Расчет числовых характеристик выборки — выборочная средняя, выборочная дисперсия и среднее квадратическое отклонение, коэффициент вариации, мода и медиана
Условие задачи
В целях изучения стажа рабочих завода проведена 36%-ная механическая выборка, в результате которой получено следующее распределение рабочих по стажу работы:
| Стаж, число лет | Число рабочих, чел. |
| до 5 | 12 |
| 5 -10 | 18 |
| 10 -15 | 24 |
| 15 -20 | 32 |
| 20 -25 | 6 |
| свыше 25 | 8 |
| Итого | 100 |
На основе этих данных вычислите:
- Средний стаж рабочих завода.
- Моду и медиану стажа рабочих.
- Средний квадрат отклонений (дисперсию), среднее квадратическое отклонение и коэффициент вариации.
- С вероятностью 0.997 предельную ошибку выборочной средней и возможные границы, в которых ожидается средний стаж рабочих всего завода.
- С вероятностью 0.954 предельную ошибку выборочной доли и границы удельного веса рабочих со стажем работы от 10 лет и выше в общей численности рабочих.
Задали объемную контрольную работу? Скоро важный зачет/экзамен? Нет времени на выполнение работы или подготовку к зачету/экзамену, но есть деньги? На сайте 100task.ru можно заказать решение контрольной работы или онлайн-помощь на зачете/экзамене 〉〉
Решение задачи
Вычисление средней
Для вычисления среднего стажа просуммируем произведения середин интервалов и соответствующих частот, и полученную сумму разделим на сумму частот.
Вычисление моды и медианы
Вычислим моду и медиану стажа:
Мода — варианта, которой соответствует наибольшая частота.
Мода вычисляется по формуле:
- начало модального интервала
- величина интервала
- частота модального интервала
- частота интервала, предшествующего модальному
- частота интервала, следующего за модальным
Таким образом, наибольшее количество рабочих имеют стаж 16.2 лет.
Медиана — варианта, находящаяся в середине ряда распределения.
Расчет медианы производится по формуле:
-начало (нижняя граница) медианного интервала
-величина интервала
-сумма всех частот ряда
-частота медианного интервала
-сумма накопленных частот вариантов до медианного
Таким образом, половина рабочих имеет стаж до 14.2 лет, другая половина — более 14.2 лет.
Вычисление дисперсии, среднего квадратического отклонения и коэффициента вариации
Вычислим дисперсию, среднее квадратическое отклонение и коэффициент вариации:
Коэффициент вариации:
Интервальная оценка выборочной средней
Вычислим предельную ошибку выборочной средней:
где -аргумент функции Лапласа.
Границы, в которых ожидается средний стаж:
Интервальная оценка выборочной доли
Вычислим предельную ошибку выборочной доли:
Число рабочих со стажем 10 лет и выше
Выборочная доля:
Возможная граница генеральной доли:
К оглавлению решебника по статистике 〉
100task.ru
3. Выборочное среднее квадратическое отклонение.
Определение. Арифметическое значение квадратного корня из выборочной дисперсии называется выборочным средним квадратическим отклонением:
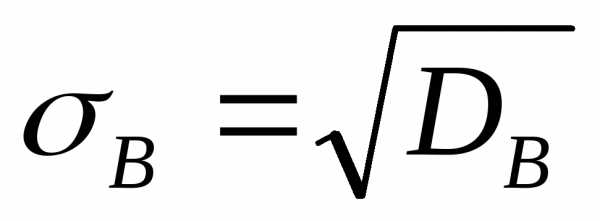(10)
Исправленное выборочное среднее квадратическое отклонение
4. Мода. Определение. Модой М0 называют значение признака, которое имеет наибольшую частоту (ni = max).
Например, для распределения, данного табл. 5, мода равна 5.
5. Медиана. Медианой те называют значение признака, которое делит статистическое распределение на две равные части:
me = xk+1, если n = 2k+1,
me =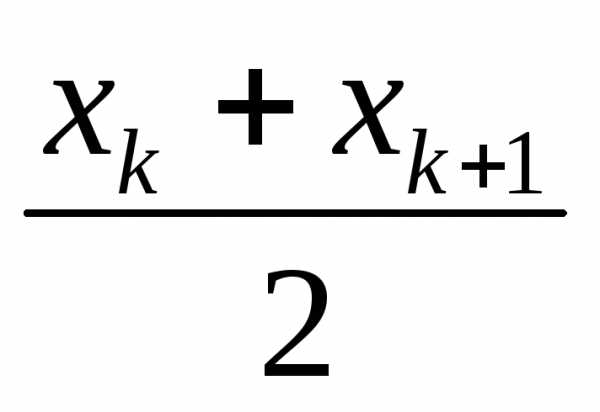 
, если n=2k
6. Коэффициент вариации. Для сравнивания меры рассеяния значений признаков около выборочной средней в разных выборках служит коэффициент вариации.
Определение. Коэффициентом вариации
V называется отношение выборочного среднего квадратического отклонения к выборочной средней, выраженное в процентах: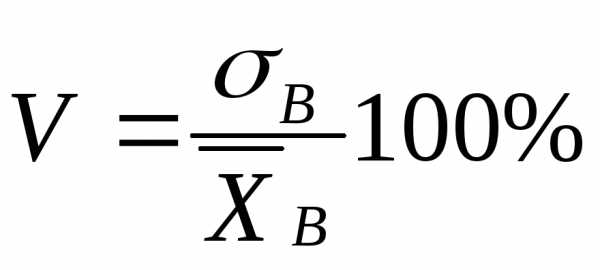 
(12)
Пусть изучается случайная величина X. Из генеральной совокупности сделана выборка объема п со значениями признака х1 х2,…, хn. Предположим, что х1, х2,…,хn различны. Их можно рассматривать как случайные величины Х1, Х2, …, Хn, имеющие то же распределение, что и случайная величина X, и, следовательно, одинаковые значения М(Х) и D(Х). Тогда
Воспользовавшись свойствами дисперсии находим
Пусть σ
– средняя
квадратическая ошибка выборочной
средней. Тогда
Вывод. Средняя
квадратическая ошибка выборочной
средней σ(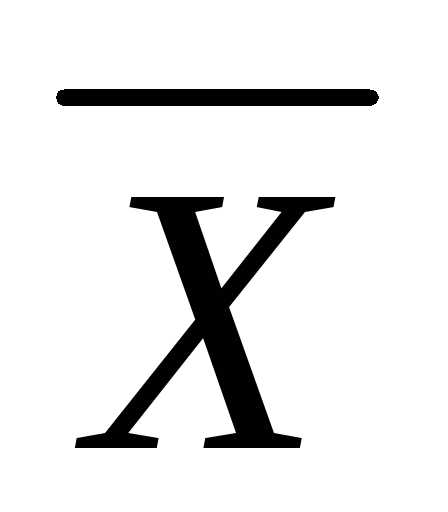
B) в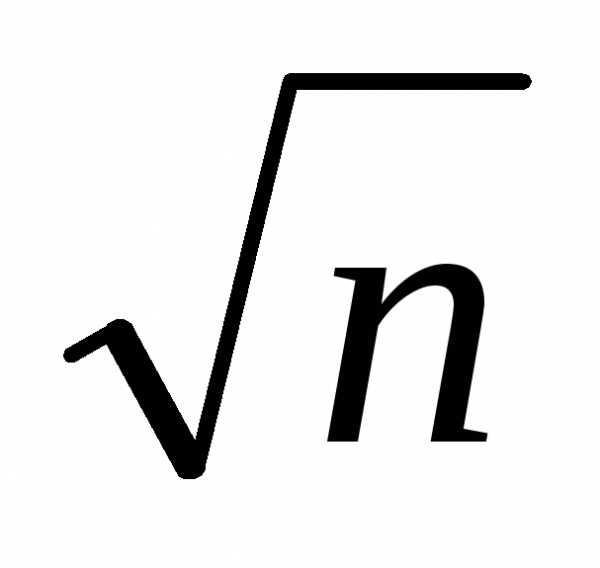 
раз меньше среднего квадратического
отклонения случайной величиныX, возможные
значения которой попали в выборочную
совокупность.
1.6. Статистические оценки параметров распределения
Оценки математического ожидания и дисперсии.
С понятием параметров распределения мы познакомились в теории вероятностей. Например, в нормальном законе распределения, задаваемом функцией плотности вероятности
параметрами служат а – математическое ожидание и а – среднее квадратическое отклонение. В распределении Пуассона параметром является число а = пр.
Определение. Статистической оценкой неизвестного параметра теоретического распределения называют его приближенное значение, зависящее от данных выборки (х1, х2, х3, …, хk; п1, п2, п3,…, пk), т. е. некоторую функцию этих величин.
Здесь х1, х2, х3, …, хk – значения признака, п1, п2, п3
Обозначим через θ – оцениваемый параметр, а через θ* – его статистическую оценку. Величину |θ*–θ| называют точностью оценки. Чем меньше |θ*–θ|, тем лучше, точнее определен неизвестный параметр.
Чтобы оценка θ* имела практическое значение, она не должна содержать систематической ошибки и вместе с тем иметь возможно меньшую дисперсию. Кроме того, при увеличении объема выборки вероятность сколь угодно малых отклонений |θ*–θ| должна быть близка к 1.
Сформулируем следующие определения.
Оценка параметра называется несмещенной, если ее математическое ожидание М(θ*) равно оцениваемому параметру θ, т. е.
М(θ*) = θ,
(1)и смещенной, если
М(θ*) ≠ θ, (2)
Оценка θ* называется состоятельной, если при любом δ > 0
(3)
Равенство (3) читается так: оценка θ* сходится по вероятности к θ.
3. Оценка θ* называется эффективной, если при заданном п она имеет наименьшую дисперсию.
Теорема 1. Выборочная средняя ХВ является несмещенной и состоятельной оценкой математического ожидания.
Доказательство. Пусть выборка репрезентативна, т. е.. все элементы генеральной совокупности имеют одинаковую возможность попасть в выборку. Значения признака х1, х2, х3,…,хn
Так как каждая из величин Х1, Х2, Х3, …, Хп имеет распределение, совпадающее с распределением генеральной совокупности, то М(Х) = а. Поэтому
Далее, на основании закона больших чисел имеем
откуда следует,
что 
–
состоятельная оценка М(Х).
Используя правило
исследования на экстремум, можно
доказать, что 
является и эффективной оценкойМ(Х).
В качестве оценки дисперсии изучаемого признака в генеральной совокупности D(Х) принимается исправленная дисперсия.
Теорема 2. Исправленная
выборочная дисперсия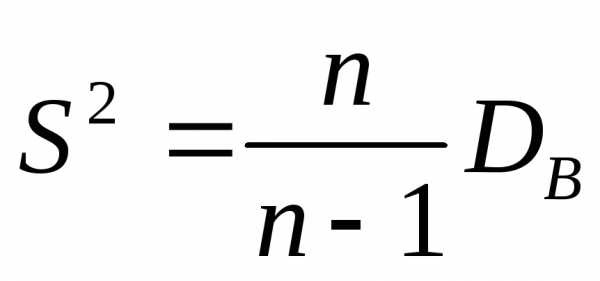 
является
несмещенной и состоятельной оценкой
дисперсии D(Х).
studfiles.net
Метод произведений вычисления выборочных средней и дисперсии
Метод произведений – это удобная техника вычислений условных моментов различных порядков вариационного ряда с равноотстоящими вариантами. Зная условные моменты, нетрудно найти начальные и центральные эмпирические моменты. В частности, методом произведений удобно вычислять выборочную среднюю и выборочную дисперсии. При этом рекомендуем пользоваться расчетной таблицей, которая составляется следующим образом:
· в первый столбец таблицы записывают выборочные (первоначальные) варианты, располагая их в возрастающем порядке;
· во второй столбец записывают частоты вариант; складывают все частоты и их сумму (объем выборки ) помещают в нижнюю клетку столбца;
· в третий столбец записывают условные варианты причем в качестве ложного нуля выбирают варианту с наибольшей частотой и полагают равным разности между любыми двумя соседними вариантами;
· умножают частоты на условные варианты и записывают их произведения в четвертый столбец; сложив все полученные числа, их сумму помещают в нижнюю клетку столбца;
· умножают частоты на квадраты условных вариант и записывают их выражения в пятый столбец; сложив все полученные числа, их сумму , помещают в нижнюю клетку столбца;
· умножают частоты на квадраты условных вариант, увеличенных каждая на единицу, и записывают произведения в шестой контрольный столбец; сложив все полученные числа, их сумму помещают в нижнюю клетку столбца.
Далее вычисляются условные моменты:
И, наконец, вычисляются:
выборочная средняя
и выборочная дисперсия
В качестве иллюстрации, рассмотрим пример.
Пример 7: Пусть дан статистический ряд распределения значений измеряемой случайной величины:
|
варианты: |
10,2 |
10,4 |
10,6 |
10,8 |
11,0 |
11,2 |
11,4 |
11,6 |
11,8 |
12,0 |
|
частоты: |
2 |
3 |
8 |
13 |
25 |
20 |
12 |
10 |
6 |
1 |
Расчеты осуществляем в таблице:
|
10,2 |
2 |
-4 |
-8 |
32 |
18 |
|
10,4 |
3 |
-3 |
-9 |
27 |
12 |
|
10,6 |
8 |
-2 |
-16 |
32 |
8 |
|
10,8 |
13 |
-1 |
-13 |
13 |
0 |
|
11,0 |
25 |
0 |
25 |
||
|
11,2 |
20 |
1 |
20 |
20 |
80 |
|
11,4 |
12 |
2 |
24 |
48 |
108 |
|
11,6 |
10 |
3 |
30 |
90 |
160 |
|
11,8 |
6 |
4 |
24 |
96 |
150 |
|
12,0 |
1 |
5 |
5 |
25 |
36 |
Контроль вычислений:
Таким образом, вычисления произведены верно.
Далее, вычислим условные моменты первого и второго порядков:
Находим шаг:
И, наконец, вычислим искомые величины:
po-teme.com.ua
ВЫБОРОЧНОЕ СРЕДНЕЕ — это… Что такое ВЫБОРОЧНОЕ СРЕДНЕЕ?
- ВЫБОРОЧНОЕ СРЕДНЕЕ
- наблюдений х1, …, хn есть
В. с. является состоятельной, несмещенной, эффективной оценкой математического ожидания случайной величины X. Если совокупность распределена нормально (см. Распределение нормальное) с параметрами (a , s ), то распределено тоже нормально с параметрами
Корректное вычисление В. с. имеет большое значение в практике геол. работ, особенно при подсчете запасов полезных ископаемых и экономической оценке м-ний.
Геологический словарь: в 2-х томах. — М.: Недра. Под редакцией К. Н. Паффенгольца и др.. 1978.
- ВЫБОРКА
- ВЫБОРОЧНЫЙ МЕТОД
Смотреть что такое «ВЫБОРОЧНОЕ СРЕДНЕЕ» в других словарях:
выборочное среднее — математическое ожидание — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность Синонимы математическое ожидание EN sample meanpopulation mean … Справочник технического переводчика
выборочное среднее — 3.19 выборочное среднее (sample mean) :Сумма n значений хi выборочных единиц, деленная на объем выборки п Источник … Словарь-справочник терминов нормативно-технической документации
Выборочное среднее — Выборочное (эмпирическое) среднее это приближение теоретического среднего распределения, основанное на выборке из него. Определение Пусть выборка из распределения вероятности, определённая на некотором вероятностном пространстве .… … Википедия
выборочное среднее — Арифметическое среднее наблюдений, составляющих выборку, т.е. сумма всех наблюдений, деленная на их количество: (x1 x2 … xn)/n. Является одной из наиболее частых оценок среднего совокупности. Это мера положения, часто обозначается . Величина… … Словарь социологической статистики
ВЫБОРОЧНОЕ СРЕДНЕЕ — математическое ожидание эмпирического распределения … Математическая энциклопедия
Выборочное среднее арифметическое — 2.25. Выборочное среднее арифметическое где n объем выборки; xi результат измерения i ой единицы. Оценка х является состоятельной и несмещенной оценкой среднего значения в совокупности Источник … Словарь-справочник терминов нормативно-технической документации
Выборочное среднее квадратическое отклонение — 2.27. Выборочное среднее квадратическое отклонение Оценка не является несмещенной Источник … Словарь-справочник терминов нормативно-технической документации
Среднее арифметическое — У этого термина существуют и другие значения, см. среднее значение. В математике и статистике среднее арифметическое одна из наиболее распространённых мер центральной тенденции, представляющая собой сумму всех наблюденных значений деленную на их… … Википедия
СРЕДНЕЕ, ИСТИННОЕ (или ПОПУЛЯЦИЯ) — Теоретическое значение, представляющее среднее полного набора всех возможных рассматриваемых значений. Полученное или выборочное среднее – всегда наилучшая оценка этого истинного среднего … Толковый словарь по психологии
Среднее значение (выборочное) — среднеарифметическое из частных значений, образующих выборку независимых друг от друга и от пространственных координат величин. Источник: ГОСТ 20522 96: Грунты. Методы статистической обработки результатов испытаний … Словарь-справочник терминов нормативно-технической документации
dic.academic.ru
Выборочное среднее как статистическая оценка среднего в генеральной совокупности
Пусть сделана выборка из распределения для случайной величины . Независимые измерения или наблюдения являются реализацией этой выборки.
Обозначим . Статистика называется выборочным средним и используется в качестве точечной оценки среднего генеральной совокупности. является также и случайной величиной. Реально для вычислений используется значение этой статистики , которое получается как среднее арифметическое значений реализации этой выборки: .
Докажем, что выборочное среднее является несмещённой оценкой среднего генеральной совокупности.
Таким образом получилось, что , т.е. математическое ожидание выборочного среднего равно математическому ожиданию или среднему значений в генеральной совокупности. Следовательно, выборочная средняя – это несмещённая оценка среднего в генеральной совокупности.
Можно доказать, что выборочное среднее является также эффективной и состоятельной оценкой средней генеральной совокупности.
Вычислим дисперсию для выборочной средней.
В результате , т.е. дисперсия средней по выборке равна одной n-ой от дисперсии генеральной совокупности. Тогда для стандартного квадратичного отклонения , где — стандартное квадратичное отклонение выборочного среднего, а — стандартное квадратичное отклонение генеральной совокупности. Получилось, что при увеличении объёма выборки до n стандартное квадратичное отклонение выборочного среднего уменьшается в корень из n раз. Следовательно, для повышения эффективности выборочного среднего как оценки среднего генеральной совокупности нужно увеличивать объём выборки. Но при больших объёмах выборки большие увеличения выборки приводят к небольшому росту эффективности этой оценки, потому что стандартное квадратичное отклонение при этом уменьшается в корень квадратный из n раз.
Эти рассуждения и доказательства проведены в предположении, что выборка является повторной, только такие выборки позволяют каждый раз отбирать элемент генеральной совокупности независимо от предыдущих выборов. В случае повторной выборки достаточно большого объёма (большего 30) можно доказать, что случайная величина выборочное среднее , являющаяся суммой достаточно большого числа одинаково распределённых случайных величин , имеет закон распределения, близкий к нормальному.
В реальной ситуации выборку чаще всего делают бесповторной, чтобы получить в выборке большее разнообразие информации. Можно доказать, что и в случае бесповторной выборки выборочное среднее является несмещённой оценкой генерального среднего. Формулы для определения выборочного среднего для бесповторной выборки не меняются. Более того, если объём бесповторной выборки достаточно велик, но при этом выборка составляет незначительную долю генеральной совокупности, что бывает в очень больших генеральных совокупностях, то и в этом случае закон распределения выборочной средней будет близок к нормальному.
Но в случае бесповторной выборки необходимо изменить формулы вычисления дисперсии и стандартного квадратичного отклонения выборочной средней : и , где, как и прежде, n – объём выборки, а N – это объём генеральной совокупности. В случае повторной выборки аналогичные формулы не зависели от объёма генеральной совокупности в силу случайности формирования такой выборки. Если объём генеральной совокупности бесконечен, очень велик или выборка составляет малую долю от генеральной совокупности, то отношение будет очень мало или стремиться к нулю. В таком случае результаты вычисления дисперсии и стандартного квадратичного отклонения не будут отличаться от тех, которые получатся для повторной выборки.
Сравнение формул для повторной и для бесповторной выборок показывает, что дисперсия и стандартное квадратичное отклонение выборочной средней для бесповторной выборки меньше при одинаковом объёме выборки. Это означает, что бесповторная выборка более эффективна, чем повторная. Но этот эффект проявляется лучше для сравнительно небольших выборок.
infopedia.su
Выборочное среднее — это… Что такое Выборочное среднее?
- Выборочное среднее
- Категория:
- Средние величины
Wikimedia Foundation. 2010.
- Порту (значения)
- Линдси, Стивен Уэйн
Смотреть что такое «Выборочное среднее» в других словарях:
ВЫБОРОЧНОЕ СРЕДНЕЕ — наблюдений х1, …, хn есть В. с. является состоятельной, несмещенной, эффективной оценкой математического ожидания случайной величины X. Если совокупность распределена нормально (см. Распределение нормальное) с параметрами (a , s ), то… … Геологическая энциклопедия
выборочное среднее — математическое ожидание — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность Синонимы математическое ожидание EN sample meanpopulation mean … Справочник технического переводчика
выборочное среднее — 3.19 выборочное среднее (sample mean) :Сумма n значений хi выборочных единиц, деленная на объем выборки п Источник … Словарь-справочник терминов нормативно-технической документации
выборочное среднее — Арифметическое среднее наблюдений, составляющих выборку, т.е. сумма всех наблюдений, деленная на их количество: (x1 x2 … xn)/n. Является одной из наиболее частых оценок среднего совокупности. Это мера положения, часто обозначается . Величина… … Словарь социологической статистики
ВЫБОРОЧНОЕ СРЕДНЕЕ — математическое ожидание эмпирического распределения … Математическая энциклопедия
Выборочное среднее арифметическое — 2.25. Выборочное среднее арифметическое где n объем выборки; xi результат измерения i ой единицы. Оценка х является состоятельной и несмещенной оценкой среднего значения в совокупности Источник … Словарь-справочник терминов нормативно-технической документации
Выборочное среднее квадратическое отклонение — 2.27. Выборочное среднее квадратическое отклонение Оценка не является несмещенной Источник … Словарь-справочник терминов нормативно-технической документации
Среднее арифметическое — У этого термина существуют и другие значения, см. среднее значение. В математике и статистике среднее арифметическое одна из наиболее распространённых мер центральной тенденции, представляющая собой сумму всех наблюденных значений деленную на их… … Википедия
СРЕДНЕЕ, ИСТИННОЕ (или ПОПУЛЯЦИЯ) — Теоретическое значение, представляющее среднее полного набора всех возможных рассматриваемых значений. Полученное или выборочное среднее – всегда наилучшая оценка этого истинного среднего … Толковый словарь по психологии
Среднее значение (выборочное) — среднеарифметическое из частных значений, образующих выборку независимых друг от друга и от пространственных координат величин. Источник: ГОСТ 20522 96: Грунты. Методы статистической обработки результатов испытаний … Словарь-справочник терминов нормативно-технической документации
dic.academic.ru