Глава 4. ФУНКЦИЯ ОДНОЙ ПЕРЕМЕННОЙ
= cos(3x +3T1) =cos3x для всех значений аргументаx . Отсюда следует, что3T1 – периодфункцииcost, гдеt =3x ,атогда3T1 ≥2π ,т.е.T1 ≥23π .
Итак, число T =23π – наименьший положительный период функции
f(x)= cos3x ;
2)период даннойфункции совпадаетспериодом функции cos4x , так как.
f(x) =sin2 2x =1−cos2 4x . Рассуждая как в пункте 1), можно показать, что
наименьший положительный период функции cos4x равен24π =π2 . Таким
образом,наименьшийположительныйпериодфункции f (x) =sin2 2x равенπ2 ;
3) наименьшие положительные периоды функций sin 2x иcos5x равны соответственноπ и25π (см. пункты 1) и 2)). Наименьший положительный
период суммы этих функций будет равен наименьшему общему кратному их периодов, т.е. числу 2π ;
4) для положительных значений аргумента x функцияf (x) =3×4 +1 определена и возрастает, поэтому периодической быть не может. Значит, и на всей числовой оси функция не является периодической.
Сложная функция. Пусть область значений функцииy =f (x) содержится в области определения функцииg(y). Тогда на множествеD( f ) определена функцияz =g( f (x)), которая называетсясложной функцией иликомпозицией функцийf иg и обозначаетсяg f .
Пример 4.4. Найти сложные функцииg f иf g , если:
1) | f (x) = x2 , g(x) = |
|
| ; | 2) | f (x)= 3×2 −1, g(x)= sinx . |
| ||||||
x |
| ||||||||||||
Решение: 1) | по |
|
|
|
| определению композиции функций имеем | |||||||
|
| x |
| , (f g)(x)= f (g(x))= ( |
| )2 =x ,x ≥0 ; |
| ||||||
(g f )(x)= g(f (x))= | x2 | = |
|
|
|
| |||||||
|
| x |
| ||||||||||
|
|
| |||||||||||
2) | аналогично |
| получаем | (g f )(x)= g(f (x))= sin(3×2 −1) | и | ||||||||
( f g)(x)= f (g(x))= 3sin2 x −1.
studfiles.net
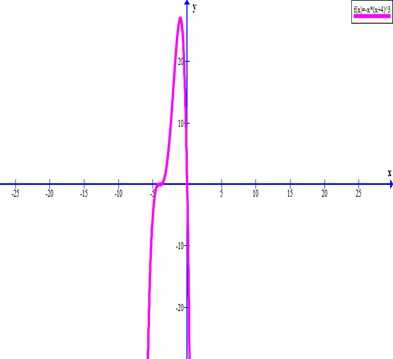
y = –x(x+4)^3 исследуйте функцию и постройте ее график
Исследуйте функцию и постройте ее график:
y = —x(x+4)^3.
Решение.
Запишем функцию:
- Функция существует для любого значения аргумента х. Это значит, что ее область определения от минус бесконечности до плюс бесконечности.
- Найдем точки пересечения функции с осями координат.
Ох: при пересечении с осью Ох у = 0. Решим уравнение:
Данное уравнение можно разбить на два более простых:
или
Найдем решение обоих уравнений и получим:
или
Таким образом, получилось 2 точки пересечения (0; 0) и (—4; 0).
Оу: при пересечении с осью Оу х = 0. После подстановки этого значения в уравнение функции, получим:
Функция пересекается с осью Оу в начале координат. Кстати, в этой же точке она пересекает и ось Ох.
- Проверим функцию на четность:
Итак, функция не является ни четной, ни нечетной.
- Степенные функции не имеют периода.
- Проверим функцию на промежутки убывания или возрастания, а также найдем точки экстремума:
Чтобы найти критические точки, приравняем производную к нулю:
или
или
Исследуем знаки производной функции на полученных промежутках:
От —∞ до —4:
— функция возрастает
От —4 до —1:
— функция возрастает
От —1 до +∞:
— функция убывает
Получили точку —1 — точка максимума.
Вычислим координату у этой точки:
- Определим промежутки вогнутости или выпуклости и точки ее перегиба. Для этого найдем вторую производную:
или
Исследуем знак этой производной на следующих промежутках:
От —∞ до —4:
— функция выпукла вверх
От —4 до —2:
— функция выпукла вниз
От —2 до +∞:
— функция выпукла вверх
Координатами точек перегиба будут:
- У функции нет точек разрыва.
- График функции.
ru.solverbook.com
Ответы@Mail.Ru: Построить график функции y=x^2+4x
Выделим квадрат двучлена y = (x^2+4x+4)-4 = (x+2)^2-4. Строишь параболу у = x^2 и переносишь ее на 2 единицы влево и на 4 единицы вниз. Вершина будет в точке (-2;-4) Либо строй по точкам. (0;0), (-4;0) Вершина по формуле (-2;-4) И добавь еще несколько точек.
можна не заморачиваться, а просто тупо береш любое х — считаеш у ставиш точку и т д, апроксимируеш точки кривой и все
<img src=»//otvet.imgsmail.ru/download/8c54c9c9ac26f1c816b415e26072f6f8_i-26.jpg» >
График — парабола, ветви направлены вверх. Вершина: х=-4/2 = -2, у = (-2)²+4*(-2) = -4. Точка (-2;-4). Таблица для построения графика: х -5 -4 -3 -2 -1 0 1 у 5 0 -3 -4 -3 0 5 Функция убывает на промежутке (-∞; -2]. Неравенство верно при х∈(-∞;-4]∪[0;+∞).
touch.otvet.mail.ru
