Теория вероятностей на ЕГЭ. Простые задачи. Часть1
Теория вероятностей на ЕГЭ по математике может быть представлена как в виде простых задач на классическое определение вероятности, так и в виде достаточно сложных, на применение соответствующих теорем.
В этой части рассмотрим задачи, для решения которых достаточно применения определения вероятности. Иногда здесь мы будем применять также формулу для вычисления вероятности противоположного события. Хотя без этой формулы здесь можно обойтись, она все равно понадобится при решении следующих задач.

Теоретическая часть
Случайным называют событие, которое может произойти или не произойти (заранее предсказать невозможно) во время наблюдения или испытания.
Пусть при проведении испытания (бросание монеты или кубика, вытягивание экзаменационного билета и т. д.) возможны равновозможных исходов. Например, при подбрасывании монеты число всех исходов равно 2, так как кроме выпадения «решки» или «орла» других исходов быть не может. При броске игрального кубика возможны 6 исходов, так как на верхней грани кубика равновозможно появление любого из чисел от 1 до 6. Пусть также некоторому событию А благоприятствуют исходов.
Вероятностью события А называется отношение числа благоприятных для этого события исходов к общему числу равновозможных исходов (это классическое определение вероятности). Пишем
Например, пусть событие А состоит в выпадении нечётного числа очков при бросании кубика. Всего возможны 6 исходов: выпадение на верхней грани кубика 1, 2, 3, 4, 5, 6. При этом благоприятными для события А являются исходы с выпадением 1, 3, 5. Таким образом, .
Заметим, что всегда выполняется двойное неравенство , поэтому вероятность любого события А лежит на отрезке [0; 1], то есть . Если у вас в ответе вероятность получается больше единицы, значит, вы где-то ошиблись и решение нужно перепроверить.
События А и В называются противоположными друг другу, если любой исход благоприятен ровно для одного из них.
Например, при бросании кубика событие «выпало нечётное число» является противоположным событию «выпало чётное число».
Событие, противоположное событию А, обозначают. Из определения противоположных событий следует , значит, .
Задачи о выборе объектов из набора
В этих задачах нужно подсчитать общее число объектов (равно общему числу исходов) и число подходящих объектов (равно числу благоприятных исходов). После этого следует воспользоваться определением вероятности.
Задача 1. В чемпионате мира участвуют 24 команды. С помощью жребия их нужно разделить на четыре группы по шесть команд в каждой. В ящике вперемешку лежат карточки с номерами групп:
1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4.
Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется в третьей группе?
Решение.
Общее число исходов равно числу карточек – их 24. Благоприятных исходов 6 (так как номер 3 написан на шести карточках). Искомая вероятность равна .
Ответ: 0,25.
Задача 2. В урне 14 красных, 9 жёлтых и 7 зелёных шаров. Из урны наугад достают один шар. Какова вероятность того, что этот шар окажется жёлтым?
Решение.
Общее число исходов равно числу шаров: 14 + 9 + 7 = 30. Число исходов, благоприятствующих данному событию, равно 9. Искомая вероятность равна равна .
Ответ: 0,3
Задача 3. На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет чётной и больше 5?
Решение.
Исходом здесь является нажатие определённой клавиши, поэтому всего имеется 10 равновозможных исходов. Указанному событию благоприятствуют исходы, означающие нажатие клавиши 6 или 8. Таких исходов два. Искомая вероятность равна .
Ответ: 0,2.
Задача 4. Какова вероятность того, что случайно выбранное натуральное число от 4 до 23 делится на три?
Решение.
На отрезке от 4 до 23 имеется 23 – 4 + 1 = 20 натуральных чисел, значит, всего возможны 20 исходов. На этом отрезке кратны трём следующие числа: 6, 9, 12, 15, 18, 21. Всего таких чисел 6, поэтому рассматриваемому событию благоприятствуют 6 исходов. Искомая вероятность равна .
Ответ: 0,3.
Задача 5. Из 20 билетов, предлагаемых на экзамене, школьник может ответить только на 17. Какова вероятность того, что школьник не сможет ответить на выбранный наугад билет?
Решение.
1 -й способ.
Так как школьник может ответить на 17 билетов, то на 3 билета он ответить не может. Вероятность получить один из этих билетов по определению равна .
2-й способ.
Обозначим через А событие «школьник может ответить на билет». Тогда . Вероятность противоположного события равна =1 – 0,85 = 0,15.
Ответ: 0,15.
Задача 6. В чемпионате по художественной гимнастике участвуют 20 спортсменок: 6 из России, 5 из Германии, остальные – из Франции. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая седьмой, окажется из Франции.
Решение.
Всего 20 спортсменок, у всех равные шансы выступать седьмой. Поэтому имеются 20 равновероятных исходов. Из Франции 20 – 6 – 5 = 9 спортсменок, поэтому имеются 9 благоприятных для указанного события исходов. Искомая вероятность равна .
Ответ: 0,45.
Задача 7. Научная конференция проводится в 5 дней. Всего запланировано 50 докладов – первые три дня по 12 докладов, остальные распределены поровну между четвёртым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора Н. окажется запланированным на последний день конференции?
Решение.
Сначала найдём, сколько докладов запланировано на последний день. На первые три дня запланировано докладов. Остаются ещё 50 – 36 = 14 докладов, которые распределяются поровну между оставшимися двумя днями, поэтому в последний день запланировано докладов.
Будем считать исходом порядковый номер доклада профессора Н. Всего таких равновозможных исходов 50. Благоприятствуют указанному событию 7 исходов (последние 7 номеров в списке докладов). Искомая вероятность равна .
Ответ: 0,14.
Задача 8. На борту самолёта 10 мест рядом с запасными выходами и 15 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажиров высокого роста. Пассажир К. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру К. достанется удобное место, если всего в самолёте 200 мест.
Решение.
Исход в этой задаче – выбор места. Всего имеется 200 равновозможных исходов. Благоприятствуют событию «выбранное место удобное» 15 + 10 = 25 исходов. Искомая вероятность равна .
Ответ: 0,125.
Задача 9. Из 1000 собранных на заводе кофемолок 7 штук бракованных. Эксперт проверяет одну наугад выбранную кофемолку из этой 1000. Найдите вероятность того, что проверяемая кофемолка окажется бракованной.
Решение.
При выборе кофемолки наугад возможны 1000 исходов, событию А «выбранная кофемолка бракованная» благоприятны 7 исходов. По определению вероятности .
Ответ: 0,007.
Задача 10. Завод производит холодильники. В среднем на 100 качественных холодильников приходится 15 холодильников со скрытыми дефектами. Найдите вероятность того, что купленный холодильник окажется качественным. Результат округлите до сотых.
Решение.
Эта задача похожа на предыдущую. Однако формулировка «на 100 качественных холодильников приходится 15 с дефектами» указывает нам, что дефектные 15 штук не входят в 100 качественных. Поэтому общее число исходов равно 100 + 15 =115 (равно общему числу холодильников), благоприятных исходов 100. Искомая вероятность равна . Для подсчёта приближённого значения дроби удобно воспользоваться делением уголком. Получаем 0,869…, что приблизительно равно 0,87.
Ответ: 0,87.
Задача 11. Перед началом первого тура чемпионата по теннису участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 16 теннисистов, среди которых 7 участников из России, в том числе Максим Зайцев. Найдите вероятность того, что в первом туре Максим Зайцев будет играть с каким-либо теннисистом из России.
Как и в предыдущей задаче, необходимо внимательно прочитать условие и понять, что является исходом, а что – благоприятным исходом (так, неосмысленное применение формулы вероятности приводит к неправильному ответу ).
Здесь исход – это соперник Максима Зайцева. Так как всего теннисистов 16, а сам с собой Максим играть не может, то имеется 16 – 1 = 15 равновероятных исходов. Благоприятный исход – соперник из России. Таких благоприятных исходов 7 – 1 = 6 (из числа россиян исключаем самого Максима). Искомая вероятность равна .
Ответ: 0,4.
Задача 12. Футбольную секцию посещают 33 человека, среди них два брата – Антон и Дмитрий. Посещающих секцию случайным образом делят на три команды по 11 человек в каждой. Найдите вероятность того, что Антон и Дмитрий окажутся в одной команде.
Решение.
Сформируем команды, последовательно помещая футболистов на свободные места, при этом начнем с Антона и Дмитрия. Сначала поместим Антона на случайно выбранное место из свободных 33. Теперь помещаем на свободное место Дмитрия (исходом будем считать выбор места для него). Всего имеется 32 свободных места (одно уже занял Антон), поэтому всего возможны 32 исхода. В одной команде с Антоном остается 10 свободных мест, поэтому событию «Антон и Дмитрий в одной команде» благоприятствуют 10 исходов. Вероятность этого события равна .
Ответ: 0,3125.
Задача 13. Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали ходить. Найдите вероятность того, что часовая стрелка застыла, достигнув отметки 11, но не дойдя до отметки 2 часа.
Решение.
Условно циферблат можно разделить на 12 секторов, располагающихся между отметками соседних чисел (между 12 и 1, 1 и 2, 2 и 3, …, 11 и 12). Исходом мы будем считать остановку часовой стрелки в одном из указанных секторов. Всего есть 12 равновозможных исходов. Указанному событию благоприятствуют три исхода (сектора между 11 и 12, 12 и 1, 1 и 2). Искомая вероятность равна .
Ответ: 0,25.
Подведем итог
После изучения материала по решению простых задач по теории вероятностей рекомендую выполнить задачи для самостоятельного решения, которые мы публикуем на нашем канале Telegram. Вы также можете проверить правильность их выполнения, внеся свои ответы в предлагаемую форму.
Также рекомендую изучить “Округление с недостатком” и другие уроки по решению заданий ЕГЭ по математике, которые представлены на нашем канале Youtube.
Спасибо, что поделились статьей в социальных сетях
Источник “Подготовка к ЕГЭ. Математика.Теория вероятностей”. Под редакцией Ф.Ф. Лысенко, С.Ю. Кулабухова
safonova-ln.ru
Решение задач профильного ЕГЭ по теме «Теория вероятности»

Вероятность. Задачи профильного ЕГЭ по математике.
Подготовила учитель математики МБОУ «Лицей №4» г. Рузаевка
Овчинникова Т.В.

Определение вероятности
Вероятностью события A называют отношение числа m благоприятствующих этому событию исходов к общему числу n всех равновозможных несовместимых событий, которые могут произойти в результате одного испытания или наблюдения:
m
Р =
n
Пусть k – количество бросков монеты, тогда количество всевозможных исходов: n = 2 k .
Пусть k – количество бросков кубика, тогда количество всевозможных исходов: n = 6 k .

В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.
Решение.
Всего 4 варианта: о; о о; р р; р р; о .
Благоприятных 2: о; р и р; о .
Вероятность равна 2/4 = 1/2 = 0,5 .
Ответ: 0,5.

В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.
Решение.
Игральные кости – это кубики с 6 гранями. На первом кубике может выпасть 1, 2, 3, 4, 5 или 6 очков. Каждому варианту выпадения очков соответствует 6 вариантов выпадения очков на втором кубике.
Т.е. всего различных вариантов 6×6 = 36.
Варианты (исходы эксперимента) будут такие:
1; 1 1; 2 1; 3 1; 4 1; 5 1; 6
2; 1 2; 2 2; 3 2; 4 2; 5 2; 6
и т.д. …………………………
6; 1 6; 2 6; 3 6; 4 6; 5 6; 6
Подсчитаем количество исходов (вариантов), в которых сумма очков двух кубиков равна 8.
2; 6 3; 5; 4; 4 5; 3 6; 2.
Всего 5 вариантов.
Найдем вероятность: 5/36 = 0,138 ≈ 0,14.
Ответ: 0,14.

В сборнике билетов по биологии всего 55 билетов, в 11 из них встречается вопрос по ботанике. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по ботанике.
Решение:
Вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по ботанике, равна 11/55 =1/5 = 0,2.
Ответ: 0,2.

В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из США, остальные − из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.
Решение.
Всего участвует 20 спортсменок,
из которых 20 – 8 – 7 = 5 спортсменок из Китая.
Вероятность того, что спортсменка, выступающая первой, окажется из Китая, равна 5/20 = 1/4 = 0,25.
Ответ: 0,25.

Научная конференция проводится в 5 дней. Всего запланировано 75 докладов − первые три дня по 17 докладов, остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
Решение:
В последний день конференции запланировано
(75 – 17 × 3) : 2 = 12 докладов.
Вероятность того, что доклад профессора М. окажется запланированным на последний день конференции, равна 12/75 = 4/25 = 0,16.
Ответ: 0,16.

Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России?
Решение:
Нужно учесть, что Руслан Орлов должен играть с каким-либо бадминтонистом из России. И сам Руслан Орлов тоже из России.
Вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России, равна 9/25 = 36/100 = 0,36.
Ответ: 0,36.

Даша дважды бросает игральный кубик. В сумме у нее выпало 8 очков. Найдите вероятность того, что при первом броске выпало 2 очка.
Решение.
В сумме на двух кубиках должно выпасть 8 очков. Это возможно, если будут следующие комбинации:
2 и 6
6 и 2
3 и 5
5 и 3
4 и 4
Всего 5 вариантов. Подсчитаем количество исходов (вариантов), в которых при первом броске выпало 2 очка.
Такой вариант 1.
Найдем вероятность: 1/5 = 0,2.
Ответ: 0,2.

В чемпионате мира участвует 20 команд. С помощью жребия их нужно разделить на пять групп по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп:
1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5.
Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется в третьей группе.
Решение:
Всего команд 20, групп – 5.
В каждой группе – 4 команды.
Итак, всего исходов получилось 20, нужных нам – 4, значит, вероятность выпадения нужного исхода 4/20 = 0,2.
Ответ: 0,2.

Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая – 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая – 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Решение:
Вероятность того, что стекло куплено на первой фабрике и оно бракованное:
р 1 = 0,45 · 0,03 = 0,0135.
Вероятность того, что стекло куплено на второй фабрике и оно бракованное:
р 2 = 0,55 · 0,01 = 0,0055.
Поэтому по формуле полной вероятности вероятность того, что случайно купленное в магазине стекло окажется бракованным равна
р = р 1 + р 2 = 0,0135 + 0,0055 = 0,019.
Ответ: 0,019.

Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,52. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3.
Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
Решение:
Возможность выиграть первую и вторую партию не зависят друг от друга. Вероятность произведения независимых событий равна произведению их вероятностей:
р = 0,52 · 0,3 = 0,156.
Ответ: 0,156.

Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два раза промахнулся. Результат округлите до сотых.
Решение:
Результат каждого следующего выстрела не зависит от предыдущих. Поэтому события «попал при первом выстреле», «попал при втором выстреле» и т.д. независимы.
Вероятность каждого попадания равна 0,8. Значит, вероятность промаха равна 1 – 0,8 = 0,2.
1 выстрел: 0,8
2 выстрел: 0,8
3 выстрел: 0,8
4 выстрел: 0,2
5 выстрел: 0,2
По формуле умножения вероятностей независимых событий, получаем, что искомая вероятность равна:
0,8 ∙ 0,8 ∙ 0,8 ∙ 0,2 ∙ 0,2 = 0,02048 ≈ 0,02.
Ответ: 0,02.

В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен.
Решение:
Найдем вероятность того, что неисправны оба автомата.
Эти события независимые, вероятность их произведения равна произведению вероятностей этих событий:
0,05 · 0,05 = 0,0025.
Событие, состоящее в том, что исправен хотя бы один автомат, противоположное.
Следовательно, его вероятность равна
1 − 0,0025 = 0,9975.
Ответ: 0,9975.

Ковбой Джон попадает в муху на стене с вероятностью 0,9, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,2. На столе лежит 10 револьверов, из них только 4 пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон промахнётся.
Решение:
Вероятность того, что Джон промахнется, если схватит пристрелянный револьвер равна:
0,4 · (1 − 0,9) = 0,04
Вероятность того, что Джон промахнется, если схватит непристрелянный револьвер равна:
0,6 · (1 − 0,2) = 0,48
Эти события несовместны, вероятность их суммы равна сумме вероятностей этих событий:
0,04 + 0,48 = 0,52.
Ответ: 0,52.

При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем – 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,98?
Решение:
Можно решать задачу «по действиям», вычисляя вероятность уцелеть после ряда последовательных промахов:
Р(1) = 0,6;
Р(2) = Р(1) · 0,4 = 0,24;
Р(3) = Р(2) · 0,4 = 0,096;
Р(4) = Р(3) · 0,4 = 0,0384;
Р(5) = Р(4) · 0,4 = 0,01536.
Последняя вероятность меньше 0,02, поэтому достаточно пяти выстрелов по мишени.
Ответ: 5.

В классе 26 человек, среди них два близнеца – Андрей и Сергей. Класс случайным образом делят на две группы по 13 человек в каждой. Найдите вероятность того, что Андрей и Сергей окажутся в одной группе.
Решение:
Пусть один из близнецов находится в некоторой группе.
Вместе с ним в группе окажутся 12 человек из 25 оставшихся одноклассников.
Вероятность того, что второй близнец окажется среди этих 12 человек, равна
P = 12 : 25 = 0,48.
Ответ: 0,48.
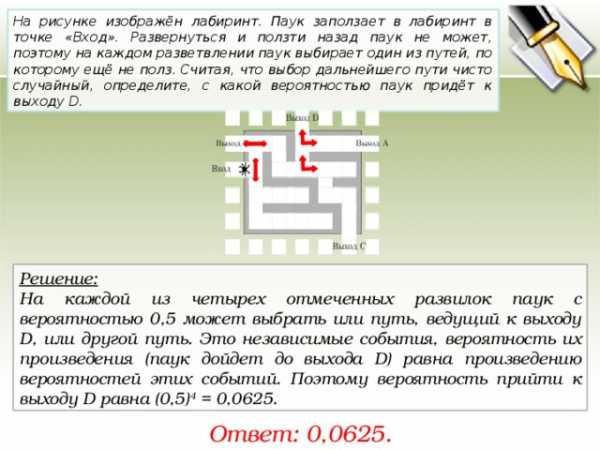
На рисунке изображён лабиринт. Паук заползает в лабиринт в точке «Вход». Развернуться и ползти назад паук не может, поэтому на каждом разветвлении паук выбирает один из путей, по которому ещё не полз. Считая, что выбор дальнейшего пути чисто случайный, определите, с какой вероятностью паук придёт к выходу D.
Решение:
На каждой из четырех отмеченных развилок паук с вероятностью 0,5 может выбрать или путь, ведущий к выходу D, или другой путь. Это независимые события, вероятность их произведения (паук дойдет до выхода D) равна произведению вероятностей этих событий. Поэтому вероятность прийти к выходу D равна (0,5) 4 = 0,0625.
Ответ: 0,0625.
multiurok.ru
Задачи на вероятность из ЕГЭ
С 2012 года организаторы ЕГЭ по математике решили внести в него дополнительное новшество. Задачи B10 отныне будут посвящены вычислению вероятностей случайных событий. При том, что выполнение этих заданий требует наличия у учеников самых элементарных знаний из области теории вероятностей, у многих старшеклассников решение этих задач вызывает серьезные затруднения. Что же нужно знать и уметь школьнику для расчета вероятностей случайных событий? Разберем несколько примеров, которые были в пробной диагностической работе по математике, прошедшей в московских школах 7 декабря 2011 года.
Решение таких задач основывается на следующих теоретических фактах:
- Случайным называется событие, исход которого невозможно точно предсказать заранее (подбрасывание монеты, игральной кости, выигрыш лотерейного билета и т. п.).
- Вероятность случайного события равна отношению числа благоприятных исходов к общему числу исходов события (к примеру, вероятность того, что при подбрасывании монеты выпадет «орел», равна 1/2. Действительно, событие является случайным, общее число исходов равно 2, так как может выпасть либо «орел», либо «решка», число благоприятных исходов равно 1. Тогда искомая вероятность по определению равна 1/2).
- Вероятность события не может быть больше 1 (число благоприятных исходов, понятно, не может превышать общее число исходов события).
- Два события называются независимыми, если появление одного из них не влияет на вероятность появления другого. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий (теорема об умножении вероятностей).
- Два события называются несовместными, если они не могут появиться одновременно в результате однократного проведения случайного эксперимента. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий (теорема о сложении вероятностей).
Пример 1. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 3 очка. Результат округлите до сотых.
Решение:
Всего возможных исходов эксперимента:
- на первом кубике выпадает число 1, на втором — 1 или 2, или 3, или 4, или 5, или 6 — шесть вариантов;
- на первом кубике выпадает число 2, на втором — 1 или 2, или 3, или 4, или 5, или 6 — шесть вариантов;
- и так далее…
- на первом кубике выпадает число 6, на втором — 1 или 2, или 3, или 4, или 5, или 6 — шесть вариантов.
Итого, 36 возможных исходов.
Всего благоприятных исходов эксперимента (то есть, что в сумме выпадет 3 очка):
- на первом кубике выпадает число 1, на втором — 2 — один вариант;
- на первом кубике выпадает число 2, на втором — 1 — один вариант.
Итого, 2 благоприятных исхода.
Факт выпадения того или иного числа на кубиках является случайным событием, следовательно, искомая вероятность определяется отношением числа благоприятных исходов к общему числу исходов эксперимента: 2/36 = 0,0(5) ≈ 0,06 (с учетом округления до сотых). Ответ: 0,06.
Пример 2. В кармане у Пети было 4 монеты по рублю и 2 монеты по 2 рубля. Петя, не глядя, переложил какие-то три монеты в другой карман. Найдите вероятность того, что обе двухрублевые монеты лежат в одном кармане.
Решение:
Вероятность того, что среди трех наугад взятых Петей монет не будет ни одной монеты по 2 рубля, равна 4/6 · 3/5 · 2/4 = 1/5 (действительно, берем монеты по одной: сначала из шести 6 вариантов подходит 4, далее из 5 вариантов подходит 3, далее из 4 вариантов подходит 2; все эти независимые события должны быть реализованы вместе, значит общая вероятность определяется произведением вероятностей каждого из событий).
Вероятность того, что среди трех наугад взятых Петей монет будет две монеты по 2 рубля, равна 2/6 · 1/5 · 4/4 + 4/6 · 2/5 · 1/4 + 2/6 · 4/5 · 1/4 = 1/5 (рассуждения аналогичны предыдущим, сложение появляется за счет того, что рассматриваемые события являются несовместными).
Первое и второе события являются несовместными, поскольку не могут быть реализованы одновременно. По теореме о сложении вероятностей искомая вероятность равняется сумме вероятностей каждого события: 1/5 + 1/5 = 2/5 = 0,4. Ответ: 0,4.
Пример 3. В чемпионате по гимнастике участвуют 76 спортсменок: 30 из России, 27 из Украины, остальные — из Белоруссии. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Белоруссии.
Решение: выбор спортсменки, выступающей первой, определяется жребием, поэтому его можно считать случайным событием. В нашем случае число благоприятных исходов этого события равно 76 — 30 — 27 = 19 (число спортсменок, выступающих за Белоруссию). Общее число возможных исходов события равно 76 (общее число спортсменок, участвующих в чемпионате). Вероятность случайного события — это отношение числа благоприятных исходов к общему числу исходов события, в нашем случае она равняется 19/76 = 0,25. Ответ: 0,25.
Современный человек должен быть знаком с основами теории вероятностей. Решение о введении в экзамен задач на вычисление вероятности событий кажется поэтому вполне оправданным. Но бояться этих заданий не стоит, успех в сдаче ЕГЭ зависит от качества подготовки ученика, а это уже напрямую зависит от преподавателя.
Репетитор по математике в Тропарёво
Сергей Валерьевич
yourtutor.info
Задание №10 ЕГЭ по математике базовый уровень
Вероятность и статистика
В задании №10 ЕГЭ по математике базового уровня нам предстоит решить задачу по теории вероятности. Задачи довольно простые и адаптированы под реальные жизненные ситуации, что делает их решение интересным для школьников. Разберем с Вами несколько подробных примеров.
Разбор типовых вариантов задания №10 ЕГЭ по математике базового уровня
Первый вариант задания (демонстрационный вариант 2018)
В чемпионате по прыжкам в воду участвуют 35 спортсменов: 7 из России, 12 из Китая, 9 из Японии и 7 из США. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий первым, окажется из России.
Алгоритм выполнения:
- Вспомнить определение вероятности.
- Определить из условия задачи необходимые величины.
- Подставить значения и вычислить вероятность.
Решение:
Вспомним определение вероятности.
Вероятность – это отношение возможности происшествия одного или нескольких конкретных событий к общему числу возможных результатов.
Для того, чтобы определить вероятность происшествия конкретного события(в данном случае – что первым будет россиянин) нужно разделить число благоприятных исходов на общее число событий.
Определим из условия задачи необходимые величины.
Вариантов благоприятного исхода 7, так как россиян 7 и каждый из них имеет равные шансы выступать первым.
Всего общее число вариантов 35, так как спортсменов всего 35 и каждый из них может выступать первым.
Подставим значения и вычислим вероятность.
7/35 = 1/5 = 0,2
Ответ: 0,2.
Второй вариант задания
Олег, Петя, Миша и Дима бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должен будет не Миша.
Алгоритм выполнения:
- Вспомнить определение вероятности.
- Определить из условия задачи необходимые величины.
- Подставить значения и вычислить вероятность.
Решение:
Вспомним определение вероятности.
Вероятность – это отношение возможности происшествия одного или нескольких конкретных событий к общему числу возможных результатов.
Для того, чтобы определить вероятность происшествия конкретного события(в данном случае – что игру должен будет начинать не Миша) нужно разделить число благоприятных исходов на общее число событий.
Определим из условия задачи необходимые величины.
Вариантов благоприятного исхода 3, так как «не Миш» трое и каждый из них имеет равные шансы начинать игру.
Всего общее число вариантов 4, так как мальчиков всего 4 и каждый из них может начинать игру.
Подставим значения и вычислим вероятность.
3/4 = 0,75
Вариант решения в общем виде:
При бросании жребия начинает игру один из 4 мальчиков. Вероятность этого события составляет P = 1/4 (для любого мальчика, в том числе и для Миши). Тогда обратная вероятность того, что Миша не будет начинать игру, равна:
Ответ: 0,75.
Третий вариант задания
Вася, Петя, Олег, Коля и Лёша бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должен будет Вася или Петя.
Алгоритм выполнения:
- Вспомнить определение вероятности.
- Определить из условия задачи необходимые величины.
- Подставить значения и вычислить вероятность.
Решение:
Вспомним определение вероятности.
Вероятность – это отношение возможности происшествия одного или нескольких конкретных событий к общему числу возможных результатов.
Для того, чтобы определить вероятность происшествия конкретного события(в данном случае – что игру должен будет начинать Вася или Петя) нужно разделить число благоприятных исходов на общее число событий.
Определим из условия задачи необходимые величины.
Вариантов благоприятного исхода 2, так как Вася и Петя – это два мальчика, каждый из них имеет равные шансы начинать игру.
Всего общее число вариантов 4, так как мальчиков всего 5 и каждый из них может начинать игру.
Подставим значения и вычислим вероятность.
2/5 = 0,4
Решение в общем виде:
Всего при бросании жребия может быть n = 5 исходов (для 5 человек). Обозначим через событие А – жребий выпал Васе или Пете. Число благоприятных исходов для события A равно m = 2. Следовательно, искомая вероятность, равна:
Ответ: 0,4.
Четвертый вариант задания
Помещение освещается фонарём с двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,1. Найдите вероятность того, что в течение года обе лампы перегорят.
Алгоритм выполнения:
- Определить вероятность каждого события в отдельности.
- Перемножить вероятности событий. Это даст вероятность того, что события произойдут последовательно.
Решение:
Определим вероятность каждого события в отдельности.
Вероятность того, что перегорит первая лампа по условию 0,1. Вероятность того, что перегорит вторая лампа по условию 0,1.
Перемножим вероятности событий. Это даст вероятность того, что события произойдут последовательно.
Ответ: 0,01.
Пятый вариант задания
Помещение освещается фонарём с двумя лампами. Вероятность перегорания одной лампы в течение года равна 0,15. Найдите вероятность того, что в течение года обе лампы перегорят.
Алгоритм выполнения:
- Определить вероятность каждого события в отдельности.
- Перемножить вероятности событий. Это даст вероятность того, что события произойдут последовательно.
Решение:
Определим вероятность каждого события в отдельности.
Вероятность того, что перегорит первая лампа по условию 0,15. Вероятность того, что перегорит вторая лампа по условию 0,15.
Перемножим вероятности событий. Это даст вероятность того, что события произойдут последовательно.
Ответ: 0,0225.
Вариант десятого задания 2017
Из каждых 100 лампочек, поступающих в продажу, в среднем 3 неисправны. Какова вероятность того, что случайно выбранная в магазине лампочка окажется исправной?
Данная задача даже проще, чем предыдущая. В начале, нам необходимо найти количество исправных лампочек:
100 — 3 = 97
После этого находим вероятность, она равна отношению количества исправных лампочек к общему количеству:
97 / 100 = 0,97
Ответ: 0,97
Вариант десятого задания 2019 года(1)
На семинар приехали 6 ученых из Норвегии, 5 из России и 9 из Испании. Каждый ученый подготовил один доклад. Порядок докладов определяется случайным образом. Найдите вероятность того, что восьмым окажется доклад ученого из России.
Алгоритм выполнения
- Поскольку событие, описанное в условии, является независимым, то вероятность того, что ученый из России выступит именно 8-м, такая же, как и вероятность выступления под любых другим номером. Поэтому для решения можем применить формулу-определение для вероятности P=Nб/N, где Nб – кол-во благоприятствующих данному событию исходов, N – общее кол-во исходов.
- Подсчитываем общее кол-во исходов. Оно равно сумме всех докладов.
- Определяем кол-во благоприятствующих исходов как число докладов от российских ученых.
- Подставляем полученные данные в формулу, вычисляем вероятность.
Решение:
P=Nб/N
N=6+5+9=20
Nб=5
P=5/20=0,25
Вариант десятого задания 2019 года(2)
В коробке вперемешку лежат чайные пакетики с черным и зеленым чаем, одинаковые на вид, причем пакетиков с черным чаем в 4 раза больше, чаем пакетиков с зеленым. Найдите вероятность того, что случайно выбранный из этой коробки пакетик окажется пакетиком с зеленым чаем.
Алгоритм выполнения
- Обозначаем через х кол-во пакетиков с зеленым чаем. Выражаем затем через х кол-во пакетиков с черным чаем.
- Записываем ф-лу для нахождения вероятности, имея в виду, что число благоприятствующих исходов равно кол-ву пакетиков зеленого чая, а общее число исходов – общему кол-ву пакетиков.
- Вычисляем вероятность.
Решение:
Пусть х – кол-во пакетиков зеленого чая. Тогда кол-во пакетиков черного составляет 4х.
Вероятность P=Nб/N. Здесь Nб=х, поскольку вероятность определяется именно для пакетиков с зеленым чаем. N=х+4х=5х.
Получаем: P=х/(5х)=1/5=0,2.
Вариант десятого задания 2019года(3)
В среднем из 1400 садовых насосов, поступивших в продажу, 14 подтекает. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
Алгоритм выполнения
- Из 1400 вычитаем 14. Получаем кол-во исправных насосов.
- По ф-ле P=Nб/N (где Nб – кол-во исправных насосов, N – общее кол-во насосов) находим искомую вероятность.
Решение:
1400 – 14 = 1386 (шт.) – исправных насосов поступило в продажу.
1386 / 1400 = 0,99 – вероятность того, что случайно подобранный насос исправен (не подтекает).
Вариант десятого задания 2019 года(4)
В кармане у Дани было пять конфет – «Ласточка», «Взлетная», «Василек», «Грильяж» и «Гусиные лапки», а также ключи от квартиры. Вынимая ключи, Даня случайно выронил из кармана одну конфету. Найдите вероятность того, что упала конфета «Взлетная».
Алгоритм выполнения
- Определяем общее кол-во конфет. Фиксируем, что упала единственная конфета.
- Применяя ф-лу для вероятности P=Nб/N, находим искомую вероятность.
Решение:
В кармане у Дани находится 6 предметов – 5 конфет и ключи. Ключи для расчета не учитываем, поскольку их извлечение из кармана не является случайным событием. Тогда общее кол-во случайных событий N=5. Кол-во благоприятных исходов для этих событий в данном случае равно 1, т.к. падает 1 конфета. Отсюда Nб=1.
Вероятность находим по ф-ле P=Nб/N. Подставляем числовые данные, получаем: P=1/5=0,2.
Вариант десятого задания 2019 года(5)
На борту самолета 26 мест рядом с запасными выходами и 10 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажира высокого роста. Пассажир Д. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру Д. достанется удобное место, если всего в самолете 300 мест.
Алгоритм выполнения
- Суммируем 26 и 10, чтобы найти общее кол-во удобных для пассажира Д. мест.
- Используя ф-лу P=Nб/N, где Nб – кол-во удобных мест, N – общее кол-во мест, находим искомую вероятность.
Решение:
26 + 10 = 36 – кол-во мест, которые удобны для пассажира Д
Р = 36 / 300 = 0,1233 – вероятность того, что при случайном выборе пассажиру достанется удобное место
Вариант десятого задания 2019 года(6)
Вероятность того, что новая шариковая ручка пишет плохо или вовсе не пишет, равна 0,21. Покупатель не глядя берет одну шариковую ручку из коробки. Найдите вероятность того, что эта ручка пишет хорошо.
Алгоритм выполнения
- Анализируем ситуацию, описанную в условии. Определяем, что существует только 2 варианта возможных событий.
- Находим искомую вероятность как разность единицы и вероятности того, что ручка пишет плохо.
Решение:
Вариантов событий в данном случае имеется два – ручка пишет хорошо или она пишет плохо. При этом ручка в любом случае будет из коробки взята, т.е. событие состоится. Это означает, что его вероятность равна 1.
Поскольку вероятность того, что ручка пишет плохо, составляет 0,21, то вероятность того, ручка будет писать хорошо, равна:
1 – 0,21 = 0,79.
Вариант десятого задания 2019 года(7)
На олимпиаде по русскому языку участников рассаживают по трем аудиториям. В первых двух по 130 человек, оставшихся проводят в запасную аудиторию в другом корпусе. При подсчете выяснилось, что всего было 400 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
Алгоритм выполнения
- Умножаем 130 на 2, получаем кол-во участников в первых двух аудиториях.
- Из 400 вычитаем полученное произведение. Узнаем, сколько участников находилось в запасной аудитории.
- Делим полученную разность на 400. Находим искомую вероятность.
Решение:
130 · 2 = 260 – участников писали олимпиаду в первых 2-х аудиториях.
400 – 260 = 140 – участников находилось в запасной аудитории.
Вероятность P = Nб / N. Здесь Nб = 140, N = 400.
Получаем: Р = 140 / 400 = 0,35.
Вариант десятого задания 2019 года(8)
В группе туристов 8 человек. С помощью жребия они выбирают двух человек, которые должны идти в село в магазин за продуктами. Какова вероятность того, что турист Д., входящий в состав группы, пойдет в магазин?
Алгоритм выполнения
- Записываем ф-лу P=Nб/N, где Nб – кол-во благоприятных исходов для ситуации, N – общее кол-во исходов.
- Благоприятным исходом в данном случае является попадание туриста Д. в группу из 2 человек, которым нужно идти в магазин. Т.е. Nб=2.
- Общее кол-во исходов – число туристов, составляющих полную группу.
- Подставляем определенные числовые величины в ф-лу, находим искомую вероятность.
Решение:
Вероятность равна: P = Nб / N.
Nб = 2, т.к. по условию для похода в магазин требуется 2 человека.
N = 8, т.к. всего в группе 8 туристов.
Р = 2 / 8 = 0,25.
Вариант десятого задания 2019 года(9)
На тарелке лежат одинаковые на вид пирожки: 1 с мясом, 12 с капустой и 3 с вишней. Петя наугад выбирает один пирожок. Найдите вероятность того, что этот пирожок окажется с капустой.
Алгоритм выполнения
- Для вычисления вероятности используем ф-лу P=Nб/N, где Nб – кол-во благоприятных исходов ситуации, N – общее кол-во исходов.
- Определяем кол-во благоприятных исходов. Здесь таковым является кол-во пирожков с капустой.
- Находим общее кол-во исходов. Это – кол-во всех (любых) пирожков.
- Подставляем числовые данные в формулы, определяем требуемую вероятность.
Решение:
Искомую вероятность найдем по ф-ле P=Nб/N.
В данном случае Nб = 12, поскольку именно столько на тарелке пирожков с капустой.
Общее число исходов N = 1 + 12 + 3 = 16 (пирожков).
Р = 12 / 16 = 0,75.
Вариант десятого задания 2019 года(10)
Конкурс исполнителей проводится в 5 дней. Всего заявлено 50 выступлений – по одному от каждой страны, участвующей в конкурсе. Исполнитель из России участвует в конкурсе. В первый день запланировано 14 выступлений, остальные распределены поровну между оставшимися днями.
Алгоритм выполнения
- Из 50 вычитаем 14. Получаем кол-во незапланированных выступлений, которые приходятся на 2–5-й дни.
- Полученную разность делим на 4, т.е. на кол-во дней, в течение которых будет заслушано выступление российского исполнителя. Получим кол-во выступлений, которые приходятся на каждый из этих дней.
- По ф-ле P=Nб/N (где Nб – кол-во выступлений в каждый из дней, кроме первого; N – общее кол-во выступлений в эти дни) находим искомую вероятность.
Решение:
50 – 14 = 36 – кол-во незапланированных выступлений, в числе которых как раз и предполагается выступление россиянина.
5 – 1 = 4 – кол-во дней, в течение которых распределены поровну 36 выступлений.
36 : 4 = 9 – кол-во выступлений, приходящихся на каждый день, начиная со 2-го.
Поскольку выступление в 3-й день, равно как и в любой другой, начиная со 2-го, является независимым и равновероятным событием, то вероятность его положит.исхода можно определить по ф-ле P=Nб/N. Здесь Nб = 9, N = 36. Тогда: Р = 9 / 36 = 0,25.
spadilo.ru
Теория вероятности. ЕГЭ задача B10.
Как решить задачу на вероятность?
Здравствуйте, дорогие учащиеся!
Задачи по теории вероятности были включены в ЕГЭ (B10), а также изучают в школьном курсе математике. Это задачи простого уровня сложности. Достаточно знать базовые понятия, чтобы решить задачи на вероятность.Теперь перейдем к разбору основных понятий теории вероятности, а также рассмотрим примеры на практике.
Вероятность — мера которой измеряют возможность наступления некоторого события.
Событие — факт который может произойти (оно называется вероятным) или не произойти (оно называется невероятным или маловероятным) при данном испытании.
Пример события:
A — выигрыш в лотерею;
A1, A2, A3, A4, A5, A6 — множество элементарных событий, допустим при бросании игральной кости рассчитать вероятность, что ни разу не выпадет 6 очков.
Событие бывает:
Случайным — событие, которое не возможно предсказать заранее. Например, бросание монеты. Может выпасть орел или решка. Такое действие в котором есть различные исходы называют испытанием.
Благоприятный исход — событие которое ожидают.
Всевозможные исходы или общее число исходов — все события которые могут произойти.
Пример, в пакете 10 яблок, из них 3 — красные, остальные — зеленые. Вы запускаете в пакет руку и наугад вынимаете яблоко. Найдите вероятность вытащить зеленое яблоко? В данной задаче количество благоприятных событий будет равно 7, так как событий — вытащить зеленое яблоко равно 10-3=7. Количество всевозможных событий равно 10, так как есть вероятность вытащить и зеленое и красное яблоко.
Невозможным — в результате опыта такое событие никогда не произойдет.
Достоверным — в результате опыта такое событие наступает всегда.
Определение вероятности:
Вероятность события равна отношению числа благоприятных исходов к общему числу исходов.
Формула нахождения вероятности:
P(A)=m:n
где m — число благоприятных исходов, n — число всевозможных исходов
Вероятность не может быть больше единицы.
Если вероятность равна единице, то событие в данном испытание наступает всегда.
Если вероятность равна нулю, то событие в данном испытание никогда не наступит.
Делаем вывод, что вероятность заключена в пределах от нуля до единицы.
Задача №1:
К каким классам событий (возможное, невозможное, достоверное) относятся:
а) расстояние между двумя произвольными населенными пунктами меньше, чем 180 тысяч километров;
б) в корзине лежат яблоки, вероятность достать из корзины грушу;
в) выиграть в лотерее?
Решение:
Первое из событий достоверное;
второе – невозможное;
третье событие может произойти, а может не произойти – оно является возможным, но не достоверным.
Задача №2:
Абонент забыл последнюю цифру номера телефона и поэтому набирает её наугад. Определить вероятность того, что ему придётся звонить не более чем в 4 раза?
Решение:
Нужный нам звонок 1, а всего цифр десять ( 0; 1; 2; 3; 4; 5; 6; 7; 8; 9).
По формуле вероятности P(A)=m:n, m=1, n=10.
Вероятность набрать верную цифру из десяти равна 1/10.
Рассмотрим случаи:
1. первый звонок оказался верным, вероятность равна 1/10 (сразу набрана нужная цифра).
2. первый звонок оказался неверным, а второй — верным, вероятность равна 9/10*1/9=1/10 (9 цифр нас не интересующих, а второй раз правильная цифра из девяти цифр).
3. первый и второй звонки оказались неподходящими , а третий — верным, P(А)=9/10*8/9*1/8=1/10 (первый раз набираем и попадаем на ненужный нам номер 9 цифр нас не интересующих, второй раз остается 8 цифр не интересующих нас и последний третий раз один нужный нам номер уже из 8 оставшихся цифр).
4. первый, второй и третий звонки оказались неподходящими , а четвертый — верным, P(А)=9/10*8/9*7/8*1/7=1/10 (аналогично рассуждаем пунктам 2-3).
P=1/10+1/10+1/10+1/10=4/10=0,4 — вероятность того, что ему придется звонить не более чем в четыре места.
Ответ: 0,4
Задача №3:
В ящике лежат шары: 6 белых, 8 красных, 3 зеленых, 13 коричневых. Из ящика вынимают один шар. Какова вероятность того что при вынимания шара из ящика наугад, шар окажется цветным (не белым) ?
Решение:
По формуле вероятности P(A)=m:n,
m=8+3+13=24 количество интересующих нас шаров,в данном случае не белых;
n=6+8+3+13=30 общее количество шаров.
Подставляем данные в формулу:
P(A)= 24:30=0,8 вероятность того, что из ящика наугад достанут цветной шар.
Ответ: 0,8.
Хочешь готовиться к экзаменам бесплатно? Репетитор онлайн бесплатно. Без шуток. ЗДЕСЬ
На сайте Вы можете в меню ПОМОГИТЕ РЕШИТЬ задавать вопросы мы Вам обязательно ответим.
Рекомендуем подписаться на новостную рассылку нашего сайта TutoMath.ru, чтобы быть в курсе всех новинок.
tutomath.ru
Задача 4: теория вероятностей
Говоря бытовым языком, теория вероятностей — это наука, изучающая события, которые могут произойти, а могут и не произойти. В школьном курсе теории вероятностей рассматриваются лишь самые примитивные задачи, решить которые может абсолютно каждый — надо лишь немного потренироваться.
Ключевым моментом теории вероятностей является понятие «благоприятствующий исход». С помощью него решаются все задачи B6, которые встречаются в ЕГЭ по математике. Что это такое и как его применять, мы разберем в данном разделе.
- § 1.
- Семинар по задачам B10: теория вероятностей
- Глава 1.
- Теория вероятностей
- § 1.
- Решение задач B6: №362—377
- § 2.
- Тест по теории вероятностей (1 вариант)
- Глава 2.
- Элементы комбинаторики
- § 1.
- Задачи B6 с монетами
- § 2.
- Правила комбинаторики в задаче B6
- § 3.
- Комбинаторика в задаче B6: легкий тест
- § 4.
- Комбинаторика в задаче B6: средний тест
- Классическое определение вероятности
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
www.berdov.com
Задачи из ЕГЭ по теории вероятности
1группа
1.По отзывам покупателей Иван Иванович оценил надёжность двух интернет-магазинов. Вероятность того, что нужный товар доставят из магазина А, равна 0,8. Вероятность того, что этот товар доставят из магазина Б, равна 0,9. Иван Иванович заказал товар сразу в обоих магазинах. Считая, что интернет-магазины работают независимо друг от друга, найдите вероятность того, что ни один магазин не доставит товар. (0,02) Решение: 1-0,8=0,2 1-0,9=0,1 0,2*0,1=0,02
2.На фабрике керамической посуды 5% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 80% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Ответ округлите до сотых.0,99 Решение:0,05*0,2=0,01 1-0,01=0,99
3.Вероятность того, что новый DVD-проигрыватель в течение года поступит в гарантийный ремонт, равна 0,045. В некотором городе из 1000 проданных DVD-проигрывателей в течение года в гарантийную мастерскую поступила 51 штука. На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?0,006
Решение:0,051-0,045=0,006
4.Агрофирма закупает куриные яйца в двух домашних хозяйствах. 60% яиц из первого хозяйства — яйца высшей категории, а из второго хозяйства — 40% яиц высшей категории. Всего высшую категорию получает 55% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства.0,75
Решение:0,6х+0,4(1-х)==0,55
5.Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая –– 55% . Первая фабрика выпускает 3% бракованных стекол, а вторая –– 1% . Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным0,019
Решение:0,45*0,03+0,55*0,01=0,019
6.При изготовлении подшипников диаметром 67 мм вероятность того, что диаметр будет отличаться от заданного не больше, чем на 0,01 мм, равна 0,965. Найдите вероятность того, что случайный подшипник будет иметь диаметр меньше, чем 66,99 мм, или больше, чем 67,01 мм.0,035 Решение:1-0,965=0,035
2группа
1. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 6 очков. Результат округлите до сотых(0,14)
Решение: 1-5,5-1,2-4,4-2,3-3 5/36
2.В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что сумма выпавших очков равна 16. Результат округлите до тысячных.0,028
Решение:556,565,655,664,646,466 6/216
3.В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 9 очков. Результат округлите до сотых.0,11
Решение:36,63,45,54 4/36
4.В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что разница выпавших очков равна 1 или 2 .0,5
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что произведение выпавших очков делится на 5 , но не делится на 30 . Ответ округлите до сотых.0,25
Решение:9/36
3группа
1. В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орёл выпадет ровно два раза.0,375
Решение:1100,0110,0011 3/8
2.Бросили шесть монет. Какова вероятность того, что число выпавших «гербов» будет больше числа выпавших «решек»? Ответ округлите до сотых.0,34
Решение:Рррррр гррррр ггрррр гггррр ггггрр гггггр гггггг 3/7
3.В случайном эксперименте симметричную монету бросают пять раз. Найдите вероятность того, что орёл выпадет ровно два раза.0,3125
Решение:5/16
4.В случайном эксперименте симметричную монету бросают семь раз. Найдите вероятность того, что количество выпавших орлов меньше 4 . Ответ округлите до сотых.0,5
4группа
1.В параллели 51 учащийся, среди них два друга — Михаил и Сергей. Учащихся случайным образом разбивают на 3 равные группы. Найдите вероятность того, что Михаил и Сергей окажутся в одной группе.0,32
Решение:16/50
2.В сборнике билетов по математике всего 20 билетов, в 16 из них встречается вопрос по логарифмам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по логарифмам.0,8
Решение:16/20
3.Из множества натуральных чисел от 58 до 82 включительно наудачу выбирают одно число. Какова вероятность того, что оно делится на 6?0,16
Решение: Чисел 25 60,66,72,78 4/25
4.За круглый стол на 5 стульев в случайном порядке рассаживаются 3 мальчика и 2 девочки. Найдите вероятность того, что обе девочки будут сидеть рядом.0,5
Решение:2/4
5. На чемпионате по прыжкам в воду выступают 40 спортсменов, среди них 6 прыгунов из Голландии и 2 прыгуна из Аргентины. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что четырнадцатым будет выступать прыгун из Аргентины.0,05
Решение:2/40
6. В группе туристов 24 человека. Их вертолётом в несколько приёмов забрасывают в труднодоступный район по 3 человека за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист A. полетит первым рейсом вертолёта.0,125
Решение:1/8
7. В классе 21 учащийся, среди них две подруги — Света и Нина. Класс случайным образом делят на семь групп, по 3 человека в каждой. Найдите вероятность того, что Света и Нина окажутся в одной группе.0,1
Решение:2/20
8. В большой партии насосов в среднем на каждые 1393 исправных приходится 7 неисправных насосов. Найдите вероятность того, что случайно выбранный насос окажется неисправным.0,005
Решение:7/1393
9.Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Химик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Химик» выиграет жребий ровно два раза.0,375
Решение:3/8
10.Перед началом волейбольного матча капитаны команд тянут честный жребий, чтобы определить, какая из команд начнёт игру с мячом. Команда «Стартер» по очереди играет с командами «Протор», «Ротор» и «Мотор». Найдите вероятность того, что «Стартер» будет начинать только вторую и последнюю игры.0,125
Решение:1/8
11.На борту самолёта 18 мест рядом с запасными выходами и 28 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажира высокого роста. Пассажир Д. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру Д. достанется удобное место, если всего в самолёте 200 мест.0,23
Решение:18+28=46 46/200
12.В группе туристов 10 человек. С помощью жребия они выбирают четырёх человек, которые должны идти в село в магазин за продуктами. Какова вероятность того, что турист Д., входящий в состав группы, пойдёт в магазин?0,4
Решение:4/10
videouroki.net
