Сборник. Задачи на составление уравнений по видам
1 вид задач.
У хозяйки было всего 20 кур и цыплят. Кур было в 4 раза меньше, чем цыплят. Сколько цыплят было у хозяйки?
У хозяйки было всего 16 уток и утят. Уток было в 3 раза меньше, чем утят. Сколько утят было у хозяйки?
Сумма трех чисел равна 80. Первое число меньше второго в 2,75 раза, а третье число составляет
В трех классах 119 учащихся. В первом учатся на 4 человека больше, чем во втором, и на 3 человека меньше, чем в третьем классе. Сколько учеников в каждом классе?
На трех полках стояло 110 книг, причем на первой было в 2 раза больше чем на второй и на 5 больше, чем на третьей. Сколько книг на каждой полке?
На первой полке было 33 книги, а на другой – 21 книга. Сколько книг нужно переставить с первой полки на вторую, чтобы книг стало поровну?
На автостоянке легковых машин в 2 раза больше грузовых. После того, как со стоянки уехало 10 легковых машин, а приехало 4 грузовых, количество легковых и грузовых машин стало поровну. Сколько легковых машин было на стоянке первоначально?
В первом бидоне в 3 раза больше молока, чем во втором. Если из первого перелить 20 литров во второй, то молока в бидонах будет поровну. Сколько молока в каждом бидоне?
На одной полке было в 3 раза больше книг, чем на другой. Когда с одной полки сняли 8 книг, а на другую положили 32 книги, то на полках книг стало поровну. Сколько книг было первоначально?
В двух бочках 725 литров бензина. Когда из первой бочки взяли бензина, а из второй бочки бензина, то в обеих бочках бензина стало поровну. Сколько бензина было первоначально в каждой бочке?
На первую автомашину погрузили на 0,6 т зерна больше, чем на вторую. Если бы на первую автомашину погрузили в 1,2 раза больше, а на вторую в 1,4 раза больше, то груза на обеих автомашинах было бы поровну. Сколько тонн груза погрузили на каждую автомашину?
На первом участке было в 3 раза больше кустов малины, чем на втором. Когда с первого участка пересадила на второй 20 кустов, то их стало поровну на обоих участках. Сколько кустов было посажено на каждом участке?
На первом катере было в 2 раза больше людей, чем во втором. Когда на ближайшей пристани с первого катера сошли 98 человек, а со второго 16 человек, то на обоих катерах людей стало поровну. Сколько человек было на каждом катере первоначально?
В одном элеваторе зерна в 3 раза больше, чем в другом. Из первого вывезли 960 т зерна, а во второй привезли 240 т, после чего в обоих элеваторах зерна стало поровну. Сколько было в каждом элеваторе зерна первоначально?
В двух вагонах поезда ехало одинаковое количество пассажиров. После того, как из первого вагона вышли 26 пассажиров, а из второго – 17 пассажиров, в первом вагоне стало в 2 раза меньше пассажиров, чем во втором вагоне. Сколько пассажиров было в каждом вагоне первоначально?
Одно число в 4 раза меньше другого, а их сумма равна 60. Найти эти числа.
Одно число в 3 раза больше другого, а их разность равна 10. Найти эти числа.
Некоторое число увеличили на 20 и оказалось, что оно увеличилось в 3 раза. Найти это число.
Некоторое число увеличили на 35 и оказалось, что оно увеличилось в 5 раза. Найти это число.
В двухзначном натуральном числе сумма цифр равна 9. Число десятков меньше числа единиц на 3. Найдите это число.
В двухзначном натуральном числе сумма цифр равна 14. Число единиц меньше числа десятков на 4. Найдите это число
В двухзначном натуральном числе разность цифр равна 6. Число единиц меньше числа десятков в 4 раза. Найдите это число
В двухзначном натуральном числе разность цифр равна 7. Число единиц меньше числа десятков в 8 раз. Найдите это число.
Турист шел 3 часа пешком и 4 часа ехал на велосипеде. Всего он проделал путь в 62 км. С какой скоростью турист шел пешком, если он шел на 5 км/ч медленнее, чем ехал на велосипеде?
Поезд шел 3,5 ч со скоростью 64,4 км/ч. На сколько надо увеличить скорость поезда, чтобы пройти это расстояние за 2,8 ч.
Теплоход проходит за 15 ч против течения столько же, сколько за 13 часов по течению Найдите скорость течения реки, если собственная скорость теплохода 70км/ч. Ответ – 5 км/ч
Из двух сел, расстояние между которыми 21 км, вышли одновременно на встречу друг другу мужчина и женщина. При встрече оказалось, что мужчина прошел в раза больше расстояние, чем женщина. Через сколько часов после выхода они встретились если скорость мужчины 6км/ч? С какой скоростью шла женщина? Ответ через 2 часа, 4.5 км/ч.
multiurok.ru
«Решение задач на составление уравнений»
Урок математики в 6-м классе по теме
«Решение задач на составление уравнений»
Цель деятельности учителя: создать условия для формирования навыков решения задач на составление уравнений.
Планируемые результаты изучения темы:
Личностные: осознают причины успеха/неуспеха учебной деятельности; понимают важность и необходимость знаний для человека.
Предметные: умеют составлять математическую модель реальной ситуации, решать уравнение по правилам.
Метапредметные результаты изучения темы (универсальные учебные действия):
познавательные: владеют общим приемом решения задач; умеют проводить информационно-смысловой анализ текста, приводить примеры;
регулятивные: различают способ и результат действия;
коммуникативные: договариваются и приходят к общему решению в совместной деятельности, в том числе в ситуации столкновения интересов.
Оборудование: компьютер, мультимедийный проектор.
Дидактические материалы:
Учебник авт. И.И. Зубарева, А.Г. Мордкович “Математика. 6 класс”. М.: Мнемозина, 2009 г.
И.И.Зубарева, М.С.Мильштейн, В.Г.Гамбарин “Мультимедийное приложение” к учебникам “Математика, 5 класс”, “Математика, 6 класс” авторов И.И.Зубаревой, А.Г.Мордковича.
Компьютерная презентация урока в POWER POINT.
Сценарий урока.
Организационный этап
Добрый день, присаживайтесь!
Этап актуализация знаний.
– Ребята. Сегодня у нас необычный урок. Мы начнём знакомство с основами математического моделирования. Узнаем, как моделирование помогает решать задачи. С моделями мы встречаемся с детства. (Примеры приводят ученики) (Слайд №1)
“Откроем тетради, запишем тему урока. В начале урока не забудьте нарисовать в тетради смайлик. Какое у вас настроение?” Вы привели несколько примеров различных моделей. Но мы будем говорить о математических моделях.
Математическая модель является приближенным представлением реальных объектов, процессов, выраженных в математических терминах и сохраняющим существенные черты оригинала. (Слайд №2)
Построение математической модели заключается в определении связей между теми или иными процессами и явлениями.
Математическое моделирование – это средство изучения реального объекта, процесса или системы путем их замены математической моделью.
– Сегодня на уроке мы научимся использовать математическое моделирование для решения задач.
Слайд №3 «Для начала мы начнем с разминки» (работа в парах с взаимной проверкой по образцу)
Один ученик получает индивидуальное задание на карточке:
Реши задачу: Мастер и ученик вместе за 1 час изготовили 120 деталей. Сколько деталей изготовил ученик за 1 час, если мастер сделал на 20 деталей больше?

Этап изучение нового материала
На прошлых уроках вы учились решать уравнения. А сегодня будите учиться решать задачи при помощи уравнения.
Прочитаем задачу (Слайд №4)
Мастер и ученик вместе за 1 час изготовили 120 деталей. Сколько деталей изготовил ученик за 1 час, если мастер сделал на 20 деталей больше?
Решая задачи в 5 классе, с чего вы начинали? (рисовали схемы, исходя из условия задачи), т.е. переводили текст задачи на математический язык и получали математическую модель ситуации.
Ученик, работавший по карточке, объясняет решение задачи:
Ученик — ?
Мастер – на 20 деталей больше
120-20 = 100 (дет.) – делает мастер и ученик
100: 2 = 50 (дет.) – делает ученик за 1 час
Ответ: 50 деталей
Но, кроме такого способа решения задач, существует еще один способ решения таких задач. И я вам сейчас о нем расскажу. В задачах, в которых обе величины неизвестны, одну из них обозначают переменной (чаще всего это меньшая из двух величин).
Составляем краткую запись в виде таблицы.
Итак получаем уравнение.х+х+20 = 120
Решаем, полученное уравнение и получаем ответ на вопрос задачи.
Итак, решим еще одну задачу(слайд №5)
В классе 24 ученика. Известно, что девочек в 2 раза меньше, чем мальчиков. Сколько девочек и сколько мальчиков в классе?
Мальчики — ?
Девочки — ?, в 2 раза меньше, чем мальчиков
Девочек в два раза меньше, чем мальчиков. Отсюда, одна часть учащихся – девочки, а еще две такие части приходится на мальчиков.
1 + 2 = 3 (части) – приходится на всех учеников класса;
24 : 3 = 8 (уч.) – девочки;
24 — 8 = 16(уч.) –мальчики.
Ответ : 8 девочек, 16 мальчиков.
Решим эту задачу другим способом.
Пусть х девочек в классе, тогда 2х — мальчиков.
Зная, что всего в классе 24 ученика, имеем уравнение:
2х + х = 24;
3х = 24;
х = 24:3;
х = 8.
8 девочек в классе;
24 – 8 = 16 мальчиков.
Ответ : 8 девочек, 16 мальчиков.
Сравните эти две задачи и назовите, что у них общего. Вывод делают ученики.
При решении задач: 1) Составили краткую запись, 2) Составили уравнение, 3) Решили уравнение и 4) Записали ответ.
Открываем учебники п.20, читаем «Проверь себя!» и делаем вывод.
Этап первичное осмысление и закрепление знаний
Слайд №6. Выполнение № 595(у доски и в тетради)
Физминутка (проводит физорг класса)
Дети, повторяйте: хлопать начинайте,
Дружно наклоняйтесь. Дружно покачайтесь.
Вместе покивайте, вместе поморгайте,
Ручки вы потрите, ручкой помашите!
(Читает стишок и все вместе выполняют то, что в нём говорится)
Этап закрепление изученного материала
Работа в парах. Выполните № 596 самостоятельно. По окончании поменяйтесь тетрадями с соседом и проверьте. Один ученик работает за доской.
Решение:
Составление математической модели
Работа с математической моделью.
1) х – 3х = 10,2 – 21,6
-2х=-11,4
х = (-11,4):-2
х =5,7 (м) – глубина 1 скважины
2) 5,7+3,4 = 9,1 (м) – глубина 2 скважины
Ответ на вопрос задачи.
Ответ: 5,7м, 9,1м.
7. Этап подведение итогов. Домашнее задание.
— Наш урок подходит к концу, с начала запишем домашнее задание, затем подведем итоги.
На доске: Домашнее задание: П. 20, № 594(разобрать по учебнику), №597, тетрадь для см.р. стр. 73, упр. 3.
— А теперь подведем итоги: Что мы хотели узнать? Что мы узнали? На все ли вопросы мы получили ответы?
— Достигли ли вы поставленной цели?
— Давайте еще раз вспомним, как решить задачу с помощью уравнения? (Выделить три этапа математического моделирования)
Оценки за урок.
— Итог урока каждый из вас подведет с помощью телеграммы; то есть в виде одного краткого предложения, которое выразит ваше отношение к уроку
“Всем спасибо, урок окончен!”
infourok.ru
Задачи на составление уравнений
Задачи на составление уравнений для 5 – 6 классов..
На полке стояло несколько книг. После того, как с неё сняли 8 книг, а затем положили 17, на ней стало 22 книги. Сколько книг было на полке первоначально?
На двух полках 120 книг. На первой полке в 4 раза больше книг, чем на второй. Сколько книг на каждой полке?
На трёх складах 72 тонны пшеницы. На первом в 3 раза больше, чем на втором, а на третьем в 4 раза больше, чем на втором. Сколько зерна на каждом складе?
Петя подарил Даше на 2 цветка больше, чем Саша. Сколько цветов подарил каждый мальчик, если вместе они подарили 8 цветов?
Лиза нашла грибов в 2 раза больше, чем Ваня. А Таня в 4 раза больше, чем Ваня. Сколько грибов нашёл каждый из ребят, если вместе они нашли 140 грибов?
Коля сказал Лере в 5 раз больше вежливых слов, чем Паша. А Сева сказал Лере в 10 раз больше вежливых слов, чем Паша. Сколько вежливых сказал каждый из мальчиков, если все вместе они сказали 32 слова?
В двух корзинах 24 кг помидоров. В первой корзине в 2 раза больше, чем во второй. Сколько килограммов помидоров было в каждой корзине?
Кирилл и Валера вместе собрали 60 грибов. Причём Кирилл в 4 раза больше, чем Валера. Сколько грибов собрал каждый?
Данила и Виталий получили вместе 40 отметок. Причём Данила в 3 раза больше, чем Виталий. Сколько отметок получил Данила?
Вика сказала в 5 раз больше вежливых слов, чем её подруга. Сколько вежливых слов сказала Вика, если вместе в этот день они сказали 24 вежливых слова?
Тимофею сделали на уроке математики в 7 раз больше замечаний, чем Ивану. Сколько замечаний получил каждый, если вместе они получили 24 замечания?
Злата исписала за год тетрадей в 4 раза больше, чем Лера. Сколько тетрадей исписала каждая, если вместе они в четвертом классе исписали 120 тетрадей?
Костя выучил за год в 10 раз больше стихотворений, чем Лера. Сколько выучил Костя, если вместе они выучили 110 стихов?
Маша прочитала на 7 книг больше, чем её подруга. Сколько книг прочитала подруга, если вместе за год они прочитали 77 книг?
В коробке красных шаров было в 7 раз больше, чем синих. А зелёных шаров на 10 больше, чем синих. Сколько шаров каждого цвета было в коробке, если всего в коробке было 100 шаров?
На одной полке в 5 раз больше книг, чем на второй. После того как с первой полки переложили на вторую 12 книг, на полках книг стало поровну. Сколько книг было первоначально на каждой полке?
На двух полках было книг поровну. Если на вторую полку положить еще 15 книг, то на ней книг станет в 2,5 раза больше, чем на первой. Сколько книг было на каждой полке первоначально?
intolimp.org
Урок по математике «Решение задач на составление уравнения»
Тема: Решение задач на составление уравнения.
Цель: — закрепление вычислительных навыков;
— закрепление умений решения уравнений;
— формирование умений решения текстовых задач путем выделения трех этапов
математического моделирования;
— формирование умений записи обоснования уравнения, получаемого в ходе
решения задачи.
Ход урока:
1.Организационный момент.
2.Разминка (устные упражнения)
Двое учащихся у доски записывают решения уравнений, которые были заданы на дом.
С остальными проводится разминка – решений уравнений (слайд 1), (слайд 2).
На экране появляются условия. Учащиеся производят вычисления устно.
Слайд 1
Разминка
1) -6х = 12 4) 
2) 2х = — 2, 4 5) 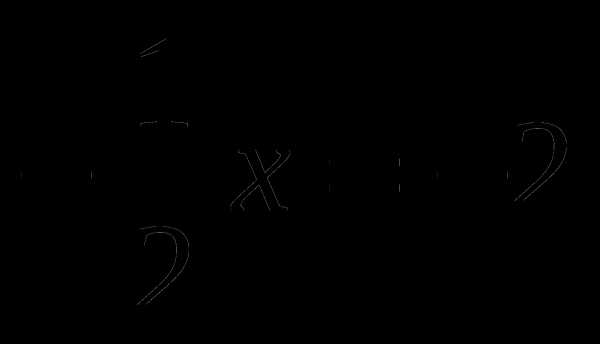
3)  6)
6) 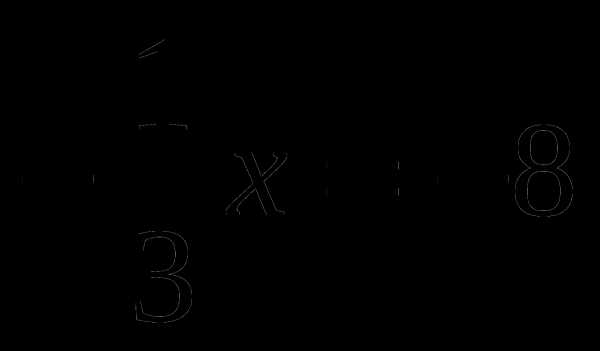
Слайд 2
1) 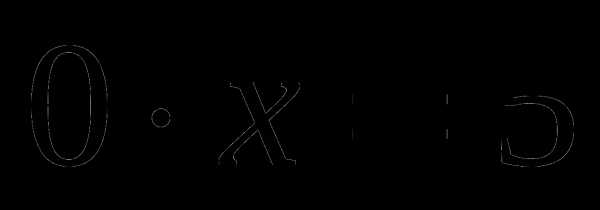
2) 
3) 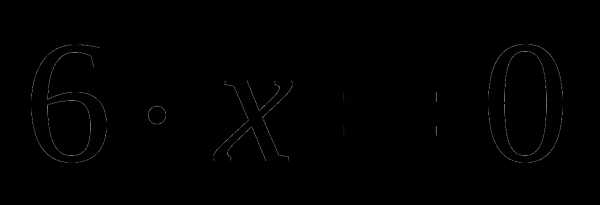
4)
3.Изучение нового материала.
Учитель: Ребята, сегодня мы рассмотрим много уравнений. Мы с вами знаем, что часто уравнения помогают решать задачи. Появляются они а процессе решения, как математические модели ситуаций, которые описываются в задачах.
Сегодня на уроке мы будем учиться правильно оформлять решения таких задач.
Решим такую задачу: В одном бидоне молока было в 3 раза больше, чем в другом. Когда из одного бидона перелили в другой 5 литров, молока в бидонах стало поровну. Сколько литров молока было в каждом бидоне первоначально?
Вопросы: 1) О каких величинах идет речь в задаче?
Что известно об этих величинах?
Что происходило, какие действия были выполнены?
Что в итоге получилось?
Учитель: Рассмотрим графическую модель ситуации, описанной в задаче, и составим ее аналитическую модель. (Демонстрируется слайд 3. В ходе демонстрации обсуждается, какую величину удобно принять за
Слайд 3
Решение задач на составление уравнений
1 бидон
5 л
2 бидон
5 л
3х – 5 = х + 5
Учитель: Теперь, когда мы обсудили, давайте посмотрим, как можно записать решение этой задачи. (Демонстрируется 4 слайд)
Слайд 4
1.Составление математической модели
Пусть х л. – количество молока во 2 бидоне до переливания.
Тогда 3х л. — количество молока в 1 бидоне до переливания;
(3х – 5)л.- осталось в 1 бидоне, (х + 5)л. – стало во 2 бидоне.
По условию задачи, после переливания молока в обоих бидонах стало поровну.
Составим уравнение:
3х – 5 = х + 5
Учитель: Сначала вы записываете, что принимаете за х. (Появляется соответствующий текст слайда, учитель его читает). Затем записываете как через х выражаются остальные величины (появляется и читается текст до уравнения). Теперь нужно записать, на основании чего составляется уравнение, а затем и само уравнение (появляется соответствующий текст). Этот этап решения задачи называется составлением математической модели ( на экране появляется название этого этапа).
Учитель: А что нужно делать дальше?
Ученики: Решить уравнение.
Учитель: Прежде, чем решать уравнение, запишем первый этап в тетради(ученики записывают). Теперь переходим к следующему этапу – работе с математической моделью, т.е. к решению уравнения. (Начинается демонстрация 5 слайда).
Слайд 5
2.Работа с математической моделью
3х – 5 = х + 5,
3х – х = 5 + 5,
2х = 10,
х = 5.
3.Ответ на вопрос задачи
5 л. – столько было молока во 2 бидоне
5
 (л) – столько было молока в 1 бидоне.
(л) – столько было молока в 1 бидоне.Ответ: 15л,5л.
Учитель: Запишите этот этап в тетради самостоятельно. (Учащиеся записывают, а затем по просьбе учителя проговаривают решение уравнения по шагам). Уравнение решено. Какую величину мы нашли? Мы ответили на вопрос задачи?
Ученики: Нет, потому что …
Учитель: Запишите название третьего этапа: «Ответ на вопрос задачи». (Решение сначала проговариваются учащимися устно, затем появляется на экране). Теперь можно записать ответ?
Ученики: Да. (появляется ответ)
Учитель: Итак, мы сейчас решили задачу, выделяя три этапа математического моделирования. Назовите, пожалуйста, еще раз эти этапы.
4. Закрепление нового материала.
Задача: Надо расставить 380 книг на полки так, чтобы на второй полке было на 6 книг больше, чем на первой, а на третьей – на 9 книг больше, чем на второй. Как это можно сделать?
Учитель: 1) О каких величинах в задаче идет речь?
2) Что известно об этих величинах?
3) Что получилось в итоге?
4) Какую величину удобно принять за х?
5) Как и каким образом через х выражаются остальные величины?
6) На основании чего можно составить уравнение?
Слайд 6
1. Составление математической модели
1 полка – х книг,
2 полка – (х + 6) книг,
3 полка – (х + 6) + 9 = х + 15 книг.
По условию задачи на 3-х полках 380 книг.
Составим уравнение: х + (х + 6) + (х + 15) = 380
2. Работа с математической моделью.
3. Ответ на вопрос задачи
Учащимся предлагается записать таблицу в тетради и завершить решение задачи самостоятельно. Учитель, проходя между рядами, наблюдает за деятельностью учащихся и, при необходимости, корректирует их. Проверка осуществляется устно.
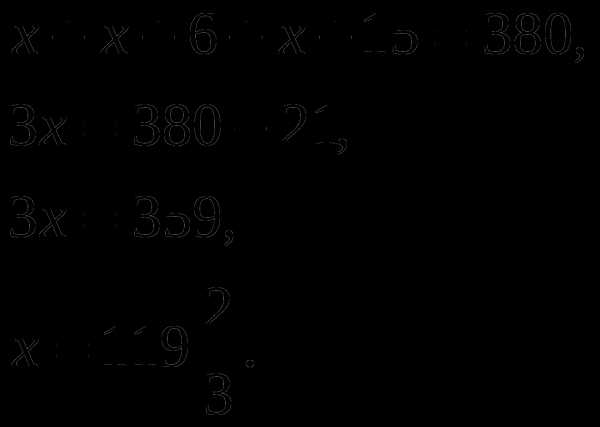
Учитель: Можно ли расставить книги на полки таким образом.
Ученики: Нет.
Учитель: Почему?
Ученики: Число книг на полке не может быть дробным.
5. Задание на дом: №158, №161.
6. Итог урока: — Что мы сегодня на уроке узнали нового?
— Что мы сегодня научились делать?
математической моделью, т. е.апишем первый этап в тетради(ученики записывают). появляется название этого этапа).
infourok.ru
Схема решения задач на составление уравнений
Все задачи на составление уравнений можно решать по схеме:
1. Анализ и краткая запись условия задачи. Построение чертежа, если он необходим.
2. Выявление оснований для составления уравнения.
3. Составление уравнения.
4. Решение уравнения.
5. Исследования корней уравнения.
6. Запись ответа.
Задачи на движение.· s = vt v = t =
Основные типы задач на движение:
1) задачи на движение по прямой (навстречу и вдогонку),
2) задачи на движение по замкнутой трассе,
3) задачи на движение по воде,
4) задачи на среднюю скорость,
5) задачи на движение протяженных тел.
Для успешного решения задач на движение нужно кое-что твёрдо держать в голове. А именно – формулу-ключ, в которой связаны путь, время и скорость. В любой задаче дают кучу информации, но эту формулу – никогда! Это должно быть ваше знание! s = vt
Чтобы эту формулу-ключ хорошо и осмысленно запомнить, достаточно ответить самому себе на простой вопрос: «Если я иду со скоростью 4 километра в час, какое расстояние я пройду за 1 час? за 2 часа?». Очевидно, умножив 4 на 1, получим 4 км за 1 час; 4 умножим на 2, получим 8 км за 2 часа. Вот вы и запомнили нехитрую формулу скорости, пути, времени: s = vt
s — это пройденный путь, или расстояние,
v – скорость движения,
t– время движения.
Зная эту формулу (для расстояния), вы можете легко получить из неё формулу для скорости
v = или времени t =
Запомнили? Если считать задачу замком, то эти формулы – ключи, который должен быть всегда при вас. Ибо без ключа замок открывать неудобно…
Что нам даёт этот ключ? Он нам даёт дополнительную информацию! Которой, как раз, и не хватает. Скажем, в задаче даны скорость и расстояние. А нам нужно найти время. Из формулы-ключа можно найти время. Если формулу-ключ помните, то любую величину можно найти, зная две другие величины.
Как составить уравнение задачи на движение? Это и есть самое интересное.
Нужно что-то взять за икс (x). Что брать за икс? В простых задачах за икс, чаще всего, можно брать вопрос задачи. Вот что надо узнать в задаче, вот это и будет иксом!
Практические советы:
1. Записываем формулу-ключ: s = vt
2. До составления уравнения, приводим (если надо) все величины задачи к единым единицам измерения.
3. Определяемся с иксом, расписываем через икс все данные. Особое внимание на величины, входящие в формулу-ключ: путь, скорость, время. Эти величины – основа решения задач на движение. Стараемся снять всю возможную информацию с задачи.
4. Записываем уравнение. Если никак не записывается, читаем задачу. Скорее всего, вы использовали не все данные из задачи или не увидели в тексте подсказки. Она, подсказка, всегда есть.
5. Решаем уравнение. При получении двух корней – за ответ берём приличный корень, несусветный и левый – отбрасываем.
Допущения, которые обычно принимаются в условиях этих задач:
1) движение на отдельных участках считается равномерным (если не указано противное),
2) величины должны быть выражены в одной системе единиц;
3) повороты движущихся тел считаются мгновенными;
4) если тело движется по течению реки, то его скорость равна сумме скорости тела в стоячей воде (собственной скорости )и скорости течения:
если тело движется против течения, то его скорость равна разности собственной скорости и скорости течения
;
5) если два тела начинают движение одновременно навстречу друг другу, и – скорости тел; s – первоначальное расстояние между телами, то время в пути до встречи у обоих тел одинаково:
6) если два тела начинают движение одновременно в одном направлении, и – скорости тел, > , s– первоначальное расстояние между телами, то время, в течение которого одно тело догонит другое (время в пути до встречи)
;
7) если в задаче отсутствуют единицы длины, то весь пройденный путь можно принять за единицу;
8) если движение двух точек со скоростями и (> ) происходит по окружности длины l, то при движении в противоположных направлениях точки будут встречаться через время, а при движении в одном направлении (при условии одновременного старта из одного положения) точка с большей скоростью догонит другую, обогнав ее на целый круг
: ; где t– время в пути до встречи.
Перед решением задачи составляем таблицу, при этом обращаем внимание на следующее, если речь идёт о двух телах:
1. При заполнении столбика «время»
вышли они одновременно или нет?
какое тело находилось в пути дольше и на сколько часов?
какое тело находилось данное время в пути или это общее время?
2. При заполнении столбика «расстояние»
какое тело прошло заданное расстояние или это общее расстояние. В зависимости от этого пройденное расстояние проставляем или напротив каждого тела, или объединяем два тела
какое тело прошло большее расстояние и на сколько, или они прошли одинаковое расстояние. На эти же самые пункты обращаем внимание, если речь идёт не о двух телах, а об одном теле, движение которого разбито на части.
infourok.ru
Мотивационно-целевой | Организационный момент Проверка готовности: -Проверьте все ли у вас готово к началу урока? На месте ли ручка, на месте тетрадка? — Здравствуйте, садитесь. -Кто сегодня отсутствует? (отмечает в журнале) 2. Актуализация знаний — что означает этот знак (С2 «+»), он объединяет числа. -Вот неизвестный компонент (С3), скажите как он называется? -А это что за элемент, какое носит он названье? (С4) -Какой недостающий компонент этой разности? (С5) -Хорошо, я вижу, вы все хорошо знаете компоненты сложения и вычитания. Подведение к теме урока — А сейчас, ребята, посмотрите на экран. Скажите, можно ли по данным рисунка составить задачу?(С6) — Давайте составим задачу. (фиксирует краткую запись на доске) было -7б. Унес — ? Осталось – 2б. Давайте решим эту задачу. Сначала откроем тетради, запишем число. Запись на доске: Решение: 7-2=5 (бутылок) Ответ: 5 бутылок унес кот. А вы знаете, что эту задачу можно было решить при помощи уравнения. Вот посмотрите: 7-х=2 Х=7-2 Х=5 Ответ: 5 бутылок унес кот. Ребята, посмотрите на решение задачи и скажите, какая тема нашего урока? Чем мы будем заниматься? Все — верно, будем решать задачи и уравнения. А вот я получила уравнение из условия задачи, если мы с вами объединим и задачи, и уравнения, то получим тему: «Решение задач на составление уравнений». Запишем тему урока. (фиксирует на доске) Цель и задачи урока Какую цель урока мы с вами поставим на данном уроке? (фиксирует цель на боковой доске). Чтобы прийти к поставленной цели, какие задачи необходимо решить? Нам нужно вспомнить, что такое уравнение? Итак, наша 1.задача: повторить понятие уравнения. (фиксирует на доске) — А мы знаем, по каким правилам выполняются решение уравнений на нахождение неизвестных компонентов сложения и вычитания? — Значит, надо вспомнить? 2.задача: повторить правила нахождение неизвестных компонентов сложения и вычитания. (фиксирует) — А зачем нам эти правила? А умеете ли вы по условию задачи составлять уравнения? Это будет нашей 3 задачей: Научиться составлять уравнения по условию задачи. (фиксирует) | 1. Организационный момент -Проверяют свою готовность к уроку (наличие тетради, ручки, учебника). -Приветствуют учителя, садятся за парты. -отчет дежурного об отсутствующих 2. Актуализация знаний — Ответы учащихся: плюс -слагаемое — уменьшаемое — вычитаемое Подведение к теме урока — да. — Составляют: у кота было 7 бутылок молока. После того как он унес несколько бутылок, осталось 2. Сколько бутылок унес кот? Записывают число Записывают решение задачи. — Как? Смотрят, подсказывают как решить полученное уравнение. — решать задачи, решать уравнения. записывают Цель и задачи урока — научиться решать задачи на составление уравнений. — да. -да. Знаем, но немного забыли — чтобы правильно решать уравнения Нет. | Слайд 1. дата Презентация Слайд 2. Слайд 3. Слайд 4. Слайд 5. Слайд 6 | Операционально-содержательный | Решение поставленных задач — Что такое уравнение? Что значит решить уравнение? Как найти неизвестное слагаемое? -уменьшаемое? -вычитаемое? Хорошо, все верно. — А вы знаете, что лес играет огромную роль для человечества? — Молодцы, а еще он поддерживает влажность воздуха. Лес называют – зеленными легкими планеты. (С7) — Поэтому наши задачи сегодня будут связаны с лесом. Итак, внимание на экран: по рисунку составим условие задачи и решим ее. (С8) !!!А вы знали, что зайцы, являясь безобидным животным, может нанести вред лесу? Он объедает кору у осин и обкусывает верхушки у подроста лиственных парод.(С9) Внимание на экран, следующая задача. (С10) А вы знаете, какую роль для леса играют птицы? (С11) Физминутка Мы чуть-чуть уже устали Ну-ка дружно все мы встали. Превратимся на полминутки в деревцо. — ветер дует нам в лицо, Закачалось деревцо. Ветер тише, тише, тише… Деревцо все выше, выше, выше… Встали ровно, подтянулись и друг другу улыбнулись. — садитесь. Продолжаем работать. Следующая задача уже на экране. (С12) -береза имеет высоту 15 метров. Клен на несколько метров ниже березы, и его высота 10 метров. На сколько метров клен ниже березы? !!!А вы знаете, что клен и береза обладают бактерицидным действием. Береза живет 100-120 лет. Внимание на экран: на аллее растут 15 тополей и несколько хвойных деревьев. Всего 38 деревьев. Сколько хвойных деревьев растут на аллее? (С13) !!! А вы знаете, что тополь лучше других деревьев очищает воздух. Гектар тополей очищает воздух в 40 раз больше, чем гектар хвойных деревьев. За сутки один тополь выделяет кислорода, столько, что хватит для дыхания трех человек в течении этого времени.(14) Работа в парах Ребята, сейчас мы с вами поработаем самостоятельно в парах. Ваша задача заключается в следующем: по рисунку составить краткую запись задачи, составить уравнение и решить его. (учитель дает консультацию ребятам по мере необходимости) — Какой неизвестный компонент вы искали? — Как найти неизвестное слагаемое? Переверните карточку и проверьте получившееся уравнение. У всех получилось? — Вы все постарались, выполняя задания, советовавшись друг с другом, поэтому у вас все получилось. | Решение поставленных задач — это равенство с неизвестным компонентом. — найти неизвестный компонент — чтобы найти неизвестное слагаемое, надо от суммы отнять разность. — чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое. — чтобы найти неизвестное вычитаемое, надо от уменьшаемого отнять разность. — да, он очищает воздух, дает нам много витаминов (ягоды, грибы, лечебные травы). — Лес – это дом для растений и животных. — белка и зайка собрали 9 грибов. Белка 4 гриба и зайка несколько. Сколько грибов собрал зайка? Учащийся решает задачу у доски, с помощью учителя. Остальные записывают в тетрадь. — комментируют
Смотрят на презентацию, составляют задачу: на ветке сидело несколько птиц. После того как 3 птицы улетело, то осталось 5. Сколько птиц сидело на ветке? Учащийся решает задачу у доски, с помощью учителя. Остальные записывают в тетрадь. — Птицы защищают деревья от вредителей-насекомых. Совы защищают корни деревьев от грызунов (мышей). Физминутка Встали. Выполняют физминутку Садятся. Смотрят. Учащийся решает задачу у доски, с помощью учителя. Остальные записывают в тетрадь. Комментируют. Учащийся решает задачу у доски. Остальные записывают в тетрадь. Комментируют. Работа в парах Работают. слагаемое — повторяют правило. -да. | Слайд 7 Слайд 8 Слайд 9 Слайд 10 Слайд 11 Слайд 12 Слайд 13 Слайд 14 Дидактический материал (карточки с разным заданием для каждой пары) | Рефлексивно-оценочный | Подведение итогов А сейчас давайте вернемся к нашим задачам. Все ли задачи решены? 1.задача: повторить понятие уравнения. 2.задача: повторить правила нахождение неизвестных компонентов сложения и вычитания. 3 задача: Научиться составлять уравнения по условию задачи. А что вы можете сказать про поставленную цель в начале урока, достигли ли ее? Что нового и полезного вы узнали на уроке? (С15) Прошу посмотреть на экран и закончить предложения. Очень хорошо. Я рада вашим успехам. Домашнее задание Когда пойдете на прогулку, посчитайте, сколько тополей растет на школьном участке. Оценивание Учитель озвучивает отметки за работу на уроке. (ответы, работа у доски, активная работа на уроке) Урок окончен, всего доброго. | Подведение итогов Мы повторили понятие уравнения и правила нахождения неизвестных компонентов сложения и вычитания. Также мы научились составлять уравнения по условию задачи и решать их. Мы ее достигли. При помощи слайда рефлексии делятся впечатлениями. Домашнее задание Записывают. Оценивание Выставляют отметки в дневники. | Слайд 15 |
xn--j1ahfl.xn--p1ai
Как решать задачи на составление уравнений?
Перед тем, как решать задачи на составление уравнений, нужно хорошо изучить теорию положения химического элемента в Периодической таблице Д.И. Менделеева, чтобы знать, как определить валентность конкретного элемента. Для того, чтобы составить уравнение химической реакции окисления алюминия кислородом запишем символы, которыми обозначаются данные химические элементы: , .
Теперь перейдем к веществам. Алюминий – металл, его молекула состоит из одного атома, кислород – неметалл, молекула которого состоит из двух атомов:
.
Пока мы точно не знаем, какой состав будет иметь образующееся соединение. Для того, чтобы его определить необходимо знать валентности алюминия и кислорода. Они равны III и II, соответственно. Индексы будут расставляться наоборот: у алюминия – II, а у киcлорода – III, т.е. формула образующегося вещества — .
Теперь уравнение реакции принимает вид:
.
Остается только расставить коэффициенты. В реакцию вступило 2 атома кислорода, а образовалось – 3. Чтобы уравнять число атомов кислорода нужно найти наименьшее общее кратное. Это 6. Следовательно, перед формулой кислороды мы должны будем поставить коэффициент 3, а перед формулой оксида алюминия – 2.
Перейдем к алюминию: в реакцию вступил 1 атом, а образовалось – 4; наименьшее общее кратное равно 4-м, следовательно, перед формулой алюминия мы должны поставить 4:
.
ru.solverbook.com

 (л) – столько было молока в 1 бидоне.
(л) – столько было молока в 1 бидоне.