Линейное Уравнение — Mathcracker.Com
Инструкции: Используйте это Калькулятор линейных уравнений вычислить график предоставленного вами линейного уравнения, показав все шаги. Пожалуйста, укажите линейное уравнение (например, \(x + 5y = 2 + \frac{2}{3}x\)) в поле ниже:
Подробнее о линейные уравнения
Этот калькулятор поможет вам построить график линейного уравнения, которое вы предоставите. Итак, первым шагом является предоставление действительного линейного уравнения, например 2x + 3y = 4, или вы можете предоставить что-то, что не упрощается напрямую, например 2/3 x + y = 4/3 x — 1/2 y + 2. Подойдет любое действительное линейное выражение. .
Подойдет любое действительное линейное выражение. .
После того, как вы предоставите действительное линейное уравнение, наступает самое легкое время, поскольку все, что вам нужно сделать, это нажать кнопку «Вычислить», и вам будут показаны этапы процесса построения графика линейной функции.
Линейные уравнения будут играть важную роль во многих операциях, в том числе для решить систему линейных уравнений .
Формула линейного уравнения
Существуют различные формы, в которых можно записать формулу линейного уравнения. Наиболее распространенными являются
стандартная форма
, который показан ниже
Наиболее распространенными являются
стандартная форма
, который показан ниже
Кроме того, существует форма пересечения наклона , который показан ниже
\[y = mx + n\]
Эти две формы могут быть преобразованы из одной в другую, за исключением пары исключений, а именно вертикальной линии, выраженной x = a. Эта линия вертикальна и пересекает ось x в точке (a, 0). Мы имеем, что x = a является стандартной формой линии, но эта линия не имеет наклонного перехвата (по крайней мере, там, где y является зависимой переменной)
Мы имеем, что x = a является стандартной формой линии, но эта линия не имеет наклонного перехвата (по крайней мере, там, где y является зависимой переменной)
Каковы этапы построения графика линейного уравнения?
- Шаг 1: Четко определите имеющееся уравнение
- Шаг 2: Посмотрите коэффициент, который умножает y, если он равен нулю, то у вас есть вертикальная линия
- Шаг 3: Если коэффициент, умножающий y, отличен от нуля, то вы решаете для y, чтобы получить форма пересечения наклона
- Шаг 4: Используя форму «наклон-пересечение», оцените функцию при x = 0 и x = 1, и тогда у вас будет две точки, через которые проходит прямая
- Шаг 5: Проведите линию, используя две найденные точки в качестве ориентира
Один из самых четких способов провести линию — это иметь две точки, через которые проходит линия, так как часто использование наклона для ориентира может ввести в заблуждение.
Решение линейного уравнения в одной переменной
Студенты знакомы с системами линейных уравнений, и они более или менее понимают, что нужно сделать. Но затем они задаются вопросом о решении линейного уравнения с одной переменной. Допустим, у вас есть линейное уравнение в форме «наклон-пересечение»:
\[y = a + bx \]Как же решить эту проблему? Ну, она уже решена: Для каждого заданного значения x решение y равно y = a + bx. Таким образом, при условии, что \(b \ne 0\), у вас есть бесконечное множество решений линейного уравнения.
Ситуация меняется, когда у вас есть два линейных уравнения, в этом случае вам нужно
решить оба уравнения одновременно
.
Так ли важны линейные уравнения?
Еще бы! Пожалуй, один из самых важных во всей математике. Это объясняется простотой и в то же время широким спектром применения.
Пример: калькулятор линейных уравнений
Получите график следующего линейного уравнения: \(\frac{1}{3} x + \frac{7}{4} y — \frac{5}{6} = 0\)
Решение:
Получите уравнение линии в форме наклон-пересечение
Нам было дано следующее уравнение. .:
.:
Упрощение констант:
\[\displaystyle \frac{1}{3}x+\frac{7}{4}y-\frac{5}{6}=0\]Теперь, положив \(y\) в левой части, \(x\) и константу в правой части, получим
\[\displaystyle \frac{7}{4}y = -\frac{1}{3}x + \frac{5}{6}\]Теперь, находя \(y\) путем деления обеих частей уравнения на \(\frac{7}{4}\), получается следующее
\[\displaystyle y=-\frac{\frac{1}{3}}{\frac{7}{4}}x+\frac{\frac{5}{6}}{\frac{7}{4}}\]и упрощая окончательно получаем следующее
\[\displaystyle y=-\frac{4}{21}x+\frac{10}{21}\]
Вывод
: На основании имеющихся данных мы делаем вывод, что уравнение линии в форме наклонная-пересечение имеет вид: \(\displaystyle y=-\frac{4}{21}x+\frac{10}{21}\), с наклоном \(\displaystyle b = -\frac{4}{21}\) и y-перехватом \(\displaystyle n = \frac{10}{21}\).
Учитывая эти данные, представленный линейный график показывает
Пример: пример калькулятора линейных уравнений
Вычислите следующее: \(\frac{1}{3}x + \frac{5}{4}y = \frac{1}{6}\)
Отвечать: Теперь мы получили следующее уравнение:
\[\displaystyle \frac{1}{3}x+\frac{5}{4}y=\frac{1}{6}\]Первый шаг — упрощение констант:
\[\displaystyle \frac{1}{3}x+\frac{5}{4}y=\frac{1}{6}\]Поместив \(y\) в левую часть, а \(x\) и постоянный член в правую часть, получим
\[\displaystyle \frac{5}{4}y = -\frac{1}{3}x +\frac{1}{6}\]Теперь нам нужно решить \(y\), что достигается делением обеих сторон уравнения на \(\frac{5}{4}\), и получается следующее
\[\displaystyle y=-\frac{\frac{1}{3}}{\frac{5}{4}}x+\frac{\frac{1}{6}}{\frac{5}{4}}\]и упрощая окончательно получаем следующее
\[\displaystyle y=-\frac{4}{15}x+\frac{2}{15}\]
Вывод
: Уравнение линии в форме наклон-пересечение, согласно представленной информации, равно \(\displaystyle y=-\frac{4}{15}x+\frac{2}{15}\), с наклоном \(\displaystyle b = -\frac{4}{15}\) и y-пересечением \(\displaystyle n = \frac{2}{15}\).
Согласно этим данным, представленный линейный график имеет вид
Пример: еще один пример калькулятора линейных уравнений
Представляет ли это линию: \( y = 5 \). Если да, то каковы ее характеристики?
Отвечать: Да, это так. Действительно, когда у вас есть выражение типа \( y = 5 \), у вас есть линейное уравнение в форме «наклон-пересечение», с a = 0 и b = 5. Следовательно, мы имеем горизонтальную линию, которая пересекает ось y в точке (0, 5).
Больше калькуляторов по алгебре
Линии
,
Линейные уравнения
и
линейные функции
всегда будет играть решающую роль в алгебре, представляя также четкую связь с некоторыми основными геометрическими свойствами.
С точки зрения применения, возможно Решение систем линейных уравнений является одним из самых распространенных применений линий и линейных уравнений.
заказ решений на аукционе за минимальную цену с максимальным качеством
Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать:
- решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
- написание лабораторных, рефератов и курсовых
- выполнение заданий по литературе, русскому или иностранному языку.
Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.
Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.
Объединение сервисов в одну систему
Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы:
- Форум, где посетители обмениваются идеями и помогают друг другу
- Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения
- Аукцион, где цена за товар или услугу определяется в результате торгов
- Система рейтингов, где участники могут оценивать ответы друг друга. Причем, чем больше рейтинг пользователя, тем более значимым становится его голос
Принцип работы
Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами.
Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания. Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.
Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например, уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели.
Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте). Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т. к. можно учитывать и другие факторы – см. выше).
к. можно учитывать и другие факторы – см. выше).
Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.
За счет чего будет развиваться сервис
Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей.
Второе – удобный сервис для заказчиков и для желающих заработать на решениях.
Преимущества для заказчиков
Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.
Преимущества для решающих задания
Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения.
Преимущества для владельца сервиса
Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике. И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.
И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.
В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.
Что необходимо для создания сервиса
- Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.
Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию.

- Выбрать платежную систему.
- Сделать подходящий движок для сайта. Нужно решить – создавать его с нуля или изменить какой-нибудь существующий движок (например, форумный) с открытой лицензией.
- Привлечь посетителей. Учитывая посещаемость exir.ru и число публикуемых на форуме вопросов, думаю, это не будет большой проблемой.
Desertai be cukraus Vilniuje: tortai, pyragaičiai, saldainiai
Калькулятор решения линейных уравнений | Узнайте, как работает решатель линейных уравнений
Калькулятор решения линейных уравнений — это онлайн-инструмент, который быстро находит переменные для заданного уравнения. Просто введите уравнение в поле ввода и нажмите кнопку «Рассчитать». Он вычисляет заданные уравнения за несколько секунд и отображает точные результаты с подробным объяснением.
Калькулятор решения линейных уравнений: Линейные уравнения — самая важная тема в математике. Изучить шаги для решения системы линейных уравнений очень легко на этой странице онлайн-калькулятора. Поскольку он охватывает решение калькулятора линейных уравнений, а также объяснение всей концепции, такой как определение, как шаг за шагом решать линейное уравнение с решенными примерами. Воспользуйтесь этим удобным и бесплатным онлайн-калькулятором линейных уравнений и найдите решения в мгновение ока.
Поскольку он охватывает решение калькулятора линейных уравнений, а также объяснение всей концепции, такой как определение, как шаг за шагом решать линейное уравнение с решенными примерами. Воспользуйтесь этим удобным и бесплатным онлайн-калькулятором линейных уравнений и найдите решения в мгновение ока.
В математике линейное уравнение определяется как выражение, в котором каждый член переменной имеет показатель степени, равный единице. Если это представить на графике, то получится прямая линия. Уравнение прямой линии y=mx+c является примером линейного уравнения.
Обычно линейное уравнение имеет форму Ax+B=C, где A, B, C — константы, а x — переменная. Более того, линейные уравнения можно записать тремя различными способами:
- Линейное уравнение с одной переменной
- Линейное уравнение с двумя переменными
- Линейное уравнение с тремя переменными
Решение калькулятора линейных уравнений позволяет найти решение переменной для заданного уравнения за секунды.
Как решить систему линейных уравнений?
Следующие шаги помогут вам лучше понять, как решать линейные уравнения. Внимательно изучите шаги и научитесь вычислять линейное уравнение:
- Во-первых, поймите данное уравнение и правильно его перестройте.
- Выполните арифметические операции, такие как сложение, вычитание и т. д., чтобы упростить уравнение.
- Если известные числа решены и переставлены в правильном порядке, вычислить неизвестную переменную в уравнении.
Решено Пример:
Решите уравнение 20 = 2x + 4.
Решение:
Данное уравнение 20 = 2x + 4
Измените уравнение, переставив переменную в одну часть и константу в другую.
2x+4 = 20
2x = 20-4
2x = 16
x = 16/2
x = 8
Следовательно, значение переменной x равно 8,9 0003
- Что такое Линейное уравнение?
Линейное уравнение — это уравнение, которое дает прямую линию при представлении на графике. Это алгебраическое уравнение вида y=mx+b.
Это алгебраическое уравнение вида y=mx+b.
- Как выразить стандартную форму линейного уравнения?
Стандартная форма линейных уравнений: Ax + By + C = 0 (A ≠ 0, B ≠ 0), где x, y — переменные, а A, B и C — константы.
- Откуда я могу узнать о решении линейных уравнений?
Концепция линейных уравнений кратко объясняется на нашей странице. Пройдите страницу и научитесь решать линейные уравнения вручную.
- Можно ли найти переменные заданных линейных уравнений с помощью онлайн-калькуляторов?
Да, с помощью онлайн-калькулятора также можно легко рассчитать переменную заданных линейных уравнений.
- Какой онлайн-инструмент лучше всего подходит для решения линейных уравнений?
Linearequationscalculator.com — это лучший и надежный веб-сайт, который предоставляет бесплатный онлайн-калькулятор для всех разделов линейных уравнений, таких как калькулятор решения линейных уравнений, калькулятор линейных уравнений с одной переменной и многое другое.
Калькулятор решения линейных уравнений
|
Наших пользователей: Я просто хотел сказать вам, что я только что купил вашу программу, и это невероятно! Большое спасибо за разработку такой программы. Перетащите сюда файлы Convert To Или выберите новый формат И согласиться с нашими Условиями Эл. адрес? You are attempting to upload a file that exceeds our 50MB free limit. You will need to create a paid Zamzar account to be able to download your converted file. Would you like to continue to upload your file for conversion? * Links must be prefixed with http or https, e. Ваши файлы. Ваши данные. Вы в контроле. Используя Zamzar можно конвертировать файлы DOC во множество других форматов DOC to PDF — Convert file now Available Translations: English
| Français
| Español
| Italiano
| Pyccĸий
| Deutsch Перетащите сюда файлы Convert To Или выберите новый формат И согласиться с нашими Условиями Эл. адрес? You are attempting to upload a file that exceeds our 50MB free limit. You will need to create a paid Zamzar account to be able to download your converted file. Would you like to continue to upload your file for conversion? * Links must be prefixed with http or https, e.g. http://48ers.com/magnacarta.pdf Ваши файлы. Используя Zamzar можно конвертировать файлы DOCX во множество других форматов DOCX to PDF — Convert file now Available Translations: English
| Français
| Español
| Italiano
| Pyccĸий
| Deutsch Главная > Слово в PDF С легкостью конвертируйте файлы Doc в PDF онлайн! Выберите файл Выбрать файл С Google Диска Из Dropbox Или перетащите файлы сюда Оцените этот инструмент () Загрузите документ Word со своего компьютера или перетащите его в окно преобразования PDF, чтобы начать процесс преобразования в PDF. Получите доступ к документу PDF, загрузив файл преобразования PDF на свой компьютер. Просмотрите преобразование PDF из файла Word в браузере. Добавьте файлы на Google Диск или отправьте электронное письмо с безопасной ссылкой, чтобы преобразовать файл Word в файл PDF. Преобразование DOC в PDF онлайн или преобразование из PDF с сохранением макета и безопасности вашего документа. Ваш документ отображается так же, как в Word, даже после преобразования Word в PDF путем перетаскивания. С нашим онлайн-конвертером Word в PDF содержимое остается доступным для редактирования независимо от формата. Изменяйте файлы, конвертируйте в PDF и конвертируйте из PDF с помощью нашего приложения Soda PDF Desktop и онлайн-инструментов PDF. Преобразование из PDF БЕСПЛАТНО с помощью нашего инструмента PDF в Word. Хотите преобразовать файл Word в документ PDF? Узнайте, как преобразовать файлы Microsoft Word в редактируемые PDF-документы за считанные секунды, используя простые в использовании инструменты преобразования PDF Soda PDF. Ссылка на статью Необходимо выполнить пакетное преобразование нескольких документов Word в файлы PDF? Попробуйте использовать мощную пакетную функцию Soda PDF, которая позволяет пользователям загружать несколько файлов Word или даже целую папку с файлами Word и быстро преобразовывать их в документы PDF. Используйте наши инструменты редактирования для изменения PDF-файлов. Ссылка на статью Быстро и легко сохраните документ Google в формате PDF. Узнайте обо всех различных способах быстрого преобразования вашего документа Google в документ PDF с помощью простого в использовании инструмента PDF-конвертера Soda PDF. Работайте прямо из вашего веб-браузера; просто загрузите документ с Google Диска и конвертируйте! Ссылка на статью *Могут применяться ограничения по размеру и ежедневному использованию. Конвертируйте DOC в PDF онлайн и бесплатно Перетаскивание файлов Преобразуйте в формат Или выберите другой формат (и принять наши условия) Электронная почта, когда закончите? Вы пытаетесь загрузить файл, размер которого превышает наш лимит в 50 МБ. Вам нужно будет создать платную учетную запись Zamzar, чтобы иметь возможность скачать преобразованный файл. * Ссылки должны иметь префикс http или https , например. http://48ers.com/magnacarta.pdf Частные лица и компании доверяют Zamzar с 2006 года. Мы обеспечиваем безопасность ваших файлов и данных и предлагаем выбор и контроль над удалением файлов. Попробовала и сразу влюбилась! Это было так легко использовать! После пары преобразований я купил ребятам чашку кофе. Еще пара и решил, что это слишком хорошо, чтобы злоупотреблять! Я присоеденился! Моя жизнь намного проще! Тилли Использовал его более года для преобразования моих банковских выписок в файлы csv. Агата Вежбицкая Я использовал этот продукт в течение многих лет. И обслуживание клиентов отличное. Только что возникла проблема, когда мне предъявили обвинение, и я не согласился с обвинением, и они позаботились об этом, хотя в этом не было необходимости. ДЖХ Очень полезный и профессиональный сайт. Сервис прост в использовании, а администраторы услужливы и вежливы. Дэвид Шелтон Я впервые им пользуюсь. У меня были некоторые сложности. Я не очень хорош в этом. Но я написал в компанию, и мне очень помогли. Я доволен обслуживанием клиентов и приложением. Ана Суарес Я использую Zamar всякий раз, когда мне нужно преобразовать аудио- и видеофайлы из нескольких отправителей в единый формат файла для редактирования аудио и видео. Кристофер Би Отлично подходит, когда вам нужно много конверсий за короткое время. Вы имеете прямой доступ и даже можете оформить подписку всего на месяц. Сабина Калис Большое спасибо всем вам за помощь в правильном преобразовании СТАРЫХ файлов. 20 лет, довольно долгий срок, просмотр файлов навевает мне много воспоминаний. Это лучший подарок, который я получил в прошлом году. Спасибо всем еще раз. Цзюнн-Ру Лай Я чувствую, что Замзар — активный член команды, особенно в проектах, над которыми я работаю, где я являюсь рабочей лошадкой, и это экономит так много времени и нервов. Я избалован Zamzar, потому что они установили очень высокую планку для преобразования файлов и обслуживания клиентов. Дебора Герман Фантастический сервис! Компьютер моей мамы умер, и у нее есть более 1000 файлов Word Perfect, которые она по какой-то причине хочет сохранить. Арон Бойетт Сотрудники некоторых из самых известных мировых брендов полагаются на Zamzar для безопасного и эффективного преобразования своих файлов, гарантируя, что у них есть форматы, необходимые для работы. Сотрудники этих организаций, от глобальных корпораций и медиа-компаний до уважаемых учебных заведений и газетных изданий, доверяют Zamzar предоставление точных и надежных услуг по конвертации, в которых они нуждаются. Мы предлагаем ряд инструментов, которые помогут вам конвертировать ваши файлы наиболее удобным для вас способом. Получить приложение Полностью интегрирован в ваш рабочий стол Преобразование более 150 различных форматов файлов Конвертируйте документы, видео, аудио файлы в один клик Изучите API Один простой API для преобразования файлов 100 форматов на ваш выбор Документы, видео, аудио, изображения и многое другое. С Zamzar конвертация файлов проста, надежна и удобна, поэтому вы можете быстро конвертировать документы, изображения, видео и многое другое в нужные вам форматы. Благодаря более быстрой загрузке преобразованных файлов и дружелюбной и полезной поддержке, когда вам это нужно, у вас будет все необходимое для работы с вашими файлами. Мы не размещаем никакой внешней рекламы, а это означает, что мы сосредоточены исключительно на быстром и точном преобразовании ваших файлов. Zamzar поддерживает более 1100 различных типов преобразования файлов, включая целый ряд преобразований документов, изображений, видео и аудио, а также многое другое! Если вам нужно преобразовать файл, вы можете быть уверены, что мы выполним эту работу правильно, быстро и надежно. Наша команда стремится предоставить самый лучший инструмент для преобразования файлов, поэтому мы всегда внедряем инновации и прислушиваемся к вашим предложениям. В Zamzar вы найдете все необходимые инструменты для преобразования и сжатия в одном месте. С поддержкой более 1100 типов преобразования файлов, независимо от того, нужно ли вам конвертировать видео, аудио, документы или изображения, вы легко найдете то, что вам нужно, и вскоре ваши файлы будут в форматах и размерах, которые вам подходят. DOC и DOCX являются наиболее распространенными форматами файлов для обработки текстов. DOC в основном использовался Microsoft для своей программы Word до 2003 года. С 2007 года Word использует DOCX в качестве стандарта, хотя вы по-прежнему можете открывать файлы DOC и сохранять их в более старом формате. DOC и DOCX используются для форматированных текстовых документов, таких как отчеты, письма или резюме. Word является частью Microsoft Office, который доступен в виде платного программного приложения или доступен в Интернете по подписке Microsoft 365. Microsoft Office был разработан для операционной системы Windows, но вы также можете установить приложения Office в других операционных системах, таких как macOS от Apple и ChromeOS от Google. Базовая бесплатная программа «Word для Интернета» также доступна в Интернете для владельцев учетных записей Microsoft. Файлы DOC легко передавать и распечатывать, и их можно открыть в большинстве программ обработки текстов, включая LibreOffice, Apple Pages и Google Docs, а также в Microsoft Word. PDF означает файл «Portable Document Format». Файлы PDF обычно не создаются с нуля, а обычно конвертируются, сохраняются или «распечатываются» из других документов или изображений перед совместным использованием, публикацией в Интернете или сохранением. Их можно просматривать практически на всех устройствах. Создание PDF-файла может включать сжатие файла, чтобы он занимал меньше места для хранения. Обычно вы создаете PDF-файл, если хотите обеспечить точность документа, сделать его более безопасным или создать копию для хранения. Используя Zamzar, можно конвертировать файлы DOC во множество других форматов: DOC в AZW3
DOC в BMP
DOC в DOCX
DOC в EPUB
DOC в FB2
DOC в GIF
DOC в HTML
DOC в HTML4
DOC в HTML5
DOC в JPG
DOC в LIT
DOC в LRF
DOC в MOBI
DOC в MP3
DOC в ODT
DOC в OEB
DOC на СТРАНИЦЫ
DOC на СТРАНИЦЫ09DOC в PCX
DOC в PDF
DOC в PML
DOC в PNG
DOC в PS
DOC в РБ
DOC в TCR
DOC в TIFF
DOC в THUMBNAIL
DOC в TXT Используя Zamzar, можно конвертировать в файлы DOC множество других форматов: BMP в DOC
CSV в DOC
DOCX в DOC
EML в DOC
GIF в DOC
JPG в DOC
MDI в DOC
MSG в DOC
ODG в DOC
ODS в DOC
ODT в DOC
СТРАНИЦ в DOC
PAGES. Если у вас есть какие-либо вопросы о преобразовании или сжатии файлов с помощью Zamzar, мы будем рады помочь! Ниже мы ответили на несколько часто задаваемых вопросов, чтобы вы могли начать работу, а дополнительную информацию о преобразовании и сжатии файлов с помощью Zamzar вы можете найти в нашем Справочном центре. Существует довольно много способов конвертировать файл DOC в PDF, в том числе с помощью веб-сайта Zamzar. Если у вас нет MS Office или у вас есть много файлов DOC для преобразования в PDF, вам может быть проще использовать бесплатный онлайн-конвертер, такой как Zamzar. Всего три шага — загрузите свои файлы, конвертируйте их в PDF и загрузите. PDF или DOC лучше, зависит от того, для чего вы используете файл. Microsoft Word является наиболее часто используемым программным обеспечением для создания и редактирования текстовых документов. Однако, если вы делитесь файлами или публикуете их, вероятно, лучше сначала преобразовать файлы DOC в PDF. Это связано с тем, что не все устройства могут открывать документы Word, и вы можете защитить форматирование или информацию в документе, прежде чем делиться им. Вы можете преобразовать DOC в PDF всего за три шага с помощью бесплатного онлайн-инструмента Zamzar для преобразования: просто загрузите файлы, выберите PDF, затем «Преобразовать сейчас», затем загрузите файлы PDF. Вы можете легко преобразовать документ в PDF на своем телефоне с помощью бесплатного онлайн-инструмента преобразования, такого как Zamzar. Сначала убедитесь, что документ сохранен в ваших файлах, затем загрузите его на веб-сайт Zamzar, выберите PDF в качестве формата для преобразования, а затем загрузите новый PDF-файл. Если вы используете телефон Android, вы также можете установить приложение Microsoft Word для Android, а затем использовать его для экспорта файла в формате PDF. Однако преимущество использования онлайн-сервиса, такого как Zamzar, заключается в том, что вам не нужно устанавливать какие-либо дополнительные приложения на свой телефон. Многие бесплатные и платные приложения для преобразования файлов могут конвертировать DOC в PDF, включая онлайн-конвертеры, такие как Zamzar. С Zamzar просто загрузите свои файлы DOC в трехэтапный инструмент преобразования на их веб-сайте, нажмите, чтобы преобразовать файлы в PDF, а затем загрузите свои файлы. Единственно верный ответ отмечен + 1 К общегосударственным налогам относят: А) налог из рекламы; + Б) НДС; В) коммунальный налог; Г) гостиничный сбор. 2 Совокупность налогов, что взимаются в государстве, а также форм и методов их построения – это: А) налоговая политика; + Б) налоговая система; В) фискальная функция; Г) принцип стабильности 3 Акцизный сбор – это налог: + А) косвенный – индивидуальный; Б) прямой – реальный; В) прямой – личный; Г) косвенный – универсальный. 4 Налоги возникли в результате: А) развития торговли; + Б) появления государства; В) становление промышленности; Г) формирование товарно-денежных отношений. 5 Налоги – это: А) денежные содержания из каждого работающего человека; Б) денежные и натуральные платежи, что выплачиваются из госбюджета; В) денежные изъятия государства из прибыли и зарплаты; + Г) обязательные платежи юридических и физических лиц в бюджет в размерах и в сроки, установленные законом. 6 Недопущение каких-либо проявлений налоговой дискриминации – обеспечение одинакового подхода к субъектам ведения хозяйства – это принцип: А) стимулирование; + Б) равенства; В) стабильность; Г) равномерности уплаты. 7 К местным налогам и сборам относят: А) рыночный сбор; Б) налог на землю; В) налог из владельцев транспортных средств; Г) коммунальный налог; + Д) верные а) и г). 8. Источником уплаты налога является: А) заработная плата; Б) прибыль; В) проценты; + Г) все ответы верны. 9 Перераспределение доходов юридических и физических лиц осуществляется путем реализации: А) стимулирующей функции налогов; Б) регулирующей функции налогов; + В) распределительной функции налогов; Г) контрольной функции налогов. 10 К личностным налогам относятся: + А) подоходный налог; Б) налог на землю; В) пошлина; Г) НДС. 11 Налог с владельцев транспортных средств — это налог: А) косвенный; + Б) прямой; В) местный; Г) универсальный. 12 Пополнение средств государственной казны осуществляется путем реализации функции налогов: А) стимулирующей; Б) фискальной; + В) регулирующей; Г) контрольной. 13 К реальным налогам относятся: А) подоходный налог; Б) пошлина; + В) налог на землю; Г) НДС. 14 Налог с рекламы — это налог: А) косвенный; Б) общегосударственный; + В) местный; Г) универсальный. 15 По способу взимания налоги подразделяются: + А) прямые и косвенные; Б) на прибыль (доход), на прибавленную стоимость, ресурсные, на имущество, на действии; В) общегосударственные и местные; Г) кадастровые, декларационные и предыдущие. 16. Налоговым периодом по акцизам признается: + А) календарный месяц Б) квартал В) календарный год 17. А) получающие прибыль, накапливающие ее и не распределяющие ее между участниками + Б) получающие прибыль и распределяющие ее между участниками В) не получающие прибыль 18. Финансовой практикой выработаны виды прогрессии: — Полная и смешанная + Простая и сложная — Линейная и каскадная 19. К прямым налогам относятся: + Подоходный налог, налог на имущество — Водный налог, акцизы — Транспортный налог, подоходный налог 20. К целевым налогам относятся: + Земельный налог, налог на восстановление минерально-сырьевой базы — Налог на транспортные перевозки, налог на недвижимость — Таможенная пошлина, водный налог 21. К специальным налоговым режимам не относится: — Система налогообложения, опирающаяся на патенты — Система налогообложения для товаропроизводителей сельскохозяйственной продукции + Единый социальный налог 22. + НДС, акцизы — Налог на прибыль, налог на наследство — Налог на имущество, земельный налог 23. Какие организации не являются плательщиками налога на прибыль? — Коммерческие банки различных видов; страховые компании, получившие лицензию на обслуживание страховой деятельности; профессиональные работники рынка ценных бумаг — Некоммерческие и благотворительные организации и фонды + Платящие единый налог на вмененный доход; применяющие упрощенную систему налогообложения, учета и отчетности; уплачивающие налог на игорный бизнес; платящие единый сельскохозяйственный налог 24. Функции налогов заключаются в: + Финансовом обеспечении расходов, которые несет государство; регулировании экономики со стороны государства; поддержании равенства между различными слоями населения; стимулировании экономики — Концентрации денежных средств в государственном бюджете; осуществлении контроля за расходованием государственных денежных средств; поддержании социального равновесия путем изменения соотношения между доходами отдельных социальных групп с целью сглаживания неравенства между ними — Равномерном распределении финансовых ресурсов государства; государственном регулировании экономики; обеспечении финансирования государственных расходов; осуществлении контроля за процессом использования государственных денежных средств 25. — Обязательные + Косвенные — Целевые 26. Классифицировать налоги можно по следующим признакам: — Способ изъятия; объект налогообложения; целевое назначение налога; субъект налогообложения; уровень бюджета, в который зачисляется налог; срок уплаты — Отношение к бюджету; иерархические уровни утверждения; отношение к бюджету; субъект налогообложения; объект налогообложения; способ отражения в бухучете + Способ взимания; орган, устанавливающий налог; целевая направленность введения; субъект-налогоплательщик; уровень бюджета, в который зачисляется налог; способ отражения в бухучете; срок уплаты тест 27. К местным налогам относятся: + Земельный налог; налог на имущество физических лиц — Транспортный налог; налог за пользование воздушным пространством — Налог на богатство; налог на добычу полезных ископаемых 28. Экономическое содержание налога выражается взаимоотношениями между: — Субъектами хозяйствования в связи с перераспределением излишка доходов + Гражданами, субъектами хозяйствования и государством в связи с формированием государственных доходов — Гражданами и государством через механизмы перераспределения доходов и расходов 29. + Налог на добычу полезных ископаемых — Налог на имущество организаций — Земельный налог 30. К налогам регионального уровня относятся: — Налог на недра земли, сбор за пользование объектами растительного мира + Налог на игорный бизнес, транспортный налог — Налог на имущество физических лиц, налог на прибыль организаций 31. Снижение налогов ведет к: — Падению благосостояния населения — Росту благосостояния населения + Росту деловой активности и объемов выпуска продукции 32. Плательщиками налога на имущество являются …, имеющие по владении имущество, признанное объектом налогообложения. — Российские компании и частные лица -Российские компании + Российские и иностранные компании 33. При росте налогов наблюдается: — Рост совокупного спроса + Сокращение совокупного предложения — Сокращение совокупного спроса 34. — Удержание и перераспределение излишка доходов граждан и субъектов хозяйствования на нужды государства — Поддержание работоспособности государственных служб и ведомств + Удержание государством в пользу общества некоторой части валового внутреннего продукта в виде обязательного взноса 35. Прямые налоги характеризуются тем, что они: — Взимаются лишь в том случае, если обнаружен дефицит госбюджета — Взимаются только с субъектов хозяйствования + Носят обязательный характер 36. Принцип универсализации налогообложения заключается в том, что: — Уплата налогов должна быть удобной — Размер налогов для граждан должен быть соразмерен с их доходами + Дифференциация налогов по территориальному, национальному и другим признакам не должна существовать тест_37. Кто является плательщиком налога на доходы физических лиц? — Только граждане РФ + Физические лица-налоговые резиденты РФ, а также физические лица, получающие доходы из источников в РФ — Граждане РФ, прожившие на ее территории 183 дня и более в отчетном налоговом периоде 38. — 1 + 2 — 3 39. Налоговая ставка 0% действует при: + Реализации товаров на экспорт — Перевозке граждан всеми видами общественного транспорта — Реализации детских товаров 40. Что из перечисленного не облагают акцизом? + Парфюмерно-косметическую продукцию, которая прошла государственную регистрацию в уполномоченном органе исполнительной власти федерального уровня — Алкогольные напитки — Топливо 41. Транспортный налог по уровню установления относится к … налогам. — Федеральным + Региональным — Местным 42. Чему посвящена первая часть налогового кодекса РФ? — Описанию и регламентации принципов исчисления и уплаты каждого вида налогов и сборов — Специальному налоговому режиму + Общим принципам налогообложения и уплаты налогов в РФ Авторам 8-800-333-85-44 Оформить заявку Выполним любые типы работ Контрольная работа от 1 дня
/ от 100 руб Курсовая работа от 5 дней
/ от 1800 руб Дипломная работа от 7 дней
/ от 7950 руб Реферат от 1 дня
/ от 700 руб Онлайн-помощь от 1 дня
/ от 300 руб Оставляй заявку — и мы пройдем все тесты за тебя! QUIZ точность воспроизведений 5 лет Персональные финансы следующего поколения воспроизведений Устройства учащихся не требуются. Узнать больше 20
вопросы См. 1. Множественный выбор 30 секунд 1 pt Кто в основном использует наши налоговые деньги? (подсказка: выберите 2 правильных ответа) Ваш работодатель Правительство штата Федеральное правительство Местные предприятия 2. Множественный выбор 20 секунд 9000 3 1 pt Наши налоговые деньги расходуются на все следующие КРОМЕ: Социальное обеспечение Вооруженные силы Частное школьное образование Национальные парки 3. Множественный выбор 20 секунд 1 балл Что из следующего НЕ относится к категории расходов федерального правительства? Обязательные расходы Дискреционные расходы Проценты по выданным кредитам Проценты по государственному долгу 4. 3 0 секунд 1 балл Какие виды налогов входят в федеральный налог доход? (подсказка: выберите 4 правильных ответа 🙂 Подоходный налог Подоходный налог Налог на недвижимость Акцизный налог 5. Множественный выбор 20 секунд 90 003 1 пункт Форма W-4 позволяет… правительство знает, сколько вы заплатили налогов в прошлом году ваш работодатель знает, сколько удерживать из вашей зарплаты 3 основных кредитных бюро знают, сколько у вас иждивенцев вы знаете, сколько вы заплатили налогов в прошлом году 6. Множественный выбор 20 секунд 1 балл Джесс 21 год, она учится в колледже, и ее работа обеспечивает 65% ее поддержки. 7. Множественный выбор 20 секунд 1 балл Какой предмет вы бы ОБЯЗАТЕЛЬНО увидели на квитанции? Пенсия Здравоохранение Заработная плата до вычета налогов Ваша профессия/должность 9 1 балл подоходный налог авансом в НАЧАЛЕ год. Вы запрашиваете отсрочку для подачи налоговой декларации Вы НЕ будете удерживать подоходный налог из своей зарплаты. Вы платите все подоходные налоги на КОНЕЦ календарного года. 9. Множественный выбор 20 секунд 1 балл Джейсон подал налоговую декларацию за 2022 год и задолжал деньги. Если он не хочет платить комиссию, до какого числа он должен заплатить эту сумму? 18 апреля 15 октября 31 декабря 1 января следующего года 10. 20 секунд 1 очко Правда или Ложь: Все зарплаты, чаевые , а бонусы облагаются налогом, если специально не исключены. 11. Множественный выбор 30 секунд 1 балл Что из следующего НЕВЕРНО в отношении формы W-2? (подсказка: выберите 2 правильных ответа) Форма W-2 высылается в апреле каждого года Она позволяет вам узнать, сколько вы заработали в прошлом году Она позволяет вам узнать, сколько было удержано из вашей зарплаты Вы получать 1 форму W-2 каждый год, даже если вы работали на нескольких работах 12. Множественный выбор 20 секунд 1 балл Джейсону 15 лет, и прошлым летом он заработал на своей работе 1450 долларов. Нет, потому что он мало зарабатывал. Нет, поскольку для подачи налоговой декларации вам должно быть не менее 16 лет. Да, потому что он может получить возмещение. Да. Вы должны подать налоги, даже если вы не заработали достаточно. 13. Множественный выбор 30 секунд 1 балл Что нужно для заполнения формы 1040? (подсказка: выберите 2 правильных ответа) Ваша форма W-2 Ваша форма W-4 Ваша налоговая декларация за предыдущий год Номер социального страхования 14. Множественный выбор 1 балл Что из перечисленного НЕ является способом подачи налоговой декларации? Через налогового специалиста Отправка бумажной налоговой декларации федеральному правительству Использование налогового программного обеспечения, такого как TurboTax Через отдел кадров вашего работодателя 15. 20 секунд 1 pt 9 0003 Верно или неверно: о заработанном доходе подростка можно сообщить в отчете родителя. налоговая декларация. 16. Множественный выбор 20 секунд 1 балл Если подросток подает налоговую декларацию, может ли родитель считать его/ее иждивенцем? Да. Все подростки являются иждивенцами, пока им не исполнится 18 лет Нет. Если подросток подает налоговую декларацию, он/она не может быть заявлен Да, если подросток отвечает требованиям иждивенцев Да, но родитель должен прибавьте доход подростка к его доходу 17. Множественный выбор 20 секунд 1 балл Луиза заработала 1200 долларов на своей работе с частичной занятостью, и 500 долларов от присмотра за детьми наличными. Она сообщит о своем общем доходе в размере 1700 долларов. Она сообщит о своем общем доходе в размере 1200 долларов. Она сообщит о своем общем доходе в размере 500 долларов. Луиза должна подать налоговую декларацию. 18. Множественный выбор 30 секунд 1 балл Что ВЕРНО в отношении заработанного и незаработанного дохода? (подсказка: выберите 2 правильных ответа) Заработанный доход — это то, сколько вы зарабатываете на работе Заработанный доход — это любые деньги, которые вы зарабатываете на процентах, дивидендах и т. д. Незаработанные деньги — это любые деньги, которые вы зарабатываете на процентах, дивидендах и т. д. Незаработанные деньги — это то, сколько вы зарабатываете на работе 19. 20 секунд 1 балл Если вы должны налоги, что из перечисленного НЕВЕРНО? Вы можете произвести оплату наличными Вы можете отсрочить срок платежа По договоренности вы можете оплатить в рассрочку Вы можете произвести оплату дебетовой, но не кредитной картой 20. Множественный выбор 20 секунд 1 балл Что ВЕРНО, если вы не платите налоги? В следующем году вы должны вдвое больше У вас больше шансов получить кредит под низкий процент Вы не можете попасть в тюрьму (но вас оштрафуют на крупный размер) Это может повлиять на вашу кредитную историю Открыть все вопросы с бесплатной учетной записью У вас уже есть учетная запись? Меню настроек Этот документ будет обновляться по мере поступления дополнительных вопросов. ОНЛАЙН-РЕГИСТРАЦИЯ Разрешения выдаются физическим лицам, а не на уровне бизнеса. Тренажер создан для помощи старшекласникам, для изучения или повторения извлечения квадратного корня в режиме реального времени. Главная цель — закрепить навыки в обработке вычислительных действий извлечения квадратного корня. Имеется три уровня сложности. Первый уровень — числа до 10. Второй уровень — числа от 10 до 20. Третий уровень от 20 до 33. Найдите квадратный корень и введите правильный ответ. Уровень сложности
1
— числа с суммой до 10 — числа с суммой от 11 до 20 — числа с суммой от 20 до 100 — числа с суммой от 100 до 1000 таблица НАТаблица до
1234567891011121314151617181920 — числа до 10 — числа от 10 до 20 — числа от 20 до 33 Правильно! · = Разбиваем цифры числа на пары, начиная с разряда единиц. =
0 Цифр после запятой
012345678910 Комплексная программа Любую программу можно преобрести отдельно Комплексная программа Любую программу можно преобрести отдельно Комплексная программа Любую программу можно преобрести отдельно Комплексная программа Любую программу можно преобрести отдельно Комплексная программа Любую программу можно преобрести отдельно Комплексная программа Любую программу можно преобрести отдельно Скачать полный прейскурант платных услуг: Прейскурант. WhatsApp кабинета платных услуг: 8 (910) 460-6017 Загрузка прейскуранта… Поликлиника является уникальным лечебно-профилактическим учреждением, по существу семейным,
поскольку в стенах его медицинскую помощь одновременно получают прикрепленные к поликлинике
взрослые и дети. Поликлиника входит в состав Управления делами Президента Российской Федерации и осуществляет
свою деятельность, используя опыт и лучшие традиции Кремлевской медицины. Высокий уровень оказания профилактической и лечебно-диагностической помощи, современная
материально-техническая база, высокий уровень врачей и средних медицинских работников,
доброжелательное отношение к своим пациентам и проблемам их здоровья создали поликлинике
хорошую репутацию и заслуженный авторитет не только у пациентов, но и у страховых
медицинских организаций и медицинской общественности. В соответствии с имеющейся лицензией, поликлиника: В составе взрослого корпуса имеются отделения терапевтического и хирургического профилей,
женская консультация, дневной стационар, стоматологическое отделение; диагностическая служба
в виде отделения лучевой диагностики, кабинета функциональной диагностики, эндоскопического
отделения, а так же клинико-диагностической лаборатории, в которой выполняются практически
все виды исследований в короткие сроки. Отделение медицинской реабилитации и спортивной
медицины представлено различным спектром оказываемых услуг (физиотерапия, бальнеотерапия,
иглорефлексотерапия, массаж, остеопатия, ЛФК и др.) В состав Детского корпуса входят: педиатрическая служба, отделение специализированной
медицинской помощи, отделение медицинской реабилитации, восстановительной и спортивной
медицины и лучевой диагностики, а также стоматология. В Педиатрической службе нашим маленьким пациентам предлагаются в том числе: Отделение специализированной педиатрической медицинской помощи оказывает комплексную
медицинскую помощь с привлечением узкопрофильных специалистов высокого уровня детям от
рождения до 18 лет. Основным уставным видом деятельности ФГБУ «Поликлиника № 4» является оказание медицинской
помощи определенному контингенту — лицам, медицинское обслуживание которых в соответствии с
законодательством возложено на Управление делами Президента Российской Федерации, в том
числе в рамках обязательного медицинского страхования. Поликлиникой оказываются платные медицинские услуги как взрослым, так и детям независимо от
места жительства — на основании договоров на оказание платных медицинских услуг. Такой
договор для получения разовых медицинских услуг или на условиях длительного медицинского
обслуживания, в том числе по специальным программам (например, по программе ведения
беременности) можно заключить непосредственно в поликлинике при наличии документа,
удостоверяющего личность (паспорт). Кроме того, медицинские услуги можно получить по
программам добровольного медицинского страхования (ДМС), прикрепившись к поликлинике через
страховые медицинские организации. В зависимости от условий медицинского обслуживания при
наличии показаний оформляются листки нетрудоспособности. используйте наш онлайн-калькулятор четвертого корня. a 4 = х. ∜x=a Определение Корень четвертой степени : четвертый корень числа x , это число r , что при возведении в степень 4 дает x : r 4 =x. топ. ссылка: n -й корень из Википедии Калькулятор Нахождение корней числа не может быть трудным , когда вас попросят найти квадратный корень из или второй корень из этого числа . Процесс становится трудным , когда вы имеете дело с вопросами , чтобы найти расширенных корней , таких как четвертый корень . Это потому, что вам нужно разделить на данное число на то же число четыре раза по . Если вы пытаетесь найти этот корень для любого числа , вам следует использовать этот калькулятор четвертого корня . Это специальный математический онлайн-калькулятор , который был разработан только для этого расчета. Вы можете найти четвертый корень любого числа без учета того, что больше или меньше. Продолжайте читать до , изучите , что это за корень и как наш калькулятор может помочь вам в найти корень четвертой степени. Содержание Если число разделить на то же число четыре раза, чтобы получить « 0 » в качестве остатка , то делитель будет называться четвертым корнем из числа . Например, , « 2 » является корнем четвертой степени из « 16 », потому что получается , когда « 2 » умножается на четыре на . . Аналогично , мы можем найти четвертый корень любого числа посредством процесса деления . Разве вы, , не знаете , как все обрабатывают ? Продолжайте читать, потому что мы будем доля процесс расчета в подробно здесь. Существует нет конкретной формулы для нахождения корня четвертой степени конкретного числа . Здесь « 4 » представляет корень четвертой степени из числа « x ». Как упомянул , найти четвертый корень не сложно, если знать как делить число. Но у нас есть решенный пример здесь для вашего лучшего понимания . Пример 1: Найдите корень четвертой степени из 216. Решение: Нам нужно разделить данное число на простые множители. Вот схема умножения, которую мы получили для «216». Решив этот четвертый корень, мы получили следующий ответ. Итак, «4» — это корень четвертой степени из «216». Calculator’s Bag разработала этот четвертый калькулятор корней с простым и удобным интерфейсом. Вы можете легко использовать его, выполнив следующие действия. Что такое квадратный корень из четвертого числа? Квадратный корень будет двойным корнем четвертой степени того же числа. Длина вектора Найти Известно, что: lxy =
Длина пространственного вектора Найти Известно, что: lxyz =
Скалярное произведение векторов Найти Известно, что: ABabα =
Скалярное произведение векторов через координаты Найти Известно, что: ABx1x2y1y2 =
Скалярное произведение пространственных векторов через координаты Найти Известно, что: ABx1x2y1y2z1z2 =
Скалярное произведение вертикальных векторов Найти Известно, что: x1x2y1y2 =
Скалярное произведение пространственных вертикальных векторов Найти Известно, что: x1x2y1y2z1z2 =
Угол между векторами Найти Известно, что: αx1x2y1y2 =
Угол между пространственными векторами Найти Известно, что: αx1x2y1y2z1z2 =
Коллинеарные векторы Найти Известно, что: x1x2y1y2 =
Расстояние между точками Найти Известно, что: ABx2x1y2y1 =
Расстояние между точками в пространстве Найти Известно, что: ABx2x1y2y1z2z1 =
Существует два способа решения задач по стереометрии Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется. Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми. Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб. Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2. Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z: Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала. Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора: Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле: Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и . Сумма векторов: Разность векторов: Произведение вектора на число: Скалярное произведение векторов: Косинус угла между векторами: Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях. 1. В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж: Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1. Прямые AE и BK — скрещиваются. Найдем угол между векторами и . Для этого нужны их координаты. Запишем координаты векторов: и найдем косинус угла между векторами и : 2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK. Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания. Координаты точек A, B и C найти легко: Из прямоугольного треугольника AOS найдем Координаты вершины пирамиды: Точка E — середина SB, а K — середина SC. Найдем координаты векторов и : и угол между ними: Покажем теперь, как вписать систему координат в треугольную призму. 3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1 Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы. Запишем координаты точек: Точка D — середина A1B1. Значит, пользуемся формулами для координат середины Найдем координаты векторов и , а затем угол между ними: Смотрите, как легко с помощью векторов и координат найти угол между прямыми. Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости. Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство. Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему. Покажем, как это делается. Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2). Уравнение плоскости выглядит так: Подставим в него по очереди координаты точек M, N и K. Для точки M: То есть A + C + D = 0. Для точки N: Аналогично для точки K: Получили систему из трех уравнений: . В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю. Пусть, например, D = −2. Тогда: ; . Выразим C и B через A и подставим в третье уравнение: . Решив систему, получим: Уравнение плоскости MNK имеет вид: Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми: Вектор — это нормаль к плоскости MNK. Уравнение плоскости, проходящей через заданную точку имеет вид: Угол между плоскостями равен углу между нормалями к этим плоскостям: Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин. Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла. Мы берем меньший из них. 4. В кубе ABCDA1B1C1D1 точки E и F — середины ребер соответственно A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1. Строим чертеж. Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1. Сначала — нормаль к плоскости BDD1. Конечно, мы можем подставить координаты точек B, D и D1 в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Итак, первый вектор нормали у нас уже есть: Напишем уравнение плоскости AEF. Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F. Упростим систему: . Пусть С = -1. Тогда A = B = 2. Уравнение плоскости AEF: Нормаль к плоскости AEF: Найдем угол между плоскостями: 5. Основание прямой четырехугольной призмы BCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3. Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂 Строим чертеж. Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти? «Расстояние между прямыми A1C1 и BD равно √3». Прямые A1C1 и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A1C1 и BD — это, очевидно, OO1, где O — точка пересечения диагоналей нижнего основания, O1 — точка пересечения диагоналей верхнего. А отрезок OO1 и равен высоте параллелепипеда. Итак, AA1 = √3 Плоскость AA1 D1 D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор . Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B1D». Координаты вектора — тоже: Находим угол между плоскостями, равный углу между нормалями к ним: Зная косинус угла, находим его тангенс по формуле Получим: Ответ: Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов. Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α. Находим синус угла между прямой m и плоскостью α по формуле: 6. В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1. Как всегда, рисуем чертеж и выбираем систему координат Находим координаты вектора . Нужно ли нам уравнение плоскости BDD1? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор . Найдем угол между прямой и плоскостью: Ответ: Расстояние от точки M с координатами x0, y0 и z0 до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле: 7. В основании прямоугольного параллелепипеда BCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA1 = . Найдите расстояние от точки A до плоскости A1DB. Построим чертеж и выпишем координаты точек: Запишем уравнение плоскости A1DB. Вы помните, как это делается — по очереди подставляем координаты точек A1, D и B в уравнение Ax + Be + Cz + D Решим эту систему. Тогда Уравнение плоскости A1DB имеет вид: Дальше все просто. Находим расстояние от точки A до плоскости A1DB: В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой. Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Векторы в пространстве и метод координат» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта. Публикация обновлена:
08.04.2023 Векторные формулы содержат список формул, полезных для выполнения многочисленных арифметических операций над одним и тем же вектором и между двумя векторами. Список векторных формул включает формулы, выполняющие операции для одного вектора и над векторами. Формулы отношений направлений, направляющих косинусов, модуля вектора, единичного вектора выполняются на одном и том же векторе. А формулы скалярного произведения, перекрестного произведения, проекции векторов выполняются по двум векторам. Формула 1 Отношения направлений вектора \(\vec A = a \hat i + b \hat j + c \hat k \) равны a, b, c соответственно. Формула 2 Направляющие косинусы вектора \(\vec A = a \hat i +b \hat j + c \hat k \): 92}\] Формула 4 \[ \hat A = \frac{\vec A}{|\vec{A}|}\] Формула 5 \[ \hat A = \frac{\vec A}{|\vec{A}|}\] Формула 6 Формула 7 \[ \vec A. \vec B = |\vec{A}|.|B|.Cos\theta\] Формула 8 \[ \vec A \times \vec B = | \vec{A}|.|\vec{B}|.Sin \theta\] Формула 9 \[\begin{align} \hat i.\hat i= \hat j. Формула 10 \(\text{Проекция вектора} \vec {A} \ \text{на вектор} \vec{B} = \dfrac{\vec{A}. \vec{B}}{| \vec{B }|}\) Разбивайте сложные концепции с помощью простых визуальных средств. Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций. Забронировать бесплатный пробный урок Решение: Учитывая \(\vec A = 3\hat i — 2\hat j + 7\hat k\) и \(\vec B = 4\hat i -\hat j + 3\hat k\) \( \vec A . Решение: Учитывая \(\vec A = \hat i + 5\hat j + 2\hat k\) и \(\vec B = 2\hat i -\hat j — k\hat k\) \( \ vec A .\vec B = ((1).(2) + (5).(-1) + 2.(-1)) = 2 — 5 — 2 = -5\) 9{-1}(\frac{-\sqrt5}{6})\end{align} \) перейти к слайдуперейти к слайду Дата последнего обновления: 20 апреля 2023 г. .9к • Просмотров сегодня: 1.74k Каждый объект, имеющий как величину, так и направление, называется вектором. Вектор можно изобразить геометрически как участок направляющей линии со стрелкой, обозначающей направление, и длиной, равной величине вектора. В математике вектор – это представление объекта, включающее как величину, так и направление. Если два вектора имеют одинаковое направление и величину, они одинаковы. Это означает, что если мы возьмем вектор и перенесем его в другое место, то получим новый вектор. Вектор, который мы получаем в конце этой фазы, выглядит так, и это тот же вектор, который был у нас в начале. В физике векторы, представляющие силу и скорость, являются двумя распространенными примерами векторов. Мощность и скорость действуют одинаково. Величина вектора будет означать интенсивность силы или относительную скорость скорости. Поскольку смещение напрямую связано с расстоянием, расстояние и смещение не совпадают. Стрелка обычно используется для обозначения вектора. Кроме того, чья длина пропорциональна величине и чье направление совпадает с количеством. Масштабированные векторные диаграммы со значениями часто используются для описания векторных величин. Вектор смещения будет описан на векторной диаграмме. [Изображение будет загружено в ближайшее время] Величина Направление Направление вектора часто выражается как угол поворота против часовой стрелки вокруг его «хвоста» строго на восток. Вектор с направлением 30 градусов — это вектор, повернутый на 30 градусов против часовой стрелки относительно строго на восток с использованием этого соглашения. Векторная сумма двух или более сил представлена равнодействующей силой, которая является единственной силой. Подобно тому, как две силы с величинами F1 и F2 действуют на частицу, эффект следующий: [Изображение скоро будет загружено] Скорость изменения направления объекта представлена вектором скорости. Величина вектора скорости указывает скорость объекта, а направление вектора указывает направление объекта. [Изображение будет загружено в ближайшее время] Треугольный закон сложения векторов гласит, что когда два вектора представлены как две стороны треугольника одного порядка величины и направления, величина и направление результирующий вектор представлен третьей стороной треугольника. Поскольку две силы, Вектор А и Вектор В, действуют в одном направлении, результирующее значение R является суммой двух векторов. [Изображение скоро будет загружено] Формула треугольного закона сложения: \[\bar{R}\] = \[\bar{A}\] + \[\bar{B}\] Когда две степени, формула вектора A вектора B, выражены противоположными сторонами параллелограмма, результирующая представлена диагональю параллелограмма, взятой из того же положения. Интегральные функции: В выражениях можно применять следующие операции: Другие функции: Постоянные: Формула замены переменного в определённом интеграле. Доказательство. Пусть — некоторая первообразная для , так что Обратим ваше внимание на важную особенность формулы: кроме подынтегрального выражения, при замене переменной меняются и пределы интегрирования. Действительно, в интеграле по новой переменной должны быть указаны пределы изменения именно (то есть и ), в то время как в исходном интеграле по переменной указаны пределы изменения (то есть и )! Советы о том, какая замена целесообразна для вычисления того или иного интеграла, — те же самые, что и при вычислении неопределённых интегралов, так что тут ничего нового изучать не придётся. Формула интегрирования по частям для определённого интеграла. Доказательство теоремы 3.15. Поскольку из условий теоремы следует, что под знаками интегралов в левой и правой частях равенства стоят непрерывные функции, то к этим интегралам можно применять формулу Ньютона — Лейбница: Пусть — некоторая первообразная для функции , а — некоторая первообразная для функции . Замечание 3.6 Советы, в каких случаях целесообразно применять формулу интегрирования по частям, остаются теми же, как в случае вычисления неопределённых интегралов. Выигрыш от применения формулы интегрирования по частям для определённого интеграла по сравнению с предварительным вычислением первообразной по формуле интегрирования по частям для неопределённого интеграла, а затем применением формулы Ньютона — Лейбница получается от того, что мы сразу, при возникновении внеинтегрального члена, можем вычислить подстановку и далее при преобразованиях использовать полученное число вместо выражения, задающего внеинтегральный член. Особенно ясно проявляется указанное в замечании преимущество в том случае, если формулу интегрирования по частям приходится применять несколько раз подряд. Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции I.
Основной прием вычисления
– приведение квадратного трехчлена к виду:
где
и
– постоянные. Для выполнения
преобразования удобнее всего из квадратного трехчлена выделить полный квадрат.
Можно также воспользоваться подстановкой
Если
, то приводя квадратный трехчлен к виду (*), получаем табличные интегралы
или
Примеры вычислений
интегралов такого вида под номерами 1-2. II. Интегралы вида
Методы вычислений
аналогичны разобранным выше. В конечном итоге интеграл
приводится к табличному интегралу
если
или
если
Примеры вычислений
интегралов такого вида под номерами 3-5. III. Интегралы вида
С помощью обратной подстановки
эти интегралы приводятся к интегралам вида II. Примеры вычислений
интегралов такого вида под номерами 6-7 IV. Интегралы вида
Путем выделения из квадратного трехчлена полного квадрата данный интеграл сводится к одному из следующих
двух основных интегралов:
Эти интегралы с помощью
тригонометрических подстановок соответственно
и
сводятся
к интегралам от выражений, рациональных относительно синуса и косинуса. Примеры вычислений
интегралов такого вида под номерами 8-9. Методы интегрирования других видов функций: Найти неопределенный
интеграл:
Решение
Найти неопределенный
интеграл:
Решение
Найти неопределенный
интеграл:
Решение
Найти неопределенный
интеграл:
Решение
Найти неопределенный
интеграл:
Решение На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. ВКонтакте Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет. Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Найти неопределенный
интеграл:
Решение Найти неопределенный
интеграл:
Решение Найти неопределенный
интеграл:
Решение Найти неопределенный
интеграл, результат проверить дифференцированием:
Решение Проверка:
удалить Этот калькулятор для решения неопределённых интегралов взят от ООО «Вольфрам Альфа». Все права принадлежат владельцу! Нахождение неопределенного интеграла — очень распространенная задача в математике и других технических науках. На самом деле решение простейших физических задач редко обходится без нескольких вычислений простых интегралов. Поэтому со школьного возраста нас учат приемам и методам решения интегралов , приводятся многочисленные таблицы интегралов простых функций. Но со временем все благополучно забывается или у нас нет времени на расчеты или нужно найти неопределенный интеграл от очень сложной функции. Наш сервис идеально подойдет для решения этих проблем. Он позволяет точно находить неопределенные интегралы онлайн. Онлайн-сервис OnSolver.com позволяет быстро и бесплатно решить интеграл онлайн. С помощью нашего сервиса вам будет легко проверить свой ответ, найти допущенную ошибку или опечатку или просто убедиться, что вы выполнили свою работу безупречно, даже если вы хотите вычислить интеграл самостоятельно. Если вы решаете задачу и должны решить неопределенный интеграл в качестве вспомогательной операции, зачем тратить время на то, что вы, возможно, делали уже тысячу раз? Более того, ненужные вычисления интеграла могут быть причиной канцелярских или других мелких ошибок, которые впоследствии приведут к неправильному ответу. Неопределенный интеграл — это обратный процесс дифференцирования. Вместо того, чтобы иметь набор предельных значений, можно найти только уравнение, которое будет давать интеграл из-за дифференцирования без необходимости использовать значения для получения определенного ответа. ‘ Indefinite Integral Calculator ‘ это онлайн-инструмент, который помогает вычислить значение неопределенных интегралов для заданной функции. Онлайн-калькулятор неопределенных интегралов поможет вам рассчитать значение неопределенных интегралов за несколько секунд. Чтобы найти значение неопределенного интеграла, выполните следующие действия: Производные определяются как нахождение скорости изменения функции по отношению к другим переменным. Он имеет дело с такими переменными, как x и y, функциями f(x) и соответствующими изменениями переменных x и y. Производная функции представлена f ‘(x). Интеграция определяется как процесс, обратный дифференциации. Интегрирование представлено как ‘ ∫ ‘ Неопределенные интегралы являются интегралами, не имеющими верхнего и нижнего пределов. Существуют общие функции и правила, которым мы следуем, чтобы найти интегрирование. Хотите найти сложные математические решения за считанные секунды? Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами. Запись на бесплатный пробный урок Пример 1: Найдите значение интегрирования 5x 3 + 2x 2 и проверьте это с помощью онлайн-калькулятора неопределенных интегралов. Решение: = ∫(5x 3 + 2x 2 ) = ∫(5x 3 ) + ∫(2x 2 ) Используя правило умножения на константу и степень, = [5 × (x 3 + 1 / 3 + 1)] + [2 × x 2 + 1 / 2 + 1] = (5x 4 / 4) + (2x 3 / 3) Пример 2: Найдите значение интегрирования 4x 2 — 6x и проверьте его с помощью онлайн-калькулятора неопределенного интеграла. Разделы: Математика, Внеклассная работа Цели: Мы будем рассматривать неравенства, правая часть которых равна нулю, а левая часть представлена в виде произведения или частного функций. Идея метода: Знак произведения или частного определяется знаком сомножителей. Рис.1 Линейная функция с ненулевым угловым коэффициентом меняет знак при переходе через нуль функции, причём справа от нуля знак функции совпадает со знаком углового коэффициента. Рис.2 Квадратный трёхчлен с D>0 при переходе через каждый нуль функции меняет свой знак, причём правее большего корня знак квадратного трёхчлена совпадает со знаком его старшего коэффициента. [1]
Эти соображения приводят к следующей схеме решения неравенства: Пример 1:[1] Рис. 3 На самом правом из них знак каждого сомножителя совпадает со знаком его старшего коэффициента: Следовательно, дробь на этом промежутке тоже отрицательна. В рассмотренном примере 1, знаки в промежутках знакопостоянства функции чередуются. Однако делать обобщение, что так будет происходить всегда, разумеется, не следует. Пример 2: -2 – нуль второй кратности Рис.4 Обозначим нуль второй кратности галочкой, чтобы не забыть. Т.к. числитель всегда принимает положительные значения, то на правом крайнем промежутке знак будет зависеть от знака старшего коэффициента знаменателя, т. Рис.5 Это поможет понять следующая геометрическая картинка (Рис.6): Рис.6 Вывод: при переходе через нуль чётной кратности, знак не меняется. Решить по вариантам, с последующим обсуждением у доски. I вариант Пример 3: Рис.7 Ответ: II вариант Пример 4: Рис. Ответ: Применение метода интервалов не ограничивается решением рациональных неравенств. Универсальность метода основана на достаточно наглядном свойстве непрерывных функций: «Если на интервале (a;b) функция f(x) непрерывна и не обращается в нуль, то на этом интервале она сохраняет знак». Пример 5: [1] , Будем решать это неравенство по той же схеме, но не на всей оси, а на области определения логарифмической функции, т.е. на промежутке (*): Рис. 9 Следовательно на этом промежутке левая часть неравенства отрицательна Ответ: . Пример 6: Рис.10 Квадратный трёхчлен в числителе не имеет корней и не меняет свой знак. Его знак совпадает со знаком старшего коэффициента, т.е. «+». Ответ:. Пример 7: ОДЗ: Приведём неравенство к такому виду, чтобы в правой части был «0»: ;;; Рис.11 Ответ:. Пример 8: ОДЗ: Рис.12 , но ОДЗ удовлетворяет только Рис.13 Ответ:. Задание на дом: (Решение предоставлено в Приложении1) Задания для факультативный занятий предоставлены в Приложении2. Вывод: Как известно, линейная, квадратичная, степенная, показательная, логарифмическая и тригонометрические функции, а так же их композиции и функции, получаемые из них с помощью арифметических действий, непрерывны в своей области определения. Поэтому метод интервалов можно применять при решении практически всех неравенств школьного курса. Метод интервалов позволяет представить множество решений неравенства в виде объединения промежутков, границы которых либо корни соответствующего уравнения, либо граничные точки области определения. Список литературы: [1] «Метод интервалов» //Журнал «Квант» No12, 1985 г. Метод интервалов — универсальный метод решения неравенств. С его помощью можно решить неравенства самого разного вида. Рассмотрим алгоритм метода интервалов, а затем перейдем к примерам решения неравенств этим методом. Алгоритм решения неравенств методом интервалов. Прежде чем применить метод интервалов для решении неравенства, необходимо все дроби привести к наименьшему общему знаменателю и все слагаемые перенести в левую часть, чтобы справа остался нуль. Для начала рассмотрим алгоритм решения неравенств вида 1. Приравниваем к нулю левую часть: (Таким образом мы находим нули функции а также ее область определения). 2.Дробь равна нулю, если числитель равен нулю, а знаменатель отличен от нуля, поэтому это уравнение равносильно системе: 3. 4. «Петля» 1)Если есть кратный корень четной степени, то в нем — «петля»: 2) Если один и тот же корень встречается четное число раз, то в нем — «петля»: так как корень x2 встречается четное количество раз (два раза). 3) Если дискриминант равен нулю, то в соответствующем корне x=-b/2a — «петля». (В этом случае x1=x2, то есть один и тот же корень встретился два раза). 4) Если корень стоит под знаком модуля, а выражение с модулем является множителем (а не слагаемым!), то в таком корне — «петля»: 5. Выбираем промежутки с нужным знаком: если в неравенстве знак > или ≥, берем промежутки с «+»; если < или ≤ — с «-«. Точки, в которых знаменатель обращается в нуль, всегда выколотые!!! В остальных случаях запомнить, выколотая точка или закрашенная, можно с помощью ассоциации. Замечание Отдельно стоящие закрашенные точки включаем в решение: (Знаки в «петлях» — «виртуальные». В этих точках функция обращается нуль либо не определена. «Петля» служит только для сохранения порядка чередования знаков). Кому принадлежит идея «петли», я не знаю. Этот способ очень удобный для расстановки знаков. Почему его нет в литературе? Именно потому, что знак в «петле»- «виртуальный». Точки, которые мы отмечаем на числовой прямой, являются либо нулями функции, либо не входят в её область определения. Поэтому использовать «петлю» можно, но ставить в неё знак — нельзя. Предлагаю бороться с этим противоречием, либо поставить знак карандашом, а потом его стереть, либо ставить знак в черновик, но не переносить его в чистовик. Далее рассмотрим различные примеры решения неравенств с помощью этого метода. 7 диагностических тестов
226 практических тестов
Вопрос дня
Карточки
Learn by Concept ← Предыдущая 1 2 3 4 Следующая → Common Core: Справка по математике для 3-го класса »
Числа и операции с дробями »
Понимание дробей как чисел »
Представление дроби на числовой прямой путем определения интервала от 0 до 1: CCSS. Какая часть числовой строки розовая? Возможные ответы: Правильный ответ: Объяснение: Числовая строка разбита на равные части. из частей розовый, что означает, что числовая линия розовая. Сообщить об ошибке Какая часть числовой строки розовая? Возможные ответы: Правильный ответ: Объяснение: Числовая строка разбита на равные части. из частей розовый, что означает, что числовая линия розовая. Сообщить об ошибке Какая часть числовой строки розовая? Возможные ответы: Правильный ответ: Объяснение: Числовая строка разбита на равные части. Сообщить об ошибке Какая часть числовой строки розовая? Возможные ответы: Правильный ответ: Объяснение: Числовая строка разбита на равные части. из частей розовый, что означает, что числовая линия розовая. Сообщить об ошибке Какая часть числовой строки розовая? Возможные ответы: Правильный ответ: Объяснение: Числовая строка разбита на равные части. из частей розовый, что означает, что числовая линия розовая. Сообщить об ошибке Какая часть числовой строки розовая? Возможные ответы: Правильный ответ: Объяснение: Числовая строка разбита на равные части. Сообщить об ошибке Какая часть числовой строки розовая? Возможные ответы: Правильный ответ: Объяснение: Числовая строка разбита на равные части. из частей розовый, что означает, что числовая линия розовая. Сообщить об ошибке Какая часть числовой строки розовая? Возможные ответы: Правильный ответ: Объяснение: Числовая строка разбита на равные части. из частей розовый, что означает, что числовая линия розовая. Сообщить об ошибке Какая часть числовой строки розовая? Возможные ответы: Правильный ответ: Объяснение: Числовая строка разбита на равные части. Сообщить об ошибке Какая часть числовой строки розовая? Возможные ответы: Правильный ответ: Объяснение: Числовая строка разбита на равные части. из частей розовый, что означает, что числовая линия розовая. Сообщить об ошибке ← Предыдущая 1 2 3 4 Следующая → Уведомление об авторских правах 7 Диагностические тесты
226 практических тестов
Вопрос дня
Карточки
Learn by Concept Представьте, что вам нужно постоянно сидеть в классе без перемены или обеденного перерыва. Большинство вещей не может продолжаться без перерыва. Между ними обычно есть промежуток. Эти промежутки известны как интервалы. Знаете ли вы, что в математике тоже есть интервалов ? Они помогают нам измерить эти пробелы в цифрах. Давайте разберемся, что такое интервал в математике подробнее. Давайте посмотрим на определение интервала в математике. Интервал — это промежуток между двумя объектами или точками. Давайте лучше разберемся в этом. Чем отличаются эти две линии? Первая строка сплошная, а во второй строке есть пробелы. Чем отличается аварийный мигающий свет машины скорой помощи от ее фары? Фары постоянно мигают. Однако аварийные проблесковые маячки мигают через определенные промежутки времени. Непрерывный означает без промежутка, тогда как интервал означает с промежутками. Давайте посмотрим на другой пример, чтобы понять интервалы: Когда автомобиль движется по дороге, он должен остановиться, когда светофор мигает красным. Интервал в математике измеряется числами. Интервал включает в себя все числа, находящиеся между двумя конкретными числами. Этот диапазон включает все действительные числа между этими двумя числами. Действительные числа — это любые числа, которые вы можете придумать. Например, интервал между 0 и 10 будет включать не только 1, 2, 3, 4, 5, 6, 7, 8 и 9, но и другие типы чисел между ними. К ним относятся десятичные числа, такие как 1,3, и дроби, такие как 1/10. Обозначение интервала — это упрощенный способ описания конкретного интервала. Давайте посмотрим, как это делается. Шаг 1: Пишем первое и последнее число интервала, которые являются конечными точками интервала. Например, если интервал от 6 до 20, мы пишем 6, 20. Шаг 2: Мы используем круглую или квадратную скобку с каждой стороны двух чисел. Итак, в этом примере мы используем: Итак, мы видим, что некоторые интервалы включают конечные точки, некоторые включают их частично, а некоторые не включают их. Исходя из этого, в математике существует три типа интервалов. Это: Этот тип интервала не включает конечные точки. Например, (5, 10) не включает конечные точки 5 и 10. Этот тип интервала включает конечные точки. Этот тип интервала включает только одну из конечных точек. Например, (6, 16] включает 16, но не включает 6, тогда как [6,16) включает 6, но не включает 16. Вот как разные типы интервалов выглядят в числовых строках: Давайте узнаем, что такое временной интервал. Предположим, вы идете из дома в школу. Вы постоянно ходите пешком и добираетесь до школы за 10 минут. Теперь, возвращаясь домой, вы устаете и решаете посидеть 2 минуты. Вы останавливаетесь на 2 минуты, а затем снова начинаете идти домой. Итак, мы говорим, что вы взяли временной интервал в 2 минуты, возвращаясь домой. Временной интервал можно определить как время между двумя событиями. Мы можем показать временные интервалы на временной шкале: Здесь временная шкала показывает интервалы в 1 час. Мы можем найти время между событиями, используя интервалы. Например, Сэм начал играть в футбол в 16:30. Он закончил игру в 18:00. Как долго он играл? Мы можем нарисовать временную шкалу следующим образом: Интервал с 16:30 до 16:30. до 17:00 составляет полчаса. Затем с 17:00 до 18:00 это час. Итак, получается полтора часа. Сэм играл в футбол полтора часа. Пример 1. Какой интервал между 14:00 и и 18:45? Решение : Вычтем значения времени: 6:45 – 2:00 = 4:45 Таким образом, между 14:00 и 2:00 4 часа 45 минут. и 18:45 Значит интервал будет 4 часа 45 минут. Пример 2. Учащиеся в возрасте от 12 до 17 лет могут быть членами школьной футбольной команды. Укажите интервал, который будет представлять эту информацию. Решение . Допустимый возраст от 12 до 17 лет. Таким образом, интервал равен [12, 17]. Пример 3: Чтобы сдать экзамен по математике, учащиеся должны набрать более 65 баллов из 100. Как это будет представлено в виде интервала? Решение . Студенты должны набрать от 65 до 100 баллов. Интервал для этого будет записан как (65, 100]. (10, 40) [10, 40] [10, 40] (10, 40) Правильный ответ: [10, 40] 2 (12, 30) [12, 30] (12, 30) [12, 30) Правильный ответ: [12, 30) 3 125 минут 85 минут 1 час 15 минут 1,5 часа Правильный ответ: 85 минут 4 3 минуты 2,5 минуты 200 секунд 2 минуты Правильный ответ: 2 минуты Permalink A tag already exists with the provided branch name. Many Git commands accept both tag and branch names, so creating this branch may cause unexpected behavior. Are you sure you want to create this branch? Go to file Cannot retrieve contributors at this time Создайте консольное приложение «Строковый калькулятор».
Приложение должно читать из консоли введенные пользователем строки, числа, арифметические операции проводимые между ними и выводить в консоль результат их выполнения. Обратите внимание на принципы ООП, постарайтесь разбить программу на логические классы. Дизайн-студия Дмитрия Борового завершила разработку нового корпоративного сайта для компании «Таск» – одной из крупейших страховых компаний Республики Беларусь. Клиент: Страховая компания «Таск». Задача: Основная задача для специалистов Дизайн-студии была сформулирована следующим образом: разработать простой, удобный, интуитивно понятный, но вместе с тем современный сайт для настоящих и потенциальных клиентов, который бы содействовал продвижению услуг компании «Таск» на рынке страхования. Решение: Новый сайт «Таск» является инструментом для выбора вида страхования и расчета стоимости страхового полиса, а также сервисом поддержки клиентов компании, позволяющим клиентам отслеживать состояние заявок через интернет. Презентационная титульная страница сайта В Студии был придуман и разработан интерактивный блок услуг компании, служащий путеводителем посетителя в различных видах страхования (страхование имущества, рисков, грузов, автострахование, Каско, медицинское страхование и др.), которые сгруппированы в два раздела: страхование частных лиц и корпоративных клиентов. Красивые иллюстрации для интерактивного блока услуг Внутренняя страница сайта. Страница описания страховой услуги Когда посетитель находит интересующую его услугу в интерактивном блоке на главной странице, он переходит на внутреннюю страницу, на которой представлена вся необходимая информация, от условий страхования по данному договору и калькулятора стоимости полиса до формы бланка заявления и рекомендаций для клиентов. Внутренняя страница сайта. Калькулятор страхования Калькуляторы стоимости сегодня становятся актуальными и практичными элементами корпоративных сайтов. Для сайта страховой компании «ТАСК» были разработаны простые и точные калькуляторы по отдельным видам страхования. Оценка стоимости страхового полиса происходит мгновенно без перезагрузки страницы. Особенностью каждого калькулятора является то, что логика расчетов и стоимость модифицируются автоматически в системе управления сайтом (CMS db.drive4). Таким образом, менеджеры компании могут настраивать расчет стоимости страхового полиса самостоятельно, без сторонней помощи, просто вводя привычные для них расчеты в Exсel или других форматах в нужные поля системы управления сайтом. На сайте реализована также система пояснений для вероятно неизвестных пользователю терминов, которые ему показываются при наведении курсора мыши. На сайте присутствует закрытый раздел для действующих клиентов компании, в котором, пройдя авторизацию, они могут наблюдать в режиме онлайн за состоянием заявок по страховым выплатам. Точки продаж Встроенный на сайте модуль «Яндекс.Карты» позволяет посетителю легко ориентироваться среди точек продаж, выбрать для себя ту, что находится ближе, а также посмотреть время работы данной точки и телефоны агентов. По завершении работ по разработке специалисты Студии приступили к поисковому продвижению сайта. Новый корпоративный сайт страховой компании «ТАСК» доступен по ссылке Страховая компания «ТАСК». О разработчике Дизайн-студия Дмитрия Борового — один из лидеров белорусского рынка интернет-разработок с 7-ми летним опытом. За это время реализовано более 250 проектов, созданные студией сайты получили более 15 дипломов и наград международных конкурсов. Среди наших клиентов: Heineken в Беларуси, ОАО «Белорусский автомобильный завод» (БелАЗ), ОАО «Борисовский молочный комбинат» (ТМ «Здравушка»), страховая компания «Таск», ОАО «Паритетбанк», Mitsubishi Motors в Беларуси, группа компаний «Трайпл», ЗАО «РРБ-Банк», комплекс «Минск-арена», сети салонов обуви «AXIS» и «Мегатоп». Основные направления деятельности студии: разработка сайтов, разработка логотипов и фирменных стилей, графическое сопровождение брендов, поисковое продвижение сайтов, разработка медийной интернет-рекламы и интерактивных презентаций. Время — самый ценный ресурс из всех, но почему-то мы склонны забывать об этом факте. Но со временем дело в том, что почти нет ограничений на то, чего мы можем достичь, если посвятим этому время. Выбор того, как мы распределяем время, формирует нашу личность и привычки, делая нас теми, кто мы есть. Как руководство, так и калькуляторы, которые мы здесь предлагаем, помогут овладеть навыками тайм-менеджмента и помогут вам правильно расставить приоритеты в своих задачах и деятельности. Мы создали 4 уникальных калькулятора тайм-менеджмента — ежедневный, еженедельный, один для штатных сотрудников и один для студентов. Итак, прежде чем вы прочитаете полное руководство и откроете для себя широкий спектр преимуществ использования калькуляторов управления временем, вот быстрый доступ ко всем 4: Калькулятор тайм-менеджмента — это инструмент, который позволяет вам понимать, планировать и организовывать свое время. Это поможет вам понять, как вы тратите свое время. Его можно применять к любому заданному периоду времени — это означает, что вы можете использовать его ежедневно, еженедельно, ежемесячно или даже ежегодно. можно использовать для двух основных целей. Оба имеют одну и ту же главную цель — помочь вам освоить навыки тайм-менеджмента. Давайте начнем эту главу с перечисления нескольких существенных преимуществ, которые могут получить все, кто использует калькулятор тайм-менеджмента: Список можно продолжать и продолжать, но большинство других предметов в нем уникальны и относятся к конкретным лицам. Так что мы не будем иметь дело с ними здесь. Однако есть и преимущества калькуляторов тайм-менеджмента, о которых можно говорить в общих чертах. Мы сосредоточимся на них и укажем вам на правильное мышление — стремиться к улучшению ваших навыков тайм-менеджмента. Важно выработать привычку отслеживать, оценивать и планировать время, необходимое для завершения задач, поскольку в планировании часто участвуют другие люди. Итак, если вы не хотите безответственно относиться к чужому времени и графикам — особенно когда вы работаете над взаимозависимыми задачами — вам помогут точные оценки, созданные с помощью приложения для управления временем и калькулятора управления временем. больше никогда не опаздывать. Если у вас нет оценок того, сколько времени потребуется для завершения определенного действия, вы не сможете эффективно планировать заранее. Как только вы лучше поймете, как распределяете время, вы сможете оценить свою личную продуктивность в разное время дня. Калькуляторы тайм-менеджмента помогут вам понять, как лучше структурировать свой день и улучшить свои организаторские способности. Этот набор навыков поможет вам лучше расставлять приоритеты, укладываться в сроки, эффективно использовать все свои ресурсы и больше никогда не опаздывать на встречи. Как только вы узнаете, сколько времени требуется, чтобы закончить действие, вы с меньшей вероятностью будете откладывать дела на потом и с большей вероятностью сосредоточитесь в течение заданного периода времени. В конце концов, сравнение со вчерашним собой, вероятно, самый здоровый способ роста и улучшения самооценки. Как только человек осознает, что он может выполнить определенное действие, скажем, за час, маловероятно, что он позволит себе потратить 2 часа на одно и то же действие в будущем. После изучения преимуществ использования калькулятора тайм-менеджмента, вот кое-что более осязаемое, чтобы помочь вам визуализировать то, о чем мы говорим, например, пример, показывающий еженедельный обзор времени, потраченного на работу по дому, поездки на работу, спорт, сон, общение и , конечно, работа. Как видите, после ввода значений для каждого дня в следующем столбце время будет переведено в проценты от вашей недели. Как мы упоминали ранее, человеку крайне важно понимать, как он распределяет этот ограниченный ресурс времени и как отслеживать этот ресурс. Кроме того, проценты — это прекрасный способ лучше визуализировать распределение времени на различные виды деятельности. Если какой-либо процент кажется слишком высоким, возможно, вы можете установить ограничение на эти действия. Это особенно касается деятельности, которая не обязательно способствует вашему росту и общему благополучию (например, социальные сети). Теперь давайте подробнее рассмотрим наш пример. Как видите, человек с регулярным режимом сна и работой полный рабочий день посвящает 33,33% и 23,81% своего времени этим двум важным видам деятельности. В сумме это составляет 57,13% их недели, оставляя менее половины времени, чтобы посвятить всем другим действиям. Это 40 часов в неделю на работе и 56 часов в неделю на сон. Оба числа адекватны и необходимы для здоровой жизни и здорового баланса между работой и личной жизнью. Итак, как только вы введете обязательные для вас действия, вы сможете распределить остальные по своему усмотрению. Удобно, правда? Теперь давайте более подробно рассмотрим каждый из 4 калькуляторов тайм-менеджмента, которые мы сделали для вас. Как мы упоминали в самом начале этого руководства, мы сделали 4 разных калькулятора тайм-менеджмента. Все они работают по одному принципу, но адаптированы к разным ситуациям. Таким образом, помимо ежедневных и еженедельных калькуляторов, мы также сделали специальные калькуляторы тайм-менеджмента для студентов и штатных сотрудников. Теперь давайте обсудим каждый из этих калькуляторов, их основные цели и способы их использования. Первый калькулятор тайм-менеджмента является ежедневным и предназначен для различных потребностей каждого дня. Как только вы введете цифры для действий, которые вы должны выполнить в определенный день, вы получите общее количество и процент часов, потраченных на эти действия. Таким образом, вы можете легко проверить, есть ли у вас дополнительное время — и когда — для других занятий в соответствии с вашими предпочтениями. Скачать калькулятор ежедневного тайм-менеджмента Чем полезен наш ежедневный калькулятор тайм-менеджмента? Ну, для начала, ведь каждый день разный, и нужно отслеживать эти отличия. Например, вы же не каждый день ходите в банк или стрижетесь, верно? Более того, как бы тщательно вы ни планировали порядок своих повседневных дел, многое может пойти не так и нарушить намеченный вами график. В конце концов, есть ограниченное количество факторов, которые вы можете предвидеть в жизни, так как многие вещи требуют сотрудничества с другими людьми. Помните тот случай, когда вы застряли в пробке или когда ваши коллеги опоздали на встречу? Некоторые вещи выйдут из-под вашего контроля, и это нормально. Однако отслеживание этих ежедневных задержек может выявить некоторые закономерности и помочь вам начать более реалистично оценивать время. Итак, причина, по которой калькулятор ежедневного управления временем полезен, заключается в том, что он помогает вам создавать структуру на ежедневной основе и, таким образом, помогает вам сосредоточиться на одной конкретной задаче, вместо того, чтобы отвлекаться между несколькими задачами. И почему так важно сосредоточиться на одной задаче за раз? Что ж, согласно последним статистическим данным о производительности, многозадачность может снизить производительность на целых 40%. Использование калькулятора ежедневного учета рабочего времени может быть ретроактивным и проактивным. В первом случае ваша роль более пассивна и больше похожа на наблюдателя. Что вам нужно сделать, так это отслеживать время, которое вы потратили на что-то. После того, как вы закончили действие или выполнили задачу, вы указываете, как долго вы это делали. Ретроактивный подход помогает вам получить четкое представление о том, как вы проводите свое время. Понимание того, сколько времени вы посвящаете каждому виду деятельности, — это первый шаг к изменению ваших привычек и улучшению распорядка дня. Только после того, как у вас появится четкое представление о том, как вы распределяете свое время, можно начать активное использование, что подразумевает принятие решения о том, сколько времени вы хотите выделить на определенную деятельность, и попытки придерживаться графика. Второе предназначение этих калькуляторов, о котором мы упоминали ранее, — отслеживание вашего прогресса и постановка четких целей. Слово «проактивный» несет в себе семантику «заранее», и вы можете составить свой ежедневный график настолько заранее, насколько пожелаете. Например, вы можете составить ежедневное расписание накануне вечером или рано утром, выпивая первую чашку кофе. И все это, наблюдая за результатами вашего ежедневного калькулятора тайм-менеджмента. Второй сделанный нами калькулятор тайм-менеджмента охватывает диапазон занятий в течение одной недели. То, как вы распределяете свое время на еженедельной основе, может легко стать вашей рутиной, поэтому вам следует обратить внимание на действия, которые вы делаете регулярно. Так создаются привычки, а именно наши привычки делают нас уникальными личностями. Скачать еженедельный калькулятор тайм-менеджмента Как только вы лучше поймете, как используете свое еженедельное время, вам будет легче проводить свободное время и планировать выходные и отпуск. Планирование недели в основном состоит из поиска способов распределить свою деятельность между рабочей неделей и выходными — для этой цели отлично подойдет недельный калькулятор тайм-менеджмента. Точно так же, как ежедневный калькулятор управления временем, вы можете использовать недельный калькулятор как проактивно, так и задним числом. Разница только во времени. А именно, как только вы закончите с повседневными делами, вам нужно ввести их в определенный день недели. Это жизненно важный шаг, так как вы постепенно научитесь различать работу с максимальной эффективностью и борьбу за выносливость, выполняя действия и задачи в «медленные» дни. Это снова ретроактивный подход, который поможет вам понять свое расписание на неделю таким, какое оно есть сейчас. Если вы уже выполнили эту часть, вы, вероятно, хотели бы сократить время, затрачиваемое на действия, если вы заметили их. Также не стоит слишком корить себя, если вы заметили, что в вашу рутину вкрадываются нездоровые привычки. Важно то, что вы заметили их и знаете, что они существуют. Имейте в виду, что работа над лучшей версией себя требует времени и усилий. Итак, пока вы можете сказать, что работаете над устранением или минимизацией времени, которое вы тратите на пожирателей времени, все хорошо. Конечная цель — составить расписание, которое оптимизирует вашу производительность в течение недели. Теперь поговорим о более конкретном виде недельного графика, касающемся всех, кто занят на условиях полной занятости. Этот калькулятор тайм-менеджмента поможет вам лучше управлять своим временем на работе. Вы можете использовать этот инструмент не только для того, чтобы получить максимальную отдачу от выходных, но и для того, чтобы улучшить распорядок рабочей недели. Скачать еженедельный калькулятор тайм-менеджмента для штатных сотрудников Быть сотрудником с полной занятостью уже означает, что ваш недельный график включает 40 часов работы. Учитывая, что в одной неделе всего 168 часов, базовое «ваше время», которое вы фактически можете выделить на другие виды деятельности, составляет 128 часов. Теперь давайте сложим время, которое вы спите, и вычтете его из этого. Итак, чтобы быть здоровым и продуктивным, взрослые должны спать от 7 до 9 часов каждый день, как утверждают эксперты. Остается 72 часа, если предположить, что человек спит в среднем 8 часов каждый день. Теперь подумайте о других важных делах, которые вы выполняете ежедневно, и попытайтесь оценить еженедельное общее количество следующих действий: Видите ли, для оптимального баланса между работой и личной жизнью необходимо научиться максимально эффективно использовать то, что остается после работы и сна. Отслеживание своей производительности и времени, необходимого для выполнения каждой из задач, — отличное начало для установления режима. Почему для штатных сотрудников важно иметь постоянный распорядок дня? Что ж, время — ограниченный ресурс, и если вы хотите иметь возможность заранее планировать и продвигать свою карьеру, вам нужно иметь временные рамки для конкретных действий. Теперь давайте посмотрим, как калькулятор тайм-менеджмента может помочь вам идеально сбалансировать работу и личную жизнь. Во-первых, планирование рабочих дней, когда вы должны ввести продолжительность: Другим видом деятельности, который вы можете считать основным, является регулярное выполнение базовых упражнений для поддержания здоровья. Это ваши основные занятия, и никакое свободное время или время, потраченное на общение, не должно влиять на продолжительность указанного основного занятия. После выполнения этого шага вы получите общее количество времени, которое у вас осталось для распределения на другие действия. Теперь вы должны ввести значения для второстепенных действий. Эта категория также должна включать работу по дому и деятельность, связанную с уходом за собой. Кроме того, сюда следует вводить действия, которые вы считаете основными только в определенные дни, например, посещение почты, запланированный визит к стоматологу и т. д. Естественно, если осталось какое-то количество времени, вы можете выбрать, хотите ли вы пообщаться или увеличить продолжительность любого действия, которое вы предпочитаете. Теперь давайте поговорим о выходных, когда вам не нужно посвящать время работе или поездкам на работу. Вы можете попробовать чередование коротких путешествий и общения, а также тратить больше времени на работу по дому и готовить еду на следующую неделю. Академический опыт включает в себя определенный набор « проблем », с которыми студенты сталкиваются, занимаясь тайм-менеджментом. Вот почему мы создали еще один специальный еженедельный калькулятор, который может помочь учащимся планировать свою социальную деятельность в соответствии с уроками, учебой и выполнением заданий. Этот инструмент значительно повысит качество каждого из этих действий. Давайте покажем вам, о чем мы говорим. Скачать еженедельный калькулятор тайм-менеджмента для студентов Почему мы выбрали учащихся в качестве целевой группы для этого инструмента? Ну, для начала, знаете ли вы, что подавляющее большинство студентов отложат свои обязанности до последней минуты? В поддержку этого утверждения мы обнаружили, что различные исследования указывают на диапазон от 50% до 95% студентов, которые регулярно прокрастинируют. На результат такого высокого процента влияет несколько важных факторов, преобладающим из которых часто является их очень активная социальная жизнь. Мы не пытаемся сказать, что учащиеся не должны общаться и участвовать в общественной деятельности. При правильной организации, учете времени и хорошо спланированной структуре у вас будет достаточно времени, чтобы уложиться во все сроки И принять участие во всех веселых мероприятиях с друзьями. Мы знаем, планирование вашей общественной жизни может показаться странным, даже нелепым. Тем не менее, просто попробуйте — укажите вечеринки, на которые вы планируете пойти, в своем календаре. Покажем это на примере. Вот как выглядит расстановка приоритетов по таким категориям, как посещение занятий, выполнение домашних заданий и сон, в калькуляторе тайм-менеджмента. Итак, в первую очередь, как мы только что упомянули, введите от 7 до 9 часов сна и добавьте продолжительность ваших академических обязанностей, включая время, потраченное на учебу и поездки на работу. После того, как вы войдете в другие запланированные заранее мероприятия, такие как волонтерство или участие в студенческой организации, вы получите оценку того, сколько времени у вас осталось для распределения. Само собой разумеется, каждую неделю будет разный набор действий, которые считаются приоритетными. Поэтому убедитесь, что вы также учитываете различные случайные задачи, такие как посещение почты, банка, подготовка к промежуточным экзаменам или запланированный визит к стоматологу. Отметьте эти действия как основные и включите их в категорию « Другое » калькулятора. Это для рабочей недели, когда у тебя есть уроки и другие обязанности в целом. Но настоящие перемены начнутся только тогда, когда вы тоже начнете планировать свои выходные. Опять же, вы должны сосредоточиться на своей академической успеваемости, поэтому вам нужно будет ввести значения для учебы, выполнения домашних заданий и любых других заданий, которые у вас есть время, чтобы закончить только в выходные дни. Только после этого планируйте любую общественную деятельность. Это единственный способ получить блестящий академический опыт и достаточно времени для общения — при условии, что вы придерживаетесь своего расписания. Как вы можете сделать вывод, предоставленные нами калькуляторы тайм-менеджмента могут значительно улучшить ваши навыки тайм-менеджмента. Они помогут вам выявить пожирателей времени и улучшить ваши навыки планирования и составления графиков, а также точность. Как только вы сможете планировать свою неделю заранее, улучшится не только то, как вы распределяете время, но и качество вашей работы. Наличие структурированного расписания разделяет большие отрезки времени на конкретные задачи и цели, что облегчает их достижение. Более того, в вашем дне будет больше маленьких побед, что крайне полезно для вашего психического здоровья. Однако, если вы считаете себя технически подкованным и хотите использовать возможности онлайн-инструментов управления временем, мы предлагаем вам сделать все это с помощью Clockify. Поскольку основной деятельностью является отслеживание времени, нет никаких причин не использовать то же решение для отслеживания вашего прогресса. Как говорится в пословице — убить двух зайцев одним выстрелом. Clockify может вам помочь: Я долго ждал этого дня. Я был очень счастлив, когда впервые сделал свой собственный калькулятор. Это был такой гордый момент, потому что в то время калькуляторы были довольно дорогими, поскольку все, что у меня было, это мои карманные деньги, и я никогда не собирался тратить их на калькулятор. Я до сих пор помню, как сильно волновался, когда мой учитель впервые дал мне задание сделать калькулятор. Это был момент, когда я говорил сам с собой: « Нет.. Вы не можете сделать калькулятор, так что просто пойдите и купите его. ’’ Что на самом деле означает для меня калькулятор? Когда перед нами появляется слово Калькулятор . Наконец я пришел домой и постоянно думал о своей задаче сделать калькулятор. Я так устал и заснул, Так как я думал, что так груз. Когда я проснулся, было ровно 2 часа ночи. Я запаниковал! Но я сказал себе перестать думать, включил ноутбук и начал писать код, а потом подумать, что можно с этим сделать, но хотя бы начать сначала. Лабораторная работа 4.1 : Я только что открыл IDE (интегрированную среду разработки) и начал писать код. Я только что написал базовую структуру программы. Это было #include Использование пространства имен std; Int main() { } Это был момент, когда я буквально застрял между этими двумя фигурными скобками. Я чувствовал, что когда-то я должен прочитать условие поставленной задачи, чтобы понять больше. Итак, я сделал это. Я открыл свою книгу, чем прочитал заявление задание 4.1 в котором указано что. Ну, это был момент, когда я почувствовал себя довольно расслабленным, потому что, по крайней мере, я знал об этих четырех операторах и действительно собирался их использовать, но как, потому что логика все еще не была найдена ни в книге, ни в моем мозгу. Поскольку я объявил переменные и сохранил в них два значения, пусть у нас есть два значения 4 и 20, вы можете изменить значения, но я просто показываю вам логику однострочного калькулятора, который состоит только из одного оператора cout . Cout << «sum = » <<20 + 4<< «\nsub =» <<20–4<< «\nmul =» <<20*4<< «\ndiv =» <<20/ 4; Вывод будет: сумма = 24 Счастливый момент Я показал свою программу своему учителю. Он оценил меня, и все в моем классе аплодировали мне, потому что я был тем, кто написал такую маленькую программу с полной эффективностью. Я был очень счастлив, и если вам, ребята, понравилась эта история, вы, ребята, также можете поблагодарить меня, нажав на значок хлопков. I вариант. 1.Что такое рынок ценных бумаг? 2.Что является главной задачей рынка ценных бумаг? 3. Кто занимается осуществлением организованного рынка ценных бумаг? 4. Фьючерсные контракты обращаются 5.Какое название носит рынок, на котором исполнение заключенных сделок происходит не позднее второго рабочего дня со дня заключения сделки? 6.Что из ниже перечисленного не является ценной бумагой? 7. Что такое конвертируемые облигации? 8. Какую функцию выполняет андеррайтер ценных бумаг? 9.Что такое акция? 10.Кто может являться инвестором государственных ценных бумаг? 11.Из чего состоит контрольный пакет акций? 12. Что используется в техническом анализе? 13. Чему может быть равна эмиссионная цена облигации? 14.Что такое инвестиционный пай? 15.Дайте определение понятию «чистые активы»: 16.Посредством чего производится уступка прав требования по именным депозитам? 17. Что происходит при покупке колл-опциона? 18.Дайте определение понятию «учетная стоимость акции (NAV)». 19.Ценная бумага (ЦБ), которая закрепляет совокупность имущественных и неимущественных прав, подлежащих удостоверению, уступке и безусловному осуществлению с соблюдением форм и порядка… 20. Могут ли освобождаться отдельные выпуски эмиссионных ценных бумаг от процедуры государственной регистрации? II вариант. 1.Как называется ничем не обусловленное обязательство векселедателя выплатить по наступлении предусмотренного срока полученную взаймы сумму? 2.Как называют юридическое лицо или органы исполнительной власти либо органы местного самоуправления, которые несут от своего имени обязательства перед владельцами ЦБ осуществлению прав, закрепленных ими? 3. Выберите, частью какого рынка является рынок ценных бумаг? 4. 5. Отметьте, к какой разновидности относятся ЦБ, которые выражают отношение совладения и предоставляющие их владельцу право долевого участия как в собственности, так и в прибыли эмитента? 6. Акция является: 7. Определите, для чего из ниже перечисленного необходим акцепт? 8. Выберите основные виды облигаций: 9. Отметьте специфическую черту валютного рынка: 10. Ценные бумаги по виду выраженных прав делятся на: 11. Определите, кто является главным и последним плательщиком по простому векселю: 12. Выберите того, кто может обязываться векселем в РФ: 13. Выберите, что может быть выписано на предъявителя по российскому законодательству: 14. 15. Эмиссионная ЦБ, которая закрепляет права её владельца на получение части прибыли в виде дивидендов: 16. Определите, каким путем осуществляется государственное регулирование рынка ценных бумаг в РФ: 17. Отметьте право, которое дает обыкновенная акция: 18. 19. Обязательства эмитента облигаций выплатить, кроме основной суммы долга, заранее обговорённые проценты, начисленные на номинал: 20. Определите, как называют именную ЦБ, которая подтверждает право её владельца на долю в имуществе фонда: Последний раз тест пройден 1 час назад.
Для учителя
Перед прохождением теста рекомендуем прочитать: Вопрос 1 из 5 Пригодность Ликвидность Экономность Эквивалентность Правильный ответ Неправильный ответ
Пояснение к правильному ответу
Одним из признаков ценных бумаг является их ликвидность. В вопросе ошибка? Вопрос 2 из 5 Эмират Эквивалент Эмитент Патент Правильный ответ Неправильный ответ
Пояснение к правильному ответу
Организацию, выпустившую ценные бумаги, называют эмитентом. Она обязана исполнять обязательства, которые обозначены в документе. В вопросе ошибка? Вопрос 3 из 5 В 1991 В 1996 В 2000 В 2020 Правильный ответ Неправильный ответ
Пояснение к правильному ответу
Владелец ценных бумаг защищён законодательством. В вопросе ошибка? Вопрос 4 из 5 Правильный ответ Неправильный ответ
Пояснение к правильному ответу
Банковский сертификат — это документ, который выдаётся человеку в тот момент, когда он совершает вклад. Ценная бумага гарантирует возврат средств с процентами. Примером может быть сберегательная книжка. В вопросе ошибка? Вопрос 5 из 5 Закладная Докладная Объяснительная Доказательная Правильный ответ Неправильный ответ
Пояснение к правильному ответу
Закладная — это ценная бумага, которая выдаётся при совершении ипотечных сделок. В вопросе ошибка? Доска почёта Чтобы попасть сюда — пройдите тест. Пока никого нет. Будьте первым! 3.7 Средняя оценка: 3.7 Всего получено оценок: 187. А какую оценку получите вы? Чтобы узнать — пройдите тест. Страница, которую вы пытались открыть по этому адресу, похоже, не существует. Обычно это результат плохой или устаревшей ссылки. Мы извиняемся за любые неудобства. Если вы впервые посещаете TechTarget, добро пожаловать! Извините за обстоятельства, при которых мы встречаемся. Вот куда вы можете пойти отсюда: Сеть Развертывание 5G на предприятии требует тщательного планирования. Подготовьтесь к достижениям в области беспроводных технологий с помощью этого руководства по 5G, которое … Сравнение стоимости SD-WAN и MPLS не всегда является решением типа «или-или». Организации часто внедряют обе технологии, чтобы … Wireshark — полезный инструмент для сбора данных о сетевом трафике. Сетевые специалисты могут извлечь максимальную пользу из этого инструмента, анализируя захваченные . ИТ-директор COVID-19 привел к широкому внедрению облачных технологий и технологий удаленной работы. Вот что ИТ-директора должны знать об инвестициях в ИИ и… У ИТ-руководителей есть возможность поддержать трансформацию бизнеса, сосредоточив внимание на людях. Узнайте, почему ИТ-директора имеют решающее значение … Команды по закупкам должны упростить процесс запроса предложений, чтобы найти подходящего поставщика. Эти советы могут помочь организации … Корпоративный настольный компьютер Организации, в управлении которых находятся настольные компьютеры с macOS, должны убедиться, что их продукты для обеспечения безопасности поддерживают компьютеры Mac. Собственный брандмауэр macOS по умолчанию отключен, поэтому ИТ-специалисты могут задаться вопросом, стоит ли настраивать функцию безопасности. Узнайте, как … Типичные обновления Apple OS являются большими и нечастыми, но функция Rapid Security Response помогает администраторам сохранять устройства Apple … Облачные вычисления Расходы на облако могут выйти из-под контроля, но такие службы, как Google Cloud Recommender, предоставляют информацию для оптимизации ваших рабочих нагрузок. Но… Йорам Новик, второй генеральный директор облачного стартапа Zadara, привносит в эту должность многолетний опыт руководства ИТ и рассказывает о . Если вы рассматриваете Amazon Route 53 как способ уменьшить задержку, вот как работает этот сервис. ComputerWeekly.com ИТ-команды, ответственные за развертывание и управление цифровым наблюдением на рабочих местах, говорят, что им неудобно «крайне … Участники контрактной отрасли задаются вопросом, почему правительству Великобритании требуется так много времени, чтобы опубликовать результаты своего… После проверки готовности к чрезвычайным ситуациям 23 апреля правительство подтвердило необходимость проверки того, почему были исключены некоторые мобильные телефоны 4G и 5G Страница, которую вы пытались открыть по этому адресу, похоже, не существует. Если вы впервые посещаете TechTarget, добро пожаловать! Извините за обстоятельства, при которых мы встречаемся. Вот куда вы можете пойти отсюда: Сеть Развертывание 5G на предприятии требует тщательного планирования. Подготовьтесь к достижениям в области беспроводных технологий с помощью этого руководства по 5G, которое … Сравнение стоимости SD-WAN и MPLS не всегда является решением типа «или-или». Wireshark — полезный инструмент для сбора данных о сетевом трафике. Сетевые специалисты могут извлечь максимальную пользу из этого инструмента, анализируя захваченные … ИТ-директор COVID-19 привел к широкому внедрению облачных технологий и технологий удаленной работы. Вот что ИТ-директора должны знать об инвестициях в ИИ и… У ИТ-руководителей есть возможность поддержать трансформацию бизнеса, сосредоточив внимание на людях. Узнайте, почему ИТ-директора имеют решающее значение … Команды по закупкам должны упростить процесс запроса предложений, чтобы найти подходящего поставщика. Корпоративный настольный компьютер Организации, в управлении которых находятся настольные компьютеры с macOS, должны убедиться, что их продукты для обеспечения безопасности поддерживают компьютеры Mac. Обзор этих … Собственный брандмауэр macOS по умолчанию отключен, поэтому ИТ-специалисты могут задаться вопросом, стоит ли настраивать функцию безопасности. Узнайте, как … Типичные обновления Apple OS являются большими и нечастыми, но функция Rapid Security Response помогает администраторам сохранять устройства Apple … Облачные вычисления Расходы на облако могут выйти из-под контроля, но такие службы, как Google Cloud Recommender, предоставляют информацию для оптимизации ваших рабочих нагрузок. Йорам Новик, второй генеральный директор облачного стартапа Zadara, привносит в эту должность многолетний опыт руководства ИТ и рассказывает о … Если вы рассматриваете Amazon Route 53 как способ уменьшить задержку, вот как работает этот сервис. ComputerWeekly.com ИТ-команды, ответственные за развертывание и управление цифровым наблюдением на рабочих местах, говорят, что им неудобно «крайне … Участники контрактной отрасли задаются вопросом, почему правительству Великобритании требуется так много времени, чтобы опубликовать результаты своего. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||



 Почти все использовали формат файла DOC каждый раз, при написании письма, при работе или вообще при написании чего-либо на компьютере вы бы использовали формат файла DOC. В 1990-х годах Microsoft выбрала расширение DOC для обработки своих файлов программы Microsoft Word. По мере развития и роста технологий ПК, первоначальное использование расширения стало менее важным и в значительной степени исчезло из мира ПК.
Почти все использовали формат файла DOC каждый раз, при написании письма, при работе или вообще при написании чего-либо на компьютере вы бы использовали формат файла DOC. В 1990-х годах Microsoft выбрала расширение DOC для обработки своих файлов программы Microsoft Word. По мере развития и роста технологий ПК, первоначальное использование расширения стало менее важным и в значительной степени исчезло из мира ПК.
 pdf
pdf Он не кодирует информацию, относящуюся к программному обеспечению, аппаратному обеспечению или операционной системе, используемой для создания или просмотра документа.
Он не кодирует информацию, относящуюся к программному обеспечению, аппаратному обеспечению или операционной системе, используемой для создания или просмотра документа. 0 File)
0 File) Выберите файлы для конвертации.
Выберите файлы для конвертации. Ваши данные. Вы в контроле.
Ваши данные. Вы в контроле.
 openxmlformats-officedocument.wordprocessingml.document
openxmlformats-officedocument.wordprocessingml.document
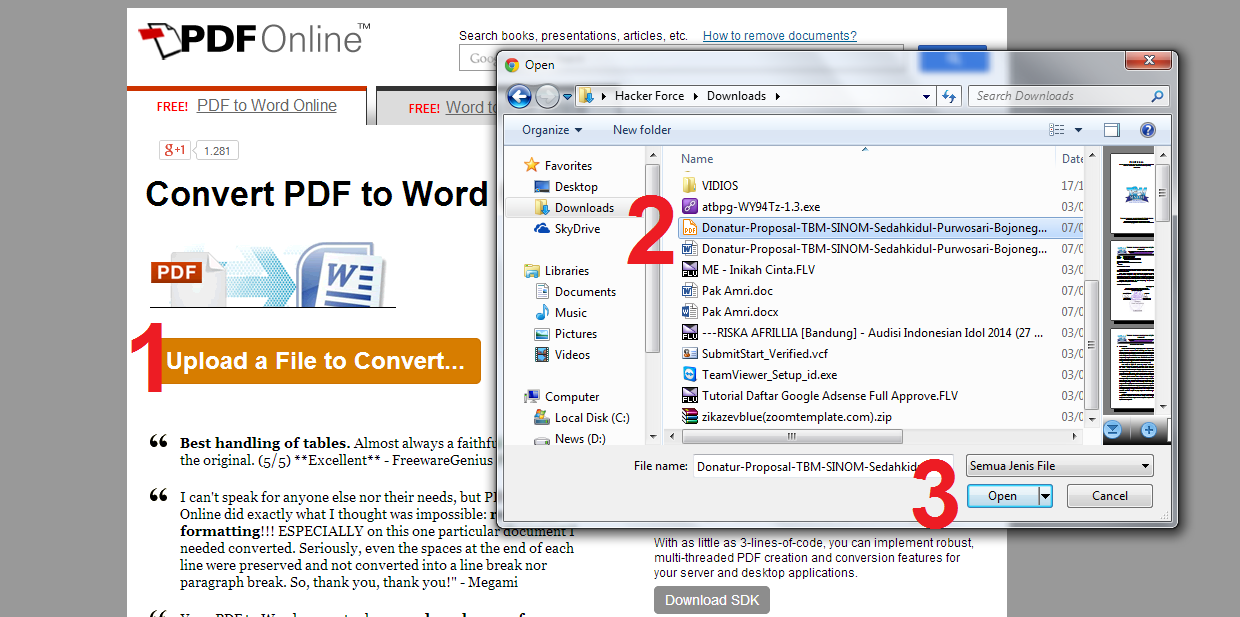 0 File)
0 File) Или загрузите файлы из облачного хранилища, такого как Google Drive или Dropbox.
Или загрузите файлы из облачного хранилища, такого как Google Drive или Dropbox.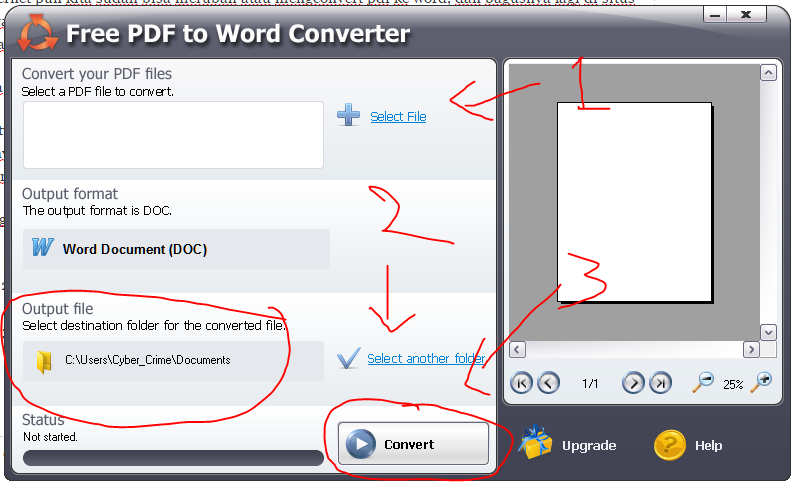 Просто загрузите файл Word в Soda PDF Desktop, чтобы преобразовать его в PDF. Это так просто!
Просто загрузите файл Word в Soda PDF Desktop, чтобы преобразовать его в PDF. Это так просто! Аванквест 2023, все права защищены.
Аванквест 2023, все права защищены. Хотите продолжить загрузку файла для конвертации?
Хотите продолжить загрузку файла для конвертации? Отличное быстрое приложение, значительно увеличило мою производительность. Также замечательная поддержка — всегда быстро помогали!
Отличное быстрое приложение, значительно увеличило мою производительность. Также замечательная поддержка — всегда быстро помогали! Я могу сделать несколько больших файлов за короткий промежуток времени.
Я могу сделать несколько больших файлов за короткий промежуток времени. Поскольку Word Perfect практически мертв, я решил конвертировать все ее файлы. Преобразователь Замзара был идеальным.
Поскольку Word Perfect практически мертв, я решил конвертировать все ее файлы. Преобразователь Замзара был идеальным. Помимо нашей онлайн-службы преобразования файлов, мы также предлагаем настольное приложение для преобразования файлов прямо с вашего рабочего стола и API для автоматического преобразования файлов для разработчиков. Какой инструмент вы используете, зависит от вас!
Помимо нашей онлайн-службы преобразования файлов, мы также предлагаем настольное приложение для преобразования файлов прямо с вашего рабочего стола и API для автоматического преобразования файлов для разработчиков. Какой инструмент вы используете, зависит от вас! Он был разработан Adobe, чтобы люди могли обмениваться документами независимо от того, какое устройство, операционную систему или программное обеспечение они используют, сохраняя при этом содержимое и форматирование. Формат эволюционировал, чтобы разрешить редактирование и интерактивные элементы, такие как электронные подписи или кнопки. Формат PDF теперь является стандартным открытым форматом, доступным не только в Adobe Acrobat. Он поддерживается Международной организацией по стандартизации (ISO).
Он был разработан Adobe, чтобы люди могли обмениваться документами независимо от того, какое устройство, операционную систему или программное обеспечение они используют, сохраняя при этом содержимое и форматирование. Формат эволюционировал, чтобы разрешить редактирование и интерактивные элементы, такие как электронные подписи или кнопки. Формат PDF теперь является стандартным открытым форматом, доступным не только в Adobe Acrobat. Он поддерживается Международной организацией по стандартизации (ISO).
 ZIP в DOC
PDF в DOC
PNG в DOC
PPS в DOC
PPSX в DOC
PPT в DOC
PPTX в DOC
PSD в DOC
PUB в DOC
RTF в DOC
TIFF в DOC
WKS в DOC
WPD в DOC
WPS в DOC
ZIP в DOC
PDF в DOC
PNG в DOC
PPS в DOC
PPSX в DOC
PPT в DOC
PPTX в DOC
PSD в DOC
PUB в DOC
RTF в DOC
TIFF в DOC
WKS в DOC
WPD в DOC
WPS в DOC Если у вас есть Microsoft Word, вы также можете преобразовать файл в самой программе. Откройте документ, щелкните вкладку «Файл» вверху, затем используйте функции «Сохранить как» или «Печать» для создания PDF-файла.
Если у вас есть Microsoft Word, вы также можете преобразовать файл в самой программе. Откройте документ, щелкните вкладку «Файл» вверху, затем используйте функции «Сохранить как» или «Печать» для создания PDF-файла.

 К коммерческим организациям относятся организации:
К коммерческим организациям относятся организации: К косвенным налогам относятся:
К косвенным налогам относятся: К какой группе налогов относятся акцизы?
К какой группе налогов относятся акцизы? Какой налог является федеральным?
Какой налог является федеральным? Сущность налога – это:
Сущность налога – это: Сколько частей имеет налоговый кодекс РФ?
Сколько частей имеет налоговый кодекс РФ? прослушиваний | Quizizz Поиск среди миллионов тестов
прослушиваний | Quizizz Поиск среди миллионов тестов предварительный просмотр
предварительный просмотр  Множественный выбор
Множественный выбор Она на иждивении?
Она на иждивении? Множественный выбор
Множественный выбор Должен ли он подавать налоговую декларацию?
Должен ли он подавать налоговую декларацию? Множественный выбор
Множественный выбор Что является правдой?
Что является правдой? Множественный выбор
Множественный выбор
 Любой волонтер в клиниках для налогоплательщиков с низким доходом, который работает с IRS для оказания помощи налогоплательщикам с низким доходом, будет освобожден от уплаты налога, и ему не нужно получать разрешение.
Любой волонтер в клиниках для налогоплательщиков с низким доходом, который работает с IRS для оказания помощи налогоплательщикам с низким доходом, будет освобожден от уплаты налога, и ему не нужно получать разрешение.  Если работник подписывает декларацию и использует свой собственный ИНН, и работник не освобожден от налогов, то этот работник обязан зарегистрироваться.
Если работник подписывает декларацию и использует свой собственный ИНН, и работник не освобожден от налогов, то этот работник обязан зарегистрироваться.  Такие сотрудники должны зарегистрироваться в качестве оплачиваемых составителей, если только они не освобождены по другой освобожденной категории.
Такие сотрудники должны зарегистрироваться в качестве оплачиваемых составителей, если только они не освобождены по другой освобожденной категории. 
 Банк может взимать комиссию RAL/RAC. Составитель не может взимать с налогоплательщика дополнительную плату за выбор одного из этих вариантов.
Банк может взимать комиссию RAL/RAC. Составитель не может взимать с налогоплательщика дополнительную плату за выбор одного из этих вариантов. 

 Извлекаем корень из 5, самое близкое число из которого можно извлечь корень 4. Из 4 извлекаем корень получится 2, записываем в ответ. Из 5 вычитаем 4 получится 1 и как в делении сносим новые цифры. Нашу первую цифру из ответа нужно умножить на 2, два умножить на два получится 4. В красном квадрате находится новая цифра искомого числа. Число нужно так подобрать чтобы при умножении получилось максимальное число, не превосходящее число 129.
Извлекаем корень из 5, самое близкое число из которого можно извлечь корень 4. Из 4 извлекаем корень получится 2, записываем в ответ. Из 5 вычитаем 4 получится 1 и как в делении сносим новые цифры. Нашу первую цифру из ответа нужно умножить на 2, два умножить на два получится 4. В красном квадрате находится новая цифра искомого числа. Число нужно так подобрать чтобы при умножении получилось максимальное число, не превосходящее число 129. pdf
pdf Поликлиника постоянно динамически
развивается и обновляется в соответствии с требованиями времени и современных научных
достижений.
Поликлиника постоянно динамически
развивается и обновляется в соответствии с требованиями времени и современных научных
достижений.





 данный номер. Другими словами слов , если число умножить четыре раза на само , это число будет назвал четвертым корнем результирующего числа .
данный номер. Другими словами слов , если число умножить четыре раза на само , это число будет назвал четвертым корнем результирующего числа . Единственная задача , которую вам нужно сделать, это разделить данное число на то же самое число четыре умноженное на . Мы можем вообще представить четвертый корень формулы как:
Единственная задача , которую вам нужно сделать, это разделить данное число на то же самое число четыре умноженное на . Мы можем вообще представить четвертый корень формулы как:


 Найдите косинус угла между прямыми AE и BK.
Найдите косинус угла между прямыми AE и BK. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.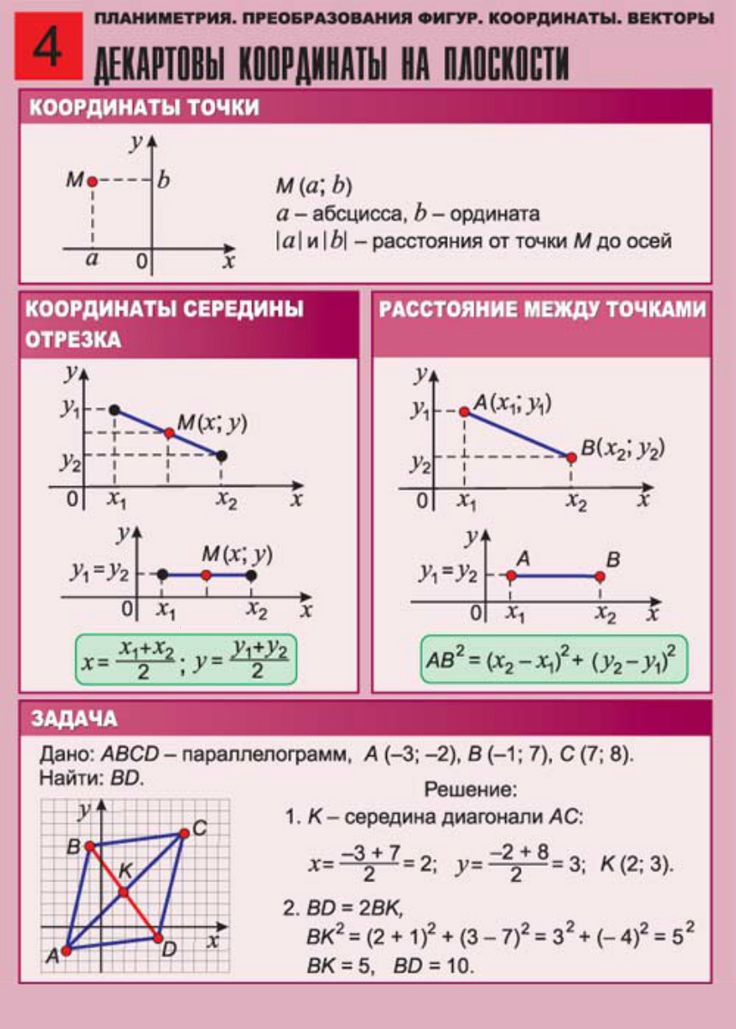 А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
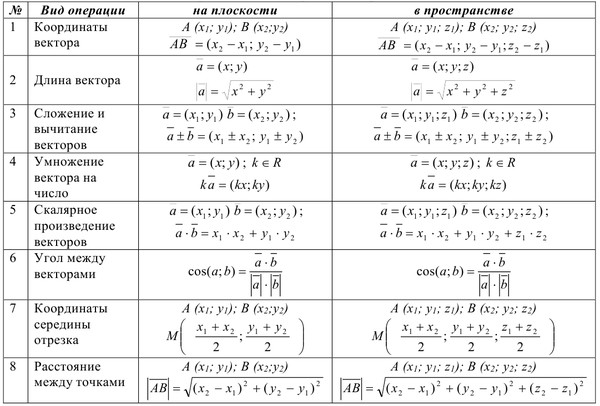 Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.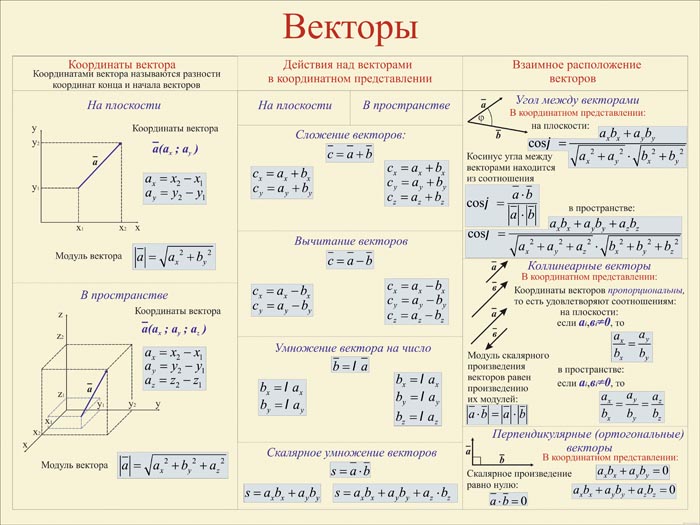 Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».
Прямую четырехугольную призму можно по-другому назвать «параллелепипед». Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
 Выберем
Выберем Векторы имеют как скалярную, так и векторную составляющую, и эти векторные формулы помогают систематически и легко выполнять многочисленные операции над векторами.
Векторы имеют как скалярную, так и векторную составляющую, и эти векторные формулы помогают систематически и легко выполнять многочисленные операции над векторами.
 \hat j = \hat k.\hat k = 1 \\ \hat i.\hat j =\hat j.\hat k=\шляпа k.\шляпа i = 0\end{align} \]
\hat j = \hat k.\hat k = 1 \\ \hat i.\hat j =\hat j.\hat k=\шляпа k.\шляпа i = 0\end{align} \]  \vec B = ((3).(4) + (-2).(-1) + 7.(3)) = 12 + 2 + 21 = 35\)
\vec B = ((3).(4) + (-2).(-1) + 7.(3)) = 12 + 2 + 21 = 35\) От хвоста к голове показана ориентация вектора. Мы рассмотрим определение вектора и некоторые векторные формулы с примерами по этой теме. Давайте посмотрим на идею!
От хвоста к голове показана ориентация вектора. Мы рассмотрим определение вектора и некоторые векторные формулы с примерами по этой теме. Давайте посмотрим на идею!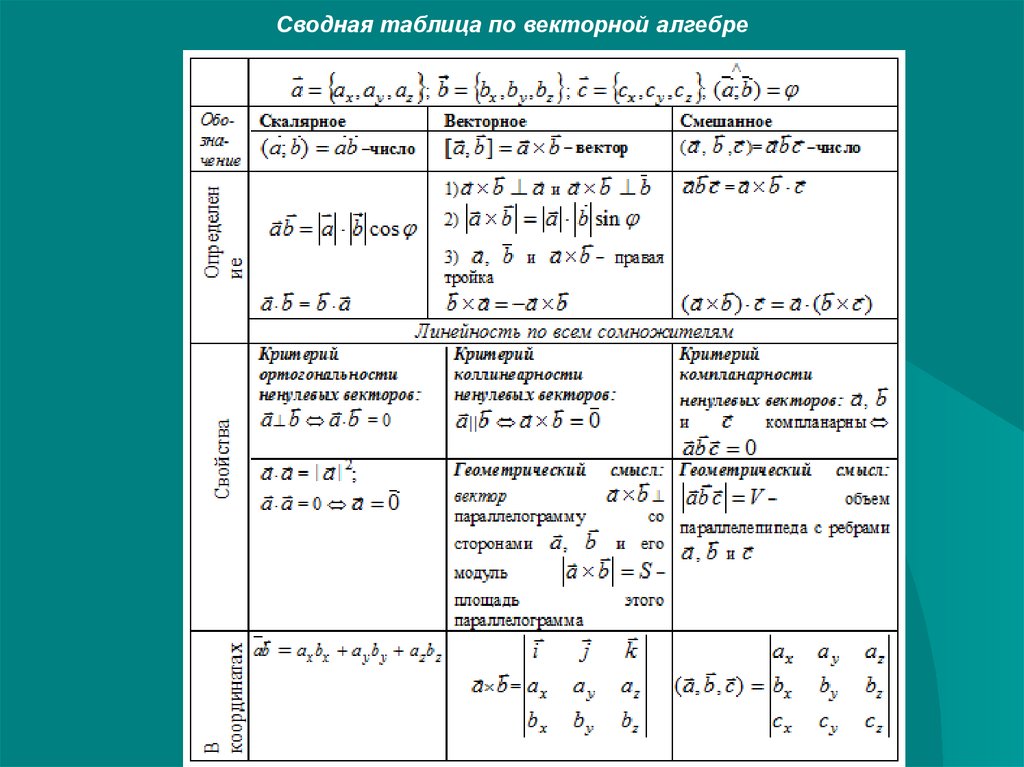




 Формула интегрирования по частям для неопределённого интеграла, то есть
Формула интегрирования по частям для неопределённого интеграла, то есть 4 Вычислим интегралВыгодно взять и , так что получаем:
4 Вычислим интегралВыгодно взять и , так что получаем:
 Интегралы вида
Интегралы вида
 Для этого вам нужно только связаться со мной:
Для этого вам нужно только связаться со мной: Вы можете заменить наш сервис на поиск нужного интеграла в таблицах. Здесь вы получите решение неопределенного интеграла в табличном виде, просто набрав нужную функцию. Не все математические сайты могут вычислить неопределенные интегралы от функций онлайн быстро и качественно, особенно если вы хотите найти неопределенный интеграл от сложных функций или функций, которые не входят в общий курс высшей математики. Веб-сайт OnSolver.com поможет решить интеграл онлайн и хорошо справиться с вашей работой. Онлайн-решение интеграла на сайте OnSolver.com всегда даст вам точный ответ.
Вы можете заменить наш сервис на поиск нужного интеграла в таблицах. Здесь вы получите решение неопределенного интеграла в табличном виде, просто набрав нужную функцию. Не все математические сайты могут вычислить неопределенные интегралы от функций онлайн быстро и качественно, особенно если вы хотите найти неопределенный интеграл от сложных функций или функций, которые не входят в общий курс высшей математики. Веб-сайт OnSolver.com поможет решить интеграл онлайн и хорошо справиться с вашей работой. Онлайн-решение интеграла на сайте OnSolver.com всегда даст вам точный ответ. Просто воспользуйтесь нашими услугами и без труда найдите неопределенный интеграл онлайн. Этот сервер очень полезен для практических задач нахождение интеграла функции онлайн. Вы должны ввести заданную функцию, получить неопределенное интегральное онлайн-решение и сравнить решение со своим ответом.
Просто воспользуйтесь нашими услугами и без труда найдите неопределенный интеграл онлайн. Этот сервер очень полезен для практических задач нахождение интеграла функции онлайн. Вы должны ввести заданную функцию, получить неопределенное интегральное онлайн-решение и сравнить решение со своим ответом.
 Он представлен как ∫f(x)dx
Он представлен как ∫f(x)dx 
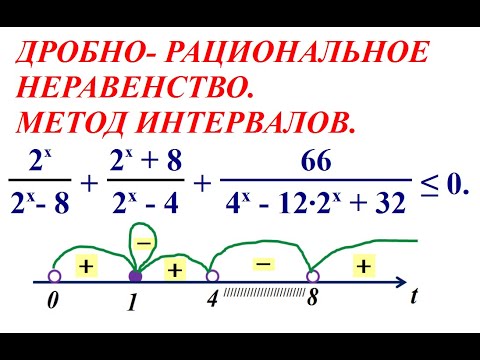 Учитывая это, расставляем в интервалах знаки (как показано на Рис.3).
Учитывая это, расставляем в интервалах знаки (как показано на Рис.3). е. «+». Левее «1» знаменатель будет отрицательным, а числитель положительным, поэтому при переходе через число -2 знак не меняется:
е. «+». Левее «1» знаменатель будет отрицательным, а числитель положительным, поэтому при переходе через число -2 знак не меняется: 8
8 Учитывая это, расставляем знаки на остальных промежутках.
Учитывая это, расставляем знаки на остальных промежутках. 13:
13: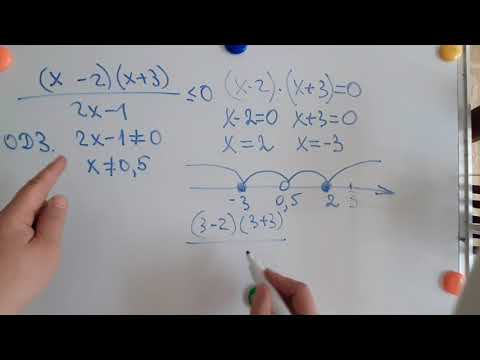
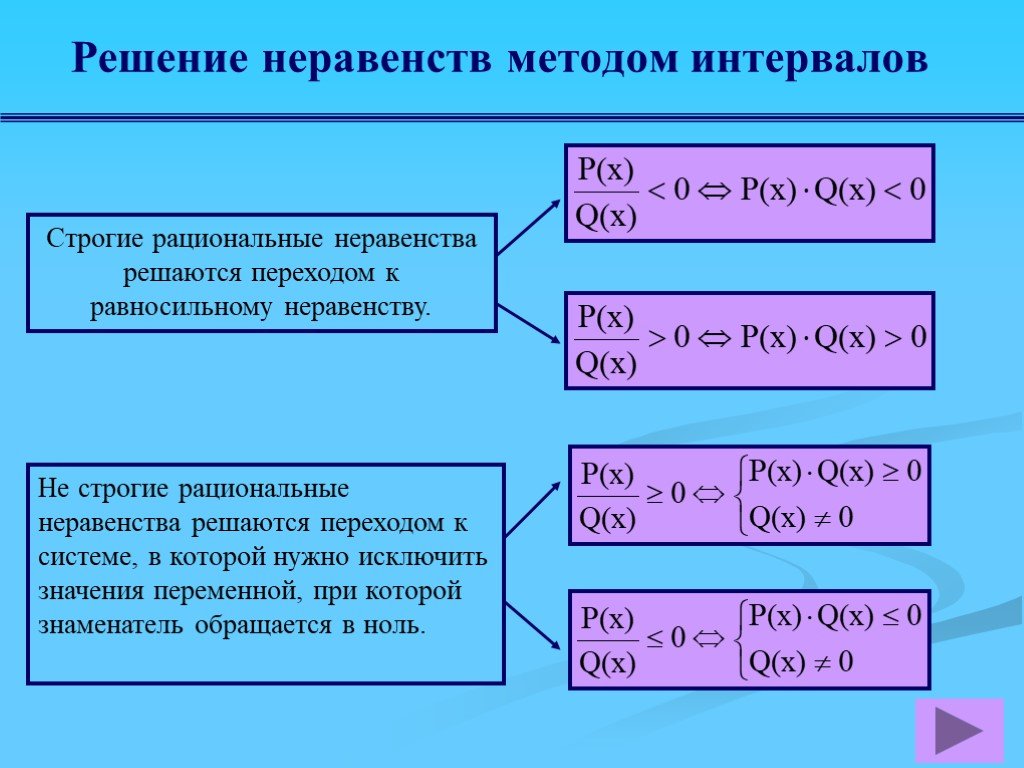 Полученные точки отмечаем на числовой прямой с учетом области определения функции. Точки разбивают числовую прямую на промежутки, в каждом из которых рассматриваемая функция имеет определенный знак. Выбираем любое число из любого промежутка (удобнее всего брать нуль, если он не входит в отмеченные точки), и подставляем это число в последнее неравенство (то есть в упрощенное неравенство, в котором все слагаемые стоят в левой части и дроби приведены к наименьшему общему знаменателю). В результате определяем знак на выбранном промежутке. Остальные знаки расставляем в шахматном порядке.
Полученные точки отмечаем на числовой прямой с учетом области определения функции. Точки разбивают числовую прямую на промежутки, в каждом из которых рассматриваемая функция имеет определенный знак. Выбираем любое число из любого промежутка (удобнее всего брать нуль, если он не входит в отмеченные точки), и подставляем это число в последнее неравенство (то есть в упрощенное неравенство, в котором все слагаемые стоят в левой части и дроби приведены к наименьшему общему знаменателю). В результате определяем знак на выбранном промежутке. Остальные знаки расставляем в шахматном порядке.
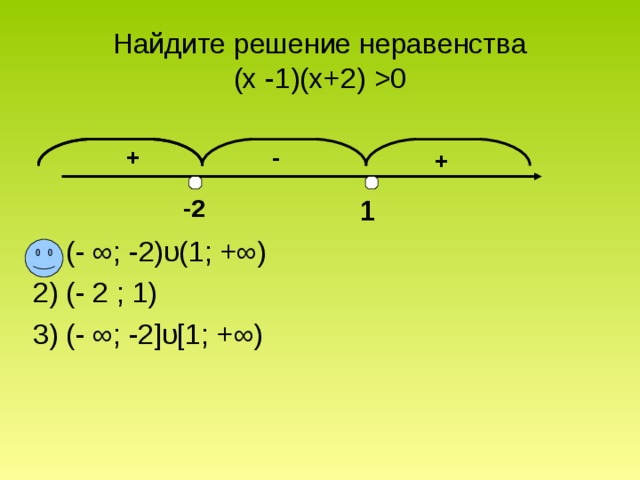 Нуль не является ни положительным, ни отрицательным числом (он отделяет положительные числа от отрицательных). Ставя знак в «петлю», мы совершаем грубую ошибку.
Нуль не является ни положительным, ни отрицательным числом (он отделяет положительные числа от отрицательных). Ставя знак в «петлю», мы совершаем грубую ошибку. Math.Content.3.NF.A.2a
Math.Content.3.NF.A.2a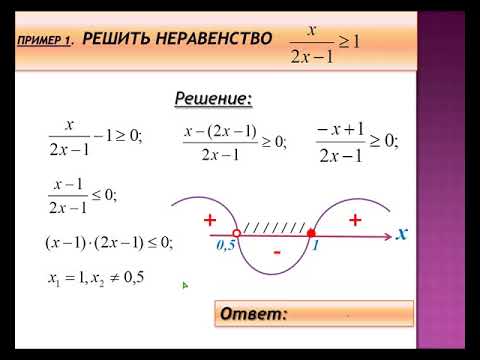 из частей розовый, что означает, что числовая линия розовая.
из частей розовый, что означает, что числовая линия розовая. из частей розовый, что означает, что числовая линия розовая.
из частей розовый, что означает, что числовая линия розовая. из частей розовый, что означает, что числовая линия розовая.
из частей розовый, что означает, что числовая линия розовая.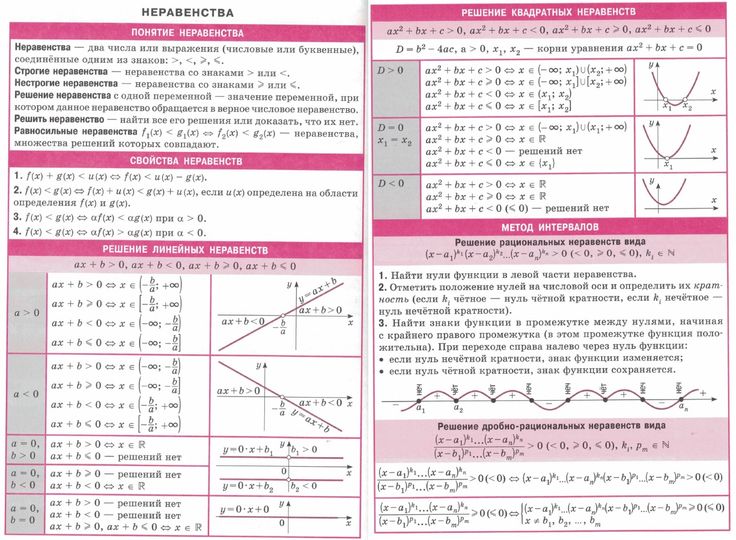 На что это будет похоже?
На что это будет похоже? Однако, если светофор горит зеленым, автомобиль будет продолжать движение, не останавливаясь.
Однако, если светофор горит зеленым, автомобиль будет продолжать движение, не останавливаясь.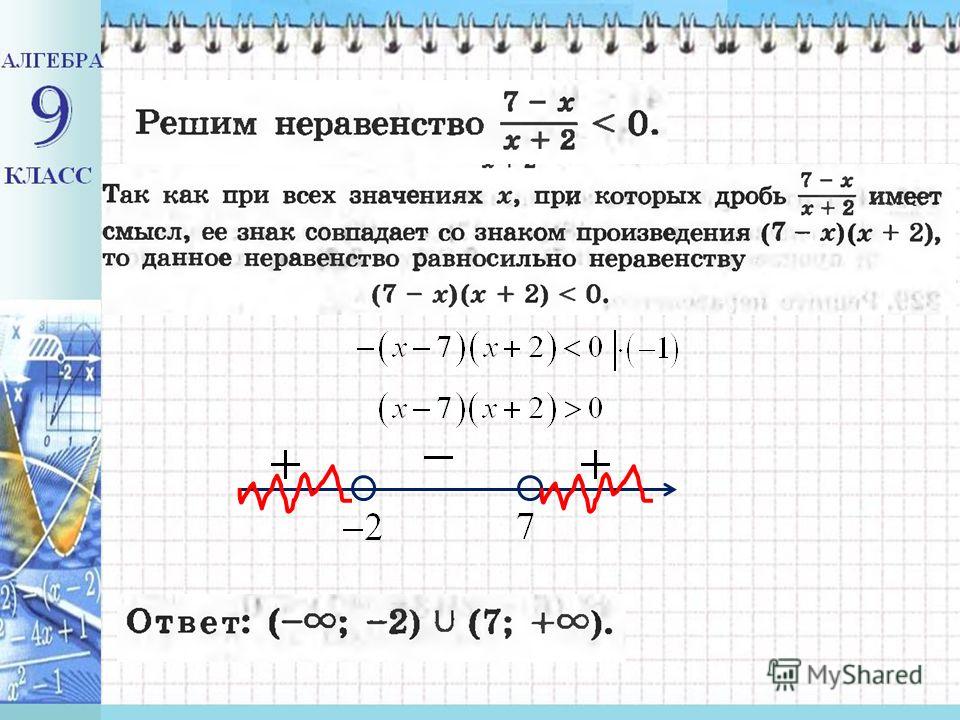 Мы используем:
Мы используем: Например, [4, 9] включает конечные точки 4 и 9.
Например, [4, 9] включает конечные точки 4 и 9. 

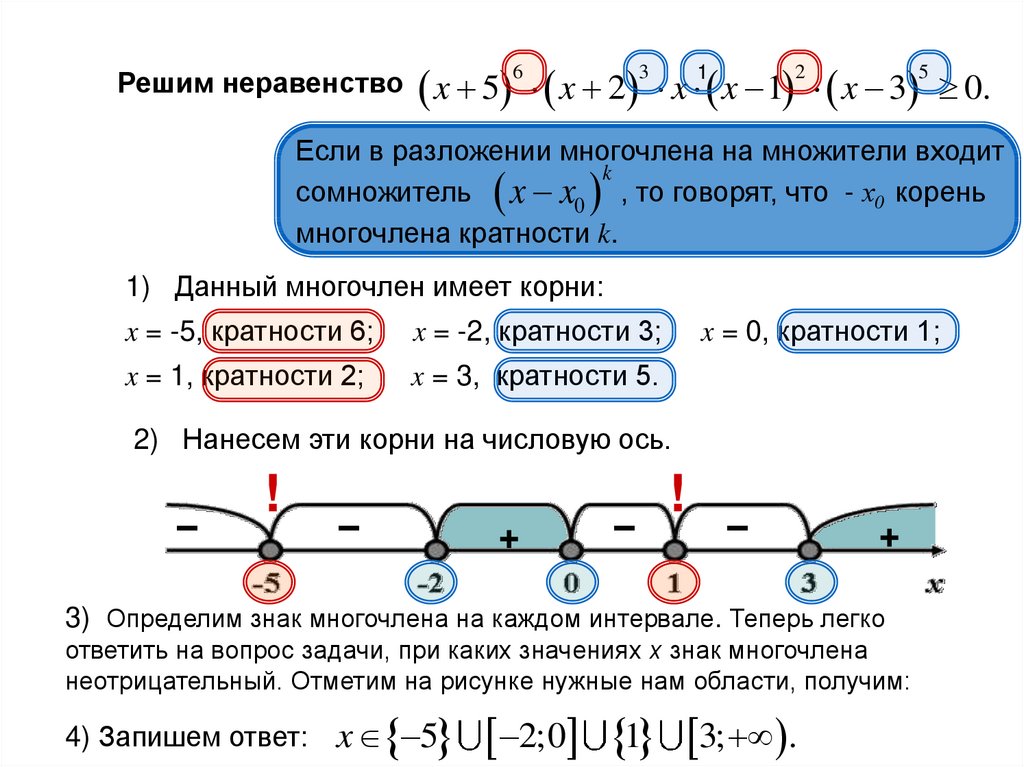 Максимальное количество участников должно быть менее 30, поэтому 30 не учитываются. Следовательно, интервал равен [12, 30).
Максимальное количество участников должно быть менее 30, поэтому 30 не учитываются. Следовательно, интервал равен [12, 30).
 ..)
..) Решения, в которых весь код программы находится в одном классе будут низко оценены. Продемонстрируйте своё умение в работе с разными синтаксическими конструкциями, не забудьте про исключительные ситуации, при которых выполнение программы невозможно из-за некорректных входных данных.
Решения, в которых весь код программы находится в одном классе будут низко оценены. Продемонстрируйте своё умение в работе с разными синтаксическими конструкциями, не забудьте про исключительные ситуации, при которых выполнение программы невозможно из-за некорректных входных данных.
 Технически блок реализован с помощью оригинального элемента, разработанного дизайнерами Студии. По своей сути этот элемент аналогичен панели задач MacOS и использует JavaScript-анимацию. Пользователь легким кликом мышки может переключаться с одного вида страхования на другой, просматривая при этом предлагаемые компанией услуги.
Технически блок реализован с помощью оригинального элемента, разработанного дизайнерами Студии. По своей сути этот элемент аналогичен панели задач MacOS и использует JavaScript-анимацию. Пользователь легким кликом мышки может переключаться с одного вида страхования на другой, просматривая при этом предлагаемые компанией услуги. Пользователям представляется очень удобным рассчитывать, сколько им придется заплатить за ту или иную услугу на сайте в режиме онлайн. Это значительно экономит их время, исключая необходимость звонка в компанию и общения с менеджером, а также дает возможность заранее планировать расходы.
Пользователям представляется очень удобным рассчитывать, сколько им придется заплатить за ту или иную услугу на сайте в режиме онлайн. Это значительно экономит их время, исключая необходимость звонка в компанию и общения с менеджером, а также дает возможность заранее планировать расходы.








 Калькулятор ежедневного учета рабочего времени
Калькулятор ежедневного учета рабочего времени
 Это потому, что только 2,5% людей могут работать в режиме многозадачности. Таким образом, для остального населения стоимость переключения задач в основном вредна.
Это потому, что только 2,5% людей могут работать в режиме многозадачности. Таким образом, для остального населения стоимость переключения задач в основном вредна.
 Это именно то, чем является калькулятор недельного тайм-менеджмента (и его цель) — инструмент для отслеживания ваших еженедельных привычек и, при необходимости, их улучшения.
Это именно то, чем является калькулятор недельного тайм-менеджмента (и его цель) — инструмент для отслеживания ваших еженедельных привычек и, при необходимости, их улучшения. Наблюдение за распределением времени в разные дни поможет вам понять свои привычки и распорядок дня.
Наблюдение за распределением времени в разные дни поможет вам понять свои привычки и распорядок дня.



 Это та часть, где вы можете проявить творческий подход и даже немного поэкспериментировать, чтобы обогатить свою личную жизнь.
Это та часть, где вы можете проявить творческий подход и даже немного поэкспериментировать, чтобы обогатить свою личную жизнь.


 Эта задача очень много значит для меня. История… | Ахмед Ясин
Эта задача очень много значит для меня. История… | Ахмед Ясин Это создает в нашем сознании образ машины, которая выполняет невообразимые вычисления за несколько секунд. Раньше я думал, что сделать калькулятор могут только профессиональные программисты. Как мог такой парень 12 класса, как я, сделать калькулятор на таком этапе. Я думал, что сделать калькулятор не так уж и просто. Но я должен был сказать себе попробовать это со всем, что я узнал с самого начала этого курса c++, и я получил ответ от себя, что « брух.. это уже начало…» .На этом этапе я знал только о cout функция, cin функция, некоторые типы данных и очень немногие основные операторы, такие как сложение (+), вычитание)(-) , умножение (*) и деление (/).
Это создает в нашем сознании образ машины, которая выполняет невообразимые вычисления за несколько секунд. Раньше я думал, что сделать калькулятор могут только профессиональные программисты. Как мог такой парень 12 класса, как я, сделать калькулятор на таком этапе. Я думал, что сделать калькулятор не так уж и просто. Но я должен был сказать себе попробовать это со всем, что я узнал с самого начала этого курса c++, и я получил ответ от себя, что « брух.. это уже начало…» .На этом этапе я знал только о cout функция, cin функция, некоторые типы данных и очень немногие основные операторы, такие как сложение (+), вычитание)(-) , умножение (*) и деление (/).
 Я действительно должен был сделать логику. Я пытался использовать эти операторы по-разному. В конце концов я получил свое достижение после двух часов напряженной работы. Наконец-то я сделал простой калькулятор в одну строку.
Я действительно должен был сделать логику. Я пытался использовать эти операторы по-разному. В конце концов я получил свое достижение после двух часов напряженной работы. Наконец-то я сделал простой калькулятор в одну строку.
 +
+

 Переводной вексель – это письменный документ, который содержит безусловный приказ векселедателя плательщику:
Переводной вексель – это письменный документ, который содержит безусловный приказ векселедателя плательщику:
 Определите, какое право предоставляет инвестиционный пай инвесторам:
Определите, какое право предоставляет инвестиционный пай инвесторам: Как называется плата за использование заемных средств:
Как называется плата за использование заемных средств: Это означает, что их стоимость выражается в денежном эквиваленте, их можно обменять на материальные средства.
Это означает, что их стоимость выражается в денежном эквиваленте, их можно обменять на материальные средства. Соответствующий закон был принят в 1996 году. В нём определено, что выпускать документы данного типа могут только лицензированные банки, юридические лица и государство.
Соответствующий закон был принят в 1996 году. В нём определено, что выпускать документы данного типа могут только лицензированные банки, юридические лица и государство. Она гарантирует владельцу получение имущества или денежных средств.
Она гарантирует владельцу получение имущества или денежных средств.
 ..
.. Обзор этих …
Обзор этих … ..
.. Обычно это результат плохой или устаревшей ссылки. Мы извиняемся за любые неудобства.
Обычно это результат плохой или устаревшей ссылки. Мы извиняемся за любые неудобства. Организации часто внедряют обе технологии, чтобы …
Организации часто внедряют обе технологии, чтобы … Эти советы могут помочь организации …
Эти советы могут помочь организации …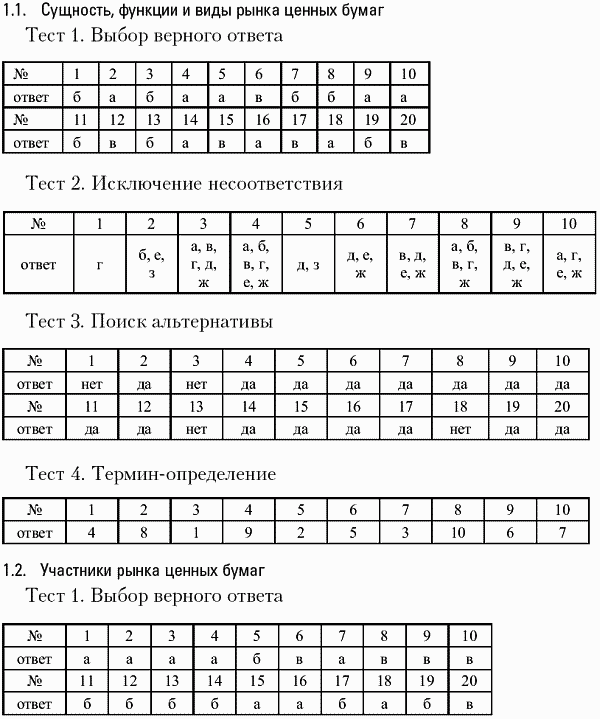 Но…
Но…