Лучший Способ Конвертировать PDF в Текст в Windows 10
Вы можете конвертировать PDF в текст используя соответствующий инструмент редактирования PDF-файлов. Хорошая программа для конвертации должна иметь возможность конвертировать сразу несколько файлов, конвертировать все страницы, выполнять распознавание текста и сохранять форматирование в вашем PDF-файле. Здесь мы покажем вам идеальный инструмент, который можно использовать для преобразования PDF в TXT.
Скачать Бесплатно Скачать Бесплатно КУПИТЬ СЕЙЧАС КУПИТЬ СЕЙЧАС
Пошаговое Руководство по Преобразованию PDF файла в Текст
Шаг 1: Откройте PDF файл с Помощью PDFelement
Скачайте и установите PDFelement на свой компьютер, чтобы конвертировать PDF в обычный текст. После установки запустите программу и нажмите кнопку «Открыть файлы», чтобы выбрать PDF-файлы, которые вы хотите превратить в текст.
Шаг 2: Редактирование PDF документа (По желанию)
После загрузки PDF-файла в PDFelement вы можете редактировать текст, изображения или страницы в файле. Чтобы отредактировать текст, нажмите на вкладку «Редактировать», перейдите в PDF-файл и дважды щелкните по тексту, который вы хотите отредактировать, после чего вокруг текста появится синее поле. Вы можете удалить этот текст или заменить его новым текстом.
Чтобы отредактировать текст, нажмите на вкладку «Редактировать», перейдите в PDF-файл и дважды щелкните по тексту, который вы хотите отредактировать, после чего вокруг текста появится синее поле. Вы можете удалить этот текст или заменить его новым текстом.
Чтобы отредактировать изображение, нажмите на вкладку «Редактировать», а затем выберите опцию «Редактировать». Теперь дважды щелкните на изображении, чтобы отредактировать его. Наконец, если вы хотите отредактировать страницы PDF-файла, нажмите на вкладку «Страница» и выберите различные варианты замены, удаления или перемещения страниц PDF в нужное место.
Шаг 3: Конвертирование PDF в Текст
Чтобы преобразовать ваш PDF-файл в текст, вернитесь на вкладку «Конвертировать» на верхней панели инструментов. Теперь нажмите на кнопку «В Текст» на той же вкладке, которая откроет окно преобразования.
В следующем окне вы можете выбрать страницы, включить распознавание текста и изменить расположение выходного текстового файла.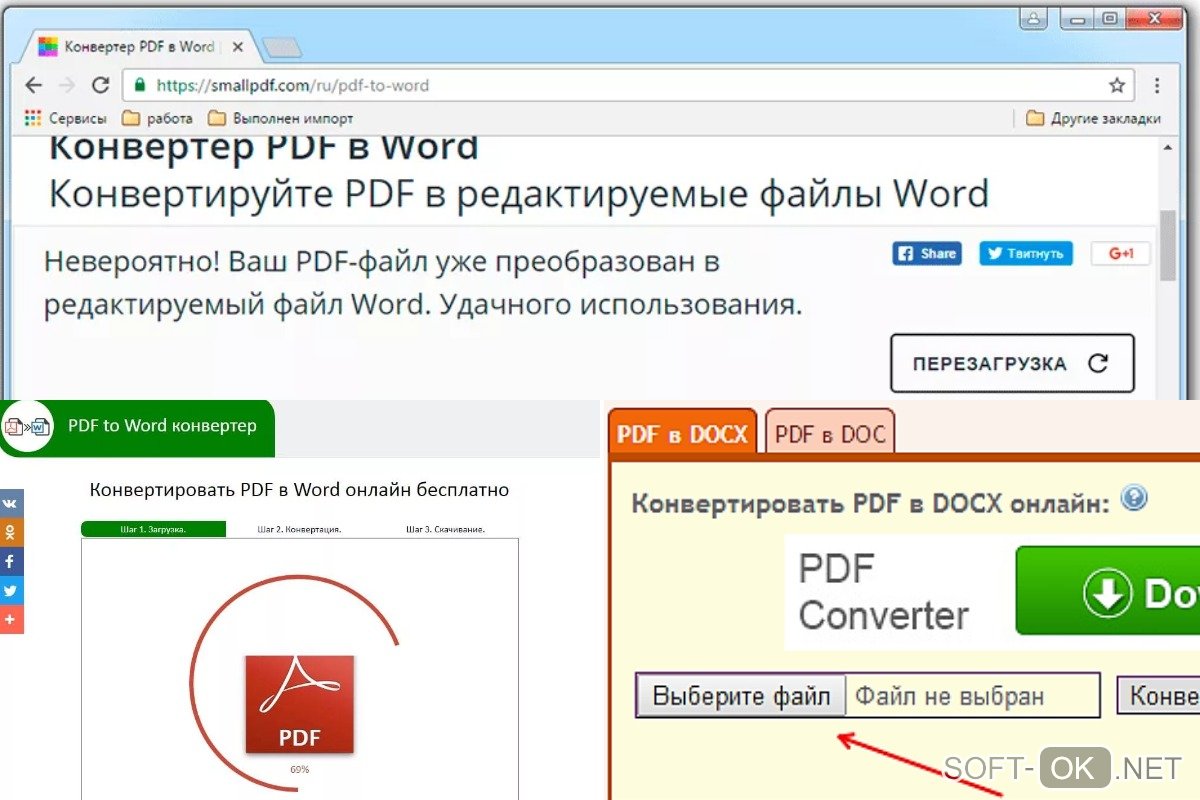 После установки всех этих параметров нажмите на кнопку «Сохранить», чтобы начать процесс. После завершения преобразования на экране появится диалоговое окно, в котором будет указано, что конвертация прошла успешно.
После установки всех этих параметров нажмите на кнопку «Сохранить», чтобы начать процесс. После завершения преобразования на экране появится диалоговое окно, в котором будет указано, что конвертация прошла успешно.
Вам нужно программное обеспечение для чтения, редактирования, преобразования, аннотирования, заполнения или объединения PDF-файлов? PDFelement-это простая в использовании программа, которая может выполнять все эти задачи в течение нескольких секунд, не жертвуя качеством вашего PDF-файла. Вы можете редактировать текст, добавлять новое изображение, удалять существующие изображения, изменять размер изображения или поворачивать его в любом направлении, не прибегая к помощи какого-либо стороннего программного обеспечения.
Новые формы могут быть созданы с использованием существующих шаблонов или пустых страниц, а пользователи также могут заполнять PDF-формы с помощью PDFelement в Windows или macOS. Для того чтобы преобразовать PDF-файлы в текст, PDFelement также оснащен множеством отличных функций. Вы можете использовать опцию «OCR» для преобразования документа на основе изображений в редактируемый текст PDF-файле, имеющем отсканированное содержание. Вы также можете выбрать четные или нечетные страницы для преобразования или ввести значение для преобразования нескольких страниц одновременно.
Для того чтобы преобразовать PDF-файлы в текст, PDFelement также оснащен множеством отличных функций. Вы можете использовать опцию «OCR» для преобразования документа на основе изображений в редактируемый текст PDF-файле, имеющем отсканированное содержание. Вы также можете выбрать четные или нечетные страницы для преобразования или ввести значение для преобразования нескольких страниц одновременно.
Скачать Бесплатно Скачать Бесплатно КУПИТЬ СЕЙЧАС КУПИТЬ СЕЙЧАС
Другие Рекомендуемые Бесплатные Программы для Конвертации PDF в Текст
1. Foxyutils
Foxyutils- это PDF-конвертер, который выделяется своей способностью обрабатывать большое количество шрифтов и структур документов в PDF-документах. Большая база данных шрифтов этого приложения означает, что оно способно подбирать даже самые необычные и редко используемые шрифты и включать их в выходной текстовый файл. Это приложение также разбивает изображения в исходном документе и обрабатывает их независимо, что приводит к хорошо организованной последовательности изображений в конечном текстовом документе.
С другой стороны, Foxyutils не имеет функции распознавания текста. Так что если у вас есть отсканированные документы, которые вы хотели бы конвертировать, Foxyutils не будет полезной. Приложение также работает в Интернете, что означает, что вам потребуется активное подключение к Интернету для загрузки и скачивания файлов.
2. Nitro Конвертер PDF в TXT
Nitro PDF-одна из самых известных альтернатив Adobe на рынке, используемая для редактирования и преобразования PDF-документов. Онлайн-версия программы обычно бесплатна, хотя вам придется заплатить за версию для ПК. С помощью Nitro PDF вы просто загружаете файл, который хотите преобразовать, вводите адрес электронной почты для отправки выходного файла и ждете. Он может конвертировать PDF-документы в Excel, PowerPoint и Word или обратно, но функция Excel не всегда работает корректно.
С точки зрения качества, Nitro PDF создант хорошие текстовые файлы с аккуратно расположенными изображениями и правильной общей структурой. Однако у пользователей отсутствует функция OCR, поэтому вам, возможно, придется искать альтернативы, если у вас есть отсканированный документ для преобразования.
Однако у пользователей отсутствует функция OCR, поэтому вам, возможно, придется искать альтернативы, если у вас есть отсканированный документ для преобразования.
3. Free File Converter
Free File Converter-это одна из самых простых и понятных в использовании бесплатных программ для преобразования PDF в Text. Он позволяет конвертировать PDF-файлы в различные форматы, включая doc, MOBI и EPUB. После загрузки файлов автоматически генерируется ссылка для загрузки, позволяющая вам загружать файлы напрямую. Помимо PDF-файлов, Free File Converter также позволяет загружать для преобразования другие форматы файлов. Еще одна интересная особенность заключается в том, что он поддерживает большие файлы. Бесплатный конвертер файлов принимает PDF-файлы размером до 300 МБ, что отлично подходит, если у вас есть большие, несложные документы, которые вам нужно конвертировать.
Помимо быстрого и простого использования, другие его функции работают немного хуже среднего, так что это может быть разочарованием для тех, кто ищет профессиональный инструмент. Текст часто получается не в том месте или плохо выровненным после всех преобразований, а приложение не имеет функции распознавания отсканированных документов. Изображения обычно преобразуются и включаются как часть фоновой графики.
Текст часто получается не в том месте или плохо выровненным после всех преобразований, а приложение не имеет функции распознавания отсканированных документов. Изображения обычно преобразуются и включаются как часть фоновой графики.
4. UniPDF
UniPDF- это один из лучших вариантов для конвертации сразу нескольких PDF файлов в текстовые. Это бесплатный конвертер PDF в TXT для настольных компьютеров Windows, который преобразует PDF-файлы во множество других форматов, включая Word, PNG и HTML. Как и Foxyutils, UniPDF отлично справляется с чтением шрифтов и сопоставлением их с ближайшими альтернативами, если шрифт в PDF-файле не существует в базе данных UniPDF. Однако в UniPDF также отсутствует OCR для преобразования отсканированных документов.
Одной из отличительных черт этого приложения является его способность конвертировать несколько PDF-файлов в текстовые файлы одновременно. Просто загрузите папку с несколькими PDF-файлами, выберите «конвертировать» и наблюдайте, как каждый файл преобразуется автоматически.
PDF в текст – Конвертация PDF-файлов в текст
ЗАГРУЗИТЬ
Перетащите файлы сюда.
PDF — это файл формата Portable Document Format. Обычно он содержит текст, но может также поддерживать гиперссылки, изображения, диаграммы и т.д. Самое лучшее в PDF — это его универсальность. Неважно, на какой платформе вы создаете PDF, например, потому что он будет работать и выглядеть одинаково на любой другой платформе. Благодаря этой универсальности PDF стал форматом по умолчанию для обмена документами в Интернете.
Текстовые файлы намного проще, чем PDF. Они могут содержать только текст или текстовый код, что означает отсутствие изображений и ссылок (однако вы можете включать некликабельные URL). Эти ограничения делают текстовые файлы менее надежными, чем PDF, однако TXT имеет некоторые преимущества. Прежде всего, текстовые файлы почти всегда меньше, чем PDF, и их легче редактировать и обрабатывать.
Почему вы должны конвертировать PDF в текст?
Если у вас нет дорогостоящего программного обеспечения для редактирования, PDF-файлы нелегко изменять. Найти текст в PDF-файле не всегда просто, а такие простые действия, как вырезать и вставить, могут оказаться невозможными.
Если, например, в PDF есть абзац, который вы хотите вырезать и вставить в другой документ, вы можете столкнуться с некоторыми проблемами. Однако если вы конвертируете PDF в текст, это будет очень просто. Это самая распространенная причина для конвертации PDF в текст!
Другой причиной может быть уменьшение PDF-файлов до более экономичного размера. Если вы сохраняете PDF-файл, наполненный изображениями, он может быть довольно большим. Но если вам важен только текст в этом документе, вы можете преобразовать его в TXT и освободить больше места на жестком диске.
Как бесплатно конвертировать PDF-файлы в текст?
Конвертировать PDF в текст с помощью нашего бесплатного онлайн-инструмента невероятно просто. Вам не нужно беспокоиться о водяных знаках, регистрироваться, отправлять нам свой email или ограничиваться несколькими загрузками. Вы можете загрузить столько файлов, сколько вам нужно!
Вам не нужно беспокоиться о водяных знаках, регистрироваться, отправлять нам свой email или ограничиваться несколькими загрузками. Вы можете загрузить столько файлов, сколько вам нужно!
Для начала загрузите один или до 20 PDF-файлов с помощью элементов управления, расположенных выше. Вы можете перетащить файлы или нажать кнопку “ЗАГРУЗИТЬ”, в зависимости от того, что вам больше подходит. Если у вас более 20 файлов, не беспокойтесь — вы сможете повторить эти шаги столько раз, сколько вам нужно.
После загрузки PDF-файлов наш сервер автоматически начнет конвертировать их в TXT-файлы. По завершении вы можете загрузить каждый из них, нажав кнопку “СКАЧАТЬ”. Однако если вы предпочитаете получить все сразу, вы можете нажать кнопку “СКАЧАТЬ ВСЕ”. В этом случае вы получите ZIP-архив со всеми текстовыми конвертациями.
Когда вы будете готовы выполнить еще одну партию преобразований, просто нажмите кнопку “ОЧИСТИТЬ” и начните сначала.
Безопасно ли конвертировать PDF в текстовые файлы?
Да, это абсолютно безопасно. Наш инструмент конвертации полностью автоматизирован, поэтому вам не нужно беспокоиться о том, что кто-то увидит ваши документы. Инструмент автоматически очищает все загруженные и конвертированные файлы через час, что означает, что ваши документы всегда в безопасности.
Наш инструмент конвертации полностью автоматизирован, поэтому вам не нужно беспокоиться о том, что кто-то увидит ваши документы. Инструмент автоматически очищает все загруженные и конвертированные файлы через час, что означает, что ваши документы всегда в безопасности.
Если вы беспокоитесь о потере оригинальных PDF-файлов, это не проблема. Наш инструмент копирует ваши PDF-файлы при загрузке, а затем конвертирует эти копии. Ваши основные PDF-файлы всегда будут в безопасности на вашем устройстве, если они вам снова понадобятся.
Преобразование PDF в текст | Онлайн и бесплатно
Преобразование PDF в текстовые документы
Работает на aspose.com и aspose.cloudПеретащите или загрузите свои файлы*
Выбрать файл
Выбрать с Google Диска Выбрать из Dropbox
Введите URL
*Загружая файлы или используя наш сервис, вы соглашаетесь с нашими Условиями обслуживания и Политикой конфиденциальности MP4AVIMOVWEBMFLVWVMMKVMPGMPEG
Ваши файлы успешно обработаны
СКАЧАТЬОтправить результат по адресу:
ПОСМОТРЕТЬ РЕЗУЛЬТАТЫПОСМОТРЕТЬ РЕЗУЛЬТАТЫ
Лучший бесплатный онлайн-конвертер PDF в текст
 Без регистрации и капчи. Здесь вы можете конвертировать документы онлайн и сохранять их в нужном вам формате на свой компьютер или любое другое устройство.
Без регистрации и капчи. Здесь вы можете конвертировать документы онлайн и сохранять их в нужном вам формате на свой компьютер или любое другое устройство.Быстро и просто
Конвертер PDF в текст — это онлайн-сервис для преобразования файлов из одного типа в другой. Мы поддерживаем множество популярных форматов для работы, все возможные форматы изображений, форматы мультимедийных файлов и т. д. Наш инструмент преобразования PDF в текст прост в использовании: выберите нужный тип файла, затем определите выходной формат вашего документа, загрузите файл и нажмите ‘Загрузить’.
Мы поддерживаем множество популярных форматов для работы, все возможные форматы изображений, форматы мультимедийных файлов и т. д. Наш инструмент преобразования PDF в текст прост в использовании: выберите нужный тип файла, затем определите выходной формат вашего документа, загрузите файл и нажмите ‘Загрузить’.
Безопасность гарантирована
Мы гарантируем безопасность и конфиденциальность. Мы не получаем права на ваш файл и ручной проверки не будет. Мы заботимся о вашей конфиденциальности и ваших файлах. В связи с этим мы также не будем передавать ваши данные другим сторонам. Крайне важно, чтобы у вас была возможность немедленно удалить загруженные вами файлы с нашего сервера. Если вы забудете это сделать, они будут автоматически удалены с нашего сервера через 24 часа. Мы полностью защищаем вашу информацию.
Универсальное преобразование
Вы можете конвертировать файлы из PDF в текст с любой ОС или устройства с подключением к Интернету. Наш сервис работает на любой ОС, включая Windows, Mac и Linux.
Наш сервис работает на любой ОС, включая Windows, Mac и Linux.
Самые популярные варианты конвертации
Мы поддерживаем самые распространенные варианты конвертации для работы и учебы. Используйте наше бесплатное приложение, чтобы уменьшить нагрузку при работе как с документами, так и с файлами изображений.
Книги о том, как преобразовать PDF в текст
- Преобразование PDF в JPG
- Преобразование PDF в Word
Как преобразовать PDF в текст
1
Откройте бесплатный веб-сайт PDF и выберите приложение Convert.2
Щелкните внутри области перетаскивания файлов, чтобы загрузить или перетащить файлы.3
Вы можете загрузить максимум 10 файлов для операции.4
Нажмите кнопку Преобразовать. Файлы будут загружены и преобразованы.
5
Ссылка для скачивания файлов результатов будет доступна сразу после конвертации.6
Вы также можете отправить ссылку на файл на свой адрес электронной почты.7
Обратите внимание, что файл будет удален с наших серверов через 24 часа, а ссылки для скачивания перестанут работать по истечении этого периода времени.
Часто задаваемые вопросы
1
❓ Как преобразовать PDF в TXT?
Во-первых, вам нужно добавить файл для преобразования: перетащите или щелкните внутри белой области. Затем нажмите кнопку «Конвертировать». Когда преобразование завершено, вы можете загрузить свой результат.
2
⏱️ Сколько времени занимает конвертация PDF в TXT?
Это приложение работает быстро.
 Вы можете получить результат в течение нескольких секунд.
Вы можете получить результат в течение нескольких секунд.3
🛡️ Безопасно ли конвертировать PDF в TXT с помощью бесплатного конвертера?
Конечно! Ссылка для скачивания файлов результатов будет доступна сразу после конвертации. Мы удаляем загруженные файлы через 24 часа, и ссылки для скачивания перестают работать по истечении этого периода времени. Никто не имеет доступа к вашим документам. Приложение абсолютно безопасно.
4
💻 Могу ли я конвертировать PDF в TXT на Linux, Mac OS или Android?
Да, вы можете использовать бесплатное приложение Converter в любой операционной системе с веб-браузером. Наше приложение работает онлайн и не требует установки какого-либо программного обеспечения.

5
🌐 Какой браузер мне использовать для преобразования PDF в TXT?
Вы можете использовать любой современный браузер для преобразования. Например, Google Chrome, Firefox, Opera, Safari.
Быстрое и простое преобразование
Загрузите документ, выберите формат сохранения и нажмите кнопку «Конвертировать». Вы получите ссылку для скачивания, как только файл будет конвертирован.
Преобразование откуда угодно
Работает на всех платформах, включая Windows, Mac, Android и iOS. Все файлы обрабатываются на наших серверах. Для вас не требуется установка плагинов или программного обеспечения.
Качество преобразования
. Все файлы обрабатываются с помощью API-интерфейсов Aspose, которые используются многими компаниями из списка Fortune 100 в 114 странах.
Конвертер PDF в текст онлайн
Конвертер PDF в текст онлайн | Преобразование PDF в обычный текстовый файлПлан обновления
Задайте параметры и нажмите кнопку «Выполнить преобразование»
Перетащите файл на кнопку «Обзор» или нажмите «Обзор», чтобы выбрать файл , rar, 7z, xz) для пакетного преобразования
Нажмите кнопку для запуска преобразования
Рейтинг
5. 0
0
— 5 голосов
Мы предлагаем разработку Custom Converter, чтобы предоставить вам полностью индивидуальное решение для преобразования файлов и обработки данных, основанное на ваших деловых или личных требованиях. Узнать больше.
Вы можете помочь другим найти этот сайт — поделитесь своим опытом!
- Вход в учетную запись пользователя — самый безопасный способ работы с вашими файлами. Зарегистрируйте свою учетную запись сейчас!
- Время, затрачиваемое на конвертацию, зависит от размера файла. Пожалуйста, будьте терпеливы, пока выполняется преобразование. Мы работаем над улучшением производительности.
- Для обеспечения надежной работы сервисов мы установили лимиты на количество конверсий и размер загружаемых файлов. Ограничения зависят от плана преобразования, который вы будете использовать. Вы можете проверить доступные планы преобразования на странице цен.

- Незарегистрированные пользователи имеют следующие ограничения: 10 конверсий в день, 10 МБ на загруженный файл. Зарегистрируйте свою учетную запись сейчас, чтобы расширить лимиты бесплатно.
- Если вы хотите конвертировать очень большие файлы или у вас возникли проблемы с конвертацией вашего файла — не стесняйтесь обращаться к нам, наша команда способна решить практически любую проблему конвертации.
Copyright © 2022
Инструменты преобразования
План обновления
Установите параметры и нажмите кнопку «Выполнить преобразование»
Перетащите файл на кнопку «Обзор» или нажмите «Обзор», чтобы выбрать файл
Обзор
Использовать один файл или архив (zip, rar, 7z, xz) для пакетного преобразования
Нажмите кнопку, чтобы запустить преобразование 5 голосов
Мы предлагаем разработку Custom Converter, чтобы предоставить вам полностью индивидуальное решение для преобразования файлов и обработки данных на основе ваших деловых или личных требований.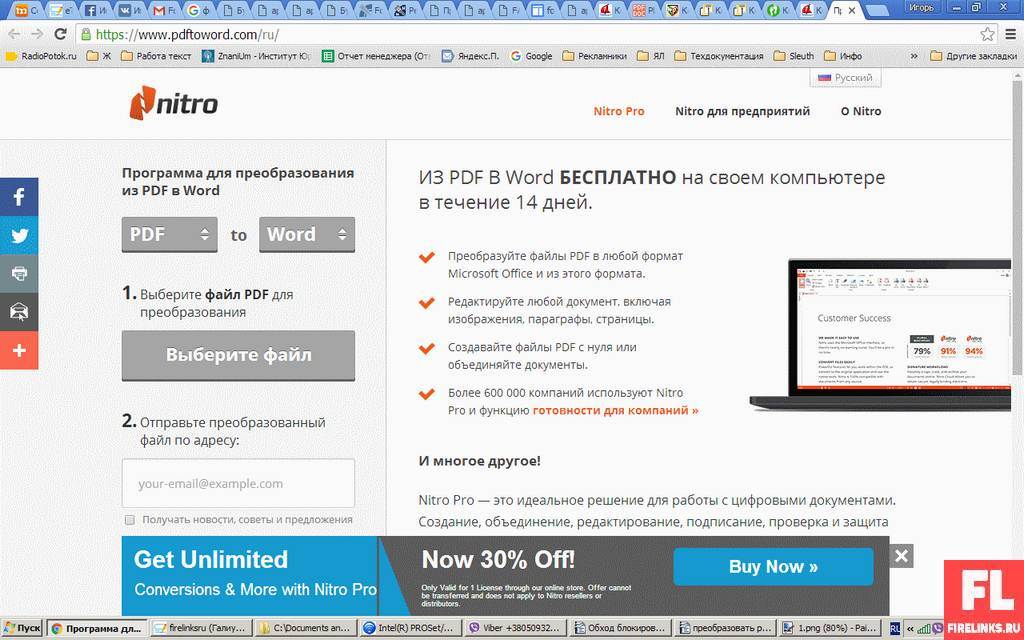 Узнать больше.
Узнать больше.
Вы можете помочь другим найти этот сайт — поделитесь своим опытом!
- Вход в учетную запись пользователя — самый безопасный способ работы с вашими файлами. Зарегистрируйте свою учетную запись сейчас!
- Время, затрачиваемое на конвертацию, зависит от размера файла. Пожалуйста, будьте терпеливы, пока выполняется преобразование. Мы работаем над улучшением производительности.
- Для обеспечения надежной работы сервисов мы установили лимиты на количество конверсий и размер загружаемых файлов. Ограничения зависят от плана преобразования, который вы будете использовать. Вы можете проверить доступные планы преобразования на странице цен.
- Незарегистрированные пользователи имеют следующие ограничения: 10 конверсий в день, 10 МБ на загруженный файл. Зарегистрируйте свою учетную запись сейчас, чтобы расширить лимиты бесплатно.


 Вы можете получить результат в течение нескольких секунд.
Вы можете получить результат в течение нескольких секунд.



 04.2021 11:00
04.2021 11:00 ном
ном Ежедневно мы получаем много вопросов о конфликте, нашей позиции и политике. В этом посте мы организовали некоторые из наиболее распространенных вопросов и связали наши ответы и политики. По мере появления новых фактов мы будем обновлять этот пост информацией и политиками по мере необходимости.
Ежедневно мы получаем много вопросов о конфликте, нашей позиции и политике. В этом посте мы организовали некоторые из наиболее распространенных вопросов и связали наши ответы и политики. По мере появления новых фактов мы будем обновлять этот пост информацией и политиками по мере необходимости. com?
com? com пожертвовал 25 000 долларов. Главный шахматист Chess.com ММ Дэнни Ренш и генеральный директор Эрик пожертвовали дополнительно по 5000 долларов каждый. GM Ben Finegold собрал чуть менее 20 000 долларов, а ChessDojo собрал чуть более 15 000 долларов; свой вклад внесли бесчисленные члены шахматного сообщества. Кроме того, весь доход от рекламы из России идет на помощь Украине.
com пожертвовал 25 000 долларов. Главный шахматист Chess.com ММ Дэнни Ренш и генеральный директор Эрик пожертвовали дополнительно по 5000 долларов каждый. GM Ben Finegold собрал чуть менее 20 000 долларов, а ChessDojo собрал чуть более 15 000 долларов; свой вклад внесли бесчисленные члены шахматного сообщества. Кроме того, весь доход от рекламы из России идет на помощь Украине. com. Мы выявили и закрыли счета нескольких российских олигархов, попавших под санкции.
com. Мы выявили и закрыли счета нескольких российских олигархов, попавших под санкции. Нам невыносимо больно видеть катастрофу, которая происходит в эти дни с нашими людьми.0006
Нам невыносимо больно видеть катастрофу, которая происходит в эти дни с нашими людьми.0006 Мы сыграли десятки матчей и сотни партий. Для нас честная конкуренция всегда была выше политики, и украинцы разделили это чувство.Мы просим вас сохранить шанс на взаимное уважение между командами, игроками и людьми из обеих стран.
Мы сыграли десятки матчей и сотни партий. Для нас честная конкуренция всегда была выше политики, и украинцы разделили это чувство.Мы просим вас сохранить шанс на взаимное уважение между командами, игроками и людьми из обеих стран. com.
com. 0.4 alpha1
0.4 alpha1 
 Согласно стандарту, powr ( ± 0 , ± 0 ) {displaystyle operatorname {powr} (pm 0,pm 0)} возвращает значение «не число» NaN.
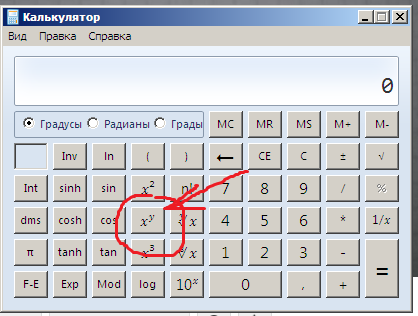
Согласно стандарту, powr ( ± 0 , ± 0 ) {displaystyle operatorname {powr} (pm 0,pm 0)} возвращает значение «не число» NaN. {0}} — это неопределённость, поведение некоторых функций, возвращающих в данном случае 1 {displaystyle 1} , не является результатом соглашения или ошибкой, оно имеет логическое обоснование. Дело в том, что в компьютерной арифметике числовые данные подразделяются на целые и вещественные. Это может неявно использоваться в некоторых функциях, реализующих операцию возведения в степень. Например, так сделано в калькуляторе Windows и функции pow в C++. Для целого и вещественного показателя степени используются различные алгоритмы, и функция возведения в степень анализирует показатель: если он равен целому числу, то вычисление степени идёт по другому алгоритму, в котором отрицательные и нулевое основания степени являются допустимыми. Если показатель степени принадлежит множеству целых чисел и равен 0, а основание — вещественное число, то операцию 0 0 {displaystyle 0^{0}} следует определять не иначе как lim x → 0 x 0 {displaystyle lim _{x o 0}x^{0}} .
{0}} — это неопределённость, поведение некоторых функций, возвращающих в данном случае 1 {displaystyle 1} , не является результатом соглашения или ошибкой, оно имеет логическое обоснование. Дело в том, что в компьютерной арифметике числовые данные подразделяются на целые и вещественные. Это может неявно использоваться в некоторых функциях, реализующих операцию возведения в степень. Например, так сделано в калькуляторе Windows и функции pow в C++. Для целого и вещественного показателя степени используются различные алгоритмы, и функция возведения в степень анализирует показатель: если он равен целому числу, то вычисление степени идёт по другому алгоритму, в котором отрицательные и нулевое основания степени являются допустимыми. Если показатель степени принадлежит множеству целых чисел и равен 0, а основание — вещественное число, то операцию 0 0 {displaystyle 0^{0}} следует определять не иначе как lim x → 0 x 0 {displaystyle lim _{x o 0}x^{0}} . {0}} .
{0}} . Например,
Например,

 ответил 10.02.14
ответил 10.02.14 ответил 09.02.14
ответил 09.02.14
 Найти вероятность что обе они фальшивые.
Найти вероятность что обе они фальшивые.

 В 1-й урне по 3 белых и черных шара, а во 2-й — 3 белых и 4 черных. Из 1-й урны во 2-ю не глядя перекладывают 2 шара, а затем из 2-й вытягивают 2 шара. Какова вероятность, что они разных цветов?
В 1-й урне по 3 белых и черных шара, а во 2-й — 3 белых и 4 черных. Из 1-й урны во 2-ю не глядя перекладывают 2 шара, а затем из 2-й вытягивают 2 шара. Какова вероятность, что они разных цветов?
 Именно поэтому количество белых шаров в этом случае равно 5 (3+2).
Именно поэтому количество белых шаров в этом случае равно 5 (3+2).
 Вычислите вероятность того, что из 1-ой урны во 2-ую были переложены шары разного цвета.
Вычислите вероятность того, что из 1-ой урны во 2-ую были переложены шары разного цвета.
 е. полная вероятность равна P(A)=13/32.
е. полная вероятность равна P(A)=13/32.


 В первом ящике 5 белых и 4 синих шарика, во втором 3 и 1, а в третьем — 4 и 5 соответственно. Наугад выбран ящик и из него вытащенный шарик, оказался синий. Какова вероятность того, что этот шарик со второго ящика?
В первом ящике 5 белых и 4 синих шарика, во втором 3 и 1, а в третьем — 4 и 5 соответственно. Наугад выбран ящик и из него вытащенный шарик, оказался синий. Какова вероятность того, что этот шарик со второго ящика?
 Найти вероятность того, что наугад взятый красный шар содержится в одном из первых пяти ящиков.
Найти вероятность того, что наугад взятый красный шар содержится в одном из первых пяти ящиков.
 Следовательно, это могло произойти в двух случаях:
Следовательно, это могло произойти в двух случаях:

 Соответственно, вероятность извлечения черного шара равна P(ч)2 = 15/20 = 3/4.
Соответственно, вероятность извлечения черного шара равна P(ч)2 = 15/20 = 3/4.
 Какова вероятность того, что вторая игра будет проводиться новыми мячами?
Какова вероятность того, что вторая игра будет проводиться новыми мячами?
 2)
2)
 2273 + 0.2273 = 0.4546
2273 + 0.2273 = 0.4546
 В одной 10 красных и 5 синих шаров, во второй 5 красных и 7 синих шаров. Какова вероятность того, что из первой урны наудачу будет вынут красный шар, а из второй синий?
В одной 10 красных и 5 синих шаров, во второй 5 красных и 7 синих шаров. Какова вероятность того, что из первой урны наудачу будет вынут красный шар, а из второй синий?
 Из обеих урн наудачу извлекается по одному шару. Какова вероятность, что оба шара одного цвета?
Из обеих урн наудачу извлекается по одному шару. Какова вероятность, что оба шара одного цвета?
 е. третий шар будет черным, а первые два — белыми).
е. третий шар будет черным, а первые два — белыми).
 После
этого наудачу по одному извлекают три
шара без возвращения. Тогда вероятность
того, что все три шара будут белыми,
равна …
После
этого наудачу по одному извлекают три
шара без возвращения. Тогда вероятность
того, что все три шара будут белыми,
равна … Тогда
Тогда Вероятности отказов
элементов равны соответственно 0,05, 0,1
и 0,20. Тогда вероятность того, что тока
в цепи не будет, равна …
Вероятности отказов
элементов равны соответственно 0,05, 0,1
и 0,20. Тогда вероятность того, что тока
в цепи не будет, равна … Тогда Учитывая,
что
получаем
Тогда Учитывая,
что
получаем  Тогда
А
так как по условию задачи
события
и
зависимы,
то
Тогда
А
так как по условию задачи
события
и
зависимы,
то  Тогда и
Тогда и  $$
$$ Итак, у нас есть $6$ черных шаров из $10$ общего количества шаров, и ответ на первый вопрос равен 9.0003
Итак, у нас есть $6$ черных шаров из $10$ общего количества шаров, и ответ на первый вопрос равен 9.0003 Вы должны добавить .
$$\begin{align}\mathsf P(B_2)&=\mathsf P(W_1\cap B_2)+\mathsf P(B_1\cap B_2)\\[1ex] &=\mathsf P(W_1)\cdot\ mathsf P(B_2\mid W_1)+\mathsf P(B_1)\cdot\mathsf P(B_2\mid B_1)\\[1ex]&=\dfrac{5}{11}\dfrac{6}{10}+ \dfrac{6}{11}\dfrac{5}{10}\\[1ex]&=\dfrac 6{11}\end{align}$$
Вы должны добавить .
$$\begin{align}\mathsf P(B_2)&=\mathsf P(W_1\cap B_2)+\mathsf P(B_1\cap B_2)\\[1ex] &=\mathsf P(W_1)\cdot\ mathsf P(B_2\mid W_1)+\mathsf P(B_1)\cdot\mathsf P(B_2\mid B_1)\\[1ex]&=\dfrac{5}{11}\dfrac{6}{10}+ \dfrac{6}{11}\dfrac{5}{10}\\[1ex]&=\dfrac 6{11}\end{align}$$
 А общее количество способов выбрать 2 шара из урны А равно $10 \выберите 2$ способа.
А общее количество способов выбрать 2 шара из урны А равно $10 \выберите 2$ способа.

 Поставляется без аккумулятора и зарядного устройства.
Поставляется без аккумулятора и зарядного устройства.

 250 (2,5 Ач) / макс. 500 (5,0 Ач)
250 (2,5 Ач) / макс. 500 (5,0 Ач) Обращаем внимание, что замену запасных частией может проводить только специально обученный персонал. Пожалуйста, обратите внимание на условия гарантии.
Обращаем внимание, что замену запасных частией может проводить только специально обученный персонал. Пожалуйста, обратите внимание на условия гарантии.
 е. 9.
е. 9. е. 18 = 2 × 3 × 3; 45 = 3 × 3 × 5,
е. 18 = 2 × 3 × 3; 45 = 3 × 3 × 5,


 Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
 3’5» — 0 градусов 3 минуты 5 секунд (выражение интерпретируется как градусы/минуты/секунды)
3’5» — 0 градусов 3 минуты 5 секунд (выражение интерпретируется как градусы/минуты/секунды) Подобрать
оптимальные пропорции поможет наш
Подобрать
оптимальные пропорции поможет наш 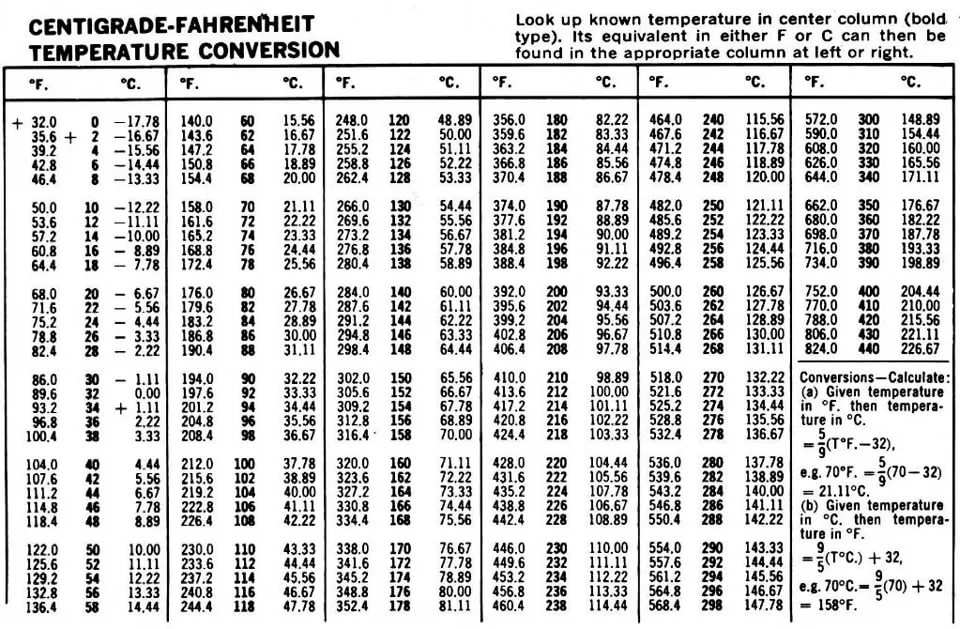




 8 Коэффициенты для единиц, перечисленных в алфавитном порядке и
B.9 Факторы для единиц, перечисленных по видам величин или областям науки.
8 Коэффициенты для единиц, перечисленных в алфавитном порядке и
B.9 Факторы для единиц, перечисленных по видам величин или областям науки.
 Обратите внимание, что второй луч всегда находится на оси x.
Обратите внимание, что второй луч всегда находится на оси x. Итак, если наш заданный угол равен 33°, то его опорный угол также равен 33°.
Итак, если наш заданный угол равен 33°, то его опорный угол также равен 33°.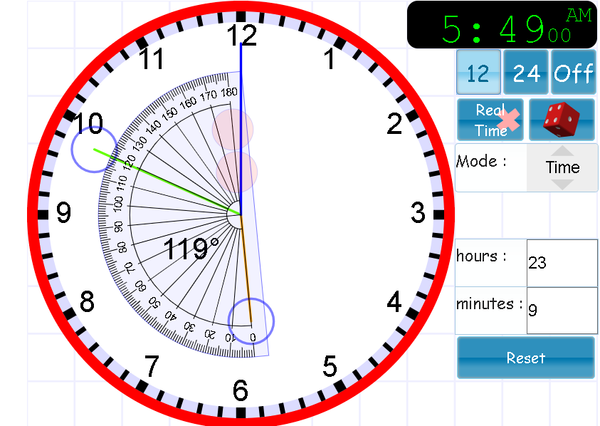


 Эта теорема имеет место для системы
Эта теорема имеет место для системы 4 = 6,8 млн усл. ед.,
4 = 6,8 млн усл. ед., 3. Системы линейных уравнений. Метод Крамера
3. Системы линейных уравнений. Метод Крамера Квадратная система линейных
неоднородных уравнений n-го
порядка с отличным от нуля определителем
основной матрицы системы (0) имеет одно и только
одно решение, и это решение вычисляется
по формулам:
Квадратная система линейных
неоднородных уравнений n-го
порядка с отличным от нуля определителем
основной матрицы системы (0) имеет одно и только
одно решение, и это решение вычисляется
по формулам: Для того чтобы матрицаАимела обратную, необходимо и достаточно,
чтобы ее определитель был отличен от
нуля:detA0.
Для того чтобы матрицаАимела обратную, необходимо и достаточно,
чтобы ее определитель был отличен от
нуля:detA0.
 2) Система имеет хотя бы одно решение.
такие системы называютсясовместными.
3) Система имеет только одно решение.
Такие системы называютсяопределёнными.
2) Система имеет хотя бы одно решение.
такие системы называютсясовместными.
3) Система имеет только одно решение.
Такие системы называютсяопределёнными. Найденные значения y и z подставляем в первое уравнение, из
которого затем находим значение x:
Найденные значения y и z подставляем в первое уравнение, из
которого затем находим значение x:


 3 em}
3 em} 
 } $
} $ 2+5a-5}{a-5} \\ y = \frac{4a+25}{a-5} \end{array} \right.} $
2+5a-5}{a-5} \\ y = \frac{4a+25}{a-5} \end{array} \right.} $ Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как как методом крамера решить систему уравнений,как найти дискриминант матрицы по методу крамера,как решать линейные уравнения методом крамера,как решать матрицу методом крамера,как решать матрицы методом крамера,как решать метод крамера,как решать методом крамера,как решать методом крамера линейные уравнения,как решать методом крамера матрицы,как решать систему уравнений методом крамера,как решить матрицу методом крамера,как решить методом крамера систему,как решить методом крамера систему уравнений,как решить систему линейных уравнений методом крамера,как решить систему методом крамера,как решить систему уравнений методом крамера,крамер матрица,крамер метод,крамер формулы,крамера,крамера матрица,крамера метод пример,крамера метод это,линейные уравнения методом крамера,матрица крамер,матрица крамера,матрица метод крамера,матрица методом крамера,матрицу решить методом крамера,матрицы метод крамера,матрицы метод крамера примеры,матрицы примеры метод крамера,матрицы теорема крамера,метод гаусса и крамера,метод гаусса и метод крамера,метод гаусса крамера и,метод гаусса крамера и матричный метод,метод гаусса метод крамера матричный метод,метод крамер,метод крамера,метод крамера 4 на 4,метод крамера 4х4,метод крамера гаусса и,метод крамера для матрицы 4 порядка,метод крамера для решения систем линейных уравнений,метод крамера для чайников,метод крамера и гаусса,метод крамера и матричный метод,метод крамера и метод гаусса,метод крамера и метод гаусса решения систем линейных уравнений,метод крамера как решать,метод крамера матрица,метод крамера матрицы,метод крамера матрицы примеры,метод крамера метод гаусса,метод крамера метод гаусса и,метод крамера метод гаусса матричный метод,метод крамера пример,метод крамера примеры,метод крамера примеры с решением,метод крамера решение,метод крамера решение матриц,метод крамера решение систем линейных уравнений,метод крамера решения,метод крамера решения систем линейных уравнений,метод крамера система линейных уравнений,метод крамера системы линейных уравнений,метод крамера слау,метод крамера теория,метод крамера формула,метод крамера формулы,метод крамера это,метод обратной матрицы метод крамера,метод решение крамера,метод решения крамера,метод слау крамера,метода крамера,методом крамера,методом крамера как решать,методом крамера матрица,методом крамера решить,методом крамера решить матрицу,методом крамера решить системы уравнений,методом крамера решить уравнение,по крамеру решение,по формулам крамера,по формулам крамера решить систему,по формулам крамера решить систему линейных уравнений,по формулам крамера решить систему уравнений,по формуле крамера решить систему,по формуле крамера решить систему линейных уравнений,по формуле крамера решить систему уравнений,правила крамера,правило крамера,правило крамера решения систем,правило крамера решения систем линейных уравнений,пример метод крамера,примеры линейных уравнений решение методом крамера,примеры метод крамера,примеры решение линейных уравнений методом крамера,примеры формула крамера,решение линейных систем уравнений по формулам крамера,решение линейных уравнений методом крамера,решение линейных уравнений методом крамера примеры,решение матриц метод крамера,решение матриц методом крамера,решение матриц по методу крамера,решение матрицы методом крамера,решение метод крамера,решение методом крамера,решение по крамеру,решение по формуле крамера,решение систем линейных уравнений метод крамера,решение систем линейных уравнений методом крамера,решение систем линейных уравнений методом крамера методом гаусса,решение систем линейных уравнений по формулам крамера,решение систем методом крамера,решение систем по формулам крамера,решение систем уравнений методом крамера,решение систем уравнений методом крамера примеры с решением,решение систем уравнений по формулам крамера,решение системных уравнений методом крамера,решение системы линейных уравнений методом крамера,решение системы методом крамера,решение системы по формулам крамера,решение системы уравнений методом крамера,решение слау методом крамера,решение уравнений методом крамера,решение уравнений по формулам крамера,решение уравнения методом крамера,решения метод крамера,решите систему линейных уравнений методом крамера,решите систему уравнений методом крамера,решите систему уравнений по формулам крамера,решить матрицу методом крамера,решить методом крамера,решить методом крамера системы уравнений,решить методом крамера слау,решить методом крамера уравнение,решить по правилу крамера систему,решить по правилу крамера систему уравнений,решить по формулам крамера систему,решить по формулам крамера систему уравнений,решить по формуле крамера систему,решить по формуле крамера систему уравнений,решить систему алгебраических линейных уравнений методом крамера,решить систему линейных уравнений методом крамера,решить систему линейных уравнений по формулам крамера,решить систему линейных уравнений по формуле крамера,решить систему методом гаусса и методом крамера,решить систему методом крамера,решить систему методом крамера и методом гаусса,решить систему по правилу крамера,решить систему по формулам крамера,решить систему по формуле крамера,решить систему уравнений методом крамера,решить систему уравнений по правилу крамера,решить систему уравнений по формулам крамера,решить систему уравнений по формуле крамера,решить системы уравнений методом крамера,решить слау методом крамера,решить уравнение методом крамера,система крамера,система линейных уравнений метод крамера,система линейных уравнений методом крамера,система уравнений методом крамера,систему линейных уравнений решить по формулам крамера,систему уравнений решить по правилу крамера,системы линейных уравнений метод крамера,слау метод крамера,слау методом крамера,способ крамера,теорема крамера матрицы,теория крамера,теория метод крамера,уравнение крамера,уравнение методом крамера,формула крамера,формула крамера для решения,формула крамера для решения системы,формула крамера для решения системы линейных уравнений,формула крамера примеры,формула метод крамера,формулам крамера,формулы крамер,формулы крамера,формулы крамера для решения систем,формулы крамера для решения систем линейных уравнений,формулы метод крамера.
Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как как методом крамера решить систему уравнений,как найти дискриминант матрицы по методу крамера,как решать линейные уравнения методом крамера,как решать матрицу методом крамера,как решать матрицы методом крамера,как решать метод крамера,как решать методом крамера,как решать методом крамера линейные уравнения,как решать методом крамера матрицы,как решать систему уравнений методом крамера,как решить матрицу методом крамера,как решить методом крамера систему,как решить методом крамера систему уравнений,как решить систему линейных уравнений методом крамера,как решить систему методом крамера,как решить систему уравнений методом крамера,крамер матрица,крамер метод,крамер формулы,крамера,крамера матрица,крамера метод пример,крамера метод это,линейные уравнения методом крамера,матрица крамер,матрица крамера,матрица метод крамера,матрица методом крамера,матрицу решить методом крамера,матрицы метод крамера,матрицы метод крамера примеры,матрицы примеры метод крамера,матрицы теорема крамера,метод гаусса и крамера,метод гаусса и метод крамера,метод гаусса крамера и,метод гаусса крамера и матричный метод,метод гаусса метод крамера матричный метод,метод крамер,метод крамера,метод крамера 4 на 4,метод крамера 4х4,метод крамера гаусса и,метод крамера для матрицы 4 порядка,метод крамера для решения систем линейных уравнений,метод крамера для чайников,метод крамера и гаусса,метод крамера и матричный метод,метод крамера и метод гаусса,метод крамера и метод гаусса решения систем линейных уравнений,метод крамера как решать,метод крамера матрица,метод крамера матрицы,метод крамера матрицы примеры,метод крамера метод гаусса,метод крамера метод гаусса и,метод крамера метод гаусса матричный метод,метод крамера пример,метод крамера примеры,метод крамера примеры с решением,метод крамера решение,метод крамера решение матриц,метод крамера решение систем линейных уравнений,метод крамера решения,метод крамера решения систем линейных уравнений,метод крамера система линейных уравнений,метод крамера системы линейных уравнений,метод крамера слау,метод крамера теория,метод крамера формула,метод крамера формулы,метод крамера это,метод обратной матрицы метод крамера,метод решение крамера,метод решения крамера,метод слау крамера,метода крамера,методом крамера,методом крамера как решать,методом крамера матрица,методом крамера решить,методом крамера решить матрицу,методом крамера решить системы уравнений,методом крамера решить уравнение,по крамеру решение,по формулам крамера,по формулам крамера решить систему,по формулам крамера решить систему линейных уравнений,по формулам крамера решить систему уравнений,по формуле крамера решить систему,по формуле крамера решить систему линейных уравнений,по формуле крамера решить систему уравнений,правила крамера,правило крамера,правило крамера решения систем,правило крамера решения систем линейных уравнений,пример метод крамера,примеры линейных уравнений решение методом крамера,примеры метод крамера,примеры решение линейных уравнений методом крамера,примеры формула крамера,решение линейных систем уравнений по формулам крамера,решение линейных уравнений методом крамера,решение линейных уравнений методом крамера примеры,решение матриц метод крамера,решение матриц методом крамера,решение матриц по методу крамера,решение матрицы методом крамера,решение метод крамера,решение методом крамера,решение по крамеру,решение по формуле крамера,решение систем линейных уравнений метод крамера,решение систем линейных уравнений методом крамера,решение систем линейных уравнений методом крамера методом гаусса,решение систем линейных уравнений по формулам крамера,решение систем методом крамера,решение систем по формулам крамера,решение систем уравнений методом крамера,решение систем уравнений методом крамера примеры с решением,решение систем уравнений по формулам крамера,решение системных уравнений методом крамера,решение системы линейных уравнений методом крамера,решение системы методом крамера,решение системы по формулам крамера,решение системы уравнений методом крамера,решение слау методом крамера,решение уравнений методом крамера,решение уравнений по формулам крамера,решение уравнения методом крамера,решения метод крамера,решите систему линейных уравнений методом крамера,решите систему уравнений методом крамера,решите систему уравнений по формулам крамера,решить матрицу методом крамера,решить методом крамера,решить методом крамера системы уравнений,решить методом крамера слау,решить методом крамера уравнение,решить по правилу крамера систему,решить по правилу крамера систему уравнений,решить по формулам крамера систему,решить по формулам крамера систему уравнений,решить по формуле крамера систему,решить по формуле крамера систему уравнений,решить систему алгебраических линейных уравнений методом крамера,решить систему линейных уравнений методом крамера,решить систему линейных уравнений по формулам крамера,решить систему линейных уравнений по формуле крамера,решить систему методом гаусса и методом крамера,решить систему методом крамера,решить систему методом крамера и методом гаусса,решить систему по правилу крамера,решить систему по формулам крамера,решить систему по формуле крамера,решить систему уравнений методом крамера,решить систему уравнений по правилу крамера,решить систему уравнений по формулам крамера,решить систему уравнений по формуле крамера,решить системы уравнений методом крамера,решить слау методом крамера,решить уравнение методом крамера,система крамера,система линейных уравнений метод крамера,система линейных уравнений методом крамера,система уравнений методом крамера,систему линейных уравнений решить по формулам крамера,систему уравнений решить по правилу крамера,системы линейных уравнений метод крамера,слау метод крамера,слау методом крамера,способ крамера,теорема крамера матрицы,теория крамера,теория метод крамера,уравнение крамера,уравнение методом крамера,формула крамера,формула крамера для решения,формула крамера для решения системы,формула крамера для решения системы линейных уравнений,формула крамера примеры,формула метод крамера,формулам крамера,формулы крамер,формулы крамера,формулы крамера для решения систем,формулы крамера для решения систем линейных уравнений,формулы метод крамера. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и как методом крамера решить систему уравнений. Просто введите задачу в окошко и нажмите
«решить» здесь (например, как решать линейные уравнения методом крамера).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и как методом крамера решить систему уравнений. Просто введите задачу в окошко и нажмите
«решить» здесь (например, как решать линейные уравнения методом крамера). Один из методов состоит в том, чтобы дополнить матрицу 3×3 повторением первых двух столбцов, получив матрицу 3×5. Затем вычисляем сумму произведений записей вниз по по каждой из трех диагоналей (слева вверху справа внизу) и вычесть произведения записей вверх по по каждой из трех диагоналей (слева внизу справа вверху). Это легче понять с визуальным и пример.
Один из методов состоит в том, чтобы дополнить матрицу 3×3 повторением первых двух столбцов, получив матрицу 3×5. Затем вычисляем сумму произведений записей вниз по по каждой из трех диагоналей (слева вверху справа внизу) и вычесть произведения записей вверх по по каждой из трех диагоналей (слева внизу справа вверху). Это легче понять с визуальным и пример. Прибавьте результат к произведению записей по второй диагонали. Добавьте этот результат к произведению записей вниз по третьей диагонали.
Прибавьте результат к произведению записей по второй диагонали. Добавьте этот результат к произведению записей вниз по третьей диагонали. Таким образом,
Таким образом, Для больших матриц лучше всего использовать графическую утилиту или компьютерное программное обеспечение.
Для больших матриц лучше всего использовать графическую утилиту или компьютерное программное обеспечение.  Если мы записываем определитель
Если мы записываем определитель
 Чтобы увидеть, какой из них, мы используем процесс исключения. Наша цель — исключить одну из переменных.
Чтобы увидеть, какой из них, мы используем процесс исключения. Наша цель — исключить одну из переменных. Настройте матрицу, дополненную первыми двумя столбцами.
Настройте матрицу, дополненную первыми двумя столбцами. Изобразив систему, мы видим, что две плоскости одинаковы и обе пересекают третью плоскость по прямой.
Изобразив систему, мы видим, что две плоскости одинаковы и обе пересекают третью плоскость по прямой.

 В правом столбце получаем решение:
В правом столбце получаем решение:



 Теорема звучит так:
Теорема звучит так:  Он равен четырем, значит будем использовать минус четыре:
Он равен четырем, значит будем использовать минус четыре: Если его дискриминант больше нуля, то оно имеет два корня, сумма которых равна второму коэффициенту с противоположным знаком, а произведение корней равно свободному члену:
Если его дискриминант больше нуля, то оно имеет два корня, сумма которых равна второму коэффициенту с противоположным знаком, а произведение корней равно свободному члену:
 Подставим это выражение вместо D.
Подставим это выражение вместо D.









 Запишем ответ.
Запишем ответ.



 .. 2 х 2 + а 1 х +а 0 — квадратное уравнение с корнями 7 н-1 , r n затем,
.. 2 х 2 + а 1 х +а 0 — квадратное уравнение с корнями 7 н-1 , r n затем,
 Если α , β являются корнями уравнения: x 2 + 10x + 2 = 0 , то найдите значение (α/β + β/α).
Если α , β являются корнями уравнения: x 2 + 10x + 2 = 0 , то найдите значение (α/β + β/α).  Если α , β и γ являются корнями уравнения и учитывая, что α + β + γ = 10, αβ + αγ + βγ = -1 и αβ γ = -6, то найдите кубическое уравнение.
Если α , β и γ являются корнями уравнения и учитывая, что α + β + γ = 10, αβ + αγ + βγ = -1 и αβ γ = -6, то найдите кубическое уравнение.  Если α и β являются корнями уравнения x 2 – 3x +2 =0, тогда найдите значение α 2 – β 2 .
Если α и β являются корнями уравнения x 2 – 3x +2 =0, тогда найдите значение α 2 – β 2 . 