Интегральные функции:
- Si(x)
- Интегральный синус от x
- Ci(x)
- Интегральный косинус от x
- Shi(x)
- Интегральный гиперболический синус от x
- Chi(x)
- Интегральный гиперболический косинус от x
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.
 3
3- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- 15/7
- — дробь
Другие функции:
- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от x
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:
- pi
- Число «Пи», которое примерно равно ~3.
 14159..
14159.. - e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
Завершение квадрата
» Завершение квадрата » вот где мы. ..
..
| … возьмем квадратное уравнение следующим образом: | и превратите его в это: | |
| топор 2 + Ьх + с = 0 | а(х+ d ) 2 + е = 0 |
Для тех из вас, кто торопится, могу сказать, что: d = b 2a
и: e = c − b 2 4a
Но если у вас есть время, позвольте мне показать вам, как « Заполнить квадрат » самостоятельно.
Завершение квадрата
Допустим, у нас есть простое выражение вида x 2 + bx. Наличие x дважды в одном и том же выражении может усложнить жизнь. Что мы можем сделать?
Что ж, немного вдохновившись геометрией, мы можем преобразовать его вот так:
Как видите x 2 + bx можно переставить почти в квадрат. ..
..
… и мы можем завершить квадрат с помощью (b/2) 2
В алгебре это выглядит так:
| x 2 + шт | + (б/2) 2 | = | (х+b/2) 2 |
| «Завершить квадрат » |
Итак, сложив (b/2) 2 , мы можем завершить квадрат.
Результат (x+b/2) 2 имеет x только один раз , что проще в использовании.
Сохранение равновесия
Теперь… мы не можем просто прибавить (b/2) 2 без вычитания ! В противном случае меняется все значение.
Итак, давайте посмотрим, как это сделать правильно на примере:
| Начните с: | |
| («b» в данном случае равно 6) | |
| Заполните квадрат: | |
| Также вычесть новый термин |
Упростите и готово. | |
Результат:
x 2 + 6x + 7 = (x+3) 2 − 2
И теперь x появляется только один раз, и наша работа сделана!
Быстрый подход
Вот быстрый способ получить ответ. Вам может понравиться этот метод.
Сначала подумайте о желаемом результате: (x+d) 2 + e
После разложения (x+d) 2 получаем: x 2 + 2dx + d 2 + e
Теперь посмотрим, сможем ли мы превратить наш пример в эту форму, чтобы обнаружить d и e
Пример: попробуйте вписать x
2 + 6x + 7 в x 2 + 2dx + d 2 + eТеперь мы можем «форсировать» ответ:
- 911 33 Мы знаем, что 6х должно закончиться вверх как 2dx, поэтому d должно быть 3
- Далее мы видим, что 7 должно стать d 2 + e = 9 + e, поэтому e должно быть −2
И мы получаем тот же результат (x+3) 2 − 2, что и выше!
Теперь давайте рассмотрим полезное приложение: решение квадратных уравнений.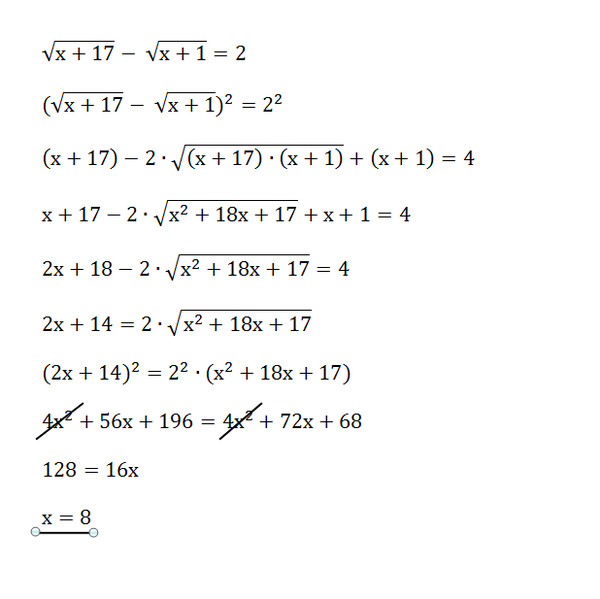 ..
..
Решение общих квадратных уравнений путем заполнения квадрата
Мы можем дополнить квадрат до , решить квадратное уравнение (найти, где оно равно нулю).
Но общее квадратное уравнение может иметь коэффициент а перед х 2 :
топор 2 + Ьх + с = 0
Но с этим легко справиться… просто разделите все уравнение сначала на «а», а затем продолжайте:
х 2 + (б/а)х + с/а = 0
шагов
Теперь мы можем решить квадратное уравнение за 5 шагов:
- Шаг 1 Разделите все члены на a (коэффициент x 2 ).
- Шаг 2 Переместите числовое выражение ( c/a ) в правую часть уравнения.
- Шаг 3 Заполните квадрат в левой части уравнения и сбалансируйте его, добавив такое же значение в правую часть уравнения.
Теперь у нас есть что-то похожее на (x + p) 2 = q, которое можно довольно легко решить:
- Шаг 4 Извлеките квадратный корень из обеих частей уравнения.

- Шаг 5 Вычтите число, оставшееся в левой части уравнения, чтобы найти x .
Примеры
Хорошо, несколько примеров помогут!
Пример 1: решить x
2 + 4x + 1 = 0Шаг 1 можно пропустить в этом примере, так как коэффициент при x 2 равен 1
Шаг 2 Переместите числовой член в правую часть уравнения: 909 09
x 2 + 4x = -1
Шаг 3 Заполните квадрат в левой части уравнения и уравновесьте его, добавив то же число в правую часть уравнения.
(б/2) 2 = (4/2) 2 = 2 2 = 4
x 2 + 4x + 4 = -1 + 4
(x + 2) 2 = 3
Шаг 4 Извлеките квадратный корень из обеих частей уравнения:
х + 2 = ±√3 = ±1,73 (до 2 знаков после запятой)
Шаг 5 Вычтите 2 с обеих сторон:
x = ±1,73 – 2 = -3,73 или -0,27
А вот еще интересная и полезная штука. В конце шага 3 у нас было уравнение: (х + 2) 2 = 3 Это дает нам вершину (точка поворота) x 2 + 4x + 1: (-2, -3) |
Пример 2: решить 5x
2 – 4x – 2 = 0Шаг 1 Разделить все члены на 5
x 2 – 0,8x – 0,4 = 0
Шаг 2 Переместите числовой член в правую часть уравнения:
x 2 – 0,8x = 0,4
Шаг 3 Заполните квадрат в левой части уравнения и уравновесьте его, добавив то же число в правой части уравнения:
(b/2) 2 = (0,8/2) 2 = 0,4 2 = 0,16
x 2 – 0,8x + 0,16 = 0,4 + 0,16
(x – 0,4) 2 = 0,56
Шаг 4 Извлеките квадратный корень из обеих частей уравнения:
x – 0,4 = ±√0,56 = ±0,748 (до 3 знаков после запятой)
Шаг 5 Вычтите (-0,4) из обеих частей (другими словами, добавьте 0,4 ):
x = ±0,748 + 0,4 = -0,348 или 1,148
Почему «Завершить квадрат»?
Зачем заполнять квадрат, если мы можем просто использовать квадратную формулу, чтобы решить квадратное уравнение?
Ну, одна причина указана выше, где новая форма не только показывает нам вершину, но и упрощает решение.
Бывают также случаи, когда форма ax 2 + bx + c может быть частью более крупного вопроса и переставлять его как a(x+ d ) 2 + 9092 8 e делает решение проще, потому что x появляется только один раз.
Например, «x» может быть функцией (например, cos(z) ), и ее изменение может открыть путь к лучшему решению.
Также завершение квадрата является первым шагом в выводе квадратичной формулы
Думайте об этом как о еще одном инструменте в вашем наборе математических инструментов.
364, 1205, 365, 2331, 2332, 3213, 3896, 3211, 3212, 1206
Сноска: значения «d» и «e»
Как я получил значения d и e из верхней части страницы?
| Начните с | |
| Разделить уравнение на a | |
| Положить c/a на другую сторону | |
| Добавить (b/2a) 2 на обе стороны | |
| «Заполните квадрат» | |
Теперь верни все назад. Конвертировать bmp в jpeg: Конвертировать BMP в JPEG онлайн — ConvertioКонвертируйте BMP в JPEG через бесплатное приложение или PHPКонвертируйте BMP в JPEG через бесплатное приложение или PHP
GroupDocs.Conversion Cloud для PHP и бесплатные приложения были разработаны, чтобы помочь вам начать работу с REST API преобразования документов. Он не только позволяет конвертировать между форматами файлов Bitmap Image File (BMP) и JPEG Image (JPEG), но и более 153 типов документов из Microsoft Office, OpenDocument , Adobe, AutoCAD, PDF, изображения и многие другие популярные категории. Бесплатные приложения для конвертации популярных форматовBMP к PPT BMP к PPS BMP к PPTX BMP к PPSX BMP к ODP BMP к OTP BMP к POTX BMP к POT BMP к POTM BMP к PPTM BMP к PPSM BMP к FODP BMP к TIFF BMP к TIF BMP к JPG BMP к JPEG BMP к PNG BMP к GIF BMP к BMP BMP к ICO BMP к PSD BMP к WMF BMP к EMF BMP к DCM BMP к DICOM BMP к WEBP BMP к SVG BMP к JP2 BMP к EMZ BMP к WMZ BMP к SVGZ BMP к TGA BMP к PSB Как преобразовать BMP в JPEG
Часто задаваемые вопросы (FAQ)Я не хочу никуда загружать свои конфиденциальные файлы BMP или JPEG? Каковы мои варианты?GroupDocs.Conversion Cloud также доступен в виде образа Docker, который можно использовать для [самостоятельного размещения] (https://purchase.groupdocs.cloud/self-hosting) сервиса. Или вы можете создавать свои собственные сервисы, используя API с высоким кодом GroupDocs.Conversion, которые в настоящее время управляют бесплатными приложениями BMP и JPEG для конвертации, а также REST-API. Могу ли я попробовать конвертировать BMP в JPEG бесплатно?Приложение GroupDocs.Conversion Cloud совершенно бесплатно. Вы можете преобразовать любое количество BMP файлов в JPEG. Если вы разработчик и хотите интегрировать эту функцию в свое собственное приложение, вы можете попробовать GroupDocs.Conversion Low-Code API без каких-либо ограничений. Я хочу создать собственное приложение, которое может конвертировать BMP в JPEG?Проверьте наши SDK на GitHub, если вы ищете исходный код для преобразования формата файла BMP в JPEG в облаке. Расширенные функции BMP и API преобразования документовПреобразование BMP в все распространенные форматыBMP API преобразования защищены и требуют аутентификацииВодяной знак BMP страницЗащита паролем JPEG выходной документПреобразование BMP в JPEG страница за страницей или настраиваемый диапазон страницBMP преобразование обозреватель API на основе коллекции swaggerБесплатные онлайн-приложения для конвертации BMPКонвертируйте неограниченное количество документов и изображений с помощью наших бесплатных онлайн-приложений для конвертации Бесплатные приложения для преобразования BMP во множество форматов документов рядом с JPEGREST API GroupDocs. Безопасность и аутентификацияОблачный API GroupDocs.Conversion защищен и требует аутентификации. Вам необходимо зарегистрироваться в облаке GroupDocs и получить идентификатор ключа доступа к приложению (appSID) и секретный ключ доступа к приложению. Для запросов с проверкой подлинности требуется подпись и параметры запроса AppSID или заголовок авторизации OAuth 2.0. Проводник APIСамый простой способ опробовать GroupDocs.Conversion Cloud API прямо в браузере — использовать проводник GroupDocs Cloud Web API, который представляет собой набор документации Swagger для облачных API GroupDocs. Он позволяет без усилий взаимодействовать и опробовать каждую операцию. наши API-интерфейсы. Бесплатные приложения для быстрого начала работы и преобразования BMP в JPEGС GroupDocs.Conversion Cloud API вы можете сразу же начать конвертировать свои файлы, так как вам не нужно ничего устанавливать. Ресурсы поддержки и обученияОбразовательные ресурсы
Поддержка продукта
Начать бесплатную пробную версию Скачать репозиторий GitHub Преобразование BMP в JPEG с помощью SDK на других популярных языкахGroupDocs.ConversionCloud SDK за Node.js GroupDocs.ConversionCloud SDK за Android GroupDocs.ConversionCloud SDK за Java GroupDocs.ConversionCloud SDK за Python GroupDocs.ConversionCloud SDK за . GroupDocs.ConversionCloud за cURL GroupDocs.ConversionCloud SDK за Ruby Как конвертировать формат bmp в pdf онлайнФормат файла – это особенность структуры данных. Узнать его тип можно по названию расширения, указанному в конце имени после точки. Знание расширения позволяет определить тип документа, и подобрать программу для работы с ним. Конвертация – это изменение расширения. Логическая структура содержания и основная информация при конвертировании не страдает. О форматах BMP и PDFГрафический формат BMP разработала компания Microsoft для хранения растрового изображения в виде точечного рисунка. Определить принадлежность файла к нему можно по названию расширения: «.bmp», «.dib» или «.rle». BMP поддерживается операционной системой Windows и большинством графических программ. Недостатком является большой размер конечного файла. Хотя для работы с PDF нужны специальные программы, он — стандарт среди электронных документов. Приложения, программыXnConvertПриложение позволяет конвертировать до 500 графических форматов, при этом количество выходных типов формата достигает 80. Поэтому с его помощью можно преобразовать не только BMP в PDF, но и работать с другими редкими форматами, которые не получается открыть обычными приложениями. Программа может конвертировать в пакетном режиме, импортировать папки, фильтры. Она снабжена полезными функциями для работы с файлами. AdapterAdapter – это простой и функциональный конвертер изображений, поддерживающий большинство популярных форматов. В этом приложении можно добавлять изображения, перетаскивая их на рабочую панель. После этого необходимо выбрать желаемый тип конвертации. Программа также отображает размеры исходного и конечного файлов. Отличительные характеристики Adapter:
Программа поддерживается операционными системами Windows и Mac. Free Image Convert and ResizeХотя эта программа не поддерживает много графических форматов, с её помощью можно легко преобразовать BMP в PDF. Преимущество программы заключается в том, что можно одновременно работать с несколькими файлами, регулировать их размер и переименовать их. Конвертер поддерживается операционной системой Windows. ФотоконвертерПриложение может преобразовывать сразу несколько файлов за раз. Программа отличается простотой функционала, но качественно конвертирует изображения BPM в PDF. Доступна работа и с другими графическими форматами. С приложением можно работать не только через меню, но и с помощью командной строки. Онлайн-сервисыZamzarОнлайн-конвертер позволяет преобразовывать до 36 графических форматов в 13 других. Image EspressoСервис позволяет работать с изображениями онлайн. Загрузив файл, можно редактировать размер изображения, обрезать лишнее и поворачивать его. При желании можно использовать весь функционал сервиса: наложить эффекты, текст, отрегулировать яркость изображения и другие характеристики. К недостаткам относится невозможность работать с файлами с размером более 10 Мб. PDF CandyСервис позволяет конвертировать изображения без потери качества. Сайт предназначен для работы с форматом PDF. На нём можно преобразовывать разные типы форматов в PDF и наоборот. Также можно загрузить сразу несколько файлов, перетащив их или нажав на кнопку «Добавить». Конвертировать BMP в JPEG онлайнКонвертер файлов / Изображения / Конвертировать в BMP / JPEG конвертер / BMP в JPEG Выберите файл для конвертации Перетащите файлы сюда. OnlineConvertFree предоставляет бесплатные услуги по конвертации изображений без установки какого-либо программного обеспечения. Легко конвертируйте файлы bmp в jpeg или любой другой формат всего за несколько кликов. С помощью этих шагов можно легко преобразовать файл JPEG в формат BMP. Шаг 1 Загрузить bmp-файлВы можете выбрать bmp-файл, который хотите конвертировать, с вашего компьютера, Google Диска, Dropbox или просто перетащить его на страницу. Шаг 2 Выберите «в jpeg»Выберите jpeg или любой другой из 200+ поддерживаемых форматов, в который вы хотите конвертировать. Шаг 3 Загрузите файл в формате jpegДождитесь завершения преобразования, затем нажмите кнопку загрузки, чтобы получить преобразованный файл в формате jpeg. Преобразование bmp в jpegБыстро и просто Просто перетащите ваши файлы bmp на веб-страницу, и вы сможете конвертировать их в jpeg или более чем в 250 различных форматов файлов без необходимости регистрации, предоставьте адрес электронной почты или добавить водяной знак. Вам не нужно беспокоиться о безопасности. Как только вы загрузите ваши bmp файлы, мы их моментально удалим. Затем преобразованные файлы удаляются через 24 часа. Кроме того, мы гарантируем, что все передачи файлов безопасны благодаря расширенному шифрованию SSL. Все хранится в облаке. Вам не нужно утруждать себя установкой какого-либо программного обеспечения. Мы обрабатываем все преобразования bmp в jpeg в облаке, что означает, что никакие ресурсы вашего компьютера не будут использоваться в процессе. Растровое изображение Microsoft WindowsJoint Photographic Experts Groupконвертер bmpbmp в curbmp в emfbmp в gifbmp в icobmp в jpegbmp в pbmbmp в pcxbmp в pfbbmp в pgmbmp в pngtgmp в ppgmbb в smbbmp в psdbmp в psdbmp в psdbmp в psdbmp в pdfbmp в docbmp в docxbmp в rtfbmp в dxfbmp в epsbmp в wmfbmp в jpgbmp в aibmp в mp4bmp в avibmp в tifbmp в ddsbmp в psbmp в rgbbmp в wbmpbmp в xpmbmp в yuv Convert to jpegarw to jpegbmp to jpegcgm to jpegcr2 to jpegcrw to jpegcur to jpegdcm to jpegdcr to jpegdjvu to jpegdng to jpegemf to jpegfax to jpeggif to jpeghdr to jpegico to jpegnef to jpegorf to jpegpbm to jpegpcx to jpegpes to jpegpgm to jpegpict to jpegpng to jpegpnm to jpegppm to jpegpsd to jpegpwp to jpegraf to jpegsfw to jpegsvg to jpegtga to jpegtiff to jpegtim to jpegwpg to jpegxcf to jpegxwd to jpeghtml to jpegpdf to jpegdoc to jpegdocx to jpegxls to jpegxlsx to jpegpptx to jpegodt to jpegwps to jpegrtf to jpegtxt в jpegcsv в jpegpps в jpegdxf в jpegeps в jpegpcd в jpegpct в jpegwmf в jpegppt в jpegjpg в jpegai в jpegmp3 в jpegmp4 в jpegxps в jpegoxps в jpegavi в jpegmov в jpegswf в jpegmpg в jpegmpeg в jpegmpeg в jpegtif в jpegwed в jpeghtm в jpeghtm в jpegcdr в jpegheic в jpegps в jpegjfif в jpegheif в jpegavif в jpegcad в jpegsid в jpegmax в jpegmix в jpegjpe в jpegjp2 в jpegrgb в jpegexr в jpegmap в jpegbin в jpegjif в jpegyuv в jpegpef в jpegrw2 в jpeg Преобразование BMP в JPEG онлайнПреобразование BMP в JPEG онлайнПреобразование изображений BMP в формат JPEG онлайн бесплатно с помощью современного браузера, такого как Chrome, Opera или Firefox. Работает на aspose.com и aspose.cloud*Загружая файлы или используя наш сервис, вы соглашаетесь с нашими Условиями обслуживания и Политикой конфиденциальности TIFF TIF GIF PNG APNG TGA EMF EMZ WMF WMZ WEBP SVG SVGZ DICOM DCM DJVU DNG ODG OTG EPS CDR CMX BASE64Поделиться на Facebook Поделиться на Twitter Поделиться на LinkedIn Посмотреть другие приложения Попробуйте наш Cloud API Посмотреть исходный код в избранное или Esc, чтобы отменить действие Преобразование Aspose.Imaging Преобразование файлов BMP в JPEG онлайн бесплатно. Мощный бесплатный онлайн-конвертер BMP в JPEG очень прост. Не требуется установка настольного программного обеспечения. Все конвертации вы можете сделать онлайн с любой платформы: Windows, Linux, macOS и Android. Мы не требуем регистрации. Этот инструмент абсолютно бесплатный. Conversion — это бесплатное приложение на базе Aspose.Imaging , профессионального .NET/Java API, предлагающего расширенные функции обработки изображений локально и готового для использования на стороне клиента и сервера. Нужно облачное решение? Aspose.Imaging Cloud предоставляет SDK для популярных языков программирования, таких как C#, Python, PHP, Java, Android, Node.js, Ruby, которые построены на базе Cloud REST API и постоянно развиваются.
Интегрируйте функцию преобразования BMP в JPG в свои собственные проекты Это бесплатное преобразование основано на Aspose.Imaging for .NET , который представляет собой быстрый API для обработки изображений, включая, помимо прочего, преобразование изображений.
Пожалуйста, посетите https://products.aspose.com/imaging/net/conversion/bmp-to-jpg, чтобы попробовать Aspose.Imaging for .NET в ваших собственных приложениях. Разработчикам Java мы предлагаем собственный API Aspose.Imaging for Java для использования в ваших приложениях Java. Посетите https://products.aspose.com/imaging/java/conversion/bmp-to-jpg, чтобы попробовать. Как конвертировать файлы BMP с помощью Aspose. Imaging Conversion Imaging Conversion
Часто задаваемые вопросы
Х в степени 3 2: как посчитать 4 в степени 3/2 — Спрашивалка 2 | |
10.2. Закон степени 3/2 и понятие первеанса.
Прежде чем переходить непосредственно к описанию характеристик электронных потоков, вспомним полезные соотношения между плотностью тока с катода jк и напряжением U между катодом и анодом в диодах разной конфигурации, которые работают в режиме ограничения тока пространственным зарядом.
Для любых диодов в режиме ограничения тока пространственным зарядом величина jк пропорциональна напряжению U в степеним 3/2. Для плоского диодного зазора шириной d эта связь имеет вид
. (11.2)
На практике для характеристики протекания токов в диодных зазорах часто используют понятие первеанса
, (11.3)
где Iк— ток катода.
Значения
первеанса сильно
меняются от расстояния между катодом
и анодом и площади катода. В маломощных системах типа осциллографа
первеанс может иметь величину порядка
10-9 А/В3/2.
В мощных же СВЧ приборах эта величина
достигает значений (10-5 -10-6 ) А/В3/2.
Поэтому для таких устройств чаще
пользуются значением микропервеанса
В маломощных системах типа осциллографа
первеанс может иметь величину порядка
10-9 А/В3/2.
В мощных же СВЧ приборах эта величина
достигает значений (10-5 -10-6 ) А/В3/2.
Поэтому для таких устройств чаще
пользуются значением микропервеанса
, (11.4)
который имеет значения порядка 1-10 для мощных приборов.
Приведенные соотношения позволяют оценить напряжения, необходимые для получения требуемых токов пучка.
В СВЧ электронике используются три основных типа электронных пучков: ленточные, сплошные по сечению цилиндрические и пучки кольцевого сечения. Оценим поля пространственного заряда для двух первых типов пучков. Начнем с ленточного пучка. Воспользуемся изображением ленточного пучка на рис.11.1.
Рис.11.1. | Предположим,
что пучок имеет достаточно большую
протяженность в направлениях z и y. |
поперечного его сечения. Выделим в пучке объем, имеющий толщину 2x и площадь поверхности S в плоскости xz (см. рис.11.1). В этом выделенном объеме величина x x /2. По теореме Гаусса
, (11.5)
Здесь
в левой части равенства поток нормальной
составляющей электрического поля Еn через
всю поверхность выделенного объема, а
в правой части — интеграл от пространственного
заряда в этом объеме. Предположим, что
пучок однороден по сечению и имеет
плотность . Тогда, учитывая равенство нулю всех
составляющих поля, кроме x-й,
получаем:
Тогда, учитывая равенство нулю всех
составляющих поля, кроме x-й,
получаем:
и .
Отсюда следует, что в пределах пучка
, (11.6)
т.е. x-ая составляющая электрического поля равна нулю в центре пучка и линейно увеличивается с ростом x вплоть до его границы xп. Дальше поле не меняется с расстоянием (рис.11.2), так как вне пучка отсутствует пространственный заряд, а линии электрического поля вне пучка не расходятся (параллельны оси x).
Полезно иметь выражение электрического поля через плотность тока пучка. Учитывая, что в моноскоростном пучке со скоростью электронов V плотность тока, а, получаем:
Рис.11.2.
(11.7)
Для полей внутри цилиндрического пучка, воспользовавшись той же теоремой Гаусса и предполагая, что в пучке отсутствуют азимутальные поля, а также поля вдоль оси Z, получаем
и , (11.8)
где r — радиальная координата, отсчитываемая
от оси пучка, а L – протяженность вдоль оси Z выделенного
кольцевого пояска диаметром 2r.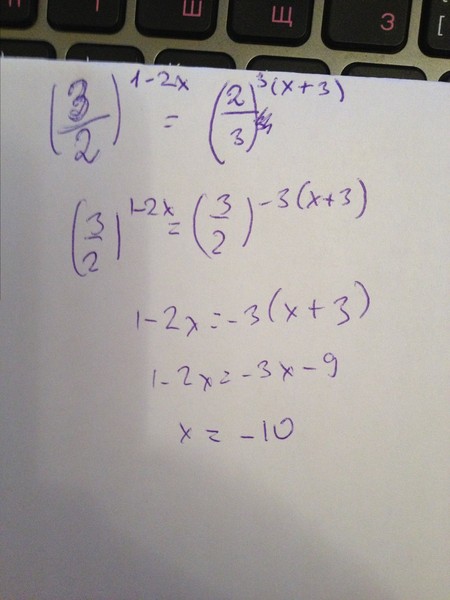 Отсюда следует, что внутри пучка
радиальная составляющая поля увеличивается
с радиусом:
Отсюда следует, что внутри пучка
радиальная составляющая поля увеличивается
с радиусом:
. (11.9)
Вне пучка пространственного заряда нет, однако, площадь в интеграле по поверхности увеличивается. Поэтому в этой области поле уменьшается (см.рис.11.3) по закону
. (11.10)
Как и для ленточного пучка, можно записать выражение для поля в пучке через его ток. Учитывая, что
, (11.11)
получаем для области внутри пучка, т.е. при r rп
. (11.12)
Рис.11.3.
Определив электрические поля, мы можем теперь определить и силы, расфокусирующие пучок.
(11.13)
Выражение для электрической силы бывает удобно записать для всей области внутри и вне цилиндрического электронного пучка в виде
при1 -1 при1 | (11. |
где =r/rп и =V/C – соответственно относительные значения координаты и скорости, а С – скорость света.
Здесь ток выражен в А, а линейные размеры в м.
Далее можно оценить и расфокусировку пучков под действием этих сил. Оценки показывают, что при нерелятивистских скоростях (1), когда можно пренебречь действием собственного магнитного поля пучка и связанной с этим самофокусировкой, расфокусировка зависит от первеанса и меняется следующим образом:
При микропервеансе р 1 пучок расширяется в два раза на пути Lx12,3rпо, где rпо — начальный радиус пучка.
Если р 3, Lx7,1rпо.
Обычно, Lx(10-102)rпо, и приходится использовать специальные системы удержания.
Как мы уже говорили при рассмотрении гироконов, при релятивистских скоростях из-за действия собственных магнитных полей пучка расфокусировка замедляется или может даже отсутствовать. Чтобы оценить возможности самофокусировки, необходимо определить не только электрические, но и магнитные поля пучка. Из закона Ампера азимутальная составляющая магнитной индукции цилиндрического пучка с током Iп и радиусом rп определяется соотношением:
при1 -1 при1 | (11.15) |
где =r/rп, ток
выражен в А, линейные размеры в м, а
магнитная индукция в Тл.
Зная магнитное поле, мы определяем и магнитную силу. Внутри пучка
. (11.16)
Сравнение соотношений (11.14) и (11.16) свидетельствует, что внутри пучка на всех радиальных координатах
, (11.17)
т.е. силы приблизительно равны только в ультрарелятивистском случае, когда .
3-8
Прогрессия арифметическая формула: Арифметическая прогрессия — урок. Алгебра, 9 класс.
Арифметическая прогрессия формулы, свойства, сумма членов, примеры и нахождение n-го члена
Арифметическая прогрессия — одно из фундаментальных понятий алгебры и математического анализа. Она имеет много применений в различных областях, включая финансы, физику, экономику и другие науки.
Арифметическая прогрессия — последовательность из чисел, в которой каждый следующий член отличается от предыдущего на определенное значение. Это значение называют разностью или шагом арифметической прогрессии и обозначают буквой d. Разность может быть и отрицательным числом и даже равняться нулю.
Например, 2,7,12,17,22… — это арифметическая прогрессия, так как второй ее член (7) отличается от первого (2) на 5, третий член (12) отличается от второго (7) тоже на 5, четвертый член (17) отличается от третьего (12) снова на 5 и т. д. Получается у этой числовой последовательности каждый следующий элемент больше предыдущего на 5 и эта последовательность является арифметической прогрессией.
А вот последовательность 3, 5, 7, 10, 15… не является арифметической прогрессией. Подумайте почему.
Таким образом, чтобы найти следующий член прогрессии, необходимо добавить к нему разность (шаг).
{a_n=a_{n-1}+d}
Для того, чтобы найти член арифметической прогрессии, необходимо знать первый член и разность. Формула для этого выглядит так:
{a_n=a_1+(n-1)d}
Характеристическое свойство арифметической прогрессии
Если для последовательности чисел выполняется следующее равенство, то такую последовательность можно назвать арифметической прогрессией:
{a_n=\frac {a_{n-1}+a_{n+1}}{2}, n\ge 2}
Сумма членов арифметической прогрессии
Для того, чтобы найти сумму первых n членов арифметической прогрессии, необходимо воспользоваться одной из формул:
{S_n=\frac {a_1+a_n}{2} \cdot n},
{S_n=\frac {2a_1+d(n-1)}{2} \cdot n}
В этих формулах a1 — первый член арифметической прогрессии, n — количество элементов для суммирования, an — член с номером n, d — разность прогрессии. На сайте вы можете найти сумму членов арифметической прогрессии онлайн.
На сайте вы можете найти сумму членов арифметической прогрессии онлайн.
Примеры арифметической прогрессии
2, 5, 8, 11, 14, 17…
Это арифметическая прогрессия, у которой первый член a1 равен 2, а разность d равна 3.
75, 70, 65, 60, 55…
В данном примере мы имеем дело с отрицательной разностью прогрессии. a1=75, d=-5.
Формулы арифметической прогрессии
| Определение арифметической прогрессии | {a_n=a_{n-1}+d} |
|---|---|
| Разность арифметической прогрессии | {d = a_{n+1}-a_n} |
| Формула n-го члена арифметической прогрессии | a_n=a_1+(n-1)d |
| Сумма первых n членов арифметической прогрессии | {S_n=\dfrac {a_1+a_n}{2} \cdot n} {S_n=\dfrac {2a_1+d(n-1)}{2} \cdot n} |
| Характеристическое свойство арифметической прогрессии | a_n=\dfrac {a_{n-1}+a_{n+1}}{2}, n\ge 2 |
Арифметические прогрессии широко применяются в финансовых расчетах, например, при расчете аннуитетов и амортизации. Они также используются в физике при описании равномерно ускоренного движения тела.
Они также используются в физике при описании равномерно ускоренного движения тела.
Понимание арифметических прогрессий может быть полезно не только в научных и технических областях, но и в повседневной жизни. Например, при планировании бюджета или распределении времени между задачами можно использовать концепцию арифметической прогрессии для более эффективного использования ресурсов.
Арифметическая прогрессия — это важное математическое понятие, которое широко используется в различных областях. Понимание ее смысла может быть полезно для решения различных задач и повышения эффективности в различных сферах деятельности.
ОглавлениеВВЕДЕНИЕЧасть первая. АРИФМЕТИКА, АЛГЕБРА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ Глава I. ДЕЙСТВИТЕЛЬНЫЕ И КОМПЛЕКСНЫЕ ЧИСЛА 2. Простые и составные числа. Признаки делимости. 3. Наибольший общий делитель и наименьшее общее кратное. 4. Целые числа. Рациональные числа. 5. Десятичные дроби. Представление рациональных чисел десятичными дробями. 6. Иррациональные числа. Действительные числа. 7. Действия с приближенными числами. 8. Числовая ось. Координаты точки на плоскости.  § 2. Степени и корни 9. Степени с натуральными показателями. 10. Степени с целыми показателями. 11. Корни. 12. Степени с рациональными показателями. Степени с действительными показателями. 13. Алгоритм извлечения квадратного корня. § 3. Комплексные числа 14. Основные понятия и определения. 15. Рациональные действия с комплексными числами. 16. Геометрическое изображение комплексных чисел. Тригонометрическая форма комплексного числа. 17. Действия с комплексными числами, заданными в тригонометрической форме. Формула Муавра. 18. Извлечение корня из комплексного числа. Глава II. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ 19. Алгебраические выражения. Одночлены и многочлены. 20. Формулы сокращенного умножения. 21. Бином Ньютона. 22. Разложение многочлена на множители. 23. Дробные алгебраические выражения. § 2. Иррациональные алгебраические выражения 24. Радикалы из алгебраических выражений. 25. Освобождение от иррациональности в знаменателе дроби.  n. n.41. Обратная пропорциональная зависимость. Степенная функция с рациональным показателем степени. 42. Показательная функция. 43. Логарифмическая функция. § 3. Преобразование графиков 44. Параллельный сдвиг графика. 45. График квадратного трех члена. 46. График дробно-линейной функции. 47. Преобразование симметрии. Сжатие и растяжение графика. 48. Построение графиков функций. 49. Сложение графиков. § 4. Некоторые сведения о рациональных функциях 50. Целые и дробные рациональные функции. Деление многочленов. 51. Схема Горнера. Теорема Безу. 52. Нули многочлена. Разложение многочлена на множители. Глава V. УРАВНЕНИЯ 53. Уравнение. Корни уравнения. 54. Равносильные уравнения. 55. Системы уравнений. 56. Графическое решение уравнений. §. 2. Алгебраические уравнения с одной неизвестной 57. Число и кратность корней. 58. Уравнения первой степени (линейные уравнения). 59. Уравнения второй степени (квадратные уравнения). 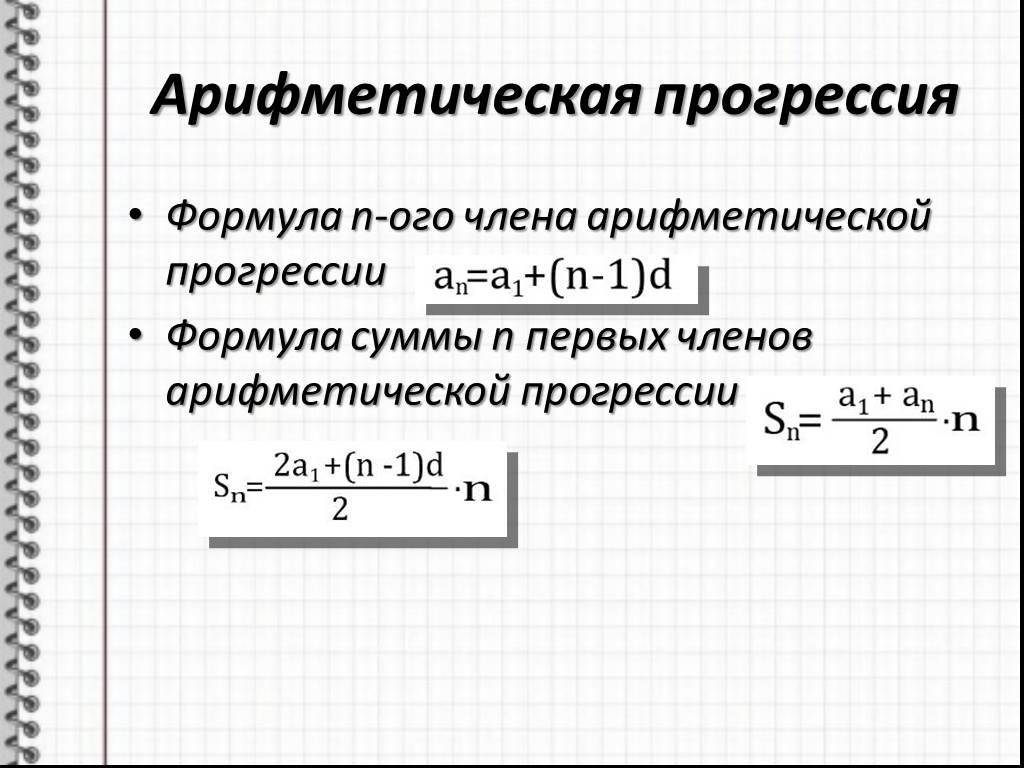 60. Формулы Виета. Разложение квадратного трехчлена на множители. 61. Исследование квадратного уравнения. 62. Уравнения высших степеней. Целые корни. 63. Двучленные уравнения. 64. Уравнения, сводящиеся к квадратным. 65. Возвратные уравнения. § 3. Системы алгебраических уравнений 66. Линейные системы. 67. Определители второго порядка. Исследование линейных систем двух уравнений с двумя неизвестными. 68. Системы, состоящие из уравнения второй степени и линейного уравнения. 69. Примеры систем двух уравнений второй степени. Системы уравнений высших степеней. § 4. Иррациональные, показательные и логарифмические уравнения 70. Иррациональные уравнения. 71. Показательные уравнения. 72. Логарифмические уравнения. 73. Разные уравнения. Системы уравнений. Глава VI. НЕРАВЕНСТВА 74. Свойства неравенств. Действия над неравенствами. 75. Алгебраические неравенства. § 2. Решение неравенств 76. Множество решений неравенства.  Равносильные неравенства. Равносильные неравенства.77. Графическое решение неравенств. 79. Квадратные неравенства. 80. Неравенства высших степеней. Неравенства, содержащие дробные рациональные функции от х. 81. Иррациональные, показательные и логарифмические неравенства. 82. Неравенства с двумя неизвестными. Глава VII. ПОСЛЕДОВАТЕЛЬНОСТИ 83. Числовая последовательность. 84. Предел числовой последовательности. 85. Бесконечно малые. Правила предельного перехода. § 2. Арифметическая прогрессия 86. Арифметическая прогрессия. Формула общего члена. 87. Свойства арифметической прогрессии. 88. Формула для суммы n членов арифметической прогрессии. § 3. Геометрическая прогрессия 89. Геометрическая прогрессия. Формула общего члена. 90. Свойства геометрической прогрессии. 91. Формулы для суммы n членов геометрической прогрессии. 92. Бесконечно убывающая геометрическая прогрессия. Глава VIII. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА (ДУГИ) 93. Вектор, проекция вектора.  94. Положительные углы и дуги, меньшие 360°. 95. Углы и дуги, большие 360°. 96. Отрицательные углы. Сложение и вычитание углов. § 2. Тригонометрические функции произвольного угла 97. Определение основных тригонометрических функций. 98. Изменение основных тригонометрических функций при изменении угла от 0 до 2pi. § 3. Соотношения между тригонометрическими функциями одного и того же угла 99. Основные тригонометрические тождества. 100. Вычисление значений тригонометрических функций по значению одной из них. 101. Значения тригонометрических функций некоторых углов. § 4. Четность, нечетность и периодичность тригонометрических функций 102. Четность и нечетность. 103. Понятие периодической функции. 104. Периодичность тригонометрических функций. § 5. Формулы приведения 105. Зависимость между тригонометрическими функциями дополнительных углов. 106. Формулы приведения. Глава IX. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА И ИХ ГРАФИКИ § 1.  Тригонометрические функции числового аргумента Тригонометрические функции числового аргумента108. Области определения и области изменения значений тригонометрических функций. 109. Некоторые неравенства и их следствия. § 2. Графики тригонометрических функций 110. Первоначальные сведения о таблицах тригонометрических функций. 111. Основные графики. 112. Примеры построения графиков некоторых других тригонометрических функций. 113. Дальнейшие примеры построения графиков функций. Глава X. ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ 114. Расстояние между двумя точками на плоскости. 115. Косинус суммы и разности двух аргументов. 116. Синус суммы и разности двух аргументов. 117. Тангенс суммы и разности двух аргументов. 118. О формулах сложения для нескольких аргументов. § 2. Формулы для двойного и половинного аргумента. Выражение sin na и cos na через степени sin a и cos a 119. Тригонометрические функции двойного аргумента. 120. Выражение sin na и cos na через степени sin a и cos a при натуральном числе n.  121. Тригонометрические функции половинного аргумента. 122. Выражение основных тригонометрических функций аргумента а через tg(a/2). § 3. Преобразование в сумму выражений вида sina•cosb, cosa•cosb и sinа•sinb § 4. Преобразование в произведение сумм вида § 5. Преобразование некоторых выражений в произведения с помощью введения вспомогательного аргумента 127. Преобразование в произведение выражения a•sina + b•cosa. 128. Преобразование в произведение выражений a•sina+b и a•cosa+b 129. Преобразование в произведение выражения a•tga+b. Глава XI. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ИХ ГРАФИКИ 130. Функция у = arcsin x (арксинус). 131. Функция y = arccos x (арккосинус). 132. Функция y = arctg x (арктангенс). 133. Функция y = arcctg x (арккотангенс). 134. Пример. § 2. Операции над обратными тригонометрическими функциями 135. Тригонометрические операции. 136. Операции сложения (вычитания). § 3. Обратные тригонометрические операции над тригонометрическими функциями 137.  Функция у = arcsin (sin x). Функция у = arcsin (sin x).138. Функция y = arctg (tg x). Глава XII. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА 139. Уравнение sin х = а. 140. Уравнение cos х = a. 141. Уравнение tg x = a. 142. Уравнение ctg x = a. 143. Некоторые дополнения. § 2. Способ приведения к одной функции одного и того же аргумента 145. Некоторые типы уравнений, приводящихся к уравнениям относительно функции одного аргумента. 146. Способ разложения на множители. 147. Решение рациональных тригонометрических уравнений с помощью универсальной тригонометрической подстановки tg(x/2) = t. § 3. Некоторые частные приемы решения тригонометрических уравнений и систем 148. Введение вспомогательного аргумента. 149. Преобразование произведения в сумму или разность. 150. Переход к функциям удвоенного аргумента. 151. Решение уравнения типа… 152. Применение подстановок sinx ± соsx = y. § 4. Решение тригонометрических неравенств 154. Простейшие тригонометрические неравенства.  155. Примеры тригонометрических неравенств, сводящихся к простейшим. Часть вторая. ГЕОМЕТРИЯ 156. Точка. Прямая. Луч. Отрезок. 157. Плоскость. Фигуры и тела. 160. Равенство фигур. Движение. 161. Равенство тел. § 2. Измерение геометрических величин 162. Сложение отрезков. Длина отрезка. 163. Общая мера двух отрезков. 164. Сравнительная длина отрезков и ломаных. 165. Измерение углов. 166. Радианная мера угла. 167. Измерение площадей. 168. Площадь прямоугольника. Объем прямоугольного параллелепипеда. Глава XIV. ПЕРПЕНДИКУЛЯРНЫЕ И ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. ЗАДАЧИ НА ПОСТРОЕНИЕ 169. Перпендикуляр и наклонные. 170. Свойство перпендикуляра, проведенного к отрезку в его середине. 171. Параллельные прямые. 172. Углы, образованные двумя параллельными прямыми и секущей. 173. Углы с параллельными или перпендикулярными сторонами. § 2. Геометрические места точек. Окружность 174. Геометрическое место точек. 175. Свойство биссектрисы угла.  176. Окружность. 177. Взаимное расположение прямой и окружности. Касательная и секущая. 178. Хорда и диаметр. Сектор и сегмент. 179. Взаимное расположение двух окружностей. § 3. Основные задачи на построение 181. Деление отрезка пополам. Построение перпендикуляров. 182. Построение углов. 183. Другие задачи на построение. Глава XV. ТРЕУГОЛЬНИКИ, ЧЕТЫРЕХУГОЛЬНИКИ 184. Стороны и углы треугольника. 185. Биссектрисы треугольника. Вписанная окружность. 186. Оси симметрии сторон треугольника. Описанная окружность. 187. Медианы и выcоты треугольника. 188. Равенство треугольников. 189. Построение треугольников. 190. Равнобедренные треугольники. 191. Прямоугольные треугольники. § 2. Параллелограммы 192. Четырехугольники. 193. Параллелограмм и его свойства. 194. Прямоугольник. § 3. Трапеция 196. Трапеция. 197. Средняя линия треугольника. 198. Средняя линия трапеции. 199. Деление отрезка на равные части.  § 4. Площади треугольников и четырехугольников 200. Площадь параллелограмма. 201. Площадь треугольника. 202. Площадь трапеции. Глава XVI. ПОДОБИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР 203. Пропорциональные отрезки. 204. Свойства биссектрис внутреннего и внешнего углов треугольника. § 2. Подобное преобразование фигур (гомотетия) 205. Определение гомотетичных фигур. 206. Свойства преобразования подобия. § 3. Общее подобное соответствие фигур 207. Подобные фигуры. 208. Периметры и площади подобных треугольников. 209. Применение подобия к решению задач на построение. Глава XVII. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ И КРУГЕ 210. Углы с вершиной на окружности. 211. Углы с вершиной внутри и вне круга. 212. Угол, под которым виден данный отрезок. 213. Четырехугольники, вписанные в окружность. 214. Пропорциональные отрезки в круге. 215. Задачи на построение. § 2. Метрические соотношения в треугольнике 216. Пропорциональные отрезки в прямоугольном треугольнике.  Теорема Пифагора. Теорема Пифагора.218. Теорема синусов. Формула Герона. 217. Квадрат стороны, лежащей против острого или тупого утла и треугольнике. Теорема косинусов. 218. Теорема синусов. Формула Герона. 219. Радиусы вписанной и описанной окружностей. § 3. Решение треугольников 220. Таблицы функций. 221. Решение треугольников. Сводка основных формул. 222. Решение прямоугольных треугольников. 223. Решение косоугольных треугольников. Глава XVIII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ. ДЛИНА окружности И ПЛОЩАДЬ КРУГА 224. Выпуклые многоугольники. 225. Правильные многоугольники. 226. Соотношения между стороной, радиусом и апофемой. 227. Периметр и площадь правильного n-угольника. 228. Удвоение числа сторон правильного многоугольника. § 2. Длина окружности. Площадь круга и его частей 229. Длина окружности. 230. Площадь круга и его частей. Глава XIX. ПРЯМЫЕ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ 231. Взаимное расположение двух прямых в пространстве.  232. Взаимное расположение прямой линии и плоскости. 233. Взаимное расположение двух плоскостей. 234. Свойства параллельных прямых и плоскостей. 235. Построения в стереометрии. § 2. Перпендикулярность прямых и плоскостей 236. Перпендикуляр к плоскости. 237. Перпендикуляр и наклонные. 238. Угол между прямой и плоскостью. 239. Связь между перпендикулярностью и параллельностью прямых и плоскостей. 240. Общий перпендикуляр двух скрещивающихся прямых. § 3. Двугранные и многогранные углы 241. Двугранный угол. 242. Взаимно перпендикулярные плоскости. 243. Трехгранные углы. 244. Многогранные углы. § 4. Многогранники 245. Многогранники. 246. Правильные многогранники. Глава XX. МНОГОГРАННИКИ И КРУГЛЫЕ ТЕЛА 247. Цилиндры и призмы. 248. Параллелепипеды. 249. Объемы призм и цилиндров. 250. Площадь боковой поверхности призмы. 251. Площадь поверхности цилиндра. § 2. Пирамида. Конус 252. Свойства пирамиды и конуса. 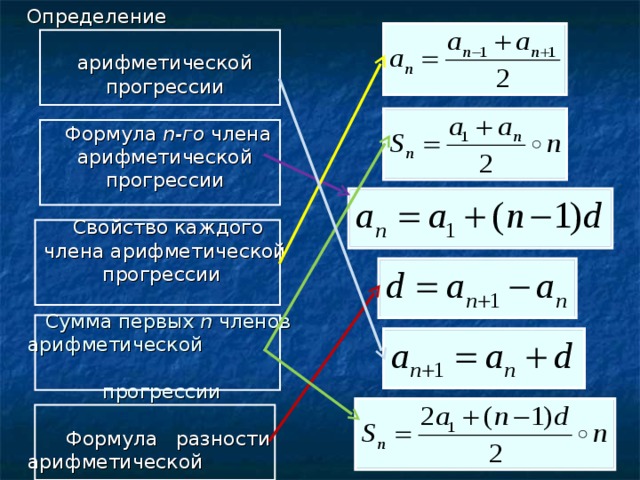 253. Объем пирамиды и конуса. 254. Площадь боковой поверхности правильной пирамиды и конуса. 255. Усеченный конус и усеченная пирамида. § 3. Шаровая поверхность. Шар 256. Шар и шаровая поверхность. 257. Объем шара и его частей. 258. Площадь поверхности шара и ее частей. 259. Понятие телесного угла. Ответы к упражнениям Приложения |
Формула арифметической последовательности — Что такое формула арифметической последовательности? Примеры
Формула арифметической последовательности используется для вычисления члена n th и суммы арифметической прогрессии. Арифметическая последовательность — это последовательность, в которой общая разность между любыми двумя последовательными членами остается постоянной. Если мы хотим найти какой-либо термин/сумму терминов в арифметической последовательности, мы можем использовать формулу арифметической последовательности. Давайте разберемся с формулой арифметической прогрессии на решенных примерах.
Что такое формула арифметической последовательности?
Арифметическая последовательность имеет вид: а, а + d, а + 2d, а + 3d, …… до n членов. Первый член — это а, общая разница — d, n = количество терминов. Для расчета с использованием формул арифметической последовательности сначала определите первый член, количество членов и общую разность последовательности. Существуют различные формулы, связанные с арифметическим рядом, используемым для вычисления члена n th , суммы или общей разности данной арифметической последовательности.
- n й срок есть, а n = а 1 + (n — 1) d
- Сумма n членов равна S n = (n/2) [2a 1 + (n — 1) d] (или) (n/2) [a 1 + a n ]
- Общая разность, d = a n — a n — 1
В этих формулах a 1 = первый член, d = общая разность и n = количество членов.
Арифметическая последовательность Формула
Формулы арифметической последовательности имеют вид 1) d
где,
- a n = n th срок,
- a 1 = первый член и
- d — общая разность
Формула 2: Сумма первых n членов арифметической последовательности вычисляется по одной из следующих формул:
- S n = (n/2) [2a 1 + (n — 1) d] (когда мы знаем первый член и общую разность)
- S n =(n/2) [a 1 + a n ] (при первом и последнем членах)
где,
- S n = сумма n слагаемых,
- a 1 = первый член,
- a n = n th срок и
- d — общая разница между последовательными терминами
Формула 3: Формула для вычисления общей разности арифметической прогрессии имеет вид н -й срок,
Применение формулы арифметической последовательности
Мы используем формулу арифметической прогрессии каждый день или даже каждую минуту, даже не осознавая этого. Ниже приведены несколько примеров практического применения формулы арифметической последовательности
Ниже приведены несколько примеров практического применения формулы арифметической последовательности
- Складывание чашек, стульев, мисок или карточного домика.
- Места на стадионе или в зрительном зале располагаются в арифметической последовательности.
- Секундная стрелка на часах движется в арифметической последовательности, а также минутная и часовая стрелки.
- Недели в месяце следуют арифметической последовательности, как и годы. Каждый високосный год можно определить, прибавив 4 к предыдущему високосному году.
- Количество свечей, задуваемых в день рождения, с каждым годом увеличивается как арифметическая прогрессия.
Cuemath — одна из ведущих мировых платформ для обучения математике, предлагающая онлайн-уроки по математике в режиме реального времени один на один для классов K-12. Наша миссия — изменить то, как дети изучают математику, чтобы помочь им преуспеть в школе и на конкурсных экзаменах. Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Запись на бесплатный пробный урок
Примеры с использованием формулы арифметической последовательности
Пример 1: Используя формулу арифметической последовательности, найдите 13 th член в последовательности 1, 3, 5, 9, 00 100 100 100
Решение:
Найти: 13 -й -й член данной последовательности.
Поскольку разница между последовательными терминами одинакова, данная последовательность образует арифметическую последовательность.
a = 1, d = 4
По формуле арифметической прогрессии 2 а n = 1 + (13 — 1)4
a n = 1 + (12)4
a n = 1 + 48
a n = 49
☛ Также проверьте: Калькулятор арифметической последовательности
Ответ: 13 th член последовательности равен 49. 90 90 4 Пример:
90 90 4 Пример:
900 0 Найдите первый член арифметической прогрессии где 35 -й -й член равен 687, а общая разность 14.
Решение:
Найти: Первый член арифметической прогрессии
Дано: a n = n
4-й 4-й член 14
Используя формулу арифметической последовательности,
a n = a 1 + (n − 1)d
687 = a 1 + (35 — 1)14
106 7 + ( 34)14
687 = a 1 + 476
a 1 = 211
Ответ: Первый член последовательности равен 211. следующей арифметики ряд: 3 + 7 + 11 + ……. (до 25 слагаемых).
Решение:
Найти сумму первых 25 членов арифметической прогрессии 3, 7, 11, …….
Дано: a 1 = 3, d = 4, n = 25
данная арифметическая последовательность равна 3, 7, 11,….
Используя формулу арифметического ряда:
S n = (n/2) [2a + (n — 1) d]
Сумма первых 25 членов
S 25 =(25/2 ) [2 x 3 + (25 — 1) 4]
= (25/2) [6 + 24 x 4]
= 25/2 × 102
= 1275
Ответ: Сумма данного арифметического ряда равна 1275.
Часто задаваемые вопросы о формуле арифметической последовательности
Что такое формула арифметической последовательности в алгебре?
Формула арифметической последовательности относится к формуле для вычисления общего члена арифметической последовательности и суммы n членов арифметической последовательности.
- Общий член арифметической последовательности: a n = a 1 + (n — 1) d
- Сумма первых n членов арифметической прогрессии равна n = (n/2) [2a 1 + (n — 1) d]
где a 1 = первый член и d = общая разность последовательности.
Что такое n в формуле арифметической последовательности?
В формуле арифметической последовательности для нахождения общего термина a n = a 1 + (n — 1) d, ‘n’ относится к номеру термина в данной арифметической последовательности. Например, 2 представляет 2 -й -й член последовательности.
Что такое формула арифметической последовательности для суммы n членов?
Сумма первых n членов арифметической последовательности определяется как S n = (n/2) [2a 1 + (n — 1) d], где S n = сумма n членов , a 1 = первый член, а d — общая разность.
Что такое формула арифметического ряда?
Арифметический ряд есть не что иное, как сумма нескольких или всех членов арифметической прогрессии. Таким образом, формула арифметического ряда:
- S n = (n/2) [2a 1 + (n — 1) d] [ИЛИ]
- S n = (n/2) [a 1 + a n ]
Здесь a 1 — первый член арифметического ряда, а d — его общая разность.
Как использовать формулу арифметической последовательности?
Чтобы использовать формулу арифметической последовательности, сначала определите первый член (a 1 ) и общую разность (d) последовательности. Затем подставьте их в соответствующую формулу (из n -й член или сумма) и упростить.
Затем подставьте их в соответствующую формулу (из n -й член или сумма) и упростить.
В чем разница между явной формулой и рекурсивной формулой арифметической последовательности?
Явная формула используется для нахождения любого члена арифметической прогрессии, если мы знаем только его первый член и общую разность. Но рекурсивная формула может быть использована для нахождения термина только тогда, когда известны его предыдущий термин и общая разность.
- Явная формула для арифметической последовательности: a n = a 1 + (н — 1) д
- Рекурсивная формула для арифметической последовательности: a n = a n — 1 + d
Арифметические и геометрические последовательности
\(\def\d{\displaystyle}
\def\курс{Математика 228}
\ новая команда {\ f} [1] {\ mathfrak # 1}
\ новая команда {\ s} [1] {\ mathscr # 1}
\def\N{\mathbb N}
\def\B{\mathbf{B}}
\def\circleA{(-.5,0) круг (1)}
\ деф \ Z {\ mathbb Z}
\def\circleAlabel{(-1. {-1}}
\def\nrml{\triangleleft}
\ деф \ ст {:}
\ деф \ ~ {\ широкая тильда}
\def\rem{\mathcal R}
\def\sigalg{$\sigma$-алгебра }
\def\Гал{\mbox{Гал}}
\def\iff{\leftrightarrow}
\def\If{\Leftrightarrow}
\ деф \ земля {\ клин}
\def\И{\bigwedge}
\защита\вход{\вход}
\def\AAnd{\d\bigwedge\mkern-18mu\bigwedge}
\def\Ви{\bigvee}
\def\VVee{\d\Vee\mkern-18mu\Vee}
\ деф \ имп {\ стрелка вправо}
\def\Imp{\Rightarrow}
\def\Fi{\Leftarrow}
\def\var{\mbox{var}}
\def\Th{\mbox{Th}}
\защита\вход{\вход}
\def\sat{\mbox{Sat}}
\def\con{\mbox{Con}}
\def\iffmodels{\bmodels\models}
\def\dbland{\bigwedge \!\!\bigwedge}
\def\дом{\mbox{дом}}
\def\rng{\mbox{диапазон}}
\def\isom{\cong}
\DeclareMathOperator{\wgt}{wgt}
\newcommand{\vtx}[2]{узел[заливка,круг,внутренний интервал=0pt, минимальный размер=4pt,метка=#1:#2]{}}
\ новая команда {\ va} [1] {\ vtx {выше} {# 1}}
\ новая команда {\ vb} [1] {\ vtx {ниже} {# 1}}
\ новая команда {\ vr} [1] {\ vtx {право} {# 1}}
\ новая команда {\ vl} [1] {\ vtx {слева} {# 1}}
\renewcommand{\v}{\vtx{выше}{}}
\def\circleA{(-.
{-1}}
\def\nrml{\triangleleft}
\ деф \ ст {:}
\ деф \ ~ {\ широкая тильда}
\def\rem{\mathcal R}
\def\sigalg{$\sigma$-алгебра }
\def\Гал{\mbox{Гал}}
\def\iff{\leftrightarrow}
\def\If{\Leftrightarrow}
\ деф \ земля {\ клин}
\def\И{\bigwedge}
\защита\вход{\вход}
\def\AAnd{\d\bigwedge\mkern-18mu\bigwedge}
\def\Ви{\bigvee}
\def\VVee{\d\Vee\mkern-18mu\Vee}
\ деф \ имп {\ стрелка вправо}
\def\Imp{\Rightarrow}
\def\Fi{\Leftarrow}
\def\var{\mbox{var}}
\def\Th{\mbox{Th}}
\защита\вход{\вход}
\def\sat{\mbox{Sat}}
\def\con{\mbox{Con}}
\def\iffmodels{\bmodels\models}
\def\dbland{\bigwedge \!\!\bigwedge}
\def\дом{\mbox{дом}}
\def\rng{\mbox{диапазон}}
\def\isom{\cong}
\DeclareMathOperator{\wgt}{wgt}
\newcommand{\vtx}[2]{узел[заливка,круг,внутренний интервал=0pt, минимальный размер=4pt,метка=#1:#2]{}}
\ новая команда {\ va} [1] {\ vtx {выше} {# 1}}
\ новая команда {\ vb} [1] {\ vtx {ниже} {# 1}}
\ новая команда {\ vr} [1] {\ vtx {право} {# 1}}
\ новая команда {\ vl} [1] {\ vtx {слева} {# 1}}
\renewcommand{\v}{\vtx{выше}{}}
\def\circleA{(-. 5,0) круг (1)}
\def\circleAlabel{(-1.5,.6) узел[выше]{$A$}}
\def\circleB{(.5,0) круг (1)}
\def\circleBlabel{(1.5,.6) узел[выше]{$B$}}
\def\circleC{(0,-1) круг (1)}
\def\circleClabel{(.5,-2) узел[справа]{$C$}}
\def\twosetbox{(-2,-1.4) прямоугольник (2,1.4)}
\def\threesetbox{(-2.5,-2.4) прямоугольник (2.5,1.4)}
\def\ansfilename{практика-ответы}
\def\shadowprops{{fill=black!50,shadow xshift=0.5ex,shadow yshift=0.5ex,path fading={круг с размытым краем 10 процентов}}}
\ новая команда {\ hexbox} [3] {
\def\x{-cos{30}*\r*#1+cos{30}*#2*\r*2}
\def\y{-\r*#1-sin{30}*\r*#1}
\рисовать (\х,\у) +(90:\r) — +(30:\r) — +(-30:\r) — +(-90:\r) — +(-150:\r) — +(150: \r) — цикл;
\draw (\x,\y) узел{#3};
}
\renewcommand{\bar}{\overline}
\newcommand{\card}[1]{\left| #1 \справа|}
\newcommand{\twoline}[2]{\begin{pmatrix}#1 \\ #2 \end{pmatrix}}
\новая команда{\lt}{<}
\новая команда{\gt}{>}
\newcommand{\amp}{&}
\)
5,0) круг (1)}
\def\circleAlabel{(-1.5,.6) узел[выше]{$A$}}
\def\circleB{(.5,0) круг (1)}
\def\circleBlabel{(1.5,.6) узел[выше]{$B$}}
\def\circleC{(0,-1) круг (1)}
\def\circleClabel{(.5,-2) узел[справа]{$C$}}
\def\twosetbox{(-2,-1.4) прямоугольник (2,1.4)}
\def\threesetbox{(-2.5,-2.4) прямоугольник (2.5,1.4)}
\def\ansfilename{практика-ответы}
\def\shadowprops{{fill=black!50,shadow xshift=0.5ex,shadow yshift=0.5ex,path fading={круг с размытым краем 10 процентов}}}
\ новая команда {\ hexbox} [3] {
\def\x{-cos{30}*\r*#1+cos{30}*#2*\r*2}
\def\y{-\r*#1-sin{30}*\r*#1}
\рисовать (\х,\у) +(90:\r) — +(30:\r) — +(-30:\r) — +(-90:\r) — +(-150:\r) — +(150: \r) — цикл;
\draw (\x,\y) узел{#3};
}
\renewcommand{\bar}{\overline}
\newcommand{\card}[1]{\left| #1 \справа|}
\newcommand{\twoline}[2]{\begin{pmatrix}#1 \\ #2 \end{pmatrix}}
\новая команда{\lt}{<}
\новая команда{\gt}{>}
\newcommand{\amp}{&}
\)
Расследуй!18
Для узоров из точек ниже нарисуйте следующий узор в последовательности. Затем дайте рекурсивное определение и замкнутую формулу для количества точек в \(n\)-м шаблоне.
Затем дайте рекурсивное определение и замкнутую формулу для количества точек в \(n\)-м шаблоне.
Обратимся теперь к вопросу о нахождении замкнутых формул для конкретных типов последовательностей.
Арифметические последовательности
Если члены последовательности отличаются на константу, мы говорим, что последовательность арифметическая . Если начальный член (\(a_0\)) последовательности равен \(a\), а общая разность равна \(d\text{,}\), то мы имеем
Рекурсивное определение: \(a_n = a_{n-1} + d\) с \(a_0 = a\text{.}\)
Замкнутая формула: \(a_n = a + dn\text{.}\)
Откуда мы это знаем? Для рекурсивного определения нам нужно указать \(a_0\text{.}\) Затем нам нужно выразить \(a_n\) в терминах \(a_{n-1}\text{.}\) Если мы вызовем первый член \(a\text{,}\), затем \(a_0 = a\text{.}\) Для рекуррентного отношения по определению арифметической последовательности разница между последовательными терминами является некоторой константой, скажем, \ (d\text{. }\) Итак, \(a_n — a_{n-1} = d\text{,}\) или, другими словами,
}\) Итак, \(a_n — a_{n-1} = d\text{,}\) или, другими словами,
Чтобы найти замкнутую формулу, сначала выпишите последовательность в общем виде:
\начать{выравнивать*} а_0 \амп = а\\ a_1 \amp = a_0 + d = a+d\\ a_2 \amp = a_1 + d = a+d+d = a+2d\\ a_3 \amp = a_2 + d = a+2d+d = a+3d\\ \amp\vdots \конец{выравнивание*}Мы видим, что для нахождения \(n\)-го члена нам нужно начать с \(a\), а затем добавить \(d\) несколько раз. Фактически, добавьте его \(n\) раз. Таким образом, \(a_n = a+dn\text{.}\)
Пример 2.2.1
Найдите рекурсивные определения и замкнутые формулы для приведенных ниже последовательностей. Предположим, что первый указанный термин равен \(a_0\text{.}\)
- \(2, 5, 8, 11, 14, \ldots\text{.}\)
- \(50, 43, 36, 29, \ldots\text{.}\)
Решение
Сначала мы должны проверить, что эти последовательности действительно являются арифметическими, взяв разности последовательных членов. Это покажет общую разницу \(d\text{.}\)
Это покажет общую разницу \(d\text{.}\)
- \(5-2 = 3\text{,}\) \(8-5 = 3\text{,}\) и т. д. Чтобы перейти от каждого термина к следующему, мы добавляем три, так что \(d = 3\text{.}\) Таким образом, рекурсивное определение \(a_n = a_{n-1} + 3\) с \(a_0 = 2\text{.}\) Замкнутая формула \(a_n = 2 + 3n\text{.}\)
Здесь общая разница: \(-7\text{,}\), так как мы прибавляем \(-7\) к 50, чтобы получить 43, и так далее. Таким образом, у нас есть рекурсивное определение \(a_n = a_{n-1} — 7\) с \(a_0 = 50\text{.}\) Замкнутая формула \(a_n = 50 — 7n\text{.} \)
Как насчет таких последовательностей, как \(2, 6, 18, 54, \ldots\text{?}\) Это не арифметика, поскольку разница между терминами непостоянна. Однако отношение 90 475 90 476 между последовательными членами является постоянным. Мы называем такие последовательности 9{п}\текст{.}\)
Пример 2.2.2
Найдите рекурсивную и замкнутую формулу для приведенных ниже последовательностей. Опять же, первый указанный термин равен \(a_0\text{. }\)
}\)
- \(3, 6, 12, 24, 48, \ldots\)
- \(27, 9, 3, 1, 1/3, \ldots\)
Решение
Опять же, мы должны сначала проверить, действительно ли эти последовательности являются геометрическими, на этот раз путем деления каждого члена на его предыдущий член. Предполагая, что это отношение постоянно, мы нашли \(r\text{.}\)
9{п}\текст{.}\)В приведенных выше примерах и формулах мы предполагали, что начальный термин был \(a_0\text{.}\). Если ваша последовательность начинается с \(a_1\text{,}\), вы можете легко найти термин, который было бы \(a_0\) и использовать это в формуле. Например, если мы хотим получить формулу для последовательности \(2, 5, 8,\ldots\) и настаиваем на том, что \(2= a_1\text{,}\), то мы можем найти \(a_0 = -1\) (поскольку последовательность арифметическая с общей разностью 3, имеем \(a_0 + 3 = a_1\)). Тогда замкнутая формула будет \(a_n = -1 + 3n\text{.}\)
Подраздел Суммы арифметических и геометрических последовательностей
¶Расследуй!19
В вашем соседнем продуктовом магазине есть кондитерский автомат, полный Skittles.
Предположим, что автомат для конфет в настоящее время содержит ровно 650 кеглей, и каждый раз, когда кто-то вставляет четвертак, из автомата выходит ровно 7 кеглей.
Сколько кеглей останется в автомате после того, как будут вставлены 20 четвертаков?
Останется ли когда-нибудь в автомате ровно ноль Skittles? Объяснять.
Что, если автомат выдает 7 Skittles первому покупателю, положившему четвертак, 10 — второму, 13 — третьему, 16 — четвертому и т. д. Сколько Skittles выдал автомат после того, как было положено 20 четвертак? в машину?
Что, если автомат выдает 4 кегли первому покупателю, 7 — второму, 12 — третьему, 19 — четвертому и т. д. Сколько кеглей выдал автомат после того, как 20 четвертаков были помещены в автомат?
Посмотрите на последовательность \((T_n)_{n\ge 1}\), которая начинается с \(1, 3, 6, 10, 15,\ldots\text{.}\) Это называется треугольных чисел.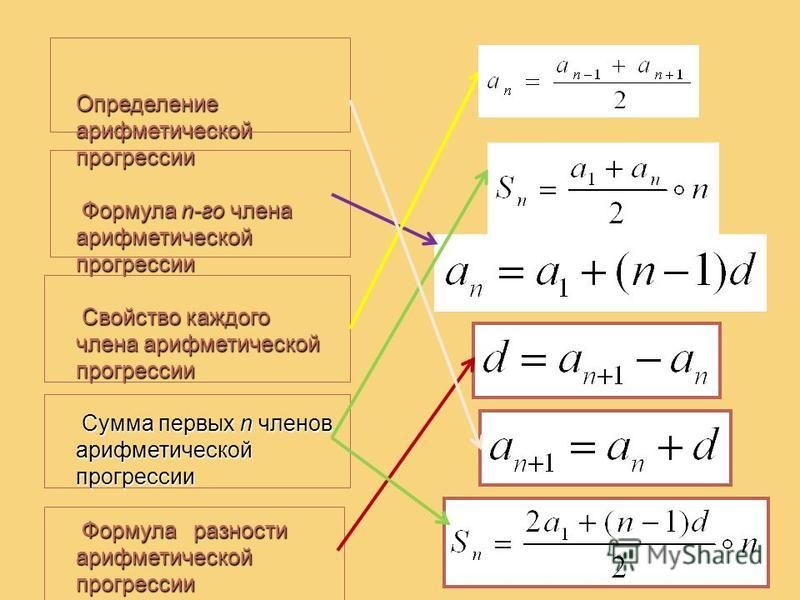 , так как они представляют собой количество точек в равностороннем треугольнике (представьте, как вы расположите 10 кеглей для боулинга: ряд из 4 плюс ряд из 3 плюс ряд из 2 и ряд из 1).
, так как они представляют собой количество точек в равностороннем треугольнике (представьте, как вы расположите 10 кеглей для боулинга: ряд из 4 плюс ряд из 3 плюс ряд из 2 и ряд из 1).
Является ли эта последовательность арифметической? Нет, поскольку \(3-1 = 2\) и \(6-3 = 3 \ne 2\text{,}\) общего различия нет. Является ли последовательность геометрической? Нет. \(3/1 = 3\), но \(6/3 = 2\text{,}\), поэтому общего соотношения нет. Что делать?
Обратите внимание, что различия между терминами образуют арифметическую последовательность: \(2, 3, 4, 5, 6,\ldots\text{.}\) Это говорит о том, что \(n\)-й член последовательности \(1 ,3,6,10,15,\ldots\) — это сумма первых \(n\) членов последовательности \(1,2,3,4,5,\ldots\text{.}\ ) Мы говорим, что первая последовательность — это последовательность 90 437 частичных сумм 90 438 второй последовательности (частичных сумм, потому что мы не берем сумму всех бесконечно многих членов). Если бы мы знали, как складывать члены арифметической последовательности, мы могли бы использовать это, чтобы найти замкнутую формулу для последовательности, разности которой являются членами этой арифметической последовательности.
Это должно стать яснее, если мы напишем треугольные числа так:
\начать{выравнивать*} 1 \амп = 1\\ 3 \амп = 1+2\\ 6 \ампер = 1 + 2 + 3\\ 10 \ампер = 1+2 + 3+ 4\\ \vdots\amp\qquad\vdots\\ T_n \amp = 1 + 2 + 3 + \cdots + n. \конец{выравнивание*}Подумайте, как найти сумму первых 100 положительных целых чисел (то есть \(T_{100}\)). Вместо того, чтобы складывать их по порядку, мы перегруппируем и добавим \(1+100 = 101\text{.}\) Следующая пара для объединения: \(2+99 = 101\text{.}\) Затем \(3+ 98 = 101\text{.}\) Продолжайте. Это дает 50 пар, каждая из которых в сумме дает \(101\text{,}\), поэтому \(T_{100} = 101\cdot 50 = 5050\text{.}\) 1 Это озарение обычно приписывают Карлу Фридриху Гауссу, одному из величайших математиков всех времен, который открыл его еще ребенком, когда его неприятный учитель начальных классов решил, что он займет класс, заставив их вычислить длинную сумму.
В общем случае, используя такую же перегруппировку, мы находим, что \(T_n = \frac{n(n+1)}{2}\text{. }\) Между прочим, это в точности то же самое, что и \({n +1 \выберите 2}\text{,}\), что имеет смысл, если вы думаете о треугольных числах как о подсчете количества рукопожатий на вечеринке с \(n+1\) людьми: первый человек пожимает \ (n\) рук, следующий пожимает еще \(n-1\) рук и так далее.
}\) Между прочим, это в точности то же самое, что и \({n +1 \выберите 2}\text{,}\), что имеет смысл, если вы думаете о треугольных числах как о подсчете количества рукопожатий на вечеринке с \(n+1\) людьми: первый человек пожимает \ (n\) рук, следующий пожимает еще \(n-1\) рук и так далее.
Суть всего этого в том, что некоторые последовательности, хотя и не являются арифметическими или геометрическими, могут быть интерпретированы как последовательности частичных сумм арифметических и геометрических последовательностей. К счастью, есть методы, которые мы можем использовать для быстрого вычисления этих сумм.
Подподраздел Суммирование арифметических последовательностей: реверс и сложение
¶Вот метод, который позволяет нам быстро найти сумму арифметической последовательности.
Пример 2.2.4
Найдите сумму: \(2 + 5 + 8 + 11 + 14 + \cdots + 470\text{.}\)
Решение
Идея состоит в том, чтобы подражать тому, как мы нашли формулу для треугольных чисел.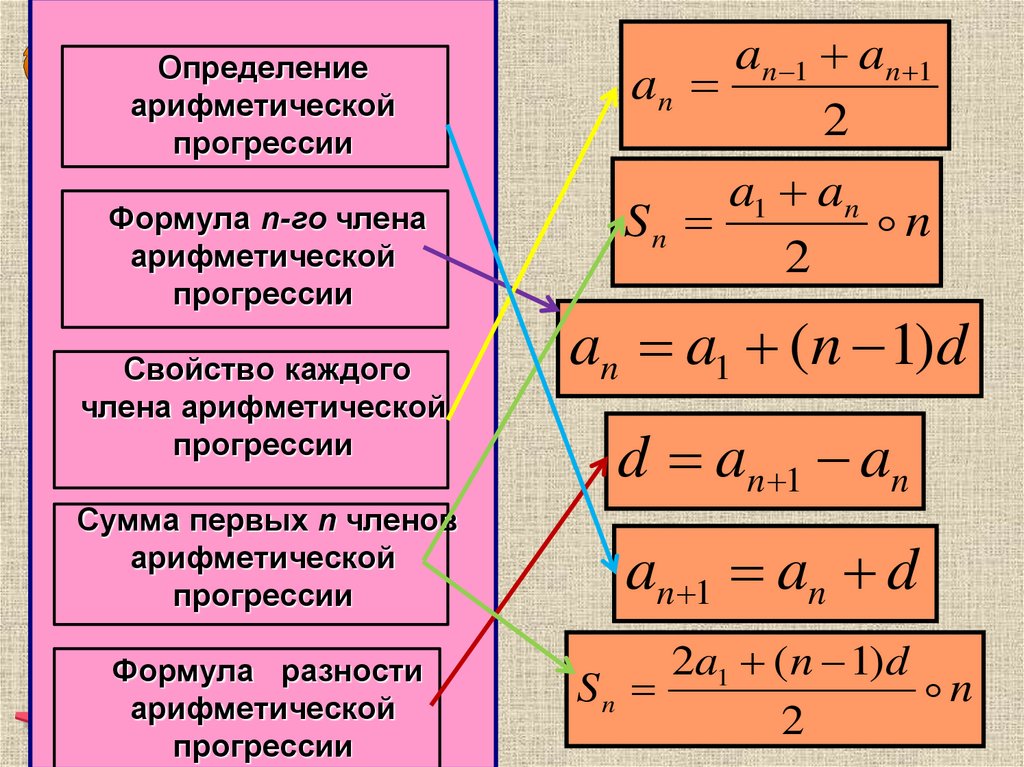 Если мы сложим первый и последний члены, мы получим 472. Второй член и предпоследний член также в сумме дают 472. Чтобы отслеживать все, мы могли бы выразить это следующим образом. Вызовите сумму \(S\text{.}\) Затем
Если мы сложим первый и последний члены, мы получим 472. Второй член и предпоследний член также в сумме дают 472. Чтобы отслеживать все, мы могли бы выразить это следующим образом. Вызовите сумму \(S\text{.}\) Затем
| \(S =\) | \(2\) | \(+\) | \(5\) | \(+\) | \(8\) | \(+ \cdots +\) | \(467\) | \(+\) | 470 |
| \(+ \quad S =\) | \(470\) | \(+\) | \(467\) | \(+\) | \(464\) | \(+ \cdots +\) | \(5\) | \(+\) | 2 |
| \(2S =\) | \(472\) | \(+\) | \(472\) | \(+\) | \(472\) | \(+ \cdots +\) | \(472\) | \(+\) | \(472\) |
Чтобы найти \(2S\), мы прибавляем 472 к самому себе несколько раз. Какой номер? Нам нужно решить, сколько слагаемых ( слагаемых ) в сумме. Поскольку термины образуют арифметическую последовательность, \(n\)-й член в сумме (считая \(2\) как 0-й член) может быть выражен как \(2 + 3n\text{.}\) Если \( 2 + 3n = 470\), тогда \(n = 156\text{.}\) Таким образом, \(n\) находится в диапазоне от 0 до 156, что дает в сумме 157 членов. Это число 472 в сумме для \(2S\text{.}\) Таким образом,
Поскольку термины образуют арифметическую последовательность, \(n\)-й член в сумме (считая \(2\) как 0-й член) может быть выражен как \(2 + 3n\text{.}\) Если \( 2 + 3n = 470\), тогда \(n = 156\text{.}\) Таким образом, \(n\) находится в диапазоне от 0 до 156, что дает в сумме 157 членов. Это число 472 в сумме для \(2S\text{.}\) Таким образом,
\begin{уравнение*} 2S = 157\cdot 472 = 74104 \end{уравнение*}
Теперь легко найти \(S\text{:}\)
\begin{уравнение*} S = 74104/2 = 37052 \end{уравнение*}
Это будет работать для любой суммы арифметических последовательностей. Вызовите сумму \(S\text{.}\) в обратном порядке и добавьте. Это дает одно число, добавленное к самому себе много раз. Найдите количество раз. Умножить. Разделить на 2. Готово.
Пример 2.2.5
Найдите замкнутую формулу для \(6 + 10 + 14 + \cdots + (4n — 2)\text{.}\)
Решение
Опять у нас есть сумма арифметической прогрессии. Нам нужно знать, сколько членов в последовательности. Ясно, что каждый член последовательности имеет вид \(4k — 2\) (о чем свидетельствует последний член). Но для каких значений \(k\)? Чтобы получить 6, \(k = 2\text{.}\) Чтобы получить \(4n-2\), возьмите \(k = n\text{.}\) Итак, чтобы найти количество терминов, нам нужно знать сколько целых чисел находится в диапазоне \(2,3,\ldots, n\text{.}\) Ответ: \(n-1\text{.}\) (есть \(n\) чисел от 1 в \(n\text{,}\), так что на единицу меньше, если мы начнем с 2.)
Нам нужно знать, сколько членов в последовательности. Ясно, что каждый член последовательности имеет вид \(4k — 2\) (о чем свидетельствует последний член). Но для каких значений \(k\)? Чтобы получить 6, \(k = 2\text{.}\) Чтобы получить \(4n-2\), возьмите \(k = n\text{.}\) Итак, чтобы найти количество терминов, нам нужно знать сколько целых чисел находится в диапазоне \(2,3,\ldots, n\text{.}\) Ответ: \(n-1\text{.}\) (есть \(n\) чисел от 1 в \(n\text{,}\), так что на единицу меньше, если мы начнем с 2.)
Теперь переверните и добавьте:
| \(S =\) | \(6\) | \(+\) | \(10\) | \(+ \cdots +\) | \(4н-6\) | \(+\) | \(4н-2\) |
| \(+ \quad S =\) | \(4н-2\) | \(+\) | \(4н-6\) | \(+ \cdots +\) | \(10\) | \(+\) | 6 |
| \(2S =\) | \(4n+4\) | \(+\) | \(4n+4\) | \(+ \cdots +\) | \(4n+4\) | \(+\) | \(4n+4\) |
Так как членов \(n-2\), мы получаем
\begin{уравнение*} 2S = (n-2)(4n+4)\qquad \mbox{ так} \qquad S = \frac{(n-2)(4n+4)}{2} \end{уравнение*}
Помимо нахождения сумм, мы можем использовать эту технику для нахождения закрытых формул для последовательностей, которые мы распознаем как последовательности частичных сумм.
Пример 2.2.6
Используйте частичные суммы, чтобы найти замкнутую формулу для \((a_n)_{n\ge 0}\), которая начинается с \(2, 3, 7, 14, 24, 37,\ldots \ldots\)
Решение
Во-первых, если вы посмотрите на различия между терминами, вы получите последовательность различий: \(1,4,7,10,13, \ldots\text{,}\), которая является арифметической последовательностью. Написано по-другому:
\начать{выравнивать*} а_0 \ампер = 2\\ a_1 \амп = 2+1\\ a_2 \amp = 2+1+4\\ а_3 \амп = 2+1+4+7 \конец{выравнивание*}
и так далее. Мы можем записать общий член \((a_n)\) в терминах арифметической последовательности следующим образом:
\begin{уравнение*} a_n = 2 + 1 + 4 + 7 + 10 + \cdots + (1 + 3 (n-1)) \end{уравнение*}
(мы используем \(1+3(n-1)\) вместо \(1+3n\), чтобы правильно выровнять индексы; для \(a_3\) мы добавляем 7, что равно \ (1+3(3-1)\)).
Мы можем перевернуть и сложить, но начальная 2 не соответствует нашему шаблону. Это просто означает, что нам нужно убрать 2 из обратной части:
Это просто означает, что нам нужно убрать 2 из обратной части:
| \(a_n =\) | \(2\) | \(+\) | \(1\) | \(+\) | \(4\) | \(+ \cdots +\) | \(1+3(n-1)\) |
| \(+ ~ a_n =\) | \(2\) | \(+\) | \(1+3(n-1)\) | \(+\) | \(1+3(n-2)\) | \(+ \cdots +\) | \(1\) |
| \(2a_n =\) | \(4\) | \(+\) | \(2+3(n-1)\) | \(+\) | \(2+3(n-1)\) | \(+ \cdots +\) | \(2+3(n-1)\) |
Не считая первого члена (4), есть \(n\) слагаемых \(2+3(n-1) = 3n-1\), поэтому правая часть становится \(2+( 3n-1)n\text{.}\)
Наконец, найдя \(a_n\), мы получим
\begin{уравнение*} a_n = \d \frac{4+(3n-1)n}{2}. \end{уравнение*}
На всякий случай проверяем \(a_0 = \frac{4}{2} = 2\text{,}\) \(a_1 = \frac{4+2}{2} = 3\text{, }\) и т. д. Имеем правильную замкнутую формулу.
д. Имеем правильную замкнутую формулу.
Подподраздел Суммирование геометрических последовательностей: умножение, сдвиг и вычитание
¶Чтобы найти сумму геометрической последовательности, мы не можем просто поменять местами и сложить. Вы понимаете, почему? Причина, по которой один и тот же термин добавлялся сам к себе много раз, заключается в том, что существовала постоянная разница. Таким образом, когда мы добавили эту разницу в одном направлении, мы вычли разницу в другом направлении, оставив постоянную сумму. Для геометрических сумм у нас есть другая техника.
Пример 2.2.7
Что такое \(3 + 6 + 12 + 24 + \cdots + 12288\text{?}\)
Решение
Умножьте каждый член на 2, обыкновенный коэффициент. Вы получаете \(2S = 6 + 12 + 24 + \cdots + 24576\text{.}\) Теперь вычтите: \(2S — S = -3 + 24576 = 24573\text{.}\) Так как \(2S — S = S\text{,}\) у нас есть ответ.
Чтобы лучше понять, что произошло в приведенном выше примере, попробуйте записать его так:
| \(S=\) | \(3\, +\) | \(6 + 12 + 24 + \cdots + 12288\) | |
| \(-~2S=\) | \(6 + 12 + 24 + \cdots + 12288\) | \(+ 24576\) | |
| \(-S = \) | \(3\, +\) | \(0 + 0 + 0 + \cdots + 0 \) | \(-24576\) |
Затем разделите обе части на \(-1\), и мы получим тот же результат для \(S\text{.}\) Идея состоит в том, что при умножении суммы на обыкновенное отношение каждый член становится следующим термином. Мы сдвигаем сумму, чтобы вычитание в основном сокращалось, оставляя только первый член и новый последний член. 9{n+1}}{-4}\)
Хотя это может показаться новой техникой, вы, вероятно, использовали ее раньше.
Пример 2.2.9
Выразите \(0,464646\ldotts\) в виде дроби.
Решение
Пусть \(N = 0,46464646\ldots\text{. }\) Рассмотрим \(0,01N\text{.}\) Получим:
}\) Рассмотрим \(0,01N\text{.}\) Получим:
| \(Н=\) | \(0,4646464\ldotts\) | |
| \(-\) | \(0,01Н =\) | \(0,00464646\ldotts\) |
| \(0,99Н =\) | \(0,46\) |
Итак, \(N = \frac{46}{99}\text{.}\) Что мы сделали? Мы рассматривали повторяющуюся десятичную дробь \(0,464646\ldots\) как сумму геометрической последовательности \(0,46, 0,0046, 0,000046, \ldots\). Обычное отношение равно \(0,01\text{.}\). Единственная реальная разница что мы сейчас вычисляем бесконечную геометрическую сумму , у нас нет дополнительного «последнего» члена для рассмотрения. На самом деле, это результат ограничения, как если бы вы вычисляли 9 в математических вычислениях.n k = n!\text{.}\)
ПодразделУпражнения
¶1
Рассмотрим последовательность \(5, 9, 13, 17, 21, \ldots\) с \(a_1 = 5\)
Дайте рекурсивное определение последовательности.

Приведите замкнутую формулу для \(n\)-го члена последовательности.
Является ли \(2013\) членом последовательности? Объяснять.
Сколько членов содержит последовательность \(5, 9, 13, 17, 21, \ldots, 533\)?
9{th}\) член \(1, 6, 15, 28, 45, \ldots\text{,}\), где \(b_0 = 1\)
Решение
- \(a_n = a_{n-1} + 4\) с \(a_1 = 5\text{.}\)
- \(a_n = 5 + 4(n-1)\text{.}\)
Да, поскольку \(2013 = 5 + 4(503-1)\) (так что \(a_{503} = 2013\)).
133
- \(\frac{538\cdot 133}{2} = 35777\text{.}\)
- \(b_n = 1 + \frac{(4n+6)n}{2}\text{.}\)
2
Рассмотрим последовательность \((a_n)_{n \ge 0}\), которая начинается с \(8, 14, 20, 26, \ldots\text{.}\) 9{99}a_k\text{.}\)
Решение
\(32\text{,}\), что равно \(26+6\text{.
 }\)
}\)- \(a_n = 8 + 6n\text{.}\)
- \(30500\text{.}\) Мы хотим \(8 + 14 + \cdots + 602\text{.}\) Перевернуть и сложить, чтобы получить 100 сумм 610, всего 61000, что в два раза больше суммы мы ищем.
3
Рассмотрим сумму \(4 + 11 + 18 + 25 + \cdots + 249\text{.}\)
Сколько членов (слагаемых) в сумме?
Подсчитать сумму. Не забудьте показать все свои работы.
Раствор
36.
- \(\frac{253 \cdot 36}{2} = 4554\text{.}\)
4
Рассмотрим последовательность \(1, 7, 13, 19, \ldots, 6n + 7\text{.}\)
Сколько элементов в последовательности?
Какой предпоследний член?
Найдите сумму всех членов последовательности.
Решение
- \(n+2\) членов, так как для получения 1 по формуле \(6n+7\) мы должны использовать \(n=-1\text{.
 }\) Таким образом, мы имеем \( n\) слагаемых плюс слагаемые \(n=0\) и \(n=-1\).
}\) Таким образом, мы имеем \( n\) слагаемых плюс слагаемые \(n=0\) и \(n=-1\). - \(6n+1\text{,}\), что на 6 меньше, чем \(6n+7\) (или подставьте \(n-1\) вместо \(n\)).
- \(\frac{(6n+8)(n+2)}{2}\text{.}\) Перевернуть и добавить. Каждая сумма дает константу \(6n+8\) и есть \(n+2\) терминов.
5
Найти \(5 + 7 + 9 + 11+ \cdots + 521\text{.}\) 9{30}}\text{.}\)
8
Найдите \(x\) и \(y\) такие, что \(27, x, y, 1\) является частью арифметической прогрессии. Затем найдите \(x\) и \(y\) так, чтобы последовательность была частью геометрической прогрессии. (Предупреждение: \(x\) и \(y\) могут быть не целыми числами.)
9
Начав с любого прямоугольника, мы можем создать новый, больший прямоугольник, присоединив квадрат к более длинной стороне. Например, если мы начнем с прямоугольника \(2\x 5\), мы склеим квадрат \(5\x 5\), сформировав прямоугольник \(5 \x 7\):
Создайте последовательность прямоугольников, используя это правило, начиная с прямоугольника \(1\times 2\).
 Затем выпишите последовательность периметров для прямоугольников (первый член последовательности будет равен 6, так как периметр прямоугольника \(1\times 2\) равен 6 — следующий член будет равен 10).
Затем выпишите последовательность периметров для прямоугольников (первый член последовательности будет равен 6, так как периметр прямоугольника \(1\times 2\) равен 6 — следующий член будет равен 10).На этот раз повторите описанную выше часть, начиная с прямоугольника \(1 \times 3\).
Найдите рекурсивные формулы для каждой из последовательностей периметров, которые вы нашли в частях (a) и (b). Не забудьте также указать начальные условия.
Являются ли последовательности арифметическими? Геометрический? Если нет, то являются ли они близкими к любому из этих (т. е. являются ли разности или отношения почти постоянными)? Объяснять.
10
Рассмотрим последовательность \(2, 7, 15, 26, 40, 57, \ldots\) (где \(a_0 = 2\)). Глядя на различия между членами, представить последовательность как последовательность частичных сумм. Затем найдите замкнутую формулу последовательности, вычислив \(n\)-ю частичную сумму.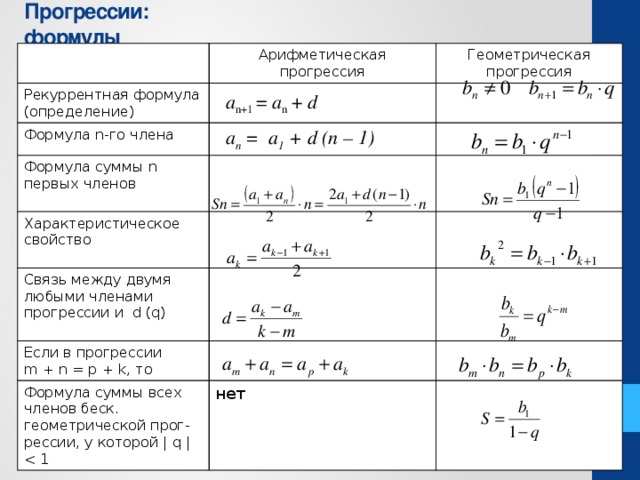 9n (2+3k)\text{.}\) Чтобы найти замкнутую формулу, мы обращаем и складываем. Получаем \(a_n = \frac{(4+3n)(n+1)}{2}\) (там у нас \(n+1\), потому что в сумме есть \(n+1\) членов для\)).
9n (2+3k)\text{.}\) Чтобы найти замкнутую формулу, мы обращаем и складываем. Получаем \(a_n = \frac{(4+3n)(n+1)}{2}\) (там у нас \(n+1\), потому что в сумме есть \(n+1\) членов для\)).
11
Если у вас достаточно зубочисток, вы можете сделать большую треугольную сетку. Ниже представлены треугольные сетки размера 1 и размера 2. Для сетки размера 1 требуется 3 зубочистки, для сетки размера 2 требуется 9 зубочисток.
Пусть \(t_n\) будет количеством зубочисток, необходимых для создания треугольной сетки размером \(n\). Выпишите первые 5 членов последовательности \(t_1, t_2, \ldots\text{.}\)
Найдите рекурсивное определение последовательности. Объясните, почему вы правы.
Является ли последовательность арифметической или геометрической? Если нет, то это последовательность частичных сумм арифметической или геометрической прогрессии? Объясните, почему ваш ответ правильный.
Используйте результаты из части (c), чтобы найти замкнутую формулу для последовательности.

Калькулятор решение систем уравнений методом крамера: Онлайн калькулятор. Решение систем линейных уравнений. Метод Крамера
code golf — Решение систем уравнений с использованием правила Крамера
спросил
Изменено 7 лет, 4 месяца назад
Просмотрено 5к раз
\$\начало группы\$
Создайте алгоритм, использующий правило Крамера (с определителями матриц) для решения системы линейных уравнений. Код должен работать для «n» переменных.
Вы можете использовать любую структуру данных для хранения матрицы и возврата результата
Примечание: Также учтите, что возможная система может не иметь решений и может иметь бесконечно много решений 🙂 🙂 , поэтому, ваше решение должно учитывать это…
Если это так, просто распечатайте или верните «нет» или «бесконечно много».
Так как это код-гольф, побеждает наименьший код…
РЕДАКТИРОВАТЬ : Чтобы сделать это более сложным, вы не можете использовать встроенные в язык библиотеки матричных операций.
Кроме того, ваш алгоритм НЕ должен иметь дело с тем, как получить ввод, только как обработать ввод и вернуть правильный вывод. Как было сказано ранее, вы можете хранить этот ввод в любой структуре.
- код-гольф
- математика
\$\конечная группа\$
2
\$\начало группы\$
Mathematica 40
Постановка задачи по ссылке:
с = {{2, 1, 1}, {1, -1, -1}, {1, 1, 1}};
г = {3, 0, 0};
Алгоритм (пробелы не нужны):
i = 1; (a = s; a[[All, i++]] = r; Det@a/Det@s) & /@ r
результат:
{1, -2, 3}
Если система имеет бесконечные решения, она возвращает Indetermined или ComplexInfinite
Обратите внимание, что Mathematica может решать линейные системы изначально. Среди других возможных способов вы можете использовать:
Среди других возможных способов вы можете использовать:
s~LinearSolve~r
или
Решить[s.{x,y,z}==r]
\$\конечная группа\$
1
\$\начало группы\$
Python3 — 310
по определению (m,n): если n==1: вернуть m[0][0] г=0 для r в диапазоне (n): к=м[:] дель к[р] z+=m[r][0]*(-1)**r*det([p[1:]для p в k],n-1) вернуть Z ш = длина (т) д = дет (ч, ш) если д==0:г=[] else:r=[det([r[0:i]+[s]+r[i+1:]для r,s в zip(h,t)],w)/d для i в диапазоне(w) ] печать (р)
Определитель вычисляется по формуле Лапласа, ничего особенного 🙂
Поместите матрицу и известные члены соответственно в массив с именами h и t, например:
h = [[2, 1, 1],[1, -1, -1],[1, 2, 1]] л = [3, 0, 0]
Что дает
[1.0, -2.0, 3.0]
\$\конечная группа\$
\$\начало группы\$
Я не уверен, какие части программы учитываются при подсчете баллов? (В настоящее время считается только алгоритм, как это сделал @belisarius. ) 9i*a(1,i)*d([a(w,1:i-1),a(w,i+1:конец)])
конец
конец
%%основной
для я = 1: число (б)
с=а
с(:,я)=б
х(я)=d(с)/d(а)
конец
%выход
если есть (isinf (d))
«нет решений»
иначе ~d(а)
«бесконечные решения»
конец
Икс
) 9i*a(1,i)*d([a(w,1:i-1),a(w,i+1:конец)])
конец
конец
%%основной
для я = 1: число (б)
с=а
с(:,я)=б
х(я)=d(с)/d(а)
конец
%выход
если есть (isinf (d))
«нет решений»
иначе ~d(а)
«бесконечные решения»
конец
Икс
Matlab, конечно, может решать линейные системы изначально:
a\b
\$\конечная группа\$
3
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Технологический центр DuPage — Решение систем уравнений
в электронике и технике. Например, при использовании Законы Кирхгофа (KCL и KVL) для анализа цепи вы в конечном итоге придёте к системе уравнений контура надо решить за ТОКИ I 1 и I 2 . Эти два неизвестных решение для сети, созданной Кирхгофом Законы.
Ссылки на Кирхгофа Законы
Кирхгофа Закон о напряжении
- Активный Эксперимент 1
- Активный Эксперимент 2
- Активный Эксперимент 3
- Активный Эксперимент 4
- Активный Эксперимент 5
Согласно диаграммам справа СУММА
Условия напряжения в петлях должны быть НУЛЕВЫМИ. Шаги к решению уравнений закона Кирхгофа. 1. Рассматривайте каждую петлю как отдельное уравнение с I 1 & I 2 как переменные для решения. 2. Решить одновременные уравнения относительно неизвестной количества. я 1 и I 2 Решение для переменных описано ниже. |
Цикл 1 — Цикл 2 = 0 |
Система уравнений имеет одно решение. Этот
решение представляет собой набор упорядоченных пар вида (x, y), которые
удовлетворяет двум или более уравнениям. Система уравнений
обычно имеет (стандартную) форму. Это полезно
расположить (переписать уравнения системы) так, чтобы
стандартная форма:
Этот
решение представляет собой набор упорядоченных пар вида (x, y), которые
удовлетворяет двум или более уравнениям. Система уравнений
обычно имеет (стандартную) форму. Это полезно
расположить (переписать уравнения системы) так, чтобы
стандартная форма:
AX + BY = C
DX + EY = F
и одна упорядоченная пара (x,y) удовлетворяет этим двум уравнения.
Или в электронике
А I 1 + B I 2 =
C
D I 1 + E I 2 =
Ф
и одна заказанная пара ( I 1 , I 2 ) удовлетворяет эти два уравнения.
Пример:
Уравнение 1. |
Используя пример, мы хотим найти способ сделать коэффициент либо I 1 либо я 2 равны, чтобы мы могли изолировать другую переменную и решить для нее. Попробуйте умножить целиком Уравнение 1. на «3», так что у нас есть
Уравнение 1.
) (3)3 I 1 + (3) I 2 =
(3)14 |
Уравнение 1.
) 9 I 1 + 3 I 2 =
42 |
7 I 1 = 35
и так,
I 1 = 5
Вставьте этот I 1 = 5 обратно в
либо уравнение 1 или уравнение 2 и тогда вы сможете решить для
X.
Подставим в уравнение. 2.
Уравнение 2. ) 2 I 1 +
3 I 2 = 7 |
Интерактивный
Решатель для I 1 и I 2
Уравнение 1. |
I 1 + I 2 =
I 1 + I 2 =
I 1 = | |
I 2 = |
топ
Системы уравнений относительно x и y и СОЛВЕР
Система уравнений имеет одно решение. Этот
решение представляет собой набор упорядоченных пар вида (x, y), которые
удовлетворяет двум или более уравнениям. Система уравнений
обычно имеет (стандартную) форму. Это полезно
расположить (переписать уравнения системы) так, чтобы
стандартная форма:
Этот
решение представляет собой набор упорядоченных пар вида (x, y), которые
удовлетворяет двум или более уравнениям. Система уравнений
обычно имеет (стандартную) форму. Это полезно
расположить (переписать уравнения системы) так, чтобы
стандартная форма:
AX + BY = C
DX + EY = F
и одна упорядоченная пара (x,y) удовлетворяет этим двум уравнения.
Одним из способов решения этой системы уравнений является построение графика оба уравнения (не забудьте установить y = уравнение) и обратите внимание на пересечение линий, которые нанесены на график. Этот точка пересечения — это упорядоченная пара, представляющая решение.
Вы можете попробовать это вручную на бумаге или с помощью графика.
утилита, такая как графический калькулятор, или даже доступный инструмент
В интернете.
Попробуйте этот пример, изобразив его в виде графика:
Уравнение 1. ) X+ 2Y = 10 |
Используя тот же пример:
Уравнение 1. ) X+ 2Y = 10 |
Попробуйте умножить все уравнение 1. на «2», чтобы мы есть
Уравнение 1. |
Уравнение 1. ) 2X+ 4Y = 20 |
5Г = 10 |
Уравнение 2. ) 2X — Y = 10 |
Попробуйте численно, введя значения здесь (не забудьте поставить «-» для отрицательного знака.
 ), а затем нажмите
Кнопка «Решить».
), а затем нажмите
Кнопка «Решить».Х + Д =
Х + Д =
х = | |
Д = |
Решатель: просто Введите значения коэффициента и нажмите решить
Х + Д =
Х + Д =
х = | |
Д = |
Матрицы и правило Крамера для решения Система уравнений
Решения систем уравнений вида
AX + BY = C
DX + EY = F
Можно найти с помощью далее:
Х = Д =
(AE — BD)
(AE – BD)
Этот метод получен из определителей матриц которое можно составить из системы уравнений
Напомним, что матрица A имеет вид
[А] = | | а | б | |
| с | д | |

a*d — c * b = определитель A
Решить систему вида
AX + BY = C
DX + EY = F
1.) Найдите определители следующие матрицы.
[А] = | | а | б | |
| д | е | |
[А х ] = | | с | б | |
| ф | е | |
[А и ] = | | а | с | |
| д | ф | |
2.
Замени двойное неравенство двумя неравенствами 9 x 18: ГДЗ учебник по математике 4 класс Петерсон. 4 урок. Двойное неравенство Номер 3
Этапы урока, содержание (задания) | Время | Деятельность учителя (описание, прямая речь) | Деятельность учащихся (описание, предполагаемые ответы) | Формы, методы и приемы обучения | Формируемые УУД |
1. Организационный момент. | 1 мин. | Приветствует учащихся. Проверяет готовность к уроку. Проверьте, чтобы у вас на партах был учебник и рабочая тетрадь. Начинается урок, | Приветствуют учителя. | Словесный (беседа) | КУУД – вступать в диалог с учителем |
2. Актуализация знаний. | 5 мин. | Повторение Давайте проверим ваши знания с прошлых уроков. Что такое неравенство? Что мы называем множеством решений неравенства? Давайте вспомним, какие виды решений неравенства существуют. Множество решений, бесконечное множество решений и пустое множество решений. — Что значит пустое множество? Теперь я вам представлю три неравенства, скажите в каком неравенстве множество решений, в каком бесконечное множество решений, а в каком пустое множество решений? B+5 10Y a 200 Запиши неравенства. Я буду говорить неравенства словами, а вы будете записывать его цифрами. а) 15 меньше или равно 34 б) 72 больше или равно 27 в) 37 больше 22 г) 46 меньше 92 д) 55 = 55 Какие знаки используются при решении неравенств? Молодцы! | Внимательно слушают учителя. Отвечают на вопросы. -выражение, показывающее, что одна величина больше или меньше другой — Пустое множество Во множестве нет элементов. — множество решений — пустое множество решений — бесконечное множество решений Слушают учителя. Выполняют задание. Выходят к доске желающие и записывают неравенства под диктовку. — Используются знаки «», «=» и «≤», и «≥». | Словесный (беседа, рассказ), наглядный (доска, рабочая тетрадь), практический (работа у доски, в тетради; ответы на вопросы) Фронтальная работа | КУУД – формулировать собственное мнение, вступать в диалог с учителем, учитывать мнение других; РУУД – принимать и сохранять учебную задачу, планировать свои действия; ЛУУД – интерес к новому содержанию; ПУУД — анализировать информацию, выбирать рациональный способ решения задачи. |
3. Целеполагание. | 3 мин. | Давайте запишем число и классная работа. Обратите внимание, сейчас я запишу на доске выражение : 5 Ребята, а что я записала? А что в нем не так? Правильно, ребята! Как вы думаете, как называются такие неравенства, в которых два знака? Кто сможет назвать тему нашего урока? Правильно. Мы будем говорить о двойном неравенстве. | Слушают учителя. Отвечают на вопросы учителя: — Неравенство. — В нем два знака неравенства. — Двойное; — Сложное. — Двойное неравенство. | Словесный (беседа), наглядный (интерактивная доска) | КУУД – формулировать собственное мнение; РУУД – принимать и сохранять учебную задачу, умение формулировать тему и цель урока; ПУУД — находить сходства, различия, закономерности. |
4. Изучение нового материала. | 10 – 12 минут | Ознакомляет с новым материалом с помощью практической работы. Откройте учебник на странице 10. Давайте прочитаем 1 задание. Я читаю, слушайте внимательно. О чем говорится в задании? Отметьте на числовом луче эти числа. Какие это числа? Назовите их. Правильно. Напишите карандашиком в учебнике эти числа. Как вы думаете, как можно записать это множество с помощью знаков неравенства? Числа 4, 5, 6 можно заменить буквой х, то есть она будет обозначать числа от 4 до 6. Это будет выглядеть так: 3 Запишите себе это неравенство в тетрадь. Теперь давайте, ознакомимся с правилом в учебнике в рамочке. Я читаю, вы слушаете. Прочитайте каждый про себя данное правило. — Кто может объяснить: Что такое двойное неравенство? Почему неравенство называется двойным? Как читают двойное неравенство, например, из нашего правила. Какие числа будут являться решением неравенства? Почему именно эти числа? Правильно. Обратите внимание на линейку, мы видим, что нам нужны числа больше 5, но меньше 10. Еще раз назовите эти числа. А что происходит, если в записи двойного неравенства используется, к примеру, знак «больше или равно»? Да, конечно. Обратите внимание на двойные неравенства, что мы видим? Молодцы! | Открывают учебник на нужной странице и внимательно слушают чтение задания учителя. — Нам нужно отметить на числовом луче множество чисел, которые одновременно больше 3 и меньше 7. — Отмечают числа. — 4, 5, 6. — 3 — 3 Слушают учителя и записывают выражение в тетрадь. Учащиеся смотрят на страницу 10 и слушают правило, прочтенное учителем. Далее читают каждый про себя данное правило. — Например, арбуз. В правиле сказано, что он тяжелее одной 5-килограммовой гири, но легче двух таких гирь. Как показано на картинке. — Потому что в нем объединили два неравенства. — х больше пяти и меньше десяти. — 6, 7, 8, 9. Потому что они входят в промежуток между числами 5 и 10. Смотрят на линейку в правиле и отвечают: 6, 7, 8, 9. — Множество решений расширяется. — Что когда появляется знак «меньше или равно», то число, которое меньше, тоже входит во множество решений данного неравенства. | Словесный (беседа, рассказ, рассуждение), наглядный (учебник, доска, презентация), практический (выполнение заданий по новому материалу | КУУД – вступать в диалог с учителем и одноклассниками, формулировать собственное мнение, учитывать мнение других; РУУД – принимать и сохранять учебную задачу, планировать этапы решения задачи; ПУУД — анализировать информацию, выбирать рациональный способ решения задачи; — устанавливать зависимости, соотношения между объектами в процессе наблюдения и сравнения; — находить сходства, различия, закономерности; ЛУУД – интерес к новому содержанию. |
5. Физическая минутка. | 1 – 2 мин. | Учитель показывает движения со словами: Поворот, наклон, прыжок, Улыбнись давай, дружок. Еще попрыгай: раз, два, три! На соседа посмотри, Руки вверх и тут же вниз И за парту вновь садись. Мульдимедийная презентация Организует выполнение гимнастики для глаз | Повторяют движения за учителем под стихотворение. Выполняют гимнастику для глаз по упражнениям презентации | Словесный (беседа), наглядный (действия учителя), практический (выполнение упражнений) | КУУД – вступать в диалог с учителем; РУУД – принимать и сохранять учебную задачу. |
6. Практическая работа | 7 – 10 минут | Давайте выполним задание на странице 10, №2. Прочитай неравенства. Первый ряд начинает читать, остальные слушают. Молодцы! Справились с заданием. Следующее задание №3. Прочитайте задание про себя. Что от нас требуют в задании? Хорошо. Два человека идут к доске, остальные решают у себя в тетради и позже мы проверим, что у вас получилось. Итак, что получилось у ребят? Проверяем. Правильно? Следующее смотрим. Верно? У всех так? Молодцы! Присаживайтесь. Справились с трудным заданием. Впереди ждет еще одно задание под номером 5. Прочитайте задание. Что нужно сделать в задании? Хорошо. Два человека выходят к доске и записывают неравенства. Один под буквами а и б, другой – под буквами – в и г. Каждый выполняет задание в тетради, и потом мы проверим, что у вас получилось. Приступайте. Смотрим на доску и проверяем. У всех такие равенства получились? Молодцы! Мы справились с еще одним трудным и интересным заданием. | Открывают учебник на странице 10. Читают неравенства по цепочке. — а больше 7 и меньше 12; — b больше 15 и меньше или равно 96 и т. — Замени двойное неравенство двумя неравенствами. — Заменить двойные неравенства двумя неравенствами. Двое идут к доске и пишут неравенства. — Первое неравенство делится на: х больше или равно 9, а второе: х меньше 18. — Правильно. — у больше 3 и второе: у меньше или равно 11. — Да, верно. Смотрят и читают задание №5. — Записать двойные неравенства. Выходят к доске и работают, остальные выполняют задание в тетради. — 4 — 5 “больше или равно» k — 10 m “меньше или равно» 25 и т.д. Да. | Словесный (беседа, рассказ), наглядный (учебник, доска, дидактический материал), практический (выполнение заданий в учебнике и в тетради) | КУУД – формулировать собственное мнение; РУУД – принимать и сохранять учебную задачу, планировать этапы решения задачи; ПУУД — анализировать информацию, выбирать рациональный способ решения задачи; ЛУУД – интерес к новому содержанию. |
7. Самостоятельная работа. | 5 мин. | Теперь я проверю, как вы усвоили наш сегодняшний материал, самостоятельно задание 5. | Получают карточки, подписывают их и решают задания. | Словесный (беседа), наглядный (дидактический материал), практический (выполнение заданий) | КУУД — вступать в диалог с учителем; РУУД – принимать и сохранять учебную задачу, планировать свои действия. |
8. Подведение итогов. | 1 – 2 мин. | — Что нового мы узнали на уроке? — Какие задания мы выполняли на уроке? Да, мы сегодня много с вами сделали. | — Мы узнали, что такое двойное неравенство. — Как они читаются. — Их состав. — Составляли двойные неравенства, читали их. — Из двойного неравенства делали два неравенства. | Словесный (беседа), наглядный (презентация) | КУУД – формулировать собственное мнение, учитывать другие мнения; ЛУУД – интерес к новому содержанию. |
9. Рефлексия. | 2 мин. | Мне хочется узнать, как вы оцените свою работу. В этом мне помогут смайлики разного цвета. На партах лежат смайлики разных цветов. Я рада, что вы честно оценили свою работу. Спасибо за урок. | Дети оценивают свою работу на уроке. | Словесный (беседа), наглядный (дидактический материал), практический (работа с карточками) | КУУД – вступать в диалог с учителем; РУУД – адекватно воспринимать оценку учителя и сверстников, принимать и сохранять учебную задачу |
Двойные неравенства. 2 способа решения
Например:
\(5<11<17\)
\(-2\leq3x+5\leq2\)
\(2x-5\leq3x+7\leq8x\)
Двойное неравенство по своей сути – это система из двух неравенств, записанных в одну строку. Поэтому их всегда можно представить в виде системы.
Например:
\(-2\leq3x+5\leq2\Leftrightarrow\begin{cases}-2\leq3x+5\\3x+5\leq2\end{cases}\)
\(2x-5\leq3x+7\leq8x\Leftrightarrow\begin{cases}2x-5\leq3x+7\\3x+7\leq8x\end{cases}\)
Но делать это нужно не всегда.
1) Если в крайней левой и крайней правой частях двойного неравенства нет неизвестных, то удобнее оставить его как есть. При этом в процессе решения стремится равносильными преобразованиями привести неравенство к виду \([число]\)\(<\)\(x\)\(<\)\([число]\).
Пример: Решите двойное неравенство:
|
\(-2\leq3x+5\leq2\) \(|-5\) |
Здесь нет неизвестных по краям, поэтому к системе переходить не будем. Вместо этого делаем такие преобразования, чтоб в центре остался голый икс, а по краям — числа. |
|
|
\(-7≤3x≤-3\) \(|:3\) |
Теперь нам мешает \(3\). Поделим все три части неравенства на \(3\). |
|
|
\(-\)\(\frac{7}{3}\)\(\leq x \leq-1\) |
Готово, наш икс «голый». Можно записывать ответ. |
Ответ: \([-\)\(\frac{7}{3}\)\(;-1]\)
2) Если в крайних частях двойного неравенства есть неизвестные лучше перевести неравенство в систему и решать его как обычную систему неравенств.
Пример: Решите двойное неравенство:
|
\(2x-5<3x+7≤8x\) |
В крайней левой и крайней правой частях есть неизвестные –значит переходим к системе. |
|
\(\begin{cases}2x-5<3x+7\\3x+7\leq8x\end{cases}\) |
Решаем обычные линейные неравенства: все, что с иксами переносим в левую сторону, все что без иксов — в правую. |
|
\(\begin{cases}2x-3x<7+5\\3x-8x\leq-7\end{cases}\) |
Приводим подобные слагаемые |
|
\(\begin{cases}-x<12 \\-5x\leq-7 \end{cases}\) |
«Оголим» иксы, поделив верхнее неравенство на \((-1)\), нижнее на \((-5)\). Не забываем при этом перевернуть знаки сравнения, так как мы делим на отрицательное число. |
|
\(\begin{cases}x>-12 \\x\geq \frac{7}{5}\end{cases}\) |
Отметим на числовой оси оба решения |
|
Так как у нас система, то мы ищем значения иксов, которые подойдут обоим неравенствам, т. |
Ответ: \([\)\(\frac{7}{5}\)\(;\infty)\)
Вопрос Видео: Решение двойных неравенств с переменными по трем сторонам
Стенограмма видео
Найдите все значения 𝑥, удовлетворяющие неравенству минус 20 минус 𝑥 меньше или равно трем 𝑥 плюс два, что меньше 18 минус два 𝑥 . Запишите ответ в виде интервала.
Для начала мы решим эту задачу, разделив ее на две части: первое неравенство слева, а затем второе неравенство справа. Итак, мы можем приступить к решению нашего первого неравенства. Итак, у нас есть минус 20 минус 𝑥 меньше или равно трем 𝑥 плюс два. Итак, мы собираемся решить это неравенство, но помня так же, как мы решаем уравнение. Итак, первое, что мы собираемся сделать, это на самом деле мы собираемся вычесть два с каждой стороны, что дает нам минус 22 минус 𝑥 меньше или равно трем 𝑥.
Хорошо, теперь наш следующий шаг, мы на самом деле собираемся добавить 𝑥 к каждой стороне, что дает нам минус 22 меньше или равно четырем 𝑥. Хорошо, теперь мы можем решить это неравенство, потому что мы собираемся разделить три на четыре, что дает минус 22, если четыре меньше или равны 𝑥. Просто чтобы привести это в порядок, мы упростим эту дробь в левой части. Таким образом, мы можем сказать, что минус 11 больше двух меньше или равно 𝑥. Большой! Итак, наше первое неравенство решено.
Хорошо, теперь мы можем решить это неравенство, потому что мы собираемся разделить три на четыре, что дает минус 22, если четыре меньше или равны 𝑥. Просто чтобы привести это в порядок, мы упростим эту дробь в левой части. Таким образом, мы можем сказать, что минус 11 больше двух меньше или равно 𝑥. Большой! Итак, наше первое неравенство решено.
Теперь мы продолжим и решим правую часть, наше второе неравенство. И это второе неравенство говорит нам, что три 𝑥 плюс два меньше, чем 18 минус два 𝑥. Хорошо, снова решим это так, как мы решаем уравнение, поэтому первое, что мы собираемся сделать, это на самом деле мы собираемся вычесть два из каждой стороны, что дает нам три 𝑥 меньше, чем 16 минус два 𝑥. Итак, теперь мы добавим по две 𝑥 с каждой стороны. Таким образом, мы получаем, что пять 𝑥 меньше 16.
И затем, наконец, чтобы решить наше неравенство, мы делим обе части на пять, что дает нам, что 𝑥 меньше 16 на пять. Так здорово! Мы решили оба неравенства. Итак, давайте теперь соберем их вместе, чтобы увидеть, какими могут быть наши возможные значения 𝑥.
Если мы объединим наши решения, мы увидим, что 𝑥 больше или равно минус 11 для двух и меньше 16 для пяти. Хорошо, давайте покажем, что это на самом деле означает. Итак, если мы посмотрим на это на числовой прямой, мы увидим это вот так, где мы фактически получили заполненную точку над нашим минусом 11 над двумя. И это потому, что он меньше или равен. И тогда у нас фактически есть открытый круг над нашими 16 против пяти. И это потому, что он просто говорит, что это больше, чем 𝑥.
Итак, мы решили эту проблему. И мы знаем, где лежат наши ценности. Но мы закончили? Ну, нет, потому что на самом деле наш вопрос просит нас записать наш ответ в виде интервала. Таким образом, в интервальной записи это будет наше решение со скобкой слева. И это потому, что он меньше или равен. И снова это то же самое, что когда мы показываем на числовой строке. У нас там другое обозначение и у нас есть цветной кружок.
Но когда мы используем обозначение интервала, мы фактически используем для этого скобки. А справа у нас скобки. И мы используем эту скобку в правой части, потому что, как мы видим, здесь просто 𝑥 меньше 16 на пять, не меньше или равно. И снова мы получили обозначение открытого круга. Итак, мы подошли к окончательному ответу. И это написано как интервал.
А справа у нас скобки. И мы используем эту скобку в правой части, потому что, как мы видим, здесь просто 𝑥 меньше 16 на пять, не меньше или равно. И снова мы получили обозначение открытого круга. Итак, мы подошли к окончательному ответу. И это написано как интервал.
1.4: Составные неравенства — Mathematics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 19681
- Дэвид Арнольд
- Колледж секвойи
В этом разделе обсуждается метод, используемый для решения составных неравенств, который представляет собой фразу, которая обычно относится к паре неравенств, соединенных либо словом «и», либо словом «или». Прежде чем мы приступим к расширенной работе по решению этих неравенств, давайте сначала потратим пару слов (в целях повторения) на обсуждение решения простых линейных неравенств.
Прежде чем мы приступим к расширенной работе по решению этих неравенств, давайте сначала потратим пару слов (в целях повторения) на обсуждение решения простых линейных неравенств.
Простые линейные неравенства
Как и при решении уравнений, вы можете прибавить или вычесть одинаковую сумму из обеих частей неравенства.
Свойство \(\PageIndex{1}\)
Пусть \(a\) и \(b\) — действительные числа с \(a \[a+c и \[a-c Эта утилита одинаково действительна, если вы замените «less чем» с \(>, \leq\) или \(\geq\). Пример \(\PageIndex{1}\) Решить неравенство \(x + 3 < 8\) для \(x.\) Решение Вычесть \(3\) с обеих сторон неравенство и упростить. \[\begin{align*} x+3 &<8 \\ x+3-3 &<8-3 \\ x &<5 \end{align*}\] Таким образом, все действительные числа меньше чем \(5\) являются решениями неравенства. Традиционно набор решений неравенств изображается на числовой прямой. Мы можем описать набор решений, используя построитель набора и нотацию интервала. Решение: \[(-\infty, 5)=\{x : x<5\}\nonumber\] Важным понятием является идея эквивалентных неравенств. Эквивалентные неравенства. Два неравенства называются эквивалентными тогда и только тогда, когда они имеют одно и то же множество решений. Обратите внимание, что это определение аналогично определению эквивалентных уравнений. То есть два неравенства эквивалентны, если все решения первого неравенства являются также решениями второго неравенства, и наоборот. Таким образом, в примере \(\PageIndex{1}\) вычитание трех из обеих частей исходного неравенства дает эквивалентное неравенство. То есть неравенства \(x+3 < 8\) и \(x < 5\) имеют одно и то же множество решений, а именно, все действительные числа, меньшие 5. Неслучайно инструменты в Свойстве \( \PageIndex{1}\) производят эквивалентные неравенства. Всякий раз, когда вы добавляете или вычитаете одинаковую сумму из обеих частей неравенства, полученное неравенство эквивалентно исходному (у них один и тот же набор решений). Давайте посмотрим на другой пример. Пример \(\PageIndex{2}\) Решите неравенство \(x-5 \geq 4\) для \(x.\) Решение Добавьте 5 к обеим частям неравенства и упрощать. \[\begin{align*} x-5 & \geq 4 \\ x-5+5 & \geq 4+5 \\ x & \geq 9 \end{align*}\] Закрасить раствор на числовой строке. В построителе наборов и интервальных обозначениях решение: \[[9, \infty)=\{x : x \geq 9\} \nonumber\] Вы также можете умножить или разделить обе стороны на одно и то же положительное число. Свойство \(\PageIndex{2}\) Пусть \(a\) и \(b\) – действительные числа с \(a \[a c и \[\frac{a}{c}<\frac{b}{c}\] Опять же, эта утилита одинаково действительна, если вы замените символ «меньше чем» на \(>, \leq, \text{или} \geq.\) Инструменты в свойстве 4 всегда производят эквивалентные неравенства. Пример \(\PageIndex{3}\) Решить неравенство \(3x \leq −18\)для \(x.\) Решение Разделить обе части неравенства на \(3 \) и упростить. \[\begin{align*} 3 x & \leq-18 \\ \frac{3 x}{3} & \leq \frac{-18}{3} \\ x & \leq-6 \end {align*}\] Нарисуйте решение на числовой прямой. В построителе наборов и интервальных обозначениях решение: \[(-\infty,-6]=\{x : x \leq-6\} \nonumber\] На данный момент нет никакой разницы между техникой решения неравенств и методикой решения уравнений. Однако есть одно важное исключение. Рассмотрим на мгновение истинное утверждение \[-2<6 \label{eq6}\] Если вы умножите обе части неравенства \ref{eq6} на \(3,\), вы все равно получите истинное утверждение; т. е. \[-6<18 \nonumber\] Но если вы умножите обе части неравенства \ref{eq6} на \(−3,\), вам нужно «обратить символ неравенства», чтобы сохранить истинное заявление; то есть \[6>-18 \nonumber\] Это обсуждение приводит к следующему свойству. Свойство \(\PageIndex{3}\) Пусть \(a\) и \(b\) — действительные числа с \(a < b\). Если \(c\) - любое действительное отрицательное число, то \[a c>b c\] и \[\frac{a}{c}>\frac{b}{c}\] Обратите внимание, что вы «переворачиваете знак неравенства», когда умножаете или делите обе части неравенства на отрицательное число. Опять же, эта утилита одинаково действительна, если вы замените символ «меньше» на \(>, \leq,\) или \(\geq\). Инструменты в Property \(\PageIndex{3}\) всегда производят эквивалентные неравенства. Пример \(\PageIndex{4}\) Решить неравенство \(−5x > 10\) для \(x.\) Решение Разделить обе части неравенства на \(−5 \) и перевернуть знак неравенства. Упрощать. \[\begin{array}{r}{-5 x>10} \\ {\dfrac{-5 x}{-5}<\dfrac{10}{-5}} \\ {\quad x <-2}\end{array} \nonumber\] Нарисуйте решение на числовой прямой. В построителе наборов и интервальной нотации решение равно \[(-\infty,-2)=\{x : x<-2\} \nonumber\] Теперь обратим наше внимание на решение составных неравенств. В этом случае лучший способ учиться — это делать. Начнем с примера. Пример \(\PageIndex{5}\) Решите следующее составное неравенство для \(x.\) \[3-2 x<-1 \quad \text { or } \quad 3-2 x >1 \nonumber\] Решение Сначала решим каждое из неравенств независимо. В первом неравенстве прибавьте \(−3\) к обеим частям неравенства, затем разделите на \(−2,\), поменяв знак неравенства на противоположный. \[\begin{align*} 3-2 x &<-1 \\-2 x &<-4 \\ x &>2 \end{align*}\] Заштрихуйте решение на числовой прямой. Точно такую же последовательность операций можно использовать для решения второго неравенства \[\begin{align*} 3-2 x &>1 \\-2 x &>-2 \\ x &<1 \end{align*}\] Хотя вы решаете каждую часть неравенства независимо друг от друга, вам нужно организовать свою работу следующим образом, расположив решение числового ряда для первого неравенства над решением второго неравенства. \[\begin{array}{rllllrll}{3-2 x}&{<}&{-1} & {\text {или}} & {\quad 3-2 x}&{>}&{ 1} \\ {-2 x}&{<}&{-4} & &{-2 x}&{>}&{-2} \\ {x}&{>}&{2} && {x }&{<}&{1}\end{массив} \nonumber\] (2, \infty)=\{x : x<1 \text { or } x>2\} \nonumber\] Давайте рассмотрим другой пример. Пример \(\PageIndex{6}\) Решите следующее составное неравенство для \(x.\) \[-1<3-2 x<1 \label{eq12}\] Решение Напомним, что \(a < x < b\) идентично утверждению \(x > a\) и \(x < b.\). Таким образом, мы можем записать составное неравенство \(−1 < 3 − 2x < 1\) в виде \[3-2 x>-1 \quad \text { and } \quad 3-2 x<1 \label{eq13}\] Решите каждое неравенство самостоятельно, организовав работу следующим образом. \[\begin{array}{rllllrll}{3-2 x}&{>}&{-1} & {\text {и}} & {\quad 3-2 x}&{<}&{ 1} \\ {-2 x}&{>}&{-4} & &{-2 x}&{<}&{-2} \\ {x}&{<}&{2} && {x }&{>}&{1}\end{array} \label{eq14}\] Заштрихуйте решение каждого неравенства на отдельных действительных линиях, одну поверх другой Решение, как в интервальных, так и в обозначениях построителя множеств, равно \[(1,2)=\{x : 1 Обратите внимание, что в нашем ответе мы использовали компактную форму составного неравенства. С тем же успехом мы могли бы использовать \[(1,2)=\{x : x>1 \text { and } x<2\} \nonumber\] Обе формы записи построителя наборов одинаково допустимы. . Вы можете использовать любой из них, но вы должны понимать оба. Альтернативный подход. Возможно, вы заметили, что при решении второго неравенства в \ref{eq14} вы повторяете те же операции, что и при решении первого неравенства. То есть вы вычли \(3\) из обеих частей неравенства, а затем разделили обе части неравенства на \(−2,\), поменяв знак неравенства на противоположный. Это повторение раздражает и предлагает возможный короткий путь в данной конкретной ситуации. Вместо того, чтобы разбивать составное неравенство \ref{eq12} на две части (как в \ref{eq13}), давайте сохраним неравенство вместе, как в \[-1<3-2 x<1 \label{eq16}\] Теперь правила работы с этой формой. Свойство \(\PageIndex{4}\) При работе с составным неравенством вида \[a можно прибавлять (или вычитать) ту же сумму к (из) все три части неравенства, как в \[a+c или \[a-c Вы также можете умножить все три части на то же самое положительное число \(c > 0,\) как в \[c a Однако, если вы умножите все три части на одно и то же отрицательное число \(c < 0,\) тогда не забудьте поменять местами знаки неравенства, как в \[c a>c x>c b\] Правила деления идентичны правилам умножения. Если \(c > 0\) (положительно), то \[\frac{a}{c}<\frac{x}{c}<\frac{b}{c}\] Если \( c < 0\) (отрицательно), то при делении знаки неравенства меняются местами. \[\frac{a}{c}>\frac{x}{c}>\frac{b}{c}\] Каждый из инструментов в свойстве \(\PageIndex{4}\) всегда производят эквивалентные неравенства. Итак, вернемся к составному неравенству \ref{eq16} и вычтем \(3\) из всех трех членов неравенства. \[\begin{array}{c}{-1<3-2 x<1} \\ {-1-3<3-2 x-3<1-3} \\ {-4<-2 x<-2}\end{array} \nonumber\] Затем разделите все три члена на \(−2,\), меняя при этом знаки неравенства. \[\begin{array}{c}{-4<-2 x<-2} \\ {\dfrac{-4}{-2}>\dfrac{-2 x}{-2}>\ dfrac{-2}{-2}} \\ {2>x>1}\end{array} \nonumber\] Принято менять порядок этого последнего неравенства. Читая неравенство справа налево, мы получаем \[1 , которое описывает действительные числа больше 1 и меньше \(2.\) Решение рисуется на следующую реальную строку. Обратите внимание, что это идентично решению, установленному на реальной линии на рисунке \(\PageIndex{2}\). Обратите также внимание, что этот второй альтернативный метод более эффективен, особенно если вы немного поработаете в уме. Рассмотрим следующую последовательность, в которой мы вычитаем три из всех трех членов, затем делим все три члена на \(−2,\), меняя знаки неравенства, а затем, наконец, читаем неравенство в противоположном направлении. \[\begin{array}{c}{-1<3-2 x<1} \\ {-4<-2 x<-2} \\ {\quad 2>x>1} \\ { \quad 1 Давайте посмотрим на другой пример. Пример \(\PageIndex{7}\) Решите следующее составное неравенство для \(x.\) \[-1 Решение Сначала умножим все три члена на \(2,\), чтобы очистить дроби. \[2(-1)<2\left(x-\frac{x+1}{2}\right) \leq 2(2) \nonumber\] \[-2<2(x) -2\left(\frac{x+1}{2}\right) \leq 4 \nonumber\] Отмена. Обратите внимание на использование круглых скобок, что очень важно, когда используется знак минус. \[-2<2 x-\cancel{2}\left(\frac{x+1}{\cancel{2}}\right) \leq 4 \nonnumber\] \[-2<2 x-(x+1) \leq 4 \nonumber\] Распределите знак минус и упростите. \[\begin{align*} -2 &< &&2x-x-1 &&\leq 4 \\ -2 &< &&x-1&& \leq 4\end{align*}\] Добавить \(1\ ) всем трем участникам. \[-1 Это решение описывает действительные числа больше \(-1\) и меньше \(5,\), включая \(5. Ответ, описанный как в нотации интервала, так и в нотации построителя множеств, следует за \[(-1,5]=\{x :-1 Давайте посмотрим на другой пример Пример \(\PageIndex{8}\) Решите следующее составное неравенство для \(x.\) \[x \leq 2 x-3 \leq 5 \nonumber\] Решение Предположим, что мы пытаемся изолировать \(x\), как мы это делали в примере \(\PageIndex{7}\). Возможно, мы попытаемся добавить \(−x\) ко всем трем элементам. \[\begin{align*} x &\leq &&2x-3 &&\leq 5 \\ x-x &\leq &&2x-3-x &&\leq 5-x \\ 0 &\leq &&x-3 &&\leq 5-x \end{align*}\] Ну, это мало помогло, просто перенес задачу с \(x\) на другой конец неравенства. Подобные попытки не помогут выделить \(x. Решение: разделим неравенство (со словом «и», разумеется). \[x \leq 2 x-3 \quad \text { и } \quad 2 x-3 \leq 5 \nonumber\] Мы можем решить первое неравенство, вычитая \(2x\) из обеих частей неравенства, затем умножая обе части на \(−1,\), обращая неравенство в процессе \[\begin{align*} x & \leq 2 x-3 \\-x & \leq-3 \\ x & \geq 3 \end{align*}\] Чтобы решить второе неравенство, прибавьте \(3\) к обеим частям, затем разделите обе стороны на \(2\): \[\begin{align*} 2 x-3 & \leq 5 \\ 2 x & \leq 8 \\ x & \leq 4 \end{align*} \] Конечно, вы, вероятно, захотите организовать свою работу следующим образом \[\begin{array}{rllrl} x & \leq 2 x-3 & \text{and} &2 x-3 & \leq 5 \\ -x & \leq-3 && 2 x & \leq 8 \\ x & \geq 3 & & x & \leq 4\end{array} \nonumber\] Таким образом, нам нужно заштриховать на числовой прямой все действительные числа, которые больше или равны \(3\) и меньше или равно \(4,\), как показано на рисунке \(\PageIndex{5}\).

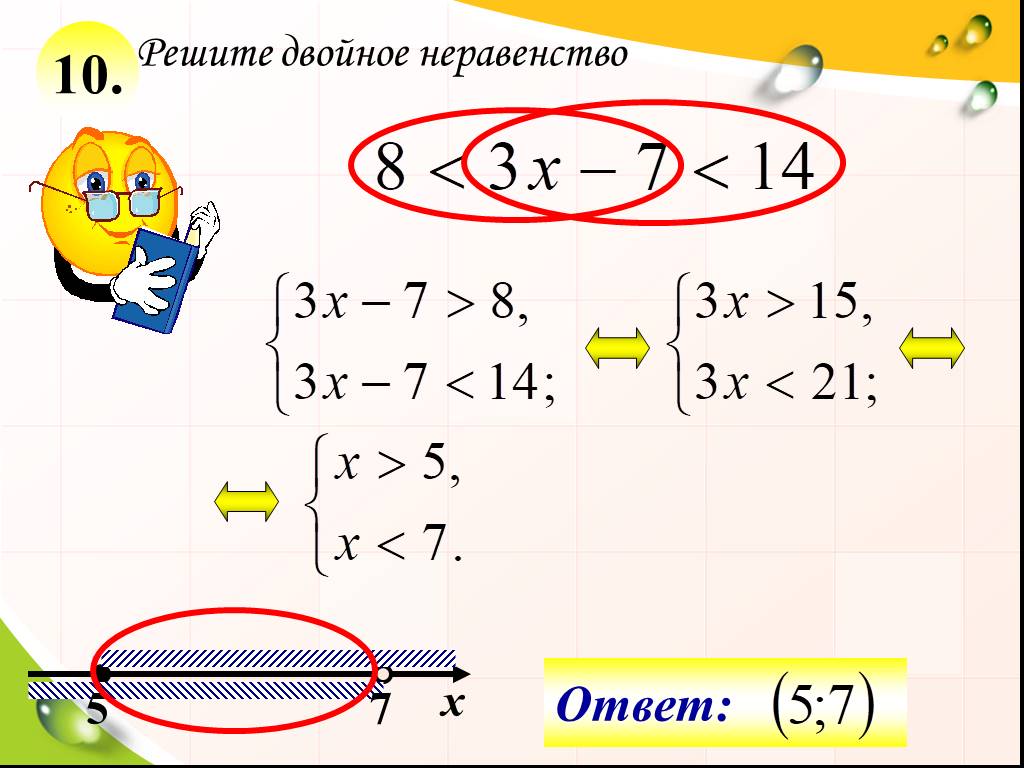
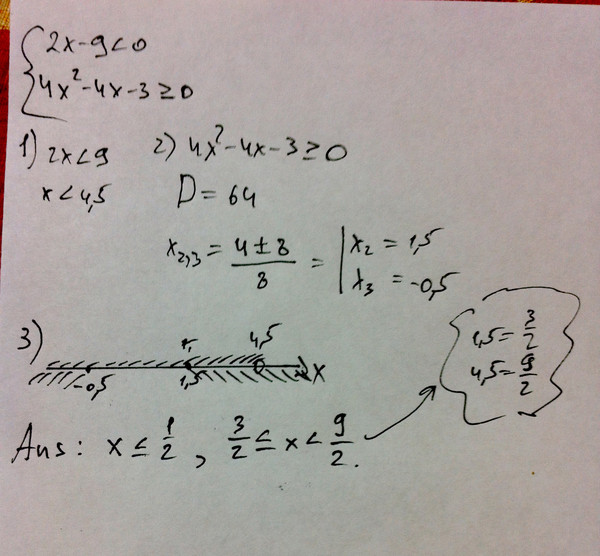
Составные неравенства
 В предыдущем разделе мы изучили тонкости «и» и «или», пересечения и объединения, а также рассмотрели некоторые простые составные неравенства. В этом разделе мы опираемся на эти основы и обращаем внимание на более сложные примеры.
В предыдущем разделе мы изучили тонкости «и» и «или», пересечения и объединения, а также рассмотрели некоторые простые составные неравенства. В этом разделе мы опираемся на эти основы и обращаем внимание на более сложные примеры.
 Решение составного неравенства \(−1 < 3 − 2x < 1.\)
Решение составного неравенства \(−1 < 3 − 2x < 1.\)


 \) Это то есть действительные числа, находящиеся между \(-1\) и \(5,\), включая \(5,\), заштрихованные на вещественной линии на рисунке \(\PageIndex{4}\).
\) Это то есть действительные числа, находящиеся между \(-1\) и \(5,\), включая \(5,\), заштрихованные на вещественной линии на рисунке \(\PageIndex{4}\). \) Итак, что же нам делать?
\) Итак, что же нам делать?
Уравнения с модулями: Уравнение с модулем
19. Уравнения с модулем
Модулем (Абсолютной величиной) Числа называется неотрицательное число:
(3.9)
Геометрическая интерпретация модуля: – это расстояние от точки А до точки Х на координатной оси, в частности, – это расстояние от точки 0 до точки Х.
Свойства модуля:
1) 2) 3)
4) 5) 6)
7) 8) 9)
Пусть – некоторое алгебраическое выражение. Тогда, используя определение модуля (3.9) при соответствующих предположениях, можно раскрыть знак абсолютной величины данного выражения:
Уравнение, содержащее выражение с неизвестной Х под знаком модуля, называется Уравнением с модулем. Рассмотрим основные типы уравнений с модулем и методы их решения.
I тип: уравнение вида
(3.10)
Где А – число, – некоторое выражение с неизвестной Х.
1. Если уравнение (3.10) решений не имеет.
2. Если уравнение (3.10) равносильно уравнению
Если уравнение (3.10) равносильно уравнению
3. Если уравнение (3.10) равносильно совокупности уравнений:
II тип: Уравнение вида
Где – некоторые выражения с неизвестной Х.
Решать это уравнение можно несколькими способами.
1-й способ – используя определения модуля:
2-й способ – используя подход к решению, как к уравнениям I типа с дополнительным условием на знак выражения
З а м е ч а н и е. 1-й или 2-й способ решения таких уравнений выбирают в зависимости от того, какое из неравенств или решается легче.
3-й способ – метод интервалов. Необходимо:
1) найти те значения Х, для которых
2) нанести полученные значения Х на числовую ось;
3) определить знаки для каждого из полученных интервалов;
4) нарисовать кривую знаков;
5) решить уравнение на каждом промежутке в отдельности, раскрывая модуль согласно рисунку;
6) для каждого конкретного промежутка проверить, принадлежат ли полученные корни этому промежутку;
7) в ответе указать совокупность всех полученных корней.
III тип: Уравнения, содержащие несколько модулей. Если их два, то это уравнение вида
(3.11)
Где – некоторые выражения с неизвестной Х.
1-й способ – можно использовать определение модуля и рассматривать 4 случая возможных знаков Этот способ, как правило, не является рациональным.
2-й способ – Метод интервалов. Необходимо нарисовать столько числовых осей и кривых знаков, сколько модулей в уравнении. Для уравнения (3.11) рисуют две оси, располагая их одна под другой (одна ось для вторая – для ). Для каждого выражения и следует изобразить кривую знаков на соответствующей оси. Затем раскрывают модули, используя рисунок, и решают уравнение отдельно на каждом промежутке. Подходят только те корни, которые принадлежат рассматриваемому промежутку. В ответе необходимо указать совокупность полученных корней.
IV тип: Уравнение вида
(3.12)
Где – некоторые выражения с неизвестной Х;
1-й способ – решение уравнения (3. 12) сводится к решению совокупности уравнений:
12) сводится к решению совокупности уравнений:
2-й способ – метод интервалов (не рационально).
3-й способ – после возведения уравнения в квадрат и использования свойства модуля уравнение сводится к равносильному:
Полученное уравнение решается в зависимости от его типа.
V тип: Уравнения, решаемые заменой переменной, например:
Где – некоторые выражения с неизвестной Х;
По свойству модуля оно записывается в виде
Вводят замену и решают полученное квадратное уравнение относительно неизвестной У. Затем необходимо вернуться к старой переменной. В случае 2-х различных корней квадратного уравнения это будет совокупность уравнений I типа:
Если корень единственный, то остается решить уравнение
Необходимо помнить, что в случае отрицательного значения уравнение с модулем не имеет решений.
Пример 1. Решить уравнение
Решение. Это уравнение I типа. Его ОДЗ:
Это уравнение I типа. Его ОДЗ:
Уравнение записывается в виде
На ОДЗ можно сократить и получаем
откуда т. е.
Получаем корни которые подходят по ОДЗ.
Пример 2. Решить уравнение
Решение. Это уравнение II типа. Его ОДЗ: Оно имеет решение, если т. е. при Таким образом, для получаем:
(3.13)
Решим отдельно полученные дробно-рациональные уравнения. Первое уравнение сводится к виду
откуда
Это квадратное уравнение решений не имеет, так как
Из второго уравнения совокупности (3.13) получаем
т. е.
Квадратное уравнение имеет корни:
Т. е. первый корень не принадлежит множеству на котором решали уравнение, следовательно, ответом является только
Пример 3. Решить уравнение
Решение. Имеем уравнение II типа, которое решим по определению модуля:
(3.14)
Решаем первую систему совокупности (3.14):
Значение не подходит по условию Следовательно, корнем является
Решаем вторую систему совокупности (3. 14):
14):
Получили ответ
Пример 4. Решить уравнение
Решение. Поскольку то уравнение записывается в виде
Это уравнение относится к III типу уравнений.
Его ОДЗ: Решим методом интервалов.
Нулями выражений, стоящих под модулем, являются и Эти значения разбивают числовую ось на три промежутка (рис. 3.1).
Рис. 3.1
Раскрыв модули на каждом из полученных промежутков, с учетом их знаков, получим совокупность систем:
Решим отдельно системы:
I. | II. |
III.
Решением данного уравнения являются значения и
Пример 5. Решить уравнение
Решение. Запишем уравнение в виде
Оно относится к IV типу. Возведем обе его части в квадрат:
После упрощения имеем:
т. е.
е.
Получаем – корень.
Пример 6. Решить уравнение
Решение. ОДЗ: т. е.
Преобразуем данное уравнение к виду
Заменяем
Уравнение приобретает вид
Решаем его как дробно-рациональное и получаем:
Последнее квадратное уравнение имеет корни:
Возвращаясь к переменной Х, получаем:
Второе уравнение совокупности решений не имеет, так как слева положительное выражение, а справа – отрицательное.
Первое уравнение совокупности сводится к I типу уравнений с модулем и равносильно совокупности при условии
Приходим к совокупности
т. е.
Решение имеет только второе уравнение совокупности, его корни:
Оба они подходят по ОДЗ.
Пришли к ответу:
Пример 7. Решить уравнение
Решение. ОДЗ:
С учетом ОДЗ данное уравнение равносильно уравнению:
Используя свойства модуля (имеем сумму двух неотрицательных величин), получаем:
Т. е. – решение полученной системы, оно подходит по ОДЗ.
е. – решение полученной системы, оно подходит по ОДЗ.
Получили ответ:
| < Предыдущая | Следующая > |
|---|
Решение уравнения с модулем онлайн · Как пользоваться Контрольная Работа РУ
Допустим, вам надо решить уравнение, содержащее модуль, а ещё лучше, если вам дано уравнение с 2 модулями.
Для примера, требуется решить
| x + 1| + |x – 5| = 20
Это уравнение мы решим с помощью калькулятора уравнений
Вы вводите уравнение, как указано на изображении ниже (знак модуля отмечается вертикальными линиями «|»)
Нажимаете кнопку «Решить уравнение!» и получаете подробное решение для своего уравнения с модулем:
Подробное решение
| Для каждого выражения под модулем в ур-нии |
| допускаем случаи, когда соотв. выражение «>= 0» или «< 0», |
решаем получившиеся ур-ния. |
x - 5 >= 0 |
x + 1 >= 0 |
5 <= x |
| получаем ур-ние |
x + 1 + x - 5 - 20 = 0 |
| упрощаем, получаем |
-24 + 2*x = 0 |
| решение на этом интервале: |
x1 = 12 |
x - 5 >= 0 |
x + 1 < 0 |
| Неравенства не выполняются, пропускаем |
x - 5 < 0 |
x + 1 >= 0 |
-1 <= x < 5 |
| получаем ур-ние |
x + 1 + 5 - x - 20 = 0 |
| решение на этом интервале: |
| Не найдены корни при этом условии |
x - 5 < 0 |
x + 1 < 0 |
x < -1 |
| получаем ур-ние |
-1 - x + 5 - x - 20 = 0 |
| упрощаем, получаем |
-16 - 2*x = 0 |
| решение на этом интервале: |
x2 = -8 |
| Тогда, окончательный ответ: |
x1 = 12 |
x2 = -8
модулей для дифференциальных уравнений
модулей для дифференциальных уравненийУчебное пособие по вспомогательному приложению
Численные решения дифференциальных уравнений
Спринты мирового класса
Модель логистического роста
Модели хищник-жертва
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Пружинное движение
Пружинные системы I
Матричные операции
Собственные значения и собственные векторы
Траектории линейных систем
Маятник
Свинец в теле
Коэффициент усиления и фазовый сдвиг
Система Ван дер Поля
Учебное пособие по вспомогательному приложению
- Назначение: Чтобы изучить основы Maple V, выпуск 4 или выпуск 5 для использования в модулях дифференциальных уравнений.

- Предпосылки: Никто
- Доступно для: Клен
Численные решения дифференциальных уравнений
- Назначение: Получить опыт работы с численными методами аппроксимации решение начальные задачи первого порядка.
- Предпосылки: Проработайте базовый учебник для вашей системы компьютерной алгебры.
- Доступно для: Клен
Спринты мирового класса
- Назначение: Чтобы изучить применимость линейного дифференциала уравнение как модель для процесс спринта, и чтобы проиллюстрировать важность параметров в моделировании.
- Предпосылки: Учебник для вашего вспомогательного приложения и умение решать линейка первого порядка дифференциальное уравнение с постоянными коэффициентами.
- Доступно для: Клен
Модель логистического роста
- Назначение: Изучить стандартную модель роста населения в
стесненная среда.

- Предпосылки: Разделение переменных.
- Доступно для: Клен
Модели хищник-жертва
- Назначение: Разработать и изучить модель Лотки-Вольтерры. для взаимодействия хищник-жертва как прототип первого порядка система дифференциальных уравнений.
- Предпосылки: Модуль Численных Решений дифференциальные уравнения.
- Доступно для: Клен
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- Назначение: Чтобы исследовать качественное поведение
решения начальных задач вида
у" + ау' + у = 0, у(0) = у0, у'(0) = у1.В частности, чтобы определить, как решения зависят от знаки и величины коэффициентов a и b и на первоначальные условия. - Предпосылки: Учебное пособие по вспомогательному приложению и
знание символической формы решений дифференциальных
уравнения вида у» + ау’ + бай = 0 .

- Доступно для: Клен
Весеннее движение
- Назначение: Расследовать математическая модель у» + (к/м)у’ + (К/м)у = 0 для пружинящего движения и изучения эффекта повышенного демпфирования.
- Предпосылки: Знание линейных однородных дифференциальные уравнения с константой коэффициенты.
- Доступно для: Клен
Системы принудительной пружины I
- Назначение: Изучить влияние внешней движущей силы. на простом линейном осцилляторе, демпфированном или незатухающем.
- Предпосылки: Модуль и знания Spring Motion символической формы решений дифференциальных уравнения вида у» + ау’ + by = f(t) , где f — функция синуса или косинуса.
- Доступно для: Клен
Матричные операции
- Назначение: Чтобы поэкспериментировать с
матричные операции, особенно
умножение, инверсия и
детерминанты и изучать
приложения к решению систем
линейные уравнения.
 В процессе
изучая эти матричные операции, мы
научитесь пользоваться помощником
приложение для выполнения матрицы
вычисления.
В процессе
изучая эти матричные операции, мы
научитесь пользоваться помощником
приложение для выполнения матрицы
вычисления. - Предпосылки: Базовое понимание линейных комбинаций векторов, Знакомство с умножением матриц.
- Доступно для: Клен
Собственные значения и собственные векторы
- Назначение: Экспериментировать и изучать свойства собственные значения и собственные векторы и их применение к дифференциальные уравнения.
- Предпосылки: Модуль операций с матрицами и концепция уменьшенной эшелонированной формы строки.
- Доступно для: Клен
Траектории линейных систем
- Назначение: Для исследования траекторий на фазовой плоскости 2×2 однородных линейных систем первого порядка дифференциальные уравнения вида X’ = AX.
- Предпосылки: Модуль операций с матрицами и
понимание смысла собственных значений и
собственные векторы матрицы A.

- Доступно для: Клен
Маятник
- Назначение: Чтобы исследовать фазовую плоскость для второго порядка нелинейное дифференциальное уравнение, в частности стандартное модель для затухающих и незатухающих маятников.
- Предпосылки: Модуль Spring Motion.
- Доступно для: Клен
Свинец в теле
- Назначение: Разработать и изучить модель отсека количества свинца в организме человека и изучить трехмерная управляемая линейная система.
- Предпосылки: Модуль по траекториям линейных Уравнения.
- Доступно для: Клен
Усиление и фазовый сдвиг
- Назначение: Чтобы изучить взаимосвязь между частотой внешней движущей силой и параметрами демпфирующего линейный осциллятор.
- Предпосылки: Модуль по принудительному пружинному движению.
- Доступно для: Клен
Система Ван дер Поля
- Назначение: Чтобы изучить модель Ван дер Поля для нелинейного
электрическая цепь — в частности, для изучения предельного цикла
явление.

- Предпосылки: Модуль по принудительному пружинному движению.
- Доступно для: Клен
| модули на math.duke.edu |
Модульный арифметический решатель — Калькулятор конгруэнтности
Поиск инструмента
Найдите инструмент в dCode по ключевым словам:Просмотрите полный список инструментов dCode
Модульный модуль решения уравнений
Инструмент/решатель для решения модульного уравнения. Модульное уравнение — это математическое выражение, представленное в виде сравнения хотя бы с одной неизвестной переменной.
Результаты
Модульный решатель уравнений — dCode
Теги: Арифметика
Поделиться
dCode и многое другое каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !
Калькулятор модульных уравнений
Уравнение для решения (по одному в строке)x+12=3
Модуль
Переменные
Решение уравнений с несколькими модулями
В частном случае с одним неизвестным с несколькими уравнениями с несколькими модулями существует китайская теорема об остатках:
⮞ Перейти к: Китайский остаток
Ответы на вопросы (FAQ)
Что такое модульная конгруэнтность? (Определение)
Модульная конгруэнтность — это своего рода уравнение (или система конгруэнтности, по крайней мере, с одной неизвестной переменной), действительное в соответствии с линейной конгруэнтностью (по модулю/модулю). По модулю принято говорить не о равенстве, а о конгруэнтности.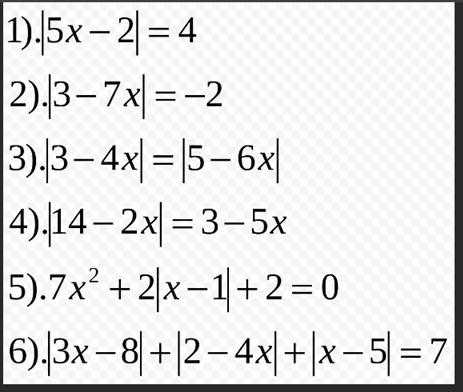
Для системы уравнений с несколькими модулями (нелинейной) это другой расчет, который можно выполнить с помощью калькулятора, решающего китайскую задачу с остатками, доступного на dCode.
Как решить модульное уравнение?
Введите уравнение/сравнение, переменные и значение по модулю. Значение модуля является глобальным и применяется ко всем уравнениям.
Пример: $$ x+12 \экв 3 \mod 5 \Стрелка вправо x = 1 $$
Как решить несколько уравнений?
Введите одно уравнение/сравнение в каждой строке или разделите их с помощью оператора && .
Как написать символ конгруэнтности ≡?
Скопируйте этот символ: ≡ (Unicode U+2261)
В LaTeX напишите: \equiv
В dCode нет необходимости писать ≡ (конгруэнтно) для решения уравнений, знак равенства =
4 достаточно.
Исходный код
dCode сохраняет за собой право собственности на исходный код «Modular Equation Solver». За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Modular Equation Solver», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Modular Equation Solver». Функции Solver (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и загрузка всех данных, сценарий или доступ к API для «Modular Equation Solver» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!
За исключением явной лицензии с открытым исходным кодом (указано Creative Commons/бесплатно), алгоритма «Modular Equation Solver», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, транслятор) или «Modular Equation Solver». Функции Solver (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и загрузка всех данных, сценарий или доступ к API для «Modular Equation Solver» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!
Напоминание: dCode можно использовать бесплатно.
Cite dCode
Копирование и вставка страницы «Modular Equation Solver» или любых его результатов разрешено, если вы цитируете dCode!
Бесплатный экспорт результатов в виде файла .
Округление чисел до сотых онлайн калькулятор: Округленные числа | Онлайн калькулятор
Калькулятор округления числа
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
Калькулятор округления чисел, округлит числа, до целого (до единиц), десятых, сотых, тысячных, десятитысячных представленные: обыкновенной либо десятичной дробью и экспоненциальной записью и отобразит подробное решение.
 Вы можете выбрать тип округления, а так же указать количество чисел после запятой. Примеры записи числа, которое необходимо округлить: 5765, -1652, 1/3, -3/6, -5/-7, 34.012, 56,23, 2.3e+5, 5.8e-123 и т.д.
Вы можете выбрать тип округления, а так же указать количество чисел после запятой. Примеры записи числа, которое необходимо округлить: 5765, -1652, 1/3, -3/6, -5/-7, 34.012, 56,23, 2.3e+5, 5.8e-123 и т.д.Число
Тип округления
До целого (до единиц)До десятыхДо сотыхДо тысячныхДо десятитысячныхУказать количество чисел после запятой
Пожалуйста, опишите возникшую ошибку.
Подтвердите, что вы не робот
Правила округления целых чисел
Правило 1. Если справа от цифры до которой необходимо округлить число, стоит цифра:
0,
1,
2,
3,
4,
то тогда необходимо просто заменить нулями все цифры до цифры до которой необходимо округлить число.
Примеры:
Красной чертой отделим округляемый разряд, а зеленым выделим цифру, которая стоит справа.
Округлим число 423012324 до десятых
42301232|4 ≈ 423012320
Округлим число 423012324 до сотых
4230123|24 ≈ 423012300
Округлим число 423012324 до тысячных
423012|324 ≈ 423012000
Округлим число 423012324 до десятитысячных
42301|2324 ≈ 423010000
Округлим число 4.230123243 до семи знаков после запятой
42|3012324 ≈ 420000000
Правило 2. Если справа от цифры до которой необходимо округлить число, стоит цифра:
5,
6,
7,
8,
9,
то тогда необходимо к цифре до которой необходимо округлить число прибавить 1.
Примеры:
Красной чертой отделим округляемый разряд, а зеленым выделим цифру, которая стоит справа.
Округлим число 94856757 до тысячных
Необходимо округлить до тысячных, значит после красной черты мы оставляем 3 цифры.
Красной чертой отделим округляемый разряд, а зеленым выделим цифру, которая стоит справа.
94856|757
Если справа от красной черты, стоит цифра: 0, 1, 2, 3, 4 то тогда необходимо заменить нулями все цифры стоящие после красной черты, а если стоит цифра: 5, 6, 7, 8, 9 то тогда необходимо тоже заменить нулями все цифры стоящие после красной черты и к цифре стоящей слева от красной черты прибавить число 1.
После красной черты у нас стоит цифра 7, значит мы должны заменить нулями все цифры стоящие после красной черты и прибавить 1 к цифре слева от красной черты.
94856 + 1 = 94857
94856757 ≈ 94857000
Правила округления десятичных чисел
Правило 1. Если справа от цифры до которой необходимо округлить число, стоит цифра:
0,
1,
2,
3,
4,
то тогда необходимо просто отбросить все цифры до цифры до которой необходимо округлить число.
Примеры:
Красной чертой отделим округляемый разряд, а зеленым выделим цифру, которая стоит справа.
Округлим число 4.23012324 до целого (до единиц)
4.|23012324 ≈ 4
Округлим число 4.23012324 до десятых
4.2|3012324 ≈ 4.2
Округлим число 4.23012324 до сотых
4.23|012324 ≈ 4.23
Округлим число 4.23012324 до тысячных
4.230|12324 ≈ 4.230
Округлим число 4.23012324 до десятитысячных
4.2301|2324 ≈ 4.2301
Округлим число 4.230123243 до семи знаков после запятой
4.2301232|43 ≈ 4.2301232
Правило 2. Если справа от цифры до которой необходимо округлить число, стоит цифра:
5,
6,
7,
8,
9,
то тогда необходимо к цифре до которой необходимо округлить число прибавить 1.
Примеры:
Красной чертой отделим округляемый разряд, а зеленым выделим цифру, которая стоит справа.
Округлим число 12.56843 до целого (до единиц)
Необходимо округлить до целого (до единиц), значит после точки мы оставляем 0 цифры.
12.|56843
Если справа от красной черты, стоит цифра: 0, 1, 2, 3, 4 то тогда необходимо просто отбросить все цифры стоящие после красной черты, а если стоит цифра: 5, 6, 7, 8, 9 то тогда необходимо тоже отбросить все цифры стоящие после красной черты и к цифре стоящей слева от красной черты прибавить число 1.
После красной черты у нас стоит цифра 5, значит мы должны отбросить все цифры стоящие после красной черты и прибавить 1 к цифре слева от красной черты.
12 + 1 = 13
12.56843 ≈ 13
Округлим число 985.0029 до тысячных
Необходимо округлить до тысячных, значит после точки мы оставляем 3 цифры.
985.002|9
Если справа от красной черты, стоит цифра: 0, 1, 2, 3, 4 то тогда необходимо просто отбросить все цифры стоящие после красной черты, а если стоит цифра: 5, 6, 7, 8, 9 то тогда необходимо тоже отбросить все цифры стоящие после красной черты и к цифре стоящей слева от красной черты прибавить число 1.
После красной черты у нас стоит цифра 9, значит мы должны отбросить все цифры стоящие после красной черты и прибавить 1 к цифре слева от красной черты.
2 + 1 = 3
985.0029 ≈ 985.003
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор упрощения выражений |
| Калькулятор со скобками |
| Калькулятор уравнений |
| Калькулятор суммы |
| Калькулятор пределов функций |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Калькулятор делителей числа |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Округление чисел онлайн
Задача округления чисел известна со школьной скамьи. Округление применяется для того, чтобы в результате получить числа более удобные для восприятия и дальнейших расчетов.
В результате округления получается приближенное число.
Для обозначения округления используют знак приблизительно равно ≈
Округление чисел онлайн калькулятор
Введите число для округления: Знаков после запятой (значащих цифр):всего расчетов — 84858
Калькулятор округляет число до заданного количество значащих цифр после запятой. Введите округляемое число и нужно количество значащих цифр. В результате вы получите округленное число и все возможные варианты округления:
Введите округляемое число и нужно количество значащих цифр. В результате вы получите округленное число и все возможные варианты округления:
- до миллионов;
- до сотен тысяч;
- до десятков тысяч;
- до тысяч;
- до сотен;
- до единиц;
- до десятых;
- до сотых;
- до тысячных;
- до десятитысячных;
- до стотысячных;
- до миллионных.
Просто выберите нужный вариант округления.
Правила округления
Первое правило
Если первая из отделяемых цифр больше или равна 5, то последняя оставляемая цифра усиливается (увеличивается на единицу).
Пример: округлим до десятых число 123,456. В разряде десятых находится цифра 4, а следом за ним цифра 5. По первому правилу округления мы должны усилить разряд десятых, то есть увеличить его на единицу. Таким образом в результате округления до десятых получим 123,456 ≈ 123,5.
Второе правило
Если первая из отделяемых цифр меньше или равна 4, то последняя оставляемая цифра записывается без изменений.
Пример: округлим до сотых число 123,4523. В разряде сотых находится цифра 5, а следом за ним цифра 2. По второму правилу округления оставляем цифру в разряде сотых без изменения. Таким образом в результате округления до сотых получим 123,4523 ≈ 123,45.
Пример: округлим число π Пи (3,14) до десятых. После числа 1, которое стоит в разряде десятых идет число 4. Соответственно, по правилам округления записываем десятые без изменения. Получаем: 3,14 ≈ 3,1.
Третье правило
Если отбрасывается цифра 5, а за ней нет значащих цифр, то округление производится к ближайшему четному числу. При этом последняя сохраняемая цифра оставляется неизменной, если она четная, и усиливается, если она нечетная. Такое округление называют банковским или бухгалтерским округлением. Оно отличается от математического округления.
Пример: округлим до целых число 2,5 используя математическое округление. В разряде десятых у нас находится цифра 5, значит по первому правилу округления мы усиливаем разряд единиц и получаем 2,5 ≈ 3.
Если же необходимо округлить по правилам банковского округления, то так как после 5 у нас нет значащих цифр, а 2 — число четное, то оставляем разряд единиц без изменения и получаем, что 2,5 ≈ 2. Вот такой парадокс. Имейте это ввиду при округлении чисел.
Ваша оценка
[Оценок: 243 Средняя: 2.9]
Округление чисел до целых, десятых, сотых, тысячных Автор admin средний рейтинг 2.9/5 — 243 рейтинги пользователей
Калькулятор округления
Создано Матеушем Мухой и Мацеем Ковальски, кандидатами наук
Отзыв от Jack Bowater
Последнее обновление: 14 декабря 2022 г.
Содержание:- Режимы округления 900 09 Краткий обзор округления
- Часто задаваемые вопросы
Этот калькулятор округления чисел можно использовать для уменьшения точности числа, чтобы сделать его короче, проще и/или легче понять, когда вы выполняете дальнейшие операции с ним. Часто бывает, что вам не нужно точное число (например, 9). 0017 3324.238576 ) и с радостью согласился бы на
0017 3324.238576 ) и с радостью согласился бы на 3324.34 , 3324 или даже 3300 ; этот калькулятор округления десятичных дробей позволит вам сделать именно это. Просто введите число и выберите нужную точность из списка. Если это не для вас, вы можете выбрать режим округления.
Режимы округления
В зависимости от ситуации вы захотите, чтобы этот алгоритм округления вел себя соответствующим образом. Иногда хочется все округлить ( 2.1 будет округлено до 3 ). Иногда вы хотите, чтобы точные половины были округлены вверх в половине случаев и вниз в другой половине, чтобы повысить вероятность того, что среднее значение будет близко к истине. Вот описание всех режимов, округлим до целого числа.
- вверх — округление от нуля.
3.2и3.6становятся4, но-3.2и-3.6становятся-4.
- вниз — округление до нуля. Вышеупомянутые числа становятся
3и-3соответственно. - ceil — округление в сторону большего числа. Он отличается от округления до способом обработки отрицательных чисел. Оба
-3.2и-3.6становятся-3. - этаж — округляется в сторону меньшего числа. Точно так же отрицательные числа идут в обратном направлении, чем в случае округления в меньшую сторону.
-3.2становится-4. На этом принципе основан наш калькулятор по модулю. - половина вверх (по умолчанию) — округление до ближайшего соседа. Если равноудалены, то округляются от нуля (так же, как в режиме до ). Например,
3,5становится4, а-3,5становится-4. Так обычно выполняется округление. - наполовину вниз — аналогично наполовину вверх, округляет до ближайшего соседа, если не равноудален — тогда округляет до нуля (так же, как в режиме вниз ).
 Вышеупомянутые числа становятся
Вышеупомянутые числа становятся 3и-3соответственно. - половина даже — интересно. Округляет до ближайшего соседа, но если они равноудалены, то округляет до четного числа. И
1,5, и2,5округляются до2.3,5и4,5округляются до4. Он предотвращает кумулятивные ошибки округления, и именно поэтому он часто используется в науке (мы используем его в качестве режима по умолчанию в нашем калькуляторе значащих цифр. Если вы все время будете округлять в большую сторону, среднее значение будет слишком высоким… вот почему мы в половине случаев округляйте вверх. То же правило (по той же причине) используется в бухгалтерском учете. Если вы хотите округлить до ближайшего цента, просто используйте получетный режим . - половина ячейки — ближайший сосед, равноудаленные значения идут в сторону большего числа.
- половина этажа — ближайший сосед, равноудаленный к меньшему номеру.

Краткий обзор округления
Если весь этот текст звучит устрашающе, вот краткая таблица, в которой вы можете проверить и понять все режимы округления, доступные в калькуляторе, а также некоторые дополнения в качестве бонуса. По заслугам: эта таблица взята из очень занимательного поста Макса Максфилда об алгоритмах округления, рекомендуемого к прочтению.
Часто задаваемые вопросы
Как округлить до ближайшего целого числа?
Чтобы округлить число до ближайшего целого числа, нужно посмотреть на значение сразу после десятичной дроби :
- Если это одно из чисел
0, 1, 2, 3 или 4, то мы округлить в меньшую сторону : вычеркнуть все , что идет после десятичной точки , и оставить часть до десятичной без изменений . - Если это одно из чисел
5, 6, 7, 8, 9, то округляем : вычеркиваем все, что стоит после десятичной и увеличить часть перед запятой на единицу .
7,5 округляется вверх или вниз?
Согласно наиболее популярному методу округления 7,5 округляется до 8 . Всякий раз, когда значение сразу после запятой меньше 5, мы округляем в меньшую сторону; в противном случае мы округляем.
Во что округляется 2,47?
- 2,47 округляется до 2,5 , если мы округляем до ближайшего десятого .
- 2,47 раунда до 2 , если мы округлим до ближайшего целого числа .
Почему мы округляем числа?
Мы округляем числа, чтобы сделать их более простыми для понимания и более удобными для выполнения дальнейших вычислений. Округление дает числа, достаточно близкие к исходным значениям, поэтому сообщение, которое они несут, в основном сохраняется. Конечно, в некоторых ситуациях требуется большая точность — поэтому иногда округляем до ближайшего целого, а иногда до сотых.
Матеуш Муха и Мацей Ковальски, кандидаты наук
Номер
Округлить до
Результат
Для нестандартных режимов округления воспользуйтесь расширенным режимом.
Пример
Ознакомьтесь с 70 похожими арифметическими калькуляторами ➗
Абсолютное изменениеАбсолютное значениеСложение и вычитание дробей… Еще 67 ближайшие, десятки , сотые, тысячные, десятки тысяч, сто тысяч и т. д.
Проще говоря, этот калькулятор округления чисел позволяет округлять числа в большую или меньшую сторону до любого десятичного знака.
До чего вы округляете?При округлении числа самое первое, на что нужно обратить внимание: до чего вы его округляете?
Цифры можно округлять до десятков, сотен, тысяч и т.д.
Пример:
Если у вас есть число 4827, то оно может быть округлено следующим образом:
- Округление до ближайшей десятой будет: 4830
- 4827 будет округлено до ближайшей сотни: 4800
- округлить до ближайших тысяч 4827 будет: 5000
Округленная таблица чисел:
| Наименование округления | Соответствующий номер | Номер до (+), после (-1) запятой |
| Миллион | 1 000 000 | 7 |
| Сотни тысяч | 100 000 | 6 |
| Десять тысяч | 10 000 | 5 |
| тысяч | 1 000 | 4 |
| Сотня | 100 | 3 |
| Десять | 10 | 2 |
| Блок | 1 | 1 |
| Десятый | 0,1 | -1 |
| Сотый | 0,01 | -2 |
| Тысячный | 0,001 | -3 |
| Десятитысячный | 0,0001 | -4 |
| Стотысячный | 0,00001 | -5 |
| Миллионный | 0,000001 | -6 |
Более реалистичный способ понять этот идентификатор метода — наблюдать за числовой линией перед округлением чисел. В соответствии с этой стратегией, если единица данного числа меньше пяти, вы будете следовать правилу «округления в меньшую сторону». Если заданное число больше 5, то будет применяться «округление».
В соответствии с этой стратегией, если единица данного числа меньше пяти, вы будете следовать правилу «округления в меньшую сторону». Если заданное число больше 5, то будет применяться «округление».
Если цифра десятков в заданном числе меньше 50, применяется правило «округления в меньшую сторону», но если цифра десятков равна 50 или больше 50, округление в большую сторону будет применяться. Например, если у вас есть число 834, то десятка будет «34», что меньше 50, поэтому вы округлите число до 800. Точно так же в случае с 871 время «71» больше. чем 50, поэтому число будет преобразовано в 900.
Округление чисел до ближайшей тысячи:Иногда необходимо округлить четырехзначное число до ближайших десятков, сотен или тысяч. Например:
- Если задано число 2431 и нужно округлить до десятка, то будет 4230.
Но если округлить до ближайшей 1000, то ваша сотня будет соблюдена; если оно меньше 50, то вы округляете число в меньшую сторону, а если оно больше 50, вы округляете число в большую сторону. Например:
Например:
- Если задано число 2839, то «83» больше 50, поэтому число будет округлено до 3000.
При округлении до ближайшего цента, копейки или сотой будет применяться та же процедура. Все, что вам нужно сделать, это искать сотые места. Найдя 100-е место, посмотрите на цифру справа. Если эта цифра 5 или больше 5, число на 100-м месте будет увеличено на 1. Все те числа, которые присутствуют после него, будут просто отброшены.
Округление чисел до ближайшей тысячной:Округление до ближайшей тысячной: 34,4317
- Сначала вычислите цифру тысячных: 1 из 34,4317
- Теперь найдите наименьшее разрядное значение: 7 из 34,4317
- Вы видите, что цифра больше пяти, поэтому округляйте
- Итак, 1 + 1 = 2
- 34,4317 округлить до тысячных будет 34,432
Округление чисел до ближайшей десятки:
Округление до ближайшей десятки: 434. 2:
2:
- Просто определите цифру десятков: 3 в 434,2
- Сразу после этого вам просто нужно вычислить следующее наименьшее значение разряда: 4 в 434,2
- Посмотрите, эта цифра больше или равна пяти? Нет, просто округлите в меньшую сторону.
- Десятки останутся такими же, как 3, и каждая последующая цифра превратится в ноль. Здесь цифры после запятой опущены
- 434,2 округлить до десятых будет 430
| Номер | Полуприподнятый | Полупух | Наполовину 0 | От половины до 0 | Получетный | Половина нечетного | Этаж | Потолок |
| 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 |
| 7,6 | 8 | 8 | 8 | 8 | 8 | 8 | 7 | 8 |
| 7,5 | 8 | 7 | 8 | 7 | 8 | 7 | 7 | 8 |
| 7,4 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 8 |
| 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 |
| -7 | -7 | -7 | -7 | -7 | -7 | -7 | -7 | -7 |
| -7,4 | -7 | -7 | -7 | -7 | -7 | -7 | -8 | -7 |
| -7,5 | -7 | -8 | -8 | -7 | -8 | -7 | -8 | -7 |
| -7,6 | -8 | -8 | -8 | -8 | -8 | -8 | -8 | -7 |
| -8 | -8 | -8 | -8 | -8 | -8 | -8 | -8 | -8 |
Все, что вам нужно сделать, это просто ввести свое число в этот калькулятор округления чисел и выбрать желаемую точность в раскрывающемся меню.
Ось z в геометрии 9 букв: Ось Z, 9 (девять) букв
Ось Oz В Математике — CodyCross ответы
Решение этого кроссворда состоит из 9 букв длиной и начинается с буквы А
Ниже вы найдете правильный ответ на Ось Oz в математике, если вам нужна дополнительная помощь в завершении кроссворда, продолжайте навигацию и воспользуйтесь нашей функцией поиска.
ответ на кроссворд и сканворд
Пятница, 20 Августа 2021 Г.
CodyCross Телестудия Rруппа 607
АППЛИКАТА
предыдущий следующий
ты знаешь ответ ?
ответ:
CODYCROSS Телестудия Группа 607 ГОЛОВОЛОМКА 4
- Сыграла дашу букину в сериале счастливы вместе
- Часть слова, расположенная перед корнем
- Государственный язык эквадора
- Фамилия юного помощника остапа из 12 стульев
- Мигающая лампочка в электронных приборах
- Норвежский рождественский пончик, пышка в смальце
- Навязчивый страх боли
- Организация, осуществляющая контроль и проверку
- Популярный в японии лопоухий советский персонаж
связанные кроссворды
- Аппликата
- Декартова координата 9 букв
- Ось oz в математике 9 букв
- Координата z 9 букв
- Аппликата
- Математический термин, в переводе «приложенная»
Наименование букв латинского алфавита:
1 – а 10 – йот 19 – эс
2 – бе 11 – ка 20 –те
3 – це 12 – эль 21 – у
4 – де 13 – эм 22 – вэ
5 – е 14 – эн 23 – дубль-вэ
6 – эф 15 – о 24 – икс
7 – ге 16 – пе 25 – ипсилон
8 – га 17 – ку 26 –зета
9 – и 18 – эр
Наименование букв греческого алфавита:
1 – альфа 9 – йота 17 – ро
2 – бета 10 – каппа 18 – сигма
3 – гамма 11 – ламбда 19 – тау
4 – дельта 12 – мю 20 – ипсилон
6 – дзета 14 – кси 22 – хи
7 – эта 15 – омикро 23 – пси
8 – тэта 16 – пи 24 – омега
латинский алфавит
Шрифт типа А с наклоном (прописные и строчные буквы)
Рис. 7
7
ГРЕЧЕСКИЙ АЛФАВИТ
Шрифт типа Б с наклоном (прописные и строчные буквы)
Рис. 8
Все графические работы должны выполняться карандашом, в том числе буквы и цифры чертежного шрифта. Необходимо выполнять надписи сначала тонкими линиями жестким карандашом (твердость 2Т), а окончательную обводку с приданием каждой букве и цифре определенной толщины выполнять карандашом средней твердости (ТМ). Применять более мягкие карандаши для обводки не следует, так как они пачкают бумагу, и чертеж теряет свежесть.
Работая карандашом, не надо проводить лишних линий при построении вспомогательной сетки. Вспомогательные линии не следует проводить за пределы буквы и цифры.
Чтобы толщина
обводки каждой буквы или цифры была
одинаковой, нужно время от времени
править карандаш на наждачной бумаге.
После этого следует обязательно
проверять, какую толщину линии на бумаге
дает правленый карандаш. Если под рукой
нет наждачной бумаги, то править карандаш
можно и на обычной бумаге. Для этого
проводят карандашом по бумаге до тех
пор, пока графиту не придадут форму
конуса или лопатки.
Если под рукой
нет наждачной бумаги, то править карандаш
можно и на обычной бумаге. Для этого
проводят карандашом по бумаге до тех
пор, пока графиту не придадут форму
конуса или лопатки.
Во избежание загрязнения поверхности чертежа его следует покрыть листом чистой бумаги, оставляя при этом ту часть, на которой в данный момент выполняют надпись.
На лекционных и практических занятиях будет принята система обозначений и символики (табл. 2,3), разработанная проф. Н.Ф.Четверухиным. Система этих обозначений широко применяется в настоящее время кафедрами начертательной геометрии и инженерной графики ведущих вузов России.
Таблица 2
ОБОЗНАЧЕНИЯ ГЕОМЕТРИЧЕСКИХ ОБЪЕКТОВ
Геометрическая фигура (объект) | Обозначение и пример |
Точка | Прописная буква
латинского алфавита: А,В,С,
… или арабская цифра:1,2,3,
… (может быть римская цифра:I,II,III,
…). Центр проецирования S. Начало координатО(буква). Точка в бесконечности:S,А,В, …. |
Линия – прямая или кривая | Строчная буква латинского алфавита: a,b,c, …. Горизонтальh; фронтальf; профильная прямая или кривая (профиль)р; ось вращенияi; направление проецирования или направление взгляда в пространстве:s– наП1,v– наП2; оси координат:x,y,z; оси проекцийx,y,zилиx12,x24и т.д. (АВ) – прямая, определяемая точкамиАиВ; ΙАВΙ – длина отрезкаАВ, натуральная величина отрезкаАВ. Скобки не даются,
если в тексте имеются соответствующие
слова (например, прямая АВ). |
Поверхность (включая плоскость) | Прописная буква греческого алфавита: Г(гамма),(сигма),(лямбда), …. |
Плоскость проекций | Прописная буква греческого алфавита: П(пи) с добавлением индекса.П1– горизонтальная плоскость проекций;П2– фронтальная плоскость проекций; П3– профильная плоскость проекций;П4,П5, … – дополнительные плоскости проекций. |
Угол | Строчная буква греческого алфавита: ,,, …. |
Проекция объекта | А1,b1,1– горизонтальные проекции точкиА, линииb, поверхности; А2,b2,2–
фронтальные проекции точкиА,
прямойb, поверхности; и т. |
Таблица 3
СИМВОЛЫ ВЗАИМОРАСПОЛОЖЕНИЯ И ЛОГИЧЕСКИХ ОПЕРАЦИЙ
Знак | Смысл знака | Пример, пояснение |
или или | Взаимная принадлежность (инцидентность) объектов как множеств, подмножеств Взаимная принадлежность (инцидентность) объектов, из которых один – множество, другой – элемент множества, т.е. точка | tГ– линияtпринадлежит поверхностиГ; поверхностьГпроходит через линиюt; Гt–
то же (знак открытой частью всегда
обращен в сторону большего множества). tА– линияtпроходит через точкуА; точкаАпринадлежит линииt; Аt– то же (знакоткрытой частью обращен в сторону множества). |
∩ | Пересечение | а∩b– линииaиbпересекаются;(a∩b) – плоскостьзадана пересекающимися прямымиaиb. |
= или | Результат Равенство Совпадение | А=а∩b– точкаАполучена в результате пересечения линийaиb.АВ=ЕF– отрезокАВравен отрезкуЕF. А2=В2–
фронтальные проекции точекАиВсовпадают. |
ΙΙ | Параллельность | (АВ) ΙΙ (СD) – прямыеАВиСDпараллельны. |
| Перпендикулярность | АВСD |
| Отображается, последовательность действий | А1А2– по горизонтальной проекции точкиАстроим фронтальную. |
X%2c Y или Z%2c в геометрии — ответы на кроссворды
Кроссворд «За 2с ___» . с 5 буквами в последний раз видели 01 января 1971 года. Мы нашли 20 возможных решений для этой подсказки. Ниже приведены все возможные ответы на эту подсказку, упорядоченные по рангу. Вы можете легко улучшить поиск, указав количество букв в ответе.
Лучшие ответы на X%2c Y или Z%2c В геометрии:
PLAIN, AXES, AXISСортировать по: Классифицировать Ранг Длина | |||
Длина | Слово | Подсказка | |
|---|---|---|---|
| 92% | 5 | ОБЫЧНЫЙ | «Для 2с ___» |
| 77% | 4 | ОСи | x, y и z по математике |
| 77% | 4 | ОСЬ | x, y или z в геометрии |
| 74% | 3 | ГЕН | Ввод в X, Y или Z |
| 66% | 4 | ОРИКС | X или Y (анаг) |
| 66% | 15 | СТРОЧНЫЕ БУКВЫ | х, у или г |
| 66% | 6 | ПИСЬМО | Х, Y или Z.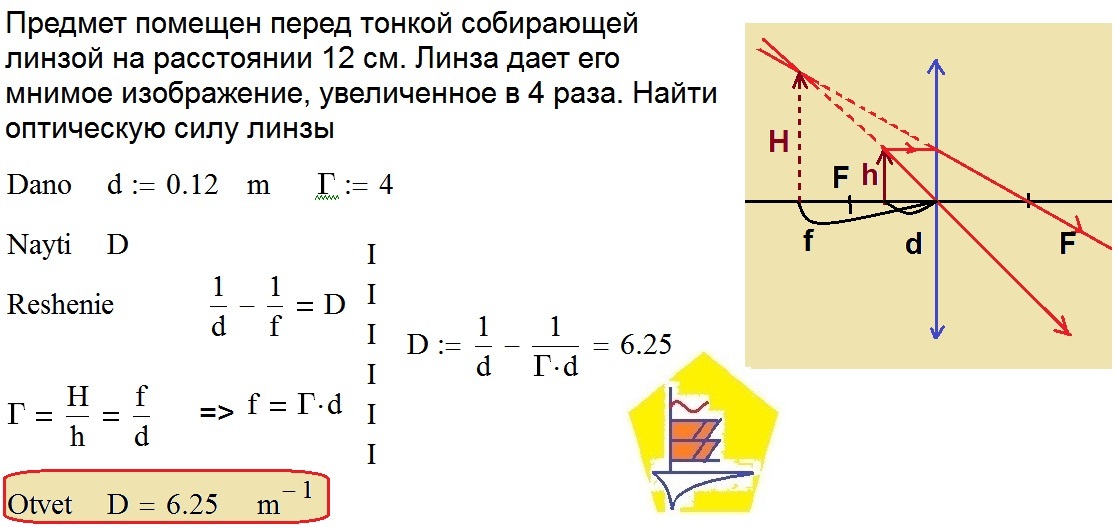 |
| 56% | 7 | АЛГЕБРА | Тема «X + Y = Z» |
| 53% | 7 | БУМЕРЫ | Поколение Z, миллениалы, поколение X, ___ |
| 53% | 5 | АКСИОМА | Если X=Y и Y=Z, то X=Z, например |
| 51% | 3 | АТО | От ___ г. |
| 51% | 3 | ТАС | Часть X-X-X |
| 51% | 14 | ПРОФИЛЬНОЕ ИЗОБРАЖЕНИЕ | «Малкольм Икс» или «Милк»? |
| 51% | 4 | ВАШ | «Y» в FYI |
| 51% | 4 | ОБЛАСТЬ | Расчет геометрии |
| 51% | 14 | ЖЕ РАЗНИЦА | х — у = х — у |
| 51% | 3 | НАБОР | {х, у, г}, например |
| 51% | 7 | ДЕЛИТЕЛЬ | В х ÷ у, у |
| 48% | 4 | POSH | Fancy-y-y |
| 48% | 5 | УСЛОВИЯ | х и у в «х + у» |
Уточните результаты поиска, указав количество букв. Если какие-то буквы уже известны, вы можете предоставить их в виде шаблона: «CA????».
Если какие-то буквы уже известны, вы можете предоставить их в виде шаблона: «CA????».
Последние подсказки
- Золотой штат, фамильярный кроссворд
- Вне книжного бизнеса, возможно, разгадка кроссворда
- Уличный хип-хоп Бит Кроссворд Подсказка
- Пули и т. д. Кроссворд
- Я прах, разложившийся в земле Кроссворд
- Звук слизи, падающей на пол Кроссворд
- Персидский правитель дает римскому королю 6 разгадку кроссворда
- Уютное и расслабляющее место для отдыха Кроссворд
- Последнее место, где вы найдете путешественников? Кроссворд
- Кроссворд «— Ты извиняешься»
- Город, где останавливаются корабли Кроссворд
- Спорим, что сыну нужно разгадать головоломки Кроссворд
- Захваченный в бронзе, высокий греческий персонаж Кроссворд
- Новый префикс, который я подготовил ранее? Кроссворд
- Встань на вершину Дейзи, вышедшей замуж ранее Кроссворд
- Проверяет измененную подсказку кроссворда Санкции
- Класс Pe, Обычно Кроссворд
- Кроссворд Страдальца
- Действуй как больной неудачник, разгадывай кроссворд
- 601, К Катону Кроссворд
- Разрезать в клочья Кроссворд
- Как подсказка кроссворда с рассчитанным ходом
- Возьмите переднее пассажирское сиденье Кроссворд Clive
- Плата за политические услуги Кроссворд
- Благодарность окружного прокурора о назначении кроссворда
- Ближневосточная федерация с 1971 года, краткий кроссворд
- Переместить границы, возможно, разгадка кроссворда
- Дочь Миноса, которая помогла Тесею разгадать кроссворд
- Кроссворд доктора, лечащего пазухи
- Отмена (Движение за права арендаторов) Кроссворд
- Глава, выпустивший крик боли, взял разгадку кроссворда
- Создатель кроссвордов Gillikins, Quadlings, Winkies и Munchkins
- Убийца может быть рядом с кормой в спасательном плавучем кроссворде
- Техас, Кроссворд Звездного штата
- Клейкая подсказка для кроссворда «Скотч» или «Канал»
- Принятие хитов Кроссворд
- Разработка сценария со старой ветчиной из Италии Кроссворд
- Память (говорите, впервые едите моллюсков?) Кроссворд
- Шикарный тип? Кроссворд
- Некоторые онлайн-помощники Кроссворд
- Что вы можете пожелать сделать с чем-то отвратительным Кроссворд
- Слишком сложно, эта подсказка будет подсказкой кроссворда
- Words With Dare, Dime or Diet Кроссворд
- Направленный (Анаг.
 ) Кроссворд
) Кроссворд - О пинте опрокинутой, Том любит это! Кроссворд
- Chipotle Extra, для разгадки короткого кроссворда
- Ошибочно расслышав день получения новой академической премии Кроссворд
- Подсказка-кроссворд о нестабильном положении дел
- Ответы от Корнуоллского чая, заваренного, но не горячего Кроссворд
- «СНЛ» Квасцы Педрад Кроссворд
Мы нашли 1 решений для X%2c Y или Z%2c В геометрии .Лучшие решения определяются по популярности, рейтингу и частоте поиска. Наиболее вероятный ответ на подсказку ОБЫЧНЫЙ .
С crossword-solver.io вы найдете 1 решения. Мы используем исторические головоломки, чтобы найти наилучшие ответы на ваш вопрос. Мы добавляем много новых подсказок на ежедневной основе.
С нашей поисковой системой для решения кроссвордов у вас есть доступ к более чем 7 миллионам подсказок. Вы можете сузить возможные ответы, указав количество букв, которые он содержит. Мы нашли более 18 ответов для X%2c Y или Z%2c в геометрии.
Вы можете сузить возможные ответы, указав количество букв, которые он содержит. Мы нашли более 18 ответов для X%2c Y или Z%2c в геометрии.
Актуальные подсказки
- 1977 Линда Ронштадт разгадывает кроссворд
- Сосед Хорватии Кроссворд
- Сайт онлайн-знакомств, кроссворд
- Цель маски для лица Кроссворд
- Частные беседы в Твиттере, для краткости Кроссворд
- Острая корейская капуста Кроссворд
- Преувеличенная мужественность Кроссворд
- Эмерсон опус Кроссворд Подсказка
- Кроссворд израильского морского порта
- Перепроверьте разгадку кроссворда
- Сухой юмор Кроссворд
- A, во французском кроссворде
- ___ (бостонский небоскреб) Кроссворд
- Разгадка кроссворда «На нем»
- Сделать много? Кроссворд
- Кроссворд канала «Акулий торнадо»
- Порт Миссисипи.
 Кроссворд
Кроссворд - Исполнительница песни How We Do (Party) Рита Кроссворд
- Актер Эфрон из фильма «Спасатели Малибу» Кроссворд
- Болотная птица Кроссворд
- Актер Эльба из кроссворда «Кошки»
- Героиня сказки «Красавица и чудовище» Кроссворд
- Единицы сетки Кроссворд
- Кроссворд отношения
- Cavs, на табло Кроссворд
- Сам по себе кроссворд
- Входить с осторожностью Кроссворд Подсказка
- Валюта Вьетнама Кроссворд
- Держатель значка за заслуги Кроссворд Clue
- Кроссворд HH Munro
- Хватит говорить Кроссворд
- Соответствует кроссворду
- Научная орг. Кроссворд
- Гонка «Машина времени» Кроссворд
- Марион ___, победительница в номинации «Лучшая женская роль» за кроссворд «Жизнь в розовом цвете»
- Кроссворд Политический беженец
- Исламское право Кроссворд Clive
- Покаялся ли кроссворд?
- Арест, как преступника Кроссворд Подсказка
- Джон Стид и Эмма Пил Кроссворд
- Место для парковки Кроссворд
- Урад дал, он же черный ___ Кроссворд
- Олимпийская гимнастка Strug Кроссворд Clue
- Партнер Фреда Астера по танцам.
 Кроссворд
Кроссворд - Очертания кроссворда
- Бостонский небоскреб, знакомый кроссворд
- Передовая разгадка кроссворда
- Система весов Кроссворд
- Сайт перископа Кроссворд
- Дочь Леды Кроссворд
Повторяющиеся подсказки
- Аксессуар к подсказке кроссворда костюма
- Покупка в магазине пакетов Кроссворд
- Разгадать кроссворд
- Отбросьте кроссворд
- Краткая подсказка кроссворда
- Судья Кроссворд
- Подсказка кроссворда соевого творога
- Кроссворд актерского мастерства
- Входит в кроссворд
- Метод Кроссворд Подсказка
- Отдых (против) Кроссворд
- Отвлечь кроссворд ключ
- Кроссворд оленя
- Бейливик Кроссворд Подсказка
- Разгадка кроссворда телесериала
- Кроссворд члена кооператива
- Кроссворд для удаления пятен
- Поверхности со стразами Кроссворд
- Разгадка кроссворда сержанта-инструктора «Один»
- Пудели, но не Schnoodles или Doodles Кроссворд Clive
- Разгадка кроссворда горького сожаления
- Разгадка кроссворда
- Отступление Кроссворд Подсказка
- Подтолкнуть к кроссворду
- Что-то взятое лучником Кроссворд
- Собери груши, разгадывай кроссворд
- Введение Кроссворд
- Кроссворд о наводнениях
- Единица работы Кроссворд
- Разве это не неправильно? Кроссворд
- Один из 64 отделов Луизианы Кроссворд
- Кроссворд французского писателя Сагана
- Блюда медленного приготовления Кроссворд
- Разделы сюжета Кроссворд
- Общались с, но не по-настоящему Кроссворд
- Подсказка кроссворда шумихи
- Найдите ключ к кроссворду русла реки
- Разгадка кроссворда
- Кроссворд Адриатической страны
- Разгадка кроссворда
- Река в Англии Кроссворд
- Отменено, в некотором роде Кроссворд
- Подражание кроссворду
- Австралийский мегаполис Кроссворд
- Кроссворд преемника Черчилля
- Подключенный кроссворд
- Кроссворд на итальянском языке «три»
- Кроссворд с маленькой картой
- Фигура Голова?: Сокр.
 Кроссворд
Кроссворд - Воображаемый кроссворд
Системы координат (Direct3D 9) — приложения Win32
Редактировать
Твиттер LinkedIn Фейсбук Электронная почта
- Статья
Обычно приложения для трехмерной графики используют два типа декартовых систем координат: левостороннюю и правостороннюю. В обеих системах координат положительная ось x направлена вправо, а положительная ось y направлена вверх. Вы можете запомнить, в каком направлении указывает положительная ось z, указав пальцами левой или правой руки в положительном направлении x и согнув их в положительном направлении y. Направление, на которое указывает ваш большой палец, к вам или от вас, является направлением, на которое указывает положительная ось Z для этой системы координат. На следующем рисунке показаны эти две системы координат.
Направление, на которое указывает ваш большой палец, к вам или от вас, является направлением, на которое указывает положительная ось Z для этой системы координат. На следующем рисунке показаны эти две системы координат.
Direct3D использует левостороннюю систему координат. Если вы переносите приложение, основанное на правосторонней системе координат, вы должны внести два изменения в данные, передаваемые в Direct3D.
- Измените порядок вершин треугольника так, чтобы система обходила их по часовой стрелке спереди. Другими словами, если вершины v0, v1, v2, передайте их в Direct3D как v0, v2, v1.
- Используйте матрицу вида для масштабирования мирового пространства на -1 в направлении z. Для этого поменяйте местами знак _31, _32, _33 и _34 элемента D3DMATRIX структура, которую вы используете для своей матрицы представления.
Чтобы получить правосторонний мир, используйте функции D3DXMatrixPerspectiveRH и D3DXMatrixOrthoRH для определения преобразования проекции. Однако будьте осторожны при использовании соответствующей функции D3DXMatrixLookAtRH , обратном порядке отбраковки обратной грани и соответствующем размещении кубических карт.
Однако будьте осторожны при использовании соответствующей функции D3DXMatrixLookAtRH , обратном порядке отбраковки обратной грани и соответствующем размещении кубических карт.
Хотя левосторонние и правосторонние координаты являются наиболее распространенными системами, существует множество других систем координат, используемых в 3D-программном обеспечении. Например, приложения для 3D-моделирования нередко используют систему координат, в которой ось Y направлена к наблюдателю или от него, а ось Z направлена вверх.
Формально ориентация набора базисных векторов (т. е. системы координат) может быть найдена путем вычисления определителя матрицы, определяемой конкретным набором базисных векторов. Если определитель положителен, говорят, что базис «положительно» ориентирован (или правосторонний). Если определитель отрицательный, говорят, что базис «отрицательно» ориентирован (или левосторонний). Объяснение того, что такое определитель, см. в любом ресурсе по линейной алгебре.
Новичкам шахматы: Шахматы для начинающих: задачи, изучение дебютов, видео
Шахматы для начинающих: задачи, изучение дебютов, видео
2023
2023
2023
Самоучители по шахматам
Самоучители
Путешествие в шахматное королевство (Авербах, Бейлин)
Сен 20, 2021 0
Книгу «Путешествие в шахматное королевство» можно отнести к одному из лучших самоучителей по шахматам. Это первая шахматная книга знаменитого гроссмейстера Бориса Гельфанда, которая до сих пор находится с ним рядом. Авторы (выдающийся гроссмейстер и известный […]
Самоучители
«Куда идет король…» Виктор Хенкин
Ноя 24, 2015
Автор: Хенкин В.Л. Издательство: Москва, 1979. — 162 стр. Несмотря на то, что книга выпущена в далеком 1979 году, она до сих пор не потеряла свою актуальность. Виктор Львович Хенкин, российский шахматист и теоретик, писал […]
Виктор Львович Хенкин, российский шахматист и теоретик, писал […]
Самоучители
«Самоучитель шахматной игры» Д. Бронштейн
Авг 31, 2015
Автор: Бронштейн,Д.И. Издательство: Физкультура и спорт, 1979. — 250 стр. Давид Иванович Бронштейн остановился в одном шаге от шахматной короны — в 1951, мачт за звание чемпиона мира по шахматам между чемпионом мира Михаилом Ботвинником […]
Биографии шахматистов
Биография шахматистов
Анатолий Карпов — двенадцатый чемпион мира по шахматам
Апр 26, 2016
Анатолий Карпов — один из величайших шахматистов современности, оставивший яркий след в любимой игре миллионов. Став символом побед и достижений советской системы, он не затерялся и в современных российских реалиях, активно проявив себя в общественной […]
Биография шахматистов
Чемпионы мира по шахматам
Июл 7, 2019
Первый чемпионат мира по шахматам состоялся в 1886 году, уже после смерти некоронованного короля Пола Морфи. Участник первого матча, Вильгельм Стейниц, считал кощунственным разыгрывать мировую корону пока был жив великий американец. Победив в матче Иоганна […]
Участник первого матча, Вильгельм Стейниц, считал кощунственным разыгрывать мировую корону пока был жив великий американец. Победив в матче Иоганна […]
Биография шахматистов
Михаил Чигорин — первый профессиональный шахматист России
Сен 1, 2016
Михаил Иванович Чигорин (1850-1908) — талантливый русский шахматист, сильнейший российский игрок рубежа XIX-XX веков, основоположник отечественной шахматной школы. Чигорин был одним из претендентов на шахматную корону, но дважды уступил Вильгельму Стейницу. В нем удивительным образом […]
Изучение дебютов
Открытые дебюты
Венская партия
Июн 26, 2022
Дебют разработан в прошлом столетии шахматистами Вены во главе с мастером Гампе. Его идея — защитив пешку e4 и пункт d5 атаковать центр ходом f2-f4. Все же проводя тематический контрудар d7-d5, черные достигают хорошей позиции. […]
[…]
Открытые дебюты
Дебют слона
Май 13, 2022 0
Дебют слона — открытый дебют, начинающийся ходами:1. e2-e4 e7-e52. Сf1-c4. История Этот дебют встречается еще в трактате Люсены (XV век). Большой популярностью начало пользовалось в средние века, его высоко оценивал Франсуа-Андре Филидор. В современной дебютной […]
Открытые дебюты
Защита двух коней
Апр 24, 2021 0
Защита двух коней — дебют, начинающийся ходами: e2-e4 e7-e5 Kg1-f3 Kb8-c6 Cf1-c4 Kg8-f6. Относится к открытым дебютам. ПОХОЖИЕ ЗАПИСИ: Защита двух коней. Контратака Тракслера (C57) Дебют четырех коней Преимущество двух слонов Восьмой тур Grand Swiss […]
Видео по дебютам
Дебюты — Шахматы для начинающих
Дебют — это начальная стадия шахматной партии. Основная задача дебюта, вывести свои фигуры на самые выгодные позиции и помещать развитию фигур противники. Если вы хотите хорошо научиться играть в шахматы, вам обязательно необходимо разучить несколько основных дебютов для игры белыми и для игры чёрными. На данный момент, благодаря развитию шахматных программ и появлению среди них настоящих «монстров» типа Deep Fritz и Houdini («Гудини»), привело к тому, что все, самые сильные ходы в дебюте изучены. По этой причине, дебют является самой малотворческой частью шахматной партии. Как бы то ни было, дебюты надо изучать.
Основная задача дебюта, вывести свои фигуры на самые выгодные позиции и помещать развитию фигур противники. Если вы хотите хорошо научиться играть в шахматы, вам обязательно необходимо разучить несколько основных дебютов для игры белыми и для игры чёрными. На данный момент, благодаря развитию шахматных программ и появлению среди них настоящих «монстров» типа Deep Fritz и Houdini («Гудини»), привело к тому, что все, самые сильные ходы в дебюте изучены. По этой причине, дебют является самой малотворческой частью шахматной партии. Как бы то ни было, дебюты надо изучать.
Процесс изучению дебютов может быть намного интересней, если вы воспользуетесь материалами сайта ChessWood.ru. Вы сможете посмотреть видеоуроки с разбором основных дебютов и посмотреть последовательность ходов в дебютах шахматных партий.
Дебюты можно разделить на три вида:
- Открытые — игра начинается ходами e2-e4, e7-5;
- Полуоткрытые — на ход e2-e4 чёрные отвечают любым ходом кроме e7-5;
- Закрытые — белые начинают партию любым ходом кроме e2-e4.

Классификация дебютов носит формальный характер, однако она проста и удобна в использовании.
Открытые дебюты
- Венгерская партия
- Венская партия
- Гамбит Эванса (1. e4 e5 2. Кf3 Кc6 3. Сc4 Сc5 4. b4)
- Дебют королевского коня
- Дебют Понциани или Английская партия (1. e2-e4 e7-e5 2. Kg1-f3 Kb8-c6 3. c2-c3)
- Дебют слона
- Дебют трёх коней
- Дебют четырёх коней
- Защита двух коней
- Защита Филидора
- Испанская партия (1. e4 e5 2. Kf3 Kc6 3. Cb5)
- Итальянская партия (1. e2-e4 e7-e5 2. Kg1-f3 Kb8-c6 3. Cf1-c4 Cf8-c5)
- Королевский гамбит (1. e2-e4 e7-e5 2. f2-f4)
- Латышский гамбит
- Русская партия (защита Петрова)
- Центральный дебют
- Шотландская партия
- Шотландский гамбит
Полуоткрытые дебюты
- Дебют Нимцовича
- Защита Алехина
- Защита Каро-Канн
- Защита Оуэна
- Защита Пирца-Уфимцева
- Защита Робача (1.
 e4 g6)
e4 g6) - Сицилианская защита
- Скандинавская защита (1. e2-e4 d7-d5)
- Французская защита
Закрытые дебюты
- Английское начало
- Атака Гроба
- Будапештский гамбит
- Вариант Чигорина
- Гамбит Блэкмара-Димера
- Голландская защита
- Дебют Берда
- Дебют Рети
- Дебют Сокольского
- Дебют ферзевых пешек
- Защита Бенони
- Защита Грюнфельда
- Защита Нимцовича
- Защита Рагозина
- Защита Чигорина
- Каталонское начало
- Контргамбит Альбина (1. d2-d4 d7-d5 2. c2-c4 e7-e5 )
- Новоиндийская защита
- Принятый ферзевый гамбит
- Славянская защита
- Староиндийская защита
- Староиндийское начало
- Ферзевый гамбит
Закрытые дебюты
Альтернативное название дебюта — Ферзевый гамбит. Меранская система. Позиция может быть получена через разный порядок ходов. История Обычно меранскую систему связывают с именем Акибы Рубинштейна, считая, что она впервые была применена в партии Грюнфельд — […]
Закрытые дебюты
Когда черные в ответ на ферзевый гамбит избирают отказанный ферзевый гамбит, то взятие белыми на d5 является интересным продолжением. Партии с комментариями Ботвинник — Керес (1-0) Москва, 1952 Корчной — Карпов (1-0) Багио, 1978 Каспаров […]
Партии с комментариями Ботвинник — Керес (1-0) Москва, 1952 Корчной — Карпов (1-0) Багио, 1978 Каспаров […]
Полуоткрытые дебюты
Вариант назван в честь сильнейшего советского и российского гроссмейстера Марка Тайманова (1926-2016), участника цюрихского турнира претендентов 1953 года, чемпиона СССР (1956). e2-e4 c7-c5 Кf3 e7-e6 d4 cxd Kxd4 Kc6 Вариант Тайманова сицилианской защиты — отличный […]
Полуоткрытые дебюты
Дебют назван в честь Николоса (Николая) Россолимо. Начинается ходами: e2-е4 c7-с5 Kg1-f3 Kb8-c6 Сb5 Сильнейшие шахматисты Специалистом по дебюту является российский шахматист Сергей Владимирович Рублевский, партии которого приведены ниже. Партии с комментариями Сабо — Авербах […]
Открытые дебюты
Дебют разработан в прошлом столетии шахматистами Вены во главе с мастером Гампе. Его идея — защитив пешку e4 и пункт d5 атаковать центр ходом f2-f4. Все же проводя тематический контрудар d7-d5, черные достигают хорошей позиции. […]
Все же проводя тематический контрудар d7-d5, черные достигают хорошей позиции. […]
Открытые дебюты
Дебют слона — открытый дебют, начинающийся ходами:1. e2-e4 e7-e52. Сf1-c4. История Этот дебют встречается еще в трактате Люсены (XV век). Большой популярностью начало пользовалось в средние века, его высоко оценивал Франсуа-Андре Филидор. В современной дебютной […]
Закрытые дебюты
Дебют Сокольского (также «польский дебют», «Дебют орангутанга») — шахматный дебют, начинающийся ходом 1. b2-b4. Относится к фланговым началам. Назван в честь Алексея Сокольского, исследовавшего этот дебют. Ранее ход 1. b2-b4 применялся Савелием Тартаковером, давшим ему […]
Закрытые дебюты
Исходная позиция закрытой системы каталонского начала (закрытого каталона) возникает после ходов: 1. d4 d5 2. c4 e6 3. Nf3 Nf6 4. g3 Be7 5. Bg2 O-O 6. O-O Самым популярным продолжением за черных является ход […]
Закрытые дебюты
Лондонская система — шахматный дебют, начинающийся ходами: 1. d2-d4 d7-d5 3. Cc1-f4 Относится к закрытым началам. Лондонская система появилась в XIX веке. Первая сохранившаяся партия — Лабурдонне — Мак-Доннелл (Лондон, 1834). Этот поединок был начат […]
d2-d4 d7-d5 3. Cc1-f4 Относится к закрытым началам. Лондонская система появилась в XIX веке. Первая сохранившаяся партия — Лабурдонне — Мак-Доннелл (Лондон, 1834). Этот поединок был начат […]
Закрытые дебюты
Атака Гроба, также Дебют Гроба (анг. Grob Opening) — дебют, начинающийся ходом 1. g2-g4. Относится к фланговым началам. Дебют назван по имени швейцарского шахматиста Генри Гроба, применявшего его.
Шахматы для начинающих | Учебный план: открытие
Каждый мастер когда-то был новичком. Вот почему гроссмейстер Сэм Шенкленд подготовил это подробное руководство, которое поможет вам сделать первые шаги в мире шахмат. Ознакомьтесь с шагами и ресурсами и начните свой путь к мастерству.
- Целевой диапазон навыков: Новичок (рейтинг 1000-1399)
- Цель : Получить знания, чтобы уверенно подойти к дебюту и добиться успеха!
Задания:
- Заучить принципы дебюта.

- Применяйте принципы в тренировочных играх.
- Выучите несколько «турнирных» дебютов.
- Посмотрите эти видеоуроки для практического повторения.
- Прочитайте эти статьи для практического обзора.
- Сыграйте в тематическом турнире открытия на Chess.com.
- Завершить вступительный урок.
- Пройди тест!
Каждый шахматист делает свои «первые шаги» в начальной стадии. Вот что мы рекомендуем для того, чтобы стать увереннее и показывать себя с лучшей стороны в каждой партии:
1. Запомните принципы дебютаКаждый шахматист должен понять эти ключевые идеи, прежде чем сможет сыграть достойный дебют.
Даже не зная какой-либо теории или конкретных дебютных вариантов, следуя приведенным ниже принципам и рекомендациям, можно добиться хороших результатов в большинстве любительских игр.
Прочтите это: Принципы открытия: для начинающих!
Смотрите это: Дебютные принципы
2. Применяйте принципы в тренировочных играх следовал принципам из статьи из Задания №1. В игры нужно играть как можно чаще. Мы полагаем, что для достижения 1400 потребуется сыграть не менее 100 практических партий (как в электронные шахматы, так и в живые шахматы), потратив время на оценку того, следовали ли вы «правилам» дебюта после 10-го хода. уровень; однако игрок должен продолжать эту практику до тех пор, пока не будет достигнуто 1400, независимо от того, сколько игр для этого потребуется.
Применяйте принципы в тренировочных играх следовал принципам из статьи из Задания №1. В игры нужно играть как можно чаще. Мы полагаем, что для достижения 1400 потребуется сыграть не менее 100 практических партий (как в электронные шахматы, так и в живые шахматы), потратив время на оценку того, следовали ли вы «правилам» дебюта после 10-го хода. уровень; однако игрок должен продолжать эту практику до тех пор, пока не будет достигнуто 1400, независимо от того, сколько игр для этого потребуется.Начни прямо сейчас!
Выберите предпочитаемый контроль времени и… → Начните игру в шахматы
или, если вы предпочитаете более медленный контроль времени…
Выберите один день до 14 дней за ход и → Начать ежедневную шахматную партию
3. Выучить несколько «турнирных» дебютов Опытные шахматисты, как правило, играют определенный набор из подготовленных открытий. Хотя этот список расширяется по мере того, как шахматист совершенствуется, не обязательно знать каждую исходную линию с самого начала. На данный момент достаточно понимать несколько избранных дебютов (или, по крайней мере, знать их достаточно, чтобы распознавать их в собственных партиях)!
Хотя этот список расширяется по мере того, как шахматист совершенствуется, не обязательно знать каждую исходную линию с самого начала. На данный момент достаточно понимать несколько избранных дебютов (или, по крайней мере, знать их достаточно, чтобы распознавать их в собственных партиях)!
Каждый шахматист со временем выберет « дебютный репертуар «, но до этого каждый шахматист должен знать следующие дебюты наизусть. В настоящее время не важно беспокоиться о том, какие варианты/ходы вы выберете, если перейдете по ссылкам ниже; просто исследуйте и наслаждайтесь просмотром нескольких игр мастеров прошлого:
С Тренером дебютов вы можете найти более 3000 дебютных строк и построить свой репертуар.
Используйте Game Explorer , чтобы просмотреть 5 партий и запомнить первые 5 ходов в следующих дебютах:
- Игра Руи Лопеса или Испанская игра
- Фортепиано Giuoco или итальянская игра
- Открытие «Четырех рыцарей»
- Два рыцаря или «Жареная печень»
- Ферзевый гамбит принят
- Отказ от ферзевого гамбита
- Отказ от ферзевого гамбита: славянин и/или полуславянин
 Посмотрите эти видеоуроки для практического ознакомления.
Посмотрите эти видеоуроки для практического ознакомления.Несмотря на то, что дебюты важны, не забывайте готовить свои навыки эндшпиля.
Делайте заметки и, возможно, просматривайте избранное несколько раз, чтобы убедиться, что вы усваиваете идеи!
- Все, что вам нужно знать: открытие! по ММ Даниэль Ренш
- Каждый шахматный дебют: первый ход! по IM Дэвид Прюсс
- Разработка, часть 1: подсчет по IM Дэвид Прюсс
- Разработка, часть 2: открытые и закрытые позиции, ММ Дэвид Прюсс
- Разработка, часть 3: гибкие позиции, IM Дэвид Прюсс
- Принципы открытия, объясненные FM Чарльз Галофре
- Открытие «Четырех рыцарей»: вступление! by ГМ Роман Дзиндзичашвили
- Легкая и Амбициозная Система против французов от МГ Романа Дзиндзичашвили Анализ участников
- : принятие решений об открытии, GM Роман Дзиндзичашвили
- Петровская оборона от FM Tiger Lilov
 Прочитайте эти статьи для практического обзора
Прочитайте эти статьи для практического обзора Гроссмейстер Колонка Грегори Серпера полна хороших дебютных советов и поучительных игр.
Мы выбрали несколько, которые, по нашему мнению, наиболее подходят для игроков этого уровня. Прочтите эти шесть статей так, как будто они были личным заданием от самого Грегори, чтобы еще больше укрепить свои новые дебютные знания!
- Обезьяна видит, обезьяна делает
- Важный урок моей юности
- Хороший, плохой и злой — Часть 2
- Типичные паттерны, которые должен знать каждый. Часть 6
- Типичные паттерны, которые должен знать каждый: самый быстрый способ проиграть игру
- Как проиграть партию за 10 ходов или меньше — Часть 2
Турниры на Chess.com начинаются и заканчиваются каждый день. Перейдите на страницу турниров, выберите «тематический» верхний фильтр и найдите предстоящий турнир, созданный/тематический для практики определенного дебюта, и присоединитесь к нему. (Их часто называют «тематических» турниров.) Вам будет предоставлена позиция для игры против других участников, и вы сможете испытать дебют с обеих сторон доски, играя белыми и черными.
(Их часто называют «тематических» турниров.) Вам будет предоставлена позиция для игры против других участников, и вы сможете испытать дебют с обеих сторон доски, играя белыми и черными.
Вы готовы к «тематической» задаче? → Присоединяйтесь к турниру сейчас!
Главный урок здесь будет заключаться в том, чтобы увидеть, как другие, скорее всего, более опытные игроки вашего турнира подходят к данной позиции. Вы увидите, что у каждого дебюта есть определенная пешечная структура, определенные тактические темы, которые часто встречаются в позициях, и другие стратегические идеи, характерные для этого дебюта. Научитесь разрабатывать планы, а не просто кусочки!
7. Пройти урок дебюта На Chess.com есть много уроков дебюта; однако мы выбрали именно этот курс для учащихся вашего уровня. Если вы можете пройти этот курс и набрать более 70%, вы должны играть на начальном этапе на уровне 1400 или выше.
Улучшите свои шахматы с помощью этих уроков → Использование типичных ошибок дебюта
ДОПОЛНИТЕЛЬНЫЙ МАТЕРИАЛ: Хотите еще советы для начинающих? Посмотрите это видео с 5 лучшими шахматными советами от чемпиона мира 9.0006 Магнус Карлсен
.Проверьте свои новые навыки.
Этот последний раздел содержит вопросы, на которые игрок должен ответить после завершения этого учебного плана!
Вопрос 1
На каком ходу ММ Даниэль Ренш сказал, что игрок должен рокироваться, хотя правило говорит 900 50 ход 10, в Принципах дебюта — — статья для начинающих?
Вопрос 2
Какая «мелочь», по словам GM Gregory Serper , могла бы помочь игроку избежать многих неудач в дебюте, о чем он затем рассказал в статье «Важный урок из моей юности»?
Вопрос 3
В его примере из открытия Свешникова, прежде чем он говорит о «качестве» разработки, кто ММ Дэвид Прюсс говорит, что лидирует в разработке в этом видео? Белый, черный или равный?
Вопрос 4
Что ММ Даниэль Ренш называет «ключом» или «секретом» к планированию на уровне мастера шахмат в статье «Принципы дебюта — для начинающих»?
Вопрос 5
Какой ход Петросян сделал на восьмом ходу против Ханса Ри, чтобы заставить сдаться в статье МГ Грегори Серпера «Как проиграть партию за 10 или менее ходов, часть 2»?
Ответы:
- 1.
 ход 7
ход 7 - 2. «здравый смысл»
- 3. равно. Само развитие было равным, основанным на принципах Дэвида, основанных на чистом счете .
- 4. пешки
- 5. 8.Фb3!
Как играть в шахматы для начинающих: правила, ходы и подготовка
Шахматы — одна из древнейших настольных игр. В нее играли и любили на протяжении веков, но в последние годы ее популярность резко возросла благодаря множеству новых игроков, желающих изучить правила шахмат.
С 2020 года интерес к шахматам резко вырос, чему способствовали люди, желающие играть онлайн во время самоизоляции, популярность шоу Netflix «Королевский гамбит» и звезды Twitch, участвующие в турнире PogChamps и шахматном боксе. После того, как фотография Лионеля Месси и Криштиану Роналду, играющих в шахматы, стала вирусной, Chess.com достиг рекордного уровня посещаемости.
Шахматы переживают возрождение, но если вы новичок в игре, изучение шахматных правил и различных стратегий может показаться ошеломляющим. Вот тут-то и пригодится наше руководство. Мы расскажем вам об основных правилах, в том числе о том, как ходить и брать фигуры, а также о важных приемах для победы, таких как проход и рокировка.
Вот тут-то и пригодится наше руководство. Мы расскажем вам об основных правилах, в том числе о том, как ходить и брать фигуры, а также о важных приемах для победы, таких как проход и рокировка.
Правила шахмат для начинающих
- Расстановка: На каком поле стоит ферзь? Узнайте, пока мы готовимся к игре, размещая свои фигуры.
- Основные правила: Узнайте, как каждая шахматная фигура ходит и бьет.
- Шах и мат: Окружите короля соперника, чтобы победить.
- Расширенные правила: Объяснение повышения, прохода и рокировки.
Независимо от того, открыли ли вы шахматы заново или впервые садитесь играть, мы составили это руководство для начинающих о том, как играть. Это руководство включает в себя все основы, которые вам нужно знать при изучении шахмат, от того, на какое поле поставить ферзя во время подготовки, до того, когда объявить «мат» и заявить о победе.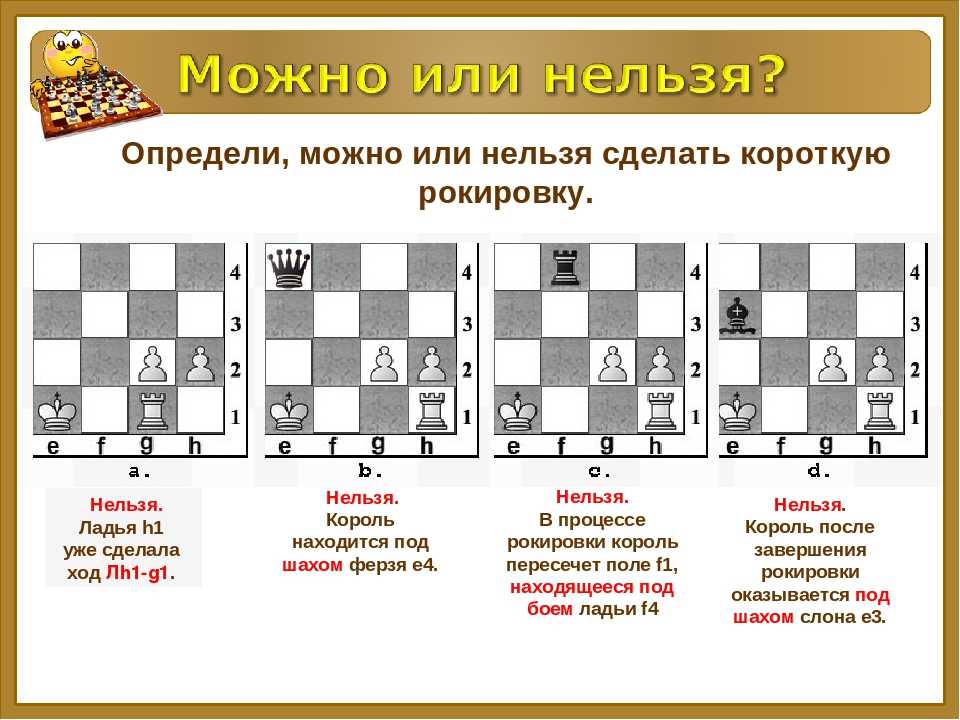
Хотя ниже вы найдете все, что вам нужно для обычной игры в шахматы, мы не углублялись в более сложные элементы, такие как определенные дебюты, позиции на доске или правила турнира. Это чистые основы, которые помогут вам играть как можно быстрее, не беспокоясь о времени своих ходов или защите от определенных дебютов. Как только вы освоите основы игры, вы сможете изучать новые стратегии, тактики и углублять свое понимание игры во время игры, постепенно совершенствуя свои навыки и опыт. Кто знает, может быть, это станет вашим первым шагом на пути к званию следующего гроссмейстера.
Как настроить шахматную доску
В шахматы играют два игрока на шахматной доске размером восемь на восемь клеток. На 64 квадратах чередуются светлые и темные цвета — традиционно черный и белый. При правильной настройке белый квадрат должен быть крайним справа на краю, ближайшем к каждому игроку.
Фишки игроков располагаются в двух горизонтальных рядах (известных как ранги), ближайших к каждому игроку. Второй ранг — т.е. второй ряд с точки зрения игрока — состоит из линии из восьми пешек, каждая из которых стоит на одной клетке.
Второй ранг — т.е. второй ряд с точки зрения игрока — состоит из линии из восьми пешек, каждая из которых стоит на одной клетке.
Ближний ряд почти симметричен: ладьи (также известные как ладьи) расположены на двух крайних левом и крайнем правом угловых полях, за ними следуют кони на внутреннем пространстве рядом с ними, а затем слоны.
Две центральные клетки ранга заняты королем и королевой. Ферзь ставится на поле своего цвета (например, черный ферзь на черном поле), а король занимает оставшееся поле противоположного цвета. Это означает, что король и королева каждого цвета обращены друг к другу, что делает правильную расстановку симметричной между двумя игроками.
Белый игрок делает первый ход, а игроки чередуют один ход, пока один из игроков не будет побежден матом или не сдастся. Ничья также может быть согласована. При игре с необязательным таймером, как в турнирах, первый игрок, у которого закончилось время, проигрывает игру.
Начальные позиции фигур в шахматах с изображением каждой королевы на поле соответствующего ее цвета. Изображение: sudowoodo/stock.adobe.com
Изображение: sudowoodo/stock.adobe.com Каковы основные правила игры в шахматы?
Хотите знать, как играть в шахматы для начинающих? Вот краткое изложение того, как работают правила. В шахматах каждый игрок по очереди делает один ход. Игроки не могут пропустить ход — они должны переместить фигуру. Каждая шахматная фигура движется определенным образом и должна двигаться в соответствии с ее законным движением.
За исключением коня, который может перепрыгивать через фигуры, фигуры не могут проходить через фигуры любого цвета, не останавливаясь (в случае фигуры того же цвета) или не захватывая их (в случае фигуры противоположного цвета).
Как захватывать фигуры
Если фигура приземляется на поле с фигурой противника, эта фигура берется и удаляется с доски. Фигуры не могут быть размещены на одной клетке с фигурой того же цвета. Когда фигура захватывает фигуру противника, она должна завершить свое текущее действие движения и завершить ход игрока.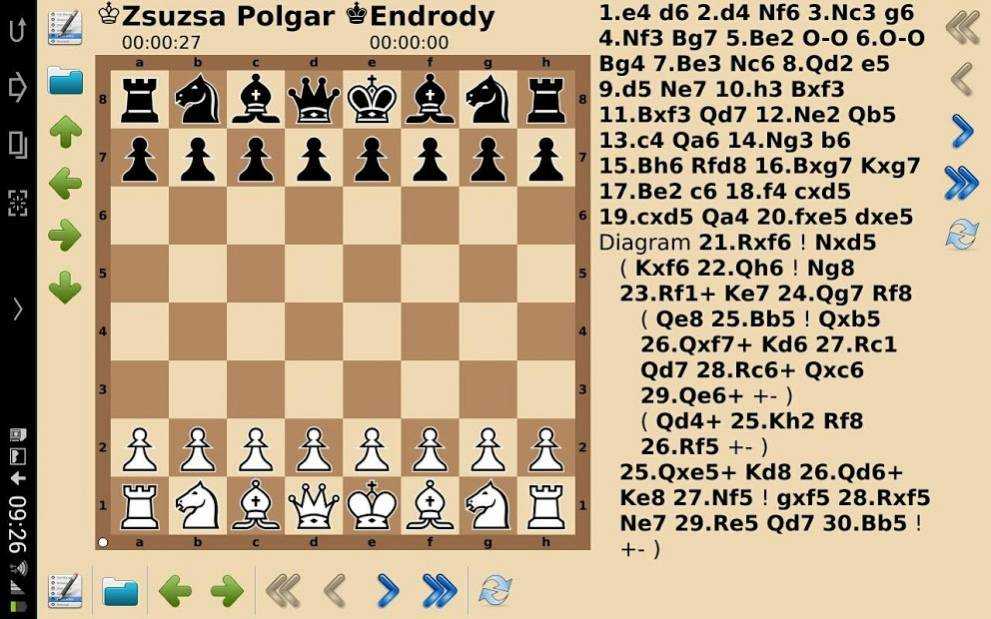
Как передвигать шахматные фигуры
Пешка
Пешки ходят на одно поле вперед по прямой. Они не могут двигаться по горизонтали, диагонали или назад.
Исключением является случай, когда пешка еще не передвинута во время игры. Если пешка еще не ходила, ее можно передвинуть на две клетки вперед за один ход. Оба квадрата должны быть пустыми. Игрок также может переместить фигуру на одну клетку.
Единственный случай, когда пешка может двигаться по диагонали, — это взятие фигуры противника. Пешки могут брать фигуру противника на любой из диагональных клеток слева или справа от фигуры. В рамках взятия фигуры пешка будет двигаться по диагонали, чтобы заменить взятую фигуру. Пешка не может брать соседнюю фигуру на любом другом поле или ходить по диагонали без взятия.
Ладья (замок)
Ладья, иногда называемая ладьей, может перемещаться на любое количество клеток по горизонтали по своему текущему ряду (линейке) или столбцу (вертикали). Он не может проходить через фигуры одного цвета и может захватывать фигуры противоположного цвета, перемещаясь на занятое место. Он не может двигаться по диагонали ни по какой причине.
Он не может проходить через фигуры одного цвета и может захватывать фигуры противоположного цвета, перемещаясь на занятое место. Он не может двигаться по диагонали ни по какой причине.
Рыцарь
Кони — единственная шахматная фигура, которую можно перемещать «сквозь» другие фигуры, «перепрыгивая» через них. Он захватывает фигуры как обычно, приземляясь на поле, занятое фигурой противоположного цвета, и не может двигаться на поле, занятое фигурой того же цвета, но может перемещаться по фигурам любого цвета во время своего хода.
Кони ходят по фиксированной схеме «L»: две клетки вперед, назад, влево или вправо, затем одна клетка по горизонтали или вертикали, или наоборот — одна клетка вперед, назад, влево или вправо, а затем две клетки по горизонтали или вертикали для завершения. форма «L».
Это означает, что конь всегда может переместиться на ближайшую клетку, которая не находится на его текущей строке (ряде), столбце (вертикали) или непосредственно примыкающей по диагонали.
Конь должен пройти все расстояние — например, он не может переместиться только на две клетки по прямой линии, не сдвинувшись на одну в сторону.
Доступные ходы коня в форме буквы «L».Бишоп
Слон может ходить на любое количество клеток по диагонали — это означает, что он всегда ходит по диагональной линии клеток, соответствующей текущему цвету его клетки. Это означает, что каждый игрок начинает игру с одним слоном, который может ходить на каждый цвет. Слон не может двигаться ни по горизонтали, ни по вертикали ни по какой причине. Он не может пройти через фигуры одного цвета и захватывает фигуру противоположного цвета, двигаясь на свою клетку.
Королева
Ферзь может ходить на любое количество клеток по горизонтали, вертикали или диагонали. Эти движения должны совершаться по одной прямой за один поворот. (Другими словами, вы не можете переместиться на три клетки по диагонали, а затем на три клетки по вертикали. ) Ферзь не может пройти через фигуры одного цвета и берет фигуру противоположного цвета, двигаясь на свое поле.
) Ферзь не может пройти через фигуры одного цвета и берет фигуру противоположного цвета, двигаясь на свое поле.
Король
Король перемещается на одно поле по горизонтали, вертикали или диагонали. Король не может переместиться на место, которое дало бы шах или мат противнику.
В отличие от всех других шахматных фигур, король никогда не берется — игрок проигрывает матч, когда королю ставится мат, что приведет к неизбежному взятию соперником на следующем ходу.
Короля никогда не берут в плен во время шахматного матча — если поставить мат, игра заканчивается. Изображение: Angela Bedürftig/PixabayЧто такое шах и мат?
Когда фигура движется таким образом, что игрок может захватить короля противника на своем следующем ходу, атакующий игрок обычно объявляет «шах».
Игрок, поставленный под шах, должен переместить своего короля или переместить другую фигуру, чтобы остановить атаку на своем следующем ходу — либо заблокировав ход, либо захватив атакующую фигуру.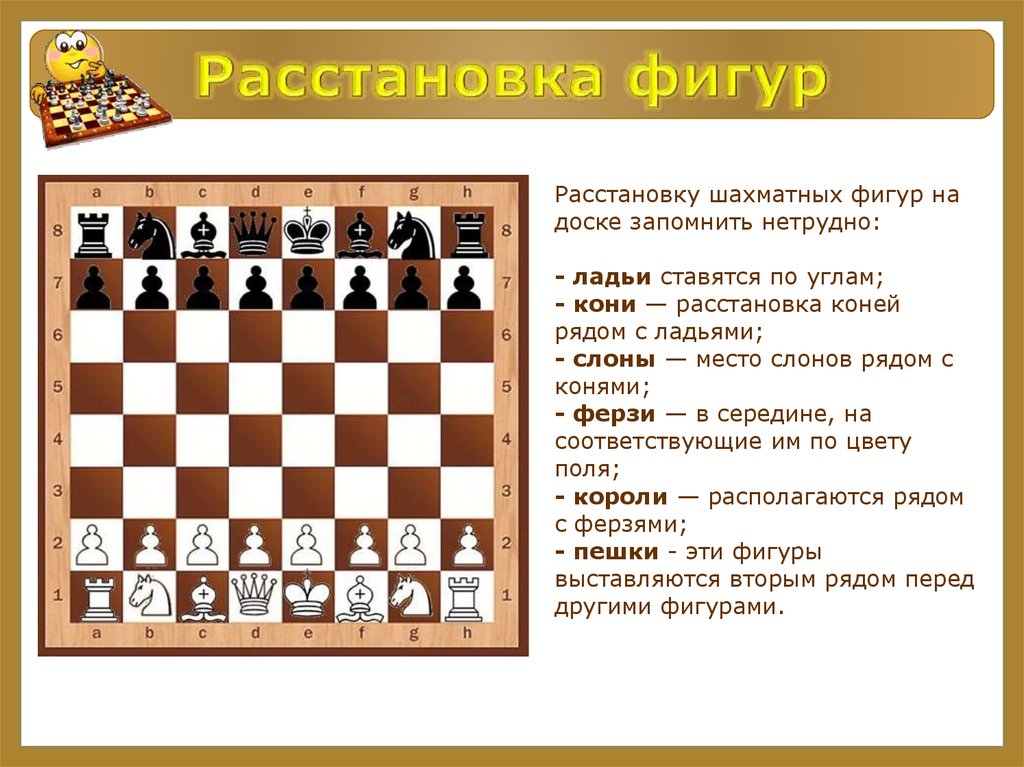
Если игрок создает ситуацию, когда его противник не может предотвратить захват своего короля на следующем ходу, атакующий игрок объявляет «мат» и немедленно выигрывает игру. Король никогда не берется в плен — игра в шахматы считается выигранной, когда объявляется успешный мат.
Мат возникает, когда игрок не может избежать проверки, а это означает, что его король будет захвачен на следующем ходу. Изображение: Steve Buissinne/PixabayИгрок также может уйти в отставку, предоставив своему противнику победу. Матчи также могут закончиться согласованной ничьей — например, в результате пата, в результате которого игрок не может сделать никаких разрешенных ходов, или если ни один игрок не может выиграть, используя доступные разрешенные ходы, ситуация, известная как «мертвая позиция». Одним из примеров мертвой позиции является ситуация, когда оба игрока остаются со своим королем в качестве единственной оставшейся фигуры на доске.
Ничьи также могут происходить в результате сложных правил, обычно используемых в профессиональных турнирах, включая одинаковые позиции на доске, встречающиеся три или пять раз (правила, известные соответственно как трехкратное повторение и пятикратное повторение), или отсутствие взятий или ходов пешек в течение последних 50 или 75 лет. движется. Точные используемые правила могут зависеть от турнира и соглашения между игроками.
движется. Точные используемые правила могут зависеть от турнира и соглашения между игроками.
Продвинутые шахматные правила
Существует ряд продвинутых правил, которые можно использовать в шахматах, наряду со специфическими дебютами и позициями на доске, известными под разными названиями, от дебюта двойной королевской пешки до знаменитого королевского гамбита и ферзевого гамбита.
Расширенные правила могут включать в себя конкретные варианты, которые изменяют основные правила игры, а также сопутствующие требования, часто используемые в настройках турнира, такие как время и правило касания-хода, которое гласит, что как только игрок коснется фигуры, она должна сделать законный ход.
Поскольку это руководство для начинающих по изучению шахмат, мы рассмотрим здесь только некоторые из основных продвинутых правил — правила, которые всегда следует использовать в сочетании с основными правилами перемещения и взятия фигур, а также со стандартной установкой и правилами. за объявление мата.
за объявление мата.
Как только вы освоите основы игры в шахматы, вы найдете сотни книг и других ресурсов, которые помогут вам открыть для себя глубокую стратегию и почти бесконечные варианты, возможные во время игры, а также местные турниры, которые помогут вам усовершенствовать свою игру и тактика.
Существуют тысячи потенциальных раскладок доски из сотен проемов и вариантов. Изображение: Steve Buissinne/PixabayКак продвигать пешку?
Если пешка достигает противоположного края доски — самого дальнего ряда (ряда) от контролирующего игрока — она превращается в другую фигуру: ладью, коня, слона или ферзя. Новая фигура заменяет пешку на своей текущей клетке и следует правилам движения для соответствующей фигуры.
В то время как большинство случайных игроков используют захваченные фигуры для обозначения превращенных фигур, пешка может быть по закону превращена в любую фигуру, независимо от того, была ли она взята. Например, у игрока может быть несколько ферзей в результате превращения пешек или несколько слонов, способных двигаться по диагональным линиям одного цвета в зависимости от поля, на котором была превращена пешка.
Количество пешек, которые можно продвигать, не ограничено.
Что такое En passant?
En passant — по-французски «мимоходом» — один из самых известных ходов в шахматах. На проходе происходит, когда пешка перемещается на две клетки вперед в результате своего дополнительного начального хода.
Если пешка противника могла бы легально взять ходящую пешку, если бы она переместилась только на одну клетку вместо двух, противник может объявить на проходе на своем следующем ходу и переместить свою пешку по диагонали на клетку, через которую прошла пешка, — взяв ход. пешка, как если бы она передвинулась только на одну клетку.
En passant должен быть объявлен и сделан как следующий ход противника, чтобы быть законным — в противном случае игрок, у которого есть шанс взять пешку, теряет эту возможность.
Что такое рокировка?
Рокировка — это, пожалуй, самое сложное основное правило в шахматах, и в результате это правило часто упускается из виду многими новичками.
Рокировка разрешена, когда фигура короля и ладья игрока еще не двигались во время игры. Рокировка может быть выполнена любой ладьей, если она не двигалась — другими словами, она все еще находится в своих начальных углах на краю, ближайшем к контролирующему игроку.
Рокировка предполагает, что игрок перемещает фигуру короля на два поля к ладье, с которой он рокирует, прежде чем переместить ладью на поле, через которое прошел король. Это фактически ставит ладью рядом с другой стороной короля, в то время как король перемещается на два поля к месту, в котором ладья начала игру. Независимо от того, выполняется ли рокировка ладьей ближе к королю (королевский фланг) или на одно поле дальше (ферзевый фланг), король перемещается только на две клетки.
Короля нельзя использовать в маневре рокировки, если он в данный момент находится под шахом, но ладью можно использовать в рокировке, даже если она находится под угрозой со стороны фигуры противника — другими словами, если она может быть взята на следующем ходу противника, или на любой из клеток, через которые он проходит при выполнении хода.
Как обычно, рокировка не может быть использована для перемещения короля, если она ставит короля под шах. Рокировка также не может быть использована, если между королем и ладьей есть какие-либо фигуры — поля между ними должны быть чистыми.
Часто задаваемые вопросы о шахматах
Повышают ли шахматы IQ?
На протяжении многих лет было проведено множество исследований, посвященных преимуществам шахмат, и ученые утверждали, что шахматы могут помочь в борьбе с деменцией и улучшить рабочую память.
А как же IQ? Поможет ли игра в шахматы стать умнее? В официальном документе Роберт Фергюсон из Американской шахматной школы процитировал исследование, проведенное с участием более 4000 школьников. Большинство проанализированных студентов продемонстрировали «значительный» прирост показателей IQ после изучения шахмат как минимум в течение четырех с половиной месяцев. Другие исследования также утверждают, что игра в шахматы может помочь улучшить IQ и познавательные способности детей.
Можно ли выиграть в шахматы за 2 хода?
В шахматы можно выиграть всего за два хода, используя Fool’s Mate. Это ставит мат ферзем за наименьшее количество возможных ходов. Это можно сделать только в том случае, если у вас есть контроль над черными и если игрок белыми допускает серьезные тактические ошибки.
В шахматы можно выиграть всего за два хода с помощью Fool’s Mate.Во-первых, игрок белыми начинал партию, перемещая пешку на поле f3 или f4 на доске. Затем игроку черными нужно будет переместить пешку на e6. Если затем белые переместят пешку на g4, может случиться мат. Черным просто нужно переместить ферзя на поле h5 и поставить мат. Король белого игрока попал в ловушку и не может выбраться.
Могут ли пешки двигаться назад?
Пешки не могут двигаться назад. На своем первом ходу пешки могут двигаться вперед на одно или два деления, но после этого их движение ограничено только одним делением вперед.
В отличие от других шахматных фигур, способ взятия пешки отличается от ее движения.

 14159..
14159..



 Conversion может выполнять преобразование документов в ряде форматов документов. Он преобразовывает точно, гарантируя, что детали сохраняются при преобразовании документа.
Conversion может выполнять преобразование документов в ряде форматов документов. Он преобразовывает точно, гарантируя, что детали сохраняются при преобразовании документа. NET
NET Конвертирование в PDF позволяет обойтись без потерь качества. Формат разработала компания Adobe Systems.
Конвертирование в PDF позволяет обойтись без потерь качества. Формат разработала компания Adobe Systems.
 Среди них можно найти даже несколько редких, что является несомненным плюсом. Программа качественно преобразует изображения в PDF. К недостаткам можно отнести скорость работы сервиса.
Среди них можно найти даже несколько редких, что является несомненным плюсом. Программа качественно преобразует изображения в PDF. К недостаткам можно отнести скорость работы сервиса. Максимальный размер файла 100 МБ или регистрация
Максимальный размер файла 100 МБ или регистрация
 Независимо от того, используете ли вы MacBook, компьютер с Windows или даже портативное мобильное устройство, для вашего удобства конвертер BMP в JPEG всегда доступен онлайн.
Независимо от того, используете ли вы MacBook, компьютер с Windows или даже портативное мобильное устройство, для вашего удобства конвертер BMP в JPEG всегда доступен онлайн.
 Поэтому можно пренебречь действием
краевых полей во всяком случае в
центральной по оси y части пучка. Тогда вблизи центра пучка
составляющие электрического поля Еz=Еy=0, а Еx0.
Пусть пучок имеет толщину x.
Выберем положение начала координат
посредине тонкой стенки
Поэтому можно пренебречь действием
краевых полей во всяком случае в
центральной по оси y части пучка. Тогда вблизи центра пучка
составляющие электрического поля Еz=Еy=0, а Еx0.
Пусть пучок имеет толщину x.
Выберем положение начала координат
посредине тонкой стенки 14)
14) Как и в первом издании, содержание ориентировано на программы вступительных экзаменов в технические вузы и, в особенности, на программы подготовительных отделений при высших учебных заведениях, для учащихся которых, как мы надеемся, книга окажется полезной.
Как и в первом издании, содержание ориентировано на программы вступительных экзаменов в технические вузы и, в особенности, на программы подготовительных отделений при высших учебных заведениях, для учащихся которых, как мы надеемся, книга окажется полезной.

 }\)
}\) }\) Таким образом, мы имеем \( n\) слагаемых плюс слагаемые \(n=0\) и \(n=-1\).
}\) Таким образом, мы имеем \( n\) слагаемых плюс слагаемые \(n=0\) и \(n=-1\). Затем выпишите последовательность периметров для прямоугольников (первый член последовательности будет равен 6, так как периметр прямоугольника \(1\times 2\) равен 6 — следующий член будет равен 10).
Затем выпишите последовательность периметров для прямоугольников (первый член последовательности будет равен 6, так как периметр прямоугольника \(1\times 2\) равен 6 — следующий член будет равен 10).
 три разных тока I 1 , я 2 и я 3 с I 3 = I 1 + I 2 .
три разных тока I 1 , я 2 и я 3 с I 3 = I 1 + I 2 .  ) 3I 1 + I 2 = 14
) 3I 1 + I 2 = 14  ) 2 I 1 +
3 I 2 = 7
) 2 I 1 +
3 I 2 = 7  ) 3I 1 + I 2 = 14
) 3I 1 + I 2 = 14  ) (2)X+ (2)2Y =
(2) 10
) (2)X+ (2)2Y =
(2) 10 



 Значит масса арбуза заключена в промежутке от 5 кг до 10 кг. И чтобы не писать два неравенства, пишут одно двойное неравенство.
Значит масса арбуза заключена в промежутке от 5 кг до 10 кг. И чтобы не писать два неравенства, пишут одно двойное неравенство.

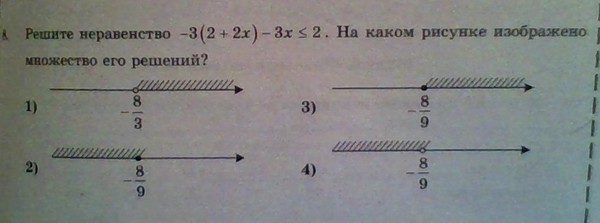 д.
д.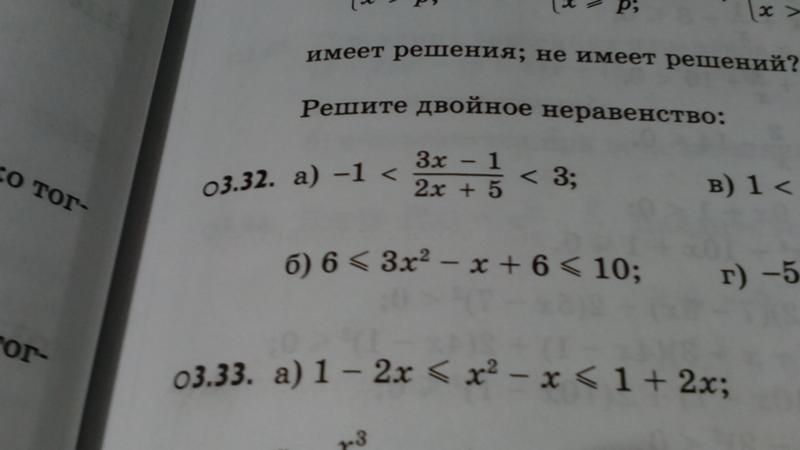



 е. интервал, где есть двойная штриховка: и сверху, и снизу. Его и запишем ответ.
е. интервал, где есть двойная штриховка: и сверху, и снизу. Его и запишем ответ.



 В процессе
изучая эти матричные операции, мы
научитесь пользоваться помощником
приложение для выполнения матрицы
вычисления.
В процессе
изучая эти матричные операции, мы
научитесь пользоваться помощником
приложение для выполнения матрицы
вычисления.


 Вышеупомянутые числа становятся
Вышеупомянутые числа становятся 


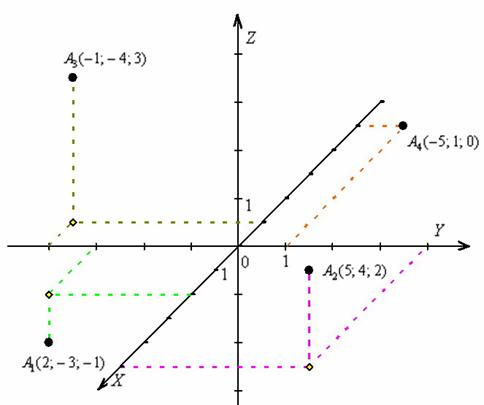
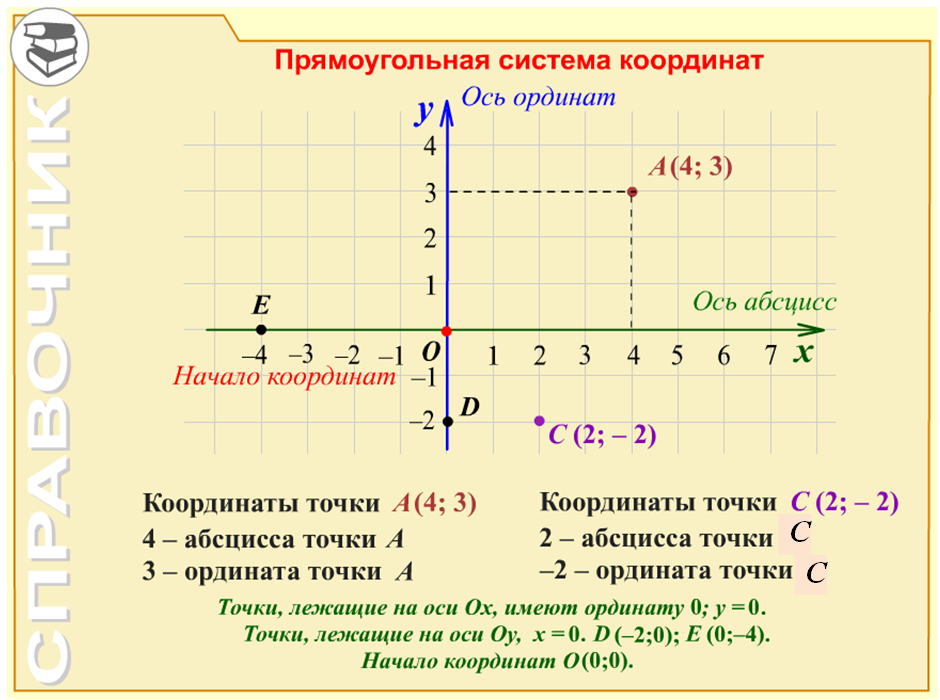 д.
д.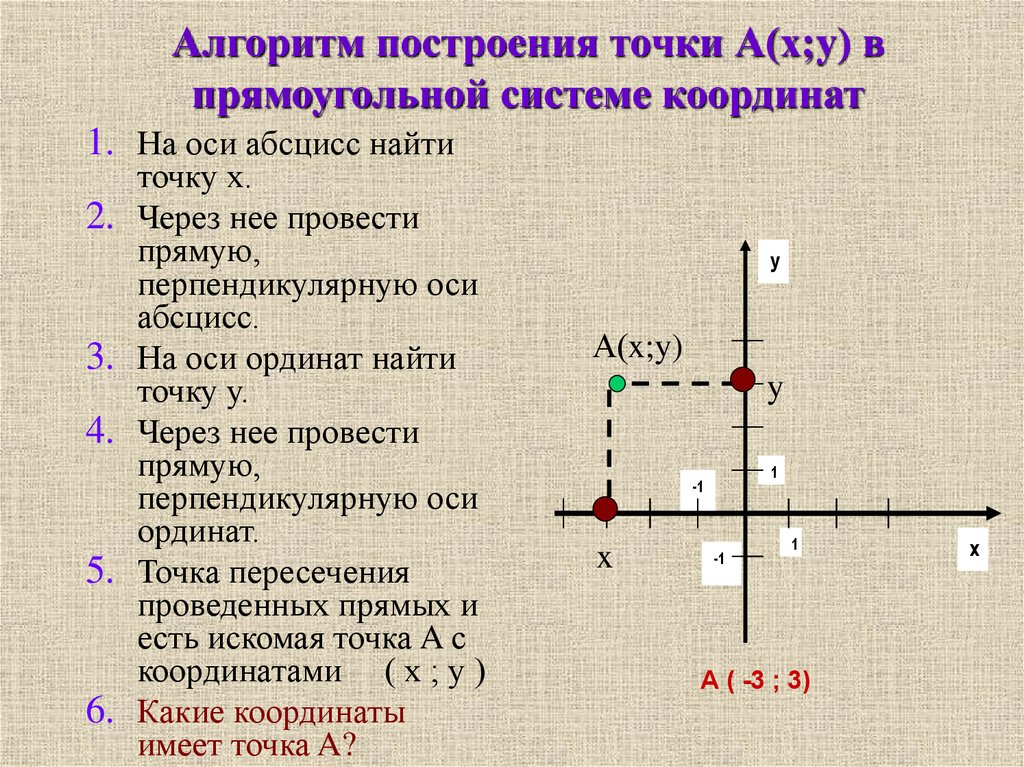

 ) Кроссворд
) Кроссворд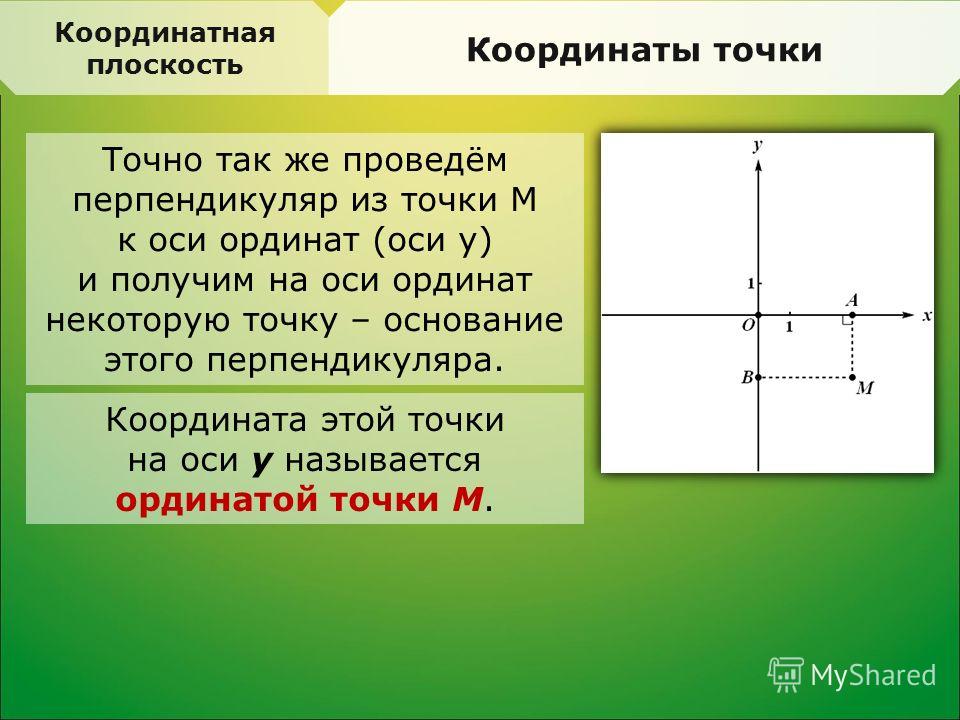 Кроссворд
Кроссворд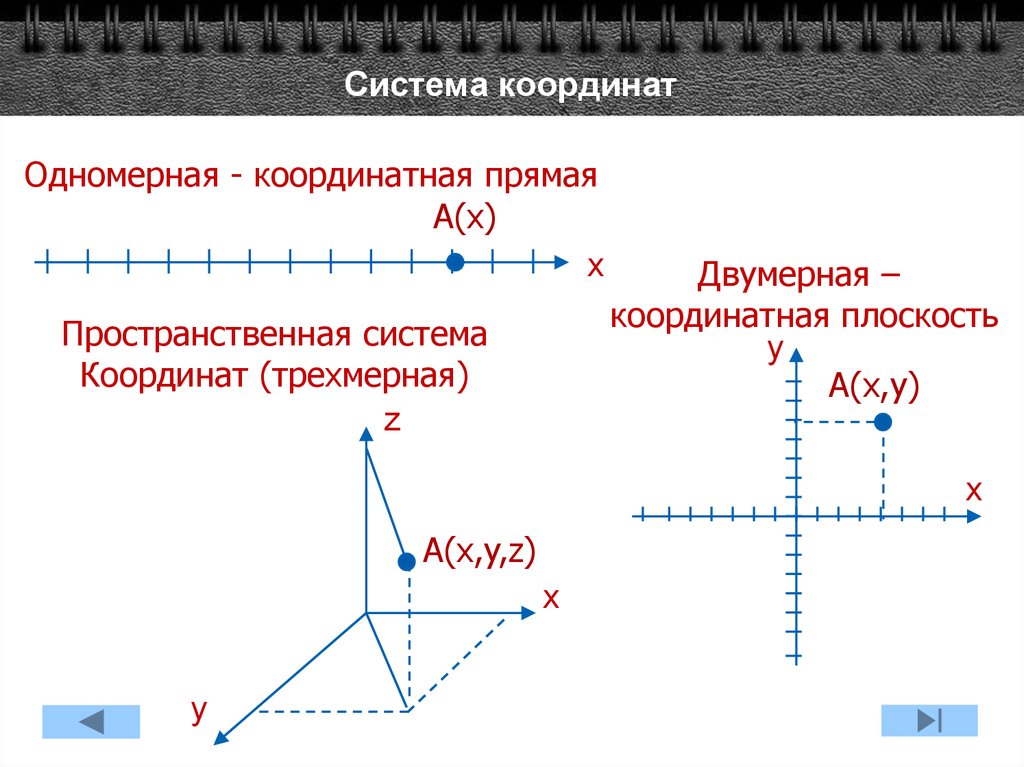 Кроссворд
Кроссворд Кроссворд
Кроссворд
 e4 g6)
e4 g6)
 ход 7
ход 7