Что такое площадь по математике: Что такое площадь? Как её найти?

Содержание

Что такое площадь в математике? Единицы площади

От Masterweb

01.07.2018 14:00

Есть проблемы с элементарной геометрией? Эта статья поможет вам решить одну из них. Здесь вы узнаете о том, что такое площадь в математике, об единицах ее измерения и других важных аспектах этой темы. Разбор некоторых конкретных примеров даст вам возможность глубже изучить вопрос.

Что такое площадь в математике?

Площадь — это мера того, сколько пространства есть на плоской поверхности. Например, есть два одинаковых куска бумаги, чья суммарная площадь, очевидно, больше чем у каждого из них по отдельности.

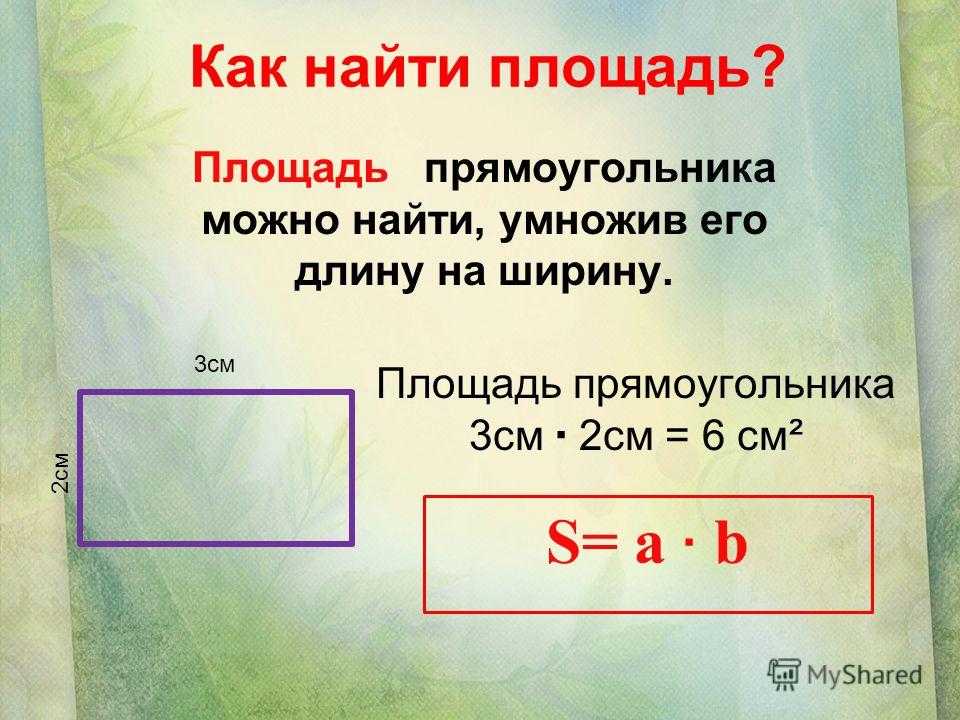
Площади фигур в математики вычисляются разными путями, зависимо от их формы. Например, в случае с прямоугольником необходимо найти произведение его высоты и ширины. Посмотрим на рисунок.

Имеем ответ: 2 × 4 = 8 см2. Задача решена.

Проверить его можно вручную подсчитав количество больших квадратиков внутри прямоугольника. Подобной задачи достаточно для того чтобы объяснить, что такое площадь в математике. Но в этой теме есть еще и другие важные нюансы.

Единица измерения площади в математике

Измеряется площадь в квадратных единицах. То есть ее можно определить как некоторое количество четырехугольников, чьи стороны равны 1. При этом если поменять местами значения длины и высоты, конечный результат не изменится.

Примечание! Все величины должны быть в одинаковых единицах измерения.

Допустим, что данные заданы в сантиметрах. Как тогда правильно обозначить это на бумаге?

Вместо того чтобы писать «восемь квадратных сантиметров», можно использовать запись вида «8 см2». Достаточно просто возвести сокращенную форму меры во вторую степень.

Перевод величин

У студента или ученика может возникнуть потребность перевести значение из одних единиц измерения в другие. Существует только один верный способ это сделать. Правда, для этого необходимо вспомнить, как правильно переводить одни единицы измерения в другие.

Допустим имеем 9000 м2. Нужно найти, сколько это гектаров. Известно что 1 га = 10 000 м2. Разделим исходную площадь на десять тысяч. В результате получим 0,9 га. Это и будет искомым значением. Главное иметь информацию об отношении двух величин между собой.

А теперь проверим.

Другие фигуры

К сожалению, для нахождения площади не всегда достаточно перемножить два числа. Ситуации бывают разные. Рабочая формула для каждой из них будет видоизменяться из раза в раз. Ниже приведены наиболее часто встречаемые вариации фигур.

Пример

Теперь вы знаете, что такое площадь в математике. Основной теоретический материал усвоен, и можно переходить к практике. Для закрепления решим конкретную задачу.

Условие. Имеется квадрат со стороной 3 сантиметра и круг с радиусом такой же длины. Найдите, чья площадь больше и на сколько.

Решение. Для начала произведем вычисления для каждой из фигур по отдельности:

Sквад = 3 × 3 = 9. Итак, площадь квадрата равна 9 см2.

А вот площадь круга вычисляется уже по другой формуле. Для ее нахождения необходимо вспомнить значение ∏:

Sкруг = ∏ × 3 × 3 ≈ 28,26 см2.

По результатам видим, что площадь круга в несколько раз больше. Осталось лишь посчитать на сколько. Для этого найдем разницу двух чисел.

Sкруг — Sквад = 28,26 — 9 = 19,26 см2.

Ответ найден.

Обычно, решая такие задачи, человек должен сводить все к готовым формулам. Затем уже искать неизвестные, выражать величины одну через другую и использовать смекалку.

Что такое площадь в математике? Единицы площади :: SYL.ru

Что такое площадь в математике?

Имеем ответ: 2 × 4 = 8 см². Задача решена.

Единица измерения площади в математике

Примечание! Все величины должны быть в одинаковых единицах измерения.

Допустим, что данные заданы в сантиметрах. Как тогда правильно обозначить это на бумаге?

Вместо того чтобы писать «восемь квадратных сантиметров», можно использовать запись вида «8 см²«. Достаточно просто возвести сокращенную форму меры во вторую степень.

Перевод величин

Допустим имеем 9000 м². Нужно найти, сколько это гектаров. Известно что 1 га = 10 000 м². Разделим исходную площадь на десять тысяч. В результате получим 0,9 га. Это и будет искомым значением. Главное иметь информацию об отношении двух величин между собой.

А теперь проверим.

Другие фигуры

Пример

Решение. Для начала произведем вычисления для каждой из фигур по отдельности:

S_квад = 3 × 3 = 9. Итак, площадь квадрата равна 9 см².

А вот площадь круга вычисляется уже по другой формуле. Для ее нахождения необходимо вспомнить значение ∏:

S_круг = ∏ × 3 × 3 ≈ 28,26 см².

S_круг — S_квад = 28,26 — 9 = 19,26 см².

Ответ найден.

Площадь — Математика 3-го класса

Площадь — это количество пространства плоской формы или поверхности.

Сколько места занимает эта доска? 🤔

👉 Чтобы это понять, найдем площадь доски !

Совет: Только двумерные объекты имеют площадь. Трехмерные объекты имеют объема .

Обложка книги плоская. Передняя часть двери шкафа плоская. Бумага плоская.

Как найти площадь чего-либо?

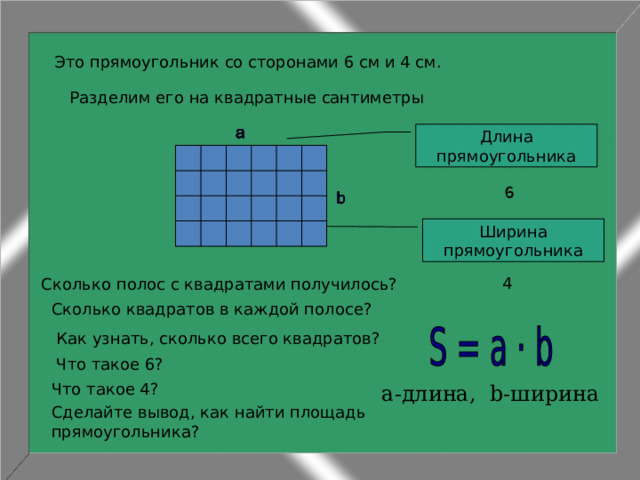
Давайте найдем площадь сетки как эта доска

Один из способов найти площадь сетки это подсчитать все квадраты в ней .

Сколько здесь квадратов?

Верно! Есть 30 квадратов.

Площадь доски 30 квадрат шт. . 😀

1 квадрат равен 1 квадратный блок .

Но счет идет довольно медленно. Давайте изучим более быстрый способ.

Использование умножения для нахождения площади

Чтобы найти площадь сетки , такой как прямоугольник или квадрат, просто умножьте на высоту на ширину .

Высота x Ширина = Площадь

Почему это работает? 🤔

Потому что сетки — это просто столбцы , умноженные на на некоторое количество строк! 🤓

Сколько строк и столбцов в нашей сетке?

Что произойдет, если мы умножим количество строк (5) на количество столбцов (6)?

5 x 6 = 30

901 😺
Так что помните:
Умножьте на длину и ширину любого прямоугольника или квадрата, чтобы получить его площадь .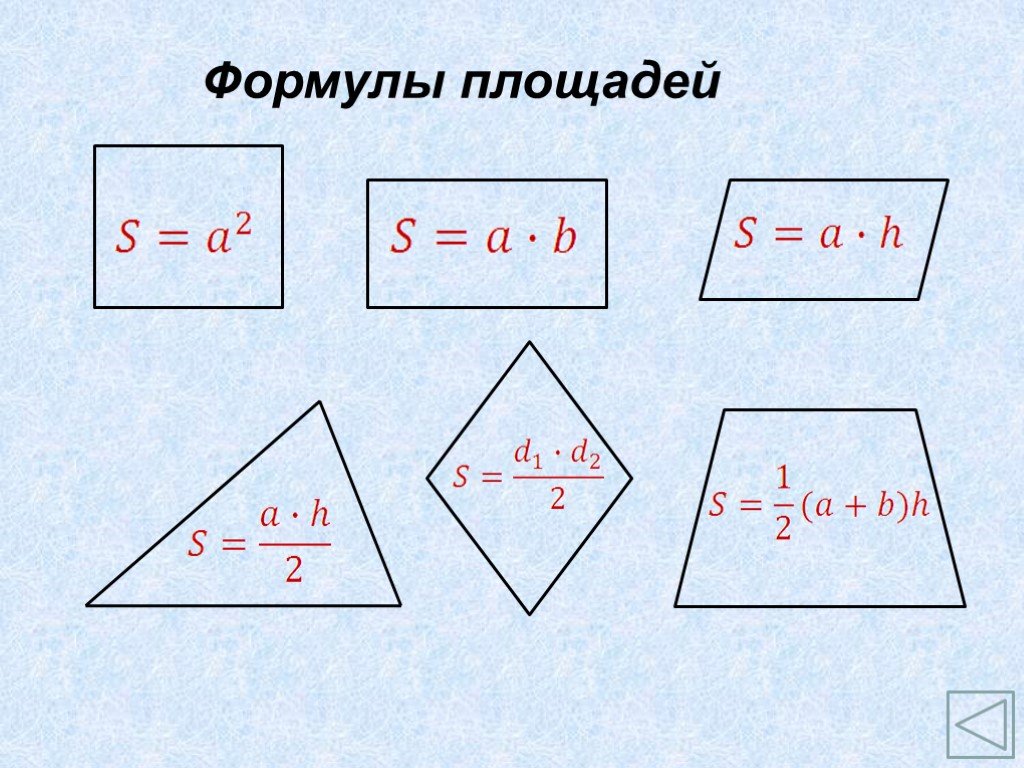
Единицы площади
Точно так же, как длина, вес и время, площадь также имеет около единиц из измерения .
Единицы из площадь говорят нам, насколько велика или мала площадь на самом деле.
Представьте, что это размер каждой клетки на доске.
Площадь квадрата шириной 1 см и высотой 1 см составляет 1 квадрат сантиметр.
Квадрат сантиметр единица измерения площади. Записывается как см² .
В Соединенных Штатах люди также иногда используют квадратных дюймов в качестве единицы измерения.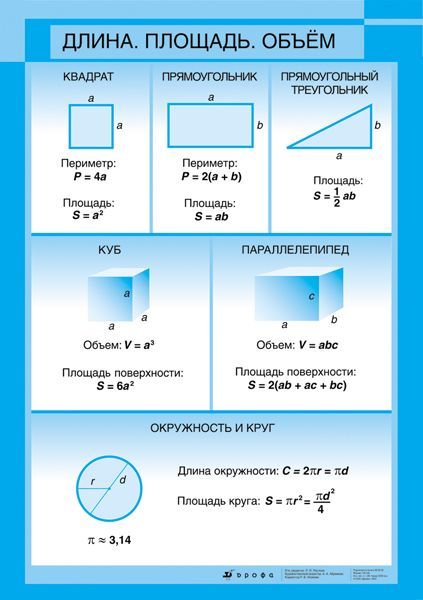 Записывается как кв . дюйма или дюйма² .
👉 Площадь квадрата шириной 1 и высотой 1 равна 1 квадратный дюйм.
Итак, какова площадь нашей доски?
Мы знаем, что это 30 квадратных единиц.
Если площадь каждого квадрата равна 1 см², то площадь доски равна 30 см². 👍
Площадь больших пространств
Что, если мы хотим измерить площадь больших пространств, таких как это травяное поле?
Какую единицу измерения следует использовать? 🤔
😌 Квадратный сантиметр будет слишком мал.
Для больших помещений часто используется единица измерения квадратных метра. Записывается как м² .
Квадрат метр – это площадь, занимаемая квадратом со стороной 1 м. 👍
Теперь измерим площадь двора.
👉 Сетка может помочь нам посчитать квадратные единицы.
Вместо подсчета умножим столбцов на строки.
5 х 9 = ?
Что мы получаем? 45 квадрат штук !
Итак, площадь двора 45 м² . 🎉
квадратных футов
В Соединенных Штатах люди часто используют квадратных футов вместо квадратных метра !
1 квадрата фута — это площадь квадрата размером 1 фут на 1 фут. Сокращенно кв. . футов или футов² .
Квадратные футы меньше квадратных метров.
1 м ² может поместиться чуть более 10 футов².
Теперь завершите практику. Вы узнаете больше и будете помнить дольше. 💪
Как найти площадь шестиугольника
Все ресурсы по математике для старших классов
8 Диагностические тесты 613 практических тестов Вопрос дня Карточки Learn by Concept
Справка по математике для старших классов » Геометрия » Плоская геометрия » Шестиугольники » Как найти площадь шестиугольника
Calculate the approximate area a regular hexagon with the following side length:
Possible Answers:
Cannot be determined
Correct answer:
Пояснение:
Есть несколько способов найти площадь шестиугольника.
В правильном шестиугольнике разделите фигуру на треугольники.
Найдите площадь одного треугольника.
Умножьте это значение на шесть.
В качестве альтернативы, площадь может быть найдена путем вычисления половины длины стороны, умноженной на апофему.

Правильные шестиугольники:
Правильные шестиугольники представляют собой интересные многоугольники. Шестиугольники представляют собой шестигранные фигуры и имеют следующую форму:
В правильном шестиугольнике все стороны имеют одинаковую длину и все внутренние углы имеют одинаковую меру; поэтому мы можем написать следующее выражение.

Один из самых простых способов найти площадь многоугольника — разбить фигуру на треугольники. Начнем с разделения шестиугольника на шесть треугольников.
На этом рисунке центральная точка равноудалена от всех вершин. В результате шесть пунктирных линий внутри шестиугольника имеют одинаковую длину. Точно так же все треугольники внутри шестиугольника конгруэнтны по правилу стороны-стороны-стороны: каждый из треугольников имеет две общие стороны внутри шестиугольника, а также сторону основания, которая составляет периметр шестиугольника. Аналогичным образом, каждый из треугольников имеет одинаковые углы. Они расположены в круге, и шестиугольник на нашем изображении разделил его на шесть равных частей; поэтому мы можем написать следующее:
Мы также знаем следующее:
Теперь давайте посмотрим на каждый из треугольников в шестиугольнике. Мы знаем, что у каждого треугольника есть две равные стороны; следовательно, каждый из углов при основании каждого треугольника должен быть одинаковым. Мы знаем, что у треугольника есть  , и мы можем найти два угла при основании каждого треугольника, используя эту информацию.
Каждый угол в треугольнике равен .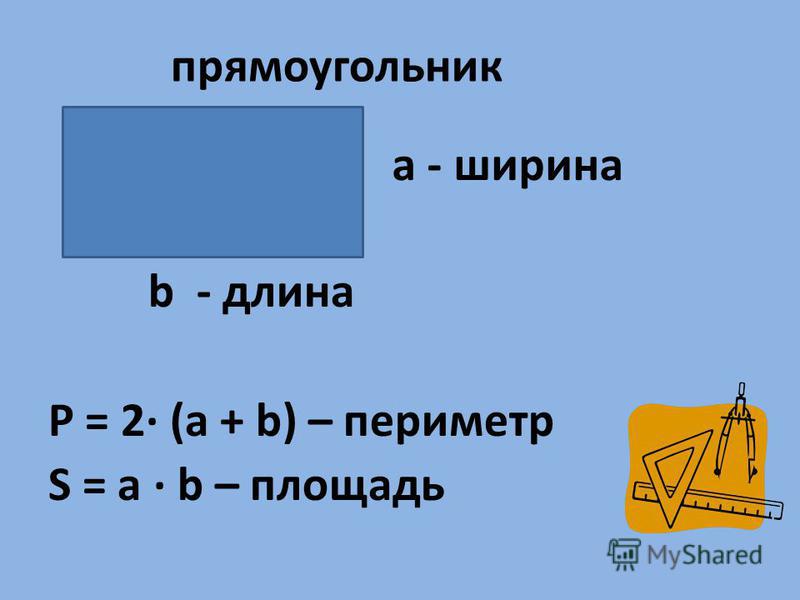 Теперь мы знаем, что все треугольники конгруэнтны и равносторонние: каждый треугольник имеет три равные длины сторон и три равных угла. Теперь мы можем использовать эту жизненно важную информацию для определения площади шестиугольника. Если мы найдем площадь одного из треугольников, то можем умножить ее на шесть, чтобы вычислить площадь всей фигуры. Начнем с анализа . Если мы проведем высоту через треугольник, то обнаружим, что создаем два  треугольника.
Найдем длину этого треугольника. Помните, что в треугольниках длины сторон находятся в следующем соотношении:
. Теперь мы можем проанализировать,  используя замещающую переменную для длины стороны, .
Мы знаем размеры основания и высоты и можем найти его площадь.
Теперь нам нужно умножить это на шесть, чтобы найти площадь всего шестиугольника.
Мы нашли площадь правильного шестиугольника с длиной стороны, .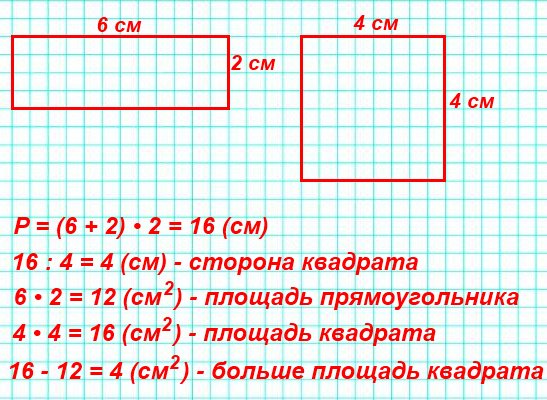 Если мы знаем длину стороны правильного шестиугольника, то можем найти площадь.
Если у нас нет правильного шестиугольника, то мы находим площадь шестиугольника, используя длину стороны (т. е. ) и апофему (т.е. ), которая является длиной линии, проведенной из центра прямой угол любой стороны. Это обозначено переменной  на следующем рисунке:

Альтернативный метод:
Если нам даны переменные и , то мы можем найти площадь шестиугольника по следующей формуле:
и является апофемой. Мы должны вычислить периметр, используя длину стороны и уравнение , где  – длина стороны.

Решение:
В данной задаче мы знаем, что длина стороны правильного шестиугольника равна:
Подставим это значение в формулу площади правильного шестиугольника и решим.
Упрощение.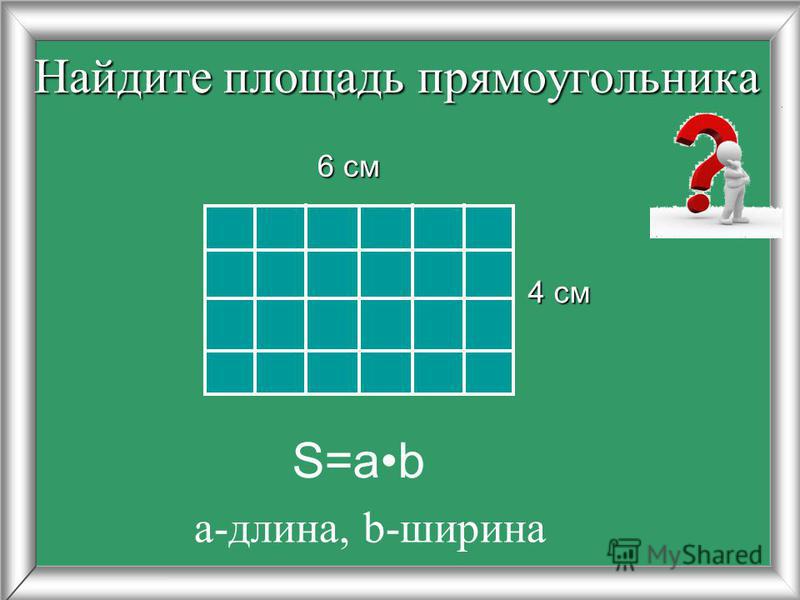

Округлите ответ до ближайшего целого числа.
Сообщить об ошибке
Одна шестиугольная ячейка сот имеет диаметр два сантиметра.

Какова площадь клетки с точностью до десятых долей сантиметра?

Возможные ответы:
Невозможно определить Пояснение:
Есть несколько способов найти площадь шестиугольника.
В правильном шестиугольнике разделите фигуру на треугольники.
Найдите площадь одного треугольника.
Умножьте это значение на шесть.
В качестве альтернативы, площадь может быть найдена путем вычисления половины длины стороны, умноженной на апофему.

Правильные шестиугольники:
Правильные шестиугольники представляют собой интересные многоугольники. Шестиугольники представляют собой шестигранные фигуры и имеют следующую форму:
В правильном шестиугольнике все стороны имеют одинаковую длину и все внутренние углы имеют одинаковую меру; поэтому мы можем написать следующее выражение.

Один из самых простых способов найти площадь многоугольника — разбить фигуру на треугольники. Начнем с разделения шестиугольника на шесть треугольников.
На этом рисунке центральная точка равноудалена от всех вершин. В результате шесть пунктирных линий внутри шестиугольника имеют одинаковую длину. Точно так же все треугольники внутри шестиугольника конгруэнтны по правилу стороны-стороны-стороны: каждый из треугольников имеет две общие стороны внутри шестиугольника, а также сторону основания, которая составляет периметр шестиугольника. Аналогичным образом, каждый из треугольников имеет одинаковые углы. Они расположены в круге, и шестиугольник на нашем изображении разделил его на шесть равных частей; поэтому мы можем написать следующее:
Мы также знаем следующее:
Теперь давайте посмотрим на каждый из треугольников в шестиугольнике.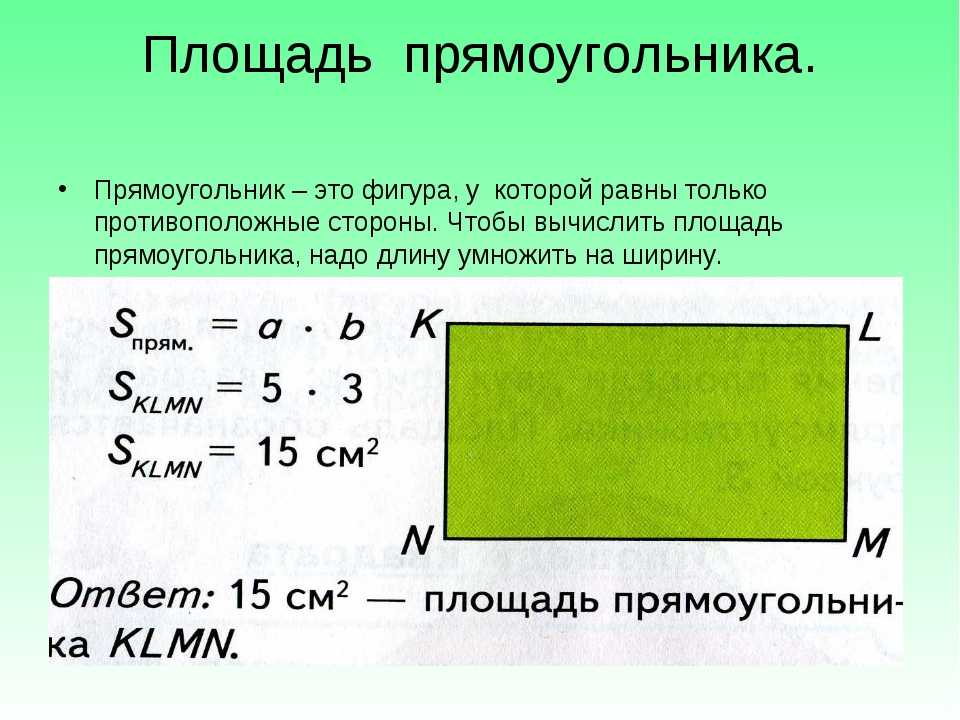 Мы знаем, что у каждого треугольника есть две равные стороны; следовательно, каждый из углов при основании каждого треугольника должен быть одинаковым. Мы знаем, что у треугольника есть  , и мы можем найти два угла при основании каждого треугольника, используя эту информацию.
Каждый угол в треугольнике равен . Теперь мы знаем, что все треугольники конгруэнтны и равносторонние: каждый треугольник имеет три равные длины сторон и три равных угла. Теперь мы можем использовать эту жизненно важную информацию для определения площади шестиугольника. Если мы найдем площадь одного из треугольников, то можем умножить ее на шесть, чтобы вычислить площадь всей фигуры. Начнем с анализа . Если мы проведем высоту через треугольник, то обнаружим, что создаем два  треугольника.
Найдем длину этого треугольника. Помните, что в треугольниках длины сторон находятся в следующем соотношении:
. Теперь мы можем проанализировать,  используя замещающую переменную для длины стороны, .
Мы знаем размеры основания и высоты и можем найти его площадь.
Теперь нам нужно умножить это на шесть, чтобы найти площадь всего шестиугольника.
Мы нашли площадь правильного шестиугольника с длиной стороны, . Если мы знаем длину стороны правильного шестиугольника, то можем найти площадь.
Если у нас нет правильного шестиугольника, то мы находим площадь шестиугольника, используя длину стороны (т. е. ) и апофему (т.е. ), которая является длиной линии, проведенной из центра прямой угол любой стороны. Это обозначено переменной  на следующем рисунке:

Альтернативный метод:
Если нам даны переменные и , то мы можем найти площадь шестиугольника по следующей формуле:
и является апофемой. Мы должны вычислить периметр, используя длину стороны и уравнение , где  – длина стороны.

Решение:
В задаче сказано, что соты имеют диаметр два сантиметра. Чтобы решить задачу, нам нужно разделить диаметр на два. Это связано с тем, что радиус этого диаметра равен длине внутренней стороны равносторонних треугольников в сотах. Найдем длину стороны правильного шестиугольника/соты.

Подставить и решить.
Нам известна следующая информация.
В итоге можем написать следующее:
Подставим это значение в формулу площади правильного шестиугольника и решим.
Упрощение.
Решить.
Округлить до десятых долей сантиметра.
Сообщить об ошибке
Какова площадь правильного шестиугольника с апофемой и длиной стороны ?
Возможные ответы:
Правильный ответ:
Пояснение:
Есть несколько способов найти площадь шестиугольника.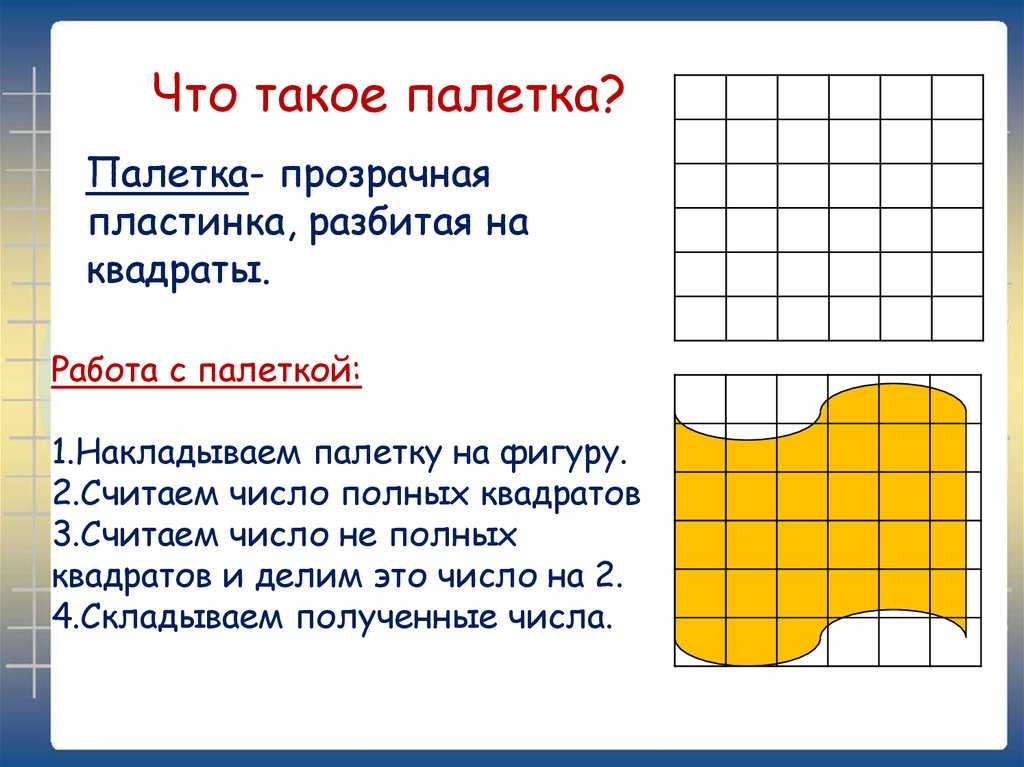
В правильном шестиугольнике разделите фигуру на треугольники.
Найдите площадь одного треугольника.
Умножьте это значение на шесть.
В качестве альтернативы, площадь может быть найдена путем вычисления половины длины стороны, умноженной на апофему.

Правильные шестиугольники:
Правильные шестиугольники представляют собой интересные многоугольники. Шестиугольники представляют собой шестигранные фигуры и имеют следующую форму:
В правильном шестиугольнике все стороны имеют одинаковую длину и все внутренние углы имеют одинаковую меру; поэтому мы можем написать следующее выражение.

Один из самых простых способов найти площадь многоугольника — разбить фигуру на треугольники. Начнем с разделения шестиугольника на шесть треугольников.
На этом рисунке центральная точка равноудалена от всех вершин. В результате шесть пунктирных линий внутри шестиугольника имеют одинаковую длину.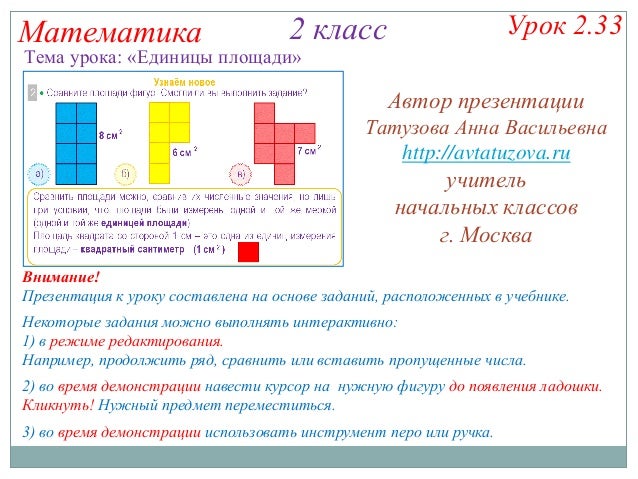 Точно так же все треугольники внутри шестиугольника конгруэнтны по правилу стороны-стороны-стороны: каждый из треугольников имеет две общие стороны внутри шестиугольника, а также сторону основания, которая составляет периметр шестиугольника. Аналогичным образом, каждый из треугольников имеет одинаковые углы. Они расположены в круге, и шестиугольник на нашем изображении разделил его на шесть равных частей; поэтому мы можем написать следующее:
Мы также знаем следующее:
Теперь давайте посмотрим на каждый из треугольников в шестиугольнике. Мы знаем, что у каждого треугольника есть две равные стороны; следовательно, каждый из углов при основании каждого треугольника должен быть одинаковым. Мы знаем, что у треугольника есть  , и мы можем найти два угла при основании каждого треугольника, используя эту информацию.
Каждый угол в треугольнике равен .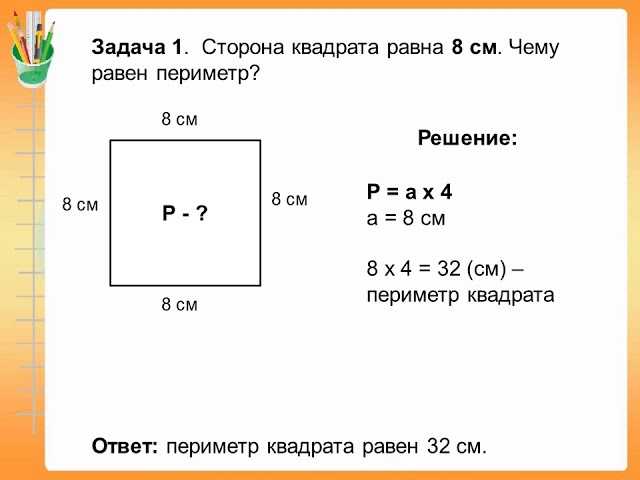 Теперь мы знаем, что все треугольники конгруэнтны и равносторонние: каждый треугольник имеет три равные длины сторон и три равных угла. Теперь мы можем использовать эту жизненно важную информацию для определения площади шестиугольника. Если мы найдем площадь одного из треугольников, то можем умножить ее на шесть, чтобы вычислить площадь всей фигуры. Начнем с анализа . Если мы проведем высоту через треугольник, то обнаружим, что создаем два  треугольника.
Найдем длину этого треугольника. Помните, что в треугольниках длины сторон находятся в следующем соотношении:
. Теперь мы можем проанализировать,  используя замещающую переменную для длины стороны, .
Мы знаем размеры основания и высоты и можем найти его площадь.
Теперь нам нужно умножить это на шесть, чтобы найти площадь всего шестиугольника.
Мы нашли площадь правильного шестиугольника с длиной стороны, .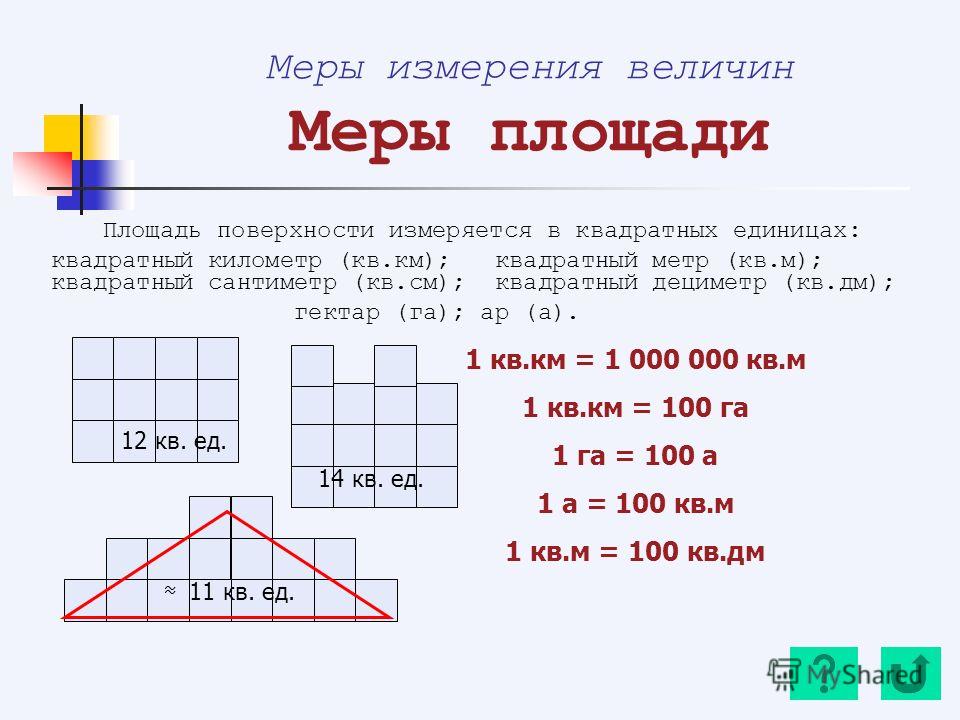 Если мы знаем длину стороны правильного шестиугольника, то можем найти площадь.
Если у нас нет правильного шестиугольника, то мы находим площадь шестиугольника, используя длину стороны (т. е. ) и апофему (т.е. ), которая является длиной линии, проведенной из центра прямой угол любой стороны. Это обозначено переменной  на следующем рисунке:

Альтернативный метод:
Если нам даны переменные и , то мы можем найти площадь шестиугольника по следующей формуле:
и является апофемой. Мы должны вычислить периметр, используя длину стороны и уравнение , где  – длина стороны.

Решение:
В шестиугольнике количество сторон , а в этом примере длина стороны .
Периметр .
Затем мы подставляем числа для апофемы и периметра в исходное уравнение.
Район .
Сообщить об ошибке
Эта фигура представляет собой правильный шестиугольник со следующей длиной стороны:

Вычислите площадь правильного шестиугольника.
Возможные ответы:
Правильный ответ:
Пояснение:
Есть несколько способов найти площадь шестиугольника.
В правильном шестиугольнике разделите фигуру на треугольники.
Найдите площадь одного треугольника.
Умножьте это значение на шесть.
В качестве альтернативы, площадь может быть найдена путем вычисления половины длины стороны, умноженной на апофему.

Правильные шестиугольники:
Правильные шестиугольники представляют собой интересные многоугольники. Шестиугольники представляют собой шестигранные фигуры и имеют следующую форму:
В правильном шестиугольнике все стороны имеют одинаковую длину и все внутренние углы имеют одинаковую меру; поэтому мы можем написать следующее выражение.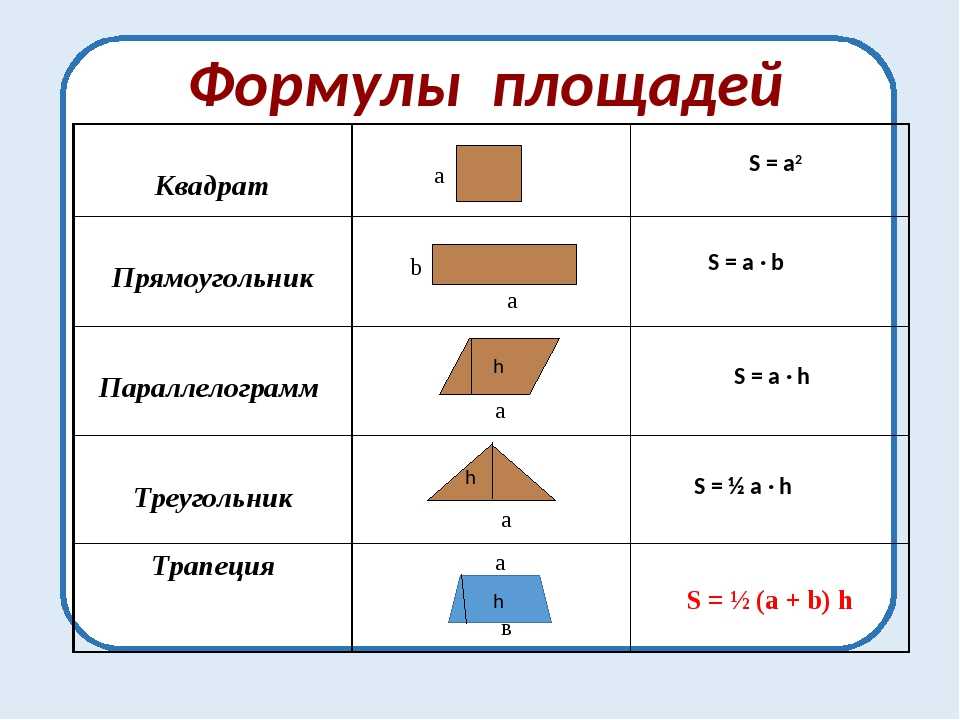

Один из самых простых способов найти площадь многоугольника — разбить фигуру на треугольники. Начнем с разделения шестиугольника на шесть треугольников.
На этом рисунке центральная точка равноудалена от всех вершин. В результате шесть пунктирных линий внутри шестиугольника имеют одинаковую длину. Точно так же все треугольники внутри шестиугольника конгруэнтны по правилу стороны-стороны-стороны: каждый из треугольников имеет две общие стороны внутри шестиугольника, а также сторону основания, которая составляет периметр шестиугольника. Аналогичным образом, каждый из треугольников имеет одинаковые углы. Они расположены в круге, и шестиугольник на нашем изображении разделил его на шесть равных частей; поэтому мы можем написать следующее:
Мы также знаем следующее:
Теперь давайте посмотрим на каждый из треугольников в шестиугольнике. Мы знаем, что у каждого треугольника есть две равные стороны; следовательно, каждый из углов при основании каждого треугольника должен быть одинаковым. Мы знаем, что у треугольника есть  , и мы можем найти два угла при основании каждого треугольника, используя эту информацию.
Каждый угол в треугольнике равен . Теперь мы знаем, что все треугольники конгруэнтны и равносторонние: каждый треугольник имеет три равные длины сторон и три равных угла. Теперь мы можем использовать эту жизненно важную информацию для определения площади шестиугольника. Если мы найдем площадь одного из треугольников, то можем умножить ее на шесть, чтобы вычислить площадь всей фигуры. Начнем с анализа . Если мы проведем высоту через треугольник, то обнаружим, что создаем два  треугольника.
Найдем длину этого треугольника. Помните, что в треугольниках длины сторон находятся в следующем соотношении:
. Теперь мы можем проанализировать,  используя замещающую переменную для длины стороны, .
Мы знаем размеры основания и высоты и можем найти его площадь.
Теперь нам нужно умножить это на шесть, чтобы найти площадь всего шестиугольника.
Мы нашли площадь правильного шестиугольника с длиной стороны, . Если мы знаем длину стороны правильного шестиугольника, то можем найти площадь.
Если у нас нет правильного шестиугольника, то мы находим площадь шестиугольника, используя длину стороны (т. е. ) и апофему (т.е. ), которая является длиной линии, проведенной из центра прямой угол любой стороны. Это обозначено переменной  на следующем рисунке:

Альтернативный метод:
Если нам даны переменные и , то мы можем найти площадь шестиугольника по следующей формуле:
и является апофемой.

No related posts.