Образец решения профессиональной задачи по математике: Решение педагогической задачи. | Методическая разработка на тему:

alexxlab / / Математике

Факультет математики, информатики и физики

Декан факультета – Харламов Олег Сергеевич, кандидат физико-математических наук, доцент кафедры высшей математики и физики

Тел.: +7(8442) 94-55-33

Подготовка бакалавров
44.03.05 Педагогическое образование (с двумя профилями подготовки)
«Математика», «Информатика»

Вступительные испытания для лиц, поступающих  на базе полного общего или высшего образования:

  1. Математика (профильного уровня) или Информатика и ИКТ
    2. Обществознание
    3. Русский язык

 

Вступительные испытания для лиц,поступающих  на базе среднего профессионального образования (СПО):

  1. Теоретические основы математики с методикой преподавания 
  2. Педагогика 
  3. Русский язык


Срок обучения: очная форма обучения – 5 лет, заочная форма – 6 лет

Программа ориентирована на тех, кто предпочитает математику, а также желает на высоком уровне освоить информатику и ИКТ.

Программа нацелена на подготовку высококвалифицированных учителей математики и информатики, готовых к профессиональной деятельности в образовательных организациях общего образования. Выпускники факультета, освоившие данную программу, готовы также работать в качестве специалистов в области цифровизации образования, использования информационных и мультимедийных технологий, вести разработку современных электронных образовательных ресурсов, ресурсов сети Интернет.

Выпускникам данной образовательной программы, успешно сдавшим все государственные итоговые испытания, присваивается квалификация «Бакалавр». Возможно дальнейшее обучение по программам магистратуры, нацеленным на углубление в проблематику педагогического образования, математики и информатики.

44.03.05 Педагогическое образование (с двумя профилями подготовки)
«Математика, Физика»

Вступительные испытания для лиц, поступающих  на базе полного общего или высшего образования:

  1. Математика (профильного уровня) или физика
    2. Обществознание
    3. Русский язык

 

Вступительные испытания для лиц, поступающих  на базе среднего профессионального образования (СПО):

  1. Теоретические основы математики с методикой преподавания 
  2. Педагогика 
  3. Русский язык


Срок обучения: очная форма обучения – 5 лет

Программа ориентирована на подготовку в области физико-математического образования – изучение фундаментальных основ математики и физики, а также методик их преподавания в образовательных организациях общего образования. Выпускники программы – высококвалифицированные учителя математики и физики, готовые к профессиональной деятельности педагога и научно-исследовательской работе в области физико-математических наук.

Выпускникам данной образовательной программы, успешно сдавшим все государственные итоговые испытания, присваивается квалификация «Бакалавр». Возможно дальнейшее обучение по программам магистратуры, нацеленным на углубление в проблематику педагогического образования, физики и математики.

09.03.03 Прикладная информатика
«Прикладная информатика»

Вступительные испытания для лиц, поступающих  на базе полного общего или высшего образования:

  1. Информатика и информационно-коммуникационные технологии (ИКТ) или Физика
    2. Математика (профильного уровня)
    3. Русский язык

Вступительные испытания для лиц, поступающих  на базе среднего профессионального образования (СПО):

1.Информационные технологии 

  1. Архитектура аппаратных средств и прикладное программное обеспечение
  2. Русский язык 

Срок обучения: очная форма обучения – 4 года

Программа нацелена на подготовку высококвалифицированных специалистов в области прикладной информатики, готовых к профессиональной деятельности, самосовершенствованию и решению прикладных задач в условиях цифровизации общества и экономики, а также информатизации разных сфер человеческой деятельности и развития информационных технологий.

Выпускники факультета, освоившие программу прикладной информатики, могут работать по таким востребованным профессиям, как специалист по внедрению информационных систем, программист информационных систем, консультант по информационным системам, сервис-инженер по информационным системам и др.

После завершения обучения по данной программе возможно дальнейшее обучение в рамках одной из предлагаемых магистерских программ, ориентированных на формирование компетенций обучающихся в области прикладной информатики. а также углубления в проблематику педагогического образования и информатизации различных областей экономики и общества.

 

09.03.03 Прикладная информатика
«Программирование и искусственный интеллект»

Вступительные испытания для лиц, поступающих  на базе полного общего или высшего образования:

  1. Информатика и информационно-коммуникационные технологии (ИКТ) или Физика
    2. Математика (профильного уровня)
    3. Русский язык

Вступительные испытания для лиц, поступающих  на базе среднего профессионального образования (СПО):

1.Информационные технологии 

  1. Архитектура аппаратных средств и прикладное программное обеспечение
  2. Русский язык 

Срок обучения: очная форма обучения – 4 года

Подготовка магистров:
44.04.01 Педагогическое образование
Магистерская программа: «Технологии обучения в физико-математическом образовании»

Вступительные испытания: комплексный экзамен: педагогика (зачет/незачет; компьютерное тестирование), технологии обучения в физико-математическом образовании (компьютерное тестирование)

Срок обучения: очная форма обучения – 2 года

Программа направлена на подготовку высококвалифицированных педагогических кадров, способных к педагогической и научно-исследовательской деятельности в образовательных организациях, реализующих основные образовательные программы на профильном и углубленном уровнях в области физико-математического образования, а также готовых к построению авторских методических систем обучения математике и физике, работе с одаренными детьми, подготовке школьников к олимпиадам.

Выпускники данной программы востребованы в лицеях, гимназиях, школах с углубленным изучением физико-математических дисциплин, в организациях среднего профессионального и высшего образования.

Выпускникам, освоившим основную профессиональную образовательную программу и успешно сдавшим все предусмотренные программой государственные итоговые испытания, присваивается квалификация «Магистр».

44.04.01 Педагогическое образование
Магистерская программа: «Технологии обучения в цифровой образовательной среде»

Вступительные испытания: комплексный экзамен: педагогика (зачет/незачет; компьютерное тестирование), технологии обучения в цифровой образовательной среде (компьютерное тестирование)

Срок обучения: очная форма обучения – 2 года

Программа направлена на подготовку высококвалифицированных педагогических кадров и специалистов в области информатизации образования, способных к педагогической и научно-исследовательской деятельности в образовательных организациях, реализующих основные образовательные программы с использованием электронного обучения и дистанционных образовательных технологий.

Выпускники данной программы готовы к педагогической деятельности, разработке онлайн-курсов и иных электронных образовательных ресурсов, консультированию обучающихся и сотрудников организаций в области онлайн-обучения и применения ресурсов цифровой образовательной среды.

Выпускникам, освоившим основную профессиональную образовательную программу и успешно сдавшим все предусмотренные программой государственные итоговые испытания, присваивается квалификация «Магистр»

44.04.01 Педагогическое образование

Магистерская программа: «Научно-исследовательская деятельность в физико-математическом образовании»

Вступительные испытания: комплексный экзамен: педагогика (зачет/незачет; компьютерное тестирование), научно-исследовательская деятельность в физико-математическом образовании (компьютерное тестирование)

Срок обучения: очная форма обучения – 2 года

Программа направлена на подготовку высококвалифицированных педагогических кадров и специалистов в области физики и математики, способных к педагогической и научно-исследовательской деятельности в образовательных организациях, реализующих основные образовательные программы на профильном и углубленном уровнях в области физико-математического образования, а также готовых к проведению самостоятельных научных исследований и руководству исследовательской работой обучающихся. Выпускники данной программы готовы применять знания современных научных направлений исследований в предметной области (физика и математика), уметь ставить задачи научно-исследовательской деятельности, формировать интерес учащихся к решению практических задач в области физики и математики.

Выпускникам, освоившим основную профессиональную образовательную программу и успешно сдавшим все предусмотренные программой государственные итоговые испытания, присваивается квалификация «Магистр»

Подготовка научно-педагогических кадров (аспирантура)
Направление: 44.06.01 «Образование и педагогические науки»
Направленность (профиль): «Теория и методика обучения и воспитания (информатика)» (13.00.02)

Вступительные испытания: теория и методика обучения и воспитания (информатика), философия, иностранный язык

Срок обучения: очная форма обучения – 3 года

Программа нацелена на подготовку научно-педагогических кадров, способных к педагогической и научно-исследовательской деятельности в образовательных организациях, реализующих основные образовательные программы всех уровней образования.

Областью профессиональной деятельности выпускников, освоивших программу аспирантуры, является исследование педагогических процессов, образовательных систем и их закономерностей, разработка и использование педагогических технологий для решения задач образования, науки, культуры и социальной сферы.

Выпускникам, освоившим основную профессиональную образовательную программу и успешно сдавшим все предусмотренные программой государственные итоговые испытания, присваивается квалификация «Исследователь. Преподаватель-исследователь».

По результатам представления научного доклада об основных результатах подготовленной научно-квалификационной работы (диссертации) организация дает заключение для представления данной работы в диссертационный совет для защиты по научной специальности 13.00.02 «Теория и методика обучения и воспитания (информатика)».

Подготовка научно-педагогических кадров (аспирантура)
Направление: 44.06.01 «Образование и педагогические науки»
Направленность (профиль): «Теория и методика обучения и воспитания (математика)» (13. 00.02)

Вступительные испытания: теория и методика обучения и воспитания (математика), философия, иностранный язык

Срок обучения: очная форма обучения – 3 года

Программа нацелена на подготовку научно-педагогических кадров, способных к педагогической и научно-исследовательской деятельности в образовательных организациях, реализующих основные образовательные программы всех уровней образования. Областью профессиональной деятельности выпускников, освоивших программу аспирантуры, является исследование педагогических процессов, образовательных систем и их закономерностей, разработка и использование педагогических технологий для решения задач образования, науки, культуры и социальной сферы.

Выпускникам, освоившим основную профессиональную образовательную программу и успешно сдавшим все предусмотренные программой государственные итоговые испытания, присваивается квалификация «Исследователь. Преподаватель-исследователь».

По результатам представления научного доклада об основных результатах подготовленной научно-квалификационной работы (диссертации) организация дает заключение для представления данной работы в диссертационный совет для защиты по научной специальности 13. 00.02 «Теория и методика обучения и воспитания (математика)».

Подготовка научно-педагогических кадров (аспирантура)
Направление: 03.06.01 «Физика и астрономия»
Направленность (профиль): «Физическая электроника» (01.04.04)

Вступительные испытания: физическая электроника, философия, иностранный язык

Срок обучения: очная форма обучения – 3 года

Программа нацелена на подготовку научно-педагогических кадров, способных к научно-исследовательской и педагогической деятельности в области физики и астрономии (физической электроники). Областью профессиональной деятельности выпускников, освоивших программу аспирантуры, является  исследование физических явлений, составляющих основу для разработок и создания новых электронных приборов и устройств. Основное внимание в ходе подготовки аспирантов по данной программе уделяется теоретическим исследованиям физических явлений в твердотельных микро- и наноструктурах; проводящих, полупроводниковых и тонких диэлектрических пленках и покрытиях.

Выпускникам, освоившим основную профессиональную образовательную программу и успешно сдавшим все предусмотренные программой государственные итоговые испытания, присваивается квалификация «Исследователь. Преподаватель-исследователь».

По результатам представления научного доклада об основных результатах подготовленной научно-квалификационной работы (диссертации) организация дает заключение для представления данной работы в диссертационный совет для защиты по научной специальности 01.04.04 «Физическая электроника».

Развитие профессиональной компетентности педагога: теория и практика

%PDF-1.5 % 1 0 obj > >> /PageLayout /OneColumn /PageMode /UseNone /Pages 6 0 R /Type /Catalog >> endobj 7 0 obj /CreationDate (D:20130305124535+06’00’) /Producer (doPDF Ver 7.2 Build 376 \(Windows 7 Business Edition — Version: 6.1.7600 \(x86\)\)) /Title >> endobj 2 0 obj > stream

  • Развитие профессиональной компетентности педагога: теория и практика
    • Печеркина А. А.1.5doPDF Ver 7.2 Build 376 (Windows 7 Business Edition — Version: 6.1.7600 (x86))2013-03-05T12:45:35+06:00 endstream endobj 3 0 obj > endobj 4 0 obj > endobj 5 0 obj > endobj 6 0 obj > endobj 8 0 obj > /ProcSet [/PDF /Text] /XObject > >> /Type /Page /Annots [255 0 R] >> endobj 9 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 10 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 11 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 12 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 13 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 14 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 15 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 16 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 17 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 18 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 19 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 20 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 21 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 22 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 23 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 24 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 25 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 26 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 27 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 28 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 29 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 30 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 31 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 32 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 33 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 34 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 35 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 36 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 37 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 38 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 39 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 40 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 41 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 42 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 43 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 44 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 45 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 46 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 47 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 48 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 49 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 50 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 51 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 52 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 53 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 54 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 55 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 56 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 57 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 58 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 59 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 60 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 61 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 62 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 63 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 64 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 65 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 66 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 67 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 68 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 69 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 70 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 71 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 72 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 73 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 74 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 75 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 76 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 77 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 78 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 79 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 80 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 81 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 82 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 83 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 84 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 85 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 86 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 87 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 88 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 89 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 90 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 91 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 92 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 93 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 94 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 95 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 96 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 97 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 98 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 99 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 100 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 101 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 102 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 103 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 104 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 105 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 106 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 107 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 108 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 109 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 110 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 111 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 112 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 113 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 114 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 115 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 116 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 117 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 118 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 119 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 120 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 121 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 122 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 123 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 124 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 125 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 126 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 127 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 128 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 129 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 130 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 131 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 132 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 133 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 134 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 135 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 136 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 137 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 138 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 139 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 140 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 141 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 142 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 143 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 144 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 145 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 146 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 147 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 148 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 149 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 150 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 151 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 152 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 153 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 154 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 155 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 156 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 157 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 158 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 159 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 160 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 161 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 162 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 163 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 164 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 165 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 166 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 167 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 168 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 169 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 170 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 171 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 172 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 173 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 174 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 175 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 176 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 177 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 178 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 179 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 180 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 181 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 182 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 183 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 184 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 185 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 186 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 187 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 188 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 189 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 190 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 191 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 192 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 193 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 194 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 195 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 196 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 197 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 198 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 199 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 200 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 201 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 202 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 203 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 204 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 205 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 206 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 207 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 208 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 209 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 210 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 211 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 212 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 213 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 214 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 215 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 216 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 217 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 218 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 219 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 220 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 221 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 222 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 223 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 224 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 225 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 226 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 227 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 228 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 229 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 230 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 231 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 232 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 233 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 234 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 235 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 236 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 237 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 238 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 239 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 240 0 obj > /ProcSet [/PDF /Text] /XObject > >> /Type /Page >> endobj 241 0 obj > /ProcSet [/PDF /Text] /XObject > >> /Type /Page >> endobj 242 0 obj > /ProcSet [/PDF /Text] >> /Type /Page >> endobj 243 0 obj > stream x^;o0w !d[ѵ:$HY6eLRx#ߛpn~B؞4տ k-#h&|k_;Yuy97oaB)]O%qO5 E!2iU0Nf uK، lh`UJ0:S!Вį=#@4>QA\:4+k @LH}DZE񳴏[E8g ŁRRJLH {l2j;s2yAC:UV9iVSCd W1FUhlZ$Z:`\kH)2g}4tOta]荍1asÈA^ċ9`»vS0,7. %7۶*t1@c*Hru(\d&vid_

    стратегий решения математических задач, которые заставят учащихся сказать: «Я понял!»

     

    Даже учащиеся, которые быстро разбираются в математических фактах, могут застрять, когда дело доходит до решения задач.

    Как только понятие переводится в словесную задачу или простое математическое предложение содержит неизвестное, они впадают в тупик.

    Это потому, что решение проблем требует от нас сознательного выбора стратегий, наиболее подходящих для решения проблемы   под рукой . И не все студенты обладают этой метакогнитивной способностью.

    Но вы можете обучить этим стратегиям решения проблем. Вам просто нужно знать, что это такое.

    Мы собрали их здесь, разделив на четыре категории:

    1. Стратегии понимания проблемы
    2. Стратегии решения проблемы
    3. Стратегии отработки
    4. Стратегии проверки решения

    Ознакомьтесь с этими стратегиями, а затем объясните их своим ученикам. В следующий раз, когда они погрузится в сложную задачу, они будут заполнять свою рабочую бумагу быстрее, чем когда-либо!

    Стратегии понимания проблемы

    Прежде чем учащиеся смогут решить задачу, они должны знать, о чем она их просит. Часто это первое препятствие для текстовых задач, в которых не указана конкретная математическая операция.

    Поощряйте учащихся:

    Читать и перечитывать вопрос

    Они говорят, что читали его, но действительно ли они ? Иногда учащиеся перескакивают вперед, как только замечают одну знакомую информацию, или отказываются от попыток понять ее, если проблема не имеет смысла на первый взгляд.

    Научите учащихся интерпретировать вопрос, используя стратегии самоконтроля, такие как:

    • Медленнее перечитывать вопрос, если он не имеет смысла с первого раза
    • Просьба о помощи
    • Выделение или подчеркивание важной информации.

    Определение важной и посторонней информации

    Джон собирает деньги на день рождения своего друга Ари. Он начинает со своих 5 долларов, затем Маркус дает ему еще 5 долларов. Сколько у него сейчас?

    Будучи взрослыми, глядя на вышеприведенную задачу, мы можем мгновенно бросить взгляд за имена и сценарий дня рождения, чтобы увидеть простую задачу на сложение. Студенты, однако, могут изо всех сил пытаться определить, что важно в информации, которую им предоставили.

    Научите учащихся сортировать и просеивать информацию в задаче, чтобы найти то, что важно. Хороший способ сделать это — попросить их поменять местами информацию, чтобы посмотреть, изменится ли решение. Если изменение имен, элементов или сценариев не повлияет на конечный результат, они поймут, что им не нужно уделять особое внимание при решении проблемы.

    Схематический подход

    Это стратегия математического вмешательства, которая может облегчить решение задач для всех учащихся, независимо от их способностей.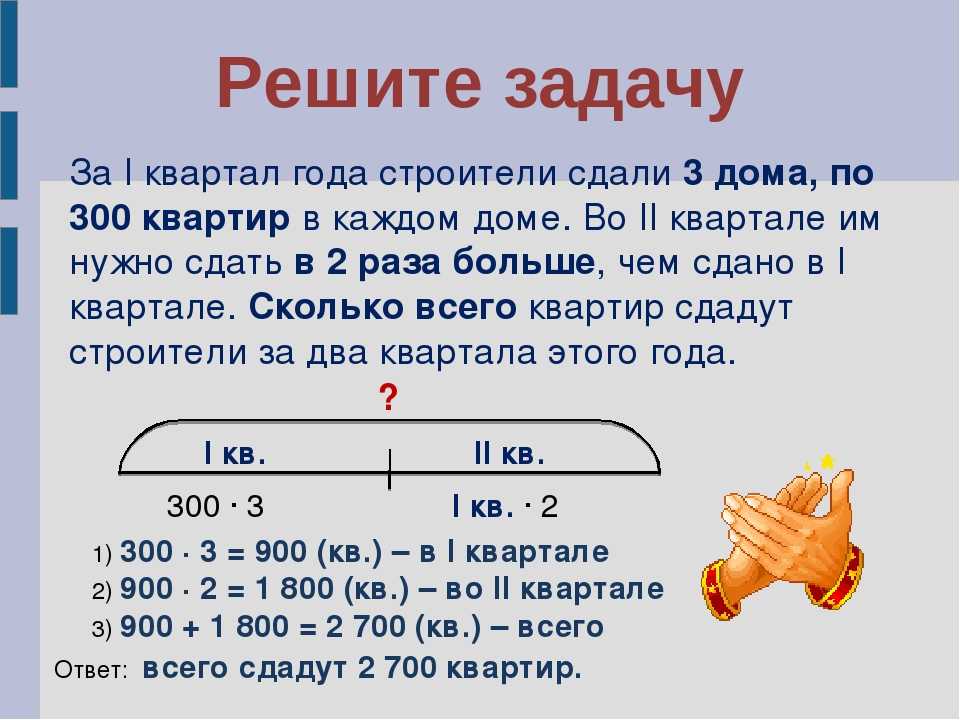

    Сравните разные текстовые задачи одного типа и составьте формулу или математическую основу предложения, которая применима ко всем ним. Например, простая задача на вычитание может быть выражена следующим образом:

    [Число/Количество A] с удаленным [Число/Количество B] становится [конечным результатом].

    Это базовая процедура или 9Схема 0043 учащихся просят использовать. Получив список схем для различных математических операций (сложение, умножение и т. д.), они могут по очереди применить их к незнакомой текстовой задаче и посмотреть, какая из них подходит.

    Стратегии решения задачи

    Отстающие ученики часто считают, что математика — это то, что вы либо делаете автоматически, либо не делаете вообще. Но это не так. Помогите учащимся понять, что у них есть выбор стратегий решения проблем, и если одна из них не сработает, они могут попробовать другую.

    Вот четыре общих стратегии, которые учащиеся могут использовать для решения задач.

    Визуализация

    Визуализация абстрактной задачи часто облегчает ее решение. Студенты могли нарисовать картинку или просто поставить отметки на листе рабочей бумаги.

    Поощряйте визуализацию, моделируя ее на доске и предоставляя графические органайзеры, в которых есть место для рисования учащимися перед тем, как они запишут окончательное число.

    Угадай и проверь

    Покажите учащимся, как сделать обоснованное предположение, а затем снова включить этот ответ в исходную задачу. Если это не сработает, они могут изменить свое первоначальное предположение соответственно выше или ниже.

    Найти закономерность

    Чтобы найти закономерности, покажите учащимся, как извлекать и перечислять все релевантные факты в задаче, чтобы их можно было легко сравнивать. Если они найдут закономерность, то смогут найти недостающую часть информации.

    Работа в обратном порядке

    Работа в обратном порядке полезна, если учащимся нужно найти неизвестное число в задаче или математическом предложении. Например, если задача 8 + x = 12, учащиеся могут найти x по:

    1. Начиная с 12
    2. Выбрать 8 из 12
    3. Осталось 4
    4. Проверка работы 4 при использовании вместо x

    Стратегии отработки

    Теперь, когда студенты поняли задачу и сформулировали стратегию, пришло время применить ее на практике. Но если они просто начнут и сделают это, они могут усложнить себе задачу. Покажите им, как эффективно решать задачу, используя:

    Документирование решения

    Смоделируйте процесс записи каждого шага, который вы предпринимаете для решения математической задачи, и раздайте рабочие листы, когда учащиеся решают задачу. Это позволит учащимся отслеживать свои мысли и выявлять ошибки до того, как они придут к окончательному решению.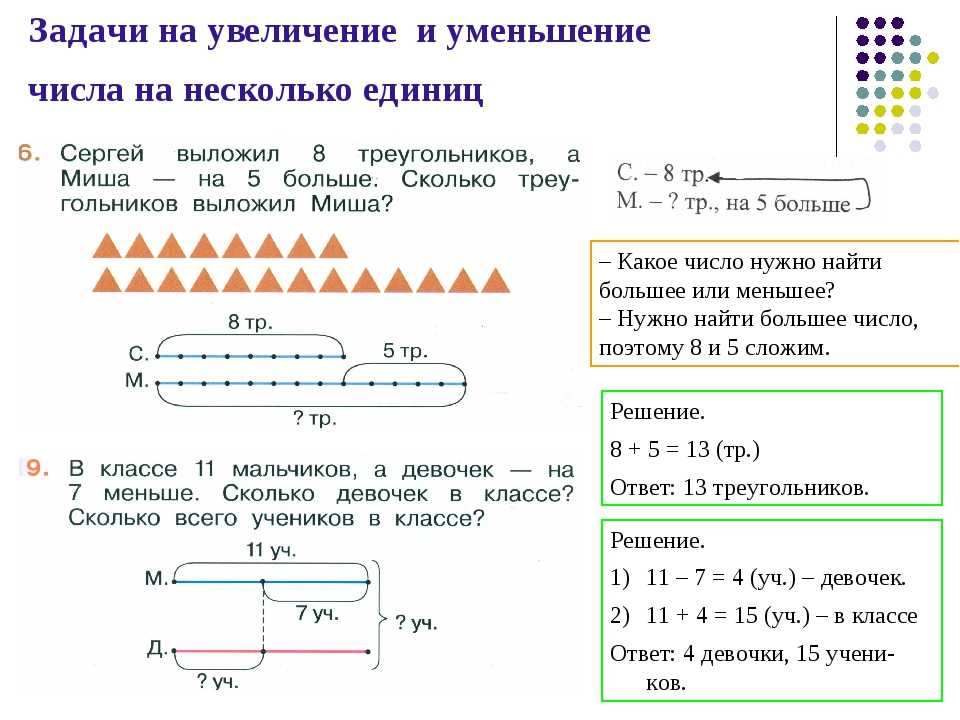

    Проверяйте по ходу дела

    Проверяйте работу по мере выполнения — еще одна важная стратегия самоконтроля для изучающих математику. Смоделируйте это для них, задавая вопросы вслух, например:

    • Последний шаг выглядит правильно?
    • Является ли это следствием предыдущего шага?
    • Вычислил ли я какие-нибудь «меньшие» суммы в рамках более крупной задачи, которую нужно проверить?

    Стратегии проверки решения

    Студенты часто ошибаются, думая, что скорость — это все в математике, поэтому они спешат записать ответ и двигаться дальше, не проверив.

    Но проверка тоже важна. Это позволяет им выявлять проблемные области по мере их возникновения и решать более сложные проблемы, требующие многократных проверок , прежде чем  дойти до окончательного ответа.

    Вот некоторые стратегии проверки, которые вы можете продвигать:

    Проверка с партнером

    Сравнение ответов с коллегами-лидами — это более осмысленный процесс, чем просто получение галочки от учителя. Если у учащихся есть два разных ответа, предложите им рассказать о том, как они к ним пришли, и сравнить методы разработки. Они выяснят, где именно они ошиблись, а что сделали правильно.

    Перечитайте задачу с вашим решением

    В большинстве случаев учащиеся смогут определить, правильный ли их ответ, вставив его обратно в исходную задачу. Если это не работает или просто «выглядит неправильно», пришло время вернуться и исправить это.

    Исправление ошибок

    Покажите учащимся, как вернуться назад во время выполнения упражнения, чтобы точно определить место, где они допустили ошибку. Подчеркните, что они не могут этого сделать, если они не записали все в первую очередь — так что один ответ без проработки не так впечатляет, как они могут подумать!

    Нужна дополнительная помощь в развитии навыков решения проблем?

    Узнайте, как настроить задачу по решению задач и рассуждению или изучите Mathseeds и Mathletics, наши отмеченные наградами онлайн-программы по математике. У них есть более 900 заданий по решению проблем, проверенных учителями!

    Категории Математика, Стратегии обучения

    Математика через решение задач | Math Goodies

    Маргарет Таплин Институт образования Сатья Саи, Гонконг

    Что такое «подход к решению проблем»?

    Поскольку акцент сместился с обучения решению проблем на обучение через решение проблем (Лестер, Масингила, Мау, Ламбдин, Дос Сантон и Раймонд, 1994), многие авторы пытались прояснить, что подразумевается под решением проблем. подход к обучению математике. Основное внимание уделяется обучению математическим темам через контексты решения проблем и ориентированные на исследования среды, которые характеризуются тем, что учитель «помогает учащимся достичь глубокого понимания математических идей и процессов, вовлекая их в занятия математикой: создание, предположение, исследование, тестирование, и проверка» (Лестер и др., 1994, с.154). Конкретные характеристики подхода к решению проблем включают:

    • взаимодействие между учениками/учениками и учителем/учениками (Van Zoest et al. , 1994)
    • математический диалог и консенсус между учащимися (Van Zoest et al., 1994)
    • учителя предоставляют ровно столько информации, сколько нужно для установления предыстории/намерения проблемы, а учащиеся разъясняют, интерпретируют и пытаются построить один или несколько процессов решения (Cobb et al., 1991)
    • учителя, принимающие правильные/неправильные ответы без оценки (Cobb et al., 1991)
    • учителя направляют, тренируют, задают проницательные вопросы и участвуют в процессе решения проблем (Lester et al., 1994)
    • учителя знают, когда уместно вмешаться, а когда отступить и позволить ученикам идти своим путем (Lester et al., 1994)
    • Еще одной характеристикой является то, что подход к решению задач может использоваться для поощрения учащихся к обобщению правил и понятий, что является центральным процессом в математике (Эван и Лаппин, 1994).

    Шенфельд (в Olkin and Schoenfeld, 1994, стр. 43) описал, как изменилось использование решения проблем в его обучении с 1970-х годов: Эвристики полиатипа: начертите схему, исследуйте частные случаи или аналогии, специализируйтесь, обобщайте и т. д. С годами курсы развивались до такой степени, что в них меньше внимания уделялось эвристике как таковой, а больше — знакомству студентов с фундаментальными идеями: важность математических рассуждений и доказательств… в качестве отправной точки для серьезных исследований, а не задач, которые необходимо выполнить).

    Шенфельд также предположил, что хорошая задача должна быть такой, которую можно расширить, чтобы привести к математическим исследованиям и обобщениям. Он описал три характеристики математического мышления:

    1. ценить процессы математизации и абстракции и иметь пристрастие к их применению
    2. развитие компетенции с инструментами торговли и использование этих инструментов для достижения цели понимания структуры — математического осмысления (Schoenfeld, 1994, с. 60).
    3. Как Cobb et al. (1991), целью участия в решении проблем является не только решение конкретных проблем, но и «поощрение интериоризации и реорганизации задействованных схем в результате деятельности» (стр. 187). Этот подход не только развивает у учащихся уверенность в своих способностях к математическому мышлению (Schifter and Fosnot, 1993), но и позволяет учащимся строить, оценивать и уточнять свои собственные математические теории и теории других (NCTM, 19).89). Поскольку это стало преобладающим требованием обучения, важно рассмотреть сами процессы более подробно.

    Роль решения задач в обучении математике как процессу

    Решение задач является важным компонентом математического образования, поскольку это единственное средство, с помощью которого можно достичь на школьном уровне всех трех перечисленных ценностей математики в начале этой статьи: функциональное, логическое и эстетическое. Давайте рассмотрим, как решение проблем является полезным средством для каждого из них.

    Уже указывалось, что математика является важной дисциплиной из-за ее практической роли для человека и общества. Этот аспект математики можно развивать с помощью подхода к решению проблем. Представление проблемы и развитие навыков, необходимых для решения этой проблемы, более мотивируют, чем обучение навыкам без контекста. Такая мотивация придает решению проблем особую ценность как средство изучения новых концепций и навыков или закрепления уже приобретенных навыков (Станик и Килпатрик, 19).89, NCTM, 1989). Подход к математике через решение проблем может создать контекст, который имитирует реальную жизнь и, следовательно, оправдывает математику, а не рассматривает ее как самоцель. Национальный совет учителей математики (NCTM, 1980) рекомендовал, чтобы решение задач было в центре внимания преподавания математики, потому что, по их словам, оно включает в себя навыки и функции, которые являются важной частью повседневной жизни. Кроме того, это может помочь людям адаптироваться к изменениям и неожиданным проблемам в их карьере и других аспектах их жизни. Совсем недавно Совет одобрил эту рекомендацию (NCTM, 1989) с утверждением, что решение задач должно лежать в основе всех аспектов преподавания математики, чтобы учащиеся могли ощутить силу математики в окружающем их мире. Они рассматривают решение задач как средство, с помощью которого учащиеся могут строить, оценивать и уточнять свои собственные математические теории и теории других.

    Согласно Resnick (1987), подход к решению проблем способствует практическому использованию математики, помогая людям развивать возможности адаптации, когда, например, технология выходит из строя. Таким образом, это также может помочь людям перейти в новую рабочую среду в то время, когда большинство из них, вероятно, столкнутся с несколькими изменениями карьеры в течение трудовой жизни (NCTM, 19).89). Резник выразил убеждение, что «школа должна сосредоточить свои усилия на подготовке людей к тому, чтобы они были хорошими адаптивными учениками, чтобы они могли эффективно работать в непредсказуемых ситуациях и задача требует изменения» (стр. 18). Кокрофт (1982) также отстаивал решение задач как средство развития математического мышления как инструмента повседневной жизни, говоря, что способность решать задачи лежит «в основе математики» (стр. 73), поскольку это средство, с помощью которого математика может применяться в различных незнакомых ситуациях.

    Решение задач, однако, больше, чем средство для обучения и закрепления математических знаний и помощи в решении повседневных задач. Это также навык, который может улучшить логическое мышление. Люди больше не могут оптимально функционировать в обществе, просто зная правила, которым нужно следовать, чтобы получить правильный ответ. Они также должны быть в состоянии решить посредством процесса логического вывода, какой алгоритм, если таковой имеется, требуется в ситуации, а иногда должны иметь возможность разработать свои собственные правила в ситуации, когда алгоритм не может быть применен напрямую. По этим причинам решение проблем можно развивать как самостоятельный ценный навык, способ мышления (NCTM, 19). 89), а не просто как средство для поиска правильного ответа.

    Многие авторы подчеркивали важность решения задач как средства развития логического мышления в математике. «Если образование не способствует развитию интеллекта, оно явно неполноценно. А между тем интеллект есть по существу способность решать задачи: бытовые проблемы, личные проблемы…» (Поля, 1980, с.1). Современные определения интеллекта (Gardner, 1985) говорят о практическом интеллекте, который позволяет «человеку решать настоящие проблемы или трудности, с которыми он или она сталкивается» (стр. 60), а также побуждает человека находить или создавать проблемы, «закладывая тем самым основу. для приобретения новых знаний» (с.85). Как указывалось ранее, стандартная математика с акцентом на приобретение знаний не обязательно удовлетворяет эти потребности. Резник (1987) описал несоответствия, существующие между алгоритмическими подходами, преподаваемыми в школах, и «изобретенными» стратегиями, которые большинство людей используют на работе для решения практических задач, которые не всегда точно вписываются в преподаваемый алгоритм. По ее словам, большинство людей разработали «практические правила» для расчета, например, количества, скидок или суммы сдачи, которую они должны дать, и они редко включают стандартные алгоритмы. Обучение методам решения проблем позволяет людям легче адаптироваться к таким ситуациям.

    Еще одна причина, по которой подход к решению проблем ценен, заключается в его эстетической форме. Решение задач позволяет учащемуся испытать ряд эмоций, связанных с различными этапами процесса решения. Математики, которые успешно решают задачи, говорят, что опыт, полученный при этом, помогает оценить «силу и красоту математики» (NCTM, 1989, стр. 77), «радость биться головой о математическую стену, а затем обнаружив, что могут быть способы обойти или преодолеть эту стену» (Олкин и Шенфельд, 1994, с.43). Они также говорят о готовности или даже желании заниматься задачей в течение длительного времени, что приводит к тому, что задача перестает быть «головоломкой» и позволяет ей стать проблемой. Однако, хотя именно это участие изначально побуждает решателя решать проблему, все же необходимо, чтобы определенные методы были доступны для успешного продолжения участия. Следовательно, необходимо больше понимать, что представляют собой эти методы и как их лучше всего сделать доступными.

    В последнее десятилетие было высказано предположение, что методы решения задач могут быть наиболее эффективно доступны, если сделать решение задач центром учебной программы по математике. Хотя математические задачи традиционно входили в учебную программу по математике, только сравнительно недавно решение задач стало рассматриваться как важное средство преподавания и изучения математики (Stanic and Kilpatrick, 1989). В прошлом решение задач имело место на уроках математики, но обычно оно использовалось символически в качестве отправной точки для получения единственного правильного ответа, обычно путем следования единственной «правильной» процедуре. Однако в последнее время профессиональные организации, такие как Национальный совет учителей математики (NCTM, 1980 и 1989) рекомендовали, чтобы учебная программа по математике была организована вокруг решения задач, уделяя особое внимание:

    • развитию навыков и способности применять эти навыки в незнакомых ситуациях
    • сбор, организация, интерпретация и передача информации
    • формулирование ключевых вопросов, анализ и концептуализация проблем, определение проблем и целей, обнаружение закономерностей и сходств, поиск соответствующих данных, экспериментирование, перенос навыков и стратегий в новые ситуации
    • развитие любознательности, уверенности и непредубежденности (NCTM, 1980, стр. 2-3).

    Одной из целей обучения через решение проблем является поощрение учащихся к совершенствованию и развитию своих собственных процессов в течение определенного периода времени, поскольку их опыт позволяет им отказаться от некоторых идей и осознать новые возможности (Carpenter, 1989). Помимо развития знаний, учащиеся также развивают понимание того, когда уместно использовать определенные стратегии. При использовании этого подхода акцент делается на том, чтобы сделать учащихся более ответственными за собственное обучение, а не позволять им чувствовать, что алгоритмы, которые они используют, являются изобретениями какого-то внешнего и неизвестного «эксперта». Значительное значение придается исследовательской деятельности, наблюдениям и открытиям, пробам и ошибкам. Студенты должны разработать свои собственные теории, проверить их, проверить теории других, отбросить их, если они не согласуются, и попробовать что-то еще (NCTM, 19).89). Студенты могут стать еще более вовлеченными в решение проблем, формулируя и решая свои собственные проблемы или переписывая проблемы своими словами, чтобы облегчить понимание. Особенно важно отметить, что их поощряют обсуждать процессы, которые они предпринимают, чтобы улучшить понимание, получить новое понимание проблемы и поделиться своими идеями (Thompson, 1985, Stacey and Groves, 1985).

    Заключение

    В этой главе было высказано предположение о том, что существует множество причин, по которым подход к решению задач может существенно повлиять на результаты математического образования. Это не только средство развития логического мышления, оно может предоставить учащимся контекст для изучения математических знаний, оно может улучшить перенос навыков в незнакомые ситуации и само по себе является эстетической формой. Подход, основанный на решении проблем, может дать учащимся возможность сформировать свои собственные представления о математике и взять на себя ответственность за собственное обучение. Нет никаких сомнений в том, что программа по математике может быть улучшена за счет создания среды, в которой учащиеся подвергаются обучению через решение задач, в отличие от более традиционных моделей обучения решению задач. Задача учителей всех уровней состоит в том, чтобы развивать процесс математического мышления наряду со знаниями и искать возможности представить даже рутинные математические задачи в контексте решения проблем.

    Ссылки

    Карпентер, Т. П. (1989). «Обучение как решение проблем». В R.I.Charles и E.A. Сильвер (редакторы), Преподавание и оценка решения математических задач, (стр. 187–202). США: Национальный совет учителей математики.

    Кларк, Д. и Макдонаф, А. (1989). «Проблемы в классе решения задач», Австралийский учитель математики, 45, 3, 20–24.

    Кобб П., Вуд Т. и Якель Э. (1991). «Конструктивистский подход к математике второго класса». В фон Глейзерфилд, Э. (ред.), Радикальный конструктивизм в математическом образовании, стр. 157-176. Дордрехт, Нидерланды: Kluwer Academic Publishers.

    Кокрофт, У.Х. (Ред.) (1982). Математика считает. Отчет Комитета по расследованию преподавания математики в школах, Лондон: Канцелярия Ее Величества.

    Эван, Р. и Лаппин, Г. (1994). «Построение осмысленного понимания содержания математики», в Aichele, D. и Coxford, A. (Eds.) Professional Development for Teachers of Mathematics, стр. 128-143. Рестон, Вирджиния: NCTM.

    Гарднер, Ховард (1985). Рамки разума. Нью-Йорк: Основные книги.

    Лестер, Ф.К.Мл., Масингила, Дж.О., Мау, С.Т., Ламбдин, Д.В., Дос Сантон, В.М. и Раймонд, А.М. (1994). «Учимся учить через решение проблем». в Aichele, D. и Coxford, A. (Eds.) Профессиональное развитие учителей математики, стр. 152-166. Рестон, Вирджиния: NCTM.

    Национальный совет учителей математики (NCTM) (1980). Программа действий: рекомендации по школьной математике 1980-х годов, Рестон, Вирджиния: NCTM.

    Национальный совет учителей математики (NCTM) (1989). Учебная программа и стандарты оценки школьной математики, Рестон, Вирджиния: NCTM.

    Олкин И. и Шенфельд А. (1994). Обсуждение главы Брюса Резника. В А. Шенфельд (ред.). Математическое мышление и решение задач. (стр. 39-51). Хиллсдейл, Нью-Джерси: Lawrence Erlbaum Associates.

    Поля Г. (1980). «О решении математических задач в средней школе». В С. Крулик (Ред.). Решение задач по школьной математике (стр. 1-2). Рестон, Вирджиния: NCTM.

    Резник, Л. Б. (1987). «Обучение в школе и за ее пределами», Исследователь в области образования, 16, 13-20..

    Ромберг, Т. (1994). Обучение в классе, которое способствует математическому мышлению и решению проблем: связь между теорией и практикой. В А. Шенфельд (ред.). Математическое мышление и решение задач. (стр. 287-304). Хиллсдейл, Нью-Джерси: Lawrence Erlbaum Associates.

    Шифтер Д. и Фоснот К. (1993). Реконструкция математического образования. Нью-Йорк: Издательство педагогического колледжа.

    Шенфельд, А. (1994). Размышления о занятиях и преподавании математики. В А. Шенфельд (ред.). Математическое мышление и решение задач. (стр. 53-69). Хиллсдейл, Нью-Джерси: Lawrence Erlbaum Associates.

    Стейси, К. и Гровс, С.

    No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *