Бесконечные периодические дроби 6 класс с ответами
Тестовые задания для 6 класса по теме: Бесконечные периодические дроби.
Правильный вариант ответа отмечен знаком +
1. Что такое бесконечная периодическая десятичная дробь?
a. дробь, у которой одна или несколько цифр повторяются +
b. дробь, которая имеет две единицы после десятичной запятой -
c. дробь, которую можно превратить в смешанное число -
d. обыкновенная дробь -
2. К бесконечной периодической десятичной дроби относится дробь …
a. ⅛ -
b. ½ -
c. ¼ -
d. 1/9 +
3. Как называют повторяющиеся цифры 3, 27, 6?
a. часом дроби -
b. интервалом дроби —
c. периодом дроби +
d. промежутком дроби -
4. Какого вида десятичных дробей не бывает?
a. бесконечного -
b.
c. периодического -
d. конечного -
5. Как нужно записать бесконечную периодическую десятичную дробь 0,272727…?
a. 0,(27) +
b. 0,<27> -
c. 0,{27} -
d. 0,|27| -
6. Как читается бесконечная периодическая десятичная дробь 0,(3)?
a. ноль и три -
b. ноль целых и три в скобках -
c. ноль и три периода -
d. ноль целых и три в период +
7. Какое число больше, чем 5/9?
a. 0,6 +
b. 0,3 -
c. 0,44-
d. 0,53 -
8. -2/15 — …
a. 2,1(3) -
b. -2,(13) -
c. -2,1(3) +
d. 2,(13) -
9. В каком варианте дробь не может быть представлена в виде бесконечной периодической десятичной дроби?
a. 7/11 -
b. ¾ +
c. 1 ⅖ -
1 ⅖ -
d. ⅓ -
тест 10. Как записать число в виде бесконечной периодической десятичной дроби?
a. 0,8(23) +
b. 0,(823) -
c. 0,82(3) -
d. 0,823
11. Как называется периодическая дробь, если ее период начинается не сразу после запятой?
a. размешанной -
b. домешанной -
c. смешанной +
d. перемешанной -
12. Какие цифры бесконечно повторяются при преобразовании обыкновенной дроби 4/11 в десятичную?
a. 3 и 6 +
b. 4 и 1 -
c. 2 и 5 -
d. 6 и 7 -
13. Какую дробь можно записать по схеме 0,(5)?
a. ⅛ -
b. 9/14 -
c. 6/7 -
d. 5/9 +
14. Ноль целых двести восемь тысячных и три в период — это обыкновенная дробь …
a. 5/24 +
b. 6/31 -
c. 7/20 -
7/20 -
d. 8/17 -
15. Какое равенство является неверным?
a. ¼ = 4/16 -
b. ⅝ = 25/40 -
c. ⅓ = 3/10 +
d. ⅖ = 8/20 -
16. Чему равна бесконечная периодическая десятичная дробь 0,(7)?
a. 7/9 +
b. ⅝ -
c. 6/11 -
d. 3/7 -
17. В какой бесконечной периодической десятичной дроби не повторяется цифра 3?
a. ⅓ -
b. 3/9 -
c. 8/24 -
d. 9/36 +
18. Ноль целых четыре десятых и шесть в периоде — …
a. 0,(46) -
b. 0,4(6) +
c. 0,46 -
d. 0,04(6) -
19. Как называют бесконечные десятичные непериодические дроби?
a. иррациональные +
b. неправильные -
c. рациональные -
d. изменчивые -
тест-20. Какую цифру в периоде содержит смешанное число 2 2/15?
a. 7 -
7 -
b. 4 -
c. 3 +
d. 5 -
21. Какая дробь является конечной?
a. 11/45 -
b. 12/13 -
c. 13/16 +
d. 14/21 -
22. Какое неравенство составлено верно?
a. 0,(3) > ⅕ +
b. 9/11 < 0,(79) -
c. 5/16 > 0,4(1) -
d. 0,(45) > ⅝ -
23. 15/16 — …
a. 0,93(75) -
b. 0,9375 +
c. 0,(93) -
d. 0,(937) -
24. Что нельзя получить при делении натурального числа на натуральное число?
a. бесконечную периодическую десятичную дробь -
b. натуральное число -
c. конечную десятичную дробь -
d. бесконечную смешанную дробь +
25. Как называется периодическая дробь, если ее период начинается сразу после запятой?
a. чистой +
b. белой -
белой -
c. приятной -
d. правильной -
26. Какая цифра бесконечно повторяется при делении дроби 21/27?
a. 5 -
b. 2 -
c. 7 +
d. 1 -
27. Какую цифру в периоде имеет обыкновенная дробь 19/22 при преобразовании в бесконечную периодическую десятичную дробь?
a. 58 -
b. 63 +
c. 49 -
d. 72 -
28. Какие делители должен иметь знаменатель дроби, чтобы получилась конечная десятичная дробь?
a. 2 и 5 +
b. 3 и 6 -
c. 4 и 7 -
d. 5 и 8 -
29. 0,5(3) — …
a. 11/16 -
b. 8/15 +
c. ¾ -
d. 7/17 -
тест_30. Какая цифра будет в периоде при превращении обыкновенной дроби на картинке в десятичную?
a. 4 +
b. 2 -
c. 5 -
d. 1 —
1 —
ГДЗ тест 5 десятичные дроби (вариант) 1 математика 5‐6 класс тесты Тульчинская
Решить моё задание
Сообщить об ошибке
Скачать решение
Решить моё задание
Сообщить об ошибке
Решить моё задание
Сообщить об ошибке
Расскажите об ошибке
ГДЗ по математике 5‐6 класс Тульчинская тесты тест 5 десятичные дроби (вариант) — 1 Оставить отзыв Предложение Жалоба Неполное решение задания Нет решения Опечатка Ошибка в ответе Не совпадает номер задания или страница учебника ДругоеСообщение должно содержать от 10 до 250 символов
Спасибо! Ваше сообщение успешно отправлено! This site is protected by reCAPTCHA and the Google
Privacy Policy and
Terms of Service apply.
Заказать решение задач
ГДЗ решит любую задачу или пример, найдет ответ за тебя.
Заполни форму ниже и получи свой уникальный ответ, быстро и качественно от наших лучших авторов.
В одном вопросе выполняется только одно упражнение! Каждое задание оформляется по отдельности.
ПРЕДМЕТ
Математика
Алгебра
Геометрия
Русский
Литература
Английский
Окружающий мир
Мир природы и человека
Химия
Физика КЛАСС
1 класс
2 класс
3 класс
4 класс
5 класс
6 класс
7 класс
8 класс
9 класс
10 класс
11 класс
ВЫБРАТЬ ФАЙЛ
КОММЕНТАРИЙ (какой номер/задание нужно решить, под какой буквой, краткой/полной записью и др. )
)
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Тест по теме Приближение десятичных дробей — Тестирование
Математика 6 класс приближение десятичных дробей тест
Внимание! Все тесты в этом разделе разработаны пользователями сайта для собственного использования. Администрация сайта не проверяет возможные ошибки, которые могут встретиться в тестах.
Список вопросов теста
Вопрос 1
Сколько значащих цифр в числе 0,8035?
Варианты ответов
Вопрос 2
Округлите число 4,5372 с точностью до 0,001.
Варианты ответов
- 4,537 4,540 4,530 другой ответ
Вопрос 3
Округлите число 935,451 с точностю до четырех значащих цифр.
Варианты ответов
- 935,4 935,5 935,0 другой ответ
Вопрос 4
Округлите число 0,6265 с точность до сотых и запишите результат в ответ.
Вопрос 5
Округлите число 0,2539 с точностью до двух значащих цифр и запишите результат в ответ.
Округлите число 0,6265 с точность до сотых и запишите результат в ответ.
Videouroki. net
18.12.2020 21:14:13
2020-12-18 21:14:13
Источники:
Https://videouroki. net/tests/tiest-po-tiemie-priblizhieniie-diesiatichnykh-drobiei. html
Математика 6 класс Тематические тесты к учебнику Никольского — Чулков П. В. » /> » /> .keyword { color: red; }
Математика 6 класс приближение десятичных дробей тест
Главная Учебники 6 класс Математика 6 класс Тематические тесты к учебнику Никольского – Чулков П. В.
В.
Пособие содержит 48 тестов (в 4 вариантах), примерно равноценных по трудности, и итоговый тест (в 2 вариантах). Тематика тестов дана на обороте обложки. Тесты (кроме итогового) сгруппированы по вариантам. Каждый вариант начинается с нечётной страницы, поэтому учитель может использовать одну книгу сразу для четырёх учащихся, разделив её по вариантам и скрепив в виде отдельных тетрадок. Ученик подписывает такую тетрадку и использует её в течение всего учебного года. Ответы, которые приведены ко всем тестовым заданиям в конце книги, остаются у учителя для возможности оперативной проверки.
Заметим, что использование тестовых заданий имеет ряд преимуществ перед традиционными формами контроля, главное из них – оперативность: тест можно провести и проверить быстрее, чем обычную самостоятельную работу, а оценки можно объявить практически сразу по окончании работы. Тем не менее авторы полагают, что тесты не могут полностью заменить традиционные формы контроля. Это связано в первую очередь с тем, что при выполнении тестового задания контроль обращён на результат, а не на ход и состав деятельности по решению задачи и далеко не всегда возможно установить (и соответственно устранить) причины, по которым допущена та или иная ошибка.
Выбор в качестве средства контроля тестов или контрольных работ целиком и полностью остаётся на усмотрение учителя. Авторы выражают признательность А. В. Шевкину и Е. Г. Лысенок, чьи замечания существенно способствовали улучшению данной книги.
В заключение напомним основные правила организации работы с тестами:
1. От учащегося не требуется предъявлять никаких записей.
2. Перед проведением теста ученик должен быть проинструктирован, как правильно указывать ответ.
3. Время выполнения работы и нормы оценок должны быть объявлены ученику заранее.
Тест 1. Отношения чисел и величин
Тест 2. Масштаб
Тест 3. Деление числа в данном отношении
Тест 4. Пропорции
Тест 5. Прямая и обратная пропорциональность
Тест 6. Понятие о проценте
Тест 7. Задачи на проценты
Тест 8. Круговые диаграммы
Тест 9. Отрицательные целые числа
Тест 10. Противоположные числа. Модуль числа
Тест 11. Сравнение целых чисел
Тест 12. Сложение целых чисел
Тест 13. Законы сложения целых чисел
Законы сложения целых чисел
Тест 14. Разность целых чисел
Тест 15. Произведение целых чисел
Тест 16. Частное целых чисел
Тест 17. Распределительный закон
Тест 18. Раскрытие скобок и заключение в скобки
Тест 19. Действия с суммами нескольких слагаемых
Тест 20. Представление целых чисел на координатной оси
Тест 21. Отрицательные дроби
Тест 22. Рациональные числа
Тест 23. Сравнение рациональных чисел
Тест 24. Сложение и вычитание дробей
Тест 25. Умножение и деление дробей
Тест 26. Законы сложения и умножения
Тест 27. Смешанные дроби произвольного знака
Тест 28. Изображение рациональных чисел на координатной оси
Тест 29. Уравнения
Тест 30. Решение задач с помощью уравнений
Тест 31. Понятие положительной десятичной дроби
Тест 32. Сравнение положительных десятичных дробей
Тест 33. Сложение и вычитание десятичных дробей
Тест 34. Перенос запятой в положительной десятичной дроби
Тест 35. Умножение положительных десятичных дробей
Умножение положительных десятичных дробей
Тест 36. Деление положительных десятичных дробей
Тест 37. Десятичные дроби и проценты
Тест 38. Сложные задачи на проценты
Тест 39. Десятичные дроби произвольного знака
Тест 40. Приближение десятичных дробей
Тест 41. Приближение суммы, разности, произведения и частного двух чисел
Тест 42. Разложение положительной обыкновенной дроби в конечную десятичную дробь
Тест 43. Бесконечные периодические десятичные дроби. Периодичность десятичного разложения обыкновенной дроби
Тест 44. Длина отрезка
Тест 45. Длина окружности. Площадь круга
Тест 46. Координатная ось
Тест 47. Декартова система координат на плоскости
Тест 48. Столбчатые диаграммы и графики
Сравнение положительных десятичных дробей Тест 33.
Znayka. win
23.12.2019 4:40:06
2019-12-23 04:40:06
Источники:
Https://znayka. win/uchebniki/6-klass/matematika-6-klass-tematicheskie-testy-k-uchebniku-nikolskogo-chulkov-p-v/
Тесты по математике 6 класс Журавлев » /> » /> . keyword { color: red; }
keyword { color: red; }
Математика 6 класс приближение десятичных дробей тест
Пособие содержит тестовые задания по математике к учебнику СМ. Никольского «Математика 6 класс», включенному в Федеральный перечень учебников. Тесты даются в двух вариантах к каждому параграфу учебника. В конце предлагается итоговый тест в двух вариантах. Ко всем заданиям имеются ответы. Пособие также может использоваться при обучении математике по другим учебникам.
1. Первый велосипедист проезжает за час 10 км, а второй – 15 км. Однажды они одновременно направились навстречу друг другу из пунктов, расположенных на расстоянии 150 км друг от друга. Какое расстояние проехал до встречи второй велосипедист?
А) 90 км
Б) 100 км
В) 60 км
Г) другой ответ
2. Число 252 разделили в отношении 3 : 4. Найдите произведение получившихся чисел.
А) 13 068
Б) 15 552
В) 10 692
Г) другой ответ
ТЕСТ 1. Отношения чисел и величин 5
ТЕСТ 2. Масштаб 7
Масштаб 7
ТЕСТ 3. Деление числа в данном отношении 9
ТЕСТ 4. Пропорции 11
ТЕСТ 5. Прямая и обратная пропорциональность 13
ТЕСТ 6. Понятие о проценте 15
ТЕСТ 7. Задачи на проценты 17
ТЕСТ 8. Круговые диаграммы 19
ТЕСТ 9. Отрицательные целые числа 23
ТЕСТ 10. Противоположные числа. Модуль числа 25
ТЕСТ 11. Сравнение целых чисел 27
ТЕСТ 12. Сложение целых чисел 29
ТЕСТ 13. Законы сложения целых чисел 31
ТЕСТ 14. Разность целых чисел 33
ТЕСТ 15. Произведение целых чисел 35
ТЕСТ 16. Частное целых чисел 37
ТЕСТ 17. Распределительный закон 39
ТЕСТ 18. Раскрытие скобок и заключение в скобки 41
ТЕСТ 19. Действия с суммами нескольких слагаемых 43
ТЕСТ 20. Представление целых чисел на координатной оси 45
ТЕСТ 21. Отрицательные дроби 47
ТЕСТ 22. Рациональные числа 49
ТЕСТ 23. Сравнение рациональных чисел 51
ТЕСТ 24. Сложение и вычитание дробей 53
ТЕСТ 25. Умножение и деление дробей 55
ТЕСТ 26. Законы сложения и умножения 57
Законы сложения и умножения 57
ТЕСТ 27. Смешанные дроби произвольного знака 59
ТЕСТ 28. Изображение рациональных чисел на координатной оси 61
ТЕСТ 29. Уравнения 63
ТЕСТ 30. Решение задач с помощью уравнений 65
ТЕСТ 31. Понятие положительной десятичной дроби 67
ТЕСТ 32. Сравнение положительных десятичных дробей 69
ТЕСТ 33. Сложение и вычитание положительных десятичных дробей 71
ТЕСТ 34. Перенос запятой в положительной десятичной дроби 73
ТЕСТ 35. Умножение положительных десятичных дробей 75
ТЕСТ 36. Деление положительных десятичных дробей 77
ТЕСТ 37. Десятичные дроби и проценты 79
ТЕСТ 38. Сложные задачи на проценты 81
ТЕСТ 39. Десятичные дроби произвольного знака 83
ТЕСТ 40. Приближение десятичных дробей 85
ТЕСТ 41. Приближение суммы, разности, произведения и частного двух чисел 87
ТЕСТ 42. Разложение положительной обыкновенной дроби в конечную десятичную дробь 89
ТЕСТ 43. Бесконечные периодические десятичные дроби 91
ТЕСТ 44. Длина отрезка 93
Длина отрезка 93
ТЕСТ 45. Длина окружности. Площадь круга 95
ТЕСТ 46. Координатная ось 97
ТЕСТ 47. Декартова система координат на плоскости 99
ТЕСТ 48. Столбчатые диаграммы и графики 102
Итоговый тест 106
Ответы 122
Какое расстояние проехал до встречи второй велосипедист.
Znayka. cc
27.07.2017 2:34:31
2017-07-27 02:34:31
Источники:
Https://znayka. cc/uchebniki/6-klass/testy-po-matematike-6-klass-zhuravlev/
Тест по математике «действия с рациональными числами». Тест по математике на тему «Все действия с рациональными числами» (6 класс)
Тест по математике для проведения контроля
по теме «Все действия с рациональными числами»
Цель: установление уровня сформированности предметных, метапредметных и личностных результатов обучающихся по теме «Рациональные числа».
Требования стандарта :
Личностные результаты:
Метапредметные результаты:
Предметные результаты:
Инструкция по выполнению работы
На выполнение всей работы отводится 30 минут.
Работа состоит из 7 заданий. Среди них 3 задания с выбором одного верного ответа из четырех предложенных (задания 2, 3, 5), 1 задание на соотнесение (задание 1), 1 задание с кратким ответом (задание 4), 1 задание на составление выражения и нахождения значения (задание 7) и 1 задание, требующее составить уравнения по заданному условию (задание 6).
Задания 2. К заданию приводится 2 варианта ответа, один из которых верный. (1 балл)
Задания 3. К заданию приводится 4 варианта ответа, один из которых верный. (1 балл)
Задание 5. К заданию приводится 4 варианта ответа, один из которых верный. (2 балла)
Задание 1 на соотнесение. Учащиеся вписывают в приведенную в ответе таблицу под каждой цифрой соответствующую букву. За каждую верно указанную пару начисляется 0,5 балл. Максимальный балл за задание 2.
Задание 4 со свободным ответом. Учащиеся представляют решение на черновике и выписывают в бланк полученный ответ. Максимальный балл за задание 3.
Задание 6 на составление уравнений имеющих заданный ответ. Максимальный балл 4.
Максимальный балл 4.
Задание 7 на составление выражения по заданным условиям, на основе имеющихся знаний по теме и нахождении значения выражения. Максимальный балл за задание 4.
Максимальное количество баллов за всю работу – 17.
Вариант 1
- Значение выражения
Установите соответствие между выражениями и их ответами. Результат запишите в таблицу.
Значение выражения
является отрицательным числом?3. Выясните корнем, какого уравнения является число 2. Выпишите правильный ответ.
1)
2)
3)
4)
4. Вычислите:
А)
Б)
Ответ_______________________
5. Выберите номер рисунка соответствующего неравенству -а>b .
6. Придумайте и запишите четыре уравнения с различными математическими действиями, корнем, которых является число -6.
__________________________________________________________________
7. Запишите выражение: модуль разности числа b и суммы чисел a и c . Найдите значение выражения при a = –5, b = –0,5 и c = –0,05.
Ответ_______________________________________________________
Критерии оценивания тестового контроля знаний
Уровни деятельностиУУД
Критерии
№ задания
Макс. балл
Эмоц.-психол.
Личностные
Регуля-тивный
Регуля-тивные
Соци-альный
Комму-
никати-вные
Анали-тичес-кий
Позна-
ватель-
ные
Знание понятия противоположного числа
Умение находить числа изображённые точками на координатной прямой.

Умение сравнивать числа изображённые на координатной прямой
Творчс-кий
Личност-ные
Умение составить выражение по заданным условиям и на основе имеющихся знаний по теме.
Самосовершенствова-ния
Регуля-
тивные
Решение составленного выражения содержащего модуль и нахождение его значения.
Ответы
Результаты тестовой работыКласс: 6А Предмет: математика Педагог: Дата проведения:
Цель: установление уровня сформированности предметных, метапредметных и личностных результатов у обучающихся в соответствии с требованиями ФГОС
Эмоц.-псих..
Регулятивный
Социальный
Аналитический
Творческий
Самосовер
шенствования
Итого баллов
% выполнения
Отметка
Номер задания
4 (а)
4 (б)
ФИО обучающихся
/баллы
17
5
6.5
3
4
2
8.
 5
5 4
6.5
3
6
3
9
4
7
3
10
4
5
3
5.5
3
9
4
12
4
3
2
3.5
2
3
2
5.5
3
14
5
2.5
2
9.5
4
8
4
4
2
4.5
2
5
3
Реал. баллы
35.5
4 0
Макс. баллы
% достижен.
77
87
13
57
36
21
УУД
Личностные
Регулятивные
Коммуникативные
Познавательные
% достижения
55.
 5
5 54
13
57
Аналитическая записка по результатам тестовой работы
по теме « Все действия с рациональными числами »
Цель : установление уровня образовательных достижений обучающихся по теме «Рациональные числа » на основе требований ФГОС.
Класс: 6 Дата проведения тестовой работы:
Тестовая работа устанавливала уровень сформированности следующих предметных, метапредметных и личностных результатов:
формирование ответственного отношения к учению,
формирование готовности и способности обучающегося к саморазвитию и самообразованию на основе мотивации к обучению и познанию.
умение осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач,
умение оценивать правильность выполнения учебной задачи.
Овладение приемами вычисления рациональных чисел,
Развитие умения использовать приёмы для решения различных математических задач.

По итогам тестирования получены следующие результаты :
Предметные результаты :
На высоком уровне сформированности
знания:Простейшие действия с рациональными числами
Умение выполнять вычисления с рациональными числами, взятыми под знак модуля.
На низком уровне сформированности
умения:Метапредметные результаты :
Наиболее сформированными являются следующие компоненты деятельности:
регулятивный,
познавательные
Наименее сформированными являются следующие компоненты деятельности:
и универсальные учебные действия:
коммуникативные.
Уровни достижения компонентов деятельности :
Эмоционально — психологический 77 %
Регулятивный 87 %
Социальный 13 %
Аналитический 57 %
Творческий 36 %
Самосовершенствования 21 %.

Уровни сформированности универсальных учебных действий:
Регулятивные УУД 54 %,
Коммуникативные УУД 13 %
Познавательные УУД 57 %
Личностные УУД 55,5 %
Выводы :
1. По результатам тестирования выявлен высокий уровень сформированности теоретических знаний по предмету, умение находить и сравнивать числа изображённые точками на координатной прямой; эмоционально-психологические и регулятивные компоненты деятельности, познавательные УУД.
2. Выявились недостатки в подготовке обучающихся:
Недостаточно сформировано умение решать выражения в несколько действий, менее сформирован творческий компонент и самосовершенствования, коммуникативные УУД.
Предложения :
В ходе учебных занятий необходимо уделить внимание формированию компонентов деятельности и универсальных учебных действий, освоению предметных и личностных результатов:
Повышать уровень сложности задания, включать задачи нестандартного характера, требующие творческого подхода к решению, создавать для обучающихся условия, способствующие самосовершенствованию.

3. Выясните корнем, какого уравнения является число 3. Выпишите правильный ответ.
1)
2)
3)
4)
4. Вычислите:
А)
Б)
Ответ_______________________
5. Выберите номер рисунка соответствующего неравенству а
6. Придумайте и запишите четыре уравнения с различными математическими действиями, корнем, которых является число -4.
7. Запишите выражение: модуль разности числа a и суммы чисел b и c . Найдите значение выражения при a = –5, b = –0,5 и c = –0,05.
Тест «Все действия с рациональными числами»
Вариант 2
2-е изд., перераб. и доп. — М.: 2015. — 128 с. М.: 2013. — 128 с.
Данное пособие полностью соответствует федеральному государственному образовательному стандарту (второго поколения). Пособие содержит тестовые задания по математике ко всем учебникам математики 6 класса, включенным в Федеральный перечень учебников. Тесты даются в двух вариантах по всем темам, изучаемым в 6 классе. В конце предлагается итоговый тест в двух вариантах. Ко всем заданиям имеются ответы.
Формат: pdf (2015, 128с.)
Размер: 2,3 Мб
Смотреть, скачать: drive.google
Формат: djvu (2013, 128с.)
Размер: 772 Кб
Смотреть, скачать: yandex.disk
Формат: pdf
Размер: 4 Мб
Смотреть, скачать: yandex.disk
ОГЛАВЛЕНИЕ
ТЕСТ 1. Отношения
чисел и величин 5
ТЕСТ 2. Масштаб 7
ТЕСТ 3. Деление числа в данном отношении 9
ТЕСТ 4. Пропорции 11
ТЕСТ 5. Прямая и обратная пропорциональность 13
Прямая и обратная пропорциональность 13
ТЕСТ 6. Понятие о проценте 15
ТЕСТ 7. Задачи на проценты 17
ТЕСТ 8. Круговые диаграммы 19
ТЕСТ 9. Отрицательные целые числа 23
ТЕСТ 10. Противоположные числа. Модуль числа 25
ТЕСТ 11. Сравнение целых чисел 27
ТЕСТ 12. Сложение целых чисел 29
ТЕСТ 13. Законы сложения целых чисел 31
ТЕСТ 14. Разность целых чисел 33
ТЕСТ 15. Произведение целых чисел 35
ТЕСТ 16. Частное целых чисел 37
ТЕСТ 17. Распределительный закон 39
ТЕСТ 18. Раскрытие скобок и заключение в скобки 41
ТЕСТ 19. Действия с суммами нескольких слагаемых 43
ТЕСТ 20. Представление целых чисел на координатной оси 45
ТЕСТ 21. Отрицательные дроби 47
ТЕСТ 22. Рациональные числа 49
ТЕСТ 23. Сравнение рациональных чисел 51
ТЕСТ 24. Сложение и вычитание дробей 53
ТЕСТ 25. Умножение и деление дробей 55
ТЕСТ 26. Законы сложения и умножения 57
ТЕСТ 27. Смешанные дроби произвольного знака 59
ТЕСТ 28. Изображение рациональных чисел на координатной оси 61
ТЕСТ 29. Уравнения 63
Уравнения 63
ТЕСТ 30. Решение задач с помощью уравнений 65
ТЕСТ 31. Понятие положительной десятичной дроби 67
ТЕСТ 32. Сравнение положительных десятичных дробей 69
ТЕСТ 33. Сложение и вычитание положительных десятичных дробей 71
ТЕСТ 34. Перенос запятой в положительной десятичной дроби 73
ТЕСТ 35. Умножение положительных десятичных дробей 75
ТЕСТ 36. Деление положительных десятичных дробей 77
ТЕСТ 37. Десятичные дроби и проценты 79
ТЕСТ 38. Сложные задачи на проценты 81
ТЕСТ 39. Десятичные дроби произвольного знака 83
ТЕСТ 40. Приближение десятичных дробей 85
ТЕСТ 41. Приближение суммы, разности, произведения и частного двух чисел
87
ТЕСТ 42. Разложение положительной обыкновенной дроби в конечную
десятичную дробь 89
ТЕСТ 43. Бесконечные периодические десятичные дроби 91
ТЕСТ 44. Длина отрезка 93
ТЕСТ 45. Длина окружности. Площадь круга 95
ТЕСТ 46. Координатная ось 97
ТЕСТ 47. Декартова система координат на плоскости 99
ТЕСТ 48. Столбчатые диаграммы и графики 102
Столбчатые диаграммы и графики 102
Итоговый тест 106
Ответы 122
|
Главная » Рабочие тетради, прописи, альбомы » Математика: 6 класс. Тестовые задания. Часть №1. Обыкновенные и десятичные дроби. ФГОС
| ||||||||||||||||||||||||||
Урок 60. умножение положительных десятичных дробей. часть 1 — Математика — 6 класс
Математика
6 класс
Урок № 60
Умножение положительных десятичных дробей. Часть 1
Перечень рассматриваемых вопросов:
- десятичная запись дробей;
- десятичная дробь;
- умножение десятичной дроби на десятичную;
- умножение десятичной дроби на натуральное число.

Тезаурус
Десятичная дробь – это дробь, у которой знаменатель является степенью числа 10.
Десятичные дроби записывают без знаменателей, выделяя целую часть (целая часть правильной дроби считается равной 0) и отделяя её запятой от числителя дробной части.
Обязательная литература:
- Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
Дополнительная литература:
- Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.
- Кордина Н. Е. Виват, математика! Занимательные задания и упражнения 5 кл. // Кордина Н. Е. — издательство «Учитель», 2009. — 112 с.
- Гельфман Э. Г., Демидова Л. Н., Зильберберг Н.
 И., Просвирова И. Г. Десятичные дроби: рабочая тетрадь по математике. 5 класс. // Томск: Изд-во Томского государственного педагогического университета, 2007. — 76 с.
И., Просвирова И. Г. Десятичные дроби: рабочая тетрадь по математике. 5 класс. // Томск: Изд-во Томского государственного педагогического университета, 2007. — 76 с.
Теоретический материал для самостоятельного изучения
Умножая натуральные числа, мы действуем по алгоритму.
Десятичная форма записи дробей позволяет умножать их практически по тем же правилам, что и натуральные числа. Отличие лишь в том, что в ответе следует правильно определять место запятой.
Рассмотрим произведение дробей 2,5 и 1,02. Переведём их в неправильные обыкновенные дроби и выполним умножение.
Выполним умножение другим способом. Переведём дроби в натуральные числа. Для этого перенесём запятую на один знак вправо в числе 2,5 и на два знака вправо в числе 1,02. Таким образом, произведение натуральных чисел 25 и 102 будет в 1000 раз больше произведения 2,5 на 1,02. Выполним умножение.
25·102=2550
Чтобы получить из него произведение дробей 2,5 на 1,02, нужно разделить 2550 на 1000. Для этого передвинем запятую на три знака влево. Получим 2,55.
Для этого передвинем запятую на три знака влево. Получим 2,55.
Таким образом, чтобы перемножить две десятичные дроби, достаточно перемножить их, не обращая внимания на запятые, как обычные натуральные числа, а потом в полученном произведении отделить запятой справа столько цифр, сколько их было после запятой в обоих множителях вместе.
Для десятичных дробей справедливы те же законы, что и для натуральных чисел.
Разбор заданий
1. Найдите произведение.
6,5 · 0,014 = 0,091
Выполняем умножение, не обращая внимания на запятые. В результате получилось число 910. Теперь определим место запятой. В дроби 6,5 – одна цифра после запятой, в дроби 0,014 – три цифры. Значит, всего мы должны отсчитать справа четыре цифры. Отсчитаем и припишем недостающий ноль. Получилось 0,091.
16 ·0,08 = 1,28
Умножив 8 на 16, получили 128. В числе 16 нет цифр после запятой, в числе 0,08 – две цифры. Значит, отсчитаем справа две цифры и поставим запятую. Получилось число 1,28.
Получилось число 1,28.
2. Найдите произведение, применяя законы умножения.
0,25·0,3·0,4
Удобнее сначала 0,25 · 0,4, получим 0,1. Умножим 0,1 на 0,3 получим 0,03.
2,4 · 4,8 + 2,6 · 4,8
Вынесем за скобку общий множитель 4,8. Получим
4,8 · (2,4+2,6) = 4,8 · 5 = 24,0 = 24
3. Вычислите площадь прямоугольника со сторонами 3,12 дм и 3,5 дм.
Чтобы найти площадь прямоугольника, нужно длину умножить на ширину. Получаем 3,12 дм·3,5 дм = 10,92 дм2
4. Вычислите объём прямоугольного параллелепипеда, длина, ширина и высота которого соответственно равны 4,5 см, 2,3 см, 10 см.
Вспомним формулу объёма прямоугольного параллелепипеда.
V = a·b·c
Получаем
V = 4,5 см · 2,3 см · 10см = 103,5 см3.
Разбор заданий тренировочного модуля
№ 1. Собственная скорость моторной лодки 11,5 км/ч, а скорость течения реки 1,6 км/ч. Какой путь пройдёт моторная лодка по течению за 3 часа?
Чтобы найти скорость движениялодки по течению, нужно к собственной скорости лодки прибавить скорость течения.
11,5 км/ч + 1,6 км/ч = 13,1 (км/ч) – скорость по течению.
Чтобы найти расстояние, нужно скорость умножить на время.
13,1 км/ч·3ч = 39,3 (км).
Ответ: 39,3 км пройдёт лодка по течению за 3 часа.
№ 2. Из двух населённых пунктов вышли навстречу друг другу два пешехода. Скорость первого пешехода 4,9 км/ч, скорость второго на 1,5 км/ч меньше. Пешеходы встретились через 2,5 часа. Найдите расстояние между пунктами.
Решение
Найдём сначала скорость второго пешехода.
4,9 км/ч– 1,5 км/ч = 3,4 (км/ч) – скорость второго пешехода.
Когда объекты движутся навстречу другу друг, мы можем найти скорость сближения, сложив их скорости.
4,9 км/ч + 3,4 км/ч = 8,3 (км/ч) – скорость сближения.
Чтобы найти расстояние между пунктами, нужно скорость сближения умножить на время до встречи.
S = vсближ. · t
Получаем: 8,3 км/ч ∙ 2,5 ч = 20,75 (км) – расстояние между пунктами.
Ответ: расстояние между пунктами равно 20,75 км.
Математика, 6 класс, дроби и десятичные дроби
CCSS.Math.Content.6.NS.A.1 6 класс, Система счисления
Кластер: Применение и расширение предыдущих знаний об умножении и делении для деления дробей на дроби
Стандарт: Интерпретация и вычисление частных дробей, а также решение текстовых задач, связанных с делением дробей на дроби, например, с помощью визуальные модели фракций и уравнения для представления проблемы. Например, создайте контекст истории для (2/3) ÷ (3/4) и используйте визуальную дробную модель, чтобы показать частное; используйте связь между умножением и делением, чтобы объяснить, что (2/3) ÷ (3/4) = 8/9потому что 3/4 от 8/9 это 2/3. (В общем, (a/b) ÷ (c/d) = ad/bc.) Сколько шоколада получит каждый, если 3 человека поделят 1/2 фунта шоколада поровну? Сколько порций по 3/4 чашки содержится в 2/3 чашки йогурта? Какой ширины прямоугольная полоса земли длиной 3/4 мили и площадью 1/2 квадратных мили?
CCSS.Math.Content. 6.NS.B.2
6 класс, Система счисления
6.NS.B.2
6 класс, Система счисления
Кластер: Свободно вычислять многозначные числа и находить общие делители и кратные
Стандарт: Быстрое деление многозначных чисел по стандартному алгоритму.
CCSS.Math.Content.6.NS.B.3 6 класс, Система счисления
Кластер: Свободно выполнять вычисления с многозначными числами и находить общие делители и кратные
Стандарт: Свободно складывать, вычитать, умножать и делить многозначные десятичные числа, используя стандартный алгоритм для каждой операции.
CCSS.Math.Practice.MP.1 Математические практики
Кластер: Математические практики
Стандарт: Разбираться в проблемах и настойчиво решать их. Подкованные в математике учащиеся начинают с того, что объясняют себе смысл задачи и ищут пути ее решения. Они анализируют данные, ограничения, отношения и цели. Они строят предположения о форме и значении решения и планируют путь решения, а не просто пытаются найти решение.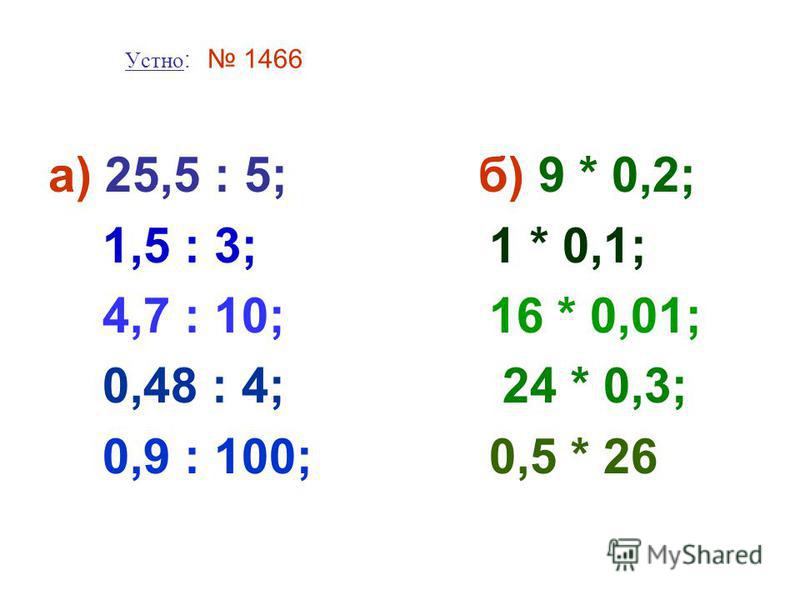 Они рассматривают аналогичные проблемы и пробуют частные случаи и более простые формы исходной задачи, чтобы получить представление о ее решении. Они контролируют и оценивают свой прогресс и при необходимости меняют курс. Учащиеся постарше могут, в зависимости от контекста задачи, преобразовывать алгебраические выражения или менять окно просмотра на своем графическом калькуляторе, чтобы получить необходимую им информацию. Подкованные в математике учащиеся могут объяснять соответствия между уравнениями, словесными описаниями, таблицами и графиками или рисовать диаграммы важных функций и взаимосвязей, графически отображать данные и искать закономерности или тенденции. Младшие школьники могут полагаться на использование конкретных объектов или изображений, чтобы помочь осмыслить и решить проблему. Подкованные в математике учащиеся проверяют свои ответы на задачи другим методом и постоянно спрашивают себя: «Имеет ли это смысл?» Они могут понять подходы других к решению сложных проблем и определить соответствие между различными подходами.
Они рассматривают аналогичные проблемы и пробуют частные случаи и более простые формы исходной задачи, чтобы получить представление о ее решении. Они контролируют и оценивают свой прогресс и при необходимости меняют курс. Учащиеся постарше могут, в зависимости от контекста задачи, преобразовывать алгебраические выражения или менять окно просмотра на своем графическом калькуляторе, чтобы получить необходимую им информацию. Подкованные в математике учащиеся могут объяснять соответствия между уравнениями, словесными описаниями, таблицами и графиками или рисовать диаграммы важных функций и взаимосвязей, графически отображать данные и искать закономерности или тенденции. Младшие школьники могут полагаться на использование конкретных объектов или изображений, чтобы помочь осмыслить и решить проблему. Подкованные в математике учащиеся проверяют свои ответы на задачи другим методом и постоянно спрашивают себя: «Имеет ли это смысл?» Они могут понять подходы других к решению сложных проблем и определить соответствие между различными подходами.
CCSS.Math.Practice.MP.2 Математические практики
Кластер: Математические практики
Стандарт: Рассуждать абстрактно и количественно. Учащиеся, обладающие математическими способностями, понимают величины и их отношения в проблемных ситуациях. Студенты привносят две взаимодополняющие способности в решение проблем, связанных с количественными отношениями: способность деконтекстуализировать — абстрагировать данную ситуацию и представлять ее символически и манипулировать репрезентирующими символами, как если бы они жили собственной жизнью, не обязательно обращая внимание на их референты — и способность контекстуализировать, делать паузы по мере необходимости в процессе манипулирования, чтобы исследовать референты для задействованных символов. Количественное рассуждение влечет за собой привычки создавать последовательное представление проблемы; рассмотрение задействованных единиц; обращать внимание на значение величин, а не только на то, как их вычислять; знание и гибкое использование различных свойств операций и объектов.
CCSS.Math.Practice.MP.3 Математические практики
Кластер: Математические практики
Стандарт: Придумывать жизнеспособные аргументы и критиковать рассуждения других. Подкованные в математике учащиеся понимают и используют заявленные предположения, определения и ранее установленные результаты при построении аргументов. Они строят предположения и выстраивают логическую последовательность утверждений, чтобы исследовать истинность своих предположений. Они способны анализировать ситуации, разбивая их на случаи, а также могут распознавать и использовать контрпримеры. Они обосновывают свои выводы, сообщают их другим и отвечают на аргументы других. Они индуктивно рассуждают о данных, выдвигая правдоподобные аргументы, учитывающие контекст, из которого эти данные возникли. Подкованные в математике учащиеся также способны сравнивать эффективность двух правдоподобных аргументов, отличать правильную логику или рассуждения от ошибочных и, если в аргументе есть изъян, объяснять, в чем он заключается. Учащиеся начальной школы могут создавать аргументы, используя конкретные референты, такие как объекты, рисунки, диаграммы и действия. Такие аргументы могут иметь смысл и быть правильными, даже если они не обобщаются и не становятся формальными до более поздних классов. Позже учащиеся учатся определять области, к которым применяется аргумент. Учащиеся всех классов могут слушать или читать аргументы других, решать, имеют ли они смысл, и задавать полезные вопросы, чтобы прояснить или улучшить аргументы.
Учащиеся начальной школы могут создавать аргументы, используя конкретные референты, такие как объекты, рисунки, диаграммы и действия. Такие аргументы могут иметь смысл и быть правильными, даже если они не обобщаются и не становятся формальными до более поздних классов. Позже учащиеся учатся определять области, к которым применяется аргумент. Учащиеся всех классов могут слушать или читать аргументы других, решать, имеют ли они смысл, и задавать полезные вопросы, чтобы прояснить или улучшить аргументы.
CCSS.Math.Practice.MP.4 Математические практики
Кластер: Математические практики
Стандарт: Модель с математикой. Учащиеся, хорошо разбирающиеся в математике, могут применять математику, которую они знают, для решения проблем, возникающих в повседневной жизни, обществе и на рабочем месте. В младших классах это может быть так же просто, как написать уравнение сложения для описания ситуации. В средних классах учащийся может применять пропорциональные рассуждения, чтобы спланировать школьное мероприятие или проанализировать проблему в сообществе. К старшей школе учащийся может использовать геометрию для решения задачи проектирования или использовать функцию для описания того, как одна интересующая величина зависит от другой. Подкованные в математике учащиеся, которые могут применять то, что они знают, спокойно делают предположения и приближения, чтобы упростить сложную ситуацию, понимая, что позже они могут потребовать пересмотра. Они способны определять важные величины в практической ситуации и отображать их отношения, используя такие инструменты, как диаграммы, двусторонние таблицы, графики, блок-схемы и формулы. Они могут математически анализировать эти отношения, чтобы делать выводы. Они обычно интерпретируют свои математические результаты в контексте ситуации и размышляют о том, имеют ли результаты смысл, возможно, улучшая модель, если она не достигла своей цели.
К старшей школе учащийся может использовать геометрию для решения задачи проектирования или использовать функцию для описания того, как одна интересующая величина зависит от другой. Подкованные в математике учащиеся, которые могут применять то, что они знают, спокойно делают предположения и приближения, чтобы упростить сложную ситуацию, понимая, что позже они могут потребовать пересмотра. Они способны определять важные величины в практической ситуации и отображать их отношения, используя такие инструменты, как диаграммы, двусторонние таблицы, графики, блок-схемы и формулы. Они могут математически анализировать эти отношения, чтобы делать выводы. Они обычно интерпретируют свои математические результаты в контексте ситуации и размышляют о том, имеют ли результаты смысл, возможно, улучшая модель, если она не достигла своей цели.
CCSS.Math.Practice.MP.5 Математические практики
Кластер: Математические практики
Стандарт: Стратегическое использование соответствующих инструментов. Подкованные в математике учащиеся рассматривают доступные инструменты при решении математической задачи. Эти инструменты могут включать карандаш и бумагу, конкретные модели, линейку, транспортир, калькулятор, электронную таблицу, систему компьютерной алгебры, статистический пакет или программное обеспечение для динамической геометрии. Профессиональные учащиеся достаточно хорошо знакомы с инструментами, соответствующими их классу или курсу, чтобы принимать обоснованные решения о том, когда каждый из этих инструментов может быть полезен, признавая как получаемое понимание, так и их ограничения. Например, математически подкованные старшеклассники анализируют графики функций и решений, построенные с помощью графического калькулятора. Они обнаруживают возможные ошибки, стратегически используя оценку и другие математические знания. Создавая математические модели, они знают, что технологии позволяют визуализировать результаты различных предположений, исследовать последствия и сравнивать прогнозы с данными.
Подкованные в математике учащиеся рассматривают доступные инструменты при решении математической задачи. Эти инструменты могут включать карандаш и бумагу, конкретные модели, линейку, транспортир, калькулятор, электронную таблицу, систему компьютерной алгебры, статистический пакет или программное обеспечение для динамической геометрии. Профессиональные учащиеся достаточно хорошо знакомы с инструментами, соответствующими их классу или курсу, чтобы принимать обоснованные решения о том, когда каждый из этих инструментов может быть полезен, признавая как получаемое понимание, так и их ограничения. Например, математически подкованные старшеклассники анализируют графики функций и решений, построенные с помощью графического калькулятора. Они обнаруживают возможные ошибки, стратегически используя оценку и другие математические знания. Создавая математические модели, они знают, что технологии позволяют визуализировать результаты различных предположений, исследовать последствия и сравнивать прогнозы с данными. Подкованные в математике учащиеся разных классов способны идентифицировать соответствующие внешние математические ресурсы, такие как цифровой контент, размещенный на веб-сайте, и использовать их для постановки или решения задач. Они могут использовать технологические инструменты для изучения и углубления своего понимания концепций.
Подкованные в математике учащиеся разных классов способны идентифицировать соответствующие внешние математические ресурсы, такие как цифровой контент, размещенный на веб-сайте, и использовать их для постановки или решения задач. Они могут использовать технологические инструменты для изучения и углубления своего понимания концепций.
CCSS.Math.Practice.MP.6 Математические практики
Кластер: Математические практики
Стандарт: Следите за точностью. Математически подкованные ученики стараются точно общаться с другими. Они стараются использовать четкие определения в обсуждениях с другими и в собственных рассуждениях. Они заявляют о значении выбранных ими символов, включая последовательное и уместное использование знака равенства. Они внимательно относятся к указанию единиц измерения и маркировке осей, чтобы прояснить соответствие с количествами в задаче. Они рассчитывают точно и эффективно, выражают числовые ответы с точностью, соответствующей контексту задачи.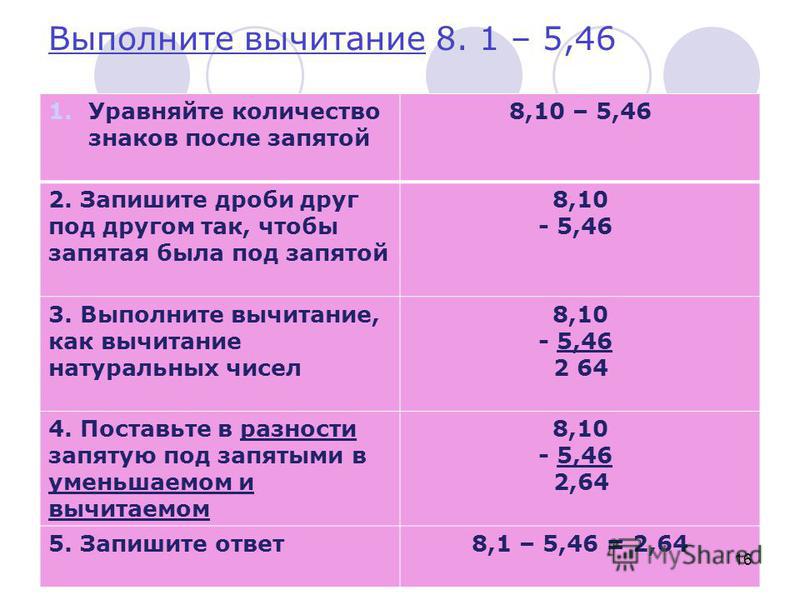 2 + x + 1) может привести их к общей формуле суммы геометрического ряда. Работая над решением задачи, математически подкованные ученики контролируют процесс, уделяя внимание деталям. Они постоянно оценивают обоснованность своих промежуточных результатов.
2 + x + 1) может привести их к общей формуле суммы геометрического ряда. Работая над решением задачи, математически подкованные ученики контролируют процесс, уделяя внимание деталям. Они постоянно оценивают обоснованность своих промежуточных результатов.
MCCRS.Math.Content.6.NS.A.1 6 класс
Область обучения: Система счисления
Стандарт: Применение и расширение предыдущего понимания умножения и деления для деления дробей на дроби
Индикатор: Интерпретация и вычисление частных дробей, а также решение текстовых задач, связанных с делением дробей на дроби, например, с помощью моделей визуальных фракций и уравнений для представления проблемы. Например, создайте контекст истории для (2/3) … (3/4) и используйте визуальную дробную модель, чтобы показать частное; используйте связь между умножением и делением, чтобы объяснить, что (2/3) Ö (3/4) = 8/9потому что 3/4 от 8/9 это 2/3. (В общем, (a/b) Ö (c/d) = ad/bc.) Сколько шоколада получит каждый, если 3 человека разделят 1/2 фунта шоколада поровну? Сколько порций по 3/4 чашки содержится в 2/3 чашки йогурта? Какой ширины прямоугольная полоса земли длиной 3/4 мили и площадью 1/2 квадратных мили?
MCCRS.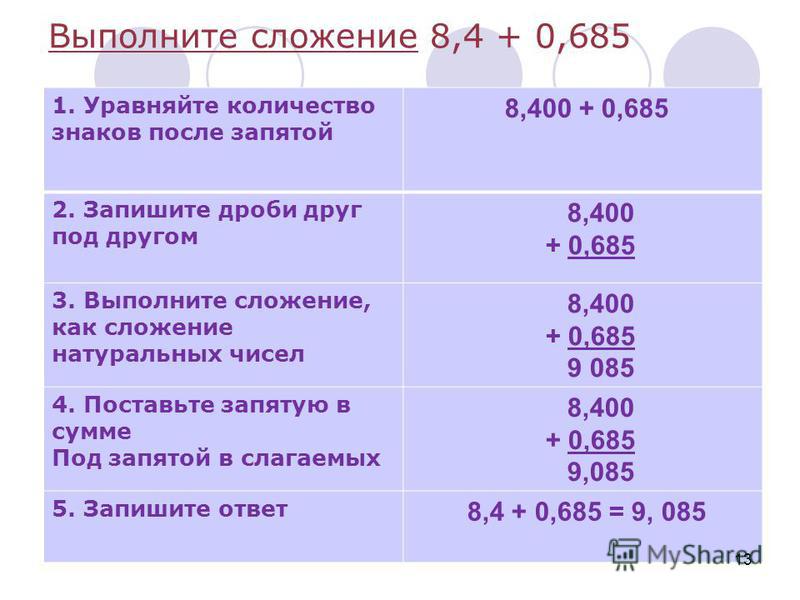 Math.Content.6.NS.B.2
6 класс
Math.Content.6.NS.B.2
6 класс
Область обучения: Система счисления
Стандарт: Быстрые вычисления с многозначными числами и нахождение общих делителей и кратных
Индикатор: Быстро делите многозначные числа по стандартному алгоритму.
MCCRS.Math.Content.6.NS.B.3 6 класс
Область обучения: Система счисления
Стандарт: Свободно считать с многозначными числами и находить общие множители и кратные
Индикатор: Свободно складывать, вычитать, умножать и делить многозначные десятичные числа, используя стандартный алгоритм для каждого операция.
MCCRS.Math.Practice.MP.1 Классы K-12
Область обучения: Математические практики
Стандарт: Математические практики
Показатель: Разбираться в задачах и настойчиво решать их. Подкованные в математике учащиеся начинают с того, что объясняют себе смысл задачи и ищут пути ее решения. Они анализируют данные, ограничения, отношения и цели. Они строят предположения о форме и значении решения и планируют путь решения, а не просто пытаются найти решение. Они рассматривают аналогичные проблемы и пробуют частные случаи и более простые формы исходной задачи, чтобы получить представление о ее решении. Они контролируют и оценивают свой прогресс и при необходимости меняют курс. Учащиеся постарше могут, в зависимости от контекста задачи, преобразовывать алгебраические выражения или менять окно просмотра на своем графическом калькуляторе, чтобы получить необходимую им информацию. Подкованные в математике учащиеся могут объяснять соответствия между уравнениями, словесными описаниями, таблицами и графиками или рисовать диаграммы важных функций и взаимосвязей, графически отображать данные и искать закономерности или тенденции. Младшие школьники могут полагаться на использование конкретных объектов или изображений, чтобы помочь осмыслить и решить проблему. Подкованные в математике учащиеся проверяют свои ответы на задачи, используя другой метод, и они постоянно спрашивают себя: «Имеет ли это смысл?».
Они строят предположения о форме и значении решения и планируют путь решения, а не просто пытаются найти решение. Они рассматривают аналогичные проблемы и пробуют частные случаи и более простые формы исходной задачи, чтобы получить представление о ее решении. Они контролируют и оценивают свой прогресс и при необходимости меняют курс. Учащиеся постарше могут, в зависимости от контекста задачи, преобразовывать алгебраические выражения или менять окно просмотра на своем графическом калькуляторе, чтобы получить необходимую им информацию. Подкованные в математике учащиеся могут объяснять соответствия между уравнениями, словесными описаниями, таблицами и графиками или рисовать диаграммы важных функций и взаимосвязей, графически отображать данные и искать закономерности или тенденции. Младшие школьники могут полагаться на использование конкретных объектов или изображений, чтобы помочь осмыслить и решить проблему. Подкованные в математике учащиеся проверяют свои ответы на задачи, используя другой метод, и они постоянно спрашивают себя: «Имеет ли это смысл?». Они могут понять подходы других к решению сложных задач и определить соответствие между различными подходами.
Они могут понять подходы других к решению сложных задач и определить соответствие между различными подходами.
MCCRS.Math.Practice.MP.2 Классы K-12
Область обучения: Математические практики
Стандарт: Математические практики
Индикатор: Рассуждать абстрактно и количественно. Учащиеся, обладающие математическими способностями, понимают величины и их отношения в проблемных ситуациях. Студенты привносят две взаимодополняющие способности в решение проблем, связанных с количественными отношениями: способность деконтекстуализировать — абстрагировать данную ситуацию и представлять ее символически и манипулировать репрезентирующими символами, как если бы они жили своей собственной жизнью, не обязательно обращая внимание на свои референты — и способность контекстуализировать, делать паузы по мере необходимости в процессе манипуляции, чтобы исследовать референты для задействованных символов. Количественное рассуждение влечет за собой привычки создавать последовательное представление проблемы; рассмотрение задействованных единиц; обращать внимание на значение величин, а не только на то, как их вычислять; знание и гибкое использование различных свойств операций и объектов.
MCCRS.Math.Practice.MP.3 Классы K-12
Область обучения: Математические практики
Стандарт: Математические практики
Показатель: Придумывать обоснованные аргументы и критиковать рассуждения других. Подкованные в математике учащиеся понимают и используют заявленные предположения, определения и ранее установленные результаты при построении аргументов. Они строят предположения и выстраивают логическую последовательность утверждений, чтобы исследовать истинность своих предположений. Они способны анализировать ситуации, разбивая их на случаи, а также могут распознавать и использовать контрпримеры. Они обосновывают свои выводы, сообщают их другим и отвечают на аргументы других. Они индуктивно рассуждают о данных, выдвигая правдоподобные аргументы, учитывающие контекст, из которого эти данные возникли. Подкованные в математике учащиеся также способны сравнивать эффективность двух правдоподобных аргументов, отличать правильную логику или рассуждения от ошибочных и «если в аргументе есть изъян» объяснять, в чем он заключается. Учащиеся начальной школы могут создавать аргументы, используя конкретные референты, такие как объекты, рисунки, диаграммы и действия. Такие аргументы могут иметь смысл и быть правильными, даже если они не обобщаются и не становятся формальными до более поздних классов. Позже учащиеся учатся определять области, к которым применяется аргумент. Учащиеся всех классов могут слушать или читать аргументы других, решать, имеют ли они смысл, и задавать полезные вопросы, чтобы прояснить или улучшить аргументы.
Учащиеся начальной школы могут создавать аргументы, используя конкретные референты, такие как объекты, рисунки, диаграммы и действия. Такие аргументы могут иметь смысл и быть правильными, даже если они не обобщаются и не становятся формальными до более поздних классов. Позже учащиеся учатся определять области, к которым применяется аргумент. Учащиеся всех классов могут слушать или читать аргументы других, решать, имеют ли они смысл, и задавать полезные вопросы, чтобы прояснить или улучшить аргументы.
MCCRS.Math.Practice.MP.4 Классы K-12
Область обучения: Математические практики
Стандарт: Математические практики
Индикатор: Модель с математикой. Учащиеся, хорошо разбирающиеся в математике, могут применять математику, которую они знают, для решения проблем, возникающих в повседневной жизни, обществе и на рабочем месте. В младших классах это может быть так же просто, как написать уравнение сложения для описания ситуации. В средних классах учащийся может применять пропорциональные рассуждения, чтобы спланировать школьное мероприятие или проанализировать проблему в сообществе. К старшей школе учащийся может использовать геометрию для решения задачи проектирования или использовать функцию для описания того, как одна интересующая величина зависит от другой. Подкованные в математике учащиеся, которые могут применять то, что они знают, спокойно делают предположения и приближения, чтобы упростить сложную ситуацию, понимая, что позже они могут потребовать пересмотра. Они способны определять важные величины в практической ситуации и отображать их отношения, используя такие инструменты, как диаграммы, двусторонние таблицы, графики, блок-схемы и формулы. Они могут математически анализировать эти отношения, чтобы делать выводы. Они обычно интерпретируют свои математические результаты в контексте ситуации и размышляют о том, имеют ли результаты смысл, возможно, улучшая модель, если она не достигла своей цели.
К старшей школе учащийся может использовать геометрию для решения задачи проектирования или использовать функцию для описания того, как одна интересующая величина зависит от другой. Подкованные в математике учащиеся, которые могут применять то, что они знают, спокойно делают предположения и приближения, чтобы упростить сложную ситуацию, понимая, что позже они могут потребовать пересмотра. Они способны определять важные величины в практической ситуации и отображать их отношения, используя такие инструменты, как диаграммы, двусторонние таблицы, графики, блок-схемы и формулы. Они могут математически анализировать эти отношения, чтобы делать выводы. Они обычно интерпретируют свои математические результаты в контексте ситуации и размышляют о том, имеют ли результаты смысл, возможно, улучшая модель, если она не достигла своей цели.
MCCRS.Math.Practice.MP.5 Классы K-12
Область обучения: Математические практики
Стандарт: Математические практики
Индикатор: Стратегически используйте соответствующие инструменты. Подкованные в математике учащиеся рассматривают доступные инструменты при решении математической задачи. Эти инструменты могут включать карандаш и бумагу, конкретные модели, линейку, транспортир, калькулятор, электронную таблицу, систему компьютерной алгебры, статистический пакет или программное обеспечение для динамической геометрии. Профессиональные учащиеся достаточно хорошо знакомы с инструментами, соответствующими их классу или курсу, чтобы принимать обоснованные решения о том, когда каждый из этих инструментов может быть полезен, признавая как получаемое понимание, так и их ограничения. Например, математически подкованные старшеклассники анализируют графики функций и решений, построенные с помощью графического калькулятора. Они обнаруживают возможные ошибки, стратегически используя оценку и другие математические знания. Создавая математические модели, они знают, что технологии позволяют визуализировать результаты различных предположений, исследовать последствия и сравнивать прогнозы с данными.
Подкованные в математике учащиеся рассматривают доступные инструменты при решении математической задачи. Эти инструменты могут включать карандаш и бумагу, конкретные модели, линейку, транспортир, калькулятор, электронную таблицу, систему компьютерной алгебры, статистический пакет или программное обеспечение для динамической геометрии. Профессиональные учащиеся достаточно хорошо знакомы с инструментами, соответствующими их классу или курсу, чтобы принимать обоснованные решения о том, когда каждый из этих инструментов может быть полезен, признавая как получаемое понимание, так и их ограничения. Например, математически подкованные старшеклассники анализируют графики функций и решений, построенные с помощью графического калькулятора. Они обнаруживают возможные ошибки, стратегически используя оценку и другие математические знания. Создавая математические модели, они знают, что технологии позволяют визуализировать результаты различных предположений, исследовать последствия и сравнивать прогнозы с данными. Подкованные в математике учащиеся разных классов способны идентифицировать соответствующие внешние математические ресурсы, такие как цифровой контент, размещенный на веб-сайте, и использовать их для постановки или решения задач. Они могут использовать технологические инструменты для изучения и углубления своего понимания концепций.
Подкованные в математике учащиеся разных классов способны идентифицировать соответствующие внешние математические ресурсы, такие как цифровой контент, размещенный на веб-сайте, и использовать их для постановки или решения задач. Они могут использовать технологические инструменты для изучения и углубления своего понимания концепций.
MCCRS.Math.Practice.MP.6 Классы K-12
Область обучения: математические практики
Стандарт: математические практики
Показатель: внимание к точности. Математически подкованные ученики стараются точно общаться с другими. Они стараются использовать четкие определения в обсуждениях с другими и в собственных рассуждениях. Они заявляют о значении выбранных ими символов, включая последовательное и уместное использование знака равенства. Они внимательно относятся к указанию единиц измерения и маркировке осей, чтобы прояснить соответствие с количествами в задаче. Они рассчитывают точно и эффективно, выражают числовые ответы с точностью, соответствующей контексту задачи. 2 + 92 как 5 минус положительное число, умноженное на квадрат, и используйте это, чтобы понять, что его значение не может быть больше 5 для любых действительных чисел x и y.
2 + 92 как 5 минус положительное число, умноженное на квадрат, и используйте это, чтобы понять, что его значение не может быть больше 5 для любых действительных чисел x и y.
MCCRS.Math.Practice.MP.8 Классы K-12
Область обучения: Математические практики
Стандарт: Математические практики
Показатель: Ищите и выражайте регулярность в повторяющихся рассуждениях. Подкованные в математике учащиеся замечают, повторяются ли вычисления, и ищут как общие методы, так и упрощения. Учащиеся старших классов могут заметить, что при делении 25 на 11 они повторяют одни и те же вычисления снова и снова, и прийти к выводу, что у них есть повторяющаяся десятичная дробь. Уделяя внимание вычислению наклона, постоянно проверяя, находятся ли точки на линии, проходящей через (1, 2) с наклоном 3, учащиеся средней школы могут абстрагироваться от уравнения (y — 2)/(x -1) = 3. Заметив регулярность в том, как члены сокращаются при расширении (x — 1) (x + 1), (x — 1) (x ^ 2 + x + 1) и (x — 1) (x ^ 3 + x ^ 2 + x + 1) может привести их к общей формуле суммы геометрического ряда. Работая над решением задачи, математически подкованные ученики контролируют процесс, уделяя внимание деталям. Они постоянно оценивают обоснованность своих промежуточных результатов.
Работая над решением задачи, математически подкованные ученики контролируют процесс, уделяя внимание деталям. Они постоянно оценивают обоснованность своих промежуточных результатов.
Математика 4 класса | Десятичные дроби
Краткое изложение единиц
Глава 6 знакомит учащихся с совершенно новой категорией чисел — десятичными дробями. Учащиеся изучат десятичные дроби и их связь с дробями, увидев, что десятые и сотые доли являются особенно важными дробными единицами, поскольку они представляют собой расширение системы позиционных значений в новый вид чисел, называемый десятичными дробями. Таким образом, студенты расширяют свое представление о том, что такое «число», чтобы охватить эту совершенно новую категорию, на которую они будут опираться до конца своего математического образования.
Учащиеся уже сталкивались с примером необходимости изменить свое понимание числа в 3 классе, когда этот термин стал включать дроби. Их понимание дробей в 3 классе (3.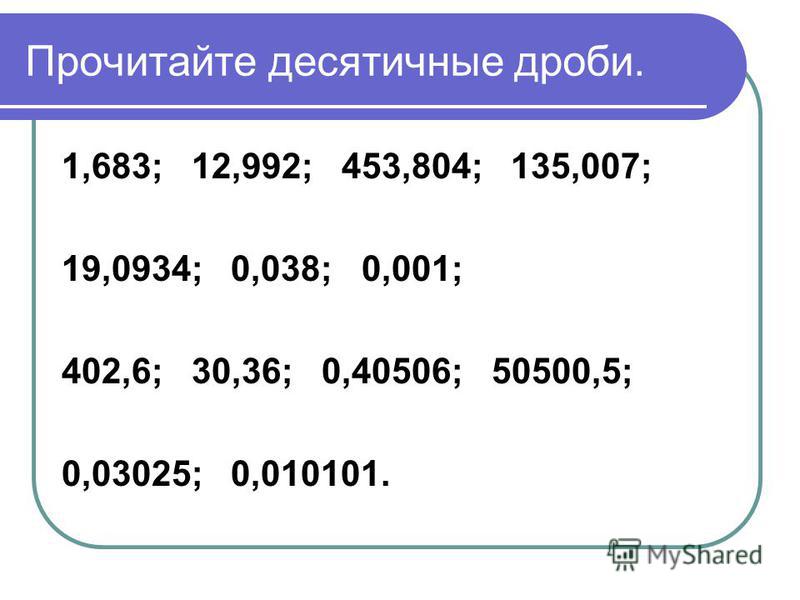 NF.A), а также их работа с дробями в этом году (4.NF.A, 4.NF.B) обеспечат основу, на которой десятичные числа, их эквивалентность дроби, их сравнение и их сложение будут построены. Учащиеся также развили понимание денег во 2-м классе, работая с суммами менее одного доллара или целыми суммами в долларах (2.MD.8). Но со знаниями, полученными в этом разделе, учащиеся смогут работать с деньгами, представленными в виде десятичных дробей, как это часто бывает.
NF.A), а также их работа с дробями в этом году (4.NF.A, 4.NF.B) обеспечат основу, на которой десятичные числа, их эквивалентность дроби, их сравнение и их сложение будут построены. Учащиеся также развили понимание денег во 2-м классе, работая с суммами менее одного доллара или целыми суммами в долларах (2.MD.8). Но со знаниями, полученными в этом разделе, учащиеся смогут работать с деньгами, представленными в виде десятичных дробей, как это часто бывает.
Таким образом, учащиеся полагаются на свою работу с дробями, чтобы увидеть важность десятых как дробной единицы как расширения системы разрядов в теме А, а затем расширить это понимание до сотых долей в теме В. В темах А и В, учащиеся конвертируют между дробью, десятичной дробью, единицей и расширенной формой, чтобы стимулировать эти связи (4.NF.6). Затем учащиеся учатся сравнивать десятичные дроби в теме C (4.NF.7) и складывать десятичные дроби в теме D (4.NF.5). Наконец, учащиеся применяют это десятичное понимание для решения текстовых задач, в том числе связанных с деньгами, в конце модуля. Таким образом, работа с деньгами (4.MD.2) поддерживает основную работу и основную направленность модуля на десятичные дроби.
Таким образом, работа с деньгами (4.MD.2) поддерживает основную работу и основную направленность модуля на десятичные дроби.
Несмотря на то, что учащиеся будут иметь широкие возможности для изучения стандартов математической практики, они будут в значительной степени полагаться на поиск и использование структуры (MP.7), особенно структуры системы разрядов. Они также будут придумывать жизнеспособные аргументы и критиковать рассуждения других (MP.3), используя различные модели десятичных дробей для поддержки своих рассуждений.
В 5 классе учащиеся будут опираться на эту прочную основу десятичных дробей, чтобы развить еще более глубокое понимание отношения десятичных дробей к разрядному значению и выполнять десятичные операции с аналогичными моделями (5.NBT.1—4, 5.NBT. 7). К концу 6-го класса учащиеся будут свободно пользоваться стандартным алгоритмом вычисления с десятичными дробями (6.NS.3). С этого момента учащиеся будут использовать свое понимание десятичных дробей как особого вида чисел в своей математической работе, включая отношения, функции и многие другие.
Темп: 16 учебных дней (14 уроков, 1 гибкий день, 1 контрольный день)
Fishtank Plus для математики
Разблокируйте функции, чтобы оптимизировать время подготовки, планировать увлекательные уроки и следить за успеваемостью учащихся.
Узнать больше
Оценка
Следующие оценки сопровождают Раздел 6.
Предварительная часть
Предложите учащимся пройти предварительную оценку и самооценку перед началом модуля. Используйте Руководство по анализу предварительной оценки, чтобы определить пробелы в фундаментальном понимании и наметить план ускорения обучения на протяжении всего модуля.
Промежуточный модуль
Предложите учащимся выполнить оценку промежуточного модуля после урока 9.
Последующий модуль
Используйте приведенные ниже ресурсы для оценки усвоения учащимися содержания модуля и плана действий для будущих модулей.
Постмодальная оценка
Ключ к ответам после модульной оценки
Руководство по анализу послемодульной оценки
92F25A3F-8529-4314-9899-6EE68694E3D0Пост-юнит самооценка
Расширенный пакет оценивания
Используйте данные учащихся для управления планированием с помощью расширенного набора модульных оценок, помогающих оценить способности учащихся с базовыми навыками и понятиями, а также их прогресс в изучении содержания модуля.
Скачать образец
Подготовка блока
Интеллектуальная подготовка
Рекомендации по подготовке к преподаванию данного модуля
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Интеллектуальная подготовка для всех модулей
- Прочтите и прокомментируйте разделы «Сводка модуля» и «Основные сведения» плана модуля.
- Выполните все целевые задачи и аннотируйте их с учетом «Сводки модуля» и «Основных сведений».
- Пройти итоговую оценку.
Интеллектуальная подготовка для конкретного модуля
- Прочтите стр. 9–10 Прогрессии для общих базовых государственных стандартов в математике Число и операции — дроби, 3–5.
- Прочтите следующую таблицу, в которой указаны модели, используемые во всем устройстве.
| Модель зоны | Пример: Следующая фигура представляет 1 целое. 0,24 из них заштриховано. |
| Числовая строка | Пример: Точка на числовой прямой ниже расположена на 0,24. |
| Основа для картин 10 блоков | Пример: Представьте число 21,53 в десятичной системе счисления. |
Основные понятия
Основные математические понятия, которые учащиеся поймут в этом модуле
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950- Дробные единицы десятые и сотые доли особенно важны, поскольку они представляют собой расширение системы разрядов до разрядов меньше одного целого.
- «Есть несколько способов читать вслух десятичные дроби. Например, 0,15 можно прочитать вслух как «1 десятая и 5 сотых» или «15 сотых», точно так же, как 1500 иногда читают как «15 сотен» или «1 тысяча, 5 сотен»» (NF Progression, p. 15).
- «Количество цифр справа от запятой указывает на количество нулей в знаменателе, поэтому $$2,70=\frac{270}{100}$$ и $$2,7=\frac{27}{10}$ $” (Прогрессия NF, стр. 15).
- В отличие от целых чисел, добавление нулей в конце десятичного числа не меняет его значения.
 Преобразование дробей можно использовать для отображения $$2,70=\frac{270}{100}=\frac{10\times27}{10\times10}=\frac{27}{10}=2,7$$.
Преобразование дробей можно использовать для отображения $$2,70=\frac{270}{100}=\frac{10\times27}{10\times10}=\frac{27}{10}=2,7$$. - Местные единицы не симметричны относительно десятичной точки; скорее, они симметричны относительно места единиц.
- При сравнении чисел, записанных в стандартной форме, используется понимание того, что единица любой единицы больше любой суммы меньшей единицы. Таким образом, наибольшие значения разрядов в каждом числе содержат наиболее важную информацию при сравнении чисел. Если оба числа имеют одинаковое количество наибольших единиц, следующее по величине разрядное значение следует рассматривать следующим, итеративно, до тех пор, пока одна цифра не станет больше другой в той же единице. Это может означать, что десятичная дробь с меньшим количеством цифр больше, чем десятичная дробь с большим количеством цифр в тех случаях, когда более крупные значения десятичных разрядов имеют большее значение (например, 0,4 > 0,13).
- Подход к сложению десятичных дробей основан на идее необходимости складывать одинаковые единицы и, таким образом, заменять дроби эквивалентными дробями, которые позволяют складывать одинаковые единицы (т.
 е. общие знаменатели).
е. общие знаменатели).
Запас слов
Термины и обозначения, которые учащиеся изучают или используют на уроке0004
дробь развернутая форма
сотая
десятая
Чтобы увидеть весь словарный запас для Раздела 6, просмотрите наш глоссарий лексики для 4-го класса.
Материалы
Материалы, изображения и инструменты, которые потребуются преподавателям и учащимся для этого раздела
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950- Базовые десять блоков (1 тысяча, 10 сотен, 10 десятков, 10 единиц на учащегося или малую группу) ) — Вы можете использовать только один набор для учителя, если материалы ограничены.
Модульная практика
Сложные задачи и упражнения на беглость речи
Получите доступ к ежедневным задачам со словами и нашим ориентированным на содержание упражнениям на беглость речи, созданным, чтобы помочь учащимся укрепить свои навыки применения и беглости речи.
Предварительный просмотр
Узнать больше
Схема урока
Тема A: Знакомство с десятыми долями
Представление десятичных долей с точностью до десятых меньше единицы в моделях площади. Преобразование между дробью, десятичной и единицей измерения.
Преобразование между дробью, десятичной и единицей измерения.
4.NF.C.6
Представлять десятичные дроби с точностью до десятых долей числовыми строками. Преобразование между дробью, десятичной и единицей измерения.
4.NF.C.6
Представляет десятичные дроби с точностью до десятых больше десяти с помощью графических блоков с основанием десять. Преобразование между дробью, десятичной дробью, единицей и дробью и десятичной расширенной формой.
4.NF.C.6
Тема B: Понимание десятых и сотых долей
Представлять десятичные дроби с точностью до сотых меньше единицы, понимая эквивалентность некоторого числа десятых и 10-кратного количества сотых. Преобразование между дробью, десятичной и единицей измерения.
4.NF.C.5 4.NF.C.6
Представляет десятичные дроби с точностью до сотых больше единицы. Преобразование между дробью, десятичной дробью, единицей и дробью и десятичной расширенной формой.
4.NF.C.5 4.NF.C.6
Перегруппируйте числа с более чем 9 десятыми или 9 сотыми в простейшую форму единицы и наоборот.
4.NF.C.5 4.NF.C.6
Тема C: Десятичное сравнение
Сравнить два десятичных знака меньше 1, записав результат сравнения символом >, = или <. Обоснуйте вывод, используя визуальную модель.
4.NF.C.7
Сравнить два десятичных знака больше 1, записав результат сравнения с помощью символа >, = или <. Обоснуйте вывод, используя визуальную модель.
4.NF.C.7
Сравните два или более десятичных знака, записанных в различных формах.
4.NF.C.7
Тема D: Десятичное сложение
Сложение десятых с сотыми, записанными в виде десятичных дробей.
4.NF.C.5
Сложение десятых с сотыми, записанными в виде десятичных дробей.
4.NF.C.5
Решите текстовые задачи на сложение десятичных знаков и десятичных дробей.
4.NF.C.5
Тема E: Деньги как десятичная сумма
Найти стоимость некоторой комбинации долларовых банкнот и монет.
4.МД.А.2
Решите текстовые задачи на деньги.
4.МД.А.2
Общие базовые стандарты
Ключ
Основной кластер
Вспомогательный кластер
Дополнительный кластер
Основные стандарты
Стандарты содержания, описанные в этом модуле
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Измерения и данные
4.МД.А.2 — Используйте четыре операции для решения текстовых задач, связанных с расстояниями, интервалами времени, объемами жидкости, массами объектов и деньгами, включая задачи с простыми дробями или десятичными дробями, а также задачи, требующие выражения измерений, данных в более крупной единице, с точки зрения меньшей. Ед. изм. Представляйте измеряемые величины с помощью диаграмм, таких как диаграммы с числовыми линиями, которые имеют шкалу измерения.
Числа и операции — дроби
4.NF.C.5 — Выразите дробь со знаменателем 10 в виде эквивалентной дроби со знаменателем 100 и используйте эту технику, чтобы сложить две дроби со знаменателями 10 и 100 соответственно.
 Учащиеся, умеющие составлять эквивалентные дроби, могут разрабатывать стратегии сложения дробей с разными знаменателями в целом. Но сложение и вычитание с разными знаменателями вообще не обязательны для этого класса.
Например, выразите 3/10 как 30/100 и добавьте 3/10 + 4/100 = 34/100.
Учащиеся, умеющие составлять эквивалентные дроби, могут разрабатывать стратегии сложения дробей с разными знаменателями в целом. Но сложение и вычитание с разными знаменателями вообще не обязательны для этого класса.
Например, выразите 3/10 как 30/100 и добавьте 3/10 + 4/100 = 34/100. 4.NF.C.6 — Используйте десятичную запись для дробей со знаменателем 10 или 100. Например, перепишите 0,62 как 62/100; описать длину как 0,62 метра; Найдите 0,62 на диаграмме с числовыми линиями.
4.NF.C.7 — Сравните две десятичные дроби с сотыми, рассуждая об их размере. Признайте, что сравнения действительны только тогда, когда два десятичных знака относятся к одному и тому же целому. Запишите результаты сравнений символами >, = или
.
Основополагающие стандарты
Стандарты, охватываемые предыдущими единицами или классами, которые являются важной основой для текущей единицы
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Измерения и данные
2.
 MD.C.8
MD.C.8
Числа и операции в десятичной системе счисления
4.НБТ.А.2
Числа и операции — дроби
3.NF.A.2
4.NF.A.1
4.NF.A.2
4.NF.B.3
Будущие стандарты
Стандарты в будущих классах или единицы, которые связаны с содержимым данного раздела
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Числа и операции в десятичной системе счисления
5.НБТ.А.1
5.НБТ.А.2
5.НБТ.А.3
5.
 НБТ.А.4
НБТ.А.45.НБТ.Б.7
Числа и операции — дроби
5.NF.A.1
Стандарты математической практики
CCSS.MATH.PRACTICE.MP1 — Разбираться в проблемах и настойчиво решать их.
CCSS.MATH.PRACTICE.MP2 — Рассуждайте абстрактно и количественно.
CCSS.MATH.PRACTICE.MP3 — Придумывайте жизнеспособные аргументы и критикуйте рассуждения других.
CCSS.MATH.PRACTICE.MP4 — Модель с математикой.
CCSS.MATH.PRACTICE.MP5 — Стратегически используйте соответствующие инструменты.
CCSS.MATH.PRACTICE.MP6 — Следите за точностью.
CCSS.MATH.PRACTICE.MP7 — Ищите и используйте структуру.
CCSS.MATH.PRACTICE.MP8 — Ищите и выражайте закономерность в повторяющихся рассуждениях.

Единица 5
Операции с дробями
значок/стрелка/вправо/большойЕдиница 7
Преобразование единиц
Десятичные дроби и дроби — GED Math
Все математические ресурсы GED
4 Диагностические тесты 263 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 5 6 Следующая →
GED Math Help » Числа и операции » Номера » Десятичные числа и дроби
Преобразуйте следующее десятичное число в дробь:
Возможные ответы:
Правильный ответ:
Объяснение:
Десятичная дробь читается как двести сорок три тысячных, что переводится как:
Сообщить об ошибке
Преобразовать следующую дробь в десятичную:
Возможные ответы: 4 4 44
4
2 Правильный ответ:
Объяснение:
Сообщить об ошибке
Умножить:
Возможные ответы:
Правильный ответ:
Умножить числители, затем умножить знаменатели. Мы можем перекрестно отменить 9 и 3, разделив оба на 3:
Мы можем перекрестно отменить 9 и 3, разделив оба на 3:
Сообщить об ошибке
Добавьте дроби ниже.
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы сложить дроби, нужно убедиться, что дроби имеют общий знаменатель — , что знаменатель обоих чисел одинаков. Поскольку у этих дробей нет общего знаменателя, вы используете правило наименьшего общего кратного, чтобы найти общий знаменатель.
Для этих дробей наименьшее общее кратное равно . а также .
Чтобы дроби остались одинаковыми, нужно умножить числитель и знаменатель в на , а числитель и знаменатель в на . Как только вы нашли общий знаменатель и умножили числитель и знаменатель для каждой дроби, вы можете сложить дроби.
Поскольку числитель больше знаменателя, вы упростите дробь, чтобы она стала смешанным числом.
Сообщить об ошибке
Выше меню кофейни; налог с продаж не взимается с покупок.
Хедвиг хочет устроить неформальную вечеринку для себя и семнадцати гостей. Она хочет подать большой эспрессо и круассан с маслом каждому посетителю, включая себя. Как назло, в магазине действует акция — на каждые два купленных круассана третий в подарок. Сколько сдачи получит Хедвиг за 100-долларовую купюру?
Возможные ответы:
Правильный ответ:
Пояснение:
На вечеринке будет восемнадцать человек, включая Хедвиг.
Она потратит на большой эспрессо.
«Купи два, получи один бесплатно» означает, что только две трети из восемнадцати круассанов — двенадцать из них — будут куплены по обычной цене, а остальные шесть будут бесплатными. Поэтому она потратит .
Общая стоимость покупки составит .
Сдача 100-долларовой купюры составит
.
Сообщить об ошибке
Разделить:
Не использовать калькулятор.
Возможные ответы:
Правильный ответ:
Объяснение:
Сообщить об ошибке
Оценка:
Не используйте калькулятор.
Возможные ответы:
Правильный ответ:
Объяснение:
, которое преобразуется следующим образом:
,
, поэтому
Сообщить об ошибке
Всего у Джима есть 13,85 долларов в пятицентовиках, десятицентовиках и четвертаках.
Предположим, у Джима 47 пятицентовых монет. Сколько копеек у него могло быть?
Возможные ответы:
Правильный ответ:
Объяснение:
Если у Джима 47 пятицентовых монет, то у него есть пятицентовые монеты. Поскольку у него всего 13,85 долларов США, у него всего десять центов и четвертаков.
Поскольку у него всего 13,85 долларов США, у него всего десять центов и четвертаков.
Количество десятицентовых монет, которое есть у Джима, должно быть равно количеству, которое можно заработать только четвертями, т. е. целому числу, кратному . Мы пробуем все четыре варианта:
64 десятицентовика: в десятицентовых монетах
Сумма в четвертях:
Разделите это на :
, которое не является целым числом.
65 десятицентовиков: в десятицентовых монетах
Сумма в четвертях:
Разделите это на :
, что является целым числом.
66 десятицентовиков: в десятицентовых монетах
Сумма в кварталах:
Разделите на :
, что не является целым числом.
67 десятицентовиков: в десятицентовых монетах
Сумма в четвертях:
Разделите это на :
, которое не является целым числом.
65 десятицентовиков — правильный выбор, поскольку только он позволяет использовать целое число четвертаков.
Сообщить об ошибке
Оценка:
Не использовать калькулятор.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы разделить числа с разными знаками, разделите их абсолютные значения и добавьте знак минус. То есть
Чтобы разделить целое число на десятичную дробь, переместите десятичные запятые в обоих числах на одинаковое количество знаков, пока делитель не станет целым числом.
Следовательно, мы перемещаем десятичную точку (письменную или подразумеваемую) через каждые два знака:
Это становится целочисленным делением:
Поскольку мы должны поставить минус, частное равно .
Сообщить об ошибке
Каждый учащийся африканской школы должен владеть одним из трех языков: суахили, хауса или йоруба. Предположим, что ни один учащийся не изучает более одного языка.
Одна треть учащихся выбрали суахили, а две пятых остальных учащихся выбрали хауса. Какая часть студентов выбрала йоруба?
Возможные ответы:
Правильный ответ:
Объяснение:
студентов выбрали суахили, поэтому
выбрали хауса или йоруба.
Так как из этих студентов выбрали хауса,
из них выбрали йоруба.
Это три пятых двух третей, поэтому мы умножаем эти дроби:
Две пятых студентов берут йоруба.
Сообщить об ошибке
← Назад 1 2 3 4 5 6 Далее →
Уведомление об авторских правах
Все ресурсы GED Math
4 Диагностические тесты 263 практических теста Вопрос дня Карточки Learn by Concept
Учебный план для 6 класса
Ниже перечислены необходимые навыки со ссылками на ресурсы, которые помогут в этом.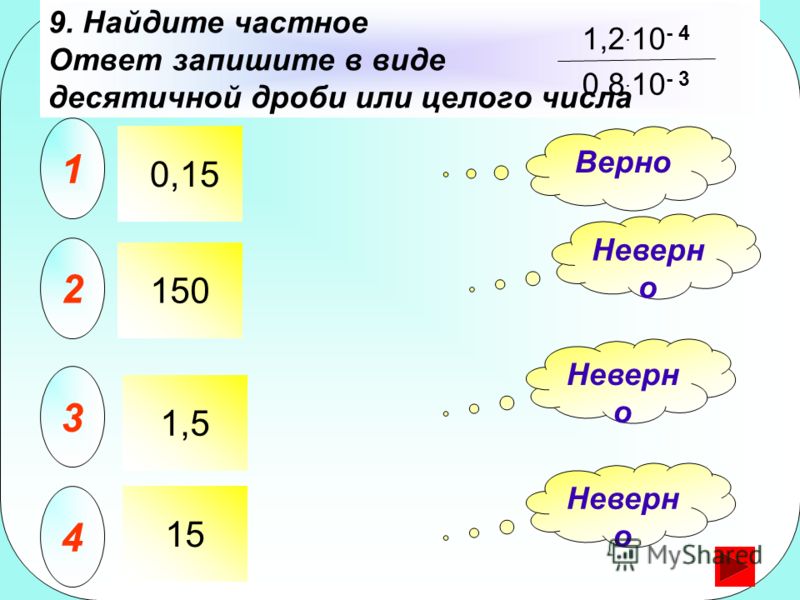 Мы также поощряем множество упражнений и работу с книгами. Учебная программа Главная
Мы также поощряем множество упражнений и работу с книгами. Учебная программа Главная
Важно: это только руководство.
Обратитесь в местное управление образования, чтобы узнать их требования.
Класс 6 | Вычитание
☐ Понять, что подразумевается под десятками, сотнями и т. д. целого числа; и использовать метод вычитания путем сложения.
☐ Сколько будет 10?
☐ Вычитание путем сложения
☐ Дополнение десятков
6 класс | Умножение
☐ Определите и определите нулевое свойство умножения
☐ Свойство нулевого продукта
☐ Свойства реального числа
☐ Умножение на ноль
6 класс | Числа
☐ Чтение и запись целых чисел до триллионов
☐ Значение разряда
☐ Определение целого числа
☐ Триллион Определение
☐ Упражнение: Досчитай до миллиарда
☐ Определение абсолютного значения и определение абсолютного значения рациональных чисел (включая положительные и отрицательные)
☐ Абсолютное значение
☐ Определение абсолютного значения
☐ Числовая строка
☐ Найдите рациональные числа на числовой прямой (включая положительные и отрицательные)
☐ Числовая строка
☐ Рациональные числа
☐ Определение рационального числа
☐ Строка номера дроби
☐ Масштабируемая числовая строка
☐ Порядок рациональных чисел (включая положительные и отрицательные)
☐ Равно меньше и больше символов
☐ Определение заказа
☐ Сравнение дробей
☐ Сравните дроби
☐ Номера для заказа
☐ Заказ игры
☐ Заказ десятичных знаков
☐ Определите и определите коммутативные и ассоциативные свойства сложения и умножения
☐ Коммутативные ассоциативные и дистрибутивные законы
☐ Умные блоки
☐ Определение ассоциативного закона
☐ Определение коммуникативного права
☐ Деятельность: Коммутативная Ассоциативная и Распределительная
☐ Свойства реального числа
☐ Вычислять числовые выражения, используя порядок операций (может включать показатели степени два и три)
☐ Порядок действий — БОДМАС
☐ Порядок действий — PEMDAS
☐ Определение порядка операций
☐ Калькулятор порядка операций
☐ Экспоненты
☐ Определите и определите распределительное свойство умножения над сложением
☐ Коммутативные ассоциативные и дистрибутивные законы
☐ Определение распределительного закона
☐ Деятельность: Коммутативная Ассоциативная и Распределительная
☐ Свойства реального числа
☐ Определите и определите тождественность и обратные свойства сложения и умножения
☐ Обратный
☐ Обратный
☐ Определение аддитивной идентичности
☐ Определение мультипликативной идентичности
☐ Определение обратного
☐ Определение обратной операции
☐ Свойства реального числа
☐ Обратное значение в алгебре
☐ Обратная дробь
6 класс | Десятичные дроби
☐ Представление дробей в виде завершающих или повторяющихся десятичных дробей
☐ Преобразование дробей в десятичные
☐ Повторяющееся десятичное определение
☐ 0,999. .. равно 1?
.. равно 1?
☐ Завершение десятичного определения
☐ Используйте различные стратегии для сложения, вычитания, умножения и деления десятичных дробей до миллионных долей
☐ Сложение десятичных знаков
☐ Вычитание десятичных дробей
☐ Умножение десятичных дробей
☐ Анимация умножения десятичных знаков
☐ Деление десятичных дробей
☐ Анимация деления десятичных дробей
☐ Десятичные рабочие листы
6 класс | Дроби
☐ Сложение и вычитание дробей с разными знаменателями
☐ Эквивалентные дроби
☐ Упрощение дробей
☐ Добавление дробей
☐ Вычитание дробей
☐ Наименьший общий знаменатель
☐ Общий знаменатель
☐ Сложение и вычитание смешанных дробей
☐ Рабочие листы дробей
☐ Использование рациональных чисел
☐ Умножать и делить дроби с разными знаменателями.
☐ Упрощение дробей
☐ Обратный
☐ Деление дробей
☐ Умножение дробей
☐ Рабочие листы дробей
☐ Использование рациональных чисел
☐ Обратная дробь
☐ Умножать и делить смешанные дроби с разными знаменателями
☐ Смешанные фракции
☐ Деление дробей
☐ Умножение смешанных чисел
☐ Определение смешанной фракции
☐ Обратный
☐ Обратная дробь
☐ Определить мультипликативное обратное (обратное) число
☐ Обратный
☐ Обратный
☐ Обратная дробь
☐ Взаимное определение
☐ Найдите несколько представлений рациональных чисел (дробей, десятичных знаков и процентов от 0 до 100)
☐ Преобразование десятичных дробей в дроби
☐ Преобразовать десятичные дроби в проценты
☐ Преобразование дробей в десятичные
☐ Преобразование дробей в проценты
☐ Преобразование процентов в десятичные дроби
☐ Десятичные дроби и проценты
☐ Рациональные числа
☐ Преобразование процентов в дроби
☐ Определение рационального числа
6 класс | Проценты
☐ Чтение, запись и определение процентов от целого (от 0% до 100%)
☐ Десятичные дроби и проценты
☐ Знакомство с процентами
☐ Определение процента
☐ Решите задачи на проценты с использованием процентов, ставок и оснований
☐ Знакомство с процентами
☐ Калькулятор процентов
☐ Проверьте свои проценты
☐ Введение в интерес
☐ Рабочие листы процентов
☐ Определение процентной ставки
6 класс | Соотношения
☐ Решение простых пропорций в контексте
☐ Соотношения
☐ Пропорции
☐ Ratio — приготовить шоколадные чипсы
☐ Пазл Стадо верблюдов
☐ Стадо верблюдов — Решение
☐ Определение коэффициента
☐ Ratio — Рецепт шоколадных чипсов
☐ Определение доли
☐ Проверьте пропорциональность, используя произведение средних, равное произведению крайних значений
☐ Соотношения
☐ Пропорции
☐ Перекрестное умножение
☐ Понимание концепции соотношения
☐ Соотношения
☐ Ratio — приготовить шоколадные чипсы
☐ Ratio — Рецепт шоколадных чипсов
☐ Определение коэффициента
☐ Выразите эквивалентные отношения в виде доли
☐ Соотношения
☐ Определение коэффициента
☐ Ratio — Рецепт шоколадных чипсов
☐ Ratio — приготовить шоколадные чипсы
☐ Определение доли
☐ Пропорции
☐ Различать скорость и отношение
☐ Определение коэффициента
☐ Определение годовой процентной ставки
☐ Решите пропорции, используя эквивалентные дроби
☐ Эквивалентные дроби
☐ Определение эквивалентных дробей
☐ Определение доли
☐ Пропорции
6 класс | Измерение
☐ Измерение емкости и расчет объема прямоугольной призмы
☐ Объем кубоида
☐ Кубоиды Прямоугольные призмы и кубы
☐ Призмы с примерами
☐ Жидкость для заливки
☐ Метрический объем
☐ Определите метрические единицы объема (миллилитры, литры)
☐ Метрические измерения с Мэгги
☐ Метрический объем
☐ Определение емкости
☐ Определение литра | Литер
☐ Миллилитр | Определение миллилитров
☐ Упражнение: Откройте для себя потенциал
☐ Определите эквивалентные метрические единицы вместимости (миллилитры в литры и литры в миллилитры или наоборот)
☐ Метрический объем
☐ Конвертер единиц измерения
☐ Метрические измерения с Мэгги
☐ Определить инструменты и методы, необходимые для измерения с соответствующим уровнем точности: емкость (метрические единицы)
☐ Точность и прецизионность
☐ Метрический объем
☐ Упражнение: Открытие потенциала
☐ Определить личные характеристики производительности (метрические единицы)
☐ Метрический объем
☐ Упражнение: Открытие потенциала
☐ Метрические измерения с Мэгги
☐ Метрическая система измерения
☐ Деятельность: Личные измерения
☐ Понимание преобразования измерений
☐ Конвертер единиц измерения
☐ Метрическая площадь
☐ Метрический объем
☐ Метрическая длина
☐ Метрическая масса
☐ Преобразование температуры — Цельсия в градусы Фаренгейта
☐ Преобразование градусов Цельсия в градусы Фаренгейта и наоборот
☐ Метрические измерения с Мэгги
☐ Знакомство со стандартными единицами измерения США
☐ Интерактивный термометр
☐ Определение температуры
☐ Определение термометра
☐ Определение
градусов по Фаренгейту☐ Определение Цельсия
☐ Преобразование температуры — Цельсия в градусы Фаренгейта
☐ Определить стандартные единицы вместимости США (жидкие унции, чашки, пинты, кварты и галлоны)
☐ Мерные стаканчики
☐ Стандартный том США
☐ Знакомство со стандартными единицами измерения США
☐ Определение стандартных единиц США
☐ Определение емкости
☐ Упражнение: Открытие потенциала
☐ Определение пинты
☐ Определение жидкой унции
☐ Определить эквивалентные единицы измерения емкости в США (жидкие унции в чашки, чашки в пинты, пинты в кварты и кварты в галлоны или наоборот)
☐ Знакомство со стандартными единицами измерения США
☐ Мерные стаканчики
☐ Стандартный том США
☐ Конвертер единиц измерения
☐ Определите инструменты и методы, необходимые для измерения с соответствующим уровнем точности: емкость (стандартные единицы США)
☐ Стандартный том США
☐ Точность и прецизионность
☐ Упражнение: Открытие потенциала
☐ Определить личные эталоны производительности (стандартные единицы США)
☐ Стандартный том США
☐ Упражнение: Откройте для себя потенциал
☐ Знакомство со стандартными единицами измерения США
☐ Деятельность: Личные измерения
6 класс | Время
☐ Понимание високосных лет
☐ Високосные годы
☐ Определение високосного года
☐ Знакомство с днями, неделями, месяцами и годами
☐ Годы
☐ 12-месячный календарь
☐ Понимание AD и BC
☐ н. э. и
э. и
☐ Знать 24-часовой формат времени и как переводить 24-часовой формат времени в формат AM/PM.
☐ Определение АМ
☐ Определение PM
☐ Определение двенадцатичасовых часов
☐ Определение 24-часовых часов
6 класс | Геометрия (плоскость)
☐ Вычислите длины соответствующих сторон подобных треугольников (или других простых подобных фигур), используя пропорциональные рассуждения
☐ Аналогичное определение
☐ Аналогичный
☐ Подобные треугольники
☐ Как определить, подобны ли треугольники
☐ Пропорции
☐ Вычислить площадь основных многоугольников, начерченных на координатной плоскости (прямоугольники и фигуры, составленные из прямоугольников со сторонами целочисленной длины)
☐ Площадь неправильных многоугольников
☐ Площадь круга Треугольник Квадрат Прямоугольник Параллелограмм Трапеция Эллипс и сектор
☐ Калькулятор площади
☐ Деятельность: Сад
☐ Что такое площадь?
☐ Площадь многоугольника по чертежу
☐ Интерактивные полигоны
☐ Определить площади треугольников и четырехугольников (квадратов, прямоугольников, параллелограммов, ромбов и трапеций) и вывести формулы
☐ Площадь круга Треугольник Квадрат Прямоугольник Параллелограмм Трапеция Эллипс и сектор
☐ Калькулятор площади
☐ Треугольники — Равнобедренные, равнобедренные и разносторонние
☐ Используйте различные стратегии, чтобы найти площадь правильных и неправильных многоугольников
☐ Площадь круга Треугольник Квадрат Прямоугольник Параллелограмм Трапеция Эллипс и сектор
☐ Площадь неправильных многоугольников
☐ Полигоны
☐ Интерактивные полигоны
☐ Определение правильного многоугольника
☐ Определение неправильного многоугольника
☐ Площадь многоугольника по чертежу
☐ Калькулятор площади
☐ Определите радиус, диаметр, хорды и центральные углы окружности
☐ Круг
☐ Определение радиуса
☐ Определение диаметра
☐ Определение аккорда
☐ Определение центра | Центр
☐ Круговой сектор и сегмент
☐ Понимать взаимосвязь между диаметром и радиусом окружности
☐ Круг
☐ Определение радиуса
☐ Определение диаметра
☐ Упражнение: Помидоры для сада
☐ Задание: Олимпийская легкоатлетическая дорожка
☐ Определите площадь и длину окружности по соответствующей формуле
☐ Пи
☐ Площадь круга Треугольник Квадрат Прямоугольник Параллелограмм Трапеция Эллипс и сектор
☐ Калькулятор площади
☐ Круг
☐ Периметр
☐ Задание: Олимпийская легкоатлетическая дорожка
☐ Площадь круга
☐ Вычислите площадь сектора круга, зная центральный угол и радиус круга
☐ Круг
☐ Площадь круга Треугольник Квадрат Прямоугольник Параллелограмм Трапеция Эллипс и сектор
☐ Круговой сектор и сегмент
☐ Калькулятор площади
☐ Упражнение: Олимпийская легкая атлетика
☐ Площадь круга
☐ Понимать взаимосвязь между длиной окружности и диаметром круга
☐ Круг
☐ Пи
☐ Упражнение: Найдите приблизительное значение числа Пи
☐ Задание: Олимпийская легкоатлетическая дорожка
☐ Периметр
☐ Определить площадь эллипса по соответствующей формуле
☐ Площадь круга Треугольник Квадрат Прямоугольник Параллелограмм Трапеция Эллипс и сектор
☐ Калькулятор площади
☐ Эллипс
☐ Определение эллипса
6 класс | Геометрия (тело)
☐ Определить объем прямоугольных призм (кубоидов) путем подсчета кубов и вывести формулу
☐ Объем кубоида
☐ Играть Считай 3D-блоки
☐ Определение прямоугольной призмы
☐ Кубоиды Прямоугольные призмы и кубы
☐ Вращающийся куб
6 класс | Алгебра
☐ Используйте подстановку для оценки алгебраических выражений (могут включать показатели степени один, два и три)
☐ Замена
☐ Экспоненты
☐ Упражнение: Суповая банка
☐ Решите и объясните двухшаговые уравнения с целыми числами, используя обратные операции
☐ Обратный
☐ Введение в алгебру: умножение
☐ Определение обратного
☐ Определение обратной операции
☐ Определение аддитивной обратной
☐ Взаимное определение
☐ Введение в алгебру
☐ Баланс при сложении и вычитании
☐ Оценить формулы для заданных входных значений (окружность, площадь, объем, расстояние, температура, проценты и т. д.)
д.)
☐ Уравнения и формулы
☐ Введение в интерес
☐ Преобразование температуры — Цельсия в градусы Фаренгейта
6 класс | Экспоненты
☐ Представление многократного умножения в экспоненциальной форме
☐ Экспоненты
☐ Обозначение индекса — степень числа 10
☐ Законы экспонентов
☐ Представление экспоненциальной формы в виде многократного умножения
☐ Экспоненты
☐ Обозначение индекса — степень числа 10
☐ Законы экспонентов
☐ Вычислить выражения, имеющие показатели степени, где степень является показателем степени одного, двух или трех
☐ Экспоненты
☐ Определение мощности
☐ Обозначение индекса — степень числа 10
6 класс | Координаты
☐ Определите и нанесите точки во всех четырех квадрантах
☐ Декартовы координаты
☐ Интерактивные декартовы координаты
☐ Изображение Тираннозавра Рекса с нанесением координат
☐ Квадрант
☐ Определение точки
☐ Нажми на координату
☐ Координаты и 4 квадранта
☐ Точка
☐ Маска пришельца из координат
☐ Диплодок, использующий координаты
6 класс | Линейные уравнения
☐ Преобразование словесных выражений, состоящих из двух шагов, в алгебраические выражения
☐ Введение в алгебру: умножение
☐ Введение в алгебру
☐ Превратить словесные предложения, состоящие из двух шагов, в алгебраические уравнения
☐ Добавьте два числа, и ответ всегда будет 1089
☐ Почему ответ всегда 1089
☐ Введение в алгебру: умножение
☐ Введение в алгебру
6 класс | Данные
☐ Разработайте концепцию выборки при сборе данных из населения и определите лучший метод сбора данных для конкретного вопроса
☐ Как сделать опрос
☐ Образец определения
☐ Определение случайной выборки
☐ Определение населения
☐ Что такое данные?
☐ Вопросы опроса
☐ Демонстрация результатов опроса
☐ Упражнение: Длина листьев
☐ Деятельность: Оценка
☐ Запишите данные в таблицу частот
☐ Демонстрация результатов опроса
☐ Случайные слова
☐ Распределение частот
☐ Упражнение: Эксперимент с кубиком
☐ Упражнение: Эксперимент с игральными костями
☐ Активность: случайная или нет?
☐ Упражнение: Длина листьев
☐ Построить диаграммы Венна для сортировки данных
☐ Наборы и диаграммы Венна
☐ Определите и обоснуйте наиболее подходящий график для отображения заданного набора данных (пиктограмма, гистограмма, линейный график, гистограмма или круговая диаграмма)
☐ Гистограммы
☐ Точечные диаграммы
☐ Графики данных
☐ Демонстрация результатов опроса
☐ Пиктограммы
☐ Круговая диаграмма
☐ Линейные графики
☐ Гистограммы
☐ Определение частотной гистограммы
☐ Сделать гистограмму
☐ Определить среднее значение, моду и медиану для заданного набора данных
☐ Подлая машина
☐ Как рассчитать среднее значение
☐ Как найти медианное значение
☐ Как рассчитать моду или модальное значение
☐ Среднее определение
☐ Определение медианы
☐ Определение режима
☐ Поиск центральной ценности
☐ Определить диапазон для заданного набора данных
☐ Определение диапазона
☐ Ассортимент
☐ Чтение и интерпретация графиков
☐ Пиктограммы
☐ Круговая диаграмма
☐ Гистограммы
☐ Гистограммы
☐ Линейные графики
☐ Обоснование прогнозов, сделанных на основе данных
☐ Как сделать опрос
☐ Запишите и интерпретируйте данные, используя график стеблей и листьев.
☐ Участки стеблей и листьев
☐ Рассчитайте относительные частоты по таблице частот.
☐ Относительная частота
☐ Активность: случайная или нет?
☐ Деятельность: Оценка
☐ Определение относительной частоты
☐ Чтение и интерпретация таблиц частот
☐ Распределение частот
☐ Групповое распределение частот
☐ Упражнение: Длина листьев
6 класс | Оценка
☐ Оценка объема, площади и окружности
☐ Оценка
☐ Определение оценки
☐ Метрическая система измерения
☐ Знакомство со стандартными единицами измерения США
☐ Жидкость для заливки
☐ Деятельность: Сад
☐ Упражнение: Исследование твердых тел
☐ Определение оценки
☐ Обоснуйте обоснованность оценок
☐ Оценка
☐ Советы и рекомендации по оценке
☐ Визуальная оценка
☐ Головоломка Band around the Earth
☐ Оценка количества в процентах (от 0% до 100%)
☐ Игры на оценку
☐ Определение оценки
☐ Определение оценки
☐ Оценка
☐ Знакомство с процентами
☐ Советы и рекомендации по оценке
☐ Обоснуйте обоснованность ответов, используя оценку (включая округление)
☐ Советы и рекомендации по оценке
☐ Округление чисел
☐ Определение оценки
☐ Определение оценки
☐ Визуальная оценка
☐ Оценка
☐ Игры на оценку
6 класс | Вероятность
☐ Определить вероятность зависимых событий
☐ Вероятность
☐ Вероятность: типы событий
☐ Условная вероятность
☐ Определите количество возможных исходов составного события, используя фундаментальный принцип подсчета, и используйте его для определения вероятностей событий, когда исходы имеют одинаковую вероятность
☐ Вероятность
☐ Условная вероятность
☐ Пазл Мешки с шариками
☐ Основной принцип счета
☐ Вероятность: типы событий
☐ Перечислите возможные исходы составных событий
☐ Вероятность
шестой класс
шестой класс
|
Copyright 2009 Дж. |
Страница не найдена — Фонд Наффилда
Страница не найдена — Фонд НаффилдаСтраница, которую вы ищете, не может быть найдена. Пожалуйста, попробуйте использовать либо главное меню, либо поиск по сайту.
Поиск проектов, новостей, воздействия, событий
Поиск
Образование 638 Когнитивные и некогнитивные навыки 32Curriculum и субъект. образование и навыки 93Начальное образование 127Q-Step 26Эффективность школы 44Среднее образование 152Особые образовательные потребности и инвалидность 52Системные проблемы образования 96justice 227 Акцент к правосудию 36 Адмизирующим правосудием 21Civil правосудие 21 Курта Опыт и доказательства 18 КРИМИНАЛЬНОЕ ПРАВДА 22DOMESTIC НАПРАВЛЕНИЕ 5 ИСПРАВЛЕНИЕ И ПРАВА ПРАВА 15 СВЯЗАНСКОЕ ПРЕДОСТАВЛЕНИЕ 130 ПРИВАТ И ПРОМЕМОЙ ЗАКОН 2SOCIAL LAWERESEALE 9-летняя юстиция 24-й. 19 326Прогнозирование преступности 2Данные для общественного блага 27Цифровой вред и дезинформация 33Цифровая интеграция и исключение 14Цифровые навыки 16Цифровое общество 46Инвалидность 13Экономика, государственные расходы и услуги 174Этническая принадлежность 47Семья и семейная динамика 114Гендер 41Глобальное неравенство в отношении здоровья дети и нуждающиеся дети 73Психическое здоровье 90Musculoskeletal conditions 11Pensions 16Physical health 43Poverty and living standards 106Productivity and innovation 6Public health 150Social media 2Socioeconomics of ageing 24Socioeconomics of early adulthood 39Sports science 1Substance misuse 11Tax 46Trust in democracy 65Valuing data 5
ProjectsNewsEventsImpactOpinionPublicationsSeriesReportsEducation 638Cognitive and non-cognitive skills 32Curriculum and subject choice 30Early years 160Education рабочая сила 73Образовательная оценка 27Высшее образование 90language и грамотность 77lifelong Learning 14nuffield Исследования.



 5
5  5
5 


 Web-мастеринг.
Web-мастеринг. Тестовые задания. Часть №1. Обыкновенные и десятичные дроби. ФГОС
Тестовые задания. Часть №1. Обыкновенные и десятичные дроби. ФГОС Б. Истоминой. Ориентируясь на цели, предваряющие каждую группу тестов, их можно использовать как на этапе самоконтроля, так и на этапе текущей и итоговой проверки, работая и по другим учебникам.
Б. Истоминой. Ориентируясь на цели, предваряющие каждую группу тестов, их можно использовать как на этапе самоконтроля, так и на этапе текущей и итоговой проверки, работая и по другим учебникам.
 И., Просвирова И. Г. Десятичные дроби: рабочая тетрадь по математике. 5 класс. // Томск: Изд-во Томского государственного педагогического университета, 2007. — 76 с.
И., Просвирова И. Г. Десятичные дроби: рабочая тетрадь по математике. 5 класс. // Томск: Изд-во Томского государственного педагогического университета, 2007. — 76 с.
 Преобразование дробей можно использовать для отображения $$2,70=\frac{270}{100}=\frac{10\times27}{10\times10}=\frac{27}{10}=2,7$$.
Преобразование дробей можно использовать для отображения $$2,70=\frac{270}{100}=\frac{10\times27}{10\times10}=\frac{27}{10}=2,7$$. е. общие знаменатели).
е. общие знаменатели). Учащиеся, умеющие составлять эквивалентные дроби, могут разрабатывать стратегии сложения дробей с разными знаменателями в целом. Но сложение и вычитание с разными знаменателями вообще не обязательны для этого класса.
Например, выразите 3/10 как 30/100 и добавьте 3/10 + 4/100 = 34/100.
Учащиеся, умеющие составлять эквивалентные дроби, могут разрабатывать стратегии сложения дробей с разными знаменателями в целом. Но сложение и вычитание с разными знаменателями вообще не обязательны для этого класса.
Например, выразите 3/10 как 30/100 и добавьте 3/10 + 4/100 = 34/100.  MD.C.8
MD.C.8 НБТ.А.4
НБТ.А.4
 Банфилл. Все права защищены. Официальное уведомление
Банфилл. Все права защищены. Официальное уведомление