Сколько формул в математике? – Обзоры Вики
Список. Формулы с 6 по 12 класс.
…
Список математических формул (для всех понятий)
| 2cosacosb Формула | 30-60-90 Формулы |
|---|---|
| Арктан Формула | Формула площади четырехугольника |
| Формулы площади | Формула площади круга |
| Площадь формулы Пентагона | Формула площади сектора круга |
| Площадь квадратной формулы | Площадь формулы трапеции |
Отсюда, Почему формулы используются в математике? Мы узнали, что математические формулы уравнения, которые показывают нам, как что-то решить. Мы используем их, чтобы помочь нам решить проблемы проще и быстрее. … Получив нашу формулу, мы сопоставляем буквы в формуле со значениями из задачи и подставляем эти значения.
Какова основная формула? 1. Формы. В Excel формула представляет собой выражение, которое работает со значениями в диапазоне клетки или ячейка.
Например, =A1+A2+A3, который находит сумму диапазона значений от ячейки A1 до ячейки A3.
Дополнительно Какова лучшая математическая формула? 11 самых красивых математических уравнений
- Теорема Пифагора. …
- 1 = 0.999999999…. …
- Специальная теория относительности. …
- Уравнение Эйлера. …
- Уравнения Эйлера-Лагранжа и теорема Нётер. …
- Уравнение Каллана-Симанзика. …
- Уравнение минимальной поверхности. …
- Линия Эйлера. (Изображение предоставлено Патриком Ионом/Mathematical Reviews/AMS)
Что такое расчетная формула? Формулы исчисления в основном описывают скорость изменения функции для данного входного значения с использованием производная функции/формулы дифференцирования. Процесс нахождения производной любой заданной функции известен как дифференцирование.
Что такое пример формулы?
Формула — это определяемая пользователем инструкция для выполнения вычислений. Это выражение, которое может включать адреса ячеек, числа, арифметические операторы и круглые скобки.
Он начинается с символа равенства (=), за которым следуют ссылки на ячейки и операторы. Например: =A2+B2*5-SUM(E3:E5)
Что является примером формулы? Формула — это выражение, сообщающее компьютеру, какую математическую операцию следует выполнить над определенным значением. На картинке ниже пример Microsoft Формула Excel = СУММ (1 австралийский доллар: 3 австралийских доллара), который складывает сумму ячеек A1, A2 и A3. … В этой формуле СУММ является функцией формулы.
Какова формула 2ab? в2 — б2 =(аб)(а+б) (а+б)2 =a2 + 2аб + б.
Как вы делаете математические формулы?
Кто изобрел пи?
Пи, в математике, отношение длины окружности к ее диаметру.
Символ π был изобретен Британский математик Уильям Джонс в 1706 году для представления отношения, а позже популяризировал швейцарский математик Леонард Эйлер.
Что означает Е в математике? В статистике этот символ математическая константа примерно равна 2.71828183. Призма переключается на экспоненциальное представление, когда значения очень большие или очень маленькие. Например: 2.3e-5 означает 2.3 умножить на десять в степени минус пять, или 0.000023.
Является ли пи действительным числом?
Независимо от размера круга это отношение всегда будет равно пи. В десятичной форме значение пи составляет примерно 3.14. Но пи — иррациональное число, что означает, что его десятичная форма не заканчивается (например, 1/4 = 0.25) и не становится повторяющейся (например, 1/6 = 0.166666…). (Всего с 18 десятичными знаками число пи равно 3.141592653589793238.)
Для чего используется алгебра?
Где используется алгебра? Алгебра широко используется в формулы, когда мы не знаем хотя бы одно из чисел, или когда одно из чисел может измениться.
Что такое Dy в dy dx? d/dx — это операция, которая означает «взять производную по x», тогда как dy/dx указывает, что «производная у была взята по х».
Является ли алгебра исчислением? Является ли алгебра тем же, что и исчисление? Нет. Хотя они тесно связаны, они оба принадлежат к разным разделам математики. В то время как исчисление имеет дело с операциями над функциями и их производными, алгебра включает операции с числами и переменными.
Какая основная формула?
Формула выражение, которое вычисляет значения в ячейке или в диапазоне ячеек. Например, = A2 + A2 + A3 + A4 — это формула, которая складывает значения в ячейках с A2 по A4. Функция — это предопределенная формула, уже доступная в Excel.
Что такое математический пример? Пример математического выражения с переменной: 2х + 3. Все переменные должны иметь коэффициент, число, которое умножается на переменную. В выражении 2х + 3 коэффициент при х равен числу 2, а это означает 2 умноженное на х плюс 3.
Являются ли уравнения алгеброй?
Давай учить!
В алгебре уравнение можно определить как математическое выражение, состоящее из символа равенства между двумя алгебраическими выражениями, имеющими одинаковое значение. Самые простые и распространенные алгебраические уравнения в математике состоят из одной или нескольких переменных.
Кто изобрел алгебру?
Мухаммед ибн Муса аль-Хорезми был мусульманским математиком и астрономом IX века. Он известен как «отец алгебры», это слово происходит от названия его книги «Китаб аль-Джабр». Его новаторская работа предлагала практические ответы на вопросы распределения земли, правил наследования и распределения заработной платы.
Какова формула 4ab?
Ответ: Формула для 4ab: ( 4ab) =( a+b )²- ( ab )² .
ФОРМУЛА ПИКА — Математика в колледже
ФОРМУЛА ПИКА Площадь искомой фигуры можно найти по формуле: М – количество узлов на границе треугольника (на сторонах и вершинах) N – количество узлов внутри треугольника *Под «узлами» имеется ввиду пересечение линий. Найдём площадь треугольника: Отметим узлы: 1 клетка = 1 см M = 15 (обозначены красным) N = 34 (обозначены синим)
Ещё пример. Найдём площадь параллелограмма: Отметим узлы: M = 18 (обозначены красным) N = 20 (обозначены синим)
Найдём площадь трапеции: Отметим узлы: M = 24 (обозначены красным) N = 25 (обозначены синим)
Найдём площадь многоугольника: Отметим узлы: M = 14 (обозначены красным) N = 43 (обозначены синим) Понятно, что находить площадь трапеции, параллелограмма, треугольника проще и быстрее по соответствующим формулам площадей этих фигур. А вот когда дан многоугольник, у которого пять и более углов эта формула работает хорошо. Теперь взгляните на следующие фигуры: Это типовые фигуры, в заданиях стоит вопрос о нахождении их площади. Такие или подобные им будут на ЕГЭ. При помощи формулы Пика такие задачи решаются за минуту. Например, найдём площадь фигуры: Отметим узлы: M = 11 (обозначены красным) N = 5 (обозначены синим) Ответ: 9,5
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах. Посмотреть решение
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах. Посмотреть решение
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Посмотреть решение
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах. Посмотреть решение
Конечно, можно и эти «микрофигурки» дробить на более простые фигуры (треугольники, трапеции). Способ решения выбирать вам. Рассмотрим подход оговоренный в статье «Площадь четырёхугольника. Универсальный способ». Найдём площадь фигуры: Опишем около неё прямоугольник: Из площади прямоугольника (в данном случае это квадрат) вычтем площади полученных простых фигур:
Ответ: 4,5 В будущем будем рассматривать задания на нахождение площади, связанные с окружностями построенными на листе в клетку, не пропустите!
|
Но знайте, что можно это делать и таким образом. 
Ответ дайте в квадратных сантиметрах.Математическая формула: примеры, производная и доказательство
Допустим, вы хотите установить на пол вашей спальни деревянную поверхность, имеющую форму прямоугольника.
Длина и ширина вашего этажа измеряются \(5\) метров на \(4\) метров. Учитывая эти размеры, есть ли способ определить, сколько деревянных панелей вам понадобится для покрытия пола?
Итак, поскольку у вас есть длина и ширина пола, вы можете просто использовать формулу площади прямоугольника, чтобы определить необходимое количество материала. Площадь прямоугольника определяется произведением его длины на ширину. В этом случае вам понадобится в общей сложности \(20\) квадратных метров деревянных панелей, чтобы покрыть пол. Это пример математической формулы.
В этой статье вы познакомитесь с математическими формулами и способами их выражения, чтобы использовать их для решения числовых задач.
Определение формулы в математике
Формула в математике — это полезный инструмент, используемый для определения решений с помощью заданного выражения. Зная общий рецепт, необходимый для решения конкретной проблемы, вы сможете воспроизвести тот же стиль работы, если столкнетесь с похожей ситуацией.
Этот процесс осуществляется с помощью различных математических операций.
Математическая формула — это правило в форме утверждения, выраженное в виде символов, помогающее легко решать задачи.
Формулы состоят из различных величин, соединенных знаком равенства. Они содержат переменные и иногда константы. Это означает, что если у вас есть значения определенных переменных в формуле, вы можете найти значение остальных переменных.
Пример математической формулы
Чтобы лучше понять, что такое математическая формула, давайте продемонстрируем ее на примере.
Допустим, прямоугольник — это участок земли, принадлежащий мистеру Паркеру. Он хочет превратить его в парк, куда дети со всего района могут приходить играть. Он хочет знать точные размеры этой земли, в частности, сумму всех длин и ширин. Это измерение известно как периметр.
Одним из способов измерения периметра прямоугольника выше является ручное измерение всего участка земли.
Однако это можно сделать математически, если известны некоторые стороны. Если вы знаете, что длина равна \(100\) метрам, а ширина — \(55\) метрам, вы можете просто использовать математическую формулу, которая даст вам общий рецепт для вычисления периметра прямоугольника.
Внимательно изучив свойства прямоугольника, вы заметите, что две противоположные стороны равны. Это означает, что если длина ниже составляет \(100\) метров, длина выше также будет \(100\) метров. По этому можно написать формулу нахождения его периметра. Пусть буква \(l\) представляет длину, а \(w\) представляет ширину:
\[ \text{Периметр прямоугольника} = l + l + w+w.\]
Далее это может быть упрощено добавлением подобных терминов
\[ \text{Периметр прямоугольника} = 2l + 2w.\]
Вы можете вынести \(2\), чтобы получить
\[ \text{Периметр прямоугольника} = 2(l + w).\]
Имея это как формулу для нахождения периметра прямоугольника, вы может заменить его числами, чтобы посмотреть, поможет ли это мистеру Паркеру эффективно решить его проблему.
\[ \begin{align} \text{Периметр прямоугольника } &= 2(l + w) \\ &= 2(100 + 55) \\ &= 2(155) \\ &= 310 \, м . \end{align}\]
Используя формулу, мистер Паркер может просто узнать периметр своего земельного участка, не измеряя его вручную.
В нескольких областях математики применяются разные формулы. Чтобы знать, где и как можно применять формулы, вы должны понимать проблему, с которой имеете дело, и знать, какие переменные являются значимыми.
Как написать математическую формулу
Как упоминалось ранее, формулы представляют собой уравнения или тождества. Они состоят из переменных и иногда констант. Фундаментальная задача написания формул состоит в том, чтобы знать, что представлять в качестве релевантной переменной.
Например, если вы хотите написать формулу для периметра прямоугольника, вы должны знать, что длина тесно связана с периметром. Вы можете взять пример того, как пишутся формулы.
Предположим, вы знаете, что \(3\) кошки едят столько же еды, сколько одна большая собака.
Напишите формулу, чтобы определить объем пищи, который вам понадобится, чтобы накормить \(27\) кошек и \(10\) крупных собак в пересчете на количество имеющихся у вас собак.
Решение
Хорошо бы сначала решить, что вы пытаетесь сделать! Вы ищете, чтобы найти формулу для объема, учитывая количество кошек и количество собак. Итак, давайте дадим этим вещам некоторые переменные.
- \(c\) — количество кошек
- \(d\) — количество собак
- \(V\) — объем пищи
Вас просят найти формулу объема корма для \(27\) кошек и \(10\) собак. Что ты знаешь? Вы знаете, что \(3\) кошки едят столько же, сколько одна большая собака. Итак,
\[3c = 1d.\]
Вам нужна формула для \(27\) кошек и \(10\) собак, или, другими словами, формула для
\[ V = 27c + 10d,\ ]
но вы хотите это с точки зрения собак, а не собак и кошек! Что делать? Что ж, вы не воспользовались тем, что \(3c = d\). Вы можете сделать небольшой факторинг, чтобы получить
\[ \begin{align} V &=27c + 10d \\ &= 9(3c) + 10d, \end{align}\]
и затем подставить в \(3c = d\), чтобы получить
\[ \begin{align} V &=9(3c) + 10d \\ &= 9d+ 10d \\ &= 19d, \end{align}\]
, что является формулой количества пищи, которое вам нужно кормить \(27\) кошек и \(10\) крупных собак по количеству имеющихся у вас собак.
Наиболее важные математические формулы
Термин «самый важный» немного вводит в заблуждение, так как это действительно зависит от того, кого вы спрашиваете! Однако в этом разделе вы обсудите некоторые общие формулы, которые используются в математике.
Области фигур
Площадь фигуры определяется двумерной областью, ограниченной данной формой.
Concept | Formula |
Area of rectangle | Area = length \(\times\) width |
Area of parallelogram | Area = основание \(\times\) высота |
Площадь треугольника | Площадь = \( \dfrac{1}{2} \times\) основание \(\times\) высота |
Площадь круга | Площадь = \(\pi\times \ ) radius\(\times\) radius |
Объемы твердых тел
Объем твердого тела – это объем трехмерного пространства, занимаемого объектом, контейнером или замкнутой поверхностью.
Концепт | Формула |
Прямоугольник | Объем = длина \(\times\) основание\(\times\) высота |
Треугольная призма | 10102 Объем ={2 \fracd 90}{0} раз\) длина \(\раз\) основание\(\раз\) высота|
Цилиндр | Объем = \(\пи\раз\) радиус\(\раз\) радиус\(\ раз\) height |
Составная мера
Составные меры — это выражения, содержащие более одной величины.
Concept | Formula |
Speed | \( \text{Speed } = \dfrac{ \text{ Distance}}{\text{time}}\) |
Density | \( \text{Density } = \dfrac{ \text{ Mass}}{\text{ Volume}}\) |
Pressure | \( \ text{Давление} = \dfrac{ \text{ Сила}}{\text{Площадь}}\) |
Алгебра перезаписи формул
Полезно знать, как переписывать формулы, так как вам могут дать площадь прямоугольника и попросить найти его длину.
Когда вы переписываете формулу, цель состоит в том, чтобы создать уравнение, эквивалентное формуле, но с отсутствующей переменной.
Для этого используется основное правило — золотое правило манипулирования уравнениями. Он говорит, что делайте с одной стороной уравнения то, что вы делаете с другой. Это означает, что если манипуляция требует, чтобы вы добавили значения к одной части уравнения, сделайте то же самое добавление к левой части уравнения. Вот пример.
Если бы были даны значения массы и плотности, то какой была бы формула для объема?
Раствор
Формула, в которой присутствуют все указанные величины, является формулой плотности.
\[\text{Плотность } = \dfrac{ \text{ Масса}}{\text{ Объем}}\]
Чтобы найти формулу для объема, вам нужно сделать объем предметом уравнения. Это будет означать, что любая форма манипуляции на любой стороне уравнения потребует ее воспроизведения на другой стороне. Для этого вам сначала нужно будет умножить обе части уравнения на объем,
\[\text{Плотность }\times \text{ Объем } = \dfrac{ \text{ Масса}}{\text{ Объем}} \times \text{ Объем}\]
и затем отмените, чтобы получить
\[\text{Плотность }\times \text{ Объем } = \text{ Масса}.
\]
Теперь вы можете разделить обе части на Плотность
\[\dfrac{\text{Плотность }\times \text { Volume }}{\text{Density} } = \dfrac{\text{ Mass}}{\text{Density} }\]
и снова отмените, чтобы получить
\[\text{ Volume } = \dfrac{ \text{ Масса}}{\text{Плотность} }.\] 92\), а его ширина равна \(6\, см\).
Решение
Прежде всего, вы можете написать формулу для нахождения площади прямоугольника вниз:
\[A = lw.\]
Чтобы найти длину, вам придется сделать ее предметом уравнения. Это означает, что вам предстоит выполнить несколько манипуляций. То, что вы делаете на одной стороне, потребует того, чтобы это было сделано на другой. Чтобы изолировать длину в одной части уравнения, вам придется разделить обе части уравнения на ширину
\[ \frac{A}{w} = \frac{lw}{w}\]
и затем отмените, чтобы получить
\[ l = \frac{A}{w}.\]
Вы теперь есть формула для нахождения длины в этом сценарии. Вы можете найти решение проблемы, подставив в формулу:
\[ \begin{align} l &= \frac{A}{w}\\ &= \frac{42}{6} \ \ &= 7.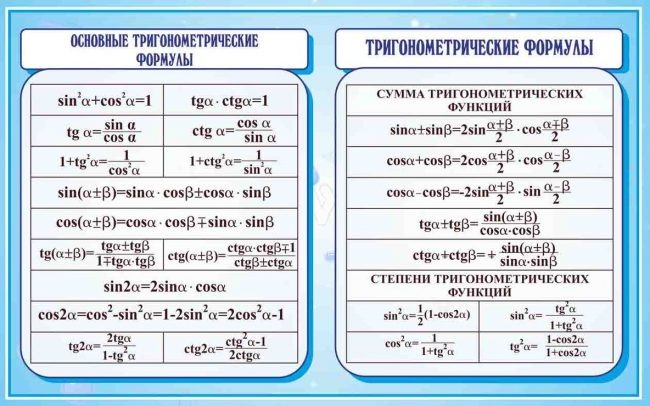
\end{align}\]
Не забудьте единицы! Длина \(7\, см\).
Замена в формулах
Замена в формулах — это процесс замены переменной ее значением в формуле. В этом разделе использование формул становится чрезвычайно очевидным. При правильных значениях переменных можно найти неизвестные переменные.
Весь процесс подстановки в формулы заключается в замене букв (переменных) их заданными значениями. Вы возьмете множество примеров, чтобы увидеть, как можно подходить к различным типам возможных ситуаций.
Найдите \(z\), когда \(x=7\) в заданной формуле
\[z = x+2.\]
Решение
Все, что вам нужно сделать, это заменить \( x\) в формуле с \(7\), так как задача говорит, что \(x\) совпадает с \(7\).
\[ \begin{align} z &= x+2 \\ &= 7 + 2 \\ &= 9.\end{align}\]
Вот вам еще один пример!
Найти \(l\), когда \(m=5\) в данной формуле
\[ l = 7m.\]
Решение
число \(5\), указанное в задаче, тогда вы можете найти \(l\).
Итак,
\[ l = 7m.\]
Связь между \(7\) и \(m\) здесь есть умножение. В целом эту формулу можно записать как
\[l = 7 \cdot m,\]
или
\[l = 7(m).\]
Подставив \(5\) вместо \(m\), вы получите
\[ \begin{align} l &= 7(5) \\ &= 35.\end{align}\]
Математическая формула — ключевые выводы
- Математическая формула — это правило в форме утверждения, выраженное в виде символов, помогающее легко решать задачи.
- Формулы состоят из различных величин, соединенных знаком равенства.
- Фундаментальное правило, используемое для переписывания формул, — это золотое правило манипулирования уравнениями, которое гласит: делайте с одной стороной уравнения то, что делаете с другой.
- Подстановка в формулы — это процесс замены переменной ее значением в формуле.
терминология — В чем разница между уравнением и формулой?
спросил
Изменено 20 дней назад
Просмотрено 136 тысяч раз
$\begingroup$
Иногда уравнение и формула используются взаимозаменяемо, но мне интересно, есть ли разница.
Например, предположим, что мы можем рассчитать топливную экономичность автомобиля как:
миль на галлон = пройденное расстояние в милях / расход топлива в галлонах
Это уравнение или формула?
- терминология
- определение
$\endgroup$
2
$\begingroup$
Уравнение — это любое выражение со знаком равенства, поэтому ваш пример по определению является уравнением. Уравнения часто появляются в математике, потому что математики любят использовать знаки равенства.
Формула представляет собой набор инструкций для получения желаемого результата. К нематематическим примерам относятся такие вещи, как химические формулы (два Н и один О составляют Н3О) или формула кока-колы (которая представляет собой просто список ингредиентов). Вы можете возразить, что эти примеры не являются уравнениями в том смысле, что водород и кислород не «равны» воде, но вы можете использовать их для получения воды.
92$ можно рассматривать как формулу для нахождения длины стороны прямоугольного треугольника, но оказывается, что такая длина всегда равна
В вашем случае «миль на галлон = расстояние/галлоны» лучше всего понимать как «формулу в виде уравнения», что означает, что в данном случае эти два слова взаимозаменяемы.
$\endgroup$
3
$\begingroup$
Уравнение нужно решить, то есть есть неизвестные. Формула предназначена для вычисления, то есть вы заменяете в ней все переменные значениями и получаете значение формулы.
Ваш пример — формула для миль на галлон . Но это может стать уравнением, если дано миль на галлон и одно из других значений, а оставшееся значение ищется.
$\endgroup$
9
$\begingroup$
Я бы сказал, что уравнение — это что угодно, в котором есть знак равенства; формула — это уравнение вида $A={\rm\stuff}$, где $A$ не входит в число веществ в правой части.
$\endgroup$
1
$\begingroup$
Пожалуйста, проголосуйте против меня, если хотите, но я бы сказал, что эти слова на самом деле являются синонимами друг друга. Оба они выражают, что между некоторыми математическими выражениями существует некоторая основная связь.
$\endgroup$
6
$\begingroup$ Формула — это уравнение, показывающее взаимосвязь между двумя или более величинами.
Это будут правила или инструкции, которые используются для демонстрации взаимосвязи между двумя или более величинами.
Уравнение — это задача, отображаемая с помощью цифр или символов, где где-то присутствует знак равенства (=); обычно ближе к концу уравнения. Если только это не отношение или деление.
$\endgroup$
$\begingroup$
Вы решаете уравнение, пока вычисляете формулу.
Между прочим, уравнение, которое содержит любые значения переменных, является тождеством.
$\endgroup$
$\begingroup$ 92$ и $f=ma$ являются «уравнениями», обычно не называемыми «формулами». Вы бы сказали не «формула силы», а «уравнение силы». Они могут иметь бесконечное количество решений. так что я бы сказал, что термины также взаимозаменяемы.
http://en.wikipedia.org/wiki/Force
$\endgroup$
$\begingroup$
Простой ответ исходит от https://www.
bbc.co.uk/bitesize/guides/zwbq6yc/revision/1
Для вашего удобства краткое объяснение по ссылке: 9{\ circ} F $)
Уравнение :
- обычно имеет только одну переменную, хотя может встречаться более одного раза
- будет правильным только для определенных значений (например, $2x = 10$ верно только для $x = 5$)
- не всегда верно.
Хотя я предлагаю вам посмотреть на 92 $
$\endgroup$
$\begingroup$
В формуле все переменные могут быть выбраны произвольно. Уравнение допускает только частные значения непостоянной переменной/s.
$\endgroup$
$\begingroup$
TL;DR Я бы сказал, что это действительно зависит от контекста.
Что я помню в старшей/средней школе:
Нам давали задачи типа
Зная длину и площадь прямоугольника, найдите его ширину.
(Не совсем прямоугольник. Это, конечно, больше подходит для начальной школы. Может быть прямоугольной призмой или чем-то еще.)
‘Формула’ $A =wl$.
«Уравнение» — это то, что вы получите, если подставите заданные значения для $A$ и $l$. Итак, если у вас есть $A=10$ и $l=7$, тогда уравнение равно $10=7w$.
В то время я думал, что это очень придирчиво/субъективно/традиционно/контекстуально. Теперь я все еще делаю это, но у меня есть 10 000+ репутации и степени бакалавра и магистра, чтобы жаловаться на это.
По словам моих учителей средней школы, то, что вы предоставили, является формулой, но это в контексте заполнения пробелов уравнения и формулы в школе.
Заключение : Я бы сказал, что это действительно зависит от контекста. Если определить уравнение как утверждение со знаком равенства, то каждая формула со знаком равенства является уравнением.
.. Кстати, в Википедии вроде бы нет неравенств, которые были бы формулами.
$\endgroup$
$\begingroup$
Мои определения будут сосредоточены на математике.
В контексте математики уравнение представляет собой математическое выражение, состоящее из чисел, переменных, операций и знака равенства, которому удовлетворяют некоторые конкретные значения желаемой переменной при заданных значениях других переменных в нем.
В контексте математики формула представляет собой уравнение, в котором желаемая переменная явно выражена в терминах (т. е. явная функция) другой переменной (переменных).
В вашем случае топливная экономичность автомобиля на галлон явно выражена с точки зрения пройденного расстояния и израсходованного топлива, т. е. соотношения расстояния и израсходованного топлива. Поэтому лучше всего использовать формулу .
ПРИМЕЧАНИЕ: В контексте математики каждая формула является уравнением, но уравнение не обязательно является формулой.
$\endgroup$
$\begingroup$
Один из способов ответить на этот вопрос был разработан на первом и втором курсах алгебры средней школы США.
В первом курсе в глоссарии формально изложены следующие определения.
уравнение : Оператор, образованный путем помещения знака равенства между двумя числовыми или переменными выражениями.
Например, $11-7=4$, $5x-1=9$ и $y+2=2+y$ являются уравнениями, поскольку все они удовлетворяют данному определению.
Следующее определение формулы также официально указано в глоссарии:
формула : Уравнение, устанавливающее правило отношения.
Вот две полезные формулы: $A=lw$, формула площади прямоугольника; $P=2l+2w$, формула периметра прямоугольника.
В то время как в начале второго курса следующее предложение резюмирует, что связь существует между двумя или более переменными:
Формула — это уравнение, которое устанавливает связь между двумя или более переменными.
