| 1 | Найти производную — d/dx | бревно натуральное х | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | Найти производную — d/dx | 92)||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 22 | Найти производную — d/dx | грех(2x) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 43 | Оценка интеграла 9бесконечность | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 45 | Найти производную — d/dx | х/2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 46 | Найти производную — d/dx | -cos(x) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 47 | Найти производную — d/dx | грех(3x) | 92+1|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 68 | Оценить интеграл | интеграл от sin(x) по x | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 69 | Найти производную — d/dx | угловой синус(х) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 85 | Найти производную — d/dx | лог х | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 86 | Найти производную — d/dx | арктан(х) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 87 | Найти производную — d/dx | бревно натуральное 5х9(logx)
Вопрос Обновлено:26/04/2023 ПУБЛИКАЦИЯ СУРЫ-ДИФФЕРЕНЦИАЛЬНОЕ ВЫЧИСЛЕНИЕ — ДИФФЕРЕНЦИРУЕМОСТЬ И МЕТОДЫ ДИФФЕРЕНЦИАЦИИ-УПРАЖНЕНИЕ 10. РЕКЛАМА Ab Padhai каро бина объявления ке Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке! Похожие видео : 412648390 02: 52 Найдите вторые производные следующих функций: 412648395 02:37 Найдите вторые производные следующих функций: 412648412 02:40 Найдите производную следующих функций: 441774538 02:06 x ਦੇ ਬਾਬਤ cosxlogx,x>0 ਦਾ ਡੈਰੀਵੇਟਿਵ ਪ ਤਾ ਕਰੋ। 642815433 01:50 x ਦੇ ਬਾਬਤ ਨਿਮਨ ਲਿਖਤ ਦਾ ਡੈਰੀਵ ੇਟਿਵ ਪਤਾ ਕਰੋ : log7(logx) 642815507 01:20 Найдите производные следующей функции. 643224474 07:00 Найдите производные следующей функции. 643224478 03:27 Найдите производную второго порядка следующих функций Найдите производные следующей функции. Роман Тургенева «Накануне»: идейно-художественное своеобразие Из каких слоев общества появятся «новые люди»? Что будет отличать их от поколения Рудиных и Лаврецких? Какую программу обновления России они примут и как приступят к освобождению народа от крепостного права? Эти вопросы волновали Тургенева давно. Еще в 1855 году, в момент работы над «Рудиным», задача, которую он поставил в «Накануне», уже начинала возникать перед ним: «Фигура главной героини, Елены, тогда еще нового типа в русской жизни, довольно ясно обрисовывалась в моем воображении,— вспоминал Тургенев,— но недоставало героя, такого лица, которому Елена, при ее еще смутном, хотя сильном стремлении к свободе, могла предаться» (XII, 306), Тогда же сосед Тургенева, отправляясь в Крым в качестве офицера дворянского ополчения, оставил писателю рукопись автобиографической повести, одним из главных героев которой был молодой болгарский революционер, студент Московского университета. Начавшаяся в 1853 году русско-турецкая война всколыхнула революционные настроения балканских славян, боровшихся за избавление от многовекового турецкого ига. В начале 1853 года Николай Катранов с русской женой Ларисой уехал на родину. Но внезапная вспышка туберкулеза спутала все планы. Пришлось вернуться в Россию, а затем ехать на лечение в Венецию, где Катранов простудился и скоропостижно скончался 5 мая 1853 года. Это был талантливый человек: он писал стихи, занимался переводами, горячо пропагандировал среди русских друзей идею освобождения родины. Вплоть до 1859 года тетрадь с рукописью Каратеева — так звали тургеневского соседа — лежала без движения, хотя, познакомившись с ней, писатель воскликнул: «Вот герой, которого я искал! Между тогдашними русскими такого еще не было». Н. А. Добролюбов, посвятивший разбору этого романа специальную статью «Когда же придет настоящий день?», дал классическое определение художественному дарованию Тургенева, увидев в нем писателя, чуткого к общественным проблемам. Очередной его роман «Накануне» еще раз блестяще оправдал эту репутацию. Добролюбов отметил четкую расстановку в нем главных действующих лиц. Центральная героиня Елена Стахова стоит перед выбором, на место ее избранника претендуют молодой ученый, историк Берсенев, будущий художник, человек искусства Шубин, успешно начинающий служебную деятельность чиновник Курнатовский и, наконец, человек гражданского подвига, болгарский революционер Инсаров. Добролюбов заметил, что в Елене Стаховой «сказалась та смутная тоска по чем-то, та почти бессознательная, но неотразимая потребность новой жизни, новых людей, которая охватывает теперь все русское общество, и даже не одно только так называемое образованное» (VI, 120). В описании детских лет Елены Тургенев обращает внимание на глубокую близость ее к народу. С тайным уважением и страхом слушает она рассказы нищей девочки Кати о жизни «на всей божьей воле» и воображает себя странницей, покинувшей отчий дом и скитающейся по дорогам. Из народного источника пришла к Елене русская мечта о правде, которую надо искать далеко-далеко, со странническим посохом в руках. Даже внешний облик Елены напоминает птицу, готовую взлететь, и ходит героиня «быстро, почти стремительно, немного наклонясь вперед». Смутная тоска и неудовлетворенность Елены тоже связаны с темой полета: «Отчего я с завистью гляжу на пролетающих птиц? Кажется, полетела бы с ними, полетела — куда, не знаю, только далеко, далеко отсюда» (VIII, 79). Устремленность к полету проявляется и в безотчетных поступках героини: «Долго глядела она на темное, низко нависшее небо; потом она встала, движением головы откинула от лица волосы и, сама не зная зачем, протянула к нему, к этому небу, свои обнаженные, похолодевшие руки…» (VIII, 35—36). Проходит тревога — «опускаются невзлетевшие крылья». И в роковую минуту, у постели больного Инсарова, Елена видит высоко над водой белую чайку: «Вот если она полетит сюда,— подумала Елена,— это будет хороший знак. Таким же окрыленным героем, достойным Елены, оказывается Дмитрий Инсаров. Что отличает его от русских Берсеневых и Шубиных? Прежде всего — цельность характера, полное отсутствие противоречий между словом и делом. Он занят не собой, все помыслы его сосредоточены на одной цели — освобождении родины, Болгарии. Тургенев верно уловил в характере Инсарова типические черты лучших людей эпохи болгарского Возрождения: широту и разносторонность умственных интересов, сфокусированных в одну точку, подчиненных одному делу — освобождению народа от векового рабства. Силы Инсарова питает и укрепляет живая связь с родной землей, чего так не хватает русским героям романа — Берсеневу, который пишет труд «О некоторых особенностях древнегерманского права в деле судебных наказаний», талантливому Шубину, который лепит вакханок и мечтает об Италии. И Берсенев, и Шубин — тоже деятельные люди, но их деятельность слишком далека от насущных потребностей народной жизни. В то же время в характере Инсарова сказывается родовая ограниченность, типичная для Дон-Кихота. В поведении героя подчеркиваются упрямство и прямолинейность, некоторый педантизм. Художественную завершенность эта двойственная характеристика получает в ключевом эпизоде с двумя статуэтками героя, которые вылепил Шубин. В первой Инсаров представлен героем, а во второй — бараном, поднявшимся на задние ноги и склоняющим рога для удара. Не обходит Тургенев в своем романе и размышлений о трагичности судьбы людей донкихотского склада. Рядом с сюжетом социальным, отчасти вырастая из него, отчасти возвышаясь над ним, развертывается в романе сюжет философский. «Накануне» открывается спором между Шубиным и Берсеневым о счастье и долге. «…Каждый из нас желает для себя счастья… Но такое ли это слово «счастье», которое соединило, воспламенило бы нас обоих, заставило бы нас подать друг другу руки? Не эгоистическое ли, я хочу сказать, не разъединяющее ли это слово?» (VIII, 14). Инсарову и Елене кажется, что их любовь соединяет личное с общественным, что она одухотворяется высшей целью. Но вот оказывается, что жизнь вступает в некоторое противоречие с желаниями и надеждами героев. На протяжении всего романа Инсаров и Елена не могут избавиться от ощущения непростительности своего счастья, от чувства виновности перед кем-то, от страха расплаты за свою любовь. Почему? Жизнь ставит перед влюбленной Еленой роковой вопрос: совместимо ли великое дело, которому она отдалась, с горем бедной, одинокой матери, которое попутно этим делом вызывается? Елена смущается и не находит на этот вопрос возражения. Ведь любовь Елены к Инсарову приносит страдание не только матери: она оборачивается невольной нетерпимостью и по отношению к отцу, к русским друзьям — Берсеневу и Шубину, она ведет Елену к разрыву с Россией. «Ведь все-таки это мой дом,—думала она,— моя семья, моя родина. Елена безотчетно ощущает, что и в ее чувствах к Инсарову счастье близости с любимым человеком временами преобладает над любовью к тому делу, которому весь, без остатка, хочет отдаться герой. Отсюда — чувство вины перед Инсаровым: «Кто знает, может быть, я его убила». В свою очередь, Инсаров задает Елене аналогичный вопрос: «Скажи мне, не приходило ли тебе в голову, что эта болезнь послана нам в наказание?» (VIII, 128). Любовь и общее дело оказываются не вполне совместимыми. В бреду, в период первой болезни, а потом в предсмертные мгновения коснеющим языком Инсаров произносит два роковых для него слова: «резеда» и «Рендич». Резеда — это тонкий запах духов, оставленный Еленой в комнате больного Инсарова; Рендич — соотечественник героя, один из организаторов готовящегося восстания балканских славян против турецких поработителей. Бред выдает глубокое внутреннее раздвоение цельного Инсарова, источником этого раздвоения является любовь. В отличие от Чернышевского и Добролюбова с их оптимистической теорией «разумного эгоизма», утверждавшей единство личного и общего, счастья и долга, любви и революции в природе человека, Тургенев обращает внимание на скрытый драматизм человеческих чувств, на вечную борьбу центростремительных (эгоистических) и центробежных (альтруистических) начал в душе каждого человека. Однако мысль о трагизме человеческого существования не умаляет, а, напротив, укрупняет в романе Тургенева красоту и величие дерзновенных, освободительных порывов человеческого духа, оттеняет поэзию любви Елены к Инсарову, придает широкий общечеловеческий смысл социальному содержанию романа. И в то же время это роман о бесконечных исканиях человечества, о постоянном стремлении его к социальному совершенству, о вечном вызове, который бросает человеческая личность «равнодушной природе»: «О, как тиха и ласкова была ночь, какою голубиною кротостию дышал лазурный воздух, как всякое страдание, всякое горе должно было замолкнуть и заснуть под этим ясным небом, под этими святыми, невинными лучами! «О боже! — думала Елена,— зачем смерть, зачем разлука, болезнь и слезы? или зачем эта красота, это сладостное чувство надежды, зачем успокоительное сознание прочного убежища, неизменной защиты, бессмертного покровительства? Что же значит это улыбающееся, благословляющее небо, эта счастливая, отдыхающая земля? Ужели это все только в нас, а вне нас вечный холод и безмолвие? Ужели мы одни. Современников Тургенева из лагеря революционной демократии, для которых главнее был социальный смысл романа, не мог не смущать его финал: неопределенный ответ Увара Ивановича на вопрос Шубина, будут ли у нас,. в России, люди, подобные Инсарову. Какие могли быть загадки на этот счет в конце 1859 года, когда дело реформы стремительно подвигалось вперед, когда «новые люди» заняли ключевые посты в журнале «Современник»? Чтобы правильно ответить на этот вопрос, нужно выяснить, какую программу действий предлагал Тургенев «русским Инсаровым». Автор «Записок охотника» вынашивал мысль о братском союзе всех антикрепостнических сил и надеялся на гармонический исход социальных конфликтов. Инсаров говорит: «Заметьте: последний мужик, последний нищий в Болгарии и я — мы желаем одного и того же. В жизни случилось другое. Добролюбов в статье «Когда же придет настоящий день?» решительно противопоставил задачи «русских Инсаровых» той программе общенационального единения, которую провозгласил в романе Тургенева болгарский революционер. «Русским Инсаровым» предстояла борьба с «внутренними турками», в число которых у Добролюбова попадали не только консерваторы, противники реформ, но и либеральные партии русского общества. Статья била в святая святых убеждений и верований Тургенева. Поэтому он буквально умолял Некрасова не печатать ее, а когда она была опубликована – покинул журнал «Современник» навсегда. В романе «Накануне» (1860) смутные светлые предчувствия и надежды, которые пронизывали меланхоличное повествование «Дворянского гнезда», превращаются в определенные решения. Само название романа «Накануне» — название «временное», в отличие от «локального» названия «Дворянское гнездо», — отражает то обстоятельство, что замкнутости, неподвижности патриархальной русской жизни приходит конец. Русский дворянский дом с вековым укладом его быта, с приживалками, соседями, карточными проигрышами оказывается на распутье мировых дорог. Русская девушка находит применение своим силам и самоотверженным стремлениям, участвуя в борьбе за независимость болгарского народа. Сразу после выхода в свет романа читатели и критики обратили внимание на то, что личностью, которую русское молодое поколение готово признать за образец, здесь представлен болгарин. Название романа «Накануне» не только отражает прямое, сюжетное его содержание (Инсаров гибнет накануне войны за независимость его родины, в которой он страстно хочет принять участие), но и содержит оценку состояния русского общества накануне реформы и мысль о значении народно-освободительной борьбы в одной стране (Болгарии) как кануна общеевропейских политических перемен (в романе косвенно затрагивается и вопрос о значении сопротивления итальянского народа австрийскому владычеству). Добролюбов считал образ Елены средоточием романа — воплощением молодой России. В этой героине, по мнению критика, воплощена «неотразимая потребность новой жизни, новых людей, которая охватывает теперь все русское общество, и даже не одно только так называемое «образованное» <.. .> «Желание деятельного добра» есть в нас, и силы есть; но боязнь, неуверенность в своих силах и, наконец, незнание: что делать? — постоянно нас останавливают <…> и мы всё ищем, жаждем, ждем… ждем, чтобы нам хоть кто-нибудь объяснил, что делать». Таким образом, Елена, представлявшая, по его мнению, молодое поколение страны, ее свежие силы, характеризуется стихийностью протеста, она ищет «учителя» — черта, присущая деятельным героиням Тургенева. Идея романа и структурное ее выражение, столь сложные и многозначные в «Дворянском гнезде», в «Накануне» предельно ясны, однозначны. Героиня, ищущая учителя-наставника, достойного любви, в «Накануне» выбирает из четырех претендентов на ее руку, из четырех идеальных вариантов, ибо каждый из героев — высшее выражение своего этико-идейного типа. Говоря о значении в романе выбора своего пути и своего «героя», который делает Елена, Добролюбов рассматривает этот поиск-выбор как некий процесс, эволюцию, аналогичную развитию русского общества за последнее десятилетие. Шубин, а затем и Берсенев соответствуют по своим принципам и характерам более архаичным, отдаленным стадиям этого процесса. Вместе с тем оба они не настолько архаичны, чтобы быть «несовместимыми» с Курнатовским (деятелем эпохи реформ) и Инсаровым (особое значение которому придает складывающаяся революционная ситуация), Берсенев и Шубин — люди 50-х гг. Ни один из них не является чистым представителем гамлетовского типа. Таким образом, Тургенев в «Накануне» как бы распростился со своим излюбленным типом. «Одарив» своего героя-художника Шубина фамилией великого русского скульптора, Тургенев придал его портрету привлекательные черты, напоминающие внешность Карла Брюллова, — он сильный, ловкий блондин. Из первого же разговора героев — друзей и антиподов (наружность Берсенева рисуется как прямая противоположность внешности Шубина: он худой, черный, неловкий), разговора, который является как бы прологом романа, выясняется, что один из них «умница, философ, третий кандидат московского университета», начинающий ученый, другой — художник, «артист», скульптор. Но характерные черты «артиста» — черты человека 50-х гг. В самом подходе Шубина к своей профессии проявляется его связь с эпохой. Сознавая ограниченность возможностей скульптуры как художественного рода, он стремится передать в скульптурном портрете не только и не столько внешние формы, сколько духовную суть, психологию оригинала, не «линии лица», а взгляд глаз. Вместе с тем ему присуща особенная, заостренная способность оценивать людей и умение возводить их в типы. Меткость характеристик, которые он дает другим героям романа, превращает его выражения в крылатые слова; Эти характеристики в большинстве случаев и являются ключом к типам, изображенным в романе. Если в уста Шубина автор романа вложил все социально-исторические приговоры, вплоть до приговора о правомерности «выбора Елены», Берсеневу он передал ряд этических деклараций. Берсенев — носитель высокого этического принципа самоотвержения и служения идее («идее науки»), как Шубин — воплощение идеального «высокого» эгоизма, эгоизма здоровой и цельной натуры. Берсеневу придана нравственная черта, которой Тургенев отводил особенно высокое место на шкале душевных достоинств: доброта. Приписывая эту черту Дон-Кихоту, Тургенев на ней основывался в своем утверждении исключительного этического значения образа Дон-Кихота для человечества. «Все пройдет, все исчезнет, высочайший сан, власть, всеобъемлющий гений, всё рассыплется прахом <…> Но добрые дела не разлетятся дымом: они долговечнее самой сияющей красоты» (VIII, 191). У Берсенева эта доброта происходит от глубоко, органически усвоенной им гуманистической культуры и присущей ему «справедливости», объективности историка, способного встать выше личных, эгоистических интересов и пристрастий и оценить значение явлений действительности безотносительно к своей личности. Отсюда и проистекает истолкованная Добролюбовым как признак нравственной слабости «скромность», понимание им второстепенного значения своих интересов в духовной жизни современного общества и своего «второго номера» в строго определенной иерархии типов современных деятелей. Тип ученого как идеал оказывается исторически дезавуированным. Это «низведение» закреплено и сюжетной ситуацией (отношение Елены к Берсеневу), и прямыми оценками, данными герою в тексте романа, и самооценкой, вложенной в его уста. Такое отношение к профессиональной деятельности ученого могло родиться лишь в момент, когда жажда непосредственного жизнестроительства, исторического общественного творчества охватила лучших людей молодого поколения. Этот практицизм, это деятельное отношение к жизни не у всех молодых людей 60-х гг. носили характер революционного или даже просто бескорыстного служения. В «Накануне» Берсенев выступает как антипод не столько Инсарова (мы уже отмечали, что он более чем кто-либо другой способен оценить значение личности Инсарова), сколько обер-секретаря Сената — карьериста Курнатовского. В характеристике Курнатовского, «приписанной» автором Елене, раскрывается мысль о принадлежности Курнатовского, как и Инсарова, к «действенному типу» и о взаимовраждебных позициях, занимаемых ими внутри этого — очень широкого — психологического типа. Вместе с тем в этой характеристике сказывается и то, как исторические задачи, необходимость решения которых ясна всему обществу (по словам Ленина, во время революционной ситуации обнаруживается невозможность «для господствующих классов сохранить в неизменном виде свое господство» и вместе с тем наблюдается «значительное повышение <…> активности масс», не желающих жить по-старому), заставляют людей самой разной политической ориентации надевать маску прогрессивного человека и культивировать в себе черты, которые приписываются обществом таким людям. «Вера» Курнатовского — это вера в государство в приложении к реальной русской жизни эпохи, вера в сословно-бюрократическое, монархическое государство. В центре романа — болгарский патриот-демократ и революционер по духу — Инсаров. Он стремится опрокинуть деспотическое правление в родной стране, рабство, утвержденное веками, и систему попрания национального чувства, охраняемую кровавым, террористическим режимом. Душевный подъем, который он испытывает и сообщает Елене, связан с верой в дело, которому он служит, с чувством своего единства со всем страдающим народом Болгарии. Любовь в романе «Накануне» именно такова, какой ее рисует Тургенев в выше цитированных словах о любви как революции («Вешние воды»). Воодушевленные герои радостно летят на свет борьбы, готовые к жертве, гибели и победе. В «Накануне» впервые любовь предстала как единство в убеждениях и участие в общем деле. Любовь Елены и ее благородная решимость разрушают аскетическую замкнутость Инсарова, делают его счастливым. Добролюбов особенно ценил страницы романа, где изображалась светлая и счастливая любовь молодых людей. В уста Шубина Тургенев вложил лирическую апологию идеала героической молодости: «Да, молодое, славное, смелое дело. Формирование
универсальных учебных
действий. (сборник
задач, 5 класс) Выполнила: Рябцева Т. А.
учитель математики МКОУ «Нижнереутская ООШ» Фатежского района Курской
области Регулятивные
универсальные учебные действия Целеполагание Задача №1Для
приготовления каши бабушка из килограммового пакета крупы трижды брала по 220 г
крупы. Комментарий: проверяется способность «удерживать» цель деятельности в ходе решения учебной
задачи: ученик должен выполнить два арифметических действия. Решение: 1)220∙3=660 (г)—потратилось на приготовление каши 2) 1000─660=340
(г)—осталось в пакете Ответ: 340 г Задача №2 Объясните
смысл предложения: а) «Из молока
получается 25% сливок»; б) «В свекле
содержится 20% сахара» Комментарий: проверяется способность преобразовывать практическую задачу в познавательную Решение: Из молока
получается 25% сливок, что составляет четвёртую часть продукта, следовательно
можно просчитать заранее, какое количество сливок будет получено из
определённого количества молока, и также количество оставшегося продукта. Т. к.
в свекле содержится 20% сахара, что составляет пятую часть продукта, можно
предположить, какое количество сахара получится из собранного урожая. Задача №3 Масса 1 л
воды равна 1 кг, а 1 л бензина—на 270 г меньше. Найдите массу 1 л бензина. Комментарий: проверяется способность преобразовывать практическую задачу в познавательную Решение: 1кг=1000г 1) 1000─270=730
(г)—масса бензина Ответ: 730 г Планирование Задача №1
Имелось 65 л фруктового сока. Из них 20 л дали детям во время завтрака, а
остальной сок разлили в трёх литровые банки. Сколько банок для этого
потребовалось? Комментарий:
Проверяется способность определять последовательности промежуточных целей и
соответствующих им действий с учётом конечного результата. Решение: 1) 65–20 = 45 (л)
– разлили в трёхлитровые банки. 2) 45꞉3= 15 (б) –
потребовалось. Ответ: потребовалось 15 банок Задача №2 Найдите
значение выражения: (37 296꞉37─17
780꞉35)꞉250 Комментарий: проверяется способность составлять план и последовательность действий Решение: 1) 37
296꞉37=1008 2) 17
780꞉35=508 3) 1008─508=500 4) 500꞉250=2 Ответ: 2 Задача №3 Выполните
действия: а) 7,8+6,9; в)
8,1─5,46; б)129+9,72; г)
96,3─0,081; Комментарий: проверяется способность применять установленные правила в планировании способа
решения Решение: а) 7, 8 б) 1 2 9, 0 0 в) 8, 1 0 г) 9 6, 3 0 0 6, 9 9, 7 2 5, 4 6 0, 0 8 1 1 4, 7 1 3 8, 7 2 2, 6 4 9 6, 2 1 9 Прогнозирование Задача №1Среди
чисел 2683; 58 643; 2482; 132 752 не считая найдите значение каждой из
сумм: 1693+789;
57854+789; 131 963+789; 1894+789; Комментарий:
проверяется умение предвосхищать результат. Решение:
Сопоставляя первые слагаемые и данные числа и учитывая, что при сложении единиц
получатся определённые результаты в единицах суммы, можно не считая определить,
что 1693+789=2482; 57854+789=58643; 131963+789=132752; 1894+789=2683. Задача №2 Длина
прямоугольника 1 м 25 см, а ширина в 5 раз меньше. Найдите длину стороны
квадрата, периметр которого равен периметру этого прямоугольника. Комментарий:проверяется
способность предвидеть возможности получения конкретного результата при решении
задачи Решение: 1)
125꞉5=25 (см)—ширина прямоугольника 2) (125+25)∙2=300
(см)—периметр прямоугольника 3) 300꞉4=75
(см)—длина стороны квадрата Ответ: 75 см Задача №3 Как
изменится сумма, если: а) одно из
слагаемых увеличить на 5; б) одно слагаемое
увеличить на 5, а второе –на 10; в) одно слагаемое
увеличить на 6, а второе уменьшить на 6; г) одно из
слагаемых увеличить вдвое? Комментарий: проверяется способность предвосхищать результат Решение: а) сумма
увеличится на 5; б) сумма
увеличится на 15; в) сумма не
изменится; г) сумма
увеличится на то слагаемое, которое увеличили вдвое Коррекция Задача №1 Ученик,
складывая числа 9875 и 6371, получил ответ 97 246. Комментарий: проверяется способность вносить необходимые коррективы в действие после его
завершения на основе его оценки и учёта сделанных ошибок. Решение:В ответе
ошибочно получено число 97 246, т. к. при сложении данных чисел результат
не может быть больше 16000. Задача №2Две лодки,
собственная скорость каждой из которых 12,5 км/ч, движутся по реке навстречу
одна другой. Через сколько часов они встретятся, если сейчас расстояние между
ними 80 км, а скорость течения 2,5 км/ч. Какоеусловие в задаче лишнее? Комментарий: проверяется способность вносить необходимые коррективы в задание. Решение: Т. к. две
лодки движутся навстречу друг другу с одинаковой собственной скоростью, то
сумма собственных скоростей лодок равна сумме скоростей лодок с учётом
движения по течению и против течения. Лишнее условие в задаче—скорость течения
реки. 1) 12,5+12,5=25(км/ч)—совместная
скорость лодок 2) 80:25=3,2 (ч)—пройдёт до встречи
лодок Ответ: через 3,2
ч Задача №3Прочитайте
задачи, какие из них имеют решение? Какие необходимо внести коррективы в
условиях задач? а) Назовите все
натуральные числа, которые лежат между: 23 и 24; б) Рост Миши 140
см, а Вити в 5 раз больше. Каков рост Вити? в) Верно ли, что
скорость велосипедиста 15 км/ч? г) Может ли быть
длина ночи 15 ч, а длина дня 11 ч? Комментарий: проверяется способность вносить коррективы в условия задач в случаях
расхождений с реальными фактами. Решение: а) Таких чисел нет. Если убрать из
условия «натуральные числа», то все числа назвать нельзя; б) Необходимо изменить условие в
части задачи «…а Вити на 5 см больше»; в) верно; г) В сутках 24 часа, а по условию
задачи получается 26. Такого быть не может Познавательные
универсальные учебные действия Общеучебные Задача №1 Подумайте, какие из чисел могут быть точными, какие— приближёнными: а) в классе 32 ученика; б) расстояние от Москвы до Киева 9800км; в) у параллелепипеда 12 ребер; г) длина стола 1,3 м; д) население Москвы 8 млн человек; е) в пакете 0,5 кг муки; ж) площадь острова Куба 105000 км2; з) в школьной библиотеке 10 000 книг. Комментарий: проверяется способность к основам смыслового восприятия художественных и
познавательных текстов, способность к выделению существенной информации из
сообщений разных видов (в первую очередь текстов). Решение: точными могут быть варианты ответов а, в, г, е; приближёнными—б, д,
ж, з. Задача №2 Существует ли натуральное число, которое равно сумме всех предшествующих ему
натуральных чисел? Комментарий: проверяется способность решать задачи исследовательского характера Решение: Такое число существует, оно равно 3, т. е. сумме чисел 1+2 Ответ:3 Задача №3Вместо
некоторых цифр поставлены звёздочки. Можно ли сравнить числа: а) 32** и 31**; б) *1** и 8**; в) **** и
***; г) *5* и 1** Комментарий: проверяется способность
применять правила и использование инструкций и освоенных закономерностей Решение:а)32**>31**;
б)*1**>8**; в) ****<***; г)*5*и 1** сравнить нельзя Задача №4В первом
вагоне трамвая ехали 46 пассажиров, а во втором –39 пассажиров. Комментарий: проверяется способность ориентироваться в разнообразии способов решения задач Решение:Iспособ 1)
46+39=85 (пас.)—было в
трамвае 2)
85–15=70 (пас.)—осталось в трамвае Ответ: 70
пассажиров II способ 1) 39–15=24 (пас.)—осталось
во втором вагоне 2) 46+24=70
(пас.)—осталось в трамвае Ответ: 70 пассажиров Знаково-символические Задача №1 В
следующей таблице указан рост учащихся. Назовите их фамилии: а) в порядке
возрастания их роста; б) в порядке убывания их роста № Фамилия Рост, см № Фамилия Рост, см 1 Антонов 124 4 Гришин 123 2 Борисов 135 5 Демина 136 3 Воронина 127 6 Ермилова 141 Комментарий: проверяется способность использовать знаково-символические средства, в том
числе модели и схемы для решения задач Решение: а)
Гришин, Антонов, Воронина, Борисов, Демина, Ермилова; б) Ермилова,
Демина, Борисов, Воронина, Антонов, Гришин Задача №2Составьте
по рисунку уравнение и решите его. 96
см 11x см 5x см Комментарий: проверяется способность преобразовывать и использовать схемы для решения задач Решение: 11x+5x=96 16x=96 x=96꞉16 x=6 Ответ: 6 см Задача №3Врачи
рекомендуют дневную норму питания распределить на 4 приёма: утренний
завтрак—25%, второй завтрак—15%, обед—45% и ужин—15%. Постройте круговую
диаграмму распределения дневной нормы питания. Комментарий: проверяется
способность создавать и преобразовывать модели и схемы для решения задач. Решение: 1)
25+15+45+15=100 долей 2) 360:100=3,6°—составляет одна
доля 3) 25•3,6=90° —составляет утренний
завтрак 4) 15•3,6=54°—составляет второй
завтрак и ужин 5) 45•3,6=162°—составляет обед Строим диаграмму Логические Задача №1Составьте
задачу с величинами «скорость», «время», «путь» по выражению: а) 150꞉5; б) 65∙4; в) 900꞉150; г)
36꞉12. Комментарий: проверяется способность строить логические рассуждения и устанавливать
причинно-следственные связи꞉ Решение: а) Мотоциклист проехал 150 км за 5 часов.
С какой скоростью двигался мотоциклист? б) Автомобиль двигался со скоростью 65
км/ч в течение 4 часов. Какой путь проделал автомобиль за это время? в) Поезд «Ласточка» проехал расстояние 900
км со скоростью150км/ч. Сколько времени поезд находился в пути? г) Турист на велосипеде двигался со
скорость 12 км/ч и преодолел расстояние в 36 км. Сколько времени находился
турист в пути? Задача №2Коля,
Петя, Женя и Сеня взвесились на весах. Получились результаты: 37,7 кг; 42,5 кг;
39,2 кг; 40,8 кг. Найдите массу каждого мальчика, если известно, что Коля
тяжелее Сени и легче Пети, а Женя легче Сени Комментарий: проверяется способность строить рассуждения в форме связи простых суждений об
объекте, его свойствах и связях Решение: 37,7
кг 39,2
кг 40,8
кг 42,5
кг Коля — — + — Петя — — — + Женя + — — — Сеня — + — — Задача №3 Привезли 12 ящиков яблок, по 30 кг в каждом, и 8 ящиков груш, по 40 кг в каждом. а) 30∙12; в) 40∙8; д) 30∙12+40∙8; б) 12─8; г) 40─30; е) 30∙12─40∙8; Комментарий: проверяется способность владеть рядом общих приёмов решения задач Решение:а)
Сколько всего привезли яблок; б) На сколько больше привезли ящиков яблок, чем
груш? в) Сколько всего привезли груш; г) На сколько больше весит ящик груш чем
яблок? д) Сколько всего привезли фруктов; е) На сколько больше привезли яблок,
чем груш? Коммуникативные
универсальные учебные действия Инициативное
сотрудничество Задача №1Вместо
звёздочек в записи вычислений цепочкой поставьте необходимые числа. а) 15∙* →90꞉* →18∙*→ 72+* →90; б) 70─* →49꞉* →7∙* →98+* →110 Комментарий:проверяется
способность контролировать действия партнёра при выполнении задания; вовремя
включаться в работу во время выполнения промежуточных вычислений Решение: а) 15∙6=90; 90꞉5=18; 18∙3=72; 72+18=90 б) 70─21=49; 49꞉7=7;
7∙14=98; 98+2=100 Задача №2 Найдите в таблице все числа по порядку от 2 до 50. 9 45 14 25 34 3 31 20 43 30 7 18 40 12 37 24 2 47 10 27 39 6 41 33 15 49 22 8 29 21 48 36 17 13 44 16 50 11 26 4 38 28 35 32 46 19 42 23 5 Комментарий: проверяется умение сотрудничать, выполнять общее дело Задача №3Восстановите
цепочки вычислений и попробуйте объяснить, почему они приводят к одному ответу: Комментарий: проверяется способность проявлять активность во взаимодействии для решения
коммуникативных задач и познавательных задач; способность формулировать
рассуждения. Решение:
50:100•0,2•10=1 50•0,01: 5: 0,1=1 1. Деление числа на 100—это то же самое,
что и умножение числа на 0,01 2. Деление числа на 5—это то же самое, что
и умножение числа на 0,2 3. Умножение числа на 10—это то же самое,
что и деление на 0,1 Модерн — маловероятная метка для каши. Твердая, утешительная и стойкая поддержка в трудные времена, она кажется старомодной. Современность — это исследование, использование прошлого в качестве пробного камня, но переворачивание привычного с ног на голову — отражение текущих вкусов, но со стильной изюминкой. Это большое давление для скромной миски вареных зерен. Исторически сложилось так, что каша чаще всего считается шотландской, приготовленной из овса или ячменя. Название, вероятно, восходит к французскому слову «potage» (что означает суп или, возможно, относится к горшку, в котором он готовится). Итак, старое снова становится новым, а овсяная каша может быть современной, крепкой и с ярко выраженным вкусом. По-видимому, постоянно растущий интерес к возвращению к семенам и злакам семейной реликвии — будь то палео-диета, употребление без глютена или просто увеличение количества клетчатки в вашем рационе — усиливает актуальность экспериментов с менее знакомыми ингредиентами. Овсяная каша может быть такой же простой, как подогрев оставшегося риса с молоком или бульоном, а затем добавление чего угодно — от ложки джема или сахара с пряностями до вчерашних жареных овощей с каплей пасты карри или нарезанным кимчи. Его отличает мягкая текстура — зерна, сваренные с большим количеством жидкости, чем вы могли бы использовать для приготовления салатов или плова. Чтобы приготовить кашу преднамеренно, выберите тип зерна в зависимости от того, хотите ли вы чего-то быстрого приготовления или планируете и готовите заранее. Для простоты выбирайте злаки быстрого приготовления, такие как овсяные хлопья, дробленый булгур, каша (жареная гречка) или лебеда. Смешивайте и сочетайте, как вам нравится, просто планируйте использовать более высокое соотношение зерна и жидкости, чтобы приготовленная текстура стала кремовой и приятной на ложку (хорошая оценка — 1 чашка зерна на 4 чашки жидкости, будь то вода, бульон, сок или даже заваренный чай). Зерна различаются по своей потребности во влаге, поэтому знайте, что у вас есть возможность играть с количеством используемой жидкости. Куда бы вы ни пошли, количество каши всегда можно варьировать. Рецепт на четыре порции (обычно с использованием 1 чашки сырых зерен) можно подавать сразу или хранить в холодильнике, чтобы раздавать в течение недели. Каши могут предложить что-то для всех, с текстурами, подходящими для любого случая — чистый холст для добавления всплесков цвета и соблазнительных ароматов, избавляющих от жжения старых скучных горячих хлопьев. Их может быть достаточно, чтобы заставить вас пообедать, стать вашим обедом или стать заманчивой основой для пикантных ужинов. Моя любимая миска состоит из нескольких злаков и украшена нарезанным авокадо, сальсой из копченых помидоров, тертым пармезаном и яйцом, сваренным всмятку, с большим количеством свежемолотого перца и щепоткой поджаренных семян тмина. А для неохотных утренних едоков, которым не нравятся сладкие хлопья в американском стиле, тарелка овсянки, заправленная каплей хорошего оливкового масла, ложечкой орехового масла или щепоткой тертого соленого сыра, будет как нельзя кстати. Насыпание: Использование контейнеров для сыпучих продуктов — это эффективный с точки зрения затрат и времени способ запастись вашими любимыми зернами каши и добавками (например, сухофруктами, орехами). , чиа, льняное семя или сердцевины конопли). Мне нравится пополнять свою постоянно растущую коллекцию пустых банок из-под консервов, маркируя их малярным скотчем. Не забудьте отметить дату покупки, чтобы следить за свежестью. Некоторые продукты (орехи и семечки) лучше всего хранить в холодильнике или морозильной камере. Надежные ресурсы: Поскольку в отделе сыпучих материалов не всегда предлагаются конкретные инструкции по хранению и приготовлению незнакомых ингредиентов, обратитесь к Совету по цельнозерновым продуктам Oldways (wholegrainscouncil.org), Совету по питанию по зерновым и бобовым (glnc.org. au) или Epicurious.com, который охватывает цельные зерна и то, что называется псевдозлаками (такими как лебеда, гречка, фонио или амарант, которые на самом деле являются семенами). Низкий и медленный: Готовьте зерна на медленном огне, плотно накрывая крышкой. Начните их с кипящей жидкости, но затем замедлите процесс. Если вы видите, что из-под крышки выходит пар, уменьшите огонь. Будьте бдительны: Часто заглядывайте внутрь кастрюли, чтобы проверить густоту каши и хорошенько ее перемешать. Добавьте больше жидкости по мере необходимости, чтобы достичь желаемой густоты и нежности зерна. Дайте постоять: Дайте каше постоять около 5 минут, накрыв ее, как только вы решите, что вас устраивает ее консистенция. Хлопья закончат приготовление и еще немного загустеют, и их будет легче выкладывать ложкой. Расслабление: Приготовьте большую порцию каши, которую можно хранить в холодильнике до 5 дней. В зависимости от зерна вы можете разогревать порции с небольшим количеством воды, молока или бульона. Или нарежьте твердую кашу, чтобы обжарить ее (например, кукурузную кашу или поленту) на сковороде и полейте соусом для жарки или макарон. На 4 порции. Пикантность этих мисок громко говорит ненавистникам сладких завтраков, предлагая более насыщенные и насыщенные вкусы. А если смешать булгур с овсянкой, получится кремообразная каша с более острым вкусом. От Лизы Голден Шредер. • 1/2 ст. сырой красный булгур или фрике • 1/2 гр. овсяные хлопья сырые старомодные • 4 гр. овощной или куриный бульон с пониженным содержанием натрия • 1/2 ч. л. молотый тмин • 1/2 ч. л. молотый кориандр • 1/4 ч. л. крупная соль • Хлопья красного перца по вкусу • 1 гр. разноцветные помидоры черри, нарезанные на четвертинки • 1 большой спелый авокадо, без косточек, нарезанный • 1/2 гр. измельченный копченый миндаль • 1/2 гр. раскрошенный соленый сыр (фета, котия или выдержанный козий сыр) или нарезанные соленые оливки без косточек • 2 гр. смесь зелени (капуста, щавель, мизуна, руккола) • 1/3 c. • 4 яичницы, по желанию Указания Смешайте булгур, овсяные хлопья, бульон, тмин, кориандр и соль в большой кастрюле. Нагреть до кипения; уменьшите огонь до средне-слабого и варите, часто помешивая, от 15 до 20 минут или до загустения. Разложите кашу по тарелкам. Сверху положите помидоры, авокадо, миндаль, сыр и немного зелени. Полить соусом чимичурри. Сверху в каждую положите по яйцу, если хотите. На 4 порции. Горячие хлопья с несколькими злаками легко найти на полке в продуктовом магазине, но их приготовление не займет много времени — и у вас всегда будут отдельные зерна в вашей кладовой для других целей. Просо, лебеда и амарант — небольшие, но очень питательные продукты с высоким содержанием белка, клетчатки и обилием антиоксидантов и минералов. Добавьте ложку молотого льняного семени, чиа или овсяных отрубей, чтобы получить еще больше клетчатки. Для каши: • 1/3 гр. сырое пшено, промытое, хорошо осушенное • 1/3 c. сырая трехцветная киноа, промытая, хорошо осушенная • 1/3 c. сырой амарант • 1 ч. л. семян фенхеля • 4-5 c. вода • 1 ч. л. тертого свежего имбиря • 1/2 ч. л. крупная соль Для начинки: • 1 ст. оливковое масло • 2 гр. нарезанный свежий ананас или твердая груша • 2 больших апельсина или мандарина, очищенных от цедры и сока • 1/4 ст. белый бальзамический уксус • Измельченный сушеный инжир или абрикос, фисташки и листья свежей кинзы по вкусу • Свежемолотый перец по вкусу • Молоко на выбор по вкусу Указания по применению Тем временем доведите до кипения 4 стакана воды в большой кастрюле. Добавьте смесь поджаренных зерен, имбирь и соль. Уменьшите огонь, накройте крышкой и варите 35-40 минут или пока зерна не станут мягкими и кремообразными. При необходимости добавьте больше воды. Снимите с огня; дать постоять 5 минут. Пока хлопья готовятся, приготовьте начинку. Нагрейте масло в сковороде на средне-сильном огне. Добавьте ананас; обжаривайте 5-6 минут или пока не начнет подрумяниваться. Добавьте апельсиновый сок, цедру и уксус. Готовьте еще несколько минут или до состояния сиропа. Разложите кашу по тарелкам. Сверху положите обжаренный ананас, немного инжира, фисташки и кинзу. В завершение щедро посыпьте перцем и при желании добавьте немного молока. На 4-6 порций. Ищите собранный вручную дикий рис, обжаренный на дровах (это хороший продукт, дорогой, но стоит вложений). Сделайте это заранее и охладите для еды по требованию. • 2 толстых ломтика бекона, нарезанных на кусочки толщиной 1/2 дюйма. штук • 3/4 гр. сырой дикий рис (см. примечание) • 1/3 c. сырая перловая крупа • 6 стаканов воды • 3/4 ч. л. крупная соль • 2 ст. подсолнечное масло или ваше любимое ореховое масло • 1/3 ст. сушеная черника • 1/3 гр. поджаренные кедровые орехи или жареные и соленые тыквенные семечки • Кленовый сахар или сироп по вкусу • Молоко на выбор по вкусу Указания Разогрейте духовку до 375 градусов. Сообщения без ответов | Активные темы | Избранное Как перевести градусы в десятичные градусы? 13/10/17 К примеру у меня есть 450 градусов, в десятичном исчислении это будет 90 градусов, или 540 а в десятичной будет 180 градусов.
Re: Как перевести градусы в десятичные градусы? 16/07/14
Re: Как перевести градусы в десятичные градусы? 07/06/17 mihaild в сообщении #1255403 писал(а):
Re: Как перевести градусы в десятичные градусы? 27/04/09
Re: Как перевести градусы в десятичные градусы? 30/01/06 wiko75 в сообщении #1255402 писал(а): Как перевести градусы в десятичные градусы? Гугль его показывает только в одном месте: так неграмотно названы десятичные доли градуса, в калькуляторе, переводящем доли градуса в минуты и секунды, и наоборот.
Re: Как перевести градусы в десятичные градусы? 12/09/10
Re: Как перевести градусы в десятичные градусы? 09/10/15 wiko75
Re: Как перевести градусы в десятичные градусы? 11/03/08
Re: Как перевести градусы в десятичные градусы? 30/01/06 Евгений Машеров в сообщении #1255980 писал(а): Я было подумал
Re: Как перевести градусы в десятичные градусы? 09/05/12 Правда, в данном случае, похоже, ТС сам не очень хорошо знает, что хочет, поскольку , и просто масштабированием тут не обойтись при любом определении «десятичного градуса».
Модераторы: Модераторы Математики, Супермодераторы Сейчас этот форум просматривают: нет зарегистрированных пользователей Преобразование координат Разбор текста Преобразовать координаты Разобрать координаты Просмотрщик Gpx онлайн
Конвертировать GPX в KML
Преобразование координат
Изображения с геотегами Nuget package
Demo Project Мы уже обработали файлы общим размером мегабайт максимум 3000 символов Десятичные градусы (DD) выражают географические координаты широты и долготы как десятичные доли градуса. DD используются во многих географических информационных системах (ГИС), веб-картографических приложениях, таких как OpenStreetMap, и устройствах GPS. Read More Вы также можете преобразовать координаты, используя многие другие пространственные привязки. См. cписок популярных ниже. Версия: 23.21.1 Email: Сделайте этот форум закрытым, чтобы он был доступен только вам и нашим разработчикам. Вы успешно сообщили об ошибке, вы получите уведомление по электронной почте, когда ошибка будет исправлена. «Отрицательное число для широты, такое как -7.48° (если оно отрицательное, минус всегда показывается ), это ЮЖНАЯ широта!» «И для долготы, если нет E или W, и если число положительное
(например, 128,3425° или +128,34°), тогда долгота будет ВОСТОЧНОЙ. Если число отрицательное, например -73,9917° (минус всегда отображается, если число отрицательное), то долгота будет ЗАПАД!» © 2000 Дэвид Дж. Левесон Чтобы преобразовать значения в Tableau напрямую, вы можете использовать вычисляемые поля. Однако, чтобы Tableau выполнил преобразование, данные должны быть представлены в виде градусов, минут и секунд в отдельные поля . Вы можете использовать два типа формул, оба подробно описаны в прилагаемой рабочей тетради. НАЖМИТЕ, ЧТОБЫ РАЗВЕРНУТЬ ШАГИ В вычисляемом поле можно использовать аналогичный набор формул для преобразования данных в десятичные градусы: Широта: ( [Градусы широты])+([Широта в минутах]/60)+([Широта в секундах]/3600)* Долгота: ([[градуса долготы])+([долготу протоколы]/60)+([долгота]/3600)* В приведенном ниже примере мы преобразуем значения для нескольких городов Индии. Как правило, десятичные градусы Индии положительные: широта: 20,59 ° северной широты и долгота: 78,96 ° восточной долготы. НАЖМИТЕ, ЧТОБЫ РАЗВЕРНУТЬ ШАГИ В вычисляемом поле вы можете использовать аналогичный набор формул для преобразования ваших данных в десятичные градусы: Широта: ([ Градусы широты])+([Широта в минутах]/60)+([Широта в секундах]/3600) Долгота: -(([Долгота в градусах])+([Долгота в минутах]/60)+([Долгота в секундах]/3600)) В приведенном ниже примере мы преобразуем значения для нескольких городов Ирландии. Нажмите здесь, чтобы вернуться на нашу страницу поддержки. Открыть новый кейс Нажмите здесь, чтобы перейти на нашу страницу поддержки. Получите подробные ответы и пошаговые инструкции по решению ваших проблем и технических вопросов. Англоязычный онлайн-сервис Onshape предлагает профессиональные решения для проектирования и создания чертежей в системе 3D-cad. К сожалению, бесплатный функционал сайта ограничен 21 днём бесплатного пользования, далее же за возможность создавать чертежи онлайн с помощью Onshape необходимо будет платить «живые» деньги. Для работы с Onshape перейдите на данный ресурс, нажмите на кнопку «I WANT TO TRY ONSHAPE» (если такой кнопки нет, просто перезагрузите главную страницу сайта). Также для осуществления черчения онлайн могут помочь такие сервисы как drawisland.com и sketch.io. Функционал указанных сервисов довольно прост, и может пригодиться, скорее, для развлекательных и бытовых целей, нежели для профессионального черчения. Рабочее окно сервиса Drawisland Сама распространенная программа у всех чертежников. Наверное, все ее возможности не знают и сами разработчики. Сотни плагинов позволяют создавать объекты любой сложности и вложенности, визуализировать их в 3-D или 2-D пространстве, есть функция создания объемного панорамного видео, где объект можно вращать мышкой в любом направлении и в любой плоскости. В сети имеется не так много веб-ресурсов для черчения и наиболее продвинутые из них предлагают свои услуги за определенную плату. Тем не менее все же есть хорошие онлайн-сервисы для проектирования — удобные и с широким набором возможностей. Именно такие инструменты будут рассмотрены нами ниже. Один из лучших среди САПР-ресурсов, выполненный в стиле веб-приложений Google. Сервис позволяет работать со схемами, диаграммами, графиками, таблицами и другими структурами. Так, если вы пользовались каким-либо офисным веб-продуктом Google, разобраться в интерфейсе и расположении необходимых элементов этого ресурса для вас не должно составить труда. Draw.io отлично справится как с созданием простых набросков с последующим экспортом в профессиональную программу, так и с полноценной работой над проектом. Этот сервис довольно специфичный. Он предназначен для работы с техническими планами строительных объектов и собрал в себе все нужные графические шаблоны для практичного и удобного создания общих чертежей помещений. Да, инструмент не самый функциональный, но содержит все необходимые возможности для создания качественного плана строительного объекта. Как видите, вы можете работать с чертежами прямо в своем браузере — без использования дополнительного ПО. Конечно, описанные решения в целом уступают десктопным аналогам, но, опять же, на их полноценную замену они и не претендуют. Опишите, что у вас не получилось. Еще один прекрасный набор инструментов, который многие специалисты советуют начинающим. Конечно, A9CAD не настолько прост как SketchUp, но все же за несколько дней его вполне можно освоить и начать делать несложные чертежи. Данная программа работает только с форматами DWG и DXF, причем файлы должны быть созданы тоже в A9CAD. Если они будут сделаны в том же КОМПАСе, то здесь их не откроешь. По крайней мере, это будет весьма затруднительно. Имеется вполне стандартный набор инструментов. Конечно, опытным юзерам или тем, кто хочет научиться чертить профессионально, этого не хватит. Здесь есть инструменты для рисования окружности, дуги, линии, квадрата/прямоугольника и кривой, а также для нанесения точек. Ниже есть кнопка для нанесения текста и изменения цвета. Конечно, измерить расстояние, копировать фигуру и выполнять подобные действия здесь тоже можно. Другие особенности A9CAD такие: Рис. №3. A9CAD Ссылка на скачивание Преимущество ABViewer состоит в том, что интерфейс здесь выполнен в духе программ от Microsoft. Имеется в виду офисный пакет, то есть Word, PowerPoint, Excel и так далее. Некоторые даже думают, что ABViewer – это тоже часть офисного ПО от создателей Windows. Все основные элементы собраны вверху. Они поделены на определенные категории. К примеру, если раскрыть блок «Рисование», можно будет увидеть инструмент для нанесения той же прямой или кривой линии, прямоугольника, окружности и других фигур. Есть также блок «Текст», который дает возможность добавить на чертеж текст в формате WordArt или в одном из обычных шрифтов. Что касается непосредственно черчения, то этот процесс здесь проходит максимально просто и гладко. Есть минимальные возможности для настройки объектов. Так пользователь может вручную ввести координаты X, Y, длину, угол и отслеживание. С этим все очень хорошо, но, опять же, только для начинающих юзеров. Еще несколько особенностей ABViewer: Рис. №4. ABViewer Итак, рассмотрим наиболее популярные электронные средства создания чертежей, их плюсы и минусы. С помощью данного продукта Вы сможете создавать двумерные и трехмерные чертежи, при том что Autodesk AutoCAD позволяет проводить рендеринг трехмерных объектов на уровне полноценных редакторов 3D-графики. Autodesk AutoCAD работает с несколькими форматами файлов. Самый распространенный формат – DWG (закрытый формат для редактирования чертежей). В качестве отрицательных моментов, опять же, отметим высокие системные требования. Программа представляет собой мультиплатформенную систему автоматизированного создания проектов в 2D и 3D графике. VariCAD разрабатывался, как софт для проектирования в машиностроительной области, а также для черчения и расчетов механических узлов. Интерфейс VariCAD разработан с учетом простой и быстрой разработки двух- или трехмерных моделей. Внедрены средства разработки трубопроводов и емкостей различного уровня сложности. Предусмотрено одностороннее конвертирование 3D макетов в 2D графику без обратного преобразования. Выбор того или иного софта зависит только от степени сложности проекта и необходимости выполнять простое задание на сложной программе. Перейдём к непосредственному описанию сетевых сервисов онлайн. Данный визуальный редактор GLIFFY обладает довольно широким инструментарием для создания чертежей и схематических изображений, включая множество шаблонов и схем для архитектурных проектов, блок-схем, сетевых диаграмм и других соответствующих целей. Для работы с данным редактором перейдите на сайт cameralabs.org, при необходимости авторизуйтесь (доступна также авторизация через социальную сеть). После этого вам станет доступен экран редактирования, где вы сможете создать ваш чертёж. Слева расположены вкладки различных шаблонов (вы можете раскрыть вкладку, кликнув на ней), сверху – панель инструментов, а справа будет размещаться непосредственное поле для создания чертежа. Для сохранения вашей работы нужно будет нажать вверху на «File» — «Сохранить» (или «Экспорт»). Англоязычный сервис draw.io поможет создать чертёж в режиме онлайн, начертав различные графики, схемы и диаграммы. Для работы с данным сервисом перейдите на сайт draw.io. Ресурс спросит, куда сохранять созданные вами работы (выберите «Device» для сохранения на жёсткий диск). Нажмите на «Create New Diagram» (создание новой диаграммы), выберите её имя, а также соответствующий шаблон для создания слева. Выберите пустую начальную диаграмму (Blanc Diagramm) или какой-либо из уже имеющихся шаблонов диаграмм (charts), инженерных схем (Engineering), блок-схем (Flowcharts), разметки (layout), карт (maps) и других видов шаблонов После того, как вы выбрали шаблон, нажмите на «Create» (Создать). Далее вы перейдёте в экран редактирования. Слева представлены различные шаблоны черчения, сверху панель вспомогательных инструментов, справа – различные настройки отображения документов. Для сохранения созданного чертежа нажмите на «File» — «Save as». Сервис drawisland.com – простой англоязычный сервис для черчения в Интернете. После перехода на него вас ждёт экран для создания чертежа с довольно ограниченным набором инструментов. Слева расположена панель инструментов, сверху вы можете выбрать размеры рисунка и повернуть его на 90 или 180 градусов, а справа доступ выбор диаметр инструмента для рисования, а также переключаться между слоями. Для сохранения созданного вами рисунка на диск нажмите на кнопку «Save» слева. Данный сервис предназначен для создания технического плана строительного объекта, который можно будет позже сохранить к себе на ПК. Как и большинство аналогичных сервисов, данный сервис обладает набором встроенных графических шаблонов, делающих процесс создания технического плана помещения практичным и удобным, позволяя легко нарисовать чертёж онлайн. «Sketch.io» — ещё один простой англоязычный ресурс для построения простых чертежей, создания графических набросков и зарисовок. Функционал сервиса довольно прост, и подойдёт, в первую очередь новичкам в деле создания чертежей. Итак, теперь переходим к изучению интерфейса и функционала софта. Все меню и названия инструментов переведены на русский язык, поэтому любой пользователь, знакомый с черчением, разберется в основах программы. В главном окне появится 3 вкладки: Если вы загрузите предыдущий проект через меню «Файл» или создадите новый чертеж, то верхняя панель инструментов станет активной. На ней вы найдете весь необходимый инструментарий в быстром доступе. Вы можете загружать во FreeCAD сторонние проекты и, наоборот, сохранять чертежи в одном из универсальных форматов для запуска в других утилитах. Некоторые задачи необходимо сделать здесь и сейчас, а под рукой не всегда есть ноутбук с предустановленным профессиональным ПО для проектирования. В этом случае пригодятся онлайн-сервисы, которые по своему функционалу не являются конкурентами для оффлайн софта, но некоторые задачи способны решить. Draw.io. Данный сервис сможет решить элементарные задачи в области черчения, но на большее он не способен. Интерфейс прост и понятен, а созданную работу можно сохранить в необходимом формате прямиком на рабочий стол. Draw.io — это англоязычная разработка, доступная . Gliffy. Этот редактор идеально подойдет для разработки простейших чертежей и схематических изображений. В нем есть уже готовые шаблоны и фигуры, что упрощает взаимодействие с программой. Существует тяжеловес в области ПО для черчения и называется он КОМПАС-3D. Им пользуется подавляющее большинство людей, занимающихся моделированием. Эта программа позволяет рисовать как 3D объекты, так и схемы, например, электрические принципиальные. Так вот, NanoCAD – это сильно обрезанная версия КОМПАС-3D. Если кто-то работал с КОМПАСом, то интерфейс этой программы ему покажется очень знакомым. Здесь есть те же объекты, те же инструменты, те же настройки. Только специализированных инструментов и возможностей для тонкой настройки нет. Если же Вы никогда не имели дело с какими-либо программами для черчения, то советуем Вам начать знакомство с удивительным миром моделирования со SketchUp, затем перейти на NanoCAD, а потом уже и на КОМПАС-3D. Вот несколько особенностей NanoCAD: Рис. №2. NanoCAD Многие советуют начинать работать с чертежами именно в NanoCAD, так как это отличная и бесплатная альтернатива КОМПАСу. Ссылка на скачивание Это программа от корпорации Google с интерфейсом на русском языке. В ней есть все самое необходимое чтобы начать работу в мире моделирования – стандартный набор инструментов, простейший интерфейс (никаких скрытых меню и непонятных функций), а также подробная справка. Что касается последнего, то помимо обычного для любой хорошей программы списка типичных вопросов и ответов, в SketchUp есть также набор видеоуроков. С их помощью каждый сможет увидеть, как работать с программой, где и какие инструменты у нее находятся, что нужно чтобы их использовать и так далее. Также в видеоуроках пользователь сможет увидеть, как работают настоящие профессионалы в данной области. В общем, для новичков здесь есть все что нужно! Вот еще несколько особенностей SketchUp: Рис. №1. SketchUp В общем, SketchUp – это лучшая программа, чтобы начать чертить! Да, в ней нет такого богатого функционала, зато все просто и понятно. После SketchUp можно переходить на что-то более сложное. Ссылка на скачивание Производителем софта выступает компания Autodesk. При работе на компьютере приложение разрешает создавать двухмерные и трехмерные проекты. Последние дают невиданную визуализацию, какой владеют продвинутые редакторы изображений. Двухмерные модели, разработанные в AutoCAD, отличаются уникальностью. На выходе получаются подробные чертежи, где будут учтены все нюансы. Эксперты отмечают, что проекты, созданные на основе цифровых технологий Autodesk, отличаются качеством. Три основных: Функции софта в полной мере реабилитируют его высокую стоимость. Компании и профессионалы-частники без сожаления расстаются с деньгами — программное обеспечение окупает вложения. Любители и новички чертежного дела предпочитают работать в издания с ограниченным функционалом или бесплатной ознакомительной версии, которая есть в сети и доступна для непосредственного скачивания. Она обширна и с каждым годом увеличивается. Продукцию Autodesk применяют в строительстве, производстве, медицине, моделировании одежды — везде, где требуются чертежи отменного качества. Учебные заведения различной направленности посвящают обучению AutoCAD немало времени. Как мной уже упоминалось выше, особой популярности среди пользователей с 2010 по 2013 год пользовался проект «CAD@Online», предоставляющий онлайн-доступ к программе «Компас-3Д» и её богатым возможностям. В рамках данного проекта пользователь получал возможность построения 2Д и 3Д моделей с помощью программного инструментария «Компас», с последующим сохранением результатов к себе на ПК. Поскольку в 2013 году проект был закрыт, то у отечественных пользователей не осталось сетевых инструментов своего производства для создания 2Д и 3Д моделей. Тем не менее англоязычный сегмент интернета располагает набором сетевых сервисов для моделирования онлайн, а некоторые из таких сервисов могут даже похвалиться русскоязычной локализацией. Тем же пользователям, которые не доверяют зарубежным решениям, можно предложить скачать стационарную программу «Компас 3Д» (отдельно доступна пробная бесплатная версия https://kompas.ru/kompas-3d/download/), и в дальнейшем пользоваться её функционалом. Давайте рассмотрим популярные сетевые сервисы, позволяющие создавать 2Д и 3Д-модели онлайн. Этот софт, разработанный на уникальном математическом ядре с запатентованными алгоритмами, хорошо известен среди проектировщиков. Программа способна решать самые сложные задачи, хотя на отечественном рынке пользуются меньшей популярностью, нежели Автокад или Нанокад. Компас — это универсальный софт, замеченный не только на высокотехнологичных производствах, но и в классических проектно-строительных компаниях, занимающихся возведением, как коммерческих, так и жилых объектов. Отечественный продукт подходит для проектирования любой объемной модели, на основании которой можно создать динамический двухмерный чертеж, реагирующий на изменения исходника. Компас хорошо интегрирован в российскую систему госстандарта, имеет отличную базу данных. Главный минус заключается в кардинальном отличии интерфейса и процедур от всем известного Автокада, поэтому пользователям достаточно непросто переходить с одного продукта на другой, если того требует работа. Компас — это «тяжелая» программа, дающая сбои при работе на слабом «железе». Еще один прекрасный набор инструментов, который многие специалисты советуют начинающим. Конечно, A9CAD не настолько прост как SketchUp, но все же за несколько дней его вполне можно освоить и начать делать несложные чертежи. Данная программа работает только с форматами DWG и DXF, причем файлы должны быть созданы тоже в A9CAD. Если они будут сделаны в том же КОМПАСе, то здесь их не откроешь. По крайней мере, это будет весьма затруднительно. Имеется вполне стандартный набор инструментов. Конечно, опытным юзерам или тем, кто хочет научиться чертить профессионально, этого не хватит. Здесь есть инструменты для рисования окружности, дуги, линии, квадрата/прямоугольника и кривой, а также для нанесения точек. Ниже есть кнопка для нанесения текста и изменения цвета. Конечно, измерить расстояние, копировать фигуру и выполнять подобные действия здесь тоже можно. А вот выполнять настройку самих объектов уже не получится. Другие особенности A9CAD такие: Рис. №3. A9CAD
Формат листа
A4A3A2A1
Ориентация листа
ВертикальныйГоризонтальный
Перв. примен.
Размер шрифта
2.53.55710
Обозначение
Размер шрифта
2.
Наименование
Размер шрифта
2.53.55710
Масса
Размер шрифта
2.53.55710
Наименование организации
Размер шрифта
2.53.55710
Масштаб
Размер шрифта
2.53.55710
Листов
Размер шрифта
2.
Материал
Размер шрифта
2.53.55710
Разраб. ФИО
Размер шрифта
2.53.55710
Разраб. Дата
Размер шрифта
2.53.55710
Пров. ФИО
Размер шрифта
2.53.55710
Пров. Дата
Размер шрифта
2.
Т.контр. ФИО
Размер шрифта
2.53.55710
Т.контр. Дата
Размер шрифта
2.53.55710
Н.контр. ФИО
Размер шрифта
2.53.55710
Н.контр. Дата
Размер шрифта
2.53.55710
Утв. ФИО
Размер шрифта
2.
Утв. Дата
Размер шрифта
2.53.55710
Инв. № подл.
Размер шрифта
2.53.55710
Подп. и дата
Размер шрифта
2.53.55710
Взам. инв. №
Размер шрифта
2.53.55710
Инв. № дубл.
Размер шрифта
2.
Подп. и дата
Размер шрифта
2.53.55710
Справ. №
Размер шрифта
2.53.55710 Создавайте великолепные рисунки логотипов с помощью нашего веб-конструктора логотипов. Независимо от того, являетесь ли вы дизайнером или у вас нет творческой стороны, вы можете создавать потрясающие логотипы для рисования. Попробуй это! Почему я должен использовать рисунок логотипа для своего бизнеса? Рисунок логотипа — отличный способ показать своим покупателям и клиентам, на что вы способны. Это также оставляет место для их собственной интерпретации бизнеса, а не заставляет их сосредоточиться на конкретных словах или мыслях. Почему я должен использовать средство для создания логотипов, а не нанимать дизайнера? Наем графического дизайнера для создания логотипа для вас может обойтись дорого. В зависимости от специальности графического дизайнера, он может не понимать ваши потребности полностью или вообще не понимать. Использование конструктора логотипов гарантирует, что стиль выполнен правильно и эффективно, оставляя больше времени для других насущных дел в вашем бизнесе. Какие цвета подходят для логотипа? Ответ на этот вопрос зависит от того, какой стиль рисования логотипа вы используете. Нарисованный логотип в плоском дизайне, вероятно, будет иметь высокий контраст с яркими цветами, тогда как эскизный, нарисованный от руки дизайн будет более тонким с менее контрастными цветами. Какие стили шрифтов подходят для моего рисунка логотипа? Опять же, это зависит от самого рисунка логотипа. Какого размера должен быть мой логотип? Это действительно то место, где может раскрыться ваш творческий потенциал. Как правило, вы захотите использовать логотип именно для того, для чего он был создан, поэтому, если у вас есть рисунок логотипа с большим количеством деталей, предназначенный для небольших визитных карточек, не взрывайте его и не помещайте. это на рекламном щите! Где я могу использовать мой новый рисунок логотипа бренда? Количество материалов для логотипов бесконечно. Традиционно рисунок логотипа используется в печатных изданиях — визитных карточках, брошюрах и т. д., но он также может хорошо работать на веб-сайте. В наши дни, с преобладанием социальных сетей и мобильных устройств, ваш логотип должен работать везде! Почему GraphicSprings лучший производитель логотипов? GraphicSprings — это бесплатное средство для создания логотипов, которое позволяет легко создавать логотипы в режиме онлайн без какого-либо опыта графического дизайна. Сложно ли создать собственный логотип с помощью GraphicSprings? Программа GraphicSprings предназначена для всех, независимо от того, являетесь ли вы новичком или опытным графическим дизайнером. Если вы еще не уверены, что GraphicSprings — это средство для создания логотипов для вас, ознакомьтесь с нашими учебными пособиями. Сколько времени занимает разработка логотипа с помощью GraphicSprings? Мы считаем, что вы сможете создать свой рисунок логотипа всего за несколько минут, а не часов или дней. Вы можете попробовать все наши функции и шаблоны без регистрации учетной записи. После того, как вы начнете, создание логотипа для рисования займет всего несколько минут. GraphicSprings разработан таким образом, что каждый может создать свой собственный творческий логотип. Могу ли я вносить неограниченное количество изменений в свой рисунок логотипа? Да! Ваше изображение сохраняется как проект на GraphicSprings после покупки логотипа. Приложение для Mac, позволяющее дизайнерам создавать, объединяться, создавать прототипы и многое другое. Веб-приложение для просмотра, отправки отзывов, проверки и передачи — в любом браузере. Полноценная дизайнерская платформа, созданная устойчивой независимой компанией с 2010 года. Узнать больше
Узнайте, что нового Product Designer Illustrator UX Designer Работа:
Прекеш,
Илья,
Тьяго,
Юхан,
Халдун,
Тапботы. Антонио Мануэль Благодаря продуманным функциям, облегчающим выполнение повседневных задач, и интуитивно понятному интерфейсу, который не прерывает ваш рабочий процесс, вы сможете делать удивительные вещи в Sketch. Контролируйте каждую точку, лежащую в основе ваших проектов. Превратите свои идеи во что-то, что каждый может проверить. Обеспечьте согласованность и масштабируемость своих проектов. Выберите между sRGB или P3, когда захотите. Работайте с лучшими современными типографскими технологиями. Новый Получите преимущество, используя стандартные блоки для каждого проекта. Работайте в одиночку или вместе с другими — решать вам. Для создания не требуется подключение к Интернету. Доступ к документам в вашем рабочем пространстве, когда вы входите в Sketch. Новый Просматривайте комментарии и отвечайте на них, не переключая приложения. Легко обменивайтесь строительными блоками вашего продукта и бренда. Упорядочивайте проекты и храните идеи в черновиках. Новый Заходите, вода в порядке! Объединяйте людей и проекты — в любом веб-браузере — чтобы заменить обмен сообщениями, вложения электронной почты и бесконечные проверки. Храните документы вместе, синхронизируйте и отслеживайте каждую веху. Пригласите клиентов, руководителей проектов и разработчиков в качестве бесплатных зрителей. Получите полный контроль над тем, кто может просматривать и редактировать проекты. Управляйте людьми, файлами и выставлением счетов — все в одном месте. Новый Приглашайте соавторов добавлять комментарии прямо на холсте. Новый Предоставьте дизайнерам мгновенный доступ к общим ресурсам. Произведением вектора x на число β (x≠0, β≠0) называется вектор, модуль которого равен |x||β| и который направлен в ту же сторону, что и вектор x, если β>0, и в противоположную, если β<0. Если x=0 и (или) β=0, то βx=0. Рис. 1 На рисунке Рис. 1 вектор x умножен на число 1.5. Полученный вектор y’ имеет то же направление, что и x т.к 1.5>0, и имеет длину 1.5 раз превысшающее длину x. Вектор q имеет противополжное к p направление, т.к. вектор p умножено на отрицательное число -0.5, и имеет длину 2 раза меньше длины p. Рассмотрим процесс умножения вектора на число. Вариант 1. Начальные точки всех векторов совпадают с началом координат. Пусть имеется вектор где координаты вектора x, и пусть β некоторое число. Тогда То есть для умножения вектора на число достаточно умножить каждый координат данного вектора на это число. На рисунке Рис. 1 вектор x имеет координаты x=(6,4). Для умножения вектора x на число 1.5, умножим каждый координат вектора x на число 1.5: Вариант 2. Начальные точки векторов произвольные. Пусть имеется вектор x, с начальной точкой и конечной точкой . Умножим вектор x на число β. Для этого проще всего параллельно переместить вектор x на начало координат, умножить на число, после чего параллельно переместить началную точку полученного вектора на точку A. Переместим вектор x на начало координат. Получим новый вектор x’ с начальными и конечными точками: Умножим x’ на β: Параллельно переместив начальную точку вектора x’ на точку A, получим вектор x» с начальными и конечными точками: На рисунке Рис. 1 вектор p=AB имеет координаты A(2,3) и B(8,1). Перемесив начальную точку вектора q’ на точку A, получим вектор q=AE, где точка E имеет координаты: Операция умножения вектора на число обладает следующими свойствами: 1.β(x+y)=βx+βy (дистрибутивность относительно сложения векторов). 2. (α+β)a=αa+βa (дистрибутивность относительно сложения чисел). 3. α(βa)=(αβ)a (ассоциативность). 4. 1·a=a (умножение на единицу). Пример 1. Умножить вектор y=(3,5,-6) на число 2.5. Пример 2. Переместим вектор AB на начало координат. Начальное и конечное точки перемещенного вектора будут: Умножив полученный вектор на число 3, изменяется расположение конечной точки B’: . Переместив вектор на точку A, получим вектор 3·x, со следующими начальной и конечной точками: Назначение. Онлайн-калькулятор предназначен для вычисления смешанного произведения векторов. Полученное решение сохраняется в файле Word. Дополнительно создается шаблон решения в Excel.
Признак компланарности. Если система Пример №1. Найти смешанное произведение.
Пример №2. Пример №3. Примечание. Определитель матрицы можно найти несколькими способами:
10. Калькулятор величины силы · Калькулятор чистой силы · Результирующие векторы Калькулятор чистой силы | Найти результирующую силу www.omnicalculator.com › физика › результирующая сила 13.02.2023 · Калькулятор чистой силы Omni позволяет определить результирующую силу, действующую на тело при одновременном действии на него нескольких сил. Калькулятор равнодействующей силы www.meracalculator.com › физика › классическая › резуль… Калькулятор равнодействующей силы определяет величину и направление равнодействующей силы. Вы можете найти результирующую не более чем для 2 векторов силы. Онлайн-калькулятор равнодействующей силы • 4 действующих силы • pickshares pickshares.com › Начало › Инструменты › Инженерное дело Этот онлайн-калькулятор равнодействующей силы определяет результирующую силу до 4 действующих сил, включая графический вывод. Векторный калькулятор — математика — это весело www.mathsisfun.com › алгебра › векторный калькулятор Векторный калькулятор. Введите значения в поле «Величина» и «Угол»… или X и Y. Он выполнит преобразования и суммирует векторы. Подробнее о векторах и скалярных произведениях … Ähnliche Fragen Как рассчитать силу вектора? Как найти результирующую силу двух векторов? Как рассчитать результат действия силы? Калькулятор равнодействующей силы — Задачи по физике с решениями Problemsphysics.com › Физика-калькуляторы-решатели Представлен онлайн-калькулятор результирующей силы. … Математически результирующая сила →Rf определяется векторной суммой всех сил, действующих на … Калькулятор чистой силы — CalcTool www.calctool.org › динамика › равнодействующая сила 30.08.2022 · Для расчета чистой силы нам нужно выполнить простую векторную сумму: для этого нам нужно знать: Величина ; и; Направление. Равнодействующая двух сил, действующих под углом — простой расчет www.easycalculation.com › физика › классическая физика Результирующая сила представляет собой векторную сумму всех сил. Воспользуйтесь нашим онлайн-калькулятором равнодействующей силы, чтобы найти равнодействующую двух сил, действующих под углом. Приложение RigRite — Калькулятор векторной силы rigriteapp.com Простой расчет сложных векторных сил. многоточечные анкеры; Редиректы/направления; Штативы и другие AHD; Хайлайны и смещения; Калькулятор силы Лоренца — Инженерные калькуляторы и инструменты www.allaboutcircuits.com › инструменты › lorentz-force-cal… заряженная частица, движущаяся как через электрическое поле, так и через магнитное поле. Ähnlichesuchanfragen Калькулятор результирующего вектора Калькулятор угла между двумя векторами Калькулятор направления вектора Калькулятор луча Калькулятор скалярного произведения Калькулятор длины вектора 900 03 Формула силы Ньютона Результирующая сила suchoptionen Калькулятор линейных комбинаций | Шаги www. 18.11.2022 · Калькулятор линейных комбинаций поможет решить систему уравнений методом комбинирования линейных уравнений. Векторный калькулятор wims.univ-cotedazur.fr › wims › en_tool~linear~vec… Эта страница позволяет выполнять вычисления над векторами. Компонентами этих векторов могут быть вещественные или комплексные числа, а также параметрические выражения. linear комбинация — Wolfram|Alpha www.wolframalpha.com › input › i=linear+combina… Вычисляйте ответы, используя революционную технологию и базу знаний Wolfram, на которые полагаются миллионы студентов и профессионалов. Для математики, естественных наук, питания, … Калькулятор линейной алгебры — Symbolab www.symbolab.com › Solver › linear-алгебра-вычисление… Бесплатный калькулятор линейной алгебры — шаг решения матричных и векторных операций -шаг. Как рассчитать линейную комбинацию? — Cuemath www.cuemath.com › калькуляторы › linear-combinatio… «Калькулятор линейных комбинаций» — это онлайн-инструмент, который помогает вычислять переменные для заданных линейных уравнений. Онлайн-калькулятор линейных комбинаций … Калькулятор линейных комбинаций: определение, формулы и примеры testbook.com › Калькуляторы 01.03.2023 · Калькулятор линейных комбинаций — это инструмент, который можно использовать для решения систем линейных уравнения. Он работает путем объединения уравнений в такой … Ähnliche Fragen Как рассчитать линейные комбинации? Что такое калькулятор линейных комбинаций? Что такое линейная комбинация двух чисел? Что такое НОД линейных комбинаций? Калькулятор линейных комбинаций calculate.academy › Калькулятор линейных комбинаций 06.10.2022 · Линейная комбинация – это отношение между двумя уравнениями в формуле ax + by = c. 4.5 Средняя оценка: 4.5 Всего получено оценок: 328. 4.5 Средняя оценка: 4.5 Всего получено оценок: 328. Решение квадратных уравнений весьма важно для решения практических задач по физике, так как многие формулы имеют старшую степень 2, в программировании и многих других смежных дисциплинах. Способов решить уравнение не так много, но чем больше уравнений вы решаете, тем быстрее и проще становится нахождение корней. Сегодня мы рассмотрим решение полных квадратных уравнений стандартной формы. Квадратное уравнение – это уравнение, старшая степень которого равняется 2. Такое уравнение всегда имеет два корня, иногда эти корни совпадают, а иногда их нет среди действительных чисел. В последнем случае, мы пишем, что действительных корней нет. В квадратном уравнении стандартной формы, есть три коэффициента: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 1 | √1 = 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | 4 | √2 = 1,414 | 9024 5|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | 9 | √3 = 1,732 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | 16 | √4 = 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | 25 | √5 = 2,236 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | 36 | 9 0249 √6 = 2,4494||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | 49 | √7 = 2,645 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | 64 | √8 = 2,828 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | 81 | √9 = 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | 9024 9 100√10 = 3,162 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Формула квадратного корня
Квадратный корень из числа имеет показатель 1/2. Формула квадратного корня используется для нахождения квадратного корня из числа.
Формула квадратного корня используется для нахождения квадратного корня из числа.
Формула квадратного корня: √x = x 1/2
| Формула квадратного корня |
|---|
| √x = x 1/2 |
| √x . √x = x |
| x√y . x√y = x 2 y |
| √(x × y) = √x × √y |
| √( х/у) = √х/√у |
| x / √y = (x / √y) × ( √y / √y) = (x . √y)/y |
| x. √y ± z. √y = (x ± z) √y |
x / (y + z. √p) = [x / (y + z√p)] × [(y – z√p)/ ( у – z√p)] = [x(y – z√p)]/[y 2 – z 2 p] Рационализировать знаменателя путем умножения на [(y – z√p)/ (y – z √p)] |
x / (y – z. = [x(y + z√p)]/[y 2 – z 2 p] 9000 3 Рационализируйте знаменатель, умножив на [(y + z√p)/ (y + z√p)] |
Примеры задач
Вопрос 1: Найдите сумму: 5√3 + 6√12
Решение:
5√3 + 6√12 = 5√3 + 6(√(4 × 3)
√3 + 6 × 2√3
= 5√3 + 12√3
= 17√3
Вопрос 2: Оцените: √64 – √25
Решение:
√64 – √25 = √(8 × 8) – √(5 × 5)
= 8 – 5 = 3
Вопрос 3: Оцените: √63 / √ 28
Решение:
√63 / √28 = √(7 × 9)/ √(7 × 4)
= √[(7 × 9 )/ (7 × 4 )]
= √(9/4)
= √9 / √4
= 3/2
Вопрос 4.

 4
4
 Почему же Тургенев обратился к этой тетради в 1859 году, когда и в России подобного типа герои уже появились? Почему в качестве образца для русских «сознательно-героических натур» Тургенев предлагает болгарина Дмитрия Инсарова? Что не устроило, наконец, Тургенева в добролюбовской интерпретации романа «Накануне», опубликованного в январском номере журнала «Русский вестник» в 1860 году?
Почему же Тургенев обратился к этой тетради в 1859 году, когда и в России подобного типа герои уже появились? Почему в качестве образца для русских «сознательно-героических натур» Тургенев предлагает болгарина Дмитрия Инсарова? Что не устроило, наконец, Тургенева в добролюбовской интерпретации романа «Накануне», опубликованного в январском номере журнала «Русский вестник» в 1860 году?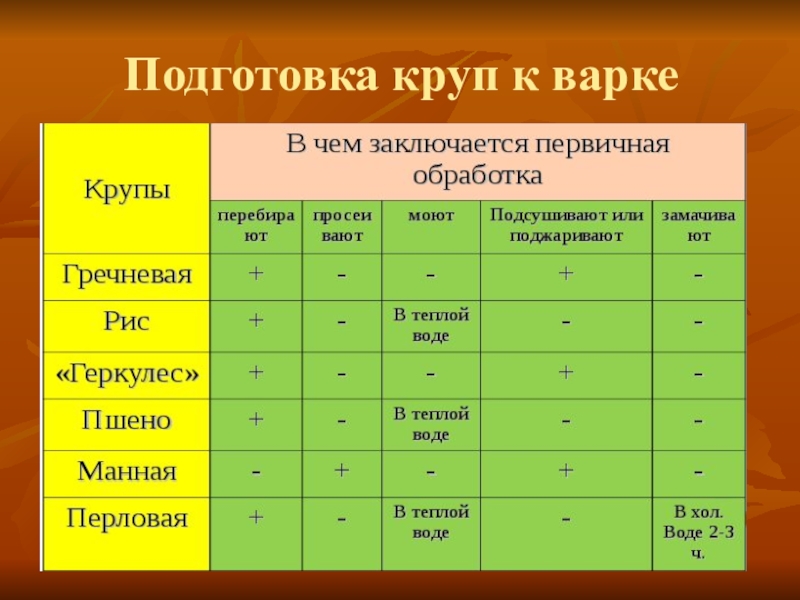 Социально-бытовой сюжет романа имеет символический подтекст: Елена Стахова олицетворяет молодую Россию «накануне» предстоящих перемен, Кто всего нужнее ей сейчас: люди науки или искусства, государственные чиновники или героические натуры, люди гражданского подвига? Выбор Еленой Инсарова дает недвусмысленный ответ на этот вопрос.
Социально-бытовой сюжет романа имеет символический подтекст: Елена Стахова олицетворяет молодую Россию «накануне» предстоящих перемен, Кто всего нужнее ей сейчас: люди науки или искусства, государственные чиновники или героические натуры, люди гражданского подвига? Выбор Еленой Инсарова дает недвусмысленный ответ на этот вопрос. Из того же источника— готовность пожертвовать собой ради других, ради высокой цели спасения людей, попавших в беду, страдающих и несчастных. Не случайно в разговорах с Инсаровым Елена вспоминает буфетчика Василия, «который вытащил из горевшей избы безногого старика и сам чуть не погиб».
Из того же источника— готовность пожертвовать собой ради других, ради высокой цели спасения людей, попавших в беду, страдающих и несчастных. Не случайно в разговорах с Инсаровым Елена вспоминает буфетчика Василия, «который вытащил из горевшей избы безногого старика и сам чуть не погиб». ..» Чайка закружилась на месте, сложила крылья — и, как подстреленная, с жалобным криком пала куда-то далеко за темный корабль» (VIII, 157).
..» Чайка закружилась на месте, сложила крылья — и, как подстреленная, с жалобным криком пала куда-то далеко за темный корабль» (VIII, 157). Это люди без крепкого корня, отсутствие которого придает их характерам или внутреннюю вялость, как у Берсенева, или мотыльковое непостоянство, как у Шубина.
Это люди без крепкого корня, отсутствие которого придает их характерам или внутреннюю вялость, как у Берсенева, или мотыльковое непостоянство, как у Шубина. Соединяют людей слова: «родина», «наука», «справедливость». И «любовь», но только если она — не «любовь-наслаждение», а «любовь-жертва».
Соединяют людей слова: «родина», «наука», «справедливость». И «любовь», но только если она — не «любовь-наслаждение», а «любовь-жертва». ..»
..» Человек, по Тургеневу, драматичен не только в своем внутреннем существе, но и в отношениях с окружающей его природой. Природа не считается с неповторимой ценностью человеческой личности: с равнодушным спокойствием она поглощает и простого смертного, и героя; все равны перед ее неразличающим взором. Этот мотив универсального трагизма жизни вторгается в роман неожиданной смертью Инсарова, исчезновением Елены на этой земле —«навсегда, безвозвратно». «Смерть, как рыбак,—с горечью говорит Тургенев,—который поймал рыбу в свою сеть и оставляет ее на время в воде: рыба еще плавает, но сеть на ней, и рыбак выхватит ее —когда захочет» (VIII, 166). С точки зрения «равнодушной природы» каждый из нас «виноват уже тем, что живет».
Человек, по Тургеневу, драматичен не только в своем внутреннем существе, но и в отношениях с окружающей его природой. Природа не считается с неповторимой ценностью человеческой личности: с равнодушным спокойствием она поглощает и простого смертного, и героя; все равны перед ее неразличающим взором. Этот мотив универсального трагизма жизни вторгается в роман неожиданной смертью Инсарова, исчезновением Елены на этой земле —«навсегда, безвозвратно». «Смерть, как рыбак,—с горечью говорит Тургенев,—который поймал рыбу в свою сеть и оставляет ее на время в воде: рыба еще плавает, но сеть на ней, и рыбак выхватит ее —когда захочет» (VIII, 166). С точки зрения «равнодушной природы» каждый из нас «виноват уже тем, что живет». Неудовлетворенность Елены современным состоянием жизни в России, ее тоска по иному, более совершенному социальному порядку в философском плане романа приобретает «продолжающийся» смысл, актуальный во все эпохи и все времена. «Накануне» — это роман о порыве России к новым общественным отношениям, пронизанный нетерпеливым ожиданием «сознательно-героических натур», которые двинут вперед дело освобождения крестьян.
Неудовлетворенность Елены современным состоянием жизни в России, ее тоска по иному, более совершенному социальному порядку в философском плане романа приобретает «продолжающийся» смысл, актуальный во все эпохи и все времена. «Накануне» — это роман о порыве России к новым общественным отношениям, пронизанный нетерпеливым ожиданием «сознательно-героических натур», которые двинут вперед дело освобождения крестьян.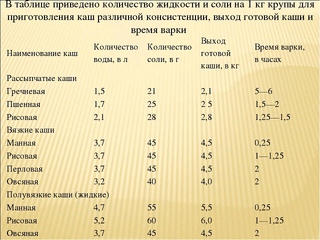 .. одни… а там, повсюду, во всех этих недосягаемых безднах и глубинах, — все, все нам чуждо? К чему же тогда эта жажда и радость молитвы?.. Неужели же нельзя умолить, отвратить, спасти… О боже! неужели нельзя верить чуду?» (VIII, 156).
.. одни… а там, повсюду, во всех этих недосягаемых безднах и глубинах, — все, все нам чуждо? К чему же тогда эта жажда и радость молитвы?.. Неужели же нельзя умолить, отвратить, спасти… О боже! неужели нельзя верить чуду?» (VIII, 156). У всех у нас одна цель. Поймите, какую это дает уверенность и крепость!» (VIII, 68). Тургеневу хотелось, чтобы все прогрессивно настроенные люди России, без различия социальных положений и оттенков в политических убеждениях, протянули друг другу руки.
У всех у нас одна цель. Поймите, какую это дает уверенность и крепость!» (VIII, 68). Тургеневу хотелось, чтобы все прогрессивно настроенные люди России, без различия социальных положений и оттенков в политических убеждениях, протянули друг другу руки.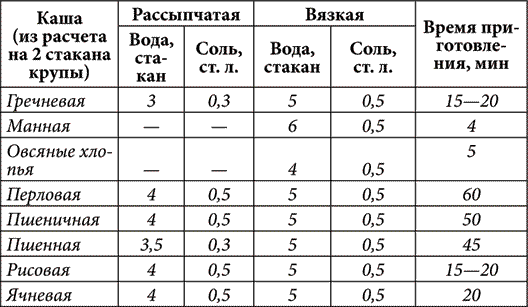 Основной для Тургенева вопрос о соотношении мысли и деятельности, человека дела и теоретика в этом романе решается в пользу практически осуществляющего идею героя.
Основной для Тургенева вопрос о соотношении мысли и деятельности, человека дела и теоретика в этом романе решается в пользу практически осуществляющего идею героя.
 Шубин и Берсенев представляют художественно-мыслительный тип (тип людей отвлеченно-теоретического или образно-художественного творчества), Инсаров и Курнатовский относятся к «деятельному» типу, т. е. к людям, призвание которых состоит в практическом «жизнетворчестве».
Шубин и Берсенев представляют художественно-мыслительный тип (тип людей отвлеченно-теоретического или образно-художественного творчества), Инсаров и Курнатовский относятся к «деятельному» типу, т. е. к людям, призвание которых состоит в практическом «жизнетворчестве».  И Берсенев, и Шубин генетически связаны с «лишними людьми», но в них нет многих главных черт героев этого рода. Оба они прежде всего не погружены в чистую мысль, анализ действительности не является их основным занятием. От рефлексии, самоанализа и бесконечного ухода в теорию их «спасает» профессионализация, призвание, живой интерес к определенной сфере деятельности и постоянный труд.
И Берсенев, и Шубин генетически связаны с «лишними людьми», но в них нет многих главных черт героев этого рода. Оба они прежде всего не погружены в чистую мысль, анализ действительности не является их основным занятием. От рефлексии, самоанализа и бесконечного ухода в теорию их «спасает» профессионализация, призвание, живой интерес к определенной сфере деятельности и постоянный труд. и идеала людей 50-х гг. — сильно рознятся от романтического представления о художнике. Тургенев нарочито дает это понять: в самом начале романа Берсенев указывает Шубину, каковы должны быть его — «артиста» — вкусы и склонности, и Шубин, шутливо «отбиваясь» от этой обязательной и неприемлемой для него позиции художника-романтика, защищает свою любовь к чувственной жизни и ее реальной красоте.
и идеала людей 50-х гг. — сильно рознятся от романтического представления о художнике. Тургенев нарочито дает это понять: в самом начале романа Берсенев указывает Шубину, каковы должны быть его — «артиста» — вкусы и склонности, и Шубин, шутливо «отбиваясь» от этой обязательной и неприемлемой для него позиции художника-романтика, защищает свою любовь к чувственной жизни и ее реальной красоте.


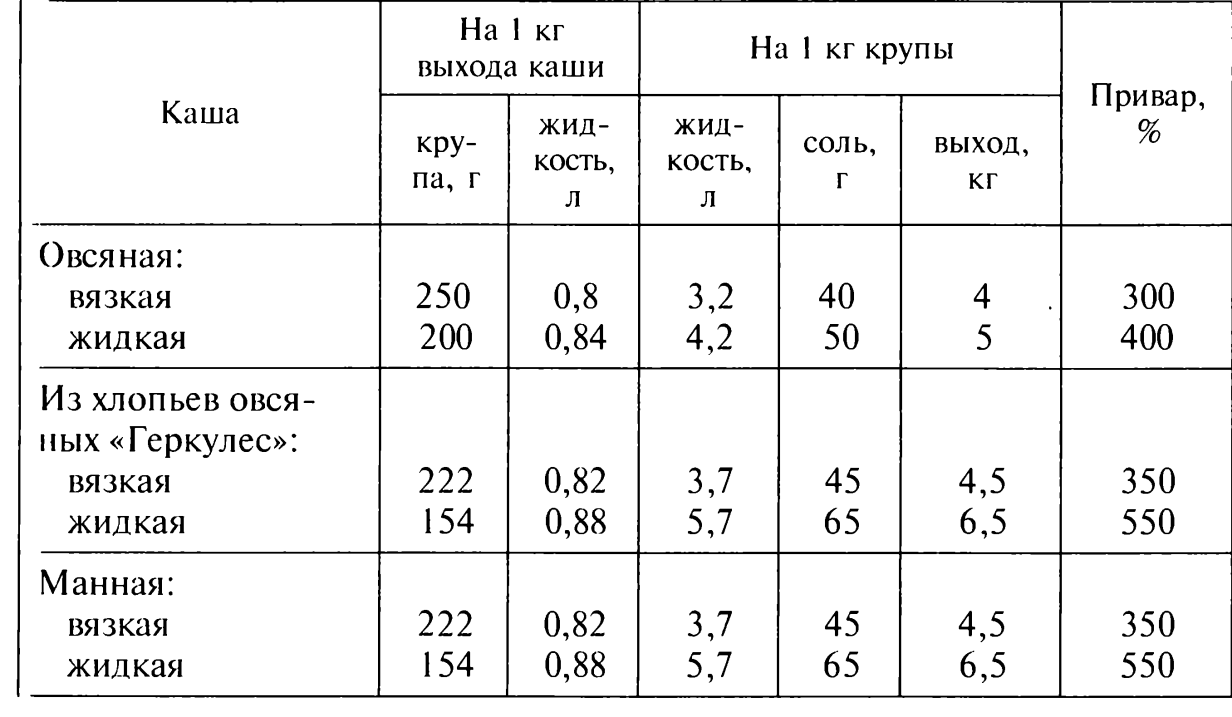 Понимая, что реформы неизбежны, деятели типа Курнатовского связывали все возможные в жизни страны изменения с функционированием сильного государства, а себя считали носителями идеи государства и исполнителями его исторической миссии, отсюда — самоуверенность, вера в себя, по словам Елены.
Понимая, что реформы неизбежны, деятели типа Курнатовского связывали все возможные в жизни страны изменения с функционированием сильного государства, а себя считали носителями идеи государства и исполнителями его исторической миссии, отсюда — самоуверенность, вера в себя, по словам Елены.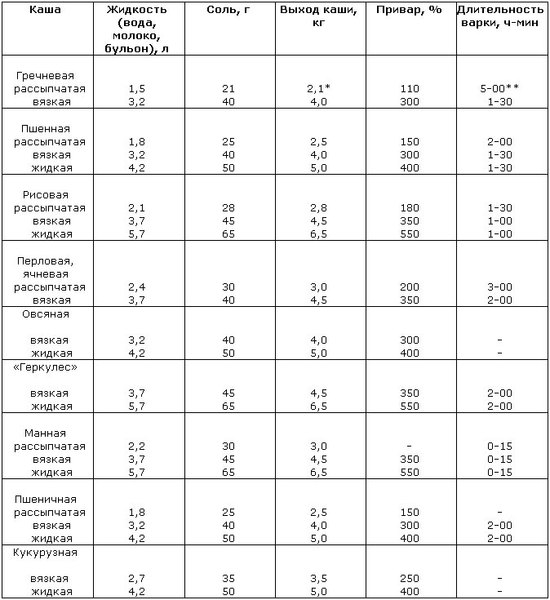 Здесь была опоэтизирована ситуация, характерная для большого периода последующей жизни русского общества и имевшая огромное значение как выражение нового этического идеала. Прежде чем соединить свою жизнь с ее жизнью, Инсаров подвергает Елену своеобразному «экзамену», предвосхищающему символический «допрос», которому подвергает таинственный голос судьбы смелую девушку-революционерку в стихотворении в прозе Тургенева «Порог». При этом герой «Накануне» вводит любимую девушку в свои планы, свои интересы и заключает с ней своеобразный договор, предполагающий с ее стороны сознательную оценку их возможной будущности, — черта отношений, характерная для демократов-шестидесятников.
Здесь была опоэтизирована ситуация, характерная для большого периода последующей жизни русского общества и имевшая огромное значение как выражение нового этического идеала. Прежде чем соединить свою жизнь с ее жизнью, Инсаров подвергает Елену своеобразному «экзамену», предвосхищающему символический «допрос», которому подвергает таинственный голос судьбы смелую девушку-революционерку в стихотворении в прозе Тургенева «Порог». При этом герой «Накануне» вводит любимую девушку в свои планы, свои интересы и заключает с ней своеобразный договор, предполагающий с ее стороны сознательную оценку их возможной будущности, — черта отношений, характерная для демократов-шестидесятников. Смерть, жизнь, борьба, падение, торжество, любовь, свобода, родина… Хорошо, хорошо. Дай бог всякому! Это не то, что сидеть по горло в болоте да стараться показывать вид, что тебе всё равно, когда тебе действительно в сущности всё равно. А там — натянуты струны, звени на весь мир или порвись!» (VIII, 141).
Смерть, жизнь, борьба, падение, торжество, любовь, свобода, родина… Хорошо, хорошо. Дай бог всякому! Это не то, что сидеть по горло в болоте да стараться показывать вид, что тебе всё равно, когда тебе действительно в сущности всё равно. А там — натянуты струны, звени на весь мир или порвись!» (VIII, 141). Сколько крупы осталось в пакете?
Сколько крупы осталось в пакете?

 Каким путём он может
сразу обнаружить свою ошибку?
Каким путём он может
сразу обнаружить свою ошибку?

 На остановке из
второго вагона вышли 15 пассажиров. Сколько всего пассажиров осталось в
трамвае? Решите задачу двумя способами
На остановке из
второго вагона вышли 15 пассажиров. Сколько всего пассажиров осталось в
трамвае? Решите задачу двумя способами

 Какой смысл имеют следующие выражения:
Какой смысл имеют следующие выражения: Это упражнение полезно
выполнить несколько раз; можно соревноваться с товарищем: кто быстрее отыщет
все числа?
Это упражнение полезно
выполнить несколько раз; можно соревноваться с товарищем: кто быстрее отыщет
все числа?
 Но горячие каши, приготовленные из риса или киноа, появились в Азии уже 12 000 лет назад. И не только в качестве еды на завтрак — кремообразные вареные зерна появляются в любое время дня.
Но горячие каши, приготовленные из риса или киноа, появились в Азии уже 12 000 лет назад. И не только в качестве еды на завтрак — кремообразные вареные зерна появляются в любое время дня. Минимально обработанные цельнозерновые продукты, такие как фарро, ржаные ягоды, овсяные хлопья или коричневый рис, требуют времени для приготовления и отлично готовятся заранее, неторопливо варятся на плите или в течение ночи в медленноварке. Если у вас есть время, замочите ягоды пшеницы, тритикале или ржи в воде на ночь перед приготовлением. Или вытащите кастрюлю быстрого приготовления или скороварку, чтобы ускорить процесс. Эти цельные зерна по своей природе будут иметь большую текстуру и вкус.
Минимально обработанные цельнозерновые продукты, такие как фарро, ржаные ягоды, овсяные хлопья или коричневый рис, требуют времени для приготовления и отлично готовятся заранее, неторопливо варятся на плите или в течение ночи в медленноварке. Если у вас есть время, замочите ягоды пшеницы, тритикале или ржи в воде на ночь перед приготовлением. Или вытащите кастрюлю быстрого приготовления или скороварку, чтобы ускорить процесс. Эти цельные зерна по своей природе будут иметь большую текстуру и вкус. В зимнее время, особенно в нашем регионе, зерновые более сухие и влаголюбивые.
В зимнее время, особенно в нашем регионе, зерновые более сухие и влаголюбивые.

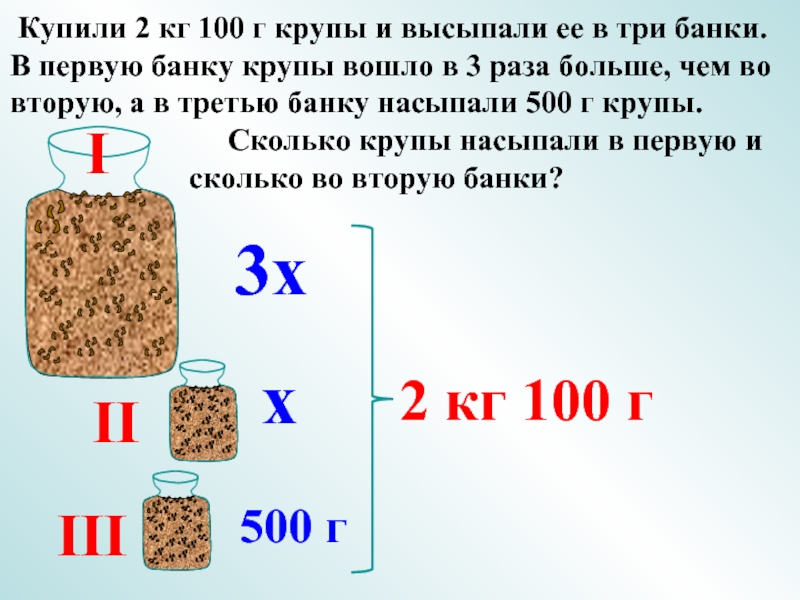
 приготовленный соус чимичурри или сальса верде
приготовленный соус чимичурри или сальса верде От Лизы Голден Шредер.
От Лизы Голден Шредер.
 Храните приготовленные кусочки бекона в герметичном контейнере. Разогрейте порции с предпочитаемым молоком. Чтобы сделать его вегетарианским, просто поджарьте зерна на оливковом масле. Обжаренные в духовке кусочки мускатной тыквы, смешанные с кленовым сиропом, хорошо сочетаются с этой кашей, если вы решите сделать ее основой для более сытного блюда. Примечание: дикий рис можно заменить или смешать с красным жасмином или пророщенным коричневым рисом. От Лизы Голден Шредер.
Храните приготовленные кусочки бекона в герметичном контейнере. Разогрейте порции с предпочитаемым молоком. Чтобы сделать его вегетарианским, просто поджарьте зерна на оливковом масле. Обжаренные в духовке кусочки мускатной тыквы, смешанные с кленовым сиропом, хорошо сочетаются с этой кашей, если вы решите сделать ее основой для более сытного блюда. Примечание: дикий рис можно заменить или смешать с красным жасмином или пророщенным коричневым рисом. От Лизы Голден Шредер.
 10.2017, 19:07
10.2017, 19:07  Десятичного в этом нет вообще ничего.
Десятичного в этом нет вообще ничего. 
 10.2017, 21:34
10.2017, 21:34  Но там не «десятичные градусы», а грады, 100 в прямом угле (также употребляется gradian или gon).
Но там не «десятичные градусы», а грады, 100 в прямом угле (также употребляется gradian или gon). А может, на каком-то из иностранных языков (по-французски) оно называется так, как могло бы быть переведено как «десятичные градусы»?
А может, на каком-то из иностранных языков (по-французски) оно называется так, как могло бы быть переведено как «десятичные градусы»? 
 com и аспозе.облако
com и аспозе.облако Просто введите свою широту и долготу и нажмите кнопку «Преобразовать». Наше приложение автоматически распознает вашу систему координат и преобразует их в желаемую.
Просто введите свою широту и долготу и нажмите кнопку «Преобразовать». Наше приложение автоматически распознает вашу систему координат и преобразует их в желаемую. 
 Далее выберите желаемый формат, в который будут преобразованы ваши координаты. Затем просто нажмите «Конвертировать» и дождитесь результата конвертации. Когда координаты преобразованы, результат будет отображаться в разделе «Преобразованные координаты».
Далее выберите желаемый формат, в который будут преобразованы ваши координаты. Затем просто нажмите «Конвертировать» и дождитесь результата конвертации. Когда координаты преобразованы, результат будет отображаться в разделе «Преобразованные координаты».

 Click this link to visit the forums.
Click this link to visit the forums. Но иногда нет N, S, E или W. Вместо этого вы можете увидеть широту, написанную как 40,665° или +40,665°. Оба эти числа являются положительными числами и означают, что широта является СЕВЕРНОЙ широтой».
Но иногда нет N, S, E или W. Вместо этого вы можете увидеть широту, написанную как 40,665° или +40,665°. Оба эти числа являются положительными числами и означают, что широта является СЕВЕРНОЙ широтой». Число положительное, значит, это СЕВЕРНАЯ широта. Итак, 40.6530190&градус — это 40,6530190&градус северной широты
Число положительное, значит, это СЕВЕРНАЯ широта. Итак, 40.6530190&градус — это 40,6530190&градус северной широты 


 ELSE 1
ELSE 1 
 Как правило, Ирландия содержит отрицательные десятичные градусы: Широта: 53,14° северной широты и долгота: -7,69° восточной долготы.
Как правило, Ирландия содержит отрицательные десятичные градусы: Широта: 53,14° северной широты и долгота: -7,69° восточной долготы.

 3-D MAX – программа бесплатная, но ее функционал значительно шире, чем у платных «AutoCAD», «NanoCAD» и «Компас» за счет бесплатных же плагинов и объемной базы заготовок моделей любой сложности и направленности.
3-D MAX – программа бесплатная, но ее функционал значительно шире, чем у платных «AutoCAD», «NanoCAD» и «Компас» за счет бесплатных же плагинов и объемной базы заготовок моделей любой сложности и направленности. Draw.io содержит огромное количество функций и продуман до мелочей. Здесь вы можете создавать даже сложные многостраничные проекты с бесконечным числом элементов.
Draw.io содержит огромное количество функций и продуман до мелочей. Здесь вы можете создавать даже сложные многостраничные проекты с бесконечным числом элементов.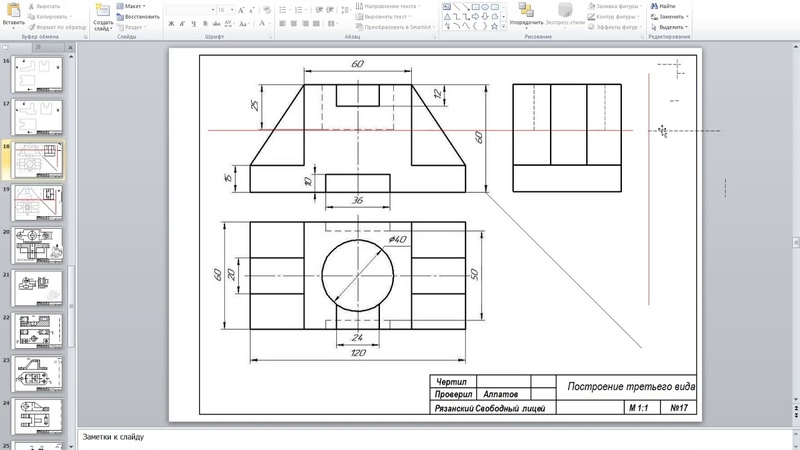

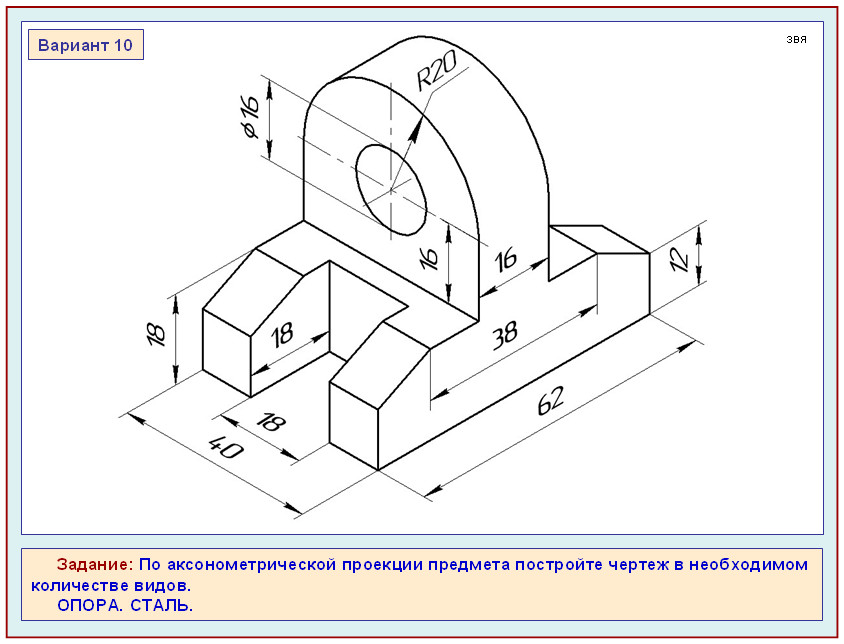 А вот выполнять настройку самих объектов уже не получится.
А вот выполнять настройку самих объектов уже не получится.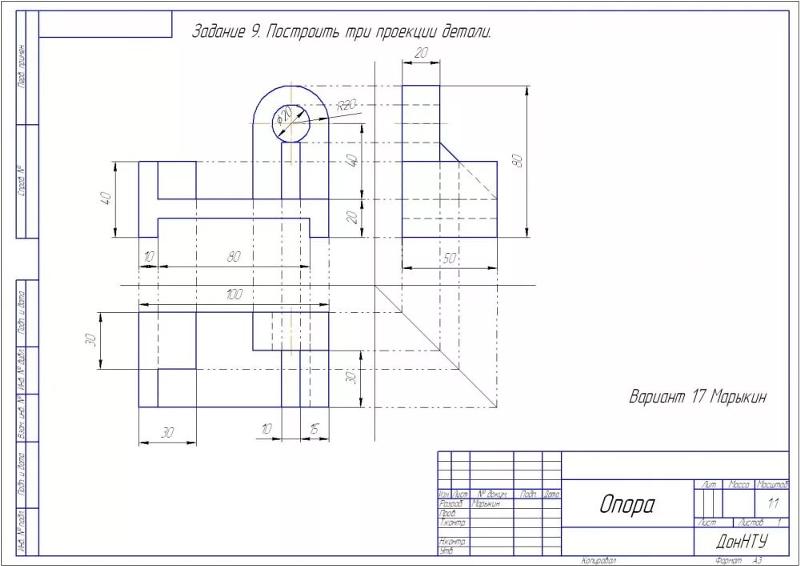
 Помимо этого Autodesk AutoCAD предоставляет возможность работы с 3D-принтерами, поистине широчайший набор функций для профессионального проектирования, возможность работы с макетами.В качестве недостатков можно отметить довольно высокие системные требования. Так, Вы не сможете использовать пакет Autodesk AutoCAD, не имея достаточно мощного ПК. При этом, однако, специалисты компании Autodesk смогли сделать свой продукт максимально доступным посредством возможности работы с Autodesk AutoCAD в режиме онлайн. Загрузив данные на сервер, Вы можете редактировать свой чертеж, просто подключившись к интернету и имея как бы портативную программу для создания чертежей на Вашем мобильном. Более того, практически ежегодно выпускается новая, усовершенствованная версия продукта.
Помимо этого Autodesk AutoCAD предоставляет возможность работы с 3D-принтерами, поистине широчайший набор функций для профессионального проектирования, возможность работы с макетами.В качестве недостатков можно отметить довольно высокие системные требования. Так, Вы не сможете использовать пакет Autodesk AutoCAD, не имея достаточно мощного ПК. При этом, однако, специалисты компании Autodesk смогли сделать свой продукт максимально доступным посредством возможности работы с Autodesk AutoCAD в режиме онлайн. Загрузив данные на сервер, Вы можете редактировать свой чертеж, просто подключившись к интернету и имея как бы портативную программу для создания чертежей на Вашем мобильном. Более того, практически ежегодно выпускается новая, усовершенствованная версия продукта.
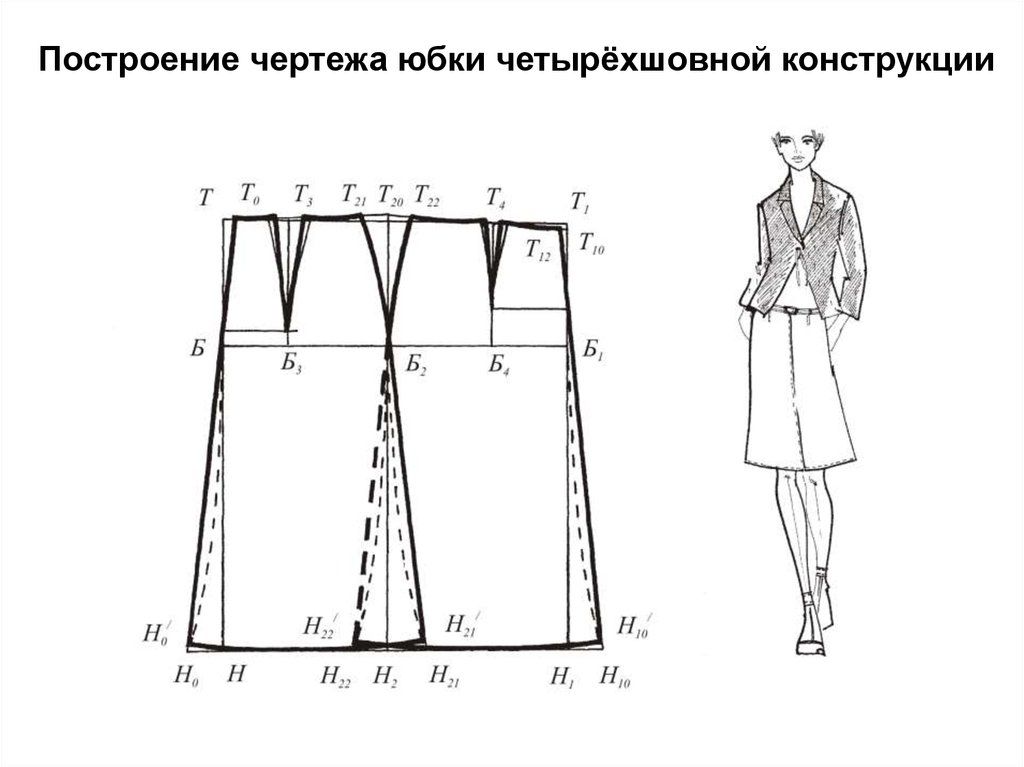 Замечу, что указанные сервисы для создания чертежей обладают довольно сжатым по сравнению с профессиональными программами функционалом, чего, впрочем, может быть достаточно для решения множества базовых задач.
Замечу, что указанные сервисы для создания чертежей обладают довольно сжатым по сравнению с профессиональными программами функционалом, чего, впрочем, может быть достаточно для решения множества базовых задач.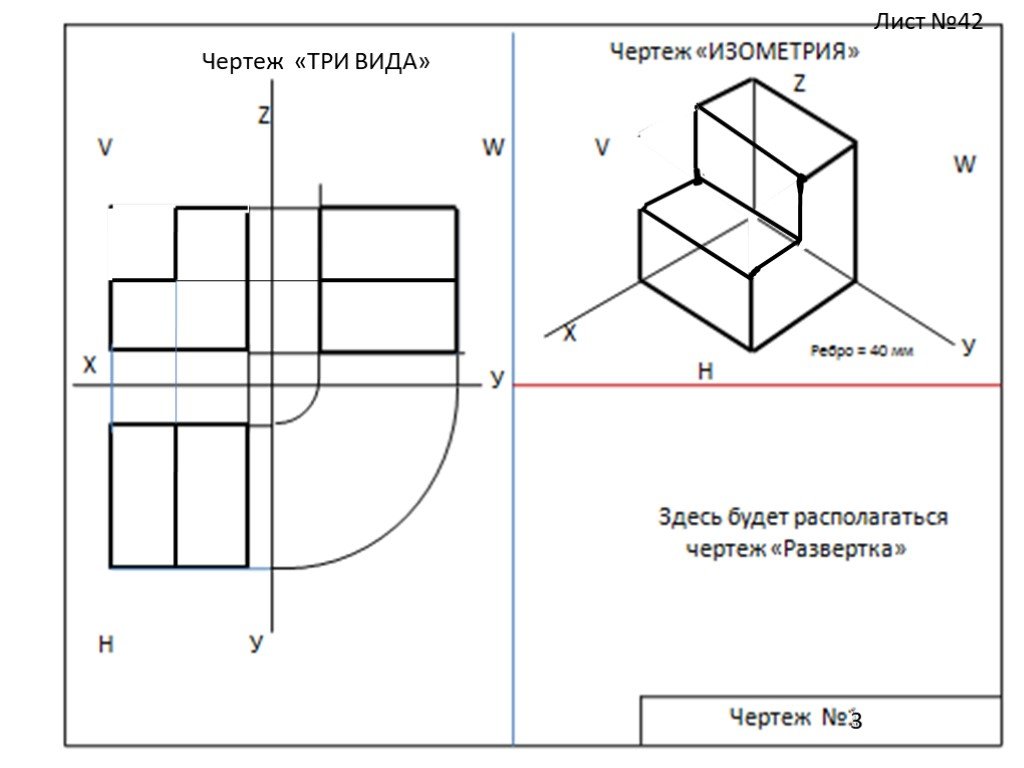
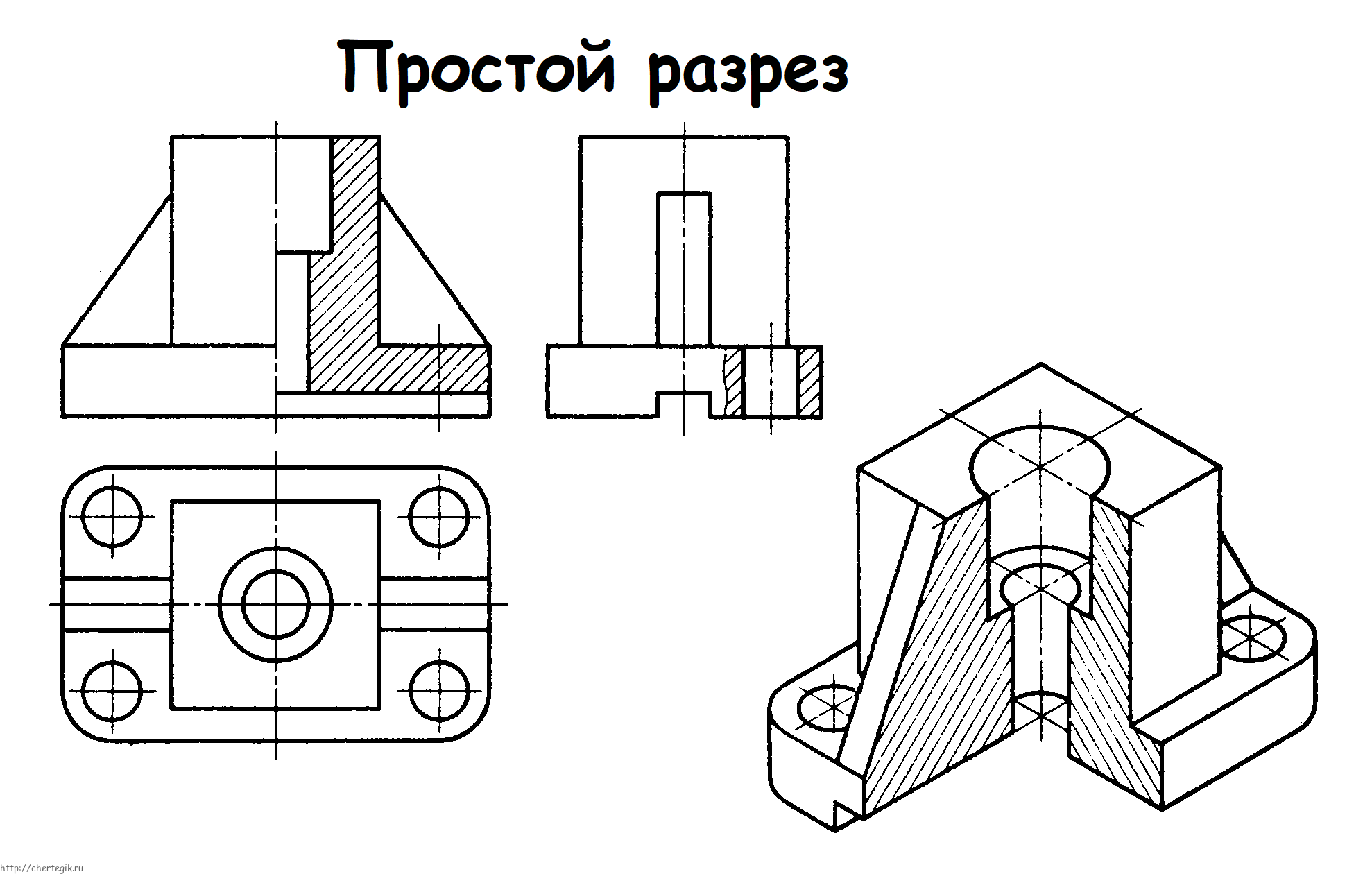
 com.ua.
com.ua.
 С помощью верхних меню открывается доступ к полному функционалу и макросам.
С помощью верхних меню открывается доступ к полному функционалу и макросам. Чтобы начать работать в нем необходимо будет авторизоваться через любую социальную сеть, после чего появится главное окно для создания и редактирования.
Чтобы начать работать в нем необходимо будет авторизоваться через любую социальную сеть, после чего появится главное окно для создания и редактирования.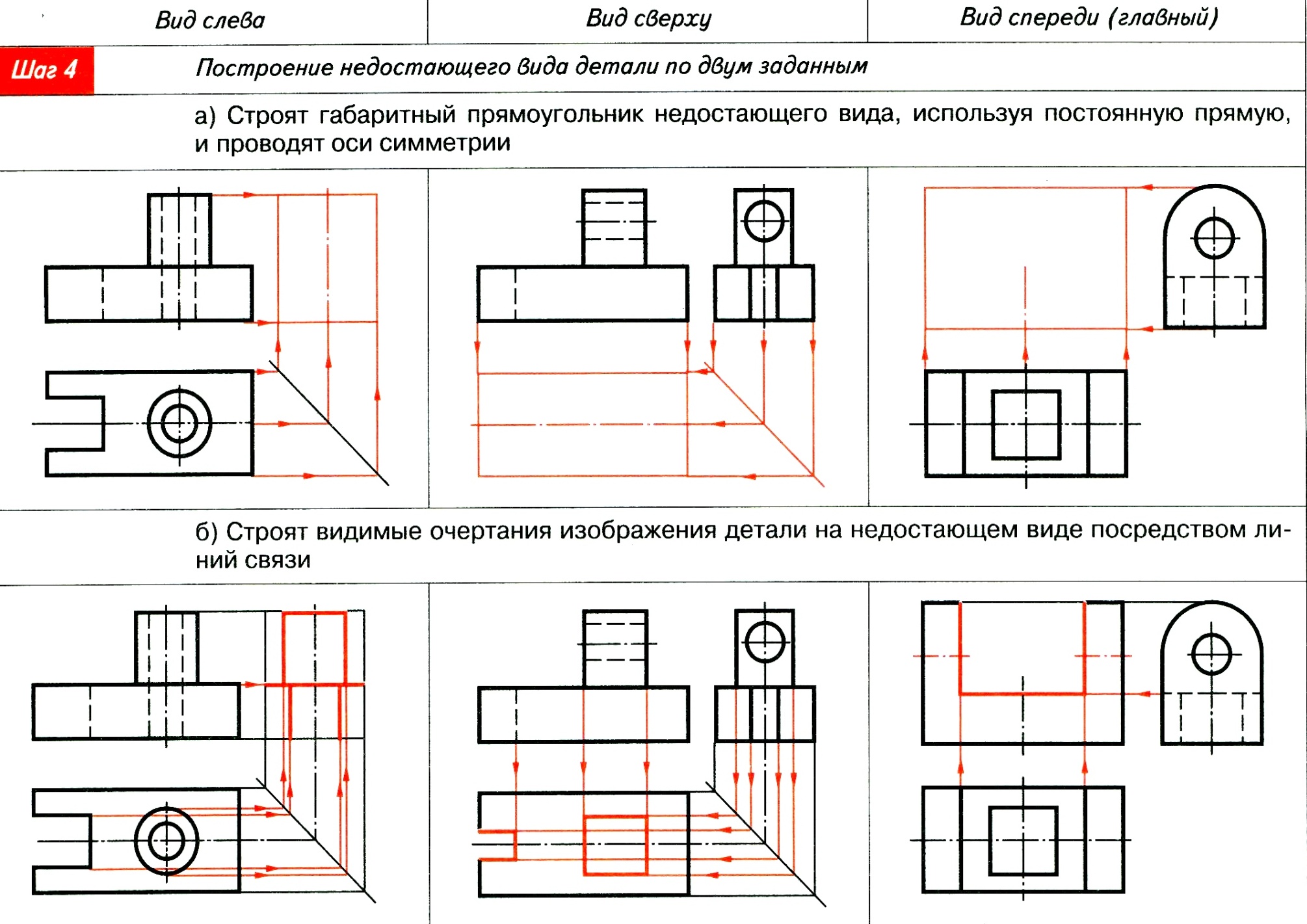 Тонкой настройки, как мы говорили выше, здесь нет.
Тонкой настройки, как мы говорили выше, здесь нет.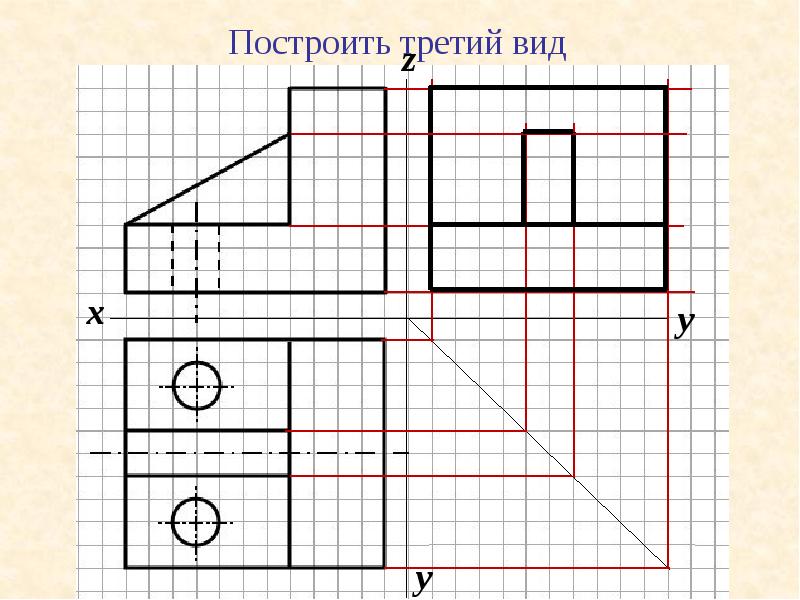 Главное, что все это наглядно, а не просто в виде текста.
Главное, что все это наглядно, а не просто в виде текста. Приложение популярно среди проектировочных отделов, автоматизированного моделирования и всего того, что связано с производством, монтажом и строительством. Устраиваясь на работу в серьезное предприятие, работнику придется иметь дело с AutoCAD. Программа доступна любителям, новичкам, профессионалам. Софт не стоит на месте, постоянно получая поддержку разработчиков. Ежегодно выходят обновленные версии с улучшенным функционалом, расширенными возможностями, усовершенствованным по замечаниям пользователей интерфейсом. Такое рачительное отношение производителя привело к популярности программного обеспечения.
Приложение популярно среди проектировочных отделов, автоматизированного моделирования и всего того, что связано с производством, монтажом и строительством. Устраиваясь на работу в серьезное предприятие, работнику придется иметь дело с AutoCAD. Программа доступна любителям, новичкам, профессионалам. Софт не стоит на месте, постоянно получая поддержку разработчиков. Ежегодно выходят обновленные версии с улучшенным функционалом, расширенными возможностями, усовершенствованным по замечаниям пользователей интерфейсом. Такое рачительное отношение производителя привело к популярности программного обеспечения.

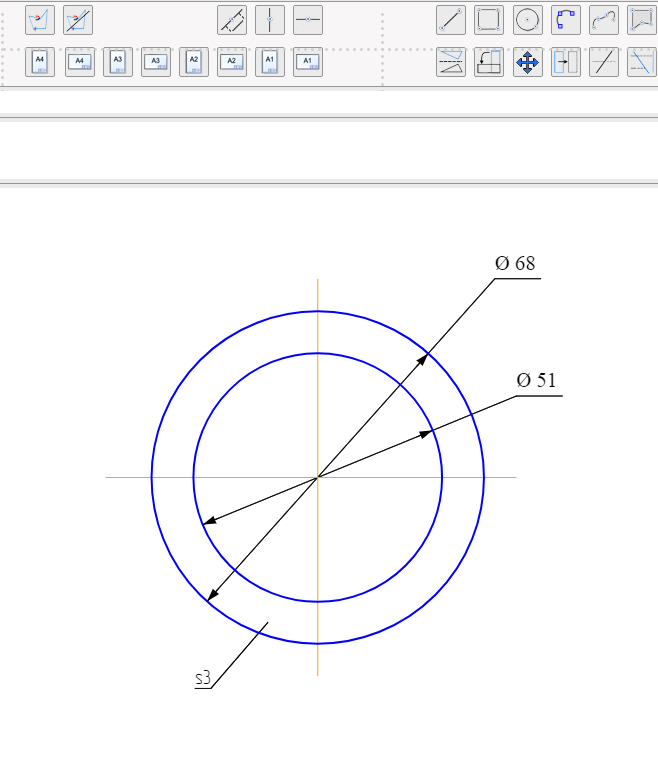
 Главное преимущество — это полное соответствие российским чертежным стандартам, поэтому программа легко встраивается в любой рабочий процесс. Но данный факт имеет и свои минусы, ведь многие специалисты работают, в том числе с иностранными заказчиками, где есть свои стандарты.
Главное преимущество — это полное соответствие российским чертежным стандартам, поэтому программа легко встраивается в любой рабочий процесс. Но данный факт имеет и свои минусы, ведь многие специалисты работают, в том числе с иностранными заказчиками, где есть свои стандарты. Соотношение цена-качество у отечественной разработки не самое лучшее, если сравнивать с основными конкурентами, при этом полностью отсутствует trial-версия, что делает невозможным ее тестирование.
Соотношение цена-качество у отечественной разработки не самое лучшее, если сравнивать с основными конкурентами, при этом полностью отсутствует trial-версия, что делает невозможным ее тестирование.
 53.55710
53.55710 53.55710
53.55710 53.55710
53.55710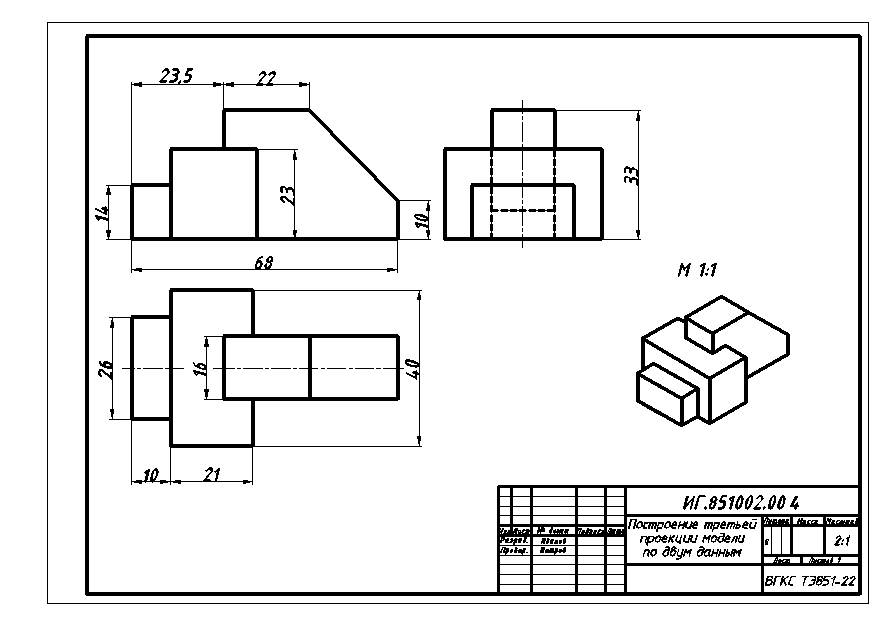 53.55710
53.55710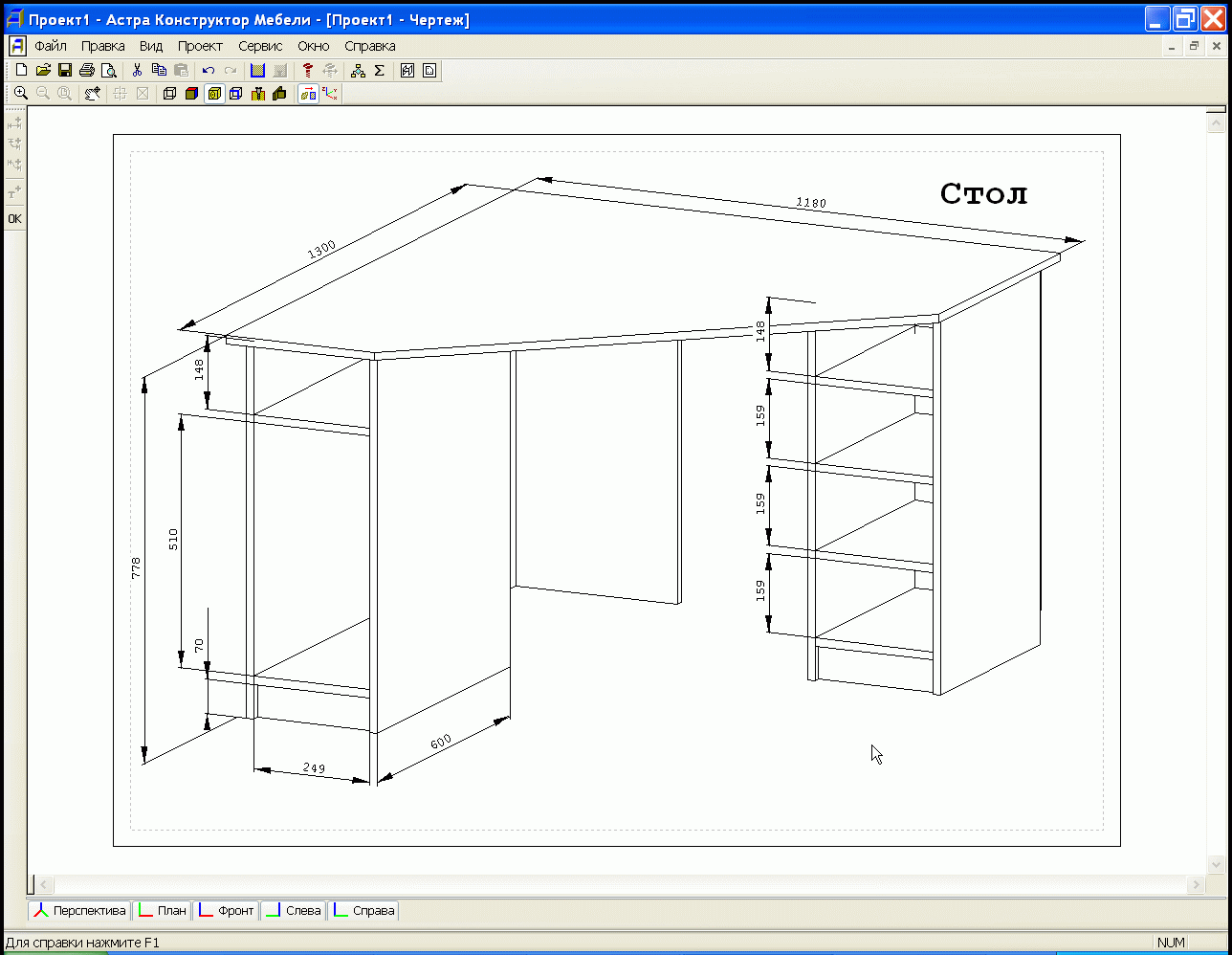 53.55710
53.55710 Рисунок логотипа может быть достаточно абстрактным, чтобы иметь значение как для вас, так и для вашей клиентуры, оставляя место для личных предпочтений.
Рисунок логотипа может быть достаточно абстрактным, чтобы иметь значение как для вас, так и для вашей клиентуры, оставляя место для личных предпочтений.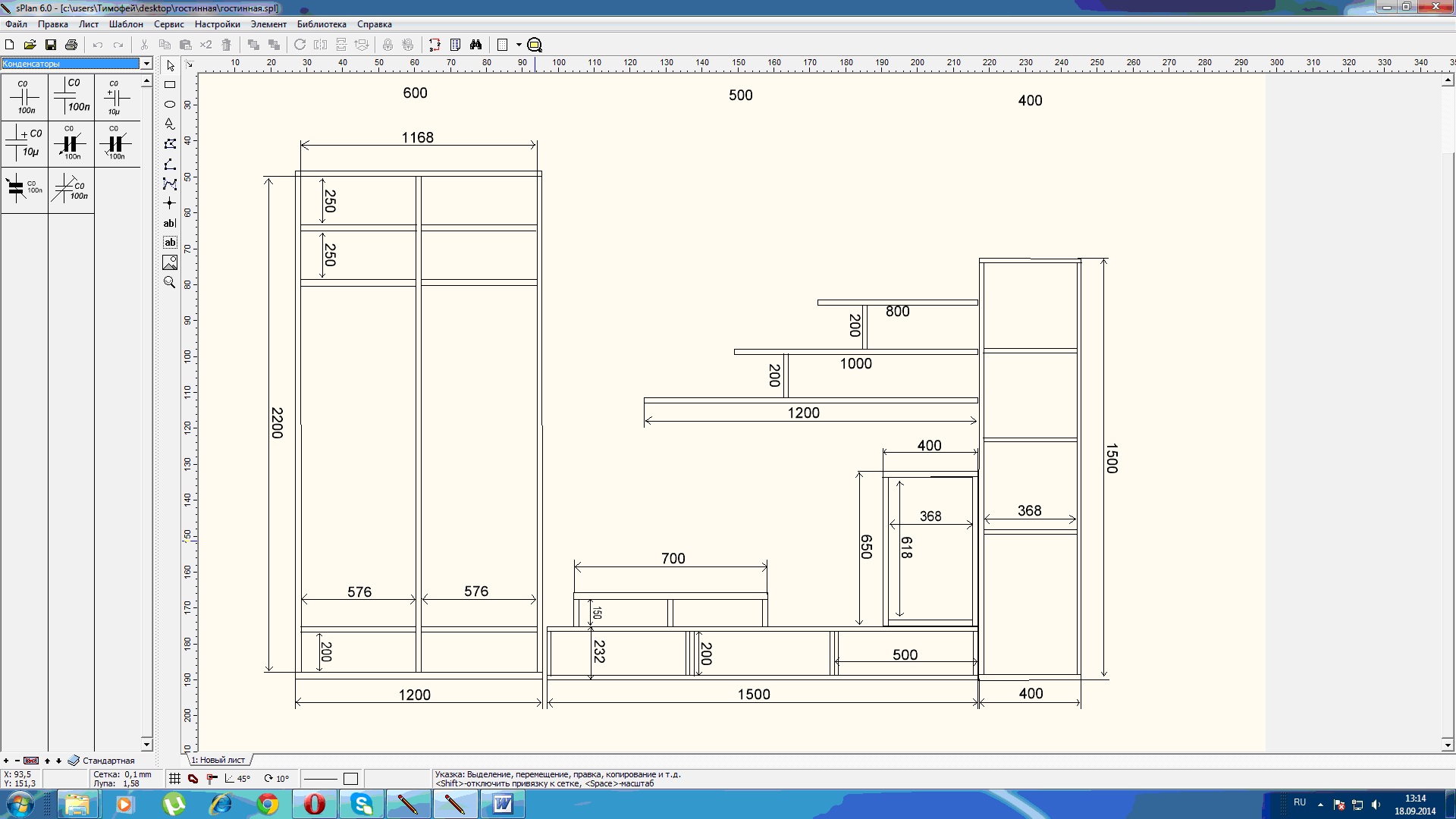 Если вы собираетесь обвести свой логотип штрихом, вы можете использовать шрифт с большим количеством вариаций, чтобы он выделялся. С эскизным логотипом в стиле рисунка ищите шрифты с меньшим единообразием и более изогнутыми формами букв.
Если вы собираетесь обвести свой логотип штрихом, вы можете использовать шрифт с большим количеством вариаций, чтобы он выделялся. С эскизным логотипом в стиле рисунка ищите шрифты с меньшим единообразием и более изогнутыми формами букв. Наша технология редактирования сложна, но проста в использовании, а наша база данных шаблонов создана профессиональными дизайнерами.
Наша технология редактирования сложна, но проста в использовании, а наша база данных шаблонов создана профессиональными дизайнерами. Вы можете вернуться к инструменту для рисования логотипа в любое время, чтобы отредактировать свой дизайн логотипа. Просто войдите в свою учетную запись и откройте проект рисования логотипа.
Вы можете вернуться к инструменту для рисования логотипа в любое время, чтобы отредактировать свой дизайн логотипа. Просто войдите в свою учетную запись и откройте проект рисования логотипа.
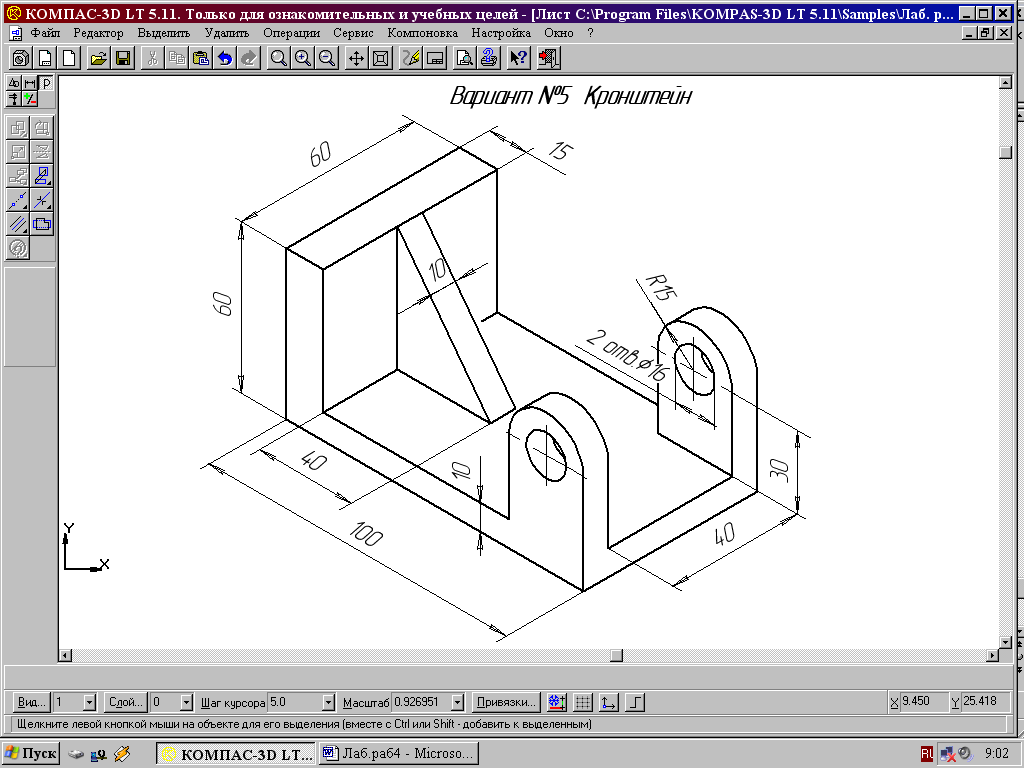



 Для умножения вектора p на число -0.5, сначала переместим параллельно вектор p так, чтобы начальная точка вектора p совпала с началом координат. Получим вектор p’=A’B’ с координатами A’(0,0) и B’(8-2, 1-3)=B’(6,-2). Умножим вектор p’ с числом -0.5:
Для умножения вектора p на число -0.5, сначала переместим параллельно вектор p так, чтобы начальная точка вектора p совпала с началом координат. Получим вектор p’=A’B’ с координатами A’(0,0) и B’(8-2, 1-3)=B’(6,-2). Умножим вектор p’ с числом -0.5: Умножить вектор x=AB на число 3, где A(2,2), B(7,6).
Умножить вектор x=AB на число 3, где A(2,2), B(7,6).

 Вычислить смешанное произведение трех векторов
Вычислить смешанное произведение трех векторов  10.2022 · Ввести силы и углы/направления до 5 различных сил в калькулятор. Калькулятор оценит и отобразит …
10.2022 · Ввести силы и углы/направления до 5 различных сил в калькулятор. Калькулятор оценит и отобразит …
 Из всех действующих сил …
Из всех действующих сил … omnicalculator.com › математика › линейно-комбинированная
omnicalculator.com › математика › линейно-комбинированная

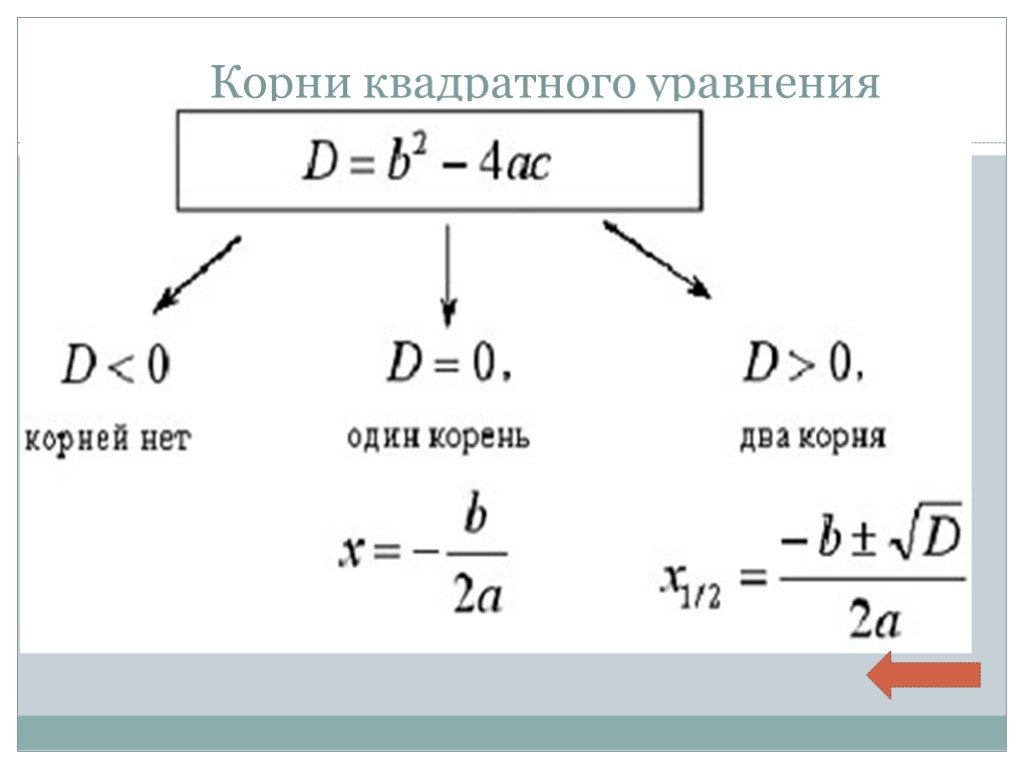 2+3х-10=0 $$– это уравнение приведенное, значит воспользуемся теоремой, обратной теореме Виета.
2+3х-10=0 $$– это уравнение приведенное, значит воспользуемся теоремой, обратной теореме Виета. Но в первом случае, корни совпадают, а во втором – действительных корней нет.
Но в первом случае, корни совпадают, а во втором – действительных корней нет. 1 Другие записи решений
1 Другие записи решений Это выражение является более удобным для практических вычислений при чётном b, то есть для уравнений вида ax2 + 2kx + c = 0.
Это выражение является более удобным для практических вычислений при чётном b, то есть для уравнений вида ax2 + 2kx + c = 0.

 Это можно выразить как √4 = ±2. Это можно проверить следующим образом: (-2) × (-2) = 4 и 2 × 2 = 4. Давайте узнаем больше о формуле квадратного корня на этой странице.
Это можно выразить как √4 = ±2. Это можно проверить следующим образом: (-2) × (-2) = 4 и 2 × 2 = 4. Давайте узнаем больше о формуле квадратного корня на этой странице.
 2 Решение:
2 Решение:  Квадратные корни чисел, отличных от полного квадрата, считаются иррациональными числами. Главный квадратный корень любого отрицательного числа, скажем -x, равен: √(-x)= i√x, где i — квадратный корень из -1.
Квадратные корни чисел, отличных от полного квадрата, считаются иррациональными числами. Главный квадратный корень любого отрицательного числа, скажем -x, равен: √(-x)= i√x, где i — квадратный корень из -1. Квадратный корень — это операция, которая используется во многих формулах и различных областях математики. Эта статья о квадратном корне и формуле квадратного корня. Квадратный корень из числа — это возведение числа в квадрат, которое дает исходное число. В этой статье обсуждаются несколько формул квадратного корня со своими проблемами.
Квадратный корень — это операция, которая используется во многих формулах и различных областях математики. Эта статья о квадратном корне и формуле квадратного корня. Квадратный корень из числа — это возведение числа в квадрат, которое дает исходное число. В этой статье обсуждаются несколько формул квадратного корня со своими проблемами. Они обсуждаются ниже.
Они обсуждаются ниже. Квадратный корень из неполных квадратов, таких как 14, 15, 18 и т. д., можно найти с помощью метода деления в длинную сторону. Чтобы найти квадратный корень с помощью метода деления в длину, мы должны выполнить определенные шаги, которые описаны ниже.
Квадратный корень из неполных квадратов, таких как 14, 15, 18 и т. д., можно найти с помощью метода деления в длинную сторону. Чтобы найти квадратный корень с помощью метода деления в длину, мы должны выполнить определенные шаги, которые описаны ниже. первую пару или цифру и перенесите следующую пару справа от напоминания, чтобы получить новый дивиденд. В приведенном выше примере 2 – 1 = 1, затем мы опускаем следующую пару, т.е. 56, и новое делимое становится 156.0003 Шаг 4. Теперь новый делитель получается путем сложения предыдущего делителя и предыдущей цифры частного и объединения его с подходящей цифрой, которая также берется в качестве следующей цифры частного, выбранной таким образом, чтобы произведение новый делитель, и эта новая цифра в частном равна или чуть меньше нового делимого. В приведенном выше примере предыдущий делитель равен 1, а предыдущая цифра частного равна 1, и их сложение дает 2, что является новым делителем. Теперь нам нужно выбрать цифру так, чтобы произведение нового делителя и новой цифры в частном было равно или меньше нового делимого, т. е. 26 — это новый делитель, а 6 — новая цифра, объединенная с предыдущей. частное. Текущее частное равно 16,9.0004
первую пару или цифру и перенесите следующую пару справа от напоминания, чтобы получить новый дивиденд. В приведенном выше примере 2 – 1 = 1, затем мы опускаем следующую пару, т.е. 56, и новое делимое становится 156.0003 Шаг 4. Теперь новый делитель получается путем сложения предыдущего делителя и предыдущей цифры частного и объединения его с подходящей цифрой, которая также берется в качестве следующей цифры частного, выбранной таким образом, чтобы произведение новый делитель, и эта новая цифра в частном равна или чуть меньше нового делимого. В приведенном выше примере предыдущий делитель равен 1, а предыдущая цифра частного равна 1, и их сложение дает 2, что является новым делителем. Теперь нам нужно выбрать цифру так, чтобы произведение нового делителя и новой цифры в частном было равно или меньше нового делимого, т. е. 26 — это новый делитель, а 6 — новая цифра, объединенная с предыдущей. частное. Текущее частное равно 16,9.0004 Повторяйте шаги 2, 3 и 4, пока не будут взяты все пары. Теперь полученное частное представляет собой квадратный корень из заданного числа. В приведенном выше примере взяты все пары, поэтому квадратный корень из числа 256 равен 16. 9 кв.
Повторяйте шаги 2, 3 и 4, пока не будут взяты все пары. Теперь полученное частное представляет собой квадратный корень из заданного числа. В приведенном выше примере взяты все пары, поэтому квадратный корень из числа 256 равен 16. 9 кв. √p) = [x / (y – z√p)]×[(y + z√p)/ (y + z√p )]
√p) = [x / (y – z√p)]×[(y + z√p)/ (y + z√p )] 
 А затем повторно запустите команду convert:
А затем повторно запустите команду convert: Кроме того, вы можете повысить свою продуктивность с помощью GIMP благодаря его параметрам настройки и сторонним плагинам.
Кроме того, вы можете повысить свою продуктивность с помощью GIMP благодаря его параметрам настройки и сторонним плагинам. archlinux.org/snapd.git
$ cd snapd
$ makepkg -si
archlinux.org/snapd.git
$ cd snapd
$ makepkg -si
 Pdftoppm читает PDF-файл как PDF-файл и записывает один файл PPM для каждой страницы, PPM-root-nnnnnn.ppm. Где nnnnnn — номер страницы
Pdftoppm читает PDF-файл как PDF-файл и записывает один файл PPM для каждой страницы, PPM-root-nnnnnn.ppm. Где nnnnnn — номер страницы
 png и т. д., Вы будете использовать следующий синтаксис:
png и т. д., Вы будете использовать следующий синтаксис: Независимо от вашей причины, вам нужен соответствующий конвертер PDF в JPG, чтобы справиться с вашими потребностями в преобразовании. JPG — это цифровой формат изображения, содержащий сжатые данные изображения.
Независимо от вашей причины, вам нужен соответствующий конвертер PDF в JPG, чтобы справиться с вашими потребностями в преобразовании. JPG — это цифровой формат изображения, содержащий сжатые данные изображения.  Онлайн-приложение использует шифрование Secure Socket Layer (SSL) для защиты загружаемых пользователями документов от киберпреступников. Он не предоставляет данные пользователей третьим лицам и удаляет их документы через час после конвертации со своих серверов.
Онлайн-приложение использует шифрование Secure Socket Layer (SSL) для защиты загружаемых пользователями документов от киберпреступников. Он не предоставляет данные пользователей третьим лицам и удаляет их документы через час после конвертации со своих серверов. Smallpdf не имеет ограничений по размеру файла.
Smallpdf не имеет ограничений по размеру файла.
 Вы также можете добавлять новые фотографии и простые фигуры, используя бесплатные инструменты для рисования.
Вы также можете добавлять новые фотографии и простые фигуры, используя бесплатные инструменты для рисования. 



 Вы также можете запросить документы у кого угодно по электронной почте для загрузки.
Вы также можете запросить документы у кого угодно по электронной почте для загрузки.

 Вам не нужно загружать какое-либо программное обеспечение или регистрироваться, чтобы пользоваться его услугами.
Вам не нужно загружать какое-либо программное обеспечение или регистрироваться, чтобы пользоваться его услугами. Он совместим с операционными системами Mac и Windows. Вы также можете загрузить его мобильное приложение для более быстрого доступа к инструментам PDF с устройств Android и iOS.
Он совместим с операционными системами Mac и Windows. Вы также можете загрузить его мобильное приложение для более быстрого доступа к инструментам PDF с устройств Android и iOS. Загрузка PDF-файлов для преобразования в формат JPG очень проста в PDF Candy. Просто нажмите кнопку «+Добавить файл», чтобы загрузить PDF-файлы прямо с вашего компьютера, или перетащите PDF-файл, который вы хотите преобразовать, в приложение.
Загрузка PDF-файлов для преобразования в формат JPG очень проста в PDF Candy. Просто нажмите кнопку «+Добавить файл», чтобы загрузить PDF-файлы прямо с вашего компьютера, или перетащите PDF-файл, который вы хотите преобразовать, в приложение. Если вы хотите получить баланс между качеством изображения и размером файла, выберите вариант «Среднее качество».
Если вы хотите получить баланс между качеством изображения и размером файла, выберите вариант «Среднее качество». Пожизненный план для рабочего стола + Интернет стоит 9 долларов.9 на пожизненную лицензию и дает вам доступ к настольному приложению PDF Candy.
Пожизненный план для рабочего стола + Интернет стоит 9 долларов.9 на пожизненную лицензию и дает вам доступ к настольному приложению PDF Candy.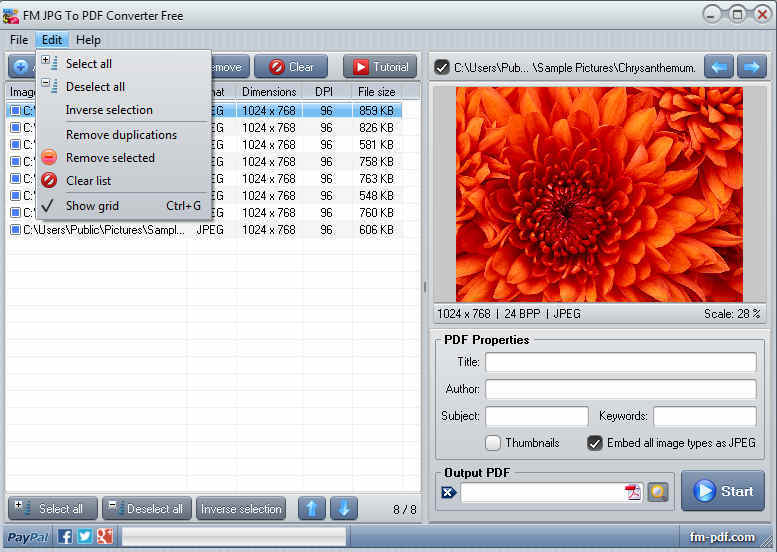
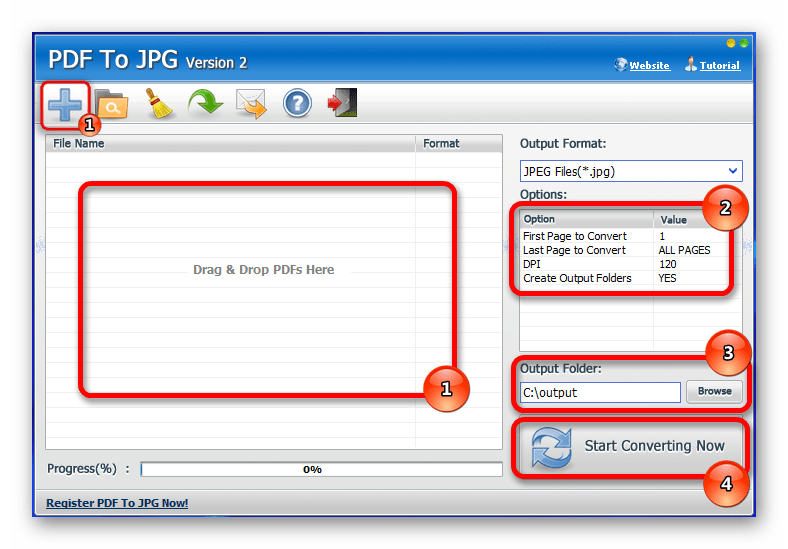
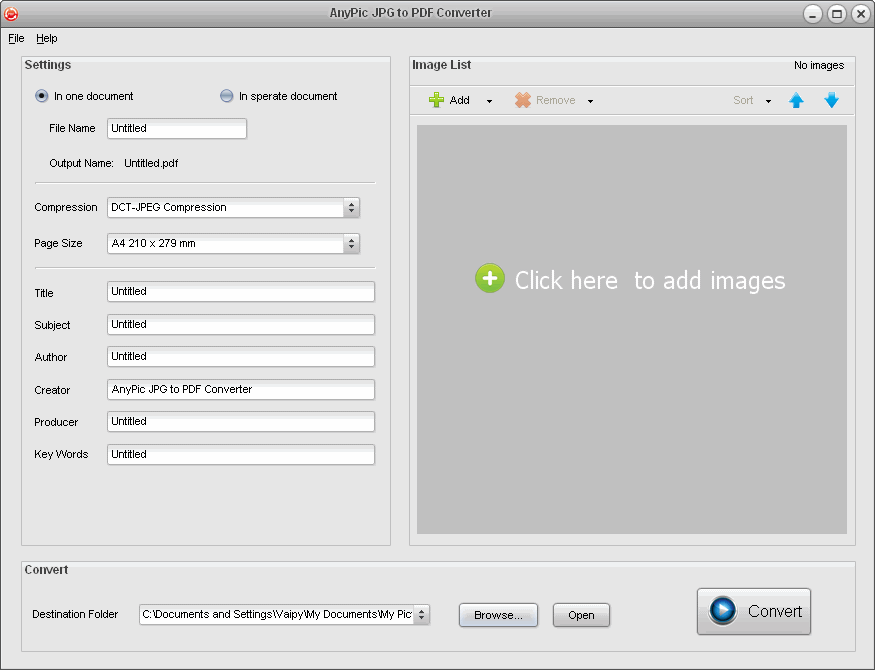 Вы также можете отметить кнопку «Включить коррекцию перекоса», чтобы исправить кривые изображения.
Вы также можете отметить кнопку «Включить коррекцию перекоса», чтобы исправить кривые изображения.
 Конвертер PDF в JPG прост в использовании для всех пользователей, включая тех, кто не знаком с онлайн-приложением.
Конвертер PDF в JPG прост в использовании для всех пользователей, включая тех, кто не знаком с онлайн-приложением.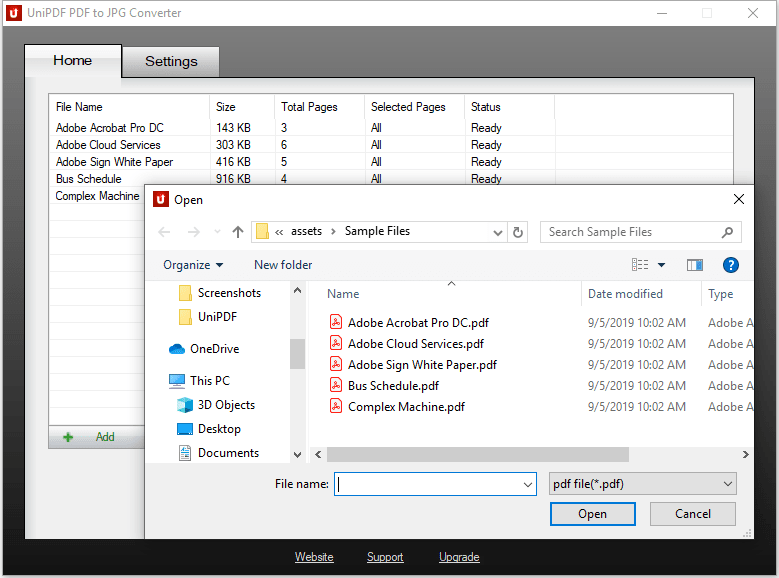 Вам не нужно загружать какое-либо программное обеспечение, чтобы использовать приложение.
Вам не нужно загружать какое-либо программное обеспечение, чтобы использовать приложение. После преобразования вашего PDF-файла в JPG Zonepdf безвозвратно удаляет все записи ваших файлов со своих серверов в течение нескольких часов.
После преобразования вашего PDF-файла в JPG Zonepdf безвозвратно удаляет все записи ваших файлов со своих серверов в течение нескольких часов. Вы можете конвертировать до 20 файлов PDF одновременно. С помощью конвертера PDF в JPG вы можете загрузить до 50 МБ файлов PDF для преобразования в файлы JPG.
Вы можете конвертировать до 20 файлов PDF одновременно. С помощью конвертера PDF в JPG вы можете загрузить до 50 МБ файлов PDF для преобразования в файлы JPG.


 Однажды я спросила у араба:
если ваши цифры арабские, то 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 какие? Он
сказал, что это английские цифры. Некоторые называют их европейскими. В
Википедии написано «современные цифры».
Однажды я спросила у араба:
если ваши цифры арабские, то 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 какие? Он
сказал, что это английские цифры. Некоторые называют их европейскими. В
Википедии написано «современные цифры». ..
..
 firebaseapp.com
https://chrono-b0e6b.firebaseio.com
chrono-b0e6b
chrono-b0e6b.appspot.com
588381206106
конквест
олтайм
оллтайм
алтайм
аллтайм
conquest
alltime
all time
firebaseapp.com
https://chrono-b0e6b.firebaseio.com
chrono-b0e6b
chrono-b0e6b.appspot.com
588381206106
конквест
олтайм
оллтайм
алтайм
аллтайм
conquest
alltime
all time
 Он написал книгу по алгебре, из названия которой слово получена алгебра , и он написал книгу по вычислениям, в которой познакомил Европу с индийско-арабскими цифрами и с тем, как с ними выполнять арифметические действия.
Он написал книгу по алгебре, из названия которой слово получена алгебра , и он написал книгу по вычислениям, в которой познакомил Европу с индийско-арабскими цифрами и с тем, как с ними выполнять арифметические действия. Дом Мудрости приобретал и переводил научные и философские трактаты, особенно греческие, а также публиковал оригинальные исследования. Работа Аль-Хорезми по элементарной алгебре, Al-Kitāb al-mukhtasar fī ḥisāb al-jabr waʾl-muqābala («Краткая книга по вычислениям путем завершения и уравновешивания») была переведена на латынь в 12 веке, от которой происходит название и термин алгебра . Алгебра представляет собой сборник правил вместе с демонстрациями для поиска решений линейных и квадратных уравнений, основанных на интуитивных геометрических аргументах, а не на абстрактных обозначениях, которые теперь связаны с предметом. Его систематический, демонстративный подход отличает его от более ранних трактовок предмета. Он также содержит разделы о вычислении площадей и объемов геометрических фигур и об использовании алгебры для решения проблем наследования в соответствии с пропорциями, предписанными исламским правом. Элементы в работе можно проследить от вавилонской математики начала 2-го тысячелетия до н.
Дом Мудрости приобретал и переводил научные и философские трактаты, особенно греческие, а также публиковал оригинальные исследования. Работа Аль-Хорезми по элементарной алгебре, Al-Kitāb al-mukhtasar fī ḥisāb al-jabr waʾl-muqābala («Краткая книга по вычислениям путем завершения и уравновешивания») была переведена на латынь в 12 веке, от которой происходит название и термин алгебра . Алгебра представляет собой сборник правил вместе с демонстрациями для поиска решений линейных и квадратных уравнений, основанных на интуитивных геометрических аргументах, а не на абстрактных обозначениях, которые теперь связаны с предметом. Его систематический, демонстративный подход отличает его от более ранних трактовок предмета. Он также содержит разделы о вычислении площадей и объемов геометрических фигур и об использовании алгебры для решения проблем наследования в соответствии с пропорциями, предписанными исламским правом. Элементы в работе можно проследить от вавилонской математики начала 2-го тысячелетия до н. э. через эллинистические, еврейские и индуистские трактаты.
э. через эллинистические, еврейские и индуистские трактаты.
 , Пиза? — умер после 1240 г.), средневековый итальянский математик, написавший Liber abaci (1202; «Книга счетов»), первая европейская работа по индийской и арабской математике, которая представила Европе индийско-арабские цифры. Его имя в основном известно из-за последовательности Фибоначчи.
, Пиза? — умер после 1240 г.), средневековый итальянский математик, написавший Liber abaci (1202; «Книга счетов»), первая европейская работа по индийской и арабской математике, которая представила Европе индийско-арабские цифры. Его имя в основном известно из-за последовательности Фибоначчи. Первые семь глав были посвящены обозначениям, объяснению принципа разрядности, согласно которому положение цифры определяет, является ли она единицей, 10, 100 и т. д., и демонстрации использования числительных в арифметических операциях. Затем эти методы были применены к таким практическим проблемам, как размер прибыли, бартер, обмен денег, преобразование мер и весов, партнерские отношения и проценты. Большая часть работы была посвящена спекулятивной математике — пропорции (представленной такими популярными средневековыми методами, как правило трех и правило пяти, которые представляют собой эмпирические методы нахождения пропорций), правилу ложного положения (метод с помощью которого проблема решается с помощью ложного предположения, затем исправляется пропорцией), извлечения корней и свойств чисел, заканчивая некоторой геометрией и алгеброй. В 1220 году Фибоначчи опубликовал короткую работу «9».0033 Practica geometriae («Практика геометрии»), который включал восемь глав теорем, основанных на элементах Евклида и о подразделениях .
Первые семь глав были посвящены обозначениям, объяснению принципа разрядности, согласно которому положение цифры определяет, является ли она единицей, 10, 100 и т. д., и демонстрации использования числительных в арифметических операциях. Затем эти методы были применены к таким практическим проблемам, как размер прибыли, бартер, обмен денег, преобразование мер и весов, партнерские отношения и проценты. Большая часть работы была посвящена спекулятивной математике — пропорции (представленной такими популярными средневековыми методами, как правило трех и правило пяти, которые представляют собой эмпирические методы нахождения пропорций), правилу ложного положения (метод с помощью которого проблема решается с помощью ложного предположения, затем исправляется пропорцией), извлечения корней и свойств чисел, заканчивая некоторой геометрией и алгеброй. В 1220 году Фибоначчи опубликовал короткую работу «9».0033 Practica geometriae («Практика геометрии»), который включал восемь глав теорем, основанных на элементах Евклида и о подразделениях .

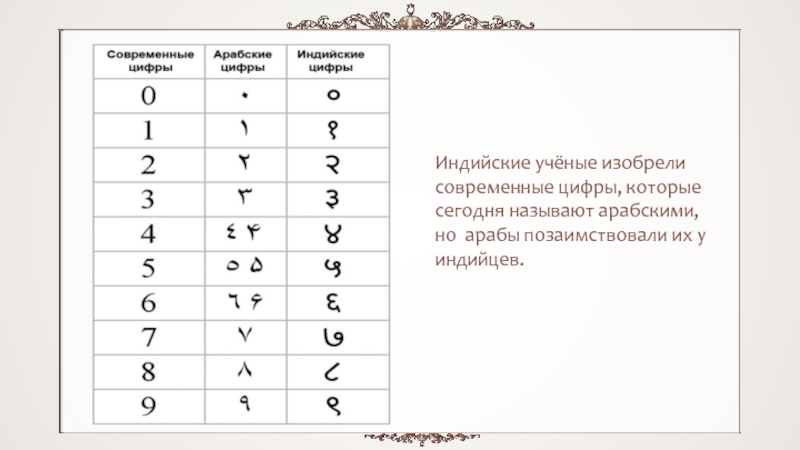 Хотя Liber abaci был более влиятельным и более широким по своему охвату, только Liber quadratorum считает Фибоначчи основным вкладом в теорию чисел между Диофантом и французским математиком 17-го века Пьером де Ферма.
Хотя Liber abaci был более влиятельным и более широким по своему охвату, только Liber quadratorum считает Фибоначчи основным вкладом в теорию чисел между Диофантом и французским математиком 17-го века Пьером де Ферма. Члены последовательности были сформулированы в формуле французским математиком Альбером Жираром в 1634 году: u n + 2 = u n + 1 + u n , где u представляет термин, а нижний индекс — его ранг в последовательности. Математик Роберт Симсон из Университета Глазго в 1753 году заметил, что по мере того, как числа увеличиваются по величине, отношение между следующими друг за другом числами приближается к числу α, , золотому сечению, значение которого равно 1,6180… или (1 + квадратный корень из √5)/2. В 19 веке французским математиком Эдуардом Лукасом был введен термин последовательность Фибоначчи , и ученые стали обнаруживать такие последовательности в природе; например, в спиралях головок подсолнуха, в сосновых шишках, в правильном происхождении (генеалогии) самца пчелы, в родственной логарифмической (равноугольной) спирали в раковинах улиток, в расположении листовых почек на стебле и в рога животных.
Члены последовательности были сформулированы в формуле французским математиком Альбером Жираром в 1634 году: u n + 2 = u n + 1 + u n , где u представляет термин, а нижний индекс — его ранг в последовательности. Математик Роберт Симсон из Университета Глазго в 1753 году заметил, что по мере того, как числа увеличиваются по величине, отношение между следующими друг за другом числами приближается к числу α, , золотому сечению, значение которого равно 1,6180… или (1 + квадратный корень из √5)/2. В 19 веке французским математиком Эдуардом Лукасом был введен термин последовательность Фибоначчи , и ученые стали обнаруживать такие последовательности в природе; например, в спиралях головок подсолнуха, в сосновых шишках, в правильном происхождении (генеалогии) самца пчелы, в родственной логарифмической (равноугольной) спирали в раковинах улиток, в расположении листовых почек на стебле и в рога животных.
 Гидроксид кальция взаимодействует со сложными веществами:
Гидроксид кальция взаимодействует со сложными веществами: 1.4. С гидроксидом кальция реагирует сероводородная кислота, образуя гидросульфид кальция и воду:
1.4. С гидроксидом кальция реагирует сероводородная кислота, образуя гидросульфид кальция и воду: 4. Гидроксид кальция реагирует с солями:
4. Гидроксид кальция реагирует с солями: ..
..

 Но сегодня другое время. Мы все больше работаем, а на досуг часто остаются вечерние или ночные часы. Да и многим очень полюбился способ игры через компьютерные программы. Как совместить интерфейс ПК, реального партнера по шахматам и возможность сражаться в любое время дня и ночи? Предлагаем вашему вниманию удобный сервис, где вы можете играть в шахматы онлайн с живыми игроками. Вам будет интересно на нашем сайте.
Но сегодня другое время. Мы все больше работаем, а на досуг часто остаются вечерние или ночные часы. Да и многим очень полюбился способ игры через компьютерные программы. Как совместить интерфейс ПК, реального партнера по шахматам и возможность сражаться в любое время дня и ночи? Предлагаем вашему вниманию удобный сервис, где вы можете играть в шахматы онлайн с живыми игроками. Вам будет интересно на нашем сайте. Это позволит вам познакомиться с другими стилями и школами шахматной игры.
Это позволит вам познакомиться с другими стилями и школами шахматной игры. Уже через несколько минут после первого посещения сайта любой пользователь легко сможет создать партию и найти достойного соперника. Если же у вас останутся вопросы, то задайте их сотрудникам нашего сайта, чтобы они смогли вам помочь.
Уже через несколько минут после первого посещения сайта любой пользователь легко сможет создать партию и найти достойного соперника. Если же у вас останутся вопросы, то задайте их сотрудникам нашего сайта, чтобы они смогли вам помочь. Кроме того, для оттачивания навыков, воспользуйтесь специальным инструментом – решение шахматных задач. Мы внедрили на наш портал разнообразные программы для решения комбинаций. Также советуем обратиться к нашей базе дебютной базе. Четкое знание первых ходов поможет вам гораздо сильнее играть в начальной стадии шахматной партии.
Кроме того, для оттачивания навыков, воспользуйтесь специальным инструментом – решение шахматных задач. Мы внедрили на наш портал разнообразные программы для решения комбинаций. Также советуем обратиться к нашей базе дебютной базе. Четкое знание первых ходов поможет вам гораздо сильнее играть в начальной стадии шахматной партии. Нет ничего лучше, чем найти единомышленников, разделяющих ваши увлечения. Шахматы онлайн как раз и являются замечательной формой коммуникации между самыми разными людьми.
Нет ничего лучше, чем найти единомышленников, разделяющих ваши увлечения. Шахматы онлайн как раз и являются замечательной формой коммуникации между самыми разными людьми. А психологический компонент обычно в игре с машиной отсутствует. С реальным противником такой проблемы нет по определению.
А психологический компонент обычно в игре с машиной отсутствует. С реальным противником такой проблемы нет по определению.

 Bullet, Blitz или Slow игры. Никаких намеков.
Bullet, Blitz или Slow игры. Никаких намеков. Фриц играет как человек и допускает тонкие тактические ошибки.
Фриц играет как человек и допускает тонкие тактические ошибки. Множество способов сокрушить соперника и улучшить свои шахматные навыки БЕСПЛАТНО.
Турниры, команды, рейтинг, лига, шахматная тактика, головоломки и многое другое.
Вам понравится играть в шахматы онлайн — обещаем!
Вы сами выбираете, как часто ходить, не нужно заканчивать шахматные партии за один присест — возвращайтесь
когда у вас есть время играть онлайн, сегодня или завтра. Играйте в несколько шахматных партий онлайн одновременно,
пробуйте разные стратегии и шахматные дебюты.
Никаких дополнительных программ для загрузки, простая навигация, бесплатная регистрация, онлайн-шахматы в лучшем виде!
Множество способов сокрушить соперника и улучшить свои шахматные навыки БЕСПЛАТНО.
Турниры, команды, рейтинг, лига, шахматная тактика, головоломки и многое другое.
Вам понравится играть в шахматы онлайн — обещаем!
Вы сами выбираете, как часто ходить, не нужно заканчивать шахматные партии за один присест — возвращайтесь
когда у вас есть время играть онлайн, сегодня или завтра. Играйте в несколько шахматных партий онлайн одновременно,
пробуйте разные стратегии и шахматные дебюты.
Никаких дополнительных программ для загрузки, простая навигация, бесплатная регистрация, онлайн-шахматы в лучшем виде! ..
.. ..
..