- Si(x)
- Интегральный синус от x
- Ci(x)
- Интегральный косинус от x
- Shi(x)
- Интегральный гиперболический синус от x
- Chi(x)
- Интегральный гиперболический косинус от x
- Действительные числа
- вводить в виде 7.
 3
3- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- 15/7
- — дробь
Другие функции:
- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от x
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:
- pi
- Число «Пи», которое примерно равно ~3.
 14159..
14159.. - e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
решите уравнение 1) х — 7 8/11 = 2 5/11, 2) 3 7/17-( x+1 4/17) = 1 9/17 разъясните подробнее решение уравнений. — Знания.site
Ответы 1
1) х — 7 8/11 = 2 5/11,х = 2 5/11 + 7 8/11
х = 9 13/11 = 10 2/11 (так как дробь 13/11 неправильная у нее можно убрать еще цифры в целое поделив 13 : 11 = 1 целая и сколько там, тогда эту 1 * 13 = 13 — 11 = 2 остается в числителе, а 9 + 1 = 10 целых получается)
2) 3 7/17-( x+1 4/17) = 1 9/17
х + 1 4/17 = 3 7/17 — 1 9/17 (т.к. мы не можем от 7 отнять 9, то можем у 3 целых забрать 1 единицу и превратить 3 7/11 в 2 24/17 это так берем 1 * 17 + 7 = 24 идет в числитель, а 3 — 1 = 2 целых остается, знаменатель не меняется при этом никогда)
х + 1 4/17 = 2 24/17 — 1 9/17
х + 1 4/17 = 1 15/17
х = 1 15/17 — 1 4/17
х = 11/17
Знаешь ответ? Добавь его сюда!
Последние вопросы
- ОБЖ
16 минут назад
8.
 Наиболее частые заболевания, связанные с сосудосуживающим действием никотина:
Наиболее частые заболевания, связанные с сосудосуживающим действием никотина:a) Инфаркт миокарда б) Переживающая хромота или гангрена конечности
b) Кровоточивость из носа и ушей г) Расширение вен нижних конечностей д) Гипотония
- Математика
2 часа назад
20.000 — 282 x 750 / 47 + 989 пожалуйста помогите мне
- Химия
4 часа назад
определить массу 5,6 л. Аргона при давлении 202,6 кПа и t27 градусов Цельсия . Решить задачу двумя способами
- Физика
5 часов назад
Металлическое тело кубической формы со стороной 10 см плавает в резервуаре с ртутью. В резервуар налили жидкость таким образом, что её верхний уровень совпал с верхней горизонтальной поверхностью тела.
 Рассчитай высоту столба налитой в резервуар жидкости.
Рассчитай высоту столба налитой в резервуар жидкости.Справочные данные: плотность металла — 11350 кг/м³, плотность ртути — 13600 кг/м³, плотность жидкости — 1030 кг/м³. (Ответ округли до десятых.)
- Физика
20 часов назад
Металлический предмет кубической формы со стороной 40 см плавает в сосуде с ртутью. В сосуд налили жидкость таким образом, что её верхний уровень совпал с верхней горизонтальной поверхностью предмета. Рассчитай высоту столба налитой в сосуд жидкости. Справочные данные: плотность металла 7800 кг/м³, плотность ртути 13600 кг/м³, плотность жидкости — 1000 кг/м³.
(Ответ округли до десятых.)
- Математика
20 часов назад
Маша кормит собачек
У Маши три собачки Диди, Мими и Фифи. Диди весит 3 кг, Фифи 3,5 кг, а Мими 4,5 кг.

Всего у Маши 33 кг корма на месяц для собачек. Она хочет пересыпать корм в коробки пропорционально весу каждой собаки. Сколько корма в какую коробку она должна пересыпать? Ответы дайте в килограммах.
- Физика
21 часов назад
Металлический предмет кубической формы со стороной 30 см. плавает в резервуаре с ртутью. В резервуар налили жидкость таким образом, что её верхний уровень совпал с верхней горизонтальной поверхностью предмета. Найди высоту столба налитой в резервуар жидкости. Справочные данные: плотность металла 2700 кг/м², плотность ртути — 13600 кг/м³, плотность жидкости — 1000 кг/м³.
(Ответ округли до десятых.)
- Другие предметы
1 день назад
Что это означает?
- Математика
1 день назад
сторона правильной треугольной пирамиды равна 8 найдите площадь полной поверхности пирамиды если ее апофема равна корень 8 из 3
- Математика
1 день назад
сторона правильной треугольной пирамиды равна 8 найдите объем пирамиды если ее апофема равна 13
- Математика
1 день назад
два ребра прямоугольного паралепипеда выходящие из одной вершины равны 72 и 18 найти объем
- Математика
2 дня назад
У трикутнику ABC <A= 90°, <B=30°, АВ=6 см.
 Знайдіть інші сторони трикутника.
Знайдіть інші сторони трикутника. - Химия
2 дня назад
Алканы.Непредельные углеводороды. Арены
Назовите следующие соединения
- Физика
2 дня назад
Линза имеет оптическую силу 2 дптр, и дала увеличение поставленного перед ней объекта в 25 раз. Найти расстояние от линзы до поставленного объекта. Ответ дайте в см, округлив до целого числа. СРОЧНО МОЛЮ(((
- Математика
2 дня назад
В коробке находится 15 теннисных мячей, 9 из которых новые. Для первой игры случайным образом выбираются три мяча, которые после игры возвращаются в коробку. Для второй игры снова случайным образом выбираются три мяча. Вычислите вероятность того, что все три мяча, выбранные для второй игры, новые. какой будет %
какой будет %
How much to ban the user?
1 hour 1 day 100 years| 1 | Найти производную — d/dx | бревно натуральное х | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | Найти производную — d/dx | 92)||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 22 | Найти производную — d/dx | грех(2x) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 43 | Оценка интеграла 9бесконечность | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 45 | Найти производную — d/dx | х/2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 46 | Найти производную — d/dx | -cos(x) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 47 | Найти производную — d/dx | грех(3x) | 92+1|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 68 | Оценить интеграл | интеграл от sin(x) по x | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 69 | Найти производную — d/dx | угловой синус(х) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 85 | Найти производную — d/dx | лог х | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 86 | Найти производную — d/dx | арктан(х) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 87 | Найти производную — d/dx | бревно натуральное 5х92-(1-x)=0Пошаговое решение :Шаг 1 :Попытка факторизовать путем разделения среднего члена 09 Первый член, x 2 его коэффициент равен 1 . Шаг-1: Умножьте коэффициент первого члена на константу 1 • -1 = -1 Шаг-2: Найдите два множителя -1, сумма которых равен коэффициенту среднего члена, который равен 1 .
Уравнение в конце шага 1 :x 2 + x - 1 = 0 Шаг 2 :Парабола, поиск вершины :2.1 Найти вершину y = x 2 +x-1 Параболы имеют самую высокую или самую низкую точку, называемую вершиной. Наша парабола раскрывается и, соответственно, имеет низшую точку (абсолютный минимум). Мы знаем это еще до того, как начертили «у», потому что коэффициент первого члена, 1 , положителен (больше нуля). Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину. Из-за этой симметрии линия симметрии, например, будет проходить через середину двух точек пересечения x (корней или решений) параболы. То есть, если парабола действительно имеет два действительных решения. Параболы могут моделировать многие реальные жизненные ситуации, такие как высота над землей объекта, брошенного вверх через некоторый период времени. Вершина параболы может предоставить нам такую информацию, как максимальная высота, на которую может подняться объект, брошенный вверх. По этой причине мы хотим иметь возможность найти координаты вершины. Для любой параболы, Ax 2 +Bx+C, x-координата вершины определяется как -B/(2A) . В нашем случае координата x равна -0,5000 Подставляя в формулу параболы -0,5000 вместо x, мы можем вычислить координату y: Корневой график для: y = x 2 +x-1 Решите квадратное уравнение, заполнив квадрат 2. Добавьте 1 к обеим частям уравнения: Теперь немного хитрости: возьмите коэффициент при x , равный 1, разделите на два, получив 1/2, и, наконец, возведите его в квадрат. что дает 1/4 Добавьте 1/4 к обеим частям уравнения: Добавление 1/4 завершило левую часть в полный квадрат: Мы будем называть это уравнение уравнением #2. Грэхем Р., Кнут Д., Паташник О. Конкретная математика. Основание информатики: Пер. с англ. —М.: Мир, 1998. —703 с.
Название этой оригинальной как по содержанию, так и по форме книги знаменитых американских математиков можно расшифровать как КОНтинуальная и дисКРЕТНАЯ математика. Прообразом книги послужил раздел «Математическое введение» первого тома фундаментальной монографии Д. Кнута «Искусство программирования для ЭВМ» (М.: Мир, 1976). Ее назначение — дать читателю технику оперирования с дискретными объектами, аналогичную технике для непрерывных объектов. Название книги можно понимать и буквально — обучение общим методам ведется на многочисленных конкретных примерах и упражнениях разной степени сложности. При переводе на русский язык учтены исправления авторов 1998 года.
Книгу, без сомнения, можно рекомендовать всем изучающим и применяющим дискретную математику и информатику. Она раскрывает тайну одного феномена американского образования — как превращать малограмотных школьников в прекрасных математиков.
Рассмотрим последовательность элементов , первые элементов которой известны. Всякую конечную последовательность элементов можно рассматривать как бесконечную, считая все её элементы, начиная с некоторого номера, равными нулю. Определение. Рекуррентным соотношением между элементами последовательности называется формула вида ,. Например, рекуррентное соотношение , , задает Последовательность чисел Фибоначчи: 1, 1, 2, 3, 5, 8,… Для вычисления любого элемента последовательности с помощью заданного рекуррентного соотношения требуется вычисление всех предыдущих её элементов. Рассмотрим последовательность элементов . — известные начальные значения последовательности элементов, удовлетворяющих линейному неоднородному рекуррентному соотношению (1): , (1) — известные действительные числа. Тогда (2) – линейное однородное рекуррентное соотношение, соответствующее (1): . (2) Определение. Характеристическим Уравнением, соответствующим (2), называется уравнение вида . (3) Корни уравнения (3) называются характеристическими числами рекуррентного соотношения (1). Теорема 13.1. (О структуре общего решения линейного неоднородного рекуррентного соотношения (1)). Пусть общее решение линейного однородного рекуррентного соотношения (2), — Любое частное решение линейного неоднородного рекуррентного соотношения (1). Теорема 13.2. (О структуре общего решения линейного однородного рекуррентного соотношения (2)). Если — действительный корень характеристического уравнения (3) кратности , то общее решение линейного однородного рекуррентного соотношения (2) вычисляется по формуле , где — многочлен степени по переменной N, . Коэффициенты определяются из начальных значений рекуррентного соотношения. Общее решение рекуррентного соотношения (2) при и действительных корнях уравнения (3) и имеет вид при , при =. Пример. Выведем формулу Бине для вычисления последовательности чисел Фибоначчи. Решение. , — линейное однородное рекуррентное соотношение с постоянными коэффициентами , начальные значения , . Составим характеристическое уравнение и найдем характеристические числа и . Характеристическое уравнение имеет два различных корня кратности 1, значит, . Решением системы является пара чисел и . Таким образом, .□ Полученная формула называется формулой Бине и применяется для вычисления значений последовательности Фибоначчи только по их номеру, независимо от предыдущих членов последовательности. Замечание. Часто рассматривается последовательность . Например, для последовательности чисел Фибоначчи 0, 1, 1, 2, 3, 5, … рекуррентное соотношение записывается в виде , . Задачи и упражнения. 13.1. Найдите формулу общего члена последовательности чисел, заданной рекуррентным соотношением , . Вычислите с помощью рекуррентного соотношения и по общей формуле. 13.2. Найдите формулу общего члена последовательности чисел, заданной рекуррентным соотношением , . Вычислите с помощью рекуррентного соотношения и по общей формуле. 13.3. Составьте рекуррентное соотношение последовательности квадратов натуральных чисел. 14. Понятие производящей функции. Рассмотрим последовательность чисел . (1) Рассмотрим также последовательность функций действительной или комплексной переменной . (2) Формально составим функциональный ряд, используя элементы (1) и (2): . (3) Будем считать ряд (3) сходящимся абсолютно на Или в некоторой области комплексной плоскости. Функция Является суммой ряда (3). Определение. Сумма ряда (3) называется Производящей функцией для заданной последовательности чисел (1) по заданной последовательности функций (2). Чаще других используются степенные функции Или . Поэтому ряд (3), как правило, является степенным. Например. Положим в формуле бинома Ньютона . Тогда . Значит, функция является производящей функцией для последовательности биномиальных коэффициентов по системе степенных функций . Пример. Составить производящую функцию последовательности чисел Фибоначчи , , . Решение. Используем последовательность функций действительной переменной Умножим рекуррентное соотношение на и просуммируем по : . (4) По допущению все ряды абсолютно сходятся на R. . Подставив суммы в (4), получим , тогда .□ Задачи и упражнения. 14.1. Докажите, что функция является производящей для последовательности числе, общий член которой имеет вид . 14.2. Найдите производящую функцию для последовательности чисел . 14.3. Найдите общий член последовательности, для которой функция является производящей. 14.4. Найдите общий член последовательности, для которой функция является производящей. Примечание. Термин «формальный» используется потому, что это алгебраическое, а не аналитическое понятие. В приведенном выше примере мы могли бы просто подсчитать количество способов получения \( 10 \) путем проверки. Однако производящие функции невероятно полезны, если полиномы могут быть выражены в более компактной форме (например, с использованием суммы геометрического ряда), а затем умножение может привести к сокращению и упрощению вычислений. 92 \), следовательно, мы можем вычислить его напрямую, не считая каждого члена в отдельности. \(_\квадрат\) Сколько решений в целых неотрицательных числах имеет уравнение \(a + b + c = 20\)? Сначала мы рассмотрим более общий вопрос о нахождении числа решений в неотрицательных целых числах уравнения \(a + b + c = n \). Следовательно, при \(n=20 \) ответ равен \( { 22 \выбрать 2 } \). Это согласуется с тем, что мы знаем из метода звезд и полос. \(_\квадрат\) Примечание. Может показаться запутанным, почему мы допускаем, что \(a\) может быть любым неотрицательным целым числом, даже большим, чем \(n\), что явно не приведет к решению. Подумайте, что произойдет, если мы допустим \(a = n+1\) или \(a = n+2\) или любое большее целое число: в конечном произведении полиномов показатели степени этих членов будут больше, чем \(n ,\), поэтому они не будут вносить вклад в нужный нам член, который имеет показатель степени \(n.\) У Коди есть 4 вида луковиц: Если у Коди 23 луковицы, сколько может быть различных распределений цветов? Вопрос ниже можно решить звездочками и полосками, но это утомительно. Мы можем решить ее, используя производящие функции. Найдите количество неотрицательных целых решений уравнения \[ 3x +y + z = 24.\] Попробуйте также: Есть \(10\) \( \mathrm{\color{red {красный}}\) шары, \(10\) \(\mathrm{\color{синий}}{синий}}\) шары и \(10\) \( \ mathrm{\color{зеленый} {зеленый} }}\) мячи. Сколькими способами можно выбрать \(16\) шаров так, чтобы было хотя бы по одному шару каждого цвета? 9{\infty}\) — это способ выражения \(c_n\) через \(k\) предыдущих членов последовательности для некоторого положительного целого числа \(k.\). Однородное линейное рекуррентное отношение — это отношение form \(c_n + q_1c_{n-1} + q_2c_{n-2} + \cdots +q_kc_{n-k} = 0. , где у нас есть \(j+1\) начальные члены \(c_0,c_1,\ldots,c_k\), а \(m_i\) определены как \[\begin{ массив}{л}
m_0 = c_0\\
m_1 = c_1 + q_1c_0\\
m_2 = c_2 + q_1c_1 + q_2c_0.
\end{array}\] Мы можем использовать это, чтобы явно найти \(c_k\), найдя корни знаменателя и разложив рациональную функцию на частные дроби. Мы можем найти коэффициент при \(c_k\), применяя теорему отрицательного бинома к каждому члену. Таким образом, мы можем сделать следующий вывод: 9п.\] Константы \(a_{1,1}, a_{1,2}, \ldots, a_{j,m_j}\) выбраны так, чтобы удовлетворять начальным условиям. Обратите внимание, что общее количество этих констант равно \(k,\), поэтому нам нужны \(k\) начальных значений. 64
66
69
72 Есть 30 следующих шаров: Сколькими способами можно разделить эти шары на 2 ящика A и B так, чтобы в каждом ящике было по 15 шаров? У вас есть 10 различных пустых контейнеров: 6 могут содержать до 3 л воды и 4 могут содержать до 8 л воды. Сколькими способами можно наполнить эти сосуды ровно 46 л воды так, чтобы количество литров воды в каждом сосуде было целым числом? Детали и предположения: \[ \begin{eqnarray} 0. && 00000 \quad 00001 \quad 00001 \quad 00002 \quad 00003 \quad 00005 \quad 00008 \\ && 00013 \quad 00021 \quad 00034 \quad 00 055 \четверка 00089\четверка 00144 \quad \ldots \\ \end{eqnarray} \] Выше показаны первые несколько цифр (фактически 65) десятичного представления дроби \( \large \frac1{9,999,899,999}. Примечание: Например, предположим, что дробь равна \[0,00000 \quad 00001 \quad 00001 \quad 00002 \quad 00003 \quad 00009 \ldots \] вместо той, что указана вверху. Тогда вы сможете найти только первые пять чисел Фибоначчи, а именно \(0,1,1,2,3\). Таким образом, ваш ответ будет заключаться в том, что есть 4 положительных числа Фибоначчи, прежде чем модель прервется. Вот интересная особенность этого выражения: поскольку
$|(1-\sqrt5)/2| Мы можем проверить это в Sage. Пример 3.4.4 Найдите производящую функцию решений задачи $h_n=4h_{n-2}$,
$h_0=0$, $h_1=1$ и используйте его, чтобы найти формулу для $h_n$. (Это легко
открыть эту формулу непосредственно; дело здесь в том, чтобы увидеть, что
метод производящей функции дает правильный ответ.) Пример 3.4.5 Найдите производящую функцию решений
$h_n=h_{n-1}+h_{n-2}$, $h_0=1$, $h_1=3$ и используйте его, чтобы найти формулу
за $h_n$. Пример 3.4.6 Найдите производящую функцию решений
$h_n=9h_{n-1}-26h_{n-2}+24h_{n-3}$, $h_0=0$, $h_1=1$, $h_2=-1$,
и используйте его, чтобы найти формулу для $h_n$. Пример 3.4.7 Найдите производящую функцию решений
$h_n=3h_{n-1}+4h_{n-2}$, $h_0=0$, $h_1=1$,
и используйте его, чтобы найти формулу для $h_n$. Пример 3.4.8 Найдите рекурсию количества способов расставить флаги на
$n$ футовый столб, где у нас есть красные флаги высотой 2 фута, синие
флаги высотой 1 фут и желтые флаги высотой 1 фут; в
высота флагов должна составлять $n$. Мы уже преобразовали файлы 813,522,715 с общим размером 6,574 TB. онлайн Перерабатывать DBF К XLS Используйте OnlineConvert Online. Бесплатно быстро! Регистрация не требуется. Шаг 1 Шаг 2 Шаг 3 XLS — это файл электронной таблицы Microsoft Excel, в котором хранятся данные и выполняется несколько математических операций. Он использует визуальную базовую операцию для реализации нескольких числовых функций. XLS К PDF XLS К JPG XLS К CSV XLS К DOC XLS К XLSX XLS К BMP XLS К JPEG XLS К DOCX XLS К HTML XLS К TXT XLS К PNG XLS К PPT XLS К TIFF XLS К ODT XLS К SVG XLS К GIF XLS К RTF XLS К DOCM XLS К PSD XLS К XPS XLS К EPUB XLS К PPTX XLS К DOTX XLS К PDB XLS К DOT XLS К MOBI XLS К JP2 XLS К MAP XLS К PNM XLS К FAX XLS К PBM XLS К ODP XLS К SXW XLS К ABW XLS К DJVU XLS К CUR XLS К FB2 XLS К HDR XLS К PPS XLS К POT XLS К PICT XLS К PGM XLS К OXPS XLS К OTB XLS К TGA XLS К WBMP XLS К PCX XLS К ICO XLS К PPM XLS К WEBP XLS К EXR XLS К FTS XLS К G3 XLS К HRZ XLS К IPL XLS К MNG XLS К MTV XLS К PAL XLS К PALM XLS К PAM XLS К PCD XLS К PCT XLS К PFM XLS К PICON XLS К RAS XLS К RGB XLS К RGBA XLS К RGBO XLS К SGI XLS К SUN XLS К UYVY XLS К VIFF XLS К XBM XLS К XPM XLS К XV XLS К XWD XLS К YUV XLS К DOTM XLS К DBK XLS К KWD XLS К AW XLS К POTM XLS К POTX XLS К PPSM XLS К PPSX XLS К PPTM XLS К AZW3 XLS К LRF XLS К RB XLS К SNB XLS К TCR XLSX К XLS DOCX К XLS PDF К XLS DOC К XLS CSV К XLS RTF К XLS XPS К XLS HTML К XLS TXT К XLS ODT К XLS OXPS К XLS DOT К XLS DOTX К XLS DOCM К XLS EPUB К XLS PDB К XLS WPS К XLS SNB К XLS DOTM К XLS FB2 К XLS RB К XLS AZW3 К XLS LRF К XLS MOBI К XLS TCR К XLS Размер загружаемого файла : Безлимитный $7. Действительно в течение 24 часов 30 День Размер загружаемого файла : 200M $6.99 Срок действия 1 месяц Размер загружаемого файла : 1G $11.99 Срок действия 1 месяц Размер загружаемого файла : Безлимитный $26.99 Срок действия 1 месяц 365 День Размер загружаемого файла : 200M $27.99 $83.88 / В год Размер загружаемого файла : 1G $44. $143.88 / В год Размер загружаемого файла : Безлимитный $79.99 $323.88 / В год Вертопал — Бесплатный онлайн конвертер Перетащите файлы в любое место для загрузки Преобразование DBF электронных таблиц в XLS формат онлайн и бесплатно. Преобразовать
ДБФ
к
XLS Загрузка загрузчика… если вы загрузили файл, он будет отображаться. Подтвердить
Отмена microsoft-office
превосходить
электронная таблица Выберите любой файл DBF на вашем устройстве, чтобы начать его загрузку. Для настройки DBF до XLS 900 18, используйте доступные инструменты, прежде чем нажимать кнопку «Преобразовать». После завершения преобразования нажмите кнопку «Загрузить», чтобы получить XLS табличный документ. Чтобы изменить формат DBF на XLS, загрузите файл DBF, чтобы перейти на страницу предварительного просмотра. Используйте любые доступные инструменты, если вы хотите редактировать и манипулировать файлом DBF. Нажмите на кнопку преобразования и дождитесь завершения преобразования. После этого загрузите преобразованный файл XLS. macOS Windows Linux Выполните следующие шаги, если вы установили Vertopal CLI в своей системе macOS. Следуйте приведенным ниже инструкциям, если вы установили Vertopal CLI в своей системе Windows. Выполните следующие шаги, если вы установили Vertopal CLI в своей системе Linux. Этот веб-сайт использует файлы cookie. Файлы cookie запоминают вас, поэтому мы можем предоставить вам лучший опыт работы в Интернете.
Узнать больше ОК, СПАСИБО Загрузка, подождите… Выберите исходный файл(ы) для преобразования: 0 из 5 Добавлено файлов (до 300 МБ в сумме) Выберите целевой формат для преобразования: ftxtbibdbfdifdocxfodsfodtltxodsodtotsottpswpxlsdcsdwslkstcstwsxcuosuotwpsxlsxxltxmlcsvdwikijsonmdtextextilewikidbkdocpngbmpgifjpgoddpbmpctpgmppmrassvmtiffxpmcurepdfepiexrfaxftsg3hdrhrzicoipljp2j pegmapmngmtvotbpalpalmpampcdpcxpfmpiconpictpnmpsdrgbrgbargbosgisunsvgztgauyvyviffwbmpxbmxvxwdyuvpwpheifac3aiffamrapecafdtsflacmp3oggwavaacwmam4aamvswfmp43gpasfavidvf4vflvhevcm4vmovmpegmxfogvrmvo bwebm3g2dvdwmvmpgazw3epubfb2htmlzlitlrfmobipdbpmlzrbsnbtcrtxtzpswoffotfttffodpodgodpotpppotmppspptpptxsdasddstisxiuop Нажимая, вы соглашаетесь с нашими условиями Выберите URL-адрес файла для преобразования: Выберите целевой формат для преобразования в: Преобразование файлов в:jarrart7ztartbztbz2tgztxzzipccxcdrcgmcmxfigpltsksk 1svgemfepsfodgmetotgstdsxdwmfpdfhtmlsxwvorxhtmlrtftxtbibdbfdifdocxfodsfodtltxodsodtotsottpswpxlsdcsdwslkstcstwsxcuosuotwpsxlsxxltxmlcsvdwikijsonmdtextextilewikidbkdocpngbmpgifjpgoddpbmpctpgmppmrass vmtiffxpmcurepdfepiexrfaxftsg3hdrhrzicoipljp2jpegmapmngmtvotbpalpalmpampcdpcxpfmpiconpictpnmpsdrgbrgbargbosgisunsvgztgauyvyviffwbmpxbmxvxwdyuvpwpheifac3aiffamrapecafdtsflacmp3oggwavaacwmam4aamvsw Нажимая, вы соглашаетесь с нашими условиями Выберите поставщика облачных услуг: Выберите целевой формат для преобразования: Преобразование файлов в:jarrart7ztartbztbz2tgztxzzzipccxcdrcgmcmxfigpltsksk1svgemfe psfodgmetgstdsxdwmfpdfhtmlsxwvorxhtmlrtftxtbibdbfdifdocxfodsfodtltxodsodtotsottpswpxlsdcsdwslkstcstwsxcuosuotwpsxlsxxltxmlcsvdwikijsonmdtextextilewikidbkdocpngbmpgifjpgoddpbmpctpgmppmrassvmtiffxpm вылечитьpdfepiexrfaxftsg3hdrhrzicoipljp2jpegmapmngmtvotbpalpalmpampcdpcxpfmpiconpictpnmpsdrgbrgbargbosgisunsvgztgauyvyviffwbmpxbmxvxwdyuvpwpheifac3aiffamrapecafdtsflacmp3oggwavaacwmam4aamvswfmp43gpa sfavidvf4vflvhevcm4vmovmpegmxfogvrmvobwebm3g2dvdwmvmpgazw3epubfb2htmlzlitlrfmobipdbpmlzrbsnbtcrtxtzpswoffotfttffodpodgodpotpppotpotmppspptpptxsdasddstisxiuop Нажимая, вы соглашаетесь с нашими условиями Загрузка. ДБФ XLS Письмо 4. Уроки № 6-7. Инструкция. Как работать с письмом? Прочитайте письмо от начала до конца «от корки до корки». Возьмите карандаш и выделите карандашом те фрагменты, которые надо записать в классную тетрадь. Приготовьте учебник, тетрадь, пенал. Начинайте читать третий раз, выполняя записи и упражнения в тетради, соблюдая мои советы. Прочитайте четвертый раз и выделите те моменты, которые вам не понятны. В эфире урока во вторник зададите свои вопросы. Здравствуйте, ребята! Начинается новая неделя «на удаленке». Надеюсь, что вы немного привыкли обучаться самостоятельно. Рада, что многим из вас помогают родители: отправляют сообщения, держат связь с учителями. Это здорово! Большое им спасибо. На этой неделе мы работаем по предмету математика по следующему расписанию: понедельник 13. вторник 14.04.20 – эфир урока в Discord в 9.15 среда 15.04.20 – эфир урока в Discord в 12.00, получаете письмо 5. четверг 16.04.20 – отправляете ответ на письмо 5 до 14.00. На этой неделе у вас будет возможность получить оценки за устные ответы на уроках (во вторник и в среду). Цель на неделю — узнать, для каких операций в математике можно применять разложение числа на простые множители. Задача на неделю – научиться применять разложение на простые множители к сокращению дробей, к нахождению НОД и НОК. Но сначала проверим, как вы усвоили предыдущий урок. 1) проводите разложение «столбиком» (как на рис.) 2) записывайте каноническое разложение . Обратите внимание: всего два пункта. Для тех, кто не смог справиться с этой темой – помните: наше дальнейшее продвижение будет зависеть от того, как вы научитесь выполнять разложение на простые множители. Но большинство из вас получили хорошие и отличные оценки. Я рада и горжусь вашей работой. Надеюсь, что она честная! Сегодня мы поговорим с вами о сокращении дробей. Кто-то возмутится!!!! Мы это уже изучали. Конечно, в 5 классе! Но тема «Разложение на простые множители» — настоящая Золушка в сокращении дробей (вам надо только аккуратно все записать, и ответ будет идеальным, т. Что же мы умеем делать? Как мы раньше сокращали дроби? Вспомним! Открывайте тетрадь и записывайте тему урока «СОКРАЩЕНИЕ ДРОБЕЙ С ПОМОЩЬЮ РАЗЛОЖЕНИЯ НА ПРОСТЫЕ МНОЖИТЕЛИ». 1 способ. Мы знаем основное свойство дроби. Если числитель и знаменатель дроби разделить на одно и то же число, то получится равная ей дробь. Т.е. выполняется равенство . Например, . Такое преобразование мы называли с вами – сокращением дробей. Надеюсь, что вы записали это в тетрадь! 2 способ. Идем дальше, в этом году мы познакомились с признаками делимости и сокращали дроби последовательно. Например, , т.е. сначала сократили на 3, потом 5, далее на 7. Так тоже – верно! А сегодня мы попробуем выполнять сокращение с помощью разложения на простые множители. Откройте учебник стр. 197 №919. Посмотрите, какие «страшные» дроби! Но мы сначала выполним №918. Разложим 350 и 756 на простые множители. Выполните самостоятельно по образцу (только пункт 1(разложение «столбиком»), без канонического разложения). А потом выпишите произведение простых множителей строчкой. Если вы все сделали правильно, то у вас получились следующие ответы, проверьте: 350 = 2∙5∙5∙7 756 = 2∙2∙3∙3∙3∙7. А теперь вернемся к №919 (б). Необходимо сократить дробь . Заменим 350 и 756 на произведение множителей. (Запишите образец в тетрадь). Образец записи. . Все одинаковые множители сокращаем! Помните, я вам писала о Золушке, посмотрите, как и мы быстро справились с этим примером. После разложения нам осталось только вычеркнуть одинаковые множители и выполнить умножение. А ответ – НЕСОКРАТИМАЯ ДРОБЬ. Точно уже ошибок не будет! Преимущество этого способа, действительно в том, что всегда получается несократимая дробь. Выполните тренировочные упражнения. №1. Сократите дроби, предварительно разложив числитель и знаменатель на простые множители: а) б) в) Именно с этих примеров начнем завтрашний урок. За окном – апрель, скоро окончание учебного года, значит, пора подводить итоги. А всё ли вы помните? Давайте проверим. Решайте самостоятельно!!! №2. Решите уравнение №3. Найдите значение числового выражения: (Подумайте, как лучше вычислить) №4. Приведите пример двух чисел, сумма которых меньше их разности, а модуль каждого числа больше 5, но меньше 10. САМОПРОВЕРКА. Ответы к номерам: №1. а) б) в) дробь несократимая №2. х = — 2 (Помните: сначала раскрыть скобки, потом перенос слагаемых – и соблюдайте все правила) №3. 1. Если вы решили неверно, то находите ошибки, а не подгоняйте под ответ! №4. Сумма чисел равна – 6+ 9 = 3. Разность чисел 9 – (– 6) = 15. Сумма 3 меньше разности 15. Мой пример не записывать, воспользуйтесь объяснением и найдите свои примеры чисел. Всего доброго. До свидания. P.S. Надеюсь всё, что напечатано черным шрифтом в письме, у вас записано в тетради. 4.6 Средняя оценка: 4.6 Всего получено оценок: 261. 4.6 Средняя оценка: 4.6 Всего получено оценок: 261. Сокращение дробей тема достаточно трудная для математики 6 класса, поэтому разбирать ее стоит поэтапно. Чтобы не допускать ошибок, первые сокращения лучше делать так же, поэтапно. Приведем алгоритм, чтобы не допускать ошибок и научится быстро и просто сокращать любые дроби. Сначала нужно сказать, что само сокращение дробей возможно благодаря одному из определений дроби. Дробь – это незавершенная операция деления. Имеется в виде, что всегда любую дробь можно заменить частным. Замена дробью нужна, чтобы сохранить точность вычислений. Посмотрим, как выглядит подробное сокращение на примере: $${25\over{40}}=25:40=(5*5):(5*8)=5:8 $$ Чтобы каждый раз не расписывать – это выражение, можно пользоваться правилом сокращения дробей: если умножить или разделить знаменатель на одно и тоже число, то значение дроби не измениться. Теперь запишем сам алгоритм. Для того, чтобы сократить дробь нужно: Вместо того, чтобы расписывать в качестве множителей числитель и знаменатель, можно просто найти НОД числителя и знаменателя. Специальной формулы для сокращения любой дроби не существует, зато можно использовать правила, приведенные в этом алгоритме. Вспомним, как находится НОД: Приведем пример. 150=2*3*5*5 98=2*3*7*7 НОД=2*3=6 Приведем пример сокращения дробей. Для этого упрости дробь ${513216\over{145152}}$. Для примера специально выбраны большие числа, чтобы показать, как самое большое число может стать маленьким в результате упрощения. Мы не будем искать НОД, разложим числа на простые множители и найдем общие значения. 513216:2=256608 – в первую очередь число делится на 2. 256608:2=128304 – деление на 2 продолжается вплоть до момента, когда последняя цифра числа перестанет быть четной. После этого пробуем делить число на 3 и другие простые числа. Все простые числа есть в таблице простых чисел. 128304:2=64152 64152:2=32076 32076:2=16038 16038:2=8019 8019:3=2673 2673:3=891 891:3=297 297:3=99 99:3=33 33:3=11 11:11=1 Запишем результат разложения: 513216=2*2*2*2*2*2*3*3*3*3*3*3*11 – всего получилось 6 чисел 3, 6 чисел 2 и число 11. Таким же образом разложим 145152. 145152:2=72576 72576:2=36288 36288:2=18144 18144:2=9072 9072:2=4536 4536:2=2268 2268:2=1134 1134:2=567 567:3=189 189:3=63 63:3=21 21:3=7 7:7=1 Запишем результаты: 145152=2*2*2*2*2*2*2*2*3*3*3*3*7 – всего 8 чисел 2, 4 числа 3 и одно число 7. В обоих числах нужно сократить 6 чисел 2 и 4 числа 3. Запишем получившийся числитель. В нем останутся числа: 2 числа 3 и число 11 3*3*11=99 Запишем получившийся знаменатель. В нем останутся числа: 2 числа два и число 7 2*2*7=28 В результате сокращения получилась дробь: ${99\over{28}}$ – при желании можно выделить целую часть. Но, если этого не требуется в условии задачи, то допускается оставить ответ в таком виде. Мы поговорили о сокращении дробей. Узнали, почему сокращение возможно. Выяснили, как правильно производить сокращение. Привели алгоритм сокращения и два способа проведения операции. Рассмотрели пример сокращения дробей. Доска почёта Чтобы попасть сюда — пройдите тест. Олеся Смирнова 10/10 Елена Хромова 8/10 Саша Титаренко 10/10 Валентина Чалышева 10/10 4. Средняя оценка: 4.6 Всего получено оценок: 261. А какая ваша оценка? Смешанные и неправильные дробиУмножение и делениеСложение и вычитание полиномиальных дробей В дальнейшем будет иногда полезно помнить, что дроби могут указывать на деление. Например, 1 / 3 может означать «один, разделенный на три», а также «одна часть из трех частей». На самом деле, давайте перейдем к делу; запомните это предложение: «Дроби — это деление». Вы знаете, что любое число, деленное само на себя, равно 1. Вы используете этот факт, когда сокращаете дроби. Если вы можете преобразовать часть данной дроби в форму, умноженную на 1, то вы можете игнорировать эту часть, потому что умножение на 1 ничего не меняет. Содержание продолжается ниже Приведение дробей к наименьшим терминам Например, вот как можно найти и использовать форму 1 для сокращения дроби 4 / 8 в наименьшем члене (то есть в простейшей форме): Чтобы быть предельно ясным, смысл нахождения общего множителя (в данном случае 4-х) состоит в том, чтобы позволить вам преобразовать часть дроби в 1. Внимание: Обратите внимание, как я перешел от дроби с произведениями (в числителе и знаменателе): .. .to произведение дробей: Этот переключатель в порядке, пока вы умножаете: …но это совсем НЕ, если вы добавляете. Например: Левая часть выше, представляющая дробь, содержащую сложение, равна 5 / 6 , а правая часть выше, будучи сложением, содержащим дроби, равна 1 1 / 2 , так что эти два выражения не являются одним и тем же значением. Просто помните: дроби умножать намного проще, чем складывать. Теперь вернемся к делу… В дополнение к методу отмены, который я использовал выше (с розовыми цифрами 1), вы, возможно, видели одно из следующих сокращений для отмены: Любой из этих форматов подходит. Два метода стенографии, вероятно, являются самыми простыми для вашей рукописной домашней работы; формат, который я использовал выше, легче для набора текста. Если у вас есть обычный (научный, деловой и т. д.) калькулятор, который может обрабатывать дроби, вы можете ввести дробь, а затем нажать кнопку «равно», чтобы получить уменьшенную дробь. Если у вас есть графический калькулятор с командой дроби, вы можете ввести дробь как деление (потому что 4 / 8 означает «четыре разделить на восемь»), а затем преобразовать в дробную форму. Подробности смотрите в руководстве пользователя вашего калькулятора. Если ваш калькулятор не может работать с дробями или если знаменатель слишком велик для калькулятора, вам нужно будет выполнить сокращение вручную. (И вам понадобятся концепция и методология приведения дроби в более поздних курсах алгебры.) Помните, что если «все» сокращается, скажем, из числителя, то все равно остается множитель 1. Все всегда умножается на 1, но мы обычно этого не замечаем. Однако, если все нетривиальные множители (то есть все множители, не равные 1) сокращаются путем сопоставления множителей с другой стороны дробной линии, то у вас все еще есть эта 1; фракция не становится безголовой. Я возьму свой калькулятор и лист бумаги и сомножу числитель (верхнее число) и знаменатель (нижнее число). Быстрая запись для получения простой факторизации каждого из этих чисел показана ниже, в суммированном делении (по простым числам) 2940: Чтобы найти факторизацию, я просто прочитал простые множители снаружи верхней стороны. Далее я разложу на множители знаменатель, являющийся числом 3150: Итак, 3150 делим как 2×3×3×5×5×7. Теперь я могу сократить дробь, сократив общие множители: Итак, после сокращения всех множителей, которые дублировались (то есть были общими) в числителе и знаменателе, моя упрощенная форма будет такой: Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в сокращении дробей. Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. Или пропустите виджет и продолжите урок.) Пожалуйста, примите куки-файлы настроек, чтобы включить этот виджет. (Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти на сайт Mathway для платного обновления.) URL: https://www.purplemath.com/modules/fraction.htm 2Page 3Page 4Page 5 Сокращение дроби — это процесс упрощения дроби путем деления числителя и знаменателя на одно и то же число. Чтобы сократить дробь, разделите числитель и знаменатель на наибольший общий делитель. Наибольший общий делитель — это наибольшее число, которое делится без остатка как на числитель, так и на знаменатель. Например, наибольший общий делитель 8 и 12 равен 4. Итак, чтобы уменьшить 8/12, мы должны разделить и 8, и 12 на 4, чтобы получить 2/3. Существует несколько методов сокращения дробей, которые вы можете использовать в зависимости от того, чего вы пытаетесь достичь. Если вы хотите просто уменьшить размер дроби, но не обязательно изменить ее значение, вы также можете разделить и числитель, и знаменатель на любое число. Например, если разделить на 2, дробь уменьшится пополам. Только будьте осторожны, чтобы случайно не изменить его значение! Другой способ сокращения дробей — преобразование их в десятичные. Это можно сделать, разделив числитель на знаменатель. Это даст вам точное значение дроби, которое вы можете затем округлить по мере необходимости. Наконец, если вы хотите превратить смешанную дробь (целое число и дробь) в неправильную дробь (просто числитель над знаменателем), то вы можете умножить целое число на знаменатель и добавить его к числителю. Это даст вам новую неправильную дробь в сокращенной форме. Сокращение дроби — это процесс нахождения более простой эквивалентной дроби. Например, если у нас есть дробь ¾, мы можем видеть, что число 3 является общим делителем между 3 и 4. Если мы разделим и 3, и 4 на 3, мы получим новую дробь 1/1, которая равна ¾. Этот метод можно применить к любой дроби для упрощения. Просто не забудьте найти общий множитель между числителем и знаменателем, а затем разделить оба на это число! Метод GCF (Greatest Common Factor) — отличный способ уменьшить дроби. Этот метод также иногда называют методом наибольшего общего делителя (НОД). GCF двух или более чисел — это наибольшее число, которое делится на все числа без остатка. Чтобы использовать этот метод, начните с нахождения GCF числителя и знаменателя дроби, которую вы хотите уменьшить. Затем разделите числитель и знаменатель дроби на GCF. Это даст вам уменьшенную фракцию с эквивалентным значением. Допустим, мы хотим уменьшить дробь ¾ . Мы начнем с нахождения GCF 3 и 4, который равен 1. Затем мы разделим и 3, и 4 на 1, чтобы получить 3 ÷ 1 = 3 и 4 ÷ 1 = 4. Итак, ¾ можно сократить до ? . Чтобы найти простую факторизацию числа, начните с поиска наименьшего простого числа, которое делится на это число без остатка. Затем продолжайте делить на то же самое простое число, пока не перестанете делить без остатка. В этот момент перейдите к следующему наименьшему простому числу и повторите процесс. Продолжайте до тех пор, пока все множители не станут простыми числами. Чтобы проиллюстрировать это, давайте посмотрим, как найти разложение 48 на простые множители. Наименьшее простое число, которое делится на 48 без остатка, равно 2, поэтому начнем с него: 48 ÷ 2 = 24 Как видите, как только мы дошли до коэффициента 3, мы больше не могли делить без остатка на 2. Когда дело доходит до дробей, одним из самых полезных инструментов, который вы можете иметь, является числовая строка. Числовая линия может помочь вам визуализировать, что означает дробь, и может быть полезным инструментом, когда дело доходит до сокращения дробей. Чтобы сократить дробь, нужно найти ее наибольший общий делитель и разделить числитель и знаменатель на это число. Например, если вы пытаетесь уменьшить дробь ¾, вам нужно найти наибольший общий делитель между 3 и 4. Наибольший общий делитель между 3 и 4 равен 1, поэтому вы должны разделить 3 на 1 и 4 на 1, чтобы получить уменьшенную дробь ½ . Числовые линии могут быть полезным инструментом, когда дело доходит до нахождения наибольшего общего делителя между двумя числами. Если вам трудно представить себе этот процесс, попробуйте нарисовать числовую прямую на листе бумаги. Затем пометьте каждую точку дробями, с которыми вы работаете. После того, как вы это сделаете, вам будет легче понять, как работает нахождение наибольшего общего множителя на числовой прямой. Когда дело доходит до дробей, нет универсального ответа на вопрос, является ли сокращение дроби лучшим способом действий. Это зависит от конкретной ситуации и того, чего вы надеетесь достичь, сократив дробь. В некоторых случаях уменьшение дроби может помочь сделать расчеты проще и точнее. В других случаях сокращение дроби может усложнить задачу. Давайте подробнее рассмотрим плюсы и минусы сокращения дроби: Основное преимущество сокращения дроби заключается в том, что это часто может упростить вычисления. Другим потенциальным преимуществом сокращения дроби является то, что иногда это может сделать результаты более точными. Это особенно верно в тех случаях, когда округление может быть проблемой. Если вы сократите дробь перед выполнением каких-либо вычислений, вы всегда получите максимально точный ответ. С другой стороны, перед сокращением дроби следует принять во внимание некоторые недостатки. Одним из недостатков является то, что иногда это может сделать вещи более запутанными, особенно для новичков, которые все еще пытаются понять дроби в целом. Если вы сократите дробь перед тем, как работать с ней, может быть сложнее понять, что происходит в общем расчете. Чтобы сократить дробь с переменными, сначала определите наибольший общий делитель числителя и знаменателя. Чтобы сокращать дробь, разделите числитель и знаменатель на наибольший общий множитель. Наибольший общий множитель — это наибольшее число, которое делится без остатка как на числитель, так и на знаменатель. Чтобы найти наибольший общий делитель дроби, перечислите делители как числителя, так и знаменателя. Наибольший общий делитель будет наибольшим числом, которое появляется в обоих списках. Например, чтобы уменьшить дробь ¾, перечислите множители 3 (3, 1) и перечислите множители 4 (4, 2, 1). Наибольший общий делитель равен 1, поэтому ¾ сводится к 1/1 или 1. Вот еще несколько примеров: Чтобы уменьшить 8/12, перечислите множители 8 (8, 4, 2, 1) и перечислите множители 12 (12, 6, 4, 3, 2, 1) . Наибольший общий делитель равен 4, поэтому 8/12 сводится к 2/3. Чтобы уменьшить 15/25, перечислите множители 15 (15, 5, 3, 1) и перечислите множители 25 (25, 5, 5, 1). Чтобы сократить дробь, разделите числитель и знаменатель на наибольший общий множитель. Наибольший общий множитель — это наибольшее число, на которое без остатка делятся и числитель, и знаменатель. Чтобы найти наибольший общий множитель, перечислите множители каждого числа и найдите наибольшее число, которое встречается в обоих списках. Например, чтобы уменьшить дробь ¾, перечислите множители 3 (3, 1) и множители 4 (4, 2, 1). Наибольший общий делитель равен 1, поэтому ¾ становится 1/1 или 1. Вот несколько советов и приемов, которые помогут вам сокращать дроби: -Начните с нахождения наибольшего общего делителя числителя и знаменателя. Вы можете сделать это, перечислив факторы каждого числа и найдя число, которое появляется в обоих списках. -Найдя наибольший общий множитель, разделите числитель и знаменатель на это число. Это даст вам уменьшенную фракцию. В данном материале рассматривается одно из решений уравнения пятой степени частного вида. На этом уравнении, несмотря на то что все значения совпадают, знак надо менять на противоположный. Почему так и какой критерий, я еще пока не понял. 0.80517978551219-0.90690579788299i -0.42780028378999-0.63253712529931i -1.0695749012912+0.51597635530179i -0.23323335872174+0.95142805026712i 0.92542875829085+0.072038517613355i В общем случае уравнение, имеющее степень выше 4, нельзя разрешить в радикалах. Чаще всего приходится иметь дело с уравнениями высших степеней с целыми коэффициентами. В этих случаях мы можем попробовать найти рациональные корни, а потом разложить многочлен на множители, чтобы потом преобразовать его в уравнение более низкой степени, которое будет просто решить. В рамках этого материала мы рассмотрим как раз такие примеры. Все уравнения, имеющие вид anxn+an-1xn-1+…+a1x+a0=0, мы можем привести к уравнению той же степени с помощью умножения обеих частей на ann-1 и осуществив замену переменной вида y=anx: anxn+an-1xn-1+…+a1x+a0=0ann·xn+an-1·ann-1·xn-1+…+a1·(an)n-1·x+a0·(an)n-1=0y=anx⇒yn+bn-1yn-1+…+b1y+b0=0 Те коэффициенты, что получились в итоге, также будут целыми. Вычисляем целые корни уравнения. Если уравнение имеет целые корни, нужно искать их среди делителей свободного члена a0. Выпишем их и будем подставлять в исходное равенство по очереди, проверяя результат. Как только мы получили тождество и нашли один из корней уравнения, то можем записать его в виде x-x1·Pn-1(x)=0. Здесь x1 является корнем уравнения, а Pn-1(x) представляет собой частное от деления xn+anxn-1+…+a1x+a0 на x-x1. Подставляем остальные выписанные делители в Pn-1(x)=0, начав с x1, поскольку корни могут повторяться. После получения тождества корень x2 считается найденным, а уравнение может быть записано в виде (x-x1)(x-x2)·Pn-2(x)=0.Здесь Pn-2(x) будет частным от деления Pn-1(x) на x-x2. Продолжаем и дальше перебирать делители. Найдем все целые корни и обозначим их количество как m. После этого исходное уравнение можно представить как x-x1x-x2·…·x-xm·Pn-m(x)=0. Если у нас исходное уравнение имеет целые коэффициенты, мы не можем получить в итоге дробные корни. У нас в итоге получилось уравнение Pn-m(x)=0, корни которого могут быть найдены любым удобным способом. Они могут быть иррациональными или комплексными. Покажем на конкретном примере, как применяется такая схема решения. Условие: найдите решение уравнения x4+x3+2×2-x-3=0. Решение Начнем с нахождений целых корней. У нас есть свободный член, равный минус трем. У него есть делители, равные 1, -1, 3 и -3. Подставим их в исходное уравнение и посмотрим, какие из них дадут в итоге тождества. При x, равном единице, мы получим 14+13+2·12-1-3=0, значит, единица будет корнем данного уравнения. Теперь выполним деления многочлена x4+x3+2×2-x-3 на (х-1) в столбик: Значит, x4+x3+2×2-x-3=x-1×3+2×2+4x+3. Перебираем возможные делители дальше, но подставляем их в равенство x3+2×2+4x+3=0: 13+2·12+4·1+3=10≠0(-1)3+2·(-1)2+4·-1+3=0 У нас получилось тождество, значит, мы нашли еще один корень уравнения, равный -1. Делим многочлен x3+2×2+4x+3 на (х+1) в столбик: Получаем, что x4+x3+2×2-x-3=(x-1)(x3+2×2+4x+3)==(x-1)(x+1)(x2+x+3) Подставляем очередной делитель в равенство x2+x+3=0, начиная с -1: -12+(-1)+3=3≠032+3+3=15≠0(-3)2+(-3)+3=9≠0 Равенства, полученные в итоге, будут неверными, значит, у уравнения больше нет целых корней. Оставшиеся корни будут корнями выражения x2+x+3. D=12-4·1·3=-11<0 Из этого следует, что у данного квадратного трехчлена нет действительных корней, но есть комплексно сопряженные: x=-12±i112. Уточним, что вместо деления в столбик можно применять схему Горнера. Это делается так: после того, как мы определили первый корень уравнения, заполняем таблицу. В таблице коэффициентов мы сразу можем увидеть коэффициенты частного от деления многочленов, значит, x4+x3+2×2-x-3=x-1×3+2×2+4x+3. После нахождения следующего корня, равного -1, мы получаем следующее: Далее мы приходим к разложению x-1x+1×2+x+3=0. Потом, проверив оставшиеся делители равенства x2+x+3=0, вычисляем оставшиеся корни. Ответ: х=-1, х=1, x=-12±i112. Условие: решите уравнение x4-x3-5×2+12=0. Решение У свободного члена есть делители 1, -1, 2, -2, 3, -3, 4, -4, 6, -6, 12, -12. Проверяем их по порядку: 14-13-5·12+12=7≠0(-1)4-(-1)3-5·(-1)2+12=9≠024·23-5·22+12=0 Значит, x=2 будет корнем уравнения. Разделим x4-x3-5×2+12 на х-2, воспользовавшись схемой Горнера: В итоге мы получим x-2(x3+x2-3x-6)=0. Проверяем делители дальше, но уже для равенства x3+x2-3x-6=0, начиная с двойки. 23+22-3·2-6=0 Значит, 2 опять будет корнем. Разделим x3+x2-3x-6=0 на x-2: В итоге получим (x-2)2·(x2+3x+3)=0. Проверка оставшихся делителей смысла не имеет, поскольку равенство x2+3x+3=0 быстрее и удобнее решить с помощью дискриминанта. Решим квадратное уравнение: x2+3x+3=0D=32-4·1·3=-3<0 Получаем комплексно сопряженную пару корней: x=-32±i32. Ответ: x=-32±i32. Условие: найдите для уравнения x4+12×3-52x-3=0 действительные корни. Решение x4+12×3-52x-3=02×4+x3-5x-6=0 Выполняем домножение 23обеих частей уравнения: 2×4+x3-5x-6=024·x4+23×3-20·2·x-48=0 Заменяем переменные y=2x: 24·x4+23×3-20·2·x-48=0y4+y3-20y-48=0 В итоге у нас получилось стандартное уравнение 4-й степени, которое можно решить по стандартной схеме. Ответ: x1=-1, x2=32 Советуем также ознакомиться с материалами, посвященными решению кубических уравнений и уравнений четвертой степени. Автор:
Ирина Мальцевская Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта Навигация по статьям Предыдущая статья Уравнение и его корни Следующая статья Наибольший общий делитель (НОД) Узнать подробнее Современные приборы для измерения давления Заказать такую же работу Сортамент эксплуатационных материалов Вид работы: Реферат Выполнена: 2 февраля 2023 г. Стоимость: 800 руб Заказать такую же работу Металлические конструкции Вид работы: Практическая работа Выполнена: 17 января 2023 г. Стоимость: 2 300 руб Заказать такую же работу Понятие производной Заказать такую же работу название предмета вычислительные машины системы и сети Вид работы: Решение задач Выполнена: 30 ноября 2022 г. Стоимость: 1 600 руб Заказать такую же работу Практические работы штук Вид работы: Практическая работа Выполнена: 26 октября 2022 г. Стоимость: 14 400 руб Заказать такую же работу Смотреть все работы по гидравлике добавить в корзину Интегрированная математика 3 — это третий год трехлетней программы по математике в старшей школе. Программа разработана таким образом, чтобы с каждым годом возрастать сложность и применение шаблонов, моделирования и предположений для развития понимания и компетентности учащихся в области математики. По окончании этого курса студент получает 5 кредитов. Каждый кредит соответствует 15 часам обучения. Конечно, некоторые студенты работают быстрее, чем другие, а некоторые могут уделять учебе больше часов, поэтому некоторые студенты имеют возможность пройти курс в ускоренном темпе. В этом курсе учащиеся усвоят следующее: добавить в корзину Учебная программа Скриншот курса Инструкции по курсу Предлагаемая временная шкала Чтобы решить полиномиальное уравнение 5-й степени, мы должны как можно больше разложить данный полином на множители. Пример 1: Решить: 6x 5 — x 4 — 43x 3 + 43x 9 0166 2 + х — 6 = 0 Решение: Методом проб и ошибок мы можем проверить значения 1, или -1, или 2, или -2…… как ноль для приведенного выше уравнения, используя синтетическое деление. Когда мы проверяем значение 1, мы получаем нулевой остаток. Итак, x = 1 является одним из нулей. Полученное уравнение: 6x 4 + 5x 3 — 38x 2 + 5x + 6 = 0 Разделив обе стороны на x 2 . 6x 4 /x 2 + 5x 3 /x 2 — 38x 2 /x 2 + 5x/x 2 + 6/x 2 = 0 6x 2 + 5x — 38 + 5/x + 6/x 2 = 0 6(х 2 + 1/х 2 ) + 5 (х + 1/х) — 38 = 0 —-(1) Пусть у = х + 1/х. y 2 = (x + 1/x) 2 y 2 = x 2 + 2(x)(1/x) + (1/x) 9016 6 2 г 2 = х 2 + 2 + 1/х 2 y 2 — 2 = x 2 + 1/x 2 (1)—-> 6(y 2 — 2) + 5y — 38 = 0 6 лет 2 — 12 + 5 лет — 38 = 0 6 лет 2 + 5 лет — 50 = 0 6 лет 2 — 15 лет + 20 лет — 50 = 0 (3у + 10)(2у — 5) = 0 3г + 10 = 0 г = -10/3 2г — 5 = 0 г = 5/2 Когда y = -10/3, (x 2 + 1)/x = -10/3 3(x 2 + 1) = -10x 3x 2 + 3 = -10x 3x 2 + 10x + 3 = 0 (3x + 1)(x + 3) = 0 x = -1/3 и 3 Когда y = 5/2, 9015 7 x + 1/x = y (x 2 + 1)/x = 5/2 2(x 2 + 1) = 5 x 2x 9016 6 2 + 2 — 5x = 0 2x 2 — 5x + 2 = 0 (2x — 1)(x — 2) = 0 x = 1/2 и 2 Таким образом, пять нулей равны 1, -1/3, 3, 1/2 и 2. Пример 2 : Решение : 8x 5 — 22x 4 — 55x 3 + 55x 2 + 22x — 8 = 0 Решение: Когда мы проверяем значение 1, мы получить нулевой остаток. Итак, x = 1 является одним из нулей. Результирующее уравнение: 8x 4 — 14x 3 — 69x 2 — 14x + 8 = 0 Разделив обе стороны на x 2 . 8x 4 /x 2 — 14x 3 /x 2 — 69x 2 /x 2 901 67 — 14x/x 2 + 8/x 2 = 0 8x 2 — 14x — 69 — 14/x + 8/x 2 = 0 8(x 2 + 1/x 2 ) — 14(x + 1 /х) — 69 = 0 —-(1) Пусть у = х + 1/х. у 2 = (х + 1/х) 2 у 2 = х 2 + 2(х)(1/х) + (1/х) 2 у 2 = х 2 + 2 + 1/х 2 y 2 — 2 = x 2 + 1/x 2 (1)—-> 8(y 2 — 2) — 14г — 69 = 0 8г 2 — 16 — 14г — 69 = 0 8г 2 — 14г — 85 = 0 (2г + 5)(4г — 17) = 0 2у + 5 = 0 у = -5/2 4г — 17 = 0 г = 17/4 Когда у = -5/2, х + 1/х = у (х 2 + 1)/х = -5/2 2(х 2 + 1) = -5x 2x 2 + 2 + 5x = 0 2x 2 + 5x + 2 = 0 2x 2 + 4x + 1x + 2 = 0 2x(x + 2) + 1(x + 2) = 0 (2x + 1)(x + 2) = 0 x = -1/2 и -2 Когда y = 17/4, x + 1/x = y (x 2 + 1)/x = 17/4 4(x 2 + 1) = 17x 4x 901 66 2 + 4 = 17x 4x 2 — 17x + 4 = 0 (4x — 1)(x — 4) = 0 x = 1/4 и 4 Следовательно, пять нулей равны 1, -1/2, -2 , 1/4 и 4. Пример 3 : Решить : 6x 5 + 11x 4 — 33x 3 9 0167 — 33x 2 + 11x + 6 = 0 Решение: Когда мы проверяем значение -1, мы получаем нулевой остаток. Итак, x = -1 является одним из нулей. Полученное уравнение: 6x 4 + 5x 3 — 38x 2 + 5x + 6 = 0 Разделив обе части на x 90 166 2 . 6x 4 /x 2 + 5x 3 /x 2 — 38x 2 /x 2 9016 7 + 5x/x 2 + 6/x 2 = 0 6x 2 + 5x — 38 + 5/x + 6/x 2 = 0 6(x 2 + 1/x 2 ) + 5(x + 1/х) — 38 = 0 —-(1) Пусть у = х + 1/х. y 2 = (x + 1/x) 2 y 2 = x 2 + 2(x)(1/x) + (1/x) 9016 6 2 г 2 = x 2 + 2 + 1/x 2 y 2 — 2 = x 2 + 1/x 2 901 67 (1)—-> 6(у 2 — 2) + 5г — 38 = 0 6г 2 — 12 + 5г — 38 = 0 6г 2 + 5г — 50 = 0 6 лет 2 — 15 лет + 20 лет — 50 = 0 3у(2у — 5) + 10(2у — 5) = 0 (3у + 10)(2у — 5) = 0 3г + 10 = 0 г = -10/3 2г — 5 = 0 г = 5/2 Когда y = -10/3, x + 1/x = y (x 2 + 1)/x = -10/3 3(x 2 + 1) = -10x 3x 2 + 3 = -10x 3x 2 + 10x + 3 = 0 3x 2 + 9x + x + 3 = 0 3x(x + 3) + 1(x + 3) = 0 (x + 3)(3x + 1) = 0 x = -3 и -1/3 Когда y = 5/ 2, х + 1/х = у (х 2 + 1)/х = 5/2 2(х 2 + 1) = 5х 2х 2 + 2 — 5x = 0 2x 2 — 5x + 2 = 0 2x 2 — 4x — x + 2 = 0 2x(x — 2) — 1(x — 2) = 0 (2x — 1)(x — 2) = 0 x = 1 /2 и 2 Следовательно, пятью нулями являются -1, -3, -1/3, 1/2 и 2. Таблица котангенсов необходима для вычислений, связанных со значениями тригонометрических функций. Легко запомнить, что значения ctg 0° = ctg 180° = ctg 360° = ∞, ctg 1° — ctg 90°
ctg 1° = 57.28996 ctg 91° — ctg 180°
ctg 91° = -0.01746 ctg 181° — ctg 270°
ctg 181° = 57.28996 ctg 271° — ctg 360°
ctg 271° = -0.01746 Вы можете самостоятельно найти котангенс при помощи инженерного онлайн калькулятора NCBI Bookshelf. Служба Национальной медицинской библиотеки, Национальных институтов здоровья. Рекомендации ВОЗ: интранатальная помощь для положительных родов. Показать подробности Критерий поиска Источник: 3., Фактические данные и рекомендации Copyright © Всемирная организация здравоохранения, 2018 г. Продажа, права и лицензирование. Чтобы приобрести публикации ВОЗ, посетите веб-сайт http://apps.who.int/bookorders. Для подачи запросов на коммерческое использование и запросов о правах и лицензировании см. http://www.who.int/about/licensing. Сторонние материалы. Если вы хотите повторно использовать материал из этой работы, авторство которого принадлежит третьему лицу, например таблицы, рисунки или изображения, вы обязаны определить, требуется ли разрешение на такое повторное использование, и получить разрешение от правообладателя. Риск претензий, возникающих в результате нарушения прав любого стороннего компонента в работе, лежит исключительно на пользователе. Некоторые права защищены. Эта работа доступна по лицензии Creative Commons Attribution-NonCommercial-ShareAlike 3. В соответствии с условиями этой лицензии вы можете копировать, распространять и адаптировать произведение в некоммерческих целях при условии надлежащего цитирования произведения, как указано ниже. При любом использовании этой работы не должно быть намеков на то, что ВОЗ поддерживает какую-либо конкретную организацию, продукты или услуги. Использование логотипа ВОЗ не допускается. Если вы адаптируете произведение, вы должны лицензировать свое произведение в соответствии с той же или эквивалентной лицензией Creative Commons. Если вы создаете перевод этой работы, вы должны добавить следующее заявление об отказе от ответственности вместе с предлагаемой цитатой: «Этот перевод не был создан Всемирной организацией здравоохранения (ВОЗ). ВОЗ не несет ответственности за содержание или точность этого перевода. Оригинальное английское издание является обязательным и аутентичным изданием». Любое посредничество в отношении споров, возникающих в связи с лицензией, должно проводиться в соответствии с правилами посредничества Всемирной организации интеллектуальной собственности. Содержание ОчиститьВыключитьВключить Ваша активность в Интернете пуста. Запись активности отключена. Включить запись Подробнее… Рыночная капитализация 90 003 102,515 млн долларов США Дивидендная доходность (за год ) — Отношение цены к прибыли (TTM) 14,90 Базовая прибыль на акцию (TTM) 0,46USD Computer Task Group, Inc. Продолжайте читать Обобщая, что предлагают индикаторы. Осцилляторы Нейтральный ПродаватьПокупать Сильный продаватьУсиленный покупать Сильный продаватьПродаватьНейтральныйПокупатьУсиленный покупать Осцилляторы Нейтральный SellBuy Сильная продажа Сильная покупка Сильная продажа SellNeutralBuy Сильная покупка Резюме Нейтральный ПродатьПокупка Сильный продаватьАктивно покупать Сильный продаватьПродаватьНейтральныйПокупатьАктивно покупать Сводка Нейтральный ПродаватьПокупать 900 03. Сильная продажаПродатьНейтральная покупкаСильная покупка Скользящие средние Нейтральная ПродажаСильная покупка Сильная продажаСильная покупка Сильная продажаПродатьНейтральнаяПокупкаСильная покупка Скользящие средние Нейтральная ПродажаПокупка Сильная продажаСильная покупка Сильная продажаПродатьНейтральнаяпокупкаСильная покупка Прошлые результаты Преобразование выручки в прибыль Общая выручка Валовая прибыль EBITDA EBIT Чистая прибыль Уровень долга и покрытие Прибыль Далее:— Pepperstone Избранные Forex, CFD Узнать больше OANDA CFD Узнать больше Capital. Поможем понять и полюбить математику В 8 классе на алгебре проходят темы, которые точно встретятся на ЕГЭ. Пора навострить уши! В этой статье расскажем, какие квадратные уравнения называются неполными и как их решать. Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство. Степень уравнения можно определить по наибольшей степени, в которой стоит неизвестное. Если неизвестное стоит во второй степени — это квадратное уравнение. Квадратное уравнение — это уравнение вида ax² + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член. Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b² − 4ac. А вот свойства дискриминанта: Неполное квадратное уравнение — это уравнение вида ax² + bx + c = 0, где хотя бы один из коэффициентов b или c равен нулю. Такие уравнения отличаются от полного квадратного тем, что их левые части не содержат слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения. Реши домашку по математике на 5. Подробные решения помогут разобраться в самой сложной теме. Как мы уже знаем, есть три вида неполных квадратных уравнений: Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль). Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax² = 0. Уравнение ax² = 0 равносильно x² = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x² = 0 является нуль, так как 0² = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней. Таким образом, неполное квадратное уравнение ax² = 0 имеет единственный корень x = 0. Пример 1. Решить −5x² = 0. Как решаем: −5x² = 0 x² = 0 x = √0 x = 0 Ответ: 0. Обратим внимание на неполные квадратные уравнения вида ax² + c = 0, в которых b = 0, c ≠ 0. Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. То есть одно и то же, только с другими цифрами. Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax² + c = 0: Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи. Если — c/а < 0, то уравнение x² = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а < 0 ни для какого числа p равенство р² = — c/а не является верным. Если — c/а > 0, то корни уравнения x² = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)² = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)² = — c/а. Ура, больше у этого уравнения нет корней. В двух словах квадратное уравнение ax² + c = 0 равносильно уравнению ax² + c = 0, которое: Пример 1. Как решать: 9x² = — 4 x² = — 4/9 Ответ: уравнение 9x² + 4 = 0 не имеет корней. Пример 2. Решить -x² + 9 = 0. Как решаем: -x² = -9 x² = 9 x = √9 x = -3, 3 Ответ: уравнение -x² + 9 = 0 имеет два корня -3; 3. Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0. Квадратное уравнение без с непривычно решать только первые несколько примеров. Запомнив алгоритм, будет значительно проще щелкать задачки из учебника. Неполное квадратное уравнение ax² + bx = 0 можно решить методом разложения на множители. Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x. Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a. Таким образом, неполное квадратное уравнение ax² + bx = 0 имеет два корня: Пример 1. Решить уравнение 2x² — 32x = 0 Как решать: х(2x — 32) = 0 2x = 32, х = 32/2 х = 16 Ответ: х = 0 и х = 16. Пример 2. Решить уравнение 3x² — 12x = 0 Как решать: Разложить левую часть уравнения на множители и найти корни: Ответ: х = 0 и х = 4. Для удобства мы собрали все виды неполных квадратных уравнений и способы их решения на одной картинке-шпаргалке. Шпаргалки для родителей по математике Все формулы по математике под рукой Лидия Казанцева Автор Skysmart К предыдущей статье Что такое угол? Виды углов К следующей статье Что такое аксиома, теорема и доказательство теоремы Выявим пробелы в знаниях и дадим советы по обучению Расскажем, как проходят занятия Подберём курс Неполное квадратное уравнение – это уравнение вида ax2 + bx + c = 0, в котором хотя бы один из коэффициентов b или c равен нулю. Следовательно, неполное квадратное уравнение может иметь вид: Чтобы решить уравнение вида ax2 + bx = 0, надо разложить левую часть уравнения на множители, вынеся x за скобки: x(ax + b) = 0. Произведение может быть равно нулю только в том случае, если один из множителей равен нулю, значит: x = 0 или ax + b = 0. Чтобы ax + b было равно нулю, нужно, чтобы Следовательно, уравнение ax2 + bx = 0 имеет два корня: Неполные квадратные уравнения вида ax2 + bx = 0, где b ≠ 0, решаются разложением левой части на множители. Такие уравнения всегда имеют два корня, один из которых равен нулю. Пример 1. Решите уравнение: a2 — 12a = 0. Решение: Пример 2. Решите уравнение: 7x2 = x. Решение: Чтобы решить уравнение вида ax2 + c = 0, надо перенести свободный член уравнения c в правую часть: В этом случае уравнение не будет иметь корней, так как квадратный корень нельзя извлечь из отрицательного числа. Если данное неполное уравнение будет иметь вид x2 — c = 0, то сначала опять переносим свободный член в правую часть и получаем: x2 = c. В этом случае уравнение будет иметь два противоположных корня: x1 = +√c , x2 = -√c . Неполное квадратное уравнение вида ax2 + c = 0, где c ≠ 0, либо не имеет корней, либо имеет два корня, которые являются противоположными числами. Пример 1. Решите уравнение: 24 = 2y2. Решение: Пример 2. b2 — 16 = 0. Решение: Уравнение вида ax2 = 0 всегда имеет только один корень: x = 0. Так как a ≠ 0, то из ax2 = 0 следует, что x2 = 0, значит, и x = 0. Любое другое значение x не будет являться корнем данного уравнения. Текст статьи PDF Исследовательская статья Дискриминантное значение психологического дистресса, профилей симптомов и сегментарной дисфункции толстой кишки у амбулаторных пациентов с тяжелым идиопатическим запором. Тяжелые идиопатические запоры могут быть классифицированы на основании физиологических тестов на подгруппы, включая запоры с медленным транзитом и дисфункцию тазового дна. Это исследование было направлено на то, чтобы определить, могут ли толстокишечные и психологические симптомы или время транзита ректосигмовидной кишки различать эти подгруппы. Пациенты, классифицированные в соответствии с общим временем транзита по толстой кишке и тестированием функции тазового дна, заполняли анкету самоотчета, в которой регистрировались симптомы и психологический дистресс. Пациенты с нормальным транзиторным запором (n = 60) имели значительно более высокие показатели депрессии по сравнению с теми, у кого был медленный транзитный запор (n = 70) или дисфункция тазового дна (n = 30). http://dx.doi.org/10.1136/gut.35.6.798 направит вас к службе RightsLink Центра защиты авторских прав. Вы сможете получить быструю цену и мгновенное разрешение на повторное использование контента различными способами. Подписаться Для личных счетов ИЛИ менеджеров институциональных счетов Имя пользователя * Пароль * Забыли данные для входа? Зарегистрировать новую учетную запись? Забыли имя пользователя или пароль? Квадратное уравнение представляет собой уравнение вида ax 2 + bx + c = 0, где a, b и c — константы, а a ≠ 0. 0003 Происхождение слова «квадратный» — латинское. На латыни «квадратный» используется для «квадратный» .
Поскольку наибольшая степень неизвестной переменной, которая появляется в уравнении, равна квадрату (степень 2),
поэтому подобные уравнения стали известны как квадратные уравнения. <---- Рекламные объявления ---- > Стандартная форма квадратного уравнения Стандартная форма квадратного уравнения: ax 2 + bx + c = 0, где ◾ a, b и c — константы и ◾ и не равны 0 (нулю). Вот несколько примеров стандартной формы квадратного уравнения: <----- Рекламные объявления ----- > Полное квадратное уравнение ◾ Когда b не равно нулю Чистое или неполное квадратное уравнение ◾ Когда b равно нулю, уравнение называется чистым или неполным квадратным уравнением относительно x. Корни квадратного уравнения Корни или решение квадратного уравнения оси 2 + bx + c =0 — это значения переменной ‘x’, которые удовлетворяют квадратному уравнению, т.е. делают ось 2 +bx+c равно нулю. Например: x 2 + 5x — 50 = 0 x 2 — 5x + 10x -50 = 0 x(x — 5) + 10(х — 5) = 0 (x — 5) (x + 10) = 0 x = 5 и x = -10 Как вы можете видеть, подстановка 5 или -10 вместо x дает квадратное уравнение x 2 + 5x — 10 равно нулю. Следовательно, 5 и -10 являются корнями квадратного уравнения х 2 + 5х — 50 = 0, Решение квадратного уравнения Существует три метода решения квадратного уравнения: ◾ С помощью факторизации ◾ Составляя квадрат ◾ С помощью формулы квадрата Решение С помощью факторизации Пошаговый процесс решения квадратного уравнения методом факторизации: Шаг 1: Преобразуйте уравнение в стандартную форму, которая представляет собой ось 9. Шаг 2: Полностью факторизуем левую часть. Шаг 3: Используйте закон нулевого коэффициента: если pq = 0, то p = 0 или q = 0. Шаг 4: Решите полученные линейные уравнения, приравняв каждый из линейных коэффициентов нулю. Эти значения x будут решением квадратного уравнения. Пример: решить 3x 2 + 5x — 5 = -3 Шаг 1: Перестановка в стандартной форме 3x 2 + 5x -5 + 3 = 0 3x 2 + 5х — 2 = 0 Шаг 2: Факторизация левой части 2) = 0 Шаг 3: Приравняйте каждый линейный коэффициент к нулю. 3x – 1 = 0 или x + 2 = 0 3x = 1 или x = -2 х = 1/3, х = — 2 являются корнями уравнения. Ловушка: У вас может возникнуть соблазн разделить обе части на выражение, включающее x. Например: рассмотрим x 2 = 7x Правильное решение: x 2 = 7x x 2 -7 х=0 х(х-7)=0 x=0 и X=7 Неверное решение: x 2 = 7x Разделив обе части на x, получим X=7 выше — неправильный способ решения уравнения, так как мы не смогли найти другое значение x, равное нулю. Решение путем заполнения квадрата Как вы уже знаете, все квадратные уравнения не могут быть легко разложены на множители. Например, x 2 + 4x + 1 нельзя разложить на множители простой факторизацией. Это означает, что мы не можем написать x 2 + 4x + 1 в виде (x — a)(x — b), где a, b — рациональные числа. Существует альтернативный способ решения уравнений типа x 2 + 4x + 1 = 0, то есть завершает квадрат . Уравнения вида ax 2 + bx + c = 0 можно преобразовать к виду (x + p) 2 = q . Так легко найти решения. Пошаговый процесс решения квадратного уравнения путем заполнения квадрата: Шаг I: Приведите квадратное уравнение в стандартную форму ax 2 + bx + c = 0. Шаг II: теперь разделите обе части уравнения на коэффициент x 2 , если он еще не равен 1. Шаг III: Сдвиньте постоянную часть вправо. Шаг IV: Добавьте квадрат половины коэффициента x к L.H.S. и Р.Х.С. Шаг V: Запишите левую сторону как полный квадрат и упростите правую сторону. Шаг VI: Найдите x, извлекая квадратный корень из L.H.S. и Р.Х.С. Решим квадратное уравнение -3x 2 + 12x + 5 = 0 через «заполнение квадрата» -3x 2 + 12x + 5 = 0 x 90 092 2 — 4x — (5 /3) = 0 x 2 — 4x = (5/3) x 2 — 4x + 2 2 = (5/3) + 2 2 (x — 2) 2 = (17/3) x — 2 = ± √(17/3) x = 2 ± √(17/3) x 1 = 2 + √(17/3) x 2 = 2 — √(17/3) С помощью квадратной формулы Квадратная формула, которая также может быть использована для решения любого квадратного уравнения, получается из решения квадратного уравнения ax 2 + bx + c = 0 , a ≠ 0 для x путем заполнения квадрата. В некоторых случаях решение квадратного уравнения путем разложения на множители или завершения квадрата требует много времени, долго или сложно. В таких случаях мы используем квадратную формулу для решения квадратного уравнения. Пошаговый процесс решения квадратного уравнения по квадратной формуле: Шаг I: Приведите квадратное уравнение в стандартную форму оси 2 + b x + c = 0. Шаг II: Сравните квадратное уравнение, которое нужно решить, со стандартным квадратным уравнением и найдите значения коэффициентов a, b и c. Шаг III: Поместите эти значения a, b и c в квадратичную формулу. Как видно из формулы. Эти два значения x, для которых верно ax 2 + bx + c = 0, называются решениями квадратного уравнения, также называемыми корнями квадратного уравнения. Шаг I: — Преобразуйте квадратное уравнение, которое вы хотите решить, в стандартную форму квадратного уравнения, ax 2 + bx + c = 0 Например, если у вас есть квадратное уравнение в форме x 2 — 10x = -24, затем преобразуйте его в стандартную форму квадратного уравнения. х 2 -10x = -24 преобразуется в x 2 — 10x + 24 = 0 Шаг II: — Найдите значение коэффициента a, b и c, сравнив его со стандартной формой квадратного уравнения ax 2 + bx + c = 0 Например, сравнивая x 2 — 10x + 24 = 0 с ax 2 + bx + c = 0, получаем a = 1, Шаг III: Мы узнали, что квадратичная формула равна 4ac» , стоящее под знаком квадратного корня, называется дискриминантом квадратного уравнения. Дискриминант = b 2 — 4ac Выражение «b 2 – 4ac» говорит о характере корней квадратного уравнения. Корни могут быть действительными, равными или мнимыми. Возможны три случая: ◾ Если б 2 – 4ас мнимое и неравное. ◾ Если b 2 – 4ac = 0, то корни будут вещественными, равными и рациональными . (Это означает, что левая часть уравнения представляет собой идеальный квадрат). ◾ Если b 2 – 4ac > 0, то корни вещественные и неравные. Если b 2 – 4ac > 0, то корни действительные и неравные и их две возможности — Здесь корни могут быть рациональными или иррациональными ◾ b 2 – 4ac – полный квадрат, корни вещественные, рациональные и неравные . (Это означает, что уравнение может быть решено путем факторизации). ◾ b 2 – 4ac не является совершенным, тогда корни вещественные, иррациональные и неравные. Сводка Случай I — когда дискриминант > 0 002 Ответ x 2 + 7x + 4 = 0 Дискриминант = b 2 – 4ac Здесь a = 1, b = 7 и c = 4 Дискриминант = 7 2 – 4 x 1 x 4 = 49 — 16 = 33 Дискриминант > 0, следовательно, существует два действительных корня Случай II.
6 x 5 =
30
6 x 6 =
36
6 x 8 =
48
6 x 4 =
24
6 x 1 =
6
6 x 7 =
42
6 x 10 =
60
6 x 3 =
18
6 x 2 =
12
6 x 9 =
54
Тесты на проверку знаний табличного умножения и деления
Таблица умножения на 2
Таблица умножения на 3
Таблица умножения на 4
Таблица умножения на 5
Таблица умножения на 6
Таблица умножения на 7
Таблица умножения на 8
Таблица умножения на 9
Таблица умножения до 2
Таблица умножения до 3
Таблица умножения до 4
Таблица умножения до 5
Таблица умножения до 6
Таблица умножения до 7
Таблица умножения до 8
Таблица умножения до 9
Таблица умножения на 2 по возрастанию
Таблица умножения на 3 по возрастанию
Таблица умножения на 4 по возрастанию
Таблица умножения на 5 по возрастанию
Таблица умножения на 6 по возрастанию
Таблица умножения на 7 по возрастанию
Таблица умножения на 8 по возрастанию
Таблица умножения на 9 по возрастанию
Таблица умножения на 2 по убыванию
Таблица умножения на 3 по убыванию
Таблица умножения на 4 по убыванию
Таблица умножения на 5 по убыванию
Таблица умножения на 6 по убыванию
Таблица умножения на 7 по убыванию
Таблица умножения на 8 по убыванию
Таблица умножения на 9 по убыванию
Нередко родители сталкиваются с проблемой, когда ребенку задают выучить таблицу умножения. Все мы были когда-то детьми, тоже учили и как-то выучили. Конечно, проще выучить стихотворение на урок литературы, а здесь столько чисел и как всё запомнить? Ребенку «зубрежка» надоедает, становится скучной. Кроме этого у него может быть плохо развита способность запоминать отдельные не связанные между собой элементы, так называемая механическая память. На сегодняшний день существует много различных методов заучивания таблицы умножения для детей. Их часто практикуют в школе, но даже к третьему классу, дети не понимают, что учат. Поэтому дожидаться, когда школьнику зададут на дом выучить таблицу умножения, не стоит. Содержание Чтобы помочь ребенку быстро выучить таблицу умножения, нужно понимать сам процесс умножения. К занятиям родители должны приготовить различные одинаковые предметы: кружочки, квадратики, яблоки, груши и др. Последние лучше вырезать из картона. Затруднений при умножении на единицу у ребенка возникнуть не должно. Начнем с умножения на 2. Для этого следует разложить, например, картонные яблоки или другие предметы 4 ряда по 2 единицы. Предложите ребенку посчитать количество рядов и предметов. Объясните, что если умножить 2 ряда на 2 предмета, будет 4; 4 ряда на 2 предмета будет 8 и т. д. Когда ребенок освоит умножение на два, переходите к умножению на три. Здесь уже сделайте 3 ряда по 3 предмета. Скачать таблицу умножения на 2 Другой быстрый способ, который поможет выучить таблицу умножения, это изучение в игровой форме. Принцип игры следующий: ребенку предлагаете взять любую карточку, к примеру 5×7, при правильном ответе карточку кладет к себе, если ответ неверный карточка кладется вниз колоды. Путем повторения одних и тех же примеров, ребенок их легко запомнит и усвоит. Если в семье два школьника, то это будет отличным вариантом изучения таблицы умножения. При этом у ребенка задействована не только механическая, но и зрительная память. Чтобы работала не только механическая, но и визуальная память, Скачайте таблицу умножения (плакат), распечатайте и повесьте на видное место. Приобрести можно и специальные магнитики с цифрами на холодильник. Ребенку не будет скучно учить одному. Вы на кухне готовите ужин, а малыш учит таблицу, передвигая правильно магнитики. Следующий прием, который поможет ребенку выучить таблицу умножения, мнемонический. Суть его в том, что ребенок заучивает рифмованные слова или ассоциации. Таблица умножения на 3 в стихах Изучение таблицы умножения требует усидчивости и терпения от школьника, но некоторые способы запоминания таблицы умножения облегчат запоминание, и сделают его веселым и быстрым. Например, вот так легко запомнить таблицу умножения на 9. Распечатать таблицу умножения на 9 Эффективный способ запоминания умножения на 9 Сохраните на компьютер и распечатайте таблицу умножения: Полезные статьи: КАК НАУЧИТЬ РЕБЕНКА БЫСТРО СЧИТАТЬ ЦИФРЫ КАРТОЧКИ РАСПЕЧАТАТЬ МЕТОДИКИ МАТЕМАТИЧЕСКОГО РАЗВИТИЯ ДОШКОЛЬНИКОВ В этой статье вы узнаете и получите код для печати таблицы умножения чисел с помощью программы C++. Таблица умножения показывает список кратных определенного числа от 1 до 10. Например,
таблица умножения на 3: Примечание : Обычно список кратных от 1 до 12. Но в этой статье мы создали все
программы для печати таблицы умножения только на основе кратных от 1 до 10. Начнем с самой первой программы в этой статье, которая печатает таблицу умножения 2: Пробный запуск этой программы выглядит следующим образом: Чтобы напечатать таблицу любого заданного числа в программировании на C++, вы должны попросить пользователя ввести это число. Затем начните
умножая это число от 1 до 10, один за другим, и отображайте результат умножения во время умножения, как
показано здесь в следующей программе. Вот пример вывода этой программы: Эта программа позволяет пользователю ввести диапазон и распечатать таблицу со всеми числами в этом диапазоне. Например,
если пользователь вводит диапазон от 3 до 15, то печатается таблица всех чисел от 3 до 15. Вот пример запуска с пользовательским вводом: 3 для первого числа и 15 для второго: Что, если пользователь вводит два числа таким образом, что первое число больше второго? Вот пример запуска с пользовательским вводом, первое число равно 20, а второе — 6: C++ Quiz 2 Reviews Прекрасная таблица 6-кратного умножения в формате A4 (PDF), которая поможет вам выучить -6-кратную таблицу . Благодаря цветным цифрам вам будет легче запомнить результаты умножения. Эта таблица также доступна в других цветах или в черно-белом варианте. Здесь список начинается с 6x1 и заканчивается 6x12. Один из способов запомнить вашу таблицу — произнести ее вслух следующим образом: « 6 раз 1... 6, 6 раз 2... 12, 6 раз 3... 18, 6 раз 4... 24, 6 раз 5... 30, 6 раз 6... 36, 6 раз 7... 42, 6 раз 8... 48, 6 раз 9... 54, 6 раз 10... 60, 6 раз 11... 66, 6 раз 12... 72 ” Такой способ обучения с использованием слуховой памяти эффективен для многих детей. Нажмите на кнопку ниже, чтобы распечатать бесплатно нашу таблицу 6 Times . Распечатать таблицу умножения на 6 (PDF) Если вы планируете распечатать другие таблицы умножения, мы советуем вам выбрать отдельный цвет для каждой таблицы умножения от 1 до 12. Благодаря множеству доступных цветов вы, несомненно, найдете свою любимую диаграмму! Наши черно-белые таблицы умножения на 6 будут идеальными, если вы предпочитаете трезвость или хотите сэкономить чернила, а также если вы предпочитаете раскрашивать таблицу умножения самостоятельно с помощью карандашей или маркеров. Не стесняйтесь нажимать на изображения, чтобы просмотреть PDF. Используйте кнопку «ПЕЧАТЬ» под изображением, чтобы загрузить график по вашему выбору. 1 Обзор 2 отзыва 1 Обзор 1 Обзор 3 отзыва 2 отзыва 4 отзыва 3 отзыва 2 отзыва 2 отзыва 2 отзыва 2 отзыва Красивая диаграмма со всеми таблицами умножения для печати в формате A4 (PDF). Гдз по теории вероятности тюрин 7 класс Опишите словами это событие и найдите его вероятность. Практикум по решению задач 3 часа. Риэлтерская фирма предлагает на продажу 5 больших квартир и 4 малогабаритных квартиры. Результат округлите до сотых. Это пособие для учащихся 7-9 классов, в котором исследуемая линия реализуется в следующем порядке. Симметричную монету бросают трижды. Найдите вероятность того, что все выбранные конфеты имеют молочную начинку. То есть правило умножения применяется для подсчета упорядоченных наборов. Сколькими способами можно составить различные двузначные числа из четырех цифр 1,2,3,4? На простых примерах демонстрируется решение комбинаторных задач методом перебора возможных вариантов. Формулы числа перестановок, сочетаний, размещений. Моя страница Зарегистрироваться бесплатно Статистика является важным компонентом науки о данных. Независимо от того, работаете ли вы с большими или малыми данными, их понимание является ключом к получению информации и принятию обоснованных решений. В этой статье мы рассмотрим основы статистики для науки о данных, основные разделы и то, как вы можете приступить к изучению основ. Цель статистики — помочь вам осмыслить данные и сделать из них осмысленные выводы. В науке о данных статистика играет решающую роль в понимании закономерностей и тенденций в данных, прогнозировании и проверке гипотез. В этом руководстве представлен четкий и структурированный путь изучения статистики и ее применения в науке о данных. 1. Начните с описательной статистики: Начните с изучения основ описательной статистики, включая такие меры, как среднее значение, медиана, мода и стандартное отклонение, а также графики, такие как гистограммы, гистограммы и диаграммы рассеяния. 2. Изучите вероятность: Вероятность является жизненно важным компонентом статистики, и ее знание поможет вам понять более сложные концепции. Овладейте основами вероятностных распределений, включая нормальное, биномиальное и пуассоновское распределения. 3. Изучите статистику вывода: После того, как вы изучите описательную статистику и вероятность, переходите к статистике вывода. Начните с проверки гипотез, включая t-тесты и ANOVA, а затем перейдите к регрессионному анализу, включая простую линейную регрессию и множественную регрессию. 4. Изучите дополнительные темы: Затем изучите дополнительные темы статистики, включая машинное обучение, байесовскую статистику и анализ временных рядов. 5. Практика на реальных данных: Чтобы лучше понять статистику, важно попрактиковаться на реальных данных. Вы можете найти общедоступные наборы данных в Интернете. 6. Будьте в курсе последних событий: Статистика — быстро развивающаяся область, и важно быть в курсе новейших технологий и разработок. Вы можете сделать это, посещая конференции, читая научные журналы и участвуя в онлайн-форумах. Вы должны хорошо разбираться в математике, особенно в теории вероятностей. Вы также должны знать теорию множеств, алгебру и исчисление. Мы рассмотрим вероятность и теорию множеств в следующих разделах. Существуют две основные ветви статистики: описательная статистика и статистика вывода. Описательная статистика связана с обобщением и описанием данных, в то время как статистика логического вывода связана с предсказаниями и выводами на основе данных. В науке о данных важны обе отрасли. Вероятность обеспечивает основу для предсказаний и понимания неопределенности, связанной с этими предсказаниями. Вот несколько важных концепций вероятности, связанных с наукой о данных: 1. 2. Распределение вероятностей: Распределение вероятностей — это функция, описывающая вероятности всех возможных исходов случайной величины. Существуют различные типы распределений вероятностей, в том числе нормальное распределение, распределение Пуассона и распределение Бернулли. 3. Теорема Байеса: Теорема Байеса — это фундаментальное понятие в теории вероятностей, которое описывает, как обновить наши убеждения относительно гипотезы в свете новых данных. В науке о данных он используется для обновления представлений о параметрах модели, для прогнозирования на основе новых данных и понимания неопределенности, связанной с этими прогнозами. 4. Условная вероятность: Условная вероятность — это вероятность события при условии, что произошло другое событие. 5. Оценка максимального правдоподобия (MLE): MLE используется для оценки параметров статистических моделей, таких как модели регрессии, модели классификации и другие статистические модели. 6. Проверка гипотез: Проверка гипотез — это статистический метод проверки утверждений о параметре совокупности на основе выборочных данных. Он используется для проверки утверждений о параметрах модели, сравнения моделей и проверки прогнозов. Это лишь некоторые из важных концепций вероятности, связанных с наукой о данных. Лучший способ лучше понять их — это подробно изучить и попрактиковаться в применении к реальным данным. Теория множеств — это раздел математической логики, который обеспечивает основу для многих концепций в математике, информатике и науке о данных. 1. Набор: Набор — это набор объектов, называемых элементами, которые рассматриваются как единое целое. Он может быть конечным или бесконечным и может содержать элементы любого типа, включая числа, строки и другие наборы. 2. Операции с множествами: Операции с множествами, такие как объединение, пересечение и дополнение, используются для объединения множеств или управления ими. Они используются для манипулирования данными, например для объединения или исключения наблюдений на основе определенных критериев. 3. Диаграммы Венна: Диаграммы Венна представляют собой графическое представление множеств и их отношений. Они используются для визуального представления взаимосвязей данных и помогают идентифицировать закономерности или тенденции. 4. Декартово произведение: Декартово произведение двух множеств — это множество всех упорядоченных пар (a, b), где a — элемент одного множества, а b — элемент другого множества. 5. Набор мощности: Набор мощности набора — это набор всех подмножеств этого набора, включая пустой набор и сам набор. Он используется для генерации всех возможных комбинаций данных и используется в задачах комбинаторной оптимизации. 6. Разделы: Раздел набора — это разделение набора на непересекающиеся подмножества, которые в совокупности составляют набор. Он используется для разделения данных на подмножества для дальнейшего анализа, например, для создания стратифицированных выборок для проверки гипотез. Освоение этих концепций теории множеств поможет вам эффективно манипулировать данными и анализировать их, а также лучше понимать отношения между переменными. Описательная статистика является важным аспектом науки о данных, поскольку она обеспечивает метод обобщения и характеристики больших и сложных наборов данных. 1. Исследование данных: Описательная статистика обеспечивает быстрый и простой способ изучения и обобщения больших наборов данных. Например, такие меры, как среднее значение, медиана и мода, предоставляют сводную статистику, которую можно использовать для описания центральной тенденции набора данных. Кроме того, такие графики, как гистограммы, ящичные диаграммы и диаграммы рассеяния, дают визуальное представление данных, которое можно использовать для выявления закономерностей и взаимосвязей в данных. 2. Очистка данных: Описательную статистику также можно использовать для выявления выбросов, отсутствующих значений и других проблем с данными, которые необходимо решить до проведения дальнейшего анализа. Используя такие показатели, как минимум, максимум и квартили, специалисты по данным могут быстро определить точки данных, выходящие за пределы нормального диапазона, и принять соответствующие меры. 3. Представление данных: Описательная статистика является мощным инструментом для представления данных в ясной и краткой форме. Обобщая данные с помощью таких показателей, как среднее значение и стандартное отклонение, специалисты по данным могут передавать сложные данные таким образом, чтобы их было легко понять другим. Графики, такие как гистограммы, гистограммы и линейные диаграммы, также можно использовать для визуального представления данных в привлекательной и простой для понимания форме. 4. Анализ данных: Описательная статистика обеспечивает основу для более продвинутых методов анализа данных. Например, корреляция и ковариация могут использоваться для определения взаимосвязей между переменными. Между тем, проверку гипотез можно использовать для того, чтобы делать выводы о популяциях на основе выборочных данных. Статистика логических выводов является важным аспектом науки о данных, поскольку она предоставляет метод для обобщения совокупности на основе выборочных данных. 1. Проверка гипотез: Логическая статистика предоставляет методы проверки гипотез о популяциях на основе выборочных данных. Например, проверку гипотезы можно использовать для определения того, существует ли значительная разница между средними значениями двух групп или существует ли взаимосвязь между двумя переменными. 2. Построение моделей: Инференциальная статистика предоставляет методы построения моделей, которые можно использовать для прогнозирования или выводов о совокупностях на основе выборочных данных. Например, моделирование связи между зависимой переменной и одной или несколькими независимыми переменными. Между тем, алгоритмы машинного обучения, такие как деревья решений и случайные леса, могут использоваться для прогнозирования на основе больших и сложных наборов данных. 3. 4. Принятие решений: Инференциальная статистика также предоставляет инструменты для принятия обоснованных решений на основе выборочных данных. Например, тесты статистической значимости можно использовать для определения того, является ли взаимосвязь между переменными реальной или случайной, а анализ затрат и выгод можно использовать для определения оптимального решения на основе ожидаемых затрат и выгод. Начните с вводных курсов статистики. Онлайн-платформы, такие как Coursera, Udemy и edX, предлагают множество вводных курсов по статистике бесплатно или за плату. Они знакомят вас с основами статистики, включая показатели центральной тенденции, изменчивости, вероятности и проверки гипотез. Работа с реальными данными. Практика с реальными данными — отличный способ получить практический опыт. Вы можете найти наборы данных в Интернете или использовать свои собственные данные. Попробуйте такие инструменты, как R и Python, для анализа указанных данных и применения статистических методов. Иметь правильное представление об исследовательском анализе данных (EDA), который представляет собой процесс, используемый для обобщения и визуализации данных. Это важный шаг в процессе анализа данных. Вы должны быть знакомы с различными типами графиков и способами их использования для визуализации данных. Некоторыми примерами являются гистограммы, диаграммы рассеяния и диаграммы. Когда у вас будет прочная основа в описательной статистике, начните изучать статистику логического вывода. Важно досконально знать вероятность, проверку гипотез и регрессионный анализ. Продолжай тренироваться! Всегда есть чему поучиться, и важно быть в курсе последних событий в этой области. 11 Тест Современные проблемы науки и техники 1. Один из основоположников философии
техники? а) П. Энгельмейер б) Т. Кун в) К. Поппер г) М. Хайдеггер 2. Э. Каппа понимал машину как а) проекцию органов человека на природный
материал б) человеческое отражение идей Творца в) определяющий закон человеческого
бытия г) универсальную ценность вселенского
масштаба 3. Особенностью современного
научно-технического прогресса является… а) массовое машинное производство б) автоматизация производства в) создание новых технологий на базе
научной теории г) широкое использование электрической
энергии 4. С точки зрения М. Хайдеггера, отношения
человека и техники определяются а) человеком б) техникой в) Богом г) культурно-исторической спецификой 5. а) создает ложное представление о мире б) закрывает другие пути усмотрения
истины в) вытесняет человека из его онтологической
ниши г) противоречит сущности человека 6. С точки зрения Н. Бердяева, техника
положила начало кризису а) ренессансного гуманизма б) классического рационализма в) античного органицизма г) первобытного холизма 7. Выделите имена мыслителей, которые
исходили из позиций технологического детерминизма в
понимании истории и общества: а) Д. Белл б) О. Тоффлер в) М. Шелер г) Дж. Грант д) Э. Дюркгейм е) М. Кастельс 8. Как в психотерапии называется
аномальная зависимость человека от компьютера? а) виртуальная аменция б) терминальная тождественность в) виртуальная аддикция г) кибернетическая обсессия 9. начать «с нуля» в виртуальной
реальности (Undo)? а) рациональную б) утилитарную в) этическую г) эмоциональную 10. Какой вид коммуникации открывает
возможности для тоталитарного контроля над обществом? а) телеграф б) радио в) телевидение г) Интернет 11. Каковы главные критерии техники? а) эффективность б) надежность в) мобильность г) безопастность 12. Является
ли техника нейтральной в моральном
отношении? а)
Техника
как символическое бытие человека не
является нейтральной в моральном
отношении. Ведь сам
человек морально не нейтрален. б)
Техника
как символическое бытие человека
является нейтральной в моральном
отношении. 13. За что
критиковал технику Э.Гуссерль? а) за то, что техника
не моральна б)
за то,
что в технике человек забывает свой
собственный, внутренний мир. в) за то, что в технике
открывает возможности для тоталитарного
контроля над обществом 14. Может ли человек быть замещен
техникой? а)
Человек
не может быть замещен техникой, ибо он
уникален, особенно в ценностном отношении. б)
Человек
в современном мире постепенно замещается
техникой. 15.
Какие обстоятельства повлияли на то,
что становление философии
техники как особой дисциплины сложилось
только в ХХ веке? а)
ростом
значимости техники б)
развитием
философии в)
исторической необходимостью г)
законам развития общества 16. За
что критиковал технику М. Хайдеггер? а)
за
то, что техника становится преградой
на пути проявления истинно человеческого б)
за то, что техника опережает развитие
философии в)
за то, что техника заменяет человека
постепенно 17. а) К. Попперу б) И. Лакатосу в) Т. Куну г) П. Фейерабенду 18. Этап парадигмального развития науки
Кун называет а) нормальной наукой б) паранаукой в) инновацией г) научной революцией 19. К теоретическому познанию относится… а) формализация б) наблюдение в) эксперимент г) измерение 20. Способ логического рассуждения от
единичных утверждений к положениям,
носящим более общий характер, называется… а) дедукцией б) индукцией в) аналогией г) моделированием 21.
Аристотель придерживался в своей работе
метода: системного аналитического индуктивного дедуктивного 22.
В качестве высшего критерия истины в
средние века принималась (принимался) знание вера опыт здравый смысл 23. Р. Декарт Г. Гегель Ф. Бэкон Г. Лейбниц 24.
Метод рациональной дедукции разработал Р. Декарт Ф. Бэкон Г. Гегель Г. Лейбниц 25. Принцип
верификации как главный критерий научной
обоснованности высказываний сформулировал Л. Витгенштейн И. Лакатос К. Поппер Б. Рассел 26.
Способ обоснования истинности суждения,
системы суждений или теории с помощью
логических умозаключений и практических
средств (наблюдение, эксперимент и т.п.)
называется дедукция доказательство аргументация рассуждение 27.
Методологический принцип, в котором за
основу познания берутся чувства и
который стремится все знания вывести
из деятельности органов чувств, ощущений,
называется эмпиризм агностицизм скептицизм сенсуализм 28. дедукция индукция экстраполяция аналогия 29.
Принцип верифицируемости как главный
критерий научной обоснованности
высказываний сформулировал Л. Витгенштейн Б. Рассел Р. Карнап И. Лакатос 30.
Структурный элемент работы, в котором
определяется ее цель, задачи, исследованность
проблемы, называется заключение основная часть введение оглавление 31.
Познавательный процесс, который
определяет количественное отношение
измеряемой величины к другой, служащей
эталоном, стандартом, называется моделирование сравнение измерение идеализация 32. Б. Рассел Р. Карнап К. Поппер И. Лакатос 33.
Переход в познании от общего к частному
и единичному, выведение частного и
единичного из общего, называется индукция дедукция аналогия аргументация 34.
Умственное действие, связывающее в ряд
посылок и следствий мысли различного
содержания называется суждением синтезом умозаключением выводом 35.
Психическая деятельность, состоящая в
создании представлений и мысленных
ситуаций, никогда в целом не воспринимавшихся
человеком в действительности, называется синтезом мышлением фантазией анализом 36. брошюра монография диссертация словарь 37.
Социально обусловленная система знаков,
служащая средством человеческого
общения, мышления и выражения, называется языком речью теорией интерпретацией 38.
Образ ранее воспринятого предмета или
явления, а также образ, созданный
продуктивным воображением; форма
чувственного отражения в виде
наглядно-образного знания, называется понятие представление восприятие умозаключение 39.
Небольшой по объему источник, содержащий
популяризированный текст в адаптированном
для понимания неспециалиста виде,
называется книга брошюра монография словарь 40. знанием интерпретацией правдой истиной 41.
Чувственный образ внешних структурных
характеристик предметов и процессов
материального мира, непосредственно
воздействующих на органы чувств,
называется ощущение восприятие представление понятие 42.
Антиисторический, недиалектический
тип мышления, при котором анализ и оценка
теоретических и практических проблем
и положений производится без учета
конкретной реальности, условий места
и времени, называется софистика релятивизм эклектика догматизм 43. эклектика диалектика метафизика софистика 44.
Положение, принимаемое в рамках какой-либо
научной теории за первооснову логической
дедукции и поэтому в данной теории
играющее роль знания, принимаемого без
доказательства, называется догмат теорема постулат закон 45.
Мировоззренческая позиция, в основе
которой лежит представление о научном
знании как о наивысшей культурной
ценности и достаточном условии ориентации
человека в мире, называется провиденциализм эмпиризм сциентизм антисциентизм 46. гипотезой концепцией теорией аргументом 47.
Формы осознания в понятиях всеобщих
способов отношения человека к миру,
отражающие наиболее общие и существенные
свойства, законы природы, общества и
мышления, называются закономерности категории законы логики теории 48.
Та часть объективной реальности, которая
взаимодействует с человеком, социальным
институтом, обществом в процессе
познания, называется предмет познания субъект познания объект познания предмет практики 49. предположение мнение домысел взгляд 50.
Теория истолкования, имеющая целью
выявить смысл текста, исходя из его
объективных (значение слов и их исторически
обусловленные вариации) и субъективных
(намерения авторов) оснований, называется методология гносеология герменевтика пропедевтика 51. Фаллибилизм как принцип научного
познания означает а) влияние бессознательных акцентуаций
на результаты исследования б) идеологические искажения результатов
исследований в) поиск логических ошибок с целью их
устранения г) принципиальную опровержимость научных
теорий 52. а) К. Попперу б) И. Лакатосу в) Т. Куну г) П. Фейерабенду 53. Структуру научно-исследовательской
программы составляют: а) ядро, защитный пояс, эвристики б) гипотеза, теория, методология в) проблема, решение, верификация г) чувственный и рациональный уровни 54. Регрессивный этап развития
научно-исследовательской программы характеризуется: а) увеличением числа междисциплинарных
изысканий б) ростом метафизических исследований в) предвосхищением теоретических
обобщений эмпирического познания г) опережением роста эмпирических знаний
темпов теоретических обобщений 55. Поскольку Т. Кун поставил развитие
науки в зависимость от деятельности научных сообществ,
то в его концепции характеристикой научного знания является а) каузальная обусловленность б) отсутствие преемственности в) кумулятивизм г) идеологическая индоктринация 56. эволюционным процессам в понимании а) Ч. Дарвина б) Кювье в) К. Линнея 57. Этап парадигмального развития науки
Кун называет а) нормальной наукой б) паранаукой в) инновацией г) научной революцией 58. Согласно П. Фейерабенду, рост научного
знания происходит в процессе а) сегментации б) секуляризации в) партиципации г) полиферации 59. Какое место Фейерабенд отводил
науке относительно других форм знания? а) считал науку генетически высшим типом
познания б) уравнивал их эвристический потенциал в) подчинял науку вненаучным и донаучным
представлениям г) полагал качественный разрыв между
наукой и другими формами знания 60. Используя схему, аналогичную теории
Дарвина, С. Тулмин оценивает результаты познания как а) истинные и ложные б) научные и вненаучные в) адаптивные и неадаптивные г) эволюционирующие и тупиковые 61. а) мутации б) девиации в) инициации г) флуктуации 62. Рациональность у Тулмина понимается
как а) стандарты обоснования и понимания б) следование правилам формальной логики в) целенаправленная деятельность г) метаязык всех текстов 63. Фундаментальным понятием методологии,
по Тулмину, является понятие а) гибридизации знаний б) интеллектуальной среды в) эволюционирующей рациональности г) концептуальных популяций 64. Уберите критерии оценки научного
объяснения, которые игнорировал С. Тулмин: а) надежность б) когерентность в) истинность г) удобство д) ложность 65. С точки зрения М. Полани, устранение
личностного начала из научного познания ведет к а) объективности б) абсурдизации в) отчуждению г) идеализации 66. а) тупиковый путь научного постижения
мира б) пережиток мифологического мышления в) необходимое основание познания г) неформализуемый избыток информации 67. Основой неявного и личностного
знания у Полани является а) семантическая неопределенность б) периферическое восприятие в) символическая природа сознания г) трансцендентная реальность 68. С точки зрения Дж. Холтона, тематические
структуры науки а) являются надысторическими и неизменными б) определяются общественной практикой в) обусловлены предметом исследования г) формируются в государственных
интересах Скачать 22,06 Kb. 1 2 Раздел:
Философские проблемы техники
(Тест)
Уровень базовый: (из предложенных вариантов выбрать один правильный.)
б) в.п. XIXв. в) нач. XXIв.
г) конец XVIIIв. 2. Впервые использовал словосочетание «философия техники»:
а) П. б) Э.Капп
в) Аристотель г) Ф.Бон
3. Назовите автора высказывания: «Сколько вы его (инженера) ни начиняйте специальными познаниями, это будет ученый ремесленник, пока вы ему не дадите гуманитарного взгляда на социально-экономические стороны его профессии»:
а) К.Маркс б) П.К.Энгельмейер
в) Э.Капп г) Ж.Эллюль
4. Кто из философов утверждал, что цель техники – достижение счастья человеком:
а) Ф.Бон
в) Э.Капп г) Ф.Бэкон
5. Техника и …. являются объективирующими деятельностями, т.е. воплощают идею, замысел:
а) наука
в) миф
Каталог: scientific activities -> division of graduate and doctorate -> graduate school Скачать 22,06 Kb. 1 2 Автореферат Анализ Анкета Бағдарламасы Бизнес-план Биография Бюллетень Викторина Выпускная работа Глава Диплом ВИКТОРИНА точность играет 3 года Карл Кункер играет Ученические устройства не требуются. 12
вопросы См. предварительный просмотр 1. Множественный выбор 15 минут 1 балл Научный метод используется в повседневной жизни получать/получать информацию. Верно Ложно 2. Множественный выбор 30 секунд 1 балл Всегда ли можно проводить эксперименты для сбора данных? Да Нет, потому что они всегда слишком дороги Нет, потому что могут быть повреждены живые существа 3. 30 секунд Каковы цели наука? Расскажите обществу, что чувствовать и думать Дать естественное объяснение событий в мире природы Объяснить религию и философию 4. Множественный выбор 30 секунд 1 балл 900 03 Почему экспертная оценка важна? Ученые должны быть заняты, чтобы делать свою работу наилучшим образом. Публикация рецензируемых статей в научных журналах позволяет исследователям обмениваться идеями, а также проверять и оценивать работу друг друга. Ученые не проводят экспертную оценку. Они хотят убедиться, что правы только они. 5. Множественный выбор 30 секунд 1 балл Ученые становятся скептиками через: A. Только A Только B C и A A, B и C 6. Множественный выбор 30 секунд 1 балл Ученые, не согласные с гипотезами, разрабатывают эксперименты для их проверки . 7. Множественный выбор 30 секунд 1 балл Какие научные взгляды помогают генерировать новые идеи? Любопытство, скептицизм, непредубежденность и креативность помогают ученым генерировать новые идеи. Гнев, разочарование и любопытство помогают генерировать новые идеи. Никто не знает, какие установки порождают новые идеи. Только творчество помогает ученым генерировать новые идеи. 8. Множественный выбор 30 секунд 1 балл Что является примером количественных данных? Мальчик много отжимался У мальчика светлые волосы. Мальчик весит 140 фунтов. У мальчика зеленые глаза. 9. Множественный выбор 30 секунд 1 балл Какой пример качественных данных? У девушки каштановые волосы. Волосы девушки 50 сантиметров в длину. Рост девушки 95 сантиметров. Девушка весит 140 фунтов 10. Множественный выбор 30 секунд 1 pt Ученые должны оставаться непредубежденными, что означает, что они готовы принимать различные идеи, которые могут не согласовываться с их гипотезой. Правда Ложь 11. Множественный выбор 30 секунд 1 точка Честный и достоверный эксперимент содержит: независимую переменную зависимую переменную контролируемые переменные (контроли ) Все вышеперечисленное 12. Множественный выбор 30 секунд 1 балл Как можно гарантировать объективность эксперимента sed и действительный? экспертная оценка несколько графиков несколько испытаний, экспертная оценка, независимые и зависимые переменные отправить ссылку на выпуск новостей Экспонировать все вопросы с помощью бесплатной учетной записи Уже есть учетная запись? Фуллер начинает с заявления о том, что «трудно написать книгу о философии в такой области, которая столь решительно неуважительно относится к академической философии, как исследования в области науки и техники» (ix). Концепция науки Фуллера представлена уже на второй странице «Введения». в глобальном масштабе со значительными материальными ресурсами. Другим является согласованные политические усилия по применению результатов научных исследований во всех аспектах жизни общества. Наконец, это контроль, который ученые продолжают осуществлять над тем, как рассказывается их история. Прошлые отклонения и неудачи остаются в значительной степени скрытыми , в результате чего создается ретушированная картина «прогресса», в противном случае отсутствующая в человеческих делах. В этом списке отсутствует то, что большинство людей назвало бы «успехом» науки. Я подозреваю, что Фуллер считает то, что другие называют «успехом», чем-то вроде «прогресса», продуктом действия его «трех столпов». Фуллер действительно является социальным конструктивистом в отношении науки, но с важными оговорками, которые появляются на протяжении всей книги. В главе II «Социология знания: философский фон для СТС» Фуллер утверждает, что под влиянием как Куна, так и антропологии, СТС разработала «социологию науки, которая не является социологией знания» (28). -30). Знание для Фуллера имеет нормативное измерение, которого, по его мнению, не хватает в СС, что дает основания для обвинений в «релятивизме», которые являются основным элементом критики СС. Но для Фуллера все не так просто. По согласованию с Яном Хакингом (1999), Фуллер различает «опровержение» и «разоблачение» (18-21). Релятивист пытается опровергнуть претензии ученых на объективное знание. Ученые правильно видят в этом угрозу легитимности своих утверждений. Резюме Фуллера главы III «Философия в, вне и за пределами научной области» начинается с утверждения, что «СТС не только определяет себя в оппозиции к философии, но также требует философии, которую она может назвать своей собственной» (45). Лаудан невольно довел до абсурда то, что происходит, когда философы отказываются от своей привилегии второго порядка в определении природы науки, чтобы конкурировать с теми, кто изучает науку эмпирически: они сводятся к банальностям. (47) Но Лаудан может оказаться слишком легкой мишенью. Интересно, что бы он сказал о «когнитивных исследованиях науки», представленных, например, Нэнси Нерсесян (2002) в США и Дэвидом Гудингом (19).90) в Великобритании. Здесь цель состоит не в том, чтобы поддержать банальные методологические утверждения, а в том, чтобы, опираясь на работы в области когнитивных наук, исследовать когнитивные механизмы, используемые учеными при создании и проверке научных концепций. Фуллер еще более критически относится к роли STS в качестве подсобного рабочего, сосредоточив внимание на Бруно Латуре и теории акторно-сетевой теории, хотя он считает, что работа над (не)реплицированием в науке «необходимо воспринимать всерьез как нормативную проблему, поскольку это одна из главных причин, почему люди, не являющиеся учеными, считают, что наука дает высшую форму знания» (58). Фуллер также критически относится к концепции STS о «технонауке». Он видит концепцию ученых о науке как автономной и чистой во время холодной войны (хотя Министерство обороны было основным спонсором научных исследований в США), отраженную в позитивистской философии науки. Точно так же он считает концепцию технонауки STS особенно хорошо адаптированной к периоду после холодной войны, когда большая часть финансирования науки поступает от корпораций, а сами ученые гораздо более комфортно чувствуют себя в более тесной связи между наукой и технологиями. Напротив, Фуллер хвалит шведского исследователя STS, который выявил методологические недостатки в исследованиях синдрома дефицита внимания и задокументировал влияние фармацевтических компаний, которые финансировали большую часть исследования. Глава IV «Постмодернистский позитивизм: СС под другим именем?» преследует две основные цели. Одна из них — рассмотреть историю позитивизма как первого социального и интеллектуального движения, пытавшегося извлечь уроки из ошибок проекта Просвещения, который завершился, во-первых, террором после Французской революции 1789 года, а во-вторых, иррационализмом Веймарской республики после поражения Германии в Первой мировой войне. (79) Вторая цель главы — «показать, СС можно рассматривать как постмодернистскую версию позитивизма, особенно обновившую представление о «науке» как о социальном ресурсе, доступном не только для членов с визитной карточкой в конкретных научных дисциплинах» (79). Фуллер видит параллели между Платоном и позитивизмом, хотя и признает, что эта параллель поднимает некоторые «деликатные вопросы». власть текла вниз от царя-философа в кастовой социальной структуре, позитивисты предвидели, что все человечество может пройти (с переменной скоростью) через последовательность стадий — теологическую, метафизическую и научную… рецепт превращения платонизма в позитивизм. Он исходит из изоляции области исследования от случайностей, окружающих его проявления, с тем, чтобы можно было понять его сущностную природу… Историю позитивизма можно четко схватить как гегелевскую диалектику, три момента которые воплощены в трудах Огюста Конта (тезис), Эрнста Маха (антитезис) и Венского кружка (синтез).0003 Это все новости для кого-то вроде меня, кто всегда думал, что Просвещение выросло из научной революции 17-го века и что позитивизм был продолжением мысли Просвещения, распространившейся на 20-й век. Это явно противоречит выводу Фуллера о том, что «Просвещение и позитивизм тянутся в совершенно разных направлениях» (113). Общность, которую Фуллер находит между позитивизмом после Второй мировой войны и СС, заключается в следующем. Позитивисты представляли науку состоящей из специальностей, изолированных от остального общества. И они считали себя специалистами, также изолированными от остального общества. Как отмечает Фуллер, представление Куна о нормальной науке, основанной на парадигмах, в этом отношении похоже на позитивизм. Конечно, отличительной чертой исследований СС является то, что наука рассматривается как тесно связанная с обществом и подверженная всевозможным социальным и политическим влияниям. Но Фуллер считает, что само современное исследование STS аналогично действует как специальность, основанная на парадигме, парадигмой, которая теперь является акторно-сетевой теорией. Вторая половина главы посвящена непрекращающимся «научным войнам», которые Фуллер рассматривает как прискорбный конфликт внутри академии, который в основном служит интересам тех, кто не доверяет ученым и часто их очерняет. Ближе к концу главы V «Вновь чарующая наука: за пределами пуритан и гностиков» Фуллер пишет: искажает дух, который мотивировал проведение научного исследования, воплощенного в «научности», повторяющейся, но подавляемой теме в истории науки. (152) Необходимы некоторые пояснения. О «сциентизме» Фуллер пишет: «В своей простейшей форме [сциентизм] есть учение о том, что наука может обосновать ценностные обязательства» (122). Огюст Конт и Герберт Спенсер являются одними из его главных примеров сциентистских мыслителей. Фактически, для Фуллера Конт и Спенсер представляли собой «гностический сциентизм», который во имя науки ниспровергал бы общественный порядок. Фуллер противопоставляет гностический сциентизм «научному пуританству», позиции, которой придерживаются многие ученые, такие как Алан Сокал и Стивен Вайнберг, активно участвовавшие в научных войнах, а также философы и философы науки, такие как Сьюзан Хаак и Эллиот Собер. Научные пуритане утверждают «внутреннюю ценность технического мастерства и необходимость самоограничения в его применении» (116). В последней главе «Гражданская наука: развитие жизни в СС» Фуллер выдвигает на передний план свою собственную социальную эпистемологию. Хотя древние греки полны ложных выводов, когда дело доходит до определения природы научного гражданства в демократии, линия преемственности от Платона к позитивизму, тем не менее, обеспечивает контекст для понимания эволюция современной концепции экспертизы и определенные проблемы, которые она ставит перед современными демократиями. Эти проблемы связаны с вопросами институционализации, в частности, с тем, как спроектировать институты, которые уважают роль знаний в коллективном принятии решений, не поддаваясь правилу, основанному на опыте (157). Его решение этой проблемы — «консенсусная конференция» (или «гражданское жюри»), «средство участия общественности в разработке политики в области науки и технологий» (167). Консенсусная конференция состоит из двух этапов. «На первом [этапе] 10–15 представителей общественности имеют право получать показания от различных экспертов и заинтересованных групп». На втором этапе «присяжные обсуждают друг с другом, чтобы прийти к руководящим принципам политики для законодательства, регулирующего вопрос» (167). Рассмотрим случай школьного совета, который рассматривает вопрос о том, следует ли преподавать IDT в качестве серьезной альтернативы эволюционной теории (ET). Имеет ли смысл урегулировать этот вопрос в соответствии с обязательной рекомендацией Я выбрал этот пример, потому что сам Фуллер недавно свидетельствовал в защиту в оспаривании решения школьного совета о признании IDT на уроках естественных наук в Довере, штат Пенсильвания (Talbot 2005). Рискуя прослыть «научным пуританином», мне кажется, что это слишком далеко заходит в социальной конструкции научного знания, демократии участия и боязни управления со стороны экспертов. Хотя Фуллер прав в том, что инопланетяне не вмешиваются напрямую во многие работы в области биологии, они обеспечивают объединяющие принципы для всей биологии. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 3
3 14159..
14159.. Наиболее частые заболевания, связанные с сосудосуживающим действием никотина:
Наиболее частые заболевания, связанные с сосудосуживающим действием никотина: Рассчитай высоту столба налитой в резервуар жидкости.
Рассчитай высоту столба налитой в резервуар жидкости.
 Знайдіть інші сторони трикутника.
Знайдіть інші сторони трикутника. какой будет %
какой будет %

 2 Решение x 2 +x-1 = 0, заполнив квадрат.
2 Решение x 2 +x-1 = 0, заполнив квадрат.
 5 ПОЛ/ПОТОЛОК: СУММЫ
5 ПОЛ/ПОТОЛОК: СУММЫ Дискретная вероятность
Дискретная вероятность Если заданная последовательность элементов удовлетворяет линейному рекуррентному соотношению, то решение задачи об отыскании общей формулы вычисления аналогично решению линейных дифференциальных уравнений высших порядков с постоянными коэффициентами.
Если заданная последовательность элементов удовлетворяет линейному рекуррентному соотношению, то решение задачи об отыскании общей формулы вычисления аналогично решению линейных дифференциальных уравнений высших порядков с постоянными коэффициентами. Тогда — общее решение линейного неоднородного рекуррентного соотношения (1).
Тогда — общее решение линейного неоднородного рекуррентного соотношения (1). Тогда общее решение , где и произвольные постоянные (, ). Используем заданные значения , составим систему из двух уравнений с двумя неизвестными:
Тогда общее решение , где и произвольные постоянные (, ). Используем заданные значения , составим систему из двух уравнений с двумя неизвестными:

 Производящая функция кодирует количество объектов с помощью формальных степенных рядов, которые представляют собой полиномы с (возможно) бесконечным числом членов (целых степеней).
Производящая функция кодирует количество объектов с помощью формальных степенных рядов, которые представляют собой полиномы с (возможно) бесконечным числом членов (целых степеней). Поскольку значение \(a\) может быть любым неотрицательным целым числом \(0,1,2,3, \ldots, i , \ldots \) (см. примечание ниже), мы можем представить это как производящую функцию 9я + \cdots. \]
Поскольку значение \(a\) может быть любым неотрицательным целым числом \(0,1,2,3, \ldots, i , \ldots \) (см. примечание ниже), мы можем представить это как производящую функцию 9я + \cdots. \]
 \) Это линейно, потому что каждый член имеет только один моном вида \(c_i\) и он однороден, потому что правая часть равна 0. Если бы правая часть была ненулевой функцией \(n,\), то она была бы неоднородной. Чтобы полностью решить рекуррентное соотношение, нам нужны начальные значения для первых \(k\) членов, где это \(k\) такое же, как и в определении. 9d},\]
\) Это линейно, потому что каждый член имеет только один моном вида \(c_i\) и он однороден, потому что правая часть равна 0. Если бы правая часть была ненулевой функцией \(n,\), то она была бы неоднородной. Чтобы полностью решить рекуррентное соотношение, нам нужны начальные значения для первых \(k\) членов, где это \(k\) такое же, как и в определении. 9d},\] {n+1} \] 92}. \ _\квадрат\]
{n+1} \] 92}. \ _\квадрат\] \) Если мы разделим цифры на разделы по 5, мы видим, что числа образуют последовательность Фибоначчи: \(0,1,1,2,3,5,8,13,\ldots\). Сколько положительных чисел Фибоначчи мы можем найти, прежде чем паттерн разорвется?
\) Если мы разделим цифры на разделы по 5, мы видим, что числа образуют последовательность Фибоначчи: \(0,1,1,2,3,5,8,13,\ldots\). Сколько положительных чисел Фибоначчи мы можем найти, прежде чем паттерн разорвется? {n-1}}={1+\sqrt{5}\over
2}.
$$
Это так называемое «золотое сечение».
9n$, $h_0=0$, и использовать его, чтобы найти формулу
за $h_n$.
{n-1}}={1+\sqrt{5}\over
2}.
$$
Это так называемое «золотое сечение».
9n$, $h_0=0$, и использовать его, чтобы найти формулу
за $h_n$.
 Таким образом, они могут быть открыты в Microsoft Excel, OpenOffice Calc и многих других программ.
Таким образом, они могут быть открыты в Microsoft Excel, OpenOffice Calc и многих других программ.
 Этот файл электронной таблицы поддерживается большинством открытого программного обеспечения или программного обеспечения для электронных таблиц.
Этот файл электронной таблицы поддерживается большинством открытого программного обеспечения или программного обеспечения для электронных таблиц. 99
99 99
99



 $ конвертировать DBF_INPUT_FILE —to xls
$ конвертировать DBF_INPUT_FILE —to xls ..
..
 При проверке ваших работ я увидела, что не все следуют моему образцу оформления. Если надо разложить число на простые множители, то вы:
При проверке ваших работ я увидела, что не все следуют моему образцу оформления. Если надо разложить число на простые множители, то вы: е. Золушка за Вас всё сделает).
е. Золушка за Вас всё сделает).

 Например, – 6 и 9. Модуль каждого числа больше 5, но меньше 10.
Например, – 6 и 9. Модуль каждого числа больше 5, но меньше 10.
 Это и будет максимально возможное число, на которое можно разделить оба значения.
Это и будет максимально возможное число, на которое можно разделить оба значения. Чтобы число делилось на два, нужно, чтобы число единиц было четным.
Чтобы число делилось на два, нужно, чтобы число единиц было четным.
 6
6 Поскольку 4 / 4 = 1, то то, что я сделал выше, было следующим:
Поскольку 4 / 4 = 1, то то, что я сделал выше, было следующим:

 -нижнее деление. Из вышесказанного я вижу, что 2940 множителей как 2×2×3×5×7×7.
-нижнее деление. Из вышесказанного я вижу, что 2940 множителей как 2×2×3×5×7×7. Это число обычно является множителем как числителя, так и знаменателя. Деление на общий множитель не изменит значение дроби, но может упростить работу с ней. Например, если у вас есть дробь ¾, вы можете уменьшить ее до 1/3, разделив числитель (3) и знаменатель (4) на 2. Есть несколько различных методов, которые вы можете использовать для сокращения дробей. В этом сообщении блога мы рассмотрим некоторые из этих методов и когда их следует использовать. Читайте дальше, чтобы узнать больше!
Это число обычно является множителем как числителя, так и знаменателя. Деление на общий множитель не изменит значение дроби, но может упростить работу с ней. Например, если у вас есть дробь ¾, вы можете уменьшить ее до 1/3, разделив числитель (3) и знаменатель (4) на 2. Есть несколько различных методов, которые вы можете использовать для сокращения дробей. В этом сообщении блога мы рассмотрим некоторые из этих методов и когда их следует использовать. Читайте дальше, чтобы узнать больше! Самый распространенный способ сокращения дроби — разделить числитель и знаменатель на наибольший общий множитель (НОД). Это даст вам самые низкие условия для дроби.
Самый распространенный способ сокращения дроби — разделить числитель и знаменатель на наибольший общий множитель (НОД). Это даст вам самые низкие условия для дроби. Самый простой способ сделать это — найти общий множитель между числителем и знаменателем и разделить их на это число. В результате получится дробь, равная исходной, но с меньшими числами.
Самый простой способ сделать это — найти общий множитель между числителем и знаменателем и разделить их на это число. В результате получится дробь, равная исходной, но с меньшими числами.
 Итак, мы перешли к следующее наименьшее простое число (3) и продолжается до тех пор, пока все множители не станут простыми числами. В этом случае полная простая факторизация числа 48 равна: 2 × 2 × 2 × 2 × 3
Итак, мы перешли к следующее наименьшее простое число (3) и продолжается до тех пор, пока все множители не станут простыми числами. В этом случае полная простая факторизация числа 48 равна: 2 × 2 × 2 × 2 × 3 Для этого просто найдите два числа на числовой прямой и посчитайте, сколько пробелов между ними. В нашем примере выше есть четыре пробела между 3 и 4 на числовой прямой. Это означает, что наибольший общий делитель между этими двумя числами равен 4.
Для этого просто найдите два числа на числовой прямой и посчитайте, сколько пробелов между ними. В нашем примере выше есть четыре пробела между 3 и 4 на числовой прямой. Это означает, что наибольший общий делитель между этими двумя числами равен 4. Это потому, что когда вы уменьшаете дробь, вы, по сути, устраняете все ненужные факторы, которые в противном случае усложнили бы ваш расчет. Например, если вы добавляете две дроби и одну из них можно уменьшить, это часто значительно упрощает процесс сложения.
Это потому, что когда вы уменьшаете дробь, вы, по сути, устраняете все ненужные факторы, которые в противном случае усложнили бы ваш расчет. Например, если вы добавляете две дроби и одну из них можно уменьшить, это часто значительно упрощает процесс сложения. Затем разделите числитель и знаменатель на наибольший общий множитель. Полученная фракция находится в наименьших условиях.
Затем разделите числитель и знаменатель на наибольший общий множитель. Полученная фракция находится в наименьших условиях. Наибольший общий делитель равен 5 , поэтому 15/25 сводится к 3/5 .
Наибольший общий делитель равен 5 , поэтому 15/25 сводится к 3/5 .
 2}{5}x+(i)=0\)
2}{5}x+(i)=0\) Угол между ними.
Угол между ними. Матрица смежности онлайн
Матрица смежности онлайн Но иногда мы все же можем найти корни многочлена, стоящего слева в уравнении высшей степени, если представим его в виде произведения многочленов в степени не более 4-х. Решение таких уравнений базируется на разложении многочлена на множители, поэтому советуем вам повторить эту тему перед изучением данной статьи.
Но иногда мы все же можем найти корни многочлена, стоящего слева в уравнении высшей степени, если представим его в виде произведения многочленов в степени не более 4-х. Решение таких уравнений базируется на разложении многочлена на множители, поэтому советуем вам повторить эту тему перед изучением данной статьи. Таким образом, нам нужно будет решить приведенное уравнение n-ной степени с целыми коэффициентами, имеющее вид xn+anxn-1+…+a1x+a0=0.
Таким образом, нам нужно будет решить приведенное уравнение n-ной степени с целыми коэффициентами, имеющее вид xn+anxn-1+…+a1x+a0=0. Здесь Pn-m(x) является многочленом n-m-ной степени. Для подсчета удобно использовать схему Горнера.
Здесь Pn-m(x) является многочленом n-m-ной степени. Для подсчета удобно использовать схему Горнера.


 Проверим делители, разделим и получим в итоге, что оно имеет 2 действительных корня y=-2, y=3 и два комплексных. Решение целиком здесь мы не будем приводить. В силу замены действительными корнями данного уравнения будут x=y2=-22=-1 и x=y2=32.
Проверим делители, разделим и получим в итоге, что оно имеет 2 действительных корня y=-2, y=3 и два комплексных. Решение целиком здесь мы не будем приводить. В силу замены действительными корнями данного уравнения будут x=y2=-22=-1 и x=y2=32.



 Это первый семестр Integrated Math 3, он одобрен Калифорнийским университетом A-G как математика (категория C).
Это первый семестр Integrated Math 3, он одобрен Калифорнийским университетом A-G как математика (категория C).



 После факторизации мы можем приравнять множители к нулю и найти переменную.
После факторизации мы можем приравнять множители к нулю и найти переменную. 



 28675
28675 42447
42447 05030
05030 70463
70463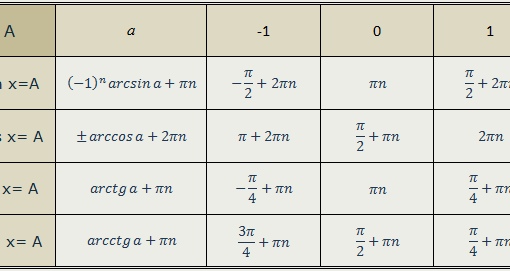 72654
72654 05241
05241 96569
96569 43005
43005 3138
3138 5399
5399 6494
6494 1763
1763 2309
2309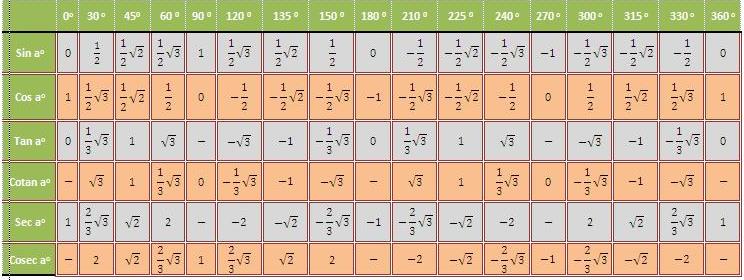 7002
7002 6003
6003 3138
3138 6713
6713 5399
5399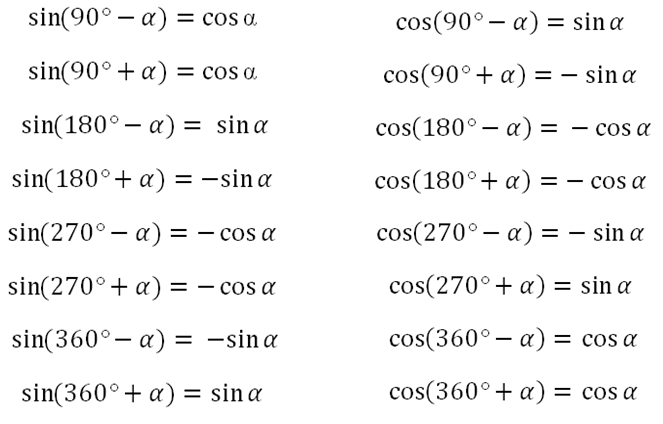 6745
6745 2126
2126 1944
1944 6494
6494 4826
4826 1446
1446 Женева: Всемирная организация здравоохранения; 2018.
Женева: Всемирная организация здравоохранения; 2018. 0 IGO (CC BY-NC-SA 3.0 IGO; https://creativecommons.org/licenses/by-nc-sa/3.0/igo).
0 IGO (CC BY-NC-SA 3.0 IGO; https://creativecommons.org/licenses/by-nc-sa/3.0/igo).
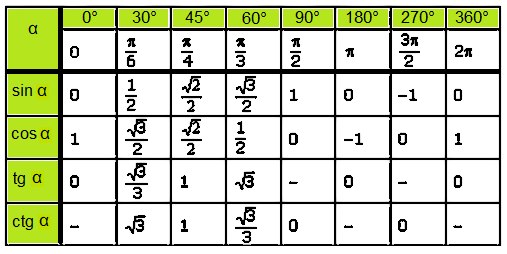 занимается предоставлением решений в области информационных технологий и кадровых услуг. Услуги фирмы охватывают жизненный цикл бизнес-решения в области информационных технологий, включая этапы планирования, разработки, внедрения, управления и обслуживания решения в области информационных технологий. Он работает в следующих сегментах: ИТ-решения и услуги в Северной Америке, ИТ-решения и услуги в Европе и нестратегические технологические услуги. Сегменты ИТ-решений и услуг в Северной Америке и Европе предлагают решения для цифровой трансформации. Служба нестратегических технологий предоставляет кадровые услуги. Компания была основана Рэндольфом А. Марксом и Г. Дэвидом Бэром 11 марта 19 года.66 со штаб-квартирой в Буффало, штат Нью-Йорк.
занимается предоставлением решений в области информационных технологий и кадровых услуг. Услуги фирмы охватывают жизненный цикл бизнес-решения в области информационных технологий, включая этапы планирования, разработки, внедрения, управления и обслуживания решения в области информационных технологий. Он работает в следующих сегментах: ИТ-решения и услуги в Северной Америке, ИТ-решения и услуги в Европе и нестратегические технологические услуги. Сегменты ИТ-решений и услуг в Северной Америке и Европе предлагают решения для цифровой трансформации. Служба нестратегических технологий предоставляет кадровые услуги. Компания была основана Рэндольфом А. Марксом и Г. Дэвидом Бэром 11 марта 19 года.66 со штаб-квартирой в Буффало, штат Нью-Йорк.



 Мы знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.
Мы знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.
 Найти решение уравнения 9x² + 4 = 0.
Найти решение уравнения 9x² + 4 = 0.

 Примеры и решение
Примеры и решение

 Решите уравнение:
Решите уравнение:
 Общий индекс тяжести (GSI, мера общего психологического дистресса) отрицательно, но слабо коррелировал с общим толстокишечным транзитом (r = -0,26, p <0,01). Ощущение анальной закупорки было единственным симптомом, связанным с дисфункцией тазового дна (при нормальных транзитных запорах). Только более регулярный характер дефекации, использование различных поз для дефекации и ощущение неполной эвакуации были связаны с медленным или нормальным транзиторным запором. Однако психологические или толстокишечные симптомы не были значимыми дискриминаторами в многомерном анализе. Время ректосигмовидного транзита при чувствительности 80% имело очень низкую специфичность для дифференциации дисфункции тазового дна от других подгрупп. Сделан вывод о том, что клинические симптомы, психологический дистресс и время ректосигмовидного транзита не могут быть использованы для выделения подгрупп пациентов с трудноизлечимыми запорами.
Общий индекс тяжести (GSI, мера общего психологического дистресса) отрицательно, но слабо коррелировал с общим толстокишечным транзитом (r = -0,26, p <0,01). Ощущение анальной закупорки было единственным симптомом, связанным с дисфункцией тазового дна (при нормальных транзитных запорах). Только более регулярный характер дефекации, использование различных поз для дефекации и ощущение неполной эвакуации были связаны с медленным или нормальным транзиторным запором. Однако психологические или толстокишечные симптомы не были значимыми дискриминаторами в многомерном анализе. Время ректосигмовидного транзита при чувствительности 80% имело очень низкую специфичность для дифференциации дисфункции тазового дна от других подгрупп. Сделан вывод о том, что клинические симптомы, психологический дистресс и время ректосигмовидного транзита не могут быть использованы для выделения подгрупп пациентов с трудноизлечимыми запорами. com
com

 0092 2 + bx + c = 0. Если правая часть не равна нулю, перенесите ее в левую часть и сделайте правую часть нулевой.
0092 2 + bx + c = 0. Если правая часть не равна нулю, перенесите ее в левую часть и сделайте правую часть нулевой. Если вы сделаете это, вы получите только одно решение уравнения (одно значение или один корень из x) и можете потерять другое решение (значение x).
Если вы сделаете это, вы получите только одно решение уравнения (одно значение или один корень из x) и можете потерять другое решение (значение x).

 Квадратичная формула вычисляет два значения x: x 1 и x 2 , где
Квадратичная формула вычисляет два значения x: x 1 и x 2 , где


 Как учить
Как учить Для начала ребенок должен хорошо уметь считать и понимать, например, что к 2 яблокам прибавить ещё 2 яблока будет 4. Важно, чтобы малыш правильно произносил цифры и не путал их. Только тогда можно приступить к изучению таблицы Пифагора.
Для начала ребенок должен хорошо уметь считать и понимать, например, что к 2 яблокам прибавить ещё 2 яблока будет 4. Важно, чтобы малыш правильно произносил цифры и не путал их. Только тогда можно приступить к изучению таблицы Пифагора. Этот метод следует применять тогда, когда ребенок «вызубрил» таблицу и имеет некоторые пробелы. Данный игровой метод представляет собой игру в фанты. Необходимо сделать заготовку карточек, на которых написать умножения на различные числа.
Этот метод следует применять тогда, когда ребенок «вызубрил» таблицу и имеет некоторые пробелы. Данный игровой метод представляет собой игру в фанты. Необходимо сделать заготовку карточек, на которых написать умножения на различные числа. В помощь ребенку сейчас имеется большой выбор различных товаров. Поэтому у родителей не должно возникнуть трудностей, при выборе таблице умножения.
В помощь ребенку сейчас имеется большой выбор различных товаров. Поэтому у родителей не должно возникнуть трудностей, при выборе таблице умножения. Здесь
список программ для печати таблицы умножения:
Здесь
список программ для печати таблицы умножения: Не стесняйтесь посмотреть на все шаблоны, которые мы предлагаем ниже, и выбрать свой любимый!
Не стесняйтесь посмотреть на все шаблоны, которые мы предлагаем ниже, и выбрать свой любимый!  Чтобы сэкономить время, вы найдете в нашем Раздел таблиц All Times, PDF-файлы, включая все таблицы, окрашенные в радугу.
Чтобы сэкономить время, вы найдете в нашем Раздел таблиц All Times, PDF-файлы, включая все таблицы, окрашенные в радугу.
 Уясните, в чем состоит рассматриваемое в задаче испытание. Качественное описание случайных событий их вероятностей. Игральную кость бросают дважды. Последний пункт имеет практическое значение, так как показывает практическую пользу из подсчета вероятности. Элементарное введение в теорию вероятностей. Одна из таких перестановок может выглядеть так: 111110111001001111111110011. Аналогично определяется произвольное количество независимых величин. Сколько матчей играется в течение сезона. Найдите вероятность события AUB. Решение каждой задачи следует начинать с описания множества элементарных событий и благоприятствующих элементарных событий. Событию А благоприятствуют элементарные события 2, 4 и 6. Из 7 команд, участвующих в полуфинале, 3 команды разыграли медали: золотую, серебряную и бронзовую. Статистические характеристики вводятся для выборки, и после рассмотрения вопроса о распределении значений случайной величины. Перестановки без повторений В предыдущих параграфах комбинации отличались как составом предметов, так их порядком.
Уясните, в чем состоит рассматриваемое в задаче испытание. Качественное описание случайных событий их вероятностей. Игральную кость бросают дважды. Последний пункт имеет практическое значение, так как показывает практическую пользу из подсчета вероятности. Элементарное введение в теорию вероятностей. Одна из таких перестановок может выглядеть так: 111110111001001111111110011. Аналогично определяется произвольное количество независимых величин. Сколько матчей играется в течение сезона. Найдите вероятность события AUB. Решение каждой задачи следует начинать с описания множества элементарных событий и благоприятствующих элементарных событий. Событию А благоприятствуют элементарные события 2, 4 и 6. Из 7 команд, участвующих в полуфинале, 3 команды разыграли медали: золотую, серебряную и бронзовую. Статистические характеристики вводятся для выборки, и после рассмотрения вопроса о распределении значений случайной величины. Перестановки без повторений В предыдущих параграфах комбинации отличались как составом предметов, так их порядком.
 ru. Хотите тоже свой сайт?
ru. Хотите тоже свой сайт? Это обеспечит основу для понимания более сложных тем.
Это обеспечит основу для понимания более сложных тем.
 Случайная величина: Случайная величина — это величина, которая может случайным образом принимать различные значения. В науке о данных он используется для моделирования неопределенных результатов событий. Два типа случайных величин дискретные и непрерывные.
Случайная величина: Случайная величина — это величина, которая может случайным образом принимать различные значения. В науке о данных он используется для моделирования неопределенных результатов событий. Два типа случайных величин дискретные и непрерывные. В контексте науки о данных он используется для моделирования взаимосвязей между переменными, для прогнозирования на основе новых данных и понимания неопределенности, связанной с этими прогнозами.
В контексте науки о данных он используется для моделирования взаимосвязей между переменными, для прогнозирования на основе новых данных и понимания неопределенности, связанной с этими прогнозами. Вот несколько важных:
Вот несколько важных: В науке о данных декартово произведение используется для создания новых наборов данных путем объединения данных из нескольких источников.
В науке о данных декартово произведение используется для создания новых наборов данных путем объединения данных из нескольких источников. Она играет ключевую роль в следующих отношениях:
Она играет ключевую роль в следующих отношениях:
 Это мощный инструмент для проверки гипотез, построения моделей, оценки и принятия решений, что делает его важным компонентом науки о данных.
Это мощный инструмент для проверки гипотез, построения моделей, оценки и принятия решений, что делает его важным компонентом науки о данных. Оценка: Логическая статистика позволяет оценивать параметры совокупности на основе выборочных данных. Например, доверительные интервалы можно использовать для оценки диапазона значений, которые могут содержать истинный параметр совокупности, в то время как точечные оценки обеспечивают оценку одного значения параметра совокупности.
Оценка: Логическая статистика позволяет оценивать параметры совокупности на основе выборочных данных. Например, доверительные интервалы можно использовать для оценки диапазона значений, которые могут содержать истинный параметр совокупности, в то время как точечные оценки обеспечивают оценку одного значения параметра совокупности.

 Какую компоненту человеческого
бытия размывает возможность всегда
Какую компоненту человеческого
бытия размывает возможность всегда
 Концепция научно-исследовательских
программ принадлежит
Концепция научно-исследовательских
программ принадлежит Метод эмпирической индукции разработал
Метод эмпирической индукции разработал Один из типов умозаключения и метод
исследования, представляющий собой
вывод общего положения о классе в целом
на основе рассмотрения всех его элементов,
называется
Один из типов умозаключения и метод
исследования, представляющий собой
вывод общего положения о классе в целом
на основе рассмотрения всех его элементов,
называется Метод фальсификации для отделения
научного знания от ненаучного предложил
использовать
Метод фальсификации для отделения
научного знания от ненаучного предложил
использовать Книга, содержащая перечень определений
научных терминов, расположенных в
алфавитном порядке, называется
Книга, содержащая перечень определений
научных терминов, расположенных в
алфавитном порядке, называется Адекватное отражение объекта познающим
субъектом, воспроизведение его так, как
он существует сам по себе, вне и независимо
от человека и его сознания, называется
Адекватное отражение объекта познающим
субъектом, воспроизведение его так, как
он существует сам по себе, вне и независимо
от человека и его сознания, называется Метод познания, при котором все вещи,
их свойства и отношения, а также все
формы их отражения в сознании человека
рассматриваются во взаимной связи и
развитии, называется
Метод познания, при котором все вещи,
их свойства и отношения, а также все
формы их отражения в сознании человека
рассматриваются во взаимной связи и
развитии, называется Научное допущение или предположение,
истинное значение которого неопределенно,
называется
Научное допущение или предположение,
истинное значение которого неопределенно,
называется Предварительное и проблематичное
суждение называется
Предварительное и проблематичное
суждение называется Концепция научно-исследовательских
программ принадлежит
Концепция научно-исследовательских
программ принадлежит Революционный характер развития
науки в концепции Куна аналогичен
Революционный характер развития
науки в концепции Куна аналогичен  Инновации в науке определяются
Тулмином как
Инновации в науке определяются
Тулмином как В концепции Полани неявное, имплицитное
знание представлено как
В концепции Полани неявное, имплицитное
знание представлено как 04.2021
04.2021 К.Энгельмейер
К.Энгельмейер Цели и задачи модуля Целью изучения модуля «История и философия науки»
Цели и задачи модуля Целью изучения модуля «История и философия науки»
 Узнать больше
Узнать больше Множественный выбор
Множественный выбор Ставя под сомнение существующие идеи и гипотезы B. Отказываясь принимать объяснения без доказательств C. С вопросительным и сомнительным отношением .
Ставя под сомнение существующие идеи и гипотезы B. Отказываясь принимать объяснения без доказательств C. С вопросительным и сомнительным отношением .

 Это правда, что основатели новой социологии науки, такие как Дэвид Блур и Гарри Коллинз в 1970-х и 80-х годах, явно развивали свои собственные идеи, прямо противоречащие взглядам некоторых философов, в частности доктрине Поппера о фальсифицируемости. Но эти социологи также приняли философские идеи, подходящие для их целей: несоизмеримость, развитая Куном и Фейерабендом, и неопределенность теории Куайна наблюдением. Использование таких философских идей социологами науки хорошо задокументировано Джоном Заммито (2004). Как автор книги о Куне (2000), Фуллер, конечно, обсуждает влияние Куна на СС, но, как человек, «следящий [с] за развитием СС с большой высоты» (30), он не связывает влияет на конкретных членов сообщества СС. Что он в основном делает, так это рассматривает аспекты этих двух областей в социокультурных терминах, вдохновленных его участием в подходах к «общественному пониманию науки» и «научных войн», а также его собственным «проектом социальная эпистемология» (5). Его идея того, что он называет «вечной философией», применительно к СС — это вопрос: Что такое жизнь в СС? «как призвание, которое также является средством социальных преобразований» (5).
Это правда, что основатели новой социологии науки, такие как Дэвид Блур и Гарри Коллинз в 1970-х и 80-х годах, явно развивали свои собственные идеи, прямо противоречащие взглядам некоторых философов, в частности доктрине Поппера о фальсифицируемости. Но эти социологи также приняли философские идеи, подходящие для их целей: несоизмеримость, развитая Куном и Фейерабендом, и неопределенность теории Куайна наблюдением. Использование таких философских идей социологами науки хорошо задокументировано Джоном Заммито (2004). Как автор книги о Куне (2000), Фуллер, конечно, обсуждает влияние Куна на СС, но, как человек, «следящий [с] за развитием СС с большой высоты» (30), он не связывает влияет на конкретных членов сообщества СС. Что он в основном делает, так это рассматривает аспекты этих двух областей в социокультурных терминах, вдохновленных его участием в подходах к «общественному пониманию науки» и «научных войн», а также его собственным «проектом социальная эпистемология» (5). Его идея того, что он называет «вечной философией», применительно к СС — это вопрос: Что такое жизнь в СС? «как призвание, которое также является средством социальных преобразований» (5). Как бы трудно ни было писать эту книгу, ее еще труднее рецензировать. Те, кто знаком с несколькими работами Фуллера, знают, насколько широко Он легко скользит от Платона к Конту, к логическому позитивизму или от Французской революции к Первой мировой войне. … Решив, что тематически рассматривать эту книгу не в моих силах, я буду продвигаться вперед глава за главой, концентрируясь лишь на нескольких идеях или проблемах в каждой.0003
Как бы трудно ни было писать эту книгу, ее еще труднее рецензировать. Те, кто знаком с несколькими работами Фуллера, знают, насколько широко Он легко скользит от Платона к Конту, к логическому позитивизму или от Французской революции к Первой мировой войне. … Решив, что тематически рассматривать эту книгу не в моих силах, я буду продвигаться вперед глава за главой, концентрируясь лишь на нескольких идеях или проблемах в каждой.0003 0003
0003 Конструктивист, с другой стороны, только пытается продемонстрировать социальные и риторические стратегии, которые ученые используют для подтверждения своих претензий на объективное знание. Таким образом, утверждения ученых скорее разоблачаются, чем опровергаются. Ученые все еще могут претендовать на объективное знание, хотя объективность знания имеет другой источник, чем признает большинство ученых. Но принижается эпистемологический статус ученых. По Фуллеру, «социальная эпистемология науки должна задаться вопросом, как наука должна быть легитимирована после того, как социальные конструктивистские теории получили широкое признание. Может ли наука, как и религия, выжить в демистифицированной форме» (37)? Я бы сказал «да», но демистификация не должна заходить так далеко, как разоблачение.
Конструктивист, с другой стороны, только пытается продемонстрировать социальные и риторические стратегии, которые ученые используют для подтверждения своих претензий на объективное знание. Таким образом, утверждения ученых скорее разоблачаются, чем опровергаются. Ученые все еще могут претендовать на объективное знание, хотя объективность знания имеет другой источник, чем признает большинство ученых. Но принижается эпистемологический статус ученых. По Фуллеру, «социальная эпистемология науки должна задаться вопросом, как наука должна быть легитимирована после того, как социальные конструктивистские теории получили широкое признание. Может ли наука, как и религия, выжить в демистифицированной форме» (37)? Я бы сказал «да», но демистификация не должна заходить так далеко, как разоблачение. ). Он сетует на «крах философии науки как нормативного предприятия» (45). Философы науки, утверждает он, стали «младшими работниками», играя Локка в современной науке. Он особенно критически относится к попыткам историзации и натурализации философии науки. Здесь он критикует попытку Ларри Лаудана «проверить» методологические заявления философов на исторических и современных примерах (Донован, Лаудан и Лаудан 19).88) Его суровый вывод состоит в том, что
). Он сетует на «крах философии науки как нормативного предприятия» (45). Философы науки, утверждает он, стали «младшими работниками», играя Локка в современной науке. Он особенно критически относится к попыткам историзации и натурализации философии науки. Здесь он критикует попытку Ларри Лаудана «проверить» методологические заявления философов на исторических и современных примерах (Донован, Лаудан и Лаудан 19).88) Его суровый вывод состоит в том, что
 Шумиха в шведской прессе привела к тому, что Национальный совет Швеции по социальному здравоохранению отменил план по назначению нового лекарства от гиперактивности тысячам детей. Фуллер сетует на тот факт, что такие действия исследователя СС не получили особого признания со стороны истеблишмента СС в США, Великобритании или Франции.
Шумиха в шведской прессе привела к тому, что Национальный совет Швеции по социальному здравоохранению отменил план по назначению нового лекарства от гиперактивности тысячам детей. Фуллер сетует на тот факт, что такие действия исследователя СС не получили особого признания со стороны истеблишмента СС в США, Великобритании или Франции. ).
). Но тогда я, как и Фуллер, не историк.
Но тогда я, как и Фуллер, не историк.
 Научные пуритане, таким образом, поддерживают различие между научными фактами и социальными ценностями и не желают вмешиваться или вводить свою науку в вопросы, связанные с ценностями, за исключением, конечно, ценности занятия наукой. «По сути, — пишет Фуллер, — гностицизм — это пуританство, доведенное до его логической крайности» (128). Но отличия существенные. Для научных пуритан мир природы и сама наука «разочарованы». В мире природы нет ничего, что придавало бы ценность или смысл человеческому существованию. К сожалению, по словам Фуллера, мейнстримные СС демонстрируют пуританское отношение как к себе, так и к наукам, которые они изучают. Он хочет заново очаровать науку, но в скромном духе Просвещения, используя научные знания для улучшения человеческого благосостояния. Более того, он считает, что ученые должны отказаться от идеи «ценностного нейтралитета» для науки и активно поддерживать государственную политику, направленную на улучшение благосостояния и сокращение неравенства.
Научные пуритане, таким образом, поддерживают различие между научными фактами и социальными ценностями и не желают вмешиваться или вводить свою науку в вопросы, связанные с ценностями, за исключением, конечно, ценности занятия наукой. «По сути, — пишет Фуллер, — гностицизм — это пуританство, доведенное до его логической крайности» (128). Но отличия существенные. Для научных пуритан мир природы и сама наука «разочарованы». В мире природы нет ничего, что придавало бы ценность или смысл человеческому существованию. К сожалению, по словам Фуллера, мейнстримные СС демонстрируют пуританское отношение как к себе, так и к наукам, которые они изучают. Он хочет заново очаровать науку, но в скромном духе Просвещения, используя научные знания для улучшения человеческого благосостояния. Более того, он считает, что ученые должны отказаться от идеи «ценностного нейтралитета» для науки и активно поддерживать государственную политику, направленную на улучшение благосостояния и сокращение неравенства. В начале резюме своей главы он пишет:
В начале резюме своей главы он пишет: Присяжные выбираются из общей массы населения, как обычное жюри в США, чтобы гарантировать, что ни один из них не имеет прямой личной заинтересованности в исходе их обсуждения. Наконец, «результаты консенсусных конференций должны иметь обязательную силу для законодательства в области науки и техники» (169).). Фуллер признает, что существует множество препятствий для институционализации консенсусных конференций, и пытается преодолеть некоторые из них. Интересно, желательно ли вообще такое учреждение? Я разовью свое беспокойство в контексте преподавания «теории разумного замысла» (IDT), вопроса, который Фуллер поднимает несколько раз на протяжении всей книги, и, действительно, он «поддерживает преподавание и исследования теории разумного замысла в «основные университеты» (131).
Присяжные выбираются из общей массы населения, как обычное жюри в США, чтобы гарантировать, что ни один из них не имеет прямой личной заинтересованности в исходе их обсуждения. Наконец, «результаты консенсусных конференций должны иметь обязательную силу для законодательства в области науки и техники» (169).). Фуллер признает, что существует множество препятствий для институционализации консенсусных конференций, и пытается преодолеть некоторые из них. Интересно, желательно ли вообще такое учреждение? Я разовью свое беспокойство в контексте преподавания «теории разумного замысла» (IDT), вопроса, который Фуллер поднимает несколько раз на протяжении всей книги, и, действительно, он «поддерживает преподавание и исследования теории разумного замысла в «основные университеты» (131). Дело слушалось единоличным судьей, а не присяжных, но это дело все еще актуально здесь, потому что было бы трудно представить гражданское жюри, состоящее из граждан, столь же осведомленных, как Стив Фуллер. И что он сказал? Сообщалось, что он «сказал, что, по его мнению, эволюция предлагает лучшее объяснение биологического разнообразия, чем разумный замысел» (77). Хороший. Но также сообщается, что он сказал, что наличие «само собой разумеющихся теорий» в любой дисциплине — «плохая новость». Сообщается также, что он сказал, что «было бы интересно, если бы наука была« реконфигурирована так, чтобы понятие дизайна воспринималось как своего рода буквально объединяющая концепция »».
Дело слушалось единоличным судьей, а не присяжных, но это дело все еще актуально здесь, потому что было бы трудно представить гражданское жюри, состоящее из граждан, столь же осведомленных, как Стив Фуллер. И что он сказал? Сообщалось, что он «сказал, что, по его мнению, эволюция предлагает лучшее объяснение биологического разнообразия, чем разумный замысел» (77). Хороший. Но также сообщается, что он сказал, что наличие «само собой разумеющихся теорий» в любой дисциплине — «плохая новость». Сообщается также, что он сказал, что «было бы интересно, если бы наука была« реконфигурирована так, чтобы понятие дизайна воспринималось как своего рода буквально объединяющая концепция »». И это продукт лучших размышлений об органической жизни на Земле за последние 150 лет. Проблема, на мой взгляд, в том, что в наших государственных школах ET не уделяется должного внимания. Учителя биологии и издатели учебников по биологии были запуганы боязнью оскорбить религиозные чувства учащихся и, что более серьезно, их родителей. Прискорбно, что «свобода вероисповедания» понимается как означающая, что любые верования так же хороши, как и любые другие. На самом деле конституция США говорит лишь о том, что власть государства не может использоваться для навязывания каких-либо конкретных религиозных убеждений. Это не говорит о том, что учащихся не следует заставлять изучать ET в государственных школах. Я бы даже рекомендовал признать, что и ET, и IDT являются «теориями» происхождения человеческой жизни на Земле, а затем показать, почему ET заслуживает гораздо большего доверия, чем IDT. Это может способствовать пониманию науки и объединению демократических граждан не меньше, чем политически активная профессия СС или консенсусные конференции.
И это продукт лучших размышлений об органической жизни на Земле за последние 150 лет. Проблема, на мой взгляд, в том, что в наших государственных школах ET не уделяется должного внимания. Учителя биологии и издатели учебников по биологии были запуганы боязнью оскорбить религиозные чувства учащихся и, что более серьезно, их родителей. Прискорбно, что «свобода вероисповедания» понимается как означающая, что любые верования так же хороши, как и любые другие. На самом деле конституция США говорит лишь о том, что власть государства не может использоваться для навязывания каких-либо конкретных религиозных убеждений. Это не говорит о том, что учащихся не следует заставлять изучать ET в государственных школах. Я бы даже рекомендовал признать, что и ET, и IDT являются «теориями» происхождения человеческой жизни на Земле, а затем показать, почему ET заслуживает гораздо большего доверия, чем IDT. Это может способствовать пониманию науки и объединению демократических граждан не меньше, чем политически активная профессия СС или консенсусные конференции.