alexxlab — Страница 22 — Таловская средняя школа

Как отмечается площадь в математике: Какой буквой обозначается площадь в математике

alexxlab / 08.08.202310.05.2023 / Математике

Почему в физике расстояние обозначается буквой s, а скорость – v?

Содержание:

Со времен возникновения различных наук и математических расчетов ученые начали использовать множество символов и сокращений. Это вполне оправданное решение, ведь длинные формулы, записанные при помощи слов, отнимали бы много времени. По какому принципу выбираются эти обозначения, в частности буквы, указывающие на скорость и расстояние?

Как обозначают физические величины и понятия?

В физике существует общепринятый список обозначений. Он включает латинские и греческие буквы, кириллицу (редко), специальные символы, надстрочные и подстрочные знаки, скобки и др. В качестве самостоятельной науки физика зародилась в 17-м веке во время научной революции, но многие идеи, физические воззрения появились еще в античный период. Отсюда и использование латыни, греческого языка.

Количество физических величин довольно большое – букв в алфавитах недостаточно для обозначения их всех. Поэтому одни и те же буквы могут обозначать разные понятия. Важно различать и стиль написания.

Впервые термин “физика” фигурирует в сочинениях Аристотеля (IV век до н. э.)

Например, латинские символы обычно пишутся курсивом, греческие – обыкновенным прямым начертанием. Строчными буквами обозначают интенсивные величины (не зависят от размеров системы, например, температура), заглавными – экстенсивные.

Интересный факт: среди всех латинских букв для обозначения понятий из области физики реже всего встречается буква о.

Ввиду исторических причин множество обозначений с использованием латинских букв – это сокращения слов, которые указывают на данные понятия. Чаще всего это латинские, английские, немецкие и французские слова. Во избежание путаницы почти не используются греческие заглавные буквы, если они похожи на латинские по манере написания.

Почему в физике расстояние обозначается буквой s?

Расстояние в физике измеряется единицами длины (метр в международной системе единиц) и имеет два значения:

степень удаленности объектов друг от друга;
длина пути, которую прошел объект.

Взаимосвязь между расстоянием, скоростью и временем

Расстояние – один из тех случаев, когда обозначающая буква является первой в слове-определении. Некоторые источники по-разному объясняют происхождение буквы s:

От английского слова «space», которое означает расстояние, пространство, площадь.
От латинского «spatium» – пространство между двумя предметами, протяжение в длину и ширину.

Фактически оба варианта являются правильными. Согласно этимологии слова «space», оно вошло в употребление в 1300-х годах и происходит от французского «espace», а оно, в свою очередь, от латинского «spatium». В значении космического пространства «space» начало употребляться лишь с конца 17-го века, после того как появилось в художественном произведении Джона Мильтона.

Почему в физике скорость обозначается буквой v?

Для обозначения скорости в физике используют строчную букву v тоже не случайно. Это первая буква в латинском слове «velocitas», французском «vitesse» и английском «velocity». Все они означают скорость, быстроту, стремительность.

Возникает другой вопрос: почему именно «velocity» стало определением скорости, а не другие английские слова с похожим значением, например, «speed»? Дело в том, что в физике скорость является векторной величиной, которая отображает быстроту и направление перемещения объекта относительно заданной системы отсчета.

Скорость – векторная величина

Слово «speed» указывает на скалярную скорость – величину, которая не зависит от системы координат. Например, скорость света – постоянная величина, поэтому на английском данный термин будет выглядеть как «the speed of light».

Кроме того, скорость и расстояние – взаимосвязанные величины наряду со временем. Эта связь в физике выражается формулой. Зная две величины, можно рассчитать и третью. Использование одинаковых букв нецелесообразно.

Если Вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

Как в Индиане чуть не узаконили π = 3.2 / Хабр

Поздравляю всех с (прошедшим) днем числа Пи! (день числа Пи отмечается 14 марта, поскольку эта дата в американском формате записывается в как 3. 14 — прим. перев.) Чтобы отметить его как следует, я хочу ненадолго отвлечься от программного обеспечения и поговорить о чем-то особом. Возможно, вы слышали байку о том, как в штате Индиана пытались законодательно приравнять число Пи к чем-то типа 3, или 4, или 3.15. Обычно ее рассказывают в качестве доказательства того, что жители Индианы — бестолковая деревенщина, но это далеко не вся история. Зачем они пытались поменять значение π и на что они рассчитывали?

_{Предвосхищая комментарии: конечно, я знаю про константу τ и считаю ее более уместной для описания свойств круга. Однако никто не пытался поменять ее значение на законодательном уровне, не так ли?}

Я занялся исследованием, и теперь могу рассказать историю целиком. Чтобы вы поняли контекст, мне придется объяснить кое-какие математические концепции.

Мне придется объяснить немало математических концепций.

Линейка и циркуль

Западная математическая традиция берет свое начало из Греции. Они были не первой цивилизацией, занимавшейся математикой, и многие приписываемые им вещи были открыты еще раньше математиками из Вавилона, Египта и Китая — однако эти исследования дошли до нас через античную Грецию. Также греки того времени имели неоспоримое превосходство в области геометрии, и особенно интересовались классом задач, называемым «Построение с помощью циркуля и линейки».

Если у вас есть бесконечно длинная неградуированная линейка и циркуль, какие формы вы можете построить и что можно получить из существующих форм? Сделать можно гораздо больше, чем вы думаете. Например, можно взять угол и получить его бисекцию, то есть провести линию, разделяющую его ровно пополам. Можно взять линию и построить из нее 32-угольник. Можно взять квадрат и построить другой квадрат, площадь которого будет ровно в 2 раза больше.

Некоторые задачи на построение греки так и не решили, однако это не значило, что задача нерешаема вообще. Некоторые слишком сложные для античности задачи были решены позже, например построение 17-угольника (решена в 1796 году). Одна из самых долго обсуждаемых задач такого рода называлась «квадратура круга»: если у вас есть круг, можно ли построить квадрат точно такой же площади?

Теперь нужно очень точно сформулировать, что это значит. Если вы можете построить квадрат с погрешностью 0.00001% — это не считается. Если вы придумаете способ, решение которого будет стремиться к точному значению за бесконечное количество шагов — это не считается. Также не считается решение, требующее что-либо еще помимо немаркированной линейки и циркуля. Греки уже знали способ найти квадратуру круга с помощью градуированной линейки или архимедовой спирали — вопрос был именно в том, можно ли получить точную площадь с минимумом инструментов.

К эпохе Возрождения математики сходились во мнении, что это скорее всего невозможно, поскольку все мыслимые попытки провалились. В 1837 году ученый Пьер Ванцель подвел под это утверждение твердый фундамент. Площадь круга с радиусом 1 будет равна π, следовательно стороны квадрата должны иметь длину, равную √π. Ванцель доказал, что это значение можно получить только в том случае, если бы π было алгебраическим числом, а математики подозревали, что оно на самом деле трансцендентное.

Алгебраическое? Трансцендентное? Я позаимствую объяснение, написанное Марком Доминусом:

Сыграем в игру. Возьмите произвольное число X. Дальше вы можете использовать сложение, вычитание, деление и умножение на любое целое число. Вы также можете умножать результат на X. Операции можно производить сколько угодно раз. Если в результате вы получите 0 — вы победили.
Например, X = 2/3. Умножаем на 3, вычитаем 2, получаем 0 — вы победили!
Допустим, X равен ∛7. Умножаем на X, потом еще раз, потом вычитаем 7. Вы снова победили!
Теперь допустим, что X = √2 + √3. Тут увидеть решение уже не так просто. Но оказывается, что если умножить на X, вычесть 10, дважды умножить на X, а потом добавить 1, то вы тоже победите. Это абсолютно неочевидно, но вы можете попробовать выполнить это на калькуляторе.
А вот если X = π — вы не можете выиграть. Нет такого способа, позволившего бы получить 0 с помощью разрешенных действий, сколько бы раз вы их не повторяли. Это также очень хитрая, неочевидная штука.
Числа, с которыми вы можете победить, называются алгебраическими. Числа вроде π, с которыми вы не можете, называются трансцендентными.

Хотя «почти все» числа являются трансцендентными, доказать что конкретное число является таковым очень сложно. Мы даже не знаем, является ли таковым значение π + e. Тем не менее, в 1882 году Фердинанд фон Линдеманн доказал трансцендентность числа π — это значит, что построить сторону квадрата длиной √π невозможно, а следовательно и построить квадратуру круга тоже нельзя.

_{Быстрый набросок доказательства: действительные числа являются неисчислимыми. Каждое алгебраическое число является корнем некого полинома. Полиномы могут быть представлены в виде кортежа коэффициентов, например: x^2 — 3 → (1, 0, -3). Множество всех конечных списков является счетным, следовательно алгебраические числа также счетны. Если вычесть из несчетного множества действительных чисел счетное множество алгебраических, останутся трансцендентные.}

Хочу еще раз подчеркнуть, что это практически не влияет на настоящие прикладные задачи. Получить приближенное решение легко, а если вам позарез необходимо получить точное значение — можно взять линейку с делениями.

Мракобесы

Даже после того, как математики доказали невозможность построения квадратуры круга, существует группа людей, продолжающих с энтузиазмом искать решения: мракобесы.

Мракобесы — это люди, глубоко и непоколебимо убежденные в чем-то внешне похожем на научные исследования, но на самом деле являющемся бредом сивой кобылы. Для завсегдатаев интернета самым известным примером наверняка является куб времени. Большинство мракобесов говорят более осмысленно, но руководствуются такой же инопланетной логикой. В любой области такие ребята есть: например, мракобесы от информатики опровергают проблему останова, доказывают равенство P и NP, и выдают вот такие охренительные шедевры _{(нет, серьезно, посмотрите — это божественно!)}.

Мракобесов в области математики также немало, и порядочное их число озабочены квадратурой круга и трисекцией угла. Я думаю, что причины следующие:

Задачу легко понять обывателю.
Задача известна за пределами математического сообщества. Мракобесов, решающих проблему Гольдбаха, гораздо меньше (но они тоже есть).
Задача выглядит так, будто ее можно «попытаться решить» без каких-либо познаний в математике: просто делай построения до тех пор, пока что-нибудь не получится.
Легко посчитать задачу решенной, если вы не понимаете нюансов насчет точного решения и использования только линейки и циркуля.

В книге «A Budget of Paradoxes» Огастес Де Морган упоминает более тридцати «квадратурщиков», с которыми он вел переписку. Читая его заметки из 1872 года, не перестаешь удивляться тому, как похожи тогдашние мракобесы на нынешних. Именно поэтому мракобесие настолько меня завораживает — в нем безумие противоречит конформизму. Какими бы ни были предметная область и эра, какие бы слова ни произносил мракобес — они всегда идут по тому же сценарию и говорят одно и то же. Именно поэтому мракобесие можно распознать, даже не вчитываясь — по соответствию форме все становится понятно. Это научная версия того, что в искусстве называют «ар-брют».

Эдвард Дж. Гудвин

Мракобесие возникает по-разному. В случае с Эдвардом Дж. Гудманом, к несчастью, причиной было психическое заболевание. Он считал, что доказательства ниспосланы ему свыше — в прямом смысле слова Бога. В 1888 году Бог рассказал ему, как построить квадратуру круга. Полное описание метода можно прочитать здесь, но вот его краткое содержание: сначала берем 90-градусную дугу и проводим хорду между ее концами. Отношение длины дуги к хорде будет равно 8:7, а длины хорды к основанию треугольника — 10:7. Из произведения этих величин следует, что длина основания равна 4/5 длины дуги, а поскольку мы рассматривали только четверть круга, то умножение на 4 даст нам искомое значение: 16/5. Далее построение является тривиальным.

Первый шаг построения квадратуры круга согласно Гудвину

Уследили за ходом мысли? Надеюсь, что нет! Я потратил три часа, разглядывая это доказательство и пытаясь понять, что, черт возьми, творилось у него в голове. Должен сказать, что заставить себя думать как мракобес отнюдь не просто. Теперь эта инопланетная логика отпечаталась у меня в голове. Я на один шаг приблизился к тому, чтобы самому стать мракобесом. Чего я только не делаю ради вас!

Самое важное для нашей истории — это соотношения, которые он использовал: 8:7 и 10:7. Они примерно на 2% и 1% отличаются от настоящих значений π/2 и √2 соответственно, и из них мы можем получить значение π c погрешностью примерно 4% (160/49). Гудвин дальше совершил еще две ошибки, которые по стечению обстоятельств отменили друг друга, и пришел к чуть более точному значению π = 3.2.

_{Во-первых, он умножил на 7/10, а не на 10/7.
Во-вторых, он умножил на 4 (окружность состоит из 4 таких дуг), но не поделил на 2 (диаметр равен удвоенному радиусу).}

Сразу оговорюсь: это не единственная его ошибка вообще, а единственная очевидная ошибка в вычислениях. Непонятно, как именно переопределение π позволяет ему построить квадратуру круга. Если предположить, что это сработает, стороны получаемого квадрата будут примерно на 1% длиннее — погрешность достаточно малая, чтобы на глазок решение казалось верным.

Гудвин отмечает расхождение между его значением 3.2 и «общепризнанным» 3.1416, а потом заявляет, что 3.1416 — ошибочное. Это, на мой взгляд, самое захватывающее и жуткое в мракобесии. Даже если это что-то несусветное и легко опровергается эмпирически, их вера в собственное утверждение непоколебима. Слабые метакогнитивные способности не позволяют им даже допустить собственную неправоту. Это не он где-то сделал ошибку, а все остальные облажались. Многим мракобесам присущи иллюзии величия, они сравнивают себя с Галиллеем или Эйнштейном. Впрочем, если бы я думал, что обладаю истинным знанием о вселенной, я бы тоже сравнивал.

Идем в правительство!

Итак, у Гудвина появился способ в прямом смысле сделать невозможное. Как о нем рассказать? Конечно, его нужно опубликовать! В 1894 году он отправил свое доказательство в Американский Ежемесячный Математический Журнал (American Mathematical Monthly, AMM), который опубликовал его в июльском выпуске.

Как оно могло туда попасть? Просто повезло. AMM был основан всего за 7 месяцев до этого, и редакторы еще не определились с курсом издания. Общее направление заключалось в том, чтобы сделать математику доступнее и интереснее для широкой аудитории, и они пробовали различные способы этого добиться. Как писал один историк, в первое время они печатали «все, что присылали — или по крайней мере то, на что хватало места». Сначала они печатали «высшую пробу», а потом уже все остальное. Доказательство Гудвина было опубликовано в разделе «Запросы и информация», который редакторы не проверяли вообще.

_{Также в этом разделе}_{постоянно}_{творилась перепалка между авторами.}

Но тонкости внутренней работы издательства для большинства недоступны: они думают, что «опубликовано» и «признано» — одно и то же. Это дало Гудвину желаемую убедительность и раздуло его мракобесские амбиции. В 1889 году он уже оформил «копирайт» на свое доказательство, и теперь, думая, что все математическое сообщество его поддерживает, решил заработать на нем денег. Он считал, что открытие такого масштаба должны проходить в каждой школе, а значит каждая школа должна платить ему отчисления за использование его доказательства. Поэтому в 1897 году он обратился в законодательные органы штата Индиана с предложением: они официально объявят его доказательство верным, а он взамен позволит им использовать его бесплатно, что сэкономит государству кучу денег.

Так что да, мотивация правительства штата Индиана была в экономии бюджетных средств.

Закон можно прочитать целиком по этой ссылке.

Новое платье короля

Не до конца понятно, как именно постановление прошло рассмотрение. Некоторые люди спекулируют, что члены палаты представителей не обладали математической грамотностью и не поняли, что фраза «диаметр относится к длине окружности, как пять четвертых к пяти» была про число π. Мне же кажется, что поначалу они догадывались, что это брехня! Вот что пишет The Telegraph:

Гаст из Блумингтона, демократ, под громкий хохот заявил, что постановление нужно отправить в Министерство Финансов, поскольку оно взяло на себя ответственность за решение глобальных задач и обладает свободным временем. Другой представитель поднялся и высказал мнение, что более уместным окажется Министерство Болот. В такой шутливой обстановке спикер отправил «Квадратуру Круга» в Министерство Болот, где, в болоте, постановление и найдет достойную могилу.

Но потом Министерство Каналов («болот») отправило его в Министерство Образования, а оттуда оно вернулось с полной поддержкой государственного управляющего. Постановление было принято с 67 голосами «за» и без единого голоса «против». Как же так? Моя догадка: никто, по иронии, не хотел показаться глупым. Большинство людей не знакомы с мракобесием и не могут с легкостью отличить бред от фактов, которые просто звучат неправдоподобно для не разбирающегося в теме человека. Вы действительно хотите быть тем человеком, который вздумал попрепираться с Эйнштейном? По крайней мере, этого хватило, чтобы убедить газету Indianapolis Journal:

Среднестатистический редактор не добьется ничего особого, поднимая на смех открытие, признанное Американским Математическим Журналом, подтвержденное профессорами Национальной Астрономической Обсерватории Вашингтона (в том числе профессором Холлом, который открыл спутники Марса), объявленное «безупречным» профессорами из университетов Энн Арбор и Джона Хопкинса, а также запатентованное в семи странах Европы. Он едва ли настолько подкован в математике, чтобы противостоять их совместному авторитету.

Может быть, это и палату представителей тоже убедило? На мой взгляд, звучит вполне правдоподобно, но это спекуляция.

_{Гудвин утверждал, что обсудил это с Аcафом Холлом, и все поверили ему на слово. Почему именно с ним? Возможно потому, что он первым публично провел}_{эксперимент Бюффона с бросанием иглы}_{— это способ вычисления π с помощью случайной выборки. Могу представить, как Гудман услышал про это и решил, что Холл тоже пытается найти его}_{истинное}_{значение — еще один ске(π)тик.}

Какими бы ни были причины, постановление прошло, и Сенат тоже собирался его принять. Но так случилось, что на той неделе в Капитолии оказался математик из университета Purdue. Кто-то из сенаторов спросил его мнение, и ученый объяснил, почему доказательство было чушью — в результате постановление ушло в стол. Думаю, что это подтверждает мою гипотезу: мракобес может сойти за эксперта и заставить людей усомниться в себе, но когда в дело вступает настоящий эксперт, заклинание рассеивается.

Гудвин умер спустя 5 лет в возрасте 77. Многие его знакомые все еще в него верили. Из его некролога:

Годы шли, а дитя его гения оставалось непринятым математическим сообществом. Он был разбит досадой, но никогда не терял надежды на то, что доживет до момента, когда мир узрит величие его замысла, а он испытает мимолетное блаженство успеха. На фоне размеренной деревенской жизни разыгралась трагедия нереализованных амбиций.

В чем мораль этой истории? Большинство людей ограничиваются выводом о том, что американцы / жители Индианы / политики — тупицы. Я же считаю, что главное в истории — мракобесие. Оно нарушает наши эпистемологические нормы, подавая абсолютную неправоту с абсолютной самоуверенностью. Мало кто оказывается к этому готов. Гудвин, по всем меркам, обладал харизмой и говорил убедительно. Он вел себя как человек, которому можно верить — люди и верили, и от его лица чуть не развалили геометрию.

Но если не брать в расчет его почти-успех, Гудвин ничем не отличался от других мракобесов. Он думал, писал и действовал точно так же.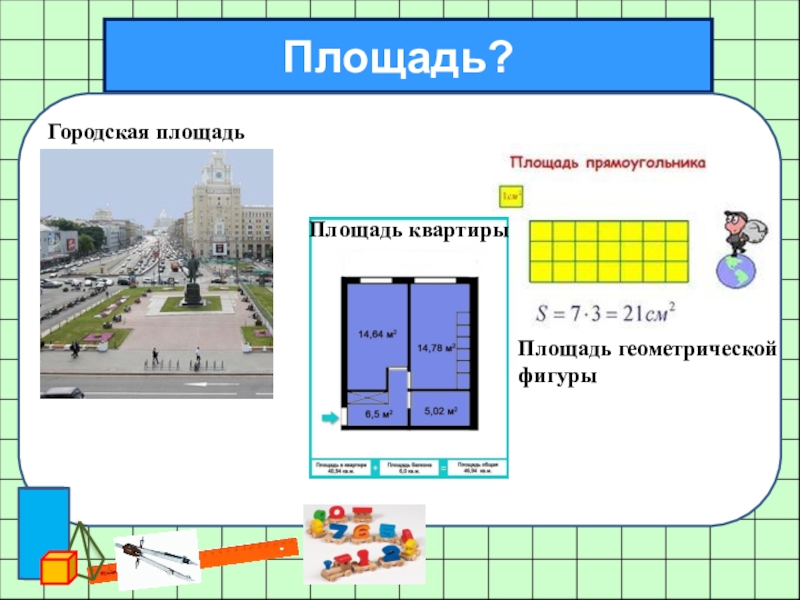 Я иногда получаю электронную почту с таким же мракобесным настроением. Сто лет прошло, а оно ни капли не поменялось.

Вычисление площади | SkillsYouNeed

Площадь — это мера того, сколько места внутри фигуры. Вычисление площади формы или поверхности может быть полезно в повседневной жизни — например, вам может понадобиться знать, сколько краски нужно купить, чтобы покрыть стену, или сколько семян травы вам нужно, чтобы посеять газон.

На этой странице собрана основная информация, которую вам необходимо знать, чтобы понимать и вычислять площади обычных фигур, включая квадраты и прямоугольники, треугольники и круги.

Расчет площади методом сетки

Когда фигура рисуется на масштабированной сетке, вы можете найти площадь, подсчитав количество квадратов сетки внутри фигуры.

В этом примере внутри прямоугольника 10 квадратов сетки.

Чтобы найти значение площади с помощью метода сетки, нам нужно знать размер, который представляет квадрат сетки.

В этом примере используются сантиметры, но тот же метод применим для любой единицы длины или расстояния. Например, вы можете использовать дюймы, метры, мили, футы и т. д.

В этом примере каждый квадрат сетки имеет ширину 1 см и высоту 1 см. Другими словами, каждый квадрат сетки равен одному «квадратному сантиметру».

Подсчитайте квадраты сетки внутри большого квадрата, чтобы найти его площадь.

Имеется 16 маленьких квадратов, поэтому площадь большого квадрата составляет 16 квадратных сантиметров.

В математике квадратные сантиметры сокращаются до см ² . ² означает «квадратный».

Каждый квадрат сетки равен 1 см ² .

Площадь большого квадрата 16см ² .

Подсчет квадратов на сетке для нахождения площади работает для всех фигур, если известны размеры сетки. Однако этот метод становится более сложным, когда фигуры не точно соответствуют сетке или когда вам нужно подсчитать доли квадратов сетки.

В этом примере квадрат не вписывается точно в сетку.

Мы все еще можем вычислить площадь, считая квадраты сетки.

Имеется 25 полных квадратов сетки (заштрихованы синим цветом).
10 половинных квадратов сетки (заштрихованы желтым цветом) – 10 половинных квадратов соответствуют 5 полным квадратам.
Также есть 1 четверть квадрата (заштриховано зеленым цветом) – (¼ или 0,25 целого квадрата).
Сложите целые квадраты и дроби вместе: 25 + 5 + 0,25 = 30,25.

Следовательно, площадь этого квадрата равна 30,25 см ² .

Вы также можете записать это как 30¼cm ² .

Хотя использование сетки и подсчет квадратов внутри формы является очень простым способом изучения понятий площади, он менее полезен для нахождения точных площадей с более сложными формами, когда может быть много долей квадратов сетки, которые нужно сложить вместе.

Площадь можно рассчитать с помощью простых формул, в зависимости от типа фигуры, с которой вы работаете.

Оставшаяся часть этой страницы объясняет и дает примеры того, как вычислить площадь фигуры без использования системы сетки.

Площади простых четырехугольников:

Квадраты, прямоугольники и параллелограммы

Простейшие (и наиболее часто используемые) вычисления площадей предназначены для квадратов и прямоугольников.

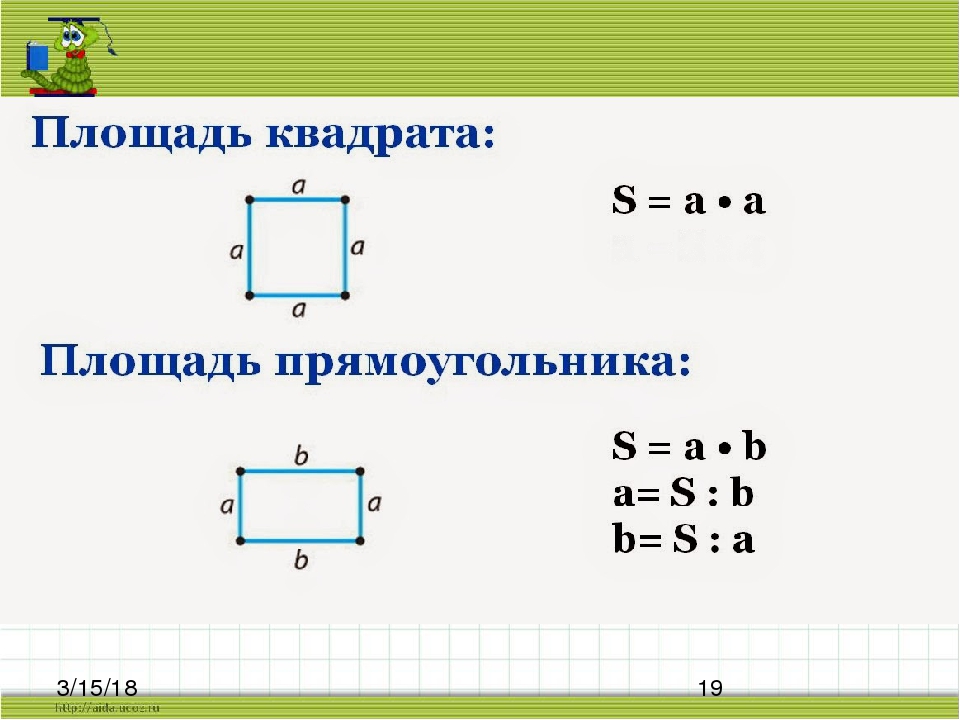
Чтобы найти площадь прямоугольника, умножьте его высоту на ширину.

Площадь прямоугольника = высота × ширина

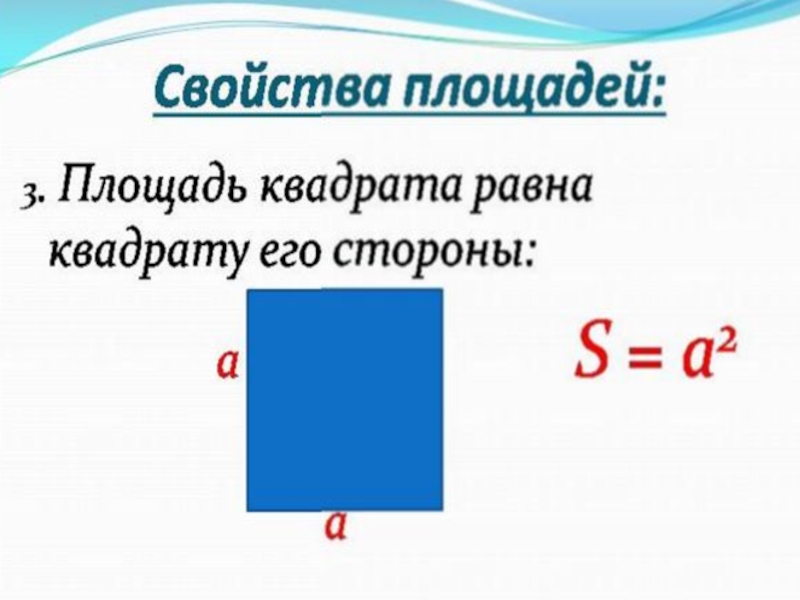
Для квадрата вам нужно только найти длину одной из сторон (поскольку каждая сторона имеет одинаковую длину), а затем умножить это само на себя, чтобы найти площадь. Это то же самое, что сказать длину ² или длина в квадрате.

Хорошей практикой является проверка того, что фигура на самом деле является квадратом, путем измерения двух сторон. Например, стена комнаты может выглядеть как квадрат, но когда вы ее измерите, вы обнаружите, что на самом деле это прямоугольник.

Часто в реальной жизни формы могут быть более сложными.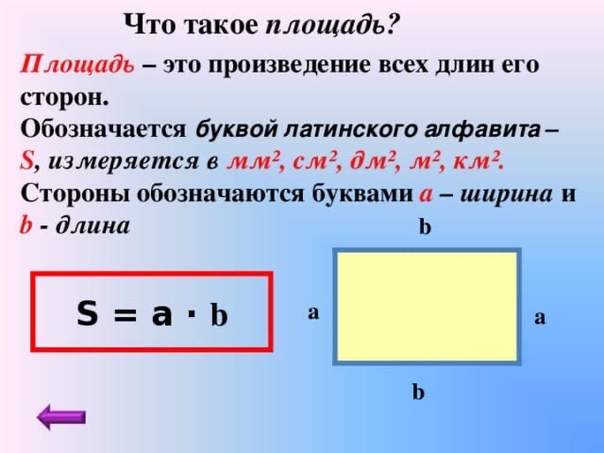 Например, представьте, что вы хотите найти площадь пола, чтобы заказать нужное количество ковра.

Типовой план помещения не может состоять из простого прямоугольника или квадрата:

В этом и других подобных примерах хитрость заключается в том, чтобы разбить фигуру на несколько прямоугольников (или квадратов). Неважно, как вы разделите фигуру — любое из трех решений приведет к одному и тому же ответу.

Решение 1 и 2 требуют, чтобы вы сделали две фигуры и сложили их площади вместе, чтобы найти общую площадь.

Для решения 3 вы делаете большую фигуру (A) и вычитаете из нее меньшую фигуру (B), чтобы найти площадь.

Другая распространенная проблема заключается в том, чтобы найти область границы — фигура внутри другой фигуры.

В этом примере показан путь вокруг поля шириной 2 метра.

Опять же, в этом примере есть несколько способов определить площадь пути.

Вы можете рассматривать путь как четыре отдельных прямоугольника, вычислять их размеры, затем их площадь и, наконец, складывать площади вместе, чтобы получить общую сумму.

Более быстрым способом было бы определить площадь всей фигуры и площадь внутреннего прямоугольника. Вычтите внутреннюю площадь прямоугольника из целого, оставив площадь пути.

Площадь всей фигуры 16 м × 10 м = 160 м ² .
Мы можем рассчитать размеры средней секции, потому что знаем, что путь по краю имеет ширину 2 м.
Ширина всей фигуры 16 м, а ширина пути по всей фигуре 4 м (2 м слева от фигуры и 2 м справа). 16м — 4м = 12м
То же самое можно сделать для высоты: 10 м — 2 м — 2 м = 6 м
Итак, мы подсчитали, что средний прямоугольник имеет размеры 12 м × 6 м.
Таким образом, площадь среднего прямоугольника равна: 12 м × 6 м = 72 м ² .
Наконец, мы отделяем площадь среднего прямоугольника от площади всей фигуры. 160 — 72 = 88м ² .

Площадь пути 88 м ² .

A Параллелограмм — это четырехсторонняя фигура с двумя парами сторон одинаковой длины — по определению прямоугольник — это разновидность параллелограмма. Однако большинство людей склонны думать о параллелограммах как о четырехгранных фигурах с наклонными линиями, как показано здесь.

Площадь параллелограмма вычисляется так же, как и для прямоугольника (высота × ширина), но важно понимать, что под высотой понимается не длина вертикальных (или не вертикальных) сторон, а расстояние между сторонами .

Из диаграммы видно, что высота — это расстояние между верхней и нижней сторонами фигуры, а не длина стороны.

Представьте воображаемую линию под прямым углом между верхней и нижней сторонами. Это высота.

Вычисление площади треугольников

Треугольник можно представить как половину квадрата или параллелограмма.

Предполагая, что вы знаете (или можете измерить) размеры треугольника, вы можете быстро вычислить его площадь, используя следующую формулу:

Площадь треугольника = (высота × ширина) ÷ 2.

Другими словами, вы можете вычислите площадь треугольника так же, как площадь квадрата или параллелограмма, а затем просто разделите ответ на 2.

Высота треугольника измеряется как прямоугольная линия от нижней линии (основания) до «вершины» (верхней точки) треугольника.

Вот несколько примеров:

Площадь трех треугольников на диаграмме выше одинакова.

Каждый треугольник имеет ширину и высоту 3 см.

Площадь вычисляется:

(высота × ширина) ÷ 2

3 × 3 = 9

9 ÷ 2 = 4,5

Площадь каждого треугольника равна 4,5 см ² .

В реальных ситуациях вы можете столкнуться с задачей, требующей нахождения площади треугольника, например:

Вы хотите покрасить фронтон сарая. Вы только хотите посетить отделочный магазин один раз, чтобы получить нужное количество краски. Вы знаете, что литр краски покроет 10м ² стены. Сколько краски нужно, чтобы покрыть фронтон?

Вам нужно три измерения:

A — Общая высота до вершины крыши.

B — Высота вертикальных стен.

C — Ширина здания.

В этом примере размеры:

A — 12,4 м

B — 6,6 м

C — 11,6 м

Следующий этап требует дополнительных расчетов. Думайте о здании как о двух формах, прямоугольнике и треугольнике. По имеющимся у вас измерениям вы можете рассчитать дополнительные измерения, необходимые для определения площади конца фронтона.

Измерение D = 12,4 — 6,6

D = 5,8 м

Теперь вы можете разрабатывать площадь двух частей стены:

Площадь прямоугольной части стены: 6,6 × 11 = 76,56 м. ²

Площадь треугольной части стены: (5,8 × 11,6) ÷ 2 = 33,64 м ²

Сложите эти две площади вместе, чтобы найти общую площадь:

76,56 + 33,64 = 110,2 м ²

Как известно, один литр краски покрывает 10 м ² стены, чтобы мы могли вычислить, сколько литров нам нужно купить:

110,2 ÷ 10 = 11,02 литра.

На самом деле вы можете обнаружить, что краска продается только в 5-литровых или 1-литровых банках, в результате получается чуть более 11 литров. У вас может возникнуть соблазн округлить до 11 литров, но если мы не разбавим краску водой, этого будет недостаточно. Таким образом, вы, вероятно, округлите до следующего целого литра и купите две 5-литровые банки и две 1-литровые банки, что в сумме составит 12 литров краски. Это позволит избежать любых потерь и оставит большую часть литра для подкрашивания позже. И не забывайте, если вам нужно нанести более одного слоя краски, вы должны умножить количество краски на один слой на необходимое количество слоев!

Площади кругов

Для вычисления площади круга необходимо знать его диаметр или радиус .

Диаметр окружности — это длина прямой линии от одной стороны окружности до другой, проходящей через центральную точку окружности. Диаметр в два раза больше длины радиуса (диаметр = радиус × 2)

Радиус окружности — это длина прямой линии от центральной точки окружности до ее края. Радиус равен половине диаметра. (радиус = диаметр ÷ 2)

Вы можете измерить диаметр или радиус в любой точке окружности – важно измерять с помощью прямой линии, которая проходит через (диаметр) или заканчивается (радиус) в центре окружности.

На практике при измерении окружностей часто бывает проще измерить диаметр, чем разделить его на 2, чтобы найти радиус.

Радиус нужен для вычисления площади круга, формула такова:

Площадь круга = πR ² .

Это означает:

π = Pi — константа, равная 3,142.

R = радиус окружности.

R ² (радиус в квадрате) означает радиус × радиус.

Следовательно, круг с радиусом 5 см имеет площадь:

3,142 × 5 × 5 = 78,55 см ² .

Круг диаметром 3м имеет площадь:

Сначала вычисляем радиус (3м ÷ 2 = 1,5м)

Затем применяем формулу:

πR ²

3,142 × 1,5 × 1,5 = 7,0695.

Площадь круга диаметром 3 м равна 7,0695 м ² .

Заключительный пример

Этот пример использует большую часть содержимого этой страницы для решения простых задач с площадями.

Это дом Рубена М. Бенджамина в Блумингтоне, штат Иллинойс, внесенный в Национальный реестр исторических мест США (регистрационный номер: 376599).

Этот пример включает в себя нахождение площади фасада дома, деревянной решетчатой части, исключая дверь и окна. Вам нужны следующие мерки:

А – 9,7 м	В – 7,6 м
С – 8,8 м	Г – 4,5 м
В – 2,3 м	В – 2,7 м
Г – 1,2 м	В – 1,0 м

Примечания:

Все измерения являются приблизительными.
О бордюре вокруг дома можно не беспокоиться – он не учитывался при измерениях.
Предполагается, что все прямоугольные окна имеют одинаковый размер.
Размер круглого окна — это диаметр окна.
Размеры двери включают ступени.

Какова площадь деревянной решетчатой части дома?

Вычисления и ответы ниже:

Ответы на приведенный выше пример

Сначала вычислите площадь основной формы дома – прямоугольника и треугольника, составляющих фигуру.

Основной прямоугольник (В × С) 7,6 × 8,8 = 66,88м ² .

Высота треугольника (A – B) 9,7 – 7,6 = 2,1.

Следовательно, площадь треугольника равна (2,1 × C) ÷ 2,
2,1 × 8,8 = 18,48. 18,48 ÷ 2 = 9,24 м ² .

Суммарная полная площадь фасада дома равна сумме площадей прямоугольника и треугольника:

66,88 + 9,24 = 76,12 м ² .

Затем определите площади окон и дверей, чтобы их можно было вычесть из общей площади.

Площадь двери и ступеней составляет (D × E) 4,5 × 2,3 = 10,35 м ² .

Площадь одного прямоугольного окна составляет (G × F) 1,2 × 2,7 = 3,24 м ² .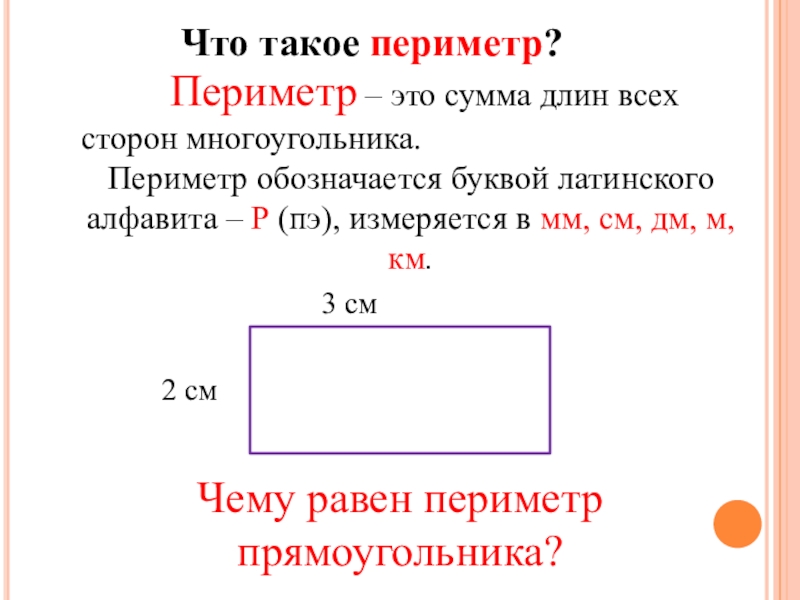

Пять прямоугольных окон. Умножьте площадь одного окна на 5.

3,24 × 5 = 16,2 м2. (общая площадь прямоугольных окон).

Круглое окно имеет диаметр 1 м, поэтому его радиус равен 0,5 м.

Используя πR ², определите площадь круглого окна: 3,142 × 0,5 × 0,5 =. 0,7855 м ² .

Затем добавьте площади дверей и окон.

(площадь дверей) 10,35 + (площадь прямоугольных окон) 16,2 + (площадь круглых окон) 0,7855 = 27,3355

Наконец, вычтите общую площадь окон и дверей из полной площади.

76,12 – 27,3355 = 48,7845

Площадь деревянного реечного фасада дома, а ответ на задачу: 48,7845м ² .

Вы можете округлить ответ до 48,8 м ² или 49 м ² .

См. нашу страницу по Оценка, приближение и округление .

Дальнейшее чтение из книги «Навыки, которые вам нужны»

Понимание геометрии
Часть руководства «Навыки, которые вам необходимы для счета»

В этой электронной книге рассматриваются основы геометрии и рассматриваются свойства фигур, линий и твердых тел. Эти концепции построены в книге, с примерами работы и возможностями для вас, чтобы попрактиковаться в ваших новых навыках.

Если вы хотите освежить свои знания или помочь своим детям в обучении, эта книга для вас.

Какова площадь фигуры? Определение, формула, примеры, факты

Площадь фигуры

Форма определяется как фигура, заключенная в границу. Мы видим вокруг себя бесчисленное множество объектов в форме квадрата, прямоугольника, круга и т. д.

Теперь, что это за площадь формы? Давайте углубимся в концепцию.

Площадь фигуры – это пространство, ограниченное периметром или границей данной формы. Мы можем рассчитать площадь формы для различных геометрических фигур, используя определенные математические формулы.

Родственные игры

Площадь основных геометрических фигур

Как найти площадь фигуры? Давайте изучим площади различных фигур и формулы их площадей. Один отличный способ понять область формул фигур — сделать диаграмму формул! Тем не менее, мы попытаемся понять их один за другим.

Прямоугольник

Площадь прямоугольника можно определить как площадь, занимаемую плоской поверхностью прямоугольника. Он рассчитывается как произведение его длины (l) и ширины (w).

Площадь прямоугольника $= \text{l} \times \text{w}$

Давайте поймем почему, разделив прямоугольник длиной 5 единиц и шириной 2 единицы на единичные квадраты. Единичные квадраты — это квадраты со стороной 1 единица и площадью, равной 1 квадратной единице.

Квадрат

Квадраты также являются прямоугольниками, длина которых равна ширине. Итак, площадь квадрата можно вычислить, умножив его сторону (а) в два раза или найдя его площадь.

Площадь квадрата 92$

Параллелограмм
Площадь параллелограмма можно вычислить, умножив его основание на высоту. Основание и высота параллелограмма перпендикулярны друг другу. Формула для вычисления площади параллелограмма может быть представлена следующим образом:
Площадь параллелограмма $= b \times h$ квадратных единиц
Где b — длина основания, а h — высота.
Вам интересно, как это так?
Давайте выполним задание, чтобы выяснить это.
Шаг 1: Вырежьте параллелограмм с основанием любой длины, скажем, b единиц.
Шаг 2: Нарисуйте высоту длины h единиц перпендикулярно основанию.
Шаг 3: Разрежьте полученный прямоугольный треугольник.
Шаг 4: Поместите разрезанный прямоугольный треугольник на противоположную сторону, чтобы получить прямоугольник длины b единиц и ширины h единиц.
Мы знаем, что площадь прямоугольника равна произведению его длины на ширину. Таким образом, площадь прямоугольника, образованного таким образом в приведенном выше упражнении, будет равна $b \times h$ кв. единиц.
Кроме того, площадь прямоугольника выше будет равна площади параллелограмма, с которого мы начали.
Поскольку мы вырезали часть параллелограмма и разместили его на другой стороне, площадь фигуры не изменится. Это означает, что площадь параллелограмма будет равна площади образованного таким образом прямоугольника. То есть $b \times h$ кв. единиц.
Треугольник
Площадь треугольника можно найти по формуле: $\frac{1}{2} \times \text{base} \times \text{height}$ 92$,
, где r — радиус окружности, а pi $(\pi)$ — константа, равная 22/7 или 3,14 (приблизительно).
Знаете ли вы, что если мы разделим длину окружности на ее диаметр, то в частном получится константа, равная значению pi $(\pi)$?
Это означает, что $\pi =$ длина окружности/диаметр
Связанные рабочие листы
Как применить формулу для нахождения площади фигуры?
Определите такие параметры, как длина, ширина, сторона, радиус и т. д., необходимые для нахождения площади фигуры.
Измерьте параметры и убедитесь, что все они имеют одинаковые единицы измерения. Например, если длина прямоугольника измеряется в дюймах, то и ширина должна быть только в дюймах.
Подставьте эти значения в формулу.
Вычислить площадь фигуры. 2$ 92$, что является необходимой площадью фигуры.
Часто задаваемые вопросы
В чем разница между площадью и периметром фигуры?
Площадь — это область, занимаемая замкнутой фигурой в двумерной плоскости, тогда как периметр — это длина внешней границы замкнутой фигуры.
В чем разница между площадью формы и площадью поверхности?
Площадь фигуры — это пространство, занимаемое границей плоских фигур, таких как круги, прямоугольники и треугольники, тогда как площадь поверхности — это площадь граней объемных фигур, таких как кубы, прямоугольные параллелепипеды, конусы и т. д.
Можем ли мы найти площадь незамкнутой фигуры?
Площадь открытой фигуры определена нечетко, так как мы не можем определить ее площадь по той части фигуры, которая открыта.
Назовите хоть один пример из жизни, где нам нужно вычислить площадь?
Нам нужно найти площадь пола перед укладкой на него плитки.

Конвертер пдф в jpeg онлайн: Конвертировать PDF в JPG — быстрый, онлайн, бесплатный

alexxlab / 07.08.202324.05.2023 / Разное

PDF в JPG_Преобразование PDF в JPG онлайн бесплатно_Конвертер PDF в JPG | Right PDF Online

PDF в JPG

PDF в JPG

Выберите файл для загрузки Или перетащите сюда

Открыть с помощью:Удаленный файл

Каждый раз можно конвертировать до файлов, а размер файла не может превышать 。
SSL используется для защиты передачи данных на сервер, и ни один файл не будет сохранен для обеспечения информационной безопасности.

Неверный формат файла. Пожалуйста, выберите еще раз。
Выбрать еще раз
Невозможно загрузить несколько файлов одновременно. Преобразование ограничено одним файлом за раз. Пожалуйста, выберите еще раз。。
Выбрать еще раз
Невозможно преобразовать файл размером более {0} МБ. Загрузите версию программного обеспечения.
Извините, похоже, с файлом возникли проблемы, поэтому его невозможно преобразовать.
Начать бесплатную пробную версию Выбрать еще раз
Попробуйте Right PDF Pro сейчас, чтобы конвертировать файлы любого размера бесплатно в течение 14 дней.
Преобразование…
Идет загрузка… (KB) / KB
Не удалось загрузить
Выбрать еще раз
Почувствуйте неограниченное преобразование с Right PDF Pro. Скачайте и попробуйте прямо сейчас!
Бесплатная пробная версия
Преобразование завершено
Загрузить Выбрать еще раз
Начать бесплатную пробную версию Выбрать еще раз

Почему я не могу редактировать конвертированный Word?

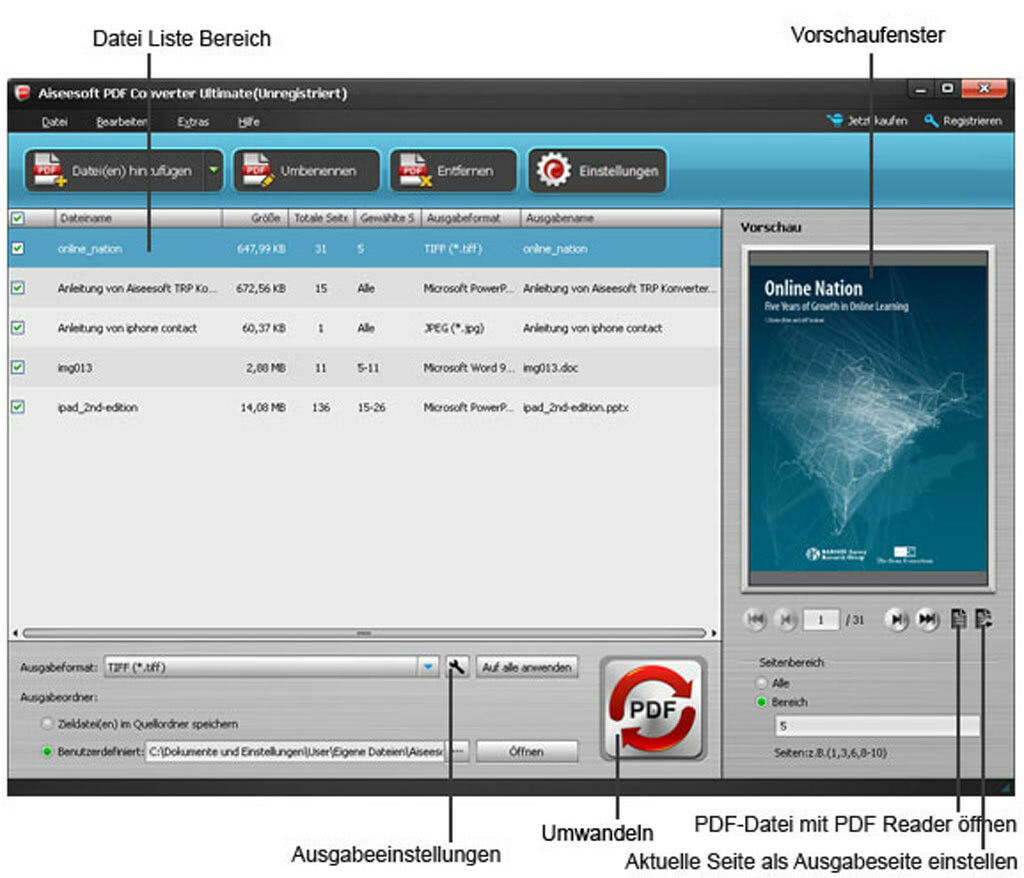Поскольку исходный PDF-файл является отсканированным или созданным из изображений, в нем нет настоящего текста. В настоящее время наши онлайн-сервисы преобразования PDF не поддерживают распознавание текста OCR.
Загрузить Конвертер Right PDF для распознавания текста в отсканированном PDF.

Почему некоторые тексты в конвертированном Word выглядят искаженными?

Сложные формулы, редко используемые языки, специальные символы и т.д. могут вызвать ошибки распознавания во время конвертации, и таких ситуаций трудно избежать。

Есть ли какие-либо опасения по поводу моей загрузки?

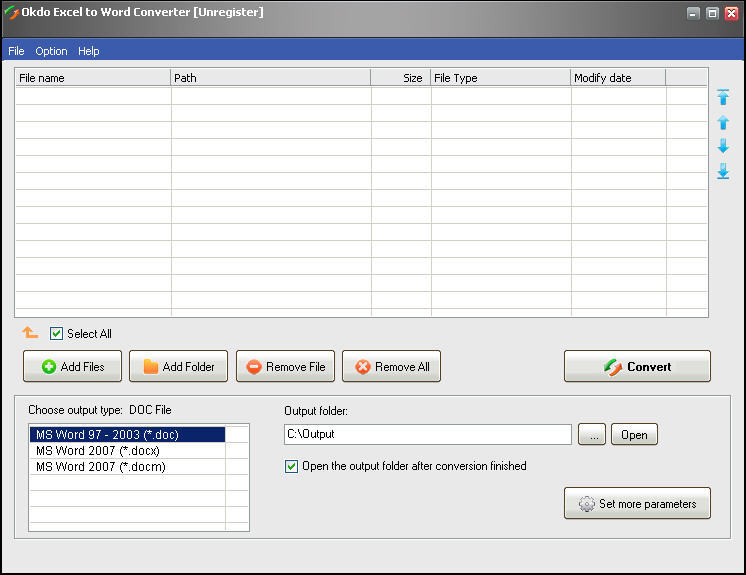Мы не будем хранить или использовать загруженные вами файлы. Чтобы у пользователей было достаточно времени для загрузки результатов, файлы будут храниться в течение 2 часов после конвертации. Тогда как исходные, так и результирующие файлы будут полностью удалены с нашего сервера.

Доступна ли настольная версия?

У нас также есть настольная версия для Right PDF Pro и Right PDF Converter. Right PDF Pro предоставляет расширенные функции, такие как редактирование, преобразование, шифрование, подписание, обработка текста, распознавание символов и т. д., которые могут значительно расширить ваши возможности обработки PDF. Скачать сейчас! Right PDF Pro
Right PDF Converter может пакетно конвертировать файлы различных форматов в PDF или преобразовывать PDF в Word, Excel, текст, изображение и т. д. Кроме того, благодаря функциям OCR (оптическое распознавание символов) вы можете легко редактировать отсканированные файлы. Загрузить Конвертер Right PDF Начать 14-дневную бесплатную пробную версию прямо сейчас

Что делать, если размер файла превышает ?

Поскольку большой файл требует более высокой скорости сетевого подключения, кроме того, загрузка и преобразование будут более сложными. В настоящее время мы не поддерживаем преобразование файла больше .
Вы можете скачать Right PDF Pro или Конвертер Right PDF и попробовать бесплатно в течение 14 дней. Во время пробного периода размер файла не ограничен, и доступны дополнительные функции редактирования и преобразования.

Конвертируйте PDF в JPG онлайн и бесплатно
Загрузите файл размером до 20 МБ, поддерживается PDF-формат
Расчетное оставшееся время：00:00 Конвертация для：00:00
Примечание: если PDF-файл защищен паролем, используйте функцию Расшифровать пароль PDF, чтобы удалить пароль. Если размер файла превышает лимит, сначала разделите его.
Пользовательские настройки следующим образом
Выбор страницы Конвертируйте каждую страницу Конвертируйте нечетные страницы Конвертируйте четные страницы Конверсия страницы спецификации
Введите номер страницы или диапазон номеров страниц, разделенных запятыми (например, 1,3-5,8-9)
Выберите формат конвертации jpg png
Качество изображения Высокая средний Низкий
Показать водяной знак да Нет
Функции：
Конвертер «Онлайн PDF в изображение» позволяет вам напрямую конвертировать PDF-файлы в файлы изображений, поддерживает форматы JPG или PNG для преобразованных файлов. Кроме того, получившийся в результате преобразования файл Word точно сохраняет все элементы страницы и форматирование исходного PDF-файла. После преобразования создается сжатый файл, который пользователь сразу же может загрузить. Пользователи могут указать диапазон номеров страниц для преобразования.
Руководство：
Нажмите или перетащите файл для загрузки, установите выходные параметры и нажмите кнопку «Пуск». После этого мы автоматически загрузим преобразованный файл, вам нужно только дождаться момента, когда появится возможность его скачать.
Рекомендация：
Pic в PDF PDF в Word PDF в Excel PDF в PPT PDF в TXT PDF в HTML PDF в длинное изображение
Безопасность документа：
Безопасность облачного хранения:файлы автоматически удаляются через 24 часа, никто не может прочитать или скачать их, ваша конфиденциальность защищена на 100 %. Вы можете вручную удалить преобразованный файл в разделе «Мои файлы».
Версия для ПК：
Наш бесплатный конвертер PDF инструмент также доступен сейчас. Как легкий автономный инструмент, он разработан с простым в использовании интерфейсом и понятной навигацией. Установив его на свой компьютер, вы получите мощный комплексный поставщик PDF-решений, включая PDF-ридер, конвертер, объединение, компрессор, разделитель, средство для удаления страниц, сумматор водяных знаков, средство защиты и многое другое. Что еще более важно, в настоящее время его можно использовать совершенно БЕСПЛАТНО. Пожалуйста, начните БЕСПЛАТНУЮ пробную версию сейчас.
Этот документ защищен паролем
Это частный файл, пожалуйста, введите пароль:
Этот документ защищен паролем
Это частный файл, пожалуйста, введите пароль:
Этот документ защищен паролем
Это частный файл, пожалуйста, введите пароль:
Этот документ защищен паролем
Это частный файл, пожалуйста, введите пароль:
Конвертер PDF в JPG онлайн [100% бесплатно]
Используйте наш быстрый и мощный конвертер PDF в JPG для извлечения изображений из документа PDF в виде отдельных файлов JPG.
Что такое онлайн-конвертер PDF в JPG?
Бесплатный онлайн-конвертер PDF в JPG — это продвинутый онлайн-инструмент, который предлагает вам функции извлечения страниц из PDF в виде отдельных файлов JPG.
Вы можете использовать этот инструмент для преобразования страниц PDF-документа в высококачественные файлы JPG всего за несколько секунд. Этот инструмент прост в использовании и помогает конвертировать PDF-файлы с несколькими страницами в высококачественные изображения JPG.
Когда вы загружаете файл PDF в инструмент, он обрабатывает документ и преобразует страницы PDF в изображения JPG онлайн. Это мощный онлайн-сервис, который работает внутри веб-браузера без каких-либо ограничений операционной системы.
Вы можете нажать кнопку загрузки файлов на калькуляторе, чтобы добавить документы PDF для обработки в конвертере PDF в JPG.
Если вместо JPG вы хотите преобразовать PDF в формат изображения PNG, вы можете воспользоваться конвертером PDF в PNG, чтобы сделать это.
Преобразование PDF в JPG онлайн бесплатно
Вы можете бесплатно конвертировать PDF в JPEG в высоком качестве онлайн, используя нашу передовую онлайн-утилиту.
Когда вы нажимаете кнопку «Загрузить файл», вы получаете доступ ко всем изображениям JPG, созданным из исходного документа PDF в zip-файле. Процесс преобразования PDF в JPG быстрый и эффективный.
Этот бесплатный конвертер PDF в JPG может преобразовывать документ PDF в различные форматы файлов изображений. Качество изображения, которое вы получаете из PDF-файлов, не имеет себе равных с этим инструментом.
Вы можете конвертировать файлы PDF в JPG без каких-либо ограничений по размеру файла. После того, как файл JPG загружен из этого онлайн-инструмента, вы можете сохранить его на своем ПК или поделиться им с кем-либо через Интернет.
Если у вас есть файл PNG и вы хотите легко преобразовать его в PDF, вы можете использовать конвертер PNG в PDF от SEO Magnifier.
Зачем использовать конвертер PDF в JPG?
Проводя исследования, вы часто сталкиваетесь в Интернете с документами в формате PDF, содержащими информацию, которую вы хотите использовать.
Если PDF-файл содержит много дополнительной информации, которая вам не нужна, нет смысла сохранять весь PDF-файл.
В этом случае вы можете преобразовать документ PDF в файлы изображений JPG и сохранить те, которые вам нужны, и отбросить те, которые вам не нужны.
Здесь на помощь приходит конвертер PDF в JPG! С помощью этого инструмента вы можете преобразовать любой PDF-документ в JPG без каких-либо ограничений по размеру или использованию инструмента.
Как преобразовать файл PDF в изображения JPG с помощью нашего конвертера PDF в JPG?
Вот как вы можете использовать конвертер PDF в JPG:
Перейдите на наш веб-сайт и выберите конвертер PDF в JPG https://seomagnifier.com/pdf-to-jpg-converter-online.
Нажмите кнопку «Загрузить файлы» и выберите документ PDF на своем ПК. Вы также можете перетащить файл PDF в конвертер.
Выберите страницы, которые вы хотите преобразовать в JPG.
Нажмите кнопку запуска, чтобы начать преобразование PDF в JPG.
Загрузите преобразованные файлы JPG и начните сначала, чтобы преобразовать больше файлов PDF в jpg.
SEO Magnifier Конвертер PDF в JPG Beat Особенности
100% бесплатное использование
Вы можете использовать конвертер PDF в JPG бесплатно 24/7. Ограничений по использованию этого инструмента нет. Как и конвертер PNG в TXT от SEO Magnifier, конвертер PDF в JPG можно использовать бесплатно.
Кроме того, если у вас есть изображение и вы хотите извлечь из него текст, вы можете использовать для этого конвертер изображения в текст.
Привлекательный дизайн пользовательского интерфейса
Все инструменты, доступные в SEO Magnifier, отличаются элегантным и привлекательным дизайном пользовательского интерфейса. Преобразование PDF в JPG вместе с генератором текста в изображение довольно интерактивны с точки зрения дизайна пользовательского интерфейса.
Кроме того, если вы хотите преобразовать документ PDF в формат .txt вместо JPG, вы можете использовать для этой цели онлайн-конвертер PDF в TXT.
Регистрация не требуется
Все инструменты обработки PDF, доступные на SEO Magnifier, работают без регистрации. Вам не нужно регистрировать учетную запись на нашем веб-сайте, чтобы использовать инструменты преобразования PDF в JPG или TXT в PDF.
Вы можете просто перейти на наш веб-сайт и начать использовать все инструменты бесплатно. Вам не нужно будет предоставлять какие-либо данные кредитной карты для использования наших онлайн-инструментов, таких как конвертер URL в PDF.
Особенности Кроссплатформенная поддержка
Конвертер PDF в JPG и JPG в pdf работает на всех подключенных к Интернету устройствах с веб-браузерами. С этим конвертером нет проблем с активностью компа с точки зрения веб-браузера или операционной системы.
Конвертер PDF в Word — еще один замечательный инструмент от SEO Magnifier, который вы можете использовать на всех настольных и мобильных устройствах с веб-браузерами.
Быстрая облачная обработка
Когда дело доходит до использования онлайн-инструмента, большое значение имеет скорость его обработки. Мы разработали этот инструмент, сделав пользовательский интерфейс и взаимодействие с пользователем нашим главным приоритетом.
PDF to JPG — один из самых быстрых онлайн-инструментов для обработки PDF-документов. Этот инструмент работает так же быстро, как конвертер Word в PDF от SEO Magnifier.
SEOMagnifier Часто задаваемые вопросы PDF в JPG
Какой лучший бесплатный онлайн-конвертер pdf в jpg?
Конвертер PDF в JPG от SEOMagnifier — лучший онлайн-конвертер PDF в JPG на рынке. Этот инструмент на 100% бесплатный, безопасный и надежный, и работает без регистрации или подписки.
Как конвертировать файл pdf в файл jpg онлайн конвертером?
Если у вас есть документ PDF и вы хотите преобразовать его в формат изображения JPG, вы можете использовать для этого наш конвертер PDF в JPG.
Как конвертировать документ pdf в формат файла jpg онлайн бесплатно?
Конвертер PDF в JPG — это бесплатный онлайн-инструмент, который вы можете использовать для бесплатного онлайн-конвертации файлов PDF в JPG. Вы можете загружать свои PDF-документы в этот инструмент, и он выполняет преобразование за короткий промежуток времени.

5 Бесплатный онлайн-конвертер PDF в JPG
Ваша работа становится чрезвычайно утомительной, и вам требуется быстрое и эффективное онлайн-программное обеспечение для преобразования файлов? Существует множество веб-сайтов, которые предоставляют эти виды услуг, помогая удовлетворить ваши потребности Конвертер PDF в JPG онлайн бесплатно .
Мы собрали несколько лучших онлайн-конвертеров PDF в JPG, чтобы ускорить вашу работу и сэкономить время. Эти инструменты также доступны в автономном режиме.
Лучший конвертер PDF в JPG в автономном режиме
Возможность работы в сети — отличная возможность для тех, у кого есть Wi-Fi или Интернет. Другим, у кого его нет, потребуется загрузить программное обеспечение на свои ПК и Mac. Одним из лучших представленных вариантов является UPDF для Mac. Это программное обеспечение работает с PDF-файлами с точным преобразованием.
UPDF — это многофункциональное программное обеспечение PDF, которое преобразует PDF в различные форматы файлов, включая DOC, XML, JPG, TIFF и другие. Он предлагает высокий уровень безопасности и не передает данные каким-либо сторонним источникам. Программное обеспечение также поставляется с руководством пользователя, которое упрощает работу.
Pros
Согласованность формата : UPDF гарантирует, что содержимое преобразованного файла примерно совпадает с исходным файлом, что означает меньшее количество ручных исправлений после преобразования. Это также помогает сэкономить время и подготовить изображения более высокого качества.
Простой пользовательский интерфейс : Это программное обеспечение предлагает удобный интерфейс, который помогает легко читать с большими значками для просмотра и использования.
Поддержка функции OCR : Это программное обеспечение поддерживает функцию OCR. Вы можете легко преобразовать отсканированные файлы PDF в редактируемые форматы PDF, такие как Word, Text и т. д.
Мощные функции : такие как редактирование, аннотирование, преобразование, объединение, объединение, защита, сведение PDF и т. д.

Топ-5 лучших онлайн-конвертеров PDF в JPG бесплатно
Поскольку на рынок преобразования файлов выходит так много инструментов, крайне важно, чтобы вам потребовался удобный инструмент, который может хорошо работать с большим набором документов. Кроме того, если вы беспокоитесь о безопасности и безопасности обмена файлами в Интернете, будьте уверены, что они останутся конфиденциальными и зашифрованными.
Вот 5 лучших онлайн-конвертеров PDF в JPG.
1. Онлайн-конвертер InvestinTech PDF в JPG
Благодаря этому впечатляющему программному обеспечению, доступному для всех, оно используется миллионами людей во всем мире и является отличным инструментом с точки зрения его функций. Во-первых, он предлагает быстрый и удобный процесс конвертации с помощью мощных серверов конвертации. Для смены формата на нужный требуется всего несколько секунд.
Pros
Преобразование отсканированных PDF-файлов : Вы можете использовать это онлайн-программное обеспечение для простой отправки информации, хранящейся в отсканированных PDF-файлах, в файлы изображений JPG с помощью механизма оптического распознавания символов (OCR). Этот инструмент помогает распознавать символы в документе и преобразовывать их в цифровой текст.
Безопасная онлайн-обработка : Конвертер PDF в JPG от InvestinTech использует шифрование SHA-256 с 2048-битным ключом RSA между серверами и веб-браузерами. Также файлы, загруженные в интернет, удаляются через несколько часов.
Работает на мобильных устройствах и ПК : Это программное обеспечение применимо для мобильных устройств, и его функции и кнопки легко просматривать. Кроме того, он работает с любой операционной системой.
Минусы
Ограниченное количество файлов для загрузки за клик: Одним из недостатков этого программного обеспечения является небольшое количество файлов, загружаемых за клик. Это может занять некоторое время, если у вас есть большая коллекция PDF-файлов, ожидающих на вашем ПК, планшете или смартфоне.
2. Конвертер PDF в JPG онлайн
Если вам нужны утонченность и ясность, то вам определенно понравится Convertio онлайн-конвертер PDF в JPG. Он предлагает простой трехэтапный процесс, с помощью которого вы можете преобразовать свои документы. Помимо загрузки файлов с ПК или планшета, вы также можете использовать Google Диск или Dropbox.
Pros
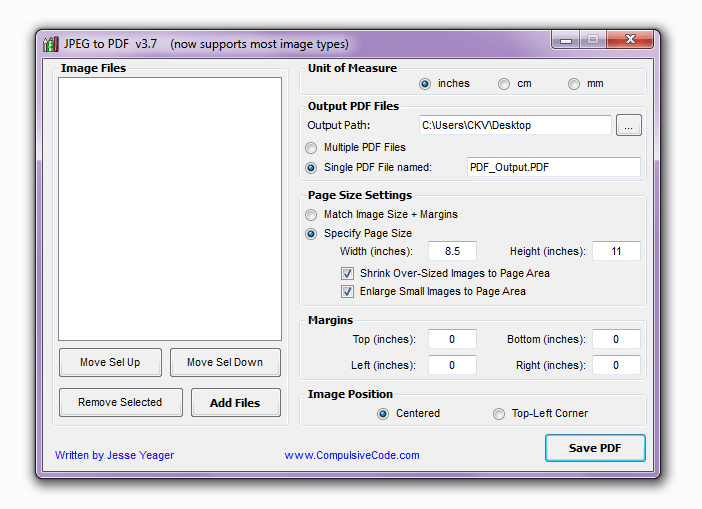Высокие оценки клиентов : Миллионы пользователей в настоящее время используют Convertio, и он признан одним из лучших программ, доступных в настоящее время в Интернете. Звездный рейтинг 4,7 из 5 показывает стандарты и процедуры безопасности, которые он впитывает.
Различные пункты выдачи : Помимо выбора PDF-файлов с вашего ПК, вы можете использовать Dropbox, URL, Google Drive или просто перетаскивать файлы на страницу. Несколько вариантов, предлагаемых Convertio, удобны для пользователей, у которых, как правило, возникают проблемы с одним программным обеспечением.
Минусы
Максимальный размер файла: Ограничение размера файла является одним из недостатков этого программного обеспечения; максимальный размер файла, которым можно поделиться на веб-сайте, составляет 100 МБ. Для обычных пользователей это может быть оптимальным, но в больших масштабах это будет неосуществимо.
3. Онлайн-конвертер PDF2JPG
Если вы ищете разнообразие в вашем файле изображения (качество) и высокую производительность, тогда PDF2JPG является оптимальным выбором для вас. Это отличный инструмент для пользователей, которые занимаются обменом файлами и процедурами конвертации. Кроме того, он не создает водяных знаков на конечном выходе. Он имеет быстрый процесс преобразования, который помогает сэкономить время и защитить файлы от любых угроз.
Плюсы
Различные типы выходного качества : При преобразовании документа онлайн вы можете изменить качество вывода. Доступны три типа качества JPG. ( Среднее , Хорошее , Отличное) . Эти типы в основном зависят от DPI (точек на дюйм) изображения. Например, изображение хорошего качества имеет разрешение 150 точек на дюйм, а изображение отличного качества — 300 точек на дюйм.
Уведомление по электронной почте: После того, как файлы будут преобразованы онлайн, вы получите уведомление по электронной почте, подтверждающее изменение. Это помогает повысить безопасность пользователя. Это также действует как напоминание для них, если они заняты другими важными задачами.
Без ограничений: Это идеальный инструмент для тех, кому требуется конвертировать огромное количество файлов ежедневно или в любое заданное время. Даже если вы хотите изменить целую книгу или журнал, то это программное обеспечение является надежным для вас. Кроме того, он обеспечивает эффективный механизм рабочего процесса.
Минусы
Низкий предел размера файла: размер файла PDF ограничен 25 МБ, что немного меньше по сравнению с другим программным обеспечением, доступным в Интернете.
4. Smallpdf Онлайн-конвертер PDF в JPG
SmallPDF Конвертер PDF в JPG — это замечательное программное обеспечение, предлагающее простой трехэтапный процесс преобразования формата в высококачественное изображение JPG. Наряду с его быстротой, он также предлагает привилегии членства и различные инструменты, позволяющие PDF-файлу выполнять различные процедуры, такие как сжатие, разделение и т. д.
Ниже приведены его плюсы и минусы, которые могут помочь вам принять решение об использовании программного обеспечения.
Профи
Защищенное шифрование : Файлы, загруженные на этот сайт, зашифрованы с использованием 256-битной технологии шифрования. Эта функция обеспечивает безопасность документов и затрудняет взлом хакеров или других лиц.
Автоматическое удаление файла :После изменения формата на нужный сервер веб-сайта полностью удалит файл(ы) через три часа. Это дает вам подходящий период для загрузки и сохранения файлов JPEG.
Типы членства : С месячной, годовой или неограниченной подпиской вы получаете немедленный доступ ко всем инструментам, ориентированным на PDF, и файлам различных типов.
Минусы
Можно управлять лучшими параметрами безопасности: веб-сайт может использовать расширенные параметры безопасности, включая тройное резервное копирование или 256-битное шифрование. Это поможет улучшить взаимодействие с клиентами и обеспечить безопасность от кибер-краж.
5. Cloud Convert PDF to JPG Converter
Cloud Convert — онлайн-конвертер документов, поддерживающий преобразование PDF-файла в нужный формат (JPG). Одной из лучших функций, которую он влечет за собой, является индивидуальная настройка желаемой плотности пикселей для вашего выходного изображения. Он обеспечивает высококачественное преобразование, поддерживает различные форматы, кроме JPEG.
Преимущества и недостатки онлайн-сервисов Cloud Convert обсуждаются ниже:
Плюсы
Мощный API : API позволяет выполнять индивидуальную интеграцию с приложением. Также предусмотрены огромные скидки для крупных клиентов. Кроме того, мы предоставляем множество функций, таких как интеграция с Amazon S3.
Подробные параметры : Cloud Convert предлагает различные переменные параметры для изменения, чтобы улучшить результат вашего изображения. Некоторые из них — это количество страниц, которые вы хотите исправить, ширина страницы, качество уровня сжатия и другие. Это помогает создавать индивидуальные выходные данные, подходящие для всех ваших приложений.
Минусы
Слишком много вариаций в форматах: Иногда у пользователя возникает некоторое недоумение относительно того, с каким форматом он работает. Выбор необходимого формата является важной задачей и требует особого внимания. Убедитесь, что вам нужен именно JPG.
Как конвертировать PDF в JPG онлайн бесплатно
Поскольку мы узнали о различных инструментах, доступных в Интернете для конвертации PDF в JPG, мы продемонстрируем один из них, чтобы дать вам ясность.
Взяв за образец Convertio, мы поможем вам изучить процесс конвертации файлов через него.
Процесс преобразования PDF в JPG онлайн
Шаг 1. Загрузите PDF
Во-первых, вам необходимо загрузить нужный файл PDF. Мы можем использовать для этого несколько вариантов, таких как Google Диск, Dropbox, URL-адрес или просто перетаскивая его на страницу.
Шаг 2: Выберите формат
Далее мы выберем формат (JPG) из выпадающего меню. Однако первым будет PDF.
Шаг 3: Загрузите файл
После завершения процесса преобразования нам нужно будет загрузить необходимые файлы на ПК, ноутбук или смартфон.
( N.B. Этот инструмент является лишь примером. Вы можете использовать любой доступный онлайн-инструмент).
Недостатки использования онлайн-конвертера PDF в JPG
Онлайн-конвертеры файлов известны своей быстрой процедурой работы и высококачественным результатом. Однако он также имеет некоторые ограничения.
Проблемы с низким уровнем безопасности
Некоторые интернет-сайты предлагают варианты с низким уровнем безопасности при работе с файловыми транзакциями и преобразованиями. Эти сайты не имеют возможности шифрования файлов и легко взламываются отдельными лицами. Во-вторых, некоторые веб-сайты склонны сохранять файлы в своих базах данных, что также является угрозой безопасности.
Ограниченный размер документа
Некоторые файлы, загруженные на определенные веб-сайты преобразования файлов, не могут соответствовать установленным критериям ограничения размера.

Парабола онлайн построение: Точки разрыва функции онлайн

alexxlab / 07.08.202303.06.2023 / Разное

Построение графика квадратичной функции — презентация онлайн

Похожие презентации:

Построение графика квадратичной функции

График квадратичной функции. Построение графика квадратичной функци

Еще один способ построения графика квадратичной функции

Квадратичная функция, ее график и свойства

Задачи ОГЭ №11, №23. Функции и их графики. Построение графика сложной функции

Построение графика квадратичной функции

Квадратичная функция и её график

Построение графика квадратичной функции. (9 класс)

Построение графиков квадратичной функции

1. Цели урока:

ТЕМА УРОКА:
Построение графика
квадратичной функции
ЦЕЛИ УРОКА:
Сформулировать алгоритм построения
графика квадратичной функции, т. е. функции
вида
y = ax2+bx+c ( у=а(х- n)2 + m)
Научиться строить график квадратичной
функции по алгоритму.
Нет ни одной области
математики, как бы
абстрактна она ни была,
которая когда-нибудь не
окажется применимой к
явлениям действительного
мира.
Н.И.Лобачевский
4. Параболический фонтан и лучи прожектора
ПАРАБОЛИЧЕСКИЙ ФОНТАН И ЛУЧИ
ПРОЖЕКТОРА
5. Библиотека с крышей в форме параболы в Норвегии и падение баскетбольного мяча
БИБЛИОТЕКА С КРЫШЕЙ В ФОРМЕ ПАРАБОЛЫ В
НОРВЕГИИ И ПАДЕНИЕ БАСКЕТБОЛЬНОГО МЯЧА
7. АЛГОРИТМ ПОСТРОЕНИЯ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ
y = ax2+bx+c
Определить направление ветвей
параболы(a>0- ветви направлены вверх, a<0ветви направлены вниз)
Определить координаты вершины параболы
(n; m) и отметить ее в координатной
плоскости: n = -b/2a; m = y(n)
Заполнить таблицу
Построить график (можно воспользоваться
шаблоном y = ax2)
y=
y
3
2
1
0
-1
1 2
– 4x – 2
График функции парабола, ветви которой
направлены вверх (a=1).
4
-3 -2 -1
2
x
3 4 5 6
-2
-3
-4
Координаты вершины:
x х = -b/2a = -(-4)/2 = 2;
y = y(2) = 22- 4∙2 – 2 = -6
Почему в таблице значения
записаны разным цветом?
-5
-6
х
0
1
2
3
4
у
-2
-5
-6
-5
-2
Сформулируйте правила построения
графиков функций у=а(х- n)2 + m.
Два параллельных переноса:
вдоль оси у на m единиц вверх,
если m>0; или на m единиц вниз,
если m<0;
вдоль оси х на n единиц вправо,
если n>0; или на m единиц влево,
если n<0
(можно воспользоваться шаблоном y =
ax2)
Построить графики функции
1)у=(х- 3)2 + 1; 2)у=(х+ 2)2 – 2; 3)у=-(х- 1)2 — 3
10. С помощью каких преобразований получили данные графики функций?
С ПОМОЩЬЮ КАКИХ
ПРЕОБРАЗОВАНИЙ ПОЛУЧИЛИ
ДАННЫЕ ГРАФИКИ ФУНКЦИЙ?

Написать формулу для
графиков квадратичной
функции
Установите соответствие
y ( x 5) 2 2
y 2( x 4) 2
y ( x 1) 2 1
y ( x 1) 2
13. ПОРЕШАЕМ. Но сначала всё выясним о коэффициентах и свободном члене.
ПОРЕШАЕМ.
НО СНАЧАЛА ВСЁ ВЫЯСНИМ О
КОЭФФИЦИЕНТАХ И СВОБОДНОМ
ЧЛЕНЕ.
14. Решение заданий из сборника «ОГЭ 3000 задач»
РЕШЕНИЕ ЗАДАНИЙ ИЗ СБОРНИКА
«ОГЭ 3000 ЗАДАЧ»
15. Решение заданий из сборника «ОГЭ 3000 задач»
РЕШЕНИЕ ЗАДАНИЙ ИЗ СБОРНИКА
«ОГЭ 3000 ЗАДАЧ»
16.
Решение заданий из сборника «ОГЭ 3000 задач»РЕШЕНИЕ ЗАДАНИЙ ИЗ СБОРНИКА
«ОГЭ 3000 ЗАДАЧ»
17. Решение заданий из сборника «ОГЭ 3000 задач»
РЕШЕНИЕ ЗАДАНИЙ ИЗ СБОРНИКА
«ОГЭ 3000 ЗАДАЧ»
18. Решение заданий из сборника «ОГЭ 3000 задач»
РЕШЕНИЕ ЗАДАНИЙ ИЗ СБОРНИКА
«ОГЭ 3000 ЗАДАЧ»
19. Самостоятельная работа !
САМОСТОЯТЕЛЬНАЯ РАБОТА !
Задания из сборника «ОГЭ 3000 задач»
1 вариант- № 1488, 1491, 1494, 1504
2 вариант-№ 1489, 1492, 1495, 1505
20. ДОМАШНЕЕ ЗАДАНИЕ : №1512-1516 (из сборника заданий «ГИА 3000 задач»)
ДОМАШНЕЕ ЗАДАНИЕ :
№1512-1516 (ИЗ СБОРНИКА ЗАДАНИЙ
«ГИА 3000 ЗАДАЧ»)
21. Итоги урока
ИТОГИ УРОКА
Сформулируйте алгоритм построения графика
квадратичной функции.
Что узнали на уроке?
Чему научились на уроке?
В чем испытывали трудности?
22. Древняя китайская мудрость Скажи мне — и я забуду, Покажи мне — и я запомню, Вовлеки меня – и я пойму.
ДРЕВНЯЯ КИТАЙСКАЯ МУДРОСТЬ
СКАЖИ МНЕ — И Я ЗАБУДУ,
ПОКАЖИ МНЕ — И Я ЗАПОМНЮ,
ВОВЛЕКИ МЕНЯ – И Я ПОЙМУ.
English Русский Правила
Преобразование графиков
Репетиторы ❯ Математика ❯ Преобразование графиков
Автор: Валентин В., онлайн репетитор по математике
●
10.10.2011
●
Раздел: Математика

Мы знаем уже несколько «стандартных» функций, например, y = х², у = f(х) и др. Теперь же рассмотрим варианты их преобразований.
Графики функций y = ах², y = ах³.
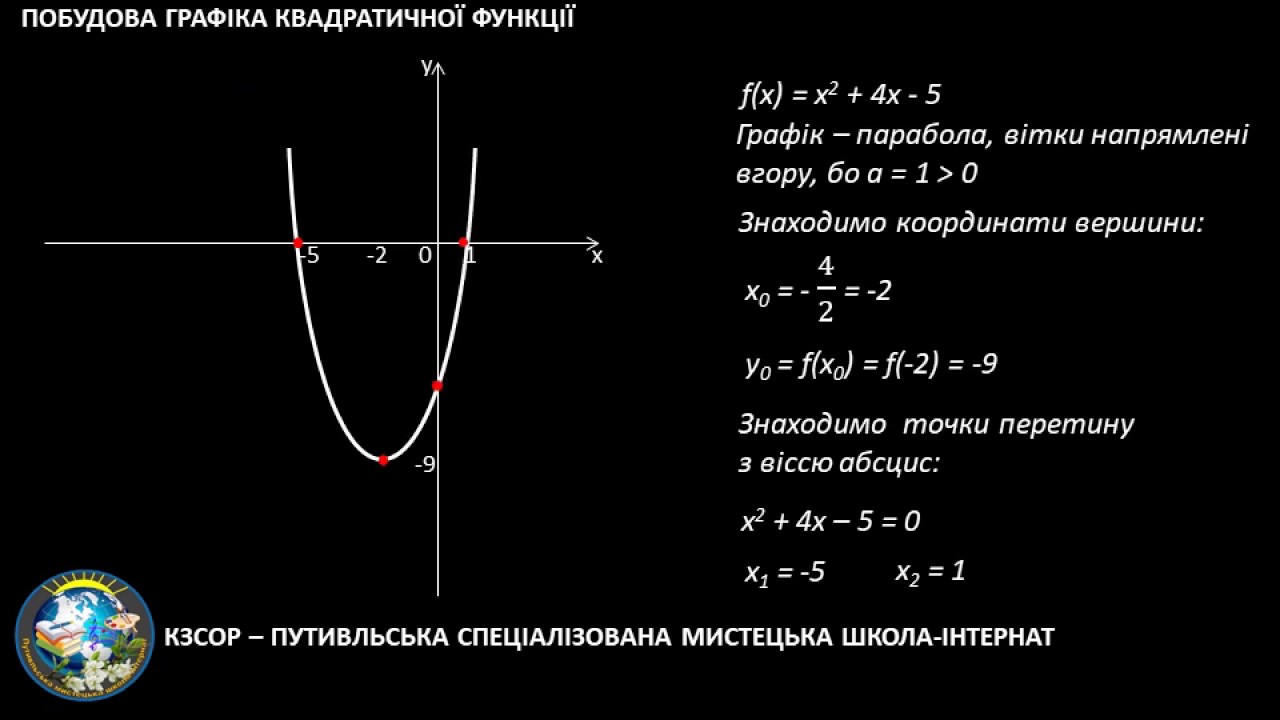
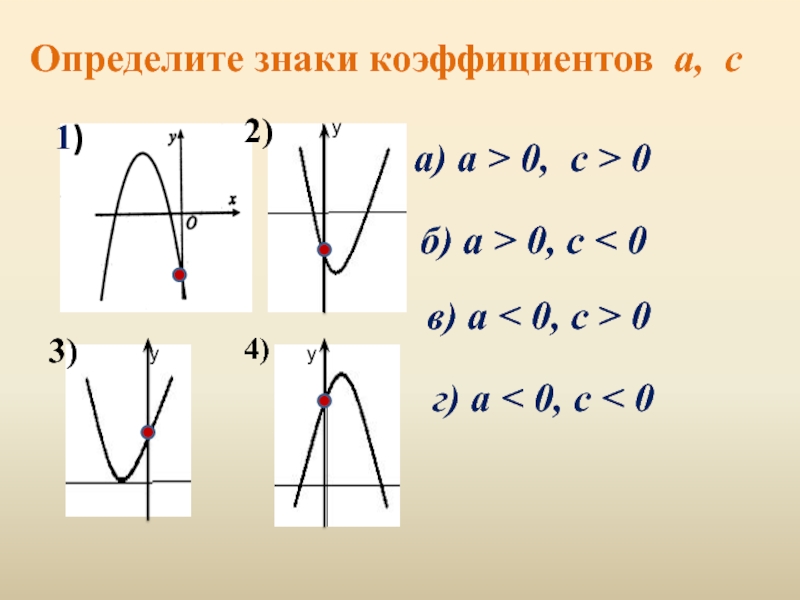
Мы знаем, что графиком функции y = ах² является парабола. Чтобы построить график функции y = ах², нужно «растянуть» или «сжать» параболу y = х² от оси х с коэффициентом |а|. Если а < 0, то график функции нужно еще симметрично отобразить относительно оси х.
Все полученные графики – так же, как и первоначальный график – называются параболами. При а > 0 ветви параболы направлены вверх, при а < 0 – вниз.
Аналогично строится и график функции y = ах³– кубическая парабола.
График функции у = f(х – m) + n
Точкой отсчета для построения графика этой функции является построение графика функции у = f(х). Итак, для создания графика функции у = f(х – m) + n нужно:
1. Выполнить параллельный перенос плоскости, выбрав началом новой системы координат х´у´ точку
О (m; n).
2. В новой плоскости построить график функции у = f(х).
Полученный график и будет графиком заданной функции, а именно – у = f(х – m) + n.
График квадратичной функции.
Квадратичной мы называем функцию вида у = ах² + bх + c, где а, b и c – любые действительные числа и
а ≠ 0.
Чтобы построить график функции у = ах² + bх + c, нам необходимо:
1. Произвести выделение полного квадрата квадратного трехчлена у = ах² + bх + c, в результате которого мы получаем
ах² + bх + c = а(х + b/2а)² + 4ас – b²/4а.
2. Построим график полученной функции, т.е. у = а(х + b/2а)² + 4ас – b²/4а.
Для этого нам нужно выполнить параллельный перенос плоскости, поместив в начало новой системы координат х´у´ точку О (-b/2а; 4ас – b²/4а), а также в плоскости х´у´ построить параболу – график функции
у´ = а (х´)².
Прямая х = -b/2а получила название ось симметрии параболы, а точка О´ (-b/2а; 4ас – b²/4а) – вершина параболы.
Если а > 0, то ветви параболы будут направлены вверх, если а < 0 – вниз.
Построить график квадратичной функции можно несколькими способами.
Способ 1.
Отыскание координат вершины параболы по формулам:
х_₀ = -b/2а
у_₀ = 4ас – b²/4а.
Используя приведенные формулы, мы сможем получить координаты вершины нашей параболы и еще нескольких точек.
Способ 2.
Построение параболы по точкам с ординатой, равной свободному члену квадратного трехчлена
ах² + bх + c. При построении графика этим способом нам нужно будет решить уравнение, чтобы найти координаты наших двух «опорных» точек. После мы сможем найти координаты вершины параболы и собственно через 3 точки построить параболу.
Способ 3.
Построение параболы по корням квадратного трехчлена. Для этого нам предстоит найти корни квадратного трехчлена х_₁ и х_₂. Далее мы определим координаты наших опорных точек и вершины. А после построим сам график.
График функции у = f(kх).
Рассмотрим случай, когда k > 0, k ≠ 1.
Сопоставляя нашу функцию с функцией у = f(х), приходим к выводу, что график функции у = f(kх) получается из графика функции у = f(х) сжатием с коэффициентом k к оси у.
Сжиматься и растягиваться могут и графики тригонометрических функций (например, у = m sin kx, у = m cos kx и др.).
Построение подобных графиков проходят в три стадии:
1. Строим график «простой», знакомой нам функции у = sin x.
2. Строим график функции у = sin kx.
3. Строим график функции у = m sin kx.
На практике же легче всего построить график для функции у = m sin kx сжатием или растяжением одной полуволны графика у = sin x, а затем построить весь график.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.
Задать вопрос

Математика

Курсы по математике 10 класс

Математика

Курсы по математике 9 класс

Математика

Математика 11 класс

Математика

Курсы по геометрии 7 класс

Математика

Курсы по алгебре 7 класс

Математика

Алгебра 8 класс

Математика

Курсы по геометрии 8 класс

Французский язык

Курсы французского языка для начинающих

Parabola Calculator
Онлайн-калькулятор параболы находит стандартные и вершинные параболические уравнения и вычисляет фокус, направление, вершину и важные точки параболы. 2 + 10y + 16 \)? 92 + 4x + 10$$
$$Без точки пересечения с осью.$$
Однако онлайн-калькулятор гиперболы поможет вам определить центр, эксцентриситет, фокусный параметр, главную и асимптоту для заданных значений в уравнение гиперболы.
Как найти директрису параболы?
Возьмем стандартную форму уравнения параболы: $ (x – h)2 = 4p (y – k) $
В этом уравнении основное внимание уделяется: $ (h, k + p)$
Принимая во внимание, что направляющая равна $ y = k – p $.
Если мы повернем параболу, то ее вершина будет: $ (h,k) $. Однако ось симметрии параллельна оси x, и ее уравнение будет таким: $ (y – k)2 = 4p (x – h)$ ,
Теперь фокус: $ (h + р, к)$
Направляющая параболы равна $ x = h – p $.
Кроме того, директриса параболы также может быть рассчитана с помощью простого уравнения: $y = c – \frac{(b² + 1)}{(4a)}$ .
Как работает калькулятор параболы?
Калькулятор уравнения параболы делает расчет быстрее и без ошибок, поскольку он использует математическое уравнение параболы. Для удобства вам необходимо выполнить следующие шаги:
Ввод:
Сначала выберите уравнение параболы из раскрывающегося списка. Вы можете выбрать стандартную форму, форму вершины, три точки или вершину и точки для ввода.
Теперь будет отображаться выбранное уравнение для параболы. Поэтому просто введите значения в данные поля соответственно.
Нажмите кнопку расчета.
Вывод:
Калькулятор уравнения параболы вычисляет:
Уравнение параболы в стандартной форме.
Уравнение параболы в вершинной форме.
Все параметры, такие как вершина, фокус, эксцентриситет, директриса, широкая прямая кишка, ось симметрии, пересечение по оси x, пересечение по оси y.
Приведите пошаговые расчеты, когда парабола проходит через разные точки.
Наряду со всеми этими математическими значениями, этот графограф параболы отображает график параболы в конце.
Часто задаваемые вопросы:
Как расстояние между фокусом и директрисой влияет на форму параболы?
Всякий раз, когда расстояние между фокусом и директрисой параболы увеличивается, |a| уменьшится. Это означает, что парабола расширяется с увеличением расстояния между двумя ее параметрами.
Как построить параболу?
Для быстрых и простых расчетов вы можете использовать онлайн-график парабол, который строит графическое представление данного уравнения параболы. Однако для ручного построения графика параболы необходимо выполнить несколько шагов:
Прежде всего, найдите следующие параметры:
y-перехват.
x-перехватов.
Ищите дополнительные точки, чтобы иметь не менее пяти точек для построения графика.
Теперь просто нанесите точки и нарисуйте график параболы.
Какие существуют два типа трансформации?
Первый тип преобразования известен как преобразование. Он перемещает узел из одного положения в другое вместе с одной из осей, связанных с его начальным положением.
Второй тип — вращение. Он перемещает узел по кругу вокруг точки вращения.
Как вы описываете преобразование параболы?
Вертикальное перемещение параболы дает возможность построить новую параболу. Это будет то же самое, что и основная парабола. Таким же образом можно перевести параболу по горизонтали.
Заключение:
Калькулятор параболы используется для получения быстрых результатов и построения графика для любого заданного параболического уравнения. Этот поиск уравнения параболы делает ваш расчет быстрее и проще, решая все связанные свойства параболического уравнения. Это также позволяет вам понять, как поместить значения в формулу параболы. Итак, этот инструмент всегда готов предоставить свои услуги всем в мгновение ока и без каких-либо затрат.
Каталожные номера:
Из источника Википедии: Декартова система координат, Сходство с единичной параболой, Положение фокуса.
Из источника онлайн-заметок Пола: Параболы, Зарисовка парабол, Направление оси.
Из источника ООР Услуги: Графики парабол с вершинами в начале координат, Стандартные формы парабол с вершинами, Ось x как ось симметрии.
Другие языки: Parabol Hesaplama, Kalkulator Parabola, Kalkulator Paraboli, Parabel Rechner, 放物線計算.
Ось симметрии — уравнение, формула, определение, примеры, парабола
Ось симметрии — это воображаемая прямая линия, которая делит фигуру на две одинаковые части, тем самым создавая одну часть как зеркальное отражение другой части. При складывании по оси симметрии две части накладываются друг на друга. Прямая линия называется линией симметрии/зеркальной линией. Эта линия может быть вертикальной, горизонтальной или наклонной.
Мы можем видеть эту ось симметрии даже в природе, такой как цветы, берега рек, здания, листья и так далее. Мы можем наблюдать это в Тадж-Махале, культовом мраморном сооружении в Индии.
1. Что такое ось симметрии?
2. Ось симметрии параболы
3. Уравнение оси симметрии
4. Ось симметрии Формула
5. Найти ось симметрии
6. Вывод оси симметрии
7. Идентификация оси симметрии
8. Часто задаваемые вопросы об оси симметрии
Что такое ось симметрии?
Ось симметрии представляет собой прямую линию, делающую форму объекта симметричной. Ось симметрии создает точные отражения на каждой из своих сторон. Он может быть горизонтальным, вертикальным или боковым. Если мы складываем и разворачиваем объект вдоль оси симметрии, две стороны идентичны. Разные фигуры имеют разные линии симметрии. У квадрата четыре оси симметрии, у прямоугольника две оси симметрии, у круга бесконечные оси симметрии, а у параллелограмма нет осей симметрии. 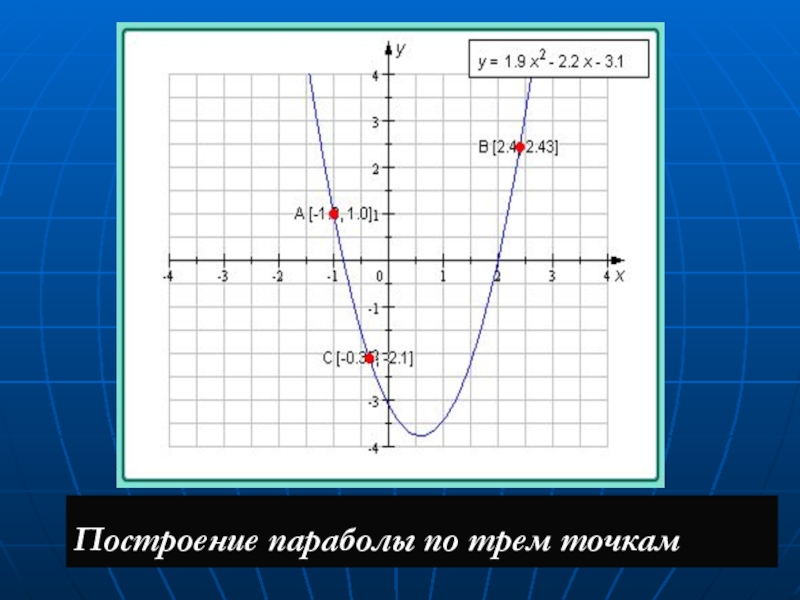Правильный многоугольник из n сторон имеет n осей симметрии.
Ось симметрии Определение
Ось симметрии — это воображаемая линия, которая делит фигуру на две одинаковые части, каждая из которых является зеркальным отражением друг друга. При складывании фигуры по оси симметрии две одинаковые части накладываются друг на друга.
Ось симметрии параболы
Парабола имеет одну линию симметрии. Ось симметрии — это прямая линия, которая делит параболу на две симметричные части. Парабола может быть четырех видов. Он может быть как горизонтальным, так и вертикальным, обращенным влево или вправо. Ось симметрии определяет форму параболы.
Если ось симметрии вертикальна, то и парабола вертикальна (раскрывается вверх/вниз).
Если она горизонтальна, то и парабола горизонтальна (открывается влево/вправо).
Горизонтальная ось симметрии имеет нулевой наклон, а вертикальная ось симметрии имеет неопределенный наклон.
Уравнение оси симметрии
Вершина — это точка пересечения оси симметрии с параболой. Это ключевой момент для определения его уравнения. Если парабола раскрывается вверх или вниз, ось симметрии вертикальна и в этом случае ее уравнением является вертикальная линия, проходящая через ее вершину. Если парабола открывается вправо или влево, ось симметрии горизонтальна, а ее уравнением является горизонтальная линия, проходящая через ее вершину. то есть
Ось уравнения симметрии параболы, вершина которой равна (h, k) и направлена вверх/вниз, равна x = h.
Ось уравнения симметрии параболы, вершина которой равна (h, k) и открывается влево/вправо, равна y = k.
Ось симметрии Формула
Формула оси симметрии применяется к квадратным уравнениям, где используется стандартная форма уравнения и линия симметрии. Линия, которая делит или раздваивает любой объект на две равные половины, обе половины которых являются зеркальным отображением друг друга, называется осью симметрии. Эта линия оси, разделяющая объекты, может быть любого из трех типов: горизонтальная (ось X), вертикальная (ось Y) или наклонная линия.
Уравнение оси симметрии может быть представлено, когда парабола имеет две формы:
Стандартная форма
Вершинная форма
Стандартная форма
Квадратное уравнение в стандартной форме : y = ax ² + b x+c
, где a, b и c — действительные числа.
Здесь формула оси симметрии: x = — b/2a.
Вершинная форма
Квадратное уравнение в вершинной форме: y = a (x-h) ² + k
где (h, k) — вершина параболы.
Здесь формула оси симметрии равна x = h.
Вывод оси симметрии параболы
Ось симметрии всегда проходит через вершину параболы. Таким образом, идентификация вершины помогает нам вычислить положение оси симметрии. Формула оси симметрии параболы: x = -b/2a. Выведем уравнение оси симметрии.
Квадратное уравнение параболы: y = ax ² + bx + c (парабола вверх/вниз).
Постоянный член ‘c’ не влияет на параболу. Поэтому рассмотрим, что y = ax ² + bx.
Ось симметрии является средней точкой двух пересечений с х. Чтобы найти точку пересечения, подставьте y = 0.
x(ax+b)=0
x = 0 и (ax+b)=0
x = 0 и x = -b/a
формула средней точки x = (x ₁ + x ₂ ) / 2
x= [0 + (-b/a)] / 2
Следовательно, x = -b/2a
Примечание: Если парабола открыта влево/вправо, то найдите середину y -перехватывает.
Найти ось симметрии
Пример 1: Найти ось симметрии квадратного уравнения y = x ² — 4x + 3.
Решение:
Дано: y = x ² — 4x + 3
Использование формула оси симметрии,
x = -b/2a
x = -(-4)/2(1)
x = 4/2
= 2
Следовательно, ось симметрии уравнения y = x ² — 4x + 3 равно x = 2.
Пример 2: Найдите ось симметрии параболы y = 4x ² .
Решение:
Используя формулу оси симметрии а у = 4x ² равно x = 0,
Идентификация оси симметрии
Определим ось симметрии данной параболы, используя формулу, изученную в предыдущем разделе.
1) Рассмотрим уравнение y = x ² — 3x + 4. Сравнивая это с уравнением стандартной формы параболы (y = ax ² + bx + c), имеем
a = 1, b = -3 и c = 4
Это вертикальная парабола. Таким образом, он имеет вертикальную ось симметрии.
Мы знаем, что x = -b/2a есть уравнение оси симметрии.
x = -(-3)/2(1) = 1,5
x = 1,5 — ось симметрии параболы y = x ² — 3x + 4.
2) Рассмотрим другой пример. х = 4у ² +5у+3.
Сравнивая со стандартной формой квадратного уравнения, получаем a = 4, b = 5 и c = 3. Эта парабола горизонтальна, и ось симметрии тоже горизонтальна.
Мы знаем, что y = -b/2a есть уравнение оси симметрии.
y = -b/2a
y = -5/2(4)
y = -0,625
3) Если даны две точки, находящиеся на одинаковом расстоянии от вершины параболы, то определяем уравнение оси симметрии путем нахождения середины этих точек. Предположим, что две точки (3, 4) и (9, 4) являются точками на параболе, тогда вершина проходит через точку пересечения, которая образует середину этих заданных точек. Таким образом, x = (3+9)/2 = 12/2 = 6. Следовательно, уравнение оси симметрии имеет вид x = 6,9.0003
Пример: Если ось симметрии уравнения y = qx ² – 32x – 10 равна 8, то найдите значение q.
Решение: Дано,
y = qx ² – 32x – 10
Ось симметрии x = 8
По формуле:
x = — б/2а
, где а = q, b = -32 и x = 8
8 = -(-32) / (2 × q)
8 = 32/2q
16q = 32
q = 2
Следовательно, значение q = 2
Важные замечания по оси симметрии
Ось симметрии — это воображаемая линия, которая делит фигуру на две одинаковые части, являющиеся зеркальным отображением друг друга.
Для параболы y = ax ² + b x+c ось симметрии определяется как x = -b/2a
Правильный многоугольник с ‘n’ сторонами имеет ‘n’ осей симметрии.
☛ Статьи по теме:
Линии симметрии в прямоугольнике
Линии симметрии параллелограмма
Часто задаваемые вопросы об оси симметрии
Что такое ось симметрии в алгебре?
Ось симметрии — это воображаемая линия, которая делит фигуру на две одинаковые части, каждая из которых является зеркальным отражением друг друга. Правильный многоугольник из n сторон имеет n осей симметрии.
Что такое определение оси симметрии?
Ось симметрии — воображаемая прямая, которая делит фигуру на две одинаковые части или делает фигуру симметричной. Например, у квадрата 4, а у прямоугольника 2 оси симметрии.
Что такое формула оси симметрии?
Формула оси симметрии использует стандартную форму квадратного уравнения, а также форму вершины. Симметрия делит любую геометрическую фигуру на две равные половины. Формула оси симметрии задается как для квадратного уравнения стандартной формы y = ax ² + bx + c: x = -b/2a. Если парабола имеет форму вершины y = a(x-h) ² + k, то формула будет следующей: x = h.
Какая формула используется для расчета оси симметрии стандартной формы?
Формула, используемая для нахождения оси симметрии квадратного уравнения стандартной формы y = ax ² + bx + c, выглядит следующим образом: x = -b/2a.
Что такое формула оси симметрии для формы вершины?
Квадратное уравнение представляется в вершинной форме как: y = a(x−h) ² + k , где (h, k) — вершина параболы. Поскольку ось симметрии и форма вершины лежат на одной линии, формула x = h.
Найдите ось симметрии квадратного уравнения y = 5x
² — 10х + 3.
Дано: у = 5х ² — 10х + 3
Используя формулу оси симметрии,
х = -b/2а
х = -(-10)/2(5)
х = 10/10
х = 1
Следовательно, ось симметрии уравнения y = 5x ² — 10x + 3 равна x = 1.
Что такое ось симметрии параболы?
Ось симметрии — это прямая линия, которая делит параболу на две симметричные части. Он проходит через вершину параболы. Ось симметрии параболы может быть горизонтальной или вертикальной.
Как найти ось симметрии, используя вершинную форму уравнения?
Квадратное уравнение в вершинной форме имеет вид y = a(x-h) ² +k. Ось симметрии находится там, где вершина пересекает параболу в точке, обозначенной вершиной (h, k). h — координата x. а в вершинной форме x = h и h = -b/2a, где b и a — коэффициенты в стандартной форме уравнения, y = ax ² + bx + c.
Что такое ось симметрии на графике?
Горизонтальная или вертикальная линия на графике, проходящая через вершину параболы, образует ось симметрии параболы. В случае любого другого графика осью симметрии является уравнение линии, которая делит фигуру на две равные части, одна из которых является зеркальным отражением другой.
Является ли ось симметрии такой же, как и линия симметрии?
Да, линия симметрии и ось симметрии совпадают.

Матрицы 3а 2в: Матричный калькулятор

alexxlab / 07.08.202326.05.2023 / Разное

404 Cтраница не найдена

Мы используем файлы cookies для улучшения работы сайта МГТУ и большего удобства его использования. Более подробную информацию об использовании файлов cookies можно найти здесь. Продолжая пользоваться сайтом, вы подтверждаете, что были проинформированы об использовании файлов cookies сайтом ФГБОУ ВО «МГТУ» и согласны с нашими правилами обработки персональных данных.

Размер:

AAA
Изображения Вкл. Выкл.
Обычная версия сайта
К сожалению запрашиваемая страница не найдена.
Но вы можете воспользоваться поиском или картой сайта ниже

Университет
Майкопский государственный технологический университет – один из ведущих вузов юга России.
История университета

Анонсы

Объявления

Медиа
Представителям СМИ

Газета «Технолог»

О нас пишут

Ректорат

Структура
Филиал

Политехнический колледж

Медицинский институт
Лечебный факультет

Педиатрический факультет

Фармацевтический факультет

Стоматологический факультет

Факультет послевузовского профессионального образования

Факультеты

Кафедры

Ученый совет

Дополнительное профессиональное образование

Бережливый вуз – МГТУ
Новости

Объявления

Лист проблем

Лист предложений (Кайдзен)

Реализуемые проекты

Архив проектов

Фабрика процессов

Рабочая группа «Бережливый вуз-МГТУ»

Вакансии

Профсоюз

Противодействие терроризму и экстремизму

Противодействие коррупции

WorldSkills в МГТУ

Научная библиотека МГТУ

Реквизиты и контакты

Автошкола МГТУ

Опрос в целях выявления мнения граждан о качестве условий оказания образовательных услуг

Управление имущественным комплексом

Работа МГТУ в условиях предотвращения COVID-19

Документы, регламентирующие образовательную деятельность

Система менеджмента качества университета

Региональный центр финансовой грамотности

Аккредитационно-симуляционный центр

Абитуриентам
Подача документов онлайн

Абитуриенту 2023
Для поступающих на обучение по программам бакалавриата, специалитета, магистратуры — Прием 2023

Для поступающих на обучение по программам среднего профессионального образования (колледж)

Для поступающих на обучение по договорам об оказании платных образовательных услуг
Образец договора

Образовательный кредит

Оплата материнским (семейным) капиталом

Банковские реквизиты для оплаты обучения

Приказ об установлении стоимости обучения для 1 курса набора 2022-2023 учебного года

Для поступающих на обучение по программам ординатуры

Для поступающих на обучение по программам аспирантуры

Часто задаваемые вопросы (бакалавриат, специалитет, магистратура)

Видеоматериалы для постуающих

Экран приёма 2022

Иностранным абитуриентам
Международная деятельность

Общие сведения

Кафедры

Новости

Центр международного образования

Академическая мобильность и международное сотрудничество
Академическая мобильность и фонды

Индивидуальная мобильность студентов и аспирантов

Как стать участником программ академической мобильности

Дни открытых дверей в МГТУ
День открытых дверей online

Университетские субботы

Дни открытых дверей на факультетах

Подготовительные курсы
Подготовительное отделение

Курсы для выпускников СПО

Курсы подготовки к сдаче ОГЭ и ЕГЭ

Онлайн-курсы для подготовки к экзаменам

Подготовка школьников к участию в олимпиадах

Малая технологическая академия
Профильный класс
Социально-экономический профиль

Медико-фармацевтический профиль

Инженерно-технологический профиль

Эколого-биологический профиль

Агротехнологический профиль

Индивидуальный проект

Кружковое движение юных технологов

Олимпиады, конкурсы, фестивали

Веб-консультации для абитуриентов и их родителей
Веб-консультации для абитуриентов

Родительский университет

Олимпиады для школьников
Отборочный этап

Заключительный этап

Итоги олимпиад

Профориентационная работа

Стоимость обучения

Студентам
Студенческая жизнь
Стипендии

Организация НИРС в МГТУ

Студенческое научное общество

Студенческие научные мероприятия

Конкурсы

Академическая мобильность и международное сотрудничество

Образовательные программы

Расписание занятий

Расписание звонков

Онлайн-сервисы

Социальная поддержка студентов

Общежития

Трудоустройство обучающихся и выпускников
Вакансии

Обеспеченность ПО

Инклюзивное образование
Условия обучения лиц с ограниченными возможностями

Доступная среда

Ассоциация выпускников МГТУ

Перевод из другого вуза

Вакантные места для перевода

Студенческое пространство
Студенческое пространство

Запись на мероприятия

Отдел по социально-бытовой и воспитательной работе

Наука и инновации
Научная инфраструктура
Проректор по научной работе и инновационному развитию

Научно-технический совет

Управление научной деятельностью

Управление послевузовского образования

Точка кипения МГТУ
О Точке кипения МГТУ

Руководитель и сотрудники

Документы

Контакты

Центр коллективного пользования

Центр народной дипломатии и межкультурных коммуникаций

Студенческое научное общество

Научные издания
Научный журнал «Новые технологии»

Научный журнал «Вестник МГТУ»

Научный журнал «Актуальные вопросы науки и образования»

Публикационная активность

Конкурсы, гранты

Научные направления и результаты научно-исследовательской деятельности
Основные научные направления университета

Отчет о научно-исследовательской деятельности в университете

Результативность научных исследований и разработок МГТУ

Финансируемые научно-исследовательские работы

Объекты интеллектуальной собственности МГТУ

Результативность научной деятельности организаций, подведомственных Минобрнауки России (Анкеты по референтным группам)

Студенческое научное общество

Инновационная инфраструктура
Федеральная инновационная площадка

Проблемные научно-исследовательские лаборатории
Научно-исследовательская лаборатория «Совершенствование системы управления региональной экономикой»

Научно-исследовательская лаборатория проблем развития региональной экономики

Научно-исследовательская лаборатория организации и технологии защиты информации

Научно-исследовательская лаборатория функциональной диагностики (НИЛФД) лечебного факультета медицинского института ФГБОУ ВПО «МГТУ»

Научно-исследовательская лаборатория «Инновационных проектов и нанотехнологий»

Научно-техническая и опытно-экспериментальная база

Центр коллективного пользования

Научная библиотека

Экспортный контроль

Локальный этический комитет

Конференции
Школа молодого врача

Международная научно-практическая конференция «Фундаментальные и прикладные аспекты геологии, геофизики и геоэкологии с использованием современных информационных технологий»

Международная научно-практическая конференция «Актуальные вопросы науки и образования»

VI Международная научно-практическая онлайн-конференция

Наука и университеты

Международная деятельность
Иностранным студентам

Международные партнеры

Академические обмены, иностранные преподаватели
Академическая мобильность и фонды

Индивидуальная мобильность студентов и аспирантов

Факультет международного образования
Новости факультета

Информация о факультете

Международная деятельность

Кафедры
Кафедра русского языка как иностранного

Кафедра иностранных языков

Центр Международного образования

Центр обучения русскому языку иностранных граждан
Приказы и распоряжения

Курсы русского языка

Расписание

Академическая мобильность

Контактная информация

Контактная информация факультета международного образования

Сведения об образовательной организации
Основные сведения

Структура и органы управления образовательной организацией

Документы

Образование

Образовательные стандарты и требования

Руководство. Педагогический (научно-педагогический) состав

Материально-техническое обеспечение и оснащённость образовательного процесса

Стипендии и меры поддержки обучающихся

Платные образовательные услуги

Финансово-хозяйственная деятельность

Вакантные места для приёма (перевода)

Международное сотрудничество

Доступная среда

Организация питания в образовательной организации

Операции над матрицами
Как вы, наверное, уже поняли матрицы ничем не отличаются от обычных чисел, по правде говоря — это просто много цифр в одном числе))) И разумеется, существуют такие же операции над матрицами, как и над числами, но не все и вычисляются немного по-другому. И именно сегодня мы этим и займемся.
Матрицей размера m x n или (m x n)-матрицей называется прямоугольная таблица из чисел

, состоящая из m-строк и n-столбцов

Сумма матриц
Суммой A+B (m x n)-матриц и называется матрица того же порядка, каждый элемент которой равен сумме соответствующих элементов матриц A и В.
Ну с этим все очень просто, а рассмотрев пример, вообще поймете, что делать нечего.
Пример №1 Вычислить сумму матриц A и В
Делаем согласно правилу: складываем элементы матрицы А и соответствующие элементы матрицы В:
Все! Сумма матриц А и В найдена! Проще простого.
Произведение матрицы на число
Произведением αA матрицы на действительное или комплексное число α называется матрица B, полученная из матрицы A умножением всех ее элементов на число α.
Как вы видите из определения, здесь также нет ничего сложного.
Пример №2 Найти произведение матрицы A на число -2.
Просто перемножаем каждое число матрицы А на число -2:
Произведение матриц
Произведением АВ (m x n)-матрицы на (n x k)-матрицу , называется (m x k)-матрица , элемент которой , стоящий в i-строке и j-столбце равен сумме произведений соответствующих элементов i-строки матрицы А и j-столбца матрицы В.
Понимаю, что в этом огромном определении вам мало, что понятно, но все таки попробуем разобраться.
Во-первых знайте: умножать матрицы можно только в том случае, если число строк первой матрицы равно числу столбцов второй матрицы!
Во-вторых знайте: переместительный закон умножения здесь не действует! Т.е. если матрицы поменять местами, то и результат изменится.
Ну а теперь давайте решим пример.
Пример №3 Найти произведение матрицы А на матрицу В.
Чтобы вам было проще и, чтобы вы не наделали глупых ошибок в вычислениях, советую сперва расписывать каждый элемент матрицы:
А теперь полученные числа, вписываем в матрицу, согласно координатам (ij):
Произведение матрицы найдено! Посложнее, конечно, но ничего поймете методику и вникните быстро).
Рассмотрим, теперь пример посложнее…
Пример №4 Найти произведение матрицы А на матрицу В.
Также распишем каждый элемент матрицы:
Вот и все, а теперь, запишем, полученную матрицу:
Возьмем немного сложнее пример дальше.
Пример №5 Вычислить 3А + ВС
Решаем это, как обычный пример, правда вместо слагаемых будут выступать матрицы.
1 действие: 3*А:
2 действие: BC:
Вставляем полученные результаты в матрицу и получаем:
Ну а теперь, выполняем последнее действие, а именно складываем матрицы 3А и ВС:
На этой хорошей ноте всем спасибо)

Если кто-то не понял или не разобрался в теме или в заданиях, задавайте вопросы в комментариях.

Уроки по теории вероятности
Продолжаем изучать матрицы и сегодня на уроке мы научимся находить и вычислять обратную матрицу. Обратная матрица Матрица называется транспонированной к матрице , если выполняется условие: , для всех , где и — элементы матриц и соответственно. Проще говоря, транспонированная матрица — это перевернутая матрица, т.е. столбцы записаны строками, а строки столбцами. Пример №1 Транспонировать матрицу
Мы рассмотрели самые основные тригонометрические функции (не обольщайтесь помимо синуса, косинуса, тангенса и котангенса существует еще целое множество других функций, но о них позже), а пока рассмотрим некоторые основные свойства уже изученных функций. Тригонометрические функции числового аргумента Какое бы действительное число ни взять, ему можно поставить в соответствие однозначно определенное число . Правда, правило соответствия
Я решил, что не будем слишком долго разжевывать теоретическую часть введения в тригонометрию так, как в любом случае мало кто ее будет читать и уж тем более маловероятно, что он там все поймет. Я считаю, что лучший способ изучения математики — это не зубрежка, а работа с конкретными примерами и чем больше тем лучше. Поэтому
Сегодня, мы рассмотрим тему «Прогрессии», которую большинство в школе либо не понимают, либо после забывают, хотя делать этого не нужно! Числовые последовательности Если каждому натуральному числу поставлено в соответствие некоторое действительное число , то говорят, что задана числовая последовательность (или просто последовательность): Кратко последовательность обозначают символом {} или (), число называют членом или элементом этой
Логика также является одним из разделов математики. Подробно во все тонкости данной дисциплины, мы, в мат. анализе вникать, конечно, не будем, но база нам понадобится, а следовательно, данный урок мы посвятим именно ей. Высказывания. Операции над высказываниями Высказывание — это любое утверждение, о котором можно сказать, что оно либо истинно либо ложно. Существует всего пять
Найдите матрицу X, если i 3A X B ii X 3B 2A…
Перейти к
Матрицы. Упражнение 8.1.
Матрицы. Упражнение 8.2.
Матрицы. Упражнение 8.3.
налог на товары и услуги
Банковское дело
Акции и дивиденды
Квадратные уравнения с одной переменной
Факторизация
Соотношение и пропорция
Матрицы
Арифметика и геометрическая прогрессия
Отражение
Формула раздела
Уравнение прямой линии
Сходство
Локус
Круги
Конструкции
Измерение
Тригонометрические тождества
Тригонометрические таблицы
Высоты и расстояния
Главная > ML Aggarwal Solutions Класс 10 Математика > Глава 8 — Матрицы > Матрицы. Упражнение 8.2. > Вопрос 5
Вопрос 5 Матрицы Упражнение 8.2
\text { If } A=\left[\begin{array}{cc} 0 и -1 \\ 1 и 2 \end{массив}\right] \text { и } B=\left[\begin{массив}{cc} 1 и 2 \\ -1 и 1 \конец{массив}\справа]
Найдите матрицу X, если:
(i) 3A + X = B
(ii) X – 3B = 2A
Ответ:
Дано
\begin{array}{l} A=\left[\begin{массив}{cc} 0 и -1 \\ 1 и 2 \конец{массив}\справа] \\ B=\left[\begin{массив}{cc} 1 и 2 \\ -1 и 1 \конец{массив}\справа] \end{array}
Теперь нам нужно найти
\begin{aligned} &\текст { (i) } 3 A+X=B\\ &Х=В-3 А \end{выровнено}
\begin{выровнено} &\text { Подставляем полученные значения }\\ &\ начало {выровнено} X &=\left[\begin{массив}{rr} 1 и 2 \\ -1 и 1 \end{массив}\right]-3\left[\begin{массив}{rr} 0 и -1 \\ 1 и 2 \конец{массив}\справа] \\ &=\left[\begin{массив}{rr} 1 и 2 \\ -1 и 1 \end{массив}\right]-\left[\begin{массив}{rr} 0 и -3 \\ 3 и 6 \конец{массив}\справа] \\ &=\left[\begin{массив}{rr} 1-0 и 2+3 \\ -1-3 и 1-6 \end{массив}\right]=\left[\begin{массив}{rr} 1 и 5 \\ -4 и -5 \конец{массив}\справа] \end{выровнено} \end{выровнено}
\begin{выровнено} &\текст { (ii) } X-3 B=2 A\\ &Х=2 А+3 В \end{выровнено}
\begin{выровнено} &\text { Теперь подставляя значения } A \text { и } B \text { получаем }\\ &X=2\left[\begin{массив}{rr} 0 и -1 \\ 1 и 2 \end{массив}\right]+3\left[\begin{массив}{rr} 1 и 2 \\ -1 и 1 \конец{массив}\справа]\\ &=\left[\begin{массив}{rr} 0 и -2 \\ 2 и 4 \end{массив}\right]+\left[\begin{массив}{rr} 3 и 6 \\ -3 и 3 \конец{массив}\справа]\\ &=\left[\begin{массив}{rr} 0+3 и -2+6 \\ 2-3 и 4+3 \end{массив}\right]=\left[\begin{массив}{rr} 3 и 4 \\ -1 и 7 \конец{массив}\справа] \end{выровнено}
Связанные вопросы
Решить матричное уравнение
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнения
Матрицы Упражнение 8. 1
Упражнение с матрицами 8.2
Упражнение с матрицами 8.3
Главы
GST
Банковское дело
Акции и дивиденды
Квадратные уравнения с одной переменной
Факторизация
Отношение и пропорция
Матрицы
Арифметика и геометрическая прогрессия
Отражение
Формула сечения
Уравнение прямой
Подобие
Геометрическое место
Окружности
Построения
Измерения
Тригонометрические тождества
Тригонометрические таблицы
Высоты и расстояния
Курсы
Быстрые ссылки
Условия и политика
Условия и политика
2022 © Quality Tutorials Pvt Ltd. Все права защищены
Для двух $3 x 3$ матриц A и B пусть A + B = 2В’ и 3А + 2B = ${I_3}$, где B’ — транспонированная матрица B, а ${I_3}$ — единичная матрица $3 \times 3$. Тогда A) $5A + 10B = 2{I_3}$B) $3A + 6B = 2{I_3}$C) $10A + 5B = 3{I_3}$D) $B + 2A = {I_3}$ 9{‘}} = \dfrac{{A + B}}{2}$

Подставьте это в предыдущее уравнение
$
   \Стрелка вправо 6B — \left( {\dfrac{{A + B}}{2}} \ right) = {I_3} \\
   \Rightarrow 12B — A — B = 2{I_3} \\
$
Подставьте значение ${I_3}$ из данного уравнения 3A + 2B = ${I_3}$
$
   \Стрелка вправо 12B — A — B = 2(3A + 2B) \\
   \Стрелка вправо 11B — A = 6A + 4B \\
   \Стрелка вправо 7A = 7B \\
   \Стрелка вправо A = B \\
$
Замена в 3A + 2B = ${I_3}$, получаем
$
   \Стрелка вправо 3A + 2A = {I_3} \\
   \Стрелка вправо 5A = {I_3} \\
$
Теперь у нас есть A = B и ${I_3}$= 5A
Мы попросили 5A +10B
$ \Rightarrow 5A + 10B = 5A + 10A = 15A = 3 \times 5A = 3{I_3}$
Следовательно, правильный вариант C.

Выполнить действия а больше 0 б больше 0: Выполнить действия ( а больше 0, b больше 0):…

alexxlab / 07.08.202310.05.2023 / Разное

ЕСЛИ (функция ЕСЛИ) — Служба поддержки Майкрософт

Формулы и функции

Общие сведения о формулах в Excel
Статья

ПРОСМОТРX
Статья

ВПР
Статья

Функция СУММ
Статья

Функция СЧЁТЕСЛИ
Статья

Функция ЕСЛИ
Статья

ЕСЛИМН
Статья

СУММЕСЛИ
Статья

СУММЕСЛИМН
Статья

ПОИСКПОЗ
Статья

Далее: Использование функций

Функция ЕСЛИ — одна из самых популярных функций в Excel. Она позволяет выполнять логические сравнения значений и ожидаемых результатов.

Поэтому у функции ЕСЛИ возможны два результата. Первый результат возвращается в случае, если сравнение истинно, второй — если сравнение ложно.

Например, функция =ЕСЛИ(C2=»Да»;1;2) означает следующее: ЕСЛИ(С2=»Да», то вернуть 1, в противном случае вернуть 2).

Функция ЕСЛИ, одна из логических функций, служит для возвращения разных значений в зависимости от того, соблюдается ли условие.
ЕСЛИ(лог_выражение; значение_если_истина; [значение_если_ложь])
Например:

Имя аргумента

Описание

лог_выражение    (обязательно)

Условие, которое нужно проверить.

значение_если_истина    (обязательно)

Значение, которое должно возвращаться, если лог_выражение имеет значение ИСТИНА.

значение_если_ложь    (необязательно)

Значение, которое должно возвращаться, если лог_выражение имеет значение ЛОЖЬ.

Простые примеры функции ЕСЛИ

=ЕСЛИ(C2=»Да»;1;2)

В примере выше ячейка D2 содержит формулу: ЕСЛИ(C2 = Да, то вернуть 1, в противном случае вернуть 2)

В этом примере ячейка D2 содержит формулу: ЕСЛИ(C2 = 1, то вернуть текст «Да», в противном случае вернуть текст «Нет»). Как видите, функцию ЕСЛИ можно использовать для сравнения и текста, и значений. А еще с ее помощью можно оценивать ошибки. Вы можете не только проверять, равно ли одно значение другому, возвращая один результат, но и использовать математические операторы и выполнять дополнительные вычисления в зависимости от условий. Для выполнения нескольких сравнений можно использовать несколько вложенных функций ЕСЛИ.

В примере выше функция ЕСЛИ в ячейке D2 означает: ЕСЛИ(C2 больше B2, то вернуть текст «Превышение бюджета», в противном случае вернуть текст «В пределах бюджета»)

На рисунке выше мы возвращаем не текст, а результат математического вычисления. Формула в ячейке E2 означает: ЕСЛИ(значение «Фактические» больше значения «Плановые», то вычесть сумму «Плановые» из суммы «Фактические», в противном случае ничего не возвращать).

В этом примере формула в ячейке F7 означает: ЕСЛИ(E7 = «Да», то вычислить общую сумму в ячейке F5 и умножить на 8,25 %, в противном случае налога с продажи нет, поэтому вернуть 0)

Примечание: Если вы используете текст в формулах, заключайте его в кавычки (пример: «Текст»). Единственное исключение — слова ИСТИНА и ЛОЖЬ, которые Excel распознает автоматически.

Распространенные неполадки

Проблема

Возможная причина

0 (ноль) в ячейке

Не указан аргумент значение_если_истина или значение_если_ложь. Чтобы возвращать правильное значение, добавьте текст двух аргументов или значение ИСТИНА/ЛОЖЬ.

#ИМЯ? в ячейке

Как правило, это указывает на ошибку в формуле.

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

См. также

Функция ЕСЛИ — вложенные формулы и типовые ошибки

Функция УСЛОВИЯ

Использование ЕСЛИ с функциями И, ИЛИ и НЕ

СЧЁТЕСЛИ

Рекомендации, позволяющие избежать появления неработающих формул

Общие сведения о формулах в Excel

Знакомство с R (молниеносное и поверхностное).
О курсе
Презентации и данные
Полезности
Собственно, сам R
RStudio — среда для разработки (IDE) на R
Онлайн IDE для R — на тот случай, если у вас не установлен R:
https://rstudio. cloud
Создайте папку, где будут храниться ВСЕ материалы курса. Например: Мы будем ее называть рабочей директорией. В эту папку помещайте ВСЕ файлы с кодом (с расширением .R).
Внутри папки linmodr создайте папку data, где будут храниться все файлы с данными для анализа.
В итоге у вас должно получиться примерно это:
C:\linmodr\ C:\linmodr\data\
Настройка RStudio
Все настройки RStudio находятся в меню Tools -> Global Options
Восстановление рабочего пространства из прошлого сеанса — это лучше отменить, т.к. обычно переменные-призраки очень мешают. На вкладке General убираем галочку Restore .RData into workspace at startup, и меняем Save workspace to .RData on exit — Never
Перенос длинных строк в окне кода — это удобно. На вкладке Code ставим галочку рядом с опцией Soft-wrap R source files
Комментарии в текстах программ обозначаются символом #
# это комментарии, они не будут выполняться
Ctrl + Shift + C — закомментировать/раскомментировать выделенный фрагмент кода
Ctrl + Enter — отправляет активную строку из текстового редактора в консоль, а если выделить несколько строк, то будет выполнен этот фрагмент кода.
Tab или Ctrl + Space — нажмите после того как начали набирать название функции или переменной, и появится список автоподстановки. Это помогает печатать код быстро и с меньшим количеством ошибок.
В RStudio можно поставить курсор на слово setwd и нажать F1
Перед названием функции можно напечатать знак вопроса и выполнить эту строку ?setwd
Можно воспользоваться функцией help()
help("setwd")
## [1] 4
1024/2
## [1] 512
## [1] 1 2 3 4 5 6 7 8 9 10
## [1] 136
## [1] 16
sqrt(27)
## [1] 5.196152
Оператор присваивания это символ стрелочки <-. Он работает справа налево, это значит, что значение выражения в его правой части присваивается объекту в левой части.
Переменные — это такие контейнеры, в которые можно положить разные данные и даже функции.
Имена переменных могут содержать латинские буквы обоих регистров, символы точки . и подчеркивания _ , а так же цифры. Имена переменных должны начинаться с латинских букв. Создавайте понятные и “говорящие” имена переменных.
var_1 <- 1024 / 2 1238 * 3 -> var_2 var_2
## [1] 3714
Как выбрать название переменной?
a — плохо, и даже b, с, или х. Но в некоторых случаях допустимо:)
var1 — плохо, но уже лучше
var_1 — плохо, но уже лучше
shelllength — говорящее, но плохо читается
shell_length, wing_colour или leg_num — хорошие говорящие и читабельные названия
Данные в R можно хранить в виде разных объектов.
В результате выполнения следующих команд числа. Одно выражение — одно значение.
## [1] 23
sqrt(25)
## [1] 5
На самом деле, эти величины — просто векторы единичной длины
Векторы — один объект, внутри которого несколько значений.
Некоторые способы создания векторов:
Оператор: используется для создания целочисленных векторов, где значения следуют одно за другим без пропусков
1:10 # от одного до 10
## [1] 1 2 3 4 5 6 7 8 9 10
-5:3 # от -5 до 3
## [1] -5 -4 -3 -2 -1 0 1 2 3
Функция seq() создает последовательности из чисел
seq(from = 1, to = 5, by = 0.5)
## [1] 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0
Функция c() — от англ. concatenate. Следите, чтобы было английское си, а не русское эс:).
?c # посмотрите хелп к функции
Функция c принимает несколько (произвольное количество) аргументов, разделенных запятыми. Она собирает из них вектор.
c(2, 4, 6)
## [1] 2 4 6
c(-9.3, 0, 2.17, 21.3)
## [1] -9.30 0.00 2.17 21.30
Векторы можно хранить в переменных для последующего использования
vect_num <- -11:12 # численный вектор от -11 до 12 сохранен в переменной vect_num vect_num_1 <- c(1. 3, 1.7, 1.2, 0.9, 1.6, 1.4) # численный вектор, сохранен в переменной vect_num_1
Адресация внутри векторов
При помощи оператора [], можно обратится к некоторым элементам вектора. В квадратных скобках вам нужно указать один или несколько порядковых номеров элементов
vect_num[1] # первый элемент в векторе vect_num
## [1] -11
vect_num[10] # 10-й элемент
## [1] -2
vect_num[22]
## [1] 10
Если вам нужно несколько элементов, то их нужно передать квадратным скобкам в виде вектора. Например, нам нужны элементы с 3 по 5. Вот вектор, который содержит значения 3, 4 и 5.
## [1] 3 4 5
Если мы его напишем в квадратных скобках, то добудем элементы с такими порядковыми номерами
vect_num[3:5]
## [1] -9 -8 -7
Аналогично, если вам нужны элементы не подряд, то передайте вектор с номерами элементов, который вы создали при помощи функции c() c(2, 4, 6) # это вектор содержащий 2, 4 и 6, поэтому
vect_num[c(2, 4, 6)] # возвращает 2-й, 4-й и 6-й элементы
## [1] -10 -8 -6
vect_num[c(1, 10, 20)] # возвращает 1-й, 10-й и 20-й элементы
## [1] -11 -2 8
Вектор — одномерный объект. У его элементов только один порядковый номер (индекс). Поэтому при обращении к элементам вектора нужно указывать только одно число или один вектор с адресами.
Правильно:
vect_num[c(1, 2, 5)] # возвращает 1-й, 3-й и 5-й элементы
## [1] -11 -10 -7
Но R выдаст ошибку, если при обращении к вектору, вы не создавали вектор, а просто перечислили номера элементов через запятую.
vect_num[1, 3, 5] # ошибка vect_num[15, 9, 1] # ошибка
vect_num[c(15, 9, 1)] # правильно
## [1] 3 -3 -11
При помощи функции c() можно объединять несколько векторов в один вектор
c(1, 1, 5:9)
## [1] 1 1 5 6 7 8 9
c(vect_num, vect_num)
## [1] -11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 ## [20] 8 9 10 11 12 -11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 ## [39] 3 4 5 6 7 8 9 10 11 12
c(100, vect_num)
## [1] 100 -11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 ## [20] 7 8 9 10 11 12
Добываем 1, 3, 5 и с 22 по 24 элементы
vect_num[c(1, 3, 5, 22:24)]
## [1] -11 -9 -7 10 11 12
Числовые данные
Уже видели в прошлом разделе.
Текстовые данные
Каждый текстовый элемент (говорят “строка” — string или character) должен быть окружен кавычками — двойными или одинарными.
"это текст"
## [1] "это текст"
'это тоже текст'
## [1] "это тоже текст"
Текстовые значения можно объединять в вектора.
Это текстовый вектор
rainbow <- c("red", "orange", "yellow", "green", "blue", "violet") rainbow # весь вектор
## [1] "red" "orange" "yellow" "green" "blue" "violet"
Добываем первый и последний элементы
В данном случае я точно знаю, что их 6, мне нужны 1 и 6.
rainbow[c(1, 6)]
## [1] "red" "violet"
Добываем элементы с 3 по 6
Если у вас вдруг слишком короткий вектор в этом задании, то можно склеить новый из двух
double_rainbow <- c(rainbow, rainbow) double_rainbow
## [1] "red" "orange" "yellow" "green" "blue" "violet" "red" "orange" ## [9] "yellow" "green" "blue" "violet"
rainbow[3:6] # элементы с 3 по 6
## [1] "yellow" "green" "blue" "violet"
Логические данные
TRUE # истина
## [1] TRUE
FALSE # ложь
## [1] FALSE
Для ленивых — можно сокращать первыми заглавными буквами. Но лучше так не делать, чтобы читать программы было легче.
c(T, T, T, T, F, F, T, T)
## [1] TRUE TRUE TRUE TRUE FALSE FALSE TRUE TRUE
Логический вектор
c(TRUE, TRUE, TRUE, FALSE, FALSE, TRUE)
## [1] TRUE TRUE TRUE FALSE FALSE TRUE
Еще логический вектор
short_logical_vector <- c(FALSE, TRUE)
Создаем длинный логический вектор.
Чтобы создавать длинные вектора из повторяющихся элементов, можно использовать функцию rep()
?rep
rep(x = 1, times = 3) # 1 повторяется 3 раза
## [1] 1 1 1
rep(x = "red", times = 5) # "red" повторяется 5 раз
## [1] "red" "red" "red" "red" "red"
rep(x = TRUE, times = 2) # TRUE повторяется 2 раза
## [1] TRUE TRUE
В R названия аргументов функций можно не указывать, если вы используете аргументы в том же порядке, что прописан в help к этой функции.
rep(TRUE, 5) # TRUE повторяется 5 раз, аргументы без названий
## [1] TRUE TRUE TRUE TRUE TRUE
Создаем логический вектор, где TRUE повторяется 3 раза, FALSE 3 раза и TRUE 4 раза. Результат сохраняем в переменной vect_log
vect_log <- c(rep(TRUE, 3), rep(FALSE, 3), rep(TRUE, 4)) vect_log
## [1] TRUE TRUE TRUE FALSE FALSE FALSE TRUE TRUE TRUE TRUE
Применение логических векторов для фильтрации данных
Логические векторы создаются при проверке выполнения каких либо условий, заданных при помощи логических операторов (>, <, ==, !=, >=, <=, !, &, |). Такие векторы можно использовать для фильтрации данных
Вспомните, у нас был вот такой текстовый вектор
double_rainbow
## [1] "red" "orange" "yellow" "green" "blue" "violet" "red" "orange" ## [9] "yellow" "green" "blue" "violet"
Задача 1. Допустим, мы хотим из этого вектора извлечь только желтый цвет.
Мы можем создать логический вектор, в котором TRUE будет только для 3-го и 9-го элементов
f_yellow <- double_rainbow == "yellow" f_yellow
## [1] FALSE FALSE TRUE FALSE FALSE FALSE FALSE FALSE TRUE FALSE FALSE FALSE
Этот логический вектор-фильтр мы можем использовать для извлечения данных из double_rainbow
double_rainbow[f_yellow]
## [1] "yellow" "yellow"
Задача 2. Допустим, мы хотим извлечь из double_rainbow желтый и синий Желтый фильтр у нас уже есть, поэтому мы создадим фильтр для синего.
f_blue <- double_rainbow == "blue"
Выражение “желтый или синий” можно записать при помощи логического “или” (|)
f_yellow | f_blue
## [1] FALSE FALSE TRUE FALSE TRUE FALSE FALSE FALSE TRUE FALSE TRUE FALSE
Задача решена, мы извлекли желтый и синий цвета.
double_rainbow[f_yellow | f_blue]
## [1] "yellow" "blue" "yellow" "blue"
То же самое можно было бы записать короче.
В одну строку — совершенно нечитабельно:
double_rainbow[double_rainbow == "yellow" | double_rainbow == "blue"]
## [1] "yellow" "blue" "yellow" "blue"
Фильтр отдельно — читается лучше:
f_colours <- double_rainbow == "yellow" | double_rainbow == "blue" double_rainbow[f_colours]
## [1] "yellow" "blue" "yellow" "blue"
У нас был числовой вектор
vect_num
## [1] -11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 ## [20] 8 9 10 11 12
Задача 3. Давайте извлечем из числового вектора vect_num только значения больше 0
vect_num[vect_num > 0]
## [1] 1 2 3 4 5 6 7 8 9 10 11 12
Задача 4. Давайте извлечем из вектора vect_num все числа, которые либо меньше или равны -8, либо больше или равны 8
f_5_8 <- (vect_num <= -8) | (vect_num >= 8) vect_num[f_5_8]
## [1] -11 -10 -9 -8 8 9 10 11 12
Факторы
Факторы — это способ хранения дискретных (=категориальных данных). Например, если вы поймали 10 улиток и посмотрели их цвет. У большого количества улиток небольшое счетное количество возможных цветов.
snail_colours <- c("red", "green", "green", "green", "yellow", "yellow", "yellow", "yellow") snail_colours # это текстовый вектор.
## [1] "red" "green" "green" "green" "yellow" "yellow" "yellow" "yellow"
Но цвет “желтый” обозначает одно и то же для каждой из улиток. Поэтому в целях экономии места можно записать цвета этих улиток в виде вектора, в котором численным значениям будут сопоставлены “этикетки” (называются “уровни” — levels) — названия цветов. Мы можем создать “фактор” цвет улиток.
factor(snail_colours)
## [1] red green green green yellow yellow yellow yellow ## Levels: green red yellow
уровни этого фактора
1 — green,
2 — red,
3 — yellow
По умолчанию, R назначает порядок уровней по алфавиту. Можно изменить порядок (см. help("factor")). Нам это пригодится позже
double_rainbow # текстовый вектор
## [1] "red" "orange" "yellow" "green" "blue" "violet" "red" "orange" ## [9] "yellow" "green" "blue" "violet"
Создаем фактор из текстового вектора и складываем его в переменную
f_double_rainbow <- factor(double_rainbow)
Как узнать, что за данные хранятся в переменной?
Чтобы узнать, что за данные хранятся в переменной, используйте функцию class()
class(f_double_rainbow)
## [1] "factor"
class(vect_log)
## [1] "logical"
class(vect_num)
## [1] "integer"
class(rainbow)
## [1] "character"
Встроенные константы в R: NA, NULL, NAN, Inf
NA — англ “not available”. Когда объект был, но его свойство не измерили или не записали.
NULL — пусто — просто ничего нет
NaN — “not a number”
Inf — “infinity” — бесконечность
Вот текстовый вектор с пропущенным значением
rainbow_1 <- c("red", "orange", NA, "green", "blue", "violet")
Кстати, если попросили добыть из вектора номер элемента, которого там точно нет, то R выдаст NA, потому, что такого элемента нет
rainbow_1[198]
## [1] NA
Поэкспериментируем с векторами. Проверим, как работают арифметические операции
vect_num + 2
## [1] -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
vect_num * 2
## [1] -22 -20 -18 -16 -14 -12 -10 -8 -6 -4 -2 0 2 4 6 8 10 12 14 ## [20] 16 18 20 22 24
vect_num * (-2)
## [1] 22 20 18 16 14 12 10 8 6 4 2 0 -2 -4 -6 -8 -10 -12 -14 ## [20] -16 -18 -20 -22 -24
vect_num ^2
## [1] 121 100 81 64 49 36 25 16 9 4 1 0 1 4 9 16 25 36 49 ## [20] 64 81 100 121 144
Теперь посмотрим на встроенные константы в действии.
Создаем новый вектор для экспериментов
NAs_NANs <- c(1, 3, NA, 7, 0, 22:24)
Вот так он выглядит
NAs_NANs
## [1] 1 3 NA 7 0 22 23 24
Что произойдет с NA?
NAs_NANs + 2 # останется NA
## [1] 3 5 NA 9 2 24 25 26
NAs_NANs * 0 # останется NA
## [1] 0 0 NA 0 0 0 0 0
NAs_NANs / 0 # останется NA
## [1] Inf Inf NA Inf NaN Inf Inf Inf
Но в последнем случае вы увидите
Inf при делении чисел на ноль
NaN при делении нуля на ноль
NaN получится, если взять корень из отрицательного числа
sqrt(-1)
## Warning in sqrt(-1): NaNs produced
## [1] NaN
Вы уже видели массу функций, их легко узнать по скобкам после ключевого слова. Познакомимся еще с несколькими и научимся писать пользовательские функции. Пользовательские функции позволяют автоматизировать повторяющиеся действия и делают код легко читаемым.
Вот наш вектор
NAs_NANs
## [1] 1 3 NA 7 0 22 23 24
Длину вектора можно вычислить при помощи функции length()
length(NAs_NANs)
## [1] 8
Сумму элементов вектора при помощи функции sum()
sum(NAs_NANs)
## [1] NA
Упс! Почему-то получилось NA
Чтобы узнать, почему и как это исправить — посмотрите в help("sum"). Выяснится, что у функции sum() есть аргумент na.rm, который по умолчанию принимает значение FALSE, то есть NA не учитываются при подсчете суммы.
Если мы передадим функции sum аргумент na.rm = TRUE, то получится правильная сумма
sum(NAs_NANs, na.rm = TRUE)
## [1] 80
Та же история с функцией mean
mean(NAs_NANs, na.rm = TRUE)
## [1] 11.42857
Попробуем написать пользовательскую функцию mmean(), которая будет по умолчанию считать среднее значение элементов в векторе с учетом пропущенных значений (NA)
mmean <- function(x){ mean(x, na.rm = TRUE) }
В этом коде: — mmean — переменная, название функции. В эту переменную мы складываем функцию, которую создает функция function() — function() — функция, которая делает функции. В скобках перечисляются аргументы (названия переменных, которые мы передаем в функцию, чтобы она что-то сделала с ними) — { } — в фигурных скобках тело функции — последовательность действий, которую нужно сделать с аргументами
У больших функций бывает еще инструкция return(), которая сообщает, что именно должна возвращать наша функция. Вот как выглядела бы наша функция с этой инструкцией
mmean <- function(x){ res <- mean(x, na.rm = TRUE) return(res) }
Проверим нашу функцию при помощи встроенной функции
mean(vect_num, na.rm = TRUE)
## [1] 0.5
mmean(vect_num)
## [1] 0.5
Работает
Датафрейм — один из способов хранения табличных данных в R. Создадим датафрейм.
Для этого, для начала, создадим векторы с данными для переменных.
len <- 1:9 # числовой col <- c(rep("green", 4), rep("red", 5)) # текстовый wid <- seq(from = 2, by = 2, to = 18) # числовой
Теперь сложим эти векторы в датафрейм
my_worms <- data.frame(Length = len, Width = wid, Colour = col)
Можно проверить, действительно мы создали объект класса data.frame
class(my_worms) # смотрим, действительно датафрейм
## [1] "data.frame"
Содержимое датафрейма можно просмотреть несколькими способами
my_worms # печать датафрейма
## Length Width Colour ## 1 1 2 green ## 2 2 4 green ## 3 3 6 green ## 4 4 8 green ## 5 5 10 red ## 6 6 12 red ## 7 7 14 red ## 8 8 16 red ## 9 9 18 red
View(my_worms) # просмотр в RStudio head(my_worms)
## Length Width Colour ## 1 1 2 green ## 2 2 4 green ## 3 3 6 green ## 4 4 8 green ## 5 5 10 red ## 6 6 12 red
tail(my_worms)
## Length Width Colour ## 4 4 8 green ## 5 5 10 red ## 6 6 12 red ## 7 7 14 red ## 8 8 16 red ## 9 9 18 red
# fix(my_worms) # ручное редактирование. осторожно! избегайте его использовать, никаких документов о нем не останется
Адресация внутри датафреймов
Вывод столбца-переменной при помощи оператора $ и имени переменной
my_worms$Length
## [1] 1 2 3 4 5 6 7 8 9
my_worms$Width
## [1] 2 4 6 8 10 12 14 16 18
У каждой ячейки в датафрейме есть координаты вида [строка, столбец]
my_worms[2, 3] # вторая строка в 3 столбце
## [1] "green"
my_worms[2, ] # вторая строка целиком
## Length Width Colour ## 2 2 4 green
my_worms[1:9, 2] # строки с 1 по 9 во втором столбце
## [1] 2 4 6 8 10 12 14 16 18
my_worms[, 2] # второй столбец целиком
## [1] 2 4 6 8 10 12 14 16 18
Базовые графики
Скаттерплот (точечный график) — по оси х и y непрерывные числовые величины
plot(x = my_worms$Width, y = my_worms$Length)
Боксплот — по оси х дискретная величина, по оси y значение непрерывной величины. Черта — медиана, коробка — 25 и 75 перцентили, усы — либо размах варьирования, либо 1.5 интерквартильных расстояния (1.5 высоты коробки), если есть “выбросы”.
plot(x = as.factor(my_worms$Colour), y = my_worms$Length)
Для настройки внешнего вида см graphical parameters в help
На самом деле, мы не будем пользоваться этой системой графики, но об этом в следующих сериях
Графики из пакета ggplot2
В R есть более удобный (но, может быть, более многословный) пакет для рисования графиков — ggplot2. Чтобы использовать функции из пакета ggplot2, нужно его сначала установить.
Установка пакета в локальную библиотеку делается один раз. Поэтому строку с install.packages() не нужно включать в финальную версию кода.
install.packages('ggplot2')
В текущей сессии работы в R пакет нужно активировать перед использованием. Когда вы в следующий раз начнете работать с R, нужные пакеты придется снова активировать. Поэтому строки с загрузкой пакетов при помощи library() обязательно должны остаться в финальной версии кода.
library(ggplot2)
Нарисуем те же самые графики при помощи пакета ggplot2.
ggplot(data = my_worms) + geom_point(aes(x = Width, y = Length))
ggplot(data = my_worms) + geom_boxplot(aes(x = Colour, y = Length))
Добавляем для точек эстетику цвет (colour) из переменной Colour
ggplot(data = my_worms) + geom_point(aes(x = Width, y = Length, colour = Colour))
Графики можно сохранять в переменных, и использовать потом
gg <- ggplot(data = my_worms) + geom_point(aes(x = Width, y = Length, colour = Colour))
Чтобы вывести график, нужно напечатать название переменной.
Можно менять темы оформления графика. Если тема нужна только один раз, то прибавляем ее к графику
gg + theme_dark()
gg + theme_light()
gg + theme_classic()
Можно установить нужную тему до конца сессии.
theme_set(theme_bw()) gg
Подписи осей и легенд задает функция labs()
gg + labs(x = "Ширина", y = "Длина", colour = "Цвет")
Графики можно делить на фасетки при помощи facet_wrap или facet_grid
gg + facet_wrap(~Colour, nrow = 1)
Чтобы изменить подписи цветов, нужно изменить уровни соотв. фактора.
my_worms$col_rus <- factor(my_worms$Colour, levels = c("green", "red"), labels = c("Зеленый", "Красный")) ggplot(data = my_worms) + geom_point(aes(x = Width, y = Length, colour = col_rus)) + labs(x = "Ширина", y = "Длина", colour = "Цвет") + facet_wrap(~col_rus, nrow = 1)
Больше или равно (>=) — JavaScript
Оператор больше или равен ( >= ) возвращает true , если левый операнд больше или равен правому операнду, и ложь в противном случае.
х >= у
Операнды сравниваются по тому же алгоритму, что и оператор «Меньше», с инвертированием результата. x >= y обычно эквивалентно !(x < y) , за исключением двух случаев, когда x >= y и x < y оба равны false :
выдает синтаксическую ошибку при передаче в BigInt() ).
Если один из операндов преобразуется в NaN . (Например, строки, которые нельзя преобразовать в числа, или undefined .)
х >= у обычно эквивалентно x > y || x == y , за исключением нескольких случаев:
Когда одно из x или y равно null , а другое не является null и становится 0 при приведении к числовому (включая 9 0004 0 , 0n , false , "" , "0" , new Date(0) и т. д.): x >= y is true , а x > y || х == у равно ложь .
Когда одно из x или y равно undefined , а другое является одним из null или undefined : x >= y равно false , а x == y равно правда .
Когда x и y являются одним и тем же объектом, который становится NaN после первого шага Меньше чем (например, new Date(NaN) ): x >= y равно false , а x == y равно true .
Когда x и y являются разными объектами, которые становятся одним и тем же значением после первого шага Меньше чем: x >= y равно true , а x > y || x == y равно false .
Сравнение строк
"a" >= "b"; // ЛОЖЬ "а" >= "а"; // истинный "а" >= "3"; // истинный
Сравнение строки с числом
"5" >= 3; // истинный "3" >= 3; // истинный "3" >= 5; // ЛОЖЬ "привет" >= 5; // ЛОЖЬ 5 >= "привет"; // ЛОЖЬ
Сравнение номеров
5 >= 3; // истинный 3 >= 3; // истинный 3 >= 5; // ЛОЖЬ
Сравнение числа с BigInt
5n >= 3; // истинный 3 >= 3н; // истинный 3 >= 5н; // ЛОЖЬ
Сравнение логических значений, null, undefined, NaN
true >= false; // истинный правда >= правда; // истинный ложь >= истина; // ЛОЖЬ правда >= 0; // истинный правда >= 1; // истинный ноль >= 0; // истинный 1 >= ноль; // истинный не определено >= 3; // ЛОЖЬ 3 >= не определено; // ЛОЖЬ 3 >= NaN; // ЛОЖЬ NaN >= 3; // ЛОЖЬ
Спецификация
Спецификация языка ECMAScript
# sec-relational-operators
Таблицы
BCD загружаются только в браузере с включенным JavaScript. Включите JavaScript для просмотра данных.
Больше, чем оператор
Меньше, чем оператор
Оператор меньше или равно
Обнаружили проблему с содержанием этой страницы?
Отредактируйте страницу на GitHub.
Сообщить о проблеме с содержимым.
Посмотреть исходный код на GitHub.
Хотите принять более активное участие?
Узнайте, как внести свой вклад.
Последний раз эта страница была изменена 30 марта 2023 г. участниками MDN.
Если еще и Вложенные, если еще
Операторы If-Else являются важной частью программирования R. В этом руководстве мы увидим различные способы применения условных операторов (If..Else вложенный IF) в R. В R есть много мощных пакетов для манипулирования данными. В более поздней части этого руководства мы увидим, как операторы IF ELSE используются в популярных пакетах.
Образец данных
Давайте создадим образец данных, чтобы показать, как выполнять функцию ЕСЛИ ИНАЧЕ. Этот фрейм данных будет использоваться далее в примерах.
x1 x2 х3
1 129 А
3 178 Б
5 140 С
7 186 Д
9 191 Э
11 104 Ф
13 150 Г
15 183 Х
17 151 я
19 142 Дж
Запустите программу ниже, чтобы создать приведенную выше таблицу в R.
сет.сид(123) mydata = data.frame(x1 = seq(1,20,by=2), x2 = выборка (100:200,10,ЛОЖЬ), x3 = БУКВЫ [1:10])
x1 = seq(1,20,by=2) : Переменная 'x1' содержит альтернативные числа от 1 до 20. Всего это 10 числовых значений.

x2 = выборка(100:200,10,FALSE) : Переменная 'x2' представляет собой 10 неповторяющихся случайных чисел в диапазоне от 100 до 200.

x3 = БУКВЫ[1:10] : Переменная 'x3' содержит 10 алфавитов, начиная с A до Z.
Синтаксис функции ifelse() :
Функция ifelse() в R работает аналогично функции MS Excel ЕСЛИ. Синтаксис см. ниже:
. ifelse(условие, значение, если условие истинно, значение, если условие ложно)
Пример 1: простой оператор IF ELSE
Предположим, вас попросили создать двоичную переменную — 1 или 0 на основе переменной «x2». Если значение переменной 'x2' больше 150, присвойте 1, иначе 0.
mydata$x4 = если еще (mydata$x2>150,1,0)
В этом случае он создает переменную x4 в том же фрейме данных «mydata». Результат показан на изображении ниже:
ifelse : Output
Создать переменную в новом фрейме данных
Предположим, вам нужно добавить созданную выше бинарную переменную в новый фрейм данных. Вы можете сделать это, используя приведенный ниже код -
х = если еще (мои данные $ х2> 150,1,0) новые данные = cbind (х, мои данные)
cbind() используется для объединения двух векторов, матриц или фреймов данных по столбцам.
Применить ifelse() к символьным переменным
Если переменная 'x3' содержит символьные значения - 'A', 'D', то переменная 'x1' должна быть умножена на 2. В противном случае она должна быть умножена на 3.
mydata$y = ifelse(mydata$x3 %in% c("A","D") ,mydata$x1*2,mydata$x1*3)
Результат показан в таблице ниже
х1 х2 х3 у 1 129 А 2 3 178 Б 9 5 140 С 15 7 186 Д 14 9191 Э 27 11 104 Ф 33 13 150 Г 39 15 183 Н 45 17 151 я 51 19 142 Дж 57
Пример 2. Вложенный оператор If ELSE в R
Несколько операторов If Else можно написать аналогично функции If в Excel. В этом случае мы говорим R умножить переменную x1 на 2, если переменная x3 содержит значения «A», «B». Если значения «C», «D», умножьте на 3. В противном случае умножьте на 4.
mydata$y = ifelse(mydata$x3 %in% c("A","B"), mydata$x1*2, ifelse(mydata$x3 %in% c("C","D"), mydata$x1*3, моиданные$x1*4))
Вы ненавидите указывать фрейм данных несколько раз для каждой переменной?
Вы можете использовать функцию with() , чтобы каждый раз не упоминать фрейм данных. Это ускоряет написание кода R.
mydata$y = with(mydata, ifelse(x3 %in% c("A","B") , x1*2, ifelse(x3 %in% c("C","D"), x1*3, x1*4)))

Специальные темы, связанные с IF ELSE
В этом разделе мы рассмотрим следующие темы -
Как обрабатывать отсутствующие (NA) значения в IF ELSE.
Как использовать операторы ИЛИ и И в IF ELSE
Агрегированные или сводные функции и оператор IF ELSE
Обработка отсутствующих значений

Неверный метод
x = NA
ifelse(x==NA,1,0)
Результат: NA
Должно было быть возвращено 1.
Правильный метод 901 58
х = нет данных
ifelse( is.na(x) ,1,0)
Результат: 1
Функция is. na() проверяет, является ли значение NA или нет.

Использование операторов ИЛИ и И
Символ & используется для выполнения условий И
ifelse(mydata$x1<10 & mydata$x2>150,1,0)
Результат: 0 1 0 1 1 0 0 0 0 0
| символ используется для выполнения условий ИЛИ
ifelse(mydata$x1<10 | mydata$x2>150,1,0)
Результат: 1 1 1 1 1 0 0 1 1 0

Подсчет случаев, когда условие выполняется 900 11
В этом примере , мы можем подсчитать количество записей, в которых выполняется условие.
sum(ifelse(mydata$x1<10 | mydata$x2>150,1,0))
Результат: 7
Оператор If Else: Другой стиль
Есть еще один способ определить if.. оператор else в R. Этот стиль написания If Else в основном используется, когда мы используем условные операторы в циклах и функциях R. Другими словами, он используется, когда нам нужно выполнить различные действия на основе условия.
Синтаксис -
если (состояние) да иначе нет
k = 99
if(k > 100) 1 else 0
Результат: 0
If..Else If..Else Операторы
k = 100
if (k > 100){
print("Больше 100")
} else if (k < 100){
print("Меньше 100")
} else 9 0199 {
печать ("Равно 100")
}
Результат: "Равно 100"
If Else в популярных пакетах
1. dplyr package
if_else( условие, значение, если условие истинно, значение, если условие ложно, значение, если нет данных)
Следующая программа проверяет, является ли значение кратным 2
библиотека (dplyr) х=с(1,Н/Д,2,3) if_else(x%%2==0, "Кратно 2", "Не кратно 2", "Отсутствует")
Результат : Не кратное 2 Отсутствующий Кратность 2 Не кратное 2
Символ %% возвращает остаток после деления значения на делитель.

Имя аргумента	Описание
лог_выражение (обязательно)	Условие, которое нужно проверить.
значение_если_истина (обязательно)	Значение, которое должно возвращаться, если *лог_выражение* имеет значение ИСТИНА.
значение_если_ложь (необязательно)	Значение, которое должно возвращаться, если *лог_выражение* имеет значение ЛОЖЬ.

Проблема	Возможная причина
0 (ноль) в ячейке	Не указан аргумент значение_если_истина или значение_если_ложь. Чтобы возвращать правильное значение, добавьте текст двух аргументов или значение ИСТИНА/ЛОЖЬ.
#ИМЯ? в ячейке	Как правило, это указывает на ошибку в формуле.

Спецификация
Спецификация языка ECMAScript # sec-relational-operators

x1	x2	х3
1	129	А
3	178	Б
5	140	С
7	186	Д
9	191	Э
11	104	Ф
13	150	Г
15	183	Х
17	151	я
19	142	Дж

Как обыкновенную дробь превратить в неправильную: Представление смешанного числа в виде неправильной дроби и наоборот — урок. Математика, 5 класс.

alexxlab / 07.08.202308.05.2023 / Разное

Как перевести в неправильную дробь – правило с примерами

4.7

Средняя оценка: 4.7

Всего получено оценок: 273.

4.7

Средняя оценка: 4.7

Всего получено оценок: 273.

Перевод неправильной дроби – это необходимая процедура для правильной записи ответа. К тому же в некоторых ситуациях, куда удобнее вести вычисления со смешанными дробями, нежели с неправильными числами. Рассмотрим правила перевода неправильных дробей в смешанные числа.

Виды дробей

Дроби можно разделить на:

Правильные, в которых числитель меньше знаменателя.
Неправильные, в которых числитель большей знаменателя.
Смешанные, в которых выделена целая часть.
Десятичные, которые записываются с помощью разделяющей запятой. В таких дробях число знаков после запятой, равняется степени числа 10, которая стоит в знаменателе. Такая форма записи позволяет как бы спрятать знаменатель за запятой, что крайне удобно при быстром счете.

Помимо этого все дроби, как и другие числа, делятся на положительные и отрицательные.

Если числитель больше знаменателя, то дробь неправильная. Если числитель меньше знаменателя – правильная. Но нет названия для дроби, у которой числитель и знаменатель равны, так как она автоматически превращается в единицу. Как только в расчетах ученик видит такую ситуацию, следует сразу же преобразовать число в 1.

Перевод неправильной дроби в смешанное число

Для того, чтобы перевести неправильную дробь в смешанное число, нужно выделить в ней целую часть. Для этого числитель делится на знаменатель с остатком. Результат такого деления это целая часть числа, а остаток это числитель дробной части. При этом знаменатель нового числа будет таким же, как и знаменатель дроби.

Приведем пример:

Дробь ${13\over{4}}$ нужно перевести в смешанное число. Для этого поделим с остатком 13 на 4:

13:4= 3, ост. 1

Значит, перевод будет выглядеть так:

$${13\over{4}}=3 {1\over{4 }}$$

Можно как перевести в неправильную дробь смешанное число, так и наоборот: выделить целую часть в неправильной дроби. Ученик выполняет эти действия для записи ответа или облегчения расчетов. Но нельзя превратить неправильную дробь в правильную и наоборот. Это два разных вида чисел, которые между собой никак не связаны.

Что мы узнали?

Мы поговорили о правиле перевода неправильной дроби в смешанное число. Сказали, как правильно выделить целую часть дроби, и привели пример. Также отметили, что нельзя превратить неправильное число в правильное.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Нина Кононова
5/5
Сева Бакиева
5/5
Эмир Субхонбердиев
5/5
Булат Зинуров
4/5
Оценка статьи
4.7
Средняя оценка: 4.7
Всего получено оценок: 273.
А какая ваша оценка?
Как перевести обычную дробь в десятичную
13 февраля 2020 Ликбез Образование
Два способа, которые помогут вам выполнить преобразование.
1. Превратите знаменатель в 10, 100 или 1 000
Этот способ очень простой, но он подходит не для каждой дроби.
Для начала умножьте числитель и знаменатель на такое число, которое преобразует нижнюю часть дроби в 10 или 100, 1 000 и так далее.
Допустим, нам нужно перевести дробь с числителем 7 и знаменателем 25. Мы можем получить в нижней части 100: достаточно умножить 25 на 4. Про верхнюю часть тоже не забываем: получаем 28.
Запишите числитель отдельно. Отсчитайте справа в нём столько же знаков, сколько нолей вы получили в знаменателе после умножения, и поставьте запятую. Это и будет искомая десятичная дробь.
В нашем примере в знаменателе 100, значит отсчитываем в числителе два знака и ставим запятую. Получаем 0,28.
Если такой множитель подобрать не удаётся, текущий способ не подходит. Воспользуйтесь следующим.
Сейчас читают 🔥
Как найти площадь любого треугольника
2.
Поделите числитель на знаменатель
Чтобы преобразовать обычную дробь в десятичную, достаточно поделить её верхнюю часть на нижнюю. Проще всего это сделать, конечно же, на калькуляторе.
Если для вас принципиально важно обойтись без вспомогательных устройств, просто поделите числитель на знаменатель столбиком.
Для примера переведём дробь с числителем 7 и знаменателем 25. Поделив 7 на 25 столбиком, получим 0,28.
Важный момент. При делении столбиком вы можете обнаружить, что процесс идёт по кругу и после запятой в результат попадают повторяющиеся цифры. В таком случае эту дробь нельзя перевести в конечную десятичную. Вместо неё у вас получится периодическая дробь. Чтобы записать результат, возьмите повторяющееся число в скобки.
Допустим, нужно перевести дробь с числителем 1 и знаменателем 3. Поделив 1 на 3 столбиком, мы получим бесконечную десятичную дробь 0,333333333… Приведём её к краткому виду 0,(3) — это и будет результат. Читается как «ноль целых и три в периоде».
Читайте также 📕📐✂️
Как научить ребёнка считать играючи
6 способов посчитать проценты от суммы с калькулятором и без
9 логических задач, которые по зубам только настоящим интеллектуалам
3 логические задачи, которые решат только самые сообразительные
11 книг, которые прокачают математическое мышление
Неправильные дроби
7 4
(семь четвертей или семь четвертей)

Неправильная дробь имеет первое число больше (или равно) нижнему числу.

Обычно » »
Другие примеры
3 2 7 3 16 15 15 15 100 5
Видите, как верхнее число больше (или равно) нижнего числа?
Это делает его неправильной дробью (но в неправильных дробях нет ничего плохого).
Три типа дробей
Существуют три типа дробей:
Дроби
Дробь (например, ⁷ / ₄ ) состоит из двух чисел:
Числитель Знаменатель
umerator) это количество частей у нас .
Нижнее число (знаменатель) — это число частей, которое делится на .
Пример: ⁷ / ₄ означает:
У нас есть 7 детали
Каждая часть равна квартал ( ¹ / ₄ ) целого
Итак, мы можем определить три типа дробей следующим образом:
Правильные дроби: Числитель меньше знаменателя
Примеры: ¹ / ₃ , ³ / ₄ , ² / ₇

Неправильные дроби: Числитель больше (или равен) знаменателю
Примеры: ⁴ / ₃ , ¹¹ / ₄ , ⁷ / ₇

Смешанные фракции: Целое число и правильная дробь вместе
Примеры: 1 ¹ / ₃, 2 ¹/₄, 16 ²/₅
Неправильная дробь
Таким образом, неправильная дробь — это дробь, в которой верхнее число (числитель) больше или равно нижнему числу (знаменатель): это верхнее тяжелое .

4 4
Могут быть равны
Что делать, если числитель равен знаменателю? Например ⁴ / ₄ ?
Ну, в целом то же самое, но записывается в виде дроби, поэтому большинство людей согласны с тем, что это разновидность неправильной дроби.

Неправильные или смешанные дроби
Мы можем использовать либо неправильную дробь, либо смешанную дробь, чтобы показать одну и ту же сумму.
Например, 1 3 4 = 7 4 , как показано здесь:

1 90 009 3 4 7 4
=

Преобразование неправильных дробей в смешанные

Чтобы преобразовать неправильную дробь в смешанную, выполните следующие действия.
Разделить числитель на знаменатель.
Запишите целое число ответ
Затем запишите любой остаток выше знаменателя.

Пример: Преобразуйте
11 4 в смешанную дробь.
Разделить:
11 ÷ 4 = 2 с остатком 3
Запишите 2, а затем запишите остаток (3) над знаменателем (4).
Ответ:
2 3 4
Этот пример можно записать так:
Пример: Преобразуйте
10 3 в смешанную дробь.
Ответ:
3 1 3

Преобразование смешанных дробей в неправильные дроби
Преобразование смешанной дроби в неправильную дробь, выполните следующие действия:
Умножить целую часть числа на знаменатель дроби.
Добавьте это к числителю
Затем запишите результат над знаменателем.

Пример: Преобразуйте 3
2 5 в неправильную дробь.
Умножьте целую часть числа на знаменатель:
3 × 5 = 15
Добавьте это к числителю:
15 + 2 = 17
Затем запишите этот результат над знаменателем:
17 5
Мы можем вычислить числитель за один раз:
Пример. неправильная дробь.

Плохие ли неправильные дроби?
НЕТ, они неплохие!
Для математики они на самом деле лучше , чем смешанные дроби. Потому что смешанные дроби могут сбивать с толку, когда мы пишем их в формуле: следует ли складывать или умножать две части?
Смешанная фракция: Что такое: 1 + 2 1 4 ?
Это: 1 + 2 + 1 4 = 3 1 4 ?
Или это: 1 + 2 × 1 4 = 1 1 2 ?

Неправильная дробь: Что такое: 1 + 9 4 ?
Это: 4 4 + 9 4 = 13 4
Но для повседневного использования люди лучше понимают смешанные дроби.
Пример: Легче сказать «Я съел 2 1 4 сосисок», чем «Я съел 9 4 сосиски»

Рекомендуем:
Для математики: неправильные дроби
Для повседневного использования: смешанные фракции

Смешанное число в неправильную дробь
Введение
Что такое преобразование смешанных чисел в неправильные дроби?
Как преобразовать смешанные числа в неправильные дроби
Рабочий лист преобразования смешанных чисел в неправильные дроби
Распространенные заблуждения
Практика преобразования смешанных чисел в неправильные дроби вопросы
Преобразование смешанных чисел в неправильные дроби Вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Индивидуальные занятия по математике, созданные для успеха KS4
Еженедельные онлайн-уроки повторения GCSE по математике теперь доступны
Узнать больше
Введение
Что такое преобразование смешанных чисел в неправильные дроби?
Как преобразовать смешанные числа в неправильные дроби
Рабочий лист преобразования смешанных чисел в неправильные дроби
Распространенные заблуждения
Практика преобразования смешанных чисел в неправильные дроби вопросы
Преобразование смешанных чисел в неправильные дроби Вопросы GCSE
Контрольный список обучения
Следующие уроки
Все еще застряли?
Здесь мы научимся преобразовывать смешанные числа в неправильные дроби.
Существуют также рабочие листы с неправильными дробями и смешанными числами, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.
Что такое смешанные числа и неправильные дроби?
Правильная дробь имеет числитель (верхнее число), который меньше знаменателя (нижнее число) дроби.
Пример правильной дроби: \frac{8}{11} \
Неправильная дробь имеет числитель больше знаменателя дроби. Иногда их называют «верхними тяжелыми» фракциями.
Примером неправильной дроби является \frac{25}{7} \
Смешанное число состоит из целой части и дробной части .
Примером смешанного числа является 3 \frac{3}{4} \times 2 \frac{5}{8}
См. также: Неправильная дробь в смешанном числе
Как происходит преобразование смешанное число в неправильную дробь?
Преобразование смешанного числа в неправильную дробь является важным навыком. При вычислениях со смешанными числами может быть намного проще выполнить необходимые арифметические действия, если смешанные числа будут преобразованы в неправильные дроби.
Правильная дробь имеет числитель (верхнее число), который меньше знаменателя (нижнее число) дроби.
Неправильная дробь имеет числитель больше знаменателя дроби. Иногда их называют «верхними тяжелыми» фракциями.
Например,
Если бы нам нужно было вычислить 1 \frac{2}{3} \times 4 \frac{3}{5}, одним из способов было бы использование метода сетки.
Это может быть очень долгий процесс, включающий множество других арифметических операций с дробями. Преобразование смешанных чисел в неправильные дроби перед умножением — это способ упрощение процесса .
Чтобы преобразовать смешанные числа в неправильные дроби, мы заменим целое число на дробь с тем же знаменателем . Затем мы складываем числители вместе и получаем новый числитель поверх исходного знаменателя .
Например,
Чтобы быстро преобразовать смешанное число в неправильную дробь, мы можем умножить целое число на знаменатель , добавить числительное r , а затем напишите над исходным знаменателем .
Например,
Это упростит процесс сложения, вычитания, умножения и деления дробей.
Что такое преобразование смешанных чисел в неправильные дроби?
Как преобразовать смешанное число в неправильную дробь
Чтобы преобразовать смешанное число в неправильную дробь:
Умножьте целое число на знаменатель.
Добавьте числитель.
Запишите неправильную дробь, используя вычисленное значение в качестве числителя над исходным знаменателем.
Объясните, как преобразовать смешанные числа в неправильные дроби
Таблица преобразования смешанных чисел в неправильные дроби
Получите бесплатную таблицу преобразования смешанных чисел в неправильные дроби, содержащую более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
Икс
Преобразование смешанных чисел в таблицу неправильных дробей
Получите бесплатную таблицу преобразования смешанных чисел в неправильные дроби, содержащую более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
Примеры преобразования смешанных чисел в неправильные дроби
Пример 1: преобразование смешанного числа в неправильную дробь
Запишите следующее смешанное число в виде неправильной дроби 2\frac{4}{5}.
Умножьте целое число на знаменатель.
Целая часть смешанного числа равна 2, а знаменатель равен 5, \2\умножить на 5 = 10.
2 Добавьте числитель.
Числитель равен 4, \ 10 + 4 = 14.
Новый числитель неправильной дроби равен 14.
3 Запишите неправильную дробь, используя вычисленное значение в качестве числителя над исходным знаменателем.
2\разрыв{4}{5}=\разрыв{14}{5}
Пример 2: заменить смешанное число неправильной дробью
Запишите следующее смешанное число в виде неправильной дроби 3\frac{1}{6}.
Умножьте целое число на знаменатель.
Целая часть смешанного числа равна 3, а знаменатель равен 6, \3 х 6 = 18.
Добавьте числитель.
Числитель равен 1, \ 18 + 1 = 19.

Новый числитель неправильной дроби равен 19.
Запишите неправильную дробь, используя вычисленное значение в качестве числителя над исходным знаменателем.
3\frac{1}{6}=\frac{19}{6}
Пример 3: замена смешанного числа неправильной дробью
Запишите следующее смешанное число как неправильную дробь: 4\frac{ 3}{7}.
Умножьте целое число на знаменатель.
Целая часть смешанного числа равна 4, а знаменатель равен 7, \ 4 \ умножить на 7 = 28,
Добавьте числитель.
Числитель равен 3, \ 28 + 3 = 31.

Новый числитель неправильной дроби равен 31.
Запишите неправильную дробь, используя вычисленное значение в качестве числителя над исходным знаменателем.
4\frac{3}{7}=\frac{31}{7}
Распространенные заблуждения
Прибавление целого числа к знаменателю вместо умножения
Распространенная ошибка может возникнуть при добавлении целого числа к знаменателю вместо умножения.
Запутанные смешанные числа и неправильные дроби
Смешанные числа записываются целым числом и дробной частью.
Например, 4 \frac{5}{6}.
Неправильные дроби не пишутся с целой частью, но числитель всегда больше знаменателя.
Например, \frac{29{6}.
Практика преобразования смешанных чисел в неправильные дроби вопросы
3\frac{2}{5}
\frac{13}{5}
\frac{23}{5}
2\frac{1}{ 5}
2\frac{3}{5}=\frac{2\times5+3}{5}=\frac{10+3}{5}=\frac{13}{5}
\frac {37}{7}
\frac{52}{7}
\frac{25}{7}
\frac{34}{7}
5\frac{2}{7}=\frac {5\times7+2}{7}=\frac{35+2}{7}=\frac{37}{7}
\frac{81}{4}
\frac{33}{8}
\frac{35}{4}
\frac{33}{4}
8\frac{1}{4}=\frac{8\times4+1}{4}=\frac{32+1 {4}=\frac{33}{4}
\frac{16}{11}
\frac{55}{11}
\frac{58}{11}
\frac{58} {3}
5\frac{3}{11}=\frac{5\times11+3}{11}=\frac{55+3}{11}=\frac{58}{11}
\ frac{21}{13}
\frac{54}{13}
\frac{19}{13}
\frac{52}{13}
4\frac{2}{13}=\ frac{4\times13+2}{13}=\frac{52+2}{13}=\frac{54}{13}
\frac{26}{9}
\frac{25}{9}
\frac{19}{9}
\frac{16}{9}
2\frac{8}{9} =\frac{2\times9+8}{9}=\frac{18+8}{9}=\frac{26}{9}
Преобразование смешанных чисел в неправильные дроби Вопросы GCSE
1. Выберите дробь, которая равна 5 \frac{3}{7}?

\frac{22}{7} \hspace{1cm} \frac{38}{7} \hspace{1cm} \frac{15}{7} \hspace{1cm} \frac{35}{7}

(1 балл)
Показать ответ
\frac{38}{7}
(1)
2. (a) Запишите 3.2 в виде неправильной дроби в ее простейшей форме.

(b) Вычислите 3\frac{1}{4}-1\frac{1}{3}.

(5 баллов)
Показать ответ
(a)

Для любого правильного смешанного числа. Например, 3\frac{2}{10}.
(1)
\фракция{16}{5}
(1)

(б)

Преобразование одной из дробей в неправильную. Например, \frac{13}{4} или \frac{4}{3}.
(1)
Обе дроби подведите к общему знаменателю. Например, \frac{39}{12}, \frac{16}{12}.

Правильные дроби:	Числитель меньше знаменателя
Примеры: ¹ / ₃ , ³ / ₄ , ² / ₇

Неправильные дроби:	Числитель больше (или равен) знаменателю
Примеры: ⁴ / ₃ , ¹¹ / ₄ , ⁷ / ₇

Смешанные фракции:	Целое число и правильная дробь вместе
Примеры: 1 ¹ / ₃, 2 ¹/₄, 16 ²/₅

Как перевести 3 в дробь: Mathway | Популярные задачи

alexxlab / 07.08.202309.05.2023 / Разное

Дробь	Десятичная
3 1/1	4
3 1/2	3,5
3 1/3	3,(3)
3 1/4	3,25
3 1/5	3,2
3 1/6	3,1(6)
3 1/7	3,(142857)
3 1/8	3,125
3 1/9	3,(1)
3 1/10	3,1
3 1/11	3,(09)
3 1/12	3,08(3)
3 1/13	3,(076923)
3 1/14	3,0(714285)
3 1/15	3,0(6)
3 1/16	3,0625
3 1/17	3,(0588235294117647)
3 1/18	3,0(5)
3 1/19	3,(052631578947368421)
3 1/20	3,05
3 1/21	3,(047619)
3 1/22	3,0(45)
3 1/23	3,(0434782608695652173913)
3 1/24	3,041(6)
3 1/25	3,04
3 1/26	3,0(384615)
3 1/27	3,(037)
3 1/28	3,03(571428)
3 1/29	3,(0344827586206896551724137931)
3 1/30	3,0(3)

2
Дробь 3 1/3 в виде десятичной дроби
Калькулятор «Конвертер обыкновенных дробей в десятичные»
Как записать 3 целых 1/3 в виде десятичной дроби?
Ответ: Дробь 3 1/3 в десятичном виде это 3,33333333333333… или 3,(3)
3
=3,33333333333333… = 3,(3)
Объяснение конвертации дроби 3 1/3 в десятичную
Для того, чтобы перевести дробь 3 1/3 (3⅓) в десятичный формат необходимо разделить числитель 1 на знаменатель 3. Результат деления:
1 ÷ 3 = 3,33333333333333…
и прибавить целую часть (3):
0.333 + 3 = 3,33333333333333…
Другой способ перевод дроби 3 целых 1/3 в десятичный формат заключается в том, чтобы перевести эту смешанную дробь в неправильную дробь. Для этого необходимо сперва умножить целую часть (3) на знаменатель (3):
3 × 3 = 9
после чего прибавить результат к числителю (1):
9 + 1 = 10
и в конце разделить результат на числитель (3):
= 10 ÷ 3 =3,33333333333333. ..
Как можно заметить, наша десятичная дробь имеет повторяющуюся группу цифр (3) после запятой, длиною в 1 цифру. Это значит, что мы имеем периодическую десятичную дробь, которую можно записать следующим образом:
3,(3)
число в скобках (3) обозначает группу цифр, повторяющихся бесконечно
Похожие расчеты
Поделитесь текущим расчетом
Печать
https://calculat.io/ru/number/fraction-as-a-decimal/3—1—3
<a href=»https://calculat.io/ru/number/fraction-as-a-decimal/3—1—3″>Дробь 3 1/3 в виде десятичной дроби — Calculatio</a>
О калькуляторе «Конвертер обыкновенных дробей в десятичные»
Данный онлайн-конвертер обыкновенных дробей в десятичные является полезным инструментом, предназначенным для легкого преобразовывания любой дроби в ее эквивалентную десятичную форму. Например, он может помочь узнать как записать 3 целых 1/3 в виде десятичной дроби? Независимо от того, являетесь ли вы учеником, студентом или профессионалом, этот конвертер может сэкономить ваше время и усилия при выполнении ручных вычислений.
Чтобы использовать этот конвертер, просто введите дробь, которую вы хотите преобразовать, в соответствующие поля. Вам необходимо ввести целую часть (если есть), числитель и знаменатель дроби. Например, если вы хотите преобразовать 3 1/3 в его десятичный эквивалент, вы введете ‘3’ как целую часть, ‘1’ как числитель и ‘3’ как знаменатель.
После того, как вы ввели дробь, нажмите кнопку ‘Конвертировать’, чтобы получить результаты. Конвертер отобразит десятичный эквивалент дроби, который в нашем случае равен 3,33333333333333…. Кроме того, он предоставит пошаговое объяснение процесса преобразования, чтобы вы могли понять, как был получен десятичный эквивалент дроби. Если результат является периодической десятичной дробью, конвертер отобразит повторяющийся шаблон, используя скобки для обозначения повторяющихся цифр.
Одной из ключевых особенностей этого конвертера является его способность выводить периодические десятичные дроби. В математике периодическая десятичная дробь — это десятичная дробь, в которой есть повторяющийся шаблон цифр, например, 0,33333. .. или 0,142857142857… Это отличает такие дроби от непериодических десятичных дробей, которые заканчиваются после определенного числа цифр, например, 0,5 или 0,75.
Использование этого онлайн-конвертера дробей в десятичные является быстрым и простым способом преобразования любой дроби в ее десятичный эквивалент. Он может быть особенно полезен тем, кто испытывает трудности с ручными вычислениями или кто часто выполняет преобразования.
Калькулятор «Конвертер обыкновенных дробей в десятичные»
Таблица конвертации обыкновенных дробей в десятичные
Дробь Десятичная
3 1/1 4
3 1/2 3,5
3 1/3 3,(3)
3 1/4 3,25
3 1/5 3,2
3 1/6 3,1(6)
3 1/7 3,(142857)
3 1/8 3,125
3 1/9 3,(1)
3 1/10 3,1
3 1/11 3,(09)
3 1/12 3,08(3)
3 1/13 3,(076923)
3 1/14 3,0(714285)
3 1/15 3,0(6)
3 1/16 3,0625
3 1/17 3,(0588235294117647)
3 1/18 3,0(5)
3 1/19 3,(052631578947368421)
3 1/20 3,05
3 1/21 3,(047619)
3 1/22 3,0(45)
3 1/23 3,(0434782608695652173913)
3 1/24 3,041(6)
3 1/25 3,04
3 1/26 3,0(384615)
3 1/27 3,(037)
3 1/28 3,03(571428)
3 1/29 3,(0344827586206896551724137931)
3 1/30 3,0(3)
FAQ
Как записать 3 целых 1/3 в виде десятичной дроби?
Дробь 3 1/3 в десятичном виде это 3,33333333333333. .. или 3,(3)
Смотрите также
Мэтуэй | Популярные задачи
92-4*-1+2 92
1 Найти том сфера (5) 
2 Найти площадь круг (5) 
3 Найдите площадь поверхности сфера (5) 
4 Найти площадь круг (7) 
5 Найти площадь круг (2) 
6 Найти площадь круг (4) 
7 Найти площадь круг (6) 
8 Найти том сфера (4) 
9 Найти площадь круг (3) 
10 9(1/2)
11 Найти простую факторизацию 741
12 Найти том сфера (3) 
13 Оценить 3 квадратный корень из 8*3 квадратный корень из 10
14 Найти площадь круг (10) 
15 Найти площадь круг (8) 
16 Найдите площадь поверхности сфера (6) 
17 Найти простую факторизацию 1162
18 Найти площадь круг (1) 
19 Найдите окружность круг (5) 
20 Найти том сфера (2) 
21 Найти том сфера (6) 
22 Найдите площадь поверхности сфера (4) 
23 Найти том сфера (7) 
24 Оценить квадратный корень из -121
25 Найти простую факторизацию 513
26 Оценка квадратный корень из 3/16* квадратный корень из 3/9
27 Найти том коробка (2)(2)(2) 
28 Найдите окружность круг (6) 
29 Найдите окружность круг (3) 
30 Найдите площадь поверхности сфера (2) 
31 Оценить 2 1/2÷22000000
32 Найдите Том коробка (5)(5)(5) 
33 Найти том коробка (10)(10)(10) 
34 Найдите окружность круг (4) 
35 Преобразование в проценты 1,7
36 Оценить (5/6)÷(4/1)
37 Оценить 3/5+3/5
38 Оценить ф(-2) 92
40 Найти площадь круг (12) 
41 Найти том коробка (3)(3)(3) 
42 Найти том коробка (4)(4)(4)
45 Найти простую факторизацию 228
46 Оценить 0+0
47 Найти площадь круг (9) 
48 Найдите окружность круг (8) 
49 Найдите окружность круг (7) 
50 Найти том сфера (10) 
51 Найдите площадь поверхности сфера (10) 
52 Найдите площадь поверхности сфера (7) 
53 Определить, является простым или составным 5
60 Преобразование в упрощенную дробь 2 1/4
61 Найдите площадь поверхности сфера (12) 
62 Найти том сфера (1) 
63 Найдите окружность круг (2) 
64 Найти том коробка (12)(12)(12) 
65 Добавить 2+2=
66 Найдите площадь поверхности коробка (3)(3)(3) 
67 Оценить корень пятой степени из 6* корень шестой из 7
68 Оценить 7/40+17/50
69 Найти простую факторизацию 1617
70 Оценить 27-(квадратный корень из 89)/32
71 Оценить 9÷4
72 Оценка 92
74 Оценить 1-(1-15/16)
75 Преобразование в упрощенную дробь 8
76 Оценка 656-521 9-2
79 Оценить 4-(6)/-5
80 Оценить 3-3*6+2
81 Найдите площадь поверхности коробка (5)(5)(5) 
82 Найдите площадь поверхности сфера (8) 
83 Найти площадь круг (14) 
84 Преобразование в десятичное число 5 ноября
85 9-2
88 Оценить 1/2*3*9
89 Оценить 4/4-17/-4
90 Оценить 11. 02+17.19
91 Оценить 3/5+3/10
92 Оценить 4/5*3/8
93 Оценить 6/(2(2+1))
94 Упростить квадратный корень из 144
95 Преобразование в упрощенную дробь 725%
96 Преобразование в упрощенную дробь 6 1/4
97 Оценить 7/10-2/5
98 Оценить 6÷3
99 Оценить 5+4
100 Оценить квадратный корень из 12- квадратный корень из 192
Как преобразовать целое число в неправильную дробь?
Числа — это математические цифры или значения, которые можно использовать для счета, измерения и выполнения других арифметических операций. Целые числа, целые числа, натуральные числа, рациональные и иррациональные числа и т. д. являются примерами чисел. Система счисления — это стандартизированный метод выражения чисел во многих форматах, включая цифры и язык. Он содержит много видов чисел, таких как простые числа, нечетные числа, четные числа, рациональные числа, целые числа и так далее. Эти числа могут быть представлены несколькими способами в зависимости от используемой системы счисления.
Система счисления включает в себя несколько типов чисел, таких как простые числа, нечетные числа, четные числа, рациональные числа, целые числа и так далее. Эти цифры и слова могут быть использованы для выражения этих чисел. Например, целые числа, такие как 50 и 35, представленные как цифры, могут альтернативно записываться как пятьдесят и тридцать пять.
Целые числа
Подмножество чисел, включающее ноль и все положительные целые числа, называется целыми числами. Общее число идет от 0 до бесконечности. Эти числа используются в повседневных вычислениях, в основном для измерения фундаментальных величин. Натуральные числа состоят исключительно из целых чисел, включая ноль. Числа 0, 1, 2, 3, 4, 5,… обозначают подмножество. Подмножество исключает дроби, десятичные числа и отрицательные целые числа.
Положительные целые числа, также называемые счетными числами, — это части целых чисел, содержащие ноль, например 0, 1, 2, 3, 4, 5 и т. д., исключая отрицательные целые числа, дроби и десятичные дроби. 10, 11, 22, 100, 1000 и так далее — примеры целых чисел.
Неправильная дробь
Неправильная дробь – это дробь, в которой числитель больше или равен знаменателю. Каждая дробь состоит из двух частей: числителя и знаменателя. Правильные дроби и неправильные дроби — это два основных типа дробей в математике, зависящие от значений числителя и знаменателя. Например, 7/2 и 9/5, неправильные дроби.
Как преобразовать целое число в неправильную дробь?
Ответ:
Чтобы преобразовать целое число в неправильную дробь, необходимо выполнить следующие шаги:
Шаг 1: Сократите целое число до правильной дроби. Числитель — это целое число, а знаменатель — 1. Например, если целое число равно 5, числитель дроби равен 5, а знаменатель — 1. В результате 5/1.
Шаг 2: Теперь выберите любую дробь, которая равна 1. Если числа в числителе и знаменателе дроби совпадают, то дробь равна 1. 4/4, 6/6 и 7/7 несколько примеров.
Шаг 3: Наконец Умножьте целое число на дробное, которое равно 1. Возьмите неправильную дробь из шага 1 выше. Умножьте его на любую дробь, равную единице. Это не влияет на исходное значение неправильной дроби. Например, умножьте 5/1 на 5/5 (числитель умножить на числитель и знаменатель на знаменатель). 5/1 разделить на 5/5 равно 25/5.
В результате после упрощения неправильной дроби мы получим то же самое целое число, которое равно 5.
Примеры вопросов 2/9, 6/3, 3/5.

Решение:

Неправильная дробь — это дробь, в которой числитель больше или равен знаменателю. Каждая дробь состоит из двух частей: числителя и знаменателя.
из приведенных выше дробей, 11/5, 6 и 6/3 являются неправильными дробями. Так как в 11/5 11 > 5, 6 можно записать как 6/1, где 6 > 1, а 6/3 можно упростить как 2/1, где 2 > 1.

Вопрос 2: Как изменить всю цифру 8 в неправильную дробь?

Решение:

Здесь 8 — целое число,
Шаг 1. Сократите целое число до неправильной дроби. мы можем записать это как 8/1
Шаг 2: Теперь выберите любую дробь, равную 1. Когда числа в числителе и знаменателе дроби совпадают, дробь равна 1. Итак, здесь дробь равна 8/ 8, так как это равно 1.
Шаг 3: Atlast Умножьте целое число на дробное, которое равно 1. Возьмите неправильную дробь из шага 1 выше. Умножьте его на любую дробь, равную единице. Это не влияет на исходное значение неправильной дроби.
Следовательно, здесь целое число 8, которое мы можем записать как 8/1, будет умножено на дробь, которая эквивалентна 1, то есть 8/8
= 8/1 × 8/8
= 64/8, это неделимая дробь.

Вопрос 3: Как преобразовать 3/5 в целое число?

Ответ:

Здесь 3/5 не является неправильной дробью, так как числитель меньше знаменателя. точное кратное их знаменателям. Следовательно, 3/5 не могут быть преобразованы в целые числа.

Вопрос 4: Как целое число 10 превратить в неправильную дробь?

Решение:

Здесь 10 — целое число,
Шаг 1: Сократите целое число до неправильной дроби. мы можем записать это как 10/1.
Шаг 2: Теперь выберите любую дробь, равную 1. Когда числа в числителе и знаменателе дроби совпадают, дробь равна 1. Итак, здесь дробь 10/10, так как она равна 1.
Шаг 3: Atlast Умножьте целое число на дробное, которое равно 1. Возьмите неправильную дробь из шага 1 выше. Умножьте его на любую дробь, равную единице. Это не влияет на исходное значение неправильной дроби. Поэтому здесь целое число 10, которое мы можем записать как 10/1, будет умножено на дробь, которая эквивалентна 1, то есть 10/10.
= 10/1 × 10/10
= 100/10, это неправильная дробь.

Вопрос 5: Упростите неправильную дробь 8/6 + 10/6 и выясните, получится целое число или нет?

Решение:

Дано: 8/6 + 10/6
Здесь с тем же знаменателем 6.
= 8/6 + 10/6
9095 0 = (8 + 10)/6
= 18/6
Здесь 18/6 — неправильная дробь после дальнейшего упрощения,
= 18/6 = 3
Следовательно, 3 — целое число.

Вопрос 6: Превратите целое число 6 в неправильную дробь.

Решение:

Здесь 6 — целое число,
Шаг 1. Сократите целое число до неправильной дроби. мы можем записать это как 6/1.
Шаг 2: Теперь выберите любую дробь, равную 1. Когда числа в числителе и знаменателе дроби совпадают, дробь равна 1. Итак, здесь дробь 6/6, так как она равна 1.
Шаг 3: Наконец, умножьте целое число на дробное, которое равно 1.

Разложить по формуле бинома ньютона онлайн: Разложение Бинома Ньютона | Онлайн калькулятор

alexxlab / 07.08.202321.05.2023 / Разное

Бином Ньютона

Бином Ньютона — формула

Определение 1
С натуральным n формула Бинома Ньютона принимает вид a+bn=Cn0·an+Cn1·an-1·b+Cn2·an-2·b2+…+Cnn-1·a·bn-1+Cnn·bn, где имеем, что Cnk=(n)!(k)!·(n-k)!=n(n-1)·(n-2)·…·(n-(k-1))(k)!- биномиальные коэффициенты, где есть n по k, k=0,1,2,…,n, а «!» является знаком факториала.
В формуле сокращенного умножения a+b2=C20·a2+C21·a1·b+C22·b2=a2+2ab+b2
просматривается формула бинома Ньютона, так как при n=2 является его частным случаем.
Первая часть бинома называют разложением (a+b)n, а Сnk·an-k·bk — (k+1)-ым членом разложения, где k=0,1,2, …,n.
Коэффициенты бинома Ньютона, свойства биномиальных коэффициентов, треугольник Паскаля
Представление биномиальных коэффициентов для различных n осуществляется при помощи таблицы, которая имеет название арифметического треугольника Паскаля. Общий вид таблицы:
Показатель степени Биноминальные коэффициенты
0 C00
1 C10 C11
2 C20 C21 C22
3 C30 C31 C32 C33
⋮ … … … … … … … … …
n Cn0 Cn1 … … … … … Cnn-1 Cnn
При натуральных n такой треугольник Паскаля состоит из значений коэффициентов бинома:
Показатель степени Биноминальные коэффициенты
0 1
1 1 1
2 1 2 1
3 1 3 3 1
4 1 4 6 4 1
5 1 5 10 10 5 1
⋮ … … … … … … … … … … … … …
n Cn0 Cn1 … … … … … … … … … Cnn-1 Cnn
Боковые стороны треугольника имеют значение единиц. Внутри располагаются числа, которые получаются при сложении двух чисел соседних сторон. Значения, которые выделены красным, получают как сумму четверки, а синим – шестерки. Правило применимо для всех внутренних чисел, которые входят в состав треугольника. Свойства коэффициентов объясняются при помощи бинома Ньютона.
Доказательство формулы бинома Ньютона
Имеются равенства, которые справедливы для коэффициентов бинома Ньютона:
коэффициента располагаются равноудалено от начала и конца, причем равны, что видно по формуле Cnp=Cnn-p, где р=0, 1, 2, …, n;
Cnp=Cnp+1=Cn+1p+1;
биномиальные коэффициенты в сумме дают 2 в степени показателя степени бинома, то есть Cn0+Cn1+Cn2+…+Cnn=2n;
при четном расположении биноминальных коэффициентов их сумма равняется сумме биномиальных коэффициентов, расположенных в нечетных местах.
Равенство вида a+bn=Cn0·an+Cn1·an-1·b+Cn2·an-2·b2+…+Cnn-1·a·bn-1+Cnn·bn считается справедливым. Докажем его существование.
Для этого необходимо применить метод математической индукции.
Для доказательства необходимо выполнить несколько пунктов:
Проверка справедливости разложения при n=3. Имеем, что
a+b3=a+ba+ba+b=a2+ab+ba+b2a+b==a2+2ab+b2a+b=a3+2a2b+ab2+a2b+2ab+b3==a3+3a2b+3ab2+b3=C30a3+C31a2b+C32ab2+C33b3
Если неравенство верно при n-1, тогда выражение вида a+bn-1=Cn-10·an-1·Cn-11·an-2·b·Cn-12·an-3·b2+…+Cn-1n-2·a·bn-2+Cn-1n-1·bn-1
считается справедливым.
Доказательство равенства a+bn-1=Cn-10·an-1·Cn-11·an-2·b·Cn-12·an-3·b2+…+Cn-1n-2·a·bn-2+Cn-1n-1·bn-1, основываясь на 2 пункте.
Доказательство 1
Выражению
a+bn=a+ba+bn-1==(a+b)Cn-10·an-1·Cn-11·an-2·b·Cn-12·an-3·b2+…+Cn-1n-2·a·bn-2+Cn-1n-1·bn-1
Необходимо раскрыть скобки, тогда получимa+bn=Cn-10·an+Cn-11·an-1·b+Cn-12·an-2·b2+…+Cn-1n-2·a2·bn-2++Cn-1n-1·a·bn-1+Cn-10·an-1·b+Cn-11·an-2·b2+Cn-12·an-3·b3+…+Cn-1n-2·a·bn-1+Cn-1n-1·bn
Производим группировку слагаемых
a+bn==Cn-10·an+Cn-11+Cn-10·an-1·b+Cn-12+Cn-11·an-2·b2+. ..++Cn-1n-1+Cn-1n-2·a·bn-1+Cn-1n-1·bn
Имеем, что Cn-10=1 и Cn0=1, тогда Cn-10=Cn0. Если Cn-1n-1=1 и Cnn=1, тогда Cn-1n-1=Cnn. При применении свойства сочетаний Cnp+Cnp+1=Cn+1p+1, получаем выражение вида
Cn-11+Cn-10=Cn1Cn-12+Cn-11=Cn2⋮Cn-1n-1+Cn-1n-2=Cnn-1
Произведем подстановку в полученное равенство. Получим, что
a+bn==Cn-10·an+Cn-11+Cn-10·an-1·b+Cn-12+Cn-11·an-2·b2+…++Cn-1n-1+Cn-1n-2·a·bn-1=Cn-1n-1·bn
После чего можно переходить к биному Ньютона, тогда a+bn=Cn0·an+Cn1·an-1·b+Cn2·an-2·b2+…+Cnn-1·a·bn-1+Cnn·bn.
Формула бинома доказана.
Бином Ньютона — применение при решении примеров и задач
Для полного понятия использования формулы рассмотрим примеры.
Пример 1
Разложить выражение (a+b)5, используя формулу бинома Ньютона.
Решение
По треугольнику Паскаля с пятой степенью видно, что биноминальные коэффициенты – это 1, 5, 10, 10, 5, 1. То есть, получаем, что a+b5=a5+5a4b+10a3b2+10a2b3+5ab4+b5 является искомым разложением.
Ответ: a+b5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
Пример 2
Найти коэффициенты бинома Ньютона для шестого члена разложения выражения вида a+b10.
Решение
По условию имеем, что n=10, k=6-1=5. Тогда можно перейти к вычислению биномиального коэффициента:
Cnk=C105=(10)!(5)!·10-5!=(10)!(5)!·(5)!==10·9·8·7·6(5)!=10·9·8·7·61·2·3·4·5=252
Ответ: Cnk=C105=252
Ниже приведен пример, где используется бином для доказательства делимости выражения с заданным числом.
Пример 3
Доказать, что значение выражения 5n+28·n-1, при n, являющимся натуральным числом, делится на 16 без остатка.
Решение
Необходимо представить выражение в виде 5n=4+1n и воспользоваться биномом Ньютона. Тогда получим, что
5n+28·n-1=4+1n+28·n-1==Cn0·4n+Cn1·4n-1·1+…+Cnn-2·42·1n-2+Cnn-1·4·1n-1+Cnn·1n+28·n-1==4n+Cn1·4n-1+…+Cnn-2·42+n·4+1+28·n-1==4n+Cn1·4n-1+…+Cnn-2·42+32·n==16·(4n-2+Cn1·4n-3+. ..+Cnn-2+2·n)
Ответ: Исходя из полученного выражения, видно, что исходное выражение делится на 16.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Метод Ньютона онлайн
Метод Ньютона используется для нахождения корней функции f(x) = 0. Если необходимо найти минимум функции f(x) → min методом Ньютона, то необходимо использовать данный калькулятор.
Назначение сервиса. Сервис предназначен для отыскания корней уравнений f(x) в онлайн режиме следующими методами:
Метод хорд, Метод итераций, Комбинированный метод, Метод половинного деления (метод дихотомии)
Метод золотого сечения, Модифицированный метод Ньютона, Метод секущих, Метод Ньютона (метод касательных)

Инструкция. Введите выражение F(x), нажмите Далее. Полученное решение сохраняется в файле Word. Также создается шаблон решения в Excel.
Решение онлайн

Видеоинструкция

Оформление Word

F(x) =
Искать в интервале от до .
Точность ξ =
Количество интервалов разбиения, n = (подробнее о влиянии на решение)
Метод решения нелинейных уравненийМетод дихотомииМетод Ньютона (метод касательных)Модифицированный метод НьютонаМетод хордКомбинированный методМетод золотого сеченияМетод итерацийМетод секущих

Правила ввода функции, заданной в явном виде

Примеры правильного написания F(x):
10•x•e^2x = 10*x*exp(2*x)
x•e^-x+cos(3x) = x*exp(-x)+cos(3*x)
x³-x²+3 = x^3-x^2+3
Выражение 0. 2+3x-12.
см. также Решение нелинейных уравнений. Примеры решений. Пусть дано уравнение f(x)=0, где f(x) определено и непрерывно в некотором конечном или бесконечном интервале a ≤ x ≤ b. Всякое значение ξ, обращающее функцию f(x) в нуль, то есть такое, что f(ξ)=0 называется корнем уравнения или нулем функции f(x). Число ξ называется корнем k-ой кратности, если при x = ξ вместе с функцией f(x) обращаются в нуль ее производные до (k-1) порядка включительно: f(ξ)=f’(ξ)= … =f^k-1(ξ) = 0. Однократный корень называется простым. Приближенное нахождение корней уравнения складывается из двух этапов: Отделение корней, то есть установление интервалов [α_i,β_i], в которых содержится один корень уравнения. f(a)•f(b)<0, т. е. значения функции на его концах имеют противоположные знаки. f’(x) сохраняет постоянный знак, т.е. функция монотонна (эти два условия достаточны, но НЕ необходимы) для единственности корня на искомом отрезке). f”(x) сохраняет постоянный знак, т.е. функция выпукла вверх, либо – вниз. Уточнение приближенных корней, то есть доведение их до заданной точности. Геометрическая интерпретация метода Ньютона (метод касательных) Пусть корень ξ уравнения f(x)=0 отделен на отрезке [a,b]. Предположим мы нашли (n-1)-ое приближение корня x_n_-1. Тогда n-ое приближение x_n мы можем получить следующим образом. Положим x_n = x_n_-1 + h_n_-1 . (3.15) Раскладывая в ряд f(x=ξ) в точке x_n_-1, получим f(x_n) = f(x_n_-1+h_n_-1) = f(x_n_-1) + f’(x_n_-1)h_n_-1=0 Отсюда следует . (3.16) Подставим (3.16) в формулу (3.15), получим (3.17) Рис.1. Геометрическая интерпретация метода Ньютона Геометрически метод Ньютона эквивалентен замене дуги кривой y=f(x) касательной, проведенной в некоторой точке кривой (см. рис.1). В точке B имеем f(x₀)f’’(x₀)>0. Здесь x₀=b. Проведем касательную в точке B, получим на пересечении касательной осью OX точку x₁. Далее проводим касательную в точке B₁, получим точку x₂ и т.д. Если положить x₀=a, то в точке x₀ будем иметь f(x₀)f’’(x₀)<0. Тогда касательная в точке A пересекла бы ось OX в точке x’₁, лежащей вне отрезка [a,b], то есть при таком выборе начальной точки, метод Ньютона оказывается расходящимся. Достаточные условия сходимости метода Ньютона определяются следующей теоремой. Теорема 5. Если f(a)f(b)<0, причем f′(x) и f″(x) отличны от нуля и сохраняют определенные знаки при a≤x≤b, то исходя из начального приближения x₀∈[a,b], удовлетворяющего неравенству f(x₀)f’’(x₀)>0 (3. 18) можно вычислить методом Ньютона (3.17) единственный корень ξ уравнения f(x)=0 с любой степенью точности. Доказательство: Пусть f(a)<0, f(b)>0, f′(x)>0, f″(x)>0, a≤x≤b. Согласно неравенству (3.18) в качестве точки x₀ мы должны взять ту границу отрезка, для которой f(x₀)>0, т.е. в данном случае т. b. Итак, имеем x₀>ξ. Докажем, что все приближения x_n> ξ и следовательно все f(x_n)>0. Пусть теперь x_n-1> ξ. Положим ξ = x_n-1 + (ξ-x_n-1). Применяя формулу Тейлора, получим где ξ <c_n_-1<x_n_-1. Так как f″(x)>0, то имеем f(x_n-1)+f′(x_n-1)(ε-x_n-1)<0 и, следовательно ч.т.д. (3.19) Из (3.19) учитывая знаки f(x_n-1) и f′(x_n-1) имеем x_n<x_n_-1, то есть получаем ограниченную монотонную убывающую последовательность x₀>x₁> . .. >x_n>x_n+1>ε. Следовательно, существует . Переходя к пределу в формуле (3.17) получим , то есть f(ξ)=0, и следовательно, ξ- корень ,ч.т.д. Оценим скорость сходимости метода Ньютона. Из (3.17) следует . (3.20) Представим f(ξ) в виде , откуда . (3.21) Подставим (3.21) в (3.20), получим Отсюда . (3.22) Здесь , Таким образом, скорость сходимости метода Ньютона квадратичная. Рис.2 Критерий завершения итерационного процесса имеет вид |x_n – x_n-1|<ε. Замечание. В общем случае совпадение с точностью до ε двух последовательных приближений x_n-1 и x_n не гарантирует, что с той же точностью совпадет x_n и ξ (см. рис. 2). Поэтому целесообразно проверять кроме разности |x_n – x_n_-1|<ε также значение функции f(x_n): |f(x_n)|< ε₁. Пример. f(x) = x⁴-3x³+75x-10000=0. Найти отрицательный корень с пятью верными знаками. Решение: Полагая x=0, -10, -100, получим f(0)=-10⁴, f(-10) = -150, f(-100) ≈ 10⁸. Таким образом -100<ξ<-10. Сузим интервал, так как f(-11)=3433, то -11< ξ <-10. В интервале [-11, -10] f(x)<0, f’’(x)>0. Так как f(-11)f’’(-11)>0, то x₀=-11. Последовательные приближения даны в таблице. n x_n f(x_n) f’(x_n) h_n=- f(x_n)/ f’(x_n) 0 -11 3453 -5183 0.7 1 -10.3 134.3 -4234 0.03 2 -10.27 37.8 -4196 0. 009 3 -10.261 0.2 4 -10.260 <0 Получим -10.261<ξ<-10.260. Метод золотого сечения Точки деления интервала выбираются таким образом, чтобы отношение длин подынтервалов удовлетворяло соотношению (см. рис.) . (3.32) Так как Δ_k = Δ_k+1 + Δ_k+2, то имеем . (3.33) С учетом (3.32) из (3.33) получим уравнение , корнем которого является золотое сечение. . Скорость сходимости МЗС имеет порядок с коэффициентом 1/γ = γ -1 = 0.618. Калькулятор биномиальной теоремы и решатель Получите подробные решения ваших математических задач с помощью нашего пошагового калькулятора Биномиальной теоремы . Практикуйте свои математические навыки и учитесь шаг за шагом с помощью нашего математического решателя. Ознакомьтесь со всеми нашими онлайн-калькуляторами здесь. 1 2 3 4 5 6 7 8 900 06 9 а б в г ж г м n u v w x y z 9 0006 . (◻) + - × ◻/◻ / ÷ ◻ 90 069 2 ◻ ^◻ √◻ √ ^◻ √ ◻ ^◻ √ ∞ e π ln бревно бревно 90 099 ◻ lim d/dx D ^□ _x ∫ ∫ 9006 9 ◻ |◻| θ = > < >= <= sin cos tan кроватка sec csc asin acos atan acot asec acsc sinh cosh 9н$. {5}$ 9{2}+405x+243$  Проблемы с математикой? Доступ к подробным пошаговым решениям тысяч проблем, число которых растет с каждым днем! Онлайн-вычисление LCM двух целых чисел — вычисление наименьшего общего кратного Биномиальный коэффициент, расчет онлайн Сводка: Калькулятор биномиального коэффициента, который позволяет вычислить биномиальный коэффициент из двух целых чисел. биномиальный_коэффициент онлайн Описание: Определение биномиального коэффициента В математике биномиальный коэффициент двух целых чисел n и k представляет собой число `(n!)/(k!(n-k)!`, где `k Калькулятор биномиального коэффициента Калькулятор биномиального коэффициента позволяет вычислять биномиальный коэффициент из двух целых чисел. К вычислить биномиальный коэффициент из двух чисел n и k, калькулятор использует следующую формулу: `(n!)/(k!(n-k)!`. Указаны шаги расчета. Например, чтобы 90 527 вычислить биномиальный коэффициент 90 528 следующих двух целых чисел 5 и 3, просто введите биномиальный_коэффициент(`5;3`), и калькулятор возвращает результат, равный 10. Биномиальные коэффициенты вмешиваются, в частности, в расширение алгебраического выражения с помощью биномиальной формулы Ньютона или в вероятности с комбинаторикой или комбинациями. Одна из особенностей 9.Калькулятор биномиальных коэффициентов 0527 предназначен для указания различных шагов вычисления , которые позволяют найти результат. Синтаксис: binomial_coefficient(n;k), n и k — целые числа. Примеры: binomial_coefficient(5;3), возвращает 10 Расчет онлайн с помощью binomial_coefficient (расчет биномиальных коэффициентов) См. также Список связанных калькуляторов: Номер расстановки комплекта калькулятор : расстановка. Вычислить онлайн количество расположения p элементов множества из n элементов. Расчет биномиальных коэффициентов: binomial_coefficient. Калькулятор биномиального коэффициента, который позволяет вычислить биномиальный коэффициент из двух целых чисел. Чтобы подсчитать количество комбинаций: комбинация. Вычислить количество k элементов части множества из n элементов. Преобразователь base-n : base_converter. Калькулятор позволяет выполнять десятичные, двоичные, шестнадцатеричные преобразования и, в более общем случае, преобразование в любое основание n от 2 до 36. Калькулятор простой факторизации: prime_factorization. Функция prime_factorization используется для онлайн-расчета разложения целого числа на простые множители. Калькулятор частного и остатка: euclidean_division. Калькулятор позволяет найти в режиме онлайн частное и остаток при евклидовом делении двух многочленов или двух целых чисел. Четность числа: is_odd. Функция Is_odd возвращает true, если переданное число нечетное, иначе false. Четность числа: is_even. Функция Is_even возвращает 1, если число четное, иначе 0. Калькулятор факториала: факториал. Факториал натурального числа n — это произведение натуральных чисел, меньших или равных n. Калькулятор факториала позволяет найти это число. Калькулятор перестановок: перестановка. Подсчитать онлайн количество перестановок набора из n элементов. Расчет НОД онлайн: НОД. Калькулятор НОД, который использует алгоритм Евклида для определения шагов вычисления НОД. Наименьшее общее кратное: lcm. Калькулятор LCM для расчета наименьшего общего кратного (НОК). Калькулятор теоремы Пифагора: пифагорейский. Калькулятор использует теорему Пифагора, чтобы проверить прямоугольность треугольника или найти длину одной стороны прямоугольного треугольника. Решатель обратного отсчета: arithmetic_solver. Этот решатель обратного отсчета позволяет найти целевое число из набора целых чисел с помощью арифметических операций.

`Построить график по функции онлайн: Построение графика функции онлайн`

alexxlab / 07.08.202309.05.2023 / Разное

`Онлайн калькулятор: График функции`

УчебаМатематикаГеометрия

Строит график функции, заданной математической формулой.

Данный онлайн калькулятор строит графики функций одной переменной. Функция задается при помощи формулы, в которой могут участвовать математические операции, константы и математические функции. Синтаксис описания формулы см. ниже.

`Построитель графиков функций одной переменной`

Функция одной переменной

Начальное значение

Конечное значение

Количество точек

Отображать таблицу

Точность вычисления

Знаков после запятой: 2

Формула

График функции

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

В формуле допускается использование одной переменной (обозначается как x), числа пи ( pi), следующих математических операторов:

+ — сложение
— — вычитание
* — умножение
/ — деление
^ — возведение в степень

и следующих функций:

sqrt — квадратный корень
rootp — корень степени p, например root3(x) — кубический корень
exp — e в указанной степени
lb — логарифм по основанию 2
lg — логарифм по основанию 10
ln — натуральный логарифм (по основанию e)
logp — логарифм по основанию p, например log7(x) — логарифм по основанию 7
sin — синус
cos — косинус
tg — тангенс
ctg — котангенс
sec — секанс
cosec — косеканс
arcsin — арксинус
arccos — арккосинус
arctg — арктангенс
arcctg — арккотангенс
arcsec — арксеканс
arccosec — арккосеканс
versin — версинус
vercos — коверсинус
haversin — гаверсинус
exsec — экссеканс
excsc — экскосеканс
sh — гиперболический синус
ch — гиперболический косинус
th — гиперболический тангенс
cth — гиперболический котангенс
sech — гиперболический секанс
csch — гиперболический косеканс
abs — абсолютное значение (модуль)
sgn — сигнум (знак)

Ссылка скопирована в буфер обмена

`Похожие калькуляторы`

• Графики функций
• Вычисление значений функции
• Производная показательно-степенной функции
• Гамма-функция
• Обратные тригонометрические функции
• Раздел: Геометрия ( 97 калькуляторов )

 Геометрия график график функции Инженерные Математика формула функция функция одной переменной

 PLANETCALC, График функции

Anton2020-11-03 14:19:28

`404 — Страница не найдена`

jpg»> Страницы Партнеры сайта _________________________________ 404: Запрошенная страница с адресом [http://primer.by/algebra/funkcii/postroit-grafik-funkcii-onlajn/] не найдена. Если Вы уверены, что набрали ссылку корректно, напишите, пожалуйста, об этом на: меню пользователя Новости 30. 11.16 17.03.15 25.03.14 29.08.13 05.05.13 jpg»> primer.by 2013-2016 Построение графика функции онлайн Функция f ( ) График: от до Точки пересечения: показывает? Введите: { здесь кусочно-определенная функция Примеры функций для построения графика График логарифмической функции у = лог(х)/х График показательной функции 9(-2*х)) Логистическая функция 1/(1 + ехр(-х)) Приведенные выше примеры также содержат: модуль или абсолютное значение: absolute(x) или |x| квадратные корни sqrt(x), кубических корней cbrt(x) тригонометрические функции: sinus sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x) экспоненциальные функции и показатели exp(x) обратные тригонометрические функции: арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс acot(x) натуральные логарифмы ln(x), десятичные логарифмы log(x) гиперболические функции: гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x) обратные гиперболические функции: гиперболический арксинус asinh(x), гиперболический арккосинус acosh(x), гиперболический арктангенс ath(x), гиперболический арккотангенс acoth(x) другие тригонометрические и гиперболические функции: секанс sec(x), косеканс csc(x), арксеканс asec(x), арккосеканс acsc(x), гиперболический секанс sech(x), гиперболический косеканс csch(x), гиперболический арксикансек asech(x), гиперболический арккосеканс acsch(x) функции округления: округлить до пола(x), округлить до потолка(x) знак числа: знак(х) для теории вероятностей: функция ошибок erf(x) (интеграл вероятности), Функция Лапласа laplace(x) Факториал х : х! или факториал(х) Гамма-функция gamma(x) Функция Ламберта LambertW(x) Тригонометрические интегралы: Si(x), Ci(х), Ши(х), Чи(х) Правила вставки Следующие операции могут быть выполнены2*x — умножение 3/х 95 — возведение в степень х + 7 — дополнение х — 6 — вычитание Реальные числа вставка как 7,5 , № 7,5 Константы Пи — число Пи и — основание натурального логарифма и — комплексный номер оо — символ бесконечности Чтобы увидеть подробное решение, поделитесь им со всеми друзьями-студентами Графическое представление функции exp(x) Программное обеспечение для построения графиков онлайн , также известное как графопостроитель , представляет собой онлайн-построитель кривых , который позволяет отображать функции в режиме онлайн. Просто введите выражение в соответствии с x функции, которую нужно построить, используя обычные математические операторы. 9Построитель кривых 0236 особенно подходит для изучения функции , позволяет получить графическое представление функции из уравнения кривой, его можно использовать для определения вариации, минимума, максимума функции. Онлайн-плоттер также может рисовать параметрические кривые. и рисовать полярные кривые, а для функций достаточно ввести выражение для представления по параметру t. 9Для мощности / Для отдела Это программное обеспечение для построения кривых позволяет использовать следующие обычных математических функций : абс (абсолютное значение), график абсолютного значения arccos (арккосинус), арккосинус графика arcsin (арксинус), арксинус графика arctan (арктангенс), арктангенс графика ч (гиперболический косинус), построить гиперболический косинус cos (косинус), график косинус cosec (косеканс), косеканс участка котан (котангенс), котангенс участка coth (гиперболический котангенс), построить гиперболический котангенс cube_root (кубический корень), построить кубический корень эксп (экспоненциальная), экспоненциальный график ln (напировский логарифм), построить напьеровский логарифм логарифм (логарифм), логарифм графика сек (секанс), секущая участка ш (гиперболический синус), построить гиперболический синус sin (синус), график синуса sqrt (квадратный корень), участок квадратный корень тангенс (тангенс), участок касательной -й (гиперболический тангенс), построить гиперболический тангенс абс. (абсолютное значение), график абсолютного значения arccos (арккосинус), арккосинус графика arcsin (арксинус), арксинус графика arctan (арктангенс), арктангенс графика ч (гиперболический косинус), построить гиперболический косинус cos (косинус), график косинус cosec (косеканс), косеканс участка котан (котангенс), котангенс участка coth (гиперболический котангенс), построить гиперболический котангенс cube_root (кубический корень), построить кубический корень эксп (экспоненциальная), экспоненциальный график ln (напировский логарифм), построить напьеровский логарифм логарифм (логарифм), логарифм графика сек (секанс), секущая участка ш (гиперболический синус), построить гиперболический синус sin (синус), график синуса sqrt (квадратный корень), участок квадратный корень тангенс (тангенс), участок касательной -й (гиперболический тангенс), построить гиперболический тангенс Графические функции онлайн Этот онлайн-плоттер позволяет вам рисовать несколько кривых одновременно , просто введите выражение функции, которую нужно построить, и нажмите «Добавить», графическое представление функции появляется мгновенно, можно повторить операцию для построения других кривых онлайн . Переменная, которая будет использоваться для представления функций, — «x». Координаты точек на кривой можно получить с помощью курсора. Для этого нажмите на кривую, чтобы появился этот курсор, а затем перетащите вдоль кривой, чтобы увидеть ее координаты. Кривые можно удалить из плоттера: Чтобы удалить кривую, выберите кривую, затем нажмите кнопку удаления в меню. Чтобы удалить все кривые с графика, нажмите кнопку удалить все в меню. Можно изменить кривую, представленную на графике, выбрав ее, отредактировав ее выражение и затем щелкнув на кнопку редактирования. онлайн-плоттер имеет несколько опций, позволяющих настроить график. Чтобы получить доступ к этим параметрам, нажмите кнопку параметров. Затем можно определить границы графов, чтобы подтвердить эти изменения, необходимо снова нажать кнопку параметров. Проведение касательной функции к точке Онлайн-плоттер позволяет провести тангенс функции в точке сделать это, вы просто рисуете нужную функцию, затем, как только функция нарисована, нажмите на меню, параметры, а затем кнопку касательной, которая появляется на экране, после чего будет нарисована касательная, можно изменить точку касательной, что приводит к перерисовке касательной. Калькулятор позволяет определить уравнение касательной очень просто, с уравнением кривой. График производной функции Онлайн-плоттер позволяет вам построить производную функции для этого, вы просто рисуете нужную функцию, затем после того, как функция нарисована, нажмите на меню, на параметры, затем на появившуюся производную кнопку, затем строится производная функции. 9Построитель кривых 0236 также можно использовать для вычисления производной функции и к участок он для этой цели, вам нужно нарисовать нужную функцию, затем, как только функция будет нарисована, выберите ее, щелкнув по ней, на кривой появится красный курсор. Затем нажмите на меню, на параметры, затем на производную кнопку «выражение», которая появляется на экране, затем строится и вычисляется производная функции. («Выражение» представляет собой выражение, которое необходимо получить и нанести на график). Построить параметрическую кривую онлайн Плоттер позволяет рисовать параметрическую кривую , для этого вам просто нужно ввести абсциссу, ординату как функцию от t, затем нажмите кнопку «Построить параметрическую кривую», кривая автоматически отображается с двумя курсорами для отображения нужных точек. Построить полярную кривую онлайн Построитель кривых можно использовать для построения полярной кривой . Для этого просто введите выражение полярной кривой в зависимости от t, затем нажмите кнопку «Построить полярную кривую», кривая автоматически отобразится с двумя курсорами для отображения нужных точек. Переместите курсор на кривую Есть возможность двигаться по кривым и получать координаты точки, на которой находится курсор, Для этого необходимо ввести курсор и перемещать его по графику, координаты X и Y отображаются под графиком. Доступные графические опции Можно изменить область графика, для этого необходимо зайти в меню, затем нажать на опции, Затем можно изменить пределы графического дисплея. Графический калькулятор предлагает возможность масштабировать и перемещать область графика. Сделать это, используйте область в правом нижнем углу графиков. Кнопка + позволяет увеличить масштаб кривых, — позволяет уменьшить масштаб кривых, Стрелки используются для перемещения кривых, Экспорт кривых Можно экспортировать построенные кривые с помощью графического калькулятора , экспорт осуществляется как изображение в формате PNG. Для этого вам нужно зайти в меню графика, затем в подменю экспорта графиков. Затем калькулятор отображает построенные кривые в виде изображения, просто щелкните правой кнопкой мыши, чтобы экспортировать изображение, также возможно скопировать изображение. Чтобы вернуться к обычному отображению калькулятора, используйте кнопку Выход из режима изображения.

`Пятьдесят восемь тысяч триста восемь рублей: Сумма Прописью Онлайн — сервис быстрого перевода`

alexxlab / 07.08.202330.05.2023 / Разное

`Карта сайта`

Размер:

A A A Цвет: CCC Изображения Вкл.Выкл. Обычная версия сайта Главная О районе Общая информация История Символика Почетные граждане Органы власти района Полезные телефоны СМИ района Расписание общественного транспорта Открытые данные Фотогалерея Видеогалерея Туризм Администрация Руководители Полномочия Структура Подведомственные организации Официальные визиты Результаты проверок Информационные системы Учрежденные СМИ Муниципальная служба и кадры ТО и представительства Статистическая информация Приоритеты Международное сотрудничество Перспективный план работы администрации Телефонный справочник План главы района Платежные реквизиты для перечисления платежей в местный бюджет Административная комиссия Новости и анонсы Новости Анонсы событий Памятные даты района Мероприятия и проекты Информационные сообщения Информация Социального фонда РФ Информация Роспотребнадзора Информация налоговой инспекции Информация прокуратуры Информация отдела МВД Информация Росреестра Документы Устав Камышловского района Постановления главы Распоряжения главы Постановления администрации Распоряжения администрации Проекты НПА внесенные в Думу Регламенты государственных и муниципальных услуг Формы обращений Порядок обжалования Муниципальные программы Проекты НПА для общественного обсуждения Профилактика нарушений Услуги Доступно об услугах Нормативные документы Подтверждение личности при регистрации на ЕПГУ Услуги Электронные услуги Технологические схемы предоставления государственных и муниципальных услуг Мониторинг муниципальных услуг Независимая оценка качества оказания услуг учреждениями соц. сферы Экономика Малое и среднее предпринимательство Муниципальные закупки Муниципальный контроль Паспорт района Доклад главы о достигнутых значениях показателей для оценки эффективности Программы развития Итоги социально-экономического развития Прогноз баланса трудовых ресурсов Легализация заработной платы Предоставляемые льготы Стратегия социально экономического развития до 2035 года Схема размещения рекламных конструкций Оценка регулирующего воздействия Предоставление платежных (банковских) услуг на территории Камышловского муниципального района Инициативное бюджетирование Защита прав потребителей Потребителю Новости Бесплатные юридические консультации Социальная сфера Образование Культура Спорт Молодежная политика Здравоохранение ВФСК ГТО Обеспечение жильем Меры социальной поддержки Социально ориентированные некоммерческие организации Доступная среда Центр занятости населения Дополнительное образование Сведения для распространителей информационной продукции, содержащей запрещенную для распространения среди детей информацию Открытый муниципалитет Оценка эффективности деятельности руководителей Общественное обсуждение Публичная декларация Общественная палата Камышловского муниципального района Референтные группы Общественные организации Публичные слушания Прозрачность Опросы Инвестиции Инвестиционный уполномоченный Инвестиционный паспорт района Законодательство и официальные документы В помощь инвестору Присоединение к сетям Инвестиционные площадки свободные Инвестиционные предложения Успешно реализованные и реализуемые проекты Полезные ссылки Содействие и развитие конкуренции Муниципально-частное партнерство Антимонопольный комплаенс Свод инвестиционных правил Свердловской области Деятельность Транспортное обеспечение населения Охрана окружающей среды Градостроительство Нормативные документы Формирование комфортной городской среды Информация о безнадзорных животных Перечень сведений подлежащих представлению с использованием координат Перечень сведений подлежащих представлению с использованием координат Обращение с твердыми коммунальными отходами (ТКО) Муниципальные леса Догазификация Финансы Бюджет для граждан Бюджет Финансовый контроль Межбюджетные отношения Администрирование доходов Контроль в сфере закупок Информация Документы финансового управления администрации Методики Инфографика Обращения Создать обращение Личный кабинет Интернет-приемная Порядок и время приема Порядок рассмотрения обращений Обзоры обращений Ответственные лица за прием граждан Нормативно-правовая база по работе с обращениями граждан Подведомственные учреждения Политика конфиденциальности Муниципальное имущество Невостребованные земельные доли Информация о проведении торгов Предоставление земельных участков бесплатно Свободные земельные участки сельскохозяйственного назначения Информация об объектах, находящихся в собственности МО Камышловский муниципальный район Информация о проведении государственной кадастровой оценки объектов недвижимости Публичный сервитут Информация о реквизитах, необходимых для заполнения платежных документов, в целях перечисления платежей в бюджет с 01. 01.2021 года Выявление правообладателей ранее учтенных объектов недвижимости, права на которые не зарегистрированы в Едином государственном реестре недвижимости Планы проведения плановых выездных и документарных проверок муниципального имущества Информация о неиспользуемом муниципальном имуществе для субъектов малого и среднего предпринимательства Свободные земельные участки, предназначенных под жилищное строительство Противодействие коррупции Нормативные правовые и иные акты в сфере противодействия коррупции Антикоррупционная экспертиза Методические материалы Формы документов, связанных с противодействием коррупции, для заполнения Сведения о доходах, расходах, об имуществе и обязательствах имущественного характера Комиссия по соблюдению требований к служебному поведению и урегулированию конфликта интересов Комиссия по противодействию коррупции Обратная связь для сообщений о фактах коррупции Антикоррупционное просвещение Часто задаваемые вопросы Телефон доверия Доклады, отчеты, обзоры и статистическая информация Опрос уровня восприятия коррупции Безопасность Мероприятия по противодействию коронавирусной инфекции Гражданская оборона Защита населения Экстренные случаи Нормативные правовые акты по вопросам безопасности Единая дежурно-диспетчерская служба (ЕДДС) Информация для населения (памятки, порядок действий, новости) Безопасность на воде Пожарная безопасность Мероприятия Комиссия по профилактике экстремизма Консультативный совет Антинаркотическая комиссия Безопасность дорожного движения Профилактика правонарушений Профилактика терроризма,минимизация и (или) ликвидация последствий его проявлений Муниципальный архив Об архиве Фонды архива Услуги Библиотека Читальный зал Государственные архивы Свердловской области Календарь памятных дат Полезные ссылки Административная комиссия Авторизация Комментарии к материалу Сын погибшего в ДТП отсудил 300 тысяч рублей морального ущерба у человека, который в ДТП не виноват | 59. ruВсе новости«Есть над чем работать»: Путин — об атаке беспилотников на Москву В Лысьве протестировали новую модель теплоснабжения Пермский банк победил в ежегодном конкурсе «Лучшая банковская программа для МСП — 2023» Не доставайся же ты никому! Бизнесмен 5 лет содержал любовницу, а затем засудил за шантаж, но продолжает признаваться ей в любви Глава Перми Алексей Дёмкин наградил студентов, представивших лучшие проекты развития города В июне в Перми пройдет экстремальный забег «Стальной характер» 300 лет Перми: как местные компании готовятся к юбилею города Собаки сиба-ину взяли в семью леопарда Мао — подробности удивительной истории В Перми спасатели начнут дежурить у воды до начала сезона «Если вам нагадят под дверь, понравится?» Крик души собачника, который убирает за своим питомцем на улице Российская компания формирует обособленный центр обслуживания в Перми и набирает бухгалтеров Какому бизнесу Пермь признается в любви: истории номинантов В Перми пропала пенсионерка, передвигающаяся на кресле-коляске В Перми завершили реконструкцию здания Благородного собрания Взрывы в жилых домах, 8 БПЛА и пострадавшие. Как беспилотники атаковали Москву и Подмосковье — видео Не сходил к нотариусу — забрали квартиру. После смерти отца дочь судится с государством за свою жилплощадь В Кремле объяснили, для чего беспилотники атаковали Москву и Подмосковье этим утром Как беспилотники смогли долететь до Москвы? Объясняют эксперты В центре Перми вместо «Рынка еды» откроется караоке-бар Пермскому бизнесу предлагают накрутить голоса в Народной премии 59.RU — объясняем, почему не стоит соглашаться Безопасность, чистота и лазерное шоу: как уральские предприниматели организуют детский досуг в крае Мать младенца, сгоревшего в коляске: «Местные хотят меня поджечь». Что произошло и происходит в Култаево, где случилась ужасная трагедия В Перми летом можно бесплатно посмотреть фильмы, снятые к 300-летию города. Публикуем программу показов Только со свидетельством о смерти: пермяки жалуются, что на кладбища не пускают без документов. Что говорят в мэрии В Перми после ремонта открыли часть набережной у речного вокзала Турнир по конному поло впервые был включен в программу спортивных игр ПМЭФ-2023 Незаконно призванные смогут дезертировать? В России снова изменили законы о службе в армии и мобилизации Делегация Алжира примет участие в ПМЭФ-2023 Детский центр решил поселиться в новостройке на берегу Данилихи Когда школьники узнают свои результаты ЕГЭ? Показываем в одной картинке В Минобороны рассказали, сколько беспилотников атаковало Москву и Подмосковье В Прикамье прогнозируют шквалистый ветер и грозы «Практически невозможная ситуация»: полиция признала 7-летнего ребенка виновником ДТП — машина сбила его возле подъезда «Прям над нашим домом, братан»: видео атаки беспилотников на Москву и Подмосковье от очевидцев В СВО погибли двое участников ЧВК «Вагнер» из Осы В Перми продают здание с баром на улице Советской В Перми перенесли автобусную остановку «Улица Папанинцев» Если хочется больше драйва. Чем хорош новый китайский полноприводный кроссовер: рассказы владельцев Второго шанса произвести первое впечатление не будет: как подготовиться к собеседованию Все новости Перейти к публикации Правильно расставьте запятые и напишите цифры: Пятьдесят восемь миллионов на Курс NCERT Класс 12 Класс 11 Класс 10 Класс 9 Класс 8 Класс 7 Класс 6 IIT JEE Exam JEE MAINS JEE ADVANCED X BOARDS XII BO ARDS NEET Предыдущий год (по годам) Физика Предыдущий год Химия Предыдущий год Биология Предыдущий год Нет Все образцы работ Образцы работ Биология Образцы работ Физика Образцы работ Химия 900 08 Скачать PDF-файлы Класс 12 Класс 11 Класс 10 Класс 9 Класс 8 Класс 7 Класс 6 Экзаменационный уголок Онлайн-класс Викторина Задать вопрос в Whatsapp Поиск Doubtnut Английский словарь Toppers Talk Блог Скачать Получить приложение Вопрос Обновлено: 26. 04.2023 NAND LAL ПУБЛИКАЦИЯ-ЗНАНИЕ НАШИХ НОМЕРОВ-ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ ДЛЯ ПРАКТИКИ 9 Текстовое решение ари видео бина kisi ad ki rukaavat ke! Видео по теме Правильно расставьте запятые и напишите цифры: (a) Семьдесят три лакха семьдесят пять тысяч триста семь. (b) Девять крор пять лакх сорок один. (c) Семь крор пятьдесят два лакха двадцать одна тысяча три. сто два. (d) Пятьдесят восемь миллионов четыреста двадцать три тысячи двести два. (e) Двадцать три лакха тридцать тысяч десять. 4193 02:25 Напишите следующие цифры на индийском система нумерации: Шесть миллионов пятьсот сорок три тысячи двести десять. Семьдесят шесть миллионов восемьдесят пять тысяч девять сто восемьдесят семь. Триста двадцать пять миллионов четыреста семьдесят девять тысяч восемьсот тридцать восемь. 1529382 02:21 Правильно расставьте запятые и напишите цифры: (a) Семьдесят три лакха семьдесят пять тысяч триста семь. (b) Девять крор пять лакхов сорок один. одна тысяча триста два. (d) Пятьдесят восемь миллионов четыреста двадцать три тысячи двести два. (e) Двадцать три лакха тридцать тысяч десять. 571223218 03:06 Следующие номера указаны в международном система нумерации. Перепишите каждое в индийской системе счисления. Восемь миллионов пятьсот сорок шесть тысяч двести восемьдесят три. Семьдесят семь миллионов сорок восемь тысяч один сто пять. Восемьдесят миллионов двадцать пять тысяч сорок восемь. 642585153 03:45 Напишите следующие числа на индийском языке система нумерации: Шесть миллионов пятьсот сорок три тысячи двести десять. Семьдесят шесть миллионов восемьдесят пять тысяч девять сто восемьдесят семь. Триста двадцать пять миллионов четыреста семьдесят девять тысяч восемьсот тридцать восемь. 642585157 04:02 Номер телефона : लाख इक्कीस हज़ार तीन सौ दो 644775755 01:33 स ही स्थानों पर अल्प विराम लगाते हुए संख्याकों क ो लिखिए: ौ दो 644775756 02:01 Правильно расставьте запятые и напишите цифры: Пятьдесят восемь миллионов четыреста двадцать три тысячи двести два. 645656962 02:05 Правильно расставьте запятые и напишите цифры: Четыре крора, тридцать пять лакхов, двадцать одна тысяча пятьсот три. 645656976 01:56 Напишите цифры и расставьте запятые. Сто восемьдесят пять миллионов триста двадцать три тысячи двести пятьдесят один 646307878 01:33 Напишите цифры и расставьте запятые. Два миллиона триста сорок шесть тысяч восемьсот двадцать пять 646307880 00:50 Напишите цифры и расставьте запятые. Сто миллионов двести тысяч триста 646307881 01:45 Правильно расставьте запятые и напишите цифры: Семь кроров пятьдесят два лакха двадцать одна тысяча триста два. 646307976 01:44 Правильно расставьте запятые и напишите цифры: Пятьдесят восемь миллионов четыреста двадцать три тысячи двести два. 646307977 03:02 Запишите числа с запятыми в каждом из следующих чисел: Восемьсот восемь миллионов восемьдесят тысяч восемьсот восемь. 646308099 01:24 Правильно расставьте запятые и напишите цифры: Пятьдесят восемь миллионов четыреста двадцать три тысячи двести два. 647000279 02:05 РЕКЛАМА NAND LAL ПУБЛИКАЦИЯ-ЗНАНИЕ НАШИХ НОМЕРОВ-ДОПОЛНИТЕЛЬНЫЕ ВОПРОСЫ ДЛЯ ПРАКТИКИ Проверьте следующие утверждения, если они верны. LXXV великолепен… 01:31 Исправьте следующие утверждения. Наименьшее четырехзначное число, имеющее… 02:01 Исправьте следующие утверждения. Расширение числа 8759 i… 01:32 Исправьте следующие утверждения. В индийской системе счисления 58,… 02:09 Исправьте следующие утверждения. Рост Ритики 65 см. В мельнице… 01:16 Исправьте следующие утверждения. Прибавив 1 к наибольшему 4-значному… 01:32 Проверьте следующие утверждения, верны они или нет В римском числе. .. 01:52 Расставьте запятые подходящим образом и напишите имена номеров для следующего: … 01:37 79200510 в Международной системе нумерации. 01:22 100400258 в индийской системе счисления. 01:11 812341905 — международная система нумерации. 01:11 Правильно расставьте запятые и напишите цифры. Семь крор семь лак… 01:18 Правильно расставьте запятые и напишите цифры: Двадцать девять миллионов на… 01:25 Правильно расставьте запятые и напишите число ералс: Пятьдесят восемь миллион на… 01:28 Правильно расставьте запятые и напишите цифры: Семь лакхов сорок три… 23 01:04 Напишите индийские арабские цифры для следующего: MDLI 01:01 Напишите индийские арабские цифры для следующего: CXVIII 01:01 9 0122 Напишите индийским арабским числительным следующее: CLIX 01:02 Ask Unlimited Doubts Видеорешения на нескольких языках (включая хинди) Видеолекции экспертов Бесплатные PDF-файлы (документы за предыдущий год, книжное решение) s и многое другое) Посетить специальное предложение Консультационные семинары для IIT-JEE, NEET и экзаменов Совета Doubtnut хочет отправлять вам уведомления. Разрешите получать регулярные обновления! Прослушивание… Числа с «и» | ИспанскийDict Ответы Привет, Нила Возможно, вам будет полезно понять, что когда мы озвучиваем числа, мы склонны группировать их из-за того, как нас учат математике в раннем возрасте; то есть мы обычно склонны группировать их в соответствии с их позиционной ценностью, т. е. кратными десяти. Делая это, мы, по сути, просто произносим список чисел в последовательном порядке, от высшего к низшему, в зависимости от их разрядности (в десятичной десятичной системе). Есть одно предостережение: когда ненулевое число встречается как в разряде десятков, так и в разряде единиц, принято (опять же, как артефакт того, как нас обычно учат числам) указывать эти числа так, как если бы они были единой единицей (или элементом списка). Другими словами, для числа вроде «23» принято говорить «двадцать три», а не что-то вроде «два десятка и три». Как ни странно, тот же эффект именования распространяется на сотые и десятые доли справа от запятой. Например, число «0,23» часто говорят как «двадцать три сотых», а не как «двадцать одна сотая и три десятых» (хотя, строго говоря, в этом нет ничего плохого) Принимая все это во внимание, правила, которым необходимо следовать при написании чисел, очень похожи на те, которые используются при написании любого другого типа списка. Обратите внимание, например, на то, как перечисляются следующие элементы в зависимости от количества элементов в каждом списке: два предмета яйца и тосты (1) яйца и (2) тосты 203 (1) двести и (2) три 223 (1) двести и (2) двадцать три три предмета бекон, яйца и тосты (1) бекон, (2) яйца и (3) тосты 2,223 (1) две тысячи , (2) двести и (3) двадцать три 9040 7 1 000 223 (1) один миллион, (2) двести и (3) двадцать три Я хочу проиллюстрировать еще одну вещь, прежде чем перейти к более сложным числам. Изучите, как сгруппированы следующие числа: 1 523 345 365 523 345 365 345 365 365 использование запятых, которое происходит, когда мы пишем числа вот так. Что мы делаем, так это группируем числа во второй раз. Помните, что первый способ, которым мы сгруппировали числа, был по степеням 10 (т. е. 10 ⁰, 10 ¹, 10 ², 10 ³, 10 ⁴, 10 ⁵, 10 ⁶ и т.д.) Теперь вторая группировка происходит после каждой третьей цифры. То есть каждая группа чисел, разделенная запятой, считается отдельным элементом списка в том, что сейчас считается основным списком. Теперь вы видите, что наш первоначальный список теперь перегруппирован, чтобы сформировать новый список (первичный список), в котором каждый элемент списка может состоять либо из одного элемента, либо из двух элементов (вторичный список). Именно здесь пригодится соглашение об именовании чисел, таких как «23», как единой единицы (элемента), потому что оно поддерживает количество элементов в каждом вторичном списке не более двух элементов. Рассмотрим следующее (я буду выделять каждый отдельный элемент списка в основном списке, используя другой цвет, а также нумеруя их, тогда как каждому элементу во вторичных списках будет присвоено либо «a», либо «b»): Три элемента 523 345 365 (1a) пятьсот (1b) двадцать три миллиона, (2a) триста (2b) сорок пять тысяч, (3a) триста (3b) шестьдесят -пять 23 345 365 (1а)двадцать три миллиона, (2а)триста (2б) сорок пять тысяч, (3а) триста (3б) шестьдесят пять 3300, 365 (1а) три миллиона, (2а) триста тысяч, (3а) триста и (3б) шестьдесят пять Когда используется десятичная дробь, ее часто заменяют словом «и», чтобы создать третий уровень исходного списка. То есть теперь иерархия вашего списка выглядит следующим образом (1) целые числа и десятичные дроби, которые можно разделить на (2) тысячи, миллионы, миллиарды и т. д. и тысячные, миллионные, миллиардные и т. д., их можно далее подразделить на сотни и единицы измерения. 323 345,365 (1a) триста (1b) двадцать три тысячи, (2a) триста (2b) сорок пять и (3а) триста (3б) шестьдесят пять тысячных 323,345365 (1а) триста (1б) двадцать три и (2а) триста (2б) сорок- пять тысяча, (3а) триста и (3б) шестьдесят пять миллионных В разговорной речи (как уже было предложено другими) в целях экономии многие из этих «и» часто опускаются, т. е. невнятно или полностью вычеркнуто. Однако обычно конечное «и» сохраняется (или, по крайней мере, в большей степени, чем другие «и»), так что, когда вы слышите его произнесенное, число вроде «523 345 365» может звучать примерно как 9.0123 «пятьсот двадцать три миллиона триста сорок пять тысяч триста шестьдесят пять» или, как сказал Гэри, «пятьсот ‘n’ двадцать три миллиона триста n сорок пять тысяч триста nd шестьдесят пять».

« Предыдущая 1 … 20 21 22 23 24 … 3 230 Следующая »