Цели, задачи, функции и экономические проблемы логистики запасов.
В движении материальных потоков неизбежно наступает момент, когда товары превращаются в запасы – накопленные, временно не используемые материальные ресурсы. Материальные запасы выполняют три основные функции:
сглаживают несоответствие между моментами производства, транспортировки и потребления товаров;
устраняют диспропорциональность объёмов и структуры спроса и предложения на рынке;
позволяют получить спекулятивную прибыль.
Запасы создаются
на всех стадиях кругооборота товаров
– в производственных, транспортных,
торговых и других логистических системах,
чему соответствует разнообразие их
видов. Часть предназначена для реализации,
другие – для потребления (в производственном
процессе, домашнем хозяйстве), а третьи
образуются в результате физического
перемещения продуктов от продавца к
покупателю в ходе купли-продажи. Производственные запасы ориентированы
на конкретную технологию и поэтому
стабильны по своему натурально-вещественному
составу. На практике, классификация
запасов помогает при выработке политики
закупок и управления запасами различных
групп. Момент перехода запасов из одной
формы в другую называется границей
запасов. При
расчёте оптимальной величины запасов
из иногда разделяют на три части: текущую,
страховую и подготовительную.
Производственные запасы ориентированы
на конкретную технологию и поэтому
стабильны по своему натурально-вещественному
составу. На практике, классификация
запасов помогает при выработке политики
закупок и управления запасами различных
групп. Момент перехода запасов из одной
формы в другую называется границей
запасов. При
расчёте оптимальной величины запасов
из иногда разделяют на три части: текущую,
страховую и подготовительную.
Текущим называется запас, обеспечивающий сбыт или производство в интервалах между поставками.
Подготовительный запас позволяет осуществить подготовку продукта к производственному потреблению или отгрузке (нарезать, высушить, снять смазку, укомплектовать, оформить отгрузочные документы).
Стразовой запас способствует непрерывности
материально-технического обеспечения
и сбыта в ситуациях непредвиденных
отклонений в условиях торговли или
производства (поставка некачественного
товара, задержка очередной партии, брак
или остановка производства).
Цели логистических запасов вытекают из общелогистических целей. Их можно классифицировать по трём группам:
минимизация затрат (текущих и инвестиций) на образование запасов;
достижение высокого уровня готовности к отпуску материалов в производство, товаров – к отгрузке и выполнению заказов клиентов;
минимизация затрат на логистическую сферу, создание системы управления запасами, стоимость которой не превышала бы эффект от её функционирования.
Задачи логистики запасов вытекают из поставленных целей. К ним относятся:
Функции логистики запасов выполняются коммерческими, маркетинговыми, логистическими и финансовыми службами организаций в процессе решения задач управления запасами. Это учёт запасов, планирование, финансовое обеспечение, контроль за состоянием, оперативное регулирование и анализ.
Издержки запасообразования, связанные с созданием и поддержанием запасов, можно разделить на две группы:
Определение этих
издержек происходит двумя основными
способами – калькулированием и в
процентах от стоимости запаса.
Задачи с решениями — логистика (укр.яз)
- Файлы
- Академическая и специальная литература
- Финансово-экономические дисциплины
- Логистика
Логистика
Закупочная логистика / логистика снабжения
Информационная логистика
Логистика в отраслях
Логистика запасов
Логистика складирования
Матметоды и моделирование в логистике
Основы логистики
Производственная логистика
Распределительная логистика
Управление цепями поставок
Финансово-экономические дисциплины
Анализ и прогнозирование временных рядов в экономике
Аудит
Банковское дело
Бизнес-курс ACCA
Бизнес-курс CIMA
Бизнес-курс MBA
Бизнес-курс СFA
Бизнес-планирование
Биржевая торговля
Бухгалтерский учет
Бюджетная система
Внешнеэкономическая деятельность
Государственное регулирование экономики
Государственные и муниципальные финансы
Государственный финансовый контроль
Деньги и кредит
Инвестиции
Инновации
Институциональная экономика
Информационные технологии в экономике
История экономики
История экономических учений
Коммерческая деятельность предприятия
Контроль и ревизия
Лизинг
Логистика
Математические методы и моделирование в экономике
Методы принятия решений в экономике
Мировая экономика
Налоги и налогообложение
Организация производства
Отраслевая экономика
Оценка и оценочная деятельность
Планирование и контроль на предприятии
Предпринимательство
Прогнозирование социально-экономических процессов
Размещение производительных сил (РПС)
Региональная и национальная экономика
Рынок финансовых услуг
Рынок ценных бумаг
Системный анализ в экономике
Системы технологий
Статистика экономическая
Статистический анализ экономических данных
Страхование
Таможенное дело
Товароведение
Торговое дело
Управление затратами
Учет и анализ банкротства
Философия экономики
Финансовая математика
Финансово-экономическая периодика
Финансовое планирование и прогнозирование
Финансовый менеджмент
Финансы
Финансы предприятий
Ценообразование
Экзамен GMAT
Эконометрика
Экономика
Экономика недвижимости
Экономика общественного сектора
Экономика предприятия
Экономика природопользования
Экономика труда
Экономическая теория
Экономический анализ
- формат doc
- размер 397 КБ
- добавлен
11 октября 2010 г.

Чала Н. Д.
НаУКМА, 2009
Задачі до іспиту із розв’язками на наступні теми:
АВС-аналіз
Визначення оптимального економічного розміру замовлення,
оптимального розміру партії
Організація виробничих ліній
Розрахування часу перебування виробу у процесі, щоденної
продуктивності процесу
Планування замовлень
Прийняття логістичного рішення щодо вибору транспорту
Похожие разделы
- Академическая и специальная литература
- Транспорт
- Транспортное обслуживание и транспортная логистика
Смотрите также
- формат doc
- размер 1.34 МБ
- добавлен 15 февраля 2011 г.
Пробное электронное неформатированное издание, МАИ, 2009 Содержание: Базисные понятия логистического менеджмента Глобальные логистические концепции управления материальным потоком Закупочная логистика Задачи транспортной логистики Логистика запасов Логистика складирования Сбытовая логистика Микрологистические концепции и технологии Оценка эффективности логистического сервиса
Курсовая работа- формат docx
- размер 377.
 24 КБ
24 КБ - добавлен 01 апреля 2011 г.
Закупочная логистика. Логистика закупок. Транспортная логистика. Транспортная логистика. Логистика распределения. Логистика распределения. Логистика запасов. Логистика запасов. Логистика складирования. Логистика складирования.rn
Статья- формат doc
- размер 468.64 КБ
- добавлен 16 декабря 2010 г.
В данном курсе рассмотрены следующие темы: Логистика: понятие, цели и задачи. Информационная логистика. Закупочная логистика. Логистика производственных процессов. Распределительная логистика. Складская логистика. Логистика запасов. Транспортная логистика. Логистика сервисного обслуживания. Методы оценки логистических затрат и пути их оптимизации.
- формат doc
- размер 2.38 МБ
- добавлен 25 января 2010 г.
Логистика, лекции для заочников, ДУЭП Логистика — инструмент развития рыночной экономики Материальные и информационные потоки и логистические операции Методология и научная база логистики Закупочная логистика Производственная логистика Распределительная логистика Логистика запасов Транспортная логистика Использование в логистике технологии автоматической идентификации штриховых кодов Основы логистики складирования
Статья- формат doc
- размер 1.3 МБ
- добавлен 06 января 2010 г.
Утверждено на заседании кафедры менеджмента организаций протокол № 1 от 31. 08.2006 г. Зав. кафедрой Дорофиенко В. В. 181 стр. Введение. Логистика и факторы её развития. Концепция логистики. Информационная логистика. Закупочная логистика. Логистика производственных процессов. Сбытовая логистика. Логистика запасов. Логистика складирования и транспорта. Организация логистического управления. Литература.
08.2006 г. Зав. кафедрой Дорофиенко В. В. 181 стр. Введение. Логистика и факторы её развития. Концепция логистики. Информационная логистика. Закупочная логистика. Логистика производственных процессов. Сбытовая логистика. Логистика запасов. Логистика складирования и транспорта. Организация логистического управления. Литература.
- формат doc
- размер 822.5 КБ
- добавлен 02 декабря 2010 г.
БелГУ, 2010 Преподаватель Захарова О. Н. 81 стр Конспект лекций: Основные понятия логистики Заготовительная логистика Производственная логистика Распределительная логистика Логистика в торговой системе. Сервис в логистике Управление запасами Транспортная логистика. Информационная логистика Приложения
Статья- формат doc
- размер 1.
 54 МБ
54 МБ - добавлен 20 августа 2010 г.
Логистика как инструмент рыночной экономики Технологические процессы и управление материальными потоками на предприятии Логистические системы Закупочная логистика Производственная логистика Распределительная логистика Транспортная логистика Информационная логистика Логистика запасов Логистика складирования
Статья- формат doc
- размер 1.27 МБ
- добавлен 07 марта 2009 г.
Введение в логистику. Научные основы логистики. Концепция логистики. Закупочная логистика. Производственная логистика. Распределительная логистика. Складская логистика. Транспортная логистика. Информационная логистика. Логистика сервисного обслуживания. Глобальная логистика. Управление запасами. Определение и оптимизация затрат. Организация логистического управления. Методы оптимизации материальных потоков. Применение методов прогнозирования в ло…
Глобальная логистика. Управление запасами. Определение и оптимизация затрат. Организация логистического управления. Методы оптимизации материальных потоков. Применение методов прогнозирования в ло…
- формат doc
- размер 454 КБ
- добавлен 11 декабря 2011 г.
М., МГУТУ, 2009. — 55с. Содержание: Логистика производственных процессов Закупочная логистика Управление материальными потоками в сфере производства Сущность и задачи транспортной логистики Задачи распределительной логистикиrn
Презентация- формат ppt
- размер 1.87 МБ
- добавлен 18 февраля 2011 г.
Логистика. Логистика и Интернет. Интернет и логистика закупок. Интернет и сбытовая логистика. Интернет и транспортная логистика. Электронный документооборот через Интернет. Заключение
Интернет и сбытовая логистика. Интернет и транспортная логистика. Электронный документооборот через Интернет. Заключение
12 Распространенные проблемы управления запасами и их решения
Запасы являются источником жизненной силы любого бизнеса, имеющего дело с продукцией, и жизненно важно, чтобы вы эффективно управляли ими для успеха и роста бизнеса.
проблем управления запасами несколько.
Правильное решение поможет вам повысить рентабельность и обеспечить превосходное обслуживание клиентов.
Независимо от того, где находится инвентарь – один склад или несколько; или даже дропшиппинг поставщика.
Надлежащее управление запасами помогает сократить расходы, повысить денежный поток и обеспечить непрерывное производство и своевременное выполнение заказов клиентов.
Партнерство с известным поставщиком услуг, таким как Tranquil, может означать разницу между хаосом и бесперебойностью.
Постоянное наличие запасов позволит вам увеличивать продажи, удовлетворять потребности клиентов и поддерживать непрерывность бизнеса.
Рассмотрим наиболее распространенные проблемы управления запасами и их решения .
ЧИТАЙТЕ ТАКЖЕ: Общие проблемы ERP в 2022 году
1. Отсутствие видимости запасов
Если вы не можете найти или идентифицировать запасы в своем запасе, своевременная доставка продукции становится очень сложной, и это может нанести ущерб вашему бизнесу репутация.
Инвентаризация, которая является неполной, труднодоступной или ошибочной, обязательно снизит вашу прибыль.
Фактически, наиболее распространенной причиной задержки, неправильной или частичной отгрузки является сложность обнаружения или идентификации запасов на складе.
Получение при поиске нужного запаса имеет решающее значение для обеспечения эффективности склада, а также хорошего опыта для клиента.
Решение: Система управления запасами в режиме реального времени
При внедрении системы управления запасами в реальном времени, такой как Tranquil ERP, вы будете иметь все точные данные о местоположении и наличии запасов.
Это поможет легко найти складские запасы, что в конечном итоге приведет к лучшему выполнению заказов и удовлетворенности клиентов.
ТАКЖЕ ПРОЧИТАЙТЕ: Инвентаризация конвейера и инвентаризация развязки
2. Неэффективный процесс или программное обеспечение управления инвентаризацией 0006 .
Многие предприятия до сих пор пытаются управлять своими запасами с помощью ручных процедур или устаревшего программного обеспечения, что может замедлить рост вашего бизнеса.
Может показаться, что использование ручных, трудоемких или низкотехнологичных систем не представляет большого труда, если у вас небольшой бизнес с одним складом, но это изменится, когда вы расширитесь.
Когда объемы продаж растут, вам необходимо расширить запасы и добавить склады.
Старые и неэффективные методы управления запасами будет трудно масштабировать, они окажутся препятствием и не дадут вам нужных результатов.
Процедуры ручного отслеживания инвентарных запасов включают либо бумажную работу, либо процедуры отслеживания в нескольких электронных таблицах и программном обеспечении, что может привести к избыточности данных, неполным данным и затратам большого количества времени на это; это также обеспечивает меньшую безопасность.
В нынешнюю эпоху конкуренции очень важно в любой момент времени знать, какие именно ресурсы у вас есть; вы больше не можете полагаться на ежегодный физический подсчет запасов с участием всех ваших сотрудников.
Еще одной большой проблемой является потеря запасов, вызванная кражей, повреждением, порчей и т.д.; эта проблема с цепочкой поставок требует способности правильно определять, отслеживать и измерять проблемные области.
Вы можете масштабировать программное обеспечение для управления запасами и поддерживать сложную логистику только в том случае, если сможете интегрировать его с существующим программным обеспечением для бизнеса.
Этого нельзя достичь с помощью устаревших, унаследованных систем.
Решение: Решение для управления запасами на базе IoT
ТАКЖЕ ПРОЧИТАЙТЕ: Что такое недозаказы и как с ними справиться или как их избежать?
Система управления запасами, использующая Интернет вещей, расширит возможности сотрудников вашего склада и поможет им эффективно и быстро управлять запасами и отслеживать их на протяжении всего времени, пока они находятся на вашем складе.
Вы можете упростить управление запасами с помощью правильного решения и повысить эффективность управления запасами.
Не только крупные корпорации, но даже малые предприятия могут извлечь выгоду из централизованной системы отслеживания запасов со встроенными функциями учета — все это можно найти в Tranquil ERP; он надежен, интуитивно понятен, экономичен, гибок и масштабируем.
3. Отслеживание устаревших материалов
Почти в каждом бизнесе вы рано или поздно столкнетесь с этой проблемой.
Будут некоторые продукты или материалы, которые останутся непроданными или неиспользованными, и они могут стать устаревшими или просроченными.
Эти материалы или продукты имеют тенденцию накапливаться со временем, так как менеджеры по запасам в основном игнорируют их.
Когда этот продукт или материал понадобится когда-нибудь в будущем, к сожалению, непроданные запасы останутся забытыми, и будут куплены новые запасы; старый может оставаться на складе так долго, что полностью выйдет из строя.
Это увеличивает расходы и потери материалов.
Решение: Эффективная система управления запасами
ЧИТАЙТЕ ТАКЖЕ: Что такое отрицательный запас?
Эта функция включена в модуль управления запасами Tranquil ERP.
Вы сможете найти мертвые запасы и правильно их использовать.
Такое программное решение может значительно помочь менеджерам по запасам в управлении запасами.
4. Идентификация неправильно расположенных материалов
Если в магазине нет надлежащей системы отслеживания продуктов, материалов или оборудования, их поиск при наличии заказов на продажу может быть обременительным и трудоемким.
В конце концов, на складе обычно могут храниться тысячи товаров. Это может задержать продажи и сделать клиентов недовольными.
Решение : Средство поиска продуктов
Все продукты, которые у вас есть, должны быть снабжены RFID-метками, штрих-кодами или QR-кодами, выгравированными с помощью лазера.
Это поможет вашим сотрудникам определить необходимые продукты.
Они должны быть оснащены только сканером. Как только сканер находит нужный продукт, загорается лампа, указывающая на совпадение.
Это поможет вашим сборщикам быстро найти товар и отправить его агентам по продажам, что сэкономит им время, ускорит цикл продаж и порадует клиентов.
ЧИТАЙТЕ ТАКЖЕ: Продажи маршрутов и фургонов – проблемы и возможности
5. Борьба с излишками
Когда вы покупаете новые материалы, а на складе остается несколько нераспроданных товаров, это может повлиять на вашу прибыльность.
Эта ситуация в основном возникает из-за неэффективности ручных процессов, что приводит к плохому контролю запасов.
Хранить слишком много запасов так же плохо, как хранить слишком мало, так как чрезмерные запасы препятствуют вашему денежному потоку и создают проблемы, связанные с запасами, такие как хранение или потеря.
Решение : Процесс аудита запасов
При внедрении процесса аудита запасов менеджеры по запасам смогут регулярно проверять запасы, чтобы быстро выявлять неиспользованные запасы.
Это значительно повышает эффективность использования запасов, позволяя вашей компании сократить расходы, устранить задержки и повысить прибыльность.
6. Управление запасами, отходами и дефектами
Хотя это может показаться незначительным, это одна из наиболее распространенных и повторяющихся проблем управления запасами, которая может привести к огромным потерям.
Чтобы своевременно выполнять заказы, необходимо поддерживать оптимальные запасы.
Без стандартных процедур и неподготовленных операторов вы можете получить поврежденный или израсходованный инвентарь, а это может оказаться не только очень дорогим, но и привести к неудовлетворенным клиентам.
Решение : Современное программное обеспечение для управления запасами
Tranquil ERP имеет надежный модуль управления запасами, который позволяет вам эффективно управлять своими запасами и контролировать их.
Благодаря оптимизации процедур и процессов вашим сотрудникам будет легче выполнять свою работу, а вы сможете сократить расходы и устранить потери.
ТАКЖЕ ПРОЧИТАЙТЕ: Руководство по проблемам закупок
7. Отсутствие централизованного узла инвентаризации
Инвентаризация становится очень сложной, когда у вас есть запасы в нескольких местах.
Дискретные данные о запасах из разных мест усложняют доставку, что приводит к задержкам.
Это одна из самых больших и постоянных проблем, с которыми сегодня сталкивается большинство предприятий.
Решение : Центральная система инвентаризации
Вы можете значительно сократить расходы и сэкономить много времени, просто создав централизованный центр инвентаризации для ваших данных, связанных с инвентаризацией, включая инвентаризацию.
Это обеспечивает полную видимость и контроль запасов и данных в одном месте, что упрощает управление запасами.
Также становится намного проще отслеживать инвентарь, который входит и выходит из вашего офиса.
8. Изменение спроса
Потребительский спрос находится в постоянном движении; это усложняет хранение инвентаря.
Сколько хранить? Слишком много, и вы можете остаться без запаса; слишком мало, и вы не сможете удовлетворить требования клиентов.
Решение : Технология планирования запасов
Вам нужна надежная технология прогнозирования запасов, которая учитывает все эти факторы и помогает более эффективно планировать запасы.
Модуль управления запасами Tranquil ERP имеет функцию прогнозирования, которая помогает создавать и реализовывать оптимальный план запасов.
Это поможет вам не отставать от меняющегося спроса клиентов.
ТАКЖЕ ЧИТАЙТЕ: Конфигурация ERP, настройка ERP и персонализация ERP
9. Сложность цепочки поставок
Международные цепочки поставок динамичны и могут создавать препятствия в управлении и планировании ваших запасов.
Производители и дистрибьюторы страдают от непредвиденных экономических подъемов и спадов, которые влияют на цены и доступность сырья.
Они также решают, когда, как и куда отправлять запасы, а это означает, что у вас есть сроки, которые вы не можете предсказать, что требует от вас большей гибкости.
Решение : Надежное приложение для управления запасами
С правильным приложением для управления запасами, внедренным в вашем бизнесе, вы можете максимально точно прогнозировать время выполнения заказов и лучше подготовиться к сложностям цепочки поставок.
10. Управление складским пространством и эффективностью
Одной из самых сложных задач для любого бизнеса является эффективное управление пространством.
Склады должны быть спланированы и спроектированы с помощью платформ управления запасами, чтобы вы могли контролировать, когда доставляется новый запас, и помочь вам наилучшим образом использовать доступное пространство.
Если вы имеете дело с хрупкими или скоропортящимися продуктами, вам необходимо организовать специализированный уход и хранение – например, холодильное хранение.
Вы должны реализовать определенные стратегии для дорогостоящего инвентаря, чтобы предотвратить кражу и повреждение.
Управление запасами на складе является трудоемким и требует выполнения нескольких шагов, таких как получение запасов, их размещение, комплектование запасов, упаковка и, наконец, отгрузка.
Крайне важно, чтобы все эти задачи выполнялись максимально эффективно.
ЧИТАЙТЕ ТАКЖЕ: Что такое улучшение бизнес-процессов (BPI)?
Решение : Система управления складом
Модули управления запасами либо имеют управление складом как функцию, либо интегрированы с модулями управления складом.
Это может помочь вам автоматизировать многие утомительные задачи и повысить эффективность всего управления складом вашего бизнеса.
11. Недостаточное управление заказами и плохое планирование производства:
Планирование производства имеет решающее значение, если вы не хотите остановки производства и перерасхода бюджета.
Если вы не спланируете это должным образом, ваши прогнозы продаж могут пойти наперекосяк, как и планирование вашего проекта.
Мысль о том, что запасов достаточно, а перепродажа товаров — обычная проблема, с которой сталкиваются многие компании.
Решение : Программное обеспечение для планирования производства
Программное обеспечение для планирования производства использует сезонные тенденции и исторические данные для получения довольно точных прогнозов, которые помогут вам лучше планировать производство.
12. Недостаток опыта и плохая коммуникация
В то время как каждая компания хотела бы иметь менеджеров по запасам, которые являются отличными коммуникаторами и технически подкованными, легко осваивающими новые технологии, правда в том, что это редко случается таким образом.
Простое развертывание наиболее многофункциональной ERP-системы не поможет, если она не используется должным образом.
Решение : Надлежащее обучение
С самого начала важно обеспечить надлежащее обучение всех тех, кто будет использовать новую систему.
Особо следует обратить внимание руководителей на то, что им необходимо как следует ознакомиться с новой системой.
Главы различных отделов также должны быть проинформированы о важности сотрудничества и обмена данными.
Разные решения для каждого процесса могут привести к путанице и неправильным данным. Универсальное решение, такое как Tranquil ERP, может помочь вам сократить потери материалов и повысить эффективность управления запасами в масштабах всей организации. Tranquil — это надежное передовое решение ERP, развернутое в облаке, которое поможет вам максимально эффективно использовать свои запасы. Запланируйте демонстрацию с нами, чтобы узнать, как работает наше программное обеспечение и какую пользу оно может принести вашему бизнесу.
Tranquil — это надежное передовое решение ERP, развернутое в облаке, которое поможет вам максимально эффективно использовать свои запасы. Запланируйте демонстрацию с нами, чтобы узнать, как работает наше программное обеспечение и какую пользу оно может принести вашему бизнесу.
20 основных проблем и решений управления запасами
By Sunith 6 мая 2022 г. Программное обеспечение CRM 0 комментариев
Управление запасами является одним из ключевых процессов в компании электронной коммерции, где необходимо обновлять ассортимент товаров. неоднократно для бесперебойного потока поставок.
Для достижения эффективного управления запасами отличным решением является внедрение новейших технологий. Использование новых технологий подобно сверхспособностям, расширяющим возможности вашего бизнеса.
Несмотря на это, многие компании сталкиваются с проблемами в управлении запасами. Итак, здесь, в этом блоге, мы обсуждаем некоторые из проблем управления запасами с решениями для их решения.
Содержание
Проблемы управления запасами 1. Невозможность определить местонахождение запасов 9 0002 Одной из самых больших проблем на складе будет отслеживание продуктов в инвентаре, которые должны быть отправлены или доставлены клиентам.Что произойдет, если запасы будут доступны? Поставки доходят до клиентов с опозданием, что в конечном итоге снижает ценность бренда и вызывает низкие рейтинги в социальных сетях.
2. Выбор процесса инвентаризации вручнуюЗнаете ли вы?
43 процента малых предприятий в США не отслеживают запасы или делают это вручную. ( Источник )
Использование процессов инвентаризации вручную для отслеживания вашего инвентаря приведет к путанице и будет рассматриваться как одна из основных проблем управления запасами .
Невозможность отследить точное местонахождение товара на складе и отсутствие обновлений о том, был ли продукт доставлен или нет, приводит к тому, что клиент не может заказать новые продукты с прогнозируемой неэффективностью.
Этот пробел в обновлениях также в основном связан с использованием быстрых процессов, таких как отслеживание нескольких заказов, и необходимостью получения сведений о запасах в режиме реального времени.
3. Устаревшие продуктыОбновление продуктов с течением времени неизбежно для того, чтобы продукты оставались свежими и соответствовали тенденциям и соответствовали ожиданиям покупателей на рынке.
Таким образом, в этом процессе все старые товары, которые не проданы, должны быть зарегистрированы для облегчения очистки и должны освободить место для новых.
Оставление старых продуктов на складе также может привести к большим потерям и занять столь необходимое место на складе.
4. Анализ рыночного спросаАнализ состояния рынка очень важен, поскольку спрос ускоряет производство, за которым следует рост складских запасов.
Никакой анализ наиболее продаваемых областей или областей спроса не приведет к нехватке продукции на рынке, что приведет к снижению удовлетворенности клиентов и потере ценности бренда.
Внесение новых запасов без освобождения старых в конечном итоге приведет к убыткам и сокращению прибыли.
Как избежать Проблемы управления запасами , такие как неправильное управление при приобретении новых запасов и ручное обновление заказов, являются первичными или могут привести к тому, что некоторые продукты не будут обновляться и в конечном итоге будут повторно заказаны.
6. Неумение управлять инвентарными отходами и дефектамиУправление отходами в отрасли является одним из самых серьезных упущений, которое приводит к повреждению инвентарных запасов на складах.
При этом необходимо эффективно отслеживать бракованные изделия, чтобы поддерживать цикл поставки на склад и своевременные поставки.
С другой стороны, затраты, связанные с инвентарными отходами и дефектами, больше и приводят к огромным потерям в отрасли, если они остаются незамеченными.
7. Отсутствие централизованного центра инвентаризации
Отсутствие централизованного центра инвентаризации Представьте себе переключение нескольких вкладок для получения сведений о заказах клиентов и отслеживание данных в режиме реального времени. Это приводит к разочарованию менеджеров по запасам и медленной доставке результатов.
Без единой панели управления все разговоры, информация о заказах и отслеживание агентов доставки не будут поступать в один почтовый ящик.
Это затрудняет для менеджеров по инвентаризации управление запросами и отслеживание продуктов в инвентаре.
8. Расширение ассортимента продукцииРасширение ассортимента продукции и создание новых складов требуют эффективного управления запасами.
Ручное обновление списка запасов и отслеживание заказов без данных в режиме реального времени приведет к бесхозяйственности.
Все менеджеры по запасам должны просматривать заказы и сведения о доставке, а также отслеживать складские запасы, чтобы распределять поставки с наибольшим спросом.
Управление заказами клиентов во избежание перепроданности и истощения запасов является одной из самых сложных задач.
Своевременная доставка заказов и рассмотрение их жалоб, если в заказе есть какие-то проблемы, сыграют большую роль в обзорах и рейтингах, которые получит бренд.
Кроме того, в приоритете должны быть оптимизация процессов заказа, отслеживание доставки и информирование клиента на протяжении всего пути его заказа.
10. Рост конкуренцииРастущая конкуренция заставила малые предприятия расширить свои складские помещения, чтобы удовлетворить растущий спрос.
Это, в свою очередь, привело к тому, что компании уделили приоритетное внимание системе управления запасами, которая держит менеджеров в курсе всех деталей заказов.
Не отставать от конкурентов, поддерживать товарные запасы и реагировать на жалобы и запросы клиентов является приоритетом.
11. Вопросы цепочки поставок
Вопросы цепочки поставок Постоянные изменения в цепочке поставок по всему миру сказываются на планировании управления запасами.
В основном это связано с тем, что производители и оптовые дистрибьюторы принимают решение о перемещении ваших запасов и требуют гибкости в поставках с длительными сроками поставки.
Кроме того, с другой стороны, ручное отслеживание всех запасов только увеличит время доставки для ваших клиентов.
12. Отсутствие планирования производстваЕсли запасы не поступают на склад вовремя, чтобы соответствовать циклу спроса-предложения, это может быть очень неприятно.
Этому могут способствовать многие факторы, такие как медленное производство, отсутствие транспорта или задержки в сроках доставки, которые могут привести к отсутствию складских запасов.
Это, в свою очередь, приводит к задержке заказов клиентов и снижению рейтинга клиентов в социальных сетях.
13. Неправильное управление процессами Использование базовых технологий или ручное управление запасами не покажется сложной задачей, если предприятие небольшое и обслуживает небольшое количество клиентов.
Но когда он увеличится в размерах, все задачи, которые изначально были легкими, станут сложными и потребуют помощи для выполнения заказов клиентов.
14. Отсутствие необходимого программного обеспеченияПервоначально малый бизнес с ограниченным количеством доставок не будет чувствовать необходимости использовать платформу управления запасами.
Без необходимого программного обеспечения отслеживание запасов, создание отчетов и отслеживание агентов доставки будет невозможно.
15. Поддержание эффективного складаДля бизнеса процессы на складе для поддержания или управления товарными запасами многочисленны и включают множество шагов.
Такие процессы, как сбор, упаковка, получение и возврат, должны быть максимально эффективными для обеспечения бесперебойной доставки.
16. Неточность данных При ручном управлении складом сбор всех данных, необходимых для отслеживания состояния запасов и составления отчетов, кажется огромной задачей.
В наши дни отслеживание деталей вашего заказа должно осуществляться одним движением пальца, а не по телефону с длинным списком номеров для звонков.
17. Меньшая видимость процессаУчтите, что размещенный вами заказ не поставляется с системой отслеживания заказов, клиенты будут разочарованы и перейдут на бренд, который обеспечивает полную прозрачность.
Инвентарь, который трудно найти или отследить на складе, приводит к задержке доставки заказов.
Подбор правильных товарных запасов и поддержание сроков доставки клиентам очень важно для бизнеса и сохранения хороших впечатлений.
18. Поддержание надлежащего уровня запасовВыполнение заказов клиентов и поддержание запасов в соответствии с потребностями имеет жизненно важное значение в управлении запасами.
Продукты, которые легко портятся, и хрупкие запасы требуют специальной помощи при хранении.
Кроме того, с другой стороны, выбор надлежащих методов управления запасами для ценных запасов повысит удовлетворенность клиентов.
Управление складскими помещениями для размещения новых запасов может оказаться непростой задачей.
Использование ручного процесса, составление плана и выделение мест для инвентаризации потребует много времени и ресурсов.
Кроме того, план должен быть синхронизирован со временем поступления запасов на склад. Таким образом, в конечном счете, без автоматизированной системы инвентаризации эту роль сложно освоить.
20. Выставление счетов и документы вручнуюВручную отслеживать все отчеты об управлении запасами, заказы на покупку и счета-фактуры будет сложной задачей.
При этом время, затрачиваемое на составление счетов и счетов-фактур, будет большим и может привести к тому, что несколько элементов будут упущены. 1. Оценка запасов ежемесячные и квартальные отчеты.
Разделите отчеты об аудите по категориям и количеству циклов инвентаризации для расчета финансов.
На платформе управления запасами можно просматривать аудиторские отчеты по регионам и областям, а также планировать последующие финансовые годы.
Для ускорения управления запасами автоматизация всего процесса установки точек повторного заказа на основе текущих запасов и доступности сделает процессы эффективными.
Платформа управления запасами делает это, предотвращая задержки заказов и повышая уровень удовлетворенности клиентов.
3. Увеличьте объем хранения и обеспечьте безопасностьДля управления складом платформа управления запасами помогает быстро очищать запасы и удалять устаревшие продукты.
Сортировка складских запасов по отсекам и автоматизация процессов заказа, таких как упаковка и отгрузка, помогает справиться с проблемами управления запасами , с которыми сталкиваются менеджеры.
4. ПрогнозированиеПлатформа управления запасами с прогнозированием спроса позволяет вам предвидеть потребности и планировать заказы.
Благодаря интеграции с учетными записями и данными о продажах прогноз для вашего бизнеса электронной коммерции может быть установлен строго.
Планирование заказов инвентаря на основе меняющихся предпочтений клиентов, наличия запасов или покупательских тенденций станет прибыльным для бренда.
5. Меры контроляСистема управления запасами, являющаяся частью платформы управления запасами, помогает управлять запасами скоропортящихся, хрупких и снятых с производства продуктов.
Кроме того, периодическое техническое обслуживание оборудования, используемого для хранения запасов, является одной из важных задач управления запасами на складе для эффективного протекания процессов.
Такие преимущества, как отслеживание местоположения проблемы с запасами с указанием стоимости и количества, могут помочь нам выявить проблему и помочь нуждающимся клиентам. Все это можно сделать с помощью платформы управления запасами.
6. Эволюция упаковкиКлассифицируйте и распределяйте запасы в соответствии со стандартами упаковки на платформе управления запасами.
Это помогает контролировать расходы на доставку в зависимости от размера продукта и направляет их в легкодоступные места хранения.
Модернизация или переход на единую платформу решения для всех ваших запасов и управления запасами будет отличным решением для вашего бизнеса.
Функции отслеживания повторных заказов и закупок будут очень полезны всем менеджерам запасов на складах.
При этом автоматическое обновление товарных запасов, доступность данных о запасах в режиме реального времени и облачное хранилище отчетов будут очень полезны для более быстрого управления вашими запасами.
8. Отслеживание расширения линейки продуктовПлатформа управления запасами может использоваться для ведения учета нескольких продуктов с просмотром полной истории запасов.
Отслеживайте агентов по доставке, непроданные товары и товары на складе с помощью платформы.
Используйте аналитику, чтобы также увидеть спрос на линейку продуктов в разных местах, автоматически распределяя запасы для этого региона.
9. Добавление инструментов повышения производительности Отслеживание доставки, отгрузок, запасов и взаимодействия с клиентами с помощью мобильной или настольной версии обеспечивает доступ к информации в любое время и в любом месте.
Вся доступная информация хранится в облаке без необходимости многократного сохранения и выполняется автоматически.
Эта постоянная доступность инструментов повышает производительность и повышает степень удовлетворенности клиентов за счет ускорения выполнения процессов. Неиспользование инструментов повышения производительности является одной из основных проблем управления запасами , с которыми сталкиваются многие начинающие компании.
10. Воспользуйтесь преимуществом сроков выполнения заказа и прогнозируйте спросПри заказе продукции с высоким спросом рассмотрение сроков выполнения заказа является решающим шагом.
Товары с высоким спросом можно легко отслеживать и управлять ими со складов с помощью платформы управления запасами.
Используя непрерывные циклы заказа, платформа автоматизирует точки повторного заказа, вычисляя среднее время выполнения заказа, чтобы предотвратить дефицит.
Система управления запасами также может помочь в прогнозировании высокого спроса и соответствующем распределении запасов.
Платформы управления запасами предлагают передовые технологии, такие как сканирование местоположения продукта и технология штрих-кода для улучшения возможностей отслеживания запасов.
При этом использование платформы на мобильных устройствах, оснащенных облачным хранилищем, может упростить управление запасами и помочь эффективно управлять складскими запасами.
12. Четкие отчеты об эффективностиОтслеживайте все данные о заказах, измеряйте уровень удовлетворенности клиентов и другую информацию, например скорость обработки заказов, чтобы лучше обслуживать клиентов.
Кроме того, получайте отчеты по областям с наибольшим объемом продаж, сегментам клиентов и времени доставки, чтобы улучшить качество обслуживания клиентов.
13. Включите изображения В базе данных инвентаризации добавление изображений будет более привлекательным фактором для покупки, улучшения процессов и приведет к лучшим результатам.
Например, добавление изображения складских запасов на платформу управления запасами позволяет нам идентифицировать, расставлять приоритеты и разделять запасы на основе запросов.
Также добавление изображений содержимого в инвентарь может увеличить продажи, подтверждая оптовую закупку и отгрузку готового товара.
14. Безбумажные транзакцииБольшое преимущество использования платформ управления запасами заключается не только в упрощении процессов, но и в сокращении использования бумаги для отчетов и счетов.
Принимая во внимание воздействие на окружающую среду, отказ от бумаги — отличный и модный шаг для компаний, желающих перейти на инструменты нового поколения.
Благодаря этому преимуществу безбумажный учет значительно ускорит процессы учета, отслеживания и отчетности.
15. Следите за сервисными процессами Самым большим преимуществом системы управления запасами является ее способность отслеживать процессы обслуживания, такие как ошибки доставки, поврежденные или дефектные продукты и пропущенные встречи по доставке.
Дополнительные функции, такие как оценка производительности поставщика, выявление и устранение проблем в цепочке поставок, а также минимизация ошибок для обеспечения бесперебойного потока процессов инвентаризации, улучшат общий процесс.
16. Отслеживание в нескольких местахУправляйте складами в разных местах с помощью функций отслеживания в нескольких местах, таких как отслеживание запасов и принятие мер по предотвращению затоваривания складов.
Такие преимущества, как планирование уведомлений для автоматического отслеживания запасов и настройка нескольких вкладок для отслеживания складских процессов и доступа к важным сведениям о транзите, ускорят процессы.
17. Техническая поддержка и обновленияПри управлении запасами список функций может быть огромным и часто сбивает с толку менеджеров по запасам.
Для этого будет назначена онлайновая или офлайновая поддержка стажеров для помощи и обучения продукту.
Это может улучшить отношения с клиентами и помочь лучше понять продукт, чтобы повысить уровень их производительности.
18. Улучшение связиС помощью платформы управления запасами можно также улучшить связь с поставщиками.
Имея встроенную информационную панель, менеджеры по инвентаризации могут просматривать все данные инвентаризации в режиме реального времени с помощью простого пользовательского интерфейса.
Расширенные инструменты, такие как Kapture предлагает автоматические сообщения для связи и помогает управлять бухгалтерией, продажами и складскими операциями в одном окне.
19. Автоматизация выставления счетов и отчетовПлатформа управления запасами может помочь предприятиям выставлять счета и отчеты, полностью автоматизируя процесс и сохраняя его.
Все счета, счета-фактуры и отчеты, связанные с товарно-материальными запасами, будут храниться в соответствии с датами и могут быть просмотрены или загружены в любое время и на любом устройстве.
Одна из самых больших проблем управления запасами , которую можно решить с помощью эффективной платформы управления.
Используя платформу управления запасами, списки запасов можно отслеживать и перемещать в соответствии с их рыночным спросом.
Запасы новых продуктов могут быть получены только в зависимости от спроса и наличия свободного места на складе.
Нужна платформа управления запасами, которая может больше?
Платформа управления запасами Kapture предлагает все, что необходимо для бизнеса в сфере электронной коммерции, не допуская неэффективного управления.
Такие функции, как доступность данных о запасах в режиме реального времени, параметры пользовательской настройки, отслеживание агентов доставки, информация о счетах и аналитика, делают это программное обеспечение хорошим вариантом.
Хотите узнать больше? Обратитесь к нам за демонстрацией.

 24 КБ
24 КБ 54 МБ
54 МБ Вместо этого будет создан пустой словарь:
Вместо этого будет создан пустой словарь: Это обусловлено тем фактом, что внутренняя реализация set основана на хеш-таблицах. Например, списки и словари – это изменяемые объекты, которые не могут быть элементами множеств. Большинство неизменяемых типов в Python (int, float, str, bool, и т.д.) – хешируемые. Неизменяемые коллекции, например tuple, являются хешируемыми, если хешируемы все их элементы.
Это обусловлено тем фактом, что внутренняя реализация set основана на хеш-таблицах. Например, списки и словари – это изменяемые объекты, которые не могут быть элементами множеств. Большинство неизменяемых типов в Python (int, float, str, bool, и т.д.) – хешируемые. Неизменяемые коллекции, например tuple, являются хешируемыми, если хешируемы все их элементы. name = name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self.name}")'
print(City("Moscow") == City("Moscow"))
# Вывод:
False
cities = {City("Moscow"), City("Moscow")}
print(cities)
# Вывод
{City("Moscow"), City("Moscow")}
name = name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self.name}")'
print(City("Moscow") == City("Moscow"))
# Вывод:
False
cities = {City("Moscow"), City("Moscow")}
print(cities)
# Вывод
{City("Moscow"), City("Moscow")} __class__):
return False
return self._name == other._name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self._name}")'
__class__):
return False
return self._name == other._name
def __repr__(self) -> str:
""" Определим метод __repr__ для наглядности следующих примеров
"""
return f'City("{self._name}")' Это один из самых распространённых вариантов использования множеств. Такая операция выполняется в среднем за
Это один из самых распространённых вариантов использования множеств. Такая операция выполняется в среднем за 
 Или другими словами, пересечение этих множеств является пустым множеством.
Или другими словами, пересечение этих множеств является пустым множеством. issuperset(fibonacci_numbers):
print("Надмножество!")
# Вывод:
Надмножество!
issuperset(fibonacci_numbers):
print("Надмножество!")
# Вывод:
Надмножество! # Отличие состоит в том, что метод union принимает не только
# объект типа set, а любой iterable-объект
you_fruit_list: list = list(your_fruits)
our_fruits: set = my_fruits.union(you_fruit_list)
print(our_fruits)
# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"}
# Отличие состоит в том, что метод union принимает не только
# объект типа set, а любой iterable-объект
you_fruit_list: list = list(your_fruits)
our_fruits: set = my_fruits.union(you_fruit_list)
print(our_fruits)
# Вывод (порядок может быть другим):
{"apple", "banana", "orange", "pear"} update(i**2 for i in [1, 2, 3])
print(numbers)
# Вывод (порядок может быть другим):
{1, 2, 3, 4, 9}
update(i**2 for i in [1, 2, 3])
print(numbers)
# Вывод (порядок может быть другим):
{1, 2, 3, 4, 9} Метод
Метод  Следует отметить, что удаление элемента, как и в аналогичном случае с добавлением элементов, изменяет исходное множество. Удаление одного элемента из множества имеет вычислительную сложность
Следует отметить, что удаление элемента, как и в аналогичном случае с добавлением элементов, изменяет исходное множество. Удаление одного элемента из множества имеет вычислительную сложность  , также существует два специальных метода –
, также существует два специальных метода –  Я буду рад, если у вас есть какие-либо конструктивные замечания и дополнения.
Я буду рад, если у вас есть какие-либо конструктивные замечания и дополнения.




 (См. также пример 10.)
(См. также пример 10.) Таким образом, пересечение с \(\overline{B}\) приводит к тому, что остаются только значения, не входящие в \(B\). То есть \(A\cap\overline{B}\) - это \(A\) со всеми удаленными значениями из \(B\). Таким образом, мы видим, что эти множества содержат одни и те же элементы. ∎
Таким образом, пересечение с \(\overline{B}\) приводит к тому, что остаются только значения, не входящие в \(B\). То есть \(A\cap\overline{B}\) - это \(A\) со всеми удаленными значениями из \(B\). Таким образом, мы видим, что эти множества содержат одни и те же элементы. ∎ Например:
Например: {n} S_i\,.\]
Студенты берут 92\,.\]
{n} S_i\,.\]
Студенты берут 92\,.\] Множество, писал Кантор, есть совокупность определенных, различимых объектов восприятия или мысли, рассматриваемых как единое целое. Объекты называются элементами или членами множества.
Множество, писал Кантор, есть совокупность определенных, различимых объектов восприятия или мысли, рассматриваемых как единое целое. Объекты называются элементами или членами множества.
 Набор может быть определен правилом членства (формулой) или перечислением его членов в фигурных скобках. Например, множество, заданное правилом «простые числа меньше 10», также может быть задано как {2, 3, 5, 7}. В принципе, любое конечное множество может быть определено явным списком его элементов, но для определения бесконечных множеств требуется правило или шаблон для указания членства; например, многоточие в {0, 1, 2, 3, 4, 5, 6, 7, …} указывает, что список натуральных чисел ℕ можно продолжать бесконечно. Пустой (или недействительный, или нулевой) набор, обозначенный {} или Ø, вообще не содержит элементов. Тем не менее, он имеет статус набора.
Набор может быть определен правилом членства (формулой) или перечислением его членов в фигурных скобках. Например, множество, заданное правилом «простые числа меньше 10», также может быть задано как {2, 3, 5, 7}. В принципе, любое конечное множество может быть определено явным списком его элементов, но для определения бесконечных множеств требуется правило или шаблон для указания членства; например, многоточие в {0, 1, 2, 3, 4, 5, 6, 7, …} указывает, что список натуральных чисел ℕ можно продолжать бесконечно. Пустой (или недействительный, или нулевой) набор, обозначенный {} или Ø, вообще не содержит элементов. Тем не менее, он имеет статус набора.
 Если
плоская кривая
определена уравнением
, причем перемещение от
точки
к точке
происходит при изменении
от
до
, то
Если
плоская кривая
определена уравнением
, причем перемещение от
точки
к точке
происходит при изменении
от
до
, то Сделать чертеж.
Сделать чертеж.

 Тогда криволинейный интеграл первого рода вдоль кривой вычисляется по формуле
Тогда криволинейный интеграл первого рода вдоль кривой вычисляется по формуле





 интеграл и может быть определен в двух, трех и более измерениях.
интеграл и может быть определен в двух, трех и более измерениях. Поясним, как это делается для кривых в R9.0044 2 .
Случай с R 3 аналогичен.
Поясним, как это делается для кривых в R9.0044 2 .
Случай с R 3 аналогичен.

 r ‘(t) = -x + 3xy + x + z = 3xy + z
r ‘(t) = -x + 3xy + x + z = 3xy + z r ‘(t)dt = Mdx + Ndy + Pdz
r ‘(t)dt = Mdx + Ndy + Pdz Линейные интегралы Показать мобильное уведомление Показать все примечания Скрыть все примечания
Линейные интегралы Показать мобильное уведомление Показать все примечания Скрыть все примечания Мы также рассмотрим одну из наиболее важных теорем, касающихся линейных интегралов, — теорему Грина.
Мы также рассмотрим одну из наиболее важных теорем, касающихся линейных интегралов, — теорему Грина.

 Инвестиция ради процентов представляет собой краткосрочную стратегию, направленную на получение
Инвестиция ради процентов представляет собой краткосрочную стратегию, направленную на получение 4. АУДИТ НАЧИСЛЕННЫХ ПРОЦЕНТОВ
4. АУДИТ НАЧИСЛЕННЫХ ПРОЦЕНТОВ =>
=> Потребность в опоре на концепцию внешней
Потребность в опоре на концепцию внешней Практика, практика и еще раз практика
Практика, практика и еще раз практика
 руб.
руб.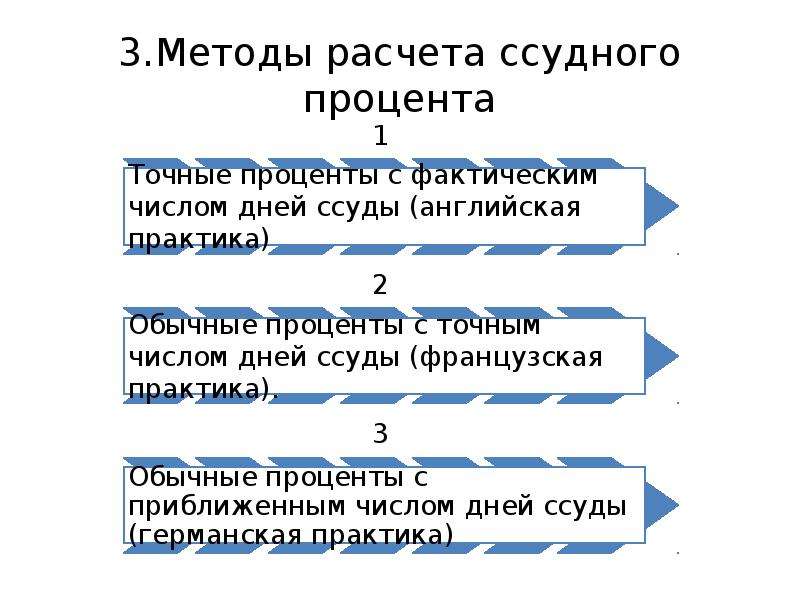
 Основное
отличие сложных процентов от
простых процентов меняется от одного
расчетного периода к другому.
Основное
отличие сложных процентов от
простых процентов меняется от одного
расчетного периода к другому.  При этом оговариваются годовая
номинальная ставка и
количество начислений за год. Фактически за базовый период
принимается часть
года со ставкой сложных
процентов , так что
При этом оговариваются годовая
номинальная ставка и
количество начислений за год. Фактически за базовый период
принимается часть
года со ставкой сложных
процентов , так что  Эта плата называется процентом. Сумма процентов, которую нам придется платить, может варьироваться в зависимости от многих факторов, в том числе от того, сколько мы взяли взаймы, сколько времени нам потребуется, чтобы погасить их, а также от общей экономической ситуации в стране. Когда экономика в плохом состоянии, люди с меньшей вероятностью будут давать деньги взаймы, поэтому плата будет выше, и наоборот, когда экономика в порядке.
Эта плата называется процентом. Сумма процентов, которую нам придется платить, может варьироваться в зависимости от многих факторов, в том числе от того, сколько мы взяли взаймы, сколько времени нам потребуется, чтобы погасить их, а также от общей экономической ситуации в стране. Когда экономика в плохом состоянии, люди с меньшей вероятностью будут давать деньги взаймы, поэтому плата будет выше, и наоборот, когда экономика в порядке. С другой стороны, сложные проценты зависят не только от основной суммы кредита, но и от процентов, которые накапливаются по нему в течение определенного периода времени. Расчет сложных процентов немного сложнее, чем расчет простых процентов.
Общая формула для расчета сложных процентов:
Сложные проценты = [P(1 + i) n ] — П. Здесь; P — основная сумма, I — процентная ставка, n — количество периодов начисления сложных процентов. Эти рабочие листы объясняют, как рассчитать простые проценты. Хотя это может показаться бесконечной задачей, она будет иметь большое значение в вашей будущей жизни при банковском обслуживании и покупке дома.
С другой стороны, сложные проценты зависят не только от основной суммы кредита, но и от процентов, которые накапливаются по нему в течение определенного периода времени. Расчет сложных процентов немного сложнее, чем расчет простых процентов.
Общая формула для расчета сложных процентов:
Сложные проценты = [P(1 + i) n ] — П. Здесь; P — основная сумма, I — процентная ставка, n — количество периодов начисления сложных процентов. Эти рабочие листы объясняют, как рассчитать простые проценты. Хотя это может показаться бесконечной задачей, она будет иметь большое значение в вашей будущей жизни при банковском обслуживании и покупке дома. Решается примерная задача и предлагаются две практические задачи.
Решается примерная задача и предлагаются две практические задачи. Дано десять задач.
Дано десять задач. 
 Предлагаются три задачи, а также место, где учащиеся могут скопировать правильный ответ, когда он будет дан.
Предлагаются три задачи, а также место, где учащиеся могут скопировать правильный ответ, когда он будет дан. 
 Это также тип процентов, которые банки выплачивают клиентам по их сберегательным счетам.
Это также тип процентов, которые банки выплачивают клиентам по их сберегательным счетам. Обычно выражаемый в процентах, он представляет собой комиссию или сбор, который заемщик платит кредитору за финансируемую сумму.
Обычно выражаемый в процентах, он представляет собой комиссию или сбор, который заемщик платит кредитору за финансируемую сумму. 
 Сумма кредита составляет 18 000 долларов США. Годовая процентная ставка по кредиту составляет 6%. Срок кредита составляет три года.
Сумма кредита составляет 18 000 долларов США. Годовая процентная ставка по кредиту составляет 6%. Срок кредита составляет три года.


 Основные условия те же: кредит в размере 10 000 долларов, процентная ставка 5% и срок 5 лет.
Основные условия те же: кредит в размере 10 000 долларов, процентная ставка 5% и срок 5 лет. Простые проценты, однако, не учитывают силу сложных процентов или процентов на проценты, где после первого года 1% фактически будет заработан на балансе в 101 доллар, что в сумме составит 1,01 доллара. В следующем году 1% будет заработан на 102,01 доллара, что составит 1,02 доллара. И так один.
Простые проценты, однако, не учитывают силу сложных процентов или процентов на проценты, где после первого года 1% фактически будет заработан на балансе в 101 доллар, что в сумме составит 1,01 доллара. В следующем году 1% будет заработан на 102,01 доллара, что составит 1,02 доллара. И так один. Когда наступает срок погашения кредита, вместо 13 000 долларов вы в конечном итоге должны 13 310 долларов. Хотя вы можете не считать 310 долларов огромной разницей, этот пример — всего лишь трехлетняя ссуда; сложные проценты накапливаются и становятся угнетающими при более длительных сроках кредита.
Когда наступает срок погашения кредита, вместо 13 000 долларов вы в конечном итоге должны 13 310 долларов. Хотя вы можете не считать 310 долларов огромной разницей, этот пример — всего лишь трехлетняя ссуда; сложные проценты накапливаются и становятся угнетающими при более длительных сроках кредита.

 А что же такое история в целом? На сегодняшний день на этот вопрос даётся два ответа.
А что же такое история в целом? На сегодняшний день на этот вопрос даётся два ответа. По мнению этих историков и философов, подход «история- единое целое» единственно верный, потому что заключается 1.в единстве происхождения человека как вида, 2. в эволюции системы родства и семейно-брачных отношений. 3.в общности языков, 4. в сходной эволюции возникновения и развития религиозных верований, 5.в единой логике движения мировой истории и т.д.
По мнению этих историков и философов, подход «история- единое целое» единственно верный, потому что заключается 1.в единстве происхождения человека как вида, 2. в эволюции системы родства и семейно-брачных отношений. 3.в общности языков, 4. в сходной эволюции возникновения и развития религиозных верований, 5.в единой логике движения мировой истории и т.д.
 Все исторические явления и процессы тесно взаимосвязаны и взаимообусловлены. Например, победа в битве на Куликовом поле 1380г. имела переломное значение в борьбе Руси с монгольским игом, а убийство Александра II в 1881 г. привело к остановке проведения реформ и т.д. и таких примеров можно привести много.
Все исторические явления и процессы тесно взаимосвязаны и взаимообусловлены. Например, победа в битве на Куликовом поле 1380г. имела переломное значение в борьбе Руси с монгольским игом, а убийство Александра II в 1881 г. привело к остановке проведения реформ и т.д. и таких примеров можно привести много. Если элементы последовательности расположены в порядке убывания, то порядок последовательности убывающий. Арифметическая последовательность, геометрическая последовательность, последовательность Фибоначчи, гармоническая последовательность, треугольная числовая последовательность, квадратная числовая последовательность и кубическая числовая последовательность — вот несколько примеров конкретных последовательностей.
Если элементы последовательности расположены в порядке убывания, то порядок последовательности убывающий. Арифметическая последовательность, геометрическая последовательность, последовательность Фибоначчи, гармоническая последовательность, треугольная числовая последовательность, квадратная числовая последовательность и кубическая числовая последовательность — вот несколько примеров конкретных последовательностей.

 . n раз) + (а n + а n + a n + ….. n раз)
. n раз) + (а n + а n + a n + ….. n раз)
 Найдите сумму арифметической последовательности 8 терминов, первый и последний термины равны 4 и 10 соответственно.
Найдите сумму арифметической последовательности 8 терминов, первый и последний термины равны 4 и 10 соответственно. 
 Первый член a 1 , общая разница
это д ,
а количество терминов n . Сумма
арифметический ряд получается путем умножения числа
термины раз
среднее значение первого и последнего членов.
Первый член a 1 , общая разница
это д ,
а количество терминов n . Сумма
арифметический ряд получается путем умножения числа
термины раз
среднее значение первого и последнего членов.

 Изучить информацию о том, как Yandex использует cookie и другие Ваши данные, можно тут: https://yandex.com/legal/confidential/?lang=ru.
Изучить информацию о том, как Yandex использует cookie и другие Ваши данные, можно тут: https://yandex.com/legal/confidential/?lang=ru. Пользователь может вносить свои записи в эти справочники.
Пользователь может вносить свои записи в эти справочники.

.jpg)






 Так что не стесняйтесь использовать и ссылаться на друзей.
Так что не стесняйтесь использовать и ссылаться на друзей. Ежедневный калькулятор может использоваться кем угодно; пары ведут обратный отсчет до своего большого дня, студенты осторожно
готовятся к датам испытаний и даже ждут мам, с тревогой наблюдая, как проходят секунды, прежде чем они встретят своего новорожденного. Дни, прошедшие с калькулятора, дают уникальное и интересное значение времени, особенно когда оно проходит.
Ежедневный калькулятор может использоваться кем угодно; пары ведут обратный отсчет до своего большого дня, студенты осторожно
готовятся к датам испытаний и даже ждут мам, с тревогой наблюдая, как проходят секунды, прежде чем они встретят своего новорожденного. Дни, прошедшие с калькулятора, дают уникальное и интересное значение времени, особенно когда оно проходит. Мы избавим вас от всех препятствий и всех ненужных тестов, предоставив вам чистый и простой
доступ к разделу ввода даты для подсчета, где вы можете определить пределы диапазона дат, который вы устанавливаете. Это буквально 1-минутный процесс, для которого вам не нужна помощь.
Мы избавим вас от всех препятствий и всех ненужных тестов, предоставив вам чистый и простой
доступ к разделу ввода даты для подсчета, где вы можете определить пределы диапазона дат, который вы устанавливаете. Это буквально 1-минутный процесс, для которого вам не нужна помощь.
 05.13
05.13  by 2013-2016
by 2013-2016

 Разрешите получать регулярные обновления!
Разрешите получать регулярные обновления! Поэтому я надеюсь, что можно ответить на мой вопрос, используя одно из этих определений.
Поэтому я надеюсь, что можно ответить на мой вопрос, используя одно из этих определений. Вы можете легко (с помощью некоторых тригонометрических формул) вычислить значения $\sin x$ для $x=0,\pi/6,\pi/3,\pi/4,\pi/2, \pi/ 12,\пи/5$. Постройте эти значения.
Вы можете легко (с помощью некоторых тригонометрических формул) вычислить значения $\sin x$ для $x=0,\pi/6,\pi/3,\pi/4,\pi/2, \pi/ 12,\пи/5$. Постройте эти значения.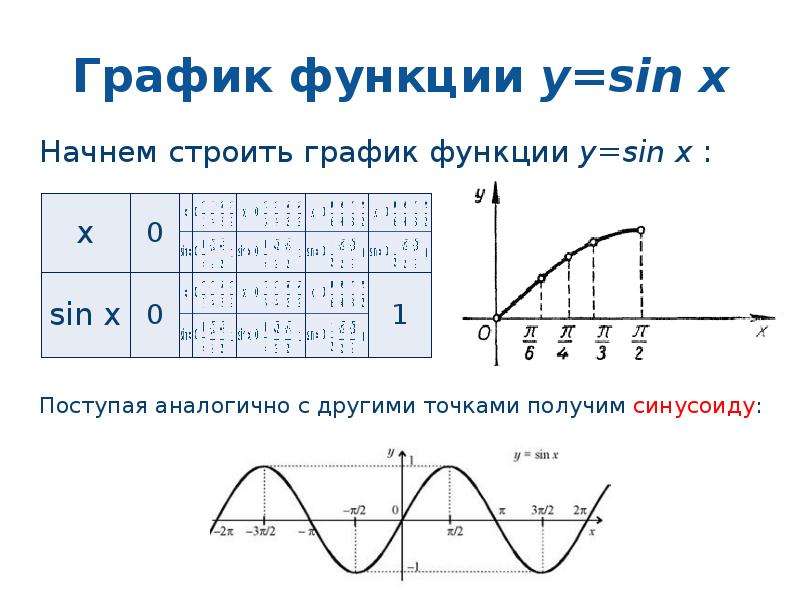 Координата $y$ точки равна $\sin\theta$, где $\theta$ – угол между точкой, началом координат и точкой $(1,0)$ (и, конечно, измеренный положительный в направлении против часовой стрелки с положительной осью $x$, соответствующей $\theta=0$).
Координата $y$ точки равна $\sin\theta$, где $\theta$ – угол между точкой, началом координат и точкой $(1,0)$ (и, конечно, измеренный положительный в направлении против часовой стрелки с положительной осью $x$, соответствующей $\theta=0$).


 00грн – 2,300.00грнКупить
00грн – 2,300.00грнКупить 00грн
00грн 00грн
00грн 00грн
00грн 80грн Купить
80грн Купить 50грн
50грн 28грн – 3,863.54грнКупить
28грн – 3,863.54грнКупить 20грн
20грн 68грн – 8,298.40грнКупить
68грн – 8,298.40грнКупить 40грнКупить
40грнКупить 00грн
00грн 00грн
00грн




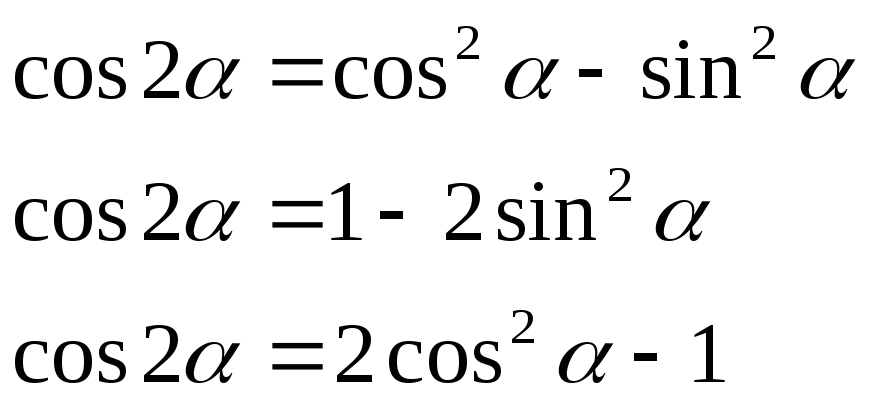 к. cos 5х: cos 5х =1, а sin 5х: cos 5х= tg 5x, то получим:
к. cos 5х: cos 5х =1, а sin 5х: cos 5х= tg 5x, то получим:
 Сразу отметим, что не стоит путать формулы суммы и разности синусов и косинусов с формулами синусов и косинусов суммы и разности. Ниже мы перечислим эти формулы, приведем их вывод и покажем примеры применения для конкретных задач.
Сразу отметим, что не стоит путать формулы суммы и разности синусов и косинусов с формулами синусов и косинусов суммы и разности. Ниже мы перечислим эти формулы, приведем их вывод и покажем примеры применения для конкретных задач.

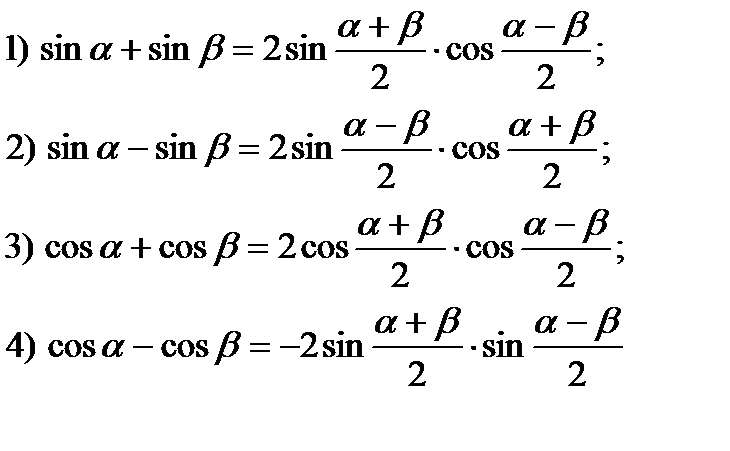 Пусть α = π 2 , β = π 6 . Вычислим значение суммы синусов этих углов. Сначала воспользуемся таблицей основных значений тригонометрических функций, а затем применим формулу для суммы синусов.
Пусть α = π 2 , β = π 6 . Вычислим значение суммы синусов этих углов. Сначала воспользуемся таблицей основных значений тригонометрических функций, а затем применим формулу для суммы синусов. Формулы суммы и разности синусов и косинусов широко используются при решении тригонометрических уравнений и при преобразовании тригонометрических выражений.
Формулы суммы и разности синусов и косинусов широко используются при решении тригонометрических уравнений и при преобразовании тригонометрических выражений.


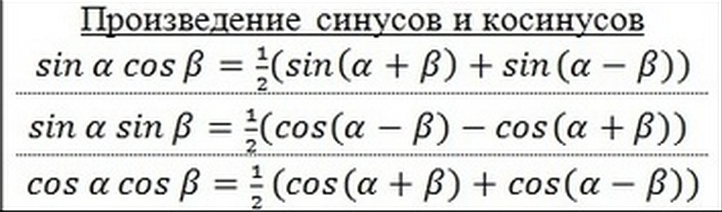 29 а – 1 учащийся решает на доске, остальные – в тетради.
29 а – 1 учащийся решает на доске, остальные – в тетради. Ответим на вопрос: достигли мы цели нашего урока?
Ответим на вопрос: достигли мы цели нашего урока?
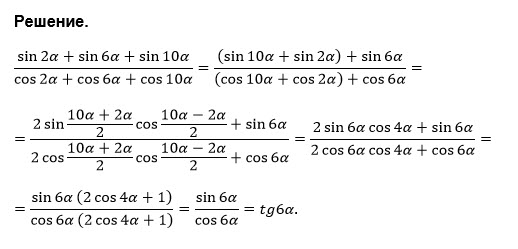 поставьте $t = -\pi/2,$, чтобы показать, что $\sin$ — нечетная функция. после всего этого вы получаете
$$\sin(t-s) = \sin t \cos t — \cos t \sin s $$ и два для сумм. 9{ix}$.
поставьте $t = -\pi/2,$, чтобы показать, что $\sin$ — нечетная функция. после всего этого вы получаете
$$\sin(t-s) = \sin t \cos t — \cos t \sin s $$ и два для сумм. 9{ix}$. Мы знаем тригонометрические углы 45° и 30°, но не знаем тригонометрический угол (45° + 30° = 75°). Таким образом, чтобы упростить эти типы проблем. Мы изучим тригонометрические формулы или тождества суммы и разности двух углов, что облегчит задачу.
Мы знаем тригонометрические углы 45° и 30°, но не знаем тригонометрический угол (45° + 30° = 75°). Таким образом, чтобы упростить эти типы проблем. Мы изучим тригонометрические формулы или тождества суммы и разности двух углов, что облегчит задачу.
 .(1)
.(1) 
 Преобразуйте каждое из следующих произведений в сумму или разность.
Преобразуйте каждое из следующих произведений в сумму или разность.  Найдите
Найдите  Выразите каждое из следующих чисел в виде произведения
Выразите каждое из следующих чисел в виде произведения  Докажите, что: 1 + cos 2x + cos 4x + cos 6x = 4 потому что x cos 2x cos 3x
Докажите, что: 1 + cos 2x + cos 4x + cos 6x = 4 потому что x cos 2x cos 3x 
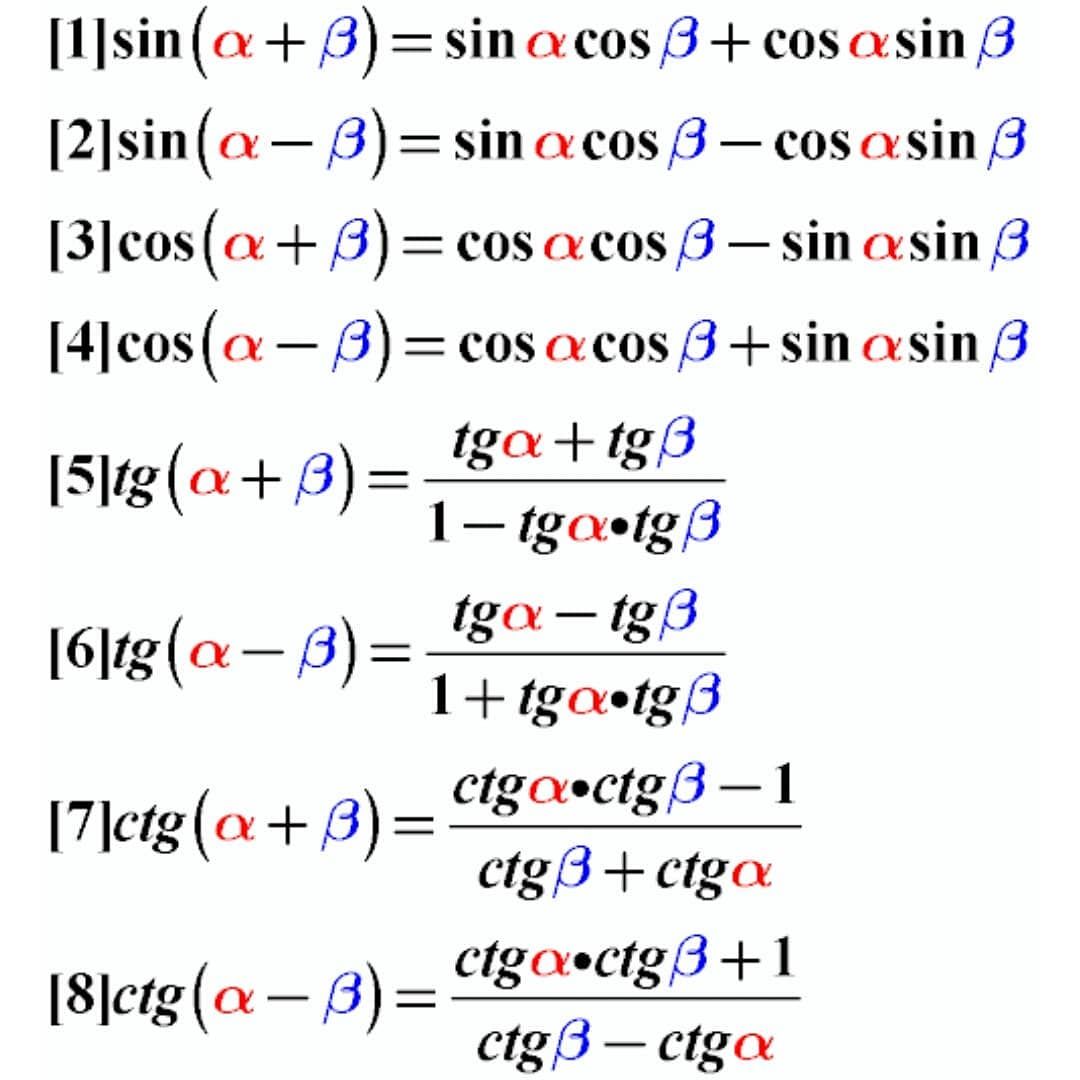 .(1)
.(1) .(1)
.(1) .(из тождества 1)
.(из тождества 1)
