250 сантиметр в миллиметры | 250 см в миллиметры
Переведите 250 сантиметров в миллиметры (см в миллиметры) с помощью нашего калькулятора перевода и таблиц перевода. Чтобы преобразовать 250 см в миллиметры, воспользуйтесь приведенной ниже формулой прямого преобразования.
250 см = 2500 мм.
Вы также можете конвертировать 250 сантиметров в другие (популярные) единицы измерения длины.
250 САНТИМЕТР
=
2500 МИЛЛИМЕТРОВ
Конвертерный калькулятор
Количество:
От:
ACR — AcresCMK — Квадратные сантиметрыFTK — Квадратные футыHAR — ГектарыINK — Квадратные дюймыKMK — Квадратные километрыMIK — Квадратные милиMTK — Квадратные метрыYDK — Квадратные ярдыANN — YearsDAY — DaysHUR — HoursMCS — MicrosecondsMIN — MinutesMLS — MillisecondsMON — MonthsSEC — SecondsWEE — WeeksBIT — BitsBYT — BytesEBI — ExabitsEBY — ExabytesGBI — GigabitsGBY — GigabytesKBI — KilobitsKBY — KilobytesMBI — MegabitsMBY — MegabytesPBI — PetabitsPBY — PetabytesTBI — TerabitsTBY — TerabytesBLL — Баррели (нефть)CMQ — Кубические сантиметрыFTQ — Кубические футыGLI — Галлоны (Великобритания)GLL — Галлоны (США, жидкость)LTR — ЛитрыMLT — МиллилитрыMTQ — Кубические метрыOZI — Унции UKBTU — BTUCAL — КалорииERG — ErgEVL — Электрон ВольтFPD — Фут-фунтHPH — Лошадиная сила-часIPD — Дюйм-фунтJOU — ДжоулиCMT — СантиметрDMT — ДециметрыFOT — ФутыINH — ДюймыKMT — КилометрыMMT — МиллиметрыMTR — МетрыSMI — МилиYRD — YardCTM — КаратыGRM — граммыKGM — килограммыLBR — фунтыMGM — миллиграммыONZ — унции TNE — тонны (метрические)DEG — градусыGRD — градыRAD - радианыFPM — футы/минутыFPS — футы/секундыKMH — километры/часKMS — километры/секундыKNT — узлыMPH — мили/часMTS — метры/секундыGCC — Граммы/кубический сантиметрKCC — килограммы/кубический сантиметрKLI — килограммы/литрKMC — килограммы/кубический метрOCI — унции/кубический дюймOGL — унции/галлонPCF — фунты/кубический футPCI — фунты/кубический дюймPGL — фунты/галлонJCM — джоули/сантиметрKGF — килограмм ForceNWN — НьютоныPFC — Фунт-силаA0 — Бор, атомная единица длиныAST — АнгстремAU — Астрономическая единицаCBL — длина кабеля (имперская)CBL(US) — Длина кабеля USCH — ЦепиF — Французский charriereFM — FermiFNG — FingerFNG(CLOTH) — Палец (ткань)FTM — FathomFUR — FurlongHH — HandLD — Световой деньLEA — лига (земля)LH — Световой часLM — Световая минутаLN — ЛинияLNK (G. S.) — Ссылка (Gunter’s; Геодезист) LNK (RE) — Link (Ramsden’s; Engineer’s) LS — Световой-секундный — Световой годM — Метр (базовая единица СИ)MIL — Мил (Швеция и Норвегия)MILE DATA — Мили (тактические или данные)MK — MickeyNAIL — Гвоздь (ткань)NL — Морская лигаNM — НанометрNMI — Морские милиNMI I — Морская миляP — PalmPC — ParsecPICA — PicaPM — Пикометр (бикрон, клеймо)POINT — точка (американский, английский)PT — PaceQUART — QuarterSHAKU — Shaku (Japan)SPT — SpatTH — Мил (тыс.) TWP — TwipUM — Микрометр (стар. микрон) XU — X единица измерения; siegbahnABA — Электромагнитная единица AbampereAMP — Ампер (базовая единица Si)ESU — Esu в секунду Статампер (CgsABC — Абкулон Электромагнитная единицаATU — Атомная единица зарядаCLM — КулонFRD — ФарадейMAH — Миллиампер-часSTT — Статкулон Франклин ЭлектростABV — Абвольт (единица Cgs)STV — Статвольт ( Cgs Unit)VLT — Вольт (Si Unit)ACF — Акр-футыACI — Акры-дюймыBIB — Баррели (нефтяные)BII — Баррели (британские)BIU — Баррели (Us Dry)BKT — Ведра (британские)BRO — Галлоны (пивные)BUD — Бушели (Us Dry Level)BUI — Бушели (Imperial)BUU — Бушели (Us Dry Heaped)CMB — CoombsCMI — Cubic MilesCP — CupsCRF — Cord-FootsCRW — Cords (Дрова)CUF — Cubic FathomsCUI — Cubic InchsCUT — Cubic FootsCUY — Cubic ЯрдыDSI — тире (имперские фунты)DSS — десертные ложки (имперские фунты)DSU — тире (США)FBM — борд-футыFFT — пятые FID — жидкие драхмы (имперские)FIS — жидкие скрукле (имперские)FLB — бочки (США, жидкие)FLU — жидкие драмы ( Us) Us FluidramFRK — FirkinsGAI — галлоны (имперские единицы)GAU — галлоны (Us Dry)GAW — галлоны (Us Fluid Wine)GLU — Teacups (gills)GTT — DropsHDI — Hogsheads (Imperial)HHU — Hogsheads (Us)JGR — Jiggers ( Bartending)KLD — KilderkinsLMD — LambdasLOD — LoadsLST — LastsM3 — Кубические метры (Si Unit)MII — Minims (Imperial)MIU — Minims (Us)OZF — Унции (Fluid Us Food NutritioPER — PerchsPKI — Pecks (Imperial)PKU — Pecks (Us) Сухой)PNI — пинчи (британские)PNU — пинчи (американские)PON — PonysPOT — Pottle QuartersPP — стыковые трубыPTI — пинты (британские)PUD — пинты (Us Dry)PUF — пинты (Us Fluid)QRF — Quart S (Us Fluid) QRT — Кварталы QTI — Кварты (британские)QTU — Кварты (Us Dry)RGS — Реестр TonsSCI — Мешки (британские) BagsSCU — Мешки(Us)SHT — Shots (Us)SM — SeamsSTK — Забастовки (Imperial)STU — Забастовки (Us) )TBC — столовые ложки (канадские)TBF — столовые ложки (обычные в США)TBM — столовые ложки (метрические)TBS — столовые ложки (в австралийских единицах измеренияTCA — чайные ложки (канадские) TFD — столовые ложки (Us Food NutritionTIM — чайные ложки (британские)TMF — Timber FootsTMT — чайные ложки ( Метрическая система)TND – тонны (водоизмещение)TNT – тонны (воды)TNW – тонны (фрахт)TSC – чайные ложки (стандарт США)TSF – чайные ложки (США Food Nutrition) WEY — Wey (Us)ACM — Атмосфера-кубический фут в минутуACS — Атмосфера-кубический фут в секунду SecoATC — Атмосфера-кубический сантиметр PeATH — Атмосфера-кубический фут в часBTJ — BTU (Международная таблица) В расчете на BTN — BTU (Международная таблица) В расчете на BTS — БТЕ (международная таблица) по CAS — Калория (международная таблица) ERS — Эрг в секундуFMF — Фут-фунт-сила в минутуFT — Фут-фунт-сила в часFTO — Фут-фунт-сила в секундуHPS — Лошадиная силаLAM — Литр-атмосфера в час MinuteLSC — LusecLTS — Литр атмосферы в секундуPNC — PonceletSQL — Прямой эквивалент квадратного фута TC — Тонна кондиционирования воздухаTMS — Атмосфера-кубический сантиметр PeTRM — Тонна охлаждения (ImperialTRR — Тонна охлаждения (It)AMU — Единица атомной массы UnifiedAT — Анализ тонны (Короткий)ATS — Ton Assay (Длинный)BAC — Bag (Coffee)BDM — Bag (Portland Cement)BRG — BargeCLV — CloveCRT — CrithCT — Carat (Metric)DA — DaltonDRT — Dram (Apothecary Troy)DWT — PennyweightGAM — GammaGR — GrainGV — GraveKIP — KipLB — Фунт (метрический)LBA — ФунтLBT — Фунт (тройской)LBV — Фунт (Avoirdupois)ME — Атомная единица массы Электрон RMRK — MarkMTE — MiteMTM — Клещ (метрический)OZ — Унция (Us Food Nutrition LabelOZT — Унция (аптечная тройка)OZZ — унция (Avoirdupois)PNN — PointQ — квинтал (метрическая система)QR — четверть (неформальная)QRI — четверть (имперская)QRL — четверть длинная (неформальная)SAP — Scruple (аптекарь)SH — тонна короткаяSLG — слаг Geepound HylSLH — SheetST — StoneSWT — Вес в сотни (центум) oTON — Тонна LongWY — WeyZTR — ZentnerARE — AresBD — BoardsBHE — Эквивалент мощности котла DBR — BarnsBRN — BaronysCDA — Cuerda Pr SurveysCRD — CordsCRI — Circular InchsCRM — Circular MilsDNM — DunamsGNT — GunthasHD — Hides РО — RoodsSCT — SectionsSHD — СараиSII — Square Link Gunters InternatiSLR — Square Link RamsdensSQC — Square Chains InternationalSQM — Square Mil Square ThousSQR — Square Rod/Pole/PerchsSRR — Square RoofingsSTR — StremmasTWN — TownshipsYLN — YardlandsARM — Arcminute MoaARS — ArcsecondCNS — Centesimal Second Of ArcCNT — Столетняя минута ArcDOA — Градус (дуги)GRA — Град Градиан GonOCT — OctantQRD — QuadrantSGN - SignSXT — Секстантµ — Угловой MilATA — Атмосфера (техническая)ATM — Атмосфера (стандартная)BAR — BarBRY — Бари (единица Cgs)CMH — Сантиметр Of MercuryCMW – сантиметр водяного столба (4 °C)FTH – фут ртутного столба (условный)FTW – фут водяного столба (392 °F)IMC — дюйм ртутного столба (условный)INW — дюйм водяного столба (392 °F)KM — килограмм-сила на квадратный метр KSI — кип на квадратный дюймLTP — длинная тонна на квадратный футMHG — микрометр ртутного столбаMMH — миллиметр ртутного столбаMMW — Миллиметр воды (398 °C)PA — Паскаль (единица Си)PD — Фунт на квадратный футPSF — Фунт на квадратный футPSI — Фунт на квадратный дюймPZ — Пьез (единица МТС)STP — Короткая тонна на квадратный футTOR — ТоррATN — Атомная единица ForceDYN — Dyne (Cgs Unit)KFF — Килограмм-сила Kilopond Grave-KI — Kip Kip-ForceMGF — Milligrave-Force Gravet-ForceOZC — Унция-силаPDL — PoundalSN — Sthene (единица Mts)TNF — Long Ton-ForceTNL — Short Ton- ForceAUC — атомная единица времениCTN — CenturyCYC — каллипический циклDEC — DecadeFN — FortnightHEL — HelekHIP — гиппархический циклJFF — JiffyKEH — Ke (четверть часа) LSR — Luster LustrumMD — MillidayMLL — MillenniumMMN — MomentMOF — Month (Full)MOG — Month (Greg) Av)MOH — месяц (полый)MOS — месяц (синодический)MTN — метонический цикл EnneadecaeterisOC — OctaeterisPLN — планковское времяSGM — SigmaSHK — ShakeSTH — сотический циклSVD — SvedbergYR — год (общий)YRG — год (григорианский)YRJ — год (юлианский) YRL – год (високосный)YRM – год (среднетропический)B39- Британская термальная единица (39 °F)B59 — Британская термальная единица (59 °F)B60 — Британская термальная единица (60 °F)B63 — Британская термальная единица (63 °F)BOE — эквивалент барреля нефтиBRT — Британская термальная единица ( Iso)BTI — Британская термальная единица (InternatBTM — Британская термальная единица (средняя)BTT — Британская термальная единица (ThermochC15 — Калория (15 °C)C20 — Калория (20 °C)C98 — Калория (398 °C)CAM — Калория ( Среднее значение)CFT — Кубический фут атмосферы CHU — Тепловая единица ЦельсияCL — Калория (Us Fda)CLTH — Калория (термохимическая)CN — Кубический фут природного газаCTA — Кубический сантиметр атмосферыCYD — Кубический ярд атмосферы StandEH — Атомная единица энергии ХартриFTD — Foot-PoundalIMG — Галлон-атмосфераKCA — Большая килокалорияKWH — Киловатт-час Board Of Trade ULTM — Литр-атмосфераQD — QuadRDB — Therm (Ec)RY — RydbergTCE — Тонна угольного эквивалентаTHR — Therm (Us)THU — ThermieTN — Тонна TntTOE — Тонна нефтяного эквивалентаBAN — Ban HartleyBSH — Bit ShannonCD — Candela (Si Base Unit) CandleCPD — Candlepower (New)JK — Si UnitNAT — Nat Nip NepitNBL — NibbleBQ — Беккерель (Si Unit)CI — CurieRD — Rutherford (H)C — Скорость света в вакуумеFPF — фарлонг в две неделиFPH — фут в часIPH — дюйм в часIPM — дюйм в минутуIPS — дюйм в секундуMCH — число МахаMPM — миля в минутуMPS — миля в секундуMS — метр в секунду (единица Си)SPS — скорость звука в AirCDF — Кандела на квадратный футCDI — Кандела на квадратный дюймCDM — Кандела на квадратный метр (Si UFL — FootlambertLMB — LambertSB — Stilb (Cgs Unit)CEL — ЦельсийDDE — Градус DelisleDNE — Градус НьютонаFAN — ФаренгейтGMR — Регулятор газа MarkKEL — Kelvin’sRAN — RankineREA — ReaumurRME — Градус RømerCFM — Кубический фут в минутуFTS — Кубический фут в секундуGPD — Галлон (жидкость США) в суткиGPH — Галлон (жидкость США) в часGPM — Галлон (жидкость США) в минутуINM — Кубический дюйм в минутуINS — Кубический дюйм в секундуLPM — Литр в минутуMQS — кубический метр в секунду (Si UniCM — кулон-метрDB — DebyeEA0 — атомная единица электрического диполяFC — фут-канделя люмен на квадрат FoLMN — люмен на квадратный дюймLX — люкс (единица Si)PH — Phot (единица Cgs)FHP — фут в секунду Час в секундуFMS — фут в минуту в секундуFP — фут в секунду в квадратеG — стандартная гравитацияGAL — галлон GalileoIP — дюйм в минуту в секунду в секундуIP2 — дюйм в секунду в квадратеKNS — узел в секундуMM — миля в минуту в секундуMP — миля в час в секундуMP2 — миля в секунду Секунда в квадратеMSA — метр на секунду в квадрате (Si UFT2 — квадратный фут в секундуM2S — квадратный метр в секунду (Si UnSTX — Стокс (единица Cgs)FTP — фут-фунт)MKG — метр-килограмм-силаNEM — ньютон-метр (единица Si)GML — грамм на секунду MillilitreLAB — фунт (эквивалентный) на галлонLBF — фунт (эквивалентный) на кубический LBI — фунт (экспериментальный) на кубический LBL — фунт (экспериментальный) на галлонOFT — унция (экспериментальный) на кубический OG — унция (эвердупуа) на галлон ) Per GallonOIN — Унция (Avoirdupois) на кубический SFT — Slug на кубический футGSS — Gauss (Cgs Unit)TSL — Tesla (Si Unit)GY — Grey (Si Unit)RDD — RadLBH — Pound Per Foot HourLBS — Фунт на фут в секундуLFT — Фунт-сила-секунда на квадрат LIN — Фунт-сила-секунда на квадрат PAS — Паскаль-секунда (единица Si)PSU — Пуаз (единица Cgs)MX — Максвелл (единица Cgs)WB — Вебер (единица Si)REM — Рентген-эквивалент ManSV — Sievert (Единица Си)
S.) — Ссылка (Gunter’s; Геодезист) LNK (RE) — Link (Ramsden’s; Engineer’s) LS — Световой-секундный — Световой годM — Метр (базовая единица СИ)MIL — Мил (Швеция и Норвегия)MILE DATA — Мили (тактические или данные)MK — MickeyNAIL — Гвоздь (ткань)NL — Морская лигаNM — НанометрNMI — Морские милиNMI I — Морская миляP — PalmPC — ParsecPICA — PicaPM — Пикометр (бикрон, клеймо)POINT — точка (американский, английский)PT — PaceQUART — QuarterSHAKU — Shaku (Japan)SPT — SpatTH — Мил (тыс.) TWP — TwipUM — Микрометр (стар. микрон) XU — X единица измерения; siegbahnABA — Электромагнитная единица AbampereAMP — Ампер (базовая единица Si)ESU — Esu в секунду Статампер (CgsABC — Абкулон Электромагнитная единицаATU — Атомная единица зарядаCLM — КулонFRD — ФарадейMAH — Миллиампер-часSTT — Статкулон Франклин ЭлектростABV — Абвольт (единица Cgs)STV — Статвольт ( Cgs Unit)VLT — Вольт (Si Unit)ACF — Акр-футыACI — Акры-дюймыBIB — Баррели (нефтяные)BII — Баррели (британские)BIU — Баррели (Us Dry)BKT — Ведра (британские)BRO — Галлоны (пивные)BUD — Бушели (Us Dry Level)BUI — Бушели (Imperial)BUU — Бушели (Us Dry Heaped)CMB — CoombsCMI — Cubic MilesCP — CupsCRF — Cord-FootsCRW — Cords (Дрова)CUF — Cubic FathomsCUI — Cubic InchsCUT — Cubic FootsCUY — Cubic ЯрдыDSI — тире (имперские фунты)DSS — десертные ложки (имперские фунты)DSU — тире (США)FBM — борд-футыFFT — пятые FID — жидкие драхмы (имперские)FIS — жидкие скрукле (имперские)FLB — бочки (США, жидкие)FLU — жидкие драмы ( Us) Us FluidramFRK — FirkinsGAI — галлоны (имперские единицы)GAU — галлоны (Us Dry)GAW — галлоны (Us Fluid Wine)GLU — Teacups (gills)GTT — DropsHDI — Hogsheads (Imperial)HHU — Hogsheads (Us)JGR — Jiggers ( Bartending)KLD — KilderkinsLMD — LambdasLOD — LoadsLST — LastsM3 — Кубические метры (Si Unit)MII — Minims (Imperial)MIU — Minims (Us)OZF — Унции (Fluid Us Food NutritioPER — PerchsPKI — Pecks (Imperial)PKU — Pecks (Us) Сухой)PNI — пинчи (британские)PNU — пинчи (американские)PON — PonysPOT — Pottle QuartersPP — стыковые трубыPTI — пинты (британские)PUD — пинты (Us Dry)PUF — пинты (Us Fluid)QRF — Quart S (Us Fluid) QRT — Кварталы QTI — Кварты (британские)QTU — Кварты (Us Dry)RGS — Реестр TonsSCI — Мешки (британские) BagsSCU — Мешки(Us)SHT — Shots (Us)SM — SeamsSTK — Забастовки (Imperial)STU — Забастовки (Us) )TBC — столовые ложки (канадские)TBF — столовые ложки (обычные в США)TBM — столовые ложки (метрические)TBS — столовые ложки (в австралийских единицах измеренияTCA — чайные ложки (канадские) TFD — столовые ложки (Us Food NutritionTIM — чайные ложки (британские)TMF — Timber FootsTMT — чайные ложки ( Метрическая система)TND – тонны (водоизмещение)TNT – тонны (воды)TNW – тонны (фрахт)TSC – чайные ложки (стандарт США)TSF – чайные ложки (США Food Nutrition) WEY — Wey (Us)ACM — Атмосфера-кубический фут в минутуACS — Атмосфера-кубический фут в секунду SecoATC — Атмосфера-кубический сантиметр PeATH — Атмосфера-кубический фут в часBTJ — BTU (Международная таблица) В расчете на BTN — BTU (Международная таблица) В расчете на BTS — БТЕ (международная таблица) по CAS — Калория (международная таблица) ERS — Эрг в секундуFMF — Фут-фунт-сила в минутуFT — Фут-фунт-сила в часFTO — Фут-фунт-сила в секундуHPS — Лошадиная силаLAM — Литр-атмосфера в час MinuteLSC — LusecLTS — Литр атмосферы в секундуPNC — PonceletSQL — Прямой эквивалент квадратного фута TC — Тонна кондиционирования воздухаTMS — Атмосфера-кубический сантиметр PeTRM — Тонна охлаждения (ImperialTRR — Тонна охлаждения (It)AMU — Единица атомной массы UnifiedAT — Анализ тонны (Короткий)ATS — Ton Assay (Длинный)BAC — Bag (Coffee)BDM — Bag (Portland Cement)BRG — BargeCLV — CloveCRT — CrithCT — Carat (Metric)DA — DaltonDRT — Dram (Apothecary Troy)DWT — PennyweightGAM — GammaGR — GrainGV — GraveKIP — KipLB — Фунт (метрический)LBA — ФунтLBT — Фунт (тройской)LBV — Фунт (Avoirdupois)ME — Атомная единица массы Электрон RMRK — MarkMTE — MiteMTM — Клещ (метрический)OZ — Унция (Us Food Nutrition LabelOZT — Унция (аптечная тройка)OZZ — унция (Avoirdupois)PNN — PointQ — квинтал (метрическая система)QR — четверть (неформальная)QRI — четверть (имперская)QRL — четверть длинная (неформальная)SAP — Scruple (аптекарь)SH — тонна короткаяSLG — слаг Geepound HylSLH — SheetST — StoneSWT — Вес в сотни (центум) oTON — Тонна LongWY — WeyZTR — ZentnerARE — AresBD — BoardsBHE — Эквивалент мощности котла DBR — BarnsBRN — BaronysCDA — Cuerda Pr SurveysCRD — CordsCRI — Circular InchsCRM — Circular MilsDNM — DunamsGNT — GunthasHD — Hides РО — RoodsSCT — SectionsSHD — СараиSII — Square Link Gunters InternatiSLR — Square Link RamsdensSQC — Square Chains InternationalSQM — Square Mil Square ThousSQR — Square Rod/Pole/PerchsSRR — Square RoofingsSTR — StremmasTWN — TownshipsYLN — YardlandsARM — Arcminute MoaARS — ArcsecondCNS — Centesimal Second Of ArcCNT — Столетняя минута ArcDOA — Градус (дуги)GRA — Град Градиан GonOCT — OctantQRD — QuadrantSGN - SignSXT — Секстантµ — Угловой MilATA — Атмосфера (техническая)ATM — Атмосфера (стандартная)BAR — BarBRY — Бари (единица Cgs)CMH — Сантиметр Of MercuryCMW – сантиметр водяного столба (4 °C)FTH – фут ртутного столба (условный)FTW – фут водяного столба (392 °F)IMC — дюйм ртутного столба (условный)INW — дюйм водяного столба (392 °F)KM — килограмм-сила на квадратный метр KSI — кип на квадратный дюймLTP — длинная тонна на квадратный футMHG — микрометр ртутного столбаMMH — миллиметр ртутного столбаMMW — Миллиметр воды (398 °C)PA — Паскаль (единица Си)PD — Фунт на квадратный футPSF — Фунт на квадратный футPSI — Фунт на квадратный дюймPZ — Пьез (единица МТС)STP — Короткая тонна на квадратный футTOR — ТоррATN — Атомная единица ForceDYN — Dyne (Cgs Unit)KFF — Килограмм-сила Kilopond Grave-KI — Kip Kip-ForceMGF — Milligrave-Force Gravet-ForceOZC — Унция-силаPDL — PoundalSN — Sthene (единица Mts)TNF — Long Ton-ForceTNL — Short Ton- ForceAUC — атомная единица времениCTN — CenturyCYC — каллипический циклDEC — DecadeFN — FortnightHEL — HelekHIP — гиппархический циклJFF — JiffyKEH — Ke (четверть часа) LSR — Luster LustrumMD — MillidayMLL — MillenniumMMN — MomentMOF — Month (Full)MOG — Month (Greg) Av)MOH — месяц (полый)MOS — месяц (синодический)MTN — метонический цикл EnneadecaeterisOC — OctaeterisPLN — планковское времяSGM — SigmaSHK — ShakeSTH — сотический циклSVD — SvedbergYR — год (общий)YRG — год (григорианский)YRJ — год (юлианский) YRL – год (високосный)YRM – год (среднетропический)B39- Британская термальная единица (39 °F)B59 — Британская термальная единица (59 °F)B60 — Британская термальная единица (60 °F)B63 — Британская термальная единица (63 °F)BOE — эквивалент барреля нефтиBRT — Британская термальная единица ( Iso)BTI — Британская термальная единица (InternatBTM — Британская термальная единица (средняя)BTT — Британская термальная единица (ThermochC15 — Калория (15 °C)C20 — Калория (20 °C)C98 — Калория (398 °C)CAM — Калория ( Среднее значение)CFT — Кубический фут атмосферы CHU — Тепловая единица ЦельсияCL — Калория (Us Fda)CLTH — Калория (термохимическая)CN — Кубический фут природного газаCTA — Кубический сантиметр атмосферыCYD — Кубический ярд атмосферы StandEH — Атомная единица энергии ХартриFTD — Foot-PoundalIMG — Галлон-атмосфераKCA — Большая килокалорияKWH — Киловатт-час Board Of Trade ULTM — Литр-атмосфераQD — QuadRDB — Therm (Ec)RY — RydbergTCE — Тонна угольного эквивалентаTHR — Therm (Us)THU — ThermieTN — Тонна TntTOE — Тонна нефтяного эквивалентаBAN — Ban HartleyBSH — Bit ShannonCD — Candela (Si Base Unit) CandleCPD — Candlepower (New)JK — Si UnitNAT — Nat Nip NepitNBL — NibbleBQ — Беккерель (Si Unit)CI — CurieRD — Rutherford (H)C — Скорость света в вакуумеFPF — фарлонг в две неделиFPH — фут в часIPH — дюйм в часIPM — дюйм в минутуIPS — дюйм в секундуMCH — число МахаMPM — миля в минутуMPS — миля в секундуMS — метр в секунду (единица Си)SPS — скорость звука в AirCDF — Кандела на квадратный футCDI — Кандела на квадратный дюймCDM — Кандела на квадратный метр (Si UFL — FootlambertLMB — LambertSB — Stilb (Cgs Unit)CEL — ЦельсийDDE — Градус DelisleDNE — Градус НьютонаFAN — ФаренгейтGMR — Регулятор газа MarkKEL — Kelvin’sRAN — RankineREA — ReaumurRME — Градус RømerCFM — Кубический фут в минутуFTS — Кубический фут в секундуGPD — Галлон (жидкость США) в суткиGPH — Галлон (жидкость США) в часGPM — Галлон (жидкость США) в минутуINM — Кубический дюйм в минутуINS — Кубический дюйм в секундуLPM — Литр в минутуMQS — кубический метр в секунду (Si UniCM — кулон-метрDB — DebyeEA0 — атомная единица электрического диполяFC — фут-канделя люмен на квадрат FoLMN — люмен на квадратный дюймLX — люкс (единица Si)PH — Phot (единица Cgs)FHP — фут в секунду Час в секундуFMS — фут в минуту в секундуFP — фут в секунду в квадратеG — стандартная гравитацияGAL — галлон GalileoIP — дюйм в минуту в секунду в секундуIP2 — дюйм в секунду в квадратеKNS — узел в секундуMM — миля в минуту в секундуMP — миля в час в секундуMP2 — миля в секунду Секунда в квадратеMSA — метр на секунду в квадрате (Si UFT2 — квадратный фут в секундуM2S — квадратный метр в секунду (Si UnSTX — Стокс (единица Cgs)FTP — фут-фунт)MKG — метр-килограмм-силаNEM — ньютон-метр (единица Si)GML — грамм на секунду MillilitreLAB — фунт (эквивалентный) на галлонLBF — фунт (эквивалентный) на кубический LBI — фунт (экспериментальный) на кубический LBL — фунт (экспериментальный) на галлонOFT — унция (экспериментальный) на кубический OG — унция (эвердупуа) на галлон ) Per GallonOIN — Унция (Avoirdupois) на кубический SFT — Slug на кубический футGSS — Gauss (Cgs Unit)TSL — Tesla (Si Unit)GY — Grey (Si Unit)RDD — RadLBH — Pound Per Foot HourLBS — Фунт на фут в секундуLFT — Фунт-сила-секунда на квадрат LIN — Фунт-сила-секунда на квадрат PAS — Паскаль-секунда (единица Si)PSU — Пуаз (единица Cgs)MX — Максвелл (единица Cgs)WB — Вебер (единица Si)REM — Рентген-эквивалент ManSV — Sievert (Единица Си)
Кому:
A0 — Бор, атомная единица длиныAST — АнгстремAU — Астрономическая единицаCBL — Длина кабеля (имперская)CBL(US) — Длина кабеля USCH — ЦепиF — Французский charriereFM — ФермиFNG — FingerFNG(CLOTH) — Палец (ткань)FTM — FathomFUR — FurlongHH — HandLD — Световой деньLEA — лига (земля)LH — Световой часLM — Световая минутаLN — ЛинияLNK (G. S.) — Ссылка (Гюнтера; Сюрвейерская)LNK (RE) — Ссылка (Рамсденская; Инженерная)LS — Световая секундаLY — Световая- yearM — метр (базовая единица СИ)MIL — мил (Швеция и Норвегия)MILE DATA — мили (тактические или данные)MK — MickeyNAIL — гвоздь (ткань)NL — морская лигаNM — нанометрNMI — морская миляNMI I — морская миляP — PalmPC — ParsecPICA — PicaPM — пикометр (бикрон, клеймо) POINT — точка (американский, английский) PT — PaceQUART — QuarterSHAKU — Shaku (японский) SPT — SpatTH — Mil (тыс.)TWP — TwipUM — микрометр (стар.: микрон)XU — единица X; siegbahnABA — Электромагнитная единица AbampereAMP — Ампер (базовая единица Si)ESU — Esu в секунду Статампер (CgsABC — Абкулон Электромагнитная единицаATU — Атомная единица зарядаCLM — КулонFRD — ФарадейMAH — Миллиампер-часSTT — Статкулон Франклин ЭлектростABV — Абвольт (единица Cgs)STV — Статвольт ( Cgs Unit)VLT — Вольт (Si Unit)ACF — Акр-футыACI — Акры-дюймыBIB — Баррели (нефтяные)BII — Баррели (британские)BIU — Баррели (Us Dry)BKT — Ведра (британские)BRO — Галлоны (пивные)BUD — Бушели (Us Dry Level)BUI — Бушели (Imperial)BUU — Бушели (Us Dry Heaped)CMB — CoombsCMI — Cubic MilesCP — CupsCRF — Cord-FootsCRW — Cords (Дрова)CUF — Cubic FathomsCUI — Cubic InchsCUT — Cubic FootsCUY — Cubic ЯрдыDSI — тире (имперские фунты)DSS — десертные ложки (имперские фунты)DSU — тире (США)FBM — борд-футыFFT — пятые FID — жидкие драхмы (имперские)FIS — жидкие скрукле (имперские)FLB — бочки (США, жидкие)FLU — жидкие драмы ( Us) Us FluidramFRK — FirkinsGAI — галлоны (имперские единицы)GAU — галлоны (Us Dry)GAW — галлоны (Us Fluid Wine)GLU — Teacups (gills)GTT — DropsHDI — Hogsheads (Imperial)HHU — Hogsheads (Us)JGR — Jiggers ( Bartending)KLD — KilderkinsLMD — LambdasLOD — LoadsLST — LastsM3 — Кубические метры (Si Unit)MII — Minims (Imperial)MIU — Minims (Us)OZF — Унции (Fluid Us Food NutritioPER — PerchsPKI — Pecks (Imperial)PKU — Pecks (Us) Сухой)PNI — пинчи (британские)PNU — пинчи (американские)PON — PonysPOT — Pottle QuartersPP — стыковые трубыPTI — пинты (британские)PUD — пинты (Us Dry)PUF — пинты (Us Fluid)QRF — Quart S (Us Fluid) QRT — Кварталы QTI — Кварты (британские)QTU — Кварты (Us Dry)RGS — Реестр TonsSCI — Мешки (британские) BagsSCU — Мешки(Us)SHT — Shots (Us)SM — SeamsSTK — Забастовки (Imperial)STU — Забастовки (Us) )TBC — столовые ложки (канадские)TBF — столовые ложки (обычные в США)TBM — столовые ложки (метрические)TBS — столовые ложки (в австралийских единицах измеренияTCA — чайные ложки (канадские) TFD — столовые ложки (Us Food NutritionTIM — чайные ложки (британские)TMF — Timber FootsTMT — чайные ложки ( Метрическая система)TND – тонны (водоизмещение)TNT – тонны (воды)TNW – тонны (фрахт)TSC – чайные ложки (стандарт США)TSF – чайные ложки (США Food Nutrition) WEY — Wey (Us)ACM — Атмосфера-кубический фут в минутуACS — Атмосфера-кубический фут в секунду SecoATC — Атмосфера-кубический сантиметр PeATH — Атмосфера-кубический фут в часBTJ — BTU (Международная таблица) В расчете на BTN — BTU (Международная таблица) В расчете на BTS — БТЕ (международная таблица) по CAS — Калория (международная таблица) ERS — Эрг в секундуFMF — Фут-фунт-сила в минутуFT — Фут-фунт-сила в часFTO — Фут-фунт-сила в секундуHPS — Лошадиная силаLAM — Литр-атмосфера в час MinuteLSC — LusecLTS — Литр атмосферы в секундуPNC — PonceletSQL — Прямой эквивалент квадратного фута TC — Тонна кондиционирования воздухаTMS — Атмосфера-кубический сантиметр PeTRM — Тонна охлаждения (ImperialTRR — Тонна охлаждения (It)ACR — AcresCMK — Квадратные сантиметрыFTK — Квадратные футыHAR — ГектарыINK — Квадратные дюймыKMK — Квадратные километрыMIK — Квадратные милиMTK — Квадратные метрыYDK — Квадратные ярдыAMU — Унифицированная атомная единица массыAT — Тонна анализа (краткая)ATS — Тонна анализа (длинная)BAC — Мешок (Кофе)BDM — Мешок (портландцемент)BRG — BargeCLV — CloveCRT — CrithCT — Carat (Metric)DA — DaltonDRT — Dram (Apothecary Troy)DWT — PennyweightGAM — GammaGR — GrainGV — GraveKIP — KipLB — Pound (Metric)LBA — PoundLBT — Pound (Troy)LBV — Pound (Avoirdupois)ME — Атомная единица массы Электрон RMRK — MarkMTE — MiteMTM — Клещ (метрический) OZ — Унция (этикетка питания США OZT — Унция (аптечная Троя) OZZ — Унция (Avoirdupois) PNN — PointQ — Квинтал (метрический) QR — Квартал (неофициальный) QRI — Quarter (Imperial)QRL — Quarter Long (Informal)SAP — Scruple (Apothecary)SH — Ton ShortSLG — Slug Geepound HylSLH — SheetST — StoneSWT — Hundredweight (центум веса oTON — Ton LongWY — WeyZTR — ZentnerANN — YearsDAY — DaysHUR — HoursMCS — MicrosecondsMIN — MinutesMLS — MillisecondsMON — MonthsSEC — SecondsWEE — WeeksARE — AresBD — BoardsBHE — эквивалент мощности котла DBR — BarnsBRN — BaronysCDA — Cuerda Pr SurveysCRD — CordsCRI — Circular InchsCRM — Circular MilsDNM — DunamsGNT — GunthasHD — HidesRO — RoodsSCT — SectionsSHD — Сараи SII — Square Link Gunters InternatiSLR — Square Link RamsdensSQC — Square Chains InternationalSQM — Square Mil Square ThousSQR — Square Rod/Pole/PerchsSRR — Square RoofingsSTR — StremmasTWN — TownshipsYLN — YardlandsARM — Arcminute MoaARS — ArcsecondCNS — Centesimal Second Of ArcCNT — Centesimal Minute Of ArcDOA — Degree (Дуги)GRA — Grad Gradian GonOCT — OctantQRD — QuadrantSGN - SignSXT — Sextantµ — Угловой MilATA — Атмосфера (Техническая)ATM — Атмосфера (Стандартная)BAR — BarBRY — Бари (единица Cgs)CMH — Сантиметр ртутного столбаCMW — Сантиметр водяного столба ( 4 °C)FTH — фут ртутного столба (условный)FTW — фут водяного столба (392 °F)IMC — дюйм ртутного столба (условный)INW — дюйм водяного столба (392 °F)KM — килограмм-сила на квадратный метр KSI — кип на квадратный дюймLTP — длинная тонна на квадратный футMHG — микрометр ртутного столбаMMH — миллиметр ртутного столбаMMW — Миллиметр воды (398 °C)PA — Паскаль (единица Си)PD — Фунт на квадратный футPSF — Фунт на квадратный футPSI — Фунт на квадратный дюймPZ — Пьез (единица МТС)STP — Короткая тонна на квадратный футTOR — ТоррATN — Атомная единица ForceDYN — Dyne (Cgs Unit)KFF — Килограмм-сила Kilopond Grave-KI — Kip Kip-ForceMGF — Milligrave-Force Gravet-ForceOZC — Унция-силаPDL — PoundalSN — Sthene (единица Mts)TNF — Long Ton-ForceTNL — Short Ton- ForceAUC — атомная единица времениCTN — CenturyCYC — каллипический циклDEC — DecadeFN — FortnightHEL — HelekHIP — гиппархический циклJFF — JiffyKEH — Ke (четверть часа) LSR — Luster LustrumMD — MillidayMLL — MillenniumMMN — MomentMOF — Month (Full)MOG — Month (Greg) Av)MOH — месяц (полый)MOS — месяц (синодический)MTN — метонический цикл EnneadecaeterisOC — OctaeterisPLN — планковское времяSGM — SigmaSHK — ShakeSTH — сотический циклSVD — SvedbergYR — год (общий)YRG — год (григорианский)YRJ — год (юлианский) YRL – год (високосный)YRM – год (среднетропический)B39- Британская термальная единица (39 °F)B59 — Британская термальная единица (59 °F)B60 — Британская термальная единица (60 °F)B63 — Британская термальная единица (63 °F)BOE — эквивалент барреля нефтиBRT — Британская термальная единица ( Iso)BTI — Британская термальная единица (InternatBTM — Британская термальная единица (средняя)BTT — Британская термальная единица (ThermochC15 — Калория (15 °C)C20 — Калория (20 °C)C98 — Калория (398 °C)CAM — Калория ( Среднее значение)CFT — Кубический фут атмосферы CHU — Тепловая единица ЦельсияCL — Калория (Us Fda)CLTH — Калория (термохимическая)CN — Кубический фут природного газаCTA — Кубический сантиметр атмосферыCYD — Кубический ярд атмосферы StandEH — Атомная единица энергии ХартриFTD — Foot-PoundalIMG — Галлон-атмосфераKCA — Большая килокалорияKWH — Киловатт-час Board Of Trade ULTM — Литр-атмосфераQD — QuadRDB — Therm (Ec)RY — RydbergTCE — Тонна угольного эквивалентаTHR — Therm (Us)THU — ThermieTN — Тонна TntTOE — Tone Of Oil EquivalentBAN — Ban HartleyBSH — Bit ShannonCD — Candela (Si Base Unit) CandleCPD — Candlepower (New)JK — Si UnitNAT — Nat Nip NepitNBL — NibbleBIT — BitsBYT — BytesEBI — ExabitsEBY — ExabytesGBI — GigabitsGBY — GigabytesKBI — KilobitsKBY — KilobytesMBI — МегабитыMBY — МегабайтыPBI — ПетабитыPBY — ПетабайтыTBI — ТерабитыTBY — ТерабайтыBLL — Баррели (нефть)CMQ — Кубические сантиметрыFTQ — Кубические футыGLI — Галлоны (Великобритания)GLL — Галлоны (жидкости США)LTR — ЛитрыMLT — МиллилитрыMTQ — Кубические метрыOZI — Унции UKBQ — Беккерели ( Si Unit)CI — КюриRD — Резерфорд (H)BTU — BTUCAL — КалорииERG — ErgEVL — Электрон ВольтFPD — Фут-фунтHPH — Лошадиная сила-часIPD — Дюйм-фунтJOU — ДжоульC — Скорость света в вакуумеFPF — Фарлонг в две неделиFPH — Фут в часIPH — Inch Per HourIPM — Inch Per MinuteIPS — Inch Per SecondMCH — Mach NumberMPM — Mile Per MinuteMPS — Mile Per SecondMS — Метр в секунду (Si Unit)SPS — Скорость звука в AirCDF — Candela Per Square FootCDI — Candela Per Square InchCDM — Candela Per Квадратный метр (Si UFL — FootlambertLMB — LambertSB — Stilb (Cgs Unit)CEL — ЦельсийDDE — Градус DelisleDNE — Градус НьютонаFAN — ФаренгейтGMR — Регулирующий газ MarkKEL — Kelvin’sRAN — RankineREA — ReaumurRME — Градус RømerCFM — Кубический фут в минутуFTS — Кубический фут в минуту SecondGPD — галлон (жидкость США) в суткиGPH — галлон (жидкость США) в часGPM — галлон (жидкость США) в минутуINM — кубический дюйм в минутуINS — кубический дюйм в секундуLPM — литр в минутуMQS — кубический метр в секунду (Si UniCM — кулоновый метрDB — DebyeEA0 — атомная единица электрического диполя CMT — сантиметр DMT — дециметрыFOT — футыINH — дюймыKMT — километрыMMT — миллиметрыMTR — метрыSMI — милиYRD — ярдыCTM — каратыGRM — граммыKGM — килограммыLBR — фунтыMGM — миллиграммыONZ — унции TNE — тонны (метрические)DEG — градусыGRD — градыRAD - RadiansFC — Фут-канд Люмен на квадрат FoLMN — Люмен на квадратный дюймLX — Люкс (Единица Si)PH — Фот (Единица Cgs)FHP — Фут в час в секундуFMS — Фут в минуту в секундуFP — Фут в секунду в квадратеdG — Стандартная сила тяжестиGAL — Gal GalileoIP — Дюйм в минуту в секундуIP2 — дюйм в секунду в квадратеKNS — узел в секундуMM — миля в минуту в секундуMP — миля в час в секундуMP2 — миля в секунду в квадратеMSA — метр в секунду в квадрате (Si UFPM — футы/минутыFPS — футы/секундыKMH — километры/ ЧасKMS — Километры/секундыKNT — УзлыMPH — Мили/часMTS — Метры/секундыFT2 — Квадратный фут в секундуM2S — Квадратный метр в секунду (Si UnSTX — Стокс (единица Cgs)FTP — Foot-PoundalMKG — Метр Килограмм-силаNEM — Ньютон-метр (Единица Si )GCC — граммы/кубический сантиметрKCC — килограммы/кубический сантиметрKLI — килограммы/литрKMC — килограммы/кубический метрOCI — унции/кубический дюймOGL — унции/галлонPCF — фунты/кубический футPCI — фунты/кубический дюймPGL — фунты/галлонGML — грамм на миллилитрLAB — фунт (Avoirdupois) Per GallonLBF — фунт (Avoirdupois) на кубический LBI — фунт (Avoirdupois) на кубический LBL — фунт (Avoirdupois) на галлонOFT — унция (Avoirdupois) на кубический OG — унция (Avoirdupois) на галлонOGA — унция (Avoirdupois) на галлонOIN — Унция (Avoirdupois) на кубический SFT — Слаг на кубический футGSS — Гаусс (единица Cgs)TSL — Тесла (единица Si)GY — Грей (единица Si)RDD — RadJCM — Джоули/сантиметрKGF — Килограмм-силаNWN — НьютоныPFC — Фунт силыLBH — Фунт Per Foot HourLBS — Фунт на фут-секундуLFT — Фунт-сила-секунда на квадрат LIN — Фунт-сила-секунда на квадрат PAS — Паскаль-секунда (единица Si)PSU — Пуаз (единица Cgs)MX — Максвелл (единица Cgs)WB — Вебер (Si) Единица)REM — Рентген-эквивалент ManSV — Зиверт (Единица Si)
S.) — Ссылка (Гюнтера; Сюрвейерская)LNK (RE) — Ссылка (Рамсденская; Инженерная)LS — Световая секундаLY — Световая- yearM — метр (базовая единица СИ)MIL — мил (Швеция и Норвегия)MILE DATA — мили (тактические или данные)MK — MickeyNAIL — гвоздь (ткань)NL — морская лигаNM — нанометрNMI — морская миляNMI I — морская миляP — PalmPC — ParsecPICA — PicaPM — пикометр (бикрон, клеймо) POINT — точка (американский, английский) PT — PaceQUART — QuarterSHAKU — Shaku (японский) SPT — SpatTH — Mil (тыс.)TWP — TwipUM — микрометр (стар.: микрон)XU — единица X; siegbahnABA — Электромагнитная единица AbampereAMP — Ампер (базовая единица Si)ESU — Esu в секунду Статампер (CgsABC — Абкулон Электромагнитная единицаATU — Атомная единица зарядаCLM — КулонFRD — ФарадейMAH — Миллиампер-часSTT — Статкулон Франклин ЭлектростABV — Абвольт (единица Cgs)STV — Статвольт ( Cgs Unit)VLT — Вольт (Si Unit)ACF — Акр-футыACI — Акры-дюймыBIB — Баррели (нефтяные)BII — Баррели (британские)BIU — Баррели (Us Dry)BKT — Ведра (британские)BRO — Галлоны (пивные)BUD — Бушели (Us Dry Level)BUI — Бушели (Imperial)BUU — Бушели (Us Dry Heaped)CMB — CoombsCMI — Cubic MilesCP — CupsCRF — Cord-FootsCRW — Cords (Дрова)CUF — Cubic FathomsCUI — Cubic InchsCUT — Cubic FootsCUY — Cubic ЯрдыDSI — тире (имперские фунты)DSS — десертные ложки (имперские фунты)DSU — тире (США)FBM — борд-футыFFT — пятые FID — жидкие драхмы (имперские)FIS — жидкие скрукле (имперские)FLB — бочки (США, жидкие)FLU — жидкие драмы ( Us) Us FluidramFRK — FirkinsGAI — галлоны (имперские единицы)GAU — галлоны (Us Dry)GAW — галлоны (Us Fluid Wine)GLU — Teacups (gills)GTT — DropsHDI — Hogsheads (Imperial)HHU — Hogsheads (Us)JGR — Jiggers ( Bartending)KLD — KilderkinsLMD — LambdasLOD — LoadsLST — LastsM3 — Кубические метры (Si Unit)MII — Minims (Imperial)MIU — Minims (Us)OZF — Унции (Fluid Us Food NutritioPER — PerchsPKI — Pecks (Imperial)PKU — Pecks (Us) Сухой)PNI — пинчи (британские)PNU — пинчи (американские)PON — PonysPOT — Pottle QuartersPP — стыковые трубыPTI — пинты (британские)PUD — пинты (Us Dry)PUF — пинты (Us Fluid)QRF — Quart S (Us Fluid) QRT — Кварталы QTI — Кварты (британские)QTU — Кварты (Us Dry)RGS — Реестр TonsSCI — Мешки (британские) BagsSCU — Мешки(Us)SHT — Shots (Us)SM — SeamsSTK — Забастовки (Imperial)STU — Забастовки (Us) )TBC — столовые ложки (канадские)TBF — столовые ложки (обычные в США)TBM — столовые ложки (метрические)TBS — столовые ложки (в австралийских единицах измеренияTCA — чайные ложки (канадские) TFD — столовые ложки (Us Food NutritionTIM — чайные ложки (британские)TMF — Timber FootsTMT — чайные ложки ( Метрическая система)TND – тонны (водоизмещение)TNT – тонны (воды)TNW – тонны (фрахт)TSC – чайные ложки (стандарт США)TSF – чайные ложки (США Food Nutrition) WEY — Wey (Us)ACM — Атмосфера-кубический фут в минутуACS — Атмосфера-кубический фут в секунду SecoATC — Атмосфера-кубический сантиметр PeATH — Атмосфера-кубический фут в часBTJ — BTU (Международная таблица) В расчете на BTN — BTU (Международная таблица) В расчете на BTS — БТЕ (международная таблица) по CAS — Калория (международная таблица) ERS — Эрг в секундуFMF — Фут-фунт-сила в минутуFT — Фут-фунт-сила в часFTO — Фут-фунт-сила в секундуHPS — Лошадиная силаLAM — Литр-атмосфера в час MinuteLSC — LusecLTS — Литр атмосферы в секундуPNC — PonceletSQL — Прямой эквивалент квадратного фута TC — Тонна кондиционирования воздухаTMS — Атмосфера-кубический сантиметр PeTRM — Тонна охлаждения (ImperialTRR — Тонна охлаждения (It)ACR — AcresCMK — Квадратные сантиметрыFTK — Квадратные футыHAR — ГектарыINK — Квадратные дюймыKMK — Квадратные километрыMIK — Квадратные милиMTK — Квадратные метрыYDK — Квадратные ярдыAMU — Унифицированная атомная единица массыAT — Тонна анализа (краткая)ATS — Тонна анализа (длинная)BAC — Мешок (Кофе)BDM — Мешок (портландцемент)BRG — BargeCLV — CloveCRT — CrithCT — Carat (Metric)DA — DaltonDRT — Dram (Apothecary Troy)DWT — PennyweightGAM — GammaGR — GrainGV — GraveKIP — KipLB — Pound (Metric)LBA — PoundLBT — Pound (Troy)LBV — Pound (Avoirdupois)ME — Атомная единица массы Электрон RMRK — MarkMTE — MiteMTM — Клещ (метрический) OZ — Унция (этикетка питания США OZT — Унция (аптечная Троя) OZZ — Унция (Avoirdupois) PNN — PointQ — Квинтал (метрический) QR — Квартал (неофициальный) QRI — Quarter (Imperial)QRL — Quarter Long (Informal)SAP — Scruple (Apothecary)SH — Ton ShortSLG — Slug Geepound HylSLH — SheetST — StoneSWT — Hundredweight (центум веса oTON — Ton LongWY — WeyZTR — ZentnerANN — YearsDAY — DaysHUR — HoursMCS — MicrosecondsMIN — MinutesMLS — MillisecondsMON — MonthsSEC — SecondsWEE — WeeksARE — AresBD — BoardsBHE — эквивалент мощности котла DBR — BarnsBRN — BaronysCDA — Cuerda Pr SurveysCRD — CordsCRI — Circular InchsCRM — Circular MilsDNM — DunamsGNT — GunthasHD — HidesRO — RoodsSCT — SectionsSHD — Сараи SII — Square Link Gunters InternatiSLR — Square Link RamsdensSQC — Square Chains InternationalSQM — Square Mil Square ThousSQR — Square Rod/Pole/PerchsSRR — Square RoofingsSTR — StremmasTWN — TownshipsYLN — YardlandsARM — Arcminute MoaARS — ArcsecondCNS — Centesimal Second Of ArcCNT — Centesimal Minute Of ArcDOA — Degree (Дуги)GRA — Grad Gradian GonOCT — OctantQRD — QuadrantSGN - SignSXT — Sextantµ — Угловой MilATA — Атмосфера (Техническая)ATM — Атмосфера (Стандартная)BAR — BarBRY — Бари (единица Cgs)CMH — Сантиметр ртутного столбаCMW — Сантиметр водяного столба ( 4 °C)FTH — фут ртутного столба (условный)FTW — фут водяного столба (392 °F)IMC — дюйм ртутного столба (условный)INW — дюйм водяного столба (392 °F)KM — килограмм-сила на квадратный метр KSI — кип на квадратный дюймLTP — длинная тонна на квадратный футMHG — микрометр ртутного столбаMMH — миллиметр ртутного столбаMMW — Миллиметр воды (398 °C)PA — Паскаль (единица Си)PD — Фунт на квадратный футPSF — Фунт на квадратный футPSI — Фунт на квадратный дюймPZ — Пьез (единица МТС)STP — Короткая тонна на квадратный футTOR — ТоррATN — Атомная единица ForceDYN — Dyne (Cgs Unit)KFF — Килограмм-сила Kilopond Grave-KI — Kip Kip-ForceMGF — Milligrave-Force Gravet-ForceOZC — Унция-силаPDL — PoundalSN — Sthene (единица Mts)TNF — Long Ton-ForceTNL — Short Ton- ForceAUC — атомная единица времениCTN — CenturyCYC — каллипический циклDEC — DecadeFN — FortnightHEL — HelekHIP — гиппархический циклJFF — JiffyKEH — Ke (четверть часа) LSR — Luster LustrumMD — MillidayMLL — MillenniumMMN — MomentMOF — Month (Full)MOG — Month (Greg) Av)MOH — месяц (полый)MOS — месяц (синодический)MTN — метонический цикл EnneadecaeterisOC — OctaeterisPLN — планковское времяSGM — SigmaSHK — ShakeSTH — сотический циклSVD — SvedbergYR — год (общий)YRG — год (григорианский)YRJ — год (юлианский) YRL – год (високосный)YRM – год (среднетропический)B39- Британская термальная единица (39 °F)B59 — Британская термальная единица (59 °F)B60 — Британская термальная единица (60 °F)B63 — Британская термальная единица (63 °F)BOE — эквивалент барреля нефтиBRT — Британская термальная единица ( Iso)BTI — Британская термальная единица (InternatBTM — Британская термальная единица (средняя)BTT — Британская термальная единица (ThermochC15 — Калория (15 °C)C20 — Калория (20 °C)C98 — Калория (398 °C)CAM — Калория ( Среднее значение)CFT — Кубический фут атмосферы CHU — Тепловая единица ЦельсияCL — Калория (Us Fda)CLTH — Калория (термохимическая)CN — Кубический фут природного газаCTA — Кубический сантиметр атмосферыCYD — Кубический ярд атмосферы StandEH — Атомная единица энергии ХартриFTD — Foot-PoundalIMG — Галлон-атмосфераKCA — Большая килокалорияKWH — Киловатт-час Board Of Trade ULTM — Литр-атмосфераQD — QuadRDB — Therm (Ec)RY — RydbergTCE — Тонна угольного эквивалентаTHR — Therm (Us)THU — ThermieTN — Тонна TntTOE — Tone Of Oil EquivalentBAN — Ban HartleyBSH — Bit ShannonCD — Candela (Si Base Unit) CandleCPD — Candlepower (New)JK — Si UnitNAT — Nat Nip NepitNBL — NibbleBIT — BitsBYT — BytesEBI — ExabitsEBY — ExabytesGBI — GigabitsGBY — GigabytesKBI — KilobitsKBY — KilobytesMBI — МегабитыMBY — МегабайтыPBI — ПетабитыPBY — ПетабайтыTBI — ТерабитыTBY — ТерабайтыBLL — Баррели (нефть)CMQ — Кубические сантиметрыFTQ — Кубические футыGLI — Галлоны (Великобритания)GLL — Галлоны (жидкости США)LTR — ЛитрыMLT — МиллилитрыMTQ — Кубические метрыOZI — Унции UKBQ — Беккерели ( Si Unit)CI — КюриRD — Резерфорд (H)BTU — BTUCAL — КалорииERG — ErgEVL — Электрон ВольтFPD — Фут-фунтHPH — Лошадиная сила-часIPD — Дюйм-фунтJOU — ДжоульC — Скорость света в вакуумеFPF — Фарлонг в две неделиFPH — Фут в часIPH — Inch Per HourIPM — Inch Per MinuteIPS — Inch Per SecondMCH — Mach NumberMPM — Mile Per MinuteMPS — Mile Per SecondMS — Метр в секунду (Si Unit)SPS — Скорость звука в AirCDF — Candela Per Square FootCDI — Candela Per Square InchCDM — Candela Per Квадратный метр (Si UFL — FootlambertLMB — LambertSB — Stilb (Cgs Unit)CEL — ЦельсийDDE — Градус DelisleDNE — Градус НьютонаFAN — ФаренгейтGMR — Регулирующий газ MarkKEL — Kelvin’sRAN — RankineREA — ReaumurRME — Градус RømerCFM — Кубический фут в минутуFTS — Кубический фут в минуту SecondGPD — галлон (жидкость США) в суткиGPH — галлон (жидкость США) в часGPM — галлон (жидкость США) в минутуINM — кубический дюйм в минутуINS — кубический дюйм в секундуLPM — литр в минутуMQS — кубический метр в секунду (Si UniCM — кулоновый метрDB — DebyeEA0 — атомная единица электрического диполя CMT — сантиметр DMT — дециметрыFOT — футыINH — дюймыKMT — километрыMMT — миллиметрыMTR — метрыSMI — милиYRD — ярдыCTM — каратыGRM — граммыKGM — килограммыLBR — фунтыMGM — миллиграммыONZ — унции TNE — тонны (метрические)DEG — градусыGRD — градыRAD - RadiansFC — Фут-канд Люмен на квадрат FoLMN — Люмен на квадратный дюймLX — Люкс (Единица Si)PH — Фот (Единица Cgs)FHP — Фут в час в секундуFMS — Фут в минуту в секундуFP — Фут в секунду в квадратеdG — Стандартная сила тяжестиGAL — Gal GalileoIP — Дюйм в минуту в секундуIP2 — дюйм в секунду в квадратеKNS — узел в секундуMM — миля в минуту в секундуMP — миля в час в секундуMP2 — миля в секунду в квадратеMSA — метр в секунду в квадрате (Si UFPM — футы/минутыFPS — футы/секундыKMH — километры/ ЧасKMS — Километры/секундыKNT — УзлыMPH — Мили/часMTS — Метры/секундыFT2 — Квадратный фут в секундуM2S — Квадратный метр в секунду (Si UnSTX — Стокс (единица Cgs)FTP — Foot-PoundalMKG — Метр Килограмм-силаNEM — Ньютон-метр (Единица Si )GCC — граммы/кубический сантиметрKCC — килограммы/кубический сантиметрKLI — килограммы/литрKMC — килограммы/кубический метрOCI — унции/кубический дюймOGL — унции/галлонPCF — фунты/кубический футPCI — фунты/кубический дюймPGL — фунты/галлонGML — грамм на миллилитрLAB — фунт (Avoirdupois) Per GallonLBF — фунт (Avoirdupois) на кубический LBI — фунт (Avoirdupois) на кубический LBL — фунт (Avoirdupois) на галлонOFT — унция (Avoirdupois) на кубический OG — унция (Avoirdupois) на галлонOGA — унция (Avoirdupois) на галлонOIN — Унция (Avoirdupois) на кубический SFT — Слаг на кубический футGSS — Гаусс (единица Cgs)TSL — Тесла (единица Si)GY — Грей (единица Si)RDD — RadJCM — Джоули/сантиметрKGF — Килограмм-силаNWN — НьютоныPFC — Фунт силыLBH — Фунт Per Foot HourLBS — Фунт на фут-секундуLFT — Фунт-сила-секунда на квадрат LIN — Фунт-сила-секунда на квадрат PAS — Паскаль-секунда (единица Si)PSU — Пуаз (единица Cgs)MX — Максвелл (единица Cgs)WB — Вебер (Si) Единица)REM — Рентген-эквивалент ManSV — Зиверт (Единица Si)
Таблица преобразования: сантиметры в миллиметры
| сантиметры | МИЛЛИМЕТРОВ | |
|---|---|---|
| 1 | = | 10 |
| 2 | = | 20 |
| 3 | = | 30 |
| 4 | = | 40 |
| 5 | = | 50 |
| 7 | = | 70 |
| 8 | = | 80 |
| 9 | = | 90 |
| 10 | = | 100 |
| МИЛЛИМЕТРОВ | сантиметр | |
|---|---|---|
| 1 | = | 0,1 |
| 2 | = | 0,2 |
| 3 | = | 0,3 |
| 4 | = | 0,4 |
| 5 | = | 0,5 |
| 7 | = | 0,7 |
| 8 | = | 0,8 |
| 9 | = | 0,9 |
| 10 | = | 1 |
Ближайшие номера для 250 сантиметров
250 см в миллиметры
250 см равняется 2500 миллиметрам
Универсальный конвертер единиц измерения
| ⇆ | ||
Пожалуйста, выберите физическую величину, две единицы, затем введите значение в любое из полей выше. | ||
Чтобы перевести значение в сантиметрах в соответствующее значение в миллиметрах, просто умножьте количество в см на 10 (коэффициент преобразования). Вот 9формула 0231 :
Значение в миллиметрах = значение в см × 10
Предположим, вы хотите преобразовать 250 см в миллиметры. Используя приведенную выше формулу преобразования, вы получите:
Значение в миллиметрах = 250 × 10 = 2500 миллиметров
Определение сантиметра
сантиметр (см) – десятичная дробь метра, международная стандартная единица длины. , что примерно эквивалентно 39,37 дюймам.
Определение миллиметра
Миллиметр (мм) – это десятичная дробь метра, международная стандартная единица длины, примерно эквивалентная 39,37 дюймам.
Этот конвертер поможет вам получить ответы на такие вопросы, как:
- Сколько сантиметров в 250 миллиметрах?
- 250 см скольким миллиметрам равны?
- Сколько 250 см в миллиметрах?
- Как перевести см в миллиметры?
- Какой коэффициент перевода см в миллиметры?
- Как перевести см в миллиметры?
- По какой формуле перевести см в миллиметры? Среди прочих.

Таблица перевода сантиметров в миллиметры около 250 см
| Таблица перевода сантиметров в миллиметры 35 | 1800 мм | ||
|---|---|---|---|
| 190 см | = | 1900 мм | |
| 200 см | = | 2000 мм | |
| 210 см | = | 2100 мм | |
| 220 см | = 9003 5 | 2200 мм | |
| 230 см | = | 2300 мм | |
| 240 см | = | 2400 мм | |
| 250 см | = | 2500 мм | |
| Таблица перевода см в миллиметры | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 250 см | = | 2500 мм | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 260 см | = | 2600 мм s | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 270 см | = | 2700 мм | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 280 см | = | 2800 мм | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 290 см | = | 2900 мм | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 300 см | = | 900 34 3000 мм|||||||||||||||||||||||||||||||||||||||||||||||||||||
| 310 см | = | 3100 мм | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| 320 см | = | 3200 мм | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| Элементы | Сторона реагента | Сторона продукта |
|---|---|---|
| Ca | 9025 2 11 | |
| S | 1 | 1 |
| O | 5 | 4 | 90 248
| H | 4 | 2 |
- Мы находим, что сторона продукта лишена 1 моля атома кислорода и 2 молей атома водорода.
- Чтобы уравнять количество молей со стороны реагента и продукта, мы добавляем 2 моля H 2 O со стороны продукта.

- Таким образом, общая сбалансированная реакция определяется выражением –
- H 2 SO 3 + Ca(OH) 2 = C a SO 3 + 2H 2 O
H
2 SO 3 + Ca(OH) 2 титрованиеКислотно-основное титрование между H 2 SO 3 и Ca(OH) 2 проводят для измерения количества ионов кальция и гидроксида. Процедура титрования описана ниже.
ПриборБюретка, держатель бюретки, пипетка, коническая колба, мерная колба, промывочная бутыль и химические стаканы.
Индикатор Фенолфталеин – кислотно-щелочной индикатор, используемый для определения конечной точки титрования.
- Стандартизированный H 2 SO 3 отбирают в бюретку, а гидроксид кальция отбирают в коническую колбу.
- Добавьте 2 капли индикатора фенолфталеина.
- H 2 SO 3 медленно добавляют из бюретки в коническую колбу при постоянном встряхивании до тех пор, пока раствор из бесцветного не станет светло-розовым.
- Описанная выше процедура повторяется для 3 согласованных показаний.
- Неизвестная нормальность Ca(OH) 2 рассчитывается по формуле V 1 S 1 = V 2 S 2 .
H
2 SO 3 + Ca(OH) 2 результирующее ионное уравнениерезультирующее ионное уравнение между H 2 SO 90 115 3 + Ca(OH) 2 это:
H 2 SO 3 (водн. ) + Ca 2+ (водн.) + 2OH – (водн.) = CaSO 3 (т) + 2 H 2 O (л)
) + Ca 2+ (водн.) + 2OH – (водн.) = CaSO 3 (т) + 2 H 2 O (л)
Для вывести результирующее ионное уравнение:
- Баланс полученное молекулярное уравнение –
- H 2 SO 3 + Ca(OH) 2 = CaSO 3 + 2H 2 O
- Укажите ионную форму каждого веществ, находящихся в водной форме и способных к полной диссоциации в воде. Н 2 SO 3 — слабый электролит, не полностью диссоциирующий на ионы в водной форме.
- Отсюда полное ионное уравнение: 6 – (водн.) = CaSO 3 ( s) + 2H 2 O (l)
- Мы находим, что полное ионное уравнение совпадает с результирующим ионным уравнением.
Н
2 SO 3 + Ca(OH) 2 сопряженные пары- H 2 SO 3 и HSO 3 9011 6 – – сопряженные кислотно-основные пары.

- OH – и H 2 O представляют собой сопряженные кислотно-основные пары.
H
2 SO 3 + Ca(OH) 2 межмолекулярные силы- In H 2 SO 9011 5 3 , силы Ван-дер-Ваальса, диполь-дипольные взаимодействия и лондоновские дисперсионные силы межмолекулярные силы, которые связывают ионы водорода и сульфита вместе.
- В Ca(OH) 2 сильные электростатические силы притяжения между ионами Ca 2+ и OH – , поскольку гидроксид кальция является ионным соединением.
H
2 SO 3 + Ca(OH) 2 энтальпия реакцииСтандартная энтальпия реакции реакции между H 2 901 16 SO 3 и Ca(OH) 2 -358,6 кДж/моль.
Is H
2 SO 3 + Ca(OH) 2 буферный раствор? H 2 SO 3 + Ca(OH) 2 представляет собой буферный раствор. Это непрямой кислый буфер, так как сульфит кальция образуется в результате реакции слабой кислоты и сильного основания.
Это непрямой кислый буфер, так как сульфит кальция образуется в результате реакции слабой кислоты и сильного основания.
Является ли H
2 SO 3 + Ca(OH) 2 полной реакцией?H 2 SO 3 + Ca(OH) 2 не является полной реакцией, так как H 2 SO 3 , слабая кислота, остается в растворе.
Является ли H
2 SO 3 + Ca(OH) 2 экзотермической реакцией?H 2 SO 3 + Ca(OH) 2 является экзотермической реакцией, поскольку энтальпия реакции отрицательна, а выделяющееся тепло запускает реакцию в прямом направлении.
Является ли H
2 SO 3 + Ca(OH) 2 окислительно-восстановительной реакцией? Реакция между H 2 SO 3 и Ca(OH) 2 не является окислительно-восстановительной реакцией, так как не происходит изменения степеней окисления элементов.
Является ли H
2 SO 3 + Ca(OH) 2 реакцией осаждения?H 2 SO 3 + C a(OH) 2 представляет собой реакцию осаждения, так как образующийся продукт представляет собой белый осадок сульфита кальция , не растворим в воде.
Ис Н
2 SO 3 + Ca(OH) 2 необратимая реакция?H 2 SO 3 + Ca(OH) 2 является необратимой реакцией, поскольку образующийся сульфит кальция является остатком, который нерастворим в воде. Значит, обратной реакции не бывает.
Является ли H
2 SO 3 + Ca(OH) 2 реакцией замещения? Реакция между H 2 SO 3 + Ca(OH) 2 является примером реакции двойного замещения, , потому что анионы и катионы меняются местами, образуя соль и воду.
Численные методы в примерах и задачах киреев пантелеев: Численные методы в примерах и задачах — Владимир Киреев, Андрей Пантелеев
Киреев В.И., Пантелеев А.В. Численные методы в примерах и задачах
- формат pdf
- размер 11,86 МБ
- добавлен 1 апреля 2015 г.
М.: Высшая школа, 2004. — 480 с. — ISBN 5-06-004763-6.
Пособие охватывает классические разделы численного анализа: методы
алгебры, теории приближения функций одной переменной с их
приложениями, разностные методы решения задач Коши и краевых задач
для обыкновенных дифференциальных уравнений, численные методы
решения уравнений математической физики с двумя и тремя
независимыми переменными. Впервые в учебной литературе наряду с
традиционными методами изложены новые экономичные, устойчивые и
простые в реализации методы приближения функций, численного
дифференцирования и интегрирования, решения задачи Коши, основанные
на применении ишегрально-дифференциальных сплайнов.
Для студентов математических, инженерно-технических и авиационных специальностей вузов и университетов, аспирантов и научных работников.
Численные методы алгебры.
Методы решения систем линейных алгебраических уравнений.
Методы решения задач о собственных значениях и собственных векторах
матриц.
Методы решения нелинейных уравнений и систем.
Численные методы теории приближений.
Методы приближения сеточных функций.
Методы численного дифференцирования и интегрирования.
Численные методы решения обыкновенных дифференциальных
уравнений.
Методы решения задачи Коши.
Методы решения краевых задач.
Численные методы решения дифференциальных уравнений в
частных производных.
Численные методы решения уравнений математической физики с двумя
независимыми переменными.
Численные методы решения уравнений математической физики с тремя
независимыми переменными.
Купить и скачать книгу «Численные методы в примерах и задачах»
Похожие разделы
- Академическая и специальная литература
- Физика
- Матметоды и моделирование в физике
- Академическая и специальная литература
- Химия и химическая промышленность
- Информационные технологии в химической промышленности
- Вычислительная химия
- Прикладная литература
- Компьютерная литература
- Matlab / Simulink
Поиск материала «Численные методы в примерах и задачах, Киреев В.
 И., Пантелеев А.В., 2015» для чтения, скачивания и покупки
И., Пантелеев А.В., 2015» для чтения, скачивания и покупкиНиже показаны результаты поиска поисковой системы Яндекс. В результатах могут быть показаны как эта книга, так и похожие на нее по названию или автору.
Search results:
- Численные методы в примерах и задачах — Пантелеев…
ПРИКЛАДНАЯ МАТЕМАТИКА для ВТУЗов В.И. КИРЕЕВ А.В. ПАНТЕЛЕЕВ ЧИСЛЕННЫЕ МЕТОДЫ В ПРИМЕРАХ И ЗАДАЧАХ Издание третье, стереотипное Рекомендовано Учебно-методическим объединением высших учебных заведений Российской Федерации по образованию в области авиаиии, ракетостроения и космоса в качестве учебного пособия для студентов высших технических учебных заведений Москва «Высшая школа» 2008.
Киреев, А.В. Пантелеев.
djvu.online
- Киреев В.И., Пантелеев А.В. Численные методы в примерах.
 ..
..Бахвалов Н.С., Лапин А.В., Чижонков Е.В. Численные методы в задачах и упражнениях. Учеб. пособие Учебное пособие содержит элементы теории, примеры решений эаддч и упражнения для самостоятельной работы. Представленные задачи разбиты по рекомендуемым темам семинарских занятий, а их подбор призван способствовать закреплению материала, излагаемого в теоретическом курсе. Типовые задачи снабжены решениями, которые могут быть использованы студентами для самостоятельного изучения предмета и овладения обидами…
vk.com
-
Купить эту книгу
- Канцтовары
Канцтовары: бумага, ручки, карандаши, тетради. Ранцы, рюкзаки, сумки. И многое другое.
my-shop.ru
- Численные методы в примерах и задачах от Киреев.
 .. — PDF Drive
.. — PDF Driveby Киреев В.И. & Пантелеев А.В.
. Введение в численные методы в задачах и упражнениях Гулин А.В.|Мажорова О.С …
Критерий фактори Вероятность и статистика в примерах и задачах. Том 1. Основные поня …
Получите самые популярные бесплатные книги в вашем почтовом ящике.
ru.pdfdrive.com
- Численные методы в примерах и задачах — Киреев В. — Скачать…
Формат: PDF (10283 Kb). СКАЧАТЬ. Currently 0/5. Рейтинг: 0/5 (Всего голосов: 0). Аннотация. Численные методы в примерах и задачах.
700 задач по математике. Все типы задач курса начальной школы. Учимся считать деньги. 1-4 классы.
www.rulit.me
- Численные методы в примерах и задачах by Киреев.
 .. — PDF Drive
.. — PDF DriveПрограммирование на C++ в примерах и задачах. 369 Pages·2017·11.54 MB·4,148 Downloads·Russian·New! обширный список задач для самостоятельного решения.
Методы оптимизации в примерах и задачах. 512 Pages·2015·7.03 MB·410 Downloads·Russian·New! , обучающихся по направлению «Прикладная математика» Методы � …
www.pdfdrive.com
- Численные методы в примерах и задачах Автор: Киреев…
Описание: Пособие охватывает классические разделы численного анализа: методы алгебры, теории приближения функций одной переменной с их приложениями, разностные методы решения задач Коши и краевых задач для обыкновенных дифференциальных уравнений, численные методы решения уравнений математической физики с двумя и тремя независимыми переменными.
vk.com
- Уважаемые коллеги ! Представляем вашему вниманию подборку.
 ..
..Представляем вашему вниманию подборку — практикум по численным методам ! В данных книгах содержатся элементы теории, примеры решений задач и упражнения для самостоятельной работы.
«Численные методы в примерах и задачах» 2015 г. Автор: Киреев В.И., Пантелеев А.В. Пособие охватывает классические разделы численного анализа: методы алгебры, теории приближения функций одной переменной с их приложениями, разностные методы решения задач Коши и краевых задач для обыкновенных…
vk.com
- Киреев В.И., Пантелеев А.В. Численные методы в примерах…
Пособие охватывает классические разделы численного анализа: методы алгебры, теории приближения функций одной переменной с их приложениями, разностные методы решения задач Коши и краевых задач для обыкновенных дифференциальных уравнений, численные методы решения уравнений математической физики с двумя и тремя независимыми переменными.

www.studmed.ru
- Киреев В.И., Пантелеев A.B. — Численные методы в примерах…
Пособие охватывает классические разделы численного анализа: методы алгебры, теории приближения функций одной переменной с их приложениями, разностные методы решения задач Коши и краевых задач для.
Название: Численные методы в примерах и задачах Авторы: Киреев В.И., Пантелеев A.B. Издательство: М.: Высшая школа Год издания: 2004 Страниц: 480 Формат: PDF Язык: Русский Размер: 11.6 Mb.
1.downfiles.ru
- Киреев В.И., Пантелеев А.В. | Численные методы в примерах…
Численные методы в примерах и задачах Название: Численные методы в примерах и задачах Автор: Киреев В.И., Пантелеев А.В. Формат: PDF Размер: 10 Мб Год: 2015 Качество: Отличное Язык: Русский Страниц: 448.

В учебнике представлены основные численные методы решения задач алгебры и анализа, теории приближений и оптимизации, задач для обыкновенных дифференциальных уравнений и уравнений математической физики.
www.arhibook.ru
- Численные методы в примерах и задачах Учебное пособие…
Здесь можно скачать «Численные методы в примерах и задачах Учебное пособие Издание четвертое исправленное», год 2015 в формате fb2 полную версию бесплатно без регистрации и SMS, а также читать онлайн книгу на сайте ПараКниг (paraknig.me).
Многие его задачи, породив обширную литературу и вызвав многочисленные подражания, вошли в ее золотой фонд. В предлагаемой книге собрано 520 задач и головоломок Дьюдени по арифметике, алгебре, геометрии, разрезанию и составлению фигур.
paraknig.me
- Скачать Численные методы в примерах и задачах
Численные методы в примерах и задачах — Численные методы — это методы приближенного решения задач прикладной математики, основанные на реализации алгоритмов, соответствующих математическим моделям.
 Наука, изучающая численные методы, называется также численным анализом, или вычислительной математикой.
Наука, изучающая численные методы, называется также численным анализом, или вычислительной математикой.Численные методы решения обыкновенных дифференциальных уравнений Глава 6. Методы решения задачи Коши Глава 7. Методы решения краевых задач Часть IV.
raznoezdes.ucoz.ru
- «Численные методы в примерах и задачах», А. В. Пантелеев…
Пособие охватывает классические разделы численного анализа: методы алгебры, теории приближения функций одной переменной с их приложениями, разностные методы решения задач Коши и краевых задач для обыкновенных дифференциальных уравнений, численные методы решения уравнений математической физики с двумя и тремя независимыми переменными.
В каждом разделе кратко изложены основные теоретические сведения, приведены решения типовых примеров и задачи для самостоятельного решения.
www.
 litres.ru
litres.ru - ЭБС Лань | Численные методы в примерах и задачах
Пособие охватывает классические разделы численного анализа: методы алгебры, теории приближения функций одной переменной с их приложениями, разностные методы решения задач Коши и краевых задач для обыкновенных дифференциальных уравнений, численные методы решения уравнений математической физики с двумя и тремя независимыми переменными.
В каждом разделе кратко изложены основные теоретические сведения, приведены решения типовых примеров и задачи для самостоятельного решения.
e.lanbook.com
- Киреев В.И., Пантелеев А.В. Численные методы в примерах…
— 480 с. Пособие охватывает классические разделы численного анализа: методы алгебры, теории приближения функций одной переменной с их приложениями, разностные методы решения задач Коши и краевых задач для обыкновенных дифференциальных уравнений, численные методы решения уравнений математической физики с двумя и тремя независимыми переменными.

Численные методы решения уравнений математической физики с двумя независимыми переменными. Постановка задачи и основные положения.
diary.ru
- ЭБС Лань | Численные методы в примерах и задачах
Пособие охватывает классические разделы численного анализа: методы алгебры, теории приближения функций одной переменной с их приложениями, разностные методы решения задач Коши и краевых задач для обыкновенных дифференциальных уравнений, численные методы решения уравнений математической физики с двумя и тремя независимыми переменными.
В каждом разделе кратко изложены основные теоретические сведения, приведены решения типовых примеров и задачи для самостоятельного решения.
e.lanbook.com
- Численные методы в примерах и задачах.
 Учебное пособие…
Учебное пособие…Скачать книгу Киреев Владимир Иванович, Пантелеев Андрей Владимирович «Численные методы в примерах и задачах. Учебное пособие» в формате бесплатно и без регистрации, а также другие книги Киреев Владимир Иванович, Пантелеев Андрей Владимирович в формате fb2.
paraknig.me
- Численные методы в примерах и задачах | Киреев…
Киреев В.И., Пантелеев А.В.
3.50 Mb. Только что пользователи скачали эти книги: #1.
libcats.org
- Численные методы в примерах и задачах — А. В. Пантелеев
Пособие охватывает классические разделы численного анализа: методы алгебры, теории приближения функций одной переменной с их приложениями, разностные методы решения задач Коши и краевых задач для обыкновенных дифференциальных уравнений, численные методы решения уравнений математической физики с двумя и тремя независимыми переменными.

В каждом разделе кратко изложены основные теоретические сведения, приведены решения типовых примеров и задачи для самостоятельного решения.
child-class.ru
- Скачать полную книгу Численные методы в примерах…
Численные методы в примерах и задачах — В. И. Киреев, А. В. Пантелеев целиком! А вы уже поделились с друзьями? Пособие охватывает классические разделы численного анализа: методы алгебры, теории приближения функций одной переменной с их приложениями, разностные методы решения задач Коши и краевых задач для обыкновенных дифференциальных уравнений, численные методы решения уравнений математической физики с двумя и тремя независимыми переменными.
litvik.net
- Книги, учебники — В. И. Киреев, А. В. Пантелеев Численные..
 .
.Книга подробно рассматривает основные вопросы базовых разделов численного анализа и применение численных методов в алгебре и теории интегрального и дифференциального исчисления. Отдельные главы посвящены теории приближения монофункций с их приложениями, решению задач Коши разностными методами, а также алгоритм решения задачи Коши интегрально-дифференциальными сплайнами. Для углубленного изучения вопроса приведена теория и практика вычисления значений функций нескольких переменных.
teor-meh.ru
- ЭБС Лань | Методы оптимизации в примерах и задачах
Рассмотрены аналитические методы решения задач поиска экстремума функций многих переменных на основе необходимых и достаточных условий. Изложены численные методы нулевого, первого и второго порядков решения задач безусловной минимизации, а также численные методы поиска условного экстремума. Описаны алгоритмы решения задач линейного программирования, целочисленного программирования, транспортных задач.

e.lanbook.com
- Киреев В.И., Пантелеев А.В. — Численные методы в примерах…
Пособие охватывает классические разделы численного анализа: методы алгебры, теории приближения функций одной переменной с их приложениями, разностные методы решения задач Коши и краевых задач для обыкновенных дифференциальных уравнений, численные методы решения уравнений математической физики с двумя и тремя независимыми переменными.
mirknig.ws
- Киреев, Владимир Иванович — Численные методы в примерах…
(Учебная литература) (Прикладная математика в примерах и задачах) Вычислительная математика — Приближенные вычисления — Численные методы — Пособие по решению задач для высшей школы Шифр хранения: FB 3 01-5/526-4 FB 3 01-5/527-2.

1# $a Киреев, Владимир Иванович. 245. 00 $a Численные методы в примерах и задачах / $c В. И. Киреев, А. В. Пантелеев.
search.rsl.ru
- Численные методы в примерах и задачах… — Google Книги
Пособие охватывает классические разделы численного анализа: методы алгебры, теории приближения функций одной переменной с их приложениями, разностные методы решения задач Коши и краевых задач для обыкновенных дифференциальных уравнений, численные методы решения уравнений математической физики с двумя и тремя независимыми переменными.
Авторы: Владимир Иванович Киреев, Андрей Владимирович Пантелеев.
books.google.ru
- Киреев В.И., Пантелеев А.В. — Численные методы в примерах…
Пособие охватывает классические разделы численного анализа: методы алгебры, теории приближения функций одной переменной с их приложениями, разностные методы решения задач Коши и краевых задач для обыкновенных дифференциальных уравнений, численные методы решения уравнений математической физики с двумя и тремя независимыми переменными.

mirknig.ws
- В.И. Киреев, А.В. Пантелеев — Численные методы в примерах…
Пособие охватывает классические разделы численного анализа: методы алгебры, теории приближения функций одной переменной с их приложениями, разностные методы решения задач Коши и краевых зада.
Для студентов математических, инженерно-технических и авиационных специальностей вузов и университетов, аспирантов и научных работников. Автор: В.И. Киреев, А.В. Пантелеев Название: Численные методы в примерах и задачах Издательство: Высшая школа Год: 2008 Страниц: 480 ISBN: 978–5–06–004763–9…
www.takelink.ru
- Численные методы в примерах и задачах, Киреев…
Пособие охватывает классические разделы численного анализа: методы алгебры, теории приближения функций одной переменной с их приложениями, разностные методы решения задач Коши и краевых задач для обыкновенных дифференциальных уравнений, численные методы решения уравнений математической физики с двумя и тремя независимыми переменными.

В каждом разделе кратко изложены основные теоретические сведения, приведены решения типовых примеров и задачи для самостоятельного решения.
lanbook.com
- Книга Численные Методы В примерах и Задачах.
В маркетплейсе СберМегаМаркет можно найти книга Численные Методы В примерах и Задачах.
Пособие охватывает классические разделы численного анализа: методы алгебры, теории приближения функций одной переменной с их приложениями, разностные методы решения задач Коши и краевых задач для обыкновенных дифференциальных уравнений, численные методы решения уравнений математической физики с двумя и тремя независимыми переменными.
sbermegamarket.ru
- Киреев, Пантелеев: Численные методы в примерах и задачах.

Пособие охватывает классические разделы численного анализа: методы алгебры, теории приближения функций одной переменной с их приложениями, разностные методы решения задач Коши и краевых задач для обыкновенных дифференциальных уравнений, численные методы решения уравнений математической физики с двумя и тремя независимыми переменными.
В каждом разделе кратко изложены основные теоретические сведения, приведены решения типовых примеров и задачи для самостоятельного решения.
www.labirint.ru
- В.И. Киреев, А.В. Пантелеев — Численные методы в примерах…
Виктор Суворов — Сборник произведений (69 книг) (1). Сергей ТТ.
subscribe.ru
- Методы оптимизации в примерах и задачах от Пантелеев…
Скачать.
 Конвертировать (EPUB, MOBI) Отправлено на электронную почту Отправлено в Kindle Report.
Конвертировать (EPUB, MOBI) Отправлено на электронную почту Отправлено в Kindle Report.— «Прикладная математика» Численные методы в примерах и задачах Киреев В.И.|Пантеле …
Методы математической физики в примерах и задачах. В 2 т. Т.II.
Получите самые популярные бесплатные книги в вашем почтовом ящике.
ru.pdfdrive.com
На данной странице Вы можете найти лучшие результаты поиска для чтения, скачивания и покупки на интернет сайтах материалов, документов, бумажных и электронных книг и файлов похожих на материал «Численные методы в примерах и задачах, Киреев В.И., Пантелеев А.В., 2015»
Для формирования результатов поиска документов использован сервис Яндекс.XML.
Нашлось 3 млн ответов. Показаны первые 32 результата(ов).
Дата генерации страницы:
Численные методы
Численные методы Версия, к которой вы обращаетесь, не является окончательной. Описание этого курса может измениться. Окончательная версия будет опубликована 1 июня.
Описание этого курса может измениться. Окончательная версия будет опубликована 1 июня.
5,00 кредитов
30,0 ч + 30,0 ч
Q2
Язык
Французский
Основные темы
Этот курс предназначен для введения в методы выполнения числовых вычислений на компьютерах.
Курс служит трем основным целям:
- понимание основных численных методов с лежащими в их основе математическими понятиями,
- способность интерпретировать надежность численных результатов,
- навыки программирования для реализации простых числовых алгоритмов с помощью Python.
Результаты обучения
По окончании этого раздела обучения учащийся способен: | |
| 1 | По окончании этого курса слушатели смогут: |
Содержание
В этом курсе представлен широкий обзор численных методов с использованием исчисления, алгебры и информатики. Учащийся должен осознавать соответствующие проблемы при выборе подходящего метода и программного обеспечения и их разумном использовании с точки зрения вычислительной стоимости, численной точности, сложности и стабильности. Чтобы сделать презентацию конкретной и привлекательной, в качестве верного компаньона принята среда программирования PYTHON.
Темы включают:
- Анализ ошибок: ошибка моделирования, ошибка усечения, порядок сходимости и аппроксимации, представление чисел с плавающей запятой (IEEE754).

Что такое контрольная работа в вузе: Специфика контрольных работ | edugid.ru
Что такое контрольная работа
Что такое контрольная работа Студенту.рф- Все компании
- Рейтинг
- Публикации
Сколько стоит написать вашу работу?
Заполните форму и узнайте стоимость
Вид работыПоиск информацииДипломнаяВКРМагистерскаяРефератОтчет по практикеВопросыКурсовая теорияКурсовая практикаДругоеКонтрольная работаРезюмеБизнес-планДиплом MBAЭссеЗащитная речьДиссертацияТестыЗадачиДиплом техническийПлан к дипломуКонцепция к дипломуПакет для защитыСтатьиЧасть дипломаМагистерская диссертацияКандидатская диссертацияКонтактные данные — строго конфиденциальны!
Указывайте телефон без ошибок! — потребуется для входа в личный кабинет.
* Нажимая на кнопку, вы даёте согласие на обработку персональных данных и соглашаетесь с политикой конфиденциальности
Подтверждение
Ваша заявка принята.
Ей присвоен номер 0000.
Просьба при ответах не изменять тему письма и присвоенный заявке номер.
В ближайшее время мы свяжемся с Вами.
Ошибка оформления заказа
Кажется вы неправильно указали свой EMAIL, без которого мы не сможем ответить вам.
Пожалуйста проверте заполнение формы и при необходимости скорректируйте данные.
Когда на горизонте начинает маячить сессия, студенты сразу вспоминают о контрольных работах. Чаще всего такая форма контроля и обучения применяется на заочном отделении. А вот если контрольную работу необходимо написать на дневном отделении, то тут поможет только тщательная подготовка и доля везения.
Что такое контрольная работа и с чем её едятКонтрольная работа – часть обучающего процесса, которая является формой проверки знаний учащегося.
Виды контрольных работ:
- аудиторные и домашние;
- экзаменационные и текущие.
Варианты заданий:
- Решение задач;
- Написание реферата;
- Ответ на вопросы;
- Тест;
- Составление таблиц;
- Чертёж;
- Выполнение упражнений;
- Рисование графиков.
Контрольная работа может включать в себя как одно задание, так и комбинацию из нескольких вариантов. Для написания теоретических заданий требуется изучение литературных источников, для решения прикладных задач необходимо ознакомиться с формулами и основными аспектами работы.
Сложность контрольной работы зависит не только от дисциплины, но и от требований преподавателя. В его силах упростить структуру и содержание, или усложнить, добавив решение задач или чертёж. Не стоит радоваться, если для допуска к зачёту или экзамену по сложной технической дисциплине нужно будет написать реферат. Поскольку в этом случае вы рискуете ничему не научиться в процессе выполнения работы. Самый лучший вариант – это подробные методические рекомендации, следуя которым можно легко справиться с работой самостоятельно.
Поскольку в этом случае вы рискуете ничему не научиться в процессе выполнения работы. Самый лучший вариант – это подробные методические рекомендации, следуя которым можно легко справиться с работой самостоятельно.
Когда контрольная работа используется в качестве формы контроля, действует несколько правил:
- Работа выполняется в аудитории и чётко ограничена во времени.
- Студентам запрещено пользоваться любыми материалами (конспектами, книгами, подсказками) кроме своей головы.
- Проверка происходит по конкретным темам.
Задача студента – подготовиться по имеющимся конспектам и учебникам. Хотя, если контрольная нагрянула неожиданно – остаётся надеяться только на студенческую смекалку.
Зачем нужна контрольная работа?Анализируя выполненные контрольные работы, преподаватель получает представление об общем уровне подготовки группы и об уровне знаний каждого учащегося. После этого он сможет сделать вывод об эффективности своей работы, о необходимости проведения дополнительных занятий по какой-либо теме, о качестве заданий.
После этого он сможет сделать вывод об эффективности своей работы, о необходимости проведения дополнительных занятий по какой-либо теме, о качестве заданий.
Для студентов же контрольная работа становится пропуском на экзамен или зачёт. Также некоторые преподаватели практикуют выставление на её основе оценок «автоматом». Причем можно отказаться, если оценка оказывается ниже ожидаемой и сдавать экзамен на общих основаниях.
Некоторые преподаватели предлагают всякие приятные бонусы: ответ только на 1 вопрос из 2, дополнительный балл к отметке, возможность самому выбрать билет. Вариантов много, но чтобы их получить придётся постараться. Обычно на вводных занятиях каждый преподаватель сообщает о том, что и как нужно сделать в контрольной работе, чтобы получить преимущество.
Если же никаких «плюшек» не было обещано, выполняя контрольную работу можно получить полезные навыки, усвоить новую информацию и оценить свои знания. Так что польза получается в любом случае, если действовать самостоятельно.
Выбор темы работы и стандартная структура
Если в качестве контрольной работы предлагается выполнить реферат, перед студентом встаёт проблема выбора темы. Сделать это можно 2 способами:
- Прогрессивный выбор. Зная тему будущей дипломной работы, можно в рамках изучаемой дисциплины подготовить некоторые вопросы.
- Формальный выбор. Из готового списка тем, предлагаемых преподавателем, студент выбирает интересную ему, или предлагает свою.
Иногда выбор осуществляется по порядковому номеру учащегося, но и в этом случае можно предложить свою тему. Обычно преподаватели стремятся поощрять инициативных студентов, и вашу тему скорее всего одобрят.
Структура контрольной работы строится по плану:
- Заглавие – тема работы.
- Оглавление – список основных разделов с указанием страниц.
- Введение – исследуемая проблема, её актуальность, используемые методы, цели и задачи работы.

- Основная часть – непосредственно сама контрольная работа (ответ на теоретические вопросы, решение задач, таблицы, схемы, чертежи).
- Заключение – подведение итогов, оценка выполнения целей, поставленных во введении, анализ полученных навыков.
- Список использованных источников – книги и статьи, которые использовались в работе.
- Приложения – всё, что не вошло в основную часть (рисунки, графики, словарь терминов, примеры и др.)
Обязательно контрольная работа должна содержать только основную часть, все остальные пункты добавляются в зависимости от конкретных требований к оформлению.
Оформление контрольной работыДля аудиторных работ – достаточно листочка с ответами или решениями, написанными от руки. Домашние контрольные работы, которые требуется выполнить в тетради, практически не требуют специального оформления.
Сложнее оформлять работы в печатной форме и чертежи. Прежде чем отправлять готовый файл на печать, необходимо тщательно изучить требования к оформлению. Иначе, велика вероятность возврата на доработку или получения заниженной оценки, потому что некоторые преподаватели требуют точного следования всем инструкциям. Подробнее про оформление контрольной работы здесь.
Иначе, велика вероятность возврата на доработку или получения заниженной оценки, потому что некоторые преподаватели требуют точного следования всем инструкциям. Подробнее про оформление контрольной работы здесь.
- Содержание плагиата. Не следует бездумно копировать готовые рефераты и курсовые.
- 50% заимствованного текста. Информация должна быть проанализирована и переработана, а не скопирована из источника.
- Отсутствие некоторых частей работы.
- Отсутствие ссылок на используемые источники.
- Неправильное оформление или нарушение требований к заглавию.
- Соблюдение всех требований и пожеланий преподавателя.
- Использование конспекта и рекомендованной литературы.
- Поиск примеров и анализ информации.
- Консультации у преподавателя.
Контрольная работа практически всегда выполняется по нескольким вариантам, поэтому поиск выполненных работ редко даёт результаты. Если же время поджимает или задание оказалось слишком сложным – лучше заказать работу у профессионалов. Только обязательно потом изучите решение. А самое главное – любая контрольная работа помогает вам повысить уровень своей квалификации.
Если же время поджимает или задание оказалось слишком сложным – лучше заказать работу у профессионалов. Только обязательно потом изучите решение. А самое главное – любая контрольная работа помогает вам повысить уровень своей квалификации.
Вам будет интересно
Типы работ
- Диплом МВА
Магистерская
ВКР
Эссе
Диссертация
Дипломные работы
Курсовые работы
Реферат
Отчет по практике
Бизнес-план
Контрольные работы
Доп. Образование
- Обучение онлайн
Второе высшее
Бизнес-образование
Развиваем мозги
Советы студентам
- Финансовая грамотность
Работа
Жизнь студенческая
Полезности в учебе
Важно знать
Учеба
- Рейтинги Вузов России
ЕГЭ
Поступление
Сессия
Форма обучения
Практика студентов
Структура контрольной работы в вузе
Контрольная работа — один из самых распространённых видов проверки знаний студентов в университете. Как правило, преподаватели проводят такие проверочные несколько раз за семестр, и оценки за контрольную существенно повлияют на итоговый балл. Чтобы контрольную работу оценили высоко, она должна иметь правильную структуру.
Как правило, преподаватели проводят такие проверочные несколько раз за семестр, и оценки за контрольную существенно повлияют на итоговый балл. Чтобы контрольную работу оценили высоко, она должна иметь правильную структуру.
Узнать больше о правильном написании контрольных, рефератов и курсовых можно, подписавшись на наш телеграм-канал со студенческими лайфхаками. А бонусы и выгодные предложения мы собрали в специальной группе.
Структура контрольной работы
Содержание контрольной зависит от дисциплины и конкретной темы, но структура работы, как правило, остаётся неизменной:
- Титульный лист.
- Содержание.
- Введение.
- Основная часть, разбитая на главы.
- Выводы.
- Список литературы.
- Приложения.
Расскажем подробнее о каждом пункте.
Титульный лист
На нём указывают:
- название вуза и структурного подразделения;
- предмет и тему работы;
- данные студента и преподавателя, который будет её проверять;
- город и год выполнения работы.

Это обложка работы и если она будет оформлена неправильно, преподаватель вряд ли поставит студенту высокую оценку.
Требования к оформлению и выполнению работ обычно изложены в методических указаниях по конкретному предмету.Содержание
Это план контрольной работы с указанием страниц, на которых размещены отдельные пункты. Не стоит пренебрегать оглавлением: оно делает проверку работы более удобным, помогает придерживаться структуры.
Введение
Во вступлении к работе описывается:
- актуальность;
- предмет и объект исследования;
- цель и задачи работы;
- краткий обзор источников;
Объём раздела — 1-2 страницы.
Это самый важный элемент структуры контрольной работы в вузе: если у преподавателя нет времени читать её полностью, он ограничится введением. Поэтому там нужно изложить всю необходимую информацию.Основная часть
Содержание этого раздела зависит от предмета и конкретной темы. Представители гуманитарных специальностей обычно анализируют материал по теме работы, будущие инженеры производят расчёты или делают чертежи.
Представители гуманитарных специальностей обычно анализируют материал по теме работы, будущие инженеры производят расчёты или делают чертежи.
Как правила, основная часть состоит из двух глав (теоретической и практической), её объём составляет 10-12 страниц.
Выводы
Этот раздел не менее важен, чем введение. Именно в заключении подводятся итоги работы, кратко излагается её суть. Выводы должны быть информативными и лаконичными, занимать 1-1.5 страницы.
Список источников
Стоит помнить, что главное — не количество литературы, а её актуальность и соответствие теме. Не стоит включать в перечень монографии и статьи, написанные более 10 лет назад, а при подборе учебников лучше брать последние издания.
В список необходимо включать только ту литературу, на которую студент ссылается в тексте контрольной.
Правила оформления источников в контрольной такие же, как для других работ.
Приложения
Большие таблицы, чертежи, схемы и иллюстрации размещают в приложениях. Каждый элемент нумеруется в алфавитном порядке.
Каждый элемент нумеруется в алфавитном порядке.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Подготовка контрольной работы обычно занимает несколько днейПравила оформления всех разделов контрольной с примерами для скачивания мы собрали в специальном материале, а в другой статье рассказали про ГОСТы для студенческих работ.Структура контрольной работы для заочников
Структура контрольных у студентов стационарной и заочной форм обучения одинаковая. При этом от заочников часто требуют работы большего объёма: не 12-15, а 20-25 страниц.
Студентам заочного отделения потребуется обработать больше источников и изложить больше теоретического материала. Если в работе есть практическая часть, она также может быть больше чем у студентов-очников: заочникам придётся выполнять те задания, которые другие делали на аудиторных занятиях.
Если у студента не хватает времени, чтобы хорошо написать контрольную, он всегда может обратиться к экспертам образовательного сервиса. Они в краткие сроки подготовят любую учебную работу: контрольную, лабораторную, самостоятельную, практическую.
Они в краткие сроки подготовят любую учебную работу: контрольную, лабораторную, самостоятельную, практическую.
вступительных экзаменов в колледж. Кто они такие? | Связанный колледж
Финансовый Академический Подготовка к колледжу Жизнь в колледже
Академический Подготовка к колледжу
4089
Вы можете слышать о SAT, ACT и CLT и думать: «Боже мой! Что это?» Давайте объясним. Это три разных вступительных экзамена в колледж, и если ваш ученик готовится в ближайшее время поступить в колледж, вы, вероятно, много о них услышите.
Что такое вступительный экзамен в колледж?
Вступительный экзамен в колледж проверяет академические навыки вашего учащегося, такие как чтение, письмо и математика. На их выполнение уходит несколько часов, и ваш ученик справится с ними за один присест (конечно, с перерывом или двумя).
На их выполнение уходит несколько часов, и ваш ученик справится с ними за один присест (конечно, с перерывом или двумя).
Требуется ли сдача вступительного экзамена в колледж для поступления в колледж?
Можно подумать, что ответ на название «вступительный экзамен в колледж» будет «да», но на самом деле это «не обязательно». Некоторые колледжи действительно требуют результатов тестов для поступления в колледж, но все больше и больше колледжей предпочитают не требовать результатов тестов для поступления. Это в основном потому, что есть некоторый вопрос о справедливости для всех студентов на экзаменах. Ваш студент должен проверить требования для каждого интересующего его колледжа.
Если для поступления в колледж не требуется вступительный экзамен, то нет смысла его сдавать, верно?
Не так быстро. Сдача вступительного экзамена в колледж по-прежнему дает преимущества, даже если он не требуется для поступления в колледж. Экзамен может использоваться для выполнения минимальных требований для определенного курса. Баллы также могут быть использованы для определения суммы, которую ваш учащийся получает от некоторых форм финансовой помощи, таких как стипендии. И даже если желаемая школа вашего ученика не требует оценок, ваш ученик может захотеть представить их в любом случае, если он наберет действительно хороший балл, поскольку это только увеличит его шансы на поступление.
Баллы также могут быть использованы для определения суммы, которую ваш учащийся получает от некоторых форм финансовой помощи, таких как стипендии. И даже если желаемая школа вашего ученика не требует оценок, ваш ученик может захотеть представить их в любом случае, если он наберет действительно хороший балл, поскольку это только увеличит его шансы на поступление.
Что делать, если мой ученик поступает в общественный колледж?
Местные колледжи обычно не требуют вступительных экзаменов, но на всякий случай уточните в школе.
Когда мой ученик сдает вступительный экзамен в колледж?
Большинство вступительных экзаменов в колледж проводятся в младших классах или в начале старшего года старшей школы. Ваш учащийся может уточнить у своего школьного консультанта даты и места проведения экзаменов или найти их на тестовых веб-сайтах (см. ниже).
Как мой ученик должен подготовиться к вступительным экзаменам в колледж?
Если ваш студент планирует сдавать вступительный экзамен в колледж, ему следует начать подготовку за несколько месяцев до даты экзамена и заниматься практически каждый день. Один из лучших вариантов — купить книгу для подготовки к экзамену, который собирается сдавать ваш ученик. Вы можете найти их на Amazon, и они дадут вашему ученику действительно хорошее представление о том, чего ожидать на экзамене, а также помогут им подготовиться к нему. Ваш ученик также должен пройти тест достаточно рано, чтобы у него было время пересдать его, если он не сдаст экзамен так хорошо, как хотел бы, с первого раза.
Один из лучших вариантов — купить книгу для подготовки к экзамену, который собирается сдавать ваш ученик. Вы можете найти их на Amazon, и они дадут вашему ученику действительно хорошее представление о том, чего ожидать на экзамене, а также помогут им подготовиться к нему. Ваш ученик также должен пройти тест достаточно рано, чтобы у него было время пересдать его, если он не сдаст экзамен так хорошо, как хотел бы, с первого раза.
Где я могу найти больше ресурсов?
Посетите веб-сайт SAT, ACT или CLT, в зависимости от того, какой тест сдает ваш учащийся.
Предыдущий
Следующий
Общие типы тестов в колледже
Цели обучения
- Определить распространенные типы тестов, проводимых в колледже, и их цели
Что тестируется
Есть много способов понять, как тесты и экзамены вписываются в академическую и студенческую культуру. Один из способов — спросить, для какой цели служат тесты (также называемые оценками). Например, чего пытается добиться ваш преподаватель, проводя для вас контрольный опрос в первый день занятий? Чем цель этого теста может отличаться от цели, скажем, пробной викторины, проводимой перед промежуточным экзаменом? И какова цель промежуточного периода?
Например, чего пытается добиться ваш преподаватель, проводя для вас контрольный опрос в первый день занятий? Чем цель этого теста может отличаться от цели, скажем, пробной викторины, проводимой перед промежуточным экзаменом? И какова цель промежуточного периода?
Очевидно, что каждый опрос, викторина, практический тест, промежуточный и итоговый экзамены могут служить разным целям. В зависимости от цели оценка относится к одной из следующих трех категорий:
- Предварительная оценка
- Формирующее оценивание
- Суммарное оценивание
Тесты этой категории используются для измерения убеждений, предположений, знаний и навыков, которые у вас есть, когда вы начинаете занятие или до того, как начнете работать над новой темой. С помощью предварительной оценки ваш преподаватель собирает исходные данные, чтобы использовать их позже для оценки изменений, то есть путем сравнения прежних знаний или навыков с тем, что вы изучаете в классе.
Один из подходов к предварительному оцениванию – это когда профессор просит студентов в начале семестра описать термин или понятие, лежащие в основе курса. Затем, позже в ходе курса, профессор пересматривает эти данные, чтобы определить, как инструкция изменила ваше понимание той же концепции. Сравнение того, что вы знаете или во что верите до и после курса или урока, — это продуктивный способ оценить, насколько успешным было ваше обучение и насколько успешным было преподавание.
Формирующее оценивание Тесты в этой категории обычно представляют собой викторины, всплывающие викторины, контрольные вопросы и практические тесты. При формирующем оценивании цель вашего преподавателя – следить за тем, что вы изучаете, и получать от вас отзывы о том, что нужно делать дальше в обучении. Хорошо ли учащиеся справились с викториной? Если да, то пора переходить к следующей теме. Если они не преуспели, это предполагает, что этой концепции следует уделить больше учебного времени. Формирующее оценивание помогает преподавателю лучше удовлетворить ваши потребности как учащегося.
Формирующее оценивание помогает преподавателю лучше удовлетворить ваши потребности как учащегося.
Тесты этой категории — это наиболее знакомые учащимся экзамены: промежуточные и выпускные экзамены. При итоговом оценивании преподаватель оценивает, сколько вы на самом деле узнали в конце учебного блока, сравнивая это с эталоном того, что вы должны были выучить. Суммарные оценки могут вызывать стресс, но они могут быть эффективным инструментом измерения. Большинство итоговых оценок оцениваются.
На курсах колледжа тесты обычно бывают устными — вас могут попросить, например, сделать устную презентацию, — или письменными — вас могут попросить отметить или записать свои ответы на бумаге или на компьютере. На специальных курсах вы также можете столкнуться с физическими тестами, в которых вас просят выполнить набор навыков (например, продемонстрировать процедуру сердечно-легочной реанимации).
Форматы тестов
Тесты различаются по стилю, строгости и требованиям. Например, в тесте с закрытой книгой испытуемый обычно должен полагаться на память, чтобы отвечать на определенные вопросы. Однако в тесте с открытой книгой испытуемый может использовать один или несколько дополнительных ресурсов, например, справочник или заметки. Тестирование по открытой книге может использоваться для предметов, по которым требуется много технических терминов или формул, чтобы эффективно отвечать на вопросы, например, по химии или физике.
Например, в тесте с закрытой книгой испытуемый обычно должен полагаться на память, чтобы отвечать на определенные вопросы. Однако в тесте с открытой книгой испытуемый может использовать один или несколько дополнительных ресурсов, например, справочник или заметки. Тестирование по открытой книге может использоваться для предметов, по которым требуется много технических терминов или формул, чтобы эффективно отвечать на вопросы, например, по химии или физике.
Кроме того, тест может проводиться официально или неофициально. В неформальном тесте вы можете просто отвечать в классе на вопросы для обсуждения, заданные преподавателем. В формальном тесте обычно ожидается, что вы будете работать в одиночку, и ставки выше.
Ниже приведен пример распространенных форматов тестов, с которыми вы можете столкнуться. Если вы знаете, какой тип теста вы будете сдавать, вы можете адаптировать свой подход к обучению в соответствии с форматом.
Общие типы тестов
Существует три распространенных типа тестов: письменные тесты, устные тесты и тесты на физические навыки. Давайте посмотрим, какие вещи вы должны будете выполнить в каждом типе теста.
Давайте посмотрим, какие вещи вы должны будете выполнить в каждом типе теста.
Письменный тест
Письменный тест может быть открытым, закрытым или любым другим. Студенты должны давать письменные ответы (как следует из названия этого типа теста). Ниже вы найдете таблицу наиболее распространенных типов вопросов в письменных тестах:
| Тип вопроса | Описание |
|---|---|
| Множественный выбор (цель) | Вам предоставляется вопрос и набор ответов на каждый вопрос, и вы должны выбрать, какой ответ или группа ответов являются правильными. Вопросы с несколькими вариантами ответов обычно требуют меньше времени для ответа тестируемым, чем другие типы вопросов, и их легко оценивать и оценивать. Они также допускают широкий диапазон сложности. |
| Верно Неверно (цель) | Вам представлено утверждение, и вы должны определить, верно оно или нет. Вопросы типа «верно/неверно», как правило, не являются преобладающими в тестах, потому что преподаватели знают, что статистически случайные догадки могут дать хороший результат. Но при умеренном использовании вопросы «верно/неверно» могут быть эффективными. Но при умеренном использовании вопросы «верно/неверно» могут быть эффективными. |
| Соответствие (цель) | Вам представлен набор конкретных терминов или идей и набор определений или идентифицирующих характеристик. Вы должны сопоставить каждый термин с его правильным определением или характеристиками. |
| Заполнение бланка (цель) | Вам представлены идентифицирующие характеристики, и вы должны вспомнить и указать правильный связанный термин или идею. Существует два типа тестов на заполнение пропусков: 1) Упрощенная версия предоставляет банк слов возможных слов, которые будут заполнять пробелы. 2) В более сложной версии нет банка слов для выбора. Тесты с заполнением бланков без банка слов могут вызывать беспокойство. |
| Эссе (субъективно) | Вам задают вопрос или концепцию, которую вы должны подробно объяснить. Вопросы-эссе подчеркивают темы и общие идеи. Вопросы для эссе позволяют учащимся продемонстрировать критическое мышление, творческое мышление и навыки письма. |
Устный тест
Устный тест (также называемый устным экзаменом или устным экзаменом) – это дискуссионный тест. Они также субъективны: на вопросы теста не может быть единственного правильного ответа.
Устный тест практикуется во многих школах и дисциплинах, в которых экзаменатор устно задает вопросы учащемуся. Студент должен ответить на вопрос таким образом, чтобы продемонстрировать достаточные знания предмета. Многие научные программы требуют, чтобы студенты, стремящиеся получить степень бакалавра, завершили программу, сдав устный экзамен или комбинацию устных и письменных экзаменов, чтобы показать, насколько хорошо студент понял материал. Обычно предоставляются учебные пособия или учебная программа, чтобы студенты могли подготовиться к экзамену, просматривая практические вопросы и темы, которые, вероятно, будут на экзамене.
Тест физических навыков
В тесте физических навыков вам предоставляется возможность выполнять определенные задачи, требующие ручного труда или физических навыков. Эти задачи измеряют физические способности, такие как сила, мышечная гибкость и выносливость. Ниже приведен пример тестов на физические способности на рабочем месте:
Эти задачи измеряют физические способности, такие как сила, мышечная гибкость и выносливость. Ниже приведен пример тестов на физические способности на рабочем месте:
Вы можете просмотреть расшифровку «Теста на физические способности» здесь (откроется в новом окне).
Цель тестирования
Вы уникальный человек. Никто другой не похож на вас. В колледже у вас есть особые способы обучения; вы интересуетесь определенными предметами; у вас есть подходы к взаимодействию с другими, которые являются особенными для вас. Вы личность.
Ваши преподаватели должны знать как можно больше о том, что вы знаете, думаете или умеете, и чем вы отличаетесь от других студентов. Тестирование — один из способов сделать это — оценить, как вы учитесь, что вы изучаете и что вы можете сделать с тем, что узнали. Зная больше об этих аспектах вас как ученика, ваши учителя смогут лучше служить вам.
Что ваши инструкторы ищут, чтобы получить подсказки о вашем индивидуальном обучении? В основном, ваши инструкторы пытаются с помощью тестирования подтвердить, что вы понимаете концепции, модели поведения или навыки, которым они обучают. Они хотят знать, что вы достигаете целей, которые они перед вами поставили. Их цели могут относиться к когнитивным навыкам, таким как запоминание, понимание, применение, анализ, оценка и создание. (Дополнительную информацию о таксономии Блума и когнитивной области обучения см. в разделе «Модели мышления».) Кроме того, ваши преподаватели всегда рады хорошей грамматике, вдумчивости, творчеству, точности и надежным ссылкам.
Они хотят знать, что вы достигаете целей, которые они перед вами поставили. Их цели могут относиться к когнитивным навыкам, таким как запоминание, понимание, применение, анализ, оценка и создание. (Дополнительную информацию о таксономии Блума и когнитивной области обучения см. в разделе «Модели мышления».) Кроме того, ваши преподаватели всегда рады хорошей грамматике, вдумчивости, творчеству, точности и надежным ссылкам.
Ваши профессора не единственные, кому нужно знать о вашем обучении. Администрации колледжей, такие как деканы и ректоры, также должны быть проинформированы. Успеваемость учащихся дает им полезную информацию, которую они используют для принятия решений об учебниках, подготовке учителей, профессиональном развитии и других образовательных или ресурсных потребностях. Многие заинтересованные стороны инвестируют в то, чтобы студенты были успешными.
Тем не менее, ваши преподаватели действительно находятся на переднем крае, когда дело доходит до сбора и интерпретации данных об обучении учащихся./Dopolnitelnye%20zadaniya/8%20klass/Kontrolnye%20raboty%20ris/Kontrolnaya%20rabota%20(8kl)%208.jpg)
Равенство треугольников признаки равенства треугольников: Первый признак равенства треугольников — урок. Геометрия, 7 класс.
Равные треугольники – определение, свойства, признаки
4.5
Средняя оценка: 4.5
Всего получено оценок: 370.
4.5
Средняя оценка: 4.5
Всего получено оценок: 370.
Изучая тему треугольников, стоит обратить внимание на признаки равенства двух фигур. Их можно использовать во время решений различных заданий. О том, как определить признаки и свойства равенства треугольников – поговорим в этой статье.
Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.
Опыт работы учителем математики — более 33 лет.
Определение
Треугольники ABC и $A_1B_1C_1$ считаются равными в том случае, если их можно совместить наложением. При этом, все стороны и вершины фигур полностью наложатся друг на друга, а все соответствующие углы совместятся.
Исходя из определения равных треугольников, в равных треугольниках все соотвествующие стороны равны и все соответствующие углы равны. Используем это свойство для доказательства признаков равенства треугольников способом наложения.
Для обозначения равенства фигур используют знак “равно”, к примеру, $Δ ABC = Δ А_1В_1С_1$
Математик Фалес, чтобы вычесть расстояние от корабля до суши построил треугольник на суше равный треугольнику на «море». Он, таким образом, узнал точное расстояние.
Признаки равенства
Выделяют три признака равенства треугольников:
1. Если две стороны и угол между ними одного треугольника равны соответствующим двум сторонам и углу между ними другого треугольника, то такие фигуры равны.
Рис. 1. Первый признак равенства2. Если сторона и два прилегающих к ней угла одного треугольника равны соответствующей стороне и двум прилегающим к ней углам другого треугольника, то такие фигуры равны.
Рис. 2. Второй признак равенства3. Если три стороны в одном треугольнике равны трем сторонам в другом треугольнике, то такие треугольники равны.
Кроме того, стоит выделить некоторые свойства:
- Сумма двух внутренних углов треугольника будет всегда меньше 1800.

- Внешний угол треугольника всегда больше внутреннего, при условии, если угол не смежный с ним.
- Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Алгоритм доказательства равенства фигур
- Необходимо сориентироваться, для каких треугольников необходимо доказать равенство. Для удобства можно выделить их разными цветами.
- На рисунке отметить, все необходимые данные в условии задания.
- Проверить есть ли у двух треугольников общая сторона либо угол.
- Далее необходимо проанализировать, имеют ли треугольники по две пары равных сторон либо углов. А также необходимо поразмышлять, как можно доказать равенство третьей стороны, либо угла между ними.
- При недостатке данных необходимо выяснить: можно ли использовать равенство других треугольников, чтобы доказать равенство нужных по условию.
- При необходимости, можно сделать дополнительное построение.
Порядок названия вершин одного треугольника должен быть одинаковым с порядком названия вершин другого треугольника.
Стойки стремянки могут свободно раздвигаться, до того момента, когда их не зафиксировали перемычкой. Жесткость такой конструкции основывается на третьем признаке равенства фигур.
Пример
Задание:
Два отрезка пересекаются в точке О и делятся этой точкой пополам. Доказать, что $Δ ABO = Δ CDO$.
Решение:
Стоит обратить внимание на рисунок
В условии задания сказано, что $BO=OD$, $AO = OС$. А углы $AOB$ и $COD$ равны, так как они вертикальные. Поэтому $Δ ABO = Δ CDO$ по первому признаку равенства треугольников.
Что мы узнали?
Для того, чтобы доказать равенство фигур необходимо использовать один из трех признаков равенства треугольников. Треугольники могут быть равными по двум сторонами и углу между ними, по стороне и двум прилегающим к ней углам, а также по трем сторонам.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Анна Ножеева
5/5
Ярик Яраслав
5/5
Данила Салин
5/5
Никита Ушаков
5/5
Оценка статьи
4.5
Средняя оценка: 4.5
Всего получено оценок: 370.
А какая ваша оценка?
Равенство треугольников. Признаки равенства треугольников – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД
Запомнить
Восстановить пароль
Регистрация
Конспект
Два треугольника называются равными, если их можно совместить наложением. Если два треугольника равны, то элементы (т. е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника.
Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Второй признак равенства треугольников. Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Третий признак равенства треугольников. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны
Признаки равенства прямоугольных треугольников
Два прямоугольных треугольника равны, если выполняется одно из следующих условий:
- равны их катеты;
- катет и гипотенуза одного треугольника равны катету и гипотенузе другого;
- гипотенуза и острый угол одного треугольника равны гипотенузе и острому углу другого;
- катет и прилежащий острый угол одного треугольника равны катету и прилежащему острому углу другого;
- катет и противолежащий острый угол одного треугольника равны катету и противолежащему острому углу другого.

Сообщить об ошибке
Обязательные
Математическая грамотность
Грамотность чтения
История Казахстана
Предметы по профилю
Биология
Химия
Английский язык
Французский язык
География
Немецкий язык
Информатика
Основы права
Русская литература
Математика
Физика
Русский язык
Всемирная история
Укажите предмет *
Скопируйте и вставьте вопрос задания *
Опишите подробнее найденную ошибку в задании *
Прикрепите скриншот
Объем файла не должен превышать 1МБ
Казахский
Русский
Обратите внимание! По выбранным Вами предметам ГРАНТЫ не предоставлены. В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен.
В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен.
1. Скачайте приложение iTest, используя QR-код или строку поиска в AppStore или Play Market
2. Авторизуйтесь в приложении и готовьтесь к экзаменам вместе с нами
Стороны равной длины — определение, формы, примеры, факты
Стороны равной длины — введение
Математика — это не только числа, она также включает изучение различных форм, таких как круги, квадраты, овалы, цилиндры, треугольники, прямоугольники и многое другое.
Включает определение размеров сторон или точных углов фигур.
Сегодня мы обсудим фигуры, имеющие сторон одинаковой длины . Мы узнаем факторы, которые отличают их друг от друга, и их соответствующие названия. Давайте начнем!
Родственные игры
Что такое Стороны равной длины?
Стороны одинаковой длины означают, что их размеры одинаковы. Проще говоря, стороны фигуры, имеющие одинаковую длину, являются сторонами равной длины.
Проще говоря, стороны фигуры, имеющие одинаковую длину, являются сторонами равной длины.
Стороны, имеющие одинаковую длину, также называются конгруэнтными сторонами. Эти стороны могут быть частью одной формы или разных форм. Давайте посмотрим на несколько примеров фигур со сторонами одинаковой длины.
В прямоугольнике ниже противоположные стороны конгруэнтны друг другу.
В двух треугольниках ниже стороны конгруэнтны друг другу.
Связанные рабочие листы
Стороны равной длины в одной форме
Треугольники
В зависимости от длины сторон треугольники можно разделить на разносторонние, равнобедренные и равносторонние.
- Разносторонний треугольник:
Это треугольник, в котором каждая сторона имеет разную длину.
- Равнобедренный треугольник:
Это треугольник, в котором две стороны имеют одинаковую длину. Угол, падающий между равными сторонами, называется углом при вершине. Углы, противолежащие двум равным сторонам треугольника, всегда будут равны. Точно так же, если два угла треугольника равны, то их соответствующие противоположные стороны также будут иметь одинаковую длину.
Точно так же, если два угла треугольника равны, то их соответствующие противоположные стороны также будут иметь одинаковую длину.
- Равносторонний треугольник:
Это треугольник, в котором все три стороны имеют одинаковую длину. Каждый угол равностороннего треугольника равен 60°. Следовательно, его также называют равноугольным треугольником.
Итак, треугольники с равными сторонами могут быть либо равнобедренными, либо равносторонними.
Четырехугольники
Четырехугольники — это многоугольники с четырьмя сторонами. Они также могут иметь равные все или некоторые из сторон. Различные категории перечислены ниже:
- Все стороны равны
В этих четырехугольниках все четыре стороны равны. Их еще называют правильными четырехугольниками. Примерами правильных четырехугольников являются квадрат и ромб.
- Три равные стороны
В этих четырехугольниках три стороны равны.
- Одна пара равных сторон
В этих четырехугольниках есть одна пара равных сторон. Стороны могут быть как противоположными, так и примыкающими друг к другу.
Стороны могут быть как противоположными, так и примыкающими друг к другу.
- Противоположные стороны равны: Примером этого является равнобедренная трапеция
- Смежные стороны равны: Примером этого является неправильный четырехугольник, у которого две смежные стороны равны.
- Две пары равных сторон
- Равные стороны противоположны: Примеры: прямоугольник и параллелограмм.
- Равные стороны смежные: Пример — воздушный змей.
Многоугольники
Многоугольники — это двумерные замкнутые фигуры, состоящие только из прямых сторон. Многоугольники могут иметь любое количество сторон. Это означает, что треугольники и четырехугольники также являются многоугольниками. Многоугольники также могут иметь равные все или некоторые стороны.
- Правильные многоугольники:
Многоугольники, у которых все стороны и все внутренние углы равны, называются правильными многоугольниками. Все их углы также равны. Обратите внимание, что ромб не имеет равных сторон, а не является правильным многоугольником, потому что все его внутренние углы не равны.
Все их углы также равны. Обратите внимание, что ромб не имеет равных сторон, а не является правильным многоугольником, потому что все его внутренние углы не равны.
- Неправильные многоугольники:
Многоугольники, у которых все стороны не равны, называются правильными многоугольниками. У них могут быть некоторые стороны одинаковой длины, но не все. Таким образом, даже если прямоугольники и параллелограммы имеют равные противоположные стороны, они являются неправильными многоугольниками.
Стороны одинаковой длины в различных формах
При сравнении различных форм, если сторона одной формы равна стороне другой, говорят, что стороны равны.
Если все стороны одной фигуры равны всем сторонам другой фигуры и углы также одинаковы, то две фигуры называются конгруэнтными.
Например, два треугольника называются конгруэнтными, если все их соответствующие стороны и углы равны.
Критерии конгруэнтности треугольников
Нам не нужно измерять все стороны и углы двух треугольников, чтобы проверить, конгруэнтны они или нет. Если они соответствуют любому из заданных критериев, то они конгруэнтны.
Если они соответствуют любому из заданных критериев, то они конгруэнтны.
- Критерии SSS (сторона-сторона-сторона)
Два треугольника $\Delta\text{ABC}$ и $\Delta\text{PQR}$ называются конгруэнтными по критерию SSS, если их соответствующие стороны равны.
- AB $=$ PQ
- до н.э. $=$ QR
- AC $=$ PR
- Критерии SAS (сторона-угол-сторона)
Два треугольника $\Delta{ABC}$ и $\Delta{PQR}$ называются конгруэнтными по критериям SAS, если две их соответствующие стороны и угол между ними равны.
- AB $=$ PQ
- ∠A $=$ ∠P
- AC $=$ PR
- Критерии AAS (угол-угол-сторона)
Два треугольника $\Delta\text{ABC}$ и $\Delta\text{PQR}$ называются конгруэнтными по критериям ААС, если любые два их соответствующих угла и любая одна сторона равны.
- ∠A $=$ ∠P
- ∠С $=$ ∠Р
- AC $=$ PR
- RHS-критерий (правая сторона гипотенузы)
Два прямоугольных треугольника $\Delta\text{ABC}$ и $\Delta\text{XYZ}$ называются конгруэнтными по RHS-критерию, если их соответствующие гипотенуза и одна пара соответствующих сторон равны..jpg)
- ∠B $=$ ∠Y (прямой угол)
- AC $=$ XZ (гипотенуза)
- AB $=$ XY (сторона)
Заключение
У некоторых фигур все стороны равны, а у других ни одна из сторон не равна. Кроме того, есть фигуры, у которых только несколько равных сторон. Мы можем сравнивать стороны и углы различных фигур, чтобы найти конгруэнтные стороны и конгруэнтные формы.
Решенные примеры
1. Назовите три фигуры, все стороны которых имеют одинаковую длину.
Решение : Три фигуры, все стороны которых имеют одинаковую длину, это ромб, квадрат и равносторонний треугольник.
2. Найдите периметр правильного шестиугольника, если одна из его сторон равна 9 дм.
Решение: Правильный шестиугольник имеет 6 сторон одинаковой длины.
Поскольку сторона равна 9 дюймам, периметр будет:
6$\умножить на 9 = 54$ дюймов.
3. Если две стороны треугольника равны, какой это треугольник?
Решение : Это равнобедренный треугольник. У равнобедренного треугольника две равные стороны.
У равнобедренного треугольника две равные стороны.
4. Если одна сторона параллелограмма 10 дюймов, а другая сторона 6 дюймов, каков общий периметр?
Решение : В параллелограмме противоположные стороны равны друг другу.
Если одна сторона 10 дюймов, а другая сторона 6 дюймов, общий периметр будет:
10$ + 10 + 6 + 6 = 32$ дюймов.
Практические задачи
1
В $\Delta\text{ABC}$ ∠A $=$ 50°, ∠ B $=$ 80° и ∠ C $=$ 50°. Определите равные стороны.
AC $=$ BC
AB $=$ AC
AB $=$ BC
Стороны не равны
Правильный ответ: AB $=$ BC
Дано, что ∠A $=$∠ В $=$ 50°. Это означает, что стороны, противолежащие этим углам, также равны. То есть AB $=$ BC.
2
$\Delta\text{ABC}$ имеет стороны 6 дюймов, 8 дюймов и 10 дюймов. $\Delta\text{DEF}$ конгруэнтно $\Delta\text{ABC}$. Что за треугольник $\Delta\text{DEF}$?
Разносторонний
Равносторонний
Равнобедренный
Невозможно определить
Правильный ответ: Разносторонний
Если $\Delta\text{DEF}$ конгруэнтно $\Delta\text{ABC}$, стороны $\ Delta\text{DEF}$ также составляет 6 дюймов, 8 дюймов и 10 дюймов. Поскольку все три стороны $\Delta\text{DEF}$ имеют разную длину, это разносторонний треугольник.
Поскольку все три стороны $\Delta\text{DEF}$ имеют разную длину, это разносторонний треугольник.
3
Какие из следующих четырехугольников являются правильными многоугольниками?
Прямоугольник
Квадрат
Воздушный змей
Ромб
Правильный ответ: Квадрат
У правильного многоугольника все стороны равны и все углы равны. Квадрат – это единственный четырехугольник с равными сторонами и равными углами.
4
Определите фигуру, у которой не все стороны равны.
Равносторонний треугольник
Ромб
Прямоугольник
Правильный пятиугольник
Правильный ответ: Прямоугольник
В прямоугольнике смежные стороны имеют разную длину, а противоположные стороны равны.
Часто задаваемые вопросы
Возможны ли конгруэнтные формы с соответствующими сторонами разной длины?
Нет, конгруэнтные фигуры должны иметь стороны одинаковой длины.
Может ли быть неправильный многоугольник со сторонами одинаковой длины?
Да, если стороны равны, но углы разные, или равны только две или некоторые из сторон, то это будет неправильный многоугольник. Например, у ромба равные стороны, но разные углы.
Поскольку все углы равностороннего треугольника равны 60°, можем ли мы сказать, что все равносторонние треугольники конгруэнтны друг другу?
Нет, чтобы треугольники были равны, все их стороны и углы должны быть равны.
2.4: Доказательство равенства линий и углов
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 34127
- Генри Африк
- CUNY Технологический колледж Нью-Йорка через Технологический колледж Нью-Йорка в CUNY Академические работы
Мы можем доказать равенство прямых и углов, если мы можем показать, что они являются соответствующими частями конгруэнтных треугольников. Мы считаем удобным представить эти доказательства в форме в два столбца с утверждениями в левом столбце и причиной каждого утверждения в правом.
Мы считаем удобным представить эти доказательства в форме в два столбца с утверждениями в левом столбце и причиной каждого утверждения в правом.
Пример \(\PageIndex{1}\)
Дано \(AB || CD\) и \(AB = CD\) доказать \(AD = BC\)
Решение
| Причины | |
| 1. \(AB = CD\). | 1. Дано. |
| 2. \(\угол ABD = \угол CDB\). | 2. Альтернативные внутренние углы параллельных прямых \((AB || CD)\) равны. |
| 3. \(BD = DB\). | 3. Личность. |
| 4. \(\треугольник ABD \cong \треугольник CDB\) | 4. \(SAS = SAS\): \(AB, \угол B, BD\) из \(\треугольник ABD = CD\), \(\угол D\), \(DB\) из \(\ треугольник CDB\). |
| 5. \(АД = ВС\) | 5. Соответствующие стороны равных треугольников равны, |
Объяснение: Каждое из первых трех утверждений говорит о том, что сторона или угол \(\треугольника ABD\) равна соответствующей стороне или углу \(\треугольника CDB\). Чтобы получить эти утверждения, мы должны сначала написать конгруэнтность, используя методы предыдущих разделов. Затем мы выбираем три пары соответствующих сторон или углов, которые равны по одной из следующих причин:0005
Чтобы получить эти утверждения, мы должны сначала написать конгруэнтность, используя методы предыдущих разделов. Затем мы выбираем три пары соответствующих сторон или углов, которые равны по одной из следующих причин:0005
Причины равенства линий
- Дано. Это означает, что в начале упражнения нас просят предположить, что строки равны. Например, в задаче будет указано «дано \(AB = CD\)» или \(AB\) и \(CD\) будут отмечены так же на схеме.
- Личность. Это означает, что в обоих треугольниках появляется один и тот же отрезок прямой. Например, \(BD\) и \(DB\) представляют один и тот же отрезок прямой. Конечно, длина отрезка равна самой себе.
Причины равенства углов
- Дано.
- Личность.
- Альтернативные внутренние углы параллельных прямых равны. Чтобы применить эту причину, мы должны иметь в виду, что прямые параллельны.
- Соответствующие углы параллельных прямых равны.
- Вертикальные углы равны.

Это не единственные возможные причины, но это все, что мы будем использовать в первую очередь.
Мы также должны выбрать три пары равных сторон или углов, чтобы одну из причин \(SAS = SAS\), \(ASA = ASA\) или \(AAS = AAS\) можно было использовать для обоснования сравнения утверждение в утверждении 4. В разделах 2.6 и 2.7 мы приведем некоторые дополнительные причины конгруэнтности двух треугольников.
Мы хотим доказать утверждение 5. Причина в том, что соответствующие стороны (или углы) конгруэнтных треугольников равны. Мы можем использовать эту причину здесь, потому что конгруэнтность треугольников уже доказана в утверждении 4,
.Последнее замечание. Обратите внимание, что решение примера \(\PageIndex{1}\) согласуется с нашим первоначальным определением доказательства. Верность каждого нового утверждения подтверждается использованием предыдущих утверждений и уже установленных причин.
Приведем другой пример:
Пример \(\PageIndex{2}\)
Учитывая \(QP || ST\) и \(QR = TR\) докажите \(PR = SR\).
Решение
| Заявления | Причины |
| 1. \(QR = TR\) | 1. Дано. |
| 2. \(\угол Q = \угол T.\) | 2. Альтернативные внутренние углы параллельных прямых (\(QP || ST\)) равны. |
| 3. \(\угол PRQ = \угол SRT\). | 3. Вертикальные углы равны. |
| 4. \(\треугольник PQR \cong \треугольник STR\). | 4. \(ASA = ASA: \угол Q, QR, \угол R\) из \(\треугольник PQR = \угол T\), \(TR, \угол R\) из \(\треугольник STR\) . |
| 5. \(PR = SR\). | 5. Соответствующие стороны равных треугольников равны, |
1. Даны \(\угол A = \угол D\), \(\угол B = \угол E\), \(AB = DE\). Докажите \(AC = DF\).
2. Даны \(AC=DF\), \(BC = EF\), \(\угол C = \угол F\).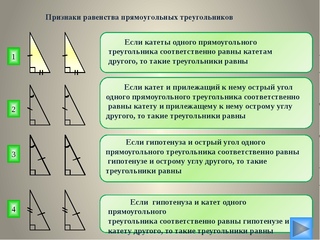 Докажите \(AB = DE\).
Докажите \(AB = DE\).
3. Даны \(AC = EC\) и \(BC = DC\). Докажите \(AB = ED\).
4. Даны \(AC = DC\), \(\угол A = \угол D\). Докажите \(BC = EC\).
5. Даны \(\угол ABD = \угол CDB\) и \(\угол ADB = \угол CBD\). Докажите \(AB = CD\).
6. Даны \(AB || CD\) и \(AD || CB\). Докажите \(AB = CD\).
7. Даны \(AC = BC\) и \(\угол ACD = \угол BCD\). Докажите \(\угол А = \угол В\).
8. Даны \(\угол A = \угол B\), \(\угол ACD = \угол BCD\). Докажите \(AC = BC\).
9. Даны \(AB || CD\) и \(AB = CD\). Докажите \(AE = CE\). (Подсказка: покажите \(\треугольник ABE \cong \треугольник CDE\))
10. Даны \(AE = CE\) и \(BE = DE\). Докажите \(\угол BAC = \угол CDB\).
11. Даны \(\угол A = \угол D\), \(AC = DE\), \(AB || DC\). Докажите \(BC = CE\).
12. Даны \(AB || DE\), \(AC || FE\) и \(DC = FE\). Докажите \(BE = EC\).
13.
Hno2 hi i2 no h2o: Используя метод электронного баланса, составьте уравнение реакции HNO2 + HI → I2 + NO + H2O Определите окислитель и восстановитель
Азотистая кислота — презентация онлайн
Похожие презентации:
Сложные эфиры. Жиры
Физические, химические свойства предельных и непредельных карбоновых кислот, получение
Газовая хроматография
Хроматографические методы анализа
Искусственные алмазы
Титриметрические методы анализа
Биохимия гормонов
Антисептики и дезинфицирующие средства. (Лекция 6)
Клиническая фармакология антибактериальных препаратов
Биохимия соединительной ткани
1. Азотистая кислота
Азотистая кислота HNO2имеет слабый характер.
Весьма неустойчива, может быть
только в разбавленных растворах:
2HNO2
NO + NO2 + h3O.
2. Атом азота в азотистой кислоте имеет промежуточную степень окисления +3
в связи с этим он может быть иокислителем, и проявлять
восстановительные свойства:
HNO2 + HI = I2 + NO + h3O,
HNO2 + h3O2 = HNO3 + h3O,
KNO2 + KMnO4 + h3SO4 = KNO3 +
K2SO4 + MnSO4 + h3O.

Нагреваясь, раствор азотистой
кислоты распадается с
выделением NO и
образованием азотной кислоты
Запишите уравнение
4. Соли азотистой кислоты называются нитритами
Нитриты гораздо более устойчивы, чем HNO2,все они токсичны. Представляют собой
кристаллические вещества, хорошо
растворимые в воде (труднее других — AgNО2)
Свойства .
1) Как и HNО2, нитриты обладают окислительновосстановительной двойственностью:
KNО2 + Н2О2 = KNО3 + Н2O
3KNО2 + 2КМпO4 + Н2O = 3KNО3 + 2MnО2↓ + 2КОН
2KNО2 + 2KI + 2h3SO4 = 2NO + I2 + 2K2SO4 + 2Н2O
2) Нитрит аммония разлагается при нагревании:
Nh5NО2 = N2↑ + 2Н2O
Состав. Строение. Свойства.
HNO3
H — O —N
O
O
степень окисления азота
валентность азота IV
+5
химическая связь
ковалентная полярная
Азотная кислота – бесцветная гигроскопичная жидкость,
c резким запахом, «дымит» на воздухе, неограниченно
растворимая в воде. tкип. = 83ºC.. При хранении на свету
разлагается на оксид азота (IV), кислород и воду,
приобретая желтоватый цвет: 4HNO3 = 4NO2 + O2 + 2h3O
Азотная кислота ядовита.

При разложении азотной кислоты
кислород, поэтому скипидар вспыхивает.
выделяется
Азотная кислота (HNO3)
Классификация
Азотная кислота по:
наличию кислорода:
основности:
растворимости в воде:
кислородсодержащая
одноосновная
растворимая
летучести:
летучая
степени электролитической
диссоциации:
сильная
Получение азотной кислоты в промышленности
Nh4
NO
NO2
1. Контактное окисление аммиака до
оксида азота (II):
4Nh4+ 5O2 = 4NO + 6h3O
2. Окисление оксида азота (II) в оксид
азота (IV):
2NO+O2 = 2NO2
3. Адсорбция (поглощение) оксида
азота (IV) водой при избытке кислорода
4NO2 + 2h3O + O2 = 4HNO3
HNO3
В лаборатории азотную кислоту получают действием
концентрированной серной кислоты на нитраты при
слабом нагревании.
Составьте уравнение реакции получения азотной кислоты.
NaNO3 + h3SO4 = NaHSO4 + HNO3
Химические свойства азотной кислоты
1. Типичные свойства кислот
2.
 Взаимодействие азотной кислоты с металлами
Взаимодействие азотной кислоты с металлами3. Взаимодействие азотной кислоты с неметаллами
Химические свойства азотной кислоты
Азотная кислота проявляет все типичные свойства
кислот.
Перечислите их:
Составьте уравнения реакций азотной кислоты:
1 с оксидом меди (II), оксидом алюминия;
2 c гидроксидом натрия, гидроксидом цинка;
3
c карбонатом аммония, силикатом натрия.
Дайте названия полученным веществам. Определите тип
реакции.
1
2HNO3 + CuO = Cu(NO3)2 + h3O
6HNO3 + Al2O3 = 2Al(NO3)3 + 3h3O
2
HNO3 + NaOH = NaNO3 + h3O
2HNO3 + Zn(OH)2 = Zn(NO3)2 + 2h3O
3
2HNO3 + (Nh5)2CO3 = 2Nh5NO3 + ↑CO2 + h3O
2HNO3 + Na2SiO3 = ↓h3SiO3 + 2NaNO3
Взаимодействие азотной кислоты с металлами
Как реагируют металлы с растворами кислот?
Металлы,
стоящие
в ряду активности
до кислоты
водорода,
вытесняют
Особенности
взаимодействия
азотной
с металлами:
его
изодин
кислот.
Металлы,
стоящие
после водорода
кислот его
1.
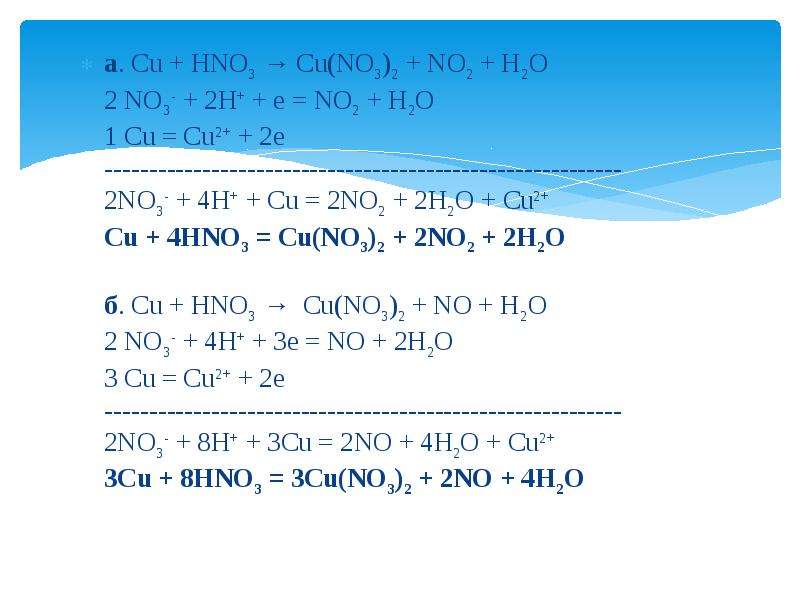 Ни
Ниметалл
никогда
не выделяет
из азотнойизкислоты
не
вытесняют,
т.е. не взаимодействуют
с кислотами,
не
водород.
Выделяются
разнообразные соединения
азота:
растворяются
них. N2+1O, N20,
N+4O2, N+2вO,
N–3h4 (Nh5NO3)
N–3h5+
N20
N2+1O
N+2O
N+4O2
концентрация кислоты
активность металлов
2. С азотной кислотой реагируют металлы, стоящие до и
после водорода в ряду активности.
3. Азотная кислота не взаимодействует с Au, Pt
4. Концентрированная азотная кислота пассивирует металлы:
Al, Fe, Be, Cr, Ni, Pb и другие (за счет образования плотной
оксидной пленки). При нагревании и при разбавлении азотной
кислоты данные металлы в ней растворяются.
Найти закономерность при взаимодействии
азотной кислоты с металлами:
Единственная общая закономерность при
взаимодействии азотной кислоты с металлами: чем
более разбавленная кислота и чем активнее металл,
тем глубже восстанавливается азот:
Увеличение
конц.
 кислоты
кислотыУвеличение
активности
металла
Допишите схемы реакций:
1)
HNO3(конц.) + Cu → Cu(NO3)2 + … + h3O
2)
HNO3(разб.) + Cu → Cu(NO3)2 + … + h3O
Рассмотрите превращения в свете ОВР
1) 4HN+5O3(конц.) + Cu0 = Cu+2(NO3)2 + 2 N+4O2 + 2 h3O
окислитель
восстановитель
N+5 + 1e → N+4 1 2
Cu0 – 2e → Cu+2 2 1
восстановление
окисление
2) 8 HN+5O3(конц.) + 3 Cu0 = 3Cu+2(NO3)2 + 2 N+2O + 4 h3O
окислитель
восстановитель
N+5 + 3e → N+2 3 2
Cu0 – 2e → Cu+2 2 3
восстановление
окисление
Взаимодействие азотной кислоты с неметаллами
Азотная кислота как сильный окислитель
Окисляет неметаллы до соответствующих кислот.
Концентрированная (более 60%) азотная кислота восстанавливается до
NO2 , а если концентрация кислоты (15 – 20%), то до NO.
Расставьте в схемах коэффициенты методом электронного баланса.
4 HNO3 + С → СO2 + 2 h3O + 4 NO2
N+5 + 1e → N+4 1 4
С0 – 4e → С+4 4 1
HNO3 (за счет N+5) – окислитель, пр.
 восстановления
восстановленияC – восстановитель, процесс окисления
5 HNO3 + P → h4PO4 + 5 NO2 + h3O
N+5 + 1e → N+4 1 5 HNO3 (за счет N+5) – окислитель, пр. восстановления
P – восстановитель, процесс окисления
P0 – 5e → P+5 5 1
5 HNO3 + 3 P + 2 h3O → 3 h4PO4 + 5 NO
N+5 + 3e → N+2 3 5 HNO3 (за счет N+5) – окислитель, пр. восстановления
P0 – 5e → P+5 5 3 P – восстановитель, процесс окисления
Применение азотной кислоты
1
Производство азотных и комплексных
удобрений.
2
Производство взрывчатых веществ
3
Производство красителей
4
Производство лекарств
5
Производство пленок,
нитролаков, нитроэмалей
6
Производство
искусственных волокон
7
Как компонент нитрующей
смеси, для траления
металлов в металлургии
Соли азотной кислоты
Как называются соли азотной кислоты?
нитраты
Нитраты K, Na, Nh5+ называют селитрами
Составьте формулы перечисленных солей.
KNO3
NaNO3
Nh5NO3
Нитраты – белые кристаллические
вещества.
 Сильные электролиты, в
Сильные электролиты, врастворах полностью диссоциируют
на ионы. Вступают в реакции обмена.
Каким способом можно определить нитрат-ион в растворе?
К соли (содержащей нитрат-ион) добавляют серную
кислоту и медь. Смесь слегка подогревают. Выделение
бурого газа (NO2) указывает на наличие нитрат-иона.
Нитрат калия (калиевая селитра)
Бесцветные кристаллы Значительно
менее гигроскопична по сравнению с
натриевой, поэтому широко применяется в пиротехнике как окислитель.
При нагревании выше 334,5ºС
плавится, выше этой температуры
разлагается с выделением кислорода.
Нитрат натрия
Применяется как удобрение; в
стекольной,
металлообрабатывающей промышленности; для получения
взрывчатых
веществ,
ракетного
топлива и пиротехнических смесей.
Нитрат аммония
Кристаллическое
вещество
белого
цвета. Температура плавления 169,6 °C,
при нагреве выше этой температуры
начинается постепенное
разложение
вещества, а при температуре 210°С
происходит полное разложение.

При нагревании нитраты разлагаются тем полнее, чем
правее в электрохимическом ряду напряжений стоит металл,
образующий соль.
Li K Ba Ca Na
Mg Al Mn Zn Cr Fe Co Sn Pb Cu
нитрит + О2
оксид металла + NO2 + O2
Ag Hg Au
Ме + NO2 + O2
Составьте уравнения реакций разложения нитрата
натрия, нитрата свинца, нитрата серебра.
2NaNO3 = 2NaNO2 + O2
2Pb(NO3)2= 2PbO + 4NO2 + O2
2AgNO3 = 2Ag + 2NO2 + O2
1. Степень окисления азота в азотной кислоте равна:
А
А) +5;
Б) +4;
В) -3.
2. При взаимодействии с какими веществами азотная кислота проявляет
особые свойства, отличающие её от других кислот:
Б
А) основными оксидами; Б) металлами;
В) основаниями.
3. В окислительно-восстановительной реакции азотная кислота может
А
участвовать в качестве:
А) окислителя; Б) восстановителя; В) окислителя и восстановителя.
4. Какое из данных соединений азота называют чилийской селитрой:
А) нитрат калия;
Б) нитрат кальция;
В) нитрат натрия;
5.
 Запишите уравнение взаимодействия меди с концентрированной
Запишите уравнение взаимодействия меди с концентрированнойазотной кислотой . Коэффициент перед формулой кислоты равен:
А) 2;
Б) 4;
В) 1.
6. Какое из перечисленных веществ не реагирует с разбавленной
азотной кислотой:
А) медь;
Б) гидроксид натрия;
В) бромид натрия.
7. Азотную кислоту получают в три стадии, окисляя атом азота по
следующей схеме:
А) N–3 →N+2 →N+4 → N+5
Б) N–3 →N0 →N+4 → N+5
В) N0 →N+2 →N+4 → N+5
В
Б
В
А
English Русский Правила
45. Азотистая кислота и ее соли.
Ответ. Азотистая кислота HNO2 — слабая одноосновная кислота,
существует только в разбавленных водных
растворах, окрашенных в слабый голубой
цвет, и в газовой фазе. Кислота весьма
токсична (в больших концентрациях). Соли
азотистой кислоты называются нитритами
или азотистокислыми. Нитриты гораздо
более устойчивы, чем HNO2, многие из них
— токсичны, канцерогенны. В газовой фазе
планарная молекула азотистой кислоты
существует в виде двух конфигураций:
цис- и транс-. При комнатной температуре
преобладает транс-изомер: эта структура
является более устойчивой. Так, для
цис-HNO2(г) ΔG°f = −42,59 кДж/моль, а для
транс-HNO2(г) ΔG°f = −44,65 кДж/моль. В водных
растворах существует равновесие: 2HNO2
↔ N2O3
+ h3O
↔ NO
+ NO2
+ h3O.
При нагревании раствора азотистая
кислота распадается с выделением NO и
образованием азотной кислоты: 3HNO2
↔ HNO3
+ 2 NO
+ h3O.
HNO2 является слабой кислотой. В водных
растворах диссоциирует (KD = 4,6⋅10−4),
немного сильнее уксусной кислоты. Легко
вытесняется более сильными кислотами
из солей: h3SO4 + 2 NaNO2 → Na2SO4 + 2HNO2. Азотистая
кислота проявляет как окислительные,
так и восстановительные свойства. При
действии более сильных окислителей
(пероксид водорода, хлор, перманганат
калия) окисляется в азотную кислоту:
HNO2 + h3O2 = HNO3 + h3O. HNO2
+ Cl2 + h3O = HNO3 + 2 HCl. 7HNO2 + 2 KMnO4 = 2 Mn(NO3)2 + 2 KNO3 +
3h3O + HNO3. В
то же время она способна окислять
вещества, обладающие восстановительными
свойствами: 2HNO2
+ 2 HI
= 2 NO
+ I2
+ 2 h3O.
При комнатной температуре
преобладает транс-изомер: эта структура
является более устойчивой. Так, для
цис-HNO2(г) ΔG°f = −42,59 кДж/моль, а для
транс-HNO2(г) ΔG°f = −44,65 кДж/моль. В водных
растворах существует равновесие: 2HNO2
↔ N2O3
+ h3O
↔ NO
+ NO2
+ h3O.
При нагревании раствора азотистая
кислота распадается с выделением NO и
образованием азотной кислоты: 3HNO2
↔ HNO3
+ 2 NO
+ h3O.
HNO2 является слабой кислотой. В водных
растворах диссоциирует (KD = 4,6⋅10−4),
немного сильнее уксусной кислоты. Легко
вытесняется более сильными кислотами
из солей: h3SO4 + 2 NaNO2 → Na2SO4 + 2HNO2. Азотистая
кислота проявляет как окислительные,
так и восстановительные свойства. При
действии более сильных окислителей
(пероксид водорода, хлор, перманганат
калия) окисляется в азотную кислоту:
HNO2 + h3O2 = HNO3 + h3O. HNO2
+ Cl2 + h3O = HNO3 + 2 HCl. 7HNO2 + 2 KMnO4 = 2 Mn(NO3)2 + 2 KNO3 +
3h3O + HNO3. В
то же время она способна окислять
вещества, обладающие восстановительными
свойствами: 2HNO2
+ 2 HI
= 2 NO
+ I2
+ 2 h3O. Азотистую кислоту можно получить при
растворении оксида азота (III) N2O3 в воде:
N2O3 + h3O = 2 HNO2. Также она получается при
растворении в воде оксида азота (IV) NO2:
2NO2
+ h3O
= HNO3
+ HNO2.
Азотистая кислота применяется для
диазотирования первичных ароматических
аминов и образования солей диазония.
Нитриты применяются в органическом
синтезе при производстве органических
красителей. Азотистая кислота (HNO2) весьма
токсична, причём обладает ярко выраженным
мутагенным действием, поскольку является
дезаминирующим агентом. Нитриты — соли азотистой кислоты HNO2, например,
нитрит натрия NaNO2, нитрит кальция
Ca(NO2)2. Известны нитриты щелочных,
щелочноземельных, 3d-металлов, а также
нитриты свинца и серебра. Кристаллическими
веществами являются только нитриты
калия, серебра, кальция и бария. Нитриты
калия, натрия и бария в воде хорошо
растворимы, малорастворимы нитриты
серебра, ртути (II), меди. С повышением
температуры растворимость нитритов
возрастает. В органических растворителях
нитриты растворяются плохо.
Азотистую кислоту можно получить при
растворении оксида азота (III) N2O3 в воде:
N2O3 + h3O = 2 HNO2. Также она получается при
растворении в воде оксида азота (IV) NO2:
2NO2
+ h3O
= HNO3
+ HNO2.
Азотистая кислота применяется для
диазотирования первичных ароматических
аминов и образования солей диазония.
Нитриты применяются в органическом
синтезе при производстве органических
красителей. Азотистая кислота (HNO2) весьма
токсична, причём обладает ярко выраженным
мутагенным действием, поскольку является
дезаминирующим агентом. Нитриты — соли азотистой кислоты HNO2, например,
нитрит натрия NaNO2, нитрит кальция
Ca(NO2)2. Известны нитриты щелочных,
щелочноземельных, 3d-металлов, а также
нитриты свинца и серебра. Кристаллическими
веществами являются только нитриты
калия, серебра, кальция и бария. Нитриты
калия, натрия и бария в воде хорошо
растворимы, малорастворимы нитриты
серебра, ртути (II), меди. С повышением
температуры растворимость нитритов
возрастает. В органических растворителях
нитриты растворяются плохо. Нитриты
являются термически малоустойчивыми
соединениями. Так, без разложения могут
плавиться только нитриты щелочных
металлов, остальные же начинают
разлагаться при 250—300 °C с выделением
металла либо его оксида, азота, оксидов
азота и кислорода. Нитриты реагируют с
солями меди, образуя комплексный
гексонитритокупрат-анион, придающий
раствору характерный зелёный цвет, что
можно использовать в лаборатории как
качественную реакцию. CuSO4 + 6NaNO2 = Na2SO4 +
Na4[Cu(NO2)6]. Нитриты медленно разлагаются
под действием кислот с выделением газа
(продуктов разложения азотистой кислоты).
2NaNO2 + h3SO4 = Na2SO4 + NO + NO2 +h3O. В горячей воде
те же вещества реагируют с образованием
оксида азота (II) и азотной кислоты: 6NaNO2
+ 3h3SO4 = 3Na2SO4 + 2HNO3 + 4NO + 4h3О. Нитриты могут
выступать как окислителями, так и
восстановителями — в кислой среде они
окисляются до нитратов, в щелочной
способны восстанавливаться до оксида
азота NO. В промышленности нитриты
получают поглощением нитрозного газа
(NO + NO2) растворами гидроксида или карбоната
натрия с образованием раствора нитрита
натрия, из которого кристаллизацией
получают сухой продукт.
Нитриты
являются термически малоустойчивыми
соединениями. Так, без разложения могут
плавиться только нитриты щелочных
металлов, остальные же начинают
разлагаться при 250—300 °C с выделением
металла либо его оксида, азота, оксидов
азота и кислорода. Нитриты реагируют с
солями меди, образуя комплексный
гексонитритокупрат-анион, придающий
раствору характерный зелёный цвет, что
можно использовать в лаборатории как
качественную реакцию. CuSO4 + 6NaNO2 = Na2SO4 +
Na4[Cu(NO2)6]. Нитриты медленно разлагаются
под действием кислот с выделением газа
(продуктов разложения азотистой кислоты).
2NaNO2 + h3SO4 = Na2SO4 + NO + NO2 +h3O. В горячей воде
те же вещества реагируют с образованием
оксида азота (II) и азотной кислоты: 6NaNO2
+ 3h3SO4 = 3Na2SO4 + 2HNO3 + 4NO + 4h3О. Нитриты могут
выступать как окислителями, так и
восстановителями — в кислой среде они
окисляются до нитратов, в щелочной
способны восстанавливаться до оксида
азота NO. В промышленности нитриты
получают поглощением нитрозного газа
(NO + NO2) растворами гидроксида или карбоната
натрия с образованием раствора нитрита
натрия, из которого кристаллизацией
получают сухой продукт. Нитриты других
металлов получают обменной реакцией с
нитритом натрия либо восстановлением
соответствующих нитратов. Нитриты
используются при получении азокрасителей,
для получения капролактама, как окисляющие
и восстанавливающие реагенты в
резинотехнической, текстильной и
металлообрабатывающей промышленности.
Нитрит натрия используется как консервант.
Нитриты других
металлов получают обменной реакцией с
нитритом натрия либо восстановлением
соответствующих нитратов. Нитриты
используются при получении азокрасителей,
для получения капролактама, как окисляющие
и восстанавливающие реагенты в
резинотехнической, текстильной и
металлообрабатывающей промышленности.
Нитрит натрия используется как консервант.
Нитрит
натрия также применяется при производстве
бетонных смесей в качестве ускорителя
твердения и противоморозной добавки.
Нитриты попадают в организм человека
двумя путями: прямым содержанием или
же нитратами, которые в пищеварительном
тракте (в основном в полости рта, также
желудке или кишечнике) человека
превращаются в нитриты под действием
фермента нитратредуктазы. Также нитриты
используются в производстве обработанных
мясных продуктов (колбасы, сосиски,
ветчина и пр.) Эпидемиологические
исследования высокого уровня потребления
нитратов из овощей выявили снижение
риска рака желудка, в то время как другие
исследования о потреблении нитратов/нитритов
из обработанных мясных продуктов, в
которых нитриты используются как
консерванты, показывают повышение
рисков. Механические исследования
показывают, что образование опасных
нитросоединений (таких как нитрозамины)
ускоряется в присутствии компонентов
мяса и подавляется витамином С и другими
антиоксидантами и фитонутриентами из
растительных продуктов. Таким образом,
нитриты ведут себя неодинаково в
зависимости от того, из каких источников
они поступают в организм. Нитриты,
добавляемые в мясные продукты для их
консервации, преобразуются в нитрозамины.
Нитриты, преобразовавшиеся из нитратов
из овощей и фруктов, далее превращаются
в оксид азота (II), которые способствует
расширению кровеносных сосудов и
нормализации кровяного давления. При
нормальном физиологическом состоянии
и поступлении нитритов в организм не
более допустимой суточной дозы,
утверждённой Министерством здравоохранения
в 0,2 мг/кг массы тела (за исключением
детей грудного возраста), в организме
человека образуется примерно 2 %
метгемоглобина, поскольку редуктазы
эритроцитов взрослого человека обладают
способностью превращать образовавшийся
метгемоглобин обратно в гемоглобин.
Механические исследования
показывают, что образование опасных
нитросоединений (таких как нитрозамины)
ускоряется в присутствии компонентов
мяса и подавляется витамином С и другими
антиоксидантами и фитонутриентами из
растительных продуктов. Таким образом,
нитриты ведут себя неодинаково в
зависимости от того, из каких источников
они поступают в организм. Нитриты,
добавляемые в мясные продукты для их
консервации, преобразуются в нитрозамины.
Нитриты, преобразовавшиеся из нитратов
из овощей и фруктов, далее превращаются
в оксид азота (II), которые способствует
расширению кровеносных сосудов и
нормализации кровяного давления. При
нормальном физиологическом состоянии
и поступлении нитритов в организм не
более допустимой суточной дозы,
утверждённой Министерством здравоохранения
в 0,2 мг/кг массы тела (за исключением
детей грудного возраста), в организме
человека образуется примерно 2 %
метгемоглобина, поскольку редуктазы
эритроцитов взрослого человека обладают
способностью превращать образовавшийся
метгемоглобин обратно в гемоглобин. В
Европейском Союзе допустимая суточная
доза нитритов принята в 0.1 мг/кг массы
(в пересчете на нитрит натрия). Продажа
нитритов для пищевых применений разрешена
в Евросоюзе только в смеси с пищевой
солью, с содержанием нитритов около 0,6
%, для уменьшения риска превышения
суточных норм.
В
Европейском Союзе допустимая суточная
доза нитритов принята в 0.1 мг/кг массы
(в пересчете на нитрит натрия). Продажа
нитритов для пищевых применений разрешена
в Евросоюзе только в смеси с пищевой
солью, с содержанием нитритов около 0,6
%, для уменьшения риска превышения
суточных норм.
Сбалансируйте следующее уравнение: $HI + HN{O_3} \to {I_2} + NO + {H_2}O$A. $6HI + 2HN{O_3} \to 3{I_2} + 2NO + 4{H_2}O$B. $6HI + 4HN{O_3} \to 3{I_2} + 2NO + {H_2}O$C. $3HI + 2HN{O_3} \to 2{I_2} + 2NO + 4{H_2}O$D. Ни один из этих
Подсказка: Мы можем сбалансировать это уравнение, используя метод степени окисления. Сначала мы записываем степени окисления каждого элемента, а затем уравновешиваем все элементы, кроме водорода и кислорода. Тогда мы можем уравнять степени восстановления и окисления. Наконец, мы можем добавить молекулы воды, чтобы сбалансировать кислород.
Полный пошаговый ответ:
Первым шагом в уравновешивании окислительно-восстановительных реакций является запись степени окисления каждого элемента над реакцией. Водород всегда имеет степень окисления $+1$, а кислород $-2$. Для нейтральных молекул (без заряда) сумма степеней окисления равна нулю. Поскольку все молекулы здесь нейтральны, сумма степеней окисления в этом случае всегда равна нулю.
Водород всегда имеет степень окисления $+1$, а кислород $-2$. Для нейтральных молекул (без заряда) сумма степеней окисления равна нулю. Поскольку все молекулы здесь нейтральны, сумма степеней окисления в этом случае всегда равна нулю.
В $HI$ водород имеет степень окисления $ + 1$. Следовательно, степень окисления йода получается вычитанием степени окисления водорода из нуля, то есть $0 — 1 = — 1$
В $HN{O_3}$ степень окисления водорода $ + 1$, кислорода $ — 2$. Поскольку атомов кислорода три, их суммарный вклад равен $(- 2 \times 3) = — 6$. Следовательно, степень окисления азота получается путем вычитания степеней окисления водорода и кислорода из нуля. Следовательно, он равен $0 — 1 — (- 6) = + 5$.
Так как ${I_2}$ является молекулой элемента в нормальном состоянии, то в этой молекуле степень окисления йода равна нулю.
В ${H_2}O$ степень окисления водорода $ + 1$, кислорода $ — 2$. 9{ — 2} $
Наш следующий шаг — сбалансировать элементы, кроме водорода и кислорода.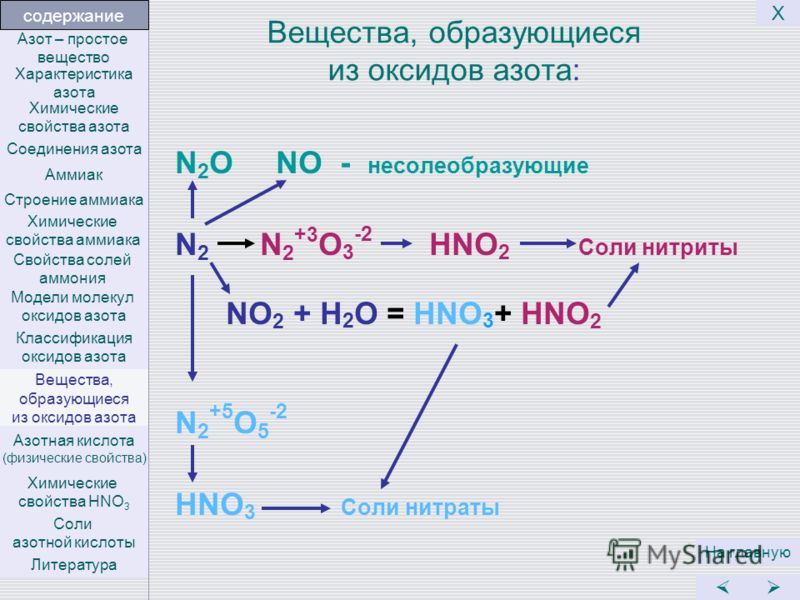 Это йод и азот. У обеих сторон есть по одному азоту, так что мы можем оставить это без внимания. В левой части находится только один йод, а в правой — два. Поэтому мы ставим $2$ рядом с $HI$:
Это йод и азот. У обеих сторон есть по одному азоту, так что мы можем оставить это без внимания. В левой части находится только один йод, а в правой — два. Поэтому мы ставим $2$ рядом с $HI$:
$2HI + HN{O_3} \to {I_2} + NO + {H_2}O$
Возвращаясь к нашим степеням окисления, мы видим, что степень окисления азота уменьшается. снижен с $+5$ до $+2$. Следовательно, он восстанавливается, и каждый атом азота претерпевает изменение $ + 5 — 2 = + 3$.
Йод окисляется (от $ — 1$ до $0$). Таким образом, изменение степени окисления составляет $ + 1$ на атом.
Мы должны уравнять изменения в процессах окисления и восстановления, чтобы сбалансировать уравнение. В процессе восстановления изменение составляет $ + 3$, а в процессе окисления — $2 \times ( + 1) = + 2$, так как участвуют две молекулы $HI$, как это получено из нашего предыдущего сбалансированного уравнения. Чтобы уравнять оба процесса, мы должны найти НОК обоих чисел, а затем соответственно умножить каждую молекулу. НОК $3$ и $2$ равен $6$. Отсюда умножаем молекулы процесса окисления ($HN{O_3}$ и $NO$) на $2$, так как $( + 3) \times 2 = 6$ и умножаем молекулы процесса окисления ($HI$ и ${I_2}$) с $3$, так как $( + 2) \times 3 = 6$ . Таким образом, мы получаем:
Отсюда умножаем молекулы процесса окисления ($HN{O_3}$ и $NO$) на $2$, так как $( + 3) \times 2 = 6$ и умножаем молекулы процесса окисления ($HI$ и ${I_2}$) с $3$, так как $( + 2) \times 3 = 6$ . Таким образом, мы получаем:
$6HI + 2HN{O_3} \to 3{I_2} + 2NO + {H_2}O$
Обратите внимание, что коэффициент $HI$ теперь становится $6$, так как ранее у нас уже было $2$.
Последним шагом является уравновешивание атомов кислорода путем добавления молекул воды там, где это необходимо. С левой стороны у нас есть шесть кислородов, а с правой стороны у нас есть три кислорода. Таким образом, мы добавляем три молекулы воды в правую часть. Поскольку с правой стороны уже есть молекула воды, общее количество молекул воды с правой стороны теперь будет четыре:
$6HI + 2HN{O_3} \to 3{I_2} + 2NO + 4{H_2}O$
Теперь мы должны сбалансировать атомы водорода. Но мы видим, что они уже уравновешены, так как с обеих сторон по восемь атомов водорода. Поскольку мы уравновесили все элементы, это окончательное уравновешенное уравнение:
$6HI + 2HN{O_3} \to 3{I_2} + 2NO + 4{H_2}O$
Итак, правильный ответ — Вариант A .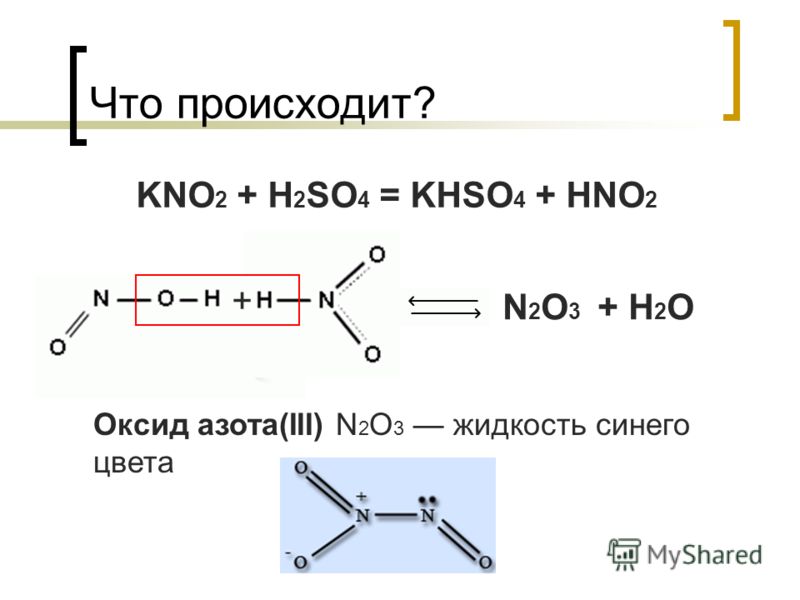
Примечание: Помимо метода степени окисления, мы также можем использовать метод полуреакции. В этом методе мы разделяем всю реакцию на половину окисления и половину восстановления и уравновешиваем их отдельно. В конце они объединяются, чтобы получить окончательное уравнение.
Обратите внимание, что окисление — это удаление электронов, а восстановление — это приобретение электронов.
Проблема разрешения в виде кислотно-основного
Проблема разрешения в виде кислотно-основного 006 1 из 22Верхний обрезанный слайд
Скачать для чтения офлайн
Образование
Разрешение de Problemas ácido-base (I)
Реклама
Реклама
Решение проблем в виде кислотно-основных
- ТЕМА 8.- РЕАКЦИИ ÁCIDO-BASE (I)
ÁCIDOS Y BASES DE BRØNSTED
1. Clasifica cada una de las siguientes especies como ácido o base de Brønsted, o
также амбо: а) h3O, б) OH-, в) h4O+, г) Nh4, д) Nh5+, е) Nh3-, ж) NO3-, з) СО32-, и) HBr,
к) ХСН.
 АСИДО ДЕ
БРЕНСТЕД
БАЗА ДЕ БРЕНСТЕД АНФОТЕРО
h4O+ OH- h3O
Кh5+ Кh3- Кh4
HBr NO3-
HCN CO32-
El NO3- (нитратный анион) представляет собой соединение основания HNO3 без содержания
пропьедадес ацидо-основа.
АСИДО ДЕ
БРЕНСТЕД
БАЗА ДЕ БРЕНСТЕД АНФОТЕРО
h4O+ OH- h3O
Кh5+ Кh3- Кh4
HBr NO3-
HCN CO32-
El NO3- (нитратный анион) представляет собой соединение основания HNO3 без содержания
пропьедадес ацидо-основа. - 3. Опишите формулу коньюгадо де када де лас сигуиентес по основаниям: а) HS-, б) HCO3-, c) CO32-, d) h3PO4-, e) HPO42-, f) PO43-, g) HSO4-, h) SO42-, i) SO32-. а) ГС-/ч3С б) HCO3- / h3CO3 в) СО32- / НСО3- г) h3PO4- / h4PO4 д) HPO42- / h3PO4- е) PO43-/HPO42- ж) HSO4-/h3SO4 з) SO42- / HSO4- и) SO32- / HSO3-
- рН: UNA MEDIDA DE LA ACIDEZ 4. Вычисление pH для основных растворов: а) HCl 0,0010 М, б) КОН. 0,76 М. а) HCl (ац) + h3O (ж) h4O+ (ац) + Cl- (ац) 𝒑𝑯 = − журнал [ 𝐻3 𝑂+ = — журнал [0,0010] = 𝟑 б) KOH (ас) K+ (ас) + OH- (ас) 𝒑𝑶𝑯 = − log [𝑂𝐻−] = − log [0,76] = 𝟎, 𝟏𝟐 𝑝𝐻 + 𝑝𝑂𝐻 = 14 ; 𝒑𝑯 = 14 − 𝑝𝑂𝐻 = 𝟏𝟑, 𝟖𝟖
- 5. Эл. рОН растворимости 9,40. Расчет концентрации ионного водорода ла растворение. 𝑝𝑂𝐻 = 9,40 𝑝𝐻 + 𝑝𝑂𝐻 = 14 𝒑𝑯 = 14 − 𝑝𝑂𝐻 = 14 − 9,40 = 𝟒, 𝟔𝟎 [𝑯 𝟑 𝑶+] = 10−4,6 = 𝟐, 𝟓 · 𝟏𝟎−𝟓 𝑴
- 6.
 Расчет числа молей KOH на 5,50 мл при растворении KOH
0,360 M. ¿Cuál es el pOH de la disolución?
𝒏 ( 𝑶𝑯−) = [ 𝑂𝐻−] · 𝑉 ( 𝑂𝐻−) = 0,360
𝑚𝑜𝑙
𝐿
· 5,50 · 10−3
𝐿 = 𝟏, 𝟗𝟖 · 𝟏𝟎−𝟑
𝒎𝒐𝒍
𝒑𝑶𝑯 = − log [𝑂𝐻−] = − log [0,360 ] = 𝟎, 𝟒𝟒
Расчет числа молей KOH на 5,50 мл при растворении KOH
0,360 M. ¿Cuál es el pOH de la disolución?
𝒏 ( 𝑶𝑯−) = [ 𝑂𝐻−] · 𝑉 ( 𝑂𝐻−) = 0,360
𝑚𝑜𝑙
𝐿
· 5,50 · 10−3
𝐿 = 𝟏, 𝟗𝟖 · 𝟏𝟎−𝟑
𝒎𝒐𝒍
𝒑𝑶𝑯 = − log [𝑂𝐻−] = − log [0,360 ] = 𝟎, 𝟒𝟒 - 7. Препарат для растворения 18,4 г HCl в 662 мл воды. Расчет эль pH де ла disolución. (Supón que el volumen permanece Constante.) [𝑯𝑪𝒍] = 18,4 𝑔 36,5 𝑔/𝑚𝑜𝑙 0,662 𝐿 = 𝟎, 𝟕𝟔𝟏𝟓 𝑴 𝒑𝑯 = − log [𝐻3 𝑂+] = − log [0,7615] = 𝟎, 𝟏𝟐
- ÁCIDOS DÉBILES Y LA CONSTANTE DE IONIZACIÓN DE UN ÁCIDO 8. ¿Cuál de las siguientes disoluciones tiene el pH más alto? а) HCOOH 0,40 М, б) HClO4 0,40 М, в) Ch4COOH 0,40 М. ДАТОС: pKa (HCOOH) = 3,77; рКа (Ch4COOH) = 4,8. а) HCOOH (а.с.) + h3O (ж) HCOO- (а.с.) + h4O+ (а.с.) 0,40 м — — 0,40 — х х х 𝐾𝑎 = [𝐻𝐶𝑂𝑂−] · [𝐻3 𝑂+ ] [𝐻𝐶𝑂𝑂𝐻] 1,7 · 10−4 «=» 𝑥2 0,40 − 𝑥 В равновесии: [НСООН) = 0,392 М; [HCOO-] = [h4O+] = 8,165·10-3 М 𝒑𝑯 = − log [𝐻3 𝑂+] = 𝟐, 𝟎𝟗 б) HClO4 (а.ч.) + h3O (ж) ClO4- (а.к.) + h4O+ (а.ч.) 𝒑𝑯 = − log [𝐻3 𝑂+] = − log [0,40] = 𝟎, 𝟒𝟎
- в)
Ch4COOH (а.
 к.) + h3O (ж) Ch4COO- (а.к.) + h4O+ (а.к.)
0,40 м — —
0,40 — х х х
𝐾𝑎 =
[𝐶𝐻3 𝐶𝑂𝑂−] · [𝐻3 𝑂+
]
[𝐶𝐻3 𝐶𝑂𝑂𝐻]
1,58 · 10−5
«=»
𝑥2
0,40 − 𝑥
«=»
𝑥2
0,40
В равновесии:
[Ch4COOH) = 0,394 М; [Ch4COO-] = [h4O+] = 6,28·10-3 М
𝒑𝑯 = − log [𝐻3 𝑂+] = 𝟐, 𝟐𝟎
к.) + h3O (ж) Ch4COO- (а.к.) + h4O+ (а.к.)
0,40 м — —
0,40 — х х х
𝐾𝑎 =
[𝐶𝐻3 𝐶𝑂𝑂−] · [𝐻3 𝑂+
]
[𝐶𝐻3 𝐶𝑂𝑂𝐻]
1,58 · 10−5
«=»
𝑥2
0,40 − 𝑥
«=»
𝑥2
0,40
В равновесии:
[Ch4COOH) = 0,394 М; [Ch4COO-] = [h4O+] = 6,28·10-3 М
𝒑𝑯 = − log [𝐻3 𝑂+] = 𝟐, 𝟐𝟎 - 9. Se disuelve una muestra de 0,0560 g de ácido acético en la cantidad suficiente de водный раствор для приготовления 50,0 мл. Расчет концентрации H+, Ch4COO- и Ch4COOH в равновесии. DATO: Ка (Ch4COOH) = 1,8·10-5. [𝐶𝐻3 𝐶𝑂𝑂𝐻] 𝑜 = 0,0560 𝑔 60 𝑔 𝑚𝑜𝑙 50,0 · 10−3 𝐿 = 0,0187 𝑀 Ch4COOH (а.к.) + h3O (ж) Ch4COO- (а.к.) + h4O+ (а.к.) 0,0187 М — — 0,0187 — х х х 1,8 · 10−5 «=» 𝑥2 0,0187 — 𝑥 [Ch4COOH]экв = 0,018129М [Ch4COO-]экв = 5,71·10-4 М [h4O+]экв = 5,71·10-4 М
- 10. ¿Cuál es la molaridad inicial de una disolución de ácido formico (HCOOH) cuyo pH, в равновесии, es de 3,26? DATO: Ка (НСООН) = 1,7·10-4. HCOOH (а.с.) + h3O (ж) HCOO- (а.с.) + h4O+ (а.с.) Ко — — Со — х х х Co – 5,5·10-4 5,5·10-4 М 5,5·10-4 М 1,7 · 10−4 «=» (5,5 · 10−4 )2 𝐶 𝑜 − 5,5 · 10−4 3,02 · 10−7 = 1,7 · 10−4 · 𝐶 𝑜 − 9,34 · 10−8 [𝑯𝑪𝑶𝑶𝑯] 𝒐 = 𝟐, 𝟑𝟐𝟔 · 𝟏𝟎−𝟑 𝑴
- 11.
 Ионизационный расчет растворения ацетилсалициловой кислоты
(аспирина) 0,20 М, как монопротез.
DATO: Ка (HA) = 3,0·10-4.
HA (а.с.) + h3O (ж) A- (а.с.) + h4O+ (а.с.)
0,20 м — —
0,20 · (1 – ) 0,20 · 0,20 ·
𝐾𝑎 =
[𝐴−] · [𝐻3 𝑂+
]
[𝐻𝐴]
3,0 · 10−4
«=»
0,202
· 𝛼2
0,20 · (1 − 𝛼)
𝜶 = 𝟎, 𝟎𝟑𝟖 (𝟑, 𝟖%)
Ионизационный расчет растворения ацетилсалициловой кислоты
(аспирина) 0,20 М, как монопротез.
DATO: Ка (HA) = 3,0·10-4.
HA (а.с.) + h3O (ж) A- (а.с.) + h4O+ (а.с.)
0,20 м — —
0,20 · (1 – ) 0,20 · 0,20 ·
𝐾𝑎 =
[𝐴−] · [𝐻3 𝑂+
]
[𝐻𝐴]
3,0 · 10−4
«=»
0,202
· 𝛼2
0,20 · (1 − 𝛼)
𝜶 = 𝟎, 𝟎𝟑𝟖 (𝟑, 𝟖%) - 12. Эль-рH дель jugo gástrico del estómago de cierto individuo es de 1,00. Después де haber ingerido algunas таблетки аспирина, ла концентрация ацидо ацетилсалицилико en su estómago es de 0,20 M. Calcula el porcentaje de ionización del ácido en esas условия. HA (а.с.) + h3O (ж) A- (а.с.) + h4O+ (а.с.) Co — 10-1 М Co · (1 – ) Co · 10-1 + Co · 0,20 м 3,0 · 10−4 «=» 0,1 · 𝐶 𝑜 · 𝛼 + 𝐶 𝑜 2 · 𝛼2 0,20 𝑦2 + 0,1 · 𝑦 − 6 · 10−5 = 0 ; 𝑦 = 6 · 10−4 𝜶 = 𝐶 𝑜 · 𝛼 𝐶 𝑜 = 𝟑 · 𝟏𝟎−𝟑 (𝟎, 𝟑%)
- BASES DÉBILES Y LA CONSTANTE DE IONIZACIÓN DE UNA BASE
13. ¿Cuál de las siguientes disoluciones tendrá un pH más alto? а) Nh4 0,20 М, б)
NaOH 0,20 М.
ДАТО: Kb (Nh4) = 1,8·10-5.
а)
Nh4 (ач) + h3O (ж) Nh5+ (ач) + OH- (ач)
0,20 м — —
0,20 — х х х
1,8 · 10−5
«=»
𝑥2
0,20 − 𝑥
«=»
𝑥2
0,20
; 𝒙 = 𝟏, 𝟗 · 𝟏𝟎−𝟑
𝑴
𝑝𝑂𝐻 = — журнал [𝑂𝐻-] = 2,72
𝒑𝑯 = 14 − 𝑝𝑂𝐻 = 𝟏𝟏, 𝟐𝟖
б)
NaOH (а.
 с.) Na+ (а.с.) + OH- (а.с.)
𝑝𝑂𝐻 = − log [𝑂𝐻−] = 0,7
𝒑𝑯 = 14 − 𝑝𝑂𝐻 = 𝟏𝟑, 𝟑
с.) Na+ (а.с.) + OH- (а.с.)
𝑝𝑂𝐻 = − log [𝑂𝐻−] = 0,7
𝒑𝑯 = 14 − 𝑝𝑂𝐻 = 𝟏𝟑, 𝟑 - 14. Расчет pH для расчетных показателей растворов: a) Nh4 0,10 M, b) C5H5N (пиридина) 0,050 М. DATO: Kb (C5H5N) = 1,7·10-9. а) Nh4 (ач) + h3O (ж) Nh5+ (ач) + OH- (ач) 0,10 М — — 0,10 — х х х 1,8 · 10−5 «=» 𝑥2 0,10 − 𝑥 «=» 𝑥2 0,10 ; 𝒙 = 𝟏, 𝟑𝟒 · 𝟏𝟎−𝟑 𝑴 𝑝𝑂𝐻 = — журнал [𝑂𝐻-] = 2,87 𝒑𝑯 = 14 − 𝑝𝑂𝐻 = 𝟏𝟏, 𝟏𝟑 б) C5H5N(а.к.) + h3O(ж) C5H5NH+(а.к.) + OH-(а.к.) 0,050 М — — 0,050 — х х х 1,7 · 10−9 «=» 𝑥2 0,050 − 𝑥 «=» 𝑥2 0,050 ; 𝒙 = 𝟗, 𝟐𝟐 · 𝟏𝟎−𝟔 𝑴 𝑝𝑂𝐻 = − log [𝑂𝐻−] = 5,04 𝒑𝑯 = 14 − 𝑝𝑂𝐻 = 𝟖, 𝟗𝟔
- 15. pH растворения разбавленного основания 0,30 M es de 10,66. ¿Cuál es la Kb de la база? B (ач) + h3O (ж) HB+ (ач) + OH- (ач) 0,30 м — — 0,30 — х х х 10−3,34 𝑀 = 4,57 · 10−4 𝑀 𝐾𝑏 = [𝐻𝐵+] · [𝑂𝐻− ] [𝐵] 𝑲 𝒃 = (4,57 · 10−4 )2 0,30 − 4,57 · 10−4 = 𝟔, 𝟗𝟕 · 𝟏𝟎−𝟕
- 16. ¿Cuál es la molaridad inicial de una disolución de amoníaco cuyo pH es de 11,22? Nh4 (ач) + h3O (ж) Nh5+ (ач) + OH- (ач) Ко — — Со — х х х 1,8 · 10−5 «=» (1,66 · 10−3 )2 𝐶 𝑜 − 1,66 · 10−3 2,76 · 10−6 = 1,8 · 10−5 · 𝐶 𝑜 − 3 · 10−8 ; 𝑪 𝒐 = 𝟎, 𝟏𝟓𝟔 𝑴
- 17.
 Расторжение Nh4 0,080 M, ¿qué porcentaje Nh4 está presente como
Кh5+?
Nh4 (ач) + h3O (ж) Nh5+ (ач) + OH- (ач)
0,080 М — —
0,080 — х х х
1,8 · 10−5
«=»
𝑥2
0,080 — 𝑥
«=»
𝑥2
0,080
; 𝒙 = 𝟏, 𝟐 · 𝟏𝟎−𝟑
𝑴
𝜶 =
1,2 · 10−3
0,080
· 100 = 𝟏, 𝟓%
Расторжение Nh4 0,080 M, ¿qué porcentaje Nh4 está presente como
Кh5+?
Nh4 (ач) + h3O (ж) Nh5+ (ач) + OH- (ач)
0,080 М — —
0,080 — х х х
1,8 · 10−5
«=»
𝑥2
0,080 — 𝑥
«=»
𝑥2
0,080
; 𝒙 = 𝟏, 𝟐 · 𝟏𝟎−𝟑
𝑴
𝜶 =
1,2 · 10−3
0,080
· 100 = 𝟏, 𝟓% - PROPIEDADES ÁCIDO-BASE DE LAS SALES 18. Especifica cuáles de las siguientes sales se hidrolizan: KF, NaNO3, Nh5NO2, MgSO4, KCN, C6H5COONa, RbI, Na2CO3, CaCl2, HCOOK. а) КФ К+ + Ф- F- (ац) + h3O (ж) HF (ац) + OH- (ац) б) NaNO3 Не гидролизуется в) Nh5NO2 Nh5+ + NO2- Nh5+ (ач) + h3O (ж) Nh4 (ач) + h4O+ (ач) NO2- (а.с.) + h3O (ж) HNO2 (а.с.) + OH- (а.с.) г) MgSO4 Mg2+ + SO42- SO42- (а.с.) + h3O (ж) HSO4- (а.с.) + OH- (а.с.) д) KCN К+ + CN- CN- (ац) + h3O (ж) HCN (ац) + OH- (ац) е) C6H5COONa C6H5COO- + Na+ C6H5COO- (а.с.) + h3O (ж) C6H5COOH (а.с.) + OH- (а.с.) г) RbI Нет гидролиза час) Na2CO3 2 Na+ + CO32- CO32- (а.с.) + h3O (ж) HCO3- (а.с.) + OH- (а.с.)
- я)
CaCl2 Не гидролизуется
к)
HCOOK HCOO- + K+
HCOO- (а.с.) + h3O (ж) HCOOH (а.с.) + OH- (а.

Y x квадрат график: Функции вида y = x², y = x³ и их свойства – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД
Алгебра Функция y= аx2, её график и свойства
Материалы к уроку
5. Функция игрек равно а икс квадрат, ее график и свойства.doc
224 KBСкачать5. Функция y= аx2, её график и свойства.ppt
2.87 MBСкачать
Конспект урока
Одной из важных функций является квадратичная функция.
Квадратичной функцией называется функция вида игрек равно а икс квадрат плюс бэ икс плюс цэ, где икс – независимая переменная, а, бэ и цэ – некоторые числа, причем а не равно нулю.
Областью определения квадратичной функции является множество всех чисел.
Примером квадратичной функции является зависимость пути от времени при равноускоренном движении. Если тело движется с ускорением а и к началу отсчета времени тэ прошло путь эс нулевое, имея в этот момент скорость вэ нулевое, то зависимость пройденного пути эс от времени тэ выражается формулой эс равно а тэ квадрат деленное на два плюс вэ нулевое тэ. . плюс эс нулевое.
. плюс эс нулевое.
Если, например, а равно восьми, вэ нулевое равно трем, эс нулевое равно восемнадцати, то эс равно четыре тэ квадрат плюс три тэ плюс восемнадцать.
Изучение квадратичной функции начнем с частного случая – функции игрек равно а икс квадрат.
При а равном единице формула игрек равно а икс квадрат принимает вид игрек равно икс квадрат. Ее графиком является парабола.
Построим график функции игрек равно три икс квадрат. Составим таблицу значений этой функции. Отметим данные точки, соединим их плавной линией и получим график функции игрек равно три икс квадрат.
При любом икс не равном нулю значение функции игрек равно три икс квадрат больше соответствующего значения функции игрек равно икс квадрат в три раза. Если переместить каждую точку графика функции игрек равно икс квадрат вверх так, чтобы расстояние от этой точки до оси иксов увеличилось в три раза, то она перейдет в точку графика функции игрек равно три икс квадрат. Таким образом, график функции игрек равно три икс квадрат можно получить из графика функции игрек равно икс квадрат растяжением от оси икс в три раза.
Таким образом, график функции игрек равно три икс квадрат можно получить из графика функции игрек равно икс квадрат растяжением от оси икс в три раза.
Построим теперь график функции игрек равно одна третья икс квадрат. Для этого составим таблицу ее значений. Отметив точки по данным координатам и соединив их плавной линией, получим график функции игрек равно одна третья икс квадрат.
При любом значении икс не равном нулю значение функции игрек равно одна третья икс квадрат меньше соответствующего значения функции игрек равно икс квадрат.. в три раза. Если переместить каждую точку графика функции игрек равно икс квадрат вниз так, чтобы расстояние от этой точки до оси икс уменьшилось в три раза, то она перейдет в точку графика функции игрек равно одна третья икс квадрат. Таким образом, график функции игрек равно одна третья икс квадрат можно получить из параболы игрек равно икс квадрат сжатием к оси икс в три раза.
Вообще график функции игрек равно а икс квадрат можно получить из параболы игрек равно икс квадрат растяжением от оси икс в а раз, если а больше единицы, и сжатием к оси икс в единица деленная на а раз, если а больше нуля и меньше единицы.
Рассмотрим теперь функцию игрек равно а икс квадрат, когда а меньше нуля.
Построим график функции игрек равно минус одна третья икс квадрат. Составим таблицу значений для этого графика и построим график функции.
Сравним графики функций минус одна третья икс квадрат и одна третья икс квадрат. При любом икс значения этих функций являются противоположными числами. Значит, соответствующие точки графиков симметричны относительно оси икс.
Таким образом, графики функций игрек равно а икс квадрат и минус а икс квадрат при а не равном нулю симметричны относительно оси икс.
График функции игрек равно а икс квадрат, где а не равно нулю называется параболой.
Сформулируем свойства функции игрек равно а икс квадрат при а большем нуля.
- Если икс равен нулю, то игрек равен нулю. График функции проходит через начало координат.
- Если икс не равен нулю, то игрек больше нуля. График функции расположен в верхней полуплоскости.
- Противоположным значениям аргумента соответствуют равные значения функции.
 График функции симметричен относительно оси игрек.
График функции симметричен относительно оси игрек. - Функция убывает в промежутке от минус бесконечности до нуля включительно и возрастает в промежутке от нуля до плюс бесконечности, включая ноль.
- Наименьшее значение, равное нулю, функция принимает при икс равном нулю, наибольшего значения функция не имеет. Областью значений функции является промежуток от нуля до плюс бесконечности, включая ноль.
Теперь сформулируем свойства функции игрек равно а икс квадрат при а меньшем нуля.
- Если икс равен нулю, то игрек равен нулю. График функции проходит через начало координат.
- Если икс не равен нулю, то игрек меньше нуля. График функции расположен в нижней полуплоскости.
- Противоположным значениям аргумента соответствуют равные значения функции. График функции симметричен относительно оси игрек.
- Функция возрастает в промежутке от минус бесконечности до нуля, включая ноль и убывает в промежутке от нуля до плюс бесконечности, включая ноль.

- Наибольшее значение, равное нулю, функция принимает при икс равном нулю, наименьшего значения функция не имеет. Областью значений функции является промежуток от минус бесконечности до нуля, включая ноль.
Из перечисленных свойств следует, что при а большем нуля ветви параболы направлены вверх, при а меньшем нуля – вниз. Ось игрек является осью симметрии параболы. Точку пересечения параболы с ее осью симметрии называют вершиной параболы. Вершиной параболы игрек равно а икс квадрат является начало координат.
К преобразованиям графика функции игрек равно а икс квадрат относят построение графика, симметричного данному относительно оси икс, растяжение графика от оси икс или сжатие графика к оси икс.
Таким образом, график функции игрек равно минус эф от икс можно получить из графика функции игрек равно эф от икс с помощью симметрии относительно оси икс. График функции игрек равно а эф от икс можно получить из графика функции игрек равно эф от икс с помощью растяжения от оси икс в а раз, если а больше единицы,. . и с помощью сжатия к оси х в единица деленная на а раз, если а больше нуля и меньше единицы.
. и с помощью сжатия к оси х в единица деленная на а раз, если а больше нуля и меньше единицы.
Остались вопросы по теме? Наши педагоги готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать педагогаОставить заявку на подбор
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
решите уравнение ((tgx+корень из 3)*log_13 (2sin^2 x))/log_31 (корень из 2 *Cosx)
Решено
Радиус вписанной в квадрат окружности равен 4√2 найти радиус окружности описанной около этого квадратаНа экзамене 20 билетов, Андрей не выучил 1 из них. Найдите вероятность того, что ему попадется выученный билет
Найдите вероятность того, что ему попадется выученный билет
Na2SO3 h3SO4 Na2S=S Na2SO4 h3O…
Геометрическая прогрессия (bn) задана условиями:b1=-6,bn+1=3bn.Найдите сумма первых пяти членов.
Пользуйтесь нашим приложениемУкажите эту страницу следующим образом:
«Как построить график х в квадрате?» eNotes Editorial , 10 октября 2020 г., https://www.enotes.com/homework-help/how-to-graph-x-squared-24739{2} = 4`; координаты этой точки (2, 4).
Найдя точки, через которые проходит парабола, мы можем теперь нанести их на график и построить через них параболу. Пожалуйста, обратитесь к приложенному графику.
Пожалуйста, обратитесь к приложенному графику.
См. eNotes без рекламы
Начните с 48-часовой бесплатной пробной версией , чтобы получить доступ к более чем 30 000 дополнительных руководств и более чем 350 000 вопросов помощи при выполнении домашних заданий, на которые наши эксперты ответили.
Получите 48 часов бесплатного доступаУже зарегистрированы? Войдите здесь.
Изображения:Это изображение было помечено как неприемлемое Нажмите, чтобы снять отметку
Изображение (1 из 1)
Утверждено редакцией eNotes Задайте вопросСвязанные вопросы
Просмотреть всеМатематика
Последний ответ опубликован 07 сентября 2010 г. в 12:47:25.
в 12:47:25.
Что означают буквы R, Q, N и Z в математике?
14 Ответы воспитателя
Математика
Последний ответ опубликован 25 февраля 2016 г. в 18:48:45.
Сколько времени (в часах) займет ваше путешествие, если вы проедете 350 км со средней скоростью 80 км/ч? Какова формула с данными: время, расстояние, скорость или скорость?
1 Ответ учителя
Математика
Последний ответ опубликован 02 сентября 2012 г. в 3:00:53.
Как ограничения (пределы исчисления) используются или применяются в повседневной жизни? Или применительно к проблемам реального мира? Мне нужно пару примеров! Спасибо!
1 Ответ учителя
Математика
Последний ответ опубликован 09 октября 2017 г. в 00:54:39
Добавьте 1 плюс 2 плюс 3 плюс 4. . . вплоть до 100.
9(2)+х-2=0.
. . вплоть до 100.
9(2)+х-2=0.
- Курс
- NCERT
- Класс 12
- Класс 11
- Класс 10
- Класс 9
- Класс 8 901 17 Класс 7
- Класс 6
- NCERT
- IIT JEE
- Экзамен
- JEE MAINS
- JEE ADVANCED
- X BOARDS
- XII BOARDS
- NEET
- Neet Предыдущий год (по годам)
- Physics Предыдущий год
- Химия Предыдущий год
- Биология Предыдущий год
- Новый Все образцы работ
- Образцы работ по биологии
- Образцы работ по физике
- Образцы работ по химии
- Скачать PDF-файлы
- Класс 12
- Класс 11
- Класс 10
- Класс 9
- Класс 8
- Класс 7
- Класс 6
- Экзаменационный уголок
- Онлайн-класс 9 0135
- Викторина
- Задать вопрос в Whatsapp
- Поиск Doubtnut
- Английский словарь
- Блог
- Скачать
- Получить приложение
- 9 0117 Toppers Talk
Вопрос
12 видео0003Khareedo DN Про и дехо сари видео бина киси объявление ки рукаават ке!
Похожие видео
Нарисуйте график y=x2−4 и, следовательно, решите x2−x−12=0.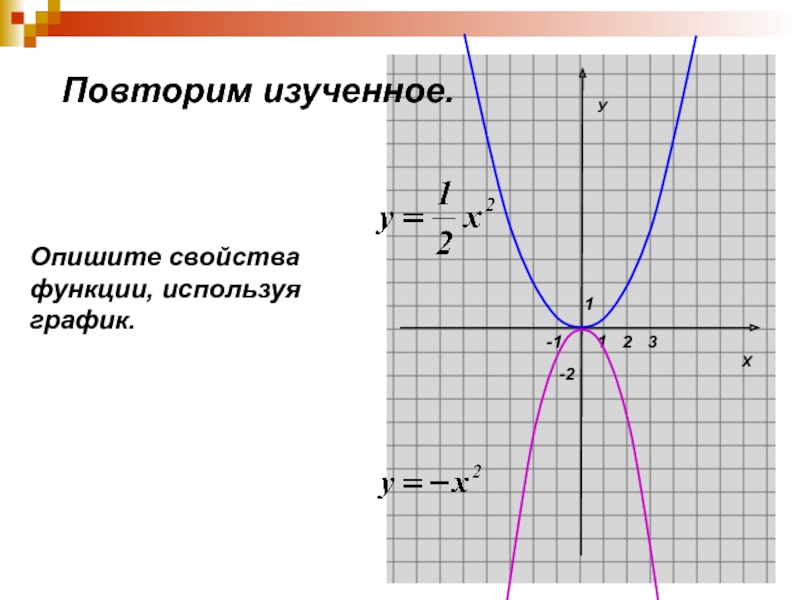
Примеры на разложение на множители: Разложение на множители — урок. Алгебра, 7 класс.
Разложение многочлена на множители: примеры, правило
Для того, чтобы разложить на множители, необходимо упрощать выражения. Это необходимо для того, чтобы можно было в дальнейшем сократить. Разложение многочлена имеет смысл тогда, когда его степень не ниже второй. Многочлен с первой степенью называют линейным.
Статья раскроет все понятия разложения, теоретические основы и способы разложений многочлена на множители.
Теория
Теорема 1Когда любой многочлен со степенью n, имеющие вид Pnx=anxn+an-1xn-1+…+a1x+a0 , представляют в виде произведения с постоянным множителем со старшей степенью an и n линейных множителей (x-xi) , i=1, 2, …, n, тогда Pn(x)=an(x-xn)(x-xn-1)·…·(x-x1) , где xi , i=1, 2, …, n – это и есть корни многочлена.
Теорема предназначена для корней комплексного типа xi ,i=1, 2, …, n и для комплексных коэффициентов ak ,k=0, 1, 2, …, n. Это и есть основа любого разложения.
Когда коэффициенты вида ak, k=0, 1, 2, …, n являются действительными числами, тогда комплексные корни, которые будут встречаться сопряженными парами. Например, корни x1 и x2 , относящиеся к многочлену вида Pnx=anxn+an-1xn-1+…+a1x+a0 считаются комплексно сопряженным, тогда другие корни являются действительными, отсюда получаем, что многочлен примет вид Pn(x)=an(x-xn)(x-xn-1)·…·(x-x3)x2+px+q , где x2+px+q=(x-x1)(x-x2).
Например, корни x1 и x2 , относящиеся к многочлену вида Pnx=anxn+an-1xn-1+…+a1x+a0 считаются комплексно сопряженным, тогда другие корни являются действительными, отсюда получаем, что многочлен примет вид Pn(x)=an(x-xn)(x-xn-1)·…·(x-x3)x2+px+q , где x2+px+q=(x-x1)(x-x2).
Замечание
Корни многочлена могут повторяться. Рассмотрим доказательство теоремы алгебры, следствия из теоремы Безу.
Основная теорема алгебры
Теорема 2Любой многочлен со степенью n имеет как минимум один корень.
Теорема Безу
После того, как произвели деление многочлена вида Pnx=anxn+an-1xn-1+…+a1x+a0 на (x-s), тогда получаем остаток, который равен многочлену в точке s, тогда получим
Pnx=anxn+an-1xn-1+…+a1x+a0=(x-s)·Qn-1(x)+Pn(s) , где Qn-1(x) является многочленом со степенью n-1.
Следствие из теоремы Безу
Когда корень многочлена Pn(x) считается s, тогда Pnx=anxn+an-1xn-1+…+a1x+a0=(x-s)·Qn-1(x) . Данное следствие является достаточным при употреблении для описания решения.
Разложение на множители квадратного трехчлена
Квадратный трехчлен вида ax2+bx+c можно разложить на линейные множители. тогда получим, что ax2+bx+c=a(x-x1)(x-x2), где x1 и x2 — это корни (комплексные или действительные).
Отсюда видно, что само разложение сводится к решению квадратного уравнения впоследствии.
Пример 1Произвести разложение квадратного трехчлена на множители.
Решение
Необходимо найти корни уравнения 4×2-5x+1=0 . Для этого необходимо найти значение дискриминанта по формуле, тогда получим D=(-5)2-4·4·1=9 . Отсюда имеем, что
x1=5-92·4=14×2=5+92·4=1
Отсюда получаем, что 4×2-5x+1=4x-14x-1.
Для выполнения проверки нужно раскрыть скобки. Тогда получим выражение вида:
4x-14x-1=4×2-x-14x+14=4×2-5x+1
После проверки приходим к исходному выражению. То есть можно сделать вывод, что разложение выполнено верно.
Пример 2Произвести разложение на множители квадратный трехчлен вида 3×2-7x-11.
Решение
Получим, что необходимо вычислить получившееся квадратное уравнение вида 3×2-7x-11=0.
Чтобы найти корни, надо определить значение дискриминанта. Получим, что
3×2-7x-11=0D=(-7)2-4·3·(-11)=181×1=7+D2·3=7+1816×2=7-D2·3=7-1816
Отсюда получаем, что 3×2-7x-11=3x-7+1816x-7-1816 .
Пример 3Произвести разложение многочлена 2×2+1 на множители.
Решение
Теперь нужно решить квадратное уравнение 2×2+1=0 и найти его корни. Получим, что
2×2+1=0x2=-12×1=-12=12·ix2=-12=-12·i
Эти корни называют комплексно сопряженными, значит само разложение можно изобразить как 2×2+1=2x-12·ix+12·i .
Пример 4Произвести разложение квадратного трехчлена x2+13x+1.
Решение
Для начала необходимо решить квадратное уравнение вида x2+13x+1=0 и найти его корни.
x2+13x+1=0D=132-4·1·1=-359×1=-13+D2·1=-13+353·i2=-1+35·i6=-16+356·ix2=-13-D2·1=-13-353·i2=-1-35·i6=-16-356·i
Получив корни, запишем
x2+13x+1=x—16+356·ix—16-356·i==x+16-356·ix+16+356·i
Замечание
Если значение дискриминанта отрицательное, то многочлены останутся многочленами второго порядка. Отсюда следует, что раскладывать их не будем на линейные множители.
Отсюда следует, что раскладывать их не будем на линейные множители.
Способы разложения на множители многочлена степени выше второй
При разложении предполагается универсальный метод. Большинство всех случаев основано на следствии из теоремы Безу. Для этого необходимо подбирать значение корня x1 и понизить его степень при помощи деления на многочлена на 1 делением на (x-x1) . Полученный многочлен нуждается в нахождении корня x2 , причем процесс поиска цикличен до тех пор, пока не получим полное разложение.
Если корень не нашли, тогда применяются другие способы разложения на множители: группировка, дополнительные слагаемые. Данная тема полагает решение уравнений с высшими степенями и целыми коэффициентами.
Вынесение общего множителя за скобки
Рассмотрим случай, когда свободный член равняется нулю, тогда вид многочлена становится как Pn(x)=anxn+an-1xn-1+…+a1x.
Видно, что корень такого многочлена будет равняться x1=0 , тогда можно представить многочлен в виде выражения Pn(x)=anxn+an-1xn-1+. ..+a1x==x(anxn-1+an-1xn-2+…+a1)
..+a1x==x(anxn-1+an-1xn-2+…+a1)
Данный способ считается вынесением общего множителя за скобки.
Пример 5Выполнить разложение многочлена третьей степени 4×3+8×2-x на множители.
Решение
Видим, что x1=0 — это корень заданного многочлена, тогда можно произвести вынесение х за скобки всего выражения. Получаем:
4×3+8×2-x=x(4×2+8x-1)
Переходим к нахождению корней квадратного трехчлена 4×2+8x-1 . Найдем дискриминант и корни:
D=82-4·4·(-1)=80×1=-8+D2·4=-1+52×2=-8-D2·4=-1-52
Тогда следует, что
4×3+8×2-x=x4x2+8x-1==4xx—1+52x—1-52==4xx+1-52x+1+52
Разложение на множители многочлена с рациональными корнями
Для начала примем за рассмотрение способ разложения, содержащий целые коэффициенты вида Pn(x)=xn+an-1xn-1+…+a1x+a0 , где коэффициента при старшей степени равняется 1.
Когда многочлен имеет целые корни, тогда их считают делителями свободного члена.
Пример 6Произвести разложение выражения f(x)=x4+3×3-x2-9x-18 .
Решение
Рассмотрим, имеются ли целые корни. Необходимо выписать делители числа -18. Получим, что ±1,±2,±3,±6,±9,±18. Отсюда следует, что данный многочлен имеет целые корни. Можно провести проверку по схеме Горнера. Она очень удобная и позволяет быстро получить коэффициенты разложения многочлена:
| xi | Коэффициенты многочленов | ||||
| 1 | 3 | -1 | -9 | -18 | |
| 1 | 1 | 3+1·1=4 | -1+4·1=3 | -9+3·1=-6 | -18+(-6)·1=-24 |
| -1 | 1 | 3+1·(-1)=2 | -1+2·(-1)=-3 | -9+(-3)·(-1)=-6 | -18+(-6)·(-1)=-12 |
| 2 | 1 | 3+1·2=5 | -1+5·2=9 | -9+9·2=9 | -18+9·2=0 |
| 2 | 1 | 5+1·2=7 | 9+7·2=23 | 9+23·2=55 | |
| -2 | 1 | 5+1·(-2)=3 | 9+3·(-2)=3 | 9+3·(-2)=3 | |
| 3 | 1 | 5+1·3=8 | 9+8·3=33 | 9+33·3=108 | |
| -3 | 1 | 5+1·(-3)=2 | 9+2·(-3)=3 | 9+3·(-3)=0 | |
Отсюда следует, что х=2 и х=-3 – это корни исходного многочлена, который можно представить как произведение вида:
f(x)=x4+3×3-x2-9x-18=(x-2)(x3+5×2+9x+9)==(x-2)(x+3)(x2+2x+3)
Переходим к разложению квадратного трехчлена вида x2+2x+3.
Так как дискриминант получаем отрицательный, значит, действительных корней нет.
Ответ: f(x)=x4+3×3-x2-9x-18=(x-2)(x+3)(x2+2x+3)
Замечание
Допускается использование подбором корня и деление многочлена на многочлен вместо схемы Горнера. Перейдем к рассмотрению разложения многочлена, содержащим целые коэффициенты вида Pn(x)=xn+an-1xn-1+…+a1x+a0, старший из которых на равняется единице.
Этот случай имеет место быть для дробно-рациональных дробей.
Пример 7Произвести разложение на множители f(x)=2×3+19×2+41x+15.
Решение
Необходимо выполнить замену переменной y=2x, следует переходить к многочлену с коэффициентами равными 1 при старшей степени. Необходимо начать с умножения выражения на 4. Получаем, что
4f(x)=23·x3+19·22·x2+82·2·x+60==y3+19y2+82y+60=g(y)
Когда получившаяся функция вида g(y)=y3+19y2+82y+60 имеет целые корни, тогда их нахождение среди делителей свободного члена. Запись примет вид:
±1,±2,±3,±4,±5,±6,±10,±12,±15,±20,±30,±60
Перейдем к вычислению функции g(y) в этих точка для того, чтобы получить в результате ноль. Получаем, что
Получаем, что
g(1)=13+19·12+82·1+60=162g(-1)=(-1)3+19·(-1)2+82·(-1)+60=-4g(2)=23+19·22+82·2+60=308g(-2)=(-2)3+19·(-2)2+82·(-2)+60=-36g(3)=33+19·32+82·3+60=504g(-3)=(-3)3+19·(-3)2+82·(-3)+60=-42g(4)=43+19·42+82·4+60=756g(-4)=(-4)3+19·(-4)2+82·(-4)+60=-28g(5)=53+19·52+82·5+60=1070g(-5)=(-5)3+19·(-5)2+82·(-5)+60
Получаем, что у=-5 – это корень уравнения вида y3+19y2+82y+60, значит, x=y2=-52 — это корень исходной функции.
Пример 8Необходимо произвести деление столбиком 2×3+19×2+41x+15 на x+52 .
Решение
Запишем и получим:
Значит,
2×3+19×2+41x+15=x+52(2×2+14x+6)==2x+52(x2+7x+3)
Проверка делителей займет много времени, поэтому выгодней предпринять разложение на множители полученного квадратного трехчлена вида x2+7x+3. Приравниванием к нулю и находим дискриминант.
x2+7x+3=0D=72-4·1·3=37×1=-7+372×2=-7-372⇒x2+7x+3=x+72-372x+72+372
Отсюда следует, что
2×3+19×2+41x+15=2x+52×2+7x+3==2x+52x+72-372x+72+372
Искусственные приемы при разложении многочлена на множители
Рациональные корни не присущи всем многочленам. Для этого необходимо пользоваться специальными способами для нахождения множителей. Но не все многочлены можно разложить или представить в виде произведения.
Для этого необходимо пользоваться специальными способами для нахождения множителей. Но не все многочлены можно разложить или представить в виде произведения.
Способ группировки
Бывают случаи, когда можно сгруппировывать слагаемые многочлена для нахождения общего множителя и вынесения его за скобки.
Пример 9Произвести разложение многочлена x4+4×3-x2-8x-2 на множители.
Решение
Потому как коэффициенты – целые числа, тогда корни предположительно тоже могут быть целыми. Для проверки возьмем значения 1, -1, 2 и -2 для того, чтобы вычислить значение многочлена в этих точках. Получаем, что
14+4·13-12-8·1-2=-6≠0(-1)4+4·(-1)3-(-1)2-8·(-1)-2=2≠024+4·23-22-8·2-2=26≠0(-2)4+4·(-2)3-(-2)2-8·(-2)-2=-6≠0
Отсюда видно, что корней нет, необходимо использовать другой способ разложения и решения.
Необходимо провести группировку:
x4+4×3-x2-8x-2=x4+4×3-2×2+x2-8x-2==(x4-2×2)+(4×3-8x)+x2-2==x2(x2-2)+4x(x2-2)+x2-2==(x2-2)(x2+4x+1)
После группировки исходного многочлена необходимо представить его как произведение двух квадратных трехчленов. Для этого нам понадобится произвести разложение на множители. получаем, что
Для этого нам понадобится произвести разложение на множители. получаем, что
x2-2=0x2=2×1=2×2=-2⇒x2-2=x-2x+2×2+4x+1=0D=42-4·1·1=12×1=-4-D2·1=-2-3×2=-4-D2·1=-2-3⇒x2+4x+1=x+2-3x+2+3
Значит:
x4+4×3-x2-8x-2=x2-2×2+4x+1==x-2x+2x+2-3x+2+3
Замечание
Простота группировки не говорит о том, что выбрать слагаемы достаточно легко. Определенного способа решения не существует, поэтому необходимо пользоваться специальными теоремами и правилами.
Пример 10Произвести разложение на множители многочлен x4+3×3-x2-4x+2 .
Решение
Заданный многочлен не имеет целых корней. Следует произвести группировку слагаемых. Получаем, что
x4+3×3-x2-4x+2==(x4+x3)+(2×3+2×2)+(-2×2-2x)-x2-2x+2==x2(x2+x)+2x(x2+x)-2(x2+x)-(x2+2x-2)==(x2+x)(x2+2x-2)-(x2+2x-2)=(x2+x-1)(x2+2x-2)
После разложения на множители получим, что
x4+3×3-x2-4x+2=x2+x-1×2+2x-2==x+1+3x+1-3x+12+52x+12-52
Использование формул сокращенного умножения и бинома Ньютона для разложения многочлена на множители
Внешний вид зачастую не всегда дает понять, каким способом необходимо воспользоваться при разложении. После того, как были произведены преобразования, можно выстроить строчку, состоящую из треугольника Паскаля, иначе их называют биномом Ньютона.
После того, как были произведены преобразования, можно выстроить строчку, состоящую из треугольника Паскаля, иначе их называют биномом Ньютона.
Произвести разложение многочлена x4+4×3+6×2+4x-2 на множители.
Решение
Необходимо выполнить преобразование выражения к виду
x4+4×3+6×2+4x-2=x4+4×3+6×2+4x+1-3
На последовательность коэффициентов суммы в скобках указывает выражение x+14.
Значит, имеем x4+4×3+6×2+4x-2=x4+4×3+6×2+4x+1-3=x+14-3.
После применения разности квадратов, получим
x4+4×3+6×2+4x-2=x4+4×3+6×2+4x+1-3=x+14-3==x+14-3=x+12-3x+12+3
Рассмотрим выражение, которое находится во второй скобке. Понятно, что там коней нет, поэтому следует применить формулу разности квадратов еще раз. Получаем выражение вида
x4+4×3+6×2+4x-2=x4+4×3+6×2+4x+1-3=x+14-3==x+14-3=x+12-3x+12+3==x+1-34x+1+34×2+2x+1+3
Пример 12Произвести разложение на множители x3+6×2+12x+6.
Решение
Займемся преобразованием выражения. Получаем, что
Получаем, что
x3+6×2+12x+6=x3+3·2·x2+3·22·x+23-2=(x+2)3-2
Необходимо применить формулу сокращенного умножения разности кубов. Получаем:
x3+6×2+12x+6==(x+2)3-2==x+2-23x+22+23x+2+43==x+2-23×2+x2+23+4+223+43
Способ замены переменной при разложении многочлена на множители
При замене переменной производится понижение степени и разложение многочлена на множители.
Пример 13Произвести разложение на множители многочлена вида x6+5×3+6.
Решение
По условию видно, что необходимо произвести замену y=x3 . Получаем:
x6+5×3+6=y=x3=y2+5y+6
Корни полученного квадратного уравнения равны y=-2 и y=-3, тогда
x6+5×3+6=y=x3=y2+5y+6==y+2y+3=x3+2×3+3
Необходимо применить формулу сокращенного умножения суммы кубов. Получим выражения вида:
x6+5×3+6=y=x3=y2+5y+6==y+2y+3=x3+2×3+3==x+23×2-23x+43x+33×2-33x+93
То есть получили искомое разложение.
Рассмотренные выше случаи помогут в рассмотрении и разложении многочлена на множители разными способами. 2 = 0 \Rightarrow (x-1-10)(x-1+10) = 0 \Rightarrow \left[ \begin{array}{cc} x_1 = 11 \\ x_2 = -9 \end{array} \right. $$
2 = 0 \Rightarrow (x-1-10)(x-1+10) = 0 \Rightarrow \left[ \begin{array}{cc} x_1 = 11 \\ x_2 = -9 \end{array} \right. $$
Ответ: -9; 11
методов факторинга с решенными примерами — Cuemath
Поэкспериментируйте со следующим моделированием, чтобы увидеть факторы нескольких выражений.
Методы факторизации
Мы обсудим некоторые систематические методы факторизации алгебраических выражений.
Метод общих множителейРассмотрим простой пример: \(3x+9\)
Факторизуя каждый член, мы получаем, \((3\times x)+(3\times 3)\)
По дистрибутивному закону \(3x+9=(3\умножить на х)+(3\умножить на 3)=3(х+3)\).
Метод перегруппировки
Перегруппировка позволяет перегруппировать члены выражения, что приводит к факторизации.
Рассмотрим выражение: \(2ab+2b+7a+7\)
Обратите внимание, что нет единого делителя, общего для всех терминов.
Запишем \(2ab+2b\) и \(7a+7\) в факторной форме отдельно.
\[\begin{align}2ab+2b&=2b(a+1)\\7a+7&=7(a+1)\end{align}\] 92+(a+b)x+ab&=0\end{align}\]
Попробуем найти \(a\) и \(b\) такие, что \((a+b)\) отображается в 5 и \(ab\) сопоставляется с 6.
Факторы \(6\) равны \(1\), \(2\), \(3\) и \(6\) . Найдите пары \(a\) и \(b\) из \(1\), \(2\), \(3\) и \(6\) такие, что \(a+b=5\) и \(ab=6\)
Это правильная пара: \(2\) и \(3\), потому что \(2+3 = 5\) и \(2 \times 3=6\)
Таким образом, квадратное уравнение можно разложить на множители как \((x+2)(x+3)=0\).
Калькулятор факторингаВот калькулятор для факторинга различных выражений.
Важные примечания
Процесс нахождения факторов называется факторингом.
Факторинг помогает найти решение любого алгебраического выражения.
Факторинг позволяет выразить выражение в более простой форме.
 9{2}\)
9{2}\)- Проверьте наличие общих членов в выражении и возьмите наибольший общий множитель.
- Проверить, применимы ли в выражении какие-либо алгебраические тождества.
- Продолжайте разлагать выражение на множители, пока не получите простейшую форму, то есть форму, которая далее не делится.
- Запишите трехчлен в стандартной форме.
- Вычесть наибольший общий делитель, если он существует.
- Найдите произведение старшего коэффициента и постоянного члена.
- Определите множители произведения, найденного на шаге 3, и проверьте, какая пара множителей даст коэффициент при \(x\).
- Выбрав подходящую пару множителей, сохраните знак в каждом числе таким образом, чтобы при работе с ними мы получили результат в виде коэффициента при \(x\), а при нахождении их произведения число было равно числу, найденному в шаге 3.
- Теперь у вас есть 4 члена в выражении, поэтому мы используем метод перегруппировки для разложения на множители.
Он говорит: «Длина фермы в два раза больше ширины».
Можно ли использовать эту информацию для записи факторизованной формы числа 528?
Решение
Пусть ширина фермы будет \(х\) футов.
Итак, длина фермы будет \(2x+1\) футов.
Площадь прямоугольника равна произведению его длины на ширину.
Согласно вопросу,
\[\begin{align}\text{Площадь фермы}&=\text{Ширина} \times \text{Длина}\\528&=x\times (2x+1)\ конец{выравнивание}\]
| Итак, факторизованная форма числа 528 равна \(x(2x+1)\) |
| Пример 2 |
Дженни попросила Джолли разложить на множители \(6xy-4y+6-9x\)
Джолли хочет разложить его на множители методом перегруппировки.
Вы можете им помочь?
Решение
Заметим, что у нас нет общего делителя среди всех слагаемых в выражении \(6xy-4y+6-9x\)
Разберемся с \(6xy-4y\) и \(6-9x\) отдельно.
\[\begin{align}6xy-4y&=2y(3x-2)\\6-9x&=-3(3x-2)\end{align}\]
Итак, данное выражение можно записать в виде
\[\begin{align}6xy-4y+6-9x&=2y(3x-2)-3(3x-2)\\&=(2y-3)(3x-2)\end{align}\ ]
| Итак, множители \(6xy-4y+6-9x\) равны \((2y-3)\) и \((3x-2)\) |
| Пример 3 |
Миа занимается фитнесом и бегает каждое утро.
Парк, в котором она бегает, имеет прямоугольную форму и имеет размеры 12 на 8 футов.
Группа защитников окружающей среды планирует обновить парк и решает построить дорожку вокруг парка.
Это увеличит общую площадь до 140 кв. футов.
Какова будет ширина дорожки?
Решение
Обозначим ширину пути как \(x\). 92+11x-x-11&=0\\x(x+11)-(x+11)&=0\\(x+11)(x-1)&=0\\x&=1,-11\ end{align}\]
Так как длина не может быть отрицательной, мы берем \(x=1\)
| Итак, ширина пути будет 1 фут. |
Иногда сложно работать с жесткими выражениями. Но не волнуйтесь!
Вот несколько советов и рекомендаций, которым вы можете следовать при факторинге.
Советы и рекомендации
Вот несколько заданий для практики.
Выберите/введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
Подведем итоги
Мини-урок был посвящен увлекательной концепции методов факторинга. Математическое путешествие по методам факторинга начинается с того, что студент уже знает, и продолжается творческим созданием новой концепции в юных умах. Сделано таким образом, что это не только понятно и легко для понимания, но и останется с ними навсегда. В этом заключается магия Cuemath.
О КуэматеВ Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов!
Благодаря интерактивному и увлекательному подходу «обучение-преподавание-обучение» учителя изучают тему со всех сторон.
Будь то рабочие листы, онлайн-классы, сеансы сомнений или любая другая форма отношений, мы в Cuemath верим в логическое мышление и разумный подход к обучению.
Часто задаваемые вопросы (FAQ)
1. Как разложить на множители трехчлены со старшим коэффициентом?
Следующие шаги показывают, как разложить на множители трехчлены со старшим коэффициентом.
2. Как разложить на множители совершенные квадратные трехчлены?
Используйте приведенные ниже алгебраические тождества, чтобы разложить на множители совершенные квадратные трехчлены.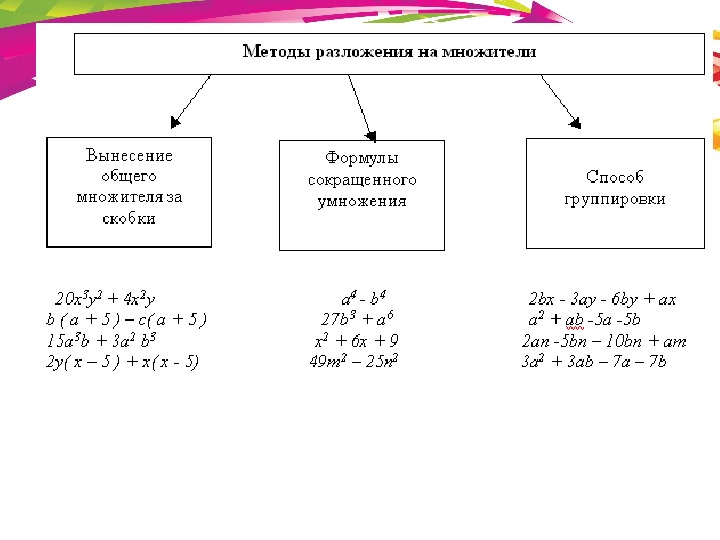 92-2аб\)
92-2аб\)
10 реальных примеров простой факторизации для лучшего понимания
Мы неосознанно используем различные основные принципы математики в нашей повседневной жизни. Мол, мы всегда используем сложение, вычитание, деление и умножение везде — от ресторанов до общественного транспорта. Когда ребенок изучает числа и основы математики, ему требуется время, чтобы определить каждое число при решении задачи. Но когда они вырастут, им может даже не понадобиться читать всю задачу, а решить ее сразу. Это происходит потому, что со временем мы знакомимся с понятиями. Первичная факторизация — аналогичный пример этого. Здесь, в этом посте, у нас есть куча примеров из реальной жизни, где мы широко используем простую факторизацию, облегчая нашу повседневную жизнь.
Что такое простая факторизация? Это будет легко понять, если мы скажем, что простая факторизация на самом деле является обратным умножением. Например, возьмем число 32. Мы можем сказать, что это результат умножения между 4 и 8. Теперь мы можем разбить число 4 на 2×2. Точно так же мы можем разбить число 8 и представить его как 2x2x2. Итак, мы можем выразить 32 как результат 2x2x2x2x2. Этот процесс называется факторизацией простых чисел, когда мы находим простые числа, из которых состоит другое число.
Теперь мы можем разбить число 4 на 2×2. Точно так же мы можем разбить число 8 и представить его как 2x2x2. Итак, мы можем выразить 32 как результат 2x2x2x2x2. Этот процесс называется факторизацией простых чисел, когда мы находим простые числа, из которых состоит другое число.
Другой пример может помочь вам лучше понять это. Возьмем, к примеру, 27. Мы можем сказать, что
27= 3×9
Но 9 не простое число. Итак, нам нужно разбить число 9 на простые числа.
9= 3×3
Итак, 27= 3x3x3
Таким образом, простая факторизация работает.
Как мы используем простую факторизацию в реальной жизни?В нашей повседневной жизни факторизация важна и используется довольно часто. Наиболее распространенные виды использования — обмен денег, оценка времени, расчет затрат и оценок во время путешествий и т. д. Более подробное описание здесь для вас.
1. Собираетесь испечь кексы? Учтите факторизацию! Предположим, у вас будет несколько друзей на ночевку у вас дома, и вы планируете удивить их нежными тающими во рту кексами. Включая вас, будет шесть человек. Вы проверяете свои формочки для маффинов и обнаруживаете, что можете испечь девять маффинов за раз. Значит, либо будет три лишних маффина, либо вы не сможете подарить всем своим друзьям по два маффина, если они попросят еще. Но что, если вы получите еще одну форму из девяти кексов? Тогда у вас получится 18 маффинов. Если разложить на множители 18, то получится 9.0003
Включая вас, будет шесть человек. Вы проверяете свои формочки для маффинов и обнаруживаете, что можете испечь девять маффинов за раз. Значит, либо будет три лишних маффина, либо вы не сможете подарить всем своим друзьям по два маффина, если они попросят еще. Но что, если вы получите еще одну форму из девяти кексов? Тогда у вас получится 18 маффинов. Если разложить на множители 18, то получится 9.0003
18= 2x3x3=6×3
Теперь на шесть человек хватит. Разделите эти кексы между друзьями, по три на каждого из них. Таким образом, факторизация облегчила вам деление кексов в равной степени.
2. Факторизация при обмене денегМы обмениваем деньги так много раз в день, верно? Но мы почти не замечаем, что используем факторизацию на каждом этапе. Вот пример.
Возьми один доллар. Все мы знаем, что 100 пенни составляют доллар. Мы также знаем, что доллар равен четырем четвертям. Не осознавая этого, вы сделали здесь факторизацию.
100= 4×25
Итак, вы видите четыре четвертака, каждый из которых стоит 25, что составляет 100 пенни или доллар.
Вот вам еще один пример. Предположим, вам нужны сдачи, а у вас есть только двадцатидолларовая купюра. При поиске сдачи вы можете разложить 20 на множители. Это даст вам следующие варианты:
20= 2×10
20= 1×20
20= 4×5
Таким образом, вы можете получить четыре купюры пять долларов, двадцать банкнот по одному доллару или две банкноты по десять долларов.
3. Выстраивание и группировкаПредположим, вы воспитатель детского сада и однажды в школе ведете детей на игровую площадку. Вам нужно сгруппировать их и вовлечь их в различные игровые действия. Итак, если в вашем классе 30 учеников, вы можете разложить это число на множители;
30= 3×10
или
30= 3x2x5
Итак, если на детской площадке три качели, можно сформировать десять групп по три ребенка в каждой и вызвать одну группу, чтобы прокатиться на качелях один раз. Как только эти трое детей закончат, вы вызываете вторую группу. Таким образом, все 30 детей смогут покататься на качелях. Вы можете удовлетворить каждого ребенка с помощью факторизации.
Вы можете удовлетворить каждого ребенка с помощью факторизации.
Если мы возьмем, например, службу доставки, мы также найдем применение факторизации. Вот как. Предположим, есть товары весом 100 фунтов, которые нужно куда-то отправить. Вы можете разложить 100 на множители следующими способами:
100 = 2 × 50
или
100 = 4 × 25
Таким образом, либо вы можете взять две упаковочные коробки, способные вместить 50 фунтов каждая, либо четыре. упаковочные коробки по 25 фунтов каждая. В любом случае, факторизация пригодится.
4. Преобразование единиц с помощью факторизацииПри решении математической задачи вас часто могут попросить выразить что-то в определенных единицах. Теперь это легко, но может быть поворот вопроса, если он просит выразить результат как произведение простых чисел. Поясним это на примере.
Допустим, вы хотите сшить себе многоцветный топ и иметь при себе две фута ткани одного цвета. Ваш портной говорит вам, что вам нужно 40 дюймов ткани, чтобы сшить топ. Итак, сколько еще вам нужно? Для начала у вас уже есть два фута, то есть 24 дюйма. Значит, нужно набрать еще 16 дюймов. Факторизуя 16, вы получаете-
Итак, сколько еще вам нужно? Для начала у вас уже есть два фута, то есть 24 дюйма. Значит, нужно набрать еще 16 дюймов. Факторизуя 16, вы получаете-
16= 2x2x2x2
Итак, вы можете купить еще четыре цвета по четыре дюйма каждый. Или вы можете купить ткань двух цветов, каждый длиной восемь дюймов. Вы можете видеть, как факторизация упрощает поиск вариантов, когда вы находитесь в исправлении.
5. Распределение времениЧасы и концепция времени очень заметно используют простую факторизацию. В сутках 24 часа, а каждый час делится на 60 минут. Итак, разложим на множители 60.
60= 5x2x2x3
Глядя на настенные часы, вы увидите пять делений между двумя числами. Начиная с 12, вы увидите, что всего 12 приращений, каждое по 5 минут. Итак, вы можете понять, как разрабатываются часы на основе концепции первичной факторизации.
Вы также можете выразить час в других формах. Используя простые множители 60, вы можете разделить час на две части по тридцать минут или четыре части по 15 минут каждая. Таким образом, если ваш врач дает вам таблетку для приема четыре раза в день, вам нужно будет разложить 24 часа на:
Таким образом, если ваш врач дает вам таблетку для приема четыре раза в день, вам нужно будет разложить 24 часа на:
24 = 2x2x2x3
Это означает, что вы должны принимать одну таблетку каждые четыре часа. Именно так простая факторизация используется и в тайм-менеджменте.
6. Куда-то далеко едете? Факторизация подсчитывает ваши часыПредположим, вы проживаете в Сан-Франциско и планируете посетить шоу American Influencer Award в Лос-Анджелесе. Расстояние между ними составляет около 380 миль. Итак, если вы едете в Лос-Анджелес, вам нужно спланировать, сколько времени вам потребуется, чтобы добраться туда, придется ли вам останавливаться где-то посередине и т. д. Это займет около шести часов, если вы проедете в среднем 65 миль в час. час. Вы фактически используете факторизацию, когда делаете этот расчет. План путешествия — это еще один пример из реальной жизни, в котором вы реализуете простую факторизацию.
7. Факторизация является основой решения головоломки Кенкен.
Kenken в наши дни очень популярен. Вы даже можете играть в нее на онлайн-сайте New York Times. Но пока вы играете с числами и решаете головоломку, вы можете подумать, что просто используете функции, упомянутые в блоках. На самом деле вы широко используете простую факторизацию. В головоломке Kenken вы разбиваете суммы на уникальные числа. Сам этот акт разрушения является первичной факторизацией или множественными факторизациями.
8. Распределение рабочей нагрузки также включает факторизацию. Предположим, у вас есть небольшой малярный бизнес и пять постоянных сотрудников, работающих с вами. Внезапно вы получаете огромный заказ и сжатые сроки, когда вам нужно покрасить помещение двухэтажного кафе. Как вам это удается? Во-первых, вы знаете своих сотрудников и их уровни эффективности и навыков. Если один может выполнить работу за шесть часов, возможно, другой сотрудник сможет сделать то же самое за четыре. Опять же, кому-то другому может понадобиться восемь часов, чтобы сделать это. Таким образом, вы можете факторизовать их время и оценить, у кого сколько времени уйдет на то, чтобы закончить ту или иную часть кафе. Таким образом, вы сможете уложиться в срок и выполнить работу с умом. То, как вы выполняете математику, представляет собой не что иное, как простую факторизацию простых чисел и другие операции, такие как H.C.F. и Л.К.М.
Таким образом, вы можете факторизовать их время и оценить, у кого сколько времени уйдет на то, чтобы закончить ту или иную часть кафе. Таким образом, вы сможете уложиться в срок и выполнить работу с умом. То, как вы выполняете математику, представляет собой не что иное, как простую факторизацию простых чисел и другие операции, такие как H.C.F. и Л.К.М.
В дополнение к приведенному выше списку, простая факторизация также используется в технологических областях. Кодировщики используют первичную факторизацию для создания уникальных кодов в криптографии для защиты и защиты информации. Используя это, они определяют, какие числа использовать в качестве кода, чтобы система стала уникальной и простой для одновременной обработки.
10. Факторизация в играх Видеоигры или компьютерные игры, в которых играют в кости на экране, используют простую факторизацию. При факторизованном программировании каждый раз, когда вы щелкаете или нажимаете, чтобы сыграть в кости, требуется определенное количество ходов и выдается результат.
Функция квадратичная онлайн: Квадратичная Функция — Mathcracker.Com
- Si(x)
- Интегральный синус от x
- Ci(x)
- Интегральный косинус от x
- Shi(x)
- Интегральный гиперболический синус от x
- Chi(x)
- Интегральный гиперболический косинус от x
- Действительные числа
- вводить в виде 7.
 3
3- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- 15/7
- — дробь
Другие функции:
- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от x
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:
- pi
- Число «Пи», которое примерно равно ~3.
 14159..
14159.. - e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
Квадратичная функция — подготовка к ЕГЭ по Математике
Все знают, как выглядит парабола y = x2. В седьмом классе мы рисовали таблицу:
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
После этого по точкам строили график:
Параболу y = ax2 + bx + c мы не станем строить каждый раз «по точкам» — для выпускника школы это просто несолидно. Ведь нам надо знать закономерности поведения данной функции. А эти закономерности таковы.
1. Знак коэффициента a отвечает за направление ветвей. При a > 0 ветви направлены вверх, при a < 0 — вниз.
Знак коэффициента a отвечает за направление ветвей. При a > 0 ветви направлены вверх, при a < 0 — вниз.
На рисунке приведены две параболы y = ax2 с равными по модулю, но противоположными по знаку значениями a.
2. Абсолютная величина коэффициента a отвечает за «раскрыв» параболы. Чем больше |a|, тем у́же парабола (больше прижата к оси Y). Наоборот, чем меньше |a|, тем шире парабола (больше прижата к оси X).
На рисунке приведены две параболы y = a1x2 и y = a2x2, у которых a2 > a1 > 0
3. Абсцисса вершины параболы y = ax2 + bx + c находится по формуле:
Для нахождения ординаты вершины y0 удобнее всего подставить x0 в уравнение параболы. Но вообще, полезно помнить, что
где D = b2 − 4ac — дискриминант.
4. Точки пересечения параболы y = ax2 + bx + c с осью X находятся с помощью решения квадратного уравнения ax2 + bx + c = 0. Если дискриминант равен нулю, то парабола касается оси X. Если дискриминант меньше нуля, то парабола не пересекает ось X.
Если дискриминант равен нулю, то парабола касается оси X. Если дискриминант меньше нуля, то парабола не пересекает ось X.
5. Точка пересечения с осью Y находится легко: мы просто подставляем x = 0 в уравнение параболы. Получается точка (0, c).
Посмотрим, как расположена квадратичная функция (парабола) в зависимости от знака коэффициента а и дискриминанта D.
Где же в реальной жизни можно увидеть параболу (квадратичную функцию)?
Мяч, брошенный под углом к горизонту, летит по параболе. Зависимость его высоты от времени — квадратичная функция. Струя воды из фонтана или шланга, направленная под углом к горизонту, рисует в пространстве именно параболу. Но это не всё. Разберите карманный фонарик. Вы увидите, что за лампочкой расположено зеркальце, имеющее параболическую форму. Спутниковая антенна или антенна телескопа имеют форму параболы. Случайно ли это?
Оказывается, параболическое зеркало обладает интереснейшим свойством — весь поток света, падающий на его поверхность, оно собирает в одной точке, называемой фокусом параболы. Вот почему форма антенн — параболическая. И наоборот, если в фокусе параболы расположен источник света, то отражённые от зеркала лучи света будут параллельны. Поэтому карманный фонарик дает направленный луч света, хорошо видимый в темноте.
Вот почему форма антенн — параболическая. И наоборот, если в фокусе параболы расположен источник света, то отражённые от зеркала лучи света будут параллельны. Поэтому карманный фонарик дает направленный луч света, хорошо видимый в темноте.
Решая задачи ЕГЭ с физическим или экономическим содержанием, мы часто будем замечать в них квадратичные зависимости одной переменной от другой. И конечно, будем пользоваться свойствами квадратичной функции.
Благодарим за то, что пользуйтесь нашими статьями. Информация на странице «Квадратичная функция» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена: 07.05.2023
Интерактивный график квадратичных функций
В предыдущем разделе «График квадратичной функции» мы изучили график квадратного уравнения в общем виде
у = ах 2 + бх + с
— это парабола .
В следующем апплете вы можете изучить, что переменные a , b и c делают с параболической кривой.
Эффекты переменных a и c довольно просты, но что делает переменная b ?
Развлечения
В этом апплете вы начинаете с простой квадратичной кривой (параболы). Вы можете исследовать кривую следующим образом:
- Используйте ползунок «a» под кривой, чтобы изменить a параметр функции и посмотреть, как это повлияет на кривую.
- Используйте ползунок «c» под кривой, чтобы изменить c параметра функции и посмотрите, как это повлияет на кривую.
- Используйте ползунок «b» под кривой, чтобы изменить b параметр функции.
- Установите флажок «Показать сегмент b /(2 a )», чтобы увидеть «перевернутую параболу», где `b=0`.
- Вы также увидите значение b /(2 a ), расстояние от оси y до (ненулевого) пересечения двух парабол, представленного горизонтальным пурпурным (розовым) сегментом.
 2 + c` (серая парабола), а значение `b` равно (2 a ), умноженное на длину пурпурного сегмента (расстояние от оси y до пересечения парабол). Чем больше значение b , тем дальше зеленая парабола движется вокруг серой.
2 + c` (серая парабола), а значение `b` равно (2 a ), умноженное на длину пурпурного сегмента (расстояние от оси y до пересечения парабол). Чем больше значение b , тем дальше зеленая парабола движется вокруг серой.Случай b > 0: Зеленая парабола движется влево и вниз (если a положительно) от своего «нормального» положения с вершиной в начале координат.
Случай b = 0: В этом случае зеленая парабола не движется вокруг серой параболы. Вершина останется на (0, с ).
Случай b < 0: Зеленая парабола движется вправо и вниз (если a положительно).
Замена
cВарьируется c просто перемещает зеленую параболу вверх или вниз.
Случай c > 0: Зеленая парабола движется вверх из своего «нормального» положения с вершиной в начале координат.
Случай c = 0: Зеленая парабола не движется ни вверх, ни вниз.
 Вершина находится в (0, 0) (если 92 + bx + c) из выражения трехчлена или значений a, b и c.
Вершина находится в (0, 0) (если 92 + bx + c) из выражения трехчлена или значений a, b и c.Результаты
Квадратичная формула — dCode
Тег(и) : Арифметика
Поделиться
dCode и многое другое
dCode бесплатен, а его инструменты оказывают ценную помощь в играх, математике, геокэшинге , головоломки и задачи, чтобы решить каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !Калькулятор квадратичных формул
Из полиномиального выражения 92+bx+c)
Извлечение значений a, b и c
См. также: Завершение квадрата — Решатель уравнений — Степень многочлена
Из значений a, b и c
Значение A=Значение B=
Значение C=
Ответы на вопросы (FAQ)
Что такое квадратичная формула? (Определение)
Квадратная формула — это название математического выражения, позволяющего находить решения квадратного уравнения (представленного в виде многочлена степени 2, равного 0). Это самый простой метод, и поэтому его чаще всего изучают. 92-4ac}}{2a} $$
Это самый простой метод, и поэтому его чаще всего изучают. 92-4ac}}{2a} $$
Исходный код
Компания dCode сохраняет за собой право собственности на исходный код «Quadratic Formula». За исключением явной лицензии с открытым исходным кодом (указывается Creative Commons/бесплатно), алгоритма «Квадратичная формула», апплета или фрагмента (преобразователь, решатель, шифрование/дешифрование, кодирование/декодирование, шифрование/дешифрование, дешифратор, транслятор) или «Квадратичной формулы». Формулы» функции (вычисление, преобразование, решение, расшифровка/шифрование, расшифровка/шифрование, декодирование/кодирование, перевод), написанные на любом информационном языке (Python, Java, PHP, C#, Javascript, Matlab и т. д.) и загрузка всех данных, сценарий или доступ к API для «Quadratic Formula» не являются общедоступными, то же самое для автономного использования на ПК, мобильных устройствах, планшетах, iPhone или в приложениях для Android!
Напоминание: dCode можно использовать бесплатно.




 Пружины вертикальны. Верхний конец пружины жёсткостью 3k и нижний конец пружины жёсткостью k закреплены. Известно, что нижняя пружина сжата на a=5 см. Ускорение свободного падения g=10 Н/кг.
Пружины вертикальны. Верхний конец пружины жёсткостью 3k и нижний конец пружины жёсткостью k закреплены. Известно, что нижняя пружина сжата на a=5 см. Ускорение свободного падения g=10 Н/кг. ВОКАЛЬНЫЕ ЖАНРЫ:
ВОКАЛЬНЫЕ ЖАНРЫ: какая электрическая величина меняется в цепи при изменении длины включенного реохорда
какая электрическая величина меняется в цепи при изменении длины включенного реохорда ..
..  pdx.edu › ~atkinsdb › учить › NAOH
pdx.edu › ~atkinsdb › учить › NAOH




 ..
.. .. — PDF Drive
.. — PDF Drive .. — PDF Drive
.. — PDF Drive ..
..

 Наука, изучающая численные методы, называется также численным анализом, или вычислительной математикой.
Наука, изучающая численные методы, называется также численным анализом, или вычислительной математикой. litres.ru
litres.ru
 Учебное пособие…
Учебное пособие…
 .
.




 Конвертировать (EPUB, MOBI) Отправлено на электронную почту Отправлено в Kindle Report.
Конвертировать (EPUB, MOBI) Отправлено на электронную почту Отправлено в Kindle Report.





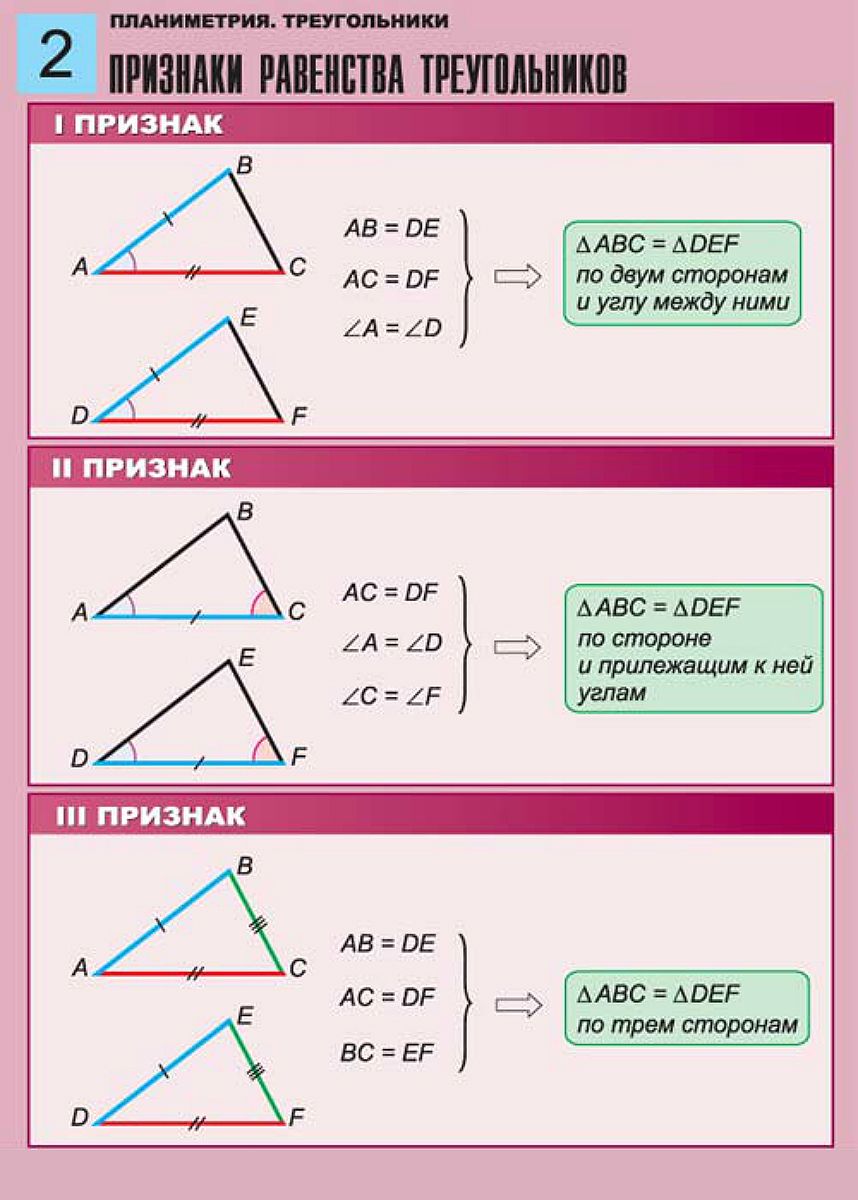
 АСИДО ДЕ
БРЕНСТЕД
БАЗА ДЕ БРЕНСТЕД АНФОТЕРО
h4O+ OH- h3O
Кh5+ Кh3- Кh4
HBr NO3-
HCN CO32-
El NO3- (нитратный анион) представляет собой соединение основания HNO3 без содержания
пропьедадес ацидо-основа.
АСИДО ДЕ
БРЕНСТЕД
БАЗА ДЕ БРЕНСТЕД АНФОТЕРО
h4O+ OH- h3O
Кh5+ Кh3- Кh4
HBr NO3-
HCN CO32-
El NO3- (нитратный анион) представляет собой соединение основания HNO3 без содержания
пропьедадес ацидо-основа. Расчет числа молей KOH на 5,50 мл при растворении KOH
0,360 M. ¿Cuál es el pOH de la disolución?
𝒏 ( 𝑶𝑯−) = [ 𝑂𝐻−] · 𝑉 ( 𝑂𝐻−) = 0,360
𝑚𝑜𝑙
𝐿
· 5,50 · 10−3
𝐿 = 𝟏, 𝟗𝟖 · 𝟏𝟎−𝟑
𝒎𝒐𝒍
𝒑𝑶𝑯 = − log [𝑂𝐻−] = − log [0,360 ] = 𝟎, 𝟒𝟒
Расчет числа молей KOH на 5,50 мл при растворении KOH
0,360 M. ¿Cuál es el pOH de la disolución?
𝒏 ( 𝑶𝑯−) = [ 𝑂𝐻−] · 𝑉 ( 𝑂𝐻−) = 0,360
𝑚𝑜𝑙
𝐿
· 5,50 · 10−3
𝐿 = 𝟏, 𝟗𝟖 · 𝟏𝟎−𝟑
𝒎𝒐𝒍
𝒑𝑶𝑯 = − log [𝑂𝐻−] = − log [0,360 ] = 𝟎, 𝟒𝟒 к.) + h3O (ж) Ch4COO- (а.к.) + h4O+ (а.к.)
0,40 м — —
0,40 — х х х
𝐾𝑎 =
[𝐶𝐻3 𝐶𝑂𝑂−] · [𝐻3 𝑂+
]
[𝐶𝐻3 𝐶𝑂𝑂𝐻]
1,58 · 10−5
«=»
𝑥2
0,40 − 𝑥
«=»
𝑥2
0,40
В равновесии:
[Ch4COOH) = 0,394 М; [Ch4COO-] = [h4O+] = 6,28·10-3 М
𝒑𝑯 = − log [𝐻3 𝑂+] = 𝟐, 𝟐𝟎
к.) + h3O (ж) Ch4COO- (а.к.) + h4O+ (а.к.)
0,40 м — —
0,40 — х х х
𝐾𝑎 =
[𝐶𝐻3 𝐶𝑂𝑂−] · [𝐻3 𝑂+
]
[𝐶𝐻3 𝐶𝑂𝑂𝐻]
1,58 · 10−5
«=»
𝑥2
0,40 − 𝑥
«=»
𝑥2
0,40
В равновесии:
[Ch4COOH) = 0,394 М; [Ch4COO-] = [h4O+] = 6,28·10-3 М
𝒑𝑯 = − log [𝐻3 𝑂+] = 𝟐, 𝟐𝟎 Ионизационный расчет растворения ацетилсалициловой кислоты
(аспирина) 0,20 М, как монопротез.
DATO: Ка (HA) = 3,0·10-4.
HA (а.с.) + h3O (ж) A- (а.с.) + h4O+ (а.с.)
0,20 м — —
0,20 · (1 – ) 0,20 · 0,20 ·
𝐾𝑎 =
[𝐴−] · [𝐻3 𝑂+
]
[𝐻𝐴]
3,0 · 10−4
«=»
0,202
· 𝛼2
0,20 · (1 − 𝛼)
𝜶 = 𝟎, 𝟎𝟑𝟖 (𝟑, 𝟖%)
Ионизационный расчет растворения ацетилсалициловой кислоты
(аспирина) 0,20 М, как монопротез.
DATO: Ка (HA) = 3,0·10-4.
HA (а.с.) + h3O (ж) A- (а.с.) + h4O+ (а.с.)
0,20 м — —
0,20 · (1 – ) 0,20 · 0,20 ·
𝐾𝑎 =
[𝐴−] · [𝐻3 𝑂+
]
[𝐻𝐴]
3,0 · 10−4
«=»
0,202
· 𝛼2
0,20 · (1 − 𝛼)
𝜶 = 𝟎, 𝟎𝟑𝟖 (𝟑, 𝟖%) с.) Na+ (а.с.) + OH- (а.с.)
𝑝𝑂𝐻 = − log [𝑂𝐻−] = 0,7
𝒑𝑯 = 14 − 𝑝𝑂𝐻 = 𝟏𝟑, 𝟑
с.) Na+ (а.с.) + OH- (а.с.)
𝑝𝑂𝐻 = − log [𝑂𝐻−] = 0,7
𝒑𝑯 = 14 − 𝑝𝑂𝐻 = 𝟏𝟑, 𝟑 Расторжение Nh4 0,080 M, ¿qué porcentaje Nh4 está presente como
Кh5+?
Nh4 (ач) + h3O (ж) Nh5+ (ач) + OH- (ач)
0,080 М — —
0,080 — х х х
1,8 · 10−5
«=»
𝑥2
0,080 — 𝑥
«=»
𝑥2
0,080
; 𝒙 = 𝟏, 𝟐 · 𝟏𝟎−𝟑
𝑴
𝜶 =
1,2 · 10−3
0,080
· 100 = 𝟏, 𝟓%
Расторжение Nh4 0,080 M, ¿qué porcentaje Nh4 está presente como
Кh5+?
Nh4 (ач) + h3O (ж) Nh5+ (ач) + OH- (ач)
0,080 М — —
0,080 — х х х
1,8 · 10−5
«=»
𝑥2
0,080 — 𝑥
«=»
𝑥2
0,080
; 𝒙 = 𝟏, 𝟐 · 𝟏𝟎−𝟑
𝑴
𝜶 =
1,2 · 10−3
0,080
· 100 = 𝟏, 𝟓%
 График функции симметричен относительно оси игрек.
График функции симметричен относительно оси игрек.
 06.17
06.17
 14159..
14159.. 2 + c` (серая парабола), а значение `b` равно (2 a ), умноженное на длину пурпурного сегмента (расстояние от оси y до пересечения парабол). Чем больше значение b , тем дальше зеленая парабола движется вокруг серой.
2 + c` (серая парабола), а значение `b` равно (2 a ), умноженное на длину пурпурного сегмента (расстояние от оси y до пересечения парабол). Чем больше значение b , тем дальше зеленая парабола движется вокруг серой. Вершина находится в (0, 0) (если 92 + bx + c) из выражения трехчлена или значений a, b и c.
Вершина находится в (0, 0) (если 92 + bx + c) из выражения трехчлена или значений a, b и c.

