Умножение матриц
Расчет умножения матриц онлайн. Умножьте матрицы порядка 2×3, 1×3, 3×3, 2×2 с 3×2, 3×1, 3×3, 2×2. Динамические расчеты, нахождения произведения матриц.
Умножение матриц возможно когда число столбцов первой матрицы равно числу строк второй матрицы.
Матрица 1
X
Матрица 2
3x33x22x33x11x32x2
X
3x33x22x33x11x32x2
В первой части мы рассмотрим умножение квадратных матриц. В следующей части Вы узнаете, как умножить разные матрицы (например, 2х3 до 3х3).
Здесь мы будем умножать матрицу 3х3 (3 ряда, 3 колонки) на другую матрицу 3х3 (3 ряда, 3 колонки).
| Матрица A | Матрица B | |||||||||||||||||||
| x |
|
В результате мы получим матрицу 3х3. Нам придется рассчитать каждую клетку результатов матрицы отдельно. Результат выразим через X.
Нам придется рассчитать каждую клетку результатов матрицы отдельно. Результат выразим через X.
Шаг 1:Рассчитаем x11
Для того, чтобы вычислить результат x11 мы будем использовать первую строку матрицы А и первый столбец матрицы В.
| Результат X | Матрица A | Матрица B | |||||||||||||||||||||||||||||
| = |
| x |
|
Мы можем представить результат x11 = a11 x b11 + a12 x b21 + a13 x b31
Шаг 2: Рассчитаем x12
Для того, чтобы вычислить результат x12 мы будем использовать первую строку матрицы А и втором столбце матрицы В.
| Результат X | Матрица A | Матрица B | |||||||||||||||||||||||||||||
| = |
| x |
|
Мы можем представить резальтат x12 = a11 x b12 + a12 x b22 + a13 x b32
По той же методике мы вычислим значения для всех ячеек.
| Результат Матрица | |||||||||
|
людей нашли эту статью полезной. А Вы?
вектор умножить на матрицу онлайн
вектор умножить на матрицу онлайнВы искали вектор умножить на матрицу онлайн? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычислить произведение матриц, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «вектор умножить на матрицу онлайн».
Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «вектор умножить на матрицу онлайн».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как вектор умножить на матрицу онлайн,вычислить произведение матриц,вычислить произведение матриц онлайн с решением,дробь умножить на матрицу онлайн,как дробь умножить на матрицу,как умножить матрицу на матрицу 3х3,как умножить обратную матрицу на матрицу,калькулятор матриц онлайн с решением умножение,калькулятор матриц онлайн умножение матриц,калькулятор матриц перемножение,калькулятор матриц произведение,калькулятор матриц умножение,калькулятор матриц умножение матриц онлайн,калькулятор матрицы онлайн умножение,калькулятор матрицы умножение,калькулятор матрицы умножение онлайн,калькулятор онлайн матрицы умножение,калькулятор онлайн умножение матрицы,калькулятор перемножения матриц,калькулятор произведение матриц,калькулятор произведения матриц,калькулятор произведения матриц онлайн,калькулятор умножение матриц,калькулятор умножение матрицу на матрицу,калькулятор умножение матрицы,калькулятор умножение матрицы на матрицу,калькулятор умножение матрицы на матрицу онлайн,калькулятор умножение матрицы онлайн,калькулятор умножения матриц,калькулятор умножения матриц онлайн,матрица на матрицу умножение,матрица на матрицу умножение онлайн,матрица онлайн умножение,матрица умножение на матрицу онлайн,матрица умножение онлайн,матрица умножить на матрицу,матрицу умножить на вектор онлайн,матрицу умножить на матрицу онлайн,матрицу умножить на обратную матрицу,матрицы калькулятор умножение,матрицы найти произведение,матрицы онлайн калькулятор умножение,матрицы перемножение,матрицы умножение калькулятор,матрицы умножение онлайн,матрицы умножение онлайн калькулятор,матрицы умножения,матрицы умножить,множення матриць,найдите произведение матриц,найти произведение матриц,найти произведение матриц калькулятор онлайн,найти произведение матриц онлайн,найти произведение матриц онлайн калькулятор,найти произведение матриц онлайн с решением,найти произведение матрицы,найти произведения матриц,обратную матрицу умножить на матрицу,онлайн калькулятор матриц умножение матриц,онлайн калькулятор матриц умножения,онлайн калькулятор матрицы умножение,онлайн калькулятор найти произведение матриц,онлайн калькулятор перемножение матриц,онлайн калькулятор произведение матриц,онлайн калькулятор произведения матриц,онлайн калькулятор умножение матриц,онлайн калькулятор умножение матриц с подробным решением,онлайн калькулятор умножение матриц с решением,онлайн калькулятор умножение матриц с решением онлайн,онлайн калькулятор умножение матрицы,онлайн калькулятор умножение матрицы на матрицу,онлайн калькулятор умножения матриц,онлайн матрица умножение,онлайн перемножение матриц,онлайн умножение двух матриц,онлайн умножение матриц на матрицу,онлайн умножение матрица,онлайн умножение матрицы,онлайн умножение матрицы на матрицу,онлайн умножение трех матриц,онлайн умножения матриц,онлайн умножить матрицу на матрицу,перемножение матриц,перемножение матриц 3 на 3,перемножение матриц калькулятор,перемножение матриц онлайн,перемножение матриц онлайн калькулятор,перемножение матрицы,перемножить матрицы,перемножить матрицы онлайн,произведение матриц онлайн,произведение матриц онлайн калькулятор,произведения матриц калькулятор,произведения матриц калькулятор онлайн,произведения матриц онлайн калькулятор,решение матриц умножение матриц,умножение двух матриц онлайн,умножение матриц,умножение матриц 2 на 2,умножение матриц калькулятор,умножение матриц калькулятор онлайн,умножение матриц на матрицу онлайн,умножение матриц онлайн,умножение матриц онлайн калькулятор,умножение матриц онлайн калькулятор с подробным решением,умножение матриц онлайн калькулятор с решением,умножение матриц онлайн с решением,умножение матриц с,умножение матриц трех онлайн,умножение матрица,умножение матрица на матрица,умножение матрица на матрица онлайн,умножение матрица на матрицу онлайн,умножение матрица онлайн,умножение матрицу на матрицу калькулятор,умножение матрицы 3х3 на матрицу 3х3,умножение матрицы калькулятор,умножение матрицы калькулятор онлайн,умножение матрицы на вектор онлайн,умножение матрицы на матрицу 3х3,умножение матрицы на матрицу калькулятор,умножение матрицы на матрицу калькулятор онлайн,умножение матрицы на матрицу онлайн,умножение матрицы на матрицу онлайн калькулятор,умножение матрицы на матрицу онлайн с решением,умножение матрицы на матрицы калькулятор,умножение матрицы онлайн,умножение матрицы онлайн калькулятор,умножение обратной матрицы на матрицу,умножение онлайн матрица,умножение трех матриц,умножение число на матриц онлайн,умножения матриц онлайн,умножения матриц онлайн калькулятор,умножения матрицу на матрицу,умножения матрицы,умножить вектор на матрицу онлайн,умножить дробь на матрицу онлайн,умножить матрицу а на матрицу в,умножить матрицу на вектор онлайн,умножить матрицу на дробь онлайн,умножить матрицу на матрицу,умножить матрицу на матрицу онлайн,умножить матрицу на матрицу онлайн с решением,умножить матрицы,умножить матрицы онлайн,умножить матрицы онлайн с решением. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и вектор умножить на матрицу онлайн. Просто введите задачу в окошко и нажмите
«решить» здесь (например, вычислить произведение матриц онлайн с решением).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и вектор умножить на матрицу онлайн. Просто введите задачу в окошко и нажмите
«решить» здесь (например, вычислить произведение матриц онлайн с решением).
Решить задачу вектор умножить на матрицу онлайн вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Преодоление трудностей с онлайн-калькулятором умножения матриц
3 мин чтения
Вы видите ряды и столбцы чисел, помещенных в наборы, и вам нужно их перемножить. Это кажется достаточно трудным. Хорошей новостью является то, что вы можете использовать онлайн-калькулятор умножения матриц, который поможет вам решить эту сложную математическую задачу. Некоторые люди могут возразить, что все дело в простом умножении и сложении, но это еще не все. Кроме того, если вы ошибетесь с одним числом, все ваши усилия будут напрасны. Давайте рассмотрим функции и преимущества этого мощного онлайн-инструмента, бесплатно доступного для студентов.
Это кажется достаточно трудным. Хорошей новостью является то, что вы можете использовать онлайн-калькулятор умножения матриц, который поможет вам решить эту сложную математическую задачу. Некоторые люди могут возразить, что все дело в простом умножении и сложении, но это еще не все. Кроме того, если вы ошибетесь с одним числом, все ваши усилия будут напрасны. Давайте рассмотрим функции и преимущества этого мощного онлайн-инструмента, бесплатно доступного для студентов.
Совершенно упрощенная задача
При использовании калькулятора вам не нужно выяснять, какие два числа нужно умножить и куда поместить произведение. Вам просто нужно ввести цифры в нужных местах и нажать кнопку. Ячейки на экране имеют те же настройки, что и числа в матрице, которую вы видите перед собой. Риск путаницы сведен к возможному минимуму. Конечно, вы должны подтвердить, что вы ввели числа правильно, чтобы получить точный результат.
Как вы знаете, чтобы перемножить две матрицы, в них должно быть одинаковое количество строк и столбцов. Пока это требование выполняется, длина строк и столбцов не имеет значения. Хорошая новость заключается в том, что учителя редко просят вас умножать матрицы размером более 4×4. Когда вы выбираете умножение матриц онлайн, вы можете легко использовать инструменты 2 × 2, 3 × 3 и 4 × 4. Они доступны вместе, поэтому вы наверняка сэкономите много времени и усилий. Вам просто нужно выбрать правильный инструмент для вашей конкретной математической задачи.
Пока это требование выполняется, длина строк и столбцов не имеет значения. Хорошая новость заключается в том, что учителя редко просят вас умножать матрицы размером более 4×4. Когда вы выбираете умножение матриц онлайн, вы можете легко использовать инструменты 2 × 2, 3 × 3 и 4 × 4. Они доступны вместе, поэтому вы наверняка сэкономите много времени и усилий. Вам просто нужно выбрать правильный инструмент для вашей конкретной математической задачи.
Калькулятор не только даст вам продукт. На самом деле вы увидите две матрицы рядом друг с другом в том виде, в котором они должны отображаться в вашем домашнем задании. Что еще более важно, вам будет представлен алгоритм решения проблемы. Это более чем полезно при подготовке к экзаменам. Вы сможете быстрее научиться делать что-то правильно, и у вас будет больше времени для практики для развития ваших навыков. Вы не должны упустить эту возможность, которую современные технологии делают доступной в любое время дня и ночи и абсолютно бесплатно.
Расширенные возможности
Вы, наверное, знаете, что уравнения можно решать с помощью матриц. Это более продвинутый метод, но он дает отличные результаты, особенно когда уравнения более сложные. Хорошей новостью является то, что вы застрахованы даже от таких математических задач. Вы можете легко использовать онлайн-калькулятор матриц с переменными. Опять же, ваша работа очень проста. Вам просто нужно правильно ввести числа и переменные, и
Если вы изучаете продвинутый курс математики в средней школе, колледже или университете, вам обязательно следует воспользоваться калькулятором умножения матриц. Это сэкономит вам много времени и усилий и поможет вам добиться еще большего успеха в этой очень сложной академической дисциплине.
Калькулятор тензорного произведения (произведение Кронекера)
Автор Анна Щепанек, доктор философии
Отзыв от Rijk de Wet
Последнее обновление: 08 февраля 2023 г.
Содержание:- Что такое тензорное произведение ma трикс?
- Как рассчитать произведение Кронекера?
- Тензорное произведение матриц 2×2
- Какова формула произведения матриц Кронекера?
- Как использовать этот калькулятор тензорного произведения?
- Свойства продукта Кронекера
- Часто задаваемые вопросы
Если вы только что наткнулись на эту причудливую матричную операцию, называемую матрично-тензорное произведение или Кронекеровское произведение матриц , больше не ищите помощи — Omni’s калькулятор тензорного произведения здесь, чтобы научить вас всему, что вам нужно нужно знать о:
- Что такое продукт Кронекера;
- Каковы основные свойства продукта Кронекера ;
- Как вычислить тензорное произведение матриц 2×2 вручную ; и
- Как выглядит наиболее общая формула продукта Кронекера .

В качестве бонуса мы объясним взаимосвязь между абстрактным тензорным произведением и произведением Кронекера двух матриц!
⚠️ Произведение Кронекера не то же самое что и обычное умножение матриц! Если вас интересует последнее, посетите калькулятор умножения матриц Omni. Чтобы узнать больше о матричных произведениях, попробуйте наш самый общий матричный калькулятор.
Что такое тензорное произведение матриц?
Произведение матричного тензора, также известное как произведение Кронекера или прямое произведение матрицы, представляет собой операцию, которая берет две матрицы произвольного размера и выводит другую матрицу, которая чаще всего намного больше любой из входных матриц.
Допустим, входные матрицы:
- AAA со строками rAr_ArA и столбцами cAc_AcA и
- BBB со строками rBr_BrB и столбцами cBc_BcB.
Результирующая матрица имеет rA⋅rBr_A \cdot r_BrA⋅rB строк и cA⋅cBc_A \cdot c_BcA⋅cB столбцов.
🔎 В частности, мы можем взять матрицы с одной строкой или одним столбцом, т. е. векторы (будь то столбец или строка по форме). В этом случае мы называем эту операцию векторным тензорным произведением .
Как рассчитать произведение Кронекера?
Когда у нас есть приблизительное представление о том, что такое тензорное произведение матриц, давайте более подробно обсудим, как его вычислить. Произведение Кронекера определяется следующим образом: блочная матрица :
A⊗B=[a11B⋯a1cAB⋮⋱⋮arA1B⋯arAcAB]\footnotesize А \otimes B = \! \begin{bматрица} a_{11} {B} & \cdots & a_{1c_A} {B} \\ \vdots &\ddots &\vdots \\a_{r_A1}{B} &\cdots &a_{r_Ac_A}{B} \end{bmatrix}A⊗B=⎣
⎡a11B⋮arA1B⋯⋱⋯a1cAB⋮arAcAB⎦
⎤
Следовательно, вычисление произведение Кронекера двух матриц сводится к многократному умножению чисел на матрицу . Как вы, наверное, помните, идея состоит в том, чтобы умножить каждый член матрицы на это число, сохраняя форму матрицы неизменной:
Как вы, наверное, помните, идея состоит в том, чтобы умножить каждый член матрицы на это число, сохраняя форму матрицы неизменной:
aijB=[aijb11⋯aijb1cB⋮⋱⋮aijbrB1⋯aijbrBcB]\footnotesize a_{ij} B =\! \begin{bматрица} a_{ij} b_{11} & \cdots & a_{ij} b_{1c_B} \\ \vdots &\ddots &\vdots \\a_{ij}b_{r_B1} &\cdots &a_{ij} b_{r_Bc_B} \end{bmatrix}aijB=⎣
⎡aijb11⋮aijbrB1⋯⋱⋯aijb1cB⋮aijbrBcB⎦
⎤
Тензорное произведение матриц 2×2
Давайте обсудим, что такое произведение Кронекера в случае матриц 2×2, чтобы убедиться, что мы действительно все прекрасно понимаем. Предположим, что
A=[a11a12a21a22], B=[b11b12b21b22]\размер сноски A = \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix}\!,\ B = \begin{bmatrix} b_{11} & b_{ 12} \\ b_{21} & b_{22} \end{bmatrix}A=[a11a21a12a22], B=[b11b21b12b22]
As мы видели выше, имеем:
A⊗B=[a11Ba12Ba21Ba22B]\footnotesize А \otimes B = \begin{bmatrix} а_{11} {В} и а_{12} {В} \\a_{21}{B} &a_{22}{B} \end{bmatrix}A⊗B=[a11Ba21Ba12Ba22B]
Записывая в явном виде члены BBB, получаем:
A⊗B=[a11[b11b12b21b22]a12[b11b12b21b22]a21[b11b12b21b22]a22[b11b12b21b22]]\размер сноски А \otimes B = \\ \begin{bmatrix} a_{11} \begin{bmatrix} б_{11} и б_{12} \\b_{21} &b_{22} \end{bmatrix} и a_{12}\begin{bmatrix} б_{11} и б_{12} \\b_{21} &b_{22} \end{bmatrix} \\a_{21}\begin{bmatrix} б_{11} и б_{12} \\b_{21} &b_{22} \end{bmatrix} &a_{22}\begin{bmatrix} б_{11} и б_{12} \\b_{21} &b_{22} \end{bmatrix} \end{bmatrix} А⊗В=⎣
⎡a11[b11b21b12b22]a21[b11b21b12b22]a12[b11b21b12b22]a22[ b11b21b12b22]⎦
⎤
Выполняя числовое умножение на матрицу, получаем окончательный результат:
A⊗B=[a11b11a11b12a12b11a12b12a11b21a1 1b22a12b21a12b22a21b11a21b12a22b11a22b12a21b21a21b22a22b21a22b22]\footnotesize А \otimes B = \\ \begin{bматрица} а_{11} б_{11} и а_{11}б_{12} и а_{12} б_{11} и а_{12} б_{12} \\ а_{11}б_{21} и а_{11}б_{22} и а_{12}б_{21} и а_{12}б_{22} \\ a_{21} b_{11} & a_{21}b_{12} & a_{22} b_{11} & a_{22} b_{12} \\ а_{21}б_{21} и а_{21}б_{22} и а_{22} б_{21} и а_{22} б_{22} \end{bmatrix} А⊗В=⎣
a22b21a12b12a12b22a22b12a22b22⎦
⎤
Следовательно, тензорное произведение матриц 2×2 является матрицей 4×4. Это совсем не сложно, не так ли? Но вы, конечно, можете себе представить, насколько грязно было бы явно записывать тензорное произведение гораздо больших матриц! К счастью, есть краткая формула для матричного тензорного произведения — давайте ее обсудим!
Это совсем не сложно, не так ли? Но вы, конечно, можете себе представить, насколько грязно было бы явно записывать тензорное произведение гораздо больших матриц! К счастью, есть краткая формула для матричного тензорного произведения — давайте ее обсудим!
Какова формула произведения матрицы Кронекера?
Мы можем вычислить элемент (A⊗B)ij(A\otimes B)_{ij}(A⊗B)ij произведения Кронекера как:
a⌈i/rB⌉,⌈j/cB⌉ ⋅b((i−1)%rB+1),((j−1)%cB+1)\footnotesize a_{\lceil i/r_B\rceil,\lceil j/c_B\rceil} \cdot b_{\ влево((i-1)\% r_B+1\вправо),\влево((j-1)\% c_B+1\вправо)}a⌈i/rB⌉,⌈j/cB⌉⋅b ((i−1)%rB+1),((j−1)%cB+1)
где ⌈x⌉\lceil x \rceil⌈x⌉ — функция потолка (т. е. наименьшая целое число, большее xxx), а %\%% обозначает операцию по модулю. Напомним также, что rBr_BrB и cBc_BcB обозначают количество строк и столбцов BBB соответственно.
Мы обсудили два метода вычисления произведения тензорных матриц. Есть и третий метод, и он наш любимый — просто используйте калькулятор тензорного произведения Omni!
Как использовать этот калькулятор тензорного произведения?
Чтобы вычислить произведение Кронекера двух матриц с помощью нашего инструмента, просто выберите размеры ваших матриц и введите коэффициенты в соответствующие поля.
🙋 Ой, вы перепутали порядок матриц? Не беспокойтесь — наш калькулятор тензорного произведения позволяет вам выбрать, хотите ли вы умножать A⊗BA \otimes BA⊗B или B⊗AB \otimes AB⊗A. Наслаждаться!
Свойства произведения Кронекера
Ассоциативность
Произведение тензорных матриц ассоциативно, т.е. для любых A,B,CA, B, CA,B,C имеем
(A⊗B)⊗C=A⊗( B⊗C)\footnotesize ({A} \otimes {B} )\otimes {C} = {A} \otimes ({B} \otimes {C})(A⊗B)⊗C=A⊗(B⊗ C)
Билинейность
Тензорное матричное произведение также билинейно, т.е. линейно по каждому аргументу в отдельности:
(A+B)⊗C=A⊗C+B⊗C,(xA)⊗B=x( A⊗B)\размер сноски (A + B)\otimes C =A \otimes C +B \otimes C, \\[0.5em] (x{A}) \otimes {B} = x({A} \otimes {B} )(A+B)⊗C=A⊗C+B⊗C,(xA)⊗B=x(A⊗B ) 9{*}.(А⊗В)∗=А∗⊗В∗.
Сингулярные значения и ранг
💡 Не беспокойтесь, если вы еще не знакомы с концепцией сингулярных значений — можете пропустить этот раздел или перейти к калькулятору сингулярных значений.
Если σ1,…,σpA\sigma_1, \ldots, \sigma_{p_A}σ1,…,σpA являются ненулевыми сингулярными значениями AAA и s1,…,spBs_1, \ldots, s_{p_B }s1,…,spB являются ненулевыми сингулярными значениями BBB, тогда ненулевых сингулярных значений A⊗BA \otimes BA⊗B являются σisj\sigma_{i}s_jσisj с i=1,…,pAi=1, \ldots, p_{A}i=1,…,pA и j=1,…,pBj=1, \ldots, p_{B}j=1,…,pB .
Напомним, что количество ненулевых сингулярных значений матрицы равно рангу этой матрицы. В результате получаем формулу ранга:
ранг(A⊗B)=ранг(A)⋅ранг(B)\footnotesize \operatorname{rank}(A \otimes B) = \operatorname{rank}(A) \cdot \operatorname{rank}(B)rank(A⊗B)=rank(A)⋅rank(B)
Инверсия тензорный продукт
В оставшейся части этого раздела мы предполагаем, что AAA и BBB являются квадратными матрицами размера mmm и nnn соответственно. 9{-1}.(А⊗В)−1=А−1⊗В−1.
Собственные значения, трассировка, определитель
💡 Нахождение собственных значений — еще одна сложная тема. Если вам нужно освежить знания, посетите наш калькулятор собственных значений и собственных векторов.
Если вам нужно освежить знания, посетите наш калькулятор собственных значений и собственных векторов.
Если α1,…,αm\alpha_1, \ldots, \alpha_mα1,…,αm и β1,…,βn\beta_1, \ldots, \beta_nβ1,…,βn являются собственными значениями AAA и BBB ( перечисленные с кратностями) соответственно, то собственные значения матрицы A⊗BA \otimes BA⊗B имеют вид
αiβj\alpha_{i}\beta_{j}αiβj с i=1,…,mi=1,\ ldots ,mi=1,…,m и j=1,…,nj=1,\ldots ,nj=1,…,n. 9mdet(A⊗B)=det(A)ndet(B)m
след(A⊗B)=след(A)след(B)\footnotesize \operatorname{trace}(A \otimes B) = \operatorname{trace}(A) \operatorname{trace}(B)trace(A⊗B)=trace(A)trace(B)
Часто задаваемые вопросы
Ассоциативный продукт Кронекера?
Да , произведение кронекеровых матриц ассоциативно: (A ⊗ B) ⊗ C = A ⊗ (B ⊗ C) для всех матриц A, B, C.
Является ли произведение Кронекера коммутативным?
No произведение матриц Кронекера не коммутативно: A ⊗ B ≠ B ⊗ A для некоторых матриц A, B.
Является ли произведение тензора таким же, как произведение Кронекера?
Тензорное произведение является более общим понятием, но если мы имеем дело с конечномерными линейными пространствами, то матрица тензорного произведения двух линейных операторов (относительно базиса, являющегося тензорным произведением исходных базисов) дается в точности произведением Кронекера матриц этих операторов по начальным основаниям.
Как найти размер матричного тензорного произведения?
Чтобы определить размер тензорного произведения двух матриц:
- Вычислить произведение количества строк входных матриц.
- Вычислить произведение количества столбцов входных матриц.
- В выходной матрице будет столько строк, сколько вы получили на шаге 1, и столько столбцов, сколько вы получили на шаге 2.
- В частности, если у вас есть матриц одинакового размера , выходная матрица имеет размеры, равные исходные размеры в квадрате .




 x
x Первые полторы тысяч разложений.
Первые полторы тысяч разложений. д) а также любых других непересекающихся многоугольников.
д) а также любых других непересекающихся многоугольников.
 Угол между ними.
Угол между ними. Матрица смежности онлайн
Матрица смежности онлайн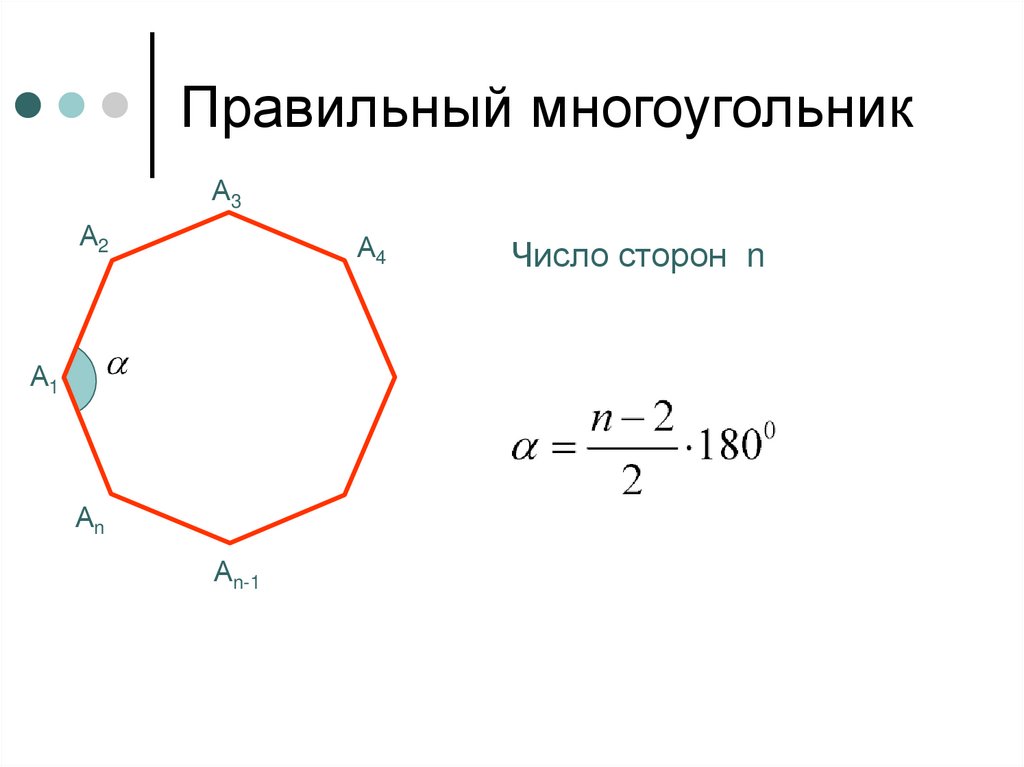 Вы можете создавать неправильные многоугольники, правильные многоугольники с равными сторонами или многоугольники от руки. Эти инструменты доступны на панели Создать объекты с шаблонами объектов для полигональных векторных слоев.
Вы можете создавать неправильные многоугольники, правильные многоугольники с равными сторонами или многоугольники от руки. Эти инструменты доступны на панели Создать объекты с шаблонами объектов для полигональных векторных слоев.


 Если исходный класс пространственных объектов поддерживает z-значения, вершинам назначаются z-значения на основе текущих настроек режима ввода высот для 3D-объектов.
Если исходный класс пространственных объектов поддерживает z-значения, вершинам назначаются z-значения на основе текущих настроек режима ввода высот для 3D-объектов.



 Как видно мы получаем неопределенность .
Как видно мы получаем неопределенность .
 Еще в статье «Замечательные пределы: Первый и второй замечательный предел» мы отдельно рассматриваем интересную группу пределов. Статья вставит еще один блок для решения большинства пределов, встречающихся не просторах обучения.
Еще в статье «Замечательные пределы: Первый и второй замечательный предел» мы отдельно рассматриваем интересную группу пределов. Статья вставит еще один блок для решения большинства пределов, встречающихся не просторах обучения. ..)
..) Он использует по определению формулу производной, чтобы найти производную функции. Он находит предельную точку функции, чтобы описать ее поведение.
Он использует по определению формулу производной, чтобы найти производную функции. Он находит предельную точку функции, чтобы описать ее поведение.



 Проводится 18 ноября 2022 года в письменном виде на площадках школ и математических кружков под руководством Проводящего. Все желающие заранее регистрируются и определяются к одному из Проводящих отборочного этапа. Подробнее о проведении отборочного тура вы можете прочитать в регламенте отборочного тура.
Проводится 18 ноября 2022 года в письменном виде на площадках школ и математических кружков под руководством Проводящего. Все желающие заранее регистрируются и определяются к одному из Проводящих отборочного этапа. Подробнее о проведении отборочного тура вы можете прочитать в регламенте отборочного тура.
 Победители Олимпиады
приглашаются в самые сильные группы, чтобы усиленно развивать свои математические способности.
Победители Олимпиады
приглашаются в самые сильные группы, чтобы усиленно развивать свои математические способности. Данный нагревательный мат рассчитан на площадь в 12,0 м2, и прекрасно подойдет для установки в гостинную, кухню, спальню и детскую. Двухжильная структура кабеля и алюмолавсановый экран, делают мат абсолютно безопасным в эксплуатации. Наличие заземления позволяет использовать электрический теплый пол Greenwich, в помещениях с повышенной влажностью: банях, саунах, душевых. Гарантия на изделие составляет 25 лет.
Данный нагревательный мат рассчитан на площадь в 12,0 м2, и прекрасно подойдет для установки в гостинную, кухню, спальню и детскую. Двухжильная структура кабеля и алюмолавсановый экран, делают мат абсолютно безопасным в эксплуатации. Наличие заземления позволяет использовать электрический теплый пол Greenwich, в помещениях с повышенной влажностью: банях, саунах, душевых. Гарантия на изделие составляет 25 лет. д.). Монтаж осуществляется как правило в плиточный клей толщиной 7-10 мм.
д.). Монтаж осуществляется как правило в плиточный клей толщиной 7-10 мм.
 10 [ Чёрный; 3,2 кВт; С датчиком пола и воздуха]
10 [ Чёрный; 3,2 кВт; С датчиком пола и воздуха] Узнать больше.
)
Узнать больше.
) Получите доступ к необходимым инструментам через M&T Mobile и Online Banking уже сегодня.
Получите доступ к необходимым инструментам через M&T Mobile и Online Banking уже сегодня.


 е. приводим подобные члены – a2 уничтожается, -3a переносим, меняя знак.
е. приводим подобные члены – a2 уничтожается, -3a переносим, меняя знак.
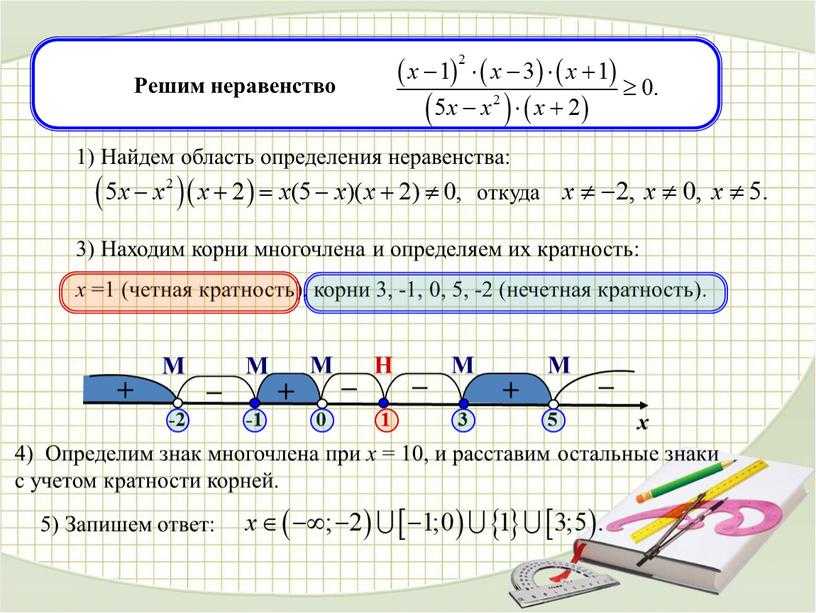
 Например, решить неравенство: 2x + 1 > 0. Рассмотрим линейную функцию y = 2x + 1, составим таблицу:
Например, решить неравенство: 2x + 1 > 0. Рассмотрим линейную функцию y = 2x + 1, составим таблицу: Эта функция сохраняет свой знак при (-∞; 2), и она положительна. И она также сохраняет свой знак при (2; ∞), и при всех этих значениях функция отрицательна. Нам нужны те x, при которых функция положительна. Получим ответ x , запишем его в виде промежутка (-∞; 2).
Эта функция сохраняет свой знак при (-∞; 2), и она положительна. И она также сохраняет свой знак при (2; ∞), и при всех этих значениях функция отрицательна. Нам нужны те x, при которых функция положительна. Получим ответ x , запишем его в виде промежутка (-∞; 2). youtube.com/watch?v=0NU3Qvs1Wuw
youtube.com/watch?v=0NU3Qvs1Wuw Что касается событий в режиме реального времени, то для более 70% матчей доступны графические трансляции и статистика в режиме реального времени. Если вы хотите сделать живую ставку на футбол, то можете рассчитывать на 40-60 рынков. Если вы выбираете хоккей или баскетбол — на 40-50 рынков. На Mostbet одни из лучших коэффициентов на рынке. Сотрудники площадки постоянно анализируют рынок и предлагает игрокам выгодные ставки на востребованные события. Но и для тех, кто любит нишевые виды спорта, найдутся интересные матчи.
Что касается событий в режиме реального времени, то для более 70% матчей доступны графические трансляции и статистика в режиме реального времени. Если вы хотите сделать живую ставку на футбол, то можете рассчитывать на 40-60 рынков. Если вы выбираете хоккей или баскетбол — на 40-50 рынков. На Mostbet одни из лучших коэффициентов на рынке. Сотрудники площадки постоянно анализируют рынок и предлагает игрокам выгодные ставки на востребованные события. Но и для тех, кто любит нишевые виды спорта, найдутся интересные матчи.  Совершив Mostbet логин, вы сможете делать ставки в тенге и установить для интерфейса казахский язык, чтобы удобно ориентироваться по сайту и в приложении.
Совершив Mostbet логин, вы сможете делать ставки в тенге и установить для интерфейса казахский язык, чтобы удобно ориентироваться по сайту и в приложении.  Мостбет регистрация доступна для всех игроков, которые исполнилось 18 лет. Есть пять вариантов, с помощью которых вы сможете создать аккаунт на этом сайте:
Мостбет регистрация доступна для всех игроков, которые исполнилось 18 лет. Есть пять вариантов, с помощью которых вы сможете создать аккаунт на этом сайте: Совершив Мостбет вход, новые игроки могут получить бонус на первый депозит или бесплатную ставку, а также участвовать в программе лояльности и получать дополнительные бонусы за активность на сайте. Вот пример бонусов, доступных в Mostbet:
Совершив Мостбет вход, новые игроки могут получить бонус на первый депозит или бесплатную ставку, а также участвовать в программе лояльности и получать дополнительные бонусы за активность на сайте. Вот пример бонусов, доступных в Mostbet: Этот Мостбет бонус доступен, если вы делаете экспресс ставку на три и более исхода. После этого вы можете получить + 40% к ставке.
Этот Мостбет бонус доступен, если вы делаете экспресс ставку на три и более исхода. После этого вы можете получить + 40% к ставке. 2 Ghz и выше;
2 Ghz и выше; 000 тенге
000 тенге

 Государственный университет Миннесоты, Манкато, магистр…
Государственный университет Миннесоты, Манкато, магистр…


 {2}}\leq 0[/latex] 9{2}}<0[/latex] и запишите свой ответ в виде интервалов.
{2}}\leq 0[/latex] 9{2}}<0[/latex] и запишите свой ответ в виде интервалов.
 Почти все использовали формат файла DOC каждый раз, при написании письма, при работе или вообще при написании чего-либо на компьютере вы бы использовали формат файла DOC. В 1990-х годах Microsoft выбрала расширение DOC для обработки своих файлов программы Microsoft Word. По мере развития и роста технологий ПК, первоначальное использование расширения стало менее важным и в значительной степени исчезло из мира ПК.
Почти все использовали формат файла DOC каждый раз, при написании письма, при работе или вообще при написании чего-либо на компьютере вы бы использовали формат файла DOC. В 1990-х годах Microsoft выбрала расширение DOC для обработки своих файлов программы Microsoft Word. По мере развития и роста технологий ПК, первоначальное использование расширения стало менее важным и в значительной степени исчезло из мира ПК.
 odt
odt Первоначально формат OpenDocument разрабатывался на базе языка XML и имел в корне , теперь же он принял форму zip архива по аналогии с форматом DOCX от Microsoft и использует преимущества технологии сжатия ZIP для уменьшения общего размера файла. Документы Writer имеют расширение .odt или .fodt.
Первоначально формат OpenDocument разрабатывался на базе языка XML и имел в корне , теперь же он принял форму zip архива по аналогии с форматом DOCX от Microsoft и использует преимущества технологии сжатия ZIP для уменьшения общего размера файла. Документы Writer имеют расширение .odt или .fodt. 0 File)
0 File) com
а также
aspose.cloud
com
а также
aspose.cloud
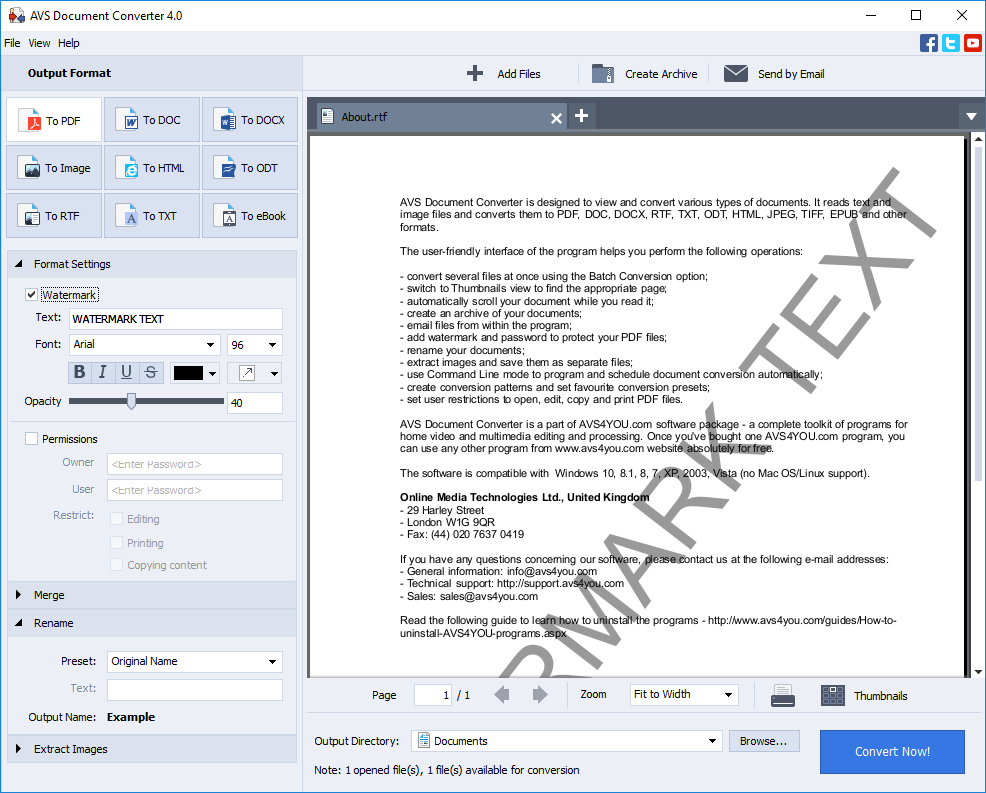 Наш конвертер файлов проанализирует содержимое исходного DOC файла до мельчайших деталей и воссоздаст содержимое в целевом ODT формате.
Наш конвертер файлов проанализирует содержимое исходного DOC файла до мельчайших деталей и воссоздаст содержимое в целевом ODT формате.

 размер файла 50MB (хотите больше?)
Как мои файлы защищены?
размер файла 50MB (хотите больше?)
Как мои файлы защищены?
 Отличное быстрое приложение, значительно увеличило мою производительность. Также замечательная поддержка — всегда быстро помогали!
Отличное быстрое приложение, значительно увеличило мою производительность. Также замечательная поддержка — всегда быстро помогали! Вы имеете прямой доступ и даже можете оформить подписку всего на месяц.
Вы имеете прямой доступ и даже можете оформить подписку всего на месяц. Преобразователь Замзара был идеальным.
Преобразователь Замзара был идеальным. Какой инструмент вы используете, зависит от вас!
Какой инструмент вы используете, зависит от вас! С поддержкой более 1100 типов преобразования файлов, независимо от того, нужно ли вам конвертировать видео, аудио, документы или изображения, вы легко найдете то, что вам нужно, и вскоре ваши файлы будут в форматах и размерах, которые вам подходят.
С поддержкой более 1100 типов преобразования файлов, независимо от того, нужно ли вам конвертировать видео, аудио, документы или изображения, вы легко найдете то, что вам нужно, и вскоре ваши файлы будут в форматах и размерах, которые вам подходят. Microsoft Office был разработан для операционной системы Windows, но вы также можете установить приложения Office в других операционных системах, таких как macOS от Apple и ChromeOS от Google. Базовая бесплатная программа «Word для Интернета» также доступна в Интернете для владельцев учетных записей Microsoft. Файлы DOC легко передавать и распечатывать, и их можно открыть в большинстве программ обработки текстов, включая LibreOffice, Apple Pages и Google Docs, а также в Microsoft Word.
Microsoft Office был разработан для операционной системы Windows, но вы также можете установить приложения Office в других операционных системах, таких как macOS от Apple и ChromeOS от Google. Базовая бесплатная программа «Word для Интернета» также доступна в Интернете для владельцев учетных записей Microsoft. Файлы DOC легко передавать и распечатывать, и их можно открыть в большинстве программ обработки текстов, включая LibreOffice, Apple Pages и Google Docs, а также в Microsoft Word. Сам файл похож на файл DOCX и может содержать текст, изображения, таблицы и фигуры, а также может быть отформатирован с использованием различных шрифтов и размеров текста.
Сам файл похож на файл DOCX и может содержать текст, изображения, таблицы и фигуры, а также может быть отформатирован с использованием различных шрифтов и размеров текста. Выберите файл DOC, который вы хотите преобразовать.
Выберите файл DOC, который вы хотите преобразовать.
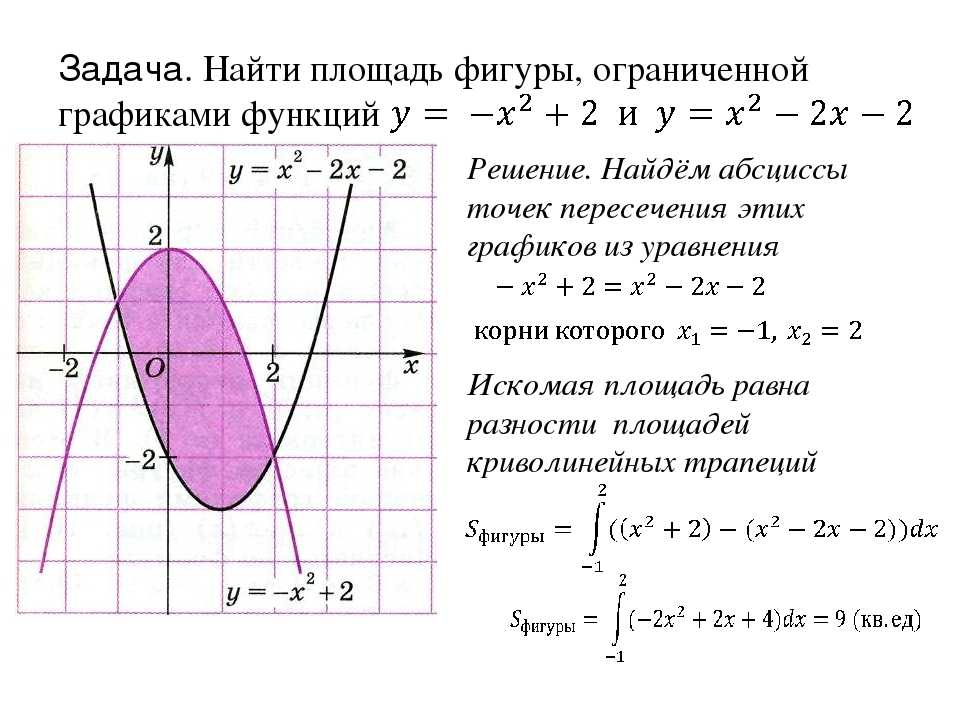
 Колмогоров Алгебра 10-11 класс упр 368 параграф 8 – Рамблер/классВычислим площадь фигуры. Колмогоров Алгебра 10-11 класс упр 368 параграф 8 – Рамблер/класс
Колмогоров Алгебра 10-11 класс упр 368 параграф 8 – Рамблер/классВычислим площадь фигуры. Колмогоров Алгебра 10-11 класс упр 368 параграф 8 – Рамблер/класс В какой момент времени (Подробнее…)
В какой момент времени (Подробнее…) .. Цыбулько И. П. Русский язык ЕГЭ-2017 ГДЗ. Вариант 13.
.. Цыбулько И. П. Русский язык ЕГЭ-2017 ГДЗ. Вариант 13.


 9b_a|f(x)−g(x)|dx. \nonumber \]
9b_a|f(x)−g(x)|dx. \nonumber \] \)
\) 92_1=\dfrac{1}{2}.\)
92_1=\dfrac{1}{2}.\) 2\) как функции \(\displaystyle y \).Однако, судя по графику, нас интересует положительный квадратный корень.) Точно так же правый график представлен функцией \(\displaystyle y=g(x)=2−x\), но также легко может быть представлен функцией \(\displaystyle x=u(y)=2−y\). Когда графики представлены как функции \(\displaystyle y\), мы видим, что область ограничена слева графиком одной функции и справа графиком другой функции. Следовательно, если мы интегрируем по \(\displaystyle y\), нам нужно вычислить только один интеграл. Разработаем формулу для этого типа интеграции.
2\) как функции \(\displaystyle y \).Однако, судя по графику, нас интересует положительный квадратный корень.) Точно так же правый график представлен функцией \(\displaystyle y=g(x)=2−x\), но также легко может быть представлен функцией \(\displaystyle x=u(y)=2−y\). Когда графики представлены как функции \(\displaystyle y\), мы видим, что область ограничена слева графиком одной функции и справа графиком другой функции. Следовательно, если мы интегрируем по \(\displaystyle y\), нам нужно вычислить только один интеграл. Разработаем формулу для этого типа интеграции.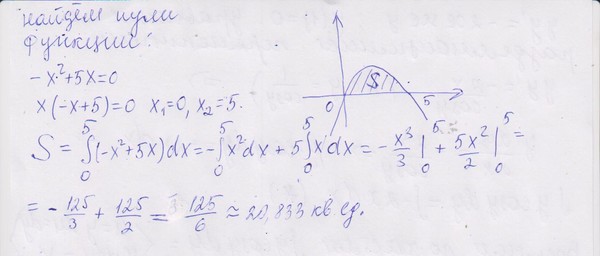 \end{align*}\]
\end{align*}\]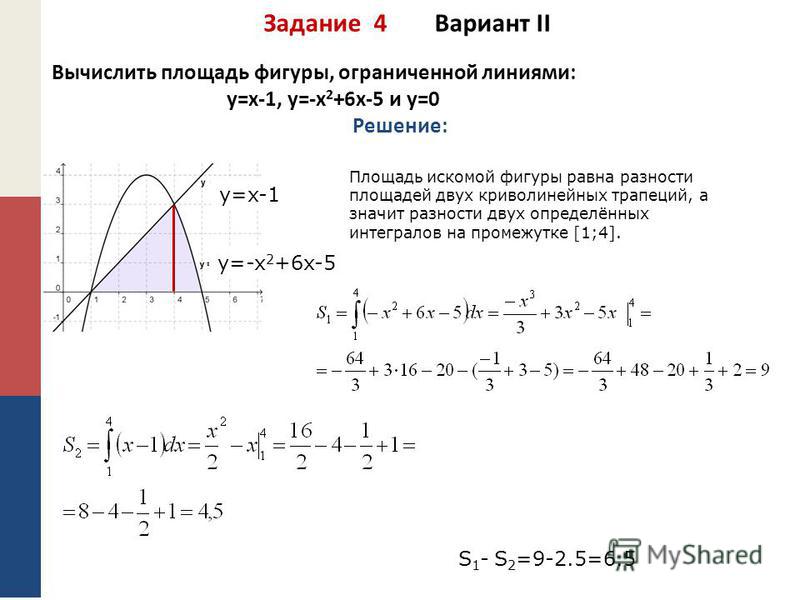
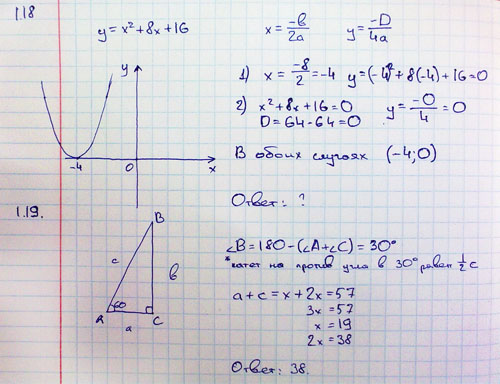 Пусть \(\textbf{R}\) будет областью, изображенной на следующем рисунке. Найдите площадь \(\textbf{R}\) путем интегрирования по \(\displaystyle y\).
Пусть \(\textbf{R}\) будет областью, изображенной на следующем рисунке. Найдите площадь \(\textbf{R}\) путем интегрирования по \(\displaystyle y\). Принципы одни и те же независимо от того, какая переменная используется в качестве переменной интегрирования.
Принципы одни и те же независимо от того, какая переменная используется в качестве переменной интегрирования.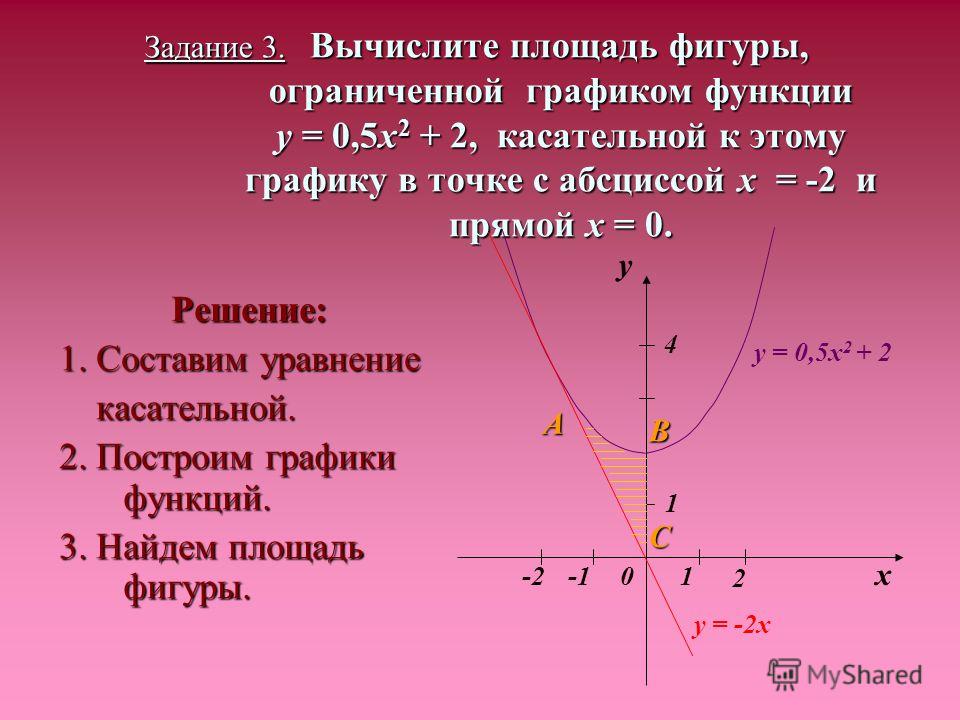 org/details/books/calculus-volume-1
org/details/books/calculus-volume-1
 Во-вторых, мы должны найти интегрирование (первообразную) кривой. Наконец, нам нужно применить верхний предел и нижний предел к интегральному ответу и взять разницу, чтобы получить площадь под кривой. 9б_а\)
Во-вторых, мы должны найти интегрирование (первообразную) кривой. Наконец, нам нужно применить верхний предел и нижний предел к интегральному ответу и взять разницу, чтобы получить площадь под кривой. 9б_а\)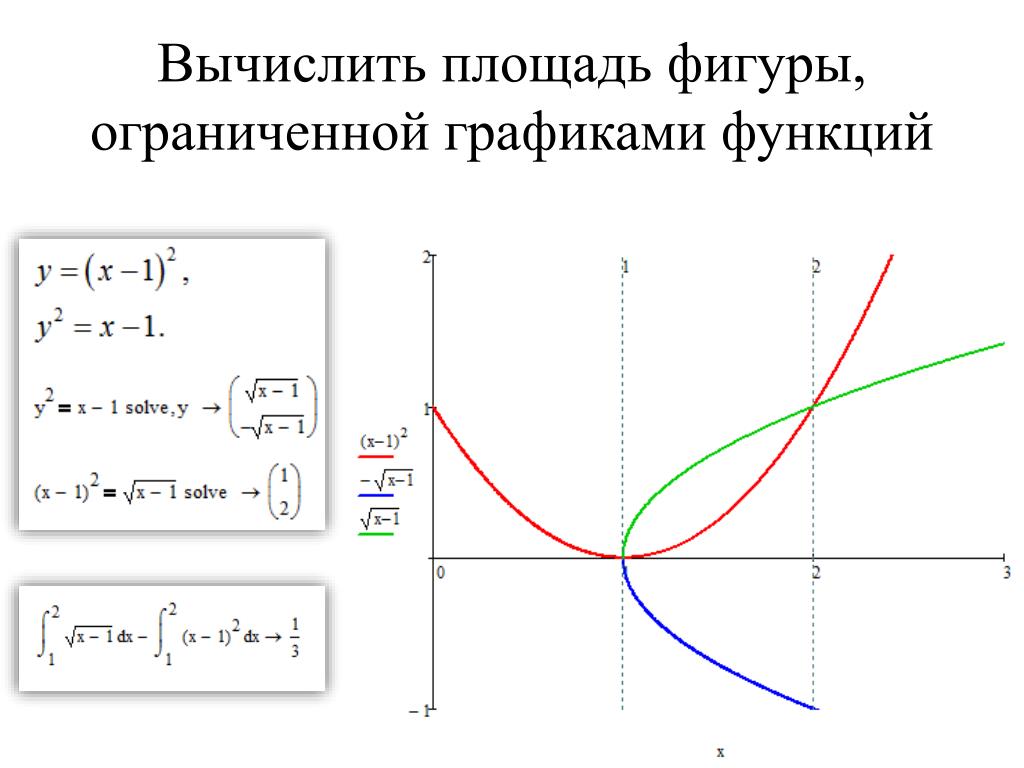 b f(x ).dx\)
b f(x ).dx\)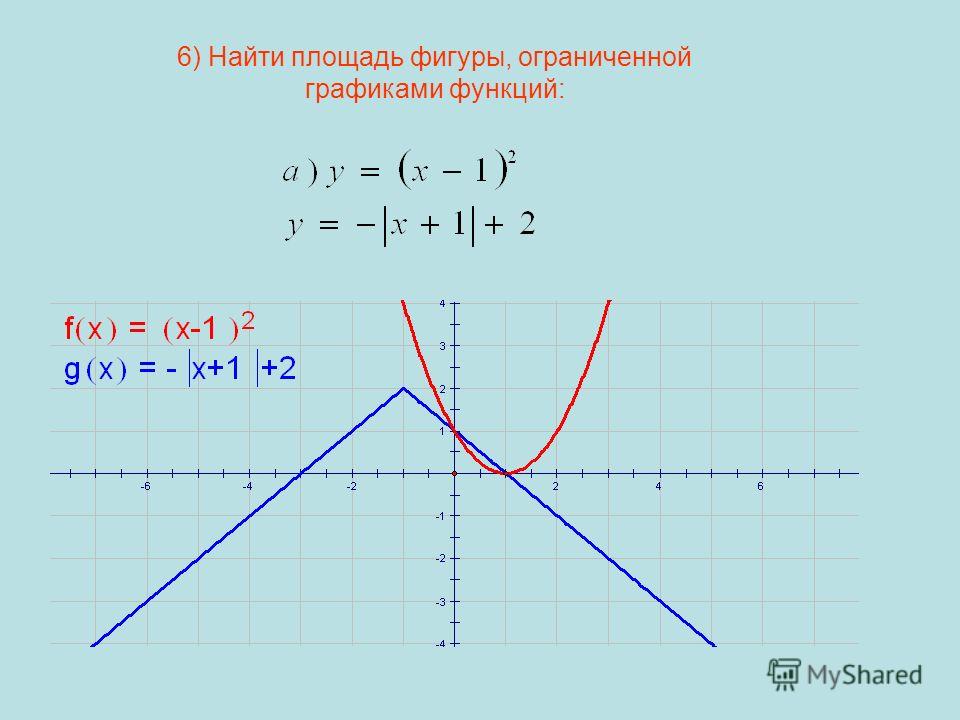
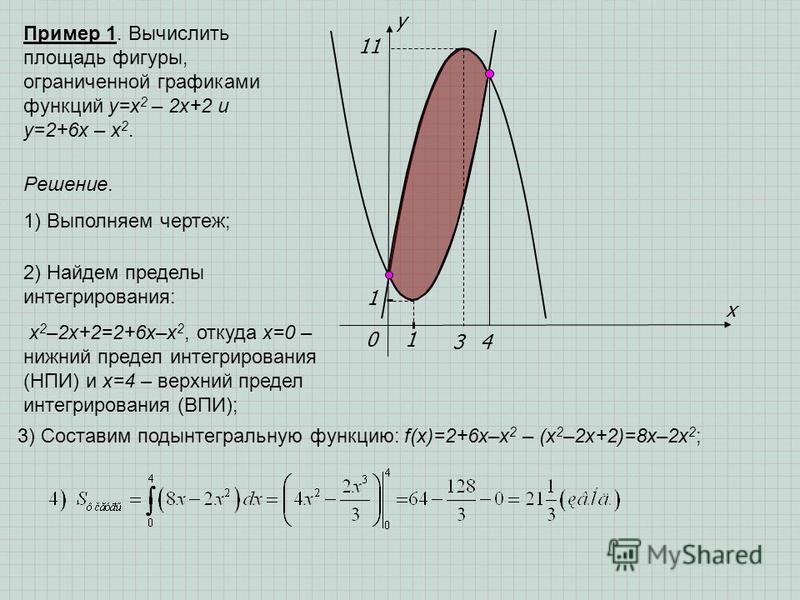 Здесь граница относительно оси и для кривой, и для линии одинакова. На рисунке ниже показаны кривая \(y_1\) = f(x) и линия \(y_2\) = g(x), и цель состоит в том, чтобы найти площадь между кривой и линией. Здесь мы берем интеграл от разности двух кривых и применяем границы, чтобы найти результирующую площадь. 9b_a [f(x) — g(x)].dx\)
Здесь граница относительно оси и для кривой, и для линии одинакова. На рисунке ниже показаны кривая \(y_1\) = f(x) и линия \(y_2\) = g(x), и цель состоит в том, чтобы найти площадь между кривой и линией. Здесь мы берем интеграл от разности двух кривых и применяем границы, чтобы найти результирующую площадь. 9b_a [f(x) — g(x)].dx\)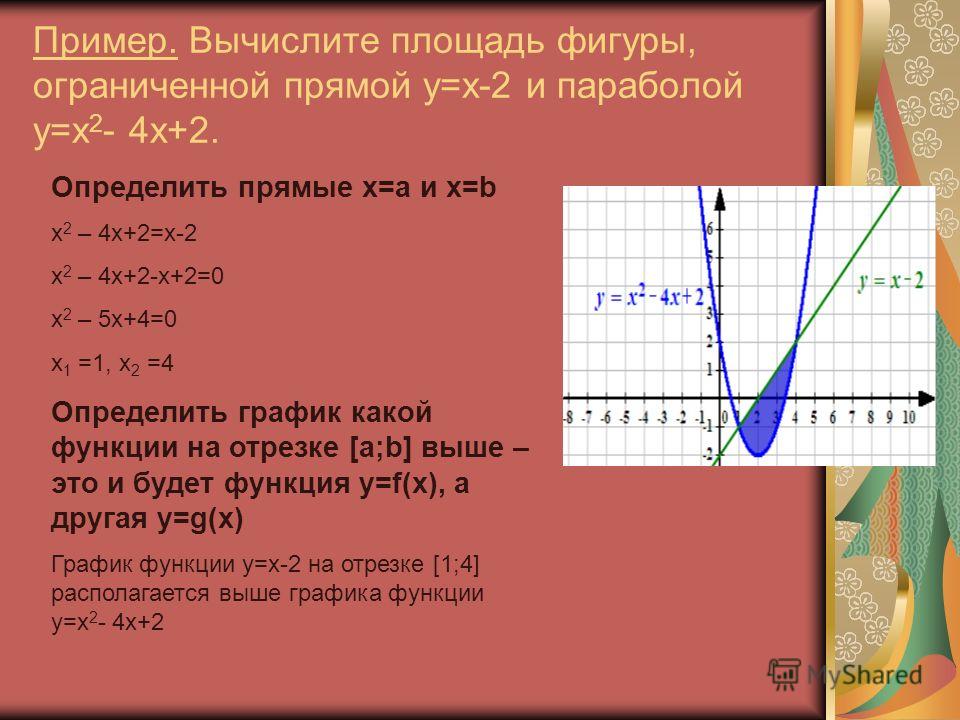
 Второй метод заключается в разделении области на несколько прямоугольников, а затем области складываются для получения необходимой площади. Третий способ – найти площадь с помощью интегрирования.
Второй метод заключается в разделении области на несколько прямоугольников, а затем области складываются для получения необходимой площади. Третий способ – найти площадь с помощью интегрирования.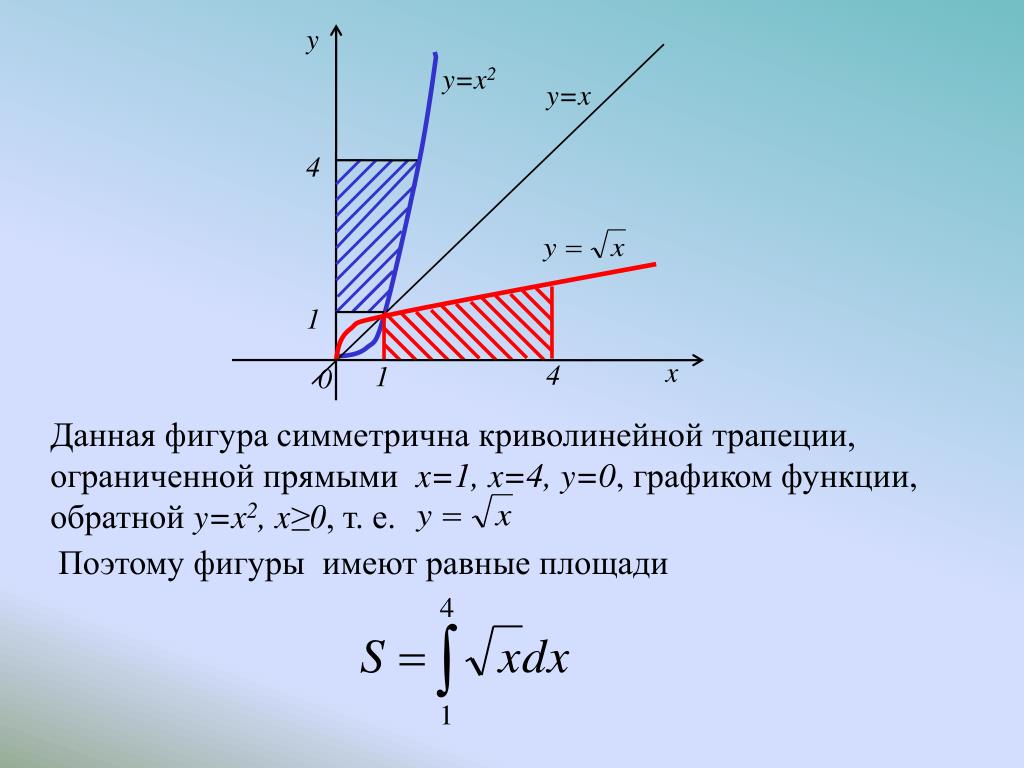
 Другой способ найти приблизительную площадь под кривой — нарисовать набор из нескольких больших прямоугольников, а затем суммировать их площади. Далее мы можем просто найти точную площадь под кривой с помощью определенных интегралов.
Другой способ найти приблизительную площадь под кривой — нарисовать набор из нескольких больших прямоугольников, а затем суммировать их площади. Далее мы можем просто найти точную площадь под кривой с помощью определенных интегралов.
 08.2005
08.2005  Я абсолютно уверен, что вам это тоже будет полезно.
Я абсолютно уверен, что вам это тоже будет полезно. Используйте его только как руководство, чтобы понять и прояснить свои концепции.
Используйте его только как руководство, чтобы понять и прояснить свои концепции. Просто напечатайте задачу из домашней работы и нажмите «Решить» — и пошаговое решение моей домашней работы по алгебре будет готово. Я использовал его на нескольких математических занятиях — алгебре в колледже, базовой математике и базовой математике. Очень рекомендую программу.
Просто напечатайте задачу из домашней работы и нажмите «Решить» — и пошаговое решение моей домашней работы по алгебре будет готово. Я использовал его на нескольких математических занятиях — алгебре в колледже, базовой математике и базовой математике. Очень рекомендую программу.

 Осталось 90 секунд
Осталось 90 секунд Время было выбрано произвольно: художница решила, что в этом положении стрелки выглядят хорошо. Через два года СССР успешно испытал свою ядерную бомбу — часы перевели на 23:57. А в 1953 году стрелку сдвинули еще на минуту ближе к полуночи: США, а вскоре и СССР создали термоядерные бомбы.
Время было выбрано произвольно: художница решила, что в этом положении стрелки выглядят хорошо. Через два года СССР успешно испытал свою ядерную бомбу — часы перевели на 23:57. А в 1953 году стрелку сдвинули еще на минуту ближе к полуночи: США, а вскоре и СССР создали термоядерные бомбы. Тогда среди угроз появилось изменение климата, вызванное деятельностью человечества. По мнению «часовщиков», с 1995 года человечество медленно, но верно движется к полуночи. За это время часы переводили вперед целых восемь раз — и только один раз на минуту назад. Это случилось в 2010 году, после того как США начали переговоры с Россией насчет нового договора о СНВ.
Тогда среди угроз появилось изменение климата, вызванное деятельностью человечества. По мнению «часовщиков», с 1995 года человечество медленно, но верно движется к полуночи. За это время часы переводили вперед целых восемь раз — и только один раз на минуту назад. Это случилось в 2010 году, после того как США начали переговоры с Россией насчет нового договора о СНВ.


 Что до изменения климата, то, судя по всему, добыча ископаемого топлива — ключевого источника нагревающих планету парниковых газов — будет только увеличиваться. Правительствам рекомендовали вспомнить о катастрофических пожарах, тропических циклонах 2020-го и постараться, чтобы выбросы сократились как можно скорее.
Что до изменения климата, то, судя по всему, добыча ископаемого топлива — ключевого источника нагревающих планету парниковых газов — будет только увеличиваться. Правительствам рекомендовали вспомнить о катастрофических пожарах, тропических циклонах 2020-го и постараться, чтобы выбросы сократились как можно скорее.
 Правительство США, их союзники по НАТО и Украина должны использовать все имеющиеся каналы связи. Попытки создать условия для мирных переговоров помогли бы снизить риск дальнейшей эскалации.
Правительство США, их союзники по НАТО и Украина должны использовать все имеющиеся каналы связи. Попытки создать условия для мирных переговоров помогли бы снизить риск дальнейшей эскалации. 
 17
17 [1]
[1] 
 Более распространенные более крупные единицы времени, не относящиеся к системе СИ, не формируются степенями десяти, вместо этого секунда умножается на 60 чтобы сформировать минуту, которая умножается на 60, чтобы сформировать час, который умножается на 24, чтобы сформировать день. Секунда также является базовой единицей времени в других системах измерения: сантиметр–грамм–секунда, метр–килограмм–секунда, метр–тонна–секунда и фут–фунт–секунда.0003
Более распространенные более крупные единицы времени, не относящиеся к системе СИ, не формируются степенями десяти, вместо этого секунда умножается на 60 чтобы сформировать минуту, которая умножается на 60, чтобы сформировать час, который умножается на 24, чтобы сформировать день. Секунда также является базовой единицей времени в других системах измерения: сантиметр–грамм–секунда, метр–килограмм–секунда, метр–тонна–секунда и фут–фунт–секунда.0003




 Cегодня разберёмся, как эти линейные уравнения решать.
Cегодня разберёмся, как эти линейные уравнения решать.



 Научившись справляться с данным видом задач, выпускники смогут рассчитывать на высокие баллы при сдаче ЕГЭ по математике.
Научившись справляться с данным видом задач, выпускники смогут рассчитывать на высокие баллы при сдаче ЕГЭ по математике.




 Выражаем. Из любого уравнения выражаем одну переменную.
Выражаем. Из любого уравнения выражаем одну переменную.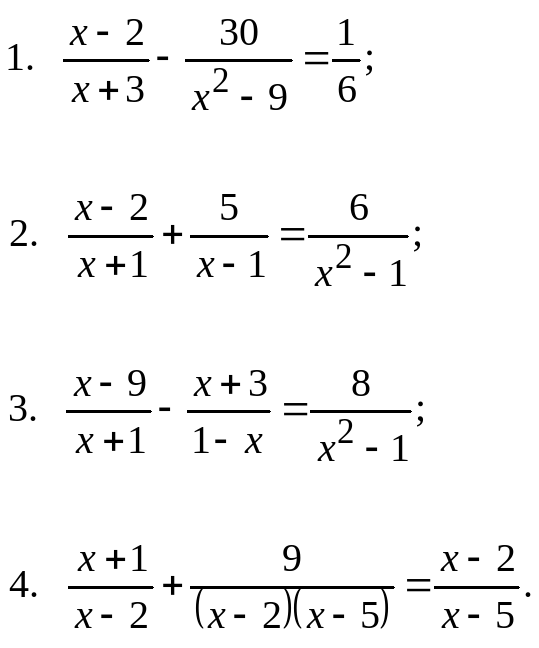
 Первое уравнение домножаем на 2, а второе на 3 и получим общий коэффициент 6.
Первое уравнение домножаем на 2, а второе на 3 и получим общий коэффициент 6. Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.сайт решение уравнений онлайн займет несколько минут. Основное преимущество www.сайт при решении математических уравнений онлайн — это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические уравнения онлайн , тригонометрические уравнения онлайн , трансцендентные уравнения онлайн , а также уравнения с неизвестными параметрами в режиме онлайн . Уравнения служат мощным математическим аппаратом решения практических задач. C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www.сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ.
Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.сайт решение уравнений онлайн займет несколько минут. Основное преимущество www.сайт при решении математических уравнений онлайн — это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические уравнения онлайн , тригонометрические уравнения онлайн , трансцендентные уравнения онлайн , а также уравнения с неизвестными параметрами в режиме онлайн . Уравнения служат мощным математическим аппаратом решения практических задач. C помощью математических уравнений можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины уравнений можно найти, сформулировав задачу на математическом языке в виде уравнений и решить полученную задачу в режиме онлайн на сайте www.сайт. Любое алгебраическое уравнение , тригонометрическое уравнение или уравнения содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами. Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы.
Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения уравнений . При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн . Поэтому для решения математических уравнений онлайн мы рекомендуем сайт www.сайт, который станет вашим незаменимым калькулятором для решения алгебраических уравнений онлайн , тригонометрических уравнений онлайн , а также трансцендентных уравнений онлайн или уравнений с неизвестными параметрами. Для практических задач по нахождению корней различных математических уравнений ресурса www.. Решая уравнения онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение уравнений на сайте www.сайт. Необходимо правильно записать уравнение и моментально получите онлайн решение , после чего останется только сравнить ответ с Вашим решением уравнения. Проверка ответа займет не более минуты, достаточно решить уравнение онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении уравнений онлайн будь то алгебраическое , тригонометрическое , трансцендентное или уравнение с неизвестными параметрами.
Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении уравнений онлайн будь то алгебраическое , тригонометрическое , трансцендентное или уравнение с неизвестными параметрами.
 Для любого значения a ≠ 2/3 значение x равно 2. Когда a = 2/ 3 уравнение становится тождеством, то есть утверждением, истинным для всех значений x.
Для любого значения a ≠ 2/3 значение x равно 2. Когда a = 2/ 3 уравнение становится тождеством, то есть утверждением, истинным для всех значений x.


 Включает рассуждения и прикладные вопросы.
Включает рассуждения и прикладные вопросы.






 Решите \frac{x-3}{7}=2
Решите \frac{x-3}{7}=2