Автор: alexxlab

Таблица значений синуса, косинуса и т.д

Соседние файлы в папке Теория по темам

• #

  12. 05.201515.87 Кб12Среднее арифметическое.doc

• #

  12.05.201518.43 Кб13Средняя линия.doc

• #

  12.05.201522.53 Кб13Степенная функция.doc

• #

  12.05.201528.16 Кб13Степень.doc

• #

  12.05.201524.06 Кб12Сумма разность векторов.doc

• #

  12.05.201530.72 Кб13Таблица значений синуса, косинуса и т.д..doc

• #

  12.05.201519.46 Кб16Теорема Виета.doc

• #

  12.05.201520.48 Кб21Теорема косинусов.doc

• #

  12.05.201520.48 Кб17Трапеция.doc

• #

  12.05.201522.02 Кб14Углы на плоскости.doc

• #

  12.05.201518.43 Кб15Уравнение движения.doc

Таблица синусов и косинусов — онлайн справочник для студентов

Таблица синусов и косинусов

Таблица 1

Используя эту таблицу, вы можете найти стандартное значение синуса или косинуса.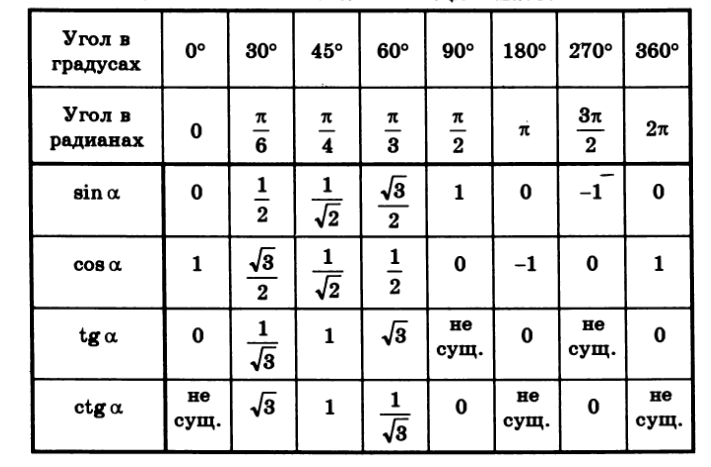 Желаемое значение будет находиться на пересечении столбца, соответствующего данному аргументу (в радианах или градусах), и строке, соответствующей заданной функции.

Примеры решения проблем

ПРИМЕР 1

Использование таблицы значений синуса и косинуса для поиска: и

Найдите значение . В таблице значений синуса и косинуса (таблица 1) во второй строке (где углы находятся в градусах) мы находим значение . Тогда на пересечении столбца, соответствующего , и линия соответствующей синусоиды (рис.1) является искомым значением

Рис. 1

Найдем значение . В таблице 1 в первой строке (где углы указаны в радианах) находим значение . Искомое значение лежит на пересечении столбца соответствующего и строки соответствующей функции косинус (рис. 2), таким образом

Рис. 2.

ПРИМЕР 2

Найти значение выражения:

Используя таблицу значений синусов и косинусов, найдем значения и (рис. 3).

Рис. 3

Подставляя найденные значения в исходное выражение, получим

Физика

166

Реклама и PR

31

Педагогика

80

Психология

72

Социология

7

Астрономия

9

Биология

30

Культурология

86

Экология

8

Право и юриспруденция

36

Политология

13

Экономика

49

Финансы

9

История

16

Философия

8

Информатика

20

Право

35

Информационные технологии

6

Экономическая теория

7

Менеджент

719

Математика

338

Химия

20

Микро- и макроэкономика

1

Медицина

5

Государственное и муниципальное управление

2

География

542

Информационная безопасность

2

Аудит

11

Безопасность жизнедеятельности

3

Архитектура и строительство

1

Банковское дело

1

Рынок ценных бумаг

6

Менеджмент организации

2

Маркетинг

238

Кредит

3

Инвестиции

2

Журналистика

1

Конфликтология

15

Этика

9

Формулы дифференцирования Свойства тригонометрических функций Графики тригонометрических функций Тригонометрические неравенства и их решения Тригонометрические формулы понижения степени

Узнать цену работы

Узнай цену

своей работы

Имя

Принимаю  Политику  конфиденциальности

Подпишись на рассылку, чтобы не пропустить информацию об акциях

Тригонометрическая таблица всех углов в радианах

Вы хотите изучать тригонометрию, но чувствуете себя запутанным с тригонометрической таблицей всех углов ? Ну, мы получили вашу спину здесь, так как мы облегчим ваше понимание.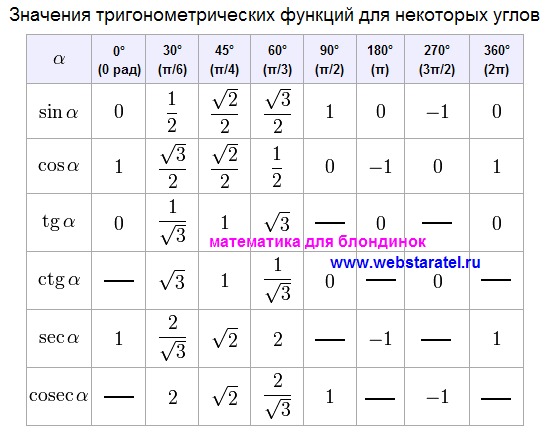 В статье будет объяснено значение таблицы тригонометрии в контексте тригонометрии.

• Формула интегрирования
• Формула тригонометрии
• Тригонометрические соотношения
• Тригонометрические функции с формулами
• Что такое тригонометрические производные
• Высота и расстояние
• Тригонометрическая формула, включающая сумму разностей идентичностей продуктов
• Триггерные идентификаторы
• Теорема Пифагора
• Формула дифференциации
• Основные идентификаторы триггеров

Таблица тригонометрии является неотъемлемой частью тригонометрии, поскольку она содержит всю структуру тригонометрии. Проще говоря, таблица тригонометрии определяет и указывает значение тригонометрических соотношений. Он включает в себя такие соотношения, как синус, косинус, секанс и т. д. Они также известны как функции тригонометрии. Таким образом, с таблицей тригонометрии можно легко узнать значение этих отношений или функций.

Таблица тригонометрии поэтому очень важна, так как без этой таблицы нельзя решать различные задачи тригонометрии. Вы можете обратиться к таблице тригонометрии, чтобы узнать значения различных тригонометрических функций. Таблица также показывает, как тригонометрические функции или отношения остаются связанными друг с другом.

Однако вариация может быть и в том случае, когда вы берете разные тригонометрические соотношения. Основное использование функций тригонометрии заключается в общем измерении прямоугольного треугольника. С помощью правильных формул тригонометрии вы можете определить общую площадь данного треугольника.

Тригонометрическая таблица в радианах

Ну, как мы все знаем, тригонометрические таблицы очень важны в области математики. Однако есть ряд других мест, где эта таблица имеет значение. До появления компьютерных технологий таблицы тригонометрии были очень полезны в области науки, техники и даже навигации. Именно после внедрения современных технологий таблица тригонометрии потеряла свою актуальность.

В настоящее время основное использование этой таблицы ограничивается только математикой. Ученые обычно запоминают таблицы, чтобы легко вводить различные значения в вопрос. У них также есть возможность понять происхождение основ тригонометрических таблиц для их окончательного понимания.

Часто задаваемые вопросы по тригонометрической таблице всех углов в радианах :

Q : Что такое тригонометрическая таблица?

A: Тригонометрическая таблица — это таблица, в которой перечислены значения тригонометрических функций для определенных углов. Эти таблицы используются в математике, естественных науках и технике для упрощения вычислений с использованием углов и треугольников.

Q : Что такое тригонометрические функции?

A: Тригонометрические функции — это шесть математических функций, которые связывают углы прямоугольного треугольника с длинами его сторон.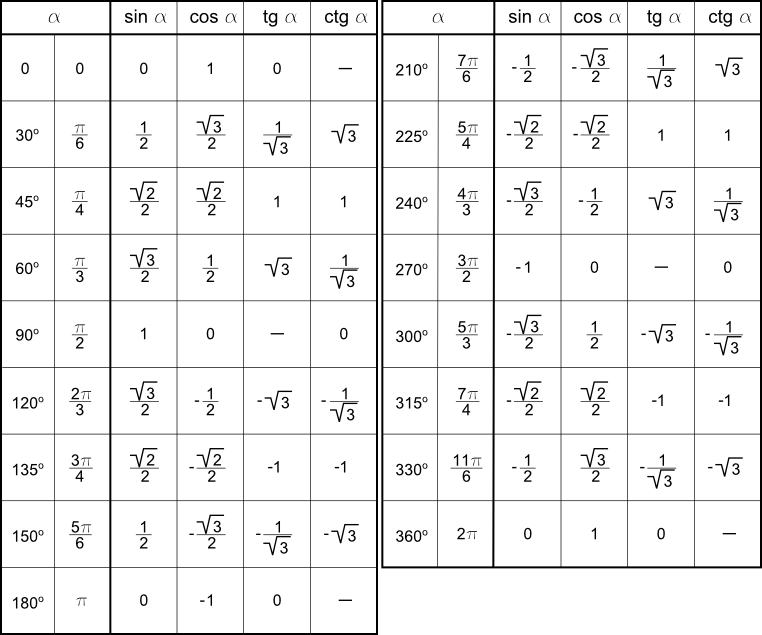 Шесть функций: синус, косинус, тангенс, косеканс, секанс и котангенс.

В: Что такое радианы?

О: Радианы — это единица измерения углов. Один радиан определяется как угол, образуемый в центре окружности дугой, длина которой равна радиусу окружности. Радианы используются в математике и естественных науках, потому что у них есть некоторые свойства, облегчающие работу с ними, чем с другими единицами измерения угла.

Q: Что такое тригонометрическая таблица всех углов в радианах?

A: Тригонометрическая таблица всех углов в радианах — это таблица, в которой перечислены значения шести тригонометрических функций для каждого угла от 0 до 2π радиан (или от 0 до 360 градусов).

В: Зачем мне тригонометрическая таблица?

О: Вы можете использовать тригонометрическую таблицу, если вам нужно выполнить вычисления с использованием углов и тригонометрических функций. Например, если вам нужно найти синус угла, вы можете найти значение синуса для этого угла в таблице, а не вычислять его самостоятельно.

Q: Как читать тригонометрическую таблицу?

О: Чтобы прочитать тригонометрическую таблицу, сначала найдите строку, соответствующую интересующему вас углу. Затем прочитайте строку, чтобы найти значения шести тригонометрических функций для этого угла.

В: Есть ли какие-нибудь хитрости или хитрости для работы с тригонометрической таблицей?

О: Да, есть некоторые хитрости и хитрости, которые можно использовать для облегчения работы с тригонометрической таблицей. Например, вы можете использовать тот факт, что функция синуса является нечетной функцией, а функция косинуса — четной функцией, чтобы быстро найти значения этих функций для определенных углов.

Q: Можно ли использовать калькулятор вместо тригонометрической таблицы?

О: Да, большинство научных калькуляторов имеют встроенные тригонометрические функции, которые можно использовать для быстрого нахождения значений синуса, косинуса, тангенса и других тригонометрических функций для любого угла. Однако в некоторых ситуациях тригонометрическая таблица может быть полезна, например, при работе с историческими или нестандартными единицами измерения углов.

В: Насколько точны тригонометрические таблицы?

О: Тригонометрические таблицы могут быть очень точными, но уровень точности зависит от количества знаков после запятой, используемых в таблице. Большинство таблиц содержат значения, округленные до нескольких знаков после запятой, но если вам нужна большая точность, вам может потребоваться выполнить собственные расчеты, используя более точный метод.

Тригонометрическая таблица — математика GCSE

Введение

Как пользоваться тригонометрической таблицей

Рабочий лист таблицы тригонометрии

Распространенные заблуждения

Практические вопросы по таблице тригонометрии

Таблица тригонометрии GCSE вопросы

Контрольный список обучения

Следующие уроки

После GCSE

Все еще застряли?

Индивидуальные занятия по математике, созданные для успеха KS4

Еженедельные онлайн-уроки повторения математики GCSE теперь доступны

Узнать больше

Введение

Как пользоваться таблицей тригонометрии

Рабочий лист таблицы тригонометрии

Распространенные заблуждения

Практические вопросы по таблице тригонометрии

Таблица тригонометрии GCSE вопросы

Контрольный список обучения

Следующие уроки

После GCSE

Все еще застряли?

Здесь мы узнаем о таблице тригонометрии.

Существуют также тригонометрические таблицы , основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.

Что такое тригонометрическая таблица?

Тригонометрическая таблица представляет собой таблицу точных значений , которые встречаются для конкретного угла для каждой из трех тригонометрических функций – синуса 9{\ круг}.

Используя эти треугольники и тригонометрические отношения синуса, косинуса и тангенса, мы можем заполнить таблицу тригонометрии.

Синус угла \textbf{θ} есть отношение противоположного и гипотенузы . {\ circ}, мы имеем, 9{2}&=3\\\\ x&=\sqrt{3} \end{выровнено}

Пошаговое руководство: Теорема Пифагора

Это означает, что высота прямоугольного треугольника равна квадратному корню из 3 \ см \ (\sqrt{3} \ см). Разметив это на прямоугольном треугольнике, мы получим

. Если бы мы использовали подобных треугольника , длина каждой стороны увеличилась бы или уменьшилась бы на один и тот же масштабный коэффициент , а углов остались бы теми же . Это означает, что даже если бы мы начали с равностороннего треугольника с длиной стороны x, мы смогли бы получить точно такой же треугольник, как и выше, разделив все длины сторон на коэффициент масштабирования. 9{2}&=2\\\\ x&=\sqrt{2} \end{выровнено}

Итак, длина гипотенузы треугольника B равна \sqrt{2} \ cm.

Длины сторон любого подобного треугольника будут увеличены, но углы останутся прежними, поэтому любой треугольник, содержащий эти углы, будет иметь такое же отношение длин сторон. {\circ}. 9{\circ}, O=\sqrt{3} и A=1, имеем \tan(60)=\frac{\sqrt{3}}{1}=\sqrt{3}.

Это означает, что точное тригонометрическое значение \tan(60) равно \sqrt{3}.

Заполнение тригонометрической таблицы этими значениями дает нам

Прежде чем мы перейдем к треугольнику B, давайте быстро рассмотрим некоторые общие значения в таблице.

Мы видим, что в приведенной выше таблице \sin(30)=\frac{1}{2} и \cos(60)=\frac{1}{2}.

Это означает, что \sin(30)=\cos(60). 9{\circ}, O=1 и A=1, имеем \tan(45)=\frac{1}{1}=1.

Это означает, что точное тригонометрическое значение для \tan(45) равно 1.

Заполнение тригонометрической таблицы этими значениями дает нам

Прежде чем мы перейдем к остальным значениям в таблице, давайте кратко рассмотрим их. новые ценности.

Мы видим, что в приведенной выше таблице \sin(45)=\frac{1}{\sqrt{2}} и \cos(45)=\frac{1}{\sqrt{2}}.

Это означает, что \sin(45)=\cos(45).

9{\circ} угол при вершине становится меньше, длина противоположной стороны должна уменьшаться, а гипотенуза должна уменьшаться, так как она стремится к длине соседней стороны. Это имеет разные результаты для каждой тригонометрической функции.

• Поскольку \sin(\theta)=\frac{O}{H} и противоположная сторона становится меньше (стремясь к 0 ), \sin(0) также должна стремиться к 0. Это дает нам значение \ грех(0)=0.
• Так как \cos(\theta)=\frac{A}{H} и гипотенуза стремится к длине прилежащей стороны, \cos(0) должно стремиться к 1, так как мы делим примыкающую сторону на прилежащую сторону. Это дает нам значение \cos(0)=1. 9{\circ} угол внизу увеличивается, длина противоположной стороны должна увеличиваться, а гипотенуза должна увеличиваться, поскольку она стремится к длине противоположной стороны. Это имеет разные результаты для каждой тригонометрической функции.
  • Поскольку \sin(\theta)=\frac{O}{H} и гипотенуза стремится к длине противоположной стороны, \sin(90) также должна стремиться к 1, так как мы разделим противоположную сторону на противоположная сторона. Это дает нам значение \sin(90)=1.
  • Так как \cos(\theta)=\frac{A}{H} и гипотенуза становится длиннее, \cos(0) должно стремиться к 0, так как мы делим смежную сторону на очень большое значение гипотенузы, что делает результат невероятно мал, как если бы он был равен 0. Это дает нам значение \cos(90)=0.
  • Поскольку \tan(\theta)=\frac{O}{A}, а противоположная сторона становится длиннее, \tan(90) не определено, например, когда мы делим очень большое число (противоположное) на относительно небольшое число ( соседние), это может мало повлиять на очень большое число. На самом деле значение может быть бесконечно большим. Это означает, что значение \tan(90) мы используем is undefined (мы не можем присвоить этому значение).

  Заполнив эти три значения в таблицу, мы получим итоговую таблицу тригонометрии.

  Глядя на таблицу, мы теперь можем определить некоторые другие значения, одинаковые для разных тригонометрических функций, в том числе

  • \sin(0)=\cos(90)=\tan(0)=0
  • \sin(90)=\cos(0)=\tan(45)=1

  Как пользоваться таблицей тригонометрии

  Для расчета с использованием точных значений тригонометрии из таблицы тригонометрии:
  

  1. Вызов точного значения триггера из таблицы.
  2. Подставить значения в уравнение/выражение.
  3. Полностью решить уравнение / упростить выражение.

  Объясните, как пользоваться таблицей тригонометрии

  Рабочий лист с точными значениями триггера (включает таблицу тригонометрии)

  Получите бесплатный рабочий лист с таблицей тригонометрических значений, содержащей более 20 вопросов и ответов по точным значениям триггера. Включает рассуждения и прикладные вопросы.

  СКАЧАТЬ БЕСПЛАТНО

  Икс

  Рабочий лист с точными значениями триггера (включает таблицу тригонометрии)

  Получите бесплатную рабочую таблицу тригонометрических значений с более чем 20 вопросами и ответами на точные тригонометрические значения. Включает рассуждения и прикладные вопросы.

  СКАЧАТЬ БЕСПЛАТНО

  Примеры таблиц тригонометрии

  Пример 1: умножение точного значения триггера на целое число

  Вычислите точное значение 4\cos(30).

  1. Вызов точного значения триггера из таблицы.

  Точное значение триггера \cos(30)=\frac{\sqrt{3}}{2}.

  2 Подставить значения в уравнение/выражение.

  Подставив значение \cos 30 в это выражение, мы получим 4\cos(30)=4\times\frac{\sqrt{3}}{2}.

  3 Полностью решить уравнение / упростить выражение.

  4 \ times \ frac {\ sqrt {3}} {2} = \ frac {4 \ sqrt {3}} {2} = 2 \ sqrt {3}

  Пример 2: упрощение выражений с помощью таблицы тригонометрии

  Упростите выражение 2\sin(45)\cos(45)-4\sin(30).

  Вызов точного значения триггера из таблицы.

  Точное значение триггера \sin(45)=\frac{1}{\sqrt{2}}.

  
  Точное значение триггера \cos(45)=\frac{1}{\sqrt{2}}.

  
  Точное значение триггера \sin(30)=\frac{1}{2}.

  Подставить значения в уравнение/выражение.

  Подставляя значение \sin{45}, значение \cos{45} и значение \sin{30} в выражение, мы имеем

  
  2\sin(45)\cos(45)-4\sin(30)=2\times\frac{1}{\sqrt{2}}\times\frac{1}{\sqrt{2} }-4\times\frac{1}{2}.

  Решить уравнение / полностью упростить выражение.

  \begin{выровнено} &2\times\frac{1}{\sqrt{2}}\times\frac{1}{\sqrt{2}}-4\times\frac{1}{2}\\\\ =&2\times\frac{1}{2}-2\\\\ =&1-2\\\\ =&-1 \end{выровнено}

  
  2\sin(45)\cos(45)-4\sin(30)=-1

  Пример 3: деление surd на точное значение триггера

  Вычислить значение \frac{2\sqrt{ 2}}{\cos(45)}.

  Вызов точного значения триггера из таблицы.

  Точное значение триггера \cos(45)=\frac{1}{\sqrt{2}}.

  Подставить значения в уравнение/выражение.

  Подставляя это в выражение, мы имеем

  
  2\sqrt{2}\div\frac{1}{\sqrt{2}}.

  Решить уравнение / полностью упростить выражение.

  \begin{выровнено} &2\sqrt{2}\div\frac{1}{\sqrt{2}}\\\\ =&2\sqrt{2}\times\sqrt{2}\\\\ =&2\times\sqrt{4}\\\\ =&2\раз{2}\\\\ =&4 \конец{выровнено}

  
  Значение \frac{2\sqrt{2}}{\cos(45)}=4.

  Пример 4: расчет с тремя точными значениями триггера

  Вычислите точное значение \sin(30)+\cos(60)-\tan(45).

  Вызов точного значения триггера из таблицы.

  Точное значение триггера \sin(30)=\frac{1}{2}.

  
  Точное значение триггера \cos(60)=\frac{1}{2}.

  
  Точное значение триггера \tan(45)=1.

  Подставить значения в уравнение/выражение. 9{2}\\\\ 3y&=3\\\\ y&=1 \end{aligned}

  Пример 6: решение уравнений с точными значениями триггера

  Учитывая, что x=\sin(45) и y=\cos( 45), определите значение \theta уравнения \tan(\theta)=\frac{x}{y}.

  Вызов точного значения триггера из таблицы.

  Точное значение триггера \sin(45)=\frac{1}{\sqrt{2}}.

  
  Точное значение триггера \cos(45)=\frac{1}{\sqrt{2}}.

  Подставить значения в уравнение/выражение. 9{\circ}).

  Распространенные заблуждения

  • Точные значения

  Если вас спросят о точном значении, вы должны оставить свой ответ в грубой форме.

  Нет необходимости записывать свой ответ в виде десятичной дроби и округлять. Это уже не будет точным значением.

  • Использование точных значений

  Если вам дали ответ, вы должны четко указать, что вы использовали точное значение триггера в своей работе. 9{\circ}

  3+\sqrt{3}

  3+\frac{2}{\sqrt{3}}

  2\sin(30)=2\times\frac{1}{2}=1.

   

  3\tan(45)=3\times{1}=3.

   

  1+3=4.

  \frac{1}{3}

  \frac{1}{2}

  0,95\text{(2dp)}

  \cos(30)=\frac{\sqrt{3}}{2}

   

  9{\ круг}. Его эскиз нарисован ниже.

   

  (a) Укажите ошибку, которую допустил Джеймс в своем наброске.

   

   

  (b) Вычислите фактическую площадь треугольника, который Джеймс должен был нарисовать.

   

  (3 балла)

  Показать ответ

  (a)

   

  Любое из следующего.

  Он ошибочно назвал гипотенузу перпендикулярной высотой.

  Высота перпендикуляра больше гипотенузы (\sqrt{2} и 1). 9{\circ}

 

 

Определить длину прямой AE = x \ см.

 

(5 баллов)

Показать ответ

\tan(60)=\sqrt{3}

(1)

AE = 0,5 \ раз \ sqrt {3} = \ frac {\ sqrt {3}} {2}

(1)

Масштабный коэффициент 1\дел 0,5=2 .

(1)

х = AD = 2 \ раз \ гидроразрыва {\ sqrt {3}} {2}

(1) 9{\circ}

Beyond GCSE

Другие тригонометрические функции, охватываемые на уровне A, включают,

• Секанс
  Функция секанса (сек) равна 1, деленной на косинус угла.

Возведение в степень онлайн ⋆ Компьютерные технологии

Предлагаемый нами бесплатный калькулятор включает такую нужную для многих функцию, как калькулятор степеней. С его помощью выполнить возведение числа в степень проще простого, задайте выражение — получите результат. Калькулятор производит возведение в степень онлайн, как и любые другие функции, прямо на нашем сайте.

Как возвести число в степень в калькуляторе?

Возведение в степень — это действие умножения числа самого на себя n раз, где число x^y — степень, x — основание степени, y=n — показатель степени. Чтобы возвести в степень на калькуляторе, используйте соответствующие кнопки на панели управления. Если вам нужна более подробная информация по работе с цифровой панелью калькулятора, перейдите на страницу кнопки онлайн калькулятора.

Функция возведения в степень в калькуляторе представлена пятью кнопками: возведение в квадрат, возведение в куб, возведение в n степень произвольного числа, возведение в степень основания равного 10-ти и возведение в степень экспоненты. (), т.е. основанием степени записывается число 10. Удобно применять, когда нужно написать возведение в какую-нибудь степень именно числа 10.

Пример, как найти степень числа 10:

Экспонента в степени

Нажав на кнопку, увидите в строке запись exp(). Чтобы посчитать число е в степени, нужно возвести число Эйлера в степень e^x = exp(x). Кому интересно знать, чему равно число е: его значение 2.71828182845905.

Пример, как возвести е в степень:

Возведение в дробную степень

Допустим, нас интересует дробная степень числа x^y1/y2. Так как возведение в степень — действие, обратное к извлечению корня, расчёт сводится к нахождению корня степени y2 из числа x в степени y1. Если значение y2 чётное, то дробную степень можно вычислить только при положительном основании, так как корень отрицательного числа не существует и калькулятор в подобной ситуации выдаст вам ошибку!

При возведении в дробную степень не забывайте закрывать основание в скобки, иначе знаменатель дроби в показателе степени уйдет в знаменатель основания!

Этот пример показывает, как возвести в дробную степень на калькуляторе:

Наш онлайн калькулятор позволяет возвести как в положительную, так и в отрицательную степень. При отрицательном значении показателя, основание должно принять вид (1/x), другими словами, числитель и знаменатель основания степени должны поменяться местами и только после этого можно начинать возведение. Калькулятор позволяет возвести число в отрицательную степень автоматически, опуская все промежуточные преобразования и выдавая сразу окончательный ответ.

При возведении в отрицательную степень всевозможных функций, в том числе тригонометрических, онлайн калькулятор автоматически учитывает их четность/нечетность по правилу знаков.

Этот пример показывает, как возвести в отрицательную степень на калькуляторе:

Дробное число в степени калькулятор тоже рассчитает.

Возведение дроби в степень с помощью калькулятора:

В калькуляторе можно рассчитать и корень в степени.

Возведение корня в степень с помощью калькулятора:

Все функции нашего бесплатного калькулятора собраны в одном разделе. Функции онлайн калькулятора >>

0 1 в степени 10

0 1 в степени 10

Вы искали 0 1 в степени 10? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 0 10 равно, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «0 1 в степени 10».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как 0 1 в степени 10,0 10 равно,0 2 в степени 2,0 2 в степени 3,0 2 в степени 4,0 25 в 5 степени,0 25 в степени 5,0 4 в 10 степени,0 4 в минус 4 степени,0 5 в степени 4,0 5 в степени 6,0 5 в степени 7,0 5 в степени 8,0 5 в степени минус 1,0 5 в степени минус 2,0 6 в минус 2 степени,0 7 в степени,0 в 7 степени,0 в степени 3 2,0 в степени 4,0 в степени 6,0 в степени 7,0 в степени 8,0 умножить на 2 в 0 степени,1 10 в степени 2,1 125 в степени,1 16 в степени,1 2 в 16 степени,1 2 в 8 степени,1 2 в минус 5 степени,1 2 в степени 10,1 2 в степени 6,1 2 в степени минус 3,1 3 в 8 степени,1 3 в 9 степени,1 3 в степени 2,1 3 в степени 5,1 4 в степени 3,1 4 в степени x,1 5 в минус 2 степени,1 5 в минус 3 степени,1 5 в степени 1 x,1 5 в степени 3,1 6 в степени 2,1 7 в степени 2,1 8 в минус 3 степени,1 8 в степени,1 8 в степени 2,1 x в 5 степени,1 x в степени 3,1 x в степени 4,1 в минус 16 степени,1 в минус 3 степени,1 в минус 5 степени,1 в минус 6 степени,1 в минус 7 степени,1 в минус 8 степени,1 в степени 0 4,1 в степени 0 6,1 в степени 12,1 в степени 16,1 в степени 2 3,1 в степени 2 равно,1 в степени 3 2,1 в степени 4 равно,1 в степени 7 3 в,1 в степени 8,1 в степени минус 3,1 в степени минус 8,1 умножить на 10 в 1 степени,1 умножить на 2 в 1 степени,1 умножить на 2 в степени 1,1 умножить на 2 в степени 2,1 х в минус 1 степени,10 в 0 4 степени,10 в 10 равно,10 в 10 степени в квадрате,10 в минус 10 степени в квадрате,10 в минус 5 степени умножить на 3,10 в степени 0 4,10 в степени 2 5,10 в степени 3 равно,10 в степени 4 3,10 в степени x 10,10 в степени минус 23,10 умножить на 10 в 4 степени,10 умножить на 10 в минус третьей степени,11 в степени 4,12 в степени 0,12 в степени 3,12 в степени 4,12 в степени 6,125 в 1 степени,125 в степени 3,13 в степени 5,15 в степени 8,16 в 0 5 степени,16 в 3 4 степени,16 в минус 2 степени,16 в степени 0,16 в степени 1,16 в степени 1 2,16 в степени 5,16 в степени 8,16 в степени минус 1,17 в 4 степени,17 в 5 степени,17 в степени 3,17 в степени 5,2 10 в степени 4,2 10 в степени 5,2 7 в минус 2 степени,2 в 0 25 степени,2 в 0 4 степени,2 в 0 8 степени,2 в 34 степени,2 в 48 степени,2 в 80 степени,2 в минус 0 5 степени,2 в минус 16 степени,2 в минус 2 степени умножить на 1,2 в степени 0 3,2 в степени 0 6,2 в степени 0 8,2 в степени 1 10,2 в степени 1 3,2 в степени 1 8,2 в степени 2 решение,2 в степени 27,2 в степени 3 2,2 в степени 34,2 в степени 36,2 в степени 37,2 в степени 38,2 в степени 4 3,2 в степени 4 5,2 в степени 42,2 в степени 47,2 в степени 49,2 в степени 5 4,2 в степени 80,2 в степени минус 0 5,2 в степени минус 16,2 умножить на 10 в 5 степени,2 умножить на 10 в степени 3,2 умножить на 10 в степени минус 2,2 умножить на 2 в минус 3 степени,2 умножить на 2 в степени,20 в степени 0 5,20 в степени 4,21 в степени 3,24 в 3 степени,24 в 4 степени,24 в степени 3,24 в степени 4,25 в степени 0 2,25 в степени 2,25 в степени 3,25 в степени 3 2,25 в степени 4,25 в степени 5,26 в 26 степени,27 в 3 степени,27 в степени 3,28 в степени 3,3 10 в минус 5 степени,3 10 в степени 5,3 в 0 8 степени,3 в 27 степени,3 в 3 степени калькулятор,3 в 3 степени равно,3 в 36 степени,3 в 5 степени равно,3 в 5 степени умножить на 3,3 в минус 5 степени умножить на 3,3 в минус 6 степени,3 в степени 0,3 в степени 0 2,3 в степени 1 4,3 в степени 1 9,3 в степени 1000,3 в степени 12,3 в степени 16,3 в степени 2 7,3 в степени 24,3 в степени 27,3 в степени 3 и в степени 2,3 в степени 36,3 в степени 4,3 в степени 4 5,3 в степени 4 равно,3 в степени 40,3 в степени 5,3 в степени 5 4,3 в степени 5 равно,3 в степени 6,3 в степени 6 5,3 в степени x умножить на 3 в степени x,3 в степени минус 1 2,3 в степени минус 6,3 в степени х 2 в степени у,3 умножить 10 в 3 степени,3 умножить на 10 в 2 степени,3 умножить на 10 в 5 степени,3 умножить на 10 в минус 5,3 умножить на 10 в минус 5 степени,3 умножить на 4 в степени 3,3 х в 5 степени,33 в степени 2,34 в степени 2,36 в 3 степени,36 в степени 2,36 в степени 3,36 в степени 5,4 в 17 степени,4 в 20 степени,4 в 24 степени,4 в 3 степени равно,4 в минус 6 степени,4 в минус 7 степени,4 в минус 9 степени,4 в степени 0,4 в степени 0 1,4 в степени 0 2,4 в степени 0 3,4 в степени 1 25,4 в степени 1 3,4 в степени 1 4,4 в степени 1 равно,4 в степени 12,4 в степени 17,4 в степени 2 3,4 в степени 20,4 в степени 24,4 в степени 25,4 в степени 3 5,4 в степени 3 вычислить,4 в степени 5 2,4 в степени 6,4 в степени минус 1 2,4 в степени минус 5,4 в степени минус 6,4 в степени минус 7,40 в степени 3,49 в степени 2,5 1 равно,5 2 в минус 1 степени,5 в 0 25 степени,5 в 0 9 степени,5 в 100 степени,5 в 17 степени,5 в 3 степени равно,5 в 32 степени,5 в 36 степени,5 в минус 4 степени,5 в минус 5 степени равно,5 в степени 0 2,5 в степени 0 25,5 в степени 0 4,5 в степени 0 6,5 в степени 1 3,5 в степени 1 равно,5 в степени 1 х,5 в степени 100,5 в степени 17,5 в степени 2 3,5 в степени 2 9,5 в степени 2 умножить на 5,5 в степени 25,5 в степени 2x 5,5 в степени 3 2,5 в степени 3 4,5 в степени 3 8,5 в степени 3 равно,5 в степени 36,5 в степени равно 3,5 в степени равно минус 5,5 умножить на 10 в 2 степени,5 умножить на 10 в 3 степени,5 умножить на 10 в минус 3,56 в степени 10,6 в минус 3 степени,6 в минус 4 степени,6 в степени 0,6 в степени 0 5,6 в степени 12,6 в степени минус 3,6 в степени минус 3 степени,6 умножить на 8 в степени минус одна третья,63 в степени 6,7 в минус 3 степени,7 в минус 4 степени,7 в степени 0,7 в степени 0 5,7 в степени 1 2,7 в степени 1 3,7 в степени 1 4,7 в степени 5,7 в степени 6 4,8 в 0 3 степени,8 в 1 4 степени,8 в степени 0,8 в степени 0 3,8 в степени 1 2,8 в степени 2 3,8 в степени 4 3,8 в степени x 4 в степени x,8 в степени минус 1 3,9 10 в минус 10 степени,9 в 0 степени,9 в степени 0,9 в степени 1 3,9 в степени 2 3,9 в степени 2 5,9 в степени 3 2,9 в степени 4 9,9 в степени минус 4,9 умножить на 10 в 9 степени,e в степени калькулятор онлайн,x в 3 степени минус x в 3 степени,x в степени 1 5,x в степени 2,x в степени 3 2,а 3 а 4 в степени,а в 3 умножить на а в 3 степени,а в степени 3 умножить на а в степени 3,в 0 8 степени,в степени 0 4,в степени 1 3,в степени калькулятор,в степени онлайн калькулятор,в степень возводить онлайн,в степень калькулятор онлайн,в степень онлайн,в степень онлайн калькулятор,в степенях калькулятор,возведение в дробную степень калькулятор онлайн,возведение в дробную степень онлайн,возведение в дробную степень онлайн калькулятор,возведение в дробную степень числа онлайн,возведение в квадрат калькулятор,возведение в квадрат онлайн,возведение в куб онлайн,возведение в отрицательную степень калькулятор,возведение в отрицательную степень онлайн,возведение в степень в калькуляторе,возведение в степень выражения онлайн,возведение в степень дробную онлайн калькулятор,возведение в степень калькулятор,возведение в степень на калькуляторе,возведение в степень онлайн,возведение в степень онлайн выражения,возведение в степень онлайн калькулятор,возведение в степень чисел онлайн,возведение в степень числа онлайн,возведение в числа в степень онлайн калькулятор,возведение выражения в степень онлайн,возведение многочлена в степень онлайн,возведение степени в степень онлайн,возведение степень числа в степень онлайн калькулятор,возведение числа в дробную степень онлайн,возведение числа в степень онлайн,возведение числа в степень онлайн калькулятор,возведите в степень,возвести в,возвести в дробную степень онлайн,возвести в квадрат онлайн,возвести в квадрат онлайн калькулятор,возвести в степень,возвести в степень в калькуляторе,возвести в степень е онлайн,возвести в степень калькулятор,возвести в степень на калькуляторе,возвести в степень онлайн,возвести в степень онлайн дробную,возвести в степень онлайн калькулятор,возвести в степень онлайн калькулятор с решением,возвести в степень с,возвести в степень число,возвести в степень число онлайн,возвести дробь в степень онлайн калькулятор,возвести е в степень онлайн,возвести число в дробную степень онлайн,возвести число в степень,возвести число в степень калькулятор,возвести число в степень онлайн,возвести число в степень онлайн калькулятор,возводить в степень онлайн,вычисление онлайн степеней,вычисление степеней онлайн,вычисление степени,вычисление степени онлайн,вычислите 2 10 в 3 степени,вычислить 2 3 в 3 степени,вычислить 4 в 3 степени,вычислить е в степени онлайн,вычислить степень онлайн,действия со степенями калькулятор,дробная степень калькулятор,дробная степень числа калькулятор,дробные степени калькулятор,е в степени калькулятор онлайн,е в степени онлайн,е возвести в степень онлайн,икс в степени 2 3,как в калькуляторе возвести в отрицательную степень,как в калькуляторе возвести в степень,как в калькуляторе возвести в степень на компьютере,как в калькуляторе возводить в степень,как в калькуляторе на компьютере возвести в степень,как возвести в отрицательную степень на калькуляторе,как возвести в степень на калькуляторе,как возвести в степень на калькуляторе в компьютере,как возвести в степень на калькуляторе на компьютере,как возвести в степень на калькуляторе обычном,как возвести в степень на обычном калькуляторе,как возвести в степень число на калькуляторе,как возвести число в дробную степень онлайн калькулятор,как возвести число в степень на калькуляторе,как возводить в степень в калькуляторе,как возводить в степень на калькуляторе,как на калькуляторе возвести в отрицательную степень,как на калькуляторе возвести в степень,как на калькуляторе возвести число в степень,как на калькуляторе возводить в степень,как на калькуляторе на компьютере возвести в степень,как на калькуляторе посчитать степень,как на калькуляторе считать степени,как на калькуляторе число возвести в степень,как перевести в степень число,как перевести число в степень,как посчитать 3 в 3 степени,как посчитать на калькуляторе степень,как посчитать на калькуляторе степень числа,как посчитать степень на калькуляторе,как посчитать степень числа на калькуляторе,как считать на калькуляторе степени,как считать степени на калькуляторе,как число возвести в степень на калькуляторе,как число перевести в степень,как число посчитать в степени,калькулятор n степени,калькулятор в степени,калькулятор в степени онлайн,калькулятор в степень онлайн,калькулятор в степенях,калькулятор возведение в дробную степень онлайн,калькулятор возведение в отрицательную степень,калькулятор возведение в степень,калькулятор возведения в степень,калькулятор возведения в степень онлайн,калькулятор возвести в степень,калькулятор возвести в степень онлайн,калькулятор возвести число в степень,калькулятор возвести число в степень онлайн калькулятор,калькулятор вычисления степеней,калькулятор действия со степенями,калькулятор для возведения числа в степень,калькулятор для вычисления степеней,калькулятор для степеней,калькулятор для степеней онлайн,калькулятор дробная степень,калькулятор дробные степени,калькулятор дробных степеней,калькулятор дробных степеней онлайн,калькулятор математический со степенями,калькулятор н степени онлайн,калькулятор онлайн в степени,калькулятор онлайн в степень,калькулятор онлайн возведение в дробную степень,калькулятор онлайн возвести число в степень онлайн,калькулятор онлайн для степеней,калькулятор онлайн дробных степеней,калькулятор онлайн примеры со степенями,калькулятор онлайн решение со степенями,калькулятор онлайн с возведением в степень,калькулятор онлайн с дробными степенями,калькулятор онлайн с отрицательными степенями,калькулятор онлайн с степенями,калькулятор онлайн со степенью,калькулятор онлайн со степенями,калькулятор онлайн степеней,калькулятор онлайн степеней дробных,калькулятор онлайн степеней онлайн с решением,калькулятор онлайн степени,калькулятор онлайн степень,калькулятор онлайн степень с рациональным показателем,калькулятор онлайн степень числа,калькулятор онлайн умножение степеней,калькулятор онлайн чисел со степенями,калькулятор отрицательная степень,калькулятор отрицательных степеней,калькулятор примеров со степенями,калькулятор с возведением в степень,калькулятор с возведением в степень онлайн,калькулятор с дробными степенями,калькулятор с дробными степенями онлайн,калькулятор с калькулятор со степенями,калькулятор с отрицательными степенями,калькулятор с отрицательными степенями онлайн,калькулятор с решением степеней,калькулятор с степенями,калькулятор с степенями онлайн,калькулятор с степенями отрицательными,калькулятор со степенью,калькулятор со степенью онлайн,калькулятор со степенями,калькулятор со степенями онлайн,калькулятор степей,калькулятор степеней,калькулятор степеней онлайн,калькулятор степеней онлайн с дробями,калькулятор степеней онлайн с решением,калькулятор степеней онлайн с решением и дробями,калькулятор степеней онлайн с решением с буквами,калькулятор степеней с рациональным показателем,калькулятор степеней с рациональным показателем онлайн,калькулятор степеней с решением,калькулятор степеней с целым показателем,калькулятор степеней умножение,калькулятор степеней умножение степеней,калькулятор степени,калькулятор степени n,калькулятор степени онлайн,калькулятор степени с рациональным показателем,калькулятор степени чисел,калькулятор степени числа,калькулятор степенів,калькулятор степенной,калькулятор степень,калькулятор степень дробная,калькулятор степень с рациональным показателем,калькулятор степень с рациональным показателем онлайн,калькулятор степень с целым показателем,калькулятор степень числа,калькулятор степень числа онлайн,калькулятор умножение со степенями,калькулятор умножение степеней,калькулятор умножение степеней онлайн,калькулятор чисел со степенями,калькулятор чисел со степенями онлайн,калькулятор чисел со степенями онлайн калькулятор,калькулятор числа в степени,калькулятор число в дробной степени,калькулятор число в степени,калькулятор число возвести в степень,калькулятор число е в степени,математический калькулятор со степенями,минус 1 в 3 степени,минус 1 в минус 8 степени,минус 10 минус 12 степени,минус 3 в 6 степени,минус 4 в 6 степени,минус 5 в 4 степени,минус 6 в 3 степени,минус 6 в 4 степени,минус 8 в 3 степени,на калькуляторе степень,найти значение выражения с степенями онлайн калькулятор с решением,найти степень числа онлайн,один в степени минус два,онлайн в куб возведение,онлайн в степень,онлайн возведение в куб,онлайн возведение в степень,онлайн возведение в степень выражения,онлайн возведение числа в степень,онлайн возвести число в степень,онлайн возводить в степень,онлайн вычисление степеней,онлайн вычисление степени,онлайн калькулятор в степени,онлайн калькулятор возведение в дробную степень,онлайн калькулятор возведение в степень,онлайн калькулятор возведения в степень,онлайн калькулятор возвести число в степень онлайн,онлайн калькулятор для степеней,онлайн калькулятор дробных степеней,онлайн калькулятор е в степени,онлайн калькулятор примеры со степенями,онлайн калькулятор решение со степенями,онлайн калькулятор с возведением в степень,онлайн калькулятор с отрицательными степенями,онлайн калькулятор с степенями,онлайн калькулятор со степенью,онлайн калькулятор со степенями,онлайн калькулятор степеней,онлайн калькулятор степеней с рациональным показателем,онлайн калькулятор степеней с решением,онлайн калькулятор степени,онлайн калькулятор степень,онлайн калькулятор степень с рациональным показателем,онлайн калькулятор степень числа,онлайн калькулятор умножение степеней,онлайн калькулятор чисел со степенями,онлайн перевести в степень,онлайн перевод в степень,онлайн перевод степеней,онлайн решение степеней,онлайн решение степени,онлайн решить пример со степенями,онлайн степени,онлайн степенной калькулятор,онлайн степень,онлайн степень числа,онлайн умножение степеней,онлайн число в степени,отрицательная степень калькулятор,перевести в степень онлайн,перевод в степень,перевод в степень калькулятор,перевод в степень онлайн,перевод из степени в число онлайн,перевод степеней онлайн,посчитать степени,посчитать степень,посчитать степень онлайн,посчитать число в степени,посчитать число в степени онлайн,примеры со степенями калькулятор онлайн,примеры со степенями онлайн калькулятор,расчет степени,решение онлайн калькулятор со степенями,решение онлайн степеней,решение онлайн степени,решение со степенями онлайн калькулятор,решение степеней онлайн,решение степеней онлайн калькулятор,решение степени онлайн,решить онлайн пример со степенями,решить пример со степенями онлайн,решить пример со степенями онлайн калькулятор с решением,с калькулятор с возведением в степень,сложение степеней калькулятор,сравнение чисел онлайн со степенями,сравнение чисел со степенями онлайн,степеней с рациональным показателем калькулятор,степени в калькулятор,степени калькулятор,степени онлайн,степени онлайн калькулятор,степени онлайн решение,степени посчитать,степени расчет,степени решение онлайн,степени считать онлайн,степени чисел калькулятор,степенной калькулятор,степенной калькулятор онлайн,степень 4 3,степень вычислить,степень вычислить онлайн,степень дробная онлайн,степень калькулятор,степень калькулятор онлайн,степень на калькуляторе,степень найти числа,степень онлайн,степень онлайн калькулятор,степень перевести в число,степень посчитать,степень рассчитать,степень с рациональным показателем калькулятор,степень с рациональным показателем калькулятор онлайн,степень с рациональным показателем онлайн калькулятор,степень с целым показателем калькулятор,степень числа калькулятор онлайн,степень числа онлайн,степень числа онлайн калькулятор,считать онлайн степени,считать степени онлайн,умножение онлайн степеней,умножение со степенями калькулятор,умножение степеней калькулятор,умножение степеней калькулятор онлайн,умножение степеней онлайн,умножение степеней онлайн калькулятор,х в 5 степени,х в 5 степени 1,х в 6 степени в 3 степени,х в степени 1 4,х в степени 1 5,х в степени 2,х в степени 3 5,х в степени 3 минус х,числа в степени калькулятор,число в дробной степени калькулятор,число в отрицательной степени калькулятор,число в степени калькулятор,число в степени калькулятор онлайн,число в степени онлайн,число в степени онлайн калькулятор,число в степени посчитать,число в степени посчитать онлайн,число в степень онлайн,число возвести в дробную степень онлайн,число возвести в квадрат онлайн,число возвести в степень,число возвести в степень калькулятор,число возвести в степень онлайн,число перевести в степень. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и 0 1 в степени 10. Просто введите задачу в окошко и нажмите «решить» здесь (например, 0 2 в степени 2).

Решить задачу 0 1 в степени 10 вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Калькулятор экспоненты

— Найдите число (основание), возведенное в степень

Онлайн-калькулятор экспоненты поможет вам решить операции с экспонентой и определить значение любого положительного или отрицательного целого числа, возведенного в энную степень. Кроме того, этот экспоненциальный калькулятор показывает результаты дробной или отрицательной степени любого числа. Здесь мы предоставляем вам все связанные данные экспоненты, ручных расчетов, правил возведения в степень и многое другое. Давайте посмотрим на некоторые основы!

Читайте дальше! 94\), 7 — основание, 4 — показатель степени. В этом примере 4 копии числа 7 перемножаются, чтобы получить 2401 как 7*7*7*7.

Очень легко выполнять вычисления с небольшими значениями, но для больших и десятичных оснований или для отрицательных или дробей, больших степеней, используйте наш калькулятор степени дроби.

Основные правила:

Есть несколько основных правил возведения в степень с их примерами. Давайте посмотрим на правила и примеры:

9x}}\)

Этот лучший и бесплатный калькулятор отрицательной степени учитывает эти свойства степени и точно вычисляет степень любого целого числа. Кроме того, вы можете попробовать наш онлайн-калькулятор журнала и антилогарифма, который является обратной функцией экспоненты.

Как вычислить степень для любого целого числа (шаг за шагом):

Вычисления мощности становятся проще с помощью этого калькулятора мощности, который помогает выполнять вычисления для всех целых чисел (отрицательных, положительных, дробей). Впереди ручной пример: 97= 2187\)

Кроме того, если у вас есть отрицательные или дробные основания или степени, попробуйте наш онлайн-калькулятор отрицательной степени, который поможет вам определить быстрые результаты отрицательных или дробных входных данных.

Как использовать онлайн-калькулятор показателей степени:

Просто следуйте приведенным шагам для получения точных результатов.

Проведите пальцем по экрану!

Ввод:

• Прежде всего, введите базовое значение.
• Затем введите степень, во сколько раз основание умножается само на себя.
• Наконец, нажмите кнопку расчета.

Выходы:

Теперь средство поиска степени показывает:

• Значение ваших входных данных.
• Пошаговые расчеты.

End-Note:

Теперь вычисление показателей степени как для отрицательных, так и для положительных целых чисел стало очень простым с помощью этого бесплатного онлайн-калькулятора степени. Этот инструмент лучше всего подходит как для студентов, так и для профессионалов, просто используйте его для решения связанных с этим проблем.

Здесь мы предлагаем вам таблицу некоторых распространенных значений целых чисел с их степенями:

0,1 в степени 3 0,00100 0,1 в степени 4 0,0001 0,2 в степени 3 0,008 0,5 в степени 3 0,12500 0,5 в степени 4 0,06250 0,5 в степени 3 0,125 1,2 в степени 4 2. 07360 1,02 в 10-й степени 1.21899 1,03 в 10-й степени 1.34392 1,2 в степени 5 2,48832 1,3 в степени 5 3,71293 1,3 в степени 3 2,197 1,4 в 10 степени 28.92547 1,05 в степени 5 1,27628 1,05 в степени 3 1.157625 1,05 в 10-й степени 1,62889 1,06 в 10-й степени 1.79085 2 в степени 3 8 2 в степени 4 16 2 в степени 5 32 2 в степени 6 64 2 в степени 7 128 2 в 9 степени 512 2 в десятой степени 1024 2 в 15 степени 32768 2 в 10-й степени 1024 2 в степени 28 268435456 3 в степени 2 9 3 в 3 степени 27 3 в 4 мощности 81 3 в степени 5 243 3 в 8 степени 6561 3 в 9 степени 19683 3 в 12 степени 531441 3 в какой степени равно 81 3 4 4 в степени 3 64 4 в степени 4 256 4,3 в степени 5 1470. 08443 4 в степени 7 16384 7 в степени 3 343 12 во второй степени 144 2,5 в степени 3 15,625 2,19 в степени 5 50.3756397099 12 в степени 3 1728 10 показатель степени 3 1000 24 во второй степени (24 2 ) 576

 

Ссылки:

Из источника Википедии: Определение и правила возведения в степень

С сайта Sciencing.com : Как найти вручную.

Другие языки: Kalkulator Potęg, Kalkulator Eksponen, Üslü Sayı Hesaplama, Potenzrechnung, 指数計算, 지수 계산기, Mocniny Kalkulačka, Calculadora De Potencia, Calcul Puissance, Calculadora De Potencias, Kalculadora De Potensias, Kalculo Lapotenza, Калькулятор кулятор.

Power Mod Calculator

Здесь мы рассмотрим несколько примеров выполнения возведения в степень по модулю вручную с использованием различных методов.

Пример 1. Прямой метод

Рассчитаем 5⁴ mod 3 .

Мы знаем, что 5⁴ = 625 , поэтому наша задача на самом деле 625 mod 3 .

Ясно, что 625 — это , а не делится на 3 , а 624 (это потому, что сумма его цифр равна 6+2+4 = 12

0 1 0 9009 на 0 делится на 0) .

Итак, 625 — 1 делится на 3 , что означает, что 5⁴ по модулю 3 = 625 по модулю 3 = 1 .

Пример 2. Интеллектуальный метод

Рассчитаем 5⁴⁴ mod 2 .

Будет очень сложно вычислить 5⁴⁴ , потому что это число очень, очень большое. Итак, мы должны быть умными. Напомним, что по модулю 2 означает, что мы спрашиваем, четное это число или нечетное: если оно четное, то оно равно 0 по модулю 2 . Если нечетное, то равно 1 mod 2 .

Когда мы вычисляем последовательные степени 5 , мы получаем 5, 25, 625,… . Как видите, у нас всегда 5 в качестве последней цифры. Действительно, если у вас есть число, последняя цифра которого равна 5 , и вы умножаете это число на 5 , то вы обязательно получите 5 на последнем месте снова. Чтобы увидеть это, представьте, что вы выполняете алгоритм длинного умножения — вы начинаете с умножения 5 × 5 и таким образом получаете 25 . Итак, 5 попадает в строку результата, а 2 переносится в следующий столбец. Что бы ни случилось дальше, у тебя есть 5 в качестве последней цифры.

Число, в котором последней цифрой является 5 , является нечетным. Итак, 5⁴⁴ мод 2 = 1 .

Пример 3.

Расчет потока и сальдо реальных денег «ПРАКТИЧЕСКОЕ ПОСОБИЕ ПО ОБОСНОВАНИЮ ИНВЕСТИЦИЙ В СТРОИТЕЛЬСТВО ПРЕДПРИЯТИЙ, ЗДАНИЙ И СООРУЖЕНИЙ (К СП-11-101-95)» (утв. Минстроем РФ)

действует Редакция от 30.06.1995Подробная информация

Расчет потока и сальдо реальных денег

Цель расчета — выявление достаточности денежных средств для финансирования всех затрат, необходимых для обеспечения деятельности предприятия в соответствии с производственной программой, погашения в установленные сроки банковской ссуды и процентов за кредит, выплаты налоговых платежей и платы за пользование природными ресурсами в соответствии с действующими законодательством, осуществления расходов по дальнейшему развитию предприятия, а также определения тенденции изменений доходов и расходов по годам расчетного периода.

При осуществлении проекта выделяется три вида деятельности:

инвестиционная (1), операционная или производственная (2) и финансовая (3).

Показатели, характеризующие финансовую устойчивость проектирования

Таблица 2.10.5.

NN пп	Наименование показателей и расчетные формулы	Краткая характеристика и область применения показателей
1	2	3
1	Коэффициент автономии (ka)	Характеризует способность предприятия сохранять финансовую независимость от заемных источников средств и не оказаться в положении банкрота в случае затруднений со сбытом продукции или длительного технического перевооружения производства.
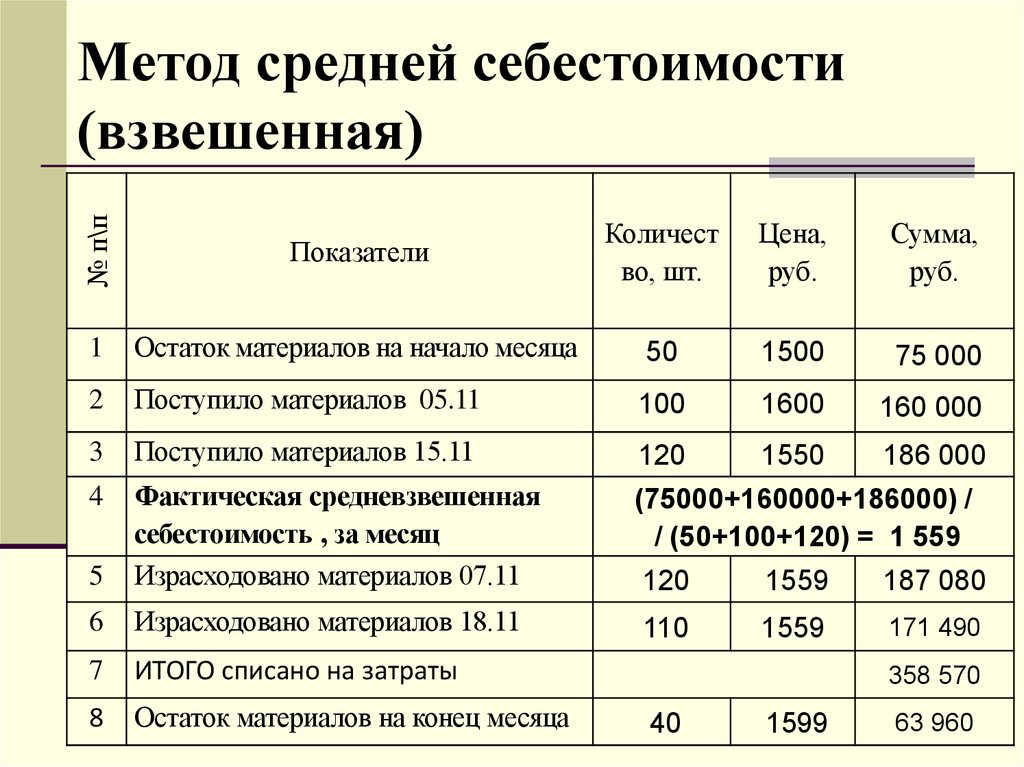		Считается нормальным ограничение ka < 0,5, что означает, что все обязательства предприятия могут быть покрыты его собственными средствами. Выполнение ограничения важно не только для самого предприятия, но и для его кредиторов. Высокий коэффициент автономии свидетельствует о гарантиях погашения предприятиями своих обязательств.
2	Коэффициент задолженности (kз)	Коэффициент kз дополняет коэффициент ka. Применяется для финансового анализа проектов в ситуациях, когда эффективность инвестиций в значительной мере зависит от конъюнктуры рынка и условий кредитования.
	, kз<1	Недостаток — невозможно установить эталонную (идеальную) пропорцию собственных и заемных средств. Обычно банками сумма занимаемых средств ограничивается 50% необходимых инвестиций. В ряде стран применяется пропорция заемного и собственного капитала 33:67 или 25:75 и даже выше [60].
3	Коэффициент маневренности (kм)	Показывает, какая часть собственных средств предприятия находится в мобильной форме. Высокие значения положительно характеризуют финансовое состояние, однако каких-либо устоявшихся в практике нормальных значений показателя не существует. Иногда в специальной литературе в качестве оптимальной величины коэффициента рекомендуется 0,5.
4	Коэффициент обеспеченности товароматериальных запасов и затрат собственными источниками (koтм)	Характеризует обеспеченность предприятия собственными источниками формирования запасов и затрат. На основе обобщения хозяйственной практики установлено нормативное ограничение koтм = 0,6 — 0,8.
5	Коэффициент оборачиваемости собственного капитала (kocк)	Показывает число оборотов собственного оборотного капитала в течение года. Скорость возврата собственного оборотного капитала зависит как от коммерческих, так и от технологических факторов. В зарубежных кампаниях машиностроительных отраслей промышленности собственный оборотный капитал совершает в среднем 4-6 оборотов в год, что обусловлено высоким уровней запасов на многих предприятиях, значительной длительностью производства технических сложных и дорогостоящих изделий.
6	Коэффициент абсолютной ликвидности (kал)	Отражает прогнозируемые платежные возможности предприятия при условии своевременного выполнения своих долговых обязательств. Считается нормальным ограничение kал = 0,8 — 1,0.
7	Показатель покрытия долгосрочной задолженности (kдз)	Характеризует возможность предприятия погашения задолженности по долгосрочным обязательствам, связанной с созданием предприятия. Уровень коэффициента зависит от отрасли производства, длительности производственного цикла, структуры оборотных активов и других факторов. За рубежом считается приемлемой пропорция 1,5 — 3,0. Она возрастает по мере погашения долгосрочного долга.

Примечания: 1. Конкретный набор показателей, используемых для оценки финансового состояния предприятия — объекта инвестирования может варьироваться в зависимости от специфики отрасли, целей проекта и других факторов.

2. Дополнительно к рассмотренным в таблице коэффициентам могут быть использованы показатели, приведенные в [37, 65, 66].

3. Указанные в таблице численные значения коэффициентов заимствованы из зарубежной практики.

4. В таблице приняты следующие обозначения:

Ксоб, Косн, Кзаем, Кобор, Ксоб. обор, К — соответственно собственный (акционерный), заемный, основной, оборотный, собственный оборотный и совокупный капитал;

Bt — выручка от продаж (реализации продукции) в t-м году;

ТМ — среднегодовая стоимость товарно-материальных запасов.

В рамках каждого вида деятельности происходит приток Пi(t) и отток Oi(t) денежных средств. Обозначим разность между ними через Фi(t)=Пi(t)-Oi(t), где i = 1, 2, 3.

Потоком реальных денег Ф(t) называется разность между притоком и оттоком денежных средств от инвестиционной и операционной (производственной) деятельности в каждом периоде осуществления проекта (на каждом шаге расчета).

Поток реальных денег Ф(t) является аналогом Rt — Зt или Эt.

Сальдо реальных денег b(t) называется разность между притоком и оттоком денежных средств от всех трех видов деятельности (также на каждом шаге расчета).

Основные составляющие потоков (и сальдо) реальных денег приведены в таблицах 10.7 — 10.10.

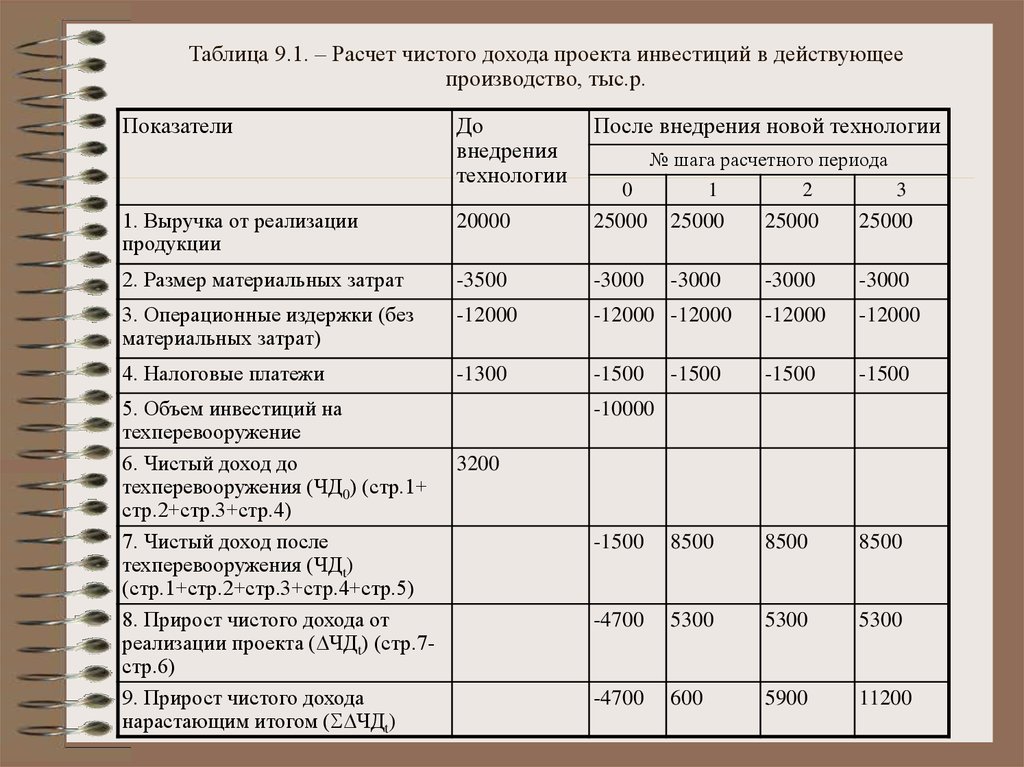
Составляется несколько различных расчетов потоков исходя из соответствующих сценариев реализации проекта. Они должны быть сформированы таким образом, чтобы сальдо накопленных реальных денег всегда принимало положительные значения.

Расчет потоков реальных денег проходит, как правило, в несколько итераций. Величина и время привлечения заемных средств определяются размерами и периодами появления дефицита реальных денег. То же относится к возврату займов, связанному с величиной накопленного сальдо реальных денег. Порядок и сроки привлечения средств и их возврата влияют на общий объем инвестиций и величины издержек, т.к. проценты по займам составляют финансовые издержки.

Учитывая сложность расчетов потоков целесообразно использовать компьютерные вычислительные системы. Краткое описание некоторых систем дано в [37].

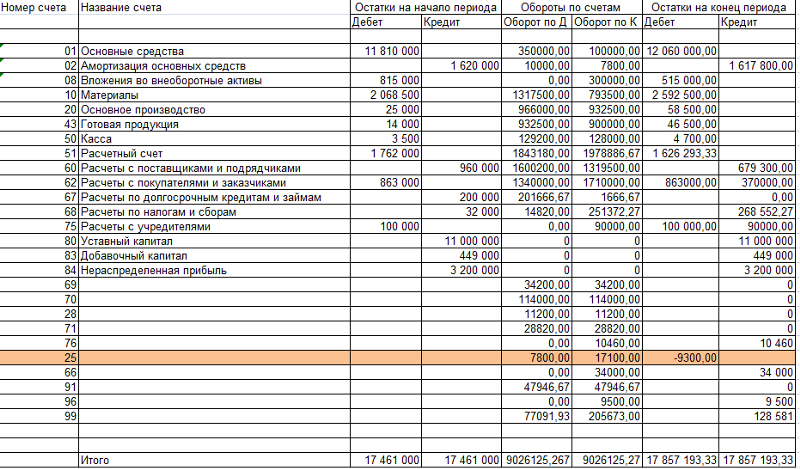При расчете потоков реальных денег следует иметь в виду принципиальное отличие понятий притоков и оттоков реальных денег от понятия доходов и расходов. Существуют определенные номинально-денежные расходы, такие как обесценение активов и амортизация основных средств, которые уменьшают чистый доход, но не влияют на потоки реальных денег, т. к. номинально-денежные расходы не предполагают операций по перечислению денежных сумм.

Все расходы вычитаются из доходов и влияют на сумму чистой прибыли, но не при всех расходах требуется реальный перевод денег. Такие расходы не влияют на поток реальных денег.

С другой стороны, не все денежные выплаты (влияющие на поток реальных денег) фиксируются как расходы. Например, покупка товарно-материальных запасов или имущества связана с оттоком реальных денег, но не является расходом.

Учет инфляции при подсчете Ф(t) и b(t) производится путем вычисления входящих в них элементов в прогнозных ценах.

Более подробно порядок расчета потоков и сальдо реальных денег изложен в [37, 60, 61].

Учитывая зарубежный опыт, прогноз потока реальных денег может составляться на год нормальной эксплуатации предприятия (работа на полную производственную мощность) и какую-либо другую дату в будущем, когда по каким-либо причинам (сокращение объемов производства и реализации продукции, рост издержек производства и др. ) предприятие может испытывать финансовые трудности. Сравнение этих двух балансовых таблиц позволит предусмотреть соответствующие «страховочные» фонды.

Расчет потока реальных денег служит основой для подготовки варианта предварительного финансового плана и расчета показателей коммерческой эффективности — простых и интегральных.

Сальдо реальных денег — определение термина

разность между притоком и оттоком денежных средств от всех видов деятельности на каждом шагу расчета.

Научные статьи на тему «Сальдо реальных денег»

Определение 2 Потоком реальных денег называется показатель, который используется для определения…
Определение 3 Сальдо – термин, который обозначает разницу между притоком денежных средств и их оттоками…
Принятие любого инвестиционного проекта включает в себя потребность положительного сальдо реальных денег. ..
В случае, если сальдо отрицательное, проект является недостаточно профинансированным и работает в убыток

Статья от экспертов

Creative Commons

Научный журнал

когда поступления больше платежей), или отрицательное (пассивное, когда платежи больше поступлений) сальдо…
Если сальдо положительное (активное), то импорт золота растет и увеличиваются валютные резервы….
Тогда происходит усиление валютной спекуляции, что приводит к появлению разрушительного потока «горячих денег…
Реальный валютный курс определяет соотношение, при котором происходит обмен товаров и услуг одного государства…
Замечание 1 Можно сказать, что посредством реального валютного курса можно измерять сравнительную

Статья от экспертов

Еще термины по предмету «Инновационный менеджмент»

Системы разработки решения «Выход»

решение, выраженное количественно или качественно, имеющее определенную степень адекватности и вероятность реализации, степень достижения запланированного результата.

Административный подход к менеджменту

подход, заключающийся в регламентации функций, нрав, обязанностей, нормативов качества, затрат, продолжительности, элементов системы менеджмента в нормативных актах (приказы, распоряжения, указания, стандарты, инструкции, положения).

Адресная специализация субъектов инновационного предпринимательства

использование значимых научных результатов путем создания дочерних научно-технических и инновационных фирм, а также инновационное обслуживание предприятий, которое может быть предметом межотраслевого использования.

• Приток реальных денег
• Сальдо
• Миграционное сальдо
• Сальдо миграции
• Туристское сальдо
• Сальдо дебетовое
• Сальдо кредитовое
• Развернутое сальдо
• Внешнеторговое сальдо
• Сальдо конверсии
• Нейтральность денег
• Стоимость денег
• Бегство от денег
• Обесценивание денег
• Функции денег
• Опцион «без денег»
• Цена денег
• Эмиссия денег
• Бегство денег
• Кругооборот денег

Смотреть больше терминов

Повышай знания с онлайн-тренажером от Автор24!

1. Напиши термин
2. Выбери определение из предложенных или загрузи свое
3. Тренажер от Автор24 поможет тебе выучить термины с помощью удобных и приятных карточек

Возможность создать свои термины в разработке

Еще чуть-чуть и ты сможешь писать определения на платформе Автор24. Укажи почту и мы пришлем уведомление с обновлением ☺️

Включи камеру на своем телефоне и наведи на qr-код. Edu24_bot откроется на устройстве

Привет! Рады, что термин оказался полезен 🤩

Для копирования текста подпишись на Telegram bot. Удобный поиск по учебным материалам в твоем телефоне

Подписаться и скачать термин

Включи камеру на своем телефоне и наведи на qr-код. Edu24_bot откроется на устройстве

Привет! Рады, что термин оказался полезен 🤩

Подписчики нашего бота Edu24_bot получают определение прямо в телеграмм! Просто перейди по ссылке ниже

Скачать термин

Включи камеру на своем телефоне и наведи на qr-код. Edu24_bot откроется на устройстве

спрос на деньги

Современная денежная теория:

Формулы интегрирования, основные формулы интегрирования для учащихся

Содержание:

• Основные формулы интегрирования
• Интегралы от рациональных функций (23 шт)
• Интегралы от трансцендентных функций (15 шт)
• Интегралы от иррациональных функций (27 шт)
• Интегралы от тригонометрических функций (31 шт)

Формулы интегрирования, таблица интегралов

• Основные формулы интегрирования
• Интегралы от рациональных функций (23 шт)
• Интегралы от трансцендентных функций (15 шт)
• Интегралы от иррациональных функций (27 шт)
• Интегралы от тригонометрических функций (31 шт)

Основные формулы интегрирования

$$ \int d x=x+c $$
$$ \mathrm{k}(\mathrm{f}(\mathrm{x})) \mathrm{d} \mathrm{x}=\mathrm{k} \cdot \int \quad \mathrm{f}(\mathrm{x}) \mathrm{d} \mathrm{x} $$
$$ \int(\mathrm{u}+\mathrm{v}+\mathrm{w}+\ldots) \mathrm{d} \mathrm{x}=\int \quad \mathrm{u} \mathrm{d} \mathrm{x}+\int_{. {1.5}+c $$
$$ \begin{array}{c} \int \frac{\mathrm{d} x}{(x+c) \cdot \sqrt{a x+b}}=\frac{1}{\sqrt{b-a c}} \cdot \ln \left|\frac{\sqrt{a x+b}-\sqrt{b-a c}}{\sqrt{a x+b}+\sqrt{b-a c}}\right|+c \\ (b-a c>0) \end{array} $$
$$ \begin{array}{r} \int \frac{d x}{(x+c) \cdot \sqrt{a x+b}}=\frac{1}{\sqrt{a c-b}} \cdot \operatorname{arctg}\left(\sqrt{\frac{a x+b}{a c-b}}\right)+c \\ (b-a c<0) \end{array} $$
$$ \int \sqrt{\frac{a x+b}{c x+d}} d x=\frac{1}{c} \cdot \sqrt{(a x+b) \cdot(c x+d)}-\frac{a d-b c}{c \cdot \sqrt{a c}} \cdot \operatorname{arctg}\left(\sqrt{\frac{a(c x+d)}{c(a x+b)}}\right)+c $$
$$ \int \frac{\mathrm{d} \mathrm{x}}{\mathrm{x} \cdot \sqrt{\mathrm{ax}+\mathrm{b}}}=\frac{1}{\sqrt{\mathrm{b}}} \cdot \ln \left|\frac{\sqrt{\mathrm{ax}+\mathrm{b}}-\sqrt{\mathrm{b}}}{\sqrt{\mathrm{ax}+\mathrm{b}}+\sqrt{\mathrm{b}}}\right|+\mathrm{c} $$
$$ \int \frac{d x}{x \cdot \sqrt{a x+b}}=\frac{2}{\sqrt{-b}} \cdot \operatorname{arctg}\left(\sqrt{\frac{a x+b}{-b}}\right)+c $$
$$ \int \frac{d x}{x^{2} \cdot \sqrt{a x+b}}=\frac{-\sqrt{a x+b}}{b x}-\frac{a}{2 b} \int \frac{d x}{x \cdot \sqrt{a x+b}} d x $$
$$ \int \frac{\sqrt{a x+b}}{x} d x=2 \cdot \sqrt{a x+b}+b \int \frac{d x}{x \cdot \sqrt{a x+b}} d x $$
$$ \int \sqrt{\frac{\mathrm{a}-\mathrm{x}}{\mathrm{b}+\mathrm{x}}} \mathrm{d} \mathrm{x}=\sqrt{(\mathrm{a}-\mathrm{x})(\mathrm{b}+\mathrm{x})}+(\mathrm{a}+\mathrm{b}) \arcsin \left(\sqrt{\frac{\mathrm{x}+\mathrm{b}}{\mathrm{a}+\mathrm{b}}}\right)+\mathrm{C} $$
$$ \int \sqrt{\frac{a+x}{b-x}} d x=-\sqrt{(a+x)(b-x)}-(a+b) \arcsin \left(\sqrt{\frac{b-x}{a+x}}\right)+c $$
$$ \int \frac{\mathrm{d} \mathrm{x}}{\sqrt{\mathrm{ax}^{2}+\mathrm{b} \mathrm{x}+\mathrm{c}}}=\frac{1}{\sqrt{\mathrm{a}}} \cdot \ln \left|2 \mathrm{ax}+\mathrm{b}+2 \sqrt{\left. {n+1}(x)}{n+1}+c $$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

11.1.1. Основные формулы и свойства неопределенного интеграла.

Главная » 11 класс. Алгебра. » 11.1.1. Основные формулы и свойства неопределенного интеграла

На чтение 2 мин. Просмотров 5.3k.

Все простейшие формулы интегралов будут иметь вид:

∫f (x) dx=F (x)+C, причем, должно выполняться равенство:

(F (x)+C)’=f (x).

Формулы интегрирования

Формулы интегрирования можно получить обращением соответствующих формул дифференцирования.

Действительно,

Показатель степени n может быть  и дробным. Часто приходится находить неопределенный интеграл от функции у=√х. Вычислим интеграл от функции f (x)=√x, используя формулу 1).

Запишем этот пример в виде формулы 2).

Так как (х+С)’=1, то ∫dx=x+C.

3) ∫dx=x+C.

Заменяя 1/х² на х^-2, вычислим интеграл от 1/х².

А можно было получить этот ответ обращением известной формулы дифференцирования:

Запишем наши рассуждения в виде формулы 4).

Умножив обе части полученного равенства на 2, получим формулу 5).

Найдем интегралы от основных тригонометрических функций, зная их производные: (sinx)’=cosx; (cosx)’=-sinx; (tgx)’=1/cos²x; (ctgx)’=-1/sin²x. Получаем формулы интегрирования 6) — 9).

6) ∫cosxdx=sinx+C;

7) ∫sinxdx=-cosx+C;

После изучения показательной и логарифмической функций, добавим еще несколько формул.

Основные свойства неопределенного интеграла

I. Производная неопределенного интеграла равна подынтегральной функции.

(∫f (x) dx)’=f (x).

II. Дифференциал неопределенного интеграла равен подынтегральному выражению.

d∫f (x) dx=f (x) dx.

III. Неопределенный интеграл от дифференциала (производной) некоторой функции равен сумме этой функции и произвольной постоянной С.

∫dF (x)=F (x)+C  или   ∫F'(x) dx=F (x)+C.

Обратите внимание: в I, II и III свойствах знаки дифференциала и интеграла (интеграла и дифференциала) «съедают» друг друга!

IV. Постоянный множитель подынтегрального выражения можно вынести за знак интеграла.

∫kf (x) dx=k·∫f (x) dx, где k — постоянная величина, не равная нулю.

V.  Интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от этих функций.

∫(f (x)±g (x)) dx=∫f (x) dx±∫g (x) dx.

VI. Если F (x) есть первообразная для f (x), а k и b — постоянные величины, причем, k≠0, то (1/k)·F (kx+b) есть первообразная для f (kx+b). Действительно, по правилу вычисления производной сложной функции имеем:

Можно записать:

неопределенный интеграл

( 2 оценки, среднее 5 из 5 )

Все формулы интегрирования — PDF, список, лист для класса 12

Содержание

Формулы интегрирования

Алгебраические выражения, тригонометрические отношения, обратные тригонометрические функции, логарифмические и экспоненциальные функции — все это можно интегрировать с помощью формул интегрирования. Основные функции, для которых были получены производные, получаются путем интегрирования функций. Эти формулы интегрирования используются для получения муравьиной производной функции. Мы получаем семейство функций из I, когда дифференцируем функцию f на интервале I. Мы можем определить функцию f, если знаем значения функций из I. Интегрирование — процесс, противоположный дифференцированию. Давайте сделаем еще один шаг и посмотрим на формулы интегрирования, которые используются в процедурах интегрирования.

Формула интеграции — что это такое?

Следующие наборы формул представляют собой общее представление формул интегрирования. Включены основные формулы интегрирования, интегрирование тригонометрических отношений, обратные тригонометрические функции, произведение функций и более сложный набор формул интегрирования. Интеграция — это, по сути, метод соединения частей для создания целого. Это действие, противоположное дифференциации. Таким образом, фундаментальное уравнение интегрирования имеет вид f'(x) dx = f(x) + C. С его помощью создаются следующие формулы интегрирования.

Формулы интегрирования для класса 12

Вычисление интеграла называется интегрированием. Интегралы используются в арифметике для вычисления множества полезных величин, таких как площади, объемы, перемещения и т. д. Когда мы говорим об интегралах, мы обычно имеем в виду определенные интегралы. Для муравьиных производных используются неопределенные интегралы. Помимо дифференцирования, интегрирование является одним из двух основных предметов исчисления в математике, который измеряет скорость изменения любой функции по отношению к ее переменным. Это широкая тема, которая изучается в классах старшего уровня, таких как класс 11 и 12.

Подробнее о:

• Штукатурка — Формула, Использование
• PM Кисан Самман Нидхи Статус 2022 @Pmkisan.Gov.In
• формула отбеливающего порошка и химическое название
• Площадь ромба – формула и примеры для класса 8

 

Формулы интегрирования — PDF

Все основные формулы интегрирования — PDF

Скачать все основные формулы интегрирования 92(θ) dθ, где x = a sin(θ) или x = a tan(θ)

разложение на неполные дроби: ∫(f(x)/(ax+b)) dx = ln|ax+b| + С

Примечание: C — постоянная интегрирования.

Формулы интегрирования – список и таблица

Основные интегральные формулы приведены ниже:

• ∫ 1 dx = x + C
• ∫ а дх = ах+ С
• ∫ x ⁿ dx = ((x ⁿ⁺¹ )/(n+1))+C ; n≠1
• ∫ sin x dx = – cos x + C
• ∫ cos x dx = sin x + C
• ∫ сек ² х dx = тангенс х + С
• ∫ cosec ² x dx = -cot x + C
• ∫ сек х (тангенс х) dx = сек х + C
• ∫ cosec x ( cot x) dx = – cosec x + C
• ∫ (1/x) dx = ln |x| + С
• ∫ e ^x dx = e ^x + C
• ∫ a ^x dx = (a ^x /ln a) + C ; а>0, а≠1
• ∫ tanx. dx =log|secx| + С
• ∫ cotx.dx = log|sinx| + С
• ∫ secx.dx = log|secx + tanx| + С
• ∫ cosecx.dx = log|cosecx – cotx| + С

 

Формулы интегрирования

обратных тригонометрических функций с пределами

• ∫ 1/(1 +x ² ).dx = -cot ^-1 x + C
• ∫ 1/x√(x ² – 1).dx = сек ^-1 x + C
• ∫ 1/x√(x ² – 1).dx = -cosec ^-1 x + C
• ∫1/√(1 – x ² ).dx = sin ^-1 x + C
• ∫ /1(1 – х ² ).dx = -cos ^-1 х + C
• ∫1/(1 + x ² ).dx = тангенс ^-1 x + C

Список сложных формул интеграции

• ∫ √ (x ² + A ² ) .dx = 1/2.x.√ (x ² + A ² ) + A ^{2 2} /2 . log|x + √(x ² + a ²  )| + С
• ∫1/(x ² + a ² ). dx = 1/a.tan ^-1 x/a + C
• ∫1/√(х ² – а ² )dx = log|x +√(x ² – a ² )| + С
• ∫ √(x ² – a ² ).dx =1/2.x.√(x ² – a ² )-a ² /2 log|x + √(x 9009 2 – а ² )| + С
• ∫1/√(a ² – x ² ).dx = sin ^-1 x/a + C
• ∫1/(x ² – a ² ).dx = 1/2a.log|(x – a)(x + a| + C
• ∫ 1/(a ² – x ² ).dx = 1/2a.log|(a + x)(a – x)| + С
• ∫1/√(x ² + a ²  ).dx = log|x + √(x ² + a ² )| + С
• ∫√(a ² – x ² ).dx = 1/2.x.√(a ² – x ² ).dx + a ² /2.sin-1 x/ а + С

 

Формулы интегрирования – Приложение

В целом существует два вида интегралов. Это интегралы, которые могут быть определенными или неопределенными.

Определенная формула интегрирования

Это интегрирования с ранее существовавшим значением пределов, приводящие к определенному конечному значению интеграла.

b∫ag(x)dx

= G(b) – G(a)

Неопределенная формула интегрирования

Это интегрирования, которые не имеют ранее существовавшего предельного значения, что делает конечное значение интеграла неопределенным. Здесь используется постоянная интегрирования C. g'(x) = g(x) + C

Мы используем обсуждавшиеся до сих пор формулы интегрирования для аппроксимации площади, ограниченной кривыми, оценки среднего расстояния, скорости и задач, ориентированных на ускорение, нахождения среднего значения функции, аппроксимации объем и площадь поверхности твердых тел, оценка длины дуги и нахождение кинетической энергии движущегося объекта с использованием несобственных интегралов.

Формулы интеграции с примерами

Пример 1: Найдите значение ∫ (9x+ 25)/ (x+ 3) ² . dx
Решение:

(9x+ 25)/ (25). x+3) ²  — рациональная функция.

Используя разложение на неполные дроби, имеем (9x+ 25)/(x+3) ²  = A/(x+3) + B/(x+3) ² 

Взяв LCD, получим

(9x+ 25)/(x+3) ²  = [A(x+3) +B]/(x+3) ² 

Приравнивая числитель, получаем

9x+ 25 = A(x+3) +B

Решая для B при x = -3, получаем B = -2

Решая для A при x = 0, получаем получить A = 9

Таким образом, неполная дробь разлагается как 9/(x+3) -2/(x+3) ²

Как указано в формулах интегрирования выше, найдите интеграл 9/(x+ 3) -2/(х+3) ²  .

∫[9/(x+3)]dx – ∫ -2(x+3) ²  .dx = 9 ln(x+3) – 2 /(x+3) +C

Пример 2 :∫ x 3+3 x +4 x √ DX
Решение:

Пример 3: ∫ x 3– x 2: ∫ x 3– x 2: ∫ x 3– x 2: ∫ x 3- x 2: ∫ x 3- x 2: ∫ x dx
Решение:

Статьи по теме

• Площадь параллелограмма – формула, определение, примеры
• uidai. Gov.In For Aadhar — новая регистрация, обновление, загрузка
• Единица силы — что такое единица силы в системе СИ и СГС?
• Спасти девочку в Индии Эссе для студентов на английском языке
• Полная форма CNG в науке и медицине

 

Формулы интеграции — КНС

Что такое интеграция с примером?

Интеграция описывается как объединение ранее изолированных объектов или людей.

Когда школы были десегрегированы и больше не существовало отдельных государственных школ для афроамериканцев, это был пример интеграции.

 

Что означает интегрирование в математике?

В математике интегрирование — это процесс нахождения функции g(x), производная которой Dg(x) равна заданной функции f. (Икс).

Представляется интегральным символом «∫», как в f(x), который обычно называют неопределенным интегралом функции.

 

Сколько существует формул интегрирования?

Существует три разных типа методов интегрирования, каждый из которых имеет собственный набор алгоритмов вычисления интегралов. Это результаты, которые были стандартизированы. Формулы интегрирования — хороший способ их запомнить.

 

Делиться заботой!

0 акции

Формулы интеграции: основные и расширенные

• Автор Вайбхав_Радж_Астхана
• Последнее изменение 24-01-2023

Список формул интегрирования:  В 12 классе по математике интегрирование — это обратный процесс дифференцирования, также известный как обратное дифференцирование. Это метод расчета общей стоимости путем сложения нескольких компонентов. Это процесс определения функции с ее производной. Формулы интегрирования могут интегрировать алгебраические уравнения, тригонометрические отношения, обратные тригонометрические функции, логарифмические и экспоненциальные функции и другие функции.

Формулы интегрирования для класса 12 используются для определения первообразной функции. Мы получим семейство функций из I, если продифференцируем функцию f на интервале I. Зная значения функций из I, мы можем вычислить функцию f. Эта обратная процедура дифференцирования известна как интегрирование. Прокрутите вниз, чтобы проверить и загрузить список формул интеграции бесплатно в формате PDF из этой статьи.

Прежде чем предоставить вам список формул, мы свели в таблицу все важные символы, термины и фразы, используемые при интеграции, и их значение:

Список формул интегрирования для класса 12

 Интеграл функции f(x)f(x) относительно xx записывается как ∫f(x)dx. Основные формулы, обычно используемые при интегрировании, перечислены ниже:

Список основных формул интегрирования:

Некоторые обобщенные результаты, полученные с использованием фундаментальных теорем об интегралах, запоминаются как формулы интегрирования при неопределенном интегрировании. Ниже приведены основные формулы интегрирования для справки:

• ∫ x ⁿ .dx = x ^{(n + 1)} /(n + 1)+ C
• ∫ 1.dx = x + C
• ∫1/x.dx = log|x| + C
• ∫ E ^x .DX = E ^x + C
• ∫ ^x .DX = A ^x /loga+ c
• ∫ E ^x [f (x)+ F ‘ (x)].dx = e ^x .f(x) + C

Тригонометрические формулы интегрирования

Список формул для тригонометрических функций приведен ниже:

• ∫ cosx.dx = sinx + C
• ∫ sinx.dx = -cosx + C
• ∫ cosec ² x.dx = -cotx + C
• ∫ sec ² x.dx = tanx + C
• ∫ cosecx.cotx.dx = -cosecx + C
∫ tg = secx + C 
• ∫ tanx.dx =log|secx| + C
• ∫ cotx.dx = log|sinx| + C
• ∫ cosecx.dx = log|cosecx – cotx| + C
• ∫ secx.dx = log|secx + tanx| + C 

Формулы обратных тригонометрических функций интегрирования

Вот список всех важных формул обратных тригонометрических функций:

• ∫1/√(1 – x ² ). dx = sin ^-1 x + C
• ∫ /1(1 – x ² ).dx = -cos ^-1 x + C
• ∫1/(1 + x ² ).dx = tan ^-1 x + C
• ∫ 1/(1 + x ²  ).dx = -cot ^-1 x + C
• ∫ 1/x√(x ²  – 1).dx = -cosec ^-1 x + C
• ∫ 1/x√(x ²  – 1).dx = sec ^{-0 x + C}

Расширенные формулы для интегрирования

Вот список некоторых важных и наиболее часто задаваемых формул для расширенных функций интегрирования:

• ∫ 1/(a ²  – x ² ).dx =1/2a.log|(a + x)(a – x)| + C
• ∫1/(x ²  – a ² ).dx = 1/2a.log|(x – a)(x + a| + C
• ∫1/(x ²  + a ² ).dx = 1/a.tan ^-1 x/a + C
• ∫1/√(x ²  – a ² )dx = log|x +√(x ² -A ² ) | + C
• ∫1/√ (A ² -x ² ) .dx = sin ^-1 x/a + c
• ∫ √ (x ² x/A + C
• ² ). dx =1/2.x.√(x ²  – a ² )-a ² /2 log|x + √(x ²  – a ² )| + C
• ∫√(a ²  – x ² ).dx = 1/2.x.√(a ²  – x ² ).dx + a ² /2 /2. 1 x/a + C
• ∫1/√(x ²  + a ²  ).dx = log|x + √(x ²  + a ² )| + C
• ∫ √(x ²  + a ²  ).dx =1/2.x.√(x ²  + a ²  )+ a ² /2 . log|x + √(x ²  + a ²  )| + C

Различные формулы интегрирования

Обычно используются три типа методов интегрирования: интегрирование по формуле частей, интегрирование по формуле подстановки и интегрирование по формуле частичных дробей. Давайте рассмотрим каждую из этих формул интегрирования одну за другой.

Интегрирование по формуле по частям

Когда любая заданная функция является произведением двух разных функций, для вычисления интеграла можно применить формулу интегрирования по частям или частичное интегрирование. Формула интегрирования методом частичного интегрирования выглядит следующим образом:

∫ f(x).g(x) = f(x).∫g(x).dx -∫(∫g(x).dx.f'(x)).dx  + c

Например : ∫ xe ^x dx имеет форму ∫ f(x).g(x). Следовательно, мы должны применить соответствующую формулу интегрирования и соответственно оценить интеграл.

f(x) = x и g(x) = e ^x

Таким образом, ∫ xe ^x dx = x∫e ^x .dx – ∫( ∫e ^x . dx+ c

= xe ^x – e ^x + c

Интегрирование по формуле подстановки

Если данная функция является функцией другой функции, мы можем применить формулу интегрирования для подстановки, чтобы решить этот интеграл. Например, если
I = ∫ f(x) dx,
, где
x = g(t), так что dx/dt = g'(t), то мы пишем dx = g'(t)
Возьмем, например,
I = ∫ f(x) dx = ∫ f(g(t)) g'(t) dt
Например: Рассмотрим ∫ (3x +2) ⁴  dx
Формула интегрирования подстановки дается следующим образом.
Возьмем u = (3x+2). ⇒ du = 3. dx
Таким образом, ∫ (3x +2) ⁴  дх = 1/3. ∫(и) ⁴ . дю
= 1/3. u ⁵  /5 = u ⁵  /15
= (3x+2) ⁵  /15

Формула интегрирования частных дробей

Чтобы найти интеграл от неправильной дроби, такой как P(x)/Q(x ), в котором степень P(x) < степени Q(x), мы можем использовать интегрирование дробями. В этом методе мы разбиваем дробь, используя разложение на частичные дроби, как P(x)/Q(x) = T(x) + P11 (x)/Q(x), где T(x) — многочлен от x, а P11 (x)/ Q(x) — правильная рациональная функция.

Предположим, что A, B и C являются действительными числами. У нас могут быть следующие типы более простых дробей, связанных с различными типами рациональных функций.

9000 Для 1 Пример: ∫ 3x+7/ x ²  -3x + 2

Разложив на неполные дроби, получим

3x+7/ x ²  -3x + 2 = A/(x-2) + B/ (x-1)

= A(x-1) + B(x-2)/ (x-2)(x-1)

Приравнивая числители, получаем 3x +7 = A(x-1)+B(x-2)

Найдите B, дав x = 1⇒ 10 = B

Найдите A, дав x = 2⇒ 13 = A

Таким образом, 3x+7/ x ²  -3x + 2 = 13/(x-2) + 10(x-1)

Применяя формулу интегрирования, получаем

∫ (3x+7/ x ²  -3x + 2) = ∫ 13/(x-2) + ∫ 10(x-1)

∫ (3x+7/ x ²  -3x + 2) = 13 log |x-2| – 10 log |x-1| + C

Формула определенного интеграла

Это интегрирование с ранее существовавшими предельными значениями, делающее окончательное значение интеграла определенным:

Формула неопределенного интеграла

Это интегрирования, в которых отсутствует ранее существовавшее значение пределов, что делает окончательное значение интеграла безграничным. C обозначает постоянную интегрирования.

∫ g'(x) = g(x) + C

Все важные формулы интегрирования PDF

Вы можете посмотреть, а также скачать PDF-файл с формулами интегрирования и дифференцирования снизу:

Ознакомьтесь с некоторыми больше формул, которые помогут вам в подготовке.

Часто задаваемые вопросы о формулах интеграции

Q.1: Что такое интеграция?

Ответ : Интеграция представляет собой процесс непрерывного суммирования и обычно рассматривается как процесс, обратный дифференцированию.

Q.2: Рассчитать ∫ 5x ⁴ dx.

Ответ : x ⁵ + C.

Q.3: Найдите  \(\int x\sqrt{1+4x}\) dx.

Как обозначается полупериметр: HTTP 429 — too many requests, слишком много запросов

alexxlab / 26.06.202320.05.2023 / Разное

Периметр прямоугольника

Периметр прямоугольника — это сумма
всех сторон прямоугольника.

Периметр прямоугольника можно рассчитать
через четыре стороны, через смежные стороны,
через диагональ, через площадь,
через радиус описанной окружности.

Самый простой способ найти периметр
прямоугольника, это сложить все стороны.

Также, исходя из свойства прямоугольника, — «противоположные
стороны равны и параллельны», можно сказать, что периметр
численно равен удвоенной сумме ширины и высоты — двух
смежных сторон прямоугольника.

Кроме этих двух способов периметр прямоугольника
можно найти через другие величины. Например, через
площадь прямоугольника, диагональ прямоугольника, и так далее.

В прямоугольник невозможно вписать окружность,
поэтому выразить периметр через вписанную
окружность не получится.

Единицы измерения периметра прямоугольника:
км, м, дм, см, мм. 2}), \]

b — любая сторона;
R — радиус описанной окружности;

Полупериметр

Полупериметр — это половина периметра.

Обозначается латинской буквой p.

Чтобы найти полупериметр нужно разделить
периметр на два, или домножить периметр на 0.5.

\[ p = \frac{P}{2} = P \cdot 0.5 \]

Полупериметр применяется в некоторых формулах
нахождения разных величин прямоугольника. Вместо того,
чтобы вычислять периметр, в таких формулах
удобней вычислять полупериметр.

Основные определения и величины

Длина прямоугольника — это длинная сторона
/ наибольшая сторона прямоугольника.

Обозначается латинской буквой a.

Ширина прямоугольника — это широкая сторона
/ наименьшая сторона прямоугольника.

Обозначается латинской буквой b.

Сторона прямоугольника — это ширина или длина прямоугольника,
в зависимости от численного значения длины стороны.

Обозначается латинской буквой a или b.

Диагональ прямоугольника — это отрезок, соединяющий
противоположные стороны прямоугольника.

Обозначается латинской буквой c или d.

Средняя линия прямоугольника — это отрезок, соединяющий
наименьшие параллельные стороны прямоугольника друг с
другом, причем делящий их пополам на равные отрезки.

Обозначается латинской буквой l.

Радиус описанной окружности прямоугольника — это отрезок,
соединяющий центр описанной около треугольника
окружности и произвольную точку на окружности.

Обозначается латинской буквой R.

Высота прямоугольника — это любая сторона прямоугольника,
а также любой отрезок в прямоугольнике, образующий угол в 90 градусов.

Обозначается латинской буквой h.

Урок 12. Периметр треугольника | Уроки математики и физики для школьников и родителей

ВИДЕОУРОК

Определение и формула периметра разностороннего треугольника.

Периметр треугольника – это сумма длин всех его сторон.Периметр обозначается буквой  Р.

Формула периметра треугольника.

Периметр треугольника зависит от длины его сторон.

Определение и формула полупериметра разностороннего треугольника.

Полупериметр треугольника – это сумма длин всех его сторон, делённая на два.

Полупериметр обозначается буквой  р.

Формула полупериметра треугольника.

Чтобы найти полупериметр треугольника нужно сложить длины всех его сторон, и полученный результат разделить на два.

Самый простой способ найти периметр треугольника заключается в том, чтобы сложить длины всех его сторон.

ЗАДАЧА:

Найти периметр разностороннего треугольника, стороны которого равны:

34 см, 12 см  и  11 см.

РЕШЕНИЕ:

Пользуясь формулойнаходим периметр:

Р = 34 + 12 + 11 = 57 (см).

ЗАДАЧА:

Сумма длин первой и второй сторон треугольника  50 см, сумма длин второй и третьей сторон  52 см, а сумма длин первой и третьей сторон  58 см. Найдите периметр треугольника.

РЕШЕНИЕ:

Обозначим длину первой стороны – П,

второй – В  и третью сторону обозначим как  Т.

Тогда:

П + В = 50, 

В + Т = 52,

П + Т = 58.

Прибавим второе равенство к первому:

П + В + В + Т = 102,

П + 2В + Т = 102, найдём 

2В = 102 – (П + Т).

Так как  П + Т = 58, то можем найти  В:

2В = 102 – (П + Т),

2В = 102 – 58 = 44, В = 22.

Тогда 

П = 50 – 22 = 28  и 

Т = 58 – 28 = 30.

Периметр треугольника равен:

Р = 28 + 22 + 30 = 80 (см).

ПРОВЕРКА:

П + В = 28 + 22 = 50, 

В + Т = 22 + 30 = 52,

П + Т = 28 + 30 = 58.

ЗАДАЧА:

Одна сторона треугольника в  2 раза длиннее другой, а третья сторона равна  15 см. Периметр треугольника равен  42 см. Найдите неизвестные стороны треугольника.

РЕШЕНИЕ:

Сначала найдём сумму первой и второй стороны треугольника:

42 –  15 = 27 (см).

Затем найдём первую сторону треугольника. Для этого полученный результат разделим на  3:

27 : 3 = 9 (см).

Тогда вторая сторона будет равна:

9 ∙ 2 = 18 (см).

ОТВЕТ:

Неизвестные стороны треугольника равны  9 см  и  18 см.

ЗАДАЧА:

Периметр треугольника больше его сторон на  32, 29  и  23 см. Определите периметр треугольника.

РЕШЕНИЕ:

Обозначим периметр треугольника  Р,

тогда

первая сторона равна: Р – 32,

вторая сторона равна: Р – 29,

третья сторона равна: Р – 23.

Найдём периметр треугольника:

Р = (Р – 32) + (Р – 29) + (Р – 23),

Р = Р – 32 + Р – 29 + Р – 23,

Р = 3Р – (32 + 29 + 23),

2Р = 32 + 29 + 23,

2Р = 84, Р = 42 (см).

ЗАДАЧА:

Стороны треугольника относятся как

7 : 6 : 4.

Найдите наибольшую сторону треугольника, если его периметр равен  51 см.

РЕШЕНИЕ:

Пусть наибольшая сторона треугольника  7х см, тогда другие стороны равны  6х см  и  4х см.

7х + 6х + 4х = 51,

17х = 51,

х = 3 (см), откуда

7х = 7 ∙ 3 = 21 (см).

Однако, если вы не знаете длину, хотя бы одной стороны треугольника, необходимо сначала найти её.

Определение и формулы периметра прямоугольного треугольника.

Для нахождения периметра прямоугольного треугольника, если известны его катеты, сначала надо найти квадраты катетов и посчитать их сумму. Затем извлечь корень из полученного числа и к результату прибавить оба катета.

ЗАДАЧА:

Найти периметр прямоугольного треугольника, у которого катеты  равны:

6 см  и  8 см.

РЕШЕНИЕ:

Сначала найдём длину гипотенузы треугольника по теореме Пифагора:

с² = 6² + 8² = 100,

с = 10 (см).

По правилу вычисления периметра разностороннего треугольника, получим:

Р = 10 + 8 + 6 = 24 (см).

Для нахождения периметра прямоугольного треугольника, если известны его катет и гипотенуза, сначала надо найти квадраты гипотенузы и катета. Затем от квадрата гипотенузы отнять квадрат катета и извлечь корень из полученного результата. К полученному результату прибавить катет и гипотенузу.

ЗАДАЧА:
В прямоугольном треугольнике один из катетов равен  3 дм, а гипотенуза – 5 дм. Найдите периметр треугольника.РЕШЕНИЕ:
Задания к уроку 12

Полупериметр треугольника – формула, определение, примеры

Полупериметр треугольника равен половине суммы всех его сторон. Треугольник — это многоугольник с тремя сторонами, тремя вершинами и тремя внутренними углами, сумма которых равна 180°. В то время как периметр треугольника рассчитывается путем сложения всех его сторон, полупериметр треугольника составляет половину значения периметра. Давайте узнаем больше о полупериметре треугольника в этой статье.

Рациональные дроби	Частичные дроби
(px + q)/(x-a)(x – b)	A/(x – a) + B/ (x-b) 1 + q)/(x-a) n	A 1 /(x-a) + A 2 /(x-a) 2  + ………. А н /(х-а) N
(PX 2 + QX + R)/(AX 2 + BX + C) N	(A 1 x + B 72).  + bx + c) + (A 2 x + B 2 )/(ax 2  + bx + c) 2  + …(A n x + B n 2 + BX + C) N
(PX 2 + QX + R)/(AX 2 + BX + C)	(AX + B)/(AX 9009 2 +	(AX + B)/(AX 9009 2 +	(AX + B)/(AX 9009 2 9019 +	(AX + B)/(AX 9009 2 9019 +	(AX + B)/(AX 9009 2 +	(AX + B)/(AX 9009 2	(AX . бх + в)
(px 2  + qx + r)/(x-a)(x-b)(x-c)	A/(x – a) + B/ (x-b) + C/ (x-c)
(px 2  + qx + r)/(x 2  +bx +c)	A/(x-a) +(Bx+C)/(x 2  +bx +c)

1.	Что такое полупериметр треугольника?
2.	Полупериметр треугольника Formula
3.	Как найти полупериметр треугольника?
4.	Часто задаваемые вопросы о полупериметре треугольника

Что такое полупериметр треугольника?

Полупериметр треугольника рассчитывается путем деления периметра треугольника на два. «Полу» означает половину, поэтому полупериметр треугольника равен половине значения периметра. Полупериметр треугольника используется для вычисления площади треугольника по формуле Герона. Полупериметр треугольника выражается в линейных единицах, таких как дюймы, ярды, сантиметры и так далее. Теперь давайте прочитаем о формуле, которая используется для нахождения полупериметра треугольника.

Полупериметр треугольника Формула

Мы знаем, что периметр треугольника равен сумме длин всех его сторон. Если мы рассмотрим треугольник с длинами сторон «a», «b» и «c», периметр можно рассчитать с помощью формулы: Периметр = a + b + c. Используя эту формулу, формула для полупериметра треугольника получается как: Полупериметр треугольника = (a + b + c)/2

Как найти полупериметр треугольника?

Если известны длины всех сторон треугольника, мы можем вычислить полупериметр, сложив стороны и разделив сумму на 2.

Пример: Найдите полупериметр треугольника со сторонами 3 единицы, 4 единиц и 5 единиц.

Решение:

Стороны треугольника равны: 3 единицы, 4 единицы и 5 единиц

Мы будем использовать формулу полупериметра треугольника )/2

Подстановка значений в формулу: Полупериметр = (a + b + c)/2 = Полупериметр = (3 + 4 + 5)/2 = 12/2 = 6 единиц.

Следовательно, полупериметр треугольника равен 6 единицам.

Использование полупериметра треугольника

Полупериметр треугольника используется для определения площади треугольников по формуле Герона, когда известны длины всех трех сторон. Эта формула зависит исключительно от длин всех сторон треугольника. Он содержит термин «s», который представляет полупериметр, который получается путем деления периметра треугольника на два. Формула Герона выражается как √[s(s-a)(s-b)(s-c)], где ‘s’ = полупериметр треугольника; а «а», «b», «с» — три стороны треугольника. Итак, после вычисления полупериметра треугольника значение «s» помещается в формулу Герона вместе с другими сторонами. Это дает площадь треугольника, три стороны которого даны.

Пример: Найдите площадь треугольника с длинами сторон 6 единиц, 7 единиц и 9 единиц.

Решение: Стороны треугольника равны «а» = 6 единицам, «b» = 7 единицам и «с» = 9 единицам.

Площадь треугольника можно рассчитать по формуле Герона √ [s(s-a)(s-b)(s-c)], где ‘s’ = полупериметр треугольника; а «а», «b», «с» — три стороны треугольника. Сначала вычислим полупериметр треугольника по формуле:

Полупериметр = (a + b + c)/2

Подставляя значения «a», «b» и «c», полупериметр (s) = (6 + 7 + 9)/2 = 22 /2 = 11 единиц.

Теперь найдем площадь треугольника по формуле Герона, Площадь треугольника = √[s(s-a)(s-b)(s-c)]

Подставив значения в формулу, где ‘s’ = 11 единиц, a = 6 единиц, ‘b’ = 7 единиц и ‘c’ = 9 единиц

Площадь треугольника = √[s(s-a)(s-b)(s-c)]

Площадь = √[11(11-6) (11-7)(11-9)] = √[11 × 5 × 4 × 2] = √440 = 20,97 квадратных единиц

 

Примеры на полупериметре треугольника

1. Пример 1: Найдите полупериметр треугольника со сторонами 15, 13 и 14 единиц.

   Решение: Стороны треугольника равны «а» = 15 единиц, «b» = 13 единиц и «с» = 14 единиц

   Мы будем использовать формулу для полупериметра треугольника, s = (a + b + c)/2

   Подставляя значения «a», «b» и «c», полупериметр (s) = (15 + 13 + 14)/2 = 42/2 = 21 единицы измерения.
   Ответ: Полупериметр треугольника равен 21 единице.

2. Пример 2: Найдите полупериметр равностороннего треугольника, длина стороны которого равна 16 единицам.

   Решение:

   Так как это равносторонний треугольник, все три стороны имеют одинаковую меру. Это означает, что значение сторон треугольника может быть записано как: «a» = 16 единиц, «b» = 16 единиц и «c» = 16 единиц

   Мы будем использовать формулу для полупериметра треугольника, с = (а + b + с)/2

   Подставляя значения «a», «b» и «c», полупериметр (s) = (16 + 16 + 16)/2 = 48/2 = 24 единицы.

   Ответ: Следовательно, полупериметр равностороннего треугольника равен 24 единицам.

перейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с нашими сертифицированными экспертами

Забронируйте бесплатный пробный урок

Практические вопросы

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о полупериметре треугольника

Что такое полупериметр треугольника?

Полупериметр треугольника равен половине периметра треугольника. «Полу» означает половину, поэтому полупериметр треугольника равен половине значения периметра. Полупериметр треугольника выражается в линейных единицах, таких как дюймы, ярды, сантиметры и так далее.

Как найти полупериметр треугольника?

Полупериметр треугольника можно рассчитать, разделив периметр треугольника на 2. Другими словами, если известны длины всех сторон треугольника, мы можем вычислить полупериметр, сложив стороны и разделив сумма на 2. Формула, используемая для нахождения полупериметра треугольника, такова: полупериметр = (a + b + c)/2, где «a», «b», «c» — три стороны треугольника. треугольник. Например, если стороны треугольника равны 4 единицам, 8 единицам и 6 единицам, полупериметр можно рассчитать следующим образом. Полупериметр = (4 + 8 + 6)/2 = 18/2 = 9единицы измерения.

Где используется полупериметр треугольника?

Полупериметр треугольника используется для нахождения площади треугольника по формуле Герона, если известны длины всех трех сторон. Формула Герона выражается как √[s(s-a)(s-b)(s-c)], где ‘s’ = полупериметр треугольника; а «а», «b», «с» — три стороны треугольника. Итак, после вычисления полупериметра треугольника значение «s» помещается в формулу Герона вместе с другими сторонами. Это дает площадь треугольника, три стороны которого даны.

Какая формула полупериметра треугольника?

Основная формула, которая используется для нахождения полупериметра треугольника: S = (a + b + c)/2, где ‘a’, ‘b’, ‘c’ — три стороны треугольника.

Чему равен полупериметр треугольника со сторонами 40 см, 24 см, 32 см?

Полупериметр треугольника можно вычислить, если известны длины трех сторон. Формула полупериметра треугольника S = (a + b + c)/2, где «a», «b», «c» — три стороны треугольника. В этом случае «а» = 40 см, «b» = 24 см и «с» = 32 см. Итак, подставим значения в формулу S = (a + b + c)/2 = (40 + 24 + 32)/2 = 96/2 = 48 см. Следовательно, полупериметр треугольника равен 48 см.

Найдите полупериметр треугольника, если стороны равны 12 единицам, 22 единицам и 15 единицам.

Формула полупериметра треугольника S = (a + b + c)/2, где ‘a’, ‘b’, ‘c’ — три стороны треугольника. В этом случае «а» = 12 единиц, «b» = 22 единицы и «с» = 15 единиц. Итак, подставим значения в формулу, S = (a + b + c)/2 = (12 + 22 + 15)/2 = 49/2 =24,5 ед.

Скачать БЕСПЛАТНЫЕ учебные материалы

Полупериметр треугольника

Полупериметр

В геометрии мы могли встретить различные типы формул, такие как периметр, площадь, высота, объем и другие подобные термины. При работе с полигонами одной из наиболее часто встречающихся метрик является полупериметр. Это измерение, связанное с плоскими фигурами, которые представляют собой двумерные формы. Простые формулы можно использовать для вычисления полупериметра множества различных плоских фигур. В этом посте вы найдете определение полупериметра, а также формулу полупериметра для различных форм, а также примеры двух используемых терминов.

Как мы все знаем, периметр фигуры — это расстояние вокруг нее, а полупериметр — это половина расстояния вокруг нее. Полупериметр данного многоугольника можно вычислить, разделив его длину окружности на два для каждого заданного многоугольника. Несмотря на то, что он получен из периметра простым способом, полупериметр часто появляется в формулах, относящихся к треугольникам и другим формам, что побудило дать ему отдельное имя. Полупериметр обозначается буквой «s» в формуле, если он является частью формулы.

 

Формула полупериметра

Формула полупериметра = периметр/2.

Однако в следующей таблице приведены расчеты полупериметра для различных форм и многоугольников: 008

Формула

Объяснение

Полу Формулы периметра треугольника

Равносторонний треугольник

3a/2

a = Длина стороны равностороннего треугольника

Равнобедренный треугольник

9 0008

а + (b/2)

а = длина равных сторон

b = длина третьей стороны

Прямоугольный треугольник

(основание + высота + гипотенуза)/2

9018 7 Высота = Перпендикуляр

Гипотенуза = самая длинная сторона меры длин трех сторон

Формулы полупериметра изогнутых фигур

Окружность

(2πr)/2 или πr

r = радиус окружности 9 0003

Полукруг

(πr + 2r)/2

r = радиус полуокружности

Полупериметр четырехугольников Формулы

9 0006

Формула прямоугольника

2(l + b)/2 или l + b

l = длина

b = ширина

квадрат

(4a/2) или 2a 90 003

а = Сторона квадрата

любой четырехугольник

(a + b + c + d)/2

a, b, c, d — длины сторон четырехугольника

9000 2  

Полупериметр треугольника

 

Можно вычислить полупериметр треугольника, разделив общий периметр треугольника на два. Из-за того, что полу’ означает половину, полупериметр треугольника равен половине значения периметра. Чтобы определить площадь треугольника по формуле Герона, необходимо знать полупериметр треугольника. Полупериметр треугольника можно выразить в линейных единицах, таких как дюймы, ярды, миллиметры и так далее. После этого мы рассмотрим формулу, которая используется для расчета полупериметра фигуры треугольной формы. Зная, что периметр треугольника равен сумме длин всех его сторон, мы можем вычислить его площадь. Возьмем, к примеру, треугольник с тремя сторонами одинаковой длины (a, b и c). Периметр треугольника можно вычислить по следующей формуле: Периметр = (a+b+c). В результате использования этой техники полупериметр треугольника равен (a + b + c)/2.

Использование полу периметра треугольника в формуле Херона

Когда длина всех трех сторон треугольника известна, полуфильт полуфи треугольник по формуле Герона. Только длины всех сторон треугольника определяют результат этого вычисления. Полупериметр обозначается буквой «s», которая получается путем деления периметра треугольника на два и обозначается буквой «s». Это формула Герона, которая записывается как √[s(s-a)(s-b)(s-c)], где s обозначает полупериметр треугольника, а буквы a’, ‘b’, ‘c’ обозначают три стороны треугольника. Это дает площадь треугольника, три стороны которого известны заранее.

Формула периметра полукруга

При расчете периметра полукруга используется формула для периметра полукруга. Мы должны знать диаметр или радиус окружности, а также длину дуги, чтобы решить эту задачу. Чтобы получить длину дуги полуокружности, мы должны сначала определить длину окружности круглой фигуры.

Длина окружности определяется формулой C = πd или C = 2πr.

Принимая во внимание значение C, мы можем придумать формулу для вычисления периметра полукруга, который определяется как сумма половины длины окружности и диаметра окружности.

Периметр полукруга вычисляется по формуле (πR + d) или (πR + 2R), или R(π + 2) единиц.

Тест с ответами по политологии для бакалавров – пройти тест онлайн бесплатно

Авторам

8-800-333-85-44

Оформить заявку

Вход

• Справочник
• Онлайн-калькуляторы
• Тесты с ответами

Выполним любые типы работ

• Дипломные работы
• Курсовые работы
• Рефераты
• Контрольные работы
• Отчет по практике
• Эссе
Узнай бесплатно стоимость работы

Политология

Политология

Политология

Политология

Политология

Политология

Политология

Политология

Политология

• Контрольная работа

  от 1 дня /

  от 100 руб

• Курсовая работа

  от 5 дней /

  от 1800 руб

• Дипломная работа

  от 7 дней /

  от 7950 руб

• Реферат

  от 1 дня /

  от 700 руб

• Онлайн-помощь

  от 1 дня /

  от 300 руб

Оставляй заявку — и мы пройдем все тесты за тебя!

Тесты по политологии с ответами

Итоговые тесты по теме Политология с ответами


Правильный вариант ответа отмечен знаком +

1. Объектом политологии является:

+ политическая жизнь общества;

— общество как совокупность социальных институтов;

— содержание внешней политики государства.

2. Прогностическая функция политологии заключается в:

+ определении различных вариантов развития общества исходя из насущного положения дел, формирование прогнозов, моделирование будущих политических процессов и отношений;

— выработке теоретических и методологических основ изучения политической действительности, а также политических категорий и законов;

— сборе и анализе конкретных явлений и процессов политической жизни общества, выявление проблем и поиск их решений.

3. Главными категориями политологии как науки являются:

+ власть, политика, демократия, политическая система, политический лидер;

— государство, право, правовая норма, принуждение, правовой статус личности;

— общество, социальный институт, общественное мнение, социальные группы.

4. Функция политологии, содержанием которой является выработка определенных рекомендаций для органов власти, называется:

+ регулятивной;

— мировоззренческой;

— прогностической.

5. К теоретическим методам политологии относится:

+ бихевиоризм;

— опрос;

— контент-анализ.

6. Предметом политологии как науки является:

+ закономерности этапов становления и развития различных политических систем, происходящие в действительности политические процессы, разработка методов ведения политической деятельности, исследование конкретных политических ситуаций, институтов, субъектов и объектов политики;

— закономерности появления и развития государства как организации политической власти, его институтов, изменения его сущности и функций на разных этапах развития;

— правотворческая деятельность уполномоченных государственных органов, законы и подзаконные нормативно-правовые акты, которые влияют на принимаемые политические решения на территории страны.

7. Что изучает политология в широком смысле?

+ политическую систему общества;

— степень соответствия проводимой государством внутренней и внешней политики реальным потребностям общества;

— политические линии поведения ключевых должностных лиц государства.

8. Большое распространение в политологии получила классификация партийных систем Д. Сартори на:

+ однопартийные, системы партии-гегемона, системы доминирующей партии, двухпартийные, системы умеренного плюрализма, системы крайнего плюрализма, атомизированные;

— гармонические, плюралистические, гегемонистские, конфликтные;

— партиципаторные, элитарные, плюралистические.

9. Второй этап развития политологии в России с конца века до 1825 г. Характеризуется:

+ распространением убеждений и взглядов Французского Просвещения;

— формированием вопросов о роли России в мировой истории, попытками преодолеть многовековые противоречия между Востоком и Западом;

— масштабные преобразования во всех сферах на фоне марксистско-ленинской идеологии.

тест 10. Какая парадигма политологии объясняет различные общественные явления природными источниками политической жизни?

+ Натуралистическая;

— Теологическая;

— Географическая.

11. Становление политологии как науки пришлось на период:

+ конца XIX – начала XX вв.;

— второй половины XVII в.;

— конца XX – начала XXI вв.

12. Место политологии в системе наук обусловлено ее наиболее тесной взаимосвязью с:

+ социологией, философией, психологией, политической теорией;

— теорией права и государства, административным правом, международным правом;

— географией, биологией, химией, физикой.

13. По теории Т. Парсонса к политической системе не относится:

+ интеграция;

— лидерство;

— регламентация.

14. Важнейшая идея либерализма заключается:

+ в признании за индивидуумом абсолютной свободы во всех возможных формах;

— в предоставлении лицу широкого набора прав и свобод со стороны государства;

— в отсутствии сдерживающих факторов поведения человека.

15. Важнейшим признаком пропорциональной избирательной системы является:

+ соответствие количества мест в парламенте числу набранных на выборах голосов;

— необходимость высокой явки на выборы;

— отсутствие возможности у мелких партий получить места в парламенте.

16. Под бюрократией в политологии понимается:

+ чиновничий аппарат, который на постоянной и профессиональной основе осуществляет политическую деятельность;

— власть толпы;

— система сложного документооборота и затрудненного доступа к общегосударственным данным.

17. Кто является основоположником политического радикализма?

+ Ж.-Ж. Руссо;

— Т. Джефферсон;

— Н. Макиавелли.

18. Поведение человека является объектом исследования в:

+ политическом бихевиоризме;

— политическом консерватизме;

— политическом радикализме.

19. Какие четыре основные парадигмы различают в политологии?

+ Теологическая, социальная, рационально-критическая, натуралистическая;

— Либеральная, консервативная, демократическая, тоталитарная;

— Позитивистская, естественная, формалистская, бихевиористская.

тест_20. Кому принадлежит теория влияния климата на политическую деятельность людей?

+ Ж. Бодену;

— Ш. Л. Монтескье;

— М. Веберу.

21. Что с точки зрения биополитической парадигмы служит главным фактором политического поведения людей?

+ Чувства, физиологические инстинкты и биологические характеристики человека как звена в природной цепи;

— Психология человека, его мотивация, цели и принципы жизни;

— Религиозность, вера в божественную сущность всех происходящих явлений, в том числе политических.

22. Что из указанного не относится к тоталитарному политическому режиму?

+ выборность главных органов власти;

— повсеместный строгий контроль политической сферы жизни;

— отсутствие контроля власти со стороны народа.

23. Какая черта не характерна для политического лидера?

+ Разовое влияние на какой-либо политический процесс;

— Распространение своего влияния на все общество или социальную группу;

— Опора влияния на авторитет, доверие и признание легитимности его деятельности.

24. Р. Такер классифицировал политических лидеров в соответствие с целями, которые они ставят, на:

+ консерваторов, реформаторов и революционеров;

— властвующих и оппозиционных;

— традиционных, рационально-легальных и харизматичных.

25. К современным моделям демократии можно отнести:

+ элитарную;

— идентитаризм;

— либерализм.

26. Демократическим транзитом в политологии называют:

+ переход различных политических режимов к демократии;

— переход политического режима из демократии в авторитарный;

— адаптация народа к смене власти после революции.

27. Что из указанного воздействует на личность на международном уровне политической социализации?

+ Международный финансовый кризис;

— Социально-экономический кризис;

— Постоянный круг общения человека.

28. По интегральному критерию политические партии делятся на:

+ левые, правые и центристов;

— кадровые и массовые;

— конституционные и революционные.

тест-29. Определенное воздействие на власть с целью принятия закона, выгодного лишь конкретной социально группе, называется:

+ лоббизмом;

— либерализмом;

— бихевиоризмом.

Вопросы по политологии — герой курса

Отображено с 1 по 8 из 1040

• • В. Как этот вопрос связан с политологией

  • Рейтинг ответа:
  • 1 файл(ы) прикреплен
  • Посмотреть ответ

• • В. Объясните, почему сравнительной политологии трудно стать наукой. Это потому, что эта область исследования относительно новая, или…

  • Рейтинг ответа:
  • Посмотреть ответ

• • В. Определите любую тему исследования в области политологии в Гане по вашему выбору и разработайте вопросник, который вы будете использовать для сбора данных по этой теме…

  • Рейтинг ответа:
  • Посмотреть ответ

• • В.

    Кто является заказчиком и поставщиком политики в области здравоохранения? Что мотивирует каждого на политическом рынке?
  • Рейтинг ответа:
  • Посмотреть ответ

• • В. Какие факторы влияют на то, как СМИ освещают политические вопросы? Как эти стандарты влияют на то, как общественность думает о политических проблемах,…

  • Рейтинг ответа:
  • Посмотреть ответ

• • Q. Как политологи подошли к теме терроризма — с точки зрения его определения, его истории и возможных политических мер. В этом…

  • Рейтинг ответа:
  • Посмотреть ответ

• • Q. Какова связь между политической наукой и политической философией, особенно между их древними и современными концепциями?

  • Рейтинг ответа:
  • Посмотреть ответ

• • Q.

    Политическая социализация начинается в молодости. Вспомните разговоры о политике, когда вы учились в начальной школе (около 10 лет). Может быть, было…
  • Рейтинг ответа:
  • Посмотреть ответ

Понятия политологии

• Американская политика
• Авторитаризм
• Баланс сил
• Капитализм
• Цивик
• Гражданские свободы
• Гражданские права
• Классический либерализм
• Колониализм
• Командно-экономический
• Коммунизм
• Сравнительная политика
• Государственный переворот
• Демократия
• Коллегия выборщиков
• Защита окружающей среды
• Фашизм
• Федерализм
• Флибустьер
• Свободный рынок
• Геополитика
• Джерримандер
• Правительство
• Империализм
• Международные организации
• Международные отношения
• Изоляционизм
• невмешательство
• Либерализм
• Марксизм
• СМИ
• Национализм
• Естественное право
• Политическая культура
• Политическая экономия
• Политическая философия
• Популярность-суверенитет
• Прецедент
• Государственная администрация
• Государственная политика
• Республика
• Социальная справедливость
• Социализм
• Суверенитет
• ООН

Политология 12 Пробный экзамен Страница

Следующие вопросы типичны для вопросов, задаваемых на промежуточные и итоговые экзамены по этому классу. Все эти вопросы были заданы на предыдущие экзамены. Я не буду знать точное количество вопросов или баллов распределяются по вопросам, пока я не сдам экзамен. Обратите внимание, что вы будете предлагается выбор, на какой вопрос эссе ответить, но вы должны ответить на все вопросы в других разделах.

* * *

Промежуточные вопросы с несколькими вариантами ответов

расовый либерализм

б) Демократическая партия, охватывающая расовый консерватизм

c) Республиканская партия, поддерживающая расовый прогрессизм

d) Демократическая партия, охватывающая расовое безразличие

e) Демократическая партия, охватывающая расовый либерализм

 

2.      Какой из следующих расширенной свободы слова в политике?

 

а) Плесси против Фергюсона и Браун против. Департамент образования

б) Бранденбург против Огайо и Техаса против Джонсона

c) Закон о шпионаже и Закон о подстрекательстве к мятежу

d) Миранда против Аризоны

e) Ничего из вышеперечисленного

 

 

4. Что из перечисленного НЕ влияет вероятность явки избирателей?

 

а) Дата закрытия или количество дней до выборов, на которых избиратель должен зарегистрироваться, чтобы проголосовать в предстоящие выборы

b) Образование

c) Возраст

d) Тесты на грамотность, необходимые для зарегистрироваться для голосования

e) Все вышеперечисленное влияет на явку избирателей

Вопросы итогового экзамена

Примечание. На итоговом экзамене будет несколько вариантов ответа. вопросы, вопросы с краткими ответами и эссе.

Вопросы с краткими ответами:

как «ретроспективный» вопрос?

2. Либерализм в экономических вопросах увеличивается или уменьшается с образованием?

3. За последние несколько десятилетий количество организаций, представленных лоббисты в Вашингтоне увеличиться, уменьшиться или остаться прежним?

4. Объясните пространственную модель выборов и гипотезу медианного избирателя.

5. Согласно Данлэпу (в книге Лестера), что такое «цикл проблема-внимание»?

6. Объясните разницу между концепцией Мэдисона «инструментальный личный интерес» и концепция Стоуна «соотношение затрат и выгод».

 

Часть III. Пожалуйста, ответьте на один из двух следующих вопросов эссе. Тщательно разработайте свой ответ, используя доказательства и ссылаясь на чтение класса и лекции, чтобы поддержать ваши утверждения везде, где это возможно. При написании эссе помните, что вы должны попытаться ответить таким образом, чтобы продемонстрировать, что вы узнали в этот курс. Например, если часть вашего ответа о Конгрессе, вы должны рассказать нам о том, как Конгресс организована, как работает комитетская и партийная системы и т. д.

Примечание. Следующий вопрос был задан, когда темой курса были гражданские права.

 

A.     Предположим, вы политический консультант поручил разработать стратегию борьбы с предложение расширить гражданские права в области, которую американское общество считает спорные — употребление наркотиков, ВИЧ/СПИД, ожирение или сексуальные предпочтения.

В МИД России назвали неприемлемыми планы Армении присоединиться к Римскому статуту МУС — Газета.Ru

В МИД России назвали неприемлемыми планы Армении присоединиться к Римскому статуту МУС — Газета.Ru | Новости

27 марта 2023, 17:57

Размер текста

А

А

А

close

100%

В Министерстве иностранных дел Российской Федерации назвали абсолютно неприемлемыми планы Армении присоединиться к Римскому статуту Международного уголовного суда (МУС) на фоне ордера на арест российского президента Владимира Путина, выданного судом в Гааге. Об этом сообщает ТАСС со ссылкой на источник в МИД России.

«В Москве считают абсолютно неприемлемыми планы официального Еревана по присоединению к Римскому статуту Международного уголовного суда на фоне недавних незаконных и юридически ничтожных «ордеров» МУС в отношении российского руководства», — заявил источник.

Он уточнил, что Москва предупредила Ереван о крайне негативных последствиях подобного решения.

24 марта стало известно, что Конституционный суд Армении признал конституционными обязательства по Римскому статуту МУС. Данное решение вступает в силу с момента опубликования. После этого Римский статут должны ратифицировать в парламенте Армении. Представитель Армении по международным правовым вопросам Егише Киракосян объяснил присоединение страны к Римскому статуту тем, что МУС обязал Азербайджан разблокировать Лачинский коридор.

Пресс-секретарь президента России Дмитрий Песков в ответ заявил, что Москва пока не обсуждала с Ереваном его позицию в связи с признанием Конституционным судом Армении обязательств, закрепленных Римским статутом Международного уголовного суда. Депутат народного собрания страны Арман Абовян выразил уверенность, что даже в случае ратификации парламентом Римского статута, никто «в здравом уме» в Армении арестовывать Путина не станет.

Страны, признающие юрисдикцию МУС (сейчас их 123), обязаны соблюдать и выполнять нормативные документы, постановления и ордеры этого органа. Армения подписала Римский статут в 1999 году, но не ратифицировала его. В 2004 году Конституционный суд страны признал его не соответствующим Основному закону.

17 марта досудебная палата МУС в Гааге выдала ордер на арест президента России Владимира Путина и уполномоченной при президенте РФ по правам ребенка Марии Львовой-Беловой.

Подписывайтесь на «Газету.Ru» в Новостях, Дзен и Telegram.
Чтобы сообщить об ошибке, выделите текст и нажмите Ctrl+Enter

Новости

Дзен

Telegram

Иван Стародубцев

Турецкий поток

Что для России означает победа Эрдогана

10:58

Георгий Бовт

Русский сезон оказался короток

О том, как скандал вокруг «Весны священной» обернулся триумфом

08:05

Алена Солнцева

Чего не может искусственный интеллект

О широте человеческого мышления и забастовке сценаристов

28. 05.2023, 08:21

Джомарт Алиев

Три буквы

О разнице поколений

27.05.2023, 08:16

Иван Глушков

А в рот не попало

О забытых русских напитках

26.05.2023, 08:10

Искусственный интеллект и римское право (17 апреля 2023)

Мы часто слышим споры об искусственном интеллекте: он заменит человека, он лишит его свободы и идентичности, он воплотившееся зло или, наоборот, ИИ — порождение технического прогресса, ведущего людей в эпоху свободы и творчества. В обоих случаях ИИ становится некой самостоятельной сущностью.

Выражу мнение, отличное от обеих позиций. ИИ — это класс программных продуктов, в которых присутствует сложная нелинейная логика. Это всего лишь инструмент, созданный человеком, это «лопата», которая без человека не может ничего, а в руках человека может стать и добром, и злом. Лопатой можно копать, а можно убивать.

Но в чем опасность ИИ? Как ни странно, я вижу ее в тотальном насаждении античеловеческой западной практики развития римского права (то есть в усилении бюрократизации и обезличивании отношений между людьми), в искоренении еще существующих в незападных странах человеческих практик, подчиненных так называемому обычному праву, то есть правилам личного взаимодействия между людьми.

Давайте посмотрим на ИИ под углом «права». «Права» в самом корневом человеческом смысле этого слова: имею право, я прав.

Обычное право против римского

Вспомним гоголевского капитана Копейкина. Он столкнулся с бюрократией, которая действует по инструкции, в соответствии с собственной железной логикой, а не в соответствии с обычным правом, которое основано на справедливости и правде. И проиграл.

Как человек он не смог добиться правды. Ему пришлось превратиться в «духа отмщения».

Почему он проиграл, будучи человеком? Потому что столкнулся с римским правом — с расчеловеченной процедурой, с механизмом, в котором главная цель — бесперебойная логичная работа самого механизма.

Ни человеческая справедливость, ни правда не являются главной целью бюрократии и любых механистичных процедур, в том числе правовых. В любом вынесении решения через процедуру, через механизм мы сталкиваемся с возможностью для судящего, решающего спрятаться за механизм, за процедуру, за ИИ, в конце концов.

Что ж делать? В обычном праве, которое изложено у разных народов в разных текстах — в «Русской правде», Второзаконии, «Салической правде» — устанавливается принцип справедливости: компенсация за нанесенный ущерб. Око за око, зуб за зуб. То есть ущерб, нанесенный пострадавшему, должен быть нанесен и причинившему ущерб.

Говорят, что Владимир Лефевр – диссидент-эмигрант, психолог и математик, написавший книгу «Алгебра совести», научил американцев, как обмануть советских руководителей.

Он разделял мир на две этические системы: западную — систему правил, и восточную — систему смыслов. По его совету западный мир, изменив своей этической системе, просто договорился «по понятиям» с восточным СССР о справедливых смыслах, например о гарантиях при демонтаже системы безопасности СССР в Восточной Европе. Но не подписал документы о правилах. В результате мы обижаемся на несправедливое расширение НАТО на восток, а Запад, теперь уже как бы вспомнив о своей этической системе, говорит, что нет никаких документов, фиксирующих правила.

Только, на мой взгляд, Лефевр был неправ в одном: всем людям — и на Востоке, и на Западе — свойственно искать справедливые и праведные смыслы. Это отражено в системах обычного права — что у восточных славян, что у западных франков.

Однако римское право, которое является порождением бюрократического государства (Римской империи) и противостоит этической системе обычного права, выстроило обезличенный механизм, в котором восстановление справедливости подменяется наказанием: наказывается само нарушение порядка, нарушение правил, установленных государством.

В обычном праве нет наказания, есть компенсаторный механизм: выколол глаз — почувствуй сам, как жить без глаза, украл яблоки — почувствуй сам, как жить без суммы, эквивалентной стоимости этих яблок. В нем отсутствует наказание тюрьмой или штрафом за нарушение предписанного механизма, но есть восстановление справедливости, «мирового» баланса — испытать на себе причиненное.

Позднее, в христианской традиции, тюрьма стала осмысляться не как наказание, а как возможность для исправления в изоляции от общества. Но сам принцип римского права тут ни при чем.

Подчинение западной модели организации общества всегда сопровождается внедрением западного правопорядка, выросшего из римского права, из слепого и бесчеловечного следования установленному порядку — dura lex, sed lex. Это римское выражение можно перевести как «черств закон, но это закон». Не в контексте неотвратимости или строгости наказания, а в том смысле, что римляне осознавали черствость и бесчеловечность бюрократического правопорядка, но считали, что в огромной империи лучше действовать по инструкции, а не искать справедливости.

Личные связи, личные пристрастия, личный опыт отторгаются западным миропорядком. Это называют коррупцией, конфликтом интересов, личной заинтересованностью. Бюрократические механизмы должны быть максимально обезличены с помощью аукционов, тендеров, камер, рейтингов.

И хотя это сильно вредит делу, но все равно внедряется до идиотизма страстно. Хотя в действительно важных случаях, когда нужен результат и нельзя допустить промах, правила обезличивания посылаются подальше, и в дело вступает личный опыт. Если б я был президентом, то окружил бы себя лично знакомыми и проверенными людьми. А как иначе доверять?

Под личную ответственность

России, как и многим незападным странам, чужды бесчеловечные бюрократические процедуры. Они не приживаются, искажаются, превращаются в карикатуру на западные институты.

Возможно, путь спасения от расчеловечивающего действия правовых бюрократизированных механизмов, частью которых все больше становятся процессы, управляемые ИИ, в том, чтобы ввести личную ответственность в среду бюрократии. Личную ответственность по принципу механизма восстановления справедливости в обычном праве: нанес ущерб — получи равный ущерб.

За каждым алгоритмом ИИ, за каждой бюрократической процедурой должна стоять конкретная личность чиновника, и ущерб, нанесенный последствиями применения этого алгоритма или процедуры, должен симметрично отразиться на карьере и благополучии чиновника.

Ведь в чем сила бюрократии, почему она засасывает и перемалывает личность любого человека? Сила бюрократии в обезличивании. Кто виноват в том, что тысячи штрафов за нарушения ПДД, зафиксированные камерами, автоматически списываются со счетов невиновных людей? Никто. Да, вы можете доказать в суде свою правоту, потратить силы, время, нервы, а вам вернут только списанные деньги.

Кто вернет? «Некто», «Оно» — безличное государство-никто.

А если бы ущерб вернул конкретный чиновник или группа чиновников, виновных в несправедливости и неправде, тогда скорость улучшения алгоритмов ИИ, бюрократических процедур, инструкций, их нацеленность на поиск справедливости и истины стремились бы к бесконечности.

Сейчас управленец спрятался за спину автоматических процедур. Впрочем, до сих пор каждое решение о наложении штрафа, зафиксированного камерой, подписывает конкретное лицо — майор или капитан. Понятно, что не лично ручкой десятки тысяч бумажек подписывает — ставится факсимильная или электронная подпись.

А сам майор или капитан ни во что не вникает, это невозможно при рассмотрении десятков тысяч случаев… Так об этом и речь, так не должно быть. Если бы выплачивал ущерб от несправедливости из собственного дохода, тогда бы и требовал справедливо организованной системы, был бы лично нацелен на исполнение правды.

Предвижу возражения христиан, которые для меня очень важны, так как и я христианин: где милость к виновным? Неужели мы вернем в правосудие дохристианский принцип око за око, зуб за зуб?

Отвечу так: не надо путать бюрократическое правосудие, порожденное Римской империей, и личную милость, к которой призывал Христос. Возможность личной милости допустимо оставить в правосудии. Например, пострадавший может простить и не взыскивать личный ущерб с причинившего.

Такой правопорядок восстановит личные отношения между людьми в свете правды и справедливости. Вернется личное измерение: я прав или я неправ, остальное не важно.

«Праведник верою жив будет.»

◄ Римлянам 1:17 ►  Context   Crossref  Комментарий   Греческий Стих   (Нажмите, чтобы открыть главу) Новая международная версия Ибо в Евангелии праведность Божья открывается – праведность по вере от начала до конца, как написано: «Праведник верою жив будет». Новый живой перевод Эта Благая Весть говорит нам, как Бог делает нас правильными в Своих глазах. Это достигается от начала до конца верой. Как сказано в Писании: «Праведник через веру имеет жизнь». English Standard Version Ибо в нем открывается праведность Божия от веры в веру, как написано: «Праведный верою жив будет». Верийская стандартная Библия Ибо Евангелие открывает Божью праведность, которая приходит по вере от начала до конца, как написано: «Праведный верою жив будет». Верийская Буквальная Библия Ибо в ней праведность Божия открывается от веры в веру, как написано: «И праведник верою жив будет». Библия короля Иакова Ибо в нем открывается правда Божия от веры в веру, как написано: праведный верою жив будет. New King James Version Ибо в нем открывается праведность Божья от веры в веру; как написано: «Праведный верою жив будет». Новая американская стандартная Библия Ибо в ней праведность Божья открывается от веры в веру; как написано: «НО ПРАВЕДНЫЙ ОДИН ЖИВЕТ ВЕРОЙ». NASB 1995 Ибо в нем открывается правда Божия от веры в веру; как написано: «ПРАВЕДНЫЙ ВЕРОЙ ЖИВ БУДЕТ». NASB 1977 Ибо в нем праведность Божия открывается от веры в веру; как написано: «НО ПРАВЕДНИК человек ДОЛЖЕН ЖИТЬ ВЕРОЙ». Стандартная Библия Наследия Ибо в ней праведность Божья раскрывается от веры в веру; как написано: «ПРАВЕДНИК ЖИВЕТ ВЕРОЙ». Расширенный перевод Библии Ибо в Евангелии открывается праведность Божья, одновременно проистекающая из веры и приводящая к вере [раскрывается таким образом, что пробуждает больше веры]. Как пишется и навсегда остается написанным, «ПРОСТО и ПРАЙТ ДОЛЖЕН ЖИТЬ ВЕРОЙ». Христианская стандартная Библия Ибо в ней открывается праведность Божия от веры в веру, как написано: Праведник верою жив будет. Holman Christian Standard Bible Ибо в ней открывается Божья праведность от веры в веру, как написано: Праведник верою жив будет. American Standard Version Ибо в нем открывается праведность Божия от веры в веру, как написано: праведный верою жив будет. Арамейская Библия на простом английском языке Ибо в ней открывается правда Божия от веры в веру, согласно написанному: «Праведный верою жив будет». Contemporary English Version Благая весть говорит о том, что Бог принимает всех, у кого есть вера, но только тех, у кого есть вера. Это точно так же, как Писание говорит: «Люди, которых Бог принимает из-за их веры, будут жить». Библия Дуэ-Реймса Ибо в ней открывается справедливость Божия от веры в веру, как написано: Праведник верою жив. English Revised Version Ибо в нем открывается праведность Божия от веры в веру, как написано: праведный верою жив будет. Перевод СЛОВА БОЖЬЕГО® Божье одобрение раскрывается в этой Благой Вести. Это одобрение начинается и заканчивается верой, как говорит Писание: «Человек, получивший Божье одобрение, будет жить верой». Перевод Благой Вести Ибо Евангелие показывает, как Бог приводит людей в порядок с Собой: через веру от начала до конца. Как сказано в Писании: «Человек, примирившийся с Богом через веру, будет жить». Версия международного стандарта Ибо в Евангелии Божья праведность открывается от веры в веру, как написано: «Праведный верою жив будет». Буквальная стандартная версия Ибо праведность Божья в нем открывается от веры в веру, как написано: «И праведник верою жив будет», Стандартная Библия большинства Ибо Евангелие открывает праведность Бога, который приходит по вере от начала до конца, как написано: «Праведный верою жив будет». Новая американская Библия Ибо в ней открывается праведность Божья от веры в веру; как написано: «Праведный верою будет жить». NET Bible Ибо праведность Божия открывается в Евангелии от веры в веру, как написано: «Праведный верою жив будет». Новая пересмотренная стандартная версия Ибо в ней открывается праведность Божья через веру для веры; как написано: «Праведный верою жив будет». New Heart English Bible Ибо в нем открывается Божья праведность от веры в веру. Как написано: «А праведник верою жив будет». Перевод Библии Вебстера Ибо в этом открывается правда Божия от веры в веру: как написано: праведный верою жив будет. Weymouth New Testament Ибо в Благой Вести открывается праведность, исходящая от Бога, зависящая от веры и стремящаяся произвести веру; как сказано в Писании: «Праведник верою жив будет». World English Bible Ибо в нем открывается Божья праведность от веры в веру. Как написано: «А праведник верою жив будет». Дословный перевод Янга Ибо праведность Божья в нем открывается от веры в веру, как написано: «И праведный верою жив будет», Дополнительные переводы … Контекст Не стыжусь благовествования 16Я не стыжусь благовествования, потому что оно есть сила Божия ко спасению всякому верующему, сперва иудею, потом эллину. 17 Ибо Евангелие открывает праведность Божию от начала до конца от веры, как написано: праведный верою жив будет. 18 Гнев Божий открывается с неба на всякое нечестие и нечестие людей, подавляющих истину нечестием своим… Верийская стандартная Библия · Скачать Перекрестные ссылки Иезекииль 18:9 Он следует Моим уставам и верно соблюдает Мои постановления. Этот человек праведен; конечно, он будет жить, говорит Господь Бог. Аввакум 2:4 Взгляни на гордого; душа его неправа — но праведник верою жив будет — Римлянам 3:21 Но ныне, независимо от закона, явилась правда Божия, о которой свидетельствуют Закон и пророки. Римлянам 3:22 И эта праведность от Бога приходит через веру в Иисуса Христа ко всем, кто верит. Нет различия, Римлянам 9:30 Что же мы скажем? Что язычники, не искавшие праведности, приобрели ее, праведность по вере; Римлянам 10:3 Поскольку они не знали о Божьей праведности и стремились утвердить свою собственную, они не покорились Божьей праведности. 2 Corinthians 3:9 Ибо если славно служение осуждения, то тем более славно служение правды! Сокровищница Писания Ибо в нем открывается правда Божия от веры в веру, как написано: праведный верою жив будет. Для там. Римлянам 3:21 Но ныне явилась правда Божия вне закона, о чем свидетельствуют закон и пророки; от веры. Римлянам 3:3 А если некоторые не уверовали? неужели их неверие сведет на нет веру в Бога? Справедливый. Аввакум 2:4 Вот, душа его которая вознеслась, не права в нем: но праведный верою своею жив будет. Иоанна 3:36 Верующий в Сына имеет жизнь вечную: а не верующий в Сына не увидит жизни; но гнев Божий пребывает на нем. Галатам 3:11 А что законом никто не оправдывается пред Богом, это очевидно: ибо праведный верою жив будет. Перейти к предыдущему В зависимости от веры Первое Божье доброе Евангелие Святые новости в прямом эфире Принцип Произвести открытое откровение Праведность Праведность Писание, имеющее в нем писания Написано Перейти к следующему праведностьПисаниеСодержащийся в немПисанияНаписано Римлянам 1 1. Павел хвалит свое призвание римляне; 9. и его желание прийти к ним. 16. Что такое его Евангелие. 18. Бог гневается на грех. 21. Каковы были грехи человечества. Комментарий Элликотта для англоязычных читателей (17) Евангелие достигает своей цели, спасения верующего, открывая праведность Бога, т. е. план или процесс, разработанный Им для того, чтобы люди стали справедливыми или праведными в Его взгляд. Существенной частью со стороны человека, началом и концом этого плана является Вера. Для чего имелся авторитет в Ветхом Завете, где сказано: «Праведный верою жив будет». Праведность Божья. Под этим не понимается, как можно было бы предположить, атрибут божественной природы, как если бы сущностная праведность Божья впервые была явлена ​​через Евангелие. Святой Павел продолжает показывать в Послании к Римлянам 1:19-20, что, по крайней мере, так много о природе Бога можно узнать без какого-либо сверхъестественного откровения. «От Бога» в данном случае означает «то, что исходит от Бога». А «праведность», которая, таким образом, «происходит от Бога», есть то состояние праведности в человеке, в которое он входит через свое участие в мессианском царстве. Вся цель пришествия Мессии состояла в том, чтобы сделать людей «праведными» перед Богом. В особенности это произошло в результате смерти Христа на кресте, которая, как мы узнаем из Римлянам 3:24-26, сделала Бога «милостивым» к людям. Выгода от этого акта гарантирована всем, кто подтверждает свое право считаться членами мессианского царства верной приверженностью Мессии. С такими людьми обращаются так, как если бы они были «праведниками», хотя приписываемая им праведность — это не какая-то их собственная заслуга, а идеальное состояние, в которое они поставлены Богом. Это известное учение об оправдании верой. (См. Экскурс A: О значении слова «праведность» в Послании к Римлянам и Экскурс E: Об доктрине оправдания верой и вмененной праведности.) Откровение.— Божья цель таким образом оправдать людей находится в процессе раскрытия или провозглашения в Евангелии. Теоретически она раскрывается в ясных утверждениях о том, каким образом человек может быть оправдан. Оно проявляется практически в сердечном принятии этих утверждений и изменении жизни, которое они влекли за собой. Для римлян момент откровения был моментом, когда они впервые услышали Евангелие. Св. Павел желает, чтобы они знали полное значение — философию, как это можно было бы назвать — того, что они слышали. От веры к вере. — Именно верой человек впервые ухватывается за Евангелие, и последним продуктом его является возросшая и усиленная вера. Помимо веры, Евангелие остается недействительным для человека. Это не осознается. Но когда оно однажды осознано и доведено до самого себя человека, оно стремится утвердить и усилить ту самую способность, с помощью которой оно было воспринято. Он делает то, о чем молились ученики, когда говорили: «Господи, умножь нашу веру» (Луки 17:5). Праведный будет жить верой. Эти слова являются частью утешительного ответа, который получает пророк Аввакум в стрессе от вторжения халдеев. Хотя его непреодолимые воинства проносятся по земле, праведник, уповающий на Бога, будет жить. Возможно, Св. Павел имел в виду, что слова «верой» должны быть поняты скорее как «праведные», чем в том виде, в каком они стоят в английской версии. «Праведный верой» или «Человек, чья праведность основана на вере», будет жить. Апостол использует слово «вера» в своем особом и многозначительном смысле. Но к этому, естественно, привело то, как его использовал Аввакум. Интенсивное личное доверие и упование, которое иудей чувствовал в Боге своих отцов, христианин направляет ко Христу и далее развивается в активную энергию благочестия. . . . Комментарий с кафедры Стих 17 — Римлянам 11:36. — II. ДОКТРИНАЛЬНАЯ ЧАСТЬ ПОСЛАНИЯ. Стих 17 — Римлянам 8:39. — C. Учение о праведности Божьей предложено, установлено и объяснено. Стих 17. Этот стих, хотя и связан последовательностью мыслей с предыдущим стихом, может быть правильно взят в связи с последующим доктринальным аргументом, фактически служа его тезисом. Ибо в нем открывается праведность Божия от (или) веры в веру, как написано: праведный же (или) верою жив будет. Следует отметить, что ἐκ является предлогом перед πίστεως в обоих предложениях предложения, хотя наша Авторизованная версия делает различие. Кроме того, в Авторизованной версии мы переводим «праведность Божью», а не «праведность», как в исправленной версии, несмотря на отсутствие артикля. Ибо имеется в виду определенная концепция, пронизывающая Послание, о праведности Божией. Если бы было место для сомнения, то оно, несомненно, было бы снято с помощью ὀργὴ Θεοῦ, также без артикля, непосредственно следующего за ним и с тем же глаголом ἀποκαλύπτεται. Ревизоры, переводящие здесь «tins wrath», дали на полях как обоснованное «a wrath», по-видимому, ради согласованности с их переводом δίκαιοσύνη. Но «гнев Божий» не имеет вразумительного значения. Выражения, кажется, просто означают Божью праведность и Божий гнев. Это выражение «праведность Божья» обсуждалось во Введении, на которое и ссылается читатель. Его внутреннее значение там принимается как собственная вечная праведность Бога, явленная во Христе для примирения мира с Собой, а не (как обычно интерпретируется) судебная праведность (так называемая), вменяемая человеку. Таким образом, нет необходимости понимать родительный падеж Θεοῦ как gen. auctoris или как эквивалент ἐνώπιον Θεοῦ. Фраза понимается в том смысле, который был бы знаком св. Павлу и его читателям из Ветхого Завета; и считается, что этот внутренний смысл пронизывает все Послание, даже когда говорится о праведности, вменяемой человеку; идея по-прежнему остается идеей Божественной праведности, объемлющей человека. Неясно, в каком именно смысле следует понимать ἐκ πίστεως εἰς πίστιν. Большинство комментаторов, принимая δικαιοσύνη за обозначение вмененной праведности человека, связывают с ним ἐκ πίστεως, как если бы было написано ἡ ἐκ (как, например, в Римлянам 10: 6). Но отсутствие ἡ, а также сочетание слов, по-видимому, скорее связывают его с ἀποκαλύπτεται. Возможно, оно предназначено для выражения субъективного условия понимания и присвоения человеком Божьей праведности. Откровение его собственной душе человека называется ἐκ πίστεως, тогда как εἰς πίστιν выражает результат; а именно веру во спасение. Подобное использование предлога εἰς встречается в Римлянам 6:19. ; 2 Коринфянам 2:15, 16; 2 Коринфянам 3:18. В последнем из этих отрывков ἀπὸ δόξης εἰς δόξαν имеет близкое сходство с выражением перед нами. Цитата из Аввакума 2:4, по-видимому, предназначена главным образом для иллюстрации того, что было сказано о вере, хотя слово δίκαιος, которое встречается в ней в связи с верой, могло также указывать на это как уместное, как, очевидно, в Галатам 3: 11, где Святой Павел цитирует его в доказательство того положения, что ἐν νόμῳ οὐδεὶς δικαιοῦται παρὰ τῷ Θεῷ. Пророк сразу же увидел испытания веры, характерные для его времени, и воскликнул: «Господи, до каких пор?» Но он стоял на страже своей, ожидая, что скажет ему Господь; и пришел к нему ответ о том, что, несмотря на видимость, его пророческое видение вскоре осуществится, Божьи обетования верным непременно исполнятся, а между тем вера должна быть их поддерживающим принципом: живи своей верой». Так на иврите. LXX. имеет Ὁ δὲ δικαιός μου ἐκ πίστεως ζήσεται (A.) или Ὁ δὲ δίκαιος ἐκ πίτεως μου ζήσεται (B). Вариации не влияют на общий смысл отрывка. Теперь некоторые, предполагая, что Св. Павел соединил ἐκ πίστεως с δίκαιος как частью подлежащего предложения, обвинили бы его в том, что он придал цитате значение, не подразумеваемое пророком, который, очевидно, имел в виду, что ἐκ πίστεως следует за ζήσεται, как часть предиката. Но нет оснований приписывать это намерение св. Павлу, кроме предположения, что он ранее соединил ἐκ πίστεως с δικαιοσύνη, в смысле ἡ ἐκ πίστεως. Но мы видели основания для вывода, что это было не так. Цитата, в том смысле, в каком ее подразумевал пророк, вполне уместна. Ибо оно выражает, что вера есть жизненный принцип праведников Божиих, тогда как весь отрывок, в конце которого оно происходит, объявляет спасение пророческого видения всецело Божьим, ожидаемым и постигаемым человеком через веру, а не вызвано его собственными действиями. Параллельные комментарии … Греческий Фор γὰρ (гар) Союз Стронга 1063: Фор. Первичная частица; правильно, с указанием причины. [евангелие] αὐτῷ (autō) Личное/притяжательное местоимение — дательный падеж среднего рода 3-е лицо единственного числа Strong’s 846: Он, она, оно, они, они, тот же самый. От частицы au; возвратное местоимение self, употребляемое в отношении третьего лица и других лиц. открывает ἀποκαλύπτεται (апокалиптический) Глагол — Настоящее Изъявительное Среднее или Пассивный — 3-е лицо единственного числа Strong’s 601: Раскрыть, выявить, выявить. От апо и калупто; снять обложку, т.е. раскрыть. [the] праведность δικαιοσύνη (dikaiosynē) Существительное в именительном падеже женского рода единственного числа Strong’s 1343: From dikaios; капитал; специально обоснование. Бога Θεοῦ (Theou) Существительное в родительном падеже Мужского рода Единственное число Strong’s 2316: Божество, особенно верховное Божество; образно говоря, магистрат; по гебраизму, очень. [то, что происходит] by ἐκ (ek) Предлог Strong’s 1537: Извне, из среди, из, намекая изнутри наружу. Первичный предлог, обозначающий происхождение, из, из. вера [от начала] πίστεως (pisteōs) Существительное в родительном падеже женского рода единственного числа Strong’s 4102: Вера, вера, доверие, доверие; верность, верность. от до εἰς (eis) Предлог Strong’s 1519: первичный предлог; в или в место, время или цель; также в деепричастных оборотах. [финиш], πίστιν (pistin) Существительное в винительном падеже женского рода единственного числа Strong’s 4102: Вера, убеждение, доверие, доверие; верность, верность. так же, как καθὼς (kathōs) Наречие Стронга 2531: В соответствии с тем, как, в той степени, что, точно так же, как. Из ката и шлюх; как раз то. написано: γέγραπται (gegraptai) Глагол — Совершенное Индикативное Среднее или Пассивный — 3-е Лицо Единственное Strong’s 1125: Первичный глагол; «могить», особенно писать; образно, описывать. «The Ὁ (Ho) Артикль — Именительный падеж мужского рода единственного числа Strong’s 3588: The, определенный артикль. Включая женский род he и средний род to во всех их вариантах; Определенный артикль; . праведный δίκαιος (dikaios) Прилагательное в именительном падеже мужского рода единственного числа Strong’s 1342: From dike; справедливый; косвенно, невинный, святой. будет жить ζήσεται (zēsetai) Глагол – Будущее Индикативное Среднее – 3-е лицо Единственное число Стронга 2198: Жить, быть живым. Основной глагол; жить. by ἐκ (ek) Предлог Strong’s 1537: Извне, из среди, из, намекая изнутри наружу. Первичный предлог, обозначающий происхождение, из, из. вера». πίστεως (pisteōs) Существительное в родительном падеже женского рода единственного числа Strong’s 4102: Вера, вера, доверие, доверие; верность, верность. Ссылки Римлянам 1:17 NIV Римлянам 1:17 NLT Римлянам 1:17 ESV Римлянам 1:17 NASB Римлянам 1:17 KJV Римлянам 1:17 BibleApps.com Римлянам 1:17 Biblia Paralela Римлянам 1:17 Китайская Библия Римлянам 1:17 Французская Библия Римлянам 1:17 Католическая Библия 90 009 NT Letters: Romans 1:17 Ибо в нем открывается правда Божия (Рим. Ro)

17 римскими цифрами — Как написать 17 римскими цифрами?

ОБЕЩАНИЕ НА 30 ДНЕЙ | ПОЛУЧИТЕ 100% ВОЗВРАТ ДЕНЕГ*

*T&C Применить

LearnPracticeDownload

17 римскими цифрами равно XVII. Чтобы преобразовать 17 в римские цифры, мы запишем 17 в расширенной форме, т.е. 17 = 10 + 5 + 1 + 1, после чего заменив преобразованные числа соответствующими римскими цифрами, мы получим 17 = X + V + I + I = XVII . В этой статье мы объясним, как правильно преобразовать 17 в римские цифры.

• 17 = 10 + 7
• Римские цифры = X + VII
• 17 римскими цифрами = XVII

1.	Как написать 17 римскими цифрами?
2.	Основные правила
3.	Номера, относящиеся к 17
4.	Часто задаваемые вопросы о 17 римскими цифрами

Как написать 17 римскими цифрами?

Римские цифры для 17 можно получить, используя метод, описанный ниже:
В этом методе мы разбиваем 17 на наименее расширяемую форму, пишем соответствующую им латинскую букву и добавляем/вычитаем их, то есть 17 = 10 + 5 + 1 + 1 = X + V + I + I = XVII.
Следовательно, значение 17 в римских цифрах равно XVII.

☛ Также проверьте: Калькулятор римских цифр

Основные правила интерпретации римских цифр

• Когда буква большего размера предшествует букве меньшего размера, буквы добавляются. Например: DI, D > I, поэтому DI = D + I = 500 + 1 = 501,
• Когда буква меньшего размера предшествует букве большего размера, буквы вычитаются. Например: IX, I < X, поэтому IX = X - I = 10 - 1 = 9.
• Когда буква повторяется несколько раз, они добавляются. Например: ХХХ = Х + Х + Х = 10 + 10 + 10 = 30
• Одну и ту же букву нельзя использовать более трех раз подряд.

Римские цифры могут показаться отличными от цифр, но они похожи. Например, 17 римскими цифрами эквивалентно XVII. Римские цифры для чисел, связанных с 17, приведены ниже:

• Х = 10
• XI = 10 + 1 = 11
• XII = 10 + 2 = 12
• XIII = 10 + 3 = 13
• XIV = 10 + 4 = 14
• XV = 10 + 5 = 15
• XVI = 10 + 6 = 16
• XVII = 10 + 7 = 17
• XVIII = 10 + 8 = 18
• XIX = 10 + 9 = 19

17 римскими цифрами Примеры

1. Пример 1: найти значение 2162 — 17.

   Решение:

   Решение данной задачи, 2162 — 17 = 2145
   Для определения значения 2162 — 17 римскими цифрами выразим 2145 в развернутом виде, т.е. 2145 = 2000 + 100 + 40 + 5 = MM + C + XL + V = MMCXLV.

2. Пример 2. Найдите разницу между 34 и 17 римскими цифрами.

   Решение:

   Решение данной задачи, 34 — 17 = 17
   Для определения значения 34 — 17 римскими цифрами выразим 17 в развернутом виде, т. е. 17 = 10 + 7 = X + VII = XVII.

3. Пример 3: Найдите значение (12 — 27) + 17 римскими цифрами.

   Решение:

   Решение (12 — 27) + 17 = -15 + 17 = 2. Теперь запишем ответ, то есть 2 = II.

4. Пример 4: Какой остаток при делении XVII на VIII?

   Решение:

   VIII = 8 и XVII = 17 в числах.
   При делении 17 на 8 в остатке остается 1,9.0398 Итак, 1 = I
   Следовательно, при делении XVII на VIII получается остаток I.

перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду

 

Готовы увидеть мир глазами математика?

Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.

Записаться на бесплатный пробный урок

Часто задаваемые вопросы по 17 римскими цифрами

Что означает 17 римскими цифрами?

Чтобы записать 17 римскими цифрами, сначала выразим 17 в развернутом виде. 17 = 10 + 5 + 1 + 1 = X + V + I + I = XVII. Следовательно, 17 в римских числах выражается как XVII.

Почему число 17 римскими цифрами пишется как XVII?

Мы знаем, что в римских цифрах мы пишем 7 как VII, а 10 как X. Следовательно, 17 римскими цифрами записывается как 17 = 10 + 7 = X + VII = XVII.

Какое значение числа 17 в римских цифрах?

Чтобы преобразовать 17 в римские цифры, преобразование включает разбиение чисел на основе разрядности (единицы, десятки, сотни, тысячи).

4.8. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами имеет вид:

у» + ру’ + ду=/ (х). (1)

Оно отличается от соответствующего линейного однородного уравнения

у» + ру’ + ду = 0. (2)

наличием в правой части некоторой функции / (х).

200

Для нахождения общего решения уравнения (1) сначала нужно найти общее решение у уравнения (2), а затем найти какое-либо частное решение у* уравнения (1). Их сумма есть общее решение данного неоднородного уравнения (1):

— * у = у + у.

Приведем правило отыскания частного решения у* уравнения (1) в следующих двух случаях: правая часть f (x) имеет вид

f (x) = ekxP„(x). (3)

где Pn(x) — многочлен степени n; правая часть f (x) имеет вид

f (x) = a cos 1x + b sin 1x. (4)

Рассмотрим каждый из этих случаев в отдельности.

I. Пусть правая часть уравнения (1) имеет вид

f (x) = (xX

причем число k не является корнем характеристического уравнения

r2 + p + q = 0, (5)

соответствующего однородному уравнению (2). Тогда частное решение уравнения (1) следует искать в форме

у* = e„(x), (6)

где Qn(x) — некоторый многочлен той же степени n с неопределенными коэффициентами.

Если же число к является корнем характеристического уравнения (5), то частное решение уравнения (1) следует искать в форме

у* = xmekx Q (x), (7)

где m — кратность корня к (т. е. m = 1, если к — однократный корень, и m = 2, если к — двукратный корень).

II. Пусть теперь правая часть уравнения (1) имеет вид:

причем числа ±1i не являются корнями характеристического уравнения (5). Тогда частное решение уравнения (1) следует искать в форме

где А и В — неопределенные коэффициенты.

Если же комплексные числа ±1i являются корнями характеристического уравнения (5), то частное решение уравнения (1) следует искать в форме

Пример 4. 21. Найти общее решение уравнения Решение:

1. Найдем общее решение у соответствующего однородного уравнения

Решая отвечающее ему характеристическое уравнение получаем корни r1 = -3, r2 = -1. Следовательно,

2. Перейдем к отысканию частного решения у* данного уравнения. Здесь правая часть f (x) = (8×2 + 84x)ex имеет вид (3): n = 2, P2(x) = 8×2 + 84x, k = 1, причем k = 1 не является корнем характеристического уравнения. Следовательно, частное решение у* нужно искать в форме

где A, B и C — некоторые коэффициенты, подлежащие определению. Для их отыскания воспользуемся тем, что у* должно быть решением данного уравнения. Найдем у*’ и у*»:

теперь подставим выражения для у*, у*’ и у*» в данное уравнение:

Сокращая обе части полученного равенства на ex и группируя члены при одинаковых степенях x, в результате получим

Это равенство выполняется тождественно только в том случае, когда коэффициенты при одинаковых степенях x в обеих частях равенства равны между собой.

Итак, имеем следующую систему уравнений для отыскания коэффициентов A, В и С:

Решая эту систему, найдем A = 1, В = 9, С = -7. Таким образом, получаем искомое частное решение

Теперь можно записать общее решение данного уравнения

Пример 4.22. Найти общее решение уравнения

Решение. 1. Найдем у.

Характеристическое уравнениеимеем корни

r = r = -3. Следовательно,

203

2. Найдем теперь у*. Здесь правая часть имеет вид (3): n = 0, P0 = 14, к = -3. Так как к = -3 является двукратным корнем характеристического уравнения, то частное решение у* следует искать в форме

у* = Ax2e-3x,

где A — коэффициент, подлежащий определению. Вычислим производные у*’ и у*»:

у* = (-3Ax2 + 2 Ax )e-3x, у*’ = (9Ax2 -12Ax + 2A)e-3x.

Подставляя выражения для у*, у*’ и у*» в данное уравнение, сокращая обе его части на e-3x и приводя подобные члены, в итоге получим 2A = 14, откуда A = 7. Следовательно, искомое частное решение имеет вид:

у* = 7x2e-3x.

Итак, общее решение данного уравнения

у = у + у* = (C1 + C2 x )e-3x + 7×2 e-3x.

Пример 4.23. Найти общее решение уравнения у» — 4у’ + 5у = 2 cos x + 6 sin x.

Решение. 1. Найдем у. Характеристическое уравнение r2 — 4r + 5 = 0

имеем корни Г1 2 = 2 ± i. Следовательно,

у = e2x(C1cosx + C2 sinx).

2. Будем теперь искать у*. Здесь правая часть f (x) имеет вид (4): а = 2, b = 6, l = ± i. Числа ± i не являются корнями характеристического уравнения, поэтому частное решение у* следует искать в форме

где A и В — неопределенные коэффициенты. Найдем производные у*’ и у*»:

подставляя теперь выражения для у*, у*’ и у*» в данное уравнение и группируя члены при cos x и sin x, в результате получим

Следовательно, для нахождения A и В имеем систему

откуда. Таким образом,

Итак, общее решение данного уравнения имеет вид:

Пример 4.24. Найти общее решение уравнения

Решение. 1. Найдем сначала у. Характеристическое уравнение г2 + 4 = 0, имеет корни Г1 2 = ± 2г. Следовательно,

2. Переходим к нахождению у*. Здесь правая часть f (x) имеет вид (4): а = 12, b = 0, I = ± 2г. Так как числа ± 2г являются корнями характеристического уравнения, то частное решение следует искать в форме

ПодставивВ данное уравнение и приведя подобные

члены, получим

откуда

т. е.Поэтому

Итак, общее решение

Пример 4.25. Найти частное решение уравнения удовлетворяющее начальным условиям у (0) = 0, у’ (0) = 1.

2

Решение. 1. Характеристическое уравнение r + 2т — 8 = 0 имеет корни T1 = -4, т2 = 2. Следовательно,

где А и В — неопределенные коэффициенты. Имеем

2. Правая часть данного уравнения имеет вид (3): n = 1, Так как к = 2 является однократным корнем характеристического уравнения, то частное решение у* ищем в форме

Подставляя у*, у*’ и у*» в данное уравнение, сокращая обе его одя подобные члены, оконч

части на е2х и приводя подобные члены, окончательно получим

12Ах + (2А + 6В) = 12х + 20.

Решая систему

Г12 А = 12,

{ 2 А + 6В = 20,

находим А = 1, В = 3. Отсюда

у* = (х2 + 3х)е2х.

Итак, найдено общее решение данного уравнения

у = у + у* = С1е-4х + С2 е2 х + (х2 + 3х)е2х.

3. Для нахождения искомого частного решения воспользуемся заданными начальными условиями. Найдем производную общего решения

у’ = -4С1е-4х + 2С2е2х + (2х2 + 8х + 3)е2х;

подставив в выражения для общего решения и его производной значения х = 0, у = 0, у’ = 1, получим систему уравнений для нахождения С1 и С2:

0 = С1 + С2,

1 = -4С1 + 2С2 + 3.

Отсюда С1 = 3, С2 = — 1. Таким образом, искомое частное решение имеет вид;

у = I е-4х -1 е2х + (х2 + 3х)е2х.

Краткий курс высшей математики

Краткий курс высшей математики

Шнейдер В. Е. и др. Краткий курс высшей математики. Учеб. пособие для втузов. М., «Высш. школа», 1972. 640 с. Данное учебное пособие предназначено для студентов вечерних факультетов втузов и заводов-втузов. Оно в основном охватывает весь материал, предусмотренный обязательной программой. Достаточное количество решенных примеров и задач способствует лучшему усвоению теоретического материала. Оглавление ПРЕДИСЛОВИЕ ГЛАВА I. МЕТОД КООРДИНАТ. ПОНЯТИЕ ФУНКЦИИ § 1. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. КООРДИНАТЫ ТОЧКИ НА ПРЯМОЙ 2. Геометрическое изображение действительных чисел. Координаты точки на прямой 3. Абсолютная величина действительного числа 4. Расстояние между двумя точками на прямой § 2. КООРДИНАТЫ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ 2. Расстояние между двумя точками на плоскости 3. Деление отрезка в данном отношении 4. Координаты точки в пространстве 5. Расстояние между двумя точками в пространстве § 3. УГОЛ МЕЖДУ ДВУМЯ ОСЯМИ. ПОЛЯРНЫЕ КООРДИНАТЫ 2. Полярные координаты 3. Зависимость между декартовыми и полярными координатами § 4. ФУНКЦИОНАЛЬНАЯ ЗАВИСИМОСТЬ 2. Понятие функции 3. График функции 4. Способы задания функций 5. Основные элементарные функции и их графики 6. Сложные функции. Элементарные функции 7. Целые и дробно-рациональные функции 8. Функции четные и нечетные. Периодические функции § 5. УРАВНЕНИЕ ЛИНИИ 2. Нахождение уравнения линии по ее геометрическим свойствам § 6 ПРЕОБРАЗОВАНИЕ КООРДИНАТ 2. Поворот осей координат ГЛАВА II. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ § 1. ПРЯМАЯ 2. Уравнение прямой с угловым коэффициентом 3. Уравнение прямой, параллельной оси ординат 4. Общее уравнение прямой и его частные случаи 5. Точка пересечения прямых. Построение прямой по ее уравнению 6. Вычисление угла между двумя прямыми. Условия параллельности и перпендикулярности двух прямых 7. Уравнение прямой, проходящей через данную точку в заданном направлении 8. Пучок прямых 9. Уравнение прямой, проходящей через две данные точки 10. Расстояние от точки до прямой § 2. КРИВЫЕ ВТОРОГО ПОРЯДКА 2. Окружность 3. Эллипс 4. Гипербола 5. Парабола 6. Окружность, эллипс, гипербола и парабола как конические сечения 7. Упрощение уравнения кривой второго порядка. График квадратного трехчлена 8. Уравнение равносторонней гиперболы, асимптоты которой приняты за оси координат 9. График дробно-линейной функции 10. Преобразование уравнения кривой второго порядка, не содержащего члена с произведением координат ГЛАВА III. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ И ВЕКТОРНОЙ АЛГЕБРЫ § 1. ЭЛЕМЕНТЫ ТЕОРИИ ОПРЕДЕЛИТЕЛЕЙ 2. Определитель третьего порядка 3. Понятие об определителях высших порядков § 2. СИСТЕМЫ УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ 2. Однородная система двух уравнений первой степени с тремя неизвестными 3. Система трех уравнений первой степени с тремя неизвестными 4. Однородная система трех уравнений первой степени с тремя неизвестными § 3. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ 2. Линейные операции над векторами 4. Проекция вектора на ось и составляются вектора по оси 5. Разложение вектора на составляющие по осям координат 6. Направляющие косинусы вектора 7. Условие коллинеарности двух векторов 8. Скалярное произведение 9. Выражение скалярного произведения через проекции перемножаемых векторов 10. Косинус угла между двумя векторами 11. Векторное произведение 12. Выражение векторного произведения через проекции перемножаемых векторов 13. Смешанное произведение трех векторов 14. Геометрический смысл смешанного произведения 15. Условие компланарности трех векторов § 4. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ 2. Равенство матриц. Действия над матрицами 3. Обратная матрица 4. Матричная запись и матричное решение системы уравнений первой степени § 5. ЛИНЕЙНЫЕ ОТОБРАЖЕНИЯ 2. Преобразование координат 3. Приведение квадратичной формы к каноническому виду 4. Упрощение общего уравнения кривой второго порядка ГЛАВА IV. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ § 1. ПЛОСКОСТЬ 2. Нормальный вектор плоскости. Уравнение плоскости, проходящей через данную точку 3. Общее уравнение плоскости и его частные случаи 4. Построение плоскости по ее уравнению 5. Угол между плоскостями. Условия параллельности и перпендикулярности двух плоскостей 6. Точка пересечения трех плоскостей § 2. ПРЯМАЯ В ПРОСТРАНСТВЕ 2. Общие уравнения прямой 3. Векторное уравнение прямой. Параметрические уравнения прямой 4. Канонические уравнения прямой 5. Уравнения прямой, проходящей через две точки 6. Угол между двумя прямыми. Условия параллельности и перпендикулярности прямых § 3. Прямая и плоскость в пространстве 2. Точка пересечения прямой с плоскостью 3. Расстояние от точки до плоскости 4. Пучок плоскостей § 4. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА 2. Цилиндрические поверхности 3. Конические поверхности 4. Поверхность вращения 6. Гиперболоиды 7. Параболоиды ГЛАВА V. ТЕОРИЯ ПРЕДЕЛОВ § 1. ПРЕДЕЛ ФУНКЦИИ 2. Предел функции при х -> -оо 3. Предел функции при х->х0 4. Бесконечно малые функции. Ограниченные функции 5. Бесконечно большие функции и их связь с бесконечно малыми функциями 6. Основные теоремы о пределах 7. Предел функции при x -> 0 8. Последовательность. Число e 9. Натуральные логарифмы 10. Сравнение бесконечно малых функций § 2. НЕПРЕРЫВНЫЕ ФУНКЦИИ 2. Операции над непрерывными функциями. Непрерывность элементарных функций 3. Свойства функций, непрерывных на сегменте 4. Понятие об обратной функции 5. Обратные тригонометрические функции 6. Показательная и логарифмическая функции 7. Понятие о гиперболических функциях ГЛАВА VI. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ 1. Приращение аргумента и приращение функции 2. Определение непрерывности функции с помощью понятии приращения аргумента и приращения функции 3. Задачи, приводящие к понятию производной 4. Определение производной и ее механический смысл 5. Дифференцируемость функции 6. Геометрический смысл производной 7. Производные некоторых основных элементарных функций 8. Основные правила дифференцирования 9. Производная обратной функции 10. Производные обратных тригонометрических функций 11. Производная сложной функции § 12. Производные гиперболических функций 13. Производная степенной функции с любым показателем 14. Сводная таблица формул дифференцирования 15. Неявные функции и их дифференцирование 16. Уравнения касательной а нормали к кривой 17. Графическое дифференцирование § 2. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ 1. Нахождение производных высших порядков 2. Механический смысл второй производной § 3. ДИФФЕРЕНЦИАЛ ФУНКЦИИ 2. Производная как отношение дифференциалов 3. Дифференциал суммы, произведения и частного функций 4. Дифференциал сложной функции. Инвариантность формы дифференциала 5. Применение дифференциала к приближенным вычислениям 6. Дифференциалы высших порядков § 4. ФУНКЦИИ, ЗАДАННЫЕ ПАРАМЕТРИЧЕСКИ, И ИХ ДИФФЕРЕНЦИРОВАНИЕ 2. Дифференцирование функций, заданных параметрически § 5. ВЕКТОРНАЯ ФУНКЦИЯ СКАЛЯРНОГО АРГУМЕНТА 2. Векторная функция скалярного аргумента и ее производная 3. Уравнения касательной прямой и нормальной плоскости к пространственной кривой 4. Механический смысл первой и второй производных векторной функции скалярного аргумента § 6. НЕКОТОРЫЕ ТЕОРЕМЫ О ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ 2. Теорема Ролля 3. Теорема Лагранжа 4. Правило Лопиталя § 7. ПРИЛОЖЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИЙ И ПОСТРОЕНИЮ ГРАФИКОВ 2. Максимум и минимум функции 3. Достаточный признак существования экстремума, основанный на знаке второй производной 4. Отыскание наибольшего и наименьшего значений функции 5. Применение теории максимума и минимума к решению задач 6. Выпуклость и вогнутость графика функции. Точки перегиба 7. Асимптоты графика функции 8. Общая схема исследования функции и построение ее графика § 8. ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ 2. Уточнение найденных значений корней методом хорд и касательных § 9. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА ЛАГРАНЖА ГЛАВА VII. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО СВОЙСТВА 2. Геометрический смысл неопределенного интеграла 3. Таблица основных интегралов 4. Основные свойства неопределенного интеграла § 2. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ 2. Интегрирование методом замены переменной 3. Интегрирование по частям § 3. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ 2. Рациональные дроби. Выделение правильной рациональной дроби 3. Интегрирование простейших рациональных дробей 4. Разложение правильной рациональной дроби на простейшие дроби 5. Метод неопределенных коэффициентов 6. Интегрирование рациональных дробей § 4. Интегрирование тригонометрических функций 2. Рациональные функции двух переменных 3. Интегралы вида § 5. ИНТЕГРИРОВАНИЕ НЕКОТОРЫХ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ 2. Интеграл вида 3. Интегралы видов 4. Интегралы вида § 6. ОБЩИЕ ЗАМЕЧАНИЯ О МЕТОДАХ ИНТЕГРИРОВАНИЯ. ИНТЕГРАЛЫ, НЕ БЕРУЩИЕСЯ В ЭЛЕМЕНТАРНЫХ ФУНКЦИЯХ 2. Понятие об интегралах, не берущихся в элементарных функциях ГЛАВА VIII. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ § 1. ЗАДАЧИ, ПРИВОДЯЩИЕ К ОПРЕДЕЛЕННОМУ ИНТЕГРАЛУ 2. Задача о работе переменной силы § 2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 2. Свойства определенного интеграла 3. Производная интеграла по переменной верхней границе 4. Формула Ньютона—Лейбница 5. Замена переменной в определенном интеграле 6. Интегрирование по частям в определенном интеграле § 3. ГЕОМЕТРИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА 2. Вычисление площади в полярных координатах 3. Вычисление объема тела по известным поперечным сечениям 4. Объем тела вращения 5. Длина дуги кривой 6. Дифференциал дуги 7. Площадь поверхности вращения 8. Общие замечания о решении задач методом интегральных сумм § 4. КРИВИЗНА ПЛОСКОЙ КРИВОЙ 2. Вычисление кривизны 3. Радиус кривизны. Круг кривизны. Центр кривизны 4. Эволюта и эвольвента § 5. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 2. Интегралы от разрывных функций 3. Признаки сходимости несобственных интегралов § 6. ПРИБЛИЖЕННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ 2. Метод трапеций 3. Метод параболических трапеций (метод Симпсона) ГЛАВА IX. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ § 1. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 2. График функции двух переменных 3. Функции трех и большего числа переменных § 2. Предел функции нескольких переменных. Непрерывность функции. Точки разрыва 2. Непрерывность функции нескольких переменных 3. Понятие области 4. Точки разрыва 5. Свойства функций, непрерывных в ограниченной замкнутой области § 3. ЧАСТНЫЕ ПРОИЗВОДНЫЕ 2. Геометрический смысл частных производных функции двух переменных 3. Частные производные высших порядков § 4. ПОЛНЫЙ ДИФФЕРЕНЦИАЛ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 2. Полный дифференциал функции 3. Приложение полного дифференциала к приближенным вычислениям § 5. Дифференцирование сложных и неявных функций 2. Инвариантность формы полного дифференциала 3. Дифференцирование неявных функций § 6. СКАЛЯРНОЕ ПОЛЕ 2. Производная по направлению 3. Градиент 4. Касательная плоскость а нормаль к поверхности 5. Геометрический смысл полного дифференциала функции двух переменных § 7. ЭКСТРЕМУМ ФУНКЦИЙ ДВУХ ПЕРЕМЕННЫХ 2. Наибольшее и наименьшее значения функции двух переменных ГЛАВА X. КРАТНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ § 1. ДВОЙНОЙ ИНТЕГРАЛ 2. Двойной интеграл. Теорема существования 3. Свойства двойного интеграла 4. Вычисление двойного интеграла в декартовых координатах 5. Вычисление двойного интеграла в полярных координатах 6. Приложения двойного интеграла § 2. ТРОЙНОЙ ИНТЕГРАЛ 2. Тройной интеграл и его свойства 3. Вычисление тройного интеграла в декартовых координатах 4. Вычисление тройного интеграла в цилиндрических координатах 5. Приложения тройного интеграла § 3. КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ 2. Задача о работе. Криволинейный интеграл 3. Вычисление криволинейного интеграла 4. Формула Остроградского — Грина 5. Независимость криволинейного интеграла от пути интегрирования 6. Отыскание первообразной по полному дифференциалу 7. Криволинейный интеграл по длине дуги ГЛАВА XI. РЯДЫ § 1. ЧИСЛОВЫЕ РЯДЫ 2. Геометрическая прогрессия 3. Простейшие свойства числовых рядов 4. Необходимый признак сходимости ряда 5. Достаточные признаки сходимости знакоположительных рядов 6. Знакопеременные ряды 7. Остаток ряда и его оценка § 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ 2. Правильно сходящиеся функциональные ряды и их свойства § 3. СТЕПЕННЫЕ РЯДЫ 2. Свойства степенных рядов 3. Ряды по степеням разности х-а 4. Разложение функций в степенные ряды. Ряд Тейлора 5. Разложение некоторых элементарных функций в ряды Тейлора и Маклорена § 4. ПРИЛОЖЕНИЕ РЯДОВ К ПРИБЛИЖЕННЫМ ВЫЧИСЛЕНИЯМ 2. Приближенное вычисление интегралов § 5. ПОНЯТИЕ О ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ. СТЕПЕННЫЕ РЯДЫ В КОМПЛЕКСНОЙ ОБЛАСТИ 2. Числовые ряды с комплексными членами 3. Степенные ряды в комплексной области § 6. РЯДЫ ФУРЬЕ 2. Ряд Фурье 3. Сходимость ряда Фурье 4. Ряды Фурье для четных и нечетных функций 5. Разложение в ряд Фурье функций с периодом 2l ГЛАВА XII. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ § 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА 2. Дифференциальные уравнения первого порядка 3. Уравнения с разделяющимися переменными 4. Однородные уравнения 5. Линейные уравнения 6. Уравнение в полных дифференциалах 7. Особые решения 8. Приближенное решение дифференциальных уравнений первого порядка методом Эйлера § 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА 2. Простейшие уравнения второго порядка, допускающие понижение порядка 3. Понятие о дифференциальных уравнениях высших порядков § 3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА 2. Линейные однородные дифференциальные уравнения второго порядка 3. Линейные неоднородные дифференциальные уравнения второго порядка 4. Метод вариации произвольных постоянных § 4. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ 2. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами 3. Приложение линейных дифференциальных уравнений второго порядка к изучению механических и электрических колебаний § 5. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ 2. Линейные дифференциальные уравнения n-го порядка с постоянными коэффициентами § 6. ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПОМОЩЬЮ РЯДОВ § 7. ПОНЯТИЕ О СИСТЕМАХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ 2. Системы линейных дифференциальных уравнений с постоянными коэффициентами ПРИЛОЖЕНИЕ 1. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА ПРИЛОЖЕНИЕ 2. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ

2.

2: Линейные ОДУ второго порядка с постоянным коэффициентом

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

350

• Йиржи Лебл
• Университет штата Оклахома

Решение уравнений с постоянными коэффициентами

Предположим, у нас есть задача

\[ y» — 6y’ + 8y = 0, y(0) = -2, y'(0) = 6 \nonumber \]

Это линейное однородное уравнение второго порядка с постоянными коэффициентами. Постоянные коэффициенты означают, что функции перед \(y»\), \(y’\) и \(y\) являются константами и не зависят от \(x\).

Чтобы угадать решение, подумайте о функции, которая, как вы знаете, остается практически неизменной, когда мы ее дифференцируем, чтобы мы могли взять функцию и ее производные, сложить вместе несколько кратных и получить ноль. {4x} \nonumber \] 92 + 1 = 0 \) не имеет действительных корней, но имеет два комплексных корня. Здесь мы рассмотрим некоторые свойства комплексных чисел.

Комплексные числа могут показаться странной концепцией, особенно из-за терминологии. В комплексных числах нет ничего воображаемого или действительно сложного. Комплексное число — это просто пара действительных чисел \((a,b)\). Мы можем думать о комплексном числе как о точке на плоскости. Мы складываем комплексные числа простым способом: \( (a, b) + (c, d) = (a + c, b + d) \). Определяем умножение на 9{3x} \sin (2x) \nonumber \]

Сноски

[1] Обоснованное предположение с некоторыми параметрами для решения является таким центральным методом в дифференциальных уравнениях, что люди иногда используют причудливое название для такого предположения : ansatz , по-немецки «начальное размещение инструмента на заготовке». Да, у немцев есть слово для этого.

---

Эта страница под названием 2. 2: Линейные ОДУ второго порядка с постоянным коэффициентом распространяется под лицензией CC BY-SA 4.0 и была создана, изменена и/или курирована Йиржи Леблом посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Йиржи Лебль

   Лицензия

   CC BY-SA

   Версия лицензии

   4,0

   Показать страницу TOC

   нет

2. Теги

   1. Формула Эйлера
   2. источник@https://www. jirka.org/diffyqs

Дифференциальные уравнения — Неоднородные дифференциальные уравнения

Онлайн-заметки Пола
Главная / Дифференциальные уравнения / DE второго порядка / Неоднородные дифференциальные уравнения

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Уведомление для мобильных устройств

Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 3.8: Неоднородные дифференциальные уравнения

Пришло время подумать о том, как решать неоднородные дифференциальные уравнения. Линейное неоднородное дифференциальное уравнение второго порядка имеет вид

. \[\begin{equation}y» + p\left( t \right)y’ + q\left( t \right)y = g\left( t \right)\label{eq:eq1}\end{ уравнение}\]

где \(g(t)\) — ненулевая функция. Обратите внимание, что мы не использовали здесь постоянные коэффициенты, потому что все, что мы собираемся сделать в этом разделе, не требует этого. Кроме того, мы используем коэффициент 1 для второй производной просто для того, чтобы часть работы было немного легче записать. Не обязательно быть 1.

Прежде чем говорить о том, как решить одну из них, нам нужно разобраться с некоторыми основами, что и является целью этого раздела.

Сначала позвоним по номеру

\[\begin{equation}y» + p\left( t \right)y’ + q\left( t \right)y = 0\label{eq:eq2}\end{equation}\]

ассоциированное однородное дифференциальное уравнение с \(\eqref{eq:eq1}\).

Теперь давайте рассмотрим следующую теорему.

Теорема

Предположим, что \(Y_{1}(t)\) и \(Y_{2}(t)\) являются двумя решениями \(\eqref{eq:eq1}\) и что \(y_ {1}(t)\) и \(y_{2}(t)\) являются фундаментальным набором решений ассоциированного однородного дифференциального уравнения \(\eqref{eq:eq2}\), тогда

\[{Y_1}\влево( t \вправо) — {Y_2}\влево( t \вправо)\]

является решением \(\eqref{eq:eq2}\) и может быть записано как

\[{Y_1}\left( t \right) — {Y_2}\left( t \right) = {c_1}{y_1}\left( t \right) + {c_2}{y_2}\left( t \right )\]

Обратите внимание на используемые здесь обозначения. Заглавными буквами обозначались решения \(\eqref{eq:eq1}\), а строчными буквами обозначались решения \(\eqref{eq:eq2}\). Это довольно распространенное соглашение при работе с неоднородными дифференциальными уравнениями. 9\prime + q\left( t \right){Y_2} & = g\left( t \right)\end{align*}\]

Итак, мы смогли доказать, что разность двух решений является решением \(\eqref{eq:eq2}\).

Доказательство того, что

\[{Y_1}\left( t \right) — {Y_2}\left( t \right) = {c_1}{y_1}\left( t \right) + {c_2}{y_2}\left( t \right )\]

еще проще. Поскольку \(y_{1}(t)\) и \(y_{2}(t)\) являются фундаментальным набором решений \(\eqref{eq:eq2}\), мы знаем, что они образуют общее решение поэтому любое решение \(\eqref{eq:eq2}\) можно записать в виде

\[y\left( t \right) = {c_1}{y_1}\left( t \right) + {c_2}{y_2}\left( t \right)\]

Итак, \(Y_{1}(t) — Y_{2}(t)\) является решением \(\eqref{eq:eq2}\), как мы показали выше, поэтому его можно записывается как

\[{Y_1}\left( t \right) — {Y_2}\left( t \right) = {c_1}{y_1}\left( t \right) + {c_2}{y_2}\left( t \right )\]

Итак, что нам дает эта теорема? Мы можем использовать эту теорему, чтобы записать форму общего решения \(\eqref{eq:eq1}\). Предположим, что \(y(t)\) является общим решением \(\eqref{eq:eq1}\) и что \(Y_{P}(t)\) является любым решением \(\eqref{eq :eq1}\), которые мы можем получить. Тогда, используя вторую часть нашей теоремы, мы знаем, что

\[y\left( t \right) — {Y_P}\left( t \right) = {c_1}{y_1}\left( t \right) + {c_2}{y_2}\left( t \right)\ ]

где \(y_{1}(t)\) и \(y_{2}(t)\) являются фундаментальным набором решений для \(\eqref{eq:eq2}\). Решение для \(y(t)\) дает,

\[y\left( t \right) = {c_1}{y_1}\left( t \right) + {c_2}{y_2}\left( t \right) + {Y_P}\left( t \right)\ ]

Мы позвоним

\[{y_c}\left( t \right) = {c_1}{y_1}\left( t \right) + {c_2}{y_2}\left( t \right)\]

дополнительное решение и \(Y_{P}(t)\) частное решение. Тогда общее решение дифференциального уравнения можно записать в виде.

\[y\left( t \right) = {y_c}\left( t \right) + {Y_P}\left( t \right)\]

Итак, чтобы решить неоднородное дифференциальное уравнение, нам нужно решить однородное дифференциальное уравнение, \(\eqref{eq:eq2}\), что для дифференциальных уравнений с постоянными коэффициентами довольно легко сделать, и нам понадобится решение \(\eqref{eq:eq1}\).

Тест Рациональные дроби и их свойства по алгебре (8 класс)

Последний раз тест пройден 14 часов назад.

Для учителя

Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.

Опыт работы учителем математики — более 33 лет.

1. Вопрос 1 из 10

   Найдите значение x, при котором дробь не имеет смысла

   • 4

   • -2

   • -4

   • нет таких значений

   Подсказка

   Правильный ответ

   Неправильный ответ

   В вопросе ошибка?

2. Вопрос 2 из 10

   Выполните сложение

   Подсказка

   Правильный ответ

   Неправильный ответ

   В вопросе ошибка?

3. Вопрос 3 из 10

   Выполните действия

   Подсказка

   Правильный ответ

   Неправильный ответ

   В вопросе ошибка?

4. Вопрос 4 из 10

   Выполните вычитание

   Подсказка

   Правильный ответ

   Неправильный ответ

   В вопросе ошибка?

5. Вопрос 5 из 10

   Выполните действия

   Подсказка

   Правильный ответ

   Неправильный ответ

   В вопросе ошибка?

6. Вопрос 6 из 10

   Выполните действия

   Подсказка

   Правильный ответ

   Неправильный ответ

   В вопросе ошибка?

7. Вопрос 7 из 10

   Выполните действия

   Подсказка

   Правильный ответ

   Неправильный ответ

   В вопросе ошибка?

8. Вопрос 8 из 10

   Найдите значение дроби

   • 2,75

   • 2,5

   • 0,2

   • 1,5

   Подсказка

   Правильный ответ

   Неправильный ответ

   В вопросе ошибка?

9. Вопрос 9 из 10

   Найдите значение x, при котором дробь не имеет смысла

   • 2

   • -2

   • -4

   • нет таких значений

   Подсказка

   Правильный ответ

   Неправильный ответ

   В вопросе ошибка?

10. Вопрос 10 из 10

    Сократите дробь

    Подсказка

    Правильный ответ

    Неправильный ответ

    В вопросе ошибка?

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Ника Дзгоева

  9/10

• Vova Pasternak

  10/10

• Николай Сенькин

  10/10

• Антонина Смышляева

  9/10

• Саша Лобач

  10/10

Рейтинг теста

3.5

Средняя оценка: 3.5

Всего получено оценок: 804.

---

А какую оценку получите вы? Чтобы узнать — пройдите тест.

Контрольная работа №1 по теме:»Рациональные дроби»

Контрольная работа №1 по теме:»Рациональные дроби»

12+  Свидетельство СМИ ЭЛ № ФС 77 — 70917 Лицензия на образовательную деятельность №0001058

Пользовательское соглашение     Контактная и правовая информация

 

Педагогическое сообщество УРОК.РФ

Бесплатные всероссийские конкурсы

Бесплатные сертификаты за публикации

Нужна помощь? Инструкции для новых участников

Бесплатная   онлайн-школа для 1-4 классов

Всё для аттестацииПубликация в сборникеВебинарыЛэпбукиПрофтестыЗаказ рецензийНовости

Библиотека

▪Учебно-дидактические материалы

▪Контрольные / проверочные работы

Материал опубликовал

0

#8 класс #Алгебра #ФГОС #Учебно-дидактические материалы #Контрольные / проверочные работы #Учитель-предметник #Школьное образование #УМК Ю. Н. Макарычева

Контрольная работа по теме: «Рациональные дроби», 8 класс

Вариант 1	Вариант 2
1. При каких значениях букв данная алгебраическая дробь имеет смысл?	1. При каких значениях букв данная алгебраическая дробь имеет смысл?
2.Сократите дробь:	2.Сократите дробь:
3. Представьте в виде дроби:	3. Представьте в виде дроби:
4. Найдите значение выражения	4. Найдите значение выражения
5. Упростите выражение:	5. Упростите выражение:
6. Постройте график функции:	6. Постройте график функции:

Опубликовано 05.01.20 в 15:26

Чтобы написать комментарий необходимо авторизоваться.

Закрыть

Решение рациональных и дробных функций

Все ресурсы SAT II Math I

6 Диагностические тесты 113 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 Следующая →

SAT II Math I Help » Функции и графики » Решающие функции » Решение рациональных и дробных функций

Упростить:

Возможные ответы:

Правильный ответ:

Объяснение:

Возведение дроби в отрицательную степень путем возведения обратной величины в степень абсолютного значения показателя степени. Затем примените свойства показателей степени следующим образом:

Сообщить об ошибке

Упростить

Возможные ответы:

Правильный ответ:

9000 4

Объяснение:

Чтобы упростить эту задачу, нам нужно найти наименьший общий знаменатель между двумя дробями. Для этого посмотрим на 5 и на 8. Наименьшее общее число между этими двумя числами равно 40.

Чтобы переписать каждую дробь в виде знаменателя 40, нам нужно умножить следующим образом:

мы можем умножить на 8/8 и 5/5, потому что эти дроби на самом деле просто 1, записанные в другом формате.

Теперь, используя порядок операций, мы получаем следующее

Теперь у нас есть общий знаменатель, и мы можем выполнить сложение, чтобы получить упрощенное число:

Сообщить об ошибке

Решите следующее уравнение, чтобы найти .

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы найти , мы должны сначала найти наименьший общий знаменатель. В этом случае это: 

Теперь уравнение можно записать в следующем виде:

Решая для , мы получаем: 

Сообщить об ошибке

Какой наименьший общий знаменатель для  и ?

Возможные ответы:

Правильный ответ:

Объяснение:

При нахождении наименьшего общего знаменателя самым быстрым способом является перемножение чисел.

В этом случае и  общий коэффициент, отличный от , который равный . Мы можем разделить эти числа на получение и остаток.

Так вот, у них нет общего множителя, так что просто умножьте их на общий множитель. Ответ 

 

Другой подход состоит в том, чтобы перечислить множители обоих чисел и найти множитель, который появляется в обоих наборах первым.

Мы видим, что в обоих наборах стоит перед любым другим числом, таким образом, это наш ответ.

 

Сообщить об ошибке

Упростите следующее:

Возможные ответы:

Правильный ответ:

 

Пояснение:

Чтобы упростить сумму двух дробей, мы должны найти общий знаменатель.

Упрощая знаменатель первой дроби, получаем

, потому что знаменатель представляет собой разность двух квадратов, которая имеет вид

Теперь мы можем переписать сумму как

9 0004 Это намного проще чтобы увидеть общий знаменатель сейчас:

 

Сообщить об ошибке

Решить:

Возможные ответы:

Правильный ответ: 9001 8

Объяснение:

Чтобы решить это уравнение, мы должны найти наименьший общий знаменатель, чтобы сложить дроби.

Имейте в виду, что знаменатель второго члена представляет собой разность квадратов, которую можно переписать как

Это наименьший общий знаменатель.

Теперь умножаем обе части уравнения на ЖК-дисплей сверху и снизу (по сути это 1):

После отмены членов получаем

Теперь находим x:

9 0005

 

Сообщить об ошибке

Упростить 

Возможные ответы:

Правильный ответ:

Объяснение:

Найдите наименьший общий знаменатель (НОД) и преобразуйте каждую дробь в НДО, а затем сложите. Упрощайте по мере необходимости.

Результатом является неправильная дробь, потому что числитель больше знаменателя и может быть упрощен и преобразован в смешанное числительное.

Сообщить об ошибке. 18

Пояснение:

Начните с приведения обеих дробей к одному знаменателю. Один из вариантов

Затем скорректируйте числители, умножив числитель каждой дроби на знаменатель другой дроби: 

Затем добавьте скорректированные числители: 

Затем мы упростим, разделив числитель и знаменатель на 2:

что дает нам окончательный результат.

Сообщить об ошибке

Упрощение:

Возможные ответы:

Правильный ответ:

Пояснение:

Чтобы разделить дроби, нужно первую дробь умножить на обратную вторую.

Теперь умножьте числители и знаменатели вместе, затем упростите.

Сообщить об ошибке

Упрощение:

Возможные ответы:

Правильный ответ:

9000 4

Пояснение:

Чтобы разделить дроби, нужно первую дробь умножить на обратную вторую.

Теперь умножьте числители и знаменатели, затем упростите.

Сообщить об ошибке

← Предыдущая 1 2 Следующая →

Уведомление об авторских правах

Все ресурсы SAT II Math I

6 Диагностические тесты 113 практических тестов Вопрос дня Карточки Learn by Concept

Руководство для преподавателей по математическим тестам для 3–8 классов 2023 г.

%PDF-1.4 % 1 0 объект >>> эндообъект 2 0 объект >поток приложение/pdf

Руководство для преподавателей по математическим тестам для 3–8 классов 2023 г.

Оценка Questar

Инк

2022-06-13T12:41:18-04:002022-06-13T12:41:26-04:002022-06-13T12:41:26-04:00Adobe InDesign 17.2 (Windows)uuid:6893e28a-f75b-46fe- be30-9246c8cbcc7fxmp.did:199c2ecd-41be-0d4a-83c7-822f3f1bf0cfxmp.id:b74310e5-898e-e347-9f17-ad5fa955cf44proof:pdfxmp. iid:6bc5e42f-a19e-2d43- a7f8-7c07a822b06axmp.did:d2ddbe5f-5fa3-7145- bc90-4d35b7db59c2xmp.did:199c2ecd-41be-0d4a-83c7-822f3f1bf0cfпо умолчанию

преобразовано из application/x-indesign в application/pdfAdobe InDesign 17.2 (Windows)/2022-06-13T12:41:18-04:00

Библиотека Adobe PDF 16.0.7False конечный поток эндообъект 14 0 объект > эндообъект 15 0 объект > эндообъект 3 0 объект > эндообъект 19 0 объект > эндообъект 20 0 объект > эндообъект 21 0 объект > эндообъект 22 0 объект > эндообъект 23 0 объект > эндообъект 24 0 объект > эндообъект 41 0 объект /LastModified/NumberOfPageItemsInPage 2/NumberofPages 1/OriginalDocumentID/PageItemUIDToLocationDataMap>/PageTransformationMatrixList>/PageUIDList>/PageWidthList>>>>>/Resources>/Font>/ProcSet[/PDF/Text]>>/TrimBox[0,0 0,0 612,0 792.0]/Тип/Страница>> эндообъект 42 0 объект /LastModified/NumberOfPageItemsInPage 2/NumberofPages 1/OriginalDocumentID/PageItemUIDToLocationDataMap>/PageTransformationMatrixList>/PageUIDList>/PageWidthList>>>>>/Resources>/Font>/ProcSet[/PDF/Text]/Properties>>>/TrimBox[0.

Глава 87. Однородные дифференциальные уравнения первого порядка

Определение

Уравнения вида

Называется Однородным, если и однородные функции степени .

Понятие однородного дифференциального уравнения связано с понятием однородной функции.

Определение

Функция называется Однородной функцией степени , если для произвольного числа выполняется равенство .

Пример

Выяснить, являются ли однородными следующие функции:

А) . Так как , то данная функция однородна степени 2.

Б) . . Функция однородна степени 0.

В) . . Данная функция неоднородная.

Дифференциальное уравнение вида (8.4.1) можно привести к виду

И при помощи подстановки ( – неизвестная функция) преобразовать в уравнение с разделяющимися переменными. Поскольку , то Þ Þ Þ .После того, как общее решение последнего уравнения будет найдено, необходимо вернуться к старой функции .

Пример

Решить уравнение .

Решение

Разделим уравнение почленно на . Получим . Выполним замену . Следовательно, . Подстановка в исходное уравнение дает Þ – уравнение с разделяющимися переменными. Решая его, получим . Возвращаясь к функции , получим общее решение уравнения: .

Логарифмирование решения дает: .

Пример

Найти частное решение уравнения в точке .

Решение

Уравнение однородное нулевой степени – или . В результате подстановки (, ) получим уравнение с разделяющимися переменными относительно функции : . Интегрирование этого уравнения дает функцию: . Следовательно, общее решение исходного уравнения имеет вид: . Частное решение, соответствующее начальному условию, имеет вид: .

Определение

Дифференциальное уравнение вида

Где и – непрерывные функции, называется Линейным дифференциальным уравнением первого порядка.

Неизвестная функция и ее производная входят в указанное уравнение линейно, что и объясняет название уравнения.

Если , то уравнение (8.4.3) называется Линейным однородным уравнением, если же , то уравнение (8.4.3) называется Линейным неоднородным уравнением.

Пусть линейное однородное уравнение.

Соответствует уравнению (8.4.3). Мы рассмотрим так называемый метод вариации постоянной – метод решения неоднородного уравнения, основанный на предварительном решении однородного уравнения (8.4.4).

Уравнение (8.4.2) можно решить методом разделения переменных:

, откуда .

Потенцируя, получаем общее решение уравнения (8.4.4):

Где .

Общее решение неоднородного уравнения (8.4.3) ищем в виде (8.4.5), полагая константу новой неизвестной функцией от аргумента.

Подставим решение (8.4.5а¢) в уравнение (8.4.3).

,

Откуда после приведения подобных получаем уравнение для :

Интегрирование уравнения (8.4.4) дает выражение для : .

Подставляя выражение для в формулу общего решения, получаем окончательное выражение для решения неоднородного уравнения:

Где – произвольная постоянная.

Следует отметить, что некоторые нелинейные уравнения приводятся к линейным уравнениям соответствующими заменами неизвестной функции . К таковым относится Уравнение Бернулли:

Где и – непрерывные функции, а – некоторое постоянное число. При имеем линейное неоднородное уравнение, а при – линейное однородное уравнение .

Пусть и . Введем новую функцию . Тогда . Поделим обе части уравнения (8.4.8) на и умножим на : .

Выполняя замену, получим линейное неоднородное уравнение относительно новой функции : . Метод решения последнего нами уже изучен.

Пример

Решить уравнение .

Решение

Это линейное неоднородное уравнение первого порядка. Сначала решим соответствующее однородное уравнение . Разделяя переменные, получим Þ .

Полагая функцией от и подставляя найденное решение в исходное неоднородное уравнение, получаем после приведения подобных дифференциальное уравнение для : .

После интегрирования этого уравнения и подстановки в уже найденное решение однородного уравнения получим искомое общее решение исходного уравнения: .

Пример

Решить уравнение .

Решение

Опять начнем с однородного уравнения . После разделения переменных и интегрирования уравнения получаем общее решение однородного уравнения . Полагая, что , получаем после подстановки в неоднородное уравнение . Откуда . Стало быть, общее решение исходного уравнения имеет вид .

Пример

Решить уравнение .

Решение

Данное нелинейное уравнение представляет собой уравнение Бернулли при . Заменой искомой функции мы получим линейное неоднородное уравнение относительно : . По формуле (8.4.7) получаем общее решение этого уравнения . Теперь выполняя обратную замену , получаем решение исходного нелинейного уравнения:

Рассмотрим еще один из возможных способов решения линейного неоднородного уравнения (8.4.3) и уравнения Бернулли (8.4.8).

Решение этих уравнений ищем в виде произведения двух функций . Тогда линейное уравнение и уравнение Бернулли сводятся к двум уравнениям с разделяющимися переменными.

Так как , то линейное уравнение (8. 4.3) преобразуется к виду .

Найдем сначала какое–нибудь частное решение уравнения . Тогда функция Решение уравнения .

Пример

Решить уравнение .

Решение

Исходное уравнение есть линейное неоднородное уравнение . Пусть , тогда . Следовательно, или . Положим . Проинтегрировав это уравнение, найдем какое–нибудь частное решение этого уравнения . Например, при получаем . Подставляя в уравнение Функцию , получим уравнение относительно функции : . Решением этого уравнения с разделяющимися переменными есть функция . Окончательное выражение для решения исходного уравнения имеет вид .

3. Однородные дифференциальные уравнения первого порядка

Понятие однородного дифференциального уравнения первого порядка связано с однородными функциями.

Определение 1.Функция f(X,y) называется однородной функцией n-ого измерения (n-ой степени) относительно переменных X и y,если при любом t справедливо тождество

Например, функция — однородная функция первого измерения, так как

;

— однородная функция третьего измерения , так как

;

— однородная функция нулевого измерения, так как

, т.е..

Определение 2.Дифференциальное уравнение первого порядкаy‘ = f(x,y) называется однородным, если функцияf(x,y) есть однородная функция нулевого измерения относительноx иy, или, как говорят,f(x,y) – однородная функция степени нуль.

Его можно представить в виде

где P(x,y) иQ(x,y) – однородные функции одинакового измерения: отношение двух однородных функций одного и того же измерения является однородной функцией нулевого измерения (см. третий из приведенных выше примеров).

Возможна следующая форма записи уравнения (3.2):

что позволяет определить однородное уравнение как такое дифференциальное, которое можно преобразовать к виду (3.3).

Замена приводит однородное уравнение к уравнению с разделяющимися переменными. Действительно, после подстановкиу = xzполучим,Разделяя переменные и интегрируя, найдем:

,

Пример 1.Решить уравнение .

 Полагаем у = zx, Подставляем эти выраженияy иdyв данное уравнение:илиРазделяем переменные:и интегрируем:,

Заменяя zна, получим.

Пример 2. Найти общее решение уравнения.

 В данном уравнении P (x,y) =x²-2y²,Q(x,y) =2xy– однородные функции второго измерения, следовательно, данное уравнение является однородным. Его можно представить в видеи решать так же, как и представленное выше. Но используем другую форму записи. Положимy = zx, откудаdy = zdx + xdz. Подставляя эти выражения в исходное уравнение, будем иметь

,

то есть

или

dx+2zxdz = 0.

Разделяем переменные, считая

.

Интегрируем почленно это уравнение

, откуда

то есть . Возвращаясь к прежней функциинаходим общее решение

Пример 3. Найти общее решение уравнения.

 Цепочка преобразований: ,y = zx,, , , , , , , , , . 

Лекция 8.

4. Линейные дифференциальные уравнения первого порядка Линейное дифференциальное уравнение первого порядка имеет вид

,

(4.1)

где ,,c(x) – непрерывные функции.

Если, то уравнение (4.1) можно записать в приведённом виде

(4. 1a)

Здесь – свободный член, называемый также правой частью уравнения. В этом виде будем рассматривать линейное уравнение в дальнейшем.

Если 0, то уравнение (4.1а) называется линейным неоднородным. Если же0, то уравнение принимает вид

(4.2)

и называется линейным однородным.

Название уравнения (4.1а) объясняется тем, что неизвестная функция y и её производнаявходят в него линейно, т.е. в первой степени.

В линейном однородном уравнении переменные разделяются. Переписав его в виде откудаи интегрируя, получаем:,т.е.

(4. 3)

При делении на теряем решение. Однако оно может быть включено в найденное семейство решений (4.3), если считать, чтоСможет принимать и значение 0.

Существует несколько методов решения уравнения (4.1а). Согласно методу Бернулли, решение ищется в виде произведения двух функций отх:

(4.4)

Одна из этих функций может быть выбрана произвольно, так как лишь произведение uv должно удовлетворять исходному уравнению, другая определяется на основании уравнения (4.1а).

Дифференцируя обе части равенства (4.4), находим .

Подставляя полученное выражение производной , а также значениеу в уравнение (4.1а), получаем, или

.

(4.5)

Так как одну из неизвестных функций можем выбрать произвольно, выберем функцию u так, чтобы

,

(4.6)

т.е. в качестве функции vвозьмём решение однородного линейного уравнения (4.6):

.

(4.3а)

Ввиду произвольности в выборе v,мы можем не учитывать произвольную постояннуюС (точнее – можем приравнять её нулю). Подставляя найденное значениеv(x) в уравнение (4.5), получим, учитывая (4.6):

,

(4. 7)

откуда

(4.8)

(Здесь Cписать обязательно, иначе получится не общее, а частное решение).

Таким образом, видим, что в результате используемой подстановки (4.4) уравнение (4.1а) сводится к двум уравнениям с разделяющимися переменными (4.6) и (4.7).

Подставляя иv(x) в формулу (4.4), окончательно получаем

,

или

.

(4.9)

Пример 1.Найти общее решение уравнения

 Положим , тогда. Подставляя выраженияив исходное уравнение, получимили(*)

Приравняем нулю коэффициент при :

Разделяя переменные в полученном уравнении, имеем (произвольную постояннуюC не пишем), отсюдаv=x. Найденное значениеvподставляем в уравнение (*):

,,.

Следовательно, общее решение исходного уравнения.

Отметим, что уравнение (*) можно было записать в эквивалентном виде:

.

Произвольно выбирая функцию u, а неv, мы могли полагать. Этот путь решения отличается от рассмотренного только заменойvнаu(и, следовательно,uнаv), так что окончательное значениеуоказывается тем же самым.

На основании изложенного выше получаем алгоритм решения линейного дифференциального уравнения первого порядка.

1. Приводим рассматриваемое уравнение к виду.

2. Используя подстановку, находими подставляем эти выражения в уравнение.

3. Группируем члены уравнения, выносим одну из функций uилиvза скобки. Находим вторую функцию, приравняв выражение в скобках нулю и решив полученное уравнение.

4. Подставляем найденную функцию в оставшееся выражение и находим вторую функцию.

5. Записываем общее решение, подставив выражения для найденных функций u иvв равенство.

6. Если требуется найти частное решение, то определяем Сиз начальных условий и подставляем в общее решение.

Отметим далее, что иногда уравнение первого порядка становится линейным, если усчитать независимой переменной, аx– зависимой, т.е. поменять ролиx иy. Это можно сделать при условии, чтоxиdxвходят в уравнение линейно.

Пример 2. Решить уравнение .

Однако если рассматривать xкак функцию оту, то, учитывая, что,его можно привести к виду

(4. 1 б)

Заменив на,получимили. Разделив обе части последнего уравнения на произведениеydy, приведем его к виду

, или. (**)

Здесь P(y)=,. Это линейное уравнение относительноx. Полагаем,. Подставляя эти выражения в (**), получаем

или.

Выберем vтак, чтобы,, откуда;. Далее имеем,,.

Т.к. , то приходим к общему решению данного уравнения в виде

.

Отметим, что в уравнение (4.1а) P(x) иQ (x) могут входить не только в виде функций от x, но и констант:P=a,Q=b. Линейное уравнение

(4. 10)

можно решать и с помощью подстановки y=uv и разделением переменных:

;.

Отсюда ;;; где. Освобождаясь от логарифма, получаем общее решение уравнения

(здесь).

При b=0 приходим к решению уравнения

(4.10а)

в виде

(4.11)

(см. уравнение показательного роста (2.4) при ).

Применим далее для интегрирования неоднородного линейного уравнения (4. 1а) метод вариации произвольной постоянной (метод Лагранжа).

Сначала интегрируем соответствующее однородное уравнение (4.2). Как указано выше, его решение имеет вид (4.3). Будем считать сомножитель Св (4.3) функцией отх, т.е. по существу делаем замену переменной

,

(4.3а)

где C(x)-новая неизвестная функцияx. Подставляя производнуюв исходное неоднородное уравнение (4.1а), получим:, или

,

(4.12)

откуда, интегрируя, находим

dx+C1,

(4. 13)

где С₁-постоянная. Следовательно,

.

(4.14)

Отметим, что согласно (4.14) (см. также (4.9)), общее решение неоднородного линейного уравнения равно сумме общего решения соответствующего однородного уравнения (4.3) и частного решения неоднородного уравнения, определяемого вторым слагаемым, входящим в (4.14) (и в (4.9)).

При решении конкретных уравнений следует повторять приведённые выше выкладки, а не использовать громоздкую формулу (4.14).

Применим метод Лагранжа к уравнению, рассмотренному в примере 1:

.

Интегрируем соответствующее однородное уравнение .

Разделяя переменные, получаем и далее. Решение выражения формулойy = Cx. Решение исходного уравнения ищем в видеy = C(x)x. Подставив это выражение в заданное уравнение, получим;;,. Общее решение исходного уравнения имеет вид

.

В заключение отметим, что к линейному уравнению приводится уравнение Бернулли

, ()

(4.15)

которое можно записать в виде

.

(4.15а)

Заменой оно приводится к линейному уравнению:

,,.

Уравнения Бернулли также решаются изложенными выше методами.

Пример 3. Найти общее решения уравнения.

 Цепочка преобразований: ,,,,,,,,,,,,,,

Число, математика и статистика — комплект академических навыков

Гомогенные уравнения по дифференциалам первого порядка

ContentStoggle Основное меню 1 Определение 2 Решение по замене 3 Работочные примеры 4 Пример 5 См. 6 Внешние ресурсы

Определение

является однородным , если оно принимает вид:

\[\frac{\mathrm{d} y}{\mathrm{d} x}=F\left(\frac{y}{x}\right),\ ]

где $F\left(\dfrac{y}{x}\right)$ — однородная функция. В данном контексте однородным называется функция от $x$ и $y$, которая остается неизменной при умножении обоих аргументов на константу, т. е. 9.2}+\frac{\mathrm{d} y}{\mathrm{d} x}+y=0.\]  

Различные типы однородных уравнений представляют собой совершенно разные объекты, и важно не путать их. два.

Решение подстановкой

Однородное дифференциальное уравнение часто можно решить, сделав замену $v(x)=\dfrac{y}{x}$, где $v=v(x)$ — функция $x .$ Перестановка дает $y=vx$.

Выражение для $\displaystyle \frac{\mathrm{d} y}{\mathrm{d} x}$ через $x$ и $v$ можно найти, продифференцировав обе части $y=xv$ относительно $x$:

\[\begin{align} \frac{\mathrm{d} y}{\mathrm{d} x} &= \frac{\mathrm{d}}{\mathrm{d} x}\Bigl[xv \Большой]\\ &= v + x \ frac{\ mathrm {d} v} {\ mathrm {d} x}. \end{align}\]

Обратите внимание, что правило произведения использовалось для различения правой части.

Это можно выразить более компактно, используя простую запись:

\[y’ = v + xv’.\]

Напомним, что общая форма однородного дифференциального уравнения первого порядка такова:

\[y’=F \left(\frac{y}{x}\right).\]

Подстановка $y’=v+xv’$ и $v(x)=\dfrac{y}{x}$ в уравнение дает:

\[v+xv’=F(v).\]

Это можно преобразовать, чтобы сформировать отделимое дифференциальное уравнение:

\[\begin{align} xv’ &= F(v)-v \\ v’ &= \frac{F(v)-v}{x} \\ \ frac {\ mathrm {d} v} {\ mathrm {d} x} &= \ frac {F (v) -v} {x} \\ \ frac {\ mathrm {d} v} {F (v) -v} & = \ frac {\ mathrm {d} x} {x}. 2}.\] 9{-2} \mathrm{d} v &= \frac{1}{2} \int \frac{1}{x} \mathrm{d} x, \\ -\frac{1}{1-v} &= \frac{1}{2}\ln(x) + C, \end{align}\]

, где $C$ — произвольная постоянная интегрирования.

Чтобы выразить это уравнение в $v$ через $y$ и $x$, подставьте обратно, используя $v = \dfrac{y}{x}$, чтобы получить:

\[-\frac{1}{1 -\frac{y}{x} } = \frac{1}{2}\ln(x) + C.\]

Наконец, это можно изменить, чтобы найти $y$ как функцию $x$:

Сначала положим $\ln(D)=C$, затем по законам логарифмов: 92,\]

с помощью замены $y = \dfrac{1}{v}$.

Решение

Первый шаг — выразить $\dfrac{\mathrm{d} y}{\mathrm{d} x}$ через $v$. Для этого продифференцируем данную замену:

\[\begin{align} y &= \frac{1}{v}, \\ \ frac {\ mathrm {d} y} {\ mathrm {d} x} & = \ frac {\ mathrm {d {\ mathrm {d} x} \left ( \ frac {1} {v} \верно). \end{align}\]

Цепное правило используется для дифференцирования правой части:

\[\begin{align} \frac{\mathrm{d} y}{\mathrm{d} x} & = \ frac {\ mathrm {d} v} {\ mathrm {d} x} \ cdot \ frac {\ mathrm {d}} {\ mathrm {d} v} \ left ( \ frac {1} {v} \ верно), \\ \ frac {\ mathrm {d} y} {\ mathrm {d} x} &= — \ frac {1} {v ^ 2} \ frac {\ mathrm {d} v} {\ mathrm {d} x}. {-\ln(x)} = \frac{1}{x},\] 92}v = -\frac{1}{x}.\]

Левая часть может быть выражена как единственная производная (в результате правила произведения), и уравнение принимает вид:

\[\ frac{\mathrm{d}}{\mathrm{d} x} \left( \frac{1}{x}v \right) = -\frac{1}{x}.\]

Интегрирование обеих частей дает решение в терминах $v$:

\[\begin{align} \int\frac{\mathrm{d}}{\mathrm{d} x} \left( \frac{1}{x}v \ справа) &=\int -\frac{1}{x} \\ \frac{1}{x}v &= -\ln(x) + C. \конец{выравнивание}\]

Решение в терминах $y$ можно найти, вспомнив исходную замену $y=\dfrac{1}{v}$. Преобразование этого дает $v = \dfrac{1}{y}$, а подстановка этого в решение для $v$ дает:

\[\frac{1}{xy} = — \ln(x) + C. \]

Преобразование дает решение, выраженное в форме $y=y(x)$:

\[\begin{align} \frac{xy}{1} &= \frac{1}{-\ln (х) + С}, \\ xy &= \frac{1}{C — \ln(x)}, \\ y &= \frac{1}{x \left( C — \ln(x) \right)}. \конец{выравнивание}\] 92$.

Пример видео

Профессор Робин Джонсон находит общее решение $\dfrac{\mathrm{d}y}{\mathrm{d}x}=\dfrac{3y-4x}{x}$.

См. также

• Разделяемые ОДУ
• Коэффициент интегрирования

Внешние ресурсы

• Видео по однородным уравнениям первого порядка в Академии Хана.

Однородные уравнения первого порядка

Функция А f ( x,y ) называется однородным степени n , если уравнение

   

выполняется для всех x,y и z (для которых определены обе стороны).

Пример 1 : Функция f ( x,y ) = x ² + y ² является однородной степени 2, так как

 

Пример 2 : Функция является однородной степени 4, так как

Пример 3 : Функция f ( x,y ) = 2 x + y является однородной степени 1, так как

Пример 4 : Функция f ( x,y ) = x ³ – y ² неоднородна, так как

, который не равен z ⁿ f ( x,y ) для любого n .

Пример 5 : Функция f ( x,y ) = x ³ sin ( y/x ) является однородной степени 3, так как

Дифференциальное уравнение первого порядка называется однородным , если M ( x,y ) и N ( x,y ) являются однородными функциями одной и той же степени.

Пример 6 : Дифференциальное уравнение

   

Число

является однородным, поскольку оба M ( x,y ) = x ² – y ² и N ( x,y ) = xy — однородные функции одного и того же степень (а именно, 2).

Из этого факта следует метод решения однородных уравнений:

Замена y = xu (и, следовательно, dy = xdu + udx ) превращает однородное уравнение в разделимое.

Пример 7 : Решите уравнение ( x ² — Y ² ) DX + XY DY = 0,

Это уравнение является однородным, как видно из примера 6. Таким образом, чтобы решить его, сделайте замены y = xu и dy = x dy + u dx :

 

Это последнее уравнение теперь разделимо (что и было задумано). Приступая к решению,

Следовательно, решение разделимого уравнения, включающего x и v , можно записать как

 

Чтобы получить решение исходного дифференциального уравнения (которое включало переменные x и y ), просто заметьте, что

 

Замена v на y / x в предыдущем решении дает окончательный результат:

 

Это общее решение исходного дифференциального уравнения.

Пример 8: Решите IVP

   

Так как функции

оба однородны степени 1, дифференциальное уравнение однородно. Подстановки y = xv и dy = x dv + v dx преобразуют уравнение в

, что упрощается следующим образом:

Теперь уравнение разделимо.