Пошаговый Калькулятор Линейной Регрессии — Mathcracker.Com
Инструкции: Проведите регрессионный анализ с помощью Калькулятор Линейной Регрессии где будет найдено уравнение регрессии и предоставлен подробный отчет о расчетах, а также диаграмма рассеяния. Все, что вам нужно сделать, это ввести данные X и Y. По желанию можно добавить заголовок и название переменных.
Подробнее об этом калькуляторе линейной регрессии
A
модель линейной регрессии
соответствует линейной модели, которая минимизирует сумму квадратов ошибок для набора пар \((X_i, Y_i)\).
Это означает, что вы предполагаете существование модели, которая в упрощенной форме имеет вид \(Y = \alpha + \beta X\), а затем вы отмечаете несоответствия (ошибки), обнаруженные при использовании этой линейной модели для прогнозирования набора заданных данных.
Для каждого \(X_i\) в данных вы вычисляете \(\hat Y_i = \alpha + \beta X_i\) и вычисляете ошибку, измеряя \(Y_i — \hat Y_i\). В частности, в этом случае вы берете квадрат каждого несоответствия/ошибки и суммируете ВСЕ эти квадраты ошибок.
Задача регрессионного калькулятора — найти наилучшие значения \(\alpha\) и \(\beta\), чтобы сумма квадратов ошибок была как можно меньше.
Формула регрессии
Уравнение линейной регрессии, также известное как уравнение наименьших квадратов, имеет следующую форму: \(\hat Y = a + b X\), где коэффициенты регрессии представляют собой значения \(a\) и \(b\).
Вопрос в том: Как рассчитать коэффициенты регрессии? Коэффициенты регрессии вычисляются этим регрессионным калькулятором следующим образом:
\[b = \frac{SS_{XY}}{SS_{XX}}\] \[a = \bar Y — \bar X \cdot b \]
Это формулы, которые вы использовали, если бы вычисляли уравнение регрессии вручную, но, вероятно, вы предпочтете использовать калькулятор (наш
Калькулятор регрессии
), который покажет вам важные шаги.
Эта формула линейной регрессии интерпретируется следующим образом: коэффициент \(b\) известен как коэффициент наклона, а коэффициент \(a\) известен как точка пересечения по оси y.
Если вместо линейной модели вы хотите использовать нелинейную модель, то вам следует рассмотреть вместо нее модель калькулятор полиномиальной регрессии , что позволяет использовать мощности независимой переменной.
Калькулятор линейной регрессии шаги
Прежде всего, вы хотите оценить, имеет ли смысл проводить регрессионный анализ. Итак, сначала вы должны запустить это
калькулятор коэффициента корреляции
чтобы увидеть, существует ли значительная степень линейной связи между переменными.
Итак, сначала вы должны запустить это
калькулятор коэффициента корреляции
чтобы увидеть, существует ли значительная степень линейной связи между переменными.
Другими словами, имеет смысл проводить регрессионный анализ только в том случае, если коэффициент корреляции достаточно силен, чтобы обосновать модель линейной регрессии. Кроме того, вы должны использовать это калькулятор точечной диаграммы чтобы убедиться, что визуальный рисунок действительно линейный.
Можно предположить, что коэффициент корреляции близок к 1, но тем не менее характер связи вовсе не линейный.
Шаги для проведения регрессионного анализа следующие:
Шаг 1: Получите данные для зависимой и независимой переменной в формате столбца.
Шаг 2: Введите данные или вставьте их, если они уже есть, например, в формате Excel.
Шаг 3:
Нажмите «Рассчитать».
Этот калькулятор уравнения регрессии с шагами предоставит вам все необходимые расчеты в организованном порядке, чтобы вы могли четко понять все этапы процесса.
Остатки регрессии
Как оценить, хороша ли модель линейной регрессии? Вы можете подумать: «Легко, просто посмотрите на scatterplot «. В действительности математика и статистика обычно выходят за пределы того, где глаз встречается с графиком. Обычно рискованно полагаться только на диаграмму рассеяния для оценки качества модели.
С точки зрения хорошего соответствия, один из способов оценки качества соответствия модели линейной регрессии заключается в следующем
вычисление коэффициента детерминации
показывает долю вариации зависимой переменной, которая объясняется независимой переменной.
В линейной регрессии выполнение предположений имеет решающее значение для того, чтобы оценки коэффициента регрессии обладали хорошими свойствами (несмещенность, минимальная дисперсия и др.).
Для того чтобы оценить предположения линейной регрессии, необходимо посмотреть на остатки. Для этого вы можете взглянуть на нашу программу калькулятор остатков .
Предсказательная сила уравнения регрессии
Как узнать, правильно ли найдено уравнение регрессии? Или лучше вопрос, как узнать, имеет ли оцениваемое уравнение регрессии хорошую предсказательную силу?
Что вам нужно сделать, это
вычислить коэффициент детерминации
, который сообщает вам величину вариации зависимой переменной, которая объясняется зависимой(ыми) переменной(ями). 2 = 0.64\), и интерпретация состоит в том, что 64% вариации зависимой переменной объясняются независимой переменной в этой модели.
2 = 0.64\), и интерпретация состоит в том, что 64% вариации зависимой переменной объясняются независимой переменной в этой модели.
Полиномиальная регрессия
Как мы упоминали ранее, бывают случаи, когда линейная регрессия просто не подходит, потому что существует четкая нелинейная модель, определяющая взаимосвязь между двумя переменными.
Ваш первый сигнал о том, что вместо линейной регрессии следует использовать полиномиальную регрессию, заключается в том, что вы видите, что в данных, представленных диаграммой рассеяния, присутствует криволинейный паттерн.
Если это так, вы можете попробовать это
калькулятор полиномиальной регрессии
, чтобы оценить нелинейную модель, которая имеет больше шансов на лучшее соответствие.
Что дает этот онлайн-калькулятор линейной регрессии?
Сначала вы получаете таблицу данных и вычисляете соответствующие квадраты и перекрестные умножения, чтобы получить требуемую сумму квадратов значений, необходимую для применения формулы регрессии.
Как только все это будет аккуратно отображено в таблице со всеми необходимыми столбцами, будут показаны формулы регрессии с подставленными правильными значениями, а затем с выводом о модели линейной регрессии, которая была оценена на основе данных.
Кроме того, строится точечная диаграмма, чтобы оценить, насколько тесна линейная связь между переменными, что дает представление о том, насколько хороша модель линейной регрессии.
Является ли r2 коэффициентом регрессии?
Нет. Технически коэффициенты регрессии — это оценочные коэффициенты, являющиеся частью регрессионной модели. Коэффициент r2 называется коэффициентом детерминации.
Коэффициент r2 также рассчитывается по выборочным данным, но это не коэффициент регрессии, но это не значит, что он не важен. Коэффициент r2 важен, потому что он дает оценку процента вариации, объясняемой моделью.
Как сделать линейную регрессию в excel?
В Excel есть возможность проводить линейную регрессию либо непосредственно с помощью команд «=НАКЛОН()» и «=ИНТЕРЦЕПТ()», либо с помощью меню «Анализ данных».
Но Excel не показывает все шаги, как это делает наш регрессионный калькулятор.
Другие калькуляторы, связанные с линейной регрессией
Этот
Калькулятор уравнения регрессии
является лишь одним из многих калькуляторов, представляющих интерес при работе с линейными моделями. Вас также могут заинтересовать
вычисление коэффициента корреляции
, или в
построить диаграмму рассеяния
с предоставленными данными. 2 = 0,67 при оценке линейной регрессии Y как функции X, тогда интерпретация заключается в том, что X объясняет 67% вариации Y.
2 = 0,67 при оценке линейной регрессии Y как функции X, тогда интерпретация заключается в том, что X объясняет 67% вариации Y.
Что происходит, когда у вас больше переменных
Потенциально у вас может быть более одной независимой переменной. Например, вы можете быть заинтересованы в оценке Y в терминах двух переменных X1 и X2. В этом случае вам необходимо рассчитать множественную линейную регрессию модель, где идея по сути та же: найти гиперплоскость, которая минимизирует сумму квадратов ошибок.
Онлайн калькулятор: Аппроксимация функции одной переменной
Данный калькулятор по введенным данным строит несколько моделей регрессии: линейную, квадратичную, кубическую, степенную, логарифмическую, гиперболическую, показательную, экспоненциальную. Результаты можно сравнить между собой по корреляции, средней ошибке аппроксимации и наглядно на графике. Теория и формулы регрессий под калькулятором.
Результаты можно сравнить между собой по корреляции, средней ошибке аппроксимации и наглядно на графике. Теория и формулы регрессий под калькулятором.
Если не ввести значения x, калькулятор примет, что значение x меняется от 0 с шагом 1.
Аппроксимация функции одной переменной
83 71 64 69 69 64 68 59 81 91 57 65 58 62
Значения x, через пробел
183 168 171 178 176 172 165 158 183 182 163 175 164 175
Значения y, через пробел
Линейная аппроксимация
Квадратичная аппроксимация
Кубическая аппроксимация
Аппроксимация степенной функцией
Показательная аппроксимация
Логарифмическая аппроксимация
Гиперболическая аппроксимация
Экспоненциальная аппроксимация
Точность вычисления
Знаков после запятой: 4
Линейная регрессия
Коэффициент линейной парной корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Квадратичная регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Кубическая регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Степенная регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Показательная регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Логарифмическая регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Гиперболическая регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Экспоненциальная регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Результат
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Сначала сформулируем задачу:
Пусть у нас есть неизвестная функция y=f(x), заданная табличными значениями (например, полученными в результате опытных измерений).
Нам необходимо найти функцию заданного вида (линейную, квадратичную и т. п.) y=F(x), которая в соответствующих точках принимает значения, как можно более близкие к табличным.
На практике вид функции чаще всего определяют путем сравнения расположения точек с графиками известных функций.
Полученная формула y=F(x), которую называют эмпирической формулой, или уравнением регрессии y на x, или приближающей (аппроксимирующей) функцией, позволяет находить значения f(x) для нетабличных значений x, сглаживая результаты измерений величины y.
Для того, чтобы получить параметры функции F, используется метод наименьших квадратов. В этом методе в качестве критерия близости приближающей функции к совокупности точек используется суммы квадратов разностей значений табличных значений y и теоретических, рассчитанных по уравнению регрессии.
Таким образом, нам требуется найти функцию F, такую, чтобы сумма квадратов S была наименьшей:
Рассмотрим решение этой задачи на примере получения линейной регрессии F=ax+b.
S является функцией двух переменных, a и b. Чтобы найти ее минимум, используем условие экстремума, а именно, равенства нулю частных производных.
Используя формулу производной сложной функции, получим следующую систему уравнений:
Откуда, выразив a и b, можно получить формулы для коэффициентов линейной регрессии, приведенные выше.
Аналогичным образом выводятся формулы для остальных видов регрессий.
Калькулятор простой линейной регрессии с шагами
В простой линейной регрессии отправной точкой является оценочное уравнение регрессии: ŷ = b 0 + b 1 x. Он обеспечивает математическое соотношение между зависимой переменной (y) и независимой переменной (x). Кроме того, его можно использовать для прогнозирования значения y для заданного значения x. Есть две вещи, которые нам нужны, чтобы получить оценочное уравнение регрессии: наклон (b 1 ) и точка пересечения (b 0 ). Формулы для наклона и точки пересечения получены методом наименьших квадратов: min Σ(y — ŷ) 2 . График оценочного уравнения регрессии известен как оценочная линия регрессии.
График оценочного уравнения регрессии известен как оценочная линия регрессии.
После оценочного уравнения регрессии вторым наиболее важным аспектом простой линейной регрессии является коэффициент детерминации. Коэффициент детерминации, обозначаемый r 2 , обеспечивает меру согласия для оцениваемого уравнения регрессии. Прежде чем мы сможем найти r 92$
Теперь, когда мы знаем сумму квадратов, мы можем вычислить коэффициент детерминации. r 2 — это отношение SSR к SST. Он принимает значение от нуля до единицы, где ноль указывает на наихудшее соответствие, а единица указывает на идеальное соответствие. Идеальная подгонка означает, что все точки на диаграмме рассеяния будут лежать на предполагаемой линии регрессии. При интерпретации r 2 первым шагом является преобразование его значения в проценты. Затем его можно интерпретировать как процент изменчивости y, объясняемый оценочным уравнением регрессии. 92 = \dfrac{\text{SSR}}{\text{SST}} $
Коэффициент корреляции выборки можно рассчитать с помощью коэффициента детерминации, указывающего на тесную связь между регрессией и корреляцией. Регрессию можно рассматривать как более сильную версию регрессии. В то время как корреляция говорит нам о знаке и силе взаимосвязи, регрессия количественно определяет взаимосвязь, чтобы облегчить предсказание. Чтобы получить коэффициент корреляции выборки, просто возьмите квадратный корень из коэффициента детерминации со знаком, совпадающим со знаком наклона.
Регрессию можно рассматривать как более сильную версию регрессии. В то время как корреляция говорит нам о знаке и силе взаимосвязи, регрессия количественно определяет взаимосвязь, чтобы облегчить предсказание. Чтобы получить коэффициент корреляции выборки, просто возьмите квадратный корень из коэффициента детерминации со знаком, совпадающим со знаком наклона.
Следующим шагом в регрессионном анализе является проверка значимости. То есть мы хотим определить, существует ли статистически значимая связь между x и y. Существует два способа проверки значимости: либо с помощью t-теста, либо с помощью F-теста. Первым шагом в обоих тестах является вычисление среднеквадратичной ошибки (MSE), которая обеспечивает оценку дисперсии ошибки. Квадратный корень из MSE называется стандартной ошибкой оценки и дает оценку стандартного отклонения ошибки.
| Среднеквадратическая ошибка | Стандартная ошибка оценки |
| $ \text{MSE} = \dfrac{\text{SSE}}{n-2}$ | $ s = \sqrt{\text{MSE}} $ |
Стьюдентный тест — это проверка гипотезы об истинном значении наклона, обозначаемом $\beta_1$. Статистика теста для этой проверки гипотезы рассчитывается путем деления расчетного наклона b 1 на расчетное стандартное отклонение b 92}} $. Затем тестовая статистика используется для проверки гипотезы с использованием t-распределения с n-2 степенями свободы. В простой линейной регрессии F-тест представляет собой тот же тест гипотезы, что и t-критерий. Единственная разница будет заключаться в тестовой статистике и используемом распределении вероятностей.
Статистика теста для этой проверки гипотезы рассчитывается путем деления расчетного наклона b 1 на расчетное стандартное отклонение b 92}} $. Затем тестовая статистика используется для проверки гипотезы с использованием t-распределения с n-2 степенями свободы. В простой линейной регрессии F-тест представляет собой тот же тест гипотезы, что и t-критерий. Единственная разница будет заключаться в тестовой статистике и используемом распределении вероятностей.
| т тест | Статистика испытаний |
| $ H_0: \beta_1 = 0 $ $ H_a: \beta_1 \neq 0 $ | $ t = \dfrac{b_1}{s_{b_1}} $ |
Доверительные интервалы и интервалы прогнозов могут быть построены вокруг оценочной линии регрессии. В обоих случаях интервалы будут наиболее узкими вблизи среднего значения x и будут расширяться по мере удаления от среднего значения. Разница между ними заключается в том, что доверительный интервал дает диапазон ожидаемого значения y. Интервал предсказания дает диапазон предсказанного значения y. Доверительные интервалы будут уже, чем интервалы прогнозирования.
Интервал предсказания дает диапазон предсказанного значения y. Доверительные интервалы будут уже, чем интервалы прогнозирования.
В простой линейной регрессии есть только одна независимая переменная (x). Однако мы можем захотеть включить более одной независимой переменной, чтобы улучшить прогностическую силу нашей регрессии. Это известно как множественная регрессия, которую можно решить с помощью нашего калькулятора множественной регрессии. Одной из наиболее важных частей регрессии является проверка значимости. Два теста значимости, t-тест и F-тест, являются примерами проверки гипотез. Проверка гипотезы может быть выполнена с помощью нашего калькулятора проверки гипотез.
Пошаговый калькулятор линейной регрессии — MathCracker.com
Инструкции: Проведите регрессионный анализ с помощью Калькулятор линейной регрессии , где будет найдено уравнение регрессии и предоставлен подробный отчет о расчетах,
вместе с точечной диаграммой. Все, что вам нужно сделать, это ввести данные X и Y. При желании вы можете добавить заголовок и добавить имя переменных.
Все, что вам нужно сделать, это ввести данные X и Y. При желании вы можете добавить заголовок и добавить имя переменных.
Подробнее об этом калькуляторе линейной регрессии
А модель линейной регрессии соответствует линейной модели, которая минимизирует сумму квадратов ошибок для набора пар \((X_i, Y_i)\).
То есть вы предполагаете существование модели, которая в упрощенной форме имеет вид \(Y = \alpha + \beta X\), а затем принимаете к сведению несоответствия (ошибки), обнаруженные при использовании этой линейной модели для прогнозирования набора заданных данных.
Для каждого \(X_i\) в данных вы вычисляете \(\hat Y_i = \alpha + \beta X_i\) и вычисляете ошибку, измеряя \(Y_i — \hat Y_i\). В частности, в этом случае вы берете квадрат каждого несоответствия/ошибки и суммируете ВСЕ эти квадраты ошибок.
В частности, в этом случае вы берете квадрат каждого несоответствия/ошибки и суммируете ВСЕ эти квадраты ошибок.
Задача калькулятора регрессии — найти наилучшие значения \(\альфа\) и \(\бета\), чтобы сумма квадратов ошибок была как можно меньше.
Формула регрессии
Уравнение линейной регрессии, также известное как уравнение наименьших квадратов, имеет следующую форму: \(\hat Y = a + b X\), где коэффициенты регрессии — это значения \(a\) и \(b\).
Вопрос: Как рассчитать коэффициенты регрессии? Коэффициенты регрессии вычисляются этим калькулятором регрессии следующим образом:
\[b = \frac{SS_{XY}}{SS_{XX}}\] \[a = \bar Y — \bar X \cdot b \]
Это формулы, которые вы использовали, если вам нужно было рассчитать уравнение регрессии вручную, но, вероятно, вы предпочтете использовать
калькулятор (наш регрессионный калькулятор), который покажет вам важные шаги.
Эта формула линейной регрессии интерпретируется следующим образом: коэффициент \(b\) известен как коэффициент наклона, и коэффициент \(a\) известен как y-перехват.
Если вместо линейной модели вы хотите использовать нелинейную модель, то вам следует вместо этого рассмотреть калькулятор полиномиальной регрессии , что позволяет использовать степени независимой переменной.
Калькулятор линейной регрессии Шаги
Прежде всего, вы хотите оценить, имеет ли смысл проводить регрессионный анализ. Итак, сначала вы
следует запустить этот калькулятор коэффициента корреляции, чтобы увидеть, есть ли
значительная степень линейной связи между переменными.
Другими словами, имеет смысл проводить регрессионный анализ только тогда, когда коэффициент корреляции достаточно силен, чтобы случай для модели линейной регрессии. Кроме того, вы должны использовать этот калькулятор точечной диаграммы, чтобы убедиться, что визуальное картина действительно линейна.
Можно предположить, что коэффициент корреляции близок к 1, но тем не менее характер связи вовсе не линейный.
Шаги для проведения регрессионного анализа:
Шаг 1: Получите данные для зависимой и независимой переменных в формате столбца.
Шаг 2: Введите данные или вставьте их, если они у вас уже есть, например, в формате Excel.
Шаг 3: Нажмите «Рассчитать».
Этот калькулятор уравнения регрессии с шагами предоставит вам все необходимые расчеты в организованном порядке, поэтому чтобы вы могли четко понимать все этапы процесса.
Остатки регрессии
Как мы оцениваем, хороша ли модель линейной регрессии? Вы можете подумать: «Легко, просто взгляните на диаграмма рассеяния «. На самом деле математика и статистика, как правило, выходят за рамки того, что видно на графике. Обычно рискованно полагаться исключительно на диаграмму рассеяния для оценки качества модели.
С точки зрения качества подгонки, один из способов оценки качества подгонки модели линейной регрессии заключается в следующем. расчет коэффициента детерминации
, указывает долю вариации зависимой переменной, которая объясняется независимой переменной.
расчет коэффициента детерминации
, указывает долю вариации зависимой переменной, которая объясняется независимой переменной.
В линейной регрессии выполнение допущений имеет решающее значение, так что оценки коэффициента регрессии иметь хорошие свойства (непредвзятость, минимальная дисперсия и т. д.).
Чтобы оценить предположения о линейной регрессии, вам нужно взглянуть на остатки. Для этой цели, вы можете взглянуть на наш остаточный калькулятор .
Предсказательная сила уравнения регрессии
Как узнать, правильно ли найдено уравнение регрессии? Или лучше вопрос, как узнать, является ли уравнение регрессии оценка обладает хорошей предсказательной силой?
Что вам нужно сделать, так это вычислить коэффициент детерминации, который говорит вам
величина вариации зависимой переменной, которая объясняется зависимой(ыми) переменной(ями). 92 = 0,64\) и
интерпретация заключается в том, что 64% вариации зависимой переменной объясняются независимой переменной в этой модели.
92 = 0,64\) и
интерпретация заключается в том, что 64% вариации зависимой переменной объясняются независимой переменной в этой модели.
Полиномиальная регрессия
Как мы упоминали ранее, бывают случаи, когда линейная регрессия просто не подходит, потому что существует четкая нелинейная модель, управляющая связь между двумя переменными.
Ваш первый сигнал о том, что вместо линейной регрессии следует использовать полиномиальную регрессию, заключается в том, что вы видите криволинейный паттерн в данные, представленные диаграммой рассеяния.
Если это так, вы можете попробовать этот калькулятор полиномиальной регрессии, чтобы оценить нелинейный модель, которая имеет больше шансов на лучшую посадку.
Что дает этот онлайн-калькулятор линейной регрессии?
Сначала вы получаете таблицу данных и вычисляете соответствующие квадраты и перекрестные умножения, чтобы получить требуемое
сумма квадратов значений, необходимых для применения формулы регрессии.
Как только все это будет аккуратно отображено в таблице со всеми необходимыми столбцами, будут показаны формулы регрессии с правильными значениями. подключается, а затем с выводом о модели линейной регрессии, которая была оценена на основе данных.
Кроме того, строится точечная диаграмма, чтобы оценить, насколько тесной является линейная связь между переменными, что дает указание того, насколько хороша модель линейной регрессии.
Является ли r2 коэффициентом регрессии?
Нет. С технической точки зрения, коэффициенты регрессии — это рассчитанные коэффициенты, являющиеся частью регрессионной модели. Коэффициент r2 называется коэффициентом детерминации.
Коэффициент r2 также рассчитывается по выборочным данным, но это не коэффициент регрессии, но это не значит, что он не важен.
Коэффициент r2 важен, потому что он дает оценку процента вариации, объясняемой моделью.
Как сделать линейную регрессию в Excel?
Excel может выполнять линейную регрессию либо непосредственно с помощью команд «=НАКЛОН()» и «=ПЕРЕЧЕСТ()», либо с помощью меню Анализ данных.
Но Excel не показывает все шаги, как это делает наш регрессионный калькулятор.
Другие калькуляторы, связанные с линейной регрессией
Этот калькулятор уравнения регрессии является лишь одним из многих калькуляторов, представляющих интерес при работе с линейными моделями.
Вас также могут заинтересовать
вычисление коэффициента корреляции
, или к
построить точечную диаграмму
с предоставленными данными.

 )
) )
) )
) )
) )
) )
) )
) )
) 4848096202
4848096202 656059029
656059029 9335804265
9335804265 8571673007
8571673007 1736481777
1736481777 984807753
984807753 5
5 3420201433
3420201433 7547095802
7547095802 8746197071
8746197071 156434465
156434465 9781476007
9781476007 4694715628
4694715628 )/3
)/3



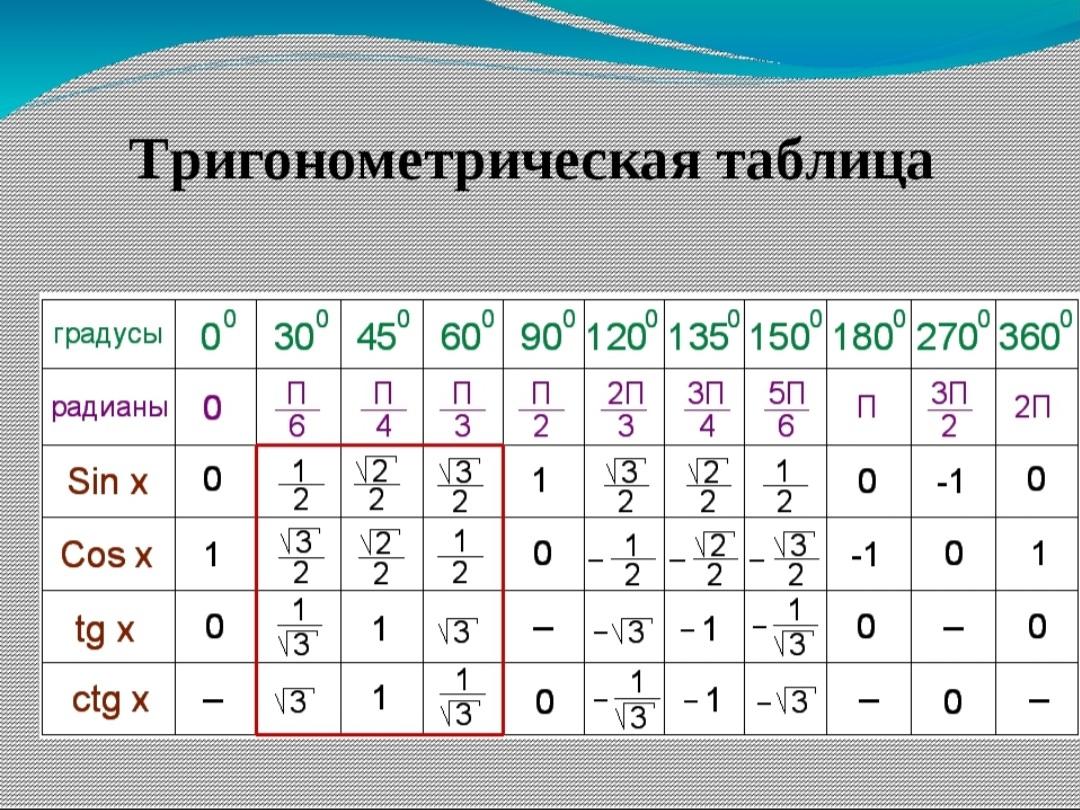
 Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.
 Поздравляем! Ваш график смен уже доступен для Вас в любое время и в любом месте.
Поздравляем! Ваш график смен уже доступен для Вас в любое время и в любом месте.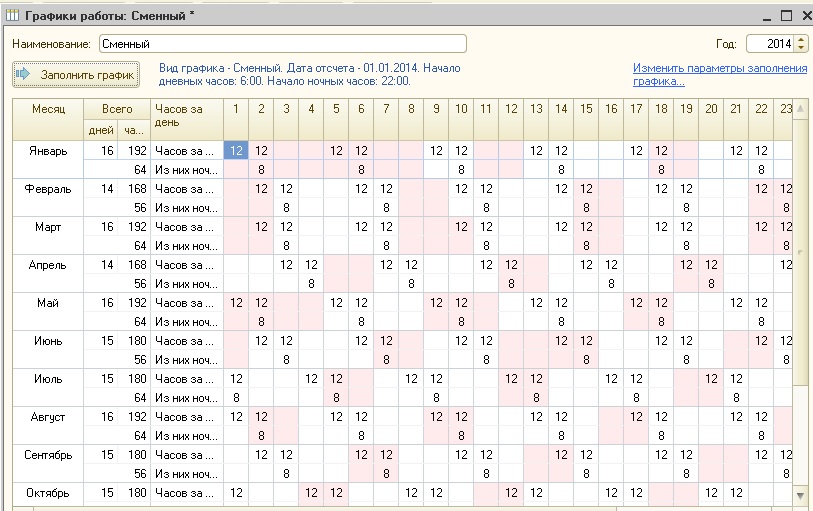 ru
ru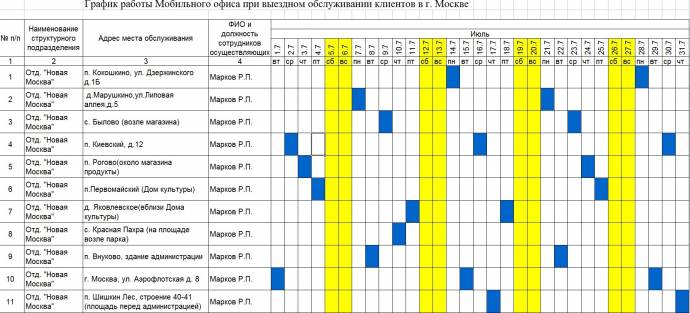 Нам нужна диаграмма, которая показывает данные за текущий месяц вместе с предыдущими 11 месяцами. Чтобы использовать приведенный ниже пример, загрузите Excel Rolling Chart.xlsx
Нам нужна диаграмма, которая показывает данные за текущий месяц вместе с предыдущими 11 месяцами. Чтобы использовать приведенный ниже пример, загрузите Excel Rolling Chart.xlsx  Имена НЕ чувствительны к регистру — «ДАННЫЕ» будут восприниматься так же, как «данные»
Имена НЕ чувствительны к регистру — «ДАННЫЕ» будут восприниматься так же, как «данные»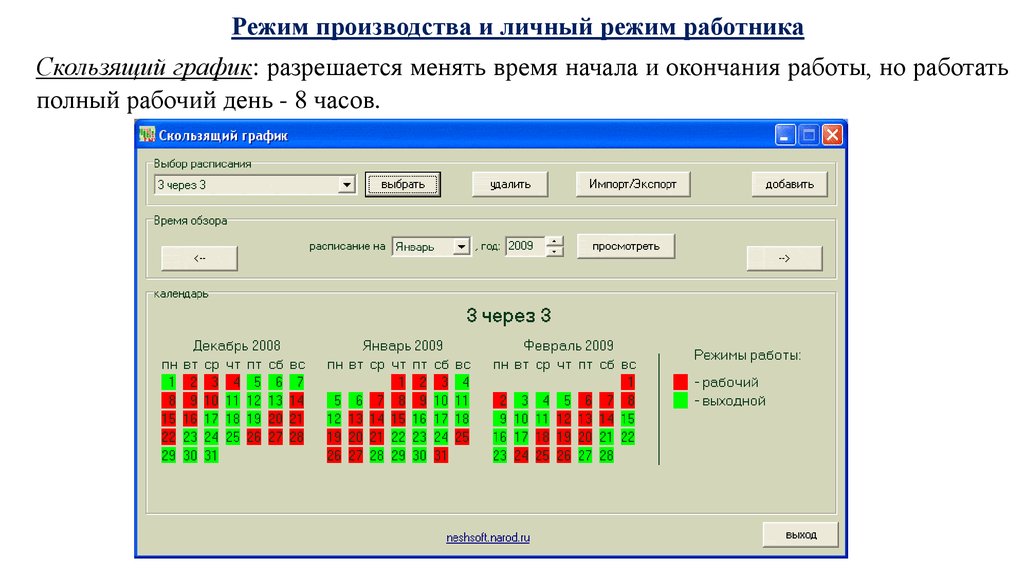 Здесь вы можете изменить количество месяцев (например), которые вы хотите включить в свою диаграмму. Если бы вместо этого вы добавляли столбцы к своим данным каждый месяц, вы бы соответствующим образом корректировали свою формулу.
Здесь вы можете изменить количество месяцев (например), которые вы хотите включить в свою диаграмму. Если бы вместо этого вы добавляли столбцы к своим данным каждый месяц, вы бы соответствующим образом корректировали свою формулу. Теперь вам нужно указать диаграмме использовать наш динамический диапазон вместо всей таблицы. Нажмите на график, чтобы активировать контекстные вкладки Chart Tools .
Теперь вам нужно указать диаграмме использовать наш динамический диапазон вместо всей таблицы. Нажмите на график, чтобы активировать контекстные вкладки Chart Tools .
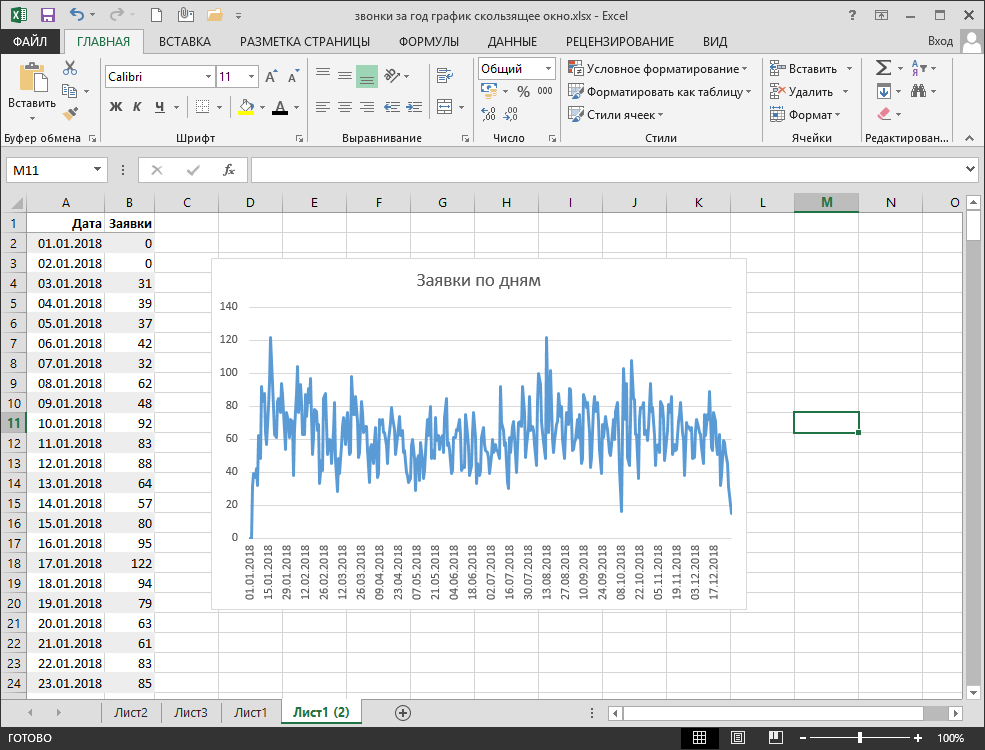 Выберите имя, которое хотите изменить, затем нажмите кнопку Изменить . Внесите изменения в диалоговое окно так же, как при первом его создании. Только будьте осторожны, чтобы не изменить само имя, если от него зависят другие формулы.
Выберите имя, которое хотите изменить, затем нажмите кнопку Изменить . Внесите изменения в диалоговое окно так же, как при первом его создании. Только будьте осторожны, чтобы не изменить само имя, если от него зависят другие формулы. l=+новая дата;ga(‘создать’, ‘UA-68417692-1’, ‘авто’);ga(‘require’, ‘eventTracker’, {attributePrefix: ‘data-‘});ga(‘отправить’, ‘просмотр страницы’);
l=+новая дата;ga(‘создать’, ‘UA-68417692-1’, ‘авто’);ga(‘require’, ‘eventTracker’, {attributePrefix: ‘data-‘});ga(‘отправить’, ‘просмотр страницы’); Позволь мне объяснить. Представьте, что у вас есть некоторые финансовые данные, подобные следующим:
Позволь мне объяснить. Представьте, что у вас есть некоторые финансовые данные, подобные следующим: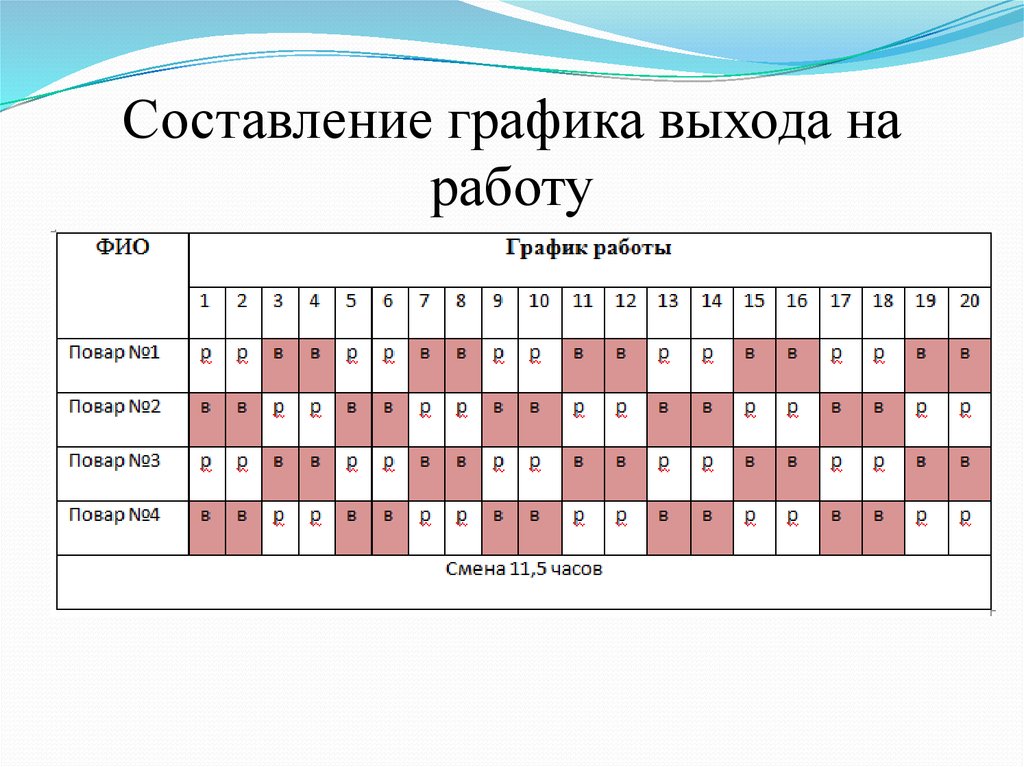 Это просто облегчает жизнь.
Это просто облегчает жизнь.

 ru/wp-content/uploads/2022/03/angles-ABCD.svg"}}}]}
ru/wp-content/uploads/2022/03/angles-ABCD.svg"}}}]} \circ$. Мы пришли к противоречию.
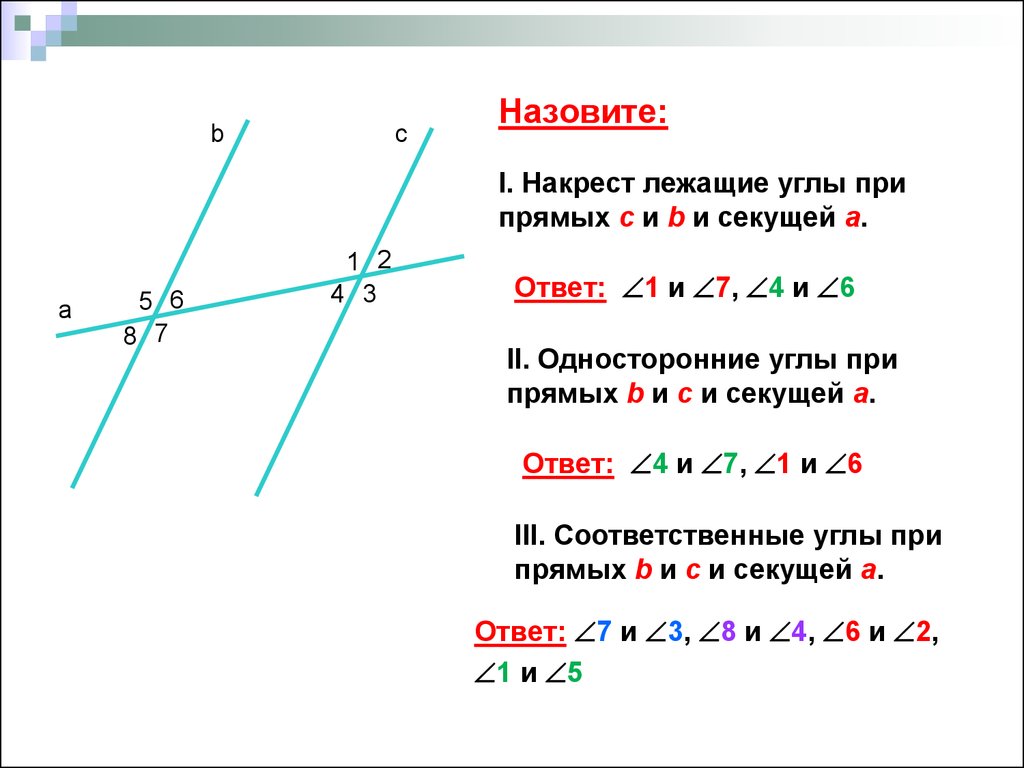
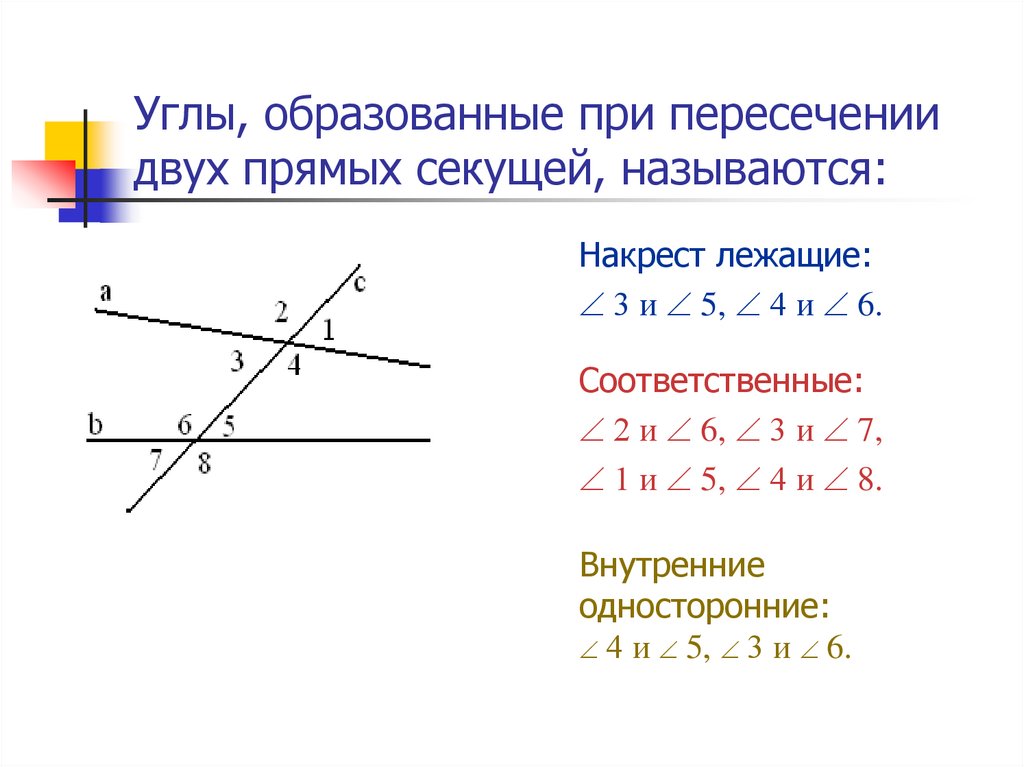
\circ$. Мы пришли к противоречию.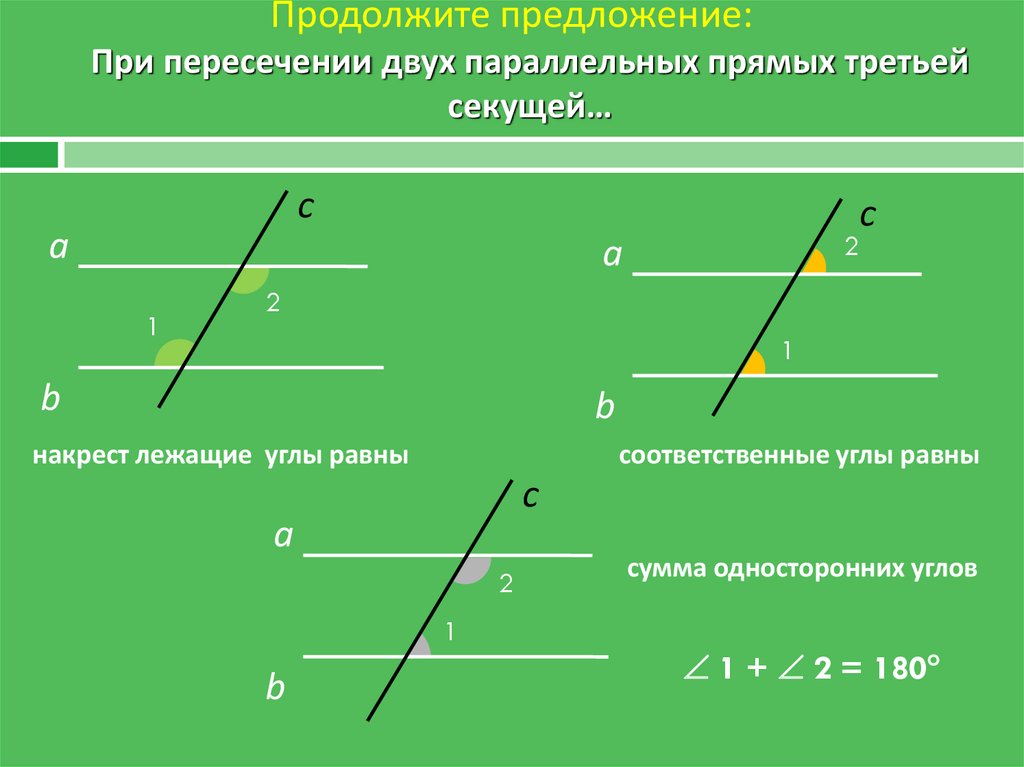 Поэтому теорема обычно доказывается по внутренним накрест углам, ведь равенство таких же внешних — прямое следствие.
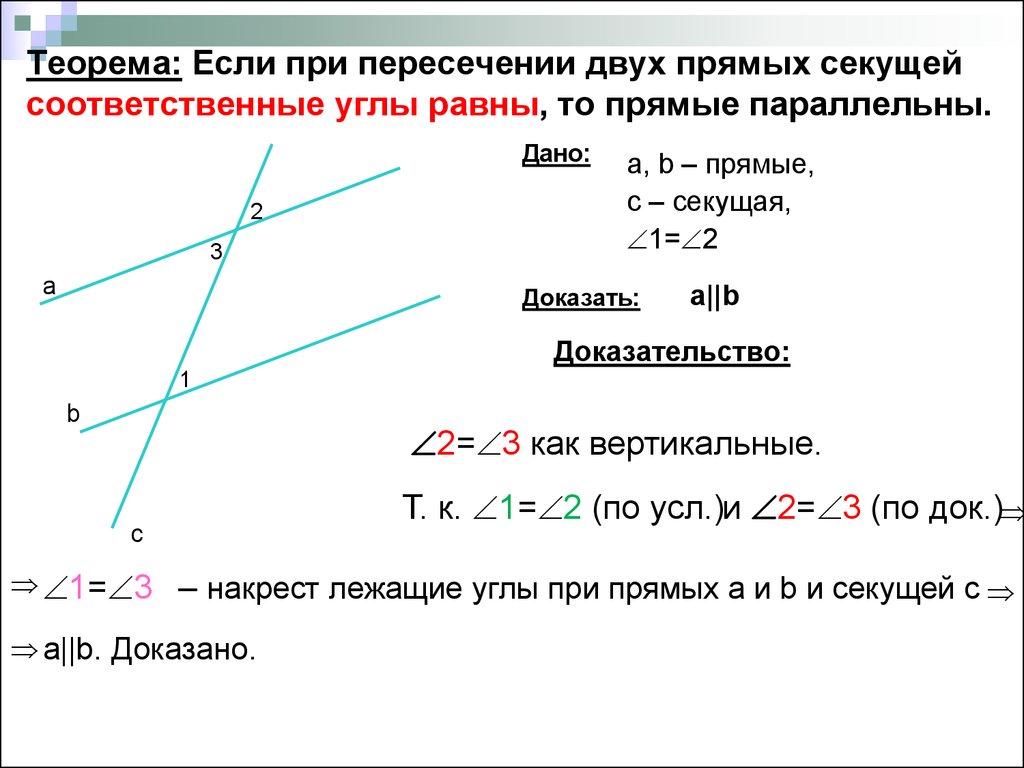
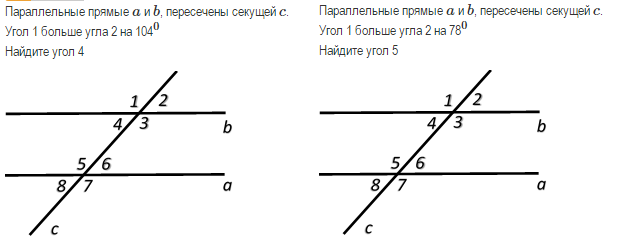
Поэтому теорема обычно доказывается по внутренним накрест углам, ведь равенство таких же внешних — прямое следствие.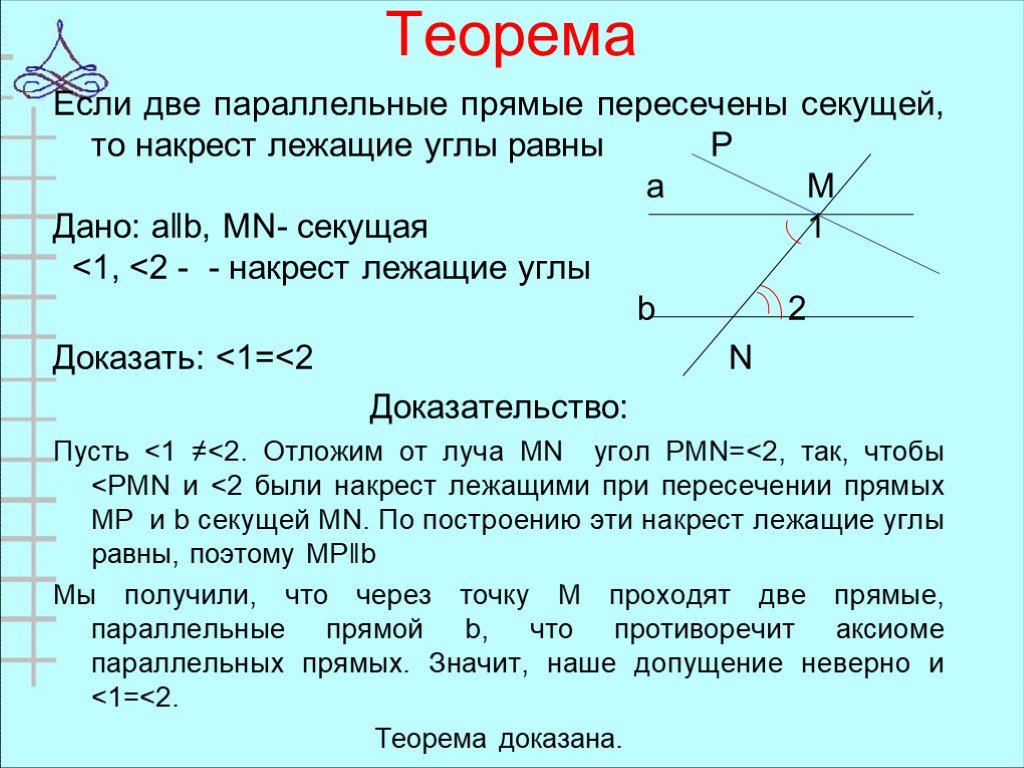 Если при пересечении двух прямых секущей соответственные углы равны, то такие прямые параллельны.
Если при пересечении двух прямых секущей соответственные углы равны, то такие прямые параллельны.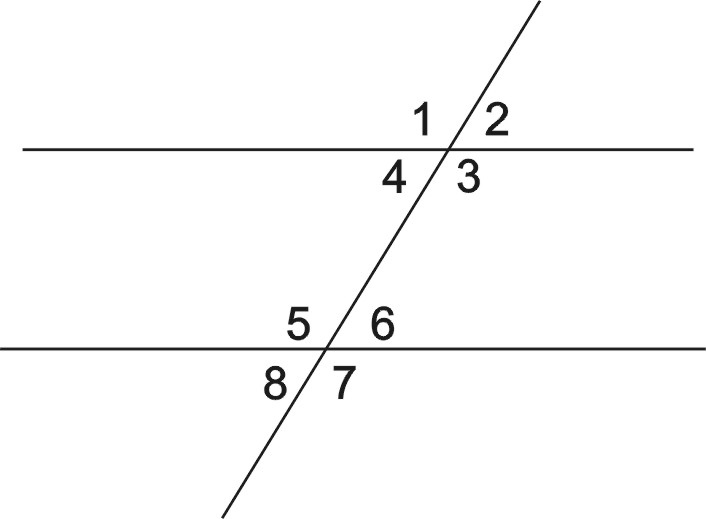 \circ$. Они являются односторонними при секущей $AB$ для отрезков $AC$ и $BD$. Следовательно $AC\parallel{BD}$.
\circ$. Они являются односторонними при секущей $AB$ для отрезков $AC$ и $BD$. Следовательно $AC\parallel{BD}$. \\circ$, то такие прямые параллельны.","Если при пересечении двух прямых секущей накрест односторонние углы равны, то такие прямые параллельны."],"answer":[0,1,2]}}}]}
\\circ$, то такие прямые параллельны.","Если при пересечении двух прямых секущей накрест односторонние углы равны, то такие прямые параллельны."],"answer":[0,1,2]}}}]}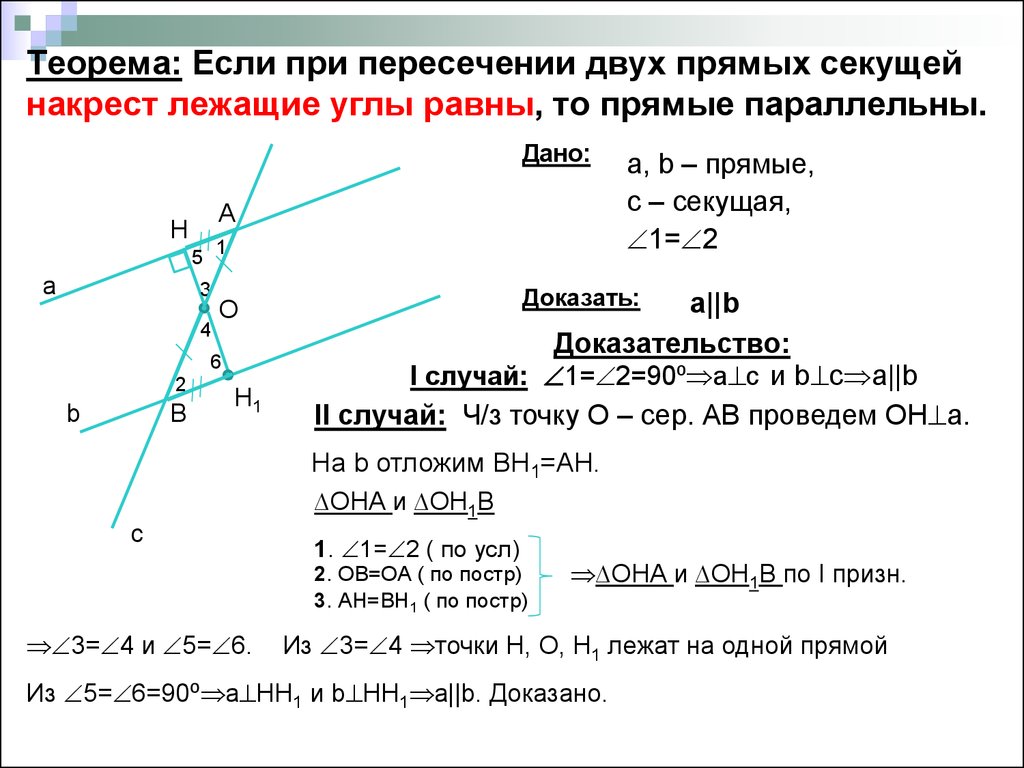 )
)
 Тригонометрическая форма комплексного числа.
Тригонометрическая форма комплексного числа. n.
n.
 Равносильные неравенства.
Равносильные неравенства.
 Тригонометрические функции числового аргумента
Тригонометрические функции числового аргумента
 Функция у = arcsin (sin x).
Функция у = arcsin (sin x).

 Теорема Пифагора.
Теорема Пифагора.





 6: Касательные и секущие Section_7_6
6: Касательные и секущие Section_7_6
 $\overleftrightarrow{AT}\parallel\overleftrightarrow{BQ}$.
$\overleftrightarrow{AT}\parallel\overleftrightarrow{BQ}$.
 $м\угол 1=м\угол 2$;
$м\угол
2=\frac{1}{2}m\overparen{TC}$; $m\overparen{TC}=m\overparen{TB}$ (поскольку
$\overline{BC}\parallel\overleftrightarrow{AT}$), поэтому
$\frac{1}{2}m\overparen{TC}=\frac{1}{2}m\overparen{TB}$. Затем
$м\угол
ATB=\frac{1}{2}m\overparen{TB}$.
$м\угол 1=м\угол 2$;
$м\угол
2=\frac{1}{2}m\overparen{TC}$; $m\overparen{TC}=m\overparen{TB}$ (поскольку
$\overline{BC}\parallel\overleftrightarrow{AT}$), поэтому
$\frac{1}{2}m\overparen{TC}=\frac{1}{2}m\overparen{TB}$. Затем
$м\угол
ATB=\frac{1}{2}m\overparen{TB}$.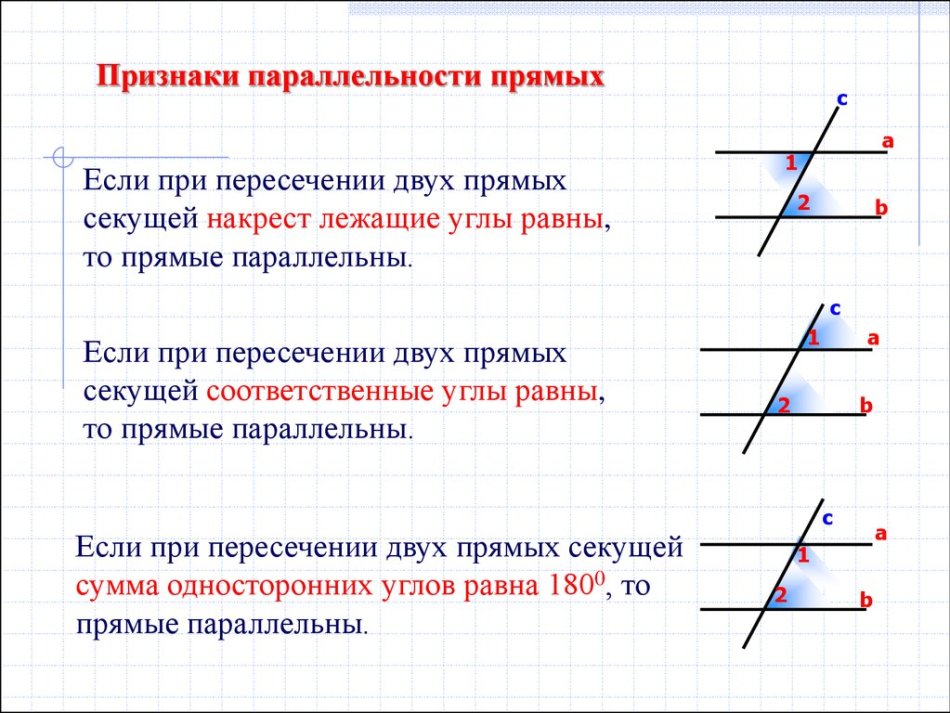
 )
) )
) )
) )
) )
) )
) )
) )
) 04.16
04.16 2 — 2x — 3. Найдите: а)наименьшее значение функции; б) значения x, при которых значение функции равно 5; в) значение…
2 — 2x — 3. Найдите: а)наименьшее значение функции; б) значения x, при которых значение функции равно 5; в) значение… . .)
. .)
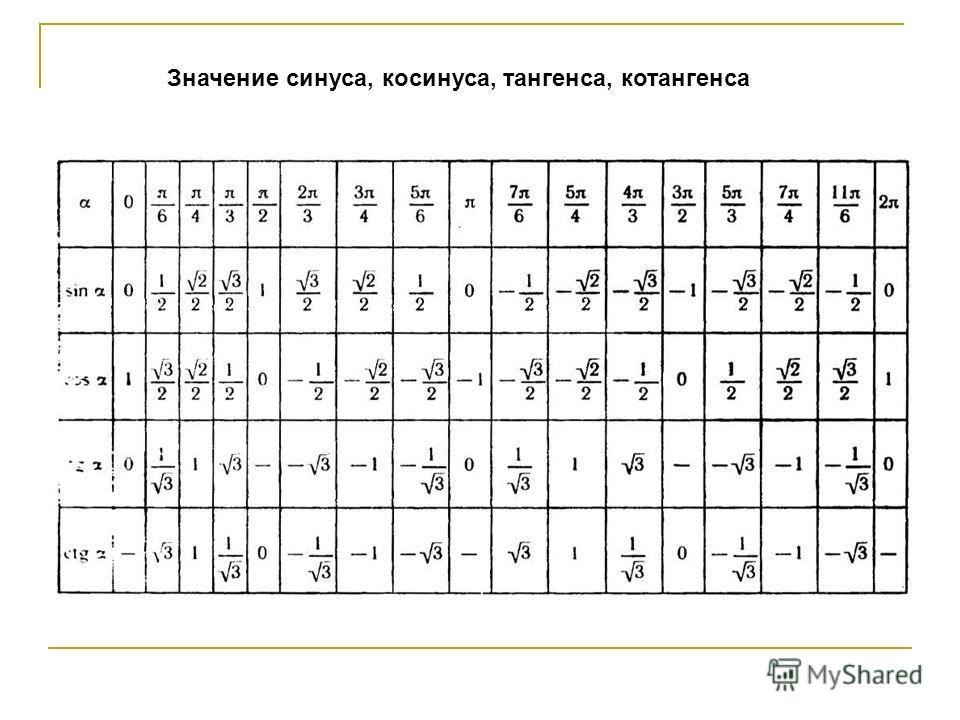
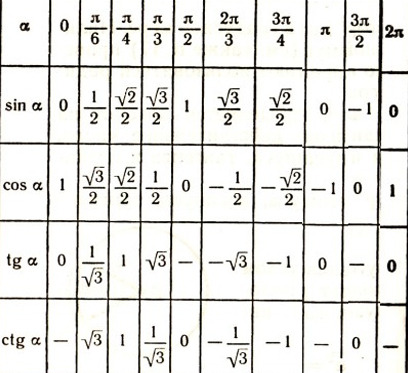 Значение cos 3° составляет 0,9986 (приблизительно)
Значение cos 3° составляет 0,9986 (приблизительно) 

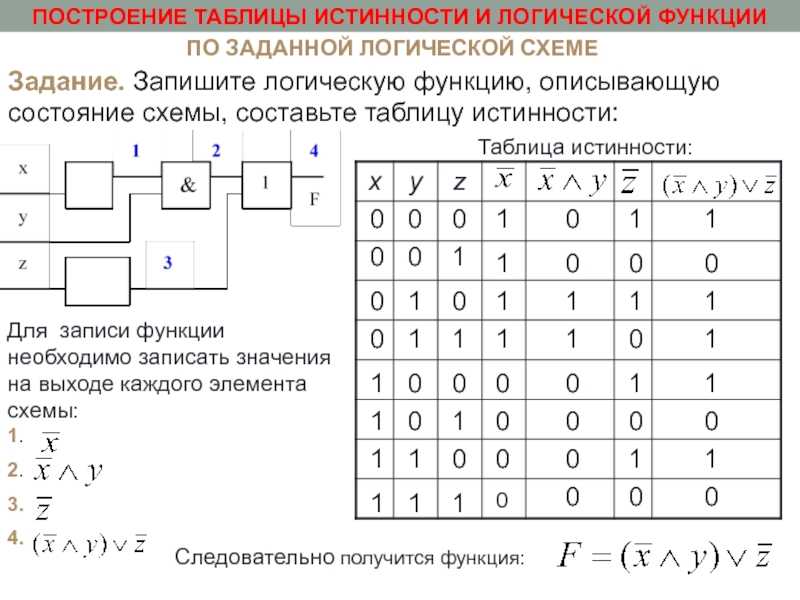 В случае противного результата, в конъюнкцию включается ее отрицание.
В случае противного результата, в конъюнкцию включается ее отрицание.
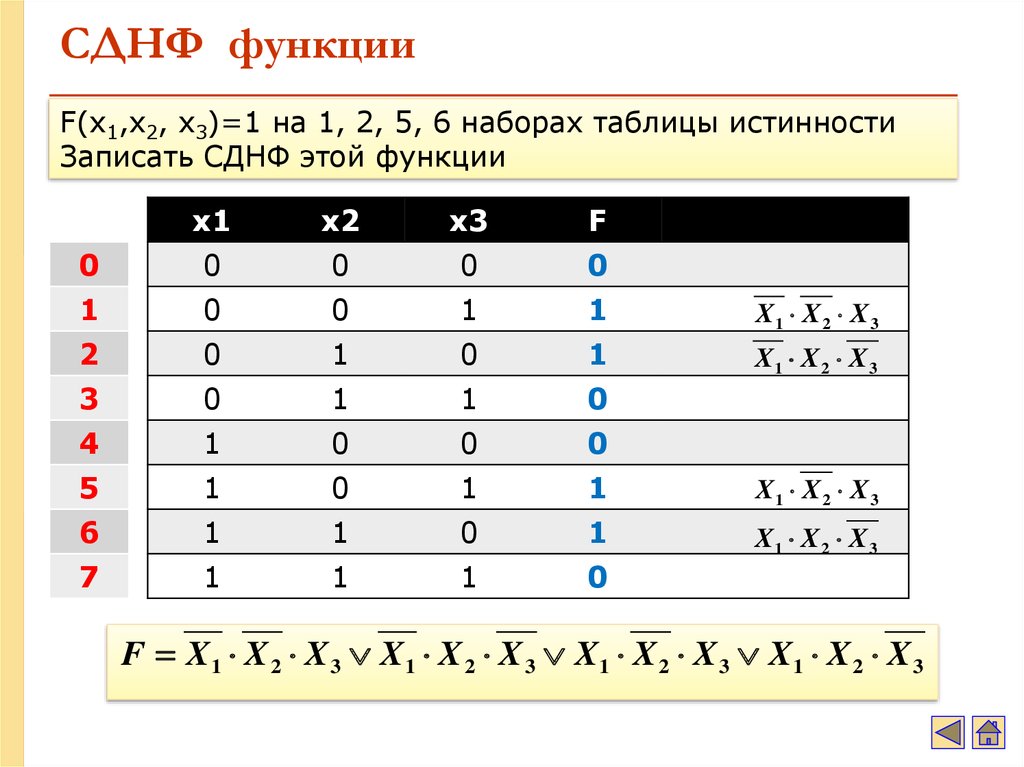 В этом случае результат будет истинным только в том случае, когда оба высказывания либо ложны, либо истинны.
В этом случае результат будет истинным только в том случае, когда оба высказывания либо ложны, либо истинны.
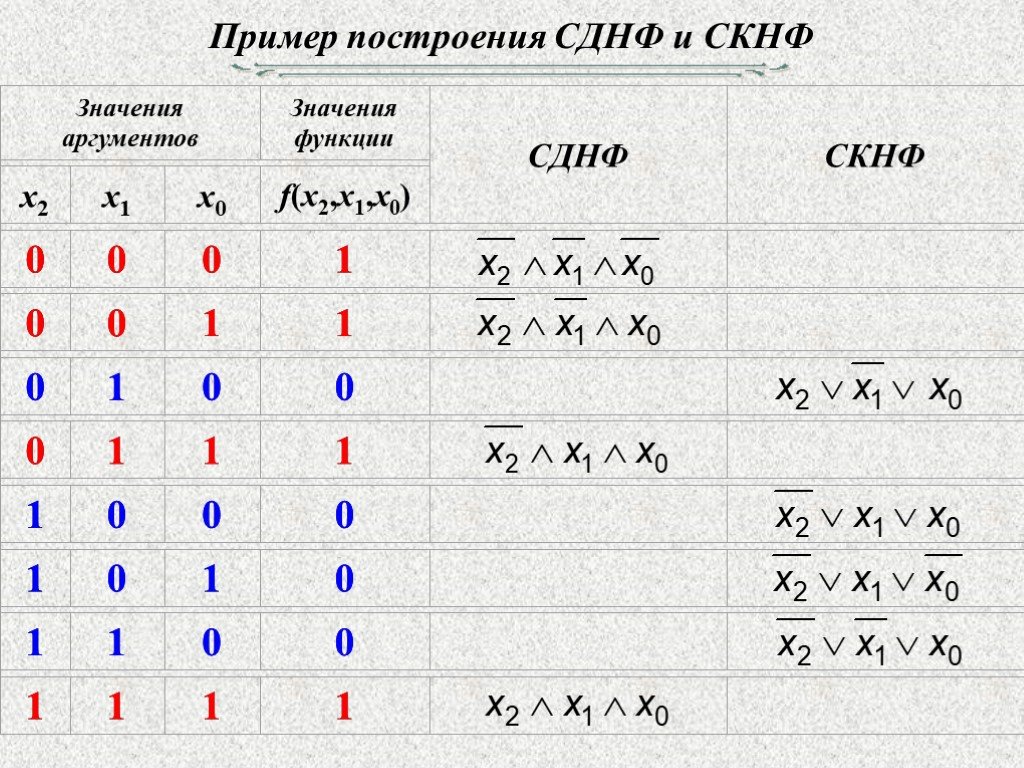
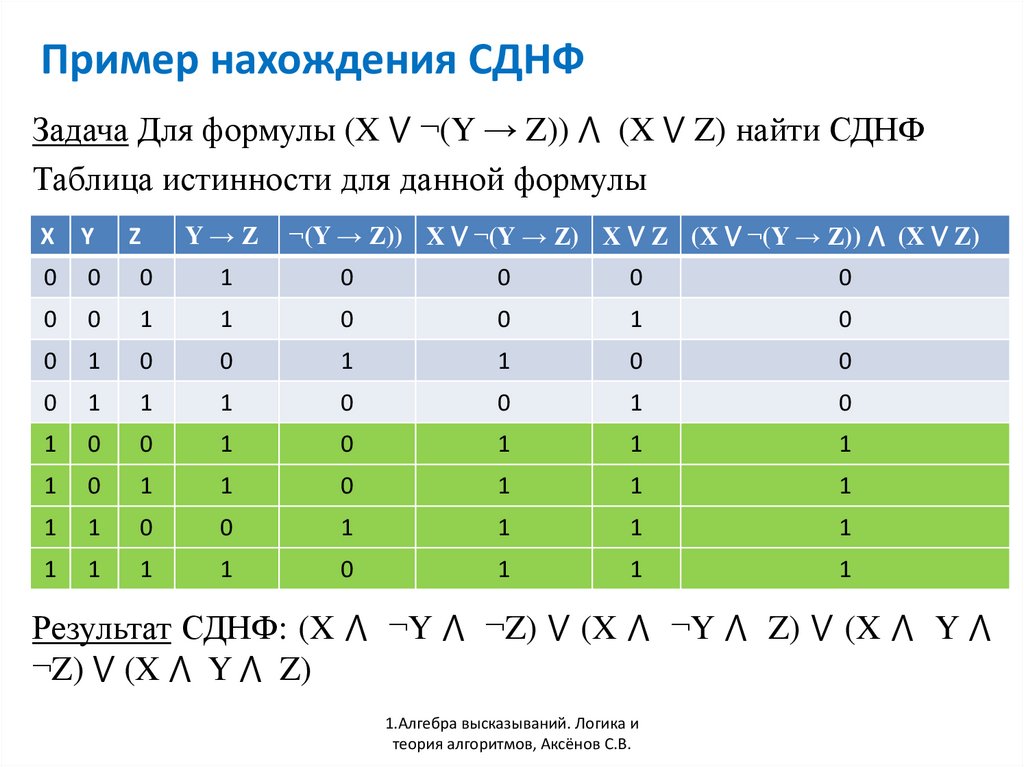
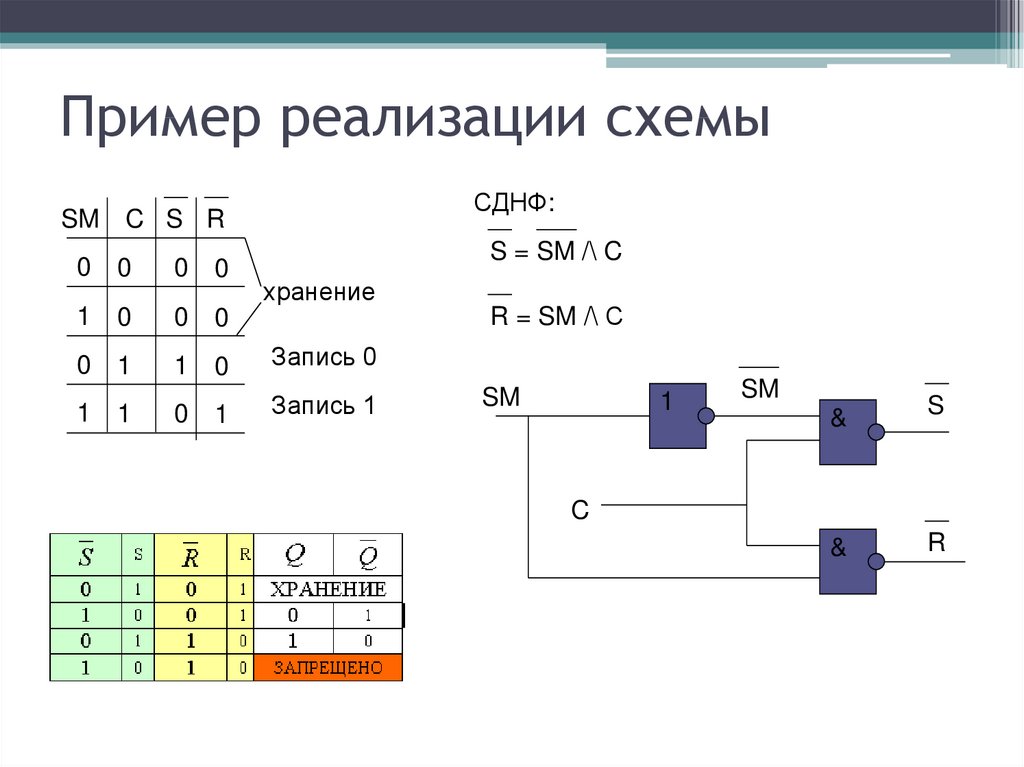 Понятие элементарного произведения; понятие дизъюнктивной нормальной формы (ДНФ). Методика построения таблицы истинности дляДНФ упрощенным методом. Понятие
Понятие элементарного произведения; понятие дизъюнктивной нормальной формы (ДНФ). Методика построения таблицы истинности дляДНФ упрощенным методом. Понятие
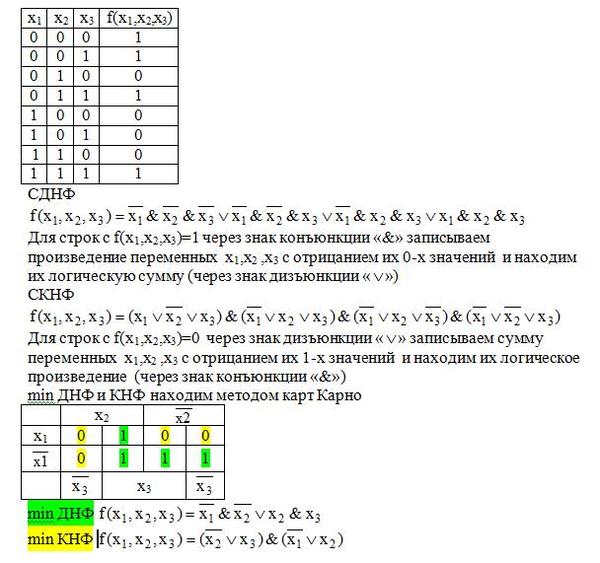
 Их
Их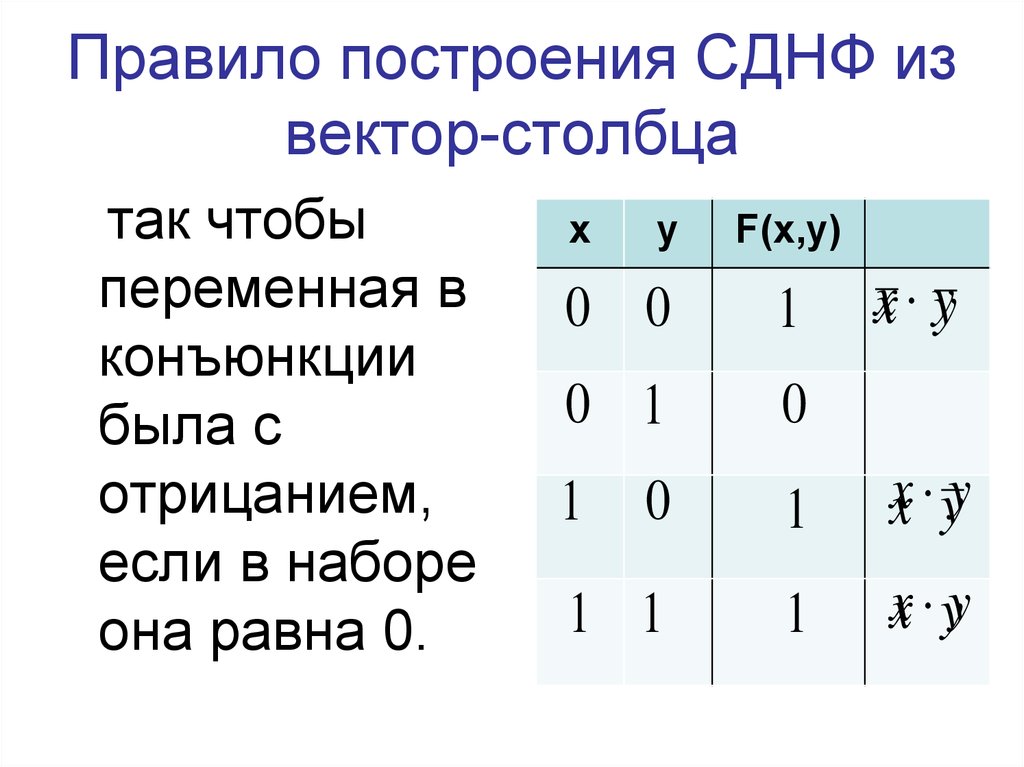 Каждая не тождественно ложная
Каждая не тождественно ложная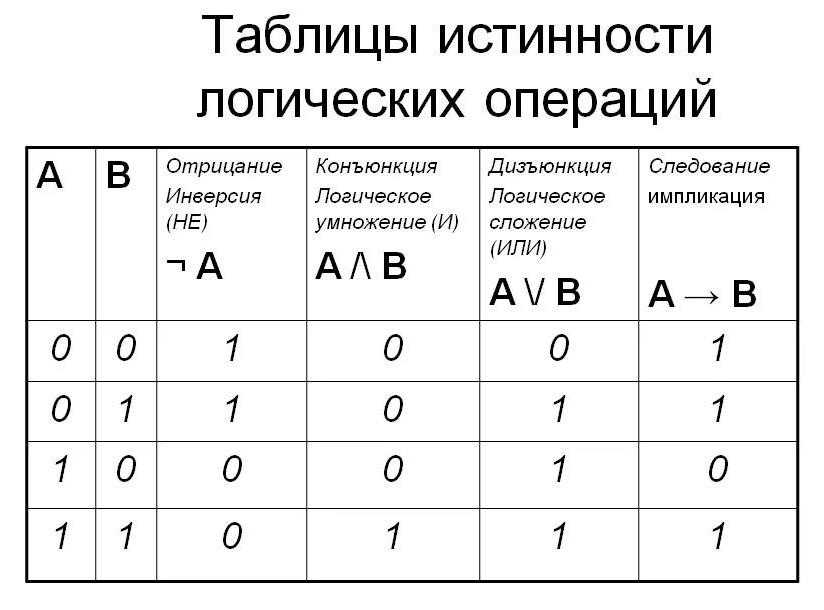
 Построить
Построить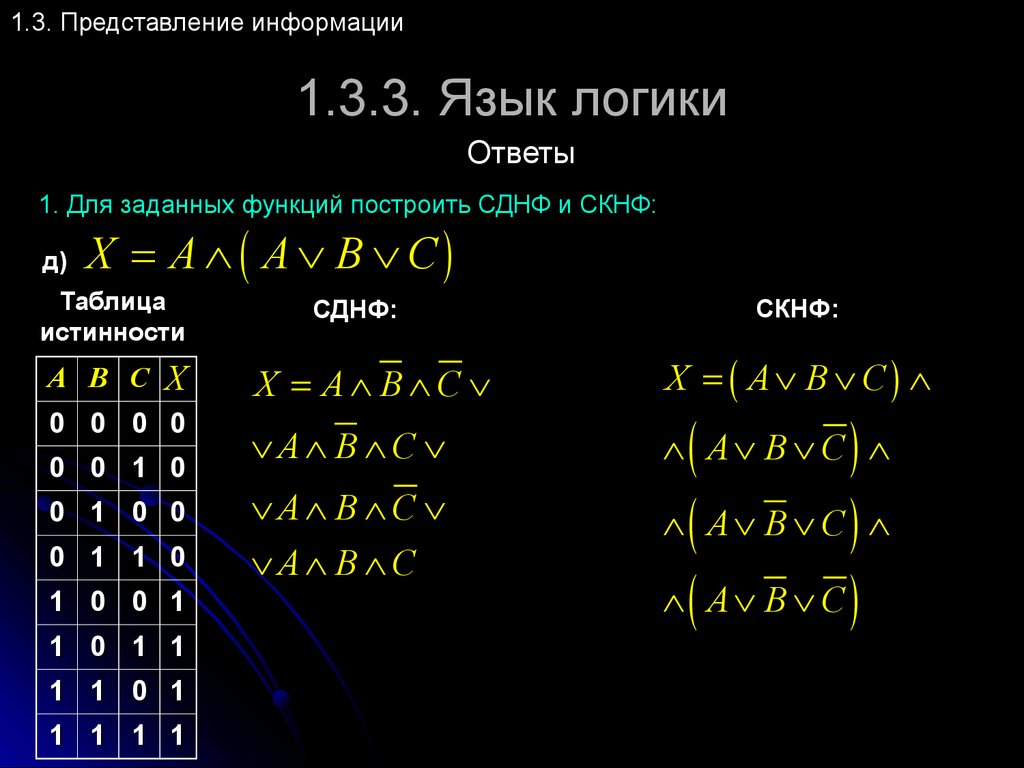 Какая
Какая ros.org/urdf
ros.org/urdf
 config model.sdf
config model.sdf  material
material launch. Это должно автоматически загрузить веб-версию беседки под названием gzweb.
launch. Это должно автоматически загрузить веб-версию беседки под названием gzweb.
 Классический подход может состоять в том, чтобы создать круг в графическом редакторе, таком как Photoshop, сохранить его как текстуру, импортировать эту текстуру в движок и поместить ее под иконку. Однако вместо этого можно использовать MATH для создания круга. Преимущества создания визуальных элементов SDF в движке включают гибкость изменения размера/градиента/анимации/штрихов и многое другое. Итак, давайте начнем с примера с кругом.
Классический подход может состоять в том, чтобы создать круг в графическом редакторе, таком как Photoshop, сохранить его как текстуру, импортировать эту текстуру в движок и поместить ее под иконку. Однако вместо этого можно использовать MATH для создания круга. Преимущества создания визуальных элементов SDF в движке включают гибкость изменения размера/градиента/анимации/штрихов и многое другое. Итак, давайте начнем с примера с кругом.



 ..) редактор по умолчанию анимирует каждый узел, в отличие от Unreal. Мы надеемся, что эти анимации помогут более четко показать, что происходит с SDF. Однако все эти узлы в следующем разделе существуют и возможны в Unreal, так что не волнуйтесь, это все равно, пока вы не перейдете к пользовательскому HLSL, но я расскажу об этом.
..) редактор по умолчанию анимирует каждый узел, в отличие от Unreal. Мы надеемся, что эти анимации помогут более четко показать, что происходит с SDF. Однако все эти узлы в следующем разделе существуют и возможны в Unreal, так что не волнуйтесь, это все равно, пока вы не перейдете к пользовательскому HLSL, но я расскажу об этом. Для этого я использую минимальный узел :
Для этого я использую минимальный узел :  Пересечение — это просто максимальный узел между двумя SDF. Я покажу это, чтобы вы могли увидеть различия, но любой, кто использует Illustrator/Photoshop и инструменты поиска пути, должен быть интуитивно знаком с этими понятиями:
Пересечение — это просто максимальный узел между двумя SDF. Я покажу это, чтобы вы могли увидеть различия, но любой, кто использует Illustrator/Photoshop и инструменты поиска пути, должен быть интуитивно знаком с этими понятиями: Чтобы заставить анимированный круг вычитаться из статического круга, вы должны превратить анимированный круг в отрицательный (с отрицательным узлом) и запустить его через максимальный узел . Что интересно, так это то, что два круга с другим методом вычитания сверху создают забавную анимацию луны/затмения. Статический круг сверху, вычитаемый из анимационного круга, как бы создает затмение — тень луны загораживает солнце — а другое вычитание выглядит как фаза луны, когда луна проходит через свои полные лунные циклы:
Чтобы заставить анимированный круг вычитаться из статического круга, вы должны превратить анимированный круг в отрицательный (с отрицательным узлом) и запустить его через максимальный узел . Что интересно, так это то, что два круга с другим методом вычитания сверху создают забавную анимацию луны/затмения. Статический круг сверху, вычитаемый из анимационного круга, как бы создает затмение — тень луны загораживает солнце — а другое вычитание выглядит как фаза луны, когда луна проходит через свои полные лунные циклы:  Вместо этого я хочу повторить итерацию, как инструмент поиска пути в Illustrator, вы можете объединять/вычитать/пересекать ваши фигуры SDF:
Вместо этого я хочу повторить итерацию, как инструмент поиска пути в Illustrator, вы можете объединять/вычитать/пересекать ваши фигуры SDF:  Lerping — не единственный способ смешивания SDF и, вероятно, не самый полезный с математической точки зрения. IQ использует настраиваемый сглаженный минимум для смешивания SDF. К
осуществлять
эта техника смешивания я сделал пользовательский узел HLSL , но я расскажу, как это сделать позже. Это показывает уравнение, которое я использовал от IQ, который вдохновил Dreams (видеоигру) на улучшение его исходного кода, и это был один из способов, которым они смешивали формы вместе в своей игре:
Lerping — не единственный способ смешивания SDF и, вероятно, не самый полезный с математической точки зрения. IQ использует настраиваемый сглаженный минимум для смешивания SDF. К
осуществлять
эта техника смешивания я сделал пользовательский узел HLSL , но я расскажу, как это сделать позже. Это показывает уравнение, которое я использовал от IQ, который вдохновил Dreams (видеоигру) на улучшение его исходного кода, и это был один из способов, которым они смешивали формы вместе в своей игре:  Смесь работает, когда круги расположены близко друг к другу, они почти сливаются в один круг, а по мере того, как они удаляются друг от друга, они превращаются в отдельные круги. В отличие от лерпа, который представляет собой вес между двумя формами, форма которых является более доминирующей для визуального отображения, эта смесь фактически будет работать, чтобы объединить две формы, когда они находятся близко, и разделить их, когда они разделены. Я также могу выбрать, сколько смешивания использовать, поэтому на этом gif-анимации выше небольшое смешивание сохраняет каждый круг своей собственной отчетливой формой, а большее смешивание объединяет круги в одну большую каплю.
Смесь работает, когда круги расположены близко друг к другу, они почти сливаются в один круг, а по мере того, как они удаляются друг от друга, они превращаются в отдельные круги. В отличие от лерпа, который представляет собой вес между двумя формами, форма которых является более доминирующей для визуального отображения, эта смесь фактически будет работать, чтобы объединить две формы, когда они находятся близко, и разделить их, когда они разделены. Я также могу выбрать, сколько смешивания использовать, поэтому на этом gif-анимации выше небольшое смешивание сохраняет каждый круг своей собственной отчетливой формой, а большее смешивание объединяет круги в одну большую каплю. Комбинации форм и анимаций кажутся бесконечными, а это всего лишь два круга… что, если я сделаю БОЛЬШЕ фигур? Хорошо давайте сделаем это!
Комбинации форм и анимаций кажутся бесконечными, а это всего лишь два круга… что, если я сделаю БОЛЬШЕ фигур? Хорошо давайте сделаем это! И GLSL, и HLSL являются языками кодирования шейдеров и очень похожи. Игровые движки, как правило, используют HLSL и Shadertoy, а некоторые веб-приложения используют GLSL. Формы IQ написаны на GLSL, поэтому мне нужно преобразовать их в HLSL для Unity или Unreal. Есть удобный сайт, который я открываю, если нахожу что-то, что я не знаю, как конвертировать из GLSL в HLSL через Microsoft. Здесь вы можете видеть, что мне нужно заменить vec2 на float2:
Я иду и преобразовываю эти GLSL в HLSL в своем блокноте, чтобы я мог легко скопировать и вставить это в движок:
И GLSL, и HLSL являются языками кодирования шейдеров и очень похожи. Игровые движки, как правило, используют HLSL и Shadertoy, а некоторые веб-приложения используют GLSL. Формы IQ написаны на GLSL, поэтому мне нужно преобразовать их в HLSL для Unity или Unreal. Есть удобный сайт, который я открываю, если нахожу что-то, что я не знаю, как конвертировать из GLSL в HLSL через Microsoft. Здесь вы можете видеть, что мне нужно заменить vec2 на float2:
Я иду и преобразовываю эти GLSL в HLSL в своем блокноте, чтобы я мог легко скопировать и вставить это в движок: Это всегда должен быть выход с плавающей запятой, а входы могут варьироваться от SDF до SDF.
Это всегда должен быть выход с плавающей запятой, а входы могут варьироваться от SDF до SDF.  Например, если я умножу на .5 , треугольник будет больше, но если я умножу на 2 , как в примере gif, треугольник уменьшится вдвое. Я предпочитаю умножение вместо деления только потому, что вы можете случайно получить деление на 0, что компьютеры ДЕЙСТВИТЕЛЬНО не любят, поэтому я склонен использовать умножение в большинстве моих приключений масштабирования UV.
Например, если я умножу на .5 , треугольник будет больше, но если я умножу на 2 , как в примере gif, треугольник уменьшится вдвое. Я предпочитаю умножение вместо деления только потому, что вы можете случайно получить деление на 0, что компьютеры ДЕЙСТВИТЕЛЬНО не любят, поэтому я склонен использовать умножение в большинстве моих приключений масштабирования UV.
 Расстояния от центра до линии окружности одинаковые.
Расстояния от центра до линии окружности одинаковые.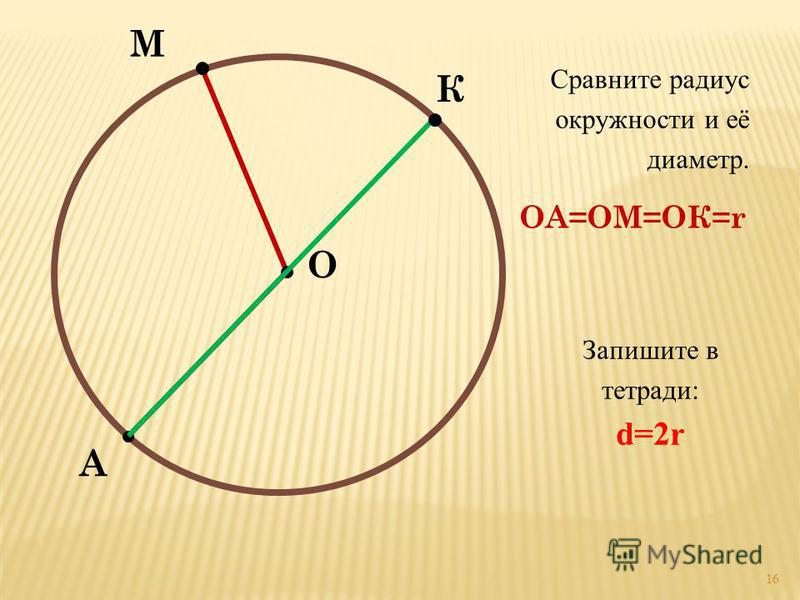
 com/watch?v=kBTkuSiGWOY
com/watch?v=kBTkuSiGWOY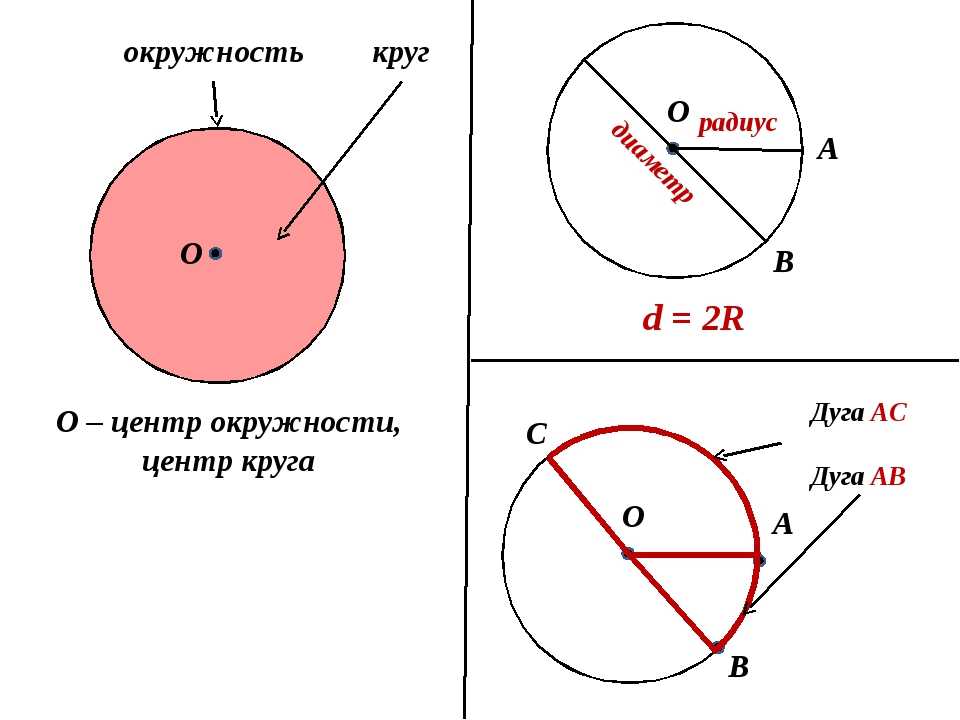
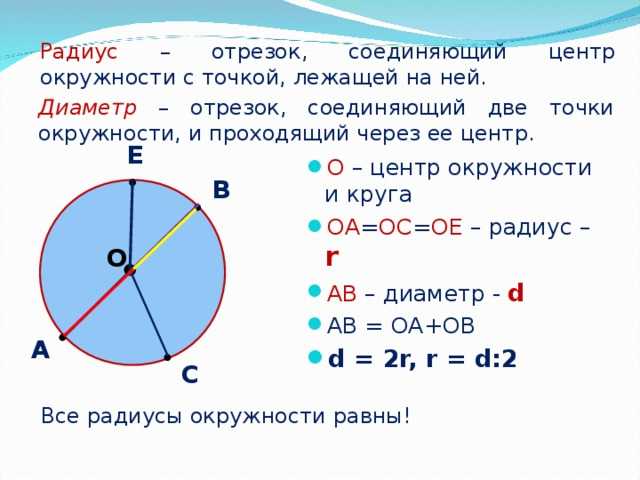 51), если R1 = 20 м, v1= 10 м/с, R2 = 10 м, v2 = 5 м/с.
51), если R1 = 20 м, v1= 10 м/с, R2 = 10 м, v2 = 5 м/с. ..)
..) Масштаб-> -50%
Масштаб-> -50%  При этом заявляя, что является профессионалом в области 3D-моделирования, конкурирующим с существующими. Заявление о профессиональном уровне на данный момент подтверждается только использованием Parasolid в качестве механизма рендеринга. Это не полный инструмент даже в некоторых областях. Он достаточно проработан, чтобы быть полезным. Если бы у меня был станок с ЧПУ, мне пришлось бы использовать Fusion 360 или какую-то другую программу или программы для создания моделей и траекторий движения инструментов. Тем не менее, я вижу большой потенциал Shapr3D, но им нужно доделать некоторые наборы функций, прежде чем добавлять новые, иначе они рискуют потерять таких людей, как я.
При этом заявляя, что является профессионалом в области 3D-моделирования, конкурирующим с существующими. Заявление о профессиональном уровне на данный момент подтверждается только использованием Parasolid в качестве механизма рендеринга. Это не полный инструмент даже в некоторых областях. Он достаточно проработан, чтобы быть полезным. Если бы у меня был станок с ЧПУ, мне пришлось бы использовать Fusion 360 или какую-то другую программу или программы для создания моделей и траекторий движения инструментов. Тем не менее, я вижу большой потенциал Shapr3D, но им нужно доделать некоторые наборы функций, прежде чем добавлять новые, иначе они рискуют потерять таких людей, как я. Но для более широкого охвата им следует сосредоточиться на таких вещах и исправить их.
Но для более широкого охвата им следует сосредоточиться на таких вещах и исправить их.
 Все-таки это не партия с человеком и не живое общение, которое тоже имеет свои преимущества. Но многим именно эта идея и нравится. В процессе игры очень быстро выясняется, что играть в шахматы с компьютером — не проще и не скучнее, чем с живым игроком, а во многих случаях это даже более интересно. Дело в том, что обыграть машину не так просто: она «держит» в памяти гигантское количество информации и анализирует ее за очень короткий срок. В результате вы имеете перед собой очень сильного противника.
Все-таки это не партия с человеком и не живое общение, которое тоже имеет свои преимущества. Но многим именно эта идея и нравится. В процессе игры очень быстро выясняется, что играть в шахматы с компьютером — не проще и не скучнее, чем с живым игроком, а во многих случаях это даже более интересно. Дело в том, что обыграть машину не так просто: она «держит» в памяти гигантское количество информации и анализирует ее за очень короткий срок. В результате вы имеете перед собой очень сильного противника.
 А если вы хотите играть в шахматы на весь экран с компьютером весь день напролет, никто не откажет вам в этом удовольствии. И это тоже очень удобно.
А если вы хотите играть в шахматы на весь экран с компьютером весь день напролет, никто не откажет вам в этом удовольствии. И это тоже очень удобно. Но на процессе самой игры это никак не отразится, тем более кардинальным образом. Вы все также сможете играть в шахматы с компьютером, получать статистику, настраивать параметры игры и выполнять массу других задач.
Но на процессе самой игры это никак не отразится, тем более кардинальным образом. Вы все также сможете играть в шахматы с компьютером, получать статистику, настраивать параметры игры и выполнять массу других задач. Развиваясь и одновременно отвлекаясь от рутинных дел, вы получите невероятный заряд бодрости, энергии, сможете переключиться, чтобы потом с новыми силами выполнять рабочие задачи.
Развиваясь и одновременно отвлекаясь от рутинных дел, вы получите невероятный заряд бодрости, энергии, сможете переключиться, чтобы потом с новыми силами выполнять рабочие задачи. Вы можете посмотреть сериал, но это вряд ли принесет хоть какую-то пользу. А шахматы на весь экран с компьютером — решение, которое оправдает себя сразу же. Подходит такая игра и в сложные жизненные периоды, когда нужно сконцентрироваться, но из-за нервов это не получается. Две-три партии шахмат онлайн — и вы уже можете решать какие-то задачи с более высоким уровнем эффективности.
Вы можете посмотреть сериал, но это вряд ли принесет хоть какую-то пользу. А шахматы на весь экран с компьютером — решение, которое оправдает себя сразу же. Подходит такая игра и в сложные жизненные периоды, когда нужно сконцентрироваться, но из-за нервов это не получается. Две-три партии шахмат онлайн — и вы уже можете решать какие-то задачи с более высоким уровнем эффективности. Вы сможете сохранить свой прогресс, получить рейтинг шахматиста, а также откроете новые опции. Не откладывайте этот шаг на потом, ведь регистрация займет у вас буквально пару минут. Достаточно лишь указать:
Вы сможете сохранить свой прогресс, получить рейтинг шахматиста, а также откроете новые опции. Не откладывайте этот шаг на потом, ведь регистрация займет у вас буквально пару минут. Достаточно лишь указать: Проблема в том, что многие пользователи просто заявляют: «хочу играть в шахматы бесплатно с компьютером здесь и сейчас». При этом они даже не утруждают себя пройти элементарный ликбез и разобраться с правилами. Не повторяйте их ошибок.
Проблема в том, что многие пользователи просто заявляют: «хочу играть в шахматы бесплатно с компьютером здесь и сейчас». При этом они даже не утруждают себя пройти элементарный ликбез и разобраться с правилами. Не повторяйте их ошибок. В последующих партиях вы наверняка сможете прийти к той же позиции и легко его обыграть.
В последующих партиях вы наверняка сможете прийти к той же позиции и легко его обыграть.
 Дело в том, что такая игра (даже в виртуальном формате) приносит очень много пользы игрокам, например:
Дело в том, что такая игра (даже в виртуальном формате) приносит очень много пользы игрокам, например: Ваше самолюбие вряд ли будет задето, как в случае с человеком. Вы видите цель и идете к ней, не отвлекаясь на свои внутренние переживания, ожидания, обиды и другие проявления. В результате вы учитесь работать над конкретной задачей, отбрасывая все лишнее. Эту стратегию затем можно использовать в жизни и добиваться больших успехов в разных сферах жизни.
Ваше самолюбие вряд ли будет задето, как в случае с человеком. Вы видите цель и идете к ней, не отвлекаясь на свои внутренние переживания, ожидания, обиды и другие проявления. В результате вы учитесь работать над конкретной задачей, отбрасывая все лишнее. Эту стратегию затем можно использовать в жизни и добиваться больших успехов в разных сферах жизни.
 Также в Chess Ultra имеется режим обучения и сценарий с 80 шахматными задачами, включая ключевые эпизоды всемирно известных партий.
Также в Chess Ultra имеется режим обучения и сценарий с 80 шахматными задачами, включая ключевые эпизоды всемирно известных партий. Так что если игра не заладилась, вы всегда можете смести в гневе все фигуры и карты на пол или даже опрокинуть стол.
Так что если игра не заладилась, вы всегда можете смести в гневе все фигуры и карты на пол или даже опрокинуть стол. Порадовали и игровые возможности Pure Chess: можно играть в одиночку против компьютера или с другом за одним ПК, а также в режиме онлайн, участвуя в турнирах и отслеживая свою позицию в глобальном рейтинге.
Порадовали и игровые возможности Pure Chess: можно играть в одиночку против компьютера или с другом за одним ПК, а также в режиме онлайн, участвуя в турнирах и отслеживая свою позицию в глобальном рейтинге. Например, в одном из режимов игрок получает сразу двух королей, в другом – призрачную армию с телепортацией и бессмертием. Играть можно против компьютера или других пользователей.
Например, в одном из режимов игрок получает сразу двух королей, в другом – призрачную армию с телепортацией и бессмертием. Играть можно против компьютера или других пользователей. После завершения партии игрок получает подробную статистику с ценным анализом.
После завершения партии игрок получает подробную статистику с ценным анализом. В 2009 году Сhessmaster 9000 получил оценку 2718 рейтинга Эло, что подвинуло его на 14 позицию среди себе подобных. Последней выпущенной частью серии стала Chessmaster XI, содержащая, помимо прочего, несколько занимательных мини-игр.
В 2009 году Сhessmaster 9000 получил оценку 2718 рейтинга Эло, что подвинуло его на 14 позицию среди себе подобных. Последней выпущенной частью серии стала Chessmaster XI, содержащая, помимо прочего, несколько занимательных мини-игр. com является сайтом хотя и бесплатным, но созданным в коммерческих целях, поэтому определенный дискомфорт создают рекламные баннеры. В остальном стандартный для подобного ресурса набор: возможность играть прямо в браузере против других пользователей или компьютера, обучающие курсы и шахматные задачи, возможность свободного общения между участниками и наблюдателями игры.
com является сайтом хотя и бесплатным, но созданным в коммерческих целях, поэтому определенный дискомфорт создают рекламные баннеры. В остальном стандартный для подобного ресурса набор: возможность играть прямо в браузере против других пользователей или компьютера, обучающие курсы и шахматные задачи, возможность свободного общения между участниками и наблюдателями игры.

 В проекте реализована система боевого пропуска, турниры и ранговые системы, кроссплатформенная и офлайн-игра. Кроме того, каждый сезон в игре меняется ротация героев и некоторых предметов.
В проекте реализована система боевого пропуска, турниры и ранговые системы, кроссплатформенная и офлайн-игра. Кроме того, каждый сезон в игре меняется ротация героев и некоторых предметов.
 Помимо геймплея приятное впечатление производит музыка и визуальное оформление, выдержанное в сказочном средневековом стиле.
Помимо геймплея приятное впечатление производит музыка и визуальное оформление, выдержанное в сказочном средневековом стиле. Игрокам под медитативный саундтрек придется манипулировать привычными фигурами, чтобы расположить нужные на ключевых местах. Средневековый сеттинг, сочная картинка и расслабленный геймплей по достойной цене.
Игрокам под медитативный саундтрек придется манипулировать привычными фигурами, чтобы расположить нужные на ключевых местах. Средневековый сеттинг, сочная картинка и расслабленный геймплей по достойной цене.

 Есть и режим классических шахмат, а также режим шахмат продвинутых, в котором фигурки, оказавшиеся под ударом, будут сражаться друг с другом в реальном времени за возможность сохранить за собой место на шахматном поле.
Есть и режим классических шахмат, а также режим шахмат продвинутых, в котором фигурки, оказавшиеся под ударом, будут сражаться друг с другом в реальном времени за возможность сохранить за собой место на шахматном поле.



 »
» »
»



 двигаться
b6 (ход
играл в игру). Это угрожает ферзю, но после …Qxc5 большой перевес белых практически исчезает. Уровни Майи
1500–1900 гг.
предсказывают, что в среднем игроки с рейтингом 1500 и выше будут правильно играть bxa6, заставляя ферзевый фланг открываться для
решающий эффект.
двигаться
b6 (ход
играл в игру). Это угрожает ферзю, но после …Qxc5 большой перевес белых практически исчезает. Уровни Майи
1500–1900 гг.
предсказывают, что в среднем игроки с рейтингом 1500 и выше будут правильно играть bxa6, заставляя ферзевый фланг открываться для
решающий эффект.
 Точность сопоставления ходов любой модели увеличивается с качеством хода, поскольку хорошие ходы легче предсказать. Но даже когда игроки совершают ужасные промахи, Майя правильно предсказывает их примерно в 25% случаев. Эта способность понимать, как и когда люди могут совершать ошибки, может сделать Maia очень полезным инструментом обучения.
Точность сопоставления ходов любой модели увеличивается с качеством хода, поскольку хорошие ходы легче предсказать. Но даже когда игроки совершают ужасные промахи, Майя правильно предсказывает их примерно в 25% случаев. Эта способность понимать, как и когда люди могут совершать ошибки, может сделать Maia очень полезным инструментом обучения. Этот график показывает, что персонализированные Майи достигают точности до 65% при прогнозировании действий конкретных игроков.
Этот график показывает, что персонализированные Майи достигают точности до 65% при прогнозировании действий конкретных игроков.
 Однако способы, которыми системы ИИ подходят к проблемам, часто отличаются от того, как это делают люди, и поэтому могут быть непонятными и трудными для изучения. Важнейшим шагом в преодолении этого разрыва между человеческим и искусственным интеллектом является моделирование отдельных действий, составляющих человеческое поведение, а не просто сопоставление совокупной человеческой деятельности.
Мы преследуем эту цель в модельной системе с долгой историей искусственного интеллекта: шахматах. Совокупная производительность шахматиста раскрывается по мере того, как он принимает решения в ходе игры. Сотни миллионов онлайн-игр, в которые играют игроки любого уровня квалификации, представляют собой богатый источник данных, в котором эти решения и их точный контекст записываются в мельчайших деталях. Применяя к этим данным существующие шахматные движки, включая реализацию AlphaZero с открытым исходным кодом, мы обнаруживаем, что они плохо предсказывают ходы человека.
Мы разрабатываем и представляем Maia, специализированную версию Alpha-Zero, обученную на человеческих шахматных играх, которая предсказывает ходы человека с гораздо большей точностью, чем существующие движки, и может достигать максимальной точности при прогнозировании решений, принимаемых игроками с определенным уровнем навыков в игре.
Однако способы, которыми системы ИИ подходят к проблемам, часто отличаются от того, как это делают люди, и поэтому могут быть непонятными и трудными для изучения. Важнейшим шагом в преодолении этого разрыва между человеческим и искусственным интеллектом является моделирование отдельных действий, составляющих человеческое поведение, а не просто сопоставление совокупной человеческой деятельности.
Мы преследуем эту цель в модельной системе с долгой историей искусственного интеллекта: шахматах. Совокупная производительность шахматиста раскрывается по мере того, как он принимает решения в ходе игры. Сотни миллионов онлайн-игр, в которые играют игроки любого уровня квалификации, представляют собой богатый источник данных, в котором эти решения и их точный контекст записываются в мельчайших деталях. Применяя к этим данным существующие шахматные движки, включая реализацию AlphaZero с открытым исходным кодом, мы обнаруживаем, что они плохо предсказывают ходы человека.
Мы разрабатываем и представляем Maia, специализированную версию Alpha-Zero, обученную на человеческих шахматных играх, которая предсказывает ходы человека с гораздо большей точностью, чем существующие движки, и может достигать максимальной точности при прогнозировании решений, принимаемых игроками с определенным уровнем навыков в игре. настраиваемый способ. Для двойной задачи прогнозирования того, совершит ли человек большую ошибку при следующем шаге, мы разрабатываем глубокую нейронную сеть, которая значительно превосходит конкурентные базовые показатели. Взятые вместе, наши результаты показывают, что существует многообещающая разработка систем искусственного интеллекта с учетом взаимодействия людей путем предварительного точного моделирования детального принятия решений человеком.
настраиваемый способ. Для двойной задачи прогнозирования того, совершит ли человек большую ошибку при следующем шаге, мы разрабатываем глубокую нейронную сеть, которая значительно превосходит конкурентные базовые показатели. Взятые вместе, наши результаты показывают, что существует многообещающая разработка систем искусственного интеллекта с учетом взаимодействия людей путем предварительного точного моделирования детального принятия решений человеком.

 В 3 года
В 3 года
 Эта теорема имеет
Эта теорема имеет
 Аппроксимации линейного сегмента лежат на выше $\tan\theta$ от $\theta\ приблизительно25$ до $\theta=45$ и на ниже в другом месте, поэтому вам следует округлить в меньшую сторону на и в большую сторону на соответственно при выполнении ментальная арифметика. Очевидно, что это возможно расширить для углов, превышающих $60$ градусов, но неясно, можно ли (и насколько далеко) сделать это с формулами, которые используют только «простые» умножения и деления.
Аппроксимации линейного сегмента лежат на выше $\tan\theta$ от $\theta\ приблизительно25$ до $\theta=45$ и на ниже в другом месте, поэтому вам следует округлить в меньшую сторону на и в большую сторону на соответственно при выполнении ментальная арифметика. Очевидно, что это возможно расширить для углов, превышающих $60$ градусов, но неясно, можно ли (и насколько далеко) сделать это с формулами, которые используют только «простые» умножения и деления. \circ = 1/5$$ 9\circ$
$$\tan a = 1/\tan(90°−a)$$
\circ = 1/5$$ 9\circ$
$$\tan a = 1/\tan(90°−a)$$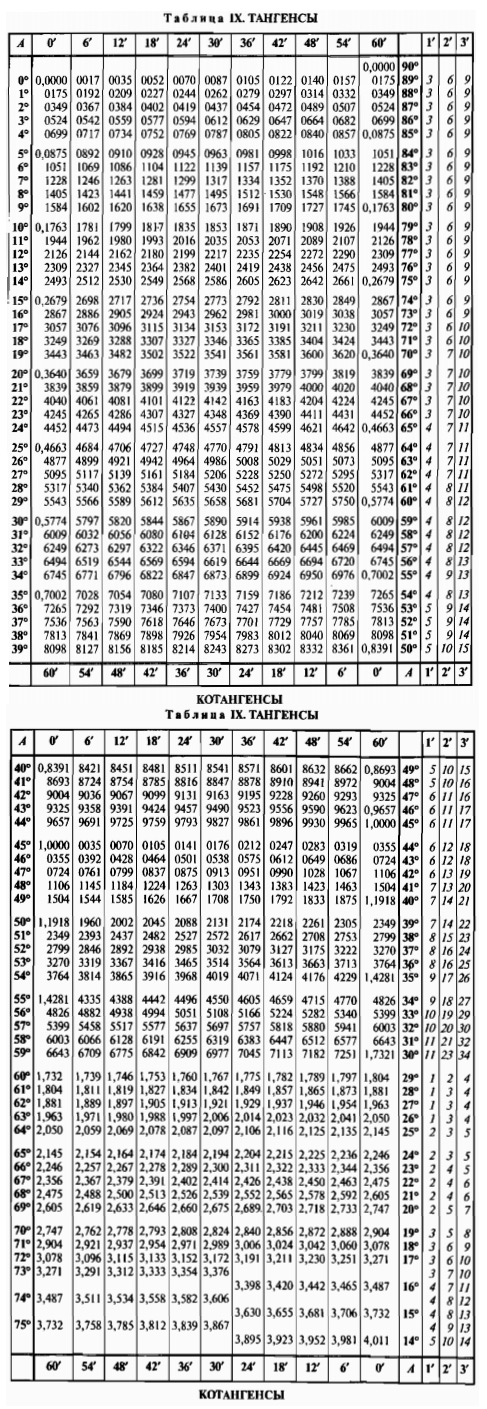
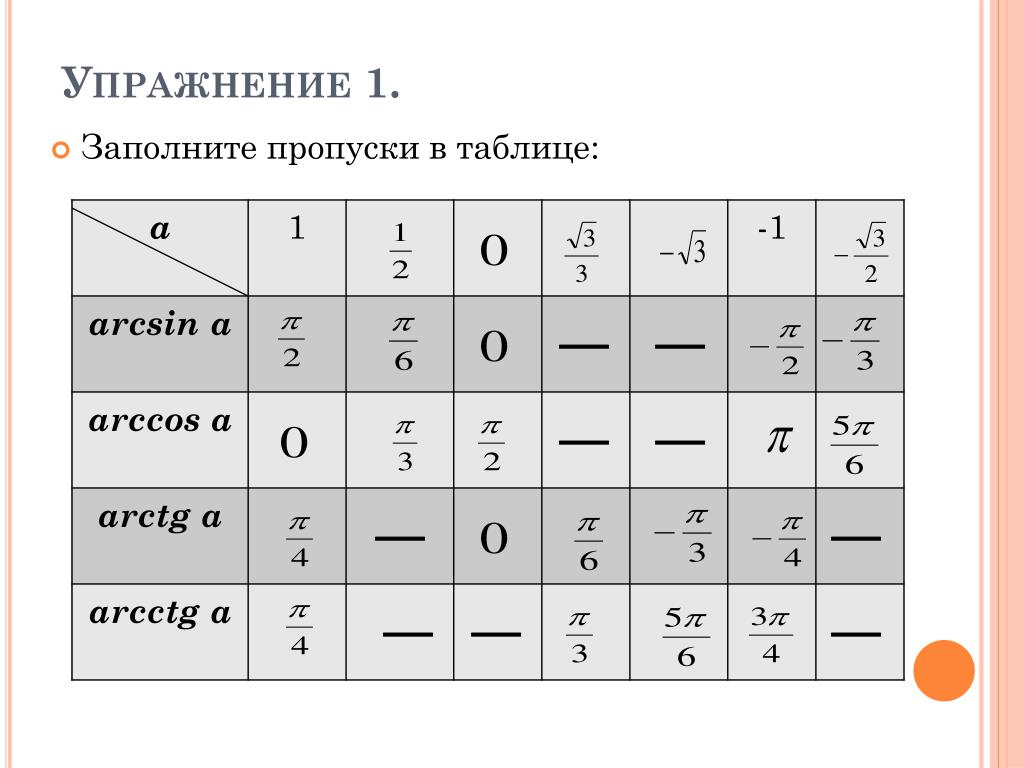 \circ$), я думаю, что можно без чрезвычайного количества механического запоминания сделать очень грубые оценки. Для большей точности или, по крайней мере, перекрестной ссылки, можно было бы составить аналогичный треугольник, оценить соотношение сторон напрямую и выполнить однократное деление. 92\свыше 90-х}$$
дает относительную ошибку менее $6\%$ во всем диапазоне $[0,{\pi\over2}[\ $. См. следующий рисунок:
\circ$), я думаю, что можно без чрезвычайного количества механического запоминания сделать очень грубые оценки. Для большей точности или, по крайней мере, перекрестной ссылки, можно было бы составить аналогичный треугольник, оценить соотношение сторон напрямую и выполнить однократное деление. 92\свыше 90-х}$$
дает относительную ошибку менее $6\%$ во всем диапазоне $[0,{\pi\over2}[\ $. См. следующий рисунок: 0175 2° 0.0349 3° 0.0524 4° 0,0699 5° 0.0875 6° 0.1051 7° 0.1228 8° 0.1405 9° 0.1584 10° 0.1763 11° 0.1944 12° 0.2126 13° 0.2309 14° 0.2493 15° 0.2679 16° 0.2867 17° 0.3057 18° 0.3249 19° 0.3443 20° 0.364 21° 0.3839 22° 0.404 23° 0.
0175 2° 0.0349 3° 0.0524 4° 0,0699 5° 0.0875 6° 0.1051 7° 0.1228 8° 0.1405 9° 0.1584 10° 0.1763 11° 0.1944 12° 0.2126 13° 0.2309 14° 0.2493 15° 0.2679 16° 0.2867 17° 0.3057 18° 0.3249 19° 0.3443 20° 0.364 21° 0.3839 22° 0.404 23° 0.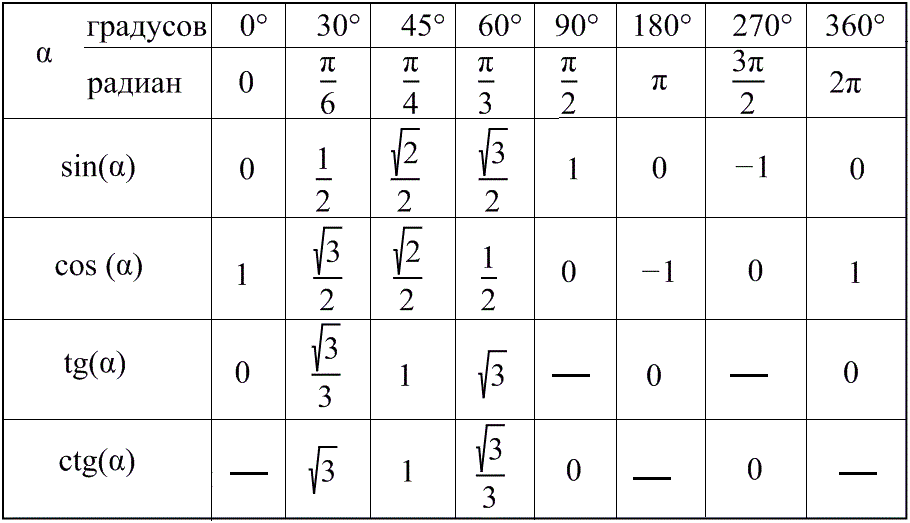 4245 24° 0.4452 25° 0.4663 26° 0.4877 27° 0.5095 28° 0.5317 29° 0.5543 30 ° 0.5774 31° 0.6009 32° 0.6249 33° 0.6494 34° 0.6745 35° 0.7002 36° 0.7265 37° 0.7536 38° 0.7813 39° 0.8098 40 ° 0.8391 41° 0.8693 42° 0.9004 43° 0.9325 44° 0.
4245 24° 0.4452 25° 0.4663 26° 0.4877 27° 0.5095 28° 0.5317 29° 0.5543 30 ° 0.5774 31° 0.6009 32° 0.6249 33° 0.6494 34° 0.6745 35° 0.7002 36° 0.7265 37° 0.7536 38° 0.7813 39° 0.8098 40 ° 0.8391 41° 0.8693 42° 0.9004 43° 0.9325 44° 0.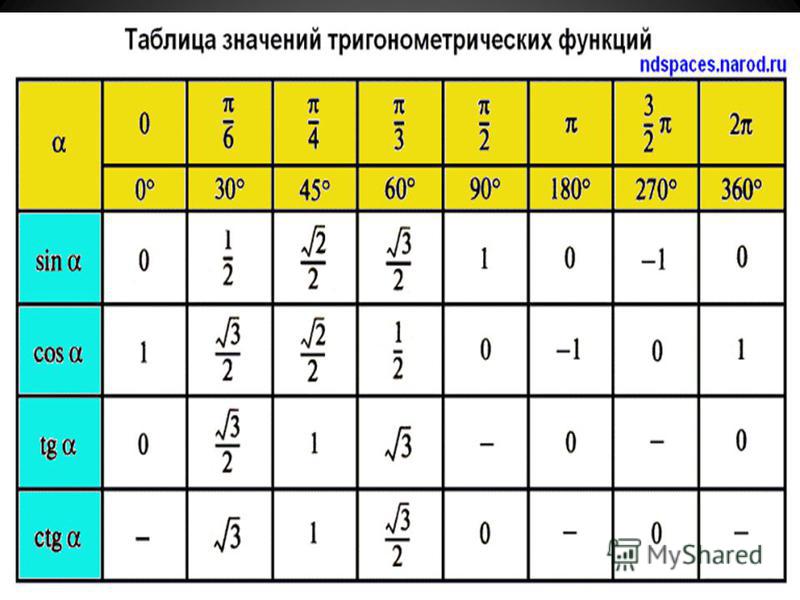 9657 45° 1 46° 1.0355 47° 1.0724 48° 1.1106 49° 1.1504 50° 1.1918 51° 1.2349 52° 1.2799 53° 1.327 54° 1.3764 55° 1.4281 56° 1.4826 57° 1.5399 58° 1.6003 59° 1.6643 60 ° 1.7321 61° 1.804 62° 1.8807 63° 1.9626 64° 2.0503 65° 2.
9657 45° 1 46° 1.0355 47° 1.0724 48° 1.1106 49° 1.1504 50° 1.1918 51° 1.2349 52° 1.2799 53° 1.327 54° 1.3764 55° 1.4281 56° 1.4826 57° 1.5399 58° 1.6003 59° 1.6643 60 ° 1.7321 61° 1.804 62° 1.8807 63° 1.9626 64° 2.0503 65° 2.