Конвертировать DOC В ПДФ Бесплатно
DOC в ПДФ
Разработано на базе программных решений от aspose.com а также aspose.cloud
Выберите DOC файлы или перетащите DOC файлы мышью
Google Drive Dropbox
Использовать пароль
Этот пароль будет применяться ко всем документам
Использовать распознавание текста Использовать распознавание текста
АнглийскийАрабскийИспанскийИтальянскийКитайский упрощенныйНемецкийПерсидскийПольскийПортугальскийРусскийФранцузский «/>
Если вам нужно преобразовать несколько DOC в один ПДФ, используйте Merger
Загружая свои файлы или используя наш сервис, вы соглашаетесь с нашими Условиями обслуживания и Политикой конфиденциальности.
Сохранить как
PDFDOCXMDPPTXPPTHTMLTXTDOCDOTDOTXRTFMHTMLXHTMLODTOTTEPUBXLSXXLSCSVTEXMOBIWPSWPT
КОНВЕРТИРОВАТЬ
Ваши файлы были успешно сконвертированы
СКАЧАТЬ
Загрузить в Google Загрузить в Dropbox
Конвертация других документов
Отправить на электронную почту
Пройдите наш опрос
Хотите сообщить об этой ошибке на форуме Aspose, чтобы мы могли изучить и решить проблему? Когда ошибка будет исправлена, вы получите уведомление на email. Форма отчета
Форма отчета
Google Sheets
Mail Merge
Облачный API
Конвертировать DOC в ПДФ онлайн
Используйте конвертер DOC в ПДФ для экспорта документов DOC в ПДФ формат онлайн. Это совершенно бесплатно.
Наш онлайн сервис может конвертировать DOC документы любой сложности. Документы DOC могут содержать таблицы и списки, верхние и нижние колонтитулы, формулы и графику, стилизованный текст и так далее. Наш конвертер проанализирует содержимое DOC файла до мельчайших деталей и воссоздаст соответствующие элементы в целевом ПДФ формате.
Конвертер DOC в ПДФ онлайн
Конвертация из DOC в ПДФ и наоборот — одна из самых востребованных операций с офисными документами. Форматы документов DOC отлично подходят, когда вы хотите, чтобы другие люди могли вносить изменения в содержимое. Напротив, ПДФ формат — отличный выбор, когда нам нужно защитить документ от изменения. Нам нужны обе уникальные функции, которые предоставляют форматы DOC и ПДФ.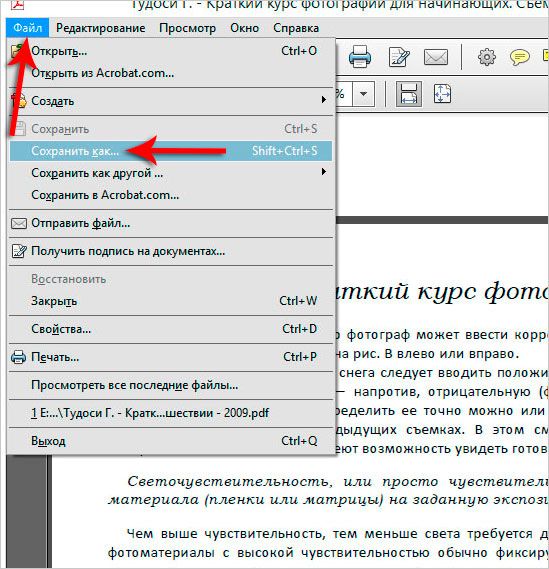 Форматы документов ПДФ и DOC в некоторых случаях дополняют друг друга и тесно связываются в современной офисной работе. Довольно часто мы хотим преобразовать редактируемый DOC документ в неизменяемый ПДФ файл. Это может быть контракт или какие-то финансовые данные, которые не следует изменять.
Форматы документов ПДФ и DOC в некоторых случаях дополняют друг друга и тесно связываются в современной офисной работе. Довольно часто мы хотим преобразовать редактируемый DOC документ в неизменяемый ПДФ файл. Это может быть контракт или какие-то финансовые данные, которые не следует изменять.
Конвертировать файл DOC в ПДФ
Чтобы конвертировать DOC в ПДФ формат, просто перетащите DOC файл в поле загрузки данных, укажите параметры преобразования, нажмите кнопку ‘Конвертировать’ и получите выходной ПДФ файл за считанные секунды. Результирующее содержимое ПДФ, структура и оформление будут идентичны исходному DOC документу.
DOC to ПДФ Converter основан на программных продуктах компании Aspose, которые широко используются во всем мире для обработки DOC файлов и ПДФ с высокой скоростью и профессиональным качеством результата.
Как преобразовать DOC в ПДФ
- Загрузите DOC файлы, чтобы преобразовать их в ПДФ формат онлайн.
- Укажите параметры преобразования DOC в ПДФ.

- Нажмите кнопку, чтобы конвертировать DOC в ПДФ онлайн.
- Загрузите результат в ПДФ формате для просмотра.
- Вы можете отправить ссылку для скачивания по электронной почте, если хотите получить результаты позже.
Вопросы-Ответы
Как конвертировать DOC в ПДФ бесплатно?
Просто используйте наш DOC в ПДФ Converter. Вы получите выходные файлы ПДФ одним кликом мыши.
Сколько DOC файлов я могу конвертировать в ПДФ формат за раз?
Вы можете конвертировать до 10 DOC файлов за раз.
Каков максимально допустимый размер DOC файла?
Размер каждого DOC файла не должен превышать 10 МБ.
Какие есть способы получить результат в ПДФ формате?
После завершения преобразования DOC в ПДФ вы получите ссылку для скачивания. Вы можете скачать результат сразу или отправить ссылку на скачивание ПДФ на свой e-mail позже.
Как долго мои файлы будут храниться на ваших серверах?
Все пользовательские файлы хранятся на серверах Aspose в течение 24 часов. По истечении этого времени они автоматически удаляются.
По истечении этого времени они автоматически удаляются.
Можете ли вы гарантировать сохранность моих файлов? Все безопасно?
Aspose уделяет первостепенное внимание безопасности и защите пользовательских данных. Будьте уверены, что ваши файлы хранятся на надежных серверах и защищены от любого несанкционированного доступа.
Почему конвертация DOC в ПДФ занимает немного больше времени, чем я ожидал?
Конвертация больших DOC файлов в ПДФ формат может занять некоторое время, поскольку эта операция включает перекодирование и повторное сжатие данных.
Преобразовать doc в pdf
Для начала определимся, что такое doc и pdf. Чтобы правильно написать указанные форматы, надо ставить перед ними точку — .doc и .pdf. Но точку часто не ставят — все торопятся…
Наличие точки означает, что после точки мы имеем дело с расширением имени файла (или иначе — форматом файла). Например,
- «расписание.doc» – это имя файла,
- а .
 doc – это расширение имени файла, которое указывает операционной системе, какой именно программой следует открывать файл.
doc – это расширение имени файла, которое указывает операционной системе, какой именно программой следует открывать файл.
.Doc (от англ. document) – это расширение означает, что документ был создан программой Microsoft Word.
.Pdf (от англ. Portable Document Format) был разработан фирмой Adobe для федеральных властей США для создания и хранения рабочих документов.
В настоящее время используется в издательском деле, для распространения факсов, в формах налоговой отчетности, в образовательных, юридических, финансовых учреждениях, а также обычными пользователями ПК в электронных письмах, в сообщениях и т.д.
Такой файл легко напечатать и использовать для совместной работы, а также трудно изменить. Принято считать, что если Вам прислали документ в формате .pdf, то Вы НЕ будете присланный документ изменять или редактировать. Точно также, если Вы отправляете документ в формате .pdf, то «по умолчанию» предполагаете, что Ваш документ не будет редактироваться получателем (Ваше резюме, налоговая отчетность и т. п.)
п.)
Поэтому если Вы вдруг решите:
- вскрыть «а-ля хакер» присланный Вам документ в формате .pdf,
- отредактировать его (внести изменения),
- потом отправить тому, кто вам прислал этот документ,
то не удивляйтесь, что с Вами обратная сторона не захочет больше иметь дела. Кроме того, на некоторые материалы в формате .pdf есть авторские права, например, на электронные книги, поэтому любое изменение в таких материалов автоматически означает нарушение авторских прав.
После «лирического отступления» по компьютерной грамотности вернемся к теме статьи: как преобразовать файл doc в pdf? Сделать это можно различными способами. Возможно применение текстового редактора Word, а также иных утилит или с помощью онлайн-сервисов.
Преобразовать doc в pdf может быть необходимо в различных случаях. Допустим, Вам требуется переслать файл по электронной почте в хорошо оформленном виде, создать резюме в виде .pdf файла или сделать простейшую электронную книгу. Существует возможность использовать для этих целей платные и бесплатные программы. Программы, призванные преобразовать doc в pdf, могут быть двух групп.
Существует возможность использовать для этих целей платные и бесплатные программы. Программы, призванные преобразовать doc в pdf, могут быть двух групп.
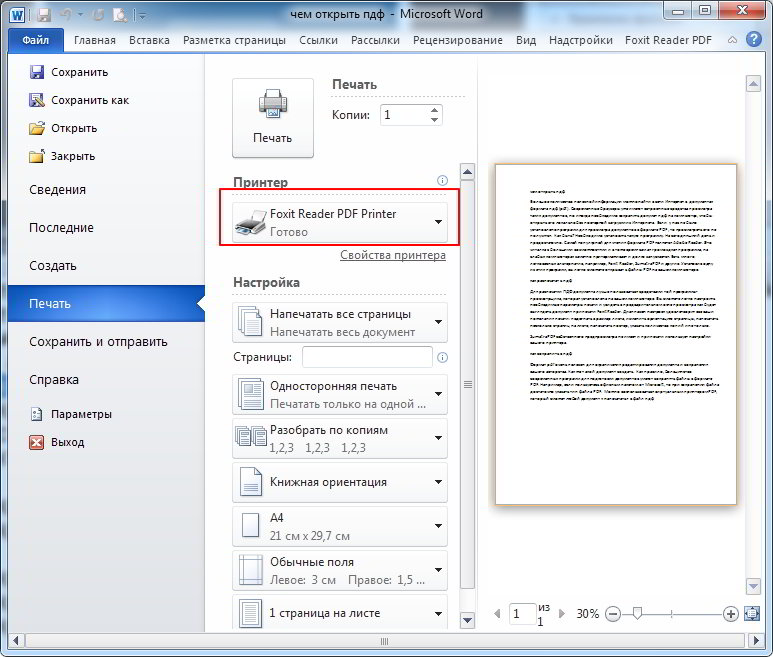
Первая программа является полноценной утилитой для того, чтобы преобразовать DOC в PDF. Программы, которые находятся во второй группе, подключаются к системе как виртуальный принтер, то есть наличие реального принтера не требуется. В этом случае Вам нужно вывести документ на печать, но выбирать нужно при этом виртуальный, а не физический принтер. Pdf документ будет определен в отдельную папку.
Не всем известно, что возможно преобразовать doc (docx) в pdf с помощью текстового редактора Word, в котором был создан исходный документ. Это поможет Вам обойтись без поиска, скачивания и установки сторонних программ.
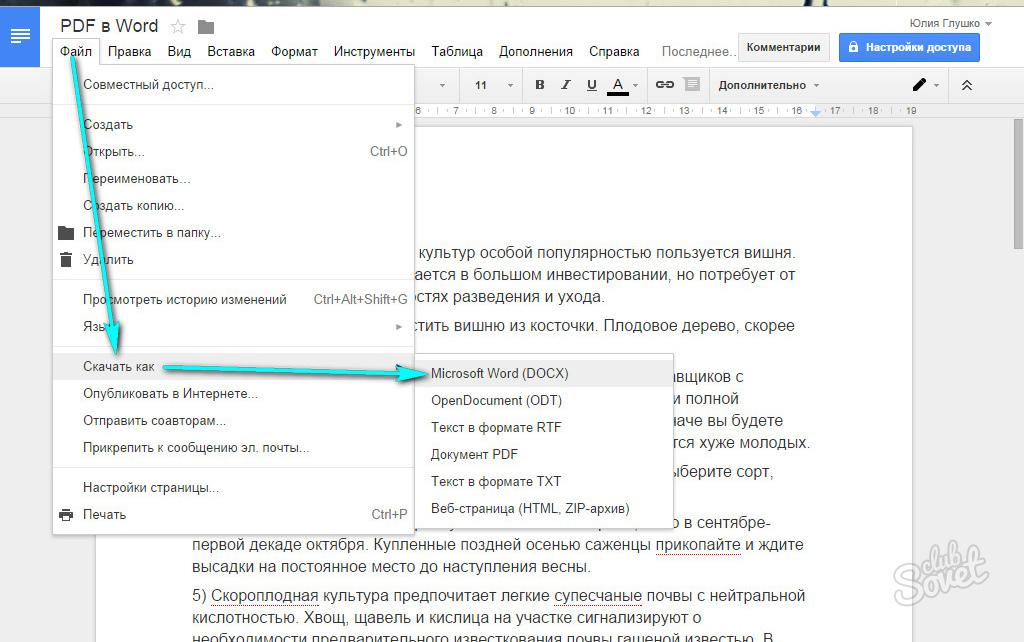
Документ можно открыть в MS Office и сохранить в формате .pdf. Чтобы это сделать, нажмите на значок Office в верхнем углу слева, выберите «Сохранить как»:
Откроется «Сохранение документа», в котором сначала выбирается папка для хранения:
Рис.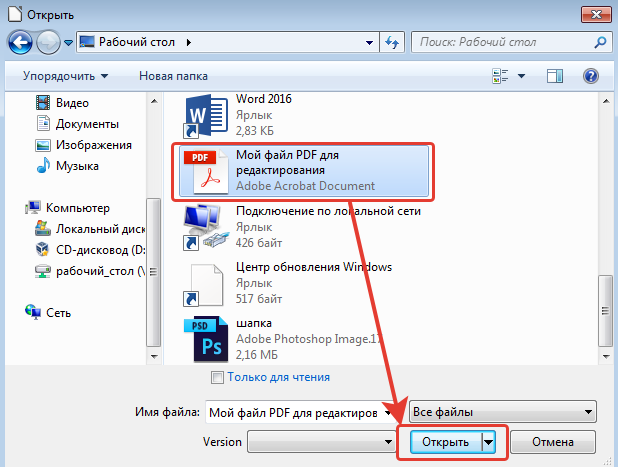 1. Сохранить документ в формате pdf в программе Word
1. Сохранить документ в формате pdf в программе Word
Далее по шагам, обозначенным на рисунке 1:
цифра 1 на рис. 1 — в поле Тип Файла кликнуть по маленькому треугольнику. Появится выпадающее меню, в котором надо найти и кликнуть по «PDF (*.pdf)».
2 на рис. 1 — ввести имя документа,
3 — вариант оптимизации «Стандартная» или «Минимальный размер»,
4 — выберите подходящие параметры. Можно сначала сохранить документ с одними параметрами , если они не понравятся или не подойдут, выбрать другие параметры и сохранить документ с новыми параметрами.
5 — в «Сервисе» есть опция «Сжать рисунки». Если ей воспользоваться, то объем документа можно уменьшить, но качество рисунков будет несколько ниже, чем до сжатия.
6 на рис. 1 — самая важная кнопка «Сохранить», на которую надо нажать, чтобы сохранить документ в формате pdf с выбранными параметрами.
Как преобразовать DOC в PDF в OpenOffice?
Word является платной программой, и он не у всех есть, поэтому есть еще вариант с бесплатным пакетом OpenOffice:
Официальный сайт OpenOffice: https://www.
openoffice.org/ru/
Чтобы скачать, нужно перейти по указанной выше ссылке на официальный сайт и затем кликнуть по кнопке «Загрузить Apache OpenOffice».
В этом пакете программа OpenOffice Writer является программой, аналогичной текстовому редактору Word. Нужно открыть Writer. Сверху есть панель инструментов и кнопка «PDF».
Когда документ загружен в редактор Writer, нужно кликнуть по кнопке «PDF».
Здесь можно настраивать разные параметры документа, допустим, поставить на него пароль или настроить параметры внешних и внутренних ссылок.
Если в первоначальном документе есть графические изображения, стоит обратить внимание на пункт «Изображение» во вкладке «Общие». Там выставляются параметры сжатия JPEG, а также разрешение изображений. Чем параметры выше, тем лучше станет качество документа, но и вес его станет больше. Здесь потребуется найти оптимальный баланс между весом документа и его качеством.
Когда Вы настроите все параметры,дальше вводится название файла, выбирается папка для хранения и нажимается «Сохранить».
Некоторые утверждают, что Writer конвертирует в PDF лучше, чем Word: получается файл меньше по объему и качество не страдает.
Как конвертировать DOC в PDF онлайн?
Если у Вас нет под рукой текстового редактора, тогда можно воспользоваться бесплатным сервисом для конвертации. Допустим, сервисом doc2pdf.net. Этот бесплатный преобразователь позволяет конвертировать документы Word (.doc/.docx) в формат Adobe PDF (.pdf).
Преобразовать DOCX (DOC) в PDF: https://www.doc2pdf.com/
Сервис работает в двух режимах:
- онлайн,
- десктопная версия.
В правом верхнем углу этого сервиса есть возможность выбрать русский язык вместо английского, который используется по умолчанию.
Режим онлайн означает, что документ загружается на сторонний сервис, там конвертируется в другой формат и возвращается Вам. НО документ должен быть НЕ более 25 МБ!
Десктопная версия означает, что программа устанавливается на Ваш компьютер, а потом с ее помощью можно конвертировать файлы по мере необходимости.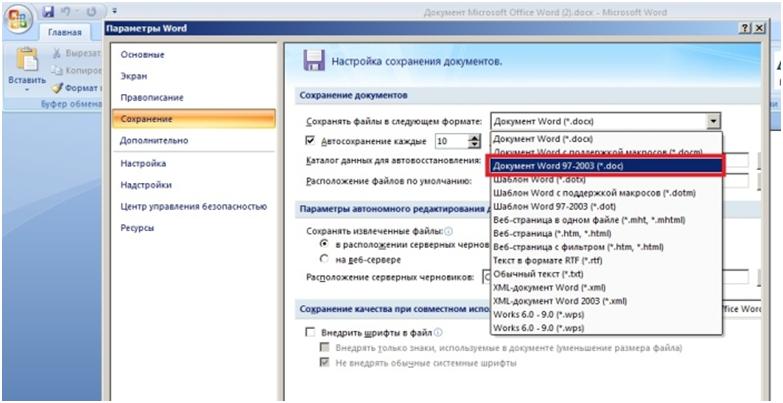
Когда Вы зайдете на сайт, то заметите в левой колонке страницы форму:
Рис. 2. Сервис doc2pdf в режиме онлайн
Цифра 1 на рис. 2 — клик по «My computer». Выбираем на своем ПК файл, подлежащий конвертации в PDF (он должен быть не более 25 Мб). После того, как файл выбран, идет его конвертация, нужно немного подождать.
Когда файл будет преобразован, появится 2 варианта для того, чтобы получить файл pdf на свой компьютер:
- скачать (цифра 1 на рис. 3),
- получить по электронной почте. Для этого варианта есть поле для ввода e-mail (2 на рис. 3). Вводите свой e-mail без ошибок, ибо на него будет выслан файл в формате PDF.
Рис. 3. Сохранить файл PDF на своем ПК или выслать файл на электронную почту
P.S. Статья закончилась, но на блоге можно еще почитать:
1. Как легко посчитать буквы в тексте
2. 4 программы проверки орфографии
3. Как сделать гиперссылку в Word?
4. Как сохранить веб-страницу в PDF-документ
5. О сходстве и различии файлов doc и docx
О сходстве и различии файлов doc и docx
Получайте новые статьи по компьютерной грамотности на ваш почтовый ящик:
Необходимо подтвердить подписку в своей почте. Спасибо!
Конвертировать DOC/DOCX в PDF в App Store
Описание
Преобразователь документов Word в PDF
В дополнение к исключительно высокому уровню безопасности файла PDF, поскольку пользователь не может редактировать исходное содержимое документа, многие люди также довольны тем, что PDF позволяет отображать документы без ошибок шрифта.
Это приложение «Конвертировать Word в PDF» поможет вам легко и быстро преобразовать файл Word в PDF.
Приложение имеет встроенный полный шрифт Unicode, индийский шрифт, арабский шрифт, бразильский шрифт, специальные шрифты ….
Приложение не только поддерживает преобразование doc в pdf или docx в pdf, но также поддерживает все форматы слов с 2003, 2007, 2013, 2016
Приложение позволяет без церемоний конвертировать ваши файлы DOC или DOCX в PDF.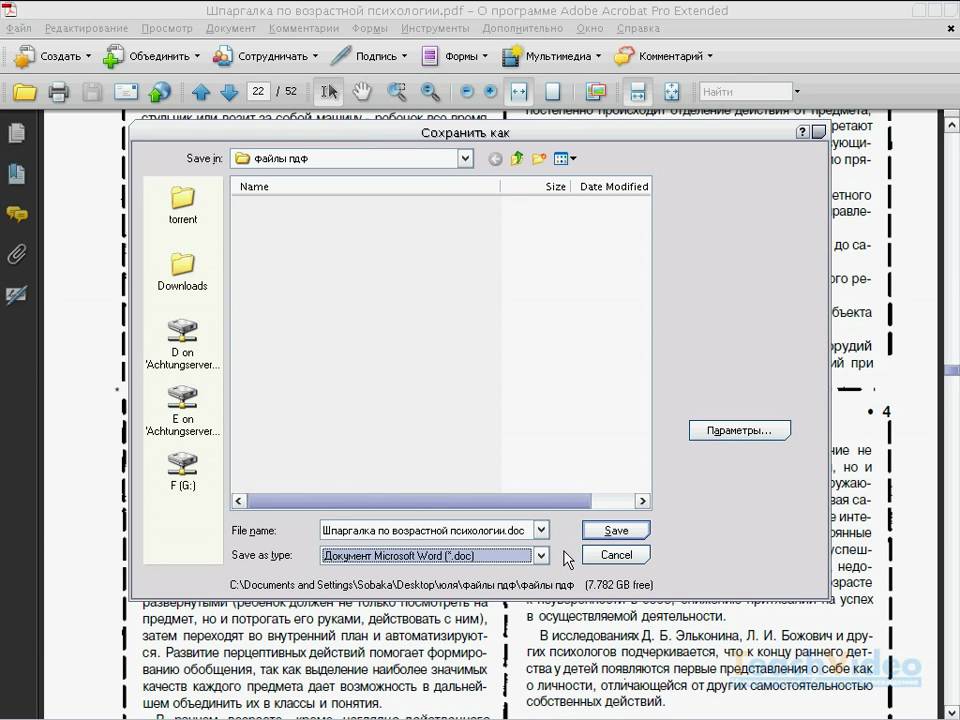
Выберите файл DOC/DOCX, выполнив поиск по имени. Коснитесь файла, подтвердите и дождитесь преобразования в PDF. Вот и все. Ваш DOC/DOCX был преобразован в файл PDF.
Предупреждение. Приложению DOC/DOCX to PDF требуется подключение к Интернету для выполнения преобразования.
Используйте надежное приложение Convert Word to PDF, чтобы легко и быстро преобразовывать файлы, отображать их в программе чтения PDF и обмениваться файлами с другими.
Ждем комментариев от пользователей, чтобы улучшить приложение.
Версия 2.0
— Разрешить пользователю удалять ADS
— Исправление ошибок на iPad с IOS > 13
Рейтинги и обзоры
282 Оценки
Преобразовать слово в PDF
Отличное приложение
Часто тормозит
Очень хорошее приложение здесь, но в остальном оно медленное, несмотря на отличное соединение и другие приложения, такие как onedrive, работают нормально
Разработчик Tu Phan не предоставил Apple подробностей о своей политике конфиденциальности и обработке данных. Для получения дополнительной информации см. политику конфиденциальности разработчика.
Для получения дополнительной информации см. политику конфиденциальности разработчика.
Сведения не предоставлены
Разработчик должен будет предоставить сведения о конфиденциальности при отправке следующего обновления приложения.
Информация
- Продавец
- Ту Фан
- Размер
- 15 МБ
- Категория
- Производительность
- Возрастной рейтинг
- 4+
- Авторское право
- © (с) 2020 Ту Фан
- Цена
- Бесплатно
- Тех. поддержка
- политика конфиденциальности
Еще от этого разработчика
Вам также может понравиться
Top 10 Best Doc to PDF Converter Бесплатное программное обеспечение для Mac или Windows
Иван Кук
• Подано в: Create PDF
Иногда вам нужно конвертировать Doc в PDF. PDF-файлы очень компактны и малы, поэтому вы сэкономите много места на своем компьютере, если конвертируете файлы Doc в формат PDF. Еще одним преимуществом преобразования документов в формат PDF является повышение их безопасности. Вы будете иметь полный контроль над своими файлами, шифруя их, добавляя пароли, используя водяные знаки и так далее. Ниже мы покажем вам топ 10 бесплатные конвертеры Doc в PDF , которые помогут вам легко изменить формат файла, включая PDFelement Pro.
PDF-файлы очень компактны и малы, поэтому вы сэкономите много места на своем компьютере, если конвертируете файлы Doc в формат PDF. Еще одним преимуществом преобразования документов в формат PDF является повышение их безопасности. Вы будете иметь полный контроль над своими файлами, шифруя их, добавляя пароли, используя водяные знаки и так далее. Ниже мы покажем вам топ 10 бесплатные конвертеры Doc в PDF , которые помогут вам легко изменить формат файла, включая PDFelement Pro.
ПОПРОБУЙТЕ БЕСПЛАТНО
- Часть 1: 5 лучших бесплатных конвертеров Doc в PDF для Windows
- Часть 2: 5 лучших бесплатных конвертеров Doc в PDF для Mac
- Часть 3: три метода преобразования документа в PDF
Часть 1: 5 лучших бесплатных конвертеров Doc в PDF для Windows
#1: PDFelement Pro для Windows — самый простой способ преобразовать Doc в PDF
PDFelement Pro — это профессиональный инструмент для редактирования PDF, который можно загрузить бесплатно. С PDFelement Pro у вас есть полный контроль над файлами PDF. Если вы хотите выполнять простые задачи, такие как вставка, поворот, удаление и обрезка файлов, или сложные задачи, такие как изменение фона или добавление водяных знаков, это позволит вам делать все это с легкостью. Он имеет оптимизированные параметры редактирования текста, которые превратят вашу рабочую среду в профессиональный редактор, в котором нет известных проблем. Вы можете использовать его для создания PDF-файлов с нуля и преобразования их в любой формат. Он также открывает доступ к широкому спектру инструментов, которые можно использовать для создания форм, которые можно очень легко заполнять с помощью стандартных приложений для просмотра документов.
С PDFelement Pro у вас есть полный контроль над файлами PDF. Если вы хотите выполнять простые задачи, такие как вставка, поворот, удаление и обрезка файлов, или сложные задачи, такие как изменение фона или добавление водяных знаков, это позволит вам делать все это с легкостью. Он имеет оптимизированные параметры редактирования текста, которые превратят вашу рабочую среду в профессиональный редактор, в котором нет известных проблем. Вы можете использовать его для создания PDF-файлов с нуля и преобразования их в любой формат. Он также открывает доступ к широкому спектру инструментов, которые можно использовать для создания форм, которые можно очень легко заполнять с помощью стандартных приложений для просмотра документов.
Основные возможности PDFelement Pro для Windows:
- Преобразование файлов Microsoft Office, EPUB, веб-страниц и других файлов в формат PDF.
- Включение мощных инструментов редактирования PDF позволяет легко редактировать PDF.
- Преобразование PDF в Word, Excel, EPUB и другие редактируемые форматы.

- Безопасный PDF с паролем, водяным знаком и цифровой подписью.
- Позволяет обмениваться файлами PDF напрямую в любом месте.
- Разрешить функции OCR редактировать и преобразовывать отсканированные файлы PDF.
ПОПРОБУЙТЕ БЕСПЛАТНО
#2: PrimoPDF
Если вы ищете бесплатный конвертер Doc в PDF, который без проблем работает с операционной системой Windows, попробуйте PrimoPDF. В нем говорится, что он может конвертировать практически любые файлы в стандартные для отрасли файлы PDF. Вы будете уверены в последовательном создании PDF при его использовании. Он также позволяет легко объединять несколько PDF-файлов в один PDF-файл.
Минусы:
- Для работы требуется Microsoft.NET Framework 2.0.
- Он загружает автоматические обновления каждый раз, когда конвертирует.
#3: 7-PDF Maker
Будучи отдельной программой, вам не нужно устанавливать PDF-принтер для использования 7-PDF Maker. Запустите этот бесплатный инструмент преобразования Doc в PDF и импортируйте файл Word, который вы хотите преобразовать, а затем измените настройки, файл PDF будет создан автоматически.
Запустите этот бесплатный инструмент преобразования Doc в PDF и импортируйте файл Word, который вы хотите преобразовать, а затем измените настройки, файл PDF будет создан автоматически.
Минусы:
- Его интерфейс немного сложен для навигации.
- При его использовании у вас будут периодически возникать проблемы с номерами страниц.
#4: doPDF
doPDF — это мощный инструмент для создания PDF-файлов, который поможет вам конвертировать PDF-файлы из форматов DOCX, XLSX, PPTX, PUBX, HTML, TXT и других форматов. Он не требует сторонних приложений и почти не использует ресурсы при преобразовании ваших файлов. Как только он будет установлен, вы сможете создавать PDF-файлы бесплатно.
Минусы:
- Дополнительное программное обеспечение будет автоматически установлено в вашей системе при использовании этого приложения.
- Основной интерфейс не имеет параметров преобразования.
#5: BullZip PDF Printer
Это бесплатное приложение Doc to PDF работает как принтер Microsoft Windows и позволяет создавать PDF-файлы из любого приложения MS Windows.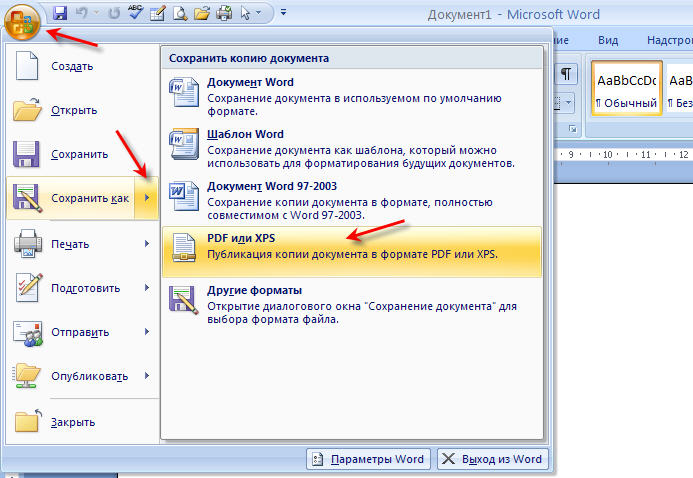 Он поддерживает широкий спектр форматов файлов. Он не имеет никаких ограничений, рекламы или всплывающих окон.
Он поддерживает широкий спектр форматов файлов. Он не имеет никаких ограничений, рекламы или всплывающих окон.
Минусы:
- Во время преобразования могут возникать сбои в работе.
- Он автоматически устанавливает надстройки в ваш браузер.
Часть 2: 5 лучших бесплатных конвертеров Doc в PDF для Mac
№1: PDFelement Pro для Mac — выбор редакции!
PDFelement Pro для Mac имеет замечательные функции, которые помогут вам очень легко создавать файлы PDF и работать с ними. Вы можете использовать его для создания PDF-файлов из Microsoft Word, Excel и PowerPoint без изменения исходного качества исходного файла. Вам не нужно будет предварительно устанавливать Microsoft Office на свой Mac для создания PDF. Это окажется действительно удобным приложением, особенно если вам постоянно приходится иметь дело со многими PDF-документами ежедневно. Вы можете импортировать в него несколько PDF-файлов, чтобы создать множество PDF-файлов одновременно.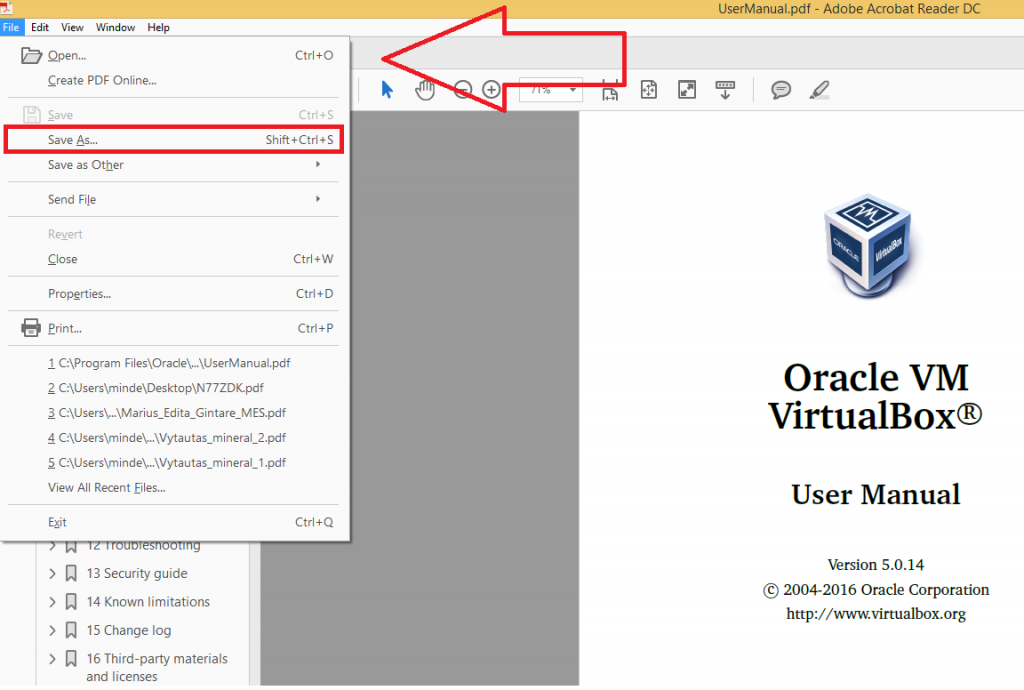 PDF-файлы, создаваемые этим приложением, могут работать с любым PDF-редактором, PDF-конвертером, PDF-ридером и другими сторонними приложениями.
PDF-файлы, создаваемые этим приложением, могут работать с любым PDF-редактором, PDF-конвертером, PDF-ридером и другими сторонними приложениями.
Основные возможности PDF Creator:
- Легко конвертируйте DOC, DOCX, XLS, XLSX, PPT и PPTX в PDF.
- Позволяет импортировать неограниченное количество файлов Microsoft и без ограничений по размеру.
- Поддержка пакетного преобразования нескольких файлов в PDF одновременно.
- Обеспечивает высококачественный вывод PDF и может поддерживаться многими приложениями PDF.
#2: Cisdem PDFMaster для Mac
Cisdem PDFMaster для Mac — это стабильный инструмент PDF, который позволяет создавать PDF-файлы из файлов различных форматов, включая Word, PowerPoint, Text, RTFD, HTML, EPUB, CHM, изображения и т. д. , Качество преобразования высокое, а изображения, подчеркнутый текст, таблицы, шрифт и стиль и другие элементы сохраняются при преобразовании. Он имеет удобный интерфейс, который не доставит вам трудностей при навигации.
Минусы:
- Поддерживаемых выходных форматов очень мало.
- Чтобы пользоваться расширенными функциями, необходимо приобрести полную версию.
#3: Coolmuster Word to PDF Converter для Mac
С помощью Coolmuster Word to PDF Converter для Mac вы можете легко создавать PDF-файлы с возможностью поиска из документов Word. Программное обеспечение имеет простой в использовании интерфейс, который позволяет завершить процесс конвертации всего за несколько кликов. После преобразования исходный макет, формат, текст и изображения сохраняются.
Минусы:
- Полная версия слишком дорога для личного использования.
- Последнее обновление выпущено в 2019 году.
#4: Doxillion Free Mac Document Converter
Этот бесплатный конвертер документов Doc в PDF помогает конвертировать файлы различных форматов, включая DOC, DOCX, XLS и XLSX. Вы можете использовать его для преобразования документов за один раз или в пакетном режиме. Он также поддерживает преобразование изображений в текст с помощью технологии OCR.
Он также поддерживает преобразование изображений в текст с помощью технологии OCR.
Минусы:
- : Вы не сможете редактировать файлы PDF напрямую, когда используете их.
- Привыкание к нему в первый раз может быть трудным и утомительным.
#5: Canyua PDF Creator Pro для Mac
С этим приложением можно сделать так много. Вы можете очень легко создавать документы PDF и конвертировать документы Word в формат PDF. Он поддерживает создание PDF-файлов напрямую с различными типами объектов, включая таблицы, текстовые поля, изображения, гиперссылки и т. д. Он также позволяет вам установить доступ к PDF-файлам и сканировать документы со сканера как PDF-файлы.
Минусы:
- Водяные знаки на преобразованных страницах при использовании пробной версии.
- Множество ограничений при конвертации.
Часть 3. Три метода преобразования Doc в PDF
Способ 1. Преобразование Doc в PDF в Windows
Немедленно загрузите и установите PDFelement Pro. В следующем руководстве я расскажу вам, как создать PDF-документ с использованием файла DOC в Windows.
В следующем руководстве я расскажу вам, как создать PDF-документ с использованием файла DOC в Windows.
ПОПРОБУЙТЕ БЕСПЛАТНО
Шаг 1. Добавьте файл в программу
Загрузите и установите PDFelement Pro для Windows, а затем запустите приложение. Когда откроется основной интерфейс, выберите опцию «Создать PDF», чтобы начать.
Как только вы нажмете «Создать PDF», должно открыться всплывающее окно, в котором вы сможете выбрать файл DOC, который нужно преобразовать в документ PDF. После того, как вы выбрали файл DOC, нажмите кнопку «Открыть».
Шаг 2. Редактирование PDF-файла и добавление примечаний (необязательно)
После загрузки файла вы можете вносить необходимые изменения (редактировать или добавлять текст и т. д.) прямо из этого интерфейса. Перейдите на вкладку «Редактировать» и выберите нужные параметры. Если вы хотите аннотировать PDF, вы можете найти соответствующие инструменты на вкладке «Комментарий».
Шаг 3. Сохранить DOC как файл PDF
Теперь щелкните вкладку «Файл» и выберите параметр «Сохранить как», чтобы сохранить файл DOC как документ PDF. Программное обеспечение попросит вас указать местоположение и имя этого недавно преобразованного PDF-документа на следующем экране. Заполнив все это, нажмите кнопку «Сохранить», чтобы, наконец, сохранить файл DOC в виде документа PDF.
Программное обеспечение попросит вас указать местоположение и имя этого недавно преобразованного PDF-документа на следующем экране. Заполнив все это, нажмите кнопку «Сохранить», чтобы, наконец, сохранить файл DOC в виде документа PDF.
Способ 2. Преобразование Doc в PDF на Mac
С официального сайта загрузите PDFelement Pro для Mac. Этот конструктор PDF идеально подходит для всех операционных систем Mac. Обычно, чтобы установить программное обеспечение, перетащите файлы в папку «Приложения» для установки программ на вашем компьютере Mac. Чтобы запустить это программное обеспечение, дважды нажмите на символ приложения, чтобы начать преобразование документов Word в PDF.
Действия по преобразованию Word в PDF на Mac
Шаг 1. Импорт файлов Word
Теперь импортируйте документы в систему. Вы можете сделать это, перетащив документы Word в программу. Затем нажмите кнопку «Файл» и нажмите «Создать» > «PDF из файла».
Шаг 2. Преобразование Word в PDF
После выбора прямого документа Word и нажатия кнопки «Открыть» документ Word будет преобразован в файл PDF и автоматически открыт в PDFelement.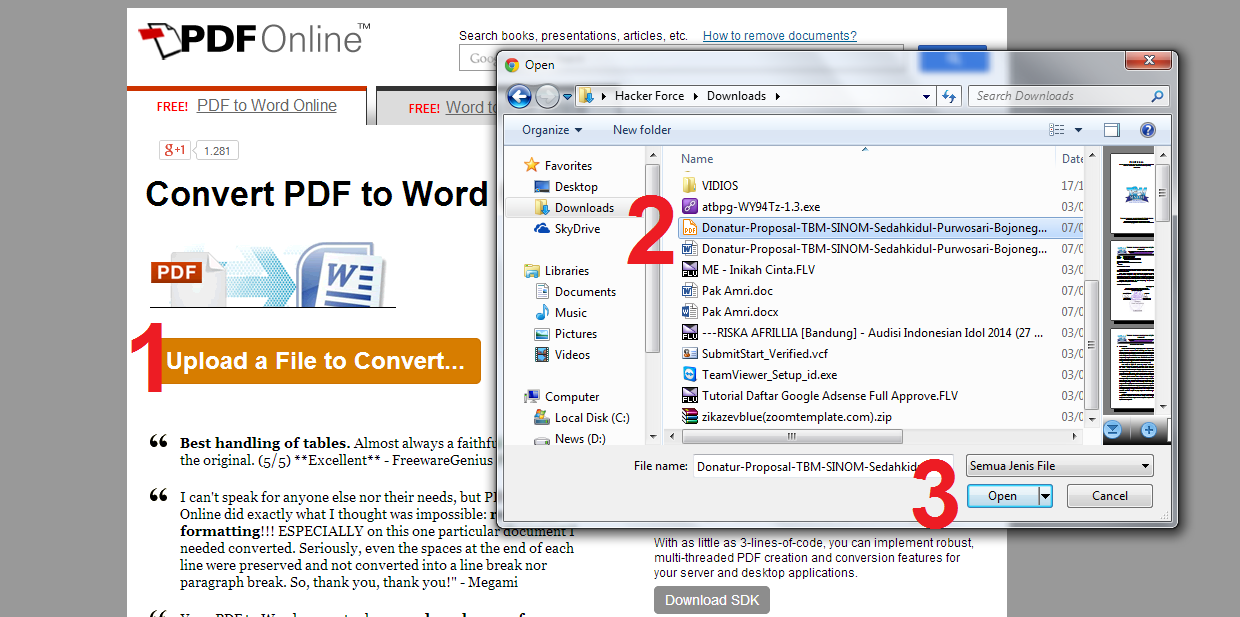

 doc – это расширение имени файла, которое указывает операционной системе, какой именно программой следует открывать файл.
doc – это расширение имени файла, которое указывает операционной системе, какой именно программой следует открывать файл.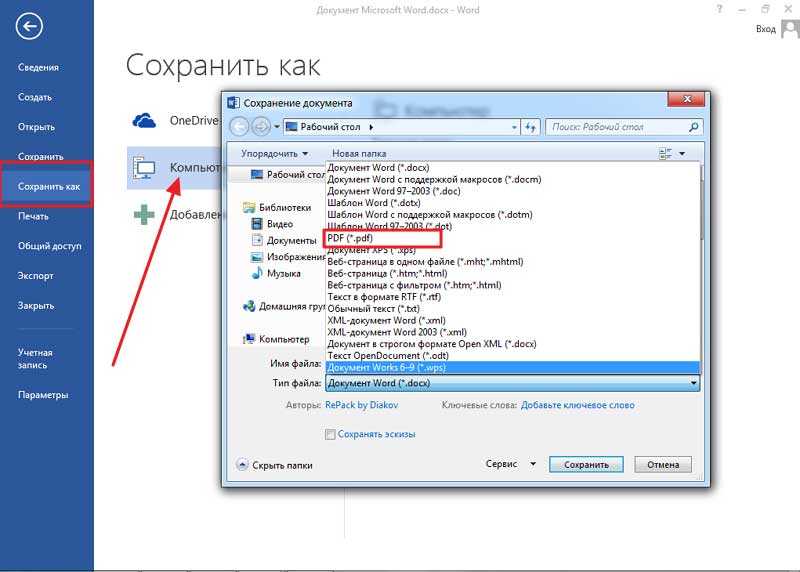 openoffice.org/ru/
openoffice.org/ru/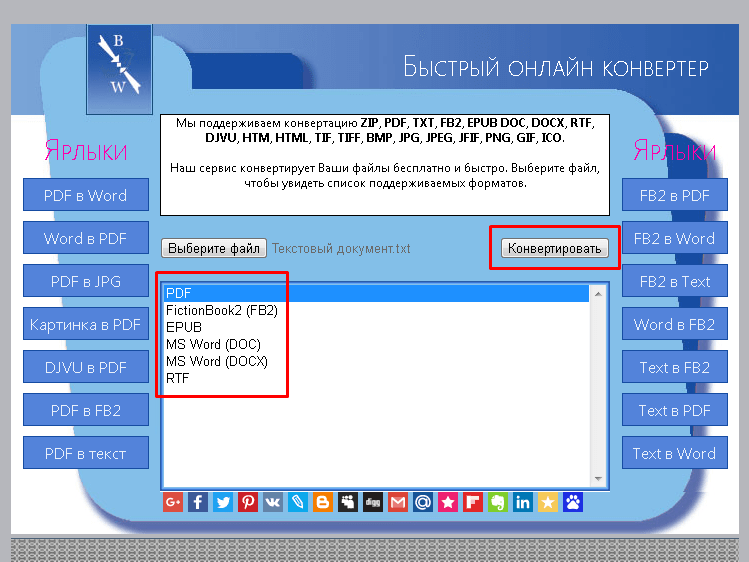

 Составим ее
Составим ее Найдем, наконец, расстояние от точки M0 до плоскости (1). Очевидно, что расстояние от точки M0 до плоскости (1) − это расстояние от точки M0 до точки M1. А это расстояние вычисляется так:
Найдем, наконец, расстояние от точки M0 до плоскости (1). Очевидно, что расстояние от точки M0 до плоскости (1) − это расстояние от точки M0 до точки M1. А это расстояние вычисляется так: Вычисления можно осуществить самостоятельно, но для этого потребуется время. Также есть вероятность ошибочного выбора алгоритма и потери данных между действиями.
Вычисления можно осуществить самостоятельно, но для этого потребуется время. Также есть вероятность ошибочного выбора алгоритма и потери данных между действиями.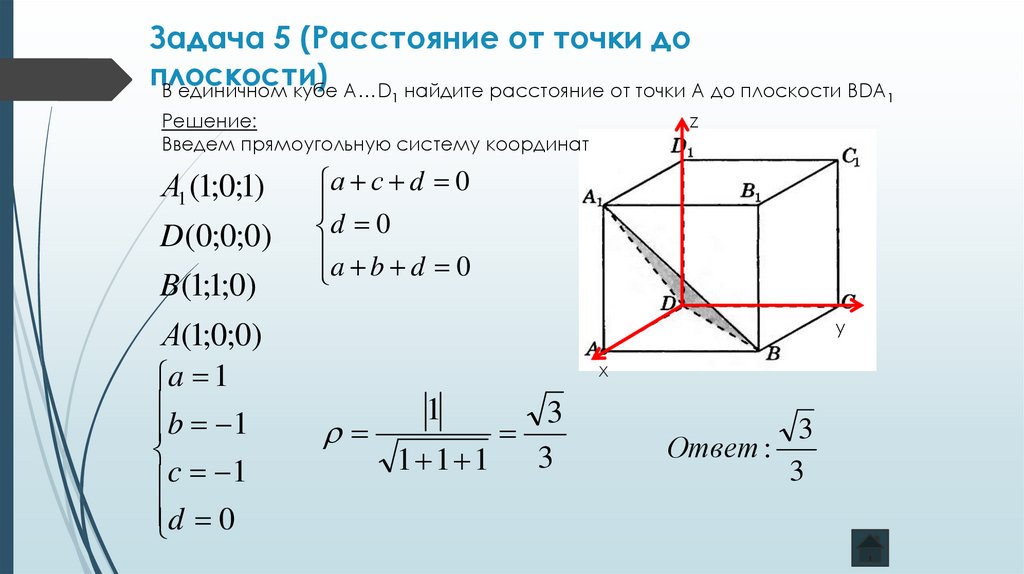 Расстояние между точками
Расстояние между точками Воспользоваться любым расчетом на сайте можно бесплатно. Школьники смогут обойтись без репетиторов при подготовке домашних заданий и повторении тем к поступлению в университет.
Воспользоваться любым расчетом на сайте можно бесплатно. Школьники смогут обойтись без репетиторов при подготовке домашних заданий и повторении тем к поступлению в университет.
 Если вы новичок в теме нахождения минимального расстояния от точки до плоскости, вы можете прочитать статью ниже, где мы обсуждаем:
Если вы новичок в теме нахождения минимального расстояния от точки до плоскости, вы можете прочитать статью ниже, где мы обсуждаем: Другими словами, это величина вектора нормали , которая начинается в данной точке и заканчивается на плоскости.
Другими словами, это величина вектора нормали , которая начинается в данной точке и заканчивается на плоскости. 92}} L=A2+B2+C2
92}} L=A2+B2+C2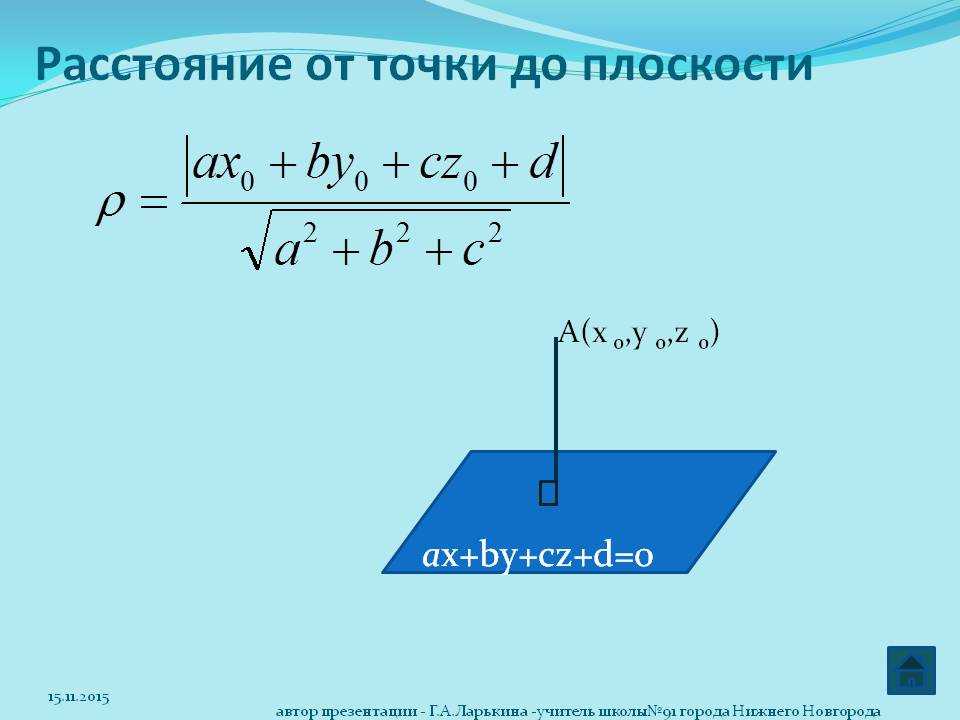 2}}Л=А2+В2+С2
2}}Л=А2+В2+С2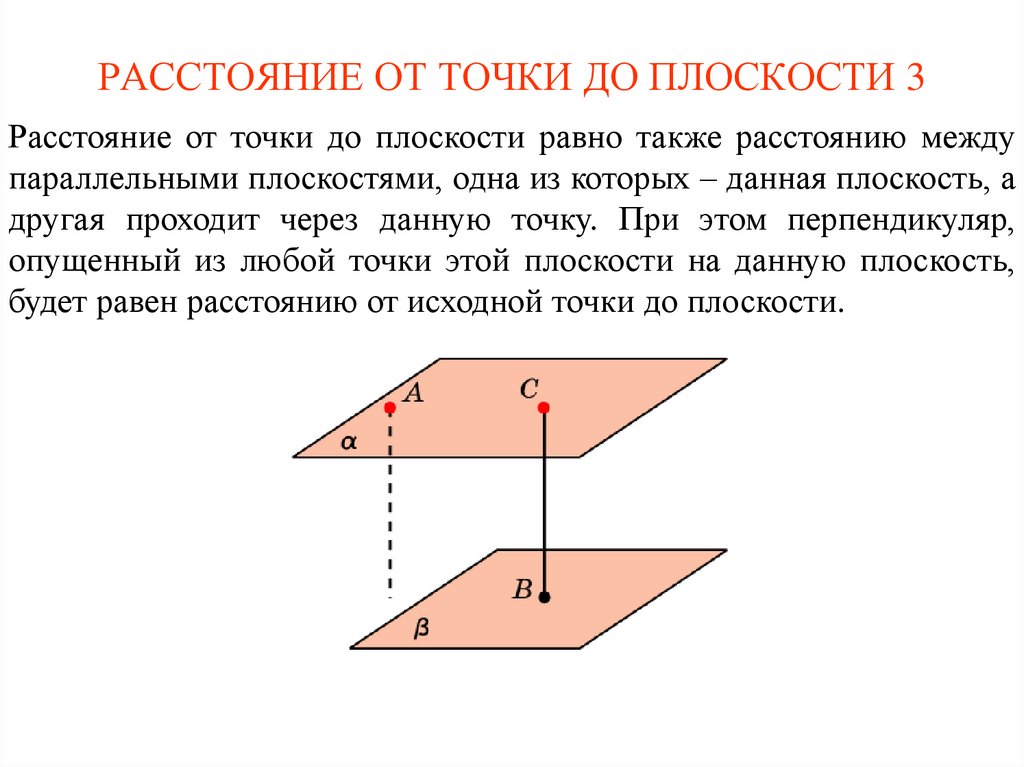 К счастью, наш калькулятор расстояния от точки до плоскости может выполнить расчеты за вас!
К счастью, наш калькулятор расстояния от точки до плоскости может выполнить расчеты за вас! Он должен быть в виде Ax+By+Cz+D=0 .
Он должен быть в виде Ax+By+Cz+D=0 .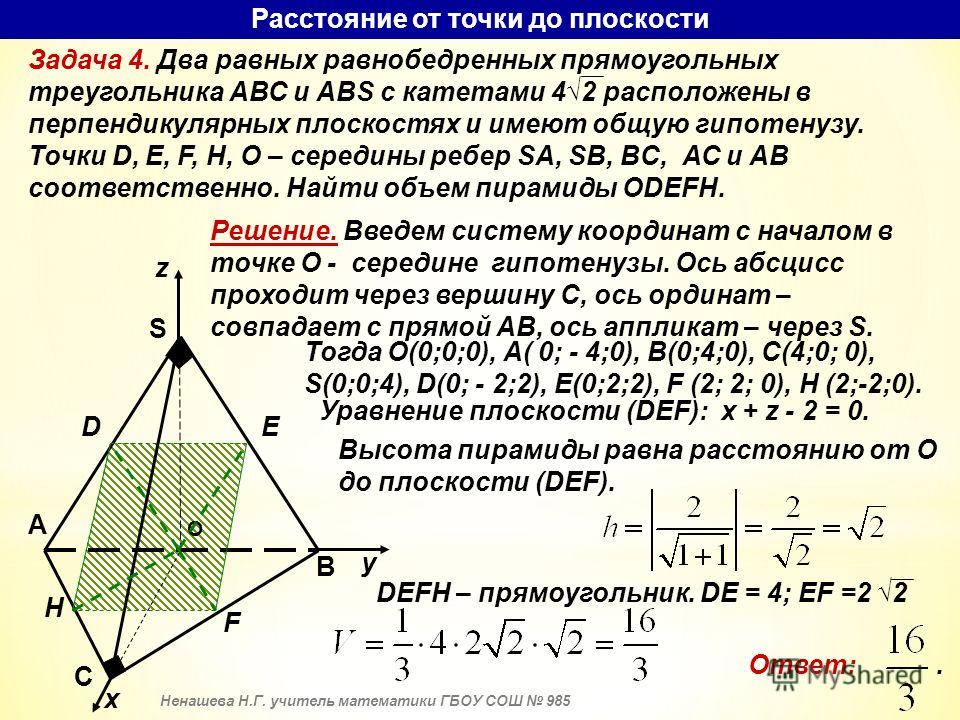 Чтобы получить этот результат, мы применяем формулу расстояние = |A×a + B×b + C×c|/√(A 2 + B 2 + C 2 ) с A=B= 1 и C=D=0 и а = b = с = 1 . Получаем расстояния = |1×1 + 1×1 + 0×1| / √(1 2 + 1 2 ) = |2| / √2 = √2 .
Чтобы получить этот результат, мы применяем формулу расстояние = |A×a + B×b + C×c|/√(A 2 + B 2 + C 2 ) с A=B= 1 и C=D=0 и а = b = с = 1 . Получаем расстояния = |1×1 + 1×1 + 0×1| / √(1 2 + 1 2 ) = |2| / √2 = √2 .
 с координатами (x, y, z) является поверхностью сферы радиусом r с центром в точке (x, y, z) . Таким образом, с точки зрения геометрии задача трилатерации состоит в том, чтобы найти координаты пересечения трех сфер. Эти координаты находятся путем решения системы уравнений, основанной на следующих рассуждениях 1 :
с координатами (x, y, z) является поверхностью сферы радиусом r с центром в точке (x, y, z) . Таким образом, с точки зрения геометрии задача трилатерации состоит в том, чтобы найти координаты пересечения трех сфер. Эти координаты находятся путем решения системы уравнений, основанной на следующих рассуждениях 1 : 


 Если же свободный член не равен нулю, то это уравнение не удовлетворяется никакими значениями неизвестных, следовательно, полученная система является несовместной. Тогда несовместна и исходная система.
Если же свободный член не равен нулю, то это уравнение не удовлетворяется никакими значениями неизвестных, следовательно, полученная система является несовместной. Тогда несовместна и исходная система.







 Например, -16 — отрицательное число.
Например, -16 — отрицательное число. Поэтому в ряду целых чисел можно заменить запятые на знак меньше:
Поэтому в ряду целых чисел можно заменить запятые на знак меньше: Например, к таким числам относят -1, -2, -3. Прочитать запись можно, как минус один, минус два, минус три.
Например, к таким числам относят -1, -2, -3. Прочитать запись можно, как минус один, минус два, минус три.
 С левой стороны от нуля отмечают отрицательные числа, а с правой — положительные.
С левой стороны от нуля отмечают отрицательные числа, а с правой — положительные. С каждым шагом в левую сторону число будет уменьшаться в меньшую сторону. При каждом шаге в правом направлении число будет увеличиваться.
С каждым шагом в левую сторону число будет уменьшаться в меньшую сторону. При каждом шаге в правом направлении число будет увеличиваться. Это объясняется тем, что -5 представляет собой отрицательное число, а 3 является положительным числом. С помощью координатной прямой достаточно просто определить положение данных чисел.
Это объясняется тем, что -5 представляет собой отрицательное число, а 3 является положительным числом. С помощью координатной прямой достаточно просто определить положение данных чисел.

 В сумме с ним число дает 0. Например:
В сумме с ним число дает 0. Например:
 положительные и отрицательные числа в нашем разделе «Счет».
положительные и отрицательные числа в нашем разделе «Счет».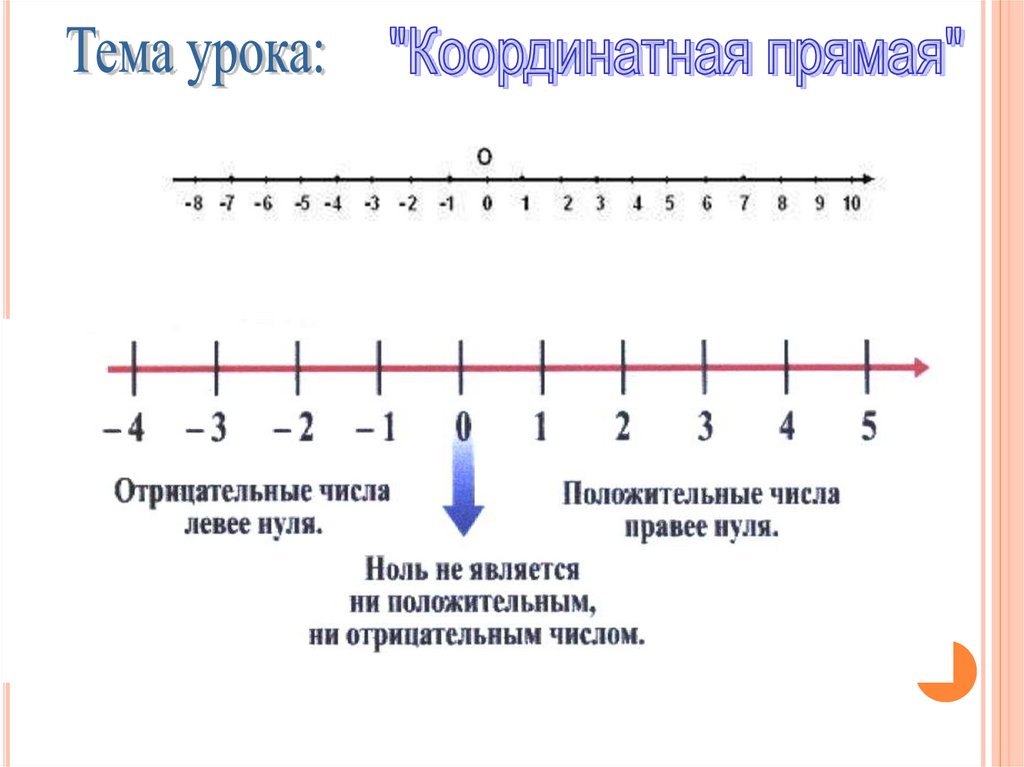 Но вы получаете всего три гранта: $\large\unicode{xA3}\normalsize1,\!000 \times 3 = \large\unicode{xA3}\normalsize3,\!000$. Следовательно, у вас есть: $\large\unicode{xA3}\normalsize20,\!000 + \large\unicode{xA3}\normalsize3,\!000 + (- \large\unicode{xA3}\normalsize24,\!750) = — \large\unicode{xA3}\normalsize1,\!750$ осталось на конец марта. Таким образом, к концу марта ваш овердрафт составит $\large\unicode{xA3}\normalsize1,\!750$.
Но вы получаете всего три гранта: $\large\unicode{xA3}\normalsize1,\!000 \times 3 = \large\unicode{xA3}\normalsize3,\!000$. Следовательно, у вас есть: $\large\unicode{xA3}\normalsize20,\!000 + \large\unicode{xA3}\normalsize3,\!000 + (- \large\unicode{xA3}\normalsize24,\!750) = — \large\unicode{xA3}\normalsize1,\!750$ осталось на конец марта. Таким образом, к концу марта ваш овердрафт составит $\large\unicode{xA3}\normalsize1,\!750$. Чтобы рассчитать количество в баке, мы вычитаем это количество $4$ раз (чтобы вернуться назад на $4$ дней).
Чтобы рассчитать количество в баке, мы вычитаем это количество $4$ раз (чтобы вернуться назад на $4$ дней). Мы не ставим перед ними знак плюс (+), потому что нам это не нужно, так как общее понимание таково, что числа без знака положительны.
Мы не ставим перед ними знак плюс (+), потому что нам это не нужно, так как общее понимание таково, что числа без знака положительны.

 Квадратный корень — это число, которое нужно умножить само на себя, чтобы получить число. Нельзя умножать число само на себя, чтобы получить отрицательное число. Чтобы получить отрицательное число, вам нужно одно отрицательное и одно положительное число.
Квадратный корень — это число, которое нужно умножить само на себя, чтобы получить число. Нельзя умножать число само на себя, чтобы получить отрицательное число. Чтобы получить отрицательное число, вам нужно одно отрицательное и одно положительное число. Вы делаете два шага вперед, останавливаетесь, затем делаете еще два шага. Вы прошли 2 × 2 шага = 4 шага.
Вы делаете два шага вперед, останавливаетесь, затем делаете еще два шага. Вы прошли 2 × 2 шага = 4 шага. 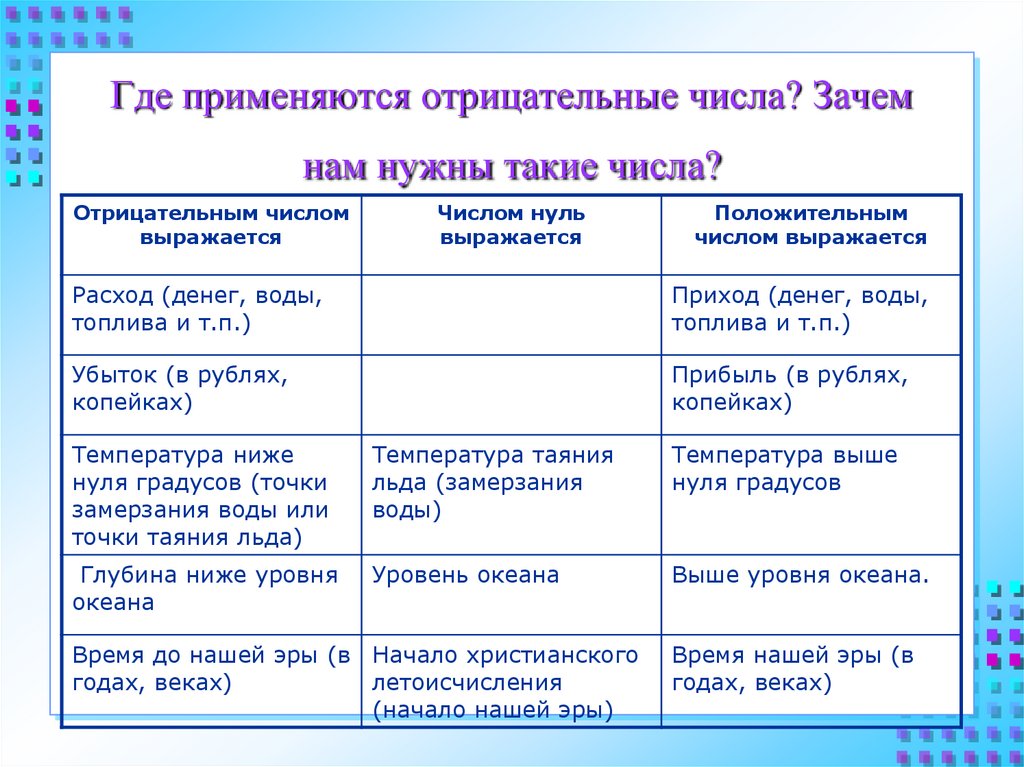 Теперь сделайте два шага назад , а затем еще два назад. Вы стоите на +4. Повернувшись лицом в отрицательном направлении и пройдя назад ( два негатива ), вы достигли положительного результата.
Теперь сделайте два шага назад , а затем еще два назад. Вы стоите на +4. Повернувшись лицом в отрицательном направлении и пройдя назад ( два негатива ), вы достигли положительного результата. 

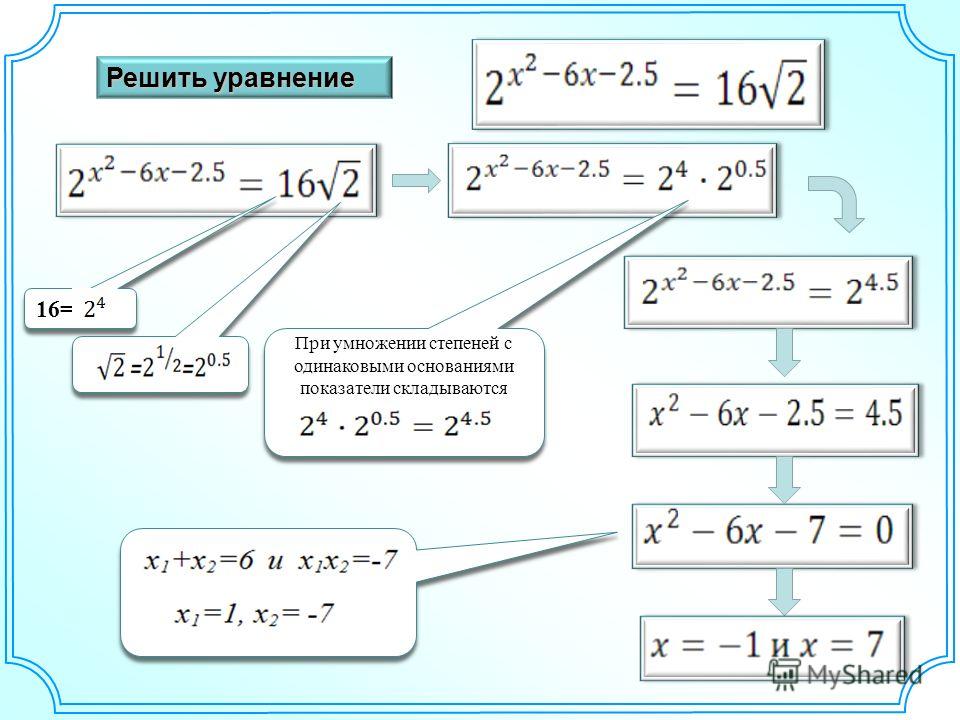
 Решить уравнение
Решить уравнение

 Так и тут. Ключевым словом в термине «показательное уравнение» является слово «показательное». Что оно означает? Это слово означает, что неизвестное (икс) находится в показателях каких-либо степеней. И только там! Это крайне важно.
Так и тут. Ключевым словом в термине «показательное уравнение» является слово «показательное». Что оно означает? Это слово означает, что неизвестное (икс) находится в показателях каких-либо степеней. И только там! Это крайне важно. Такие уравнения не имеют чётких правил решения. Поэтому в данном уроке мы их рассматривать не будем. На радость ученикам.) Здесь мы будем рассматривать только показательные уравнения в «чистом» виде.
Такие уравнения не имеют чётких правил решения. Поэтому в данном уроке мы их рассматривать не будем. На радость ученикам.) Здесь мы будем рассматривать только показательные уравнения в «чистом» виде.
 Здорово, правда?
Здорово, правда? Лишняя тройка мешает: коэффициент, понимаешь.)
Лишняя тройка мешает: коэффициент, понимаешь.) Или, в некоторых случаях, к совокупности уравнений такого вида. Тогда наше простейшее уравнение можно в общем виде переписать вот так:
Или, в некоторых случаях, к совокупности уравнений такого вида. Тогда наше простейшее уравнение можно в общем виде переписать вот так: Поскольку именно показательная функция и её свойства лежат в основе решения показательных уравнений, да.) Развёрнутый ответ на этот вопрос будет дан в отдельном спецуроке, посвящённом решению сложных нестандартных уравнений с использованием монотонности разных функций.)
Поскольку именно показательная функция и её свойства лежат в основе решения показательных уравнений, да.) Развёрнутый ответ на этот вопрос будет дан в отдельном спецуроке, посвящённом решению сложных нестандартных уравнений с использованием монотонности разных функций.) Иначе несладко вам придётся, да…
Иначе несладко вам придётся, да… Эти преобразования (целых два!) — основа решения всех уравнений математики вообще. И не только показательных. Так что, кто забыл, тоже прогуляйтесь по ссылочке: я их не просто так ставлю.
Эти преобразования (целых два!) — основа решения всех уравнений математики вообще. И не только показательных. Так что, кто забыл, тоже прогуляйтесь по ссылочке: я их не просто так ставлю. Есть там такая очень полезная формулка:
Есть там такая очень полезная формулка: Смело убираем тройки и получаем:
Смело убираем тройки и получаем: А это уже посложнее, чем простое возведение, согласитесь. Почувствуйте разницу, что называется!
А это уже посложнее, чем простое возведение, согласитесь. Почувствуйте разницу, что называется!
 Вот мы и добрались до одинакового основания — пятёрки. Заменяем теперь в уравнении неудобное нам число 0,04 на 5-2 и получаем:
Вот мы и добрались до одинакового основания — пятёрки. Заменяем теперь в уравнении неудобное нам число 0,04 на 5-2 и получаем: )
) )
) Ибо теперь уже отчётливо видно, что 1/4 — это 2-2. Отлично, и число 0,25 тоже сроднили с двойкой.)
Ибо теперь уже отчётливо видно, что 1/4 — это 2-2. Отлично, и число 0,25 тоже сроднили с двойкой.) Заменяем в нашем уравнении числа 4, 0,25 и корень из двух на степени двойки:
Заменяем в нашем уравнении числа 4, 0,25 и корень из двух на степени двойки: Как? С помощью тождественных преобразований, вестимо.) Дорешайте, чего уж там! Умножайте обе части на двойку (чтобы убрать дробь 3/2), переносите слагаемые с иксами влево, без иксов вправо, приводите подобные, считайте — и будет вам счастье!
Как? С помощью тождественных преобразований, вестимо.) Дорешайте, чего уж там! Умножайте обе части на двойку (чтобы убрать дробь 3/2), переносите слагаемые с иксами влево, без иксов вправо, приводите подобные, считайте — и будет вам счастье! Хотя бы с точки зрения визуального восприятия и, особенно, распознавания справа налево!
Хотя бы с точки зрения визуального восприятия и, особенно, распознавания справа налево! Ну, если не любой, то процентов 80 всех показательных уравнений — уж точно! Да-да, я не шучу!
Ну, если не любой, то процентов 80 всех показательных уравнений — уж точно! Да-да, я не шучу! ) Значит, урок прошёл не напрасно, и начальный уровень решения показательных уравнений можно считать успешно освоенным. Впереди — следующие уровни и более сложные уравнения! И новые приёмы и подходы. И нестандартные примеры. И новые сюрпризы.) Всё это — в следующем уроке!
) Значит, урок прошёл не напрасно, и начальный уровень решения показательных уравнений можно считать успешно освоенным. Впереди — следующие уровни и более сложные уравнения! И новые приёмы и подходы. И нестандартные примеры. И новые сюрпризы.) Всё это — в следующем уроке! Нам может понадобиться использовать связь между показателями степени и логарифмами для решения экспоненциальных уравнений.
Нам может понадобиться использовать связь между показателями степени и логарифмами для решения экспоненциальных уравнений. Например, 3 x = 81, 5 x — 3 = 625, 6 2y — 7 = 121 и т. д. — некоторые примеры экспоненциальных уравнений. Мы можем столкнуться с использованием экспоненциальных уравнений при решении задач алгебры, сложных процентов, экспоненциального роста, экспоненциального распада и т. д.
Например, 3 x = 81, 5 x — 3 = 625, 6 2y — 7 = 121 и т. д. — некоторые примеры экспоненциальных уравнений. Мы можем столкнуться с использованием экспоненциальных уравнений при решении задач алгебры, сложных процентов, экспоненциального роста, экспоненциального распада и т. д. Другими словами, мы можем сказать, что алгебраические уравнения, в которых переменные входят в качестве показателей, известны как уравнения с показателями. Некоторые из примеров такого уравнения: 3 x + 4 = 81, -2 3y-7 = -64 и т. д.
Другими словами, мы можем сказать, что алгебраические уравнения, в которых переменные входят в качестве показателей, известны как уравнения с показателями. Некоторые из примеров такого уравнения: 3 x + 4 = 81, -2 3y-7 = -64 и т. д.  Следовательно, показательное уравнение может быть преобразовано в логарифмическую функцию. Это помогает в процессе решения показательного уравнения с разными основаниями. Вот формула для преобразования показательных уравнений в логарифмические уравнения.
Следовательно, показательное уравнение может быть преобразовано в логарифмическую функцию. Это помогает в процессе решения показательного уравнения с разными основаниями. Вот формула для преобразования показательных уравнений в логарифмические уравнения.
 Например, 5 x = 3 не имеет одинаковых оснований с обеих сторон, и основания не могут быть одинаковыми. В таких случаях мы можем сделать одну из следующих вещей.
Например, 5 x = 3 не имеет одинаковых оснований с обеих сторон, и основания не могут быть одинаковыми. В таких случаях мы можем сделать одну из следующих вещей. Разделив обе части на log 5,
Разделив обе части на log 5, Например, 5 2x — 3 = 125, 3 7 — 2x = 91 и т. д. являются показательными уравнениями.
Например, 5 2x — 3 = 125, 3 7 — 2x = 91 и т. д. являются показательными уравнениями.

 Другими словами, правило журнала позволит нам переместить переменную обратно на землю, где мы сможем ее заполучить.
Другими словами, правило журнала позволит нам переместить переменную обратно на землю, где мы сможем ее заполучить. 0005
0005 Тогда:
Тогда:
 ..или около 3,328, округленное до трех знаков после запятой.
..или около 3,328, округленное до трех знаков после запятой.
 Решение различных логических задач дает возможность детям научиться анализировать ситуацию, находить взаимосвязи, сравнивать, отличать главное и второстепенное, формировать стратегию, применять в нужном месте свои знания и навыки. Овладение этими методами и означает умение мыслить.
Решение различных логических задач дает возможность детям научиться анализировать ситуацию, находить взаимосвязи, сравнивать, отличать главное и второстепенное, формировать стратегию, применять в нужном месте свои знания и навыки. Овладение этими методами и означает умение мыслить. Почти у любой задачи есть несколько вариантов решения. Чтобы легко справляться даже с самыми непростыми заданиями, надо знать, какой способ будет наиболее подходящим в той или иной ситуации.
Почти у любой задачи есть несколько вариантов решения. Чтобы легко справляться даже с самыми непростыми заданиями, надо знать, какой способ будет наиболее подходящим в той или иной ситуации.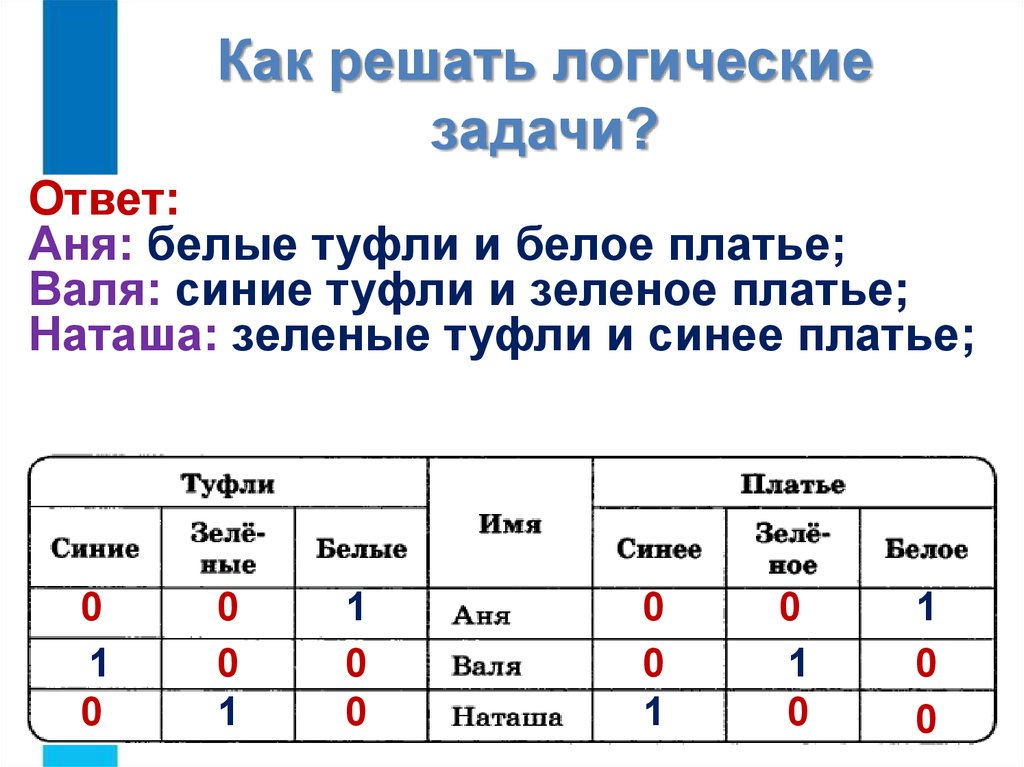
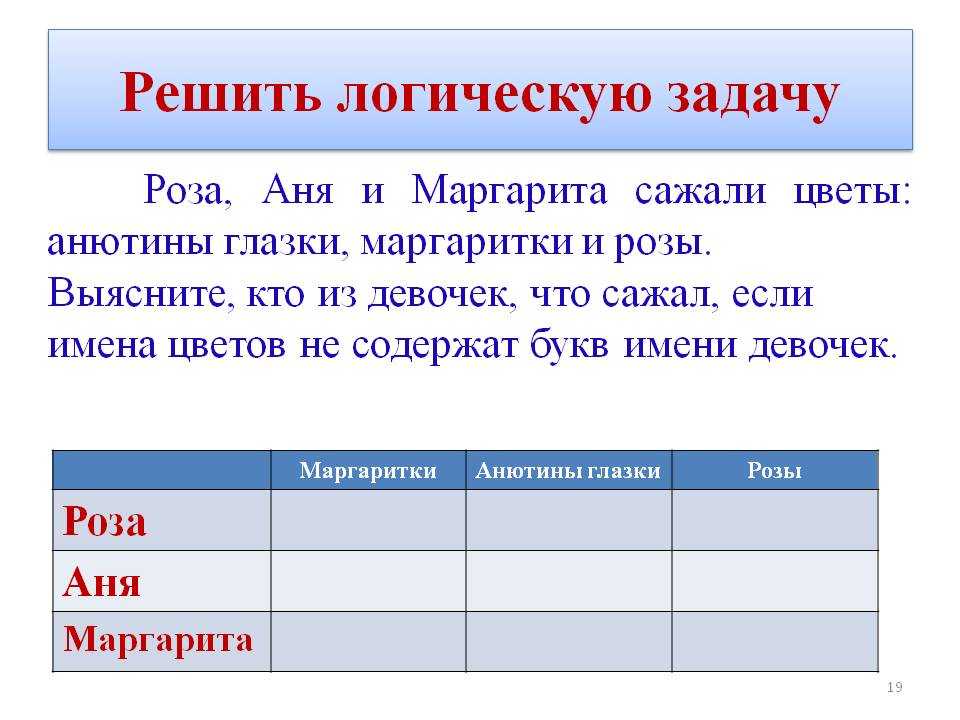 Далее решаем последний пример 7+3=10.
Далее решаем последний пример 7+3=10.

 Главное – подобрать подходящий способ решения, который быстро приведет к правильному результату.
Главное – подобрать подходящий способ решения, который быстро приведет к правильному результату. Это позволит видеть разные способы решения задач и вариантов ее оформления. Это делает ученика свободным, спокойным, появляется возможность его успеха и уверенность, что всегда можно найти выход из сложной ситуации.
Это позволит видеть разные способы решения задач и вариантов ее оформления. Это делает ученика свободным, спокойным, появляется возможность его успеха и уверенность, что всегда можно найти выход из сложной ситуации.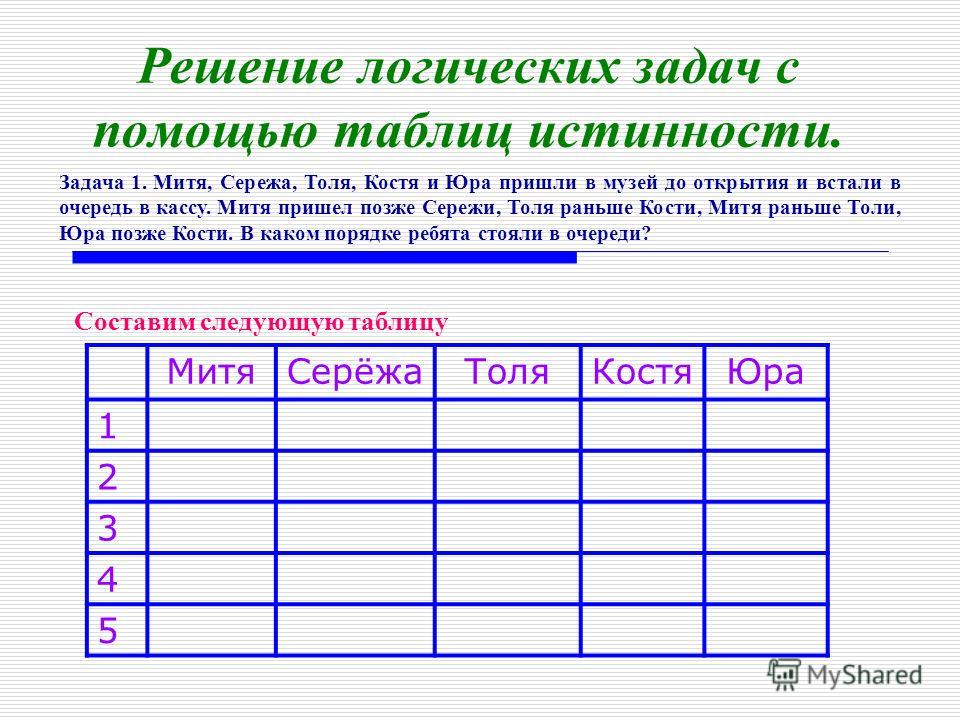 ru/blog/all-articles/kak-reshat-zadachi-na-logiku
ru/blog/all-articles/kak-reshat-zadachi-na-logiku

 Приносим извинения за неудобства.
Приносим извинения за неудобства. , 9:31
, 9:31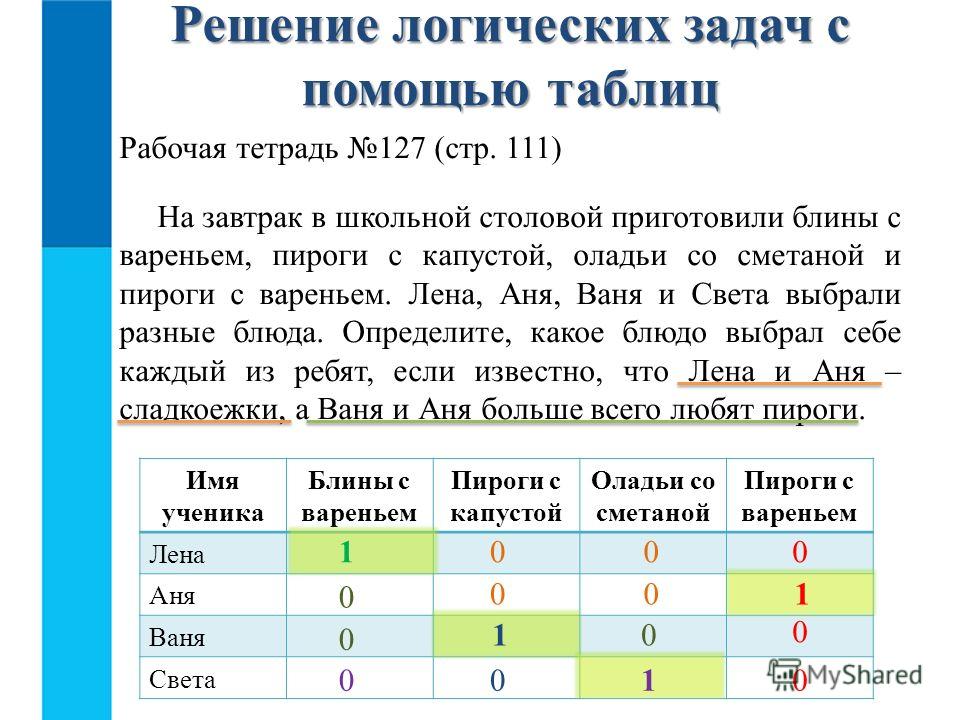 , 21:57.
, 21:57. Приносим извинения за неудобства.
Приносим извинения за неудобства. , 9:31
, 9:31
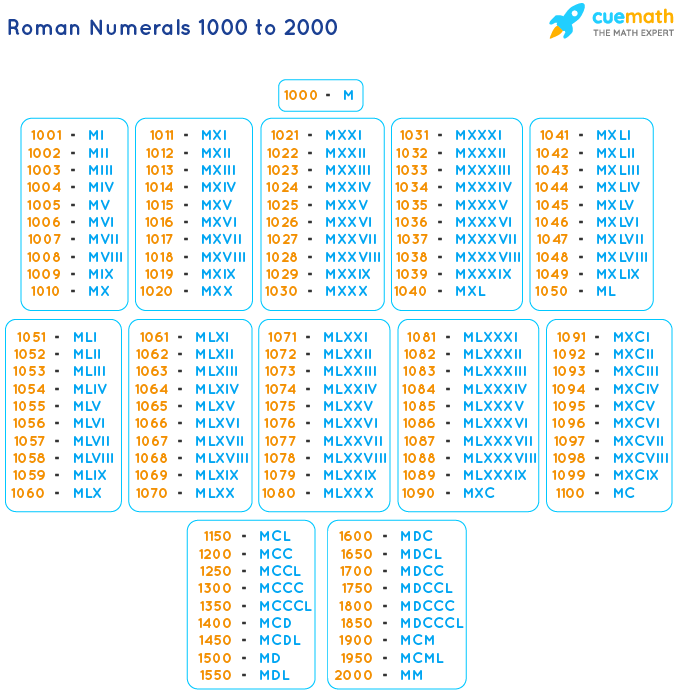

 Работаем с текстом в оранжевой
рамке.
Работаем с текстом в оранжевой
рамке.
 к. 50 –L, то L+II=
LII (52)
к. 50 –L, то L+II=
LII (52)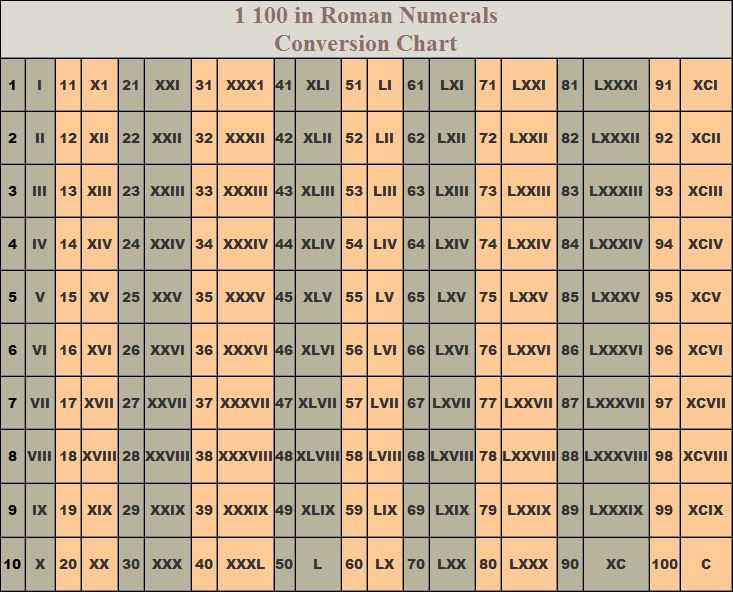
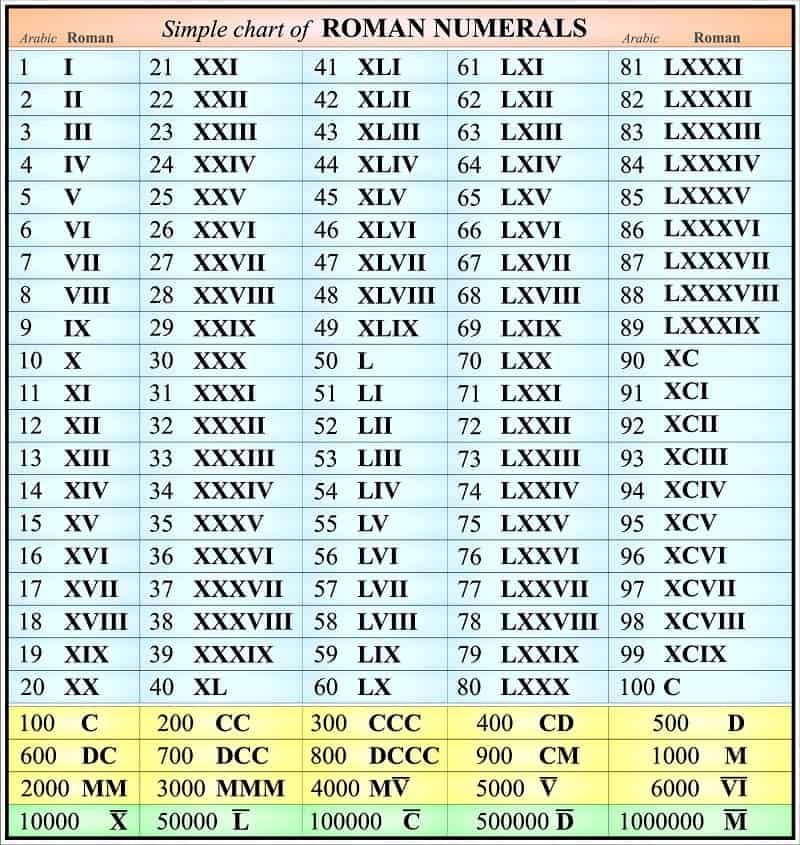 15
15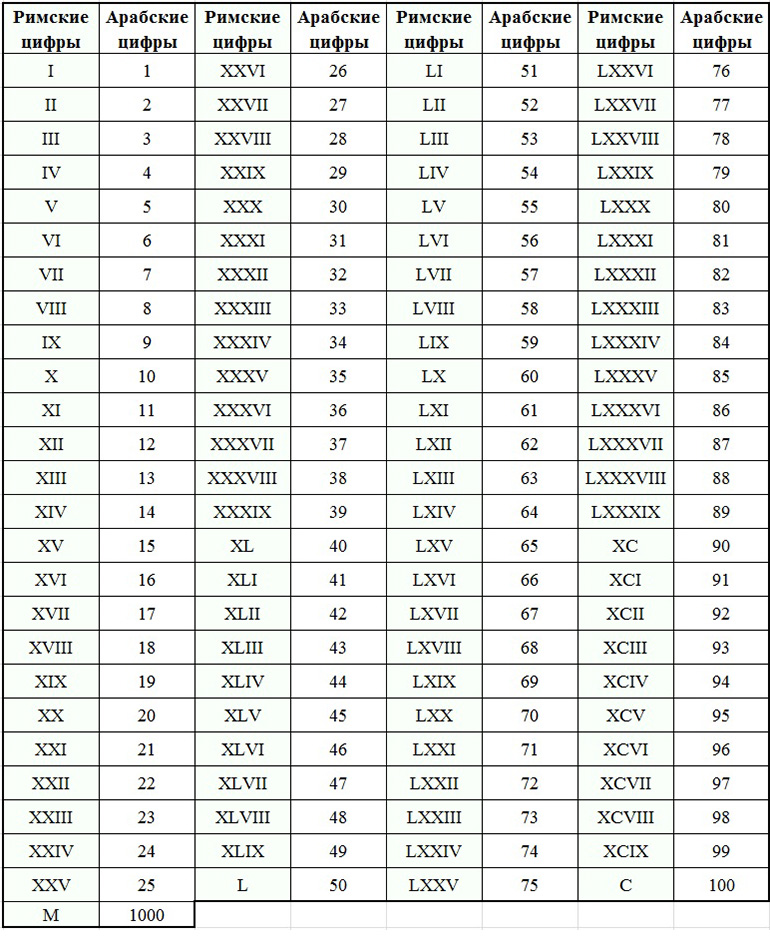 к. у него на
часах: 6ч. 15 мин.
к. у него на
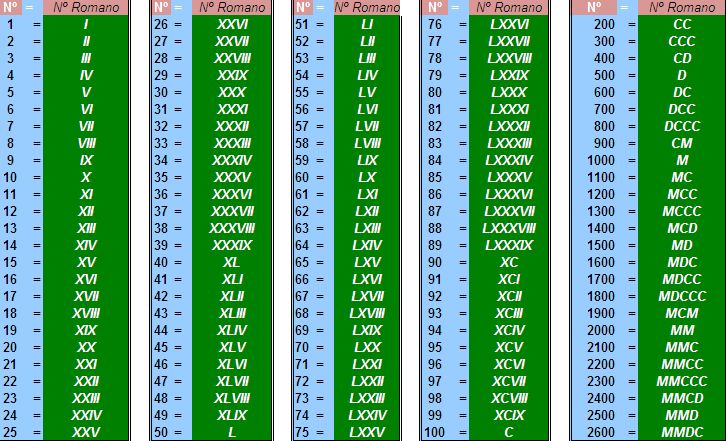
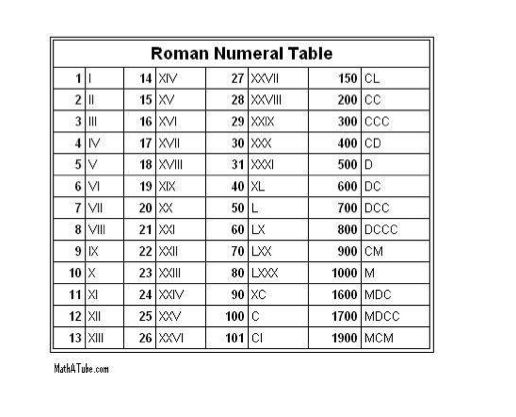
часах: 6ч. 15 мин.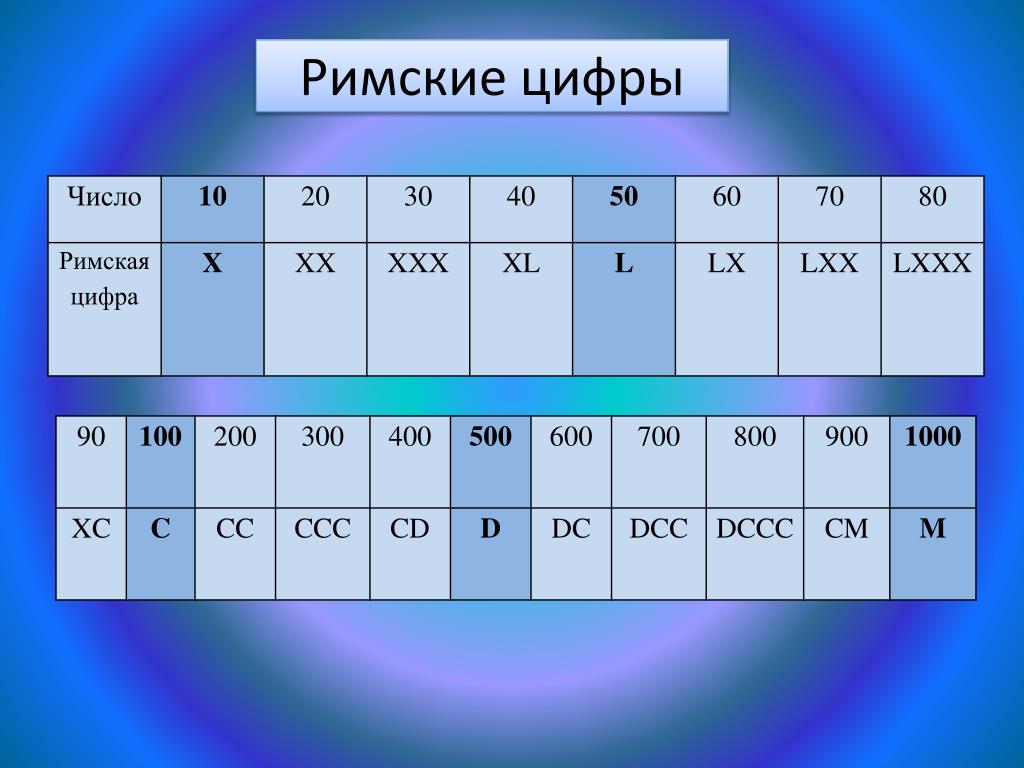 Мы видим римские цифры на циферблате часов. Знаменитая башня с часами Биг-Бен также имеет римские цифры в качестве циферблата. Этот инструмент является самым простым способом конвертировать современные числа в римские числа.
Мы видим римские цифры на циферблате часов. Знаменитая башня с часами Биг-Бен также имеет римские цифры в качестве циферблата. Этот инструмент является самым простым способом конвертировать современные числа в римские числа.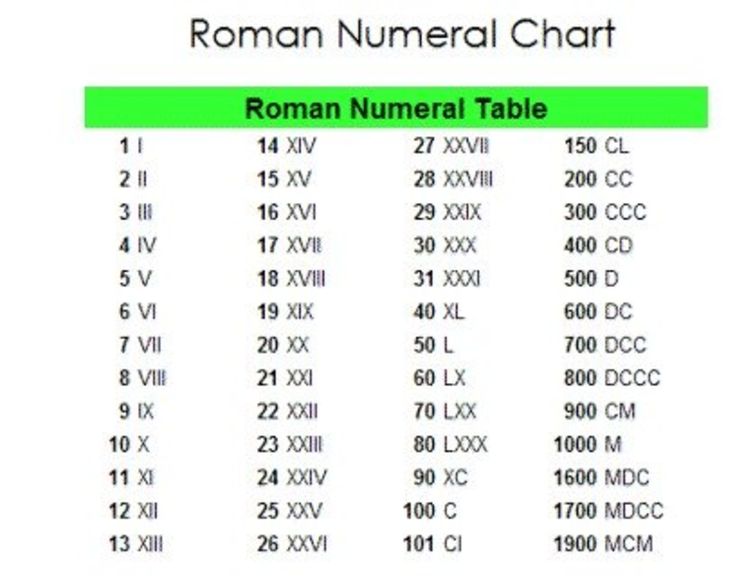 Чтобы преобразовать 600 в римские цифры, запишем 600 в развернутом виде, т.е. 600 = 500 + 100, после чего заменив преобразованные числа соответствующими им римскими цифрами, получим 600 = D + C = DC. В этой статье мы объясним, как правильно преобразовать 600 римскими цифрами.
Чтобы преобразовать 600 в римские цифры, запишем 600 в развернутом виде, т.е. 600 = 500 + 100, после чего заменив преобразованные числа соответствующими им римскими цифрами, получим 600 = D + C = DC. В этой статье мы объясним, как правильно преобразовать 600 римскими цифрами.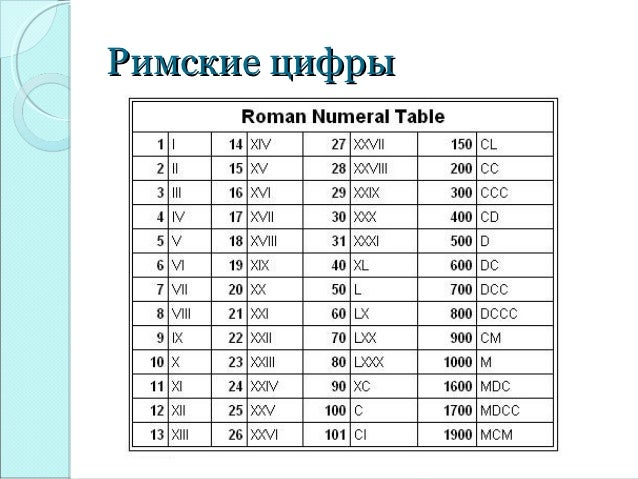

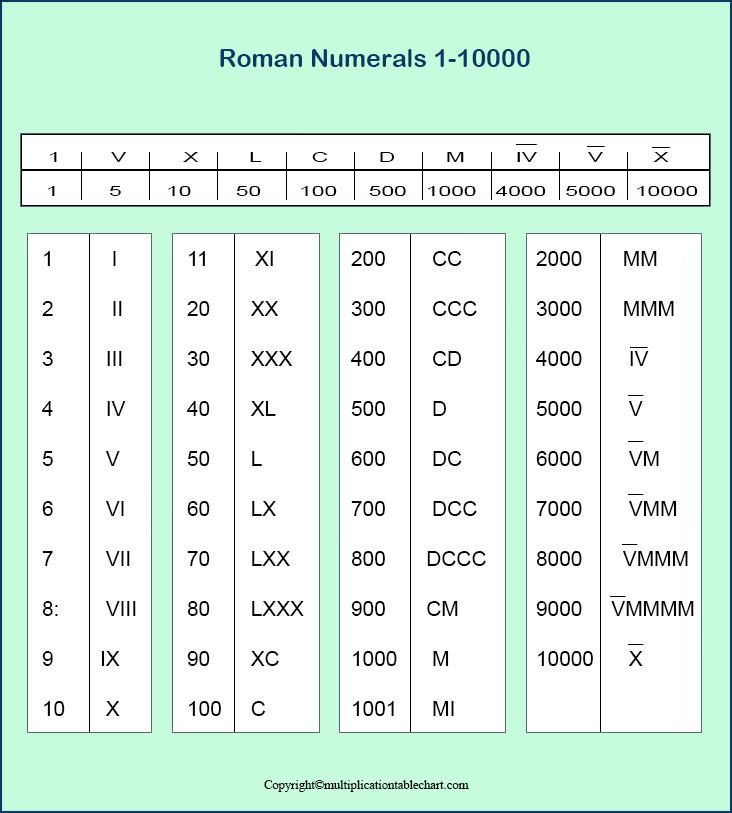 е. 599 = 500 + 90 + 9 = D + XC + IX = DXCIX.
е. 599 = 500 + 90 + 9 = D + XC + IX = DXCIX.
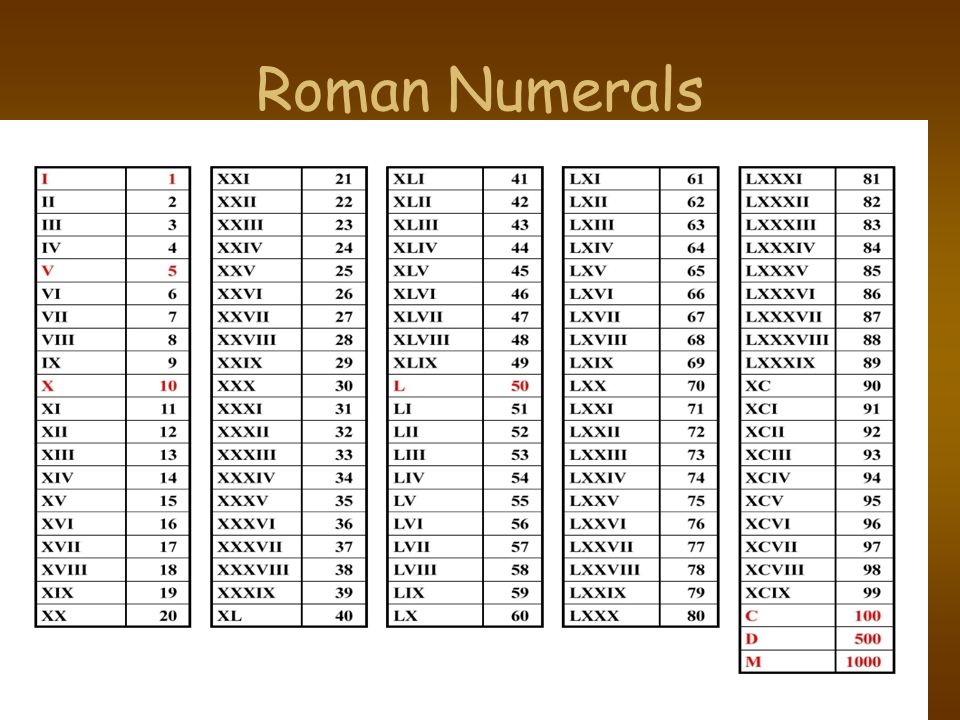 Римские цифры от 500 до 600 помогут учащимся легко выучить числа для перевода римских цифр. В этой статье мы упростили все правила, которым следуют при написании римских цифр от 500 до 600.
Римские цифры от 500 до 600 помогут учащимся легко выучить числа для перевода римских цифр. В этой статье мы упростили все правила, которым следуют при написании римских цифр от 500 до 600.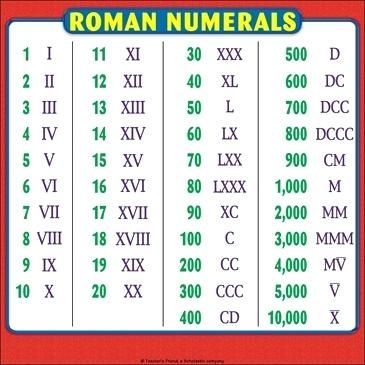 Студентам рекомендуется практиковать римские цифры от 500 до 600 для простых математических вычислений.
Студентам рекомендуется практиковать римские цифры от 500 до 600 для простых математических вычислений.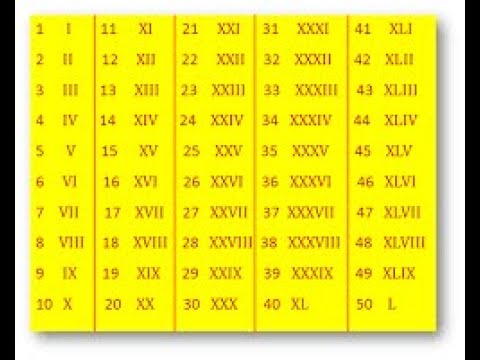 Например: LX, L > X, поэтому LX = L + X = 50 + 10 = 60,9.0008
Например: LX, L > X, поэтому LX = L + X = 50 + 10 = 60,9.0008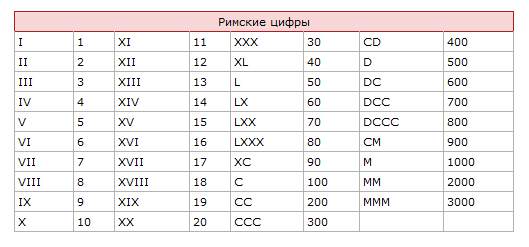
 Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
 Какую массу оксида никеля (ll) , выделившимся при растворении цинка водородом, можно восстановить?
Какую массу оксида никеля (ll) , выделившимся при растворении цинка водородом, можно восстановить? 2 … …)на месте точек должны быть цифры или знаки + и —
2 … …)на месте точек должны быть цифры или знаки + и — Найдите высоту данного параллелепипеда.
Найдите высоту данного параллелепипеда. Какую массу оксида никеля (ll) , выделившимся при растворении цинка водородом, можно восстановить?
Какую массу оксида никеля (ll) , выделившимся при растворении цинка водородом, можно восстановить?
 От тебя требуется лишь позволить нам поделиться с тобой нашими знаниями и применять их для своего наилучшего будущего.
От тебя требуется лишь позволить нам поделиться с тобой нашими знаниями и применять их для своего наилучшего будущего.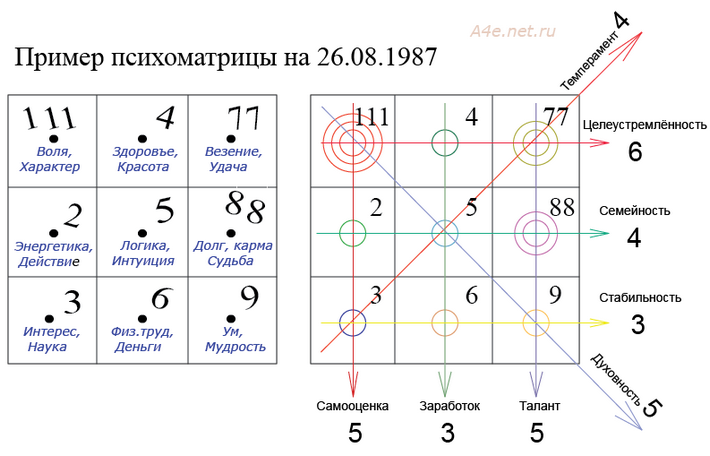 Совместимость по Матрице судьбы поможет выстроить гармоничные и счастливые отношения.
Совместимость по Матрице судьбы поможет выстроить гармоничные и счастливые отношения.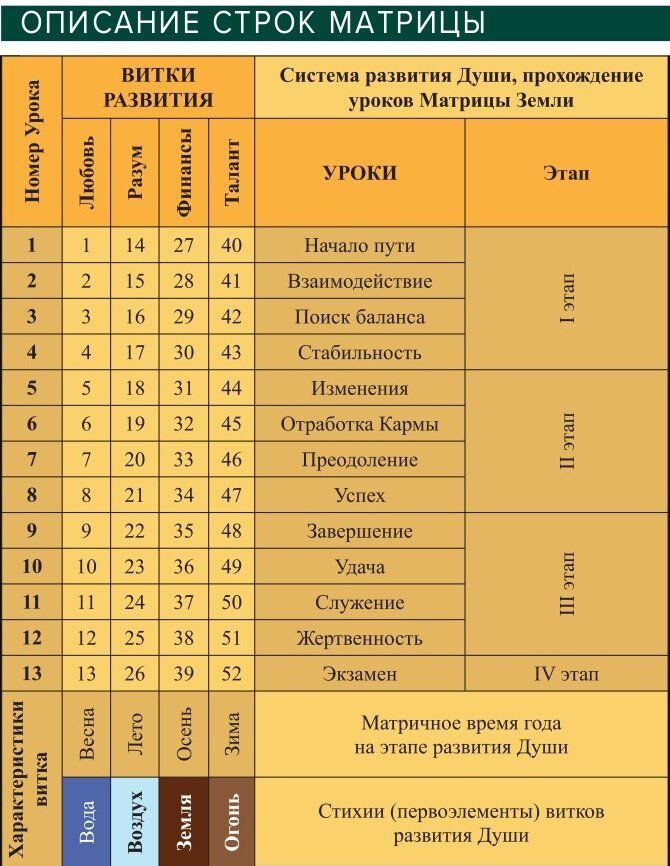
 Стоимость обучения окупается буквально за несколько консультаций.
Стоимость обучения окупается буквально за несколько консультаций. Исключён человеческий фактор.
Исключён человеческий фактор. 9 Энергия, Аркан “Отшельник”
9 Энергия, Аркан “Отшельник” Карта здоровья в Матрице Судьбы (урок 3)
Карта здоровья в Матрице Судьбы (урок 3) При открытии раздела видно какие цифры в матрице участвуют в описании.
При открытии раздела видно какие цифры в матрице участвуют в описании. И соединили в подробное руководство по составлению и расшифровке Матрицы, а также создали сервис по автоматическому расчёту с полным описанием по каждой дате.
И соединили в подробное руководство по составлению и расшифровке Матрицы, а также создали сервис по автоматическому расчёту с полным описанием по каждой дате.

 Калькулятор матриц позволяет производить расчеты с матрицами онлайн.
Калькулятор матриц позволяет производить расчеты с матрицами онлайн.
 В отличие от обычного умножения, умножение матриц не является коммутативным. Умножение A x B и B x A даст разные результаты. Матрицы 2×2 чаще всего используются для описания основных геометрических преобразований в двумерном векторном пространстве.
В отличие от обычного умножения, умножение матриц не является коммутативным. Умножение A x B и B x A даст разные результаты. Матрицы 2×2 чаще всего используются для описания основных геометрических преобразований в двумерном векторном пространстве. Умножение матриц в общем случае НЕ коммутативно
Умножение матриц в общем случае НЕ коммутативно 