Интегральные функции:
- Si(x)
- Интегральный синус от x
- Ci(x)
- Интегральный косинус от x
- Shi(x)
- Интегральный гиперболический синус от x
- Chi(x)
- Интегральный гиперболический косинус от x
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.
 3
3- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- 15/7
- — дробь
Другие функции:
- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от x
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:
- pi
- Число «Пи», которое примерно равно ~3.
 14159..
14159.. - e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
Тесты по теме «Производная» онлайн
-
Производная. Формулы.
25.10.2020 11284
Данный тест будет полезным учителю для осуществления быстрого контроля на уроке, а также ребятам, которые желают проверить свои знания по данной теме.
-
Вычисление производной
03.04.2020 6354
Данный тест может быть использован в качестве контроля знаний учащихся после изучения темы «Производная»
-
Геометрический смысл производной
03.
 12.2022
356
0
12.2022
356
0
Данный тест предназначен для отработки навыков нахождения тангенса угла наклона касательной к графику функции и навыков нахождения уравнения касательной в заданной точке.
-
Производная простейших функций
04.03.2021 594 0
Тест по алгебре и началам математического анализа на применение знаний таблицы производных
-
Наибольшее и наименьшее значения функций
23.12.2018 2182
Контрольный тест по алгебре и началам анализа в 11 классе. По материалам профильного ЕГЭ 2019 года (№12)
-
Производная элементарных функций
18.
 04.2020
15384
04.2020
15384
Перед Вами тренировочный тест, проверяющий усвоение небольшой, логически завершенной части темы «Производная». Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по специальностям технического профиля. Планируется, что на выполнение этого теста Вы потратите не более 5 минут.
-
Тест «Вторая производная. Физический смысл производной»
05.06.2022 297 0
Тест «Вторая производная. Физический смысл производной». Тест по теме «Вторая производная. Физический смысл производной» проверяет знание определения первой и второй производной, понимание физического смысла первой и второй производной функции, умения вычислять первую и вторую производные функций.
 умения вычислять значения производных функций в точке.
Тест содержит 10 вопросов с выбором единичного верного ответа и вопросы с вводом верного ответа в виде числа.
умения вычислять значения производных функций в точке.
Тест содержит 10 вопросов с выбором единичного верного ответа и вопросы с вводом верного ответа в виде числа. -
Производная и ее применение
25.12.2019 9011 0
Данный тест создан для проверки знаний по темам «Функция», «Производная»
-
Производная сложной функции
02.02.2022 1097 0
Образовательный тест по теме «Производная сложной функции» позволяет проверить знания школьников или студентов. В тесте требуется как найти сложную функцию из предложенных, так и самостоятельно вычислить производную некоторой сложной функции.
 Для выполнения заданий необходимо знать таблицу производных и правило вычисления производной сложной функции.
Тест одновариантный, состоит из 14 заданий.
Для выполнения заданий необходимо знать таблицу производных и правило вычисления производной сложной функции.
Тест одновариантный, состоит из 14 заданий. -
Тест «Геометрический смысл производной. Уравнение касательной и нормали»
05.06.2022 706 0
Тест по теме «Геометрический смысл производной. Уравнение касательной и нормали» проверяет знание геометрического смысла производной, алгоритм нахождения уравнения касательной и нормали к графику функции в точке; умения составлять уравнение касательной и нормали к графику функции в заданной точке, находить угловой коэффициент касательной к графику функции, угол между касательной к графику и осью Ох. Тест содержит 10 вопросов с выбором единичного и верного ответа, установление верной последовательности и вопросы с вводом верного ответа в виде числа.

-
Производные некоторых элементарных функций
18.10.2021 796
Тест по теме «Производные некоторых элементарных функций» предназначен для проверки усвоения указанной темы обучающимися 11 класса. Составитель: Инютина Н.В.
-
Тест «Правила дифференцирования»
03.06.2022 1532 0
Тест «Правила дифференцирования». Тест по теме «Правила дифференцирования» проверяет знание правил дифференцирования — правило дифференцирования суммы двух функций, правило вынесения постоянного множителя за знак производной, правило нахождения производной произведения функций, частного функций, нахождения производной сложной функции.
 Тест содержит 10 вопросов.
В тесте присутствуют вопросы с единичным верным ответом, вопросы на установление соответствия функции и ее производной и вопрос, в котором нужно записать верный ответ в виде числа.
Тест содержит 10 вопросов.
В тесте присутствуют вопросы с единичным верным ответом, вопросы на установление соответствия функции и ее производной и вопрос, в котором нужно записать верный ответ в виде числа.
-
Исследование функции с помощью производной
13.12.2022 359 0
Тест по математике на тему «Исследование функции с помощью производной» представляет собой 10 вопросов теоретической и практической направленности. Тест можно использовать при повторении изученного материала или актуализации знаний.
-
Применение производной к исследованию функций и построению графиков.
14.04.2022 867 0
Перед Вами тренировочный тест, проверяющий усвоение небольшой, логически завершенной части по теме производная.
 Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по специальностям технического профиля.
Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по специальностям технического профиля. -
Производная функции
14.03.2023 38 0
Здраствуйте! Предлагаем вашему вниманию тест по теме ПРОИЗВОДНАЯ ФУНКЦИИ. В нем вы сможите проверить свои знания! Удачи!
-
Правила дифференцирования
03.12.2022 258 0
Уважаемые учащиеся! В данном тесте вы можете проверить свои знания по теме Правила дифференцирования. Желаю всем удачи!
-
Урок №6 «Признаки возрастания и убывания функции»
27.
 05.2020
2393
0
05.2020
2393
0
Данный тест предназначен для закрепления материала по теме «Признак возрастания и убывыания функции». Очень внимательно читайте задание и инструкцию к работе. Желаю удачи!!!
-
Производная. Геометрический смысл производной
03.03.2021 554 0
Данный тест предназначен для проверки знаний обучающихся по теме «Производная. Геометрический смысл производной»
-
Нахождение производной суммы. Формулы дифференцирования.
18.04.2020 2317 0
Использование формул дифференцирования и правила суммы для нахождения производных.

-
Производная сложной функции.
31.10.2020 7362 0
Данный тест будет полезным учителю для осуществления быстрого контроля на уроке, а также ребятам, которые желают проверить свои знания по данной теме.
-
Итоговый тест по дисциплине «Математика» 1 ВАРИАНТ 38.02.01 Экономика и бухгалтерский учет (по отраслям)
19.12.2022 21 0
Тест по разделам: комплексные числа, производная, интеграл, дифференциальные уравнения.
-
Выполнение задания №7 формата ЕГЭ (профильный уровень)
09.
 01.2021
225
0
01.2021
225
0
В тесте представлены задания на применение геометрического, физического смыслов производной и при исследовании функции
-
Производная функции (высшая математика)
07.12.2021 359 0
Тест по курсу высшей математики на тему «Производная функции». Тест создан с целью проверки элементарных теоретических знаний производной и умения решать простейшие задачи производной.
-
Тест «Производные элементарных функций»
04.06.2022 160 0
Тест «Производные элементарных функций».
 Тест по теме «Производные элементарных функций» проверяет знание формул нахождения производных элементарных функций — степенной, показательной, логарифмической, тригонометрических функций, а также их различных комбинаций и умения вычислять производные функций.
Тест содержит 10 вопросов с единичным верным ответом.
Тест по теме «Производные элементарных функций» проверяет знание формул нахождения производных элементарных функций — степенной, показательной, логарифмической, тригонометрических функций, а также их различных комбинаций и умения вычислять производные функций.
Тест содержит 10 вопросов с единичным верным ответом.
-
Производные элементарных функций
16.11.2018 1443 0
Тест рекомендуется использовать при изучении темы «Производные элементарных функций» по учебнику Ю.М. Колягина, 11 класс
-
Дифференцирование алгебраической суммы
18.04.2020 555 0
Перед Вами тренировочный тест, проверяющий усвоение небольшой, логически завершенной части темы «Правила дифференцирования».
 Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по специальностям технического профиля. Планируется, что на выполнение этого теста Вы потратите не более 5 минут.
Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по специальностям технического профиля. Планируется, что на выполнение этого теста Вы потратите не более 5 минут. -
Применение производной к исследованию функций в заданиях ЕГЭ №1
27.12.2020 496 0
Тест предназначен для обучающихся средней школы для подготовки к ЕГЭ и проверки уровня знаний по теме «Применение производной к исследованию функций и построению графиков».
-
Примеры использования производной для нахождения наилучшего решения в прикладных задачах.
29.
 04.2022
199
0
04.2022
199
0
Перед Вами тренировочный тест, проверяющий усвоение небольшой, логически завершенной части темы «Начала математического анализа». Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по специальностям технического профиля.
-
Производная функции в школьном курсе математике
19.09.2018 1335 0
Тест состоит из 10 вопросов раскрывающих тему «Производная функции»
-
Математика тест для 11 класса по теме производная
30.
 01.2019
316
0
01.2019
316
0
Тест предназначен для учащихся 11 классов или студентов 1 и 2 курса. Содержит задания по теме «Производная и её приложения», «Интеграл», «Первообразная», «Пределы». Включает в себя 19 заданий
-
Тест для обучающихся 11 класс в форме ЕГЭ (профильный уровень)
08.02.2020 13 0
Тест состоит из 12 вопросов 1 части ЕГЭ профильного уровня обучающихся 11 класса
-
Нахождение производной
29.02.2020 3602 0
тренировочный тест на нахождение производной сложной функции, производная частного и произведения
-
Дифференцирование произведения
18.
 04.2020
1566
0
04.2020
1566
0
Перед Вами тренировочный тест, проверяющий усвоение небольшой, логически завершенной части темы «Правила дифференцирования». Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по специальностям технического профиля. Планируется, что на выполнение этого теста Вы потратите не более 5 минут.
-
Нахождение значений производных в точке
22.04.2020 246 0
Тест направлен на формирования навыков поиска производных различных функций и нахождение значений производных
-
Дифференцирование частного
27.
 04.2020
1709
0
04.2020
1709
0
Перед Вами тренировочный тест, проверяющий усвоение небольшой, логически завершенной части темы «Правила дифференцирования». Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по специальностям технического профиля. Планируется, что на выполнение этого теста Вы потратите не более 5 минут.
-
УД Математика Производная (вариант 2)
06.05.2020 246 0
Тест по математике «Вычисление производной» для студентов 1 курса СПО
-
Производная тригонометрической функции
06.
 05.2020
1251
0
05.2020
1251
0
Тест предназначен для проверки зананий по теме «Производная тригонометрических функций и их комбинации с элементарными функциями»
-
Нахождение значения производной тригонометрической функции в точке
08.05.2020 201 0
Тест предназначен для проверки зананий по теме «Нахождение значения производной тригонометрической функции в точке»
-
Производная y’ (нахождение производных функций)
18.05.2020 735 0
Найти производные заданных функций. Решите задание, сверьте свой ответ с предложенными.
 выберите верный
выберите верный -
Производная и ее приложения
29.05.2020 713 0
Тест предназначен для проверки знания физического и геометрического смысла производной, формул производных элементарных функций, правил вычисления производной, уения применять производную для составления уравнения касательной, исследования функции на монотонность и экстремумы
-
ОУД.03 Математика. Итоговое тестирование
11.06.2020 254 0
Перед Вами тренировочный тест, проверяющий усвоение небольшой, логически завершенной части учебной дисциплины математика. Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по специальностям технического профиля.

-
Производная функции
06.10.2020 441 0
Проверка усвоения учащимися темы «Производная функции», умение применять полученные знания на конкретных примерах и задачам физики и геометрии.
-
Применение производной к исследованию функций в заданиях ЕГЭ №2
15.01.2021 1106 0
Тест для обучающихся средней школы, предназначен для подготовки к ЕГЭ и проверки уровня знаний по теме «Физический, геометрический смысл призводной и применение производной к исследованию функций «.
-
Математический анализ.
 Вычисление производных.
Вычисление производных.
12.03.2021 213 0
Данный тест рассчитан на выпускников школ и первокурсников ВУЗов. Проверьте свои знания в теории производных.
-
Геометрический смысл производной в задачах ЕГЭ
30.03.2021 417 0
Тест для обучающихся средней школы, предназначен для подготовки к ЕГЭ и проверки уровня знаний по теме «Производная. Геометрический смысл производной».
-
Механический смысл производной
23.10.2021 853 0
Тест состоит из 7 вопросов по теме «Физический смысл производной», содержит прямые и обратные задания, аналогичные заданию №6 ЕГЭ.

-
Итоговый тест за 1 четверть, 11 класс, математика
30.10.2021 285 0
Тест по математике 11 класса за 1 четверть по УМК Алимова Ш. А. (алгебра и начала анализа) и Атанасяна Л. С. (геометрия). Базовый уровень.
-
Производные функции
05.12.2021 382 0
Тест для проработки темы -производная. Предназначен для решения и проработки темы учников и их родителей.
-
Правила дифференцирования
18.
 03.2022
142
0
03.2022
142
0
Тест предназначен для проверки знаний по теме «Правила дифференцирования».
-
Тест по теме «Производная»
23.04.2022 74 0
Тест по теме «Производная» состоит из четырнадцати вопросов, девять из которых тестовые, остальные с записью ответа
-
Проверка знаний по теме «Производные»
27.04.2022 22 0
Данный тест содержит материалы для проверки знаний по теме «Производная», время на выполнение теста ограничено
-
Производная.
 Понятие производной
Понятие производной
02.06.2022 67 0
Алгебра и начала анализа. Тема «Производная» Тест №1 по теме «Понятие производной. Физический смысл производной»
-
Тест на соответствие «Производные элементарных функций»
05.06.2022 23 0
Тест на соответствие «Производные элементарных функций». Тест по теме «Производные элементарных функций» проверяет знание формул нахождения производных элементарных функций — степенной, тригонометрических функций, умения вычислять производные функций. Тест содержит 10 функций и 10 производных функций. При выполнении теста необходимо установить соответствие между функцией и ее производной.
-
Производная.
 Геометрический смысл производной.
Геометрический смысл производной.
05.06.2022 81 0
Алгебра и начала анализа. Тема «Производная» Тест по теме «Производная. Геометрический смысл производной».
-
Монотонность функции, если задан график производной функции
05.10.2022 195 0
Тест базового уровня. Тест предназначен для повторения понятия монотонности функции через понятие производной.
-
Вычисление производной простейшей функции
29.11.2022 432 0
Тест предназначен для проверки знаний таблицы производных простейших фкнкций, а также применения правил дифференцирования.

-
Итоговый тест по дисциплине «Математика» 1 ВАРИАНТ
18.12.2022 96 0
Тест по разделам: комплексные числа, множества, графы, производная, интеграл, дифференциальные уравнения, ряды, теория вероятностей.
-
Итоговый тест по дисциплине «Математика» 2 ВАРИАНТ
18.12.2022 35 0
Тест по разделам: комплексные числа, множества, графы, производная, интеграл, дифференциальные уравнения, ряды, теория вероятностей.
-
Итоговый тест по дисциплине «Математика» 2 ВАРИАНТ 38.
 02.01 Экономика и бухгалтерский учет (по отраслям)
02.01 Экономика и бухгалтерский учет (по отраслям)
19.12.2022 49 0
Тест по разделам: комплексные числа, производная, интеграл, дифференциальные уравнения.
Критические точки и первый производный тест — Криста Кинг Математика
Что такое критические точки и как их найти?
Процесс оптимизации заключается в поиске наименьшего и наибольшего значений функции. Если мы воспользуемся калькулятором, чтобы нарисовать график функции, мы обычно сможем определить наименьшее и наибольшее значения.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Например, для функции, показанной ниже, мы можем увидеть, просто взглянув на график, что функция достигает своего наименьшего значения в точке ???A???. Эта нижняя возможная точка является глобальным минимумом функции .
Эта нижняя возможная точка является глобальным минимумом функции .
Есть причина, по которой важно уметь находить этот глобальный минимум. Давайте на мгновение представим, что функция, показанная на графике, на самом деле моделирует вероятность того, что продукты испортятся в морозильной камере ресторана при различных температурах.
Если я владелец этого ресторана и хочу свести к минимуму вероятность того, что моя еда испортится, то мне очень интересно найти этот глобальный минимум. Если я знаю, как посчитать это значение, то я буду знать точную температуру, на которую следует установить морозильник, чтобы свести к минимуму вероятность того, что моя еда испортится.
И это действительно ценно! Правильное соблюдение этого правила может сэкономить мне время и деньги, а также поможет обеспечить бесперебойную работу моего ресторана и добиться успеха в долгосрочной перспективе.
Вот что такое оптимизация. Это позволяет нам рассчитать точку, в которой функция максимизируется или минимизируется, и у этого есть все виды реальных приложений, о которых мы подробно поговорим позже в курсе.
Это позволяет нам рассчитать точку, в которой функция максимизируется или минимизируется, и у этого есть все виды реальных приложений, о которых мы подробно поговорим позже в курсе.
В этом разделе мы поговорим о процессе оптимизации, начиная с того, как найти наименьшее и наибольшее значения функции. Мы закончим раздел, переведя эти шаги оптимизации в изучение того, как рисовать график функции.
Локальные и глобальные экстремумы
В общем случае наименьшее и наибольшее значения функции являются ее экстремумами . Думайте об экстремумах как о «экстремальных точках» функции.
Экстремумы функции состоят из ее наименьших точек, которые мы называем минимумов , и ее наибольших точек, которые мы называем максимумов .
Внутри минимумов функции различают локальные (относительные) минимумы и глобальные (абсолютные) минимумы. А внутри максимумов функции мы различаем локальные (относительные) максимумы и глобальные (относительные) максимумы.
В качестве примера давайте снова посмотрим на тот же график, что и раньше.
Мы уже сказали, что абсолютный/глобальный минимум функции находится в точке ???A???, и это потому, что ???A??? это точка, в которой функция имеет наименьшее значение во всей области определения. Но функция также имеет локальный минимум при ???C???, потому что ???C??? является низшей точкой функции в области вблизи ???C???.
Функция также имеет локальный максимум в точке ???B???, потому что ???B??? является наивысшей точкой функции в районе ???B???.
Мы бы не определили абсолютный максимум для функции, потому что он стремится к ???\infty??? оба слева от ???A??? и справа от ???C???, так что мы не можем назвать конечную точку, которая описывала бы наибольшее значение, которое когда-либо достигает функция.
Таким образом, в общем случае
локальный/относительный максимум существует везде, где функция меняет направление с возрастания на убывание.
 Если локальный максимум также оказывается наивысшей точкой функции в любом месте ее области определения, то это также глобальный/абсолютный максимум . Функция может иметь бесконечно много локальных/относительных максимумов, но у нее будет только один (или ни одного) глобальный/абсолютный максимум.
Если локальный максимум также оказывается наивысшей точкой функции в любом месте ее области определения, то это также глобальный/абсолютный максимум . Функция может иметь бесконечно много локальных/относительных максимумов, но у нее будет только один (или ни одного) глобальный/абсолютный максимум.Локальный/относительный минимум существует везде, где функция меняет направление с убывающего на возрастающее. Если локальный минимум также оказывается самой низкой точкой функции в любом месте ее области определения, то это также глобальный/абсолютный минимум . У функции может быть бесконечно много локальных/относительных минимумов, но у нее будет только один (или ни одного) глобальный/абсолютный минимум. 92???, которая представляет собой параболу с вершиной в начале координат, которая раскрывается. Эта парабола имеет только один локальный минимум при ???x=0???, этот локальный минимум также является глобальным минимумом, но парабола не имеет ни локального максимума, ни глобального максимума.

Возьмем другой пример: строка ???y=x??? это линия, которая проходит через начало координат с наклоном ???m=1???, и у нее вообще нет экстремумов (нет локальных максимумов или минимумов, а также нет глобальных максимумов или минимумов), потому что она никогда не меняет направление.
Итак, какие экстремумы вы сможете классифицировать, всегда будет зависеть от конкретной функции, с которой вы работаете.
Критические точки
Первым шагом в любом процессе оптимизации всегда является поиск критических точек функции.
Критические точки существуют, где производная равна ???0??? (или, возможно, где производная не определена), и они представляют собой точки, в которых график функции изменит направление либо с убывания на возрастание, либо с увеличения на убывание.
Поскольку функция меняет направление в критических точках, функция всегда будет иметь по крайней мере локальный максимум или минимум в критической точке, если не глобальный максимум или минимум там.

Чтобы найти критические точки, мы просто берем производную, устанавливаем ее равной ???0???, а затем находим переменную.
Как использовать критические точки для поиска локальных и глобальных экстремумов
Пройти курс
Хотите узнать больше об исчислении 1? У меня есть пошаговый курс для этого. 🙂
Узнать больше
Пошаговый пример поиска критических точек и применения теста первой производной 92=4???
???x=\pm2???
Это критические точки ???f(x)???.
Критические точки существуют там, где производная равна 0, и представляют собой точки, в которых график функции меняет направление с убывающего на возрастающее и наоборот.
Увеличение и уменьшение
Поскольку критические точки — это точки, в которых функция меняет направление с возрастания на убывание или с убывания на возрастание, следующим шагом является исследование поведения между критическими точками.

Если производная положительна, функция возрастает. Функция — это , увеличивающая , когда она движется вверх по мере нашего движения слева направо.
Если производная отрицательна, функция убывает. Функция на уменьшается на , когда она движется вниз по мере нашего движения слева направо.
Чтобы проверить знак производной, мы просто выберем значение между каждой парой критических точек и подставим это тестовое значение в производную, чтобы посмотреть, получим ли мы положительный или отрицательный результат. Если тестовое значение дает положительный результат, это означает, что функция возрастает на этом интервале, а если тестовое значение дает отрицательный результат, это означает, что функция на этом интервале убывает.
Если мы найдем одну критическую точку для функции, то нам просто нужно посмотреть на знак производной слева и справа от этой одной критической точки.

Но если мы находим несколько критических точек, то нам нужно найти знак производной слева от самой левой критической точки, справа от самой правой критической точки и между каждой критической точкой.
Продолжим один из предыдущих примеров, взглянув на знак производной между каждой критической точкой.
Пример
Критические точки функции: ???x=\pm2???. Где функция возрастает, а где убывает?
???f(x)=x+\frac{4}{x}???
Ранее мы использовали производную, чтобы найти, что функция имеет критические точки в ???x=\pm2???. Когда у нас есть критические точки, полезно нанести их на числовую линию от наименьшего к наибольшему, слева направо.
Из этой диаграммы видно, что нам нужно протестировать три интервала. 92}???
???f'(3)=1-\frac{4}{9}???
???f'(3)=\frac{9}{9}-\frac{4}{9}???
???f'(3)=\frac{5}{9}>0???
Производная была положительной на первом интервале, отрицательной на втором интервале и положительной на третьем интервале.
 Нанесите эти знаки на диаграмму критических точек, которую мы нарисовали ранее.
Нанесите эти знаки на диаграмму критических точек, которую мы нарисовали ранее.Помните, что исходная функция ???f(x)??? увеличивается там, где мы нашли положительный результат, и уменьшается там, где мы нашли отрицательный результат. Так что можно сказать
???f(x)??? увеличивается на ???-\infty
???f(x)??? убывает на ???-2
???f(x)??? увеличивается на ???2
Проверка первой производной
После того, как мы нашли интервалы, на которых функция возрастает и убывает, мы фактически уже завершили проверку первой производной, если не считать явных формулировок выводов о максимальном и минимальном значениях функции. .
Потому что тест первой производной — это просто тест для нахождения максимума и минимума функции.
Другими словами, если у нас есть диаграмма критических точек, заполненная знаками производной,
критерий первой производной позволяет сделать следующие выводы:
Если слева от критической точки производная отрицательна, а справа от нее положительна, то график имеет в этой точке локальный минимум (возможно, это местный минимум может быть глобальным минимумом).

Если производная положительна слева от критической точки и отрицательна справа от нее, график имеет локальный максимум в этой точке (и, возможно, этот локальный максимум может быть глобальным максимумом).
Итак, для предыдущего примера проверка первой производной позволяет сделать вывод, что функция имеет локальный максимум в точке ???x=-2??? и локальный минимум при ???x=2???.
Получите доступ к полному курсу исчисления 1
Начать
Изучайте математикуКриста Кинг математика, учитесь онлайн, онлайн-курс, онлайн-математика, исчисление 1, исчисление i, вычисление 1, вычисление i, приложения производных, приложения дифференцирования, производные приложения, рисование графиков, рисование кривых, зарисовка кривых, зарисовка графиков, критические точки, поиск критических точек, тест первой производной, локальный максимум, локальные максимумы, локальные экстремумы, локальный экстремум, локальный минимум, локальные минимумы, глобальные экстремумы, глобальные максимумы, глобальный максимум, глобальные минимумы, глобальный минимум, относительный экстремум, относительный экстремум, относительный максимум, относительный максимум, относительный минимум, относительный минимум, абсолютный экстремум, абсолютный экстремум, абсолютный максимум, абсолютный максимум, абсолютный минимум, абсолютный минимум, оптимизация
0 лайковНайти первую производную функции
Все ресурсы для предварительного исчисления
12 диагностических тестов 380 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 5 Следующая →
Precalculus Help » Вводный расчет » Производные » Найдите первую производную функции
Рассмотрим функцию
Какая первая производная от ?
Возможные ответы:
Правильный ответ:
Объяснение:
Обратите внимание, что определено для всех
Используя законы логарифмирования, мы можем записать как .

Использование цепного правила и правила произведения . У нас есть:
.
Обратите внимание,
.
Теперь заменим и получим окончательный ответ:
Сообщить об ошибке
Найти производную от .
Возможные ответы:
Правильный ответ:
Объяснение:
Здесь используется простое экспоненциальное правило производных.
Умножьте значение показателя степени на функцию, затем вычтите 1 из старого показателя степени, чтобы получить новый показатель степени.
Формула выглядит следующим образом:
.
Используя нашу функцию,
где и мы получаем следующую производную,
.
Сообщить об ошибке
Найдите производную от .
Возможные ответы:
Правильный ответ:
Объяснение:
Для этой задачи нам нужно использовать цепное правило.

Цепное правило гласит, что нужно работать снаружи внутрь. В этом случае внешняя функция и внутренняя функция . Затем производная становится внешней функцией, умноженной на производную внутренней функции.
Таким образом, мы используем следующую формулу
.
В нашем случае и .
Следовательно, результат
.
Сообщить об ошибке
Найдите первую производную следующей функции:
Возможные ответы:
Правильный ответ:
5
5 Объяснение:
Чтобы найти первую производную полинома, все, что нам нужно знать, это как применить правило степени к простому члену с показателем степени:
Приведенная выше формула говорит нам, что для получения производной члена с коэффициентом и показателем степени , мы просто умножаем член на и вычитаем 1 из показателя степени.
 С учетом этого возьмем производную функции в задаче почленно:
С учетом этого возьмем производную функции в задаче почленно:Сообщить об ошибке
Найдите производную следующей функции:
Возможные ответы:
Правильный ответ:
Объяснение:
Мы видим, что наша функция включает ряд членов, возведенных в степень, поэтому нам нужно будет применить правило степени, а также правило цепочки, чтобы найти производную функции. Сначала мы применяем правило степени ко всем терминам в скобках, а затем применяем цепное правило, умножая весь результат на производную только от выражения в скобках:
Сообщить об ошибке
Какая первая производная от
по отношению к ?
Возможные ответы:
Правильный ответ:
Объяснение:
Поскольку мы берем производную по , мы применяем степенное правило только к терминам, которые содержат .
 Поскольку все термины содержат , мы рассматриваем как константу.
Поскольку все термины содержат , мы рассматриваем как константу.Производная константы всегда .
Итак, производная от
это ноль.
Сообщить об ошибке
Найдите первую производную от
относительно
Возможные ответы:
Правильный ответ:
5
5 Объяснение:
Производная константы равна .
Сообщить об ошибке
Найдите первую производную от
относительно
Возможные ответы:
Правильный ответ:
Объяснение:
Вспомните правило степени, согласно которому нужно умножить на показатель степени перед константой, а затем вычесть показатель степени на 1.
Результат:
Возьмем производную от следующего члена:
Производную от :
Сила чего-то есть.

Наш результат:
Сообщить об ошибке
Найти первую производную функции
.
Возможные ответы:
Правильный ответ:
Объяснение:
Для функции
первая производная равна
Итак, для
первая производная равна
Сообщить об ошибке
Найти первую производную от
относительно .
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти производную этого уравнения, вспомните правило степени, которое гласит: умножьте показатель степени перед константой, а затем вычтите единицу из показателя степени.


 14159..
14159.. 12.2022
356
0
12.2022
356
0
 04.2020
15384
04.2020
15384
 умения вычислять значения производных функций в точке.
Тест содержит 10 вопросов с выбором единичного верного ответа и вопросы с вводом верного ответа в виде числа.
умения вычислять значения производных функций в точке.
Тест содержит 10 вопросов с выбором единичного верного ответа и вопросы с вводом верного ответа в виде числа. Для выполнения заданий необходимо знать таблицу производных и правило вычисления производной сложной функции.
Тест одновариантный, состоит из 14 заданий.
Для выполнения заданий необходимо знать таблицу производных и правило вычисления производной сложной функции.
Тест одновариантный, состоит из 14 заданий.
 Тест содержит 10 вопросов.
В тесте присутствуют вопросы с единичным верным ответом, вопросы на установление соответствия функции и ее производной и вопрос, в котором нужно записать верный ответ в виде числа.
Тест содержит 10 вопросов.
В тесте присутствуют вопросы с единичным верным ответом, вопросы на установление соответствия функции и ее производной и вопрос, в котором нужно записать верный ответ в виде числа. Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по специальностям технического профиля.
Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по специальностям технического профиля. 05.2020
2393
0
05.2020
2393
0

 01.2021
225
0
01.2021
225
0
 Тест по теме «Производные элементарных функций» проверяет знание формул нахождения производных элементарных функций — степенной, показательной, логарифмической, тригонометрических функций, а также их различных комбинаций и умения вычислять производные функций.
Тест содержит 10 вопросов с единичным верным ответом.
Тест по теме «Производные элементарных функций» проверяет знание формул нахождения производных элементарных функций — степенной, показательной, логарифмической, тригонометрических функций, а также их различных комбинаций и умения вычислять производные функций.
Тест содержит 10 вопросов с единичным верным ответом. Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по специальностям технического профиля. Планируется, что на выполнение этого теста Вы потратите не более 5 минут.
Содержание и уровень сложности включенных в него заданий, в основном, отвечают обязательным требованиям к математической подготовке студентов, обучающихся по специальностям технического профиля. Планируется, что на выполнение этого теста Вы потратите не более 5 минут. 04.2022
199
0
04.2022
199
0
 01.2019
316
0
01.2019
316
0
 04.2020
1566
0
04.2020
1566
0
 04.2020
1709
0
04.2020
1709
0
 05.2020
1251
0
05.2020
1251
0
 выберите верный
выберите верный
 Вычисление производных.
Вычисление производных.

 03.2022
142
0
03.2022
142
0
 Геометрический смысл производной.
Геометрический смысл производной.

 02.01 Экономика и бухгалтерский учет (по отраслям)
02.01 Экономика и бухгалтерский учет (по отраслям)
 Если локальный максимум также оказывается наивысшей точкой функции в любом месте ее области определения, то это также глобальный/абсолютный максимум . Функция может иметь бесконечно много локальных/относительных максимумов, но у нее будет только один (или ни одного) глобальный/абсолютный максимум.
Если локальный максимум также оказывается наивысшей точкой функции в любом месте ее области определения, то это также глобальный/абсолютный максимум . Функция может иметь бесконечно много локальных/относительных максимумов, но у нее будет только один (или ни одного) глобальный/абсолютный максимум.


 Нанесите эти знаки на диаграмму критических точек, которую мы нарисовали ранее.
Нанесите эти знаки на диаграмму критических точек, которую мы нарисовали ранее.


 С учетом этого возьмем производную функции в задаче почленно:
С учетом этого возьмем производную функции в задаче почленно: Поскольку все термины содержат , мы рассматриваем как константу.
Поскольку все термины содержат , мы рассматриваем как константу.

 Қышқылдармен және негіздермен әрекеттесуі:
Қышқылдармен және негіздермен әрекеттесуі: Бейтараптану реакция
Бейтараптану реакция
 тұз + қышқыл = жаңа тұз + жаңа қышқыл
тұз + қышқыл = жаңа тұз + жаңа қышқыл
 Қышқыл (артық) + негіз = қышқылдық тұз + су
Қышқыл (артық) + негіз = қышқылдық тұз + су ..
.. Назвіть продукти реакції.
Назвіть продукти реакції.
 Як їх можна розрізнити, використовуючи хімічні реакції? Кальцій оксид є основним оксидом, тому реагує з кислотами, але не реагує з лугами. Алюміній оксид є амфотерним оксидом, тому реагує з кислотами і лугами. Достатньо подіяти лугом. В реакцію вступить алюміній оксид.
Як їх можна розрізнити, використовуючи хімічні реакції? Кальцій оксид є основним оксидом, тому реагує з кислотами, але не реагує з лугами. Алюміній оксид є амфотерним оксидом, тому реагує з кислотами і лугами. Достатньо подіяти лугом. В реакцію вступить алюміній оксид. ) = K2ZnO2 + 2H2O Калій цинкат і вода
) = K2ZnO2 + 2H2O Калій цинкат і вода
 Записуємо рівняння реакції: Ba(ОH)2 + ZnО = BaZnО2 + H2O
Записуємо рівняння реакції: Ba(ОH)2 + ZnО = BaZnО2 + H2O 
 Записуємо рівняння реакції:
Записуємо рівняння реакції: 
 Які сполуки є амфотерними? Сполуки, для яких характерні і кислотні, і основні властивості, тобто оксиди і гідроксиди деяких хімічних елементів у ступенях окиснення +2, +3 та +4.
Які сполуки є амфотерними? Сполуки, для яких характерні і кислотні, і основні властивості, тобто оксиди і гідроксиди деяких хімічних елементів у ступенях окиснення +2, +3 та +4. Hy vọng tài liệu giup ich cho ac bạn học sinh trong quá trình lam bài tập, cung như học tap. Mời cac bạn tham khảo.
Hy vọng tài liệu giup ich cho ac bạn học sinh trong quá trình lam bài tập, cung như học tap. Mời cac bạn tham khảo. Có kết tủa trắng xanh
Có kết tủa trắng xanh (1), (2), (3)
(1), (2), (3) Trung hòa vừa đủ 250 мл навоза dịch Ba(OH) 2 1M với dung dịch H 2 SO 4 15%. Khối lượng dung dịch H 2 SO 4 đã dùng là:
Trung hòa vừa đủ 250 мл навоза dịch Ba(OH) 2 1M với dung dịch H 2 SO 4 15%. Khối lượng dung dịch H 2 SO 4 đã dùng là:

 Отбросьте единицу
Отбросьте единицу Перейдем к другому методу – сравнение дробей приводя их к общему… числителю.
Перейдем к другому методу – сравнение дробей приводя их к общему… числителю. Однако, для того, чтобы сравнить эти две дроби, тебе не обязательно искать общий знаменатель. Хотя… найди его и посмотри, вдруг знак сравнения все же неправильный?
Однако, для того, чтобы сравнить эти две дроби, тебе не обязательно искать общий знаменатель. Хотя… найди его и посмотри, вдруг знак сравнения все же неправильный?
 Внимательно посмотреть ход решения и случайно не перепутать знаки. Мы отнимали от второго числа первое и получили отрицательный ответ, значит?..
Внимательно посмотреть ход решения и случайно не перепутать знаки. Мы отнимали от второго числа первое и получили отрицательный ответ, значит?..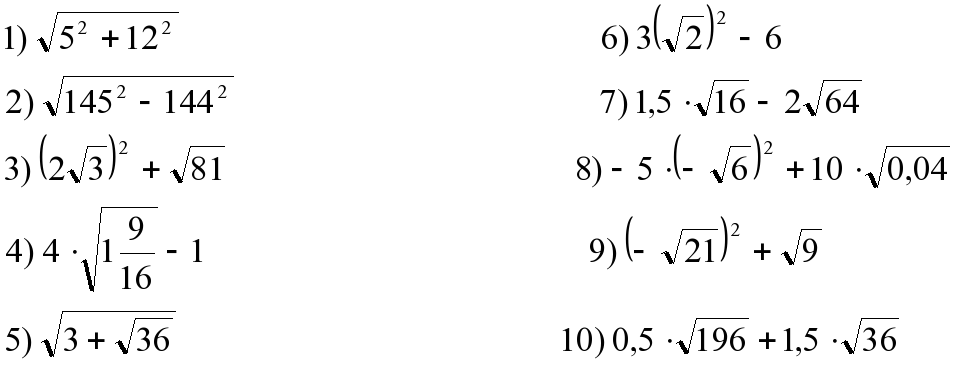 {3}}=6\)
{3}}=6\) {6}}=12\)
{6}}=12\) \( {{\log }_{\frac{1}{3}}}12\vee {{\log }_{\frac{1}{3}}}24\) – основания одинаковы.
\( {{\log }_{\frac{1}{3}}}12\vee {{\log }_{\frac{1}{3}}}24\) – основания одинаковы.
 b}\;{\rm{при}}\;0 < a < 1}\end{array}} \right. \) или \( {\log _a}x \vee {\log _a}y{\rm{ }} \Leftrightarrow {\rm{ }}\left[ {\begin{array}{*{20}{l}}{x \vee y\;{\rm{при}}\;a > 1}\\{x \wedge y\;{\rm{при}}\;0 < a < 1}\end{array}} \right. \)
b}\;{\rm{при}}\;0 < a < 1}\end{array}} \right. \) или \( {\log _a}x \vee {\log _a}y{\rm{ }} \Leftrightarrow {\rm{ }}\left[ {\begin{array}{*{20}{l}}{x \vee y\;{\rm{при}}\;a > 1}\\{x \wedge y\;{\rm{при}}\;0 < a < 1}\end{array}} \right. \) {2}14<2,25}}\end{array}\)
{2}14<2,25}}\end{array}\) \circ }}\)
\circ }}\)
 МНОЖЕСТВО ЦЕЛЫХ ЧИСЕЛ
МНОЖЕСТВО ЦЕЛЫХ ЧИСЕЛ СТЕПЕНЬ ДРОБИ
СТЕПЕНЬ ДРОБИ ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК
ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ
ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ СВОЙСТВА ФУНКЦИ И у=tg(x) И ЕЕ ГРАФИК
СВОЙСТВА ФУНКЦИ И у=tg(x) И ЕЕ ГРАФИК ПРЕДЕЛ ФУНКЦИИ
ПРЕДЕЛ ФУНКЦИИ ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК
ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК ФОРМУЛА НЬЮТОНА—ЛЕЙБНИЦА
ФОРМУЛА НЬЮТОНА—ЛЕЙБНИЦА Но для тех из нас, кому не так повезло, вот один конкретный метод, в котором используется то, что называется деревом факторов.
Но для тех из нас, кому не так повезло, вот один конкретный метод, в котором используется то, что называется деревом факторов.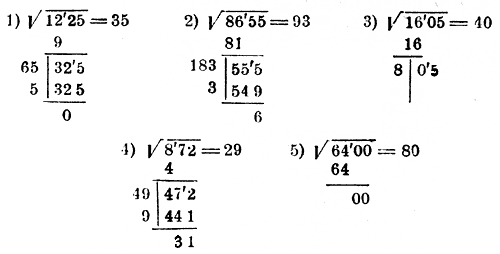 Это означает, что одна 3 выходит за пределы квадратного корня. Для каждого под радикалом без пары мы помещаем это число в квадратный корень, что означает, что одна 5 входит в квадратный корень. Это дает окончательный ответ .
Это означает, что одна 3 выходит за пределы квадратного корня. Для каждого под радикалом без пары мы помещаем это число в квадратный корень, что означает, что одна 5 входит в квадратный корень. Это дает окончательный ответ . Это неизменно дает следующее дерево факторов.
Это неизменно дает следующее дерево факторов. Радикальный или сурд, термины, которые не
упростить можно комбинировать или собирать в алгебраические выражения почти таким же образом
что вы будете собирать переменные термины, такие как три 𝑥 и пять 𝑥 или два 𝑦 и семь
𝑦 и так далее.
Радикальный или сурд, термины, которые не
упростить можно комбинировать или собирать в алгебраические выражения почти таким же образом
что вы будете собирать переменные термины, такие как три 𝑥 и пять 𝑥 или два 𝑦 и семь
𝑦 и так далее. И вы должны быть осторожны, чтобы не
спутать это с этим выражением, которое представляет собой маленькую двойку в этом знаке квадратного корня,
что означает квадратный корень из семи.
И вы должны быть осторожны, чтобы не
спутать это с этим выражением, которое представляет собой маленькую двойку в этом знаке квадратного корня,
что означает квадратный корень из семи.
 Итак, корень восемь минус корень два может
можно переписать как два корня два минус один корень два. И два корня два минус один корень два
всего один корень два. Хотя, очевидно, мы бы не
потрудитесь написать единицу перед ним, так что это просто квадратный корень из двух.
Итак, корень восемь минус корень два может
можно переписать как два корня два минус один корень два. И два корня два минус один корень два
всего один корень два. Хотя, очевидно, мы бы не
потрудитесь написать единицу перед ним, так что это просто квадратный корень из двух.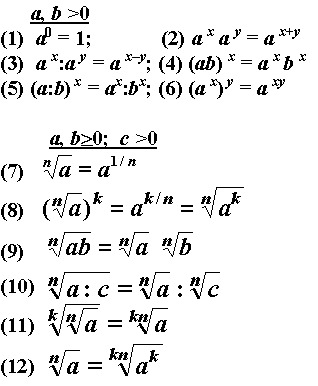


 ко второй строке прибавим первую строку умноженную на -21 1 5
ко второй строке прибавим первую строку умноженную на -21 1 5  Решить систему уравнений методом Гаусса3 x 2 y z 4
Решить систему уравнений методом Гаусса3 x 2 y z 4 Методы оптимизации
Методы оптимизации

 На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника. На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. 
 25
25 com/id286009794
com/id286009794
 Приведенные ниже данные по умолчанию являются примером системы с бесконечным числом решений:
Приведенные ниже данные по умолчанию являются примером системы с бесконечным числом решений: 
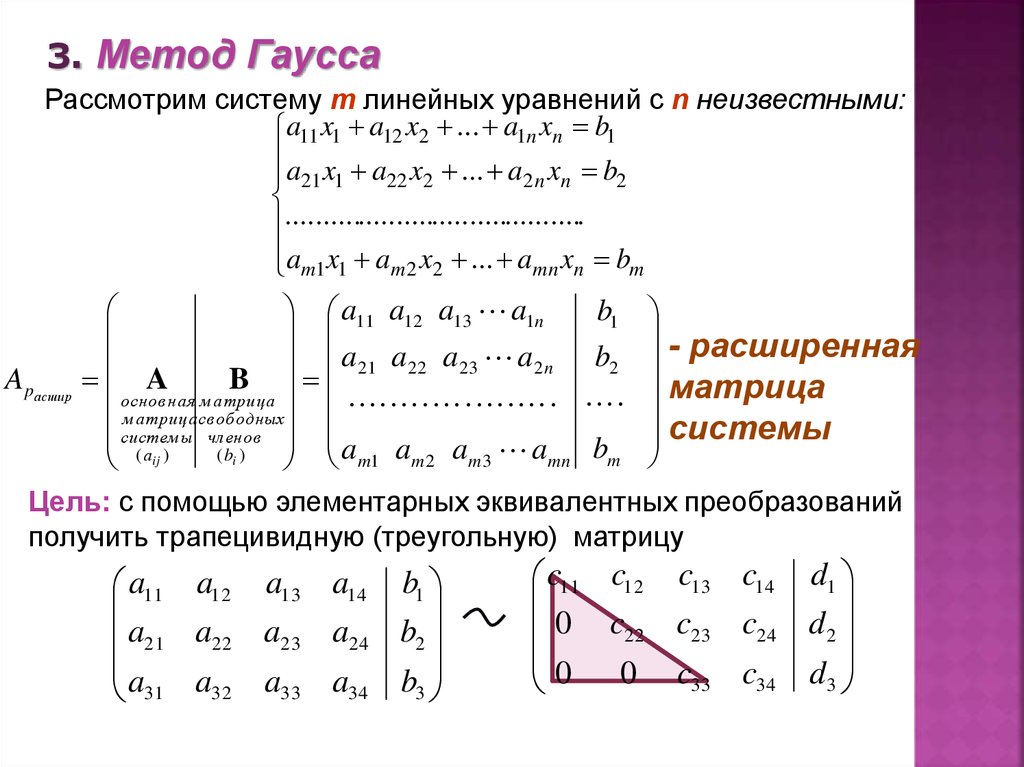 Также в результате преобразований можно получить те же уравнения, «лишнее» из которых тоже можно отбросить — и опять задача сводится к случаям 1 или 2.
Также в результате преобразований можно получить те же уравнения, «лишнее» из которых тоже можно отбросить — и опять задача сводится к случаям 1 или 2. е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
 Затем мы преобразуем нашу новую расширенную матрицу обратно в уравнения, и на этом этапе решение системы станет очень простым.
Затем мы преобразуем нашу новую расширенную матрицу обратно в уравнения, и на этом этапе решение системы станет очень простым. Итак, давайте решим пару систем.
Итак, давайте решим пару систем.
 Мы можем выполнить обе эти операции одновременно, так что давайте сделаем это.
Мы можем выполнить обе эти операции одновременно, так что давайте сделаем это. Технически 5 во втором столбце можно оставить. Тем не менее, это облегчит нашу жизнь в будущем, если это будет 1. Мы можем использовать операцию второй строки, чтобы позаботиться об этом. Мы можем разделить всю строку на 5. Это даст
Технически 5 во втором столбце можно оставить. Тем не менее, это облегчит нашу жизнь в будущем, если это будет 1. Мы можем использовать операцию второй строки, чтобы позаботиться об этом. Мы можем разделить всю строку на 5. Это даст
 Затем мы можем использовать первое уравнение, чтобы получить \(x_{1}\). Обратите также внимание, что наличие единиц вдоль главной диагонали несколько помогло в этом процессе.
Затем мы можем использовать первое уравнение, чтобы получить \(x_{1}\). Обратите также внимание, что наличие единиц вдоль главной диагонали несколько помогло в этом процессе. Вот работа для этой расширенной матрицы.
Вот работа для этой расширенной матрицы. Тут один из трех вариантов. Во-первых, нам каким-то образом удалось доказать, что 0 равно 8, и мы знаем, что это невозможно. Во-вторых, мы допустили ошибку, но, проанализировав нашу работу, не видно, что мы допустили ошибку.
Тут один из трех вариантов. Во-первых, нам каким-то образом удалось доказать, что 0 равно 8, и мы знаем, что это невозможно. Во-вторых, мы допустили ошибку, но, проанализировав нашу работу, не видно, что мы допустили ошибку.
 Выполнение этого дает,
Выполнение этого дает, В этих случаях мы обычно записываем решение следующим образом:
В этих случаях мы обычно записываем решение следующим образом:




 Наш онлайн-калькулятор определителей матриц использует все эти формулы для точных вычислений определителей. Просто вы можете использовать наш онлайн-математический калькулятор, который поможет вам легко выполнять различные математические операции за короткий промежуток времени.
Наш онлайн-калькулятор определителей матриц использует все эти формулы для точных вычислений определителей. Просто вы можете использовать наш онлайн-математический калькулятор, который поможет вам легко выполнять различные математические операции за короткий промежуток времени. Кроме того, в нем есть поля для создания матрицы и очистки матрицы, он автоматически сгенерирует матрицу и очистит все значения из матрицы соответственно.
Кроме того, в нем есть поля для создания матрицы и очистки матрицы, он автоматически сгенерирует матрицу и очистит все значения из матрицы соответственно.
 д. Когда дело доходит до решения определителя для матрицы более высокого порядка, это очень сложная задача. Просто попробуйте этот онлайн-калькулятор определителя, который позволяет вам найти определитель матриц с помощью различных методов расчета с полным расчетом. Как правило, студенты и профессионалы используют этот калькулятор определителя матрицы для решения своих математических задач.
д. Когда дело доходит до решения определителя для матрицы более высокого порядка, это очень сложная задача. Просто попробуйте этот онлайн-калькулятор определителя, который позволяет вам найти определитель матриц с помощью различных методов расчета с полным расчетом. Как правило, студенты и профессионалы используют этот калькулятор определителя матрицы для решения своих математических задач.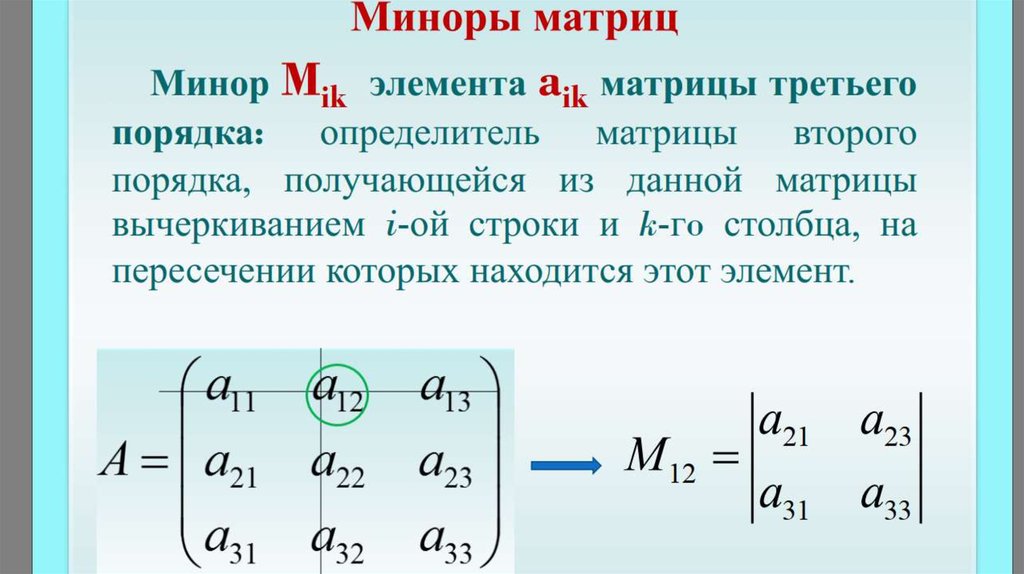 Калькулятор вычисляет определитель для матриц размерности от 1 × 1 до 9 × 9
Калькулятор вычисляет определитель для матриц размерности от 1 × 1 до 9 × 9


 Онлайн калькулятор расстояния между точками
Онлайн калькулятор расстояния между точками Найди правильный ответ.
Найди правильный ответ. Калькулятор вычисления силы, массы и ускорения.
Калькулятор вычисления силы, массы и ускорения. Для плоского, цилиндрического и сферического конденсаторов
Для плоского, цилиндрического и сферического конденсаторов Он также может вычислять матричные произведения, ранг, недействительность, сокращение строк, диагонализацию, собственные значения, собственные векторы и многое другое.
Он также может вычислять матричные произведения, ранг, недействительность, сокращение строк, диагонализацию, собственные значения, собственные векторы и многое другое.
 Некоторые полезные методы разложения включают QR, LU и разложение Холецкого. Для более сложных матриц для вычисления определителя необходимо использовать формулу Лапласа (разложение кофакторов), исключение Гаусса или другие алгоритмы.
Некоторые полезные методы разложения включают QR, LU и разложение Холецкого. Для более сложных матриц для вычисления определителя необходимо использовать формулу Лапласа (разложение кофакторов), исключение Гаусса или другие алгоритмы.



 Отсюда следует:
Отсюда следует:
 ru
ru ru
ru 5.3: Формулы тройного угла и линейные комбинации
5.3: Формулы тройного угла и линейные комбинации {\circ} \). 9{2/3}}{8}\right) \\ &=\dfrac{3\sqrt{2} −2\sqrt{2} }{2} \\ &=\dfrac{\sqrt{2}} }{ 2} \end{aligned}\)
{\circ} \). 9{2/3}}{8}\right) \\ &=\dfrac{3\sqrt{2} −2\sqrt{2} }{2} \\ &=\dfrac{\sqrt{2}} }{ 2} \end{aligned}\)
 2\theta}\).
2\theta}\). ck12.org/c/trigonometry
ck12.org/c/trigonometry
 Э.
Э. Cos-функции выводятся таким же образом. Шаблон остается верным, если заменить sin на cos.
Cos-функции выводятся таким же образом. Шаблон остается верным, если заменить sin на cos.
 Один из обычно используемых методов — который мы сделали здесь — это правило подстановки с тригонометрической функцией, а затем упрощение результата с помощью простого разбиения.
Один из обычно используемых методов — который мы сделали здесь — это правило подстановки с тригонометрической функцией, а затем упрощение результата с помощью простого разбиения.
 Пожалуйста, смотрите полный список ниже.
Пожалуйста, смотрите полный список ниже.
 Adobe создала этот формат в конце 90-х годов, и он стал основным продуктом обмена документами в Интернете. PDF-файлы почти всегда содержат текст, но они также могут содержать диаграммы, изображения и гиперссылки.
Adobe создала этот формат в конце 90-х годов, и он стал основным продуктом обмена документами в Интернете. PDF-файлы почти всегда содержат текст, но они также могут содержать диаграммы, изображения и гиперссылки. д., у вас могут возникнуть проблемы с передачей его другим пользователям или его загрузкой в приложения и на веб-сайты. Преобразовывая этот файл в PDF, вы снимаете эти ограничения, поскольку большинство людей знают, что такое PDF, и знают, как открыть его на всех своих устройствах.
д., у вас могут возникнуть проблемы с передачей его другим пользователям или его загрузкой в приложения и на веб-сайты. Преобразовывая этот файл в PDF, вы снимаете эти ограничения, поскольку большинство людей знают, что такое PDF, и знают, как открыть его на всех своих устройствах.
 pitt.edu/. Вы, как автор, несете ответственность за полную проверку PDF-документа на предмет точности преобразования и соблюдение требований к электронной версии. Подробную информацию о требованиях к PDF см. в Руководстве по форматированию ETD.
pitt.edu/. Вы, как автор, несете ответственность за полную проверку PDF-документа на предмет точности преобразования и соблюдение требований к электронной версии. Подробную информацию о требованиях к PDF см. в Руководстве по форматированию ETD. technology.pitt.edu/software/student). Следует отметить, что версии Word для Mac не полностью интегрируют функции PDFMaker, и вам может потребоваться найти компьютер для окончательного преобразования.
technology.pitt.edu/software/student). Следует отметить, что версии Word для Mac не полностью интегрируют функции PDFMaker, и вам может потребоваться найти компьютер для окончательного преобразования. 

 Выберите вкладку Acrobat и нажмите кнопку «Настройки» (второй вариант на ленте Acrobat). Появится диалоговое окно Acrobat PDFMaker. Просмотрите каждую вкладку; Настройки, Безопасность, Word и Закладки. (Если вы не видите вкладку Acrobat, не выполняйте простое преобразование в PDF с помощью преобразования Microsoft Word. Вам потребуется загрузить Acrobat.)
Выберите вкладку Acrobat и нажмите кнопку «Настройки» (второй вариант на ленте Acrobat). Появится диалоговое окно Acrobat PDFMaker. Просмотрите каждую вкладку; Настройки, Безопасность, Word и Закладки. (Если вы не видите вкладку Acrobat, не выполняйте простое преобразование в PDF с помощью преобразования Microsoft Word. Вам потребуется загрузить Acrobat.) Многие элементы обработки текста, такие как сноски, концевые сноски и гиперссылки, должны быть сохранены при преобразовании в PDF, если эти параметры выбраны на вкладке Word.
Многие элементы обработки текста, такие как сноски, концевые сноски и гиперссылки, должны быть сохранены при преобразовании в PDF, если эти параметры выбраны на вкладке Word.
 Вы также можете использовать меню «Пуск», «Все программы», чтобы найти приложение Adobe Acrobat или Reader, а затем открыть файл PDF с помощью кнопки «Открыть» на панели инструментов.
Вы также можете использовать меню «Пуск», «Все программы», чтобы найти приложение Adobe Acrobat или Reader, а затем открыть файл PDF с помощью кнопки «Открыть» на панели инструментов. Лучше использовать подчеркивание ( _ ) на случай, если при загрузке возникнут проблемы с файловой системой.
Лучше использовать подчеркивание ( _ ) на случай, если при загрузке возникнут проблемы с файловой системой. е. фотографические изображения, графические объекты, диаграммы) может отображаться в ETD как цветная, так и черно-белая. Тем не менее, черно-белые или заштрихованные объекты могут лучше всего отображаться в процессе микрофильмирования для архивирования диссертаций. Перекрестную штриховку можно использовать для различения цветов внутри объекта (например, графика Excel), если объект не является полноцветным. Если используется черно-белая графика, при желании в файле PDF можно установить ссылку на цветную копию. Обратитесь к Руководству по форматированию ETD для получения подробной информации о графике в ETD.
е. фотографические изображения, графические объекты, диаграммы) может отображаться в ETD как цветная, так и черно-белая. Тем не менее, черно-белые или заштрихованные объекты могут лучше всего отображаться в процессе микрофильмирования для архивирования диссертаций. Перекрестную штриховку можно использовать для различения цветов внутри объекта (например, графика Excel), если объект не является полноцветным. Если используется черно-белая графика, при желании в файле PDF можно установить ссылку на цветную копию. Обратитесь к Руководству по форматированию ETD для получения подробной информации о графике в ETD.


 д., и любую допустимую операцию с дробями, показывая все шаги. Вам необходимо предоставить правильное выражение с дробями. Это может быть что-то простое, как «1/2 + 1/3», или что-то более сложное, как ‘(1/3+1/4)(1/5+1/6)’.
д., и любую допустимую операцию с дробями, показывая все шаги. Вам необходимо предоставить правильное выражение с дробями. Это может быть что-то простое, как «1/2 + 1/3», или что-то более сложное, как ‘(1/3+1/4)(1/5+1/6)’.
 Обычно нужно начинать с нахождения общего знаменателя, но часто для сложения дробей используется следующая формула:
Обычно нужно начинать с нахождения общего знаменателя, но часто для сложения дробей используется следующая формула:


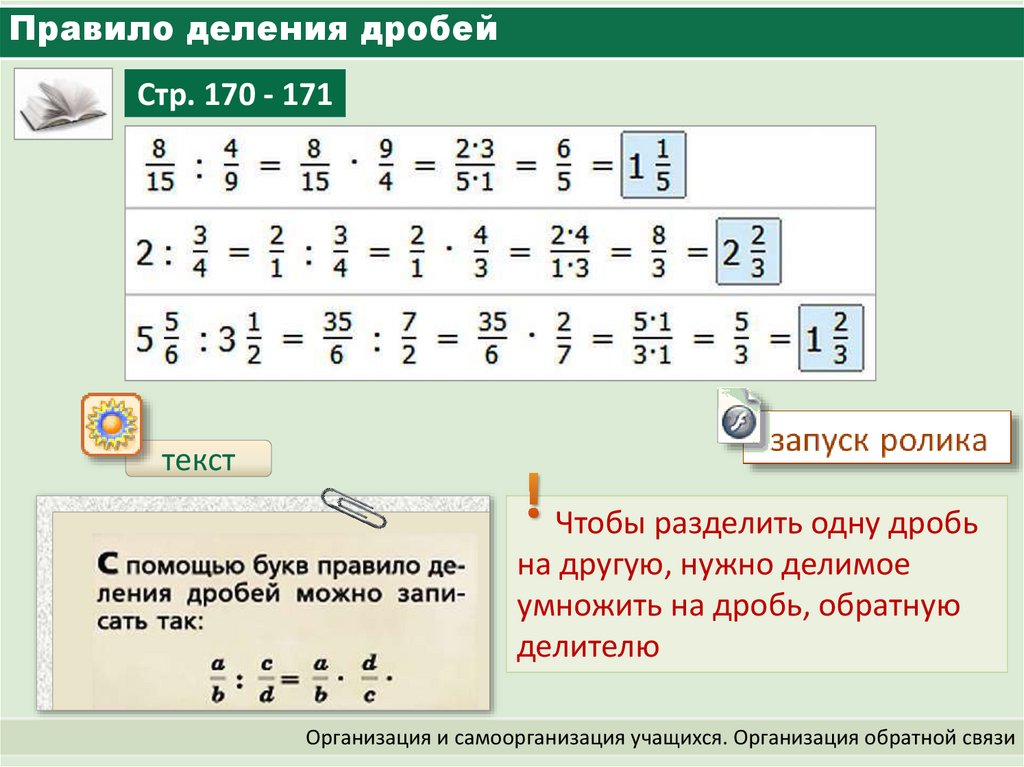

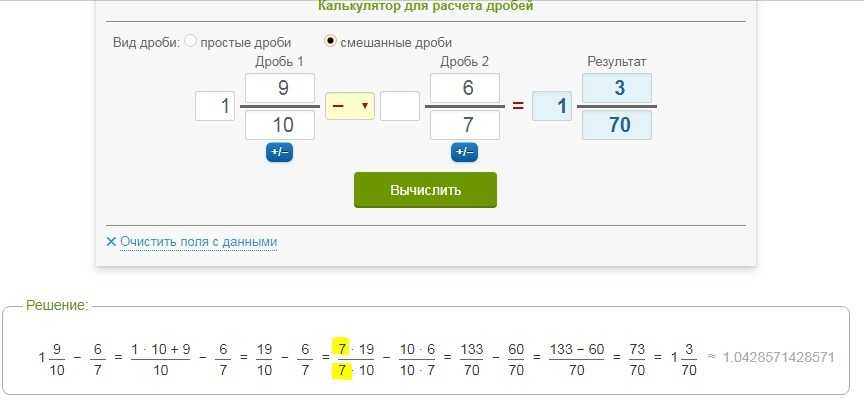
 В более элементарных условиях смешанные числа рассматриваются как важные объекты, в то время как в более продвинутых условиях смешанные числа просто представляются в их дробной нотации.
В более элементарных условиях смешанные числа рассматриваются как важные объекты, в то время как в более продвинутых условиях смешанные числа просто представляются в их дробной нотации.
 Пример отрицательной смешанной дроби: -5 1/2 .
Пример отрицательной смешанной дроби: -5 1/2 .  Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций: 
 4 { \left( { 6-\frac { 3 } { 2 } y }\right)ydy } = 5(48-32) = 80$
4 { \left( { 6-\frac { 3 } { 2 } y }\right)ydy } = 5(48-32) = 80$ 2-\frac { 250 } { 3 } x+178 }\right)dx= } } \\=\frac { 1 } { 4 } \left( { 644-1500+1068 }\right)=\frac { 212 } { 4 } =53$
2-\frac { 250 } { 3 } x+178 }\right)dx= } } \\=\frac { 1 } { 4 } \left( { 644-1500+1068 }\right)=\frac { 212 } { 4 } =53$ Теорема о представлении в виде СКНФ. Построение СКНФ по таблице
Теорема о представлении в виде СКНФ. Построение СКНФ по таблице Процесс вычисления определенного интеграла может быть утомительным и трудоемким, но калькулятор определенного интеграла делает этот процесс быстрым и легким.
Процесс вычисления определенного интеграла может быть утомительным и трудоемким, но калькулятор определенного интеграла делает этот процесс быстрым и легким.
 Точность аппроксимации можно повысить, увеличив количество подинтервалов, но это также может увеличить вычислительную сложность расчета.
Точность аппроксимации можно повысить, увеличив количество подинтервалов, но это также может увеличить вычислительную сложность расчета. Независимо от того, работаете ли вы над академическим заданием, проводите научные исследования или выполняете инженерные расчеты, калькулятор определенного интеграла поможет вам сэкономить время и избежать ошибок в расчетах.
Независимо от того, работаете ли вы над академическим заданием, проводите научные исследования или выполняете инженерные расчеты, калькулятор определенного интеграла поможет вам сэкономить время и избежать ошибок в расчетах.
 Затем нажмите кнопку рассчитать, и калькулятор покажет вам результаты расчета.
Затем нажмите кнопку рассчитать, и калькулятор покажет вам результаты расчета.
 14159..
14159.. 1) 24. 2).
1) 24. 2). 6. 7. 8. 9. Добавить или вычесть. 30. Активность стены; 31. Задание:
6. 7. 8. 9. Добавить или вычесть. 30. Активность стены; 31. Задание: it
it 2
2 Квадраты и квадратные корни
>
Упражнение 6.3
>
Вопрос 8
Квадраты и квадратные корни
>
Упражнение 6.3
>
Вопрос 8 ..
..