d°m′s″ Конвертер угловой меры, Общеупотребительные единицы
d°m′s″ — Градусы, минуты, секунды. Конвертер величин. / Конвертер угловой меры, Общеупотребительные единицыEN ES PT RU FR
Ой… Javascript не найден.
Увы, в вашем браузере отключен или не поддерживается JavaScript.
К сожалению, без JavaScript этот сайт работать не сможет. Проверьте настройки браузера, может быть JavaScript выключен случайно?
d°m′s″ — Градусы, минуты, секунды. Конвертер и таблица перевода величины.
Всё очень просто: Нужна помощь? x Этот конвертер величин очень простой. Правда.
|
| ||||||||||
?Настройки конвертера:
x
Объяснение настроек конвертера
Кстати, пользоваться настройками не обязательно. Вам вполне могут подойти настройки по умолчанию.
Количество значащих цифр
Для бытовых целей обычно не нужна высокая точность, удобнее получить округлённый результат. В таких случаях выберите 3 или 4 значащих цифры. Максимальная точность — 9 значащих цифр. Точность можно изменить в любой момент.
Разделитель групп разрядов
Выберите, в каком виде вам будет удобно получить результат:
1234567. 89 89 | нет |
|---|---|
| 1 234 567.89 | пробел |
| 1,234,567.89 | запятая |
| 1.234.567,89 | точка |
- Значащих цифр: 1 23456789
- Разделитель разрядов: нет пробел запятая точка
Укажите значение (градусы, минуты, секунды, d°m′s″):
» открыть »
» свернуть »
Общеупотребительные единицы
Чтобы ввести комбинированную единицу градусы, минуты, секунды, вы можете набрать * или o вместо символа градуса °.
| градусы, минуты, секунды → окружность (circle) | |
| градусы, минуты, секунды → секстант | |
| градусы, минуты, секунды → радиан (rad) | |
| градусы, минуты, секунды → градус (deg) | |
| градусы, минуты, секунды → град (grad) | |
| градусы, минуты, секунды → минута (′) | |
| градусы, минуты, секунды → секунда (″) |
Единицы: окружность (circle) / секстант / радиан (rad) / градус (deg) / / град (grad) / минута (′) / секунда (″)
» открыть »
» свернуть »
Единицы уклона
Уклон в процентах часто используют для обозначения уклона дорог или строительных объектов.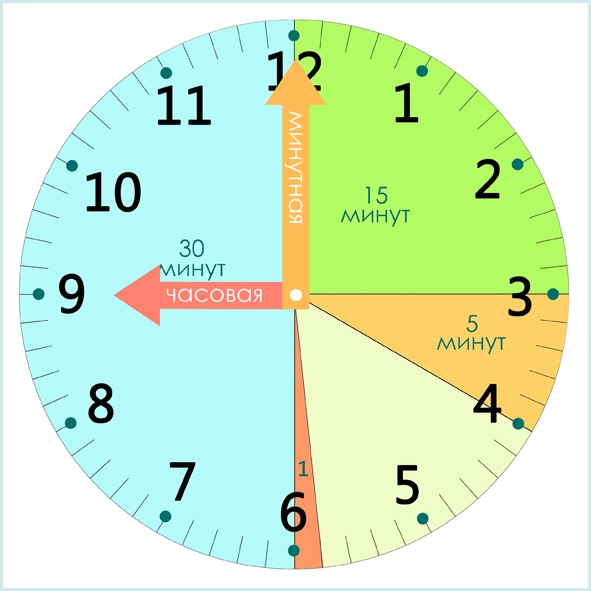 Нулевой уклон означает горизонтальную поверхность. Уклон в 100% означает подъём на 1 метр на каждый метр расстояния, т.е. угол наклона 45 градусов. Вертикальная линия имеет бесконечное значение уклона.
Нулевой уклон означает горизонтальную поверхность. Уклон в 100% означает подъём на 1 метр на каждый метр расстояния, т.е. угол наклона 45 градусов. Вертикальная линия имеет бесконечное значение уклона.
| градусы, минуты, секунды → уклон в процентах (%) | |
| градусы, минуты, секунды → уклон в промилле (‰) |
Единицы: уклон в процентах (%) / уклон в промилле (‰)
» открыть »
» свернуть »
Морские единицы
| градусы, минуты, секунды → румб |
Единицы: румб
» открыть »
» свернуть »
Артиллерийские единицы
Эти шкалы используются в артиллерийских прицелах и некоторых военных приборах. Происхождение названия ‘тысячная’ связано с тем, что величина близка к 1/1000 радиана.
| градусы, минуты, секунды → Русская тысячная | |
| градусы, минуты, секунды → Немецкая тысячная | |
| градусы, минуты, секунды → Угловой мил | |
| градусы, минуты, секунды → Шведская тысячная |
Единицы: Русская тысячная / Немецкая тысячная / Угловой мил / Шведская тысячная
Не можете найти нужную единицу?
Попробуйте поискать:
Другие варианты:
Посмотрите алфавитный список всех единиц
Задайте вопрос на нашей странице в facebook
< Вернитесь к списку всех конвертеров
Надеемся, Вы смогли перевести все ваши величины,
и Вам у нас на Convert-me. Com понравилось. Приходите снова!
Com понравилось. Приходите снова!
!
Значение единицы приблизительное.
Либо точного значения нет,
либо оно неизвестно. ?
Пожалуйста, введите число. (?)
Простите, неизвестное вещество. Пожалуйста, выберите что-то из списка. ***
Нужно выбрать вещество.
От этого зависит результат.
Совет: Не можете найти нужную единицу? Попробуйте поиск по сайту. Поле для поиска в верхней части страницы.
Нашли ошибку? Хотите предложить дополнительные величины? Свяжитесь с нами в Facebook.
Действительно ли наш сайт существует с 1996 года? Да, это так. Первая версия онлайнового конвертера была сделана ещё в 1995, но тогда ещё не было языка JavaScript, поэтому все вычисления делались на сервере — это было медленно. А в 1996г была запущена первая версия сайта с мгновенными вычислениями.
Для экономии места блоки единиц могут отображаться в свёрнутом виде. Кликните по заголовку любого блока, чтобы свернуть или развернуть его.
Слишком много единиц на странице? Сложно ориентироваться? Можно свернуть блок единиц — просто кликните по его заголовку. Второй клик развернёт блок обратно.
Наша цель — сделать перевод величин как можно более простой задачей. Есть идеи, как сделать наш сайт ещё удобнее? Поделитесь!
? Пожалуйста, введите градусы, минуты и секунды, например 5°10’5″
Минуточку, загружаем коэффициенты…
Градус, минута, секунда | это… Что такое Градус, минута, секунда?
Толкование
- Градус, минута, секунда
Градус, минута, секунда — общепринятые единицы измерения плоских углов и земного шара.
Содержание
- 1 Градус
- 2 Минуты и секунды
- 3 Угловая секунда
- 3.1 Использование
- 3.
 2 Дольные единицы
2 Дольные единицы
- 4 Примечания
- 5 Литература
- 6 См. также
Градус
Градус (от лат. gradus — деление шкалы, шаг, ступень) обозначается °. Один оборот равен 360°. В прямом углу, таким образом, 90°, в развёрнутом — 180°.
Деление окружности на 360° придумали аккады (вавилоняне) — соответственно делению года в вавилонском календаре на 360 дней.
- 1° = радиан ≈ 0,017453293 радиан
- 1° = оборота ≈ 0,002777 оборота
- 1° = градов ≈ 1,111111 градов
Минуты и секунды
В измерении углов традиционно используется шестидесятеричная система счисления. По аналогии с делением часа как интервала времени градус делят на 60 минут (′), а минуту — на 60 секунд (″).
- 1′ = ≈ 2,9088821×10-4 радиан.
- 1″ = ≈ 4,8481368×10-6 радиан.
Угловая секунда
Одна угловая секунда примерно соответствует углу, под которым виден футбольный мяч с расстояния около 45 километров.

Углова́я секу́нда (англ. arcsecond, arc second, as, second of arc; синонимы: дуговая секунда, секунда дуги[1]) — внесистемная астрономическая единица измерения малых углов, тождественная секунде плоского угла[2].
Использование
Угловая секунда (обозначается ″) используется в астрономии при измерении плоских углов в градусных мерах. При измерении углов в часовых мерах (в частности, для определения прямого восхождения) используется единица измерения «секунда» (обозначается с). Соотношение между этими величинами определяется формулой 1c = 15″.[3]
Иногда угловую секунду (и производные от неё дольные единицы) ошибочно называют арксекундой[1][4], что является простой транслитерацией с англ. arcsecond.
Дольные единицы
По аналогии с международной системой единиц (СИ), наряду с угловой секундой применяются и её дольные единицы измерения: миллисекунды (англ.
 milliarcseconds, mas), микросекунды (англ. microarcseconds, µas) и пикосекунды (англ. picoarcseconds, pas). Они не входят в СИ (СИ рекомендует миллирадианы и микрорадианы), но допускаются к применению[2]. Однако, согласно ГОСТ 8.417-2002, наименование и обозначения единиц плоского угла (градус, минута, секунда) не допускается применять с приставками[5], в связи с чем такие дольные величины должны приводиться либо к единицам СИ (миллирадианам и т.п.), либо к угловым секундам, либо обозначаться исходными единицами (mas, µas и pas соответственно).
milliarcseconds, mas), микросекунды (англ. microarcseconds, µas) и пикосекунды (англ. picoarcseconds, pas). Они не входят в СИ (СИ рекомендует миллирадианы и микрорадианы), но допускаются к применению[2]. Однако, согласно ГОСТ 8.417-2002, наименование и обозначения единиц плоского угла (градус, минута, секунда) не допускается применять с приставками[5], в связи с чем такие дольные величины должны приводиться либо к единицам СИ (миллирадианам и т.п.), либо к угловым секундам, либо обозначаться исходными единицами (mas, µas и pas соответственно).Дольные единицы могут использоваться для обозначения собственного движения звёзд и галактик, годичного параллакса и углового диаметра звёзд.[6]
Для наблюдения астрономических объектов под такими сверхмалыми углами астрономы прибегают к методу интерферометрии, при котором сигналы, принимаемые несколькими разнесёнными радиотелескопами, комбинируются в процессе апертурного синтеза.
 Так, используя методику интерферометрии со сверхдлинной базой (VLBI), астрономы получили возможность измерить собственное движение галактики Треугольника.
Так, используя методику интерферометрии со сверхдлинной базой (VLBI), астрономы получили возможность измерить собственное движение галактики Треугольника.В видимом свете существенно труднее достичь миллисекундного разрешения. Тем не менее, спутник Hipparcos справился с этой задачей в процессе астрометрических измерений, по результатам которых были составлены наиболее точные (по состоянию на 1997 год) каталоги звёзд Tycho (TYC) и Hipparcos (HIP).[7][8]
Примечания
- ↑ 1 2 Англо-русско-английский астрономический словарь. Astronet. Проверено 23 декабря 2007.
- ↑ 1 2 Non-SI units accepted for use with the International System of Units (англ.). SI brochure (8th ed.). Bureau International des Poids et Mesures. — Описание СИ на сайте Международного бюро мер и весов. Проверено 23 декабря 2007.
- ↑ Справочник.
 Некоторые внесистемные единицы. ASTROLAB. Проверено 23 декабря 2007.
Некоторые внесистемные единицы. ASTROLAB. Проверено 23 декабря 2007. - ↑ Glossary entry for English term «arcsecond» (англ.). Справочник по услугам профессионального перевода, предоставляемым независимыми переводчиками и бюро перевода. ProZ.com. Проверено 23 декабря 2007.
- ↑ ГОСТ 8.417-2002. Единицы величин. Введён в действие с 1 сентября 2003 г. // Информационная система по оборудованию «Прибор.Инфо» : справочник. — 2003.
- ↑ Источник: статья Minute of arc в en-wiki.
- ↑ Гурьянов С. Почему звезды называются именно так?. проект «Астрогалактика» (29 октября 2005 года). Проверено 26 декабря 2007.
- ↑ Цветков А. С. Общие сведения о проекте Hipparcos // Руководство по практической работе с каталогом Hipparcos. — СПб.: АИ СПбГУ.
Литература
- Гельфанд И. М., Львовский С. М., Тоом А. Л. Малые углы // Тригонометрия.
 — М.: МЦНМО, 2002. — 199 с. — ISBN 5-94057-050-X
— М.: МЦНМО, 2002. — 199 с. — ISBN 5-94057-050-X
См. также
- Град, минута, секунда
- Оборот
- Радиан
Wikimedia Foundation. 2010.
Игры ⚽ Нужен реферат?
- Градско (община Градско)
- Градус цельсия
Полезное
Символы единиц измерения
Если у вас есть современный компьютер и быстрое подключение к Интернету, это сообщение вскоре должно быть заменено веб-страницей, которую вы хотите просмотреть. Если это сообщение отображается в течение длительного периода времени, это может быть связано со следующими причинами:
Символы единиц СИ представляют собой сокращенные версии полного названия единицы измерения. Существуют строгие правила в отношении написания, использования заглавных букв, пунктуация, шрифт и стиль шрифта для символов.
Символы единиц СИ обычно являются сокращенными версиями названия единицы измерения. Например,
основные единицы секунд, метров, килограммов, ампер, кельвинов, молей и кандел имеют
символы единиц с, м, кг, А, К, моль и
CD.
Например,
основные единицы секунд, метров, килограммов, ампер, кельвинов, молей и кандел имеют
символы единиц с, м, кг, А, К, моль и
CD.
Названия юнитов могут быть расширены путем добавления префикса, указывающего степень десяти. Пока базовой единицей длины является метр, также можно использовать единицы измерения километры, мегаметры, сантиметры, миллиметров и др. Они имеют символы единиц км, мм, см и мм.
Некоторые символы единиц СИ представляют собой один символ, например с, символ секунд.
Некоторые символы единиц СИ состоят из нескольких символов, например моль, символ родинок, и км на километры.
Пробелы появляются в некоторых символах единиц измерения, таких как «Н·м», символ ньютон-метров.
Ограниченное количество математических символов может отображаться в символах единиц измерения. Например
м 2 — условное обозначение квадратных метров,
км/ч» — это обозначение километров в час,
и
${\rm{nV/}}\sqrt {{\rm{Гц}}} $ — единица
используется для описания интенсивности случайного шума.
Символы единиц СИ аналогичны, но отличаются от аббревиатуры, инициализмы и акронимы. Поскольку все эти могут появляться в технических и научных документах, они кратко изложены ниже.
Руководства по стилю обычно позволяют сокращать документы на замена общеизвестных слов и фраз несколькими символами, известна как аббревиатура. Например, латинская фраза «и так далее» обычно появляется как и т. д., в то время как термин «против» заменяется на «в.» или «против». Аббревиатуры иногда применяется к единицам СИ, с сек. замена секунд и темп. использовал вместо температуры.
При чтении текста вслух сокращения обычно преобразуются вернуться к полному слову. Если табличка на чьем-то столе показывает Доктор Нет, мы приветствуем человека как доктор Нет. Мы не пытаемся произнести аббревиатуру как двухсимвольное слово dr, и мы не прочитать отдельные буквы ди-а.
Хотя символы единиц СИ не являются аббревиатурами, они читаются одинаково
как сокращения. Когда мы видим символ Па
мы произносим слово паскаль, а не буквы горо-ай или
неофициальный термин для человека, который породил нас, наш папа.
Как правило, следует избегать сокращения названий единиц СИ. Используйте полное название единицы СИ, например секунды и килограммы, или используйте символы единиц измерения, такие как песок кг. Не используйте сокращения, такие как сек. за секунду и килограмм за килограмм.
| Приемлемо? | Примеры сокращений |
|---|---|
| № | Карточный домик рухнул, когда выпало 20 на него упал килограммовый груз. |
| Да | Карточный домик рухнул, когда выпало 20 килограммовая масса упала на него. |
| Да | Карточный домик рухнул, когда выпало 20. на него упала масса кг. |
Многие сокращения имеют точку как неотъемлемую часть выражения. Аббревиатура и т. д. всегда имеет точку в конце, даже если она стоит в середине предложения. Напротив, точка никогда не используется в символе единицы СИ, если только символ появляется в конце предложения.
| Приемлемо? | Пунктуация с символами единиц |
|---|---|
| Да | Карточный домик рухнул, когда
20
кг
на него упала масса. |
| № | Карточный домик рухнул, когда 20 кг. на него упала масса. |
| Да | Тяжело, похоже 20 кг. |
Когда группа слов заменяется набором (обычно) их первого буквы, это известно как инициализм. Условия RSVP, PS, QED, CEO, UK, UN, FBI и SI — все инициализмы. При чтении вслух мы обычно произносим каждое отдельное слово письмо, как будто нас просят произнести его по буквам. Например, мы произносим SI как ess-eye. Мы не пытаемся произнесите это как двухбуквенное испанское слово, означающее «да», и мы не заменяем его именем, которое оно представляет — Международная система единиц.
В нетехнической связи некоторые названия единиц заменяются на
инициализмы. Это особенно часто встречается, когда слово «за» является частью
имени подразделения. Километры в час часто выражаются в км/ч,
мили в час как mph, а частей на миллион как ppm. В качестве примечания, SI
система не позволяет даже прописанные названия миль в час и частей
за миллион, который будет использован.
В технических и научных сообщениях не используйте инициализм названий единиц СИ. Допускаются инициализмы других фраз, но не для названий единиц СИ.
| Приемлемо? | Пример использования инициализма |
|---|---|
| Да | Десять самых популярных автомобилей, продаваемых в США имеют среднюю максимальную скорость 200 километров в час. |
| Да | Десять самых популярных автомобилей, продаваемых в США, имеют среднюю максимальную скорость 200 км/ч. |
| № | Десять самых популярных автомобилей, продаваемых в США, имеют среднюю максимальную скорость 200 км/ч. |
| № | Десять самых популярных автомобилей, продаваемых в США, имеют среднюю максимальную скорость 200 км/ч. |
Иногда список символов, представляющих фразу, произносится как слово. Например, NASA, NATO, AWOL, SWAT, NASDAQ, FIFO и LIFO — все они сокращения.
Правила использования заглавных букв и пунктуации в аббревиатурах часто неясны и со временем меняются. Они могут начинаться с заглавных букв, иногда разделенных точками.
Если название относится к организации, оно, как правило, сохраняет все заглавные буквы.
формат. Но если аббревиатура относится к приему или фразе, которые становятся общепринятыми
используется, то аббревиатура в конечном итоге повышается до статуса слова. Радар, сонар, акваланг,
Laser и snafu изначально были аббревиатурами, но сегодня считаются словами.
Они могут начинаться с заглавных букв, иногда разделенных точками.
Если название относится к организации, оно, как правило, сохраняет все заглавные буквы.
формат. Но если аббревиатура относится к приему или фразе, которые становятся общепринятыми
используется, то аббревиатура в конечном итоге повышается до статуса слова. Радар, сонар, акваланг,
Laser и snafu изначально были аббревиатурами, но сегодня считаются словами.
Иногда говорящий сам решает, нужно ли что-то говорить. рассматривается как аббревиатура, инициализм или акроним. Термин ASAP может произноситься как можно скорее, или да-эс-да-горох, или да-сок.
| Срок | Предпочтительный Символ единицы измерения | Приемлемый Символ единицы измерения | Не использовать как символ или в тексте |
|---|---|---|---|
| секунд (время) | с | сек. | |
| минут (время) | мин | мин. | |
| час | ч | час. | |
| секунд (время) | ▮″ | сек | |
| минута (угол) | ▮′ | мин | |
| градус (угол) | ▮° | град | |
| градусов Цельсия | ℃ | С | по Цельсию |
| метр в секунду | м/с | м/с, м/с | |
| килограмм | кг | кг | |
| километров в час | км/ч | км/ч, км/ч | |
| миль в час | Нет | миль в час, миль в час | |
| кубических сантиметров | см 3 | куб.см, куб.см. | |
| квадратных метров | м 2 | кв.м. | |
| Ом | Ом | Ом | Р |
| милли | м | млн. | |
| микро | мк | и | |
| часть на сотню | % | процентов | |
| тысячная часть | Нет | пт, ‰ | |
| часть на десять тысяч | Нет | ‱ | |
| частей на миллион | частей на миллион | ||
| частей на миллиард | Нет | частей на миллиард | |
| частей на триллион | Нет | стр.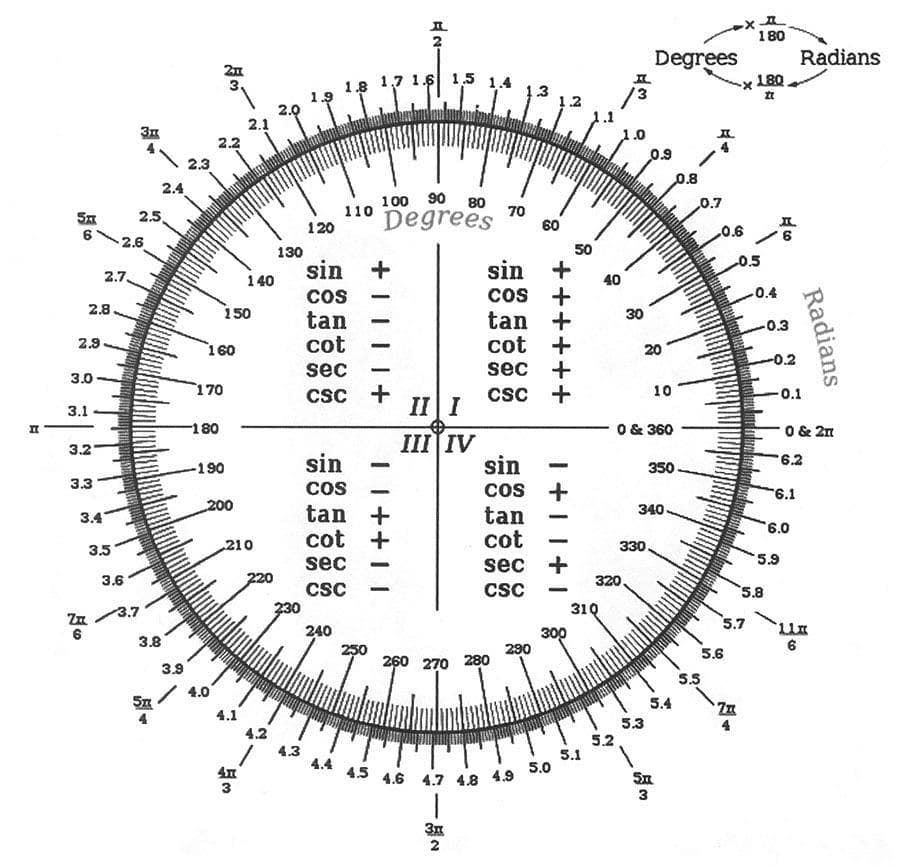 |
Если вы собираетесь создавать документы, содержащие символы SI, вам потребуется доступ как к прописным, так и к строчным буквам в Латинский и греческий алфавиты. Латинский алфавит это \[\начать{массив}{с} {\ rm {abcdefghijklmnopqrstuvwxyz}} \\ {\rm{ABCDEFGHIJKLMNOPQRSTUVWXYZ}} \конец{массив}\] и греческий алфавит \[\начать{массив}{с} \альфа\бета\гамма\дельта\варепсилон\дзета\эта\тета\йота\каппа\лямбда\мю\ню\ксио\пи\ро\сигма\тау\ипсилон\варфи\хи\пси\омега\\ {\ rm A} {\ rm B} \ Gamma \ Delta {\ rm E} {\ rm Z} {\ rm H} \ Theta {\ rm I} {\ rm K} \ Lambda {\ rm M} {\ rm N} \ Xi {\ rm O} \ Pi {\ rm P} \ Sigma {\ rm T} \ Upsilon \ Phi {\ rm X} \ Psi \ Omega \конец{массив}\]
Система СИ крайне требовательна к шрифту и стилю шрифта
для символов единиц.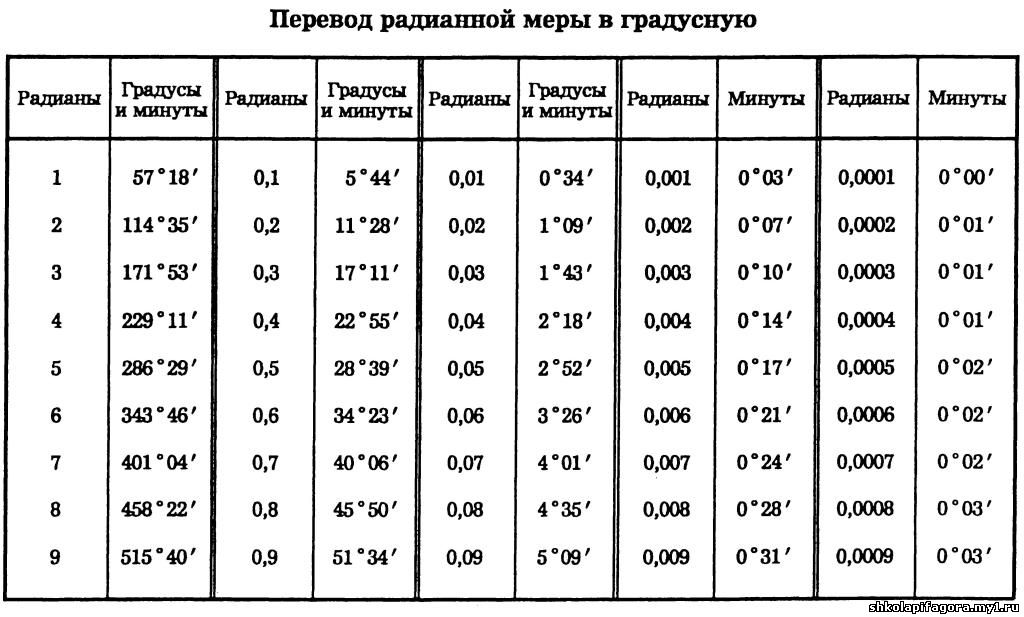 Все символы единиц СИ должны быть написаны латинскими буквами.
шрифт и обычный вес. Они никогда не могут быть написаны на
курсивный шрифт. Они никогда не могут быть написаны жирным шрифтом.
У них может никогда не быть индексов.
Они никогда не могут быть украшены полосами, штрихами, знаками ударения и т. д.
Все символы единиц СИ должны быть написаны латинскими буквами.
шрифт и обычный вес. Они никогда не могут быть написаны на
курсивный шрифт. Они никогда не могут быть написаны жирным шрифтом.
У них может никогда не быть индексов.
Они никогда не могут быть украшены полосами, штрихами, знаками ударения и т. д.
Правила, перечисленные выше, применяются каждый раз, когда символ единицы СИ появляется, даже если находится в предложении, окруженном текстом другой шрифт или стиль шрифта.
| Приемлемо? | Примеры шрифта символа единицы СИ и стиля шрифта |
|---|---|
| № | Несмотря на занос 80 м, водитель сказал:» я только ехал 50 км/ч офицер. » |
| Да | Несмотря на юз 80 м, водитель сказал: Я только собирался 50 км/ч офицер. » » |
Символы единиц СИ определяются с использованием заглавных букв. на каждом персонаже. Вы никогда не должны изменять эту заглавную букву, так как это может существенно изменить значение символа. Например, строчный символ s представляет собой базовую единицу времени, секунды — в то время как символ верхнего регистра S представляет собой базу единица электропроводности Сименс.
Некоторые заголовки пишутся заглавными буквами. Это допустимо иметь символ единицы СИ в таком названии, но он должен сохранить свой правильный регистр, даже если он в нижнем регистре.
Никогда не начинайте предложение с символа единицы СИ. Грамматическое правило которые требуют, чтобы первая буква предложения была заглавной, может быть несовместимым с правилами SI о капитализации.
| Приемлемо? | Примеры использования заглавных букв в символах единиц СИ |
|---|---|
| Да | Котел взорвался, когда давление достигло
100 МПа. . . |
| Да | ВЛИЯНИЕ ДАВЛЕНИЙ БОЛЕЕ 100 МПа В НЕАРМИРОВАННЫХ КОТЛАХ. |
| № | ВЛИЯНИЕ ДАВЛЕНИЙ СВЫШЕ 100 МПа В НЕАРМИРОВАННЫХ КОТЛАХ. |
Первый символ символа единицы СИ пишется с большой буквы только тогда, когда название подразделения чествует человека. Сюда входят единицы, соответствующие написание имени лауреата в ваттах, ньютонах и герцах. Это также включает такие единицы, как фарад и бел, где единица написана иначе, чем имя лауреата (в данном случае Фарадей и Белл).
Единственным исключением из правила предыдущего абзаца является литр. Он не назван в честь человека, поэтому изначально использовался символ нижнего регистра. л. Это можно легко спутать с цифрой один, 1. Из-за этого заглавный символ L теперь является приемлемым символом единицы для литров. Строчная версия по-прежнему считается приемлемой. символ, если вы предпочитаете использовать его.
Электрическая единица сопротивления, ом, названа в честь Георга Ома. Нахождение
разумный символ единицы сложен, как заглавная буква
О может быть трудно различить
от числительного для числа ноль, 0. Использование двух букв не так много
лучше, так как О может ошибаться
для английского слова, о. Есть два решения этой проблемы.
Наиболее распространенным является использование греческого алфавита для символа единицы,
используя заглавную букву омега,
Ом. Если
Греческий алфавит недоступен, тогда Ом
считается приемлемым символом единицы для ома. Обратите внимание на первую букву
полное имя — строчная буква «о», а первая буква символа — буква «о».
заглавная О.
Нахождение
разумный символ единицы сложен, как заглавная буква
О может быть трудно различить
от числительного для числа ноль, 0. Использование двух букв не так много
лучше, так как О может ошибаться
для английского слова, о. Есть два решения этой проблемы.
Наиболее распространенным является использование греческого алфавита для символа единицы,
используя заглавную букву омега,
Ом. Если
Греческий алфавит недоступен, тогда Ом
считается приемлемым символом единицы для ома. Обратите внимание на первую букву
полное имя — строчная буква «о», а первая буква символа — буква «о».
заглавная О.
Имя единицы измерения, например метр, может быть указано во множественном числе. символ единицы, такие как m, никогда не может быть сделано множественное число.
Помните, что s в нижнем регистре — это символ единицы СИ для секунд.
Добавление s в конец другого символа единицы измерения может сделать его похожим на
вы умножаете на время, или меняете саму единицу.
| Приемлемо? | Примеры множественного числа |
|---|---|
| Под вопросом | Таблица двойная метр длинный. |
| Да | Таблица двойная метров длинный. |
| Да | Таблица 2 м длинный. |
| № | Таблица 2 мс длинный. |
| № | Таблица 2 м длинный. |
Никогда не разрешается изменять символ единицы СИ с помощью добавление индекса. Вы можете определить символы количества SI с помощью индексов.
| Приемлемо? | Примеры символов и индексов единиц СИ |
|---|---|
| Да | Среднеквадратичное давление оказалось равным ${P_{{\rm{rms}}}} = 6\;{\rm{кПа}}$ . |
| № | Среднеквадратичное давление оказалось равным $P = 6\;{\rm{kP}}{{\rm{a}}_{{\rm{rms}}}}$ . |
| № | Среднеквадратичное давление оказалось равным ${P_{{\rm{rms}}}} = 6\;{\rm{kP}}{{\rm{a}}_{{\rm{rms}}}}$
. |
Между числом и символом единицы измерения должен быть один условный пробел. Не пропускайте этот пробел и не используйте для его заполнения дефис, точку, знак умножения или любой другой символ. Не допускайте перевода строки или разрыва страницы между числом и символом единицы измерения.
| Приемлемо? | Примеры символа единицы измерения Пробел |
|---|---|
| Да | Таблица 2 м длинный. |
| № | Таблица 2м длинный. |
| № | Таблица 2-м длинный. |
| № | Таблица 2‧м длинный. |
| № | Таблица 2×м длинный. |
| № | Стол 2 м длинный. |
Единицами можно управлять с помощью умножения, деления и возведения в степень
операции, но вообще не сложение, вычитание и другие математические
операции. Эти операции могут быть показаны с помощью символов, перечисленных ниже.
Эти операции могут быть показаны с помощью символов, перечисленных ниже.
Любой символ единицы может быть умножен на другой символ единицы. Эти умножение обычно изображается точкой в центре или обычной космос. Центрированная точка предпочтительнее, когда есть вероятность, что единицу можно спутать с другой единицей.
| Приемлемо? | Примеры символа единицы, умноженного на символ единицы |
|---|---|
| Да | Н·м или Н м |
| Под вопросом | Два метра-секунды 2 м с а две миллисекунды — это 2 мс. |
| Да | Два метра-секунды 2 м·с а две миллисекунды — это 2 мс. |
| № | Нм или Н-м или Н×м или Н*м |
| Да — Исключения из обычного правила | Втч, кВтч, ВА, кВА |
Любой символ единицы может быть разделен любым другим символом единицы. Есть
три способа показать это: с косой чертой (технически называемой солидусом),
с отрицательным показателем или со знаком горизонтального деления.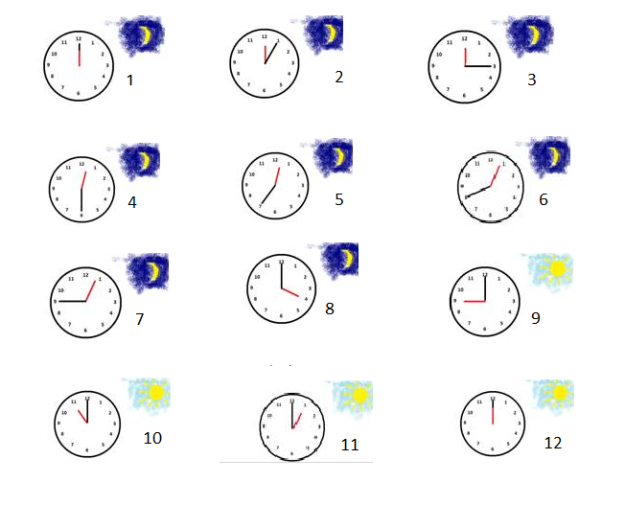 Эти
те же параметры доступны для символов количества и чисел.
Эти
те же параметры доступны для символов количества и чисел.
За косой чертой может следовать только один символ единицы измерения, если не используются круглые скобки чтобы смысл был ясен.
Слово per может использоваться с названиями единиц для обозначения деления, например, в километрах в час. Однако буква p не может использоваться для обозначения деления, как в kph.
| Приемлемо? | Примеры символа единицы, разделенного символом единицы |
|---|---|
| Да | м/с или Н·м -1 или $\frac{{\rm{m}}}{{\rm{s}}}$ или кг· м/с 2 или кг·м×с -2 или ${\rm{nV/}}\sqrt {{\rm{Гц}}} $ или кг/(с 2 · А) |
| № | Н÷м или кг/с 2 × A или кг/с 2 /А |
Допустимо возводить символы единиц в степени. Показатели могут
быть либо положительным, либо отрицательным.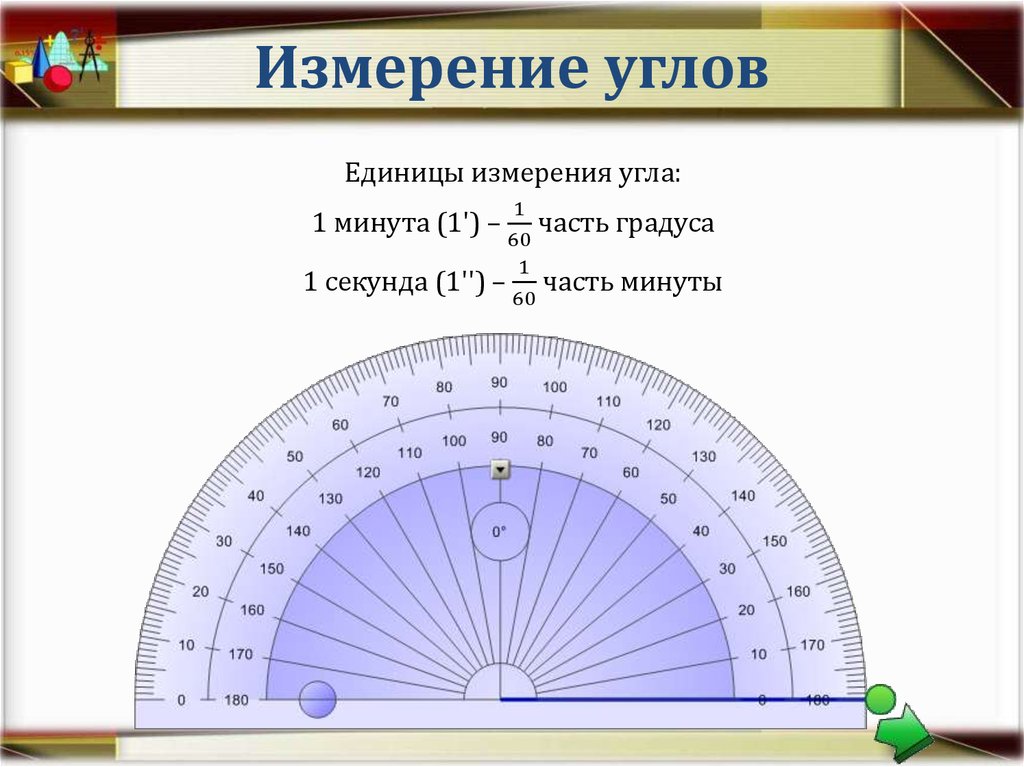 Хотя обычно это целые числа,
приложения, в которых имеет смысл говорить о нецелочисленных степенях. Экспоненты
нуля не используются, потому что это можно сделать, опустив единицу
символ целиком. Показатель степени +1 обычно не записывается, так как предполагается, что
ни один показатель степени не совпадает с показателем степени +1. Знаки плюс обычно
опущены в показателях, как они предполагаются.
Хотя обычно это целые числа,
приложения, в которых имеет смысл говорить о нецелочисленных степенях. Экспоненты
нуля не используются, потому что это можно сделать, опустив единицу
символ целиком. Показатель степени +1 обычно не записывается, так как предполагается, что
ни один показатель степени не совпадает с показателем степени +1. Знаки плюс обычно
опущены в показателях, как они предполагаются.
Никогда не помещайте имя устройства в то же выражение, что и символ устройства. Используйте либо все имена, либо все символы, а не их сочетание.
Слово «за» используется вместо «разделено на» в именах единиц измерения. Не используйте слово «за» с символами единиц измерения.
Названия единиц измерения могут использоваться без чисел, с числами, выраженными словами, или с числами, написанными цифрами.
Символы единиц измерения всегда должны иметь связанный с ними номер, и этот номер должен быть выражен цифрами (а не словами).
| Приемлемо? | Примеры названий блоков смешивания, символов блоков и математических символов |
|---|---|
| Возможно | Скорость самолета пятьсот километров в час. |
| Возможно | Скорость самолета 500 километров в час. |
| Да | Скорость самолета 500 км/ч. |
| № | Скорость самолета пятьсот км/ч. |
| № | Скорость самолета 500 км в час. |
| № | Скорость самолета 500 км в час. |
| № | Скорость самолета 500 км/час. |
| Да | Спидометр отображал скорость в километров в час. |
| № | Спидометр отображал скорость в км/ч. |
time — английское обозначение часов, минут и секунд
Задавать вопрос
спросил
Изменено 7 лет, 1 месяц назад
Просмотрено 288 тысяч раз
Я часто вижу английские обозначения времени с использованием символов "» и «" .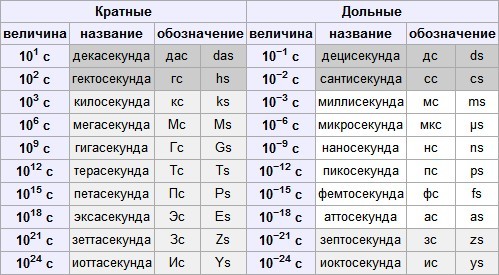 Я всегда ошибался насчет этих двух и даже их значения.
Я всегда ошибался насчет этих двух и даже их значения.
Я больше привык к «01:05:56», например.
Как представить часы, минуты и секунды с помощью апострофа и знаков препинания в кавычках? Что для часов, что для минут, а что для секунд?
Является ли обычным способом записи прошедшего времени? У них особое произношение?
- время
- символы
3
Это не особенно распространенный для выражения времени.
Аналогично градусам-минутам-секундам: вместо десятичных градусов (38,897212°, -77,036519°) пишется (38° 53′ 49,9632″, -77° 2′ 11,4678″). Оба произошли от шестидесятеричной системы счисления, подобной той, что была разработана в Древнем Вавилоне: одно простое число представляет первое шестидесятеричное деление, второе — следующее и так далее. Астрономы 17 века использовали третье деление 1/60 секунды.
Преимущество использования символов минут и секунд для обозначения времени состоит в том, что оно явно выражает продолжительность , а не время .

 Щёлкните по кнопке «Посчитать».
Щёлкните по кнопке «Посчитать». 2 Дольные единицы
2 Дольные единицы
 milliarcseconds, mas), микросекунды (англ. microarcseconds, µas) и пикосекунды (англ. picoarcseconds, pas). Они не входят в СИ (СИ рекомендует миллирадианы и микрорадианы), но допускаются к применению[2]. Однако, согласно ГОСТ 8.417-2002, наименование и обозначения единиц плоского угла (градус, минута, секунда) не допускается применять с приставками[5], в связи с чем такие дольные величины должны приводиться либо к единицам СИ (миллирадианам и т.п.), либо к угловым секундам, либо обозначаться исходными единицами (mas, µas и pas соответственно).
milliarcseconds, mas), микросекунды (англ. microarcseconds, µas) и пикосекунды (англ. picoarcseconds, pas). Они не входят в СИ (СИ рекомендует миллирадианы и микрорадианы), но допускаются к применению[2]. Однако, согласно ГОСТ 8.417-2002, наименование и обозначения единиц плоского угла (градус, минута, секунда) не допускается применять с приставками[5], в связи с чем такие дольные величины должны приводиться либо к единицам СИ (миллирадианам и т.п.), либо к угловым секундам, либо обозначаться исходными единицами (mas, µas и pas соответственно). Так, используя методику интерферометрии со сверхдлинной базой (VLBI), астрономы получили возможность измерить собственное движение галактики Треугольника.
Так, используя методику интерферометрии со сверхдлинной базой (VLBI), астрономы получили возможность измерить собственное движение галактики Треугольника. Некоторые внесистемные единицы. ASTROLAB. Проверено 23 декабря 2007.
Некоторые внесистемные единицы. ASTROLAB. Проверено 23 декабря 2007. — М.: МЦНМО, 2002. — 199 с. — ISBN 5-94057-050-X
— М.: МЦНМО, 2002. — 199 с. — ISBN 5-94057-050-X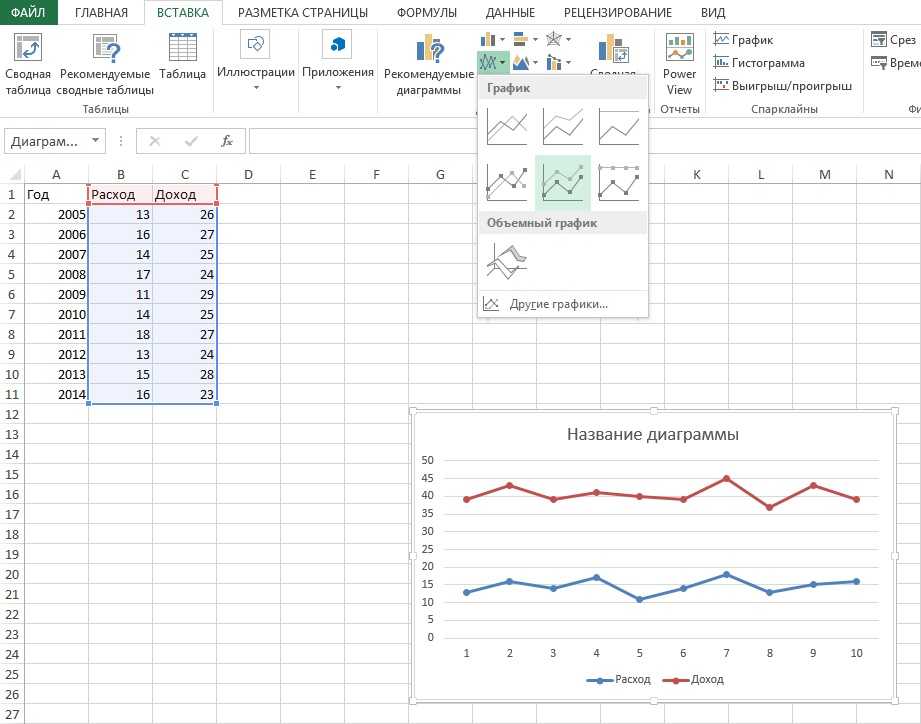 Вы получите ссылку для скачивания.
Вы получите ссылку для скачивания.
 .. можно мне не мешать…
.. можно мне не мешать…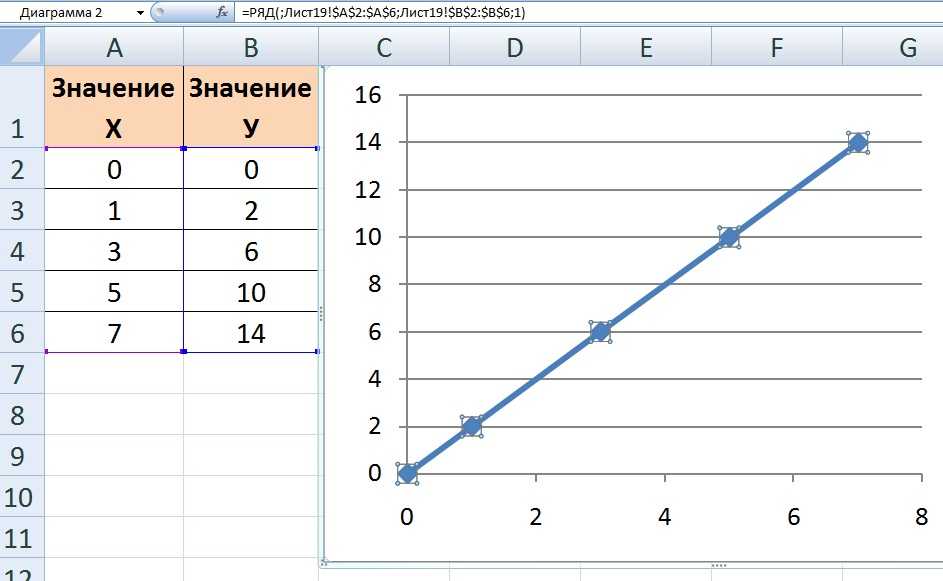


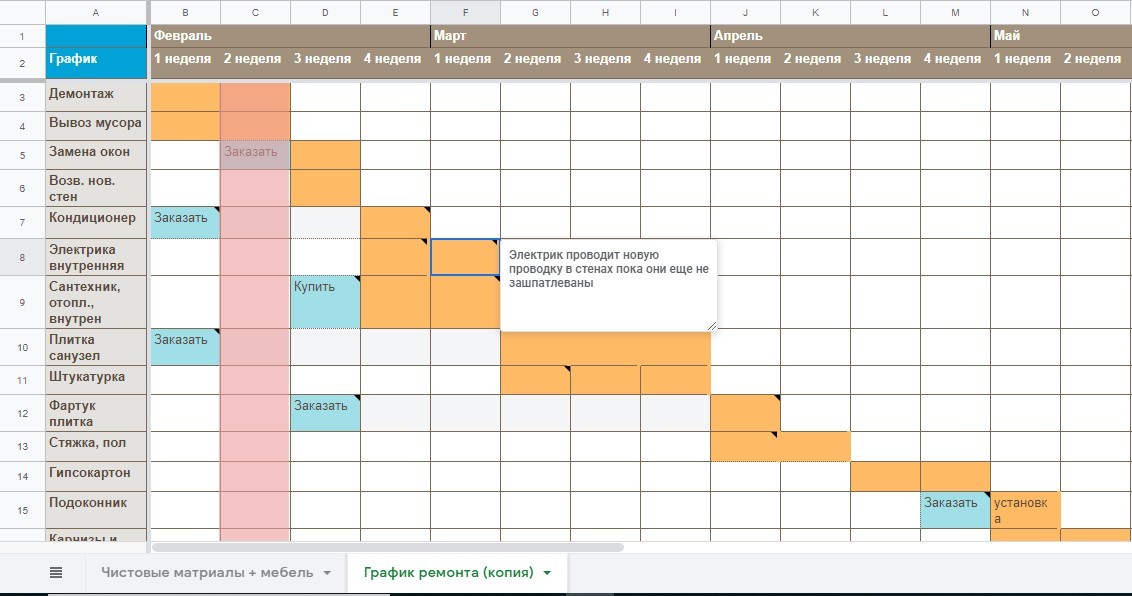
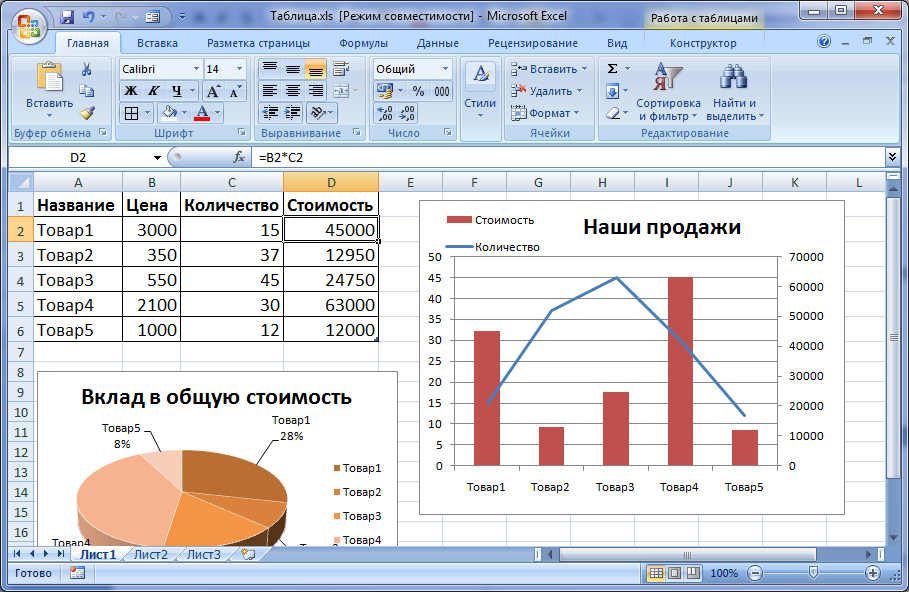
 Просто выберите рамку таблицы и используйте панель быстрого доступа, чтобы добавить или удалить строки и столбцы.
Просто выберите рамку таблицы и используйте панель быстрого доступа, чтобы добавить или удалить строки и столбцы.
 60 шт.)
60 шт.)
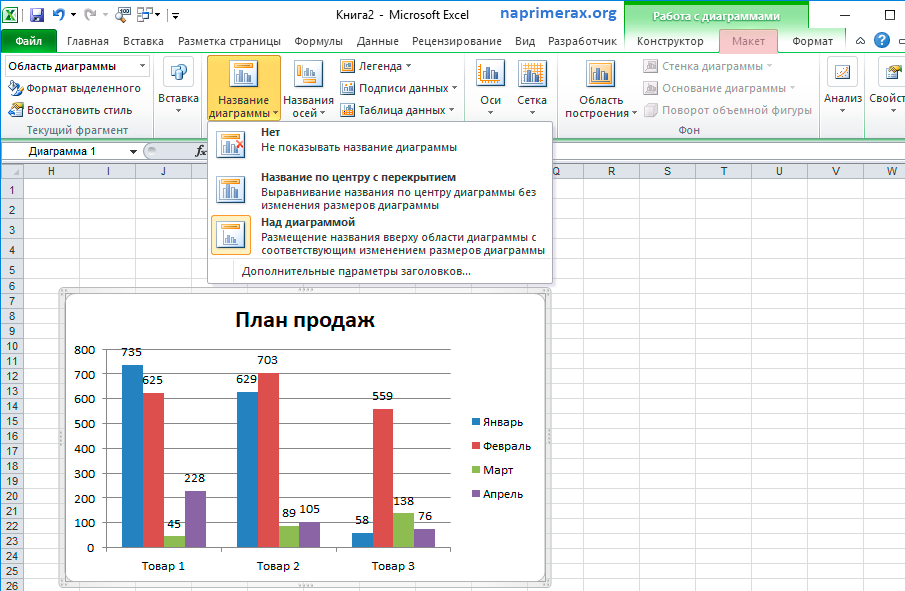
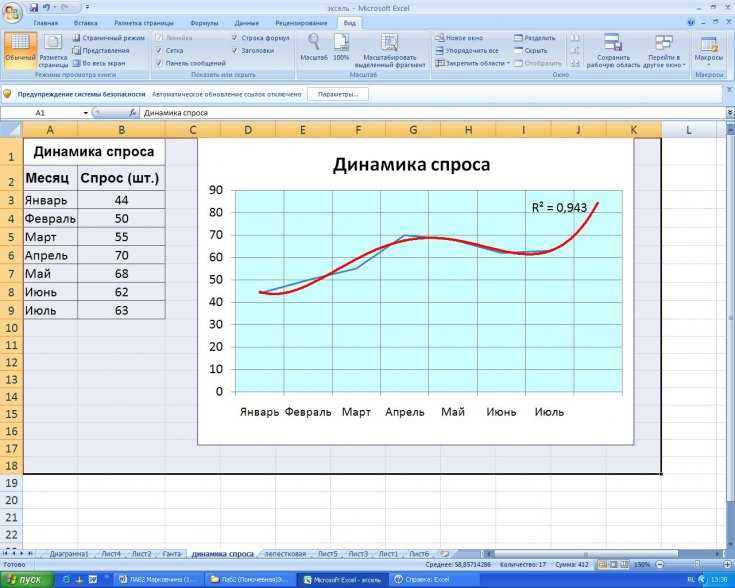
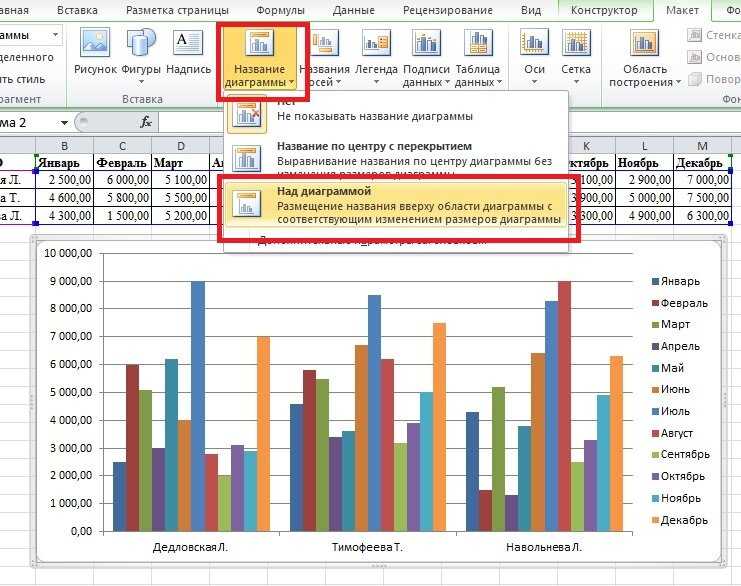
 Таблицы также можно использовать для подготовки необработанных данных перед созданием других диаграмм, таких как гистограммы, круговые диаграммы или временные шкалы.
Таблицы также можно использовать для подготовки необработанных данных перед созданием других диаграмм, таких как гистограммы, круговые диаграммы или временные шкалы.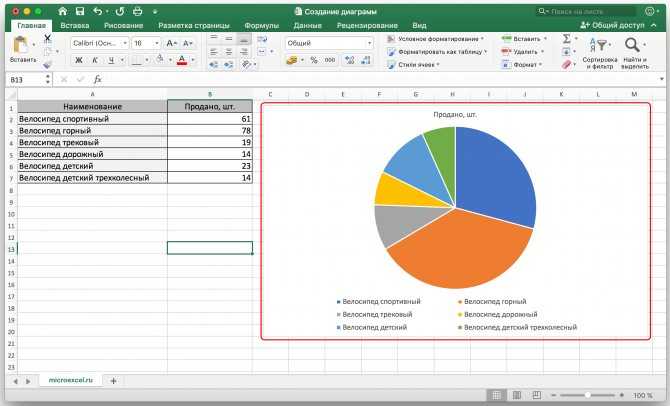
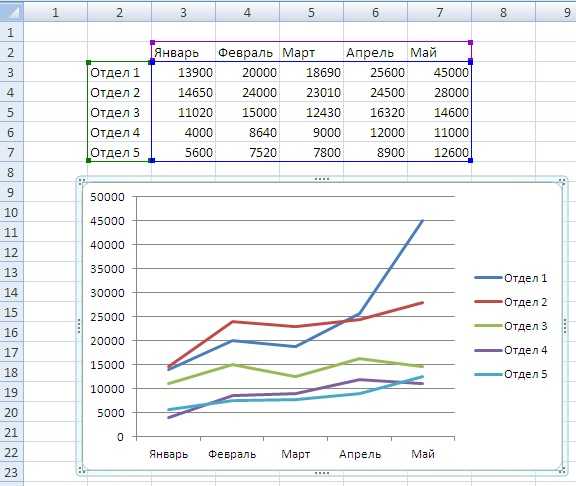 Введите информацию и данные
Введите информацию и данные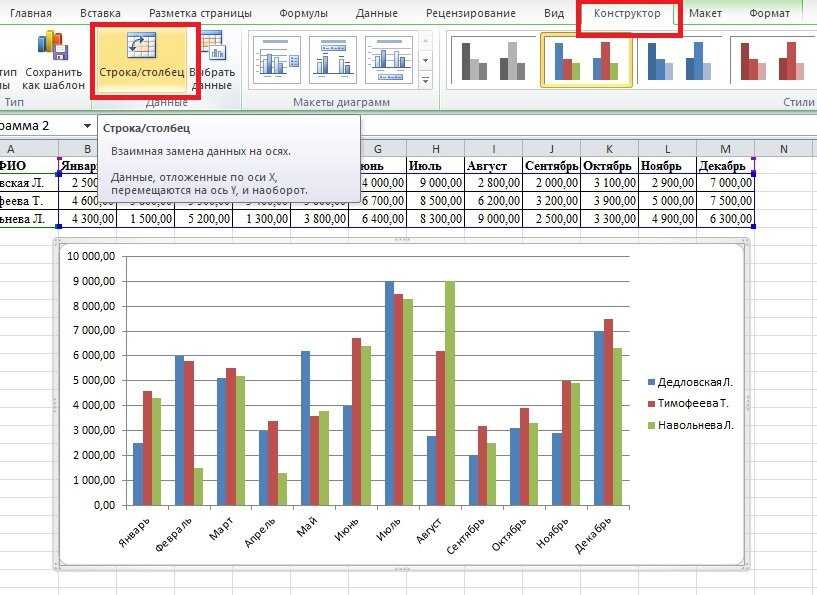

 2
2 05.14
05.14

 В ответе запишите найденное значение.
В ответе запишите найденное значение.
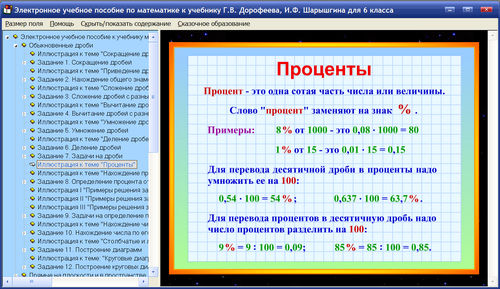
 Найдите значение выражения
Найдите значение выражения Найдите значение выражения
Найдите значение выражения Давайте посмотрим, как Роб и Пэтти пытались упростить заданное числовое выражение, применяя порядок или правило операций.
Давайте посмотрим, как Роб и Пэтти пытались упростить заданное числовое выражение, применяя порядок или правило операций.
 Чтобы определить, какую операцию выполнять первой, мы прибавляем или вычитаем то, что идет первым слева направо, что в данной ситуации означает прибавление, 1 + 3 = 4.
Чтобы определить, какую операцию выполнять первой, мы прибавляем или вычитаем то, что идет первым слева направо, что в данной ситуации означает прибавление, 1 + 3 = 4.



 , Мнемозина, 2014 г.
, Мнемозина, 2014 г. 


 ), прямые и обратные теоремы;
), прямые и обратные теоремы;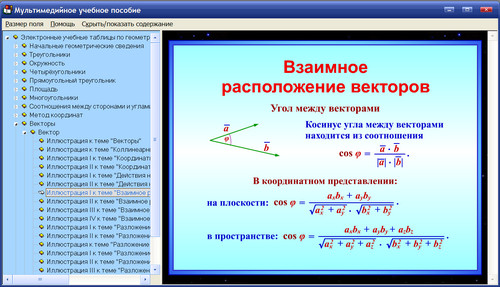

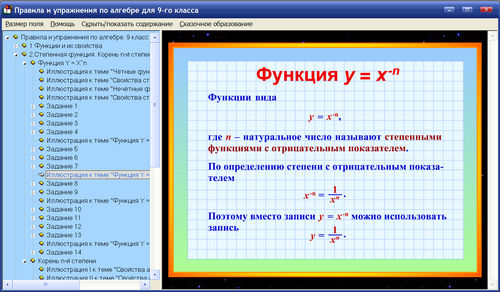

 Познакомить учащихся с производной показательной и логарифмической функций, сформировать у учащихся навыки вычисления производной показательной и логарифмической функции, через решение различных типов заданий. Вывод формулы производной показательной функции провести на наглядно-интуитивной основе. При рассмотрении вопроса о дифференциальном уравнении показательного роста и показательного убывания показательная функция должна выступать как математическая модель, находящая широкое применение при изучении реальных процессов и явлений действительности.
Познакомить учащихся с производной показательной и логарифмической функций, сформировать у учащихся навыки вычисления производной показательной и логарифмической функции, через решение различных типов заданий. Вывод формулы производной показательной функции провести на наглядно-интуитивной основе. При рассмотрении вопроса о дифференциальном уравнении показательного роста и показательного убывания показательная функция должна выступать как математическая модель, находящая широкое применение при изучении реальных процессов и явлений действительности. Познакомить учащихся с интегрированием как операцией, обратной дифференцированию; научить использовать свойства и правила при нахождении первообразных различных функций.
Познакомить учащихся с интегрированием как операцией, обратной дифференцированию; научить использовать свойства и правила при нахождении первообразных различных функций. Особое место занимает уравнения и неравенства с двумя переменными и уравнения с параметрами. Научатся решать системы уравнений, неравенства с одной переменной и их системы.
Особое место занимает уравнения и неравенства с двумя переменными и уравнения с параметрами. Научатся решать системы уравнений, неравенства с одной переменной и их системы. Тригонометрические уравнения
Тригонометрические уравнения Показательная и логарифмическая функции — 30 ч.
Показательная и логарифмическая функции — 30 ч. Первообразная и интеграл-16 ч.
Первообразная и интеграл-16 ч. Элементы математической статистики, комбинаторики и теории вероятностей- 16 ч.
Элементы математической статистики, комбинаторики и теории вероятностей- 16 ч. Уравнения, неравенства, их системы-16 ч.
Уравнения, неравенства, их системы-16 ч. Это программа обучения алгебре с самым высоким рейтингом , которая помогает учащимся всех уровней способностей
узнать и освоить элементарную алгебру.
Это программа обучения алгебре с самым высоким рейтингом , которая помогает учащимся всех уровней способностей
узнать и освоить элементарную алгебру.




 Для реализации на практике невозможно сохранить бесконечность такого разложения: его приближенность должна быть сбалансирована с требуемой точностью восстановления.
Для реализации на практике невозможно сохранить бесконечность такого разложения: его приближенность должна быть сбалансирована с требуемой точностью восстановления. Это позволило описывать данные в виде столбцов, а само математическое преобразование в виде матрицы. Для того чтобы сопоставить этой матрице некоторое распределение диэлектрической проницаемости, физики решали задачу оптимизации для целевой функции, собранной из ошибок преобразования для всех компонент разложения.
Это позволило описывать данные в виде столбцов, а само математическое преобразование в виде матрицы. Для того чтобы сопоставить этой матрице некоторое распределение диэлектрической проницаемости, физики решали задачу оптимизации для целевой функции, собранной из ошибок преобразования для всех компонент разложения. Модель показала устойчивость даже тогда, когда авторы добавили шум к частоте и к распределению диэлектрической проницаемости. Физики отмечают, что если расширить описанный метод до трехмерного случая, это позволит решать задачи для двумерных функций. В данный момент они работают над экспериментальной реализацией предложенного аналогового вычислителя в рамках оптики и акустики.
Модель показала устойчивость даже тогда, когда авторы добавили шум к частоте и к распределению диэлектрической проницаемости. Физики отмечают, что если расширить описанный метод до трехмерного случая, это позволит решать задачи для двумерных функций. В данный момент они работают над экспериментальной реализацией предложенного аналогового вычислителя в рамках оптики и акустики.


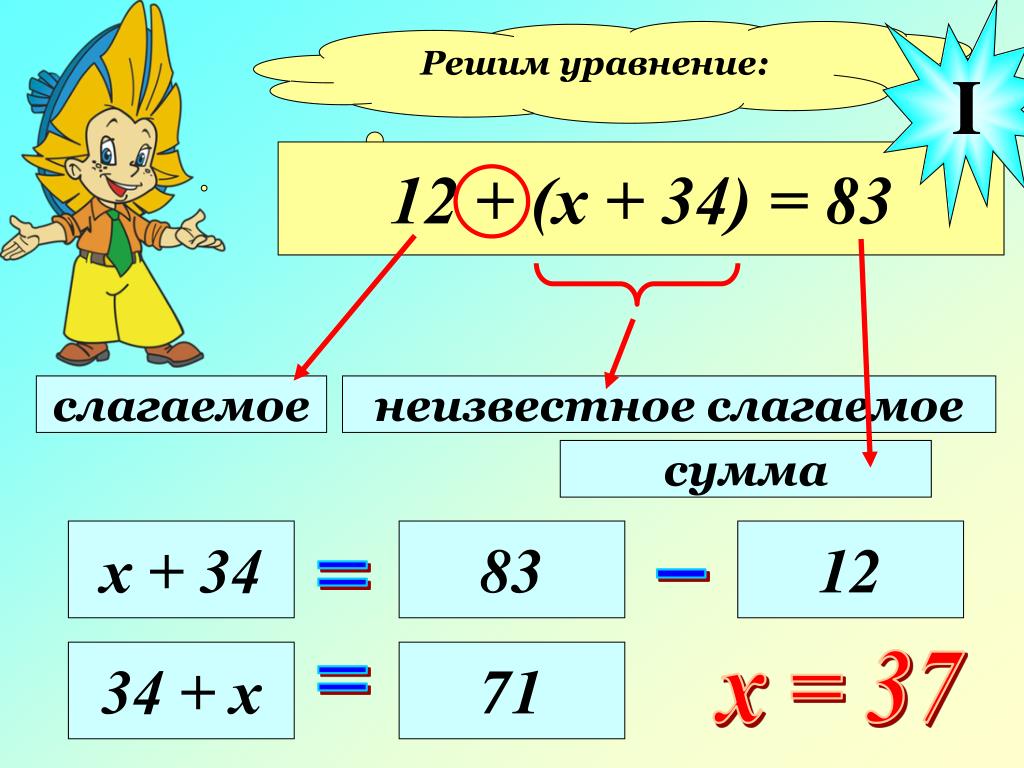


 В более подготовленных классах даже для первичного закрепления могут быть использованы выражения, в которых не два, а три и более действий, но их решение требует большего числа шагов с каждым шагом упрощая уравнение, до тех пор пока не получится простое уравнение. И каждый раз можно наблюдать, как меняется неизвестный компонент действий.
В более подготовленных классах даже для первичного закрепления могут быть использованы выражения, в которых не два, а три и более действий, но их решение требует большего числа шагов с каждым шагом упрощая уравнение, до тех пор пока не получится простое уравнение. И каждый раз можно наблюдать, как меняется неизвестный компонент действий.

 SymPy
SymPy 

 com, отмечает, что все умножение и деление должны выполняться слева направо, а затем сложение и вычитание. , над которым также следует работать слева направо.
com, отмечает, что все умножение и деление должны выполняться слева направо, а затем сложение и вычитание. , над которым также следует работать слева направо.


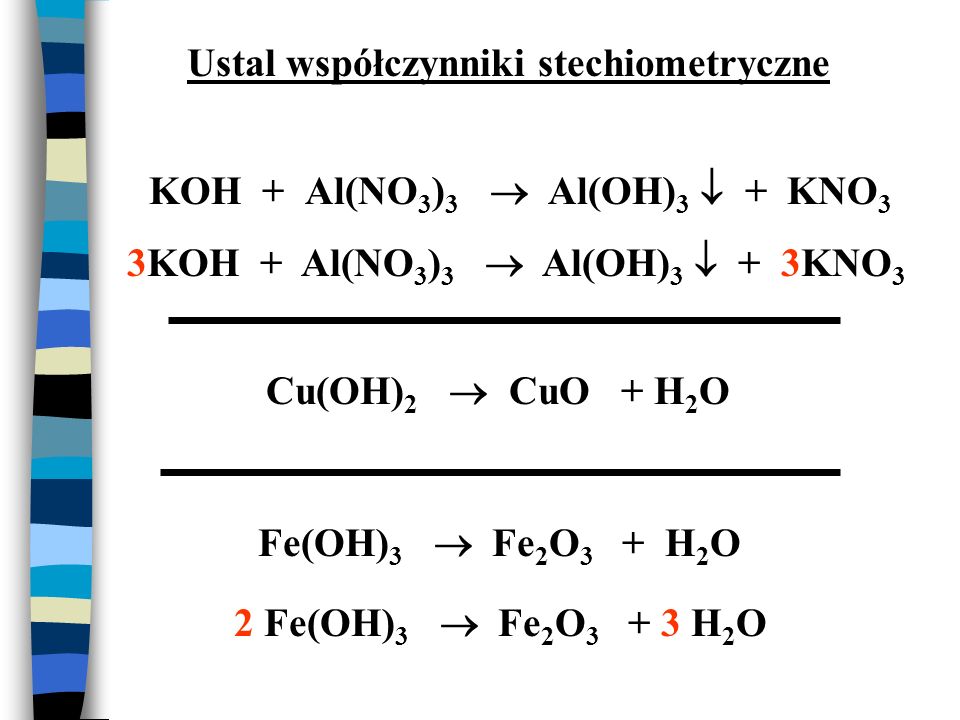 Каким не может быть самое
Каким не может быть самое Có nhiều trường hợp để từ chất A sang chất B phai đi qua nhiều phương trình Khac nhau.
, hay con gọi la chuỗi phương trình. Hãy xem tiep ben dưới một số gợi ý cac phương trình phản ứng có thể giup bạn лам được điều này.
Có nhiều trường hợp để từ chất A sang chất B phai đi qua nhiều phương trình Khac nhau.
, hay con gọi la chuỗi phương trình. Hãy xem tiep ben dưới một số gợi ý cac phương trình phản ứng có thể giup bạn лам được điều này.

 8670
8670  2 SO 4 + 2AL (№ 3 ) 3 → AL 2 (SO 4 ) 3 + 2CU (№ 3 ) 2 + 4HA 2 2 + 4H + 4H + 4H + 4. + 4H + 4H + 4H + 4H + 4. + 4H + 4H + 4H + 4. + 4H + 4H + 4H + 4. + 4. + 4. + 4. NO + CuSO 4 Xem tất cả phương trình sử dụng Al(NO3)3
2 SO 4 + 2AL (№ 3 ) 3 → AL 2 (SO 4 ) 3 + 2CU (№ 3 ) 2 + 4HA 2 2 + 4H + 4H + 4H + 4. + 4H + 4H + 4H + 4H + 4. + 4H + 4H + 4H + 4. + 4H + 4H + 4H + 4. + 4. + 4. + 4. NO + CuSO 4 Xem tất cả phương trình sử dụng Al(NO3)3 Катализаторы — это вещества, которые ускоряют темп (скорость) химической реакции, не потребляясь и не становясь частью конечного продукта.
Катализаторы не влияют на равновесные ситуации.
Катализаторы — это вещества, которые ускоряют темп (скорость) химической реакции, не потребляясь и не становясь частью конечного продукта.
Катализаторы не влияют на равновесные ситуации.


 Определим функцию
равенством
Определим функцию
равенством 3: Определение предела функции
3: Определение предела функции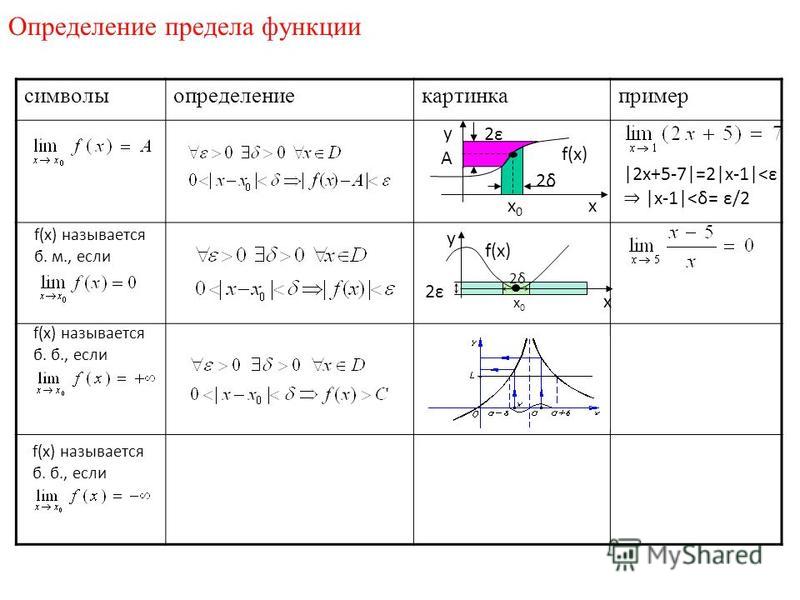 По этой причине логично сделать ее первой темой в курсе исчисления. 92}{h} = 2x + h\]
По этой причине логично сделать ее первой темой в курсе исчисления. 92}{h} = 2x + h\] Рассмотрим график разностного отношения \(D(x) = \dfrac{\sin x}{x}\).
Рассмотрим график разностного отношения \(D(x) = \dfrac{\sin x}{x}\). На самом деле мы легко можем видеть, что \(f\) непрерывно в \(x = a\) тогда и только тогда, когда \( \displaystyle \lim_{x \to a} f(x) = f(a)\).
На самом деле мы легко можем видеть, что \(f\) непрерывно в \(x = a\) тогда и только тогда, когда \( \displaystyle \lim_{x \to a} f(x) = f(a)\).
 Это приводит к парадоксальному заключению, что нам не нужен континуум (\(\mathbb{R}\)) для непрерывности. Это кажется странным. 92 -1}{x-1} — 2 \справа | &= \влево | (x+1) — 2 \справа | \\[4pt] &= \влево | х — 1 \право | < \delta = \varepsilon \end{align*}\]
Это приводит к парадоксальному заключению, что нам не нужен континуум (\(\mathbb{R}\)) для непрерывности. Это кажется странным. 92 -1}{x-1} — 2 \справа | &= \влево | (x+1) — 2 \справа | \\[4pt] &= \влево | х — 1 \право | < \delta = \varepsilon \end{align*}\] Мы уже видели в теореме 6.2.1 один из способов сделать это. Вот еще один. Ключевым является наблюдение, которое мы сделали после определения предела:
Мы уже видели в теореме 6.2.1 один из способов сделать это. Вот еще один. Ключевым является наблюдение, которое мы сделали после определения предела:
 По теореме 4.2.1 главы 4 имеем \(\displaystyle \lim_{n \to \infty } f(x_n) + g(x_n) = L + M\). Поскольку {\(x_n\)} была произвольной последовательностью с \(x_n \neq a\) и \(\displaystyle \lim_{n \to \infty}x_n = a\), мы имеем
По теореме 4.2.1 главы 4 имеем \(\displaystyle \lim_{n \to \infty } f(x_n) + g(x_n) = L + M\). Поскольку {\(x_n\)} была произвольной последовательностью с \(x_n \neq a\) и \(\displaystyle \lim_{n \to \infty}x_n = a\), мы имеем 2.4) из главы 4.
2.4) из главы 4. 0 и была создана, изменена и/или курирована Юджином Боманом и Робертом Роджерсом (OpenSUNY) через исходный контент, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
0 и была создана, изменена и/или курирована Юджином Боманом и Робертом Роджерсом (OpenSUNY) через исходный контент, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу. org/how-we-got-from-there-to-here-a-story-of-real-analysis
org/how-we-got-from-there-to-here-a-story-of-real-analysis
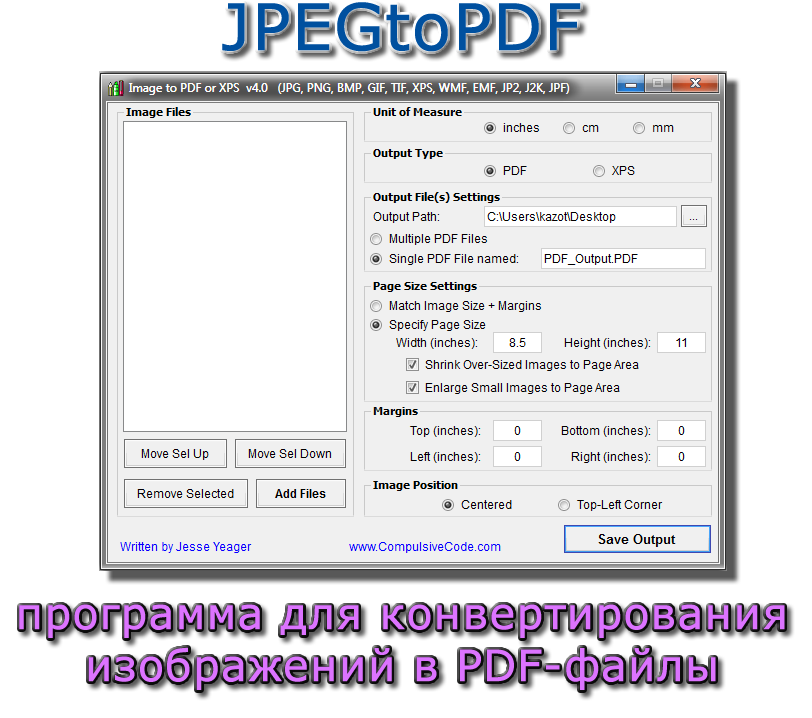
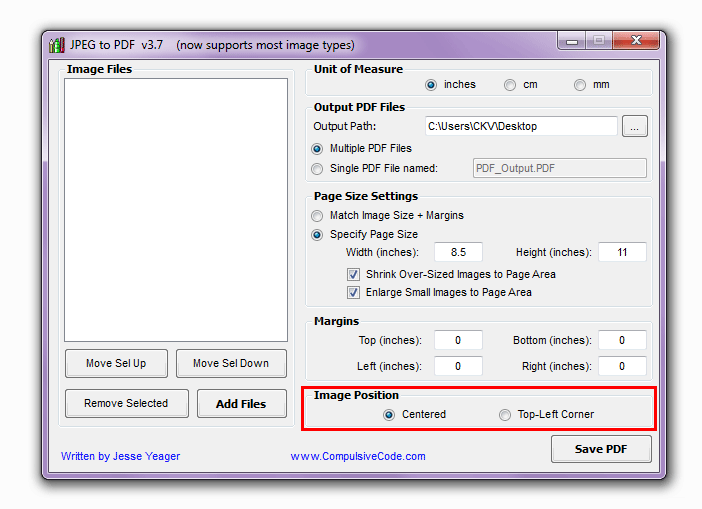
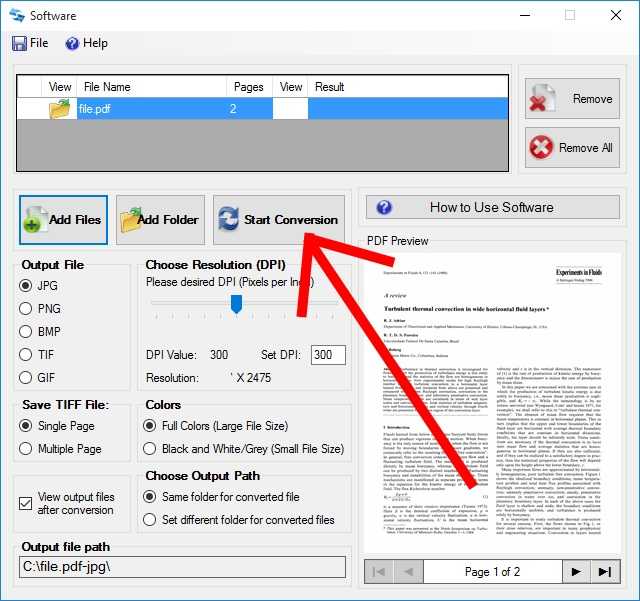 Программа оснащена множеством функций, от основных до продвинутых, таких как распознавание текста . Он поддерживает пакетное преобразование и работает на основных операционных системах и устройствах.
Программа оснащена множеством функций, от основных до продвинутых, таких как распознавание текста . Он поддерживает пакетное преобразование и работает на основных операционных системах и устройствах. Он имеет несколько основных и расширенных функций, необходимых для создания качественной продукции. С легкостью защищайте, сжимайте и редактируйте свои PDF-файлы в нескольких операционных системах.
Он имеет несколько основных и расширенных функций, необходимых для создания качественной продукции. С легкостью защищайте, сжимайте и редактируйте свои PDF-файлы в нескольких операционных системах.
 Д.
Д. После выбора изображений JPG в инструменте теперь вы можете форматировать предварительный просмотр JPG. Например, вы можете установить размер страницы PDF, ориентацию страницы PDF, а также установить поля страницы. Эти настройки можно применить из раскрывающегося списка. Кроме того, вы можете определить качество PDF-файла с помощью ползунка этого инструмента. Проще говоря, вы можете соответствующим образом настроить качество файла. Вы также можете вращать изображения JPG с помощью ротатора этого инструмента JPG в PDF. Кроме того, вы можете изменить порядок изображений JPG в соответствии с вашими предпочтениями. Вы можете перемещать изображения в формате JPG, перетаскивая карточку. Также доступны варианты добавления или удаления JPG из списка. Теперь нажмите кнопку «Преобразовать в PDF», а затем загрузите преобразованный PDF на свое устройство. Наконец, используйте этот инструмент JPG в PDF и легко конвертируйте JPG в PDF онлайн.
После выбора изображений JPG в инструменте теперь вы можете форматировать предварительный просмотр JPG. Например, вы можете установить размер страницы PDF, ориентацию страницы PDF, а также установить поля страницы. Эти настройки можно применить из раскрывающегося списка. Кроме того, вы можете определить качество PDF-файла с помощью ползунка этого инструмента. Проще говоря, вы можете соответствующим образом настроить качество файла. Вы также можете вращать изображения JPG с помощью ротатора этого инструмента JPG в PDF. Кроме того, вы можете изменить порядок изображений JPG в соответствии с вашими предпочтениями. Вы можете перемещать изображения в формате JPG, перетаскивая карточку. Также доступны варианты добавления или удаления JPG из списка. Теперь нажмите кнопку «Преобразовать в PDF», а затем загрузите преобразованный PDF на свое устройство. Наконец, используйте этот инструмент JPG в PDF и легко конвертируйте JPG в PDF онлайн. Вы можете конвертировать несколько изображений JPG в PDF с помощью этого инструмента JPG в PDF. Вы можете легко выбрать JPG, конвертировать в PDF и загрузить его из JPG в PDF инструмент.
Вы можете конвертировать несколько изображений JPG в PDF с помощью этого инструмента JPG в PDF. Вы можете легко выбрать JPG, конвертировать в PDF и загрузить его из JPG в PDF инструмент. Существует бесчисленное множество причин для создания PDF с коллекцией файлов JPG, независимо от того, что у вас есть, вы можете сделать все это с помощью онлайн-конвертера JPEG в PDF.
Существует бесчисленное множество причин для создания PDF с коллекцией файлов JPG, независимо от того, что у вас есть, вы можете сделать все это с помощью онлайн-конвертера JPEG в PDF.

 Несмотря на небольшую цену, Adobe Acrobat DC — идеальное решение для работы с файлами PDF, которое удовлетворит все ваши потребности.
Несмотря на небольшую цену, Adobe Acrobat DC — идеальное решение для работы с файлами PDF, которое удовлетворит все ваши потребности. Nitro PDF Pro
Nitro PDF Pro
 Конвертер PDF
Конвертер PDF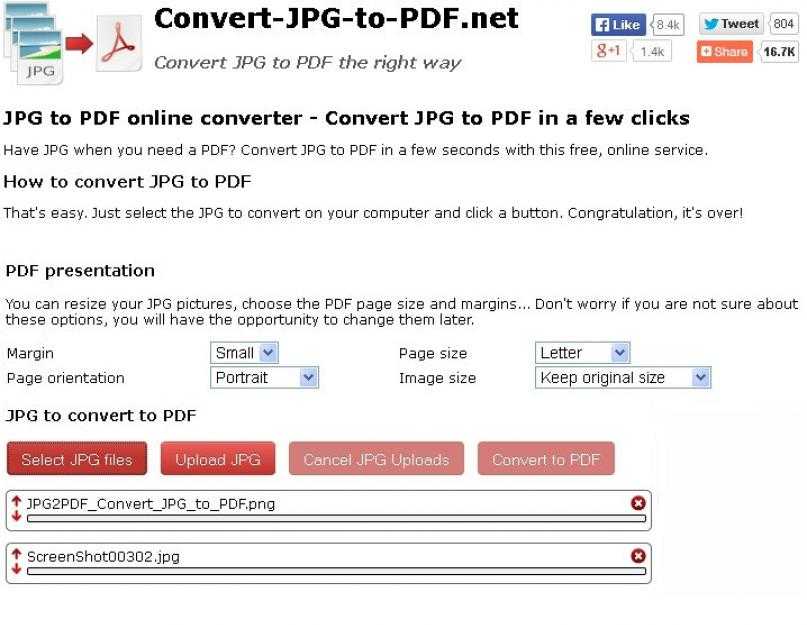


 JPG2PNG
JPG2PNG Теперь вы можете тщательно изучить достоинства и недостатки каждого из этих преобразователей, если вы выберете их. Кроме того, вы, возможно, изучали, почему и чем HiPDF лучше, чем каждый из этих конвертеров JPG в PNG? HiPDF популярен из-за своей конфиденциальности в отношении пользователей, что делает его надежным и заслуживающим доверия.
Теперь вы можете тщательно изучить достоинства и недостатки каждого из этих преобразователей, если вы выберете их. Кроме того, вы, возможно, изучали, почему и чем HiPDF лучше, чем каждый из этих конвертеров JPG в PNG? HiPDF популярен из-за своей конфиденциальности в отношении пользователей, что делает его надежным и заслуживающим доверия.