Урок математики по теме «Деление дробей в уравнениях»
Форма урока: объяснение нового материала.
Цели урока:
- Обучающая: выработать навыки учащихся умножать и делить обыкновенные дроби, решать и оформлять задачи на уравнения.
- Воспитательная: воспитывать самостоятельность, аккуратность
- Развивающая: развивать внимание, математическую речь, вычислительные навыки учащихся, интерес к математике.
Ожидаемые результаты: дети научаться решать задачи и уравнения на дроби.
Этапы урока |
Время (мин) | Слайды |
Организационный момент. |
2 | Слайд 1 |
| Устная работа и повторение ранее изученного | 8 | Слайды 2, 3, 4, 5,6 |
| Формирование новых знаний и умений | 10 | Слайды 7, 8 |
| Физкультминутка | 2 | Слайды 9, 10 |
| Закрепление нового материала | 5 | Слайд 11 |
| Проверка знаний (с/р) | 10 | Слайд 12 |
| Постановка домашнего задания | 1 | Слайд 13 |
| Подведение итогов урока | 2 |
ХОД УРОКА
I. Организационный этап
– Здравствуйте, мы проведем сегодня урок по
теме «Деление дробей в уравнених». Откройте
тетради, запишите число, классная работа и тему
урока.
Откройте
тетради, запишите число, классная работа и тему
урока.
Целью нашего урока является закрепление и
проверка умений умножать и делить обыкновенные
дроби, а также повторить навыки решения задач и
уравнений.
II. Устный опрос учащихся
Чтобы умным в жизни стать
Надо дроби изучать
1) Переведите смешанную дробь в неправильную (Приложение 1, слайд 3)
2) Выделите целую часть (Приложение 1, слайд 4)
3) Умножьте дроби (Приложение 1, слайд 5)
– Повторим правило умножения двух дробей: Чтобы умножить дробь на дробь нужно перемножить их числители и знаменатели и первое произведение записать числителем, а второе знаменателем.
4) Выполните деление (в тетрадях с последующей взаимопроверкой, сосед у соседа) (Приложение 1, слайд 6)
– Повторим правило деления двух дробей: Чтобы
разделить одну дробь на другую, нужно первую
дробь умножить на дробь, обратную второй.
III. Формирование новых знаний и умений
– При изучении темы деление большое значение имеет умение решать уравнения. Рассмотрим пример и запишем его в тетрадь. (Приложение 1, слайд 7)
– Чтобы решить уравнение необходимо
определить какой компонент в уравнении является
неизвестным.
– Какой?
– 1 множитель
– Правильно! Чтобы найти неизвестный множитель,
что нужно сделать?
– Чтобы найти неизвестный множитель необходимо
произведение разделить на известный множитель.
– Находим корень уравнения, выполняя деление.
Выполним проверку и запишем ответ.
– А теперь давайте проверим ваше умение решать задачи.
№ 597 (Приложение 1, слайд 7)
– Сколько всего прошел лыжник ? (26 км)
– Сколько километров прошел в первый день?
(неизвестно)
– Сколько километров прошел во второй день?
(неизвестно)
– Какую величину, с какой сравнивают?
– Что возьмем за х?
– Как найти дробь от числа?
– Сколько километров прошел за два дня?
– Как найти?
– Составим уравнение.
– 14 км лыжник прошел во второй день
26 – 14 = 12 км лыжник прошел в первый день.
№ 598 (Приложение 1, слайд 8)
– Вспомним что такое 1% (одна сотая)
– Какой дробью запишем 75% (75/100 = 3/4)
– Сколько грибов собрала белка? (неизвестно)
– Сколько грибов собрал бельчонок? (неизвестно)
– Какую величину, с какой сравнивают?
– Что обозначим за икс?
– Как найти дробь от числа?
– Сколько собрали вместе белка и бельчонок?
– Составим уравнение.
200 грибов собрала белка
350 – 200 = 150 грибов собрал бельчонок
IV. Физкультминутка
– Встаем и выполняем несколько упражнений.
А теперь, ребята, встали,
Быстро руки вверх подняли,
В стороны, вперёд, назад
Повернулись вправо, влево,
Тихо сели, вновь за дело.
V. Закрепление нового материала
№ 594
– Сколько собрал Митя?
– Сколько собрал Коля?
– Какую величину, с какой сравнивают?
– Что обозначим за икс?
– Как найти дробь от числа?
– Сколько собрали вместе мальчики?
28 грибов собрал Митя
64 – 28 = 36 грибов собрал Коля
VI. «Математический выбор»
Уравнения, оцениваемые в 3 балла: Уравнения, оцениваемые в 5 баллов:
1) 1)
2) 2)
3) 3)
4) 4)
Уравнения, оцениваемые в 6 баллов:
1)
2)
3)
4)
Оценки: 5 – 12 баллов; 4 – 9 баллов; 3 – 6 баллов.
Каждый выбирает себе уравнения по «плечу».
Учитель во время работы оценивает учеников.
VII. Итог урока
– С каким настроением вы сегодня работали на
уроке?
– Какая задача для вас была самой интересной?
– Ребята чему мы научились на сегодняшнем уроке?
– Как найти часть от числа?
– Как найти неизвестный множитель?
Оценки за урок.
VIII. Домашнее задание
– С листов решить любые три уравнения, из тех которые не решали в классе.
«Дроби». Математика 4 класс — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
«Дроби».
Математика
4 класс
Ц ЕЛИ :
закрепить знание понятий «дроби»правильные и неправильные; смешанные
числа;
повторить свойства сложения и
вычитания дробей
формирование умений решать
составные задачи на нахождение третьей
части;
развивать речь, внимание, память;
навыки устных и письменных вычислений,
самоанализа.
ДЕВИЗ УРОКА.
«
Начнешь в учении
с малого,
постигнешь и
большее».
А КТУАЛИЗАЦИЯ
ЗНАНИЙ .
1 7 5 2 16 7 13 4 9
6 9 6 9 9 6
6 9
Тема: «Дроби»
Т ЕМА «Д РОБИ »
План.
1. Виды дробей.
2. Сложение и вычитание
дробей.
3. Решение задач.
Д РОБИ .
1 числитель
знаменатель
6
Сколько частей
взяли.
На сколько
частей
разделили.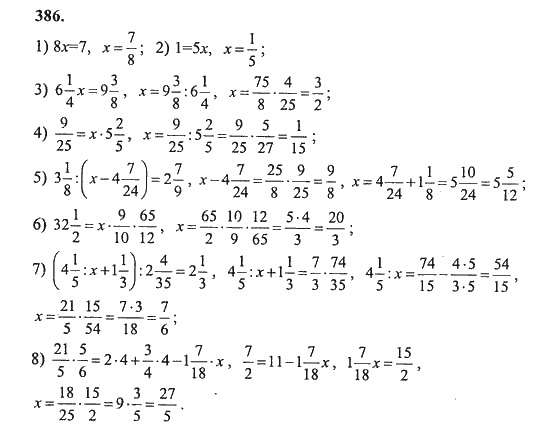
К ЛАССИФИКАЦИЯ ДРОБЕЙ .
правильные
неправильные
1
5
2
4
7
9
16
7
6
6
9
6
9
9
9
6
Числитель
меньше
знаменателя
Числитель
больше
знаменателя
К ЛАССИФИКАЦИЯ
ДРОБЕЙ
Дроби
со знаменателем 6
со знаменателем 9
*
РАБОТА
ПО ВАРИАНТАМ .
Вариант1: расположить дроби со
знаменателем 6 в порядке возрастания;
Вариант2: расположить дроби со
знаменателем 9 в порядке убывания.
Проверка:
1в. 1; 4;
6
6
5; 7
6
6
2в. 16;
9
9;
7; 2
9
9
9
Д РОБИ .
правильные
неправильные
смешанные
Уровень А – составить выражение с дробями на сложение
и вычитание по схеме:
а
n
в
n
а
n
в
n
Уровень В – составить выражение в несколько действий с
дробями по схеме
а
n
в
n
с
n
а
n
Уровень С – составить уравнение с дробями.
а х в
n
n
а х в
n
n
в
n
с
n
с
n
При сложении дробей с одинаковыми
знаменателями, числители
складываются, а знаменатели остаются
без изменения.
При вычитании дробей с одинаковыми
знаменателями, из числителя первой
дроби вычесть числитель второй дроби,
знаменатель остается без изменения.
С ЛОЖЕНИЕ И ВЫЧИТАНИЕ
ДРОБЕЙ .
а + в = а+в
n n
n
а–в =а-в
n n
n
Р ЕШЕНИЕ
ЗАДАЧ .
Длина трех рек России Волги,
Дуная и Днепра составляет 8100км.
Длина реки Волги составляет -4\9всей
длины, длина Дуная составляет 1\3
всей длины. Какова длина Днепра?
1 СПОСОБ :
План решения задачи:
1) : х
2) : х
3) — :
Проверка
1) 8100: 9х4
2) 8100:3 х1
3)8100- 3600 -2700
2
СПОСОБ :
8100 – (8100:9х4 + 8100:3х1)= 1800(км)
Вывод: При решении задачи на
нахождение третьей части, нужно из целого
вычесть первую часть, а потом – вторую. Или
из целого вычесть сумму двух частей.
.
Г ЕНИЙ СОСТОИТ ИЗ
1% ВДОХНОВЕНИЯ И 99% ПОТЕНИЯ .
Словарная работа:
Гений – высшая творческая
способность. (Человек,
обладающий такой
способностью).
Вдохновение – творческий
подъем, прилив творческих сил.
И ТОГ
УРОКА .
— Назовите тему урока.
-Что мы повторили?
— Что понравилось ? Что нового для себя открыли?
Д\З : по выбору:
1)тренажер
2) по учебнику
3) Составить и решить задачу с дробями
English Русский Правила
Рабочие листы для дробей
Половины, трети и четверти
Откройте дверь к пониманию дробей для младших школьников до 3-го класса с помощью наших листов для половин, третей и четвертей! Удобные для детей иллюстрации, увлекательные упражнения и практические занятия позволяют детям впитывать все, что касается половинок, третей и четвертей.
Визуальные модели дробей
Помогите учащимся 3-х и 4-х классов понять дроби как равные части целого, используя фигуры, реальные объекты, кусочки пиццы и множество визуальных моделей дробей! Они определяют правильные дроби, единичные дроби, смешанные числа и многое другое.
Определение дробей
Хотите, чтобы ребенок научился определять дроби в один миг? Приложите все усилия, чтобы найти числители и знаменатели, заполнить таблицу, составив дроби, и многое другое с помощью этих динамических рабочих листов в формате PDF.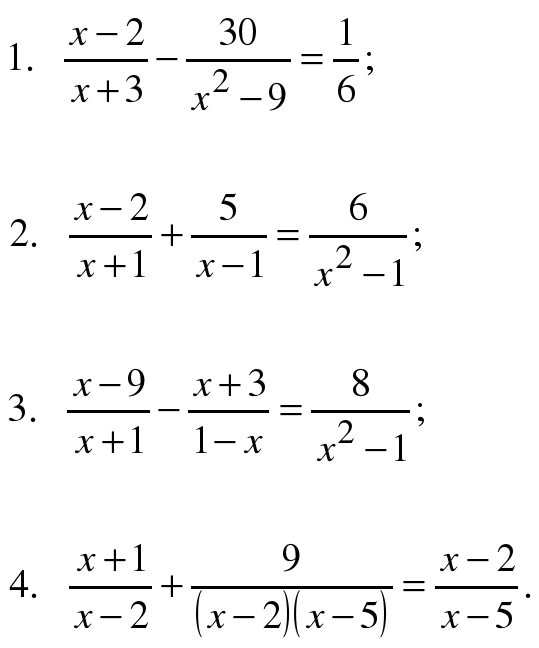
Типы дробей
Какой дробью является 1/4? Да, это единичная дробь. Определите правильную дробь, неправильную дробь, смешанное число, единичную дробь, например дроби, в отличие от дробей, как профессионал, с этими печатными листами дробей.
Упрощение дроби
Сократите правильную дробь, неправильную дробь и смешанные числа до наименьшего члена.
Преобразование неправильных дробей в смешанные числа
Что легче интерпретировать, 1 1/4 или 5/4? Некоторым учащимся может быть сложнее работать со смешанными числами, чем с неправильными дробями, для других неправильные дроби могут показаться более легкими. Подготовьтесь к преобразованию между ними с помощью этих рабочих листов в формате PDF!
Эквивалентная дробь
Интерактивные рабочие листы, в которых используются полосы дробей, круговая модель, визуальная графика и многое другое.
Дроби на числовой прямой
Эти рабочие листы с дробями на числовой прямой помогают детям визуально понимать дроби.
Сложение дробей
Сложение одинаковых, непохожих, правильных, неправильных и смешанных дробей. Включены специальные дроби, такие как единица и обратная дробь.
Вычитание дробей
Бесплатные рабочие листы по вычитанию включают в себя все типы дробей, построенные с различными уровнями навыков.
Умножение дробей
Распознавание умножения дробей на целые числа с использованием повторного сложения, массивов, моделей числовых рядов, равных групп и моделей площадей; выполнять умножение двух и трех дробей, умножение дробей на смешанные числа и т. д.; решить ряд задач на умножение дробей.
Деление дробей
Подключитесь к нашим печатным листам деления дробей и попрактикуйтесь в делении дробей на целые числа, дроби на дроби, смешанного числа на дроби и т. д.!
Проблемы со словами на дроби
Узнайте, как дроби применяются и используются в реальной жизни, выполняя эти задачи со словами.
Сравнение дробей
Изучите наши листы сравнения дробей, чтобы без труда сравнить две дроби с одинаковыми и разными знаменателями. Благодаря большому количеству моделей и упражнений, эти PDF-файлы являются отличным учебным пособием для детей.
Благодаря большому количеству моделей и упражнений, эти PDF-файлы являются отличным учебным пособием для детей.
Сравнение смешанных чисел
Что больше, 1 2/5 или 2 5/6? Сравните такие смешанные числа мгновенно и безошибочно с помощью наших рабочих таблиц сравнения смешанных чисел!
Упорядочивание дробей
Расположите дроби в возрастающем или убывающем порядке.
Округление дробей
Округление дробей до ближайшего целого числа или до ближайшей половины. Числовые строки также включены.
Оценка дробей
Оценить сумму, разность, произведение и частное с дробями.
Рабочие листы «Преобразование дробей в десятичные числа»
Поддержите знания ребенка, связанные с преобразованием дробей в десятичные числа, включив множество увлекательных упражнений и стремительно повышая их силу!
Преобразование между дробями, десятичными знаками и процентами Рабочие листы
Помогите учащимся сделать большой прорыв в выполнении преобразования между процентами, десятичными знаками и дробями. Обширный набор упражнений направлен на улучшение при проверке их понимания темы.
Обширный набор упражнений направлен на улучшение при проверке их понимания темы.
Иллюстративная математика
Иллюстративная математикакласс 4
4 класс
- Сравнение роста, вариант 1
- Сравнение роста, вариант 2
- Тысячи и миллионы четвероклассников
- Находящиеся под угрозой исчезновения
- Сравнение привлеченных денег
- Билеты на карнавал
- Сад Карла
- Идентификация множественных
- Кратные числа 3, 6 и 7
- Числа в таблице умножения
- Игра в шкафчик
- Кратные числа 3, 6 и 7
- Двойной плюс один
- Кратность девяти
4.ОА. 4 класс — Операции и алгебраическое мышление
4.ОА.А. Используйте четыре операции с целыми числами для решения задач.
4.ОА.А.1. Интерпретируйте уравнение умножения как сравнение, например, интерпретируйте $35 = 5 \times 7$ как утверждение, что 35 в 5 раз больше, чем 7, и в 7 раз больше, чем 5. Представьте вербальные утверждения мультипликативных сравнений в виде уравнений умножения.
4.ОА.А.2. Умножьте или разделите, чтобы решить текстовые задачи, включающие мультипликативное сравнение, например, используя рисунки и уравнения с символом неизвестного числа для представления проблемы, отличая мультипликативное сравнение от аддитивного сравнения.
 См. Глоссарий, Таблица 2.
См. Глоссарий, Таблица 2.4.ОА.А.3. Решите многошаговые словесные задачи, поставленные с целыми числами и имеющие ответы с целыми числами, используя четыре операции, включая задачи, в которых необходимо интерпретировать остатки. Представьте эти проблемы, используя уравнения с буквой, обозначающей неизвестную величину. Оцените обоснованность ответов, используя вычисления в уме и стратегии оценки, включая округление.
4.ОА.Б. Знакомство с множителями и множителями.
4.ОА.Б.4. Найдите все пары множителей для целого числа в диапазоне от 1 до 100. Признать, что целое число является кратным каждого из его делителей. Определить, является ли заданное целое число в диапазоне от 1 до 100 кратным заданному однозначному числу.
 Определите, является ли заданное целое число в диапазоне от 1 до 100 простым или составным.
Определите, является ли заданное целое число в диапазоне от 1 до 100 простым или составным.4.ОА.С. Создавайте и анализируйте шаблоны.
4.ОА.С.5. Создайте шаблон числа или формы, который следует заданному правилу. Определите очевидные особенности шаблона, которые не были явными в самом правиле. Например, учитывая правило «Добавить 3» и начальный номер 1, создайте термины в результирующей последовательности и обратите внимание, что термины чередуются между нечетными и четными числами. Неформально объясните, почему числа будут продолжать чередоваться таким образом.
- Какой у меня номер?
- Тысячи и миллионы четвероклассников
- Находящиеся под угрозой исчезновения
- Заказ 4-значных номеров
- Округление в числовой строке
- Округление до ближайшей 1000
- Округление до ближайших 100 и 1000
- Перегруппировывать или не перегруппировывать
- Тысячи и миллионы четвероклассников
- Стратегия ментального подразделения
4.НБТ. 4 класс — Числа и операции с основанием десять
4.НБТ.А. Обобщить понимание разряда для многозначных целых чисел.
4.
 НБТ.А.1. Знайте, что в многозначном целом числе цифра на одном месте в десять раз больше, чем на месте справа от нее. Например, поймите, что 700 долларов \дел 70 = 10 долларов, применив концепции разряда и деления.
НБТ.А.1. Знайте, что в многозначном целом числе цифра на одном месте в десять раз больше, чем на месте справа от нее. Например, поймите, что 700 долларов \дел 70 = 10 долларов, применив концепции разряда и деления.4.НБТ.А.2. Читать и писать многозначные целые числа, используя числа с основанием десять, имена чисел и расширенную форму. Сравните два многозначных числа на основе значений цифр в каждом разряде, используя символы $>$, = и $
<$, чтобы записать результаты сравнения.4.НБТ.А.3. Используйте понимание разрядности для округления многозначных целых чисел до любого места.
4.НБТ.Б. Используйте понимание позиционного значения и свойства операций для выполнения многоразрядной арифметики.

4.НБТ.Б.5. Умножьте целое число до четырех цифр на однозначное целое число и умножьте два двузначных числа, используя стратегии, основанные на разрядности и свойствах операций. Проиллюстрируйте и объясните расчет, используя уравнения, прямоугольные массивы и/или модели площадей.
4.НБТ.Б.6. Находите целые числа в частных и остатках с до четырехзначными делителями и однозначными делителями, используя стратегии, основанные на разрядном значении, свойствах операций и/или взаимосвязи между умножением и делением. Проиллюстрируйте и объясните расчет, используя уравнения, прямоугольные массивы и/или модели площадей.
- Деньги в копилку
- Забеги
- Объяснение эквивалентности дробей с помощью изображений
- Дроби и прямоугольники
- Сравнение дробей с использованием игры эталонов
- Удвоение числителей и знаменателей
- Список дробей в возрастающем размере
- Использование контрольных показателей для сравнения дробей
- Сравнение двух разных пицц
- Запись смешанного числа в виде эквивалентной дроби
- Сравнение сумм единичных дробей
- Делаем 22 семнадцатых разными способами
- Идеальный удар Синтии
- Персики
- Пластиковые строительные блоки
- Запись смешанного числа в виде эквивалентной дроби
- Пока нет задач, иллюстрирующих этот стандарт.
- Расширение умножения целых чисел на дроби
- Пока нет задач, иллюстрирующих этот стандарт.

- Пока нет задач, иллюстрирующих этот стандарт.
- Сахар в шести банках газировки
- Добавление десятых и сотых
- Даймс и Пенни
- Расширенные дроби и десятичные дроби
- Эквивалентность дроби
- Сколько десятых и сотых?
- Даймс и Пенни
- Расширенные дроби и десятичные дроби
- Сколько десятых и сотых?
- Использование значения места
4.НФ. 4 класс — Числа и операции — Дроби
4.НФ.А. Расширьте понимание дробной эквивалентности и порядка.

4.НФ.А.1. Объясните, почему дробь $a/b$ эквивалентна дроби $(n \times a)/(n \times b)$, используя визуальные модели дробей, обращая внимание на то, как количество и размер частей различаются, несмотря на то, что сами две фракции имеют одинаковый размер. Используйте этот принцип для распознавания и создания эквивалентных дробей.
4.НФ.А.2. Сравните две дроби с разными числителями и разными знаменателями, например, создав общие знаменатели или числители, или сравнив с эталонной дробью, такой как 1/2. Признайте, что сравнения допустимы только тогда, когда две дроби относятся к одному и тому же целому. Запишите результаты сравнений символами $>$, = или $
<$ и обоснуйте выводы, например, с помощью визуальной фракционной модели.4.
 НФ.Б. Создавайте дроби из единичных дробей, применяя и расширяя предыдущее понимание операций над целыми числами.
НФ.Б. Создавайте дроби из единичных дробей, применяя и расширяя предыдущее понимание операций над целыми числами.4.NF.B.3. Под дробью $a/b$, где $a > 1$, понимается сумма дробей $1/b$.
4.NF.B.3.а. Понимать сложение и вычитание дробей как соединение и разделение частей, относящихся к одному и тому же целому.
4.NF.B.3.б. Разложите дробь на сумму дробей с одинаковым знаменателем более чем одним способом, записывая каждое разложение уравнением. Обоснуйте разложения, например, с помощью визуальной дробной модели. Примеры: $\frac38 = \frac18 + \frac18 + \frac18$; $\frac38 = \frac18 + \frac28$; $2 \frac18 = 1 + 1 + \frac18 = \frac88 + \frac88 + \frac18.$
4.NF.B.3.c. Складывать и вычитать смешанные числа с одинаковыми знаменателями, например, заменяя каждое смешанное число эквивалентной дробью и/или используя свойства операций и отношения между сложением и вычитанием.

4.NF.B.3.d. Решайте текстовые задачи, включающие сложение и вычитание дробей, относящихся к одному и тому же целому и имеющих одинаковые знаменатели, например, используя визуальные модели дробей и уравнения для представления задачи.
4.NF.B.4. Применяйте и расширяйте прежнее понимание умножения, чтобы умножить дробь на целое число.
4.NF.B.4.а. Под дробью $a/b$ следует понимать кратное $1/b$. Например, используйте модель визуальной дроби, чтобы представить $5/4$ как произведение $5 \times (1/4)$, записав вывод уравнением $5/4 = 5 \times (1/4).$
4.NF.B.4.b. Понимайте кратное $a/b$ как кратное $1/b$ и используйте это понимание, чтобы умножить дробь на целое число. Например, используйте модель визуальной дроби, чтобы выразить $3 \times (2/5)$ как $6 \times (1/5)$, распознав этот продукт как $6/5$. (Вообще, $n \times (a/b) = (n \times a)/b.$)
4.NF.B.4.c. Решайте текстовые задачи, связанные с умножением дроби на целое число, например, используя визуальные модели дробей и уравнения для представления задачи. Например, если каждый человек на вечеринке съест 3/8 фунта ростбифа, а на вечеринке будет 5 человек, сколько фунтов ростбифа потребуется? Между какими двумя целыми числами лежит ваш ответ?
4.Н.Ф.К. Понимать десятичную запись дробей и сравнивать десятичные дроби.
4.NF.C.5. Выразите дробь со знаменателем 10 в виде эквивалентной дроби со знаменателем 100 и используйте эту технику, чтобы сложить две дроби со знаменателями 10 и 100 соответственно.
 Но сложение и вычитание с разными знаменателями вообще не обязательны для этого класса. Например, выразите $3/10$ как $30/100$ и добавьте $3/10 + 4/100 = 34/100$.
Но сложение и вычитание с разными знаменателями вообще не обязательны для этого класса. Например, выразите $3/10$ как $30/100$ и добавьте $3/10 + 4/100 = 34/100$.4.NF.C.6. Используйте десятичную запись для дробей со знаменателем 10 или 100. Например, перепишите $0,62$ как $62/100$; описать длину как $0,62$ метра; найдите $0,62$ на диаграмме с числовыми линиями.
4.NF.C.7. Сравните два десятичных знака с сотыми, рассуждая об их размере. Признайте, что сравнения действительны только тогда, когда два десятичных знака относятся к одному и тому же целому. Запишите результаты сравнений символами $>$, = или $
<$ и обосновывайте выводы, например, с помощью визуальной модели.
- Кто самый высокий?
- Марджи покупает яблоки
- Сад Карла
- Диаметр кнопки
- Пока нет задач, иллюстрирующих этот стандарт.
- Пока нет задач, иллюстрирующих этот стандарт.
- Пока нет задач, иллюстрирующих этот стандарт.
- Измерение углов
- Нахождение неизвестного угла
- Измерение углов
4.МД. 4 класс — Измерения и данные
4.МД.А. Решайте задачи, связанные с измерением и преобразованием измерений из большей единицы в меньшую.
4.МД.А.1. Знать относительные размеры единиц измерения в пределах одной системы единиц, в том числе км, м, см; кг, г; фунт, унция; л, мл; ч, мин, сек. В рамках единой системы измерения выражайте измерения в большей единице через меньшую. Запишите эквиваленты измерений в таблицу из двух столбцов. Например, известно, что 1 фут в 12 раз длиннее 1 дюйма. Выразите длину змеи длиной 4 фута как 48 дюймов. Создайте таблицу преобразования для футов и дюймов, перечислив пары чисел $(1, 12)$, $( 2, 24)$, $(3, 36)$, …
4.МД.А.2. Используйте четыре операции для решения текстовых задач, связанных с расстояниями, интервалами времени, объемами жидкостей, массами объектов и деньгами, включая задачи с простыми дробями или десятичными знаками, а также задачи, требующие выражения измерений, выраженных в более крупной единице, через меньшую единицу.
 . Представляйте измеряемые величины с помощью диаграмм, таких как диаграммы с числовыми линиями, которые имеют шкалу измерения.
. Представляйте измеряемые величины с помощью диаграмм, таких как диаграммы с числовыми линиями, которые имеют шкалу измерения.4.МД.А.3. Применяйте формулы площади и периметра для прямоугольников в реальных и математических задачах. Например, найдите ширину прямоугольной комнаты, зная площадь пола и длину, рассматривая формулу площади как уравнение умножения с неизвестным коэффициентом.
4.МД.Б. Представлять и интерпретировать данные.
4.МД.Б.4. Создайте линейный график для отображения набора данных измерений в долях единицы $(1/2, 1/4, 1/8)$. Решайте задачи на сложение и вычитание дробей, используя информацию, представленную в виде линейных графиков. Например, по линейному графику найдите и интерпретируйте разницу в длине между самым длинным и самым коротким экземпляром в коллекции насекомых.
4.
 МД.К. Геометрические измерения: понимать понятия угла и измерять углы.
МД.К. Геометрические измерения: понимать понятия угла и измерять углы.4.МД.С.5. Распознавать углы как геометрические фигуры, которые образуются там, где два луча имеют общую конечную точку, и понимать принципы измерения углов:
4.MD.C.5.а. Угол измеряется по отношению к окружности с центром в общей конечной точке лучей, принимая во внимание долю дуги окружности между точками, где два луча пересекают окружность. Угол, который проходит через 1/360 окружности, называется «углом в один градус» и может использоваться для измерения углов.
4.MD.C.5.b. Угол, который проходит через $n$ углов в один градус, называется угловой мерой, равной $n$ градусам.
4.МД.
 С.6. Измерьте углы в целых числах с помощью транспортира. Эскиз углов заданной меры.
С.6. Измерьте углы в целых числах с помощью транспортира. Эскиз углов заданной меры.4.МД.С.7. Признать угловую меру аддитивной. Когда угол разлагается на непересекающиеся части, угловая мера целого равна сумме угловых мер частей. Решите задачи на сложение и вычитание, чтобы найти неизвестные углы на диаграмме в реальном мире, и математические задачи, например, используя уравнение с символом для неизвестной меры угла.
- Измерение углов
- Геометрия букв
- В чем смысл?
4.Г. 4 класс — Геометрия
4.Г.А. Рисуйте и идентифицируйте линии и углы, а также классифицируйте фигуры по свойствам их линий и углов.
4.Г.А.1. Рисовать точки, прямые, отрезки, лучи, углы (прямые, острые, тупые), перпендикулярные и параллельные прямые. Определите их на двумерных фигурах.
4.
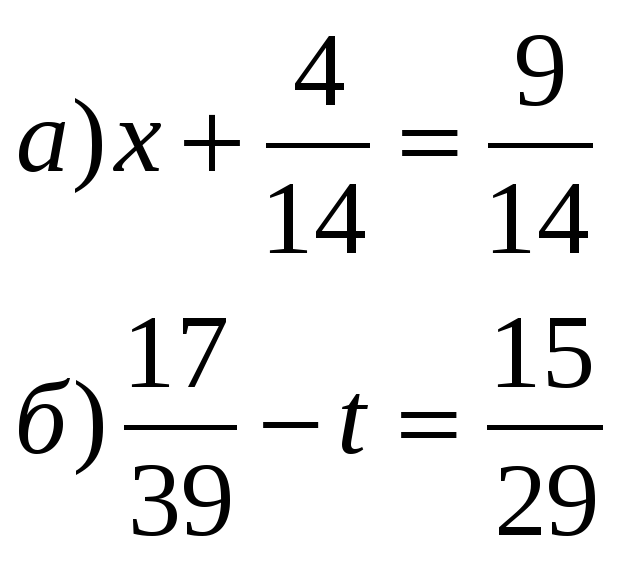



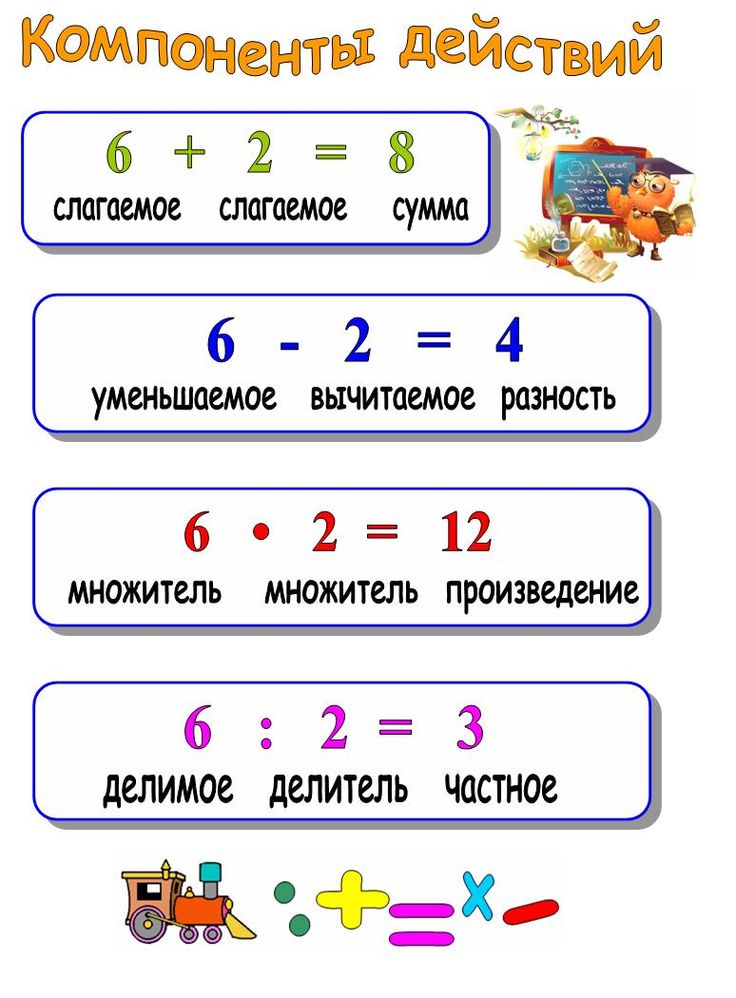 Эта точка и
есть знак умножения.
Эта точка и
есть знак умножения. А теперь посчитаем,
сколько троек — их 6, поэтому второе число — 6. Между ними ставлю знак
умножения — точку. Получилось новое числовое выражение:
А теперь посчитаем,
сколько троек — их 6, поэтому второе число — 6. Между ними ставлю знак
умножения — точку. Получилось новое числовое выражение: Второй множитель
— 2. Он показывает, сколько таких слагаемых. Это значит, по шесть надо взять
два раза. Поэтому действие умножения мы можем заменить вот таким действием
сложения:
Второй множитель
— 2. Он показывает, сколько таких слагаемых. Это значит, по шесть надо взять
два раза. Поэтому действие умножения мы можем заменить вот таким действием
сложения: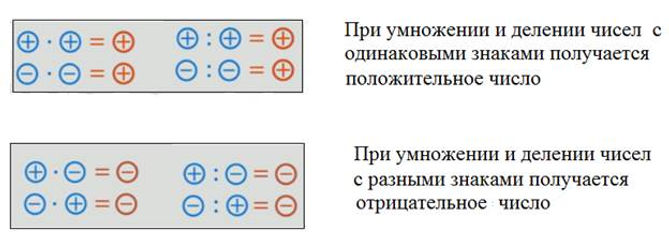 При этом:
При этом: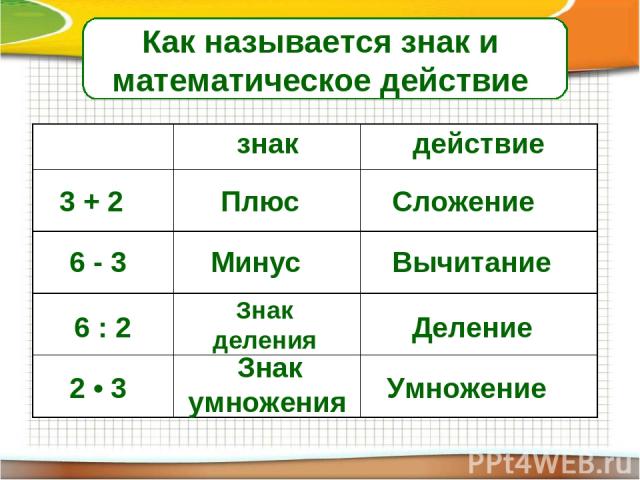
 Последние буквы в алфавите сдвигаются в начало, поэтому «я» с ключом 4 превратится в «г». Один участник переписки прибавляет k к каждой букве в сообщении, чтобы его зашифровать. Второй — расшифровывает его, отнимая от каждой буквы то же число. Таким образом слово «яблоко», зашифрованное методом Цезаря с ключом 4 превратится в «гептот».
Последние буквы в алфавите сдвигаются в начало, поэтому «я» с ключом 4 превратится в «г». Один участник переписки прибавляет k к каждой букве в сообщении, чтобы его зашифровать. Второй — расшифровывает его, отнимая от каждой буквы то же число. Таким образом слово «яблоко», зашифрованное методом Цезаря с ключом 4 превратится в «гептот». Но встает вопрос: как передать ключ? Этот вопрос не потерял своей актуальности с появлением телеграфа, телефона и интернета. С античности и до изобретения асимметричной криптографии в 70-х годах XX века хорошего решения у нас не было. Передача ключей шифрования была дорогим и сложным в организации мероприятием.
Но встает вопрос: как передать ключ? Этот вопрос не потерял своей актуальности с появлением телеграфа, телефона и интернета. С античности и до изобретения асимметричной криптографии в 70-х годах XX века хорошего решения у нас не было. Передача ключей шифрования была дорогим и сложным в организации мероприятием.
 По определению конечной группы оба слагаемых и результат всегда принадлежат группе.
По определению конечной группы оба слагаемых и результат всегда принадлежат группе.  В нашем случае сумма равна 13, и n = 1. Поскольку оба слагаемых в конечной группе меньше модуля, n может принять всего два значения.
В нашем случае сумма равна 13, и n = 1. Поскольку оба слагаемых в конечной группе меньше модуля, n может принять всего два значения. 1024, подбор такого ключа на самом мощном современном компьютере займет миллиарды лет, и считается на практике невозможным.
1024, подбор такого ключа на самом мощном современном компьютере займет миллиарды лет, и считается на практике невозможным. ba mod N
ba mod N

 Во-первых, коммутативные свойства. Начнем с коммутативного свойства сложения. Коммутативное свойство сложения гласит, что порядок сложения двух чисел не меняет их суммы. Переменное представление этого 𝑎 плюс 𝑏 — это то же самое, что сказать 𝑏 плюс 𝑎. Или четыре плюс три — это то же самое, что три плюс четыре. Порядок здесь не имеет значения. Свойство коммутативности можно применить и к умножению.
Во-первых, коммутативные свойства. Начнем с коммутативного свойства сложения. Коммутативное свойство сложения гласит, что порядок сложения двух чисел не меняет их суммы. Переменное представление этого 𝑎 плюс 𝑏 — это то же самое, что сказать 𝑏 плюс 𝑎. Или четыре плюс три — это то же самое, что три плюс четыре. Порядок здесь не имеет значения. Свойство коммутативности можно применить и к умножению.
 И третье в нашем списке — свойства идентичности. Начиная со свойства идентичности сложения, это свойство утверждает, что сумма слагаемого и нуля является слагаемым. 𝑎 плюс ноль равно 𝑎. Семь плюс ноль будет семь. Переходя к тождественному свойству умножения, давайте внимательно посмотрим на все изменения. Свойство идентичности умножения говорит, что произведение фактора и один является этим фактором. В нашем примере 𝑎 умножить на один равно 𝑎. Обратите внимание, что тождественное свойство умножения умножает множитель на единицу.
И третье в нашем списке — свойства идентичности. Начиная со свойства идентичности сложения, это свойство утверждает, что сумма слагаемого и нуля является слагаемым. 𝑎 плюс ноль равно 𝑎. Семь плюс ноль будет семь. Переходя к тождественному свойству умножения, давайте внимательно посмотрим на все изменения. Свойство идентичности умножения говорит, что произведение фактора и один является этим фактором. В нашем примере 𝑎 умножить на один равно 𝑎. Обратите внимание, что тождественное свойство умножения умножает множитель на единицу. Распределительное свойство говорит об этом. Чтобы умножить сумму на число, умножьте каждое слагаемое суммы на число за скобками. Это много слов. Давайте посмотрим, как это выглядит. Начнем с примера, в котором используются числа.
Распределительное свойство говорит об этом. Чтобы умножить сумму на число, умножьте каждое слагаемое суммы на число за скобками. Это много слов. Давайте посмотрим, как это выглядит. Начнем с примера, в котором используются числа. Вот этот пример с цифрами. Пять раз два плюс пять раз три — это то же самое, что сказать пять раз пять или пять раз два плюс три. Вот диаграмма, которая поможет вам обобщить все различные свойства. Эти свойства лягут в основу решения всевозможных уравнений.
Вот этот пример с цифрами. Пять раз два плюс пять раз три — это то же самое, что сказать пять раз пять или пять раз два плюс три. Вот диаграмма, которая поможет вам обобщить все различные свойства. Эти свойства лягут в основу решения всевозможных уравнений.
 И мы обычно выражаем эти Заметки словами Плюс (или больше ) и Минус (или меньше ). Таким образом, $2+3$, или на $2$ больше $3$, обозначает сумму чисел $2$ и $3$, то есть $5$. А $5-3$ или $5$ меньше $3$ обозначают разницу, которая возникает при вычитании $3$ из $5$, то есть $2$. [ Обратите внимание на четкое различие между двумя употреблениями знаков $+$ и $-$ .]
И мы обычно выражаем эти Заметки словами Плюс (или больше ) и Минус (или меньше ). Таким образом, $2+3$, или на $2$ больше $3$, обозначает сумму чисел $2$ и $3$, то есть $5$. А $5-3$ или $5$ меньше $3$ обозначают разницу, которая возникает при вычитании $3$ из $5$, то есть $2$. [ Обратите внимание на четкое различие между двумя употреблениями знаков $+$ и $-$ .] — латинский оригинал: 1727 г.), стр. 9:
— латинский оригинал: 1727 г.), стр. 9:


 До этого у этого пациента мы уже удаляли один зуб мудрости с фолликулярной кистой.
До этого у этого пациента мы уже удаляли один зуб мудрости с фолликулярной кистой.

 Но лучше сохранить зуб мудрости в целости и сохранности.
Но лучше сохранить зуб мудрости в целости и сохранности.
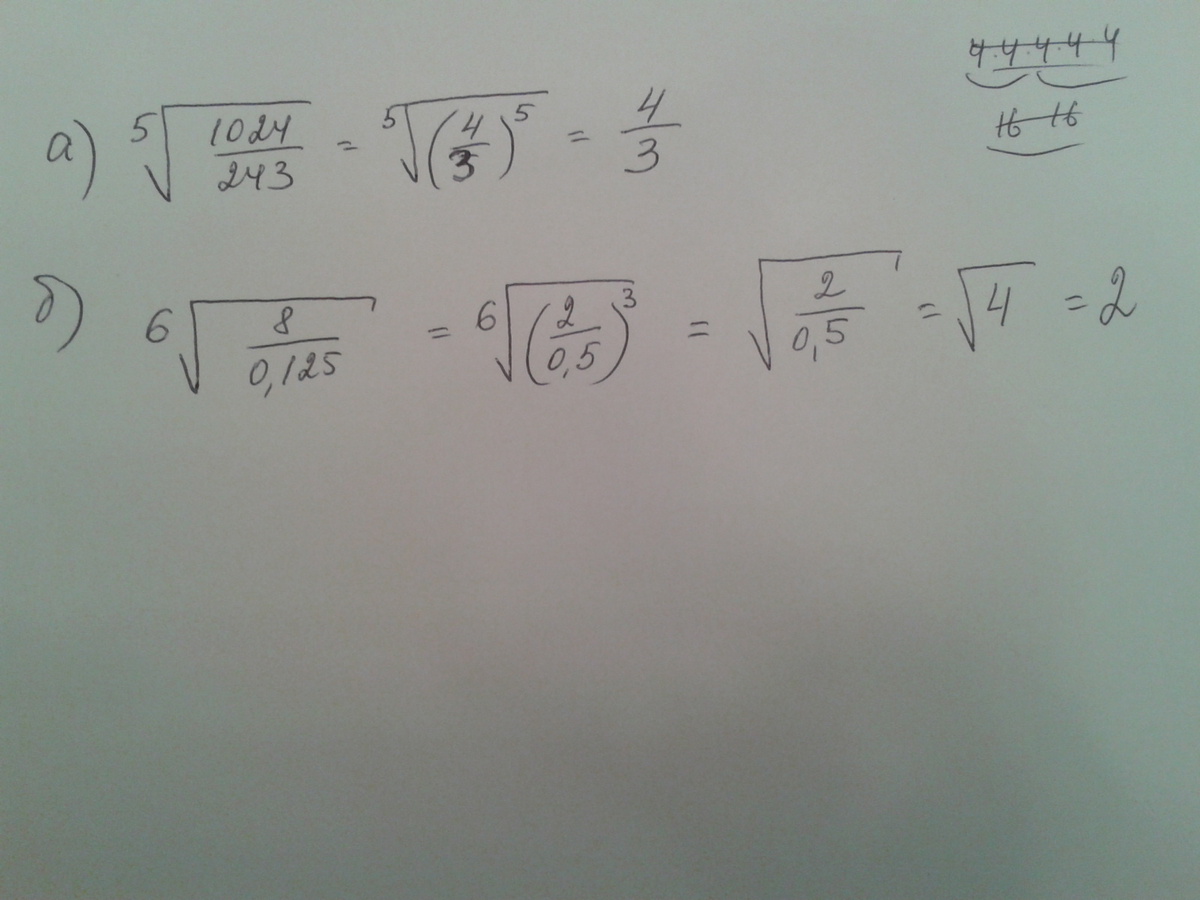 А форма этого корня не соответствует пока лункам зуба, в которых находились корни шестерки. Поэтому лунки в месте удаления зуба корректируются бором до получения нами необходимого размера и конфигурации под стереолитографическую модель, которая, в свою очередь, обеспечивает сохранение места для нового зуба в целости.
А форма этого корня не соответствует пока лункам зуба, в которых находились корни шестерки. Поэтому лунки в месте удаления зуба корректируются бором до получения нами необходимого размера и конфигурации под стереолитографическую модель, которая, в свою очередь, обеспечивает сохранение места для нового зуба в целости.
 Так как в текущий момент это место занимает стериолитографическая модель, то пока ее мой помощник извлекает, у меня было несколько секунд сфотографировать восьмерку, наш зуб-донор:
Так как в текущий момент это место занимает стериолитографическая модель, то пока ее мой помощник извлекает, у меня было несколько секунд сфотографировать восьмерку, наш зуб-донор:
 8, пока скрыт, находится под десной. Как можно видеть на фотографии, пока в месте размещения восьмерки сделан аккуратный разрез. Вот так этот зуб выглядит на томографии:
8, пока скрыт, находится под десной. Как можно видеть на фотографии, пока в месте размещения восьмерки сделан аккуратный разрез. Вот так этот зуб выглядит на томографии:
 н. «зуб нового поколения». Польза зубов-восьмерок в век цифровых технологий становится очевидной и востребованной.
н. «зуб нового поколения». Польза зубов-восьмерок в век цифровых технологий становится очевидной и востребованной.


 Пересадка зуба
Пересадка зуба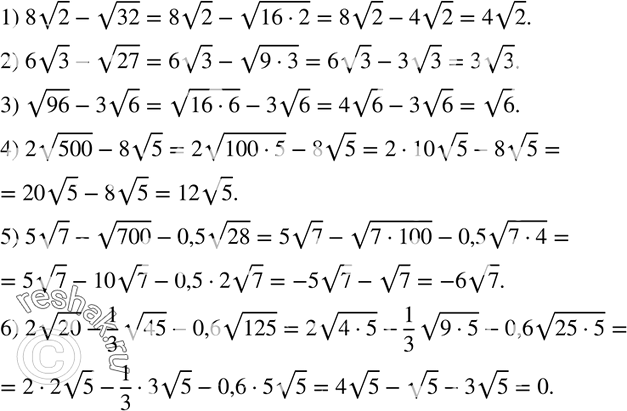 немного. Я объясню, как мы идем.
немного. Я объясню, как мы идем.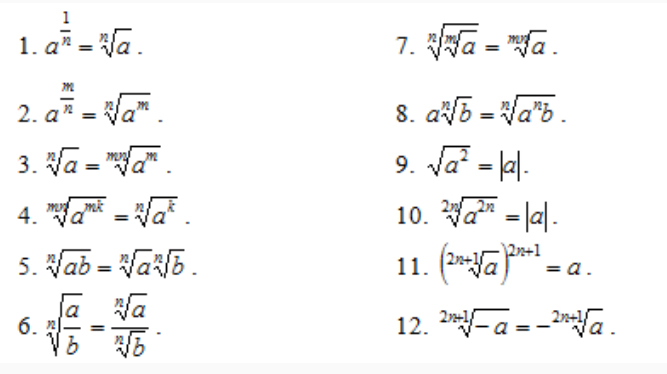 Затем я могу вытащить из радикала любой фактор, который встречается три раза. Так как 8 = 2 3 , то этот радикал полностью упростится.
Затем я могу вытащить из радикала любой фактор, который встречается три раза. Так как 8 = 2 3 , то этот радикал полностью упростится.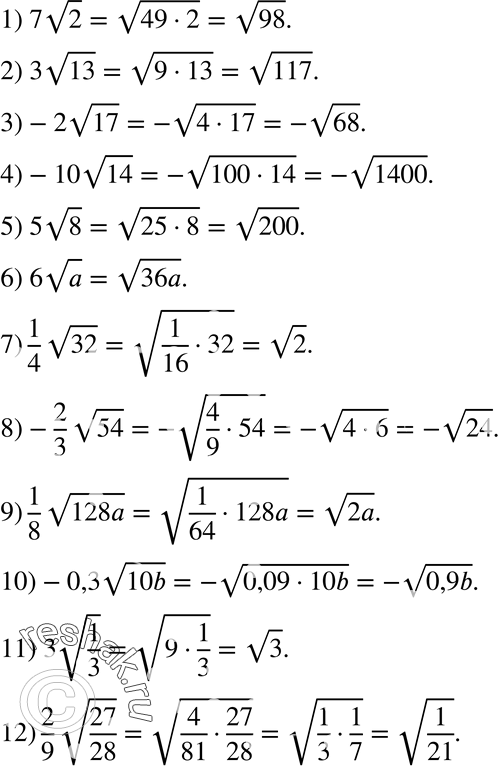 Я беру корень пятой степени, поэтому я могу вытащить из корня все, для чего у меня есть пять копий.
Я беру корень пятой степени, поэтому я могу вытащить из корня все, для чего у меня есть пять копий. Это делается для того, чтобы не принимать во внимание, нужны ли в вашем ответе столбцы абсолютных значений. Если вы не уверены, о чем я говорю, проверьте здесь.
Это делается для того, чтобы не принимать во внимание, нужны ли в вашем ответе столбцы абсолютных значений. Если вы не уверены, о чем я говорю, проверьте здесь. Сейчас это не так. Так что я сначала упрощу радикалы, а потом посмотрю, смогу ли я пойти дальше.
Сейчас это не так. Так что я сначала упрощу радикалы, а потом посмотрю, смогу ли я пойти дальше. Для кубического корня мне понадобится три копии. Вот что я умножу на эту дробь.
Для кубического корня мне понадобится три копии. Вот что я умножу на эту дробь.
 potenzieren, возведение в степень) — это нахождение числа по известному значению его логарифма, то есть решение уравнения:
potenzieren, возведение в степень) — это нахождение числа по известному значению его логарифма, то есть решение уравнения:
 f)))).
f)))).
 Проверка домашнего задания
Проверка домашнего задания
 Название,
которой узнаем, ответив на вопросы.
Название,
которой узнаем, ответив на вопросы.
 Какой вывод мы можем сделать?
Какой вывод мы можем сделать?

 а) (с4)5 = с4·5 = с20 2.
а) (х2)7 = х2·7=
х14
а) (с4)5 = с4·5 = с20 2.
а) (х2)7 = х2·7=
х14
 а7(а6)2 =
а7(а6)2 =  а7(а6)2 =
а7(а6)2 =  а7(а6)2 =
а7(а6)2 =  — Журнал Кванта , 29 января 2018 г.
— Журнал Кванта , 29 января 2018 г. Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/exponentiation. Доступ 9 мая. 2023.
Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/exponentiation. Доступ 9 мая. 2023. Определения и примеры »
Определения и примеры » 2}\) и \(\theta\) — это угол между вектором в комплексной плоскости и осью \(x\), как определено на этом рисунке: 92}.\)
2}\) и \(\theta\) — это угол между вектором в комплексной плоскости и осью \(x\), как определено на этом рисунке: 92}.\) 9{i\theta}.\]
9{i\theta}.\]
 9{i\omega t},\]
9{i\omega t},\] Таким образом, приведенное выше интегро-дифференциальное уравнение может быть гораздо проще записано как
Таким образом, приведенное выше интегро-дифференциальное уравнение может быть гораздо проще записано как
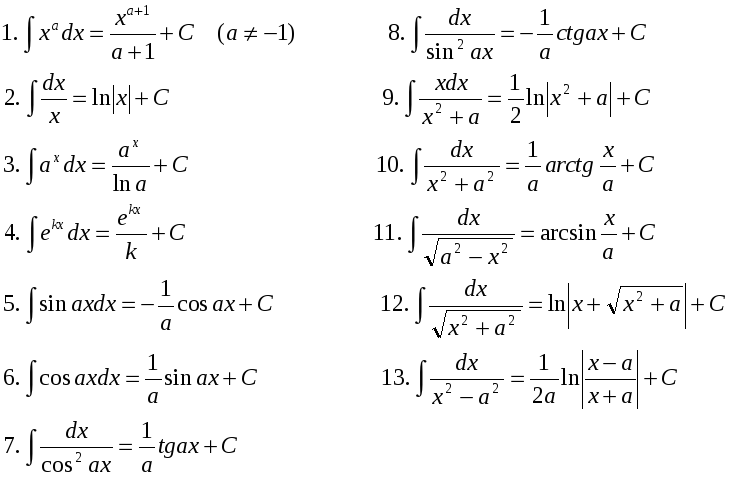 Эта тень и есть проекция тела птицы на ось х. А если бы Солнце находилось справа от птицы, мы бы увидели ее тень на оси у, в районе цифры 8. Это есть проекция тела птицы на ось ординат. Она показывает, на какой высоте летит птица. То есть, расстояние от «земли» (от оси х) до нее.
Эта тень и есть проекция тела птицы на ось х. А если бы Солнце находилось справа от птицы, мы бы увидели ее тень на оси у, в районе цифры 8. Это есть проекция тела птицы на ось ординат. Она показывает, на какой высоте летит птица. То есть, расстояние от «земли» (от оси х) до нее. То есть, его тень перемещается вправо на 6 единиц (клеточек). Такое же изменение проекции происходит по оси у. То есть, он одновременно поднимается вверх также на 6 единиц.
То есть, его тень перемещается вправо на 6 единиц (клеточек). Такое же изменение проекции происходит по оси у. То есть, он одновременно поднимается вверх также на 6 единиц. Если человек будет находиться, например, в точке, тень от которой падает на ось х в точке 15, он будет находиться на высоте 15. Два параметра — положение тени человека на оси абсцисс и высота, на которой он находится, жестко связаны между собой вышеуказанной формулой.
Если человек будет находиться, например, в точке, тень от которой падает на ось х в точке 15, он будет находиться на высоте 15. Два параметра — положение тени человека на оси абсцисс и высота, на которой он находится, жестко связаны между собой вышеуказанной формулой. В то же самое время, его тень (проекция на ось х) переместилась вправо всего на 5 единиц. Разделив 10 на 5, мы получаем цифру 2. Эта цифра — соотношение высоты и удаленности от нуля по оси х — есть показатель крутизны дороги. Понятно?
В то же самое время, его тень (проекция на ось х) переместилась вправо всего на 5 единиц. Разделив 10 на 5, мы получаем цифру 2. Эта цифра — соотношение высоты и удаленности от нуля по оси х — есть показатель крутизны дороги. Понятно? 5. Соответственно, формулы, которыми мы опишем две последние дороги будут выглядеть как у = 2х и у = 0.5х.
5. Соответственно, формулы, которыми мы опишем две последние дороги будут выглядеть как у = 2х и у = 0.5х. 5x. Не очень сложно, да?
5x. Не очень сложно, да?
 Точнее, мы можем это сделать, но полученная цифра не будет соответствовать крутизне в средней точке между ними. Смотрите:
Точнее, мы можем это сделать, но полученная цифра не будет соответствовать крутизне в средней точке между ними. Смотрите:
 Мы подставляем в производную значение проекции на ось х, точки дороги, крутизна которой нас интересует. Допустим, мы хотим узнать, насколько круто поднимается дорога в точке, находящейся над цифрой 1 по оси х. Мы подставляем эту единицу в производную, и вычисляем значение:
Мы подставляем в производную значение проекции на ось х, точки дороги, крутизна которой нас интересует. Допустим, мы хотим узнать, насколько круто поднимается дорога в точке, находящейся над цифрой 1 по оси х. Мы подставляем эту единицу в производную, и вычисляем значение: То есть, в указанных точках дороги подниматься так же тяжело, как по соответствующим этим точкам прямым. «Здесь так же круто, как там».
То есть, в указанных точках дороги подниматься так же тяжело, как по соответствующим этим точкам прямым. «Здесь так же круто, как там».
 Но дорога не может висеть в воздухе, она же должна опираться на ось х?
Но дорога не может висеть в воздухе, она же должна опираться на ось х?

 Если мы найдем производную этой функции, то обнаружим, что она выглядит точно так же, как производная от функции f (x) = x2! То есть, как f ‘(x) = 2x. Ибо при нахождении производной четверка (постоянная) будет отброшена.
Если мы найдем производную этой функции, то обнаружим, что она выглядит точно так же, как производная от функции f (x) = x2! То есть, как f ‘(x) = 2x. Ибо при нахождении производной четверка (постоянная) будет отброшена.

 Для проверки вы можете примерно посчитать закрашенные клетки на картинке.
Для проверки вы можете примерно посчитать закрашенные клетки на картинке. Результат вычитания и есть искомая площадь.
Результат вычитания и есть искомая площадь.
 .. Читать дальше
.. Читать дальше Сам процесс воплощения и его результат имеет обратное влияние на саму изначальную Идею, так Идея меняется. Вот так вот всё в нашем Мире и волнуется, колеблется, воюет и успокаивается, что бы потом опять Идеей изменений прийти к стабильному равновесию. Всё равно!
Сам процесс воплощения и его результат имеет обратное влияние на саму изначальную Идею, так Идея меняется. Вот так вот всё в нашем Мире и волнуется, колеблется, воюет и успокаивается, что бы потом опять Идеей изменений прийти к стабильному равновесию. Всё равно!  .. Читать далее
.. Читать далее Вы же смотрите на спидометр иногда?
Вы же смотрите на спидометр иногда?  .. Читать далее
.. Читать далее




 6 степени 8 равно, 6 в, 3-й, степени это 1-й пример тогда степени. Приравниваются, 8 минут сексановый так 11 из, 8 что то надо поднять чтобы получилось 35 да экстренная суперномер дальше 2-й 5. Степень 12 и справа сразу тоже делаем дать в какой то степени 1 лет на 1 0 0 Угу так посмотрим что у нас Здесь варианта 16 степень 8 некрона 200
Да 4,5, почти 3,5 да 3,5, так, дальше 81 справа тройка. Ну, тоже вспоминаю, что 81 это 9 в квадрате, а 9 и 3 тоже связаны между собой. А тариф в квадрате это 9. Поэтому записываю вот так 1 делить на 81 это значит 3 4-й на Иксмен 6 равно 3. Тогда это можно вот так приписать 3 в минус, 4-й на минус 6. Кстати, вам там оформление важно. Ну, то есть то, что ты сейчас пишешь или только ответы? Так, главное, чтобы подробно было расписано все так просто. В каждом из этих примеров можно все проверки делать-то нет, если не требуется. Ладно так минус 4 на минеть 3 в 1-й степени все теперь можем всего не приравнять. Из скобочки раскрыть минус 4 х + 24 равна одному.
6 степени 8 равно, 6 в, 3-й, степени это 1-й пример тогда степени. Приравниваются, 8 минут сексановый так 11 из, 8 что то надо поднять чтобы получилось 35 да экстренная суперномер дальше 2-й 5. Степень 12 и справа сразу тоже делаем дать в какой то степени 1 лет на 1 0 0 Угу так посмотрим что у нас Здесь варианта 16 степень 8 некрона 200
Да 4,5, почти 3,5 да 3,5, так, дальше 81 справа тройка. Ну, тоже вспоминаю, что 81 это 9 в квадрате, а 9 и 3 тоже связаны между собой. А тариф в квадрате это 9. Поэтому записываю вот так 1 делить на 81 это значит 3 4-й на Иксмен 6 равно 3. Тогда это можно вот так приписать 3 в минус, 4-й на минус 6. Кстати, вам там оформление важно. Ну, то есть то, что ты сейчас пишешь или только ответы? Так, главное, чтобы подробно было расписано все так просто. В каждом из этих примеров можно все проверки делать-то нет, если не требуется. Ладно так минус 4 на минеть 3 в 1-й степени все теперь можем всего не приравнять. Из скобочки раскрыть минус 4 х + 24 равна одному. Так получается 4 угу так минус 4 х равна 1 минус 24 минус 23 на минус умножаем левой правой части. Вот здесь плюс здесь прос равна 23 4-е это 5 целых 3 4-й 5-75 нужно записать. Ну вроде так так, 7-е пример 7 степени, 2 плюс оставим пока, а с правой части 3 4 0 3 3 4 3 Если поделим на 7428 и 63 остается 949-77-71, то 73-й 72 так теснопер все встречи вот так приравниваем 2 плюс экстра. Да 4,5 почти 3,5 да 3,5 так дальше 81 справа тройка, ну тоже вспоминаю что 81 это 9 в квадрате, а 9 и 3 тоже связаны между собой. А тариф в квадрате, это 9 поэтому записываю вот. Так 1 делить на 81 это значит 3 4-й на иксмен 6 равно 3 тогда это Можно вот так. Приписать 3 в минус, 4-й на минус, 6 кстати вам там оформление важно, ну то есть то что ты сейчас пишешь или только. Ответы, так, главное, чтобы подробно, было расписано все. Так, просто в каждом из этих. Примеров можно все проверки делать то. Нет если не, требуется ладно так минус 4 на минеть 3 в 1-й степени все теперь можем всего не приравнять из скобочки раскрыть минус 4 х + 24 равна одному так, получается, 4 угу так минус 4 х равна, 1 минус 24 минус 23.
Так получается 4 угу так минус 4 х равна 1 минус 24 минус 23 на минус умножаем левой правой части. Вот здесь плюс здесь прос равна 23 4-е это 5 целых 3 4-й 5-75 нужно записать. Ну вроде так так, 7-е пример 7 степени, 2 плюс оставим пока, а с правой части 3 4 0 3 3 4 3 Если поделим на 7428 и 63 остается 949-77-71, то 73-й 72 так теснопер все встречи вот так приравниваем 2 плюс экстра. Да 4,5 почти 3,5 да 3,5 так дальше 81 справа тройка, ну тоже вспоминаю что 81 это 9 в квадрате, а 9 и 3 тоже связаны между собой. А тариф в квадрате, это 9 поэтому записываю вот. Так 1 делить на 81 это значит 3 4-й на иксмен 6 равно 3 тогда это Можно вот так. Приписать 3 в минус, 4-й на минус, 6 кстати вам там оформление важно, ну то есть то что ты сейчас пишешь или только. Ответы, так, главное, чтобы подробно, было расписано все. Так, просто в каждом из этих. Примеров можно все проверки делать то. Нет если не, требуется ладно так минус 4 на минеть 3 в 1-й степени все теперь можем всего не приравнять из скобочки раскрыть минус 4 х + 24 равна одному так, получается, 4 угу так минус 4 х равна, 1 минус 24 минус 23.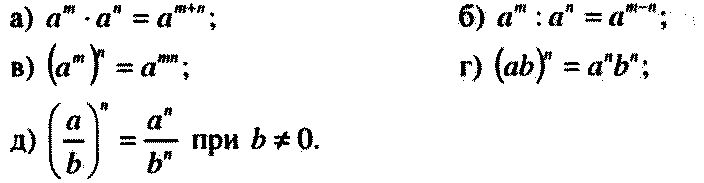 На минус умножаем левой правой, части вот здесь +. Здесь, прос равна 23 4-е это 5 целых 3 4-й 5-75 нужно записать ну вроде, так.
Так, 6 равна а там же 8 икс. То есть там и два-два в 3-й. Умножить на вик да, то есть, получается, будет 23 икс да угу в степени перемножаются 3 0 0 Ну, слева то, что будет здесь 1/2 это 2 минус, 1-й минус 1-е и * х мин 6. Ну а справа, как ты сказал, 2 степени 3 икс угу. Так что же это будет? Нината нет, получается, выписатся просто икс + 6 минус + 6 минус 1 икс это минусик Угу Мензиес, страна транексам, а не травматина. Как же это сделать можно? А как решить икс собираем вместе либо слева, либо справа на коровна, куда тебе нравится спать будет минус 4 икс рано с 6 а минус 6 да ну и получается, что икс равен 24 почти то есть от минусов уничтожаем вот так плюс плюс делаем слева и справа, потому что мы можем на минус 1 * обе части 6 поделить надо на 4 поделить. Пасть. Ну, это 1,5, так дальше был 9-й, что 9 здесь 81 тоже что можно делать, на это будет получается справа 9 во 2-й да я Огу немножк на 2 икс угу, вот я с его только не вижу, что там 9 в какой степени 6 на 1 что-то лохтората сейчас? Так 6 равна а там же 8 икс то есть там и 22 в 3-й * вик да, то-есть получается будет 23 икс да угу в степени.
На минус умножаем левой правой, части вот здесь +. Здесь, прос равна 23 4-е это 5 целых 3 4-й 5-75 нужно записать ну вроде, так.
Так, 6 равна а там же 8 икс. То есть там и два-два в 3-й. Умножить на вик да, то есть, получается, будет 23 икс да угу в степени перемножаются 3 0 0 Ну, слева то, что будет здесь 1/2 это 2 минус, 1-й минус 1-е и * х мин 6. Ну а справа, как ты сказал, 2 степени 3 икс угу. Так что же это будет? Нината нет, получается, выписатся просто икс + 6 минус + 6 минус 1 икс это минусик Угу Мензиес, страна транексам, а не травматина. Как же это сделать можно? А как решить икс собираем вместе либо слева, либо справа на коровна, куда тебе нравится спать будет минус 4 икс рано с 6 а минус 6 да ну и получается, что икс равен 24 почти то есть от минусов уничтожаем вот так плюс плюс делаем слева и справа, потому что мы можем на минус 1 * обе части 6 поделить надо на 4 поделить. Пасть. Ну, это 1,5, так дальше был 9-й, что 9 здесь 81 тоже что можно делать, на это будет получается справа 9 во 2-й да я Огу немножк на 2 икс угу, вот я с его только не вижу, что там 9 в какой степени 6 на 1 что-то лохтората сейчас? Так 6 равна а там же 8 икс то есть там и 22 в 3-й * вик да, то-есть получается будет 23 икс да угу в степени. Перемножаются 300 ну слева то, что будет здесь-одна 2-я это 2 минус, 1-й минус 1-е и *, х мин 6 ну а, справа как, ты сказал 2 степени 3 икс угу так что, же это будет нината нет получается выписатся просто. Икс + 6 минус + 6 минус 1 икс это минусик угу мензиес страна, транексам а не травматина как же. Это сделать, можно а как, решить икс, собираем вместе, либо слева-либо справа на, коровна? Куда тебе, нравится спать будет минус 4 икс, рано с 6 а минус. 6 да ну и, получается что икс равен 24 почти то есть от минусов уничтожаем вот.
Ну давай лучше, 10 сек, не 3 на 10 степени мин секс-десятку можно сократить. Но что нам это дает, тоже не очень красиво, так сейчас посмотрим. 6 степени 3 минус секс 6 на 10 в квадрате. Ну, я сейчас моносекс, шестерки. Если сократим все равно разные основания, получается, то страх какой-то странный. Например, сейчас надо подумать на 6:10, 3 минусес ага, ну давай тогда дальше, прости здесь шей степени 3 на 6 Ганимеде 6 на 10 в квадрате на 10 минус. Вот эту шестерку можно с этой слева сократитесь, будет 6 во 2-й, так, значит, так, двойка теперь все, что связано с, наверное, в 1 сторону перемещаемом на 10 в степени умножим на 10 в степени х слева и справа.
Перемножаются 300 ну слева то, что будет здесь-одна 2-я это 2 минус, 1-й минус 1-е и *, х мин 6 ну а, справа как, ты сказал 2 степени 3 икс угу так что, же это будет нината нет получается выписатся просто. Икс + 6 минус + 6 минус 1 икс это минусик угу мензиес страна, транексам а не травматина как же. Это сделать, можно а как, решить икс, собираем вместе, либо слева-либо справа на, коровна? Куда тебе, нравится спать будет минус 4 икс, рано с 6 а минус. 6 да ну и, получается что икс равен 24 почти то есть от минусов уничтожаем вот.
Ну давай лучше, 10 сек, не 3 на 10 степени мин секс-десятку можно сократить. Но что нам это дает, тоже не очень красиво, так сейчас посмотрим. 6 степени 3 минус секс 6 на 10 в квадрате. Ну, я сейчас моносекс, шестерки. Если сократим все равно разные основания, получается, то страх какой-то странный. Например, сейчас надо подумать на 6:10, 3 минусес ага, ну давай тогда дальше, прости здесь шей степени 3 на 6 Ганимеде 6 на 10 в квадрате на 10 минус. Вот эту шестерку можно с этой слева сократитесь, будет 6 во 2-й, так, значит, так, двойка теперь все, что связано с, наверное, в 1 сторону перемещаемом на 10 в степени умножим на 10 в степени х слева и справа. Тогда здесь будет слева 10 степени икс длитесь степени икс так напишем, потому что 6 степени минус. Как бы делим на шесте? А справа будет 10 в квадрате, поделить на 6 в квадрате? Вот что-то получается и смотри слева 106 в степени икс 10 шестых степеней справа, 10 шестых в квадрате основания получились одинаковыми. 10 шестых, следовательно, Экс равно двум брать, так нет, попросив пока что нет, давай 12-й так и оставляем КСПпт 7-й, а 128100 дозачислили. Если разложить или так, может, знаешь, 128 завтра да, да, да. Ну-давай, лучше 10 сек не 3 на 1 0 Степени, мин секс десятку можно сократить но. Что нам это дает тоже не очень красиво так сейчас посмотрим 6 степени 3 минус, секс 6 на 10 в квадрате ну я сейчас. Моносекс шестерки Если сократим все, равно, разные основания получается то страх. Какой то странный например сейчас Надо подумать на. 6103 минусес, ага ну. Давай, тогда Дальше прости здесь шей степени 3 на 6 ганимеде 6 на 10 в квадрате, на 10? Минус, вот эту шестерку можно с. Этой слева сократитесь будет 6 во, 2-й, так значит так, двойка теперь все что связано с наверное в 1 сторону перемещаемом на 10 в степени умножим на 10 в степени х слева.
Тогда здесь будет слева 10 степени икс длитесь степени икс так напишем, потому что 6 степени минус. Как бы делим на шесте? А справа будет 10 в квадрате, поделить на 6 в квадрате? Вот что-то получается и смотри слева 106 в степени икс 10 шестых степеней справа, 10 шестых в квадрате основания получились одинаковыми. 10 шестых, следовательно, Экс равно двум брать, так нет, попросив пока что нет, давай 12-й так и оставляем КСПпт 7-й, а 128100 дозачислили. Если разложить или так, может, знаешь, 128 завтра да, да, да. Ну-давай, лучше 10 сек не 3 на 1 0 Степени, мин секс десятку можно сократить но. Что нам это дает тоже не очень красиво так сейчас посмотрим 6 степени 3 минус, секс 6 на 10 в квадрате ну я сейчас. Моносекс шестерки Если сократим все, равно, разные основания получается то страх. Какой то странный например сейчас Надо подумать на. 6103 минусес, ага ну. Давай, тогда Дальше прости здесь шей степени 3 на 6 ганимеде 6 на 10 в квадрате, на 10? Минус, вот эту шестерку можно с. Этой слева сократитесь будет 6 во, 2-й, так значит так, двойка теперь все что связано с наверное в 1 сторону перемещаемом на 10 в степени умножим на 10 в степени х слева. И, справа тогда здесь будет слева 10 степени икс длитесь степени, икс так, напишем потому, что 6 степени. Минус как бы делим. На, шесте а справа будет 10 в квадрате поделить на 6 в квадрате вот. Что то получается и смотри слева 106 в степени икс 10 шестых степеней справа 10 шестых в квадрате, основания, получились одинаковыми 10 шестых следовательно экс равно.
Угу, Иксина 4 справа приходит плюсом, да, минус 3 а ничего, ничотак 14-й. Ну там справа 4 в квадрате да записываем слева логарифма опять с непонятными основаниями логарифм, что 88125 эксентри справа 2 в квадрате основания равны приравниваем степени логарифм Посоне 85 икс минус 3 равно 2 отсюда 5 минус 3 равно 8 в квадрате определение логарифма то есть о логарифме основание возводится в степень, которая справа однокомнат 5 равно 8 квадрате 64 и + 3-67. Что-то как тут раньше не делится? Ну ладно, их равно да, написать засчитай 67 делить на 5065, делим на 5 это 13-13, еще 25134 что ли? Донократия, проверим 6 7 Делейна 5-13 целых 4 пятнарик взятьесли так это 14-й номер.
И, справа тогда здесь будет слева 10 степени икс длитесь степени, икс так, напишем потому, что 6 степени. Минус как бы делим. На, шесте а справа будет 10 в квадрате поделить на 6 в квадрате вот. Что то получается и смотри слева 106 в степени икс 10 шестых степеней справа 10 шестых в квадрате, основания, получились одинаковыми 10 шестых следовательно экс равно.
Угу, Иксина 4 справа приходит плюсом, да, минус 3 а ничего, ничотак 14-й. Ну там справа 4 в квадрате да записываем слева логарифма опять с непонятными основаниями логарифм, что 88125 эксентри справа 2 в квадрате основания равны приравниваем степени логарифм Посоне 85 икс минус 3 равно 2 отсюда 5 минус 3 равно 8 в квадрате определение логарифма то есть о логарифме основание возводится в степень, которая справа однокомнат 5 равно 8 квадрате 64 и + 3-67. Что-то как тут раньше не делится? Ну ладно, их равно да, написать засчитай 67 делить на 5065, делим на 5 это 13-13, еще 25134 что ли? Донократия, проверим 6 7 Делейна 5-13 целых 4 пятнарик взятьесли так это 14-й номер. Дальше все записал угу, если что, это пересмотрю. Просто, конечно, да так. Вариант 2-й. Тут номеров нет, не удобно так ну смотри 7 степени семьи справа тоже надо какой-то сделать степень 3403343. На что делится Анриале + 4 + 31010 неделитило слева семерка у нас в основании давай попробуем на 7 поделить 343 поделить на 77 на 4 2 0 Угу иксина, 4 справа приходит плюсом да минус 3 а ничего ничотак 14-й, ну, там справа 4 В квадрате да, записываем слева логарифма опять с непонятными основаниями логарифм что 88125 эксентри справа 2 в Квадрате основания равны приравниваем, степени логарифм посоне 8 пять-икс минус 3 равно 2 отсюда 5 минус 3. Равно 8 в квадрате Определение Логарифма то есть о логарифме основание возводится в Степень которая справа однокомнат 5 равно 8 квадрате 64 и + 3-67 что то как тут раньше не делится ну ладно их равно да, написать засчитай 67. Делить на 5065 делим на 5 это 13-13 еще 25134 что ли донократия проверим 67 делейна 5-13 целых 4 пятнарик взятьесли так это 14-й номер Дальше, все, записал угу если что это пересмотрю просто конечно да так вариант 2-й тут номеров нет.
Дальше все записал угу, если что, это пересмотрю. Просто, конечно, да так. Вариант 2-й. Тут номеров нет, не удобно так ну смотри 7 степени семьи справа тоже надо какой-то сделать степень 3403343. На что делится Анриале + 4 + 31010 неделитило слева семерка у нас в основании давай попробуем на 7 поделить 343 поделить на 77 на 4 2 0 Угу иксина, 4 справа приходит плюсом да минус 3 а ничего ничотак 14-й, ну, там справа 4 В квадрате да, записываем слева логарифма опять с непонятными основаниями логарифм что 88125 эксентри справа 2 в Квадрате основания равны приравниваем, степени логарифм посоне 8 пять-икс минус 3 равно 2 отсюда 5 минус 3. Равно 8 в квадрате Определение Логарифма то есть о логарифме основание возводится в Степень которая справа однокомнат 5 равно 8 квадрате 64 и + 3-67 что то как тут раньше не делится ну ладно их равно да, написать засчитай 67. Делить на 5065 делим на 5 это 13-13 еще 25134 что ли донократия проверим 67 делейна 5-13 целых 4 пятнарик взятьесли так это 14-й номер Дальше, все, записал угу если что это пересмотрю просто конечно да так вариант 2-й тут номеров нет. Дальше 1/4 сеген 2 экс мес 19 а здесь 1 делит на 6 4 Ну, в принципе, можно в степень основание оставить 1/4. То есть здесь, как есть в степени 2 ксидент ой удобно, так, а справа 1 делить на 64-64 это 4 в какой степени 4 в квадрате это 1643 это как раз-таки 64 поэтому 14 в кубе есть еще сколько. Желательно добавить и есть скобки, да так, так, все степени приравнивай мне писать не удобно. 2 икс на 12 равнородства Икс Тимуровна 19 + 3 2 0 2 2 2 2 Да ну, их все равно 11 конечно, да, но агентство так дальше слева 16936. Возможно, на самом деле по-разному сделать либо либо основание 6 выбрали, либо основание 1/6 давай на что сделаем. Значит, слева 16 так остается в степени 15 минус икс, то есть от 15 минус никс так, а справа 36 это 6 в квадрате. Но если 16 берем, то 1 штаев минус 2-я получится не старай, приравниваем степени 15 минут Иксанова отсюда минус равно 15 справа, хоть с минусом минус 15 минус 2 минус 172012 посмотри 15 пришла вправо, станет с минусом минус 15 минус 2 станена отсюда х равно 17-17.
Дальше 1/4 сеген 2 экс мес 19 а здесь 1 делит на 6 4 Ну, в принципе, можно в степень основание оставить 1/4. То есть здесь, как есть в степени 2 ксидент ой удобно, так, а справа 1 делить на 64-64 это 4 в какой степени 4 в квадрате это 1643 это как раз-таки 64 поэтому 14 в кубе есть еще сколько. Желательно добавить и есть скобки, да так, так, все степени приравнивай мне писать не удобно. 2 икс на 12 равнородства Икс Тимуровна 19 + 3 2 0 2 2 2 2 Да ну, их все равно 11 конечно, да, но агентство так дальше слева 16936. Возможно, на самом деле по-разному сделать либо либо основание 6 выбрали, либо основание 1/6 давай на что сделаем. Значит, слева 16 так остается в степени 15 минус икс, то есть от 15 минус никс так, а справа 36 это 6 в квадрате. Но если 16 берем, то 1 штаев минус 2-я получится не старай, приравниваем степени 15 минут Иксанова отсюда минус равно 15 справа, хоть с минусом минус 15 минус 2 минус 172012 посмотри 15 пришла вправо, станет с минусом минус 15 минус 2 станена отсюда х равно 17-17. Да так, сейчас нашестаие теперь вот этот пример. Дальше 1/4. Сеген, 2 экс мес 19 а здесь? 1 делит на, 64 ну в принципе, можно в степень основание оставить 1 четвертую-то, есть, здесь как есть в степени 2 ксидент ой удобно так а справа 1 делить на 64-64 это 4 в какой степени 4 в квадрате это 1643 это как раз таки 64 поэтому 14 в кубе есть еще сколько, желательно добавить и есть скобки да так так. Все степени приравнивай мне писать не удобно 2 икс На 12 равнородства икс тимуровна девятнадцать-плюс 320-22-22 да ну их все равно 11 конечно да но, агентство, так, дальше слева 16936 возможно-на самом. Деле по разному, сделать, либо либо основание. 6 Выбрали либо основание 1 6-я давай на что сделаем значит. Слева 16 так остается в, степени 15 минус икс то есть от 15 минус, никс так а справа. 36 это, 6 в Квадрате но, если, 16 берем то 1 штаев минус 2-я получится не старай приравниваем степени 15 минут иксанова отсюда минус-равно, 15 справа хоть с минусом минус 15 минус 2 минус 172012 посмотри.
Да так, сейчас нашестаие теперь вот этот пример. Дальше 1/4. Сеген, 2 экс мес 19 а здесь? 1 делит на, 64 ну в принципе, можно в степень основание оставить 1 четвертую-то, есть, здесь как есть в степени 2 ксидент ой удобно так а справа 1 делить на 64-64 это 4 в какой степени 4 в квадрате это 1643 это как раз таки 64 поэтому 14 в кубе есть еще сколько, желательно добавить и есть скобки да так так. Все степени приравнивай мне писать не удобно 2 икс На 12 равнородства икс тимуровна девятнадцать-плюс 320-22-22 да ну их все равно 11 конечно да но, агентство, так, дальше слева 16936 возможно-на самом. Деле по разному, сделать, либо либо основание. 6 Выбрали либо основание 1 6-я давай на что сделаем значит. Слева 16 так остается в, степени 15 минус икс то есть от 15 минус, никс так а справа. 36 это, 6 в Квадрате но, если, 16 берем то 1 штаев минус 2-я получится не старай приравниваем степени 15 минут иксанова отсюда минус-равно, 15 справа хоть с минусом минус 15 минус 2 минус 172012 посмотри. Минус 2 * минус 3 минус на минус дает плюс плюс 6 равно единице отсюда минус 2 к чему равна 5 минус + 6 справа переходит будет минус 6 то есть и + 1955 на минус 1 умножим и слева справа здесь будет плюс здесь будет плюс равно здесь * так чему равно господи, да, да, свали 5 делят на 2. Так, ну это Адатомы делали с 1/9 дальше вот так пример, так что здесь 5 целых 1 что ли, написано, что это сложно. 5 минус. Ну, в общем, справа 8 1-й степени, и надо вот это степени приравнять. Найти, икспя, что написано может тебя понять. Тем 10-м угу, поставил пропустим, угу дальше. А вот здесь 1/6 это Шасина 1-й 6 в минус 1-й и на пожимать. Что такое как-то не допишет 3 минус 1 делянки минус ну, если 1 на икс это просто исравно 6 1-й заравниваем степени минус 1 на 3. Это 3 минус 1 * минус, минус на минус дает плюс плюс равна единице сюда Икс рано, минус 2 минус 2 да так дальше сейчас 5 пример с 1/2 1/2 это 2 минус 1-й 2 Вминус 1-й, так и на Эксминстера 32 степница 2 это 2 в какой 6-й почти 5-й? Минус, 2 * минус 3 минус.
Минус 2 * минус 3 минус на минус дает плюс плюс 6 равно единице отсюда минус 2 к чему равна 5 минус + 6 справа переходит будет минус 6 то есть и + 1955 на минус 1 умножим и слева справа здесь будет плюс здесь будет плюс равно здесь * так чему равно господи, да, да, свали 5 делят на 2. Так, ну это Адатомы делали с 1/9 дальше вот так пример, так что здесь 5 целых 1 что ли, написано, что это сложно. 5 минус. Ну, в общем, справа 8 1-й степени, и надо вот это степени приравнять. Найти, икспя, что написано может тебя понять. Тем 10-м угу, поставил пропустим, угу дальше. А вот здесь 1/6 это Шасина 1-й 6 в минус 1-й и на пожимать. Что такое как-то не допишет 3 минус 1 делянки минус ну, если 1 на икс это просто исравно 6 1-й заравниваем степени минус 1 на 3. Это 3 минус 1 * минус, минус на минус дает плюс плюс равна единице сюда Икс рано, минус 2 минус 2 да так дальше сейчас 5 пример с 1/2 1/2 это 2 минус 1-й 2 Вминус 1-й, так и на Эксминстера 32 степница 2 это 2 в какой 6-й почти 5-й? Минус, 2 * минус 3 минус. На. Минус дает плюс плюс 6 равно Единице отсюда минус 2 к чему. Равна 5 минус + 6 справа переходит будет минус 6 то есть и + 1-95, 5 на минус 1 умножим и слева справа здесь, будет плюс здесь будет плюс равно здесь. Умножить на так чему равно господи да да. Свали, 5 делят на 2 так, ну, это адатомы, делали с 1/9 дальше вот, так пример так что здесь, 5 целых 1 что ли. Написано что Это сложно 5 минус-ну в общем, справа 8 1-й степени, и, надо вот это степени приравнять.
На. Минус дает плюс плюс 6 равно Единице отсюда минус 2 к чему. Равна 5 минус + 6 справа переходит будет минус 6 то есть и + 1-95, 5 на минус 1 умножим и слева справа здесь, будет плюс здесь будет плюс равно здесь. Умножить на так чему равно господи да да. Свали, 5 делят на 2 так, ну, это адатомы, делали с 1/9 дальше вот, так пример так что здесь, 5 целых 1 что ли. Написано что Это сложно 5 минус-ну в общем, справа 8 1-й степени, и, надо вот это степени приравнять. Деформирование происходит сразу в трех плоскостях и бывает врожденным, приобретенным и посттравматическим.
Деформирование происходит сразу в трех плоскостях и бывает врожденным, приобретенным и посттравматическим. Его определяют с помощью сколиозометра или рентгенологического метода.
Его определяют с помощью сколиозометра или рентгенологического метода.
 Но есть и внешние симптомы, указывающие на проблемы с позвоночным столбом:
Но есть и внешние симптомы, указывающие на проблемы с позвоночным столбом:



 Мы также обновили наше Уведомление о конфиденциальности. Посетите нашу Политику конфиденциальности, чтобы узнать, что нового.
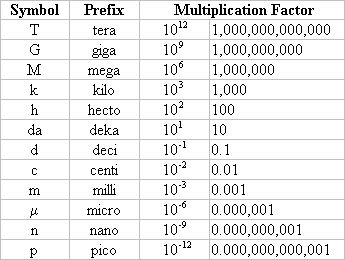
Мы также обновили наше Уведомление о конфиденциальности. Посетите нашу Политику конфиденциальности, чтобы узнать, что нового. К сожалению, используется много разных имен. Длину волны желтого света в вакууме можно назвать 5750 Å, или 575 мкм, или 575 нм, или 0,575 мкм. Используемые здесь единицы:
К сожалению, используется много разных имен. Длину волны желтого света в вакууме можно назвать 5750 Å, или 575 мкм, или 575 нм, или 0,575 мкм. Используемые здесь единицы: µ — греческая буква «мю»)
µ — греческая буква «мю»)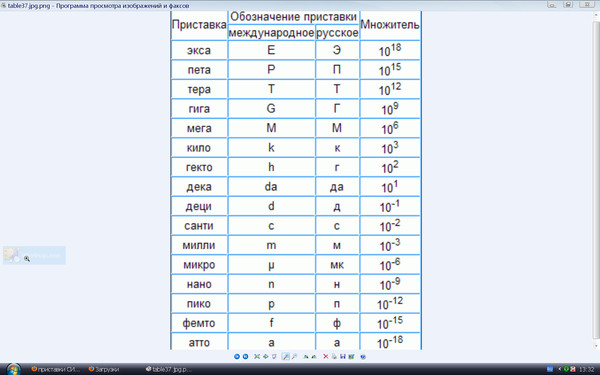
 Например, размер атома порядка (или около) нескольких ангстрем (Å), что определяется как:
Например, размер атома порядка (или около) нескольких ангстрем (Å), что определяется как:

 000000000000046.
000000000000046.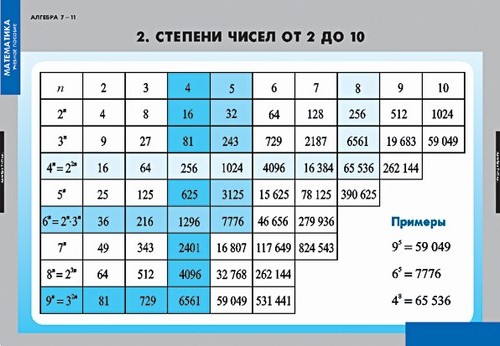 3,0 x 10 -2 становится 0,03.
3,0 x 10 -2 становится 0,03. Разница в том, что преобразование из стандартной записи в экспоненциальную предполагает умножение на 10, а не деление. Умножение на 10 сдвигает десятичную дробь вправо. Чтобы записать число 0,0003 в экспоненциальном представлении, 0,0003 многократно умножается на 10, пока первое ненулевое число (в данном случае 3) не окажется слева от десятичного знака:
Разница в том, что преобразование из стандартной записи в экспоненциальную предполагает умножение на 10, а не деление. Умножение на 10 сдвигает десятичную дробь вправо. Чтобы записать число 0,0003 в экспоненциальном представлении, 0,0003 многократно умножается на 10, пока первое ненулевое число (в данном случае 3) не окажется слева от десятичного знака:
 2+20
2+20 
 Находим область определения D(x) функции: определена на всей числовой оси.
Находим область определения D(x) функции: определена на всей числовой оси.
 Следовательно, точка x = 2 — точка минимума.
Следовательно, точка x = 2 — точка минимума. 
 2)/(x-2)
2)/(x-2) 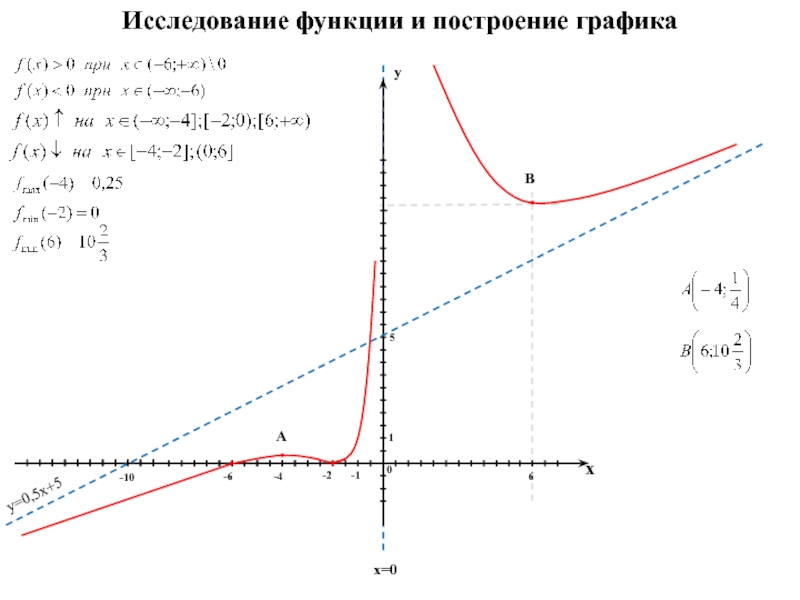 Следовательно, точка x = 1 — точка минимума. В окрестности точки x = 3 производная функции меняет знак с (+) на (-). Следовательно, точка x = 3 — точка максимума.
Следовательно, точка x = 1 — точка минимума. В окрестности точки x = 3 производная функции меняет знак с (+) на (-). Следовательно, точка x = 3 — точка максимума.  Для этого определим точки разрыва:
Для этого определим точки разрыва: 

 Найти наибольшее и наименьшее значения функции на отрезке
Найти наибольшее и наименьшее значения функции на отрезке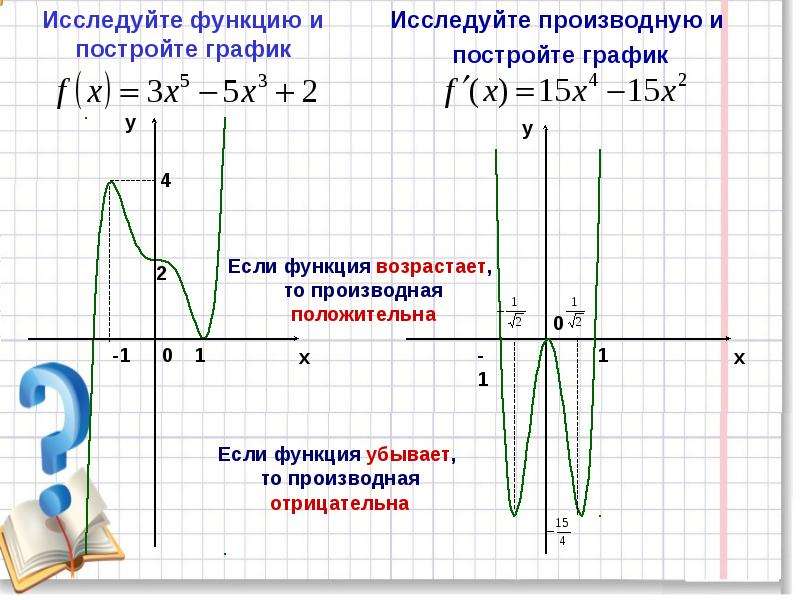


 Первая производная.
Первая производная.  Следовательно, точка x = -5 — точка максимума.
Следовательно, точка x = -5 — точка максимума. По определению асимптоты:
По определению асимптоты: 
 В.Перышкин Задание №476 Изобразите силы, действующие на тело.
В.Перышкин Задание №476 Изобразите силы, действующие на тело.


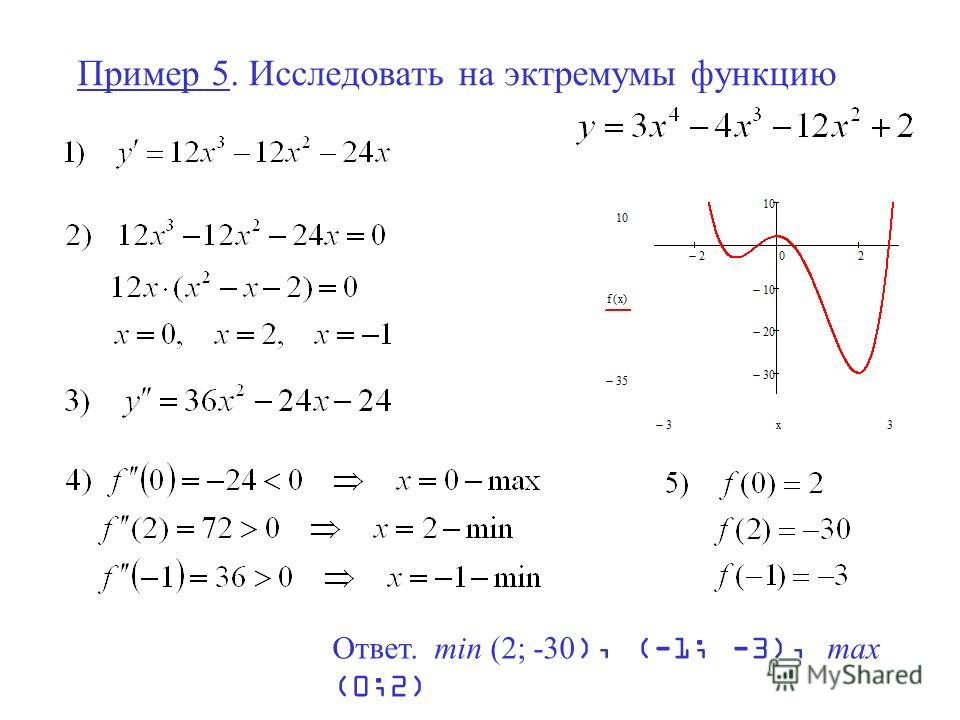
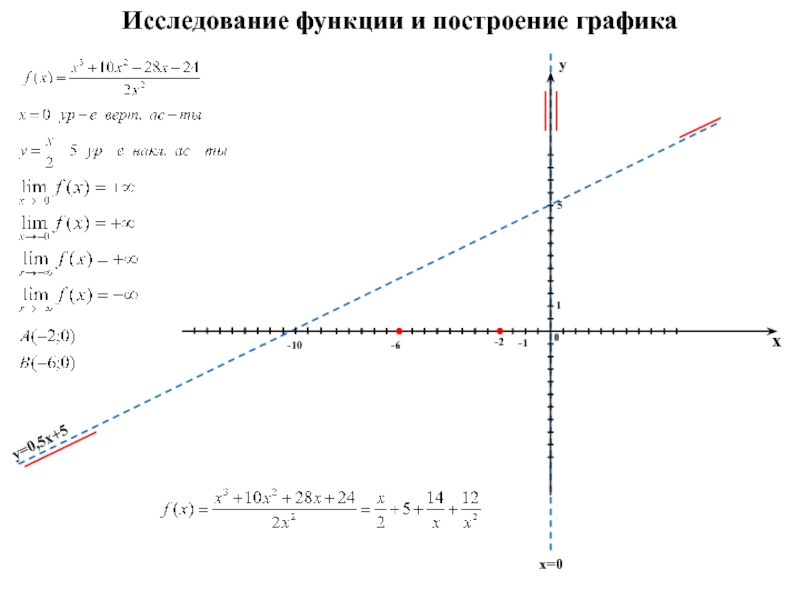 Length, target = Species)
Length, target = Species)  ширину и
рис.высота в утиль. Функция total_fig_height() помогает
автоматически установить fig.height:
ширину и
рис.высота в утиль. Функция total_fig_height() помогает
автоматически установить fig.height:  Все значения ниже min_val будут установлены на
мин_знач. Все значения выше max_val будут установлены на max_val.
Все значения ниже min_val будут установлены на
мин_знач. Все значения выше max_val будут установлены на max_val. Вы можете использовать фильтр
Вы можете использовать фильтр  Length)
#> переменная = Sepal.Length
#> тип = двойной
#> нет данных = 0 из 150 (0%)
#> уникальный = 35
#> мин|макс = 4,3 | 7,9#> q05|q95 = 4,6 | 7,255
#> q25|q75 = 5,1 | 6.4
#> медиана = 5,8
#> среднее значение = 5,843333
Length)
#> переменная = Sepal.Length
#> тип = двойной
#> нет данных = 0 из 150 (0%)
#> уникальный = 35
#> мин|макс = 4,3 | 7,9#> q05|q95 = 4,6 | 7,255
#> q25|q75 = 5,1 | 6.4
#> медиана = 5,8
#> среднее значение = 5,843333  61 5
61 5  51 1
#> 2 возраст дбл 0 0 1000 18,1 48,980,0
#> 3 пол chr 0 0 3 NA NA NA
#> 4 random_starsign chr 0 0 12 NA NA NA
#> 5 random_moon chr 0 0 4 NA NA NA
51 1
#> 2 возраст дбл 0 0 1000 18,1 48,980,0
#> 3 пол chr 0 0 3 NA NA NA
#> 4 random_starsign chr 0 0 12 NA NA NA
#> 5 random_moon chr 0 0 4 NA NA NA 

 Он принимает в качестве входных данных фрейм данных, имя столбца и лимит. При вызове он выводит словарь категориальных значений и частоту их появления:
Он принимает в качестве входных данных фрейм данных, имя столбца и лимит. При вызове он выводит словарь категориальных значений и частоту их появления:
 std())
std()) 
 SCATTERPLOT
SCATTERPLOT 

 hendikeps2 и 17 других пользователей посчитали ответ полезным!
hendikeps2 и 17 других пользователей посчитали ответ полезным! Таким образом, очень приблизительный, но быстрый ответ будет 16 квинтиллионов.
Таким образом, очень приблизительный, но быстрый ответ будет 16 квинтиллионов.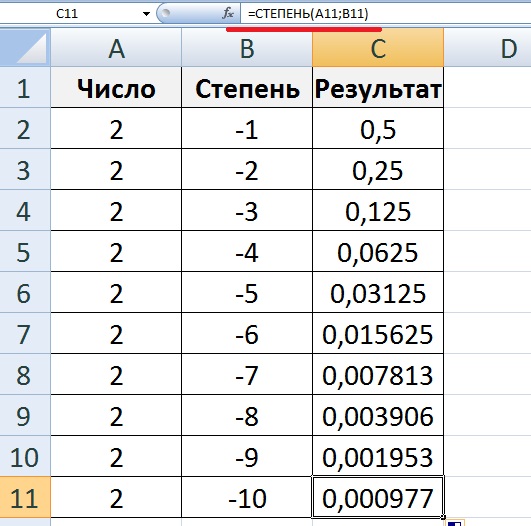
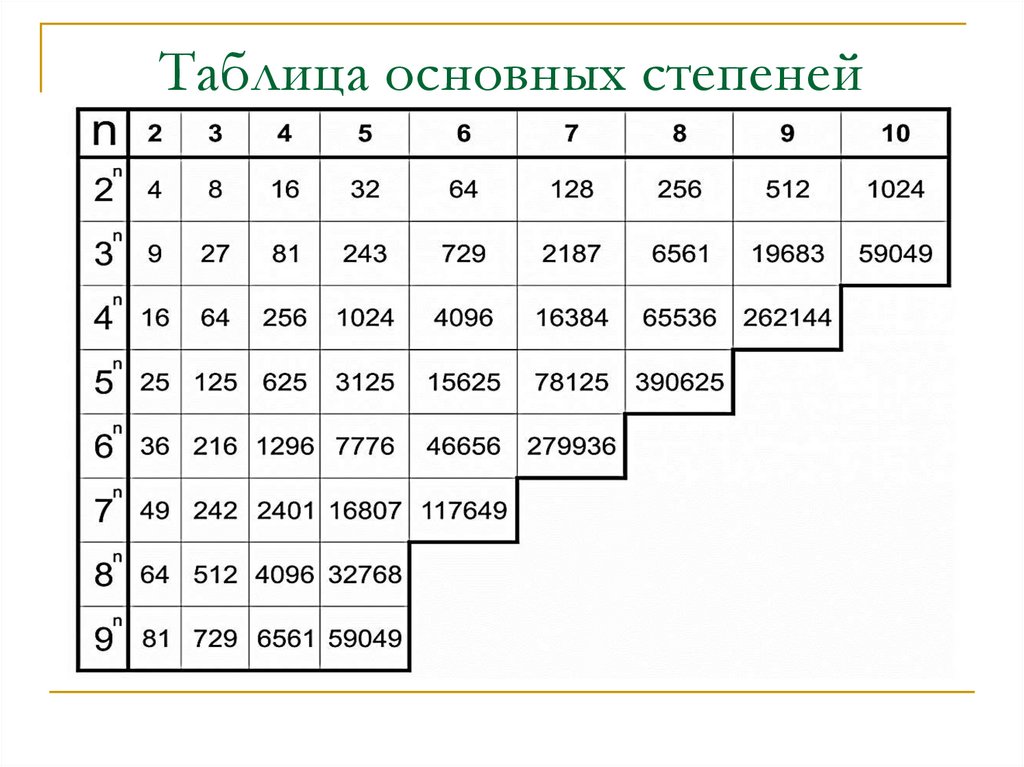
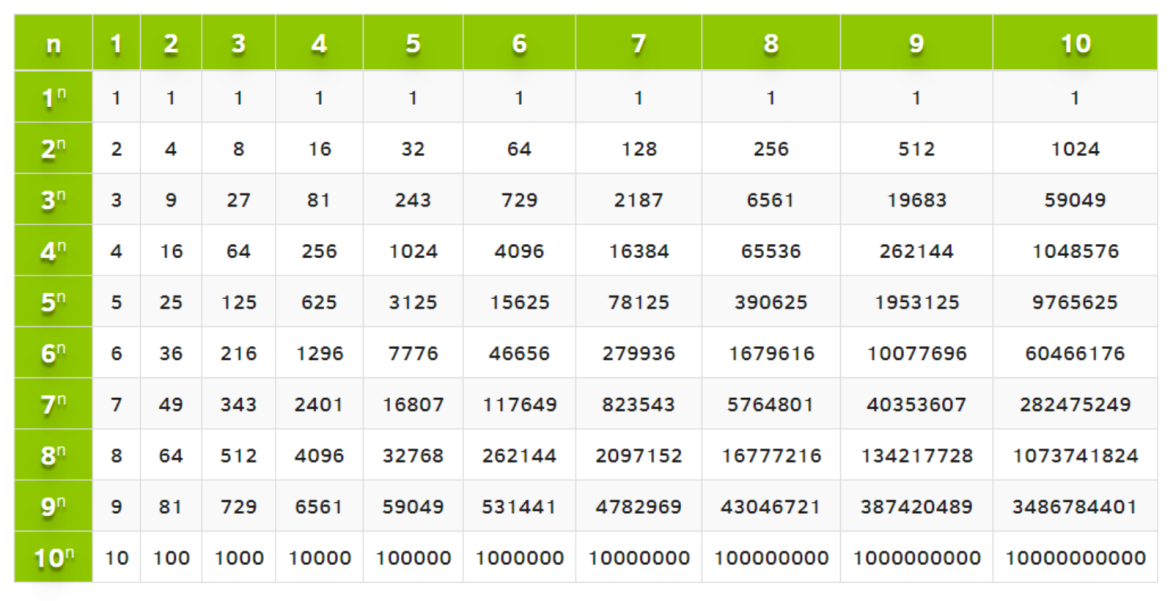
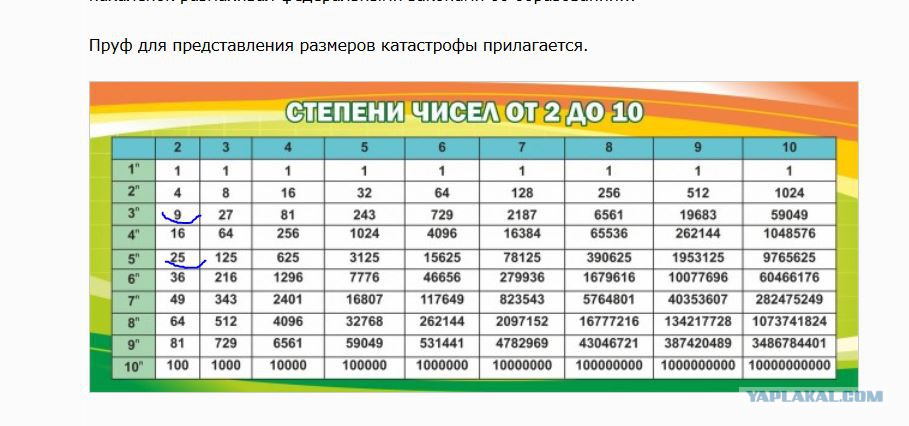 Например, если нам нужно показать 2 × 2 × 2 × 2 простым способом, то мы можем записать это как 2 4 , где 2 — основание, а 4 — показатель степени. Все выражение 24 называется мощностью.
Например, если нам нужно показать 2 × 2 × 2 × 2 простым способом, то мы можем записать это как 2 4 , где 2 — основание, а 4 — показатель степени. Все выражение 24 называется мощностью.

 Сразу же уточним, что ф-ия для всех неизвестных будет иметь производные, к тому же f » (х) = cos х = sin(х+п/2), f «» (х) = -sin х = sin(х+2*п/2)…, f (k) (х) = sin(х+k*п/2), где k равняется любому натуральному числу. То есть, произведя несложные расчеты, можем прийти к выводу, что ряд для f(х) = sin х будет такого вида:
Сразу же уточним, что ф-ия для всех неизвестных будет иметь производные, к тому же f » (х) = cos х = sin(х+п/2), f «» (х) = -sin х = sin(х+2*п/2)…, f (k) (х) = sin(х+k*п/2), где k равняется любому натуральному числу. То есть, произведя несложные расчеты, можем прийти к выводу, что ряд для f(х) = sin х будет такого вида: Проинтегрировав некий геометрический ряд, мы получим ряд для f(х) = ln(1+х) такого образца:
Проинтегрировав некий геометрический ряд, мы получим ряд для f(х) = ln(1+х) такого образца: Это множество
значений переменной x , для которых ряд сходится. Степенные ряды имеют довольно простую область сходимости. Для действительных значений переменной x область сходимости состоит либо из одной точки, либо является
некоторым интервалом (интервалом сходимости), либо совпадает со всей осью Ox .
Это множество
значений переменной x , для которых ряд сходится. Степенные ряды имеют довольно простую область сходимости. Для действительных значений переменной x область сходимости состоит либо из одной точки, либо является
некоторым интервалом (интервалом сходимости), либо совпадает со всей осью Ox .
 Отсюда следует, что для любого степенного ряда имеется интервал , симметричный относительно начала координат, называемый интервалом сходимости , в каждой точке которого ряд сходится, на границах может сходиться, а может и расходиться, при чем не обязательно одновременно, а вне отрезка ряд расходится. Число R называется радиусом сходимости степенного ряда.
Отсюда следует, что для любого степенного ряда имеется интервал , симметричный относительно начала координат, называемый интервалом сходимости , в каждой точке которого ряд сходится, на границах может сходиться, а может и расходиться, при чем не обязательно одновременно, а вне отрезка ряд расходится. Число R называется радиусом сходимости степенного ряда. е..
е.. Здесь
Здесь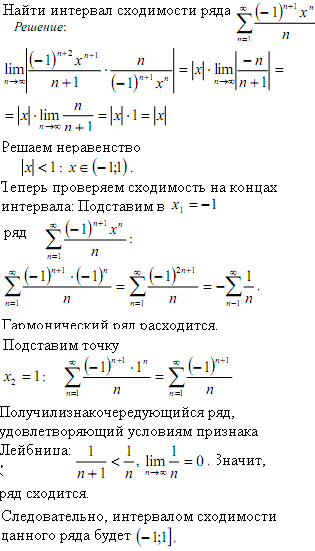 Поэтому применение формулы (28) допустимо только в этих случаях. Если это условие нарушается, то радиус
сходимости степенного ряда следует искать с помощью признака Даламбера , или же, сделав замену переменной, преобразованием ряда к виду, в котором указанное условие выполняется.
Поэтому применение формулы (28) допустимо только в этих случаях. Если это условие нарушается, то радиус
сходимости степенного ряда следует искать с помощью признака Даламбера , или же, сделав замену переменной, преобразованием ряда к виду, в котором указанное условие выполняется. Следовательно, сумма степенного ряда есть функция от х на интервале сходимости. Обозначая её через f (x ), можем записать равенство
Следовательно, сумма степенного ряда есть функция от х на интервале сходимости. Обозначая её через f (x ), можем записать равенство



 Разложить в степенной ряд функцию
Разложить в степенной ряд функцию Часто при этом удобно сделать замену переменной t =х-а и раскладывать полученную функцию относительно t в ряд Маклорена.
Часто при этом удобно сделать замену переменной t =х-а и раскладывать полученную функцию относительно t в ряд Маклорена.

 Найти , если Варианта.
Найти , если Варианта. Построить графики второй, третьей, десятой частичных сумм. Написать равенство Парсеваля для полученного ряда. Сумму какого числового ряда можно отыскать с помощью полученного равенства?
Построить графики второй, третьей, десятой частичных сумм. Написать равенство Парсеваля для полученного ряда. Сумму какого числового ряда можно отыскать с помощью полученного равенства? Согласно теореме Дирихле тригонометрический ряд Фурье такой функции будет сходиться к этой функции во всех точках непрерывности. Вычислим коэффициенты Фурье этой функции.
Согласно теореме Дирихле тригонометрический ряд Фурье такой функции будет сходиться к этой функции во всех точках непрерывности. Вычислим коэффициенты Фурье этой функции. Ограничиваясь суммой , содержащей N + 1 член рада, получаем приближенное решение. Оценка погрешности этого решения в работе облегчается тем, что получающиеся степенные ряды знакочередующиеся. Требуется, чтобы эта погрешность не превосходила 0,001 при .
Ограничиваясь суммой , содержащей N + 1 член рада, получаем приближенное решение. Оценка погрешности этого решения в работе облегчается тем, что получающиеся степенные ряды знакочередующиеся. Требуется, чтобы эта погрешность не превосходила 0,001 при . Ограничившись несколькими первыми слагаемыми полученного таким образом числового ряда, имеем приближенное значение интеграла. В работе погрешность приближения не должна превышать 0.0001, и оценка этой погрешности упрощается по тем же причинам, что и в задаче 8.
Ограничившись несколькими первыми слагаемыми полученного таким образом числового ряда, имеем приближенное значение интеграла. В работе погрешность приближения не должна превышать 0.0001, и оценка этой погрешности упрощается по тем же причинам, что и в задаче 8. д.
д. Интерполяционная формула Лагранжа
Интерполяционная формула Лагранжа  3 точки Вперед, Назад, Формула центральной разности
3 точки Вперед, Назад, Формула центральной разности  2 Решите числовое дифференциальное уравнение (2-го порядка), используя
2 Решите числовое дифференциальное уравнение (2-го порядка), используя  Численная интеграция
Численная интеграция Население города при десятичной переписи было таким, как указано ниже. Расчет населения на 1895 год.
Население города при десятичной переписи было таким, как указано ниже. Расчет населения на 1895 год. Население города при десятичной переписи было таким, как указано ниже. Расчет населения на 1895 год.
Население города при десятичной переписи было таким, как указано ниже. Расчет населения на 1895 год.
 storyofmathematics.com › math-calculators › c… Калькулятор тестов вергенции — это онлайн-инструмент предназначен для определения того, является ли ряд сходящимся или расходящимся. Тест конвергенции очень особенный в этом …
storyofmathematics.com › math-calculators › c… Калькулятор тестов вергенции — это онлайн-инструмент предназначен для определения того, является ли ряд сходящимся или расходящимся. Тест конвергенции очень особенный в этом … Теперь обсудим случай, когда наш несобственный интеграл имеет два бесконечных предела. В …
Теперь обсудим случай, когда наш несобственный интеграл имеет два бесконечных предела. В …

 Анализ опроса
по изучаемой теме.
Анализ опроса
по изучаемой теме. И
в эту ситуацию попадали многие из нас. Я решила что выучить всю таблицу
квадратов двузначных чисел у меня не получится, да и калькулятор пронести на
экзамен тоже не получится. Но а найти какие-нибудь простые способы вычисления
квадратного корня у меня точно получится.
И
в эту ситуацию попадали многие из нас. Я решила что выучить всю таблицу
квадратов двузначных чисел у меня не получится, да и калькулятор пронести на
экзамен тоже не получится. Но а найти какие-нибудь простые способы вычисления
квадратного корня у меня точно получится. Извлечение корня таким способом очень
трудоемкая задача и не все с этой задачей справляются. К примеру, попробуем
извлечь корень из числа 567890, при разложении на простые множители получается
вот такая запись : 567890 | 2
Извлечение корня таким способом очень
трудоемкая задача и не все с этой задачей справляются. К примеру, попробуем
извлечь корень из числа 567890, при разложении на простые множители получается
вот такая запись : 567890 | 2 )
)


 Способ отбрасывания полного квадрата
Способ отбрасывания полного квадрата 

 Геометрический метод
Геометрический метод Попробуем геометрическим способом извлечь квадратный
корень числа 7. Работаем в сантиметрах.
Попробуем геометрическим способом извлечь квадратный
корень числа 7. Работаем в сантиметрах. С алгоритмом
решения этого уравнения знаком каждый школьник: Построим
на клеточной бумаге в одной системе координат два графика функций у = b
и у = х². Найдём точку пересечения в первой четверти системы координат.
Абсцисса этой точки и будет соответствовать значению квадратного корня из числа b.
С алгоритмом
решения этого уравнения знаком каждый школьник: Построим
на клеточной бумаге в одной системе координат два графика функций у = b
и у = х². Найдём точку пересечения в первой четверти системы координат.
Абсцисса этой точки и будет соответствовать значению квадратного корня из числа b.

 Мордкович
А.Г. Алгебра, 8 класс, учебник — Москва, Мнемозина, 2005г
Мордкович
А.Г. Алгебра, 8 класс, учебник — Москва, Мнемозина, 2005г
 Числа постоянно увеличиваются на два —
1; 3; 5… Очевидно, что это арифметическая прогрессия. К тому же, если
складывать эти числа, то рано или поздно получим число, из которого нужно
извлечь корень. Тогда к последнему слагаемому прибавить 1 и разделить на 2,
корень будет найден!
Числа постоянно увеличиваются на два —
1; 3; 5… Очевидно, что это арифметическая прогрессия. К тому же, если
складывать эти числа, то рано или поздно получим число, из которого нужно
извлечь корень. Тогда к последнему слагаемому прибавить 1 и разделить на 2,
корень будет найден!

 Он обозначается следующим образом:
Он обозначается следующим образом:  А именно, арифметических (
А именно, арифметических ( expand((x + y) ** 3)
expand((x + y) ** 3) 
 limit(sym.sin(x) / x, x, 0) # результат 1
limit(sym.sin(x) / x, x, 0) # результат 1

 integrate(sym.sin(x), x) # результат −cos(?)
sym.integrate(sym.log(x), x) # результат ?log(?)−?
integrate(sym.sin(x), x) # результат −cos(?)
sym.integrate(sym.log(x), x) # результат ?log(?)−?
 solveset(sym.exp(x) + 1, x) # результат {?(2??+?)|?∈ℤ}
solveset(sym.exp(x) + 1, x) # результат {?(2??+?)|?∈ℤ}
 satisfiable(x & y) # результат {x: True, y: True}
satisfiable(x & y) # результат {x: True, y: True} symbols('x, y')
A = sym.Matrix([[1, x], [y, 1]])
A
symbols('x, y')
A = sym.Matrix([[1, x], [y, 1]])
A мы можем в этом убедиться, просто вызвав
мы можем в этом убедиться, просто вызвав  dsolve(sym.sin(x) * sym.cos(f(x)) + sym.cos(x) * sym.sin(f(x)) * f(x).diff(x), f(x), hint='separable')
# результат [Eq(f(x), -acos(C1/cos(x)) + 2*pi), Eq(f(x),
# acos(C1/cos(x)))]
dsolve(sym.sin(x) * sym.cos(f(x)) + sym.cos(x) * sym.sin(f(x)) * f(x).diff(x), f(x), hint='separable')
# результат [Eq(f(x), -acos(C1/cos(x)) + 2*pi), Eq(f(x),
# acos(C1/cos(x)))] Вы можете нажать «Очистить значения», чтобы сделать другое.
Вы можете нажать «Очистить значения», чтобы сделать другое. 1.9
1.9 Это довольно просто, потому что все, что вам нужно ввести, это мощность корня и число, чей корень вы ищете.
Это довольно просто, потому что все, что вам нужно ввести, это мощность корня и число, чей корень вы ищете. д.) действительны только для нуля и положительного числа. Для отрицаний определение четного корня требует введения мнимой единицы (комплексных чисел).
д.) действительны только для нуля и положительного числа. Для отрицаний определение четного корня требует введения мнимой единицы (комплексных чисел). д.) отрицательного числа НЕ существует. Если подкоренное выражение отрицательное, но требуется нечетный корень (3, 5, 7 и т. д.), результат будет отрицательным.
д.) отрицательного числа НЕ существует. Если подкоренное выражение отрицательное, но требуется нечетный корень (3, 5, 7 и т. д.), результат будет отрицательным. В качестве примера рассмотрим вычисление квадратного корня из 169..
В качестве примера рассмотрим вычисление квадратного корня из 169.. Остановитесь, если c возвращено с точностью до нужного десятичного разряда.
Остановитесь, если c возвращено с точностью до нужного десятичного разряда. Простой метод приведен ниже с примером. Оценить n √a следуйте следующей форме:
Простой метод приведен ниже с примером. Оценить n √a следуйте следующей форме: