Преобразовать Word в PDF — Конвертируйте текстовые документы в PDF онлайн
Онлайн-конвертер поможет преобразовать вордовский файл в PDF. Конвертируйте документы MS Word в один из самых ходовых и практичных форматов Adobe PDF. Конвертировать DOC в PDF или DOCX в PDF.
Перетащите файлы сюда
Преобразовать
Сканы будут сохранены в виде изображений.
Премиум
Преобразовать с помощью OCR
Сканы будут преобразованы в редактируемый текст.
Исходный язык файла
Чтобы получить оптимальный результат, выберите все языки, которые есть в файле.
Применить фильтр: Обратите внимание, что получившийся документ утратит первоначальные цвета»/> Применить фильтр No FilterGray Filter
Версия PDF без изменений 1.41.51.61.72.0
Информация: Включите поддержку JavaScript, чтобы обеспечить нормальную работу сайта.
Публикация рекламы
300,000+ users
18,000+ users
Оставайтесь на связи:
Как преобразовать Word в PDF?
- Загрузите документ Microsoft Word.

- Выберите «Оптическое распознавание символов», если хотите извлечь текст после сканирования (по желанию).
- Выберите язык (по желанию).
- Нажмите «Начать».
Преобразовать Word в PDF онлайн
бесплатно в любом месте
Лучший инструмент для преобразования Word в PDF
Преобразование документов Word в PDF на сайте PDF2Go — это быстро и удобно. Просто подключитесь к сети и загрузите файл.
Загрузите Word: можно перетащить документ, указать путь к файлу на устройстве или дать ссылку на облачное хранилище. Затем нажмите на «Сохранить изменения» и подождите, пока мы преобразуем файл.
После этого можно скачать, сохранить или отредактировать PDF-файл.
Преобразование Word в PDF онлайн
При установке программного обеспечения есть риск нарваться на вирус. Мобильные приложения менее опасны, но не защищают от навязчивой рекламы или, что ещё более подозрительно, запрашивают доступ к телефону.
Поэтому PDF2Go позволяет конвертировать онлайн! Без установки программы и без вирусов. Просто подключитесь к сети.
Зачем вообще конвертировать?
У формата PDF много преимуществ. Если вы распечатаете PDF-документ или с кем-нибудь им поделитесь, форматирование останется неизменным. PDF-файлы открываются на любых компьютерах, телефонах и устройствах для чтения электронных книг.
Надёжный PDF-конвертер PDF2Go позволяет использовать эти и другие преимущества.
Безопасный PDF-конвертер
Загрузите документ Word для конвертации в PDF — это безопасно, как никогда прежде. Ваш файл в надёжных руках. Не беспокойтесь, все права на документ остаются за вами.
Ваш файл в надёжных руках. Не беспокойтесь, все права на документ остаются за вами.
См. подробности в Политике конфиденциальности.
Что можно преобразовать?
Мы специализируемся на конвертации документов Word в PDF. Но это далеко не всё. Наряду с форматами DOC и DOCX у нас можно преобразовать и другие текстовые документы, презентации и изображения!
Например:
ODT, RTF, TXT, Microsoft PowerPoint PPT, JPG, PNG, GIF и другие
Преобразовать файл в формат PDF онлайн
Вы не привязаны к компьютеру. PDF2Go конвертирует PDF-файлы онлайн. Вы можете работать с любого устройства, дома или на работе, даже в отпуске!
PDF2Go работает и на мобильных устройствах!
Оцените инструмент 4. 7 / 5
7 / 5
Чтобы оставить отзыв, преобразуйте и скачайте хотя бы один файл
Отзыв отправлен
Спасибо за оценку
конвертирование документов DOCX онлайн (БЕСПЛАТНО)
+ —
Мгновенно преобразуйте документ Word в формат PDF, которым удобно делиться.
Выберите документ WordВыбрать конвертер:
ЗагрузитьНачать сначала
Больше действий:
Выбрать другой файл
Как конвертировать документ Word в PDF
- Выберите документ Word, который нужно конвертировать. org/HowToStep»> Наш бесплатный конвертер Word в PDF скопирует форматирование и текст из документа Word и преобразует его в PDF.
- PDF сейчас будет готов к загрузке. Все оставшиеся копии отправленных вами файлов удаляются с нашего сервера, что обеспечивает безопасность ваших данных.
Лучший конвертер Word в PDF
Если необходимо преобразовать документ Word в PDF или другой формат, наш онлайн-конвертер PDF справится с этой задачей лучше всех. Наш PDF-конвертер быстро конвертирует документы Word в PDF, сохраняя все форматирование, таблицы, изображения и текст без изменений, чтобы они выглядели точно так же, как в Word.
Да, и сколько инструментов!
Предоставляя множество инструментов для преобразования и редактирования в ваше распоряжение, онлайн-конвертер Word в PDF поможет вам с легкостью конвертировать файлы. Инструменты, которые позволяют вращать, сжимать и объединять два разных PDF-файла или разбивать один PDF-файл на два, значительно упрощают их редактирование.
Шифрование файлов и автоматическое удаление
Мы придаем большое значение конфиденциальности ваших данных. При конвертации Word в PDF онлайн с помощью бесплатного конвертера PDF ваши файлы защищаются 256-битным шифрованием SSL. Кроме того, отправленные вами данные не передаются, не продаются и недоступны третьим лицам.
Автоматическое удаление файлов
Можно удалить любые отправленные файлы с сервера после завершения конвертации. Если вы забудете удалить файлы, они будут удалены автоматически, что обеспечивает конфиденциальность ваших данных.
Конвертируйте файлы в любое время на любом устройстве
Поскольку наш онлайн-конвертер Word DOC в PDF работает на любых ОС (включая Linux, Windows и Mac), можно конвертировать файлы на любом устройстве когда и где угодно.
Воспользоваться бесплатным пробным периодом
Начните с пробного периода либо оформите одномесячную, годовую или бессрочную подписку, чтобы получить неограниченный доступ ко всем удобным инструментам, не заботясь о превышении максимального размера файлов или ограничений объема данных. Можно даже одновременно конвертировать несколько документов Word, PDF или других форматов.
Можно даже одновременно конвертировать несколько документов Word, PDF или других форматов.
Работайте более продуктивно
Подписка
- Мгновенная конвертация
- Неограниченные конверсии
- Неограниченный размер файла
- Расширенные возможности
Пожалуйста, подождите или подпишитесь, чтобы конвертировать следующий файл.
Зарегистрироваться- Мгновенная конвертация
- Неограниченные конверсии
- Неограниченный размер файла
- Расширенные возможности
Пожалуйста, зарегистрируйтесь
Для использования всех возможностей PDF-конвертера вам необходима версия PRO.
Подписка
- Мгновенная конвертация
- Неограниченные конверсии
- Неограниченный размер файла
- Расширенные возможности
Продолжайте пользоваться бесплатными
Конвертировать Word в PDF — Конвертируйте документ Word в PDF онлайн
Этот PDF-конвертер — идеальное решение для онлайн-конвертации Word в PDF.
 Преобразуйте документы Microsoft Word в популярный и практичный формат Adobe PDF. Конвертируйте DOC в PDF или DOCX в PDF.
Преобразуйте документы Microsoft Word в популярный и практичный формат Adobe PDF. Конвертируйте DOC в PDF или DOCX в PDF.Перетащите файлы сюда
Преобразовать
Отсканированные страницы будут изображениями.
Премиум
Преобразовать с помощью OCR
Отсканированные страницы будут преобразованы в текст, который можно редактировать.
Исходный язык вашего файла
Чтобы получить наилучшие результаты, выберите все языки, содержащиеся в вашем файле.
Применить фильтр: Применить фильтр Без фильтраСерый фильтр
Версия PDF So please only use this feature, if you are aware of what changing the version of your PDF does.»/> без изменений 1.41.51.61.72.0
Информация: Пожалуйста, включите JavaScript для корректной работы сайта.
Реклама
Как преобразовать Word в PDF?
- Загрузите документ Microsoft Word.
- Выберите «Использовать OCR», если хотите извлечь текст из отсканированных страниц (необязательно).
- Выберите язык (необязательно).
- Нажмите «Пуск».
Преобразование Word в PDF онлайн
бесплатно и куда угодно
Лучший конвертер Word в PDF
Использование PDF2Go для преобразования документа Word в PDF происходит быстро, легко и мгновенно. Все, что вам нужно, это стабильное подключение к Интернету и ваш файл.
Все, что вам нужно, это стабильное подключение к Интернету и ваш файл.
Загрузите документ Word с помощью перетаскивания, просмотра, облачного хранилища или предоставления ссылки. Затем все, что вам нужно сделать, это нажать «Сохранить изменения» и подождать, пока мы не конвертируем ваш файл для вас.
После этого вы можете загрузить, сохранить или отредактировать PDF-файл.
Конвертировать Word в PDF онлайн
Установка программы на компьютер сопряжена с риском. Вредоносные программы и вирусы просто ждут открытия. Хотя мобильные приложения кажутся более безопасными, они часто содержат раздражающую рекламу или подозрительный доступ к вашему телефону.
Вот почему PDF2Go позволяет конвертировать онлайн! Никаких вирусов, никаких установок. Все, что вам нужно, это подключение к Интернету.
Зачем мне конвертировать?
Формат документа PDF имеет множество преимуществ. Он сохраняет форматирование и поэтому выглядит так же, когда вы распечатываете его или делитесь им с другими. Он очень совместим, и есть ридеры, доступные для всех компьютерных систем, телефонов и даже для чтения электронных книг.
Он сохраняет форматирование и поэтому выглядит так же, когда вы распечатываете его или делитесь им с другими. Он очень совместим, и есть ридеры, доступные для всех компьютерных систем, телефонов и даже для чтения электронных книг.
Воспользуйтесь этими и многими другими преимуществами, используя надежный конвертер PDF, такой как PDF2Go.
Безопасный конвертер PDF
Загрузка документа Word для преобразования в PDF еще никогда не была такой безопасной. Мы заботимся о безопасности вашего файла на каждом этапе пути. Кроме того, мы не получаем никаких прав на ваш файл, он остается вашим и только вашим.
Дополнительную информацию можно найти в нашей Политике конфиденциальности.
Что я могу преобразовать?
Мы специализируемся на преобразовании Word в PDF. Но это не наш предел! Наряду с DOC и DOCX вы можете конвертировать другие текстовые документы, презентации и даже изображения!
Например:
ODT, RTF, TXT, Microsoft PowerPoint PPT, JPG, PNG, GIF и др.
Convert To PDF Online
Вы не привязаны к своему компьютеру! PDF2Go — это онлайн-конвертер PDF. Это значит, что вы можете пользоваться сервисом с любого компьютера, на работе, дома и даже в отпуске!
PDF2Go также работает на планшетах и смартфонах!
Оцените этот инструмент 4,7 /5
Вам нужно преобразовать и загрузить хотя бы 1 файл, чтобы оставить отзыв
Отзыв отправлен
Спасибо за ваш голос
Преобразование Word в PDF онлайн
Ваши файлы останутся конфиденциальными.
 Безопасная загрузка файлов по HTTPS.
Безопасная загрузка файлов по HTTPS.Как конвертировать Word в PDF за 3 простых шага
Нужно преобразовать документ в PDF? Преобразование Word в PDF — нечастый запрос, который мы получаем в DocFly. Тем не менее, мы разработали наше программное обеспечение так, чтобы оно включало столько функций, сколько необходимо. С помощью нашего онлайн-инструмента для преобразования Word в PDF многим людям нравится управлять всеми своими потребностями редактирования в одном централизованном месте. DocFly позволяет пользователям вносить сложные изменения, а также простые, такие как преобразование документов Word в формат PDF.
Самый простой способ конвертировать Word в PDF онлайн
Быстрое преобразование документов Word в PDF
Ищете способ быстрого преобразования документов Word в PDF? Не ищите ничего, кроме DocFly! С помощью нашего бесплатного онлайн-конвертера вы преобразуете документ Word в формат PDF менее чем за минуту.
Простой в использовании онлайн-конвертер Word в PDF
Хотите быть уверенным, что документ Word, которым вы делитесь, выглядит великолепно и его легко отправить по электронной почте? Преобразование Word в PDF для улучшения контроля версий.
Точное преобразование Word в PDF
Конвертер Word в PDF от DocFly является одним из самых точных. Наш конвертер преобразует PDF-файл, максимально приближенный к исходному документу Word.
Безопасная загрузка и хранение файлов
Все загружаемые файлы шифруются через HTTPS для защиты вашего контента. Файлы хранятся в защищенной базе данных, управляемой облачным хостингом Amazon. Вы можете удалить свои файлы из нашей системы в любое время.
Доступ к файлам из любого места
DocFly — это онлайн-сервис, доступный через любое устройство, подключенное к Интернету. Вы можете получить доступ к своему файлу из дома, офиса или любого другого места.
Всегда актуальная версия
DocFly находится в облаке, поэтому всякий раз, когда вы заходите на сайт, вы получаете доступ к последней версии программного обеспечения. Никаких длительных обновлений или загрузок программного обеспечения не требуется.
Готовы конвертировать Word в PDF онлайн?
Совет DocFly Pro: другие варианты преобразования файла Word в PDF
После запуска MS Word 2010 наиболее распространенным способом бесплатного преобразования Word в PDF является простое сохранение файла в формате PDF.

 3
3 2
2 3
3 14159..
14159.. Перепишите полиномиальное разбиение среднего члена с использованием двух множителей, найденных на шаге 2 выше, -30 и -10 похожие факторы :
Перепишите полиномиальное разбиение среднего члена с использованием двух множителей, найденных на шаге 2 выше, -30 и -10 похожие факторы :  Давайте теперь решим уравнение, заполнив квадрат и используя квадратичную формулу
Давайте теперь решим уравнение, заполнив квадрат и используя квадратичную формулу По этой причине мы хотим иметь возможность найти координаты вершины.
По этой причине мы хотим иметь возможность найти координаты вершины.
 2.1 получаем:
2.1 получаем:  е. второй корень).
е. второй корень).
 Чтобы поддержать наших студентов в этот кризис, мы теперь предоставляем услуги тестирования как онлайн, так и на территории кампуса.
Чтобы поддержать наших студентов в этот кризис, мы теперь предоставляем услуги тестирования как онлайн, так и на территории кампуса. Мы работали над тем, чтобы перевести многие из наших служб поддержки в онлайн, чтобы вы могли получить помощь, необходимую для достижения успеха.
Мы работали над тем, чтобы перевести многие из наших служб поддержки в онлайн, чтобы вы могли получить помощь, необходимую для достижения успеха.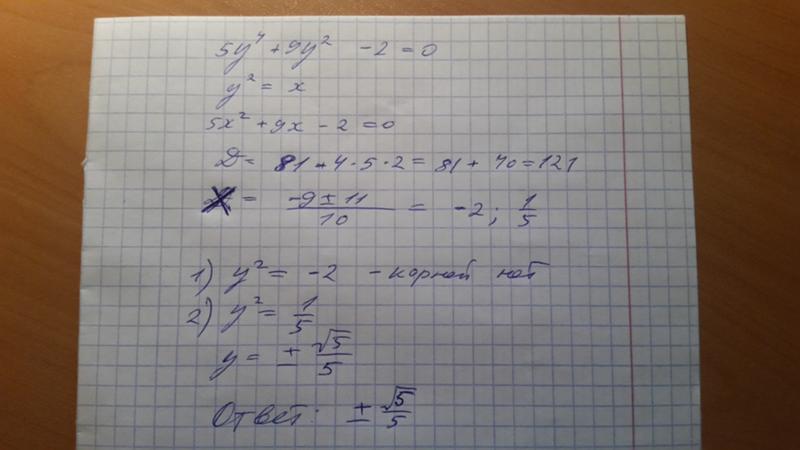



 Хотя бы потому, что российская часть мировой науки о принятии решений — очень сильная, она развивается, и на мировом уровне нас знают и уважают.
Хотя бы потому, что российская часть мировой науки о принятии решений — очень сильная, она развивается, и на мировом уровне нас знают и уважают. То есть благодаря этому ученому мы знаем, что демократические выборы возможны и необходимы, но корректное определение победителя на демократических выборах возможно не всегда.
То есть благодаря этому ученому мы знаем, что демократические выборы возможны и необходимы, но корректное определение победителя на демократических выборах возможно не всегда.
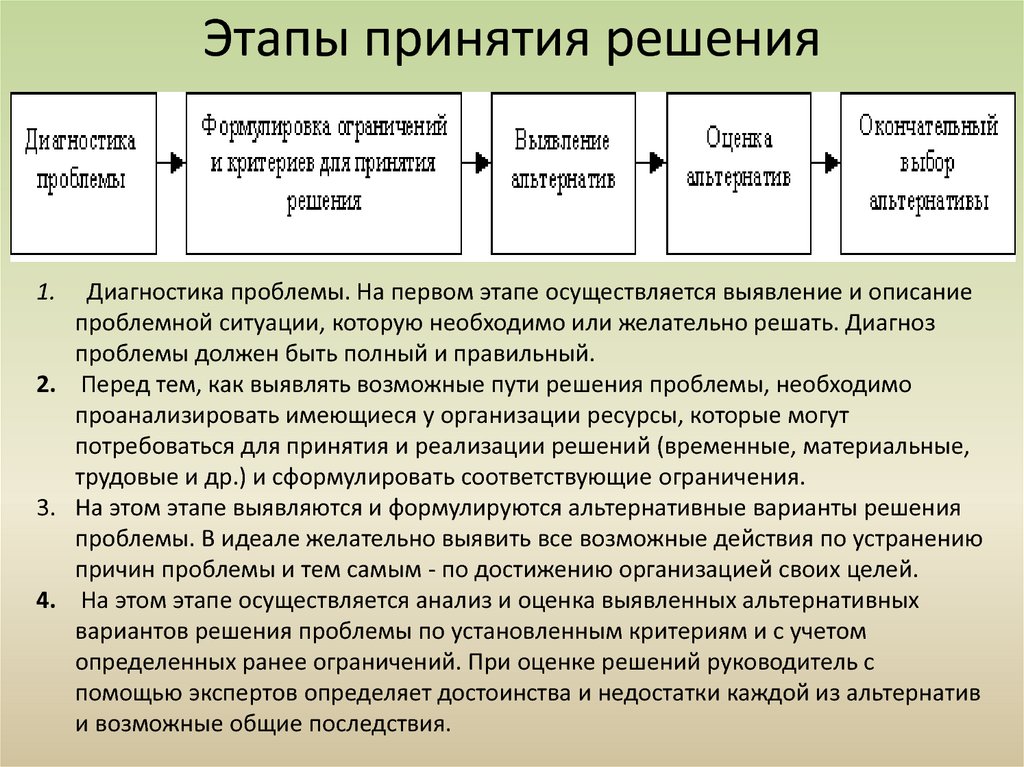
 Они представляют собой
заведомое упрощение ситуации с выявлением
и сохранением основных закономерностей.
Изменяя значения переменных модели,
соответствующих факторам, характеризующим
ситуацию, можно осуществить более полный
ее анализ.
Они представляют собой
заведомое упрощение ситуации с выявлением
и сохранением основных закономерностей.
Изменяя значения переменных модели,
соответствующих факторам, характеризующим
ситуацию, можно осуществить более полный
ее анализ.


 Кристоф Райзингер Оксфордский университет
Кристоф Райзингер Оксфордский университет Scheinkman (Колумбийский университет)
Scheinkman (Колумбийский университет)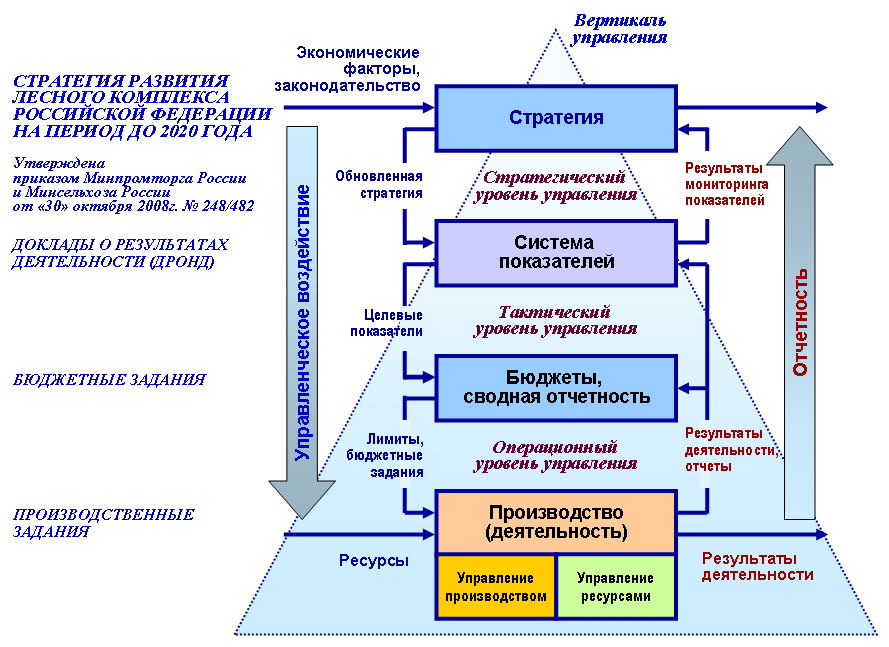



 Новый Версия обобщенного распределения Рэлея с копулой, свойствами, приложениями и различными методами оценки
Новый Версия обобщенного распределения Рэлея с копулой, свойствами, приложениями и различными методами оценки  Гибрид простой модели и новой несвязанной модели вопросов для двух чувствительных характеристик
Гибрид простой модели и новой несвязанной модели вопросов для двух чувствительных характеристик  Патель
Патель 





 Загрузить или вставить свой Excel
Загрузить или вставить свой Excel
 3.5
3.5 3.1
3.1 2.1
2.1 1.3
1.3 0.1
0.1 2.5
2.5 3
3 1.8
1.8 1.4
1.4 1.1
1.1 0.7
0.7 0.2
0.2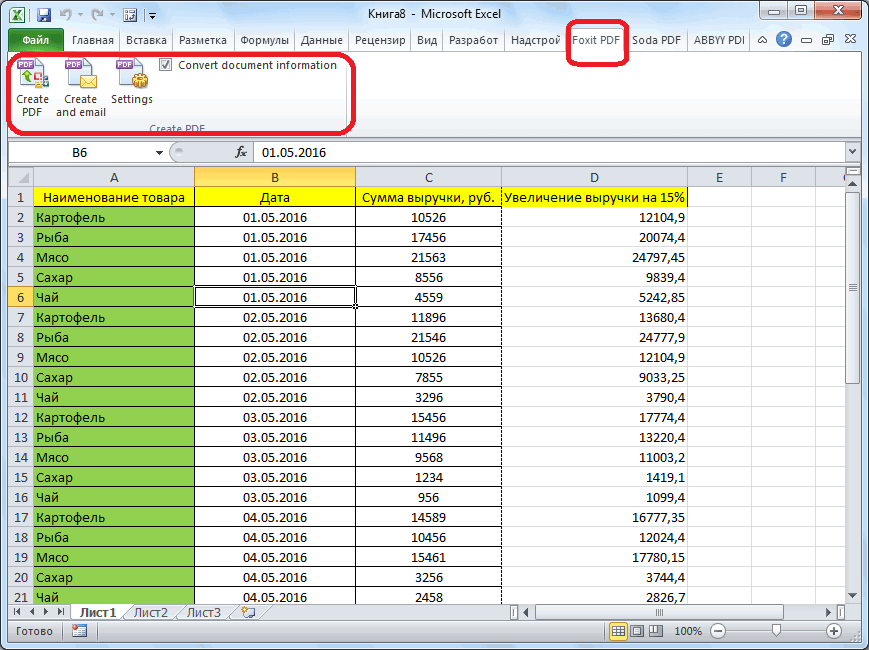
 форматы.
форматы. Cells для Python через Java в Windows. Видеть
Документация
Cells для Python через Java в Windows. Видеть
Документация в части 2 стандарта OOXML ECMA-376 новый формат представляет собой zip-пакет, содержащий ряд XML-файлов. Базовую структуру и файлы можно изучить, просто разархивировав файл .xlsx.
в части 2 стандарта OOXML ECMA-376 новый формат представляет собой zip-пакет, содержащий ряд XML-файлов. Базовую структуру и файлы можно изучить, просто разархивировав файл .xlsx.


 Во время игры the lottery, Всегда рекомендуется проверить свои результаты у официального лотерейного агента, прежде чем предпринимать какие-либо дальнейшие действия.. Это делается для того, чтобы убедиться, что вы правильно интерпретировали результаты и что вы не собираетесь принимать необдуманных решений на основе неверной информации.
Во время игры the lottery, Всегда рекомендуется проверить свои результаты у официального лотерейного агента, прежде чем предпринимать какие-либо дальнейшие действия.. Это делается для того, чтобы убедиться, что вы правильно интерпретировали результаты и что вы не собираетесь принимать необдуманных решений на основе неверной информации.




 результаты супер розыгрыша
результаты супер розыгрыша
 3 кг
3 кг Калькулятор вычисления силы, массы и ускорения.
Калькулятор вычисления силы, массы и ускорения. Для плоского, цилиндрического и сферического конденсаторов
Для плоского, цилиндрического и сферического конденсаторов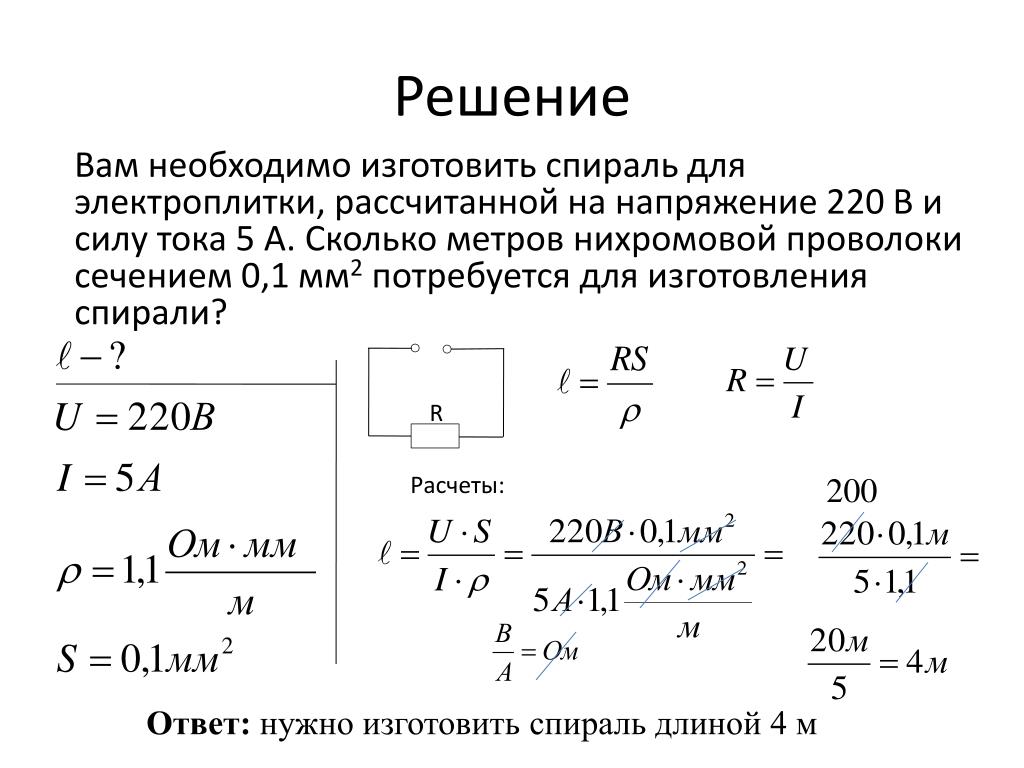 Онлайн калькулятор расстояния между точками
Онлайн калькулятор расстояния между точками Найди правильный ответ.
Найди правильный ответ. М.Онджеля, г. Бугульма
М.Онджеля, г. Бугульма Физика как учебная дисциплина отлично поддается процессу компьютеризации. Информационные технологии в процессе обучения физики можно использовать для изучения теоретического материала, тренинга, в качестве средства моделирования и визуализации, а также при решении физических задач.
Физика как учебная дисциплина отлично поддается процессу компьютеризации. Информационные технологии в процессе обучения физики можно использовать для изучения теоретического материала, тренинга, в качестве средства моделирования и визуализации, а также при решении физических задач.
 В конце каждого раздела физики находятся контрольные тесты и задачи, которые разделены на три уровня сложности.
В конце каждого раздела физики находятся контрольные тесты и задачи, которые разделены на три уровня сложности.
 Калькулятор представит подробное решение с различными комментариями, в котором учащийся сможет полностью разобраться.
Калькулятор представит подробное решение с различными комментариями, в котором учащийся сможет полностью разобраться. Т. Решение задач по физике с использованием программы Mathcad / Н. Т. Авласевич, Ж. В. Царикович // Образовательная среда сегодня: стратегии развития: материалы VIII Междунар. науч.–практ. конф. — Чебоксары: ЦНС «Интерактив плюс», 2016. — № 4. — С. 85-88.
Т. Решение задач по физике с использованием программы Mathcad / Н. Т. Авласевич, Ж. В. Царикович // Образовательная среда сегодня: стратегии развития: материалы VIII Междунар. науч.–практ. конф. — Чебоксары: ЦНС «Интерактив плюс», 2016. — № 4. — С. 85-88. 2023 г.
2023 г. Воспользуйтесь пошаговой процедурой, упомянутой ниже, чтобы решить вопросы смещения.
Воспользуйтесь пошаговой процедурой, упомянутой ниже, чтобы решить вопросы смещения. Что такое перемещение объекта?
Что такое перемещение объекта? 

 Знаете ли вы, что существует существенная разница между скоростью и скоростью? Мы написали об этом с точки зрения физика в тексте ниже.
Знаете ли вы, что существует существенная разница между скоростью и скоростью? Мы написали об этом с точки зрения физика в тексте ниже. Когда объект имеет только угловую скорость, он не смещается (расстояние равно нулю), и вы не можете использовать формулу средней скорости.
Когда объект имеет только угловую скорость, он не смещается (расстояние равно нулю), и вы не можете использовать формулу средней скорости. ..
..  Первое определяется разницей между конечным и начальным положением и направлением движения, а второе требует только пройденного расстояния. Другими словами, скорость — это вектор (с величиной и направлением), а скорость — скаляр (только с величиной).
Первое определяется разницей между конечным и начальным положением и направлением движения, а второе требует только пройденного расстояния. Другими словами, скорость — это вектор (с величиной и направлением), а скорость — скаляр (только с величиной).
 Конечная скорость возникает в жидкостях (например, в воздухе или воде) и зависит от плотности жидкости. Знание того, как рассчитать скорость, также имеет особое значение в астрофизике, поскольку результаты должны быть очень точными.
Конечная скорость возникает в жидкостях (например, в воздухе или воде) и зависит от плотности жидкости. Знание того, как рассчитать скорость, также имеет особое значение в астрофизике, поскольку результаты должны быть очень точными. Для европейского вида это будет примерно 11 м/с, или 24 мили в час . Если вы ищете нашего знакомого африканского птичьего полета, то, боюсь, вам не повезло, присяжные еще не вынесены.
Для европейского вида это будет примерно 11 м/с, или 24 мили в час . Если вы ищете нашего знакомого африканского птичьего полета, то, боюсь, вам не повезло, присяжные еще не вынесены. Это время изменится, если человек изменит положение тела.
Это время изменится, если человек изменит положение тела.


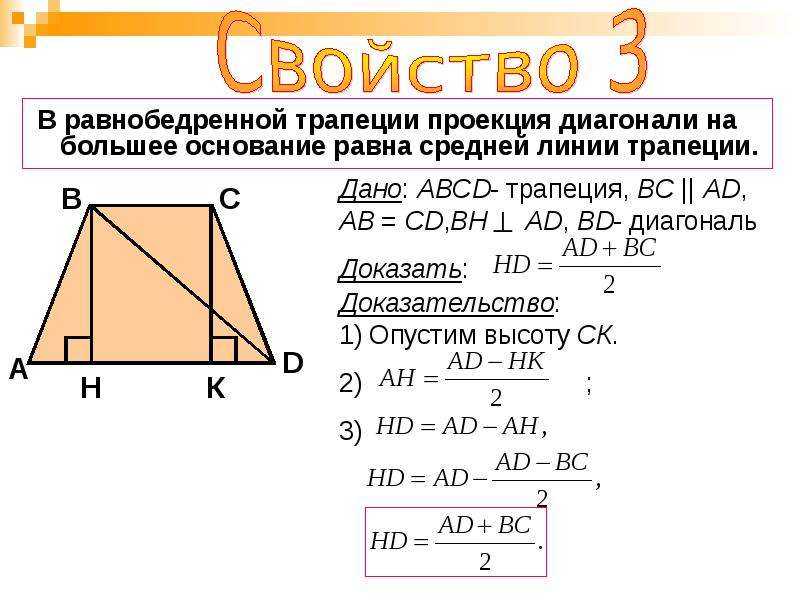 Если диагонали взаимно перпендикулярны, то площадь трапеции равна квадрату высоты:
Если диагонали взаимно перпендикулярны, то площадь трапеции равна квадрату высоты: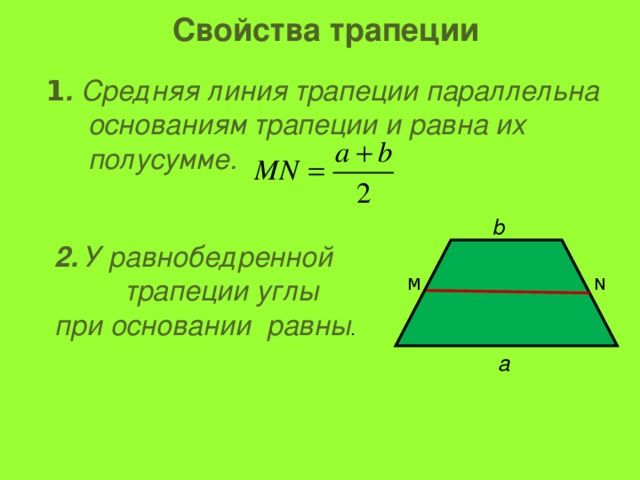 Также смотрите свойства трапеции
Также смотрите свойства трапеции Формулы длины боковой стороны через площадь, среднюю линию и угол при основе:
Формулы длины боковой стороны через площадь, среднюю линию и угол при основе:
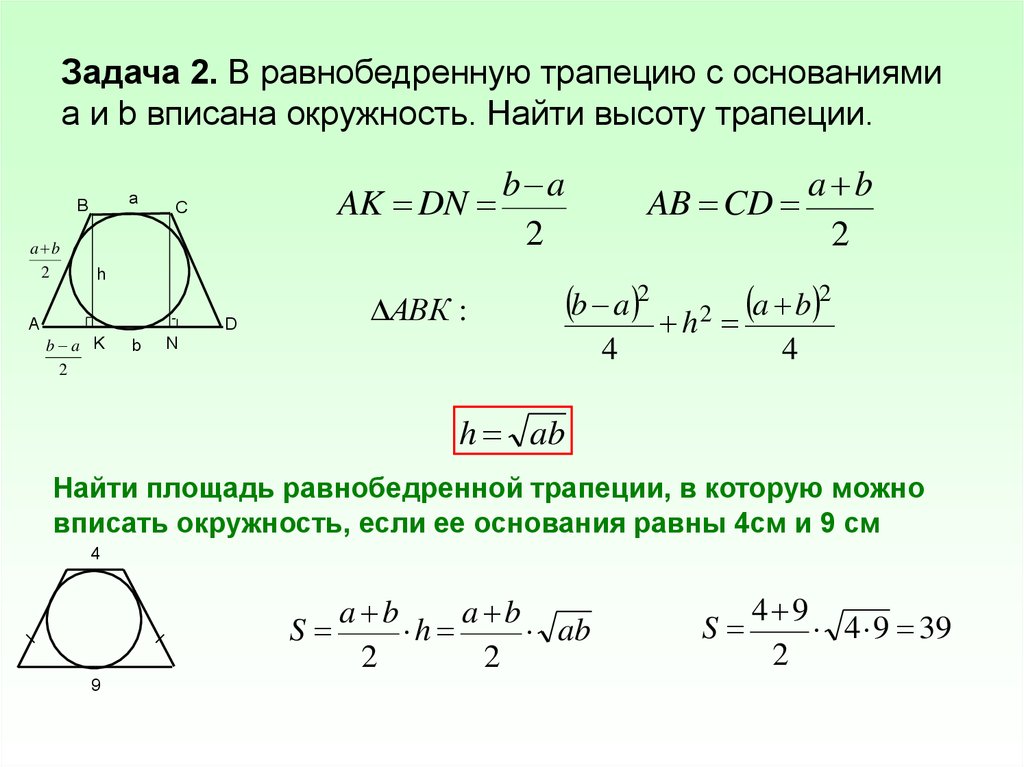 Формула высоты через стороны:
Формула высоты через стороны:
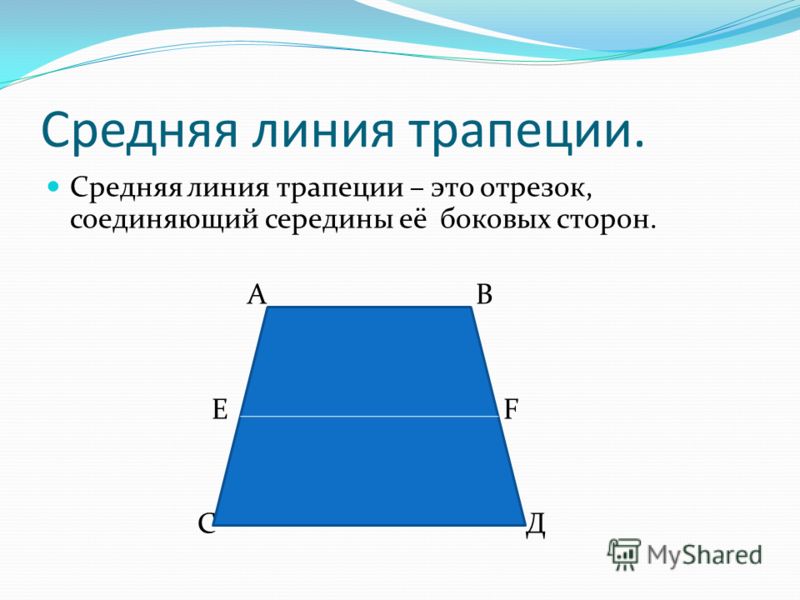 Формула длины диагонали через высоту и среднюю линию:
Формула длины диагонали через высоту и среднюю линию:
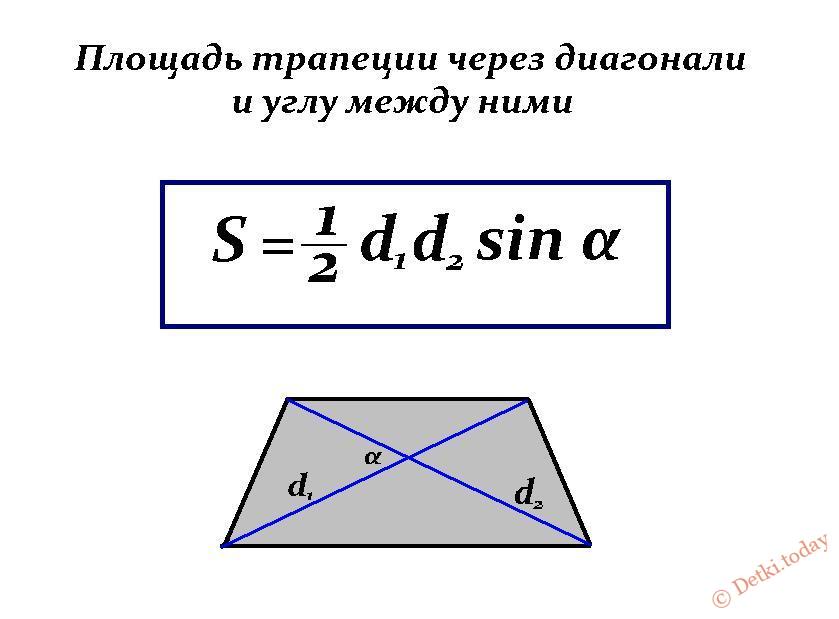 Формула площади через основания и угол между основой и боковой стороной:
Формула площади через основания и угол между основой и боковой стороной:
 Формула радиуса через стороны и диагональ:
Формула радиуса через стороны и диагональ:
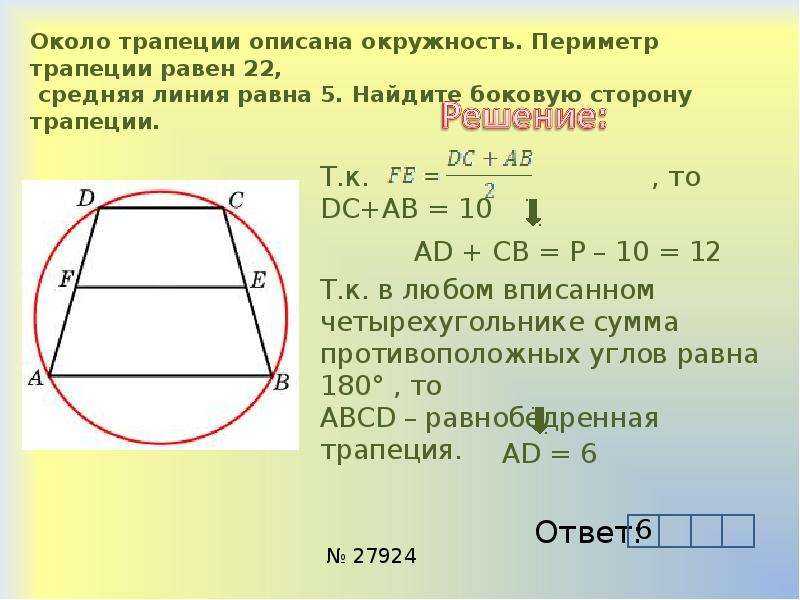
 Если в равнобедренную трапецию можно вписать окружность, то боковая сторона равна средней лини трапеции:
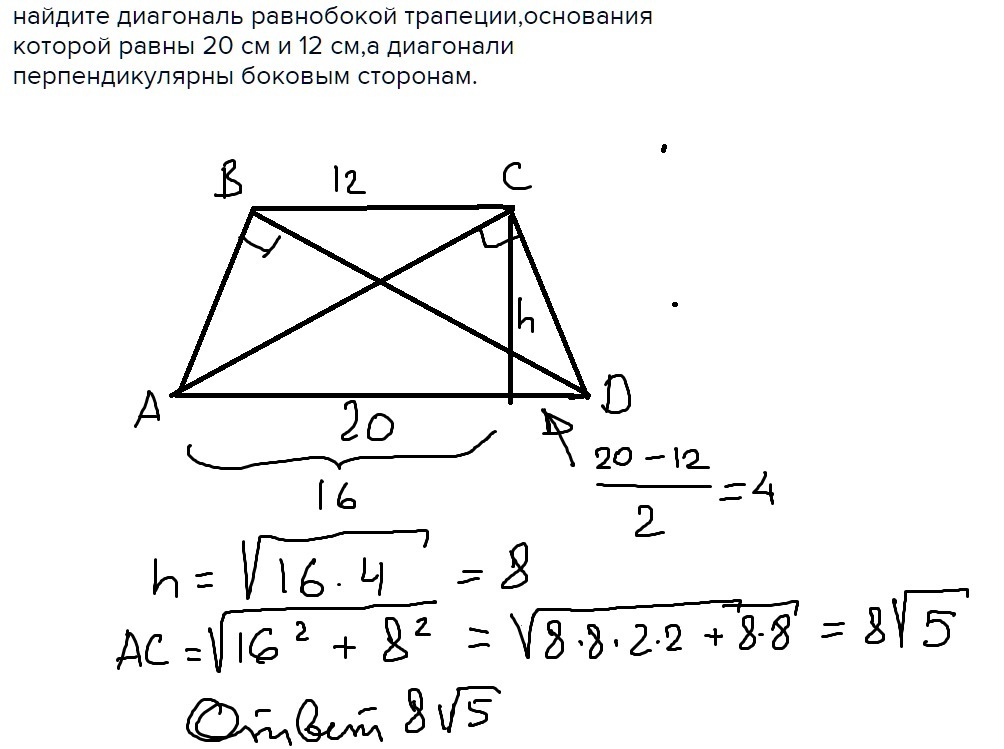
Если в равнобедренную трапецию можно вписать окружность, то боковая сторона равна средней лини трапеции: Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньшый (PD) — равен полуразности оснований:
Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньшый (PD) — равен полуразности оснований: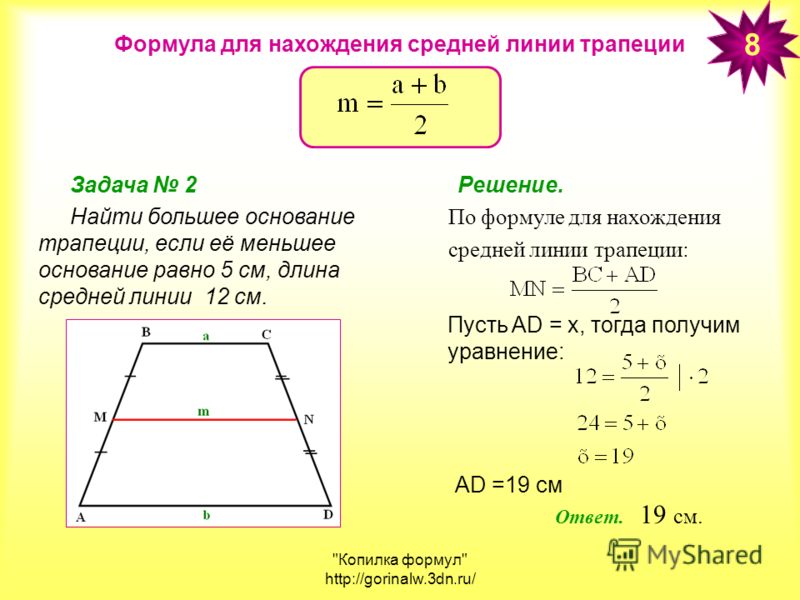 Формулы длины основ через площадь, высоту и другую основу:
Формулы длины основ через площадь, высоту и другую основу: Формула высоты через стороны:
Формула высоты через стороны: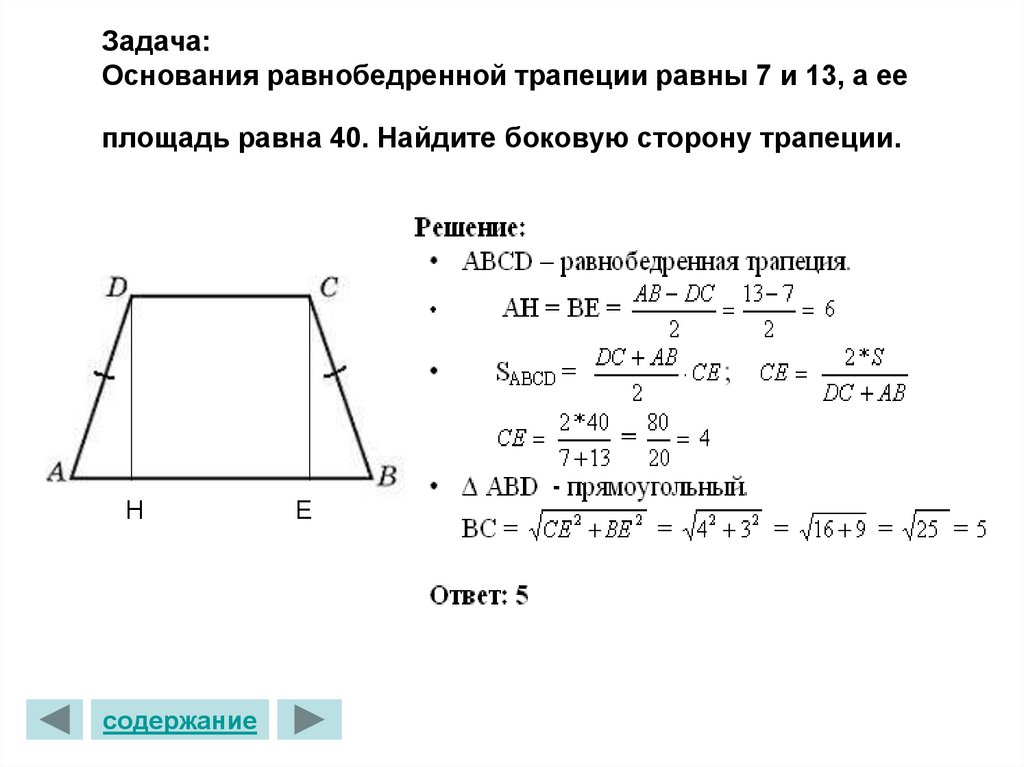 Формула длины диагонали через высоту и среднюю линию:
Формула длины диагонали через высоту и среднюю линию: Формула площади через основания и угол между основой и боковой стороной:
Формула площади через основания и угол между основой и боковой стороной: Формула радиуса через стороны и диагональ:
Формула радиуса через стороны и диагональ: Трапеция – это четырехугольник, у которого параллельна только одна сторона. Равнобедренная трапеция обладает многими интересными свойствами, которые делают ее уникальной и помогают нам отличить ее от других четырехугольников. Давайте обсудим их подробно.
Трапеция – это четырехугольник, у которого параллельна только одна сторона. Равнобедренная трапеция обладает многими интересными свойствами, которые делают ее уникальной и помогают нам отличить ее от других четырехугольников. Давайте обсудим их подробно.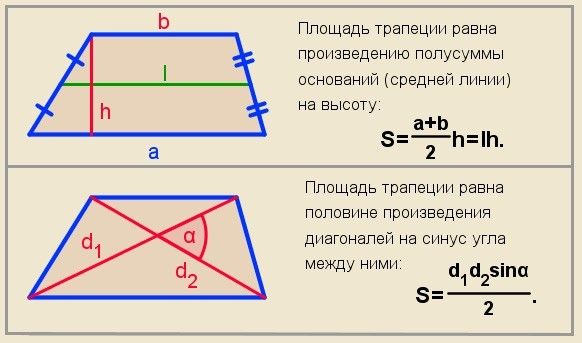 Посмотрите на изображение ниже: стороны c и d равны по длине, а противоположные стороны a и b (основания трапеции) параллельны друг другу.
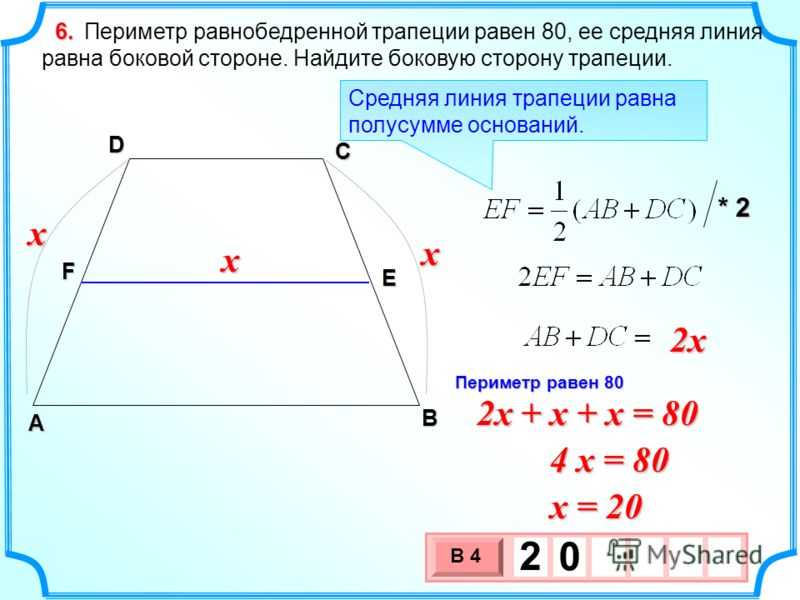
Посмотрите на изображение ниже: стороны c и d равны по длине, а противоположные стороны a и b (основания трапеции) параллельны друг другу.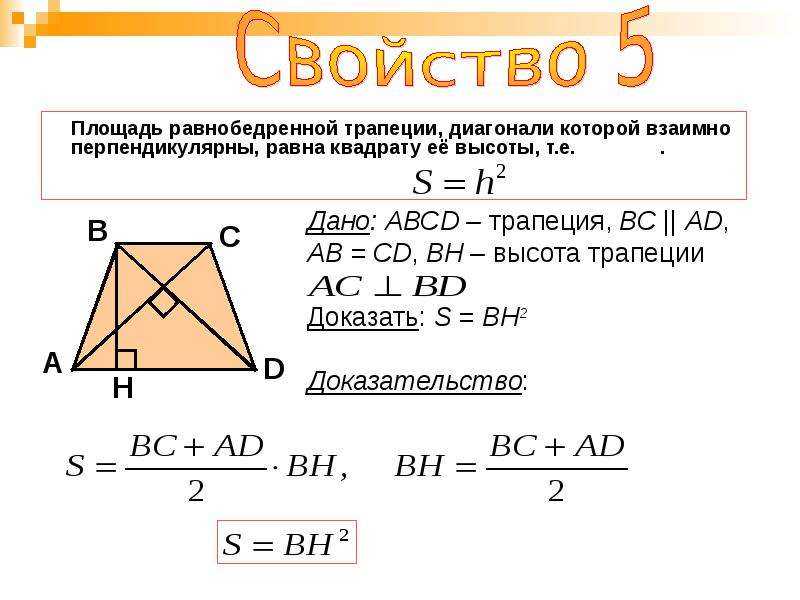

 С Cuemath вы будете учиться визуально и будете удивлены результатами.
С Cuemath вы будете учиться визуально и будете удивлены результатами.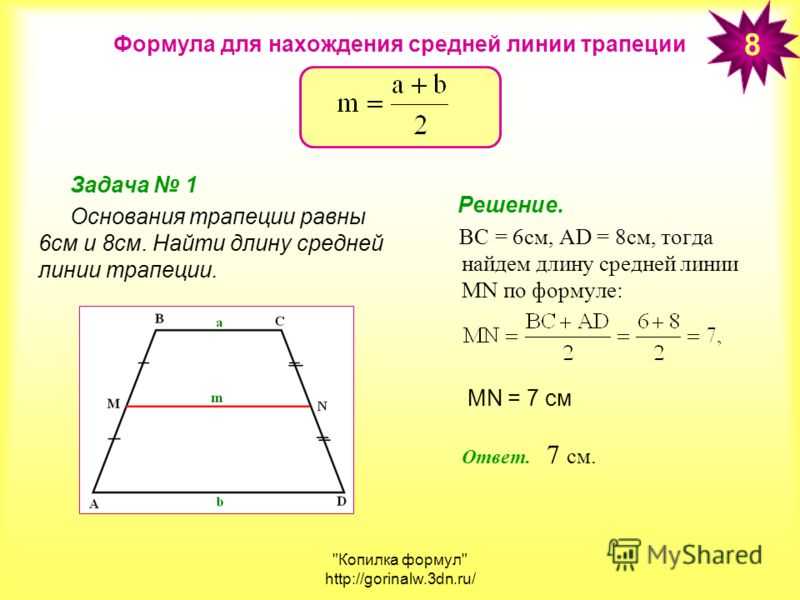

 на рисунке ниже). Или просто воспользуйтесь нашим калькулятором площади равнобедренной трапеции!
на рисунке ниже). Или просто воспользуйтесь нашим калькулятором площади равнобедренной трапеции!
 Н.Алгебра
Н.Алгебра )
) )
) )
) )
) )
) )
) )
) )
) )
)

 """
@обертывания(ф)
def wrapper_f(*args, **kwargs):
f_globals = f.__globals__
save_values = f_globals.copy() # поверхностная копия
# Добавляем контекст создания объекта
если self.kwargs:
f_globals.update(self.kwargs)
# Добавить контекст вызова функции
если кварги:
f_globals.update(kwargs)
пытаться:
результат = f()
окончательно:
f_glabals = save_values # Отменить изменения
вернуть результат
вернуть завернутый_f
"""
@обертывания(ф)
def wrapper_f(*args, **kwargs):
f_globals = f.__globals__
save_values = f_globals.copy() # поверхностная копия
# Добавляем контекст создания объекта
если self.kwargs:
f_globals.update(self.kwargs)
# Добавить контекст вызова функции
если кварги:
f_globals.update(kwargs)
пытаться:
результат = f()
окончательно:
f_glabals = save_values # Отменить изменения
вернуть результат
вернуть завернутый_f
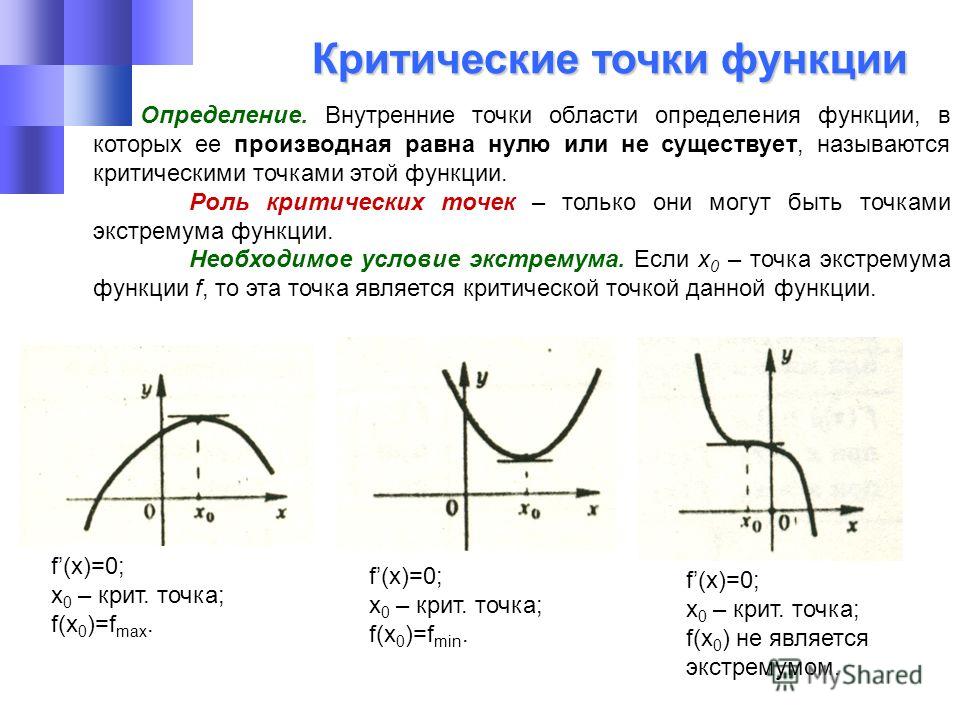
 Что означает «локальные переменные в самой внешней области действия функции не могут использовать то же имя, что и любой параметр»?
Что означает «локальные переменные в самой внешней области действия функции не могут использовать то же имя, что и любой параметр»? Вы можете поместить в него другие (внутренние) блоки и объявить переменные в тех, которые являются локальными для этого блока. Переменные во внутренних блоках могут иметь то же имя, что и во внешнем блоке, или параметры функции; они скрывают имена во внешней области. Переменные во внешнем блоке не могут иметь то же имя, что и параметр функции.
Вы можете поместить в него другие (внутренние) блоки и объявить переменные в тех, которые являются локальными для этого блока. Переменные во внутренних блоках могут иметь то же имя, что и во внешнем блоке, или параметры функции; они скрывают имена во внешней области. Переменные во внешнем блоке не могут иметь то же имя, что и параметр функции.



 Примеры текстовых значений включают: Отлично, Очень хорошо, Хорошо, Удовлетворительно и Плохо -ИЛИ- Удовлетворительно и Неудовлетворительно. Если схемы оценки текста не существует и вы выбрали параметр «Текст», вы можете ввести текст в ячейки столбца. Если вы решите предоставить учащимся доступ к результатам столбца в разделе «Мои оценки», они увидят текстовые значения своих оценок.
Примеры текстовых значений включают: Отлично, Очень хорошо, Хорошо, Удовлетворительно и Плохо -ИЛИ- Удовлетворительно и Неудовлетворительно. Если схемы оценки текста не существует и вы выбрали параметр «Текст», вы можете ввести текст в ячейки столбца. Если вы решите предоставить учащимся доступ к результатам столбца в разделе «Мои оценки», они увидят текстовые значения своих оценок. По умолчанию установлено значение «Нет». В столбце Центра оценок дополнительное значение отображается в скобках. Второстепенное значение не отображается для учащихся.
По умолчанию установлено значение «Нет». В столбце Центра оценок дополнительное значение отображается в скобках. Второстепенное значение не отображается для учащихся.






 Затем система делит результат на максимально возможное количество баллов, чтобы получить процентное соотношение для каждого элемента во взвешенном столбце. Полученные проценты сохраняют пропорциональный вес каждого элемента, поэтому элементы с более высоким значением в баллах оказывают большее влияние на составную оценку.
Затем система делит результат на максимально возможное количество баллов, чтобы получить процентное соотношение для каждого элемента во взвешенном столбце. Полученные проценты сохраняют пропорциональный вес каждого элемента, поэтому элементы с более высоким значением в баллах оказывают большее влияние на составную оценку. Знаменатель 80 — это сумма весов только тех категорий, которые содержат баллы (40 + 40 = 80).
Знаменатель 80 — это сумма весов только тех категорий, которые содержат баллы (40 + 40 = 80). Процентные значения для всех выбранных столбцов суммируются. Результат делится на количество столбцов, включенных в расчет. Результат отображается в соответствии с параметрами первичного и вторичного отображения.
Процентные значения для всех выбранных столбцов суммируются. Результат делится на количество столбцов, включенных в расчет. Результат отображается в соответствии с параметрами первичного и вторичного отображения.