iPhone 13 Pro и iPhone 13 Pro Max – Apple (RU)
Просто. Нереально.
- Значительно более мощная система камер.
- Абсолютно новые ощущения от дисплея.
- Самый быстрый
чип для iPhone. - Исключительная прочность.
- И огромный
прирост ресурса аккумулятора.
Всё это Pro.
Дизайн
Дисплей Super Retina XDR1 с технологией ProMotion
iPhone 13 Pro Max
6,7″
iPhone 13 Pro
6,1″
Хирургическая нержавеющая сталь
Передняя панель Ceramic Shield радикально повышает прочность
Надёжная защита от воды (IP68)2
Система камер
Система камер Pro получила самое масштабное обновление. Улучшенная аппаратная часть позволяет передать ещё больше деталей. Интеллектуальное программное обеспечение открывает новые возможности для съёмки фото и видео. Супербыстрый чип поддерживает все эти инновации. Так вы ещё не снимали.
Интеллектуальное программное обеспечение открывает новые возможности для съёмки фото и видео. Супербыстрый чип поддерживает все эти инновации. Так вы ещё не снимали.
Макросъёмка
Ммм, макро.
Теперь на iPhone.
Новая сверхширокоугольная камера с обновлённым объективом и мощной системой автофокуса теперь может
снимать на расстоянии всего 2 см от объекта. Самые мелкие детали будут выглядеть масштабно — узор листа,
лапки насекомого или капля росы.
Великая красота.
И даже макровидео.
Макрофотографии — это только начало. Теперь вы можете снимать и макровидео, даже замедленное или таймлапс. Приготовьтесь удивляться.
Минимум света
Скорей
бы ночь.
iPhone 13 Pro создан для съёмки при слабом освещении. Широкоугольная камера с увеличенной диафрагмой и нашей самой большой матрицей использует возможности сканера LiDAR для портретов в Ночном режиме. У сверхширокоугольной камеры с новым автофокусом диафрагма стала значительно больше, а матрица — быстрее. А у телефотокамеры появился Ночной режим.
У сверхширокоугольной камеры с новым автофокусом диафрагма стала значительно больше, а матрица — быстрее. А у телефотокамеры появился Ночной режим.
Широкоугольная камера улавливает до 2,2 раза больше света при съёмке фото и видео
Сверхширокоугольная
камера улавливает на 92% больше света при съёмке фото и видео
Ночной режим теперь
на всех камерах
Фото и видео становятся чётче и детальнее при любом освещении
Оптический зум
Зум идёт вперёд.
У новой телефотокамеры фокусное расстояние 77 мм и трёхкратный оптический зум — идеальные параметры для классических портретных кадров или съёмки фото и видео издалека. А если объект находится вблизи, можно настраивать степень размытия фона и экспериментировать с эффектами студийного освещения в Портретном режиме.
- Оптический зум 3x для телефотокамеры Крупный план ещё крупнее
- Диапазон оптического зума 6x для всей системы камер Ещё больше вариантов кадрирования
Режим «Киноэффект»
Фокус переводится. Эффект производится.
Представляем режим «Киноэффект».
Теперь iPhone может снимать видео с малой глубиной резкости и делать плавный автоматический перевод фокуса с объекта на объект. Режим «Киноэффект» распознаёт, когда новый объект готов появиться в кадре, и сразу же переводит фокус на него —
ваше видео становится ещё выразительнее. Перевести фокус на другой объект или отрегулировать бокэ можно и после съёмки. Попробуйте, нам очень интересно, что у вас получится.
- Режим «Киноэффект» позволяет регулировать глубину резкости после съёмки
- Снимайте на любую камеру: широкоугольную, сверхширокоугольную или телефото
- Поддерживает стандарт Dolby Vision HDR
Создавая режим «Киноэффект» для iPhone, мы тщательно изучали, как профессиональные кинооператоры используют перевод фокуса, чтобы добавить сюжету интриги и сделать фильм более зрелищным.
На съёмках в Голливуде над этим работает целая команда специалистов. Кинооператор решает, что будет в фокусе и в какой момент его нужно перевести. А ассистент по фокусу следит, чтобы это было сделано плавно, в нужный момент и с точной фокусировкой на нужном объекте. Мы поставили себе большую задачу: научить iPhone переводить фокус автоматически.
Для начала требовалось сгенерировать данные глубины резкости в высоком качестве: нужно было научить режим «Киноэффект» точно измерять расстояние до объекта в кадре, будь то человек, животное или предмет. А поскольку речь идёт о видео, эти данные должны были поступать непрерывно: с частотой 30 кадров в секунду.
Работу целой команды кинооператоров мы поручили системе Neural Engine. Именно она автоматически принимает решение о том, что должно быть в фокусе в данный момент, и в нужное время обеспечивает его плавный перевод на другой объект. Но если вы хотите управлять процессом вручную, фокус можно переводить самостоятельно — как во время съёмки, так и при редактировании.
И для таких серьёзных вычислительных мощностей нам был нужен процессор, который мог справиться с этой работой. Такой, как A15 Bionic.
Сложно даже представить объёмы вычислительной мощности, необходимые для работы алгоритмов машинного обучения, рендеринга смены автофокусировки, поддержки ручного изменения фокуса и перевода каждого кадра в формат Dolby Vision — и всё это в режиме реального времени.
Теперь целый Голливуд у вас в кармане.
Фотографические стили
Выберите
свои настройки.Найдите свой взгляд.
Представляем
Фотографические стили.
Фотографические стили позволяют применить к вашим кадрам выбранные параметры тона и теплоты. При этом оттенки неба и кожи остаются естественными — достичь такого эффекта с обычными фильтрами не получится. Выберите шаблон Apple: Красочный, Насыщенный контрастный, Тёплый или Прохладный. Если захотите, можно выставить более точные параметры для нужного стиля. Настроить стиль съёмки по вашему вкусу достаточно один раз, и он будет применяться автоматически.
Настроить стиль съёмки по вашему вкусу достаточно один раз, и он будет применяться автоматически.
- Наши передовые средства обработки изображения воспроизводят ваш стиль в реальном времени
- Оттенок
- Увеличивайте для более ярких насыщенных цветов. Уменьшайте для более выраженных теней и контраста.
- Теплота
- Увеличивайте, чтобы подчеркнуть золотистые полутона. Уменьшайте, чтобы добавить больше голубоватых оттенков.
Формат ProRes
Снимайте.Редактируйте.Отправляйте.
Всё это в ProRes.
- Это наш первый смартфон, на котором можно полностью снять и отредактировать фильм в формате ProRes или в стандарте Dolby Vision
ProRes подразумевает высокую чёткость изображения и низкую степень сжатия. Поэтому прямо на ходу вы можете создавать видеоконтент, готовый к публикациям и презентациям. Теперь проект в ProRes можно начать и закончить прямо на iPhone. Или открыть видео с iPhone в формате ProRes прямо в Final Cut Pro на Mac.
Теперь проект в ProRes можно начать и закончить прямо на iPhone. Или открыть видео с iPhone в формате ProRes прямо в Final Cut Pro на Mac.
Масса
технологий в каждом снимке.
Smart HDR 4 оптимизирует сцену по частям.
Технология Smart HDR 4 использует вычислительную мощность Neural Engine для машинного обучения и настройки индивидуальных параметров для нескольких человек в кадре. Наше программное обеспечение совместно с процессором обработки сигнала изображения автоматически регулирует контрастность, освещение и оттенок кожи для каждого человека. Чтобы все получились просто идеально.
Если в кадре недостаточно света, на помощь приходит технология Deep Fusion. Вместе с системой Neural Engine она анализирует все пиксели изображения, снятого с различными экспозициями. Из самых удачных областей формируется финальное изображение, в котором максимум деталей и самые тончайшие текстуры.
Телефото
- Фокусное расстояние 77 мм
- Оптический зум 3x
- Диафрагма ƒ/2.
 8
8 - Поддержка Focus Pixels
- Шестилинзовый объектив
- Оптическая стабилизация изображения
Сверхширокоугольная
- Фокусное расстояние 13 мм
- Диафрагма ƒ/1.8
- Более быстрая матрица
- Поддержка Focus Pixels
- Шестилинзовый объектив
Широкоугольная
- Фокусное расстояние 26 мм
- Размер пикселя 1,9 мкм
- Диафрагма ƒ/1.5
- Поддержка Focus Pixels на всей матрице
- Семилинзовый объектив
- Оптическая стабилизация
изображения сдвигом матрицы
Три наши самые мощные камеры
Камера TrueDepth
Система камер TrueDepth тоже на высоте:
- Режим «Киноэффект»
- Фотографические стили
- Видео в формате ProRes
- HDR-видео в Dolby Vision
- Портретный режим
- Селфи в Ночном режиме
- Smart HDR 4
- Deep Fusion
- и многое другое
Ничего
себе
селфи.
- Процессор A15 Bionic и камера TrueDepth также обеспечивают работу Face ID, исключительно надёжной технологии аутентификации
Ёмкость
До
для всех ваших фото и видео
До
1 ТБ
для всех ваших фото и видео
Дисплей
Привет, ProMotion.
Дисплей с адаптивной частотой обновления до 120 Гц — прикоснитесь и удивитесь.
Частота обновления для нового дисплея Super Retina XDR с технологией ProMotion может изменяться от 10 до 120 раз в секунду. Она автоматически становится выше, когда вам требуется быстрая обработка графики, и снижается при выполнении других задач для экономии энергии. Частота обновления зависит даже от скорости движения вашего пальца при прокрутке контента. Почувствуйте разницу.
- iOS 15 оптимизирована для ProMotion, поэтому всё работает феноменально плавно
Серьёзный
подход к игре.
Способность дисплея обновляться с частотой до 120 Гц в сочетании с потрясающей графической производительностью нового 5‑ядерного графического процессора на базе чипа A15 Bionic делают iPhone 13 Pro незаменимым устройством
для настоящих геймеров.
До 25% ярче
на улице Ваш контент будет
лучше виден на солнце
Особая
технология OLED раскрывает возможности разрешения и цветопередачи дисплея по максимуму
Яркость до 1200 кд/м² в пиковом режиме для фото и видео HDR
Область дисплея больше благодаря уменьшенной
камере TrueDepth
Невероятно точная цветопередача Ваш контент выглядит совершенно реалистично
Потрясающие контрастность и разрешение позволяют передать чёрные и белые цвета без искажений, мельчайшие детали и чёткий текст
Работа дисплея, который обновляется 120 раз в секунду, — очень энергозатратный процесс. Но такая частота обновления нужна не всегда.
Но такая частота обновления нужна не всегда.
Поэтому хороший способ повысить энергоэффективность — задать стандартную частоту обновления для различных типов контента. Например, 10 кадров в секунду для чтения книг и 120 кадров в секунду для игр. Основная сложность такого подхода в том, что частота кадров всё время меняется. Если частота обновления для экрана меню в игре составляет 30 кадров в секунду, но дисплей при этом настроен на обновление с частотой 120 кадров в секунду, драгоценный заряд аккумулятора будет расходоваться впустую, а вы никак не сможете оценить высокую частоту обновления.
Мы решили, что незачем тратить заряд аккумулятора на пустые кадры и разработали более сложную технологию работы дисплея. Такую, которая постоянно адаптируется под постоянно меняющуюся частоту обновления контента.
Никаких настроек. Частота обновления напрямую зависит от того, что происходит на экране. Если во время игры частота обновления снижается до 30 кадров в секунду, то же делает и технология ProMotion. Если вы смотрите видео, снятое с частотой 24 кадра в секунду, именно с этой частотой оно и воспроизводится на дисплее. И всё это значительно экономит энергию.
Если вы смотрите видео, снятое с частотой 24 кадра в секунду, именно с этой частотой оно и воспроизводится на дисплее. И всё это значительно экономит энергию.
С технологией ProMotion вы словно ныряете через дисплей прямо в приложение.
Мы учли даже то, как замедляется и ускоряется палец при прокрутке контента и смахивании по экрану. А скорость движения пальца определяет скорость каждого жеста. В iOS 15 вам часто будет казаться, что при частоте 120 Гц контент буквально следует за пальцем. С невероятной скоростью. При этом технология ProMotion использует частоту 120 кадров в секунду только в те моменты, когда она вам действительно нужна.
Конечно, было бы проще просто встроить в iPhone постоянную частоту обновления 120 Гц и не думать о расходе аккумулятора. Но в Apple другой подход. Нам было важно убедиться, что дисплей работает с высокой частотой обновления именно тогда, когда эта частота нужна. И что в другие моменты заряд аккумулятора не расходуется напрасно.
Чип A15 Bionic
В нём сила Pro.
A15 Bionic — самый быстрый чип для iPhone.
Новый 5‑ядерный графический процессор обрабатывает графику до 50% быстрее, чем любой другой процессор iPhone
Новые ядра производительности и эффективности позволяют решать самые сложные задачи с экономией аккумулятора
Сверхбыстрая система Neural Engine обрабатывает до 15,8 триллиона операций в секунду и обеспечивает работу режима «Киноэффект», технологии Smart HDR 4 и многих других функций
Обновлённый процессор обработки сигнала изображения уменьшает шумы и настраивает тональную компрессию на совершенно новом уровне
Технология Secure Enclave защищает вашу личную информацию: данные Face ID, контакты и многое другое
Обработка данных на устройстве защищает такой контент, как ваши запросы к Siri и взаимодействие с текстом в функции «Онлайн‑текст»
Год за годом чип iPhone менял представления о пределах возможного для смартфона. В основе всего лежит наш уникальный подход к разработке: долгий путь к созданию каждого продукта и по‑настоящему слаженная работа всех наших команд.
В основе всего лежит наш уникальный подход к разработке: долгий путь к созданию каждого продукта и по‑настоящему слаженная работа всех наших команд.
Такая тесная интеграция наших команд позволяет развивать функции, которые были бы невозможны при другом подходе.
Именно так мы создаём новые технологии, например ProMotion, начиная планировать их заранее — за несколько лет. Команда, создававшая чип A15 Bionic, отлично знала, что именно требуется для функционирования аппаратного и программного обеспечения дисплея, и учитывала это в своих процессах.
Например, мы оптимизировали модуль дисплея, чтобы он поддерживал различную частоту кадров, и создали систему, при которой технология ProMotion может обеспечивать потрясающую графическую производительность и использовать потенциал нового энергоэффективного 5‑ядерного графического процессора.
Тем временем команды, разрабатывающие программное обеспечение для дисплея и систему iOS, выяснили, для каких задач такая высокая частота обновления подходит лучше всего и в каких случаях можно оптимизировать частоту кадров для экономии заряда аккумулятора. Мы начали не просто с идеи создания быстрого чипа, на базе которого строились бы различные функции. Вместо этого мы подумали о том, каким должно быть идеальное устройство, которое мы были бы рады предложить пользователям. И затем объединили наши усилия для его создания.
Мы начали не просто с идеи создания быстрого чипа, на базе которого строились бы различные функции. Вместо этого мы подумали о том, каким должно быть идеальное устройство, которое мы были бы рады предложить пользователям. И затем объединили наши усилия для его создания.
Аккумулятор
iPhone 13 Pro Max
работает от аккумулятора дольше любого другого iPhone.
- До 2,5 часа дольше работает без подзарядки iPhone 13 Pro Max3
- До 1,5 часа дольше работает без подзарядки iPhone 13 Pro3
А с зарядным устройством MagSafe
они будут заряжаться ещё быстрее.
iOS 15
На связи.
В моменте.
В iOS 15 вы можете делиться с собеседниками фильмами, музыкой и другим контентом с вашего экрана прямо во время разговора по FaceTime. Уведомления легко настроить так, чтобы видеть только актуальные на данный момент и фокусироваться на главном. А чтобы мгновенно отправить электронное письмо или сделать звонок, достаточно коснуться соответствующего текста на фото.
А чтобы мгновенно отправить электронное письмо или сделать звонок, достаточно коснуться соответствующего текста на фото.
Подробнее об iOS 15
Ваши данные под защитой.
iPhone даёт вам возможность полностью контролировать свои личные данные и доступ к ним. Наглядная информация о конфиденциальности помогает
выбирать приложения в зависимости от того, как они используют ваши
данные. Приложения должны получить разрешение пользователя, прежде чем начать отслеживать его действия в сторонних приложениях и на сайтах.
И это только начало.
Подробнее об Apple и конфиденциальности
Хороший дизайн полезен для планеты.
Все наши магазины, офисы, дата-центры и операционные отделы уже работают с нулевым уровнем выбросов углерода. К 2030 году нейтральный углеродный след будет и у всех наших продуктов — а значит, и при их использовании.
В этом году мы отказались от пластиковых обёрток для коробок с iPhone 13 и iPhone 13 Pro, что позволило сэкономить 600 метрических тонн пластика. А наши заводы по сборке устройств перешли на полностью безотходное производство.
Подробнее об Apple
и окружающей среде
Целый телефон
развлечений.
Слушайте онлайн песни, альбомы и подборки от наших музыкальных редакторов. Смотрите сериалы, о которых все говорят. Открывайте для себя увлекательные новые игры. Сервисы Apple — это самый интересный контент, который всегда у вас под рукой. А Apple One объединяет их все в формате удобной единой подписки.
Подробнее об Apple One
Магия умножается.
Всё, за что вы любите iPhone, работает ещё лучше вместе с Mac, iPad и Apple Watch — автоматически, как по волшебству. Вы можете отвечать на звонки с любого удобного устройства. Делать на iPhone фотографии, которые будут тут же появляться на Mac. И читать любые сообщения на всех ваших устройствах. Проще простого.
И читать любые сообщения на всех ваших устройствах. Проще простого.
Подробнее о совместной
работе продуктов Apple
Дополненная реальность
Как он
выглядит.
Со всех сторон и во всех цветах.
- Небесно-голубой
- Серебристый
- Золотой
- Графитовый
Посмотрите на iPhone 13 Pro в дополненной реальности
Посмотрите на iPhone 13 Pro Max в дополненной реальности
Посмотрите на iPhone 13 Pro и iPhone 13 Pro Max в дополненной реальности.
Откройте эту страницу в Safari
на iPhone или iPad.
Аксессуары
Что к нему добавить.
AirPods
Идеальный аксессуар для iPhone может стать персональным — с бесплатной гравировкой при покупке в Apple.
AirTag
Прикрепите один AirTag к ключам, а другой — к рюкзаку. И если они потеряются, вы cможете легко их найти с помощью приложения «Локатор».
MagSafe
Один момент — и на месте. Плюс быстрая беспроводная зарядка.
Где купить iPhone?
Вы можете купить iPhone у реселлера или оператора сотовой связи. Выбирайте любой удобный вариант.
Подробнее о покупке iPhone
Ремонт iPhone 13 | Качественные услуги с гарантией в сервисе Pedant
Дмитрий Стыров
Мастер Антон в кратчайшие сроки выполнил диагностику и выявил проблему с 7 IPhone! В течении 2 часов была произведена замена всех поврежденных/неисправных деталей! Телефон функционирует, а гарантия на ремонт 90 дней страхует! Возможность оплаты картой приятно удивила! Пункт приема/ремонта в шаговой доступности от станции метро Бабушкинская! Рекомендую!
Евгений
Дважды обращался, и дважды за переделкой после криворуких «мастеров». Внимание к клиенту и работа выполненная на 5+ поразили. Рекомендую и сам буду обращаться!
Внимание к клиенту и работа выполненная на 5+ поразили. Рекомендую и сам буду обращаться!
Михаил
Сломался телефон, сенсор не реагировал на касание. Обратился в вашу компанию. Очень быстро, качественно, недорого сделали. Понравилось хорошее отношение сотрудников. Большое спасибо.
Дарья
Отличная компания, и главное рядом с домом. Мастер сделал все быстро и качественно. Цены приемлемые. В общем все супер ,советую ☺️
YULIYA ROSSIEVA
Благодарю за оперативный ремонт смартфона. Заменили стекло, наклеили гидрогелевую пленку и все это ща час работы ! Ещё и сделали бесплатную диагностику! Большое спасибо за качественную и быструю работу. \
Данил
Очень хороший сервис, сотрудники уважительно относятся к покупателям. Починили очень быстро по дешевой цене, а самое главное качественно.Всем советую!
Починили очень быстро по дешевой цене, а самое главное качественно.Всем советую!
Отличный сервис- быстро, качественно и бюджетно, все сделали при мне, запчасти в наличии, цена супер. Все объяснили, дали гарантию, все работает отлично.
Полина Солодова
Здравствуйте хотела посоветовать данную компанию так как тут очень приятные цены и качественное обслуживание. я не раз буду обращаться в эту компанию так как она мне очень нравиться как клиенту
Екатерина
Очень хороший сервис. Однозначно приду ещё , посоветую всем своим знакомым и друзьям.\Все сделали быстро, качественно и не дорого. Ну очень давольна. Спасибо вам огромное.\Поставлю 5 звёзд!
Милена
Здравствуйте, месяц назад у меня телефон выключился и не включался, обратилась к вам (мне вас посоветовали)\На следующий день забрала, и теперь телефон работает как прежде. Хочу сказать вам спасибо, за качественную работу! Я очень довольна!
Хочу сказать вам спасибо, за качественную работу! Я очень довольна!
parchina
Отличный сервис по ремонту айфонов.Быстрый ремонт,умеренная цена.Доброжелательный персонал.Замечательные ребята.Буду рекомендовать.Благодарю
Эдуард
Хорошый сервис, мой телефон починили довольно быстро. Посоветую ваш сервис родным и близким. Особое внимание заслуживает низкие цены.
Лена
Очень хороший сервис . Телефон отремонтировали . Результат на лицо. Может и дорого , но качественно.
Алексей Черничко
Спасибо мастерам за такую внимательную работу.Относил телефон на починку,очень быстро и качественно починили за недорогую цену. Буду всем советовать именно этот сервисный центр
Буду всем советовать именно этот сервисный центр
Карина
Рекомендую данный сервис. Вся работы была выполнена на высшем уровне. Мне крайне понравился персонал и скорость работы. Добрые, вежливые, не всегда встретишь подобное отношение к клиентам. Буду обращаться за услугой лишь сюда.
Виталий
Все супер, пришел с уверенностью, что гнездо type-c в моем телефоне разбито из-за использования в машине растягивающегося провода, т.к. большая осевая нагрузка, но мастер первым делом прочистил гнездо, продул и проверил, все стало отлично! 5 мину и готово)
Александра Кривенкова
Недавно заглючил телефон, провод перестал заряжать. Нашла рядом данный сервисный центр, ребята оперативно оказали помощь, подобрали новый зарядный шнур и подзарядили сам телефон! Мастера вежливые, доброжелательные и клиентоориентированые. Спасибо
Спасибо
Полина Владимировна солодова
Здравствуйте хотела посоветовать данную компанию так как тут очень приятные цены и качественное обслуживание. я не раз буду обращаться в эту компанию так как она мне очень нравиться как клиенту
Елена
Сегодня обратилась в филиал возле м. Чеховская. Очень благодарна Андрею и Илье за оперативную помощь. Сотрудники проявили высокий профессионализм, оперативность и мастерство. Всем советую!
Расулжон
Стекло бесплатно поклеили, отличный сервис рекомендую, буду обращаться ещё не раз
Сергей
Отличный сервис!!!! Мастер Влад профессионал своего дела. Сделал всё быстро качественно. Фирме Педант, в лице мастера Влада огромное спасибо за работу!
Сделал всё быстро качественно. Фирме Педант, в лице мастера Влада огромное спасибо за работу!
Иваненков Роман
Не могу назвать этот сервис хорошим…. Это слишком бледное слово. Сервис на Домодедовской — СУПЕР ВОСХИТИТЕЛЬНЫЙ!!! Мастер Игорь просто маг и волшебник! Чётко, буквально за минуту сделал предположение об неисправности. Сориентировал по цене. Не успел доехать до дома, после сдачи телефона в ремонт, как поступило сообщение об успешном выполнении ремонта. Причина неисправности и стоимость ремонта полностью соответствовали заявленным при сдаче в ремонт. Я не являюсь молодой восторженной девушкой, более того сам являюсь сервисменом в другой области, могу объективно оценить качество услуг. Я в восторге. Отдельный респект и уважуха Игорю. Человек своё дело знает.
Алина Сатюкова
Первое что хочу сказать — спасибо за оперативное решение моего вопроса и за стремление ребят максимально помочь. Ремонтировала свой любимый Samsung. Шла из соседнего бара по утру и разбила телефон. Подняла голову в слезах и увидела вывеску Pedant.ru через дорогу. В обед я уже была там и на следующий день забрала свой телефон как новый. Были разные варианты по цене / качеству дисплея, но ребята посоветовали именно оригинал — то есть точь в точь, что стоял у меня. Еще, мне кажется, я понравилась менеджеру и он мне сделал какую то защиту дисплея в подарок — она практически не заметна, но уже, после этого, роняла телефон моя дочь, я с замиранием сердца подняла его и дисплей оказался жив. \
Ремонтировала свой любимый Samsung. Шла из соседнего бара по утру и разбила телефон. Подняла голову в слезах и увидела вывеску Pedant.ru через дорогу. В обед я уже была там и на следующий день забрала свой телефон как новый. Были разные варианты по цене / качеству дисплея, но ребята посоветовали именно оригинал — то есть точь в точь, что стоял у меня. Еще, мне кажется, я понравилась менеджеру и он мне сделал какую то защиту дисплея в подарок — она практически не заметна, но уже, после этого, роняла телефон моя дочь, я с замиранием сердца подняла его и дисплей оказался жив. \
VM
Стал плохо работать динамик на телефоне, кого-то хорошо слышу при разговоре, некоторых просто отвратительно. Думал уже менять телефон, но зашел в ваш центр на Новослободской. За 2 минуты почистили динамик и стало все отлично. Был очень приятно удивлен. Спасибо! Так держать!
Ольга
Телефон починили быстро за небольшую стоимость. Очень довольна, спасибо большое.
Очень довольна, спасибо большое.
Виктор Петрович
Выражаю огромную благодарность Сервису! И, лично, мастеру Алексею! Прекрасно разобрался и решил мою проблему! Спасибо! Отремонтировали два смартфона Samsung.
Николай
Мне понравился интерьер офиса.Сотрудники грамотные.Решают все вопросы по гаджету.Сделали ремонт в течении часа.Понравилась гарантия: у меня 3 месяца.Так что рекомендую.Цена , кстати, вменяемая.
Илья
Огромное спасибо сервису на м. Новослободская! Обратился 24.04.2022. Все как для себя сделано! Честно, быстро, качественно с гарантией!
Olga
Cпасибо большое, за отличное обслуживание. Довольна ремонтом. Все оперативно и доброжелательно.
Довольна ремонтом. Все оперативно и доброжелательно.
Анастасия
Спасибо большое сервисному центру. Удобный график работы. Можно записаться через социальные сети. Дают гарантию,что самое главное при ремонте телефона. Сломался телефон мастер приехал в назначенное время и место. Оценил поломку и предпринял все меры по устранению причины поломки. Мастер вежливый и видно грамотный. Время его работы заняло не больше 20 минут.
Ирек
Обратился сегодня с банальной проблемой для спеца, коим я не являюсь) Реакция на обращение моментальная, так сказать «бросив все». Получил обратно свой смартфон исправным буквально через 5 минут. Мастер одним словом! Спасибо. Рекомендую, зачёт!
Евгения
Добрый день! Рекомендую сервис на Маяковской. Профессиональные, отзывчивые и неравнодушные сотрудники, готовые прийти на помощь «блондинке со смартфоном». Настроили, актуализировали и подробно объяснили что к чему, за что заслуживают большого человеческого спасибо!
Профессиональные, отзывчивые и неравнодушные сотрудники, готовые прийти на помощь «блондинке со смартфоном». Настроили, актуализировали и подробно объяснили что к чему, за что заслуживают большого человеческого спасибо!
Александр
Приятный сервис, вежливые сотрудники работают качественно и оперативно. Нареканий нет, всё классно.
Артем
После падения телефон начал постоянно выключаться,пришел в данный сервис,специалист оперативно нашел проблему,быстро и качественно все сделал,за что ему огромная благодарность.причем даже денег не взял.пол года назад я менял корпус и аккумулятор в этом же сервисе, тогда тоже скидку большую сделали)))в общем сервис рекомендую,лучше специалистов в городе у нас не найти!!!
Алиса
Хочу выразить благодарность сотруднику Тимофею за качественную и быструю работу. Хороших вам клиентов!
Хороших вам клиентов!
Тимур
Добрый день! Спасибо большое за быструю и качественную работу по замене дисплея на iphone и защитное стекло в подарок, очень приятно, теперь мой телефон как новенький.
Игорь
Большое спасибо Ростиславу за быстро выполненную работу, за честность и качество. Не ожидали, что так быстро все сделают и даже денег не возьмут.
Лариса
Сервис действительно хорош, помощь своевременная, хорошее обслуживание, всё объяснил и рассказал, маленький минус что не укладываются в заявленные 90 минут, но всё равно сделали всё на высшем уровне. Естественно буду обращаться ещё раз и всем так же советую. Цены оправдывают себя и усилия сотрудников. Всё вполне народно и доступно.
Светлана
всего за несколько минут снова ожил в мой телефончик!!!! спасибо,молодой человек!Вы очень внимателен и толковый в своем деле!!! рекомендую в ТЦ Арена!!!!
Алексей
Доброго всем дня! Еще зимой обратилась в этот сервис с серьезной проблемой своего тогда еще нового Xiaomi Redmi-8 (полгода со дня покупки) В моем мобильном глючил экран, причем так, что некоторые операции совершались сами по себе и не поддавались контролю. Были даже случаи, когда, зайдя в приложение Сбербанк Онлайн, автоматически мог осуществиться перевод. Набор любого текста в СМС стал не возможен: получалась какая-то АБРАКАДАБРА… Короче, телефон стал создавать мне проблемы во всем. И я вынуждена была обратиться к специалистам. Адрес нашла в интернете. Из детального разговора с мастером, я сразу поняла, что мне здесь не будут ничего навязывать, поэтому доверилась ему. Мне было предложено несколько вариантов решения проблемы с подробным описанием расходов (цены были те же, что и на сайте). Я выбрала замену экрана… И не пожалела! На следующий же день, когда все было сделано. мои проблемы сошли на НЕТ, как будто их не было… RESPECT и УВАЖЕНИЕ !!! Рекомендую!
Мне было предложено несколько вариантов решения проблемы с подробным описанием расходов (цены были те же, что и на сайте). Я выбрала замену экрана… И не пожалела! На следующий же день, когда все было сделано. мои проблемы сошли на НЕТ, как будто их не было… RESPECT и УВАЖЕНИЕ !!! Рекомендую!
Максим
К счастью редко пользуюсь услугами ремонта смартфонов, но….все бывает в первый раз. И очень важен первый положительный опыт в этом деле. Первый раз пришел с тем что не заряжался телефон от зарядки. За 2 минуты !!! мастер почистил разъем на телефоне и не взял за это ни копейки. Шок . На радиорынке сказали бы наверное что ты парень попал — там полно работы с заменой полтелефона. Поэтому выбор центра во второй раз ( утопил айфон в бассейне ) был очевиден, хотя ехать на машине из Одинцово в центр Москвы ещё то удовольствие. И снова всё супер. И дело не только в стоимости старенького уже айфона, а в том что я очень не люблю процесс переноса данных на новый. В общем быстро, качественно и за разумные деньги. И огромная благодарность Коноваловой Лидии за то , что постоянно держала меня в курсе этапов ремонта. Так приятно когда такие симпатичные люди помогают решить твои временные жизненные неприятности.
С телефоном пока всё нормально. Надеюсь что надолго. Спасибо, ребята.
В общем быстро, качественно и за разумные деньги. И огромная благодарность Коноваловой Лидии за то , что постоянно держала меня в курсе этапов ремонта. Так приятно когда такие симпатичные люди помогают решить твои временные жизненные неприятности.
С телефоном пока всё нормально. Надеюсь что надолго. Спасибо, ребята.
Андрей
Добрый день! В который раз обратился в Ваш сервисный центр и остался в очередной раз доволен. Детали всегда в наличии, ремонт занимает минимум времени, не успеешь кофе до пить как уже все будет готово. Отличные мастера, благодарю! Всем советую!
Лали
Грамотный и вежливый персонал, качественный ремонт! Лучшая точка в городе, всем рекомендую!
Николай Юрьевич Полянский
Очень приятный коллектив, цены не кусаются) Мастера своего дела! Советую всем сервис
Екатерина Романова
Очень рада что попала именно к ним
Лилия
Очень вежливый персонал, все быстро и оперативно, оказанными услугами осталась довольна
Денис
Обращались в сервис на Алексеевской неоднократно, всегда быстро, качественно, доброжелательно. Всем рекомендую
Всем рекомендую
Карим
Очень понравилось качество обслуживания в этом сервисном центре. За пару минут устранили проблему с зарядкой телефона, бесплатно, вежливо и качественно. Рекомендую этот центр.
Anastasia
Пришла заменить вход для зарядки. Молодой человек посмотрел, и просто почистил его. Заняло меньше 5 минут. Денег не взяли. Очень рекомендую
Кира
Сильно разбила телефон, перед походом в салон проконсультировалась по телефону о ценах и времени работы, очень понравилось общение в чате, вежливость и быстрый ответ на любые вопросы. Сам ремонт занял меньше обещанного времени. На сайте и в салоне написано, что в подарок бесплатное защитное стекло, к сожалению, стекло мне не поставили, потому что его не было в наличии, но сделали бонусом чистку телефона. Больше всего меня удивили бумаги, которые я подписывала, в предыдущем салоне, в котором я ремонтировала уже другой телефон, не было никаких гарантий и договоров, мне очень понравилась ответственность работы салона!
Цены средние, но качество работы замечательное!
Я смело могу рекомендовать данный салон
Больше всего меня удивили бумаги, которые я подписывала, в предыдущем салоне, в котором я ремонтировала уже другой телефон, не было никаких гарантий и договоров, мне очень понравилась ответственность работы салона!
Цены средние, но качество работы замечательное!
Я смело могу рекомендовать данный салон
Иван
Обратился с проблемой на iPhone 7, не заряжался телефон, на месте все объяснили и рассказали, очень компетентный сотрудник Александр, ответил на все вопросы, предложил альтернативные варианты, сделал свою работу качественно и быстро, обязательно обращусь ещё раз
Обзор Dell XPS 13 Plus: XPS plus, батарея минус
Компания Dell шокировала всех, кто следит за рынком ноутбуков, анонсировав XPS 13 Plus. После того, как в декабре прошлого года я опубликовал свои первые впечатления, я получил всевозможные личные сообщения и электронные письма от людей, которые спрашивали, что это за штука. Этот ноутбук не похож ни на что, что когда-либо видели, и многие из нас провели последние полгода, задаваясь вопросом, хорошо это или плохо.
Этот ноутбук не похож ни на что, что когда-либо видели, и многие из нас провели последние полгода, задаваясь вопросом, хорошо это или плохо.
Обычный XPS 13 (плюс не найден) уже давно входит в число наших лучших рекомендуемых ноутбуков с Windows. Он выдающийся во многих отношениях, главным из которых является качество сборки. Dell продолжает продавать эту модель и обновила ее до процессоров 12-го поколения. XPS 13 Plus — это отдельная модель, и, насколько я понимаю, она предназначена для людей, которые хотят вывести производительность XPS на новый уровень — для тех, кто хочет получить столько сырых мышц, сколько они могут получить в 13-дюймовой машине.
С этой целью Dell вытащила все шнурки, чтобы сделать XPS 13 Plus настолько тонким, насколько это возможно. Тачпад тактильный и полностью интегрирован в упор для рук. Портов практически нет. Клавиатура стала плоской, а ряд функций заменен рядом сенсорных светодиодов. И Plus стоит на 300 долларов дороже, чем его аналог без Plus. В случае Dell это все компромиссы, направленные на создание самого тонкого и самого мощного ноутбука.
В случае Dell это все компромиссы, направленные на создание самого тонкого и самого мощного ноутбука.
К сожалению, XPS 13 Plus не такой. Он дороже и намного горячее, чем ноутбуки того же размера и веса, которые обеспечивают аналогичную или лучшую мощность, значительно лучшее время автономной работы, лучшие веб-камеры и более удобный выбор портов — и это даже не вдаваясь в различные привередливые вещи с клавиатурой. . Я не могу быть единственным, у кого здесь возникает дежа вю. Вся эта ситуация напоминает 2016 год, когда Apple внесла всевозможные изменения в MacBook во имя тонкости, что в конечном итоге… не совсем сработало.
Как и MacBook 2016 года, этот XPS 13 Plus — красивый компьютер с отличным экраном. Но даже среди людей, которым действительно нужна торговая марка Dell и операционная система Windows, я не вижу в этом выбора.
6верг.0022
Плохой
- Роскошная цена
- Сильно нагревается при не очень интенсивных нагрузках
- Недостаточное время автономной работы
- Очень мало портов (и нет разъема для наушников)
- Светодиодные функциональные клавиши выглядят немного странно
- 2 Touch ispad 90 невидимый и немного неглубокий
1299,00 долларов США в Dell 1849,99 долларов США в Best Buy
Как мы оцениваем и рассматриваем продукты
Начнем с положительной ноты: XPS 13 Plus изысканно изготовлен из алюминия и стекла. Крышка настолько прочная, насколько это возможно. Держите его закрытым, и вы не увидите большой разницы между ним и XPS старой школы. По мере того, как устройства становятся тоньше, долговечность может иногда отходить на второй план, но здесь Dell не пошла на компромисс. Вы не найдете более прочного ноутбука в 13-дюймовом пространстве. Это также довольно симпатичная машина с плоской клавиатурой, создающей цельную эстетику, которая кажется явно футуристической. Моя единственная претензия к корпусу моего графитового блока для обзора заключается в том, что он притягивает отпечатки пальцев. Если это проблема для вас, также доступен платиновый цвет.
Крышка настолько прочная, насколько это возможно. Держите его закрытым, и вы не увидите большой разницы между ним и XPS старой школы. По мере того, как устройства становятся тоньше, долговечность может иногда отходить на второй план, но здесь Dell не пошла на компромисс. Вы не найдете более прочного ноутбука в 13-дюймовом пространстве. Это также довольно симпатичная машина с плоской клавиатурой, создающей цельную эстетику, которая кажется явно футуристической. Моя единственная претензия к корпусу моего графитового блока для обзора заключается в том, что он притягивает отпечатки пальцев. Если это проблема для вас, также доступен платиновый цвет.
В отличие от нынешнего MacBook Air, здесь есть небольшой клин.
Другим важным моментом является дисплей. Я протестировал модель OLED с разрешением 3456 x 2160 и соотношением сторон 16:10. Это удовольствие от просмотра с яркими и живыми цветами и очень небольшим бликом. Благодаря крошечным рамкам (соотношение экрана к корпусу составляет 91,9 процента) панель более чем заслуживает знаменитого титула Dell InfinityEdge. Обратите внимание, что это всего лишь 60 Гц, что не всем будет интересно, но некоторым точно понравится. (Я столкнулся с проблемой на моем первом устройстве для обзора, когда экран перестал работать после того, как его сбили с дивана на ковер, несмотря на отсутствие видимых внешних повреждений. Dell прислала сменный блок, в котором мы не обнаружили никаких проблем с экраном. )
Обратите внимание, что это всего лишь 60 Гц, что не всем будет интересно, но некоторым точно понравится. (Я столкнулся с проблемой на моем первом устройстве для обзора, когда экран перестал работать после того, как его сбили с дивана на ковер, несмотря на отсутствие видимых внешних повреждений. Dell прислала сменный блок, в котором мы не обнаружили никаких проблем с экраном. )
Я стер отпечатки пальцев, как мог, для всех вас.
Я также был приятно удивлен массивом динамиков, который включает в себя два направленных вверх высокочастотных динамика под клавиатурой и два направленных вниз динамика в основании. Перкуссия была немного жестяной, но в остальном качество звука было отличным, с заметным улучшением по сравнению с прошлогодним XPS 13 (и без искажений на максимальной громкости, что было проблемой, которая была у меня с предшественником). Я бы сказал, что он соответствует звуку M2 MacBook Air, что довольно хорошо для этой категории и намного опережает то, что типично для ноутбуков с Windows. Настройки эквалайзера можно настроить в предустановленной программе MaxxAudio.
Настройки эквалайзера можно настроить в предустановленной программе MaxxAudio.
Посмотрите на все порты этой штуки.
Но в других местах очевидны жертвы Dell во имя тонкости. Прежде чем я перейду к ним, я хочу рассмотреть размер этой машины в контексте. Его толщина составляет 0,6 дюйма, а вес — 2,77 фунта. (Модель без OLED весит 2,71 фунта.) Конечно, он довольно портативный, но в 13-дюймовом пространстве есть много более тонких и легких ноутбуков с Windows, включая варианты OLED и продукты, которые намного дешевле, чем этот. MacBook Air M2 также заметно тоньше и легче этой конфигурации.
Первый компромисс: здесь есть только два порта Thunderbolt 4 USB-C. Нет даже разъема для наушников. Один из этих USB-C требуется для зарядки ноутбука. Это фактор, потому что прилагаемый адаптер на 60 Вт не заряжает устройство особенно быстро. Помимо небольшого использования Chrome, моему устройству потребовалось час и 14 минут, чтобы достичь 60 процентов. Вы должны учитывать цену док-станции или концентратора USB в цене этого устройства.
Тачпад там точно есть — обещаем.
Второй: сенсорная панель. На самом деле это не сенсорная панель, как настраиваемая (и теперь фактически заброшенная) сенсорная панель Apple — это «ряд емкостных сенсорных функций». Но, как и та полоска сенсорного экрана, она заменяет ряд физических функций, которые есть на других клавиатурах. Это ряд светодиодов, которые включают такие параметры, как яркость, громкость, отключение звука микрофона, выход из положения, вставка и т. д. Удерживая нажатой клавишу Fn на клавиатуре, светодиоды меняются на обычные функциональные клавиши.
Моя первая проблема с этим, как и многие жалобы на сенсорную панель Apple, заключается в том, что нет тактильной обратной связи, поэтому я часто не совсем уверен, действительно ли я нажал клавишу. Во-вторых, если что-то попадало в ряд (пыль, волосы, что угодно), я никогда не мог смахнуть это, не нажимая при этом кучу кнопок и не испортив все, что я делал посередине. В-третьих, я не был готов к тому, насколько сбивающим с толку может быть то, что сочетания клавиш, включающие такие вещи, как Delete и Escape, требуют сочетания настоящих и поддельных клавиш. Может быть, это то, к чему вы привыкли, но в данный момент это кажется очень странным.
Может быть, это то, к чему вы привыкли, но в данный момент это кажется очень странным.
Посмотрите на эту маленькую клавишу Backspace. Милый!
Третье: трекпад. Когда вы открываете XPS 13 Plus, первое, что вы, вероятно, заметите, это отсутствие тачпада — под клавиатурой находится сплошная стеклянная полоса. Теперь на самом деле там, где вы ожидаете, есть емкостный сенсорный трекпад; это просто никак не очерчено, и вы полагаетесь на мышечную память, чтобы убедиться, что вы щелкаете в нужном месте.
У меня не было проблем с ежедневной навигацией здесь; моя правая рука инстинктивно знала, куда щелкнуть. К сожалению, моя левая рука не развила эту мышечную память, и это становилось проблемой в тех случаях, когда мне нужно было, чтобы она подстраивалась. Это было особенно громоздко, когда мне нужно было щелкать и перетаскивать объекты или выделять текст, для чего мне обычно требуется две руки. . Я очень часто промахивался в невидимую зону с первого выстрела левой рукой.
Щелчок скрытого трекпада неглубокий, и его трудно найти на ощупь
Отдельно щелчки трекпада кажутся поверхностными. Dell фактически призвал рецензентов, чтобы их семьи протестировали устройство. (Нам сказали, что они не поверят, что это сплошной кусок стекла.) Поэтому я попросил маму щелкнуть по нему. «Это странно», — заметила она. Я объяснил, что это тактильная сенсорная панель. — О, это имеет смысл, — сказала она.
Я также отдал устройство своему младшему брату, заранее сказав ему, что оно тактильное. «Разве Apple не такая?» он спросил. Я подтвердил, что они были. «Apple лучше», — сказал он, щелкая XPS. Думаю, это зависит от семьи.
Последняя вещь с трекпадом — он выходил из строя, когда мои руки были даже слегка влажными, часто думая, что он нажат, когда я не нажимал на него (что делало его практически непригодным для использования). Я спросил об этом Dell, и они сказали, что это обычное явление для всех емкостных трекпадов (включая большинство современных трекпадов), и порекомендовали высушить руки перед использованием ноутбука. Достаточно справедливо, но я использую несколько моделей ноутбуков каждую неделю и редко, если вообще когда-либо, сталкиваюсь с такими проблемами.
Достаточно справедливо, но я использую несколько моделей ноутбуков каждую неделю и редко, если вообще когда-либо, сталкиваюсь с такими проблемами.
Сзади выглядит нормально.
У меня не так много проблем с новой клавиатурой с нулевой решеткой, которая была полностью плоской. Теперь это буквально от края до края, между клавишами почти нет места. Если изображения заставляют вас беспокоиться о том, что у нас на руках второе пришествие клавиатуры-бабочки, не волнуйтесь — все не так уж и плохо. Ход клавиш всего 1 мм, но клавиши на самом деле кажутся довольно упругими, оставаясь при этом довольно тихими. Заглавные буквы достаточно широкие, поэтому у меня не было проблем с быстрым и точным набором текста, хотя к общему ощущению потребовалось некоторое время, чтобы привыкнуть. Есть пара привередливых особенностей компоновки, которые могут беспокоить некоторых людей: клавиши со стрелками имеют половинную высоту, а кнопка питания сжата рядом с клавишей Backspace.
Совершенно не клавиатура-бабочка.
Наконец, веб-камера является улучшением по сравнению с предыдущим поколением (что является низкой планкой), но все же не удивительно. Вместо того, чтобы пойти по пути Apple и вырезать выемку камеры из крошечной рамки, Dell сохранила эту крошечную рамку, но отделила инфракрасную камеру (для распознавания лиц) от обычной веб-камеры 720p. Мои коллеги могли видеть такие детали, как пряди волос, пока я разговаривал по видеосвязи, и я не был темным или размытым, но изображение все еще было довольно зернистым и шумным.
В этой крошечной рамке спрятана маленькая веб-камера.
В основе всего этого лежит самое большое обещание XPS 13 Plus: процессор Core P-серии 12-го поколения. Большинство ноутбуков такого размера используют серию U, которая предназначена для тонкого и легкого форм-фактора, но Plus не возится с ними. Базовая модель за 1299 долларов включает i5-1240P, 8 ГБ ОЗУ, 512 ГБ памяти (твердотельный накопитель M.2 Gen 4 PCIe) и несенсорный дисплей с разрешением 1920 x 1200. Устройство, которое мне прислали, значительно шикарнее, с Core i7-1280P, 16 ГБ ОЗУ, 512 ГБ памяти и OLED-экраном с более высоким разрешением. Тот аппарат с не-OLED, 19Экран 20 x 1200 стоит 1749 долларов. SSD можно обновить, а все остальное припаяно.
Устройство, которое мне прислали, значительно шикарнее, с Core i7-1280P, 16 ГБ ОЗУ, 512 ГБ памяти и OLED-экраном с более высоким разрешением. Тот аппарат с не-OLED, 19Экран 20 x 1200 стоит 1749 долларов. SSD можно обновить, а все остальное припаяно.
Эта модель стоит 1949 долларов, что, разумеется, делает этот компьютер дорогим. MacBook Air M2 (опять же, тоньше и легче, с большим количеством портов, лучшей веб-камерой, рядом физических функций и более удобным трекпадом) с сопоставимыми характеристиками может быть на 350 долларов дешевле, чем моя модель — модель, которую мы рассмотрели. 10-ядерный процессор дешевле на 250 долларов. (Оба дешевле, чем модель без сенсорного экрана XPS Plus без OLED). Core-i7, XPS 13 U-серии (который поставляется только с 19дисплей 20 x 1200) обойдется на 600 долларов дешевле.
Технические характеристики Dell XPS 13 Plus (после обзора)
- 13,4-дюймовый сенсорный OLED-дисплей с разрешением 3456 x 2160
- Intel Core i7-1280P 12-го поколения (24 МБ кэш-памяти, до 6 ГБ LDR 902 ГГц, 142 ядра) 128-бит, двухканальный, 5200 МГц
- 512 ГБ PICe 4 x4 SSD
- Два Thunderbolt 4 USB Type-C с DisplayPort и Power Delivery
- Один адаптер USB-C на USB-A v3.
 0 в коробке, один дополнительный USB-C адаптер для гарнитуры 3,5 мм
0 в коробке, один дополнительный USB-C адаптер для гарнитуры 3,5 мм - Конструкция с четырьмя динамиками общей выходной мощностью 8 Вт, двойной массив микрофонов
- Клавиатура с нулевой решеткой и подсветкой, ход 1,0 мм
- Камера Windows Hello 720p
- Intel Killer Wi-Fi 6E 1675 (AX211) (2×2), Bluetooth 5.2
- 11,63 x 7,84 x 0,6 дюйма (295,3 x 199,04 x 15,28 мм)
- 2,77 фунта (1,26 кг)
Что касается производительности, это устройство, безусловно, лучше, чем XPS 13 11-го поколения, и оно определенно более мощное. чем любая машина 12-го поколения U-серии, которую вы можете купить. У меня не было проблем с производительностью в большинстве моих офисных работ, и редактирование фотографий было в порядке. Premiere Pro вовсе не была забавной — несколько версий программы открывались целую вечность и работали медленно, время от времени зависая — но это не редкость в этом сегменте рынка.
Это устройство, безусловно, лучше, чем XPS 13 11-го поколения. Тем не менее, он не приближается к M2 в одноядерных или графических сценариях использования, которые мы запускали. Другим явным преимуществом XPS 13 Plus перед Air является вентилятор, который теоретически поможет ему лучше выдерживать длительные нагрузки. Но вентилятор XPS 13 Plus действительно боролся с этим, потому что, черт возьми, эта штука стала горячей.
Тем не менее, он не приближается к M2 в одноядерных или графических сценариях использования, которые мы запускали. Другим явным преимуществом XPS 13 Plus перед Air является вентилятор, который теоретически поможет ему лучше выдерживать длительные нагрузки. Но вентилятор XPS 13 Plus действительно боролся с этим, потому что, черт возьми, эта штука стала горячей.
После нескольких часов регулярного использования (в моем случае это дюжина или около того вкладок Chrome с запущенным сверху Slack) этот ноутбук стал кипящим . Мне стало неудобно держать руки на упорах для рук и печатать на клавиатуре. Положить его мне на колени не стоило.
Обычно я работаю в тихом режиме, но я перепробовал все различные профили вентиляторов, и ничего не изменилось. В Оптимизированном корпусе было немного прохладнее, но все еще жарко. Режим Cool, безусловно, сделал вентиляторы раздражающе громкими, но на самом деле корпус не стал комфортно холодным. Я использовал Ultra Performance во время тестирования производительности (что заставило вентиляторы громко громко, как уровни громкости Intel MacBook Pro), а процессор по-прежнему часто достигал (а иногда и зависал) 100 градусов Цельсия. Несмотря на свою впечатляющую мощность, это устройство по-прежнему кажется наиболее подходящим для краткосрочной деятельности, если вы не хотите жарить свое шасси и процессор — и снижение оценок в Cinebench подряд подтверждает это.
Несмотря на свою впечатляющую мощность, это устройство по-прежнему кажется наиболее подходящим для краткосрочной деятельности, если вы не хотите жарить свое шасси и процессор — и снижение оценок в Cinebench подряд подтверждает это.
Тесты Dell XPS 13 Plus
| Geekbench 5.3 CPU Single | 1665 |
| Geekbench 5.3 CPU Multi | 10708 |
| Geekbench 5.3 Open CL / Compute | 20483 |
| Cinebench R23 Single | 1404 |
| Cinebench R23 Multi | 8817 |
| Cinebench R23 Multi 30-минутный цикл | 8509 |
| ProgetBench для Premiere | 393 |
| Shadow of the Tomb Raider (1920 x 1200, highest) | 19fps |
| 4K Export (Adobe Premiere Pro 15) | 6:54 |
А еще есть время автономной работы. У меня было всего пять часов и две минуты непрерывного использования с экраном около 200 нит. Экран с высоким разрешением, без сомнения, является важным фактором, так как мы часто видим разочаровывающую долговечность моделей OLED XPS. (Хотя теоретически OLED-технология должна способствовать увеличению времени автономной работы.) Тем не менее, я всегда пересматриваю конфигурацию, которая у меня есть, и эта не прослужила достаточно долго, чтобы оправдать цену в 2000 долларов.
У меня было всего пять часов и две минуты непрерывного использования с экраном около 200 нит. Экран с высоким разрешением, без сомнения, является важным фактором, так как мы часто видим разочаровывающую долговечность моделей OLED XPS. (Хотя теоретически OLED-технология должна способствовать увеличению времени автономной работы.) Тем не менее, я всегда пересматриваю конфигурацию, которая у меня есть, и эта не прослужила достаточно долго, чтобы оправдать цену в 2000 долларов.
Это усугубляет проблему с подключением, потому что этой штуке нужно будет проводить много времени подключенной — так что вы действительно прощаетесь с 50 процентами вашего выбора портов. Я знаю, что звучу здесь как заезженная пластинка, но я просто хочу подчеркнуть — MacBook Air служит мне в два раза дольше.
Согласиться на продолжение: Dell XPS 13 Plus
Как и в случае с другими компьютерами с Windows, Dell XPS 13 Plus предлагает вам несколько условий, с которыми вы можете согласиться или отклонить их при настройке.
Обязательные политики, для которых требуется соглашение:
- Запрос вашего региона и раскладки клавиатуры
- Подключение к сети Wi-Fi
- Условия лицензионного соглашения на программное обеспечение Microsoft и условия продажи Dell/лицензионное соглашение с конечным пользователем
- Войдите в учетную запись Майкрософт
- Создайте PIN-код
- Политика конфиденциальности Dell и уведомление о телеметрии
Кроме того, есть множество необязательных условий, с которыми нужно согласиться:
- Настройка Windows Hello
- Параметры конфиденциальности устройства: «Найти мое устройство», рукописный ввод и ввод текста, рекламный идентификатор, местоположение, диагностические данные, индивидуальные возможности McAfee для отправки вам связанных с обслуживанием электронных писем и текстовых уведомлений
Это девять обязательных соглашений и 11 дополнительных.
XPS 13 Plus впечатляет своей готовностью бросить вызов статусу-кво. Вы не часто видите ноутбук, который пытается сделать то, чего достигли очень немногие продукты. Я уважаю цель Dell поместить процессор серии P в такой тонкий и красивый корпус.
Вы не часто видите ноутбук, который пытается сделать то, чего достигли очень немногие продукты. Я уважаю цель Dell поместить процессор серии P в такой тонкий и красивый корпус.
Но все инновации в мире не изменили сути этого ноутбука. Это OLED XPS. И в конечном итоге я рассказываю здесь ту же историю, что и о моделях OLED XPS на протяжении многих лет. Он красивый и мощный, но слишком горячий, а экран с высоким разрешением убивает время автономной работы.
Я до сих пор использую MacBook Pro 2019 года для работы, и я удивлен, насколько похоже использование XPS 13 Plus на тот опыт. Как и этот MacBook, Plus тонкий и легкий, но он также всегда горячий, ему не хватает портов и у него нет практического срока службы батареи. Apple внесла эти непопулярные изменения во имя худобы, и, возможно, это говорит о том, что за последние несколько лет она решила отменить многие из них. Изменения Dell были менее радикальными в некоторых областях (клавиатура) и более радикальными в других (порты), но я беспокоюсь, что в целом повествование движется в том же направлении.
Я еще не рассматривал обычный XPS 13, но мне кажется, что Dell намерена сделать его доступным для большинства людей, а Plus — ноутбуком для «продвинутых пользователей». Но с ее ограниченными возможностями подключения и сомнительной способностью выдерживать нагрузки «опытного пользователя», я бы не стал рекомендовать эту модель этой группе. Я подозреваю, что людям, которым нужна полная мощность Core i7-1280P, может понадобиться как минимум что-то с USB-A.
Фотография Моники Чин / The Verge
Dell XPS 13 Plus Accessibility
Dell XPS 13 Plus (обзор)
- Буквенные клавиши имеют размер 1,8 x 1,7 сантиметра, расстояние между ними 0,1 сантиметра. Все клавиши имеют подсветку. Только клавиша Caps Lock имеет световой индикатор. Кнопка питания 1 х 1,7 сантиметра. Клавиши регулировки громкости представляют собой сенсорные светодиоды. Клавиши черные с белым текстом, и для их нажатия требуется небольшое усилие.
- В моем тестировании громкость динамиков достигла в среднем 80 децибел.

- Ноутбук весит 2,77 фунта.
- Имеется два порта Thunderbolt 4 USB Type-C с DisplayPort и Power Delivery.
- Крышку можно открыть одной рукой. Его можно откинуть назад на 140 градусов.
- Экран 13,4 дюйма с разрешением 3546 x 2160. В моем тестировании он достиг яркости 380 нит и коэффициента контрастности 181 940: 1. Есть сенсорный вариант.
- Тачпад не очерчен и поддерживает точные жесты.
- Настройка включает в себя включение устройства и просмотр нескольких меню.
- XPS 13 Plus поддерживает вход в систему с помощью отпечатков пальцев и распознавания лиц.
Windows 11
- Windows 11 включает специальное меню специальных возможностей.
- Windows 11 включает встроенное средство чтения с экрана (экранный диктор). Он поддерживает сторонние программы чтения с экрана, включая NVDA от NV Access и Jaws от Freedom Scientific. Полный список совместимого программного обеспечения можно найти на веб-сайте Microsoft.

- Windows 11 поддерживает голосовой ввод (доступ осуществляется с помощью Windows + H) и распознавание речи (переключается с помощью Windows + Ctrl + S).
- Цветовые фильтры, включая инвертированный, оттенки серого, красно-зеленый и сине-желтый, можно переключать с помощью Windows + Ctrl + C. Контрастные темы переключаются с помощью Alt + Shift влево + Print Screen. Стандартный темный режим и пользовательские цвета также доступны в разделе «Персонализация».
- Цвет и размер титров можно настроить, и они будут отображаться ближе к нижней части экрана.
- Клавиатуру можно переназначить с помощью Microsoft PowerToys. Залипание клавиш поддерживается. Доступна экранная клавиатура.
- Размер и скорость курсора можно настроить, а жесты можно переназначить в настройках сенсорной панели.
- Windows 11 поддерживает управление глазами с помощью внешних устройств отслеживания взгляда.
- Windows 11 включает функцию Snap Layout, доступ к которой можно получить, наведя указатель мыши на кнопку «Развернуть» в любом открытом окне.

Обзор Dell XPS 13 Plus: просто получите обычный XPS
Контент создается командой редакторов CNN Underscored, которые работают независимо от отдела новостей CNN. Когда вы покупаете по ссылкам на нашем сайте, мы можем получать комиссию. Узнать больше
отзывов
Майк Андронико/CNNDell XPS 13 Plus — доказательство того, что не стоит пытаться починить то, что не сломано. Этот ноутбук полностью переосмысливает Dell XPS 13 — наш давний лучший выбор для ноутбуков с Windows — с поразительно минималистичным дизайном, который обязательно станет ярким акцентом в вашем домашнем офисе. Но как только вы преодолеете причудливую эстетику XPS 13 Plus и действительно возьмете его в руки, вы можете быстро понять, что «Плюс» не обязательно означает «лучше».
Несмотря на то, что в XPS 13 сохранено многое из того, что делает его великолепным (потрясающий дисплей, великолепная клавиатура и высокая производительность), а также добавлены некоторые изящные штрихи (например, невидимый трекпад, который действительно работает), XPS 13 Plus имеет некоторые серьезные конструктивные недостатки, которые сделали его прямым. -up неудобно использовать на протяжении всей недели тестирования. Если вы не женаты на его, по общему признанию, изящном дизайне — и не заботитесь о благополучии своих больших пальцев — те, кто ищет отличный ноутбук премиум-класса с Windows, могут пропустить этот. Вот почему.
-up неудобно использовать на протяжении всей недели тестирования. Если вы не женаты на его, по общему признанию, изящном дизайне — и не заботитесь о благополучии своих больших пальцев — те, кто ищет отличный ноутбук премиум-класса с Windows, могут пропустить этот. Вот почему.
Dell XPS 13 Plus
Футуристический взгляд на классику
Красивый внешний вид и великолепный дисплей Dell XPS 13 Plus сдерживаются неудобной конструкцией, которая сильно нагревается. Если вы не женаты на его уникальном дизайне и дополнительном OLED-дисплее, вам лучше пропустить его и вместо этого получить стандартный XPS 13 за 999 долларов.
1299 долларов в Dell
Майк Андронико/CNN Хотя мне не все нравится в дизайне XPS 13 Plus, нельзя отрицать, что он красивый. Открыв крышку ноутбука, вы обнаружите поразительно минималистичный интерьер, без видимой сенсорной панели, без физических функциональных клавиш и с по-настоящему бесшумной клавиатурой, которая не занимает ни сантиметра пространства. Он выглядит как что-то из современного научно-фантастического фильма — одновременно знакомое и футуристическое — и почти гарантированно привлечет внимание, когда вы используете его на публике.
Открыв крышку ноутбука, вы обнаружите поразительно минималистичный интерьер, без видимой сенсорной панели, без физических функциональных клавиш и с по-настоящему бесшумной клавиатурой, которая не занимает ни сантиметра пространства. Он выглядит как что-то из современного научно-фантастического фильма — одновременно знакомое и футуристическое — и почти гарантированно привлечет внимание, когда вы используете его на публике.
К счастью, привлекательный дизайн XPS 13 Plus не только для галочки. Меня по-прежнему поражает невидимая стеклянная сенсорная панель ноутбука, которая, несмотря на то, что у нее нет четких границ или даже физического щелчка под ней, просто работает так, как вы хотели бы, чтобы тачпад работал. Прокрутка веб-страниц и масштабирование с помощью щипков сразу стали естественными, и, как и на последних MacBook от Apple, тактильная обратная связь ноутбука отлично справляется с имитацией ощущения традиционного щелчка мыши. Хотя я думаю, что некоторые из ультраминималистских функций XPS 13 Plus идут ему во вред, бесшовная сенсорная панель является доказательством того, что вы можете иметь форму 9.0055 и работают одновременно.
Хотя я думаю, что некоторые из ультраминималистских функций XPS 13 Plus идут ему во вред, бесшовная сенсорная панель является доказательством того, что вы можете иметь форму 9.0055 и работают одновременно.
То же самое можно сказать и о клавиатуре ноутбука, которая кажется такой же быстрой и отзывчивой, как я и ожидал от ноутбука XPS. Дизайн от края до края позволяет клавишам быть даже больше, чем у стандартного XPS 13, а их легкое покрытие soft-touch позволяет моим рукам чувствовать себя комфортно в течение долгих дней работы.
Майк Андронико/CNN Как и многие современные ноутбуки, XPS 13 Plus, к сожалению, ограничен двумя портами Thunderbolt 4 USB-C для подключения к дисплеям и аксессуарам. На этот раз нет даже разъема для наушников! К счастью, Dell по-прежнему остается одной из немногих компаний, выпускающих адаптер USB-C на USB-A для старых периферийных устройств, а также адаптер USB-C на разъем 3,5 мм для тех, кто заботится о проводном звуке.
На этот раз нет даже разъема для наушников! К счастью, Dell по-прежнему остается одной из немногих компаний, выпускающих адаптер USB-C на USB-A для старых периферийных устройств, а также адаптер USB-C на разъем 3,5 мм для тех, кто заботится о проводном звуке.
XPS 13 Plus довольно удобен в поездках, весит всего 2,7 фунта и имеет тонкие края размером чуть более половины дюйма. Он не кажется таким же легким, как новый MacBook Air M2, несмотря на тот же вес — возможно, потому, что XPS сжимает весь этот вес в более коротком корпусе — но у вас не должно возникнуть особых проблем с тем, чтобы бросить его в сумку для повседневного использования. добираться.
Майк Андронико/CNN Хотя XPS 13 Plus полностью переосмысливает классический дизайн XPS 13, он сохраняет одну важную вещь: дисплей. Яркий, почти безрамочный экран Dell InfinityEdge по-прежнему остается чуть ли не лучшим дисплеем для ноутбуков, предлагая великолепные цвета и практически не отвлекая вас от работы или полного погружения в любимые шоу и фильмы. Будет еще лучше, если вы выберете дополнительную модель OLED, с которой поставляется наш обзорный образец.
Яркий, почти безрамочный экран Dell InfinityEdge по-прежнему остается чуть ли не лучшим дисплеем для ноутбуков, предлагая великолепные цвета и практически не отвлекая вас от работы или полного погружения в любимые шоу и фильмы. Будет еще лучше, если вы выберете дополнительную модель OLED, с которой поставляется наш обзорный образец.
Невероятно четкая панель XPS 13 Plus с разрешением 3456 x 2160 доставляла мне удовольствие, когда я использовала ее в качестве основного рабочего дисплея, предлагая глубокий черный цвет и богатую контрастность, что позволяло с легкостью концентрироваться на огромных фрагментах текста при написании и редактировании обзоров. А когда пришло время взглянуть на новый трейлер «Звездных войн: Андор», меня сразу же поразили ярко-зеленые лазерные разряды и ярко-оранжевые взрывы, которые заполнили экран, когда корабль повстанцев уничтожал истребители СИД. Я также ценю, что дисплей является сенсорным, что позволяет легко увеличивать масштаб веб-страниц или быстро прокручивать их, когда мне не хочется возиться с сенсорной панелью.
Я также ценю, что дисплей является сенсорным, что позволяет легко увеличивать масштаб веб-страниц или быстро прокручивать их, когда мне не хочется возиться с сенсорной панелью.
Великолепный дисплей ноутбука дополнен четырьмя встроенными динамиками, которые идеально подходят для прослушивания видеозвонков или просмотра видео на YouTube. Вы захотите подключить наушники или компьютерные колонки для серьезного прослушивания музыки — мои любимые рок-песни звучали слишком жестяно — но они сделают свою работу для ваших ежедневных встреч в Zoom.
Майк Андронико/CNN Dell называет XPS 13 Plus своим самым мощным 13-дюймовым XPS, и, основываясь на моем тестировании, это довольно точное утверждение. Новейший ноутбук Dell никогда не поддавался моей обычной рабочей нагрузке, позволяя мне с комфортом переключаться между десятками вкладок Chrome, отвечая на видеозвонки или выполняя легкое редактирование фотографий. Это в немалой степени благодаря высококлассным характеристикам нашего тестового устройства, которые включают в себя новейший процессор Intel Core i7 12-го поколения, быстрый твердотельный накопитель (SSD) на 512 ГБ и 16 ГБ ОЗУ, а также улучшенные внутренние компоненты, которые позволяют до процессора мощностью 28 Вт по сравнению с 15 Вт на предыдущем XPS 13.
Новейший ноутбук Dell никогда не поддавался моей обычной рабочей нагрузке, позволяя мне с комфортом переключаться между десятками вкладок Chrome, отвечая на видеозвонки или выполняя легкое редактирование фотографий. Это в немалой степени благодаря высококлассным характеристикам нашего тестового устройства, которые включают в себя новейший процессор Intel Core i7 12-го поколения, быстрый твердотельный накопитель (SSD) на 512 ГБ и 16 ГБ ОЗУ, а также улучшенные внутренние компоненты, которые позволяют до процессора мощностью 28 Вт по сравнению с 15 Вт на предыдущем XPS 13.
Эта высокая повседневная производительность была отражена в наших тестах производительности, где XPS 13 Plus очень хорошо выдержал конкуренцию, продемонстрировав при этом значительный прирост по сравнению с предыдущими моделями XPS. В Geekbench 5 (который измеряет общую производительность) многоядерные результаты XPS 13 Plus были сразу после MacBook Air M2 и примерно на 57% лучше, чем у стандартного Dell XPS 13 с процессором 11-го поколения. Процессор Core i7.
Процессор Core i7.
Dell XPS 13 Plus | Dell XPS 13 OLED (модель 2021 г.) | Макбук Эйр М2 | |
|---|---|---|---|
| Процессор | Intel Core i7 12-го поколения | Intel Core i7 11-го поколения | Яблоко M2 |
| Geekbench 5 (многоядерный) | 0.cl6do54ev00013b6oycn86iv6″> | 5 372 | 8 872 |
| Shadow of the Tomb Raider (1080p, максимальные настройки) | 17 | Н/Д | 24 |
| Тест батареи (воспроизведение видео 4K) | 5:33 | 1.cl6do68k600053b6opfb4qnpl»> | 5:21 |
XPS 13 Plus показал себя не очень хорошо в наших игровых тестах, чего и следовало ожидать от машины без выделенной видеокарты. Системе удалось набрать невоспроизводимые 17 кадров в секунду (fps) при запуске Shadow of the Tomb Raider в разрешении 1080p с максимальными настройками, что значительно отстает от новейших MacBook Air и MacBook Pro с процессором M2. Тем не менее, игра подскочила до вполне играбельных 28 кадров в секунду с минимальными настройками графики. Вы сможете играть в менее требовательные игры, если повозитесь с некоторыми настройками, но это, как правило, не машина, предназначенная для игр или изнурительной работы с графикой.
Несмотря на привлекательный внешний вид, великолепный дисплей и отличную производительность, XPS 13 Plus может быть невероятно разочаровывающим в использовании. Самым большим нарушителем является невероятно острый передний край ноутбука, который часто прижимался к моему большому пальцу и запястьям таким образом, что это было неудобно, а иногда и болезненно. Другие края XPS 13 Plus также довольно острые на ощупь, что иногда делало неприятными такие простые вещи, как поднятие ноутбука или регулировка дисплея.
Это может быть связано с тем, как я лично использую ноутбуки (мой правый большой палец часто ложится на край, когда я прокручиваю), но этого было достаточно, чтобы заставить меня сделать перерыв, и оставил меня с мозолистым большим пальцем после более длительного времени. сессии. Это определенно ноутбук, который вы должны попробовать в магазине, прежде чем покупать.
сессии. Это определенно ноутбук, который вы должны попробовать в магазине, прежде чем покупать.
Мне также не нравится ряд емкостных функций прямо над клавиатурой, который заменяет физические кнопки сенсорными светодиодами, которые управляют такими вещами, как яркость, громкость и воспроизведение музыки. Хотя эти сенсорные элементы управления работают очень хорошо, я все же предпочитаю ощущать физический щелчок, когда пытаюсь отключить звук динамиков или сделать экран ярче на лету. Там нет тактильной обратной связи, чтобы вы знали, когда вы нажимаете команду, и я иногда обнаруживал, что случайно активировал некоторые светодиодные кнопки только потому, что моя рука лежала на ноутбуке. И в отличие от сенсорной панели на 13-дюймовом MacBook Pro, который я тоже не люблю, здесь нет никаких настраиваемых элементов управления или элементов управления для конкретных приложений. К счастью, Apple поумнела и вернула физические функциональные клавиши почти на все свои другие MacBook. Это вызывает особое недоумение, что Dell пошла в противоположном направлении.
К счастью, Apple поумнела и вернула физические функциональные клавиши почти на все свои другие MacBook. Это вызывает особое недоумение, что Dell пошла в противоположном направлении.
Говоря о дискомфорте, нижняя часть XPS 13 Plus может сильно нагреваться. У вас есть несколько вариантов управления температурой системы в приложении My Dell (например, есть прохладный режим, в котором приоритет отдается производительности в пользу температуры), но из коробки ноутбук сильно нагревается даже при обычном рабочая нагрузка, которая в основном включает вкладки Chrome и несколько приложений. Вы захотите использовать этот ноутбук на столе, когда это возможно.
Горячая нижняя часть — не единственная причина, по которой вы захотите оставить XPS 13 Plus на своем столе. Новый ноутбук Dell не очень долго работает без подзарядки, выдержав всего пять часов и 33 минуты непрерывного воспроизведения видео 4K в нашем тесте батареи. К чести OLED-экранов с высоким разрешением, как правило, потребляется больше энергии, и XPS 13 Plus все же удалось опередить MacBook Air M2 на несколько минут. Но ноутбук Dell отставал примерно на 30 минут от MacBook Pro M2 с аналогичной ценой, а также от стандартного Dell XPS 13, который мы тестировали с OLED-дисплеем. Лучше держать это зарядное устройство под рукой.
Новый ноутбук Dell не очень долго работает без подзарядки, выдержав всего пять часов и 33 минуты непрерывного воспроизведения видео 4K в нашем тесте батареи. К чести OLED-экранов с высоким разрешением, как правило, потребляется больше энергии, и XPS 13 Plus все же удалось опередить MacBook Air M2 на несколько минут. Но ноутбук Dell отставал примерно на 30 минут от MacBook Pro M2 с аналогичной ценой, а также от стандартного Dell XPS 13, который мы тестировали с OLED-дисплеем. Лучше держать это зарядное устройство под рукой.
Веб-камера XPS 13 Plus с разрешением 720p отлично подходит для моих ежедневных видеозвонков, но это далеко не лучшее, что вы можете получить на ноутбуке такого типа. Хотя это заставило меня выглядеть ярче и красочнее, чем на обычной тусклой камере XPS 13 с разрешением 720p, мои снимки были перенасыщенными и по-прежнему довольно пикселизированными — и далеко не такими четкими, как те, которые я получил с превосходной веб-камерой 1080p MacBook Air M2.
Dell XPS 13 Plus за 1299 долларов — это ноутбук, который мне нравился гораздо больше, чем на самом деле. У него тот же иммерсивный дисплей, хорошая производительность и удобство набора текста, которые сделали XPS 13 одним из моих любимых ноутбуков, и все это в новом красивом минималистичном дизайне. Если бы только это буквально не оставило меня с больным пальцем.
Неудобно острые края XPS 13 Plus, неудобные сенсорные кнопки и горячая нижняя часть делают ноутбук неудобным в использовании, и это позор, учитывая все остальное, что он делает правильно. Подавляющему большинству людей лучше со стандартным Dell XPS 13 за 999 долларов, который может быть оснащен практически теми же характеристиками, что и Plus (за исключением OLED-экрана), и только что получил несколько новых приятных цветовых вариантов. И если вы не женаты на Windows, новый MacBook Air M2 за 1199 долларов — лучший ноутбук, который вы можете получить в этом ценовом диапазоне.
И если вы не женаты на Windows, новый MacBook Air M2 за 1199 долларов — лучший ноутбук, который вы можете получить в этом ценовом диапазоне.
Если вы особенно очарованы привлекательным дизайном XPS 13 Plus и OLED-дисплеем, вы должны хотя бы попытаться получить его в руки перед покупкой — в конце концов, то, что мне показалось неудобным, может не быть проблемой для вас. . Но для всех остальных есть гораздо лучшие варианты за эти деньги.
Dell XPS 13 Plus | Dell XPS 13 | Макбук Эйр М2 | |
|---|---|---|---|
| 0.name»> Процессор | Intel Core i5/i7 12-го поколения | Intel Core i5-1230U / i7-1250U 12-го поколения | Apple M2 |
| Память | 8 ГБ / 16 ГБ / 32 ГБ | 8 ГБ / 16 ГБ / 32 ГБ | 8 ГБ / 16 ГБ / 24 ГБ |
| Хранение | 0.cl6dohzgy00003b6ole35zrg5″> | Твердотельный накопитель 512 ГБ / 1 ТБ | Твердотельный накопитель 256 ГБ / 512 ГБ / 1 ТБ / 2 ТБ |
| Дисплей | 13,4-дюймовый OLED-дисплей 1200p / 3,5K / 4K (сенсорный опционально) | 13,4-дюймовый дисплей 1200p (сенсорный экран опционально) | 13,6-дюймовый дисплей Liquid Retina с разрешением 2560 x 1664 |
| 4.name»> Камера | 720p | 720p | 1080p |
| Динамики | Четыре динамика | Стереодинамики | Четыре динамика |
| Порты | Thunderbolt 4 USB-C (2), переходник с USB-C на USB-A в комплекте | 1.cl6doi6vj00043b6oa3k846er»> | Thunderbolt 4 USB-C (2), порт зарядки MagSafe, разъем для наушников |
| Срок службы батареи (номинальный) | До 13 часов | До 12 часов | До 18 часов |
| Размер и вес | 11,63 x 7,84 x 0,6 дюйма, 2,71 фунта | 1.cl6dojn1q00063b6oezkwoejd»> | 11,97 x 8,46 x 0,44 дюйма, 2,7 фунта |
| Цена | 1299 долларов США | 999 долларов США | 1199 долларов США |
Примечание. Приведенные выше цены отражают цены розничных продавцов на момент публикации.

 8
8 1 Найдите вершину y = x 2 -x-4
1 Найдите вершину y = x 2 -x-4 В нашем случае координата x равна 0,5000
В нашем случае координата x равна 0,5000  С
С  3 Решение x 2 -x-4 = 0 с помощью квадратной формулы .
3 Решение x 2 -x-4 = 0 с помощью квадратной формулы . eNotes Ad-Free
eNotes Ad-Free

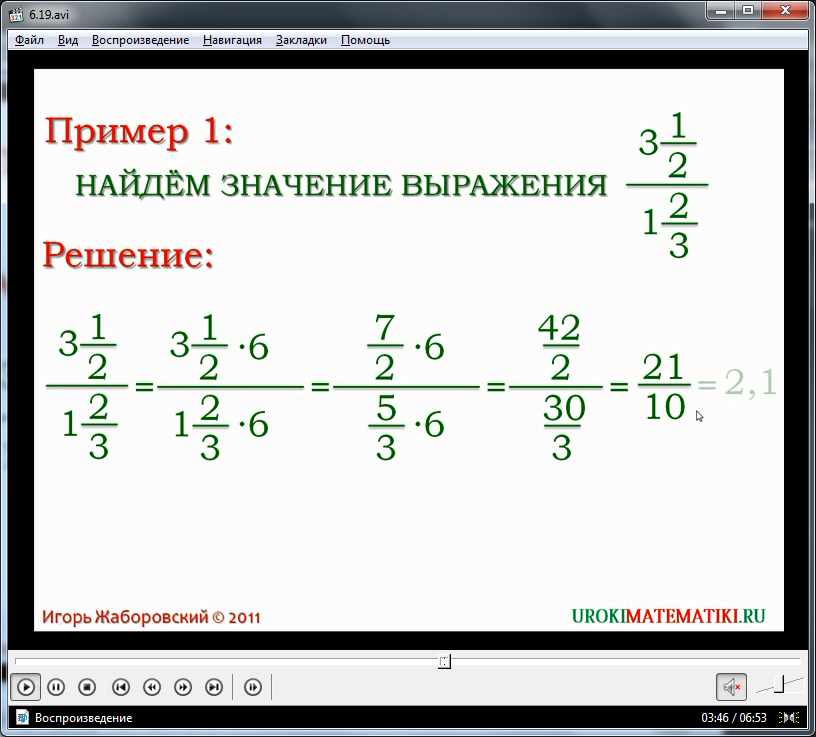
 То есть, когда у вас есть вычитания, вы не можете просто убрать скобки, потому что результат действительно может измениться. Действительно, например, если у вас есть \(1-(3-1)\), которое правильно упрощается как \(1-(3-1) = 1 — 2 = -1 \), что не то же самое, что получается при простом удалении скобок: \(1-3-1\), которое упрощается до -3, поэтому результат меняется.
То есть, когда у вас есть вычитания, вы не можете просто убрать скобки, потому что результат действительно может измениться. Действительно, например, если у вас есть \(1-(3-1)\), которое правильно упрощается как \(1-(3-1) = 1 — 2 = -1 \), что не то же самое, что получается при простом удалении скобок: \(1-3-1\), которое упрощается до -3, поэтому результат меняется.






 Калькулятор нок
Калькулятор нок Площадь круга
Площадь круга Александр Кумор
Александр Кумор Научиться находить НОК самостоятельно можно в теме нахождение
наименьшего общего кратного.
Научиться находить НОК самостоятельно можно в теме нахождение
наименьшего общего кратного. Посмотри на это!
Посмотри на это!
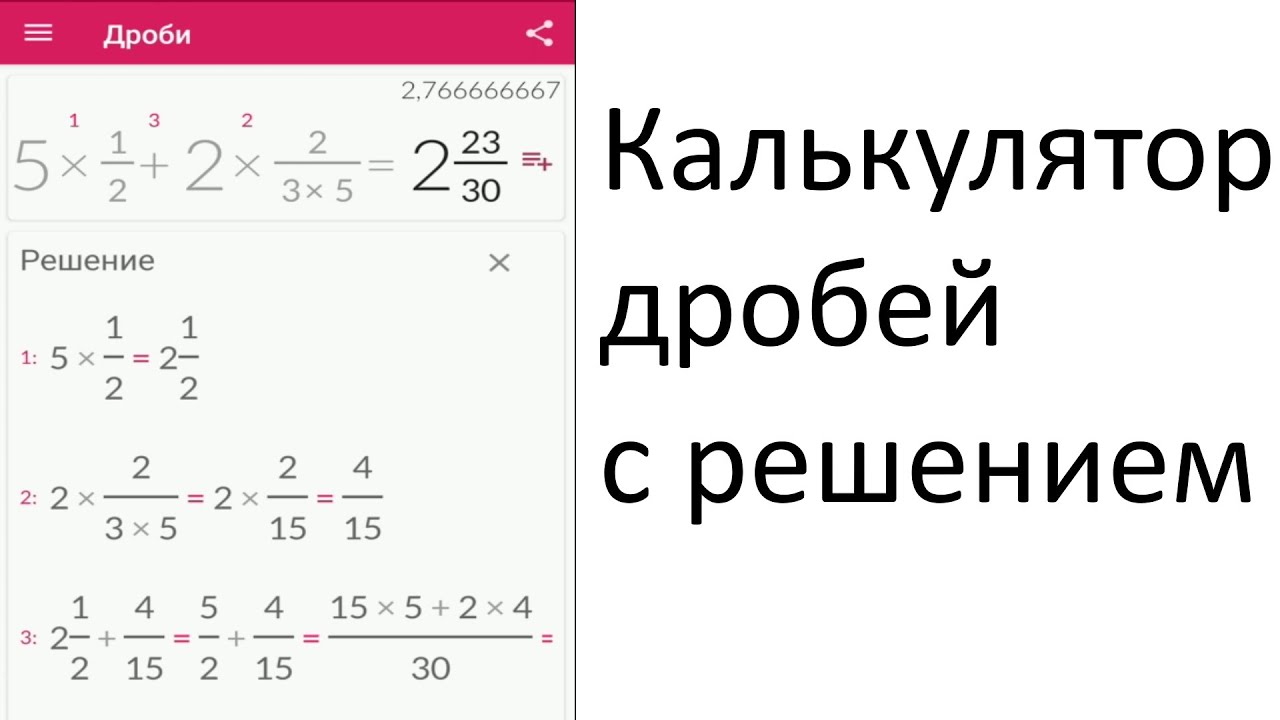 Кроме того, вы должны следовать этим правилам, чтобы вычитать рациональные функции.
Кроме того, вы должны следовать этим правилам, чтобы вычитать рациональные функции.
 Но когда это нужно упростить вручную, мы определили все правила и положения для этого выше. Например, давайте решим несколько примеров, соответствующих каждой из вышеперечисленных операций. 9{2}} $$
Но когда это нужно упростить вручную, мы определили все правила и положения для этого выше. Например, давайте решим несколько примеров, соответствующих каждой из вышеперечисленных операций. 9{2}} $$

 Математики, специалисты по данным, инженеры и физики широко используют рациональные выражения, используя бесплатный онлайн-калькулятор рациональных функций для выполнения быстрых вычислений.
Математики, специалисты по данным, инженеры и физики широко используют рациональные выражения, используя бесплатный онлайн-калькулятор рациональных функций для выполнения быстрых вычислений.




 Онлайн калькулятор расстояния между точками
Онлайн калькулятор расстояния между точками Найди правильный ответ.
Найди правильный ответ. Калькулятор вычисления силы, массы и ускорения.
Калькулятор вычисления силы, массы и ускорения. Для плоского, цилиндрического и сферического конденсаторов
Для плоского, цилиндрического и сферического конденсаторов Например, «вектор длина».
Например, «вектор длина». На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и вектор длина. Просто введите задачу в окошко и нажмите
«решить» здесь (например, вычисление длины вектора по его координатам).
На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и вектор длина. Просто введите задачу в окошко и нажмите
«решить» здесь (например, вычисление длины вектора по его координатам).
 ..
.. просмотров
просмотров

 1 . Пусть у нас имеются векторы a и b. Пусть по длине один из них равен 4, а другой 8. Скалярное произведения наших векторов равно (-12). Подставляя указанные значения в формулу для косинуса, можно легко провести его вычисление
1 . Пусть у нас имеются векторы a и b. Пусть по длине один из них равен 4, а другой 8. Скалярное произведения наших векторов равно (-12). Подставляя указанные значения в формулу для косинуса, можно легко провести его вычисление {2}}}
\]
{2}}}
\]


 В результате будем иметь
В результате будем иметь Таким образом, любой луч из данного множества сонаправленных лучей вполне определяет это направление (подобно тому, как любой направленный отрезок вполне определяет вектор, который он изображает). Поэтому направление в пространстве обычно задают при помощи только одного луча.
Таким образом, любой луч из данного множества сонаправленных лучей вполне определяет это направление (подобно тому, как любой направленный отрезок вполне определяет вектор, который он изображает). Поэтому направление в пространстве обычно задают при помощи только одного луча.
 2}} = -\frac{4}{9} $$
2}} = -\frac{4}{9} $$
 matrix[нижний.tri(result.matrix)] <- нижний.t
diag(результат.матрица) <- 0
результирующая.матрица[верхняя.три(результат.матрица)] <- t(результат.матрица)[верхняя.три(т(результат.матрица))]
## Получить результирующую матрицу
возврат (результат.матрица)
}
matrix[нижний.tri(result.matrix)] <- нижний.t
diag(результат.матрица) <- 0
результирующая.матрица[верхняя.три(результат.матрица)] <- t(результат.матрица)[верхняя.три(т(результат.матрица))]
## Получить результирующую матрицу
возврат (результат.матрица)
}
 cosine.angles <- angles(matrix = mt.c)
> центр.косинус.углы
[1] [2] [3] [4] [5]
[1,] 0,000000 1,620349 1,700334 1,614890 1,764721
[2,] 1,620349 0,000000 1,540213 1,526950 1,701793
[3,] 1,700334 1,540213 0,000000 1,615677 1,595647
[4,] 1,614890 1,526950 1,615677 0,000000 1,5
cosine.angles <- angles(matrix = mt.c)
> центр.косинус.углы
[1] [2] [3] [4] [5]
[1,] 0,000000 1,620349 1,700334 1,614890 1,764721
[2,] 1,620349 0,000000 1,540213 1,526950 1,701793
[3,] 1,700334 1,540213 0,000000 1,615677 1,595647
[4,] 1,614890 1,526950 1,615677 0,000000 1,5 equal (cos (углы (матрица = mt.c)), cor (mt))
[1] ИСТИНА
equal (cos (углы (матрица = mt.c)), cor (mt))
[1] ИСТИНА

 Разной сложности, для разных возрастов.
Именно решая задачи человек может подружиться с математикой. И именно решая задачи можно ощутить всю
радость общения с математикой.
Разной сложности, для разных возрастов.
Именно решая задачи человек может подружиться с математикой. И именно решая задачи можно ощутить всю
радость общения с математикой.
 этапов (с 2009), книги
этапов (с 2009), книги
 07.2018
07.2018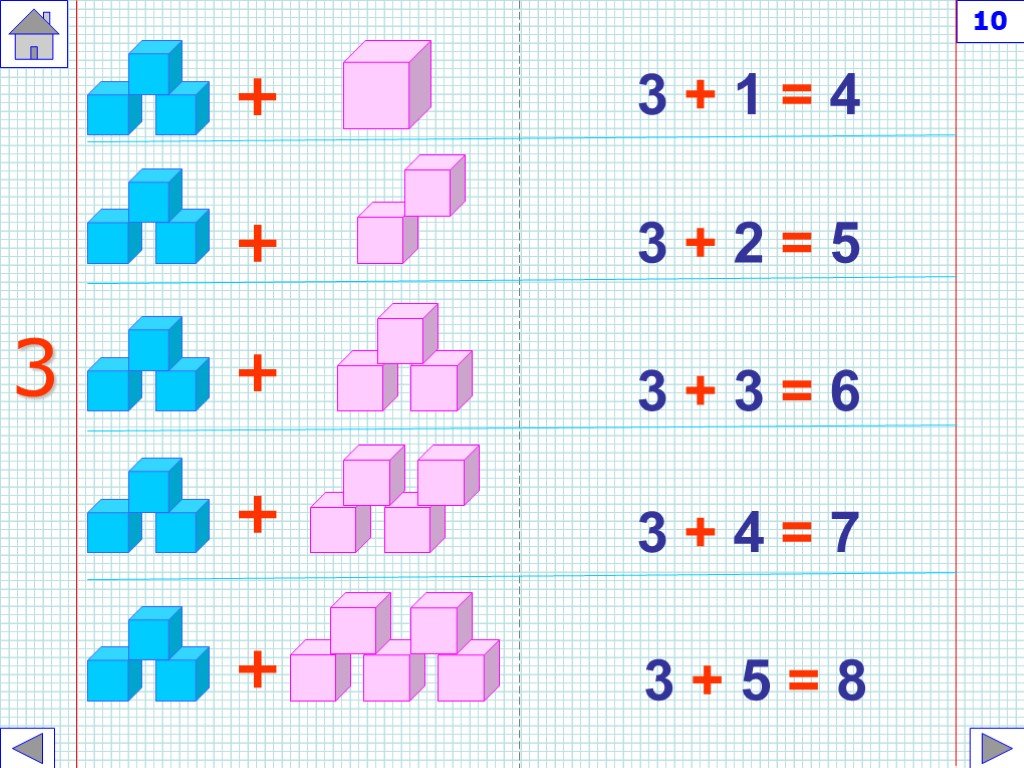 Темы включают линейную и матричную алгебру (с особым акцентом на анализ спроса/предложения и затрат/доходов) и дифференциальное исчисление. Студентам предлагается привести примеры математических приложений, основанные на их профессиональном опыте. Передается для кредита UC.
Темы включают линейную и матричную алгебру (с особым акцентом на анализ спроса/предложения и затрат/доходов) и дифференциальное исчисление. Студентам предлагается привести примеры математических приложений, основанные на их профессиональном опыте. Передается для кредита UC. ..
..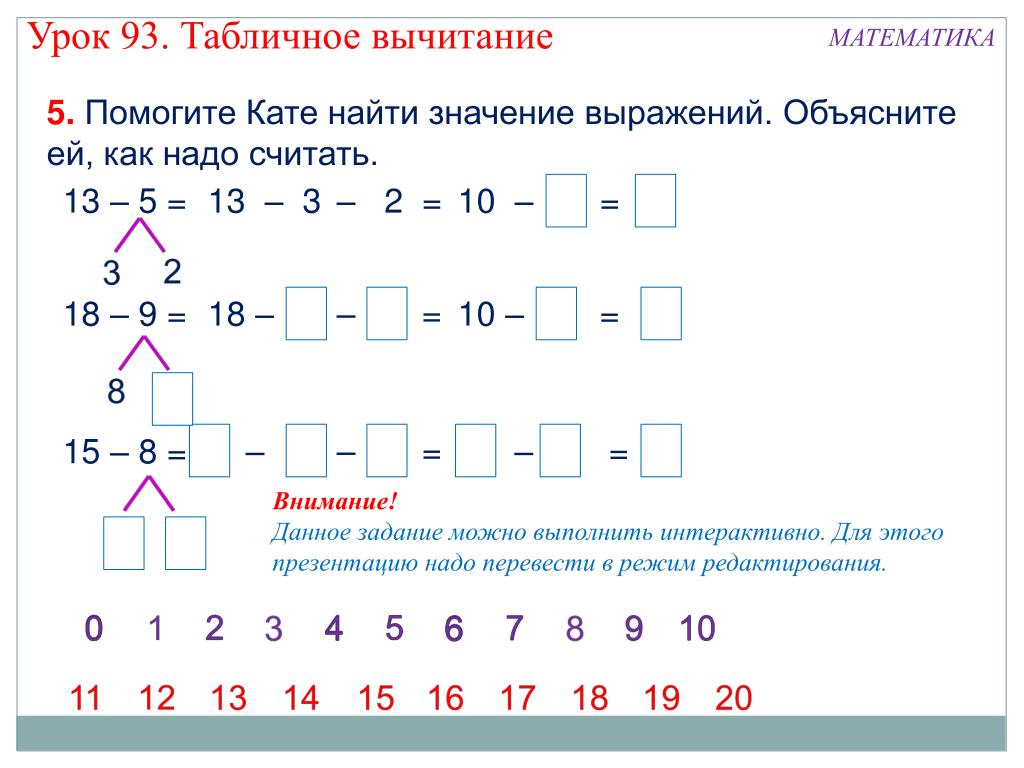
 Требуемые материалы.
Требуемые материалы.
 Поскольку школьные округа готовятся нанять большее количество
заменители и профессионалы на пенсии, практически не имеющие формального математического образования
обучения, необходимо, чтобы школьное руководство также разработало план того, как
Поддержите этих специалистов. Институт замены математики предоставит
заменить учителей математики постоянной поддержкой, инструментами и математическим контентом
знания, чтобы обеспечить учащимся полный математический опыт.
Поскольку школьные округа готовятся нанять большее количество
заменители и профессионалы на пенсии, практически не имеющие формального математического образования
обучения, необходимо, чтобы школьное руководство также разработало план того, как
Поддержите этих специалистов. Институт замены математики предоставит
заменить учителей математики постоянной поддержкой, инструментами и математическим контентом
знания, чтобы обеспечить учащимся полный математический опыт. Помимо того, что вы часами сидите за кухонным столом, решая вместе с ребенком одни и те же математические задачи, существует ряд эффективных и практичных подходов, которые родители могут использовать для поддержки математического образования своих детей. Этот институт предоставит родителям и опекунам инструменты и основы, необходимые для вовлечения их детей в критическое мышление, помогая им развивать позитивное математическое мышление. Этот тренинг также предоставит родителям навыки, позволяющие сделать математику увлекательной и увлекательной, чтобы их ребенок был готов решать проблемы и понимать новые концепции, независимо от их стиля обучения.
Помимо того, что вы часами сидите за кухонным столом, решая вместе с ребенком одни и те же математические задачи, существует ряд эффективных и практичных подходов, которые родители могут использовать для поддержки математического образования своих детей. Этот институт предоставит родителям и опекунам инструменты и основы, необходимые для вовлечения их детей в критическое мышление, помогая им развивать позитивное математическое мышление. Этот тренинг также предоставит родителям навыки, позволяющие сделать математику увлекательной и увлекательной, чтобы их ребенок был готов решать проблемы и понимать новые концепции, независимо от их стиля обучения. Через
на интерактивных сессиях профессионального развития учителя узнают, как использовать точный математический язык и методы вопросов, чтобы стимулировать студенческий дискурс, методы повышения вовлеченности во время дистанционного обучения и как обеспечить, чтобы учащиеся могли применять свои концептуальные знания для решения реальных проблем.
Через
на интерактивных сессиях профессионального развития учителя узнают, как использовать точный математический язык и методы вопросов, чтобы стимулировать студенческий дискурс, методы повышения вовлеченности во время дистанционного обучения и как обеспечить, чтобы учащиеся могли применять свои концептуальные знания для решения реальных проблем.
 Самое интересное, что FMS создала «линейку продуктов Dope Math», состоящую из тетрадей, карандашей и линеек, чтобы отдать дань уважения учащимся, которые освещают уроки математики.
Самое интересное, что FMS создала «линейку продуктов Dope Math», состоящую из тетрадей, карандашей и линеек, чтобы отдать дань уважения учащимся, которые освещают уроки математики.
 Актуализация знаний
Актуализация знаний

 Актуализация знаний5
Актуализация знаний5
 {2} x=\frac{x}{2}
\)
{2} x=\frac{x}{2}
\) {2}}=\frac{1}{2}
\)
{2}}=\frac{1}{2}
\) Тогда, окончательно имеем, что
Тогда, окончательно имеем, что

 совсем).
совсем). Беспроигрышный вариант!
Беспроигрышный вариант! д.
д.


 д. … и т. д.
д. … и т. д. Вот несколько способов свести к минимуму усталость от принятия решений и повысить продуктивность и креативность.
Вот несколько способов свести к минимуму усталость от принятия решений и повысить продуктивность и креативность. (Больше идей о формулах здесь.)
(Больше идей о формулах здесь.) Эти жесткие ограничения не позволяют задачам занимать больше времени, чем нужно, и не отвлекают вас от другой важной работы. Они также помогают вам избежать трудоголизма, который гораздо менее продуктивен, чем кажется».
Эти жесткие ограничения не позволяют задачам занимать больше времени, чем нужно, и не отвлекают вас от другой важной работы. Они также помогают вам избежать трудоголизма, который гораздо менее продуктивен, чем кажется». Я никогда не мог понять, когда идти, и я думал об этом много . (Теперь, когда они открыли второй магазин гораздо ближе к тому месту, где мы живем, это уже не так нервирует.)
Я никогда не мог понять, когда идти, и я думал об этом много . (Теперь, когда они открыли второй магазин гораздо ближе к тому месту, где мы живем, это уже не так нервирует.) Я беспомощен против всего Pinterest. На прошлой неделе я решил ограничить свои возможности и решил сосредоточиться только на одной области (кладовой) и разместить заказ только в одном магазине (The Container Store). И теперь наша кладовая выглядит довольно здорово. Есть ли варианты лучше и дешевле? Вероятно. Но работа сделал , и этого мне достаточно.
Я беспомощен против всего Pinterest. На прошлой неделе я решил ограничить свои возможности и решил сосредоточиться только на одной области (кладовой) и разместить заказ только в одном магазине (The Container Store). И теперь наша кладовая выглядит довольно здорово. Есть ли варианты лучше и дешевле? Вероятно. Но работа сделал , и этого мне достаточно.


 Например, можно интегрировать приложение для создания электронной подписи или инструмент для управления проектами.
Например, можно интегрировать приложение для создания электронной подписи или инструмент для управления проектами.
 80 USD
80 USD
 Это займет всего несколько кликов, если вы используете лучший создатель PDF для сохранить документ Word как PDF . Ниже приведены советы и рекомендации по сохранению документа Word в формате PDF с помощью PDFelement Pro.
Это займет всего несколько кликов, если вы используете лучший создатель PDF для сохранить документ Word как PDF . Ниже приведены советы и рекомендации по сохранению документа Word в формате PDF с помощью PDFelement Pro.
 com. Следующее, что вам нужно будет сделать.
com. Следующее, что вам нужно будет сделать. Если вы используете Word Perfect, вам необходимо убедиться, что в настройках публикации в PDF задано преобразование гиперссылок.
Если вы используете Word Perfect, вам необходимо убедиться, что в настройках публикации в PDF задано преобразование гиперссылок.

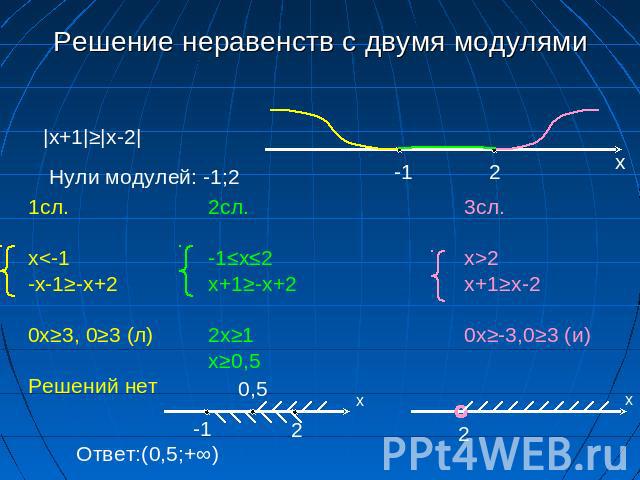 Обоим этим условиям соответствует только один из двух полученных ответов – число 2. Значит, только оно и является корнем исходного уравнения.
Обоим этим условиям соответствует только один из двух полученных ответов – число 2. Значит, только оно и является корнем исходного уравнения.
 Для этого наше неравенство надо представить в следующем виде:
Для этого наше неравенство надо представить в следующем виде:
 Для этого приравняем левые части неравенств к нулю.
Для этого приравняем левые части неравенств к нулю.
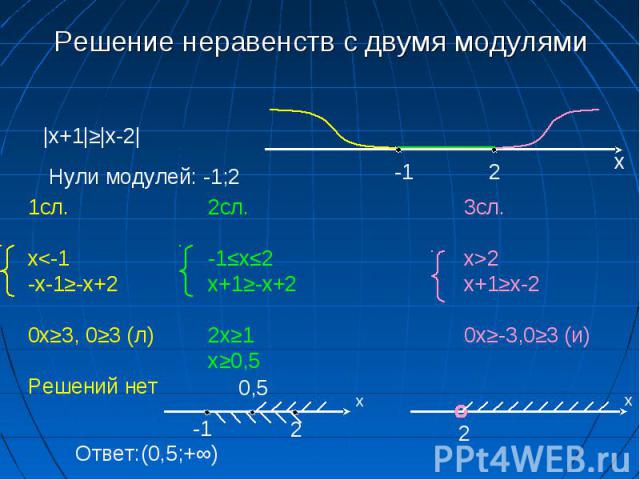 $\endgroup$
$\endgroup$ Вы можете взять это отсюда?
Вы можете взять это отсюда? А на самом деле это всегда равно .
А на самом деле это всегда равно .
 равно нулю и здесь вы получите возьмем общее от числителя и приведем его к правой части так как вы получите минус 1 разделить на Х + 1 должно быть больше или равно нулю теперь найдите решение этого неравенства для этого неделя была критическими точками, чтобы поставить x + 1 равно нулю X + 1 равно нулю отсюда мы получаем -1 как критическую точку, и здесь также получаем критические точки, необходимые для x минус 1 равные это даст X равно 1 и критическая точка, и снова X + 1 равно нулю, что даст X равно минус 1 критической
равно нулю и здесь вы получите возьмем общее от числителя и приведем его к правой части так как вы получите минус 1 разделить на Х + 1 должно быть больше или равно нулю теперь найдите решение этого неравенства для этого неделя была критическими точками, чтобы поставить x + 1 равно нулю X + 1 равно нулю отсюда мы получаем -1 как критическую точку, и здесь также получаем критические точки, необходимые для x минус 1 равные это даст X равно 1 и критическая точка, и снова X + 1 равно нулю, что даст X равно минус 1 критической
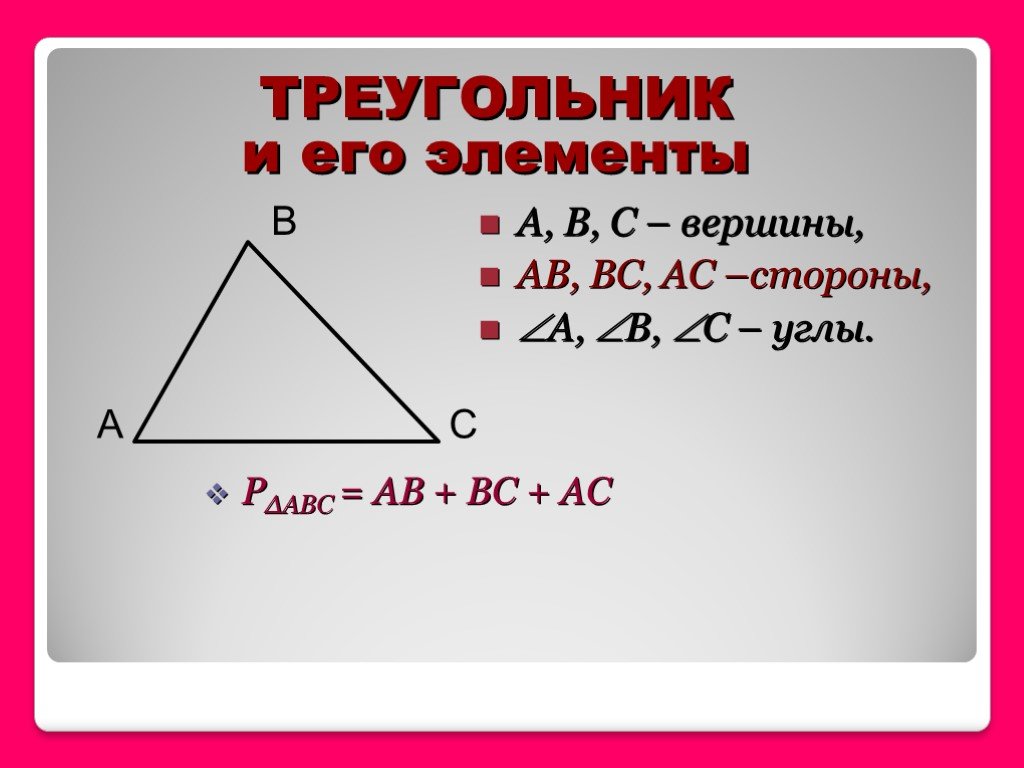 В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и AC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (BC).
В такой фигуре две стороны, которые образуют прямой угол, называются катетами (AB и AC). Третья сторона, расположенная напротив прямого угла – это гипотенуза (BC).

 Треугольник с вершиной, соединенной с такой же геометрической фигурой, ацтеки использовали в качестве эмблемы временного цикла. Герменевтической традиции известно множество видов треугольников, имеющих различные толкования: например, данная геометрическая фигура с горизонтальной чертой почиталась ими пассивным символом, который означает воздух, а перевернутая является олицетворением чаши, которая готова принять воду, а также соответствует женскому началу.
Треугольник с вершиной, соединенной с такой же геометрической фигурой, ацтеки использовали в качестве эмблемы временного цикла. Герменевтической традиции известно множество видов треугольников, имеющих различные толкования: например, данная геометрическая фигура с горизонтальной чертой почиталась ими пассивным символом, который означает воздух, а перевернутая является олицетворением чаши, которая готова принять воду, а также соответствует женскому началу.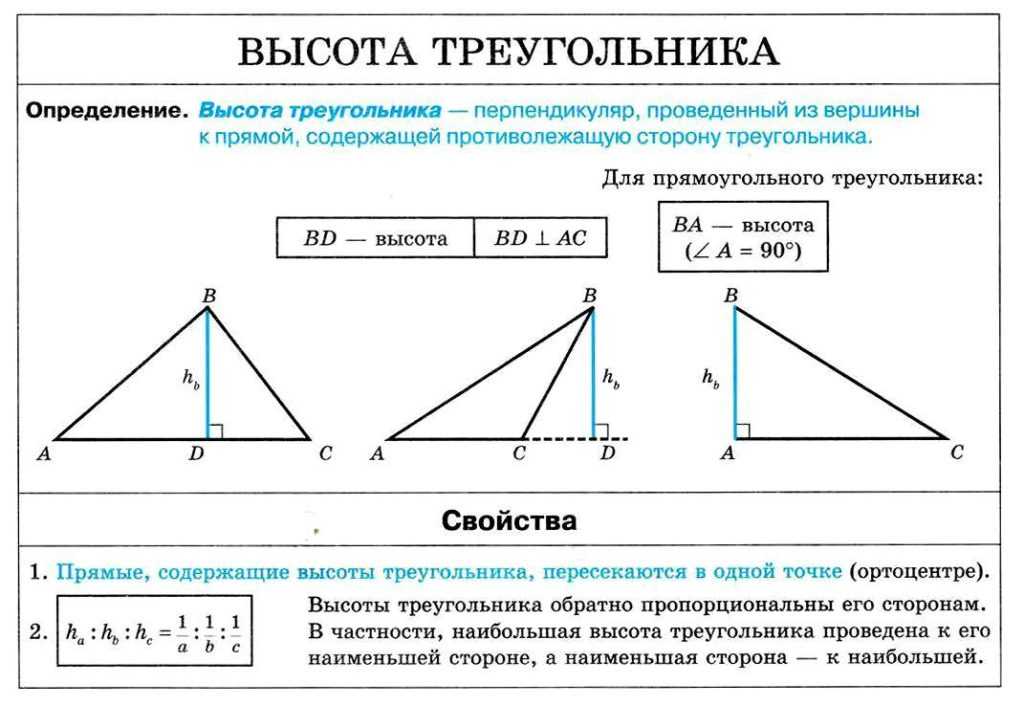 Треугольники могут выступать и в качестве лунного символа, тогда они располагаются горизонтально и соприкасаются своими вершинами. Общая точка этих треугольников символически обозначает смерть и новолуние.
Треугольники могут выступать и в качестве лунного символа, тогда они располагаются горизонтально и соприкасаются своими вершинами. Общая точка этих треугольников символически обозначает смерть и новолуние.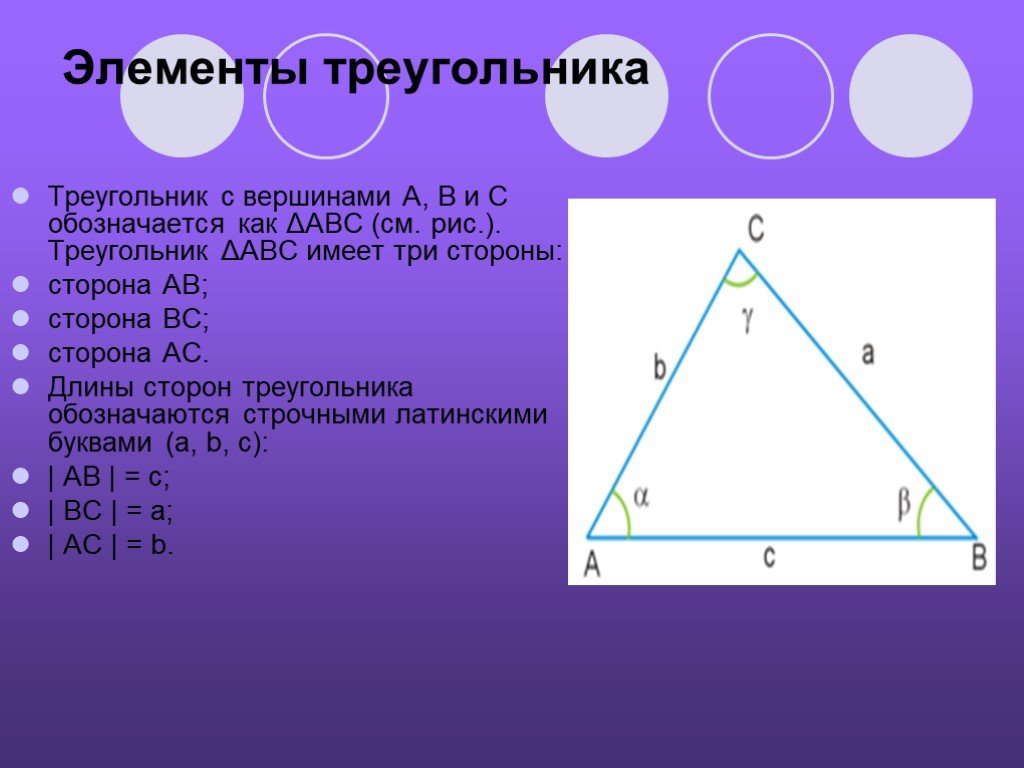
 Равносторонний треугольник толковался как равенство и единая божественная сущность Бога Отца, Бога Сына и Духа Святого. Иногда этот символ составляли из трех переплетенных между собой рыб. Символ Троицы по католической традиции составлялся из трех малых треугольников, вписанных в один большой с кругами на вершинах. Три этих круга означают триединство, но каждый круг независим и совершенен сам по себе. Эта схема иллюстрировала принцип триединства и вместе с тем индивидуальности каждого составляющего Святой Троицы.
Равносторонний треугольник толковался как равенство и единая божественная сущность Бога Отца, Бога Сына и Духа Святого. Иногда этот символ составляли из трех переплетенных между собой рыб. Символ Троицы по католической традиции составлялся из трех малых треугольников, вписанных в один большой с кругами на вершинах. Три этих круга означают триединство, но каждый круг независим и совершенен сам по себе. Эта схема иллюстрировала принцип триединства и вместе с тем индивидуальности каждого составляющего Святой Троицы. В Древней Греции был теплый климат и снега зимой не было.
В Древней Греции был теплый климат и снега зимой не было. Свое название оно получило на Древнем Востоке, его знали и использовали в навигации финикийские мореходы. Для них оно символизировало священный камень пирамидальной формы. Треугольник входил в число 48 классических созвездий античности. Древние греки считали, что это — перенесенная на небо дельта Нила, что указывает на египетские корни названия созвездия. Уже в Новое время на звездном небе были выделены созвездия Южного Треугольника и Наугольника.
Свое название оно получило на Древнем Востоке, его знали и использовали в навигации финикийские мореходы. Для них оно символизировало священный камень пирамидальной формы. Треугольник входил в число 48 классических созвездий античности. Древние греки считали, что это — перенесенная на небо дельта Нила, что указывает на египетские корни названия созвездия. Уже в Новое время на звездном небе были выделены созвездия Южного Треугольника и Наугольника.
 д.
д.
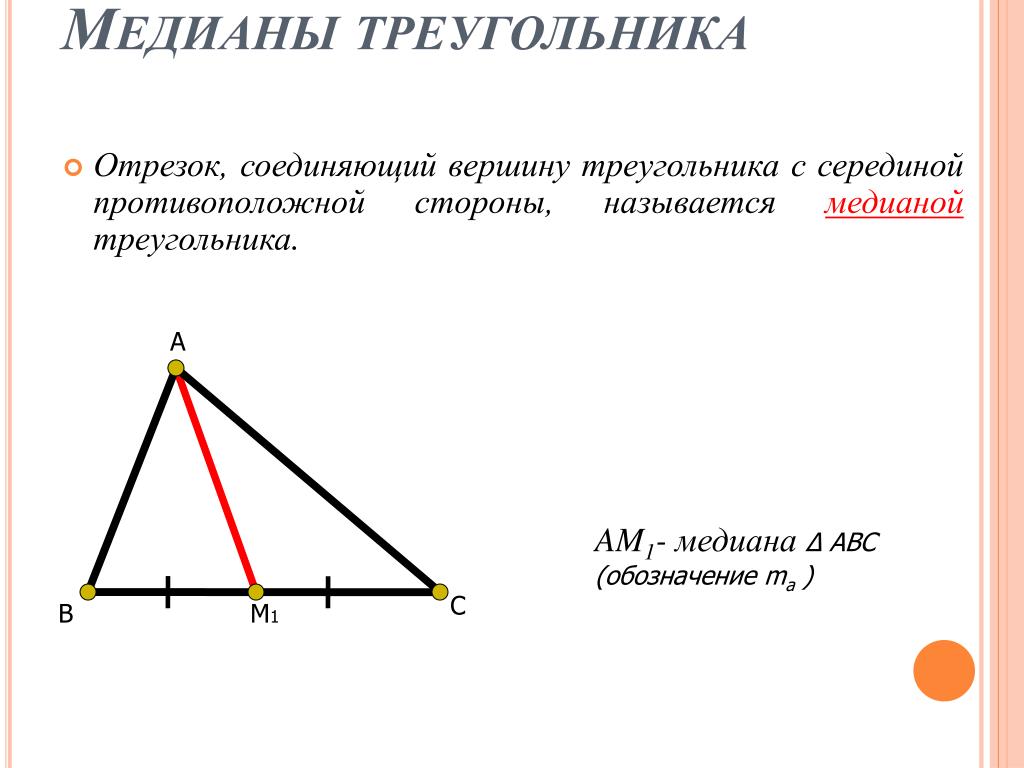
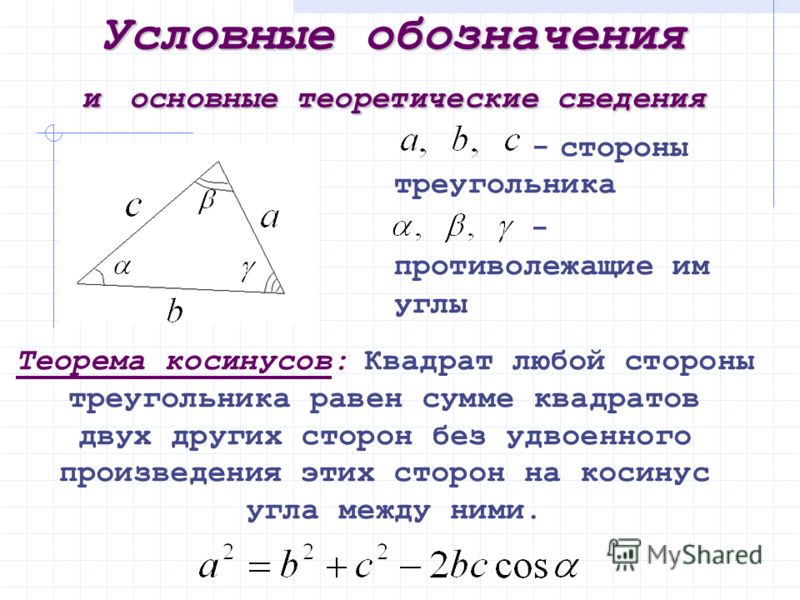



 $
$
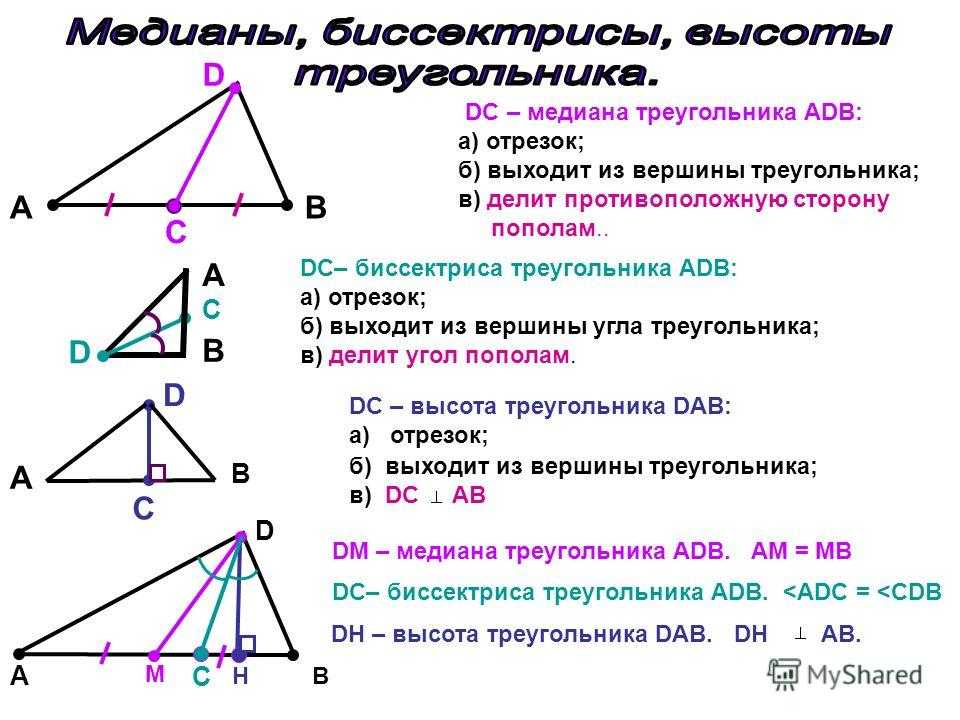

 $
Следовательно, не существует углов $\,\beta\,$ с $\,\sin\beta = 1,34\,.$
$
Следовательно, не существует углов $\,\beta\,$ с $\,\sin\beta = 1,34\,.$ \circ — D\,$’,
тогда $\,D\,$ относится к мера угла при вершине $\,D\,.$
\circ — D\,$’,
тогда $\,D\,$ относится к мера угла при вершине $\,D\,.$
 $
$ 
