 2+n-72)=1/(n+9)
2+n-72)=1/(n+9)Решите уравнение sin2x-2sin(-x)=1+cos(-x)
Главная » ЕГЭ по математике профильный уровень » Решите уравнение sin2x-2sin (-x)=1+cos (-x)
ЕГЭ по математике профильный уровень
На чтение 4 мин. Просмотров 1.7k.
В задании нужно решить тригонометрическое уравнение, затем определить какие корни попали в указанный отрезок на тригонометрическом круге. Для решения данного уравнения необходимо знать некоторые тригонометрические формулы и четность и нечетность тригонометрических функций, откладывать на круге отрезок и определять значения корней. Поскольку мы работаем с периодическими функциями, то в каждом периоде значения корней будут разными.
a) Решите уравнение .
б) Укажите корни этого уравнения, принадлежащие отрезку .
Решение.
a) Прежде чем решать данное уравнение, нам нужно упростить его: либо свести все к одной тригонометрической функции и к одному аргументы (или к или к ), либо разложить на множители, произведение которых будет равно нулю.
Начнем применять известные нам формулы.
Синус двойного аргумента
Формула синуса двойного аргумента:
Четность и нечетность тригонометрических функций
Формулы четности и нечетности тригонометрических функций:
Применим эти формулы к нашему уравнению:
Вот мы и разложили левую часть на множители. И наше уравнение распадается на два простых уравнения.
Получаем:
или
Решим первое уравнение:
Посмотрим, где на тригонометрическом круге это значение и какой угол мы получаем:
Решение уравнения sinx=½ на тригонометрическом круге
, где .
, где .
Решим второе уравнение:
.
Решением этого уравнения будет , где .
На тригонометрическом круге решение второго уравнения:
Решение тригонометрического уравнения cosx=-1 на тригонометрическом круге
Ответ на пункт a) задания будет такой:
, где ,
, где ,
, где .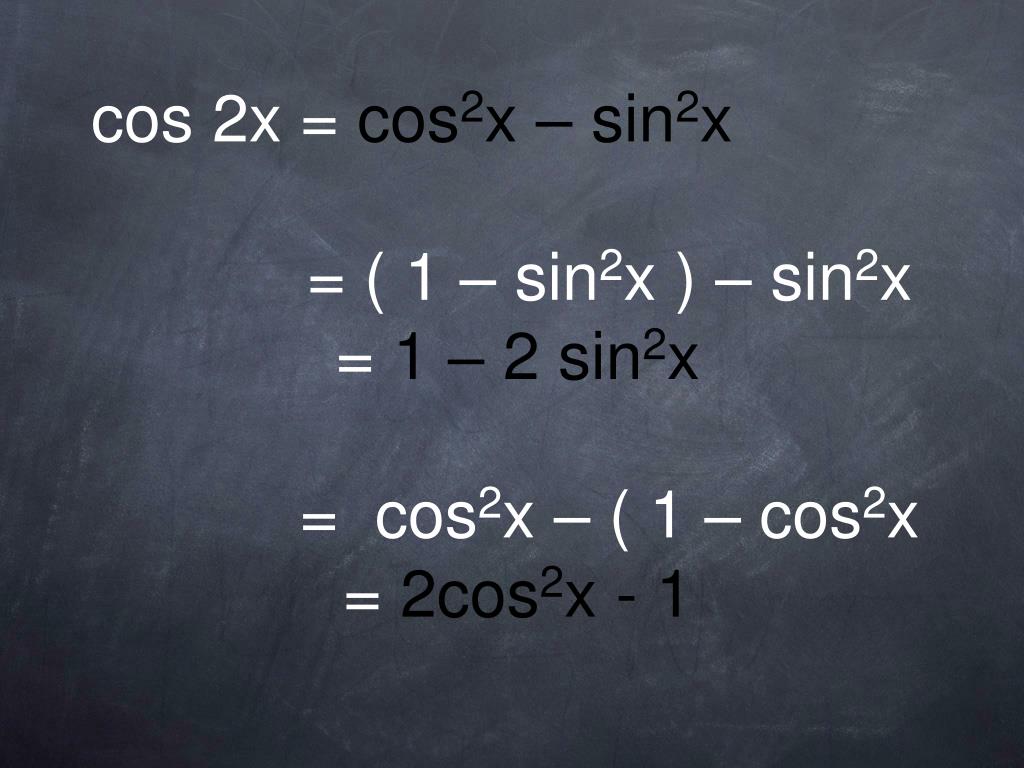
б) Найдем корни уравнения, которые принадлежат отрезку .
На помощь нам придет тригонометрический круг. Отметим на нем отрезок и нанесем корни, которые в него попали. Затем вычислим их значения.
Отрицательные углы на тригонометрическом круге откладываются по часовой стрелке. Начинаем двигаться от нуля — это единица на оси x и затем откладываем по часовой стрелке по четвертинке круга и считаем:
- ,
- ,
- ,
- (замечаем эту точку и от нее начинаем отмечать отрезок),
- ,
- ,
- .
Тригонометрический круг с отмеченным отрезком
Теперь отметим на этом отрезке точки — корни уравнения, заметим, что корень в отрезок не вошел.
Корни уравнения, входящие в указанный отрезок.
Если первый корень сразу виден: , то второй корень надо определить. Он расположен на расстоянии от корня , если двигаться по часовой стрелке.
Тогда второй корень можно найти:
.
Ответ на пункт б) будет: и .
Ответ: а), где , , где , , где .
б) ; .
( 3 оценки, среднее 5 из 5 )
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
| 1 | Найти точное значение | грех(30) | |||||
| 2 | Найти точное значение | грех(45) | |||||
| 3 | Найти точное значение | грех(30 градусов) | |||||
| 4 | Найти точное значение | грех(60 градусов) | |||||
| 5 | Найти точное значение | загар (30 градусов) | |||||
| 6 | Найти точное значение | угловой синус(-1) | |||||
| 7 | Найти точное значение | грех(пи/6) | |||||
| 8 | Найти точное значение | cos(pi/4) | |||||
| 9 | Найти точное значение | грех(45 градусов) | |||||
| 10 | Найти точное значение | грех(пи/3) | |||||
| 11 | Найти точное значение | арктан(-1) | |||||
| 12 | Найти точное значение | cos(45 градусов) | |||||
| 13 | Найти точное значение | cos(30 градусов) | |||||
| 14 | Найти точное значение | желтовато-коричневый(60) | |||||
| 15 | Найти точное значение | csc(45 градусов) | |||||
| 16 | Найти точное значение | загар (60 градусов) | |||||
| 17 | Найти точное значение | сек(30 градусов) | |||||
| 18 | Найти точное значение | cos(60 градусов) | |||||
| 19 | Найти точное значение | соз(150) | |||||
| 20 | Найти точное значение | грех(60) | |||||
| 21 | Найти точное значение | cos(pi/2) | |||||
| 22 | Найти точное значение | загар (45 градусов) | |||||
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |||||
| 24 | Найти точное значение | csc(60 градусов) | |||||
| 25 | Найти точное значение | сек(45 градусов) | |||||
| 26 | Найти точное значение | csc(30 градусов) | |||||
| 27 | Найти точное значение | грех(0) | |||||
| 28 | Найти точное значение | грех(120) | |||||
| 29 | Найти точное значение | соз(90) | |||||
| 30 | Преобразовать из радианов в градусы | пи/3 | |||||
| 31 | Найти точное значение | желтовато-коричневый(30) | |||||
| 32 | Преобразование градусов в радианы 92 | ||||||
| 35 | Преобразовать из радианов в градусы | пи/6 | |||||
| 36 | Найти точное значение | детская кроватка(30 градусов) | |||||
| 37 | Найти точное значение | арккос(-1) | |||||
| 38 | Найти точное значение | арктан(0) | |||||
| 39 | Найти точное значение | детская кроватка(60 градусов) | |||||
| 40 | Преобразование градусов в радианы | 30 | |||||
| 41 | Преобразовать из радианов в градусы | (2 шт. Вычислить log: Math.Log Метод (System) | Microsoft LearnВычислить логарифмическую базу 2 числа в КотлинеВ этой статье рассматриваются различные способы расчета 1. Использованиеln() функцияИдея состоит в том, чтобы использовать
Вот рабочий пример:
Скачать код результат: 2. ИспользованиеInteger.numberOfLeadingZeros() функцияThe
Скачать код результат: Это все о расчете Оценить этот пост Средний рейтинг 5/5. Подсчет голосов: 10 Голосов пока нет! Будьте первым, кто оценит этот пост. Сожалеем, что этот пост не оказался для вас полезным! Расскажите, как мы можем улучшить этот пост? Спасибо за чтение. Пожалуйста, используйте наш онлайн-компилятор размещать код в комментариях, используя C, C++, Java, Python, JavaScript, C#, PHP и многие другие популярные языки программирования. Когда упрощаются коэффициенты путем деления на множители факториала, они являются своего рода гармоническим рядом, который не сходится очень быстро. Числители — это последовательные степени х, а знаменатели простые числа, не факториалы. Вы захотите логарифмы чисел больших, чем 2. Здесь скорость сходимости показана в нахождении логарифма 2 этим методом. На сходимость влияет: единственный уменьшающийся фактор гармонического ряда интегральных обратных чисел. Он колеблется между наивысшим значением, а значит, должен сходиться гораздо дальше, чтобы достичь своего наивысшего значения. Логарифмические ряды: изменениеВот трюк, для чего введены логарифмы. Если вы изменяете переменную снова, используя (1 + x)/(1 — x), по принципу логарифмов, логарифм этой переменной будет логарифмом (1 + x) минус логарифм (1 — x). Во-первых, ряд логарифмов (l — x) был последовательностью степеней x разделенных на гармоническую последовательность интегральных чисел, меняющих свой знак. Этот метод делает две вещи: удаляет четные степени x и и объединяет их. Эти ряды заключены в большие скобки, умноженные на 2. Чтобы показать, насколько быстрее эти ряды сходятся, используйте это для вычисления log 2, что при применении первого метода заняло бы вечность. Решите (x + 1)/(x — 1) = 2. Здесь еще одна переменная изменится. Решая этого уравнения, переменная в ряде не 1, а 1/3. Так как каждый другой член выпал, последовательные члены уменьшаются на х (или 1/9). Это соотношение приводит к гораздо быстрому схождению. Он сходится так быстро, что только 4 члена необходимы для получения log2 c четырьмя цифрами после запятой. Расчет логарифмов Здесь вы рассчитываете два логарифма, чтобы найти сравнения в скорости сходимости. Для расчета log1,1 сделайте х = 1 / 21. Как вы уже видели, для вычисления log2, х = 1/3, где сходимость около одной десятой за каждый дополнительный член. Для точности до шести цифр, требуется семь членов. Теперь попробуйте найти значение log 3; x = 1/2. Этот ряд сходится более медленно, но попробуйте по-другому. Вы уже посчитали log 2. Log 3 = log 2 + log 1.5, потому что 3 = 2.1,5. Поэтому, найдите log1.5 и сложите его значение с log2. Log 1.5 использует x = 1/5 и его ряд сходится быстрее чем в случае с log 2. Теперь у вас есть значение с 6-ю цифрами для log 3. В примере выше вы пробовали найти значение логарифмов до 10. Обратите внимание, что есть способы для упрощения вычислений. Log 4 есть удвоенный log 2. Вы можете получить его либо из 4 = 2.2 или из 4 = 22. Log 5 есть log 4 + log 1.25. Log 6 есть log 2 + log 3. Log 7 есть log 4 + log 1.75. Log 8 есть log 2 взятый 3 раза, потому что 8 есть 23. Общие логарифмы Хотя все алгоритмы должны быть вычислены в их основной форме с основанием e, иногда называемыми гиперболическими или логарифмами Непера (от имени изобретателя логарифмов). Но более распространенное названия натуральные логарифмы или логарифмы с основанием e. Если у логарифма основание 10, тогда логарифм 10 по основанию 10 равен 1. Вы можете изменить основание, разделив натуральный логарифм на логарифм 10. Использование логарифмов: умножение и деление Конечно, нахождение логарифмов с помощью карманных калькуляторов намного проще, чем использование таблиц. Калькулятор вычисляет логарифмы обоих видов, натуральные и общие. Примеры, которые мы здесь приводим, взяты из таблиц с логарифмами с четырьмя цифрами. Ваш калькулятор, возможно, показывает больше цифр, чем таблица. На своем калькуляторе я ввел логарифм 32 и получил 1.505149978; значение логарифма 256 равно 2.408239965. Суммируя их, получим 3.9133889944. Используя сдвиг, ответ равен точно 8192! Последний пример показывает еще одну разницу с таблицами. Таблица дала только мантиссу — дробную часть. Вам необходимо вставить характеристику — целое число слева от запятой. 0.0969 есть мантиссой (в четырехзначных таблицах) для чисел 125. Риска над 1 указывает, что характеристика отрицательная. Поэтому, log есть -1 + 0.0969. Мой калькулятор пишет -0.903089987. Однако, если я ввожу 1.25 вместо 0.125, калькулятор пишет 0.096910013. Если число больше 1, мантисса не меняется, только характеристика изменяется и смещается десятичная точка. Использование логарифмов: индексы Здесь снова примеры, которые были приготовлены с помощью четырехзначных логарифмических таблиц. Логарифм 12 считается калькулятором как 1.079181246. Умножая на 3, получаем 3.23764 3738. Используя смещение и логарифм дает точно 1728. Вводим 12 снова. Нажимаем xy, затем 3, и =. Калькулятор снова высвечивает 1728. В следующем примере log 2 равен 0.301029995, правильный ответ снова. Однако, если ввести log 1024, высвечивается предыдущее значение 3.010299957 с одной дополнительной цифрой. Выше использованы логарифмы или xy клавиши, где индексы были очевидны. Иногда ответ не такой простой. Возьмем следующее: 354/5. С использованием калькулятора: Log 35 = 1.544068044. Используя клавиши xy, получаем тот же ответ. Кроме того, можно вычислить это значение используя биномиальное разложение, если калькулятор оснащен достаточной памятью. Биноминальным разложениемБиноминальным разложениемВ этот раз, 4-х значные логарифмы довольно ограниченны. Используя тот же калькулятор с клавишами логарифмов или с xy, результат равен 353.5533906. Биноминальное разложение дает тот же результат за исключением последних двух цифр. Конечно, ваш калькулятор не сделает биномиальный ряд для вас. Для того-то и упражнения, чтобы показать, что биномиальный ряд работает. Как калькулятор это делает? Он имеет встроенные программы, которые вычисляют логарифмические ряды очень быстро — за доли секунды. Помните, что калькулятор работает в двоичной системе, даже если он высвечивает десятичные цифры. Использование логарифмов с формулами Формула здесь связывает давление и объем в физическом расширение и сжатии газа. В таблице приведены значения v от 10 до 30 (предполагается, что этот диапазон охватывает необходимые значения в нашей конкретной задаче) и используются логарифмы для расчета соответствующего значения р (в последнем столбце). В 3-й колонке приведены значения 0,4logv в качестве помощи нахождения log1,4v. Табулирование с помощью этого метода облегчало процесс до появления калькуляторов. Четвертая колонка есть вычитание из 3, что есть log1000. Чтобы сделать это на калькуляторе, у вас есть выбор: использовать клавишу logs или xy. В любом случае, вы должны вставить k в это. Если k было другим, чем степень 10, это немного усложнит вычисление. Метод: использовать клавишу 1/x (обратное значение) а потом умножить на 1000 (или на соответсвующее значение к). Поиск закона логарифмов Вы знаете, что v и p относится друг к другу по закону типа: pvn = k. Возьмем логарифмы значения p: 1.361727836 и 1.176091259. После вычитания получим 0.185636579. Возьмем логарифмы значения v: 1.176091259 и 1.301029996. После вычитания получим: 0.124938736. Разделим первое значение на второе: 0.185636579/0.124938736= 1.485820827 — значение n. Такое вычисление требовало использование ячейки памяти вашего калькулятора. И все эти цифры после запятой точные, но необязательные. Числа, с которыми вам необходимо работать, скорее всего, имеют две значащие цифры. Вопросы и задачи 1. Рассмотрим следующий рисунок. Эти функции нарисованы на логарифмической шкале. Перерисуйте приближения этих функций в полулогарифмическом масштабе (ось х — линейные, ось у — логарифмическая). Выберите масштаб, который является обоснованными для угла значения в каждом конкретном случае. 2. Нарисуйте приблизительные значения функции в прямоугольных координатах поверх приведенного графика. Выберите масштаб, который является наиболее подходящим для диапазона значений в каждом случае. Масштабы могут быть неодинаковыми на каждой оси, но обе оси должны быть линейными. 3. Рассмотрите следующий рисунок. Эти функции нарисованы в прямоугольных координатах. Нарисуйте приблизительные значения функции в полулогарифмическом масштабе (ось х — линейная и ось у — логарифмическая). Выберите подходящий масштаб для диапазона значений в каждом случае. 4. Нарисуйте приблизительные значения функции в логарифмическом масштабе . Выберите подходящий масштаб для диапазона значений в каждом случае. Масштабы могут быть неодинаковыми на каждой оси, но обе оси должны быть линейными. 5. Используя формулу log10xy = log10x + log10y, найдите значения следующих множителей путем сложений чисел. Вы можете использовать калькулятор. Запишите ответы с тремя цифрами после запятой. 6. Используя формулу log10xy = ylog10x, найдите значения (стремя цифрами после запятой). Вы можете использовать калькулятор. 7. Если бы в решении задачи №6 натуральные логарифмы (с основанием e) были бы использованы вместо логарифмов с основанием 10 был бы результат верным? 8. Если бы в решении задачи №6 логарифмы по основанию 7 были бы использованы вместо десятичных логарифмов, был бы результат верным? 3 = 1000\), поэтому \(\log 1000 = 3\) Логарифмы часто используются в математике, но редко при вычислениях в уме — отчасти из-за их сложности! На самом деле, самый продвинутый метод, который я преподавал, проводя различные занятия по ментальной арифметике, — это использование логарифмов (вычисляемых в уме) для вычисления сложных корней и степеней. Математики узнают, что всегда верно следующее:
Следовательно, если мы знаем приблизительные значения \(\log 2 = 0,30103\) и \(\log 3 = 0,47712\), мы можем вычислить следующие примеры:
Наш метод вычисления логарифмов основан на запоминании различных значений логарифмов и их объединении для нахождения значения требуемого логарифма. Подготовка:Изучите следующие значения логарифмов – и, возможно, больше: \(\log 2 = 0,30103\) \(\log 3 = 0,47712\) 0\7 4 \(0,8 log 4 )\(\log 1,1 = 0,04139\) \(\log 1,3 = 0,11394\) \(\log 1,7 = 0,23045\) \((\log 1,01 = 0,00432)\) Метод:
Это простой пример: \(510 = 1,7 * 3 * 100\), и приближение не требуется. \(\log 510 = \log{1,7} + \log{3} + \log{100} = 0,23045 + 0,47712 + 2 = 2,70757\) Пример, требующий приближения: \(\log{511.28}\) Здесь есть несколько разумных подходов: \(511,28 = 510 + 0,25\%\) \(\log{511,28} = \log{1,7} + \log{3} + \log{100} + 0,00432 * 0,25 = 2,70757 + 0,00108 = 2,70865\) 9x\) для любого числа \(x\)) см. статью о вычислении антилогарифмов. При объединении алгоритмов для логарифмов и антилогарифмов мы получаем алгоритм общего назначения для всех степеней и корней. Как считать логарифмы в умеОпубликовано автором John В предыдущем посте рассматривались приближения для триггерных функций, которые достаточно просты для вычисления без калькулятора. Мне было интересно, смогу ли я придумать что-то подобное для логарифмов. Я начинаю с базы логов 10. Позже в посте я покажу, как найти логи в других базах из базы логов 10. Пусть х = м х 10 р . , где 1 ≤ м ≤ 10. Тогда log 10 ( x ) = log 10 ( м ) + без потерь и p общности можно считать 1 ≤ x ≤ 10.Но мы можем еще немного сузить наш диапазон. Если x > 3, вычислите логарифм x ‘ = x /10, а если x < 0,3, то вычислите логарифм 10 х . Таким образом, мы примем 0,3 ≤ x ≤ 3. Для x в этом диапазоне log 10 ( x ) ≈ + 1) — очень хорошее приближение. Абсолютная ошибка менее 0,0327 на интервале [0,3, 3]. Примерыlog 10 0,6 ≈ (0,6 – 1)/(0,6 + 1) = -1/4 = -0,25. Точно: -0,2218 log 10 1776 = 3 + log 10 1,776 ≈ 3 + 0,776/2,776 = 3,2795. Точно: 3,2494 log 10 9000 = 4 + log 10 0,9 ≈ 4 – 0,1/1,9 = 3,9473. Точно: 3,9542 Другие базыЛогарифмы по всем базам пропорциональны, поэтому вы можете преобразовать между логарифмической базой 10 и логарифмической в любую другую базу, умножив на константу пропорциональности. логарифм b ( x ) = логарифм 10 ( x ) / логарифм 10 ( b ). Итак, предположим, например, что вы хотите вычислить log 2 48. Поскольку 48 = 32 × 1,5, мы имеем log 2 48 = log 2 32 + log 2 1,5 = 4 + log 1901 1,5 / log 10 2 Мы можем аппроксимировать log 10 1,5 как 1/5, а log 10 2 как 1/3, чтобы получить log 2 48 = ,5/5. Точное значение 5,585. Если вы хотите использовать это для натуральных бревен, вы можете запомнить 1/log 10 e = log e 10 = 2,3. Обновление : есть лучший способ работать с другими базами. Смотрите этот пост. В том же посте объясняется, почему аппроксимация особенно проста для логарифмов с основанием 10. Больше точностиАбрамовиц и Стеган уточняют аппроксимацию t = ( x – 1)/( x + 1). Они используют интервал [1/√10, √10], а не [0,3, 3]. Этот немного другой интервал симметричен относительно 0 при преобразовании в 9.0005 т . Уравнение 4.1.41 прогоняет t через кубический полином и снижает абсолютную ошибку до значения менее 6 × 10 -4 . Уравнение 4.1.42 использует полином 9-й степени от до , чтобы уменьшить абсолютную ошибку ниже 10 -9 . Next В следующем посте я покажу, как аналогично вычислить 10 x . 2 cos y: Mathway | Популярные задачи 2 |
| 1 | Найти точное значение | грех(30) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | Найти точное значение | грех(45) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | Найти точное значение | грех(30 градусов) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | Найти точное значение | грех(60 градусов) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | Найти точное значение | загар (30 градусов) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | Найти точное значение | угловой синус(-1) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | Найти точное значение | грех(пи/6) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | Найти точное значение | cos(pi/4) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | Найти точное значение | грех(45 градусов) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | Найти точное значение | грех(пи/3) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11 | Найти точное значение | арктан(-1) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12 | Найти точное значение | cos(45 градусов) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13 | Найти точное значение | cos(30 градусов) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14 | Найти точное значение | желтовато-коричневый(60) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15 | Найти точное значение | csc(45 градусов) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16 | Найти точное значение | загар (60 градусов) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 17 | Найти точное значение | сек(30 градусов) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18 | Найти точное значение | cos(60 градусов) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19 | Найти точное значение | cos(150) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20 | Найти точное значение | грех(60) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 21 | Найти точное значение | cos(pi/2) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 22 | Найти точное значение | загар (45 градусов) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 24 | Найти точное значение | csc(60 градусов) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 25 | Найти точное значение | сек(45 градусов) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 26 | Найти точное значение | csc(30 градусов) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 27 | Найти точное значение | грех(0) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 28 | Найти точное значение | грех(120) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 29 | Найти точное значение | соз(90) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 30 | Преобразовать из радианов в градусы | пи/3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 31 | Найти точное значение | желтовато-коричневый(30) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 32 | 92|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 35 | Преобразовать из радианов в градусы | пи/6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 36 | Найти точное значение | детская кроватка(30 градусов) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 37 | Найти точное значение | арккос(-1) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 38 | Найти точное значение | арктан(0) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 39 | Найти точное значение | детская кроватка(60 градусов) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 40 | Преобразование градусов в радианы | 30 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 41 | Преобразовать из радианов в градусы | (2 шт. Как найти пери прямоугольника: Как найти периметр прямоугольника? Ответ на webmath.ru {2}}
\) \(\ A D=\sqrt{45-9}=\sqrt{36}=6(\mathrm{см}) \) Чтобы найти периметр прямоугольника, воспользуемся формулой \(\ P_{A B C D}=2(a+b) \) Для этой задачи он примет форму \(\ P_{A B C D}=2(A B+A D) \) Подставляя значения сторон прямоугольника, получим \(\ P_{A B C D}=2 \cdot(3+6)=18_{(\mathrm{см})} \) \(\ P_{A B C D}=18 \mathrm{см} \) Физика 166 Реклама и PR 31 Педагогика 80 Психология 72 Социология 7 Астрономия 9 Биология 30 Культурология 86 Экология 8 Право и юриспруденция 36 Политология 13 Экономика 49 Финансы 9 История 16 Философия 8 Информатика 20 Право 35 Информационные технологии 6 Экономическая теория 7 Менеджент 719 Математика 338 Химия 20 Микро- и макроэкономика 1 Медицина 5 Государственное и муниципальное управление 2 География 542 Информационная безопасность 2 Аудит 11 Безопасность жизнедеятельности 3 Архитектура и строительство 1 Банковское дело 1 Рынок ценных бумаг 6 Менеджмент организации 2 Маркетинг 238 Кредит 3 Инвестиции 2 Журналистика 1 Конфликтология 15 Этика 9 Формулы дифференцирования Периметр параллелограмма Периметр трапеции Периметр окружности Периметр круга Узнать цену работы Узнай цену своей работы Имя Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругоеПринимаю Политику конфиденциальности Подпишись на рассылку, чтобы не пропустить информацию об акциях Как найти периметр прямоугольника без длины и ширины? – Обзоры Викиcom/embed/dmWWomPSw_s» frameborder=»0″ allowfullscreen=»allowfullscreen» data-original-w=»720″ data-original-h=»520″>Итак, как найти длину прямоугольника, зная только периметр? Точно так же, если известны периметр и ширина, длину можно рассчитать по формуле: Длина (L) = P/2 – w. Где P = периметр прямоугольника; и w = ширина прямоугольника. Как найти периметр прямоугольника без ширины? Складываем l + l + w + w. Вместо того, чтобы складывать две стороны вашего прямоугольника и умножать на два, вы можете просто сложить все четыре стороны вместе, чтобы найти периметр вашего прямоугольника. Дополнительно Каковы формулы площади и периметра? Таблица формул площади и периметра
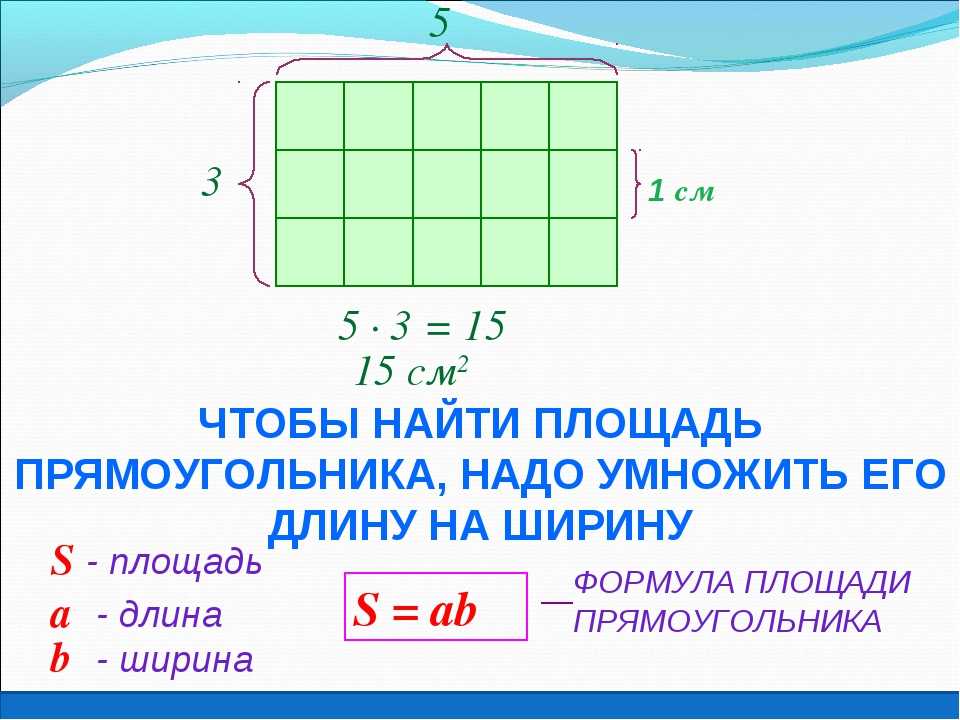
• 30 сентября 2020 г. Как измерить площадь прямоугольника? Чтобы найти площадь прямоугольника, мы умножьте длину прямоугольника на ширину прямоугольника. Как определить длину прямоугольника, зная его площадь?Чтобы найти длину или ширину, когда задана площадь прямоугольника
Как найти ширину прямоугольника, если известны периметр и длина? Чтобы найти ширину, умножьте полученную длину на 2 и вычтите результат из периметра.. Теперь у вас есть общая длина оставшихся 2 сторон. Это число, разделенное на 2, и есть ширина. Как можно ввести формулу периметра прямоугольника и квадрата? Чтобы найти периметр прямоугольника, сложите длины четырех сторон прямоугольника. Как найти ширину прямоугольника, если известны периметр и длина?Пояснение: Чтобы найти ширину, умножьте полученную длину на 2 и вычтите результат из периметра.. Теперь у вас есть общая длина оставшихся 2 сторон. Это число, разделенное на 2, и есть ширина. Также Как найти ширину прямоугольника, если известна его площадь? Чтобы сначала рассчитать длину и ширину прямоугольника, вычислите значение ширины «w», используя формулу площади прямоугольника, то есть ‘w = A / l’. Какая формула прямоугольника? Формула площади прямоугольника
23 февраля, 2020 Каковы периметр и площадь квадрата и прямоугольника? Периметр прямоугольника равен P=2b+2h, где b — основание (или ширина), а h — высота (или длина). Что такое единицы площади и периметра?Единицы периметра такие же, как и длины, т.е. м, см, мм и т.д.. Площадь: помимо плоскости, заключенной в простую замкнутую фигуру, называется плоской областью, а измерение замкнутой плоской области называется ее площадью. Площадь измеряется в квадратных единицах. Какими тремя способами найти площадь прямоугольника? Чтобы найти площадь прямоугольника, умножьте длину на ширину. Формула: A = L * W, где A — площадь, L — длина, W — ширина, а * означает умножение. где A — площадь, s — длина стороны, а · означает умножение. Как найти площадь прямоугольника с 4 сторонами? Это то же самое, что умножить основание квадрата на его высоту, потому что основание и высота просто всегда одинаковы. Используйте следующее уравнение: Площадь = сторона × сторона или A = s. Как получается площадь прямоугольника? Чтобы получить площадь прямоугольника, мы используем единичные квадраты. Разделите прямоугольник ABCD на единичные квадраты., как показано. Площадь прямоугольника ABCD — это общее количество содержащихся в нем единичных квадратов. Таким образом, общая площадь прямоугольника ABCD составляет 48 кв. Как найти длину и ширину прямоугольника, если у меня есть площадь?Чтобы сначала вычислить длину и ширину прямоугольника, вычислите значение ширины ‘w’, используя формулу площади прямоугольника, а именно: ‘w = A / l’. Как найти площадь прямоугольника без длины? com/embed/5AsqWPdUS5I» frameborder=»0″ allowfullscreen=»allowfullscreen» data-original-w=»720″ data-original-h=»520″>Как научить периметр прямоугольника?Может ли формула периметра прямоугольника использоваться для нахождения периметра любого квадрата? Периметр прямоугольника — это сумма длин всех сторон прямоугольника. Следовательно, мы можем найти периметр по сложение всех четырех сторон прямоугольника.
Математическая задача: Периметр прямоугольника Найдите периметр прямоугольника. Правильный ответ:x = 12 11 ⁄ 21 = 263/21 мПошаговое объяснение:a=3+65=3+65=3+65 =63⋅ 6+5=618+5=623≐3,8333 м b=273=2+73=72⋅ 7+3=714+3=717 ≐2,4286 м х=2⋅ ( a+b)=2⋅ (623+717)=21263 m=122111 m=12,5238 м Нашли ошибку или неточность? Смело звоните по номеру , пишите нам. Спасибо! Советы по использованию связанных онлайн-калькуляторов Нужна помощь со смешанными числами? Попробуйте наш калькулятор смешанных чисел. Для решения этой математической задачи вам необходимо знать следующие знания:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 numberOfLeadingZeros(n)
numberOfLeadingZeros(n) 5}{5}….$
5}{5}….$ Ряды для log(l — x) используют те же численные члены, но все их знаки — отрицательные. Помните, что вы собираетесь вычесть их из log(l + x), вследствие чего все отрицательные знаки в конце станут позитивными.
Ряды для log(l — x) используют те же численные члены, но все их знаки — отрицательные. Помните, что вы собираетесь вычесть их из log(l + x), вследствие чего все отрицательные знаки в конце станут позитивными. Последовательные члены сейчас сходятся более чем 400:1. Три члена ряда теперь производят логарифм с шестью знаками после запятой.
Последовательные члены сейчас сходятся более чем 400:1. Три члена ряда теперь производят логарифм с шестью знаками после запятой. Log 9 есть удвоенной log 3 потому что 9 = 32. Наконец, log 10 есть log 2+ log 5.
Log 9 есть удвоенной log 3 потому что 9 = 32. Наконец, log 10 есть log 2+ log 5.  Общие логарифмы обозначаются log, а натуральные логарифмы обозначаются ln.
Общие логарифмы обозначаются log, а натуральные логарифмы обозначаются ln. Карманный калькулятор может найти ответы намного быстрее. Действительно, большинство калькуляторов имеют одну клавишу, xy. Однако, давайте посмотрим как обработать эти примеры с помощью калькулятора.
Карманный калькулятор может найти ответы намного быстрее. Действительно, большинство калькуляторов имеют одну клавишу, xy. Однако, давайте посмотрим как обработать эти примеры с помощью калькулятора. Вам не нужно повторно вычислять каждый член. После второго члена, вы можете умножить/разделить на дополнительные множители. Например, чтобы получить третий член на второй, умножте на 3 и разделите на 320 и так далее. Этот ряд сходится очень быстро.
Вам не нужно повторно вычислять каждый член. После второго члена, вы можете умножить/разделить на дополнительные множители. Например, чтобы получить третий член на второй, умножте на 3 и разделите на 320 и так далее. Этот ряд сходится очень быстро.  Это характерно для многих формул. Величины р и v являются переменными, k и индекс n являются константами. В этой таблице к = 1000 и n = 1,4.
Это характерно для многих формул. Величины р и v являются переменными, k и индекс n являются константами. В этой таблице к = 1000 и n = 1,4. Это показывает, как это делались вычисления с помощью логарифмов до появления калькуляторов. Вы можете использовать ваш калькулятор, но использование клавиши xy является не таким легким; использование клавиши log есть более легким.
Это показывает, как это делались вычисления с помощью логарифмов до появления калькуляторов. Вы можете использовать ваш калькулятор, но использование клавиши xy является не таким легким; использование клавиши log есть более легким.







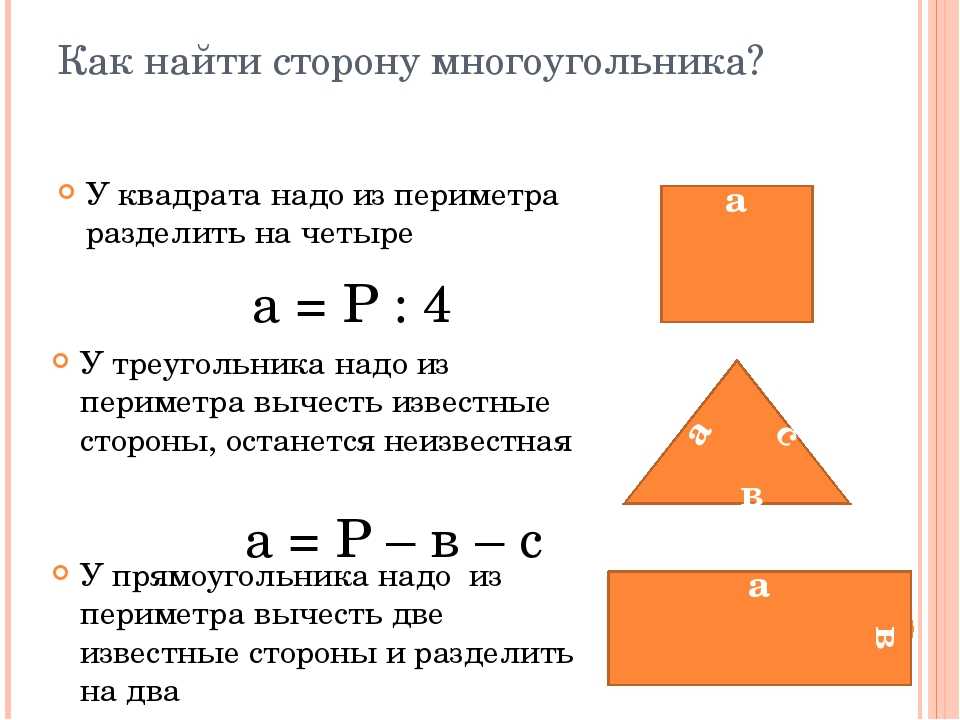 Если у вас есть только ширина и высота, вы можете легко найти все четыре стороны (каждая из двух сторон равна высоте, а две другие стороны равны ширине). Умножьте высоту и ширину на два и сложите результаты.
Если у вас есть только ширина и высота, вы можете легко найти все четыре стороны (каждая из двух сторон равна высоте, а две другие стороны равны ширине). Умножьте высоту и ширину на два и сложите результаты. Если прямоугольник является квадратом со сторонами длиной s, формула для периметра будет Psquare=2s+2s=4s, а формула площади будет Квадрат=s⋅s=s2.
Если прямоугольник является квадратом со сторонами длиной s, формула для периметра будет Psquare=2s+2s=4s, а формула площади будет Квадрат=s⋅s=s2.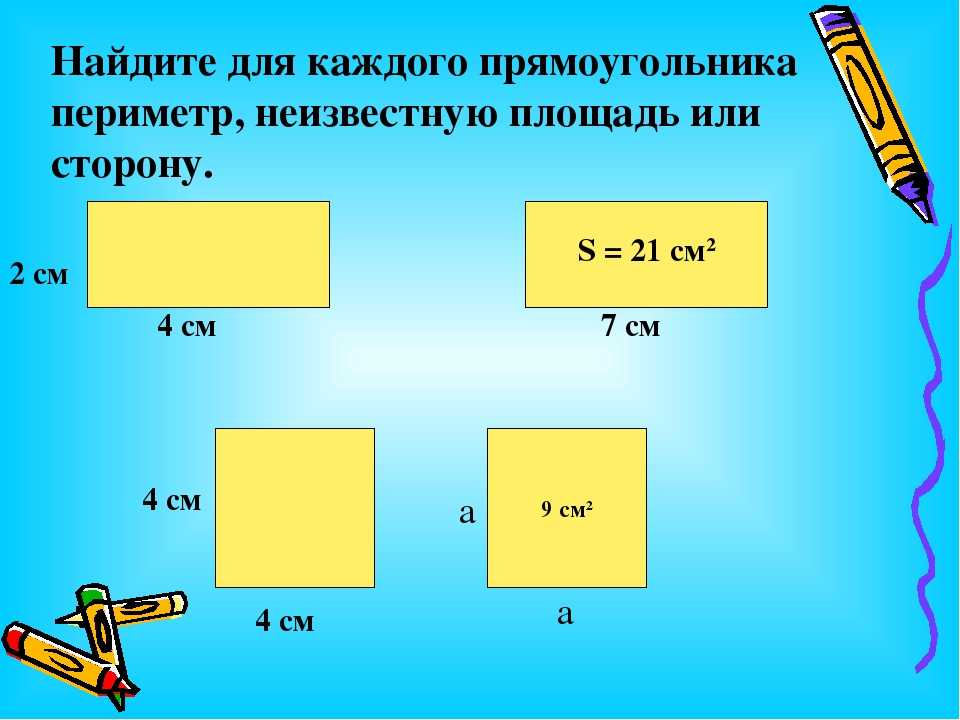 Пример: если одна сторона квадрата имеет длину 4 фута (t = 4), то площадь этого квадрата равна просто t2, или 4 х 4 = 16 квадратных футов.
Пример: если одна сторона квадрата имеет длину 4 фута (t = 4), то площадь этого квадрата равна просто t2, или 4 х 4 = 16 квадратных футов. 11.
11. Прямоугольник с основанием (3 5/6) м и высотой (2 3/7) м
Прямоугольник с основанием (3 5/6) м и высотой (2 3/7) м  Запишите ответ в виде дроби в простейшей форме. -5 2/3+3 1/4+(-7 1/3)=
Запишите ответ в виде дроби в простейшей форме. -5 2/3+3 1/4+(-7 1/3)= M см, где M — месяц вашего рождения. Плотность дуба 680 кг/м³.
M см, где M — месяц вашего рождения. Плотность дуба 680 кг/м³.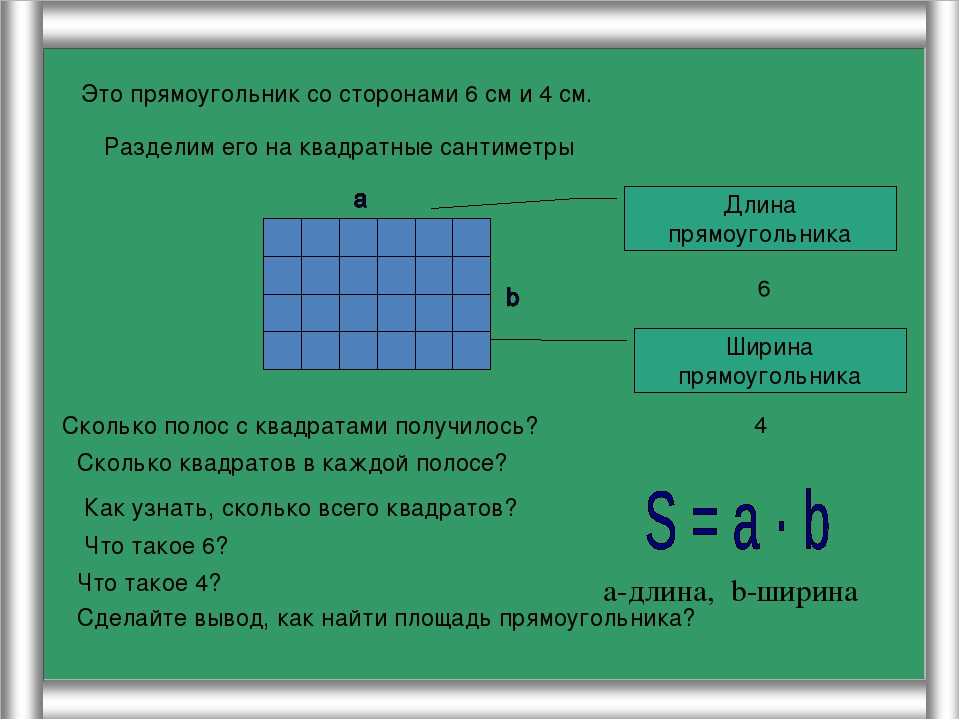


 Чтобы получилось круглое число нужно из 32 вычесть 2 получится 30.Чтобы получить второе число нужно к 32 прибавить 2 получится 34. То есть нужно вычитать и прибавлять одинаковое число. Умножаем 30 на 34 получается 1020, и прибавляем число которое вычитали и прибавляли в квадрате, то есть 2² = 4, получится 1024.
Чтобы получилось круглое число нужно из 32 вычесть 2 получится 30.Чтобы получить второе число нужно к 32 прибавить 2 получится 34. То есть нужно вычитать и прибавлять одинаковое число. Умножаем 30 на 34 получается 1020, и прибавляем число которое вычитали и прибавляли в квадрате, то есть 2² = 4, получится 1024. Число в экспоненциальной части — это количество раз, которое вам нужно умножить на это число. Калькулятор математической мощности — это простой математический калькулятор, который подскажет, чему равно число в экспоненциальной форме. Здесь мы говорим о квадратах, кубах и высших экспоненциальных степенях.
Число в экспоненциальной части — это количество раз, которое вам нужно умножить на это число. Калькулятор математической мощности — это простой математический калькулятор, который подскажет, чему равно число в экспоненциальной форме. Здесь мы говорим о квадратах, кубах и высших экспоненциальных степенях.

 в школе? Учитель просто спросил вас: «Чему равно число 3, возведенное в степень 4?» А ты просто умножил 3 на себя 4 раза, да? iCalculator разработал математический калькулятор мощности, используя ту же концепцию.
в школе? Учитель просто спросил вас: «Чему равно число 3, возведенное в степень 4?» А ты просто умножил 3 на себя 4 раза, да? iCalculator разработал математический калькулятор мощности, используя ту же концепцию. Так что теперь вам просто нужно знать, насколько велика ваша комната на самом деле. Ну так что ты делаешь? Вы умножаете 12 на 12, то есть 12² = 144 квадратных фута.
Так что теперь вам просто нужно знать, насколько велика ваша комната на самом деле. Ну так что ты делаешь? Вы умножаете 12 на 12, то есть 12² = 144 квадратных фута.











 7.2022, 2:24
7.2022, 2:24 9.2022, 19:30
9.2022, 19:30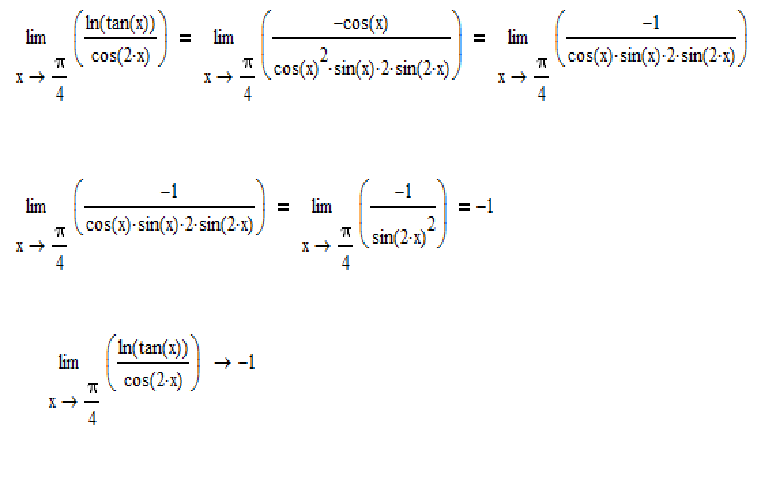 9BettpersCommXVIILastPuccMonACircBigbSkarFredAstrGorgWishMakiBonuFeliDekoZoneNorvDineGIOACurv
9BettpersCommXVIILastPuccMonACircBigbSkarFredAstrGorgWishMakiBonuFeliDekoZoneNorvDineGIOACurv 10.2022, 14:49
10.2022, 14:49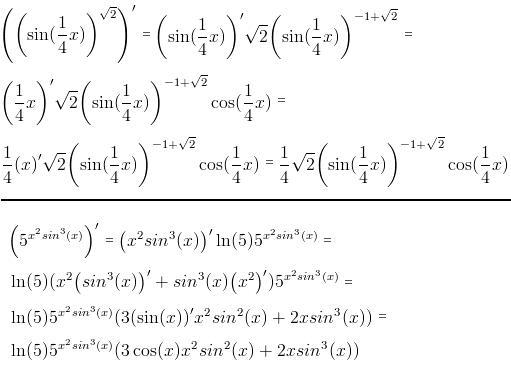 ruhandsfreetelephone.ruhangonpart.ruhaphazardwinding.ruhardalloyteeth.ruhardasiron.ru
ruhandsfreetelephone.ruhangonpart.ruhaphazardwinding.ruhardalloyteeth.ruhardasiron.ru rukleinbottle.rukneejoint.ruknifesethouse.ruknockonatom.ruknowledgestate.rukondoferromagnet.rulabeledgraph.rulaborracket.rulabourearnings.rulabourleasing.rulaburnumtree.rulacingcourse.rulacrimalpoint.ru
rukleinbottle.rukneejoint.ruknifesethouse.ruknockonatom.ruknowledgestate.rukondoferromagnet.rulabeledgraph.rulaborracket.rulabourearnings.rulabourleasing.rulaburnumtree.rulacingcourse.rulacrimalpoint.ru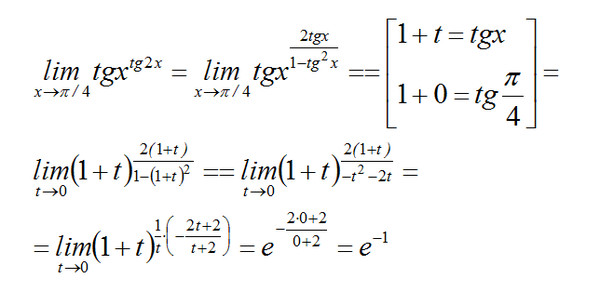 rumajorconcern.rumammasdarling.rumanagerialstaff.rumanipulatinghand.rumanualchoke.rumedinfobooks.rump3lists.runameresolution.runaphtheneseries.runarrowmouthed.runationalcensus.runaturalfunctor.runavelseed.runeatplaster.runecroticcaries.runegativefibration.runeighbouringrights.ruobjectmodule.ruobservationballoon.ru
rumajorconcern.rumammasdarling.rumanagerialstaff.rumanipulatinghand.rumanualchoke.rumedinfobooks.rump3lists.runameresolution.runaphtheneseries.runarrowmouthed.runationalcensus.runaturalfunctor.runavelseed.runeatplaster.runecroticcaries.runegativefibration.runeighbouringrights.ruobjectmodule.ruobservationballoon.ru ru
ru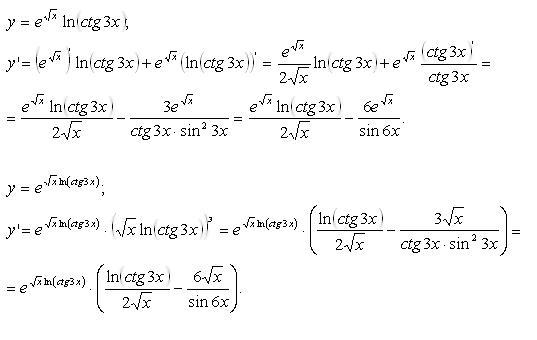 3+4 — вопрос №3701814 — Учеба и наука
3+4 — вопрос №3701814 — Учеба и наука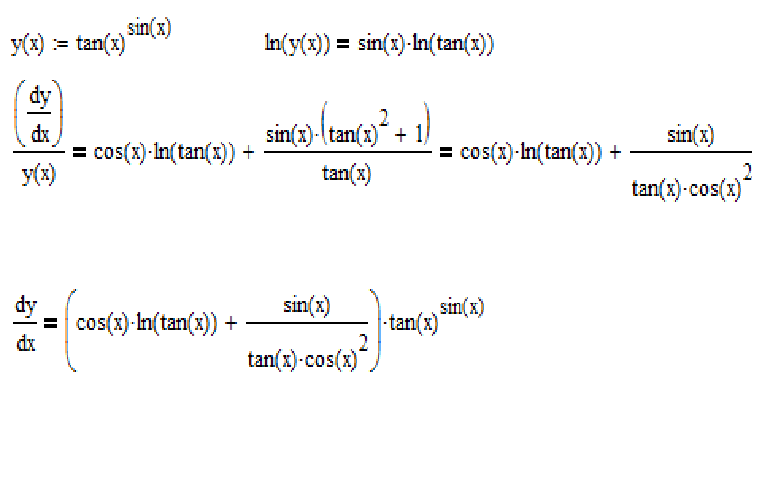

 )/3
)/3
 ..
..

 ..
..



 ..
..


 ..
..


 ..
..

 ..
..

 ..
..
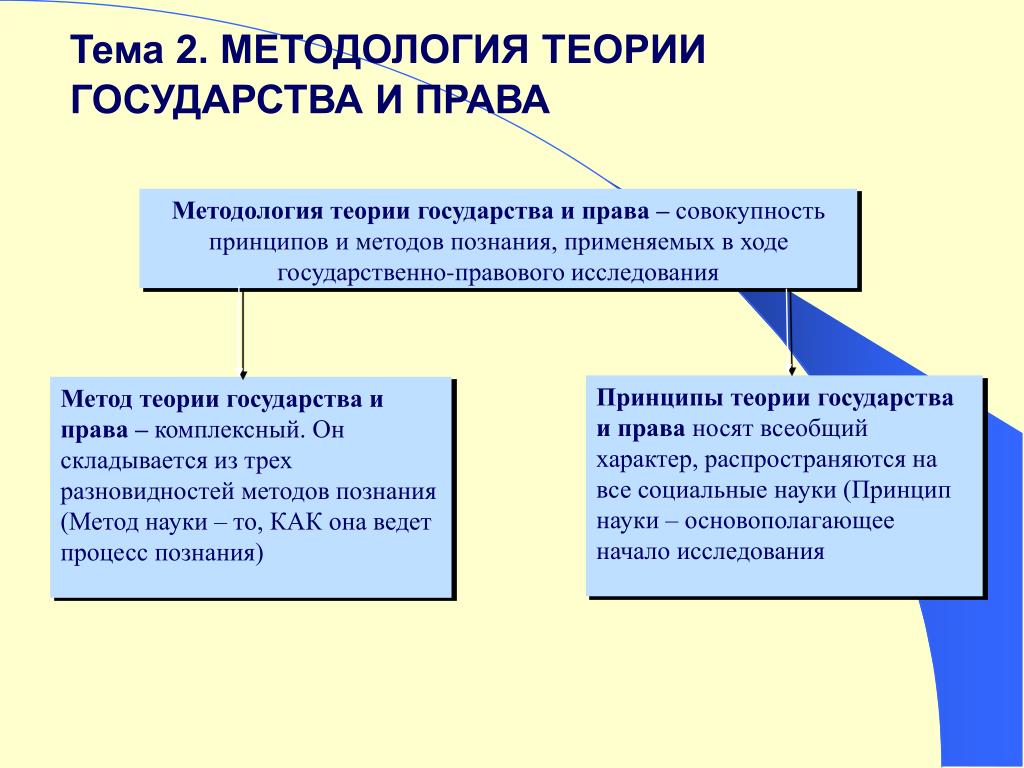
 3. Основные подходы к типологии государства…
3. Основные подходы к типологии государства…


 ..
..

 ..
..


 — 2012. — №29. — Ст. 3978.
— 2012. — №29. — Ст. 3978. от 2 октября 2012 года №159-ФЗ) // Собрание законодательства Российской Федерации. — 2005. — №1 (часть 1). — Ст. 15; Собрание законодательства Российской Федерации. — 2012. — №41. — Ст. 5524.
от 2 октября 2012 года №159-ФЗ) // Собрание законодательства Российской Федерации. — 2005. — №1 (часть 1). — Ст. 15; Собрание законодательства Российской Федерации. — 2012. — №41. — Ст. 5524. — 2011. — №50. — Ст. 7347.
— 2011. — №50. — Ст. 7347. — 1996. — №22. — Ст. 2663; Собрание законодательства Российской Федерации. — 2011. — №47. — Ст. 6621.
— 1996. — №22. — Ст. 2663; Собрание законодательства Российской Федерации. — 2011. — №47. — Ст. 6621. — 2012. — №5. – С. 33-37.
— 2012. — №5. – С. 33-37. В их деле Ли против Вейсмана судья Энтони Кеннеди ввел тест на принуждение, заявив, что учащихся государственных школ принуждали участвовать в спонсируемых государством религиозных мероприятиях, когда государственные школы пригласил духовенство произнести призывы и благословения на таких мероприятиях, как выпускной. Третий слева — генеральный юрисконсульт Объединенного комитета баптистов Оливер «Базз» Томас, который подал заявление по этому делу. (Фотография перепечатана с разрешения Объединенного баптистского комитета.)
В их деле Ли против Вейсмана судья Энтони Кеннеди ввел тест на принуждение, заявив, что учащихся государственных школ принуждали участвовать в спонсируемых государством религиозных мероприятиях, когда государственные школы пригласил духовенство произнести призывы и благословения на таких мероприятиях, как выпускной. Третий слева — генеральный юрисконсульт Объединенного комитета баптистов Оливер «Базз» Томас, который подал заявление по этому делу. (Фотография перепечатана с разрешения Объединенного баптистского комитета.) ) для определения того, имеет ли закон светский характер. законодательной цели, независимо от того, является ли ее основной эффект продвижением или сдерживанием религии, или ведет ли она к чрезмерному запутыванию между церковью и государством.
) для определения того, имеет ли закон светский характер. законодательной цели, независимо от того, является ли ее основной эффект продвижением или сдерживанием религии, или ведет ли она к чрезмерному запутыванию между церковью и государством. диплома».
диплома». Можно сомневаться, что для многих, если не для большинства студентов на выпускном акт стояния или молчания был выражением участия в молитве раввина».
Можно сомневаться, что для многих, если не для большинства студентов на выпускном акт стояния или молчания был выражением участия в молитве раввина». Скалиа утверждал: «Принуждение, которое было отличительной чертой исторических учреждений религии, было принуждением религиозной ортодоксальности и финансовой поддержки силой закона и угрозой наказания». В данном случае он не видел доказательств ни того, ни другого.
Скалиа утверждал: «Принуждение, которое было отличительной чертой исторических учреждений религии, было принуждением религиозной ортодоксальности и финансовой поддержки силой закона и угрозой наказания». В данном случае он не видел доказательств ни того, ни другого. , стр. 186).
, стр. 186). FEC (2014 г.), отчасти потому, что закон не был наименее ограничительным средством борьбы с коррупцией в политической системе. Этот наименее ограничительный критерий нуждаемости является частью «строгой проверки», применяемой судами к закону, который ограничивает права Первой поправки. (AP Photo/Susan Walsh, использовано с разрешения Associated Press)
FEC (2014 г.), отчасти потому, что закон не был наименее ограничительным средством борьбы с коррупцией в политической системе. Этот наименее ограничительный критерий нуждаемости является частью «строгой проверки», применяемой судами к закону, который ограничивает права Первой поправки. (AP Photo/Susan Walsh, использовано с разрешения Associated Press) ) суд отменил федеральный закон, требующий от кабельных операторов полностью зашифровывать программы откровенно сексуального характера или переводить их на ночные часы.
) суд отменил федеральный закон, требующий от кабельных операторов полностью зашифровывать программы откровенно сексуального характера или переводить их на ночные часы. Этот подход обеспечивает меньшую защиту свободы выражения мнений отдельных лиц, чем наименее ограничительный тест на нуждаемость.
Этот подход обеспечивает меньшую защиту свободы выражения мнений отдельных лиц, чем наименее ограничительный тест на нуждаемость. ), Верховный суд ограничил применение наименее ограничительного проверку нуждаемости, утверждая, что нейтральные и общеприменимые законы — законы, которые конкретно не касаются религиозной практики, но применяются повсеместно — должны оцениваться с минимальной тщательностью.
), Верховный суд ограничил применение наименее ограничительного проверку нуждаемости, утверждая, что нейтральные и общеприменимые законы — законы, которые конкретно не касаются религиозной практики, но применяются повсеместно — должны оцениваться с минимальной тщательностью.


 Синтаксис использования POW: POW(число,мощность), где число — это число, мощность которого вы хотите вычислить, а мощность — это количество раз, которое вы хотите вычислить. Например, если вы хотите вычислить степень числа 9 в 3-й степени, вы должны использовать следующую формулу: POW(9,3).
Синтаксис использования POW: POW(число,мощность), где число — это число, мощность которого вы хотите вычислить, а мощность — это количество раз, которое вы хотите вычислить. Например, если вы хотите вычислить степень числа 9 в 3-й степени, вы должны использовать следующую формулу: POW(9,3). В этом случае вместо этого вы должны использовать функцию XOR. В другой раз вам не следует использовать функцию POW, когда вы пытаетесь вычислить степень числа, которое больше или равно 1 000 000. В этом случае вы должны использовать функцию EXP.
В этом случае вместо этого вы должны использовать функцию XOR. В другой раз вам не следует использовать функцию POW, когда вы пытаетесь вычислить степень числа, которое больше или равно 1 000 000. В этом случае вы должны использовать функцию EXP.
 Например, =POW(-2, 3) вернет -8, так как -2 * -2 * -2 = -8.
Например, =POW(-2, 3) вернет -8, так как -2 * -2 * -2 = -8. Например, =POW(27, 1/3) вернет 3, так как кубический корень из 27 равен 3.
Например, =POW(27, 1/3) вернет 3, так как кубический корень из 27 равен 3. Ввод аргументов в неправильном порядке приведет к неверным вычислениям.
Ввод аргументов в неправильном порядке приведет к неверным вычислениям.
 2, равное примерно 7,389..
2, равное примерно 7,389..
 23: Экспоненты и научная нотация Часть I и Учебное пособие
24: Экспоненты и научная запись, часть II . Давай двигаться
на рациональные показатели и корни.
23: Экспоненты и научная нотация Часть I и Учебное пособие
24: Экспоненты и научная запись, часть II . Давай двигаться
на рациональные показатели и корни.

 Опять же, я думаю, что проще сначала сделать корневую часть, если это возможно.
С цифрами будет легче работать.
Опять же, я думаю, что проще сначала сделать корневую часть, если это возможно.
С цифрами будет легче работать. Опять же, я думаю, что проще сначала сделать корневую часть, если это возможно.
С цифрами будет легче работать.
Опять же, я думаю, что проще сначала сделать корневую часть, если это возможно.
С цифрами будет легче работать. Опять же, я думаю, что проще сначала сделать корневую часть
если возможно. С цифрами будет легче работать.
Опять же, я думаю, что проще сначала сделать корневую часть
если возможно. С цифрами будет легче работать. Пишите только с положительными показателями.
Пишите только с положительными показателями. 26: Умножение многочленов .
26: Умножение многочленов . Предположим, что переменная представляет положительное число.
Предположим, что переменная представляет положительное число.


 Если около каждого дома посадить по 9 саженцев, то не зватит 100 саженцев, а если по 5 саженцев, то 20 саженцев останется. Сколько домов? Сколько
Если около каждого дома посадить по 9 саженцев, то не зватит 100 саженцев, а если по 5 саженцев, то 20 саженцев останется. Сколько домов? Сколько