Трапеция. Формулы, признаки и свойства трапеции
Навигация по странице: Определение трапеции Элементы трапеции Виды трапеций Основные свойства трапеции Стороны трапеции Средняя линия трапеции Высота трапеции Диагонали трапеции Площадь трапеции Периметр трапеции Окружность описанная вокруг трапеции Окружность вписанная в трапецию Другие отрезки трапеции
Определение.
Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны называются основами трапеции, а две другие боковыми сторонами
Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
Элементы трапеции:
- Основы трапеции — параллельные стороны
- Боковые стороны — две другие стороны
- Средняя линия — отрезок, соединяющий середины боковых сторон.

Виды трапеций:
- Равнобедренная трапеция — трапеция, у которой боковые стороны равны
- Прямоугольная трапеция — трапеция, у которой одна из боковых сторон перпендикулярна основам
| Рис.1 | Рис.2 |
Основные свойства трапеции
1. В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:
AB + CD = BC + AD
2. Средняя линия трапеции разделяет пополам любой отрезок, который соединяет основы, так же делит диагонали пополам:
AK = KB, AM = MC, BN = ND, CL = LD
3. Средняя линия трапеции параллельна основаниям и равна их полусумме:
| m = | a + b |
| 2 |
4. Точка пересечения диагоналей трапеции и середины оснований лежат на одной прямой.
Точка пересечения диагоналей трапеции и середины оснований лежат на одной прямой.
5. В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.
6. Каждая диагональ в точке пересечения делится на две части с таким соотношением длины, как соотношение между основаниями:
BC : AD = OC : AO = OB : DO
7. Диагонали трапеции d1 и d2 связаны со сторонами соотношением:
d12 + d22 = 2ab + c2 + d2
Сторона трапеции
Формулы определения длин сторон трапеции:
1. Формула длины оснований трапеции через среднюю линию и другую основу:
a = 2m — b
b = 2m — a
2. Формулы длины основ через высоту и углы при нижнем основании:
a = b + h · (ctg α + ctg β)
b = a — h · (ctg α + ctg β)
3. Формулы длины основ через боковые стороны и углы при нижнем основании:
Формулы длины основ через боковые стороны и углы при нижнем основании:
a = b + c·cos α + d·cos β
b = a — c·cos α — d·cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:
| с = | h | d = | h |
| sin α | sin β |
Средняя линия трапеции
Определение.
Средняя линия — отрезок, соединяющий середины боковых сторон трапеции.
Формулы определения длины средней линии трапеции:
1. Формула определения длины средней линии через длины оснований:
| m = | a + b | |
| 2 |
2. Формула определения длины средней линии через площадь и высоту:
| m = | S |
| h |
Высота трапеции
Формулы определения длины высоты трапеции:
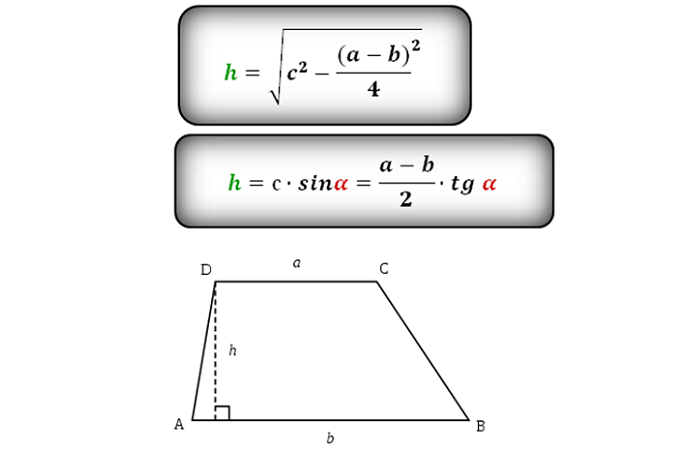
1. Формула высоты через сторону и прилегающий угол при основании:
Формула высоты через сторону и прилегающий угол при основании:
h = c·sin α = d·sin β
2. Формула высоты через диагонали и углы между ними:
| h = | sin γ · | d1 d2 | = | sin δ · | d1 d2 |
| a + b | a + b |
3. Формула высоты через диагонали, углы между ними и среднюю линию:
| h = | sin γ · | d1 d2 | = | sin δ · | d1 d2 |
| 2m | 2m |
4. Формула высоты трапеции через площадь и длины оснований:
| h = | 2S |
| a + b |
5. Формула высоты трапеции через площадь и длину средней линии:
| h = | S |
| m |
Диагонали трапеции
Формулы определения длины диагоналей трапеции:
1. Формулы диагоналей по теореме косинусов:
Формулы диагоналей по теореме косинусов:
d1 = √a2 + d2 — 2ad·cos β
d2 = √a2 + c2 — 2ac·cos α
2. Формулы диагоналей через четыре стороны:
| d1 = | √ | d 2 + ab — | a(d 2 — c2) |
| a — b |
| d2 = | √ | c2 + ab — | a(c2 — d 2) | a — b |
3. Формула длины диагоналей через высоту:
d1 = √h2 + (a — h · ctg β)2 = √h2 + (b + h · ctg α)2
d2 = √h2 + (a — h · ctg α)2 = √h2 + (b + h · ctg β)2
4. Формулы длины диагонали через сумму квадратов диагоналей:
d1 = √c2 + d 2 + 2ab — d22
d2 = √c2 + d 2 + 2ab — d12
Площадь трапеции
Формулы определения площади трапеции:
1. Формула площади через основания и высоту:
Формула площади через основания и высоту:
| S = | (a + b) | · h |
| 2 |
2. Формула площади через среднюю линию и высоту:
S = m · h
3. Формула площади через диагонали и угол между ними:
| S = | d1d2 | · sin γ | = | d1d2 | · sin δ |
| 2 | 2 |
4. Формула площади через четыре стороны:
| S = | a + b | √ | c2 — | ( | (a — b)2 + c2 — d 2 | ) | 2 |
| 2 | 2(a — b) |
5. Формула Герона для трапеции
| S = | a + b | √(p — a)(p — b)(p — a — c)(p — a — d) |
| |a — b| |
| p = | a + b + c + d | — полупериметр трапеции.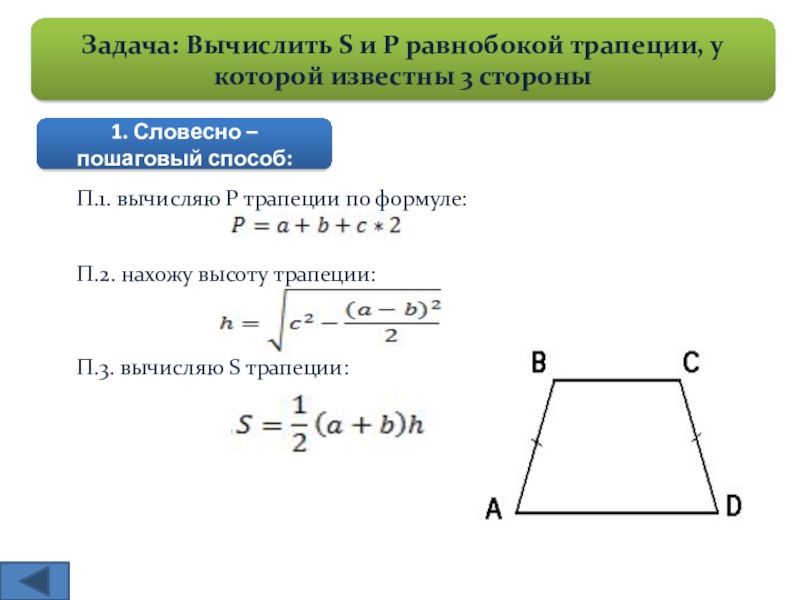 |
| 2 |
Периметр трапеции
Формула определения периметра трапеции:
1. Формула периметра через основания:
P = a + b + c + d
Окружность описанная вокруг трапеции
Окружность можно описать только вокруг равнобедренной трапеции!!!
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d1 |
| 4√p(p — a)(p — c)(p — d1) |
где
| p = | a + c + d1 |
| 2 |
a — большее основание
Окружность вписанная в трапецию
В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:
a + b = c + d
Формула определения радиуса вписанной в трапецию окружности
1. Формула радиуса вписанной окружности через высоту:
Формула радиуса вписанной окружности через высоту:
| r = | h |
| 2 |
Другие отрезки разносторонней трапеции
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
Все таблицы и формулы
Площадь трапеции: формулы, определения, элементы
Площадь трапеции, формулы расчета, определение,
способы найти площадь, нахождение площади
через величины и примеры площади трапеции.
Все формулы расчета площади трапеции
через основания и угол, периметр, радиус,
синус и две стороны, диагональ,
высоту, среднюю линию.
Площадь трапеции, можно измерить, в единицах
измерения в квадрате: мм2, см2, м2 и км2 и так далее.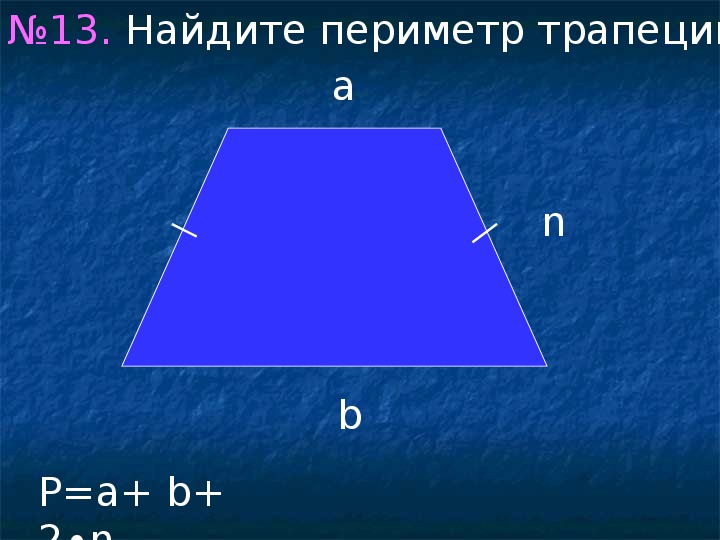
Площадь трапеции через окружность вписанную можно
найти, зная радиус окружности вписанной в трапецию
и некоторые другие величины.
Содержание
- Формулы площади трапеции
- Площадь любых трапеций
- Площадь равнобедренной трапеции
- Определения трапеции
- Элементы трапеции
Формулы площади трапеции
Площадь любых трапеций
Ⅰ. Площадь трапеции через основания и высоту:
\[ S = \frac{a+b}{2} \cdot h \]
a,b — основания трапеции;
h — высота трапеции;
Ⅱ. Площадь трапеции через высоту и среднюю линию:
\[ S = mh \]
m — средняя линия трапеции;
h — высота трапеции;
Ⅲ. Площадь трапеции через диагонали и угол между ними:
\[ S =\frac{1}{2}d_1d_2 \cdot \sin \alpha \]
\( d_1, d_2 \)- диагонали трапеции;
sin α — синус угла альфа в трапеции;
Ⅳ. 2}{2} \cdot \frac{\sin α \cdot \sin β}{\sin( α + β)} \]
2}{2} \cdot \frac{\sin α \cdot \sin β}{\sin( α + β)} \]
a,b — основания трапеции;
α — угол при основании a в трапеции;
β — угол при основании b в трапеции;
sin α — синус угла альфа в трапеции;
sin β — синус угла бетта в трапеции;
Площадь равнобедренной трапеции
Ⅰ. Площадь трапеции через синус угла, среднюю линию и боковую сторону:
\[ S = ld \cdot \sin α \]
l — средняя линия равнобедренной трапеции;
d — боковая сторона равнобедренной трапеции;
α — угол альфа при боковой стороне d равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;
Ⅱ. Площадь трапеции через диагонали и синус угла:
\[ S = \frac{d^2}{2} \cdot \sin α \]
d — диагональ равнобедренной трапеции;
α — угол между двумя диагоналями в равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;
Ⅲ. Площадь трапеции через радиус вписанной окружности и основания:
Площадь трапеции через радиус вписанной окружности и основания:
\[ S = r( a+b) \]
r — радиус вписанной окружности равнобедренной трапеции;
a, b — основания равнобедренной трапеции;
Ⅳ. Площадь трапеции через основания:
\[ S = \sqrt{ab} \cdot {\frac{a+b}{2}} \]
a, b — основания равнобедренной трапеции;
Ⅴ. Площадь трапеции через основания и среднюю линию:
\[ S = l\sqrt{ab} \]
l — средняя линия равнобедренной трапеции;
a, b — основания равнобедренной трапеции;
Ⅵ. Площадь трапеции через синус угла и стороны:
\[ S = c \cdot \sin α \cdot (a-c \cdot \cos α) \]
a — нижнее основание равнобедренной трапеции;
с — боковая сторона равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;
cos α — косинус угла альфа в равнобедренной трапеции;
Ⅶ.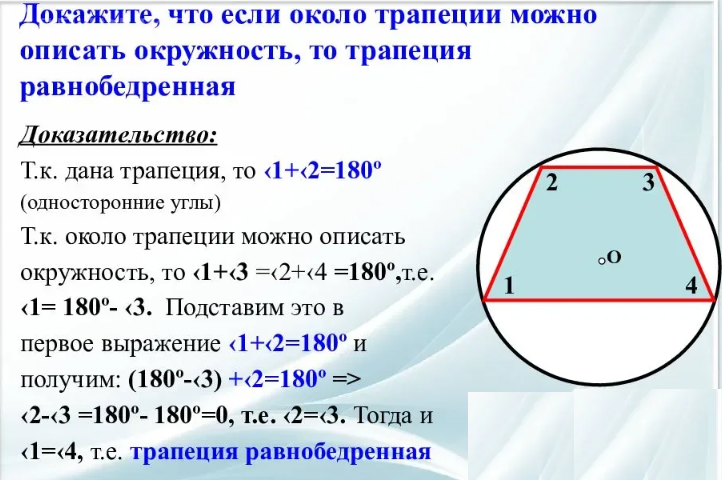 2}{\sin α} \]
2}{\sin α} \]
r — радиус вписанной окружности равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;
Определения трапеции
Трапеция — это четырехугольник, у которого две
стороны параллельны а две другие нет.
Зная углы трапеции, можно определить, к какому виду
она относится. Всего различают три вида трапеций:
- Обычная / стандартная трапеция: четыре угла и четыре стороны не равны.
- Равнобедренная / равнобочная / равнобоковая трапеция:
два угла при основании равны, две боковые стороны равны. - Прямоугольная / прямая трапеция: один из углов прямой.
Площадь равнобедренной, прямоугольной трапеции,
можно найти через формулы площади обычной трапеции.
Формул, с помощью которых, можно найти площадь трапеции
через описанную окружность около трапеции, не существует.
Элементы трапеции
Любая трапеция является четырехугольником,
поэтому у трапеции 4 угла и 4 стороны.
Основание трапеции — это сторона, противолежащая
сторона которой параллельна.
Боковая сторона трапеции — это сторона, противолежащая
сторона которой не параллельна.
Средняя линия трапеции — это отрезок, соединяющий
середины боковых сторон трапеции.
Диагональ трапеции — это отрезок, соединяющий две
вершины, которые лежат в разных концах трапеции.
Высота трапеции — это отрезок, соединяющий меньшее основание с большим,
образуя при этом два угла по 90 градусов на большей стороне.
Основания у трапеции не могут быть никогда равны.
Боковые стороны могут быть равны только,
если трапеция — равнобедренная.
Площадь трапеции — это площадь геометрической фигуры,
у которой четыре стороны и четыре угла, причем только
две стороны параллельны а остальные нет.
Калькулятор площади трапеции
Создано Bogna Szyk
Отзыв Стивена Вудинга
Последнее обновление: 18 декабря 2022 г.
Содержание:- Что такое трапеция?
- Как найти площадь трапеции?
- Как найти периметр трапеции?
- Использование калькулятора площади трапеции: пример
- Часто задаваемые вопросы
Если у вас когда-либо возникали проблемы с запоминанием формул на уроках геометрии, эта область калькулятора трапеции обязательно вам поможет. Всего за несколько простых шагов вы сможете найти площадь трапеции и определить все остальные ее свойства, например длины сторон внутренних углов. Итак, если вас беспокоят такие вопросы, как «как найти периметр трапеции», не смотрите дальше — просто продолжайте читать, чтобы узнать!
Вы также можете воспользоваться нашим калькулятором длины окружности, чтобы более подробно проанализировать геометрию круга, или нашим калькулятором формулы окружности, чтобы узнать больше об уравнениях, лежащих в основе этой геометрии.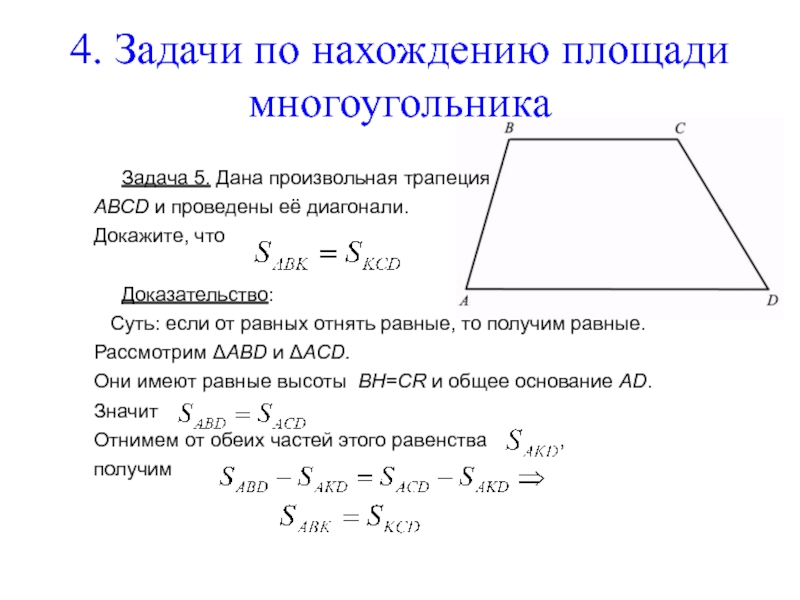
Что такое трапеция?
Трапеция – это четырехсторонняя геометрическая фигура, две стороны которой параллельны друг другу. Эти две стороны ( a и b на схеме) называются основаниями трапеции. Две другие стороны ( c и d ) называются ножками. h высота трапеции.
Сумма всех внутренних углов трапеции дает 360°. Кроме того, углы на одной стороне катета называются смежными и всегда дают в сумме 180°:
α + β = 180°
γ + δ = 180°
Как найти площадь трапеции?
Чтобы найти площадь трапеции ( A ), выполните следующие действия:
- Найдите длину каждого основания (
aиb). - Найдите высоту трапеции (
h). - Подставьте эти значения в формулу площади трапеции:
A = (a + b) × h / 2.
Вы можете заметить, что для трапеции с a = b (и, следовательно, c = d = h) формула упрощается до A = a × h , что в точности соответствует формуле площади прямоугольника.
Как найти периметр трапеции?
Чтобы быстро найти периметр трапеции, выполните следующие действия:
- Найдите длину всех сторон трапеции (
a,b,cи 9 0043 д ). - Сложите их вместе, чтобы получить периметр трапеции:
P = a + b + c + d. - Вот оно! Это так просто.
В качестве альтернативы вы можете использовать калькулятор площади трапеции, который автоматически найдет для вас площадь и периметр трапеции.
Использование калькулятора площади трапеции: пример
Предположим, вы хотите вычислить площадь некоторой трапеции. Все данные приведены:
α = 30°γ = 125°В = 6 сма = 4 смР = 25 см
Вычислите оставшиеся внутренние углы.
 Как
Как α + β = 180°,β = 180° - 30° = 150°.Аналогично, как
γ + δ = 180°,δ = 180° - 125° = 55°.Найдите длины катетов трапеции, используя формулу синуса угла:
sin 30° = c / hsin 55° = д/чc = sin 30° × 6 = 12 смd = sin 55° × 6 = 7,325 смВычтите значения a, c и d из периметра трапеции, чтобы найти длину второго основания:
b = P - a - c - d = 25 - 4 - 12 - 7,325 = 1,675 смНаконец, применим формулу площади трапеции:
A = (a + b) × h / 2 = (4 + 1,675) × 6 / 2 = 17,026 см²
Не забудьте также взглянуть на шестигранный калькулятор!
Часто задаваемые вопросы
Чем трапеция отличается от других четырехугольников?
Трапеции отличаются от других четырехугольников тем, что они имеют ровно одну пару параллельных сторон .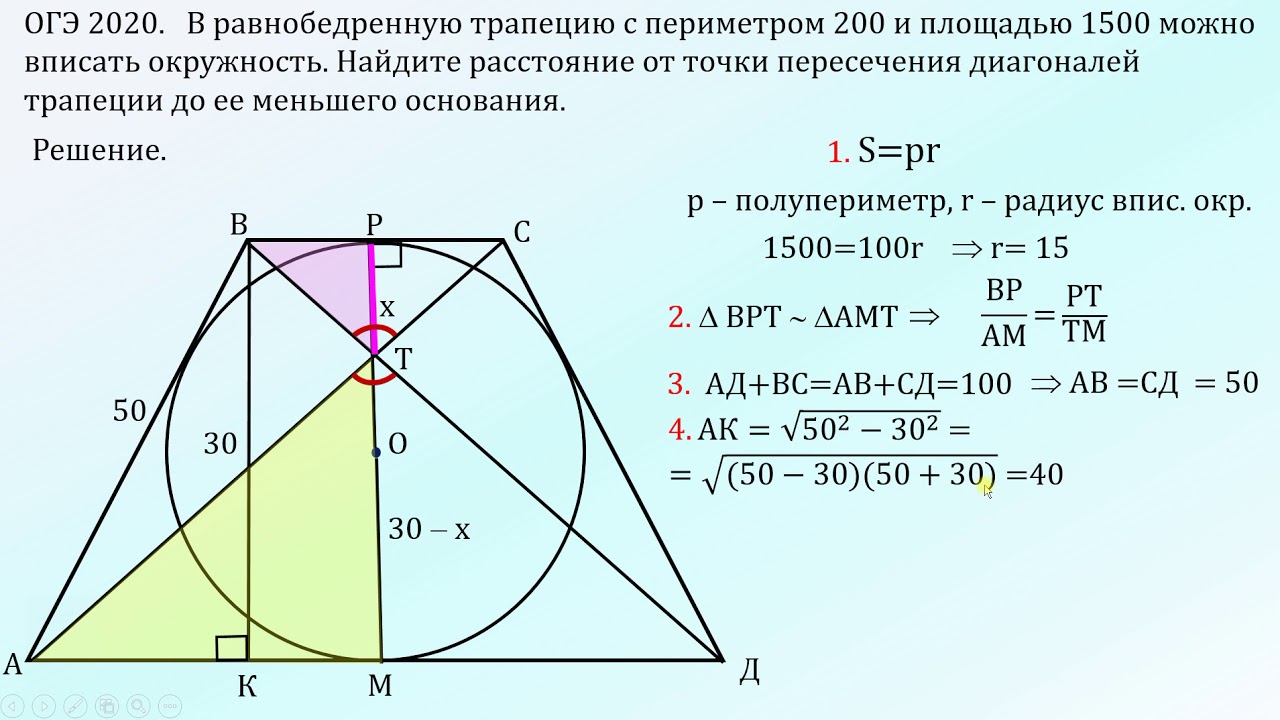 Они, по сути, четырехугольники, как прямоугольники и квадраты, но не параллелограммы.
Они, по сути, четырехугольники, как прямоугольники и квадраты, но не параллелограммы.
Какова площадь трапеции с высотой 5 м и основаниями 8 м и 1 м?
Площадь этой трапеции равна 22,5 метра в квадрате . Для получения результата воспользуемся формулой площади трапеции: A = (a + b) × h / 2 и положим a = 8 м , b = 1 м , а h = 5 м внутри него.
Bogna Szyk
a (основание)
b (основание)
h (высота)
Периметр
Периметр
У углов
Проверьте 23 аналогичные 2D Геометрические калькуляторы 📏
Площадь с прямоугольником полумесяца… еще 20
Область трапеции — формула, примеры, решения
Студенты должны выполнять различные геометрические домашние работы. Однако больше всего трудностей возникает у учащихся средних классов, поскольку они изучали только математику и алгебру, и геометрию. Например, им нужно найти перпендикулярное расстояние, площадь поверхности или параллельные стороны трапеции.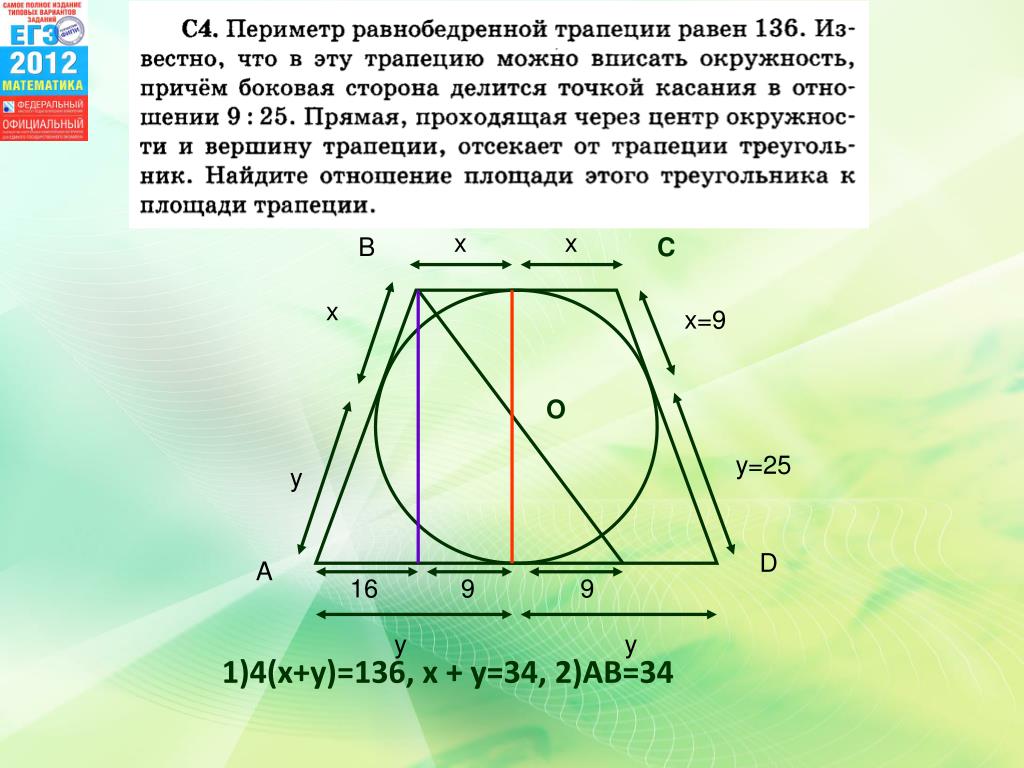 Сегодня мы поговорим именно о трапециях, нахождении площади и рассмотрении ее как одной из важнейших теорем.
Сегодня мы поговорим именно о трапециях, нахождении площади и рассмотрении ее как одной из важнейших теорем.
- Трапеция — что это за фигура?
- Элементы трапеции
- Теорема: площадь трапеции
- Расчет площадей в прошлом
- Расчет площадей в современном мире
- Формула площади трапеции по основанию и высоте
- Формула площади ловушки эзоид на Басе
- Формула площади трапеции через
- Формула площади трапеции через
- Трапеция и созвездия
- Трапеции в экспериментальной физике
Трапеция — что это за фигура?
Трапеция – это четырехугольник, имеющий две параллельные стороны и две непараллельные стороны. Параллельные стороны называются основаниями трапеции, а две другие — боковыми сторонами. Высота трапеции – это расстояние между прямыми, на которых лежат основания трапеции, любым общим перпендикуляром этих прямых. Средняя линия трапеции – это отрезок, соединяющий середины сторон.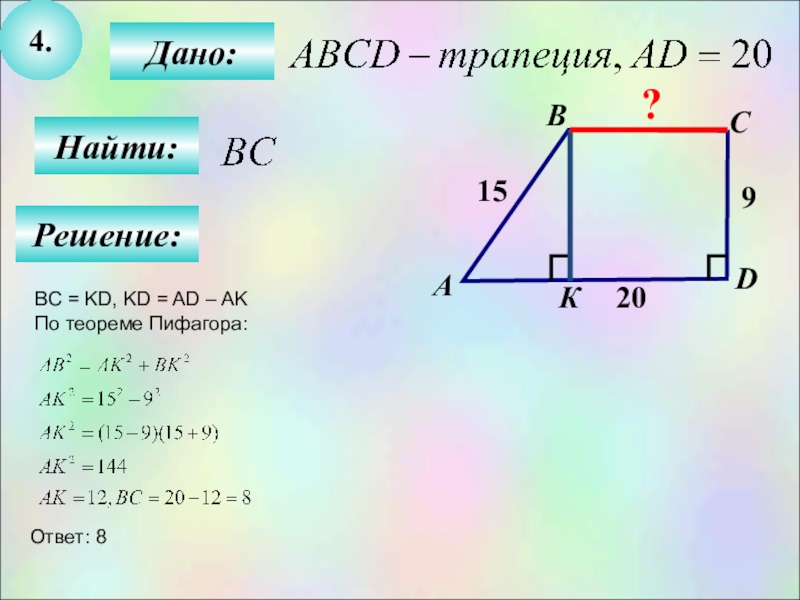
Черты трапеции
Если в трапецию вписана окружность, то сумма основ всегда совпадает с суммой сторон: a+b=c+d, а средняя линия всегда равна полусумме сторон:
Равнобедренной трапецией называется трапеция, стороны которой равны AB = CD. Тогда диагонали AC = BD и углы при основании равны:
Из всех трапеций только около равнобедренной трапеции можно описать окружность, если сумма противоположных прямых углов равна 180°. В равнобедренной трапеции расстояние от вершины одного основания до проекции противоположной вершины, которая непосредственно связана с основанием, всегда совпадает с осевой линией.
Прямоугольная трапеция — это разновидность трапеции, угол основания которой равен 90°.
Теорема: площадь трапеции
Чтобы вычислить площадь произвольного многоугольника, мы делаем следующее: делим многоугольник на треугольники и находим площадь треугольника. Сумма площадей этих треугольников равна площади многоугольника. С помощью этой методики выводим формулу расчета площади запасной части трапеции. Условимся называть высотой трапеции перпендикуляр, проведенный из любой точки одного из оснований на прямую, содержащую другое основание. На рисунке ниже мы указали, что отрезок линии BH является высотой трапеции ABCD:
С помощью этой методики выводим формулу расчета площади запасной части трапеции. Условимся называть высотой трапеции перпендикуляр, проведенный из любой точки одного из оснований на прямую, содержащую другое основание. На рисунке ниже мы указали, что отрезок линии BH является высотой трапеции ABCD:
Исходя из этого, получаем теорему: «Площадь трапеции равна произведению полусуммы ее оснований на высоту». Используя формулу площади, мы можем доказать эту теорему.
Дана трапеция: ABCD, AD, BC — длины оснований, BH — высота.
Докажите: площадь этой трапеции ABCD будет равна S = ½ (AD + BC) · BH.
Доказательство: проведите диагональ BD. Он делит трапецию на два треугольника ABD и BCD. Это означает, что периметр трапеции ABCD будет равен сумме площадей этих треугольников.
В треугольнике ABD: AD — основание, BH — высота. В треугольнике BCD: BC является основанием.
Нарисуем высоту DK. Площадь S треугольника ABD = 1/2 AD · BH; площадь S треугольника BCD = 1/2 BC · DK. Так как BH = DK, то площадь S треугольника BCD = 1/2 BC · BH. Таким образом, площадь S трапеции ABCD = 1/2 AD · BH + 1/2 BC · BH = 1/2 (AD + BC) · BH. Что требовалось доказать.
Так как BH = DK, то площадь S треугольника BCD = 1/2 BC · BH. Таким образом, площадь S трапеции ABCD = 1/2 AD · BH + 1/2 BC · BH = 1/2 (AD + BC) · BH. Что требовалось доказать.
Вычисление площадей в прошлые времена
Еще 4-5 тысяч лет назад вавилоняне умели определять площадь трапеции в квадратных единицах. Древние египтяне 4000 лет назад использовали почти те же приемы, что и мы: сумму параллельных сторон делили пополам и умножали на высоту.
Определение площадей геометрических фигур — одна из древнейших практических задач. Люди не сразу нашли правильный подход к их решению. Один из самых простых и доступных способов вычисления площадей открыл Евклид. При расчете площадей он использовал простой прием, называемый методом разбиения.
Вычисление площадей в современном мире
Сегодня существует множество формул для вычисления длин сторон, вершин, параллельных оснований и площади трапеции. Мы рассмотрим самые основные из них. Приведенные ниже формулы просты в использовании, но если вам сложно их понять и вам нужна помощь с домашним заданием, вы всегда можете обратиться в нашу службу. Опытные авторы проконсультируют вас по всем заданиям, и вы значительно улучшите свою успеваемость.
Опытные авторы проконсультируют вас по всем заданиям, и вы значительно улучшите свою успеваемость.
Формула площади трапеции по основанию и высоте
Дана произвольная трапеция. Для нахождения его площади используем следующую формулу:
В этой формуле:
- а, b — основания трапеции;
- hh — высота трапеции.
Представим, что нам нужно найти площадь трапеции, у которой известны основания, численно равные 10 см и 8 см. Также известный рост, 6 см в длину.
Решение:
- а = 8;
- б = 10;
- ч = 6;
Сразу подставляем цифры в полученную формулу и вычисляем значение:
Ответ: 54 квадратных сантиметра.
Формула площади основания и центральной линии трапеции
Следует отметить, что средняя линия трапеции равна половине суммы ее оснований. Таким образом, нахождение площади через центральную линию есть не что иное, как метод, аналогичный первому. Насколько:
Насколько:
В этой формуле:
- S = l ⋅ h;
- l — средняя линия трапеции;
- h – высота.
Предположим, нам нужно найти площадь трапеции, если известно, что средняя линия равна 5 см, а высота трапеции в два раза больше ее высоты.
Решение:
- л = 5;
- ч = 2 ⋅ л.
Найдите высоту трапеции:
h = 2 ⋅ 5 = 10
Площадь:
S = l ⋅ h = 5 ⋅ 10 = 50 см.кв.
Ответ: 50 квадратных сантиметров
Формула площади трапеции через радиус и угол вписанной окружности
Этот случай подходит только для равнобедренной трапеции:
В этой формуле:
- р это радиус вписанной окружности;
- α — угол между основанием и стороной.
Предположим, нам дан радиус вписанной окружности в трапецию, равный 4 см. Угол α равен 90 градусов. Нам нужно найти площадь трапеции.
Решение:
- r = 4;
- α = 90,
По формуле:
Ответ: 64 квадратных сантиметра.
Формула площади трапеции через диагонали и угол между ними
Существует простая формула для нахождения площади трапеции через диагонали и угол между ними:
В этой формуле:
- d1, d2 — диагонали трапеций;
- α — угол между диагоналями.
Пусть две диагонали трапеции равны 20 см и 7 см. При пересечении они образуют угол 30 градусов. Нам нужно найти площадь трапеции.
Решение:
- d1 = 20;
- д2 = 7;
- α = 30°.
Площадь:
Ответ: 35 квадратных сантиметров.
Трапеция и созвездия
Трапеция встречается не только в домашних заданиях по математике. Эту цифру можно найти при изучении созвездий. Выдающимся астеризмом весеннего неба является трапеция Льва, которую можно наблюдать по вечерам с февраля по май. Эта фигура расположена в зодиакальном созвездии Льва, образуя тело животного, и по форме напоминает трапецию.
Четыре яркие звезды созвездия α, β, γ и δ расположены на вершинах трапеции – туловища льва. А голову льва образуют звезды, расположенные в виде серпа. Отсюда и название — трапеция Льва.
А голову льва образуют звезды, расположенные в виде серпа. Отсюда и название — трапеция Льва.
Трапеции в экспериментальной физике Посмотреть
Союз физики и математики предполагает непрерывное движение науки вперед. В физике ученые проводят опыты, суть которых становится полностью ясной только после математического анализа. Многие разделы математики обязаны своим возникновением и дальнейшим развитием новым физическим опытам. В качестве примера рассмотрим школьную лабораторную работу по физике.
Постановка вопроса: Рассмотрим фигуру — произвольную трапецию ABCD. Проведите две его диагонали AC и BD, которые делят трапецию на четыре треугольника — ABO, BCO, CDO и DAO. Треугольники ABO и CDO равны:
Формулировка цели опытной работы: с помощью взвешивания доказать, что массы треугольников, полученных диагоналями и сторонами трапеции, равны.
Ход лабораторной работы:
- Учащимся необходимо взять: лист бумаги, линейку, карандаш, ластик, ножницы.




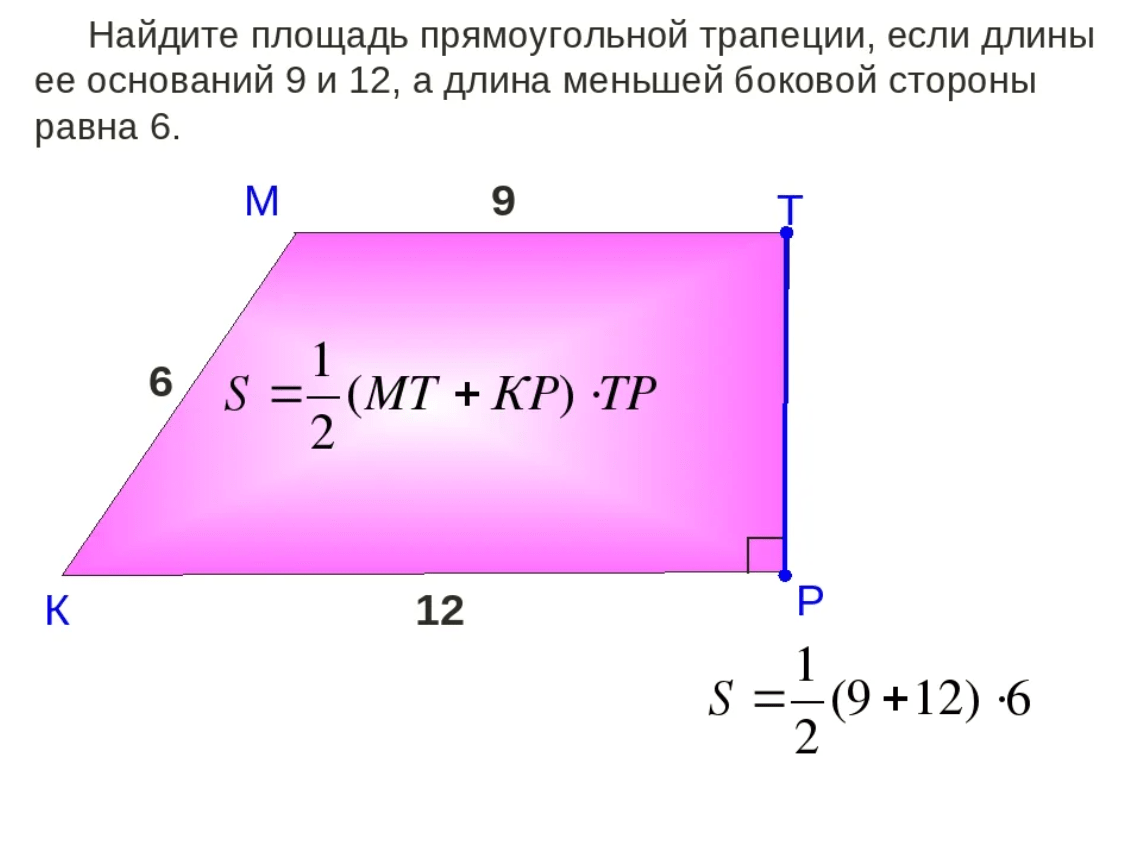
 Как
Как 
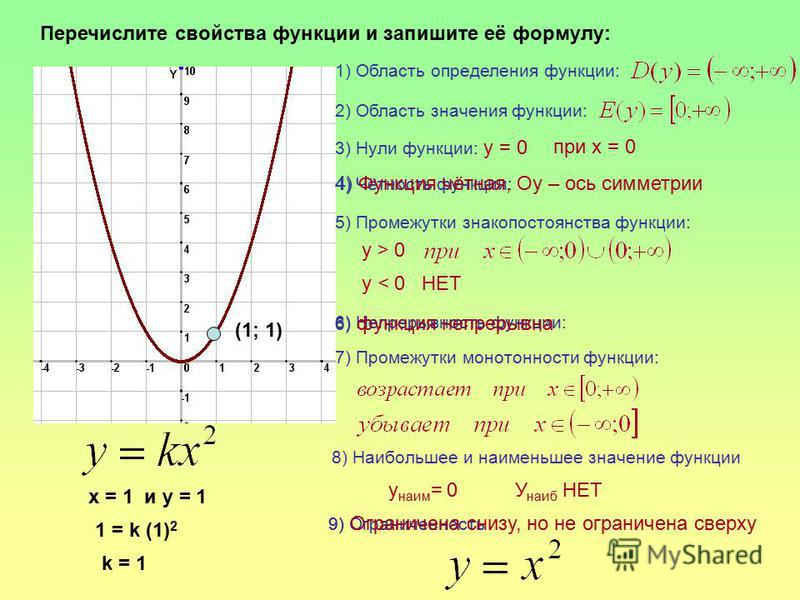
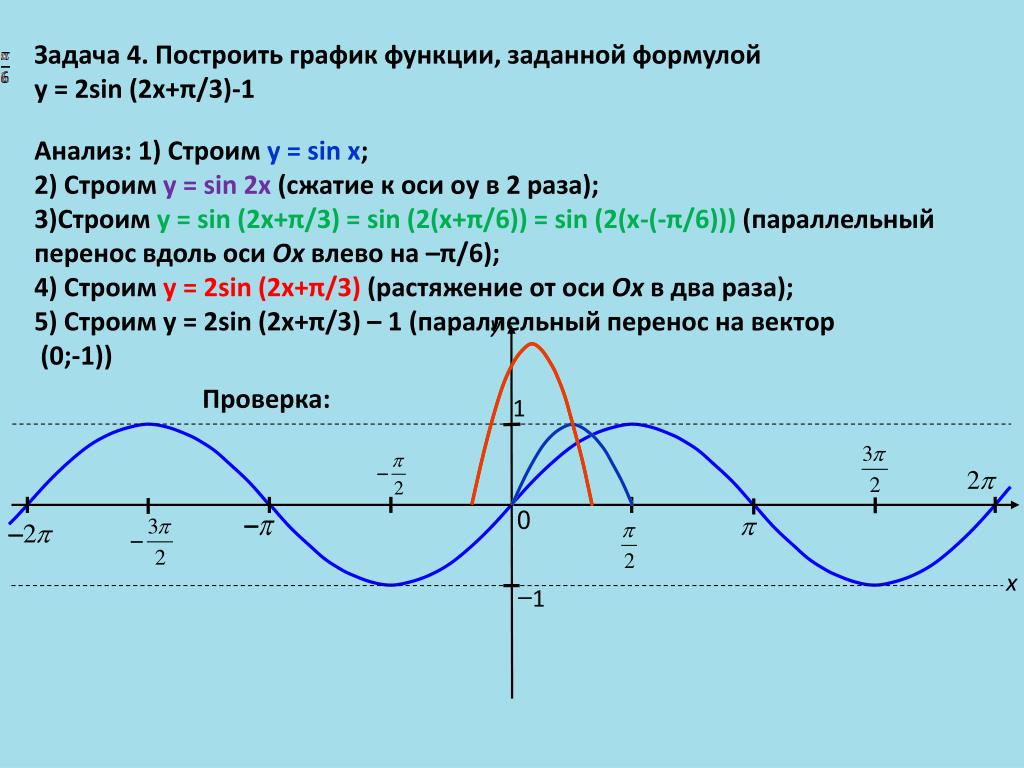 2 — 2x — 3. Найдите: а)наименьшее значение функции; б) значения x, при которых значение функции равно 5; в) значение…
2 — 2x — 3. Найдите: а)наименьшее значение функции; б) значения x, при которых значение функции равно 5; в) значение…
 д.
д. Также данный материал рекомендуется использовать учителю, осуществляющему дистанционное обучение для повышения наглядности объяснения. Видео может быть рекомендовано отстающему ученику для углубления понимания темы.
Также данный материал рекомендуется использовать учителю, осуществляющему дистанционное обучение для повышения наглядности объяснения. Видео может быть рекомендовано отстающему ученику для углубления понимания темы.
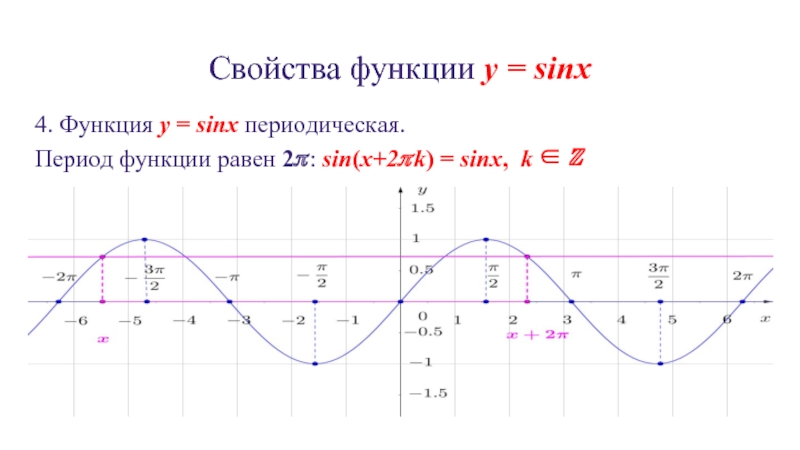
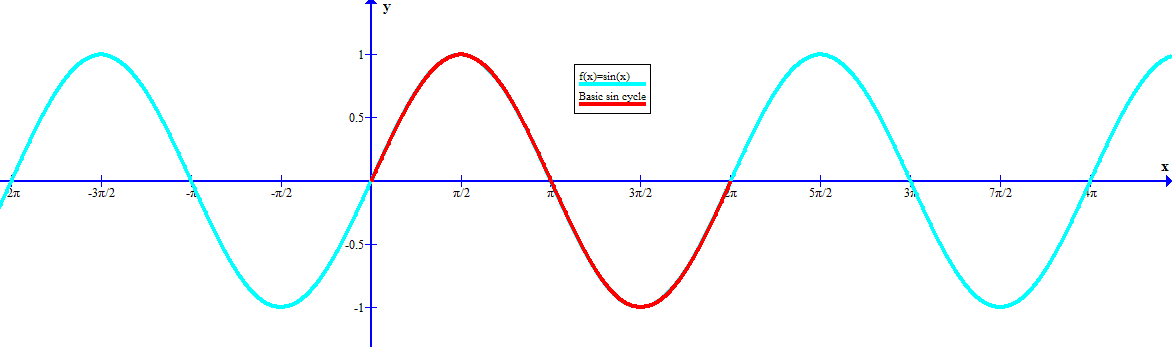
 Обычно стараются выделить наименьший положительный период, который называют основным периодом.
Обычно стараются выделить наименьший положительный период, который называют основным периодом.


 2х, то стандартный период 2П уменьшится в 2 раза, таким образом, период будет равен П. Обратите , функции tg, ctg в любой степени периодичны П.
2х, то стандартный период 2П уменьшится в 2 раза, таким образом, период будет равен П. Обратите , функции tg, ctg в любой степени периодичны П. Минимальное значение Т, при котором оно выполняется, 2П, это и будет задачи.
Минимальное значение Т, при котором оно выполняется, 2П, это и будет задачи. Сначала переносим все члены влево и раскладываем на множители.
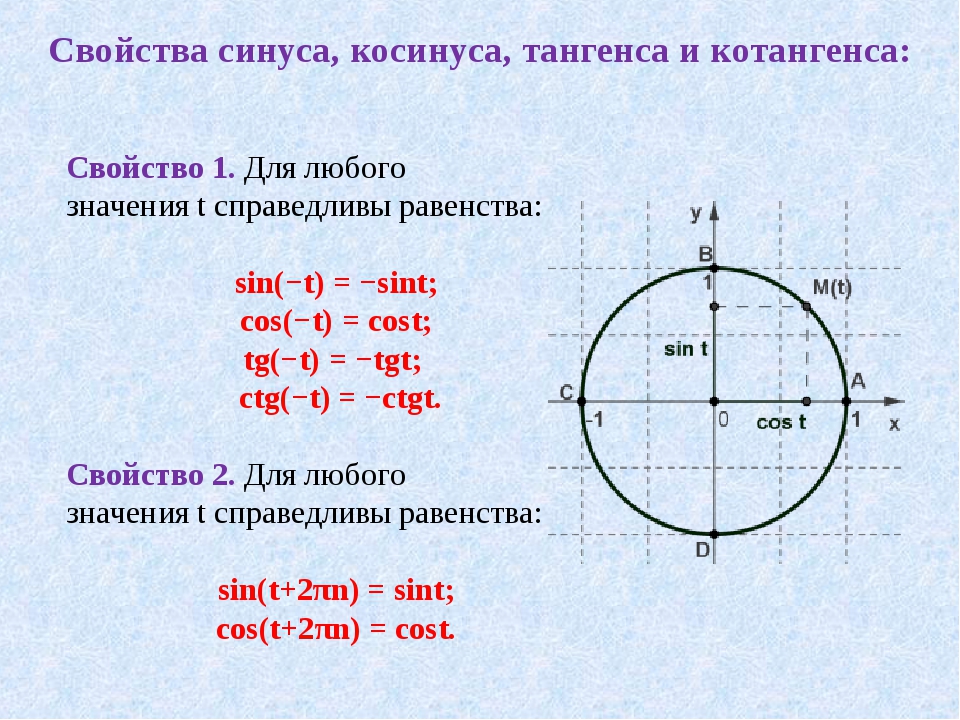
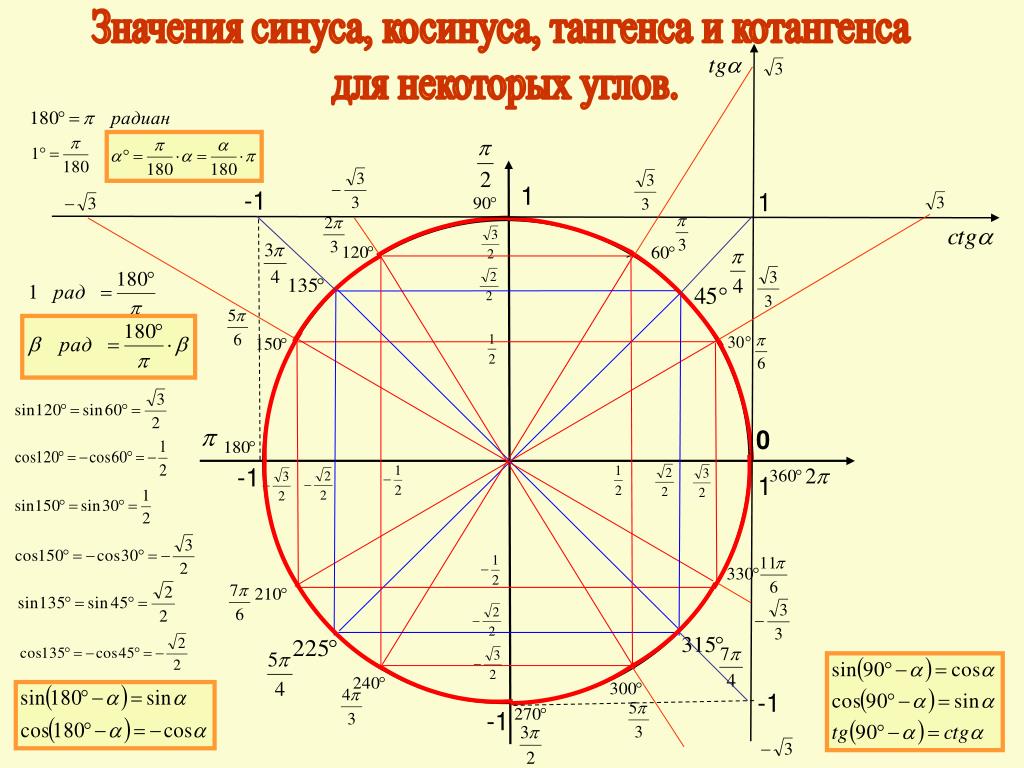
Сначала переносим все члены влево и раскладываем на множители. К таким функциям относят в первую очередь синус и косинус, во вторую — обратные этим функциям секанс и косеканс, производные от них тангенс и котангенс, а также обратные функции арксинус, арккосинус и др. Правильнее говорить не о «решении» таких функций, а об их «вычислении», то есть о нахождении численного значения.
К таким функциям относят в первую очередь синус и косинус, во вторую — обратные этим функциям секанс и косеканс, производные от них тангенс и котангенс, а также обратные функции арксинус, арккосинус и др. Правильнее говорить не о «решении» таких функций, а об их «вычислении», то есть о нахождении численного значения.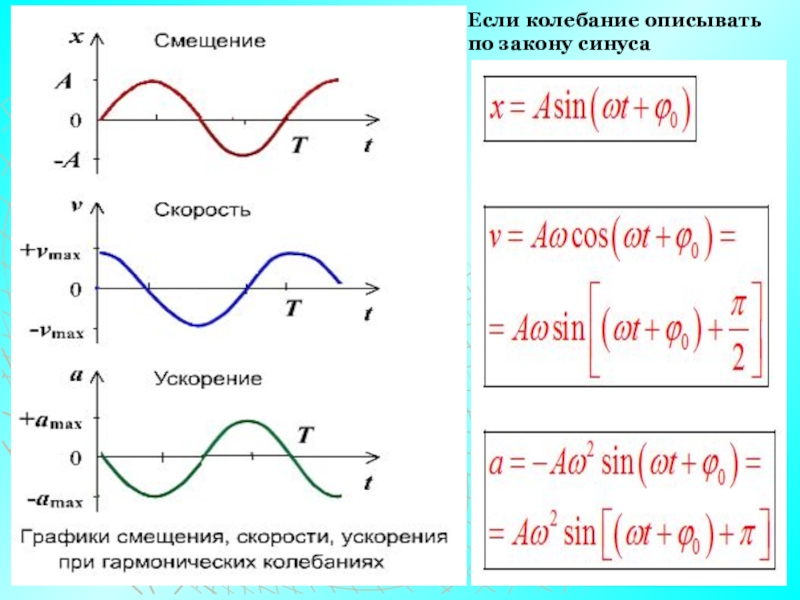 Для вычисления секанса острого угла надо найти отношение длины гипотенузы к длине прилежащего к нужному углу катета, а косеканс определяется отношением длины гипотенузы к длине противолежащего катета.
Для вычисления секанса острого угла надо найти отношение длины гипотенузы к длине прилежащего к нужному углу катета, а косеканс определяется отношением длины гипотенузы к длине противолежащего катета. 47). Эти поисковики имеют встроенные калькуляторы, поэтому после отправки такого запроса вы получите значение введенной вами тригонометрической функции.
47). Эти поисковики имеют встроенные калькуляторы, поэтому после отправки такого запроса вы получите значение введенной вами тригонометрической функции.


 Точно так же, как
вы увеличиваете b , период уменьшится.
Точно так же, как
вы увеличиваете b , период уменьшится.
 вместе.
вместе.








 4 класс. Канакина В.П., Горецкий В.Г. ГДЗ
4 класс. Канакина В.П., Горецкий В.Г. ГДЗ

 )
)
 Следовательно, велосипедист на путь, пройденный пешеходом, потратит в 3 раза меньше времени, чем пешеход: 2 ч : 3 = 2/3 ч = 40 мин.
Следовательно, велосипедист на путь, пройденный пешеходом, потратит в 3 раза меньше времени, чем пешеход: 2 ч : 3 = 2/3 ч = 40 мин.
 . . Он был в этом уверен.
. . Он был в этом уверен. Моя борьба — это ваша борьба, ваше бремя — это мое бремя.
Моя борьба — это ваша борьба, ваше бремя — это мое бремя. Бескорыстная любовь, пламенная любовь, высшее, что только может быть. Он призывал свою негритянскую аудиторию культивировать эту чистую любовь к своим угнетателям, чтобы она могла привести их на другую сторону борьбы.
Бескорыстная любовь, пламенная любовь, высшее, что только может быть. Он призывал свою негритянскую аудиторию культивировать эту чистую любовь к своим угнетателям, чтобы она могла привести их на другую сторону борьбы.
 «Говорят, время от времени они берут сюда черного мальчика и приковывают его к этим… Потом они берут хлыст и рвут его на куски».
«Говорят, время от времени они берут сюда черного мальчика и приковывают его к этим… Потом они берут хлыст и рвут его на куски».  «Вне дома» символизирует неравную систему правосудия, с которой чернокожие сталкивались на протяжении всей американской истории, вплоть до сегодняшнего дня.
«Вне дома» символизирует неравную систему правосудия, с которой чернокожие сталкивались на протяжении всей американской истории, вплоть до сегодняшнего дня. Отсутствие интереса к происходящему в «Никеле» — это напоминание о том, что ужасные акты расизма и сегрегации происходят по всей стране, и что для общества в целом проще игнорировать это, чем остановить.
Отсутствие интереса к происходящему в «Никеле» — это напоминание о том, что ужасные акты расизма и сегрегации происходят по всей стране, и что для общества в целом проще игнорировать это, чем остановить. Автор противопоставляет обнадеживающую сторону активизма, которой подражал Элвуд, реалистической стороне, которой подражал Тернер. Надежда и стремление продолжать работать ради лучшего будущего — вот что двигало Элвудом на протяжении всей его жизни. Здесь Элвуд продолжает пытаться следовать этой траектории после того, как сначала оплакивал полное опустошение и несправедливость, которые привели его к Никелю.
Автор противопоставляет обнадеживающую сторону активизма, которой подражал Элвуд, реалистической стороне, которой подражал Тернер. Надежда и стремление продолжать работать ради лучшего будущего — вот что двигало Элвудом на протяжении всей его жизни. Здесь Элвуд продолжает пытаться следовать этой траектории после того, как сначала оплакивал полное опустошение и несправедливость, которые привели его к Никелю. Люди могут говорить, что заботятся о вас, но если они постоянно показывают вам обратное, вы должны этому верить.
Люди могут говорить, что заботятся о вас, но если они постоянно показывают вам обратное, вы должны этому верить. Так и случилось — открыли прилавок. В любом случае у Тернера не было денег, чтобы поесть там. Вы можете изменить закон, но вы не можете изменить людей и то, как они относятся друг к другу. Никель был чертовски расистским — половина людей, которые работали здесь, вероятно, одевались по выходным, как члены Клана, — но, с точки зрения Тернера, порочность была глубже, чем цвет кожи.
Так и случилось — открыли прилавок. В любом случае у Тернера не было денег, чтобы поесть там. Вы можете изменить закон, но вы не можете изменить людей и то, как они относятся друг к другу. Никель был чертовски расистским — половина людей, которые работали здесь, вероятно, одевались по выходным, как члены Клана, — но, с точки зрения Тернера, порочность была глубже, чем цвет кожи. В целом, законы не изменили чувства некоторых людей, и если человек расист и злой, никакие законы не могут изменить его сердце.
В целом, законы не изменили чувства некоторых людей, и если человек расист и злой, никакие законы не могут изменить его сердце. Они слушают радио и шутят друг с другом, а Тернер делится своими идеями о том, как устроен мир. Тернер говорит Элвуду, что он должен понять, что люди злые и расистские, и что ему следует стараться избегать конфликтов. Элвуд, однако, считает, что реформы происходят через Движение за гражданские права, и что люди изменятся и будут действовать справедливо, когда они столкнутся с несправедливостью. Вылечившись, Элвуд видит шрамы на своих ногах и ему становится стыдно. Он не рассказывает бабушке об избиении, когда она приходит в гости.
Они слушают радио и шутят друг с другом, а Тернер делится своими идеями о том, как устроен мир. Тернер говорит Элвуду, что он должен понять, что люди злые и расистские, и что ему следует стараться избегать конфликтов. Элвуд, однако, считает, что реформы происходят через Движение за гражданские права, и что люди изменятся и будут действовать справедливо, когда они столкнутся с несправедливостью. Вылечившись, Элвуд видит шрамы на своих ногах и ему становится стыдно. Он не рассказывает бабушке об избиении, когда она приходит в гости. Бизнесмены дают Харперу конверты с деньгами, которые он передает суперинтенданту Спенсеру, который затем передает их своему боссу, директору Харди. Покончив с доставкой, Харпер подвозит Элвуда и Тернера к дому миссис Дэвис, жены начальника пожарной охраны, которая входит в совет директоров Nickel. Харпер идет к своей девушке, пока Элвуд и Тернер красят беседку Дэвисов.
Бизнесмены дают Харперу конверты с деньгами, которые он передает суперинтенданту Спенсеру, который затем передает их своему боссу, директору Харди. Покончив с доставкой, Харпер подвозит Элвуда и Тернера к дому миссис Дэвис, жены начальника пожарной охраны, которая входит в совет директоров Nickel. Харпер идет к своей девушке, пока Элвуд и Тернер красят беседку Дэвисов.
 Эта вера будет становиться все более важной по мере развития романа. Когда Элвуд знакомится с Тернером, он узнает, что Тернер — индивидуалист и считает, что люди должны следить за собой. Как и Харриет, Тернер считает, что отстаивание интересов других приводит к неприятностям. Когда Элвуд решает скрыть шрамы от побоев от бабушки, это указывает на то, что ему стыдно и, кроме того, он решил не останавливаться на насилии, как было показано о его персонаже в прологе. В этом смысле Никелевой академии уже удалось контролировать Элвуда, заставляя его молчать.
Эта вера будет становиться все более важной по мере развития романа. Когда Элвуд знакомится с Тернером, он узнает, что Тернер — индивидуалист и считает, что люди должны следить за собой. Как и Харриет, Тернер считает, что отстаивание интересов других приводит к неприятностям. Когда Элвуд решает скрыть шрамы от побоев от бабушки, это указывает на то, что ему стыдно и, кроме того, он решил не останавливаться на насилии, как было показано о его персонаже в прологе. В этом смысле Никелевой академии уже удалось контролировать Элвуда, заставляя его молчать.

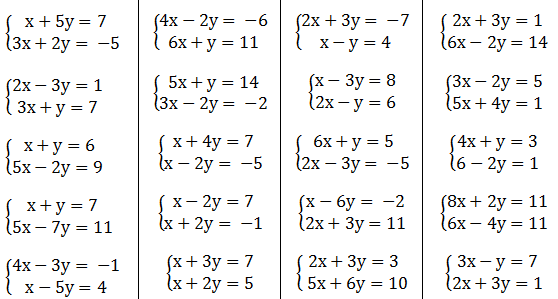
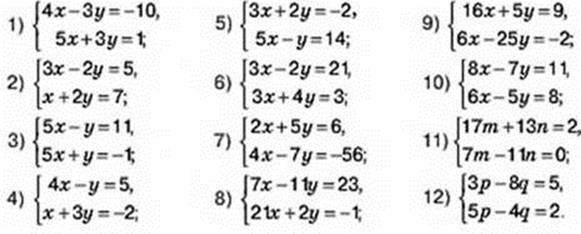
 (x-y)=0,25} і вказати компонент x0 її розв’язку (x0;y0).
(x-y)=0,25} і вказати компонент x0 її розв’язку (x0;y0).

 У математицi iснує цiла галузь — лiнiйна алгебра, яка вивчає системи рiвнянь.
У математицi iснує цiла галузь — лiнiйна алгебра, яка вивчає системи рiвнянь.

 2-2x-3 Найдите: а) наименьшее значение функции; б) значения х, при которых значение функции равно 5; в) значения х, при которых функция принимает положительные
2-2x-3 Найдите: а) наименьшее значение функции; б) значения х, при которых значение функции равно 5; в) значения х, при которых функция принимает положительные Прописные буквы, цифры, знаки препинания eps
Прописные буквы, цифры, знаки препинания eps Кисть шрифта. Прописные буквы, цифры, знаки препинания eps
Кисть шрифта. Прописные буквы, цифры, знаки препинания eps
 2}, \\ & = \sqrt{80}, \\ & = 4\sqrt{5}, \ \ & = 8,9{\circ} \text{ (3 s.f.).} \end{align}
2}, \\ & = \sqrt{80}, \\ & = 4\sqrt{5}, \ \ & = 8,9{\circ} \text{ (3 s.f.).} \end{align}

 Убеждаемся в этом прямой подстановкой в исходное уравнение. Но x1* x2 =
Убеждаемся в этом прямой подстановкой в исходное уравнение. Но x1* x2 = Если запомнить ход рассуждений, находить целые корни можно научиться очень быстро.
Если запомнить ход рассуждений, находить целые корни можно научиться очень быстро. Поэтому x1+x2 показывает, на сколько одно отличаются корни x1 и x2, то есть, на сколько один корень больше другого (по модулю).
Поэтому x1+x2 показывает, на сколько одно отличаются корни x1 и x2, то есть, на сколько один корень больше другого (по модулю). Это 1 и 16, 2 и 8, 4 и 4. Сумма 2 и 8 равна 10, а раз нужны отрицательные числа, то искомые корни — это -2 и -8.
Это 1 и 16, 2 и 8, 4 и 4. Сумма 2 и 8 равна 10, а раз нужны отрицательные числа, то искомые корни — это -2 и -8.
 $$ 92 – 4ac.$$
$$ 92 – 4ac.$$ $$
$$ $$
$$ Виета был французским математиком, чья работа над многочленами проложила путь современной алгебре.
Виета был французским математиком, чья работа над многочленами проложила путь современной алгебре. (1)
(1) Например, мы строим полиномиальное уравнение, увеличивая
корни данного полиномиального уравнения на два, как указано ниже.
Например, мы строим полиномиальное уравнение, увеличивая
корни данного полиномиального уравнения на два, как указано ниже.

 Формула периметра круга (длины окружности)
Формула периметра круга (длины окружности) также: Программа для расчета площади трапеции.
также: Программа для расчета площади трапеции.
 Прямоугольник, все стороны которого равны (a = b) называется квадратом.
Прямоугольник, все стороны которого равны (a = b) называется квадратом. «Пи» до сих пор уточняется. И используется чаще всего округленное значение. Степень точности выбирается такой, чтобы дать максимально верный ответ.
«Пи» до сих пор уточняется. И используется чаще всего округленное значение. Степень точности выбирается такой, чтобы дать максимально верный ответ. Узнать длину окружности, радиус которой равен 5 см.
Узнать длину окружности, радиус которой равен 5 см. Аналогично предыдущей задаче потребуется разделить известную длину на значение &pi-, округленное до сотых. В результате такого действия получается число 18. Результат получен.
Аналогично предыдущей задаче потребуется разделить известную длину на значение &pi-, округленное до сотых. В результате такого действия получается число 18. Результат получен.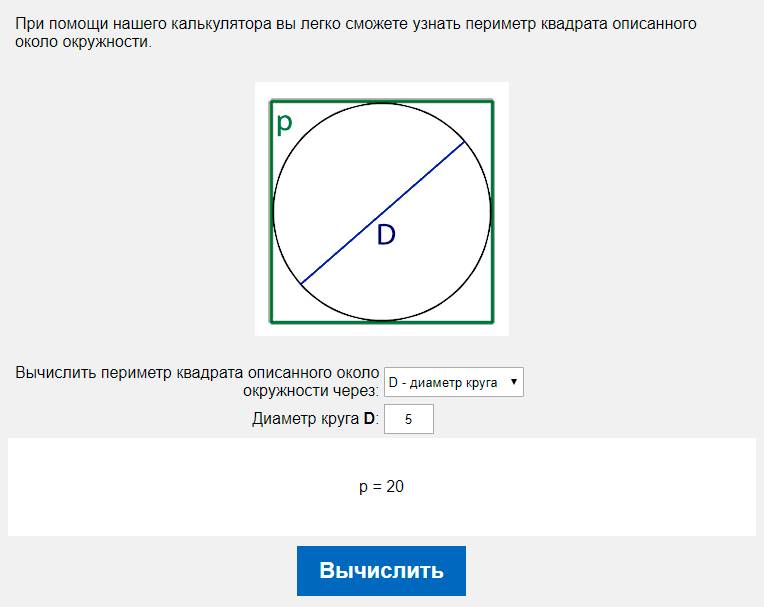 А именно перемножить значение &pi- и 2 м. Подсчеты дают результат: 6,28 м.
А именно перемножить значение &pi- и 2 м. Подсчеты дают результат: 6,28 м.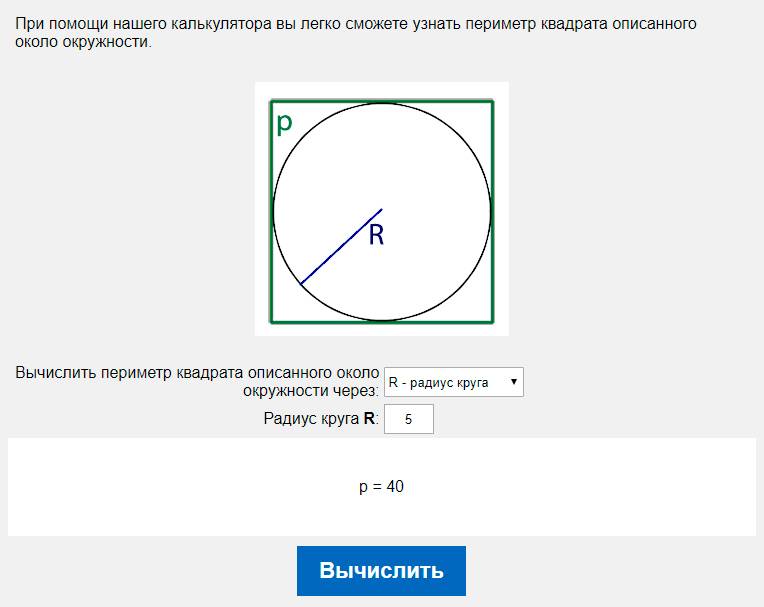 Так как диаметр равен удвоенному радиусу (r), если известна эта величина, добавьте в формулу соответствующий множитель: L=2*r*?.
Зная площадь круга (S), тоже можно вычислить длину окружности (L). Соотношение и этих двух величин выражается через число Пи, поэтому удвойте квадратный корень из произведения площади на эту математическую константу: L = 2*v(S*?).
Если известна площадь (s) не всего круга, а лишь сектора с заданным центральным углом (?), то при вычислении длины окружности (L) исходите из формулы предыдущего шага. Если угол выражен в градусах, площадь сектора будет составлять?/360 от общей площади круга, которую можно выразить формулой s*360/?. Подставьте ее в приведенное выше равенство: L = 2*v((s*360/?)*?) = 2*v(s*360*?/?). Однако чаще для измерения центрального угла используют не градусы, а радианы. В этом случае площадь сектора будет составлять?/(2*?) от общей площади круга, а формула вычисления длины окружности приобретет такой вид: L = 2*v((s*2*?/?)*?) = 2*v(s*2*??/?) = 2*?*v(2*s/?).
Так как диаметр равен удвоенному радиусу (r), если известна эта величина, добавьте в формулу соответствующий множитель: L=2*r*?.
Зная площадь круга (S), тоже можно вычислить длину окружности (L). Соотношение и этих двух величин выражается через число Пи, поэтому удвойте квадратный корень из произведения площади на эту математическую константу: L = 2*v(S*?).
Если известна площадь (s) не всего круга, а лишь сектора с заданным центральным углом (?), то при вычислении длины окружности (L) исходите из формулы предыдущего шага. Если угол выражен в градусах, площадь сектора будет составлять?/360 от общей площади круга, которую можно выразить формулой s*360/?. Подставьте ее в приведенное выше равенство: L = 2*v((s*360/?)*?) = 2*v(s*360*?/?). Однако чаще для измерения центрального угла используют не градусы, а радианы. В этом случае площадь сектора будет составлять?/(2*?) от общей площади круга, а формула вычисления длины окружности приобретет такой вид: L = 2*v((s*2*?/?)*?) = 2*v(s*2*??/?) = 2*?*v(2*s/?).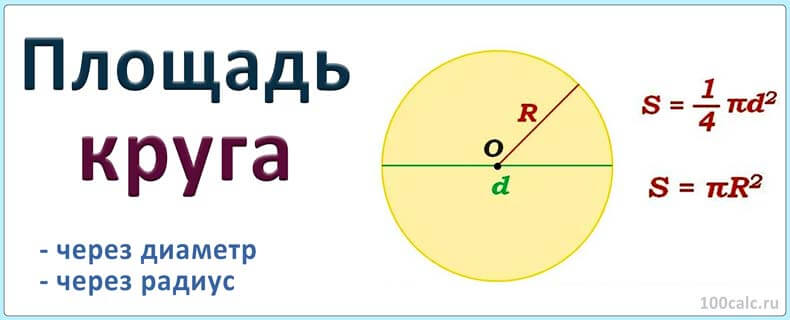 Аналогичные пропорции применяйте и при вычислении длины окружности (L) по известным длине дуги (l) и соответствующему ей центральному углу (?) — в этом случае формулы будут проще. При центральном угле, выраженном в градусах, используйте такое тождество: L = l*360/?, а если он дан в радианах, формула должна быть такой: L = l*2*?/?.
Как просто
Аналогичные пропорции применяйте и при вычислении длины окружности (L) по известным длине дуги (l) и соответствующему ей центральному углу (?) — в этом случае формулы будут проще. При центральном угле, выраженном в градусах, используйте такое тождество: L = l*360/?, а если он дан в радианах, формула должна быть такой: L = l*2*?/?.
Как просто Существует всего одно значение радиуса круга, при котором его можно
Существует всего одно значение радиуса круга, при котором его можно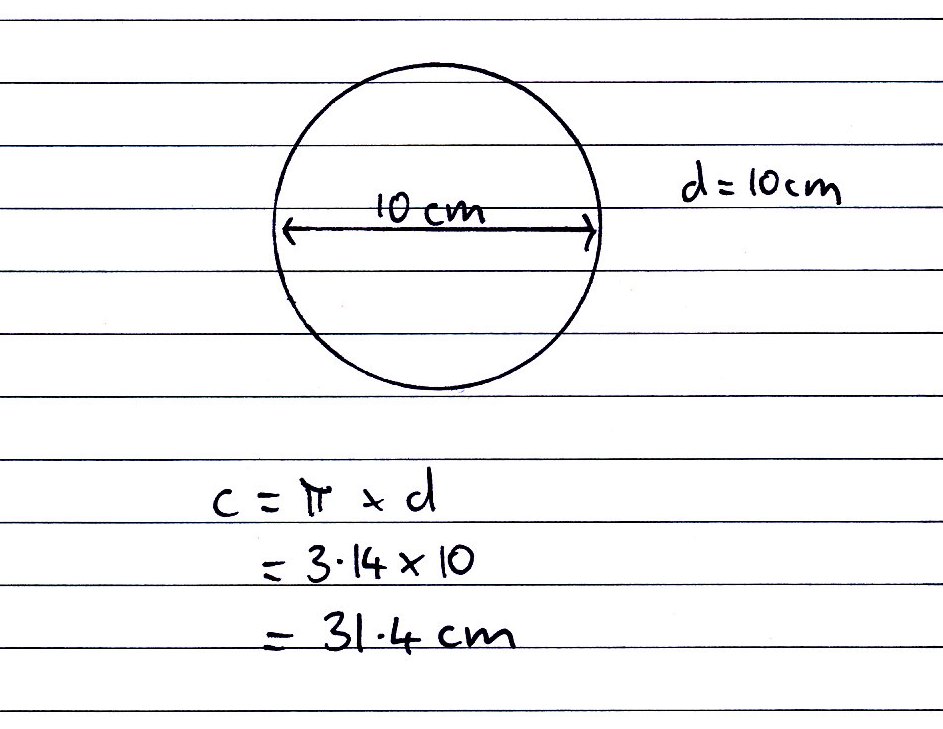 Зато можно вычислить площадь круга, ограниченного этой окружностью. Для решения задачи надо знать радиус. Спонсор размещения P&G Статьи по теме «Как вычислить площадь окружности» Как найти площадь
Зато можно вычислить площадь круга, ограниченного этой окружностью. Для решения задачи надо знать радиус. Спонсор размещения P&G Статьи по теме «Как вычислить площадь окружности» Как найти площадь Зачастую такая необходимость возникает у родителей, к которым дети-школьники обращаются за помощью по домашнему заданию по геометрии, а также ученикам, которые сейчас изучают материал.
Зачастую такая необходимость возникает у родителей, к которым дети-школьники обращаются за помощью по домашнему заданию по геометрии, а также ученикам, которые сейчас изучают материал.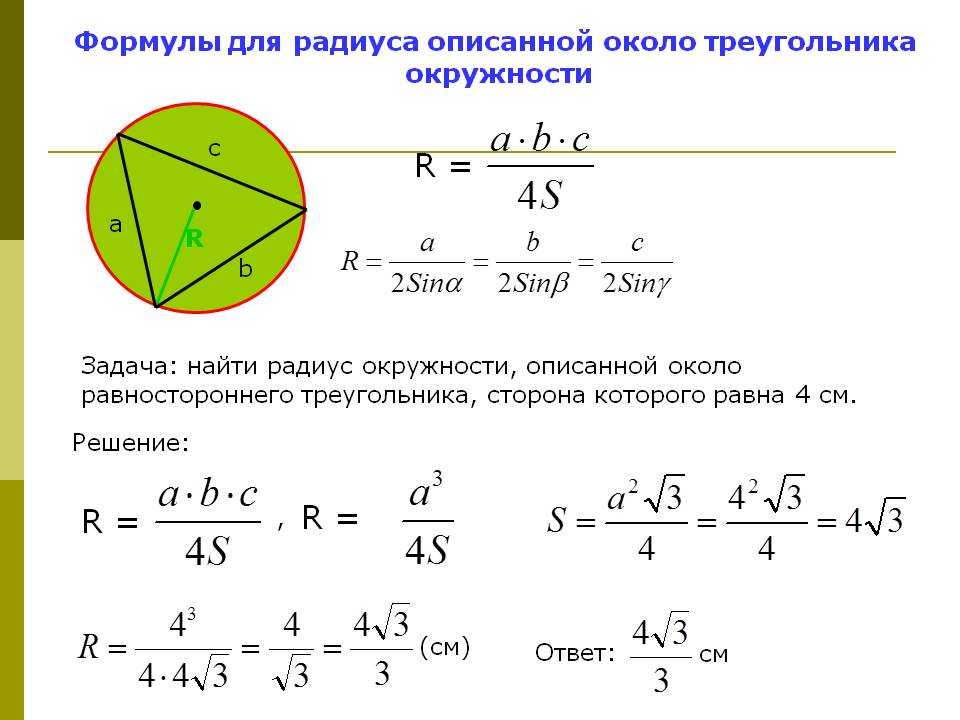 Расстояние, которое мы получим, будет диаметром . Он равен двум радиусам, поэтому формула, приведенная немного дальше, остается актуальной.
Расстояние, которое мы получим, будет диаметром . Он равен двум радиусам, поэтому формула, приведенная немного дальше, остается актуальной.

 Найдите периметр (длину окружности) круга.
Найдите периметр (длину окружности) круга. Какое расстояние проедет тележка, если колесо сделает один оборот?
Какое расстояние проедет тележка, если колесо сделает один оборот?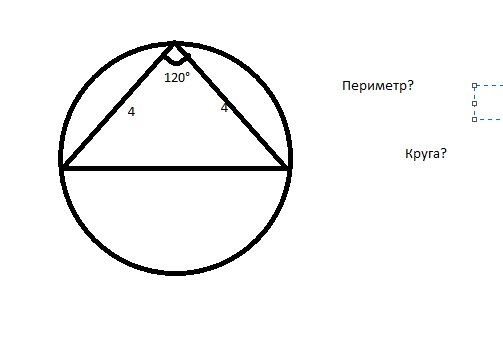 Знаете ли вы о частях круга? И как область связана с ними? Как рассчитать площадь круга формула ?
Знаете ли вы о частях круга? И как область связана с ними? Как рассчитать площадь круга формула ?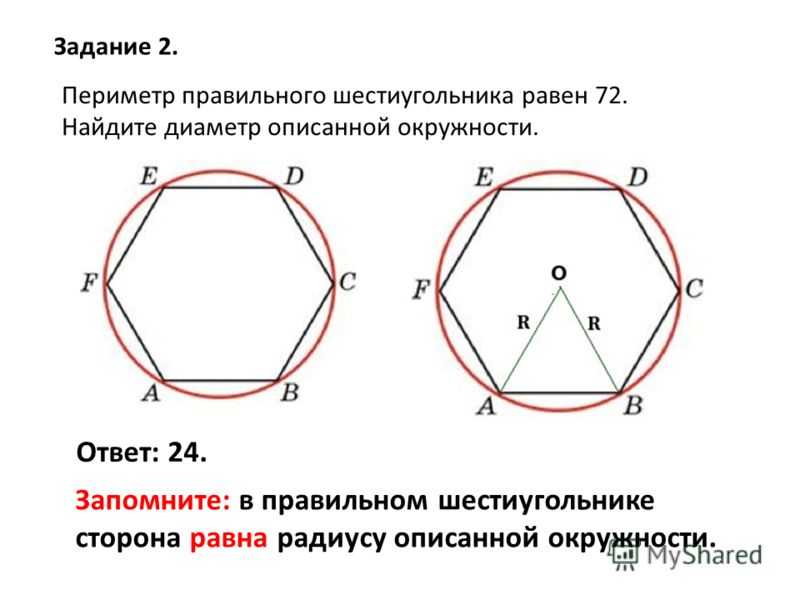 Как площадь круга связана с этими частями круга? Какая формула площади круга?
Как площадь круга связана с этими частями круга? Какая формула площади круга? Итак, если нам нужно поместить круглый диск в шкаф, нам нужно найти площадь, т. е. сколько места потребуется. После площади круг имеет объем? Поскольку круг — двумерная фигура, он не имеет объема. А как насчет площади его поверхности?
Итак, если нам нужно поместить круглый диск в шкаф, нам нужно найти площадь, т. е. сколько места потребуется. После площади круг имеет объем? Поскольку круг — двумерная фигура, он не имеет объема. А как насчет площади его поверхности?
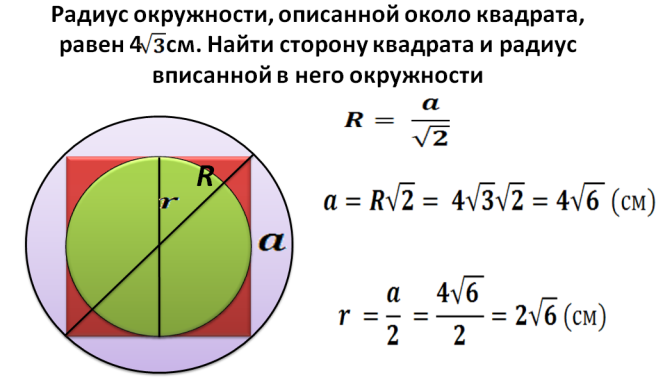
 = 11304 м².
= 11304 м².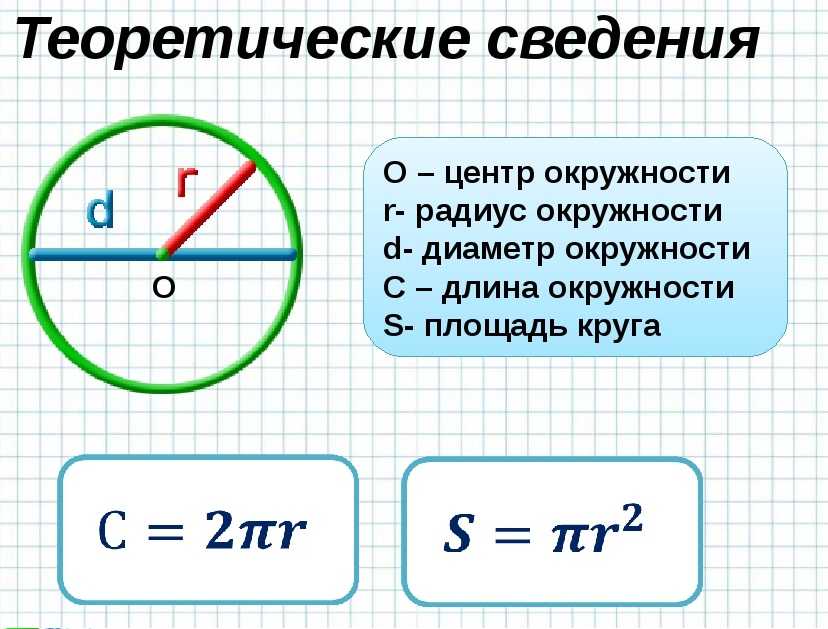


 Найдите сумму координат вектора АВ.
Найдите сумму координат вектора АВ. .
. Базовый уровень Сложные задачи
Базовый уровень Сложные задачи

 На сколько метров
На сколько метров В первой главе рассматривались положение, скорость и ускорение. Во второй главе рассматривалось решение кинематики в одном измерении. Теперь мы собираемся сделать небольшой экскурс в векторную область, чтобы быть готовыми подойти к кинематике в двух (и даже трех) измерениях.
В первой главе рассматривались положение, скорость и ускорение. Во второй главе рассматривалось решение кинематики в одном измерении. Теперь мы собираемся сделать небольшой экскурс в векторную область, чтобы быть готовыми подойти к кинематике в двух (и даже трех) измерениях.

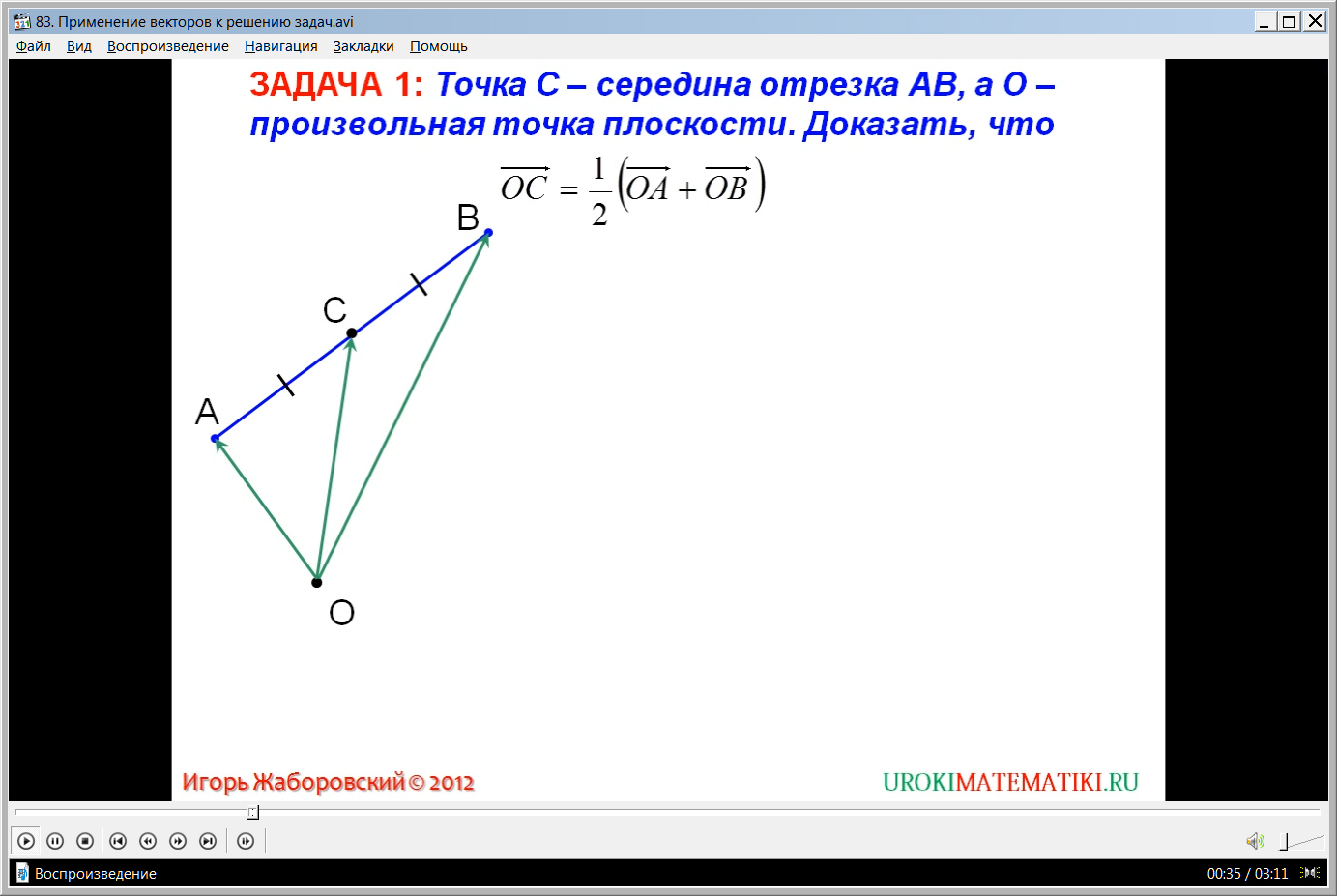
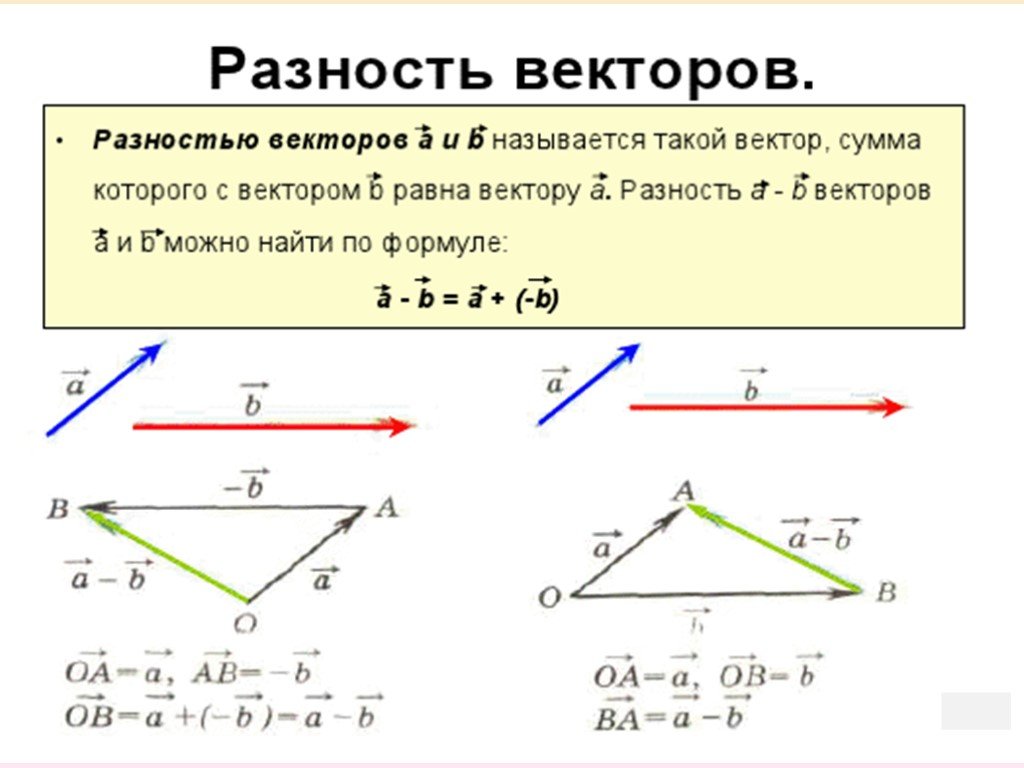


 Мы рассмотрим два метода векторного разрешения:
Мы рассмотрим два метода векторного разрешения:
 Обозначьте величину на схеме.
Обозначьте величину на схеме. Теперь в этой части урока 1 тригонометрические функции будут использоваться для определения компонентов одного вектора. Вспомните из предыдущего обсуждения, что тригонометрические функции связывают отношение длин сторон прямоугольного треугольника с мерой острого угла внутри прямоугольного треугольника. Таким образом, тригонометрические функции можно использовать для определения длины сторон прямоугольного треугольника, если известна мера угла и длина одной стороны.
Теперь в этой части урока 1 тригонометрические функции будут использоваться для определения компонентов одного вектора. Вспомните из предыдущего обсуждения, что тригонометрические функции связывают отношение длин сторон прямоугольного треугольника с мерой острого угла внутри прямоугольного треугольника. Таким образом, тригонометрические функции можно использовать для определения длины сторон прямоугольного треугольника, если известна мера угла и длина одной стороны.
 Поскольку сила натяжения в 60 ньютонов действует на Фидо вверх и вправо под углом 40 градусов, компоненты этой силы можно определить с помощью тригонометрических функций.
Поскольку сила натяжения в 60 ньютонов действует на Фидо вверх и вправо под углом 40 градусов, компоненты этой силы можно определить с помощью тригонометрических функций.

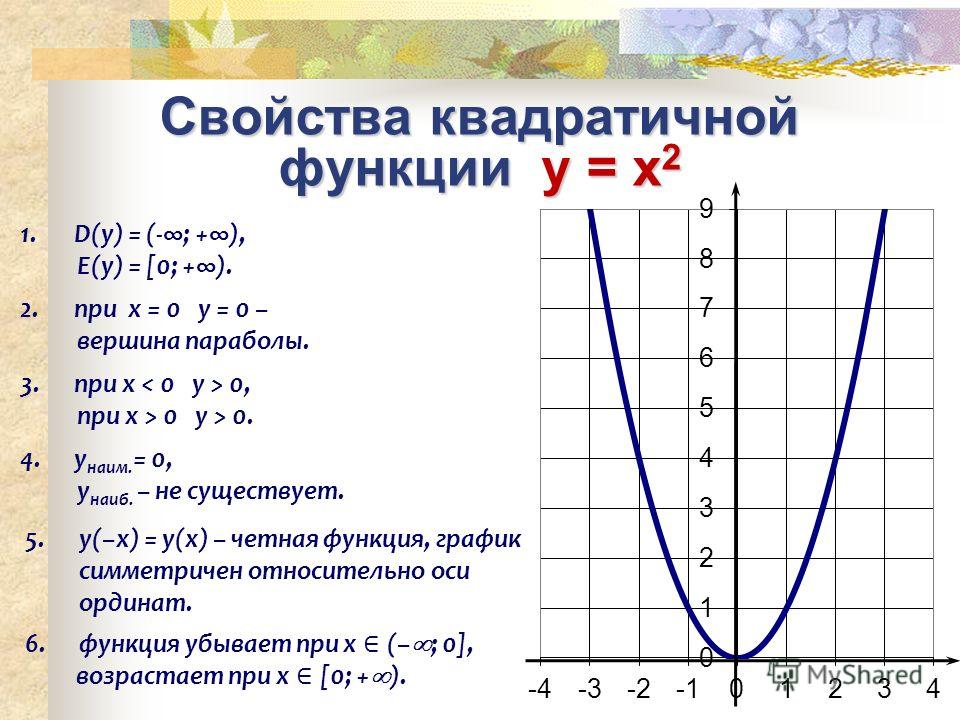 Наибольшее значение функции равно 9 при х = 3.
Наибольшее значение функции равно 9 при х = 3. Это означает, что каждая точка графика у= х2 смещается параллельно
оси абсцисс на 7 единиц влево. Построим график.
Это означает, что каждая точка графика у= х2 смещается параллельно
оси абсцисс на 7 единиц влево. Построим график. е. g+1.
Это означает, что каждая точка графика у=х2 смещается параллельно оси
ординат на 1 единицу вверх. Построим график функции у = х2+1, сдвигая
точки построенного графика у = х2.
е. g+1.
Это означает, что каждая точка графика у=х2 смещается параллельно оси
ординат на 1 единицу вверх. Построим график функции у = х2+1, сдвигая
точки построенного графика у = х2.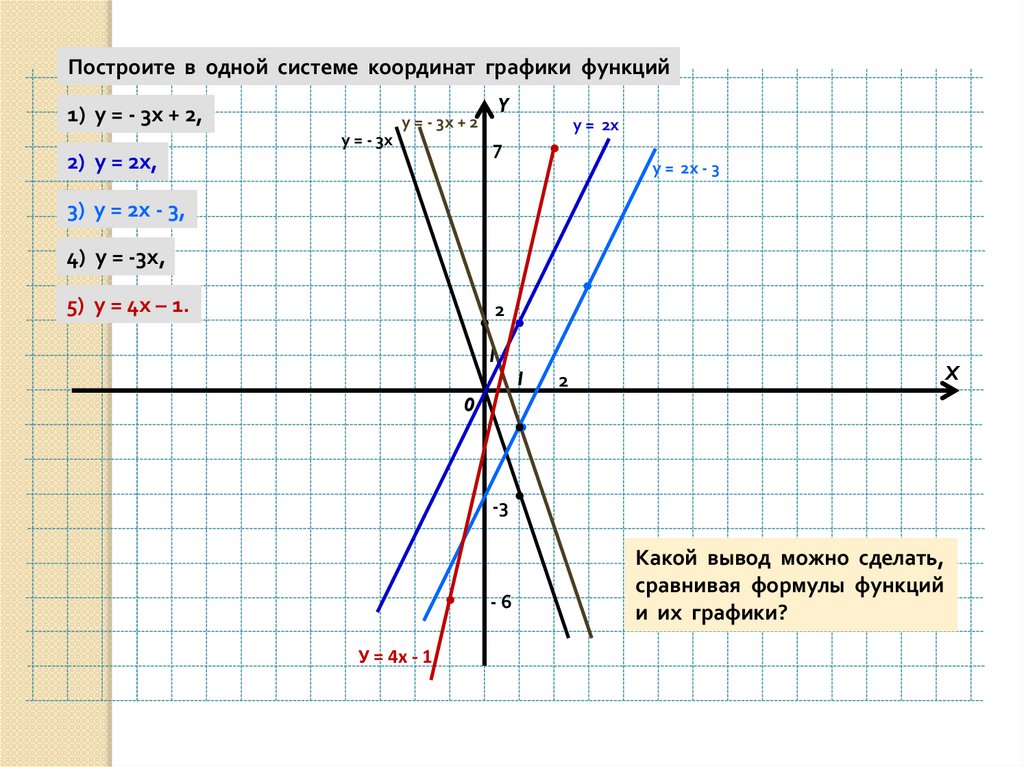 Постройте графики.
Постройте графики. 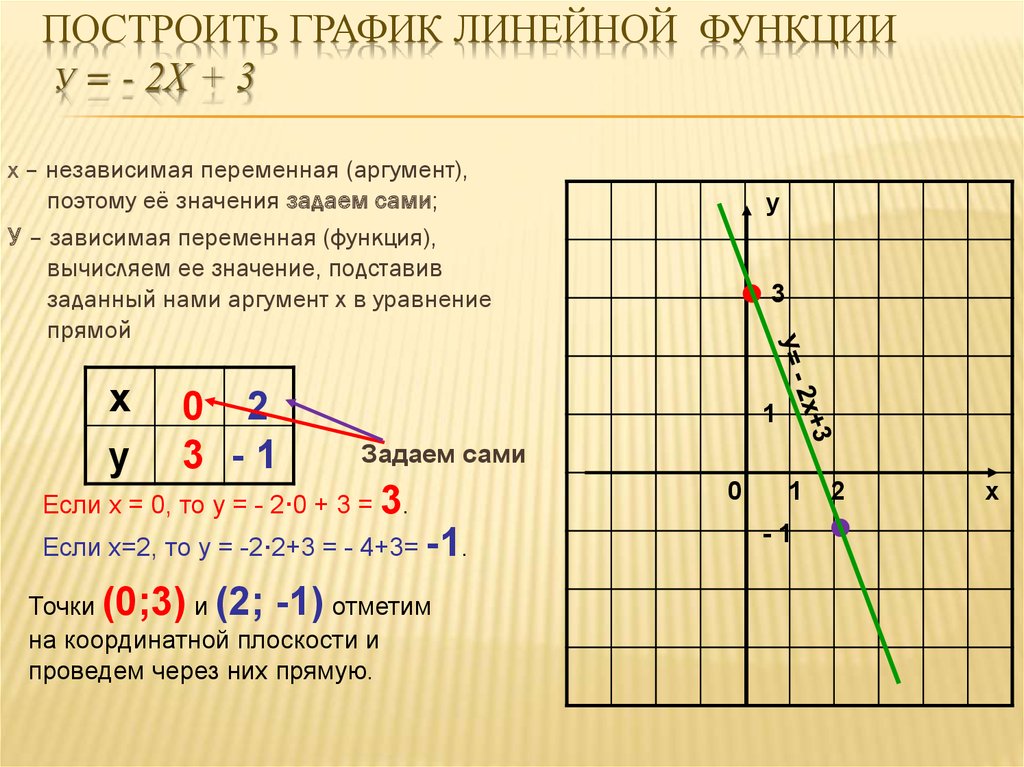 В данном случае l=
— 4 (l<0),
значит, сдвигаем вправо на 4 единицы график функции у = х2.
В данном случае l=
— 4 (l<0),
значит, сдвигаем вправо на 4 единицы график функции у = х2.
 Где функция возрастает, где – убывает?
Где функция возрастает, где – убывает?