Ряд Фурье. Разложение функции в ряд Фурье.Разложение функции в ряд синусов и косинусов.
|
|
Ряд Фурье позволяет изучать периодические (непериодические) функции, разлагая их на компоненты. Переменные токи и напряжения, смещения, скорость и ускорение кривошипно-шатунных механизмов и акустические волны — это типичные практические примеры применения периодических функций в инженерных расчетах.
Переменные токи и напряжения, смещения, скорость и ускорение кривошипно-шатунных механизмов и акустические волны — это типичные практические примеры применения периодических функций в инженерных расчетах.
Разложение в ряд Фурье основывается на предположении, что все имеющие практическое значение функции в интервале -π ≤x≤ π можно выразить в виде сходящихся тригонометрических рядов (ряд считается сходящимся, если сходится последовательность частичных сумм, составленных из его членов):
Стандартная (=обычная) запись через сумму sinx и cosxf(x)=ao+ a1cosx+a2cos2x+a3cos3x+…+b1sinx+b2sin2x+b3sin3x+…,
где ao, a1,a2,…,b1,b2,.. — действительные константы, т.е.
(1)
Где для диапазона от -π до π коэффициенты ряда Фурье рассчитываются по формулам:Коэффициенты ao,an и bn называются коэффициентами Фурье, и если их можно найти, то ряд (1) называется рядом Фурье, соответствующим функции f(x). Для ряда (1) член (a1cosx+b1sinx) называется первой или основной гармоникой,
Для ряда (1) член (a1cosx+b1sinx) называется первой или основной гармоникой,
f(x)=ao+c1sin(x+α1)+c2sin(2x+α2)+…+cnsin(nx+αn)
Где ao — константа, с 1=(a12+b12)1/2 , с n=(an2+bn2)1/2— амплитуды различных компонент, а фазовый угол равен an=arctg an/bn.
Для ряда (1) член (a1cosx+b1sinx) или c1sin(x+α1) называется первой или основной гармоникой, (a2cos2x+b2sin2x) или c2sin(2x+α2) называется второй гармоникой и так далее.
Для точного представления сложного сигнала обычно требуется бесконечное количество членов. Однако во многих практических задачах достаточно рассмотреть только несколько первых членов.
Ряд Фурье непериодических функций с периодом 2π. Разложение непериодических функций в ряд Фурье.Если функция f(x) непериодическая, значит, она не может быть разложена в ряд Фурье для всех значений х. Однако можно определить ряд Фурье, представляющий функцию в любом диапазоне шириной 2π.
Если задана непериодическая функция, можно составить новую функцию, выбирая значения f(x) в определенном диапазоне и повторяя их вне этого диапазона с интервалом 2π. Поскольку новая функция является периодической с периодом 2π, ее можно разложить в ряд Фурье для всех значений х. Например, функция f(x)=x не является периодической. Однако, если необходимо разложить ее в ряд Фурье на интервале от о до 2π, тогда вне этого интервала строится периодическая функция с периодом 2π (как показано на рис. ниже) .
ниже) .
Для непериодических функций, таких как f(x)=х, сумма ряда Фурье равна значению f(x) во всех точках заданного диапазона, но она не равна f(x) для точек вне диапазона. Для нахождения ряда Фурье непериодической функции в диапазоне 2π используется все таже формула коэффициентов Фурье.
Четные и нечетные функции.Говорят, функция y=f(x) четная, если f(-x)=f(x) для всех значений х. Графики четных функций всегда симметричны относительно оси у (т.е. являются зеркально отраженными). Два примера четных функций: у=х2 и у=cosx.
Говорят, что функция y=f(x) нечетная, если f(-x)=-f(x) для всех значений х. Графики нечетных функций всегда симметричны относительно начала координат.
Многие функции не являются ни четными, ни нечетными.
Разложение в ряд Фурье по косинусам.Ряд Фурье четной периодической функции f(x) с периодом 2π содержит только члены с косинусами (т. е. не содержит членов с синусами) и может включать постоянный член. Следовательно,
е. не содержит членов с синусами) и может включать постоянный член. Следовательно,
где коэффициенты ряда Фурье,
Разложение в ряд Фурье по синусам.Ряд Фурье нечетной периодической функции f(x) с периодом 2π содержит только члены с синусами (т.е. не содержит членов с косинусами).
Следовательно,
где коэффициенты ряда Фурье,
Ряд Фурье на полупериоде.Если функция определена для диапазона, скажем от 0 до π, а не только от 0 до 2π, ее можно разложить в ряд только по синусам или тольо по косинусам. Полученный ряд Фурье называется рядом Фурье на полупериоде.
Если требуется получить разложение Фурье на полупериоде по косинусам функции f(x) в диапазоне от 0 до π, то необходимо составить четную периодическую функцию. На рис. ниже показана функция f(x)=х, построенная на интервале от х=0 до х=π. Поскольку четная функция симметрична относительно оси f(x), проводим линию АВ, как показано на рис. ниже. Если предположить, что за пределами рассмотренного интервала полученная треугольная форма является периодической с периодом 2π, то итоговый график имеет вид, показ. на рис. ниже. Поскольку требуется получить разложение Фурье по косинусам, как и ранее, вычисляем коэффициенты Фурье ao и an
На рис. ниже показана функция f(x)=х, построенная на интервале от х=0 до х=π. Поскольку четная функция симметрична относительно оси f(x), проводим линию АВ, как показано на рис. ниже. Если предположить, что за пределами рассмотренного интервала полученная треугольная форма является периодической с периодом 2π, то итоговый график имеет вид, показ. на рис. ниже. Поскольку требуется получить разложение Фурье по косинусам, как и ранее, вычисляем коэффициенты Фурье ao и an
Если требуется получить разложение Фурье на полупериоде по синусам функции f(x) в диапазоне от 0 до π, то необходимо составить нечетную периодическую функцию. На рис. ниже показана функция f(x)=x, построенная на интервале от от х=0 до х=π. Поскольку нечетная функция симметрична относительно начала координат, строим линию CD, как показано на рис. Если предположить, что за пределами рассмотренного интервала полученный пилообразный сигнал является периодическим с периодом 2π, то итоговый график имеет вид, показанный на рис. Поскольку требуется получить разложение Фурие на полупериоде по синусам, как и ранее, вычисляем коэффициент Фурье. b
Поскольку требуется получить разложение Фурие на полупериоде по синусам, как и ранее, вычисляем коэффициент Фурье. b
Разложение периодической функции с периодом L.
Периодическая функция f(x) повторяется при увеличении х на L, т.е. f(x+L)=f(x). Переход от рассмотренных ранее функций с периодом 2π к функциям с периодом L довольно прост, поскольку его можно осуществить с помощью замены переменной.
Чтобы найти ряд Фурье функции f(x) в диапазоне -L/2≤x≤L/2, введем новую переменную u таким образом, чтобы функция f(x) имела период 2π относительно u. Если u=2πх/L, то х=-L/2 при u=-π и х=L/2 при u=π. Также пусть f(x)=f(Lu/2π)=F(u). Ряд Фурье F(u) имеет вид
Где коэффициенты ряда Фурье,
Однако чаще приведенную выше формулу приводят к зависимости от х. Поскольку u=2πх/L, значит, du=(2π/L)dx, а пределы интегрирования — от -L/2 до L/2 вместо — π до π. Следовательно, ряд Фурье для зависимости от х имеет вид
Поскольку u=2πх/L, значит, du=(2π/L)dx, а пределы интегрирования — от -L/2 до L/2 вместо — π до π. Следовательно, ряд Фурье для зависимости от х имеет вид
где в диапазоне от -L/2 до L/2 коэффициенты ряда Фурье,
(Пределы интегрирования могут быть заменены на любой интервал длиной L, например, от 0 до L)
Ряд Фурье на полупериоде для функций, заданных в интервале L≠2π.Для подстановки u=πх/L интервал от х=0 до х=L соответствует интервалу от u=0 до u=π. Следовательно, функцию можно разложить в ряд только по косинусам или только по синусам, т.е. в ряд Фурье на полупериоде.
Разложение по косинусам в диапазоне от 0 до L имеет вид
Ряд Фурье. Разложение функции в ряд Фурье.Разложение функции в ряд синусов и косинусов.
|
|
Ряд Фурье позволяет изучать периодические (непериодические) функции, разлагая их на компоненты. Переменные токи и напряжения, смещения, скорость и ускорение кривошипно-шатунных механизмов и акустические волны — это типичные практические примеры применения периодических функций в инженерных расчетах.
Разложение в ряд Фурье основывается на предположении, что все имеющие практическое значение функции в интервале -π ≤x≤ π можно выразить в виде сходящихся тригонометрических рядов (ряд считается сходящимся, если сходится последовательность частичных сумм, составленных из его членов):
Стандартная (=обычная) запись через сумму sinx и cosxf(x)=ao+ a1cosx+a2cos2x+a3cos3x+…+b1sinx+b2sin2x+b3sin3x+…,
где ao, a1,a2,…,b1,b2,.. — действительные константы, т.е.
(1)
Где для диапазона от -π до π коэффициенты ряда Фурье рассчитываются по формулам:Коэффициенты ao,an и bn называются коэффициентами Фурье, и если их можно найти, то ряд (1) называется рядом Фурье, соответствующим функции f(x). Для ряда (1) член (a1cosx+b1sinx) называется первой или основной гармоникой,
Для ряда (1) член (a1cosx+b1sinx) называется первой или основной гармоникой,
f(x)=ao+c1sin(x+α1)+c2sin(2x+α2)+…+cnsin(nx+αn)
Где ao — константа, с 1=(a12+b12)1/2 , с n=(an2+bn2)1/2— амплитуды различных компонент, а фазовый угол равен an=arctg an/bn.
Для ряда (1) член (a1cosx+b1sinx) или c1sin(x+α1) называется первой или основной гармоникой, (a2cos2x+b2sin2x) или c2sin(2x+α2) называется второй гармоникой и так далее.
Для точного представления сложного сигнала обычно требуется бесконечное количество членов. Однако во многих практических задачах достаточно рассмотреть только несколько первых членов.
Ряд Фурье непериодических функций с периодом 2π. Разложение непериодических функций в ряд Фурье.Если функция f(x) непериодическая, значит, она не может быть разложена в ряд Фурье для всех значений х. Однако можно определить ряд Фурье, представляющий функцию в любом диапазоне шириной 2π.
Если задана непериодическая функция, можно составить новую функцию, выбирая значения f(x) в определенном диапазоне и повторяя их вне этого диапазона с интервалом 2π. Поскольку новая функция является периодической с периодом 2π, ее можно разложить в ряд Фурье для всех значений х. Например, функция f(x)=x не является периодической. Однако, если необходимо разложить ее в ряд Фурье на интервале от о до 2π, тогда вне этого интервала строится периодическая функция с периодом 2π (как показано на рис. ниже) .
ниже) .
Для непериодических функций, таких как f(x)=х, сумма ряда Фурье равна значению f(x) во всех точках заданного диапазона, но она не равна f(x) для точек вне диапазона. Для нахождения ряда Фурье непериодической функции в диапазоне 2π используется все таже формула коэффициентов Фурье.
Четные и нечетные функции.Говорят, функция y=f(x) четная, если f(-x)=f(x) для всех значений х. Графики четных функций всегда симметричны относительно оси у (т.е. являются зеркально отраженными). Два примера четных функций: у=х2 и у=cosx.
Говорят, что функция y=f(x) нечетная, если f(-x)=-f(x) для всех значений х. Графики нечетных функций всегда симметричны относительно начала координат.
Многие функции не являются ни четными, ни нечетными.
Разложение в ряд Фурье по косинусам.Ряд Фурье четной периодической функции f(x) с периодом 2π содержит только члены с косинусами (т.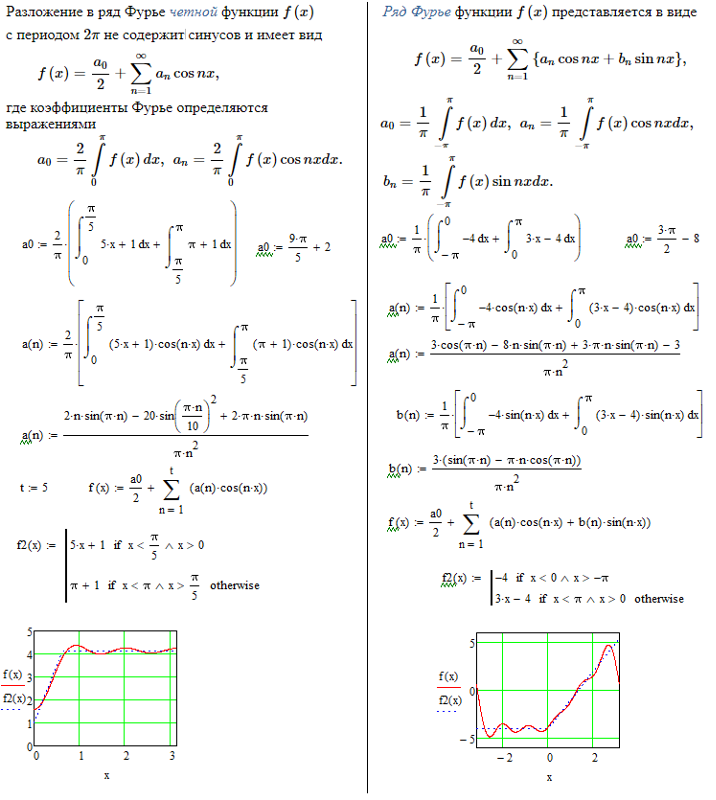 е. не содержит членов с синусами) и может включать постоянный член. Следовательно,
е. не содержит членов с синусами) и может включать постоянный член. Следовательно,
где коэффициенты ряда Фурье,
Разложение в ряд Фурье по синусам.Ряд Фурье нечетной периодической функции f(x) с периодом 2π содержит только члены с синусами (т.е. не содержит членов с косинусами).
Следовательно,
где коэффициенты ряда Фурье,
Ряд Фурье на полупериоде.Если функция определена для диапазона, скажем от 0 до π, а не только от 0 до 2π, ее можно разложить в ряд только по синусам или тольо по косинусам. Полученный ряд Фурье называется рядом Фурье на полупериоде.
Если требуется получить разложение Фурье на полупериоде по косинусам функции f(x) в диапазоне от 0 до π, то необходимо составить четную периодическую функцию.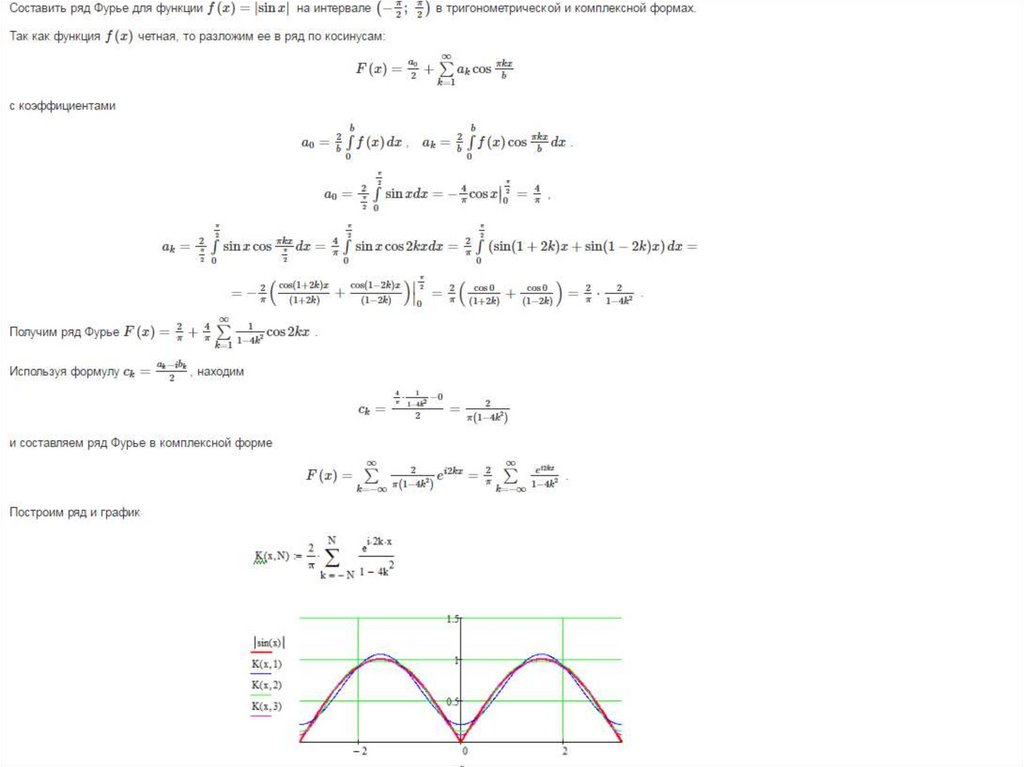 На рис. ниже показана функция f(x)=х, построенная на интервале от х=0 до х=π. Поскольку четная функция симметрична относительно оси f(x), проводим линию АВ, как показано на рис. ниже. Если предположить, что за пределами рассмотренного интервала полученная треугольная форма является периодической с периодом 2π, то итоговый график имеет вид, показ. на рис. ниже. Поскольку требуется получить разложение Фурье по косинусам, как и ранее, вычисляем коэффициенты Фурье ao и an
На рис. ниже показана функция f(x)=х, построенная на интервале от х=0 до х=π. Поскольку четная функция симметрична относительно оси f(x), проводим линию АВ, как показано на рис. ниже. Если предположить, что за пределами рассмотренного интервала полученная треугольная форма является периодической с периодом 2π, то итоговый график имеет вид, показ. на рис. ниже. Поскольку требуется получить разложение Фурье по косинусам, как и ранее, вычисляем коэффициенты Фурье ao и an
Если требуется получить разложение Фурье на полупериоде по синусам функции f(x) в диапазоне от 0 до π, то необходимо составить нечетную периодическую функцию. На рис. ниже показана функция f(x)=x, построенная на интервале от от х=0 до х=π. Поскольку нечетная функция симметрична относительно начала координат, строим линию CD, как показано на рис. Если предположить, что за пределами рассмотренного интервала полученный пилообразный сигнал является периодическим с периодом 2π, то итоговый график имеет вид, показанный на рис. Поскольку требуется получить разложение Фурие на полупериоде по синусам, как и ранее, вычисляем коэффициент Фурье. b
Поскольку требуется получить разложение Фурие на полупериоде по синусам, как и ранее, вычисляем коэффициент Фурье. b
Разложение периодической функции с периодом L.
Периодическая функция f(x) повторяется при увеличении х на L, т.е. f(x+L)=f(x). Переход от рассмотренных ранее функций с периодом 2π к функциям с периодом L довольно прост, поскольку его можно осуществить с помощью замены переменной.
Чтобы найти ряд Фурье функции f(x) в диапазоне -L/2≤x≤L/2, введем новую переменную u таким образом, чтобы функция f(x) имела период 2π относительно u. Если u=2πх/L, то х=-L/2 при u=-π и х=L/2 при u=π. Также пусть f(x)=f(Lu/2π)=F(u). Ряд Фурье F(u) имеет вид
Где коэффициенты ряда Фурье,
Однако чаще приведенную выше формулу приводят к зависимости от х. Поскольку u=2πх/L, значит, du=(2π/L)dx, а пределы интегрирования — от -L/2 до L/2 вместо — π до π. Следовательно, ряд Фурье для зависимости от х имеет вид
Поскольку u=2πх/L, значит, du=(2π/L)dx, а пределы интегрирования — от -L/2 до L/2 вместо — π до π. Следовательно, ряд Фурье для зависимости от х имеет вид
где в диапазоне от -L/2 до L/2 коэффициенты ряда Фурье,
(Пределы интегрирования могут быть заменены на любой интервал длиной L, например, от 0 до L)
Ряд Фурье на полупериоде для функций, заданных в интервале L≠2π.Для подстановки u=πх/L интервал от х=0 до х=L соответствует интервалу от u=0 до u=π. Следовательно, функцию можно разложить в ряд только по косинусам или только по синусам, т.е. в ряд Фурье на полупериоде.
Разложение по косинусам в диапазоне от 0 до L имеет вид
11.3: Серия Фурье II — Mathematics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 9462
- Уильям Ф.
 Тренч
Тренч - Университет Тринити
В этом разделе мы обсуждаем разложения Фурье по собственным функциям задач 1-4 раздела 11.1.
Косинусный ряд Фурье
Из Упражнение 11.1.20 собственные функции
\[1,\, \cos{\pi x\over L}, \, \cos{2\pi x\over L},\ точки, \, \cos{n\pi x\over L},\dots\nonumber \]
краевой задачи
\[\label{eq:11.3.1} y»+\lambda y= 0,\quad y'(0)=0,\quad y'(L)=0\]
(задача 2) ортогональны на \([0,L]\). Если \(f\) интегрируема на \([0,L]\), то разложение Фурье \(f\) по этим функциям называется 9Lf(x)\cos{n\pi x\over L}\,dx,\quad n=1,2,3,\dots.\nonumber \]
Сравнение этого определения с теоремой 11.2.6a показывает, что функция Фурье Косинусный ряд \(f\) на \([0,L]\) — это ряд Фурье функции
\[f_{1}(x)=\left\{\begin{array}{cc}{ f(-x),}&{-L получается расширением \(f\) на \([-L,L]\) как четная функция (рис. 11.3.1). Применение теоремы 11.2.4 к \(f_1\) дает следующую теорему. 9Lf(x)\cos{n\pi x\over L}\,dx,\quad n=1,2,3,\dots,\nonumber \] сходится для всех \(x\) в \([0,L];\), причем \[C(x)=\left\{\begin{array}{cl}{f(0+),}&{\text{if}x=0}\\[5pt]{f(x), } & {\ text {если} 0 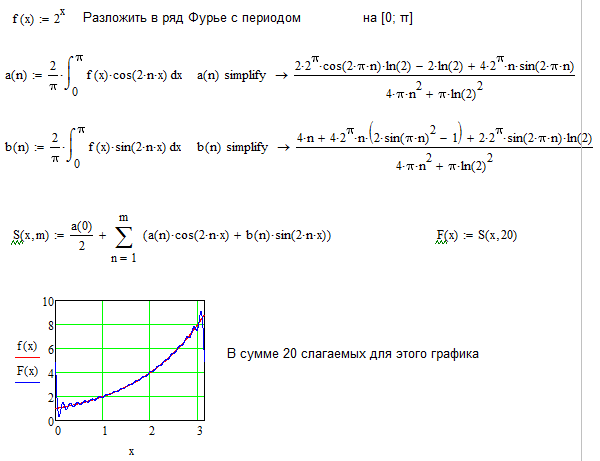 ).
). Пример 11.3.1
Теорема 11.3.1 подразумевает, что
\[C(x)=x,\quad 0\le x\le L.\nonnumber \]
Ряд синусов Фурье
Из Упражнение 11.1.19 , собственные функции
\[\sin{\pi x\over L}, \, \sin{2\pi x\over L},\dots, \, \sin{n\pi x\over L},\dots\nonumber \]
краевой задачи
\[y»+\lambda y=0,\quad y(0)=0,\quad y(L)=0\nonumber \]
(задача 1) ортогональны на \([0,L]\). Если \(f\) интегрируема на \([0,L]\), то разложение Фурье \(f\) по этим функциям называется 9Lf(x)\sin{n\pi x\over L}\,dx,\quad n=1,2,3,\dots.\nonumber \]
Если \(f\) интегрируема на \([0,L]\), то разложение Фурье \(f\) по этим функциям называется 9Lf(x)\sin{n\pi x\over L}\,dx,\quad n=1,2,3,\dots.\nonumber \]
Сравнение этого определения с теоремой 11.2.6b показывает, что функция Фурье ряд синусов \(f\) на \([0,L]\) — это ряд Фурье функции
\[f_{2}(x)=\left\{\begin{array}{cc}{ -f(-x),}&{-L , полученное расширением \(f\) над \([-L,L]\) как нечетной функцией (рис. 11.3.2).
). Применение теоремы 11.2.4 к \(f_2\) дает следующую теорему. 9Lf(x)\sin{n\pi x\over L}\,dx,\nonumber \] сходится для всех \(x\) в \([0,L];\), причем \[S (x) = \ left \ {\ begin {array} {cl} {0} & {\ text {if} x = 0} \\ [5pt] {f (x),} & {\ text {если}0 Найдите ряд Фурье по синусу \(f(x)=x\) на \([0,L]\). 9n\over n} \sin{n\pi x\over L}.\nonumber \] Теорема 11.3.2
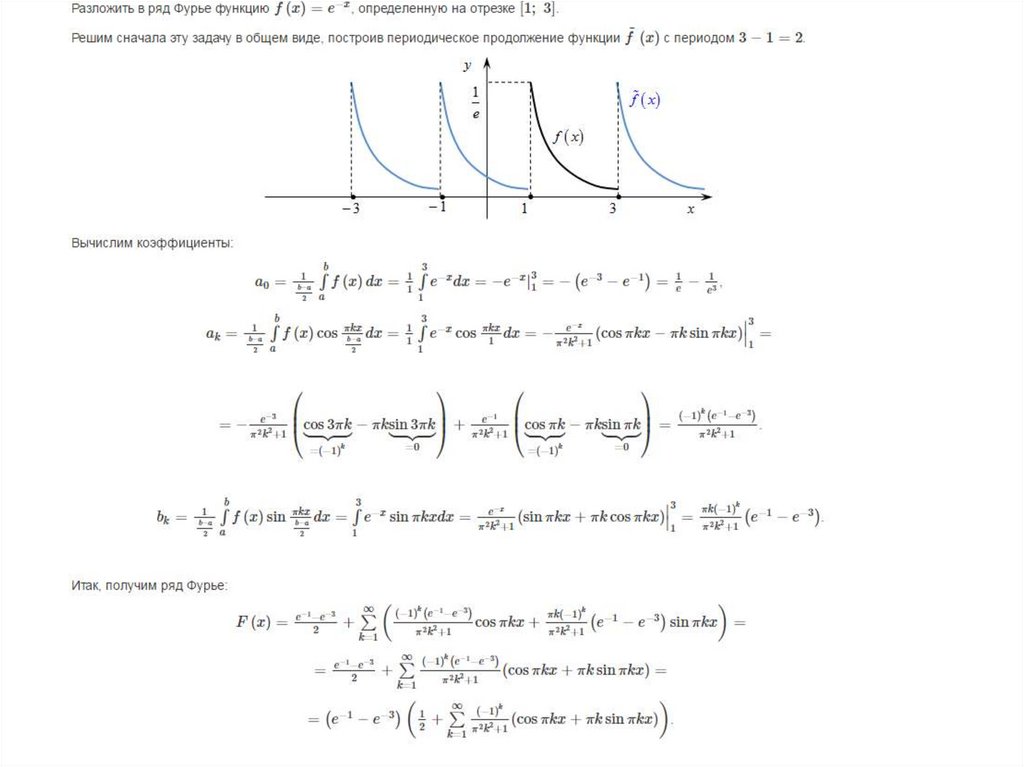
следует, что \[S(x)= \left\{\begin{array}{cl} x,&0\le x< L,\\0,& x=L. \end{array}\right.\nonumber \] Из Упражнение 11.1.22 собственные функции \[\cos{\pi x\over 2L}, \, \cos{ 3\pi x\over 2L},\dots, \, \cos{(2n-1)\pi x\over 2L},\dots\nonumber \] краевой задачи \[\label{ eq:11.3.2} y»+\lambda y=0,\quad y'(0)=0,\quad y(L)=0\] 9Lf(x)\cos{(2n-1)\pi x\over2L}\,dx.\nonumber \] Мы будем называть это разложение смешанным косинусным рядом Фурье функции \(f\) на \( [0,L]\), потому что граничные условия (Уравнение \ref{eq:11.3.2}) «смешанные» в том смысле, что они требуют, чтобы \(y\) было равно нулю в одной граничной точке и \(y’ \) быть равным нулю на другом. Напротив, «обычный» ряд косинусов Фурье связан с ( Уравнение \ref{eq:11.3.1}), где граничные условия требуют, чтобы \(y’\) было равно нулю в обеих конечных точках. Можно показать ( Упражнение 11.3.57 ), что смешанный ряд косинусов Фурье \(f\) на \([0,L]\) является просто ограничением на \([0,L]\) ряда косинусов Фурье \[f_3(x)=\left\{\begin{array}{cl} f(x),&0\le x\le L,\\-f(2L-x), &L< x\le 2L \end{array}\right.\nonumber \] on \([0,2L]\) (рис. 11.3.3).
). Применение теоремы 11.3.1
с заменой \(f\) на \(f_3\) и \(L\) на \(2L\) получается следующая теорема. 9Lf(x)\cos{(2n-1)\pi x\over2L}\,dx,\nonumber \] сходится для всех \(x\) в \([0,L];\), причем \[C_{M}(x)=\left\{\begin{array}{cl}{f(0+),}&{\text{if}x=0}\\[5pt]{f( x),} & {\ text {если} 0 Найдите смешанный ряд косинусов Фурье для \(f(x)=x-L\) на \([0,L]\). 92} \cos{(2n-1)\pi x\over2L}. Теорема 11.3.3
следует, что \[C_M(x)= x-L,\quad 0\le x\le L.\nonumber \] Из Упражнение 11.1.21 собственные функции \[\ sin{\pi x\over 2L}, \, \sin{3\pi x\over 2L},\dots, \, \sin{(2n-1)\pi x\over 2L},\dots\nonumber \ ] краевой задачи \[y»+\lambda y=0,\quad y(0)=0,\quad y'(L)=0\nonnumber \] (задача 3) ортогональны на \([0,L]\). Если \(f\) интегрируема на \([0,L]\), то Фурье-разложение \(f\) по этим функциям равно 9Lf(x)\sin{(2n-1)\pi x\over2L}\,dx.\nonumber \] Мы назовем это разложение смешанным рядом синусов Фурье функции \(f\) на \( [0,L]\). Можно показать ( Упражнение 11.3.58 ), что смешанный ряд Фурье по синусам \(f\) на \([0,L]\) является просто ограничением на \([0,L]\) ряда синусов Фурье \[f_4(x)=\left\{\begin{array}{cl} f(x),&0\le x\le L,\\f(2L-x),&L < x\le 2L, \end{array}\right.\nonumber \] on \([0,2L]\) (рис. сходится для всех \(x\) в \([0,L];\), причем \[S{M}(x)=\left\{\begin{array}{cl}{0,}&{\text{if}x=0}\\[5pt]{f(x),} &{\ text{if}0 Найдите смешанный ряд Фурье по синусам \(f(x)=x\) на \([0,L]\). 92} \sin{(2n-1)\pi x\over2L}.\nonumber \] Теорема 11.3.4
следует, что \[S_M(x)=x,\quad 0\le x\le L.\nonumber \] В приложениях, включающих разложение по собственным функциям задач 1-4, разлагаемые функции часто являются полиномами, удовлетворяющими граничным условиям рассматриваемой задачи. В этом случае следующая теорема предлагает эффективный способ получения коэффициентов в разложении. Мы докажем (а), а остальное предоставим вам ( Упражнения 11. Эта страница под названием 11.3: Серия Фурье II распространяется под лицензией CC BY-NC-SA 3.0 и была создана, изменена и/или курирована Уильямом Ф. Тренчем посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу. Формула ряда Фурье дает разложение периодической функции f(x) через бесконечную сумму синусов и косинусов. Он используется для разложения любой периодической функции или периодического сигнала на сумму набора простых осциллирующих функций, а именно синусов и косинусов. Давайте разберемся с формулой ряда Фурье на решенных примерах. В рядах Фурье используются ортогональные соотношения функций косинуса и синуса. Формула ряда Фурье для функции имеет вид 9{\pi}f(x)sin\;nx\;dx\) Есть вопросы по основным математическим понятиям? Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами. 9{2}}\) Ряд Фурье представляет собой разложение периодической функции f(x) по бесконечной сумме синусов и косинусов. Пример 11.
 3.2
3.2 Смешанный ряд косинусов Фурье
Пример 11.3.3
 \nonumber \]
\nonumber \] Смешанный ряд по синусу Фурье
 11.3.4
). 9Lf(x)\sin{(2n-1)\pi x\over2L}\,dx,\nonumber \]
11.3.4
). 9Lf(x)\sin{(2n-1)\pi x\over2L}\,dx,\nonumber \] Пример 11.3.4
Полезное наблюдение
 2(3L-2x)\) на \([0,L]\). 9{n}\frac{4}{(2n-1)\pi } \right]\sin\frac{(2n-1)\pi x}{2L}\nonumber\]
2(3L-2x)\) на \([0,L]\). 9{n}\frac{4}{(2n-1)\pi } \right]\sin\frac{(2n-1)\pi x}{2L}\nonumber\] trinity.edu/mono/9
trinity.edu/mono/9 Формула ряда Фурье. Что такое формула ряда Фурье?
Что такое формулы ряда Фурье?
Примеры формул ряда Фурье
Часто задаваемые вопросы о формулах ряда Фурье
Что подразумевается под рядом Фурье?



 Тренч
Тренч Создать собственный Курс обучения Таро. В нем мы подробно рассказываем не только о каждой карте, но и развеиваем мифы о Таро, раскрываем Путь Героя, на конкретном примере показываем расклад для определения Луча Миссии, а также даем сборник лучших рабочих раскладов и все сочетания Лучей с методами проработки.
Создать собственный Курс обучения Таро. В нем мы подробно рассказываем не только о каждой карте, но и развеиваем мифы о Таро, раскрываем Путь Героя, на конкретном примере показываем расклад для определения Луча Миссии, а также даем сборник лучших рабочих раскладов и все сочетания Лучей с методами проработки. Таро. Предназначение. Нумерология в ВК – самое большое в этой социальной сети на тему Матрицы, а наш блог Matrix_date в Instagram* – один из самых популярных, познавательных и комментируемых блогов по нумерологии (*соц. сеть заблокирована на территории РФ).
Таро. Предназначение. Нумерология в ВК – самое большое в этой социальной сети на тему Матрицы, а наш блог Matrix_date в Instagram* – один из самых популярных, познавательных и комментируемых блогов по нумерологии (*соц. сеть заблокирована на территории РФ). 11). Так возникла идея онлайн калькулятора. Благодаря чему, для того, чтобы разобраться в методе и расшифровать матрицу теперь не нужно проходить дорогостоящие обучения и смотреть многочасовые вебинары – всё есть в одном сервисе.
11). Так возникла идея онлайн калькулятора. Благодаря чему, для того, чтобы разобраться в методе и расшифровать матрицу теперь не нужно проходить дорогостоящие обучения и смотреть многочасовые вебинары – всё есть в одном сервисе. Благодаря ее опыту и умению соединять воедино большое количество информации, пользователи нашего сервиса и студенты образовательных курсов получают уникальные знания, которые легко применить на практике. Галине всегда хочется донести до пользователей сервиса и аудитории соцсетей максимум пользы, при чем сделать это интересно, доступно и креативно.
Благодаря ее опыту и умению соединять воедино большое количество информации, пользователи нашего сервиса и студенты образовательных курсов получают уникальные знания, которые легко применить на практике. Галине всегда хочется донести до пользователей сервиса и аудитории соцсетей максимум пользы, при чем сделать это интересно, доступно и креативно. Девиз Жени: «Сделать непонятное – понятным, а сложное – простым». Благодаря этому подходу пользователи сайта, студенты курсов и аудитория социальных сетей регулярно отмечают, что наконец поняли то, что не удавалось самостоятельно или на других обучениях.
Девиз Жени: «Сделать непонятное – понятным, а сложное – простым». Благодаря этому подходу пользователи сайта, студенты курсов и аудитория социальных сетей регулярно отмечают, что наконец поняли то, что не удавалось самостоятельно или на других обучениях. Надежда регулярно пополняет библиотеку новой литературой, помогает клиентам сервиса найти необходимую им книгу, а также может проконсультировать в какой литературе содержится информация о которой хочется почитать подробнее.
Надежда регулярно пополняет библиотеку новой литературой, помогает клиентам сервиса найти необходимую им книгу, а также может проконсультировать в какой литературе содержится информация о которой хочется почитать подробнее. S-5.com («Веб-сайт»). Использование Веб-сайта и Калькулятора, а также всей связанной с ними информации строго регулируется Условиями использования – Общие и настоящими дополнительными Условиями использования и Лицензионным соглашением. Получая доступ, загружая и/или используя Калькулятор, вы заключаете с MRIL юридически обязывающий договор о соблюдении общих Условий использования и настоящих Условий использования и Лицензионного соглашения. Если вы не согласны с Условиями использования и Лицензионным соглашением, вы не имеете права использовать Калькулятор, и вам будет предложено немедленно выйти из Веб-сайта. Каждый раз, когда вы используете какой-либо аспект Калькулятора, вы принимаете Условия использования и Лицензионное соглашение, действующие на данный момент. Считается, что Калькулятор является полезным помощником при разработке адекватной конструкции различных систем снегозадержания и солнечных батарей («Системы») с использованием производимых или распространяемых MRIL продуктов и компонентов («Продукты») и может использоваться только в сочетании с ними («Продукты»).
S-5.com («Веб-сайт»). Использование Веб-сайта и Калькулятора, а также всей связанной с ними информации строго регулируется Условиями использования – Общие и настоящими дополнительными Условиями использования и Лицензионным соглашением. Получая доступ, загружая и/или используя Калькулятор, вы заключаете с MRIL юридически обязывающий договор о соблюдении общих Условий использования и настоящих Условий использования и Лицензионного соглашения. Если вы не согласны с Условиями использования и Лицензионным соглашением, вы не имеете права использовать Калькулятор, и вам будет предложено немедленно выйти из Веб-сайта. Каждый раз, когда вы используете какой-либо аспект Калькулятора, вы принимаете Условия использования и Лицензионное соглашение, действующие на данный момент. Считается, что Калькулятор является полезным помощником при разработке адекватной конструкции различных систем снегозадержания и солнечных батарей («Системы») с использованием производимых или распространяемых MRIL продуктов и компонентов («Продукты») и может использоваться только в сочетании с ними («Продукты»). Разрешенное использование»). Если Архитектор или Инженер («Квалифицированный специалист») использует Калькулятор, он/она будет указывать использование Продуктов только для своих проектов и заверять, что они (1) имеют право проектировать Системы с помощью «Продуктов»; (2) распознавать специфические для проекта переменные, которые следует учитывать при разработке системы; и (3) может разработать адекватный проект в рамках Разрешенного использования и соответствовать применимым строительным нормам, правилам и общепринятой отраслевой практике. Калькулятор содержит и представляет конфиденциальную информацию MRIL и защищен различными законами США и международными законами. MRIL обладает исключительными правами на использование товарных знаков С-5! ® , ColorGard , DualGard , X-Gard и другие знаки, представленные на сайте и связанные с ее деятельностью и продажей продукции, производимой или продаваемой MRIL. Вы соглашаетесь не нарушать и не будете нарушать права MRIL в соответствии с любыми такими законами, а также использовать или копировать любую часть Веб-сайта, включая, помимо прочего, любые товарные знаки или знаки обслуживания или оригинальные авторские работы, найденные на сайте.
Разрешенное использование»). Если Архитектор или Инженер («Квалифицированный специалист») использует Калькулятор, он/она будет указывать использование Продуктов только для своих проектов и заверять, что они (1) имеют право проектировать Системы с помощью «Продуктов»; (2) распознавать специфические для проекта переменные, которые следует учитывать при разработке системы; и (3) может разработать адекватный проект в рамках Разрешенного использования и соответствовать применимым строительным нормам, правилам и общепринятой отраслевой практике. Калькулятор содержит и представляет конфиденциальную информацию MRIL и защищен различными законами США и международными законами. MRIL обладает исключительными правами на использование товарных знаков С-5! ® , ColorGard , DualGard , X-Gard и другие знаки, представленные на сайте и связанные с ее деятельностью и продажей продукции, производимой или продаваемой MRIL. Вы соглашаетесь не нарушать и не будете нарушать права MRIL в соответствии с любыми такими законами, а также использовать или копировать любую часть Веб-сайта, включая, помимо прочего, любые товарные знаки или знаки обслуживания или оригинальные авторские работы, найденные на сайте. Вы соглашаетесь с тем, что любое фактическое или потенциальное нарушение настоящих Условий использования и Лицензионного соглашения приведет к немедленному непоправимому ущербу для MRIL, что любые действия, предпринятые для обеспечения соблюдения этого соглашения, могут быть предприняты только в Колорадо, и, таким образом, вы отказываетесь от любой защиты в связи с отсутствием личной юрисдикции. или неподходящее место и любое право на суд присяжных. Если вы нарушаете или угрожаете нарушить какое-либо обязательство по настоящему соглашению, MRIL имеет право добиваться вынесения судебного приказа о запрете ваших незаконных действий и вынесения судебного решения против вас за весь ущерб, понесенный в связи с вашим нарушением или угрозой нарушения, включая все гонорары адвокатов и понесенные рассходы. Использование Калькулятора ограничено действительными и потенциальными клиентами S-5! и их коммерческое использование любым физическим или юридическим лицом, которое не является клиентом или потенциальным клиентом S-5! запрещено.
Вы соглашаетесь с тем, что любое фактическое или потенциальное нарушение настоящих Условий использования и Лицензионного соглашения приведет к немедленному непоправимому ущербу для MRIL, что любые действия, предпринятые для обеспечения соблюдения этого соглашения, могут быть предприняты только в Колорадо, и, таким образом, вы отказываетесь от любой защиты в связи с отсутствием личной юрисдикции. или неподходящее место и любое право на суд присяжных. Если вы нарушаете или угрожаете нарушить какое-либо обязательство по настоящему соглашению, MRIL имеет право добиваться вынесения судебного приказа о запрете ваших незаконных действий и вынесения судебного решения против вас за весь ущерб, понесенный в связи с вашим нарушением или угрозой нарушения, включая все гонорары адвокатов и понесенные рассходы. Использование Калькулятора ограничено действительными и потенциальными клиентами S-5! и их коммерческое использование любым физическим или юридическим лицом, которое не является клиентом или потенциальным клиентом S-5! запрещено. Использование калькулятора любым лицом или для любых целей, кроме Разрешенного использования, запрещено. С-5! может расторгнуть настоящее Соглашение в любое время и по любой причине или без таковой. Пользователи Калькулятора заявляют, гарантируют и понимают, что: предельные нагрузки по нормали к шву металлической панели крыши (как положительные, так и отрицательные) зависят от прочности балки панели крыши, и эти факторы могут повлиять на конструкцию Систем; силы, которые выдерживает хомут, могут быть больше, чем порог разрушения крыши ниже; состояние и материалы крыши, а также расстояние между креплениями крыши/подложки могут привести к обрушению крыши, но используемые зажимы могут остаться незатронутыми; можно предположить, что положительная нормаль (или направленная вниз сила) хомута к удерживающей силе шва такая же, как и отрицательная нормаль (или восходящая сила) хомута к удерживающей силе шва; что, когда речь идет о положительных нормальных силах, крыша со стоячим фальцем и конструкция под ней должны оцениваться отдельно, чтобы гарантировать, что крыша и конструкция могут противостоять нисходящим силам, создаваемым солнечной системой; расчеты положительных нормальных нагрузок основаны на различных допущениях и могут неадекватно учитывать влияние этих прижимных сил; отдельные инженерные расчеты положительных нормальных нагрузок выходят за рамки того, что здесь можно привести; монтажные зоны модуля, которые составляют от 1/8 до 1/4 длины длинной стороны модуля, начиная с угла модуля, устанавливаются по умолчанию и могут не совпадать с предписанными монтажными зонами всех производителей модулей; боковая или горизонтальная нагрузка вступает в игру с сейсмическими нагрузками и, как правило, очень минимальна по сравнению с другими нагрузками, воздействующими на систему, и не всеми S-5! хомуты испытаны в боковом направлении; и С-5! не дает никаких обещаний или заявлений в отношении силы удержания зажимов на швах, когда речь идет о направленных вниз или боковых силах.
Использование калькулятора любым лицом или для любых целей, кроме Разрешенного использования, запрещено. С-5! может расторгнуть настоящее Соглашение в любое время и по любой причине или без таковой. Пользователи Калькулятора заявляют, гарантируют и понимают, что: предельные нагрузки по нормали к шву металлической панели крыши (как положительные, так и отрицательные) зависят от прочности балки панели крыши, и эти факторы могут повлиять на конструкцию Систем; силы, которые выдерживает хомут, могут быть больше, чем порог разрушения крыши ниже; состояние и материалы крыши, а также расстояние между креплениями крыши/подложки могут привести к обрушению крыши, но используемые зажимы могут остаться незатронутыми; можно предположить, что положительная нормаль (или направленная вниз сила) хомута к удерживающей силе шва такая же, как и отрицательная нормаль (или восходящая сила) хомута к удерживающей силе шва; что, когда речь идет о положительных нормальных силах, крыша со стоячим фальцем и конструкция под ней должны оцениваться отдельно, чтобы гарантировать, что крыша и конструкция могут противостоять нисходящим силам, создаваемым солнечной системой; расчеты положительных нормальных нагрузок основаны на различных допущениях и могут неадекватно учитывать влияние этих прижимных сил; отдельные инженерные расчеты положительных нормальных нагрузок выходят за рамки того, что здесь можно привести; монтажные зоны модуля, которые составляют от 1/8 до 1/4 длины длинной стороны модуля, начиная с угла модуля, устанавливаются по умолчанию и могут не совпадать с предписанными монтажными зонами всех производителей модулей; боковая или горизонтальная нагрузка вступает в игру с сейсмическими нагрузками и, как правило, очень минимальна по сравнению с другими нагрузками, воздействующими на систему, и не всеми S-5! хомуты испытаны в боковом направлении; и С-5! не дает никаких обещаний или заявлений в отношении силы удержания зажимов на швах, когда речь идет о направленных вниз или боковых силах. ВЫ ПРИЗНАЕТЕ И СОГЛАШАЕТЕСЬ С ТЕМ, ЧТО (1) ВСЕ ОПРЕДЕЛЕНИЯ, КАСАЮЩИЕСЯ СООТВЕТСТВИЯ ПРОЕКТУ СИСТЕМЫ, ЯВЛЯЮТСЯ ВАШЕЙ ОТВЕТСТВЕННОСТЬЮ; (2) ПРОЕКТИРОВАНИЕ СИСТЕМ, КОТОРОЕ НЕ УЧИТЫВАЕТ ЗДАНИЕ, КРЫШУ И ПРОЕКТ И КОНСТРУКЦИЮ (ВКЛЮЧАЯ КОНКРЕТНЫЕ ПЕРЕМЕННЫЕ ПРОЕКТА), МОЖЕТ БЫТЬ И, ВЕРОЯТНО, НЕДОСТАТОЧНО; И (3) НАСТОЯЩИМ ОТКАЗЫВАЮТСЯ ОТ ЛЮБЫХ ПРЕТЕНЗИЙ, КОТОРЫЕ МОГУТ ПОДАТЬ ИЛИ ЛЮБЫМ ИЗ ЕЕ КОНСУЛЬТАНТОВ, АФФИЛИРОВАННЫХ СТРАХОВЫХ ЛИЦ, АДВОКАТОВ ИЛИ ЛЮБЫМ ЛИЦАМ, СВЯЗАННЫМ С ЛЮБЫМ ИЗ НИХ, И ВЫ ОБЯЗУЕТЕСЬ НЕ ПОДАТЬ ИСК В ОТНОШЕНИИ НИХ. ЗА ЛЮБОЕ ДЕЙСТВИЕ ИЛИ БЕЗДЕЙСТВИЕ ИЛИ ИСПОЛЬЗОВАНИЕ ВЕБ-САЙТА. ВЫ СОГЛАШАЕТЕСЬ И НАСТОЯЩИМ ОБЯЗАТЕЛЬНО ВОЗМЕЩАЕТЕ MRIL, ЕЕ АГЕНТАМ, ДОЛЖНОСТНЫМ ЛИЦАМ, ДИРЕКТОРАМ, АДВОКАТАМ, СТРАХОВЩИКАМ И ВСЕМ УЧАСТНИКАМ ОТ ЛЮБЫХ ПРЕТЕНЗИЙ ИЛИ ТРЕБОВАНИЙ, ВЫТЕКАЮЩИХ ИЛИ ПРЯМО ИЛИ КОСВЕННО ИЗ ЛЮБОГО ДОСТУПА К ИЛИ ИСПОЛЬЗОВАНИЮ КАЛЬКУЛЯТОРА И MRIL ПО ПРАВУ ВСЕМ ВОЗНАГРАЖДЕНИЯМ И РАСХОДАМ АДВОКАТОВ, А ТАКЖЕ КОСВЕННЫМ УБЫТКАМ, ВЫТЕКАЮЩИМ ИЛИ ПОНЕСЕННЫМ В СВЯЗИ С ПРИМЕНЕНИЕМ НАСТОЯЩЕГО ПОЛОЖЕНИЯ О ВОЗМЕЩЕНИИ, ПРАВ, ЕГО ОБЕСПЕЧИВАЮЩИХ, И/ИЛИ НАСТОЯЩИМ СОГЛАШЕНИЕМ ИЛИ ПРАВАМИ.
ВЫ ПРИЗНАЕТЕ И СОГЛАШАЕТЕСЬ С ТЕМ, ЧТО (1) ВСЕ ОПРЕДЕЛЕНИЯ, КАСАЮЩИЕСЯ СООТВЕТСТВИЯ ПРОЕКТУ СИСТЕМЫ, ЯВЛЯЮТСЯ ВАШЕЙ ОТВЕТСТВЕННОСТЬЮ; (2) ПРОЕКТИРОВАНИЕ СИСТЕМ, КОТОРОЕ НЕ УЧИТЫВАЕТ ЗДАНИЕ, КРЫШУ И ПРОЕКТ И КОНСТРУКЦИЮ (ВКЛЮЧАЯ КОНКРЕТНЫЕ ПЕРЕМЕННЫЕ ПРОЕКТА), МОЖЕТ БЫТЬ И, ВЕРОЯТНО, НЕДОСТАТОЧНО; И (3) НАСТОЯЩИМ ОТКАЗЫВАЮТСЯ ОТ ЛЮБЫХ ПРЕТЕНЗИЙ, КОТОРЫЕ МОГУТ ПОДАТЬ ИЛИ ЛЮБЫМ ИЗ ЕЕ КОНСУЛЬТАНТОВ, АФФИЛИРОВАННЫХ СТРАХОВЫХ ЛИЦ, АДВОКАТОВ ИЛИ ЛЮБЫМ ЛИЦАМ, СВЯЗАННЫМ С ЛЮБЫМ ИЗ НИХ, И ВЫ ОБЯЗУЕТЕСЬ НЕ ПОДАТЬ ИСК В ОТНОШЕНИИ НИХ. ЗА ЛЮБОЕ ДЕЙСТВИЕ ИЛИ БЕЗДЕЙСТВИЕ ИЛИ ИСПОЛЬЗОВАНИЕ ВЕБ-САЙТА. ВЫ СОГЛАШАЕТЕСЬ И НАСТОЯЩИМ ОБЯЗАТЕЛЬНО ВОЗМЕЩАЕТЕ MRIL, ЕЕ АГЕНТАМ, ДОЛЖНОСТНЫМ ЛИЦАМ, ДИРЕКТОРАМ, АДВОКАТАМ, СТРАХОВЩИКАМ И ВСЕМ УЧАСТНИКАМ ОТ ЛЮБЫХ ПРЕТЕНЗИЙ ИЛИ ТРЕБОВАНИЙ, ВЫТЕКАЮЩИХ ИЛИ ПРЯМО ИЛИ КОСВЕННО ИЗ ЛЮБОГО ДОСТУПА К ИЛИ ИСПОЛЬЗОВАНИЮ КАЛЬКУЛЯТОРА И MRIL ПО ПРАВУ ВСЕМ ВОЗНАГРАЖДЕНИЯМ И РАСХОДАМ АДВОКАТОВ, А ТАКЖЕ КОСВЕННЫМ УБЫТКАМ, ВЫТЕКАЮЩИМ ИЛИ ПОНЕСЕННЫМ В СВЯЗИ С ПРИМЕНЕНИЕМ НАСТОЯЩЕГО ПОЛОЖЕНИЯ О ВОЗМЕЩЕНИИ, ПРАВ, ЕГО ОБЕСПЕЧИВАЮЩИХ, И/ИЛИ НАСТОЯЩИМ СОГЛАШЕНИЕМ ИЛИ ПРАВАМИ. MRIL НЕ ДАЕТ НИКАКИХ ГАРАНТИЙ ИЛИ ЗАЯВЛЕНИЙ, ЯВНЫХ ИЛИ ПОДРАЗУМЕВАЕМЫХ В ОТНОШЕНИИ КАЛЬКУЛЯТОРА. ИСПОЛЬЗОВАНИЕ КАЛЬКУЛЯТОРА ОСУЩЕСТВЛЯЕТСЯ НА РИСК ПОЛЬЗОВАТЕЛЯ, И ОН ПРЕДОСТАВЛЯЕТСЯ НА УСЛОВИЯХ «КАК ЕСТЬ», «ГДЕ ЕСТЬ» И «СО ВСЕМИ ОШИБКАМИ». НЕТ ПОДРАЗУМЕВАЕМЫХ ГАРАНТИЙ, И ВСЕ ПРЕДПОЛАГАЕМЫЕ СУЩЕСТВУЮЩИЕ ПОДРАЗУМЕВАЕМЫЕ ГАРАНТИИ, ВКЛЮЧАЯ ПОДРАЗУМЕВАЕМЫЕ ГАРАНТИИ КОММЕРЧЕСКОЙ ПРИГОДНОСТИ И ПРИГОДНОСТИ ДЛЯ ОПРЕДЕЛЕННОЙ ЦЕЛИ, НАСТОЯЩИМ ЯВНО ИСКЛЮЧАЮТСЯ И ОТКАЗЫВАЮТСЯ И НЕ БУДУТ ПРИНЯТЫ В СИЛУ ПОЛЬЗОВАТЕЛЕМ. КОМПАНИЯ MRIL НЕ ЗАЯВЛЯЕТ, НЕ ГАРАНТИРУЕТ И УТВЕРЖДАЕТ, ЧТО КАЛЬКУЛЯТОР НЕ ЯВЛЯЕТСЯ (1) БЕЗОШИБОЧНЫМ, (2) ДОСТУПНЫМ ДЛЯ ИСПОЛЬЗОВАНИЯ, (3) БЕЗОПАСНЫМ, (4) РАБОТОСПОСОБНЫМ ИЛИ ФУНКЦИОНАЛЬНЫМ ИЛИ (5) СПОСОБНЫМ ОТВЕЧАТЬ ТРЕБОВАНИЯМ ЛЮБОЙ ПОЛЬЗОВАТЕЛЬ. ПРЕДУПРЕЖДЕНИЕ! ВЫ МОЖЕТЕ ПОЛУЧИТЬ СЕРТИФИКАТ ОТ КВАЛИФИЦИРОВАННОГО СПЕЦИАЛИСТА В ОТНОШЕНИИ ИНФОРМАЦИИ, ПРЕДОСТАВЛЯЕМОЙ КАЛЬКУЛЯТОРОМ, НО ЛЮБОЙ ТАКОЙ СЕРТИФИКАТ ОГРАНИЧИВАЕТСЯ ТОЧНОСТЬЮ ИНФОРМАЦИИ, ИСПОЛЬЗУЕМОЙ И ОЦЕНЯЕМОЙ КВАЛИФИЦИРОВАННЫМ СПЕЦИАЛИСТОМ, А НЕ НА ИНФОРМАЦИИ, ПРЕДОСТАВЛЯЕМОЙ КАЛЬКУЛЯТОРУ ИЛИ ЕГО.
MRIL НЕ ДАЕТ НИКАКИХ ГАРАНТИЙ ИЛИ ЗАЯВЛЕНИЙ, ЯВНЫХ ИЛИ ПОДРАЗУМЕВАЕМЫХ В ОТНОШЕНИИ КАЛЬКУЛЯТОРА. ИСПОЛЬЗОВАНИЕ КАЛЬКУЛЯТОРА ОСУЩЕСТВЛЯЕТСЯ НА РИСК ПОЛЬЗОВАТЕЛЯ, И ОН ПРЕДОСТАВЛЯЕТСЯ НА УСЛОВИЯХ «КАК ЕСТЬ», «ГДЕ ЕСТЬ» И «СО ВСЕМИ ОШИБКАМИ». НЕТ ПОДРАЗУМЕВАЕМЫХ ГАРАНТИЙ, И ВСЕ ПРЕДПОЛАГАЕМЫЕ СУЩЕСТВУЮЩИЕ ПОДРАЗУМЕВАЕМЫЕ ГАРАНТИИ, ВКЛЮЧАЯ ПОДРАЗУМЕВАЕМЫЕ ГАРАНТИИ КОММЕРЧЕСКОЙ ПРИГОДНОСТИ И ПРИГОДНОСТИ ДЛЯ ОПРЕДЕЛЕННОЙ ЦЕЛИ, НАСТОЯЩИМ ЯВНО ИСКЛЮЧАЮТСЯ И ОТКАЗЫВАЮТСЯ И НЕ БУДУТ ПРИНЯТЫ В СИЛУ ПОЛЬЗОВАТЕЛЕМ. КОМПАНИЯ MRIL НЕ ЗАЯВЛЯЕТ, НЕ ГАРАНТИРУЕТ И УТВЕРЖДАЕТ, ЧТО КАЛЬКУЛЯТОР НЕ ЯВЛЯЕТСЯ (1) БЕЗОШИБОЧНЫМ, (2) ДОСТУПНЫМ ДЛЯ ИСПОЛЬЗОВАНИЯ, (3) БЕЗОПАСНЫМ, (4) РАБОТОСПОСОБНЫМ ИЛИ ФУНКЦИОНАЛЬНЫМ ИЛИ (5) СПОСОБНЫМ ОТВЕЧАТЬ ТРЕБОВАНИЯМ ЛЮБОЙ ПОЛЬЗОВАТЕЛЬ. ПРЕДУПРЕЖДЕНИЕ! ВЫ МОЖЕТЕ ПОЛУЧИТЬ СЕРТИФИКАТ ОТ КВАЛИФИЦИРОВАННОГО СПЕЦИАЛИСТА В ОТНОШЕНИИ ИНФОРМАЦИИ, ПРЕДОСТАВЛЯЕМОЙ КАЛЬКУЛЯТОРОМ, НО ЛЮБОЙ ТАКОЙ СЕРТИФИКАТ ОГРАНИЧИВАЕТСЯ ТОЧНОСТЬЮ ИНФОРМАЦИИ, ИСПОЛЬЗУЕМОЙ И ОЦЕНЯЕМОЙ КВАЛИФИЦИРОВАННЫМ СПЕЦИАЛИСТОМ, А НЕ НА ИНФОРМАЦИИ, ПРЕДОСТАВЛЯЕМОЙ КАЛЬКУЛЯТОРУ ИЛИ ЕГО.
 эскалация или деэскалация.
эскалация или деэскалация. Прежде чем вы начнете отслеживать успехи и неудачи, ваша команда должна быть в курсе того, что именно вы отслеживаете, и убедиться, что все понимают, что они говорят об одном и том же.
Прежде чем вы начнете отслеживать успехи и неудачи, ваша команда должна быть в курсе того, что именно вы отслеживаете, и убедиться, что все понимают, что они говорят об одном и том же.

 Он включает в себя как время ремонта, так и любое время тестирования. Часы не останавливаются на этом показателе, пока система снова не станет полностью функциональной.
Он включает в себя как время ремонта, так и любое время тестирования. Часы не останавливаются на этом показателе, пока система снова не станет полностью функциональной.
 Потому что между неудачей и восстановлением происходит не одно и то же.
Потому что между неудачей и восстановлением происходит не одно и то же. Сюда входит не только время, затраченное на обнаружение сбоя, диагностику проблемы и ее устранение, но и время, затраченное на то, чтобы сбой не повторился.
Сюда входит не только время, затраченное на обнаружение сбоя, диагностику проблемы и ее устранение, но и время, затраченное на то, чтобы сбой не повторился. Всего потрачено на решение проблемы. Это означает, что ваш MTTR составляет четыре часа.
Всего потрачено на решение проблемы. Это означает, что ваш MTTR составляет четыре часа. Это не включает время задержки в вашей системе предупреждений.
Это не включает время задержки в вашей системе предупреждений.

 И поэтому метрика ломается в таких случаях.
И поэтому метрика ломается в таких случаях.
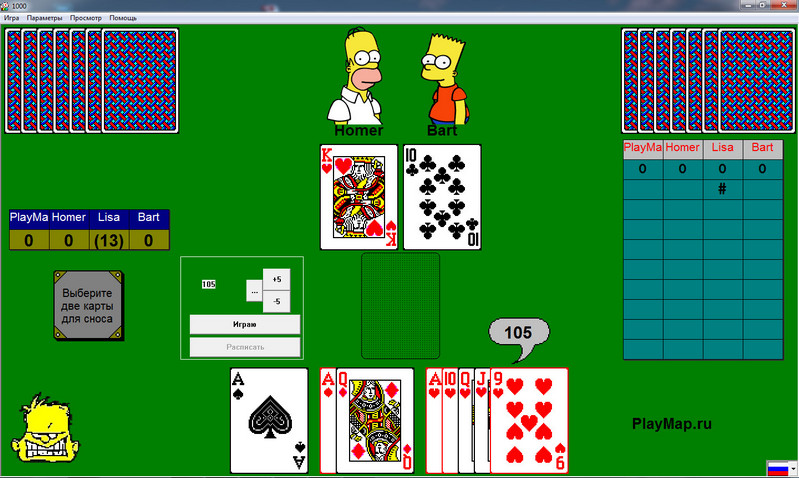 После того, как участник взял взятку, он может объявить козырный марьяж. Оценивание марьяжа зависит от масти (пиковый — 40, трефовый — 60, бубновый — 80, червовый — 100). Интересно, что все марьяжи, кроме пикового, имеют название “хваленка”. Пиковый же называют “гнилью”, т.к. много очков на нем не заработаешь.
После того, как участник взял взятку, он может объявить козырный марьяж. Оценивание марьяжа зависит от масти (пиковый — 40, трефовый — 60, бубновый — 80, червовый — 100). Интересно, что все марьяжи, кроме пикового, имеют название “хваленка”. Пиковый же называют “гнилью”, т.к. много очков на нем не заработаешь.

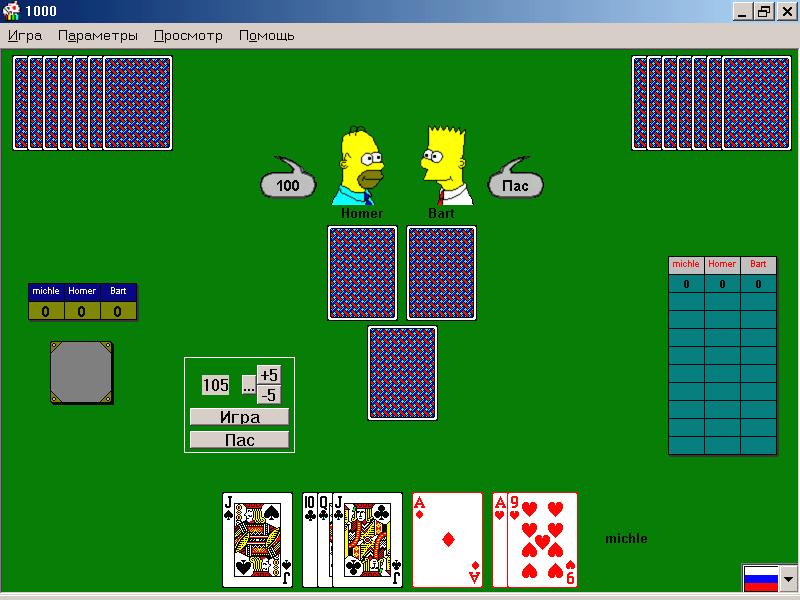
 В каждом раунде есть игрок, который обязан набрать минимум 100 очков. Такой игрок называется «сидящий на сотне»
Принудительная ставка в 100 очков передается между игроками по часовой стрелке с на каждом раунде.
В каждом раунде есть игрок, который обязан набрать минимум 100 очков. Такой игрок называется «сидящий на сотне»
Принудительная ставка в 100 очков передается между игроками по часовой стрелке с на каждом раунде. Объявление марьяжа при первом ходе невозможно.
Марьяж можно объявить первым ходом, имея на руках хотя бы одну взятку. Объявления марьяжа влечет за собою получения очков, в соответствии с номиналом марьяжа и установку козырей, соответсвующей масти.
Внимание, если на руках у игрока нет взяток, но он ходит с одной из карт марьяжа, то такой ход допустим, но объявления марьяжа и, соответсвенно, козырей не происходит.
Объявление марьяжа не происходит, если игрок вынужден скинуть одну из карт марьяжа.
Объявление марьяжа при первом ходе невозможно.
Марьяж можно объявить первым ходом, имея на руках хотя бы одну взятку. Объявления марьяжа влечет за собою получения очков, в соответствии с номиналом марьяжа и установку козырей, соответсвующей масти.
Внимание, если на руках у игрока нет взяток, но он ходит с одной из карт марьяжа, то такой ход допустим, но объявления марьяжа и, соответсвенно, козырей не происходит.
Объявление марьяжа не происходит, если игрок вынужден скинуть одну из карт марьяжа. Очки складываются из номиналов карт, которые игрок взял за раунд, и номиналов объявленных игроком марьяжей.
Игрок, заказавший игру, обязан набрать не меньше очков, чем он заказал. В противном случае с него списывается очки в размере заказанной игры
Игрок не взявший ни одной взятки, получает «палку», если игрок набрал три «палки», то его штрафуют на 120 очков.
Очки складываются из номиналов карт, которые игрок взял за раунд, и номиналов объявленных игроком марьяжей.
Игрок, заказавший игру, обязан набрать не меньше очков, чем он заказал. В противном случае с него списывается очки в размере заказанной игры
Игрок не взявший ни одной взятки, получает «палку», если игрок набрал три «палки», то его штрафуют на 120 очков. При этом при двух неудачных попытках ему не начисляются штрафные очки.
При этом при двух неудачных попытках ему не начисляются штрафные очки. 
 е. такой марьяж нельзя объявить на первом ходе.
е. такой марьяж нельзя объявить на первом ходе.

 , Спортивные игры и Лучшие игры, BuzzMavo предоставляет вам все необходимое.
, Спортивные игры и Лучшие игры, BuzzMavo предоставляет вам все необходимое.


 com предлагает вам отличные автомобильные игры, специально созданные для вас, такие как Parking Fury 3D , Extreme OffRoad Cars 2 и множество парковочных игр. У нас есть идеальная игра для вас!
com предлагает вам отличные автомобильные игры, специально созданные для вас, такие как Parking Fury 3D , Extreme OffRoad Cars 2 и множество парковочных игр. У нас есть идеальная игра для вас! А с новыми играми, которые регулярно добавляются, вы всегда найдете что-то новое и интересное для игры.
А с новыми играми, которые регулярно добавляются, вы всегда найдете что-то новое и интересное для игры. Благодаря потрясающей графике и захватывающему геймплею эта игра будет развлекать вас часами подряд. А если вы ищете что-то более образовательное, ознакомьтесь с нашими математическими играми для детских площадок. Эти игры — отличный способ улучшить свои математические навыки и в то же время весело провести время.
Благодаря потрясающей графике и захватывающему геймплею эта игра будет развлекать вас часами подряд. А если вы ищете что-то более образовательное, ознакомьтесь с нашими математическими играми для детских площадок. Эти игры — отличный способ улучшить свои математические навыки и в то же время весело провести время. Вот почему мы предлагаем наш контент на нескольких языках, включая английский, испанский, французский, португальский, турецкий и русский. Мы считаем, что это облегчит людям со всего мира возможность наслаждаться нашими играми и общаться друг с другом. Мы постоянно работаем над улучшением нашего веб-сайта и предоставлением наилучших возможностей для наших пользователей. В будущем мы планируем добавить еще больше языков на нашу платформу, чтобы еще больше людей могли присоединиться к нашему сообществу и наслаждаться нашими играми. Независимо от того, являетесь ли вы носителем языка или изучаете новый язык, наш веб-сайт предлагает отличный способ попрактиковаться в своих навыках и в то же время повеселиться. Поэтому, если вы ищете разблокированные бесплатные игры, в которые вы можете играть в любое время и в любом месте, вам подойдет наш веб-сайт. С такими играми, как unblocked games 76, трехмерными гоночными играми и Lows Adventure 2, а также образовательными играми, такими как математическая площадка, каждый найдет что-то для себя.
Вот почему мы предлагаем наш контент на нескольких языках, включая английский, испанский, французский, португальский, турецкий и русский. Мы считаем, что это облегчит людям со всего мира возможность наслаждаться нашими играми и общаться друг с другом. Мы постоянно работаем над улучшением нашего веб-сайта и предоставлением наилучших возможностей для наших пользователей. В будущем мы планируем добавить еще больше языков на нашу платформу, чтобы еще больше людей могли присоединиться к нашему сообществу и наслаждаться нашими играми. Независимо от того, являетесь ли вы носителем языка или изучаете новый язык, наш веб-сайт предлагает отличный способ попрактиковаться в своих навыках и в то же время повеселиться. Поэтому, если вы ищете разблокированные бесплатные игры, в которые вы можете играть в любое время и в любом месте, вам подойдет наш веб-сайт. С такими играми, как unblocked games 76, трехмерными гоночными играми и Lows Adventure 2, а также образовательными играми, такими как математическая площадка, каждый найдет что-то для себя.

 Решение уравнений с модулем
Решение уравнений с модулем


 Это примеры уравнений, которые вы, возможно, видели.
Это примеры уравнений, которые вы, возможно, видели.
 Интерактив откроется в новой вкладке или окне браузера. Если вам нужно, нажимайте «Новая проблема», пока не получите двухшаговое уравнение или уравнение вида 9.0037 ах + б = с . Используйте следующие шаги, чтобы помочь вам перемещаться по интерактивному интерфейсу, когда вы настраиваете и решаете данное уравнение.
Интерактив откроется в новой вкладке или окне браузера. Если вам нужно, нажимайте «Новая проблема», пока не получите двухшаговое уравнение или уравнение вида 9.0037 ах + б = с . Используйте следующие шаги, чтобы помочь вам перемещаться по интерактивному интерфейсу, когда вы настраиваете и решаете данное уравнение. Если вам нужны дополнительные указания, см. ниже.
Если вам нужны дополнительные указания, см. ниже.
 В этом разделе вы будете использовать и исследовать третью модель — плитки алгебры.
В этом разделе вы будете использовать и исследовать третью модель — плитки алгебры.
 Поскольку выражения должны иметь эквивалентные значения, шкала должна быть сбалансирована. Любые изменения, внесенные в одно выражение, также должны быть внесены в другое, чтобы сохранить баланс.
Поскольку выражения должны иметь эквивалентные значения, шкала должна быть сбалансирована. Любые изменения, внесенные в одно выражение, также должны быть внесены в другое, чтобы сохранить баланс.









 Теперь мы будем использовать уравнения для решения прикладных задач. Мы начнем с того, что переформулируем задачу всего в одном предложении, назначим переменную, а затем переведем предложение в уравнение, которое нужно решить. При назначении переменной выберите букву, которая напоминает вам о том, что вы ищете.
Теперь мы будем использовать уравнения для решения прикладных задач. Мы начнем с того, что переформулируем задачу всего в одном предложении, назначим переменную, а затем переведем предложение в уравнение, которое нужно решить. При назначении переменной выберите букву, которая напоминает вам о том, что вы ищете.
 Вместе у них есть книги. У Сэма есть книги. Сколько книг у Генри?
Вместе у них есть книги. У Сэма есть книги. Сколько книг у Генри?
 Это меньше, чем цена в ночное время. Сколько стоит фильм ночью?
Это меньше, чем цена в ночное время. Сколько стоит фильм ночью?
 На три меньше, чем есть.
На три меньше, чем есть. Сколько лет ее дочери?
Сколько лет ее дочери? Учебник по математике Мелиссы стоил меньше, чем стоил ее учебник по искусству. Ее учебник по математике стоил . Сколько стоила ее художественная книга?
Учебник по математике Мелиссы стоил меньше, чем стоил ее учебник по искусству. Ее учебник по математике стоил . Сколько стоила ее художественная книга?

 Например: стол, компьютер, лук / корова, ручка, кастрюля / село, знамя, перо — это существительные, классифицированные по родам. Определите основания классификаций:
Например: стол, компьютер, лук / корова, ручка, кастрюля / село, знамя, перо — это существительные, классифицированные по родам. Определите основания классификаций:
 Разновидности объектов и их классификация
Разновидности объектов и их классификация
 д. (рис. 1.2).
д. (рис. 1.2).


 1.9). Такие схемы используются в учебниках, каталогах и энциклопедиях для описания самых разных объектов, например растений, животных, сложных предложений, транспортных средств и т. д.
1.9). Такие схемы используются в учебниках, каталогах и энциклопедиях для описания самых разных объектов, например растений, животных, сложных предложений, транспортных средств и т. д.
 Подмножества объектов выделяет и обозначает человек, потому что ему так удобнее усваивать и передавать информацию. Дело в том, что человек одновременно может концентрировать свое внимание лишь на 5-9 объектах. Для упрощения работы с множеством объектов его делят на несколько частей; каждую из этих частей опять делят на части; те, в свою очередь, еще раз и т. д. Деление большого множества на подмножества происходит не стихийно, а по некоторым признакам его объектов.
Подмножества объектов выделяет и обозначает человек, потому что ему так удобнее усваивать и передавать информацию. Дело в том, что человек одновременно может концентрировать свое внимание лишь на 5-9 объектах. Для упрощения работы с множеством объектов его делят на несколько частей; каждую из этих частей опять делят на части; те, в свою очередь, еще раз и т. д. Деление большого множества на подмножества происходит не стихийно, а по некоторым признакам его объектов.
 Каждое царство разделено на уровни — систематические единицы. Высший уровень называется типом. Каждый тип делится на классы, классы — на отряды, отряды — на семейства, семейства — на роды, а роды — на виды.
Каждое царство разделено на уровни — систематические единицы. Высший уровень называется типом. Каждый тип делится на классы, классы — на отряды, отряды — на семейства, семейства — на роды, а роды — на виды.


 С ее помощью еще раз просмотрите файлы и папки, расположенные на диске С:. Проследите за изменениями, происходящими в правой части окна.
С ее помощью еще раз просмотрите файлы и папки, расположенные на диске С:. Проследите за изменениями, происходящими в правой части окна.

 Откройте файл Описание.doc из папки Заготовки.
Откройте файл Описание.doc из папки Заготовки.

 Подведем итоги.
Подведем итоги.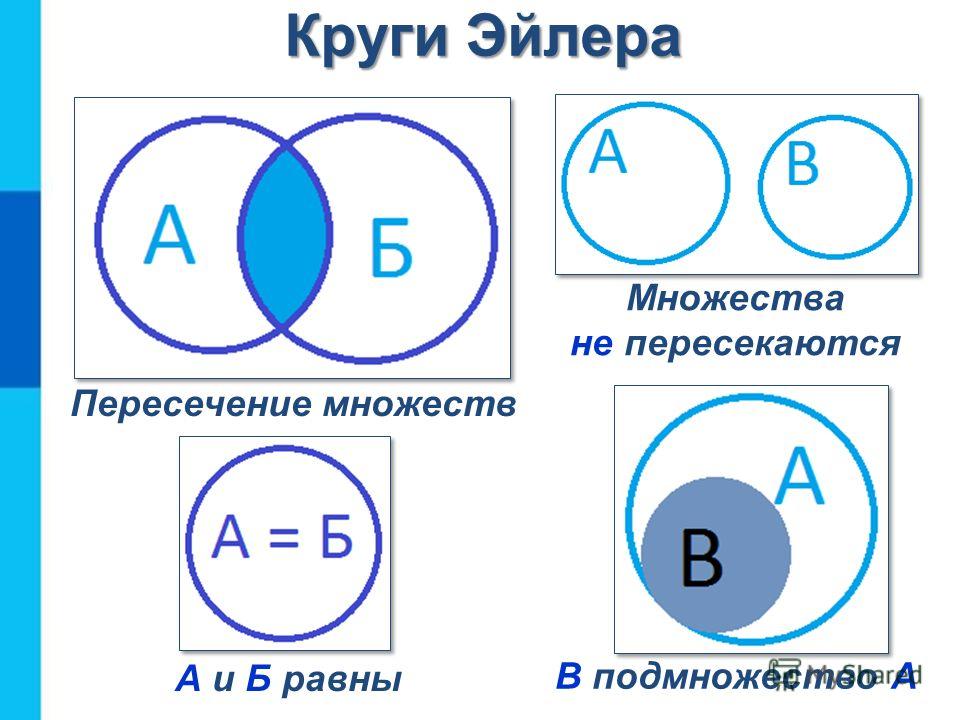 Итак, рассмотрим множество с небольшим количеством элементов. Сколько мы должны взять? Возьмем n = 1. Множество всех подмножеств {1} состоит из двух множеств — пустого множества {} и {1}. Чтобы содержать более половины всех подмножеств , B обязательно будет содержать их оба. В этом случае он явно содержит два набора, из которых один {} является подмножеством другого {1}.
Итак, рассмотрим множество с небольшим количеством элементов. Сколько мы должны взять? Возьмем n = 1. Множество всех подмножеств {1} состоит из двух множеств — пустого множества {} и {1}. Чтобы содержать более половины всех подмножеств , B обязательно будет содержать их оба. В этом случае он явно содержит два набора, из которых один {} является подмножеством другого {1}. Меньше будет
достаточно.
Меньше будет
достаточно.
 версия).
версия).

 Вы можете
хотеть
более техническое определение
.
Вы можете
хотеть
более техническое определение
. Чтобы увидеть доказательство, нажмите на
соответствующее заявление.
Чтобы увидеть доказательство, нажмите на
соответствующее заявление. Это
удивительный! Все натуральные числа являются рациональными числами,
но интуитивно большинство рациональных чисел не
натуральные числа. Так как же может быть столько
натуральные числа как бывают рациональные числа? Помещать
иначе: как любое множество может быть эквивалентно
«намного меньшее» подмножество?
Это
удивительный! Все натуральные числа являются рациональными числами,
но интуитивно большинство рациональных чисел не
натуральные числа. Так как же может быть столько
натуральные числа как бывают рациональные числа? Помещать
иначе: как любое множество может быть эквивалентно
«намного меньшее» подмножество? Это
называется кардиналом из S . Для конечных
множеств, кардинал — это просто количество элементов. Для
бесконечные множества, которые определить сложнее. Однако,
кажется, ясно, что мы имеем в виду. Мы можем думать о кардинале
как некоторая мера размера набора.
Это
называется кардиналом из S . Для конечных
множеств, кардинал — это просто количество элементов. Для
бесконечные множества, которые определить сложнее. Однако,
кажется, ясно, что мы имеем в виду. Мы можем думать о кардинале
как некоторая мера размера набора. гипотеза континуума утверждает, что такие
это не так. Правда это или ложь, не
известно, но неизвестно в более тонком смысле, чем то, что мы
просто не могу понять!
гипотеза континуума утверждает, что такие
это не так. Правда это или ложь, не
известно, но неизвестно в более тонком смысле, чем то, что мы
просто не могу понять!

 \)
\)
 \)≤1\)
\)≤1\)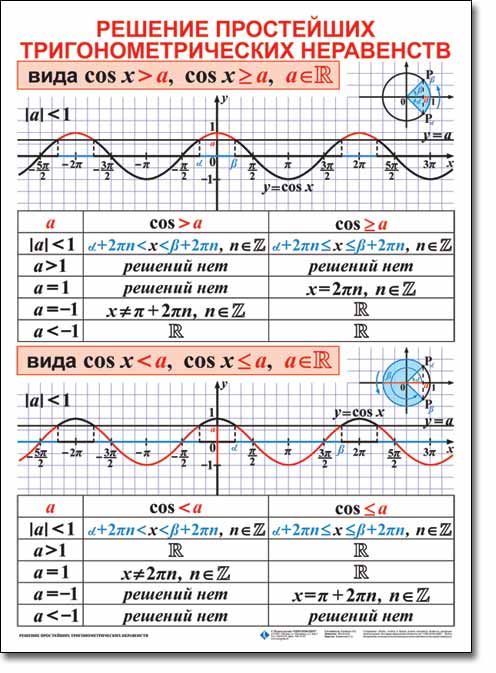 \)
\)
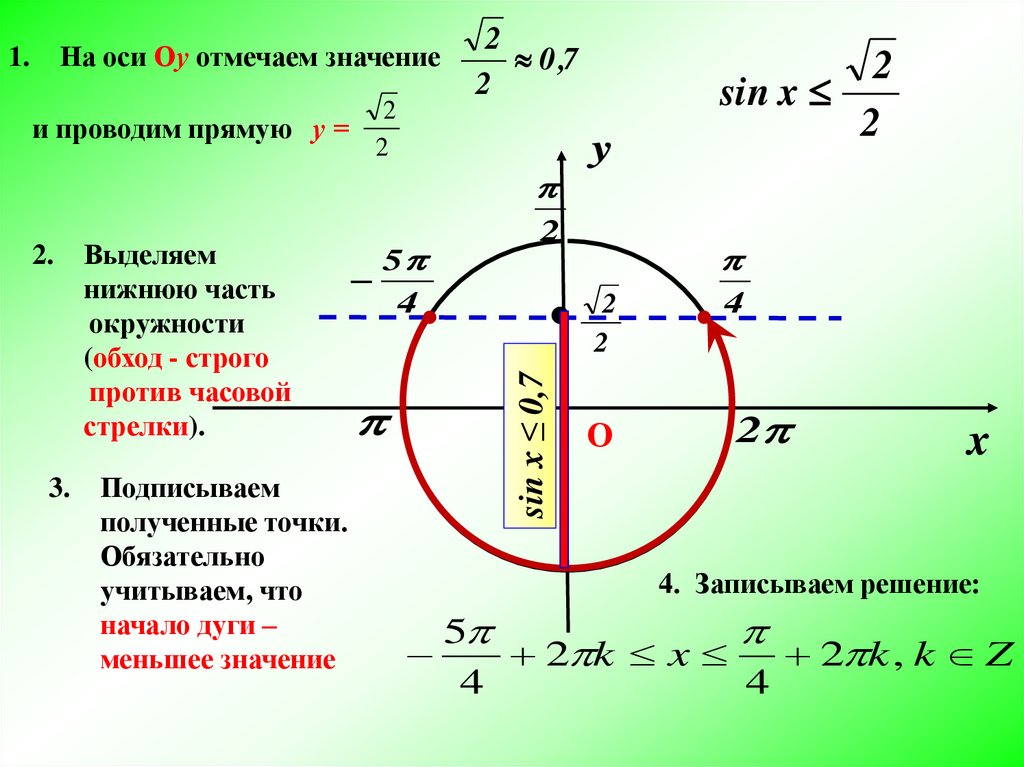
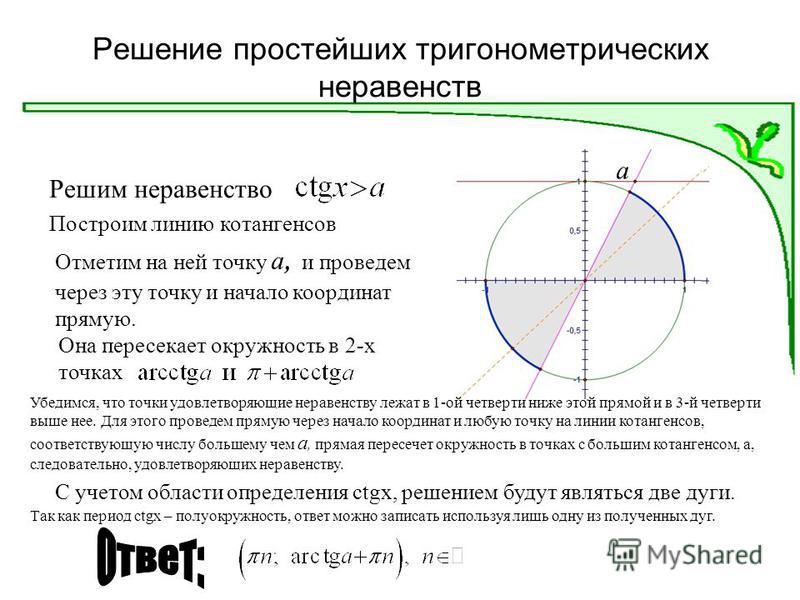 Обозначим \(P_{x_1}\ и \ P_{x_2}\) – точки пересечения прямой и единичной окружности. Решением исходного уравнения будет множество точек абсциссы, которых меньше \(\frac12\). Найдем значение \(x_1 \ и \ x_2\), совершая обход против часовой стрелки так, чтобы \(x_1<x_2\): \)
Обозначим \(P_{x_1}\ и \ P_{x_2}\) – точки пересечения прямой и единичной окружности. Решением исходного уравнения будет множество точек абсциссы, которых меньше \(\frac12\). Найдем значение \(x_1 \ и \ x_2\), совершая обход против часовой стрелки так, чтобы \(x_1<x_2\): \)
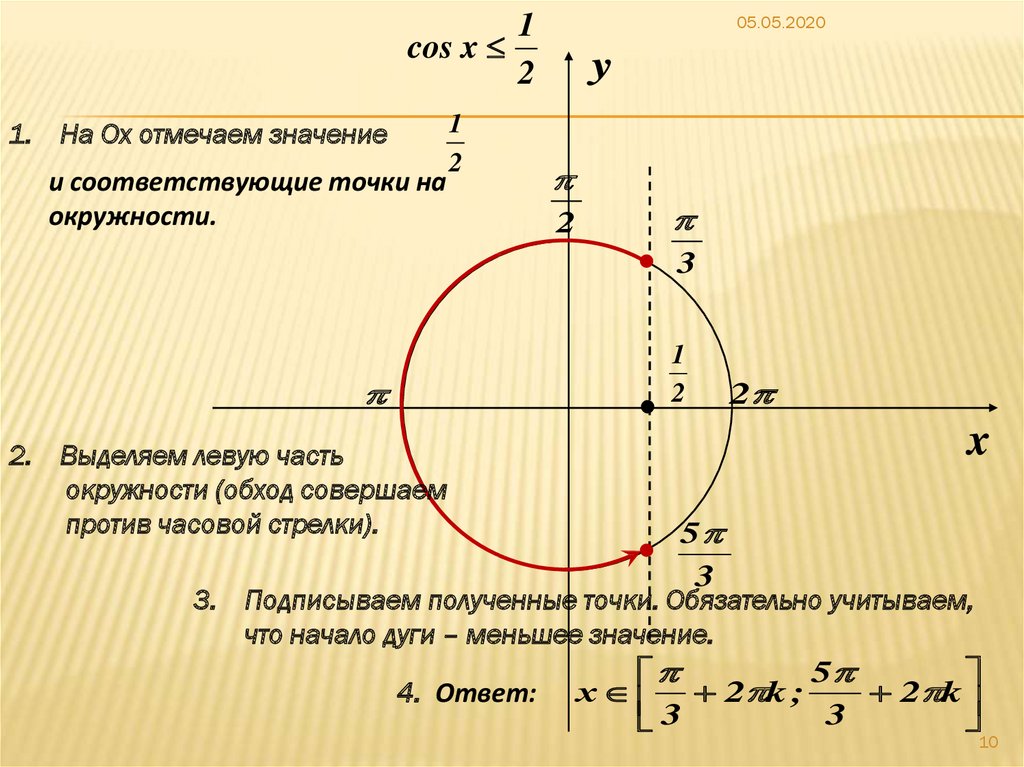
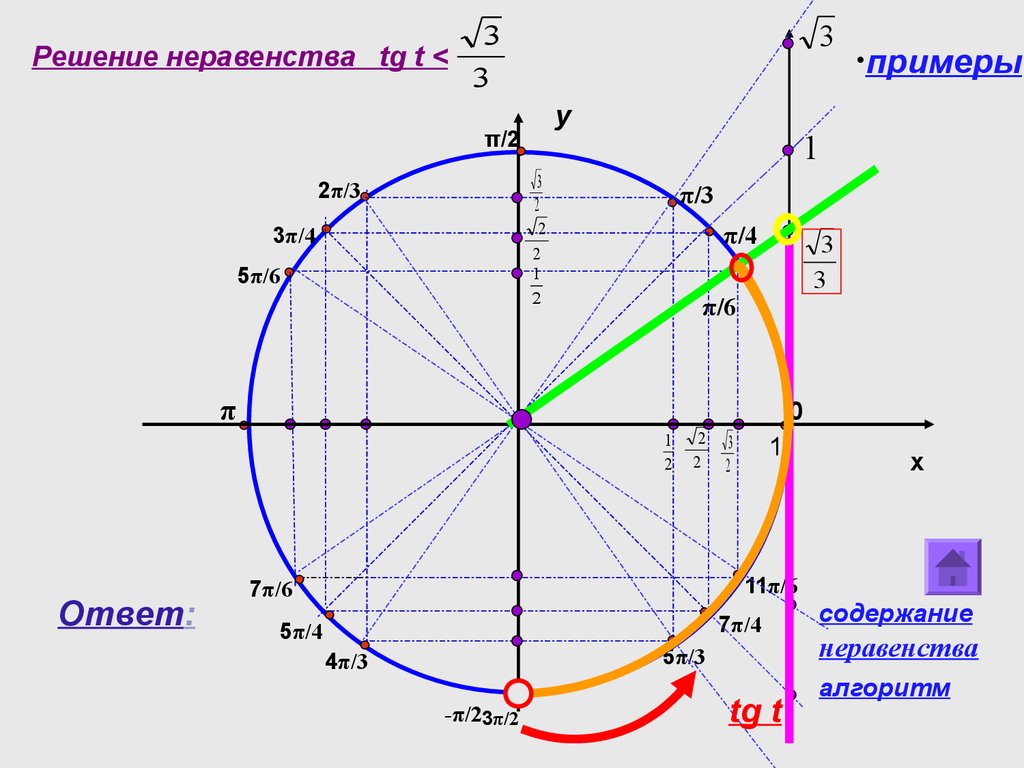
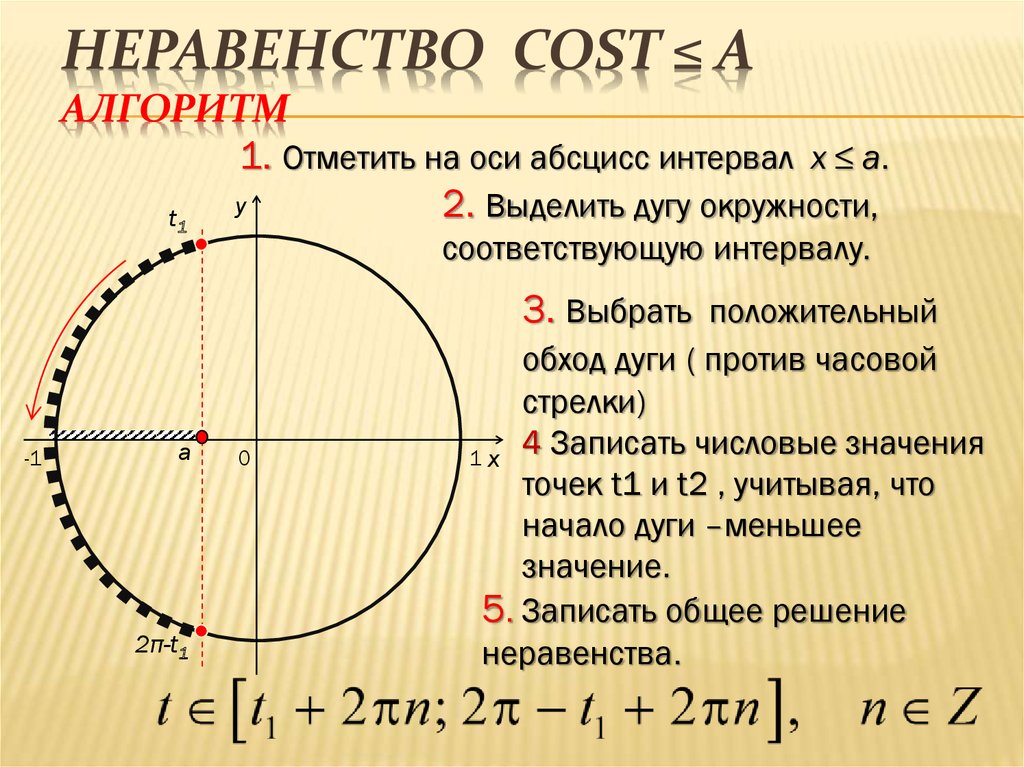
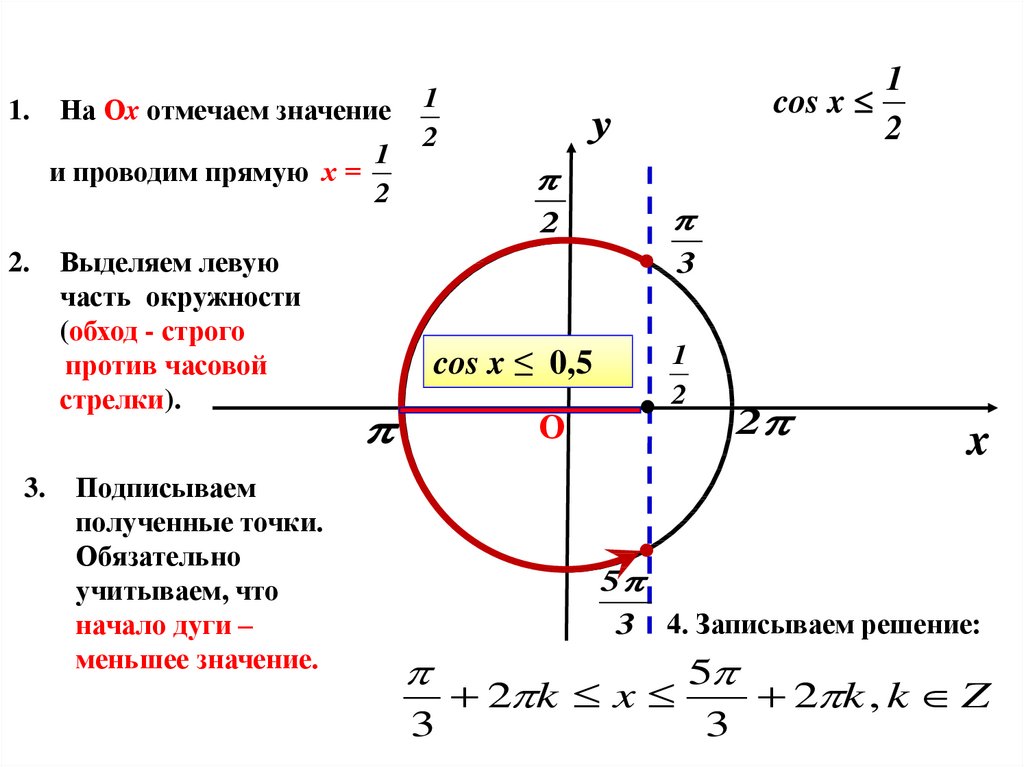 Используя следующие шаги, мы можем найти решение любого простого тригонометрического неравенства:
Используя следующие шаги, мы можем найти решение любого простого тригонометрического неравенства: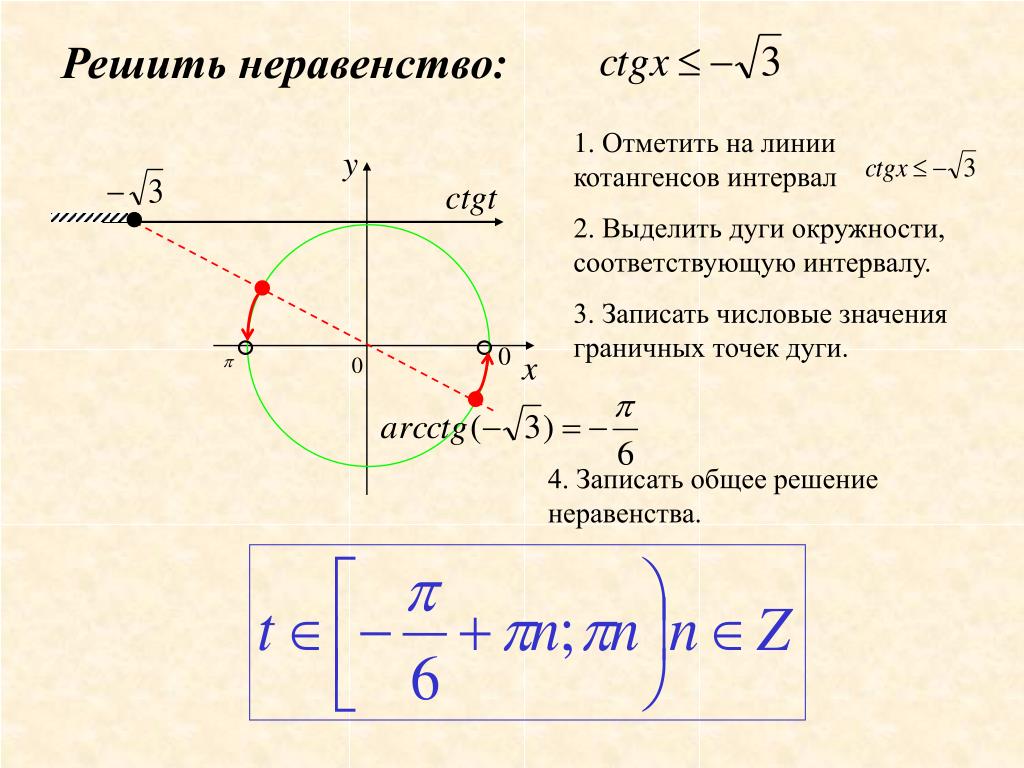

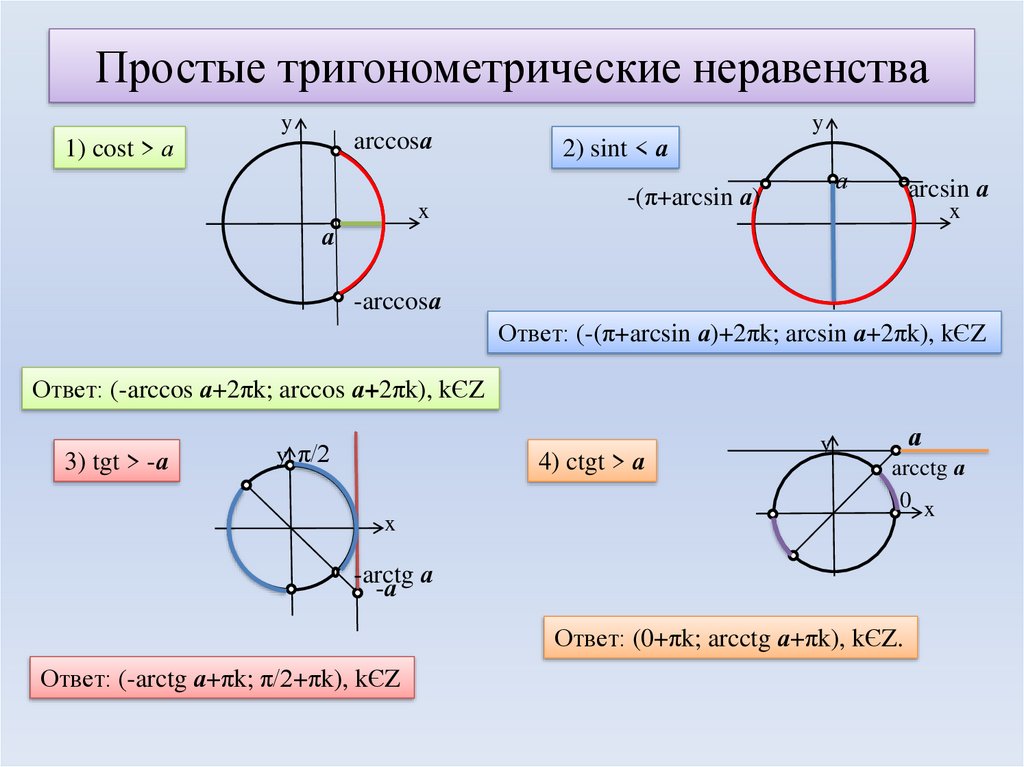

 В.Перышкин Задание №476 Изобразите силы, действующие на тело.
В.Перышкин Задание №476 Изобразите силы, действующие на тело. Укажите номера предложений, в которых сделаны ошибки, исправьте их.( 1)КореньНайдите три ошибки в тексте «Корень». Укажите номера предложений, в которых сделаны ошибки, исправьте их.( 1)Корень — осевой вегетативный орган. (2)Корень укрепляет растение в почве, всасывает из почвы воду с органическими веществами, запасает питательные вещества, осуществляет бесполое размножение и обеспечивает связь растения с бактериями и грибами, обитающими в почве. (3)Совокупность корней растения называют корневой системой. (4)Различают три вида корней: стержневой (развивается из зародышевого корешка семени), боковые (отрастают от стеблей, побегов, листьев) и придаточные (отрастают от главного и боковых корней). (5)Различают три типа корневых систем: главная (хорошо развит главный корень), мочковатая (состоит из придаточных и боковых корней) и смешанная. (6)В корне различают следующие участки: корневой чехлик, зона деления, зона роста (растяжения), зона всасывания и зона проведения. (7)В связи с изменением функций корня происходит его видоизменение; формируются корнеплоды, корневые шишки, корневые клубни, воздушные корни, клубеньки, микориза.
Укажите номера предложений, в которых сделаны ошибки, исправьте их.( 1)КореньНайдите три ошибки в тексте «Корень». Укажите номера предложений, в которых сделаны ошибки, исправьте их.( 1)Корень — осевой вегетативный орган. (2)Корень укрепляет растение в почве, всасывает из почвы воду с органическими веществами, запасает питательные вещества, осуществляет бесполое размножение и обеспечивает связь растения с бактериями и грибами, обитающими в почве. (3)Совокупность корней растения называют корневой системой. (4)Различают три вида корней: стержневой (развивается из зародышевого корешка семени), боковые (отрастают от стеблей, побегов, листьев) и придаточные (отрастают от главного и боковых корней). (5)Различают три типа корневых систем: главная (хорошо развит главный корень), мочковатая (состоит из придаточных и боковых корней) и смешанная. (6)В корне различают следующие участки: корневой чехлик, зона деления, зона роста (растяжения), зона всасывания и зона проведения. (7)В связи с изменением функций корня происходит его видоизменение; формируются корнеплоды, корневые шишки, корневые клубни, воздушные корни, клубеньки, микориза.
 Укажите номера предложений, в которых сделаны ошибки, исправьте их.
Укажите номера предложений, в которых сделаны ошибки, исправьте их.
 S.S. Для вас готово следующее случайное задание. Мы сами не знаем, но вас ждет что-то интересное!
S.S. Для вас готово следующее случайное задание. Мы сами не знаем, но вас ждет что-то интересное!



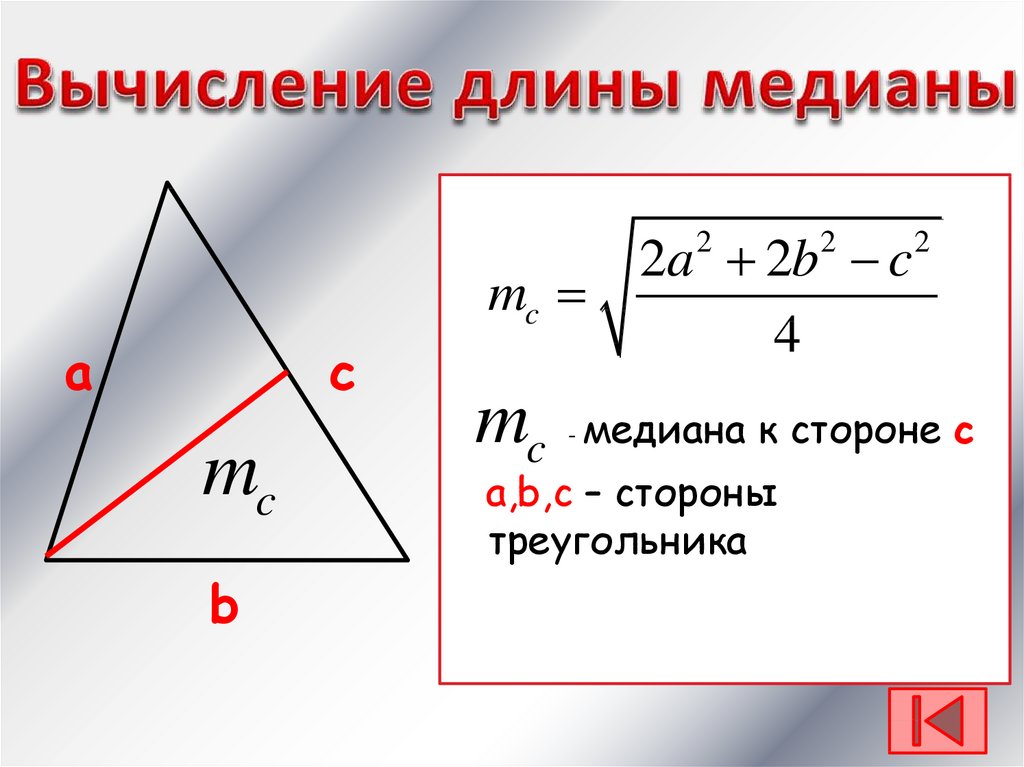
 ru Математика Геометрия Определение и свойства медианы треугольника
ru Математика Геометрия Определение и свойства медианы треугольника
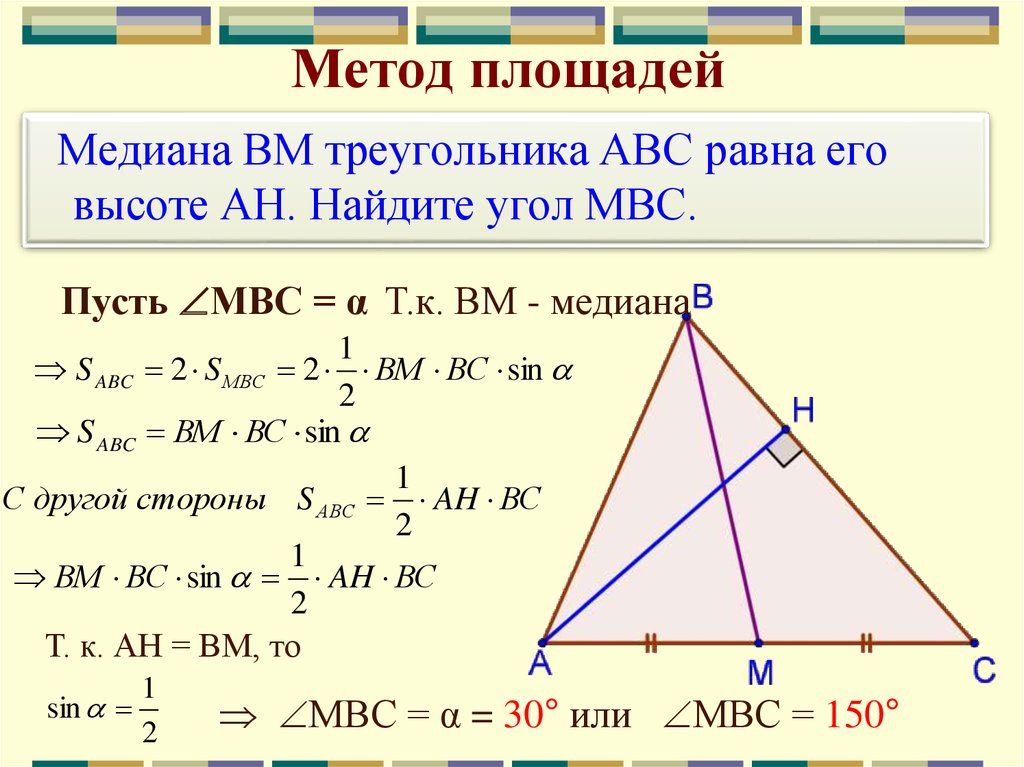
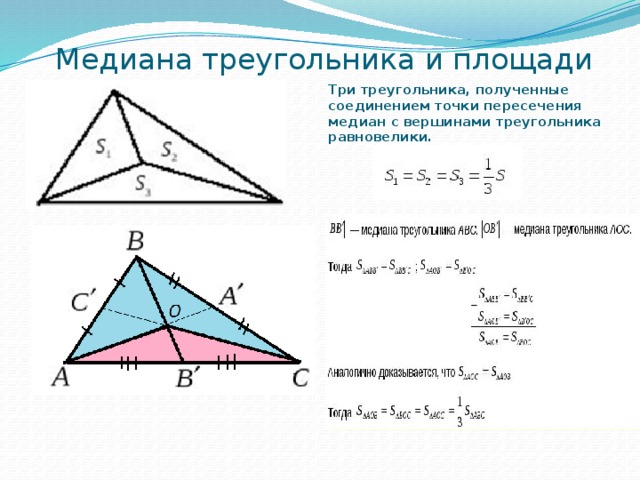 И ни один из вас не хочет получить меньший кусок. Чтобы избежать драки между вами и вашим братом из-за торта, ваша мать отрезает треугольный кусок торта от его медианы , чтобы вы оба получили одинаковый размер торта. Но что это за медиана? Как твоя мама решила, где разрезать торт?
И ни один из вас не хочет получить меньший кусок. Чтобы избежать драки между вами и вашим братом из-за торта, ваша мать отрезает треугольный кусок торта от его медианы , чтобы вы оба получили одинаковый размер торта. Но что это за медиана? Как твоя мама решила, где разрезать торт?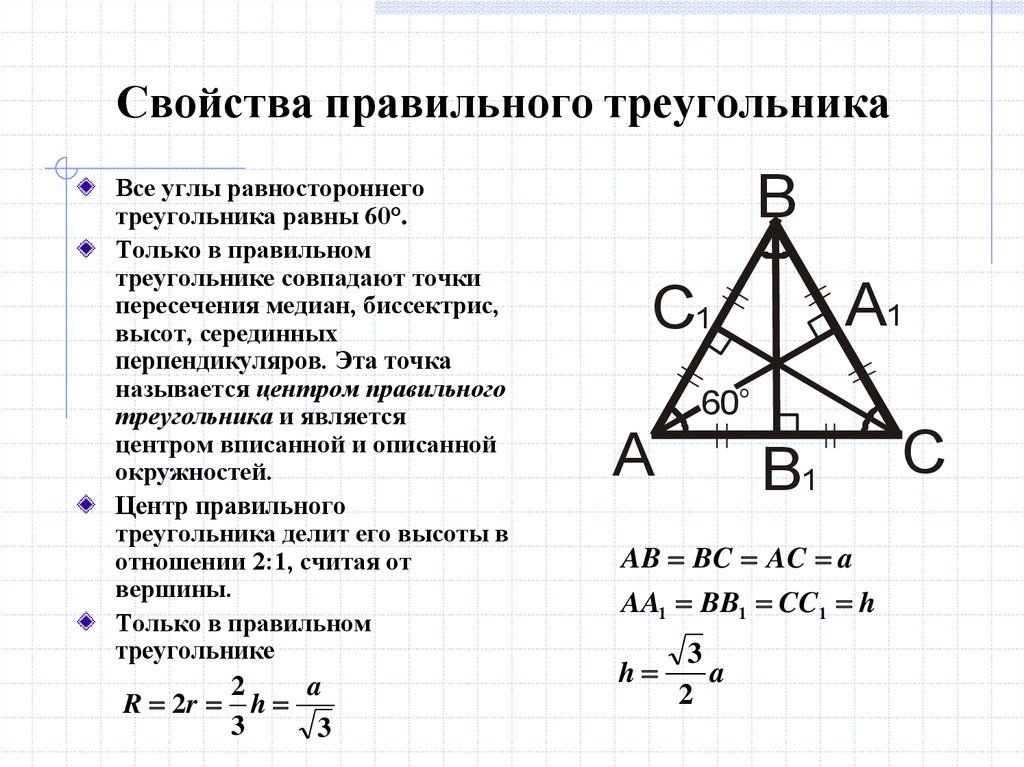 Для простоты назовем эту пиццу \(\bigtriangleup ABC\). Теперь имейте в виду, что вам нужно разделить пиццу поровну между своими друзьями. Здесь может помочь медиана .
Для простоты назовем эту пиццу \(\bigtriangleup ABC\). Теперь имейте в виду, что вам нужно разделить пиццу поровну между своими друзьями. Здесь может помочь медиана . Точка пересечения трех медиан называется центроидом . Центроид представляет собой точки параллелизма. Точка параллелизма — это точка, в которой пересекаются две или более линий. Например, точка пересечения медиан, серединных перпендикуляров и высот. Центроид всегда будет лежать внутри треугольника, в отличие от других точек параллелизма.
Точка пересечения трех медиан называется центроидом . Центроид представляет собой точки параллелизма. Точка параллелизма — это точка, в которой пересекаются две или более линий. Например, точка пересечения медиан, серединных перпендикуляров и высот. Центроид всегда будет лежать внутри треугольника, в отличие от других точек параллелизма.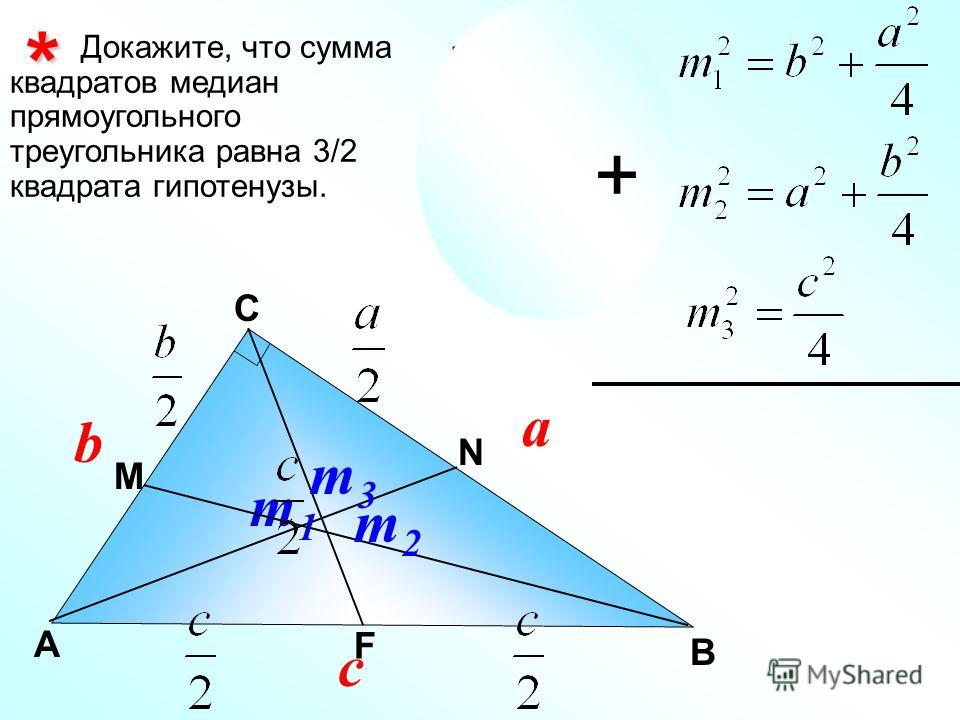


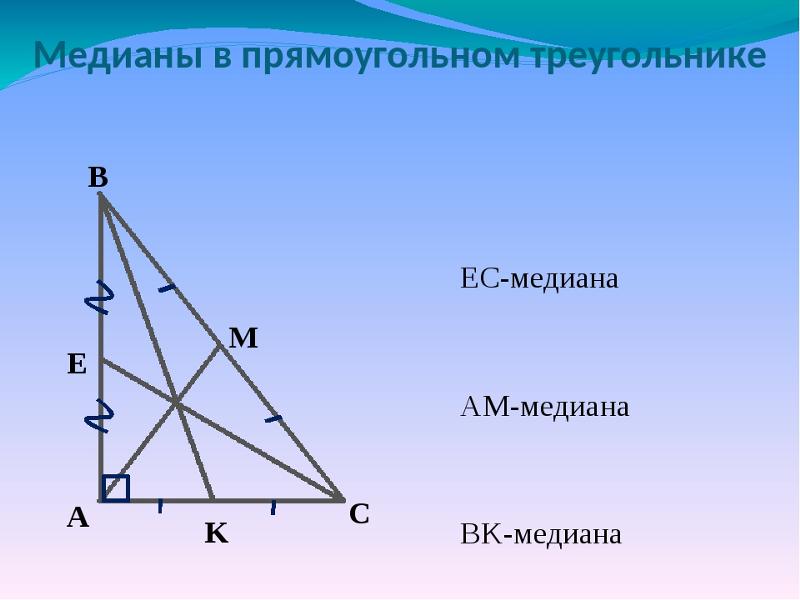
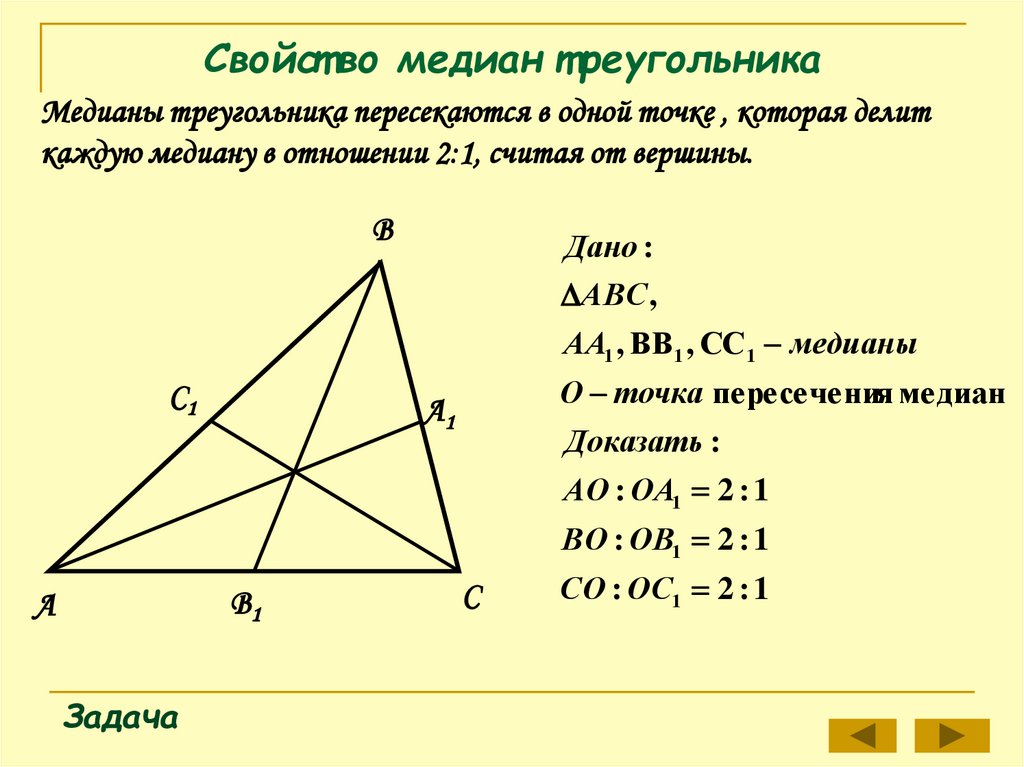
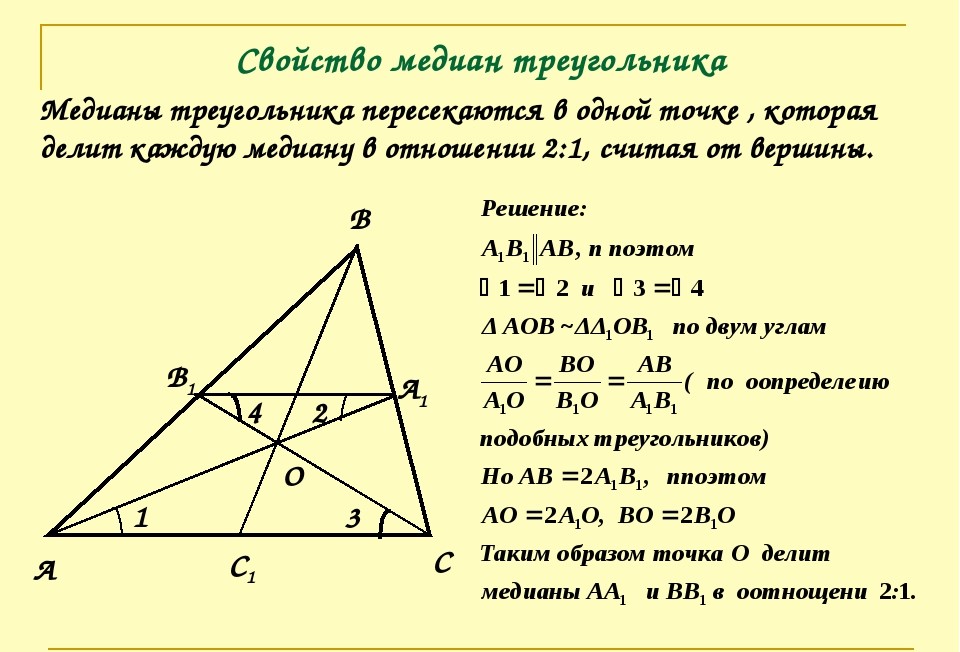

 {2}$. 9{2}=100-36=64$
{2}$. 9{2}=100-36=64$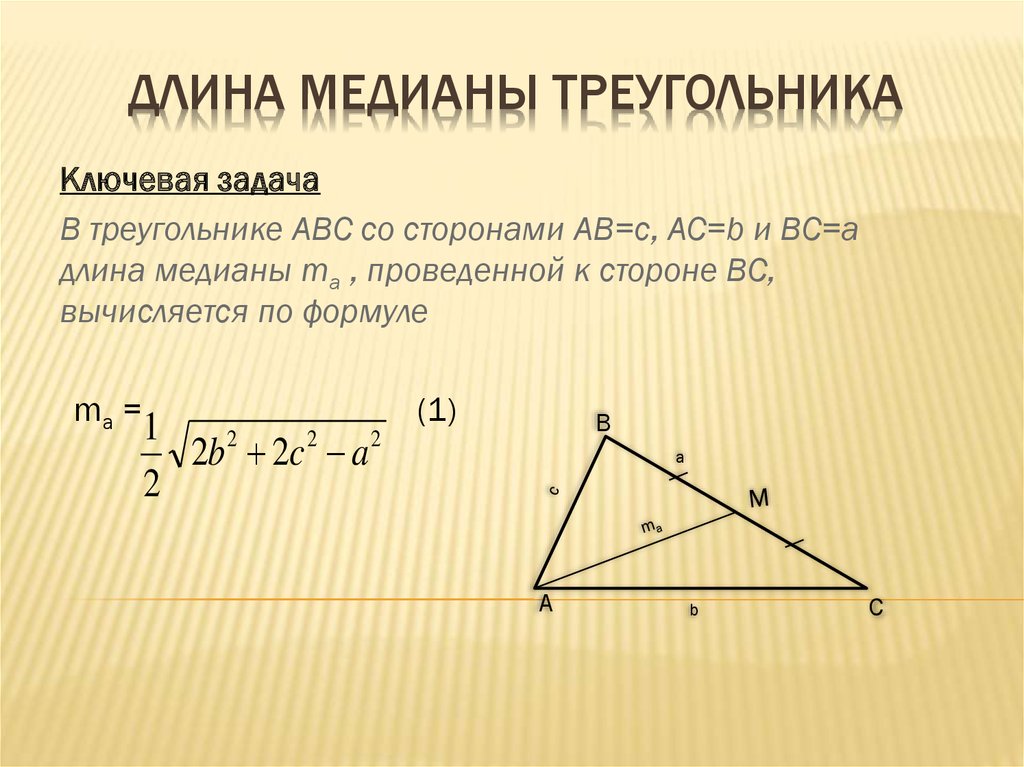
 д.
д. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. Способов разложения может быть несколько. При любом способе получается один и тот же результат.
Способов разложения может быть несколько. При любом способе получается один и тот же результат.

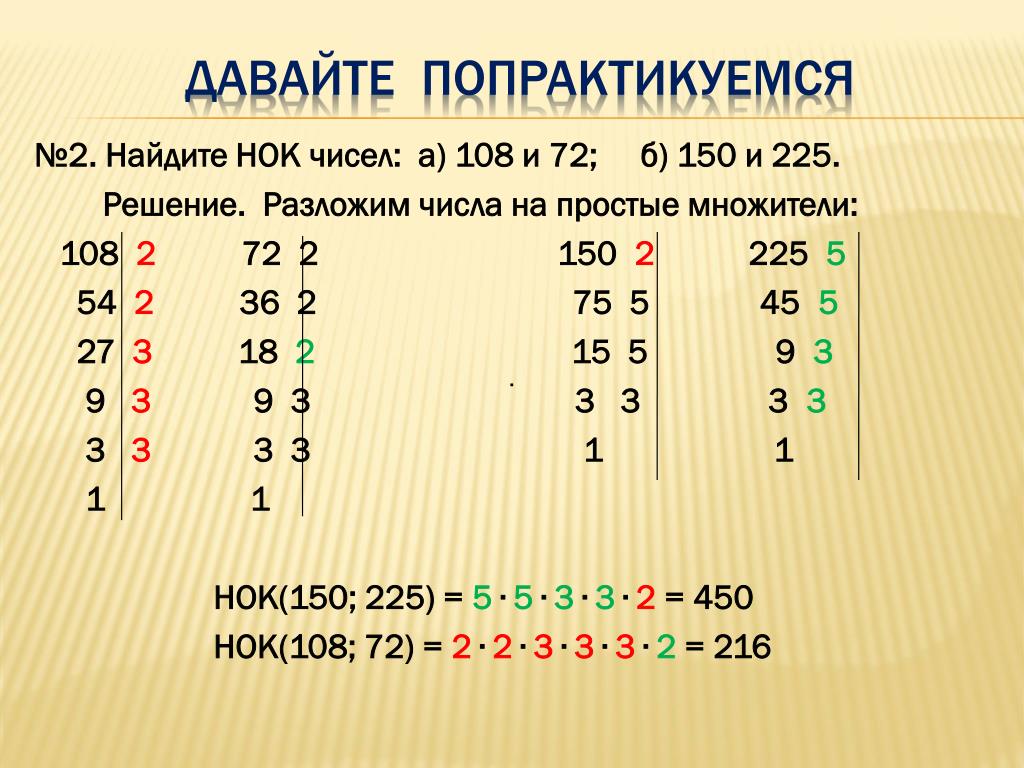 Например, 150 — это произведение чисел 5 и 30.
Например, 150 — это произведение чисел 5 и 30.
 Это так, потому что разложение числа 75 полностью содержится в разложении числа 11550.
Это так, потому что разложение числа 75 полностью содержится в разложении числа 11550. Я. За страницами учебника математики. — М.: Просвещение, 1989.
Я. За страницами учебника математики. — М.: Просвещение, 1989.
 В левой колонке запишите 2, а в правой — 819.
В левой колонке запишите 2, а в правой — 819.

 Но в задании сказано «разложить на простые множители число 24», т.е. нужны именно простые множители. А в нашем разложении 3 является простым множителем, а 8 не является простым множителем.
Но в задании сказано «разложить на простые множители число 24», т.е. нужны именно простые множители. А в нашем разложении 3 является простым множителем, а 8 не является простым множителем.

 Чтобы получить простые множители числа 6552, разделите число 6552 на наименьшие простые числа. Продолжайте процесс, пока не получите 1.
Чтобы получить простые множители числа 6552, разделите число 6552 на наименьшие простые числа. Продолжайте процесс, пока не получите 1.
 Запишите, на сколько двоек вы смогли разделить без остатка.
Теперь попробуйте разделить на следующий простой множитель, который равен 3. Цель состоит в том, чтобы получить частное 1.
Запишите, на сколько двоек вы смогли разделить без остатка.
Теперь попробуйте разделить на следующий простой множитель, который равен 3. Цель состоит в том, чтобы получить частное 1.
 Б. В.
Б. В.  (4,4; + ∞)
(4,4; + ∞) Б. В.
Б. В. ..
.. …
… ..
.. ..)
..) 1 Решение линейных неравенств
1 Решение линейных неравенств Например, решением неравенства x + 3 < 5 является множество всех значений x, меньших 2 (поскольку 5 – 3 = 2). Решением неравенства y ≥ 10 является множество всех значений y, которые больше или равны 10.
Например, решением неравенства x + 3 < 5 является множество всех значений x, меньших 2 (поскольку 5 – 3 = 2). Решением неравенства y ≥ 10 является множество всех значений y, которые больше или равны 10. Неравенства абсолютного значения можно решить, разбив их на два отдельных неравенства и решив каждое отдельно.
Неравенства абсолютного значения можно решить, разбив их на два отдельных неравенства и решив каждое отдельно.