Автор: 
- Самой функции
- Частичные суммы ряда Тейлора
Подробнее про Ряд Тейлора
.
Указанные выше примеры содержат также:
- модуль или абсолютное значение: absolute(x) или |x|
- квадратные корни sqrt(x),
кубические корни cbrt(x) - тригонометрические функции:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x) - показательные функции и экспоненты exp(x)
- обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x), арккотангенс acot(x) - натуральные логарифмы ln(x),
десятичные логарифмы log(x) - гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x), гиперболический тангенс и котангенс tanh(x), ctanh(x) - обратные гиперболические функции:
гиперболический арксинус asinh(x), гиперболический арккосинус acosh(x), гиперболический арктангенс atanh(x), гиперболический арккотангенс acoth(x) - другие тригонометрические и гиперболические функции:
секанс sec(x), косеканс csc(x), арксеканс asec(x), арккосеканс acsc(x), гиперболический секанс sech(x), гиперболический косеканс csch(x), гиперболический арксеканс asech(x), гиперболический арккосеканс acsch(x) - функции округления:
в меньшую сторону floor(x), в большую сторону ceiling(x) - знак числа:
sign(x) - для теории вероятности:
функция ошибок erf(x) (интеграл вероятности), функция Лапласа laplace(x) - Факториал от x:
x! или factorial(x) - Гамма-функция gamma(x)
- Функция Ламберта LambertW(x)
- Тригонометрические интегралы: Si(x), Ci(x), Shi(x), Chi(x)
Правила ввода
Можно делать следующие операции
- 2*x
- — умножение
- 3/x
- — деление
- x^2
- — возведение в квадрат
- x^3
- — возведение в куб
- x^5
- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- Действительные числа
- вводить в виде 7.
5, не 7,5
5, не 7,5Постоянные
- pi
- — число Пи
- e
- — основание натурального логарифма
- i
- — комплексное число
- oo
- — символ бесконечности
Чтобы увидеть подробное решение,
помогите рассказать об этом сайте:
Реализация ряда Тейлора на Python / Хабр
Ряд Тейлора для функции представляет собой бесконечную сумму членов, которая использует информацию о производных этой функции для создания полинома, аппроксимирующего эту функцию. Более точные аппроксимации можно вывести, взяв производные более высокого порядка и используя полиномы более высокой степени. В интернете уже есть много статей (и видео на YouTube) о рядах Тейлора, которые помогут вам сформировать хорошее понимание процесса построения бесконечного ряда с упоминанием того, как члены более высоких порядков дают вам более близкие аппроксимации базовой функции (при условии, что ряд сходится).
(n)(x) — для определения коэффициентов полинома. Следовательно, ряд Тейлора может быть определен для f(x), только если она бесконечно дифференцируема. Члены ряда определяются выражением
Где а является центром ряда Тейлора (прим. ред.: этот термин используется англоязычным сообществом, а русскоязычное в основном оперирует окрестностью точки а). Если центр ряда равен 0, т. е. a=0, то ряд называют рядом Маклорена.
Чтобы программно сформировать ряд Тейлора для функции, все, что от нас требуется, это вычислить коэффициенты
для достаточного количества членов. Опять же напомню, что чем больше членов ряда Тейлора мы будем использовать, тем точнее будет аппроксимация. К счастью, в пакете Python scipy уже есть встроенная функция для вычисления производной функции в заданной точке. Именно ее мы и будем использовать для определения коэффициентов искомого полинома.
from scipy.misc import derivative
import math
class TaylorSeries():
def __init__(self, function, order, center=0):
self. center = center
self.f = function
self.order = order
self.d_pts = order*2
self.coefficients = []
# количество точек (order) для scipy.misc.derivative
if self.d_pts % 2 == 0: # must be odd and greater than derivative order
self.d_pts += 1
self.__find_coefficients()
def __find_coefficients(self):
for i in range(0, self.order+1):
self.coefficients.append(round(derivative(self.f, self.center, n=i, order=self.d_pts)/math.factorial(i), 5))
center = center
self.f = function
self.order = order
self.d_pts = order*2
self.coefficients = []
# количество точек (order) для scipy.misc.derivative
if self.d_pts % 2 == 0: # must be odd and greater than derivative order
self.d_pts += 1
self.__find_coefficients()
def __find_coefficients(self):
for i in range(0, self.order+1):
self.coefficients.append(round(derivative(self.f, self.center, n=i, order=self.d_pts)/math.factorial(i), 5))
Приведенная выше логика начинается с определения класса для хранения информации о ряде Тейлора. Конструктор принимает указатель на функцию (function) для которой мы формируем ряд Тейлора, порядок (order) ряда Тейлора (то есть количество членов) и центр (center) ряда, который по умолчанию соответствует ряду Маклорена (т.е. равен нулю). Некоторые переменные, которые используются в функции scipy.misc.derivative, вычисляются на лету из уже предоставленных нами данных.
{}».format(self.center, i) if i > 0 else «») + » + »
eqn_string = eqn_string[:-3] if eqn_string.endswith(» + «) else eqn_string
print(eqn_string)
def print_coefficients(self):
print(self.coefficients)
def get_coefficients(self):
«»»
Возвращает коэффициенты ряда Тейлора
«»»
return self.coefficients
Первая функция, print_equation(…), выводит ряд Тейлора как уравнение с центром в центре ряда. print_coefficients(…) просто выведет список с коэффициентами, а get_coefficients(…) вернет его.
Приведенный ниже код используется для нахождения коэффициентов ряда Тейлора, представляющего функцию f(x):
from TaylorSeries import TaylorSeries
def f(x):
return 2 + x**3 + x**7 + x**2
if __name__ == '__main__':
terms = 15
center = 0
precision = 3
ts = TaylorSeries(f, terms, center)
ts.print_coefficients()
ts.print_equation()Выполнение этой логики сформирует список размером в 15 элементов, который содержит коэффициенты ряда Тейлора, а также выведет полиномиальное уравнение.
x и т. д., также дают правильные результаты в этой реализации. Далее, в приведенных ниже применениях, мы будем использовать именно эти функции.
Применения ряда Тейлора
Поскольку с полиномами обычно легче работать, чем с большинством функций, аппроксимация с помощью ряда Тейлора может помочь определить приблизительные значения для различных операций, связанных с этими функциями.
Бесполезное
Дифференцирование
Ряд Тейлора функции можно использовать для аппроксимации ее производной в конкретной точке. Члены ряда Тейлора можно дифференцировать по отдельности, тогда они примут форму
которая представляет собой просто производную степенной функции, умноженного на коэффициент ряда Тейлора. Обратите внимание, что в коде это отбросит члены, не представленные в ряде Тейлора, поскольку их коэффициенты будут равны 0.
В нашей Python-логике эти вычисления будут выполняются с помощью функции, приведенной ниже:
def approximate_derivative(self, x):
"""
Приблизительно вычисляет производную функции f(x) по ее ряду Тейлора. (n-1)
return value
(n-1)
return valueВ этой функции аппроксимация производной функции находится путем перебора коэффициентов, вычисления значений производной, как описано выше, и их суммирования. Подстановка значений в эту функцию обеспечивает точную аппроксимацию производной базовой функции. Ниже приведены результаты для cos(x):
x | f(x) | Approx. f'(x) |
0 | 1.0 | 0.0 |
pi/6 | 0.866 | -0.5 |
pi/4 | 0.707 | -0.707 |
pi/3 | 0.5 | -0.866 |
pi/2 | 0. | -1.0 |
pi | -1 | -0.042 |
0Выше приведены значения аппроксимированной функции cos(x) и ее производной (обратите внимание, что фактическая производная равна -sin(x)) в точках 0, 𝝿/6, 𝝿/4, 𝝿/3, 𝝿/2 и 𝝿. Глядя на значения в нескольких этих точках, мы видим, что в целом получили хорошую аппроксимацию производной cos(x). Например, в точке 𝝿/4 значение функции равно 0,707 = sqrt(2)/2, как и его производная -0,707, что является правильным значением.
К сожалению, это практически бесполезно, так как ряду Тейлора требует информация о производной функции, чтобы определить свои коэффициенты. Зачем нам нужна аппроксимация f'(x), которой требуется сама f'(x) общего вида (а значит, фактическое значение) для получения этой аппроксимации. Кроме того, существует множество различных численных методов, которые могут аппроксимировать производные без аналитического нахождения производной функции (например, методы конечных разностей), которые больше подходят для этой задачи.
Полезные
Аппроксимация значений
Одной из широко используемых целей ряда Тейлора является аппроксимация значений базовой функции. Для того, чтобы получить приблизительное значение функции, в члены ряда Тейлора подставляется x, а затем они складываются вместе. В Python-логике это выглядит следующим образом:
def approximate_value(self, x):
"""
Аппроксимирует значение f(x) с помощью полинома Тейлора.
x = точка аппроксимации f(x)
"""
fx = 0
for i in range(len(self.coefficients)):
fx += self.coefficients[i] * ((x - self.center)**i) # coefficient * nth term
return fxОпределенный интеграл
Ряд Тейлора можно использовать для аппроксимации интеграла базовой функции, поскольку члены ряда Тейлора можно интегрировать по отдельности, как мы делали это при дифференцировании. При аппроксимации интеграла члены ряда примут вид
Здесь мы опять сталкиваемся со степенной функцией, но на этот раз интегрируем ее и умножаем на соответствующий коэффициент ряда Тейлора.
Однако численно мы можем рассчитать только определенный интеграл функции, так как в противном случае отсутствие значения для константы интегрирования может привести к неправильным результатам. Рассмотрим ряд Тейлора для f(x) = sin(x) с центром в 0:
интегрирование этого полинома член за членом дает следующий полином
Теперь предположим, что это корректная аппроксимация интеграла sin(x) (для которой мы знаем фактический интеграл -cos(x)) и попытаемся вычислить эту функцию в 0. Значение от этого равно 0. В этом случае это можно скорректировать, установив константу интегрирования C = -1. Но нам нужно определить эту константу для каждого значения в области определения функции только для того, чтобы “исправить” интегралы, что делает бесконечное интегрирование бесполезным.
С другой стороны, определенные интегралы можно легко вычислить, интегрируя ряд Тейлора почленно и подставляя пределы интегрирования, как показано в Python-коде ниже.
x*sin(x). В целях сокращения длины этой статьи эти результаты будут опущены. Для тех, кто сомневается, полный код будет приведен ниже. Меняйте def f(x) и проверяйте результаты самостоятельно.
Лимиты
Вместо того, чтобы показывать, как численно аппроксимировать лимиты и реализовывать это в Python, я просто приведу пример лимита, который может быть трудно определить аналитически, но его легко найти в форме ряда Тейлора.
Рассмотрим такой лимит:
Этот лимит можно легко определить, применяя правило Лопиталя, так как он имеет форму 0/0, но давайте предположим на минуту, что мы этого не знаем (или что мы ничего не знаем о правиле Лопиталя). Как нам тогда определить этот предел? Оказывается, в этом нам может помочь ряд Тейлора, заменяющий sin(x) в пределе аппроксимацией. В этом примере будет использоваться ряд Тейлора с тремя членами:
Поскольку лимит x²/120 стремится к 0, результат равен -1/6, как и ожидалось, при оценке по правилу Лопиталя.
Заключение
Выше была представлена идея ряда Тейлора, который представляет собой математический инструмент, используемый для аппроксимации любой непрерывно дифференцируемой функции полиномом, используя только информацию о производной этой функции.
Была предоставлена реализация на Python и обсуждены применения ряда Тейлора. Полный код с некоторыми примерами использования приведен ниже, и я советую всем, кто заинтересован в работе с этим инструментом, скопировать и потестировать этот код самим, чтобы лучше понять ряд Тейлора.
Листинг кода
usage.py
from TaylorSeries import TaylorSeries
import math
def f(x):
return math.cos(x) #(math.e**x)*math.sin(x)*math.cos(x)
if __name__ == '__main__':
pts = [0, math.pi/6, math.pi/4, math.pi/3, math.pi/2, math.pi]
# pts = [-5, -4, -3, -2, -1, -0.1, 0, 0.1, 1, 2, 3, 4, 5]
terms = 15
center = 0
precision = 3
ts = TaylorSeries(f, terms, center)
ts.print_coefficients()
ts.print_equation()
print("x\tf(x)\tApprox. f(x)\tIntegral f(x)\tDerivative f(x)")
for x in pts:
print("{:.3f}\t{:.3f}\t{:.3f}\t{:.3f}\t{:.3f}".format(x, f(x), ts.approximate_value(x), ts.approximate_integral(0, x), ts.approximate_derivative(x)))
TaylorSeries.
{}».format(self.center, i) if i > 0 else «») + » + »
eqn_string = eqn_string[:-3] if eqn_string.endswith(» + «) else eqn_string
print(eqn_string)
def print_coefficients(self):
print(self.coefficients)
def approximate_value(self, x):
«»»
Аппроксимирует значение f(x) с помощью полинома Тейлора.
x = точка аппроксимации f(x)
«»»
fx = 0
for i in range(len(self.coefficients)):
fx += self.coefficients[i] * ((x — self.center)**i) # coefficient * nth term
return fx
def approximate_derivative(self, x):
«»»
Приблизительно вычисляет производную функции f(x) по ее ряду Тейлора.
Бесполезно, так как нам нужна производная самой функции, чтобы построить ряд Тейлора.
«»»
value = 0
for i in range(1, len(self.coefficients)): # skip the first value (constant) as the derivative is 0
value += self.coefficients[i] * i * ((x — self.center)**(i-1)) # differentiate each term: x^n => n*x^(n-1)
return value
def approximate_integral(self, x0, x1):
«»»
Вычисляет определенный интеграл функции, используя разложение в ряд Тейлора.
(n+1)
return value
def get_coefficients(self):
«»»
Возвращает коэффициенты ряда Тейлора
«»»
return self.coefficientsОдин из способов сделать вывод из статистического исследования — проверка гипотез. Это помогает нам проверить значения параметров популяции, которые угадываются на основе предварительно собранной информации. Многие области анализа данных включают в себя некоторое количество статистических испытаний, и почти всегда там используется проверка гипотез. Завтра в 16:00 в OTUS состоится открытый урок, на котором мы познакомимся с базовыми понятиями статистики и теории вероятностей, поймём, чем задачи этих областей отличаются друг от друга, концептуально рассмотрим методы проверки гипотез, и как они применяется в науке о данных на простых практических примерах. Регистрация для всех желающих — по ссылке.
| Модуль 24 — силовая серия |
| Введение | Урок 1 | Урок 2 | Урок 3 | Самооценочный тест |
Урок 24. 3: Тейлор, серия |
В уроке 24.2 вы нашли ряды Маклорена, которые аппроксимируют функции вблизи x = 0. В этом уроке вы узнаете, как найти ряд, который аппроксимирует функцию вблизи x = a, где a — любое действительное число. Серия Тейлора Для функции f , имеющей все производные более высокого порядка, ряд , где называется рядом Тейлора для f с центром в . Ряд Тейлора — это степенной ряд, который аппроксимирует функцию f около x = a . Частичная сумма называется полиномом Тейлора n-го порядка для f с центром в a . Каждый ряд Маклорена, в том числе изученный в уроке 24.2, представляет собой ряд Тейлора с центром в нуле. Полином Тейлора e x С центром в 1 Полином Тейлора второго порядка с центром в 1 для функции f ( x ) = e x можно найти с помощью процедуры, аналогичной процедуре, описанной в уроке 24. Коэффициент при сроке (х — 1) к в полиноме Тейлора задается выражением . Эта формула очень похожа на формулу для нахождения коэффициента x k в полиноме Маклорена, где производная оценивается в 0. В этом полиноме Тейлора производная оценивается в 1, центре ряда . Коэффициенты полинома Тейлора второго порядка с центром в 1 для e x равны е (1) = е е (1) = е Таким образом, полином Тейлора второго порядка для e x с центром в 1 равен , и около x = 1, e x P 2 ( x ). Ряд Тейлора для e x с центром в 1 аналогичен ряду Маклорена для e x из урока 24.2. Однако члены ряда Тейлора имеют степени ( x — 1), а не степени x , а коэффициенты содержат значения производных, оцененные при x = 1, а не оцененные при x = 0. График функции и полинома показывает, что полином является хорошим приближением около х = 1.
Многочлен Маклорена второго порядка, который вы нашли в уроке 24.2, , касается f ( x ) = e x при x = 0 и имеет ту же вогнутость, что и f ( x ) = e x в этой точке. Полином , с центром в точке x = 1, касается f ( x ) = e x при x = 1 и имеет ту же вогнутость, что и x ( ) e x в этой точке. 24.3.1 Найдите полином Тейлора второго порядка с центром в 1 для функции f ( х ) = ln х . Начертите этот многочлен вместе с f ( x ) = ln x . Щелкните здесь, чтобы получить ответ. Другая серия Тейлора Ряд Тейлора для одной функции можно использовать для нахождения ряда Тейлора для связанной функции. Полином Тейлора третьего порядка с центром в 1 для f ( x ) = ln x . Производная от f ( x ) = ln x равна . Производная p ( x ) дает полином Тейлора второго порядка для с центром в 1. 24.3.2 Найдите полином Тейлора второго порядка для с центром в 1 с использованием производной p ( x ) и изобразите его с помощью . Щелкните здесь, чтобы получить ответ. Серия Тейлора для cos x 2 Другие модификации ряда Тейлора дают другие ряды Тейлора. Например, замена каждого x на x 2 в ряду Тейлора на f ( x ) = cos( x ) дает ряд Тейлора для г ( x ) = f ( x 2 ) = cos( x 2 ).
|
| < Назад | Далее > |
©Авторское право
2007 Все права защищены. | Товарные знаки
| политика конфиденциальности
| Политика ссылок |
2.
.
Ряд Тейлора для $\sqrt{x}$? — Математический стек Exchange
спросил
Изменено 5 месяцев назад
Просмотрено 154 тыс. раз
$\begingroup$
Я пытаюсь вычислить ряд Тейлора для $\sqrt{x}$. К сожалению, все веб-страницы и книги содержат примеры для $\sqrt{x+1}$. Есть ли какая-то особая причина, по которой никто не показывает ряды Тейлора ровно для $\sqrt{x}$?
- расширение Тейлора
$\endgroup$
2
$\begingroup$
Краткий ответ: Ряд Тейлора $\sqrt x$ при $x_0 = 0$ не
существует, потому что $\sqrt x$ не дифференцируемо в $0$.
Для любого $x_0 > 0$ можно вычислить ряд Тейлора $\sqrt x$ в точке $x_0$
используя ряд Тейлора $\sqrt{1 + u}$ при $u_0 = 0$.
Длинный ответ: 92 + \ldots \quad . $$ Поэтому:
- Запрашивать «ряд Тейлора для $f$» имеет смысл только в том случае, если вы укажете точка $x_0$. (Часто эта точка неявно принимается как $x_0 = 0$, в в этом случае его также называют рядом Маклорена $f$.)
- Ряд Тейлора для $f$ в точке $x_0$ определяется, только если $f$ бесконечно дифференцируема в $x_0$. (Но серии Тейлора нужно не сходится ни при каком $x \ne x_0$, и даже если он сходится в окрестности $x_0$ предел может отличаться от заданной функции $f$.) 9{(n)}(x_0)}/{n!}$ для всех $n$, т.е. степенной ряд именно ряд Тейлора.
Теперь применим это к вашему вопросу: Вы запрашиваете ряд Тейлора для $f(x) = \sqrt{x}$.
Если вы имели в виду ряд Тейлора при $x_0 = 0$: это не , определенный , потому что
$\sqrt {x}$ не дифференцируем при $x_0 = 0$.
По той же причине существует
нет степенного ряда, сходящегося к $f$ в окрестности $0$.
Но $f(x) = \sqrt{x}$ можно разложить в ряд Тейлора при любом $x_0 > 0$. Общая формула приведена в Ответ Мхенни Бенгорбал. Причина, по которой часто приводится только ряд Тейлора для $\sqrt{1 + x}$ в книгах заключается в том, что для функции извлечения квадратного корня общий случай может быть легко сводится к частному случаю: $$ \ sqrt {\ mathstrut x} = \ sqrt {\ mathstrut x_0 + x — x_0} = \ sqrt {\ mathstrut x_0} \ sqrt {1 + \ frac {\ mathstrut x-x_0} {x_0}} $$ и теперь вы можете использовать ряд Тейлора $\sqrt{1+u}$ при $u_0 = 0$. 92}2+\точки $$ $f(0)=0$, но $f'(x)=\frac1{2\sqrt{x}}$ взрывается при $x=0$. Поскольку $\sqrt{x}$ не имеет первой производной в $0$, у него нет там ряда Тейлора.
$\endgroup$
1
$\begingroup$
Примечание.
Строго говоря, ниже доказывается, что $\sqrt{x}$ не может иметь асимптотического разложения вида $a_0 + a_1 x + o(x)$ при $x \to 0$.
Очевидно, что $a_0$ должно быть равно $0$, но $\sqrt{x}$ намного больше при $x \to 0$, чем любое разложение, начинающееся с $a_1 x$. Например, у нас было бы $$\frac{1}{\sqrt{x}} = \frac{\sqrt{x}}{x} = a_1 + a_2 x + \dots \rightarrow a_1,$$ при $x \to 0$, но $\frac{1}{\sqrt{x}}$ не имеет конечного предела при $x \to 0$.
С другой стороны, легко получить разложение Тейлора для $\sqrt{x}$ при $a > 0$ из разложения для $\sqrt{1 + x}$ при $0$. Установив $h = x — a$, вы получите $$\sqrt{x} = \sqrt{a + h} = \sqrt{a}\sqrt{1 + h/a},$$ а затем вы расширяете $\sqrt{1 + h/a}$ по степеням $h/a$. 92+\точки $$ и если вы хотите, чтобы теорема тождества выполнялась, это невозможно, потому что $a_0=0$ означало бы, что коэффициент $x$ равен нулю
$\endgroup$
0
$\begingroup$
Ну, я знаю, что это старый пост с ответом, но ссылаясь на вопрос, что все веб-страницы и книги не показывают примеры для $\sqrt{x}$, в книге, Исчисление Томаса, двенадцатое издание, в упражнениях раздела 10.
8, задача 9вопрос: найти многочлен Тейлора порядка 0,1,2 и 3, порожденный $f$ в $a$, и упражнения следующие
И книга также дает ответы, это следующие
Я разместил изображения книги, чтобы показать, что есть по крайней мере одна книга с проработанным упражнением.
Интернет — очень полезное место, но в хороших книгах по математическому анализу можно найти множество упражнений и примеров, разработанных экспертами. 9+\bigcup\{0\};\,f(x)=\sqrt{x}$ не имеет производной в $x=0$, поэтому нет разложения Тейлора в районе $x=0$.
Однако стоит отметить, что сигулярность в точке $x=0$ отличается от сингулярности $g:\mathbb{R}\to\mathbb{R}\{0\};\,g (x)=\frac{1}{x}$, что лишает нас разложения Тейлора для $g$ при $x=0$. Этот проще для понимания и называется полюс .
Но ваша сингулярность называется Точкой Ветвления , и именно здесь существенным образом соединяются две «ветви» многозначной функции. Напомним, что обе функции $f_\pm(x)=\pm\sqrt{x}$ являются частично обратными к $x\mapsto x^2$.
Отсюда имеем, что есть число μ∈m; M, которое удовлетворяет равенству ∫abf(x)·g(x)dx=μ·∫abg(x)dx.
Формула Ньютона-Лейбница
— М.: Наука. Главная редакция физико-математической литературы, 1985. — 432 с.
n при n целом и положительном
x, sin x, cos x
Радиус и круг кривизны. Центр кривизны. Эволюта и эвольвента
Геометрическое изображение функции двух переменных
Получение функции на основании экспериментальных данных по методу наименьших квадратов
Интегрирование по частям
Формула Чебышева
Определенные интегралы также обладают свойствами, относящимися к пределам интегрирования. Эти свойства вместе с правилами интегрирования, которые мы рассмотрим позже в этой главе, помогают нам манипулировать выражениями для вычисления определенных интегралов. 92 f(x) dx[/латекс].
Однако следующие свойства относятся только к случаю [латекс]а \le b[/латекс] и используются, когда мы хотим сравнить размеры интегралов. 92}[/latex] и [latex]g(x)=\sqrt{1+x}[/latex] на интервале [latex][0,1][/latex].
Если двойка отрицательная возводится во 2 степень, -2 в квадрате, это тоже равно четыре. Дважды два равно четыре — эта классика детской математики показывает результат возведения числа 2 в квадрат.
Нам требуется возвести в квадрат сумму двух чисел: первое число есть 3ab, второе 1. Должно получиться: 1) квадрат первого числа, т. е. (3ab)², что равно 9a²b²; 2) произведение двойки на первое число и на второе, т. е. 2 ∙ 3ab ∙ 1 = 6ab; 3) квадрат 2-го числа, т. е. 1² = 1 – все эти три члена должно сложить между собою.
п.
Это ясно, потому что наши равенства можно переписать в виде:
Значит, его площадь:
Что именно означает квадрат в математике?
Это полезно для определения вершины параболы или других графических решений.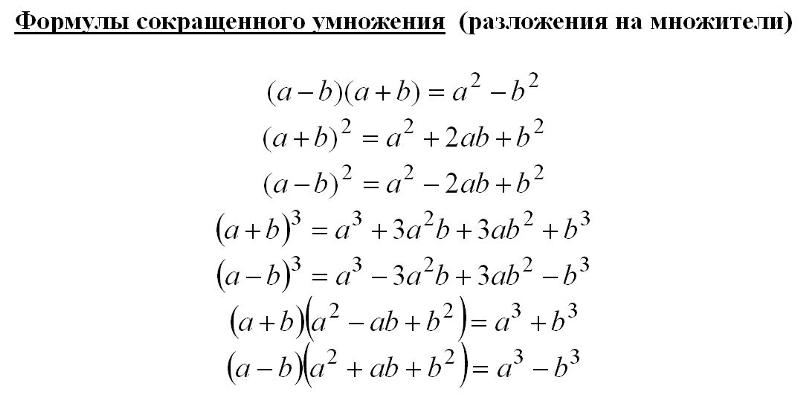
Например, рисование квадрата, каждая сторона которого имеет длину в одну единицу, показывает, что когда вы возводите в квадрат число в одну единицу длины, площадь равна четырем единицам. 92 может помочь вам вспомнить, что это означает возведение числа в квадрат.
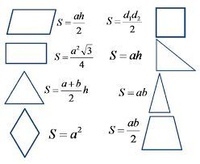
Площадь треугольника равна половине
произведения его основания на высоту.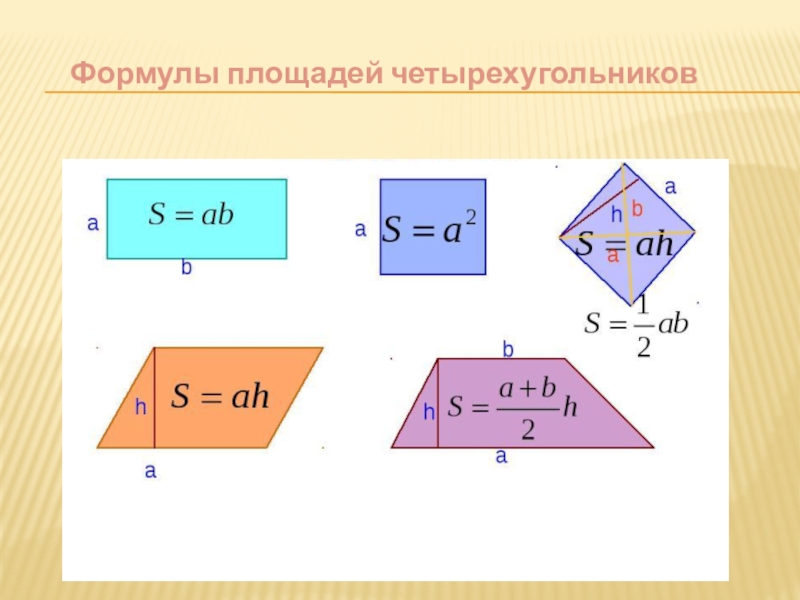
Биссектриса
угла параллелограмма отсекает от него равнобедренный треугольник.
Тогда .
5. Свойство
медианы треугольника:
(переместительный
закон)
7k.
Математика.
2
2
Алгебра.
Тесты.
Что касается студентов, изучающих геометрию, так это геометрическая формула. Геометрия — это вещь, которую мы используем каждый день в жизни, поэтому ее формулы составляют ее основу, и их очень важно знать.
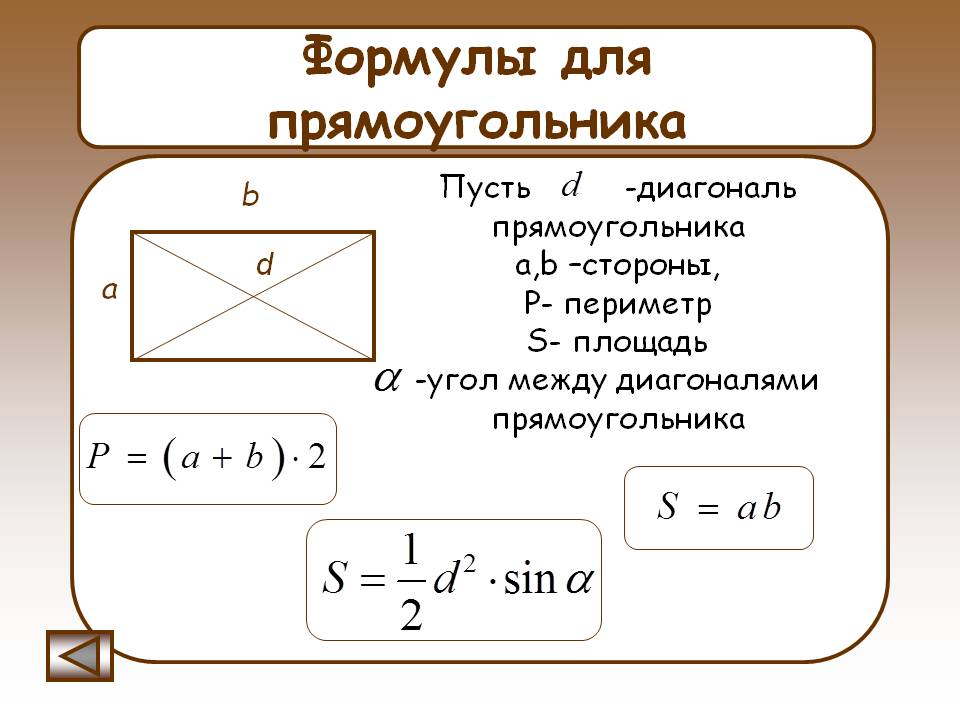д. геометрических фигур. Геометрия — это часть математики, которая имеет дело с отношениями точек, линий, углов, поверхностей, измерением тел и свойствами. Существует два типа геометрии: 2D или плоскостная геометрия и 3D или объемная геометрия.
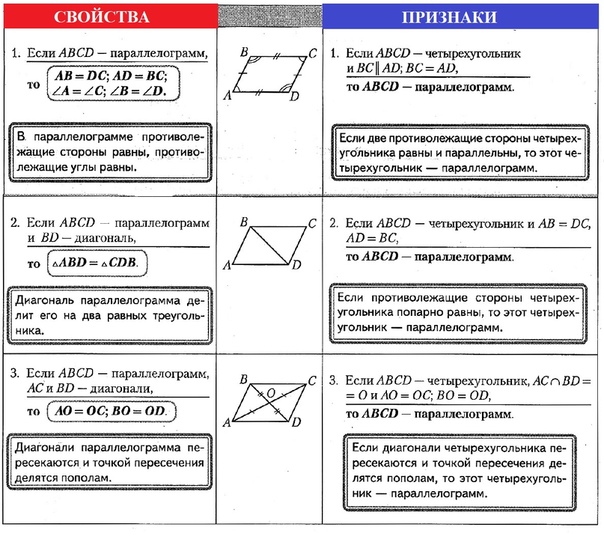д. являются некоторыми примерами трехмерных форм. Основные формулы геометрии даны следующим образом:
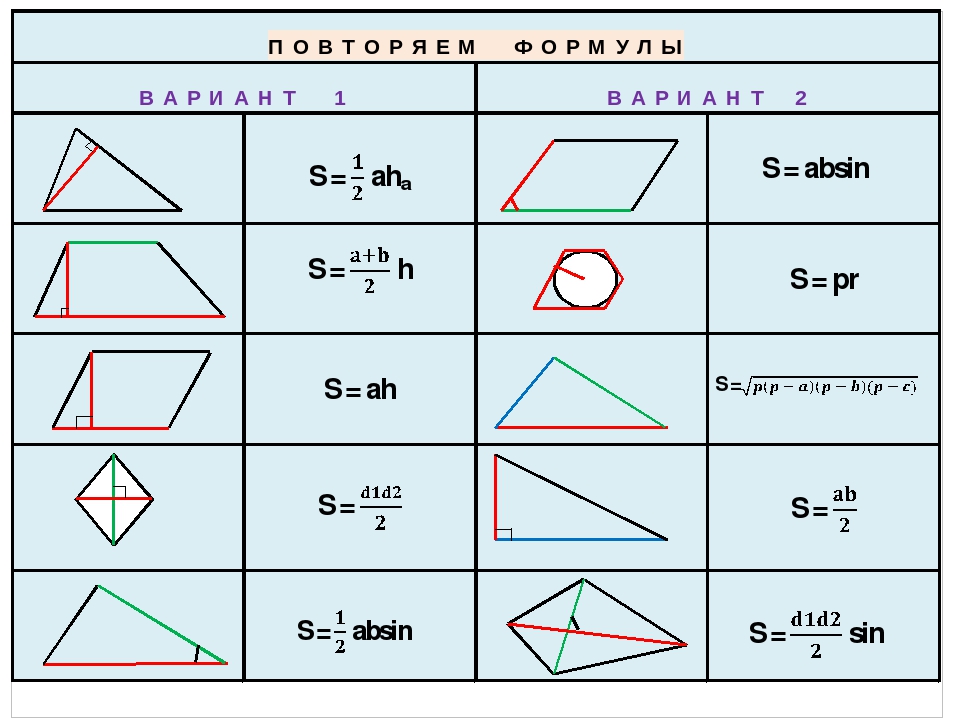и,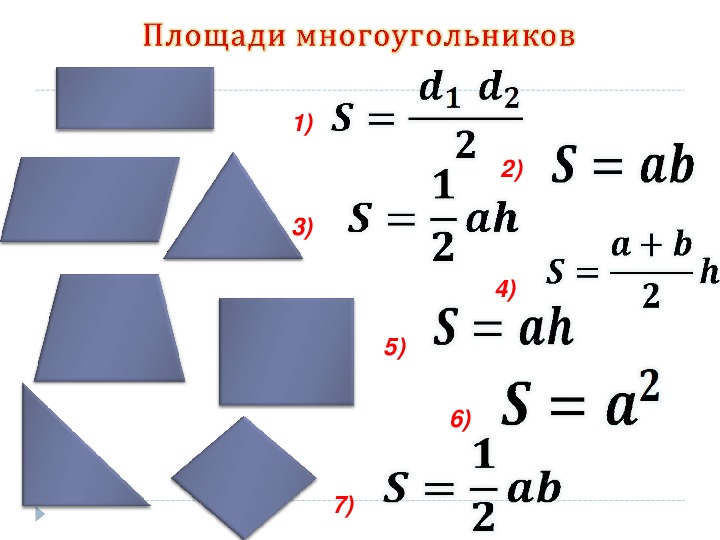
Трапеция
Прямоугольный
Сфера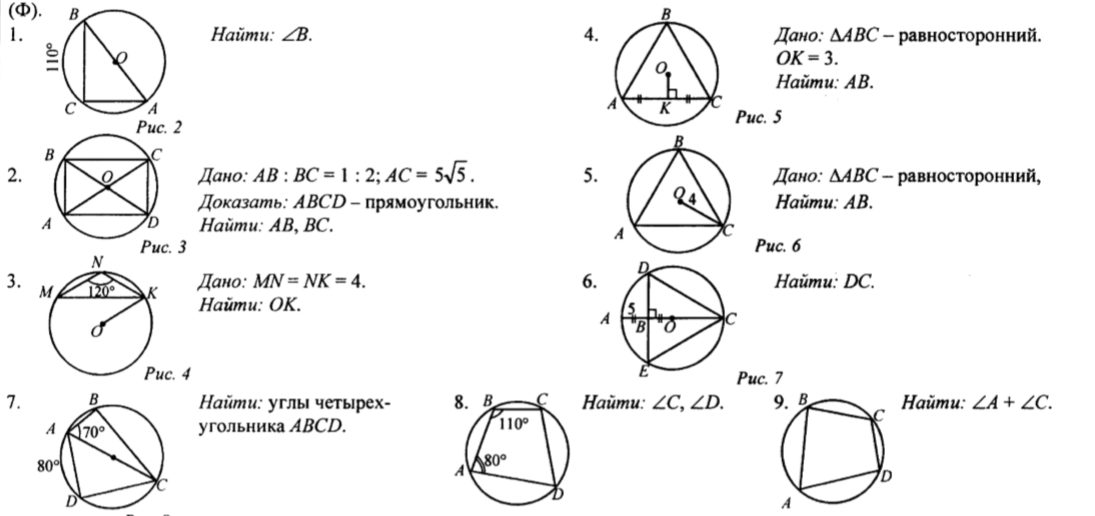
)
)
)
)
)
)
)
)
Функция y=cosx
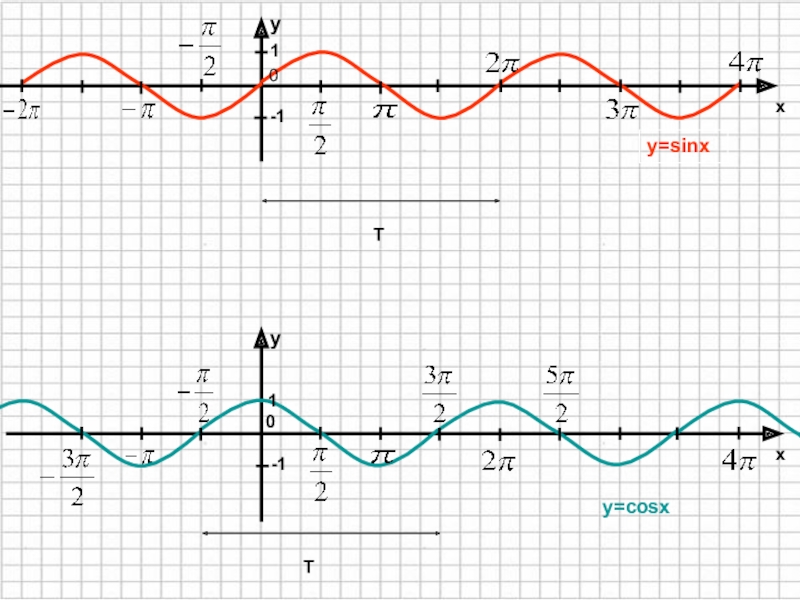Функция y=sinx
)/3
Сначала загрузите исходный файл для преобразования: перетащите TXT в форму конвертации или нажмите кнопку «Выбрать файл». После этого нажмите кнопку «Конвертировать». Когда конвертация TXT в DOC завершится, вы сможете скачать файл DOC.
txt
DOC-файлы читаются и редактируются в Android c помощью приложений (например, Kingsoft Office). Начиная с Word 2007 используется новая улучшенная версия формата – DOCX.
9 (1490 голосов)
$ vertopal convert TEXT_INPUT_FILE —to doc
Он может производить высококачественные документы при сохранении оригинального макета.
Измените настройки конвертации и нажмите на «OK». Выберите выходную папку, и когда вы закончите, нажмите «Конвертировать», чтобы начать процесс. Преобразование завершится через несколько секунд.
Чтобы узнать больше, ознакомьтесь с руководством о том, как Nitro конвертирует PDF в Word.
Эти документы можно создавать и распространять независимо от операционной системы, аппаратной платформы и прикладной программы, отвечающей за создание оригиналов. Посмотрите подробное руководство преобразования PDF в Word в Adobe Acrobat, чтобы узнать больше
Это инструмент, который может делать все, — от создания и редактирования PDF-файлов, до подписания и печати PDF-файлов, — как в Word. Foxit PDF в Word конвертер позволяет конвертировать файлы из формата PDF в формат Word, среди множества других функций.
doc,.docx), Excel(,xls,.xlsx), PowerPoint(.ppt), Text, Image, HTML
С помощью этой онлайн-программы вы можете конвертировать PDF в Word онлайн, не загружая никаких прикладных инструментов.
1 / 5
Вы не можете использовать расширенные функции, такие как пакетный инструмент или предварительный просмотр вывода файла перед преобразованием.
Мы гарантируем 100% безопасное преобразование PDF в Word и никогда не делимся вашими файлами с кем-либо еще.
Кафедра бизнес-информатики Российского университета транспорта
Непосредственные расчеты просто не позволяют в точности это установить, какими бы мощными вычислительными средствами мы ни располагали. Алгебраическая операция недопустима. Но рассмотреть предельный переход в такой ситуации возможно. Теория пределов характеризует этот случай как раскрытие неопределенности, обозначаемой
Используя этот факт, получим:
Поэтому, решая более простое неравенство (9.29), получаем
Когда Радд Тритри и Карнден Кроу прибыли, ожидая найти фермы сожженными, они обнаружили, что люди Бетода попали в засаду, а Чудотворец во главе. Тридеревья сказали: « Удивительно странно, что во главе стоит женщина. Некоторое время они называли ее Чудесной Стрэндж, но вскоре странность исчезла.
После битвы Кроу уходит с поста второго, а Уандерфул назначает нового секунданта Доу. Когда Кроу уходит, она рассказывает, что ее муж и дети собрали вещи и уехали много лет назад, и она не могла никому рассказать.
Однако их планы прерываются, когда Великий Волк решает, что больше не хочет быть будущим королем, убивает Чешуйчатого Железнорукого и забирает цепь Бетода. Затем Стаур насмехается над Клевером, говоря, что он начал уважать его, но ему нужно продемонстрировать лояльность. Вы должны распознать свой момент, когда он наступит, и воспользоваться им. Клевер сразу же наносит удар Чудесной в сердце и держит ее, пока она умирает.
Когда Радд Тритри и Карнден Кроу прибыли, ожидая найти фермы сожженными, они обнаружили, что люди Бетода попали в засаду, а Чудотворец во главе. Тридеревья сказали: « Удивительно странно, что во главе стоит женщина. Некоторое время они называли ее Чудесной Стрэндж, но вскоре странность исчезла.
После битвы Кроу уходит с поста второго, а Уандерфул назначает нового секунданта Доу. Когда Кроу уходит, она рассказывает, что ее муж и дети собрали вещи и уехали много лет назад, и она не могла никому рассказать.
Лицензия на осуществление аудиторской деятельности может быть аннулирована, если …
Основной целью аудита не является …
Аудиторская проверка может быть …
Под первоначальным аудитом понимается …
Вид сопутствующих аудиту услуг, совместимых с проведением аудита бухгалтерской отчетности
Организация, бухгалтерская отчетность которой подлежит обязательному аудиту:
Положение, верно устанавливающее задачи, стоящие перед аудитом
Без четких критериев объект аудита, скорее всего, будет сопротивляться вашим рекомендациям аудита. Я знаю, что делал, когда меня проверяли.
Но не мы! Я знал, что аудиторы не могут стоять на ногах без твердых критериев, и я успешно возражал против каждого предложения в отчете.
Подходящие критерии являются релевантными, надежными, объективными и понятными и не приводят к упущению важной информации, если применимо, в контексте целей аудита. Относительная важность каждой из этих характеристик для конкретного задания является вопросом профессионального суждения. В тех случаях, когда законы, нормативные акты или политики предписывают критерии, которые должны использоваться для задания, такие критерии считаются подходящими при отсутствии указаний на обратное. 
Применительно к финансовому аудиту применимая концепция подготовки финансовой отчетности, такая как общепринятые принципы бухгалтерского учета, представляет собой один набор критериев. 
К концу года у аудиторов были критерии для проверки.
Например, при проверке программы патронатного воспитания вы можете использовать критерии безопасных приемных домов, изложенные в последней публикации Американской ассоциации патронатного воспитания. Что было бы прискорбно и сделало бы большую часть, если не всю, аудиторскую работу недействительной, так это заявление клиента на заключительной конференции: «Мы думаем, что Американская ассоциация приемных родителей — это кучка либеральных идиотов, и мы никогда не подписывались на их стандарты. Они чокнутые!» Да, признаюсь, это случилось со мной! Упс! Поскольку клиент не согласился с критериями, я остался без авторитетной поддержки своих выводов и выводов!
Установление подходящих критериев является ключом к успеху аудита. Без определения критериев может быть утрачена направленность выполняемых процедур, и намеченный результат аудита может быть не достигнут. Подходящие критерии необходимы для того, чтобы аудитор мог разумно измерить или оценить предмет проверки, как это определено в контексте профессионального суждения. Это относится к любому типу аудита, например:
Критерии встречаются во многих формах. Иногда клиенты задают нам вопросы: «Какие критерии используются при аудите финансовой отчетности?» или «Каковы критерии внутреннего аудита?» Критерии аудита, перечисленные ниже, могут использоваться для всех различных типов аудита, обсуждаемых в этой статье. Некоторые примеры критериев аудита:
Для успешного аудита критерии должны быть согласованы соответствующими сторонами до начала задания. В большинстве случаев это проверяемая сторона и аудиторы. В некоторых случаях третьи стороны также соглашаются с критериями. Эти критерии обычно излагаются в письме об аудиторском соглашении.
Институт внутреннего аудитора заявил в стандарте IPPF 2210.A3:
Ответственной стороной обычно является заказчик, в отношении которого должны быть выполнены аудиторские процедуры.
системы обслуживающей организации, пригодность схемы средств контроля, направленных на достижение целей контроля, указанных в описании системы, и, в случае отчета типа 2, операционную эффективность таких средств контроля». (взято из SSAE 18). Другими словами, критерии должны быть доступны для организаций-пользователей и их аудиторов. Без этого получатели отчета не могут определить, соответствует ли он их потребностям. Эта информация содержится в отчете с описанием средств контроля, предоставленных обслуживающей организацией.
2-1)/x
В этой статье мы найдем производную кубического корня из x, применив степенное правило производных. Мы также будем использовать определение предела для вычисления производной кубического корня из x.
{2/3}} \cdot \dfrac{d} {dx}(x+2)$ по уравнению (I) 9x]$