Автор: 
как считать по столбцу, как вычислить от треугольной матрицы
Определитель матрицы 4 порядка
ОпределениеМатрица представляет собой прямоугольную таблицу скаляров, то есть элементов некоторого поля, которая состоит из определенного числа столбцов и определенного числа строк.
Существует разные типы матриц. При рассмотрении данной темы важно уточнить понятия некоторых из них:
- в том случае, когда матрица обладает единственным элементом, она является совпадающей со своим единственным скаляром;
- квадратная матрица представляет собой такую матрицу, которая имеет равное число столбцов и строк.
Алгебраические действия с матрицами характеризуются определенным алгоритмом и порядком. Подобные операции отличаются от манипуляций с простыми числами. Кроме алгебраических действий, над матрицами выполняют и другие операции. К примеру, транспортирование матрицы.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления).
Если нет возможности написать самому, закажите тут.
В задачах часто встречаются примеры нахождения определителя матриц разных порядков. Матрицы первого, второго, третьего, четвертого и других порядков относят к квадратным матрицам.
ОпределениеОпределитель или детерминант матрицы является определенным числом, которое можно поставить в соответствие некой квадратной матрице.
В том случае, когда элементы матрицы имеют вид действительных чисел, то и определитель является действительным числом. Определитель обозначают detA или |A|. Определитель первого порядка соответствует скаляру рассматриваемой матрицы.
Определители второго и третьего порядка определяются в соответствии со стандартным алгоритмом, то есть с помощью известных формул. Для того чтобы вычислить определитель больше третьего порядка, требуется ознакомиться с понятием минора матрицы (М).
ОпределениеМинор матрицы третьего порядка является определителем второго порядка, который получен из заданной матрицы третьего порядка путем вычеркивания i-ой степени и j-го столбца.
Изучая материалы по теме матричного определителя, можно встретить термин «детерминант». Фактически данные понятия идентичны. Однако детерминант обладает множеством значений в других научных областях, что объясняет использование его русского перевода в математике.
Свойства определителя:
- при перестановке местами двух строк или столбцов знак определителя меняется;
- при умножении строки или столбца на число, весь определить также умножится на число;
- в том случае, когда одну строку сколько угодно раз прибавляют или вычитают из другой, определитель не меняется;
- при наличии одинаковых, пропорциональных или заполненных нулями двух строк определителя весь определитель равен нулю;
- все перечисленные свойства справедливы в случае столбцов;
- транспортирование матрицы не сопровождается изменением определителя;
- определитель произведения матриц равен произведению определителей.
{N (a_{1},a_{2},…a_{n})}}*a_{1a_{1}}a_{2a_{2}}…a_{na_{n}}\)Каждое слагаемое является произведением n-элементов, которые взяли по одному из каждой строки и каждого столбца, умноженное на (-1) в степени Np, определяемое, как количество инверсий.
Геометрический смысл понятия заключается в том, что определитель представляет собой объем параллелепипеда, получаемый в том случае, если рассмотреть строки, как вектора, образующие ребра геометрической фигуры.
При этом число строк или столбцов соответствует количеству векторов. Таким образом, в случае матрицы А = (2*2), получается двухмерный параллелограмм, а детерминант является площадью рассматриваемой фигуры. Если А = (3*3), то геометрическая фигура будет иметь вид трехмерного параллелепипеда, а определитель – являться его объемом.
Правильная расстановка индексов в матрице
ОпределениеИндексы являются координатами элемента в системе.
Каждый элемент обладает парой индексов:
- первый – определяет строку;
- второй – указывает столбец.
Так как порядок представляет собой число строк или столбцов в квадратной матрице, то он определяется с помощью m-индекса нижней строки или n-индекса крайнего правого столбца. Данный метод используют при очень больших таблицах, когда считать строки или столбы неудобно.
Матрица представляет собой таблицу, заполненную числами. Одной из ее ключевых характеристик является размерность, то есть число строк и столбцов, из которых она состоит. Как правило, говорят, что какая-то матрица A имеет размер \(\left[ m\times n \right]\), если в ней имеется m строк и n столбцов. Запись имеет следующий вид:
\(A=\left[ m\times n \right]\)
или \(A=\left( {{a}_{ij}} \right),\quad 1\le i\le m;\quad 1\le j\le n.\)
Существуют и другие обозначения для матрицы. В любом случае, при разных \(\left[ m\times n \right]\) и \({{a}_{ij}}\) возникает вопрос расстановки индексов. В этом случае целесообразно обратиться к обычной системе координат:
Источник: berdov. comДанная система имеет начало координат (точка \( O=\left( 0;0 \right)\)) оси x и y, а каждая точка на плоскости однозначно определяется по координатам:
\(A=\left( 1;2 \right)\)
\(B=\left( 3;1 \right)\) и так далее.
Следует поставить рассматриваемую систему рядом с матрицей, таким образом, чтобы начало координат совпадало с левым верхним углом, что существенно облегчит задачу определения индексов. Оси должны быть направлены так, чтобы охватить всю систему. При этом необходимо повернуть систему координат. Правильный вариант расположения представлен на рисунке:
Источник: berdov.comПолучается, что любая клетка матрицы обладает однозначными координатами х и у. К примеру, запись \({{a}_{24}}\) означает, что мы обращаемся к элементу с координатами x=2 и y=4. Размеры матрицы также однозначно заданы двумя числами:
Источник: berdov.comОбщая схема вычисления определителей
ОпределениеТеорема Лапласа о разложении определителя: пусть в матрице размера выбрано k строк или столбцов, причем .
{i+j}}\cdot {{M}_{ij}}}\)Таким образом удалось вывести формулу для разложения определителя по строке. Аналогичный метод можно использовать для того, чтобы разложить определитель по столбцам.
Данное следствие позволяет сделать несколько выводов:
- методика подходит для строк и столбцов;
- число слагаемых в разложении в любом случае составляет n;
- вместо одного определителя \(\left[ n\times n \right]\) необходимо вычислить несколько определителей размера на единицу меньше \(\left[ \left( n-1 \right)\times \left( n-1 \right) \right].\)
Практическое применение алгоритма можно продемонстрировать, решая задачу по нахождению определителя матрицы:
\(\left| \begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\\end{matrix} \right|\)
В первую очередь необходимо разложить данный определитель по первой строке:
\(\begin{align} \left| A \right|=1\cdot {{\left( -1 \right)}^{1+1}}\cdot \left| \begin{matrix} 5 & 6 \\ 8 & 9 \\\end{matrix} \right|+ & \\ 2\cdot {{\left( -1 \right)}^{1+2}}\cdot \left| \begin{matrix} 4 & 6 \\ 7 & 9 \\\end{matrix} \right|+ & \\ 3\cdot {{\left( -1 \right)}^{1+3}}\cdot \left| \begin{matrix} 4 & 5 \\ 7 & 8 \\\end{matrix} \right|= & \\\end{align}\)
Отсюда следует:
\(\begin{align} &=1\cdot \left( 45-48 \right)-2\cdot \left( 36-42 \right)+3\cdot \left( 32-35 \right)= \\ &=1\cdot \left( -3 \right)-2\cdot \left( -6 \right)+3\cdot \left( -3 \right)=0.
{4+4}}\cdot \left| \begin{matrix} 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\\end{matrix} \right| & \\\end{align}\)От пары слагаемых можно избавиться. В результате останется пара определителей 3х3:
\(\begin{align} & \left| \begin{matrix} 0 & 1 & 1 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \\\end{matrix} \right|=0+0+1-1-1-0=-1; \\ & \left| \begin{matrix} 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 1 \\\end{matrix} \right|=0+1+1-0-0-1=1. \\\end{align}\)
\(\left| \begin{matrix} 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \\\end{matrix} \right|=1\cdot \left( -1 \right)+\left( -1 \right)\cdot 1=-2\)
В результате вычислений получен ответ: -2
Метод понижения порядка
Упростить расчеты при вычислении определителей можно, используя их свойства.
Например, требуется вычислить определитель:\(\begin{vmatrix}6&3&8&-4\\5&6&4&2\\0&3&4&2\\4&1&-4&6\end{vmatrix}\)
Следует вынести из третьего столбца множитель 4:
\(\begin{vmatrix}6&3&8&-4\\5&6&4&2\\0&3&4&2\\4&1&-4&6\end{vmatrix}=4\cdot\begin{vmatrix}6&3&2&-4\\5&6&1&2\\0&3&1&2\\4&1&-1&6\end{vmatrix}\)
Далее следует вынести из четвертого столбца множитель 2:
\(4\cdot\begin{vmatrix}6&3&2&-4\\5&6&1&2\\0&3&1&2\\4&1&-1&6\end{vmatrix}=4\cdot2\cdot\begin{vmatrix}6&3&2&-2\\5&6&1&1\\0&3&1&1\\4&1&-1&3\end{vmatrix}=8\cdot\begin{vmatrix}6&3&2&-2\\5&6&1&1\\0&3&1&1\\4&1&-1&3\end{vmatrix}\)
Затем можно прибавить к строке №1 строку №2, умноженную на (-2):
\(8\cdot\begin{vmatrix}6&3&2&-2\\5&6&1&1\\0&3&1&1\\4&1&-1&3\end{vmatrix}=8\cdot\begin{vmatrix}-4&-9&0&-4\\5&6&1&1\\0&3&1&1\\4&1&-1&3\end{vmatrix}\)
Следующим шагом будет сложение строки №3 и строки №2, умноженной на (-1):
\(8\cdot\begin{vmatrix}-4&-9&0&-4\\5&6&1&1\\0&3&1&1\\4&1&-1&3\end{vmatrix}=8\cdot\begin{vmatrix}-4&-9&0&-4\\5&6&1&1\\-5&-3&0&0\\4&1&-1&3\end{vmatrix}\)
Далее нужно прибавить к четвертой строке вторую, умноженную на 1:
\(8\cdot\begin{vmatrix}-4&-9&0&-4\\5&6&1&1\\-5&-3&0&0\\4&1&-1&3\end{vmatrix}=8\cdot\begin{vmatrix}-4&-9&0&-4\\5&6&1&1\\-5&-3&0&0\\9&7&0&4\end{vmatrix}\)
Можно разложить определитель по третьему столбцу:
\(8\cdot\begin{vmatrix}-4&-9&0&-4\\5&6&1&1\\-5&-3&0&0\\9&7&0&4\end{vmatrix}=8\cdot1\cdot(-1)^{2+3}\begin{vmatrix}-4&-9&-4\\-5&-3&0\\9&7&4\end{vmatrix}=8\cdot(-1)^{5}\begin{vmatrix}-4&-9&-4\\-5&-3&0\\9&7&4\end{vmatrix}=-8\begin{vmatrix}-4&-9&-4\\-5&-3&0\\9&7&4\end{vmatrix}\)
Если прибавить к первой строке третью, умноженную на 1, получим:
\(-8\begin{vmatrix}-4&-9&-4\\-5&-3&0\\9&7&4\end{vmatrix}=-8\begin{vmatrix}5&-2&0\\-5&-3&0\\9&7&4\end{vmatrix}\)
Затем необходимо разложить определитель по третьему столбцу и вычислить его:
\(-8\begin{vmatrix}5&-2&0\\-5&-3&0\\9&7&4\end{vmatrix}=-8\cdot4\cdot(-1)^{3+3}\begin{vmatrix}5&-2\\-5&-3\end{vmatrix}=-32\cdot(-1)^{6}\begin{vmatrix}5&-2\\-5&-3\end{vmatrix}=-32\begin{vmatrix}5&-2\\-5&-3\end{vmatrix}\)
Далее следует прибавить к строке №2 строку №1, умноженную на 1:
\(-32\begin{vmatrix}5&-2\\-5&-3\end{vmatrix}=-32\begin{vmatrix}5&-2\\0&-5\end{vmatrix}\)
При разложении определителя по столбцу №1 и замене определителя 1-го порядка единственным его элементом получим:
\(-32\begin{vmatrix}5&-2\\0&-5\end{vmatrix}=-32\cdot5\cdot(-1)^{1+1}\cdot(-5)=-32\cdot5\cdot1\cdot(-5)=800\)
Приведение к треугольному виду
Методика заключается в приведении определителя к треугольнику.
После этого остается вычислить произведение элементов, расположенных на главной диагонали. С помощью данного способа вычислим определитель:\(\begin{vmatrix}4&-2&0&5\\3&2&-2&1\\-2&1&3&-1\\2&3&-6&-3\end{vmatrix}\)
В первую очередь следует поменять местами первую и третью строки:
\(\begin{vmatrix}4&-2&0&5\\3&2&-2&1\\-2&1&3&-1\\2&3&-6&-3\end{vmatrix}=-\begin{vmatrix}-2&1&3&-1\\3&2&-2&1\\4&-2&0&5\\2&3&-6&-3\end{vmatrix}\)
Далее первую строку, умноженную на 1, можно прибавить к четвертой:
\(-\begin{vmatrix}-2&1&3&-1\\3&2&-2&1\\4&-2&0&5\\2&3&-6&-3\end{vmatrix}=-\begin{vmatrix}-2&1&3&-1\\3&2&-2&1\\4&-2&0&5\\0&4&-3&-4\end{vmatrix}\)
Затем нужно к строке №3 прибавить строку №1, умноженную на 2:
\(-\begin{vmatrix}-2&1&3&-1\\3&2&-2&1\\4&-2&0&5\\0&4&-3&-4\end{vmatrix}=-\begin{vmatrix}-2&1&3&-1\\3&2&-2&1\\0&0&6&3\\0&4&-3&-4\end{vmatrix}\)
Следующий шаг – умножение второй строки на 2:
\(\begin{vmatrix}-2&1&3&-1\\3&2&-2&1\\0&0&6&3\\0&4&-3&-4\end{vmatrix}=-\frac{1}{2}\begin{vmatrix}-2&1&3&-1\\6&4&-4&2\\0&0&6&3\\0&4&-3&-4\end{vmatrix}\)
Сложим вторую и первую строку, умноженную на 3:
\(-\frac{1}{2}\begin{vmatrix}-2&1&3&-1\\6&4&-4&2\\0&0&6&3\\0&4&-3&-4\end{vmatrix}=-\frac{1}{2}\begin{vmatrix}-2&1&3&-1\\0&7&5&-1\\0&0&6&3\\0&4&-3&-4\end{vmatrix}\)
После умножения строки №4 на 7 получим:
\(-\frac{1}{2}\begin{vmatrix}-2&1&3&-1\\0&7&5&-1\\0&0&6&3\\0&4&-3&-4\end{vmatrix}=-\frac{1}{2}\cdot\frac{1}{7}\begin{vmatrix}-2&1&3&-1\\0&7&5&-1\\0&0&6&3\\0&28&-21&-28\end{vmatrix}\)
Затем следует прибавить к четвертой строке вторую строку, умноженную на (-4):
\(-\frac{1}{2}\cdot\frac{1}{7}\begin{vmatrix}-2&1&3&-1\\0&7&5&-1\\0&0&6&3\\0&28&-21&-28\end{vmatrix}=-\frac{1}{2}\cdot\frac{1}{7}\begin{vmatrix}-2&1&3&-1\\0&7&5&-1\\0&0&6&3\\0&0&-41&-24\end{vmatrix}\)
В результате смены мест столбцов №3 и №4 получим:
\(-\frac{1}{2}\cdot\frac{1}{7}\begin{vmatrix}-2&1&3&-1\\0&7&5&-1\\0&0&6&3\\0&0&-41&-24\end{vmatrix}=\frac{1}{2}\cdot\frac{1}{7}\begin{vmatrix}-2&1&-1&3\\0&7&-1&5\\0&0&3&6\\0&0&-24&-41\end{vmatrix}\)
После того, как третья строка, умноженная на 8, будет прибавлена к четвертой строке, получится вычислить определитель:
\(\frac{1}{2}\cdot\frac{1}{7}\begin{vmatrix}-2&1&-1&3\\0&7&-1&5\\0&0&3&6\\0&0&-24&-41\end{vmatrix}=\frac{1}{2}\cdot\frac{1}{7}\begin{vmatrix}-2&1&-1&3\\0&7&-1&5\\0&0&3&6\\0&0&0&7\end{vmatrix}=\frac{1}{2}\cdot\frac{1}{7}\cdot(-2)\cdot7\cdot3\cdot7=-21\)
Решение высшей математики онлайн
‹— НазадС понятием определителя мы уже сталкивались при изучении векторного произведения в разделе 10. Там были введены определители матриц второго и третьего порядка. В этом разделе мы дадим определение определителя квадратной матрицы любого порядка. Это определение будет рекуррентным, то есть чтобы установить, что такое определитель матрицы порядка , нужно уже знать, что такое определитель матрицы порядка . Такое рекуррентное определение и было использовано для введения определителя матрицы третьего порядка . Отметим также, что определитель существует только у квадратных матриц.Определитель квадратной матрицы будем обозначать или .
Определение 14.6 Определителем квадратной матрицы второго порядка называется число . Определителем квадратной матрицы порядка , , называется числогде — определитель матрицы порядка , полученной из матрицы вычеркиванием первой строки и столбца с номером . Легко проверить, что это определение для определителей второго и третьего порядка совпадает с данным ранее в разделе 10.
Для наглядности запишем, как можно вычислить определитель матрицы четвертого порядка:
Замечание 14.7 Реальное вычисление определителей для матриц выше третьего порядка на основе определения используется в исключительных случаях. Как правило, вычисление ведется по другим алгоритмам, которые будут рассмотрены позже и которые требуют меньше вычислительной работы.
Замечание 14.8 В определении 14.6 было бы точнее сказать, что определитель есть функция, определенная на множестве квадратных матриц порядка и принимающая значения в множестве чисел. Замечание 14.9 В литературе вместо термина «определитель» используется также термин «детерминант», имеющий тот же самый смысл. От слова «детерминант» и появилось обозначение .Рассмотрим некоторые свойства определителей, которые сформулируем в виде предложений.
Предложение 14.6 При транспонировании матрицы определитель не меняется, то есть . Предложение 14.7 Определитель произведения квадратных матриц равен произведению определителей сомножителей, то есть . Предложение 14.8 Если в матрице поменять местами две строки, то ее определитель сменит знак.Ввиду ограниченности курса доказательства этих трех свойств мы опускаем. Читатель может найти их в учебниках по линейной алгебре [3], [5] или же может без особых сложностей проверить их на матрицах второго и третьего порядков.
Предложение 14.9 Если матрица имеет две одинаковые строки, то ее определитель равен нулю. Доказательство. Поменяем местами две одинаковые строки. В силу предложения 14.8 определитель сменит знак. С другой стороны, так как строки были одинаковыми, то матрица не изменилась и, следовательно, не изменился и ее определитель. Получим, что , откуда следует, что . В дальнейшем нам потребуется складывать строки и умножать строку на число. Эти действия над строками (столбцами) мы будем выполнять так же, как действия над матрицами-строками (матрицами-столбцами), то есть поэлементно. Результатом будет служить строка (столбец), как правило, не совпадающая со строками исходной матрицы. При наличии операций сложения строк (столбцов) и умножения их на число мы можем говорить и о линейных комбинациях строк (столбцов), то есть суммах с числовыми коэффициентами.
Предложение 14.10 Если строку матрицы умножить на число , то ее определитель умножится на это число. Доказательство. Пусть — исходная матрица, — матрица, полученная из умножением первой строки на число :Тогдагде — определитель матрицы, полученной из матрицы или, что то же самое, из матрицы вычеркиванием первой строки и -ого столбца.Вынесем множитель за знак суммы и получим
Пусть теперь матрица получается из матрицы умножением -ой строки на число . Поменяем местами первую и -ую строки в матрице и то же самое проделаем в матрице . Получим две новых матрицы и . По предложению 14.8(14.10)
Очевидно, что матрица получается из матрицы умножением первой строки на число . Как только что было доказано, . Таким образом, из второго равенства (14.10) находим , отсюда с помощью первого равенства (14.10) получаем .Предложение 14.11 Если матрица содержит нулевую строку, то ее определитель равен нулю.
Доказательство. Нулевую строку можно рассматривать как строку из единиц, умноженную на число ноль. По предложению 14.10 определитель такой матрицы равен нулю, умноженному на определитель матрицы, содержащей строку из единиц. Результат такого умножения всегда будет ноль. Предложение 14.12 Если одна из строк матрицы равна другой, умноженной на число (строки пропорциональны), то определитель матрицы равен нулю. Доказательство. По предложению 14.10 определитель исходной матрицы равен числу , умноженному на определитель матрицы, у которой есть две одинаковые строки. По предложению 14.9 определитель последней матрицы равен нулю. Поэтому и определитель исходной матрицы равен нулю. Предложение 14.13 Пусть в матрице -ая строка имеет вид . Тогда , где матрица получается из матрицы заменой -ой строки на строку , а матрица — заменой -ой строки на строку . Доказательство. Пусть первая строка матрицы имеет вид . Тогда
Для случая утверждение доказано.Пусть . Обозначим через , , матрицы , , и , в которых поменяли местами первую и -ую строки. По только что доказанному (для ) утверждению . По предложению 14.8 , , . Следовательно, . Умножив обе части последнего равенства на , получим требуемое утверждение.
Предложение 14.14 Если к одной из строк матрицы добавить другую, умноженную на число, то определитель матрицы не изменится.
Доказательство. Пусть к -ой строке матрицы прибавлена -ая строка, умноженная на число . Новую матрицу обозначим . В матрице элементы -ой строки имеют вид . По предложению 14.13 , где — матрица, полученная из матрицы заменой -ой строки на -ую строку, умноженную на число . По предложению 14.12 , то есть .Предложение 14.15 Если одна из строк матрицы является линейной комбинацией других ее строк, то определитель матрицы равен нулю.
Доказательство. По предложению 14.13 определитель исходной матрицы равен сумме определителей матриц, в каждой из которых есть пропорциональные строки. По предложению 14.12 все эти определители равны нулю. Следовательно, и определитель исходной матрицы тоже равен нулю. Определение 14.7 Алгебраическим дополнением к элементу матрицы называется число, равное , где — определитель матрицы, полученной из матрицы вычеркиванием -ой строки и -ого столбца. Алгебраическое дополнение к элементу матрицы обозначается .
Пример 14.4 Пусть . Тогда Замечание 14.10 Используя алгебраические дополнения, определение 14.6 определителя можно записать так: Предложение 14.16 Разложение определителя по произвольной строке. Для определителя матрицы справедлива формула Доказательство. Если , положим . Пусть . Тогда -ую строку поменяем местами со строкой с номером . Определитель сменит знак. Затем строку с номером поменяем местами со строкой с номером . Определитель снова сменит знак. Процесс перестановки строк будем продолжать до тех пор, пока -ая строка матрицы не станет первой строкой новой матрицы, которую мы обозначим . Отметим, что в матрице , начиная со второй строки, стоят строки матрицы , причем порядок их следования не изменился.При переходе от матрицы к матрице определитель сменит знак раз (проверьте для случая ). Таким образом
(14.11)
Это соотношение верно и при . По определению 14.6 определителя,где — определитель матрицы, полученной из матрицы вычеркиванием первой строки и -ого столбца. Первая строка матрицы совпадает с -ой строкой матрицы , поэтому . Результат вычеркивания в матрице первой строки и -ого столбца будет таким же, как при вычеркивании в матрице -ой строки и -ого столбца. Поэтому , где — определитель матрицы, полученной при вычеркивании в матрице -ой строки и -ого столбца. Следовательно,В силу равенства (14.11) получимПо определению 14.7 алгебраического дополнения получим . Тогда из предыдущего равенства вытекаетчто и требовалось доказать. Пример 14.5 Вычислите .Решение. Воспользуемся разложением по третьей строке, так выгоднее, поскольку в третьей строке два числа из трех — нули. Получим
Предложение 14.17 Для квадратной матрицы порядка при выполнено соотношение(14.12)
Доказательство. Пусть — матрица, полученная из матрицы , в которой -ая строка заменена -ой строкой этой же матрицы, а сама -ая строка осталась без изменения. Таким образом, в матрице есть две одинаковые строки и в силу предложения 14.9 .С другой стороны, используя разложение определителя по -ой строке (предложение 14.16), получим
где — алгебраическое дополнение к элементу . Так как все строки матрицы , кроме -ой, совпадают со строками матрицы , то . Так как по построению матрицы , тоТак как , то равенство (14.12) доказано. Предложение 14.18 Все свойства определителя, сформулированные для строк ( предложения 14.8-14.17), справедливы и для столбцов, в частности, справедливо разложение определителя по -ому столбцу(14.13)
и равенство при . Доказательство. В силу предложения 14.6 определитель не меняется при транспонировании матрицы, а ее столбцы становятся строками транспонированной матрицы, для которой доказываемые свойства имеют место. Предложение 14.19 Определитель треугольной матрицы равен произведению элементов ее главной диагонали.
Доказательство. Воспользуемся индукцией по порядку матрицы. Для :утверждение верно. Предположим, что доказываемое утверждение верно для матриц порядка . Покажем, что оно верно для матрицы порядка .Если — верхняя треугольная матрица, то используем разложение по первому столбцу (равенство (14.13) при ):
Справа стоит определитель треугольной марицы порядка . По предположению индукции этот определитель равен . Поэтому .Если — нижняя треугольная матрицы, то нужно воспользоваться разложением по первой строке.
В остальном рассуждения аналогичны.Итак, утверждение верно для матрицы порядка . Предложение доказано.
Следствие 14.1 Определитель единичной матрицы равен единице, .Перечисленные выше свойства позволяют находить определители матриц достаточно высоких порядков при сравнительно небольшом объеме вычислений. Алгоритм вычислений следующий.
Алгоритм создания нулей в столбце.
Пусть требуется вычислить определитель матрицы порядка . Если , то поменяем местами первую строку и любую другую, в которой первый элемент не нуль. В результате определитель , будет равен определителю новой матрицы с противоположным знаком. Если же первый элемент каждой строки равен нулю, то матрица имеет нулевой столбец и по предложениям 14.11, 14.18 ее определитель равен нулю.
Итак, считаем, что уже в исходной матрице . Первую строку оставляем без изменений.
Остальные элементы новой второй строки обозначим , . Определитель новой матрицы по предложению 14.14 равен . Прибавим ко второй строке первую строку, умноженную на число . Тогда первый элемент второй строки будет равенПервую строку умножим на число и прибавим к третьей. Первый элемент новой третьей строки будет равен
Остальные элементы новой третьей строки обозначим , . Определитель новой матрицы по предложению 14.14 равен .Процесс получения нулей вместо первых элементов строк продолжим дальше. Наконец, первую строку умножим на число и прибавим к последней строке. В результате получается матрица, обозначим ее , которая имеет вид
причем . Для вычисления определителя матрицы используем разложение по первому столбцуТак как , тоВ правой части стоит определитель матрицы порядка . К нему применим тот же алгоритм, и вычисление определителя матрицы сведется к вычислению определителя матрицы порядка . Процесс повторяем до тех пор, пока не дойдем до определителя второго порядка, который вычисляется по определению. Если матрица не обладает какими-то специфическими свойствами, то заметно уменьшить объем вычислений по сравнению с предложенным алгоритмом не удается. Еще одна хорошая сторона этого алгоритма — по нему легко составить программу для компьютера для вычисления определителей матриц больших порядков. В стандартных программах вычисления определителей используется этот алгоритм с не принципиальными изменениями, связанными с минимизацией влияния ошибок округления и погрешностей входных данных при вычислениях компьютера.
Пример 14.6 Вычислите определитель матрицы.Решение. Первую строку оставляем без изменения. Ко второй строке прибавляем первую, умноженную на число :
Определитель не меняется. К третьей строке прибавляем первую, умноженную на число :Определитель не меняется. К четвертой строке прибавляем первую, умноженную на число :Определитель не меняется. В результате получаемПо тому же алгоритму считаем определитель матрицы порядка 3, стоящий справа. Первую строку оставляем без изменений, ко второй строке прибавляем первую, умноженную на число :К третьей строке прибавляем первую, умноженную на число :В результате получаемОтвет. .
Замечание 14.11 Внимательный читатель, наверное, отметил, что хотя при вычислениях использовались дроби, результат оказался целым числом. Действительно, используя свойства определителей и то, что исходные числа — целые, операций с дробями можно было бы избежать. Но в инженерной практике числа крайне редко бывают целыми. Поэтому, как правило, элементы определителя будут десятичными дробями и применять какие-то ухищрения для упрощения вычислений нецелесообразно.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
Определитель матрицы 4×4 – Как вычислить определитель матрицы 4×4?
Определитель матрицы 4×4 — это уникальное число, которое также рассчитывается по определенной формуле.
Если порядок матрицы равен n x n, то это квадратная матрица. Итак, здесь 4×4 — это квадратная матрица, состоящая из четырех строк и четырех столбцов. Если A — квадратная матрица, то определитель матрицы A представлен как |A|.Найдите определитель матрицы 4×4? мы будем использовать нормальный метод, есть формула определителя матрицы 4 × 4, которую мы обычно используем для нахождения определителя матрицы 3 × 3.
Определение определителя
Самый простой способ — сформулировать определитель, учитывая верхний ряд элементов и соответствующие миноры. Возьмите первый элемент верхней строки и затем умножьте его на минор, после чего вычтите произведение второго элемента на минор. Продолжайте поочередно складывать и вычитать произведение каждого элемента верхней строки с заданным минором, пока не будут учтены все элементы верхней строки.
Детерминанты также играют очень важную роль при нахождении обратной матрицы, а также при решении систем линейных уравнений.
В следующей части мы также предполагаем, что у нас есть квадратная матрица (m равно n). Определитель матрицы A будет стоять через det(A) или |A|. Сначала вводится определитель матрицы 2×2 и 3×3, затем ставится случай n×n.Что такое Матрица?
Прежде чем изучать операции над матрицей, давайте обсудим, что такое матрица. Матрица может быть определена как прямоугольный массив чисел или символов, которые обычно располагаются в строках и столбцах. Порядок матрицы также может быть определен как количество строк и количество. столбцов. Элементы также являются числами в матрице, и каждое из чисел называется элементом. Множественное число слова матрица известно как матрицы.
Размер матрицы называется матрицей «n на m» и записывается как m×n, где n — количество строк, а m — количество столбцов. Например, у нас есть матрица 3×2, потому что количество строк здесь равно 3, а количество столбцов здесь равно 2.
[Изображение скоро будет загружено]
Размеры матрицы также может быть определено как количество строк и столбцов матрицы в указанном порядке.
Поскольку приведенная выше матрица А имеет 2 строки и 3 столбца, она известна как матрица 2 × 3.Ярлык для определения ранга матрицы
Общее количество линейно независимых векторов в матрице равно общему количеству ненулевых строк в ее строке, присутствующей в ступенчатой матрице. Итак, чтобы узнать ранг матрицы, мы должны в общем случае преобразовать матрицу в ее эшелонированную форму строк, а затем подсчитать общее количество ненулевых строк.
Символ определителя
Символ определителя представляет собой две вертикальные линии с обеих сторон.
Пример:
|А| обозначает определитель матрицы A
(тот же символ, что и абсолютное значение)
Для матрицы 2×2
Для матрицы 2×2 (2 строки, 2 столбца):
A = \[\begin {bmatrix} a & b \\ c & d \end{bmatrix}\]
Определитель записывается как:
|A| = ad − bc
Очень легко запомнить, когда вы думаете о кресте:
Определитель матрицы 2×2
Если A — произвольная матрица 2×2 A, элементы задаются следующим образом:
A = \[\begin{bmatrix} a_{11} & a_{12} \ \ a_{21} & a_{22} \end{bmatrix}\]
, то определитель матрицы a и этой матрицы представляется следующим образом:
det(A) = lAl = \[\begin{vmatrix} a_ {11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix}\] = a\[_{11}\]a\[_{22}\] — a\[_ {21}\]a\[_{12}\]
Для матрицы 3×3
Для матрицы 3×3 (3 строки, 3 столбца):
A = \[\begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix}\]
Определитель записывается как:
|A| будет равно a(ei − fh) − b(di − fg) + c(dh − eg)
Это может показаться сложным, но есть известная закономерность:
[Изображение скоро будет загружено]
To вычислить определитель матрицы 3×3 вот точки:
Умножить a на определитель матрицы 2×2, которая не находится ни в строке, ни в столбце a.
Также для b, и для c тоже
Сложите их, но также помните о минусе перед b
Что касается формулы (помните, что вертикальные черточки || определитель»):
lAl = a . \[\begin{vmatrix} e & f \\ h & i \end{vmatrix}\] — b . \[\begin{vmatrix} d & f \\ g & i \end{vmatrix}\] + c . \[\begin{vmatrix} d & e \\ g & h \end{vmatrix}\]
Как вычислить определитель матрицы 4×4?
Прежде чем мы попытаемся найти определитель матрицы 4×4, давайте сначала проверим несколько условий, приведенных ниже.
Если присутствует какое-либо условие, где определитель матрицы 4×4 может быть равен 0 (например, полная строка или полный столбец равен 0)
возможный.
Если элементы матрицы одинаковы, но затем переупорядочены в любом из столбцов или строк.
В любом из трех случаев, приведенных выше, используются соответствующие методы вычисления определителей 3 x 3. Мы меняем строку или столбец, чтобы заполнить их 0, за исключением одного элемента. Определитель матрицы 4 × 4 будет эквивалентен произведению этого элемента и его кофактора. В этой ситуации кофактор представляет собой детерминант 3 × 3, который оценивается по своей конкретной формуле.
Как рассчитать определитель 4X4? Посчитайте с нашим экспертом
Мы продолжаем готовить уроки по математике. Надеюсь, это будет полезно для вас, и вам не нужно будет спрашивать наших экспертов что-то вроде «Сделай мне домашнее задание по математике, пожалуйста! Я застрял..» Это вторая часть нашего руководства, объясняющая, как вычислять определители. Нас просят вычислить определитель следующей матрицы 4 × 4:
A=\begin{pmatrix}-1 & {1} & 4 & 2 \\2 & -1 & 2 & 5 \\1 &2 & 3& 4\\3& 4& -1 & 2\end{pmatrix} 9{4+1}a_{41}M_{41}\\&=a_{11}M_{11}-a_{21}M_{21}+a_{31}M_{31}-a_{41}M_{ 41}=-1\cdot M_{11}-2 \cdot M_{21}+1\cdot M_{31}-3 \cdot M_{41} \end{aligned}
Вот видеоверсия этого руководства:
youtube.com/embed/lJkDUP4n5hI?list=UUn_YObR-sCBGWwEOdCbLzxg» frameborder=»0″ allowfullscreen=»allowfullscreen»> Чтобы найти значение \Delta , нам нужно вычислить миноры M_{11}, M_{21}, M_{31}, M_{41}. Это определители порядка 3×3:
Вычислим их таким же образом, но выбрав первую строку. Это означает, что мы устанавливаем i=1, в то время как j меняется от 1 до 3. Обратите внимание, что на этот раз верхний предел равен 3 вместо 4 для исходного определителя, потому что это определители размера 3×3. Как правило, мы можем выбрать любую строку или столбец:
\begin{align} M_{11}&=\begin{vmatrix}-1&2 &5 \\2& 3 &4 \\4&-1 &2\end{vmatrix}=-1 \cdot\begin{vmatrix}3&4 \\ -1&2 \end{vmatrix}-2\cdot\begin{vmatrix}2&4 \\4&2 \end{vmatrix}+5\begin{vmatrix}2&3 \\4&-1\end{vmatrix}\\&=-1\ cdot (6+4)-2\cdot (4-16)+5\cdot(-2-12)=-10+24-70=-56\end{aligned}
Аналогично вычисляем остальные три минора:
\begin{выровнено} M_{21}&=\begin{vmatrix}1&4&2 \\2& 3 &4 \\4&-1 &2\end{vmatrix}=1 \cdot\begin{vmatrix}3&4 \\-1&2 \ end{vmatrix}-4\cdot\begin{vmatrix}2&4 \\4&2 \end{vmatrix}+2\begin{vmatrix}2&3 \\4&-1\end{vmatrix}\\&=1\cdot (6+ 4)-4\cdot (4-16)+2\cdot (-2-12)=10+48-28=30\end{выровнено}
\begin{align} M_{31}&=\begin{vmatrix}1&4&2 \\-1& 2 &5 \\4&-1 &2\end{vmatrix}=1 \cdot\begin{vmatrix}2&5 \\-1&2 \end{vmatrix}-4\cdot\begin{vmatrix}-1&5 \\4&2 \end{vmatrix}+2\begin{vmatrix}-1&2 \\4&-1\end{vmatrix}\\&=1\cdot (4+5)-4\cdot (-2-20)+2\cdot (1-8)=9+88-14=83\end{выровнено}
M_{41}=\begin{vmatrix}1&4&2 \\-1& 2 &5 \\2&3 &4\end{vmatrix}=1\cdot (8-15)-4\cdot (-4-10)+2\cdot (-3-4)=-7+56- 14=35
Наконец, у нас есть все необходимые данные для нахождения нужного определителя.
Подставим значения в выражение для \det A:\begin{aligned} \Delta& =-1\cdot M_{11}-2 \cdot M_{21}+1\cdot M_{31}-3 \cdot M_{41}\\&=-1\cdot (-56)-2\cdot 30+1\cdot 83-3\cdot 35=56-60+83-105=-26\end{выровнено}
Таким образом , ответ:
\det A =-26
Подводим итоги. Если вас просят вычислить определитель какой-либо матрицы, прежде всего убедитесь, что вы имеете дело с квадратной матрицей, т.е. количество строк и количество столбцов совпадают. Если это так, то можно продолжить и применить общую формулу для вычисления определителей, которая выглядит следующим образом: 9{i+j}a_{ij}M_{ij}
Здесь $n$ — размер вашей квадратной матрицы. Затем вы выбираете некоторую строку или столбец и выполняете расширение, получая, таким образом, множество меньших определителей для вычисления. Для удобства выберите строку или столбец с наименьшими значениями или лучше с нулями, если это возможно. Такой подход сэкономит ваше время и позволит быстрее выполнить домашнее задание по математике.
{N (a_{1},a_{2},…a_{n})}}*a_{1a_{1}}a_{2a_{2}}…a_{na_{n}}\)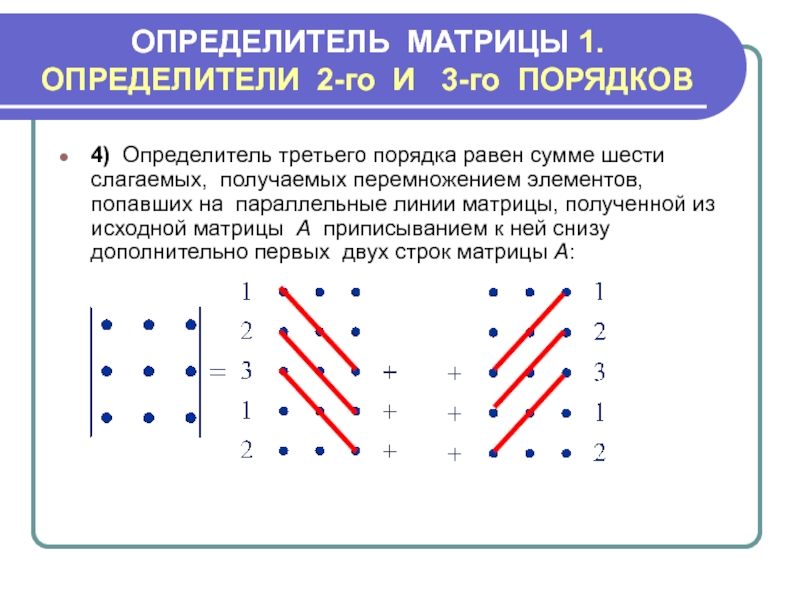
com
{i+j}}\cdot {{M}_{ij}}}\)
{4+4}}\cdot \left| \begin{matrix} 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\\end{matrix} \right| & \\\end{align}\)
Например, требуется вычислить определитель:
После этого остается вычислить произведение элементов, расположенных на главной диагонали. С помощью данного способа вычислим определитель:
Там были введены определители матриц второго и третьего порядка. В этом разделе мы дадим определение определителя квадратной матрицы любого порядка. Это определение будет рекуррентным, то есть чтобы установить, что такое определитель матрицы порядка , нужно уже знать, что такое определитель матрицы порядка . Такое рекуррентное определение и было использовано для введения определителя матрицы третьего порядка . Отметим также, что определитель существует только у квадратных матриц.
Получим, что , откуда следует, что . 
Поменяем местами первую и -ую строки в матрице и то же самое проделаем в матрице . Получим две новых матрицы и . По предложению 14.8
Предложение 14.12 Если одна из строк матрицы равна другой, умноженной на число (строки пропорциональны), то определитель матрицы равен нулю. Доказательство. По предложению 14.10 определитель исходной матрицы равен числу , умноженному на определитель матрицы, у которой есть две одинаковые строки. По предложению 14.9 определитель последней матрицы равен нулю. Поэтому и определитель исходной матрицы равен нулю. Предложение 14.13 Пусть в матрице -ая строка имеет вид . Тогда , где матрица получается из матрицы заменой -ой строки на строку , а матрица — заменой -ой строки на строку . Доказательство. Пусть первая строка матрицы имеет вид . Тогда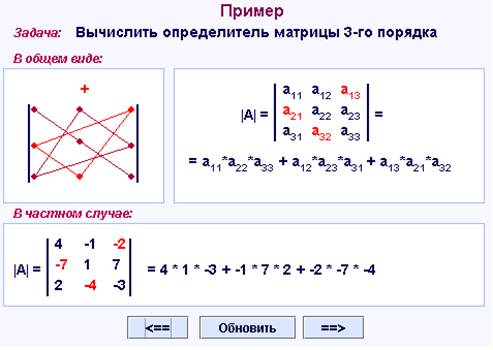
Если , положим . Пусть . Тогда -ую строку поменяем местами со строкой с номером . Определитель сменит знак. Затем строку с номером поменяем местами со строкой с номером . Определитель снова сменит знак. Процесс перестановки строк будем продолжать до тех пор, пока -ая строка матрицы не станет первой строкой новой матрицы, которую мы обозначим . Отметим, что в матрице , начиная со второй строки, стоят строки матрицы , причем порядок их следования не изменился.
Результат вычеркивания в матрице первой строки и -ого столбца будет таким же, как при вычеркивании в матрице -ой строки и -ого столбца. Поэтому , где — определитель матрицы, полученной при вычеркивании в матрице -ой строки и -ого столбца. Следовательно,В силу равенства (14.11) получимПо определению 14.7 алгебраического дополнения получим . Тогда из предыдущего равенства вытекаетчто и требовалось доказать. Пример 14.5 Вычислите .
Пусть — матрица, полученная из матрицы , в которой -ая строка заменена -ой строкой этой же матрицы, а сама -ая строка осталась без изменения. Таким образом, в матрице есть две одинаковые строки и в силу предложения 14.9 .
Доказательство. В силу предложения 14.6 определитель не меняется при транспонировании матрицы, а ее столбцы становятся строками транспонированной матрицы, для которой доказываемые свойства имеют место. 
В остальном рассуждения аналогичны.
Прибавим ко второй строке первую строку, умноженную на число . Тогда первый элемент второй строки будет равен
К нему применим тот же алгоритм, и вычисление определителя матрицы сведется к вычислению определителя матрицы порядка . Процесс повторяем до тех пор, пока не дойдем до определителя второго порядка, который вычисляется по определению. 
К четвертой строке прибавляем первую, умноженную на число :Определитель не меняется. В результате получаемПо тому же алгоритму считаем определитель матрицы порядка 3, стоящий справа. Первую строку оставляем без изменений, ко второй строке прибавляем первую, умноженную на число :К третьей строке прибавляем первую, умноженную на число :В результате получаем
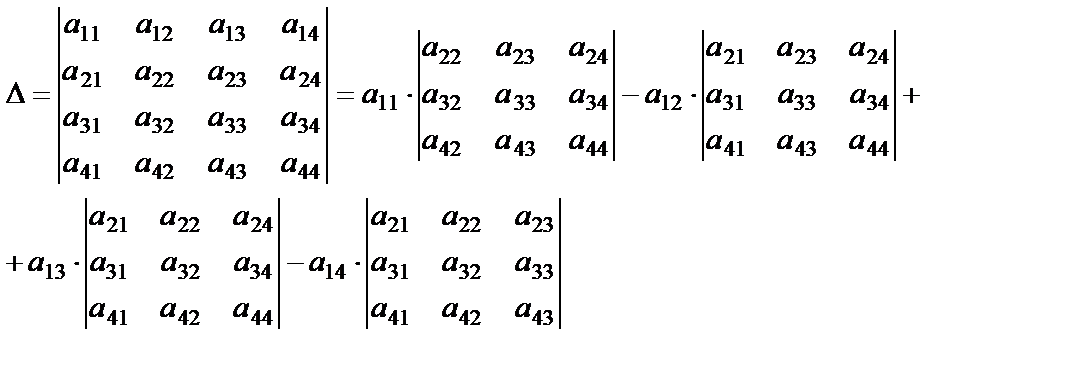Если порядок матрицы равен n x n, то это квадратная матрица. Итак, здесь 4×4 — это квадратная матрица, состоящая из четырех строк и четырех столбцов. Если A — квадратная матрица, то определитель матрицы A представлен как |A|.
В следующей части мы также предполагаем, что у нас есть квадратная матрица (m равно n). Определитель матрицы A будет стоять через det(A) или |A|. Сначала вводится определитель матрицы 2×2 и 3×3, затем ставится случай n×n.
Поскольку приведенная выше матрица А имеет 2 строки и 3 столбца, она известна как матрица 2 × 3.
Подставим значения в выражение для \det A:
Это самый простой способ одержать победу, но практически все знают, как от него защититься. 
Несмотря на кажущуюся простоту этой фигуры, у новичков возникает много вопросов относительно нее.
Но лишь с массовым приходом компьютеров эта проблема стала очень серьезной
в Гамбурге.
Другой участник операции имел возможность скрытно общаться с игроком по радио, находясь в удобной и незаметной точке наблюдения, которая была расположена в зоне для прессы на балконе, окаймлявшем зал, где проходил турнир.
Следовательно, для шустрых проходимцев – из разряда любителей срубить где-нибудь денег без особого напряга – появились новые заманчивые возможности.
..
Молодой шахматист был явно к этому готов. Он предъявил жюри все, что было в карманах, и даже разделся до пояса, сняв майку. Абсолютно ничего компрометирующего у него не обнаружили.
д.) быстро превратят шахматы в уродливое и никому не интересное занятие. Удовольствие от него не получит уже никто – ни участники, ни поклонники игры.
Если вы хотите связаться с нами, начните чат на нашем сайте, чтобы сдвинуться с мертвой точки.
Однако, несмотря на то, что количество конкретных уровней может измениться, вы все равно попадете в один из трех уровней, самый высокий из которых — 66 2/3%, второй — фиксированная ставка, а последний — 9.0%.
Этот навык пригодится им и в настоящем, и в будущем.
.
Понятный. Небольшой.
Легкие вещи.
.. 9000 5
Умножение
Он также имеет все ответы, разработанные в полном объеме. Этот учебник в твердом переплете, состоящий из 108 ежедневных уроков, охватывает все, что вам нужно для первого года обучения алгебре в старшей школе.
. . все соответствует правилу «i перед e»
Об иррациональности некоторых чисел знали с давних времен: античные геометры определили проблему несоизмеримости стороны квадрата и его диагонали, что соответствует иррациональности корня из 2. Кроме того, древние ученые впервые встретились с проблемой подсчета иррационального числа Пи, которое определяется как соотношение длины окружности к ее диаметру.
В повседневной жизни мы оперируем натуральными числами, то есть целыми и положительными числами, которые используем при счете. Рациональные числа используются при измерениях, а иррациональные практически не находят распространения в быту — область их применения лежит в высокой науке. При помощи нашего онлайн-калькулятора вы можете проверить принадлежность любого числа к определенному множеству.
15 Пусть r — рациональное число, α — иррациональное число. Рациональным или иррациональным является число:
..)
П.
Рациональное число — это число, которое можно записать как отношение двух целых чисел.
Самый простой способ сделать это — записать дробь со знаменателем один.
Итак,
0,1.0,2.0,3.0
\overline{6}0,8,-0,875,3,25,-6,6
Его десятичная форма не прерывается и не повторяется.
Автор : Джеймс Соуза (Mathispower4u.com). Лицензия : CC BY: Атрибуция 
Немного сложнее показать почему, поэтому я сделаю это в другом месте.
2020020002 …$$
Вы не можете упростить $$ \sqrt{3} $$, что означает, что мы можем , а не выразить это число как частное двух целых чисел.
Давайте посмотрим, что такое квадратный корень из 289 .
Мы видели, что √ 289 = 17. 17 — целое число. Это можно легко выразить в форме p/q. Следовательно, √ 289 – рациональное число.
Число в квадратном корне, которое повторяется, равно 17. Следовательно, квадратный корень из 289 равен 17.
Рациональные числа можно записать в виде дроби, а иррациональные — нет.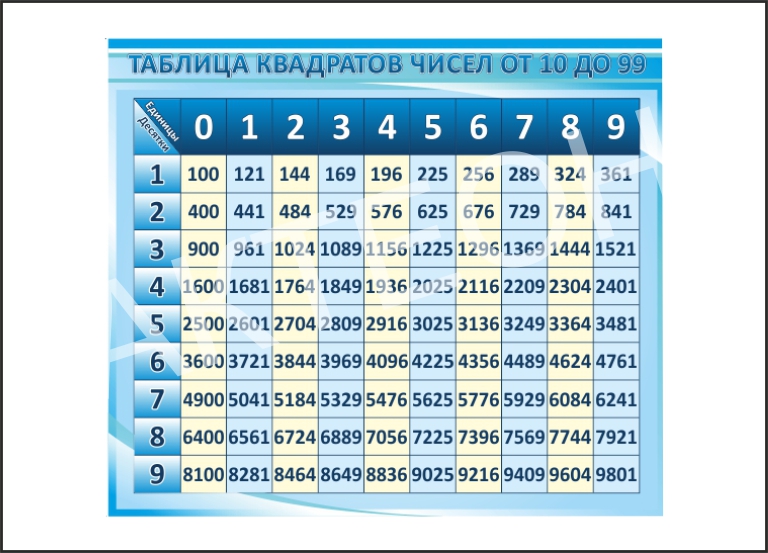
Именно так математики вычисляли его задолго до того, как были изобретены калькуляторы и компьютеры.
Затем используйте 2 и нижнее число, чтобы решить эту задачу: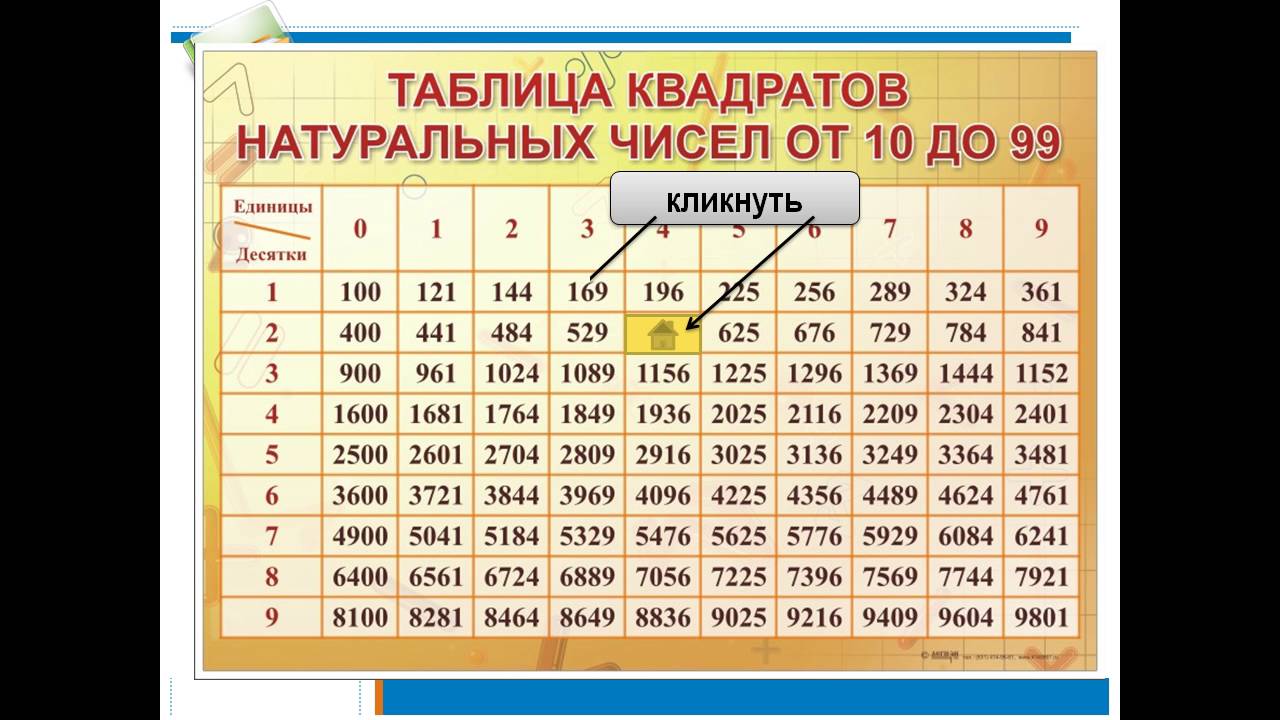
..Меньше
Такие числа будут иметь текстовый формат.
Например, при вводе десятизначного кода продукта Excel по умолчанию изменяет число 0784367998 на 784367998. В данном случае можно создать пользовательский числовой формат с кодом 0000000000, чтобы в Excel отображались все десять знаков кода продукта, включая начальный ноль. Дополнительные сведения об этой проблеме см. в статьях Создание и удаление пользовательских числовых форматов и Сохранение начальных нулей в числовых кодах.
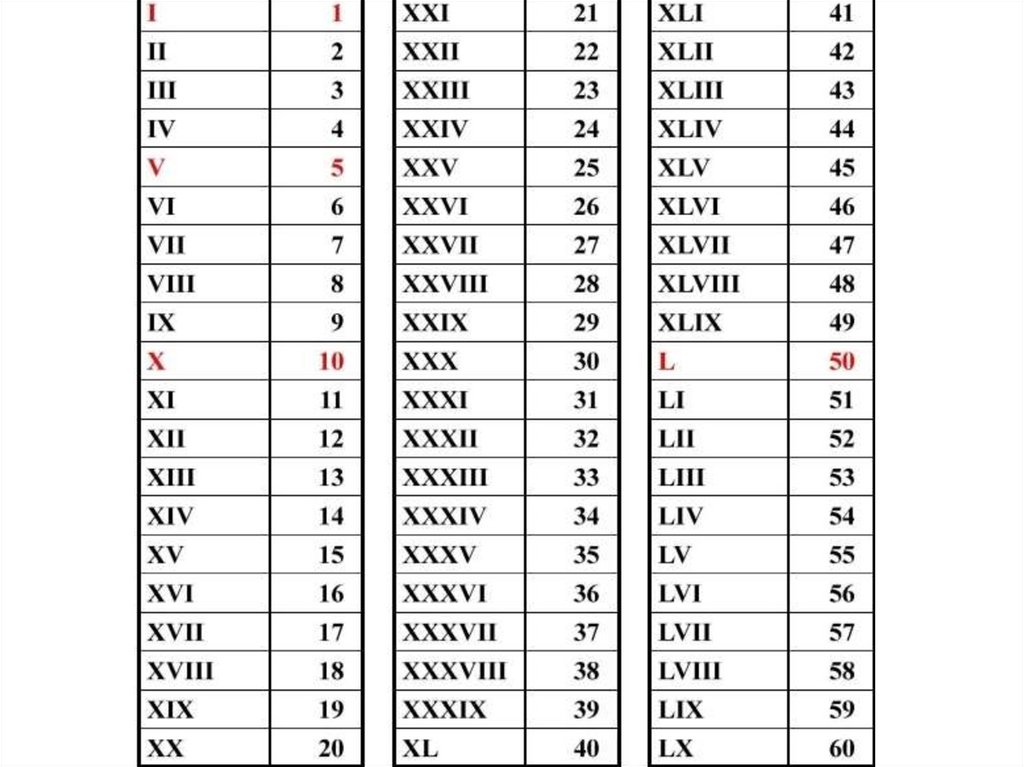
Может показаться, что они отличаются от цифр, но они похожи. Например, римские цифры XLI эквивалентны числу 41. Римские цифры, относящиеся к XLI, приведены ниже:
75 + 41 = 3016 
Поэтому 41 римскими цифрами записывается как XLI = XL + I = 40 + 1 = XLI.
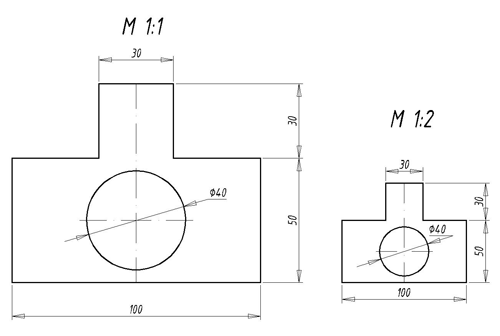
на рисунке выше).
location=’d0e23291.htm»>Процедура
Подробнее о работе с аннотативными объектами и автоматическом
масштабировании аннотаций см.
Масштабирование аннотаций.
Необходимые размеры этих элементов
сохраняются и после масштабирования при выводе окончательного
чертежа на печать.
5″
20 x 12 = Масштабный коэффициент 240 
25″ = 1′-0″
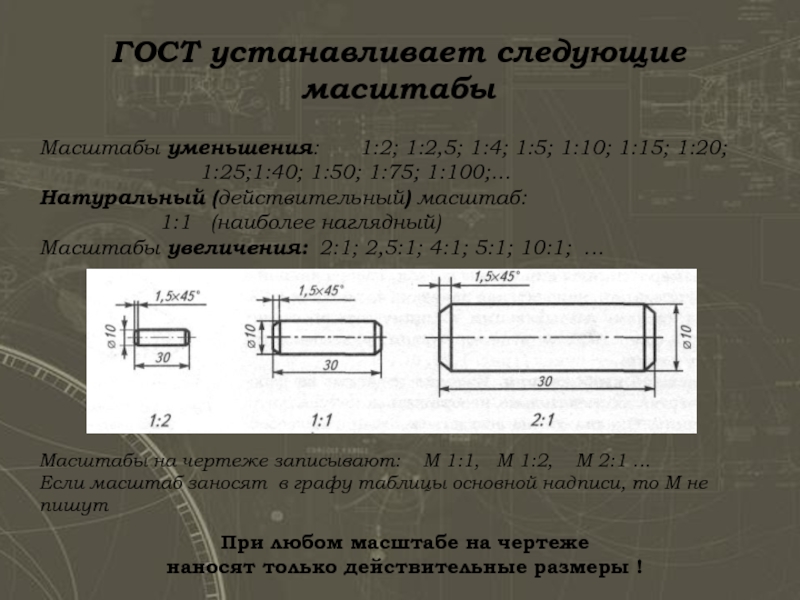То есть: 
Ожиданием
Снижением доходов
Если вкратце, то это задача про то, как с наименьшими затратами доставить продукцию или товары от производителей к покупателям, учитывая предложение первых и спрос вторых. В статье я дам основные определения транспортной задачи, покажу, как правильно сформулировать её условие, а также приведу пример решения на Python.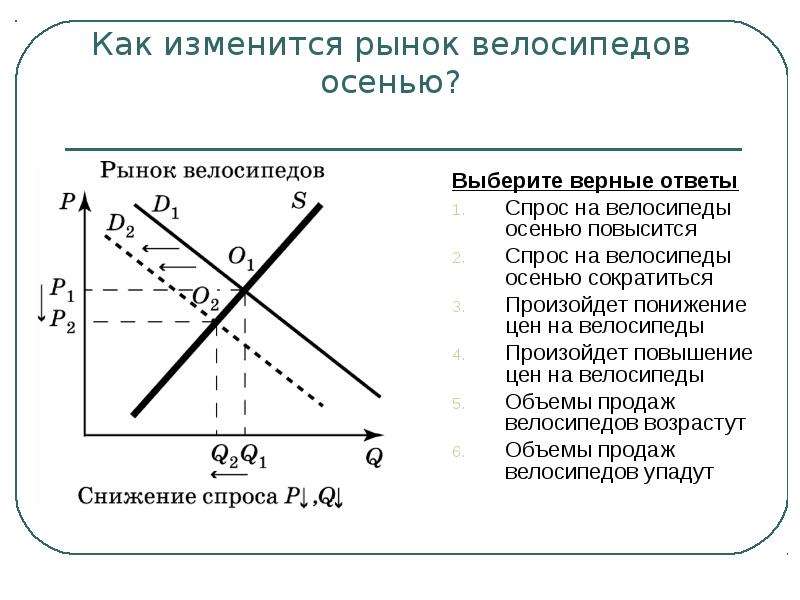
Как оказалось позднее, транспортная задача и является одной из задач линейного программирования.
Допустим, что имеется три производителя данного продукта и четыре крупных покупателя, другие покупатели являются слишком мелкими и их влиянием можно пренебречь. Предположим, что все три производителя создают абсолютно одинаковый продукт, и у покупателей на внутреннем рынке нет никаких предпочтений относительно выбора того или иного производителя кроме цены.
Давайте для лучшего понимания условий задачи и большей наглядности изобразим схему возможных взаимодействий производителей с покупателями и морским портом.
Ограничения должны быть записаны в виде математических соотношений (уравнений или неравенств).
д. перевозку и производство 1-ой тонны продукта от -го производителя в порт;
Количество поставляемого продукта для любого покупателя не может быть отрицательным.
Получается, каждый производитель должен выбрать стратегию снижения цены продукта согласно следующему условию.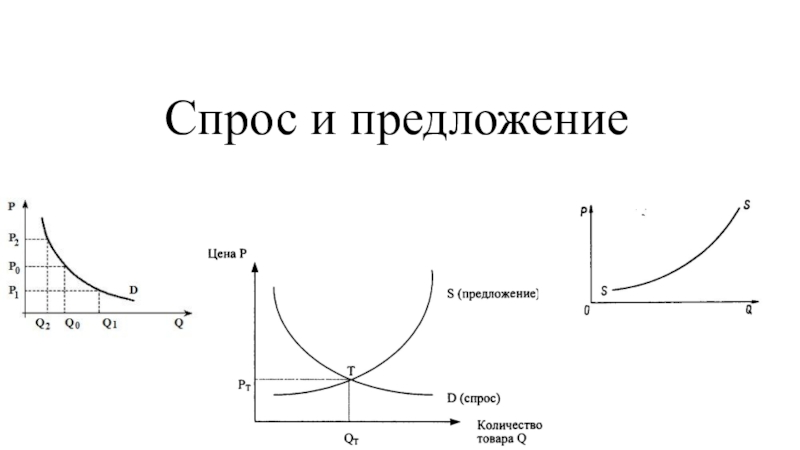
Также в комплект программного продукта IBM ILOG CPLEX Optimization Studio входит Python библиотека DOcplex и примеры её использования в Jupyter Notebook. Ниже рассмотрим ход моего решения задачи в Jupyter Notebook.
append('P'+ str(i+1))
ProdData = {'Possibilities': [890,534,1153],
'SupplyPort': [18,13,18],
'ProdCost': [12,21,10],
'PortPrice': [d,d,d],
'Overhead': [18+12,13+21,18+10]
}
Producers = pd.DataFrame(ProdData, ProdIndex)
# Покупатели
BuyIndex = ['B1','B2','B3','B4']
BuyData = {'Scenario1': [78,121,94,85], 'Scenario2': [117,670,193,279]}
Buyers = pd.DataFrame(BuyData, BuyIndex)
#выбор сценария
Scenario = Buyers.columns[0] # 0 - Scenario1
# 1 - Scenario2
print(Scenario)
# Тарифы на железнодорожные перевозки
RailData = {'P1':[14,23,21,42], 'P2':[26,10,19,36], 'P3':[15,38,18,15]}
RailFares = pd.DataFrame(RailData, BuyIndex)
totCost = RailFares + Producers['ProdCost']
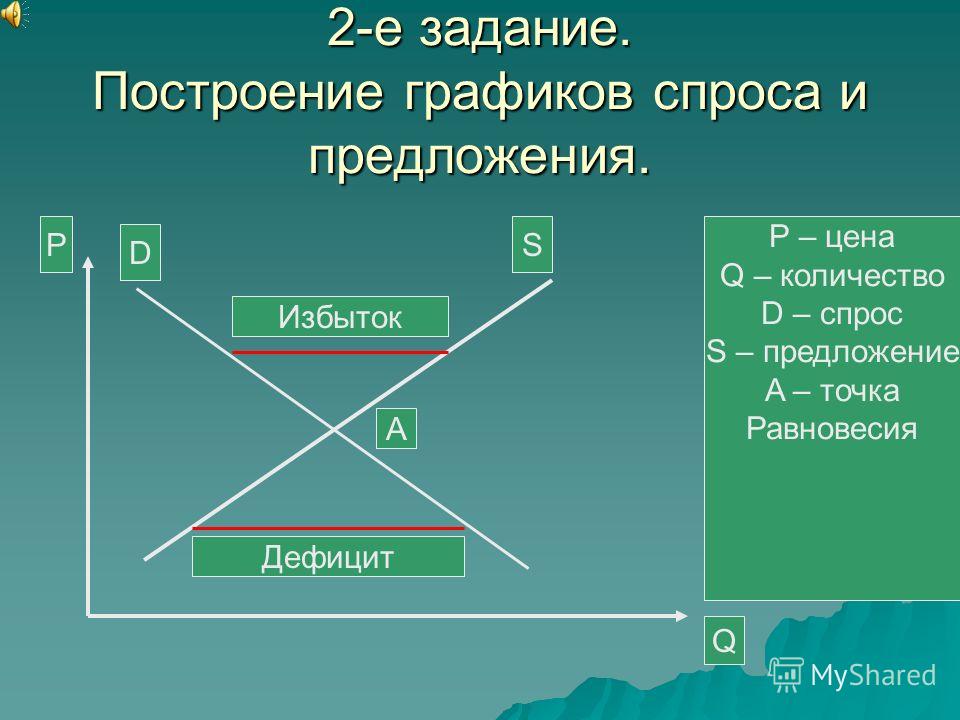index):
mdl.add_constraint(mdl.sum(x[i,j] for j in range(NBuyers)) + p[i] <= possib, ctname='Possib'+cts_name)
sum( (y[i,j]-k[i,j] )*x[i,j]*h[i,j] for i in range(NProds) for j in range(NBuyers) )
#Доставка в порт
SalesPort = mdl.sum( (d-z[i])*p[i] for i in range(NProds) )
#Целевая функция
mdl.maximize(SalesBuyers + SalesPort)
DataFrame(VolData, BuyIndex)
#Количество тонн продукта от i-го производителя в порт
VolPricePortData = dict(zip(ProdIndex, (VolPricePort)))
DecisionVolPort = pd.DataFrame(VolPricePortData, index=['Pt'])
#Цена за тонну продукта i-го производителя j-му покупателю
PriceData = dict(zip(ProdIndex, prodsPrice))
DecisionPrice = pd.DataFrame(PriceData, BuyIndex)
#Объём продаж i-го производителя j-му покупателю за вычетом затрат на доставку товара
VolPriceData = dict(zip(ProdIndex, VolPrice))
DecisionVolPrice = pd.DataFrame(VolPriceData, BuyIndex)
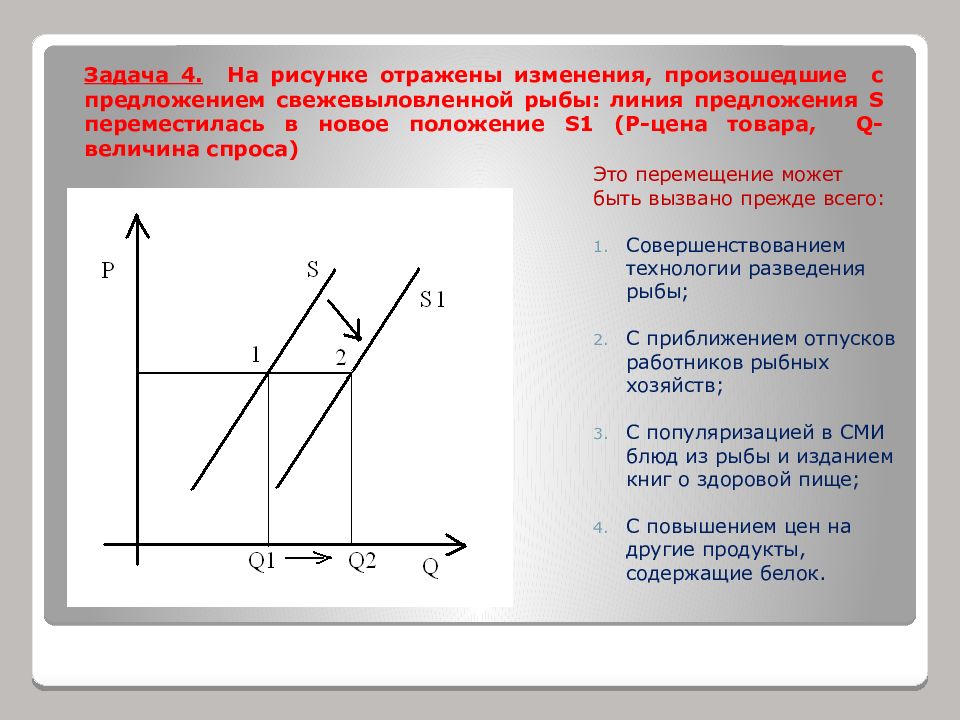add_edge(p, b, w=DecisionVolPrice[p][b])
nodeKeys = []
nodePos = []
num_buy = 0
num_prod = 0
for p in ProdIndex:
x_prod = int(-NProds/2)+num_prod
num_prod+=1
nodeKeys.append(p)
nodeKeys.append('Pt')
nodePos.append([x_prod,1])
nodePos.append([0,2])
for b in BuyIndex:
num_prod = 0
x_buy = int(-NBuyers/2)+num_buy
num_buy+=1
for p in ProdIndex:
x_prod = int(-NProds/2)+num_prod
num_prod+=1
nodeKeys.append(p)
nodeKeys.append(b)
nodePos.append([x_prod,1])
nodePos.append([x_buy+0.5,0])
pos = dict(zip(nodeKeys, nodePos))
elarge = [(u, v) for (u, v, d) in G.edges(data=True) if d['w'] > 0]
esmall = [(u, v) for (u, v, d) in G.edges(data=True) if d['w'] == 0]
plt.figure(figsize=(16, 8))
plt.subplot(1,2,1)
nx.draw_networkx_nodes(G, pos=pos, node_size=7000/((NProds+NBuyers)/2))
nx.draw_networkx_edges(G, pos=pos, edgelist=elarge, width=2, edge_color='black')
nx.
draw_networkx_edges(G, pos=pos, edgelist=esmall, width=2, alpha=0.3, edge_color='gray',)
edge_values = []
for (u, v, d) in G.edges(data=True):
if d['w']>0:
edge_values.append(int(d['w']))
labels = dict(zip(elarge, edge_values))
nx.draw_networkx_edge_labels(G, pos=pos, edge_labels=labels, font_size=12, font_color='black')
# labels
nx.draw_networkx_labels(G, pos=pos, font_size=70/((NProds+NBuyers)/2), font_color='white')
plt.axis('off')
plt.subplot(1,2,2)
plt.grid(True)
sns.barplot(x=DecisionVolPrice.columns,
y=sumBuyPort,
palette="deep").set_title('Суммарный объём продаж')
plt.show()
В своей статье я собрал и обобщил минимальный теоретический материал, необходимый для общего понимания подхода в решении подобных задач, а также привёл пример такой задачи и минимальный набор инструментов для её решения. Описанный подход позволяет получить масштабируемое решение с возможностью варьирования исходных условий задачи.
Возможно, вы прошли вводный курс по экономике. Вы пришли к пониманию того, как кривая предложения и кривая спроса пересекаются, чтобы получить равновесную цену и количество. Как мы знаем, эти точки равновесия меняются по мере смещения кривых спроса и предложения.
Эта линия позволяет нам узнать, сколько будет поставлено по любой цене, о которой мы могли бы спросить.
Затем предположим, что я решил, что для меня оптимально произвести 1000 единиц кукурузы по этой цене в 2 доллара. Моя дополнительная тысяча единиц вряд ли повлияет на рыночный спрос таким образом, чтобы привести к изменению цены. Это отсутствие «рыночной силы» позволяет нам выделить эту конкретную рыночную цену и точно записать, что я буду производить.
Но когда мы снова включим эти уровни выпуска в функцию спроса, результирующая рыночная цена составит
Наконец, предположим, что фирмы имеют предельные издержки производства, которые мы обозначим буквой 9.0034 c (что, как мы предполагаем, меньше K , чтобы облегчить жизнь). После небольшого расчета и алгебры для решения равновесия Нэша мы можем определить, что рыночная цена и количество будут даны следующим образом: если вы присмотритесь, то заметите, что они полностью оправдывают нашу старую, знакомую и технически неправильную модель спроса и предложения. Давайте разберемся, почему:
Следовательно, модель спроса и предложения дает те же качественный прогноз равновесия, как и наши уравнения равновесия. Это верно, хотя первое технически неверно.
На нашем традиционном графике спроса и предложения это будет представлено увеличением или сдвигом наружу кривой предложения, которую мы можем изобразить графически следующим образом:0003
Однако, несмотря на это, это остается чрезвычайно полезным «эмпирическим правилом». Это согласуется со всеми качественными предсказаниями, которые мы получаем из более точных расчетов. Таким образом, мы прекрасно объясняем экономический феномен как если бы кривая предложения действительно существовала.
Нарисуйте ситуацию спроса и предложения, когда существует излишек (и определите, что
излишек есть). Четко показать
где избыток находится на графике.
Обязательно правильно пометьте свои оси и сделайте
ясно, в какую сторону вы сдвигаете свои графики. Предположим при прочих равных условиях . 
Что будет на рынке спама
если доходы людей, покупающих спам, упадут?
Что произойдет на рынке
крупного рогатого скота, если правительство субсидирует производство говядины?
Вы замечаете, что, делая это, вы могли бы продать 650 обедов со стейками, но
хотят и могут продать только 400. Нарисуйте эту ситуацию на графике.
Поместите все числа, данные на вашем графике. Что будет на этом рынке?
Будет дефицит или избыток? Покажите это на своем графике. Затем
объясните, что произойдет на этом рынке (предположим, что ценовой контроль отсутствует).
Обязательно правильно пометьте свои оси и сделайте
ясно, в какую сторону вы сдвигаете свои графики. Предположим при прочих равных условиях . 
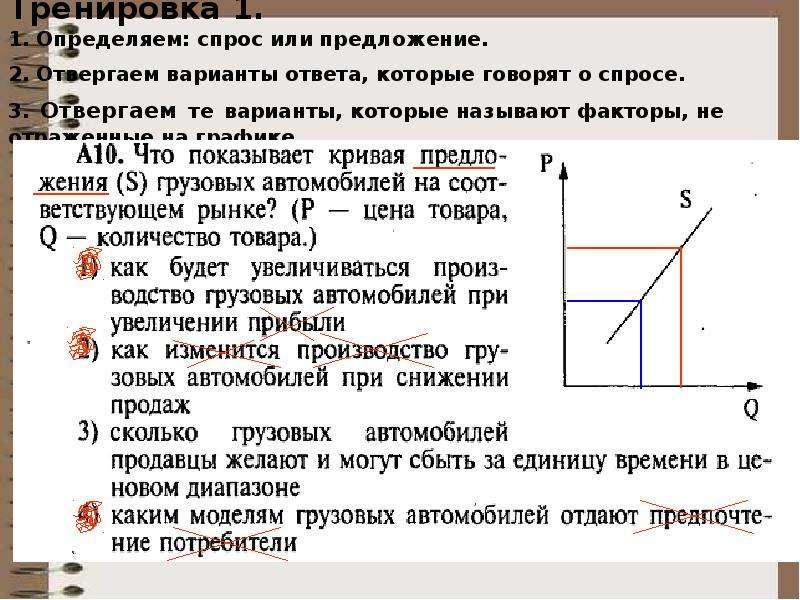Что будет на рынке спама
если доходы людей, покупающих спам, упадут?
Фактические характеристики продукта могут отличаться.
1, BLE / BR / EDR
Фактическая емкость может отличаться. Указана номинальная
емкость. Фактическая емкость батареи может быть выше или
ниже номинальной. Фактическое время работы устройства может
отличаться в зависимости от настроек устройства и
особенностей его использования.)
Фактическая емкость может отличаться. Указана номинальная
емкость. Фактическая емкость батареи может быть выше или
ниже номинальной. Фактическое время работы устройства может
отличаться в зависимости от настроек устройства и
особенностей его использования.)
4 и выше
Его производит компания Sabic – лидер инновационной химической
промышленности.
Процент
пластика в упаковке телефона также сократился с 21,7% до 0,3%. Для печати используются экологически
чистые чернила на основе соевого масла.
0
Устойчивость к царапинам стекла Gorilla Glass Victus вдвое выше, чем у Gorilla Glass 6.
0
Используя таблицу, задайте функцию формулой
Кто же из братьев разбил окно?
В AlmaU, Университете Нархоз и Каспийском Университете представлены специальности, где профильными предметами являются математика, физика, география, иностранный язык, Человек. Общество. Право, всемирная история, биология, химия и творческий экзамен.
Эти тесты могут различаться по содержанию и стилю, но в конечном итоге они оценивают базовые вычислительные способности, а также более сложное логическое мышление.
Проще говоря, это тест по математике, который оценивается так же, как и школьные тесты. Однако в некоторых случаях неправильные ответы могут уменьшить ваш общий балл.
Вам будет удобно использовать свои собственные знания о кнопках, что позволит вам сэкономить пару решающих секунд по сравнению с другими конкурентами. В любом случае, если ваш психометрический тест есть в сети, вы можете использовать свой собственный калькулятор.
Уотсон Глейзер
org/Review»>
Идеально, если вам нужно перестроиться и вернуться в игру.
org/Review»>
org/Review»>
Пожалуйста, установите современный браузер, такой как Chrome, Firefox или Edge, чтобы использовать все функции, которые может предложить Michigan.gov.
