Единицы измерения величин для школьников
Опубликовано:
- nur.kz/family/school/1904238-edinitsy-izmereniya-velichin-dlya-shkolnikov/»>
Какие существуют единицы измерения и для чего они нужны? Люди часто используют в оценках числа, а потом сравнивают их. Меры величин помогают сделать этот процесс одинаковым для всех. Вот почему школьники по всему миру изучают одни и те же единицы измерения.
Меры длины
Величинами называют все, что поддается измерению. Так говорят о длине, площади, объеме, массе, времени, скорости. Величины — результат измерений, число, выраженное в определенных единицах. Последние известны как единица измерения.
Чтобы обозначить величину, пишут число, а рядом с ним указывают единицу, в которой проводилось измерение. К примеру, 3 см, 15 кг, 20 км, 2 мин. Для каждой величины общее число возможных значений не ограничено. Так, длина может быть 1 см, 10 см, 100 см и т. д. Одну и ту же величину в разных единицах выражают с помощью разных чисел.
Кроме того, одну и ту же величину могут выражать по-разному. Например, используются различные единицы измерения длины в зависимости от того, насколько она маленькая или большая. В школе используются такие из них:
- Наименьшая единица — миллиметр (мм). Его легко увидеть на самой обычной линейке, которая есть у каждого школьника. Это самое маленькое деление, а точнее расстояние между ними.
- Следующей единицей стал сантиметр (см). На линейках сантиметры обозначаются числами. Один сантиметр состоит из десяти миллиметров. Между этими величинами ставится знак равенства, так как с их помощью обозначается одна и та же длина: 1 см = 10 мм.
- За сантиметром следует дециметр (дм). Один дециметр состоит из десяти сантиметров. Эти величины также равны, что обозначается следующим уравнением: 1 дм = 10 см.
- За дециметром следует метр (м), который содержит десять дециметров, то есть 1 м = 10 дм. В домашних условиях метр проще всего увидеть, если взять рулетку, длина которой часто составляет 1 метр.
 Сколько сантиметров в нем и как переводят сантиметры в метры? Один метр содержит десять дециметров, а они, в свою очередь, сто сантиметров (1 м = 10 дм = 100 см).
Сколько сантиметров в нем и как переводят сантиметры в метры? Один метр содержит десять дециметров, а они, в свою очередь, сто сантиметров (1 м = 10 дм = 100 см). - Самая большая единица в этой категории в рамках стандартной школьной программы — километр. Один километр состоит из тысячи метров, что обозначается так: 1 км = 1000 м. Километры используются для измерений расстояний между странами и городами. Можно, конечно, переводить миллиметры в метры и далее, но более крупные величины все же удобнее.
Существуют и более крупные меры, например мегаметры, гигаметры, тераметры, но они выходят за рамки знаний, необходимых школьнику.
Сантиметры и миллиметры: FreepickТаким образом, меры величин, с помощью которых можно измерить длину, таковы:
Меры длины: NUR.KZМеры веса
Массой называют величину, которая обозначает, сколько вещества содержит тело. В обиходе масса получила название вес. Часто при взвешивании говорят: «Вес этого вещества (материала, предмета) такой-то». Но на самом деле это не вес, а масса данного тела.
Но на самом деле это не вес, а масса данного тела.
Таким образом, масса и вес — не одно и то же. Весом называют силу, которую тело прилагает к горизонтальной опоре. Вес измеряют в ньютонах. Масса же как величина отражает количество.
Как же выразить значение массы и что для этого надо знать? Основные единицы измерения массы таковы:
- Самая маленькая единица — миллиграмм (мг). Миллиграммы редко применяются на практике. Их используют химики и другие ученые, работа которых связана с маленькими количествами веществам. В обычной жизни редко отмеряем что-либо миллиграммами.
- Следующей единицей стал грамм (г). В граммах часто измеряют количество продуктов, когда составляют рецепты. Один грамм состоит из тысячи миллиграммов. Между этими величинами ставят знак равенства, так как они тождественны: 1 г = 1000 мг.
- Следующая единица — килограмм (кг). Это общепринятая единица измерения в мире, включенная в международную систему. Один килограмм содержит тысячу граммов, то есть: 1 кг = 1000 г.

- За килограммом следует центнер (ц). В центнерах измеряется масса урожая, который собирают с небольших участков или масса различных грузов. Один центнер — это сто килограммов (1 ц = 100 кг).
- Тонна (т) — самое большое значение, с которым сталкиваются школьники, когда изучают массу предметов. Тонны используют, чтобы измерить большой груз и массу больших тел, таких как космические корабли или автомобили. Одна тонна состоит из тысячи килограмм (1 т = 1000 кг).
Если обобщить представленную выше информацию, то для измерения массы существует:
Меры веса: NUR.KZМеры объема
В каждом государстве устанавливают определенные единицы для измерений различных величин. Единица измерения, которую рассчитали точно, принимается как образец. Ее называют эталоном или образцом.
Существует стандарт килограмма, метра и т. п., на которые равняются во всех странах. Единицы, которые вошли в употребление и утверждены на государственном уровне, называют меры.
Меры могут быть однородными, если с их помощью измеряют величины одного рода. К примеру, ряд однородных мер для измерения объема таков:
- 1 куб. метр = 1000 куб. дециметров;
- 1 куб. дециметр = 1000 куб. сантиметров;
- 1 куб. сантиметр = 1000 куб. миллиметров.
Кроме того, широко используется такая величина, как литр. С его помощью удобно обозначать вместимость сосудов. Литр — это объем, который соответствует одному кубическому дециметру (1 литр = 1 куб. дециметру). Эта единица получила свое название в память о виноделе Литре из Франции.
В древности объемы измерялись самыми разными единицами: сиеками, горстками, тинами, пурами, цибами, штофами, ложками (1 тина = 3 пуры = 9 сиеков = 720 горсток = 162 штофа = 208 литров). Но сейчас о них уже забыли, так как распространение получила единая унифицированная система.
Меры площади
Для удобства страны мира пользуются международной системой единиц СИ. Это французское сокращение, которое расшифровывается так: Le Système International d’Unités, SI.
Это система, в которой для наиболее распространенных величин определены общепринятые единицы измерения. Так, ученые пришли к соглашению измерять длину в метрах. Поэтому когда в задачах длины даются в других единицах измерения (например, в миллиметрах), то их переводят в метры.
Как измеряют площадь? С этой целью применяют разнообразные меры:
- Квадратным сантиметром обозначается квадрат, сторона которого равна одному сантиметру.
- Для квадратного дециметра следует представить квадрат со стороной длиной в один дециметр.
- Соответственно, квадратный метр — квадрат, сторона которого 1 м в длину.
- Очень большие площади измеряют квадратными километрами. У такого квадрата сторона равняется одному километру.
Словосочетание «квадратный километр» сокращенно на письме отражается так: 2 км², 5 км², 15 км². В этих единицах обычно измеряют площади городов.
Для измерения площади используются:
Меры площади: NUR.KZТаковы основные единицы измерения, но в науке их арсенал гораздо шире. Людям нравится все измерять, а мир очень многогранен. Отсюда и разнообразие мер величин. К счастью, освоить и использовать их под силу каждому из нас.
Людям нравится все измерять, а мир очень многогранен. Отсюда и разнообразие мер величин. К счастью, освоить и использовать их под силу каждому из нас.
Оригинал статьи: https://www.nur.kz/family/school/1904238-edinitsy-izmereniya-velichin-dlya-shkolnikov/
Сколько сантиметров в дюйме — таблицы перевода дюймовых размеров в СМ и ММ
Обновлено 26 февраля 2023 Просмотров: 123 853 Автор: Дмитрий ПетровЗдравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы расскажем, что такое ДЮЙМ.
Хотя многие наверняка и так знают, что это некая мера длины, как привычные нам сантиметры, метры и километры.
Но вот рассказать, чему конкретно равен 1 дюйм (в сантиметрах или миллиметрах), далеко не все смогут.
Дюймы в сантиметры и другие единицы измерения
Дюйм – это неметрическая мера длины, которая используется в некоторых странах, например, в Великобритании, Канаде и Соединенных Штатах Америки. В переводе на российские исчисления – 1 дюйм равен 2,54 сантиметра.
В переводе на российские исчисления – 1 дюйм равен 2,54 сантиметра.
Слово «дюйм» имеет голландские корни. И в дословном переводе означает «большой палец». И по одной из версий изначально длиной 1 дюйма считали длину фаланги большого пальца у взрослого мужчины.
Но естественно, не может быть такого, чтобы у всех мужчин на планете были одинаковые размеры больших пальцев. А потому эта версия происхождения слова «дюйм» хоть и является основной, вызывает определенную критику у целого ряда ученых.
Поэтому есть еще несколько версии происхождения этой меры длины:
- Дюйм равен трем высушенным зернам ячменя, положенным рядом друг с другом. Причем зерна необходимо было брать из центра колоса. Это определение даже было закреплено указом английского короля Эдуарда I. А в документе фигурировало название «законный дюйм», то есть подкрепленный законом.
Интересно, что среди английских фермеров до сих пор в ходу такая мера длины как «barleycorn», что в переводе означает «ячменное зерно».
 Соответственно, она равна трети дюйма.
Соответственно, она равна трети дюйма. - Дюйм равен 1/36 части ярда. Это определение было дано за сотню лет до короля Эдуарда I – его предшественником Генрихом I. Этот монарх ввел понятие ярда в британском Королевстве.
Вот только до нашего времени дошло сразу два определения этой меры длины. По одной, ярд равен расстоянию от носа до большого пальца вытянутой вперед руки. А вот по другой, длина ярда равнялась длине меча, который король Генрих I носил всегда с собой.
Сегодня, говоря слово ДЮЙМ, автоматически подразумевается та мера длины, которая используется в США. И которую называют «английским дюймом».
В математике эта величина имеет обозначение «in» и «inch», плюс ее часто отмечают просто двойными кавычками «”».
Чему точно равен один дюйм
Мы уже сказали, что дюйм равен 2,54 сантиметра. Но так было не всегда. Из-за путаницы в определениях, эта мера длины на протяжении нескольких столетий по-разному переводилась в метрику.
Так,
- В начале XIX века (1819 год) один дюйм равнялся 2,5400438 сантиметра;
- В начале XX века (1922 год) один дюйм — 2,5399956 сантиметра;
- В середине XX века (1947 год) — 2,5399931 сантиметра.
Как видно, все эти значения примерно равны и отличаются только на втором и последующих знаках после запятой. Но это касалось только европейских стран.
А вот, например, в Мексике за один дюйм принимали 2,32 сантиметра. И совсем интересно считали в Китае. Там 1 дюйм равнялся целых 3,33 сантиметра.
И лишь в 1958 году Международной организацией законодательной метрологии признано считать 2,54 сантиметра. Более точная цифра выглядит как 2,5399599194324, но ее решили округлить до сотых. И эта величина одинакова теперь для всех стран.
Наверняка вам попадались вот такие линейки, на которых одновременно обозначены и сантиметры (сверху), и дюймы (снизу). И здесь вот наглядно видно, что 1 дюйм равен примерно 2,5 сантиметра.
А вот как выглядят значения разного количество дюймов в переводе в сантиметры.
И наконец, английский дюйм можно представить не только в соотношении к метрам или миллиметрам. Есть и другие величины, которые по-прежнему используются в разных странах.
- 1 дюйм = 0,03 ярда
- 1 дюйм = 0,08 фута
- 1 дюйм = 0,000016 мили
- 1 дюйм = 0,000014 морской мили
Кстати, Международная организация законодательной метрологии уже много лет выступает за то, чтобы окончательно отменить дюймы и прочие «старые» меры длины, а оставить только метры и их производные. Но пока эти попытки терпят неудачу, особенно в тех странах, где те же дюймы до сих пор в ходу.
Перевод долей дюйма (½, ¾ и других) в мм
Даже в России, где повсеместно используется метрическая система измерения длины, дюймы время от времени встречаются. Например, их можно найти на полках в строительных магазинах.
Многие инструменты и изделия, имеющие форму стержня, измеряются в дюймах.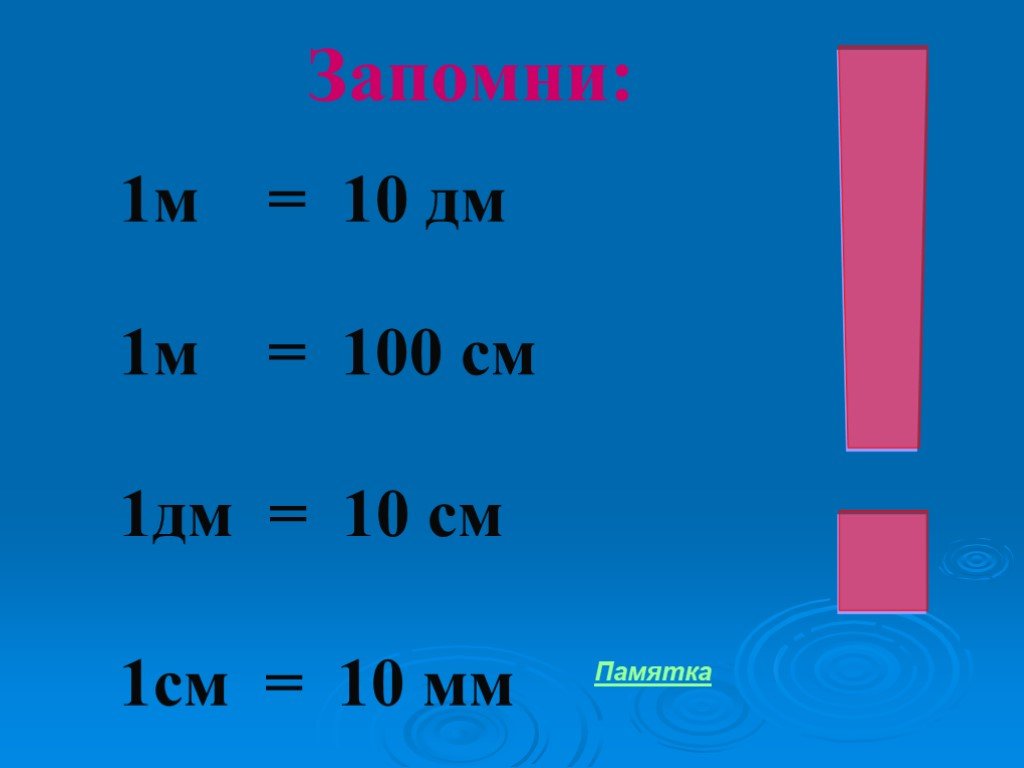 Чаще всего это касается труб.
Чаще всего это касается труб.
Так, на трубах, с помощью которых подключаются стиральные машины и другая бытовая техника, вы никогда не увидите диаметр в миллиметрах. А будет написано ½ или ¾ дюйма.
Таблица пересчета долей дюйма в миллиметры приведена ниже:
Диагонали экранов в дюймах
Также в дюймах часто измеряется диагональ телевизоров, мониторов компьютеров, планшетов и телефонов. И чтобы перевести в привычные нам сантиметры, надо умножить исходное значение на все те же 2,54. Правда, учитывайте, что производители округляют полученные значения.
Например, телевизор диагональю 20 дюймов равен не 50,8 сантиметров (20×2.54), а ровно 51 сантиметру. И все остальные дюймовые значения при переводе в сантиметры также округляются в меньшую или большую сторону.
Вот и все, что мы хотели рассказать вам о дюймах.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Сколько метров в 1 см?
Свяжитесь с нами!
Пожалуйста, свяжитесь с нами, если вы:
- Есть предложения
- Есть вопросы
- Нашли ошибку/ошибку
- Что-нибудь еще.
 ..
..
Чтобы связаться с нами, нажмите ЗДЕСЬ.
1 сантиметр равен 0,01 метра, потому что 1 умножить на 0,01 (коэффициент преобразования) = 0,01
Определение сантиметра
A сантиметр (см) — десятичная дробь метра, единица длины в Международной системе единиц (СИ), примерно равная 0,39 дюйма. Сантиметр (см) — единица длины, которая ранее была базовой единицей длины в системе единиц сантиметр-грамм-секунда (СГС). Хотя технические специалисты предпочитают префиксы SI для коэффициентов 10 3 , сантиметр остается практической единицей длины для повседневных измерений. Ширина ногтя среднего взрослого человека примерно равна одному сантиметру, что делает его удобным для измерения небольших предметов или расстояний. Узнайте больше о сантиметре и его использовании в повседневной жизни.
Ширина ногтя среднего взрослого человека примерно равна одному сантиметру, что делает его удобным для измерения небольших предметов или расстояний. Узнайте больше о сантиметре и его использовании в повседневной жизни.Вот несколько примеров вещей размером около одного сантиметра (порядок величины):
Ширина ногтя взрослого человека
Диаметр стандартного стержня карандаша
Толщина кредитной карты
Высота маленького кубика Lego
Диаметр батарейки АА
Длина муравья
Ширина маленькая кнопка
Толщина защитной пленки для экрана смартфона
Ширина рисового зерна
Высота маленькой скрепки.
Определение метра
Метр – это длина пути, пройденного светом в вакууме за промежуток времени 1/299 792 458 секунды. Один метр примерно на 3 3/8 дюйма длиннее ярда, то есть примерно 39 3/8 дюйма.
Вот некоторые распространенные способы преобразования метров в другие единицы измерения длины:
1 метр = 100 сантиметров
1 метр = 3,28084 фута
1 метр = 1,09361 ярда
1 метр = 0,000621371 мили
1 метр = 39,3701 дюйма
И наоборот, чтобы преобразовать эти другие единицы длины в метры, вы должны использовать соответствующее преобразование коэффициент, либо путем умножения, либо деления исходной величины на коэффициент.
Таким образом, метр является единицей длины в системе СИ и обычно используется для измерения расстояния и длины в различных контекстах. Его основа в единицах 10 позволяет легко преобразовать его в другие единицы длины.
Вот несколько примеров вещей размером около одного метра (порядка величины):
Типичный размах человеческих рук
Метровая палка или линейка
Размер велосипедной рамы
Большая пицца
Рыба длиной три фута (1 метр)
Стандартная кухонная столешница
Собака среднего размера
Высота баскетбольного кольца
Длина типичного бильярдного кия
Стандартная трость для ходьбы
Небольшая лестница или табурет-ступенька
Микроволны с частотой 300 ГГц имеют длину волны 1 мм
Как преобразовать 1 сантиметр в метры
Чтобы рассчитать значение в метрах, вам просто нужно использовать следующую формулу :
Значение в метрах = значение в сантиметрах × 1 / 100
Другими словами, вам нужно умножить значение емкости в сантиметрах на 1 / 100 для получения эквивалента в метрах.
Например, чтобы преобразовать см в метры, вы можете подставить значение 1 в приведенную выше формулу, чтобы получить
метра = 1 × 1 / 100 = 1 / 100
Таким образом, емкость конденсатора 1 / 100 метр. Обратите внимание, что полученное значение, возможно, придется округлить до практического или стандартного значения, в зависимости от приложения.
С помощью этого конвертера вы сможете получить ответы на такие вопросы, как:
- Сколько 1 сантиметр в метрах;
- Как перевести сантиметры в метры и
- Какая формула для перевода сантиметров в метры, среди прочего.
сантиметры в метры. 04 метр
Примечание. Значения округлены до 4 значащих цифр. Дроби округляются до ближайшей восьмой дроби.
Значения округлены до 4 значащих цифр. Дроби округляются до ближайшей восьмой дроби.
Преобразование образцов
Отказ от ответственности
Несмотря на усилия по предоставлению точной информации на этом веб-сайте, ее точность не гарантируется. Поэтому контент не должен использоваться для принятия решений, касающихся здоровья, финансов или имущества.
О нас | Свяжитесь с нами | КонфиденциальностьCopyright © 2016 — 2023 HowMany.wiki
Метрическая длина – объяснение, преобразование, единица СИ и проблемы
Метрическая система может быть определена как система измерения, использующая литр, метр и грамм в качестве основных единиц метрической длины (расстояния), вместимости (объема) и вес (масса) соответственно.
Для измерения больших или меньших величин мы используем единицы, производные от метрических единиц.
Единицы справа от базы меньше базовой единицы.
 Когда мы движемся вправо, каждая единица становится в десять раз меньше или составляет одну десятую единицы слева от нее. Итак, слово «деци» означает одну десятую базовой единицы, «сенти» — одну десятую «деци» или одну сотую базовой единицы, а «милли» — одну десятую «санти» или одну- тысячная базовой единицы.
Когда мы движемся вправо, каждая единица становится в десять раз меньше или составляет одну десятую единицы слева от нее. Итак, слово «деци» означает одну десятую базовой единицы, «сенти» — одну десятую «деци» или одну сотую базовой единицы, а «милли» — одну десятую «санти» или одну- тысячная базовой единицы.Блоки слева от базового блока больше основного блока. Когда мы движемся влево, каждая единица в 10 раз больше, чем единица справа от нее. Таким образом, «дека» означает 10-кратную базовую единицу, «гекто» — это десятикратную «дека» или стократную базовую единицу, а «килло» — десятикратную «гекто» или тысячекратную базовую единицу.
Килограмм | Hecto | Deca | Базовый блок | Deci | Центи | Милли |
1000 | 100 | 10 | 1 | 1/10 | 1/100 | 1/1000 |
Итак, единицы измерения длины, вместимости (объема) и веса (массы) в метрике системы:
Метрическая длина: сантиметр (см), миллиметр (мм), метр (м), дециметр (дм) и километр (км) используются для измерения ширины, длины или высоты объекта.
Что такое метрическая единица длины в системе СИ?
В метрической системе единицей длины в системе СИ является метр, который определяется следующим образом:
«Метрическая длина пути, который проходит свет в вакууме за 1⁄299792458 секунд».
Некоторые другие единицы также включают:
Километры
Нанометры
Миллиметры
Сантиметры
Метры
900 08Дециметры
Чтобы понять, насколько велики метрические единицы, посмотрите на таблицу ниже:
Метрическая система | Пример |
Миллиметр | Толщина кредитной карты или пластикового удостоверения личности имеет толщину около миллиметра |
Сантиметр | Ноготь шириной около сантиметра |
Метр | Гитара длиной метр |
Километр | Расстояние между городами измеряется в километрах |
Другие метрические единицы длины, не относящиеся к системе СИ
Если мы посмотрим на имперскую и американскую обычные системы, то основной единицей метрической длины является ярд. Некоторые другие единицы включают:
Некоторые другие единицы включают:
Тысяча (1/1000 дюйма)
Линия (1/12 дюйма)
Дюйм (25,4 мм)
Фут (12 дюймов, 0,3048 м)
Метрическая мера длины
10 миллиметров (мм) = | 1 сантиметр (см) |
10 сантиметров (см) = | 1 дециметр (дм) = 100 миллиметров |
100 сантиметров (см) = | 1 метр (м) = 1000 миллиметров |
1000 метров (м) = | 1 километр (км) |
Примеры включают измерение толщины или метрической длины ткани, дебетовой карты или расстояния между двумя городами.
Километр (км) (Киран) | 1000 |
Гектометр (hm) (Had) | 100 |
Декаметр (плотина) (Drawed) | 10 |
Метр (м) (Много) | 1 |
Дециметр (дм) (другой) | 1/10 |
Сантиметр (см) (цветной) | 1/100 |
Миллиметр (мм) (маски) | 1/1000 |
Преобразование больших единиц в меньшие
- 902 79 1 сантиметр = 10 миллиметров
1 метр = 100 сантиметров
1 метр = 1000 миллиметров
1 километр = 1000 метров
Чтобы преобразовать большие единицы в меньшие, мы умножаем количество больших единиц на коэффициент преобразования для соответствующих меньших единиц.
Таблица, приведенная ниже, упрощает преобразование:
Если у вас есть это | Сделайте это 9000 5 | Чтобы получить |
Миллиметры (мм) | Разделить на 10 (мм/10) | Сантиметры (см) |
Сантиметры (см) | Умножить на 10 (см * 10) | Миллиметры (мм) |
Метры (м) | Умножьте на 100 (м * 100) | Сантиметры (см ) |
Сантиметры (см) | Разделить на 100 (см/100) | Метры (м) |
Миллиметры (мм) | Разделить на 1000 (мм/100) 0) | Метры (м) |
Решенные примеры преобразования единиц измерения
Пример 1. Преобразование 5 км в м.
Преобразование 5 км в м.
Поскольку 1 км = 1000 м
Следовательно, 5 км равно 5 × 1000 равно 5000 м.
Пример 2: Как преобразовать м в см и мм?
В этом упражнении вы будете преобразовывать метрические единицы метрической длины: километры, метры, сантиметры и миллиметры.
1 км = 1000 м
1 м = 100 см
1 м = 1000 мм
1 см = 10 мм
Почему учащиеся должны знать о метрической системе?
Метрическая система важна, так как без нее мы бы полностью запутались в единицах измерения. Он полностью научный и имеет воспроизводимые стандарты измерения. Он использует такие единицы, как метр, литр и грамм, для измерения длины, жидкости, объема и массы. Учащимся необходимо знать о метрической системе, чтобы понять все различные концепции, которые будут применяться в математике и естественных науках. Наличие стандартной системы измерения — единственный способ измерять вещи, поскольку это устраняет все недоразумения.
Как учащиеся могут делать записи для метрической системы?
Они могут пойти в Vedantu и затем найти Metric Length — Explanation, Conversions, SI Unit, Measures, Problems, и FAQs на странице выделив все важные части
Сравните то, что вы написали, с тем, что на странице
Пройдите все до экзаменов
Не пропускайте информацию на странице
Интересные факты
Тонна равна 1000 килограммам.
Метрическая система была создана еще в 1670 году математиком по имени Габриэль Мутон.
С 1960-х годов метрическая система известна как «Международная система единиц» или «СИ» (от французского «Système International»).


 Сколько сантиметров в нем и как переводят сантиметры в метры? Один метр содержит десять дециметров, а они, в свою очередь, сто сантиметров (1 м = 10 дм = 100 см).
Сколько сантиметров в нем и как переводят сантиметры в метры? Один метр содержит десять дециметров, а они, в свою очередь, сто сантиметров (1 м = 10 дм = 100 см).
 Соответственно, она равна трети дюйма.
Соответственно, она равна трети дюйма. ..
.. Когда мы движемся вправо, каждая единица становится в десять раз меньше или составляет одну десятую единицы слева от нее. Итак, слово «деци» означает одну десятую базовой единицы, «сенти» — одну десятую «деци» или одну сотую базовой единицы, а «милли» — одну десятую «санти» или одну- тысячная базовой единицы.
Когда мы движемся вправо, каждая единица становится в десять раз меньше или составляет одну десятую единицы слева от нее. Итак, слово «деци» означает одну десятую базовой единицы, «сенти» — одну десятую «деци» или одну сотую базовой единицы, а «милли» — одну десятую «санти» или одну- тысячная базовой единицы.
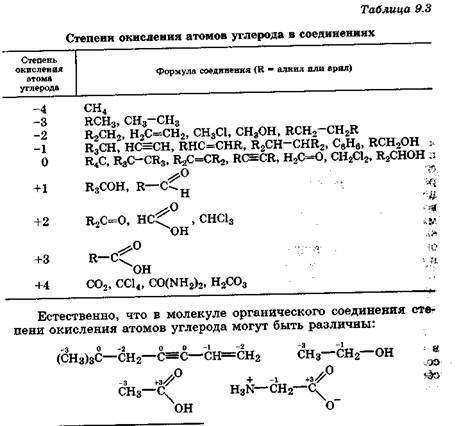
 2-4*-1+2
2-4*-1+2 2
2 Вы также можете выразить 78/2 в виде смешанной дроби: 39 0/2.
Вы также можете выразить 78/2 в виде смешанной дроби: 39 0/2. 5.
5.



 com , http://visualfractions.com/calculator/long-division/what-is-78-divided-by-6-using-long-division/. По состоянию на 24 мая 2023 г.
com , http://visualfractions.com/calculator/long-division/what-is-78-divided-by-6-using-long-division/. По состоянию на 24 мая 2023 г. Вот следующая задача, которую вам нужно решить:
Вот следующая задача, которую вам нужно решить: Для общего ознакомления с подразделением ознакомьтесь с этой статьей.
Для самостоятельного расчета деления, возможно, стоит также ознакомиться с нашим разделом о длинном делении.
Для общего ознакомления с подразделением ознакомьтесь с этой статьей.
Для самостоятельного расчета деления, возможно, стоит также ознакомиться с нашим разделом о длинном делении. сам.
сам.
 3;a1*1.1)
3;a1*1.1) Сначала мы изучали основы: сложение с умножением, извлечение корня, преобразование тригонометрических выражений. А затем учились применять изученные базовые принципы и свойства для решения математических моделей реальных задач.
Сначала мы изучали основы: сложение с умножением, извлечение корня, преобразование тригонометрических выражений. А затем учились применять изученные базовые принципы и свойства для решения математических моделей реальных задач.

 Получаем ответ:
Получаем ответ: Теперь рассмотрим уравнения, в которых неизвестная стоит в показателе степени – показательные уравнения. Идея их решения очень похожа на ту, что мы использовали при решении степенных уравнений. Нужно свести уравнение к виду:
Теперь рассмотрим уравнения, в которых неизвестная стоит в показателе степени – показательные уравнения. Идея их решения очень похожа на ту, что мы использовали при решении степенных уравнений. Нужно свести уравнение к виду: Применяя свойства степени, получаем:
Применяя свойства степени, получаем: Если вы не помните методы решения неравенств, можете их повторить, посмотрев уроки Линейные неравенства. Системы и совокупности неравенств; Решение квадратных неравенств. Метод интервалов.
Если вы не помните методы решения неравенств, можете их повторить, посмотрев уроки Линейные неравенства. Системы и совокупности неравенств; Решение квадратных неравенств. Метод интервалов. Поэтому записываем неравенство для показателей степени и меняем знак:
Поэтому записываем неравенство для показателей степени и меняем знак:
 Общая идея решения нам уже знакома – привести левую и правую части к логарифмам с одинаковым основанием:
Общая идея решения нам уже знакома – привести левую и правую части к логарифмам с одинаковым основанием:
 Что ж, можете его использовать. Но обратите внимание, что он не такой универсальный. Он подойдет только в случае, если в одной из частей уравнения стоит число.
Что ж, можете его использовать. Но обратите внимание, что он не такой универсальный. Он подойдет только в случае, если в одной из частей уравнения стоит число. Решить уравнение:
Решить уравнение:
 Решение квадратных и дробно-рациональных уравнений. Практика. Тригонометрические уравнения и неравенства. Базовый уровень).
Решение квадратных и дробно-рациональных уравнений. Практика. Тригонометрические уравнения и неравенства. Базовый уровень). Давайте сначала приведем их к одинаковому основанию:
Давайте сначала приведем их к одинаковому основанию: Вы уже знаете, как решать такие неравенства. Попробуйте решить его самостоятельно, свериться можно ниже.
Вы уже знаете, как решать такие неравенства. Попробуйте решить его самостоятельно, свериться можно ниже. Тогда первое неравенство превращается в . Решаем его:
Тогда первое неравенство превращается в . Решаем его: Но и их мы уже умеем решать:
Но и их мы уже умеем решать:
 А это, напомним, влияет на смену знака неравенства. Поэтому нужно будет рассмотреть два случая: когда основание больше и когда меньше 1. С примером решения подобного неравенства вы можете ознакомиться в ответвлении.
А это, напомним, влияет на смену знака неравенства. Поэтому нужно будет рассмотреть два случая: когда основание больше и когда меньше 1. С примером решения подобного неравенства вы можете ознакомиться в ответвлении.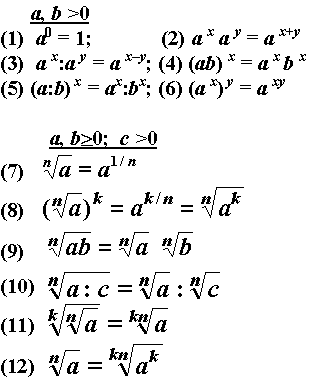 рис. 2).
рис. 2). Записываем неравенство для подлогарифмических выражений и меняем знак неравенства:
Записываем неравенство для подлогарифмических выражений и меняем знак неравенства: рис. 1).
рис. 1). М., Потапов М. К., Решетников Н.Н. Алгебра и начала математического анализа, геометрия. 10 класс. Учебник. – АО «Издательство “Просвещение”»
М., Потапов М. К., Решетников Н.Н. Алгебра и начала математического анализа, геометрия. 10 класс. Учебник. – АО «Издательство “Просвещение”» Когда вы используете несколько терминов, показатели складываются вместе.
Когда вы используете несколько терминов, показатели складываются вместе. Сложение просто определяется как оно есть, и если у вас есть несколько одночленов разной степени, вы не можете их сложить. Если я совершенно не осознаю этого, там нет ничего глубокого. Суть в том, чтобы рассматривать полиномы как формальные объекты, а не как соответствующие им карты, если только для этого нет веской причины. 92=?$$
Сложение просто определяется как оно есть, и если у вас есть несколько одночленов разной степени, вы не можете их сложить. Если я совершенно не осознаю этого, там нет ничего глубокого. Суть в том, чтобы рассматривать полиномы как формальные объекты, а не как соответствующие им карты, если только для этого нет веской причины. 92=?$$ Переписывание числа в экспоненциальной записи с использованием другой экспоненциальной базы технически «нарушает» правило записи в экспоненциальной записи: наш коэффициент a должен быть больше или равен 1, но меньше 10. Почему и должны быть между этими номерами? Потому что это просто обычный способ написать это.
Переписывание числа в экспоненциальной записи с использованием другой экспоненциальной базы технически «нарушает» правило записи в экспоненциальной записи: наш коэффициент a должен быть больше или равен 1, но меньше 10. Почему и должны быть между этими номерами? Потому что это просто обычный способ написать это. Ты прав. Мы будем использовать специальное свойство экспонент, модифицированное под наши нужды:
Ты прав. Мы будем использовать специальное свойство экспонент, модифицированное под наши нужды:


 В этом используется вся та работа, которую вы проделали, изменяя экспоненциальные основания.
В этом используется вся та работа, которую вы проделали, изменяя экспоненциальные основания.
 2\alpha\)
2\alpha\)
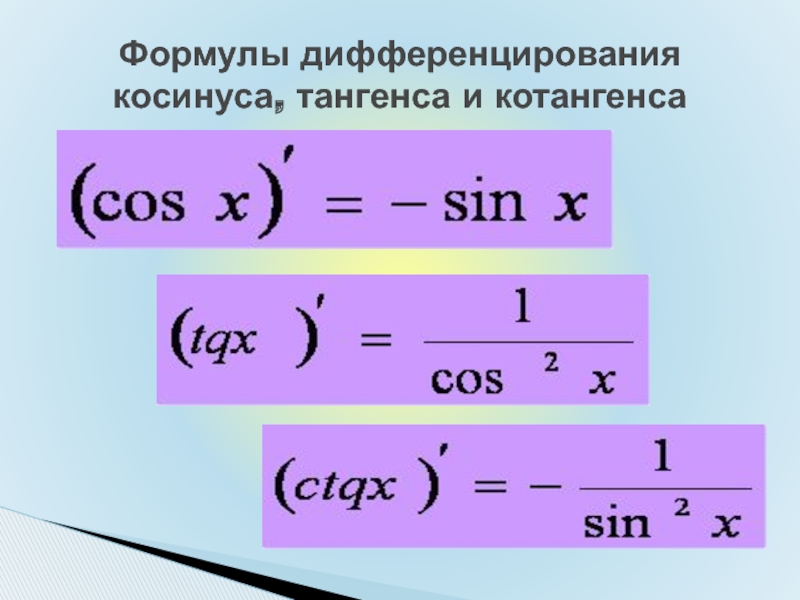 27.
27.
 Другими словами, это мера того, насколько острым является угол.
Другими словами, это мера того, насколько острым является угол.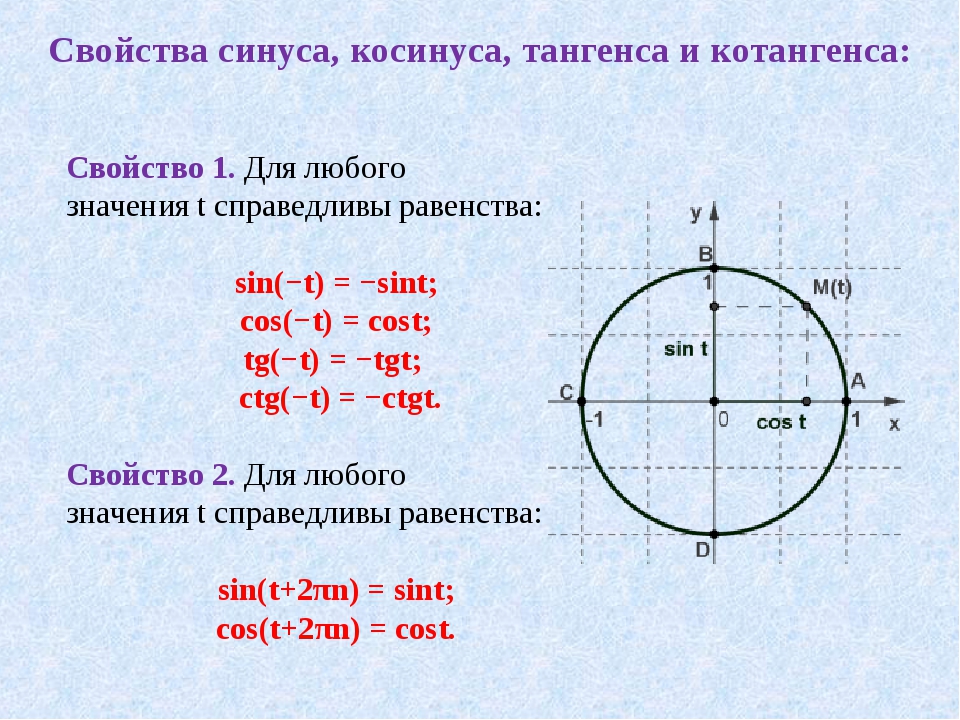 Он используется в исчислении для вычисления производных и интегралов, и он появляется во многих формулах в физике.
Он используется в исчислении для вычисления производных и интегралов, и он появляется во многих формулах в физике.
 Например, если y = cot(x), то период будет равен 2 * пи / 1 или просто 2 * пи.
Например, если y = cot(x), то период будет равен 2 * пи / 1 или просто 2 * пи. Он имеет вертикальные асимптоты при x=0 и x=(-n)*pi, где n — любое целое число.
Он имеет вертикальные асимптоты при x=0 и x=(-n)*pi, где n — любое целое число.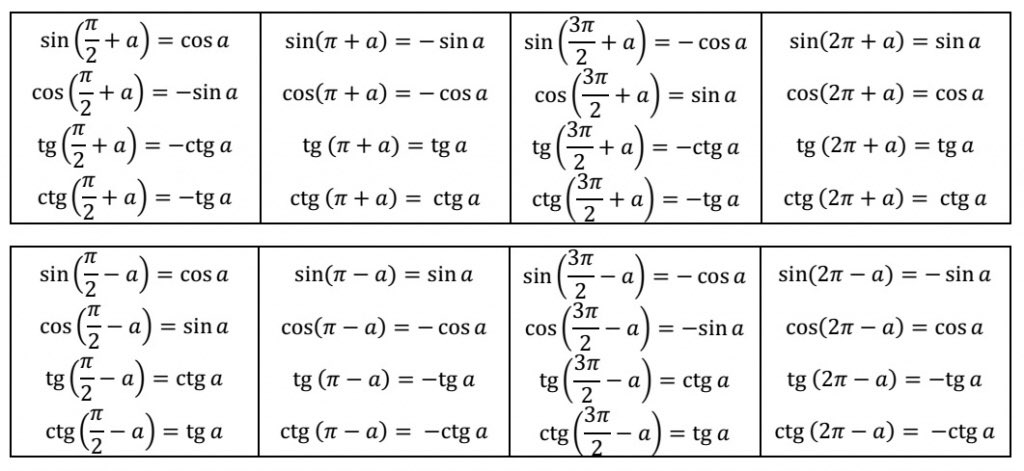 Котангенс угла определяется как отношение косинуса угла к синусу этого угла. Эту формулу часто записывают как cot x = cos x sin x.
Котангенс угла определяется как отношение косинуса угла к синусу этого угла. Эту формулу часто записывают как cot x = cos x sin x. Котангенс угла равен косинусу угла, деленному на синус угла. Математически это можно выразить как cot x = cos x / sin x. Чтобы найти котангенс угла, нужно сначала вычислить косинус и синус этого угла, а затем разделить одно на другое. Например, если у нас есть угол θ с косинусом и синусом, равными 0,5 и 0,866 соответственно, то его котангенс будет рассчитан как 0,5/0,866 = 0,57735.
Котангенс угла равен косинусу угла, деленному на синус угла. Математически это можно выразить как cot x = cos x / sin x. Чтобы найти котангенс угла, нужно сначала вычислить косинус и синус этого угла, а затем разделить одно на другое. Например, если у нас есть угол θ с косинусом и синусом, равными 0,5 и 0,866 соответственно, то его котангенс будет рассчитан как 0,5/0,866 = 0,57735. Это означает, что котангенс угла равен обратной величине тангенса этого угла. Второе выражение для cot θ – это tan(90° – θ). Это означает, что котангенс угла равен тангенсу дополнительного угла (180° – θ). В обоих случаях cot θ можно рассчитать, взяв обратное (или обратное) значение тангенса θ.
Это означает, что котангенс угла равен обратной величине тангенса этого угла. Второе выражение для cot θ – это tan(90° – θ). Это означает, что котангенс угла равен тангенсу дополнительного угла (180° – θ). В обоих случаях cot θ можно рассчитать, взяв обратное (или обратное) значение тангенса θ. Детскую кроватку можно использовать для вычисления углов и сторон треугольника. Кроме того, кроватку можно использовать в более сложных вычислениях, таких как вектора и комплексные числа. Чтобы использовать кроватку в калькуляторе, ее часто выражают как COT(x), где x представляет собой угол, выраженный в радианах. Чтобы преобразовать градусы в радианы, вы можете использовать функцию РАДИАНЫ. Выход COT(x) будет котангенсом x.
Детскую кроватку можно использовать для вычисления углов и сторон треугольника. Кроме того, кроватку можно использовать в более сложных вычислениях, таких как вектора и комплексные числа. Чтобы использовать кроватку в калькуляторе, ее часто выражают как COT(x), где x представляет собой угол, выраженный в радианах. Чтобы преобразовать градусы в радианы, вы можете использовать функцию РАДИАНЫ. Выход COT(x) будет котангенсом x.
 Таким образом, для любой заданной степени, если мы обозначим ее как ‘x’, то cot(x) = cos(x)/sin(x). Однако в тех случаях, когда синус заданного угла равен 0, тогда значение cot неопределенно или равно бесконечности (∞), так как потребовалось бы взять отношение, где знаменатель равен 0. Это происходит при 0°, 180° и 360°.
Таким образом, для любой заданной степени, если мы обозначим ее как ‘x’, то cot(x) = cos(x)/sin(x). Однако в тех случаях, когда синус заданного угла равен 0, тогда значение cot неопределенно или равно бесконечности (∞), так как потребовалось бы взять отношение, где знаменатель равен 0. Это происходит при 0°, 180° и 360°.
 Решение квадратных неравенств
Решение квадратных неравенств Кто упадёт первым?
Кто упадёт первым? .. ⋅ a
n разів
для a ∈ R, n ∈ N, n 2
a0
= 1, де а ≠ 0 a2
= а
a–n
=
1
—
аn для а ≠ 0, n ∈ N
a
m
—
n
= am
n
, а > 0, m ∈ Z, n ∈ N, n 2
ax
⋅ ay
= ax + y аx
—
аy = ax – y
(ax
)y
= ax ⋅ y
(ab)x
= ax
⋅ bx
(a
–
b)
x
=
аx
—
bx
a > 0, а ≠ 1, b > 0, c > 0, k ≠ 0
alogab
= b logаа = 1 logа1 = 0
logа(b ⋅ c) = logаb + logаc
logа
b
–
c = logаb – logаc
logаbn
= n ⋅ logаb
logаk b = 1
–
k
⋅ logаb
an = a1 + d(n – 1) Sn =
a1 + аn
—
2
⋅ n
Pn = 1 ⋅ 2 ⋅ 3 ⋅ … ⋅ n = n! C
k
n =
n!
—
k! ⋅ (n – k)!
Ak
n =
n!
—
(n – k)!
P(A) =
k
–
n
bn = b1 ⋅ qn – 1
Sn =
b1(qn
– 1)
—
q – 1
, (q ≠ 1)
a =
a, якщо а 0,
–a, якщо а < 0
.. ⋅ a
n разів
для a ∈ R, n ∈ N, n 2
a0
= 1, де а ≠ 0 a2
= а
a–n
=
1
—
аn для а ≠ 0, n ∈ N
a
m
—
n
= am
n
, а > 0, m ∈ Z, n ∈ N, n 2
ax
⋅ ay
= ax + y аx
—
аy = ax – y
(ax
)y
= ax ⋅ y
(ab)x
= ax
⋅ bx
(a
–
b)
x
=
аx
—
bx
a > 0, а ≠ 1, b > 0, c > 0, k ≠ 0
alogab
= b logаа = 1 logа1 = 0
logа(b ⋅ c) = logаb + logаc
logа
b
–
c = logаb – logаc
logаbn
= n ⋅ logаb
logаk b = 1
–
k
⋅ logаb
an = a1 + d(n – 1) Sn =
a1 + аn
—
2
⋅ n
Pn = 1 ⋅ 2 ⋅ 3 ⋅ … ⋅ n = n! C
k
n =
n!
—
k! ⋅ (n – k)!
Ak
n =
n!
—
(n – k)!
P(A) =
k
–
n
bn = b1 ⋅ qn – 1
Sn =
b1(qn
– 1)
—
q – 1
, (q ≠ 1)
a =
a, якщо а 0,
–a, якщо а < 0
 Cos2x выражается через различные тригонометрические функции, и каждая из его формул используется для упрощения сложных тригонометрических выражений и решения задач интегрирования. Это тригонометрическая функция двойного угла, которая помогает узнать значение cos при удвоении угла x.
Cos2x выражается через различные тригонометрические функции, и каждая из его формул используется для упрощения сложных тригонометрических выражений и решения задач интегрирования. Это тригонометрическая функция двойного угла, которая помогает узнать значение cos при удвоении угла x.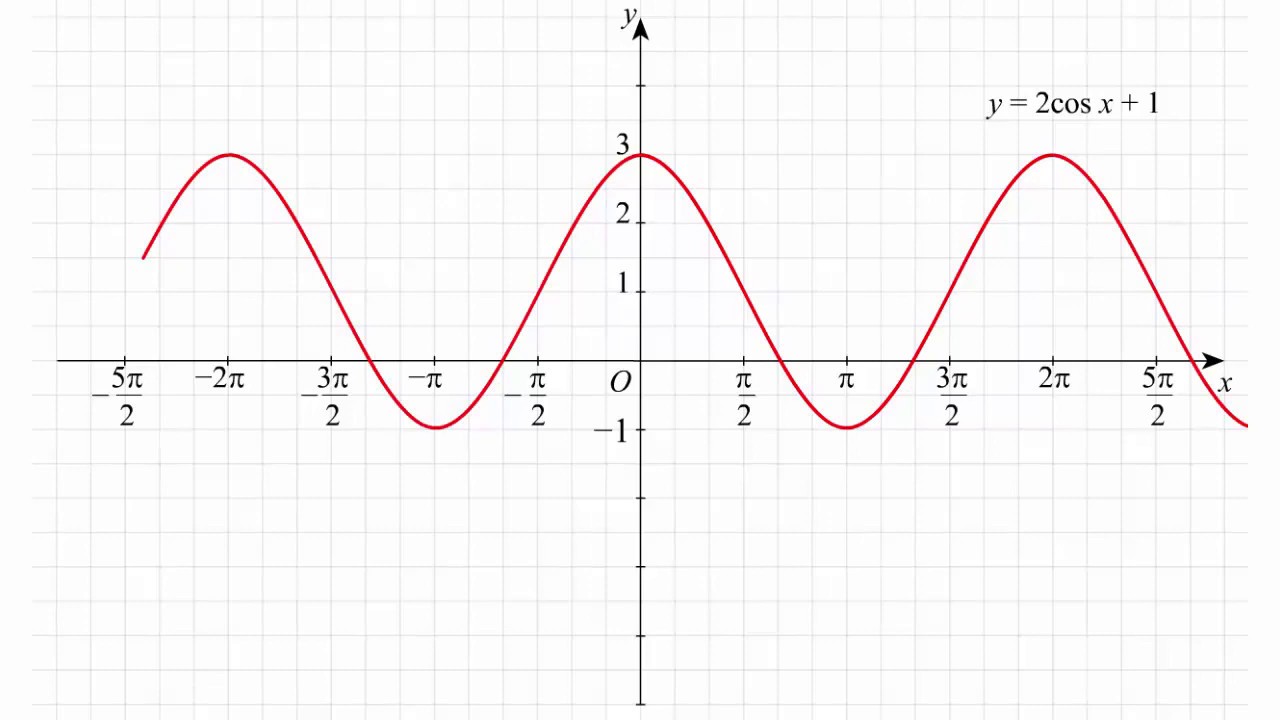 Используя формулу сложения углов для функции косинуса, мы можем заменить a = x и b = x в формуле для cos (a + b).
Используя формулу сложения углов для функции косинуса, мы можем заменить a = x и b = x в формуле для cos (a + b).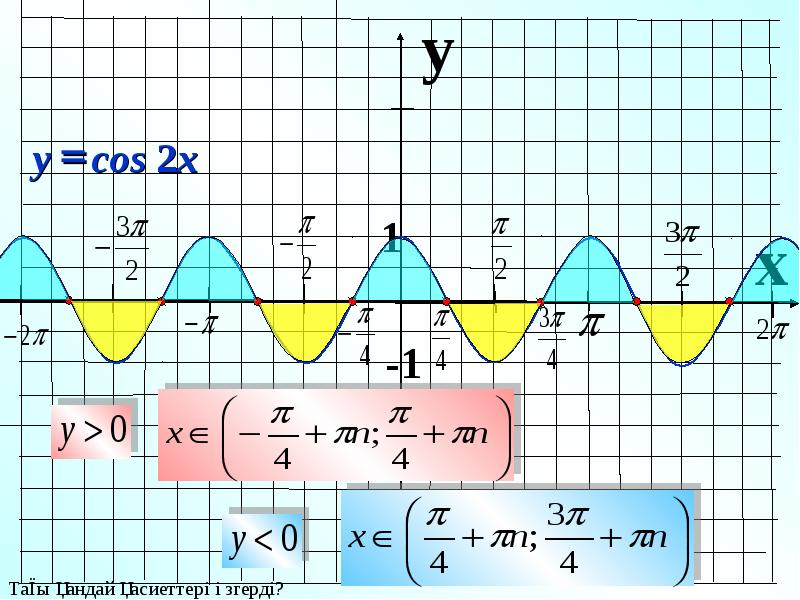
 Рассмотрим пример, демонстрирующий применение формулы cos2x.
Рассмотрим пример, демонстрирующий применение формулы cos2x.
 Это важное тригонометрическое тождество, которое можно использовать для решения различных задач тригонометрии и интегрирования. Значение cos 2x повторяется через каждые π радиан, cos 2x = cos (2x + π). Он имеет значительно более узкий график, чем cos x. Это тригонометрическая функция, которая возвращает значение функции cos двойного угла.
Это важное тригонометрическое тождество, которое можно использовать для решения различных задач тригонометрии и интегрирования. Значение cos 2x повторяется через каждые π радиан, cos 2x = cos (2x + π). Он имеет значительно более узкий график, чем cos x. Это тригонометрическая функция, которая возвращает значение функции cos двойного угла.

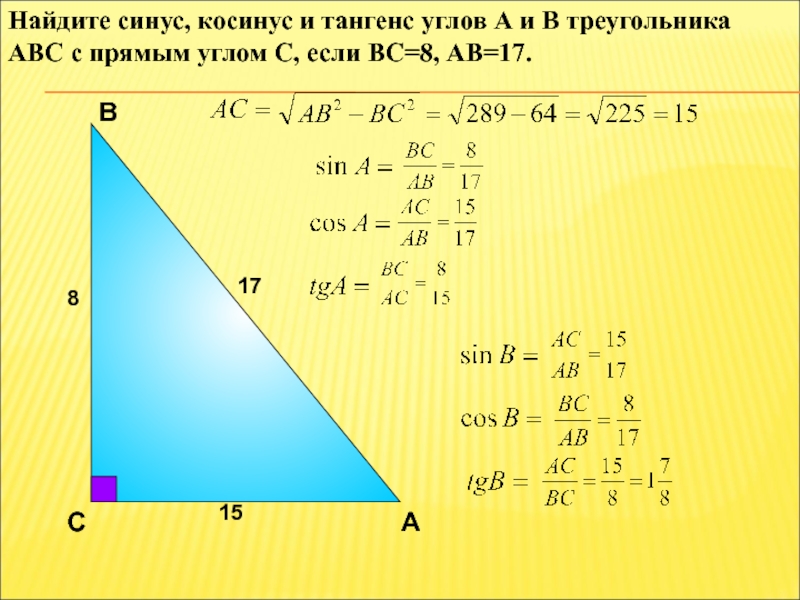
 Если sec x = 17/8, найдите значение cos 2x по формуле.
Если sec x = 17/8, найдите значение cos 2x по формуле. 
 Пересмотр ответов не допускается.
Пересмотр ответов не допускается. Квалификационный аттестат переоформляется на новом бланке на основании письменного заявления.
Квалификационный аттестат переоформляется на новом бланке на основании письменного заявления.
 Сведения об этом хранятся на протяжении 3 лет. В течение этого периода повторно сдать квалификационный экзамен нельзя. Постановление о дисквалификации можно оспорить в суде.
Сведения об этом хранятся на протяжении 3 лет. В течение этого периода повторно сдать квалификационный экзамен нельзя. Постановление о дисквалификации можно оспорить в суде. Долетят ли дроны до Челябинска?
Долетят ли дроны до Челябинска? После смерти отца москвичка судится с государством за свою жилплощадь
После смерти отца москвичка судится с государством за свою жилплощадь Кто из южноуральцев попал в топ-20 богатейших наследников России
Кто из южноуральцев попал в топ-20 богатейших наследников России Внедрен новый налог для самозанятых — налог на профессиональный доход. Появятся новые формы 2-НДФЛ и 3-НДФЛ.
Внедрен новый налог для самозанятых — налог на профессиональный доход. Появятся новые формы 2-НДФЛ и 3-НДФЛ. Поддержка в «1С.Практика автоматизации с пользой для бизнеса»;
Поддержка в «1С.Практика автоматизации с пользой для бизнеса»; Челябинск».
Челябинск». Конкурирующие предприятия
Конкурирующие предприятия 
 США U
США U  Чистая приведенная стоимость инвестиционного проекта представляет собой
Чистая приведенная стоимость инвестиционного проекта представляет собой com › тема › everfi-module-3-answers
com › тема › everfi-module-3-answers Лоренцо Аранда … Nishtha 2.0 Модуль 2 ответы || ICT …
Лоренцо Аранда … Nishtha 2.0 Модуль 2 ответы || ICT … 
 Педагогический (научно-педагогический) состав
Педагогический (научно-педагогический) состав {2}}\).
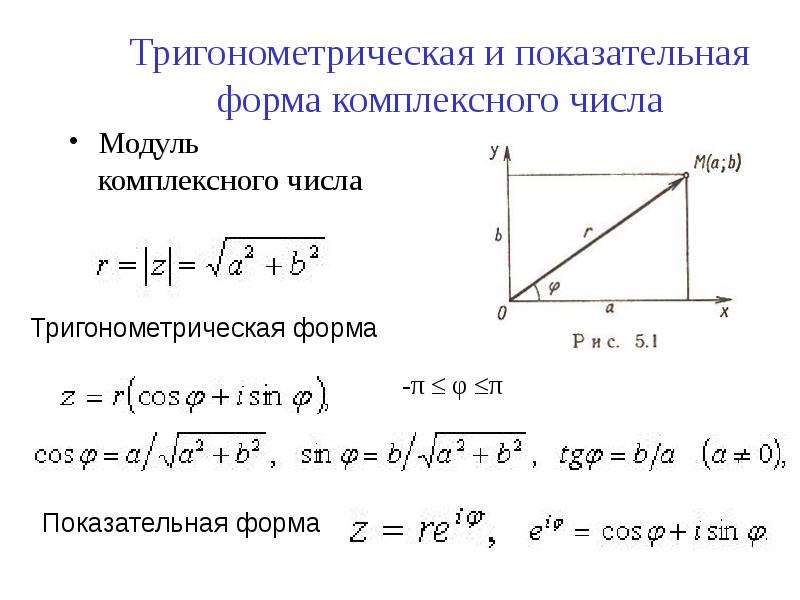
{2}}\). {i \theta}\): 9{i\theta}=\cos\theta+i\sin\theta\).
{i \theta}\): 9{i\theta}=\cos\theta+i\sin\theta\). Его также можно представить в виде диаграммы ниже.
Его также можно представить в виде диаграммы ниже.



 Так как e i∅ = cos∅ + isin∅ мы знаем это уже в тригонометрии.
Так как e i∅ = cos∅ + isin∅ мы знаем это уже в тригонометрии.



 youtube.com/watch?v=GSpjM5XSxwE
youtube.com/watch?v=GSpjM5XSxwE
 – Гродно : ГГАУ, 2016. – 26 с.
– Гродно : ГГАУ, 2016. – 26 с. Использование таких пособий, в которых рассмотрены важнейшие теоретические вопросы в доступной и сжатой форме, позволит студентам быстрее и эффективнее изучить материал.
Использование таких пособий, в которых рассмотрены важнейшие теоретические вопросы в доступной и сжатой форме, позволит студентам быстрее и эффективнее изучить материал. Лекция по курсу «Общая химия» для студентов инженерно-технологического факультета / З.В. Апанович. – Гродно : ГГАУ, 2016. – 31 с.
Лекция по курсу «Общая химия» для студентов инженерно-технологического факультета / З.В. Апанович. – Гродно : ГГАУ, 2016. – 31 с. Использование такого пособия, в котором рассмотрены важнейшие вопросы в доступной и сжатой форме, позволит студентам быстрее и эффективнее изучить материал.
Использование такого пособия, в котором рассмотрены важнейшие вопросы в доступной и сжатой форме, позволит студентам быстрее и эффективнее изучить материал. 12.2016 12:03
12.2016 12:03

 Целью данного пособия является оказание помощи в изучении теоретического материала, а также выработка навыков экспериментальной работы.
Целью данного пособия является оказание помощи в изучении теоретического материала, а также выработка навыков экспериментальной работы. ст.
ст. A. и Grassian, V.H. : Угольная кислота: важное промежуточное соединение в химии поверхности карбоната кальция, J. Am. хим. Soc., 126, 8068–8069, https://doi.org/10.1021/ja04, 2004.
A. и Grassian, V.H. : Угольная кислота: важное промежуточное соединение в химии поверхности карбоната кальция, J. Am. хим. Soc., 126, 8068–8069, https://doi.org/10.1021/ja04, 2004.
 2006. Т. 75. С. 105–153.
2006. Т. 75. С. 105–153. Б. : Эксперименты по активации CCN адипиновой кислотой: влияние фазы частиц и покрытий из адипиновой кислоты на растворимые и нерастворимые частицы, Atmos. хим. Phys., 8, 3735–3748, https://doi.org/10.5194/acp-8-3735-2008, 2008.
Б. : Эксперименты по активации CCN адипиновой кислотой: влияние фазы частиц и покрытий из адипиновой кислоты на растворимые и нерастворимые частицы, Atmos. хим. Phys., 8, 3735–3748, https://doi.org/10.5194/acp-8-3735-2008, 2008. Am. хим. Соц., 30, 1711–1714, 1908.
Am. хим. Соц., 30, 1711–1714, 1908.
 , and Friedrich, J. : TEM-Untersuchungen der Mikrostrukturen von Verbrennungsaerosolen, Berichte des Forschungszentrums Jülich; JUEL-2700, ISSN 0366-0885, 1992.
, and Friedrich, J. : TEM-Untersuchungen der Mikrostrukturen von Verbrennungsaerosolen, Berichte des Forschungszentrums Jülich; JUEL-2700, ISSN 0366-0885, 1992. Aerosol Sci., обзор, 2010 г.
Aerosol Sci., обзор, 2010 г. хим. Phys., 7, 1961–1971, https://doi.org/10.5194/acp-7-1961-2007, 2007.
хим. Phys., 7, 1961–1971, https://doi.org/10.5194/acp-7-1961-2007, 2007. Окружающая среда, 39, 359–369, 2005.
Окружающая среда, 39, 359–369, 2005. К., и Пратер, К. А. : Влияние метода генерации частиц на кажущуюся гигроскопичность нерастворимых минеральных частиц, Aerosol Sci. Технологии, 44, 830–846, 2010.
К., и Пратер, К. А. : Влияние метода генерации частиц на кажущуюся гигроскопичность нерастворимых минеральных частиц, Aerosol Sci. Технологии, 44, 830–846, 2010.


 По истечении этого времени они автоматически удаляются.
По истечении этого времени они автоматически удаляются. Наш конвертер файлов проанализирует содержимое исходного HTML файла до мельчайших деталей и воссоздаст содержимое в целевом DOC формате.
Наш конвертер файлов проанализирует содержимое исходного HTML файла до мельчайших деталей и воссоздаст содержимое в целевом DOC формате.

 Наша бесплатная служба преобразования проанализирует содержимое исходного HTML-файла до мельчайших деталей и воссоздаст содержимое в целевом формате Word.
Наша бесплатная служба преобразования проанализирует содержимое исходного HTML-файла до мельчайших деталей и воссоздаст содержимое в целевом формате Word.
 Вы можете скачать результат сразу или отправить ссылку на скачивание ворда на почту позже.
Вы можете скачать результат сразу или отправить ссылку на скачивание ворда на почту позже. Он отлично подходит для преобразования любых документов, таких как Microsoft Word, Excel, PowerPoint, PDF, Google Docs, Sheets и многих других. Вы также можете использовать этот инструмент для создания веб-контента с нуля или просто для очистки грязной разметки.
Он отлично подходит для преобразования любых документов, таких как Microsoft Word, Excel, PowerPoint, PDF, Google Docs, Sheets и многих других. Вы также можете использовать этот инструмент для создания веб-контента с нуля или просто для очистки грязной разметки.  Создавайте контент прямо в окне браузера, не устанавливая никаких расширений или плагинов для управления подсветкой синтаксиса и другими функциями редактирования текста.
Создавайте контент прямо в окне браузера, не устанавливая никаких расширений или плагинов для управления подсветкой синтаксиса и другими функциями редактирования текста.
 Особенно рекомендовано для турбодизельных двигателей с прямым впрыском. Разработано в соответствии с требованиями концерна VW.
Свойства продукта:
— Исключительная топливная экономичность за счет оптимальных антифрикционных свойств;
— Высокоэффективный пакет присадок и маловязкая синтетическая основа обеспечивают уверенный холодный пуск в любых условиях, благодаря чему значительно снижается пусковой износ двигателя;
— За счет превосходных моюще-диспергирующих свойств и высочайшей термоокислительной стабильности эффективно борется со всеми видами отложений и поддерживает в чистоте детали двигателя на протяжении всего интервала между заменами;
— Эстеровые компоненты масла обеспечивают отличные противоизносные свойства за счёт исключительной прочности масляной плёнки, что в сочетании с превосходной прокачиваемостью значительно увеличивает срок службы двигателя даже в режимах движения «Start-stop»;
— Совместимо со всеми системами нейтрализации отработавших газов, DPF, TWC, EGR и SCR за счет применения технологии Mid SAPS;
— Современный пакет присадок в сочетании с синтетической основой сохраняет мощностные параметры двигателя на протяжении всего интервала между заменами.
Особенно рекомендовано для турбодизельных двигателей с прямым впрыском. Разработано в соответствии с требованиями концерна VW.
Свойства продукта:
— Исключительная топливная экономичность за счет оптимальных антифрикционных свойств;
— Высокоэффективный пакет присадок и маловязкая синтетическая основа обеспечивают уверенный холодный пуск в любых условиях, благодаря чему значительно снижается пусковой износ двигателя;
— За счет превосходных моюще-диспергирующих свойств и высочайшей термоокислительной стабильности эффективно борется со всеми видами отложений и поддерживает в чистоте детали двигателя на протяжении всего интервала между заменами;
— Эстеровые компоненты масла обеспечивают отличные противоизносные свойства за счёт исключительной прочности масляной плёнки, что в сочетании с превосходной прокачиваемостью значительно увеличивает срок службы двигателя даже в режимах движения «Start-stop»;
— Совместимо со всеми системами нейтрализации отработавших газов, DPF, TWC, EGR и SCR за счет применения технологии Mid SAPS;
— Современный пакет присадок в сочетании с синтетической основой сохраняет мощностные параметры двигателя на протяжении всего интервала между заменами. Предназначено для дизельных и бензиновых двигателей легковых автомобилей, легких внедорожников, микроавтобусов и легких грузовиков, где требуется уровень эксплуатационных свойств API SN/CH-4 и ACEA C2/C3 данного класса вязкости.
Масло не предназначено для использования в тяжелых грузовиках и иной подобной технике!
Допуски: API SN/SM/CFИзготовитель:MANNOL В наличии на складе 10 974 ₽Артикул: 3038Трансмисионное масл MANNOL 8208 O.E.M. for Toyota Lexus ATF T-IV 20лF Type T-IV
ПродуктыТрансмиссионные масла и жидкостиСерия O.E.M.MANNOL O.E.M. ATF Type T-IV
MANNOL O.E.M. ATF Type T-IV 8208
Специальное трансмиссионное синтетическое масло (ATF) для автоматических коробок передач (АКПП) автомобилей TOYOTA/LEXUS c коробками TOYOTA и AISIN AW нового поколения. Обеспечивает бесперебойную работу АКПП, гарантирует минимальный износ, продолжительный срок службы трансмиссий и экономию топлива. Разработано на основании требований компании AISIN WARNER.
Свойства продукта:
— Синтетическая основа высочайшего качества со стабильно высоким индексом вязкости в комбинации с многофункциональным пакетом присадок сохраняет все свои свойства в широком диапазоне температур: обеспечивает хорошие смазочные свойства при низких (-45°C) температурах зимой и обеспечивает стабильную масляную плёнку при экстремальных нагрузках и температурах летом;
— Высокотехнологичная комбинация присадок обеспечивает хорошие антифрикционные свойства для зубчатых зацеплений и необходимые фрикционные свойства для фрикционных элементов, что обеспечивает существенную экономию топлива, плавное без рывков переключение передач и увеличение срока службы всех элементов трансмиссии.
Предназначено для дизельных и бензиновых двигателей легковых автомобилей, легких внедорожников, микроавтобусов и легких грузовиков, где требуется уровень эксплуатационных свойств API SN/CH-4 и ACEA C2/C3 данного класса вязкости.
Масло не предназначено для использования в тяжелых грузовиках и иной подобной технике!
Допуски: API SN/SM/CFИзготовитель:MANNOL В наличии на складе 10 974 ₽Артикул: 3038Трансмисионное масл MANNOL 8208 O.E.M. for Toyota Lexus ATF T-IV 20лF Type T-IV
ПродуктыТрансмиссионные масла и жидкостиСерия O.E.M.MANNOL O.E.M. ATF Type T-IV
MANNOL O.E.M. ATF Type T-IV 8208
Специальное трансмиссионное синтетическое масло (ATF) для автоматических коробок передач (АКПП) автомобилей TOYOTA/LEXUS c коробками TOYOTA и AISIN AW нового поколения. Обеспечивает бесперебойную работу АКПП, гарантирует минимальный износ, продолжительный срок службы трансмиссий и экономию топлива. Разработано на основании требований компании AISIN WARNER.
Свойства продукта:
— Синтетическая основа высочайшего качества со стабильно высоким индексом вязкости в комбинации с многофункциональным пакетом присадок сохраняет все свои свойства в широком диапазоне температур: обеспечивает хорошие смазочные свойства при низких (-45°C) температурах зимой и обеспечивает стабильную масляную плёнку при экстремальных нагрузках и температурах летом;
— Высокотехнологичная комбинация присадок обеспечивает хорошие антифрикционные свойства для зубчатых зацеплений и необходимые фрикционные свойства для фрикционных элементов, что обеспечивает существенную экономию топлива, плавное без рывков переключение передач и увеличение срока службы всех элементов трансмиссии.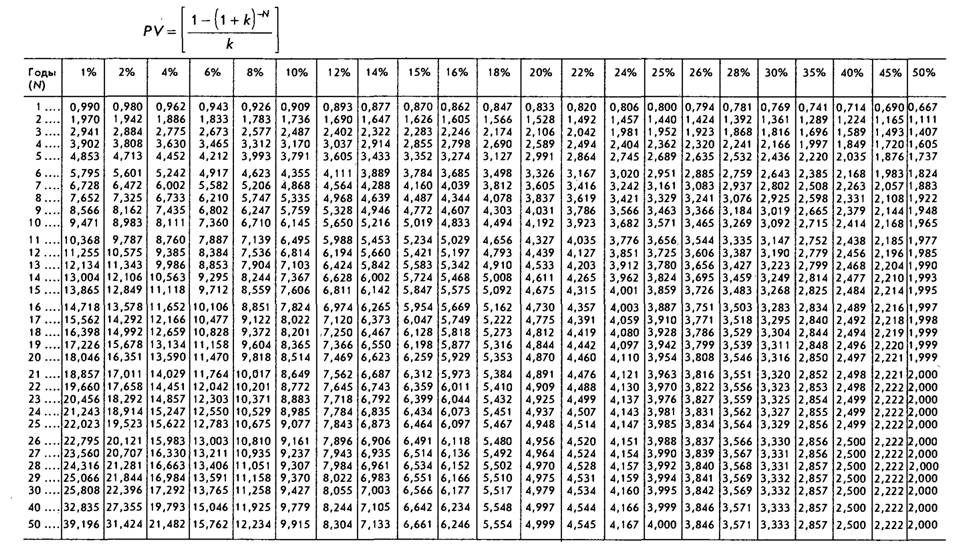 Обеспечивает слаженную и плавную работу сцеплений;
— Обладает повышенной термоокислительной и химической стабильностью и стойкостью к высокотемпературной термической деградации на протяжении всего срока эксплуатации. Это позволяет снизить образование шлама, лака, нагара и других углеродистых отложений, увеличить интервал замены масла и обеспечить долговечность деталей трансмиссии, что снижает затраты на обслуживание техники;
— Защищает от коррозии металлические детали из черных и цветных сплавов как в процессе работы, так и в нерабочем состоянии;
— Эффективно противостоит аэрации и пенообразованию;
— Обеспечивает совместимость со всеми материалами уплотнений, предотвращает их разбухание, затвердевание и усадку, что позволяет снизить затраты на запчасти и предотвращает утечки;
— Снижает шум.
Рекомендуется для АКПП Toyota и Aisin AW где требуется соответствие требованиям TOYOTA TYPE-IV. Может заменять жидкости T, T-II T-III.Изготовитель:MANNOL В наличии на складе 9 263 ₽Артикул: 1934Масло компрессорное MANNOL Compressor Oil ISO 100 20лДопуски: DIN 51 506 VBL, VCL & VDL
ISO 100
ISO L DAA, DAB, DAG & DAHИзготовитель:MANNOL В наличии на складе 9 188 ₽Артикул: 1382Трансмисионное масло MANNOL 8103 Extra Getriebeoel 75W-90 20лДопуски: SAE 75W-90 API GL 4/GL 5 LS MAN 342 Type M1/M2/M3 MACK GO-J/GO-J PlusSCANIA STO 1:0
Универсальное энергосберегающее всесезонное синтетическое трансмиссионное масло последнего поколения для всех типов механических коробок передач.
Обеспечивает слаженную и плавную работу сцеплений;
— Обладает повышенной термоокислительной и химической стабильностью и стойкостью к высокотемпературной термической деградации на протяжении всего срока эксплуатации. Это позволяет снизить образование шлама, лака, нагара и других углеродистых отложений, увеличить интервал замены масла и обеспечить долговечность деталей трансмиссии, что снижает затраты на обслуживание техники;
— Защищает от коррозии металлические детали из черных и цветных сплавов как в процессе работы, так и в нерабочем состоянии;
— Эффективно противостоит аэрации и пенообразованию;
— Обеспечивает совместимость со всеми материалами уплотнений, предотвращает их разбухание, затвердевание и усадку, что позволяет снизить затраты на запчасти и предотвращает утечки;
— Снижает шум.
Рекомендуется для АКПП Toyota и Aisin AW где требуется соответствие требованиям TOYOTA TYPE-IV. Может заменять жидкости T, T-II T-III.Изготовитель:MANNOL В наличии на складе 9 263 ₽Артикул: 1934Масло компрессорное MANNOL Compressor Oil ISO 100 20лДопуски: DIN 51 506 VBL, VCL & VDL
ISO 100
ISO L DAA, DAB, DAG & DAHИзготовитель:MANNOL В наличии на складе 9 188 ₽Артикул: 1382Трансмисионное масло MANNOL 8103 Extra Getriebeoel 75W-90 20лДопуски: SAE 75W-90 API GL 4/GL 5 LS MAN 342 Type M1/M2/M3 MACK GO-J/GO-J PlusSCANIA STO 1:0
Универсальное энергосберегающее всесезонное синтетическое трансмиссионное масло последнего поколения для всех типов механических коробок передач. Рекомендуется для использования во всех типах синхронизированных механических коробок передач (включая тяжелые), в дифференциалах (включая LS с избыточным трением), в рулевом оборудовании и других деталях трансмиссии, где встречаются чрезмерное давление и ударная нагрузка и в которых использование Стандарты GL-4 и / или GL-5 предписаны.Изготовитель:MANNOL В наличии на складе 11 388 ₽Артикул: 3074Трансмисионное масло MANNOL 8219 O.E.M. ATF SP-IV 20лACURA DW-1, тип ATF 3.0, тип ATF 3.1
BENTLEY PY112995PA
BMW 83 22 0 142 516, 83 22 0 397 114, 83 22 2 152 426,
CHRYSLER 05127382AA, 68043742AA, 68157995AA
DODGE 05127382AA, 68043742AA, 68157995AA
FORD XT-10-QLVC, XT-6-QSP, XT-6-DSP
HONDA DW-1, тип ATF 3.0, тип ATF 3.1
HYUNDAI NWS-9638 T-5, SP-IV, SPH-IV, SP-IV-RR
INFINITI Matic S, Matic W
JAGUAR Fluid 8432
JEEP 05127382AA, 68043742AA, 68157995AA
KIA NWS-9638 T-5, SP-IV, SPH-IV, SP-IV-RR
LAND ROVER TYK500050, LR0022460
LEXUS Scion FZ, тип WS, JWS 3324
LINCOLN XT-10-QLVC, XT-6-QSP, XT-6-DSP
MASERATI 231603
MAZDA FZ, FW 6A EL, FW 6AX EL
MB 236,12, 236,14, 236,15, 236,41
MERCURY XT-10-QLVC, XT-6-QSP, XT-6-DSP
MINI 83 22 0 142 516, 83 22 0 397 114, 83 22 2 152 426,
MITSUBISHI ATF-J3, Dia Queen ATF-PA
NISSAN Matic S / W
OPEL GM SATURN GMC AW1 / VI, GM SATURN GMC 88863400, GM SA
ПОРШЕ 000 043 304 00
SAAB 93 165 147 AW-1
TOYOTA Scion FZ, тип WS, JWS 3324
ZF Lifeguardfluid 6/8Изготовитель:MANNOL В наличии на складе 11 612 ₽0Избранное
Рекомендуется для использования во всех типах синхронизированных механических коробок передач (включая тяжелые), в дифференциалах (включая LS с избыточным трением), в рулевом оборудовании и других деталях трансмиссии, где встречаются чрезмерное давление и ударная нагрузка и в которых использование Стандарты GL-4 и / или GL-5 предписаны.Изготовитель:MANNOL В наличии на складе 11 388 ₽Артикул: 3074Трансмисионное масло MANNOL 8219 O.E.M. ATF SP-IV 20лACURA DW-1, тип ATF 3.0, тип ATF 3.1
BENTLEY PY112995PA
BMW 83 22 0 142 516, 83 22 0 397 114, 83 22 2 152 426,
CHRYSLER 05127382AA, 68043742AA, 68157995AA
DODGE 05127382AA, 68043742AA, 68157995AA
FORD XT-10-QLVC, XT-6-QSP, XT-6-DSP
HONDA DW-1, тип ATF 3.0, тип ATF 3.1
HYUNDAI NWS-9638 T-5, SP-IV, SPH-IV, SP-IV-RR
INFINITI Matic S, Matic W
JAGUAR Fluid 8432
JEEP 05127382AA, 68043742AA, 68157995AA
KIA NWS-9638 T-5, SP-IV, SPH-IV, SP-IV-RR
LAND ROVER TYK500050, LR0022460
LEXUS Scion FZ, тип WS, JWS 3324
LINCOLN XT-10-QLVC, XT-6-QSP, XT-6-DSP
MASERATI 231603
MAZDA FZ, FW 6A EL, FW 6AX EL
MB 236,12, 236,14, 236,15, 236,41
MERCURY XT-10-QLVC, XT-6-QSP, XT-6-DSP
MINI 83 22 0 142 516, 83 22 0 397 114, 83 22 2 152 426,
MITSUBISHI ATF-J3, Dia Queen ATF-PA
NISSAN Matic S / W
OPEL GM SATURN GMC AW1 / VI, GM SATURN GMC 88863400, GM SA
ПОРШЕ 000 043 304 00
SAAB 93 165 147 AW-1
TOYOTA Scion FZ, тип WS, JWS 3324
ZF Lifeguardfluid 6/8Изготовитель:MANNOL В наличии на складе 11 612 ₽0Избранное При использовании данного сайта вы даете свое согласие на использование cookie-файлов.
При использовании данного сайта вы даете свое согласие на использование cookie-файлов. )/3
)/3 Рабочая тетрадь для чайников с онлайн-практикой Explore Book Купить на Amazon.
Рабочая тетрадь для чайников с онлайн-практикой Explore Book Купить на Amazon. 0, 5.0), в формат величина/угол.
0, 5.0), в формат величина/угол.