Автор: Степенные выражения (выражения со степенями) и их преобразование
Рассмотрим тему преобразования выражений со степенями, но прежде остановимся на ряде преобразований, которые можно проводить с любыми выражениями, в том числе со степенными. Мы научимся раскрывать скобки, приводить подобные слагаемые, работать с основанием и показателем степени, использовать свойства степеней.
Что представляют собой степенные выражения?
В школьном курсе мало кто использует словосочетание «степенные выражения», зато этот термин постоянно встречается в сборниках для подготовки к ЕГЭ. В большинства случаев словосочетанием обозначаются выражения, которые содержат в своих записях степени. Это мы и отразим в нашем определении.
Определение 1Степенное выражение – это выражение, которое содержит степени.
Приведем несколько примеров степенных выражений, начиная со степени с натуральным показателем и заканчивая степенью с действительным показателем.
Самыми простыми степенными выражениями можно считать степени числа с натуральным показателем: 32, 75+1, (2+1)5, (−0,1)4, 2233, 3·a2−a+a2, x3−1, (a2)3.
А также степени с нулевым показателем: 50, (a+1)0, 3+52−3,20. И степени с целыми отрицательными степенями: (0,5)2+(0,5)-22.
Чуть сложнее работать со степенью, имеющей рациональный и иррациональный показатели: 26414-3·3·312, 23,5·2-22-1,5, 1a14·a12-2·a-16·b12, xπ·x1-π, 233+5.
В качестве показателя может выступать переменная 3x-54-7·3x-58 или логарифм x2·lgx−5·xlgx.
С вопросом о том, что такое степенные выражения, мы разобрались. Теперь займемся их преобразованием.
Основные виды преобразований степенных выражений
В первую очередь мы рассмотрим основные тождественные преобразования выражений, которые можно выполнять со степенными выражениями.
Пример 1Вычислите значение степенного выражения 23·(42−12).
Решение
Все преобразования мы будем проводить с соблюдением порядка выполнения действий. В данном случае начнем мы с выполнения действий в скобках: заменим степень на цифровое значение и вычислим разность двух чисел.
Имеем 23·(42−12)=23·(16−12)=23·4.
Нам остается заменить степень 23 ее значением 8 и вычислить произведение 8·4=32. Вот наш ответ.
Ответ: 23·(42−12)=32.
Пример 2Упростите выражение со степенями 3·a4·b−7−1+2·a4·b−7.
Решение
Данное нам в условии задачи выражение содержит подобные слагаемые, которые мы можем привести: 3·a4·b−7−1+2·a4·b−7=5·a4·b−7−1.
Ответ: 3·a4·b−7−1+2·a4·b−7=5·a4·b−7−1.
Пример 3Представьте выражение со степенями 9-b3·π-12 в виде произведения.
Решение
Представим число 9 как степень 32 и применим формулу сокращенного умножения:
9-b3·π-12=32-b3·π-12==3-b3·π-13+b3·π-1
Ответ: 9-b3·π-12=3-b3·π-13+b3·π-1.
А теперь перейдем к разбору тождественных преобразований, которые могут применяться именно в отношении степенных выражений.
Работа с основанием и показателем степени
Степень в основании или показателе может иметь и числа, и переменные, и некоторые выражения.
Например, (2+0,3·7)5−3,7 и (a·(a+1)−a2)2·(x+1). Работать с такими записями сложно. Намного проще заменить выражение в основании степени или выражение в показателе тождественно равным выражением.
Проводятся преобразования степени и показателя по известным нам правилам отдельно друг от друга. Самое главное, чтобы в результате преобразований получилось выражение, тождественное исходному.
Цель преобразований – упростить исходное выражение или получить решение задачи. Например, в примере, который мы привели выше, (2+0,3·7)5−3,7 можно выполнить действия для перехода к степени 4,11,3. Раскрыв скобки, мы можем привести подобные слагаемые в основании степени (a·(a+1)−a2)2·(x+1) и получить степенное выражение более простого вида a2·(x+1).
Использование свойств степеней
Свойства степеней, записанные в виде равенств, являются одним из главных инструментов преобразования выражений со степенями. Приведем здесь основные из них, учитывая, что a и b – это любые положительные числа, а r и s — произвольные действительные числа:
Определение 2- ar·as=ar+s;
- ar:as=ar−s;
- (a·b)r=ar·br;
- (a:b)r=ar:br;
- (ar)s=ar·s.
В тех случаях, когда мы имеем дело с натуральными, целыми, положительными показателями степени, ограничения на числа a и b могут быть гораздо менее строгими. Так, например, если рассмотреть равенство am·an=am+n, где m и n – натуральные числа, то оно будет верно для любых значений a, как положительных, так и отрицательных, а также для a=0.
Применять свойства степеней без ограничений можно в тех случаях, когда основания степеней положительные или содержат переменные, область допустимых значений которых такова, что на ней основания принимают лишь положительные значения. Фактически, в рамках школьной программы по математике задачей учащегося является выбор подходящего свойства и правильное его применение.
При подготовке к поступлению в Вузы могут встречаться задачи, в которых неаккуратное применение свойств будет приводить к сужению ОДЗ и другим сложностям с решением. В данном разделе мы разберем всего два таких случая. Больше информации по вопросу можно найти в теме «Преобразование выражений с использованием свойств степеней».
Представьте выражение a2,5·(a2)−3:a−5,5 в виде степени с основанием a.
Решение
Для начала используем свойство возведения в степень и преобразуем по нему второй множитель (a2)−3 . Затем используем свойства умножения и деления степеней с одинаковым основанием:
a2,5·a−6:a−5,5= a2,5−6:a−5,5=a−3,5:a−5,5= a−3,5−(−5,5)=a2.
Ответ: a2,5·(a2)−3:a−5,5=a2.
Преобразование степенных выражений согласно свойству степеней может производиться как слева направо, так и в обратном направлении.
Пример 5Найти значение степенного выражения 313·713·2123.
Решение
Если мы применим равенство (a·b)r=ar·br, справа налево, то получим произведение вида 3·713·2123 и дальше 2113·2123. Сложим показатели при умножении степеней с одинаковыми основаниями: 2113·2123=2113+23=211=21.
Есть еще один способ провести преобразования:
313·713·2123=313·713·(3·7)23=313·713·323·723==313·323·713·723=313+23·713+23=31·71=21
Ответ: 313·713·2123=31·71=21
Пример 6
Дано степенное выражение a1,5−a0,5−6, введите новую переменную t=a0,5.
Решение
Представим степень a1,5 как a0,5·3 . Используем свойство степени в степени (ar)s=ar·s справа налево и получим (a0,5)3: a1,5−a0,5−6=(a0,5)3−a0,5−6. В полученное выражение можно без проблем вводить новую переменную t=a0,5: получаем t3−t−6.
Ответ: t3−t−6.
Преобразование дробей, содержащих степени
Обычно мы имеем дело с двумя вариантами степенных выражений с дробями: выражение представляет собой дробь со степенью или содержит такую дробь. К таким выражениям применимы все основные преобразования дробей без ограничений. Их можно сокращать, приводить к новому знаменателю, работать отдельно с числителем и знаменателем. Проиллюстрируем это примерами.
Пример 7Упростить степенное выражение 3·523·513-5-231+2·x2-3-3·x2.
Решение
Мы имеем дело с дробью, поэтому проведем преобразования и в числителе, и в знаменателе:
3·523·513-5-231+2·x2-3-3·x2=3·523·513-3·523·5-23-2-x2==3·523+13-3·523+-23-2-x2=3·51-3·50-2-x2
Поместим минус перед дробью для того, чтобы изменить знак знаменателя: 12-2-x2=-122+x2
Ответ: 3·523·513-5-231+2·x2-3-3·x2=-122+x2
Дроби, содержащие степени, приводятся к новому знаменателю точно также, как и рациональные дроби.
Для этого необходимо найти дополнительный множитель и умножить на него числитель и знаменатель дроби. Подбирать дополнительный множитель необходимо таким образом, чтобы он не обращался в нуль ни при каких значениях переменных из ОДЗ переменных для исходного выражения.
Приведите дроби к новому знаменателю: а) a+1a0,7 к знаменателю a, б) 1×23-2·x13·y16+4·y13 к знаменателю x+8·y12.
Решение
а) Подберем множитель, который позволит нам произвести приведение к новому знаменателю. a0,7·a0,3=a0,7+0,3=a, следовательно, в качестве дополнительного множителя мы возьмем a0,3. Область допустимых значений переменной а включает множество всех положительных действительных чисел. В этой области степень a0,3 не обращается в нуль.
Выполним умножение числителя и знаменателя дроби на a0,3:
a+1a0,7=a+1·a0,3a0,7·a0,3=a+1·a0,3a
б) Обратим внимание на знаменатель:
x23-2·x13·y16+4·y13==x132-x13·2·y16+2·y162
Умножим это выражение на x13+2·y16, получим сумму кубов x13 и 2·y16, т.
е. x+8·y12. Это наш новый знаменатель, к которому нам надо привести исходную дробь.
Так мы нашли дополнительный множитель x13+2·y16. На области допустимых значений переменных x и y выражение x13+2·y16 не обращается в нуль, поэтому, мы можем умножить на него числитель и знаменатель дроби:
1×23-2·x13·y16+4·y13==x13+2·y16x13+2·y16x23-2·x13·y16+4·y13==x13+2·y16x133+2·y163=x13+2·y16x+8·y12
Ответ: а) a+1a0,7=a+1·a0,3a , б) 1×23-2·x13·y16+4·y13=x13+2·y16x+8·y12.
Пример 9Сократите дробь: а) 30·x3·(x0,5+1)·x+2·x113-5345·x0,5+12·x+2·x113-53, б) a14-b14a12-b12.
Решение
а) Используем наибольший общий знаменатель (НОД), на который можно сократить числитель и знаменатель. Для чисел 30 и 45 это 15. Также мы можем произвести сокращение на x0,5+1 и на x+2·x113-53.
Получаем:
30·x3·(x0,5+1)·x+2·x113-5345·x0,5+12·x+2·x113-53=2·x33·(x0,5+1)
б) Здесь наличие одинаковых множителей неочевидно.
Придется выполнить некоторые преобразования для того, чтобы получить одинаковые множители в числителе и знаменателе. Для этого разложим знаменатель, используя формулу разности квадратов:
a14-b14a12-b12=a14-b14a142-b122==a14-b14a14+b14·a14-b14=1a14+b14
Ответ: а)30·x3·(x0,5+1)·x+2·x113-5345·x0,5+12·x+2·x113-53=2·x33·(x0,5+1), б) a14-b14a12-b12=1a14+b14.
К числу основных действий с дробями относится приведение к новому знаменателю и сокращение дробей. Оба действия выполняют с соблюдением ряда правил. При сложении и вычитании дробей сначала дроби приводятся к общему знаменателю, после чего проводятся действия (сложение или вычитание) с числителями. Знаменатель остается прежним. Результатом наших действий является новая дробь, числитель которой является произведением числителей, а знаменатель есть произведение знаменателей.
Пример 10Выполните действия x12+1×12-1-x12-1×12+1·1×12.
Решение
Начнем с вычитания дробей, которые располагаются в скобках.
Приведем их к общему знаменателю:
x12-1·x12+1
Вычтем числители:
x12+1×12-1-x12-1×12+1·1×12==x12+1·x12+1×12-1·x12+1-x12-1·x12-1×12+1·x12-1·1×12==x12+12-x12-12×12-1·x12+1·1×12==x122+2·x12+1-x122-2·x12+1×12-1·x12+1·1×12==4·x12x12-1·x12+1·1×12
Теперь умножаем дроби:
4·x12x12-1·x12+1·1×12==4·x12x12-1·x12+1·x12
Произведем сокращение на степень x12, получим 4×12-1·x12+1.
Дополнительно можно упростить степенное выражение в знаменателе, используя формулу разности квадратов: квадратов: 4×12-1·x12+1=4×122-12=4x-1.
Ответ: x12+1×12-1-x12-1×12+1·1×12=4x-1
Пример 11Упростите степенное выражение x34·x2,7+12x-58·x2,7+13.
Решение
Мы можем произвести сокращение дроби на (x2,7+1)2. Получаем дробь x34x-58·x2,7+1.
Продолжим преобразования степеней икса x34x-58·1×2,7+1. Теперь можно использовать свойство деления степеней с одинаковыми основаниями: x34x-58·1×2,7+1=x34—58·1×2,7+1=x118·1×2,7+1.
Переходим от последнего произведения к дроби x138x2,7+1.
Ответ: x34·x2,7+12x-58·x2,7+13=x138x2,7+1.
Множители с отрицательными показателями степени в большинстве случаев удобнее переносить из числителя в знаменатель и обратно, изменяя знак показателя. Это действие позволяет упростить дальнейшее решение. Приведем пример: степенное выражение (x+1)-0,23·x-1 можно заменить на x3·(x+1)0,2.
Преобразование выражений с корнями и степенями
В задачах встречаются степенные выражения, которые содержат не только степени с дробными показателями, но и корни. Такие выражения желательно привести только к корням или только к степеням. Переход к степеням предпочтительнее, так как с ними проще работать. Такой переход является особенно предпочтительным, когда ОДЗ переменных для исходного выражения позволяет заменить корни степенями без необходимости обращаться к модулю или разбивать ОДЗ на несколько промежутков.
Пример 12Представьте выражение x19·x·x36 в виде степени.
Решение
Область допустимых значений переменной x определяется двумя неравенствами x≥0 и x·x3≥0 , которые задают множество [0, +∞).
На этом множестве мы имеем право перейти от корней к степеням:
x19·x·x36=x19·x·x1316
Используя свойства степеней, упростим полученное степенное выражение.
x19·x·x1316=x19·x16·x1316=x19·x16·x1·13·6==x19·x16·x118=x19+16+118=x13
Ответ: x19·x·x36=x13.
Преобразование степеней с переменными в показателе
Данные преобразования достаточно просто произвести, если грамотно использовать свойства степени. Например, 52·x+1−3·5x·7x−14·72·x−1=0.
Мы можем заменить произведением степени, в показателях которых находится сумма некоторой переменной и числа. В левой части это можно проделать с первым и последним слагаемыми левой части выражения:
52·x·51−3·5x·7x−14·72·x·7−1=0, 5·52·x−3·5x·7x−2·72·x=0.
Теперь поделим обе части равенства на 72·x.
Это выражение на ОДЗ переменной x принимает только положительные значения:
5·5-3·5x·7x-2·72·x72·x=072·x,5·52·x72·x-3·5x·7×72·x-2·72·x72·x=0,5·52·x72·x-3·5x·7x7x·7x-2·72·x72·x=0
Сократим дроби со степенями, получим: 5·52·x72·x-3·5x7x-2=0.
Наконец, отношение степеней с одинаковыми показателями заменяется степенями отношений, что приводит к уравнению 5·572·x-3·57x-2=0 , которое равносильно 5·57×2-3·57x-2=0.
Введем новую переменную t=57x, что сводит решение исходного показательного уравнения к решению квадратного уравнения 5·t2−3·t−2=0.
Преобразование выражений со степенями и логарифмами
Выражения, содержащие с записи степени и логарифмы, также встречаются в задачах. Примером таких выражений могут служить: 141-5·log23 или log3279+5(1-log35)·log53. Преобразование подобных выражений проводится с использованием разобранных выше подходов и свойств логарифмов, которые мы подробно разобрали в теме «Преобразование логарифмических выражений».
Степенные выражения (выражения со степенями) и их преобразование
Рассмотрим тему преобразования выражений со степенями, но прежде остановимся на ряде преобразований, которые можно проводить с любыми выражениями, в том числе со степенными.
Мы научимся раскрывать скобки, приводить подобные слагаемые, работать с основанием и показателем степени, использовать свойства степеней.
Что представляют собой степенные выражения?
В школьном курсе мало кто использует словосочетание «степенные выражения», зато этот термин постоянно встречается в сборниках для подготовки к ЕГЭ. В большинства случаев словосочетанием обозначаются выражения, которые содержат в своих записях степени. Это мы и отразим в нашем определении.
Определение 1Степенное выражение – это выражение, которое содержит степени.
Приведем несколько примеров степенных выражений, начиная со степени с натуральным показателем и заканчивая степенью с действительным показателем.
Самыми простыми степенными выражениями можно считать степени числа с натуральным показателем: 32, 75+1, (2+1)5, (−0,1)4, 2233, 3·a2−a+a2, x3−1, (a2)3. А также степени с нулевым показателем: 50, (a+1)0, 3+52−3,20. И степени с целыми отрицательными степенями: (0,5)2+(0,5)-22.
Чуть сложнее работать со степенью, имеющей рациональный и иррациональный показатели: 26414-3·3·312, 23,5·2-22-1,5, 1a14·a12-2·a-16·b12, xπ·x1-π, 233+5.
В качестве показателя может выступать переменная 3x-54-7·3x-58 или логарифм x2·lgx−5·xlgx.
С вопросом о том, что такое степенные выражения, мы разобрались. Теперь займемся их преобразованием.
Основные виды преобразований степенных выражений
В первую очередь мы рассмотрим основные тождественные преобразования выражений, которые можно выполнять со степенными выражениями.
Пример 1Вычислите значение степенного выражения 23·(42−12).
Решение
Все преобразования мы будем проводить с соблюдением порядка выполнения действий. В данном случае начнем мы с выполнения действий в скобках: заменим степень на цифровое значение и вычислим разность двух чисел. Имеем 23·(42−12)=23·(16−12)=23·4.
Нам остается заменить степень 23 ее значением 8 и вычислить произведение 8·4=32.
Вот наш ответ.
Ответ: 23·(42−12)=32.
Пример 2Упростите выражение со степенями 3·a4·b−7−1+2·a4·b−7.
Решение
Данное нам в условии задачи выражение содержит подобные слагаемые, которые мы можем привести: 3·a4·b−7−1+2·a4·b−7=5·a4·b−7−1.
Ответ: 3·a4·b−7−1+2·a4·b−7=5·a4·b−7−1.
Пример 3Представьте выражение со степенями 9-b3·π-12 в виде произведения.
Решение
Представим число 9 как степень 32 и применим формулу сокращенного умножения:
9-b3·π-12=32-b3·π-12==3-b3·π-13+b3·π-1
Ответ: 9-b3·π-12=3-b3·π-13+b3·π-1.
А теперь перейдем к разбору тождественных преобразований, которые могут применяться именно в отношении степенных выражений.
Работа с основанием и показателем степени
Степень в основании или показателе может иметь и числа, и переменные, и некоторые выражения. Например, (2+0,3·7)5−3,7 и (a·(a+1)−a2)2·(x+1).
Работать с такими записями сложно. Намного проще заменить выражение в основании степени или выражение в показателе тождественно равным выражением.
Проводятся преобразования степени и показателя по известным нам правилам отдельно друг от друга. Самое главное, чтобы в результате преобразований получилось выражение, тождественное исходному.
Цель преобразований – упростить исходное выражение или получить решение задачи. Например, в примере, который мы привели выше, (2+0,3·7)5−3,7 можно выполнить действия для перехода к степени 4,11,3. Раскрыв скобки, мы можем привести подобные слагаемые в основании степени (a·(a+1)−a2)2·(x+1) и получить степенное выражение более простого вида a2·(x+1).
Использование свойств степеней
Свойства степеней, записанные в виде равенств, являются одним из главных инструментов преобразования выражений со степенями. Приведем здесь основные из них, учитывая, что a и b – это любые положительные числа, а r и s — произвольные действительные числа:
Определение 2- ar·as=ar+s;
- ar:as=ar−s;
- (a·b)r=ar·br;
- (a:b)r=ar:br;
- (ar)s=ar·s.
В тех случаях, когда мы имеем дело с натуральными, целыми, положительными показателями степени, ограничения на числа a и b могут быть гораздо менее строгими. Так, например, если рассмотреть равенство am·an=am+n, где m и n – натуральные числа, то оно будет верно для любых значений a, как положительных, так и отрицательных, а также для a=0.
Применять свойства степеней без ограничений можно в тех случаях, когда основания степеней положительные или содержат переменные, область допустимых значений которых такова, что на ней основания принимают лишь положительные значения. Фактически, в рамках школьной программы по математике задачей учащегося является выбор подходящего свойства и правильное его применение.
При подготовке к поступлению в Вузы могут встречаться задачи, в которых неаккуратное применение свойств будет приводить к сужению ОДЗ и другим сложностям с решением. В данном разделе мы разберем всего два таких случая. Больше информации по вопросу можно найти в теме «Преобразование выражений с использованием свойств степеней».
Представьте выражение a2,5·(a2)−3:a−5,5 в виде степени с основанием a.
Решение
Для начала используем свойство возведения в степень и преобразуем по нему второй множитель (a2)−3 . Затем используем свойства умножения и деления степеней с одинаковым основанием:
a2,5·a−6:a−5,5= a2,5−6:a−5,5=a−3,5:a−5,5= a−3,5−(−5,5)=a2.
Ответ: a2,5·(a2)−3:a−5,5=a2.
Преобразование степенных выражений согласно свойству степеней может производиться как слева направо, так и в обратном направлении.
Пример 5Найти значение степенного выражения 313·713·2123.
Решение
Если мы применим равенство (a·b)r=ar·br, справа налево, то получим произведение вида 3·713·2123 и дальше 2113·2123. Сложим показатели при умножении степеней с одинаковыми основаниями: 2113·2123=2113+23=211=21.
Есть еще один способ провести преобразования:
313·713·2123=313·713·(3·7)23=313·713·323·723==313·323·713·723=313+23·713+23=31·71=21
Ответ: 313·713·2123=31·71=21
Пример 6
Дано степенное выражение a1,5−a0,5−6, введите новую переменную t=a0,5.
Решение
Представим степень a1,5 как a0,5·3 . Используем свойство степени в степени (ar)s=ar·s справа налево и получим (a0,5)3: a1,5−a0,5−6=(a0,5)3−a0,5−6. В полученное выражение можно без проблем вводить новую переменную t=a0,5: получаем t3−t−6.
Ответ: t3−t−6.
Преобразование дробей, содержащих степени
Обычно мы имеем дело с двумя вариантами степенных выражений с дробями: выражение представляет собой дробь со степенью или содержит такую дробь. К таким выражениям применимы все основные преобразования дробей без ограничений. Их можно сокращать, приводить к новому знаменателю, работать отдельно с числителем и знаменателем. Проиллюстрируем это примерами.
Пример 7Упростить степенное выражение 3·523·513-5-231+2·x2-3-3·x2.
Решение
Мы имеем дело с дробью, поэтому проведем преобразования и в числителе, и в знаменателе:
3·523·513-5-231+2·x2-3-3·x2=3·523·513-3·523·5-23-2-x2==3·523+13-3·523+-23-2-x2=3·51-3·50-2-x2
Поместим минус перед дробью для того, чтобы изменить знак знаменателя: 12-2-x2=-122+x2
Ответ: 3·523·513-5-231+2·x2-3-3·x2=-122+x2
Дроби, содержащие степени, приводятся к новому знаменателю точно также, как и рациональные дроби.
Для этого необходимо найти дополнительный множитель и умножить на него числитель и знаменатель дроби. Подбирать дополнительный множитель необходимо таким образом, чтобы он не обращался в нуль ни при каких значениях переменных из ОДЗ переменных для исходного выражения.
Приведите дроби к новому знаменателю: а) a+1a0,7 к знаменателю a, б) 1×23-2·x13·y16+4·y13 к знаменателю x+8·y12.
Решение
а) Подберем множитель, который позволит нам произвести приведение к новому знаменателю. a0,7·a0,3=a0,7+0,3=a, следовательно, в качестве дополнительного множителя мы возьмем a0,3. Область допустимых значений переменной а включает множество всех положительных действительных чисел. В этой области степень a0,3 не обращается в нуль.
Выполним умножение числителя и знаменателя дроби на a0,3:
a+1a0,7=a+1·a0,3a0,7·a0,3=a+1·a0,3a
б) Обратим внимание на знаменатель:
x23-2·x13·y16+4·y13==x132-x13·2·y16+2·y162
Умножим это выражение на x13+2·y16, получим сумму кубов x13 и 2·y16, т.
е. x+8·y12. Это наш новый знаменатель, к которому нам надо привести исходную дробь.
Так мы нашли дополнительный множитель x13+2·y16. На области допустимых значений переменных x и y выражение x13+2·y16 не обращается в нуль, поэтому, мы можем умножить на него числитель и знаменатель дроби:
1×23-2·x13·y16+4·y13==x13+2·y16x13+2·y16x23-2·x13·y16+4·y13==x13+2·y16x133+2·y163=x13+2·y16x+8·y12
Ответ: а) a+1a0,7=a+1·a0,3a , б) 1×23-2·x13·y16+4·y13=x13+2·y16x+8·y12.
Пример 9Сократите дробь: а) 30·x3·(x0,5+1)·x+2·x113-5345·x0,5+12·x+2·x113-53, б) a14-b14a12-b12.
Решение
а) Используем наибольший общий знаменатель (НОД), на который можно сократить числитель и знаменатель. Для чисел 30 и 45 это 15. Также мы можем произвести сокращение на x0,5+1 и на x+2·x113-53.
Получаем:
30·x3·(x0,5+1)·x+2·x113-5345·x0,5+12·x+2·x113-53=2·x33·(x0,5+1)
б) Здесь наличие одинаковых множителей неочевидно.
Придется выполнить некоторые преобразования для того, чтобы получить одинаковые множители в числителе и знаменателе. Для этого разложим знаменатель, используя формулу разности квадратов:
a14-b14a12-b12=a14-b14a142-b122==a14-b14a14+b14·a14-b14=1a14+b14
Ответ: а)30·x3·(x0,5+1)·x+2·x113-5345·x0,5+12·x+2·x113-53=2·x33·(x0,5+1), б) a14-b14a12-b12=1a14+b14.
К числу основных действий с дробями относится приведение к новому знаменателю и сокращение дробей. Оба действия выполняют с соблюдением ряда правил. При сложении и вычитании дробей сначала дроби приводятся к общему знаменателю, после чего проводятся действия (сложение или вычитание) с числителями. Знаменатель остается прежним. Результатом наших действий является новая дробь, числитель которой является произведением числителей, а знаменатель есть произведение знаменателей.
Пример 10Выполните действия x12+1×12-1-x12-1×12+1·1×12.
Решение
Начнем с вычитания дробей, которые располагаются в скобках.
Приведем их к общему знаменателю:
x12-1·x12+1
Вычтем числители:
x12+1×12-1-x12-1×12+1·1×12==x12+1·x12+1×12-1·x12+1-x12-1·x12-1×12+1·x12-1·1×12==x12+12-x12-12×12-1·x12+1·1×12==x122+2·x12+1-x122-2·x12+1×12-1·x12+1·1×12==4·x12x12-1·x12+1·1×12
Теперь умножаем дроби:
4·x12x12-1·x12+1·1×12==4·x12x12-1·x12+1·x12
Произведем сокращение на степень x12, получим 4×12-1·x12+1.
Дополнительно можно упростить степенное выражение в знаменателе, используя формулу разности квадратов: квадратов: 4×12-1·x12+1=4×122-12=4x-1.
Ответ: x12+1×12-1-x12-1×12+1·1×12=4x-1
Пример 11Упростите степенное выражение x34·x2,7+12x-58·x2,7+13.
Решение
Мы можем произвести сокращение дроби на (x2,7+1)2. Получаем дробь x34x-58·x2,7+1.
Продолжим преобразования степеней икса x34x-58·1×2,7+1. Теперь можно использовать свойство деления степеней с одинаковыми основаниями: x34x-58·1×2,7+1=x34—58·1×2,7+1=x118·1×2,7+1.
Переходим от последнего произведения к дроби x138x2,7+1.
Ответ: x34·x2,7+12x-58·x2,7+13=x138x2,7+1.
Множители с отрицательными показателями степени в большинстве случаев удобнее переносить из числителя в знаменатель и обратно, изменяя знак показателя. Это действие позволяет упростить дальнейшее решение. Приведем пример: степенное выражение (x+1)-0,23·x-1 можно заменить на x3·(x+1)0,2.
Преобразование выражений с корнями и степенями
В задачах встречаются степенные выражения, которые содержат не только степени с дробными показателями, но и корни. Такие выражения желательно привести только к корням или только к степеням. Переход к степеням предпочтительнее, так как с ними проще работать. Такой переход является особенно предпочтительным, когда ОДЗ переменных для исходного выражения позволяет заменить корни степенями без необходимости обращаться к модулю или разбивать ОДЗ на несколько промежутков.
Пример 12Представьте выражение x19·x·x36 в виде степени.
Решение
Область допустимых значений переменной x определяется двумя неравенствами x≥0 и x·x3≥0 , которые задают множество [0, +∞).
На этом множестве мы имеем право перейти от корней к степеням:
x19·x·x36=x19·x·x1316
Используя свойства степеней, упростим полученное степенное выражение.
x19·x·x1316=x19·x16·x1316=x19·x16·x1·13·6==x19·x16·x118=x19+16+118=x13
Ответ: x19·x·x36=x13.
Преобразование степеней с переменными в показателе
Данные преобразования достаточно просто произвести, если грамотно использовать свойства степени. Например, 52·x+1−3·5x·7x−14·72·x−1=0.
Мы можем заменить произведением степени, в показателях которых находится сумма некоторой переменной и числа. В левой части это можно проделать с первым и последним слагаемыми левой части выражения:
52·x·51−3·5x·7x−14·72·x·7−1=0, 5·52·x−3·5x·7x−2·72·x=0.
Теперь поделим обе части равенства на 72·x.
Это выражение на ОДЗ переменной x принимает только положительные значения:
5·5-3·5x·7x-2·72·x72·x=072·x,5·52·x72·x-3·5x·7×72·x-2·72·x72·x=0,5·52·x72·x-3·5x·7x7x·7x-2·72·x72·x=0
Сократим дроби со степенями, получим: 5·52·x72·x-3·5x7x-2=0.
Наконец, отношение степеней с одинаковыми показателями заменяется степенями отношений, что приводит к уравнению 5·572·x-3·57x-2=0 , которое равносильно 5·57×2-3·57x-2=0.
Введем новую переменную t=57x, что сводит решение исходного показательного уравнения к решению квадратного уравнения 5·t2−3·t−2=0.
Преобразование выражений со степенями и логарифмами
Выражения, содержащие с записи степени и логарифмы, также встречаются в задачах. Примером таких выражений могут служить: 141-5·log23 или log3279+5(1-log35)·log53. Преобразование подобных выражений проводится с использованием разобранных выше подходов и свойств логарифмов, которые мы подробно разобрали в теме «Преобразование логарифмических выражений».
{\frac{1}{2}}}[/latex] А поскольку вы знаете, что возведение числа в степень [latex] \frac{1}{2}[/latex] равносильно возведению в квадрат корень этого числа, вы также можете записать его таким образом.
{2}} }[/латекс].
Квадратный корень из правила произведения поможет нам упростить несовершенные корни, как показано в следующем примере.
Пример
Упрощение. [латекс] \sqrt{63}[/латекс]
Показать решениеОкончательный ответ [латекс] 3\sqrt{7}[/латекс] может показаться немного странным, но он в упрощенной форме. Вы можете прочитать это как «три радикальных семи» или «три умножить на квадратный корень из семи».
В следующем видео показано больше примеров того, как упростить квадратные корни, которые не имеют идеальных квадратных корней. 9{2}}[/латекс]
Один из советов, чтобы узнать, когда применять абсолютное значение после упрощения любого даже индексированного корня, — посмотреть на конечный показатель степени в ваших переменных терминах. Если показатель степени нечетный, включая [latex]1[/latex], добавьте абсолютное значение. Это относится к упрощению любого корня с четным индексом, как мы увидим в последующих примерах.В следующем видео вы увидите больше примеров того, как упростить радикальные выражения с переменными.
Мы покажем еще один пример, где упрощенное выражение содержит переменные как с нечетными, так и с четными степенями.
В нашем следующем примере мы начнем с выражения, записанного с рациональным показателем. Вы увидите, что вы можете использовать аналогичный процесс — разложение членов на множители и сортировку по квадратам — для упрощения этого выражения.
Вот еще один пример с идеальными квадратами.
Упрощение кубических корней
Мы можем использовать те же методы, которые мы использовали для упрощения квадратных корней, для упрощения корней более высокого порядка. Например, чтобы упростить кубический корень, цель состоит в том, чтобы найти множители под радикалом, которые являются идеальными кубами , чтобы вы могли извлечь из них кубический корень. Нам больше не нужно беспокоиться о том, определили ли мы главный корень, поскольку теперь мы находим кубические корни. Сосредоточьтесь на поиске идентичных трио факторов по мере упрощения. 9{3}}\end{array}[/latex]
Вы также можете пропустить шаг разложения на множители отрицательного числа, когда освоитесь с определением кубов.
В следующем видео мы покажем больше примеров упрощения кубических корней.
Упрощение корней четвертой степени
Теперь давайте перейдем к упрощению корней четвертой степени.
Независимо от того, какой корень вы упрощаете, применяется одна и та же идея: найдите кубы для кубических корней, степени четырех для четвертых корней и т. д. Вспомните, что когда ваше упрощенное выражение содержит четный индексный радикал и переменный множитель с нечетным показателем, вам нужно применить абсолютное значение.
Альтернативный метод факторизации состоит в том, чтобы переписать выражение с рациональными показателями, а затем использовать правила показателей для упрощения. Вы можете обнаружить, что предпочитаете один метод другому. В любом случае приятно иметь варианты. Мы снова покажем последний пример, используя эту идею.
В следующем видео мы покажем еще один пример того, как упростить корень четвертой и пятой степени.
В нашем последнем примере мы упростим более сложное выражение, [латекс]\dfrac{10{{b}^{2}}{{c}^{2}}}{c\sqrt[3] {8{{b}^{4}}}}[/латекс] . 1
2
3
4
5
6
7
8
9
0
.
C Ответить <table>
<tr>
<td>
<p>6</p> <p>8</p>
</td>
<td> + </td>
<td>
<p>9</p> <p>9</p>
</td>
<td> = </td>
</tr>
</table> <table>
<tr>
<td>
<p>1</p> <p>10</p>
</td>
<td> + </td>
<td>
<p>2</p> <p>2</p>
</td>
<td> = </td>
</tr>
</table> <table>
<tr>
<td>
<p>1</p> <p>10</p>
</td>
<td> + </td>
<td>
<p>5</p> <p>4</p>
</td>
<td> = </td>
</tr>
</table> <table>
<tr>
<td>
<p>1</p> <p>9</p>
</td>
<td> + </td>
<td>
<p>9</p> <p>7</p>
</td>
<td> = </td>
</tr>
</table> <table>
<tr>
<td>
<p>8</p> <p>10</p>
</td>
<td> + </td>
<td>
<p>7</p> <p>1</p>
</td>
<td> = </td>
</tr>
</table> <table>
<tr>
<td>
<p>1</p> <p>8</p>
</td>
<td> + </td>
<td>
<p>2</p> <p>9</p>
</td>
<td> = </td>
</tr>
</table> <table>
<tr>
<td>
<p>4</p> <p>7</p>
</td>
<td> + </td>
<td>
<p>10</p> <p>3</p>
</td>
<td> = </td>
</tr>
</table> <table>
<tr>
<td>
<p>3</p> <p>6</p>
</td>
<td> + </td>
<td>
<p>1</p> <p>5</p>
</td>
<td> = </td>
</tr>
</table> <table>
<tr>
<td>
<p>1</p> <p>5</p>
</td>
<td> + </td>
<td>
<p>2</p> <p>6</p>
</td>
<td> = </td>
</tr>
</table> <table>
<tr>
<td>
<p>4</p> <p>6</p>
</td>
<td> + </td>
<td>
<p>1</p> <p>5</p>
</td>
<td> = </td>
</tr>
</table> Тема «дробные числа» в математике одна из самых сложных для восприятия школьниками.
Также эта тема очень большая, поскольку охватывает сразу несколько разделов.
При изучении дробей в математике очень важно не упустить момент если ребенок
что-то хоть немного недопонял или сомневается или не уверен В данном случае главное объяснить где применяется «дробная часть числа», а также наглядность примеров.
Само слово «Дробь» уже подразумевает дробление, деление, часть от чего-то.
В школьной программе к изучению дробей приступают только после изучения всех операций
над целыми числами и начинают изучении дробей только в 4 классе. Но объяснить ребенку что такое обыкновенные дроби и решать задания,
и познакомиться с примерами решения дробей лучше гораздо раньше.
Это сформирует пространственное представление и логическое мышление. Наш тренажер сложения дробей в этом, конечно, поможет.
А в 5 классе изучении дробей со сверстниками не составит труда!
Но если надо решить уже имеющуюся дробь, ту придет на помощь калькулятор решающий дроби Дробь в математике – число, состоящее из одной или нескольких равных частей (долей) единицы. Дробь — число не целое, оно обозначает количество долей целого Обыкновенная дробь состоит из двух частей: числитель и знаменатель Дроби бывают правильные и неправильные. У правильных дробей числитель меньше знаменателя.
У неправильных дробей наоборот, числитель больше знаменателя,
а значит любую неправильную дробь можно перевести в смешанную,
выделив у нее целую часть и отняв ее из числителя Мер величин много и в них легко запутаться. Скорей заниматься Множество примеров различной сложности помогут ребенку быстро запомнить римские цифры Скорей заниматься Решение задач на применение формул объем, площадь, периметр Скорей заниматься Задачи на части (на дроби) в 5 — 6 классе, безусловно, тяжелейшая тема для преподавания. Возможно даже самая тяжелая за весь школьный курс. Как может построить свою работу с ней репетитор по математике? Рассмотрим некоторые приемы обучения решению таких задач, опишем связанные с темой проблемы и поговорим о ее дидактике. Причиной большинства обращений к репетитору в 5 классе является повальное непонимание законов разделения на части. Это естественно, ибо задачи, на которых формируется представление о долях, предъявляют достаточно высокие (для этого возраста) требования к уровню развития ученика, часто связанные с его физиологией. Несмотря на влияние физиогогии родители ребенка обычно стараются повлиять на ситуацию как можно быстрее. Большинству из них нужен репетитор по математике для скорейшего исправления текущей отметки. Иногда это мешает планомерно и неспешно объяснять математические законы и выстраивать темы в логически правильном порядке. Долгое время я не решался написать об этих задачах. И дело не только в сложности восприятия материала школьниками. В изучении темы выделяется несколько этапов с различными ограничениями в использовании чисел. Не случайно дроби проходят не один год. Программа 5 класса переплетается с программой 6-го класса (а по Петерсону еще и с четвертым). Поэтому даже при одном и том же характере работы преподавателя с дробями разница в индивидуальных особенностях учеников и программах не позволяют описать методы работы репетитора по математике с темой точно и коротко. Много раз я сталкивался с проблемами задач на дроби и уяснил для себя главное: тема требуют постепенного и долгого изучения. Ее нельзя проработать за один-два урока. Поэтому первое, что я делаю, — объясняю родителям ситуацию и прошу предоставить дополнительные часы для занятий. Не менее двух раз в неделю. Для репетитора по математике это стандартный график, позволяющий в большинстве случаев полноценно заниматься пробелами. Формально мой подход не отличается от того, что предлагают другие репетиторы, а именно — решение задач в большом количестве. Однако к ним еще нужно поготовить ученика, предложить ему некий план или даже алгоритм подбора пути решения. Попробую изложить … Первый этап работы репетитора — знакомство ученика с базовыми задачами, обучение составлению для них кратких записей. Очень важно вложить в ученика мысль о том, что сложная задача на дроби состоит из нескольких упакованных в нее простых, с определенной последовательных элементарных операций. Их выделением и проработкой репетитор по математике занимается на первом уроке. Выделяется 3 типа простейших задач на дроби: Для каждой из них подбирается реальная ситуация, которую удобно моделировать рисунком. Распространены примеры деления яблока или плошади. Например: Яблоко имеет массу 160 грамм, найдите вес яблока. Пример стандартный, но подходит не всех ученикам, ибо для проверки правильности демонстрируемых репетитором ариметических действий приходится делить то, что нельзя взять в руки, именно вес. При низком интеллектуальном уровене развития ученика репетитор по математике оказывается бессильным что-либо ему объяснить, ибо проблемы уходят далеко от темы «дроби». Если такое происходит, я использую пример с полом: Пол выложен одинаковыми плитками как показано на рисунке. На каждую плитку положили по шарику. Сколько шариков лежит на пола? Cлабого ребенку можно еще и полдвести к выполнению действий. Для этого репетитор по математике задает ему систему наводящих вопросов, например: Репетитор: сколько колонок на рисунке? Главное преимущество задачи на плитки и шарики состоит в использовании арифметических действий, каждое из которых удается проверить простым пересчетом. После того, как репетитор по математике убедился в понимании действий, он диктует ученику проверенное правило: «делим на знаменатель и умножаем на числитель». Несмотря на то, что можно пересчитывать количество не шариков, а самих плиток, я намеренно оставляю шары в сюжете задачи. Почему? На их примере изучается ситуация, когда какой-нибудь целый объект удерживает внутри себя (или на себе) мелкие объекты (в нашем случае пол удерживает шарики). Это широко распространено в дидактике математики 5-6 класса. Часто что-то куда-то засыпается, заливается, вкладывается и равномерно распределяется по объекту. В мешки засыпают сахар, в бидоны заливают молоко и т.д. Репетитор по математике на примере шариков помогает ребенку быстрее разобраться в числовых особеннностях этих ситуаций и понять законы измерения частей объектов. Далее … На том же рисунке с шариками нужно поставить обратную задачу: Допустим, мы знаем, что на 5/8 пола лежит 20 шаров. Как найти их общее количество? И здесь репетитору по математике тоже помогает рисунок, на котором можно просто пересчитать кружочки. Легко подбирать и комментировать выполняемые действия: . Все ясно и прозрачно. Репетитору по математике важно остановиться на терминологии и оформлении краткой записи.От того, насколько как она будет зависит идентификация правил. Ученик должен усвоить, что целый объект — это такая же величина, как и его часть, измеряемая двумя единицами: привычной (метрами, сантиметрами, килограммами, литрами, страницами, деревьями, шариками и т.д.) и «особой». В роли последней выступает целая величина. Рядом с ней в кратких записях можно поставить 1ед. Все участники элементарной задачи получают названия. То, от чего ищется часть называется целой величиной, сама дробь так и остается дробью, а часть, которую находят от целого репетитор по математике называет «частью» или «значением» дроби». Я предпочитаю второй вариант. Как правило, к репетитору обращаются в момент, когда тема набрала обороты и в классе решают в перемешку задачи на разные базовые правила. Поэтому, их приходится включать в один урок. Задача 2-го типа: целая величина неизвестна. Задача 3-го типа: неизвестна дробь. В третьей задаче для 5 класса репетитором по математике должны быть выбраны другие числа, ибо сократить дробь пятиклашки еще не могут. Обратите внимание на то, что обыгрывается один и тот же комплект чисел. В первой задаче репетитор по математике находит целого яблока, а во второй выполняет обратные действия: по той же дроби и найденному ранее значению 100 восстановливает число 160 (его даже можно в определенный помент стереть ластиком). Под каждой краткой записью оформляется решение и записывается правило: 1) чтобы найти значение дроби, нужно целую величину разделить на знаменатель и умножить на числитель. Чаще всего они встречаются в 6 классе, хотя в учебнике Петерсона сочетания двух и даже трех типов задач предлагаются уже в 5 классе. Прежде всего ученик должен знать с чего начинать исследование задачи. Краткая запись к задаче — важнейший и незаменимый элемент методики любого хорошего репетитора по математике. Она является одновременно и опорой и средством заставить ученика перечитывать условие как минимум — два три раза. Правильно составленная краткая запись в сочетании с четкими правилами «трех типов» позволяют разложить комбинированную задачу на несколько элементарных. Поэтому репетитору чрезвычайно важно научить правильно ее составлять. Как репетитор по математике работает с текстами? Если внимание ребенка ослаблено, на первых порах ему лучше предлагать уже размеченные тексты, с выделенными целыми величинами и стрелочками. Для того, чтобы не пропустить ни одну из участвующих величин репетитору по математике нужно задать вопрос: Что в задаче можно измерить? Пок ученик думато, репетитор подчеркивает в тексте соответствующие им слова. В нашем случае это показано синим цветом. Важно отработать поиск и применение типовых задач внутри комбинированной. Дети часто путают когда им делить на знаменатель, а когда на числитель. Например, краткая запись к задаче про вишню может быть следующей: Попрбуйте составить краткую запись к олимпиадной задачке: мама испекла булочки. Аня съеха 2/3 всех булочек и еще 2. Петр съел 2/3 остатка и еще 2 булочки, а Денис съел 2/3 последнего остатки и последние 2 булочки. Сколько булочек испекла мама? Александр Николаевич, репетитор по математике Москва (м.Щукинская, Строгино) Метки:
Работа репетитора,
Репетиторам по математике Классные задачи — это уроки, которые помогают учителям в формирующем оценивании. Если под рукой есть калькулятор, извлечь кубический корень из любого числа не составит никаких проблем. Но если калькулятора нет или вы просто хотите произвести впечатление на окружающих, извлеките кубический корень вручную. Большинству людей описываемый здесь процесс покажется довольно сложным, но с практикой извлекать кубические корни станет намного легче. Перед тем как приступить к чтению данной статьи, вспомните основные математические операции и вычисления с числами в кубе. Часть 1 Запишите задачу. Извлечение кубического корня вручную похоже на деление в столбик, но с некоторыми нюансами. Сначала запишите задачу в определенной форме. Умножьте и вычтите. Умножьте последнюю цифру ответа (в нашем примере это 1) на найденный множитель (1261): 1*1261 = 1261. Запишите это число под 2000 и вычтите его из 2000. Вы получите 739 (это второй остаток). Подумайте, является ли полученный ответ достаточно точным. Делайте это каждый раз, после того как завершите очередное вычитание. После первого вычитания ответ был равен 2, что не является точным результатом. После второго вычитания ответ равен 2,1. Найдите второй множитель. Чтобы попрактиковаться в вычислениях и получить более точный результат, повторите действия, которые описаны выше. Оцените второе число. Первое число вы нашли благодаря знанию кубов целых чисел. Теперь целое число превратите в десятичную дробь, приписав к нему (после десятичной запятой) некоторую цифру от 0 до 9. Необходимо найти десятичную дробь, куб которой будет близок, но меньше исходного числа. Сравните куб полученного числа с исходным числом. Если куб полученного числа больше исходного числа, попробуйте оценить меньшее число. Если же куб полученного числа намного меньше исходного числа, оценивайте большие числа до тех пор, пока куб одного из них не превысит исходное число. Если нужно, оцените другое число. Сравните куб полученного числа с исходным числом. Если куб полученного числа больше исходного числа, попробуйте оценить меньшее число. Короче говоря, нужно найти такие два числа, кубы которых чуть больше и чуть меньше исходного числа. Выполняйте описанный процесс до тех пор, пока не получите ответ, точность которого вас устроит. Оцените следующее число, сравните его с исходным, затем, если нужно, оцените другое число и так далее. Корень n-ной степени из числа x — это такое неотрицательное число z, которое при возведении в n-ную степень превращается в x. Определение корня входит в список основных арифметических операций, с которыми мы знакомимся еще в детстве. «Корень» произошел от латинского слова radix и сегодня слово «радикал» используется как синоним данного математического термина. С 13-го века математики обозначали операцию извлечения корня буквой r с горизонтальной чертой над подкоренным выражением. В 16-веке было введено обозначение V, которое постепенно вытеснило знак r, однако горизонтальная черта сохранилась. Его легко набирать в типографии или писать от руки, но в электронных изданиях и программировании распространилось буквенное обозначение корня — sqrt. Именно так мы и будем обозначать квадратные корни в данной статье. Квадратным радикалом числа x называется такое число z, которое при умножении на самого себя превращается в x. Своеобразный дуализм таких корней важен для решения квадратных уравнений, поэтому при поиске ответов в таких задачах требуется указывать оба корня. При решении алгебраических выражений используются арифметические квадратные корни, то есть только их положительные значения. Числа, квадратные корни которых являются целыми, называются идеальными квадратами. Существует целая последовательность таких чисел, начало которой выглядит как: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256… Квадратные корни других чисел представляют собой иррациональные числа. К примеру, sqrt(3) = 1,73205080757… и так далее. Школьный курс математики утверждает, что нельзя извлекать квадратные корни из отрицательных чисел. Как мы узнаем в вузовском курсе матанализа, делать это можно и нужно – для этого и нужны комплексные числа. Однако наша программа рассчитана для извлечения действительных значений корней, поэтому она не вычисляет радикалы четной степени из отрицательных чисел. Кубический радикал числа x — это такое число z, которое при умножении на себя три раза дает число x. Например, если мы умножим 2 × 2 × 2, то получим 8. Следовательно, двойка является кубическим корнем восьми. Умножим три раза на себя четверку и получим 4 × 4 × 4 = 64. Очевидно, что четверка является кубическим корнем для числа 64. Существует бесконечная последовательность чисел, кубические радикалы которых являются целыми. Ее начало выглядит как: 1, 8, 27, 64, 125, 216, 343, 512, 729, 1000, 1331, 1728, 2197, 2744… Для остальных чисел кубические корни являются иррациональными числами. Однако программа калькулятора работает иначе. По сути, извлечение корня – это возведение в обратную степень. Квадратный корень рассматривается как возведение в степень 1/2, а кубический – 1/3. Формулу возведения в степень 1/3 можно переиначить и выразить как 2/6. Результат один и тот же, но извлекать такой корень из отрицательного числа нельзя. Таким образом, наш калькулятор вычисляет арифметические корни только из положительных чисел. Столь витиеватый способ вычисления радикалов позволяет определять корни любой степени из любого выражения. Иррациональность диагонали квадрата была известна еще древним греками. Они столкнулись с проблемой вычисления диагонали плоского квадрата, так как ее длина всегда пропорциональна корню из двух. Формула для определения длины диагонали выводится из и в конечном итоге принимает вид: d = a × sqrt(2). Давайте определим квадратный радикал из двух при помощи нашего калькулятора. Введем в ячейку «Число(x)» значение 2, а в «Степень(n)» также 2. В итоге получим выражение sqrt(2) = 1,4142. Таким образом, для грубой оценки диагонали квадрата достаточно умножить его сторону на 1,4142. Поиск радикала – стандартная арифметическая операция, без которой не обходятся научные или конструкторские вычисления. Конечно, нам нет нужды определять корни для решения бытовых задач, но наш онлайн-калькулятор определенно пригодится школьникам или студентам для проверки домашних заданий по алгебре или математическому анализу. При решении некоторых технических задач бывает нужно посчитать корень третьей степени . Иногда это число еще называют кубическим корнем. Корнем третьей степени из данного числа называют такое число, куб (третья степень) которого равняется данному. То есть если y – корень третьей степени числа x, то должно выполняться условие: y?=x (икс равно игрек куб). Сколько гневных слов произнесено в его адрес? Порой кажется, что кубический корень невероятно сильно отличается от квадратного. На самом деле разница не настолько велика. Особенно, если понять, что они только частные случаи общего корня n-ой степени. Зато с его извлечением могут возникнуть проблемы. Но чаще всего они связаны с громоздкостью вычислений. Во-первых, определение этого понятия. Причем бывают четные и нечетные степени у корней. Если n — четное, то подкоренное выражение может быть только нулем или положительным числом. В противном случае вещественного ответа не будет. Когда же степень нечетная, то существует решение при любом значении «а». Оно вполне может быть и отрицательным. Во-вторых, функцию корня всегда можно записать, как степень, показателем которой является дробь. Иногда это бывает очень удобным. Например, «а» в степени 1/n как раз и будет корнем n-ой степени из «а». В этом случае основание степени всегда больше нуля. Аналогично «а» в степени n/m будет представлено, как корень m-ой степени из «а n ». В-третьих, для них справедливы все действия со степенями. Они похожи, как родные братья, только степень у них разная. И принцип их вычисления одинаков, различие только в том, сколько раз должно число на себя умножиться, чтобы получить подкоренное выражение. А о существенном отличии было сказано чуть выше. Но повториться не будет лишним. Квадратный извлекается только из неотрицательного числа. В то время, как вычислить кубический корень из отрицательной величины не составит труда. Каждый человек хоть раз делал это для квадратного корня. А как быть если степень «3»? На обычном калькуляторе имеется только кнопочка для квадратного, а кубического — нет. Здесь поможет простой перебор чисел, которые трижды умножаются на себя. Получилось подкоренное выражение? Значит, это ответ. Не получилось? Подбирать снова. А что в инженерном виде калькулятора в компьютере? Ура, здесь есть кубический корень. Эту кнопочку можно просто нажать, и программа выдаст ответ. Но это не все. Здесь можно вычислить корень не только 2 и 3 степени, но и любой произвольной. Потому что есть кнопка у которой в степени корня стоит «у». То есть после нажатия этой клавиши потребуется ввести еще одно число, которое будет равно степени корня, а уже потом «=». Этот способ потребуется, когда калькулятора под рукой нет или воспользоваться им нельзя. Тогда для того чтобы вычислить кубический корень из числа, потребуется приложить усилия. Сначала посмотреть, а не получается ли полный куб от какого-нибудь целого значения. Может быть под корнем стоит 2, 3, 5 или 10 в третьей степени? Он нужен потому, что описание может показаться сложным. На рисунке ниже показано, как извлечь кубический корень из 15 с точностью до сотых. Единственной сложностью, которую имеет этот метод, заключается в том, что с каждым шагом числа увеличиваются многократно и считать в столбик становится все сложнее. Ответом получается число: 2, 466. Поскольку ответ должен быть дан до сотых, то его нужно округлить: 2,47. Его можно использовать тогда, когда ответом является целое число. Тогда кубический корень извлекается разложением подкоренного выражения на нечетные слагаемые. К примеру, 8 представляется суммой 3 и 5. А 64 = 13 + 15 + 17 + 19. Ответом будет число, которое равно количеству слагаемых. Так корень кубический из 8 будет равен двум, а из 64 — четырем. Если под корнем стоит 1000, то его разложением на слагаемые будет 91 + 109 + 93 + 107 + 95 + 105 + 97 + 103 + 99 + 101. Всего 10 слагаемых. Это и есть ответ. Из большого числа без калькулятора мы уже разобрали. В этой статье рассмотрим как извлечь кубический корень (корень третьей степени). Оговорюсь, что речь идёт о натуральных числах. Как вы думаете, сколько времени нужно, чтобы устно вычислить такие корни как: Совсем немного, а если потренируетесь два-три раза минут по 20, то любой такой корень вы сможете извлечь за 5 секунд устно. *Нужно отметить, что речь идёт о таких числах стоящих под корнем, которые являются результатом возведения в куб натуральных чисел от 0 до 100. Мы знаем, что: Так вот, число а, которое мы будем находить – это натуральное число от 0 до 100. Вы без труда сможете извлечь кубический корень из любого числа в этой таблице. Что нужно знать? 1. Это кубы чисел кратных десяти: Я бы даже сказал, что это «красивые» числа, запоминаются они легко. Выучить несложно. 2. Это свойство чисел при произведении. Его суть заключается в том, что при возведении в третью степень какого-либо определённого числа, результат будет иметь особенность. Какую? Например, возведём в куб 1, 11, 21, 31, 41 и т.д. Можно посмотреть по таблице. 1 3 = 1, 11 3 = 1331, 21 3 = 9261, 31 3 = 26791, 41 3 = 68921 … То есть, при возведении в куб числа с единицей на конце в результате у нас всегда получится число с единицей в конце. При возведении в куб числа с двойкой на конце в результате всегда получится число с восьмёркой в конце. Покажем соответствие в табличке для всех чисел: Знания представленных двух моментов вполне достаточно. Рассмотрим примеры: Извлечь кубический корень из 21952. Данное число находится в пределах от 8000 до 27000. Это означает, что результат корня лежит в пределах от 20 до 30. Число 29952 заканчивается на 2. Такой вариант возможен только тогда, когда в куб возводится число с восьмёркой в конце. Таким образом, результат корня равен 28. Извлечь кубический корень из 54852. Данное число находится в пределах от 27000 до 64000. Это значит, что результат корня лежит в пределах от 30 до 40. Число 54852 заканчивается на 2. Такой вариант возможен только тогда, когда в куб возводится число с восьмёркой в конце. Таким образом, результат корня равен 38. Извлечь кубический корень из 571787. Данное число находится в пределах от 512000 до 729000. Это значит, что результат корня лежит в пределах от 80 до 90. Число 571787 заканчивается на 7. Такой вариант возможен только тогда, когда в куб возводится число с тройкой в конце. Таким образом, результат корня равен 83. Извлечь кубический корень из 614125. Данное число находится в пределах от 512000 до 729000. Это значит, что результат корня лежит в пределах от 80 до 90. Число 614125 заканчивается на 5. Такой вариант возможен только тогда, когда в куб возводится число с пятёркой в конце. Таким образом, результат корня равен 85. Думаю, что вы теперь без труда сможете извлечь кубический корень из числа 681472. Конечно, чтобы извлекать такие корни устно, нужна небольшая практика. Но восстановив две указанные таблички на бумаге, вы без труда в течение минуты, в любом случае, такой корень извлечь сможете. После того, как нашли результат обязательно сделайте проверку (возведите его с третью степень). *Умножение столбиком никто не отменял 😉 На самом ЕГЭ задач с такими «страшненькими» корнями нет. Например, в требуется извлечь кубический корень из 1728. Думаю, что это теперь для вас не проблема. Если вы знаете какие-то интересные приёмы вычислений без калькулятора, присылайте, со временем опубликую. С уважением, Александр Крутицких. P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях. 246. Было показано, каким образом любая степень или корень может быть выражена посредством индекса. Индекс мощности — целое число. Корень — это дробь, числитель которой равен 1. Существует также другой класс величин, которые можно рассматривать либо как степени корней, либо как корни степеней. Предположим, что 1/2 умножается само на себя, чтобы повториться три раза как множитель. Продукт a 1/2+1/2+1/2 или 3/2 (ст. 243), очевидно, является кубом 1/2 , то есть кубом квадратного корня из а. Этот дробный индекс обозначает, таким образом, степень корня . Знаменатель выражает корень, а числитель степень. Знаменатель показывает, на сколько равных делителей или корней разлагается данная величина; а числитель показывает, сколько из этих корней нужно перемножить. Знаменатель показывает, что а делится на три множителя или корня: 1/3 , 1/3 и 1/3 . И числитель показывает, что четыре из них должны быть умножены вместе; что даст четвертую степень числа 1/3 ; то есть, 247. Как 3/2 есть степень корня, так есть корень степени . Возведем в третью степень a 3 . Квадратный корень из этого равен 3/2 . Корень 3 есть количество, которое, умножив само на себя, даст 3 . Но согласно ст. 243, а 3/2 = а 1/2 .а 1/2 .а 1/2 ; и это, умноженное само на себя (ст. 100), есть Таким же образом можно показать, что m/n есть m-я степень n-го корня из a; или n-й корень m-й степени: то есть корень степени равен той же степени того же корня . Например, четвертая степень кубического корня из а равна кубическому корню из четвертой степени из а. 248. Корни и степени одной буквы можно умножить на 9.0015 добавляя свои показатели степени . (Статья 243.) Легко видеть, что тот же принцип может быть распространен на степени корней, когда показатели имеют общий знаменатель. Таким образом, а 2/7 .а 3/7 = а 2/7+3/7 = а 5/7 . Первый числитель показывает, как часто 1/7 берется в качестве множителя для получения 2/7 . (Статья 246.) А второй числитель показывает, как часто 1/7 берется в качестве множителя для получения 3/7 . Таким образом, сумма числителей показывает, как часто нужно извлекать корень для произведения . (Статья 100.) 249. Значение количества не меняется от применения к нему дробного показателя, числитель и знаменатель которого равны. Таким образом, а = 2/2 = а 3/3 = а н/н . Ибо знаменатель показывает, что а разлагается на определенное число множителей; и числитель показывает, что все эти факторы включены в n/n . С другой стороны, когда числитель дробного индекса становится равным знаменателю, выражение можно сделать более простым, отбросив индекс. Вместо n/n мы можем написать a. 250. Индекс степени или корня может быть заменен на любой другой индекс того же значения. Ибо в последнем из этих выражений предполагается, что а разлагается на вдвое больше множителей, чем в первом; а числитель показывает, что умножить на — столько этих множителей нужно перемножить. Так что вся стоимость не изменена. Таким образом, х 2/3 = х 4/6 = х 6/9 . то есть квадрат кубического корня такой же, как четвертая степень шестого корня, шестая степень девятого корня. Таким образом, 2 = 4/2 = 6/3 = 2н/н . Ибо значение каждого из этих индексов равно 2. 251. Из предыдущей статьи легко увидеть, что дробный индекс может быть выражен в десятичных знаков . 1. Таким образом, 1/2 = 5/10 или 0,5 ; то есть квадратный корень равен 5-й степени десятого корня. 2. 1/4 = 25/100 или 0,25 ; то есть корень четвертой степени равен 25-й степени корня из 100-й степени. 3. а 2/5 = а 0,4 . 4. а 7/2 = а 3,5 . 5. 9/5 = 1,8 Однако во многих случаях десятичная дробь может быть только приближением к истинному индексу. Таким образом, 1/3 = 0,3 почти. а 1/3 = а 0,333334 очень близко. Таким образом, аппроксимация может быть доведена до любой требуемой степени точности. Таким образом, 5/3 = 1,66666 . Эти десятичные индексы образуют очень важный класс чисел, называемый логарифмами . Часто удобно варьировать обозначение степеней корней, используя винкулум или радикальный знак √. При этом мы должны помнить, что сила корня такая же, как и корень силы; (ст. 247,), а также, что 9Знаменатель 0015 дробной степени выражает корень , а числитель — степень . (Статья 246.) Следовательно, вместо 2/3 мы можем написать (a 1/3 ) 2 или (a 2 ) 1/3 или 3 √a 900. 05 2 . Первая из этих трех форм обозначает квадрат кубического корня из а; и каждый из двух последних, кубический корень из квадрата a. Итак, m/n = (a 1/n ) m = (a m ) 1/n = n √a m . Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью Sign in Password recovery Восстановите свой пароль Ваш адрес электронной почты MicroExcel.ru Математика Алгебра Экспонента: определение, формула, свойства, график В данной публикации мы рассмотрим, что такое экспонента, как выглядит ее график, приведем формулу, с помощью которой задается экспоненциальная функция, а также перечислим ее основные свойства. Экспонента – это показательная функция, формула которой выглядит следующим образом: f (x) = exp(x) = e x где e – число Эйлера. Экспоненциальная функция (так часто называют экспоненту) может быть определена: Через предел (lim): Через степенной ряд Тейлора: Ниже представлен график экспоненциальной функции y = e x. Как мы видим график (синяя линия) является выпуклым, строго возрастающим, т.е. при увеличении x увеличивается значение y. Асимптотой является ось абсцисс, т.е. график во II четверти координатной плоскости стремится к оси Ox, но никогда не пересечет и не коснется ее. Пересечение с осью ординат Oy – в точке (0, 1), так как e0 = 1. Касательная (зеленая линия) к экспоненте проходит под углом 45 градусов в точке касания. Таблица знаков зодиака Нахождение площади трапеции: формула и примеры Нахождение длины окружности: формула и задачи Римские цифры: таблицы Таблица синусов Тригонометрическая функция: Тангенс угла (tg) Нахождение площади ромба: формула и примеры Нахождение объема цилиндра: формула и задачи Тригонометрическая функция: Синус угла (sin) Геометрическая фигура: треугольник Нахождение объема шара: формула и задачи Тригонометрическая функция: Косинус угла (cos) Нахождение объема конуса: формула и задачи Таблица сложения чисел Нахождение площади квадрата: формула и примеры Что такое тетраэдр: определение, виды, формулы площади и объема Нахождение объема пирамиды: формула и задачи Признаки подобия треугольников Нахождение периметра прямоугольника: формула и задачи Формула Герона для треугольника Что такое средняя линия треугольника Нахождение площади треугольника: формула и примеры Нахождение площади поверхности конуса: формула и задачи Что такое прямоугольник: определение, свойства, признаки, формулы Разность кубов: формула и примеры Степени натуральных чисел Нахождение площади правильного шестиугольника: формула и примеры Тригонометрические значения углов: sin, cos, tg, ctg Нахождение периметра квадрата: формула и задачи Теорема Фалеса: формулировка и пример решения задачи Сумма кубов: формула и примеры Нахождение объема куба: формула и задачи Куб разности: формула и примеры Нахождение площади шарового сегмента Что такое окружность: определение, свойства, формулы Одной из самых известных показательных функций в математике является экспонента. Она представляет собой число Эйлера, возведенное в указанную степень. В Экселе существует отдельный оператор, позволяющий её вычислить. Давайте разберемся, как его можно использовать на практике. Экспонента является числом Эйлера, возведенным в заданную степень. Само число Эйлера приблизительно равно 2,718281828. Иногда его именуют также числом Непера. Функция экспоненты выглядит следующим образом: где e – это число Эйлера, а n – степень возведения. Для вычисления данного показателя в Экселе применяется отдельный оператор – EXP . Кроме того, эту функцию можно отобразить в виде графика. О работе с этими инструментами мы и поговорим далее. EXP(число) То есть, эта формула содержит только один аргумент. Он как раз и представляет собой степень, в которую нужно возвести число Эйлера. Хотя синтаксис расчета экспоненты предельно прост, некоторые пользователи предпочитают применять Мастер функций . Рассмотрим, как это делается на примере. Если в качестве аргумента используется ссылка на ячейку, которая содержит показатель степени, то нужно поставить курсор в поле «Число» и просто выделить ту ячейку на листе. Её координаты тут же отобразятся в поле. После этого для расчета результата щелкаем по кнопке «OK» . Кроме того, в Экселе существует возможность построить график, взяв за основу результаты, полученные вследствие вычисления экспоненты. Для построения графика на листе должны уже иметься рассчитанные значения экспоненты различных степеней. Произвести их вычисление можно одним из способов, которые описаны выше. Приведены график и основные свойства экспоненты (е в степени х): область определения, множество значений, основные формулы, производная, интеграл, разложение в степенной ряд, действия с комплексными числами. Пусть y(x)
= e x
.
Тогда Экспонента обладает свойствами показательной функции с основанием степени е > 1
. Экспонента y(x)
= e x
определена для всех x
. Экспонента является монотонно возрастающей функцией, поэтому экстремумов не имеет. Основные ее свойства представлены в таблице. Обратной для экспоненты является натуральный логарифм . Производная е в степени х равна е в степени х : Действия с комплексными числами осуществляются при помощи формулы Эйлера : ;
; ;
; Использованная литература: Допустим, Ахиллес бежит в десять раз быстрее, чем черепаха, и находится позади неё на расстоянии в тысячу шагов. За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Это рассуждение стало логическим шоком для всех последующих поколений. Аристотель, Диоген, Кант, Гегель, Гильберт… Все они так или иначе рассматривали апории Зенона. Шок оказался настолько сильным, что «… дискуссии продолжаются и в настоящее время, прийти к общему мнению о сущности парадоксов научному сообществу пока не удалось… к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса… » [Википедия, » Апории Зенона «]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман. С точки зрения математики, Зенон в своей апории наглядно продемонстрировал переход от величины к . Этот переход подразумевает применение вместо постоянных. Насколько я понимаю, математический аппарат применения переменных единиц измерения либо ещё не разработан, либо его не применяли к апории Зенона. Если перевернуть привычную нам логику, всё становится на свои места. Ахиллес бежит с постоянной скоростью. Каждый последующий отрезок его пути в десять раз короче предыдущего. Соответственно, и время, затрачиваемое на его преодоление, в десять раз меньше предыдущего. Если применять понятие «бесконечность» в этой ситуации, то правильно будет говорить «Ахиллес бесконечно быстро догонит черепаху». Как избежать этой логической ловушки? Оставаться в постоянных единицах измерения времени и не переходить к обратным величинам. На языке Зенона это выглядит так: За то время, за которое Ахиллес пробежит тысячу шагов, черепаха в ту же сторону проползёт сто шагов. Этот подход адекватно описывает реальность без всяких логических парадоксов. Но это не полное решение проблемы. На Зеноновскую апорию «Ахиллес и черепаха» очень похоже утверждение Эйнштейна о непреодолимости скорости света. Эту проблему нам ещё предстоит изучить, переосмыслить и решить. И решение нужно искать не в бесконечно больших числах, а в единицах измерения. Другая интересная апория Зенона повествует о летящей стреле: Летящая стрела неподвижна, так как в каждый момент времени она покоится, а поскольку она покоится в каждый момент времени, то она покоится всегда. В этой апории логический парадокс преодолевается очень просто — достаточно уточнить, что в каждый момент времени летящая стрела покоится в разных точках пространства, что, собственно, и является движением. Здесь нужно отметить другой момент. Очень хорошо различия между множеством и мультимножеством описаны в Википедии . Смотрим. Как видите, «во множестве не может быть двух идентичных элементов», но если идентичные элементы во множестве есть, такое множество называется «мультимножество». Когда-то инженеры, построившие мост, во время испытаний моста находились в лодке под мостом. Если мост обрушивался, бездарный инженер погибал под обломками своего творения. Если мост выдерживал нагрузку, талантливый инженер строил другие мосты. Как бы математики не прятались за фразой «чур, я в домике», точнее «математика изучает абстрактные понятия», есть одна пуповина, которая неразрывно связывает их с реальностью. Этой пуповиной являются деньги. Применим математическую теорию множеств к самим математикам. Мы очень хорошо учили математику и сейчас сидим в кассе, выдаем зарплату. Вот приходит к нам математик за своими деньгами. Отсчитываем ему всю сумму и раскладываем у себя на столе на разные стопки, в которые складываем купюры одного достоинства. В первую очередь, сработает логика депутатов: «к другим это применять можно, ко мне — низьзя!». Дальше начнутся уверения нас в том, что на купюрах одинакового достоинства имеются разные номера купюр, а значит их нельзя считать одинаковыми элементами. Хорошо, отсчитываем зарплату монетами — на монетах нет номеров. Здесь математик начнет судорожно вспоминать физику: на разных монетах имеется разное количество грязи, кристаллическая структура и расположение атомов у каждой монеты уникально… А теперь у меня самый интересный вопрос: где проходит та грань, за которой элементы мультимножества превращаются в элементы множества и наоборот? Такой грани не существует — всё решают шаманы, наука здесь и близко не валялась. Вот смотрите. Мы отбираем футбольные стадионы с одинаковой площадью поля. Площадь полей одинакова — значит у нас получилось мультимножество. Но если рассматривать названия этих же стадионов — у нас получается множество, ведь названия разные. Как видите, один и тот же набор элементов одновременно является и множеством, и мультимножеством. Как правильно? А вот здесь математик-шаман-шуллер достает из рукава козырный туз и начинает нам рассказывать либо о множестве, либо о мультимножестве. В любом случае он убедит нас в своей правоте. Чтобы понять, как современные шаманы оперируют теорией множеств, привязывая её к реальности, достаточно ответить на один вопрос: чем элементы одного множества отличаются от элементов другого множества? Я вам покажу, без всяких «мыслимое как не единое целое» или «не мыслимое как единое целое». Сумма цифр числа — это пляска шаманов с бубном, которая к математике никакого отношения не имеет. Да, на уроках математики нас учат находить сумму цифр числа и пользоваться нею, но на то они и шаманы, чтобы обучать потомков своим навыкам и премудростям, иначе шаманы просто вымрут. Вам нужны доказательства? Откройте Википедию и попробуйте найти страницу «Сумма цифр числа». Её не существует. Нет в математике формулы, по которой можно найти сумму цифр любого числа. Ведь цифры — это графические символы, при помощи которых мы записываем числа и на языке математики задача звучит так: «Найти сумму графических символов, изображающих любое число». Математики эту задачу решить не могут, а вот шаманы — элементарно. Давайте разберемся, что и как мы делаем для того, чтобы найти сумму цифр заданного числа. И так, пусть у нас есть число 12345. Что нужно сделать для того, чтобы найти сумму цифр этого числа? Рассмотрим все шаги по порядку. 1. Записываем число на бумажке. Что же мы сделали? Мы преобразовали число в графический символ числа. Это не математическое действие. 2. Разрезаем одну полученную картинку на несколько картинок, содержащих отдельные цифры. Разрезание картинки — это не математическое действие. 3. Преобразовываем отдельные графические символы в числа. 4. Складываем полученные числа. Вот это уже математика. Сумма цифр числа 12345 равна 15. Вот такие вот «курсы кройки и шитья» от шаманов применяют математики. Но это ещё не всё. С точки зрения математики не имеет значения, в какой системе счисления мы записываем число. Так вот, в разных системах счисления сумма цифр одного и того же числа будет разной. В математике система счисления указывается в виде нижнего индекса справа от числа. С большим числом 12345 я не хочу голову морочить, рассмотрим число 26 из статьи про . Запишем это число в двоичной, восьмеричной, десятичной и шестнадцатеричной системах счисления. Мы не будем рассматривать каждый шаг под микроскопом, это мы уже сделали. Посмотрим на результат. Как видите, в разных системах счисления сумма цифр одного и того же числа получается разной. Подобный результат к математике никакого отношения не имеет. Это всё равно, что при определении площади прямоугольника в метрах и сантиметрах вы получали бы совершенно разные результаты. Ноль во всех системах счисления выглядит одинаково и суммы цифр не имеет. Это ещё один аргумент в пользу того, что . Вопрос к математикам: как в математике обозначается то, что не является числом? Что, для математиков ничего, кроме чисел, не существует? Для шаманов я могу такое допустить, но для ученых — нет. Реальность состоит не только из чисел. Полученный результат следует рассматривать как доказательство того, что системы счисления являются единицами измерения чисел. Ведь мы не можем сравнивать числа с разными единицами измерения. Если одни и те же действия с разными единицами измерения одной и той же величины приводят к разным результатам после их сравнения, значит это не имеет ничего общего с математикой. Что же такое настоящая математика? Это когда результат математического действия не зависит от величины числа, применяемой единицы измерения и от того, кто это действие выполняет. Ой! А это разве не женский туалет? Женский… Нимб сверху и стрелочка вниз — это мужской. Если у вас перед глазами несколько раз в день мелькает вот такое вот произведение дизайнерского искусства, Тогда не удивительно, что в своем автомобиле вы вдруг обнаруживаете странный значок: Лично я делаю над собой усилие, чтобы в какающем человеке (одна картинка), увидеть минус четыре градуса (композиция из нескольких картинок: знак минус, цифра четыре, обозначение градусов). И я не считаю эту девушку дурой, не знающей физику. Просто у неё дугой стереотип восприятия графических образов. И математики нас этому постоянно учат. Вот пример. 1А — это не «минус четыре градуса» или «один а». Это «какающий человек» или число «двадцать шесть» в шестнадцатеричной системе счисления. Те люди, которые постоянно работают в этой системе счисления, автоматически воспринимают цифру и букву как один графический символ. Когда снежный ком катится с горы, он постоянно увеличивается. Чем больше он становится, тем быстрее катится, чем быстрее катится, тем быстрее растет. Математики и физики очень любят описывать мир при помощи чисел. А еще больше — при помощи функций. Функция — это правило, по которому одному числу (например, x ) ставится в соответствие другое (например y ). Функции бывают простые, вроде y=10x или y=x 2 , а бывают посложнее вроде y=10*sin(7×2+3x-9) . Если вместо x и y подставить определенные физические параметры и найти функцию, которая их связывает, то получится закон природы. Еще у функций есть производная. Это — скорость изменения функции. То есть то, насколько изменится y при небольшом изменении x . Например, в случае функции y=10x производная всегда постоянная: y всегда будет расти в 10 раз быстрее, чем x . А в случае функции y=x 2 производная будет меняться. Если мы увеличим x c 0 до 1, то y тоже увеличится с 0 до 1. А если увеличим x с 1 до 2, то y увеличится с 1 до 4. То есть, производная с ростом x увеличилась. Экспонентой называется функция y=e x , где e — хитрое математическое число, которое примерно равно 2,72. Она обладает замечательным свойством: ее производная равна ей самой. То есть, если расстояние, которое проходит снежный ком, зависит от времени как экспонента, то и его скорость выражается той же самой экспонентой. Это свойство очень помогает математикам решать разные дифференциальные уравнения. Они очень любят с ней работать и стараются разные другие функции путем сдвига, растяжения, или переворачивания графика превратить в экспоненту. Все такие функции можно назвать экспоненциальными.
У экспоненциально протекающих процессов есть одно общее свойство: за одинаковый интервал времени их параметры меняются в одинаковое число раз. Банковский вклад каждый год увеличивается на 7%, снежный ком за минуту увеличивается в три раза, а количество урана-235 на атомных электростанциях уменьшается вдвое каждые 700 миллионов лет.
Экспоненциальные функции окружают нас повсюду. Экспоненциально развиваются все явления, в которых присутствует обратная связь, когда результат влияет на скорость процесса. Бывает, что обратная связь отрицательная: чем больше результат, тем медленнее идет процесс. Например, когда мы голодны, мы начинаем быстро поглощать еду, но как только чувство голода уменьшается, мы начинаем есть спокойно, потом лениво доедаем десерт. Чай остывает тоже по экспоненте: чем больше разность температур между чаем и воздухом, тем быстрее он остывает. Чем быстрее движется струна гитары, тем быстрее она тормозится о воздух, поэтому громкость звука после дерганья за струну экспоненциально уменьшается.
Еще один пример — ядерный распад. Каждое ядро может распасться в случайный момент времени, но чем ядер больше, тем больше распадов будет происходить за одну минуту. Чем быстрее ядра распадаются, тем меньше их становится, а значит и интенсивность радиации со временем падает. Поскольку производная e x равна e x , график производной e x выглядит идентично e x . Чтобы дифференцировать экспоненциальную функцию, скопируйте экспоненциальную функцию и умножьте ее на производную степени. Например, чтобы дифференцировать f(x)=e 2x , возьмите функцию e 2x и умножьте ее на производную степени 2x. Производная от 2x равна 2. Следовательно, производная от f(x)=e 2x равно f'(x)=2e 2x . Производная от e 2x равна 2e 2x . Правило дифференцирования экспоненциальной функции состоит в том, что для f(x)=e u производная равна f'(x)=u’.e u . u — функция, находящаяся в степени экспоненты, а u’ — производная этой функции. Другими словами, правило дифференцирования показательной функции заключается в умножении исходной показательной функции на производную от ее степени. Правило дифференцирования экспоненциальных функций таково: если f(x)=e u , то f'(x)=u’.e u , где u — функция в степени экспоненты, а u’ — производная этой функции. Для f(x)=e 2x , u = 2x и u’ = 2. Следовательно, f'(x)=2e 2x . Чтобы дифференцировать любую экспоненциальную функцию, продифференцируйте степень и умножьте ее на исходную функцию. Это может быть записано математически как когда , . В качестве альтернативы это можно записать как когда , . Например, продифференцируйте f(x) = e 3x . u — степень экспоненты, равная 3x. u’ — производная от u. Дифференцируя 3x, получаем u’ = 3. Подставляя u = 3x и u’ = 3 в f’(x) = u’.e u , получаем f’(x) = 3e 3x . Например, дифференцировать f(x)=e x 2 . u = x 2 и так, u’ = 2x. Следовательно, f'(x) = u’ . e u становится f'(x) = (2x).e x 2 . Например, дифференцировать f(x)=e x 2 +3x . u = x 2 +3x и, следовательно, u’ = 2x+3. Следовательно, f'(x) = (2x+3).e x 2 +3x . Например, дифференцировать f(x) = e 1 / x . Если степень экспоненциальной функции представляет собой дробь, перепишите ее в виде индекса. 1 / x можно переписать как x -1 . u = x -1 и так, u’ = -x -2 . Следовательно, f'(x) = (-x -2 )e x -1 . Это также может быть записано как или . Например, продифференцируйте e sin(x) . u = sin(x) и, следовательно, u’ = cos(x). Следовательно, f'(x) = cos(x).e sin(x) . Вот несколько примеров дифференцирования показательных функций с решениями. Цепное правило используется для дифференциации функции от функции. Цепное правило гласит, что . Правило дифференцирования экспоненциальных функций можно использовать в сочетании с цепным правилом. Например, продифференцируйте y = sin(e x ). Мы можем записать это как y = sin(u), где u = e x . Поэтому и . Использование цепного правила и так далее. Правило произведения утверждает, что для функции производная равна . Наше правило дифференцирования экспонент можно использовать вместе с правилом произведения. Например, продифференцируйте y=xe x . Здесь u = x и v = e x . Поэтому и . Используя правило произведения, производная равна . Мы можем разложить член e x так, чтобы . Правило частных . Вот пример использования правила отношения для дифференцирования экспоненциальных функций. Дифференцировать . Согласно правилу частных, u — это функция от числителя, а v — это функция от знаменателя. u = e х и так далее. v = x и так, . Подставляя эти значения в правило отношения, . Это можно упростить, разложив член e x . . Чтобы дифференцировать e xy , используйте f'(x)=u’.e u , где u = xy. Используйте правило произведения, чтобы неявно дифференцировать мощность «xy». Неявное дифференцирование говорит нам, что производная от y равна y’. Если u = xy, правило произведения дает нам u’ = (1)(y)+(x)(y’), что упрощается до u’ = y + xy’. Следовательно, производная от e xy равна (y+xy’)e xy . Если , то . Вот алгебраическое доказательство того, почему производная e x равна себя. Производная e x может быть найдена с помощью дифференцирования по первым принципам. Формула первых принципов гласит, что функцию градиента можно найти с помощью . e x можно записать в виде степенного ряда как Каждый термин можно дифференцировать, чтобы получить термин перед ним. Например, 1 дифференцируется в 0, x дифференцируется в 1, x 2 / 2 дифференцируется в x и так далее. Поскольку в этом степенном ряду бесконечное число членов, ряд остается неизменным после его дифференцирования. дифференцируется в Производным от x является x ln(a). Это правило верно для любого значения больше 0. Например, если y=2 x , то dy / dx = 2 x ln(2). Например, если y = 5 x , то dy / dx = 5 x ln(5). Производная от y=a x может быть доказана заменой a на e пер.(а) . y=a x становится и мощность может быть снижена перед ln, чтобы сделать . Мы можем дифференцировать это, используя наше правило дифференцирования экспонент: становится . Вот так вот, . Получаем . Мы можем переместить перед числом (а) обратно в степень числа (а). Мы получаем . Теперь и так. Наш первый контакт с числом e и экспоненциальной функцией был на странице о непрерывных сложных процентах и числе e. На этой странице мы дали интуитивное определение числа e, а также интуитивное определение экспоненциальной функции. Мы также вывели альтернативное выражение для показательной функции. Новым выражением экспоненциальной функции был ряд, т. е.0609 бесконечная сумма . Вы можете спросить, определение предела намного компактнее и проще, чем эта уродливая бесконечная сумма, зачем беспокоиться? Мы можем обобщить идею многочлена, допустив бесконечное число членов, как в выражении экспоненциальной функции. Отличительной чертой степенного ряда является то, что для вычисления его производной вы действуете точно так же, как и для многочлена. То есть вы берете производную почленно. Сделаем это с экспоненциальной функцией. Рассмотрим рядовое выражение экспоненциальной функции Мы можем вычислить производную левой части, применяя правило для производной суммы. То есть производная суммы равна сумме производных каждого члена Мы знаем производные от каждого из этих членов. Теперь есть некоторые числа, которые сокращаются Мы получили удивительный результат. Выражение для производной такое же, как и для исходной функции. это Теперь можно на время забыть о выражении ряда для экспоненты. Он нам нужен только здесь, чтобы доказать результат выше. Теперь мы можем применить это для вычисления производной других функций, включающих экспоненту. Вычислим производную функции На первый взгляд может быть не очевидно, но это составная функция. Это означает, что нам нужно применить цепное правило. Внешняя функция экспоненциальная. Его производная равна самому себе. Внутренняя функция — это ax: Это было просто. Может потребоваться еще несколько примеров, чтобы привыкнуть к тому факту, что производная экспоненты — это та же экспонента. Рассмотрим теперь другую составную функцию Для вычисления ее производной снова применим цепное правило. Теперь это выглядит сложнее Здесь мы имеем продукт, поэтому мы должны использовать правило продукта. Для этого мы выделяем два фактора И применяем правило продукта Рассмотрим следующую функцию. Давайте посмотрим, что я имею в виду. Во-первых, мы применяем правило произведения . Теперь, чтобы вычислить u’, нам нужно применить цепное правило . Мы подключаем его к правилу произведения 9.0025 Теперь давайте рассмотрим экспоненту с основанием, отличным от e. Как вычислить производную этой функции? Мы используем прием, который регулярно используется при работе с логарифмами. Вопрос Рекомендуемые вопросы РЕКЛАМА Text Solution Ab Padhai karo bina ads ke Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке! Значение sin500−sin700+sin100
равно
а.
Дробь, в которой числитель меньше знаменателя называется правильной, например, Дробь, в которой числитель больше знаменателя или равен знаменателю называется неправильной, например, После преобразовании неправильной дроби в смешанную, получается дробь, у которой есть целая часть и дробная часть является правильной. Любая правильная дробь всегда будет меньше единицы, например, возьмём правильную дробь и поделим числитель на знаменатель, получим примерно 0.333.
Чтобы преобразовать неправильную дробь в смешанную нужно: Приведем примеры, преобразуем неправильную дробь в смешанную: Для того, чтобы преобразовать неправильную дробь в смешанную необходимо: 1. Поделить числитель дроби на знаменатель 55 : 3 = 18 (остаток 1) Приведем примеры, преобразуем неправильную дробь в смешанную: Для того, чтобы преобразовать неправильную дробь в смешанную необходимо: 1. 7 : 3 = 2 (остаток 1) Механика Оптика Электричество и магнетизм Конденсаторы
У нас есть функция, вычисляющая непрерывные, цепные дроби, а следовательно, сейчас нет ничего сложного что бы реализовать универсальный калькулятор для вычисления дробей.
Универсальность калькулятора в том, что он считает действительно произвольное выражение и ответ выражает в виде дроби.
Если выражение не содержит иррациональные числа, то ответ будет выражен в дробях с точностью в 100 процентов.
Вообще то это настолько элементарно, что удивительно, как так можно «не включать мозги»
Пригодится для преподавателей, для формирования задач для учеников, и для школьников для проверки своих расчетов и тех задач, которые печатаются в задачниках.
1. Калькулятор высчитывает число в виде дроби, при произвольно заданных численных данных
2. Язык написания выражения, если он включает в себя какие либо функции, синус, косинус, корень квадратный, должны быть написаны на языке PHP
4. Из предыдущего пункта, делаем вывод, что желательно не использовать иррациональные числа (то есть числа, которые нельзя выразить с абсолютной точностью в виде дроби). Ошибки никакой не произойдет, просто дробь будет большая, и естественно с какой то погрешностью ( очень маленькой, но тем не менее)
5. Бот позволяет конвертировать число с десятичной точкой в дробь.
1. 1/2+3+1/2-3/117+6/113-117/241
2. Синус 60 градусов разделить на корень из трех и прибавить число 0.125
sin(PI()/3)/sqrt(3)+0.125
Удачных расчетов!
Онлайн-калькулятор неправильных дробей в смешанные числа специально разработан для быстрого преобразования неправильных дробей в смешанные числа. Давайте прочитаем статью ниже, чтобы понять, как преобразовать дробь в смешанное число. Просто сосредоточься! В контексте математики: «Особая дробь, у которой числитель больше знаменателя, называется неправильной дробью» Например: неправильные дроби: $$ \frac{3}{2} \hspace{0,25in} \frac{9}{7} \hspace{0,25in} \frac{65}{34} $$ Все вышеперечисленное дроби считаются неправильными и могут быть преобразованы в форму смешанных чисел с помощью нашего лучшего калькулятора неправильных дробей для смешанных чисел. Давайте вспомним шаги, которые необходимо выполнить, чтобы выполнить преобразование неправильных дробей в смешанные числа: Всякий раз, когда вы хотите упростить дроби, вам нужно запомнить несколько правил, которые перечислены ниже: Здесь мы будем решать пару примеров для выполнения преобразований между неправильными дробями и смешанными числами. Давайте двигаться вперед! Пример № 01: Как преобразовать неправильные дроби в смешанные числа, указанные ниже: $$ \frac{8}{3} \hspace{0,25in} и \frac{9}{2} $$ Решение: Заменим неправильные дроби на смешанные числа следующим образом: $$ \frac{8}{3} $$ Шаг № 01: Шаг № 02: Шаг № 03: $$ Частное \frac{Остаток}{Знаменатель} $$ $$ 2\frac{2}{3} $$ Какая искомая смешанная числовая форма данного доля. Теперь имеем: Шаг № 01: Шаг № 02: 9 0014 Шаг № 03: $$ Частное \frac{Остаток}{Знаменатель} $$ $$ 2\frac{1}{4} $$ Вы также можете проверить результаты с помощью калькулятора неправильной дроби для смешанного числа. Получите мгновенные и наилучшие упрощенные результаты, используя наш бесплатный калькулятор в один клик. Ввод: Вывод: Упрощенная форма данного уравнения: \(\frac{2}{2}\), что равно 1. Таким образом, это не неправильная дробь. Эквивалентная неправильная дробь данного смешанного числа задается как: $$ \frac{5}{2} $$ Вы можете определить соответствующую неправильную дробь смешанного числа с помощью бесплатного онлайн калькулятора смешанных чисел для неправильных дробей. Да, обе эти величины всегда дают одинаковый результат. Замена неправильных дробей на смешанные числа упрощает применение к ним арифметических операций. Таким образом, сложные дроби могут быть упрощены за очень короткое время. Но чтобы сделать этот процесс еще быстрее, математики используют этот бесплатный онлайн-калькулятор преобразования неправильных дробей в смешанные числа. Из источника Википедии: Дробь, Формы дробей, Арифметика с дробями, Дроби в абстрактной математике, Алгебраические дроби, Подкоренные выражения, Типографские вариации Из источника Khan Academy: неправильные дроби как смешанные числа Из источника Lumen Learning: Преобразование неправильных дробей в смешанные числа, эквивалентные дроби Создано Ханной Памула, доктором философии 900 03 Отзыв от Dominik Czernia, PhD и Jack Bowater Последнее обновление: 02 февраля 2023 г. Добро пожаловать в калькулятор смешанных чисел в неправильную дробь — инструмент, который может преобразовать дроби в мгновение ока 😉 Если вам интересно как превратить смешанное число в неправильную дробь , вы попали по адресу — ниже вы найдете краткое объяснение того, как это сделать вручную . Кроме того, калькулятор имеет пошаговое руководство 👣, так что не беспокойтесь о домашнем задании — мы протянем вам руку помощи при преобразовании смешанных чисел в неправильные дроби! Проверьте наш калькулятор неправильных дробей в смешанные числа, если вам нужно обратное преобразование. Кроме того, если ваше число по-прежнему является десятичным, вы можете преобразовать его в смешанное число с помощью нашего калькулятора смешанных чисел. Для преобразования смешанных чисел в неправильные дроби требуется всего три шага. В качестве примера возьмем 2 ⅗ и преобразуем его в неправильную дробь: Шаг 1 Умножить целое число на знаменатель дробной части: Шаг 2 Добавьте результат к числителю: Шаг 3 Число, которое вы только что вычислили, является вашим новым числителем — поместите его поверх исходного знаменателя: ¹³⁄₅ В этом случае неправильная дробь уже стоит в своем простейшая форма. Однако может случиться так, что вам потребуется уменьшить дробь. Например, если результат равен ²⁸⁄₁₀ , вам нужно вычислить наибольший общий делитель (НОД) и разделить на него оба числа: ²⁸⁄₁₀ = ¹⁴⁄₅ Или, что еще лучше, вы можете использовать наш калькулятор упрощенных дробей. Вы все еще не знаете, как превратить смешанное число в неправильную дробь? Давайте посмотрим на наглядный пример… Чтобы было легче понять и запомнить, мы еще раз проиллюстрируем преобразование 2 ⅗. Окунемся в мир шоколада: В начале нужно узнать, сколько рядов в целых плитках шоколада: 2 целые плитки шоколада, в каждой плитке 5 рядов: Далее добавляем 3 ряда из неполного столбика: Наконец, запишите число в виде неправильной дроби: ¹³⁄₅ Зачем нужно делить на 5 (или, другими словами, умножать на ⅕)? Это потому, что каждый ряд — это ⅕ всей плитки шоколада! Так почему преобразование смешанных чисел в неправильные дроби так полезно и важно ? Представьте, что у вас есть шоколадные батончики с картинки, ровно 2 ⅗ полных шоколадных батончика. Уверены, вы уже догадались — 13 человек! Ровно 13 детей могут съесть один ряд шоколада. Использование этого смешанного числа в калькулятор неправильной дроби — это кусок пирога 🍰, но мы хотим быть уверены, что это кристально ясно для вас. Мы покажем вам, как работает инструмент, на одном примере: допустим, вы хотите преобразовать 3 ¼ в форму неправильной дроби: Смешанное число Неправильная дробь 3 ¼ = ¹³⁄₄ Решение этого кроссворда состоит из 6 букв длиной и начинается с буквы Р Воскресенье, 15 Марта 2020 Г. РАНЖИР предыдущий
следующий другие решения РАНЖИР НЕМА РІШЕНЯ ФІГНЯ решения, предлагаемые пользователями НЕМА РІШЕНЯ ФІГНЯ ты знаешь ответ ? ответ: Для рассмотренных в предыдущих практикумах бактерий были получены последовательности РНК малой субъединицы рибосомы (16S rRNA). Для этого использовась база данных полных геномов NCBI[1], из которой были извлечены файлы [frn],
содержащие последовательности тРНК и рРНК. Создание единого файла, в который входят именно необходимые нам 16S рРНК последовательности, было автоматизировано при помощи cкрипта на Python. Он извлекает по заданному списку мнемоник нужные
последовательности из соответствующих файлов [frn] и записывает их в объединенный файл формата [fasta]. Выравнивание нуклеотидных последовательностей выполнялось при помощи онлайн-сервиса Muscle[2], после чего построенное выравнивание переводилось в [fasta]-формат и методом Analyze открывалось в программе MEGA. Для построения дерева в MEGA был выбран метод Neighbor-Joining, результат работы которого приведен на Рис. 1. Построенное по нуклеотидной последовательности дерево обладает четырьмя нетривиальными ветвями, из которых три соответствуют аналогичным ветвям на эталонном дереве. Для ветви, создающей различие данных деревьев, разбиение выделено оранжевым цветом. В целом, сравнивая дерево с тем, что было получено в ходе выполнения Практикума 3, стоит отметить приближение топологии дерева к эталонной: при использовании белковых последовательностей дерево вообще получалось неразрешенным,
что не позволяет адекватно провести его сравнение с эталонным. Файлы, относящиеся к данному заданию, находятся в директории В данном задании требовалось построить дерево гомологов белка CLPX_BACSU[3], имеющихся у рассматриваемых бактерий. Этот белок является АТФ-связывающей субъединицей Clp-протеаз и выполняет функцию фактора специфичности, обеспечивающего соединение протеазы с
нужным субстратом[4]. В этом качестве зачастую, помимо белков с неправильным фолдингом, выступают белки, помеченные ssrA-хвостом в результате процесса транс-трансляции и, таким образом, подлежащие деградации. Из файлов, содержащих полные протеомы исследуемых бактерий, был собран единый файл Далее был запущен blastp последовательности белка Выдачу blastp можно видеть на Рис. 3. После этого для удобства представления результатов и дальнейшей работы с ними был создан файл [xlsx], и из него извлечены мнемоники белков, соответствующие найденным гомологам. Также на отдельном листе составлена таблица, наглядно представляющая группы мнемоник, соответствующих одной и той же функции белка. Список, включавший в себя 34 мнемоники, был использован для получения последовательностей белков средствами Jalview. Далее 34 полученные последовательности были сохранены в отдельный файл и затем выровнены средствами веб-сервиса Muscle[2]. Для построения дерева был использован метод Neighbor-Joining в программе MEGA. Полученное дерево приведено ниже на Рис. 5. Также показаны ортологичные группы, пары паралогов в двух разных организмах, некоторые примеры актов видообразования и дупликаций, произошедших в ходе эволюции. строительство многоквартирных домов Смотреть все СМИ Просмотреть весь связанный контент → строительство , также называемое строительство зданий , методы и отрасли, связанные со сборкой и возведением конструкций, в первую очередь тех, которые используются для обеспечения жилья. Строительство — древнее занятие человека. Все началось с чисто функциональной потребности в контролируемой среде для смягчения воздействия климата. Построенные убежища были одним из средств, с помощью которых люди смогли приспособиться к широкому разнообразию климата и стать глобальным видом. Поначалу убежища людей были очень простыми и, возможно, существовали всего несколько дней или месяцев. Однако со временем даже временные постройки превратились в такие изысканные формы, как иглу. Постепенно стали появляться более прочные постройки, особенно после появления земледелия, когда люди стали подолгу оставаться на одном месте. Первые приюты были жилищами, но позже другие функции, такие как хранение пищи и церемония, были размещены в отдельных зданиях. Некоторые постройки стали иметь как символическое, так и функциональное значение, положив начало различию между архитектурой и строительством. История строительства отмечена рядом направлений. Одним из них является увеличение долговечности используемых материалов. Нынешнее состояние строительства сложное. Существует широкий спектр строительных продуктов и систем, предназначенных, прежде всего, для групп типов зданий или рынков. Строительство сегодня является важной частью промышленной культуры, проявлением ее разнообразия и сложности, а также мерой ее мастерства в отношении природных сил, которые могут создавать самую разнообразную застроенную среду для удовлетворения разнообразных потребностей общества. Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Охотники-собиратели позднего каменного века, кочевавшие на обширных территориях в поисках пищи, строили самые ранние временные жилища, появившиеся в археологическая запись. Палатка иллюстрирует основные элементы контроля за состоянием окружающей среды, которые являются задачей строительства. Палатка создает мембрану для защиты от дождя и снега; холодная вода на коже человека поглощает тепло тела. Мембрана также снижает скорость ветра; воздух над кожей человека также способствует потере тепла. Он контролирует теплопередачу, не пропуская горячие солнечные лучи и удерживая нагретый воздух в холодную погоду. Он также блокирует свет и обеспечивает визуальное уединение. Мембрана должна быть защищена от сил гравитации и ветра; структура необходима. Мембраны шкур сильны на растяжение (напряжения, вызванные силами растяжения), но необходимо добавить стержни, чтобы выдерживать сжатие (напряжения, вызванные силами уплотнения). Сельскохозяйственная революция, произошедшая примерно за 10 000 лет до н. э., дала большой толчок строительству. Люди больше не путешествовали в поисках дичи и не следовали за своими стадами, а оставались на одном месте, чтобы возделывать свои поля. Жилища стали более постоянными. Археологические данные скудны, но на Ближнем Востоке находят остатки целых деревень с круглыми жилищами, называемыми толои, стены которых сложены из утрамбованной глины; все следы крыш исчезли. В Европе толосы строились из сырых камней с куполообразными крышами; в Альпах до сих пор сохранились образцы (более поздней постройки) этих ульев. Доказательства композитного строительства из глины и дерева, так называемого метода плетения и мазка, также обнаружены в Европе и на Ближнем Востоке. Стены были сделаны из небольших деревцев или камыша, которые легко резать каменными орудиями. Их вкапывали в землю, связывали по бокам растительными волокнами, а затем обмазывали влажной глиной для придания дополнительной жесткости и защиты от атмосферных воздействий. Крыши не сохранились, но постройки, вероятно, были покрыты грубой соломой или связками тростника. Встречаются как круглые, так и прямоугольные формы, обычно с центральными очагами. Более тяжелые деревянные постройки также появились в культурах эпохи неолита (новый каменный век), хотя трудности рубки больших деревьев каменными орудиями ограничивали использование больших бревен для каркасов. Эти рамы обычно были прямоугольными в плане, с центральным рядом колонн для поддержки конька и соответствующими рядами колонн вдоль длинных стен; стропила шли от конька к балкам стен. Боковая устойчивость каркаса достигалась заглублением колонн в землю; затем конек и стропила были привязаны к колоннам растительными волокнами. Обычным кровельным материалом была солома: сухая трава или тростник, связанные вместе в небольшие пучки, которые, в свою очередь, были привязаны внахлест к легким деревянным шестам, протянутым между стропилами. Горизонтальные соломенные крыши плохо пропускают дождь, но, если они расположены под правильным углом, дождевая вода стекает до того, как успевает впитаться. Первобытные строители вскоре определили уклон крыши, который будет сбрасывать воду, но не солому. Перейти к содержимому Перейти к навигации По странеПо типуПо региону Приведенные выше данные, созданные базой данных PRIS. Excel для Microsoft 365 для Mac Excel 2021 для Mac Excel 2019 для Mac Excel 2016 для Mac Excel для Mac 2011 Еще…Меньше В Excel есть несколько функций, позволяющих подсчитать число пустых ячеек или ячеек с данными определенного типа в диапазоне. Щелкните ячейку, в которой должен выводиться результат. На вкладке Формулы щелкните Другие функции, наведите указатель мыши на пункт Статистические и выберите одну из следующих функции:
СЧЁТЗ: подсчитывает количество непустых ячеек.
СЧЁТ: подсчитывает количество ячеек, содержащих числа.
СЧИТАТЬПУСТОТЫ: подсчитывает количество пустых ячеек.
СЧЁТЕСЛИ: подсчитывает ячейки, отвечающие заданным условиям. Совет: Чтобы ввести нескольких условий, используйте вместо этого функцию СЧЁТЕСЛИМН. Выделите диапазон ячеек и нажмите клавишу RETURN. Щелкните ячейку, в которой должен выводиться результат. На вкладке Формулы щелкните Вставить, наведите указатель мыши на пункт Статистические и выберите одну из следующих функции:
СЧЁТЗ: подсчитывает количество непустых ячеек.
СЧЁТ: подсчитывает количество ячеек, содержащих числа.
СЧИТАТЬПУСТОТЫ: подсчитывает количество пустых ячеек.
СЧЁТЕСЛИ: подсчитывает ячейки, отвечающие заданным условиям. Совет: Чтобы ввести нескольких условий, используйте вместо этого функцию СЧЁТЕСЛИМН. Выделите диапазон ячеек и нажмите клавишу RETURN.
Подсчет уникальных значений среди повторяющихся
Подсчет количества вхождений значения
Функция СЧЁТ
Функция СЧЁТЗ
Функция СЧИТАТЬПУСТОТЫ
СЧЁТЕСЛИ (функция СЧЁТЕСЛИ)
Формулы и функции
Далее:
Использование функций
С помощью статистической функции СЧЁТЕСЛИ можно подсчитать количество ячеек, отвечающих определенному условию (например, число клиентов в списке из определенного города). Самая простая функция СЧЁТЕСЛИ означает следующее: Например:
СЧЁТЕСЛИ(диапазон;критерий)
Имя аргумента
Описание
диапазон (обязательный) Группа ячеек, для которых нужно выполнить подсчет. Диапазон может содержать числа, массивы, именованный диапазон или ссылки на числа. Пустые и текстовые значения игнорируются. Узнайте, как выбирать диапазоны на листе.
критерий (обязательный) Число, выражение, ссылка на ячейку или текстовая строка, которая определяет, какие ячейки нужно подсчитать. Например, критерий может быть выражен как 32, «>32», В4, «яблоки» или «32». В функции СЧЁТЕСЛИ используется только один критерий. Чтобы провести подсчет по нескольким условиям, воспользуйтесь функцией СЧЁТЕСЛИМН. Чтобы использовать эти примеры в Excel, скопируйте данные из приведенной ниже таблицы и вставьте их на новый лист в ячейку A1.
Данные
Данные
яблоки 32 апельсины 54 персики 75 яблоки 86
Формула
Описание
=СЧЁТЕСЛИ(A2:A5;»яблоки») Количество ячеек, содержащих текст «яблоки» в ячейках А2–А5. =СЧЁТЕСЛИ(A2:A5;A4) Количество ячеек, содержащих текст «персики» (значение ячейки A4) в ячейках А2–А5. Результат — 1. =СЧЁТЕСЛИ(A2:A5;A2)+СЧЁТЕСЛИ(A2:A5;A3) Количество ячеек, содержащих текст «яблоки» (значение ячейки A2) и «апельсины» (значение ячейки A3) в ячейках А2–А5. Результат — 3. В этой формуле для указания нескольких критериев, по одному критерию на выражение, функция СЧЁТЕСЛИ используется дважды. Также можно использовать функцию СЧЁТЕСЛИМН. =СЧЁТЕСЛИ(B2:B5;»>55″) Количество ячеек со значением больше 55 в ячейках В2–В5. =СЧЁТЕСЛИ(B2:B5;»<>»&B4) Количество ячеек со значением, не равным 75, в ячейках В2–В5. Знак амперсанда (&) объединяет оператор сравнения «<>» (не равно) и значение в ячейке B4, в результате чего получается формула =СЧЁТЕСЛИ(B2:B5;»<>75″). Результат — 3. =СЧЁТЕСЛИ(B2:B5;»>=32″)-COUNTIF(B2:B5;»<=85″) Количество ячеек со значением, большим или равным 32 и меньшим или равным 85, в ячейках В2–В5. Результат — 1. =СЧЁТЕСЛИ(A2:A5;»*») Количество ячеек, содержащих любой текст, в ячейках А2–А5. =СЧЁТЕСЛИ(A2:A5;»????ки») Количество ячеек, строка в которых содержит ровно 7 знаков и заканчивается буквами «ки», в диапазоне A2–A5. Подставочный знак «?» обозначает отдельный символ. Результат — 2.
Проблема
Возможная причина
Для длинных строк возвращается неправильное значение. Функция СЧЁТЕСЛИ возвращает неправильные результаты, если она используется для сопоставления строк длиннее 255 символов. Для работы с такими строками используйте функцию СЦЕПИТЬ или оператор сцепления &. Пример: =СЧЁТЕСЛИ(A2:A5;»длинная строка»&»еще одна длинная строка»). Функция должна вернуть значение, но ничего не возвращает. Аргумент критерий должен быть заключен в кавычки. Формула СЧЁТЕСЛИ получает #VALUE! ошибка при ссылке на другой лист. Эта ошибка возникает при вычислении ячеек, когда в формуле содержится функция, которая ссылается на ячейки или диапазон в закрытой книге.
Действие
Результат
Помните о том, что функция СЧЁТЕСЛИ не учитывает регистр символов в текстовых строках.
Критерий
не чувствителен к регистру. Например, строкам «яблоки» и «ЯБЛОКИ» будут соответствовать одни и те же ячейки. Использование подстановочных знаков В критериях можно использовать подстановочные знаки — вопросительный знак (?) и звездочку (*). Например, =СЧЁТЕСЛИ(A2:A5;»яблок?») возвращает все вхождения слова «яблок» с любой буквой в конце. Убедитесь, что данные не содержат ошибочных символов. При подсчете текстовых значений убедитесь в том, что данные не содержат начальных или конечных пробелов, недопустимых прямых и изогнутых кавычек или непечатаемых символов. В этих случаях функция СЧЁТЕСЛИ может вернуть непредвиденное значение. Попробуйте воспользоваться функцией ПЕЧСИМВ или функцией СЖПРОБЕЛЫ. Для удобства используйте именованные диапазоны. ФУНКЦИЯ СЧЁТЕСЛИ поддерживает именованные диапазоны в формуле (например, =COUNTIF(fruit;»>=32″)-COUNTIF(fruit;»>85″). Именованный диапазон может располагаться на текущем листе, другом листе этой же книги или листе другой книги. Чтобы одна книга могла ссылаться на другую, они обе должны быть открыты. Примечание: С помощью функции СЧЁТЕСЛИ нельзя подсчитать количество ячеек с определенным фоном или цветом шрифта. Однако Excel поддерживает пользовательские функции, в которых используются операции VBA (Visual Basic для приложений) над ячейками, выполняемые в зависимости от фона или цвета шрифта. Вот пример подсчета количества ячеек определенного цвета с использованием VBA. Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.
Функция СЧЁТЕСЛИМН
ЕСЛИ
СЧЁТЗ
Полные сведения о формулах в Excel
Функция УСЛОВИЯ
Функция СУММЕСЛИ
Опубликовано 21 сентября 2017 г. + Подписаться Существует множество методов расчета количества материалов. Какой из них подходит к вашему плану, зависит от дизайна и формы здания. Каждый метод характерно отличается от других. Расчет количества материалов требует надлежащего технического понимания материалов и конструкции. Здесь для вас описаны пять основных методов, и они обеспечивают правильное измерение необходимых вам материалов. 1. Метод центральной линии: Метод центральной линии применим к квадратному зданию с симметричными смещениями. Чтобы рассчитать количество материалов, необходимо умножить общую длину осевой линии на ширину и глубину конструкции. Длина осевой линии будет уменьшена на половину ширины каждого стыка, где основная стена соединяется с поперечными стенами, перегородками или верандой. Соединения должны быть приняты во внимание при расчете длины центральной линии стены. Оценка количества, произведенная этим методом, является точной и быстрой. 2. Крестовый метод: Крестовый метод предназначен для расчета материалов, необходимых для кладки стен. В этом методе учитываются длина и ширина стен на уровне цоколя (основание, на котором возвышается колонна). Внутренний размер помещения и толщина стен также важны для расчета количества. Следует учитывать симметричные смещения, так как они играют важную роль в расчете количества материалов. 3. Метод «вне-вне-в-внутрь»: этот метод следует системе PWD для расчета материалов и кажется наиболее точным из всех методов. 4. Метод пролетов: Этот метод пролетов применим в гаражах, на заводах и на железнодорожных платформах, где видны одинаковые конструкции. Бухта в строительном термине означает отсек здания. Сначала рассчитывается стоимость одного номера и умножается на количество пролетов. 5. Метод служебных помещений: Метод срочных служебных помещений предназначен для зданий с одинаковыми помещениями. Этот метод применим при строительстве колледжей, больниц, кинотеатров, тюрем и т. Расчет количества материалов осуществляется с помощью вышеупомянутых методов. Каждая из которых показывает различную перспективу расчета, и они также сосредоточены на различных типах конструкции. Подробнее Увидеть все Обновлено 26 окт. 2020 г. В экономике рыночное равновесие определяется как состояние рынка, при котором нет давления на изменения. То есть нет никакого давления на цену, чтобы она двигалась вверх или вниз. Основными силами, стоящими за этим, являются спрос и предложение. Пока спрос превышает предложение (или наоборот), цена вынуждена двигаться вверх (или вниз). Этот процесс продолжается до тех пор, пока рынок не достигнет равновесия, т. е. пока объем предложения не сравняется с объемом спроса и пока покупатели и продавцы не будут удовлетворены. В следующих параграфах мы рассмотрим, как математически рассчитать равновесную цену и количество. Чтобы сделать это, мы следуем простому пятиэтапному процессу: (1) вычисляем функцию предложения, (2) вычисляем функцию спроса, (3) устанавливаем количество предложения равным количеству спроса и находим равновесную цену, (4) подставляем равновесную цену в функцию предложения и (5) подтвердить результат, подставив равновесную цену в функцию спроса (необязательно). Обратите внимание: для простоты в этой статье мы используем линейные функции спроса и предложения. Однако, хотя этот процесс немного сложнее, его можно применить к любому другому типу функций спроса и предложения. В самом общем виде линейная функция предложения выглядит следующим образом: QS = mP + b. В этом уравнении x и y представляют собой независимые и зависимые переменные, m показывает наклон функции, а b представляет ее пересечение по оси y. Мы можем использовать эту базовую форму для расчета фактических функций предложения. Все, что нам нужно для этого, это две упорядоченные пары цены и количества (например, при цене A спрос равен B, а при цене C спрос равен D) . Имея эту информацию, мы можем вычислить наклон функции (который обычно положительный), а затем найти пересечение по оси Y, подставив два начальных значения в обновленную функцию. Чтобы получить более подробное пошаговое руководство по этому вопросу, ознакомьтесь с нашей статьей о том, как рассчитать линейную функцию предложения. Давайте рассмотрим пример, чтобы проиллюстрировать это. Представьте себе воображаемый бургерный ресторан (Deli Burger). По цене 3 доллара США за бургер Deli Burger хочет и может продать 600 бургеров. Если цена бургера увеличивается до 4,00 долларов США, продавать их становится выгоднее, поэтому ресторан расширяет производство и продает 800 бургеров. Имея эту информацию, мы можем рассчитать функцию предложения фирмы, как описано выше. Следовательно, функция предложения Deli Burger выглядит следующим образом: QS = 200P + 0 (т. е. QS = 200P). Подобно функции предложения, мы можем рассчитать функцию спроса с помощью базовой линейной функции QD = mP + b и двух упорядоченных пар цены и количества. Фактически процесс вычисления линейной функции спроса точно такой же, как и процесс вычисления линейной функции предложения. Однако, в отличие от большинства функций предложения, большинство функций спроса имеют отрицательный наклон. Чтобы понять, почему это так, обязательно прочитайте наше пошаговое руководство о том, как рассчитать линейную функцию спроса. С учетом сказанного давайте вернемся к нашему примеру сверху. На данный момент мы уже знаем, сколько бургеров Deli Burger готов и может продать по разным ценам. Теперь нам нужно выяснить, сколько гамбургеров на самом деле купят покупатели по этим ценам. Предположим, что они хотят и могут купить 1000 гамбургеров по цене 2 доллара США. Между тем, если цена вырастет до 4 долларов США, они купят только 800 бургеров. С помощью этой информации мы можем рассчитать следующую функцию рыночного спроса: QD = -100P + 1200. После того, как мы рассчитали функции спроса и предложения, мы можем установить объем предложения (QS) равным объему спроса (QD). По определению, пересечение кривой спроса и предложения представляет собой рыночное равновесие. В этот момент объем предложения равен объему спроса (т. е. QS = QD), что означает, что покупатели покупают все, что продавцы хотят продать. Начиная с этого простого уравнения, мы можем заменить обе его части соответствующими функциями (см. Давайте применим это к нашему примеру. Мы знаем, что согласно условию равновесия QS = QD. Теперь мы можем просто заменить QS на 200P (поскольку QS = 200P) и QD на -100P + 1200 (поскольку QD = -100P + 1200). Это приводит к следующему уравнению: 200P = -100P +1200. Если мы решим это уравнение для P, мы обнаружим, что P = 4. Или, другими словами, рынок достигает своего равновесия при цене 4 доллара США. Обратите внимание, что цена ниже 4,00 долларов США приведет к избыточному спросу (покупатели хотят купить больше, чем продавцы хотят продать), а цена выше равновесной приведет к избыточному предложению (покупатели хотят купить меньше, чем продавцы хотят продать ). Теперь, когда мы знаем равновесную цену, мы наконец можем рассчитать равновесное количество. Для этого мы просто подставляем только что рассчитанную нами равновесную цену (см. В нашем примере это означает, что мы подставляем равновесную цену (т.е. 4 доллара США) в функцию первоначального предложения Deli Burger QS = 200P. Это приводит к следующему уравнению QS = 200*4. Следовательно, равновесное количество составляет 800 бургеров. И последнее, но не менее важное: мы можем проверить наш результат, подставив только что рассчитанные количество и цену в функцию спроса. Как упоминалось выше, обе функции всегда должны возвращать одно и то же равновесное количество и цену. Этот шаг не является обязательным, но это отличный способ проверить свой результат во время экзаменов и тестов и убедиться, что ваши расчеты верны. Углом называется геометрическая фигура, которая состоит из двух различных лучей, исходящих из одной точки. В данном случае, эти лучи называются сторонами угла. Точка, являющаяся началом лучей, называется вершиной угла. На рисунке вы можете увидеть угол с вершиной в точке О , и сторонами k и m . На сторонах угла отмечены точки А и С. Этот угол можно обозначить как угол AOC. В середине обязательно должно стоять название точки, в которой находится вершина угла. Также существуют и другие обозначения, угол О или угол km. В геометрии вместо слова угол часто пишут специальный значок. Если у угла обе стороны лежат на одной прямой, то такой угол называется развернутым углом. То есть одна сторона угла является продолжением другой стороны угла. На рисунке нижк представлен развернутый угол О. Следует отметить, что любой угол, разделяет плоскость на две части. В случае с развернутым углом любую из двух частей, на которые он делит плоскость, можно считать внешней областью угла. Можно говорить о положении точки относительно угла. Точка может лежать вне угла (во внешней области), может находится на одной из его сторон, либо может лежать внутри угла (во внутренней области). На рисунке ниже, точка А лежит вне угла О, точка B лежит на одной из сторон угла, а точка С лежит внутри угла. Для измерения углов существует прибор называемый транспортиром. Единицей измерения угла является градус . Следует отметить, что каждый угол имеет определенную градусную меру, которая больше нуля. В зависимости от градусной меры углы делятся на несколько групп. «Основные понятия геометрии» — Признак равенства треугольника. «Геометрия в таблицах» — Координаты точки и координаты вектора в пространстве Скалярное произведение векторов в пространстве Движение Цилиндр Конус Сфера и шар Объем прямоугольного параллелепипеда Объем прямой призмы и цилиндра Объем наклонной призмы Объем пирамиды Объем конуса Объем шара и площадь сферы. Таблицы геометрия. «Геометрия 8 класс» — Каждое утверждение опирается на уже доказанные. У любого здания есть фундамент. Понятие теоремы. Аксиома -утверждение, истинность которых принимается без доказательств. Каждое математическое утверждение, получаемое путем логического доказательства, есть теорема. Так перебирая теоремы, можно добраться до аксиом. «Геометрия это наука» — Геометрия состоит из двух разделов: планиметрии и стереометрии. «Геометрические термины» — Конус. Пирамида. Радиус и центр. Диагональ. Геометрия. Квадрат. Ромб. Куб. Трапеция. Возникновение геометрических терминов. Точка. Линия. Цилиндр. Гипотенуза и катет. Сфера. Призма. Из истории геометрических терминов. «Что изучает геометрия» — Слово «параллельный» происходит от греческого «параллелос» — идти рядом. История геометрии. Преобразования в основном ограничивались подобием. L=(Р1+Р2)/2 L – длина окружности Р1 — периметр большого квадрата Р2 — периметр малого квадрата. Vпрям. Геометрия в Древней Греции. Муза геометрии, Лувр. Мы узнаем откуда пришла, и какой раньше была геометрия. Всего в теме
24 презентации Угол в измеряют в градусной мере (градус, минута, секунда), в оборотах — отношение длины дуги s к длине окружности L , в радианах — отношение длины дуги s к радиусу r ; исторически применялась также градовая мера измерения углов, в настоящее время она почти нигде не используется. 1 оборот = 2π радианам = 360° = 400 градам . В морской терминологии углы обозначаются румбами . Смежные углы — острый (a) и тупой (b). Развёрнутый угол (c) Кроме этого, рассматривается угол между гладкими кривыми в точке касания: по определению, его величина равна величине угла между касательными к кривым. Wikimedia Foundation
.
2010
. Угол, равный двум прямым. *РАЗВЕРТКА поверхности фигура, получающаяся в плоскости при таком совмещении точек данной поверхности с этой плоскостью, при котором длины линий остаются неизменными. Развертка кривой см. Эвольвента … Большой Энциклопедический словарь угол — ▲ разность направление (в пространстве) угол протяженность поворота от одного направления к другому; разность направлений; часть полного оборота (# наклона. образовывать #). наклон. наклонный. отклонение. уклониться (дорога уклонилась вправо).… … Угол — Углы: 1 общего вида; 2 смежные; 3 прилежащие; 4 вертикальные; 5 развернутый; 6 прямой, острый и тупой; 7 между кривыми; 8 между прямой и плоскостью; 9 между скрещивающимися прямыми (не лежащими в одной плоскостью) прямыми. Геометрическая фигура, состоящая из двух различных лучей, выходящих из одной точки. Лучи наз. сторонами У., а их общее начало вершиной У. Пусть [ ВА),[ ВС) стороны угла, В его вершина, плоскость, определяемая сторонами У. Фигура делит плоскость… … Математическая энциклопедия Угол, равный двум прямым. * * * РАЗВЕРНУТЫЙ УГОЛ РАЗВЕРНУТЫЙ УГОЛ, угол, равный двум прямым … Энциклопедический словарь Раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера 1) Замкнутая ломаная линия, именно: если различные точки, никакие последовательные три из к рых не лежат на одной прямой, то совокупность отрезков наз. многоугольником (см. рис. 1). М. могут быть пространственными или плоскими (ниже… … Математическая энциклопедия поперек — ▲ под углом максимум, косой угол поперечный. градус — а, м. 1) Единица измерения плоского угла, равная 1/90 прямого угла или соответственно 1/360 окружности. Угол в 90 градусов называется прямым углом. Развернутый угол составляет 180 градусов. 2) Единица измерения температурного интервала, имеющая… … Популярный словарь русского языка Теорема Шварца Кристоффеля важная теорема в теории функций комплексного переменного, носит название немецких математиков Карла Шварца и Элвина Кристоффеля. Очень важной с практической точки зрения является проблема о конформном… … Википедия Углом называют фигуру, образованную двумя лучами, выходящими из одной точки (рис. 160). При записи угла в середине пишут букву, обозначающую его вершину. Угол можно обозначить и одной буквой — названием его вершины. Например, вместо «угол АОВ» пишут короче: «угол О». Вместо слова «угол» пишут знак . Например, AОВ, O. На рисунке 161 точки С и D лежат внутри угла АОВ, точки X и У лежат вне этого угла, а точки М и Н — на сторонах угла. Как и все геометрические фигуры, углы сравниваются с помощью наложения. Если один угол можно наложить на другой так, что они совпадут, то эти углы равны. Например, на рисунке 162 ABC = MNK. Из вершины угла СОК (рис. 163) проведен луч ОР. Он разбивает угол СОК на два угла — СОР и РОК. Каждый из этих углов меньше угла СОК. Пишут: COP Два дополнительных друг другу луча образуют развернутый угол. Стороны этого угла вместе составляют прямую линию, на которой лежит вершина развернутого угла (рис. Часовая и минутная стрелки часов образуют в 6 ч развернутый угол (рис. 165). Согнем два раза пополам лист бумаги, а потом развернем его (рис. 166). Линии сгиба образуют 4 равных угла. Каждый из этих углов равен половине развернутого угла. Такие углы называют прямыми. Прямым углом называют половину развернутого угла. Для построения прямого угла пользуются чертежным треугольником (рис. 167). Чтобы построить прямой угол, одной из сторон которого является луч ОЛ, надо: а) расположить чертежный треугольник так, чтобы вершина его прямого угла совпала с точкой О, а одна из сторон пошла по лучу ОА; б) провести вдоль второй стороны треугольника луч ОВ. В результате получим прямой угол АОВ. Вопросы к теме 1.Что такое угол? Нам с вами уже известно, что любой угол делит плоскость на две части. Теперь давайте посмотрим на рисунок, на котором как раз и изображен развернутый угол О. Если мы возьмем и проведем из вершины развернутого угла луч, то он разделит данный развернутый угол еще на два угла, которые будут иметь одну общую сторону, а другие два угла будут составлять прямую. То есть, с одного развернутого угла мы получили два смежных. Если мы возьмем развернутый угол и проведем биссектрису, то эта биссектриса разделит развернутый угол на два прямых угла. А, в том случае, если мы из вершины развернутого угла проведем произвольный луч, который не является биссектрисой, то такой луч разделит развернутый угол на два угла, один из которых будет острым, а другой тупым. Развернутый угол обладает такими свойствами: Во-первых, стороны развёрнутого угла являются антипараллельными и образуют прямую; Чтобы измерить любой угол, для этих целей чаще всего используют транспортир, у которого единица измерения равна одному градусу. При измерении углов следует помнить, что любой угол имеет свою определенную градусную меру и естественно эта мера больше нуля. А развернутый угол, как нам уже известно, равен 180 градусам. То есть, если мы с вами возьмем любую плоскость круга и разделим ее радиусами на 360 равных частей, то 1/360 часть данного круга будет являться угловым градусом. Как вы уже знаете, что градус обозначается определенным значком, который имеет такой вид:
« ° ». Теперь мы также знаем, что один градус 1° = 1/360 части круга. Если угол равен плоскости круга и составляет 360 градусов, то такой угол является полным. А теперь мы возьмем, и плоскость круга поделим с помощью двух радиусов, лежащих на одной прямой линии, на две равные части. То в этом случае, плоскость полукруга составит половину полного угла, то есть 360: 2 = 180°. Мы с вами получили угол, который равен полуплоскости круга и имеет 180°. 1613. Назовите углы, изображенные на рисунке 168. Запишите их обозначения. 1614. Начертите четыре луча: ОА, ОВ, ОС и OD. Запишите названия шести углов, сторонами которых являются эти лучи. На сколько частей эти лучи делят плоскость ? 1615. Укажите, какие точки на рисунке 169 лежат внутри угла КОМ, Какие точки лежат вне этого угла? Какие точки лежат на стороне OK, a какие — на стороне ОМ? 1616. Начертите угол MOD и проведите внутри него луч ОТ. Назовите и обозначьте углы, на которые этот луч делит угол MOD. 1617. Минутная стрелка за 10 мин повернулась на угол АОВ, за следующие 10 мин — на угол ВОС, а еще за 15 мин — на угол COD. Сравните углы АОВ и ВОС, ВОС и COD, АОС и АОВ, АОС и COD (рис. 170). 1618. Изобразите с помощью чертежного треугольника 4 прямых угла в разных положениях. 1619. С помощью чертежного треугольника найдите на рисунке 171 прямые углы. Запишите их обозначения. 1620. Укажите прямые углы в классной комнате. а) 0,09 200; б) 208 0,4; в) 130 0,1 + 80 0,1. 1629. Сколько процентов от 400 составляет число 200; 100; 4; 40; 80; 400; 600? 1630. Найдите пропущенное число: а) 2 5 3 б) 2 3 5 1631. Начертите квадрат, сторона которого равна длине 10 клеток тетради. Пусть этот квадрат изображает поле. Рожь занимает 12% поля, овес — 8%, пшеница — 64%, а остальная часть поля занята гречихой. Покажите на рисунке часть поля, занятую каждой культурой. Сколько процентов поля занимает гречиха? 1632. За учебный год Петя израсходовал 40% купленных в начале года тетрадей, и у него осталось 30 тетрадей. Сколько тетрадей было куплено для Пети в начале учебного года? 1633. Бронза является сплавом олова и меди. Сколько процентов сплава составляет медь в куске бронзы, состоящем из 6 кг олова и 34 кг меди? 1634. Построенный в древности Александрийский маяк, который называли одним из семи чудес света, выше башен Московского Кремля в 1,7 раза, но ниже здания Московского университета на 119 м. 1635. Найдите с помощью микрокалькулятора: а) 4,5% от 168; в) 28,3% от 569,8; 1636. Решите задачу: 1) Площадь огорода 6,4 а. В первый день вскопали 30% огорода, а во второй день — 35% огорода. Сколько аров осталось еще вскопать? 2) У Сережи было 4,8 ч свободного времени. 35% этого времени он потратил на чтение книги, а 40% на просмотр передач по телевизору. Сколько времени у него еще осталось? 1637. Выполните действия: 1) ((23,79: 7,8 — 6,8: 17) 3,04 — 2,04) 0,85; 1638. Начертите угол ВАС и отметьте по одной точке внутри угла, вне угла и на сторонах угла. 1639. Какие из отмеченных на рисунке 172 точек лежат внутри угла АМК.Какая точка лежит внутри угла АМВ> но вне угла АМК.Какие точки лежат на сторонах угла АМК? 1640. 1641. Постройте квадрат со стороной 43 мм. Вычислите его периметр и площадь. 1642. Найдите значение выражения: а) 14,791: а + 160,961: b, если а = 100, b = 10; 1643. Рабочий должен был изготовить 450 деталей. В первый день он изготовил 60% деталей, а остальные — во второй. Сколько деталей изготовил рабочий во второй день? 1644. В библиотеке было 8000 книг. Через год число их увеличилось на 2000 книг. На сколько процентов увеличилось число книг в библиотеке? 1645. Грузовики в первый день проехали 24% намеченного пути, во второй день — 46% пути, а в третий — остальные 450 км. Сколько километров проехали эти грузовики? 1646. Найдите, сколько составляют: а) 1% от тонны; в) 5% от 7 т; 1647. Масса детеныша моржа в 9 раз меньше массы взрослого моржа. Какова масса взрослого моржа, если вместе с детенышем их масса равна 0,9 т? 1648. Н.Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей. Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения . Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости. Определение 2 Дана прямая a на плоскости. На ней обозначим некоторую точку O . Прямая разделена точкой на две части, каждая из которых имеет название луч , а точка O – начало луча . Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O . Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже. Перейдем к понятию определения угла. Определение 3 Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон. Имеет место случай, когда стороны угла могут выступать в роли прямой линии. Определение 4 Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым . На рисунке ниже изображен развернутый угол. Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O . Угол в математике обозначается знаком « ∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h , то угол обозначается как ∠ k h или ∠ h k . Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия O A и O B . В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной — ∠ A O B и ∠ B O A . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы. Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла , другая – внешняя область угла . Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние. При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла. Внутренняя область угла – элемент, служащий для второго определения угла. Определение 5 Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла. Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью. Два угла называют смежными , если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол. На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого. Определение 7 Два угла называют вертикальными , если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов. При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке. Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов. Даны два угла. Необходимо прийти к выводу, равные эти углы или нет. Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении. Развернутые углы являются равными. Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла. Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях. Чаще всего используют понятие градус . Определение 8 Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла. Стандартное обозначение градуса идет при помощи « ° », тогда один градус – 1 ° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим. Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина. Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты. Определение 9 Минутой называют одну шестидесятую часть градуса. Определение 10 Секундой называют одну шестидесятую часть минуты. Градус содержит 3600 секунд. Минуты обозначают « » », а секунды « «» ». 1 ° = 60 » = 3600 «» , 1 » = (1 60) ° , 1 » = 60 «» , 1 «» = (1 60) » = (1 3600) ° , а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17 ° 3 » 59 «» . Определение 11 Приведем пример обозначения градусной меры угла равного 17 ° 3 » 59 «» . Запись имеет еще один вид 17 + 3 60 + 59 3600 = 17 239 3600 . Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠ A O B и его градусной мере в 110 градусов применяют более удобную запись ∠ A O B = 110 ° , которая читается «Угол А О В равен 110 градусам». В геометрии используется мера угла из интервала (0 , 180 ] , а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше. Острый угол измеряется в интервале (0 , 90) , а тупой – (90 , 180) . Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так: ∠ A O B = ∠ A O C + ∠ D O B = 45 ° + 30 ° + 60 ° = 135 ° . Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол. Отсюда следует, что любые вертикальные углы равны . Если рассмотреть это на примере, мы получим, что угол А О В и С О D – вертикальные (на чертеже), тогда пары углов А О В и В О С, С О D и В О С считают смежными. В таком случает равенство ∠ A O B + ∠ B O C = 180 ° вместе с ∠ C O D + ∠ B O C = 180 ° считаются однозначно верными. Отсюда имеем, что ∠ A O B = ∠ C O D . Ниже приводится пример изображения и обозначения вертикальных улов. Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом . Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом. Определение 12 Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги. На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой, с двумя точками на окружности, соединенными и преобразованными в радиусы О А и О В. По определению данный треугольник A O B является равносторонним, значит длина дуги A B равна длинам радиусов О В и О А. Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса. На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно. Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов. Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение. Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку. Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter Давайте начнем с определения того, что такое угол. Во-первых, он является Во-вторых, он образован двумя лучами, которые называются сторонами угла. В-третьих, последние выходят из одной точки, которую называют вершиной угла. Исходя из этих признаков, мы можем составить определение: угол — геометрическая фигура, которая состоит из двух лучей (сторон), выходящих из одной точки (вершины). Их классифицируют по градусной величине, по расположению относительно друг друга и относительно окружности. Начнем с видов углов по их величине. Существует несколько их разновидностей. Основных типов углов всего четыре — прямой, тупой, острый и развернутый угол. Прямой Он выглядит так: Его градусная мера всегда составляет 90 о, иначе говоря, прямой угол — это угол 90 градусов. Только они есть у таких четырехугольников, как квадрат и прямоугольник. Тупой Он имеет такой вид: Градусная мера всегда больше 90 о, но меньше 180 о. Он может встречаться в таких четырехугольниках, как ромб, произвольный параллелограмм, во многоугольниках. Острый Он выглядит так: Градусная мера острого угла всегда меньше 90 о. Он встречается во всех четырехугольниках, кроме квадрата и произвольного параллелограмма. Развернутый Развернутый угол имеет такой вид: В многоугольниках он не встречается, но не менее важен, чем все остальные. Развернутый угол — это геометрическая фигура, градусная мера которой всегда равняется 180º. На нем можно построить проведя из его вершины один или несколько лучей в любых направлениях. Есть еще несколько второстепенных видов углов. Их не изучают в школах, но знать хотя бы об их существовании необходимо. Второстепенных видов углов всего пять: 1. Нулевой Он выглядит так: Само название угла уже говорит о его величине. Его внутренняя область равняется 0 о, а стороны лежат друг на друге так, как показано на рисунке. 2. Косой Косым может быть и прямой, и тупой, и острый, и развернутый угол. Главное его условие — он не должен равняться 0 о, 90 о, 180 о, 270 о. 3. Выпуклый Выпуклыми являются нулевой, прямой, тупой, острый и развернутый углы. Как вы уже поняли, градусная мера выпуклого угла — от 0 о до 180 о. 4. Невыпуклый Невыпуклыми являются углы с градусной мерой от 181 о до 359 о включительно. 5. Полный Полным является угол с градусной мерой 360 о. Это все типы углов по их величине. Теперь рассмотрим их виды по расположению на плоскости относительно друг друга. 1. Дополнительные Это два острых угла, образовывающие один прямой, т.е. их сумма 90 о. 2. Смежные Смежные углы образуются, если через развернутый, точнее, через его вершину, провести луч в любом направлении. Их сумма равна 180 о. 3. Вертикальные Вертикальные углы образуются при пересечении двух прямых. Их градусные меры равны. Теперь перейдем к видам углов, расположенным относительно окружности. Их всего два: центральный и вписанный. 1. Центральный Центральным является угол с вершиной в центре окружности. Его градусная мера равна градусной мере меньшей дуги, стянутой сторонами. 2. Вписанный Вписанным называется угол, вершина которого лежит на окружности, и стороны которого ее пересекают. Его градусная мера равна половине дуги, на которую он опирается. Это все, что касается углов. Теперь вы знаете, что помимо наиболее известных — острого, тупого, прямого и развернутого — в геометрии существует много других их видов. Углом называют фигуру, образованную двумя лучами, выходящими из одной точки (рис. 160). При записи угла в середине пишут букву, обозначающую его вершину. Угол можно обозначить и одной буквой — названием его вершины. Например, вместо «угол АОВ» пишут короче: «угол О». Вместо слова «угол» пишут знак . Например, AОВ, O. На рисунке 161 точки С и D лежат внутри угла АОВ, точки X и У лежат вне этого угла, а точки М и Н — на сторонах угла. Как и все геометрические фигуры, углы сравниваются с помощью наложения. Если один угол можно наложить на другой так, что они совпадут, то эти углы равны. Например, на рисунке 162 ABC = MNK. Из вершины угла СОК (рис. 163) проведен луч ОР. Пишут: COP Два дополнительных друг другу луча образуют развернутый угол. Стороны этого угла вместе составляют прямую линию, на которой лежит вершина развернутого угла (рис. 164). Часовая и минутная стрелки часов образуют в 6 ч развернутый угол (рис. 165). Согнем два раза пополам лист бумаги, а потом развернем его (рис. 166). Линии сгиба образуют 4 равных угла. Каждый из этих углов равен половине развернутого угла. Такие углы называют прямыми. Прямым углом называют половину развернутого угла. Для построения прямого угла пользуются чертежным треугольником (рис. 167). Чтобы построить прямой угол, одной из сторон которого является луч ОЛ, надо: а) расположить чертежный треугольник так, чтобы вершина его прямого угла совпала с точкой О, а одна из сторон пошла по лучу ОА; б) провести вдоль второй стороны треугольника луч ОВ. В результате получим прямой угол АОВ. Вопросы к теме 1.Что такое угол? Нам с вами уже известно, что любой угол делит плоскость на две части. Но, в случае, если у угла его обе стороны лежат на одной прямой, то такой угол называется развернутым. То есть, у развернутого угла одна его сторона является продолжением его другой стороны угла. Теперь давайте посмотрим на рисунок, на котором как раз и изображен развернутый угол О. Если мы возьмем и проведем из вершины развернутого угла луч, то он разделит данный развернутый угол еще на два угла, которые будут иметь одну общую сторону, а другие два угла будут составлять прямую. То есть, с одного развернутого угла мы получили два смежных. Если мы возьмем развернутый угол и проведем биссектрису, то эта биссектриса разделит развернутый угол на два прямых угла. А, в том случае, если мы из вершины развернутого угла проведем произвольный луч, который не является биссектрисой, то такой луч разделит развернутый угол на два угла, один из которых будет острым, а другой тупым. Развернутый угол обладает такими свойствами: Во-первых, стороны развёрнутого угла являются антипараллельными и образуют прямую; Чтобы измерить любой угол, для этих целей чаще всего используют транспортир, у которого единица измерения равна одному градусу. При измерении углов следует помнить, что любой угол имеет свою определенную градусную меру и естественно эта мера больше нуля. А развернутый угол, как нам уже известно, равен 180 градусам. То есть, если мы с вами возьмем любую плоскость круга и разделим ее радиусами на 360 равных частей, то 1/360 часть данного круга будет являться угловым градусом. Как вы уже знаете, что градус обозначается определенным значком, который имеет такой вид:
« ° ». Теперь мы также знаем, что один градус 1° = 1/360 части круга. Если угол равен плоскости круга и составляет 360 градусов, то такой угол является полным. А теперь мы возьмем, и плоскость круга поделим с помощью двух радиусов, лежащих на одной прямой линии, на две равные части. То в этом случае, плоскость полукруга составит половину полного угла, то есть 360: 2 = 180°. Мы с вами получили угол, который равен полуплоскости круга и имеет 180°. Это и есть развернутый угол. 1613. Назовите углы, изображенные на рисунке 168. Запишите их обозначения. 1614. Начертите четыре луча: ОА, ОВ, ОС и OD. Запишите названия шести углов, сторонами которых являются эти лучи. На сколько частей эти лучи делят плоскость ? 1615. 1616. Начертите угол MOD и проведите внутри него луч ОТ. Назовите и обозначьте углы, на которые этот луч делит угол MOD. 1617. Минутная стрелка за 10 мин повернулась на угол АОВ, за следующие 10 мин — на угол ВОС, а еще за 15 мин — на угол COD. Сравните углы АОВ и ВОС, ВОС и COD, АОС и АОВ, АОС и COD (рис. 170). 1618. Изобразите с помощью чертежного треугольника 4 прямых угла в разных положениях. 1619. С помощью чертежного треугольника найдите на рисунке 171 прямые углы. Запишите их обозначения. 1620. Укажите прямые углы в классной комнате. а) 0,09 200; б) 208 0,4; в) 130 0,1 + 80 0,1. 1629. Сколько процентов от 400 составляет число 200; 100; 4; 40; 80; 400; 600? 1630. Найдите пропущенное число: а) 2 5 3 б) 2 3 5 1631. Начертите квадрат, сторона которого равна длине 10 клеток тетради. 1632. За учебный год Петя израсходовал 40% купленных в начале года тетрадей, и у него осталось 30 тетрадей. Сколько тетрадей было куплено для Пети в начале учебного года? 1633. Бронза является сплавом олова и меди. Сколько процентов сплава составляет медь в куске бронзы, состоящем из 6 кг олова и 34 кг меди? 1634. Построенный в древности Александрийский маяк, который называли одним из семи чудес света, выше башен Московского Кремля в 1,7 раза, но ниже здания Московского университета на 119 м. Найдите высоту каждого из этих сооружений, если башни Московского Кремля на 49 м ниже Александрийского маяка. 1635. Найдите с помощью микрокалькулятора: а) 4,5% от 168; в) 28,3% от 569,8; 1636. Решите задачу: 1) Площадь огорода 6,4 а. 2) У Сережи было 4,8 ч свободного времени. 35% этого времени он потратил на чтение книги, а 40% на просмотр передач по телевизору. Сколько времени у него еще осталось? 1637. Выполните действия: 1) ((23,79: 7,8 — 6,8: 17) 3,04 — 2,04) 0,85; 1638. Начертите угол ВАС и отметьте по одной точке внутри угла, вне угла и на сторонах угла. 1639. Какие из отмеченных на рисунке 172 точек лежат внутри угла АМК.Какая точка лежит внутри угла АМВ> но вне угла АМК.Какие точки лежат на сторонах угла АМК? 1640. Найдите с помощью чертежного треугольника прямые углы на рисунке 173. 1641. Постройте квадрат со стороной 43 мм. Вычислите его периметр и площадь. 1642. Найдите значение выражения: а) 14,791: а + 160,961: b, если а = 100, b = 10; 1643. Рабочий должен был изготовить 450 деталей. В первый день он изготовил 60% деталей, а остальные — во второй. Сколько деталей изготовил рабочий во второй день? 1644. В библиотеке было 8000 книг. Через год число их увеличилось на 2000 книг. На сколько процентов увеличилось число книг в библиотеке? 1645. Грузовики в первый день проехали 24% намеченного пути, во второй день — 46% пути, а в третий — остальные 450 км. Сколько километров проехали эти грузовики? 1646. Найдите, сколько составляют: а) 1% от тонны; в) 5% от 7 т; 1647. Масса детеныша моржа в 9 раз меньше массы взрослого моржа. Какова масса взрослого моржа, если вместе с детенышем их масса равна 0,9 т? 1648. Во время маневров командир оставил 0,3 всех своих солдат охранять переправу, а остальных разделил на 2 отряда для обороны двух высот. В первом отряде было в 6 раз больше солдат, чем во втором. Сколько солдат было в первом отряде, если всего было 200 солдат? Н. Углом называется геометрическая фигура, которая состоит из двух различных лучей, исходящих из одной точки. В данном случае, эти лучи называются сторонами угла. Точка, являющаяся началом лучей, называется вершиной угла. На рисунке вы можете увидеть угол с вершиной в точке О , и сторонами k и m . На сторонах угла отмечены точки А и С. Этот угол можно обозначить как угол AOC. В середине обязательно должно стоять название точки, в которой находится вершина угла. Также существуют и другие обозначения, угол О или угол km. В геометрии вместо слова угол часто пишут специальный значок. Если у угла обе стороны лежат на одной прямой, то такой угол называется развернутым углом. То есть одна сторона угла является продолжением другой стороны угла. На рисунке нижк представлен развернутый угол О. Следует отметить, что любой угол, разделяет плоскость на две части. Если угол не является развернутым, то одна из частей называется внутренней областью угла, а другая внешней областью этого угла. На рисунке ниже представлен неразвернутый угол и отмечены внешняя и внутренняя области этого угла. В случае с развернутым углом любую из двух частей, на которые он делит плоскость, можно считать внешней областью угла. Можно говорить о положении точки относительно угла. Точка может лежать вне угла (во внешней области), может находится на одной из его сторон, либо может лежать внутри угла (во внутренней области). На рисунке ниже, точка А лежит вне угла О, точка B лежит на одной из сторон угла, а точка С лежит внутри угла. Для измерения углов существует прибор называемый транспортиром. Единицей измерения угла является градус . Следует отметить, что каждый угол имеет определенную градусную меру, которая больше нуля. В зависимости от градусной меры углы делятся на несколько групп. В этой статье будет рассматриваться одна из основных геометрических фигур — угол. После общего введения в это понятие мы уделим основное внимание отдельному виду такой фигуры. Развернутый угол — важное понятие геометрии, которое и будет основной темой этой статьи. В геометрии существует ряд объектов, которые составляют основу всей науки. Угол как раз относиться к ним и определяется с помощью понятия луча, поэтому начнем именно с него. Также перед тем, как приступать к определению самого угла, нужно вспомнить о нескольких не менее важных объектах в геометрии — это точка, прямая на плоскости и собственно сама плоскость. Прямой называют самую простую геометрическую фигуру, у которой нет ни начала, ни конца. Плоскостью — поверхность, которая имеет два измерения. Ну и луч (или же полупрямая) в геометрии — это часть прямой, у которой есть начало, но нет конца. Используя данные понятия, можем составить утверждение, что углом является геометрическая фигура, которая полностью лежит в некоторой плоскости и состоит из двух несовпадающих лучей с общим началом. Мы знаем о том, что углы могут быть совсем разными. А потому немного ниже будет приведена небольшая классификация, которая поможет лучше разобраться в видах углов и их главных особенностях. Итак, существует несколько видов углов в геометрии: Теперь давайте рассмотрим развернутый угол более подробно. Это тот случай, когда обе стороны лежат на одной прямой, что можно четко увидеть на рисунке немного ниже. Значит, мы можем с уверенностью сказать, что у развернутого угла одна из его сторон по сути есть продолжением другой. Стоит запомнить тот факт, что такой угол всегда можно разделить с помощью луча, который выходит из его вершины. В результате мы получим два угла, которые в геометрии называются смежными. Также развернутый угол имеет несколько особенностей. Для того, чтобы рассказать о первой из них, нужно вспомнить понятие «биссектриса угла». Напомним, что это луч, который делит любой угол строго пополам. Что касается развернутого угла, то его биссектриса разделяет его таким образом, что образуется два прямых угла по 90 градусов. Это очень легко просчитать математически: 180˚ (градус развернутого угла) : 2 = 90˚. Если же разделять развернутый угол совсем произвольным лучом, то в результате мы всегда получаем два угла, один из которых будет острым, а другой — тупым. Будет удобно рассматривать этот угол, собрав воедино все его главные свойства, что мы и сделали в данном списке: Итак, зная все эти характеристики данного вида углов, мы можем использовать их для решения ряда геометрических задач. Для того, чтобы понять, усвоили ли вы понятие развернутого угла, попытайтесь ответить на несколько следующих вопросов. Решения и ответы: Если у вас получилось ответить на все эти вопросы без подсказок и не подглядывая в ответы, значит вы готовы переходить к следующему уроку по геометрии. После того, как вы узнали о точках, прямых, отрезках и плоскости, следующее, что нужно знать, это то, что происходит, когда две прямые пересекаются в одной точке. То есть когда образуется угол. Углы — одно из основных понятий геометрии. Мы не можем думать об определении какой-либо формы, будь то треугольники, четырехугольники или многоугольники, без их углов. Таким образом, угол образует часть каждой геометрической формы. Математически угол определяется как фигура, которая образуется, когда два луча встречаются в одной точке. Обозначается символом ∠. Угол обычно измеряется в градусах, обозначаемых знаком «°». Термин «угол» происходит от латинского слова «angulus», что означает «угол». Градус — это мера поворота. Полный оборот вокруг точки дает нам полный круг, равный 360°, половинный оборот дает нам полукруг, равный 180°, а четверть оборота дает нам прямой угол, равный 90°. Угол может быть назван двумя способами: Метод – 1 : Символ угла, за которым следуют три точки, определяющие угол. Средняя буква — вершина. Таким образом, приведенную выше цифру можно записать как ∠XOY или ∠YOX. Метод – 2 : Просто запишите вершину. Пишется как ∠O. Иногда греческие буквы, такие как α, β, γ, θ и φ, или строчные латинские буквы, такие как a, b, c, x, y и z, также используются для обозначения угла или его размера. Размер угла измеряется с помощью транспортира, который обычно имеет полукруглую форму и является прозрачным. Все углы обычно классифицируются в зависимости от их величины или степени вращения на шесть основных типов: Углы также иногда классифицируют на основе их положения, направления вращения, суммы их пар или их поперечной на следующие типы: В нашей повседневной жизни мы видим углы почти повсюду вокруг нас. Некоторые из примеров приведены ниже: Геометрия является неотъемлемой частью развития современного мира, поскольку она применима к проектированию, строительным работам, архитектуре при выборе материала для строительства и многому другому. Геометрия — это раздел математики, который занимается изучением форм и их свойств. Подход к геометрии прослеживается с древних времен в их конструкциях с использованием различных форм очень специфическим образом. Термин первоначально произошел от греческих слов «ге» и «материя», что означает землю и измерение соответственно. Данная статья представляет собой исследование углов, их видов и свойств, в основном сосредоточенное на прямых углах или углах 180°. Углы — это пространство между двумя пересекающимися линиями, встречающимися в определенной точке. Они состоят из двух ответвлений, известных как стороны угла, и точки пересечения, где угол образует вершину. Углы измеряются в градусах от 0° до 360°. Углы делятся на различные типы на основе измерения и поворота. Уголки на основе измерения: Углы на основе вращения: 180 углов, широко известных как прямые углы, это углы, которые точно измеряют 180°. Прямые углы имеют две стороны, направленные в противоположные стороны. Прямой угол также измеряется как угол (пи). Это прямая линия с двумя концами, где одно плечо движется в противоположном направлении от вершины. Прямые углы также могут быть взяты как сумма двух прямых углов, то есть 90° + 90° = 180° Мера прямого угла может быть положительной или отрицательной. Если мы будем двигаться против часовой стрелки, прямой угол будет равен 180°, а если мы будем двигаться по часовой стрелке, угол будет равен -180°. которые называются вершинами, а OA и OB — две стороны угла. Рассмотрим пошагово построение прямого угла. Шаг 1: Нарисуйте прямую ОХ, в которой О будет вершиной угла. Шаг 2: Возьмите протектор и поместите его базовую линию на линию, где точка А должна находиться под углом 0°. Шаг 3: Соедините точки O и B так, чтобы образовалось другое плечо угла, указывающее в направлении, противоположном OA. Вопрос 1. Можно ли сказать, что треугольник является прямым углом? Ответ: Нет, потому что, как мы знаем, треугольник представляет собой замкнутую фигуру, три стороны которой соединяются вместе, а прямой угол образует прямую, равную 180°. Следовательно, они оба разные. Вопрос 2: Все ли прямые являются прямыми углами? Ответ: Прямые линии с двумя концами, обращенными в противоположном направлении от вершины, представляют собой прямой угол. 12 апреля 2023 г. Документы Google — отличный вариант для групп, которые хотят совместно работать над документом в режиме реального времени. К счастью, теперь вы можете загрузить документ Word и преобразовать его в документ Google с минимальными трудностями. Мы покажем вам, как конвертировать Word в Google Doc как на ПК, так и на мобильных устройствах. Содержание: Шаг 1. Откройте drive.google.com и войдите в систему, используя свою учетную запись Google. Шаг 2. Нажмите New на левой панели. Шаг 3. Нажмите Загрузка файла и найдите документ Word, который вы хотите преобразовать в документ Google. Шаг 4. Теперь ваш файл будет сохранен на Google Диске. Шаг 5. Чтобы открыть его, щелкните правой кнопкой мыши документ, нажмите Откройте с помощью и выберите Документы Google в раскрывающемся меню. Шаг 6. Теперь вам нужно убедиться, что документ сохранен в правильном формате файла. Чтобы преобразовать его, нажмите Файл в верхнем левом углу, а затем Сохранить как Документы Google. Шаг 1. Откройте приложение Google Диска на смартфоне. Шаг 2. Коснитесь значка + в правом нижнем углу экрана. Шаг 3. Коснитесь значка Загрузить . Шаг 4. Найдите документ Word, выбрав Обзор. Шаг 5. Выберите документ Word, который вы хотите преобразовать. Шаг 6. Появится всплывающее окно с надписью «Все отложенные загрузки завершены». Шаг 7. Нажмите Найдите. Шаг 8. Нажмите на документ, который откроется в Google Docs. Шаг 9. Чтобы убедиться, что файл сохранен в правильном формате, коснитесь трех точек в правом верхнем углу экрана и выберите Общий доступ и экспорт. Шаг 10. Выберите Сохранить как файл Google Docs. Да, к счастью, вы можете преобразовать документ Word в документ Google за несколько простых шагов. Сначала загрузите файл на Google Диск. Отсюда вы хотите открыть его с помощью Google Docs, используя раскрывающееся меню после щелчка правой кнопкой мыши. Сначала вам понадобится приложение Google Drive на вашем смартфоне. Затем нажмите значок плюса, а затем значок загрузки. После загрузки нажмите «Поделиться и поддержать», «Экспорт». Затем нажмите Сохранить как файл Документов Google. Если вы используете Google Docs больше, чем Microsoft Word, вам нужно преобразовать его в правильный формат. В противном случае вы можете столкнуться с проблемами форматирования, которые не проявляются при редактировании документа. Когда дело доходит до работы в Интернете, вам нужен цифровой мир на работе. Возможность быстро преобразовать документ Word в документ Google поможет вам избежать ошибок, проблем с форматированием и проблем с читабельностью. Таким образом, вы можете сотрудничать с коллегами, отправлять необходимую информацию в финансовые учреждения и многое другое. Дополнительное чтение: Как общаться в Google Docs 13.04.2023, 17:06:35 • Подано по адресу:
Гугл документы
• Проверенные решения Документы Google зарекомендовали себя как очень простое и впечатляющее программное обеспечение для обработки текстов. Оно предоставляет вам соответствующие функции для разработки документа, соединяя разных пользователей в вашем офисе в режиме реального времени, где они могут обновлять различия без задержек. Однако иногда возникает необходимость преобразовать файл Google Doc в файл Word. В этой статье представлены наиболее подходящие методы, которые помогут вам преобразовать Документы Google в Word . Преобразование Google Docs в файл Word может оказаться несложной задачей; однако обычно у вас возникает стресс при выборе наиболее эффективного метода, который сэкономит ваше время и энергию для преобразования Документов Google в Word. Первоначально, после открытия файла, вы можете нажать кнопку «Файл», чтобы продолжить. Теперь в раскрывающемся меню вы можете нажать кнопку «Загрузить», а затем выбрать вариант «Microsoft Word». Наконец, файл будет загружен в формате Word. Как мы все знаем, PDF как жесткий формат для отправки и чтения в другие файлы является еще одним важным расширением файла. Однако, когда дело доходит до обработки и редактирования PDF-файлов, мы не найдем много людей, выбирающих редакторы PDF, которые предоставляют им ряд функций для работы. Учитывая список PDF-редакторов, доступных онлайн, вы можете выбрать Wondershare PDFelement — PDF Editor в качестве удобного варианта управления вашими PDF-файлами. Попробуйте бесплатно
Попробуйте бесплатно
КУПИТЬ СЕЙЧАС
КУПИТЬ СЕЙЧАС Наряду с этим, вы даже можете защитить свои документы с помощью паролей и редактирования информации, чтобы уберечь файлы от краж и незаконного плагиата данных. С цифровыми подписями вы даже можете ратифицировать свои документы и проверять их на предмет подтверждения. Это также позволяет вам комментировать и просматривать PDF-файлы непосредственно на платформе без существенной необходимости конвертировать PDF-файл в какой-либо другой формат. С помощью PDFelement вы можете вносить различные изменения в свои PDF-файлы без преобразования. Помимо понимания процесса экспорта Google Doc в Word, вы также можете конвертировать PDF-файлы в Word с помощью PDFelement, выполнив следующие действия.
Задачи 6 класс с дробями: Урок по теме «Решение задач на дроби». 6-й класс
//действия с обыкновенными дробями 6 класс
Примеры: действия с обыкновенными дробями 6 классПопробуй другие онлайн тренажеры с дробями
Примеры на обыкновенные дроби 6 класс на все действия
Задания на дроби 6 класс.
Решать примерыЧто такое часть от целого?
Вначале дети тренируются
на простых операциях
сложения и вычитания обыкновенных дробей.
Затем, приступают к примерам сложнее на умножение дробей. Их
также легко можно отработать на тренажере умножения дробейКак рассказать про часть, чтобы ребенок понял?
Правильные дроби – это дроби, в которых числитель меньше знаменателя
Неправильные дроби – это дроби, в которых числитель равен или больше знаменателяПознакомься с другими тренажерами курса
Меры измерения
Изучайте меры длины, времени и массы на тренажереРимские цифры
Задачи на объем, площадь, периметр
Репетитор по математике о задачах на дроби в 5-6 классе — Колпаков Александр Николаевич
Этот обстоятельство часто не позволяет репетитору математики действовать стандартно, опираясь на традиционые объяснения.
Более того, в разных учебниках «доли» изучаются в разное время, по-разному «обкладываются» задачами и по-разному интегрируются в дидактику смежных тем. Поэтому очень сложно охватить все проблемы. Надеюсь, что репетиторы по математике со стажем меня понимают.Репетитор по математике о своей методике
К сожалению, его точность и прозрачность не всегда соответствует желаемому. Репетитор по математике должен понимать, какие задачи и с каким учеником следует разбирать, в каком порядке и в каком количестве. Подходы разных преподавателей могут отличаться порядком разбора задач, пояснениями, терминологией, сопровождениями в рисунках, схемах и даже их полным отсутствием. Я использую собственную базу типовых примеров и наводящих вопросов, систему записей, оформлений и обозначений (немного схожую с Петерсоновской). Оптимизирую краткие записи к задачам, делаю их удобными, информативными и ориентированными на поиск решения.Разбор элементарных задач
1) Целая величина известна
2) Целая величина неизвестна
3) Неизвестна дробь
Преимущество этого примера в том, что ребенок может не только выделить (закрасить) 5/8 пола, но и пересчитать количество шариков непосредственно.
При этом репетитор по математике указывает на возможность ответить на вопрос через простые арифметические действия (на рядах и колонках).Наводящие вопросы репетитора по математике
Ученик: 8 колонок
Репетитор: сколько шариков расположено в одной колонке?
Ученик: 4 шарика
Репетитор: Каким действием это можно найти?
Ученик: 32:8=4
Репетитор: сколько колонок в 5/8 пола?
Ученик: 5 колонок
Рептитор: Если в одной колонке 32:8=4 шарика, то в пяти колонках шаров будет …
Ученик: шариков.
Привильно !!!!!
Наводящие вопросы (если они нужны) аналогичны первому случаю.
Если ребенок не самый слабый, то вместо плиток я применяю яблоко, причем с одним и тем же набором значений величин для всех типов задач. Выписываю из образцы в отведенную для этого теоретическую тетрадь (или на форзац рабочей тетради). Каждую запись отдельно комментирую и специальным образом оформляю:
Задача 1-го типа: целая величина известна.
(г) -вес части яблока.
Чтобы найти значение дроби нужно целую величину разделить на знаменатель и умножить на числитель.
(г) — вес яблока.
Чтобы найти целую величину нужно значение дроби разделеить на числитель и умножить на знаменатель.
(яблока) -вес его части
Прием обратных действий полезен для работы с невнимательными школьниками. Он позволяет быстро сконцентрироваться на правилах, а не на изучении нового условия новой задачи. Более того, при заранее изветном ответе ребенок убеждается в правильности выбора этих действий. Действительно, как можно в них усомниться, если репетитор по математике получает в ответе то, что и должно получиться?
2) Чтобы найти целую величну нужно разделить на числитель и умножить на знаменатель.
3) Чтобы найти дробь нужно разделить ее значение на целую величину.Как репетитор математики работает с комбинированными задачами
Важно отработать каждый его этап в отдельности.Краткая запись
Главной проблемой составления краткой записи является проблема анализа текста задачи. Практика показывает, что дети крайне невнимательно и низкоэффективно с ним работают. Не умеют выделять ценную информацию о величинах и сами величины, сортировать главное и второстепенное. Для борьбы с такими проблемами репетитор математики может взять на вооружение метод слежения. Что такое краткая запись? — всего лишь короткий текст условия, из которого выброшены лишние слова, а названия величин и их значения записаны отдельными строками.
Что мешает репетитору по математике выделять эти слова в тексте? Особенно важно научить поиску целых величин, на которые в краткой записи будут указывать стрелки. Репетитор должен обратить внимание ученика на то, что слово или фраза, написанная сразу после дроби, указывает на единицу измерения дроби, то есть на ее целую величину. Репетитору по математике никто не запрещает выделить ее в тексте (подчеркнуть или записать другим цветом) и поставить к ней стрелочку. Пример оформления:
В 6 классе путают умножать ли на дробь или делить на нее. Проблема усугубляется когда в задачу встревает еще и сумма (разность) величин. Ребенок пытается запомнить эти ситуации, но от их многообразия пухнет голова. Чем может помочь ему репетитор по математике? Самое эффективное запоминание — зрительное. При многократном зрительрном анализе ребенок «фотографирует» расположение известных и неизвестных компонент выделенных репетитором строк (связанных «дробной стрелкой») и распознает эту же комбинацию величин в другой задаче. по нему в другой задаче что именно надо лелать. Для увеличения числа обращений к правилам типовых задач я рекоментдую репетиторам по математике использовать визуальные образы задач (без текстов). Репетитор подает ученику задачу ее краткой записью с полной информацией о всех известных взаимосвязях между величинами . Сложности возникают с суммами нескольких величин. В таком случае репетитору по математике приходится искать дополнительные обозначения для суммы. Я решил это пробьлему так: поле суммы закрашивается, а поля ее слагаемых обводятся тем же цветом по периметру.
Очень удобно. Если какое-то из слагаемых тоже равно сумме других, более мелких величин, то его внутренняя частсь закрашивается другим цветом, а поля слагаемых этим же цветом обводятся по контуру. И таких вложений может быть сколько угодно. Math Performance Tasks — Mrs. Reimer
Number Talks
Математические заблуждения
Сборники заданий на выполнение заданий
Число и операции в базе 10
Числа и операции — дроби
Геометрия
Измерения и данные
Операции и алгебраическое мышление
Ресурсы по математике на каждый день Уроки формирующего оценивания
Корень из 1 2 в 3 степени: Mathway | Популярные задачи
//Корень из 2 в 3 степени. Кубический корень (извлечение без калькулятора)
Шаги
2 = 1. Таким образом, первый множитель равен сумме следующих чисел: 1200 + 60 + 1 = 1261. Запишите это число слева от вертикальной черты.
{3}=729}
, то значение кубического корня из 600 лежит между 8 и 9. Поэтому используйте числа 512 и 729 в качестве верхнего и нижнего пределов ответа.
{3}=614,1}
. Исходное число 600 ближе к 592, чем к 614. Поэтому к последнему числу, которое вы оценили, припишите цифру, которая ближе к 0, чем к 9. Например, таким числом является 4. Поэтому возведите в куб число 8,44.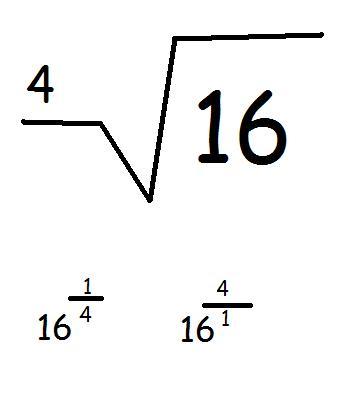
{3}=599,93}
, то есть результат меньше исходного числа менее чем на 0,1.Математическое обозначение
Квадратный корень
Например, если мы умножим 2 на 2, то получим 4. Двойка в этом случае и есть квадратный корень из четырех. Умножим 5 на 5, получим 25 и вот мы уже знаем значение выражения sqrt(25). Мы можем умножить и – 12 на −12 и получить 144, а радикалом 144 будет как 12, так и −12. Очевидно, что квадратные корни могут быть как положительными, так и отрицательными числами.
Это число бесконечно и не периодично, что вызывает некоторые затруднения при вычислении таких радикалов.Кубический корень
В отличие от квадратных радикалов, кубические корни, как и любые нечетные корни, можно извлекать из отрицательных чисел. Все дело в произведении чисел меньше нуля. Минус на минус дает плюс – известное со школьной скамьи правило. А минус на плюс – дает минус. Если перемножать отрицательные числа нечетное количество раз, то результат будет также отрицательным, следовательно, извлечь нечетный радикал из отрицательного числа нам ничего не мешает.Корень n-ной степени
Вы можете извлечь корень пятой степени из куба числа или радикал 19 степени из числа в 12 степени. Все это элегантно реализовано в виде возведения в степени 3/5 или 12/19 соответственно.Рассмотрим пример
Диагональ квадрата
Заключение
Вам понадобится
Инструкция
y.Что нужно знать о корне произвольной степени?
Корнем n-ой степени из некоторого «а» называется такое число, которое при возведении в степень n дает исходное «а».
Тогда их следует перемножить. То есть ту степень, которая была, на ту, в которую возводят.В чем сходства и различия квадратного и кубического корней?
Извлечение кубического корня на калькуляторе
Извлечение кубического корня вручную
Его записать в промежуточный ответ над знаком корня. А под этой группой расположить его куб.Наглядный пример вычисления кубического корня
Необычный способ извлечения кубического корня
Причем таких слагаемых должно быть минимально возможное число.
Посмотрите на таблицу кубов этих чисел (результаты возведения в третью степень):
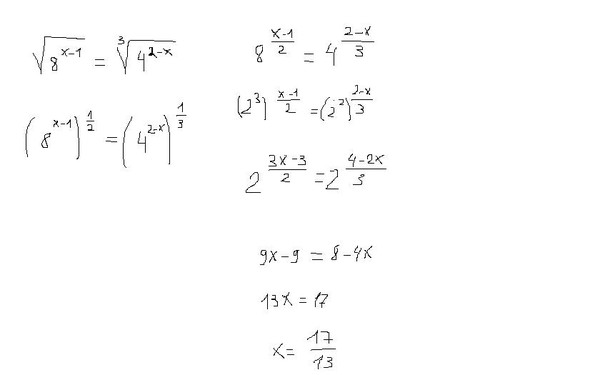
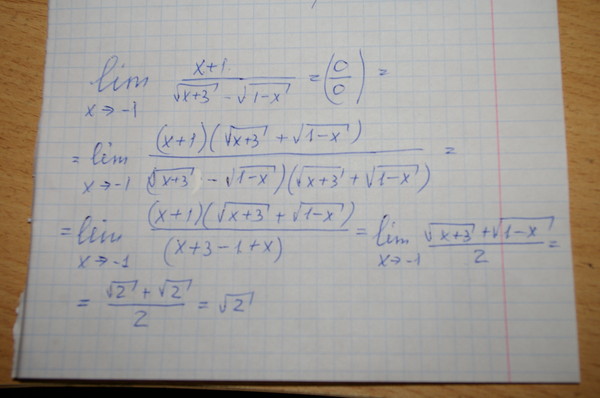На этом всё. Успеха Вам! Сил Корней, Сила
Таким образом, 4/3 — это четвертая степень кубического корня из a.
a 1/3 .a 1/3 .a 1/3 .a 1/3 = a 4/3 .
a 1/2 .a 1/2 .a 1/2 .a 1/2 .a 1/2 .
a 1/2 = а 3 .
Следовательно, 3/2 — это квадратный корень из куба a.
Или, таким образом, 2/7 = 1/7 .a 1/7 .
А 3/7 = 1/7 .а 1/7 .а 1/7 .
Следовательно, a 2/7 .a 3/7 = a 1/7 .a 1/7 .a 1/7 .a 1/7 .a 1/7 = а 5/7 .
Таким образом, a 3/3 = a 1/3 .a 1/3 .a 1/3 , что равно a.
И н/н = а 1/н .
а 1/н ….. n раз.
Вместо 2/3 мы можем поставить 4/6 .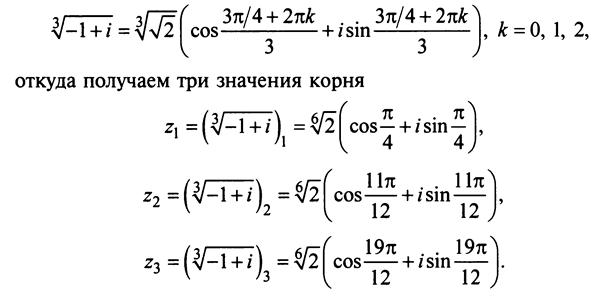
(Статья 132.)
NBSP; а 7 11 = а 1,87142 .
А (бх) 3/4 = (б 3 х 3 ) 1/4 = 4 √б 3 х 3 9 0006 .
И (а + у) 3/5 = [(а + у) 3 ] 1/5 = 5 √(а + у) 3 . Калькулятор дробей
Этот калькулятор дробей выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении. Правила выражений с дробями:
Дроби — для деления числителя на знаменатель используйте косую черту, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной части и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически конвертируются в дроби — т.е. 1.45 . Математические символы
Символ Название символа Символ Значение Пример + плюс сложение 1/2 + 1/3 — минус вычитание 90 368 1 1/2 — 2/3 * звездочка умножение 2/3 * 3/4 × знак умножения умножение 2/3 × 5/6 : знак деления деление 91/2
• сложение дробей и смешанных чисел: 8/5 + 6 2/7
• деление целых чисел и дробей: 5 ÷ 1/2
• сложные дроби: 5/8 : 2 2/3
• десятичная дробь: 0,625
• Преобразование дроби в десятичную: 1/4
• Преобразование дроби в процент: 1/8 %
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4
• квадратный корень дроби: sqrt(1/16)
• сокращение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение со скобками: 1/3 * (1/2 — 3 3/8)
• составная дробь: 3/4 от 5/7
• кратные дроби: 2/3 от 3/5
• разделить, чтобы найти частное: 3/5 ÷ 2/3
Калькулятор следует известным правилам для порядка операций .
Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — Скобки, Экспоненты, Умножение, Деление, Сложение, Вычитание.
BEDMAS — скобки, экспоненты, деление, умножение, сложение, вычитание
BODMAS — Скобки, Порядок, Деление, Умножение, Сложение, Вычитание.
GEMDAS — символы группировки — скобки (){}, показатели степени, умножение, деление, сложение, вычитание.
MDAS — Умножение и деление имеют тот же приоритет, что и сложение и вычитание. Правило MDAS является частью порядка операций правила PEMDAS.
Будь осторожен; всегда выполняйте умножение и деление перед сложением и вычитанием . Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны оцениваться слева направо.
Четверть числа 72:
Запишите дробь и десятичную дробь. Один и два плюс три и пять сотых
Упростить {1/3 + 1/12} ÷ {2/3 — 5/8}
В школе 420 учеников.
Двести пятьдесят два ученика переходят на 1-й уровень. Напишите дробью, какая часть учеников идет в 1-й класс, а какая во 2-й. Сократите обе дроби до их основной формы.
У Мэтью восемь карандашей. У трех из них нет ластика на конце. Какая часть карандашей не имеет ластика на конце?
На ферме 20 животных. Есть четыре курицы. Какую часть животных составляют куры? Выразите ответ дробью в простейшей форме.
Следующая дробь сокращена до наименьшего члена, кроме единицы. Какой из них: A.98/99 B.73/179 C.1/250 D.81/729
Саманта сделала 72 снимка во время пляжного отдыха. 3/4 этих фотографий на пляже. Сколько фотографий с ее отпуска на пляже?
Энди неправильно ответил на пять из 15 вопросов в тесте по математике. На какую часть вопроса Энди ответил правильно?
Компания имеет 860 сотрудников, из которых 500 женщин. Напишите дробь, обозначающую сотрудниц компании.
Функция е в степени х: Интеграл от е в степени х
//Что такое экспонента: определение, формула, свойства, график
Определение и формула экспоненты
График экспоненты
Свойства экспоненциальной функции
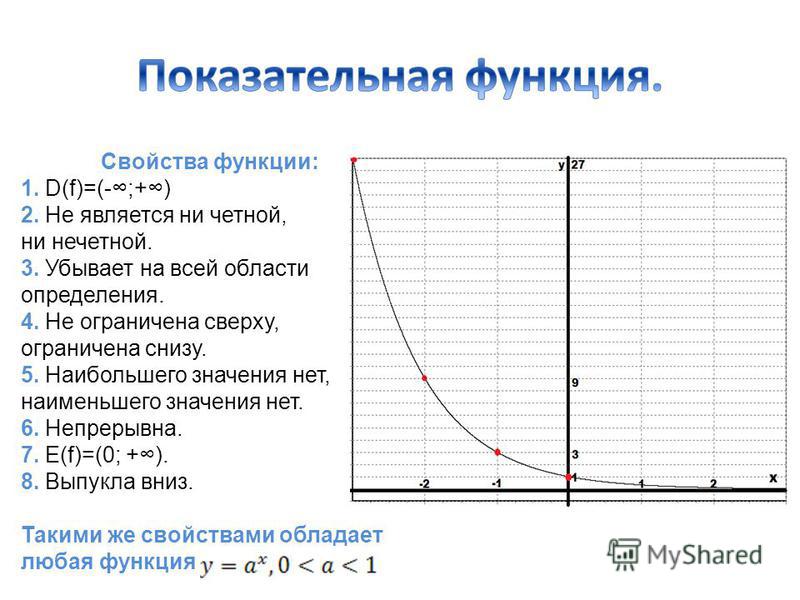
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Экспонента равна 0 в какой степени.
Производная e в степени x и показательной функцииСпособ 1: вычисление экспоненты при помощи ручного ввода функции
Этот аргумент может быть как в виде числового значения, так и принимать вид ссылки на ячейку, содержащую в себе указатель степени.Способ 2: использование Мастера функций
Способ 3: построение графика
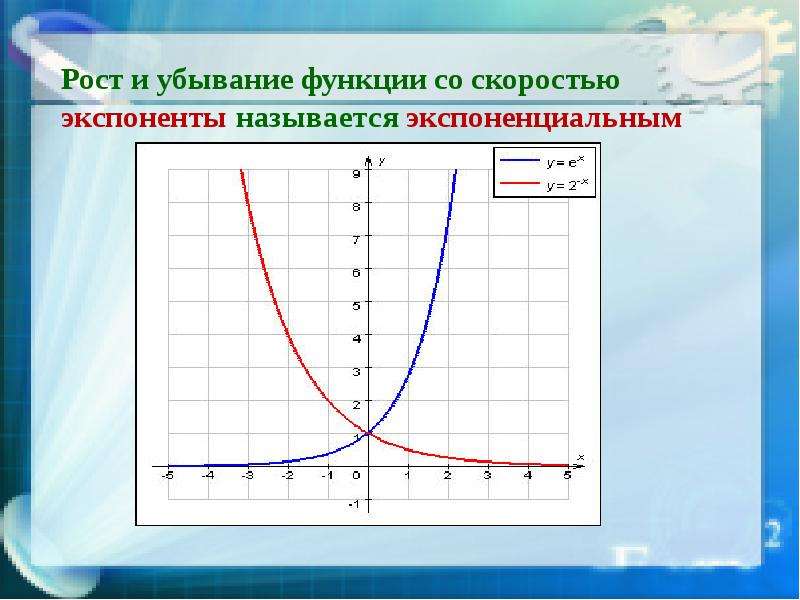
Определение
Частные значения
.Область определения, множество значений
Ее область определения:
— ∞ Ее множество значений:
0Экстремумы, возрастание, убывание
Обратная функция
;
.Производная экспоненты
.
Производная n-го порядка:
.
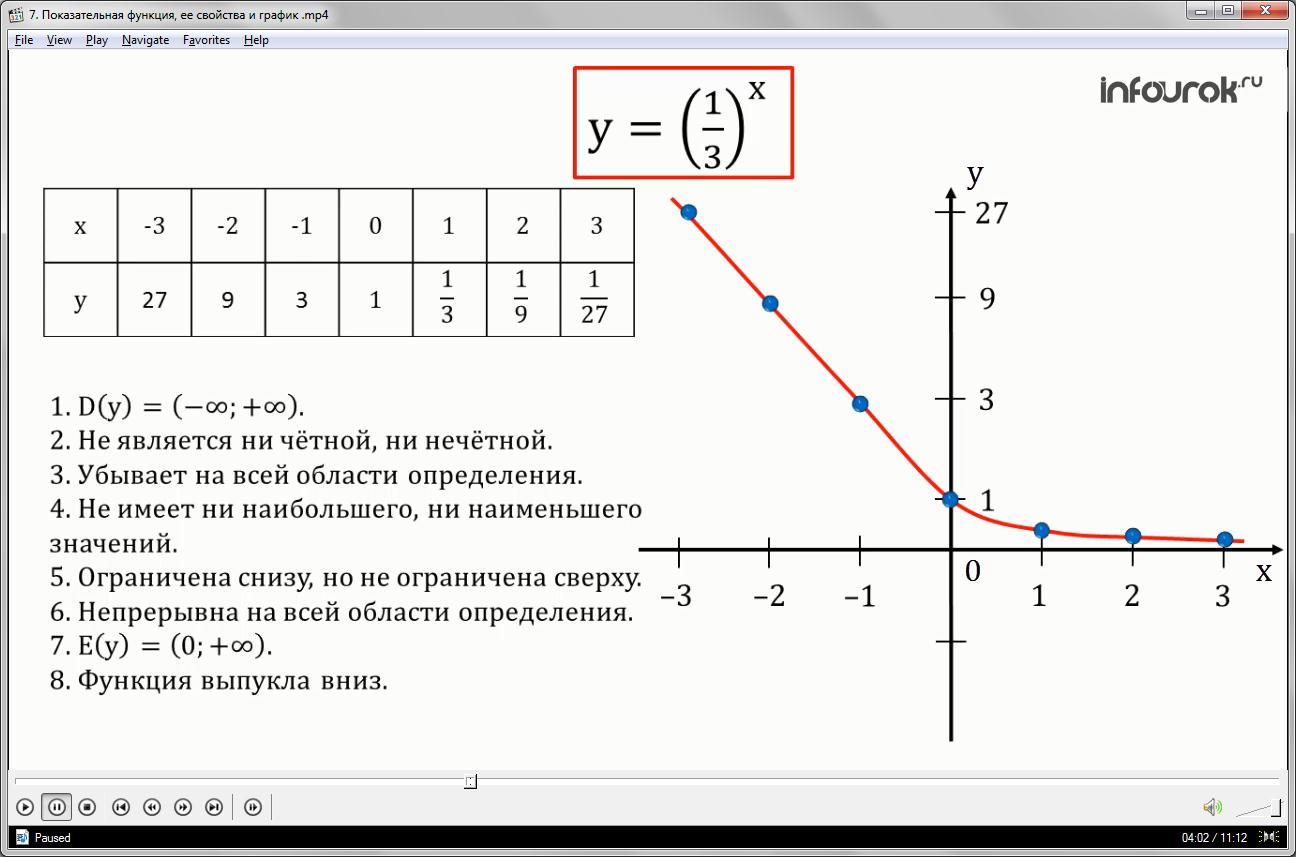
Вывод формул > > >Интеграл
Комплексные числа
,
где есть мнимая единица:
.Выражения через гиперболические функции
.Выражения через тригонометрические функции
;
.Разложение в степенной ряд
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху. 
Применение же нашей обычной логики приводит нас в ловушку. Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху.
За следующий интервал времени, равный первому, Ахиллес пробежит ещё тысячу шагов, а черепаха проползет сто шагов. Теперь Ахиллес на восемьсот шагов опережает черепаху. 
По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.среда, 4 июля 2018 г.
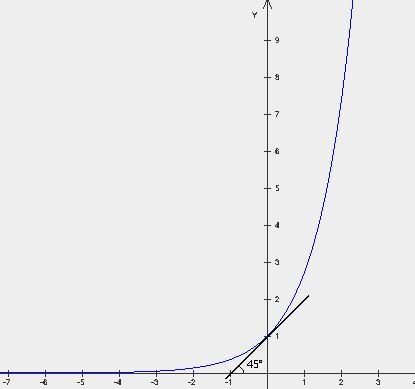Подобную логику абсурда разумным существам не понять никогда. Это уровень говорящих попугаев и дрессированных обезьян, у которых разум отсутствует от слова «совсем». Математики выступают в роли обычных дрессировщиков, проповедуя нам свои абсурдные идеи.
Затем берем с каждой стопки по одной купюре и вручаем математику его «математическое множество зарплаты». Поясняем математику, что остальные купюры он получит только тогда, когда докажет, что множество без одинаковых элементов не равно множеству с одинаковыми элементами. Вот здесь начнется самое интересное.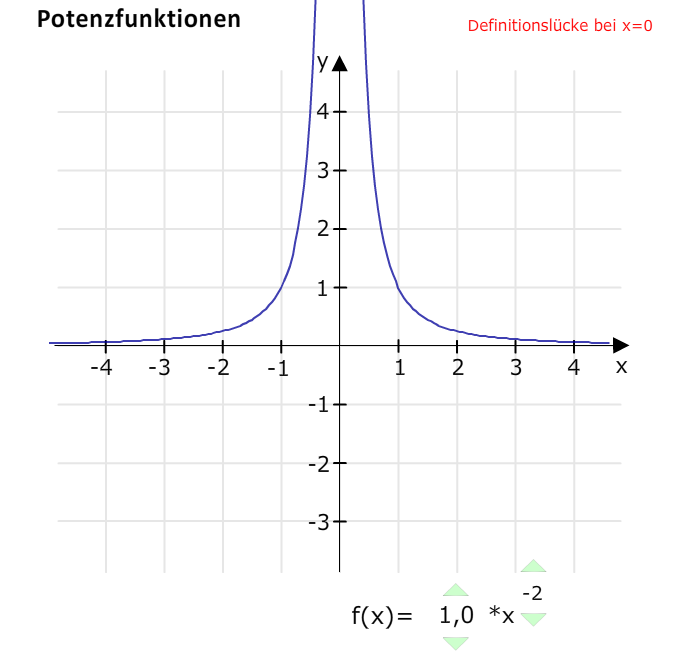
воскресенье, 18 марта 2018 г.
Это не математическое действие.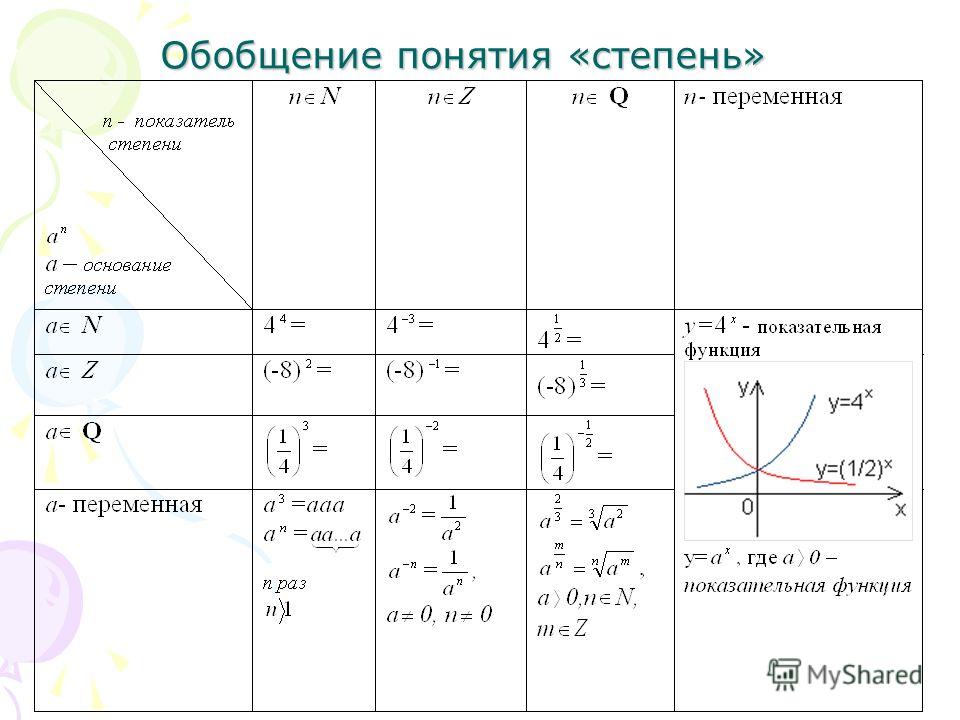
Табличка на двери
— Девушка! Это лаборатория по изучению индефильной святости душ при вознесении на небеса! Нимб сверху и стрелочка вверх.
Какой еще туалет?
В случае со снежным комом обратная связь положительная: чем больше результат, тем быстрее протекает процесс. А масса и скорость снежного кома y экспоненциально возрастают со временем x . Аналогично ведут себя деньги в банке при фиксированной процентной ставке. Чем больше денег, тем больше ежегодный прирост — и тем быстрее денег хватит на домик на Мальдивах. Так же увеличивается численность животных при отсутствии внешних угроз: чем больше популяция, тем больше размножающихся особей, тем быстрее она увеличивается.
А еще, когда микрофон подносишь близко к динамику, то самый тихий шорох через секунду превратится в звонкий гул.
Так что, если вам надо срочно отвлечься на 15 минут, а горячего чаю выпить хочется — налейте в него холодного молока или воды. Тогда разница температур уменьшится, и чай не остынет так быстро, как если бы он был горячим. Как дифференцировать экспоненциальные функции — mathsathome.com
Производные экспоненциальных функций: видео-урок 005 х
. Поэтому е в степени х остается неизменным при дифференцировании. Это единственная функция, имеющая это свойство. Производная от e kx равна ke kx . Для e x k=1 и, следовательно, производная e x это e x.
Экспоненциальная функция Производная y=e x y’=e x 9 0040 y=e kx y’=k.e kx у=е f(x) y’=f'(x).e f(x) y=a x y’=ln(a).a x Как дифференцировать экспоненту Функция
Примеры дифференцирования экспоненциальных функций
Запись этой дроби в виде индекса позволяет нам дифференцировать ее. Экспоненциальная функция Производная e x e x 90 043 e kx ke kx e 3x 3e 3x 5e 2x 10e 2x e x 2 (2x).e x 2 e (2x 9000 5 3 -x 2 ) (6x 2 -2x) . 
e (2x 3 -x 2 ) e -x -e -x 9004 0 e sin(x) cos(x). e sin(x) Цепное правило с экспоненциальными функциями
Правило произведения с экспоненциальными функциями
Правило частных с экспоненциальными функциями
Неявное дифференцирование e
xy 
Доказательство производной e
𝑥 Производная e
𝑥 с использованием первых принципов
Доказательство производной e
𝑥 с использованием ряда
Как отличить f(𝑥) = a
𝑥 Доказательство производной от a
𝑥 Вычисление производных экспоненциальных функций
Показательная функция является одной из самых важных функций в исчислении.
На этой странице мы выведем выражение для производной e x и применить его для вычисления производной других экспоненциальных функций.
Бесконечный многочлен называется0609 силовая серия. Производная e
x 
Это одно из свойств, которое делает экспоненциальную функцию действительно важной.
Поскольку внешняя функция экспоненциальная, ее производная равна самой себе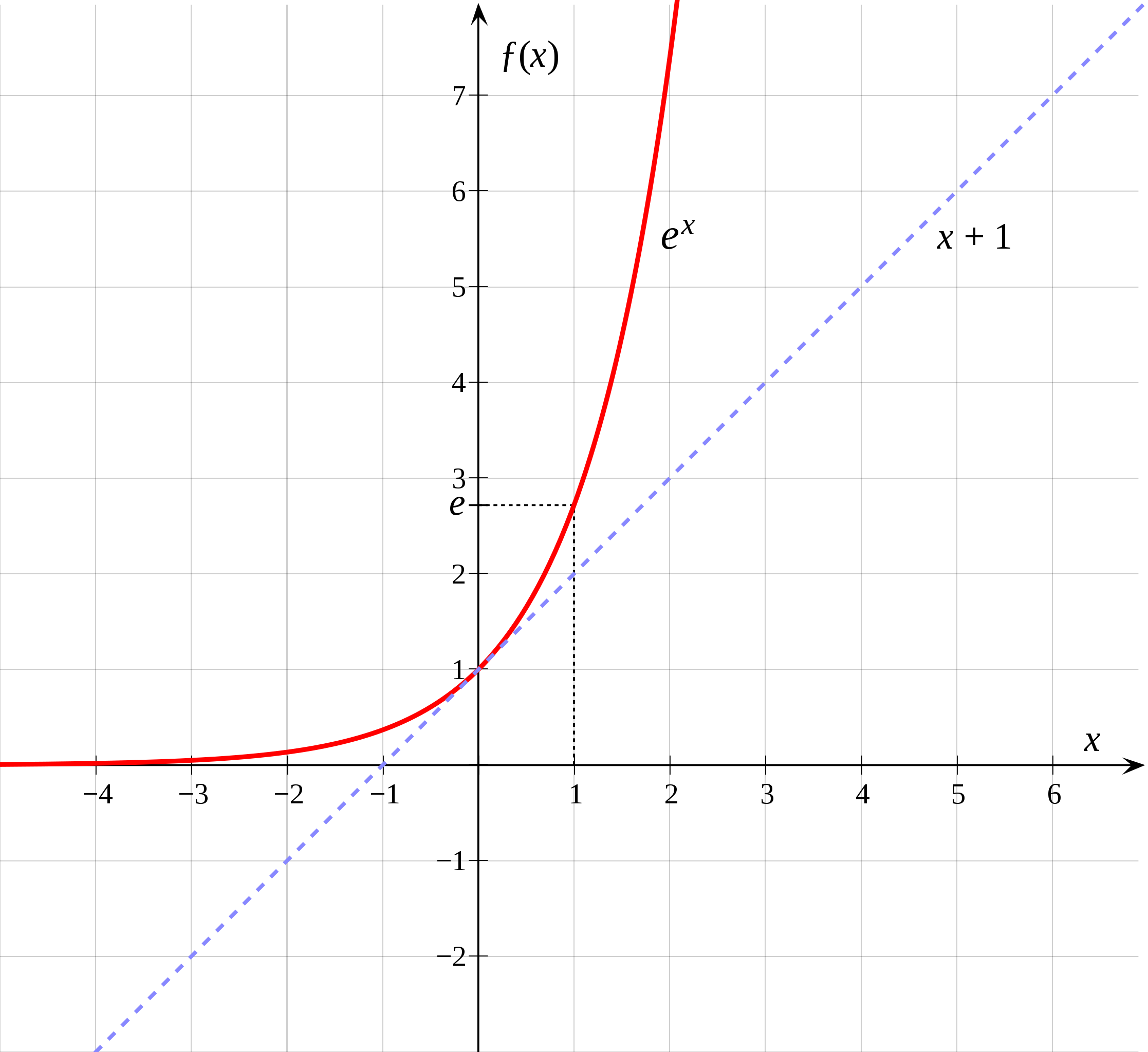
Sin 1 0: Mathway | Популярные задачи
//Mathway | Популярные задачи
1 Найти точное значение sin(30) 2 Найти точное значение sin(45) 3 Найти точное значение sin(30 град. ) 4 Найти точное значение sin(60 град. ) 5 Найти точное значение tan(30 град. ) 6 Найти точное значение arcsin(-1) 7 Найти точное значение sin(pi/6) 8 Найти точное значение cos(pi/4) 9 Найти точное значение sin(45 град. )10 Найти точное значение sin(pi/3) 11 Найти точное значение arctan(-1) 12 Найти точное значение cos(45 град. ) 13 Найти точное значение cos(30 град. ) 14 Найти точное значение tan(60) 15 Найти точное значение csc(45 град. ) 16 Найти точное значение tan(60 град. ) 17 Найти точное значение sec(30 град. 
)18 Найти точное значение cos(60 град. ) 19 Найти точное значение cos(150) 20 Найти точное значение sin(60) 21 Найти точное значение cos(pi/2) 22 Найти точное значение tan(45 град. ) 23 Найти точное значение arctan(- квадратный корень из 3) 24 Найти точное значение csc(60 град. ) 25 Найти точное значение sec(45 град.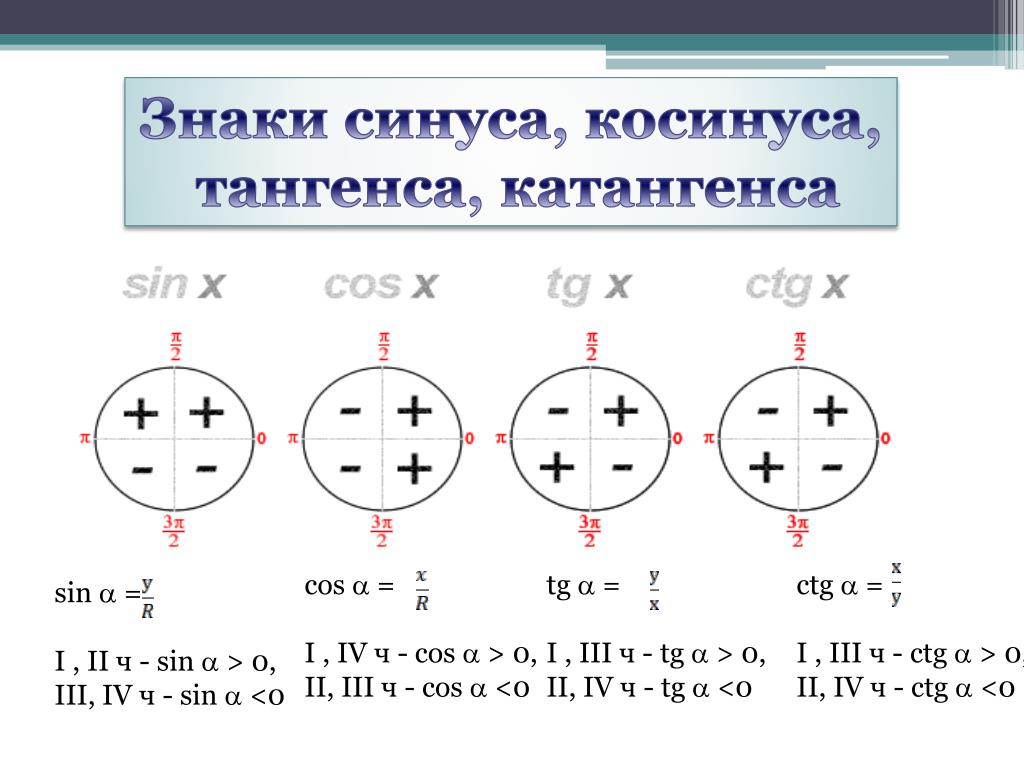 
)26 Найти точное значение csc(30 град. ) 27 Найти точное значение sin(0) 28 Найти точное значение sin(120) 29 Найти точное значение cos(90) 30 Преобразовать из радианов в градусы pi/3 31 Найти точное значение tan(30) 32 Преобразовать из градусов в радианы 45 33 Найти точное значение cos(45) 34 Упростить sin(theta)^2+cos(theta)^2 35 Преобразовать из радианов в градусы pi/6 36 Найти точное значение cot(30 град.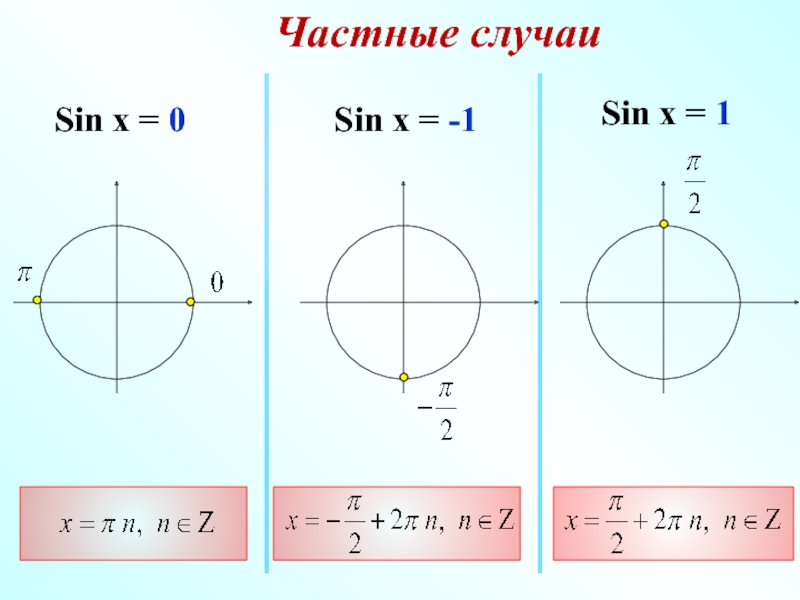 
)37 Найти точное значение arccos(-1) 38 Найти точное значение arctan(0) 39 Найти точное значение cot(60 град. ) 40 Преобразовать из градусов в радианы 30 41 Преобразовать из радианов в градусы (2pi)/3 42 Найти точное значение sin((5pi)/3) 43 Найти точное значение sin((3pi)/4) 44 Найти точное значение tan(pi/2) 45 Найти точное значение sin(300) 46 Найти точное значение cos(30) 47 Найти точное значение cos(60) 48 Найти точное значение cos(0) 49 Найти точное значение cos(135) 50 Найти точное значение cos((5pi)/3) 51 Найти точное значение cos(210) 52 Найти точное значение sec(60 град. 
)53 Найти точное значение sin(300 град. ) 54 Преобразовать из градусов в радианы 135 55 Преобразовать из градусов в радианы 150 56 Преобразовать из радианов в градусы (5pi)/6 57 Преобразовать из радианов в градусы (5pi)/3 58 Преобразовать из градусов в радианы 89 град. 59 Преобразовать из градусов в радианы 60 60 Найти точное значение sin(135 град. 
)61 Найти точное значение sin(150) 62 Найти точное значение sin(240 град. ) 63 Найти точное значение cot(45 град. ) 64 Преобразовать из радианов в градусы (5pi)/4 65 Найти точное значение sin(225) 66 Найти точное значение sin(240) 67 Найти точное значение cos(150 град. ) 68 Найти точное значение tan(45) 69 Вычислить sin(30 град.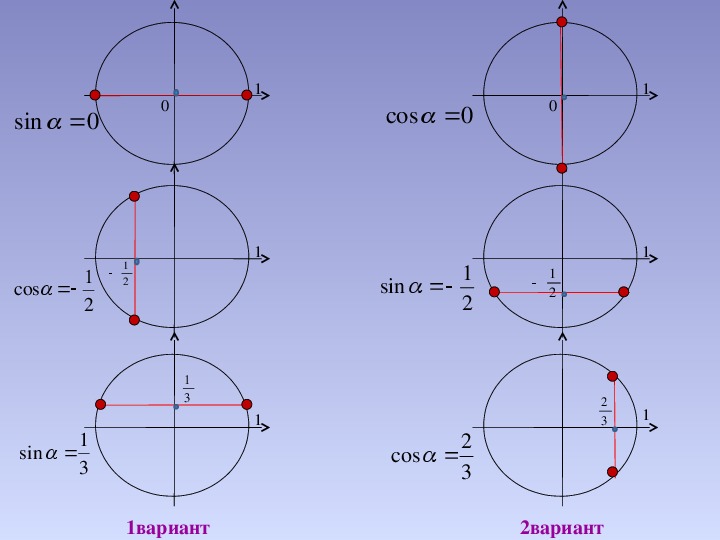 
)70 Найти точное значение sec(0) 71 Найти точное значение cos((5pi)/6) 72 Найти точное значение csc(30) 73 Найти точное значение arcsin(( квадратный корень из 2)/2) 74 Найти точное значение tan((5pi)/3) 75 Найти точное значение tan(0) 76 Вычислить sin(60 град. ) 77 Найти точное значение arctan(-( квадратный корень из 3)/3) 78 Преобразовать из радианов в градусы (3pi)/4 79 Найти точное значение sin((7pi)/4) 80 Найти точное значение arcsin(-1/2) 81 Найти точное значение sin((4pi)/3) 82 Найти точное значение csc(45) 83 Упростить arctan( квадратный корень из 3) 84 Найти точное значение sin(135) 85 Найти точное значение sin(105) 86 Найти точное значение sin(150 град. 
)87 Найти точное значение sin((2pi)/3) 88 Найти точное значение tan((2pi)/3) 89 Преобразовать из радианов в градусы pi/4 90 Найти точное значение sin(pi/2) 91 Найти точное значение sec(45) 92 Найти точное значение cos((5pi)/4) 93 Найти точное значение cos((7pi)/6) 94 Найти точное значение arcsin(0) 95 Найти точное значение sin(120 град. 
)96 Найти точное значение tan((7pi)/6) 97 Найти точное значение cos(270) 98 Найти точное значение sin((7pi)/6) 99 Найти точное значение arcsin(-( квадратный корень из 2)/2) 100 Преобразовать из градусов в радианы 88 град. кубических, тригонометрических, логарифмических и др. уравнений · Калькулятор Онлайн для чайников 🫖🤓
Учитель очень удивится увидев твоё верное решение😉
Введите уравнение с неизвестным, для которого требуется найти корни.
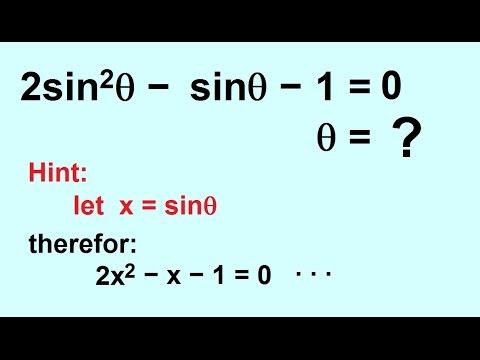2
В выражениях можно применять следующие операции:
3
Другие функции:
Постоянные: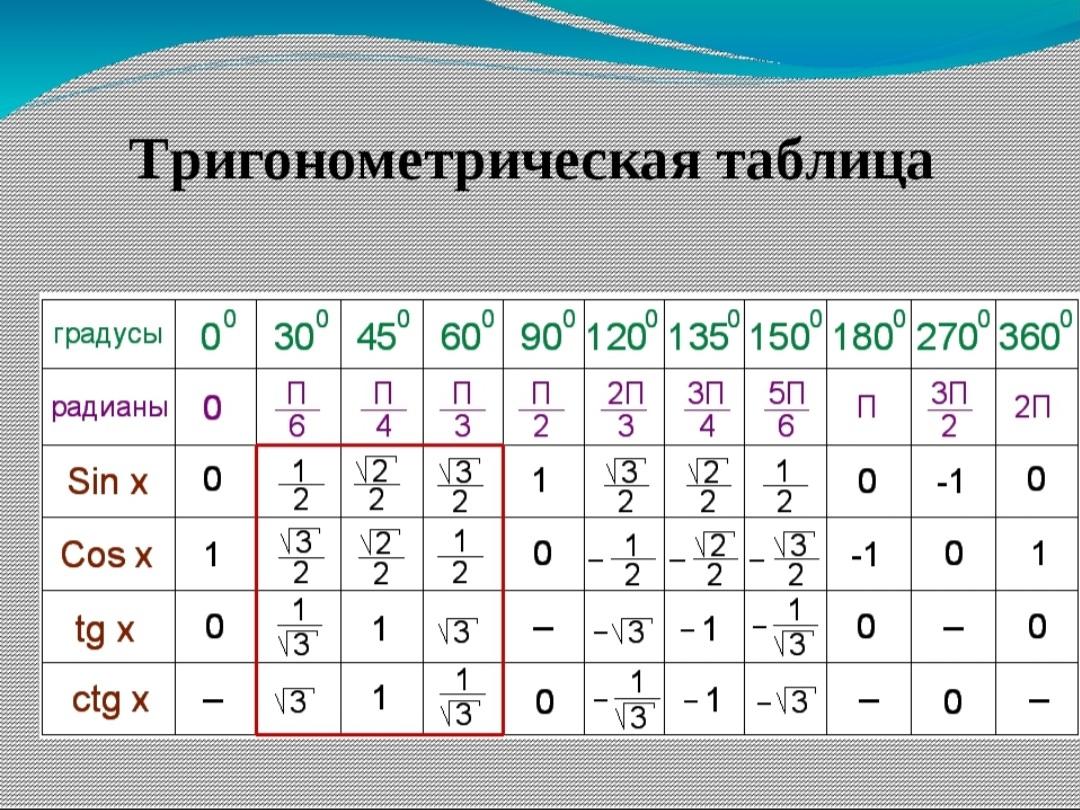
14159.. Мэтуэй | Популярные задачи
1 Найти точное значение грех(30) 2 Найти точное значение грех(45) 3 Найти точное значение грех(30 градусов) 4 Найти точное значение грех(60 градусов) 5 Найти точное значение загар (30 градусов) 6 Найти точное значение угловой синус(-1) 7 Найти точное значение грех(пи/6) 8 Найти точное значение cos(pi/4) 9 Найти точное значение грех(45 градусов) 10 Найти точное значение грех(пи/3) 11 Найти точное значение арктан(-1) 12 Найти точное значение cos(45 градусов) 13 Найти точное значение cos(30 градусов) 14 Найти точное значение желтовато-коричневый(60) 15 Найти точное значение csc(45 градусов) 16 Найти точное значение загар (60 градусов) 17 Найти точное значение сек(30 градусов) 18 Найти точное значение cos(60 градусов) 19 Найти точное значение cos(150) 20 Найти точное значение грех(60) 21 Найти точное значение cos(pi/2) 22 Найти точное значение загар (45 градусов) 23 Найти точное значение arctan(- квадратный корень из 3) 24 Найти точное значение csc(60 градусов) 25 Найти точное значение сек(45 градусов) 26 Найти точное значение csc(30 градусов) 27 Найти точное значение грех(0) 28 Найти точное значение грех(120) 29 Найти точное значение соз(90) 30 Преобразовать из радианов в градусы пи/3 31 Найти точное значение желтовато-коричневый(30) 32 92 35 Преобразовать из радианов в градусы пи/6 36 Найти точное значение детская кроватка(30 градусов) 37 Найти точное значение арккос(-1) 38 Найти точное значение арктический(0) 39 Найти точное значение детская кроватка(60 градусов) 40 Преобразование градусов в радианы 30 41 Преобразовать из радианов в градусы (2 шт. 
)/3 42 Найти точное значение sin((5pi)/3) 43 Найти точное значение sin((3pi)/4) 44 Найти точное значение тан(пи/2) 45 Найти точное значение грех(300) 46 Найти точное значение соз(30) 47 Найти точное значение соз(60) 48 Найти точное значение соз(0) 49 Найти точное значение cos(135) 50 Найти точное значение cos((5pi)/3) 51 Найти точное значение cos(210) 52 Найти точное значение сек(60 градусов) 53 Найти точное значение грех(300 градусов) 54 Преобразование градусов в радианы 135 55 Преобразование градусов в радианы 150 56 Преобразовать из радианов в градусы (5 дюймов)/6 57 Преобразовать из радианов в градусы (5 дюймов)/3 58 Преобразование градусов в радианы 89 градусов 59 Преобразование градусов в радианы 60 60 Найти точное значение грех(135 градусов) 61 Найти точное значение грех(150) 62 Найти точное значение грех(240 градусов) 63 Найти точное значение детская кроватка(45 градусов) 64 Преобразовать из радианов в градусы (5 дюймов)/4 65 Найти точное значение грех(225) 66 Найти точное значение грех(240) 67 Найти точное значение cos(150 градусов) 68 Найти точное значение желтовато-коричневый(45) 69 Оценить грех(30 градусов) 70 Найти точное значение сек(0) 71 Найти точное значение cos((5pi)/6) 72 Найти точное значение КСК(30) 73 Найти точное значение arcsin(( квадратный корень из 2)/2) 74 Найти точное значение загар((5pi)/3) 75 Найти точное значение желтовато-коричневый(0) 76 Оценить грех(60 градусов) 77 Найти точное значение arctan(-( квадратный корень из 3)/3) 78 Преобразовать из радианов в градусы (3 пи)/4 79 Найти точное значение sin((7pi)/4) 80 Найти точное значение угловой синус(-1/2) 81 Найти точное значение sin((4pi)/3) 82 Найти точное значение КСК(45) 83 Упростить арктан(квадратный корень из 3) 84 Найти точное значение грех(135) 85 Найти точное значение грех(105) 86 Найти точное значение грех(150 градусов) 87 Найти точное значение sin((2pi)/3) 88 Найти точное значение загар((2pi)/3) 89 Преобразовать из радианов в градусы пи/4 90 Найти точное значение грех(пи/2) 91 Найти точное значение сек(45) 92 Найти точное значение cos((5pi)/4) 93 Найти точное значение cos((7pi)/6) 94 Найти точное значение угловой синус(0) 95 Найти точное значение грех(120 градусов) 96 Найти точное значение желтовато-коричневый ((7pi)/6) 97 Найти точное значение соз(270) 98 9-1 (0) равно: 9 0907 Toppers Talk
Видео по теме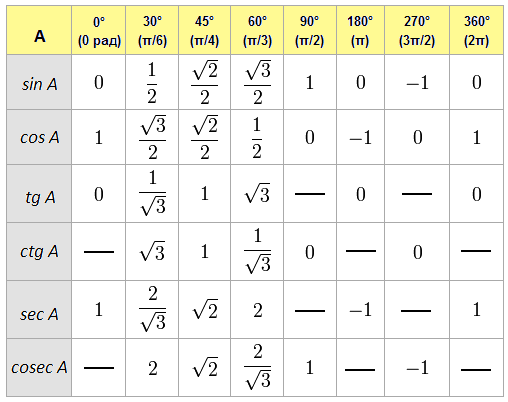
Калькулятор дробей неправильных: Калькулятор рациональных выражений
//Калькулятор преобразования неправильной дроби в смешанную
0
AC
+/-
÷
7
8
9
×
4
5
6
—
1
2
3
+
0
00
,
=
При помощи калькулятора преобразования неправильной дроби в
смешанную вы можете привести неправильную дробь к смешанному числу, а так же получить подробное решение.
Введите целые неотрицательные числа в числитель и знаменатель, если у дроби нет целой части оставьте это поле пустым.
Дробь
Правильные и неправильные дроби
Как преобразовать неправильную дробь в смешанную
1. Разделить числитель дроби на знаменатель.
2.
Числитель представить, как остаток от деления.
3. Частное представить в виде целой части.
4. Знаменатель оставить прежним.
5. Если у неправильной дроби была целая часть, то целые части необходимо сложить.
2. Остаток от деления записать в числитель
3. Частное представить в виде целой части
4. Знаменатель оставить прежним
18 — целая часть
1 — числитель
3 — знаменатель
Поделить числитель дроби на знаменатель
2. Остаток от деления записать в числитель
3. Частное представить в виде целой части
4. Знаменатель оставить прежним
5. Сложить целые части
2 + 1 — целая часть
1 — числитель
3 — знаменательВам могут также быть полезны следующие сервисы Дроби Калькулятор интервальных повторений Учим дроби наглядно Калькулятор сокращения дробей Калькулятор преобразования неправильной дроби в смешанную Калькулятор преобразования смешанной дроби в неправильную Калькулятор сложения, вычитания, умножения и деления дробей Калькулятор возведения дроби в степень Калькулятор перевода десятичной дроби в обыкновенную Калькулятор перевода обыкновенной дроби в десятичную Калькулятор сравнения дробей Калькулятор приведения дробей к общему знаменателю Калькуляторы (тригонометрия) Калькулятор синуса угла Калькулятор косинуса угла Калькулятор тангенса угла Калькулятор котангенса угла Калькулятор секанса угла Калькулятор косеканса угла Калькулятор арксинуса угла Калькулятор арккосинуса угла Калькулятор арктангенса угла Калькулятор арккотангенса угла Калькулятор арксеканса угла Калькулятор арккосеканса угла Калькулятор нахождения наименьшего угла Калькулятор определения вида угла Калькулятор смежных углов Калькуляторы систем счисления Калькулятор перевода чисел из арабских в римские и из римских в арабские Калькулятор перевода чисел в различные системы счисления Калькулятор сложения, вычитания, умножения и деления двоичных чисел Системы счисления теория N2 | Двоичная система счисления N3 | Троичная система счисления N4 | Четырехичная система счисления N5 | Пятеричная система счисления N6 | Шестеричная система счисления N7 | Семеричная система счисления N8 | Восьмеричная система счисления N9 | Девятеричная система счисления N11 | Одиннадцатиричная система счисления N12 | Двенадцатеричная система счисления N13 | Тринадцатеричная система счисления N14 | Четырнадцатеричная система счисления N15 | Пятнадцатеричная система счисления N16 | Шестнадцатеричная система счисления N17 | Семнадцатеричная система счисления N18 | Восемнадцатеричная система счисления N19 | Девятнадцатеричная система счисления N20 | Двадцатеричная система счисления N21 | Двадцатиодноричная система счисления N22 | Двадцатидвухричная система счисления N23 | Двадцатитрехричная система счисления N24 | Двадцатичетырехричная система счисления N25 | Двадцатипятеричная система счисления N26 | Двадцатишестеричная система счисления N27 | Двадцатисемеричная система счисления N28 | Двадцативосьмеричная система счисления N29 | Двадцатидевятиричная система счисления N30 | Тридцатиричная система счисления N31 | Тридцатиодноричная система счисления N32 | Тридцатидвухричная система счисления N33 | Тридцатитрехричная система счисления N34 | Тридцатичетырехричная система счисления N35 | Тридцатипятиричная система счисления N36 | Тридцатишестиричная система счисления Калькуляторы (Теория чисел) Калькулятор выражений Калькулятор упрощения выражений Калькулятор со скобками Калькулятор уравнений Калькулятор суммы Калькулятор пределов функций Калькулятор разложения числа на простые множители Калькулятор НОД и НОК Калькулятор НОД и НОК по алгоритму Евклида Калькулятор НОД и НОК для любого количества чисел Калькулятор делителей числа Представление многозначных чисел в виде суммы разрядных слагаемых Калькулятор деления числа в данном отношении Калькулятор процентов Калькулятор перевода числа с Е в десятичное Калькулятор экспоненциальной записи чисел Калькулятор нахождения факториала числа Калькулятор нахождения логарифма числа Калькулятор квадратных уравнений Калькулятор остатка от деления Калькулятор корней с решением Калькулятор нахождения периода десятичной дроби Калькулятор больших чисел Калькулятор округления числа Калькулятор свойств корней и степеней Калькулятор комплексных чисел Калькулятор среднего арифметического Калькулятор арифметической прогрессии Калькулятор геометрической прогрессии Калькулятор модуля числа Калькулятор абсолютной погрешности приближения Калькулятор абсолютной погрешности Калькулятор относительной погрешности Калькуляторы площади геометрических фигур Площадь квадрата Площадь прямоугольника КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ Калькуляторы (Комбинаторика) Калькулятор нахождения числа перестановок из n элементов Калькулятор нахождения числа сочетаний из n элементов Калькулятор нахождения числа размещений из n элементов Генератор Pdf с примерами Тренажёры решения примеров Тренажёр таблицы умножения Тренажер счета для дошкольников Тренажер счета на внимательность для дошкольников Тренажер решения примеров на сложение, вычитание, умножение, деление. 
Найди правильный ответ. Тренажер решения примеров с разными действиями Тренажёры решения столбиком Тренажёр сложения столбиком Тренажёр вычитания столбиком Тренажёр умножения столбиком Тренажёр деления столбиком с остатком Калькуляторы решения столбиком Калькулятор сложения, вычитания, умножения и деления столбиком Калькулятор деления столбиком с остатком Калькуляторы линейная алгебра и аналитическая геометрия Калькулятор сложения и вычитания матриц Калькулятор умножения матриц Калькулятор транспонирование матрицы Калькулятор нахождения определителя (детерминанта) матрицы Калькулятор нахождения обратной матрицы Длина отрезка. Онлайн калькулятор расстояния между точками Онлайн калькулятор нахождения координат вектора по двум точкам Калькулятор нахождения модуля (длины) вектора Калькулятор сложения и вычитания векторов Калькулятор скалярного произведения векторов через длину и косинус угла между векторами Калькулятор скалярного произведения векторов через координаты Калькулятор векторного произведения векторов через координаты Калькулятор смешанного произведения векторов Калькулятор умножения вектора на число Калькулятор нахождения угла между векторами Калькулятор проверки коллинеарности векторов Калькулятор проверки компланарности векторов Конвертеры величин Конвертер единиц длины Конвертер единиц скорости Конвертер единиц ускорения Цифры в текст Калькуляторы (физика) Калькулятор вычисления скорости, времени и расстояния Калькулятор вычисления ускорения, скорости и перемещения Калькулятор вычисления времени движения Калькулятор времени Второй закон Ньютона. 
Калькулятор вычисления силы, массы и ускорения. Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. Импульс тела. Калькулятор вычисления импульса, массы и скорости Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения Калькулятор отражения и преломления света Калькулятор Закона Ома Калькулятор Закона Кулона Калькулятор напряженности E электрического поля Калькулятор нахождения точечного электрического заряда Q Калькулятор нахождения силы F действующей на заряд q Калькулятор вычисления расстояния r от заряда q Калькулятор вычисления потенциальной энергии W заряда q Калькулятор вычисления потенциала φ электростатического поля Калькулятор вычисления электроемкости C проводника и сферы Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе Калькулятор вычисления энергии W заряженного конденсатора
Калькулятор вычисления энергии W заряженного конденсатора. 
Для плоского, цилиндрического и сферического конденсаторов
Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов Калькуляторы по астрономии Вес тела на других планетах Ускорение свободного падения на планетах Солнечной системы и их спутниках Генераторы Генератор примеров по математике Генератор случайных чисел Генератор паролей Калькулятор правильных и неправильных дробей
Первые полторы тысяч разложений.
Арифметическое выражение Вы ввели следующее выражение Полученный результат в виде дроби
Описание
Особенности
Бот, рассчитывает такую дробь, что бы погрешность была минимальна. Поэтому не удивляйтесь если при попытке посчитать формулу вы получите число
Примеры
Поиск по сайту
Угол между ними.
Матрица смежности онлайнОнлайн расчеты Подписаться письмом Калькулятор / конвертер неправильных дробей в смешанные числа
Не только это, вы также можете решить правильные дроби, используя калькулятор дроби для смешанного числа. Что такое неправильная дробь?
Шаги, необходимые для преобразования неправильных дробей в смешанные числа:
Правила упрощения дробей:
Как преобразовать неправильные дроби в смешанные числа?
Когда мы разделим эту дробь, мы получить остаток 2 .
Частное представляет целое число, равное 2 в нашем случае.
Теперь следующим шагом будет запись остатка в числителе. Кроме того, выберите первый в истории знаменатель, равный 3 , и считайте его таким, какой он здесь. Наконец, умножьте дробь на целое число, которое является частным.
Весь процесс показан ниже:
$$ \frac{9}{2} $$
Разделив данную дробь, получим остаток от 1
Второй шаг — найти целое число, которое есть не что иное, как частное 4 .
Наконец, возьмите остаток в числитель, знаменатель не изменится и снова будет равен 2 . После этого умножьте целое число на дробь, как показано ниже: Как работает калькулятор преобразования неправильных дробей в смешанные числа?
Позвольте нам помочь вам должным образом о его использовании!
Калькулятор бесплатного преобразования неправильных дробей в смешанные числа определяет: Часто задаваемые вопросы:
Является ли \(1\frac{0}{2}\) неправильной дробью?
Как выглядит неправильная дробь смешанного числа \(2\frac{1}{2}\)?
Как преобразовать смешанные дроби в неправильные дроби?
Могут ли неправильная дробь и смешанное число показывать одно и то же значение?
Вывод:
Ссылки:
Смешанное число в калькулятор неправильных дробей
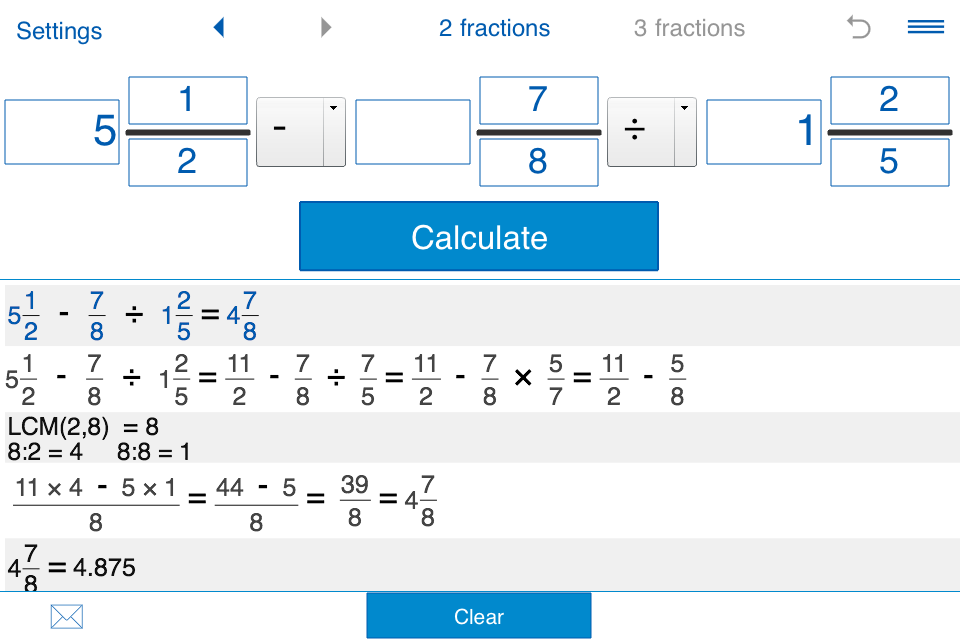
Как смешанное число превратить в неправильную дробь?
2 × 5 = 10 10 + 3 = 13 НОД(28,10) = 2 
Преобразование смешанных чисел в неправильные дроби — визуально 👀
2 × 5 = 10 10 + 3 = 13 
Вы хотите поделиться своей едой с одноклассниками 🧒🧒🏻🧒🏽. Если каждый человек получит по одной строке, на сколько человек вы сможете ее разделить? Пример: преобразовать 3 ¹/₄ в неправильную дробь с помощью калькулятора смешанного числа в неправильную дробь
3 . 1 в числителе и 4 в знаменателе.
Построение по: Построение по росту, 6 (шесть) букв
//Построение По Росту 6 Букв
Ниже вы найдете правильный ответ на Построение по росту 6 букв, если вам нужна дополнительная помощь в завершении кроссворда, продолжайте навигацию и воспользуйтесь нашей функцией поиска.ответ на кроссворд и сканворд
связанные кроссворды
Построение по нуклеотидным последовательностям | Учебный сайт Мишель Б.
Для сравнения с эталонным деревом, изображенным на Рис. 2, также приведены соответствующие нетривиальные ветви каждого дерева.Рис. 1. Дерево, построенное на основе 16S рРНК методом NJ {STAAR, STAES}
против{GEOKA, ENTFA, LACAC, LACDA, FINM2}{LACDA, LACAC}
против{FINM2, ENTFA, GEOKA, STAAR, STAES}{GEOKA, LACDA, LACAC, ENTFA}
против{STAAR, STAES, FINM2}{LACDA, LACAC, ENTFA}
против{FINM2, GEOKA, STAAR, STAES}Рис. 2. Эталонное дерево {STAAR, STAES}
против{GEOKA, ENTFA, LACAC, LACDA, FINM2}{LACDA, LACAC}
против{FINM2, ENTFA, GEOKA, STAAR, STAES}{GEOKA, STAAR, STAES}
против{ENTFA, LACAC, LACDA, FINM2}{LACDA, LACAC, ENTFA}
против{FINM2, GEOKA, STAAR, STAES}
Здесь же эта проблема не возникла, и, хоть это и можно было бы списать на случайность, на самом деле можно уверенно говорить о том, что построение
деревьев на основе 16S рРНК является более надёжным методом реконструкции. Это связано с повышенной консервативностью соответствующих генов рРНК, что и позволяет в конечном итоге более точно определить систематическое положение
организмов и оценить время расхождения близких видов.emkeller/term4/.
В отсутствие протеолитической субъединицы (CLPP) CLPX также может выступать в роли шаперона.proteomes.fasta. На его основе далее была создана база данных db.fasta: makeblastdb -in proteomes.fasta -out db.fasta -dbtype prot
CLPX_BACSU.fasta по этой базе данных с порогом evalue = 0.001. Вывод осуществлялся в текстовый файл res.txt: blastp -query CLPX_BACSU.fasta -db db.fasta -evalue 0.001 -out res.txt
Рис. 3. Находки blastp
Рис. 4. Функции белков-гомологов
Рис.5. Паралоги, ортологи и эволюционные события на древе гомологов
[1] NCBI Genomes
[2] MUSCLE Web Service
[3] Uniprot: CLPX
[4] Uniprot: CLPP Строительство | История, типы, примеры и факты
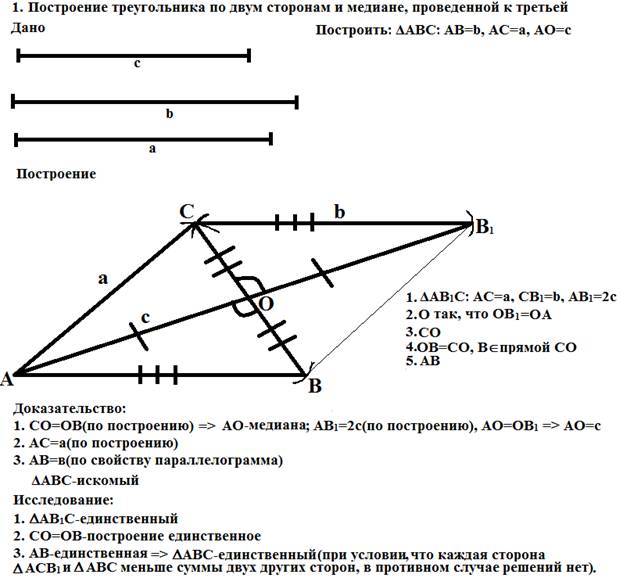
Ранние строительные материалы, такие как листья, ветки и шкуры животных, были скоропортящимися. Позже стали использовать более прочные природные материалы, такие как глина, камень и древесина, и, наконец, синтетические материалы, такие как кирпич, бетон, металлы и пластмассы. Другой — поиск зданий все большей высоты и пролета; это стало возможным благодаря разработке более прочных материалов и знанию того, как ведут себя материалы и как использовать их с большей выгодой. Третья основная тенденция связана со степенью контроля над внутренней средой зданий: стало возможным более точное регулирование температуры воздуха, уровня света и звука, влажности, запахов, скорости движения воздуха и других факторов, влияющих на комфорт человека. Еще одной тенденцией является изменение энергии, доступной для процесса строительства, начиная с силы человеческих мышц и заканчивая мощной техникой, используемой сегодня.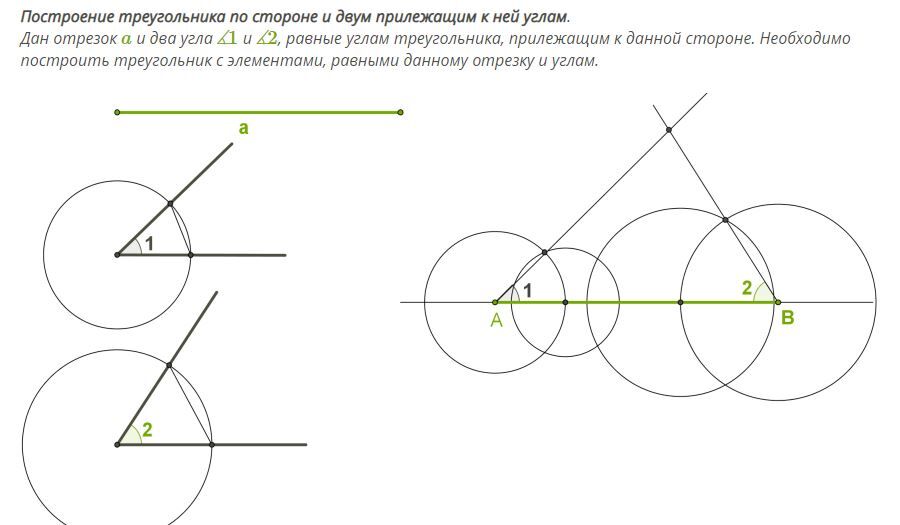
Процесс проектирования зданий хорошо организован и опирается на исследовательские институты, которые изучают свойства и характеристики материалов, должностных лиц по нормам и правилам, которые принимают и обеспечивают соблюдение стандартов безопасности, и специалистов по проектированию, которые определяют потребности пользователей и проектируют здание для удовлетворения этих потребностей. Процесс строительства также высоко организован; в нее входят производители строительных изделий и систем, мастера, собирающие их на строительной площадке, подрядчики, нанимающие и координирующие работу мастеров, и консультанты, специализирующиеся в таких аспектах, как управление строительством, контроль качества и страхование.
В данной статье сначала прослеживается история строительства, затем делается обзор его развития в настоящее время. Для рассмотрения эстетических соображений проектирования зданий см. архитектура. Для дальнейшего рассмотрения исторического развития см. искусство и архитектура, анатолийская; искусство и архитектура, арабский язык; искусство и архитектура египетские; искусство и архитектура, иранский язык; искусство и архитектура Месопотамии; искусство и архитектура сиро-палестинская; архитектура, африканская; искусство и архитектура, Oceanic; архитектура, вестерн; искусства, среднеазиатские; искусства, Восточной Азии; искусство, исламское; искусство, коренной американец; искусство, Южная Азия; искусство, Юго-Восточная Азия. История строительства
Первобытное строительство: каменный век
Раскопки в ряде мест в Европе, датируемых до 12 000 г. до н.э., показывают круглые кольца из камней, которые, как полагают, составляли часть таких убежищ. Они могли скреплять грубые хижины из деревянных шестов или утяжелять стены палаток из шкур животных, предположительно поддерживаемых центральными шестами.
Действительно, большая часть истории строительства — это поиск более сложных решений тех же основных проблем, для решения которых и предназначалась палатка. Палатка используется до сих пор. Шатер из козьей шерсти из Саудовской Аравии, монгольская юрта со складным деревянным каркасом и войлочным покрытием, а также вигвам американских индейцев с многочисленными опорами для шестов и двойной мембраной являются более изысканными и элегантными потомками грубых убежищ ранних охотников-собирателей.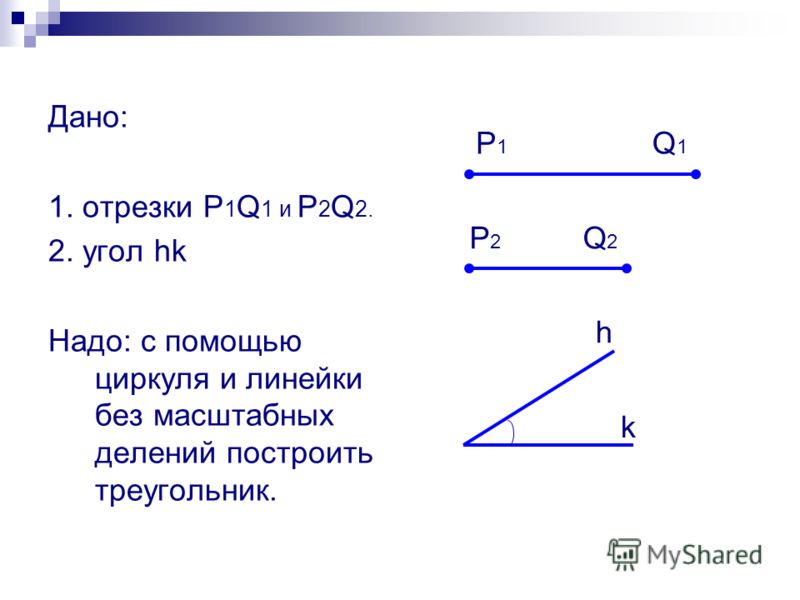
В более поздних ближневосточных толоях появилась прямоугольная прихожая или вестибюль, примыкающая к главной круглой камере — первые примеры прямоугольной формы в плане в здании. Еще позже от круглой формы отказались в пользу прямоугольной, поскольку жилища были разделены на большее количество комнат, а в поселениях было размещено больше жилищ. Толои стали важным шагом в поисках долговечности; они были началом каменного строительства.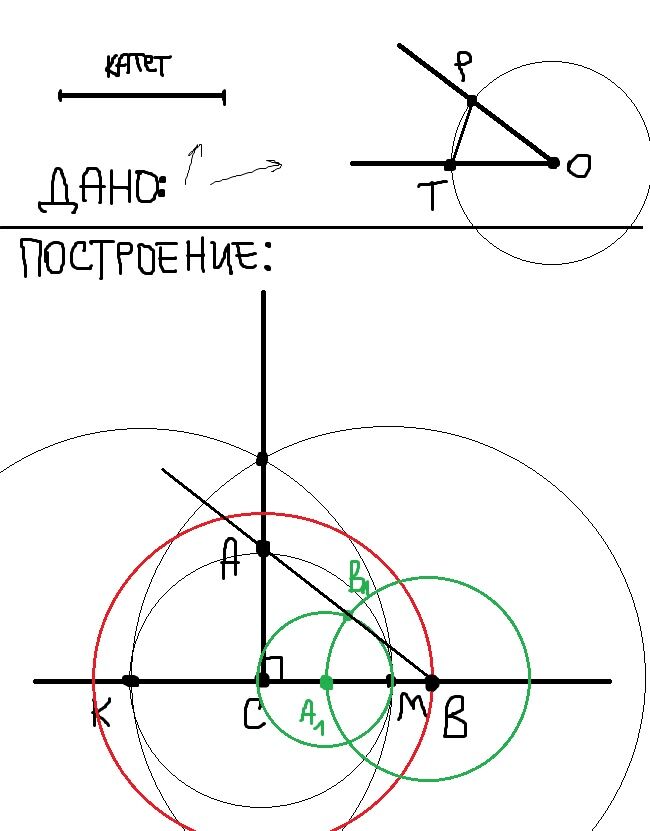
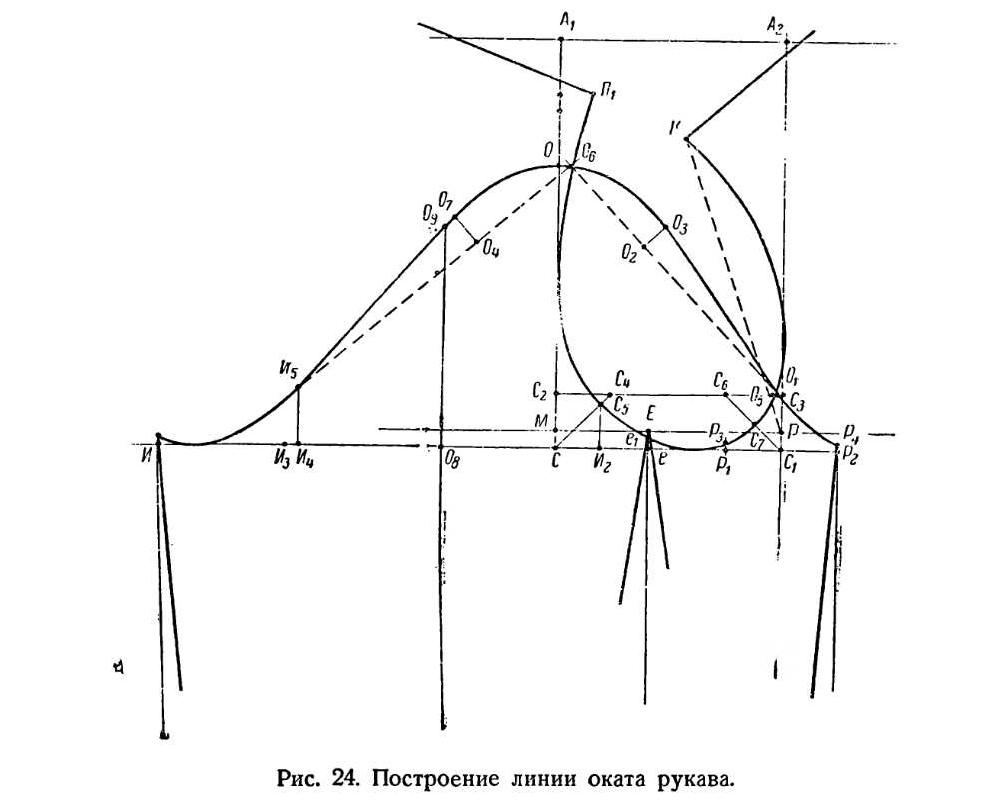В стенах этих каркасных домов использовались многие типы заполнения, в том числе глина, плетень и мазня, кора дерева (излюбленная американскими лесными индейцами) и солома. В Полинезии и Индонезии, где такие дома строят до сих пор, их приподнимают над землей на сваях для безопасности и сухости; кровля часто сделана из листьев, а стены в значительной степени открыты, чтобы обеспечить движение воздуха для естественного охлаждения. Другой вариант рамы был найден в Египте и на Ближнем Востоке, где связки тростника заменялись бревнами. PRIS — Отчеты о состоянии реактора — Строится
Строится
Страна Общая полезная электрическая мощность
[МВт] Количество реакторов АРГЕНТИНА 25 1 БАНГЛАДЕШ 2160 2 БРАЗИЛИЯ 1340 1 КИТАЙ 21608 21 ЕГИПЕТ 3300 3 ФРАНЦИЯ 1630 1 ИНДИЯ 6028 8 ИРАН, ИСЛАМСКАЯ РЕСПУБЛИКА 974 1 ЯПОНИЯ 2653 2 КОРЕЯ, РЕСПУБЛИКА 4020 3 РОССИЯ 2700 3 СЛОВАКИЯ 440 1 ТУРЦИЯ 4456 4 УКРАИНА 2070 2 ОБЪЕДИНЕННЫЕ АРАБСКИЕ ЭМИРАТЫ 1310 1 ВЕЛИКОБРИТАНИЯ 3260 2 СОЕДИНЕННЫЕ ШТАТЫ АМЕРИКИ 1117 1 Общий 59091 57 
Как вычислить количество: Количество вещества, масса и молярная масса — урок. Химия, 8 класс.
//Способы подсчета количества ячеек в диапазоне с данными
org/ListItem»>
org/ListItem»>
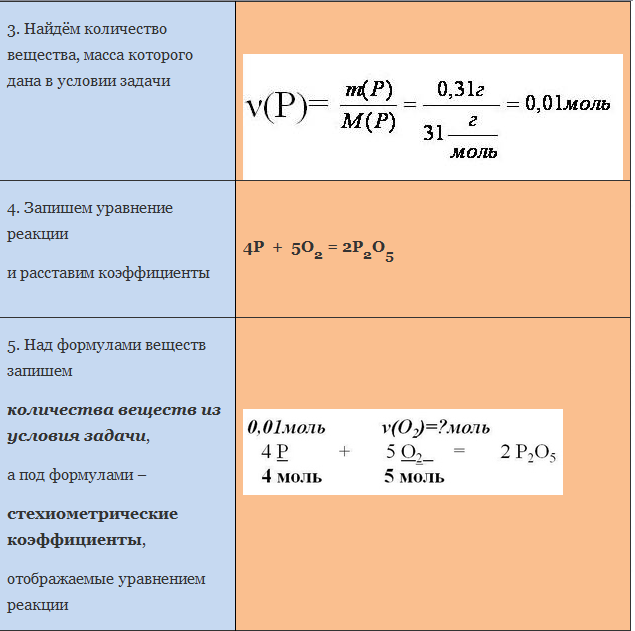
СЧЁТЕСЛИ (функция СЧЁТЕСЛИ) — Служба поддержки Майкрософт
Статья
Статья
Статья
Статья
Статья
Статья
Статья
Статья
Статья
Статья
Примеры
Результат — 2.
Результат — 2.
Подстановочный знак «*» обозначает любое количество любых символов. Результат — 4.
Распространенные неполадки
Для работы этой функции необходимо, чтобы другая книга была открыта.Рекомендации
Вопросительный знак соответствует любому отдельно взятому символу. Звездочка — любой последовательности символов. Если требуется найти именно вопросительный знак или звездочку, следует ввести значок тильды (~) перед искомым символом.
Дополнительные сведения
См. также
5 Методы расчета количества материалов
Г К Г К
Инженер-строитель на стройке
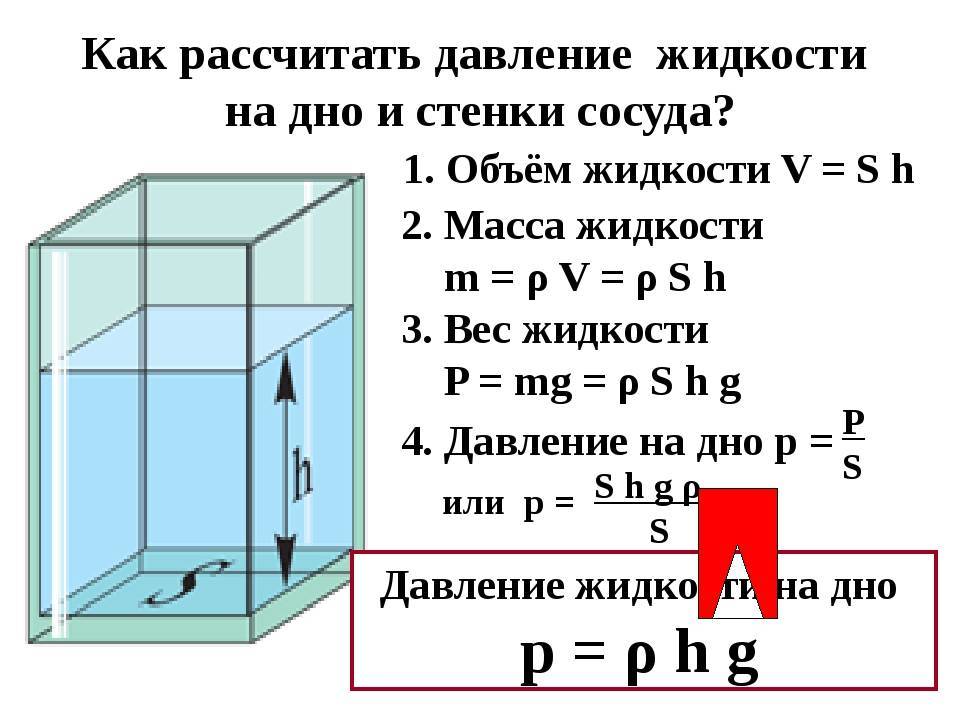
д. При строительстве больницы сервисным блоком будет кровать. Точно так же для кинотеатра/стадиона это места. Архитектурные приложения: лучшие архитектурные приложения для iPad и iPhone в 2023 году
3 мая 2023 г.
Лучшие плагины для BIM для использования в 2023 году
27 апр.
2023 г. Преобразуйте свою компанию с помощью 3D-проектов Solid-Works CAD
14 апр. 2023 г.
LOD (уровень разработки) в BIM и разница между уровнями детализации
12 апр. 2023 г.
Советы по портфолио BIM, которые помогут вам в будущей карьере
4 апр. 2023 г.
Типы и форматы файлов, наиболее часто используемые в программном обеспечении 3D CAD
28 марта 2023 г.
Полы из травертина: преимущества и недостатки
23 марта 2023 г.
Revit против Revit LT: каковы преимущества и недостатки?
21 марта 2023 г.
BIMX для ArchiCAD: технология, о которой вы должны знать в 2023 году
18 марта 2023 г.
Преимущества интеграции Verifi3D и Dropbox в строительной отрасли
17 марта 2023 г.
Как рассчитать равновесную цену и количество
1) Расчет функции предложения
2) Рассчитать функцию спроса
3) Установить объем предложения равным объему спроса и найти равновесную цену
разделы 2 и 3). Это позволяет нам решить полученное уравнение для P и найти равновесную цену. 4) Подставьте равновесную цену в функцию предложения
раздел 3) обратно в функцию предложения (см. шаг 1). Затем мы решаем полученное уравнение для QS, чтобы найти равновесное количество. Обратите внимание, что не имеет значения, используем ли мы функцию предложения или функцию спроса для этого шага. Обе функции вернут одно и то же равновесное количество, потому что, как мы узнали выше, в равновесии QS всегда равно QD. 5) Проверка путем подстановки равновесной цены в функцию спроса (необязательно)
Какой угол называется развернутый: Что такое развёрнутый угол? Ответ на webmath.ru
//Какой угол называют развернутым. Угол называется развернутым, если его стороны лежат на одной прямой
Развернутый и неразвернутый угол
Если угол не является развернутым, то одна из частей называется внутренней областью угла, а другая внешней областью этого угла. На рисунке ниже представлен неразвернутый угол и отмечены внешняя и внутренняя области этого угла.Измерение углов
Отрезки. Геометрия. Смежные и вертикальные углы. Построение параллельных прямых. Построение треугольника. Выводы. Прямые параллельны. Вершины. Простейшие геометрические фигуры. Какая фигура называется треугольником. Равные отрезки имеют равные длины. Угол – это геометрическая фигура, которая состоит из точки и двух лучей.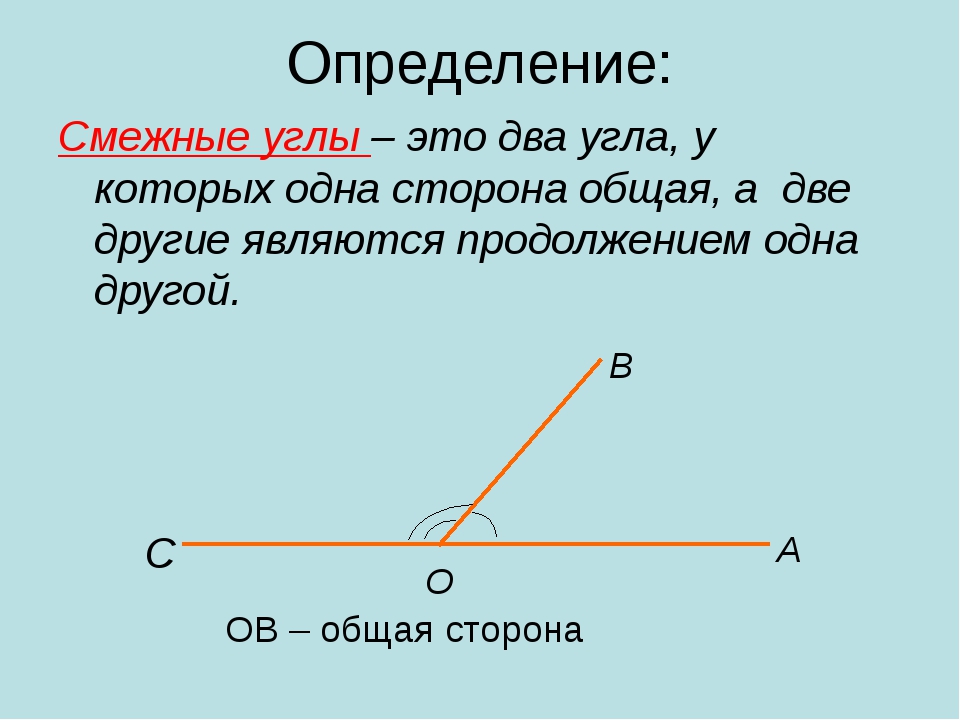
Какая геометрическая фигура была отличительным знаком пифагорейцев? Какую форму, по мнению пифагорейцев, имела вся Вселенная? Ответ: 580 – 500 гг. до н. эры. Когда существовала Древняя Греция? Введение. Ответ: «Плоскомерие». Объяснение устройства мира пифагорейцы тесно связывали с геометрией.Угловая мера
Типы углов
Смотреть что такое «Развернутый угол» в других словарях:
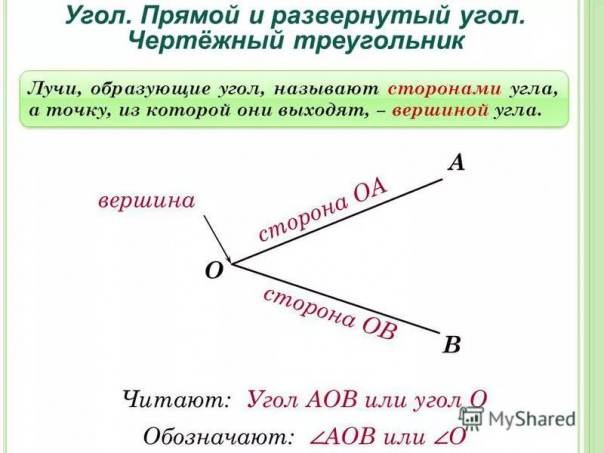УГОЛ, геометрическая… … Иллюстрированный энциклопедический словарь
поперек под прямым углом. . прямой угол угол максимального отклонения; угол, равный своему смежному; четверть оборота. перпендикуляр. перпендикулярный находящийся под прямым углом. перпендикулярно.… … Идеографический словарь русского языкаЧто такое угол?
Лучи, образующие угол , называют сторонами угла, а точку, из которой они выходят, — вершиной угла.
На рисунке 160 сторонами угла являются лучи ОА и ОБ, а его вершиной — точка О. Этот угол обозначают так: АОВ.Прямой и развернутый угол
164).Чертежный треугольник
2.Какой угол называют развернутым?
3.Какие углы называют равными?
4.Какой угол называют прямым?
5.Как строят прямой угол с помощью чертежного треугольника?
Но, в случае, если у угла его обе стороны лежат на одной прямой, то такой угол называется развернутым. То есть, у развернутого угла одна его сторона является продолжением его другой стороны угла.Свойства развернутого угла
во-вторых, развернутый угол равен 180°;
в-третьих, два смежных угла образуют развернутый угол;
в-четвертых, развернутый угол составляет половину полного угла;
в-пятых, полный угол будет равен сумме двух развёрнутых углов;
в-шестых, половина развернутого угла составляет прямой угол.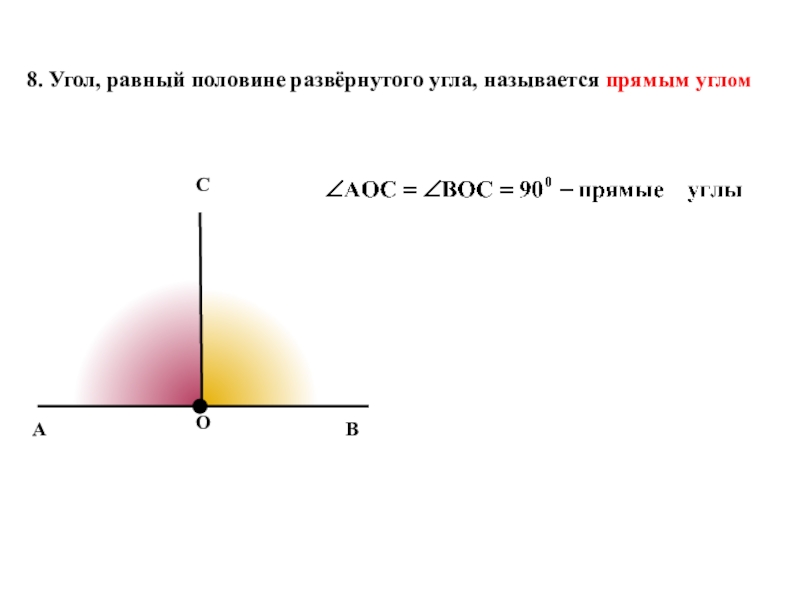
Измерение углов
Это и есть развернутый угол.Практическое задание
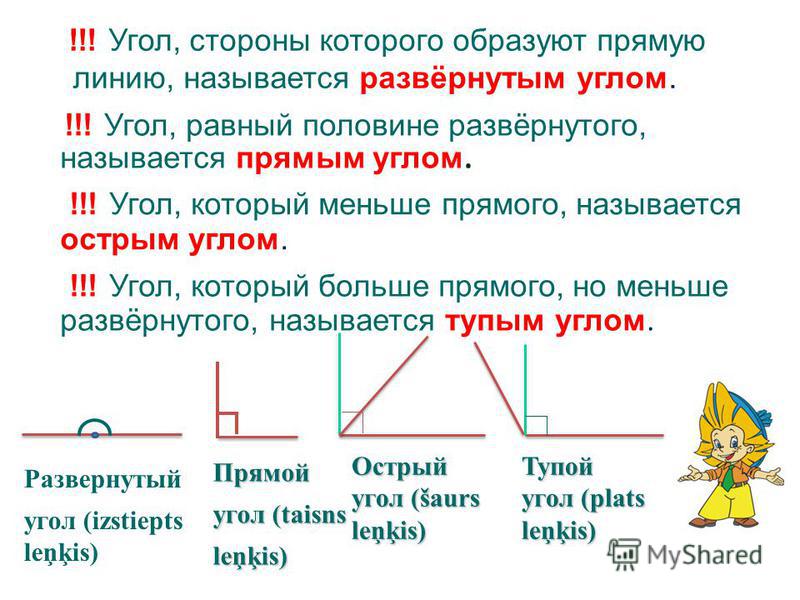
13 6 12 1
2 3? 42?
Найдите высоту каждого из этих сооружений, если башни Московского Кремля на 49 м ниже Александрийского маяка.
б) 147,6% от 2500; г) 0,09% от 456 800.
2) (3,42: 0,57 9,5 — 6,6) : ((4,8 — 1,6) (3,1 + 0,05)).
Найдите с помощью чертежного треугольника прямые углы на рисунке 173.
б) 361,62с + 1848: d, если с = 100, d =100.
б) 1% от литра; г) 6% от 80 км.
Во время маневров командир оставил 0,3 всех своих солдат охранять переправу, а остальных разделил на 2 отряда для обороны двух высот. В первом отряде было в 6 раз больше солдат, чем во втором. Сколько солдат было в первом отряде, если всего было 200 солдат? 
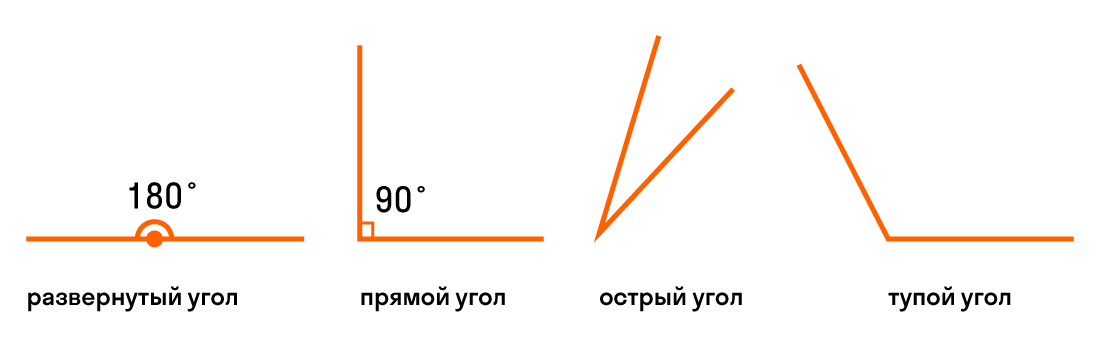
То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные .
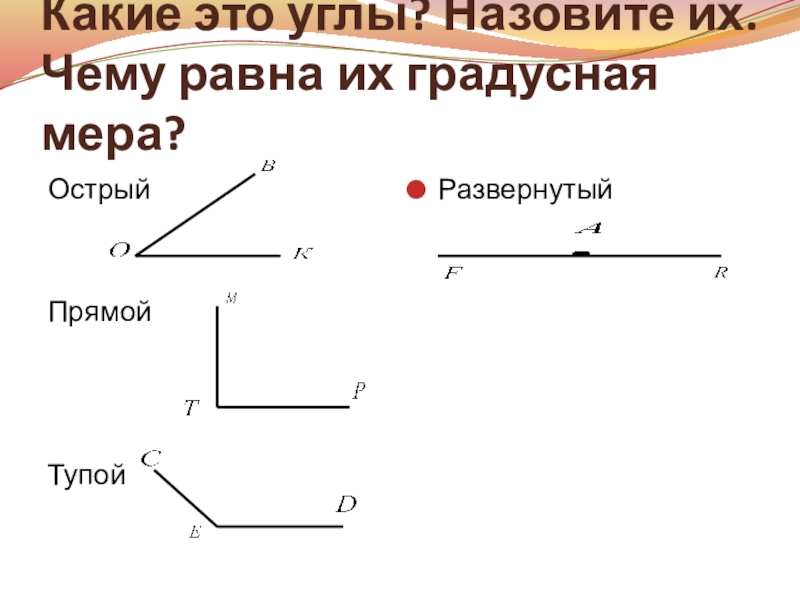Имеет место обозначение:
Ниже наглядно изображены три вида углов.
Они считаются подобными.
Угол называется развернутым если его стороны. Развернутый угол в геометрии
Рассмотрим подробнее каждый вид.
Что такое угол?
Лучи, образующие угол , называют сторонами угла, а точку, из которой они выходят, — вершиной угла.
На рисунке 160 сторонами угла являются лучи ОА и ОБ, а его вершиной — точка О. Этот угол обозначают так: АОВ.
Он разбивает угол СОК на два угла — СОР и РОК. Каждый из этих углов меньше угла СОК.Прямой и развернутый угол
Чертежный треугольник
2.Какой угол называют развернутым?
3.Какие углы называют равными?
4.Какой угол называют прямым?
5.Как строят прямой угол с помощью чертежного треугольника?
Свойства развернутого угла
во-вторых, развернутый угол равен 180°;
в-третьих, два смежных угла образуют развернутый угол;
в-четвертых, развернутый угол составляет половину полного угла;
в-пятых, полный угол будет равен сумме двух развёрнутых углов;
в-шестых, половина развернутого угла составляет прямой угол.Измерение углов
Практическое задание
Укажите, какие точки на рисунке 169 лежат внутри угла КОМ, Какие точки лежат вне этого угла? Какие точки лежат на стороне OK, a какие — на стороне ОМ?
13 6 12 1
2 3? 42?
Пусть этот квадрат изображает поле. Рожь занимает 12% поля, овес — 8%, пшеница — 64%, а остальная часть поля занята гречихой. Покажите на рисунке часть поля, занятую каждой культурой. Сколько процентов поля занимает гречиха?
б) 147,6% от 2500; г) 0,09% от 456 800.
В первый день вскопали 30% огорода, а во второй день — 35% огорода. Сколько аров осталось еще вскопать?
2) (3,42: 0,57 9,5 — 6,6) : ((4,8 — 1,6) (3,1 + 0,05)).
б) 361,62с + 1848: d, если с = 100, d =100.
б) 1% от литра; г) 6% от 80 км.
Я. ВИЛЕНКИН, B. И. ЖОХОВ, А. С. ЧЕСНОКОВ, C. И. ШВАРЦБУРД, Математика 5 класс, Учебник для общеобразовательных учреждений Развернутый и неразвернутый угол
Измерение углов
Введение в понятие геометрического угла
Такие лучи называются сторонами угла, а общее начало сторон — это его вершина.Виды углов и геометрии
Понятие развернутого угла
Свойства развернутых углов
Задачи с развернутыми углами
Угол – определение и типы с примерами
Что такое угол
Части угла
Части угла
Присвоение имени углу Как найти угол
Типы углов
Другие типы углов
Примеры из реальной жизни
Как называется угол 180°?
Это также жизненно важная часть технической основы для расчета различных конструкций, производства, создания чертежей, программирования и т. д. Что такое углы?
Типы уголков
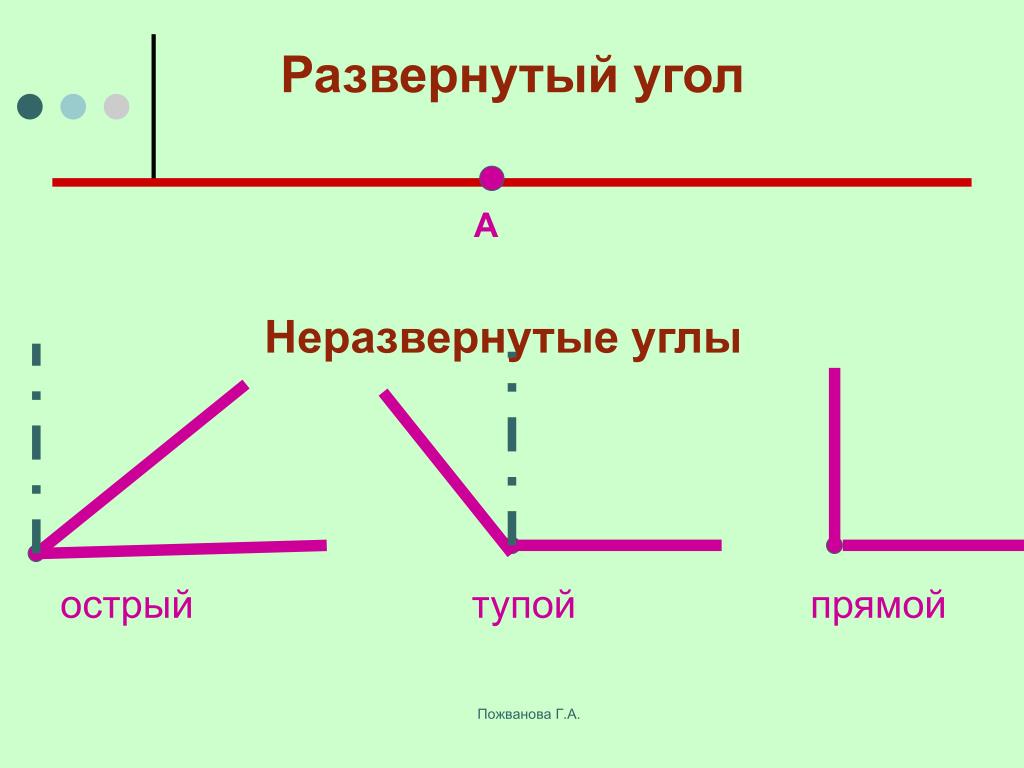
Как называется угол 180°?
Построение прямого угла
И следуйте по протектору на 180°, чтобы отметить точку Y. Свойства прямого угла
Примеры вопросов
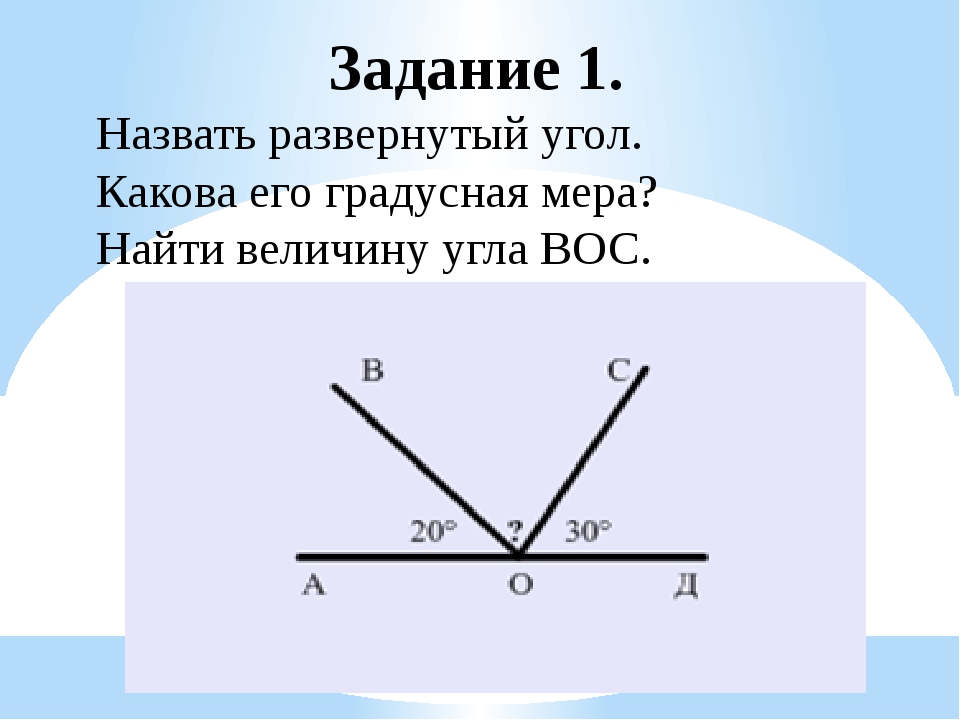
Convert doc to doc online free: DOCX (WORD) to DOC (WORD) (Online & Free) — Convertio
// Как преобразовать Word в документ Google [скриншоты + часто задаваемые вопросы включены]
Метод 1: Преобразование Word в Google Doc на рабочем столе
Способ 2. Как преобразовать Word в Google Doc на мобильном телефоне
Как преобразовать Word в Google Docs Часто задаваемые вопросы (часто задаваемые вопросы)
Можете ли вы преобразовать документ Word в документ Google?
Затем вы можете сохранить его как Google Docs. Как преобразовать документ Word в документ Google на мобильных устройствах?
Каковы преимущества преобразования документа Word в документ Google?
Подведение итогов
Итак, следуйте приведенным выше инструкциям, и вскоре вы станете мастером преобразования Word в Google Doc. Быстрый способ конвертировать Google Doc в Word
Элиза Уильямс
Как преобразовать Google Doc в Word
В этой статье мы попытаемся представить наиболее эффективный способ легко преобразовать ваши документы в любой желаемый формат. Шаг 1. Доступ к опции «Вставка»
Шаг 2. Сохранить документ Google как Word
Лучшее программное обеспечение для работы с файлами PDF
PDFelement предоставляет вам ряд инструментов, с помощью которых можно редактировать и преобразовывать документы по вашему выбору. Благодаря расширенным возможностям форматирования вы можете добиться эффективных результатов после форматирования документов непосредственно в PDFelement. Как конвертировать PDF в Word
