\(\cos\)\(\frac{π}{3}\)\(=\)\(\frac{1}{2}\)
\(\cos2=-0,416…\)
Содержание:
- Аргумент и значение
- Коcинус острого угла
- Косинус числа
- Косинус любого угла
- Знаки по четвертям
- Связь с другими функциями
- Функция
Аргумент и значение
Косинус острого угла
Косинус острого угла можно определить с помощью прямоугольного треугольника — он равен отношению прилежащего катета к гипотенузе.
Пример:
1) Пусть дан угол и нужно определить косинус этого угла.
2) Достроим на этом угле любой прямоугольный треугольник.
3) Измерив, нужные стороны, можем вычислить косинус.
Косинус острого угла больше \(0\) и меньше \(1\)
Если при решении задачи косинус острого угла получился больше 1 или отрицательным, то значит где-то в решении есть ошибка.
Косинус числа
Косинус числа можно определить с помощью числовой окружности – косинус числа равен абсциссе соответствующей точки на ней.
Числовая окружность позволяет определить косинус любого числа, но обычно находят косинус чисел как-то связанных с Пи: \(\frac{π}{2}\), \(\frac{3π}{4}\), \(-2π\).
Например, для числа \(\frac{π}{6}\) — косинус будет равен \(\frac{\sqrt{3}}{2}\). А для числа \(-\)\(\frac{3π}{4}\) он будет равен \(-\)\(\frac{\sqrt{2}}{2}\) (приблизительно \(-0,71\)).
Косинус для других часто встречающихся в практике чисел смотри в тригонометрической таблице.
Значение косинуса всегда лежит в пределах от \(-1\) до \(1\).
 При этом вычислен косинус может быть для абсолютно любого угла и числа.
При этом вычислен косинус может быть для абсолютно любого угла и числа.
Косинус любого угла
Благодаря числовой окружности можно определять косинус не только острого угла, но и тупого, отрицательного, и даже большего, чем \(360°\) (полный оборот). Как это делать — проще один раз увидеть, чем \(100\) раз услышать, поэтому смотрите картинку.
Теперь пояснение: пусть нужно определить косинус угла КОА с градусной мерой в \(150°\). Совмещаем точку О с центром окружности, а сторону ОК – с осью \(x\). После этого откладываем \(150°\) против часовой стрелки. Тогда ордината точки А покажет нам косинус этого угла.
Если же нас интересует угол с градусной мерой, например, в \(-60°\) (угол КОВ), делаем также, но \(60°\) откладываем по часовой стрелке.
И, наконец, угол больше \(360°\) (угол КОС) — всё аналогично тупому, только пройдя по часовой стрелке полный оборот, отправляемся на второй круг и «добираем нехватку градусов». Конкретно в нашем случае угол \(405°\) отложен как \(360° + 45°\).
Конкретно в нашем случае угол \(405°\) отложен как \(360° + 45°\).
Несложно догадаться, что для откладывания угла, например, в \(960°\), надо сделать уже два оборота (\(360°+360°+240°\)), а для угла в \(2640°\) — целых семь.
Стоит запомнить, что:
Косинус прямого угла равен нулю. Косинус тупого угла — отрицателен.
Знаки косинуса по четвертям
С помощью оси косинусов (то есть, оси абсцисс, выделенной на рисунке красным цветом) легко определить знаки косинусов по четвертям числовой (тригонометрической) окружности:
— там, где значения на оси от \(0\) до \(1\), косинус будет иметь знак плюс (I и IV четверти – зеленая область),
— там, где значения на оси от \(0\) до \(-1\), косинус будет иметь знак минус (II и III четверти – фиолетовая область).
Пример. Определите знак \(\cos 1\).
Решение: Найдем \(1\) на тригонометрическом круге. 2x}\)
2x}\)
—
Другие наиболее часто применяемые формулы смотри здесь.
Функция \(y=\cos{x}\)
Если отложить по оси \(x\) углы в радианах, а по оси \(y\) — соответствующие этим углам значения косинуса, мы получим следующий график:
График данной функции называется косинусоида и обладает следующими свойствами:
— область определения – любое значение икса: \(D(\cos{x} )=R\)
— область значений – от \(-1\) до \(1\) включительно: \(E(\cos{x} )=[-1;1]\)
— четная: \(\cos(-x)=\cos{x}\)
— периодическая с периодом \(2π\): \(\cos(x+2π)=\cos{x}\)
— точки пересечения с осями координат:
ось абсцисс: \((\)\(\frac{π}{2}\)\(+πn\),\(;0)\), где \(n ϵ Z\)
ось ординат: \((0;1)\)
— промежутки знакопостоянства:
функция положительна на интервалах: \((-\)\(\frac{π}{2}\)\(+2πn;\) \(\frac{π}{2}\)\(+2πn)\), где \(n ϵ Z\)
функция отрицательна на интервалах: \((\)\(\frac{π}{2}\)\(+2πn;\)\(\frac{3π}{2}\)\(+2πn)\), где \(n ϵ Z\)
— промежутки возрастания и убывания:
функция возрастает на интервалах: \((π+2πn;2π+2πn)\), где \(n ϵ Z\)
функция убывает на интервалах: \((2πn;π+2πn)\), где \(n ϵ Z\)
— максимумы и минимумы функции:
функция имеет максимальное значение \(y=1\) в точках \(x=2πn\), где \(n ϵ Z\)
функция имеет минимальное значение \(y=-1\) в точках \(x=π+2πn\), где \(n ϵ Z\).
Смотрите также:
Синус
Тангенс
Котангенс
Решение уравнения \(\cosx=a\)
1.cos в квадрате x — cos x 2. 3cos в квадрате x 3.3 sin в квадрате x
1. Определите, какое причастие употреблено в предложении: к каждой позиции из первого столбца подберите соответствующую позицию из второго столбца, обозначенную цифрой. ПРЕДЛОЖЕНИЕ ПРИЧАСТИЕ A) Замёрзшие за ночь цветы оживали. Б) Не закрытая тучей заря освещала окна. В) Мы опускаем руки в воду, струящуюся между пальцев. Г) Облака, гонимые ветром, быстро неслись по небу 1) действительное причастие настоящего времени 2) действительное причастие прошедшего времени 3) страдательное причастие настоящего времени 4) страдательное причастие прошедшего времени Запишите в таблицу выбранные цифры под соответствующими буквами. А Б В Г 2. Укажите варианты ответов, в которых в обоих словах одного ряда пропущена одна и та же буква. 1) вяж_щий, держ_щийся 2) обтека_мый, реша_мый, 3) потрач_нный, развеш_нный, 4) улаж_нный, услыш_нный. 5) ищ_щий, караул_щий 3. Выпишите слово, в суффиксе которого пишется буква Е: раста..в постав…в развес…в прикле..в обид…в 4. Выпишите наречие, в суффиксе которого пишется буква О. 1) изредк… интересоваться 2) начать занов…, 3) засидеться допоздн… 4) вылизать дочист… 5. Укажите варианты ответов, в которых выделенные слова пишутся слитно. 1) (на)отрез отказался 2) ушли (по)одиночке, 3) поговорить (с)глазу(на)глаз, 4) уйти (по)добру (по)здорову, 6. Укажите цифры, на месте которых пишется НН. В тума(1)ой дали песча(2)ого берега тускло светились огни стари(3)ого дома. В гости(4)ой на полу, украше(5)ом затейливым орнаментом, стоял мастерски сдела(6)ый стол с цветами в стекля(7)ой вазе. 7. Определите словосочетание, в котором НЕ с выделенным словом пишется СЛИТНО. Раскройте скобки и выпишите это слово. (не)сомневающийся в успехе, абсолютно (не)возмутимый; (не)далёкий, а близкий; работа (не)сделана; ещё (не)снятый фильм, 8. Расставьте знаки препинания: укажите цифру(-ы), на месте которой(-ых) должна(- ы) стоять запятая(-ые).
5) ищ_щий, караул_щий 3. Выпишите слово, в суффиксе которого пишется буква Е: раста..в постав…в развес…в прикле..в обид…в 4. Выпишите наречие, в суффиксе которого пишется буква О. 1) изредк… интересоваться 2) начать занов…, 3) засидеться допоздн… 4) вылизать дочист… 5. Укажите варианты ответов, в которых выделенные слова пишутся слитно. 1) (на)отрез отказался 2) ушли (по)одиночке, 3) поговорить (с)глазу(на)глаз, 4) уйти (по)добру (по)здорову, 6. Укажите цифры, на месте которых пишется НН. В тума(1)ой дали песча(2)ого берега тускло светились огни стари(3)ого дома. В гости(4)ой на полу, украше(5)ом затейливым орнаментом, стоял мастерски сдела(6)ый стол с цветами в стекля(7)ой вазе. 7. Определите словосочетание, в котором НЕ с выделенным словом пишется СЛИТНО. Раскройте скобки и выпишите это слово. (не)сомневающийся в успехе, абсолютно (не)возмутимый; (не)далёкий, а близкий; работа (не)сделана; ещё (не)снятый фильм, 8. Расставьте знаки препинания: укажите цифру(-ы), на месте которой(-ых) должна(- ы) стоять запятая(-ые). 1. Смотритель выпросил отпуск (1) и (2)не сказав никому ни слова о своём намерени.. пешком(3) отправ..лся за своей дочерью. 2. Подр..стая (4)ребёнок сам читает стихи о зелёном дубе (5) выр..сш..м у лукоморья. 9. Укажите предложение, в котором допущена грамматическая ошибка. 1) Это рассказ о человеке, возвратившемся после войны в родной город. 2) Приготовленные мамой оладьи были необыкновенно вкусны. 3) Изображая любой предмет, художник передает его собственное мироощущение. 4) Пользуясь автомобильными справочниками, требуется много времени на ремонт машины. 10. В каком ряду все предлоги пишутся слитно? 1) (на)подобие пирамиды, (из)под сугроба, (от)лени 2) (во)преки желанию, (в)следствие урагана, (на)встречу мечте 3) (ко)мне, (под)ле скамейки, (из)под стола 4) (в)течение занятия, (в)продолжение триместра (не)смотря на угрозы 11. Укажите правильный вариант объяснения написания выделенного слова (выделенных слов) в предложении «Мы чувствовали, что отцу не хочется разговаривать. Инна (то)же молчала».
1. Смотритель выпросил отпуск (1) и (2)не сказав никому ни слова о своём намерени.. пешком(3) отправ..лся за своей дочерью. 2. Подр..стая (4)ребёнок сам читает стихи о зелёном дубе (5) выр..сш..м у лукоморья. 9. Укажите предложение, в котором допущена грамматическая ошибка. 1) Это рассказ о человеке, возвратившемся после войны в родной город. 2) Приготовленные мамой оладьи были необыкновенно вкусны. 3) Изображая любой предмет, художник передает его собственное мироощущение. 4) Пользуясь автомобильными справочниками, требуется много времени на ремонт машины. 10. В каком ряду все предлоги пишутся слитно? 1) (на)подобие пирамиды, (из)под сугроба, (от)лени 2) (во)преки желанию, (в)следствие урагана, (на)встречу мечте 3) (ко)мне, (под)ле скамейки, (из)под стола 4) (в)течение занятия, (в)продолжение триместра (не)смотря на угрозы 11. Укажите правильный вариант объяснения написания выделенного слова (выделенных слов) в предложении «Мы чувствовали, что отцу не хочется разговаривать. Инна (то)же молчала». 1) тоже — всегда пишется слитно; 2) то же — всегда пишется раздельно; 3) тоже — здесь сочинительный союз, поэтому пишется слитно; 4) то же — здесь местоимение то с частицей же, поэтому пишется раздельн 12. Укажите предложение, в котором частица пишется через дефис. 1) Всё те(же) мы, но время уже не то. 2) На безлюдной барже не слишком(то) уютно. 3) Всё вроде(бы) отлично и здорово.
1) тоже — всегда пишется слитно; 2) то же — всегда пишется раздельно; 3) тоже — здесь сочинительный союз, поэтому пишется слитно; 4) то же — здесь местоимение то с частицей же, поэтому пишется раздельн 12. Укажите предложение, в котором частица пишется через дефис. 1) Всё те(же) мы, но время уже не то. 2) На безлюдной барже не слишком(то) уютно. 3) Всё вроде(бы) отлично и здорово.

Задавать вопрос
спросил
Изменено 4 года, 3 месяца назад
Просмотрено 355 раз
$\begingroup$ Мне нужно доказать, что это личность: 92\тета=1$)
Сделав это, я получу $\cos x + 1$. Но это должно быть неверно, поскольку окончательный ответ равен $\dfrac{\cos x}{2\sin x-1} = \dfrac{\cos x}{2\sin x-1}$. Это означает, что косинус должен быть умножен на $1$. Как же так?
Но это должно быть неверно, поскольку окончательный ответ равен $\dfrac{\cos x}{2\sin x-1} = \dfrac{\cos x}{2\sin x-1}$. Это означает, что косинус должен быть умножен на $1$. Как же так?
(Вот фото проблемы)
- алгебра-предварительное исчисление
- тригонометрия
Когда $x=0$, левая сторона равна 1, а правая сторона равна 2, поэтому это не тождество.
$\endgroup$ $\begingroup$ $\sin(2x)=2\sin(x)\cos(x)$. Следовательно, вы решаете :
$ $ \ гидроразрыва {\ соз (х)} {2 \ грех (х) + 1} = \ гидроразрыва {\ соз (х) + 1} {2 \ грех (х) + 1} $ $
Что приводит к бессмысленному уравнению:
$$\cos(x)=\cos(x)+1$$, которая заведомо не имеет решений. Похожие презентации: Элементы комбинаторики ( 9-11 классы) Применение производной в науке и в жизни Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде» Знакомство детей с математическими знаками и монетами Тренажёр по математике «Собираем урожай». Счет в пределах 10 Методы обработки экспериментальных данных Лекция 6. Корреляционный и регрессионный анализ Решение задач обязательной части ОГЭ по геометрии Дифференциальные уравнения Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи к учебнику «математика» 1 класс English
Русский
Правила Числовые неравенства и их свойства. Мы можем сравнить любые числа а и b и результат сравнения записать в виде равенства или неравенства, используя знаки =, <, >. Для произвольных чисел а и b выполняется одно и только одно из соотношений: a=b, a<b, a>b. Пример 1. Сравним обыкновенные дроби 58 и 47. Для этого приведем их к общему знаменателю: 58=3556; 47=3256. Так как 35>32, то 58>47. Пример 2. Сравним десятичные дроби 3,6748 и 3,675. Цифры в разрядах единиц, десятых и сотых совпадают, а в разряде тысячных в первой дроби стоит цифра 4, а во второй – цифра 5. Так как 4<5, то 3,6748<3,675. Пример 3. Сравним обыкновенную дробь 920 и десятичную дробь 0,45. Обратив дробь 920 в десятичную, получим, что 920=0,45. Пример 4. Сравним отрицательные числа -15 и -23. Модуль первого числа меньше модуля второго. Значит, первое число больше второго, -15>-23. В зависимости от вида числа мы использовали тот или иной способ сравнения. Число а больше числа b, если разность а-b – положительное число; число а меньше числа b, если разность a-b – отрицательное число. Если разность а-b = 0, то числа а и b равны. На координатной прямой большее число изображается точкой, лежащей правее, а меньшее – точкой, лежащей левее. Рассмотрим некоторые свойства числовых неравенств. Если a>b, то b<a, если a<b, то b>a. Действительно, если разность a-b – положительное число, то разность b-a – отрицательное число, и наоборот. Если a<b и b<c, то а<c. Докажем, что разность а-с – отрицательное число. Прибавим к этой разности числа b и –b и сгруппируем слагаемые: а-с = а-с+b-b = (а-b)+(b+c). По условию а<b и b<c. Поэтому слагаемые а-b и b-c – отрицательные числа. Если a<b и c – любое число, то а+с<b+c. Преобразуем разность (а+с)-(b+c) = а-b По условию а<b, поэтому a-b – отрицательное число. Значит, и разность (а+с)-(b+c) отрицательна. Следовательно, a+c<b+c. Если к обеим частям верного неравенства прибавить одно и то же число, то получится верное неравенство. Если a<b и c – положительное число, то aс<bс. Если a<b и c – отрицательное число, то aс>bc. Представим разность ас-bc в виде произведения: ас-bc = с(а-b). Так как a<b, то a-b – отрицательное число. Если с>0, то произведение с(а-b) отрицательно, и, следовательно, ас<bc. Если с<0, то произведение с(а-b) положительно, и, следовательно, ас>bc. Так как деление можно заменить умножением на число, обратное делителю, то аналогичное свойство справедливо и для деления. Если обе части верного неравенства умножить или разделить на одно и то же положительное число, то получится верное неравенство. Если обе части верного неравенства умножить или разделить на одно и то же отрицательное число и изменить знак неравенства на противоположный, то получится верное неравенство. Если а и b – положительные числа и а<b, то 1a>1b. Разделим обе части неравенства a<b на положительное число ab: aab<bab. Сократив дроби, получим, что 1b<1a, т.е. 1а>1b. Приведем пример использования рассмотренных свойств неравенств. Пример 5. Оценим периметр равностороннего треугольника со стороной а мм, если известно, что 54,2<a и a<54,3, и запишем результат в виде двойного неравенства. 54,2·3 < 3a < 54,3·3, 162,6 < 3a < 162,9. Значит, периметр Р данного треугольника больше 162,6 мм, но меньше 162,9 мм. Рассмотрим теперь, как выполняется сложение и умножение числовых неравенств. Если a<b и c<d, то a+c<b+d. Прибавив к обеим частям неравенства a<b число с, получим а+с<b+с. Прибавив к обеим частям неравенства с<d число b, получим b+c<b+d. То есть а+с<b+с<b+d. Из этого следует, что a+c<b+d. Если почленно сложить верные неравенства одного знака, то получится верное неравенство. Если a<b и c<d, где а,b,c,d – положительные числа, то ac<bd. Умножим обе части неравенства a<b на положительное число с, получим ac<bс. Умножив обе части неравенства c<d на положительное число b, получим bc<bd. Получим ac<bс<bd. Следовательно ac<bd. Если почленно перемножить верные неравенства одного знака, левые и правые части которых – положительные числа, то получится верное неравенство. Из этой теоремы следует, что Если числа а и b положительны и a<b, то an<bn, где n – натуральное число. Доказанные свойства используют для оценки суммы, разности, произведения и частного. Пример 6. Известно, что 15<x<16 и 2<y<3. Требуется оценить сумму х+у, разность х-у, произведение ху и частное х/у. Сложим почленно неравенства 15<x<16 и 2<y<3, получим 17<x+y<19. Оценим разность. Для этого умножим 2<y<3 почленно на (-1). Получим -3<-y<-2. Теперь сложим почленно неравенства 15<x<16 и -3<-y<-2. Получим 12<x-y<14. Оценим произведение ху. Перемножим почленно неравенства 15<x<16 и 2<y<3. Получим 30<xy<48. Оценим частное. Для этого сначала запишем неравенство для 1у. Получится 13<1y<12. В математике неравенство представляет собой математическое выражение, в котором стороны не равны. Если отношение делает неодинаковое сравнение между выражениями или двумя числами, то это известно как неравенство в математике. В этом примере знак равенства «=» в выражении заменяется любым из символов неравенства, например символом больше, чем (>), намного меньше, чем символ (<), больше или равно символу (≥), меньше или идентично символу (≤) или больше не совпадает с изображением (≠). Исключительными формами неравенств в математике являются полиномиальное неравенство, рациональное неравенство и абсолютное неравенство. Символы «<» и «>» обозначают строгие неравенства, а символы «≤» и «≥» обозначают слабые неравенства. Неравенство является строгим, если замена любых знаков «меньше» и «больше» на одинаковые знаки никоим образом не дает истинного выражения. Например, x<=y не является строгим, тогда как x Примером хорошо известного строгого неравенства является неравенство треугольника, которое утверждает, что в невырожденном треугольнике ABC выполняется следующее соотношение: al Неравенство, которое утверждает что если х является реальной величиной, то х2 >= ноль. Это неравенство не всегда является строгим, так как имеет случай равенства: пока x = ноль, x2 = 0. Математические выражения, содержащие наиболее эффективные ‘≤’ или ‘≥’, называются неравенствами слабости. Экземпляр: 2x + 8 ≤ 9 , 2x+ 4y ≥ 6 В приведенных выше примерах 2x + 8 ≤ 9 — это линейное неравенство с одной переменной, поскольку «x» — лучшая переменная, присутствующая в выражении. Кроме того 2x+ 4y ≥ 6, является линейным неравенством в переменных из-за того, что в выражении присутствуют переменные «x» и «y». Неравенство описывает отношение между двумя уникальными значениями. Обозначение x Обозначение x ≤ y означает, что x меньше или равно y, а обозначение x ≥ y означает, что x больше или равно y. Неравенства особенно полезны для решения проблем, связанных с минимальными или максимальными возможными значениями. Если каждую часть строгого или слабого неравенства умножить или разделить на одно и то же положительное число, то полученное неравенство будет истинным. Если каждую сторону строгого или слабого неравенства умножить или разделить на одно и то же отрицательное число, то направление полученного неравенства изменится. Строгие неравенства колеблются от обозначения а, не равного b, из-за этого, что а не равно b. Символ «не равно» теперь не говорит о том, что одно значение больше другого или даже о том, что их можно сравнивать по длине. В двух видах строгих неравенств a не совпадает с b. Обозначение x < y подразумевает, что x меньше y. Обозначение x > y подразумевает, что x больше y. Любые математические выражения, содержащие только символы < или >, называются строгими неравенствами. Принимая во внимание, что любые математические выражения, которые включают символы ≤ или ≥, как известно, являются слабыми неравенствами. Здесь мы подробно обсудили слабое неравенство и строгое неравенство. Мы также обсудили несколько важных фактов, связанных с слабым и строгим неравенством. Строгое неравенство — это отношение, которое содержит значения, когда они одного вида. Символы неравенства — это символы, которые используются для обозначения отношений неравенства. Вместе с другими математическими символами, такими как знак равенства (=), который указывает на отношение равенства, их иногда называют символами отношения. Строгие неравенства включают менее () символов, описанных ниже. Хотя знак равенства технически не является символом неравенства, он обсуждается вместе с символами неравенства, поскольку он включен как часть нестрогих неравенств, таких как больше или равно (≥) и меньше или равно (≤) . Знак равенства, обозначенный символом «=», указывает на равенство. Выражения по обе стороны от знака равенства либо имеют одинаковое значение, либо имеют одинаковое значение для определенных значений. Равенство (как и неравенство) является основой для решения алгебраических уравнений и неравенств. 2 = 2 5 + 3 = 1 + 7 x = x Все приведенные выше уравнения верны. В случаях, когда значения не равны, мы можем использовать ряд различных символов неравенства, например, знак не равно. Знак не равно, также называемый знаком не равно, представляет собой символ, указывающий на неравенство значений или выражений по обе стороны от символа. 12 ≠ 17 x 2 ≠ x 3 x — 7 ≠ x + 7 не говорите нам многого, кроме этого выражения по обе стороны от символа не равны. Существуют и другие, более конкретные отношения неравенства, подобные приведенным ниже. Знак «больше» — это символ, указывающий на строгое неравенство между двумя значениями; в частности, что значение слева от знака «больше» больше, чем значение справа. Больше — это строгое неравенство, означающее, что значение слева от знака должно быть больше значения справа; они не могут быть равны. Допустимы следующие варианты использования знака «больше»: 5 > 4 x 2 > x x + 12 > x + 7 Как правило, при заданном a > b a должно быть больше b. Таким образом, если бы b было равно 4, то а могло бы быть любым значением больше 4, но не 4. В случаях, когда а также может равняться 4, вместо этого мы использовали бы знак больше или равно. Знак больше или равно — это символ, указывающий, что значение в левой части символа больше или равно значению справа. Это также можно прочитать, поскольку значение в левой части как минимум равно значению в правой части. Учитывая a ≥ b a может равняться b, в отличие от знака больше. Это связано с тем, что ≥ не означает строгого неравенства. Это единственная разница между «>» и «≥». Знак «меньше» соответствует знаку «больше». Это указывает на строгое неравенство между двумя значениями; в частности, значение слева от знака «меньше» меньше значения справа. Ниже приведены допустимые варианты использования знака «меньше»: 3 х 2 4 х — 12 Как правило, учитывая а значение a должно быть меньше значения b. Они не могут быть равны. Если мы хотим обозначить, что a может быть меньше или равно b, мы должны вместо этого использовать знак меньше или равно (≤).
Неравенства знаки: Знаки неравенств — урок. Алгебра, 8 класс.
Неравенства. Знаки «»
по программе «Гармония»
Н.Б. Истоминой.2. Цели урока:
• Познакомить со знаками «< » «>»;
с понятием неравенство;
• Учиться сравнивать числа с
помощью знаков «< » «>».3. Неравенство
В математике вместо слова «больше»
между числами ставят знак «>», а вместо
слова «меньше» – знак «< ».
Неравенство
Уголок знака всегда указывает на
меньшее число.4. Работаем с предметами.
5. Сравни. Какой предмет больше?
><
Нажми на знак6. Сравни. Какой предмет меньше?
><
Нажми на знак
Сравни количество предметов на картинках.
Подбери правильный знак.
><
Нажми на знак
Сравни количество предметов на картинках.
Подбери правильный знак.
><
Нажми на знак
Сравни количество предметов на картинках.
Подбери правильный знак.
><
Нажми на знак
Сравни количество предметов на картинках.
Подбери правильный знак.
><
Нажми на знак
Сравни количество предметов на картинках.
Подбери правильный знак.
<>
Нажми на знак
Сравни количество предметов на картинках.
Подбери правильный знак.
><
Нажми на знак
Сравни количество предметов на картинках.
Подбери правильный знак.
><
Нажми на знак
Сравни количество предметов на картинках.
Подбери правильный знак.
><
Нажми на знак15. Работаем с числами.
16. Рассмотрите числовой луч.
<
>
0 1 2 3 4 5 6 7 8 9 10
Запомни: Чем ближе число к нулю, тем
оно меньше.
Соответственно, чем дальше число от
нуля, тем оно больше17. Выражения, в которых используются знаки «< » «>» называют – неравенствами.
Рассмотри запись. Замени слова «больше»
и «меньше» на знаки «<» «>»
5 меньше
5<6 6
7 больше
7>3 3
6 больше
6>0 0
3 меньше
3<7 7
2 меньше
2<9 9
9 больше
9>7 7
Выражения, в которых используются
знаки «< » «>» называют – неравенствами.18. Выбери числа больше 4
Нажми на число
0 1 2 3 4 5 6 7 8 9 10
Выбери числа больше 419. Для этого выбери числа меньше 5.
Подбери ключи к двери.
8 1 6 5 4 10 2 7 0 3 9
Нажми на
число
Для этого выбери числа меньше 5.
>
<
5
Выбери верный знак и запиши получившиеся неравенства.
20. Найди неверное неравенство на вагончиках паровозика и он продолжит свой путь.
4>2
Молодцы!
2<4
Нажми на
паровозик21. Чтобы узнать кто здесь живет найди числа меньше 6
Нажми на число
Сравни числа. Поставь
правильно знак
4
Нажми на знак
<
6
Сравни числа. Поставь
правильно знак
>
Нажми на знак
7
3
Сравни числа. Поставь
правильно знак
5
Нажми на знак
<
9
Сравни числа. Поставь
правильно знак
>
Нажми на знак
8
1
Сравни числа. Поставь
правильно знак
3
Нажми на знак
<
4
• Автор: Аксенова Нина Вадимовна,
учитель начальных классов МОУ «СОШ
№ 26» г. Энгельса Саратовской области
[email protected]
«Вы скачали эту презентацию на сайте — viki.rdf.ru»Числовые неравенства и их свойства. Сложение и умножение числовых неравенств 8 класс онлайн-подготовка на Ростелеком
Тема 8: Неравенства
Заметили ошибку? Сложение и умножение числовых неравенств.
Сложение и умножение числовых неравенств. Но есть универсальный способ сравнения, который охватывает все случаи.
Но есть универсальный способ сравнения, который охватывает все случаи. Значит, и их сумма является отрицательным числом. Следовательно, а<c.
Значит, и их сумма является отрицательным числом. Следовательно, а<c.


 Теперь перемножим почленно 15<x<16 и 13<1y<12. Получим 5<xy<8.
Теперь перемножим почленно 15<x<16 и 13<1y<12. Получим 5<xy<8.Заметили ошибку?
Расскажите нам об ошибке, и мы ее исправим. Простое примечание о символах неравенства

Строгое неравенство
Неравенство слабости

Некоторые моменты, связанные со строгим и слабым неравенством

Символ строгого неравенства меньше чем символ Подобно тому, как уравнения используют знак равенства =, чтобы показать, что значения равны, неравенства используют знаки, чтобы показать, что значения не идентичны, и объяснить их взаимосвязь. Символами строгого неравенства являются
< и >. Для оценки шкалы значений существуют типы отношений:
Для оценки шкалы значений существуют типы отношений: Заключение
Символы неравенства

Знак равенства: =
Знак не равно: ≠

Знак «больше»: >

Знак «больше» или «равно»: ≥
Знак меньше:

Корень из х 3 4: Решите уравнение: √x−3= 4. — Школьные Знания.com
СУНЦ УрФУ
Расписание
Электронный журнал
Поступающим
Олимпиады, турниры, конкурсы
Планы работы
Подготовительные курсы
Новости:
27.05.2023
Астрономы СУНЦ наблюдают
Демонстрационные наблюдения являются важной частью учебной программы по астрономии.
25.05.2023
Прозвенел последний звонок!
В СУНЦ УрФУ 23 мая для 237 выпускников прозвенел последний звонок.
21.05.2023
Два диплома на театральном фестивале
Литературный театр СУНЦ с успехом принял участие в региональном фестивале-конкурсе школьных театров «СоБытие».
15.05.2023
Проект из «магии и кирпичей»
Литературный театр СУНЦ показал спектакль «История одного рассказчика».
15.05.2023
«Милосердие сильнее мести»
Состоялась премьера спектакля литературного театра СУНЦ.
12.05.2023
И снова май, цветы, салют и слёзы
В преддверии Дня Победы в СУНЦ состоялся концерт, подготовленный учащимися и педагогами.
Больше новостей
Видеогалерея:
Дом в котором (Литературный театр СУНЦ УрФУ, май 2023)
День Победы (04.05.2023)
Игра в Шекспира (Литературный театр СУНЦ УрФУ, апрель 2023)
Больше видео
О нас:
Специализированный учебно-научный центр (СУНЦ) — структурное подразделение ФГАОУ ВО «УрФУ имени первого Президента России Б.Н. Ельцина», созданное в 1990 году как нетиповое структурное подразделение вуза, осуществляющее углубленное дифференцированное обучение по программам основного общего и среднего общего образования. Всего в России 10 СУНЦев. До мая 2011 года СУНЦ работал в составе Уральского государственного университета имени А. М. Горького (УрГУ).
В настоящее время СУНЦ имеет в своем составе 8 кафедр, укомплектованных профессорско-преподавательским составом УрФУ и учителями. Обучение производится по авторским программам, разработанным в соответствии с федеральными государственными образовательными стандартами; в составе СУНЦ — 8–11 классы различных профилей.
Иногородние обучающиеся проживают в уютном общежитии.
Прием производится в 8, 9, 10 и 11 классы. Работают подготовительные курсы.
Подробнее о правилах приема в СУНЦ можно узнать в отделе конкурсного отбора
по телефону +7 343 367-82-22 и в разделе нашего сайта «Поступающим».
Как нас найти:
Данилы Зверева ул., 30, Екатеринбург. N56°52´4˝ E60°39´16˝
Проезд:
- автобусами № 48, 52, 81 до остановки «Фирма Авангард»;
- автобусами № 28, 58 до остановки «Данилы Зверева», далее 7 минут пешком по улице Данилы Зверева;
- троллейбусом № 18 до остановки «Данилы Зверева», далее 14 минут пешком по улицам Сулимова, Данилы Зверева;
- троллейбусами № 4 до остановки «Сулимова», № 19, 32 до остановки «Боровая», далее 15 минут пешком по улицам Боровая, Вилонова, Данилы Зверева.
| 1 | Найдите количество возможностей | 7 выбрать 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 | Найдите количество возможностей | 8 выбрать 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 | Найдите количество возможностей | 5 выбрать 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 | Найдите количество возможностей | 4 выбрать 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 | Найдите количество возможностей | 8 выбрать 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | Найдите количество возможностей | 10 выбрать 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | Найдите количество возможностей | 7 выбрать 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | Найдите количество возможностей | 6 выбрать 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | Найдите количество возможностей | 9 выбрать 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | Найдите количество возможностей | 3 выбрать 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11 | Найдите количество возможностей | 6 выбрать 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12 | Найдите количество возможностей | 5 выбрать 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13 | Найдите количество возможностей | 7 переставить 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14 | Найдите количество возможностей | 7 выбрать 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15 | Найдите количество возможностей | 10 выбрать 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16 | Найдите количество возможностей | 10 выбрать 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 17 | Найдите количество возможностей | 13 выбрать 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18 | Найдите количество возможностей | 3 выбрать 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19 | Найдите количество возможностей | 4 выбрать 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20 | Найдите количество возможностей | 4 выбрать 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 21 | Найдите количество возможностей | 5 выбрать 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 22 | Найдите количество возможностей | 6 переставить 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 23 | Найдите количество возможностей | 8 выбрать 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 24 | Найдите количество возможностей | 9переставить 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 25 | Найдите количество возможностей | 13 выбрать 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 26 | Найдите количество возможностей | 12 выбрать 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 27 | Найдите количество возможностей | 12 выбрать 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 28 | Найдите количество возможностей | 12 выбрать 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 29 | Найдите количество возможностей | 9 выбрать 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 30 | Найдите количество возможностей | 9 выбрать 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 31 | Найдите количество возможностей | 7 выбрать 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 32 | Найдите количество возможностей | 6 переставить 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 33 | Найдите количество возможностей | 8 переставить 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 34 | Найдите количество возможностей | 8 переставить 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 35 | Найдите количество возможностей | 7 переставить 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 36 | Найдите количество возможностей | 52 выбрать 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 37 | Найдите количество возможностей | 5 переставить 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 38 | Найдите количество возможностей | 12 выбрать 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 39 | Найдите количество возможностей | 3 выбрать 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 40 | Найдите количество возможностей | 11 выбрать 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 41 | Найдите количество возможностей | 10 выбрать 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 42 | Найдите количество возможностей | 15 выбрать 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 43 | Найдите количество возможностей | 52 выбрать 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 44 | Найдите количество возможностей | 9 выбрать 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 45 | Найдите количество возможностей | 9 переставить 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 46 | Найдите количество возможностей | 7 переставить 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 47 | Найдите количество возможностей | 7 переставить 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 48 | Найдите количество возможностей | 11 выбрать 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 49 | Найдите количество возможностей | 11 выбрать 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 50 | Найдите количество возможностей | 11 выбрать 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 51 | Найдите количество возможностей | 10 переставить 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 52 | Найдите количество возможностей | 5 выбрать 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 53 | Найдите количество возможностей | 6 выбрать 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 54 | Найдите количество возможностей | 8 переставить 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 55 | Найдите количество возможностей | 8 выбрать 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 56 | Найдите количество возможностей | 13 выбрать 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 57 | Оценить | и | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 58 | Найти любое уравнение, перпендикулярное прямой | -7x-5y=7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 59 | Найдите количество возможностей | 13 выбрать 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 60 | Найдите количество возможностей | 10 переставить 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 61 | Найдите количество возможностей | 10 переставить 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 62 | Найдите количество возможностей | 10 выбрать 7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 63 | Найдите количество возможностей | 20 выбрать 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 64 | Найдите количество возможностей | 6 переставить 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 65 | Найдите количество возможностей | 5 переставить 4 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 66 | Найдите количество возможностей | 6 выбрать 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 67 | Найдите количество возможностей | 52 выбрать 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 68 | Найдите количество возможностей | 4 выбрать 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 69 | Найдите количество возможностей | 9переставить 7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 70 | Найдите количество возможностей | 6 выбрать 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 71 | Найдите количество возможностей | 5 переставить 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 72 | Найдите количество возможностей | 5 переставить 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 73 | Найдите количество возможностей | 6 выбрать 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 74 | Найдите количество возможностей | 7 выбрать 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 75 | Найдите количество возможностей | 8 переставить 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 76 | Найдите количество возможностей | 7 переставить 7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 77 | Найдите количество возможностей | 9 переставить 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 78 | Найдите количество возможностей | 2 переставить 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 79 | Найдите количество возможностей | 10 выбрать 8 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 80 | Найдите количество возможностей | 12 выбрать 7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 81 | Найдите количество возможностей | 15 выбрать 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 82 | Найдите обратное | [[1,0,1],[2,-2,-1],[3,0,0]] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 83 | Найти диапазон | 1/4x-7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 84 | Найдите количество возможностей | 10 переставить 7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 85 | Найдите количество возможностей | 12 выбрать 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 86 | Найдите количество возможностей | 2 выбрать 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 87 | Найдите количество возможностей | 30 выбрать 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 88 | Найдите количество возможностей | 9 выбрать 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 89 | Найдите количество возможностей | 8 переставить 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 90 | Найдите количество возможностей | 7 выбрать 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 91 | Найдите количество возможностей | 6 перестановка 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 92 | Найдите количество возможностей | 4 переставить 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 93 | Найдите количество возможностей | 4 переставить 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 94 | Найдите количество возможностей | 3 переставить 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 95 | Найдите количество возможностей | 46 выбрать 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 96 | Найдите количество возможностей | 5 переставить 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 97 | Найдите количество возможностей | 52 выбрать 7 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 98 | Найдите количество возможностей | 52 переставить 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 99 | Найдите количество возможностей | 93 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | Решить для ? | cos(x)=1/2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | Найти x | sin(x)=-1/2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | Преобразование градусов в радианы | 225 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | Решить для ? | cos(x)=(квадратный корень из 2)/2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | Найти x | cos(x)=(квадратный корень из 3)/2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11 | Найти x | sin(x)=(квадратный корень из 3)/2 | 92=9 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14 | Преобразование градусов в радианы | 120 градусов | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 15 | Преобразование градусов в радианы | 180 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16 | Найти точное значение | желтовато-коричневый(195) | 92-4|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 38 | Найти точное значение | грех(255) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 39 | Оценить | лог база 27 из 36 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 40 | Преобразовать из радианов в градусы | 2 шт. 18 разделить на 1: 18 разделить на 1 равно и я не знаю
Деление столбикомПаскалина — школьный онлайн калькулятор С остатком {{_dividend}} : {{_divisor}} = {{response.dividend}} : {{response.divisor}} ={{response.result}}{{_dividend}} : {{_divisor}} = {{response.result}} (остаток {{response.remainder}})Проверка умножением{{response.resultNormal}} × {{_divisor}} = {{_dividend}}
{{response.resultNormal}} × {{_divisor}} + {{response.remainder}} = {{response.resultNormal.mul(_divisor)}} + {{response.remainder}}= {{_dividend}} ОПИСАНИЕ Калькулятор деление столбиком онлайн поможет Вам быстро и правильно поделить натуральные числа. РУКОВОДСТВО Введите в соответствующие поля натуральные числа и нажмите кнопку «Рассчитать» ТЕОРИЯ ДЕЛЕНИЕ Действие деление определяют с помощью действия умножения. Например, разделить число 54 на 18 — значит найти такое число, которое при умножении на 18 дает число 54. Имеем: 18 * 3 = 54, поэтому 54 : 18 = 3. Вообще, для натуральных чисел a, b и c равенство a : b = c верно, если верно равенство b * c = a. Рассмотрим еще несколько примеров: 156 : 12 = 13, так как 12 * 13 = 156; 345 : 15 = 23, так как 15 * 23 = 345. В равенство a : b = c число a называют делимым, число b — делителем, число c и запись a : b — частным. Частное a : b показывает, во сколько раз число a больше числа b или во сколько раз число b меньше числа a. Можно ли например, вычислить частное 12 : 0? Если предположить, что такое частное существует и равно некоторому числу c, то должно выполнять равенство 0 * c = 12, но на самом деле 0 * c = 0. Следовательно, вычислить частное 12 : 0 нельзя. А можно ли вычислить частное 0 : 0? Пусть 0 : 0 = c. Тогда 0 * c = 0. Такое равенство справедливо при любом c. А это означает, что значением числового выражения 0 : 0 может быть любое число, то есть такое частное вычислить нельзя. Вывод: на нуль делить нельзя. Вместе с тем, поскольку a * 0 = 0, то для любого натурального числа a верно равенство: 0 : a = 0 Также для любого натурального числа a верны равенства: a : a = 1 a : 1 = a Эти равенства легко проверить с помощью умножения. АЛГОРИТМ ДЕЛЕНИЯ СТОЛБИКОМ Рассмотрим алгоритм деления столбиком на примере: 18231 : 3, где: 18231 — делимое; 3 — делитель. 1. Запишем делимое и делитель с помощью уголка следующим образом: 2. Определим первое неполное делимое. Для этого будем сравнивать слева направо цифры делимого с делителем, до тех пор, пока неполное делимое не станет больше делителя. Первая цифра слева у делимого это 1. Сравним ее с делителем: 1 < 3 — цифра делимого меньше делителя, поэтому 1 не может быть первым неполным делимым. В этом случае добавим к первой цифре делимого следующую за ней, получим 18. Сравним ее с делителем: 18 > 3 — значит 18 — первое неполное делимое. 3. Разделим первое неполное делимое на делитель: 18 : 3 = 6 (остаток 0), запишем найденное частное 6 под делителем (под линией), получим: 4. Проверяем деление умножением, для этого умножаем найденную цифру частного на делитель: 6 * 3 = 18, записываем произведение под первым неполным делимым и находим их разность, получаем: 5. Сравниваем разность с делителем: 0 < 3, значит, деление первого неполного делимого мы выполнили правильно и первая цифра частного верна. 6. Определим второе неполное делимое. Для этого снесем следующую, нами не использованную цифру делимого, вниз к найденной разности, получим: Сравним полученное число с делителем: 2 < 3, значит 2, не может быть неполным делимым. Снесем вниз следующую цифру, но при этом запишем в частное 0, так как мы сносим уже вторую цифру. Важно! Если при нахождении неполного делимого мы сносим вниз более одной цифры, то при сносе каждой цифры после первой в частное необходимо записать 0. Получаем: Сравним полученное число с делителем: 23 > 3, значит 23 — второе неполное делимое. 7. Разделим второе неполное делимое на делитель: 23 : 3 = 7 (остаток 2), запишем найденное неполное частное 7 под делителем (под линией), получим: 8. Проверяем деление умножением, для этого умножаем найденную цифру частного на делитель: 7 * 3 = 21, записываем произведение под вторым неполным делимым и находим их разность, получаем: 9. 2 < 3, значит, деление второго неполного делимого мы выполнили правильно и первая цифра частного верна. Важно! Если бы разность оказалась больше делимого, то это бы означало, что второе неполное делимое мы поделили неверно. 10. Определим третье неполное делимое. Для этого снесем следующую, нами не использованную цифру делимого, вниз к найденной разности, получим: Сравним полученное число с делителем: 21 > 3, значит 21 — третье неполное делимое. 11. Разделим третье неполное делимое на делитель: 21 : 3 = 7 (остаток 0), запишем найденное частное 7 под делителем (под линией), получим: 12. Проверяем деление умножением, для этого умножаем найденную цифру частного на делитель: 7 * 3 = 21, записываем произведение под третьим неполным делимым и находим их разность, получаем: 13. Сравниваем разность с делителем: 0 < 3, значит, деление третьего неполного делимого мы выполнили правильно и первая цифра частного верна. 14. Так как, мы использовали все цифры делимого (сносить вниз больше нечего), значит деление завершено. Получаем: Таким образом, итоговый результат будет выглядеть следующим образом: 18231 : 3 = 6077 Мы рассмотрели пример деления столбиком на однозначное число. Аналогично выполняется деление на многозначное число. Проверка деления Проверить деление можно следующими способами: 1) Умножением, для этого необходимо частное умножить на делитель. Если в результате получится делимое, значит, деление было выполнено верно. 6077 * 3 = 18231 2) Делением, для этого необходимо делимое разделить на частное. Если в результате получится делитель, значит, деление было выполнено верно. 18231 : 6077 = 3 ДЕЛЕНИЕ С ОСТАТКОМ Как разделить число 20 на число 6? Ответ на этот вопрос можно получить, решив следующую задачу. Скорее всего, каждому достанется по 3 конфеты, но при этом 2 конфеты останутся. Такое распределение конфет иллюстрирует следующее равенство: 20 = 6 * 3 + 2. Заметим, что 3 — это наибольшее число, произведение которого на делитель 6 меньше делимого 20. В записи 20 = 6 * 3 + 2 число 3 называют неполным частным, а число 2 — остатком. Также говорят, что при делении числа 20 на число 6 получили неполное частное, равное 3, и остаток — 2. Заметит, что остаток 2 меньше делителя 6. Конфеты можно было разделить и другим способом, например, дать каждому по 2 конфеты и оставить 8. Ведь 20 = 6 * 2 + 8. Но здесь число 2 не является неполным частным, а число 8 — остатком. Остаток всегда меньше делителя. Разделим число 189 на число 13: Поскольку 7 < 13, то мы вынуждены прекратить процесс деления. Это означает, что при делении числа 189 на число 13 получили неполное частное, равное 14, и остаток — 7. Этот пример иллюстрирует такое правило. Чтобы найти делимое, надо делитель умножить на неполное частное и прибавить остаток. В буквенном виде это правило записывают так: a = bq + r, где: a — делимое, b — делитель, q — неполное частное, r — остаток, r < b. Рассмотрим равенство 21 = 7 * 3. Его можно переписать так: 21 = 7 * 3 + 0. Говорят, что при делении числа 21 на число 7 остаток равен нулю. Также можно сказать, что число 21 делится нацело на число 7. Проверка деления с остатком: Чтобы проверить деление с остатком, нужно неполное частное умножить на делитель и к произведению прибавить остаток. Если в результате получится делимое, значит, деление с остатком было выполнено верно. 13 * 14 + 7 = 182 + 7 = 189 Как рассчитать 1/18 разделить на 1/3 (Что такое 1/18 ÷ 1/3?) Вы ищете, как разделить 1/18 на 1/3? В этом очень простом руководстве мы точно научим вас, что такое 1/18 ÷ 1/3, и пошагово проведем вас через процесс деления дробей. Прежде чем мы углубимся в вычисления, давайте вспомним некоторые основы дробей. Число над разделительной чертой называется числителем, а число над разделительной чертой называется знаменателем. Хотите быстро научиться или освежить в памяти, как делить дроби, посмотрите это очень быстрое и информативное видео прямо сейчас! Для деления дробей также полезно знать, что первая дробь (1/18) называется делимым , а вторая дробь (1/3) называется делителем . Поставим рядом 1/18 и 1/3, чтобы их было лучше видно: 1 / 18 / 1 / 3 Вот действительно быстрый способ разделить дроби. В делителе (вторая дробь) поменять местами числитель и знаменатель . Это известно как , обратное , и в основном это означает обратную дробь. Когда мы найдем обратную величину, мы также должны изменить знак деления на знак умножения: 1 / 18 Икс 3 / 1 После того, как вы перевернули вторую дробь и изменили символ деления на умножение, мы можем перемножить числители вместе и знаменатели вместе, и мы получим наше решение: 1 x 3 / 18 х 1 «=» 3 / 18 Готово! Теперь вы точно знаете, как вычислить 1/18 — 1/3. 1/6 Вот небольшой бонусный расчет, который поможет вам легко определить десятичный формат дроби, которую мы рассчитали. Все, что вам нужно сделать, это разделить числитель на знаменатель, и вы можете преобразовать любую дробь в десятичную: 3 / 18 «=» 0,1667 Процитируйте, дайте ссылку или ссылку на эту страницуЕсли вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большую услугу и используйте приведенный ниже инструмент, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали. Мы очень ценим вашу поддержку!
Примеры предустановленного списка дробейНиже приведены ссылки на некоторые предустановленные вычисления, которые обычно ищут: Что такое 1/2, деленное на 1/2? Сколько 1/2 разделить на 1/3? Сколько 1/2 разделить на 1/4? Сколько 1/2 разделить на 1/5? Сколько 1/2 разделить на 1/6? Сколько 1/2 разделить на 1/7? Сколько 1/2 разделить на 2/3? Сколько 1/2 разделить на 2/4? Сколько 1/2 разделить на 2/5? Сколько 1/2 разделить на 2/6? Сколько 1/2 разделить на 2/7? Сколько 1/2 разделить на 3/4? Сколько 1/2 разделить на 3/5? Сколько 1/2 разделить на 3/6? Сколько 1/2 разделить на 3/7? Сколько 1/2 разделить на 4/5? Сколько 1/2 разделить на 4/6? Сколько 1/2 разделить на 4/7? Сколько 1/2 разделить на 5/6? Сколько 1/2 разделить на 5/7? Сколько 1/2 разделить на 6/7? Сколько 1/3 разделить на 1/2? Сколько 1/3 разделить на 1/3? Сколько 1/3 разделить на 1/4? Сколько 1/3 разделить на 1/5? Сколько 1/3 разделить на 1/6? Сколько 1/3 разделить на 1/7? Сколько 1/3 разделить на 2/3? Сколько 1/3 разделить на 2/4? Сколько 1/3 разделить на 2/5? Сколько 1/3 разделить на 2/6? Сколько 1/3 разделить на 2/7? Сколько 1/3 разделить на 3/4? Сколько 1/3 разделить на 3/5? Сколько 1/3 разделить на 3/6? Сколько 1/3 разделить на 3/7? Сколько 1/3 разделить на 4/5? Сколько 1/3 разделить на 4/6? Сколько 1/3 разделить на 4/7? Сколько 1/3 разделить на 5/6? Сколько 1/3 разделить на 5/7? Сколько 1/3 разделить на 6/7? Сколько 1/4 разделить на 1/2? Сколько 1/4 разделить на 1/3? Сколько 1/4 разделить на 1/4? Сколько 1/4 разделить на 1/5? Сколько 1/4 разделить на 1/6? Сколько 1/4 разделить на 1/7? Сколько 1/4 разделить на 2/3? Сколько 1/4 разделить на 2/4? Сколько 1/4 разделить на 2/5? Сколько 1/4 разделить на 2/6? Сколько 1/4 разделить на 2/7? Сколько 1/4 разделить на 3/4? Сколько 1/4 разделить на 3/5? Сколько 1/4 разделить на 3/6? Сколько 1/4 разделить на 3/7? Сколько 1/4 разделить на 4/5? Сколько 1/4 разделить на 4/6? Сколько 1/4 разделить на 4/7? Сколько 1/4 разделить на 5/6? Сколько 1/4 разделить на 5/7? Сколько 1/4 разделить на 6/7? Сколько 1/5 разделить на 1/2? Сколько 1/5 разделить на 1/3? Сколько 1/5 разделить на 1/4? Сколько 1/5 разделить на 1/5? Сколько 1/5 разделить на 1/6? Сколько 1/5 разделить на 1/7? Сколько 1/5 разделить на 2/3? Сколько 1/5 разделить на 2/4? Сколько 1/5 разделить на 2/5? Сколько 1/5 разделить на 2/6? Сколько 1/5 разделить на 2/7? Сколько 1/5 разделить на 3/4? Сколько 1/5 разделить на 3/5? Сколько 1/5 разделить на 3/6? Сколько 1/5 разделить на 3/7? Сколько 1/5 разделить на 4/5? Сколько 1/5 разделить на 4/6? Сколько 1/5 разделить на 4/7? Сколько 1/5 разделить на 5/6? Сколько 1/5 разделить на 5/7? Сколько 1/5 разделить на 6/7? Сколько 1/6 разделить на 1/2? Сколько 1/6 разделить на 1/3? Сколько 1/6 разделить на 1/4? Сколько 1/6 разделить на 1/5? Сколько 1/6 разделить на 1/6? Сколько 1/6 разделить на 1/7? Сколько 1/6 разделить на 2/3? Сколько 1/6 разделить на 2/4? Сколько 1/6 разделить на 2/5? Сколько 1/6 разделить на 2/6? Сколько 1/6 разделить на 2/7? Сколько 1/6 разделить на 3/4? Сколько 1/6 разделить на 3/5? Сколько 1/6 разделить на 3/6? Сколько 1/6 разделить на 3/7? Сколько 1/6 разделить на 4/5? Сколько 1/6 разделить на 4/6? Сколько 1/6 разделить на 4/7? Сколько 1/6 разделить на 5/6? Сколько 1/6 разделить на 5/7? Сколько 1/6 разделить на 6/7? Сколько 1/7 разделить на 1/2? Сколько 1/7 разделить на 1/3? Сколько 1/7 разделить на 1/4? Сколько 1/7 разделить на 1/5? Сколько 1/7 разделить на 1/6? Сколько 1/7 разделить на 1/7? Сколько 1/7 разделить на 2/3? Сколько 1/7 разделить на 2/4? Сколько 1/7 разделить на 2/5? Сколько 1/7 разделить на 2/6? Сколько 1/7 разделить на 2/7? Сколько 1/7 разделить на 3/4? Сколько 1/7 разделить на 3/5? Сколько 1/7 разделить на 3/6? Сколько 1/7 разделить на 3/7? Сколько 1/7 разделить на 4/5? Сколько 1/7 разделить на 4/6? Сколько 1/7 разделить на 4/7? Сколько 1/7 разделить на 5/6? Сколько 1/7 разделить на 5/7? Сколько 1/7 разделить на 6/7? Сколько 2/3 разделить на 1/2? Сколько 2/3 разделить на 1/3? Сколько 2/3 разделить на 1/4? Сколько 2/3 разделить на 1/5? Сколько 2/3 разделить на 1/6? Сколько 2/3 разделить на 1/7? Сколько 2/3 разделить на 2/3? Сколько 2/3 разделить на 2/4? Сколько 2/3 разделить на 2/5? Сколько 2/3 разделить на 2/6? Сколько 2/3 разделить на 2/7? Сколько 2/3 разделить на 3/4? Сколько 2/3 разделить на 3/5? Сколько 2/3 разделить на 3/6? Сколько 2/3 разделить на 3/7? Сколько 2/3 разделить на 4/5? Сколько 2/3 разделить на 4/6? Сколько 2/3 разделить на 4/7? Сколько 2/3 разделить на 5/6? Сколько 2/3 разделить на 5/7? Сколько 2/3 разделить на 6/7? Сколько 2/4 разделить на 1/2? Сколько 2/4 разделить на 1/3? Сколько 2/4 разделить на 1/4? Сколько 2/4 разделить на 1/5? Сколько 2/4 разделить на 1/6? Сколько 2/4 разделить на 1/7? Сколько 2/4 разделить на 2/3? Сколько 2/4 разделить на 2/4? Сколько 2/4 разделить на 2/5? Сколько 2/4 разделить на 2/6? Сколько 2/4 разделить на 2/7? Сколько 2/4 разделить на 3/4? Сколько 2/4 разделить на 3/5? Сколько 2/4 разделить на 3/6? Сколько 2/4 разделить на 3/7? Сколько 2/4 разделить на 4/5? Сколько 2/4 разделить на 4/6? Сколько 2/4 разделить на 4/7? Сколько 2/4 разделить на 5/6? Сколько 2/4 разделить на 5/7? Сколько 2/4 разделить на 6/7? Сколько 2/5 разделить на 1/2? Сколько 2/5 разделить на 1/3? Сколько 2/5 разделить на 1/4? Сколько 2/5 разделить на 1/5? Сколько 2/5 разделить на 1/6? Сколько 2/5 разделить на 1/7? Сколько 2/5 разделить на 2/3? Сколько 2/5 разделить на 2/4? Сколько 2/5 разделить на 2/5? Сколько 2/5 разделить на 2/6? Сколько 2/5 разделить на 2/7? Сколько 2/5 разделить на 3/4? Сколько 2/5 разделить на 3/5? Сколько 2/5 разделить на 3/6? Сколько 2/5 разделить на 3/7? Сколько 2/5 разделить на 4/5? Сколько 2/5 разделить на 4/6? Сколько 2/5 разделить на 4/7? Сколько 2/5 разделить на 5/6? Сколько 2/5 разделить на 5/7? Сколько 2/5 разделить на 6/7? Сколько 2/6 разделить на 1/2? Сколько 2/6 разделить на 1/3? Сколько 2/6 разделить на 1/4? Сколько 2/6 разделить на 1/5? Сколько 2/6 разделить на 1/6? Сколько 2/6 разделить на 1/7? Сколько 2/6 разделить на 2/3? Сколько 2/6 разделить на 2/4? Сколько 2/6 разделить на 2/5? Сколько 2/6 разделить на 2/6? Сколько 2/6 разделить на 2/7? Сколько 2/6 разделить на 3/4? Сколько 2/6 разделить на 3/5? Сколько 2/6 разделить на 3/6? Сколько 2/6 разделить на 3/7? Сколько 2/6 разделить на 4/5? Сколько 2/6 разделить на 4/6? Сколько 2/6 разделить на 4/7? Сколько 2/6 разделить на 5/6? Сколько 2/6 разделить на 5/7? Сколько 2/6 разделить на 6/7? Сколько 2/7 разделить на 1/2? Сколько 2/7 разделить на 1/3? Сколько 2/7 разделить на 1/4? Сколько 2/7 разделить на 1/5? Сколько 2/7 разделить на 1/6? Сколько 2/7 разделить на 1/7? Сколько 2/7 разделить на 2/3? Сколько 2/7 разделить на 2/4? Сколько 2/7 разделить на 2/5? Сколько 2/7 разделить на 2/6? Сколько 2/7 разделить на 2/7? Сколько 2/7 разделить на 3/4? Сколько 2/7 разделить на 3/5? Сколько 2/7 разделить на 3/6? Сколько 2/7 разделить на 3/7? Сколько 2/7 разделить на 4/5? Сколько 2/7 разделить на 4/6? Сколько 2/7 разделить на 4/7? Сколько 2/7 разделить на 5/6? Сколько 2/7 разделить на 5/7? Сколько 2/7 разделить на 6/7? Сколько 3/4 разделить на 1/2? Сколько 3/4 разделить на 1/3? Сколько 3/4 разделить на 1/4? Сколько 3/4 разделить на 1/5? Сколько 3/4 разделить на 1/6? Сколько 3/4 разделить на 1/7? Сколько 3/4 разделить на 2/3? Сколько 3/4 разделить на 2/4? Сколько 3/4 разделить на 2/5? Сколько 3/4 разделить на 2/6? Сколько 3/4 разделить на 2/7? Сколько 3/4 разделить на 3/4? Сколько 3/4 разделить на 3/5? Сколько 3/4 разделить на 3/6? Сколько 3/4 разделить на 3/7? Сколько 3/4 разделить на 4/5? Сколько 3/4 разделить на 4/6? Сколько 3/4 разделить на 4/7? Сколько 3/4 разделить на 5/6? Сколько 3/4 разделить на 5/7? Сколько 3/4 разделить на 6/7? Сколько 3/5 разделить на 1/2? Сколько 3/5 разделить на 1/3? Сколько 3/5 разделить на 1/4? Сколько 3/5 разделить на 1/5? Сколько 3/5 разделить на 1/6? Сколько 3/5 разделить на 1/7? Сколько 3/5 разделить на 2/3? Сколько 3/5 разделить на 2/4? Сколько 3/5 разделить на 2/5? Сколько 3/5 разделить на 2/6? Сколько 3/5 разделить на 2/7? Сколько 3/5 разделить на 3/4? Сколько 3/5 разделить на 3/5? Сколько 3/5 разделить на 3/6? Сколько 3/5 разделить на 3/7? Сколько 3/5 разделить на 4/5? Сколько 3/5 разделить на 4/6? Сколько 3/5 разделить на 4/7? Сколько 3/5 разделить на 5/6? Сколько 3/5 разделить на 5/7? Сколько 3/5 разделить на 6/7? Сколько 3/6 разделить на 1/2? Сколько 3/6 разделить на 1/3? Сколько 3/6 разделить на 1/4? Сколько 3/6 разделить на 1/5? Сколько 3/6 разделить на 1/6? Сколько 3/6 разделить на 1/7? Сколько 3/6 разделить на 2/3? Сколько 3/6 разделить на 2/4? Сколько 3/6 разделить на 2/5? Сколько 3/6 разделить на 2/6? Сколько 3/6 разделить на 2/7? Сколько 3/6 разделить на 3/4? Сколько 3/6 разделить на 3/5? Сколько 3/6 разделить на 3/6? Сколько 3/6 разделить на 3/7? Сколько 3/6 разделить на 4/5? Сколько 3/6 разделить на 4/6? Сколько 3/6 разделить на 4/7? Сколько 3/6 разделить на 5/6? Сколько 3/6 разделить на 5/7? Сколько 3/6 разделить на 6/7? Сколько 3/7 разделить на 1/2? Сколько 3/7 разделить на 1/3? Сколько 3/7 разделить на 1/4? Сколько 3/7 разделить на 1/5? Сколько 3/7 разделить на 1/6? Сколько 3/7 разделить на 1/7? Сколько 3/7 разделить на 2/3? Сколько 3/7 разделить на 2/4? Сколько 3/7 разделить на 2/5? Сколько 3/7 разделить на 2/6? Сколько 3/7 разделить на 2/7? Сколько 3/7 разделить на 3/4? Сколько 3/7 разделить на 3/5? Сколько 3/7 разделить на 3/6? Сколько 3/7 разделить на 3/7? Сколько 3/7 разделить на 4/5? Сколько 3/7 разделить на 4/6? Сколько 3/7 разделить на 4/7? Сколько 3/7 разделить на 5/6? Сколько 3/7 разделить на 5/7? Сколько 3/7 разделить на 6/7? Сколько 4/5 разделить на 1/2? Сколько 4/5 разделить на 1/3? Сколько 4/5 разделить на 1/4? Сколько 4/5 разделить на 1/5? Сколько 4/5 разделить на 1/6? Сколько 4/5 разделить на 1/7? Сколько 4/5 разделить на 2/3? Сколько 4/5 разделить на 2/4? Сколько 4/5 разделить на 2/5? Сколько 4/5 разделить на 2/6? Сколько 4/5 разделить на 2/7? Сколько 4/5 разделить на 3/4? Сколько 4/5 разделить на 3/5? Сколько 4/5 разделить на 3/6? Сколько 4/5 разделить на 3/7? Сколько 4/5 разделить на 4/5? Сколько 4/5 разделить на 4/6? Сколько 4/5 разделить на 4/7? Сколько 4/5 разделить на 5/6? Сколько 4/5 разделить на 5/7? Сколько 4/5 разделить на 6/7? Сколько 4/6 разделить на 1/2? Сколько 4/6 разделить на 1/3? Сколько 4/6 разделить на 1/4? Сколько 4/6 разделить на 1/5? Сколько 4/6 разделить на 1/6? Сколько 4/6 разделить на 1/7? Сколько 4/6 разделить на 2/3? Сколько 4/6 разделить на 2/4? Сколько 4/6 разделить на 2/5? Сколько 4/6 разделить на 2/6? Сколько 4/6 разделить на 2/7? Сколько 4/6 разделить на 3/4? Сколько 4/6 разделить на 3/5? Сколько 4/6 разделить на 3/6? Сколько 4/6 разделить на 3/7? Сколько 4/6 разделить на 4/5? Сколько 4/6 разделить на 4/6? Сколько 4/6 разделить на 4/7? Сколько 4/6 разделить на 5/6? Сколько 4/6 разделить на 5/7? Сколько 4/6 разделить на 6/7? Сколько 4/7 разделить на 1/2? Сколько 4/7 разделить на 1/3? Сколько 4/7 разделить на 1/4? Сколько 4/7 разделить на 1/5? Сколько 4/7 разделить на 1/6? Сколько 4/7 разделить на 1/7? Сколько 4/7 разделить на 2/3? Сколько 4/7 разделить на 2/4? Сколько 4/7 разделить на 2/5? Сколько 4/7 разделить на 2/6? Сколько 4/7 разделить на 2/7? Сколько 4/7 разделить на 3/4? Сколько 4/7 разделить на 3/5? Сколько 4/7 разделить на 3/6? Сколько 4/7 разделить на 3/7? Сколько 4/7 разделить на 4/5? Сколько 4/7 разделить на 4/6? Сколько 4/7 разделить на 4/7? Сколько 4/7 разделить на 5/6? Сколько 4/7 разделить на 5/7? Сколько 4/7 разделить на 6/7? Сколько 5/6 разделить на 1/2? Сколько 5/6 разделить на 1/3? Сколько 5/6 разделить на 1/4? Сколько 5/6 разделить на 1/5? Сколько 5/6 разделить на 1/6? Сколько 5/6 разделить на 1/7? Сколько 5/6 разделить на 2/3? Сколько 5/6 разделить на 2/4? Сколько 5/6 разделить на 2/5? Сколько 5/6 разделить на 2/6? Сколько 5/6 разделить на 2/7? Сколько 5/6 разделить на 3/4? Сколько 5/6 разделить на 3/5? Сколько 5/6 разделить на 3/6? Сколько 5/6 разделить на 3/7? Сколько 5/6 разделить на 4/5? Сколько 5/6 разделить на 4/6? Сколько 5/6 разделить на 4/7? Сколько 5/6 разделить на 5/6? Сколько 5/6 разделить на 5/7? Сколько 5/6 разделить на 6/7? Сколько 5/7 разделить на 1/2? Сколько 5/7 разделить на 1/3? Сколько 5/7 разделить на 1/4? Сколько 5/7 разделить на 1/5? Сколько 5/7 разделить на 1/6? Сколько 5/7 разделить на 1/7? Сколько 5/7 разделить на 2/3? Сколько 5/7 разделить на 2/4? Сколько 5/7 разделить на 2/5? Сколько 5/7 разделить на 2/6? Сколько 5/7 разделить на 2/7? Сколько 5/7 разделить на 3/4? Сколько 5/7 разделить на 3/5? Сколько 5/7 разделить на 3/6? Сколько 5/7 разделить на 3/7? Сколько 5/7 разделить на 4/5? Сколько 5/7 разделить на 4/6? Сколько 5/7 разделить на 4/7? Сколько 5/7 разделить на 5/6? Сколько 5/7 разделить на 5/7? Сколько 5/7 разделить на 6/7? Сколько 6/7 разделить на 1/2? Сколько 6/7 разделить на 1/3? Сколько 6/7 разделить на 1/4? Сколько 6/7 разделить на 1/5? Сколько 6/7 разделить на 1/6? Сколько 6/7 разделить на 1/7? Сколько 6/7 разделить на 2/3? Сколько 6/7 разделить на 2/4? Сколько 6/7 разделить на 2/5? Сколько 6/7 разделить на 2/6? Сколько 6/7 разделить на 2/7? Сколько 6/7 разделить на 3/4? Сколько 6/7 разделить на 3/5? Сколько 6/7 разделить на 3/6? Сколько 6/7 разделить на 3/7? Сколько 6/7 разделить на 4/5? Сколько 6/7 разделить на 4/6? Сколько 6/7 разделить на 4/7? Сколько 6/7 разделить на 5/6? Сколько 6/7 разделить на 5/7? Сколько 6/7 разделить на 6/7? Сколько 6 разделить на 1/18 (6 ÷ 1/18?) Если у вас есть целое число 6 и вы хотите разделить его на дробь 1/18, то вы нашли идеальный артикль. Хотите быстро научиться или показать учащимся, как делить целое число на дробь? Включи это очень быстрое и веселое видео прямо сейчас! Теперь запомните дети, число над дробью называется числителем, а число под ним называется знаменателем. Мы будем использовать эти термины на протяжении всего руководства. Довольно простые вещи, но всегда приятно быстро подвести итоги. Давайте поставим целое число и дробь рядом, чтобы мы могли визуализировать проблему, которую пытаемся решить: 6 ÷ 1 / 18 Уловка для вычисления числа 6, деленного на 1/18, похожа на метод, который мы используем для деления дроби на целое число. Все, что нам нужно сделать здесь, это умножить целое число на числитель и сделать это число новым числителем . Тогда старый числитель становится новым знаменателем. 6 x 18 / 1 «=» 108 / 1 Итак, ответ на вопрос «сколько будет 6 разделить на 1/18?» есть: 108 / 1 Иногда после вычисления ответа мы можем упростить полученную дробь до меньших членов. В этом примере 108/1 уже находится в самой низкой возможной форме. Если вы дочитали до этого места, значит, вам очень нравятся дроби и деление на них целых чисел. Надеюсь, вам было легко следовать этому простому руководству, и теперь вы можете идти дальше и делить больше целых чисел на столько дробей, сколько душе угодно. Преобразовать 6, деленное на 1/18, в десятичное числоПоследнее небольшое вычисление, прежде чем вы пойдете. Обычно вы хотите выразить свой результат в виде десятичной дроби, и для этого все, что вам нужно сделать, это разделить числитель на знаменатель: 108 / 1 «=» 108 Процитируйте, дайте ссылку или ссылку на эту страницу Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большую услугу и используйте приведенный ниже инструмент, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали. Онлайн калькулятор десятичных дробей вычитание: Онлайн калькулятор. Сложение, вычитание, умножение и деление столбикомСложение и вычитание в столбикПаскалина — школьный онлайн калькулятор
Проверка вычитанием: Проверка сложением: ОПИСАНИЕ Данный калькулятор складывает и вычитает в столбик, как натуральные числа, так и десятичные дроби. РУКОВОДСТВО Введите в соответствующие поля натуральные числа, либо десятичные дроби и нажмите кнопку «Рассчитать» ТЕОРИЯ Сложение в столбик натуральных чисел Чтобы сложить в столбик натуральные числа, нужно: 1. 2. Сложить одинаковые разряды чисел, начиная с единиц (с правого края), затем десятки, сотни и так далее. Результаты сложения каждого разряда записываем ниже, в тот же столбец, где стоят те же разряды складываемых чисел. То есть результат сложения единиц записываем под единицами, десятков под десятками, сотен под сотнями и так далее. Обратим внимание, что если в результате сложения получается двузначное число, то в результат ниже мы записываем праву цифру, а левую прибавим к результату сложения цифр следующего разряда. 3. После сложения всех разрядов складываемых чисел и записи результатов, мы получим итоговую сумму. Например: Сложим столбиком числа 1286 и 132. 1. Запишем числа друг под другом, выравнивая их по правому краю: 2. Начнем складывать одинаковые разряды, начиная с правого края, и записывать результат сложения ниже в тот же столбик, что и складываемые разряды: Складываем единицы: 6 + 2 = 8. Получаем: Складываем десятки: 8 + 3 = 11. Так как в результате сложения получилось двузначное число, то записываем только правую цифру 1, а левую цифру запоминаем и прибавим ее к результату сложения цифр следующего разряда, в данном случае сотен. Получаем: Складываем сотни: 2 + 1 = 3 и прибавляем единицу, которую запомнили при сложении десятков: 3 + 1 = 4. Получаем: Складываем тысячи: 1 + 0 = 1. Записываем единицу под разрядом тысяч и получаем итоговый результат: Таким образом, 1286 + 132 = 1418 Вычитание в столбик натуральных чисел Чтобы вычесть в столбик натуральные числа, нужно: 1. 2. Произвести вычитание одинаковых разрядов чисел, начиная с единиц (с правого края), затем десятки, сотни и так далее, причем нужно вычитать из цифр верхнего числа (уменьшаемого) цифры нижнего числа (вычитаемого). Результаты вычитания каждого разряда нужно записывать ниже, в тот же столбец, где стоят те же разряды вычитаемых чисел. То есть результат вычитания единиц нужно записать под единицами, десятков под десятками, сотен под сотнями и так далее. В случае, если цифра верхнего числа меньше цифры нижнего числа, то для того, чтобы произвести вычитание необходимо занять единицу из цифры следующего разряда уменьшаемого числа. 3. После вычитания всех разрядов и записи результатов, мы получим итоговую разность. Например: Вычтем столбиком числа 1038 и 956. 1. Запишем числа друг под другом, выравнивая их по правому краю, причем большее число ставим сверху: 2. Начнем вычитать одинаковые разряды, начиная с правого края, и записывать результат вычитания ниже в тот же столбик, что и складываемые разряды: Вычитаем единицы: 8 — 6 = 2. Получаем: Вычитаем десятки: так как 3 меньше 5, то занимаем единицу из следующего разряда (сотен) верхнего числа. Следующий разряд равен 0, а единицу из нуля мы занять не можем. В этом случае занимаем единицу из следующего разряда тысяч для разряда сотен. И получаем, что в разряде сотен уже не 0, а 10. Вычитаем: 13 — 5 = 8 Чтобы запомнить! Над разрядами, из которых занимали единицы, ставим точки. Получаем: Вычитаем сотни. В разряде сотен стоит 0, но мы помним, что в разряд сотен занимали единицу из разряда тысяч и получили 10 сотен, а затем из разряда сотен занимали единицу для разрядов десятков. Таким образом, в разряде сотен осталось 9 сотен. Тогда: 9 — 9 = 0, получаем: Вычитаем тысячи. В разряде тысяч стоит 1, но помним, что мы занимали единицу из разряда тысяч для разряда сотен. Тогда: 0 — 0 = 0, получаем: Важно! Если в результате вычитания слева стоит нуль, либо несколько нулей, то они не записываются. Таким образом, итоговый результат вычитания будет выглядеть следующим образом: 1038 — 956 = 82 Проверка результатов Результат сложения можно проверить вычитанием: 1) Из суммы вычесть первое слагаемое. 2) Из суммы вычесть второе слагаемое. Если разность будет равна первому слагаемому, значит сложение было выполнено верно. Результат вычитания можно проверить как сложением, так и вычитанием: 1) Проверка сложением. К разности прибавить вычитаемое. Если сумма будет равна уменьшаемому, значит вычитание было выполнено верно. 2) Проверка вычитанием. Из уменьшаемого вычесть разность. Если результат будет равен вычитаемому, значит вычитание было выполнено верно. как вычитать десятичные дробиКак вычитать десятичные дроби!? На самом деле есть несколько вариантов. Как вычесть одну десятичную дробь из другой десятичной дроби… , как вычитать обыкновенную дробь из десятичной, как из натурального числа вычесть десятичную дробьНо лучше всего вычитать десятичные дроби на калькуляторе.  . И… мы делаем калькулятор, на котором будет можно будет проделывать все математические действия не только с десятичными дробями, но и с обыкновенными… . И… мы делаем калькулятор, на котором будет можно будет проделывать все математические действия не только с десятичными дробями, но и с обыкновенными…Вычитание десятичных дробей.Чтобы вычесть одну десятичную дробь от другой можно воспользоваться калькулятором. Если вам требуется разобраться, как они отнимаются, то продолжим…Самая большая проблема в вычитании десятичных дробей. Что мы немного начинаем путаться, когда пытаемся отнять одну десятично дробь от другой, и нас смущает запятая или точка (как хотите…)НО! Если ваши десятичные дроби превратить в целые числа, то проблема… как-то сразу улетучивается. И потом просто отнимаем столбиком… Давайте рассмотрим вариант номер один…Для примера возьмем самое …самое простое… от одной десятой отнять одну сотую. Обе стороны умножим на 100, чтобы оба числа стали не дробями, получим 10 и 1, вычитаем получаем 9, теперь делим на 100 и получим 9 сотых0. Вычитание десятичных дробей столбиком… Kак вычитать обыкновенную дробь из десятичнойДля того, чтобы вычесть десятичную дробь от обыкновенной, или обыкновенную дробь отнять от десятичной, то нужно, либо десятичную дробь привести к обыкновенной, либо обыкновенную дробь привести в десятичной.Кстати, в обыкновенном калькуляторе такой возможности нет… , (когда пишется эта статья, данная идея, пока только идея… но мы хотим её добавить) Для понимания как прибавить десятичную к обыкновений дроби нам нужен пример…И желательно не совсем простой, давайте вычтем из 5/6 десятичную дробь 0.5 Нам нужно перевести десятичную дробь 0.5 в обычную = 5/10. Далее нам нужен общий знаменатель, чтобы можно было продолжить… Не будем сейчас заниматься подбором наименьшего кратного множителя, просто перемножим противостоящие числа на знаменатели.  Первую дробь умножим на 10, а вторую на 6 – получим 50/60 — 30/60, вычитаем числитель = 20/60, далее нужно сократить… наибольший делитель 20… делим оба числа на 20 = 1/356- 0.5 => 5060-510=>5060-3060=>2060=>13 Kак из натурального числа вычесть десятичную дробьДля иллюстрации. Как отнимать от натурального числа десятичную дробь – этот вариант ничем вообще не отличается от самого первого случая вычитания дробей десятичных друг от друга.И не буду заново все повторять это подробно описано – как отнимать столбиком. Единственное. Что нужно сделать… это натуральное, целое число превратить в десятичную дробь! Как это сделать!? После целого числа нужно поставить точку и добавить столько нулей … сколько требуется…(нули красного цвета) И … самый простой пример… отнимем от двух 1 сотую. К двум добавляем точку и два нуля. По точке выравниваем целое и десятичную дробь и отнимаем, как я уже сказал точно так же.  Как обычное отнимание числе в столбик… только потом ставим точку Как обычное отнимание числе в столбик… только потом ставим точкуНаписать что-нибудь…как вычитать десятичные дроби , как вычесть десятичную дробь из десятичной дроби , как из числа вычесть десятичную дробь , как вычитать десятичные дроби из числа , как из целого вычесть десятичную дробь , как вычитать из целого числа десятичную дробь , как из целого числа вычесть десятичную дробь , как вычитать десятичные дроби столбиком , как вычесть из десятичной дроби обыкновенную дробь , как вычитать обыкновенную дробь из десятичной , правила как вычесть десятичные дроби , правило как вычитать десятичные дроби , как из натурального числа вычесть десятичную дробь , как из обычной дроби вычесть десятичную , как сложить и вычесть десятичные дроби , как из смешанной дроби вычесть десятичную дробь , сравнивают вычитают складывают десятичные дроби , как вычесть десятичную дробь онлайн , как вычитать отрицательные десятичные дроби ,Калькулятор вычитания дробей | Онлайн-инструмент для поиска разности дробей В математике дробь — это значение, определяющее часть целого. Действия по вычитанию дробей аналогичны сложению дробей. Следуйте процедуре, указанной для одинаковых знаменателей и разных знаменателей. Вычитание дробей с одинаковыми знаменателями Для одинаковых дробей значение числителя можно вычесть напрямую. Если вы вычитаете дроби с одинаковыми знаменателями, вы можете просто вычесть числители и оставить знаменатели одинаковыми. Пример Вычесть 2/5 и 1/5? Решение: Даны входные данные 2/5 и 1/5 Поскольку знаменатели одинаковы, просто вычтите числители, и вы получите следующий результат (2/5 )- (1/5)=1/5 Вычитание дробей с разными знаменателями Вычитание дробей с разными знаменателями не так просто. Для тех, у которых разные знаменатели, следуйте приведенным ниже рекомендациям
Пример Вычесть 2/3 и 1/5? Решение: Даны входные значения 2/3 и 1/5 Поскольку знаменатели не совпадают, найдите НОК знаменателей. Насколько нам известно, НОК 3 и 5 равно 15. 3 входит в число 15 5 раз умножается верхнее и нижнее 2/3 на 5 5 входит в 15 3 раза умножается верхнее и нижнее 1/5 на 3 Здесь вы найдете несколько простых советов и поможет научиться вычитанию дробей. Они следующие
1. Как вычитать дроби с разными знаменателями? Для вычитания дробей с разными знаменателями возьмите НОК знаменателей. 2. Как вычитать дроби с одинаковыми знаменателями? Чтобы вычесть дроби с одинаковыми знаменателями, просто вычтите числители и оставьте знаменатели одинаковыми. 3. Где я могу найти решенные примеры по вычитанию дробей в деталях? Вы можете получить пошаговую работу по вычитанию дробей, подробно описанную на нашей странице. 4. Как легко вычитать дроби? Вы можете легко вычитать дроби, используя Калькулятор вычитания дробей. Вы можете получить разницу дробей за меньшее время. Калькулятор вычитания дробейGENERATE WORK сообщить об этом объявленииGENERATE WORK Вычитание дробей — работа с шагами 105использует две правильные или неправильные дроби, $\frac{a}{b }$ и $\frac{c}{d}$ для $b,d\ne0$ и вычисляет их разность. Это онлайн-инструмент для нахождения разницы в простейшей форме двух правильных или неправильных дробей. Необходимо выполнить следующие шаги:
Результат: Простейшая дробь. Правило вычитания дробей:
Как вычитать дроби? Результатом вычитания чисел является \underline{разность}. Разница двух чисел зависит от их порядка, т.е.
вычитание является некоммутативной операцией. Например, $\frac 53-\frac 13\ne \frac 13-\frac 53$.
Подобно коммутативному свойству, ассоциативное свойство не выполняется для вычитания чисел.
$$\frac{a}{b}-\frac{c}{b}=\frac{a-c}{b},\quad \mbox{for}\;b\ne0$ $
$$\frac{a}{b}-\frac{c}{d}=\frac{a\times \frac{LCM(b,d)}{b }-c\times \frac{LCM(b,d)}{d}}{LCM(b,d)},\quad \mbox{for}\;b,d\ne0$$ Если $LCM( b,d)=b\times d$, то предыдущая формула принимает вид$$\frac{a}{b}-\frac{c}{d}=\frac{a\times d-c\times b}{b\times d},\quad \mbox{for}\;b ,d\ne0$$ Например, найдем разницу между $\frac 76$ и $\frac 3 4$. Поскольку $LCM(6,4)=12$, то$$\frac 76-\frac 3 4=\frac {7\times 2-3\times 3}{12}=\frac {8}{12 }$$ Чтобы записать разницу в простейшей форме, найдите GCF числителя и знаменателя разницы. $GFC(8,12)=4$, поэтому при делении числителя и знаменателя разницы на 4 окончательный результат равен$$\frac{8\div4}{12\div 4}=\frac 23$$ Аналогичное рассмотрение можно применить при вычитании алгебраических дробей.Работа по вычитанию дробей с шагами показывает полный пошаговый расчет для нахождения разности двух дробей $\frac{7}{6}$ и $\frac{3}{4}$ с использованием правила вычитания дробей.  Для любых других дробей просто укажите две правильные или неправильные дроби и нажмите кнопку СОЗДАТЬ РАБОТУ. Учащиеся начальной школы могут использовать этот калькулятор вычитания, как или в отличие от дробей, для выполнения работы, проверки результатов вычитания двух или более чисел, полученных вручную, или эффективного решения домашних задач. Для любых других дробей просто укажите две правильные или неправильные дроби и нажмите кнопку СОЗДАТЬ РАБОТУ. Учащиеся начальной школы могут использовать этот калькулятор вычитания, как или в отличие от дробей, для выполнения работы, проверки результатов вычитания двух или более чисел, полученных вручную, или эффективного решения домашних задач.Реальные задачи с использованием вычитания дробей Поскольку во многих реальных ситуациях приходится иметь дело с дробями, вычитание дробей очень полезно. Вычитание дробей можно представить моделью площади. Например, найдем разность $\frac 2 5-\frac 16$.  Поскольку обе дроби имеют общий знаменатель, мы можем найти разницу между первой дробью $\frac{12}{30}$ и второй дробью $\frac {5}{30}$. Если вычесть прямоугольники на первом изображении с прямоугольником на втором изображении, мы получим $7$ общих прямоугольников. Таким образом, разница составляет $\frac {7}{30}.$ Поскольку обе дроби имеют общий знаменатель, мы можем найти разницу между первой дробью $\frac{12}{30}$ и второй дробью $\frac {5}{30}$. Если вычесть прямоугольники на первом изображении с прямоугольником на втором изображении, мы получим $7$ общих прямоугольников. Таким образом, разница составляет $\frac {7}{30}.$Практические задачи на вычитание дробей Практическая задача 1: Практическая задача 2: Калькулятор вычитания дробей, формулы, примеры вычислений (работа с шагами), задачи из реальной жизни и практические задачи будут очень полезны учащимся начальной школы (K-12 образование), чтобы понять вычитание двух чисел, представленных в виде дробей. Используя эту концепцию, они могут решать сложные алгебраические задачи и уравнения, а также задачи из реальной жизни. Сколько в натрии нейтронов: «Сколько в натрии электронов, протонов, нейтронов?» — Яндекс КьюРеактор на быстрых нейтронах
Число нейтронов в атоме натрия равно A) 10B) 11C) 13D) 12Ответ Verified 302. Количество протонов равно атомному номеру (Z) элемента. Сумма числа протонов и числа нейтронов равна массовому числу (А) элемента. Полный пошаговый ответ: Дополнительная информация: Примечание : Для решения таких вопросов учащиеся должны хорошо знать периодическую таблицу. Изучение периодической таблицы необходимо для получения хороших результатов по таким вопросам, особенно на конкурсных экзаменах. Дата последнего обновления: 02 июня 2023 • Всего просмотров: 302.7k • Просмотров сегодня: 7.60k Недавно обновленных страниц 900 03 Расчет изменения энтропии при преобразовании химии класса 11 JEE_Main Закон, сформулированный доктором Нернстом, представляет собой Первый закон термодинамики Химический класс 11 JEE_Main Для реакции при rm0rm0rmC и нормальном давлении Химический класс 11 JEE_Main Двигатель, работающий между rm15rm0rm0rmC и rm2rm5rm0rmC Химический класс 11 JEE_Main Для реакции rm2Clg в rmCrmlrm2rmg знаки химического класса 11 JEE_Main Изменение энтальпии перехода жидкой воды в химический класс 11 JEE_Main Рассчитать изменение энтропии, связанное с преобразованием химического класса 11 JEE_Main 900 02 Закон, сформулированный Д-р Нернст — это Первый закон термодинамики. Химический класс 11 JEE_Main Химический класс 11 JEE_MainДля реакции при rm0rm0rmC и нормальном давлении.0003 Для реакции rm2Clg в rmCrmlrm2rmg признаки 11 класса химии JEE_Main Изменение энтальпии перехода жидкой воды 11 класса химии JEE_Main Актуальные сомнения 9000 3 Из чего состоит элемент? Франкенштейн из натрия содержит подсказкиПотребовалось около 20 лет, чтобы подтвердить ядерные пределы фтора и неона, потому что эксперименты очень сложны, говорит физик Артемис Спайроу из Мичиганского государственного университета, который не участвовал в работе. Чтобы доказать, что частица является самой тяжелой в своем роде, недостаточно просто ее создать. Вы должны показать, что ничего тяжелее не существует. «Это самая сложная часть, — говорит Спайроу. «Если вы этого не видите, значит, этого не существует? Или это потому, что ваш эксперимент был недостаточно хорош?» После столкновения ядер кальция с металлической мишенью физики используют машину длиной с футбольное поле (на фото), которая сортирует обломки на наличие интересных частиц с помощью магнитов. «Количество фтора-31, которое они произвели, заставило мои глаза вылезти из орбит», — говорит физик Кейт Джонс из Университета Теннесси, ссылаясь на цифру в статье, в которой исследователи указали, что они создали 4000 ядер. «Это много фтора-31. Я был как, эй. С помощью этих экспериментов физики надеются лучше понять границу между возможным и невозможным в природе. В качестве дополнительного бонуса измерения могут помочь астрофизикам изучать экстремальные условия в космосе, такие как нейтронные звезды, говорит Спайроу. Нейтронная звезда — это коллапс ядра мертвой звезды, и оно настолько плотное, что его чайная ложка весит около миллиарда тонн. Экстремальные условия нейтронной звезды могут привести к образованию причудливых короткоживущих ядер, которые Кубо создает в своей лаборатории. Эти переходные частицы играют роль в загадочных взрывах рентгеновского излучения, которые наблюдались на поверхности некоторых нейтронных звезд, говорит Джонс. Названные рентгеновскими сверхвспышками, они происходят, когда гравитация нейтронной звезды всасывает вещество из обычной звезды, вокруг которой она вращается. Астрофизики могут использовать эти новые лабораторные измерения для создания более точных моделей таких рентгеновских взрывов. Как определить область значения функции по формуле: виды, свойства, примеры решения задачФункции — что это, определение и ответФункция – это соответствие между двумя множествами, при котором каждому элементу одного множества соответствует единственный элемент второго множества. СУТЬ ФУНКЦИИ: Чтобы понять суть функции, можно рассмотреть формулу периметра квадрата. Мы знаем, что периметр квадрата находится так: \(P = 4a\), где a – это сторона квадрата. Мы можем сами подставить любую длину стороны квадрата, чтобы получить соответствующий ей периметр. Если между двумя какими-либо величинами есть такое соответствие, то между ними существует функция. Рассмотрим это соответствие на примере квадрата: Если \(а = 1\), то \(Р = 1 \bullet 4 = 4\) и так далее. Мы говорим, что чтобы получить периметр квадрата, нужно его сторону умножить на 4. Это будет верно для любой стороны квадрата, которую мы сами зададим. ОПРЕДЕЛЕНИЯ, СВЯЗАННЫЕ С ФУНКЦИЕЙ: Величина, которую мы подставляем в формулу, называется переменной величиной или аргументом.Та величина, которая получается в итоге преобразования переменной, называется зависимой величиной или значением функции.Закон (или принцип) по которому меняется переменная, превращаясь в зависимую, называется функцией.В нашем примере a – это переменная, P – это зависимая, а действие ( \(\bullet 4\)) – функция. В общем виде переменную, зависимую и функцию записывают следующим образом: \(y = f(x)\) Она означает, что чтобы получить y, нужно преобразовать x по функции f. Такую запись можно читать как «\(y\ \)равен \(f\) от\(\ x\)». При этом не только сама закономерность, по которой меняется \(x\), называется функцией. Для краткости функцией называют всё выражение, в котором есть зависимость. Далее, когда мы будем говорить о функции, мы будем иметь в виду целое выражение, подобно формуле площади квадрата, а не только действие преобразования аргумента. Также каждая функция имеет свою область значений и область определения. Область определения – это множество чисел, которые могут являться аргументами данной функции.Область значений – это множество чисел, которые могут являться значением функции. Например, в случае с периметром квадрата мы можем точно сказать, что сторона квадрата должна быть положительным числом. Потому что длина не может иметь отрицательное значение и не может быть равна 0, ведь в таком случае, квадрата не получится. А если аргумент функции должен быть положительным, то при умножении положительного числа на 4 получится тоже только положительное число. Таким образом область значений и областью определений в данном примере являются множества положительных чисел. СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ: Описать суть функции можно по-разному. Также можно по-разному описать зависимость, чтобы какую-либо функцию задать. Рассмотрим различные способы задания одной и той же функции.
«У Даши есть яблоки. При этом у её старшего брата Вани всегда на два яблока больше.» Чтобы словесно задать функцию, нужно описать, как изменяется аргумент. В данном случае в описании ситуации уже словесно задана функция словами «у Вани всегда на два яблока больше, чем у Даши». Эти слова определяют конкретную зависимость количества яблок у Вани от количества яблок у Даши.
Посмотрим на таблицу аргументов и зависимых от них величин. Можем заметить, что каждый y больше своего x на 2. Эта зависимость есть у каждой из пар «аргумент – значение функции».
Этот способ мы рассматривали ранее через формулу периметра квадрата. Рассмотрим более общий вид функции, заданной формулой – через \(x\ \)и \(y\): \(y = x + 2\) По формуле мы видим, что каждый y на 2 больше, чем соответствующий ему x. Пример №1 Найдите значение функции: \(y = \frac{x\ –\ 2}{5}\) при \(x = 2;\ x = 27\). 1. Чем являются значение и аргумент функции мы знаем, это y и x. А вот именно функцией является более сложное действие – «вычесть 2, разделить на 5». Найдем значение этой функции при \(x = 2\): \(y = f(x) = \frac{x\ –\ 2}{5}\) \(f(2) = \frac{2\ –\ 2}{5} = \frac{0}{5} = 0\) Таким образом мы узнали, что аргументу 2 соответствует значение функции 0. 2. Аналогично найдем значение функции при \(x = 27\): \(f(27) = \frac{27\ –\ 2}{5} = \frac{25}{5} = 5\) Значит аргументу 27 соответствует значение функции 5. Ответ: 0; 5. ГРАФИК ФУНКЦИИ: Любую функцию можно изобразить на координатной плоскости. Если координатная плоскость состоит из точек, каждая из которой имеет две координаты, то одна координата будет равна аргументу, а вторая координата значению функция, который ей соответствует. Из этого следует, что точка принадлежит графику некоторой функции, если её координаты равны аргументу и соответствующему ей значению функции. Пример №2: Постройте график функции \(y = x + 2.\) 1. Для построения графиков удобнее всего задавать функцию таблицей. Выберем несколько любых аргументов и найдем для них значения функции: 2. У нас есть координаты для четырех точек – А\((–2;\ 0)\), В(\(0;\ 2),\) С\((3;\ 5)\), D\((6;\ 8).\) Построим их на координатной плоскости и соединим. Полученный рисунок будет являться графиком функции \(y = x + 2:\) График функции не обязательно должен быть прямой линией. 1. Выберем любые аргументы и найдем им соответствующие значения функции. Запишем их в таблице: 2. Построим и соединим на координатной плоскости получившиеся точки: На данном графике мы видим что одно значение функции может быть у двух аргументов, например точки В\((–2;\ 0)\) и F(\(2;\ 0)\) или С\((–1;\ –3)\) и Е(\(1;\ –3)\) имеют разные аргументы, но одинаковые значения функции. Это не противоречит определению функции. Для разных аргументов могут совпадать значения функции Но при этом, НЕ может быть такой ситуации, когда одному аргументу соответствуют несколько значений функций. Так нарушается принцип соответствия и рисунок на координатной плоскости перестает быть графиком функций по определению Для одного аргумента НЕ может существовать несколько значений функции Например, вот такой график нельзя назвать графиком функций, потому что одному аргументу соответствует несколько значений: Пример №4: Определите без построения графика, принадлежат ли точки А\((2;\ 10)\) и В(\(–3;\ 6)\) графику функций \(y\ = \ 8\ + \ x\)? 1. 2. Определим принадлежность точки А к графику данной функции. Для этого подставим координату её абсциссы в функцию и найдем соответствующее ей значение: \({y = 8 + x }{y\left( 2 \right) = 8 + 2 = 10}\) Мы получили некую точку графика с координатами \((2;\ 10)\). Такие же координаты и у точки А Получается, что точка А\((2;\ 10)\) – это точка графика функции. Значит А принадлежит графику. 3. Аналогично определим принадлежность точки В к графику функции. \({y = 8 + x }{y(–3) = 8\ –\ 3 = 5}\) Мы получили точку графика \((–3;\ 5),\) а у точки В координаты \((–3;\ 6)\), значит тока В НЕ принадлежит графику. Ответ: да; нет. Как находится область определения функции заданной формулойСтатьи › Находится Как найти область определения функции по формуле? Если a — положительное целое число, то область определения функции есть множество действительных чисел: (−∞, +∞).
Как обозначается область определения функции fМножество всех значений, которые принимает аргумент функции, называется областью определения функции: D(f) т. Как найти область определения функции y 4x 8Так как в формуле функции y = 4x — 8 нет ни деления, ни корня, значит допустимы любые значения переменной х. Ответ: D(f) = (-∞; +∞). Что считают областью определения функции Если она задана формулойЕсли функция задана формулой, то считают, что область определения состоит из всех значений переменной, при которых эта формула имеет смысл. Графиком функции называется множество всех точек на координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции. Как найти область определения функции y sin2xY = sin 2x. Синус — тригонометрическая функция, непрерывная, значит, область определения функции — любое число. Функция независимо от своего аргумента принимает значения, находящиеся в промежутке от -1 до 1. Как найти область определения функции sinИтак, Областью определения функций y = sin x и y = cos x является множество R всех действительных чисел. Как найти область определения и значения функцииОбластью определения функции являются все значения Х, на которых существует функция. Иными словами, те Х, которые можно подставить в уравнение функции и получить в результате Y. Область значения функции определяется значениями, которое принимает Y на всей своей области определения. Что такое область определения функцииОбласть определения — множество, на котором задаётся функция. В каждой точке этого множества значение функции должно быть определено. Что такое F В функцииФункция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой. Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f. Что такое область определения функции 9 классОбласть определения —- множество всех значений аргумента (переменной x). Область значений —- множество всех значений функции (переменной y). Как найти область определения функции y 3x 7Функции y=3x-7 — является линейной функцией. Областью определения функции y=3x-7 является множество всех действительных чисел, то есть при любом значении х — функция будет существовать. Ответ: область определения функции y=3x-7 — множество всех действительных чисел. Как найти область определения функции с двумя переменнымиОбластью определения функции двух переменных называется множество всех пар, для которых существует значение. Графически область определения представляет собой всю плоскость либо её часть. Так, областью определения функции является вся координатная плоскость — по той причине, что для любой точки существует значение. Какое число не входит в область определения функции заданной формулойОтветы1. Областью определения функции называют все допустимые значения аргумента (то есть х). Недопустимыми считаются такие значения х, при подстановке которых в формулу функции получается деление на ноль или извлечение корня из отрицательного числа. Что понимают под областью определения функции заданной аналитическиПри аналитическом способе задания функции, т. е. с помощью некоторого аналитического выражения, под областью определения функции понимают множество всех значений независимых переменных, при которых это выражение имеет смысл. Как найти значение функцииЧтобы найти значение функции при заданном значении аргумента, надо значение аргумента подставить в уравнение функции вместо x и вычислить ее значение. Как найти область определения квадратичной функцииГрафиком квадратичной функции является парабола, вершина которой находится в точке (− b 2 a; − b 2 − 4 a c 4 a). Область определения функции — вся числовая прямая: D (f) = R = (− ∞; ∞). Область значений функции зависит от знака коэффициента. Что такое область определения уравненияОбластью определения уравнения f (x) = g (x) называют множество всех тех значений переменной x, при которых и выражение f (x), и выражение g (x) имеют смысл. Что такое функция в графикеПонятие графика функции График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу. Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x. Что такое область определения функции своими словамиОбласть определения — множество, на котором задаётся функция. В каждой точке этого множества значение функции должно быть определено. Как найти область определения функции гиперболыОбласть определения — любое число, кроме нуля. Область значения — любое число, кроме нуля. Функция не имеет наибольших или наименьших значений.
pine script — Функция должна вызываться при каждом расчете для согласованности, вывод консоли?спросил Изменено 6 месяцев назад Просмотрено 11 тысяч раз Недавно мой скрипт начал показывать эти строки в консоли, когда я добавляю на график или сохраняю. "Функция 'anonym_function_10' должна вызываться при каждом вычислении для согласованности. Рекомендуется извлекать вызов из тернарного оператора или из области видимости." «Функция« anonym_function_11 »должна вызываться при каждом расчете для согласованности. Рекомендуется извлекать вызов из тернарного оператора или из области». Нужна помощь, чтобы понять это, скомпрометирована ли точность кода, или это может стать возможной проблемой в будущем? Каким было бы решение, чтобы исправить это? // @версия=4 f_top_fractal(src) => src[4] < src[2] и src[3] < src[2] и src[2] > src[1] и src[2] > src[0] f_bot_fractal(src) => src[4] > src[2] и src[3] > src[2] и src[2] < src[1] и src[2] < src[0] f_fractalize(src) => f_top_fractal(src) ? 1: f_bot_fractal(источник)? -1 : 0 Последняя строка вызывает вопросы…
Если ваш код похож на этот, вы, вероятно, получите эту ошибку. мав = na(xem[1]) ? sma(src, длина): (xem[1] / длина)` попробуй так. _sma= sma(src, len) mav = na(xem[1]) ? _sma : (xem[1] / длина)3 Функции, использующие переменные серии, должны выполняться на каждом баре, чтобы у функции была полная история серии; иначе индексы серий внутри функции будут неверными. Поэтому Pine выдает предупреждение для таких функций, когда они встроены в условное выражение, что может привести к тому, что они не будут выполняться на каждом такте. Чтобы решить эту проблему, либо выполните функцию в глобальном масштабе, вне любых условных выражений, либо переопределите функцию, чтобы она принимала значения отдельных рядов в качестве аргументов функции. Последнее решение будет работать в случае OP. См. объяснение в разделе «Выполнение функций Pine и исторический контекст внутри функциональных блоков» по адресу https://www.tradingview.com/pine-script-docs/en/v4/language/Functions_and_annotations.html f_fractalize(_src) => f_top_fractal(_src) ? 1: f_bot_fractal(_src)? -1 : 0
Ниже альтернатива
f_fractalize(_src)=>
bool rhign = f_top_fractal(_src)
логический rlow = f_bot_fractal(_src)
если прав
1
иначе, если rlow
-1
еще
0
1Зарегистрируйтесь или войдите в системуЗарегистрируйтесь с помощью Google Зарегистрироваться через Facebook Зарегистрируйтесь, используя электронную почту и парольОпубликовать как гостьЭлектронная почтаТребуется, но не отображается Опубликовать как гостьЭлектронная почтаТребуется, но не отображается Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания и подтверждаете, что прочитали и поняли нашу политику конфиденциальности и кодекс поведения. R функция add1, аргумент области для ссылки на все переменныеЗадавать вопрос спросил Изменено 9 лет, 6 месяцев назад Просмотрено 2к раз Часть R Language CollectiveПри использовании функции add1 для учета новых переменных я хотел бы сослаться на все переменные (либо в каком-то фрейме данных, либо в глобальной среде), но я не могу понять, как использовать для этого аргумент области видимости. Я знаю, что могу использовать это так X = data.frame(replicate(4,rnorm(20))) ; у = rn(20) lm1 = lm(y ~ 1) out = add1(lm1, область видимости= ~X$X1 + X$X2 + X$X3) , но я не хочу вручную записывать каждую переменную. Как я уже видел в других вопросах, я знаю . символ не будет работать, но я не уверен, почему. Это означает то, что уже есть, поэтому, если я сделаю x1 = rnorm(20) ; x2 = rnorm(20) ; x3 = rnorm(20) ; x4 = rnorm(20) ; у = rn(20) out = add1(lm1, область видимости= ~ . ) не использует то, что уже есть в глобальной среде. Я знаю, что в документации говорится, что объем должен быть «формулой, дающей условия для рассмотрения», но обычно это происходит там, где . может использоваться для ссылки на все переменные. Заранее спасибо. Также обратите внимание, что я прочитал главу 7 MASS, и эти связанные темы область действия команды add1() в R http://tolstoy.newcastle.edu.au/R/help/02b/3588.html 2Это еще более простой ответ, который я нашел после просмотра этого вопроса. http://r.789695.n4.nabble.com/glm-formula-vs-character-td2543061.html )
х2 = рнорм(100)
х3 = рнорм(100)
у = рнорма(100)
BaseReg = lm(y ~ 1)
newdf = data. Озадачивает, что такой простой способ получить это не был указан в документации для add1. Как сказано на странице справки для add1, формула as.formula(paste("~", paste(names(YX)[-c(1,5)],collapse="+" )))
#~Х1 + Х2 + Х3
YX <- cbind(y,X)
form <- as.formula(paste("~", paste(names(YX)[-c(1,5)],collapse="+")))
add1(lm1, форма)
Кажется, вы наткнулись на более эффективную стратегию. При использовании объекта данных с именами столбцов: "y" "X1" "X2" "X3" "X4: > формула (YX) у ~ Х1 + Х2 + Х3 + Х4 > формула(YX)[-2] ~Х1 + Х2 + Х3 + Х4 > as.list(формула(YX)) [[1]] `~` [[2]] у [[3]] Х1 + Х2 + Х3 + Х4 > имена (YX) [1] «у» «Х1» «Х2» «Х3» «Х4» Вы можете видеть, что объект-формула имеет в качестве первого элемента определяющую формулу тильду, которая на самом деле является функцией R. X 2y 3x y: Mathway | Popular Problems 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 | Risolvere per ? | cos(x)=1/2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | Risolvere per x | sin(x)=-1/2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 | Преобразовать из градусов в радианы | 225 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 | Risolvere per ? | cos(x)=( квадратный корень из 2)/2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | Risolvere per x | cos(x)=( квадратный корень из 3)/2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11 | Risolvere per x | sin(x)=( квадратный корень из 3)/2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12 | График | g(x)=3/4* корень пятой степени из x | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 13 | Найти центр и радиус | x^2+y^2=9 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 14 | Преобразовать из градусов в радианы | 120 град. 2+n-72)=1/(n+9) 2+n-72)=1/(n+9) |
Задачи с системами уравнений
Задача 1 Две следующие системы уравнений имеет решение (1, 3). Найдите их, выполняя проверку.
a)
|x + y = 5
|2x — y = 7;
b)
|2x + y = 5
|x — y = 2
c)
|3x + y = 6
|4x — 3y = -5
d)
|1/(x — 1) = y — 3
|x — y = -2
e)
|(9x + 4y)/3 — (5x — 11)/2 = 13 — y
|13x — 7y = -8
Ответ:c) и e).
Задача 2 Равны ли системы уравнений?
|4x + 5y = 11
|x — y = 5
and
|4x — 5y = 11
|2x + y = 9 ?
Ответ: Нет.
(3-32) Решите систему уравнений:
Задача 3
|2y — x = -5
|y = 1 — 3x
Ответ:(1; -2).
Задача 4
|3x — y = 13
|3y — 2x = -4
Ответ:(5; 2).
Задача 5
|6x — y = 11
|12x — 2y — 22 = 0
Ответ: Решением является каждая пара чисел, которая есть решениея уравнения 6x — y = 11.
Задача 6
|5u — 6v = -2
|7u + 18v = 2
Ответ:(-1; 1/2).
Задача 7
|8x — 5y + 16 = 0
|1x + 3y — 17 = 0
Ответ:(1/2; 4).
Задача 8
|4(x + 2) — 7(x — y) = 7
|7(x + y) + 10(x — 2) = 79
Ответ:(5; 2).
Задача 9
|3x + 4(x — 3) = 3(2y — 3) — 3y
|3y + 2(x — 4) = 5(y + 2) — 28
Ответ:(-4; 1).
Задача 10
|(x + 3)(x — 1) = 4y + x2 + 5
|(x — 3)(3x + 2) = 3x2 — 14y + 15
Ответ: Нет решения.
Задача 11
|(x — 1)(y + 2) — (x — 2)(y + 5) = 0
|(x + 4)(y — 3) — (x + 7)(y — 4) = 0
Ответ:(5; 7)
Задача 12
|(x + 2)2 — (x + 3)(x — 3) — 3(y + 5) = 0
|(2y — 3)2 — y(4y — 3) + 12x — 15 = 0
Ответ: Решением является каждая пара чисел, которая есть решением уравнения 4x — 3y — 2 = 0.
Задача 13
|(y + 2)/6 — (y — 4)/2 = x/3
|(4/3)(y — 1) — 2x = -2
Ответ:(3; 4)
Задача 14
|0,25x — 0,04y = 1
|0,4x + 1,5y = 40,7
Ответ:(8; 25)
Задача 15
|(5x — 3y)/4 = (x — 5y)/3
|7x + y = 12
Ответ:(2; -2)
Задача 16
|(3x + 1)/5 + 2y -3 = 0
|(4y — 5)/6 + 3y — 9 = -1/2
Ответ:(-42/11; 28/11)
Задача 17
|(3x — 1)/5 + 3y — 4 = 15
|(3y — 5)/6 + 2x — 8 = 23/3
Ответ:(7; 5)
Задача 18
|(2x — z)/6 + (2x — z)/9 = 3
|(x + z)/3 — (x — z)/4 = 4
Ответ:(6; 6)
Задача 19
|(x — 1)/3 + (5y + 1)/2 = (x + 10y — 8)/6
|(x + 2)(5y — 2)/2 = 5 + 5xy/2 — 2(x + 1)
Ответ: Нет решения.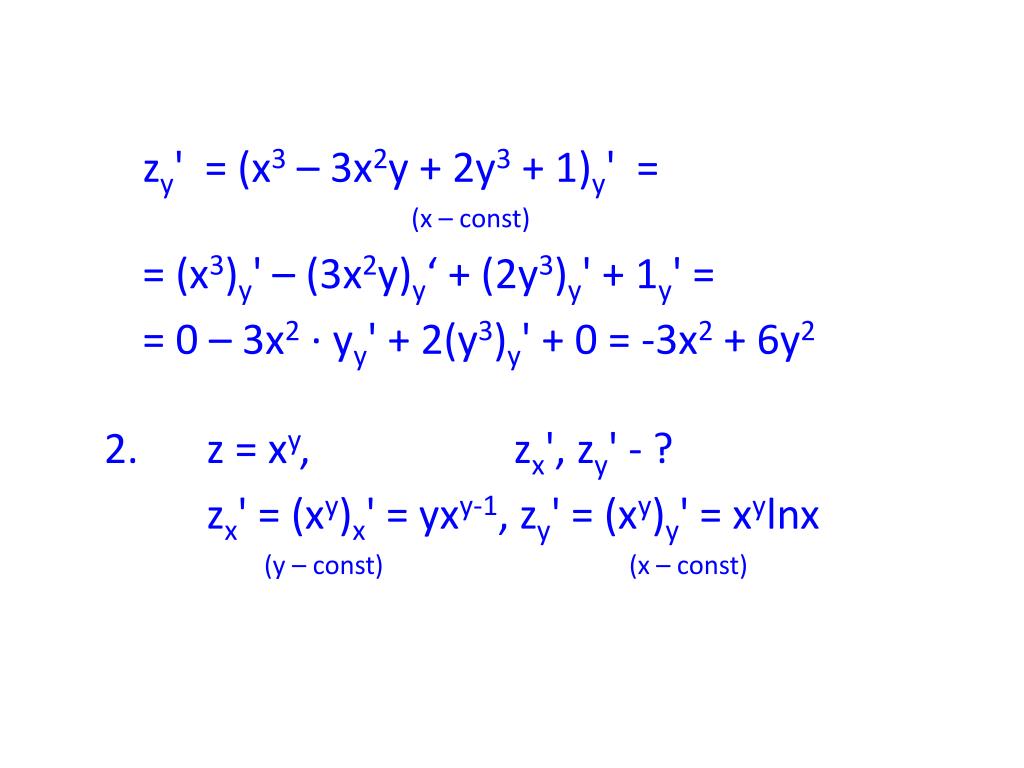
Задача 20
|(5x — 1)/6 + (3y — 1)/10 = 3
|(11 — x)/6 + (11 + y)/4 = 3
Ответ:(5; -3).
Задача 21
|y — 0,2(x — 2) = 1,4
|5/2 — (2y — 3)/4 = (4x — y)/8
Ответ:(5; 2).
Задача 22
|x/5 + 0,03(10y — 20) = 0,8
|(2x + 4,5)/20 — 0,75 = (y — 3)/8
Ответ:(4; 2).
Задача 23
|y — x — (5x — 4)/2 = 3 — (11y + 17)/4
|x + (9y + 11)/4 — (3y + 4)/7 = 6
Ответ:(2; 1).
Задача 24
|(5x — 3y)/3 — (2y — 3x)/5 = x + 1
|(2x — 3y)/3 — (3y — 4x)/2 = y + 1
Ответ:(3; 2).
Задача 25
|(x — 1)/4 (1 + y)/2 = 1/6 — (x + 2y)/6
|(x — 2)/3 + x/15 = (y + 4)/5 — (4x — y)/15
Ответ: Решением является каждая пара чисел, которая есть решением уравнения 5x — 2y = 11.
Задача 26
|(x + 2y)/4 — (x — 2y)/2 = 1 — [x — (7 — 2y)/3]
|3x — 2y = 8
Ответ:(3; 1/2).
Задача 27
|(7 + x)/5 — (2x — y)/4 — 3y = -5
|(5y — 7)/2 + (4x — 3)/6 — 18 = -5x
Ответ:(3; 2).
Задача 28
|11y/20 — 0,8(x/4 + 2,5) = 5/2
|(6x — 0,3y)/2 — 3/2 = 2(1 + x)
Ответ:(5; 10).
Задача 29
|0,5x — (y — 4)/5 = 0,3x — (y — 4)/2
|0,5y — (x — 4)/6 = 7y/12 — (x — 3)/3
Ответ:(3; 2).
Задача 30
|2(x — y)/3 + 1,6 = 8x/15 — (3y — 10)/5
|(3x + 4)/4 + y/8 = 5x/6 — (y — 17)/12
Ответ:(5; 4).
Задача 31
|(2 + x)(5y — 2)/2 = 5 + 5xy/2 — 2(1 + x)
|(x — 1)2 + (2y + 1)2 = 2(1 + 2y)(x — 1)
Ответ: Решением является каждая пара чисел, которая есть решением уравнения x + 5y = 5

Решите следующее алгебраическое выражение: [5z-(x+2y)]-[3x-(y-2z)]
Выберите область веб-сайта для поискаMathAllУчебные пособияПомощь по выполнению домашних заданийПланы уроков
Искать на этом сайте
Цитата страницы Начать эссе значок-вопрос Задайте вопрос Начать бесплатную пробную версию Скачать PDF PDF Цитата страницы Цитировать Поделиться ссылкой ДелитьсяСсылайтесь на эту страницу следующим образом:
«Решите следующее алгебраическое выражение: [5z-(x+2y)]-[3x-(y-2z)]» eNotes Editorial , 21 декабря 2009 г. , https://www.enotes.com/homework-help /алгебраическое-выражение-124719.
По состоянию на 21 мая 2023 г.
, https://www.enotes.com/homework-help /алгебраическое-выражение-124719.
По состоянию на 21 мая 2023 г.
Ответы экспертов
Привет. Это алгебраическое выражение (кстати, в чем разница между выражением и уравнением? Ответ следует далее) требует, чтобы вы увидели, что отрицательный знак можно интерпретировать как (-1) и распределять с помощью распределительного свойства умножения.
Используя стратегию решения проблем «Упрости и реши», мы сначала пытаемся определить, можем ли мы комбинировать похожие термины. Еще нет. Итак, давайте обратимся к этим неприятным (-) знакам минус. Чтобы устранить путаницу, которую они создают, изменим ли мы все знаки операций на (+) знаки сложения? Сделаем так:
[5z + -1(x + 2y)] + -1[3x + -1(y + -2z)]
= 5z + -1x + -2y + -1[3x + -1y + 2z]
= 5z + -1x + -2y + -3x + 1y + -2z Теперь объединим похожие термины
= -4x + -y + 3z
(О да! В выражении нет знака равенства, но в уравнении он есть).
Утверждено редакцией eNotesПримечание:
Многие учебники по алгебре предлагают записывать переменные в алфавитном порядке с убывающими показателями степени, а вторичные переменные имеют возрастающие степени.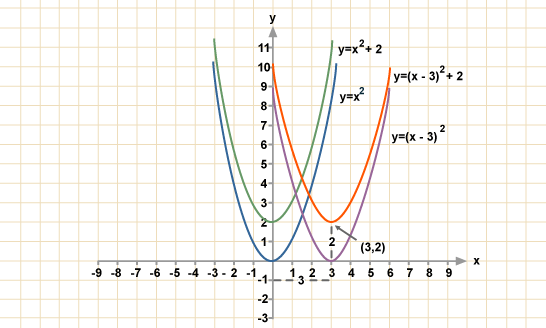 Например, 92 +2xy – нет.
Например, 92 +2xy – нет.
Для исходной задачи, описанной выше, лучшим ответом будет
— 4x — y + 3z
вместо того, чтобы требовать, чтобы первый член всегда был положительным.
Утверждено редакцией eNotesЭта проблема заключается в перемещении знака минус внутри скобки, чтобы сохранить порядок операций.
[5z-(x+2y)]-[3x-(y-2z)]
5z — x — 2y — (3x — y + 2z)
5z — x — 2y — 3x + y — 2z
3z — 4x — y
См. eNotes без рекламы
Начните 48-часовую бесплатную пробную версию , чтобы получить доступ к более чем 30 000 дополнительных руководств и более чем 350 000 вопросов помощи при выполнении домашних заданий, на которые ответили наши эксперты.
Получите 48 часов бесплатного доступаУже зарегистрированы? Войдите здесь.
Утверждено редакцией eNotes Задайте вопросПохожие вопросы
Просмотреть всеМатематика
Последний ответ опубликован 07 сентября 2010 г. в 12:47:25.
в 12:47:25.
Что означают буквы R, Q, N и Z в математике?
14 Ответы педагога
Математика
Последний ответ опубликован 07 октября 2013 г. в 20:13:27.
Как определить, является ли это уравнение линейной или нелинейной функцией?
84 Ответы педагога
Математика
Последний ответ опубликован 25 февраля 2016 г. в 18:48:45.
Сколько времени (в часах) займет ваше путешествие, если вы проедете 350 км со средней скоростью 80 км/ч? Какова формула с данными: время, расстояние, скорость или скорость?
1 Ответ воспитателя
Математика
Последний ответ опубликован 02 сентября 2012 г. в 3:00:53.
Как ограничения (пределы исчисления) используются или применяются в повседневной жизни? Или применительно к проблемам реального мира? Мне нужно пару примеров! Спасибо!
1 Ответ учителя
Математика
Последний ответ опубликован 09 октября 2017 г.

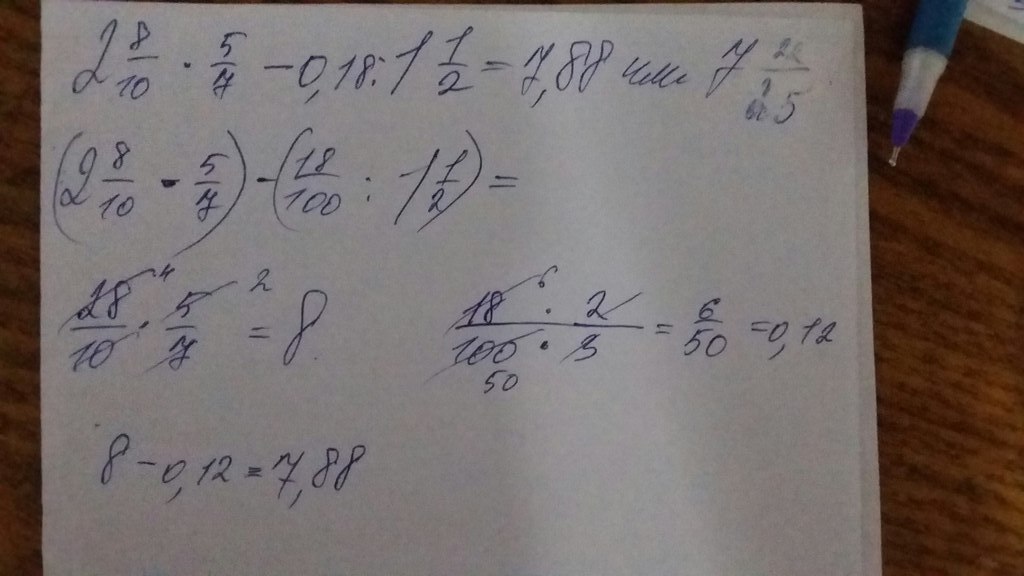 2
2 Калькулятор поделит число как нацело, так и выполнит деление с остатком. Кроме того, результаты деления будут проверены умножением.
Калькулятор поделит число как нацело, так и выполнит деление с остатком. Кроме того, результаты деления будут проверены умножением.

 Важно! Если бы разность оказалась больше делимого, то это бы означало, что первое неполное делимое мы поделили неверно.
Важно! Если бы разность оказалась больше делимого, то это бы означало, что первое неполное делимое мы поделили неверно. Сравниваем разность с делителем:
Сравниваем разность с делителем: Важно! Если бы разность оказалась больше делимого, то это бы означало, что третье неполное делимое мы поделили неверно.
Важно! Если бы разность оказалась больше делимого, то это бы означало, что третье неполное делимое мы поделили неверно. Как разделить поровну 20 конфет между шестерыми друзьями?
Как разделить поровну 20 конфет между шестерыми друзьями? Имеем: 189 = 13 * 14 + 7.
Имеем: 189 = 13 * 14 + 7.
 Надеюсь, вы поняли этот процесс и можете использовать те же методы для сложения других дробей. Полный ответ приведен ниже (упрощенный до самой низкой формы):
Надеюсь, вы поняли этот процесс и можете использовать те же методы для сложения других дробей. Полный ответ приведен ниже (упрощенный до самой низкой формы): com . По состоянию на 1 июня 2023 г. http://visualfractions.com/calculator/divide-fractions/what-is-1-18-divided-by-1-3/.
com . По состоянию на 1 июня 2023 г. http://visualfractions.com/calculator/divide-fractions/what-is-1-18-divided-by-1-3/. В этом кратком уроке по математике мы покажем вам, как можно разделить любое целое число на дробь. Если вам нравится делить числа на дроби, читайте дальше, друг мой!
В этом кратком уроке по математике мы покажем вам, как можно разделить любое целое число на дробь. Если вам нравится делить числа на дроби, читайте дальше, друг мой! Запишем это визуально:
Запишем это визуально:

 Записать числа друг под другом, причем так чтобы одинаковые разряды чисел стояли в столбик, то есть единицы одного числа под единицами второго числа, десятки под десятками, сотни под сотнями и так далее. Проще говоря, нужно записать числа друг под другом, выравнивая их по правому краю. Важно! Большее число (уменьшаемое) записывается сверху, а меньшее (вычитаемое) снизу.
Записать числа друг под другом, причем так чтобы одинаковые разряды чисел стояли в столбик, то есть единицы одного числа под единицами второго числа, десятки под десятками, сотни под сотнями и так далее. Проще говоря, нужно записать числа друг под другом, выравнивая их по правому краю. Важно! Большее число (уменьшаемое) записывается сверху, а меньшее (вычитаемое) снизу. Занятую цифру ставим в уме слева от верхней цифры и производим вычитание. Для того, чтобы не забыть, что цифра следующего разряда уменьшилась на 1, нужно поставить над ней точку.
Занятую цифру ставим в уме слева от верхней цифры и производим вычитание. Для того, чтобы не забыть, что цифра следующего разряда уменьшилась на 1, нужно поставить над ней точку.  Теперь из 10 занимаем единицу для разряда десятков и получаем, что в разряде десятков не 3, а 13.
Теперь из 10 занимаем единицу для разряда десятков и получаем, что в разряде десятков не 3, а 13. Если разность будет равна второму слагаемому, значит сложение было выполнено верно.
Если разность будет равна второму слагаемому, значит сложение было выполнено верно. 1 – 0.01 = > (0.1 – 0.01)* 100 = > (10 — 1) / 100 => 0.09
1 – 0.01 = > (0.1 – 0.01)* 100 = > (10 — 1) / 100 => 0.09 При вычитании дробей нужно проверять, подобна дробь или нет. Дроби с одинаковым знаменателем называются похожими дробями, тогда как дроби с разными дробями называются непохожими дробями.
При вычитании дробей нужно проверять, подобна дробь или нет. Дроби с одинаковым знаменателем называются похожими дробями, тогда как дроби с разными дробями называются непохожими дробями.
 Теперь измените значение знаменателя на значение НОК и умножьте числитель и знаменатель на одно и то же число. Вычтите дробные значения.
Теперь измените значение знаменателя на значение НОК и умножьте числитель и знаменатель на одно и то же число. Вычтите дробные значения.


 Этот тип
реакторов может работать на плутониевом топливе, произведенном на тепловых реакторах, и эксплуатироваться в замкнутом
цикле с собственным заводом по переработке отработанного топлива.
Они могут быть сконструированы так,
чтобы производить больше делящихся изотопов (239Pu, 241Pu),
чем используют − реакторы
размножители (бридеры). Использование бридеров позволит обеспечить нас энергией
на многие миллионы лет. Однако быстрые реакторы дороже и в
постройке и в эксплуатации. Их неоспоримое преимущество перед реакторами на
тепловых нейтронах заключается в том, что они
позволяют сжигать актиниды, которые составляют долгоживущую и высокоактивную
часть ядерных отходов реакторов на медленных нейтронах.
Этот тип
реакторов может работать на плутониевом топливе, произведенном на тепловых реакторах, и эксплуатироваться в замкнутом
цикле с собственным заводом по переработке отработанного топлива.
Они могут быть сконструированы так,
чтобы производить больше делящихся изотопов (239Pu, 241Pu),
чем используют − реакторы
размножители (бридеры). Использование бридеров позволит обеспечить нас энергией
на многие миллионы лет. Однако быстрые реакторы дороже и в
постройке и в эксплуатации. Их неоспоримое преимущество перед реакторами на
тепловых нейтронах заключается в том, что они
позволяют сжигать актиниды, которые составляют долгоживущую и высокоактивную
часть ядерных отходов реакторов на медленных нейтронах.  В случае быстрых нейтронов для реализации цепной реакции
необходимо больше делящихся изотопов. Обычно быстрые реакторы в качестве
базового топлива используют 239Pu. При делении 239Pu выделяется на 25%
больше нейтронов, чем у 235U. Таким образом, при делении 239Pu
получается столько нейтронов (даже с учетом потерь), чтобы не только
поддерживать цепную реакцию, но и конвертировать 238U
в 239Pu. В реакторе на тепловых нейтронах отношение делящихся ядер к «новым»
делящимся ядрам приблизительно 0.6. В быстрых реакторах это отношение может быть
больше 1. Таким образом, запустив быстрый реактор, заложив в него достаточное
количество делящихся изотопов, в результате бридинга через некоторое время в
него можно будет добавлять естественный и даже обедненный уран.
В случае быстрых нейтронов для реализации цепной реакции
необходимо больше делящихся изотопов. Обычно быстрые реакторы в качестве
базового топлива используют 239Pu. При делении 239Pu выделяется на 25%
больше нейтронов, чем у 235U. Таким образом, при делении 239Pu
получается столько нейтронов (даже с учетом потерь), чтобы не только
поддерживать цепную реакцию, но и конвертировать 238U
в 239Pu. В реакторе на тепловых нейтронах отношение делящихся ядер к «новым»
делящимся ядрам приблизительно 0.6. В быстрых реакторах это отношение может быть
больше 1. Таким образом, запустив быстрый реактор, заложив в него достаточное
количество делящихся изотопов, в результате бридинга через некоторое время в
него можно будет добавлять естественный и даже обедненный уран. В этом случае он применяется, чтобы сжигать оружейный плутоний и другие
трансураны.
В этом случае он применяется, чтобы сжигать оружейный плутоний и другие
трансураны. 
 Электрическая мощность −
Электрическая мощность −  Переработка
использованного топлива, особенно в бланкете, типична для циклов в
быстрых реакторах. Обычно, выделенный с помощью переработки,
плутоний вводится в активную зону как MOX-топливо.
Причем, такая переработка топлива бланкета может осуществляться до
трех раз.
Переработка
использованного топлива, особенно в бланкете, типична для циклов в
быстрых реакторах. Обычно, выделенный с помощью переработки,
плутоний вводится в активную зону как MOX-топливо.
Причем, такая переработка топлива бланкета может осуществляться до
трех раз. Кроме того, натрий обладает
прекрасными теплофизическими свойствами: он хорошо принимает,
проводит и отдает тепло. Натрий практически не снижает энергию
нейтронов и не является замедлителем, что существенно для быстрых
реакторов.
Кроме того, натрий обладает
прекрасными теплофизическими свойствами: он хорошо принимает,
проводит и отдает тепло. Натрий практически не снижает энергию
нейтронов и не является замедлителем, что существенно для быстрых
реакторов. Разведанных запасов урана для
обеспечения топливом столь большого числа атомных энергоблоков не
хватало. В сценариях с одними только тепловыми реакторами быстро
наступил бы топливный голод. Поэтому во всех странах,
развивавших быстрые программы, в конечном итоге было выбрано
натриевое направление. Однако строительство тепловых реакторов пошло
гораздо более медленными темпами, чем предполагалось и на
сегодняшний день отсутствует острая необходимость достижения высоких
значений КВ, так как природный уран всё ещё относительно доступен и
дёшев, а на складах скопились значительные запасы ОЯТ/плутония.
Таким образом, можно считать, что выбор в пользу натрия перестал
быть безальтернативным, и стало возможным вернуться к
рассмотрению других теплоносителей для быстрых реакторов.
Возникла потребность в скорейшем развитии быстрых реакторов и
замкнутого топливного цикла. Причём для быстрых реакторов
требовались высокие параметры воспроизводства.
Разведанных запасов урана для
обеспечения топливом столь большого числа атомных энергоблоков не
хватало. В сценариях с одними только тепловыми реакторами быстро
наступил бы топливный голод. Поэтому во всех странах,
развивавших быстрые программы, в конечном итоге было выбрано
натриевое направление. Однако строительство тепловых реакторов пошло
гораздо более медленными темпами, чем предполагалось и на
сегодняшний день отсутствует острая необходимость достижения высоких
значений КВ, так как природный уран всё ещё относительно доступен и
дёшев, а на складах скопились значительные запасы ОЯТ/плутония.
Таким образом, можно считать, что выбор в пользу натрия перестал
быть безальтернативным, и стало возможным вернуться к
рассмотрению других теплоносителей для быстрых реакторов.
Возникла потребность в скорейшем развитии быстрых реакторов и
замкнутого топливного цикла. Причём для быстрых реакторов
требовались высокие параметры воспроизводства.
 Кроме того, свинец удерживает в теплоносителе особо неприятных
летучих продукты деления урана — йод и цезий. У свинца высокая
температура кипения (1745°C), что исключает аварии с кризисом
теплообмена и быстрым разрушением тепловыделяющих элементов. Минус
свинца — высокая температуры плавления
327о С превращается в плюс — при возможной аварии с
разрушением корпуса, свинец застынет.
Кроме того, свинец удерживает в теплоносителе особо неприятных
летучих продукты деления урана — йод и цезий. У свинца высокая
температура кипения (1745°C), что исключает аварии с кризисом
теплообмена и быстрым разрушением тепловыделяющих элементов. Минус
свинца — высокая температуры плавления
327о С превращается в плюс — при возможной аварии с
разрушением корпуса, свинец застынет. Высокая теплопроводность обеспечивает надежность и
температурную стойкость топлива, позволяют работать при температуре
до 700о С. Выход агрессивных продуктов деления (цезий,
йод, селен, теллур и др.) из таблеток нитрида значительно меньше,
чем из оксидного топлива, — меньше коррозия оболочек твэлов.
Недостатком мононитридного топлива является образование
бета-активного улерода-14 по реакции 14N(n,p)14С.
Высокая теплопроводность обеспечивает надежность и
температурную стойкость топлива, позволяют работать при температуре
до 700о С. Выход агрессивных продуктов деления (цезий,
йод, селен, теллур и др.) из таблеток нитрида значительно меньше,
чем из оксидного топлива, — меньше коррозия оболочек твэлов.
Недостатком мононитридного топлива является образование
бета-активного улерода-14 по реакции 14N(n,p)14С. Ограничение температуры бетона поддерживается
естественной циркуляцией воздуха.
Ограничение температуры бетона поддерживается
естественной циркуляцией воздуха.
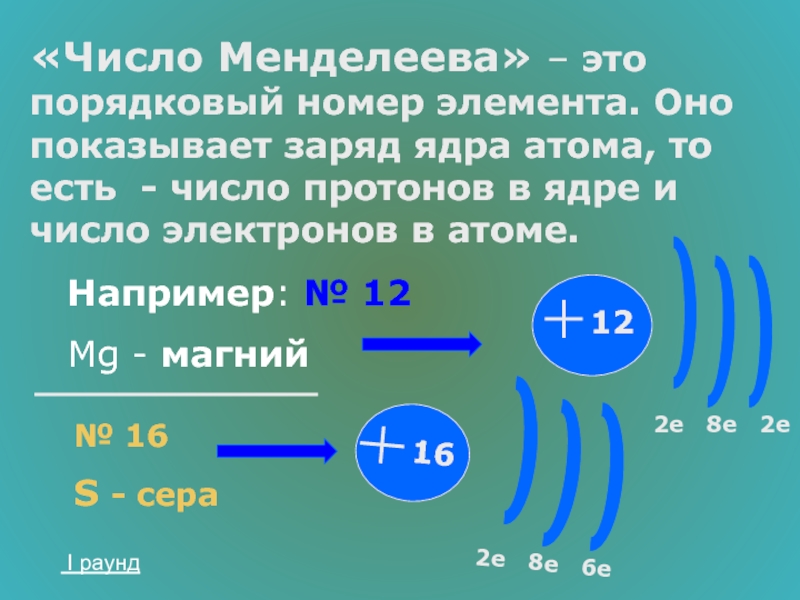 Допускается также подмешивание к регенерату сторонних МА из ОЯТ
тепловых реакторов. При добавлении 241Am в количестве 3-5% от массы
загружаемого топлива за каждую кампанию будет выжигаться до 30%
этого радионуклида.
Допускается также подмешивание к регенерату сторонних МА из ОЯТ
тепловых реакторов. При добавлении 241Am в количестве 3-5% от массы
загружаемого топлива за каждую кампанию будет выжигаться до 30%
этого радионуклида. Таким образом, уже к началу четвертого цикла
(через три года) в активную зону загружаются ТВС из собственного
регенерированного топлива, которое было выгружено после облучения в
течение первого цикла. Расчеты показывают, что уже к началу восьмого
цикла реактор, загруженный только регенератом собственного
облученного топлива с добавкой отвального урана, начинает работать в
равновесном топливном режиме.
Таким образом, уже к началу четвертого цикла
(через три года) в активную зону загружаются ТВС из собственного
регенерированного топлива, которое было выгружено после облучения в
течение первого цикла. Расчеты показывают, что уже к началу восьмого
цикла реактор, загруженный только регенератом собственного
облученного топлива с добавкой отвального урана, начинает работать в
равновесном топливном режиме. Следовательно, нет необходимости поддерживать высокое давление в
первом контуре реакторной установки.
Следовательно, нет необходимости поддерживать высокое давление в
первом контуре реакторной установки. Это позволяет
существенно расширить диапазон рабочих температур для реакторов
со свинцом-висмутом).
Это позволяет
существенно расширить диапазон рабочих температур для реакторов
со свинцом-висмутом).
 ) размещено в
едином корпусе. Тракт теплоносителя первого контура сформирован
внутри корпуса моноблока без трубопроводов и арматуры. Утечки из
первого контура за пределы моноблока исключаются.
) размещено в
едином корпусе. Тракт теплоносителя первого контура сформирован
внутри корпуса моноблока без трубопроводов и арматуры. Утечки из
первого контура за пределы моноблока исключаются. Реактор СВБР-100 при
использовании МОКС-топлива (коэффициент воспроизводства в активной
зоне КВА~1) может работать в режиме топливного самообеспечения без
потребления природного урана.
Реактор СВБР-100 при
использовании МОКС-топлива (коэффициент воспроизводства в активной
зоне КВА~1) может работать в режиме топливного самообеспечения без
потребления природного урана. 7k+ views
7k+ views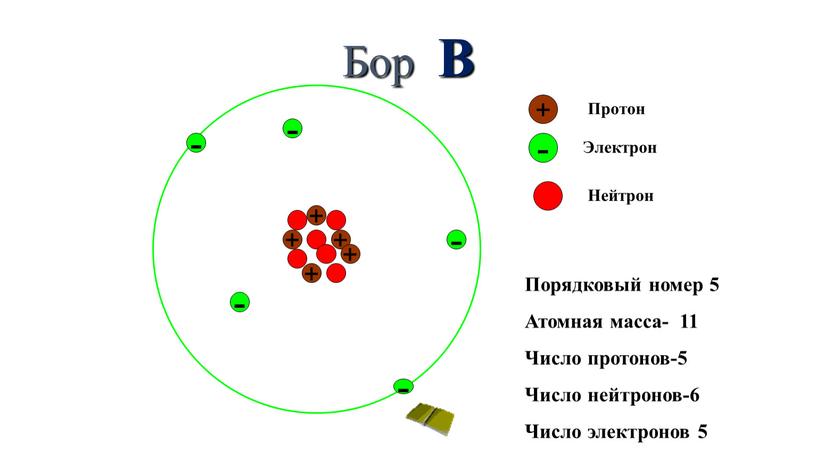
 Такие виды известны как изотопы.
Такие виды известны как изотопы. задание. Им пришлось повысить мощность ускорителя. Кубо также построил сложный фильтр частиц, машину длиной почти с футбольное поле, которая использует магниты для отделения атомных ядер друг от друга. Затем, чтобы показать, что фтор-31, версия с 22 нейтронами, является самым тяжелым типом фтора, команда провела столкновения частиц, которые, согласно теоретическим моделям, должны производить фтор-32 и фтор-33. Когда они не видели этих более тяжелых фторов, они могли почти с уверенностью подтвердить, что преобладает фтор-31. (Neon-34 получил статус чемпиона по аналогичному протоколу.) Команда не легкомысленно сделала эти официальные заявления: они анализировали свои результаты почти пять лет, прежде чем опубликовать их на этой неделе.
задание. Им пришлось повысить мощность ускорителя. Кубо также построил сложный фильтр частиц, машину длиной почти с футбольное поле, которая использует магниты для отделения атомных ядер друг от друга. Затем, чтобы показать, что фтор-31, версия с 22 нейтронами, является самым тяжелым типом фтора, команда провела столкновения частиц, которые, согласно теоретическим моделям, должны производить фтор-32 и фтор-33. Когда они не видели этих более тяжелых фторов, они могли почти с уверенностью подтвердить, что преобладает фтор-31. (Neon-34 получил статус чемпиона по аналогичному протоколу.) Команда не легкомысленно сделала эти официальные заявления: они анализировали свои результаты почти пять лет, прежде чем опубликовать их на этой неделе. Судя по этому графику, если бы там был фтор-32, они бы его увидели. И они этого не видят».
Судя по этому графику, если бы там был фтор-32, они бы его увидели. И они этого не видят».
 То есть мы можем сказать, что \(Р = 4a\) – это функция, хотя формально это выражение, содержащее аргумент, зависимую и функцию.
То есть мы можем сказать, что \(Р = 4a\) – это функция, хотя формально это выражение, содержащее аргумент, зависимую и функцию.


 {2}–\ 4.\)
{2}–\ 4.\) Точка принадлежит графику функций, если её координате x соответствует координата соответствует координата y именно как \(y\ = \ 8\ + \ x.\)
Точка принадлежит графику функций, если её координате x соответствует координата соответствует координата y именно как \(y\ = \ 8\ + \ x.\) Для нецелых действительных положительных показателей степени: D(f) = [0, +∞). Если a — отрицательное целое число, то область определения функции представляет собой множество (−∞, 0) ∪ (0, +∞).
Для нецелых действительных положительных показателей степени: D(f) = [0, +∞). Если a — отрицательное целое число, то область определения функции представляет собой множество (−∞, 0) ∪ (0, +∞).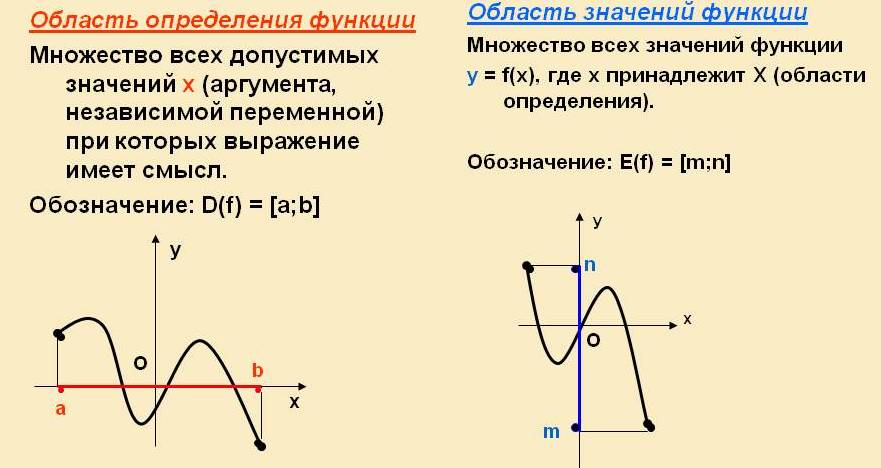



 Область определения уравнения иногда называют областью допустимых значений переменной (аргумента).
Область определения уравнения иногда называют областью допустимых значений переменной (аргумента).
 ..
..

 frame(x1,x2,x3)
out = add1 (BaseReg, имена (newdf))
frame(x1,x2,x3)
out = add1 (BaseReg, имена (newdf)) 
 92+z+1=0.$$ Теперь я почти уверен, что вы знаете, как решать квадратные уравнения, не так ли?
92+z+1=0.$$ Теперь я почти уверен, что вы знаете, как решать квадратные уравнения, не так ли?
 Задачи с прикладным содержанием (вариант 2)
Задачи с прикладным содержанием (вариант 2) Правила алгебраических преобразований позволяют выполнять некоторые манипуляции с выражениями, следуя которым можно получить в левой части равенства выражение, стоящее в правой части, или преобразовать правую часть равенства (чтобы получить выражение, стоящее в левой части после знака равенства).
Правила алгебраических преобразований позволяют выполнять некоторые манипуляции с выражениями, следуя которым можно получить в левой части равенства выражение, стоящее в правой части, или преобразовать правую часть равенства (чтобы получить выражение, стоящее в левой части после знака равенства). В виде выражения данное правило выглядит следующим образом: (а — с)² = а² — 2ас + с².
В виде выражения данное правило выглядит следующим образом: (а — с)² = а² — 2ас + с². Известны лишь величины их сторон.
Известны лишь величины их сторон. 2\right)\]
2\right)\]



 Но не волнуйтесь, мы здесь, чтобы помочь. В этом сообщении блога мы познакомим вас с некоторыми определениями и примерами алгебры, чтобы вы могли лучше понять предмет. Вооружившись этими знаниями, вы с легкостью справитесь с материалом и в мгновение ока окажетесь на пути к покорению алгебры!
Но не волнуйтесь, мы здесь, чтобы помочь. В этом сообщении блога мы познакомим вас с некоторыми определениями и примерами алгебры, чтобы вы могли лучше понять предмет. Вооружившись этими знаниями, вы с легкостью справитесь с материалом и в мгновение ока окажетесь на пути к покорению алгебры!
 Этот закон часто используется для упрощения выражений.
Этот закон часто используется для упрощения выражений. Допустим, у вас есть куча яблок, и вы хотите разделить их на две кучки. Вы можете сделать это, взяв по одному яблоку из каждой стопки и разделив их пополам. Но что, если вы хотите разделить их на четыре стопки? Вы все еще можете сделать это, взяв по одному яблоку из каждой кучи и разделив его пополам, но теперь останется три яблока. Если бы вы хотели разделить их на восемь кучек, вам нужно было бы взять по два яблока из каждой кучки и все равно разделить их пополам. Это потому, что коммутативное правило умножения гласит, что при умножении двух вещей результат всегда один и тот же, независимо от того, сколько раз они умножаются.
Допустим, у вас есть куча яблок, и вы хотите разделить их на две кучки. Вы можете сделать это, взяв по одному яблоку из каждой стопки и разделив их пополам. Но что, если вы хотите разделить их на четыре стопки? Вы все еще можете сделать это, взяв по одному яблоку из каждой кучи и разделив его пополам, но теперь останется три яблока. Если бы вы хотели разделить их на восемь кучек, вам нужно было бы взять по два яблока из каждой кучки и все равно разделить их пополам. Это потому, что коммутативное правило умножения гласит, что при умножении двух вещей результат всегда один и тот же, независимо от того, сколько раз они умножаются. Это правило можно проиллюстрировать следующей таблицей:
Это правило можно проиллюстрировать следующей таблицей: Это операция сложения (+), операция вычитания (–), операция умножения (×) и операция деления (÷). Есть также несколько менее часто используемых операций, таких как операция возведения в степень exp(-), обратная операция inverse(x) и операция степени pow(x, y).
Это операция сложения (+), операция вычитания (–), операция умножения (×) и операция деления (÷). Есть также несколько менее часто используемых операций, таких как операция возведения в степень exp(-), обратная операция inverse(x) и операция степени pow(x, y). В этом посте мы рассмотрим некоторые основные правила алгебры и примеры.
В этом посте мы рассмотрим некоторые основные правила алгебры и примеры. Например, в уравнении x2 – 4x + 10 = 0, когда x появляется дважды (один раз внутри круглых скобок и один раз снаружи), его значение внутри круглых скобок равно 10, а его значение вне круглых скобок равно 4. Этот принцип часто снова называют дистрибутивностью, потому что он говорит, что каждый член в
Например, в уравнении x2 – 4x + 10 = 0, когда x появляется дважды (один раз внутри круглых скобок и один раз снаружи), его значение внутри круглых скобок равно 10, а его значение вне круглых скобок равно 4. Этот принцип часто снова называют дистрибутивностью, потому что он говорит, что каждый член в Шаг 3: Сложите десятичные числа На этом шаге вы сложите все десятичные числа без каких-либо общих цифр (например, 10 + 5 = 15). Шаг 4. Проверьте свою работу Если вы получили ответ, который отличается от того, что вы ожидали, проверьте свою работу, умножив или разделив обе части уравнения на 10 и проверив, не изменится ли что-нибудь. Вот пример того, как вычесть два целых числа, используя эти четыре шага: Ален играл в футбол с Луи в полдень. Ален играл в футбол три часа, а Луи — один час. Как долго Al
Шаг 3: Сложите десятичные числа На этом шаге вы сложите все десятичные числа без каких-либо общих цифр (например, 10 + 5 = 15). Шаг 4. Проверьте свою работу Если вы получили ответ, который отличается от того, что вы ожидали, проверьте свою работу, умножив или разделив обе части уравнения на 10 и проверив, не изменится ли что-нибудь. Вот пример того, как вычесть два целых числа, используя эти четыре шага: Ален играл в футбол с Луи в полдень. Ален играл в футбол три часа, а Луи — один час. Как долго Al Порядок операций обычно обозначается аббревиатурой PEMDAS: скобки, экспоненты, умножение и деление (слева направо), сложение и вычитание (слева направо). Порядок операций может быть сокращен до PEMDAS+: скобки, показатели степени, умножение и деление (слева направо), сложение и вычитание (слева налево). При работе с комплексными числами порядок операций меняется: Скобки, Показатель степени, Умножение и деление (слева направо), Сложение и вычитание по мнимой оси (умножение и деление выполняются только над мнимыми элементами), Асимметрия/Асимметрия по мнимой оси. реальная/мнимая ось.
Порядок операций обычно обозначается аббревиатурой PEMDAS: скобки, экспоненты, умножение и деление (слева направо), сложение и вычитание (слева направо). Порядок операций может быть сокращен до PEMDAS+: скобки, показатели степени, умножение и деление (слева направо), сложение и вычитание (слева налево). При работе с комплексными числами порядок операций меняется: Скобки, Показатель степени, Умножение и деление (слева направо), Сложение и вычитание по мнимой оси (умножение и деление выполняются только над мнимыми элементами), Асимметрия/Асимметрия по мнимой оси. реальная/мнимая ось.
 Выражение, состоящее из 4 основных частей, переменных, операторов, показателей степени, коэффициентов и констант вместе с символом равенства, известно как алгебраическое уравнение. Возьмем уравнение: ax 2 + bx + c = d. В алгебре в начале записывается член с наибольшим показателем, а далее члены записываются с уменьшающими степенями.
Выражение, состоящее из 4 основных частей, переменных, операторов, показателей степени, коэффициентов и констант вместе с символом равенства, известно как алгебраическое уравнение. Возьмем уравнение: ax 2 + bx + c = d. В алгебре в начале записывается член с наибольшим показателем, а далее члены записываются с уменьшающими степенями. Уравнение для того же записывается как (a + b) = (b + a). Например, (x 3 + 2x) = (2x + x 3 )
Уравнение для того же записывается как (a + b) = (b + a). Например, (x 3 + 2x) = (2x + x 3 ) Уравнение для того же записывается как a × (b × c) = (a × b) × c. Например, х 3 × (2x 4 × x) = (x 3 × 2x 4 ) × x.
Уравнение для того же записывается как a × (b × c) = (a × b) × c. Например, х 3 × (2x 4 × x) = (x 3 × 2x 4 ) × x. Мы всегда добавляем похожие термины и неодинаковые термины отдельно, так как они рассматриваются как две разные величины. Математически две разные величины не могут быть сложены вместе.
Мы всегда добавляем похожие термины и неодинаковые термины отдельно, так как они рассматриваются как две разные величины. Математически две разные величины не могут быть сложены вместе. При умножении одинаковых или разных терминов мы используем законы экспоненты.
При умножении одинаковых или разных терминов мы используем законы экспоненты.