Тесты по экономике с правильными вариантами ответов онлайн
- Справочник
- Онлайн-калькуляторы
- Тесты с ответами
Оставляй заявку — и мы пройдем все тесты за тебя!
Проверку своих знаний по экономике вы можете провести в этом разделе. Здесь представлено большинство вопросов по этой специальности, с которыми можно столкнуться при тестировании в учебном заведении. Эта научная дисциплина довольно сложная, поэтому возможность несколько раз пройти тесты онлайн будет не лишней.
Здесь представлено большинство вопросов по этой специальности, с которыми можно столкнуться при тестировании в учебном заведении. Эта научная дисциплина довольно сложная, поэтому возможность несколько раз пройти тесты онлайн будет не лишней.
Экономические тесты подобраны по всем сферам, которые предусматривает дисциплина. Все очень просто: вы отвечаете на вопрос и проверяете, было решение правильным или нет. В качестве подсказки существует возможность открыть верный вариант, который предусматривают тесты по экономике. Все ответы вы можете открыть сразу и регулярно тренироваться в прохождении тестов по экономической специальности.
1. Проблемы «Что, как и для кого производить?» в условиях рыночной экономики решаются: |
| При помощи системы централизованно устанавливаемых цен и конкуренции; |
| При помощи централизованного распределения ресурсов и продуктов в пользу тех, кто больше всего в них нуждается; |
| При помощи централизованного распределения ресурсов и продуктов в пользу тех, кто лучше всех работает; |
При помощи системы свободно устанавливаемых рыночных цен и конкуренции. |
2. Экономические затраты получения данного блага измеряются: |
| Политической целесообразностью экономических реформ; |
| Ценностью других благ, которыми приходится ради этого пожертвовать; |
| Суммой денег, ранее уплаченной при приобретении данного блага; |
| Количеством других благ, которые были куплены до приобретения этого блага. |
3. Если спрос на товар и его предложение упадут, то: |
| И равновесная цена, и равновесное количество обязательно упадут; |
| Равновесная цена возрастет, а равновесное количество может возрасти, упасть, |
| Равновесное количество возрастет, а цена может возрасти, упасть, либо остаться |
| Равновесное количество упадет, а цена может возрасти, упасть, либо остаться |
4.  Цена товара снизилась на 10%, при этом спрос на него вырос на 7%. Отсюда следует, что: Цена товара снизилась на 10%, при этом спрос на него вырос на 7%. Отсюда следует, что: |
| Это нормальный товар; |
| Это малоценный товар; |
| Спрос на товар неэластичен по цене; |
| Спрос на товар эластичен по цене. |
5. Экономисты называют переменными такие затраты, которые: |
| Меняются при изменении объема выпуска; |
| Меняются в течение длительного промежутка времени; |
| Зависят от решений органов государственного управления; |
| Меняются при изменении цен на станки и оборудование. |
6. Совокупные издержки предприятия равны: |
| Сумме общих постоянных и общих переменных издержек; |
| Сумме затрат на оборудование и сырье; |
| Сумме затрат на оплату труда; |
Сумме затрат на сырье и топливо. |
7. Какое из следующих утверждений означает, что на рынке функционирует совершенно конкурентная фирма? |
| Кривая спроса на продукт фирмы имеет отрицательный наклон; |
| Кривая спроса на продукт фирмы абсолютно эластична; |
| Кривые средних и предельных издержек имеет U-образную форму; |
| Кривая спроса на продукт фирмы представляет собой вертикальную линию. |
МАКРОЭКОНОМИКА |
| в ВНД США и ВНД России; |
| в ВНД США и ВВП России; |
| в ВВП США и ВНД России; |
| в ВВП США и ВВП России; |
9.  Рост какой статьи госрасходов не увеличивает совокупный спрос: Рост какой статьи госрасходов не увеличивает совокупный спрос: |
| военные расходы; |
| пенсии; |
| оплата труда советников президента; |
| закупка импортной техники для строительства автострады. |
10. Недостаточный совокупный спрос приводит к увеличению: |
| фрикционной безработицы; |
| структурной безработицы; |
| скрытой безработицы; |
| циклической безработицы; |
11. Какое утверждение НЕВЕРНО: |
| ликвидность МЗ меньше, чем ликвидность М2; |
| в составе М2 есть элементы со 100%-й ликвидностью; |
| доходность М2 меньше, чем доходность M1; |
| в состав M1 входят элементы с нулевой доходностью; |
12.  Денежная масса возрастает, если коммерческие банки: Денежная масса возрастает, если коммерческие банки: |
| увеличивают свои вклады в центральном банке; |
| увеличивают объемы кредитов, предоставляемых домохозяйствам и фирмам; |
| увеличивают свои обязательства по текущим счетам путем получения наличных и безналичных денег от населения по вкладам; |
| уменьшают свои обязательства по текущим счетам, выплачивая наличные или безналичные деньги по вкладам. |
13. Основными инструментами монетарной политики являются: |
| государственные расходы, налоги и норма обязательных резервов; |
| предложение денег, государственные закупки и налоги; |
| учетная ставка процента, рыночная ставка процента и операции на открытом рынке; |
операции на открытом рынке, норма обязательных резервов и учетная ставка процента. |
14. Инструментом фискальной политики не является: |
| изменение величины государственных расходов; |
| регулирование рыночной ставки процента; |
| регулирование трансфертов; |
| изменение налоговых льгот. |
МИРОВАЯ ЭКОНОМИКА |
| США |
| Саудовская Аравия |
| Малайзия |
| Монголия |
| Россия |
| Великобритания |
| Германия |
| Китай |
16.  Высокий уровень конкурентоспособности американского производства достигается за счет (один ответ): Высокий уровень конкурентоспособности американского производства достигается за счет (один ответ): |
| высокого уровня развития фундаментальных исследований; |
| активной скупки иностранных лицензий; |
| совместных разработок с партнерами по научно-техническому сотрудничеству; |
| дешевой рабочей силы. |
17. Отметить страны, входящие в ЕС (несколько ответов): |
| Швейцария |
| Исландия |
| Португалия |
| Люксембург |
| Норвегия |
| Мальта |
| Швеция |
| Молдавия |
18. В развивающихся странах проявляются тенденции (несколько ответов): |
| ускорения темпов роста населения; |
| быстрый рост численности населения; |
| сокращение численности населения; |
активная миграция населения. |
19. Выберите страны, наиболее привлекательные на данный момент для иностранного инвестирования (несколько ответов): |
| Камбоджа |
| Египет |
| Ливия |
| Украина |
| США |
| Индонезия |
20. Основным фактором высокого уровня экономического развития стран Юго-Восточной Азии является: |
| богатые природные ресурсы; |
| емкий внутренний рынок; |
| дешевая рабочая сила; |
| большой объем накопленных финансовых ресурсов. |
21. ВВП мира в 2014 году составил по данным Всемирного Банка: |
38 трлн. долл. долл. |
| 74 трлн.долл. |
| 108 трлн.долл. |
| 200 трлн.долл. |
Экономика | 2,1 тыс. прослушиваний | Quizizz
Поиск среди миллионов тестовQUIZ
История
72%точность
2.1Kвоспроизведений
Андреа Шарп _ Персонал — CarrollMS6 лет
История
Андреа Шарп _ Персонал — CarrollMS
2.1Kвоспроизведений
14 вопросов
Устройства учащихся не требуются. Узнать больше
Узнать больше
14 вопросы
Показать ответыСм. предварительный просмотр
1. Множественный выбор
30 секунд
1 балл
Что такое товар?
Продукт
Ванная комната
2. Множественный выбор
30 секунд
1 точка
Количество означает
лучший товар
количество
3. Несколько- выбор
30 секунд
1 балл
Отношение между количеством товара, которое производители желают продать по различным ценам, и количеством, которое потребители желают купить.

Дефицит
Спрос и предложение
4. Множественный выбор
30 секунд
1 точка
9000 4 Если ресурсов не хватаетв мире ограниченных ресурсов есть нехватка и неограниченные потребности
очень редкий и дорогой
5. Множественный выбор
30 секунд
1 pt
Пластик, необходимый для изготовления чехлов для iphone, считается _________ ____ ____________, потому что он используется для изготовления iphone ( хороший).
Человеческие ресурсы
Капитал Ресурсы
6. Множественный выбор
30 секунд
1 балл
Исследование того, как люди принимают решения, учитывая предоставленные им ресурсы.

Экономика
Командная экономика
7. Множественный выбор
30 секунд
1 балл
добровольный обмен товарами и услугами без какого-либо вмешательства государства.
Рыночная экономика
Традиционная экономика
8. Множественный выбор
30 секунд
1 балл
Продукция s разнообразие товаров и услуг, а также поддерживает новые идеи, услуги и товары.
Преимущества рыночной экономики
Преимущества командной экономики
9. Множественный выбор
30 секунд
1 балл
Если засуха серьезно сократит количество доступной для потребителей спаржи, что вы ожидаете?
Спрос на спаржу снизится.

Цена на спаржу вырастет.
10. Множественный выбор
30 секунд
1 балл
Мои новые кроссовки Nike были представлены в мае по цене 129,99 долларов, но к декабрю они продаются по 69 долларов. 0,99. По закону спроса и предложения, что, скорее всего, верно для Nike.
Предложение кроссовок Nike было высоким, но спрос был низким.
Предложение кроссовок Nike было низким, но спрос был высоким.
11. Множественный выбор
30 секунд
1 балл
Не всегда обеспечивает основные потребности всех членов общества (слабых, больных, инвалидов или пожилых людей).
Недостаток традиционной экономики
Недостаток рыночной экономики
12.
 Множественный выбор
Множественный выбор30 секунд
1 балл
Какой тип экономической системы в США?
Рынок
Командный
Традиционный
13. Множественный выбор
30 секунд
1 балл
Что является примером капитального ресурса?
лодки
лесоматериалы (древесина)
врачи
продавцы
14. Множественный выбор
30 секунд
1 балл
Если предложение товара ограничено, но спрос высок, как повлияет цена?
Повысится
Понизится
Узнайте все вопросы с бесплатной учетной записью
У вас уже есть учетная запись?
Вопросы по экономике для тестов и рабочих листов
Из них можно создавать печатные тесты и рабочие листы. Экономика вопросов!
Выберите один или несколько вопросов, установив флажки над каждым вопросом.
Затем нажмите кнопку добавить выбранные вопросы в тест , прежде чем перейти на другую страницу.
Экономика вопросов!
Выберите один или несколько вопросов, установив флажки над каждым вопросом.
Затем нажмите кнопку добавить выбранные вопросы в тест , прежде чем перейти на другую страницу.
Предыдущий Страница 1 из 54 Далее
Выбрать все вопросыДва продавца, предлагающие один и тот же товар, конкурируют друг с другом.
Предметы или понятия, используемые для увеличения экономического влияния, называются капитал .
Система, в которой частные лица могут проводить операции без государственного регулирования, называется laissez-faire .
- торговый договор
- налоги на импорт и/или экспорт
- досмотр судов, проходящих таможню
- лицензия, гарантирующая возможность компании импортировать в страну
- Дас Капитал
- Здравый смысл
- Что такое собственность?
- Богатство народов

- Истинный
- ЛОЖЬ
- валовой внутренний продукт
- паритет покупательной способности
- валовой национальный доход
- валовой национальный продукт

- Истинный
- ЛОЖЬ
- услуга
- хочет
- потребности
- товары

- Истинный
- ЛОЖЬ
- Истинный
- ЛОЖЬ
- Истинный
- ЛОЖЬ
- бюджет
- банк
- голосование
- тест

- Истинный
- ЛОЖЬ
- ценить
- альтернативные стоимость
- избыток
- дефицит

- Истинный
- ЛОЖЬ
Если спрос высокий предложение будет низким.
Прибыль от акций будет облагаться налогом по какому типу налога?- подоходный налог
- налог на имущество
- инвестиционный налог
- налог на прирост капитала





 Множественный выбор
Множественный выбор




 .. ; an} можно найти воспользовавшись следующей формулой:
.. ; an} можно найти воспользовавшись следующей формулой: Найти длину вектора a = {1; -3; 3; -1}.
Найти длину вектора a = {1; -3; 3; -1}.
 Я представлю здесь оба метода.
Я представлю здесь оба метода. Получаем 9.0003
Получаем 9.0003
 Эти три вектора (A, B и результирующий) образуют треугольник.
Эти три вектора (A, B и результирующий) образуют треугольник. Задайте вопрос бесплатно
Задайте вопрос бесплатно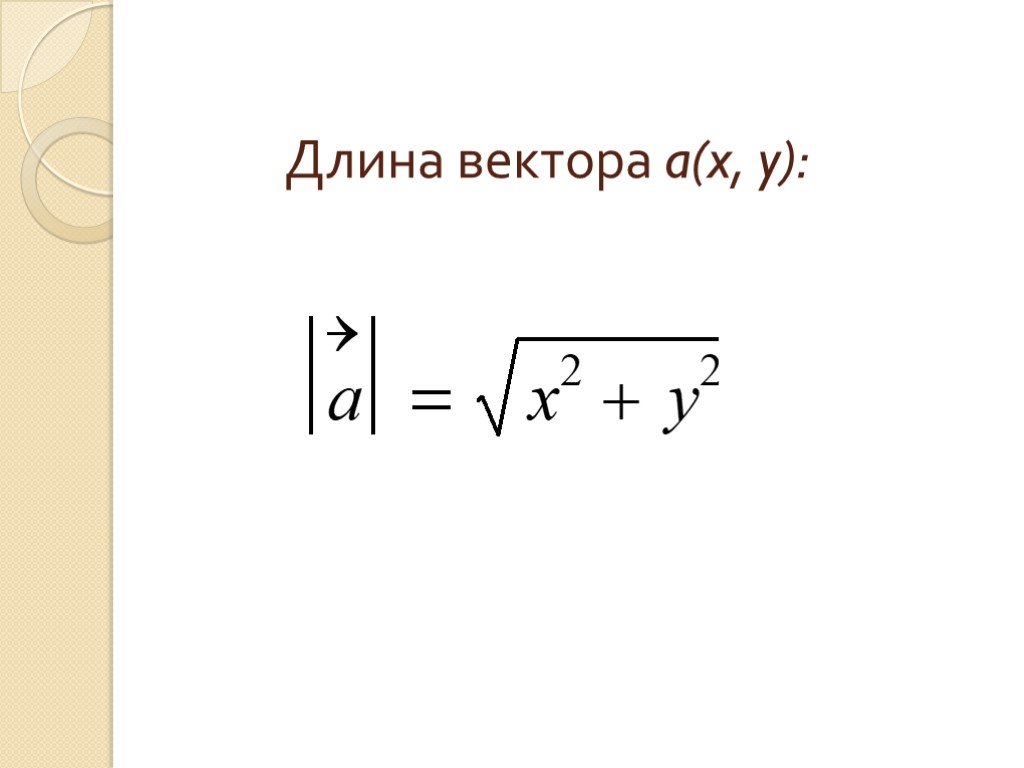 b|{\bf r}'(t)|\,dt.$$
(Ну, иногда. Это работает, если между $a$ и $b$ отрезок кривой
трассируется ровно один раз.)
92}\,дх.$$
К сожалению, такие интегралы часто невозможно вычислить точно и
должны быть приближены.
b|{\bf r}'(t)|\,dt.$$
(Ну, иногда. Это работает, если между $a$ и $b$ отрезок кривой
трассируется ровно один раз.)
92}\,дх.$$
К сожалению, такие интегралы часто невозможно вычислить точно и
должны быть приближены. 2(s/\sqrt2)\over2}+{1\over2}}=
\sqrt{{1\over2}+{1\over2}}=1.$$
Таким образом, в общем случае ${\bf r}’$ является единичным касательным вектором.
2(s/\sqrt2)\over2}+{1\over2}}=
\sqrt{{1\over2}+{1\over2}}=1.$$
Таким образом, в общем случае ${\bf r}’$ является единичным касательным вектором. Вычисляя вторые производные, находим
$|{\bf r}»(t)|=1$, $|{\bf s}»(t)|=4$.
$\квадрат$
Вычисляя вторые производные, находим
$|{\bf r}»(t)|=1$, $|{\bf s}»(t)|=4$.
$\квадрат$ Вместо этого давайте представим, что у нас есть
сделали это, поэтому мы нашли $t=g(s)$ и затем сформировали
$\шляпа{\bf r}(s)={\bf r}(g(s))$. Первая производная $\hat{\bf r}'(s)$
является единичным касательным вектором, поэтому он совпадает с единичным касательным вектором
${\bf T}(t)={\bf T}(g(s))$. Взяв производную от этого, мы получим
$${d\over ds}{\bf T}(g(s))= {\bf T}'(g(s)) g'(s)={\bf T}'(t){dt\ над
дс}.$$
Кривизна — это длина этого вектора:
$$\каппа = |{\bf T}'(t)||{dt\over ds}|={|{\bf T}'(t)|\over|ds/dt|}=
{|{\bf T}'(t)|\over|{\bf r}'(t)|}.$$
(Вспомним, что мы видели, что $ds/dt=|{\bf r}'(t)|$.) Таким образом, мы можем
вычислить кривизну, вычислив только производные по
$т$; нам не нужно делать преобразование в длину дуги.
Вместо этого давайте представим, что у нас есть
сделали это, поэтому мы нашли $t=g(s)$ и затем сформировали
$\шляпа{\bf r}(s)={\bf r}(g(s))$. Первая производная $\hat{\bf r}'(s)$
является единичным касательным вектором, поэтому он совпадает с единичным касательным вектором
${\bf T}(t)={\bf T}(g(s))$. Взяв производную от этого, мы получим
$${d\over ds}{\bf T}(g(s))= {\bf T}'(g(s)) g'(s)={\bf T}'(t){dt\ над
дс}.$$
Кривизна — это длина этого вектора:
$$\каппа = |{\bf T}'(t)||{dt\over ds}|={|{\bf T}'(t)|\over|ds/dt|}=
{|{\bf T}'(t)|\over|{\bf r}'(t)|}.$$
(Вспомним, что мы видели, что $ds/dt=|{\bf r}'(t)|$.) Таким образом, мы можем
вычислить кривизну, вычислив только производные по
$т$; нам не нужно делать преобразование в длину дуги. Затем
${\bf T}'(t)=\langle -\cos t,-\sin t,0\rangle/\sqrt2$ и
$|{\bf T}'(t)|=1/\sqrt2$. Наконец, $\kappa=1/\sqrt2/\sqrt2=1/2$,
как прежде.
$\квадрат$
Затем
${\bf T}'(t)=\langle -\cos t,-\sin t,0\rangle/\sqrt2$ и
$|{\bf T}'(t)|=1/\sqrt2$. Наконец, $\kappa=1/\sqrt2/\sqrt2=1/2$,
как прежде.
$\квадрат$

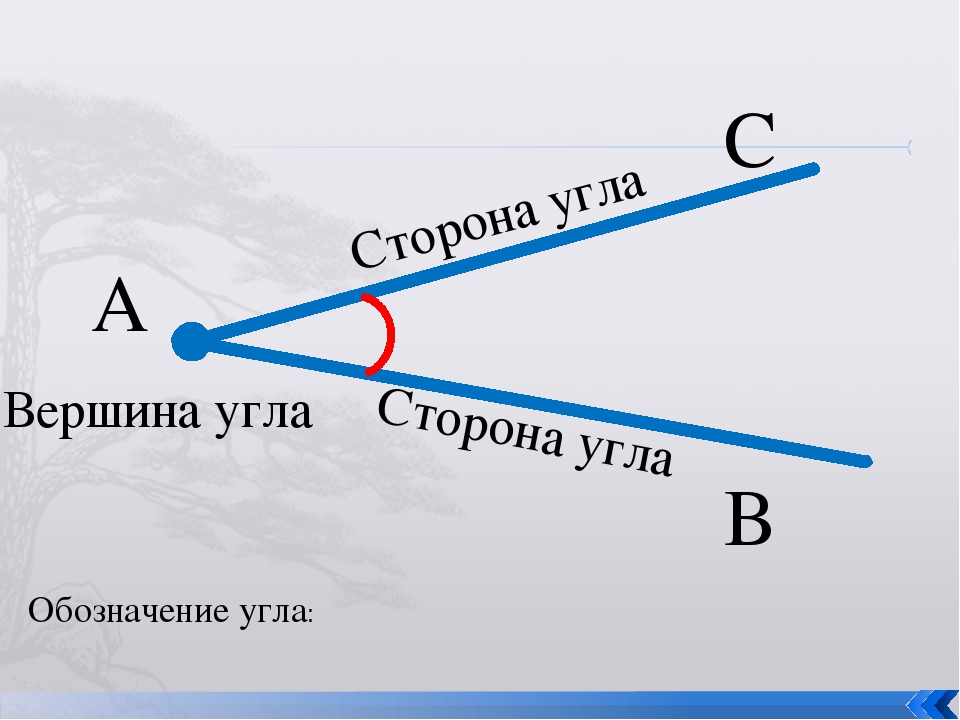
 Смежные углы между собой дополняемые, так как являются продолжением один другого.
Смежные углы между собой дополняемые, так как являются продолжением один другого.

 Линии могут быть как параллельными, так и непараллельными.
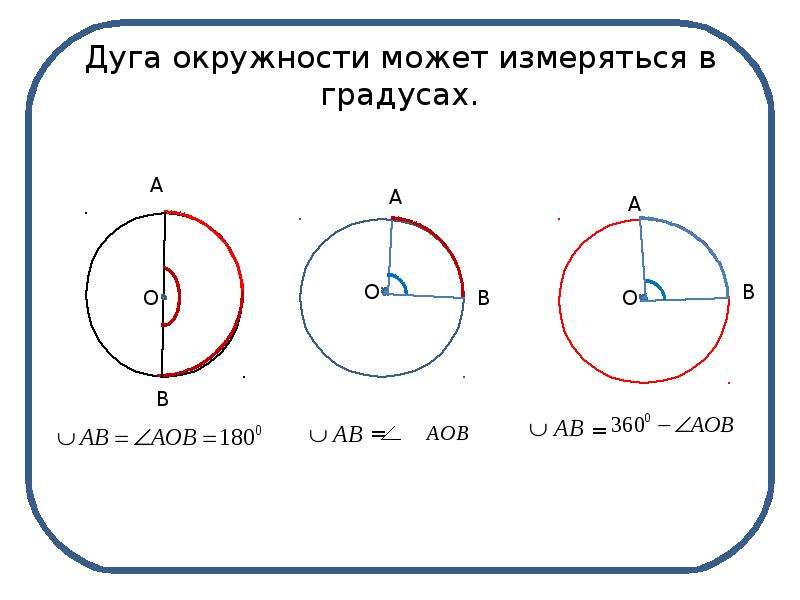
Линии могут быть как параллельными, так и непараллельными. Далее представьте дугу окружности длиной 1 единицу. Угол, образуемый этой дугой в центре окружности, имеет меру 1 радиан. Вот как это выглядит:
Далее представьте дугу окружности длиной 1 единицу. Угол, образуемый этой дугой в центре окружности, имеет меру 1 радиан. Вот как это выглядит: {\prime}=\frac{\pi}{180} \times \frac{121}{3}=\frac{121 \pi}{540}\] радиан.
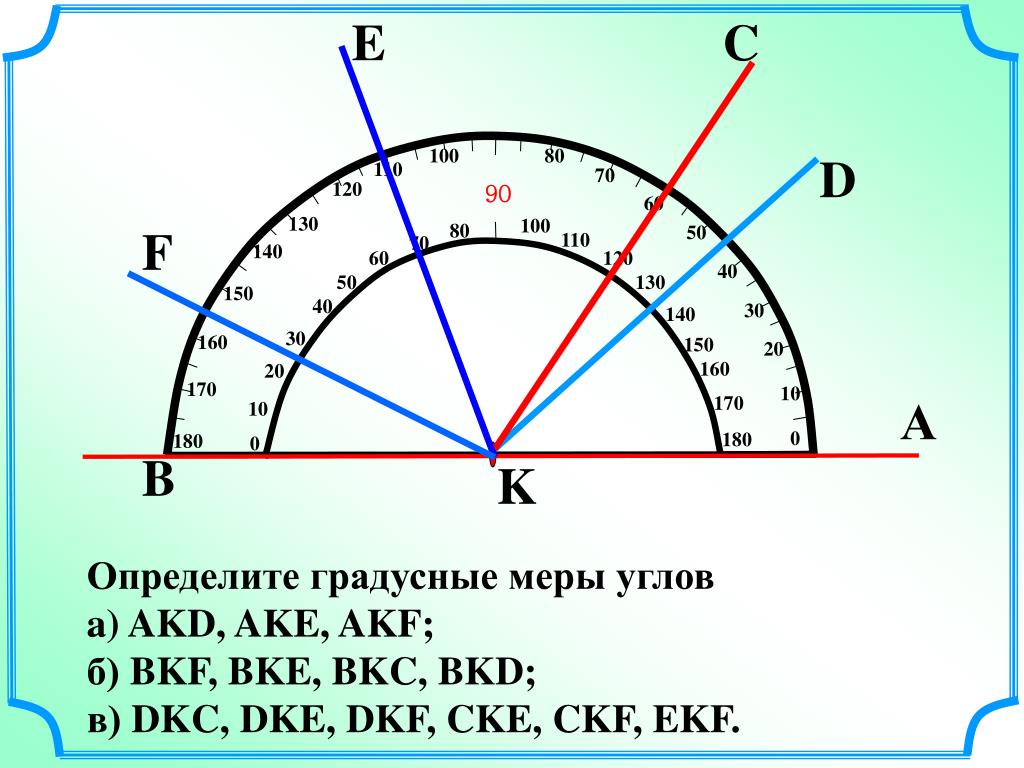
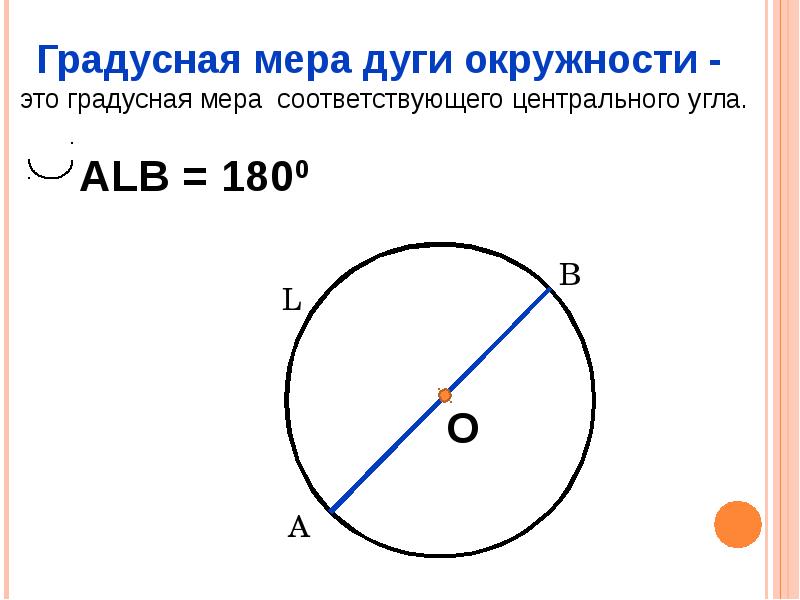
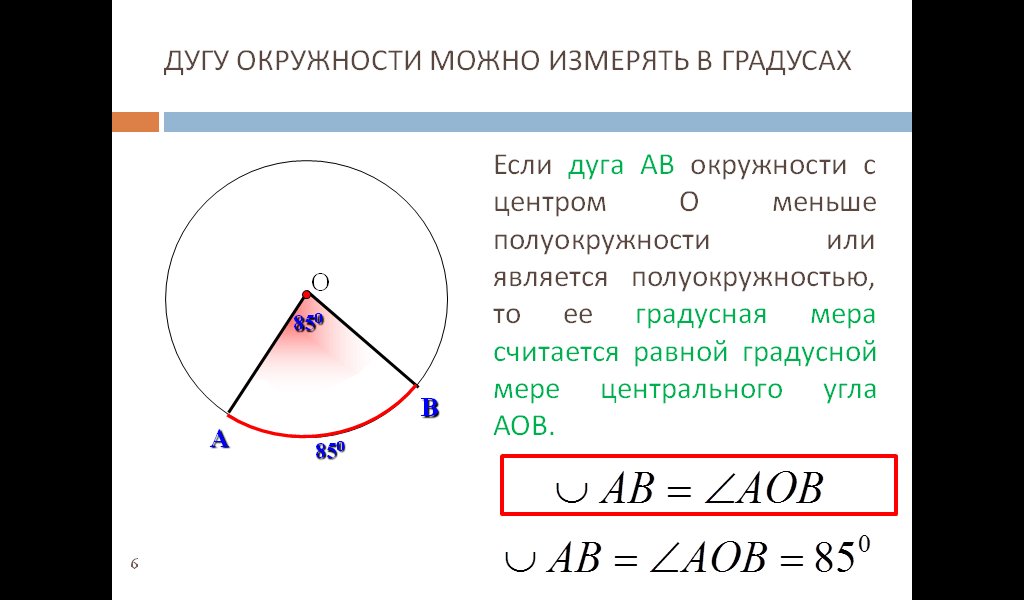
{\prime}=\frac{\pi}{180} \times \frac{121}{3}=\frac{121 \pi}{540}\] радиан. Таким образом, ∠ AOC = 143°
Таким образом, ∠ AOC = 143°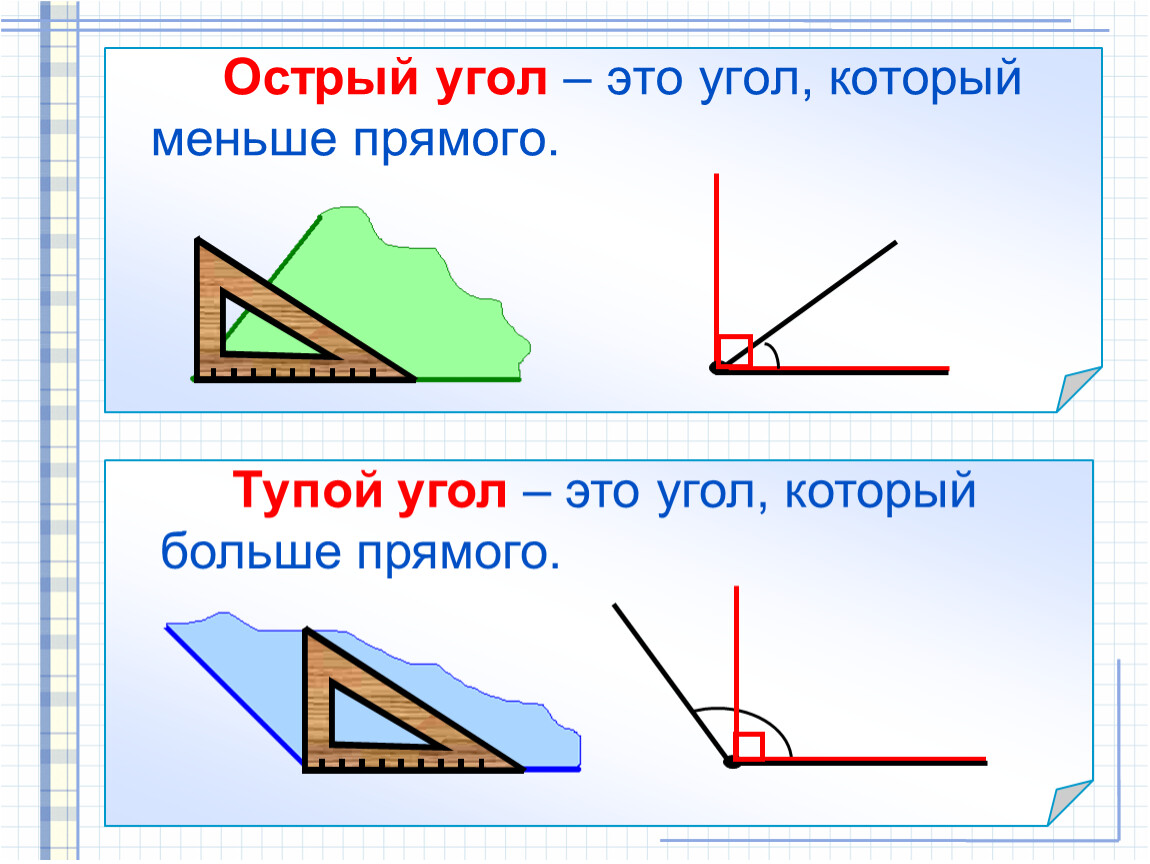
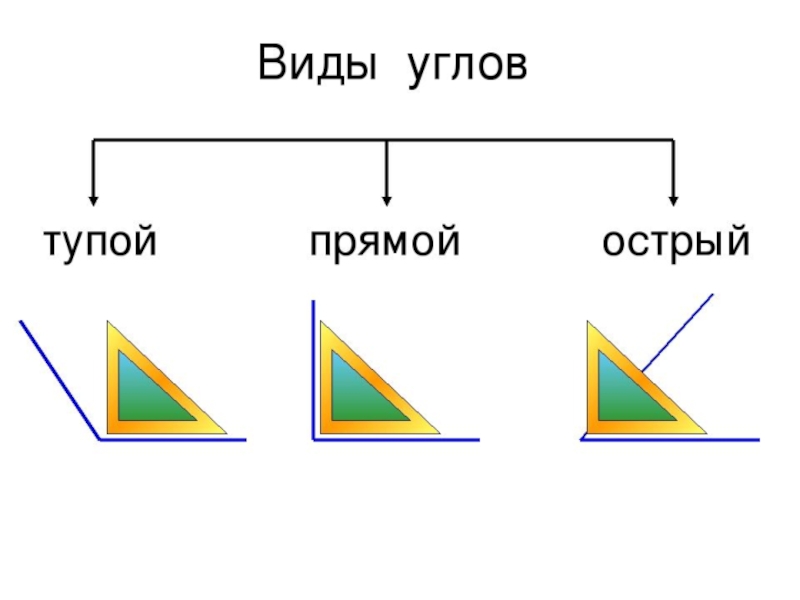
 Один градус — это \(\frac{1}{360}\) полного круга. \(90\) градусов — это четверть круга, \(180\) – половина круга (это то, сколько градусов развернутый угол), \(270\) — три четверти круга (это то, сколько градусов тупой угол) и \(360\) это целый круг.
Один градус — это \(\frac{1}{360}\) полного круга. \(90\) градусов — это четверть круга, \(180\) – половина круга (это то, сколько градусов развернутый угол), \(270\) — три четверти круга (это то, сколько градусов тупой угол) и \(360\) это целый круг. Деление градуса на минуты и секунды аналогично делению часа на минуты и секунды времени.
Деление градуса на минуты и секунды аналогично делению часа на минуты и секунды времени. Запишитесь на пробное занятие прямо сейчас!
Запишитесь на пробное занятие прямо сейчас! 3 Приблизительные значения
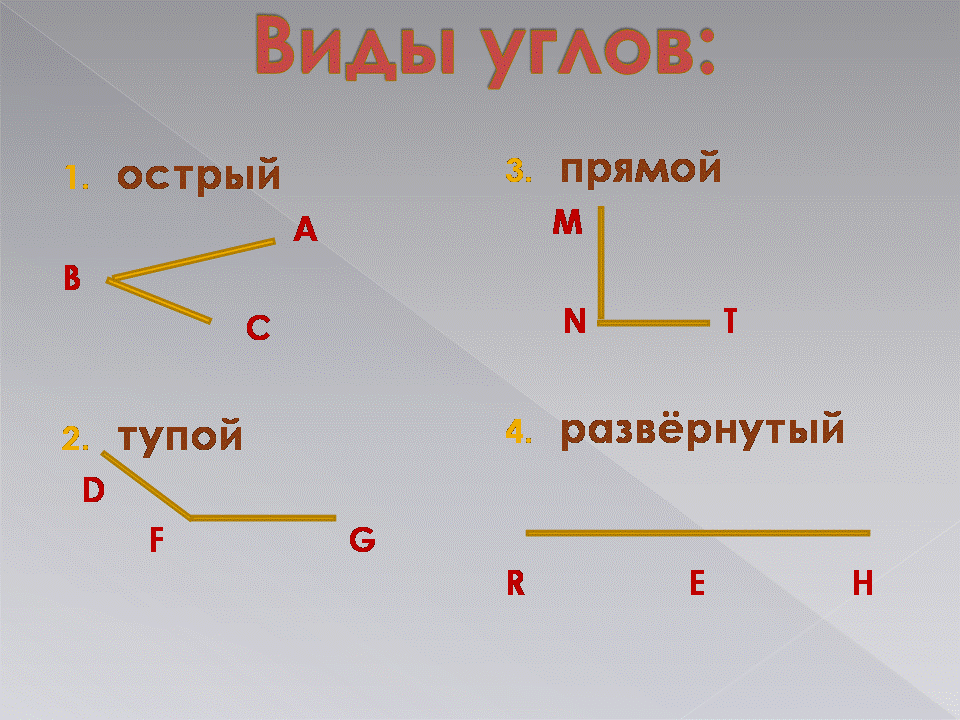
3 Приблизительные значения Согласно Проклу, угол должен быть либо качеством, либо количеством, либо отношением. Первое понятие использовал Евдем, рассматривавший угол как отклонение от прямой линии; второй — Карпом Антиохийским, который рассматривал его как промежуток или пространство между пересекающимися линиями; Евклид принял третью концепцию, хотя и свои определения прямых, острых и тупых углов.
Согласно Проклу, угол должен быть либо качеством, либо количеством, либо отношением. Первое понятие использовал Евдем, рассматривавший угол как отклонение от прямой линии; второй — Карпом Антиохийским, который рассматривал его как промежуток или пространство между пересекающимися линиями; Евклид принял третью концепцию, хотя и свои определения прямых, острых и тупых углов.
 (Чтобы понять почему, обратите внимание, что один полный круг соответствует дуге, равной длине окружности, которая равна 2 πr , поэтому s = 2 πr . Подставляя, мы получаем θ = ks / r = 2 πk . Но если один полный круг должен иметь числовое угловое значение n , то нам нужно θ = n . Это достигается установкой k = n /2 π .)
(Чтобы понять почему, обратите внимание, что один полный круг соответствует дуге, равной длине окружности, которая равна 2 πr , поэтому s = 2 πr . Подставляя, мы получаем θ = ks / r = 2 πk . Но если один полный круг должен иметь числовое угловое значение n , то нам нужно θ = n . Это достигается установкой k = n /2 π .) Он обозначается одним штрихом ( ′ ). Например, 3° 30′ равно 3 + 30/60 градусам или 3,5 градусам. Также иногда используется смешанный формат с десятичными дробями, например, 3° 5,72′ = 3 + 5,72/60 градусов. Морская миля исторически определялась как минута дуги вдоль большого круга Земли.
Он обозначается одним штрихом ( ′ ). Например, 3° 30′ равно 3 + 30/60 градусам или 3,5 градусам. Также иногда используется смешанный формат с десятичными дробями, например, 3° 5,72′ = 3 + 5,72/60 градусов. Морская миля исторически определялась как минута дуги вдоль большого круга Земли. Радиан используется практически во всех математических работах, помимо простой практической геометрии, благодаря, например, приятным и «естественным» свойствам, которые демонстрируют тригонометрические функции, когда их аргументы выражены в радианах. Радиан — это (производная) единица измерения угла в системе СИ.
Радиан используется практически во всех математических работах, помимо простой практической геометрии, благодаря, например, приятным и «естественным» свойствам, которые демонстрируют тригонометрические функции, когда их аргументы выражены в радианах. Радиан — это (производная) единица измерения угла в системе СИ. Это устройство использовали вавилоняне, и его особенно легко построить с помощью линейки и циркуля. Градус, угловая минута и угловая секунда являются шестидесятеричными единицами вавилонской единицы измерения. Одна вавилонская единица = 60° = π /3 рад ≈ 1,047197551 рад.
Это устройство использовали вавилоняне, и его особенно легко построить с помощью линейки и циркуля. Градус, угловая минута и угловая секунда являются шестидесятеричными единицами вавилонской единицы измерения. Одна вавилонская единица = 60° = π /3 рад ≈ 1,047197551 рад. Шестидесятеричные единицы назывались минут времени и секунд времени (хотя они и являются единицами измерения угла). 1 час = 15° = π /12 рад = 1/6 прямого угла ≈ 16,667 гон.
Шестидесятеричные единицы назывались минут времени и секунд времени (хотя они и являются единицами измерения угла). 1 час = 15° = π /12 рад = 1/6 прямого угла ≈ 16,667 гон. Если линия не указана, можно предположить, что это ось x в декартовой плоскости. Во многих геометрических ситуациях отрицательный угол — θ фактически эквивалентен положительному углу «один полный оборот меньше θ ». Например, поворот по часовой стрелке на 45° (то есть угол -45°) часто фактически эквивалентен повороту против часовой стрелки на 360° — 45° (то есть угол 315°).
Если линия не указана, можно предположить, что это ось x в декартовой плоскости. Во многих геометрических ситуациях отрицательный угол — θ фактически эквивалентен положительному углу «один полный оборот меньше θ ». Например, поворот по часовой стрелке на 45° (то есть угол -45°) часто фактически эквивалентен повороту против часовой стрелки на 360° — 45° (то есть угол 315°).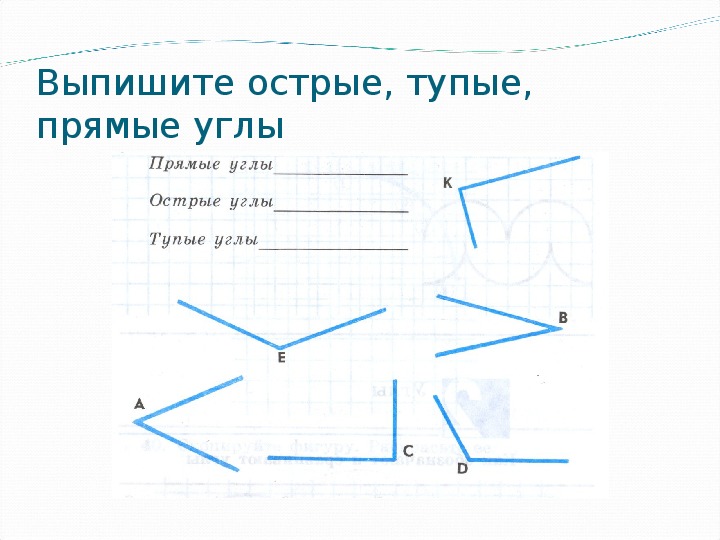


 {2}}}}} = {\ frac {y} {x}} = {\ frac {-y} {-x}} = {\ frac {\ sin (\ theta + \ pi)} {\ cos (\тета +\пи )}}} 9{2}}. Угол между двумя векторами будет просто углом поворота, который отображает один на другой. У нас пока нет численного способа определения угла. Для этого мы выбираем вектор (1,0) {\ displaystyle (1,0)}, затем для любой точки M на T {\ displaystyle \ mathbb {T}} на расстоянии θ {\ displaystyle \ theta} от ( 1,0){\displaystyle (1,0)} (на окружности), пусть u→=OM→{\displaystyle {\vec {u}}={\overrightarrow {OM}}}. Если мы назовем rθ{\displaystyle r_{\theta}} вращение, которое преобразует (1,0){\displaystyle (1,0)} в u→{\displaystyle {\vec {u}}}, то [rθ] ↦θ{\displaystyle \left[r _{\theta}\right]\mapsto \theta} — это биекция, что означает, что мы можем идентифицировать любой угол с числом от 0 до 2π{\displaystyle 2\pi}.
{2}}}}} = {\ frac {y} {x}} = {\ frac {-y} {-x}} = {\ frac {\ sin (\ theta + \ pi)} {\ cos (\тета +\пи )}}} 9{2}}. Угол между двумя векторами будет просто углом поворота, который отображает один на другой. У нас пока нет численного способа определения угла. Для этого мы выбираем вектор (1,0) {\ displaystyle (1,0)}, затем для любой точки M на T {\ displaystyle \ mathbb {T}} на расстоянии θ {\ displaystyle \ theta} от ( 1,0){\displaystyle (1,0)} (на окружности), пусть u→=OM→{\displaystyle {\vec {u}}={\overrightarrow {OM}}}. Если мы назовем rθ{\displaystyle r_{\theta}} вращение, которое преобразует (1,0){\displaystyle (1,0)} в u→{\displaystyle {\vec {u}}}, то [rθ] ↦θ{\displaystyle \left[r _{\theta}\right]\mapsto \theta} — это биекция, что означает, что мы можем идентифицировать любой угол с числом от 0 до 2π{\displaystyle 2\pi}. Частным случаям давались различные названия (теперь редко, если вообще когда-либо) давались: амфикиртик (греч. ἀμφί , с обеих сторон, κυρτόσ , выпуклый) или циссоидальный (гр. κισσόσ , плющ), двояковыпуклый; ксистроидальный или систроидальный (гр. ξυστρίσ , инструмент для шабрения), вогнуто-выпуклый; амфицельный (гр. κοίλη , впадина) или angulus lunularis , двояковогнутый.
Частным случаям давались различные названия (теперь редко, если вообще когда-либо) давались: амфикиртик (греч. ἀμφί , с обеих сторон, κυρτόσ , выпуклый) или циссоидальный (гр. κισσόσ , плющ), двояковыпуклый; ксистроидальный или систроидальный (гр. ξυστρίσ , инструмент для шабрения), вогнуто-выпуклый; амфицельный (гр. κοίλη , впадина) или angulus lunularis , двояковогнутый.
 ISBN 0768202620 .
ISBN 0768202620 . Чтобы процитировать эту статью, щелкните здесь, чтобы просмотреть список допустимых форматов цитирования. История более ранних вкладов википедистов доступна исследователям здесь:
Чтобы процитировать эту статью, щелкните здесь, чтобы просмотреть список допустимых форматов цитирования. История более ранних вкладов википедистов доступна исследователям здесь:
 Каждый треугольник имеет сумму углов 180 градусов. Следовательно, сумма углов четырехугольника равна 360 градусов.
Каждый треугольник имеет сумму углов 180 градусов. Следовательно, сумма углов четырехугольника равна 360 градусов.

 ): GASTAT-navi
): GASTAT-navi 04.2011 (Бессрочно)
04.2011 (Бессрочно) [3] На количество растворенного кислорода, присутствующего в клетках и тканях, влияют многие факторы, например [4]
[3] На количество растворенного кислорода, присутствующего в клетках и тканях, влияют многие факторы, например [4] Таким образом, на уровне моря, где атмосферное давление составляет 760 мм рт. ст., парциальные давления различных газов можно оценить так, чтобы парциальные давления азота составляли приблизительно 593 мм рт. ст., кислорода — 160 мм рт. ст., аргона — 7,6 мм рт. ст.
Таким образом, на уровне моря, где атмосферное давление составляет 760 мм рт. ст., парциальные давления различных газов можно оценить так, чтобы парциальные давления азота составляли приблизительно 593 мм рт. ст., кислорода — 160 мм рт. ст., аргона — 7,6 мм рт. ст. Уравнение альвеолярного газа используется для расчета парциального давления кислорода в альвеолах:
Уравнение альвеолярного газа используется для расчета парциального давления кислорода в альвеолах: На уровне моря без дополнительной вдыхаемой оксигенации альвеолярное парциальное давление кислорода (PAO2) составляет:
На уровне моря без дополнительной вдыхаемой оксигенации альвеолярное парциальное давление кислорода (PAO2) составляет: [7] Было обнаружено, что мозгу требуется парциальное давление кислорода от 30 до 48 мм рт. Ст. [7] [3].
[7] Было обнаружено, что мозгу требуется парциальное давление кислорода от 30 до 48 мм рт. Ст. [7] [3]. ст. и 34,53 мм рт.ст. Почки составляют еще одну систему органов с высокой потребностью в кислороде из-за высокой энергии и последующей метаболической потребности, вовлеченной в активные транспортные процессы систем реабсорбции нефронов. Таким образом, парциальное давление кислорода в мозговом веществе составляет от 10 до 20 мм рт. ст., а коре требуется от 52 до 9 мм рт.2 мм рт.ст. Мышечная потребность в кислороде сильно варьирует в зависимости от интенсивности и продолжительности активности мышц. В исходном состоянии мышечное парциальное давление кислорода находится в диапазоне от 27 до 31 мм рт. ст. [8]. В процессе потребления кислорода различными тканями содержание кислорода в крови падает так, что 100 мм рт.ст. в артериальной крови снижается до 40 мм рт.ст. в венозной [9].
ст. и 34,53 мм рт.ст. Почки составляют еще одну систему органов с высокой потребностью в кислороде из-за высокой энергии и последующей метаболической потребности, вовлеченной в активные транспортные процессы систем реабсорбции нефронов. Таким образом, парциальное давление кислорода в мозговом веществе составляет от 10 до 20 мм рт. ст., а коре требуется от 52 до 9 мм рт.2 мм рт.ст. Мышечная потребность в кислороде сильно варьирует в зависимости от интенсивности и продолжительности активности мышц. В исходном состоянии мышечное парциальное давление кислорода находится в диапазоне от 27 до 31 мм рт. ст. [8]. В процессе потребления кислорода различными тканями содержание кислорода в крови падает так, что 100 мм рт.ст. в артериальной крови снижается до 40 мм рт.ст. в венозной [9]. Все они полезны для оценки и лечения различных болезненных состояний.
Все они полезны для оценки и лечения различных болезненных состояний. Это снижает парциальное давление кислорода в альвеолярном пространстве, что приводит к уменьшению градиента диффузии, снижая парциальное давление кислорода в крови.
Это снижает парциальное давление кислорода в альвеолярном пространстве, что приводит к уменьшению градиента диффузии, снижая парциальное давление кислорода в крови. При болезненных состояниях, таких как заболевания легочных сосудов, интерстициальное заболевание или обструктивное заболевание легких, отношение доступной вентиляции легких к капиллярной перфузии искажено. Это приводит к неэффективному переносу кислорода в капиллярное пространство, что приводит к снижению парциального давления кислорода в крови.
При болезненных состояниях, таких как заболевания легочных сосудов, интерстициальное заболевание или обструктивное заболевание легких, отношение доступной вентиляции легких к капиллярной перфузии искажено. Это приводит к неэффективному переносу кислорода в капиллярное пространство, что приводит к снижению парциального давления кислорода в крови. Во время отдыха кровоток через легочные артериолы достаточно медленный, чтобы обеспечить правильную диффузию независимо от повышенного градиента А-а. Однако в условиях физической нагрузки сердечный выброс увеличивается. Когда это происходит, в легких меньше времени для оксигенации, что приводит к транзиторной гипоксии. Примеры болезни с ограниченной диффузией включают фиброз легких и хроническую обструктивную болезнь легких. Результатом является нормальное парциальное давление кислорода в альвеолярном пространстве, но низкое парциальное давление кислорода в артериальном пространстве.
Во время отдыха кровоток через легочные артериолы достаточно медленный, чтобы обеспечить правильную диффузию независимо от повышенного градиента А-а. Однако в условиях физической нагрузки сердечный выброс увеличивается. Когда это происходит, в легких меньше времени для оксигенации, что приводит к транзиторной гипоксии. Примеры болезни с ограниченной диффузией включают фиброз легких и хроническую обструктивную болезнь легких. Результатом является нормальное парциальное давление кислорода в альвеолярном пространстве, но низкое парциальное давление кислорода в артериальном пространстве. ][20]
][20] Сюда входят клиницисты, специалисты, медсестры и пульмонологи. Знание того, как использовать это значение, может помочь в диагностике и помочь сформировать стратегию лечения и ведения этих пациентов, что приведет к лучшим результатам. [Уровень 5]
Сюда входят клиницисты, специалисты, медсестры и пульмонологи. Знание того, как использовать это значение, может помочь в диагностике и помочь сформировать стратегию лечения и ведения этих пациентов, что приведет к лучшим результатам. [Уровень 5]
 J Wilderness Med. 1993 г., февраль; 4(1):17-26. [PubMed: 11538296]
J Wilderness Med. 1993 г., февраль; 4(1):17-26. [PubMed: 11538296]
 , Плеус С., Джендрике Н., Либинг С., Хинцманн Р., Хауг С., Фрекманн Г. Проверка концепции для оценки влияния парциального давления кислорода в капиллярной крови на измерения SMBG. J Diabetes Sci Technol. 2019 ноябрь;13(6):1105-1111. [Бесплатная статья PMC: PMC6835173] [PubMed: 30841739]
, Плеус С., Джендрике Н., Либинг С., Хинцманн Р., Хауг С., Фрекманн Г. Проверка концепции для оценки влияния парциального давления кислорода в капиллярной крови на измерения SMBG. J Diabetes Sci Technol. 2019 ноябрь;13(6):1105-1111. [Бесплатная статья PMC: PMC6835173] [PubMed: 30841739] [PubMed: 15521702]
[PubMed: 15521702]
 Нормальный диапазон составляет от 35 до 45 мм рт.
Нормальный диапазон составляет от 35 до 45 мм рт.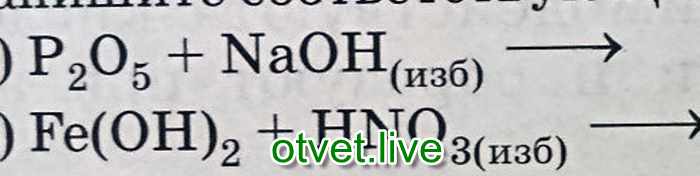 ст. [6]
ст. [6]  clinicalcorrelations.org/?p=5608
https://lifeinthefastlane.com/ccc/vbg-versus-abg/
clinicalcorrelations.org/?p=5608
https://lifeinthefastlane.com/ccc/vbg-versus-abg/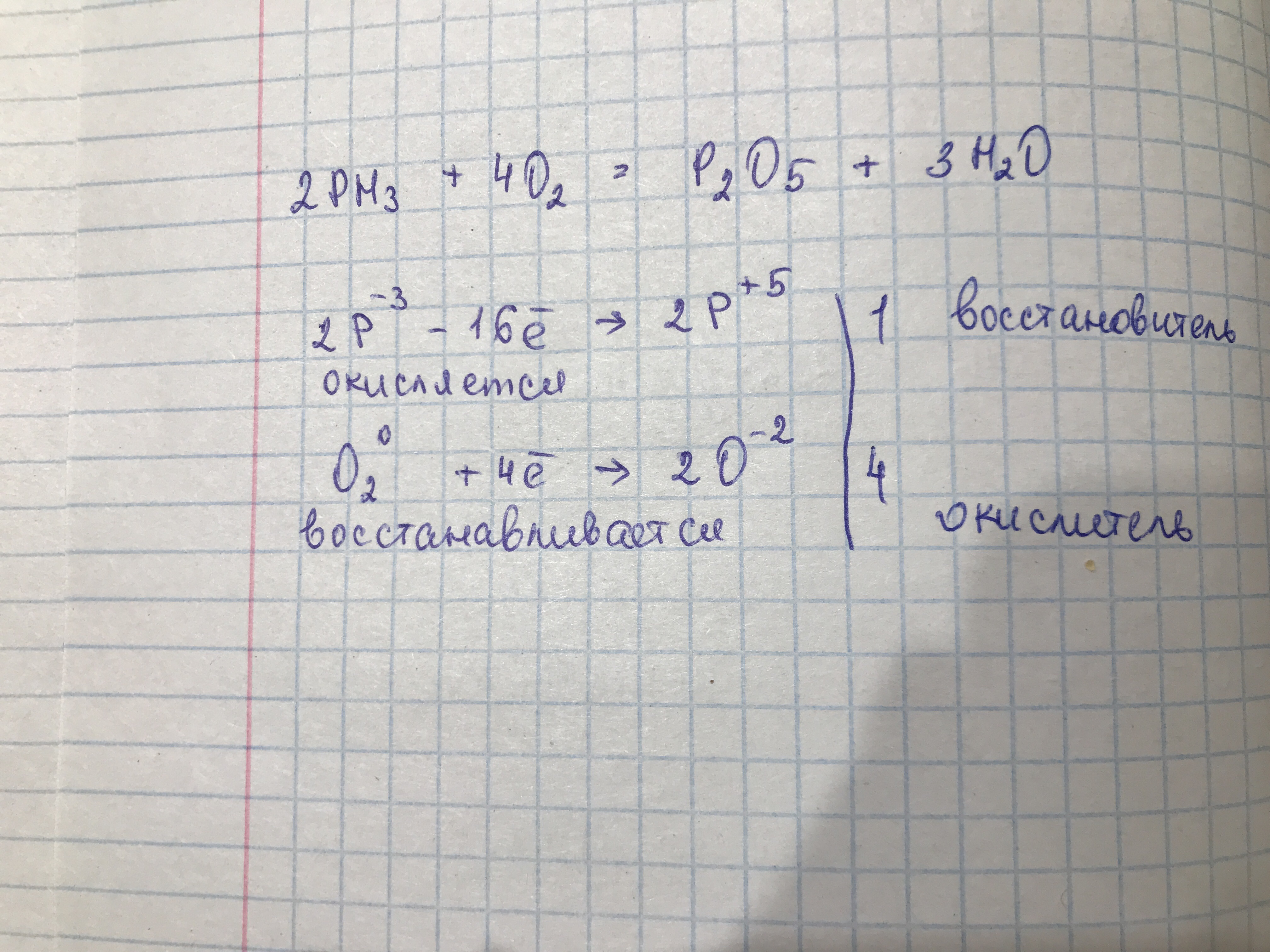
 Следует всегда аккуратно записывать ОДЗ
Следует всегда аккуратно записывать ОДЗ Мы
говорим о том, как развиваются и изменяются
образование и наука.
Мы
говорим о том, как развиваются и изменяются
образование и наука.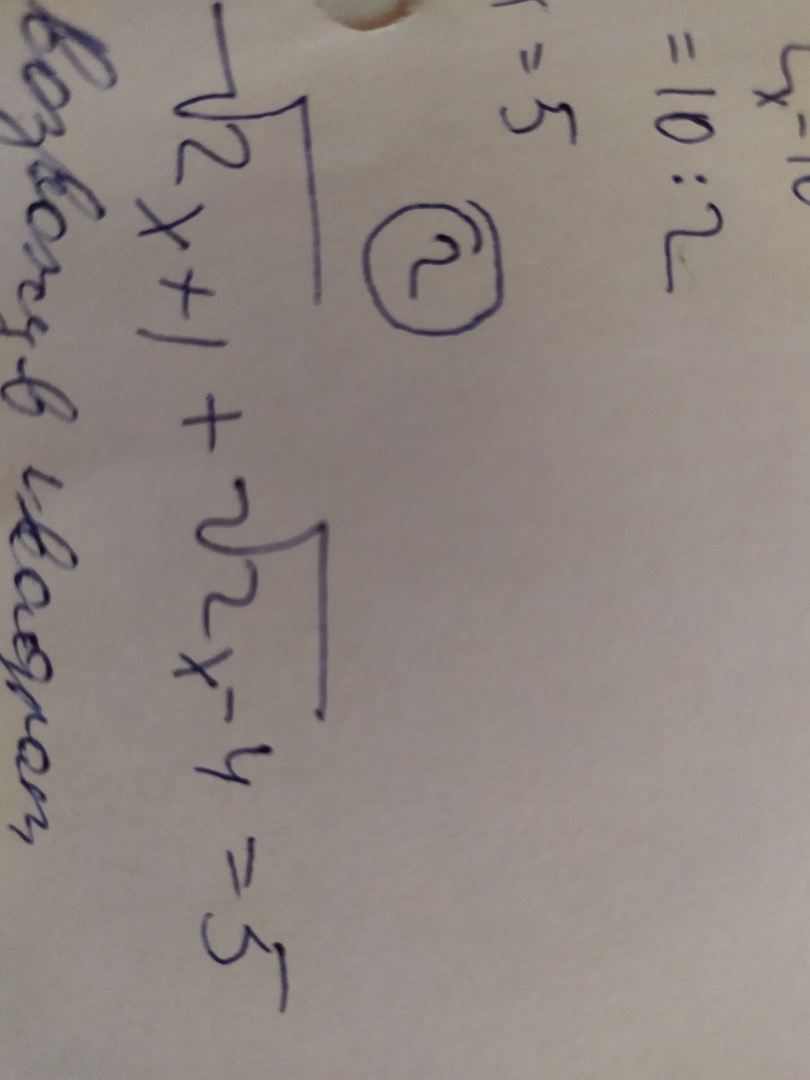
 е. выход функции извлечения квадратного корня положителен. Если выход квадратного корня всегда положителен, то диапазон $\sqrt{x-1}$, очевидно, равен $[0, \infty)$ $$$$
е. выход функции извлечения квадратного корня положителен. Если выход квадратного корня всегда положителен, то диапазон $\sqrt{x-1}$, очевидно, равен $[0, \infty)$ $$$$
 исходный код
Оставить отзыв
Добавить это приложение в закладки
исходный код
Оставить отзыв
Добавить это приложение в закладки




 Используя технологию конвертации online-convert.com, вы получите очень точные результаты конверсии.
Используя технологию конвертации online-convert.com, вы получите очень точные результаты конверсии. Это стандартный формат документов, и разработчиков программного обеспечения часто просят найти способ конвертировать файлы Microsoft Excel в документы PDF.
Это стандартный формат документов, и разработчиков программного обеспечения часто просят найти способ конвертировать файлы Microsoft Excel в документы PDF. Метод Сохранить обеспечивает SaveFormat.Pdf член перечисления, который преобразует исходные файлы Excel в формат PDF.
Метод Сохранить обеспечивает SaveFormat.Pdf член перечисления, который преобразует исходные файлы Excel в формат PDF.
 В следующем коде показано использование свойства PdfSaveOptions.CreatedTime для установки времени создания файла PDF.
В следующем коде показано использование свойства PdfSaveOptions.CreatedTime для установки времени создания файла PDF.
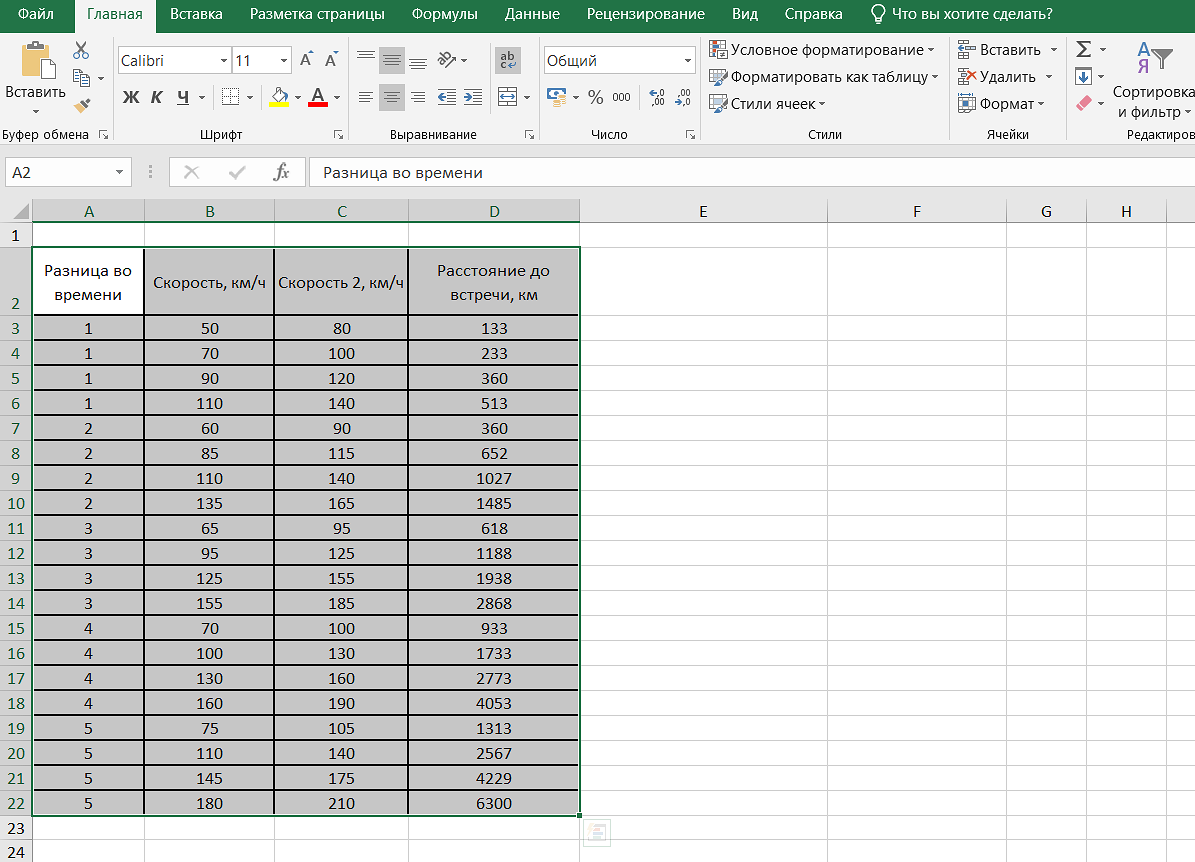
 CalculateFormula() непосредственно перед преобразованием электронной таблицы в формат PDF. Это гарантирует, что значения, зависящие от формулы, будут пересчитаны, а в PDF-файле отобразятся правильные значения.
CalculateFormula() непосредственно перед преобразованием электронной таблицы в формат PDF. Это гарантирует, что значения, зависящие от формулы, будут пересчитаны, а в PDF-файле отобразятся правильные значения.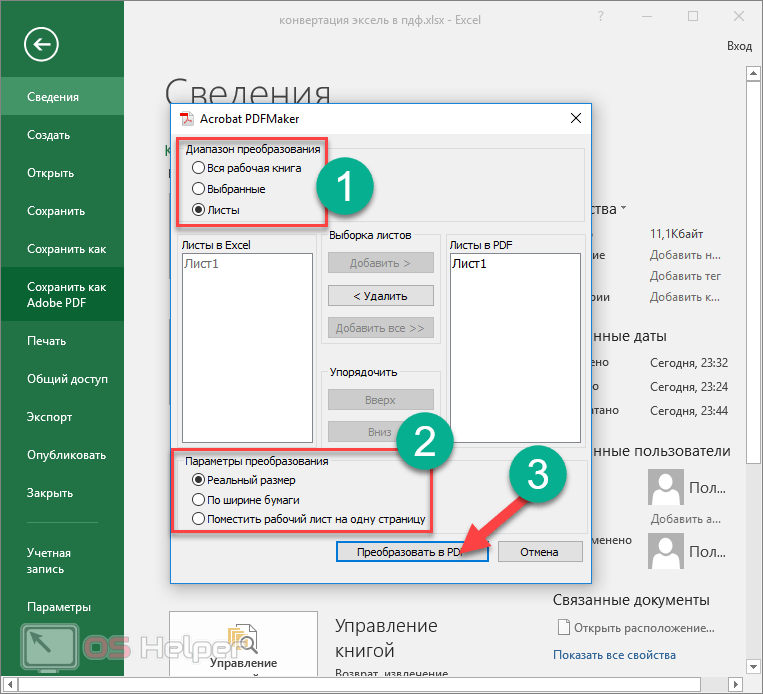
 Это связано с тем, что формула Гюйгенса дает погрешность при вычислении. Хоть величина погрешности невелика, знать об этом надо.
Это связано с тем, что формула Гюйгенса дает погрешность при вычислении. Хоть величина погрешности невелика, знать об этом надо.
 Они доступны на панели инструментов построения и в контекстном меню при создании объекта.
Они доступны на панели инструментов построения и в контекстном меню при создании объекта.





 Любое расстояние вдоль изогнутой линии, образующей дугу, называется длиной дуги. Часть кривой или часть окружности окружности называется Дугой. Все они имеют кривую форму. Длина дуги больше, чем любое расстояние по прямой линии между ее концами (хорда).
Любое расстояние вдоль изогнутой линии, образующей дугу, называется длиной дуги. Часть кривой или часть окружности окружности называется Дугой. Все они имеют кривую форму. Длина дуги больше, чем любое расстояние по прямой линии между ее концами (хорда). Дуга окружности – это любая часть окружности. Угол, образуемый дугой в любой точке, — это угол, образованный между двумя отрезками, соединяющими центр с конечными точками дуги. Например, в окружности, показанной ниже, OP — это дуга окружности с центром Q. Длина дуги этой дуги OP равна L.
Дуга окружности – это любая часть окружности. Угол, образуемый дугой в любой точке, — это угол, образованный между двумя отрезками, соединяющими центр с конечными точками дуги. Например, в окружности, показанной ниже, OP — это дуга окружности с центром Q. Длина дуги этой дуги OP равна L.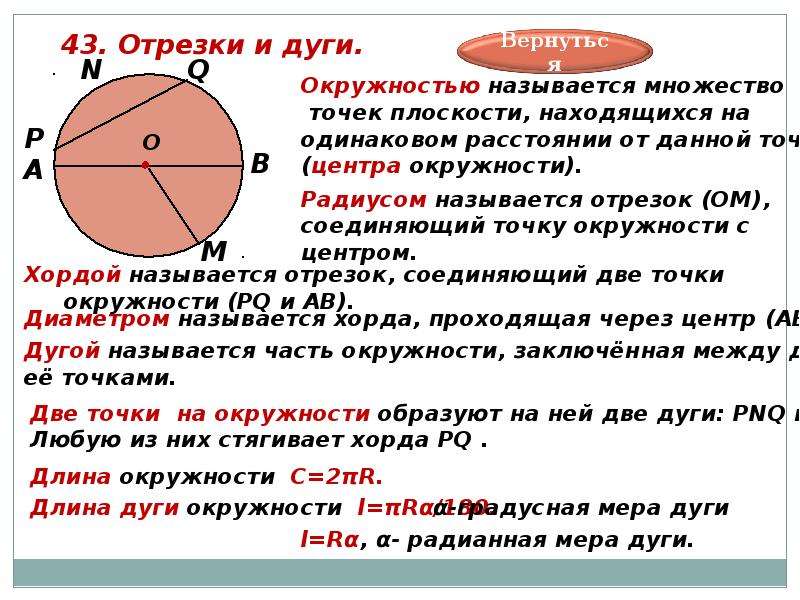
 Некоторые важные случаи приведены ниже,
Некоторые важные случаи приведены ниже,

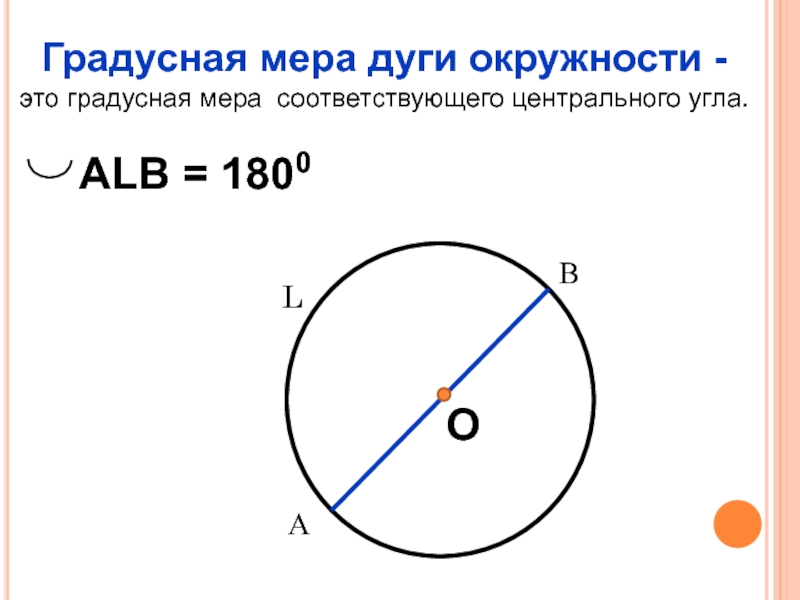
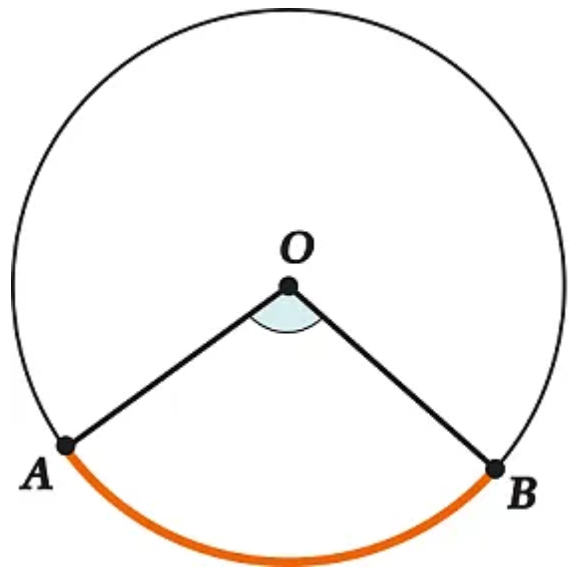
 т. е. дуга окружности — это любая часть окружности. Угол, образуемый дугой в любой точке, — это угол, образованный между двумя отрезками прямой, соединяющими эту точку с конечными точками дуги.
т. е. дуга окружности — это любая часть окружности. Угол, образуемый дугой в любой точке, — это угол, образованный между двумя отрезками прямой, соединяющими эту точку с конечными точками дуги. Ниже приведены два уравнения длины дуги.
Ниже приведены два уравнения длины дуги. Центральный угол больше 180°. Используя формулу ℓ = rθ, мы можем найти длину дуги окружности, где θ в радианах.
Центральный угол больше 180°. Используя формулу ℓ = rθ, мы можем найти длину дуги окружности, где θ в радианах. Следовательно, поскольку пропорция между углом и длиной дуги постоянна, мы можем сказать, что:
Следовательно, поскольку пропорция между углом и длиной дуги постоянна, мы можем сказать, что:
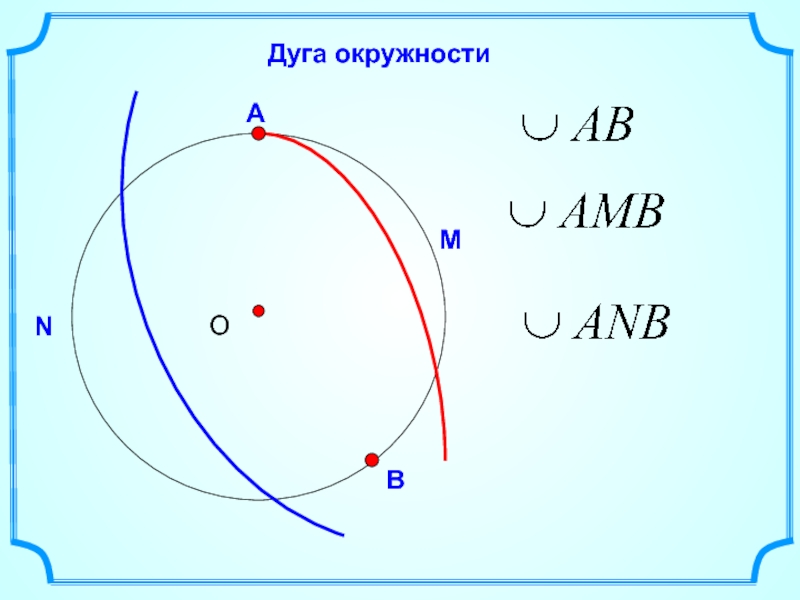
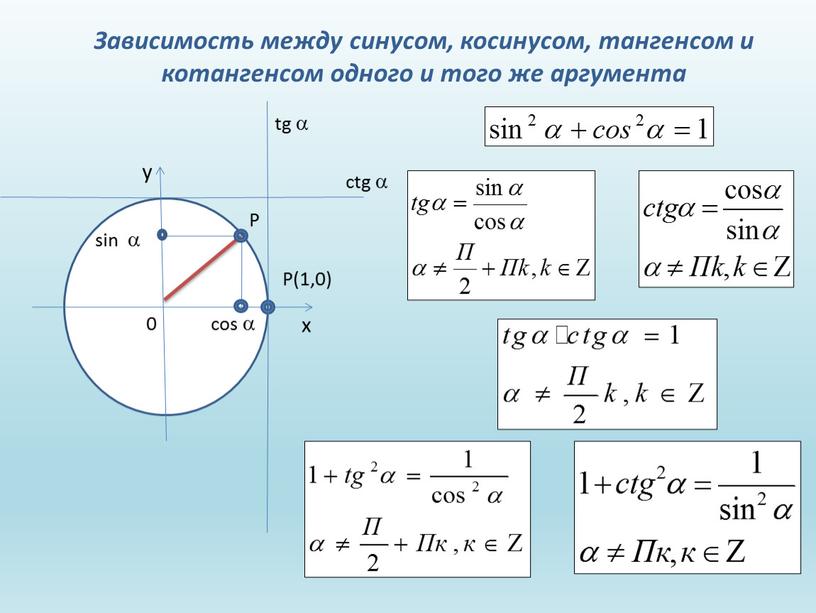
 Следовательно, справедливы формулы:
Следовательно, справедливы формулы:




 )
Если
, мы определяем
)
Если
, мы определяем
 7)
7) Позволять
Позволять  13)
13) 16) заменить на
и получить
16) заменить на
и получить  22)
22) 25).
25). Для
оставшиеся значения
вам не нужно включать объяснение.
Для
оставшиеся значения
вам не нужно включать объяснение. и позже был сокращен до jya означает «аккорд». Индус
слово было переведено на арабский язык как jîba , что было бессмысленным
слово фонетически происходит от jya , но (поскольку гласные
по-арабски не писались) было написано так же, как jaib , что значит грудь. Когда араб был
в переводе на латынь это стало sinus . ( Jaib означает грудь, залив,
или грудь: sinus означает грудь, залив или складку тоги вокруг
грудь.) английское слово sine происходит от sinus фонетически.
и позже был сокращен до jya означает «аккорд». Индус
слово было переведено на арабский язык как jîba , что было бессмысленным
слово фонетически происходит от jya , но (поскольку гласные
по-арабски не писались) было написано так же, как jaib , что значит грудь. Когда араб был
в переводе на латынь это стало sinus . ( Jaib означает грудь, залив,
или грудь: sinus означает грудь, залив или складку тоги вокруг
грудь.) английское слово sine происходит от sinus фонетически. Отношение длин стороны, прилежащей к углу, и гипотенузы прямоугольного треугольника называется функцией косинуса, которая изменяется при изменении угла. Он определяется в контексте прямоугольного треугольника для острых углов. Косинус используется для моделирования многих реальных сценариев — радиоволн, приливов и отливов, звуковых волн, музыкальных тонов, электрических токов.
Отношение длин стороны, прилежащей к углу, и гипотенузы прямоугольного треугольника называется функцией косинуса, которая изменяется при изменении угла. Он определяется в контексте прямоугольного треугольника для острых углов. Косинус используется для моделирования многих реальных сценариев — радиоволн, приливов и отливов, звуковых волн, музыкальных тонов, электрических токов.
 Математически формула функции косинуса относительно сторон прямоугольного треугольника записывается как:
Математически формула функции косинуса относительно сторон прямоугольного треугольника записывается как: P впоследствии перемещается из 9от 0° до положения 180°. В этой фазе движения длина или величина OQ увеличивается, а значение косинуса уменьшается со значения 0 при 90° до минимума -1 при 180°.
P впоследствии перемещается из 9от 0° до положения 180°. В этой фазе движения длина или величина OQ увеличивается, а значение косинуса уменьшается со значения 0 при 90° до минимума -1 при 180°. Объединив реакцию изменения значения PQ для всех четырех квадрантов, мы получили полный график зависимости cos x от x для одного полного цикла от 0 до 2π радиан (от 0° до 360°). Полученный таким образом график показан ниже:
Объединив реакцию изменения значения PQ для всех четырех квадрантов, мы получили полный график зависимости cos x от x для одного полного цикла от 0 до 2π радиан (от 0° до 360°). Полученный таким образом график показан ниже: Функция косинуса является специальной тригонометрической функцией и имеет множество свойств. Некоторые из них перечислены ниже:
Функция косинуса является специальной тригонометрической функцией и имеет множество свойств. Некоторые из них перечислены ниже:
 Он дает значение функции косинуса для угла x, обозначаемое как cos x.
Он дает значение функции косинуса для угла x, обозначаемое как cos x.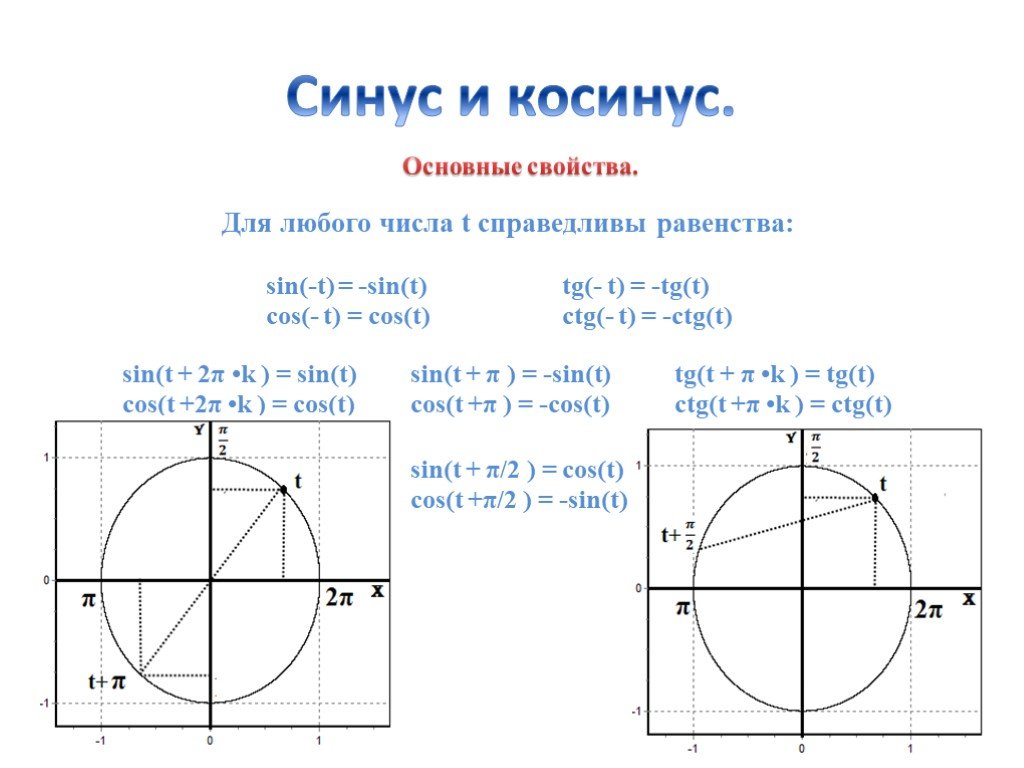

 RU
RU 2+4x-3$ на отрезке $[-5;2]$.
2+4x-3$ на отрезке $[-5;2]$. Термин вершина также относится к высшей точке параболы, которая открывается вниз.
Термин вершина также относится к высшей точке параболы, которая открывается вниз. Старший коэффициент говорит вам, в каком направлении открывается парабола, а именно
Старший коэффициент говорит вам, в каком направлении открывается парабола, а именно е. нет значения x , которое нельзя было бы подставить в уравнение y ( x ) = ах 2 + bx + c ). Однако диапазон квадратичных функций составляет , а не всех действительных чисел, а скорее варьируется в зависимости от формы кривой. В частности,
е. нет значения x , которое нельзя было бы подставить в уравнение y ( x ) = ах 2 + bx + c ). Однако диапазон квадратичных функций составляет , а не всех действительных чисел, а скорее варьируется в зависимости от формы кривой. В частности,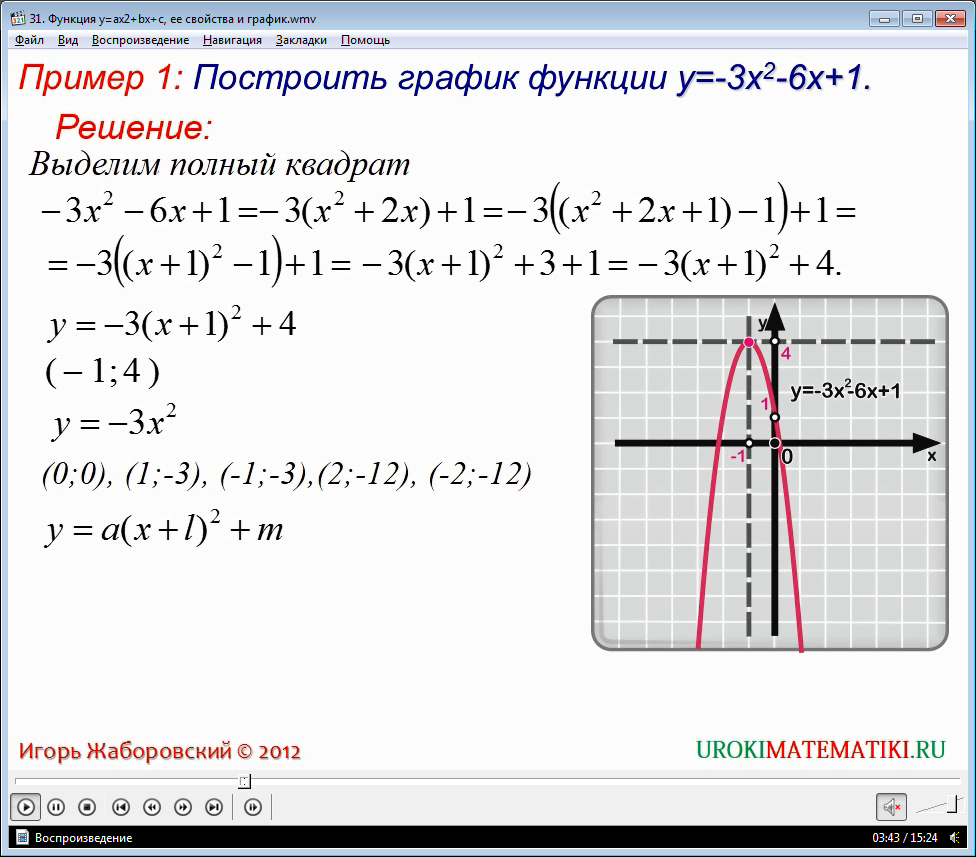 Вы можете нанести эти точки на плоскость xy- и провести через них плавную кривую, чтобы сформировать параболу, как показано ниже,
Вы можете нанести эти точки на плоскость xy- и провести через них плавную кривую, чтобы сформировать параболу, как показано ниже,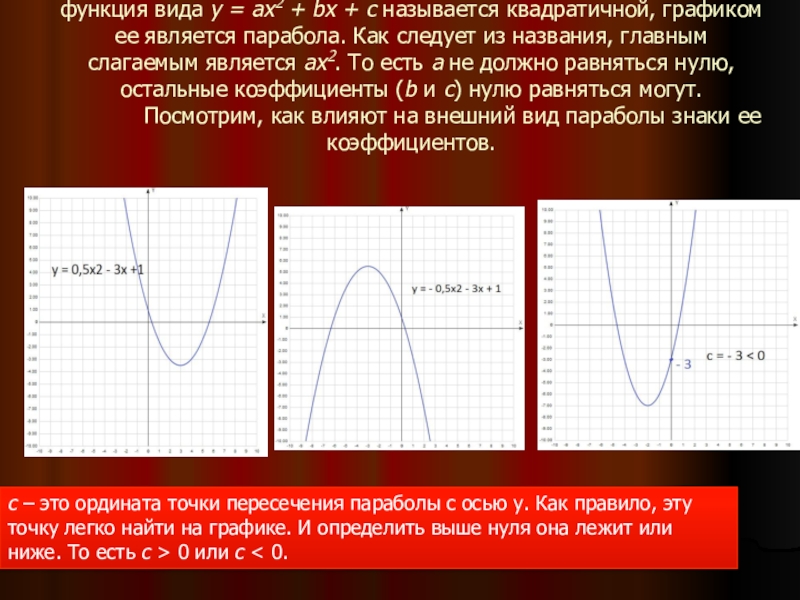 Мы можем сделать это, используя метод «Завершение квадратов».
Мы можем сделать это, используя метод «Завершение квадратов». Для функции F(x) = 7x 2 + 5x + 8 найти значение x, при котором оно возрастает.
Для функции F(x) = 7x 2 + 5x + 8 найти значение x, при котором оно возрастает.  33).
33).