Что такое вектор, как найти длину? Координаты? Формулы
Определение и обозначение вектора
Вектор в геометрии — это отрезок, для которого указано, какая из его граничных точек считается началом, а какая — концом. В некоторых учебниках вектор могут называть направленным отрезком.
Вектор обозначается одной строчной буквой латинского алфавита или двумя заглавными со стрелкой (в некоторых случаях — прямой линией) сверху.
Интересно, что порядок букв в названии вектора имеет значение! Первая буква отвечает за начало вектора, а последняя — за его конец. Поэтому и — абсолютно разные векторы.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Виды векторов
Во-первых, векторы бывают коллинеарными и неколлинеарными.
Коллинеарными называют те векторы, которые лежат на одной прямой или параллельных прямых. На рисунке
и
и
являются коллинеарными, а
и
относительно друг друга — нет.
На рисунке
и
и
являются коллинеарными, а
и
относительно друг друга — нет.
Векторы различаются и по направлению. Если векторы уже являются коллинеарными, они могут быть сонаправленными или противоположно направленными. Сонаправленные векторы обозначаются так: Если же они противоположно направлены, мы можем записать это следующим образом:
Равными являются те векторы, которые одновременно и коллинеарны, и сонаправлены, а также имеют одинаковую длину.
Нулевой вектор — вектор, длина которого равна нулю. Чаще всего его обозначают так: Он считается коллинеарным любому вектору.
Иногда в геометрии вводят дополнительные понятия, рассмотрим и их:
Закреплённый вектор — отрезок с упорядоченными концами: если С — точка начала вектора, а Е — точка конца, тогда (это то, что мы понимаем под обычным вектором в школьной геометрии).
Свободный вектор — вектор, начало и конец которого не закреплены.
 Его можно перемещать как вдоль прямой, на которой он находится, так и параллельно этой прямой. По сути под свободным вектором понимают множество закреплённых векторов.
Его можно перемещать как вдоль прямой, на которой он находится, так и параллельно этой прямой. По сути под свободным вектором понимают множество закреплённых векторов.
Сложение и вычитание векторов
Действия с векторами описываются и в алгебре, и в геометрии. Сегодня мы рассмотрим способы, благодаря которым можно сложить и вычесть векторы, не зная их координат.
Сложение: метод треугольника
Представим, что в пространстве заданы векторы и которые нам необходимо сложить. Эта задача особенно актуальна для физиков, поскольку такие векторные величины, как сила, часто приложены к одному и тому же телу. В таком случае возникает вопрос: а как же рассчитать результирующее действие всех этих сил?
В этом на помощь физикам приходит математика — царица наук! Чтобы сложить два вектора, необходимо:
Отложить начало одного вектора от конца другого.
Вектор их суммы будет совпадать с вектором , который соединяет начало вектора с концом вектора
Сложение: метод параллелограмма
Сложить векторы можно и по-другому, используя метод параллелограмма:
Совместим между собой концы и
Отложим от конца вектор, равный
Отложим от конца вектор, равный
Благодаря пунктам 2 и 3 мы получили параллелограмм (четырёхугольник, противоположные стороны которого параллельны и равны).

Проведём диагональ параллелограмма между и на которой будет лежать вектор, равный сумме и
Задача решена, вы великолепны!
Обратите внимание
Как метод параллелограмма, так и метод треугольника подразумевает перемещение векторов в пространстве: мы или совмещаем их концы, или откладываем от конца одного вектора начало другого. Получить сумму векторов, не имеющих общей точки, с этими методами не представляется возможным.
Сложение: метод многоугольника
А что если векторов больше, чем два? На эту проблему математика уже подготовила решение: воспользуемся расширенным методом треугольника, который получил название «метод многоугольника».
Согласно этому методу мы последовательно совмещаем конец и начало векторов, а после изображаем суммирующий вектор, начало которого совпадает с началом первого вектора, а конец — с концом последнего. Лучше всего рассмотреть это на чертеже:
Вычитание векторов
Продолжаем проделывать с векторами всевозможные действия, на этот раз вычитание.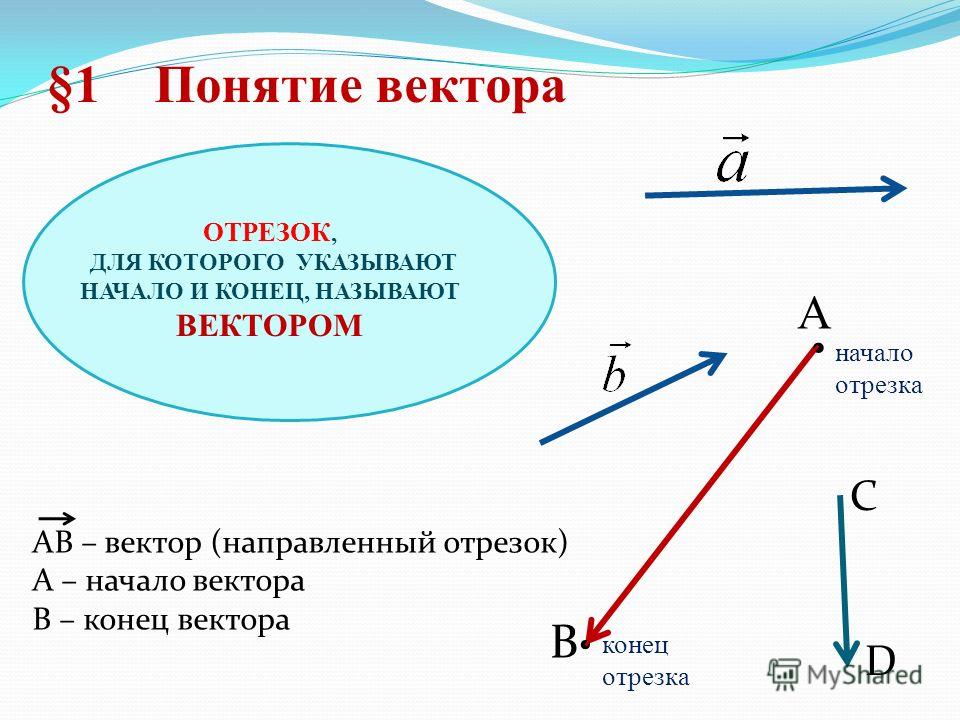 Математики знают, что вычитание — это по своей сути то же сложение, но с обратным числом.
Математики знают, что вычитание — это по своей сути то же сложение, но с обратным числом.
С векторами работает та же штука: вместо вычитания попробуем прибавить вектор, противоположно направленный исходному:
Изобразим разность векторов с помощью уже знакомого нам правила треугольника:
Боитесь запутаться в векторах сонаправленных и противоположно направленных? Существует отдельное правило для их вычитания:
Отложим один вектор от начала другого.
Тогда вектор их разности совпадает с вектором, начало которого совмещено с концом вычитаемого вектора, а начало — с концом уменьшаемого.
Этот метод схож и с методом параллелограмма, но в этом случае мы берём другую диагональ.
Учёба без слёз (бесплатный гайд для родителей)
Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.
Координаты вектора на плоскости и в пространстве
Для выполнения остальных действий с векторами нам необходимо поместить их в такую систему координат, чтобы можно было определить их положение относительно друг друга. Для этого используют декартову систему координат, которой можно пользоваться как на плоскости с осями X и Y, так и в пространстве с осями X, Y, Z.
Тогда, если находится на плоскости, его координаты можно выразить как если в пространстве —
Базисные векторы — это векторы, каждый из которых направлен вдоль своей оси координат, в трёхмерном пространстве их обозначают
Любой вектор в трёхмерном пространстве можно разложить по трём базисным векторам.
с координатами можно записать так:
Умножение вектора на число
Представьте, что нам необходимо растянуть вектор в два раза или же сжать, но уже в три. За все эти действия отвечает
одна простая задача: умножение вектора на число.
За все эти действия отвечает
одна простая задача: умножение вектора на число.
Для того чтобы увеличить или уменьшить вектор в некоторое количество раз, необходимо умножить все координаты вектора на это число.
Таким образом, если задан координатами то — Кстати, подобным образом можно перевернуть вектор, направив его в противоположную сторону:
Длина вектора
Длина вектора — одно из основных понятий в этом разделе. И неудивительно, ведь она характеризует его протяженность в пространстве и выражается числом.
Итак, длина вектора — это расстояние между его началом и концом. Её часто называют модулем, что отражается и в обозначении. Если нам необходимо найти длину мы так и запишем:
Длину вектора можно найти разными способами, вот основные:
через координаты вектора;
через координаты точек начала и конца вектора;
через теорему косинусов.

Давайте вместе разберём все методы!
Длина вектора через его координаты
Если задан через координаты то его длину можно найти как
Почему мы можем быть уверены, что эта формула правильная? Рассмотрим вектор в декартовой системе координат.
Отложим вектор от точки с координатами Тогда этот вектор можно назвать , и так как мы строили его из начала координат, координаты вектора могут быть найдены как
Рассчитаем длину через теорему Пифагора:
Задача 1
Посчитайте, чему равен модуль , если его координаты
Решение:
Модуль вектора — это его длина, а значит,
Задача 2
Длина Чему равна координата по оси , если координата по оси
Решение:
Длина вектора через координаты точек начала и конца
Для начала давайте вспомним, как задать координаты вектора через координаты его начала и конца.
Рассмотрим где и Тогда координаты вектора можно выразить так:
Мы уже знаем, как найти длину вектора через его координаты, поэтому подставим полученное выражение в формулу:
Задача 3
Найдите длину если и
Решение:
Задача 4
Рассчитайте координату по точки вектора , если его длина равна а
Решение:
Остановимся здесь и подставим известные числа в формулу:
или
Длина вектора через теорему косинуса
К сожалению, в задачах не всегда даны координаты точек вектора или его самого.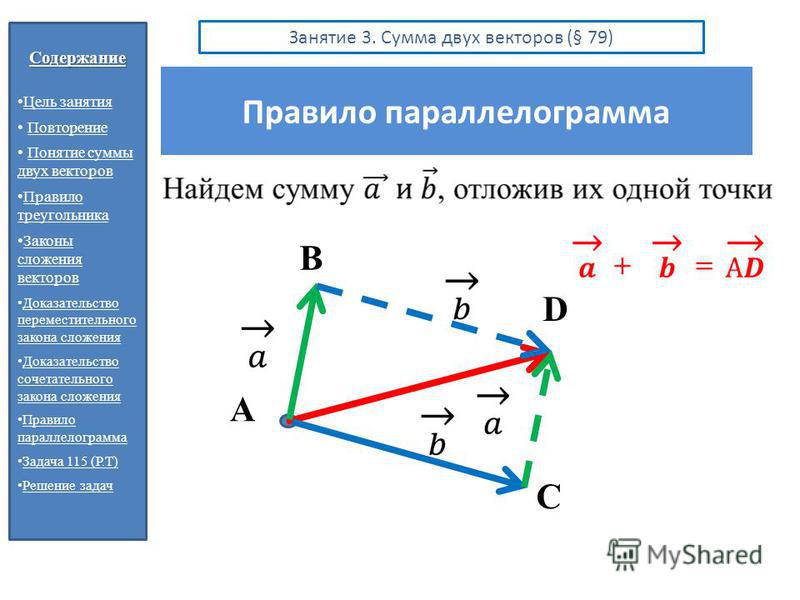 В таком случае мы воспользуемся
теоремой косинуса.
Давайте вспомним её формулировку.
В таком случае мы воспользуемся
теоремой косинуса.
Давайте вспомним её формулировку.
Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Формула теоремы косинусов:
Эту теорему можно применить и в векторной форме. Немного изменим рисунок:
Тогда, чтобы найти длину , необходимо знать (или иметь возможность вычислить) длины и , знать угол между ними, а также уметь рассчитать произведение длин этих векторов.
Задача 5
Длины и равны 4 и 6 соответственно, а угол между ними равен Вычислите длину
Решение:
Задача 6
Рассчитайте модуль вектора в треугольнике, если длина = 8, длина = 10, а угол между ними равен
Решение:
Скалярное произведение векторов
Мы практически дошли до финала нашего путешествия по царству векторов.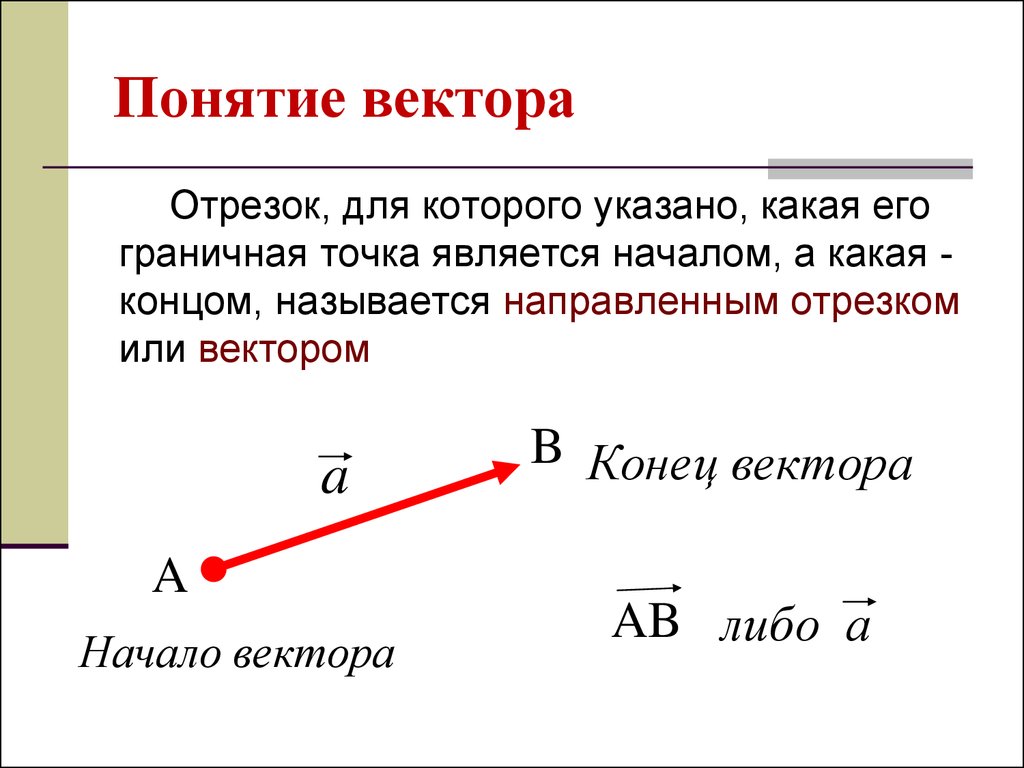 👑 Нам осталось изучить только скалярное
произведение векторов. Что это?
👑 Нам осталось изучить только скалярное
произведение векторов. Что это?
Скалярное произведение — это операция над двумя векторами, результатом которой является скаляр, то есть число, которое не зависит от выбора системы координат.
Скалярным произведением и будет скалярная величина, равная произведению модулей этих векторов, умноженная на косинус угла между ними:
Вспомним, что в той же физике величины делятся на скалярные (не имеющие направления, например, масса) и векторные (имеющие направление, например, сила, ускорение, скорость). В математике под вектором подразумевают направленный отрезок, а понятие скаляра хоть и не равно, но очень близко к понятию числа.
Скалярное произведение показывает, насколько синхронизированы, скоординированы направления векторов. Так, чем больше угол между векторами, тем меньше согласованности, а значит, скалярное произведение будет уменьшаться с ростом угла:
Скалярное произведение вектора на само себя равно квадрату его модуля: В данном случае значение скалярного произведения является наибольшим из возможных.

Если угол между векторами острый и векторы ненулевые, то скалярное произведение положительно, так как
Если угол между векторами прямой, то скалярное произведение равно 0, так как
Если угол между векторами тупой и векторы ненулевые, то скалярное произведение отрицательно, так как
Cкалярное произведение вектора на противоположно направленный ему вектор равно отрицательному произведению их длин . В данном случае значение скалярного произведения является наименьшим из возможных.
Конечно, вы можете возразить: «Согласованность направлений отлично показывает угол, для чего нам эти сложные
вычисления?». А всё дело в том, что в пространстве порой очень сложно измерить угол, а вот посчитать скалярное
произведение — просто, особенно если рассмотреть его через координаты.
Если выражен координатами а то скалярное произведение этих векторов описывается формулой: В пространстве скалярное произведение через координаты векторов будет задаваться так:
Где применяется скалярное произведение? Благодаря ему выполняется большое количество математических операций, таких как нахождение угла между векторами и любых расстояний, если они заданы через координаты. Благодаря скалярному произведению можно описать даже характеристику криволинейных поверхностей, но это мы обсудим как-нибудь в другой раз. 🙂
Чтобы закрепить пройденный материал, нужно больше, чем пара заданий. Поэтом приглашаем на онлайн-уроки математики в школу Skysmart. За короткое время благодаря особенной платформе и учителям-профессионалам вы сможете улучшить школьные отметки, подготовиться к экзаменам и олимпиадам, и самое главное — понять и полюбить математику.
Векторы — Умскул Учебник
На этой странице вы узнаете- Что вектор украл у точки?
- Какими могут быть коллинеарные векторы?
Невероятная эффективность: каждый раз, когда мы двигаем стул, мы строим сразу четыре вектора.
Вектор – это отрезок, для которого указано, какой из его концов считается началом, а какой концом.
Записывается вектор по следующим правилам: первая буква – это буква начала вектора, а вторая буква – буква конца вектора.
| Что вектор украл у точки? Практически всё! Это вообще законно? Существует такой необычный вектор, который называется нулевым. На плоскости он обозначается как точка. |
Что такое коллинеарные векторы?
Коллинеарные векторы – это векторы, лежащие на одной прямой или на параллельных.
По данной картинке \(\vec{AB}\), \(\vec{CD}\) и \(\vec{EF}\) являются коллинеарными векторами
| Какими могут быть коллинеарные векторы? Коллинеарные векторы бывают сонаправленными и противоположно направленными. |
Сонаправленные векторы – это коллинеарные векторы, направленные в одну сторону.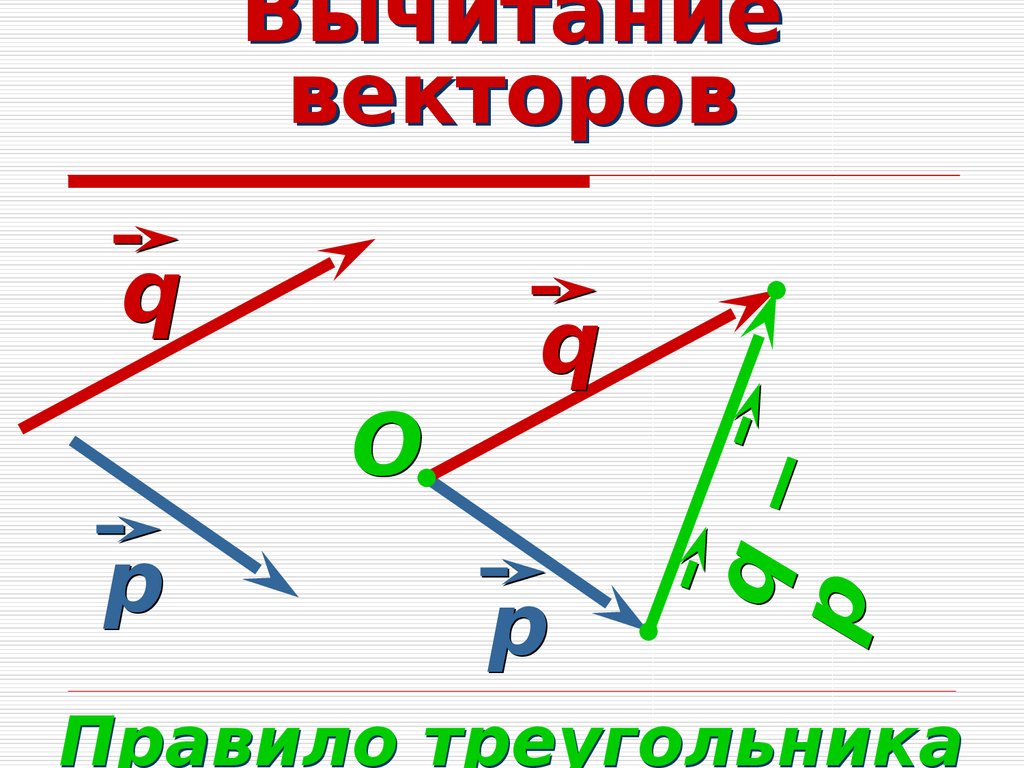
Противоположно направленные векторы – это коллинеарные векторы, направленные в противоположные стороны.
Важно: нулевой вектор сонаправлен с любым вектором.
Как можно записать длину вектора?
Длина вектора – это длина отрезка. Она не зависит от направления вектора и всегда неотрицательна, поэтому записывается в модульных скобках.
|\(\vec{AB}\)| и |\(\vec{DC}\)| — длины векторов \(\vec{AB}\) и \(\vec{DC}\)
Теперь давайте рассмотрим равенство векторов.
Векторы называются равными, если они сонаправлены и их длины равны.
А противоположными называют векторы с равными длинами и противоположными направлениями.
Играя в футбол или бильярд, мы не задумываясь совершаем множество действий с векторами. Давай разберем их с точки зрения геометрии.
Сложение векторов
Сумма векторов – это перемещение.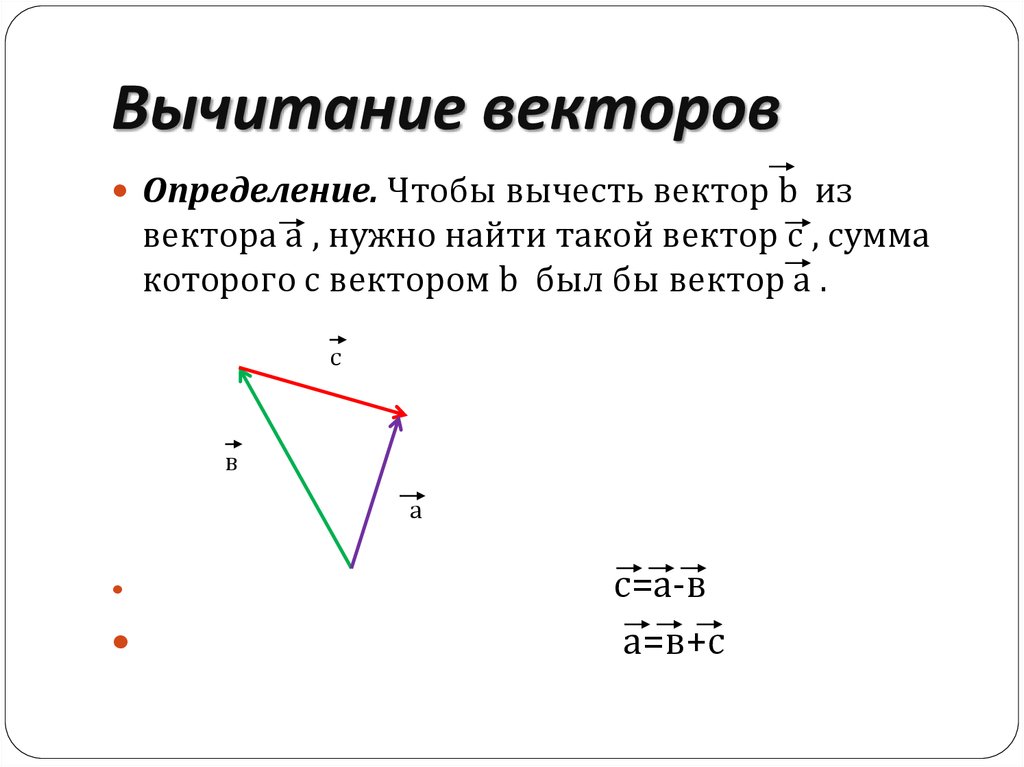
Для сложения векторов используют специальные правила, одним из них является правило треугольника.
Правило треугольника
Если начало одного вектора находится в конце другого вектора, тогда можно из начала первого вектора провести вектор в конец второго. Данное перемещение будет суммой векторов.
Что делать, если векторы отложены не друг за другом?
В таком случае можно сделать параллельный перенос. Это означает, что вектор можно сдвигать в пространстве, не меняя его направления и размера.
Существует еще одно правило сложения векторов.
Правило параллелограмма
Если оба вектора отложены от одной точки, тогда можно достроить данный рисунок до параллелограмма и провести вектор по диагонали из начальной точки. Полученный вектор будет суммой двух изначальных векторов.
Для сложения большего количества векторов применяются те же правила. Сначала складываются первый со вторым вектором, далее складывается сумма с третьим вектором и т. д.
д.
Вычитание векторов
Чтобы вычесть из одного вектора другой, нужно привести их разность к сумме одного изначального вектора и одного противоположного вектора. А далее воспользоваться методами сложения.
Умножение на число
Произведением ненулевого вектора \(\vec{a}\) на число k называется такой вектор \(\vec{b}\), длина которого равна |k| * |\(\vec{a}\)|.
При k > 0, \(\vec{a}\) и \(\vec{b}\) – сонаправлены.
При k < 0, \(\vec{a}\) и \(\vec{b}\) – противоположно направленные.
Например:
Существуют также специальные законы сложения и умножения для векторов, аналогично законам для обычных чисел.
| Законы сложения и умножения для векторов: \(\vec{a}\) + \(\vec{b}\) = \(\vec{b}\) + \(\vec{a}\) (\(\vec{a}\) + \(\vec{b}\)) + \(\vec{c}\) = \(\vec{a}\) + (\(\vec{b}\) + \(\vec{c}\)) (\(\vec{a}\) + \(\vec{b}\)) * k = \(\vec{a}\) * k + \(\vec{b}\) * k (с + b) * \(\vec{a}\) = \(\vec{a}\) * с + \(\vec{a}\) * b |
- Вектор – это отрезок, для которого указано, какой из его концов считается началом, а какой концом.

- Коллинеарные векторы бывают сонаправленными и противоположно направленными.
- Векторы могут быть равными и противоположными.
- Для сложения векторов применяется правило треугольника и правило параллелограмма.
- Также векторы можно вычитать и умножать на число.
- Существуют законы сложения и умножения для векторов, подобно законам сложения и умножения для обычных чисел.
Задание 1.
Какие векторы изображены на картинке?
- Сонаправленные
- Противоположно направленные
- Равные
- Противоположные
Задание 2.
Какие векторы изображены на картинке?
- Сонаправленные
- Противоположно направленные
- Равные
- Противоположные
Задание 3.
Выберите верное утверждение для векторов на картинке
- Вектора сонаправленные
- Вектора равные
- Это нулевые вектора
- Длины данных векторов равны
Задание 4.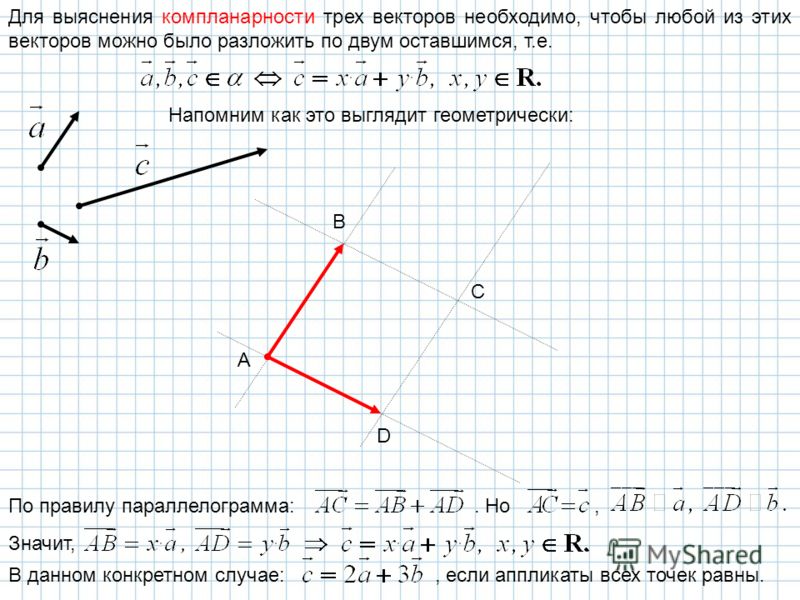
Какие векторы изображены на картинке?
- Равные
- Противоположно направленные
- Сонаправленные
- Противоположные
Ответы: 1. – 2; 2. – 1; 3. – 4; 4. – 3
Векторы на плоскости и в пространстве: основные определения
Определение вектора
В статье пойдет речь о том, что такое вектор, что он из себя представляет в геометрическом смысле, введем вытекающие понятия.
Для начала дадим определение:
Определение 1Вектор – это направленный отрезок прямой.
Исходя из определения, под вектором в геометрии отрезок на плоскости или в пространстве, который имеет направление, и это направление задается началом и концом.
В математике для обозначения вектора обычно используют строчные латинские буквы, однако над вектором всегда ставится небольшая стрелочка, например a→. Если известны граничные точки вектора – его начало и конец, к примеру A и B, то вектор обозначается так AB→.
Нулевой вектор
Определение 2Под нулевым вектором 0→ будем понимать любую точку плоскости или пространства.
Из определения становится очевидным, что нулевой вектор может иметь любое направление на плоскости и в пространстве.
Длина вектора
Определение 3Под длиной вектора AB→ понимается число, большее либо равное 0, и равное длине отрезка АВ.
Длину вектораAB→ принято обозначать так AB→.
Понятия модуль вектора и длина вектора равносильны, потому что его обозначение совпадает со знаком модуля. Поэтому длину вектора также называют его модулем. Однако грамотнее использовать термин «длина вектора». Очевидно, что длина нулевого вектора принимает значение ноль.
Коллинеарность векторов
Определение 4Два вектора лежащие на одной прямой или на параллельных прямых называются коллинеарными.
Определение 5Два вектора не лежащие на одной прямой или на параллельных прямых называются неколлинеарными.
Следует запомнить, что Нулевой вектор всегда коллинеарен любому другому вектору, так как он может принимать любое направление.
Коллиниарные векторы в свою очередь тоже можно разделить на два класса: сонаправленные и противоположно направленные.
Направление векторов
Определение 6Сонаправленными векторами называют два коллинеарных вектора a→ и b→, у которых направления совпадают, такие векторы обозначаются так a→↑↑b→.
Определение 7Противоположно направленными векторами называются два коллинеарных вектора a→ и b→, у которых направления не совпадают, т.е. являются противоположными, такие векторы обозначаются следующим образом a→↑↓b→.
Считается, что нулевой вектор является сонаправленым к любым другим векторам.
Равные и противоположные векторы
Определение 8Равными называются сонаправленные вектора, у которых длины равны.
Определение 9Противопожными называются противоположно направленные вектора, у которых их длины равны.
Введенные выше понятия позволяют нам рассматривать векторы без привязки к конкретным точкам.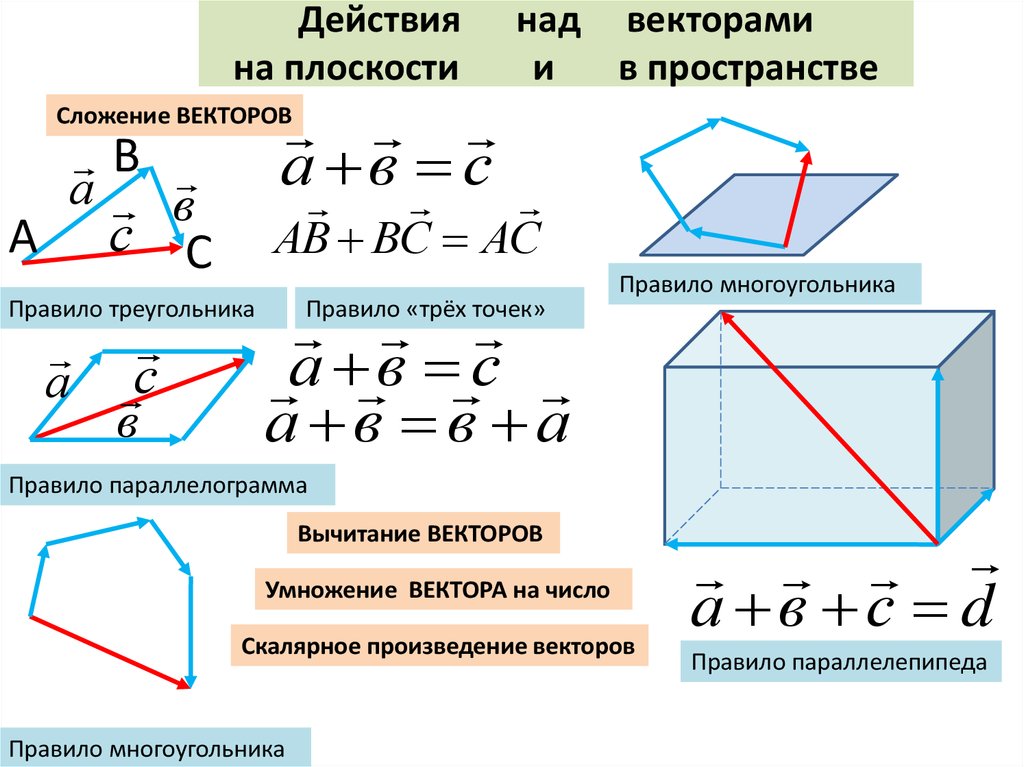 Иначе говоря, можно заменить вектор равным ему вектором, отложенным от любой точки.
Иначе говоря, можно заменить вектор равным ему вектором, отложенным от любой точки.
Пусть заданы два произвольных вектора на плоскости или в пространстве a→ и b→. Отложим от некоторой точки O плоскости или пространства векторы OA→=a→ и OB→=b→. Лучи OA и OB образуют угол ∠AOB=φ.
Углы между векторами
Определение 9Угол φ=∠AOB называется углом между векторами a→=OA→ и b→=OB→.
Очевидно, что угол между сонаправленными векторами равен нулю градусам (или нулю радиан), так как сонаправленные векторы лежат на одной или на параллельных прямых и имеют одинаковое направление, а угол между противоположно направленными векторами равен 180 градусам (или π радиан), так как противоположно направленные векторы лежат на одной или на параллельных прямых, но имеют противоположные направления.
Определение 10Перпендикулярными называются два вектора, угол между которыми равен 90 градусам (или π2 радиан).
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Навигация по статьям
Предыдущая статья
Координаты вектора в ДСК
Следующая статья
Длина вектора
- Векторное произведение
- Векторное пространство
- Геометрическая фигура угол
- Деление отрезка в заданном соотношении
- Длина вектора
- Все темы по математике
- Курсовые работы
- Рефераты
- Контрольные работы
- Отчет по практике
- Эссе
Узнать подробнее
Технологии программирования работы выполнить все обьем по заданию
Вид работы:
Контрольная работа
Выполнена:
14 июня 2022 г.

Стоимость:
3 000 руб
Заказать такую же работу
строительномонтажный чертеж
Заказать такую же работу
надо будет решить задачи за мин
Вид работы:
Онлайн-помощь
Выполнена:
24 мая 2022 г.

Стоимость:
3 600 руб
Заказать такую же работу
Предмет защита конфиденциальной информаци
Заказать такую же работу
Задание по электротехнике Технической механике по каждому предмету вариант
Вид работы:
Контрольная работа
Выполнена:
29 января 2022 г.

Стоимость:
4 000 руб
Заказать такую же работу
Сопряжение дуг Детали с внутренними и внешними сопряжениями
Вид работы:
Чертёж
Выполнена:
26 января 2022 г.

Стоимость:
2 000 руб
Заказать такую же работу
Смотреть все работы по c/c++
Урок геометрии в 9-м классе «Действия над векторами». Тема: «Умножение вектора на число»
- Гордеева Марина Эвальдовна
Разделы: Математика, Урок с использованием электронного учебника
Класс: 9
Ключевые слова: Действия над векторами
УМК: «Геометрия: 9 класс» Атанасян Л. Г. и др.
Г. и др.
Основные дидактические цели урока:
- Формирование новых знаний и умений по теме: «Умножение вектора на число».
Задачи:
Для реализации поставленной цели учитель должен решить следующие задачи:
- Актуализировать знания и умения учащихся выполнять сложение и вычитание векторов; актуализировать умения строить данные векторы из одной точки; использовать правило треугольника, многоугольника;
- Подвести учащихся к выводу алгоритма нахождения результата умножения вектора на число;
- Сформировать умение нахождения результата произведения вектора на число;
- Создать условия для применения правила в различных ситуациях;
- Произвести первичный контроль усвоения знаний.
Формируемые результаты.
Предметные результаты:
- Знать: алгоритм умножения вектора на число.

- Уметь: находить произведение вектора на число; уметь строить исходный и полученный векторы.
Метапредметные результаты:
- уметь обобщать и делать выводы,
- уметь применять правило в различных ситуациях,
- уметь разрабатывать алгоритм действий,
- уметь использовать математические знания на уроках физики и др. наук.
Личностные результаты:
- уметь ставить перед собой цели, планировать свою деятельность,
- оценивать результаты своей работы и работы одноклассников, достигать поставленных целей.
Структура урока
- мотивация
- актуализация знаний и умений учащихся
- создание проблемной ситуации
- постановка темы и целей урока
- формирование новых знаний (введение понятия «произведение вектора на число» и свойств данного произведения)
- разработка алгоритма нахождения результата произведения вектора на число, вывод алгоритма определения одинакового и противоположного направления данного вектора и вектора, полученного при умножении его на положительное и отрицательное число; алгоритма определения длины результирующего вектора.

- первичное закрепление: отработка навыка нахождения результата умножения вектора на число с использованием свойств; самоконтроль усвоения новых знаний
- контроль усвоения, самооценка результатов своей деятельности
- рефлексия
- домашнее задание
Этап урока | Деятельность учителя | Деятельность учащихся |
Организационный | Приветствует учащихся. Предлагает записать дату в тетрадь | Записывают дату |
Мотивационный | Предлагает ответить на вопрос: «Как вы понимаете слова: «Каждый человек может ошибаться, каждый имеет право на ошибку, но при этом очень важно найти её, признать её и исправить». | Поясняют услышанное высказывание. |
| Актуализация знаний и умений: — выполнять сложение и вычитание векторов | Предлагает ответить на вопросы: — что такое вектор? | — направленный отрезок…. |
| — какие векторные величины вы знаете? | — сила, скорость…. | |
| — что такое сила тяжести и от чего она зависит? | — сила тяжести — это сила, с которой…., она зависит от массы тела. | |
| — что такое сила трения? | — сила трения — это сила……. | |
| — что такое сила упругости? | — сила упругости — это сила…… | |
Предлагает выполнить задания, записанные на доске: | Выполняют задания: №2. №3. Рассмотрите рисунок и ответьте на вопрос: будет ли тело двигаться вниз по наклонной плоскости? №4. Масса первого тела 2 кг. Сила тяжести, действующая на 1 тело 20H. Изобразите ее отрезком 4 см. Изобразите вектор силы тяжести, действующей на 2 и 3 тела, если их массы соответственно 4 кг и 0,5кг. Учащиеся легко выполняют задания 1-3, но при выполнении задания №4 испытывают затруднения. | |
| Постановка темы и целей урока | Учитель, используя методику проблемного диалога, учитель подводит учащихся к постановке темы урока. | |
| Какова формула силы тяжести? | F=mg | |
| Если для 1 тела массой 2 кг сила тяжести изображается вектором, длиной 4см, то какова длина вектора силы тяжести для тела массой 4кг, если она прямо пропорционально зависит от массы тела? | Если масса тела увеличена в 2 р, то и длина вектора увеличится в 2р и будет 8 см.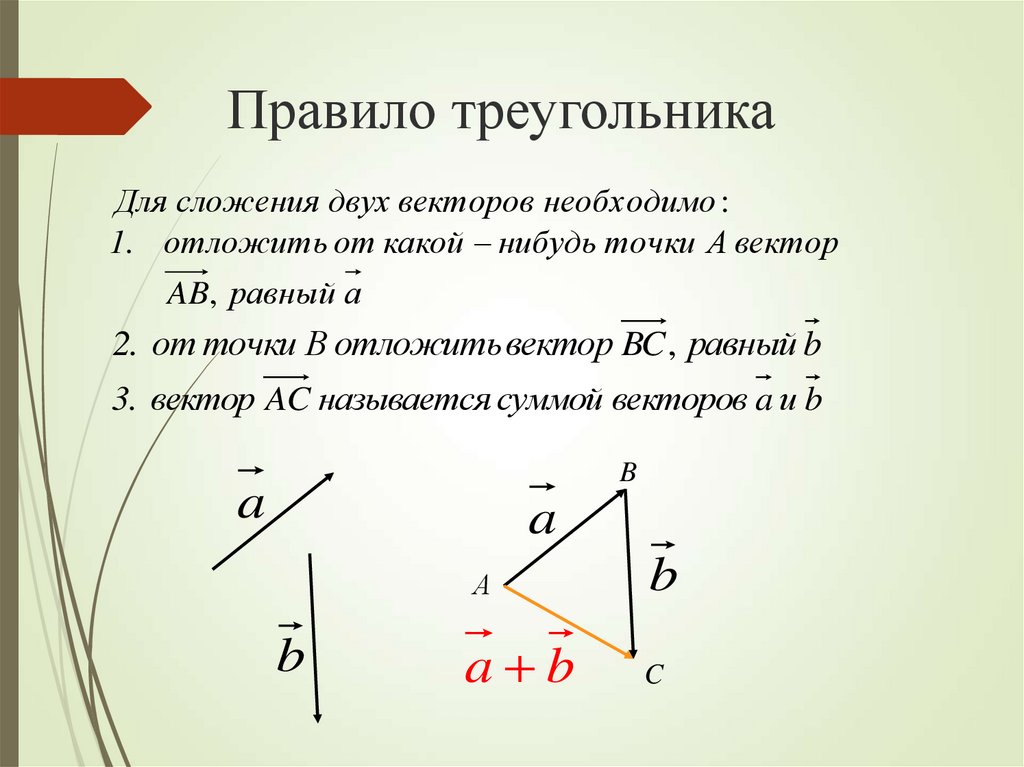 | |
| А для тела, массой 0,5кг? | Соответственно в 2 р меньше и будет 2 см. | |
| Какое действие с векторами мы сейчас производили? | Умножение и деление вектора на число. | |
| Можно ли деление на число, заменить умножением? | Деление на число, можно заменить умножением на число, обратное делителю. | |
| Какова же тема урока? (учитель на доску прикрепляет лист А-4 с темой урока) | Умножение вектора на число. | |
Какие цели урока «Умножение вектора на число»? (учитель прикрепляет на доску лист А-4 с целями урока) и уточняет цели урока (при необходимости) | Узнать, как умножать вектор на число. | |
Формирование новых знаний | Предлагает просмотреть видео с сайта Инфоурок, с целью введения понятия «произведение вектора на число». Что такое произведение вектора на число? | Смотрят фильм. |
Работа с учебником | Чтобы узнать свойства произведения, откройте учебник на стр.202-203 прочтите и запишите свойства. | Читают и записывают свойства. Читают свойства произведения чисел и свойства произведения векторов и находят аналогии, которые помогают осознать, понять свойства произведения векторов. |
Первичное закрепление | Предлагает открыть конверты, лежащие на столе, достать оттуда векторы. И показать их. Теперь предлагает изобразить вектор -0,5 данного вектора, -0,25 данного вектора, -2 данного вектора, -1/3 и 5/6 данного вектора. | Достают, показывают. Выполняют задания, уточняя направление данных векторов. |
Контроль усвоения | Предлагает выполнить самостоятельную работу. | Учащиеся, обучающиеся на 4-5 в парах садятся за ноутбуки, заходят на сайт ЯКЛАСС, выполняют тренировочную работу «Умножение вектора на число». По окончании работы учащихся оценивает программа сайта, и в итоге учитель видит на экране оценку. |
Самооценка результатов своей деятельности | Предлагает оценить свою деятельность на уроке. | Отвечают на вопросы. |
Домашнее задание | п.86 стр. 202-203 №775, 776 | Записывают задания. |
Вектор (геометрия) | это… Что такое Вектор (геометрия)?
Под направленным отрезком в геометрии понимают упорядоченную пару точек, первая из которых — точка A — называется его началом, а вторая — B — его концом.
Содержание
|
Определение
Вектором в простейшем случае называется направленный отрезок, а в других случаях различные векторы — это разные классы эквивалентности направленных отрезков, определяемые неким конкретным отношением эквивалентности. Причем отношение эквивалентности может быть разным, определяя тип вектора («свободный», «фиксированный» итд). Проще говоря, внутри класса эквивалентности все входящие в него направленные отрезки рассматриваются как совершенно равные, и каждый может равно представлять весь класс.
Учитывая изоморфизм между множеством свободных векторов и множеством их параллельных переносов пространства, если операцию сложения отождествить с композицией переносов, можно использовать множество параллельных переносов пространства даже для определения вектора.
Большую роль играют векторы в изучении бесконечно малых трансформаций пространства.
- Вектор, начало которого совпадает с его концом, называют нулевым:
- Вектор называют противоположным вектору .
- Длиной вектора, или модулем вектора, называют длину соответствующего направленного отрезка: .
Свободные, скользящие и фиксированные векторы
Иногда, вместо того, чтобы рассматривать в качестве векторов множество всех равных направленных отрезков, берут только некоторую модификацию этого множества (фактормножество). Так, говорят о «свободных» (когда отождествляются все равные по длине и направлению направленные отрезки, считаясь полностью равными или одним и тем же вектором), «скользящих» (отождествляются между собой все направленные отрезки, равные в смысле свободных векторов, начала и концы которых расположены на одной прямой) и «фиксированных» векторах (по сути дела, просто о направленных отрезках, когда разное начало означает уже неравенство векторов).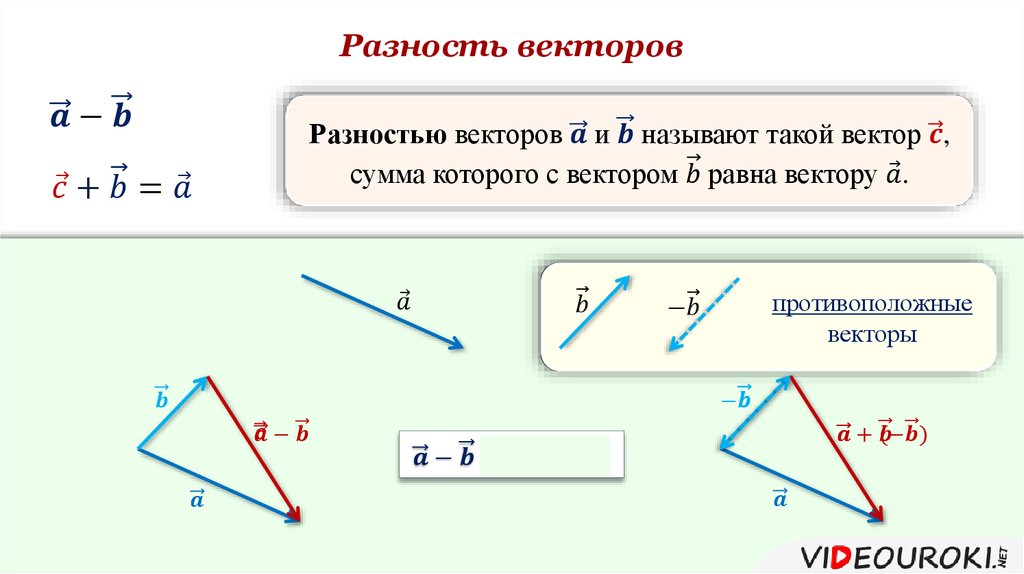
Определение. Говорят, что свободные векторы и равны, если найдутся точки E и F такие, что четырёхугольники ABFE и CDFE — параллелограммы.
- Замечание. «Ухищрение» (введение дополнительных точек) в определении равенства касается, прежде всего, случая, когда точки A,B,C,D располагаются на одной прямой. В противном случае определение выглядит проще:
Определение. Говорят, что свободные векторы и , не лежащие на одной прямой, равны, если четырёхугольник ABDC — параллелограмм.
Определение. Говорят, что скользящие векторы и равны, если
- точки A,B,C,D располагаются на одной прямой,
- векторы и равны между собой как свободные векторы.
Неформально говоря, скользящему вектору разрешено двигаться вдоль его прямой без изменения величины и направления.
- Замечание. Скользящие векторы особо употребимы в механике. Простейший пример скользящего вектора в механике — сила. Перенос такого начала вектора вдоль прямой, на котой он лежит, не меняет момента силы ни относительно какой точки; перенос же его на другую прямую, даже если не менять величины и направления вектора, может вызвать изменение его момента (скорее даже почти всегда вызовет): поэтому нельзя рассматривать силу как свободный вектор.
Определение. Говорят, что фиксированные векторы и равны, если попарно совпадают точки A и C, B и D.
Операции над векторами
Сложение векторов
Два вектора u, v и вектор их суммы
Сложение двух свободных векторов можно осуществлять как по правилу параллелограмма, так и по правилу треугольника.
Правило треугольника. Для сложения двух векторов и по правилу треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора.
Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора.
Правило параллелограмма. Для сложения двух векторов и по правилу параллелограмма оба эти вектора переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.
Сложение двух скользящих векторов определено лишь в случае, когда прямые, на которых они расположены, пересекаются. Тогда каждый из векторов переносится вдоль своей прямой в точку пересечения этих прямых, после чего сложение осуществляется по правилу параллелограмма.
Сложение двух фиксированных векторов определено лишь в случае, когда они имеют общее начало. Их сложение в этом случае осуществляется по правилу параллелограмма.
Сложение коллинеарных скользящих векторов
Если скользящие векторы параллельны, то при их сложении главная трудность состоит в определении прямой, на которой будет расположена их сумма. (Величину и направление вектора суммы было бы естественно определить точно так же, как и в случае сложения свободных векторов.) В механике при изучении статики для решения вопроса о сложении параллельных сил, которые, как известно, задаются скользящими векторами, вводится дополнительная гипотеза: к системе векторов можно добавить два вектора, равных по величине, противоположных по направлению и расположенных на одной прямой, пересекающей прямые, на которых расположены данные вектора. Пусть, например, надо сложить скользящие векторы и , расположенные на параллельных прямых. Добавим к ним векторы и , расположенные на одной прямой. Прямые, на которых расположены векторы и , и пересекаются. Поэтому определены векторы
(Величину и направление вектора суммы было бы естественно определить точно так же, как и в случае сложения свободных векторов.) В механике при изучении статики для решения вопроса о сложении параллельных сил, которые, как известно, задаются скользящими векторами, вводится дополнительная гипотеза: к системе векторов можно добавить два вектора, равных по величине, противоположных по направлению и расположенных на одной прямой, пересекающей прямые, на которых расположены данные вектора. Пусть, например, надо сложить скользящие векторы и , расположенные на параллельных прямых. Добавим к ним векторы и , расположенные на одной прямой. Прямые, на которых расположены векторы и , и пересекаются. Поэтому определены векторы
Прямые, на которых расположены векторы и , пересекаются всегда, за исключением случая, когда векторы и равны по величине и противоположны по направлению, в котором говорят, что векторы и образуют пару (векторов).
Таким образом, под суммой векторов и можно понимать сумму векторов и , и эта сумма векторов определена корректно во всех случаях, когда векторы и не образуют пару.
Произведение вектора на число
Произведением вектора и числа λ называется вектор, обозначаемый (или ), модуль которого равен , а направление совпадает с направлением вектора , если , и противоположно ему, если . Если же , или вектор нулевой, тогда и только тогда произведение — нулевой вектор.
- Обычно принято в записи произведения числа и вектора число записывать слева, но в принципе допустим и обратный порядок, хотя все же обычное соглашение состоит в том, чтобы его избегать, если нет прямой необходимости. Так или иначе, .
Из определения произведения вектора на число легко вывести следующие свойства:
- если , то . Наоборот, если , то при некотором λ верно равенство ;
- всегда °, то есть каждый вектор равен произведению его модуля на орт.
Скалярное произведение
Основная статья: Скалярное произведение
Скалярным произведением векторов и называют число, равное , где — угол между векторами и .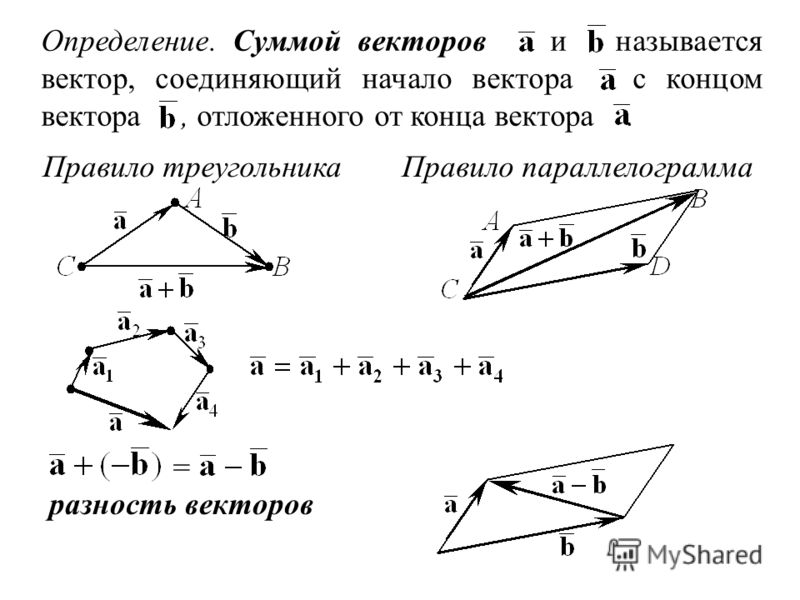 Обозначения: или .
Обозначения: или .
Если один из векторов является нулевым, то несмотря на то, что угол не определён, произведение равно нулю.
Свойства скалярного произведения векторов:
- — коммутативность.
- — дистрибутивность.
- — линейность по отношению к умножению на число.
- — норма вектора.
Геометрически скалярное произведение есть произведение длины одного из сомножителей на ортогональную проекцию другого на направление первого (или наоборот). Скалярное произведение какого-то вектора с единичным вектором есть ортогональная проекция вектора на направление единичного вектора.
Векторное произведение
Основная статья: Векторное произведение
Векторным произведением вектора a на вектор b называется вектор c, удовлетворяющий следующим требованиям:
- длина вектора c равна произведению длин векторов a и b на синус угла φ; между ними
- вектор c ортогонален каждому из векторов a и b
- вектор c направлен так, что тройка векторов abc является правой.

Обозначение:
Геометрически векторное произведение есть ориентированная площадь параллелограмма, построенного на векторах , представленная псевдовектором, ортогональным этому параллелограмму.
Свойства векторного произведения:
- При перестановке сомножителей векторное произведение меняет знак (антикоммутативность), т.е
- Векторное произведение обладает сочетательным свойством относительно скалярного множителя, то есть
- Векторное произведение обладает распределительным свойством:
Смешанное произведение
Основная статья: Смешанное произведение
Сме́шанное произведе́ние векторов — скалярное произведение вектора на векторное произведение векторов и :
(равенство записано для разных обозначений скалярного и векторного произведения).
Иногда смешанное произведение называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).
Геометрически смешанное произведение есть (ориентированный) объем параллелепипеда, построенного на векторах .
Условие перпендикулярности векторов
Векторы являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю.
Пример
Даны два вектора и . Эти векторы будут перпендикулярны, если выражение x1x2 + y1y2 = 0.
Условие коллинеарности векторов
Векторы являются коллинеарными тогда и только тогда, когда их векторное произведение равно нулю.
Пример
Даны два вектора и . Эти векторы коллинеарны, если x1 = λx2и y1 = λy2, где
См. также
- Нулевой вектор
- Вектор (алгебра)
- Радиус-вектор
- Тензор
- Момент силы
- Псевдовектор
Ссылки
- Г. С. М. Коксетер, С.
 П. Грейтцер. Новые встречи с геометрией, 1978
П. Грейтцер. Новые встречи с геометрией, 1978
Сложение векторов — свойства, правила и примеры решения задач
Отрезок, который имеет направление, называется вектором. По сути, эта линия, характеризующаяся определённой длиной. Так как с математической точки зрения это выражение, то с ним можно выполнять различные операции. Простейшими являются действия вычитания двух и более векторов и их сложение. Выполняются они по правилам геометрии и алгебры.
Содержание
- Общие сведения
- Сложение координат
- Правило параллелограмма
- Альтернативные методы
Общие сведения
Понятие вектор используется как в физике, так и в математике. С его помощью обозначают действие различных сил, указывают их направление, определяют движение. По сути, это величина, противопоставляемая массе, объёму, плотности, температуре, то есть «скалярам». Согласно определению вектор — это отрезок, имеющий строгое направление. Точку, из которой он выходит, называют начальной, а в которой заканчивается — конечной.
Точку, из которой он выходит, называют начальной, а в которой заканчивается — конечной.
Обозначают отрезок помощью заглавных латинских букв, сверху которых ставится чёрточка. Рисуют же его с помощью прямой ограниченной линии.
Например, запись AB обозначает, что точка A является началом, а B концом. В некоторых случаях для кратности отрезки допустимо обозначать одной маленькой буквой, так: AB = a.
Векторная запись используется тогда, когда невозможно величины описать с помощью одного числа. Численное значение выражение определяется длиной отрезка или его модулем. Эта величина является скалярной. В том случае если начало и конец ограниченной линии совпадают, то говорят о нулевой линии. Обозначают её цифрой 0.
Векторы, расположенные на плоскости или в пространстве, по отношению друг к другу могут быть:
- коллинеарными — отрезки лежат на одной линии или ей параллельны;
- соноправленными — замкнутые линии направление которых одинаковое;
- противоположными — вектора направлены в разные стороны;
- ортогональными — перпендикулярными друг другу;
- компланарными — лежащими на одной плоскости или ей параллельные;
- равными — ограниченными прямыми, совпадающими как по направлению, так и по величине.

Так как вектора — это выражения, то с ними можно выполнять различные действия. Их возможно складывать, вычитать, умножать на число. При работе с векторными величинами используют декартовую систему координат. В ней прямую замкнутую линию раскладывают по базису и определяют координаты её точек. Другими словами, выполняют проекции отрезков на оси. Непосредственно за базис берут орты.
Если известны начальные координаты и конечные, то текущие вычисляют путём вычитания из последних первые. Существующая возможность записать любое геометрическое свойство, используя координаты, позволяет отойти от геометрии и использовать для вычислений алгебру.
Сложение координат
Существует простое правило применимое для направленных отрезков и позволяющее найти их сумму. Заключается оно в следующем: если необходимо прибавить один вектор к другому описывающийся каждый своими координатами, достаточно сложить соответствующие их орты. Например, предположим есть два вектора a и b. Первый отрезок имеет координаты (ax; ay), а второй (bx;by). При их сложении получится новый вектор c. В результате действия его координаты будут c (ax + bx; ay + by).
Например, предположим есть два вектора a и b. Первый отрезок имеет координаты (ax; ay), а второй (bx;by). При их сложении получится новый вектор c. В результате действия его координаты будут c (ax + bx; ay + by).
Это теорема доказывается просто. Пусть даны отрезки f (x 1; y 1) и g (x 2; y 2). В системе координат относительно рассматриваемых векторов получится: f = x 1 a + y 1 b; g = x 2 a + y 2 b. Тогда искомая сумма будет: f + g = x1a + y1b + x2a + y2b = a (x 1 + x 2) + b (y 1 + y 2). Что и нужно было доказать. Это правило применимо к векторам имеющим любые координаты. Например, пусть есть a (1; 2), b (-3; 1). Нужно найти их сумму. С помощью формулы сложения получится новый направленный отрезок с координатами a + b = (1 — 3; 2 + 1) = (-2; 3).
Как и при операциях с простыми числами при работе с векторными выражениями используют различные их свойства. Существует три правила сложения векторов:
 То есть от перемены мест слагаемых результат не изменится.
То есть от перемены мест слагаемых результат не изменится.Приведённые свойства соответственно называют переместительным, сочетательным, нулевым законом. Например, предположим есть два направленных отрезка a (2; 2) и b (-4; 1). Согласно первому свойству, очерёдность значения не имеет, поэтому что при прибавлении b к a, что при a к b результат будет одинаковый: a + b = (2 -4; 2 + 1) = (-2; 3), b + a = (-4 + 2; 1 +2) = (-2; 3). По аналогии можно проверить правильность утверждения и двух оставшихся свойств.
Следует отметить, что при сложении двух противоположных ограниченных прямых сумма будет равняться нуль-вектору: a + (-a) = 0. Это утверждение не требует доказательства, так как здесь используется фундаментальный закон алгебры — правило знаков.
Правило параллелограмма
По сути, все операции с векторными выражениями сводятся к их приращению или уменьшению. Если координаты точек неизвестны, то алгебраический метод складывания не подходит. В таком случае используют геометрические операции. Одним из способов, позволяющих сложить два неколлинеарных вектора, является правило параллелограмма или прямоугольника при перпендикулярном направлении складываемых отрезков.
Сформулировать способ можно следующим образом: если имеются два отрезка не лежащие на параллельной прямой и не принадлежащие ей, то нужно достроить данные вектора до параллелограмма. Для этого необходимо взять произвольную точку и отложить от неё отрезок AB равный первому вектору, и AD совпадающий со вторым. При этом необходимо придерживаться соотношения геометрии наклона. Затем достроить необходимые параллельные прямые таким образом, чтобы образовался параллелограмм ABCD. Если в такой фигуре провести диагональ, то её длина и будет равняться сумме складываемых отрезков.
Доказать правильность утверждения можно следующими доводами. Пусть имеются две ограниченные линии a и b. От точки A можно отложить первый отрезок конец, которого обозначить как B, и второй, с точкой D. Теперь через D и B возможно провести соответственно параллельные прямые AB и AD. Место, в которой они пересекутся, пусть будет обозначено как С. Тогда используя признак параллельности двух пар прямых в фигуре ABCD, можно утверждать, что это параллелограмм. Вектор AC = a + b. Это следует из равенства отрезков AD = BC и теоремы о подобных треугольниках.
Пример задания. Определить, чему равна сумма двух отрезков длиной 2 см и 1 см расположенные друг к другу под углом 45. Для того чтобы воспользоваться правилом, нужно взять листочек в клеточку и построить два вектора, исходящие из одной точки O. Тогда первый отрезок будет OA, а второй OB. Затем достроить прямые таким образом, чтобы на рисунке получился параллелограмм. Новая полученная точка пусть будет D. Теперь с помощью линейки можно измерить диагональ фигуры, длина которой и будет искомой суммой. В ответе должно получиться, что OA + OB = OD = 3 см.
Новая полученная точка пусть будет D. Теперь с помощью линейки можно измерить диагональ фигуры, длина которой и будет искомой суммой. В ответе должно получиться, что OA + OB = OD = 3 см.
Простыми словами это правило можно рассказать так: сумма двух отрезков будет равняться диагонали параллелограмма, построенного на исходных векторах. Эта теорема чаще используется не в геометрии, а физике, например, при сложении сил.
Альтернативные методы
Операцию по сложению двух векторов можно выполнить и с помощью правила треугольника. Делается это так. Выбирается любая точка на плоскости, от которой откладываются два вектора. При этом необходимо соблюдать их размерность и наклон по отношению друг к другу. Затем две конечные точки соединяют прямой. Её длина и будет искомой величиной. То есть в итоге должна получиться равнобедренная фигура.
Применение метода сложения векторов по правилу треугольника позволяет довольно легко находить сумму для трёх и более отрезков. Для этого сначала вычисляют результат сложения для двух любых линий, а после прибавляют к полученной ограниченной прямой третью и так далее.
Для этого сначала вычисляют результат сложения для двух любых линий, а после прибавляют к полученной ограниченной прямой третью и так далее.
При сложении нескольких векторов удобно выполнять следующую последовательность построений:
- от выбранной точки пространства рисуется вектор, равняющийся первому слагаемому;
- от конечной точки откладывается вектор, совпадающий со вторым слагаемым;
- приведённая последовательность потеряется необходимое число раз;
- прямой линией соединяется точка, с которой началось построение с конечной последнего вектора;
- длина полученного отрезка и будет являться результатом сложения.
Этот способ получил название метод многоугольника. Он довольно часто применяется на практике, позволяя, довольно просто выполнить нахождение суммы. Из правила треугольника, а, следовательно, и многоугольника, вытекает следствие, которое подтверждает, что если складывается отрезок с нулевым векторным выражением, то в ответе получится длина, совпадающая со значимым слагаемым.
Следует отметить, что методы используются только, если направление отрезков является сонаправленным.
Если же отрезки неколлинеарные, то от конца одного откладывается другой. Тогда искомая сумма будет равняться длине линии, первой точкой которой будет начало одной векторной прямой, а конец совпадать с точкой, завершающей другую. То есть сумма — это отрезок, начало которого совпадает с началом обеих линий, а длина равна разности их длин, при этом направление его будет совпадать с тем что больше по длине.
Предыдущая
ГеометрияПлощадь треугольника по координатам вершин — формулы для расчета
Следующая
ГеометрияПлощадь прямоугольной трапеции через угол и основания
Объяснение урока: Векторы: геометрический подход
В этом объяснении мы узнаем, как определять векторы, записывать векторы и определять геометрическую интерпретацию основных векторных операций.
Начнем с того, что вспомним, что скаляр — это математическое объект, у которого есть размер, но нет направления; Например, у нас может быть длина 4 м или скорость 5 м/с. Для представления величин, которые иметь направление, а также размер, например, смещение на 4 м на восток или скорость 5 м/с вверх, нам нужна другая концепция: вектор.
Обратите внимание, что в этом объяснении мы будем работать с векторами в 2D-плоскости.
Определение: Вектор
Вектор — это математический объект, который имеет как величину (размер), так и направление.
Геометрически мы можем представить вектор как направленный отрезок, где длина отрезка обозначает величину, а ориентация стрелки указывает направление.
Некоторые векторы определяются с точки зрения их начальной и конечной точек; Итак, первый вектор выше равен 𝑆𝑇.
Для других векторов мы используем жирные строчные буквы, как показано выше; это обычно пишется от руки как 𝑎.
Мы также встречаем векторы, которые сочетают в себе оба вида маркировки, такие как 𝐴𝐵=c выше.
Фактическое положение вектора в 2D-плоскости не имеет значения, поскольку вектор представляет собой перемещение а не объект с фиксированным положением. Так, например, три вектора, помеченные 𝑃𝑄 ниже все рассматриваются как эквивалентные.
Если два вектора эквивалентны, они должны быть параллельны и иметь одинаковые величины и направления. Наоборот, если два вектора параллельны и имеют одинаковые величины и направления, они должны быть эквивалентны.
Для любого вектора 𝑃𝑄=⃑𝑎 вектор с той же величиной но противоположное направление, которое, следовательно, имеет стрелку, указывающую в противоположном направлении, есть 𝑄𝑃=-𝑃𝑄=-⃑𝑎.
В общем, для любого ненулевого скаляра 𝑘 вектор 𝑘⃑𝑎 является вектором с
|𝑘| раз превышает величину ⃑𝑎. Если 𝑘>0,
вектор 𝑘⃑𝑎 имеет то же направление, что и ⃑𝑎;
если 𝑘0, вектор 𝑘⃑𝑎 имеет направление, противоположное
⃑𝑎. Ниже показано несколько примеров для случаев 𝑘=−1, 2 и −12.
Ниже показано несколько примеров для случаев 𝑘=−1, 2 и −12.
Два вектора классифицируются как параллельные, если они имеют одинаковое или противоположное направление. Следовательно, все указанные выше векторы параллельны. Параллельные векторы всегда можно записать как ненулевые скаляры, кратные друг другу.
Далее рассмотрим, как совмещать векторы.
Закон: Закон треугольника для сложения векторов
Мы складываем два вектора вместе, помещая голову первого вектора в хвост второго вектора, как показано на левой диаграмме ниже.
Результирующий вектор определяется как одиночный вектор, эффект которого такой же, как комбинированный эффект двух (или более) векторов. Результирующая двух векторов начинается с хвоста первого вектора и заканчивается на вершине второго, образуя третью сторону треугольника. Он представляет собой сумму двух векторов.
В этом случае, как показано на правой диаграмме,
результирующий вектор идет от хвоста вектора ⃑𝑎 к вершине вектора ⃑𝑏,
образуя треугольник. Он представляет собой сумму ⃑𝑎+⃑𝑏.
Он представляет собой сумму ⃑𝑎+⃑𝑏.
Эта конструкция демонстрирует закон треугольника для сложения векторов, который гласит, что когда два вектора представлены по величине и направлению как две стороны треугольника, взятые по порядку, третья сторона треугольника, направленная в противоположные стороны, представляет величину и направление их суммы.
Используя этот метод, мы можем складывать столько векторов, сколько захотим, многократно применяя закон треугольника. На приведенной ниже диаграмме показано, как мы можем расширить описанный выше процесс, чтобы сложить вместе три вектора.
Давайте теперь попробуем пример со сложением векторов.
Пример 1. Графическое представление сложения векторов
𝐴𝐵𝐶𝐷 — параллелограмм с 𝐴𝐷=⃑𝑞.
Найти 𝐴𝐶.
Ответ
Напомним, что параллелограмм имеет две пары параллельных сторон, причем противоположные стороны имеют одинаковую длину. Кроме того, вспомните, что вектор — это математический объект, который имеет как величину, так и направление и не определяется своим местоположением.
В параллелограмме 𝐴𝐵𝐶𝐷 вектор ⃑𝑝 представлен в виде направленного отрезка 𝐴𝐵. Поскольку сторона 𝐴𝐵 параллелограмма противоположна стороне 𝐷𝐶, эти стороны должны быть параллельны и равны по длине. Следовательно, соответствующие векторы должны быть параллельны и равны по величине.
Аналогично, вектор ⃑𝑞 представляется в виде направленного отрезка 𝐴𝐷. Поскольку сторона 𝐴𝐷 параллелограмма противоположна стороне 𝐵𝐶, эти стороны должны быть параллельны и равны по длине. Опять же, соответствующие векторы должны быть параллельны и равны по величине.
Напомним, что если два вектора параллельны и равны по величине, они должны быть эквивалентны. Следовательно, из приведенных выше замечаний следует, что 𝐴𝐵=𝐷𝐶=⃑𝑝 а также 𝐴𝐷=𝐵𝐶=⃑𝑞. Это означает, что мы можем заполнить еще два вектора на диаграмме, как показано ниже.
Теперь вспомним закон треугольника для сложения векторов, который гласит, что когда два вектора представлены по величине
и направление как две стороны треугольника, взятые по порядку, третья сторона треугольника, направленная противоположно,
представляет величину и направление их суммы.
Чтобы найти 𝐴𝐶, обратите внимание, что это результирующий вектор 𝐴𝐵 и 𝐵𝐶 в △𝐴𝐵𝐶. Поэтому, применяя закон треугольника, имеем 𝐴𝐶=𝐴𝐵+𝐵𝐶=⃑𝑝+⃑𝑞. Эквивалентно, в △𝐴𝐷𝐶 вектор 𝐴𝐶 является результирующий вектор 𝐴𝐷 и 𝐷𝐶. На этот раз, применяя закон треугольника, мы имеем 𝐴𝐶=𝐴𝐷+𝐷𝐶=⃑𝑞+⃑𝑝=⃑𝑝+⃑𝑞. Как и ожидалось, это дает тот же результат.
Отвечая на поставленный выше вопрос, мы фактически показали, как доказать закон параллелограмма сложения векторов . Этот закон гласит, что если два вектора представлены двумя смежными сторонами параллелограмма, направленные от общей вершины, с величинами, пропорциональными соответствующим длинам сторон, то их результирующий вектор изображается диагональю, проходящей через общую вершину и направленной от нее.
Далее мы исследуем, как вычитать векторы. Как мы продемонстрируем, оказывается, что мы все еще можем применить треугольник
закон сложения векторов в этом контексте. Например, предположим, что у нас есть векторы ⃑𝑎 и ⃑𝑏,
как показано ниже, и мы хотим получить ⃑𝑎−⃑𝑏.
Например, предположим, что у нас есть векторы ⃑𝑎 и ⃑𝑏,
как показано ниже, и мы хотим получить ⃑𝑎−⃑𝑏.
Во-первых, мы меняем направление ⃑𝑏 на противоположное, чтобы получить −⃑𝑏. Затем, поместив начало вектора ⃑𝑎 в хвост вектора −⃑𝑏, теперь мы можем рассматривать это как дополнение. Применяя закон треугольника для сложения векторов, мы получаем результирующий вектор ⃑𝑎+−⃑𝑏=⃑𝑎−⃑𝑏.
Обратите внимание, что особый случай этого правила возникает при вычитании ⃑𝑎
от ⃑𝑎. Позиционирование головы первого вектора ⃑𝑎 в конце второго
вектор −⃑𝑎 означает, что
мы меняем направление и возвращаемся туда, откуда начали, когда достигаем конца вектора ⃑𝑎. Следовательно,
в этом случае
результирующий вектор равен ⃑𝑎+−⃑𝑎=⃑𝑎−⃑𝑎=⃑0,
нулевой вектор. Другой способ думать об этой операции состоит в том, что если ⃑𝑎=𝑃𝑄, то
−⃑𝑎=𝑄𝑃;
Итак, мы идем от 𝑃 к 𝑄, а затем обратно от 𝑄 к 𝑃,
возвращаясь туда, откуда мы начали, с нулевым водоизмещением.
Давайте теперь попробуем пример с вычитанием векторов.
Пример 2. Графическое представление векторного вычитания
На приведенной ниже диаграмме 𝑉𝑊=⃑𝑎, 𝑌𝑉=⃑𝑐, и 𝑌𝑍=⃑𝑑.
Запишите следующие векторы через ⃑𝑎, ⃑𝑏, ⃑𝑐, и ⃑𝑑:
-
- 𝑊𝑋
- 40086
- 40086
Ответ
Напомним, что вектор является математическим объектом, обладающим как величиной, так и направлением.
I. Начнем с поиска 𝑍𝑌. Обратите внимание, что на диаграмме изображен вектор 𝑌𝑍=⃑𝑑, который идет от 𝑌 к 𝑍. Следовательно, чтобы перейти от 𝑍 к 𝑌, мы просто меняем направление этого вектора, чтобы получить его отрицательное значение, поэтому 𝑍𝑌=−⃑𝑑.
II. Далее мы должны найти 𝑊𝑋. Во-первых, вспомним закон треугольника для сложения векторов, который гласит, что когда
два вектора представлены по величине и направлению
как две стороны треугольника, взятые по порядку, третья сторона треугольника, направленная в противоположные стороны, представляет собой величину и направление их
сумма.
Обратите внимание, что в △𝑊𝑉𝑋 вектор 𝑊𝑋 будет результатом 𝑊𝑉 и 𝑉𝑋. Нам дан вектор 𝑉𝑊=⃑𝑎, который идет от 𝑉 до 𝑊. Перейти от 𝑊 на 𝑉, мы меняем направление этого вектора, чтобы получить его отрицательное значение, поэтому 𝑊𝑉=−⃑𝑎. Более того, мы также сказал, что 𝑉𝑋=⃑𝑏. Следовательно, мы можем применить закон треугольника, чтобы получить 𝑊𝑋=𝑊𝑉+𝑉𝑋=−⃑𝑎+⃑𝑏=⃑𝑏−⃑𝑎.
III. Чтобы найти 𝑍𝑉, обратите внимание, что в △𝑍𝑌𝑉 вектор 𝑍𝑉 будет результатом 𝑍𝑌 и 𝑌𝑉. У нас есть 𝑍𝑌=−⃑𝑑 из части I, и вопрос говорит нам, что 𝑌𝑉=⃑𝑐. Применяя закон треугольника, имеем 𝑍𝑉=𝑍𝑌+𝑌𝑉=−⃑𝑑+⃑𝑐=⃑𝑐−⃑𝑑.
IV. Наконец, мы должны найти 𝑍𝑊. На этот раз обратите внимание, что если бы мы образовали треугольник 𝑍𝑉𝑊, как показано ниже, то вектор 𝑍𝑊 будет результатом 𝑍𝑉 и 𝑉𝑊.
Мы уже знаем, что 𝑉𝑊=⃑𝑎, и в части III мы обнаружили, что
𝑍𝑉=⃑𝑐−⃑𝑑. Поэтому, применяя закон треугольника, имеем
𝑍𝑊=𝑍𝑉+𝑉𝑊=⃑𝑐−⃑𝑑+⃑𝑎=⃑𝑎+⃑𝑐−⃑𝑑.
Поэтому, применяя закон треугольника, имеем
𝑍𝑊=𝑍𝑉+𝑉𝑊=⃑𝑐−⃑𝑑+⃑𝑎=⃑𝑎+⃑𝑐−⃑𝑑.
В нашем следующем примере мы исследуем параллельные векторы.
Пример 3. Поиск неизвестного в векторе по заданному параллельному вектору
Предположим, что ⃑𝑚 и ⃑𝑛 — пара непараллельных векторов и что векторы 4⃑𝑚+𝜆⃑𝑛 и 14⃑𝑚+3⃑𝑛 параллельны. Определите значение 𝜆.
Ответ
Напомним, что параллельные векторы всегда можно записать как ненулевые скалярные числа, кратные друг другу. Следовательно, в этом случае мы можем написать 14⃑𝑚+3⃑𝑛=𝑘4⃑𝑚+𝜆⃑𝑛 для некоторого ненулевого скаляра 𝑘. Раскрывая скобки в правой части, получаем уравнение 14⃑𝑚+3⃑𝑛=4𝑘⃑𝑚+𝜆𝑘⃑𝑛. Начнем с определения значения 𝑘. Для этого мы приравниваем коэффициенты при ⃑𝑚 по обе стороны приведенного выше уравнения, что дает 14=4𝑘.
Разделив обе части на 4 и упростив полученную дробь, получим 𝑘=144=72.
Чтобы найти значение 𝜆, приравняем коэффициенты ⃑𝑛
по обе стороны нашего исходного уравнения, что дает
3=𝜆𝑘. Поскольку 𝑘=72, мы можем подставить это значение, чтобы получить
3=72𝜆.
Умножив обе части на 2, а затем разделив на 7, получаем, что 𝜆=67.
Поскольку 𝑘=72, мы можем подставить это значение, чтобы получить
3=72𝜆.
Умножив обе части на 2, а затем разделив на 7, получаем, что 𝜆=67.
Способность складывать или вычитать векторы путем многократного применения закона треугольника для сложения векторов чрезвычайно полезна. В частности, это позволяет нам записывать отдельные векторы в терминах других, которые помечены на той же векторной диаграмме. Если попросить найти вектор 𝐴𝐵, пока мы можем найти направленный путь из точки 𝐴 в точку 𝐵 (для чего может потребоваться изменить направление некоторых векторов вдоль пути, взяв их отрицательные значения), тогда 𝐴𝐵 будет результирующей суммой всех векторов вдоль этого направленного пути.
Например, предположим, что нас попросили найти вектор 𝑃𝑆 на диаграмме ниже.
На данный момент нет направленного пути из 𝑃 в 𝑆
потому что некоторые стрелки идут не в ту сторону. Однако, если мы поменяем направления векторов ⃑𝑏
и ⃑𝑐, заменив их их отрицаниями, мы
создайте направленный путь от 𝑃 к 𝑆, как показано на следующей диаграмме.
Таким образом, мы получаем результирующий вектор 𝑃𝑆=𝑃𝑄+𝑄𝑅+𝑅𝑆=⃑𝑎+−⃑𝑏+−⃑𝑐=⃑𝑎−⃑𝑏−⃑𝑐. Обратите внимание, что в этом расчете скрыты два применения закона треугольника для сложения векторов:
- В △𝑃𝑄𝑅 имеем 𝑃𝑅=𝑃𝑄+𝑄𝑅=⃑𝑎+−⃑𝑏=⃑𝑎−⃑𝑏.
- В △𝑃𝑅𝑆,
имеем 𝑃𝑆=𝑃𝑅+𝑅𝑆.
Как 𝑃𝑅=⃑𝑎−⃑𝑏 и 𝑅𝑆=−⃑𝑐, это становится 𝑃𝑆=⃑𝑎−⃑𝑏+−⃑𝑐=⃑𝑎−⃑𝑏−⃑𝑐 как заявлено.
Приведенное выше обсуждение свойств направленных путей поможет нам решить следующую задачу.
Пример 4. Нахождение суммы трех векторов в треугольнике
В треугольнике 𝐴𝐵𝐶, 𝐴𝐵=⃑𝑝, 𝐵𝐶=⃑𝑞, и 𝐶𝐴=⃑𝑟. Какой из следующих векторов равно ⃑𝑝+⃑𝑞+⃑𝑟?
- 40086
- 𝐵𝐴
- ⃑0
-
- 2 40086
Ответ
Мы начинаем с рисования эскиза треулеущего, описанного в вопросе.
Нам нужно найти вектор, равный ⃑𝑝+⃑𝑞+⃑𝑟.
Поскольку 𝐴𝐵=⃑𝑝, 𝐵𝐶=⃑𝑞 и
𝐶𝐴=⃑𝑟,
тогда
⃑𝑝+⃑𝑞+⃑𝑟=𝐴𝐵+𝐵𝐶+𝐶𝐴. Ссылаясь на приведенный выше эскиз и отслеживая этот направленный путь, мы видим, что мы начинаем с вершины 𝐴 и движемся к 𝐵,
затем в 𝐶 и, наконец, обратно в 𝐴, прибыв туда, откуда мы начали. Поскольку мы начинаем и заканчиваем в 𝐴, результирующая
вектор просто 𝐴𝐴, поэтому
⃑𝑝+⃑𝑞+⃑𝑟=𝐴𝐴.
Однако очевидно, что любой вектор из точки в саму себя является просто нулевым вектором ⃑0,
потому что общий эффект таков, что мы остаемся на том же месте. Так как 𝐴𝐴=⃑𝑝+⃑𝑞+⃑𝑟 и
𝐴𝐴=⃑0,
два правых выражения должны быть равны, что дает нам
⃑𝑝+⃑𝑞+⃑𝑟=⃑0.
Ссылаясь на приведенный выше эскиз и отслеживая этот направленный путь, мы видим, что мы начинаем с вершины 𝐴 и движемся к 𝐵,
затем в 𝐶 и, наконец, обратно в 𝐴, прибыв туда, откуда мы начали. Поскольку мы начинаем и заканчиваем в 𝐴, результирующая
вектор просто 𝐴𝐴, поэтому
⃑𝑝+⃑𝑞+⃑𝑟=𝐴𝐴.
Однако очевидно, что любой вектор из точки в саму себя является просто нулевым вектором ⃑0,
потому что общий эффект таков, что мы остаемся на том же месте. Так как 𝐴𝐴=⃑𝑝+⃑𝑞+⃑𝑟 и
𝐴𝐴=⃑0,
два правых выражения должны быть равны, что дает нам
⃑𝑝+⃑𝑞+⃑𝑟=⃑0.
Просмотрев доступные варианты, мы видим, что правильный ответ — ⃑0.
Используя наш метод определения вектора из одной точки в другую путем нахождения направленного пути, мы также можем ответить на вопросы, связанные с серединами сторон или точками, которые находятся на полпути вдоль стороны. Ниже приведен пример такого типа.
Пример 5.
 Запись векторов, заданных как середины и соотношения сегментов линий в треугольнике с точки зрения других векторов
Запись векторов, заданных как середины и соотношения сегментов линий в треугольнике с точки зрения других векторов𝑃 является серединой 𝑋𝑌 и 𝑄 делит 𝑋𝑍 в соотношении 4∶1.
Напишите следующие векторы с точки зрения ⃑𝑎 и ⃑𝑏:
- 𝑌𝑍
- 𝑋𝑃
- 40086
- 𝑃𝑄
Ответ
I. сложение векторов, в котором говорится, что когда два вектора представлены по величине и направлению как две стороны треугольника, взятого по порядку третья сторона треугольника, направленная в противоположные стороны, представляет величину и направление их суммы.
Заметим, что в △𝑌𝑋𝑍 вектор 𝑌𝑍 будет результатом 𝑌𝑋 и 𝑋𝑍.
Учитывая 𝑌𝑋, нам дан вектор 𝑋𝑌=⃑𝑎, который выходит из
𝑋 к 𝑌. Чтобы перейти от 𝑌 к 𝑋,
мы меняем направление этого вектора, чтобы получить его отрицательное значение, поэтому 𝑌𝑋=−⃑𝑎. Более того,
нам говорят, что 𝑋𝑍=⃑𝑏.
Следовательно, мы можем применить закон треугольника, чтобы получить 𝑌𝑍=𝑌𝑋+𝑋𝑍=−⃑𝑎+⃑𝑏=⃑𝑏−⃑𝑎.
II. Далее прорабатываем 𝑋𝑃. Нам говорят, что 𝑃 является серединой отрезка 𝑋𝑌, поэтому 𝑋𝑃=12𝑋𝑌, и, следовательно, 𝑋𝑃=12𝑋𝑌.
Поскольку 𝑋𝑌=⃑𝑎, это означает, что 𝑋𝑃=12𝑋𝑌=12⃑𝑎.
III. Чтобы вычислить 𝑋𝑄, в вопросе говорят, что 𝑄 делит 𝑋𝑍 в соотношении 4∶1. Это означает, что точка 𝑄 будет составлять четыре пятых пути вдоль отрезок 𝑋𝑍, поэтому 𝑋𝑄=45𝑋𝑍 и, следовательно, 𝑋𝑄=45𝑋𝑍.
Поскольку 𝑋𝑍=⃑𝑏, заключаем, что 𝑋𝑄=45𝑋𝑍=45⃑𝑏.
IV. Наконец, чтобы вычислить 𝑃𝑄, вспомните, что на векторной диаграмме, если мы можем найти
направленный путь из 𝑃 в 𝑄, то вектор 𝑃𝑄
будет результирующей суммой всех векторов вдоль этого направленного пути. Мы можем легко найти подходящий направленный путь из
𝑃 к 𝑄 как
показано на диаграмме ниже.
Это означает, что у нас есть 𝑃𝑄=𝑃𝑋+𝑋𝑄. Во второй части мы выяснили, что 𝑋𝑃=12⃑𝑎. Таким образом, найти 𝑃𝑋, мы изменим направление этого вектора, чтобы получить его отрицательное значение, поэтому 𝑃𝑋=−12⃑𝑎. Кроме того, из части III имеем 𝑋𝑄=45⃑𝑏.
Заменив 𝑃𝑋 и 𝑋𝑄 в приведенном выше уравнении, мы получим 𝑃𝑄=−12⃑𝑎+45⃑𝑏=45⃑𝑏−12⃑𝑎.
Давайте закончим повторением некоторых ключевых моментов этого объяснения.
Ключевые точки
- Векторы — это математические объекты, имеющие как величину (размер), так и направление; это в отличие от скаляров, которые имеют только величину. Геометрически мы можем представить вектор как направленный отрезок, где длина отрезка обозначает величину, а ориентация стрелки указывает направление.
- Закон треугольника для сложения векторов гласит, что когда два вектора представлены по величине и направлению как две стороны треугольника, взятые по порядку, третья сторона треугольника, направленная противоположно, представляет величину и направление их суммы.

- Если мы обратим направление вектора ⃑𝑎, то получим его отрицательное значение −⃑𝑎. Вычитание вектора равносильно добавлению его отрицательного значения.
- Если дана векторная диаграмма, мы можем найти направленный путь из точки 𝐴 в точку 𝐵 (для чего может потребоваться изменить направление некоторых векторов вдоль пути, взяв их отрицательные значения), мы можем заключить, что вектор 𝐴𝐵 будет результирующей суммой всех векторов вдоль этого направленного пути.
- Вышеупомянутый метод также позволяет нам запишите векторы, заданные как середины или соотношения отрезков прямых с точки зрения других векторов.
Геометрическая алгебра в трех измерениях
Геометрическая алгебра в трех измерениях Геометрическая алгебра — это математическая система, расширяющая традиционную
скалярной алгебры в многомерные конструкции, такие как векторы и направленные
плоские сегменты, используя операцию, известную как Clifford product . Определены понятия из традиционной векторной алгебры, такие как векторное произведение.
таким образом, который расширяется до более высоких измерений, обеспечивая понимание
геометрические отношения, которые делают неудобными соглашения, такие как
правило правой руки для завитков и перекрестных произведений не нужно. Он также обеспечивает
конкретная интерпретация ранее абстрактных идей, таких как воображаемая единица
в комплексном анализе.
Определены понятия из традиционной векторной алгебры, такие как векторное произведение.
таким образом, который расширяется до более высоких измерений, обеспечивая понимание
геометрические отношения, которые делают неудобными соглашения, такие как
правило правой руки для завитков и перекрестных произведений не нужно. Он также обеспечивает
конкретная интерпретация ранее абстрактных идей, таких как воображаемая единица
в комплексном анализе.
Геометрическая алгебра особенно хорошо подходит для релятивистских теории поля в четырехмерном пространстве-времени (как описано в моей книге, Релятивистская теория поля для микроволновых инженеров ) и ее сторонники утверждают, что он может обобщать и улучшать другие математические формализмов, объединяющих практически все физические теории и их связанных математических методов на одном очень гибком языке.
Хотя я согласен с этим стремлением в целом, я считаю, что его сторонники
ошибка слишком быстрого перехода к узкоспециализированным дисциплинам, таким
как квантовая физика и общая теория относительности. Хотя хорошо знать, что каждый
из этих важных предметов можно охватить набором инструментов геометрической алгебры,
истинное принятие в качестве стандартного языка математической физики должно начаться с
гораздо более базовый уровень. Предпочтительнее, на мой взгляд, его следует представить
студентов, как только они будут готовы выйти за рамки чисто скалярных
математике и начинают говорить о многомерных объектах, таких как векторы.
Хотя хорошо знать, что каждый
из этих важных предметов можно охватить набором инструментов геометрической алгебры,
истинное принятие в качестве стандартного языка математической физики должно начаться с
гораздо более базовый уровень. Предпочтительнее, на мой взгляд, его следует представить
студентов, как только они будут готовы выйти за рамки чисто скалярных
математике и начинают говорить о многомерных объектах, таких как векторы.
Ниже приводится попытка обобщить правила геометрической алгебры в этого контекста, используя трехмерное пространство в качестве базовой линии.
Базисные векторы
Геометрическая алгебра не имеет координат в том смысле, что фундаментальные выражения могут
быть записана в общем виде, не зависящем от конкретной координаты
используемая система. Тем не менее, полезно иметь ссылку на стандарт
на векторной основе, так что смысл различных операций можно исследовать в
знакомые термины, когда это необходимо. 92 = 1
\]
Следует понимать, что основные операции, выполняемые над такими
векторы выходят за пределы любого конкретного координатного представления. Например,
скалярное произведение векторов \(a\) и \(b\) имеет следующий вид в декартовой системе
координаты,
\[
a\cdot b = a_xb_x+a_yb_y+a_zb_z
\]
и имеет разные формы в цилиндрических и сферических координатах, но
геометрическая интерпретация скалярного произведения во всех трех случаях одинакова,
показано графически ниже,
Например,
скалярное произведение векторов \(a\) и \(b\) имеет следующий вид в декартовой системе
координаты,
\[
a\cdot b = a_xb_x+a_yb_y+a_zb_z
\]
и имеет разные формы в цилиндрических и сферических координатах, но
геометрическая интерпретация скалярного произведения во всех трех случаях одинакова,
показано графически ниже,
Клин Продукт
Как правило, на этом этапе традиционного векторного анализа мы вводим векторное произведение, дающее третий вектор, который перпендикулярен другому два. Но у этого подхода есть несколько недостатков.
Во-первых, в то время как значение скалярного произведения однозначно для векторов
иметь любое количество измерений (например, два измерения, три измерения, четыре
размеры и т. д.), перекрестное произведение может быть определено только в трехмерном
пространство. В общем случае нельзя определить третий вектор, перпендикулярный двум
другие в двухмерном пространстве, а в четырехмерном пространстве есть
бесконечное число векторов, удовлетворяющих этому условию.
Второй проблемой перекрестных произведений является их зависимость от так называемого правило правой руки , неудобное соглашение, необходимое для определения ориентации результирующего вектора относительно двух других. Эта конвенция в конечном счете связано с ручностью системы координат и необходимо потому что векторы перекрестного произведения известны как осевых векторов вместо более типичных полярных векторов .
Хотя нам не нужно вдаваться в подробности того, что подразумевается под этими терминами, я хотел бы утверждают, как и большинство сторонников геометрической алгебры, что они возникают потому, что результат внешнего произведения двух векторов на самом деле не должен быть вектором в все, а скорее направленный плоский сегмент, совпадающий с двумя входными векторами. (Учитывайте тот факт, что единицы, связанные с произведением двух длин вектора должны быть площадью, а не другой длиной.) Это результат, возвращаемый клин изделия ,
\[ Р = а\клин б \] Объект \(P\) известен как бивектор и представляет собой направленный
плоского отрезка так же, как векторы \(a\) и \(b\) представляют направленные
сегменты линии. Традиционное перекрестное произведение было бы вектором, нормальным к этому
поверхности и задается правилом правой руки. Ориентация в этом случае не требуется.
ссылаются на правило правой руки и вместо этого задаются направлением \(a\)
стремясь к \(b\).
Традиционное перекрестное произведение было бы вектором, нормальным к этому
поверхности и задается правилом правой руки. Ориентация в этом случае не требуется.
ссылаются на правило правой руки и вместо этого задаются направлением \(a\)
стремясь к \(b\).
Площадь плоского участка, определяемого бивектором \(P\), определяется его величина, которая представляет собой площадь параллелограмма с ребрами \(a\) и \(b\), \[ \text{область}=|P|=|a||b|\sin\theta \] Важно отметить, что бивектор не кодирует форму плоского участка, а только его положение в пространстве (плоскость, содержащая как \(a\), так и \(b\)), его ориентация (в направлении \(a\) к \(b\)) и его площадь. Таким образом, пока площадь эквивалентна площади параллелограмма, описанного выше, эта форма сам по себе не подразумевается бивектором.
Скаляры называются объектами класса 0 , а векторы относятся к классу 1, а бивекторы относятся к 2-му классу. Предмет 3-го уровня можно получить, взяв клин произведение снова с третьим вектором, \(c\), \[ V = P\клин c = a\клин b\клин c \] Тривектор , \(V\), представляет собой ориентированное твердое тело, заметаемое \(a\), \(b\) и \(c\), и имеет объем, равный объему параллелепипеда, имеющего эти три вектора как его ребра,
\[ \text{объем}=|a\клин b\клин c| \] Обратите внимание, что если какие-либо из \(a\), \(b\) и \(c\) коллинеарны, то объем
и связанный с ним тривектор равны нулю. По расширению невозможно
определить объект класса 4 в трехмерном пространстве, потому что никакие четыре вектора
может быть линейно независимым.
По расширению невозможно
определить объект класса 4 в трехмерном пространстве, потому что никакие четыре вектора
может быть линейно независимым.
Наконец, из-за ориентации, унаследованной от последовательности вектора операндов, произведение клина антикоммутативно, \[ а\клин b = -b\клин а \] Это контрастирует с точечным произведением, которое является коммутативным, \[ а\cточка б = б\cточка а \] Мы также можем отметить, что произведение клина ассоциативно, т.е. \[ a\клин (b\клин c) = (a\клин b)\клин c = a\клин b\клин c \] в то время как скалярный продукт не является.
Продукт Клиффорда
Теперь мы готовы определить произведение Клиффорда, также называемое геометрическим произведением .
продукт , ключевая операция в геометрической алгебре. Написано просто как
сопоставление \(ab\), это сумма точечных и клиновых произведений его
операнды,
\[
ab = a\cdot b+a\клин b
\]
Но что это представляет? Скалярное произведение \((a\cdot b)\) является скаляром и
произведение клина \((a\клин b)\) является бивектором. 2 = 1
\]
\[
\mathbf{x}\mathbf{y} = \mathbf{x}\wedge\mathbf{y} = -\mathbf{y}\wedge\mathbf{x} = -\mathbf{y}\mathbf{x}
\]
93\лангле\mathcal{M}\rangle_k
\]
Нулевая (скалярная) часть \(\mathcal{M}\) иногда сокращается
\(\langle\mathcal{M}\rangle\), без нижнего индекса.
2 = 1
\]
\[
\mathbf{x}\mathbf{y} = \mathbf{x}\wedge\mathbf{y} = -\mathbf{y}\wedge\mathbf{x} = -\mathbf{y}\mathbf{x}
\]
93\лангле\mathcal{M}\rangle_k
\]
Нулевая (скалярная) часть \(\mathcal{M}\) иногда сокращается
\(\langle\mathcal{M}\rangle\), без нижнего индекса.
Геометрическое произведение, определенное выше только для векторов, может быть обобщено до
лопатки следующим образом. Для \(k\)-лезвия \(K\) и \(l\)-лезвия \(L\)
\[
KL = \langle KL\rangle_{k+l}+\langle KL\rangle_{k+l-2}+\cdots+\langle KL\rangle_{|k-l|}
\]
Другими словами, произведение представляет собой многовектор, состоящий из лопастей, имеющих градации
в диапазоне между суммой и разностью оценок своих операндов, пропуская
на 2. Мы сохраняем обозначение точки и клина для самого низкого и самого высокого порядка
термины в этом суммировании,
\[
K\cdot L = \langle KL\rangle_{|k-l|}\quad k\ge1,l\ge1
\]
\[
K\клин L = \langle KL\rangle_{k+l}\quad k\ge0,l\ge0
\]
Обратите внимание, что мы исключили для скалярного произведения случай, когда один из
операнды — это скаляр (уровень 0). В таких случаях результирующее суммирование
имеет только один термин, одно лезвие, и это лезвие имеет тот же класс, что и другое
операнд. Определение здесь как точечного, так и клиновидного произведений привело бы к двойному учету этого
срок. 92 = \mathbf{xyzxyz} = -\mathbf{xyzzyx} = -1
\]
В таких случаях результирующее суммирование
имеет только один термин, одно лезвие, и это лезвие имеет тот же класс, что и другое
операнд. Определение здесь как точечного, так и клиновидного произведений привело бы к двойному учету этого
срок. 92 = \mathbf{xyzxyz} = -\mathbf{xyzzyx} = -1
\]
Единица Псевдоскаляр
Хотя можно идентифицировать до трех взаимно независимых единичных бивекторов
плоскости, (\(\mathbf{xy}\), \(\mathbf{yz}\) и \(\mathbf{zx}\)), существует
только один самостоятельный блок трехобъемный, или тривектор, в трехмерном
пространство (все остальные тривекторы просто являются его скалярными кратными). Мы даем
этот единичный тривектор специальный символ \(i\),
\[
я = \mathbf{xyz}
\]
Обычно его называют блоком 9.2=-1\), но поскольку он коммутирует со всеми другими скалярами, векторами,
бивекторы и тривекторы, как и любой другой скаляр. Бивекторные плоскости
тоже возводят в минус единицу, как мы только что показали, однако они не коммутируют в
геометрические произведения с другими элементами так же, как скаляры и
псевдоскаляры делают.
Подалгебра, включающая геометрические произведения только скаляров и псевдоскаляры (то есть исключая векторы и бивекторы) точно повторяет комплексный анализ. Это всего лишь один простой пример того, как геометрическая алгебра и содержит, и заменяет другие знакомые формы математического анализа.
Алгебраическая область
Таким образом, полная алгебраическая область геометрической алгебры состоит из скаляры, векторы, бивекторы и тривекторы, \[ \lbrace 1\rbrace, \lbrace\mathbf{x},\mathbf{y},\mathbf{z}\rbrace, \lbrace\mathbf{xy},\mathbf{yz},\mathbf{zx}\rbrace, \lbrace\mathbf{xyz}\rbrace \] показано графически ниже,
Все количества могут быть выражены как скалярные кратные этому набору и всем операции, выполняемые над этими величинами, дают результаты в пределах этого множества.
Можно показать, что бивекторы задаются произведениями векторов и
псевдоскаляр. Например,
\[
\mathbf{xy} = \mathbf{xyzz} = я\mathbf{z}
\]
Сходным образом,
\[
\mathbf{yz} = я\mathbf{х}
\]
\[
\mathbf{zx} = я\mathbf{y}
\]
Следовательно, алгебраическая область также может быть записана
\[
\lbrace 1\rbrace, \lbrace\mathbf{x},\mathbf{y},\mathbf{z}\rbrace, \lbrace i\mathbf{x},i\mathbf{y},i\mathbf{z} \rbrace, \lbrace i\rbrace
\]
Бивекторы \(i\mathbf{x}\), \(i\mathbf{y}\) и \(i\mathbf{z}\) равны
иногда называют псевдовекторов в знак признания этой формы. {-1}
\]
При этом остаточный вектор после проектирования, тот вектор, который соединяет
\(\text{proj}_ba\) обратно в \(a\), называется 92}
\]
Это показано ниже,
{-1}
\]
При этом остаточный вектор после проектирования, тот вектор, который соединяет
\(\text{proj}_ba\) обратно в \(a\), называется 92}
\]
Это показано ниже,
Напомним, что декартовы бивекторные плоскости являются двойственными векторам, которые служат их нормалями к поверхности, т.е. \(\mathbf{xy}=i\mathbf{z}\). Этот общий тренд сохраняется для всех бивекторов и нормалей к поверхности, а не только для тех, с карецевскими осями. Следовательно, проекция вектора на плоскость также является отклонением от нормали к поверхности этой плоскости, которая оказывается ее двойной. Общий вывод состоит в том, что операции проектирования и отбраковки двойственны друг другу, \[ а_\отмена{К} = а_{iК} \] 9{-1} \] Опять же, исходная плоскость \(K\) является суммой ее проекции и отклонения из заданного вектора
\[ К = К_а+К_\отмена{а} \]Примеры применения
В качестве примера того, насколько простым может быть геометрический анализ с использованием этого набора инструментов,
теперь мы получим некоторые известные результаты. Рассмотрим треугольник ниже
образованные произвольными векторами \(a\), \(b\) и \(c\), стянутыми
углы \(A\), \(B\) и \(C\).
Рассмотрим треугольник ниже
образованные произвольными векторами \(a\), \(b\) и \(c\), стянутыми
углы \(A\), \(B\) и \(C\).
Векторы \(a\) и \(b\) расположены головой к хвосту и соединяется с \(c\), так что мы можем написать \[ а + б = с \] Теперь возьмем клиновое произведение обеих сторон с \(с\), \[ а \ клин с + б \ клин с = \ отмена {с \ клин с} = 0 \] где мы указали, что клиновое произведение \(с\) само на себя равно нулю. Следовательно, \[ а\клин с = с\клин б \] \[ |a||c|\sin B = |c||b|\sin A \] \[ \ гидроразрыва {\ греха А} {| а |} = \ гидроразрыва {\ греха В} {| б |} \] то есть закон синусов. Мы могли бы прийти к этому результату даже больше быстро, заметив, что \(a\клин c\) и \(c\клин b\) заметают одно и то же бивектор (или, по крайней мере, такой же полубивектор, так как треугольник является половиной соответствующий параллелограмм в каждом случае), что позволяет нам сразу написать \(а\клин с = с\клин b\). 92 \] это закон косинусов.
В качестве последнего примера рассмотрим неправильный многоугольник, показанный ниже. Оно имеет
\(N\) вершин, помеченных от \(p_1\) до \(p_N\) (плюс последняя вершина
\(p_{N+1}\), совпадающий с первым), и мы выбрали произвольное
точка где-то в центре, обозначенная \(c\).
Оно имеет
\(N\) вершин, помеченных от \(p_1\) до \(p_N\) (плюс последняя вершина
\(p_{N+1}\), совпадающий с первым), и мы выбрали произвольное
точка где-то в центре, обозначенная \(c\).
Для расчета площади разделим внутреннюю часть на треугольники, образованные соседними вершинами и точкой \(c\). Каждый треугольник можно считать половиной бивекторного параллелограмма, образованного прямыми, исходящими из точки \(c\) к соседним вершинам, как показано. 9N\влево(x_ky_{k+1}-x_{k+1}y_k\вправо) \] За исключением префактора бивектора, \(\mathbf{xy}\), некоторые могут распознать это как так называемая формула шнурка или формула землемера для площадь неправильного многоугольника при заданных координатах его вершин.
Дополнительное чтение
Хотя эта статья посвящена геометрической алгебре в обычном евклидовом
пространства, одни и те же общие принципы применимы к неевклидовой геометрии и к
также более высокие измерения. Одно из самых интересных применений этого
понятие относится к электромагнетизму в рамках специальной теории относительности. Для этого мы
построить геометрическую алгебру на основе четырехмерного пространства-времени, где
базисные векторы имеют следующую нормализацию, или 92 = \pm1
\]
Эта конструкция известна как алгебра пространства-времени . Чтобы получить больше информации,
читатель отсылается к моей книге «Релятивистская теория поля».
для инженеров-микроволновиков :
Для этого мы
построить геометрическую алгебру на основе четырехмерного пространства-времени, где
базисные векторы имеют следующую нормализацию, или 92 = \pm1
\]
Эта конструкция известна как алгебра пространства-времени . Чтобы получить больше информации,
читатель отсылается к моей книге «Релятивистская теория поля».
для инженеров-микроволновиков :
Теперь доступно на BookBaby и Amazon.com.
Личности
Некоторые полезные тождества приведены ниже, чтобы помочь читателю в изучении понятия геометрической алгебры далее.
В следующих тождествах:
- \(\пси\) является скаляром 9кК\клин а \]
- Определение вектора
- Векторный символ
- Сложение и вычитание векторов
- Векторы смещения
- Умножение векторов на скаляр
- Величина вектора
- Скаляр против векторов
- Примеры векторов
- Все векторы называются хвост (начальная точка) до конца стрелки, поэтому у нас есть вектор AB, а не вектор BA
- Если вы маркируете свои векторы, решение использовать прописные или строчные буквы остается за вами; если вам даны векторы, обратите внимание на направление вектора (смотрите на стрелки)
- Векторы могут быть параллельны и указывать в одном и том же или противоположном направлении (посмотрите на стрелки) 9
Сложение и вычитание векторов
Простая математика векторов не слишком сложна.
Чтобы добавить векторы, мы соединяем хвост одного вектора с головой другого, используя стрелку.
 Прямой луч, соединяющий два вектора, является результирующей r, как показано на этом рисунке:
Прямой луч, соединяющий два вектора, является результирующей r, как показано на этом рисунке:Мы добавляем вектор CD к вектору EF и получаем результирующую r.
Вот загадка: эта цифра дает те же результаты, что и предыдущая цифра?
Здесь мы добавляем вектор EF к вектору CD и еще получить результирующий r. Векторы подчиняются тем же правилам арифметики, что и целые числа (в данном случае свойство коммутативности).
В реальном мире два путешествия вдоль векторов могут показать совершенно разные пейзажи. В математике, поскольку два вектора не изменили своего направления или величины, результаты идентичны: CD + EF = EF + CD = r.
Вычитание вектора состоит всего из двух шагов:
- отрицание вектора, который вы хотите вычесть
- , затем сложите два вектора вместе
Вот векторы SA и IL, показывающие маршрут, по которому, как мы думали, мы идем на парусной лодке:
Мы не осознавали, что течение было сильным; мы заблудились в тумане; солнце ослепляло.
 По какой-то причине вместо того, чтобы следовать вектору IL, мы пошли в направлении , противоположном . Поэтому вместо добавления вектора IL нам нужно его вычесть. Мы делаем это, инвертируя вектор IL и добавляя его к вектору SA:
По какой-то причине вместо того, чтобы следовать вектору IL, мы пошли в направлении , противоположном . Поэтому вместо добавления вектора IL нам нужно его вычесть. Мы делаем это, инвертируя вектор IL и добавляя его к вектору SA:SA + (-IL) = r
Умножение векторов на скаляр
Умножение вектора на скаляр (действительное число) называется скалярным умножением .
Векторы имеют две части (величину и направление), но мы не можем умножить направление. Это не имеет смысла: два «юга» не обращены к югу больше, чем один «юг». Но мы можем умножить величину вектора:
- Умножение вектора на положительный целочисленный скаляр > 1 дает больший вектор
- Умножение вектора на отрицательный целочисленный скаляр <-1 дает больший вектор в противоположном направлении
- Умножение векторов на 1 возвращает тот же вектор (0 смещения)
- Умножение вектора на положительный дробный скаляр < 1 дает меньший вектор
- Умножение вектора на отрицательный дробный скаляр > -1 дает меньший вектор в направлении , противоположном
Два вектора также можно умножать друг на друга с помощью векторного произведения или скалярного произведения.

Умножение двух векторов методом перекрестного произведения дает новый вектор, а скалярное произведение дает число, иногда называемое скалярным произведением.
Величина вектора
Величина вектора отображается в виде абсолютного значения: a или двумя линиями, чтобы не спутать его с абсолютным значением: ∥a∥.
Если вы знаете значения оси x и оси y вектора (как если бы он был на карте или в декартовой системе координат), вы можете легко вычислить его величину, применив теорему Пифагора к изменению положения от хвоста к наконечнику :
Итак, здесь, с хвостом в (1, 4) и стрелкой в (7, 8), у нас есть изменение значения x на 6 и изменение значения y на 4, поэтому:
∥u∥ = 62 + 42
∥u∥ = 36 + 16
∥u∥ = 52
∥u∥ = 7,2111 единиц
Величина вектора1 равна 7,1 единицам.
Единица измерения определяется тем, что вы измеряете; дюймы, километры, мили в час (миль/ч) и т. д. Итак, если бы мы просто измерили расстояние в милях, то длина вектора составила бы 7,2111 мили.

Скаляр против векторов
Для ясности, скалярные величины являются только величинами: масса, температура, скорость, объем, расстояние, энергия, работа и так далее. Думайте о них как о чистых числах.
Слушайте или читайте внимательно : Слушайте или читайте две величины, такие как скорость и направление? Тогда вы имеете дело с вектором. Не читаешь и не слышишь две величины? Вероятно, вы имеете дело со скаляром.
Векторы смещения
Летающие супергерои редко выбирают кратчайший путь от Daily Bugle или Daily Planet до места катастрофы. Они налетают, петляют, прыгают и перекатываются, прежде чем, наконец, прибывают в самый последний момент.
Если бы мы использовали векторы для определения курса летающего супергероя, нам могло бы понадобиться пять или шесть векторов, чтобы учесть все эти обходные пути. Вектор смещения пересекает от начала до конца прямую линию:
Смещение в этом смысле исходит из физики, означая изменение положения по сравнению с начальным положением.

Вы суете правую руку; вы убираете правую руку: нулевое смещение. Ты ча-ча три шага влево и два шага вправо: Вектор смещения на один шаг влево.
На этом рисунке мы видим, что вектор смещения также является результирующим.
Вычисление смещения по-прежнему вектор n + вектор v = r, потому что векторы a и y отрицают друг друга!
Вы можете подумать, что мы потратили много усилий, чтобы преодолеть такое небольшое расстояние, но что, если бы мы находились на корабле ВМФ и должны были бы перемещаться вокруг пристани или охраняемого заповедника? Тогда мы можем увидеть, что это действительно был кратчайший маршрут
Примеры векторов
Все эти измерения являются примерами векторов, поскольку все они включают расстояние или размер силы и направление:
- Скорость
- Сила
- Ускорение
- Импульс
- Рабочий объем
Коммерческие авиалайнеры, истребители, лодки, автомобили, велосипедисты, бегуны, падающие объекты, ракеты, воздушные шары, бумажные самолетики и подводные лодки — все это примеры движущихся объектов, использующих векторы в повседневной жизни.

Пилоты и штурманы должны использовать векторы, чтобы добраться до места назначения. Ученые-ракетчики и аэрокосмические инженеры используют векторы для управления ракетами.
Существует одно исключение для векторов, имеющих длину и направление, и это нулевой вектор. Нулевой вектор не имеет длины, поэтому он не указывает ни в каком конкретном направлении. Это означает, что нулевой вектор имеет неопределенное направление.
Основные задачи с векторами
- Что произойдет, если мы умножим вектор на 4?
- Является ли «25 узлов к югу от юго-запада» скаляром или вектором?
- Что произойдет с вектором, если его умножить на -12?
- Два вектора параллельны, но направлены в противоположные стороны.
 Один из них — вектор z. Какой другой вектор?
Один из них — вектор z. Какой другой вектор?
Надеемся, вы сказали, что он будет указывать в том же направлении, но будет в четыре раза длиннее!
Это вектор, поскольку он дает величину и направление.
Мы надеемся, вы сказали, что он будет вдвое короче и пойдет в противоположном направлении!
Надеемся, вы помните об инвертировании векторов, назвав его -z.
Следующий урок:
Поперечные линии (углы и определение)
5.2 Сложение и вычитание векторов: аналитические методы — физика
Раздел Цели обучения
К концу этого раздела вы сможете делать следующее:
- Определять компоненты векторов
- Описать аналитический метод сложения и вычитания векторов
- Использовать аналитический метод сложения и вычитания векторов для решения задач
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:
- (3) Научные процессы. Учащийся использует критическое мышление, научные рассуждения и решение проблем для принятия обоснованных решений в классе и за его пределами.
 Ожидается, что студент:
Ожидается, что студент:- (F) символически выражать и интерпретировать отношения в соответствии с общепринятыми теориями, делать прогнозы и решать задачи математически, включая задачи, требующие пропорционального рассуждения и графического сложения векторов
- (4) Научные концепции. Учащийся знает и применяет законы, управляющие движением в двух измерениях, в различных ситуациях. Ожидается, что студент:
- (E) разработка и интерпретация диаграмм силы свободного тела;
- (F) определяют и описывают движение относительно разных систем отсчета.
Кроме того, руководство по физике для средней школы рассматривает содержание этого раздела лабораторной работы под названием «Движение в двух измерениях», а также следующие стандарты:
- (3) Научные процессы. Учащийся использует критическое мышление, научные рассуждения и решение проблем для принятия обоснованных решений в классе и за его пределами.
 Ожидается, что студент:
Ожидается, что студент:- (F) выражать и интерпретировать отношения символически в соответствии с принятыми теориями, чтобы делать прогнозы и решать проблемы математически, включая проблемы, требующие пропорционального рассуждения и графического сложения векторов.
Основные термины раздела
аналитический метод компонент (двумерного вектора) Компоненты векторов
Для аналитического метода сложения и вычитания векторов мы используем простую геометрию и тригонометрию вместо использования линейки и транспортира, как мы использовали для графических методов. Однако графический метод все же пригодится для визуализации задачи путем рисования векторов методом «голова к хвосту». Аналитический метод более точен, чем графический метод, который ограничен точностью чертежа.
 Чтобы освежить в памяти определения синуса, косинуса и тангенса угла, см. рис. 5.17.
Чтобы освежить в памяти определения синуса, косинуса и тангенса угла, см. рис. 5.17.Рисунок 5.17 Для прямоугольного треугольника синус, косинус и тангенс θ определяются с точки зрения прилежащей стороны, противолежащей стороны или гипотенузы. На этом рисунке х — это прилежащая сторона, х — противолежащая сторона, а х — гипотенуза.
Поддержка учителей
Поддержка учителей
[BL][OL] Повторить тригонометрические понятия синуса, косинуса, тангенса и теоремы Пифагора.
Поскольку по определению cosθ=x/hcosθ=x/h, мы можем найти длину x , если мы знаем h и θθ, используя x=hcosθx=hcosθ . Точно так же мы можем найти длину y , используя y=hsinθy=hsinθ . Эти тригонометрические отношения полезны для сложения векторов.

Когда вектор действует более чем в одном измерении, полезно разбить его на компоненты x и y. Для двумерного вектора компонент — это часть вектора, которая указывает либо в направлении x, либо в направлении y. Каждый двумерный вектор может быть выражен как сумма его компонентов x и y.
Например, имея такой вектор, как AA на рис. 5.18, мы можем захотеть найти, какие два перпендикулярных вектора, AxAx и AyAy, складываются для его получения. В этом примере AxAx и AyAy образуют прямоугольный треугольник, а это означает, что угол между ними составляет 90 градусов. Это обычная ситуация в физике, и с точки зрения тригонометрии это наименее сложная ситуация.
Рисунок 5.18 Вектор AA с хвостом в начале координат x — y показан вместе с его x — и y — компоненты, AxAx и Ay.Ay. Эти векторы образуют прямоугольный треугольник.

AxAx и AyAy определяются как компоненты AA вдоль осей x и y . Три вектора AA, AxAx и AyAy образуют прямоугольный треугольник.
Ax + Ay = AAx + Ay = A
Если вектор AA известен, то известны его модуль AA (его длина) и его угол θθ (его направление). Чтобы найти AxAx и AyAy, его компоненты x и y , мы используем следующие соотношения для прямоугольного треугольника:0003
Ax=AcosθAx=Acosθ
и
Ay=Asinθ,Ay=Asinθ,
, где AxAx — величина A в направлении x , AyAy — величина A в направлении y , а θθ — угол равнодействующая относительно оси x , как показано на рисунке 5.19.
Рисунок 5.19 Величины компонент вектора AxAx и AyAy можно связать с результирующим вектором AA и углом θθ тригонометрическими тождествами.
 Здесь мы видим, что Ax=AcosθAx=Acosθ и Ay=Asinθ.Ay=Asinθ.
Здесь мы видим, что Ax=AcosθAx=Acosθ и Ay=Asinθ.Ay=Asinθ.Поддержка учителей
Поддержка учителей
[BL][OL][AL] Выведите формулу для получения величины и направления вектора.
Предупреждение о заблуждении
Учащиеся могут запутаться между отношением Ax + Ay = AAx + Ay = A, которое показывает сложение векторов, и A=Ax2+Ay2A=Ax2+Ay2, которое показывает сложение величин векторов.
Предположим, например, что AA — это вектор, представляющий общее перемещение человека, идущего по городу, как показано на рис. 5.20.
Рисунок 5.20 Мы можем использовать соотношения Ax=AcosθAx=Acosθ и Ay=AsinθAy=Asinθ для определения величины векторов горизонтальной и вертикальной составляющих в этом примере.
Тогда A = 10,3 блока и θ=29,1∘θ=29,1∘, так что
Ax=Acosθ=(10,3 блока)(cos29,1∘)=(10,3 блока)(0,874)=9,0 блока.
 Ax=Acosθ=(10,3 блока)(cos29,1∘)=(10,3 блока)(0,874)= 9,0 блоков.
Ax=Acosθ=(10,3 блока)(cos29,1∘)=(10,3 блока)(0,874)= 9,0 блоков.5,6
Эта величина указывает на то, что ходок прошел 9блоков на восток, другими словами, смещение на восток на 9 блоков. Аналогично,
Ay=Asinθ=(10,3 блока)(sin29,1∘)=(10,3 блока)(0,846)=5,0 блока,Ay=Asinθ=(10,3 блока)(sin29,1∘)=(10,3 блока)(0,846)= 5,0 блоков,
5,7
, указывающее, что ходок переместился на 5 блоков к северу — смещение на 5 блоков к северу.
Аналитический метод сложения и вычитания векторов
Вычисление результирующего вектора (или сложения векторов) является обратным разбиением результирующего на его компоненты. Если известны перпендикулярные компоненты AxAx и AyAy вектора AA, то AA можно найти аналитически. как нам это сделать? Поскольку по определению
tanθ=y/x (или в этом случае tanθ=Ay/Ax),tanθ=y/x (или в этом случае tanθ=Ay/Ax),
мы находим θθ, чтобы найти направление равнодействующей.

θ=tan−1(Ay/Ax)θ=tan−1(Ay/Ax)
Поскольку это прямоугольный треугольник, для нахождения гипотенузы применима теорема Пифагора (x 2 + y 2 = h 2 ). В этом случае он становится
A2=Ax2+Ay2.A2=Ax2+Ay2.
Решение для А дает
А=Ах2+Ау2.А=Ах2+Ау2.
Таким образом, чтобы найти величину AA и направление θθ вектора по его перпендикулярным компонентам AxAx и AyAy, как показано на рис. 5.21, мы используем следующие соотношения:
A=Ax2+Ay2θ=tan−1(Ay/ Ax)A=Ax2+Ay2θ=tan−1(Ay/Ax)
Рисунок 5.21 Величина и направление результирующего вектора AA могут быть определены после определения горизонтальных составляющих AxAx и AyAy.
Поддержка учителей
Поддержка учителей
[BL][OL][AL] Продемонстрируйте задачу, связанную с перемещением, физически пройдясь в заданном направлении. Покажите, как это можно изобразить на графике.
 Объясните, что даже при аналитическом решении задач; представление его на графике облегчило бы визуализацию проблемы.
Объясните, что даже при аналитическом решении задач; представление его на графике облегчило бы визуализацию проблемы.Иногда добавляемые векторы не идеально перпендикулярны друг другу. Примером этого является приведенный ниже случай, когда векторы AA и BB складываются для получения результирующих R,R, как показано на рис. 5.22.
Рисунок 5.22 Векторы AA и BB — это два этапа ходьбы, а RR — равнодействующее или полное перемещение. Вы можете использовать аналитические методы для определения величины и направления RR.
Если AA и BB представляют собой два этапа ходьбы (два перемещения), то RR представляет собой общее перемещение. Человек, совершающий прогулку, оказывается на вершине RR. Есть много способов добраться до одной и той же точки. Человек мог идти прямо сначала в направлении x , а затем в г -направление. Эти пути являются x — и y -компонентами результирующего, RxRx и Ry.
 Ry. Если мы знаем RxRx и RyRy, мы можем найти RR и θθ, используя уравнения R=Rx2+Ry2R=Rx2+Ry2 и θ=tan–1(Ry/Rx)θ=tan–1(Ry/Rx) .
Ry. Если мы знаем RxRx и RyRy, мы можем найти RR и θθ, используя уравнения R=Rx2+Ry2R=Rx2+Ry2 и θ=tan–1(Ry/Rx)θ=tan–1(Ry/Rx) .- Нарисуйте компоненты x и y каждого вектора (включая результирующий) пунктирной линией. Используйте уравнения Ax=AcosθAx=Acosθ и Ay=AsinθAy=Asinθ, чтобы найти компоненты. На рис. 5.23 это компоненты AxAx, AyAy, BxBx и By.By. Вектор AA образует угол θAθA с x -ось, а вектор BB образует угол θBθB с собственной осью x (которая немного выше оси x , используемой вектором A ).
Рисунок 5.23 Чтобы сложить векторы AA и B,B, сначала определите горизонтальную и вертикальную составляющие каждого вектора. Это точечные векторы Ax,Ax,AyAyByBy, показанные на изображении.
- Найдите компонент результирующего размера x путем сложения компонентов векторов размером x .

Rx=Ax+BxRx=Ax+Bx
и найдите компонент y результирующей (как показано на рис. 5.24) путем сложения компонентов y векторов.
Ry=Ay+By.Ry=Ay+By.
Рисунок 5.24 Векторы AxAx и BxBx складываются, чтобы получить величину результирующего вектора в горизонтальном направлении, Rx.Rx. Точно так же векторы AyAy и ByBy складываются, чтобы получить величину результирующего вектора в вертикальном направлении, Ry.Ry.
Теперь, когда мы знаем компоненты R,R, мы можем найти его величину и направление.
- Чтобы получить величину равнодействующей R, используйте теорему Пифагора.
R=Rx2+Ry2R=Rx2+Ry2
- Чтобы получить направление результирующего
θ=tan-1(Ry/Rx).θ=tan-1(Ry/Rx).
Смотреть физику
Пример классификации векторов и величин
В этом видео сравниваются три вектора по величине, положению и направлению.

Три вектора, \overrightarrow{\text{u}}, \overrightarrow{\text{v}} и \overrightarrow{\text{w}}, имеют одинаковую величину 5\,\text{единиц}. Вектор \overrightarrow{\text{v}} указывает на северо-восток. Вектор \overrightarrow{\text{w}} указывает на юго-запад точно напротив вектора \overrightarrow{\text{u}}. Вектор \overrightarrow{\text{u}} указывает на северо-запад. Если сложить векторы \overrightarrow{\text{u}}, \overrightarrow{\text{v}} и \overrightarrow{\text{w}}, какой будет величина результирующего вектора? Почему?
0\,\текст{единицы}. Все они будут компенсировать друг друга.
5\,\текст{единиц}. Два из них будут компенсировать друг друга.
10\,\текст{единиц}.
 Два из них будут складываться вместе, чтобы дать равнодействующую.
Два из них будут складываться вместе, чтобы дать равнодействующую.15 шт. Все они будут складываться вместе, чтобы дать равнодействующую.
Советы для успеха
В видео векторы были представлены стрелкой над ними, а не жирным шрифтом. Это обычное обозначение на уроках математики.
Использование аналитического метода сложения и вычитания векторов для решения задач
На рис. 5.25 для добавления векторов используется аналитический метод.
Рабочий пример
Ускоряющийся поезд метро
Добавьте вектор AA к вектору BB, показанному на рис. 5.25, используя шаги, описанные выше. 9Ось 1104 x проходит в направлении восток-запад, а ось y — в направлении север-юг.
 Сначала человек проходит 53,0 м53,0 м в направлении 20,0°20,0° к северу от востока, представленном вектором А.А. Затем человек проходит 34,0 м34,0 м в направлении 63,0°63,0° к северу от востока, представленном вектором B.B.
Сначала человек проходит 53,0 м53,0 м в направлении 20,0°20,0° к северу от востока, представленном вектором А.А. Затем человек проходит 34,0 м34,0 м в направлении 63,0°63,0° к северу от востока, представленном вектором B.B.Рисунок 5,25 Вы можете использовать аналитические модели для добавления векторов.
Стратегия
Компоненты АА и ВВ вдоль х — и y -оси представляют ходьбу строго на восток и строго на север, чтобы добраться до одной и той же конечной точки. Мы найдем эти компоненты, а затем добавим их в направлениях x и y, чтобы найти результат.
Решение
Сначала найдем компоненты AA и BB по осям x — и y . Из задачи мы знаем, что A=53,0 м, A=53,0 м, θA=20,0∘, θA=20,0∘, BB = 34,0 м34,0 м и θB=63,0∘θB=63,0∘. Мы находим x -компоненты, используя Ax=AcosθAx=Acosθ, что дает
Ax=AcosθA=(53,0 м)(cos20,0∘)=(53,0 м)(0,940)=49,8 мAx=AcosθA=(53,0 м)(cos20,0∘)=(53,0 м)(0,940)=49,8 м
и
Bx=BcosθB=(34,0 м)(cos63,0∘)=(34,0 м)(0,454)=15,4 м.
 Bx=BcosθB=(34,0 м)(cos63,0∘)=(34,0 м )(0,454)=15,4 м.
Bx=BcosθB=(34,0 м)(cos63,0∘)=(34,0 м )(0,454)=15,4 м.Аналогичным образом, y -компоненты находятся с использованием Ay=AsinθAAy=AsinθA
Ay=AsinθA=(53,0 m)(sin20,0∘)=(53,0 m)(0,342)=18,1 мAy=Asinθ0A=(53,0002) m)(sin20,0∘)=(53,0 м)(0,342)=18,1 м
и
By=BsinθB=(34,0 м)(sin63,0∘)=(34,0 м)(0,891)=30,3 м. By=BsinθB=(34,0 м)(sin63,0∘)=(34,0 м)(0,891)=30,3 м.
x — и y -компоненты равнодействующей равны
Rx=Ax+Bx=49,8 м+15,4 м=65,2 mRx=Ax+Bx=49,8 м+15,4 м=65,2 м
Ry=Ay+By=18,1 м+30,3 м=48,4 м.Ry=Ay+By=18,1 м+30,3 м=48,4 м.
Теперь мы можем найти величину равнодействующей по теореме Пифагора
R=Rx2+Ry2=(65,2)2+(48,4)2 mR=Rx2+Ry2=(65,2)2+(48,4)2 m
5,8
так что
R=6601 м=81,2 м.R=6601 м=81,2 м.
Наконец, находим направление равнодействующей
θ=tan−1(Ry/Rx)=+tan−1(48,4/65,2).
 θ=tan−1(Ry/Rx)=+tan−1( 48,4/65,2).
θ=tan−1(Ry/Rx)=+tan−1( 48,4/65,2).Это
θ=tan−1(0,742)=36,6∘.θ=tan−1(0,742)=36,6∘.
Обсуждение
В этом примере показано сложение векторов с использованием аналитического метода. Вычитание вектора с использованием аналитического метода очень похоже. Это просто добавление отрицательного вектора. То есть A−B≡A+(−B)A−B≡A+(−B) . Компоненты – BB являются минусами компонентов BB. Следовательно, x — и y -компоненты результата A−B=RA−B=R равны
Rx=Ax+-BxRx=Ax+-Bx
и
Ry=Ay+-ByRy=Ay+-By
3
3 а остальная часть метода, описанного выше, идентична методу сложения.
Практические задачи
5.
Какова величина вектора, у которого x -компонента равна 4 см, а y -компонента равна 3 см?
- 1 см
- 5 см
- 7 см
- 25 см
6.

Какова величина вектора, составляющего угол 30° с горизонтом и чья x -компонента равна 3 единицам?
- 2,61 шт.
- 3,00 шт.
- 3,46 шт.
- 6,00 шт.
Проверьте свое понимание
7.
Между аналитическим и графическим методами сложения векторов, что точнее? Почему?
- Аналитический метод менее точен, чем графический, поскольку первый включает геометрию и тригонометрию.
- Аналитический метод является более точным, чем графический метод, поскольку последний включает в себя некоторые обширные вычисления.
- Аналитический метод менее точен, чем графический, потому что первый включает рисование всех фигур в правильном масштабе.
- Аналитический метод более точен, чем графический, поскольку последний ограничен точностью чертежа.
8.

Что является компонентом двумерного вектора?
- Компонент — это часть вектора, которая указывает либо в направлении x , либо в направлении y .
- Компонент — это часть вектора, которая имеет половину величины исходного вектора.
- Компонент — это часть вектора, указывающая в направлении, противоположном исходному вектору.
- Компонент — это часть вектора, указывающая в том же направлении, что и исходный вектор, но с удвоенной величиной.
- |A→|=Ax+Ay|A→|=Ax+Ay
- |A→|=Ax2+Ay2|A→|=Ax2+Ay2
- |A→|=Ax2+Ay2|A→|=Ax2+Ay2
- |A→|=(Ax2+Ay2)2|A→|=(Ax2+Ay2)2
- $v\cdot w\in\Re$. То есть скалярное произведение двух векторов — это просто действительное число, скаляр (не вектор).
- $\forall\ v, v\cdot v=0 \mathrm{~iff~} v=\vec{0}$. то есть точка произведение вектора на самого себя равно нулю тогда и только тогда, когда вектор является нулевой вектор. В 3D нулевой вектор равен (0,0,0).
- (коммутативность) $v \cdot w = w \cdot v$.
 {n} v_i w_i \]
{n} v_i w_i \]На самом деле, поскольку мы используем только 3 измерения, $x$, $y$ и $z$: \[ v \cdot w = v_x w_x + v_y w_y + v_z w_z \]
Вы можете легко проверить, что это определение скалярного произведения удовлетворяет требуемые свойства.
Обратите внимание, что вычисление одного элемента матричного умножения — это то же самое, что и скалярное произведение: результирующий элемент является скалярным произведением строка из первой матрицы со столбцом из второй матрицы.
Пример
Предположим, у нас есть следующие два вектора: \[ \begin{выравнивание*} v &=& (1,2,3) \\ ш &=& (6,5,4) \\ \end{выравнивание*} \]
Скалярное произведение этих векторов равно: \[ v \cdot w = 1\ast6+2\ast5+3\ast4 = 6+10+12 = 28 \]
Обратите внимание, что скалярное произведение двух векторов является скаляром : действительное число, а не вектор.
Длина
Учитывая скалярное произведение, мы можем определить длину вектора: \[ |v| = \sqrt{v\cdot v} \]
Это всего лишь наш старый друг, замаскированная теорема Пифагора! Почему? Поскольку скалярное произведение вектора на самого себя в конечном итоге приводит к квадрату каждого элемент и суммировать их.
 2} = \sqrt{4+9+36} = \sqrt{49} = 7 \]
2} = \sqrt{4+9+36} = \sqrt{49} = 7 \]Если мы нормализуем $v$, что мы получим? Пусть $w=v/|v|$, получаем \[w = (2,3,6)/7 = (2/7,3/7,6/7) \ приблизительно (0,28,0,43,0,86) \]
Легко проверить, что $|w|=1$. Вектор $w$ точно такой же направление как $v$, но это одна единица длины.
Углы между векторами
Угол между двумя векторами $v$ и $w$ можно найти с помощью следующая формула: \[ \cos(\theta) = \frac{v\cdot w}{|v||w|} \]
, который мы также можем представить как: \[ \cos(\theta) = \frac{v}{|v|} \cdot \frac{w}{|w|} \]
Другими словами, это просто скалярное произведение двух единичных векторов. То есть, если оба из двух векторов $v$ и $w$ нормализованы (длина одна единица), формула косинуса угла между ними принимает вид следующее, что удивительно просто: \[ \cos(\theta) = v\cdot w \]
Это хорошая новость, потому что скалярное произведение вычисляется очень быстро: в 3D, это всего лишь 3 умножения и 2 сложения.
 Получается, что косинус
угол часто требуется в компьютерной графике, поэтому возможность вычислить его
так просто чрезвычайно ценно. На самом деле бывают случаи, когда
хвост виляет собакой: используется косинус угла, потому что он такой быстрый
вычислить. Он часто используется в расчетах освещения.
92} = \sqrt{81+36+4} = \sqrt{121} = 11 \]
Получается, что косинус
угол часто требуется в компьютерной графике, поэтому возможность вычислить его
так просто чрезвычайно ценно. На самом деле бывают случаи, когда
хвост виляет собакой: используется косинус угла, потому что он такой быстрый
вычислить. Он часто используется в расчетах освещения.
92} = \sqrt{81+36+4} = \sqrt{121} = 11 \]Следовательно, косинус угла между $v$ и $w$ равен: \[ \cos(\theta) = \frac{v\cdot w}{7\ast 11} = \frac{2\ast9+3\ast6+6\ast2}{77} = \frac{18+18+12}{77} = \ гидроразрыва {48} {77} \ приблизительно 0,62 \]
Если по какой-то причине нам нужен фактический угол, мы можем вычислить дугу косинус, но нам это почти никогда не понадобится. (Этот угол составляет около 51 градусов.)
Пример 2
Предположим, у нас есть векторы $x=(1,0,0)$ и $y=(0,1,0)$. То есть эти являются единичными векторами, которые указывают в направлении осей X и Y. Это легко видеть, что скалярное произведение между ними равно нулю.
Что это значит? Если косинус угла равен нулю, то угол — прямой угол (девяносто градусов).
 То есть эти два вектора перпендикулярно . (Мы не удивлены, что они перпендикулярны,
но приятно видеть, что расчет это подтверждает.) В линейном
В алгебре термин ортогональный используется для векторов, которые
перпендикуляр. На гиковском языке мы говорим, что две вещи «ортогональны».
если одно не влияет на другое. Это имеет смысл, потому что мы можем
перевести объект на кратное вектору $x$, не затрагивая его Y
координаты, и переведем ее на кратные вектору $y$ без
влияет на его координату X.
То есть эти два вектора перпендикулярно . (Мы не удивлены, что они перпендикулярны,
но приятно видеть, что расчет это подтверждает.) В линейном
В алгебре термин ортогональный используется для векторов, которые
перпендикуляр. На гиковском языке мы говорим, что две вещи «ортогональны».
если одно не влияет на другое. Это имеет смысл, потому что мы можем
перевести объект на кратное вектору $x$, не затрагивая его Y
координаты, и переведем ее на кратные вектору $y$ без
влияет на его координату X.Пример 3
Что мы можем сказать об угле $\theta$ между векторами: \[ \begin{выравнивание*} v &=& (2,3,6)\\ и &=& (-6,10,-3)\\ \end{выравнивание*} \]
Косинус угла находится по формуле: \[ \cos(\theta) = \frac{(2,3,6)\cdot(-6,10,-3)}{|v||u|} = \frac{-12+30-18}{|v||u|} = \frac{0}{|v||u|} = 0 \]
Итак, эти векторы перпендикулярны (ортогональны).
Применение закона косинусов
В этом разделе доказывается, что скалярное произведение нормализованных векторов равно угол между ними.
 Можете пропустить, если вам не интересно.
два вектора, v и w, и их разность, v-w, которая
стрелка между конечными точками 9п v_i w_i}{|v| |ш|} \]
Можете пропустить, если вам не интересно.
два вектора, v и w, и их разность, v-w, которая
стрелка между конечными точками 9п v_i w_i}{|v| |ш|} \], но этот числитель — просто скалярное произведение $v$ и $w$, поэтому \[ \cos(\theta) = \frac{v\cdot w}{|v| |ш|} \]
Перекрестное произведение
Как мы знаем, скалярное произведение двух векторов дает скаляр . Перекрестное произведение дает вектор : тот, который перпендикулярен оба из них. В 3D перекрестное произведение равно: \[ \begin{выравнивание*} \vec{n} &=& \vec{v}\times\vec{w} \\ &=& \vecIII{v_x}{v_y}{v_z}\times\vecIII{w_x}{w_y}{w_z} \\ &=& \vecIII{v_yw_z-v_zw_y}{v_zw_x-v_xw_z}{v_xw_y-v_yw_x} \end{выравнивание*} \]
Обратите внимание, что порядок имеет значение: $v \times w = — w \times v$. Заметьте также, что при вычислении $n_x$ вы используете только члены из компонентов Y и Z, и аналогично для $n_y$ и $n_z$. Есть хороший графический способ запомнить способ вычислить это.
 Глядя на следующие цифры, умножьте
термины, соединенные линиями, и вычесть одну строку из другой. Для Х
и Z, вы вычитаете большую диагональ (с наклоном вправо) из
малой диагонали, а для Y вы вычитаете их в обратном порядке (или
просто отрицать результат).
Как вычислить перекрестный продукт
Глядя на следующие цифры, умножьте
термины, соединенные линиями, и вычесть одну строку из другой. Для Х
и Z, вы вычитаете большую диагональ (с наклоном вправо) из
малой диагонали, а для Y вы вычитаете их в обратном порядке (или
просто отрицать результат).
Как вычислить перекрестный продуктНаправление векторного произведения
В каком направлении указывает вектор? Для этого нам понадобится правило правой руки : направьте пальцы правой руки в направлении первого вектора, проведите их ко второму, и ваш большой палец указывает в направлении поперечного произведения. В качестве альтернативы укажите большой палец в направлении первого вектора, указательный в направлении направлении второго, а средний палец в направлении перекрестный продукт.
Интересно, что $z=x\times y$, $x = y \times z$ и $y = z \times x$. Что — нормированный вектор, параллельный оси $z$, (0,0,1) — крест произведение векторов для оси $x$ (1,0,0) и оси $y$ (0,1,0).
Длина поперечного произведения
Длина перекрестного произведения, деленная на длины двух vectors дает синус угла между двумя векторами: \[ \sin(\theta) = \frac{|v\times w|}{|v| |ш|} \]
Пример перекрестного продукта
Найдите векторное произведение следующих двух векторов: \[ \begin{выравнивание*} v &=& (2,3,6)\\ ш &=& (9,6,2)\\ \end{выравнивание*} \]
Напишем векторы вертикально, чтобы найти результат.

След:
\[ \langle\mathcal{MN}\rangle = \langle\mathcal{NM}\rangle \]Двойственность:
\[ я \ лангле \ mathcal {M} \ rangle_k = \ лангле я \ mathcal {M} \ rangle_ {3-k} \] \[ а_\отмена{К} = а_{iК} \] \[ K_\cancel{a} = K_{ia}\quad k=1,2 \] \[ я (\ mathcal {M} \ cdot а) = (я \ mathcal {M}) \ клин а \] \[ я (\ mathcal {M} \ клин а) = (я \ mathcal {M}) \ cdot а \]Проекция и отклонение:
\[ (\mathcal{M}+\mathcal{N})_K = \mathcal{M}_K + \mathcal{N}_K \] \[ (\mathcal{M}+\mathcal{N})_\cancel{K} = \mathcal{M}_\cancel{K} + \mathcal{N}_\cancel{K} \] \[ \mathcal{M} = \mathcal{M}_a + \mathcal{M}_\cancel{a} \] \[ а = а_К + а_\отменить{К} \] \[ a_b\cdot\mathcal{M}_b = a_b\cdot\mathcal{M} \] \[ a_b\cdot\mathcal{M}_\cancel{b} = 0 \] \[ a_\cancel{b}\cdot\mathcal{M}_b = (a\cdot\mathcal{M})_b \] \[ a_\cancel{b}\cdot\mathcal{M}_\cancel{b} = a\cdot\mathcal{M}_\cancel{b} \] \[ a_b\клин\mathcal{M}_b = 0 \] \[ a_b\клин\mathcal{M}_\cancel{b} = a_b\клин\mathcal{M} \] \[ a_\cancel{b}\wedge\mathcal{M}_b = a\wedge\mathcal{M}_b \] \[ a_\cancel{b}\wedge\mathcal{M}_\cancel{b} = (a\wedge\mathcal{M})_\cancel{b} \] \[ a_b\mathcal{M}_b = a_b\cdot\mathcal{M} \] \[ a_b\mathcal{M}_\cancel{b} = a_b\wedge\mathcal{M} \] \[ a_b\mathcal{M} = a_b\cdot\mathcal{M}_b + a_b\wedge\mathcal{M}_\cancel{b} \] \[ a_{KL} = a_K + a_L\quad\text{if}\quad KL= K\клин L \] \[ \left(\mathcal{M}_K\right)_L = \left(\mathcal{M}_L\right)_K\quad\text{if}\quad KL=K\wedge L \] 9кКа\право) \] \[ K\cdot L = \langle KL\rangle_{|k-l|}\quad k,l\ge1 \] \[ K\клин L = \langle KL\rangle_{k+l}\quad (k+l)\le4 \] \[ a\cdot(bc) = a\cdot(b\клин c) = (a\cdot b)c — (a\cdot c)b \] \[ a\клин (bc) = a(b\cdot c) + a\клин b\клин c \] \[ a(b\клин c) = (a\cdot b)c — (a\cdot c)b + a\клин b\клин c \] \[ abc = (a\cdot b)c — (a\cdot c)b + (b\cdot c)a + a\клин b\клин c \] \[ a\cdot(b\cdot K) = -b\cdot(a\cdot K) = (K\cdot a)\cdot b \] \[ а\cdot(bK) = (a\cdot b)K — b(a\cdot K) \] \[ a\cdot(b\cdot K) = (a\cdot b)K — b\wedge(a\cdot K) \] \[ а\клин(b\cdot K) = (a\cdot b)K — b\cdot(a\клин K) \] \[ а\cdot(K\клин L) = (a\cdot K)\клин L+(-1)^kK\клин (a\cdot L) \] \[ (a\клин b)\cdot(c\клин d) = (a\cdot d)(b\cdot c) — (a\cdot c)(b\cdot d) \] \[ a\cdot(b\клин c\клин d) = (a\cdot b)(c\клин d) — (a\cdot c)(b\клин d) + (a\cdot d)(b\клин c ) \]Вырожденные формы:
\[ \left(\mathcal{M}_K\right)_\cancel{K} = \left(\mathcal{M}_\cancel{K}\right)_K = 0 \] \[ (\mathcal{M}\cdot а)\cdot а = 0 \] \[ \mathcal{M}\клин a\клин a = 0 \] \[ (\mathcal{M}\cdot a)\клин a = (\mathcal{M}\cdot a)a = (\mathcal{M}a)\клин a \] \[ (\mathcal{M}\клин а)\cdot а = (\mathcal{M}\клин а)а = (\mathcal{M}а)\cdot а \] \[ K_i = K_\cancel{1} = K\quad k\ge 1 \] \[ K_\cancel{i} = K_1 = 0\quad k\ge 1 \]The SpaceR3
Если три взаимно перпендикулярные копии реальной прямой пересекаются в начале своих координат, то любая точка в получившемся пространстве задается упорядоченной тройной действительных чисел ( х 1 , х 2 , х 3 ). Множество всех упорядоченных троек действительных чисел называется 3-пространственное и обозначается как R 3 («R три»). См. рис.
Множество всех упорядоченных троек действительных чисел называется 3-пространственное и обозначается как R 3 («R три»). См. рис.
Рисунок 1
Операции сложения и скалярного умножения, определенные на R 2 , переносятся на R 3 :
Векторы в R 3 называются 3-векторами (поскольку есть 3 компонента), а геометрические описания сложения и скалярного умножения, данные для 2-векторов, также переносятся на 3-векторы.
Пример 1 : Если x = (3, 0, 4) и y = (2, 1, −1), то
Стандартные базисные векторы в R 3 . Поскольку для любого вектора x = ( x 1 , x 2 , x 3 ) в R 3 0 , 3 стандартные базисные векторы в R 3 равны Любой вектор x в R 3 поэтому может быть записан как См. Рисунок 2 Пример 2 : Какой вектор нужно добавить к a = (1, 3, 1), чтобы получить b = (3, 1, 5)? Пусть c — искомый вектор; тогда a + c = b . Следовательно, Обратите внимание, что c является вектором ab ; см. рисунок . Рисунок 3 Перекрестное произведение . До сих пор вы видели, как можно сложить (или вычесть) два вектора и как вектор умножается на скаляр. Можно ли как-то «перемножить» два вектора? Один из способов определить произведение двух векторов, который делается только с векторами в R 3 — это их перекрестное произведение . Let x = ( x 1 , x 2 , x 3 ) and y =( y 1 , y 2 , y 3 ) — два вектора в R 3 . Перекрестное произведение двух векторов является вектором, и, возможно, наиболее важной характеристикой этого векторного произведения является то, что оно перпендикулярно обоим множителям . (Это будет продемонстрировано, когда будет введено скалярное произведение.) То есть вектор x x y будет перпендикулярен как x , так и y ; см. рисунок . [Здесь есть неясность: плоскость на рис. , содержащая векторы x и y , имеет два перпендикулярных направления: «вверх» и «вниз». Какой из них выбирает векторное произведение? Ответ дается правилом правой руки : Поместите запястье правой руки в общую начальную точку x и y , с вашими пальцами, указывающими вдоль x ; когда вы сгибаете пальцы в направлении y , ваш большой палец будет указывать в направлении x x y . Рисунок 4 Длина вектора x = ( x 1 , x 2 , x 3 ) в R  рис.
рис. Перекрестное произведение (или векторное произведение ) x и y определяется следующим образом:
Перекрестное произведение (или векторное произведение ) x и y определяется следующим образом: Это показывает, что векторное произведение антикоммутативно: y x х = — ( х х у ).]
Это показывает, что векторное произведение антикоммутативно: y x х = — ( х х у ).]
результат, который следует из теоремы Пифагора (см. обсуждение перед рис. ниже). В то время как направление векторного произведения x и y определяется ортогональностью и правилом правой руки, величина (то есть длина) x x y равна площади параллелограмма, натянутого на вектора х и у .
Так как площадь параллелограмма на рисунке равна
выполняется следующее уравнение:
, где θ — угол между x и y .
Рисунок 5
Пример 3 : Пусть x = (2, 3, 0) и y = (−1, 1, 4) будут векторами положения в R 3 . Вычислите площадь треугольника, вершины которого являются началом и концами x и y , и определите угол между векторами x и y .
Поскольку площадь треугольника равна половине площади параллелограмма, натянутого на х и у ,
Теперь, поскольку ‖ x x y ‖ = ‖ x ‖·‖ y ‖ sin θ, угол между x и y Следовательно, θ = sin −1 √233/234. Векторы в математике — это величины с двумя атрибутами: величина и направление . Здесь вы можете узнать о векторах, о том, как складывать и вычитать векторы, как умножать векторы на скалярные величины и как векторы указывают путь в реальной жизни. Вектор — это величина в математике, которая имеет величину (расстояние, скорость или размер) и 
Вектор в математике | Определение, умножение и примеры (видео)
Содержание
Определение вектора
Переплывая бухту на лодке, вы можете думать, что плывете прямо на юг со скоростью 3 узла, но если приливы отступают, вы можете двигаться со скоростью 5 узлов на юго-восток.
Вектор или несколько векторов, работающих вместе, будут учитывать расстояние, которое вы гребете, вашу скорость и фактическое направление.
Символ вектора
Для представления векторов математики, физики и инженеры используют лучи, обозначая их строчными или прописными буквами, например:
Советы по маркировке векторов:
10.
Как мы можем определить величину вектора, если мы знаем величины его компонент?
Поддержка учителей
Поддержка учителей
Используйте Проверьте свое понимание вопросов, чтобы оценить, достигают ли учащиеся целей обучения в этом разделе. Если учащиеся испытывают затруднения при выполнении определенной задачи, форма Check Your Understanding поможет определить, какая цель вызывает проблему, и направит учащихся к соответствующему содержанию.
Если учащиеся испытывают затруднения при выполнении определенной задачи, форма Check Your Understanding поможет определить, какая цель вызывает проблему, и направит учащихся к соответствующему содержанию.
CS307: Введение в компьютерную графику
При автоматической настройке задействовано значительное количество 3D-геометрии. камера. (Еще больше задействовано использование мыши для перетаскивания камеры к другой точке зрения, но мы пока отложим это.) Нам также нужно чтобы понять некоторую геометрию векторов, чтобы сделать вычисления для материала и освещение.
Итак, сейчас мы атакуем его. Это чтение объясняет
соответствующую математику. Наиболее важной частью нижеследующего является
понимание скалярного произведения. Скалярный продукт используется несколькими способами в
модель освещения, поэтому чем вам с ней удобнее, тем лучше.
Мы не будем использовать кросс-произведения в материале и освещении, но позже в
семестр, и здесь он вполне подходит, но если вы заблудитесь в
понимая перекрестный продукт, не волнуйтесь.
Векторная математика
Интуитивно и геометрически вектор представляет собой стрелку . Это имеет длину и направление . В системе координат мы может представить вектор как тройку чисел $(\Delta x, \Delta y, \Дельта г)$.
Конечно, тройка чисел также используется для представляют точек . Есть ли разница? Да. Точка имеет местоположение , но не длину и вектор имеет длину , но не местоположение. Вы можете получить одно от другого, хотя. Если у нас есть две точки, A и B, мы можем найти вектор из A в B с помощью вычитания: \[ \vecIII{\Delta x}{\Delta y}{\Delta z} = \vec{v} = В — А = \vecIII{b_x}{b_y}{b_z} — \vecIII{a_x}{a_y}{a_z} = \vecIII{b_x-a_x}{b_y-a_y}{b_z-a_z} \]
Векторы и точки в однородных координатах
Интересно, мы можем отличить векторы от точек
в однородных координатах , о которых мы узнали в
контекст аффинных преобразований. Очки имеют $w=1$, и (как вы можете
см. из вычитания выше) векторы имеют $w=0$:
\[ \vecIV{\Delta x}{\Delta y}{\Delta z}{0}
= \vec{v}
= В — А
= \vecIV{b_x}{b_y}{b_z}{1} — \vecIV{a_x}{a_y}{a_z}{1}
\]
Очки имеют $w=1$, и (как вы можете
см. из вычитания выше) векторы имеют $w=0$:
\[ \vecIV{\Delta x}{\Delta y}{\Delta z}{0}
= \vec{v}
= В — А
= \vecIV{b_x}{b_y}{b_z}{1} — \vecIV{a_x}{a_y}{a_z}{1}
\]

 Его можно перемещать как вдоль прямой, на которой он находится, так и параллельно этой прямой. По сути под свободным вектором понимают множество закреплённых векторов.
Его можно перемещать как вдоль прямой, на которой он находится, так и параллельно этой прямой. По сути под свободным вектором понимают множество закреплённых векторов.
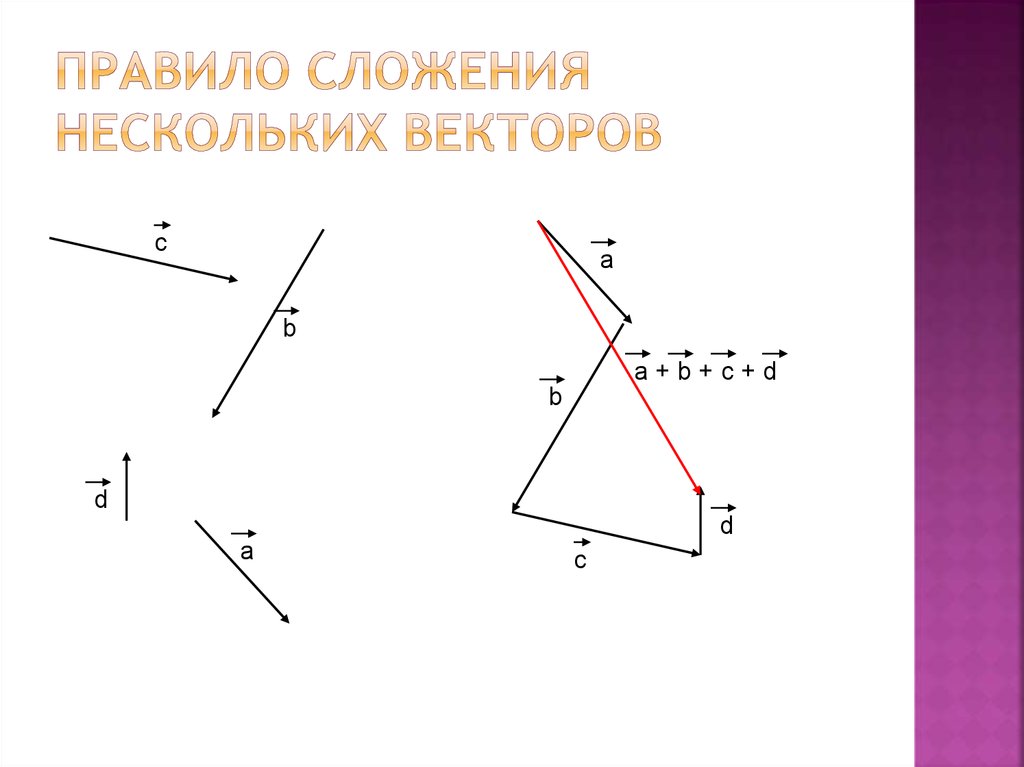

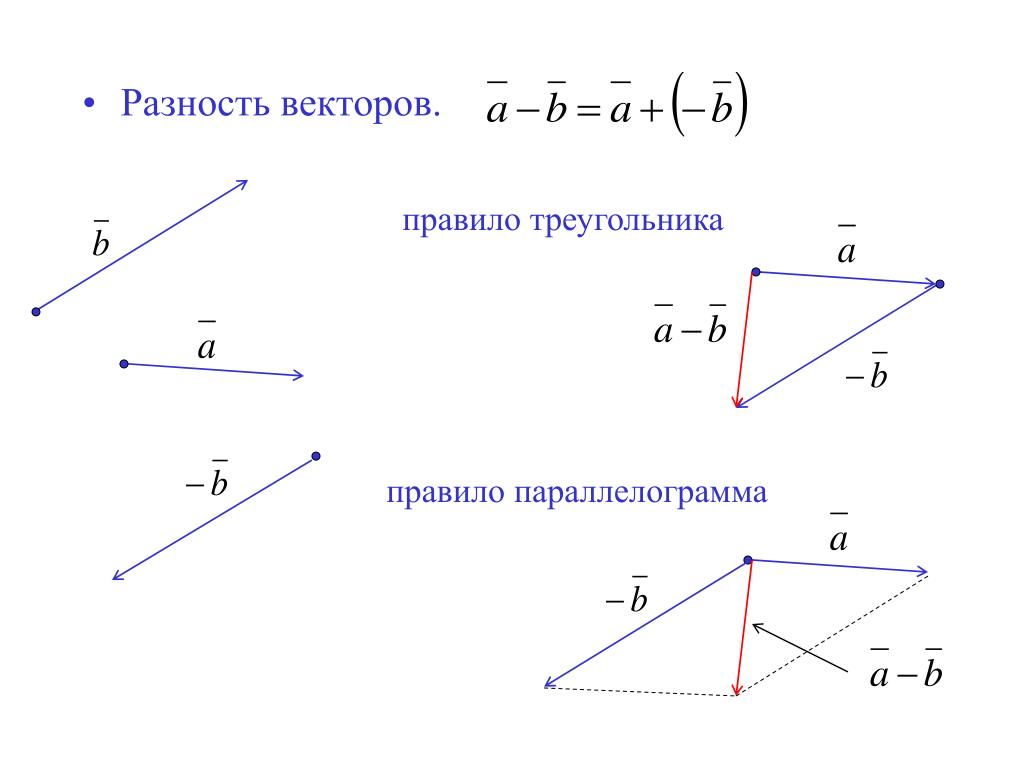
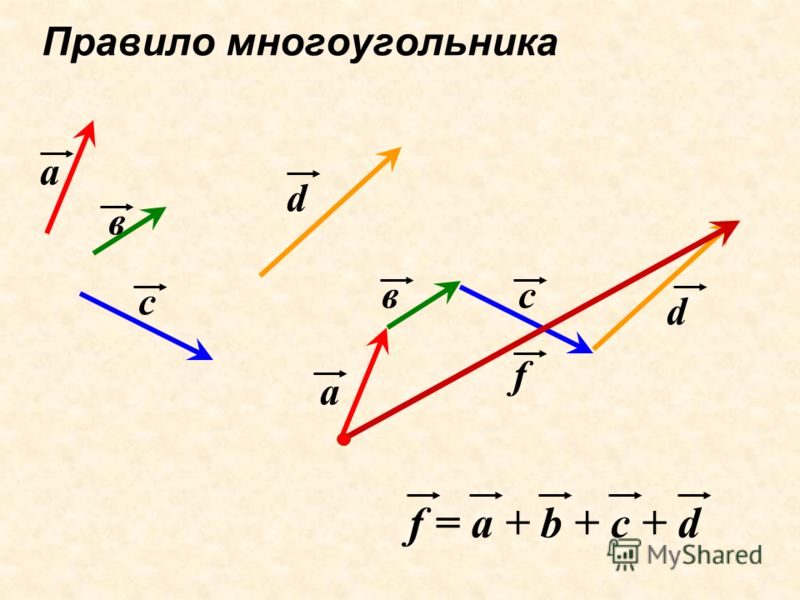




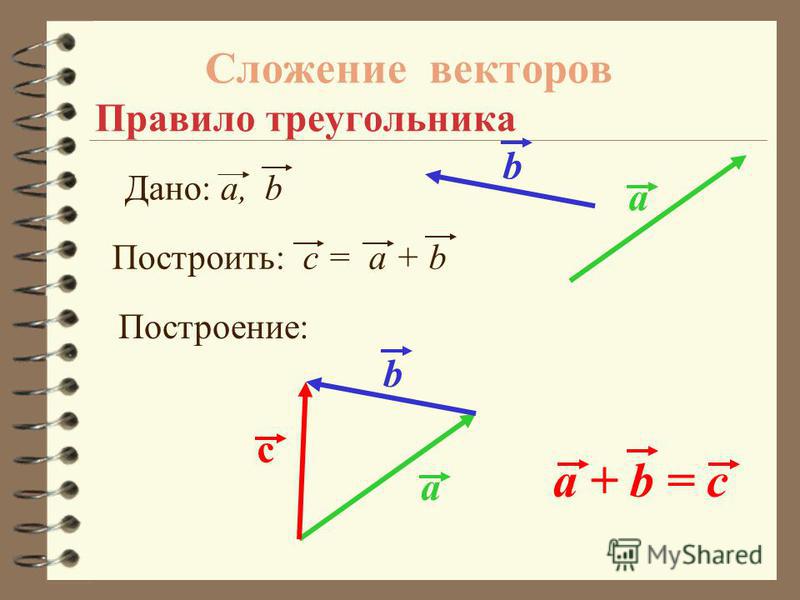
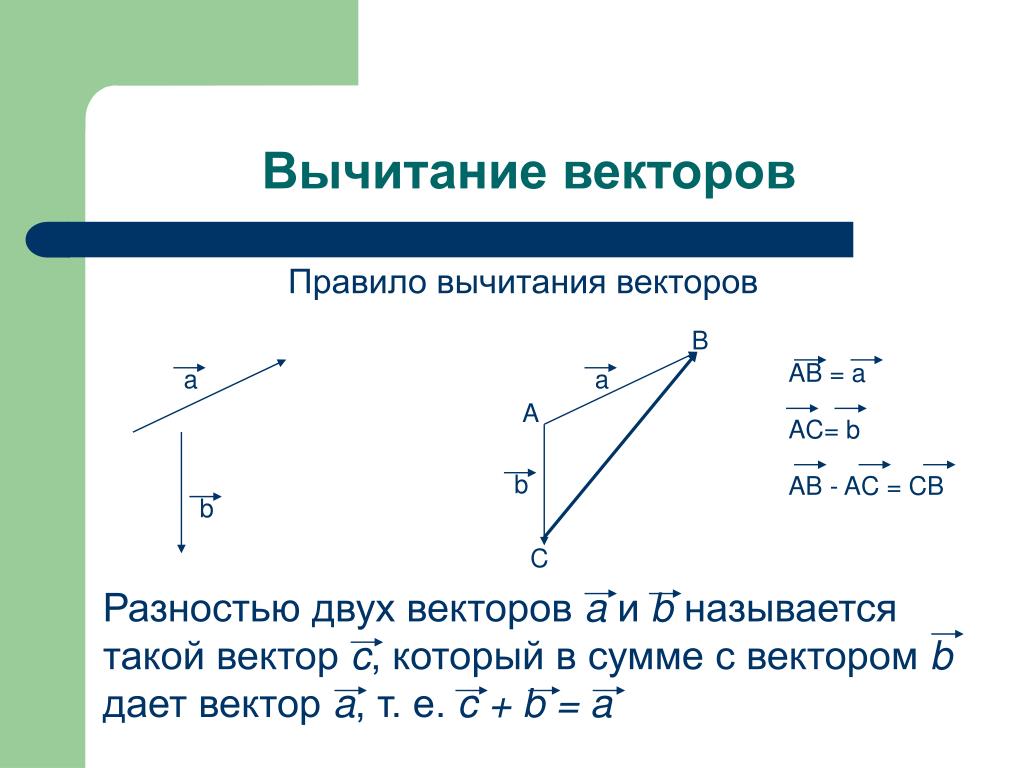
 Вектор FA обозначили вектором a, вектор ED обозначили вектором b. Выразите через векторы а и b векторы: ЕF, CD, AB, DA,OC.
Вектор FA обозначили вектором a, вектор ED обозначили вектором b. Выразите через векторы а и b векторы: ЕF, CD, AB, DA,OC.
 Предлагает рассмотреть свойства и найти сходство.
Предлагает рассмотреть свойства и найти сходство.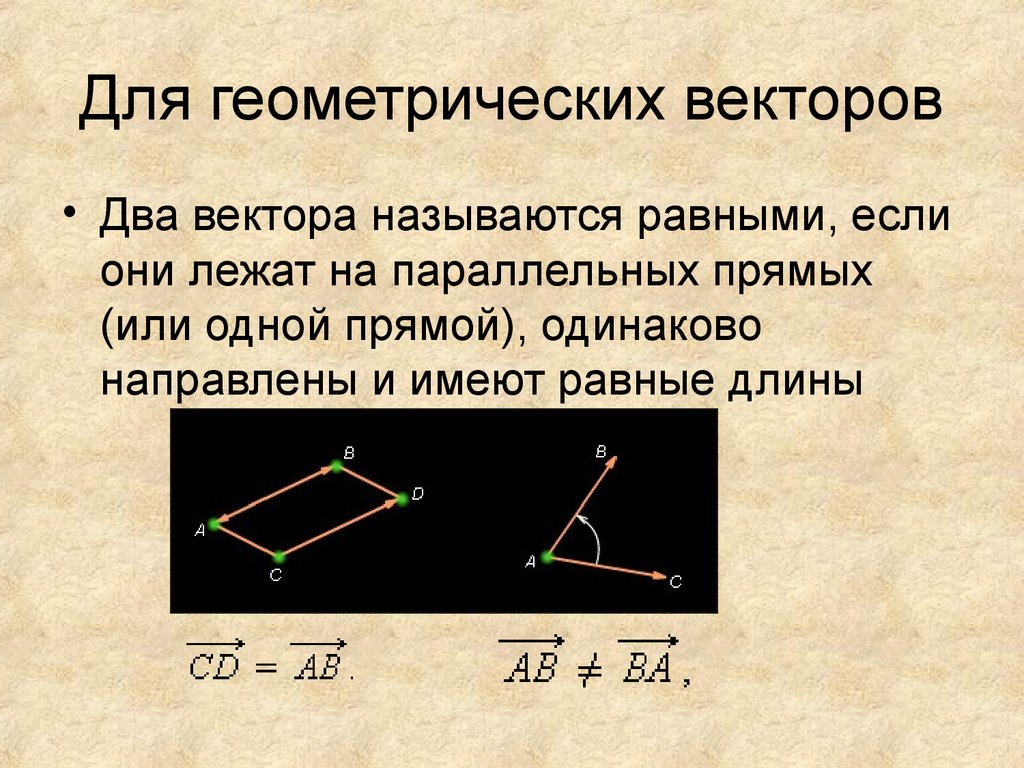

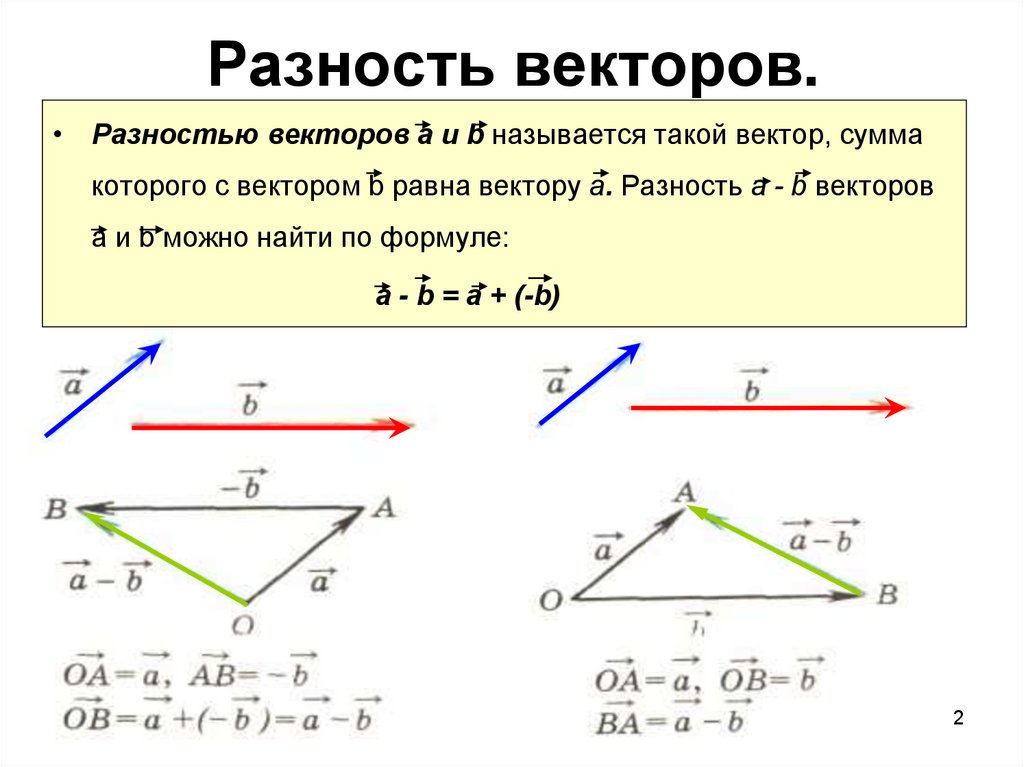 3 Скалярное произведение
3 Скалярное произведение
 Готовлю к ОГЭ, ЕГЭ. Окончила Пермский государственный университет в 2009 году. Педагогический стаж 10 лет. Квалификационная категория Первая. Педагогическое кредо: Скажи мне, и я забуду, покажи мне, и я, может быть запомню, вовлеки меня, и я пойму. Алгоритмика для начальных классов: могу научить детей начальной школы правильно составлять алгоритмы. Составлять алгоритмы для простых исполнителей, рисовать картинки определенные с помощью алгоритма исполнителю и др.
Готовлю к ОГЭ, ЕГЭ. Окончила Пермский государственный университет в 2009 году. Педагогический стаж 10 лет. Квалификационная категория Первая. Педагогическое кредо: Скажи мне, и я забуду, покажи мне, и я, может быть запомню, вовлеки меня, и я пойму. Алгоритмика для начальных классов: могу научить детей начальной школы правильно составлять алгоритмы. Составлять алгоритмы для простых исполнителей, рисовать картинки определенные с помощью алгоритма исполнителю и др. Математика дисциплинирует и воспитывает ум, это основа для всех наук. Очень люблю работать с детьми! Уроки проходят в комфортной обстановке, к каждому ученику подхожу индивидуально, объясняю доступно и понятно. На занятиях применяю игровые приемы, схемы, графики и презентации, для того, чтобы учащимся было интересно.
Математика дисциплинирует и воспитывает ум, это основа для всех наук. Очень люблю работать с детьми! Уроки проходят в комфортной обстановке, к каждому ученику подхожу индивидуально, объясняю доступно и понятно. На занятиях применяю игровые приемы, схемы, графики и презентации, для того, чтобы учащимся было интересно.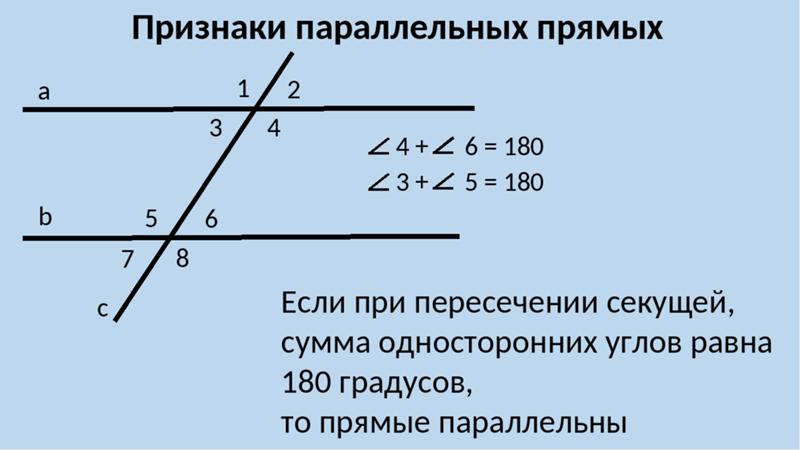 Всегда готова поделиться знаниями! Считаю, что учить наизусть скучные правила необязательно. Главное — понимать что и как, тогда ученик и без скучных заучиваний сможет свободно сформулировать любое правило, а полученные знания будут прочными и навсегда.
Готовлю к ОГЭ и ЕГЭ, мои ученики показывают хорошие и отличные результаты на экзаменах.
На уроках придерживаюсь трех единств: наглядно, понятно, просто.
Всегда готова поделиться знаниями! Считаю, что учить наизусть скучные правила необязательно. Главное — понимать что и как, тогда ученик и без скучных заучиваний сможет свободно сформулировать любое правило, а полученные знания будут прочными и навсегда.
Готовлю к ОГЭ и ЕГЭ, мои ученики показывают хорошие и отличные результаты на экзаменах.
На уроках придерживаюсь трех единств: наглядно, понятно, просто. Точка, прямая, луч, отрезок и уголНа этой странице вы узнаете
Точка, прямая, луч, отрезок и уголНа этой странице вы узнаете Но и тот, и другой имеет начало и не имеет конца.
Но и тот, и другой имеет начало и не имеет конца. 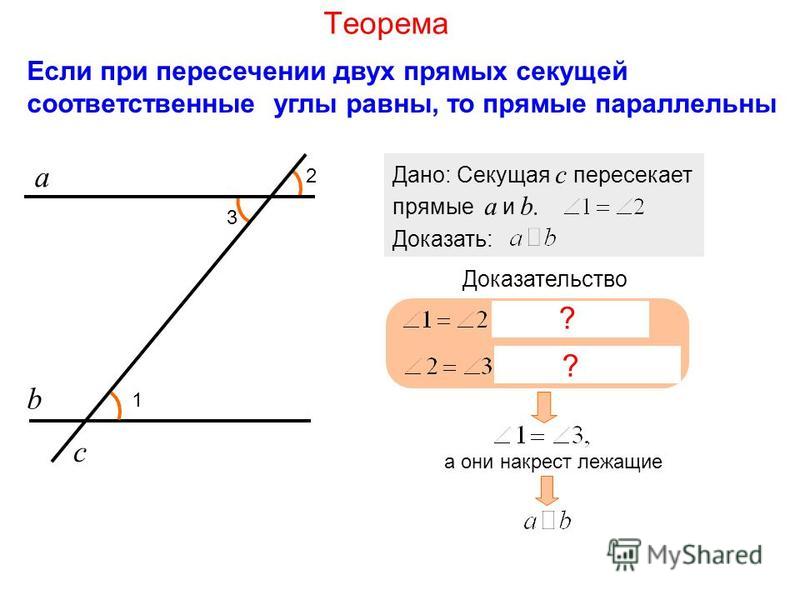


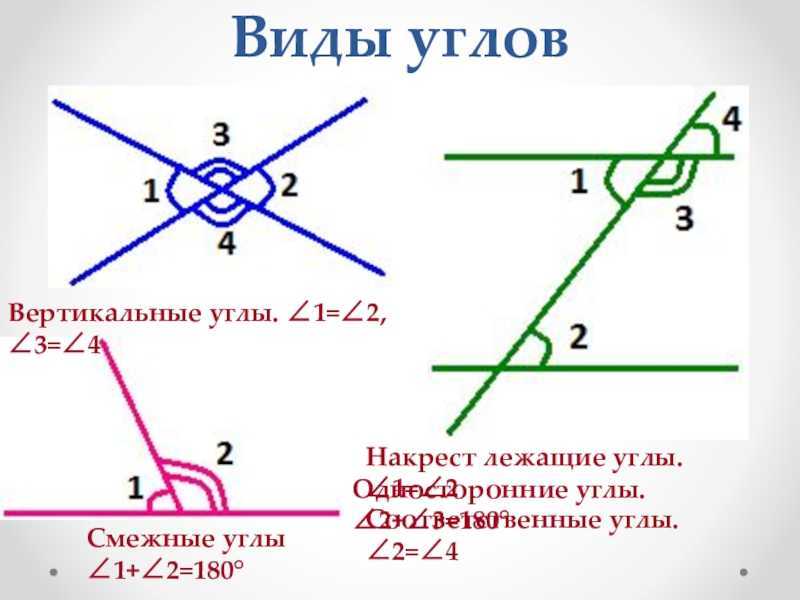

 Если у вас не получается скачать их, открыть или вы допустили ошибку, просьба написать нам на электронную почту
Если у вас не получается скачать их, открыть или вы допустили ошибку, просьба написать нам на электронную почту 
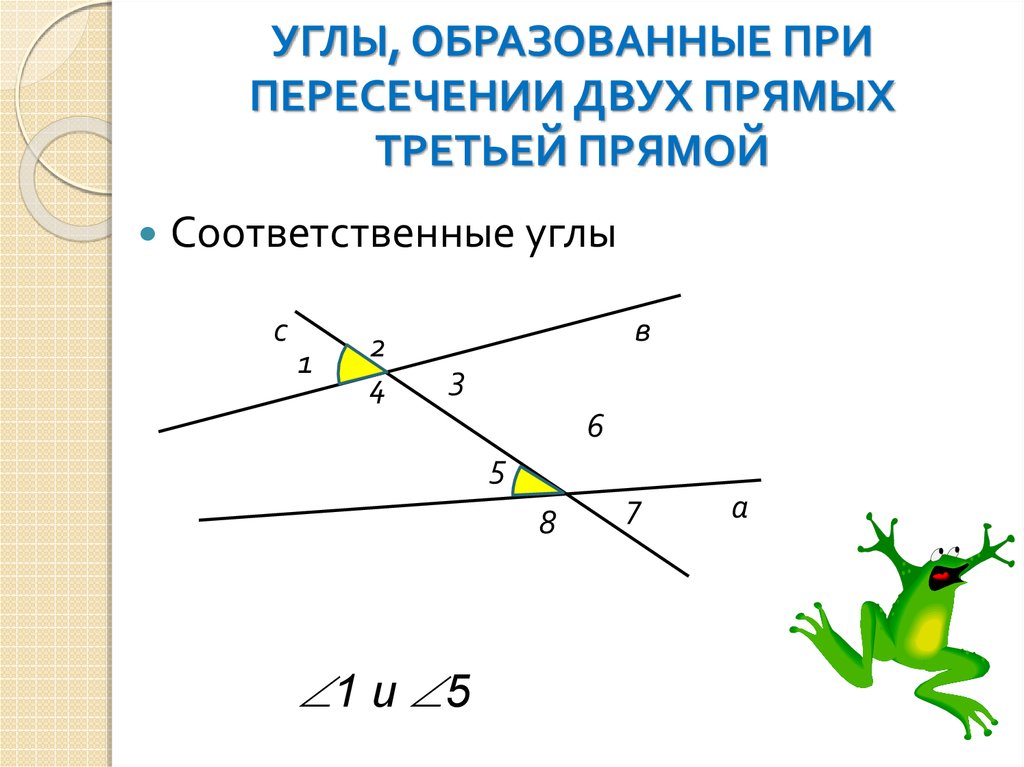 Прямая а делить плоскость на две полуплоскости. Давайте раскрасим наши полуплоскости в разные цвета и дадим им имена: β и γ, а также поставим точки с именами как на доске. Что мы можем сказать про эти точки?
Прямая а делить плоскость на две полуплоскости. Давайте раскрасим наши полуплоскости в разные цвета и дадим им имена: β и γ, а также поставим точки с именами как на доске. Что мы можем сказать про эти точки?



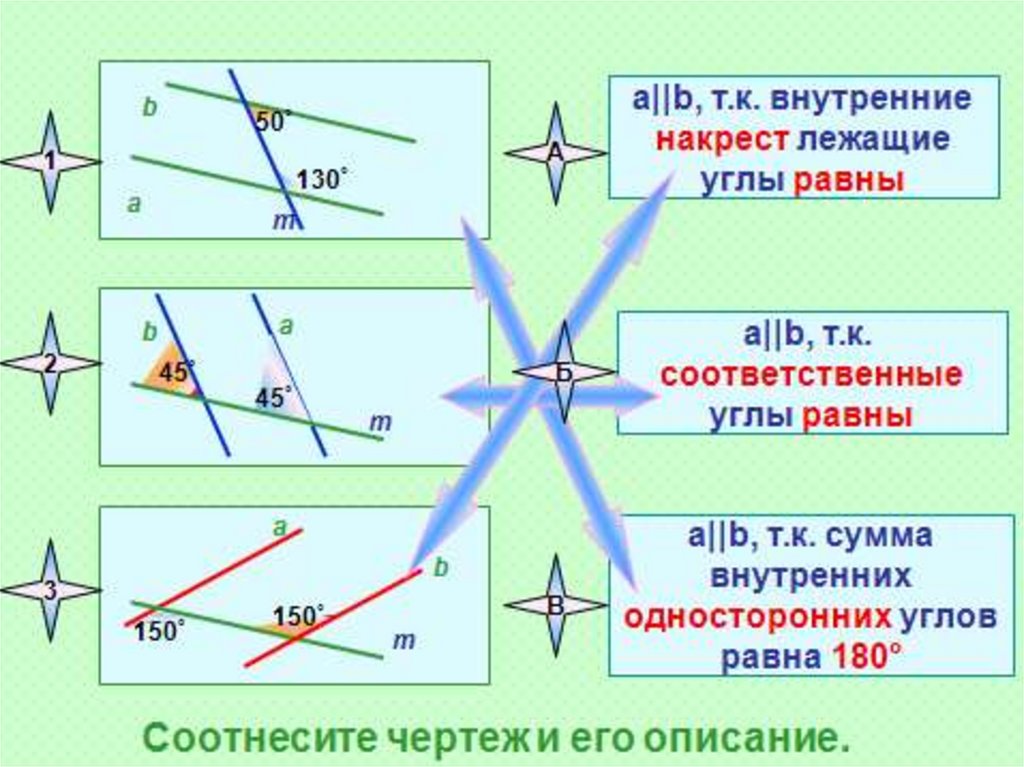

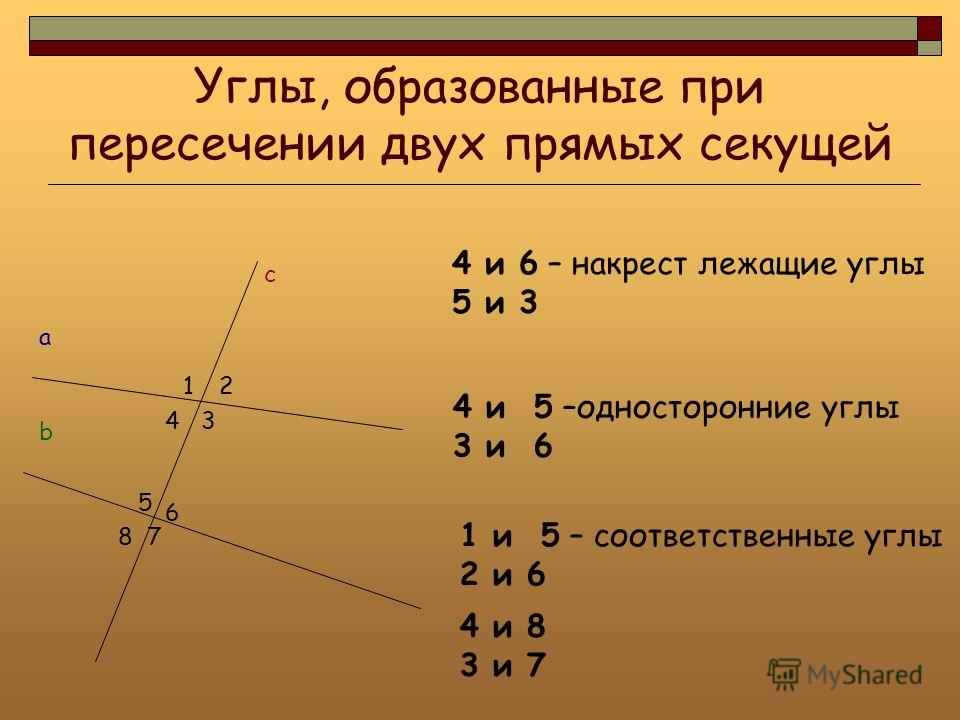 +
+
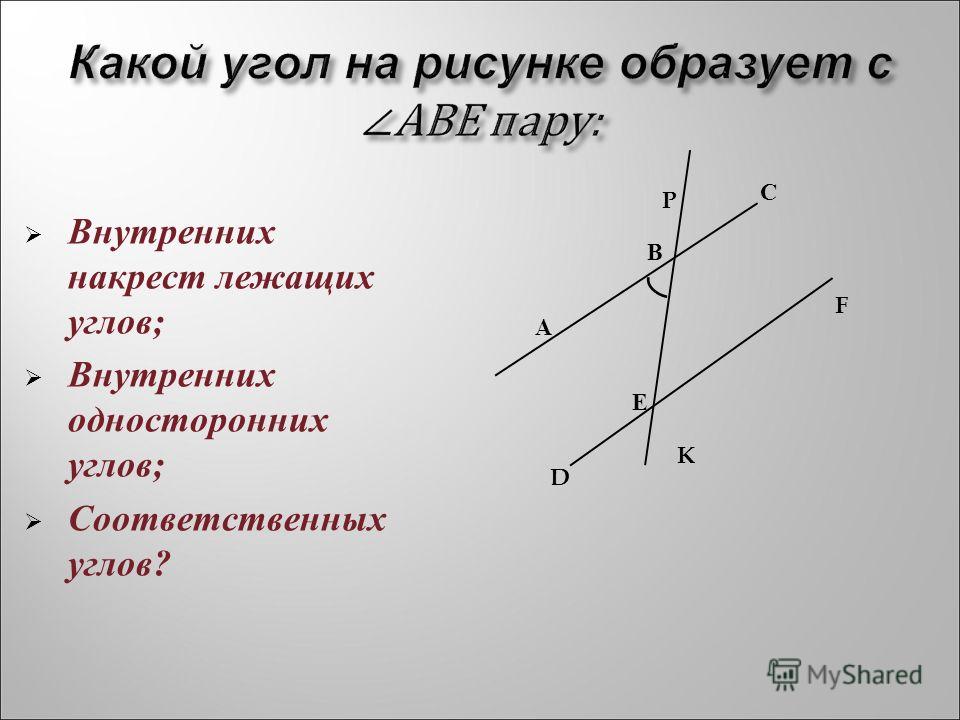


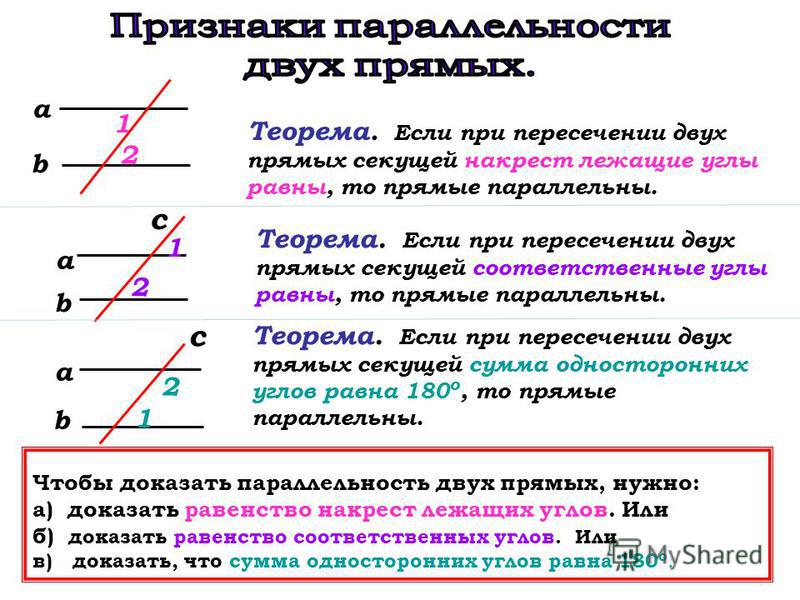 Их объединяет то, что они могут быть образованы двумя параллельными прямыми и пересекающей их линией. Утверждение о том, что сумма внутренних односторонних углов составляет 180 градусов, позволяет доказать теорему о параллельности прямых.
Их объединяет то, что они могут быть образованы двумя параллельными прямыми и пересекающей их линией. Утверждение о том, что сумма внутренних односторонних углов составляет 180 градусов, позволяет доказать теорему о параллельности прямых.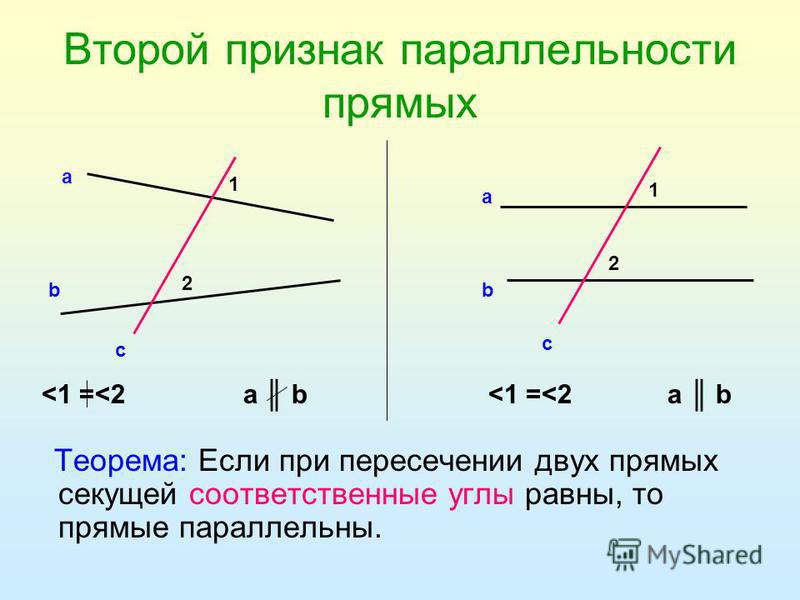 Их сумма должна быть 180 градусов.
Их сумма должна быть 180 градусов.
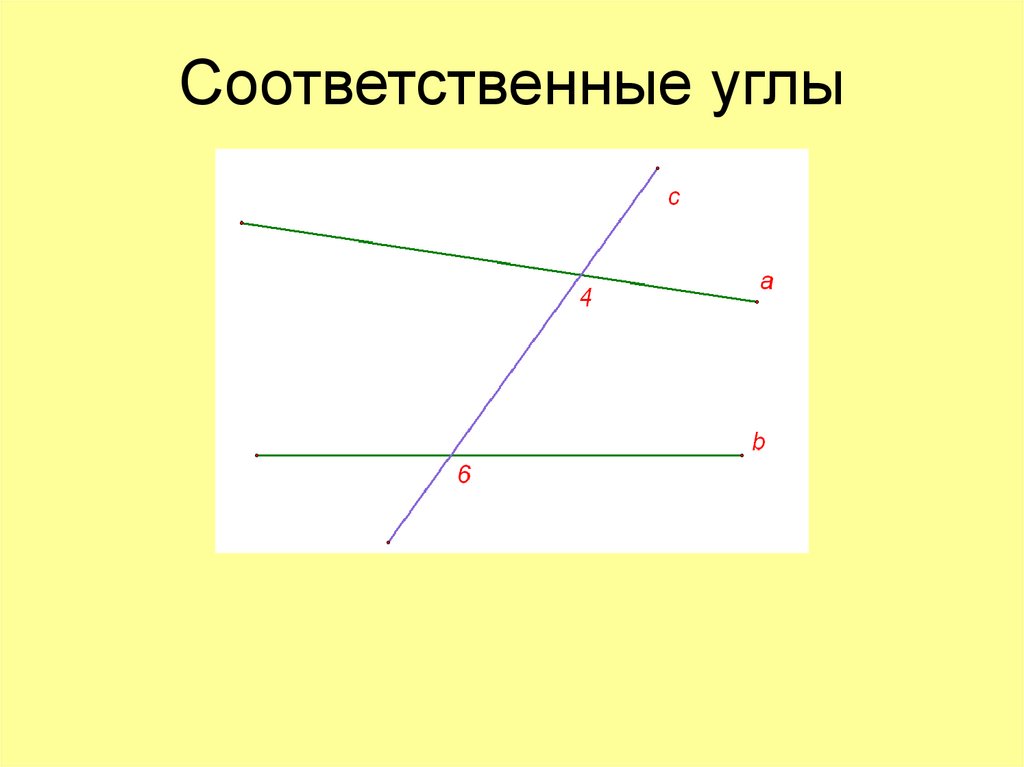

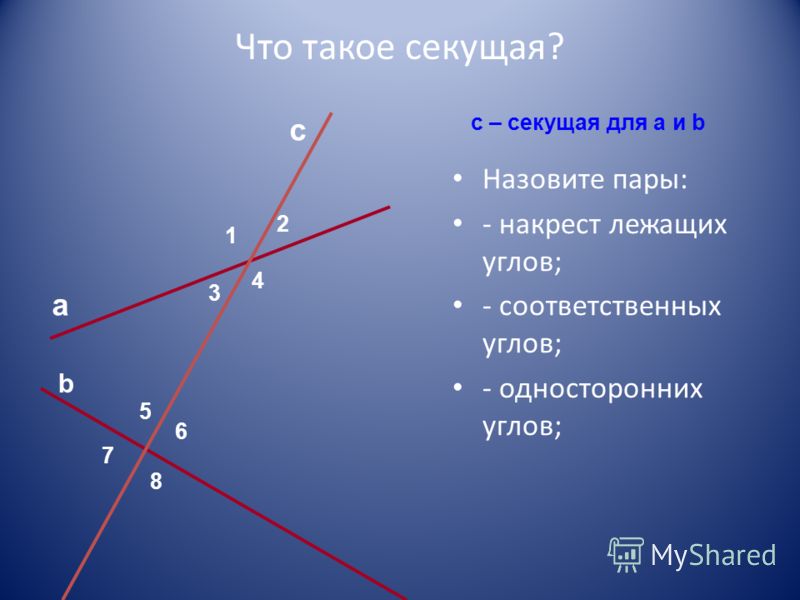 Это следствие из аксиомы параллельности открывает нам возможность сформулировать конкретные признаки параллельности прямых, по которым можно доказательно заключать о параллельности тех или иных прямых. Вы все правильно поняли: от аксиом мы наконец переходим к теоремам.
Это следствие из аксиомы параллельности открывает нам возможность сформулировать конкретные признаки параллельности прямых, по которым можно доказательно заключать о параллельности тех или иных прямых. Вы все правильно поняли: от аксиом мы наконец переходим к теоремам. Некоторые пары углов при секущей настолько важны, что за ними даже закреплены отдельные названия:
Некоторые пары углов при секущей настолько важны, что за ними даже закреплены отдельные названия:
 ru/wp-content/uploads/2022/03/angles-ABCD.svg"}}}]}
ru/wp-content/uploads/2022/03/angles-ABCD.svg"}}}]} \circ$. Мы пришли к противоречию.
\circ$. Мы пришли к противоречию.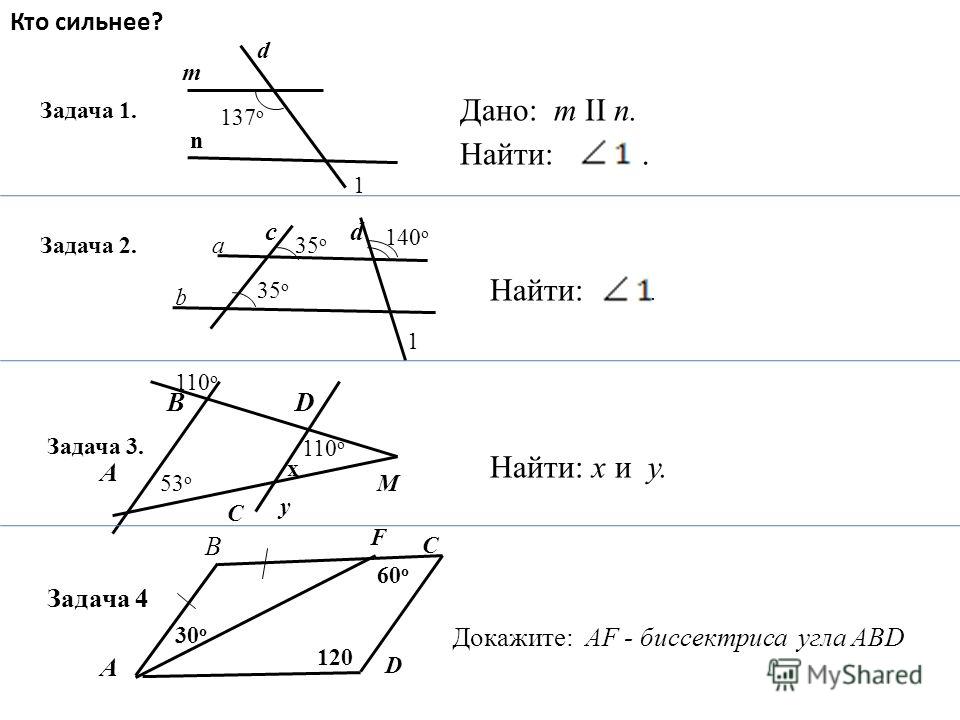 Поэтому теорема обычно доказывается по внутренним накрест углам, ведь равенство таких же внешних — прямое следствие.
Поэтому теорема обычно доказывается по внутренним накрест углам, ведь равенство таких же внешних — прямое следствие. Если при пересечении двух прямых секущей соответственные углы равны, то такие прямые параллельны.
Если при пересечении двух прямых секущей соответственные углы равны, то такие прямые параллельны. \circ$. Они являются односторонними при секущей $AB$ для отрезков $AC$ и $BD$. Следовательно $AC\parallel{BD}$.
\circ$. Они являются односторонними при секущей $AB$ для отрезков $AC$ и $BD$. Следовательно $AC\parallel{BD}$.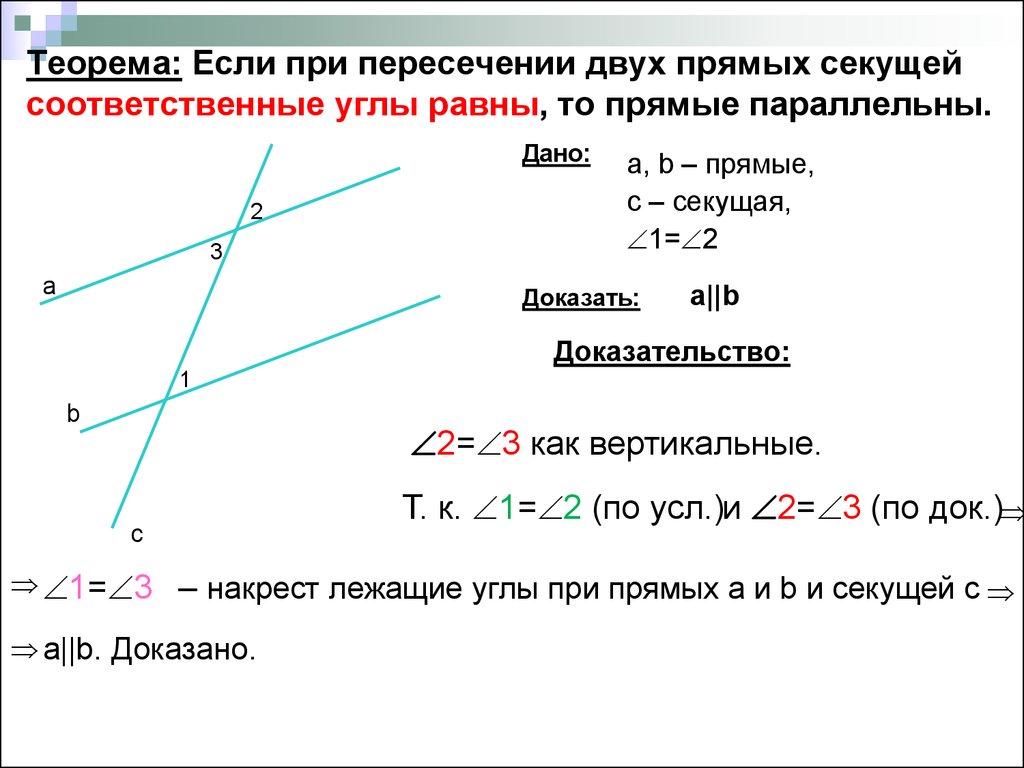 \\circ$, то такие прямые параллельны.","Если при пересечении двух прямых секущей накрест односторонние углы равны, то такие прямые параллельны."],"answer":[0,1,2]}}}]}
\\circ$, то такие прямые параллельны.","Если при пересечении двух прямых секущей накрест односторонние углы равны, то такие прямые параллельны."],"answer":[0,1,2]}}}]}
 Таким образом доказано, ∠ABC и ∠DEF.
Таким образом доказано, ∠ABC и ∠DEF.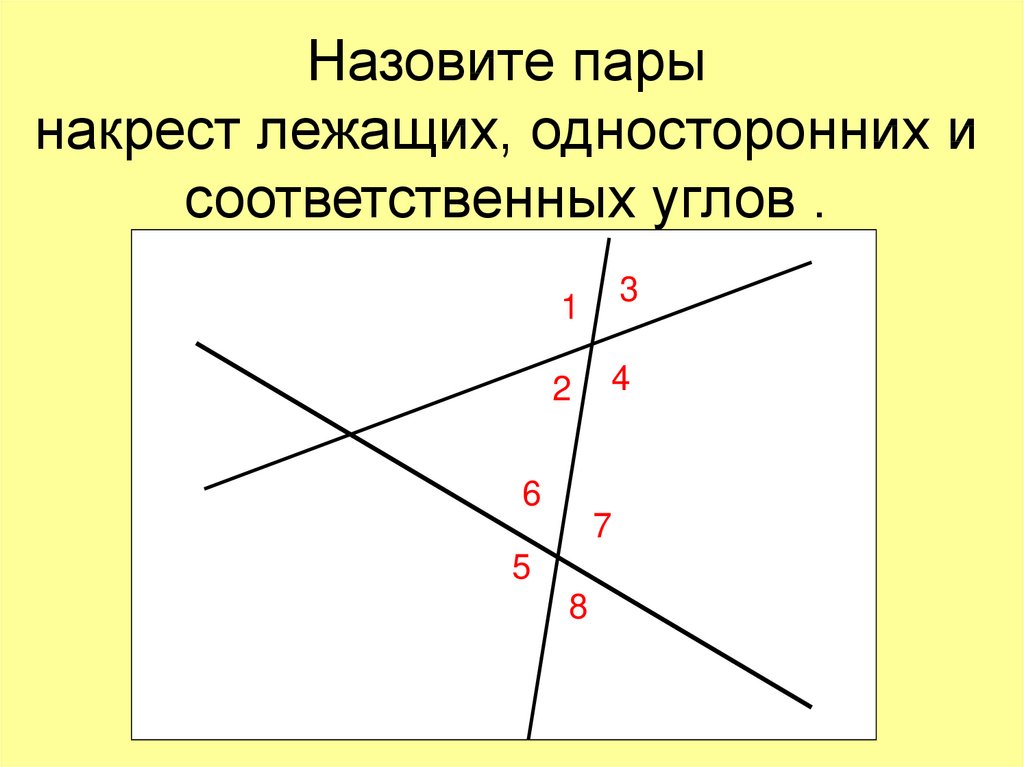
 Поскольку слагаемые углы равны друг другу (т. к. образуются биссектрисой), то угол ABC можно представить как произведение одного из них и числа 2: ∠ABC = ∠GBH * 2.
Поскольку слагаемые углы равны друг другу (т. к. образуются биссектрисой), то угол ABC можно представить как произведение одного из них и числа 2: ∠ABC = ∠GBH * 2.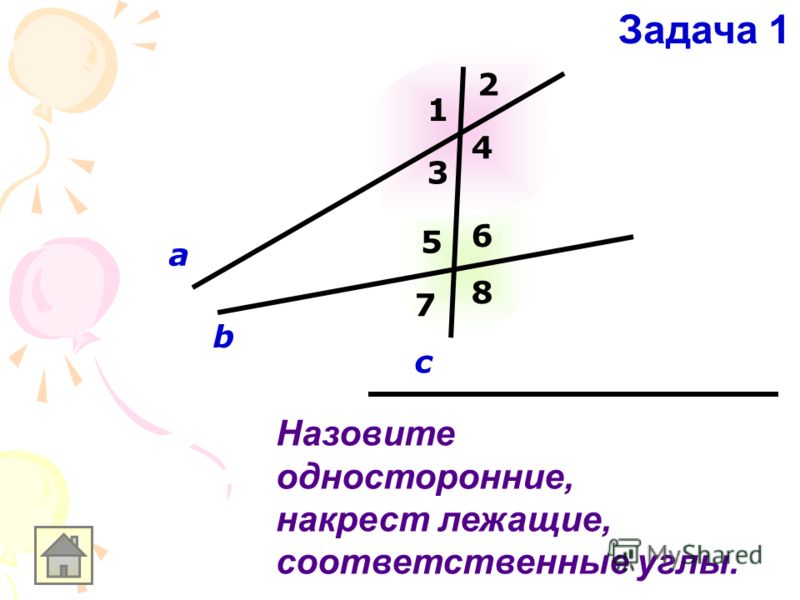 А как известно, прямые, которые перпендикулярны одной и той же прямой, параллельны друг другу. По этой же самой причине DE || GH.
А как известно, прямые, которые перпендикулярны одной и той же прямой, параллельны друг другу. По этой же самой причине DE || GH. Открытие и закрытие коробки для завтрака, сборка кубика Рубика и бесконечные параллельные железнодорожные пути — вот несколько повседневных примеров соответствующих углов. Они формируются в соответствующих углах или соответствующих углах с поперечной.
Открытие и закрытие коробки для завтрака, сборка кубика Рубика и бесконечные параллельные железнодорожные пути — вот несколько повседневных примеров соответствующих углов. Они формируются в соответствующих углах или соответствующих углах с поперечной. Таким образом имеем две параллельные линии
Таким образом имеем две параллельные линии Теперь каждый из четырех углов в первой области пересечения будет иметь еще один с таким же относительным положением во второй области пересечения.
Теперь каждый из четырех углов в первой области пересечения будет иметь еще один с таким же относительным положением во второй области пересечения.

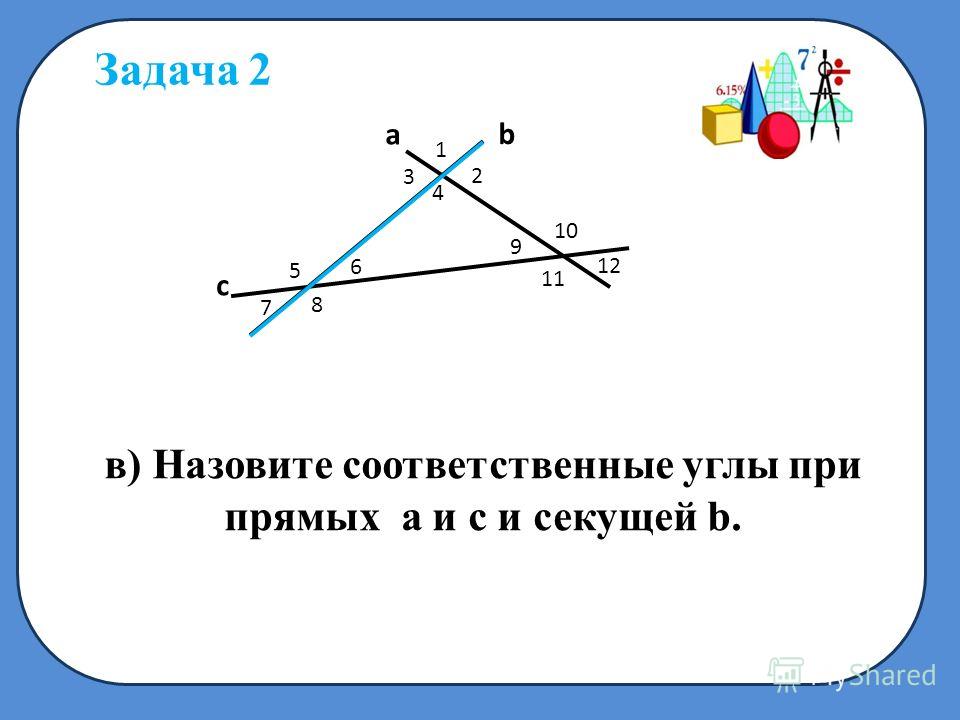 Сравните углы, образованные пересечением.
Сравните углы, образованные пересечением.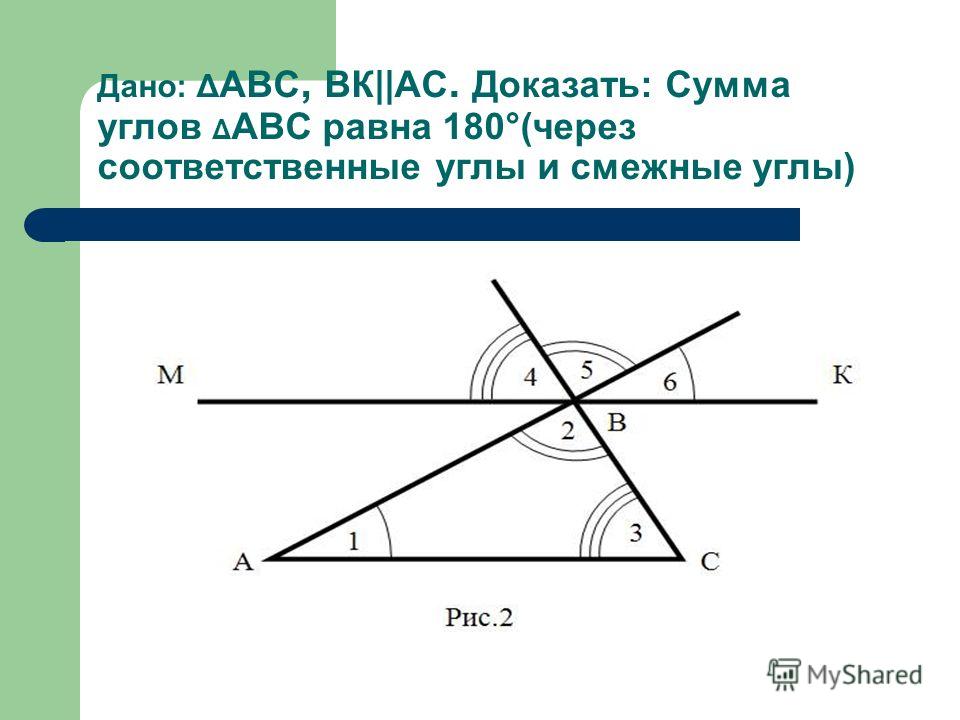 Вы увидите, что по нашему определению эти углы совпадают!
Вы увидите, что по нашему определению эти углы совпадают! При пересечении двух параллельных прямых секущая образует пару соответствующих углов.
При пересечении двух параллельных прямых секущая образует пару соответствующих углов.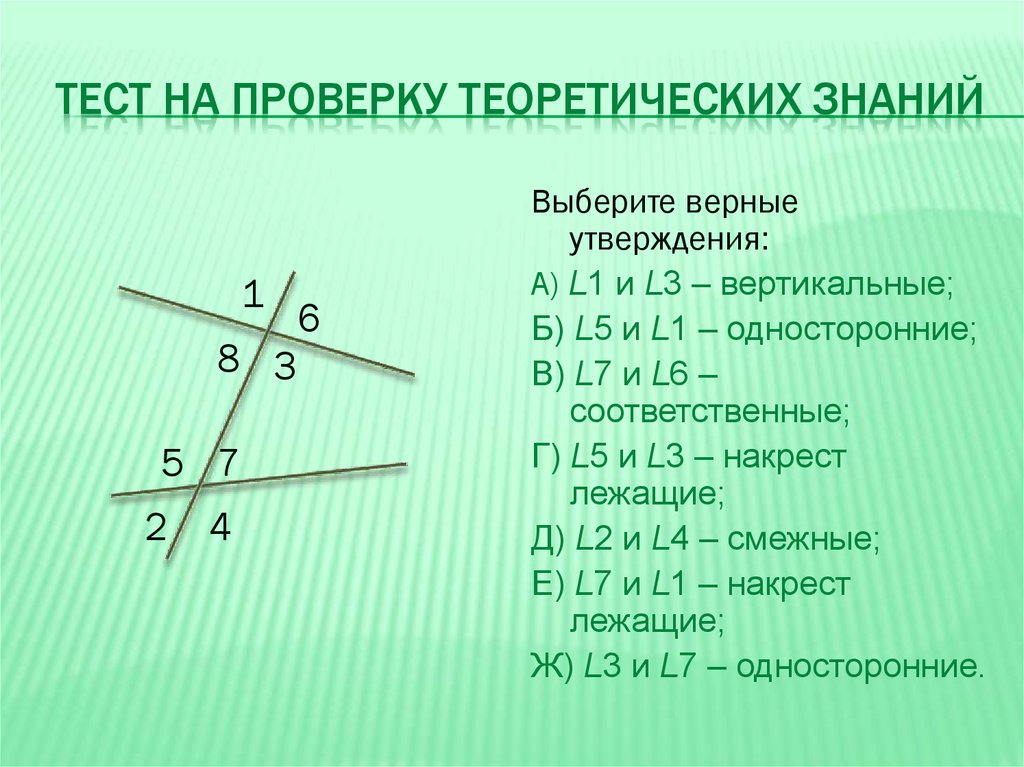
 Когда две параллельные прямые пересекаются секущей, то углы в одних и тех же углах каждой прямой называются соответствующими углами, и секущая будет выглядеть как прямая.
Когда две параллельные прямые пересекаются секущей, то углы в одних и тех же углах каждой прямой называются соответствующими углами, и секущая будет выглядеть как прямая.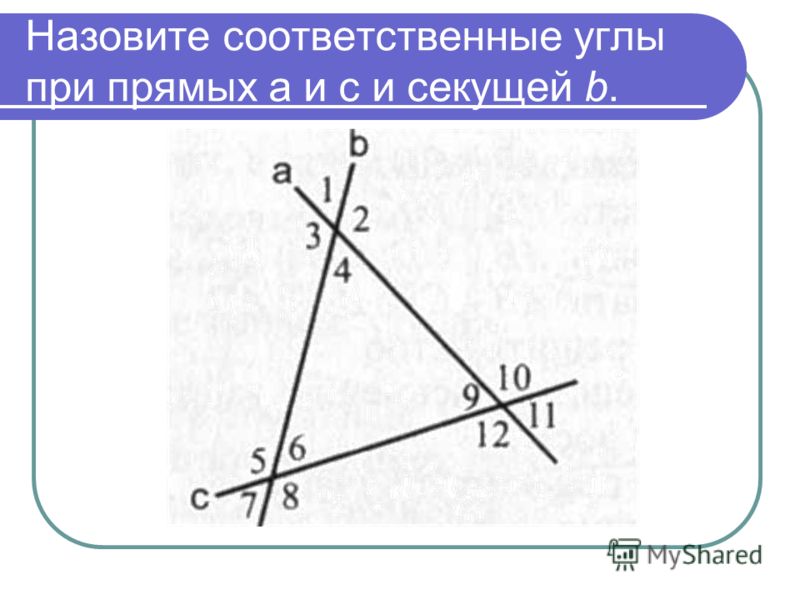
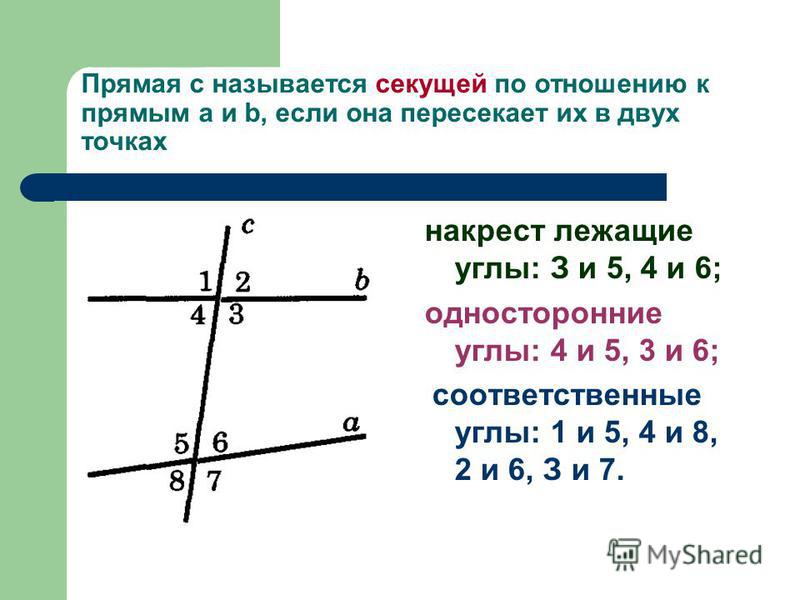 Соответствующие углы расположены в одном и том же взаимном положении, на пересечении поперечной и двух или более прямых.
Соответствующие углы расположены в одном и том же взаимном положении, на пересечении поперечной и двух или более прямых.
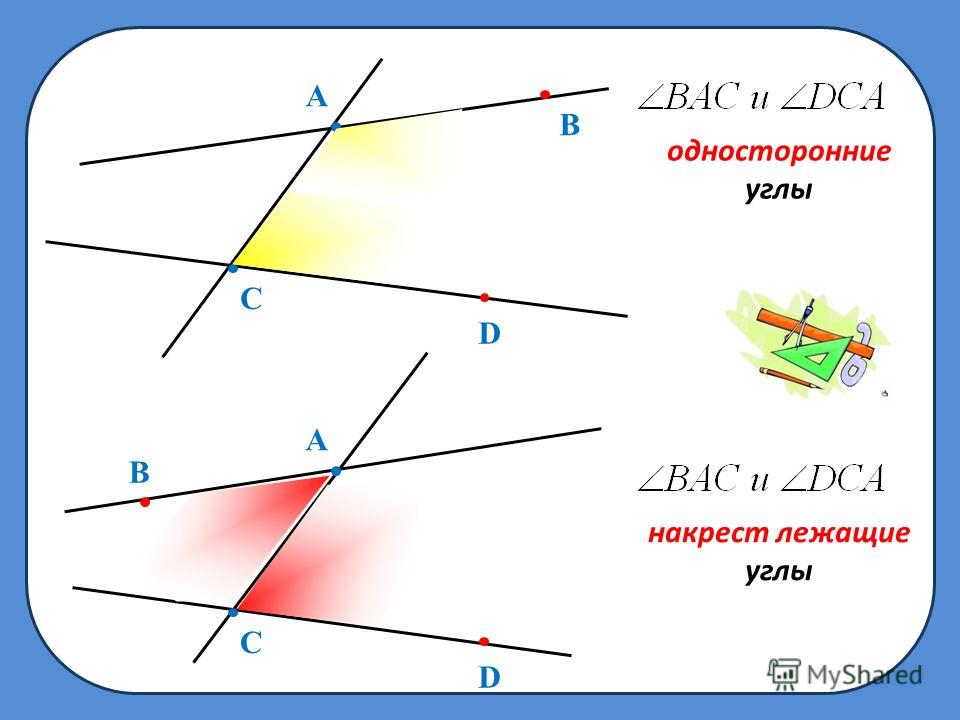 Соответственные углы равны, если секущая пересекает две параллельные прямые. Если секущая пересекает непараллельные прямые, то образующиеся соответствующие углы не равны и никак не связаны.
Соответственные углы равны, если секущая пересекает две параллельные прямые. Если секущая пересекает непараллельные прямые, то образующиеся соответствующие углы не равны и никак не связаны.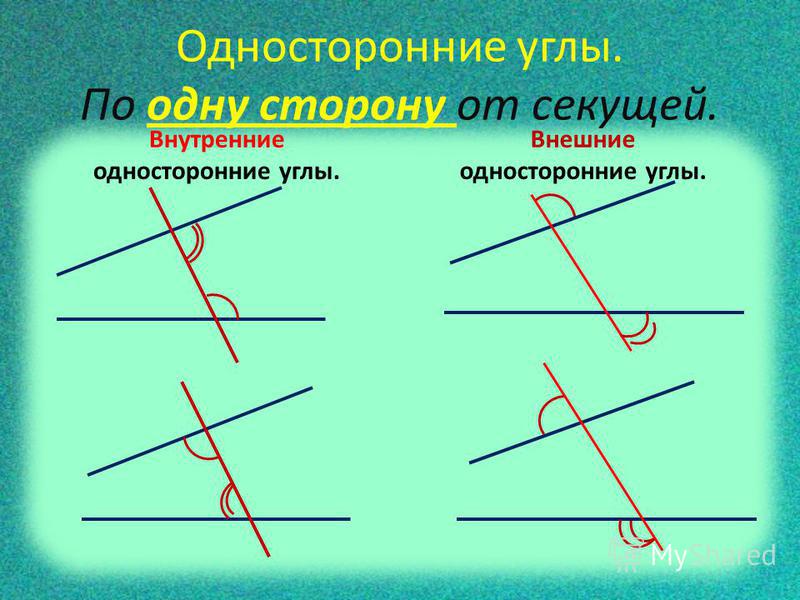 Тий G = 30 ° (соответствующие углы)
Тий G = 30 ° (соответствующие углы)  Найдите модуль соответствующего угла.
Найдите модуль соответствующего угла.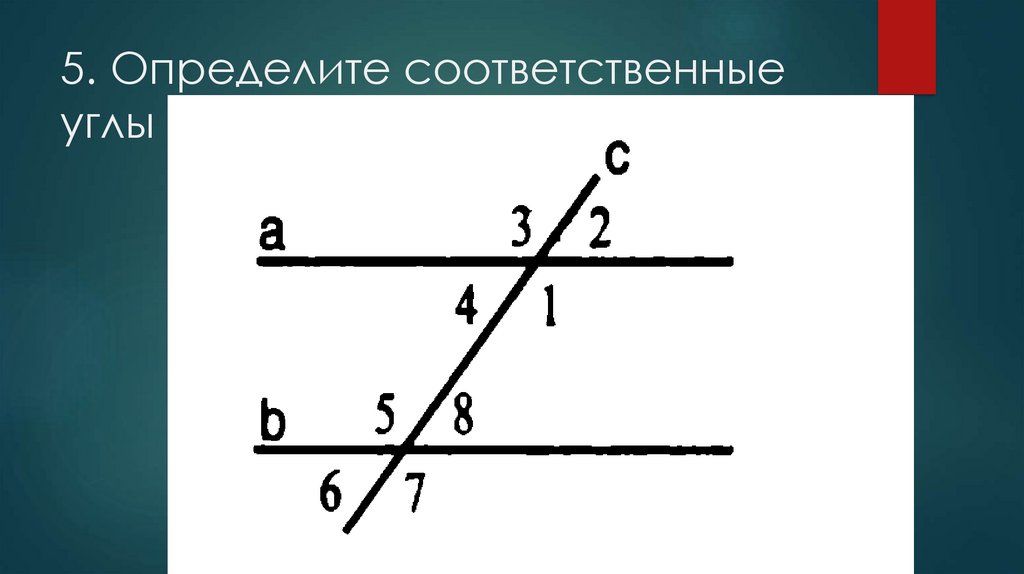
 дополнительный
.
дополнительный
.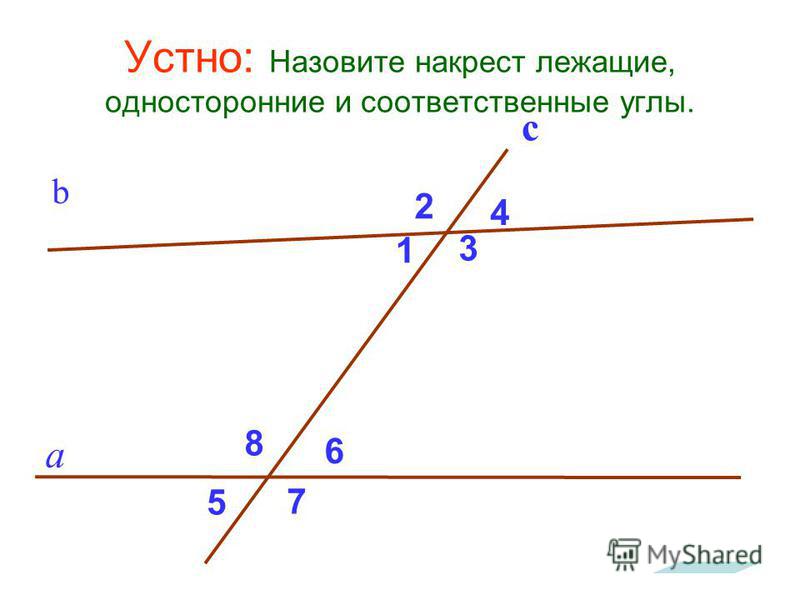
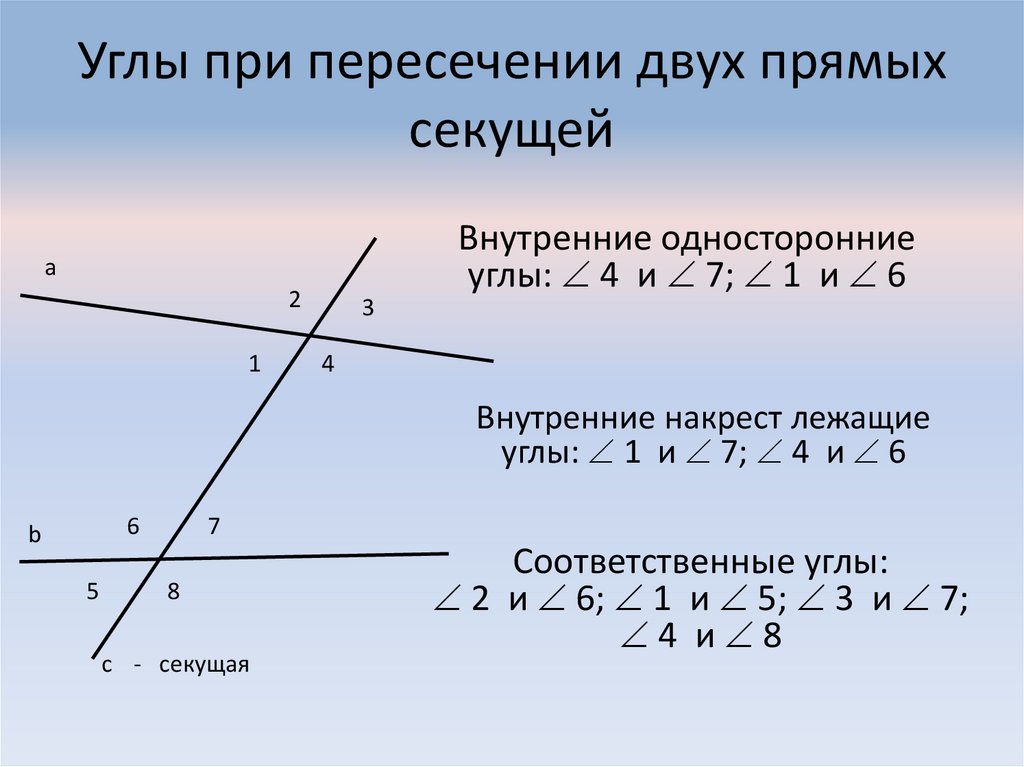 Значит, это последовательные внутренние углы.
Значит, это последовательные внутренние углы.
 То же самое и с внутренними углами.
То же самое и с внутренними углами.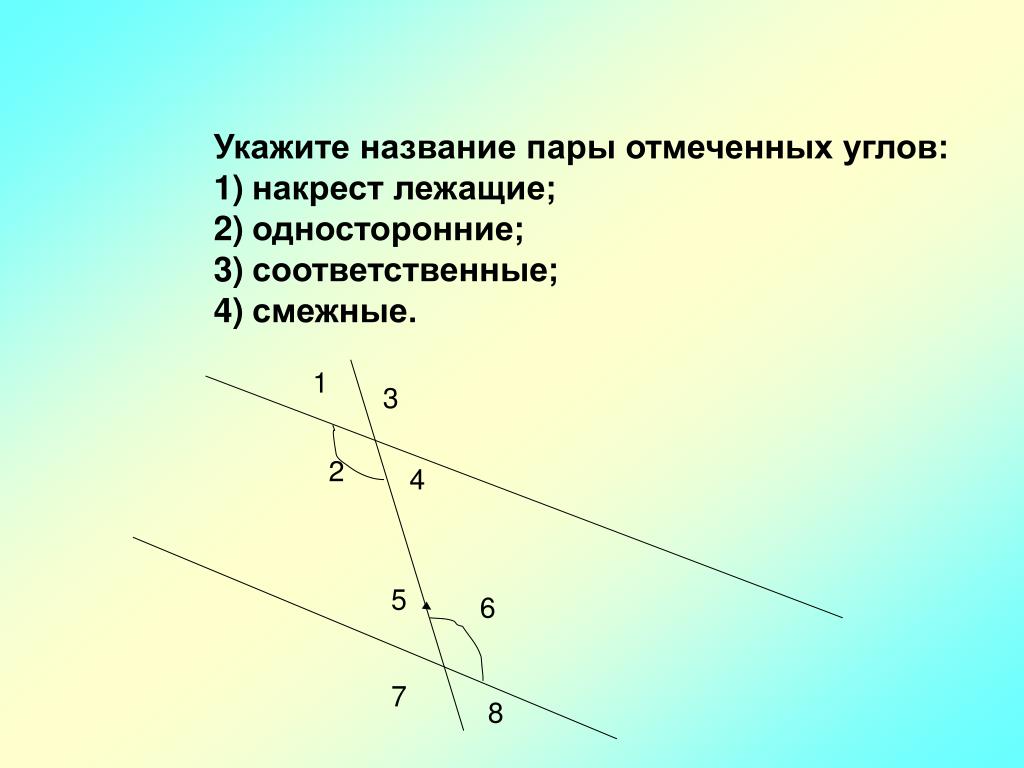 Тогда по теореме, обращенной к внутренним углам,
Тогда по теореме, обращенной к внутренним углам,  Найдите значение х.
Найдите значение х.  Соответствующие углы дополнительные
Соответствующие углы дополнительные 


 Чтобы этого не произошло, представьте, что соответствующие углы находятся под буквой F.
Чтобы этого не произошло, представьте, что соответствующие углы находятся под буквой F.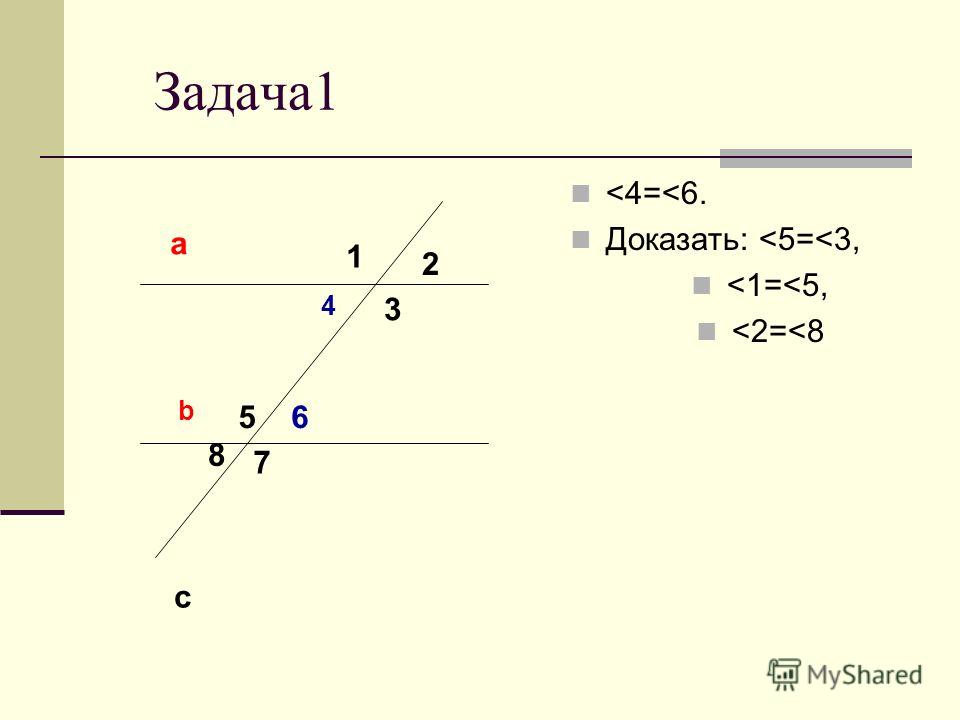
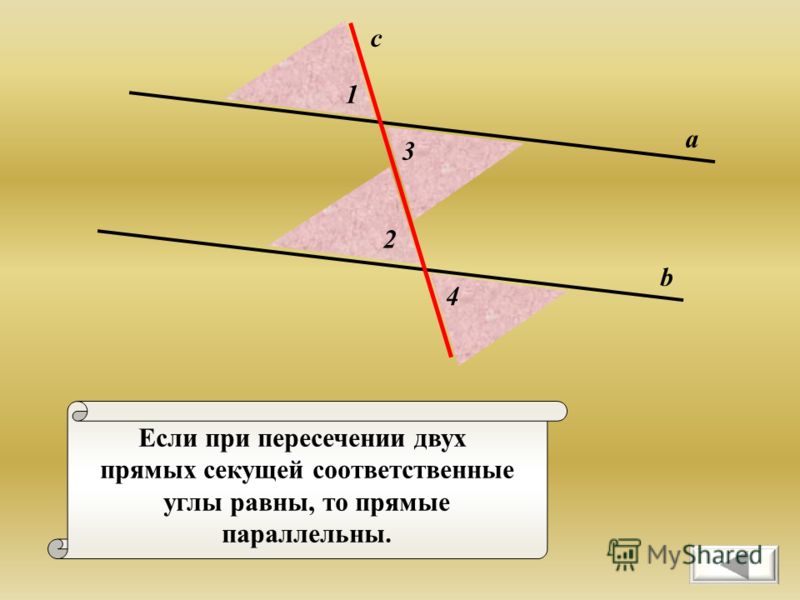

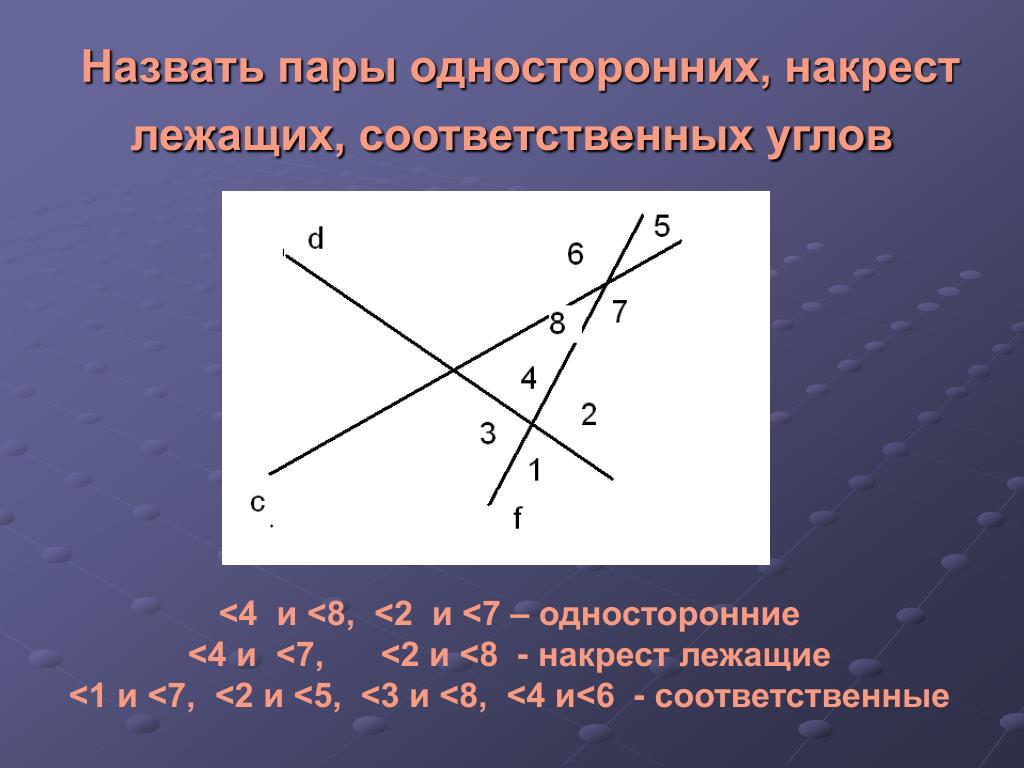

 5 842.25]
/Contents 134 0 R
/Group >
/Tabs /S
/StructParents 6
>>
endobj
13 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 135 0 R
/Group >
/Tabs /S
/StructParents 7
>>
endobj
14 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 137 0 R
/Group >
/Tabs /S
/StructParents 8
>>
endobj
15 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 138 0 R
/Group >
/Tabs /S
/StructParents 9
>>
endobj
16 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 139 0 R
/Group >
/Tabs /S
/StructParents 10
>>
endobj
17 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 140 0 R
/Group >
/Tabs /S
/StructParents 11
>>
endobj
18 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
5 842.25]
/Contents 134 0 R
/Group >
/Tabs /S
/StructParents 6
>>
endobj
13 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 135 0 R
/Group >
/Tabs /S
/StructParents 7
>>
endobj
14 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 137 0 R
/Group >
/Tabs /S
/StructParents 8
>>
endobj
15 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 138 0 R
/Group >
/Tabs /S
/StructParents 9
>>
endobj
16 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 139 0 R
/Group >
/Tabs /S
/StructParents 10
>>
endobj
17 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 140 0 R
/Group >
/Tabs /S
/StructParents 11
>>
endobj
18 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 5 842.25]
/Contents 141 0 R
/Group >
/Tabs /S
/StructParents 12
>>
endobj
19 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 142 0 R
/Group >
/Tabs /S
/StructParents 13
>>
endobj
20 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 143 0 R
/Group >
/Tabs /S
/StructParents 14
>>
endobj
21 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 144 0 R
/Group >
/Tabs /S
/StructParents 15
>>
endobj
22 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 145 0 R
/Group >
/Tabs /S
/StructParents 16
>>
endobj
23 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 146 0 R
/Group >
/Tabs /S
/StructParents 17
>>
endobj
24 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
5 842.25]
/Contents 141 0 R
/Group >
/Tabs /S
/StructParents 12
>>
endobj
19 0 obj
>
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 142 0 R
/Group >
/Tabs /S
/StructParents 13
>>
endobj
20 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 143 0 R
/Group >
/Tabs /S
/StructParents 14
>>
endobj
21 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 144 0 R
/Group >
/Tabs /S
/StructParents 15
>>
endobj
22 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 145 0 R
/Group >
/Tabs /S
/StructParents 16
>>
endobj
23 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 146 0 R
/Group >
/Tabs /S
/StructParents 17
>>
endobj
24 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 5 842.25]
/Contents 147 0 R
/Group >
/Tabs /S
/StructParents 18
>>
endobj
25 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 149 0 R
/Group >
/Tabs /S
/StructParents 19
>>
endobj
26 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 150 0 R
/Group >
/Tabs /S
/StructParents 20
>>
endobj
27 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 151 0 R
/Group >
/Tabs /S
/StructParents 21
>>
endobj
28 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 152 0 R
/Group >
/Tabs /S
/StructParents 22
>>
endobj
29 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 153 0 R
/Group >
/Tabs /S
/StructParents 23
>>
endobj
30 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
5 842.25]
/Contents 147 0 R
/Group >
/Tabs /S
/StructParents 18
>>
endobj
25 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 149 0 R
/Group >
/Tabs /S
/StructParents 19
>>
endobj
26 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 150 0 R
/Group >
/Tabs /S
/StructParents 20
>>
endobj
27 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 151 0 R
/Group >
/Tabs /S
/StructParents 21
>>
endobj
28 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 152 0 R
/Group >
/Tabs /S
/StructParents 22
>>
endobj
29 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 153 0 R
/Group >
/Tabs /S
/StructParents 23
>>
endobj
30 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 5 842.25]
/Contents 154 0 R
/Group >
/Tabs /S
/StructParents 24
>>
endobj
31 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 155 0 R
/Group >
/Tabs /S
/StructParents 25
>>
endobj
32 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 156 0 R
/Group >
/Tabs /S
/StructParents 26
>>
endobj
33 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 157 0 R
/Group >
/Tabs /S
/StructParents 27
>>
endobj
34 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 158 0 R
/Group >
/Tabs /S
/StructParents 28
>>
endobj
35 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 159 0 R
/Group >
/Tabs /S
/StructParents 29
>>
endobj
36 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
5 842.25]
/Contents 154 0 R
/Group >
/Tabs /S
/StructParents 24
>>
endobj
31 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 155 0 R
/Group >
/Tabs /S
/StructParents 25
>>
endobj
32 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 156 0 R
/Group >
/Tabs /S
/StructParents 26
>>
endobj
33 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 157 0 R
/Group >
/Tabs /S
/StructParents 27
>>
endobj
34 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 158 0 R
/Group >
/Tabs /S
/StructParents 28
>>
endobj
35 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 159 0 R
/Group >
/Tabs /S
/StructParents 29
>>
endobj
36 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 5 842.25]
/Contents 161 0 R
/Group >
/Tabs /S
/StructParents 30
>>
endobj
37 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 162 0 R
/Group >
/Tabs /S
/StructParents 31
>>
endobj
38 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 163 0 R
/Group >
/Tabs /S
/StructParents 32
>>
endobj
39 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 164 0 R
/Group >
/Tabs /S
/StructParents 33
>>
endobj
40 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 165 0 R
/Group >
/Tabs /S
/StructParents 34
>>
endobj
41 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 166 0 R
/Group >
/Tabs /S
/StructParents 35
>>
endobj
42 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
5 842.25]
/Contents 161 0 R
/Group >
/Tabs /S
/StructParents 30
>>
endobj
37 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 162 0 R
/Group >
/Tabs /S
/StructParents 31
>>
endobj
38 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 163 0 R
/Group >
/Tabs /S
/StructParents 32
>>
endobj
39 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 164 0 R
/Group >
/Tabs /S
/StructParents 33
>>
endobj
40 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 165 0 R
/Group >
/Tabs /S
/StructParents 34
>>
endobj
41 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 166 0 R
/Group >
/Tabs /S
/StructParents 35
>>
endobj
42 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 5 842.25]
/Contents 168 0 R
/Group >
/Tabs /S
/StructParents 36
>>
endobj
43 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 169 0 R
/Group >
/Tabs /S
/StructParents 37
>>
endobj
44 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 170 0 R
/Group >
/Tabs /S
/StructParents 38
>>
endobj
45 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 171 0 R
/Group >
/Tabs /S
/StructParents 39
>>
endobj
46 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 173 0 R
/Group >
/Tabs /S
/StructParents 40
>>
endobj
47 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 175 0 R
/Group >
/Tabs /S
/StructParents 41
>>
endobj
48 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
5 842.25]
/Contents 168 0 R
/Group >
/Tabs /S
/StructParents 36
>>
endobj
43 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 169 0 R
/Group >
/Tabs /S
/StructParents 37
>>
endobj
44 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 170 0 R
/Group >
/Tabs /S
/StructParents 38
>>
endobj
45 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 171 0 R
/Group >
/Tabs /S
/StructParents 39
>>
endobj
46 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 173 0 R
/Group >
/Tabs /S
/StructParents 40
>>
endobj
47 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 175 0 R
/Group >
/Tabs /S
/StructParents 41
>>
endobj
48 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 5 842.25]
/Contents 176 0 R
/Group >
/Tabs /S
/StructParents 42
>>
endobj
49 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 177 0 R
/Group >
/Tabs /S
/StructParents 43
>>
endobj
50 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 178 0 R
/Group >
/Tabs /S
/StructParents 44
>>
endobj
51 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 179 0 R
/Group >
/Tabs /S
/StructParents 45
>>
endobj
52 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 181 0 R
/Group >
/Tabs /S
/StructParents 46
>>
endobj
53 0 obj
>
/ExtGState >
/Pattern >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 184 0 R
/Group >
/Tabs /S
/StructParents 47
>>
endobj
54 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
5 842.25]
/Contents 176 0 R
/Group >
/Tabs /S
/StructParents 42
>>
endobj
49 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 177 0 R
/Group >
/Tabs /S
/StructParents 43
>>
endobj
50 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 178 0 R
/Group >
/Tabs /S
/StructParents 44
>>
endobj
51 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 179 0 R
/Group >
/Tabs /S
/StructParents 45
>>
endobj
52 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 181 0 R
/Group >
/Tabs /S
/StructParents 46
>>
endobj
53 0 obj
>
/ExtGState >
/Pattern >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 184 0 R
/Group >
/Tabs /S
/StructParents 47
>>
endobj
54 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 5 842.25]
/Contents 185 0 R
/Group >
/Tabs /S
/StructParents 48
>>
endobj
55 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 186 0 R
/Group >
/Tabs /S
/StructParents 49
>>
endobj
56 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 187 0 R
/Group >
/Tabs /S
/StructParents 50
>>
endobj
57 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 188 0 R
/Group >
/Tabs /S
/StructParents 51
>>
endobj
58 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 189 0 R
/Group >
/Tabs /S
/StructParents 52
>>
endobj
59 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 190 0 R
/Group >
/Tabs /S
/StructParents 53
>>
endobj
60 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
5 842.25]
/Contents 185 0 R
/Group >
/Tabs /S
/StructParents 48
>>
endobj
55 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 186 0 R
/Group >
/Tabs /S
/StructParents 49
>>
endobj
56 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 187 0 R
/Group >
/Tabs /S
/StructParents 50
>>
endobj
57 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 188 0 R
/Group >
/Tabs /S
/StructParents 51
>>
endobj
58 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 189 0 R
/Group >
/Tabs /S
/StructParents 52
>>
endobj
59 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 190 0 R
/Group >
/Tabs /S
/StructParents 53
>>
endobj
60 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 5 842.25]
/Contents 191 0 R
/Group >
/Tabs /S
/StructParents 54
>>
endobj
61 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 192 0 R
/Group >
/Tabs /S
/StructParents 55
>>
endobj
62 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 193 0 R
/Group >
/Tabs /S
/StructParents 56
>>
endobj
63 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 194 0 R
/Group >
/Tabs /S
/StructParents 57
>>
endobj
64 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 195 0 R
/Group >
/Tabs /S
/StructParents 58
>>
endobj
65 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 196 0 R
/Group >
/Tabs /S
/StructParents 59
>>
endobj
66 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
5 842.25]
/Contents 191 0 R
/Group >
/Tabs /S
/StructParents 54
>>
endobj
61 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 192 0 R
/Group >
/Tabs /S
/StructParents 55
>>
endobj
62 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 193 0 R
/Group >
/Tabs /S
/StructParents 56
>>
endobj
63 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 194 0 R
/Group >
/Tabs /S
/StructParents 57
>>
endobj
64 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 195 0 R
/Group >
/Tabs /S
/StructParents 58
>>
endobj
65 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 196 0 R
/Group >
/Tabs /S
/StructParents 59
>>
endobj
66 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 5 842.25]
/Contents 197 0 R
/Group >
/Tabs /S
/StructParents 60
>>
endobj
67 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 198 0 R
/Group >
/Tabs /S
/StructParents 61
>>
endobj
68 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 199 0 R
/Group >
/Tabs /S
/StructParents 62
>>
endobj
69 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 200 0 R
/Group >
/Tabs /S
/StructParents 63
>>
endobj
70 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 201 0 R
/Group >
/Tabs /S
/StructParents 64
>>
endobj
71 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 202 0 R
/Group >
/Tabs /S
/StructParents 65
>>
endobj
72 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
5 842.25]
/Contents 197 0 R
/Group >
/Tabs /S
/StructParents 60
>>
endobj
67 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 198 0 R
/Group >
/Tabs /S
/StructParents 61
>>
endobj
68 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 199 0 R
/Group >
/Tabs /S
/StructParents 62
>>
endobj
69 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 200 0 R
/Group >
/Tabs /S
/StructParents 63
>>
endobj
70 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 201 0 R
/Group >
/Tabs /S
/StructParents 64
>>
endobj
71 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 202 0 R
/Group >
/Tabs /S
/StructParents 65
>>
endobj
72 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 5 842.25]
/Contents 203 0 R
/Group >
/Tabs /S
/StructParents 66
>>
endobj
73 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 204 0 R
/Group >
/Tabs /S
/StructParents 67
>>
endobj
74 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 205 0 R
/Group >
/Tabs /S
/StructParents 68
>>
endobj
75 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 206 0 R
/Group >
/Tabs /S
/StructParents 69
>>
endobj
76 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 207 0 R
/Group >
/Tabs /S
/StructParents 70
>>
endobj
77 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 208 0 R
/Group >
/Tabs /S
/StructParents 71
>>
endobj
78 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/Annots [209 0 R 210 0 R 211 0 R 212 0 R 213 0 R 214 0 R]
/MediaBox [0 0 595.
5 842.25]
/Contents 203 0 R
/Group >
/Tabs /S
/StructParents 66
>>
endobj
73 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 204 0 R
/Group >
/Tabs /S
/StructParents 67
>>
endobj
74 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 205 0 R
/Group >
/Tabs /S
/StructParents 68
>>
endobj
75 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 206 0 R
/Group >
/Tabs /S
/StructParents 69
>>
endobj
76 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 207 0 R
/Group >
/Tabs /S
/StructParents 70
>>
endobj
77 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 208 0 R
/Group >
/Tabs /S
/StructParents 71
>>
endobj
78 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/Annots [209 0 R 210 0 R 211 0 R 212 0 R 213 0 R 214 0 R]
/MediaBox [0 0 595. 5 842.25]
/Contents 215 0 R
/Group >
/Tabs /S
/StructParents 72
>>
endobj
79 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/Annots [216 0 R 217 0 R 218 0 R]
/MediaBox [0 0 595.5 842.25]
/Contents 219 0 R
/Group >
/Tabs /S
/StructParents 79
>>
endobj
80 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/Annots [220 0 R]
/MediaBox [0 0 595.5 842.25]
/Contents 221 0 R
/Group >
/Tabs /S
/StructParents 83
>>
endobj
81 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 222 0 R
/Group >
/Tabs /S
/StructParents 85
>>
endobj
82 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 223 0 R
/Group >
/Tabs /S
/StructParents 86
>>
endobj
83 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 224 0 R
/Group >
/Tabs /S
/StructParents 87
>>
endobj
84 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
5 842.25]
/Contents 215 0 R
/Group >
/Tabs /S
/StructParents 72
>>
endobj
79 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/Annots [216 0 R 217 0 R 218 0 R]
/MediaBox [0 0 595.5 842.25]
/Contents 219 0 R
/Group >
/Tabs /S
/StructParents 79
>>
endobj
80 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/Annots [220 0 R]
/MediaBox [0 0 595.5 842.25]
/Contents 221 0 R
/Group >
/Tabs /S
/StructParents 83
>>
endobj
81 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 222 0 R
/Group >
/Tabs /S
/StructParents 85
>>
endobj
82 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 223 0 R
/Group >
/Tabs /S
/StructParents 86
>>
endobj
83 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 224 0 R
/Group >
/Tabs /S
/StructParents 87
>>
endobj
84 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 5 842.25]
/Contents 225 0 R
/Group >
/Tabs /S
/StructParents 88
>>
endobj
85 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 226 0 R
/Group >
/Tabs /S
/StructParents 89
>>
endobj
86 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 227 0 R
/Group >
/Tabs /S
/StructParents 90
>>
endobj
87 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 228 0 R
/Group >
/Tabs /S
/StructParents 91
>>
endobj
88 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 230 0 R
/Group >
/Tabs /S
/StructParents 92
>>
endobj
89 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 232 0 R
/Group >
/Tabs /S
/StructParents 93
>>
endobj
90 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
5 842.25]
/Contents 225 0 R
/Group >
/Tabs /S
/StructParents 88
>>
endobj
85 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 226 0 R
/Group >
/Tabs /S
/StructParents 89
>>
endobj
86 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 227 0 R
/Group >
/Tabs /S
/StructParents 90
>>
endobj
87 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 228 0 R
/Group >
/Tabs /S
/StructParents 91
>>
endobj
88 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 230 0 R
/Group >
/Tabs /S
/StructParents 92
>>
endobj
89 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 232 0 R
/Group >
/Tabs /S
/StructParents 93
>>
endobj
90 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 5 842.25]
/Contents 233 0 R
/Group >
/Tabs /S
/StructParents 94
>>
endobj
91 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 234 0 R
/Group >
/Tabs /S
/StructParents 95
>>
endobj
92 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 235 0 R
/Group >
/Tabs /S
/StructParents 96
>>
endobj
93 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 236 0 R
/Group >
/Tabs /S
/StructParents 97
>>
endobj
94 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 240 0 R
/Group >
/Tabs /S
/StructParents 98
>>
endobj
95 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 242 0 R
/Group >
/Tabs /S
/StructParents 99
>>
endobj
96 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
5 842.25]
/Contents 233 0 R
/Group >
/Tabs /S
/StructParents 94
>>
endobj
91 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 234 0 R
/Group >
/Tabs /S
/StructParents 95
>>
endobj
92 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 235 0 R
/Group >
/Tabs /S
/StructParents 96
>>
endobj
93 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 236 0 R
/Group >
/Tabs /S
/StructParents 97
>>
endobj
94 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 240 0 R
/Group >
/Tabs /S
/StructParents 98
>>
endobj
95 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 242 0 R
/Group >
/Tabs /S
/StructParents 99
>>
endobj
96 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 5 842.25]
/Contents 243 0 R
/Group >
/Tabs /S
/StructParents 100
>>
endobj
97 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 244 0 R
/Group >
/Tabs /S
/StructParents 101
>>
endobj
98 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 245 0 R
/Group >
/Tabs /S
/StructParents 102
>>
endobj
99 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 246 0 R
/Group >
/Tabs /S
/StructParents 103
>>
endobj
100 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 247 0 R
/Group >
/Tabs /S
/StructParents 104
>>
endobj
101 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 248 0 R
/Group >
/Tabs /S
/StructParents 105
>>
endobj
102 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
5 842.25]
/Contents 243 0 R
/Group >
/Tabs /S
/StructParents 100
>>
endobj
97 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 244 0 R
/Group >
/Tabs /S
/StructParents 101
>>
endobj
98 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 245 0 R
/Group >
/Tabs /S
/StructParents 102
>>
endobj
99 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 246 0 R
/Group >
/Tabs /S
/StructParents 103
>>
endobj
100 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 247 0 R
/Group >
/Tabs /S
/StructParents 104
>>
endobj
101 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 248 0 R
/Group >
/Tabs /S
/StructParents 105
>>
endobj
102 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. 5 842.25]
/Contents 249 0 R
/Group >
/Tabs /S
/StructParents 106
>>
endobj
103 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 250 0 R
/Group >
/Tabs /S
/StructParents 107
>>
endobj
104 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 251 0 R
/Group >
/Tabs /S
/StructParents 108
>>
endobj
105 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 252 0 R
/Group >
/Tabs /S
/StructParents 109
>>
endobj
106 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 253 0 R
/Group >
/Tabs /S
/StructParents 110
>>
endobj
107 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 254 0 R
/Group >
/Tabs /S
/StructParents 111
>>
endobj
108 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.
5 842.25]
/Contents 249 0 R
/Group >
/Tabs /S
/StructParents 106
>>
endobj
103 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 250 0 R
/Group >
/Tabs /S
/StructParents 107
>>
endobj
104 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 251 0 R
/Group >
/Tabs /S
/StructParents 108
>>
endobj
105 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 252 0 R
/Group >
/Tabs /S
/StructParents 109
>>
endobj
106 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 253 0 R
/Group >
/Tabs /S
/StructParents 110
>>
endobj
107 0 obj
>
/ExtGState >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595.5 842.25]
/Contents 254 0 R
/Group >
/Tabs /S
/StructParents 111
>>
endobj
108 0 obj
>
/ExtGState >
/XObject >
/ProcSet [/PDF /Text /ImageB /ImageC /ImageI]
>>
/MediaBox [0 0 595. Wb37c
Aώ
Wb37c
Aώ




 Сделайте это.
Сделайте это.



 Можно изменять радиус всех углов прямоугольника одновременно: удерживайте клавишу Alt (Win) или Option (Mac) во время перетаскивания для изменения радиуса одного угла. У треугольников изменяются все углы, даже если перетащить только один из них. С легкостью поворачивайте фигуру с помощью маркера поворота на холсте, который появляется при наведении курсора мыши на фигуру.
Можно изменять радиус всех углов прямоугольника одновременно: удерживайте клавишу Alt (Win) или Option (Mac) во время перетаскивания для изменения радиуса одного угла. У треугольников изменяются все углы, даже если перетащить только один из них. С легкостью поворачивайте фигуру с помощью маркера поворота на холсте, который появляется при наведении курсора мыши на фигуру.
 Можно перетащить ее в окне изображения, чтобы переместить центр градиента.
Можно перетащить ее в окне изображения, чтобы переместить центр градиента. Появится список доступных фигур. Выберите любую произвольную фигуру на свое усмотрение.
Появится список доступных фигур. Выберите любую произвольную фигуру на свое усмотрение.


 Одна из составляющих этого процесса развития – приобщение детей к познанию, исследованию изучаемых явлений. Для этого в образовательных учреждениях создаются благоприятные условия, способствующие реализации творческих идей обучающихся и их педагогов.Предлагаю вашему вниманию проект ученицы 7 класса.
Одна из составляющих этого процесса развития – приобщение детей к познанию, исследованию изучаемых явлений. Для этого в образовательных учреждениях создаются благоприятные условия, способствующие реализации творческих идей обучающихся и их педагогов.Предлагаю вашему вниманию проект ученицы 7 класса.


 Сейчас актуально развитие способности переноса знаний и навыков, полученных в одной области, в любую другую сферу человеческой деятельности.
Сейчас актуально развитие способности переноса знаний и навыков, полученных в одной области, в любую другую сферу человеческой деятельности.
 Практические навыки пригодятся им на уроках геометрии и технической графики. Проект дал возможность каждому ученику применить свои знания и умения, раскрыть свои способности и возможности.
Практические навыки пригодятся им на уроках геометрии и технической графики. Проект дал возможность каждому ученику применить свои знания и умения, раскрыть свои способности и возможности. 13,21,34,55,89 и т.д.. В этом ряду каждое последующее число является суммой двух предыдущих чисел.
13,21,34,55,89 и т.д.. В этом ряду каждое последующее число является суммой двух предыдущих чисел. Отношение поверхности граней к площади основания также равно золотой пропорции.
Отношение поверхности граней к площади основания также равно золотой пропорции.
 Золотое сечение»»
Золотое сечение»» Геометрические головоломки любимое занятие вечерами и в любую свободную минутку!
Геометрические головоломки любимое занятие вечерами и в любую свободную минутку!
 (Использован материал из журнала «Квант» «Методическое пособие в одном акте» Д. В. ФОМИН) Ведущий:.
(Использован материал из журнала «Квант» «Методическое пособие в одном акте» Д. В. ФОМИН) Ведущий:. Об геометрических фигурах в природе я уже писал в другой своей статье, но в ней больше посвящено все треугольникам: Изучаем с ребёнком треугольники (периметр, виды треугольников) с помощью цветной бумаги .
Об геометрических фигурах в природе я уже писал в другой своей статье, но в ней больше посвящено все треугольникам: Изучаем с ребёнком треугольники (периметр, виды треугольников) с помощью цветной бумаги .
 Кроме уже знакомых вам тел здесь представлены плашки и палочки. Плашки – дополнительные плоские квадратные, круглые и шестиугольные элементы, высота которых равна одной восьмой ребра куба. Палочки – линейные элементы композиции, длина которых равна ребру куба. Кроме того в композиции могут быть использованы тела одних пропорций, но разных размеров. Это так называемые композиции с масштабированием (поскольку на листе в таком случае присутствуют одинаковые тела, но как бы взятые в разном масштабе). Рассмотрите композиции, выполненные абитуриентами в последние годы (рис. 6.2-6.20).
Кроме уже знакомых вам тел здесь представлены плашки и палочки. Плашки – дополнительные плоские квадратные, круглые и шестиугольные элементы, высота которых равна одной восьмой ребра куба. Палочки – линейные элементы композиции, длина которых равна ребру куба. Кроме того в композиции могут быть использованы тела одних пропорций, но разных размеров. Это так называемые композиции с масштабированием (поскольку на листе в таком случае присутствуют одинаковые тела, но как бы взятые в разном масштабе). Рассмотрите композиции, выполненные абитуриентами в последние годы (рис. 6.2-6.20). Однако будем надеяться, что суть задания будет сохранена, и вы сможете воспользоваться нашими советами и рекомендациями.
Однако будем надеяться, что суть задания будет сохранена, и вы сможете воспользоваться нашими советами и рекомендациями. Это верно, но вы уже знаете, что в экзаменационном задании пропорции и соотношения выражаются простыми пропорциями 1:1 или 1:1,5 – и это неслучайно -их просто изобразить и просто проверить. Изменять их нельзя. Это – задание, если вы изменили задание – вы сдаете какой-то другой экзамен. Для большей убедительности этого утверждения представьте, что на экзамене по математике вы умножаете не 2 на 2, как этого требует задание, а 3 на 3, потому что это гармоничнее, интереснее и выразительнее.
Это верно, но вы уже знаете, что в экзаменационном задании пропорции и соотношения выражаются простыми пропорциями 1:1 или 1:1,5 – и это неслучайно -их просто изобразить и просто проверить. Изменять их нельзя. Это – задание, если вы изменили задание – вы сдаете какой-то другой экзамен. Для большей убедительности этого утверждения представьте, что на экзамене по математике вы умножаете не 2 на 2, как этого требует задание, а 3 на 3, потому что это гармоничнее, интереснее и выразительнее. Зачастую экзаменационные работы превращаются в навал предметов, которые хотя и взаимодействуют друг с другом, но не создают ничего, кроме некоего сложного хаоса. Из всех возможных путей составления композиции этот представляется наихудшим. Архитектурная композиция – вещь многообразная, точнее, может быть таковой, поскольку путей обретения гармонии множество. Но композиция – не хаос. Гармония может быть парадоксальной, но никогда она не возникает из хаоса. Хаос – энтропия, рассеяние, смешение всего. Гармония всегда закономерна, упорядочена, она противостоит энтропии, борется с ней, и цель человека разумного – победа гармонии над хаосом. Композиция там, где гармония.
Зачастую экзаменационные работы превращаются в навал предметов, которые хотя и взаимодействуют друг с другом, но не создают ничего, кроме некоего сложного хаоса. Из всех возможных путей составления композиции этот представляется наихудшим. Архитектурная композиция – вещь многообразная, точнее, может быть таковой, поскольку путей обретения гармонии множество. Но композиция – не хаос. Гармония может быть парадоксальной, но никогда она не возникает из хаоса. Хаос – энтропия, рассеяние, смешение всего. Гармония всегда закономерна, упорядочена, она противостоит энтропии, борется с ней, и цель человека разумного – победа гармонии над хаосом. Композиция там, где гармония. В ней может присутствовать равномерное распространение массы или резкие, выделенные акценты. Перечисленные свойства могут комбинироваться (кроме тех, конечно, которые исключают друг друга в одной работе). Следует помнить, что ощущение сложности композиции возникает от восприятия сложной гармонии некоего нетривиального замысла, а не только от сложности врезок и уж точно не от нагромождения множества тел.
В ней может присутствовать равномерное распространение массы или резкие, выделенные акценты. Перечисленные свойства могут комбинироваться (кроме тех, конечно, которые исключают друг друга в одной работе). Следует помнить, что ощущение сложности композиции возникает от восприятия сложной гармонии некоего нетривиального замысла, а не только от сложности врезок и уж точно не от нагромождения множества тел. Лист надо плотно, но не переуплотнено. Силуэт композиции из геометрических тел должен быть живым и певучим как линия в рисунке, выражая общий замысел работы. Все свободные, незанятые телами поля должны быть уравновешены, красивы по пятну и по пропорциям. Вообще, понятия «композиция на листе» и «композиция самого листа» связаны так плотно, что совершенно невозможно определить, где заканчивается одно и начинается другое. Лист – это условное пространство, композиция тоже занимает пространство (иллюзорное). Эти два пространства не только должны находиться в одном месте, но и гармонично существовать, взаимно учитывая характер друг друга. Лист (имеется в виду формат А-3) имеет определенные границы – вертикали и горизонтали. Эти линии вместе с диагоналями задают основные направления, по которым развивается пространство листа. Кроме того это пространство имеет глубину, причем неоднородную: наибольшую – в центре, наименьшую – по краям, самые плоские участки листа – в его углах (стремление убрать эти плоские места привело к арочной и овальной формам изобразительных поверхностей).
Лист надо плотно, но не переуплотнено. Силуэт композиции из геометрических тел должен быть живым и певучим как линия в рисунке, выражая общий замысел работы. Все свободные, незанятые телами поля должны быть уравновешены, красивы по пятну и по пропорциям. Вообще, понятия «композиция на листе» и «композиция самого листа» связаны так плотно, что совершенно невозможно определить, где заканчивается одно и начинается другое. Лист – это условное пространство, композиция тоже занимает пространство (иллюзорное). Эти два пространства не только должны находиться в одном месте, но и гармонично существовать, взаимно учитывая характер друг друга. Лист (имеется в виду формат А-3) имеет определенные границы – вертикали и горизонтали. Эти линии вместе с диагоналями задают основные направления, по которым развивается пространство листа. Кроме того это пространство имеет глубину, причем неоднородную: наибольшую – в центре, наименьшую – по краям, самые плоские участки листа – в его углах (стремление убрать эти плоские места привело к арочной и овальной формам изобразительных поверхностей). Композиция из геометрических тел должна учитывать эти особенности и некоторым образом подчиняться им. Так, композиция, учитывающая в своей структуре прежде всего края листа, имеет прямоугольные очертания. В такой композиции, когда лист заполнен почти до предела, лучше не размещать в углах листа геометрические тела, имеющие наибольшие объемные характеристики, например, шары. Такие прямоугольные композиции – корпусные, массивные, уравновешенные, но, как правило, не очень интересные – они часто вызывают ощущение, что автор старался не создать композицию, а просто равномерно заполнить лист. Лучше, когда в композиции на листе остается больше поля, которое взаимодействует с пространством между геометрическими телами внутри самой композиции. Так, например, композиция в форме овала, как правило, хорошо гармонирует с пространством листа, располагаясь в наиболее глубоком месте, оставляя незанятыми «плоские» углы. «Х»-образная композиция подчинена диагоналям листа. Эти направления могут быть равными по силе и, таким образом, уравновешивать друг друга, а в другом случае одна из диагоналей может доминировать.
Композиция из геометрических тел должна учитывать эти особенности и некоторым образом подчиняться им. Так, композиция, учитывающая в своей структуре прежде всего края листа, имеет прямоугольные очертания. В такой композиции, когда лист заполнен почти до предела, лучше не размещать в углах листа геометрические тела, имеющие наибольшие объемные характеристики, например, шары. Такие прямоугольные композиции – корпусные, массивные, уравновешенные, но, как правило, не очень интересные – они часто вызывают ощущение, что автор старался не создать композицию, а просто равномерно заполнить лист. Лучше, когда в композиции на листе остается больше поля, которое взаимодействует с пространством между геометрическими телами внутри самой композиции. Так, например, композиция в форме овала, как правило, хорошо гармонирует с пространством листа, располагаясь в наиболее глубоком месте, оставляя незанятыми «плоские» углы. «Х»-образная композиция подчинена диагоналям листа. Эти направления могут быть равными по силе и, таким образом, уравновешивать друг друга, а в другом случае одна из диагоналей может доминировать. Возможны также Б и Л – образные композиции, которые строятся на особо сложном, как правило, непогашенном движении, или погашенном, но не до конца. Иногда встречаются интересные композиции в виде восьмерки, совсем редко – построенные в виде «бублика» (кольцеобразные). Возможны и другие принципы компоновки, но перечислять их все нет смысла, поскольку композиция листа рождается совместно с общим замыслом – он вам и должен подсказать наиболее интересное, грамотное, выигрышное решение. Запомните одно главное правило: не может быть хорошей экзаменационной работы, если сам лист некрасив, если он перекошен массами тел, неравномерно и бессмысленно перегружен в отдельных местах и пуст – в других.
Возможны также Б и Л – образные композиции, которые строятся на особо сложном, как правило, непогашенном движении, или погашенном, но не до конца. Иногда встречаются интересные композиции в виде восьмерки, совсем редко – построенные в виде «бублика» (кольцеобразные). Возможны и другие принципы компоновки, но перечислять их все нет смысла, поскольку композиция листа рождается совместно с общим замыслом – он вам и должен подсказать наиболее интересное, грамотное, выигрышное решение. Запомните одно главное правило: не может быть хорошей экзаменационной работы, если сам лист некрасив, если он перекошен массами тел, неравномерно и бессмысленно перегружен в отдельных местах и пуст – в других. Отследить их и поправить достаточно сложно, особенно в первых композициях, когда опыт и практические навыки еще невелики. Именно поэтому для верного определения раскрытия всех граней и направления всех линий на листе используют различные способы упорядочения всех этих взаимосвязанных позиций, приведения их в единую систему. Одна из таких систем подробно описана в следующем задании. Это так называемая сетка – пространственная структура, определяющая раскрытие граней геометрических тел и направление линий в перспективе по всему листу. В процессе подготовки к экзамену «сетка» поможет вам собрать воедино все многообразие задач, связанных с процессом построения композиции, и разом, легко решить их. Безусловно, «сетка» – вещь полезная, но и в ней, конечно, есть свои плюсы и минусы. С одной стороны, изображая композиции на основе «сетки», вы, конечно, тратите некоторое (порой довольно значительное) время на подготовительный этап (рисунок самой «сетки»), тем самым уменьшая время работы над собственно композицией.
Отследить их и поправить достаточно сложно, особенно в первых композициях, когда опыт и практические навыки еще невелики. Именно поэтому для верного определения раскрытия всех граней и направления всех линий на листе используют различные способы упорядочения всех этих взаимосвязанных позиций, приведения их в единую систему. Одна из таких систем подробно описана в следующем задании. Это так называемая сетка – пространственная структура, определяющая раскрытие граней геометрических тел и направление линий в перспективе по всему листу. В процессе подготовки к экзамену «сетка» поможет вам собрать воедино все многообразие задач, связанных с процессом построения композиции, и разом, легко решить их. Безусловно, «сетка» – вещь полезная, но и в ней, конечно, есть свои плюсы и минусы. С одной стороны, изображая композиции на основе «сетки», вы, конечно, тратите некоторое (порой довольно значительное) время на подготовительный этап (рисунок самой «сетки»), тем самым уменьшая время работы над собственно композицией. С другой стороны, «сетка» может значительно сократить время на решение чисто технических задач, связанных с определением направлений горизонтальных прямых и раскрытием различных поверхностей. Конечно, определенный навык позволит вам свести к минимуму временные затраты на «сетку», но если в «сетке» будет допущена ошибка (что в стрессовых условиях экзамена вполне вероятно), то заметить эту ошибку вы сможете, только нарисовав первое геометрическое тело. Что делать в таком случае – исправлять сетку или отказаться от нее вовсе, чтобы наверстать упущенное время? Очевидно лишь то, что начинать работу над экзаменационной композицией с «сетки» следует, только если к экзамену вы научились делать «сетку» быстро и качественно, доведя этот процесс почти до автоматизма, и легко строите композицию на ее основе.
С другой стороны, «сетка» может значительно сократить время на решение чисто технических задач, связанных с определением направлений горизонтальных прямых и раскрытием различных поверхностей. Конечно, определенный навык позволит вам свести к минимуму временные затраты на «сетку», но если в «сетке» будет допущена ошибка (что в стрессовых условиях экзамена вполне вероятно), то заметить эту ошибку вы сможете, только нарисовав первое геометрическое тело. Что делать в таком случае – исправлять сетку или отказаться от нее вовсе, чтобы наверстать упущенное время? Очевидно лишь то, что начинать работу над экзаменационной композицией с «сетки» следует, только если к экзамену вы научились делать «сетку» быстро и качественно, доведя этот процесс почти до автоматизма, и легко строите композицию на ее основе. Не забывайте, что вашу композицию будут оценивать в ряду других, а следовательно, делая композицию без врезок, вы заведомо снижаете конкурентоспособность собственной (заботы. Конечно, год от года уровень экзаменационной композиции растет, и это диктует включение в композицию сложных врезок, которые делают экзаменационную работу выразительнее и интереснее. Однако их выполнение требует дополнительного времени, которое в условиях экзамена ограничено. В этой ситуации все зависит от вашего опыта – если вы усердно готовились к экзамену по композиции, скорее всего у вас уже есть свои любимые врезки, которые могут быть достаточно сложными, но, обрисованные много раз, они изображаются легко и, следовательно, быстро. Но не стоит увлекаться сложными врезками, переусложнить работу – помните, что даже композиция, выполненная с применением простых врезок, может быть достаточно сложной и выразительной. Важно также сказать о том, насколько геометрические тела должны врезаться друг в друга. Порой в композициях геометрические тела врезаны так незначительно, что создается ощущение, будто они не врезаны друг в друга, а лишь едва соприкасаются.
Не забывайте, что вашу композицию будут оценивать в ряду других, а следовательно, делая композицию без врезок, вы заведомо снижаете конкурентоспособность собственной (заботы. Конечно, год от года уровень экзаменационной композиции растет, и это диктует включение в композицию сложных врезок, которые делают экзаменационную работу выразительнее и интереснее. Однако их выполнение требует дополнительного времени, которое в условиях экзамена ограничено. В этой ситуации все зависит от вашего опыта – если вы усердно готовились к экзамену по композиции, скорее всего у вас уже есть свои любимые врезки, которые могут быть достаточно сложными, но, обрисованные много раз, они изображаются легко и, следовательно, быстро. Но не стоит увлекаться сложными врезками, переусложнить работу – помните, что даже композиция, выполненная с применением простых врезок, может быть достаточно сложной и выразительной. Важно также сказать о том, насколько геометрические тела должны врезаться друг в друга. Порой в композициях геометрические тела врезаны так незначительно, что создается ощущение, будто они не врезаны друг в друга, а лишь едва соприкасаются. Такие композиции, как правило, вызывают ощущение нестабильности, неустойчивости и незавершенности. У зрителя появляется непреодолимое желание сделать такую композицию плотнее, глубже врезать друг в друга геометрические тела. Анализируя такую работу, трудно говорить о ней как о композиции – группе гармонично соподчиненных объемов. В других композициях тела так глубоко врезаны друг в друга, что уже непонятно – какие же это тела? Такая композиция, как правило, похожа на сложную массу с торчащими из нее частями геометрических тел и не создает у зрителя ощущения гармонии. Тела в ней перестают существовать как самостоятельные объекты, превращаясь в геометрическую смесь. Если не рассматривать такие крайние случаи (когда геометрические тела почти не врезаются друг в друга или когда они превращаются в единую плотную массу), для создания композиции средней плотности следует придерживаться следующего правила: геометрическое тело должно врезаться в другое (или другие) геометрические тела не более чем наполовину, лучше – на одну треть.
Такие композиции, как правило, вызывают ощущение нестабильности, неустойчивости и незавершенности. У зрителя появляется непреодолимое желание сделать такую композицию плотнее, глубже врезать друг в друга геометрические тела. Анализируя такую работу, трудно говорить о ней как о композиции – группе гармонично соподчиненных объемов. В других композициях тела так глубоко врезаны друг в друга, что уже непонятно – какие же это тела? Такая композиция, как правило, похожа на сложную массу с торчащими из нее частями геометрических тел и не создает у зрителя ощущения гармонии. Тела в ней перестают существовать как самостоятельные объекты, превращаясь в геометрическую смесь. Если не рассматривать такие крайние случаи (когда геометрические тела почти не врезаются друг в друга или когда они превращаются в единую плотную массу), для создания композиции средней плотности следует придерживаться следующего правила: геометрическое тело должно врезаться в другое (или другие) геометрические тела не более чем наполовину, лучше – на одну треть. Кроме того, желательно, чтобы зритель всегда мог определить основные размеры геометрического тела по его видимой части. Иными словами, если в какое-либо тело врезается конус, на рисунке должна остаться видимой его вершина, значительная часть боковой поверхности и окружности основания. Если в какое-либо тело врезается цилиндр, то видимыми должны остаться части боковой поверхности цилиндра и окружностей его оснований. Особо следует сказать о врезках кубов и четырехгранников – в композиции эти геометрические тела составляют фон или, своего рода, каркас для расположения и врезки других, более сложных в построении геометрических тел. Поэтому допускаются врезки, когда видимые части кубов и четырехгранников составляют менее половины их объемов.
Кроме того, желательно, чтобы зритель всегда мог определить основные размеры геометрического тела по его видимой части. Иными словами, если в какое-либо тело врезается конус, на рисунке должна остаться видимой его вершина, значительная часть боковой поверхности и окружности основания. Если в какое-либо тело врезается цилиндр, то видимыми должны остаться части боковой поверхности цилиндра и окружностей его оснований. Особо следует сказать о врезках кубов и четырехгранников – в композиции эти геометрические тела составляют фон или, своего рода, каркас для расположения и врезки других, более сложных в построении геометрических тел. Поэтому допускаются врезки, когда видимые части кубов и четырехгранников составляют менее половины их объемов. Определяя количество геометрических тел в композиции, помните, что чем меньше тел в композиции, тем крупнее они должны быть, тем сложнее их организовать по законам гармонии и красоты, так как каждая связка должна быть обрисована очень точно. Когда количество тел возрастает и уменьшаются их размеры, значительно упрощается задача создания красивых и гармоничных сочетаний геометрических тел вследствие больших возможностей по перемещению отдельных элементов относительно друг друга. Особую роль могут сыграть в композиции плашки. Композиция, в которую включены плашки, выглядит сложнее, интереснее и богаче по сравнению с композицией, где плашек нет. Плашки могут выполнять в композиции самые разнообразные функции. Так, при помощи плашек можно создавать различные объемы. Например, когда необходимо дополнить композицию каким-нибудь геометрическим телом, но все предлагаемые кубы, шестигранники, цилиндры и пр. либо слишком крупны и массивны для этого, либо слишком сложны и нарушают композиционный замысел, привлекая к себе излишнее внимание.
Определяя количество геометрических тел в композиции, помните, что чем меньше тел в композиции, тем крупнее они должны быть, тем сложнее их организовать по законам гармонии и красоты, так как каждая связка должна быть обрисована очень точно. Когда количество тел возрастает и уменьшаются их размеры, значительно упрощается задача создания красивых и гармоничных сочетаний геометрических тел вследствие больших возможностей по перемещению отдельных элементов относительно друг друга. Особую роль могут сыграть в композиции плашки. Композиция, в которую включены плашки, выглядит сложнее, интереснее и богаче по сравнению с композицией, где плашек нет. Плашки могут выполнять в композиции самые разнообразные функции. Так, при помощи плашек можно создавать различные объемы. Например, когда необходимо дополнить композицию каким-нибудь геометрическим телом, но все предлагаемые кубы, шестигранники, цилиндры и пр. либо слишком крупны и массивны для этого, либо слишком сложны и нарушают композиционный замысел, привлекая к себе излишнее внимание. В этом случае следует использовать плашки. Одинарная плашка является наименьшим объемом, участвующим в композиции – варьируя количество плашек и их взаимное расположение, можно создавать объемы, самые разные по массе, конфигурации, плотности и сложности.
В этом случае следует использовать плашки. Одинарная плашка является наименьшим объемом, участвующим в композиции – варьируя количество плашек и их взаимное расположение, можно создавать объемы, самые разные по массе, конфигурации, плотности и сложности. Если есть необходимость усилить движение в глубину композиции, с этим хорошо справятся включенные в композицию парные плашки, перпендикулярные фронтальной плоскости.
Если есть необходимость усилить движение в глубину композиции, с этим хорошо справятся включенные в композицию парные плашки, перпендикулярные фронтальной плоскости.

 Что касается тона, то в реальной ситуации насколько легким или, напротив, насыщенным будет тон вашей композиции, определяется, прежде всего, ее сложностью. Сильный или слабый тон – не цель, а лишь средство выявления объемных характеристик композиции. Если композиция проста, тогда, действительно, хватит и легкого тона, но для создания сложного объема тональная шкала должна быть шире, а максимальный тон – соответственно, сильнее. Не увлекайтесь сильным тоном, помните, что сильный тон потребует большего времени для его технического выполнения, хотя таким тоном проще смоделировать сложный объем. Слабый тон, напротив, требует меньше времени на техническую работу, но моделировать сложный объем таким тоном не просто. Как видите, и в этом случае следует искать «золотую середину». Вообще создание красивой графики на листе требует долгой, кропотливой, внимательной и настойчивой работы. Не все получается сразу, часто ученик делает линейную композицию, затем наносит тон и видит, что линия «ушла», затерлась.
Что касается тона, то в реальной ситуации насколько легким или, напротив, насыщенным будет тон вашей композиции, определяется, прежде всего, ее сложностью. Сильный или слабый тон – не цель, а лишь средство выявления объемных характеристик композиции. Если композиция проста, тогда, действительно, хватит и легкого тона, но для создания сложного объема тональная шкала должна быть шире, а максимальный тон – соответственно, сильнее. Не увлекайтесь сильным тоном, помните, что сильный тон потребует большего времени для его технического выполнения, хотя таким тоном проще смоделировать сложный объем. Слабый тон, напротив, требует меньше времени на техническую работу, но моделировать сложный объем таким тоном не просто. Как видите, и в этом случае следует искать «золотую середину». Вообще создание красивой графики на листе требует долгой, кропотливой, внимательной и настойчивой работы. Не все получается сразу, часто ученик делает линейную композицию, затем наносит тон и видит, что линия «ушла», затерлась. Тогда ученик «поднимает линию», вновь критически оценивает свою работу и понимает, что теперь тон слабоват, и его необходимо усилить…, затем опять линию и опять – тон. В конце концов, когда вполне довольный результатом ученик приносит свою работу на консультацию педагогу или сравнивает ее с работами других учеников – его удовлетворенность куда-то исчезает. Если вам знакома такая ситуация – не отчаивайтесь, она абсолютно нормальна. Постепенно с опытом придет понимание не только того, какую силу тона и линии необходимо создать на вашем листе, но вы также научитесь чувствовать материал, работать им, и уж конечно тогда из вашего рисунка уйдут эти изнуряющие стадии приближения к идеалу. И если этого пока не произошло, позвольте дать еще один совет: не бойтесь делать ошибки – с ними приходит опыт и приобретаются навыки.
Тогда ученик «поднимает линию», вновь критически оценивает свою работу и понимает, что теперь тон слабоват, и его необходимо усилить…, затем опять линию и опять – тон. В конце концов, когда вполне довольный результатом ученик приносит свою работу на консультацию педагогу или сравнивает ее с работами других учеников – его удовлетворенность куда-то исчезает. Если вам знакома такая ситуация – не отчаивайтесь, она абсолютно нормальна. Постепенно с опытом придет понимание не только того, какую силу тона и линии необходимо создать на вашем листе, но вы также научитесь чувствовать материал, работать им, и уж конечно тогда из вашего рисунка уйдут эти изнуряющие стадии приближения к идеалу. И если этого пока не произошло, позвольте дать еще один совет: не бойтесь делать ошибки – с ними приходит опыт и приобретаются навыки. Однако найденную в небольшом эскизе гармонию не всегда удается полностью сохранить при переносе замысла на полный лист – так стоит ли вообще делать эскиз композиции?
Однако найденную в небольшом эскизе гармонию не всегда удается полностью сохранить при переносе замысла на полный лист – так стоит ли вообще делать эскиз композиции? Постепенно рисовальщик формирует свои собственные представления о том, как должна выглядеть композиция, выявляет и определяет любимые связки геометрических тел, наиболее выразительные и эффектные врезки и композиционные приемы. Тогда опыт позволяет обходиться и без стадии предварительного эскизирования. Рисовальщик, достигший такого уровня, получив исходное экзаменационное задание, строит композицию, опираясь на многократно отработанные блоки и элементы.
Постепенно рисовальщик формирует свои собственные представления о том, как должна выглядеть композиция, выявляет и определяет любимые связки геометрических тел, наиболее выразительные и эффектные врезки и композиционные приемы. Тогда опыт позволяет обходиться и без стадии предварительного эскизирования. Рисовальщик, достигший такого уровня, получив исходное экзаменационное задание, строит композицию, опираясь на многократно отработанные блоки и элементы. И пытаясь таким образом обмануть приемную комиссию, абитуриент обманывает, прежде всего, самого себя. Кроме того, каждый год экзаменационное задание хоть и незначительно, но меняется. Вводятся новые элементы (например, буквы или геометрические тела другого масштаба), задаются определенный ракурс (сверху или снизу) и точка зрения, определяются обязательные геометрические тела или их связки. Как правило, эти изменения становятся известны только на экзамене. И если вы пришли на экзамен с готовой, окончательно сложившейся композицией, эти новые вводные в лучшем случае не позволят вам реализовать «домашнюю заготовку», а в худшем – выведут вас из рабочего состояния, заставляя судорожно перекраивать вашу композицию под новые условия.
И пытаясь таким образом обмануть приемную комиссию, абитуриент обманывает, прежде всего, самого себя. Кроме того, каждый год экзаменационное задание хоть и незначительно, но меняется. Вводятся новые элементы (например, буквы или геометрические тела другого масштаба), задаются определенный ракурс (сверху или снизу) и точка зрения, определяются обязательные геометрические тела или их связки. Как правило, эти изменения становятся известны только на экзамене. И если вы пришли на экзамен с готовой, окончательно сложившейся композицией, эти новые вводные в лучшем случае не позволят вам реализовать «домашнюю заготовку», а в худшем – выведут вас из рабочего состояния, заставляя судорожно перекраивать вашу композицию под новые условия. Создавая новую композицию, воспользуйтесь как основой предыдущей работой. Наверняка, заканчивая ее, вы сокрушались, что не смогли «дотянуть» композицию, не подвинули то или иное геометрическое тело, не исправили слишком поздно замеченные ошибки во врезках, не довели до совершенства графику и т. д. Это обычная практика. Идея может быть зафиксирована в рисунке на определенный момент ее существования, но остановить ее невозможно, она живет и развивается дальше. Когда же рисунок закончен, часто оказывается, что он хуже, чем идея, лежащая в его основе. В таком случае браться за принципиально новую композицию преждевременно. Следует нарисовать новую работу на ту же тему. В ней вы сможете осуществить все, что не удалось сделать в предыдущей работе.
Создавая новую композицию, воспользуйтесь как основой предыдущей работой. Наверняка, заканчивая ее, вы сокрушались, что не смогли «дотянуть» композицию, не подвинули то или иное геометрическое тело, не исправили слишком поздно замеченные ошибки во врезках, не довели до совершенства графику и т. д. Это обычная практика. Идея может быть зафиксирована в рисунке на определенный момент ее существования, но остановить ее невозможно, она живет и развивается дальше. Когда же рисунок закончен, часто оказывается, что он хуже, чем идея, лежащая в его основе. В таком случае браться за принципиально новую композицию преждевременно. Следует нарисовать новую работу на ту же тему. В ней вы сможете осуществить все, что не удалось сделать в предыдущей работе. Другие тела перемещайте в соответствии с вашим замыслом, двигая кальку по композиции, или же меняйте их на другие. Если за один раз вам не удастся внести в композицию все задуманные изменения, возьмите следующий лист кальки. Так продолжайте до тех пор, пока вы не будете удовлетворены результатом. Окончательный вариант изобразите на листе бумаги, предварительно перенеся на него с кальки место и основные габариты всех геометрических тел. Такая последовательная работа очень похожа на процесс архитектурного проектирования, когда архитектор шаг за шагом улучшает, уточняет, совершенствует свой замысел, пока не достигнет идеала. Так и вы улучшайте и совершенствуйте свою композицию, не бросая ее, разрабатывая тему до конца, как золотую жилу пока она не иссякнет. Скорее всего, в этот момент у вас появится новая идея. Она появится сама, рожденная вашими усердием, прилежанием и опытом. Со временем новые идеи потекут потоком, одна интереснее другой. Вы едва будете успевать выбирать лучшие композиции, чтобы их нарисовать.
Другие тела перемещайте в соответствии с вашим замыслом, двигая кальку по композиции, или же меняйте их на другие. Если за один раз вам не удастся внести в композицию все задуманные изменения, возьмите следующий лист кальки. Так продолжайте до тех пор, пока вы не будете удовлетворены результатом. Окончательный вариант изобразите на листе бумаги, предварительно перенеся на него с кальки место и основные габариты всех геометрических тел. Такая последовательная работа очень похожа на процесс архитектурного проектирования, когда архитектор шаг за шагом улучшает, уточняет, совершенствует свой замысел, пока не достигнет идеала. Так и вы улучшайте и совершенствуйте свою композицию, не бросая ее, разрабатывая тему до конца, как золотую жилу пока она не иссякнет. Скорее всего, в этот момент у вас появится новая идея. Она появится сама, рожденная вашими усердием, прилежанием и опытом. Со временем новые идеи потекут потоком, одна интереснее другой. Вы едва будете успевать выбирать лучшие композиции, чтобы их нарисовать. Тогда и вступительный экзамен не застанет вас врасплох, у вас сразу найдется достойный ответ на экзаменационное задание – красивый и выразительный. Но помните, чтобы это было именно так, необходимо упорно и старательно готовиться.
Тогда и вступительный экзамен не застанет вас врасплох, у вас сразу найдется достойный ответ на экзаменационное задание – красивый и выразительный. Но помните, чтобы это было именно так, необходимо упорно и старательно готовиться. Малевича с его квадратами, кругами, прямыми и ломаными линиями.
Малевича с его квадратами, кругами, прямыми и ломаными линиями.
 Регулярность подразумевает общее стремление к упорядоченности и организованности, что придется по вкусу педантичным натурам.
Регулярность подразумевает общее стремление к упорядоченности и организованности, что придется по вкусу педантичным натурам.

 п. элементов.
п. элементов. Такую конструкцию будет уместно обыгрывать треугольными формами и конусовидными объемными элементами в дальнейшем озеленении участка. Например, цветник перед домом может быть выполнен как разделенный от угла к углу квадрат или четырехугольник. Таким образом, фактически правильная и симметричная фигура будет зрительно соотноситься с треугольником.
Такую конструкцию будет уместно обыгрывать треугольными формами и конусовидными объемными элементами в дальнейшем озеленении участка. Например, цветник перед домом может быть выполнен как разделенный от угла к углу квадрат или четырехугольник. Таким образом, фактически правильная и симметричная фигура будет зрительно соотноситься с треугольником. Общее ощущение порядка и организованности подойдет педантичным натурам.
Общее ощущение порядка и организованности подойдет педантичным натурам. Начинающим следует основывать свою работу на какой-то одной форме, сочетая между собой либо шары, круги, овалы и дуги, либо кубы, квадраты, прямоугольники и прямые линии, либо пирамиды, конусы и треугольники и т.п. Разнообразия в таком случае можно достигать за счет совмещения фигур разных размеров. Так, хорошо будет смотреться круглая ваза или фонтан в центре округлого газона или цветника.
Начинающим следует основывать свою работу на какой-то одной форме, сочетая между собой либо шары, круги, овалы и дуги, либо кубы, квадраты, прямоугольники и прямые линии, либо пирамиды, конусы и треугольники и т.п. Разнообразия в таком случае можно достигать за счет совмещения фигур разных размеров. Так, хорошо будет смотреться круглая ваза или фонтан в центре округлого газона или цветника.

 Привлечь жителей села к проблеме сохранения и благоустройства памятника, к его состоянию. Организовать практическую деятельность школьников.
Привлечь жителей села к проблеме сохранения и благоустройства памятника, к его состоянию. Организовать практическую деятельность школьников. Симметрия и геометрические фигуры придают ландшафту порядок, гармонию, закономерность, которые применяются в регулярном стиле. Благоустраиваемая территория пригодна для осуществления задуманного проекта; элементы дизайна, изображенные в эскизах, реально выполнимы.
Симметрия и геометрические фигуры придают ландшафту порядок, гармонию, закономерность, которые применяются в регулярном стиле. Благоустраиваемая территория пригодна для осуществления задуманного проекта; элементы дизайна, изображенные в эскизах, реально выполнимы. Результаты исследований…………………………………………15
Результаты исследований…………………………………………15
 История развития человечества выдвинула два главных направления в садовом дизайне – регулярный и пейзажный. Каждая историческая эпоха вносила свои черты в эти направления. Не осталось в стороне и наше время. Пейзажный стиль пришел в Европу из Китая, где всегда абсолютизировалась красота природы. Здесь большое значение придавалось тому, чтобы здания органично вписывались в искусно обработанный природный ландшафт.
История развития человечества выдвинула два главных направления в садовом дизайне – регулярный и пейзажный. Каждая историческая эпоха вносила свои черты в эти направления. Не осталось в стороне и наше время. Пейзажный стиль пришел в Европу из Китая, где всегда абсолютизировалась красота природы. Здесь большое значение придавалось тому, чтобы здания органично вписывались в искусно обработанный природный ландшафт. Модный нынче японский пейзажный сад невелик по площади, каждая его деталь – будь то мостик, фонарик или зонтик – несет сложный внутренний смысл. Для европейца японский сад излишне театрален, но очень привлекателен. Основной его принцип – ощущение спокойствия и отдыха, созерцания природы и миниатюризация.
Модный нынче японский пейзажный сад невелик по площади, каждая его деталь – будь то мостик, фонарик или зонтик – несет сложный внутренний смысл. Для европейца японский сад излишне театрален, но очень привлекателен. Основной его принцип – ощущение спокойствия и отдыха, созерцания природы и миниатюризация. Здесь редко можно встретить сооружения из натуральной необработанной древесины, природные валуны, альпийские горки, клумбы.
Здесь редко можно встретить сооружения из натуральной необработанной древесины, природные валуны, альпийские горки, клумбы. Русский сад всегда удачно совмещал два направления – декоративное и утилитарное. Огороды в этих садах не в пример французским были красивы не изысканным оформлением, а богатым урожаем самых разнообразных овощей.
Русский сад всегда удачно совмещал два направления – декоративное и утилитарное. Огороды в этих садах не в пример французским были красивы не изысканным оформлением, а богатым урожаем самых разнообразных овощей. Сегодня наивысшим достижением ландшафтного дизайнера может считаться сочетание геометрии форм цветников и таинственное волнение злаков, высокотехнологичных садовых изделий из стали и стекла с пришедшими в сады зарослями рогоза, бамбука. На пике моды нынче имитация старого заброшенного сада, воссоздание картины первозданной природы. Правда, создание атмосферы запущенности дело очень дорогое, а привнесение в сад наиболее эффектных дикоросов сопряжено с тем, что многие из них значатся в Красной книге.
Сегодня наивысшим достижением ландшафтного дизайнера может считаться сочетание геометрии форм цветников и таинственное волнение злаков, высокотехнологичных садовых изделий из стали и стекла с пришедшими в сады зарослями рогоза, бамбука. На пике моды нынче имитация старого заброшенного сада, воссоздание картины первозданной природы. Правда, создание атмосферы запущенности дело очень дорогое, а привнесение в сад наиболее эффектных дикоросов сопряжено с тем, что многие из них значатся в Красной книге.
 Ведь для того, чтобы всё правильно сделать необходимо, знать, что каким будет по размеру и по форме. Так же нужно предполагать какой будет участок – симметричный или ассиметричный. В составлении плана тоже может помочь геометрия .
Ведь для того, чтобы всё правильно сделать необходимо, знать, что каким будет по размеру и по форме. Так же нужно предполагать какой будет участок – симметричный или ассиметричный. В составлении плана тоже может помочь геометрия . Можно заметить и то, что невысокие растения на переднем плане могут казаться выше более высоких, расположенных вдали. Этот эффект носит название линейной перспективы.
Можно заметить и то, что невысокие растения на переднем плане могут казаться выше более высоких, расположенных вдали. Этот эффект носит название линейной перспективы. Линейной формой, которая неизменно присутствует во многих элементах сада, можно считать дорожки, бордюры, ограждения сада.
Линейной формой, которая неизменно присутствует во многих элементах сада, можно считать дорожки, бордюры, ограждения сада. Напротив, нам предоставлена свобода самим исследовать и открывать в ландшафте то, что красиво, привлекательно или полезно, и, что особенно важно, асимметричная компоновка влечёт за собой меньше нарушений природы.
Напротив, нам предоставлена свобода самим исследовать и открывать в ландшафте то, что красиво, привлекательно или полезно, и, что особенно важно, асимметричная компоновка влечёт за собой меньше нарушений природы. Итак, чтобы стать знатоком геометрии, читайте дальше.
Итак, чтобы стать знатоком геометрии, читайте дальше.
 В этих сценариях перпендикулярные линии создают крест. Тем не менее, края квадрата или прямоугольника также будут перпендикулярными линиями.
В этих сценариях перпендикулярные линии создают крест. Тем не менее, края квадрата или прямоугольника также будут перпендикулярными линиями.
 Матрицы используют числовые массивы, состоящие из набора чисел в квадратных скобках. Мы видим ⊥ в декартовых плоскостях.
Матрицы используют числовые массивы, состоящие из набора чисел в квадратных скобках. Мы видим ⊥ в декартовых плоскостях.


 Касательные линии появляются на графиках с кривой. Они показывают, когда определенная точка касается кривой, но сразу после этого дуга отклоняется от линии, и они больше не встречаются.
Касательные линии появляются на графиках с кривой. Они показывают, когда определенная точка касается кривой, но сразу после этого дуга отклоняется от линии, и они больше не встречаются. Однако это не единственные символы, которые используют Т-образную форму. Давайте посмотрим на несколько других.
Однако это не единственные символы, которые используют Т-образную форму. Давайте посмотрим на несколько других.
 При измерении фигур и вычислении площади перпендикулярные линии точно говорят нам, с чем мы имеем дело на фигуре. Хотя маловероятно, что вы встретите символ ⊥, если только вы не занимаетесь геометрией, всегда полезно знать, что вы ищете.
При измерении фигур и вычислении площади перпендикулярные линии точно говорят нам, с чем мы имеем дело на фигуре. Хотя маловероятно, что вы встретите символ ⊥, если только вы не занимаетесь геометрией, всегда полезно знать, что вы ищете.



 Аналог: Пуля
точка
Аналог: Пуля
точка 
 Похожий:
Похожий: 

 Соответствует
Соответствует 
 Похожий:
двухлинейная двунаправленная стрелка
Похожий:
двухлинейная двунаправленная стрелка  Похожие: длинные
двойная стрелка влево
Похожие: длинные
двойная стрелка влево  Аналогично: более длинная версия
Аналогично: более длинная версия 


 Синоним:
Синоним: 

 Аналогично: правая двойная линия
стрелка
Аналогично: правая двойная линия
стрелка 

 Аналогично: синонимы звездочка
Аналогично: синонимы звездочка 


 Аналогично: двойная линия, направленная вверх и вниз.
стрелка
Аналогично: двойная линия, направленная вверх и вниз.
стрелка 
 Аналогично: турникет повернулся
полукруг
Аналогично: турникет повернулся
полукруг  Аналогично: переменный размер
оператор
Аналогично: переменный размер
оператор  Эти формы имеют только 2 измерения: длину и ширину.
Эти формы имеют только 2 измерения: длину и ширину. Угол обозначается символом ∠. Углы измеряются в градусах (°) с помощью транспортира. Например, 45 градусов представляются как 45°.
Угол обозначается символом ∠. Углы измеряются в градусах (°) с помощью транспортира. Например, 45 градусов представляются как 45°.
 д.
д. У него одинаковые начальная и конечная точки.
У него одинаковые начальная и конечная точки. Его также можно использовать в таких областях, как наука, для разработки проектов или программ по исследованию космоса.
Его также можно использовать в таких областях, как наука, для разработки проектов или программ по исследованию космоса. Это одна из старейших областей математики, возникшая в ответ на такие практические задачи, как геодезия, и ее название происходит от греческих слов, означающих «измерение Земли». В конце концов стало понятно, что геометрия не должна ограничиваться изучением плоских поверхностей (геометрия плоскостей) и жестких трехмерных объектов (геометрия тел), но что даже самые абстрактные мысли и образы могут быть представлены и развиты в геометрических терминах.
Это одна из старейших областей математики, возникшая в ответ на такие практические задачи, как геодезия, и ее название происходит от греческих слов, означающих «измерение Земли». В конце концов стало понятно, что геометрия не должна ограничиваться изучением плоских поверхностей (геометрия плоскостей) и жестких трехмерных объектов (геометрия тел), но что даже самые абстрактные мысли и образы могут быть представлены и развиты в геометрических терминах. до н.э. на основе 10 аксиом или постулатов, из которых несколько сотен теорем были доказаны дедуктивной логикой. Элементов олицетворяли аксиоматико-дедуктивный метод на протяжении многих веков.
до н.э. на основе 10 аксиом или постулатов, из которых несколько сотен теорем были доказаны дедуктивной логикой. Элементов олицетворяли аксиоматико-дедуктивный метод на протяжении многих веков.
 Непрерывное развитие топологии началось с 1911 г., когда голландский математик Л.Э.Й. Брауэр (1881–1966) представил методы, обычно применимые к этой теме.
Непрерывное развитие топологии началось с 1911 г., когда голландский математик Л.Э.Й. Брауэр (1881–1966) представил методы, обычно применимые к этой теме. э.), приписывает египтянам изобретение геодезии для восстановления стоимости собственности после ежегодного разлива Нила. Точно так же стремление узнать объемы твердых цифр проистекало из необходимости оценивать дань, хранить нефть и зерно, строить плотины и пирамиды. Даже три непонятные геометрические задачи древности — удвоить куб, разделить угол на три части и возвести в квадрат круг, все из которых будут обсуждаться позже — вероятно, возникли из практических вопросов, из религиозного ритуала, хронометража и строительства, соответственно, в догреческих обществ Средиземноморья. И главный предмет позднейшей греческой геометрии, теория конических сечений, обязан своим общим значением, а может быть, и своим происхождением, своему применению к оптике и астрономии.
э.), приписывает египтянам изобретение геодезии для восстановления стоимости собственности после ежегодного разлива Нила. Точно так же стремление узнать объемы твердых цифр проистекало из необходимости оценивать дань, хранить нефть и зерно, строить плотины и пирамиды. Даже три непонятные геометрические задачи древности — удвоить куб, разделить угол на три части и возвести в квадрат круг, все из которых будут обсуждаться позже — вероятно, возникли из практических вопросов, из религиозного ритуала, хронометража и строительства, соответственно, в догреческих обществ Средиземноморья. И главный предмет позднейшей греческой геометрии, теория конических сечений, обязан своим общим значением, а может быть, и своим происхождением, своему применению к оптике и астрономии. Однако о Евклиде известно гораздо меньше, чем о Моисее. На самом деле, единственное, что известно с достаточной степенью достоверности, это то, что Евклид преподавал в Александрийской библиотеке во времена правления Птолемея I (323–285/283 до н. э.). Евклид писал не только по геометрии, но и по астрономии и оптике, а может быть, и по механике и музыке. Только Элементы , которые были тщательно скопированы и переведены, сохранились нетронутыми.
Однако о Евклиде известно гораздо меньше, чем о Моисее. На самом деле, единственное, что известно с достаточной степенью достоверности, это то, что Евклид преподавал в Александрийской библиотеке во времена правления Птолемея I (323–285/283 до н. э.). Евклид писал не только по геометрии, но и по астрономии и оптике, а может быть, и по механике и музыке. Только Элементы , которые были тщательно скопированы и переведены, сохранились нетронутыми. Учение придавало математике первостепенное значение в исследовании и понимании мира. Платон развил подобный взгляд, и философы, находившиеся под влиянием Пифагора или Платона, часто восторженно писали о геометрии как о ключе к толкованию вселенной. Таким образом, древняя геометрия ассоциировалась с возвышенным, дополняя свое земное происхождение и свою репутацию образца точного рассуждения.
Учение придавало математике первостепенное значение в исследовании и понимании мира. Платон развил подобный взгляд, и философы, находившиеся под влиянием Пифагора или Платона, часто восторженно писали о геометрии как о ключе к толкованию вселенной. Таким образом, древняя геометрия ассоциировалась с возвышенным, дополняя свое земное происхождение и свою репутацию образца точного рассуждения. Однако египетские писцы не оставили нам указаний об этих процедурах, а тем более намеков на то, что они знали, как их обобщить, чтобы получить теорему Пифагора: квадрат на прямой, противоположной прямому углу, равен сумме квадратов на двух других. стороны. Точно так же ведические писания древней Индии содержат разделы, называемые sulvasutra s, или «правила веревки», для точного расположения жертвенных алтарей. Требуемые прямые углы были сделаны из веревок, размеченных для получения триад (3, 4, 5) и (5, 12, 13).
Однако египетские писцы не оставили нам указаний об этих процедурах, а тем более намеков на то, что они знали, как их обобщить, чтобы получить теорему Пифагора: квадрат на прямой, противоположной прямому углу, равен сумме квадратов на двух других. стороны. Точно так же ведические писания древней Индии содержат разделы, называемые sulvasutra s, или «правила веревки», для точного расположения жертвенных алтарей. Требуемые прямые углы были сделаны из веревок, размеченных для получения триад (3, 4, 5) и (5, 12, 13). Этот факт, который был шокирован, когда его обнаружили пифагорейцы, породил концепцию и теорию несоизмеримости.
Этот факт, который был шокирован, когда его обнаружили пифагорейцы, породил концепцию и теорию несоизмеримости. В нем также есть упражнение с круглыми ограждениями с подразумеваемым значением π = 3. Подрядчик бассейна царя Соломона, который построил пруд 10 локтей в поперечнике и 30 локтей вокруг (3 Царств 7:23), использовал то же значение. Однако евреи должны были взять свое π у египтян до того, как переплыли Красное море, ибо папирус Райнда ( с. 2000 г. до н.э.; наш основной источник древнеегипетской математики) подразумевает π = 3,1605.
В нем также есть упражнение с круглыми ограждениями с подразумеваемым значением π = 3. Подрядчик бассейна царя Соломона, который построил пруд 10 локтей в поперечнике и 30 локтей вокруг (3 Царств 7:23), использовал то же значение. Однако евреи должны были взять свое π у египтян до того, как переплыли Красное море, ибо папирус Райнда ( с. 2000 г. до н.э.; наш основной источник древнеегипетской математики) подразумевает π = 3,1605.

 Для выполнения этого требования можно использовать не более одного года курсов типа ESL.
Для выполнения этого требования можно использовать не более одного года курсов типа ESL.
 Один переводной курс колледжа не будет соответствовать требованиям по математике за три года.
Один переводной курс колледжа не будет соответствовать требованиям по математике за три года.  (Рекомендуется три года/3-й уровень обучения в средней школе). Курсы должны подчеркивать разговорную речь и понимание, а также включать обучение грамматике, лексике, чтению, сочинению и культуре. Допустимы американский язык жестов и классические языки, такие как латынь и греческий, а также языки коренных американцев. Курсы, пройденные в седьмом и восьмом классах, могут использоваться для выполнения части или всего этого требования, если средняя школа признает их эквивалентными своим собственным курсам.
(Рекомендуется три года/3-й уровень обучения в средней школе). Курсы должны подчеркивать разговорную речь и понимание, а также включать обучение грамматике, лексике, чтению, сочинению и культуре. Допустимы американский язык жестов и классические языки, такие как латынь и греческий, а также языки коренных американцев. Курсы, пройденные в седьмом и восьмом классах, могут использоваться для выполнения части или всего этого требования, если средняя школа признает их эквивалентными своим собственным курсам.



 Упорядоченные пары записываются в скобках (координата x, координата y).
Упорядоченные пары записываются в скобках (координата x, координата y). Игроки называют номер строки и столбца, пытаясь найти спрятанный линкор противника.
Игроки называют номер строки и столбца, пытаясь найти спрятанный линкор противника. Когда классу дают печатный или цифровой кроссворд, научите своего ученика отвечать на кроссворд, сначала используя бумажные сетки, где вы можете быстро тактильно отметить пустые места. Не забудьте указать номера строк и столбцов. При необходимости используйте тактильный маркер (например, крошечную пенопластовую точку на липкой основе), чтобы обозначить начало слова.
Когда классу дают печатный или цифровой кроссворд, научите своего ученика отвечать на кроссворд, сначала используя бумажные сетки, где вы можете быстро тактильно отметить пустые места. Не забудьте указать номера строк и столбцов. При необходимости используйте тактильный маркер (например, крошечную пенопластовую точку на липкой основе), чтобы обозначить начало слова.
 Поместите буквы, чтобы написать загадочное слово.
Поместите буквы, чтобы написать загадочное слово. Пример. Если вы используете бумажную сетку 4 × 5, отрежьте дополнительные строки и столбцы. Для физических досок закройте области, которые не используются, так как это поможет учащимся развить представление о размере. Учащиеся узнают, что доска 4×5 намного меньше, чем доска 10×12.
Пример. Если вы используете бумажную сетку 4 × 5, отрежьте дополнительные строки и столбцы. Для физических досок закройте области, которые не используются, так как это поможет учащимся развить представление о размере. Учащиеся узнают, что доска 4×5 намного меньше, чем доска 10×12. Затем учащийся может поместить фигурку на доску Lego и назвать числа, и/или учитель может назвать числа, а учащийся помещает фигурку на это место. Следующий шаг может состоять в том, чтобы учащиеся разгадывали очень простой кроссворд с пятью просматриваемыми словами. Учащимся не следует знакомить с сетками, когда они изучают алгебру и должны рисовать уравнения!
Затем учащийся может поместить фигурку на доску Lego и назвать числа, и/или учитель может назвать числа, а учащийся помещает фигурку на это место. Следующий шаг может состоять в том, чтобы учащиеся разгадывали очень простой кроссворд с пятью просматриваемыми словами. Учащимся не следует знакомить с сетками, когда они изучают алгебру и должны рисовать уравнения! Пример. Район имеет размеры 3 на 4 квартала. Школа находится в верхнем левом углу. Заправка находится в правом верхнем углу. Сколько улиц вам нужно пересечь?
Пример. Район имеет размеры 3 на 4 квартала. Школа находится в верхнем левом углу. Заправка находится в правом верхнем углу. Сколько улиц вам нужно пересечь?
 В «Пути к технологии» есть множество постов о программировании. Swift Playgrounds, бесплатная игра Apple по программированию, доступна; однако Swift Playgrounds немного более продвинутый и не предназначен для обучения основным понятиям сетки.
В «Пути к технологии» есть множество постов о программировании. Swift Playgrounds, бесплатная игра Apple по программированию, доступна; однако Swift Playgrounds немного более продвинутый и не предназначен для обучения основным понятиям сетки. Узнайте больше о CodeQuest здесь.
Узнайте больше о CodeQuest здесь.
 ru
ru
 свойства кривых и поверхностей, сохраняющиеся при преобразованиях аффинной группы или ее подгрупп. Наиболее полно изучена дифференциальная геометрия эквиаффинного пространства. В эквиаффинной … Математическая энциклопедия
свойства кривых и поверхностей, сохраняющиеся при преобразованиях аффинной группы или ее подгрупп. Наиболее полно изучена дифференциальная геометрия эквиаффинного пространства. В эквиаффинной … Математическая энциклопедия дисциплина, изучающая геометрич. образы, находящиеся на сфере, подобно тому как планиметрия изучает геометрич. образы, находящиеся на плоскости. Всякая плоскость, пересекающая сферу, дает в сечении нек рую окружность; если секущая… … Математическая энциклопедия
дисциплина, изучающая геометрич. образы, находящиеся на сфере, подобно тому как планиметрия изучает геометрич. образы, находящиеся на плоскости. Всякая плоскость, пересекающая сферу, дает в сечении нек рую окружность; если секущая… … Математическая энциклопедия Содержание 1 Элементарная геометрия 2 Параметрические определения 3 Кривая Жордана … Википедия
Содержание 1 Элементарная геометрия 2 Параметрические определения 3 Кривая Жордана … Википедия Пример: пусть угол AOB = 90 0 , тогда градусная мера дуги ACB равна 360 0 — 90 0 = 270 0 .
Пример: пусть угол AOB = 90 0 , тогда градусная мера дуги ACB равна 360 0 — 90 0 = 270 0 .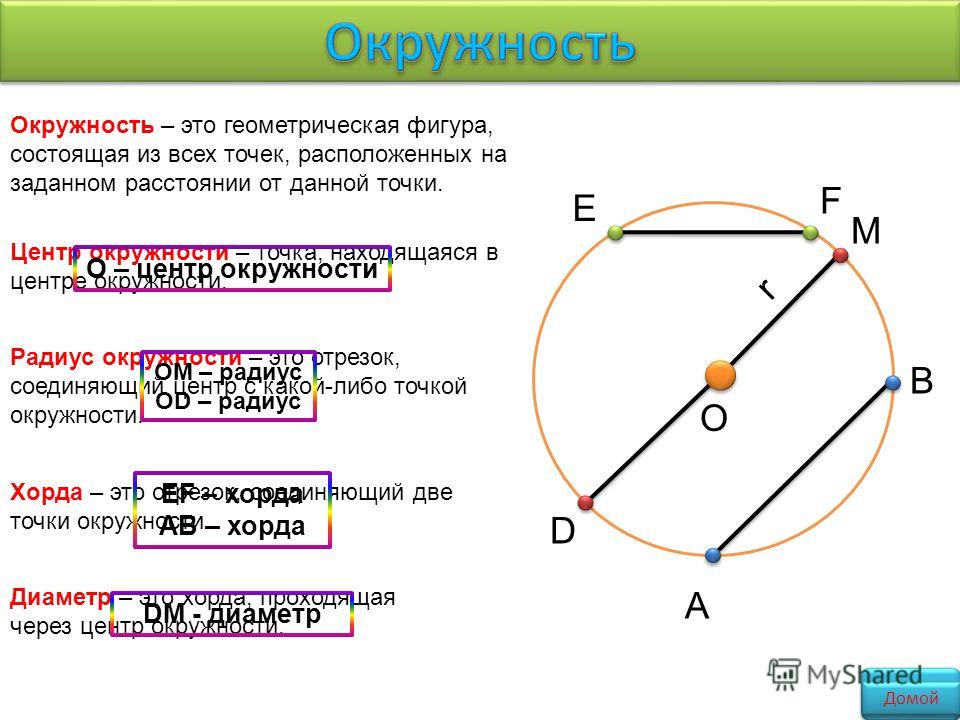 Ru Ответы Mail. ru Почта Mail. ru Прочие проекты Новости Mail. Ru Агент Mail. ru Мой Мир Mail. ru ICQ Облако Mail. ru Красота и Здоровье Коррекция веса Здоровый образ жизни Врачи, Клиники, Страхование Болезни, Лекарства Косметика, Парфюмерия Баня, Массаж, Фитнес Уход за волосами Маникюр, Педикюр Детское здоровье Салоны красоты и СПА Прочее о здоровье и красоте Животные, Растения Домашние животные Комнатные растения Сад-Огород Дикая природа Прочая живность Города и Страны Вокруг света Карты, Транспорт, GPS Климат, Погода, Часовые пояса Коды, Индексы, Адреса ПМЖ, Недвижимость Прочее о городах и странах Общество, Политика, СМИ Общество Политика Прочие социальные темы Средства массовой информации Еда, Кулинария Закуски и Салаты Первые блюда Вторые блюда Напитки Десерты, Сладости, Выпечка Консервирование Торжество, Праздник Готовим детям Готовим в … Покупка и выбор продуктов На скорую руку Прочее кулинарное Фотография, Видеосъемка Обработка и печать фото Обработка видеозаписей Выбор, покупка аппаратуры Уход за аппаратурой Техника, темы, жанры съемки Прочее фото-видео Товары и Услуги Идеи для подарков Техника для дома Прочие промтовары Сервис, уход и ремонт Прочие услуги Досуг, Развлечения Хобби Концерты, Выставки, Спектакли Охота и Рыбалка Клубы, Дискотеки Рестораны, Кафе, Бары Советы, Идеи Игры без компьютера Прочие развлечения Новый Год День Святого Валентина Восьмое марта Наука, Техника, Языки Гуманитарные науки Естественные науки Лингвистика Техника Работа, Карьера Написание резюме Подработка, временная работа Кадровые агентства Отдел кадров, HR Профессиональный рост Смена и поиск места работы Обстановка на работе Трудоустройство за рубежом Прочие карьерные вопросы Гороскопы, Магия, Гадания Гороскопы Гадания Сны Прочие предсказания Магия Юридическая консультация Административное право Гражданское право Конституционное право Семейное право Трудовое право Уголовное право Финансовое право Жилищное право Право социального обеспечения Военная служба Паспортный режим, регистрация Прочие юридические вопросы Юмор Золотой фонд Искусство и Культура Музыка Литература Кино, Театр Живопись, Графика Архитектура, Скульптура Прочие искусства Компьютерные и Видео игры Прочие Браузерные Клиентские Консольные Мобильные Программирование Другие языки и технологии Java JavaScript jQuery MySQL Perl PHP Python Веб-дизайн Верстка, CSS, HTML, SVG Системное администрирование Домашние задания Другие предметы Литература Математика Алгебра Геометрия Иностранные языки Химия Физика Биология История География Информатика Экономика Русский язык Обществознание Плесский колледж бизнеса и туризма Компания «Azimyt-K»
Ru Ответы Mail. ru Почта Mail. ru Прочие проекты Новости Mail. Ru Агент Mail. ru Мой Мир Mail. ru ICQ Облако Mail. ru Красота и Здоровье Коррекция веса Здоровый образ жизни Врачи, Клиники, Страхование Болезни, Лекарства Косметика, Парфюмерия Баня, Массаж, Фитнес Уход за волосами Маникюр, Педикюр Детское здоровье Салоны красоты и СПА Прочее о здоровье и красоте Животные, Растения Домашние животные Комнатные растения Сад-Огород Дикая природа Прочая живность Города и Страны Вокруг света Карты, Транспорт, GPS Климат, Погода, Часовые пояса Коды, Индексы, Адреса ПМЖ, Недвижимость Прочее о городах и странах Общество, Политика, СМИ Общество Политика Прочие социальные темы Средства массовой информации Еда, Кулинария Закуски и Салаты Первые блюда Вторые блюда Напитки Десерты, Сладости, Выпечка Консервирование Торжество, Праздник Готовим детям Готовим в … Покупка и выбор продуктов На скорую руку Прочее кулинарное Фотография, Видеосъемка Обработка и печать фото Обработка видеозаписей Выбор, покупка аппаратуры Уход за аппаратурой Техника, темы, жанры съемки Прочее фото-видео Товары и Услуги Идеи для подарков Техника для дома Прочие промтовары Сервис, уход и ремонт Прочие услуги Досуг, Развлечения Хобби Концерты, Выставки, Спектакли Охота и Рыбалка Клубы, Дискотеки Рестораны, Кафе, Бары Советы, Идеи Игры без компьютера Прочие развлечения Новый Год День Святого Валентина Восьмое марта Наука, Техника, Языки Гуманитарные науки Естественные науки Лингвистика Техника Работа, Карьера Написание резюме Подработка, временная работа Кадровые агентства Отдел кадров, HR Профессиональный рост Смена и поиск места работы Обстановка на работе Трудоустройство за рубежом Прочие карьерные вопросы Гороскопы, Магия, Гадания Гороскопы Гадания Сны Прочие предсказания Магия Юридическая консультация Административное право Гражданское право Конституционное право Семейное право Трудовое право Уголовное право Финансовое право Жилищное право Право социального обеспечения Военная служба Паспортный режим, регистрация Прочие юридические вопросы Юмор Золотой фонд Искусство и Культура Музыка Литература Кино, Театр Живопись, Графика Архитектура, Скульптура Прочие искусства Компьютерные и Видео игры Прочие Браузерные Клиентские Консольные Мобильные Программирование Другие языки и технологии Java JavaScript jQuery MySQL Perl PHP Python Веб-дизайн Верстка, CSS, HTML, SVG Системное администрирование Домашние задания Другие предметы Литература Математика Алгебра Геометрия Иностранные языки Химия Физика Биология История География Информатика Экономика Русский язык Обществознание Плесский колледж бизнеса и туризма Компания «Azimyt-K»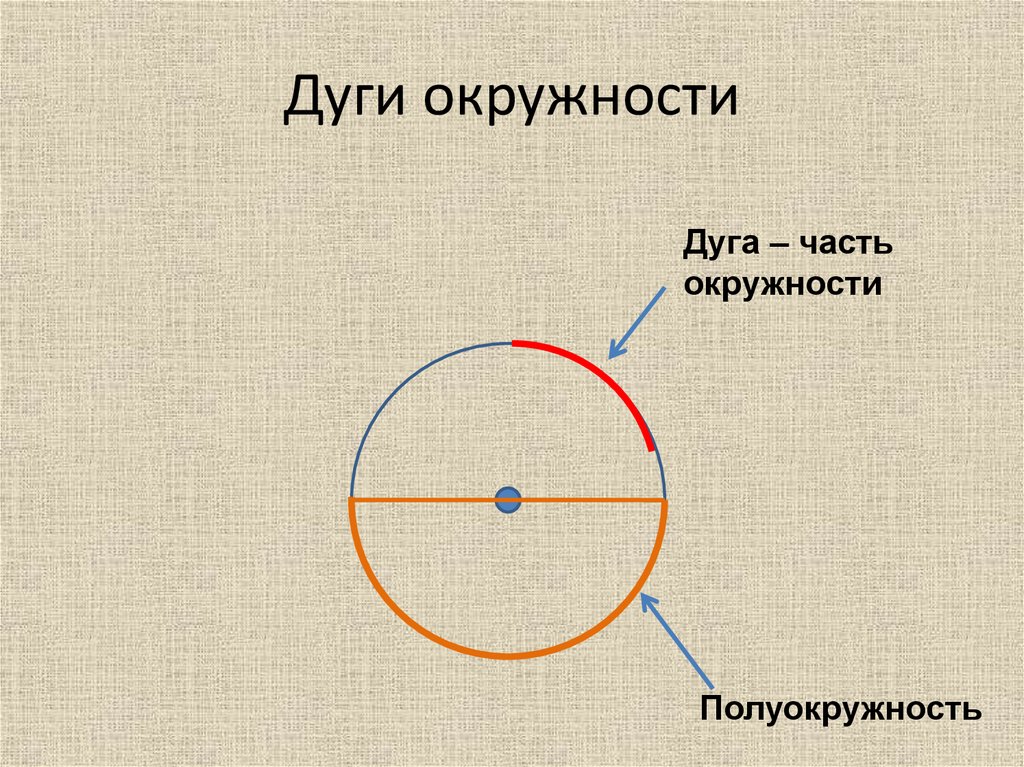 RuПочтаМой МирИгрыНовостиЗнакомстваПоискВсе проекты Вход в личный кабинет Помощь Обратная связь Полная версия Главная Все проекты
RuПочтаМой МирИгрыНовостиЗнакомстваПоискВсе проекты Вход в личный кабинет Помощь Обратная связь Полная версия Главная Все проекты была введена… … Энциклопедический словарь Ф. А. Брокгауза и И. А. Ефрона
была введена… … Энциклопедический словарь Ф. А. Брокгауза и И. А. Ефрона Хорда. 1 секущая, 2 хорда … Википедия
Хорда. 1 секущая, 2 хорда … Википедия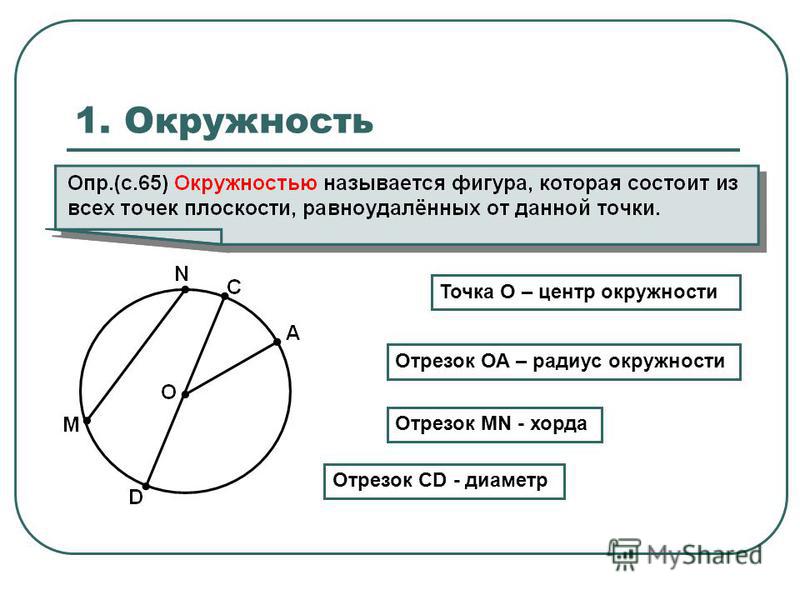 Содержание 1 Элементарная геометрия 2 Параметрические определения 3 Кривая Жордана … Википедия
Содержание 1 Элементарная геометрия 2 Параметрические определения 3 Кривая Жордана … Википедия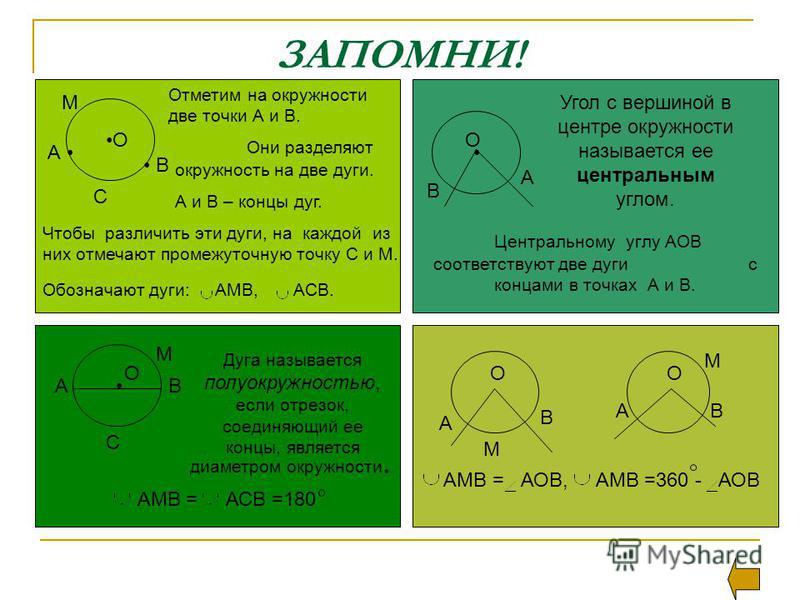 Геометрическая фигура, ограниченная окружностью, — это Круг:
Геометрическая фигура, ограниченная окружностью, — это Круг: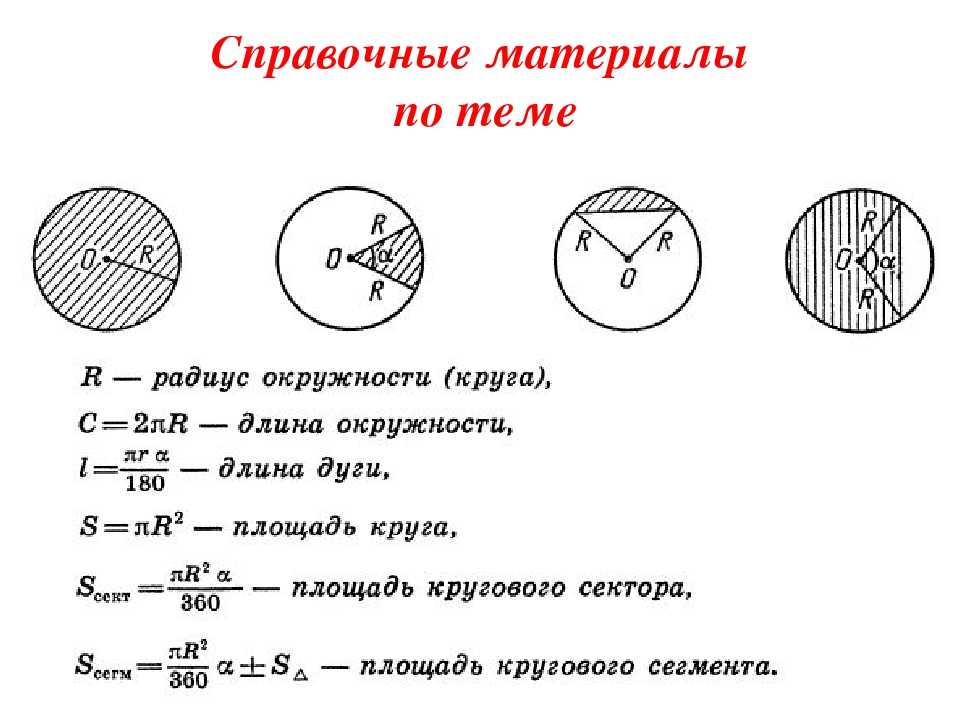
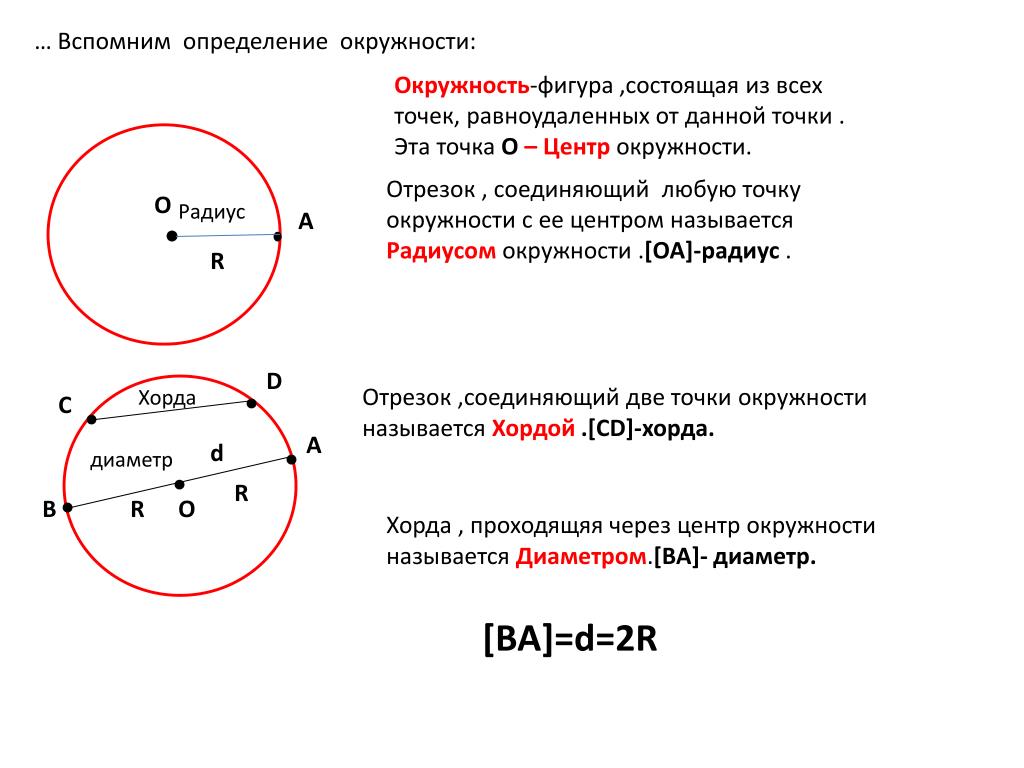 Дуга (теория графов) Другое Дуга (география) Дуга (анатомия) Дуга (физика) Дуга… … Википедия
Дуга (теория графов) Другое Дуга (география) Дуга (анатомия) Дуга (физика) Дуга… … Википедия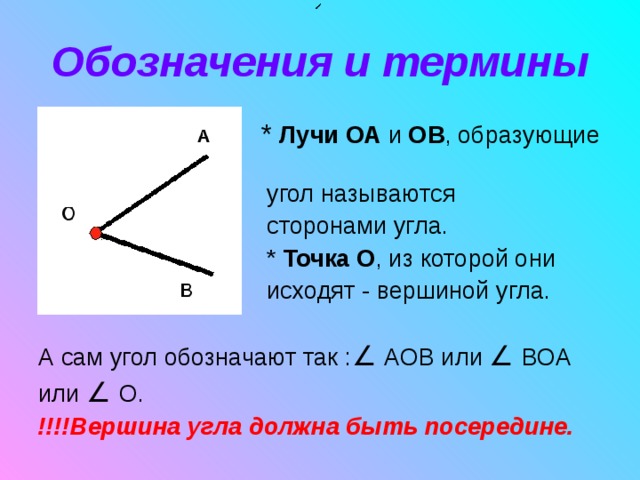 Всякая плоскость, пересекающая сферу, даёт в сечении… … Большая советская энциклопедия
Всякая плоскость, пересекающая сферу, даёт в сечении… … Большая советская энциклопедия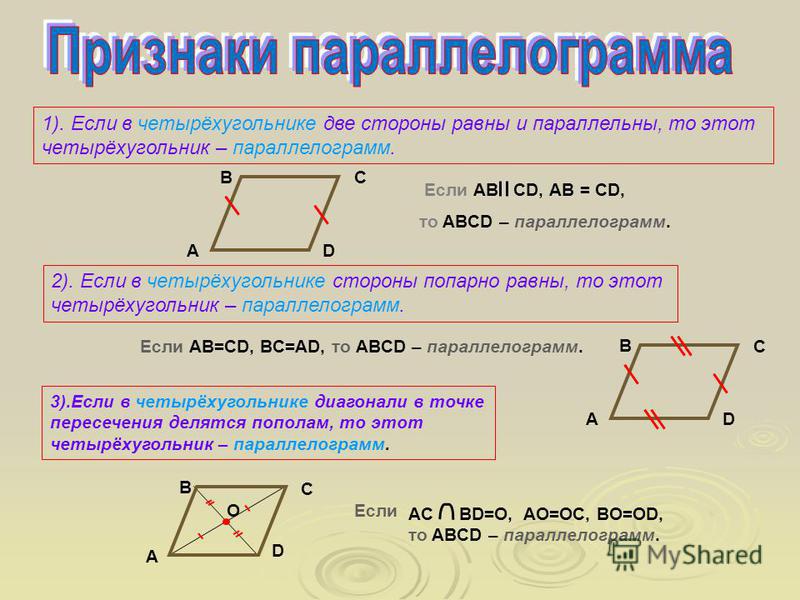 С 1629 в Нидерландах. Заложил основы аналитической геометрии, дал понятия переменной величины и функции, ввёл многие алгебраические… … Энциклопедический словарь
С 1629 в Нидерландах. Заложил основы аналитической геометрии, дал понятия переменной величины и функции, ввёл многие алгебраические… … Энциклопедический словарь
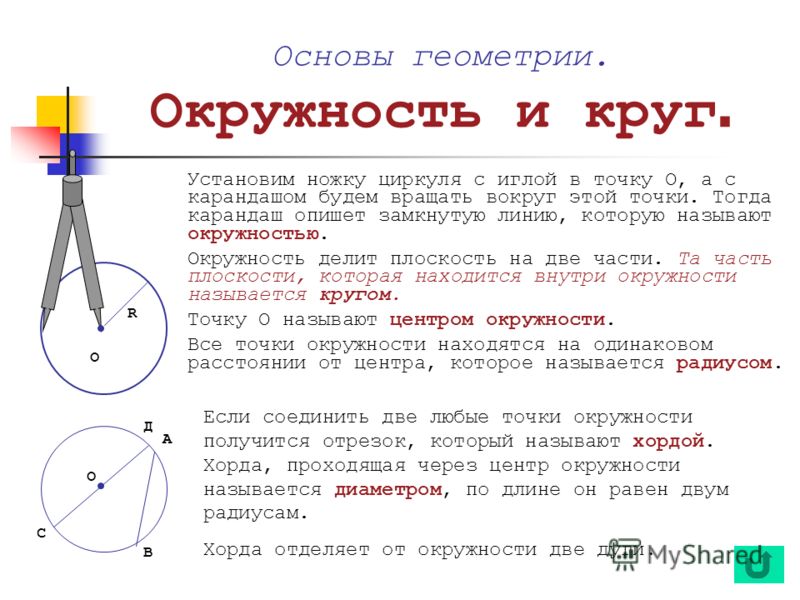 Весь представленный набор можно разделить на несколько групп:
Весь представленный набор можно разделить на несколько групп: Высвечивается несколько наименования разделов, необходимо нажать на «Символ» , где можно путем перелистывания за счет колеса мыши искать необходимый знак, либо в строке поиска выбрать категорию (статистические или математические) и найти знак. Прописной или заглавный символ высветится в рабочей области окна вставки , вам только стоит нажать правой кнопкой мыши «вставить» или «окей».
Высвечивается несколько наименования разделов, необходимо нажать на «Символ» , где можно путем перелистывания за счет колеса мыши искать необходимый знак, либо в строке поиска выбрать категорию (статистические или математические) и найти знак. Прописной или заглавный символ высветится в рабочей области окна вставки , вам только стоит нажать правой кнопкой мыши «вставить» или «окей».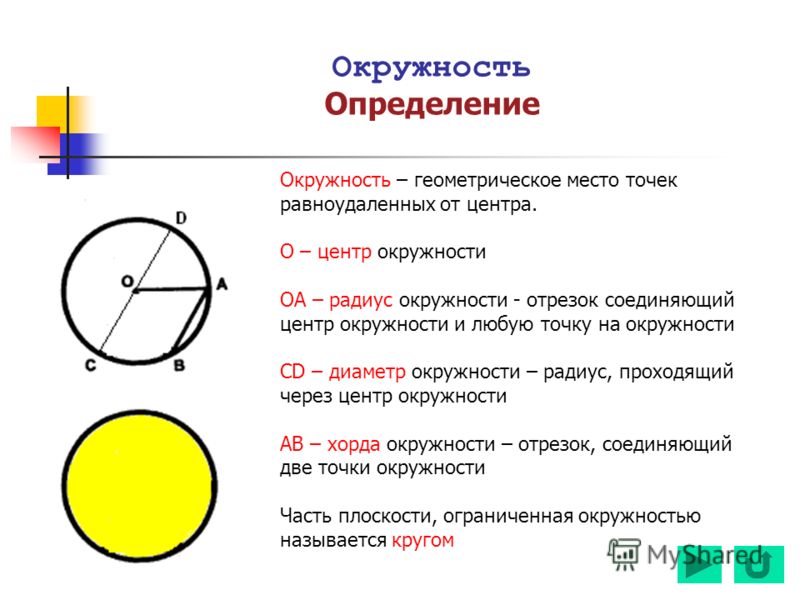

 д. Первые металлические аналоги современных подков (гиппосандалии) начали использоваться в Древнем Риме, а современный вид подкова приобрела, и их крепить металлическими гвоздями начали только в Средние века. У разных европейских народов есть собственное повествование о значении подковы, как символа удачи, благодати и счастья. Самая известная из них- это англосаксонская легенда о Св. Дунстане и Дьяволе. К будущему Кентерберийскому архиепископу Дунстану (909-988) явился сам дьявол и попросил подковать ему копыто. Дунстан, который был ещё и кузнецом, согласился на такую сделку. Однако подковал дьявола так крепко (по другому варианту легенды — приковал дьявола к стене), что тот, испытывая невероятную боль, попросил пощады. Взамен на свободу дьявол поклялся, что никогда не войдет в дверь, над которой висит подкова.
д. Первые металлические аналоги современных подков (гиппосандалии) начали использоваться в Древнем Риме, а современный вид подкова приобрела, и их крепить металлическими гвоздями начали только в Средние века. У разных европейских народов есть собственное повествование о значении подковы, как символа удачи, благодати и счастья. Самая известная из них- это англосаксонская легенда о Св. Дунстане и Дьяволе. К будущему Кентерберийскому архиепископу Дунстану (909-988) явился сам дьявол и попросил подковать ему копыто. Дунстан, который был ещё и кузнецом, согласился на такую сделку. Однако подковал дьявола так крепко (по другому варианту легенды — приковал дьявола к стене), что тот, испытывая невероятную боль, попросил пощады. Взамен на свободу дьявол поклялся, что никогда не войдет в дверь, над которой висит подкова. Весьма вероятно, что эта христианская версия значения подковы как оберегающего предмета, была перенята христианами у древних языческих кельтов, которые верили, что над дверьми прибита подкова в силе отразить вторжение Faery и других потусторонних гостей. На Британских островах это поверие очень сильно и до сих пор. Например, чтобы отогнать дьявола, подкова была зарыта в портале Стейнинфилдской церкви в Суффолке, шотландские моряки верят, что прибита к мачте подкова защищает его от бурь, такую же к мачте своего корабля распорядился прибить и легендарный адмирал Нельсон. Подкова спасала от попадания молнии и налёта ведьм, потому её вешали не только над дверьми или на дверях, но и везде, где злая сила могла попасть в дом (окна, камин, печь и т.д.).
Весьма вероятно, что эта христианская версия значения подковы как оберегающего предмета, была перенята христианами у древних языческих кельтов, которые верили, что над дверьми прибита подкова в силе отразить вторжение Faery и других потусторонних гостей. На Британских островах это поверие очень сильно и до сих пор. Например, чтобы отогнать дьявола, подкова была зарыта в портале Стейнинфилдской церкви в Суффолке, шотландские моряки верят, что прибита к мачте подкова защищает его от бурь, такую же к мачте своего корабля распорядился прибить и легендарный адмирал Нельсон. Подкова спасала от попадания молнии и налёта ведьм, потому её вешали не только над дверьми или на дверях, но и везде, где злая сила могла попасть в дом (окна, камин, печь и т.д.). Практически же, например, в Германии, подкову, для предотвращения возрождения казнённых ведьм, помещали на крышке гроба.
Практически же, например, в Германии, подкову, для предотвращения возрождения казнённых ведьм, помещали на крышке гроба. Интуитивная основа архетипичных глубин всплывает в простом народе не до конца осознанными повериями, за которыми кроется символизм первообразов, первосимволов, первосмыслов. И здесь по сути речь идёт не о подкове как о предмете для ковки лошадей, а о символическом образе «Подковы». Неком ограждённом пространстве, в котором обитает Нечто.
Интуитивная основа архетипичных глубин всплывает в простом народе не до конца осознанными повериями, за которыми кроется символизм первообразов, первосимволов, первосмыслов. И здесь по сути речь идёт не о подкове как о предмете для ковки лошадей, а о символическом образе «Подковы». Неком ограждённом пространстве, в котором обитает Нечто.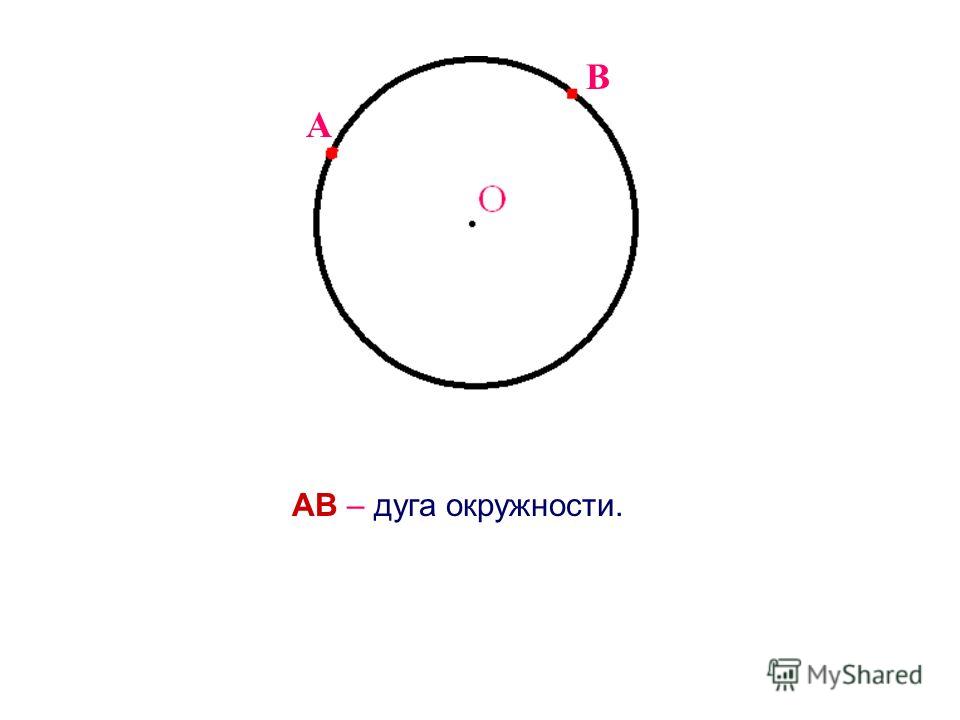 Таким образом человек, его родичи и дом находится как бы под священной защитой богини, а точнее — её материнской женственности.
Таким образом человек, его родичи и дом находится как бы под священной защитой богини, а точнее — её материнской женственности.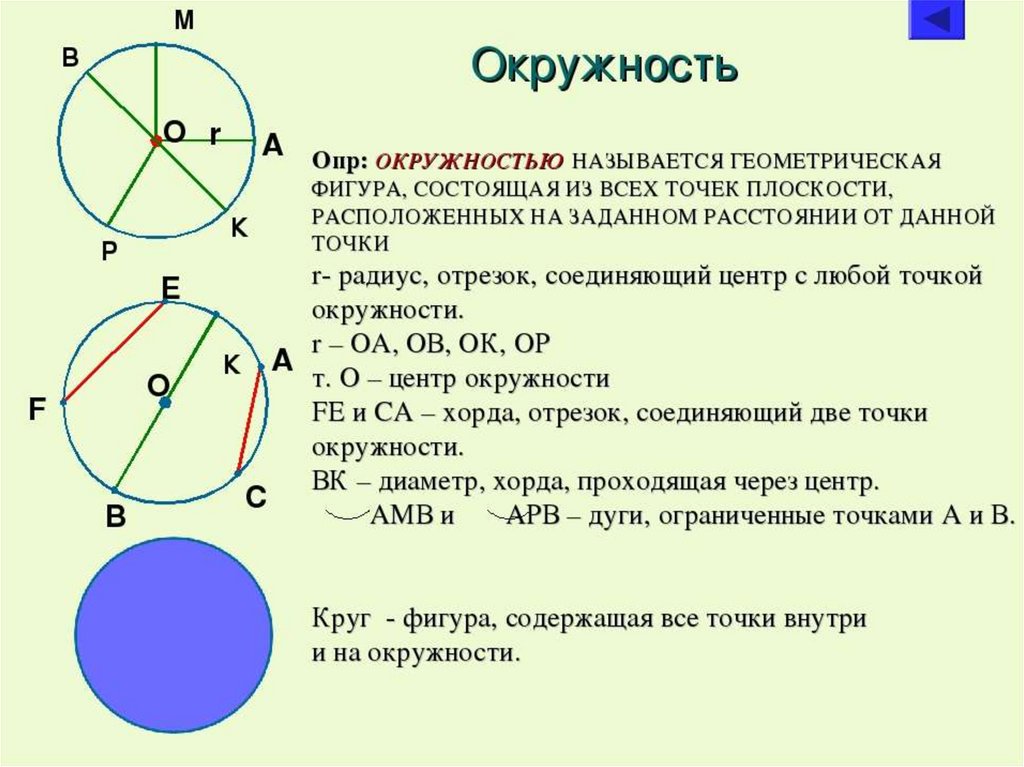
 Наличие кованых лошадей (о символике лошади во всех её аспектах можно написать сотни, тысячи страниц. Это была бы отдельная и гигантская по своим масштабам работа) показывало социальный статус владельца, богатство, стремление. Польский исследователь Папроцкий написал даже особое сочинение о подковах, как эмблемах в гербах, под заглавием «Strom czyli о herbach ze znakiem podkow». Большое об этом предмете рассуждение есть в конце Силезского гербовника (Stambuch szlezkie) того же автора (1609 г.). На различных гербах присутствуют как «одиночные подковы», так и подковы, как один из элементов герба: подкова и стрела, подкова в когтях сокола, подкова и кресты, подкова поверх восьмиконечной звезды и т.д.
Наличие кованых лошадей (о символике лошади во всех её аспектах можно написать сотни, тысячи страниц. Это была бы отдельная и гигантская по своим масштабам работа) показывало социальный статус владельца, богатство, стремление. Польский исследователь Папроцкий написал даже особое сочинение о подковах, как эмблемах в гербах, под заглавием «Strom czyli о herbach ze znakiem podkow». Большое об этом предмете рассуждение есть в конце Силезского гербовника (Stambuch szlezkie) того же автора (1609 г.). На различных гербах присутствуют как «одиночные подковы», так и подковы, как один из элементов герба: подкова и стрела, подкова в когтях сокола, подкова и кресты, подкова поверх восьмиконечной звезды и т.д. Математическое уравнение или выражение имеет одиночную пару квадратных, фигурных и других скобок, а также может использовать их некоторое количество.
Математическое уравнение или выражение имеет одиночную пару квадратных, фигурных и других скобок, а также может использовать их некоторое количество.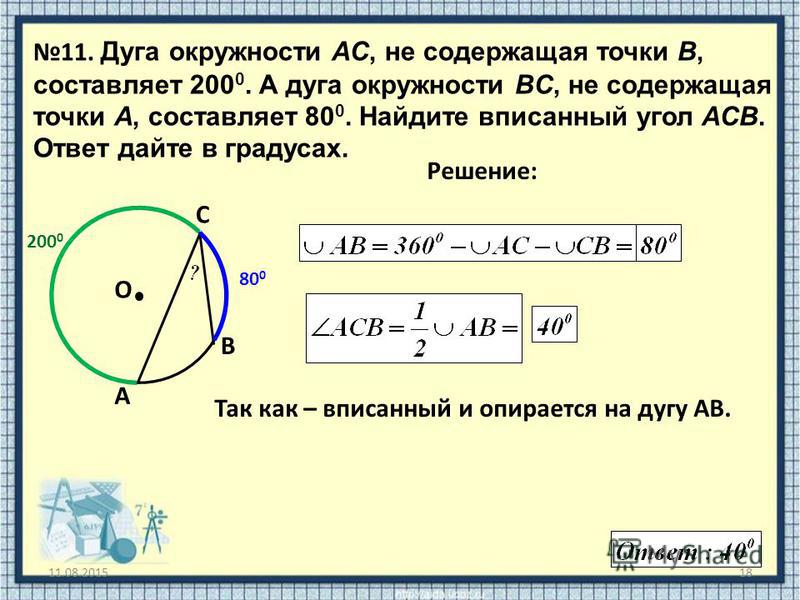 На компьютерной клавиатуре представлены все виды знаков препинания.
На компьютерной клавиатуре представлены все виды знаков препинания.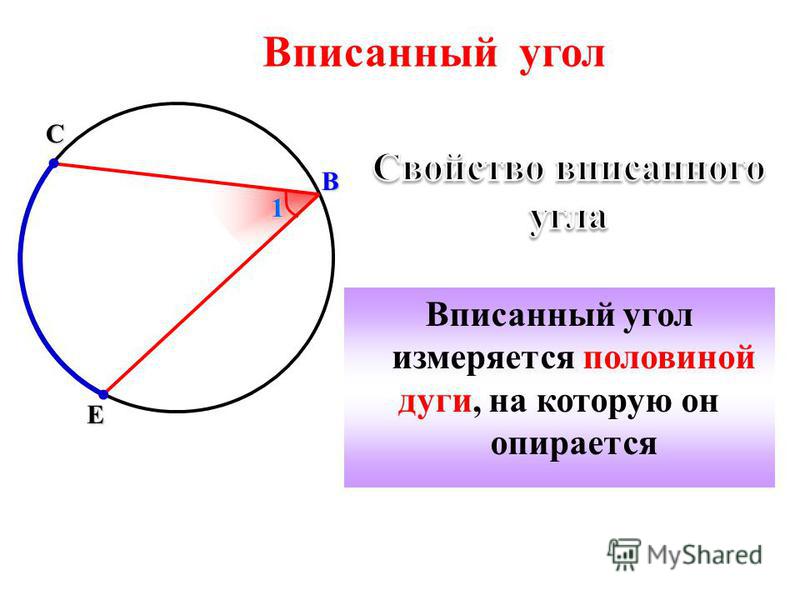
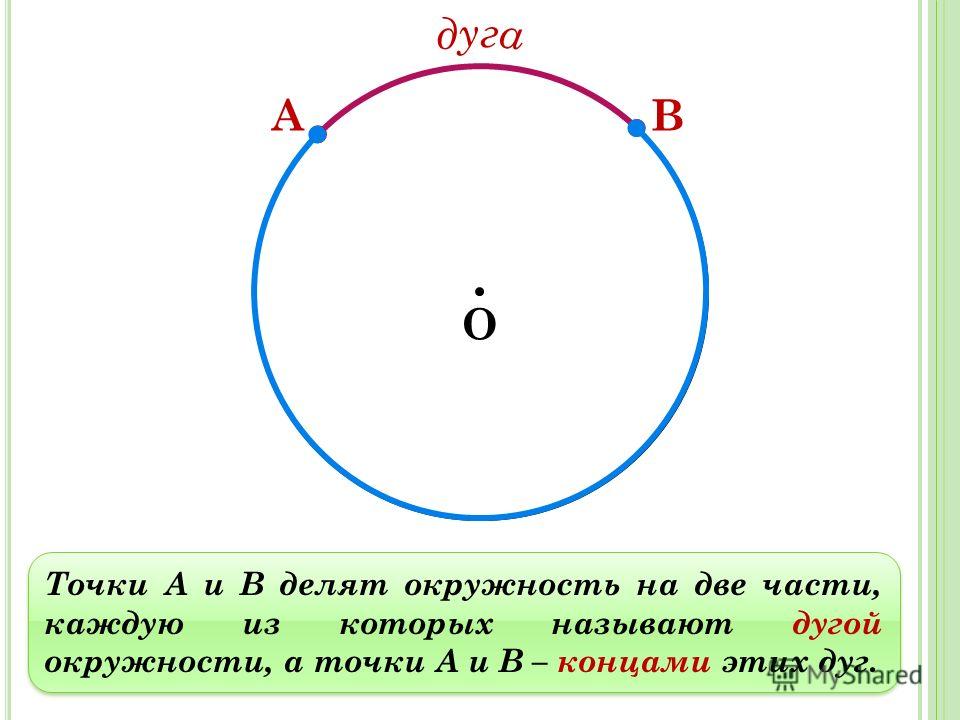

 Например, [x+11=2yy2−12=0
Например, [x+11=2yy2−12=0 Весь представленный набор можно разделить на несколько групп:
Весь представленный набор можно разделить на несколько групп: Математическое уравнение или выражение имеет одиночную пару квадратных, фигурных и других скобок, а также может использовать их некоторое количество.
Математическое уравнение или выражение имеет одиночную пару квадратных, фигурных и других скобок, а также может использовать их некоторое количество.