Шпаргалка: площадь многоугольников для геометрии 8 класса, формулы нахождения площади треугольника, квадрата, ромба, параллелограмма
31 августа, 2022
1 мин
Треугольник
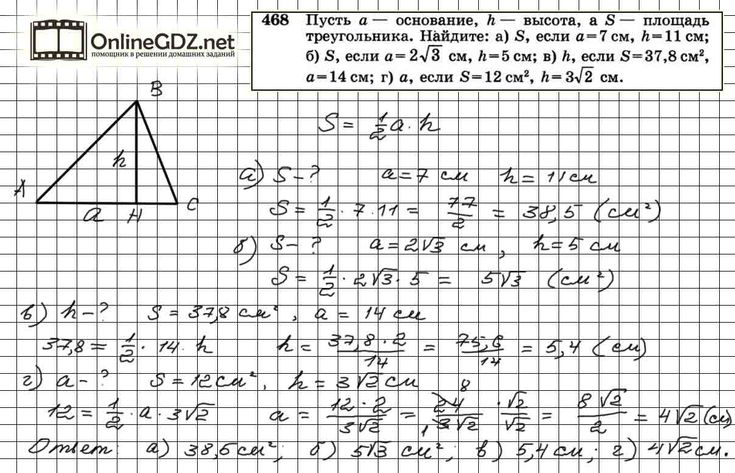
- Площадь треугольника по основанию и высоте: S=1/2 a⋅h
- Площадь треугольника по двум сторонам и углу между ними: S=1/ a⋅b⋅sinα
- Площадь треугольника по радиусу описанной окружности и трём сторонам: S = 4R/a⋅b⋅c
- Площадь треугольника по формуле Герона: S = √p(p — a)(p — b)(p — c). Где p — полупериметр, a,b,c — стороны треугольника.
- Площадь равностороннего треугольника по стороне: S = √3/4a²
- Площадь прямоугольного треугольника по двум катетам: S= ½ a • b
- Площадь прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность: S = d • e. Где d и e — отрезки гипотенузы.
Параллелограмм
- Площадь параллелограмма по основанию и высоте: S = a • h
- Площадь параллелограмма по двум сторонам и углу между ними: S = a⋅b⋅sinα
- Площадь параллелограмма по двум диагоналям и углу между этими диагоналями: S = 1/2⋅d1⋅d2⋅sinα
Ромб (он же параллелограмм, у которого все стороны равны и в который можно вписать окружность)
- Площадь ромба по вписанной окружности и стороне: S = 2 • a • r
Прямоугольник и квадрат
- Площадь прямоугольника через две стороны: S = a • b
- Площадь квадрата: S = a²
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!
Мы обязательно поправим!
Редакция Без Сменки
Честно. Понятно. С душой.
44 подписчиков
+ Подписаться
Редакция Без Сменки
15 июня, 2022
1 мин
Физ 🔬
Угловая скорость
Каждая точка вращающегося вокруг оси тела, проходящей через точку О, движется по окружности, и. ..
..
Редакция Без Сменки
13 июня, 2022
1 мин
Био 🦠
Эксперимент на догадках
Что здесь происходит? Давайте всмотримся детально в рисунок: 1️⃣ Солнышко в углу — значит…
Редакция Без Сменки
15 июня, 2022
1 мин
Инф 💻
Дел
📌 Необходимо найти наименьшее А при котором следующее неравенство будет истинно: (Дел(х, А)/\Дел…
Редакция Без Сменки
01 июля, 2022
1 мин
Лит 📚
Как отличить ямб от хорея?
Жили-были два потомственных котика 🐈🐈: старый, пожилой, очень знаменитый котик Иван и совсем ещё. ..
..
Подпишитесь на еженедельную рассылку полезных материалов про ЕГЭ, высшее образование и вузы и получите скидку на курсы Вебиума
Домашняя работа по геометрии за 9 класс к учебнику «Геометрия. 7-9 класс» А.В.Погорелов§14. Площади фигур
Решебники и ГДЗ
Начните вводить часть условия (например, могут ли, чему равен или найти):
- № 1. Докажите, что сумма площадей квадратов, построенных на катетах прямоугольного треугольника, равна площади квадрата, построенного на гипотенузе.
- № 2. Стороны двух участков земли квадратной формы равны 100 ми 150 м. Найдите сторону квадратного участка, равновеликого им.
- № 3. Найдите площадь квадрата S по его диагонали а.
- № 4. Во сколько раз площадь квадрата, описанного около окружности, больше площади квадрата, вписанного в ту же окружность?
- № 5. Как изменится площадь квадрата, если каждую его сторону увеличить в 3 раза?
- № 6.
 Во сколько раз надо уменьшить стороны квадрата, чтобы его площадь уменьшилась в 25 раз?
Во сколько раз надо уменьшить стороны квадрата, чтобы его площадь уменьшилась в 25 раз? - № 7. Чему равны стороны прямоугольника, если они относятся как 4:9, а его площадь 144 м2?
- № 8. Чему равны стороны прямоугольника, если его периметр 74 дм, а площадь 3 м2 ?
- № 9. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если площадь его равна половине площади прямоугольника.
- № 10. Квадрат и ромб имеют одинаковые периметры. Какая из фигур имеет большую площадь? 0бъясните ответ.
- № 11. Найдите площадь ромба, если его высота 10 см, а острый угол 30°.
- № 12. Найдите площадь ромба, если его высота 12 см, а меньшая диагональ 13 см.
- № 13. Докажите, что площадь ромба равна половине произведения диагоналей.
- № 14. Найдите, стороны ромба, зная, что его диагонали относятся как 1:2, а площадь ромба равна 12 см2.
- № 15. Разделите данный треугольник на три равновеликие части прямыми, проходящими через одну вершину.

- № 16*. Решите предыдущую задачу, взяв вместо треугольника параллелограмм.
- № 17. Чему равна площадь равнобедренного треугольника, если его основание 120 м, а боковая сторона 100 м? ΔАВС — равнобедренный, АВ = ВС = 100 м, АС = 120 м.
- № 18. Найдите площадь равнобедренного прямоугольного треугольника с гипотенузой а. Рассмотрим ΔАВС, ∠С = 90°, ВС = АС, АВ = а — гипотенуза.
- № 19. У треугольника со сторонами 8 см и 4 см проведены высоты к этим сторонам. Высота, проведенная к стороне 8 см, равна 3 см. Чему равна высота, проведенная к стороне 4 см?
- № 20. Докажите, что стороны треугольника обратно пропорциональны его высотам, т.е.:
- № 21. Найдите площадь равностороннего треугольника со стороной а.
- № 22. Найдите площадь правильного треугольника, вписанного вкруг радиуса 5.
- № 23. Найдите площадь прямоугольного треугольника, если его высота делит гипотенузу на отрезки 32 см и 18 см.
- № 24.
 Чему равны катеты прямоугольного треугольника, если его гипотенуза равна 73 см, а площадь равна 1320 см2?
Чему равны катеты прямоугольного треугольника, если его гипотенуза равна 73 см, а площадь равна 1320 см2? - № 25. У треугольника ABС АС = а, ВС = E. При каком угле С площадь треугольника будет наибольшей?
- № 26. Найдите площадь равнобедренного треугольника, у которого боковые стороны равны 1 м, а угол между ними равен 70°.
- № 27. Найдите площадь параллелограмма, если его стороны 2 ми 3 м, а один из углов равен 70°.
- № 28*. Найдите площадь треугольника по стороне a и прилежащим к ней углам а и b.
- № 29. Выведите формулу Герона для площади треугольника:
- № 30. Найдите площадь треугольника по трем сторонам:
- № 31. Стороны треугольника а, b, с. Найдите высоту треугольника, опущенную на сторону с.
- № 32. Боковые стороны треугольника 30 см и 25 см. Найдите высоту треугольника, опущенную на основание, равное: 1) 25 см; 2) 11 см.
- № 33. Периметр равнобедренного треугольника равен 64 см, а его боковая сторона на 11 см больше основания.
 Найдите высоту треугольника, опущенную на боковую сторону.
Найдите высоту треугольника, опущенную на боковую сторону. - № 35. Найдите высоту треугольника со сторонами
- № 36. Найдите наименьшую высоту треугольника со сторонами: 1) 5, 5, 6; 2) 17,65, 80 и наибольшую высоту
- № 37. Найдите площадь трапеции, у которой параллельные стороны 60 см и 20 см, а непараллельные — 13 см и 37 см.
- № 38. В равнобокой трапеции основания равны 10 см и 24 см, боковая сторона 25 см. Найдите площадь трапеции.
- № 39. В равнобокой трапеции большее основание равно 44 м, боковая сторона 17 ми диагональ 39 м. Найдите площадь трапеции.
- № 41*. Докажите, что среди всех параллелограммов сданными диагоналями наибольшую площадь имеет ромб.
- № 42. Выведите следующие формулы для радиусов описанной (R) и вписанной (r) окружностей треугольника:
- № 43. Найдите радиусы описанной (5) и вписанной (г) окружностей для треугольника со сторонами: 1) 13, 14, 15; 2) 15, 13, 4; 3) 35, 29, 8; 4) 4, 5, 7.
 1) а = 13, b = 14, с = 15. Полупериметр треугольника:
1) а = 13, b = 14, с = 15. Полупериметр треугольника: - № 44. Боковая сторона равнобедренного треугольника 6 см, высота, проведенная к основанию, 4 см. Найдите радиус описанной окружности. Пусть АВС — равнобедренный треугольник, АВ = ВС =
- № 45. Найдите радиусы окружностей описанной около равнобедренного треугольника с основанием а и боковой стороной b и вписанной в него.
- № 46. Найдите радиус г вписанной и радиус 5 описанной окружностей для равнобедренного треугольника с основанием 10 см и боковой стороной 13 см.
- № 47. Докажите, что в прямоугольном треугольнике радиус вписанной окружности равен половине разности между суммой катетов и гипотенузой.
- № 48. Катеты прямоугольного треугольника равны 40 см и 42 см. Найдите радиусы описанной и вписанной окружностей.
- № 49. Докажите, что площадь многоугольника, описанного около окружности, равна половине произведения периметра многоугольника на радиус окружности.
- № 50.
 Через середину высоты треугольника проведена перпендикулярная к ней прямая. В каком отношении она делит площадь треугольника? Пусть ΔАВС, ВН — высота, ВО = ОН.
Через середину высоты треугольника проведена перпендикулярная к ней прямая. В каком отношении она делит площадь треугольника? Пусть ΔАВС, ВН — высота, ВО = ОН. - № 51. Прямая, перпендикулярная высоте треугольника, делит его площадь пополам. Найдите расстояние от этой прямой до вершины треугольника, из которой проведена высота, если она равна А.
- № 52. Периметры правильных n-угольников относятся как а:b. Как относятся их площади?
- № 53. Найдите площадь круга, если длина окружности l.
- № 54. Найдите площадь кругового кольца, заключенного между двумя окружностями с одним и тем же центром и радиусами: 1) 4 см и 6 см; 2) 5,5 ми 6,5 м; 3) а и b, а > b.
- № 55. Во сколько раз увеличится площадь круга, если его диаметр увеличить: 1) в 2 раза; 2) в 5 раз; 3) в m раз? Если диаметр увеличить в n раз, то радиус увеличится тоже в n раз, тогда площадь увеличится в n2 раз.
- № 56. Найдите отношение площади круга к площади вписанного в него: 1) квадрата; 2) правильного треугольника; 3) правильного шестиугольника.
 1) Пусть ABCD — квадрат, вписанный вкруг.
1) Пусть ABCD — квадрат, вписанный вкруг. - № 57. Найдите отношение площади круга, вписанного в правильный треугольник, к площади круга, описанного около него.
- № 58. Найдите отношение площади круга, описанного около квадрата, к площади круга,вписанного в него.
- № 59. Найдите площадь сектора круга радиуса R, если соответствующий этому сектору центральный угол равен: 1) 40°; 2) 90°; 3) 150°; 4) 240°; 5) 300°; 6) 330°.
- № 60. Дана окружность радиуса 5. Найдите площадь сектора, соответствующего дуге с длиной, равной: 1) R, 2) l.
- № 61*. Найдите площадь кругового сегмента с основанием a√3 и высотой — a/2.
- № 62. Найдите площадь той части круга, которая расположена вне вписанного в него: 1) квадрата; 2) правильного треугольника; 3) правильного шестиугольника. Радиус круга 5. 1)
Поиск по сайту
Геометрия Часть 7: Площадь и периметр
Автор: cindyelkins
C. Elkins, OK Math and Reading Lady
Сегодняшняя тема — измерение площади и периметра.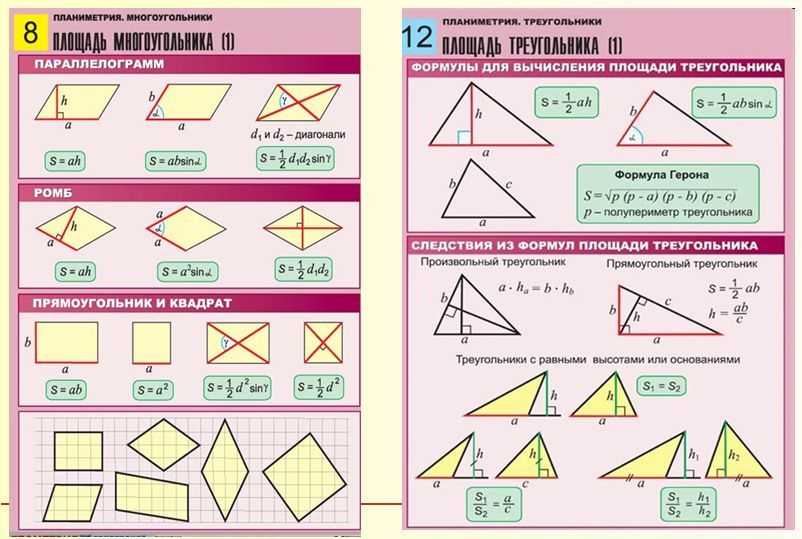 Хотя их можно считать стандартами измерения, они тесно связаны с геометрией (например, атрибуты прямоугольника). Прочтите предыдущие посты в моей серии «Геометрия» (составление и разложение), чтобы узнать о других упоминаниях площади и периметра.
Хотя их можно считать стандартами измерения, они тесно связаны с геометрией (например, атрибуты прямоугольника). Прочтите предыдущие посты в моей серии «Геометрия» (составление и разложение), чтобы узнать о других упоминаниях площади и периметра.
Неправильные представления открывают окно в детское мышление. Если мы заранее узнаем о неправильных представлениях, мы можем направить наше обучение и направления, чтобы помочь студентам избежать их. Я рассмотрю несколько неправильных представлений и некоторые стратегии и/или уроки, которые могут их исправить. Заблуждения № 1-2 появляются в этом посте. Заблуждения № 3-5 будут представлены в посте на следующей неделе.
Заблуждение №1: Учащийся слышит это: «Мы используем площадь для измерения внутри фигуры и периметр для измерения вокруг фигуры».
- Проблема: Учащийся не знает, как применить это определение к реальным ситуациям, требующим измерения площади и/или периметра.
- Проблема: Учащийся может подумать: «Поскольку периметр измеряет внешний край, то площадь означает измерение внутреннего края».

- Проблема: Учащиеся путают два термина.
Идеи:
Заблуждение № 2 : Учащийся слышит это: «Чтобы найти площадь, умножьте длину на ширину».
- Проблема: Учащийся не знает правила умножения.
- Проблема: Учащийся не знает, какие размеры являются длиной и шириной.
Идеи:
- Хорошее руководство: длина l — это l верхняя сторона. Ширина — самая короткая сторона.
- Длина и ширина равны двум , примыкающих к сторонам (не противоположным сторонам).
- Покажите, как разбить прямоугольник на квадраты. Если прямоугольник имеет размер 4″ x 2″, покажите им, как сделать 4 столбца и 2 строки. Смотрите, как они это делают. Многие ученики рисовали внутри 4 вертикальные линии, чтобы получились столбцы, и 2 горизонтальные линии, чтобы получились строки. Это, очевидно, приведет к набору квадратов 5 x 3, но учащиеся не всегда проверяют.
 Знают ли они — «Чтобы разделить прямоугольник на 4 столбца, мне нужно провести всего 3 линии». Теперь подсчет квадратов — не самый эффективный метод, но он может помочь учащимся, которые борются с концепцией или фактами умножения.
Знают ли они — «Чтобы разделить прямоугольник на 4 столбца, мне нужно провести всего 3 линии». Теперь подсчет квадратов — не самый эффективный метод, но он может помочь учащимся, которые борются с концепцией или фактами умножения. - Некоторые прямоугольники слишком велики, чтобы в них можно было рисовать квадраты. Если учащиеся не знают фактов умножения, прямоугольник можно разделить на 2 (или более) меньших прямоугольника, используя известные им факты. Затем площадь каждого меньшего прямоугольника складывается вместе, чтобы найти общую площадь. Для примера см. изображение под . Опять же, учащиеся должны подключиться к геометрии, чтобы понять, что противоположные стороны прямоугольника равны.
- Пример. Прямоугольник имеет размеры 8 x 7. Используя более известные факты, разбейте одно из измерений на 2 слагаемых (например, разбейте 7 на 5 + 2). Разделите прямоугольник на 2 прямоугольника и используйте 5 + 2, чтобы обозначить одну сторону (вместо 7). Используя концепцию распределительного свойства, учащийся вычисляет следующее: 8 x 7 = 8 (5 + 2) = (8 x 5) + (8 x 2) = 40 + 16 = 56 кв.
 единиц.
единиц.
- Пример. Прямоугольник имеет размеры 8 x 7. Используя более известные факты, разбейте одно из измерений на 2 слагаемых (например, разбейте 7 на 5 + 2). Разделите прямоугольник на 2 прямоугольника и используйте 5 + 2, чтобы обозначить одну сторону (вместо 7). Используя концепцию распределительного свойства, учащийся вычисляет следующее: 8 x 7 = 8 (5 + 2) = (8 x 5) + (8 x 2) = 40 + 16 = 56 кв.
Заблуждение №3: Учащийся видит только 2 заданных числа на изображении прямоугольника и не знает, складывать их или умножать.
- Проблема: Учащийся не знает свойств прямоугольника, применимых к этой ситуации, — что противоположные стороны равны по размеру.
- Проблема: Учащийся не понимает, как подсчет квадратов может помочь в вычислении площади и периметра.
Заблуждение № 4: Учащийся слышит следующее: «Запишите размер площади как квадратных дюймов , а размер периметра как дюймов». Примечание. Это относится к использованию таких единиц измерения, как см, футы, метры, ярды, мили и т. д.
- Проблема: Учащийся не понимает разницы между квадратными и неквадратными измерениями.
Заблуждение №5: Учащиеся думают, что между площадью и периметром может существовать связь.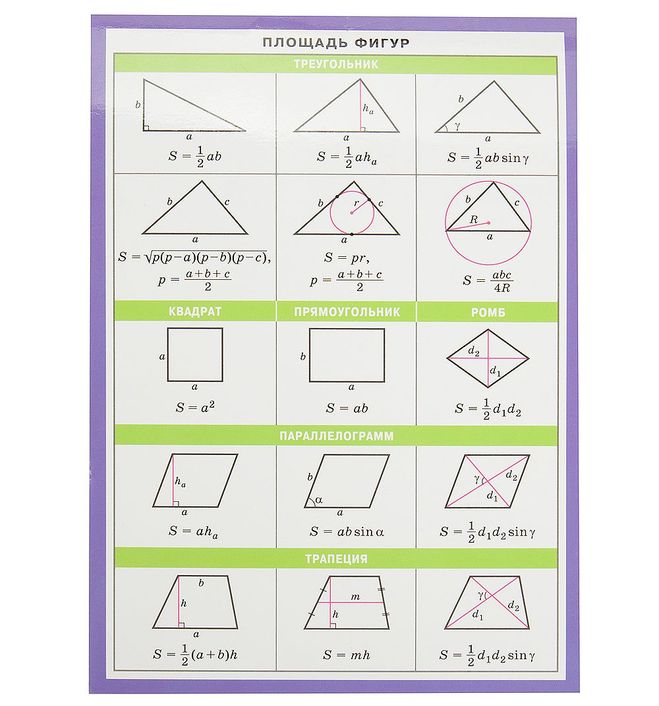 Они могут думать, что все фигуры с одинаковой площадью имеют одинаковый периметр.
Они могут думать, что все фигуры с одинаковой площадью имеют одинаковый периметр.
- Проблема. Это означает, что если одна фигура имеет площадь 12 квадратных дюймов и периметр 16 дюймов, они могут подумать, что все фигуры с площадью 12 имеют периметр 16 дюймов.
Следующее сообщение: Идеи по устранению заблуждений № 3, 4 и 5 и ссылки на действия в области и по периметру!! Оставайтесь с нами
Рубрика: Площадь и периметр, Геометрия / Измерение, Математика
Tagged площадь, геометрия, математические заблуждения, измерение, периметр
· 16 февраля
Базовая геометрия – Как найти площадь сложных фигур – Complete Test Preparation Inc.
- Сообщение от Брайан Стокер
- Дата 9 октября 2017 г.
Как найти площадь сложных фигур
Сложные фигуры можно разделить на несколько меньших фигур, для которых известна формула периметра или площади, а затем сложить их.
Пример.
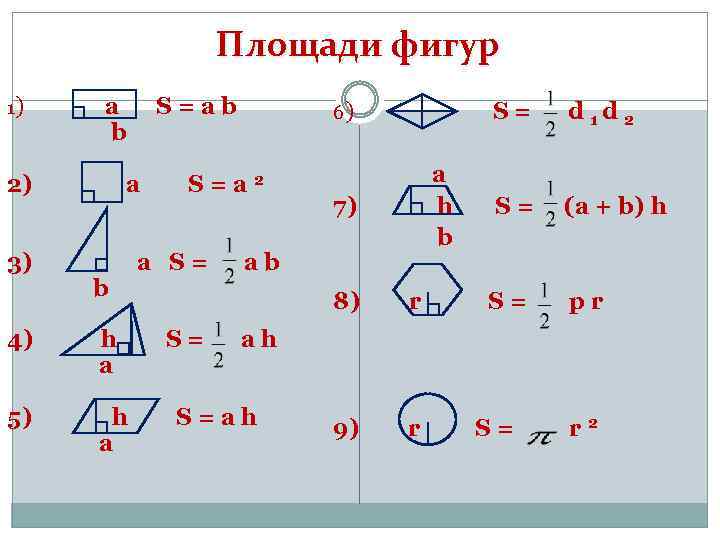 Составные двухмерные фигуры
Составные двухмерные фигуры
Чтобы определить площадь любой составной фигуры, просто введите ADD площади каждой составной базовой фигуры. Обязательно запишите свой окончательный ответ в квадратных единицах.
Определить площадь заданной фигуры.
Исходную форму можно перерисовать как прямоугольник и треугольник. У прямоугольников противоположные стороны конгруэнтны (совершенно одинаковые).
Площадь Составной = Площадь Треугольник + Площадь Прямоугольник
Площадь Треугольник = (1/2)(Основание)(Высота) = (1/2)(3м)(1,5м) = 2,25 м 2
Площадь Прямоугольник = (Основание)(Высота) = (3 м)(1,5 м) = 4,5 м 2
Площадь Композит = (2,25 м 2 ) + (4,5 м 2 ) = 6,75 м
06 2 Как найти площадь сложной фигуры Чтобы определить площадь поверхности любого составного тела, просто добавьте площадей поверхности каждого составного основного тела. Вы также должны вычесть площадь любой внутренней грани. Обязательно запишите свой окончательный ответ в квадратных единицах.
Вы также должны вычесть площадь любой внутренней грани. Обязательно запишите свой окончательный ответ в квадратных единицах.
Пример. Определить площадь поверхности данной фигуры. Оставьте окончательный ответ в терминах числа пи.
Исходная форма может быть перерисована в виде цилиндра и конуса. Нам придется вычесть площадь круга, где встречаются фигуры, из каждого уравнения площади поверхности, потому что они находятся «внутри» твердого тела.
SurfaceArea Composite = S.Area Конус + S.Area Цилиндр
S.Area Cone = (Basic Area)+(1/2)(ightPerimeter) )(dπ)(h) = (1/2)(6π)(2) = 6π футов 2
S. Площадь Цилиндр = 2(Площадь основания)+(Периметр)(Высота) = (πr 2 )+(dπ)(h) = (π3 2 )+(6π)( 5) = 39π FT 2
S.Area Композит = (6π FT 2 ) + (39π FT 2 ) = 45π FT 2
.
 вопросы по геометрии на стандартизированных тестах:
вопросы по геометрии на стандартизированных тестах: - Решить недостающий угол или сторону
- Нахождение площади или периметра различных фигур (например, треугольников, прямоугольников, кругов)
- Задачи с использованием теоремы Пифагора
- Расчет свойств геометрических фигур, таких как углы, прямые углы или параллельные стороны
- Расчет объема или площади поверхности сложных форм, например сфер, цилиндров или конусов
- Решение геометрических преобразований, таких как вращение, перемещение или отражение
Самые популярные вопросы по геометрии
Общие вопросы по геометрии в стандартизированных тестах:
- Найдите недостающий угол или сторону
- Нахождение площади или периметра различных фигур (например, треугольников, прямоугольников, кругов)
- Задачи с использованием теоремы Пифагора
- Расчет свойств геометрических фигур, таких как углы, прямые углы или параллельные стороны
- Расчет объема или площади поверхности сложных форм, например сфер, цилиндров или конусов
- Решение геометрических преобразований, таких как вращение, перемещение или отражение
Автор: , Брайан Стокер, Массачусетс, Complete Test Preparation Inc.

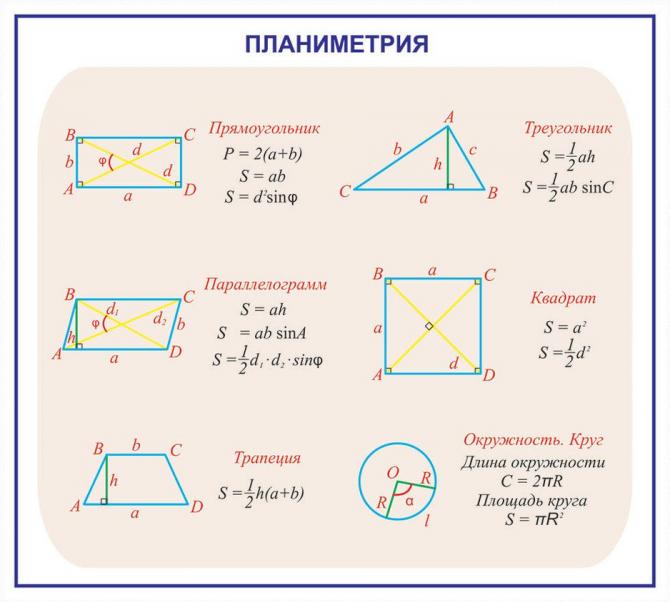 Во сколько раз надо уменьшить стороны квадрата, чтобы его площадь уменьшилась в 25 раз?
Во сколько раз надо уменьшить стороны квадрата, чтобы его площадь уменьшилась в 25 раз?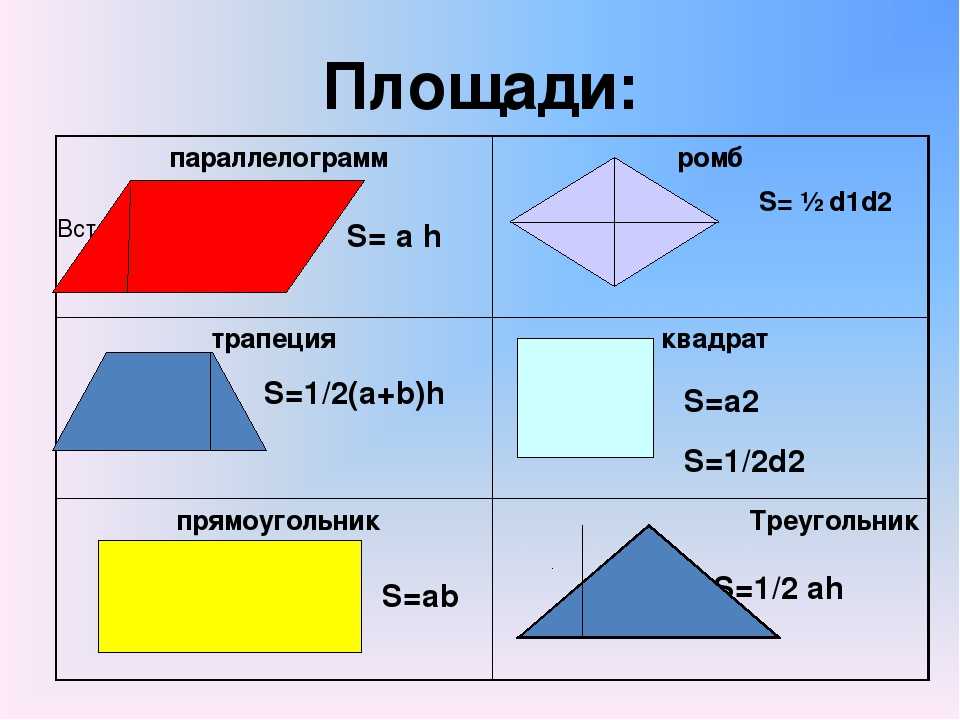
 Чему равны катеты прямоугольного треугольника, если его гипотенуза равна 73 см, а площадь равна 1320 см2?
Чему равны катеты прямоугольного треугольника, если его гипотенуза равна 73 см, а площадь равна 1320 см2? Найдите высоту треугольника, опущенную на боковую сторону.
Найдите высоту треугольника, опущенную на боковую сторону.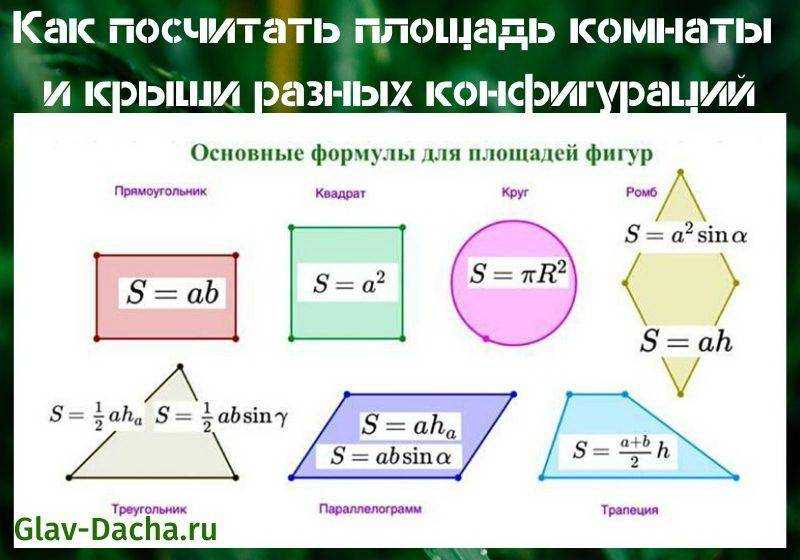 1) а = 13, b = 14, с = 15. Полупериметр треугольника:
1) а = 13, b = 14, с = 15. Полупериметр треугольника: Через середину высоты треугольника проведена перпендикулярная к ней прямая. В каком отношении она делит площадь треугольника? Пусть ΔАВС, ВН — высота, ВО = ОН.
Через середину высоты треугольника проведена перпендикулярная к ней прямая. В каком отношении она делит площадь треугольника? Пусть ΔАВС, ВН — высота, ВО = ОН.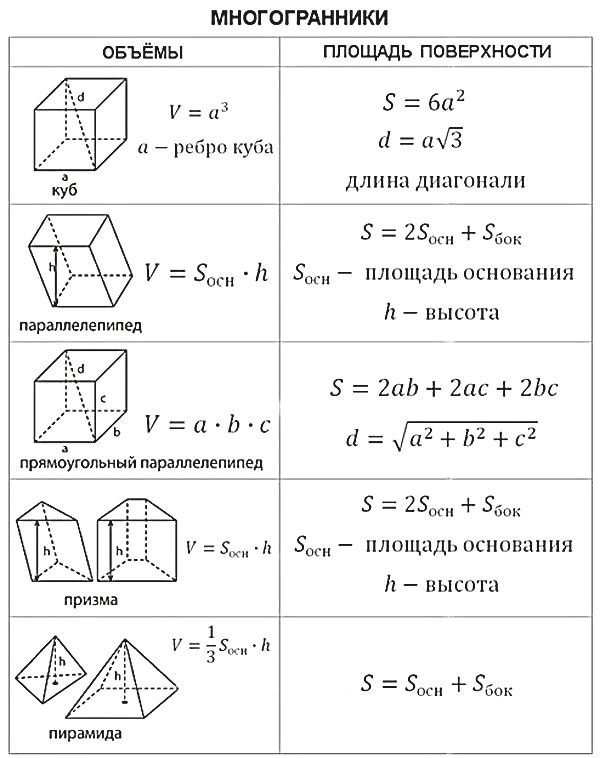 1) Пусть ABCD — квадрат, вписанный вкруг.
1) Пусть ABCD — квадрат, вписанный вкруг.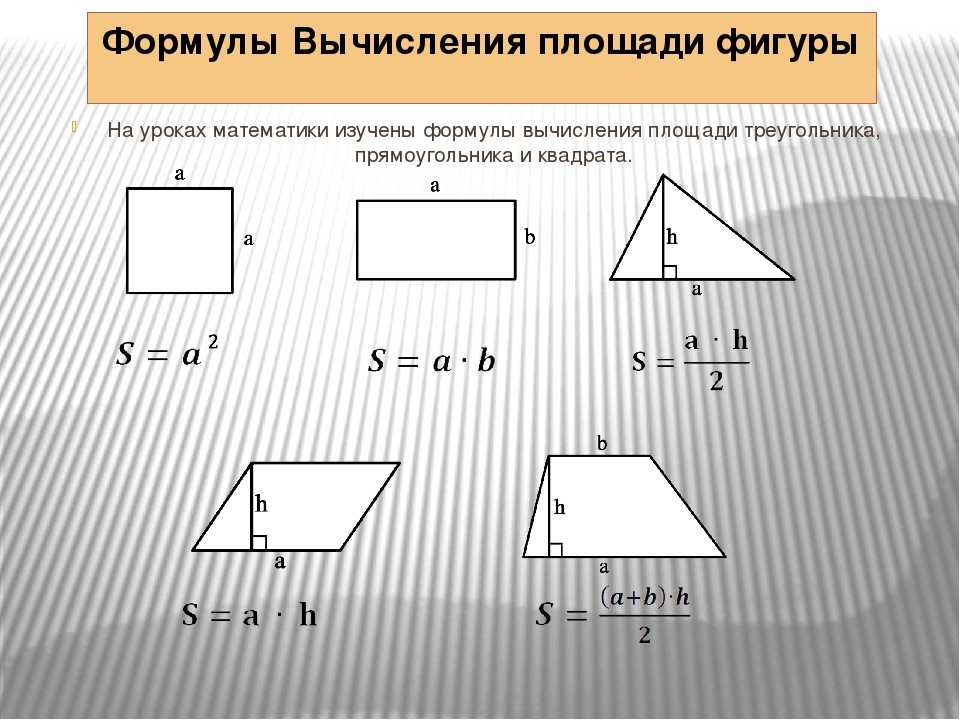
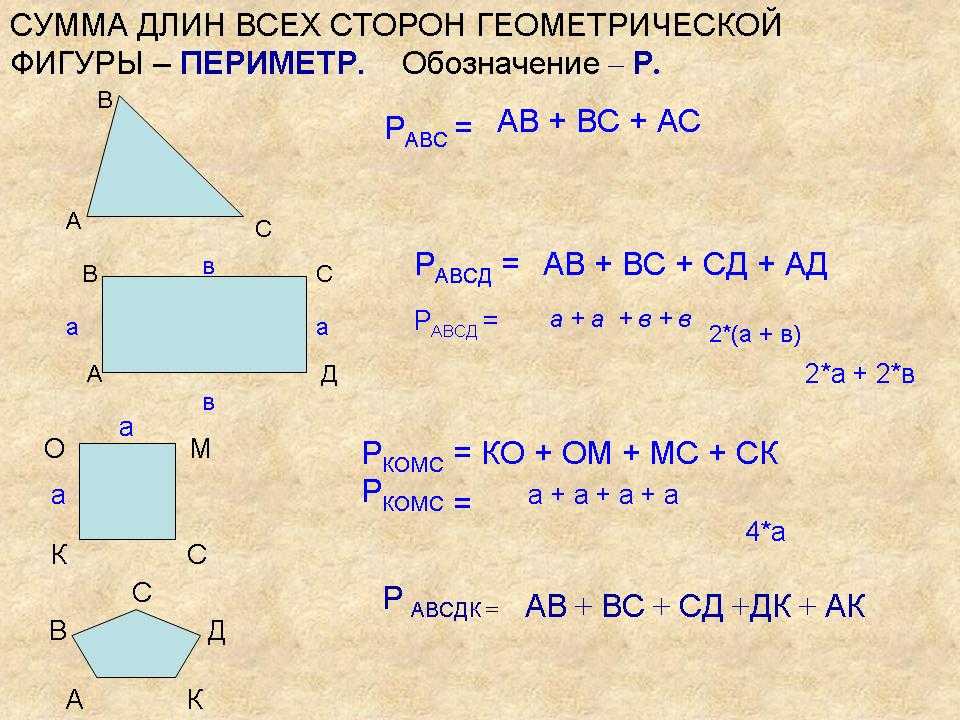 Знают ли они — «Чтобы разделить прямоугольник на 4 столбца, мне нужно провести всего 3 линии». Теперь подсчет квадратов — не самый эффективный метод, но он может помочь учащимся, которые борются с концепцией или фактами умножения.
Знают ли они — «Чтобы разделить прямоугольник на 4 столбца, мне нужно провести всего 3 линии». Теперь подсчет квадратов — не самый эффективный метод, но он может помочь учащимся, которые борются с концепцией или фактами умножения. единиц.
единиц.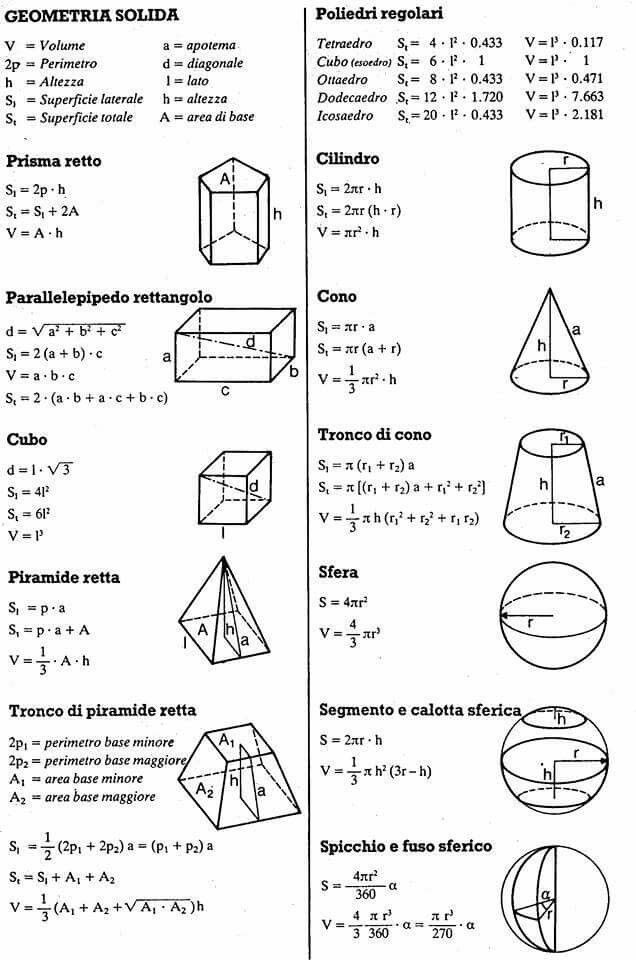
 Введите свой запрос:
Введите свой запрос: Free xml sitemap generator
Free xml sitemap generator Формула площади прямоугольника
Формула площади прямоугольника Формула площади квадрата
Формула площади квадрата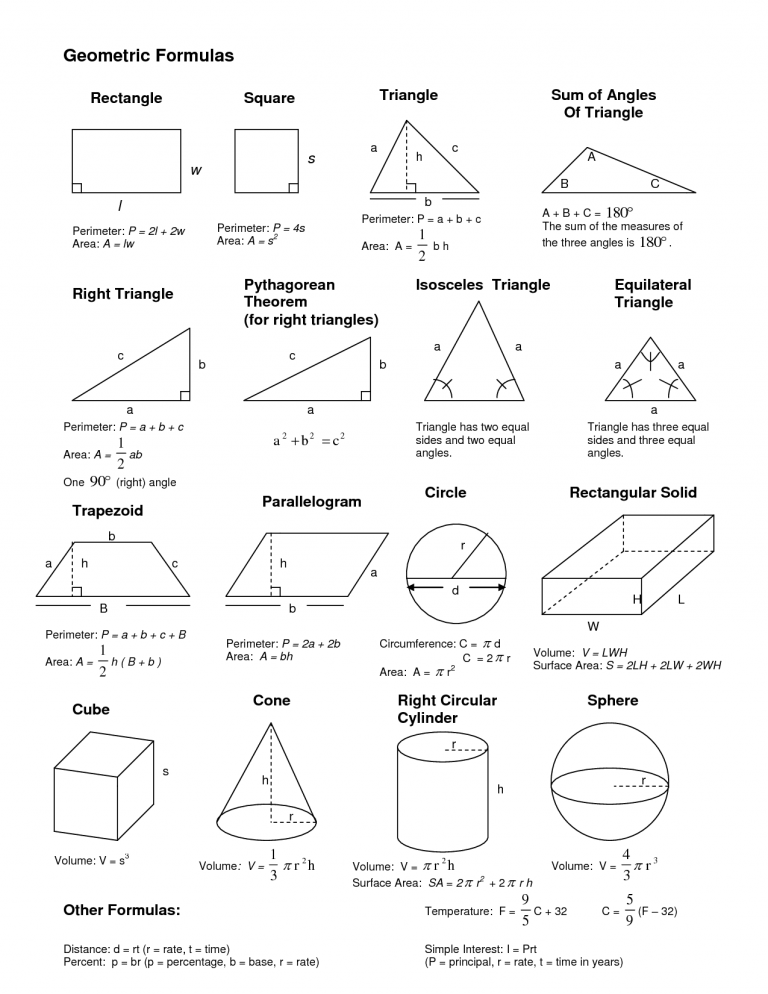 Назовите единицы измерения площадей.
Назовите единицы измерения площадей.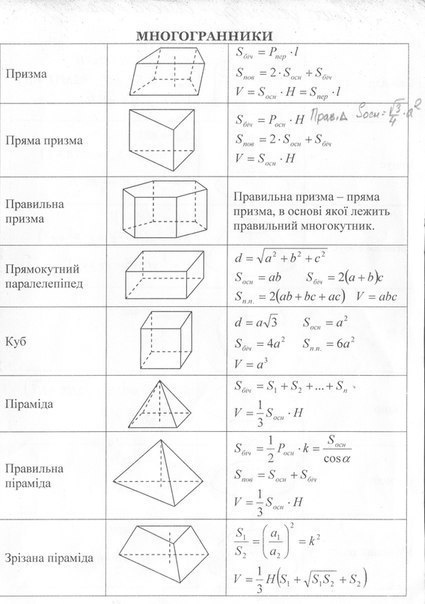
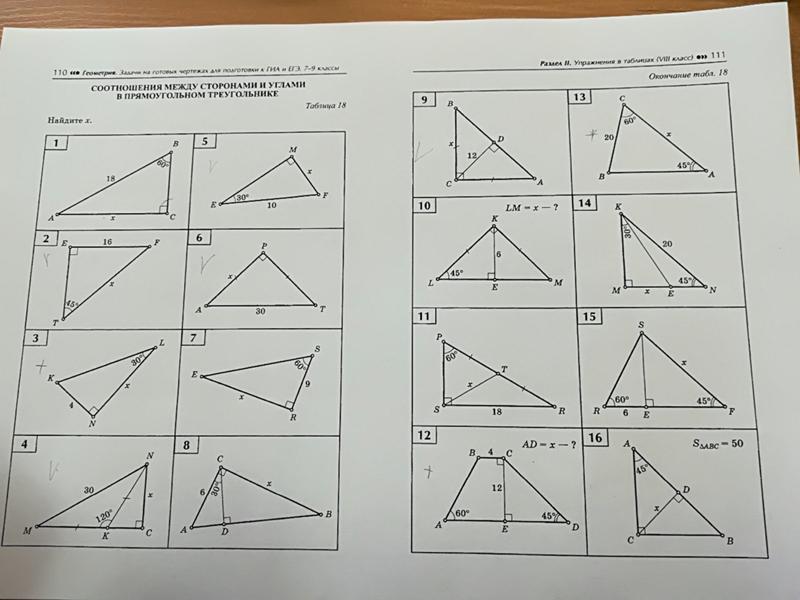
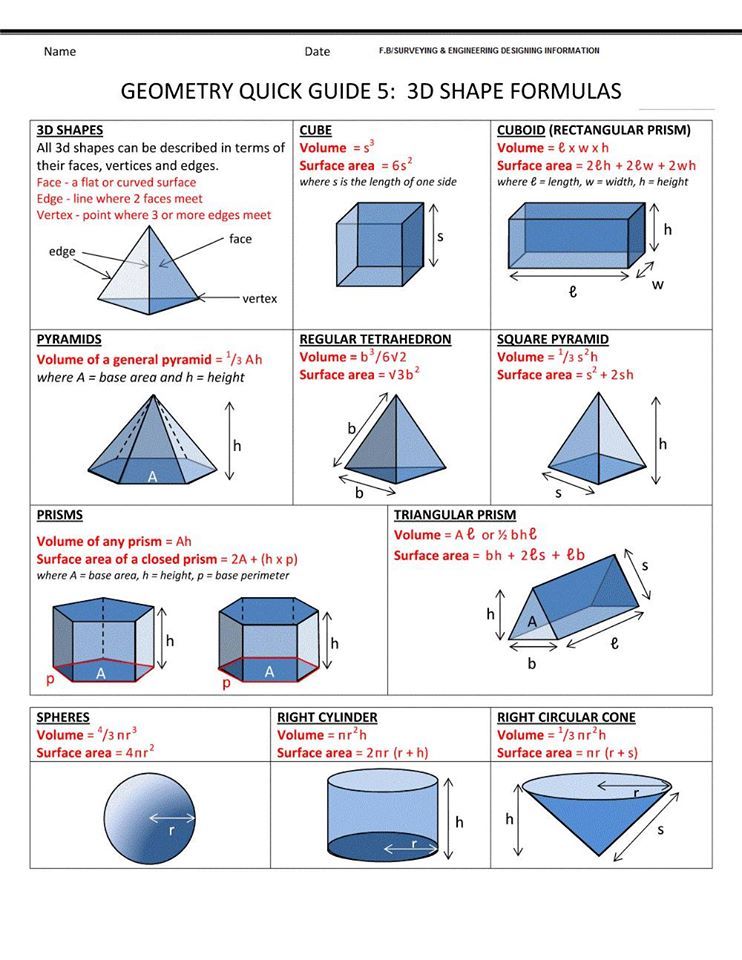 ЗАДАЧА4
ЗАДАЧА4
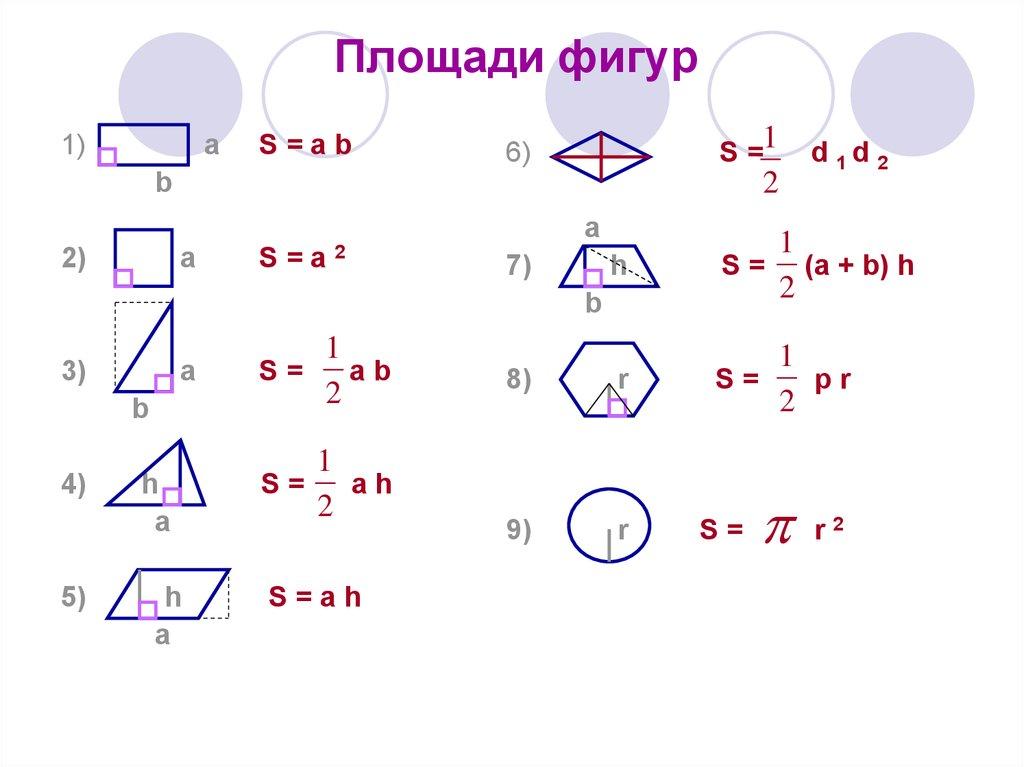 Важно уметь находить объемы таких твердых тел.
Важно уметь находить объемы таких твердых тел.
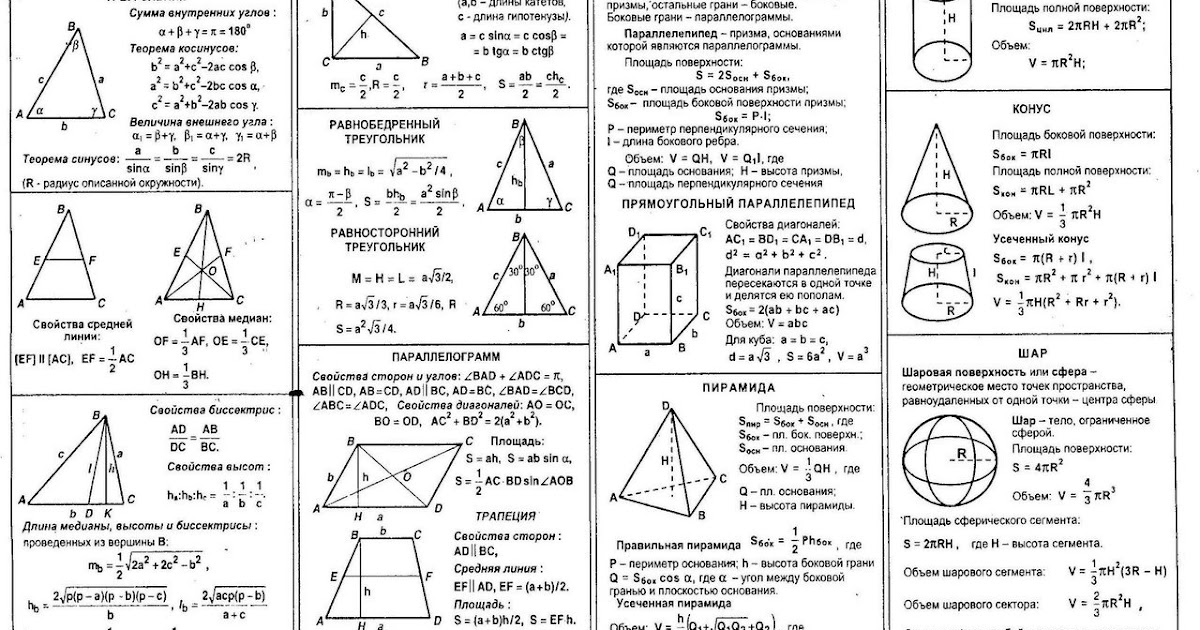 У нас тогда есть два треугольника, оба с высотой h, и один с основанием a, и один с основанием b.
У нас тогда есть два треугольника, оба с высотой h, и один с основанием a, и один с основанием b.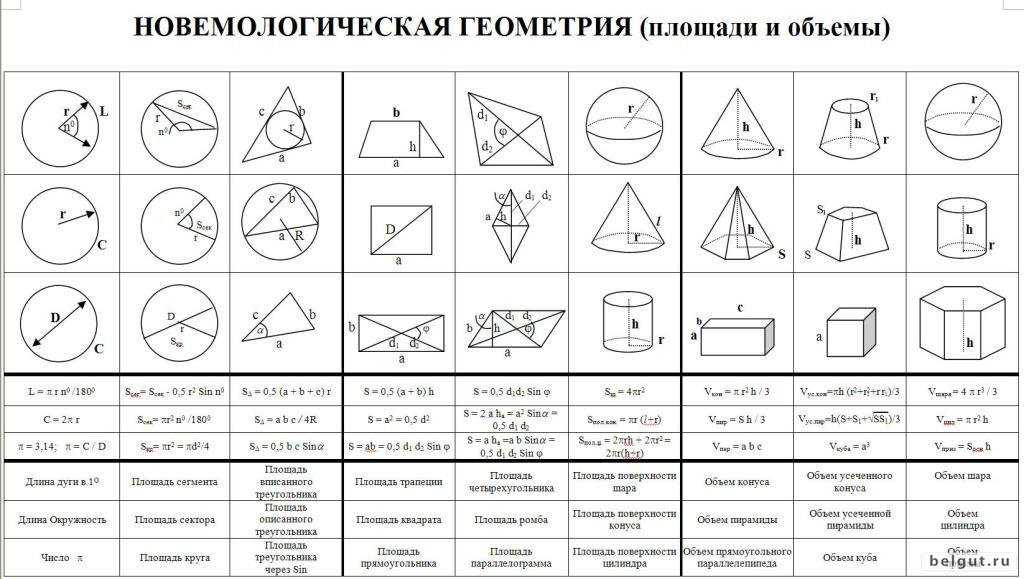

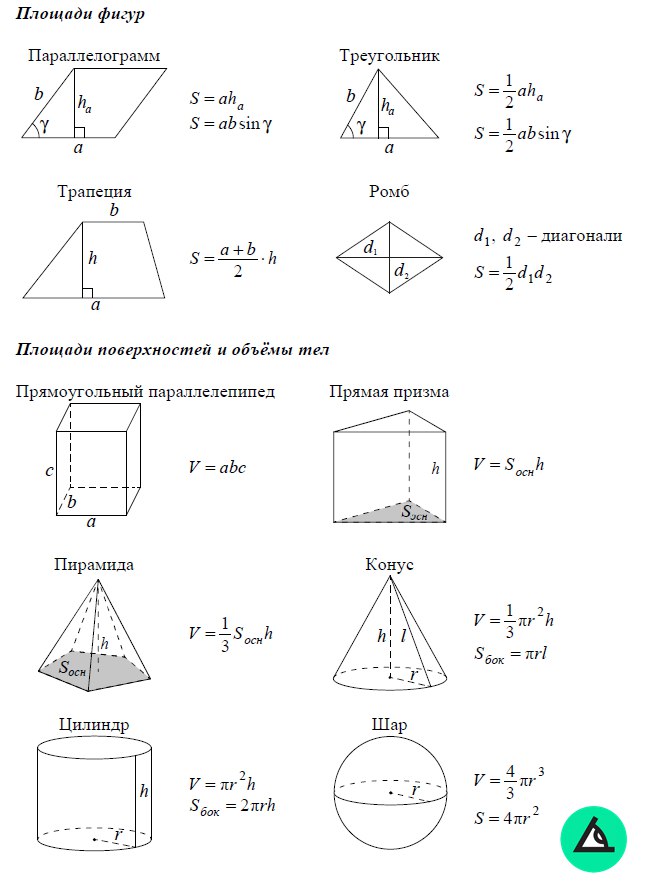
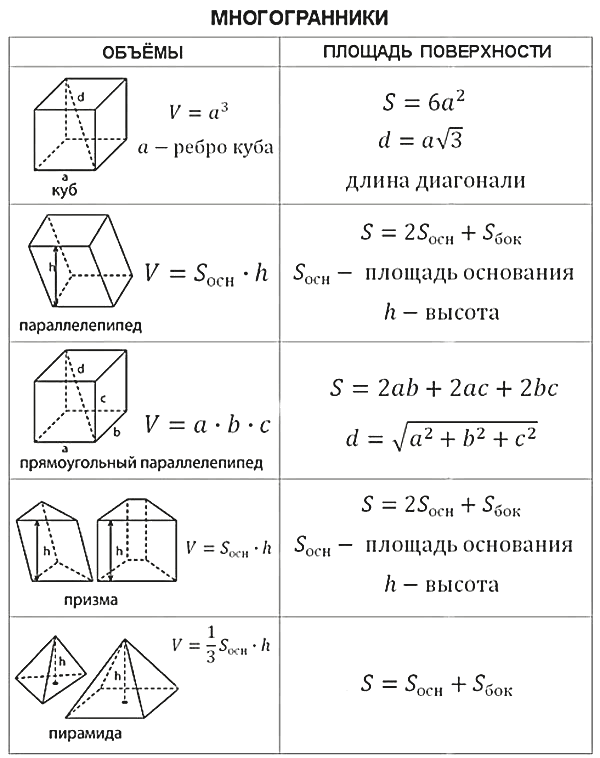 Это означает, что когда на основание поставлена прямая призма, все стенки представляют собой вертикальные прямоугольники. Обычно мы говорим «призма», когда на самом деле имеем в виду «правильную призму». Призма имеет однородное поперечное сечение. Это означает, что когда вы делаете срезы твердого тела параллельно основанию, вы получаете многоугольники, конгруэнтные основанию. Таким образом, площадь каждого среза всегда одинакова. В прямоугольной призме поперечное сечение всегда прямоугольник.
Это означает, что когда на основание поставлена прямая призма, все стенки представляют собой вертикальные прямоугольники. Обычно мы говорим «призма», когда на самом деле имеем в виду «правильную призму». Призма имеет однородное поперечное сечение. Это означает, что когда вы делаете срезы твердого тела параллельно основанию, вы получаете многоугольники, конгруэнтные основанию. Таким образом, площадь каждого среза всегда одинакова. В прямоугольной призме поперечное сечение всегда прямоугольник.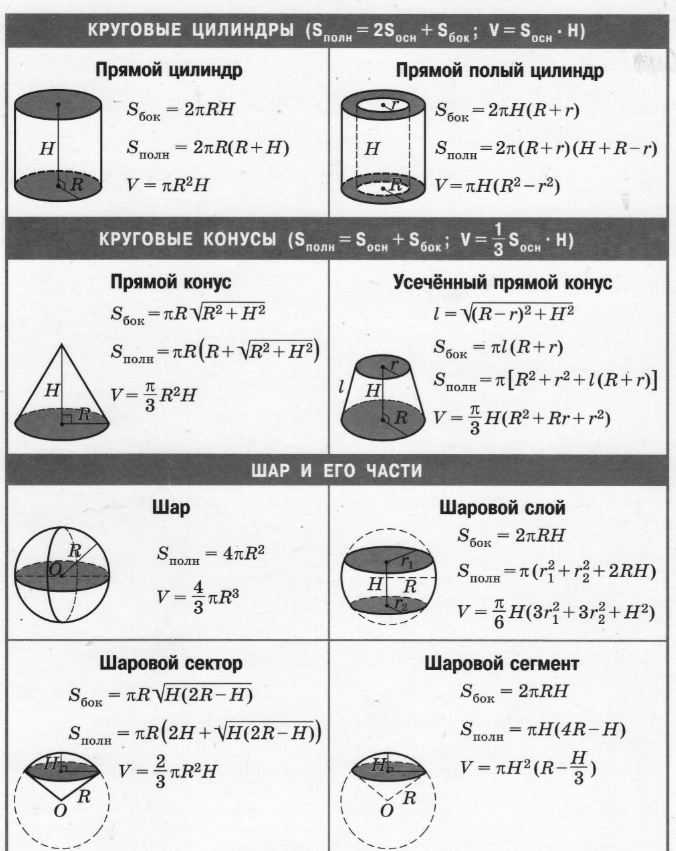

 Например, консервы обычно поставляются в банках цилиндрической формы.
Например, консервы обычно поставляются в банках цилиндрической формы.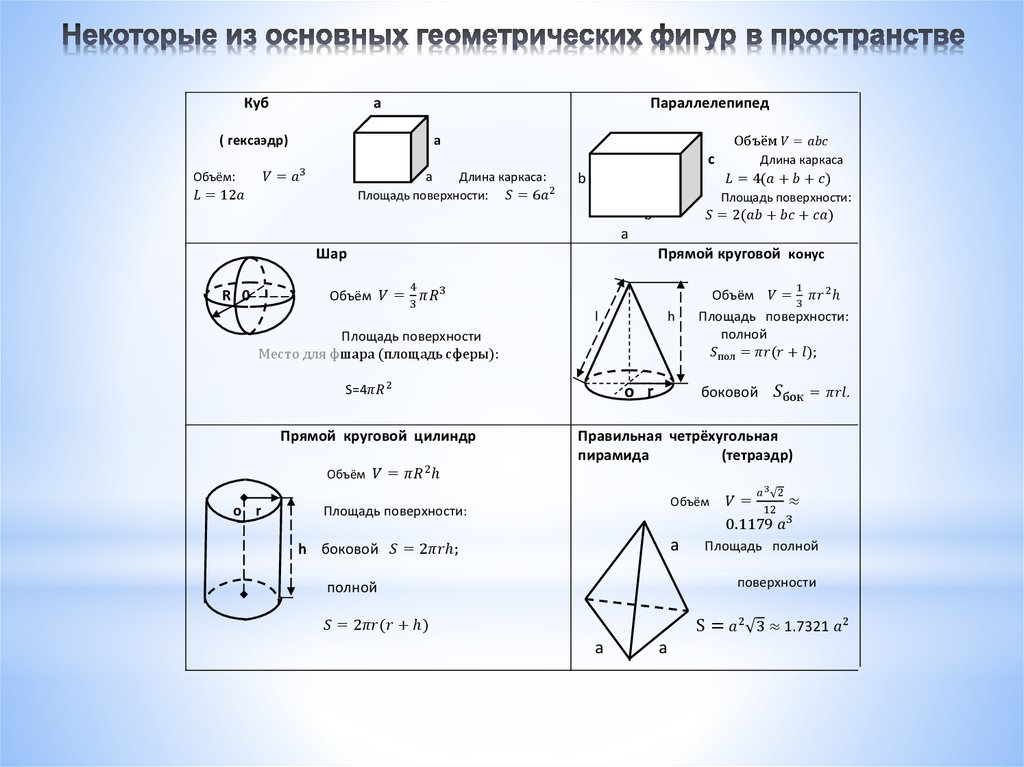

 Мы также видели в модуле по кругам, что площадь круга определяется выражением A = π r2, где r — радиус. Чтобы понять площадь фигуры, которая не ограничена ни прямыми линиями, ни дугами окружности, нам понадобится интегральное исчисление. Хотя эти идеи восходят к Архимеду и Евдоксу, систематическое развитие интегрального исчисления принадлежит Ньютону и Лейбницу.
Мы также видели в модуле по кругам, что площадь круга определяется выражением A = π r2, где r — радиус. Чтобы понять площадь фигуры, которая не ограничена ни прямыми линиями, ни дугами окружности, нам понадобится интегральное исчисление. Хотя эти идеи восходят к Архимеду и Евдоксу, систематическое развитие интегрального исчисления принадлежит Ньютону и Лейбницу. Объем конуса равен одной трети объема соответствующего цилиндра той же высоты и радиуса.
Объем конуса равен одной трети объема соответствующего цилиндра той же высоты и радиуса.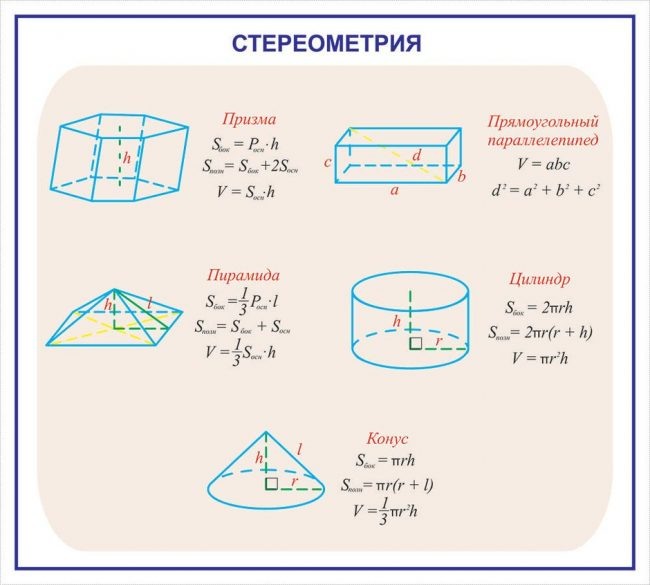
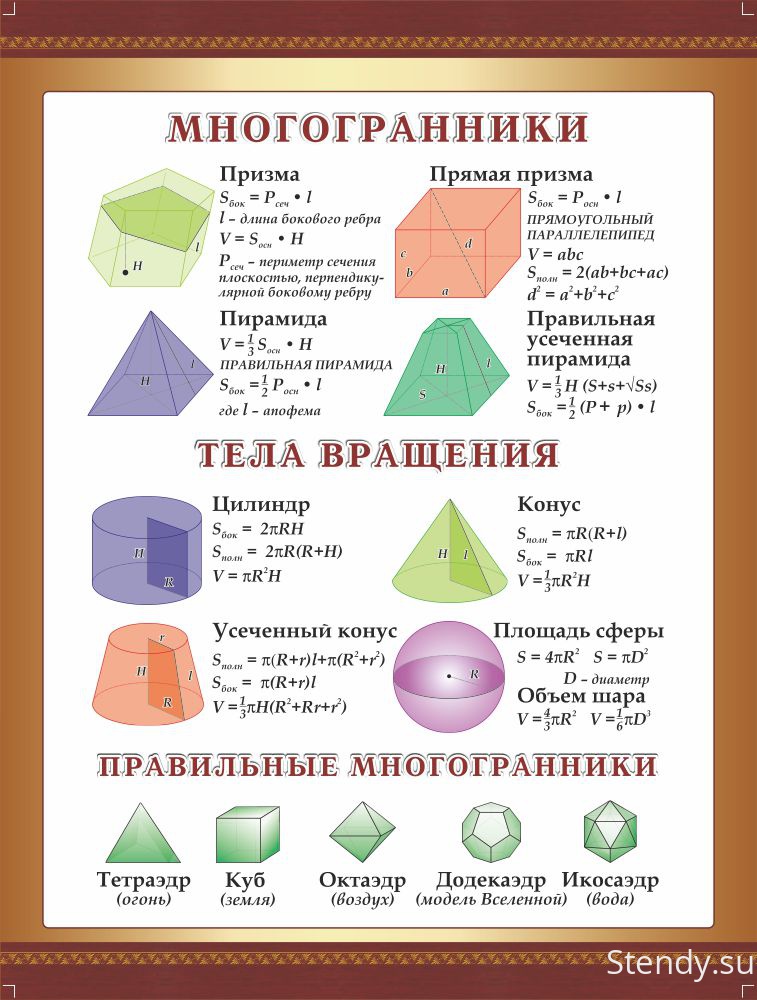 (Тот же принцип был ранее открыт Цзу Гэнчжи (480–525 гг.) в Китае.) Умное использование этого метода показывает, что объем полусферы радиусом r равен объему твердого тела, полученного путем удаления конуса из радиуса r и высоты r из цилиндра той же высоты и радиуса, таким образом показывая, что объем полушария равен π r3.
(Тот же принцип был ранее открыт Цзу Гэнчжи (480–525 гг.) в Китае.) Умное использование этого метода показывает, что объем полусферы радиусом r равен объему твердого тела, полученного путем удаления конуса из радиуса r и высоты r из цилиндра той же высоты и радиуса, таким образом показывая, что объем полушария равен π r3.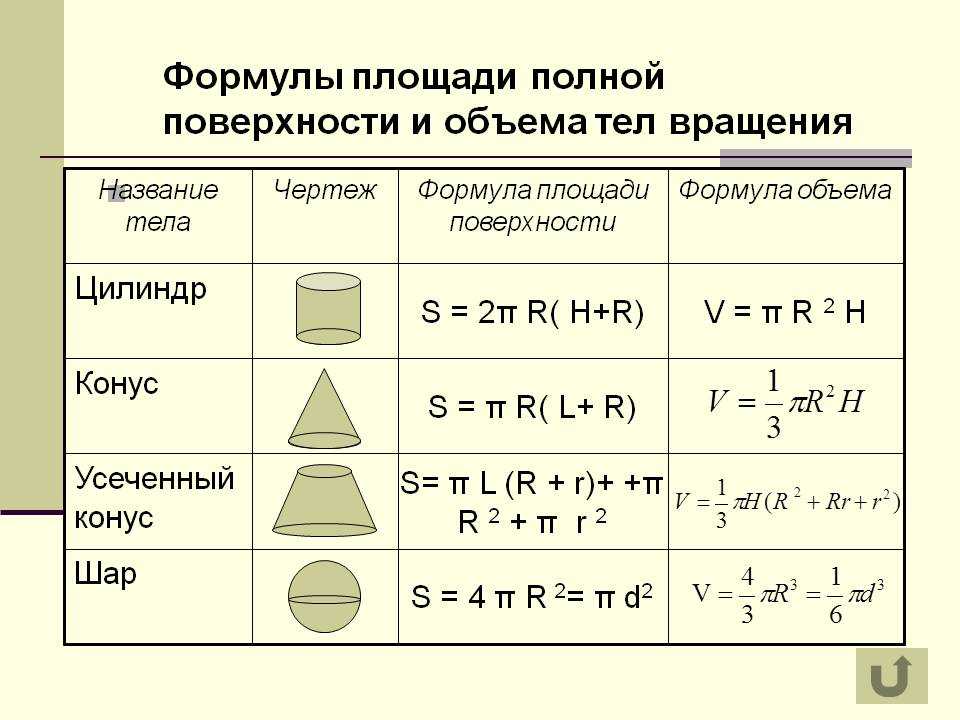 Одно довольно точное из них называется правилом Симпсона, которое было известно Кавальери, заново открыто Грегори (1638-1675) и приписано Томасу Симпсону (1710-1761). Это правило позволяет найти приблизительное значение площади неправильной фигуры, производя измерения поперек фигуры в различных точках вдоль некоторой оси. Сегодня он используется кардиологами для измерения, например, объема правого желудочка (ПЖ), связанного с кровотоком в сердце.
Одно довольно точное из них называется правилом Симпсона, которое было известно Кавальери, заново открыто Грегори (1638-1675) и приписано Томасу Симпсону (1710-1761). Это правило позволяет найти приблизительное значение площади неправильной фигуры, производя измерения поперек фигуры в различных точках вдоль некоторой оси. Сегодня он используется кардиологами для измерения, например, объема правого желудочка (ПЖ), связанного с кровотоком в сердце. ADG и BCK вместе образуют треугольник ACD ( B и A совпадают). E и F являются средними точками AC и AD соответственно. Треугольник AFE подобен треугольнику ACD и, таким образом, EF параллелен DC (соответствующие углы равны).
ADG и BCK вместе образуют треугольник ACD ( B и A совпадают). E и F являются средними точками AC и AD соответственно. Треугольник AFE подобен треугольнику ACD и, таким образом, EF параллелен DC (соответствующие углы равны).
 0 Unported License.
0 Unported License. 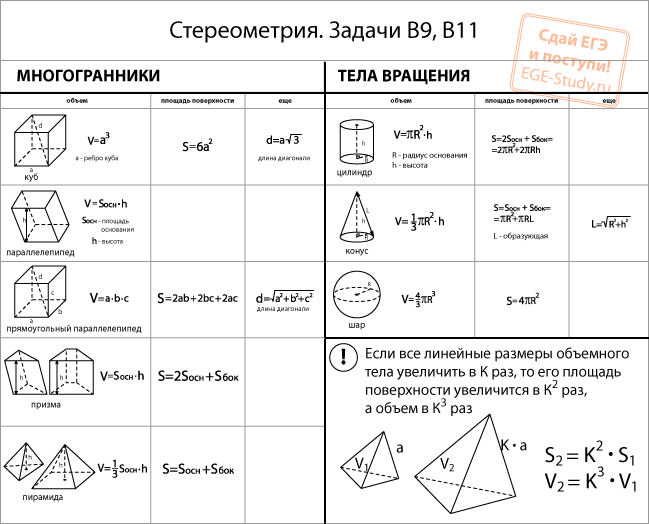 Объем измеряется в кубических единицах, например, м³, см³ и так далее. Объем можно рассматривать как способность контейнера вмещать некоторое количество жидкости (газа или жидкости).
Объем измеряется в кубических единицах, например, м³, см³ и так далее. Объем можно рассматривать как способность контейнера вмещать некоторое количество жидкости (газа или жидкости).



 Но это очень плохо (мое мнение).Так ведь это не только в 10 классе. У нас теперь предмет «Математика» во всех классах.Оценку за четверть ставим одну.И экзамен по математике, а не по алгебре или геометрии. В экзаменационную работу включили задания и по алгебре, и по геометрии, поэтому и назвали «математика».
Но это очень плохо (мое мнение).Так ведь это не только в 10 классе. У нас теперь предмет «Математика» во всех классах.Оценку за четверть ставим одну.И экзамен по математике, а не по алгебре или геометрии. В экзаменационную работу включили задания и по алгебре, и по геометрии, поэтому и назвали «математика». Очень неудобно.
Очень неудобно. На мой взгляд, когда алгебра и геометрия модулями в математике, то уменьшается уровень подготовки у детей к геометрии. Но и преподавая математику КТП я составляла, чтобы на неделе была и алгебра, и геометрия. А так на нас, математиках и филологах, какой только видимости работы не создают разные уровни руководства.
На мой взгляд, когда алгебра и геометрия модулями в математике, то уменьшается уровень подготовки у детей к геометрии. Но и преподавая математику КТП я составляла, чтобы на неделе была и алгебра, и геометрия. А так на нас, математиках и филологах, какой только видимости работы не создают разные уровни руководства.
 Я запуталась.. Кажется это моя последняя неделя.
Я запуталась.. Кажется это моя последняя неделя. В разных школах, не взирая на одинаковую программу, — разные нагрузки,требования и душевная обстановка. Ваша ситуация не является безнадежной! Поверьте, большинство студентов — гуманитариев имеют 3-йки по математике! Лично я себе, когда оказываюсь в непонятной ситуации, повторяю: «Даже если тебя съели, у тебя есть два естественных выхода!»
В разных школах, не взирая на одинаковую программу, — разные нагрузки,требования и душевная обстановка. Ваша ситуация не является безнадежной! Поверьте, большинство студентов — гуманитариев имеют 3-йки по математике! Лично я себе, когда оказываюсь в непонятной ситуации, повторяю: «Даже если тебя съели, у тебя есть два естественных выхода!» Это психологически важно — понимать, что делаешь все возможное. Не нужно ругать себя и обзывать, это вообще бессмысленно. Впереди каникулы, есть время, нужно его правильно распределить. Оставить не только на прогулки, но и занятия. Определи свои главные пробелы. Не пожалей времени и вернись назад по школьной программе. Только понимая предыдущие темы, сможешь легче понять следующие. Выучи по геометрии теоремы вместе с доказательствами, запомни примеры решений типичных задач. В свое время мне это очень помогло. Поищите с Мамой нового репетитора, лучше чтобы это был Твой школьный учитель. Или учитель, работающий в вашей школе и знающий требования Твоего учителя. Для этого Маме можно подойти к учителю и спросить, какой выход из ситуации видит он. Или задать этот же вопрос директору. Не бывает безвыходных ситуаций, работая в школе, знаю это точно. Ну а второй возможный вариант для Тебя — поступить после этого учебного года в колледж. Сдать экзамены, думаю, не станет большой проблемой, ведь Ты серьезно относишься к учебе.
Это психологически важно — понимать, что делаешь все возможное. Не нужно ругать себя и обзывать, это вообще бессмысленно. Впереди каникулы, есть время, нужно его правильно распределить. Оставить не только на прогулки, но и занятия. Определи свои главные пробелы. Не пожалей времени и вернись назад по школьной программе. Только понимая предыдущие темы, сможешь легче понять следующие. Выучи по геометрии теоремы вместе с доказательствами, запомни примеры решений типичных задач. В свое время мне это очень помогло. Поищите с Мамой нового репетитора, лучше чтобы это был Твой школьный учитель. Или учитель, работающий в вашей школе и знающий требования Твоего учителя. Для этого Маме можно подойти к учителю и спросить, какой выход из ситуации видит он. Или задать этот же вопрос директору. Не бывает безвыходных ситуаций, работая в школе, знаю это точно. Ну а второй возможный вариант для Тебя — поступить после этого учебного года в колледж. Сдать экзамены, думаю, не станет большой проблемой, ведь Ты серьезно относишься к учебе. Уже через три или четыре года Ты получишь диплом юриста, после чего поступишь в институт. Может, даже на вечернее отделение, а параллельно будешь работать по специальности. В результате будет два диплома — о среднем образовании и высшем. Это сделает Тебя более привлекательной при поиске работы. Ты выбрала очень распространенную специальность, лишние знания и навыки пригодятся Тебе. Кстати, точные науки в колледже не так трудно будет изучать. Там профильные предметы начнутся уже через год. Так что подумай, какой из вариантов Тебе лучше подойдет. Не думай о роковой ошибке. Желаю Тебе больших успехов!
Уже через три или четыре года Ты получишь диплом юриста, после чего поступишь в институт. Может, даже на вечернее отделение, а параллельно будешь работать по специальности. В результате будет два диплома — о среднем образовании и высшем. Это сделает Тебя более привлекательной при поиске работы. Ты выбрала очень распространенную специальность, лишние знания и навыки пригодятся Тебе. Кстати, точные науки в колледже не так трудно будет изучать. Там профильные предметы начнутся уже через год. Так что подумай, какой из вариантов Тебе лучше подойдет. Не думай о роковой ошибке. Желаю Тебе больших успехов! Если вам неуд не грозит, то слова учителя — пустые угрозы (Приказ Минобрнауки РФ от 28.11.2008 N 362)». Так что, Тань, не паникуй, если у тебя твердая четверка по истории, то она не может не допустить тебя к экзамену и она это знает, просто сейчас ей не хочется с тобой возиться и думает, что ее слова заставят тебя не сдавать экзамен, потому что ты не знаешь, что она блефует. В общем, историю ты сдавать будешь! 🙂
Если вам неуд не грозит, то слова учителя — пустые угрозы (Приказ Минобрнауки РФ от 28.11.2008 N 362)». Так что, Тань, не паникуй, если у тебя твердая четверка по истории, то она не может не допустить тебя к экзамену и она это знает, просто сейчас ей не хочется с тобой возиться и думает, что ее слова заставят тебя не сдавать экзамен, потому что ты не знаешь, что она блефует. В общем, историю ты сдавать будешь! 🙂 Так что ты подумай хорошенько о том, действительно ли это то, чем ты можешь заниматься в будущем? Просто очень часто подростки заблуждаются в своих представлениях о профессии, они часто пребывают в фантазиях и нереальных представлениях о ней. Поэтому подумай о том, насколько ты успешна в профильных предметах для юрфака, насколько они тебе интересны.
Так что ты подумай хорошенько о том, действительно ли это то, чем ты можешь заниматься в будущем? Просто очень часто подростки заблуждаются в своих представлениях о профессии, они часто пребывают в фантазиях и нереальных представлениях о ней. Поэтому подумай о том, насколько ты успешна в профильных предметах для юрфака, насколько они тебе интересны. Но это не означает, что дальше будет также. Все-таки, начни заниматься с преподавателем, пусть он будет уже восьмым, но ты не сдавайся, будь сильной, нужно разрешить все пробелы с предыдущих классов, планомерно все подтягивать и результат однозначно будет, его не может не быть. Главное, не паникуй и не переставай заниматься с преподавателем.
Но это не означает, что дальше будет также. Все-таки, начни заниматься с преподавателем, пусть он будет уже восьмым, но ты не сдавайся, будь сильной, нужно разрешить все пробелы с предыдущих классов, планомерно все подтягивать и результат однозначно будет, его не может не быть. Главное, не паникуй и не переставай заниматься с преподавателем. Так что перестань себя принижать, оценивай себя адекватно, не зацикливайся на неудачах и настраивайся на намеченные цели, у тебя обязательно все получится! 🙂
Так что перестань себя принижать, оценивай себя адекватно, не зацикливайся на неудачах и настраивайся на намеченные цели, у тебя обязательно все получится! 🙂 Школьная оценка не дает никаких гарантий на счастливую или несчастливую жизнь. Поговорите с мамой, скажите, что не получается. Милая, я Вам желаю счастья и незабываемого волшебного Нового года!!!
Школьная оценка не дает никаких гарантий на счастливую или несчастливую жизнь. Поговорите с мамой, скажите, что не получается. Милая, я Вам желаю счастья и незабываемого волшебного Нового года!!! Вот это надо уточнить. Потому что можно просто подготовиться к сдаче ОГЭ, совсем не обязательно сдавать его на 5. Тебе достаточно тройки. А на тройку ты написать сможешь, если тебя будут готовить.
Вот это надо уточнить. Потому что можно просто подготовиться к сдаче ОГЭ, совсем не обязательно сдавать его на 5. Тебе достаточно тройки. А на тройку ты написать сможешь, если тебя будут готовить. 12.2016
12.2016 Мы также знаем, что Геометрия — это область математики, изучающая точки, линии, многомерные объекты и формы, поверхности и твердые тела. Но так ли уж они отличаются друг от друга??
Мы также знаем, что Геометрия — это область математики, изучающая точки, линии, многомерные объекты и формы, поверхности и твердые тела. Но так ли уж они отличаются друг от друга?? Иногда мы также используем формулы, чтобы найти недостающие измерения, переставляя формулу. Нам нужно использовать много наших алгебраических навыков в этой области!
Иногда мы также используем формулы, чтобы найти недостающие измерения, переставляя формулу. Нам нужно использовать много наших алгебраических навыков в этой области!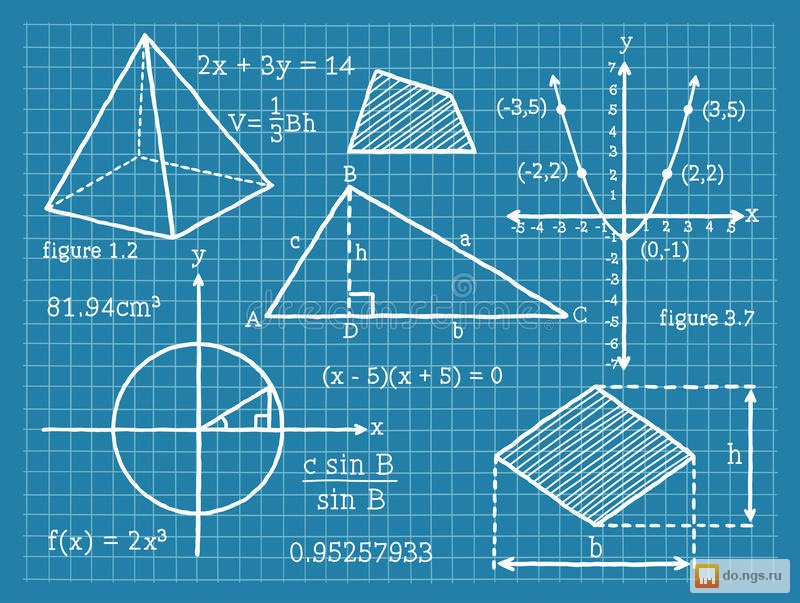 В алгебре многие уравнения на самом деле являются функциями, потому что когда мы подставляем одно значение в уравнение, мы получаем другое значение. Как мы видели в разделе «Координатная геометрия» вверху, мы можем графически изобразить эти уравнения или функции. После того, как мы нарисуем уравнения, мы можем перемещать график вверх или вниз или из стороны в сторону, добавляя константу (значение) либо к x, либо к y в функции. Ниже приведены некоторые примеры того, как функции могут «преобразовываться»:
В алгебре многие уравнения на самом деле являются функциями, потому что когда мы подставляем одно значение в уравнение, мы получаем другое значение. Как мы видели в разделе «Координатная геометрия» вверху, мы можем графически изобразить эти уравнения или функции. После того, как мы нарисуем уравнения, мы можем перемещать график вверх или вниз или из стороны в сторону, добавляя константу (значение) либо к x, либо к y в функции. Ниже приведены некоторые примеры того, как функции могут «преобразовываться»:  Чтобы применить алгебру в этом контексте, вам не нужны какие-либо новые навыки алгебры, но вам нужно иметь некоторое понимание геометрии и способность переводить несколько абстрактные идеи алгебры в более конкретное использование в геометрии. Давайте начнем с пары практических задач для иллюстрации.
Чтобы применить алгебру в этом контексте, вам не нужны какие-либо новые навыки алгебры, но вам нужно иметь некоторое понимание геометрии и способность переводить несколько абстрактные идеи алгебры в более конкретное использование в геометрии. Давайте начнем с пары практических задач для иллюстрации. обработки этого типа уравнения. Воспользуемся факторинговым подходом (впрочем, вполне законны и другие подходы).
обработки этого типа уравнения. Воспользуемся факторинговым подходом (впрочем, вполне законны и другие подходы). Немного более строгая версия этой задачи потребует от вас найти периметр прямоугольника площадью 63 квадратных единицы и длиной, в семь раз превышающей ширину. Эта формулировка вопроса заставит вас присвоить переменную в дополнение к решению проблемы.
Немного более строгая версия этой задачи потребует от вас найти периметр прямоугольника площадью 63 квадратных единицы и длиной, в семь раз превышающей ширину. Эта формулировка вопроса заставит вас присвоить переменную в дополнение к решению проблемы. На рисунке r — это радиус окружности и половина диагонали квадрата. Поскольку указано r , мы уже можем вычислить площадь круга.
На рисунке r — это радиус окружности и половина диагонали квадрата. Поскольку указано r , мы уже можем вычислить площадь круга.


 Значение числа π в данном случае округлено до 15 знаков после запятой и составляет 3,141592653589793. Таким образом, приложение Easy Geometry Calculator предложит два варианта решения задачи.
Значение числа π в данном случае округлено до 15 знаков после запятой и составляет 3,141592653589793. Таким образом, приложение Easy Geometry Calculator предложит два варианта решения задачи.
 Это приложение совместимо с iOS 10.0 или более поздней версии и требует 109MB свободного места для установки на вашем устройстве.
Это приложение совместимо с iOS 10.0 или более поздней версии и требует 109MB свободного места для установки на вашем устройстве.
 23
23

 208.2045645645645.208.204564564564. Odersuchen Sie nach формула oder школа, um noch mehr faszinierende Stock-Bilder zu entdecken.
208.2045645645645.208.204564564564. Odersuchen Sie nach формула oder школа, um noch mehr faszinierende Stock-Bilder zu entdecken. — математические фотографии и изображения
— математические фотографии и изображения …
… formeln zur berechnung von summen und winkeldifferenzen. bildung, unterricht bekommen, schulprogramm höhere mathematik — математическая графика, -clipart, -cartoons und -symbole
formeln zur berechnung von summen und winkeldifferenzen. bildung, unterricht bekommen, schulprogramm höhere mathematik — математическая графика, -clipart, -cartoons und -symbole glyphenvektor isoliert auf weißemhintergrund — математическая графика, -клипарт, -мультфильмы и -символ
glyphenvektor isoliert auf weißemhintergrund — математическая графика, -клипарт, -мультфильмы и -символ lerne wörter, die zu bildern passen. wie in der kategorie spielzeug gezeigt — math stock-grafiken, -clipart, -cartoons und -symbole
lerne wörter, die zu bildern passen. wie in der kategorie spielzeug gezeigt — math stock-grafiken, -clipart, -cartoons und -symbole Вектор
Вектор вектор — математика стоковые графики, -клипарты, -мультфильмы и -символы
вектор — математика стоковые графики, -клипарты, -мультфильмы и -символы Вектор
Вектор winzige männliche und weibliche schüler charaktere in work oder schule klasse lernen mathematik and riesigen tafel. menschen, die bildung und schreiben formel. мультипликационная векторная иллюстрация — математическая графика, клипарт, мультфильмы и символы
winzige männliche und weibliche schüler charaktere in work oder schule klasse lernen mathematik and riesigen tafel. menschen, die bildung und schreiben formel. мультипликационная векторная иллюстрация — математическая графика, клипарт, мультфильмы и символы
 kluger kleiner schuljunge, der eine multiplikationssumme macht und eine losung im unterricht berechnet — math stock-fotos und bilder
kluger kleiner schuljunge, der eine multiplikationssumme macht und eine losung im unterricht berechnet — math stock-fotos und bilder ..
.. Winzige…
Winzige…


 02KB )
02KB ) 74MB
74MB 55KB
55KB 03KB
03KB 68KB
68KB 12KB
12KB
 Значения, находящиеся ниже или за пределами этого диапазона, отображаются с наименьшими и наибольшими символами соответственно.
Значения, находящиеся ниже или за пределами этого диапазона, отображаются с наименьшими и наибольшими символами соответственно. Вы можете использовать компенсацию внешнего вида, только если у вас есть пропорциональные символы относительного размера (пропорциональные символы без указания единицы измерения) и не указан Максимальный размер. Поскольку исследование Флэннери относится именно к восприятию кругов, компенсацию внешнего вида следует использовать только с круглыми символами.
Вы можете использовать компенсацию внешнего вида, только если у вас есть пропорциональные символы относительного размера (пропорциональные символы без указания единицы измерения) и не указан Максимальный размер. Поскольку исследование Флэннери относится именно к восприятию кругов, компенсацию внешнего вида следует использовать только с круглыми символами. Вы также должны указать, должно ли это значение соответствовать площади, радиусу (половина ширины в случае квадрата) или высоте символа в свойстве «Данные представляют». Высота может быть указана только тогда, когда вы работаете в сцене.
Вы также должны указать, должно ли это значение соответствовать площади, радиусу (половина ширины в случае квадрата) или высоте символа в свойстве «Данные представляют». Высота может быть указана только тогда, когда вы работаете в сцене.
 Или установите для параметра Максимальный размер значение Нет. При необходимости отрегулируйте шаблон и фоновые символы.
Или установите для параметра Максимальный размер значение Нет. При необходимости отрегулируйте шаблон и фоновые символы. На вкладке «Классы» разверните «Нулевые значения», чтобы указать символ, метку легенды и описание легенды. Если поле атрибута, используемое для определения символов пропорционального размера, содержит нулевые значения, символы для этих объектов не будут отображаться, если только вы явно не выберете их отображение с помощью выделенного символа.
На вкладке «Классы» разверните «Нулевые значения», чтобы указать символ, метку легенды и описание легенды. Если поле атрибута, используемое для определения символов пропорционального размера, содержит нулевые значения, символы для этих объектов не будут отображаться, если только вы явно не выберете их отображение с помощью выделенного символа.

 Некоторые из этих частей настолько особенные, что имеют собственные имена и символы.
Некоторые из этих частей настолько особенные, что имеют собственные имена и символы. 2).
2). 6).
6).
 (ОГЭ). Анализ геометрических высказываний.
(ОГЭ). Анализ геометрических высказываний.

 Метапредметные результаты:
умение осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач,
умение оценивать правильность выполнения учебной задачи.
Предметные результаты:
Овладение приемами решения геометрических задач о сумме углов треугольника,
Развитие умения использовать рисунки для решения различных математических задач.
Инструкция по выполнению работы
На выполнение всей работы отводится 40 минут.
Работа состоит из 15 заданий с выбором одного верного ответа.
Метапредметные результаты:
умение осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач,
умение оценивать правильность выполнения учебной задачи.
Предметные результаты:
Овладение приемами решения геометрических задач о сумме углов треугольника,
Развитие умения использовать рисунки для решения различных математических задач.
Инструкция по выполнению работы
На выполнение всей работы отводится 40 минут.
Работа состоит из 15 заданий с выбором одного верного ответа. Координаты вектора на плоскости. Задачи.
Координаты вектора на плоскости. Задачи.
 Время на прохождение – 20 минут.
Время на прохождение – 20 минут. 9 класс. В тесте 5 вопросов. В каждом вопросе только один правильный вариант ответа.
9 класс. В тесте 5 вопросов. В каждом вопросе только один правильный вариант ответа.  Надеюсьон получился интересным и познавательным
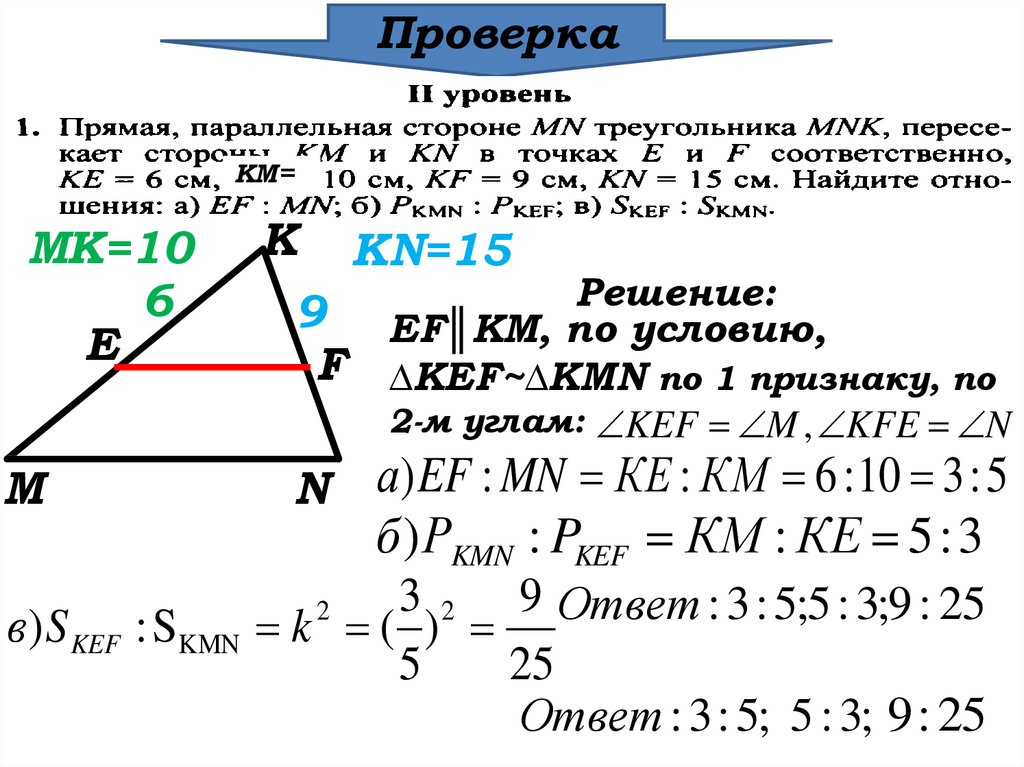
Надеюсьон получился интересным и познавательным Треугольники
Треугольники
 Данный тест представляет собой модуль «Геометрия».
Данный тест представляет собой модуль «Геометрия».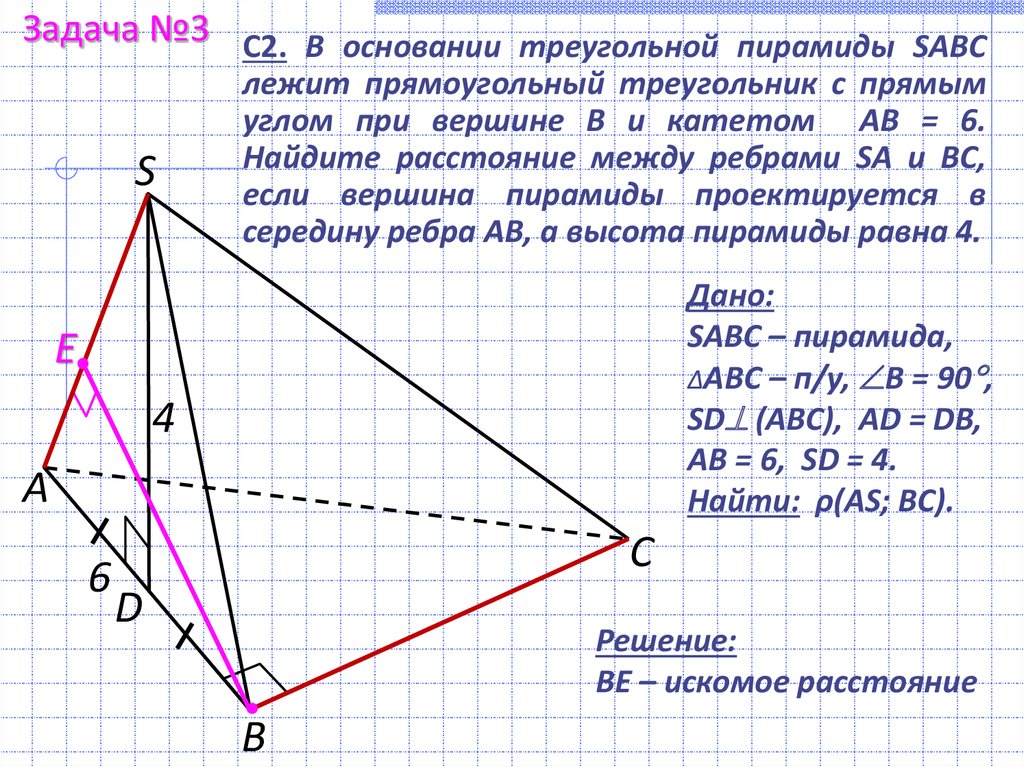 Состоит из 25 вопросов базового уровня. Лучше тестировать учащихся в конце учебного года, при повторении изученного материала.
Состоит из 25 вопросов базового уровня. Лучше тестировать учащихся в конце учебного года, при повторении изученного материала. Заданий базового уровня сложности 20, повышенного — 4, высокого — 2. Максимальное количество баллов — 30.
Заданий базового уровня сложности 20, повышенного — 4, высокого — 2. Максимальное количество баллов — 30.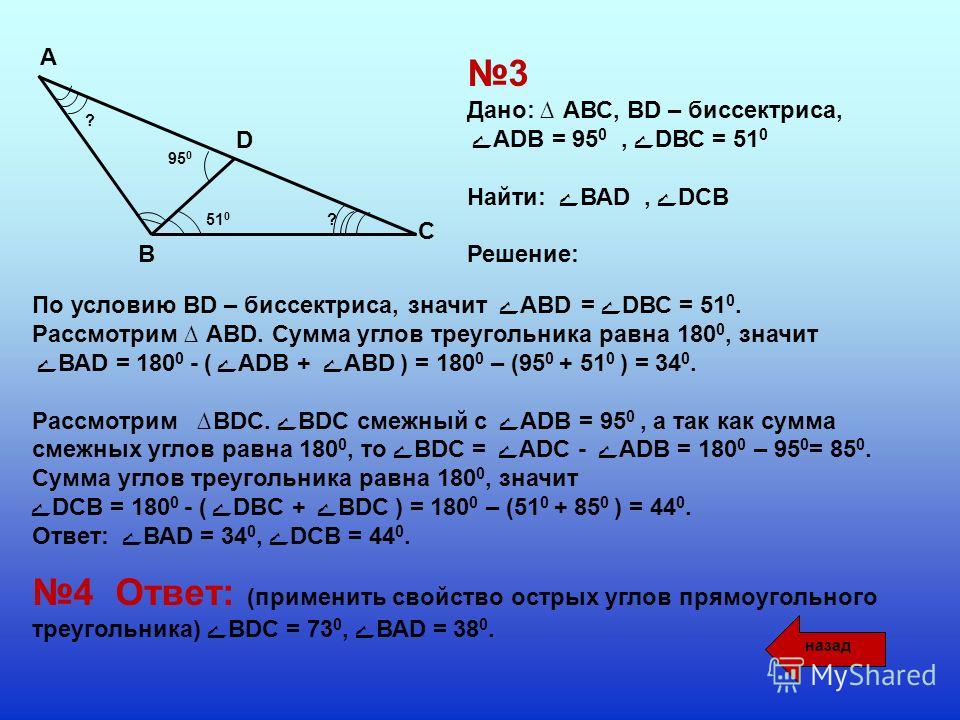
 11.2020
204
0
11.2020
204
0
 12.2020
42
0
12.2020
42
0
 Геометрия 9 класс. 4/05/2021
Геометрия 9 класс. 4/05/2021

 Учащимся нужна комплексная программа, которая привлекает постепенно усложняющимися уроками, чтобы избежать пробелов в обучении.
Учащимся нужна комплексная программа, которая привлекает постепенно усложняющимися уроками, чтобы избежать пробелов в обучении. Удаленные математические ресурсы, в том числе:
Удаленные математические ресурсы, в том числе: 

 Все ресурсы будут доступны на французском и английском языках и в конечном итоге будут размещены на веб-сайте.
Все ресурсы будут доступны на французском и английском языках и в конечном итоге будут размещены на веб-сайте.
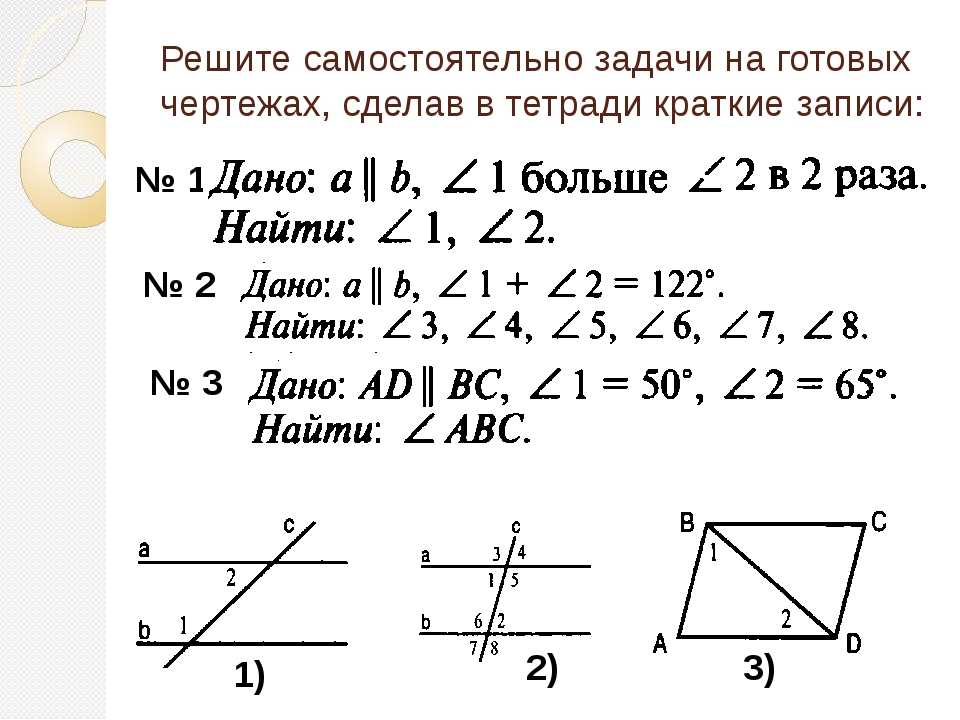

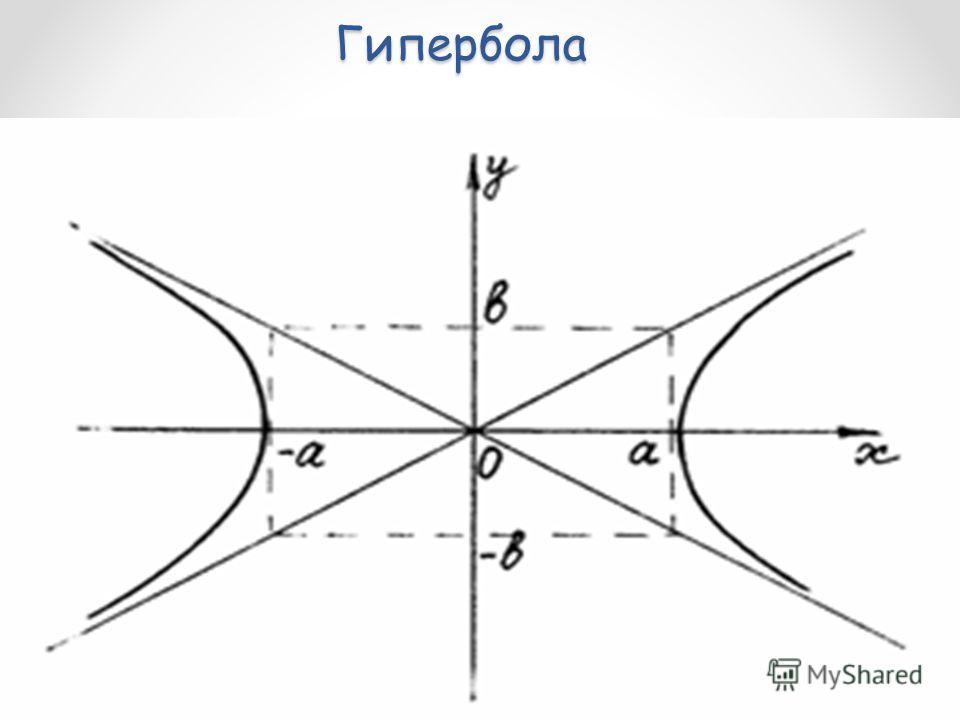
 рис.).
Если гипербола задана уравнением (2), то
директрисы определяются уравнениями
рис.).
Если гипербола задана уравнением (2), то
директрисы определяются уравнениями .. Что такое Гипербола (математика)?
.. Что такое Гипербола (математика)?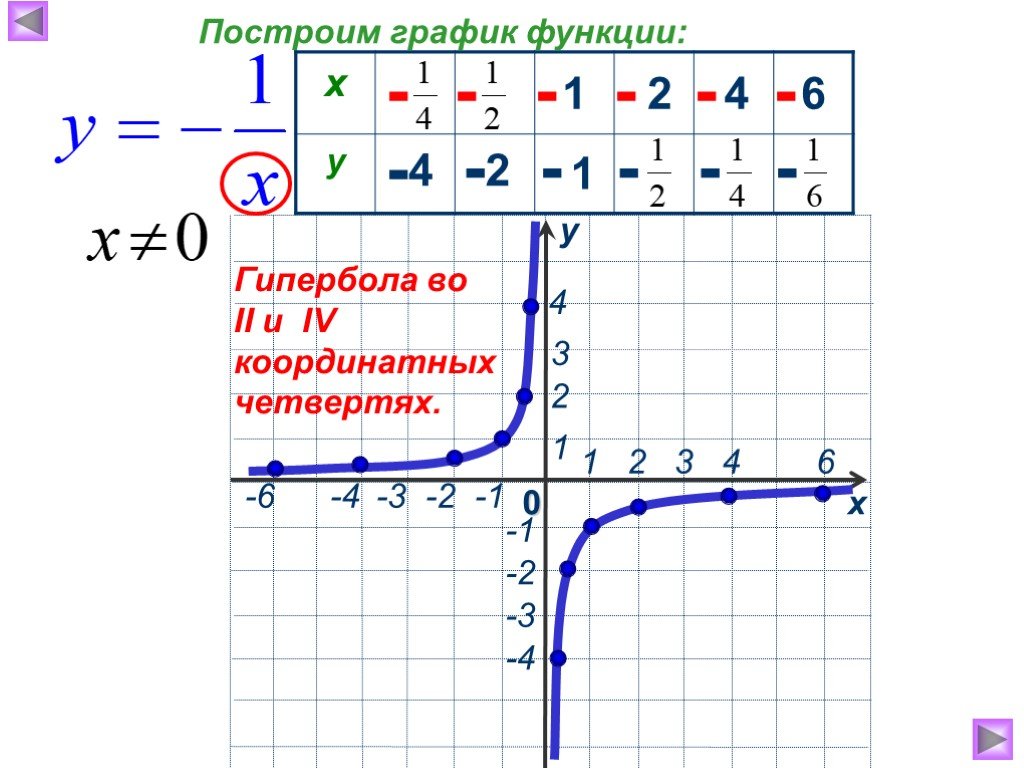 1 Соотношения
1 Соотношения Другими результатами сечения конуса плоскостью являются парабола, эллипс, а также такие вырожденные случаи, как пересекающиеся и совпадающие прямые и точка, возникающие, когда секущая плоскость проходит через вершину конуса. В частности, пересекающееся прямые можно считать вырожденной гиперболой, совпадающей со своими асимптотами.
Другими результатами сечения конуса плоскостью являются парабола, эллипс, а также такие вырожденные случаи, как пересекающиеся и совпадающие прямые и точка, возникающие, когда секущая плоскость проходит через вершину конуса. В частности, пересекающееся прямые можно считать вырожденной гиперболой, совпадающей со своими асимптотами.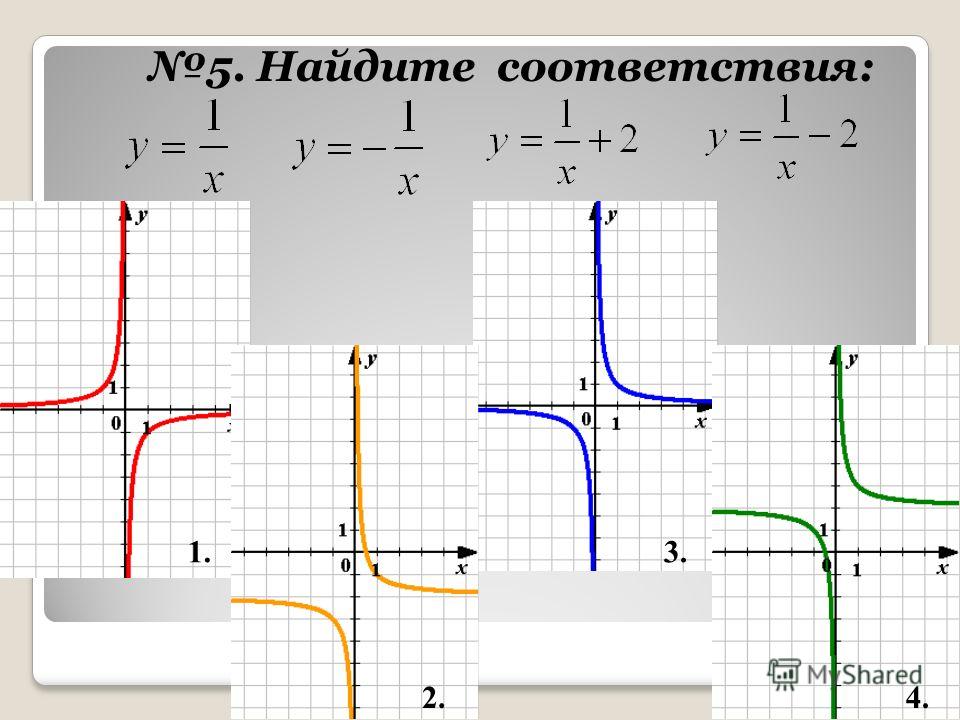
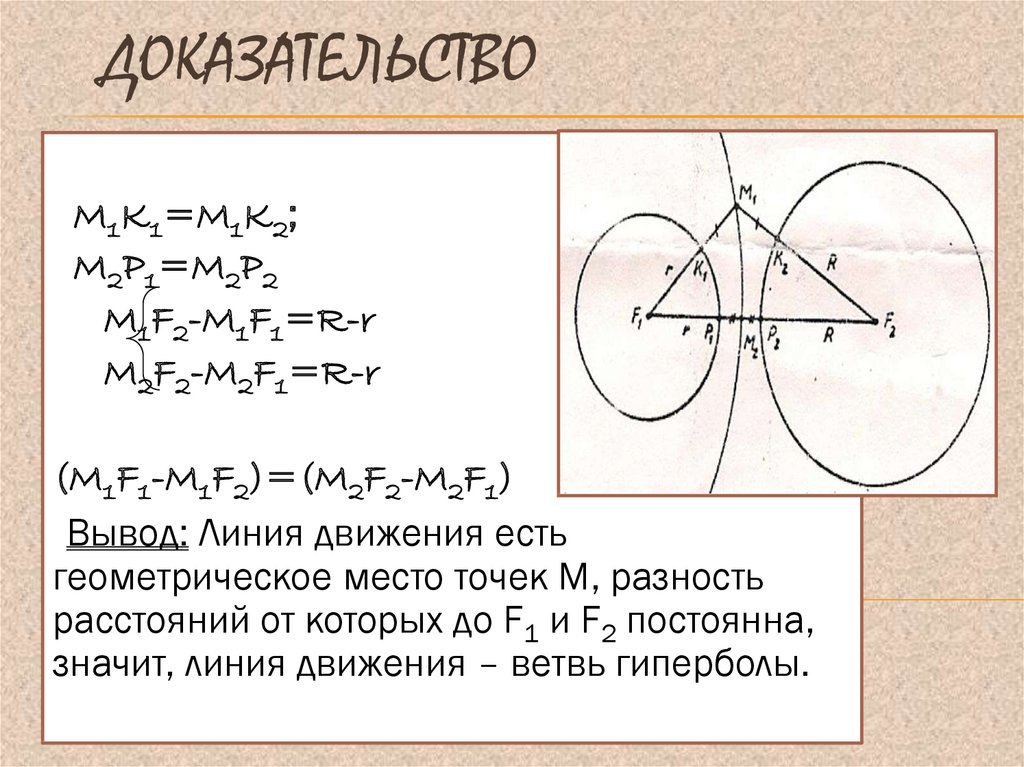
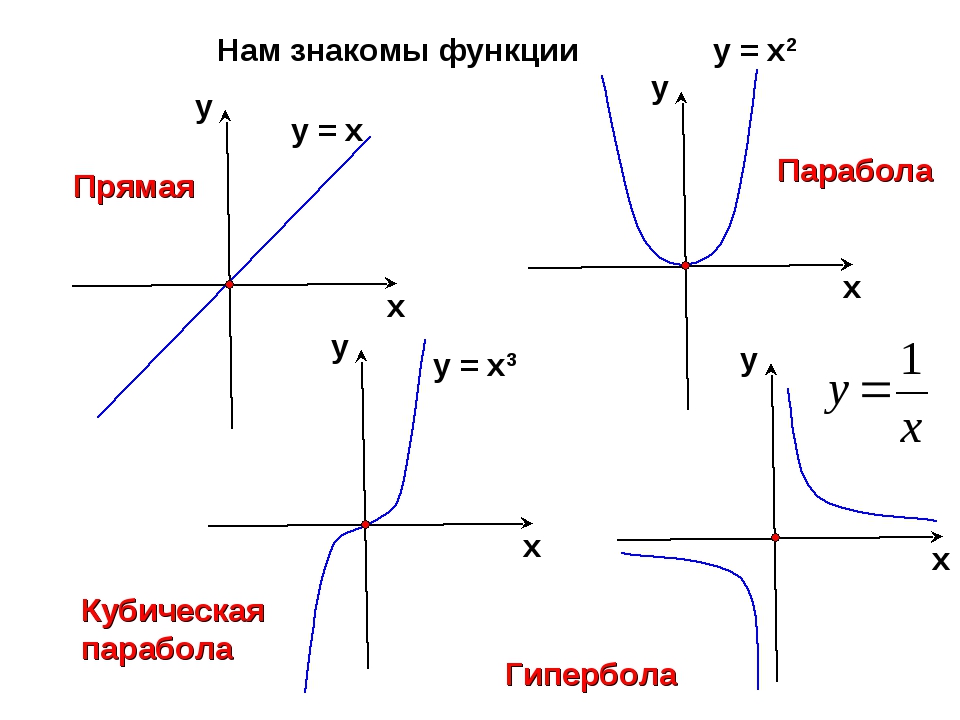

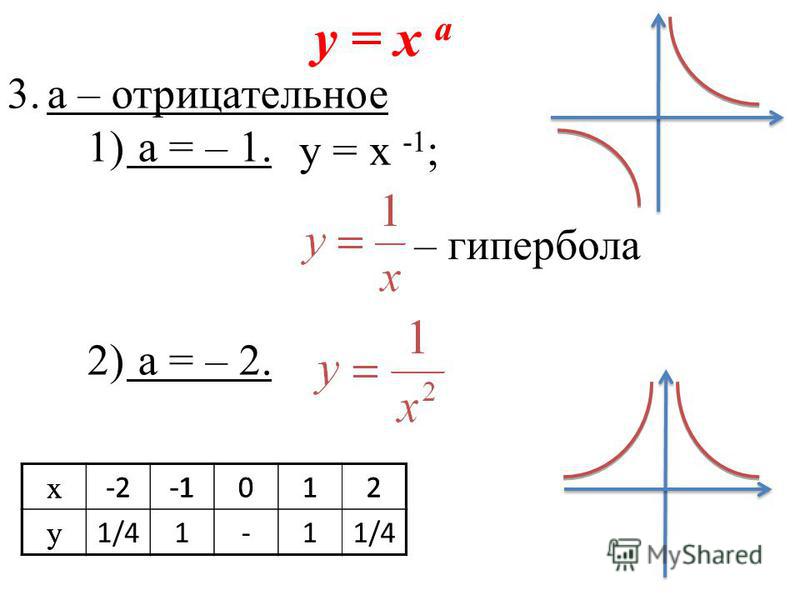
 Сопряженная гипербола не является результатом поворота начальной гиперболы на угол 90°; обе гиперболы различаются формой.
Сопряженная гипербола не является результатом поворота начальной гиперболы на угол 90°; обе гиперболы различаются формой.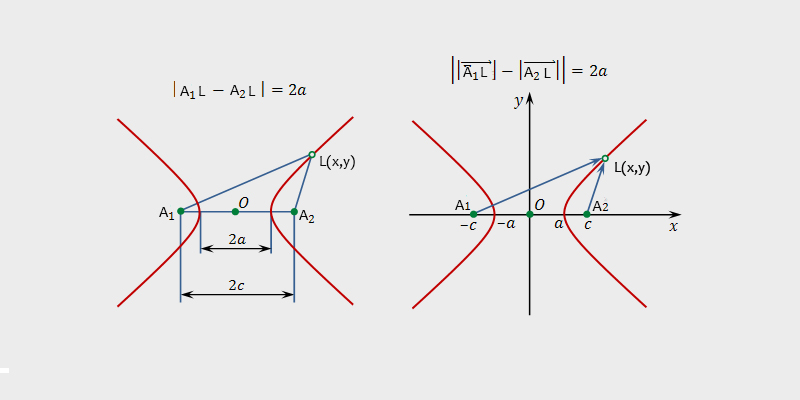 Такие диаметры называются взаимно сопряженными. Главными диаметрами называются взаимно сопряженные и взаимно перпендикулярные диаметры. У гиперболы есть только одна пара главных диаметров — действительная и мнимая оси.
Такие диаметры называются взаимно сопряженными. Главными диаметрами называются взаимно сопряженные и взаимно перпендикулярные диаметры. У гиперболы есть только одна пара главных диаметров — действительная и мнимая оси.

 Например, преобразование w = z² отображает декартовы координаты в два семейства ортогональных гипербол.
Например, преобразование w = z² отображает декартовы координаты в два семейства ортогональных гипербол.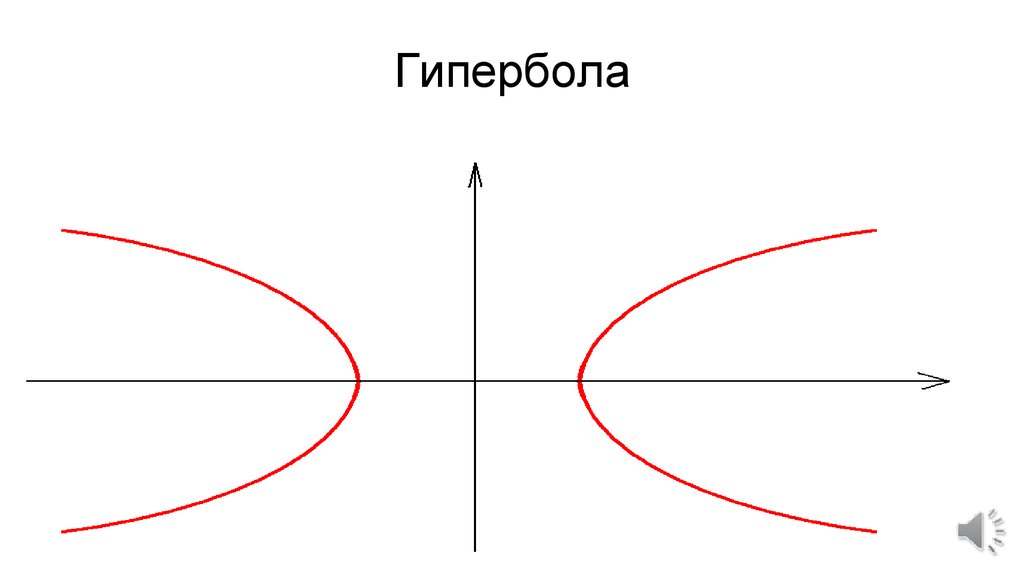



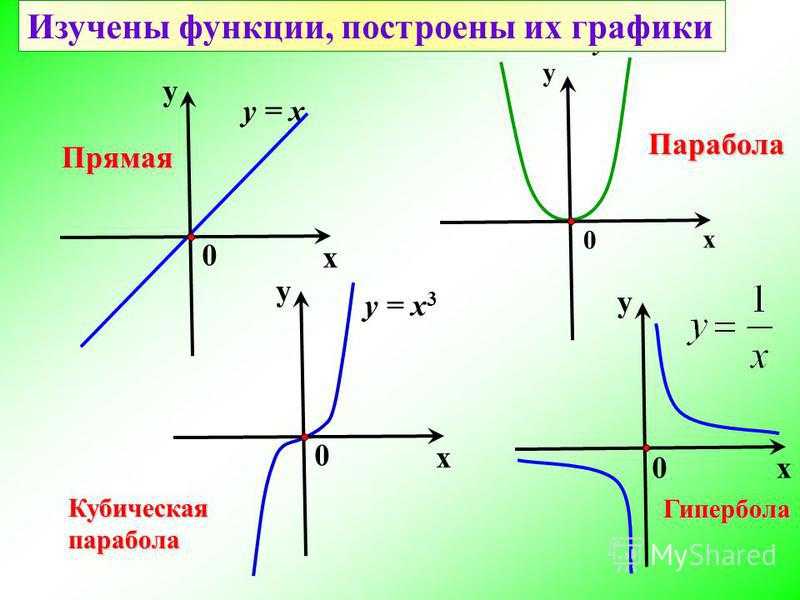
 д.? Есть ли между ними аналогия?
д.? Есть ли между ними аналогия?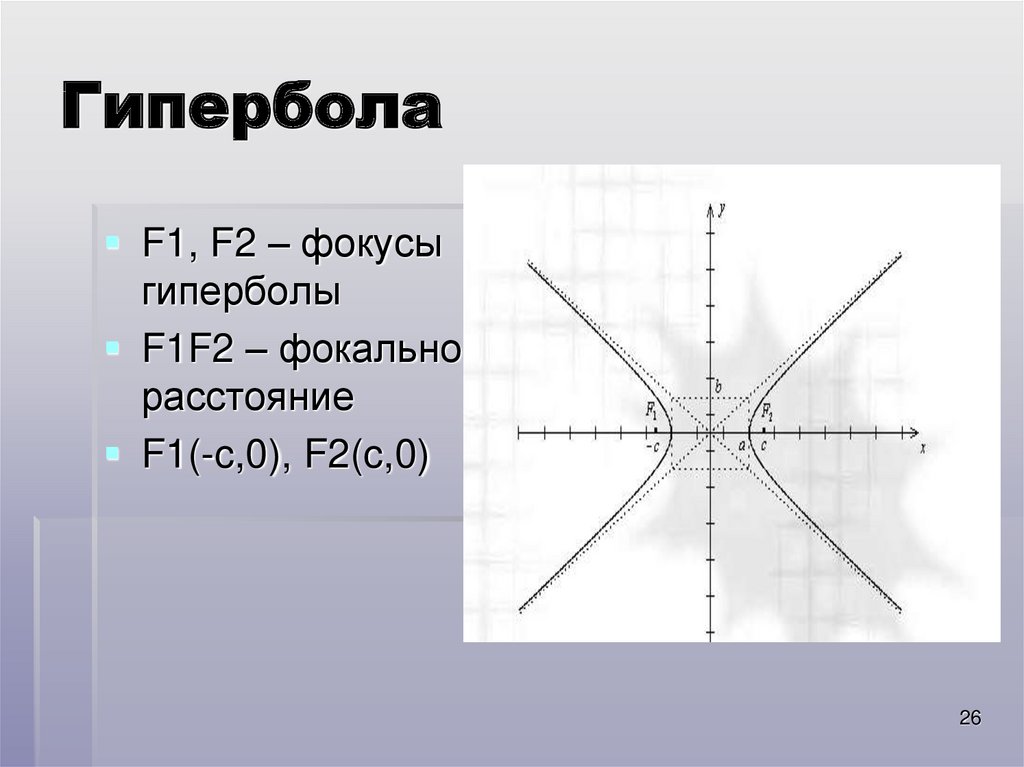 В риторике это означает опущение одного или нескольких слов, необходимых для полноты смысла — таким образом, высказывание не достигает завершенности. В геометрии это коническое сечение, в котором наклон секущей плоскости меньше — меньше — наклона стороны конуса.
В риторике это означает опущение одного или нескольких слов, необходимых для полноты смысла — таким образом, высказывание не достигает завершенности. В геометрии это коническое сечение, в котором наклон секущей плоскости меньше — меньше — наклона стороны конуса. Точная причина, по которой были выбраны эти слова, также является предметом обоснованных предположений; Джефф Миллер цитирует некоторые источники.
Точная причина, по которой были выбраны эти слова, также является предметом обоснованных предположений; Джефф Миллер цитирует некоторые источники.
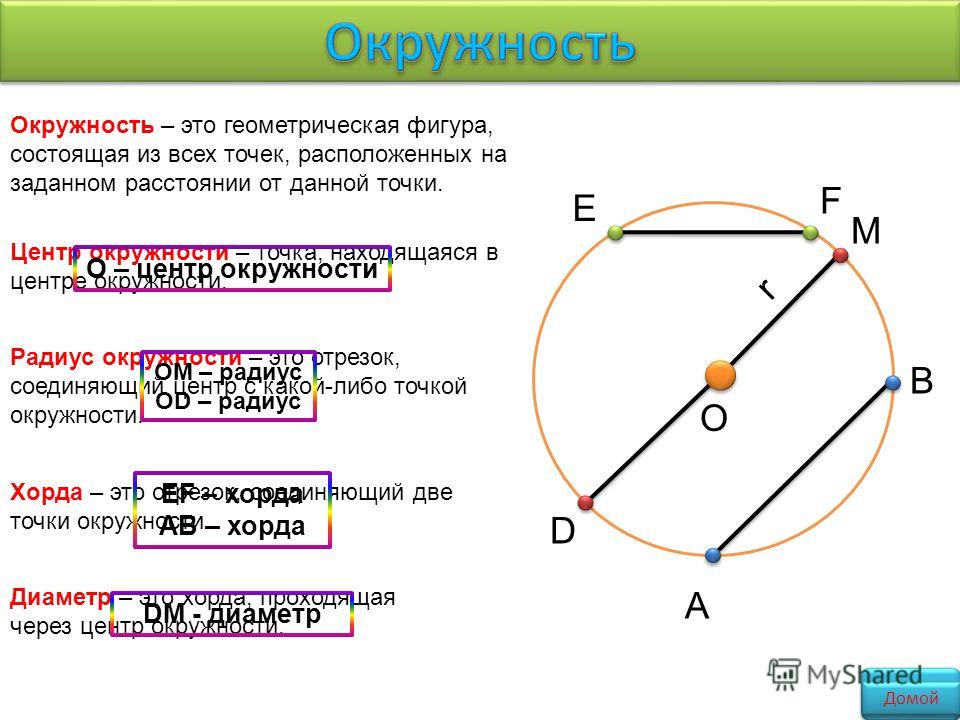
 Это – перечеркнутая буква «О».
Это – перечеркнутая буква «О». Это расстояние всей дуги окружности. Оно обозначается буквой «С». Чтобы рассчитать ее, нужно пользоваться простой формулой:
Это расстояние всей дуги окружности. Оно обозначается буквой «С». Чтобы рассчитать ее, нужно пользоваться простой формулой: И записано оно было в морском уставе. Хотя это неудивительно, так как моряки просто обязаны были разбираться в подобных математических задачах.
И записано оно было в морском уставе. Хотя это неудивительно, так как моряки просто обязаны были разбираться в подобных математических задачах. Однако часто составляет его один человек, а занимается изготовлением чего-либо по этой схеме другой.
Однако часто составляет его один человек, а занимается изготовлением чего-либо по этой схеме другой.
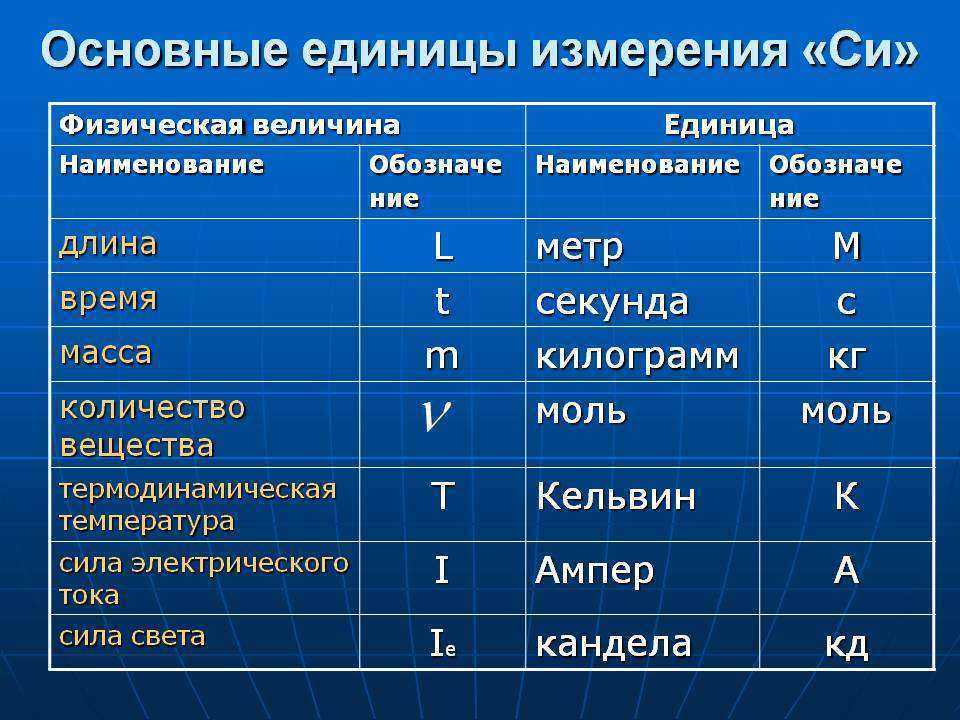 В этой науке, описывая фигуры, часто длину, ширину, высоту обозначают буквами «а», «b», «с». Согласно этой традиции, при выборе литера «В» (или «b») была заимствована системой СИ (хотя для других двух измерений стали применять отличные от геометрических символы).
В этой науке, описывая фигуры, часто длину, ширину, высоту обозначают буквами «а», «b», «с». Согласно этой традиции, при выборе литера «В» (или «b») была заимствована системой СИ (хотя для других двух измерений стали применять отличные от геометрических символы). Рассматривая ее как величину физики можно понять, что под этим словом подразумевается численная характеристика протяжности линий.
Рассматривая ее как величину физики можно понять, что под этим словом подразумевается численная характеристика протяжности линий.
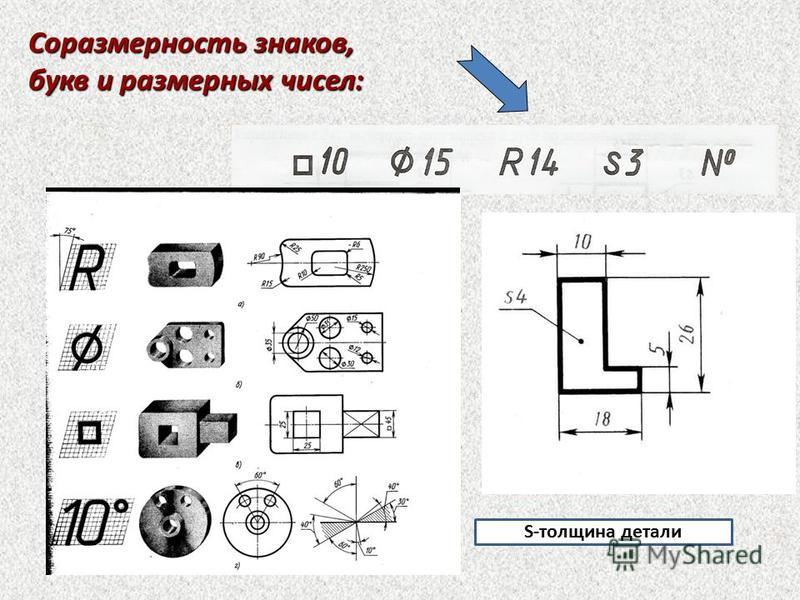
 Ещё тогда учителя рассказывали, что, латинской литерой «s» принято обозначать такую величину, как площадь. Однако, согласно общепринятым нормам, на чертежах таким способом записывается совсем другой параметр – толщина.
Ещё тогда учителя рассказывали, что, латинской литерой «s» принято обозначать такую величину, как площадь. Однако, согласно общепринятым нормам, на чертежах таким способом записывается совсем другой параметр – толщина.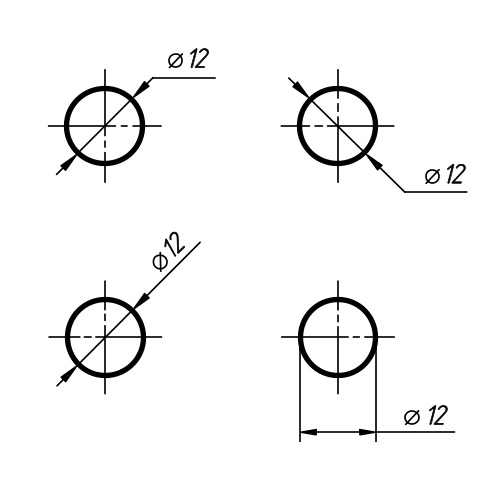

 Иными словами, если вы сомневаетесь в интерпретации того или иного сокращения, загляните в ГОСТы. Таким образом вы узнаете, как правильно обозначается высота, ширины, длина, диаметр, радиус и так далее.
Иными словами, если вы сомневаетесь в интерпретации того или иного сокращения, загляните в ГОСТы. Таким образом вы узнаете, как правильно обозначается высота, ширины, длина, диаметр, радиус и так далее.
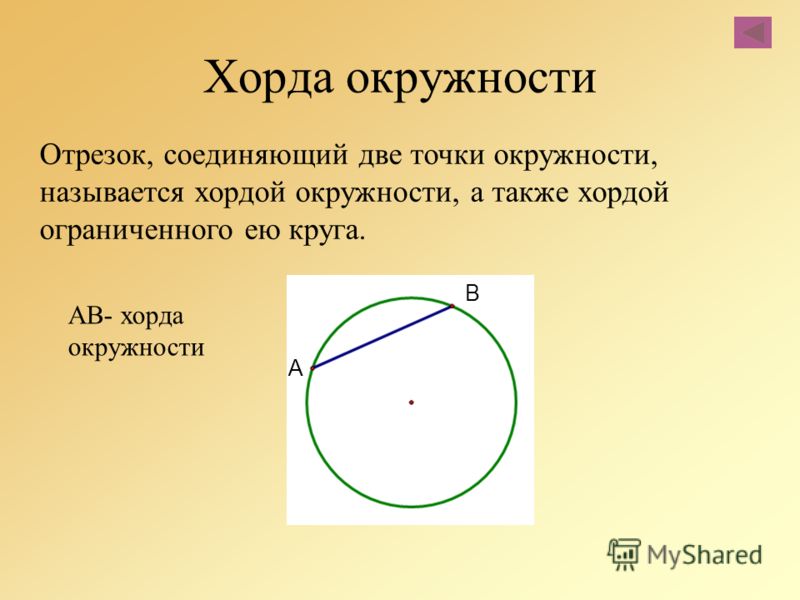
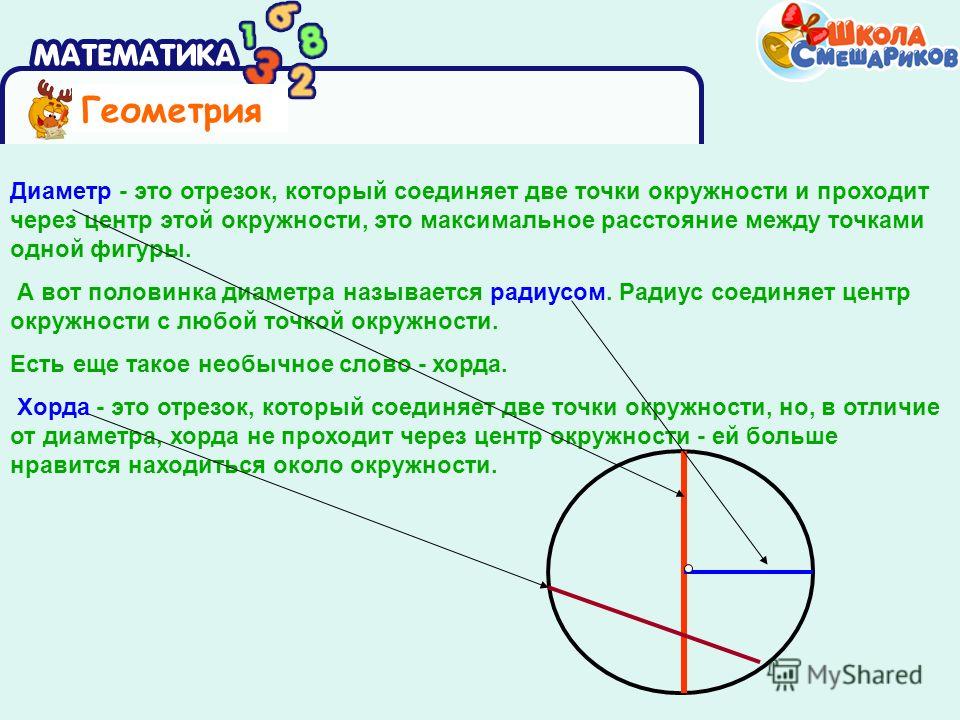
 Точно так же расстояние, измеренное от одной точки на поверхности круга до другой точки на поверхности круга, проходящей через центр, называется диаметром. Иными словами, диаметр в два раза больше радиуса. Следовательно, можно сказать, что диаметр — это самая длинная хорда окружности. Обозначения, которые используются для обозначения диаметра: «d», «φ», «D», «Dia».
Точно так же расстояние, измеренное от одной точки на поверхности круга до другой точки на поверхности круга, проходящей через центр, называется диаметром. Иными словами, диаметр в два раза больше радиуса. Следовательно, можно сказать, что диаметр — это самая длинная хорда окружности. Обозначения, которые используются для обозначения диаметра: «d», «φ», «D», «Dia».
 Здесь, следуя определению, формула для диаметра: $\mathtt{Диаметр} = \mathtt{Радиус}\times 2$. Мы подробно обсудим формулу диаметра в следующем разделе. 9{2}$.
Здесь, следуя определению, формула для диаметра: $\mathtt{Диаметр} = \mathtt{Радиус}\times 2$. Мы подробно обсудим формулу диаметра в следующем разделе. 9{2}$.
 Найдите радиус и диаметр следующего круга.
Найдите радиус и диаметр следующего круга.
 Следующим этапом идет использование циркуля – инструмента для черчения, который состоит из двух частей с закрепленными на каждой из них либо иглой, либо пишущим элементом.
Следующим этапом идет использование циркуля – инструмента для черчения, который состоит из двух частей с закрепленными на каждой из них либо иглой, либо пишущим элементом.
 Если натянуть на хула-хуп ткань, то мы уже не сможем его крутить, ведь он будет уже не окружностью – его пустота замещена тканью, куском пространства.
Если натянуть на хула-хуп ткань, то мы уже не сможем его крутить, ведь он будет уже не окружностью – его пустота замещена тканью, куском пространства.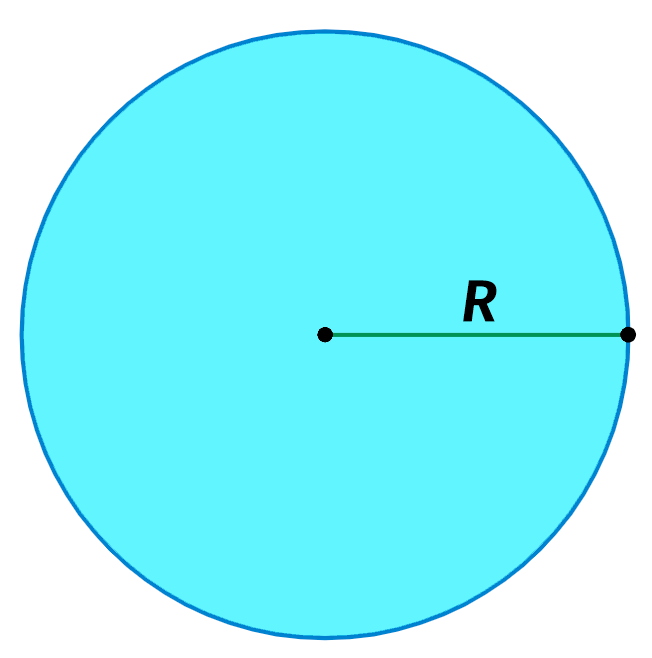
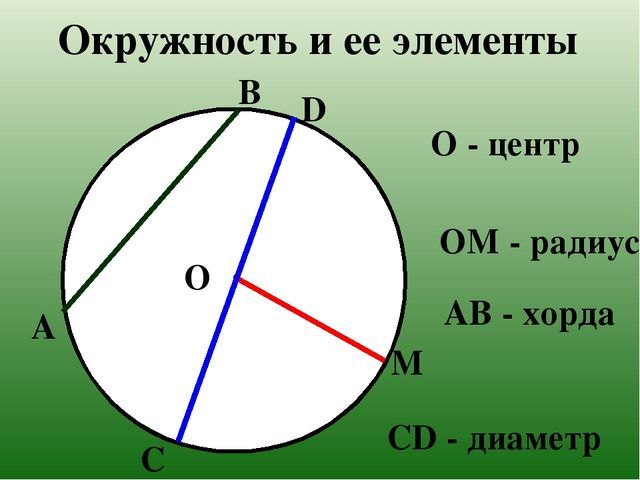 Сделав нехитрые подсчеты и, даже просто взглянув на окружность, можно практически сразу сказать, что диаметр окружности равен двум радиусам.
Сделав нехитрые подсчеты и, даже просто взглянув на окружность, можно практически сразу сказать, что диаметр окружности равен двум радиусам.
 Периметр заштрихованной области состоит из двух отрезков прямой линии AC и BC , а также дуга AB . Чтобы найти периметр всей области, мы должны сложить длины AC , BC и дугу AB .
Периметр заштрихованной области состоит из двух отрезков прямой линии AC и BC , а также дуга AB . Чтобы найти периметр всей области, мы должны сложить длины AC , BC и дугу AB .
 Уравнение площади круга:
Уравнение площади круга: 5π in 2
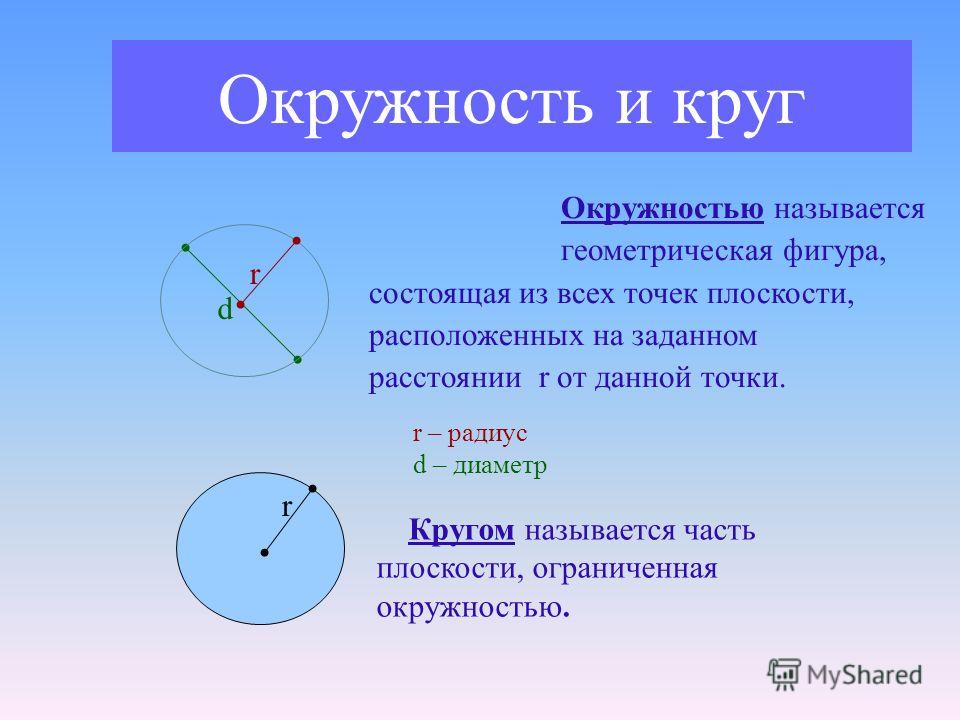
5π in 2  Чему равна площадь заштрихованного участка круга?
Чему равна площадь заштрихованного участка круга?

 Разница лишь в том, что пицца 1 разрезается на куски под углом 30°, а пицца 2 — под углом 45°. Они продаются поштучно, первые по 1,95 доллара за ломтик, а вторые по 2,25 доллара за ломтик. Какова разница в общем доходе между Pizza 2 и Pizza 1?
Разница лишь в том, что пицца 1 разрезается на куски под углом 30°, а пицца 2 — под углом 45°. Они продаются поштучно, первые по 1,95 доллара за ломтик, а вторые по 2,25 доллара за ломтик. Какова разница в общем доходе между Pizza 2 и Pizza 1?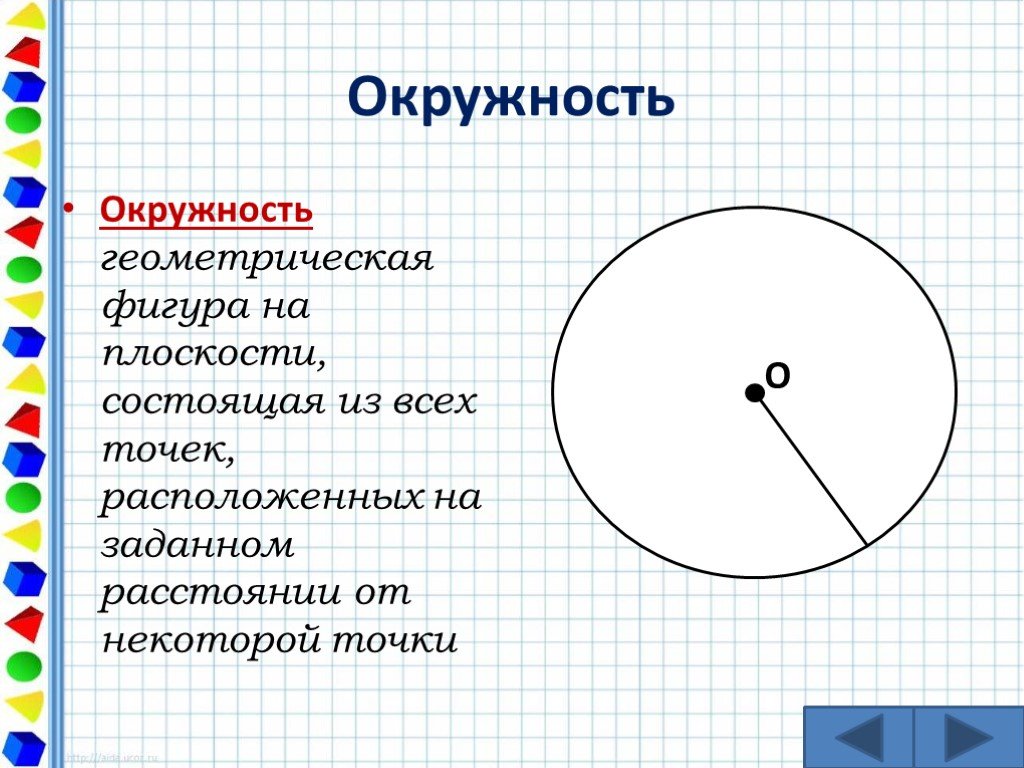 США
США
 Используйте формулу площади:
Используйте формулу площади:

 S,
S,

 Парабола
Парабола

 Вы можете копировать, распечатывать и распространять их столько раз, сколько захотите. Вы можете загрузить их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете каким-либо образом адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, логотипы спонсоров и одобрены Департаментом базового образования. Для получения дополнительной информации посетите сайт Creative Commons Attribution-NoDerivs 3.0 Unported.
Вы можете копировать, распечатывать и распространять их столько раз, сколько захотите. Вы можете загрузить их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете каким-либо образом адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, логотипы спонсоров и одобрены Департаментом базового образования. Для получения дополнительной информации посетите сайт Creative Commons Attribution-NoDerivs 3.0 Unported. Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported. В большинстве случаев трудность заключается в том, чтобы понять вопрос, а затем найти правильную стратегию для доказательства требуемого результата.
В большинстве случаев трудность заключается в том, чтобы понять вопрос, а затем найти правильную стратегию для доказательства требуемого результата.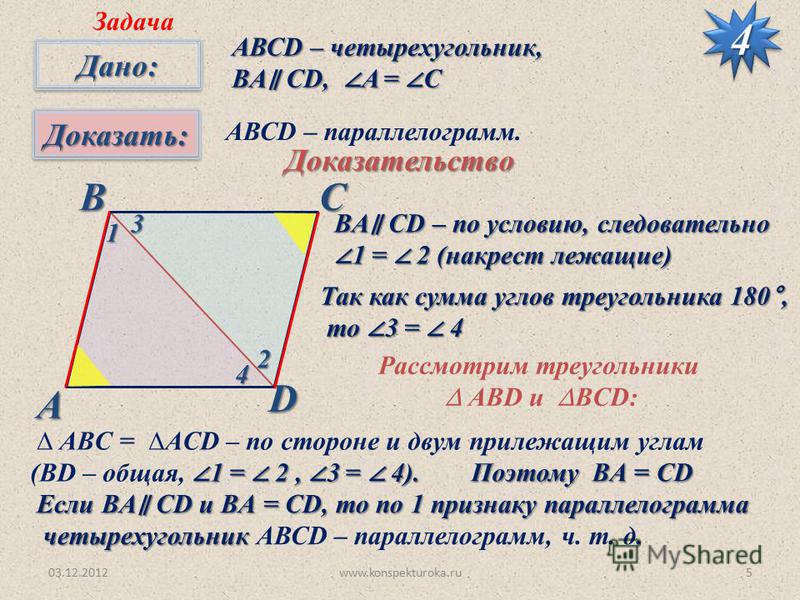 Нам нужно доказать, что PQRS — прямоугольник.
Нам нужно доказать, что PQRS — прямоугольник. е. (P, R) или (Q, S) равны 90 градусов.
е. (P, R) или (Q, S) равны 90 градусов.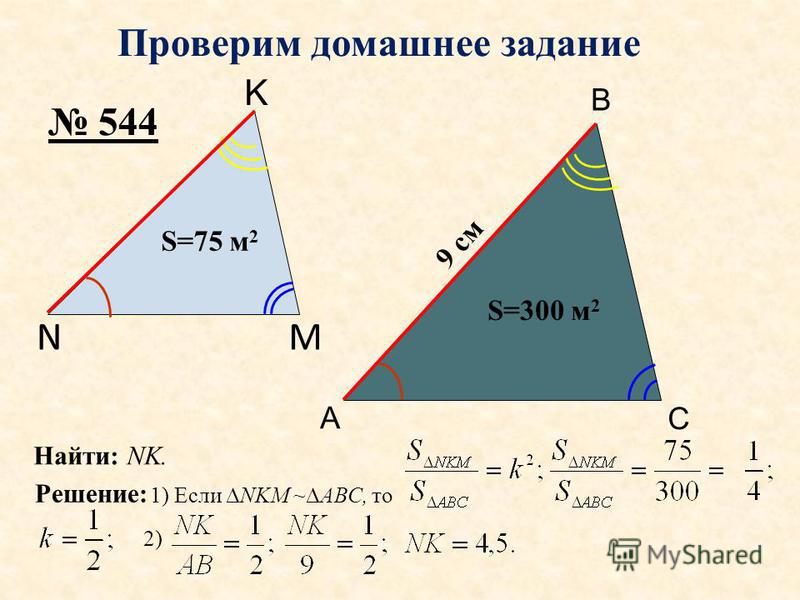 Это означает, что имеющейся информации недостаточно. Нам нужна дополнительная информация, т.е. высота. Теперь вы пойдете на строительство, как показано ниже.
Это означает, что имеющейся информации недостаточно. Нам нужна дополнительная информация, т.е. высота. Теперь вы пойдете на строительство, как показано ниже.