Ответы на задачи по технической механике
Рейтинг ↑ не забываем
Порядок действий при демонтаже кондиционеров (посмотреть)
Свод правил вентиляции и кондиционирования 2017 год (посмотреть)
Условные обозначения систем вентиляции и кондиционирования (посмотреть)
Требования к пожарной безопастности по вентиляции и кондиционированию (посмотреть).
Если Вы не нашли свой вариант ответа, обращайтесь перейдя по ссылке в группу ВК опубликовав Ваши задачи прям в ленту группы ,по возможности постараемся Вам помочь. На данной странице не все ответы, перейдя по ссылке попадаете на другую страницу с ответами
Задача № 29 Найти реакцию опор
Ответ к задачи №29
Задача № 20 Натяжка троса
Ответ к задачи № 20
Задача №7 Найти реакцию опор
Ответ к задаче №7
Задача № 9 Распределение нагрузки
Ответ к задачи № 9
Задача № 11 Определить координаты центра тяжести сечения
Ответ к задачи № 11 С решением
Задача № 12 Найти реакцию опор
Ответ к задачи №12
Задача № 13 Решить графически
Ответ к задаче №13
Задача № 33 Решить графически
Ответ к задачи № 33
Задача № 33 Силы давящие на шар
Ответ к задачи № 33 Силы давящие на шар
Задача № Задача №21 Определить координат центра тяжести
Ответ к задаче № 21 Определить координат центра тяжести
Ответ № 21 /2 Определить координат центра тяжести 30А Ответ на координат центр тяжести № 21 -27
Задача № 20 Определить опорные реакции балки. Проверить правильность их определения
Проверить правильность их определения
Ответ к задачи № 20 Определить опорные реакции балки.Проверить правильность их определения
Задача № 22 Задача № 22 найти R(a) и R(b)
Ответ к задачи Задача № 22 найти R(a) и R(b)
Задача Определить координаты центра тяжести сечения.Показать положение центра тяжести на чертеже
Ответ к задачи Определить координаты центра тяжести сечения.Показать положение центра тяжести на чертеже
Задача № 10 Найти реакцию опор
Ответ к задачи №10 Найти реакцию опор
Задача № 16 Определить опорные реакции балки.Проверить правильность их определения
Ответ к задачи № 16
Задача № 22 Определить опорные реакции балки. Проверить правильность их определения
Ответ к задачи № 22 Определить опорные реакции балки Проверить правильность их определения
Задача № 27 Определить опорные реакции балки Проверить правильность их определения
Ответ к задачи № 27 Определить опорные реакции балки Проверить правильность их определения
Задача № 26 Определить опорные реакции балки Проверить правильность их определения
Ответ к задачи № 26 Определить опорные реакции балки Проверить правильность их определения
Вариант 32 задача № 1Определить опорные реакции балки на двух опорах. Проверить правильность их определения
Проверить правильность их определения
Ответ к варианту 32 задача №1Определить опорные реакции балки на двух опорах. Проверить правильность их определения
Вариант 32 задача №2 Определить координаты центра тяжести сечения Показать положение центра на чертеже
Ответ к варианту 32 №2 Определить координаты центра тяжести сечения Показать положение центра на чертеже
Решение к варианту 32 № 2
Вариант 24 задача № 2 Определить координаты центра тяжести сечения Показать положения центра тяжести на чертеже
Ответ к варианту 24 задача № 2 Определить координаты центра тяжести сечения
Задача Указать положение центра тяжести на рисунке, придерживаясь определенного масштаба
Ответ к задачи Указать положение центра тяжести на рисунке, придерживаясь определенного масштаба
Задача — Определить величину и направления реакцию связей
Ответ к задаче -Определить величину и направления реакций связей
Задача- Определить опорные реакции балки на 2-х опорах
Ответ к задачи Определить опорные реакции балки на 2-х опорах
Задача № 9 Найти центр тяжести
Ответ к задаче № 9 найти центр тяжести
Найти центр тяжести
Решение к задаче Найти центр тяжести
Задача № 7
Решение к задаче № 7
28 задача Определить положение координаты центра тяжести
Ответ к 28 задачи Определить положение координаты центра тяжести
Задача Найти центр тяжести
Ответ к задаче Найти центр тяжести
Задача № 16 Определить положение координаты центра тяжести
Ответ к задаче № 16 Определить положение координаты центра тяжести
Ответ к задаче № 16 Определить положение координаты центра тяжести
Задача №23 Определить кординаты центра тяжести сечения
Ответ к задаче № 23 Определить координаты центра тяжести сечения
Определить опорные реакции балки
Ответ к задаче Определить опорные реакции балки
Определить опорные реакции балки
Ответ к задаче Определить опорные реакции балки
Определить координат центр тяжести
Ответ к задаче определить координат центр тяжести
Задача №20 Найти центр тяжести
Ответ к Задаче №20 Найти центр тяжести
Задача: Определить опорные реакции балки на двух опорах.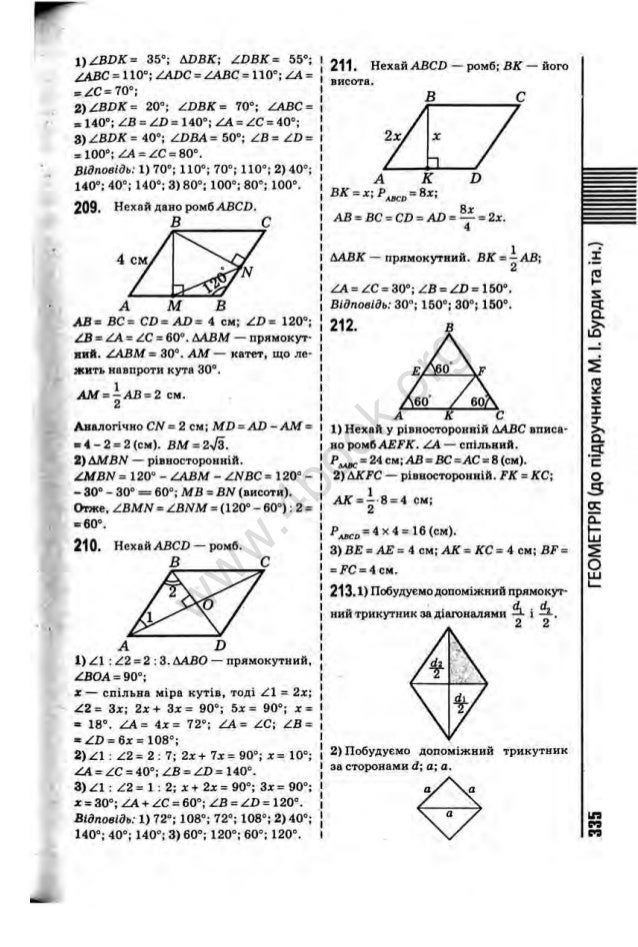 Проверить правильность их определения
Проверить правильность их определения
Ответ к задаче: Определить опорные реакции балки на двух опорах. Проверить правильность их определения
Задача Определить центр тяжести
Ответ к задаче — Определить центр тяжести
Здравствуйте, помогите пожалуйста решить задачу по расчету прочности при расстяжении, сжатии
Ответ к задаче по расчету прочности при расстяжении, сжатии
Задача- Определить координат центра тяжести
Ответ к задаче Определить координат центра тяжести
Задача — Подобрать сечение стержня подвески поддерживающего брус
Ответ к задаче Подобрать сечение стержня подвески поддерживающего брус
Задача — Подобрать сечение стержня подвески поддерживающего брус
Ответ к задаче — Подобрать сечение стержня подвески поддерживающего брус
Задача: построить эпюры Qy и Mx для балки по данным в задании
Ответ построить эпюры Qy и Mx для балки по данным в задании
Задача: номер 1. Определить реакции в опорах для балки
Определить реакции в опорах для балки
Ответ к задаче номер 1. Определить реакции в опорах для балки
Задача: построить эпюр Qy и Mx для балки, по данным в задании
Ответ к Задачи: построить эпюр Qy и Mx для балки, по данным в задании
Вариант № 3
Задание № 1 Определить изгибающий момент в точке С (справа)
Вариант № 2 Задание 1
Определить изгибающий момент в точке С . Построить эпюры поперечной силы и изгибающего момента
Вариант № 2 Задание 2
Ответ к Заданию № 2 рассчитать осевой момент инерции швеллера относительно оси Х
Задача № 3 Определить координаты центра тяжести
Ответ к задаче № 3
Задача 7
Ответ к задаче 7
Задача Проверить несущую способность балки
Ответ к задаче Проверить несущую способность балки
Задача — Момент силы относительно точки
Ответ к задаче — Момент силы относительно точки
Задача — Понятие о внецентренном растяжении ( сжатии)
Ответ к задаче — Понятие о внецентренном растяжении ( сжатии)
Задание
Ответ к заданию для Натальи Добринской
Задача: Определить реакцию опор двухопорной балки
Ответ
Задача
Ответ
Задача — столбец под номером 1
Ответ к задаче
Рисунок Д вариант чисел 1 Задача
Ответ к задаче
ПЕРЕХОДИ НА ДРУГУЮ СТРАНИЦУ САЙТА
ПО ССЫЛКЕ НИЖЕ
ОТВЕТЫ ПО ТЕХ-МЕХУ НА СЛЕДУЮЩЕЙ СТРАНИЦЕ
ОК ГДЗ — Тысячи топ решебников в клике от тебя.
 Получить за д/з 5
Получить за д/з 5Сегодня все большее число специалистов, даже те, кто недавно скептически относился к гдз, находит их удобными и полезными в своей практике. Минимум времени, которое тратится на нахождение нужного ответа, возможность воспользоваться решебником в любое время суток – вот далеко не все плюсы и преимущества, которые отличают эти материалы. Повысить собственную успеваемость, узнать что-то новое, взяв комплект учебник-решебник из иной, отличной от школьной, программы по предмету – каждый пользователь находит свой собственный метод и принцип применения этих источников.
Что выгодно отличает онлайн справочник?
По своей сути готовые домашние задания представляют собой грамотно, в соответствии с требованиями Стандартов образования, оформленные варианты решения ко всем заданиям, упражнениям и вопросам, представленным в том учебном пособии, к которому они предназначены. В готовых ответах, представленных на сайте еуроки.орг:
- рассматриваются все возможные варианты решения задания, если в нем они предполагаются;
- присутствуют наглядные инструменты – графики, рисунки, схемы, чтобы пользователь как можно более точно понял смысл представленного решения;
- даны подробные комментарии – для понимания логики, сути, алгоритма нахождения верного решения к каждому заданию сборника.

- представлен широкий выбор решебников по всем предметам школьной программы, а именно по математике, алгебре. русскому, а также английскому, биологии, истории, географии и т.д. Ресурс постоянно обновляется для организации максимально полной и качественной работы с ним заинтересованных пользователей, содержит самую актуальную информацию.
Преимущества применения ГДЗ в учебном процессе
Среди основных целей, которым служат онлайн сборники готовых ответов, такие:
- организация самопроверки, выработка навыков эффективной и результативной самостоятельной работы;
- возможность понять, как решаются сложные задания, что особенно важно тем школьникам, которые по той или иной причине пропустили занятие, блок занятий или находятся на дистанционной, семейной/домашней формах обучения;
- помощь родителям школьников – используя эти данные, они смогут быстро и качественно проверить знания своего ребенка по любой дисциплине;
- это удобный инструмент для педагогов и репетиторов для грамотной организации, систематизации своей работы – по планированию, контролю, оценке качества знаний учеников.
 Сборник готовых решений – прекрасный мотиватор, позволяющий сбалансировать интенсивную работу и необходимый полноценный отдых, получить высокую оценку и впоследствии стремиться удержать полученный результат.
Сборник готовых решений – прекрасный мотиватор, позволяющий сбалансировать интенсивную работу и необходимый полноценный отдых, получить высокую оценку и впоследствии стремиться удержать полученный результат.
Качественный инструмент для самоподготовки и отработки навыков самоконтроля — с помощью решебника можно заниматься регулярно и системно, осваивая материал школьных дисциплин по различным УМК и программам. Или — применять его только тогда, когда возникают серьезные сложности в освоении материала. Так можно не только улучшить оценки, получив более высокий балл, но и приобрести ценные и полезные навыки анализа собственных ошибок, самоподготовки. Затратив минимум времени, каждый пользователь сможет рассчитывать на высокий результат!
© 2021 Copyright. Все права защищены. Правообладатель SIA Ksenokss.
Адрес: 1069, Курземес проспект 106/45, Рига, Латвия.
Тел.: +371 29-851-888 E-mail: [email protected]
Как геометрия используется в фотографии? 10 советов, которые стоит попробовать
Вы когда-нибудь задумывались, как геометрия может улучшить ваши навыки фотографа и вывести ваши фотографии на новый уровень?
Геометрия играет жизненно важную роль в фотографии, от кадрирования объектов до создания глубины и перспективы на изображениях. Включая геометрические фигуры, линии и узоры в свои фотографии, вы можете создавать привлекательные и визуально привлекательные композиции.
Включая геометрические фигуры, линии и узоры в свои фотографии, вы можете создавать привлекательные и визуально привлекательные композиции.
Независимо от того, являетесь ли вы новичком или опытным фотографом, освоение геометрии может значительно улучшить качество ваших фотографий.
Это полезное руководство по использованию геометрии в фотографии.
Мы рассмотрим следующие темы (нажмите на маркер, чтобы перейти к этому разделу):
Содержание
Что такое геометрическая фотография?Геометрическую фотографию можно определить как тип фотографии, в котором особое внимание уделяется захвату уникальных форм, линий и других форм для создания определенного ракурса на фотографии.
Они не всегда связаны с домами или архитектурой, хотя идеи геометрической фотографии также могут исходить из зданий.
Знание того, как использовать геометрические фигуры и воплощать их в своих фотографиях, поможет вам специализироваться или даже расширить свои навыки фотографа. 1. Архитектурная фотография конкретная форма с определенной точки зрения; эта комбинация может считаться геометрической фотографией
1. Архитектурная фотография конкретная форма с определенной точки зрения; эта комбинация может считаться геометрической фотографией
Абстрактные экспрессионисты, такие как Джексон Поллок, любят создавать абстрактные работы, которые что-то значат в определенном контексте.
Фотография также может выделять определенные эмоции и чувства с помощью форм, линий или узоров.
Формы и линии 3. Фэшн-фотографияИдеи геометрической фотографии можно найти в моде в дизайнерских проектах высокого класса.
Дизайнерам моды нужны фотографы, которые понимают, на чем нужно сосредоточиться.
Геометрическая фотография — это подчеркивание узоров, правильной позы, композиции и т. д.
fashion photo Как форма используется в фотографии?Так как форма используется в геометрической фотографии или в любой из идей геометрической фотографии?
Формирование геометрии — это один из методов фотографии, используемых для создания подходящих хороших динамичных фотокомпозиций.
Такие фигуры, как квадраты, круги, треугольники и другие, можно использовать в качестве ориентиров при съемке фотографий.
Различные формы могут придать фотографии различный вид.
Фотография также может создавать впечатление симметрии, ритма и голосовых акцентов, чтобы люди, которые видят фотографию, чувствовали себя более связанными с фотографией, ссылаясь на геометрические формы.
Дальнейшая реализация: вы можете использовать геометрические фигуры в качестве ориентира при расположении нескольких объектов на фотографиях, чтобы ваши фотографии выглядели более динамично и организованно.
Предположим, вам нужно сфотографировать сразу трех человек на одном снимке.
Если поставить все три на одинаковую высоту, получится жесткое и неприглядное фото.
Если вы расположите их треугольником, ваша фотография в целом будет выглядеть более динамичной, сбалансированной и привлекательной.
образуют треугольник Зачем использовать геометрию в фотографии?Итак, как геометрия используется в фотографии? И почему?
На самом деле это связано с позиционированием и композицией.
Согласно нескольким исследованиям, наши глаза и разум больше привлекают более симметричные объекты.
Левая и правая стороны человека не на 100% одинаковы. Но некоторые люди сталкивались с почти одинаковыми левой и правой сторонами.
Они считаются красивыми и более привлекательными для противоположного пола.
Потому что симметрия свидетельствует о хорошей генетике, особенно с точки зрения репродуктивного здоровья.
Таким образом, нам нужно упаковать геометрическую фотографию в композицию, чтобы придать ощущение порядка самой неестественной или неинтересной стороне наших объектов.
10 советов по включению геометрии в вашу фотографию 1. Правило третейПравило третей — одна из самых основных фотокомпозиций, и фотографы должны знать ее.
По правилу третей фотограф просто делит область фотографии на девять равных квадратов и помещает POI (достопримечательность) в точку или линию на плоскости, которая делится на 3 x 3.
Есть четыре интересные точки (IP), а интересные линии состоят из 2 горизонтальных и вертикальных линий.
Принцип ROT заключается в размещении POI на точке или линии.
Фотография будет выглядеть более привлекательно, чем любая другая точка/линия.
Точка интереса, расположенная на четырех точках или линиях выше, может быть объектом или частью глаза фотообъекта.
правило третейСегодня многие цифровые камеры имеют функцию правила третей (сетка) либо на экране режима просмотра в реальном времени, либо в видоискателе.
Наше предложение для разделения полей между положительным и отрицательным с использованием соотношения 50: 50 или 30: 50, в зависимости от вкуса.
Чтобы лучше изучить правило третей, рекомендуем ознакомиться с нашим руководством по правилу третей, а также посмотреть это видео Джулиана Дискаверса:
2. Золотая форма Золотая форма, также называемая Золотое сечение — это геометрическая фотокомпозиция, состоящая в разделении области фотографии, окаймленной реальными линиями или виртуальными краями, на положительное и отрицательное.
Кажется, что между двумя полями существует контраст, который образует гармоничное единство.
Принцип Золотой формы заключается в правильном разделении положительных и отрицательных областей.
В сбалансированном виде фотография будет выглядеть хорошо скомпонованной.
золотая спираль/соотношениеДля дальнейшего изучения золотого сечения/формы мы рекомендуем ознакомиться с нашим руководством по золотому сечению, а также посмотреть это видео от Reg Does Stuff:
3. СимметричныйЭта фотокомпозиция размещает объект и делит область фотографии одинаково справа и слева, чтобы выглядеть удивительно симметрично.
симметричные линии 4. Шаблон и повторениеИнстинктивно люди инстинктивно интересуются гармоничными узорами или узорами.
Таким образом, фотография с узорчатой или закольцованной композицией может стать отличной фотоработой.
Паттерн (паттерн) и повтор (повторение) можно получить, подобрав правильный ракурс фото и выбрав таким образом расстояние между объективом и объектом.
5. Кадр в кадреС помощью техники «кадр в кадре» мы создаем геометрическую композицию фотографии, направляя или направляя взгляд на то, что находится внутри «кадра», игнорируя то, что находится за пределами «кадра». ».
Рамка здесь не фоторамка в физической форме, а вы ищете объект, который можно использовать как «рамку» в виде реальных или виртуальных линий.
Ищите такие элементы, как окна, двери, коридоры, зеркала, колонны зданий, арки или любой объект, который обычно представляет собой замкнутую геометрическую форму для обрамления POI.
кадр внутри кадраРамка также не должна окружать всю POI.
Для дальнейшего изучения техники создания кадра в кадре мы рекомендуем это видео от FotoCollab:
6. Направляющие линии Еще один альтернативный ответ на вопрос о том, как геометрия используется в фотографии, — это направляющие линии.
Одна из самых интересных фотокомпозиций, на мой взгляд, — «Направляющие линии».
Линии или линии могут быть виртуальными или реальными. Они приводят наш взгляд к объекту, который становится POI, или сама линия становится POI на фотографии.
направляющие линииИщите такие объекты, как дороги, стены, мосты и т. д., которые могут образовывать виртуальную очередь и направлять взгляд на реальный объект (POI).
Для дальнейшего изучения того, как использовать направляющие линии, мы рекомендуем это видео от J.M. Wilyat:
7. Композиция негативного пространстваКомпозиция негативного пространства — это творческая композиция, которая оставляет на фотографии много свободного или негативного пространства.
Областью здесь может быть небо, бескрайняя пустыня, луг или что-то еще, что может дать «свободное пространство» фотографии.
Предусмотрев правильное пустое пространство, ваши фотографии могут выглядеть очень интересно и креативно.
Отражение на фото может быть основным элементом (достопримечательностью) или исследоваться только как дополнение.
Если фотоотражение является основным элементом, оно должно содержать фотографию, рассказывающую историю, даже если это всего лишь отражение.
Отражение обычно знакомо фотографам, которые любят абстрактную красоту или минимализм с композицией отражения в качестве основного POI.
Предметы, которые можно использовать для отражения, могут быть самые разные, например, лужи, спокойные озера, незасаженные рисовые поля, реки, окна, зеркала, зеркала и даже стекла и другие.
Между тем, объекты, которые можно использовать, это объекты, живые существа, люди и другие.
9. Захват текстурыТекстура — это фотокомпозиция, отображающая текстуру фотографируемого объекта.
При наличии текстуры детали объектов будут более заметными, особенно если этому способствует хорошее освещение.
Примерами объектов, обычно используемых для текстурных композиций, являются камни, асфальт, полосы костей на листьях, дерево, кожа, глаза, ткань и многое другое.
Используемая техника проста, чтобы получить текстуру и сфотографировать объект с близкого расстояния с помощью телеобъектива или 50 мм и выше.
Текстура 10. Глубина резкостиКомпозиция, изолирующая объекты за счет размытия фона, обычно используется для фотографирования людей, изображений или любого другого предмета, цель которого состоит в том, чтобы фотографическая аудитория сосредоточилась только на выделенном объекте.
размытие глубины резкости Заключительные замечанияЭто десять альтернативных ответов и методов использования геометрии в фотографии, которые вы можете применить, чтобы сделать свои фотографии более творческими и интересными.
Фотокомпозиция, как и композиция в любой области искусства, подобна вкусу еды.
Все зависит от личных предпочтений. Итак, не существует стандартных правил композиционных приемов в области фотографии.
Еще Стив МакКарри сказал, что для создания чего-то творческого необходимо нарушить существующие правила.
Проявите творческий подход, чтобы ваши фотографии выглядели не небрежно, а изучали теорию композиционных приемов в фотографии. И если вы хотите узнать больше о творчестве в фотографии, у нас есть руководство по этому вопросу.
Часто задаваемые вопросы
Какие фигуры часто встречаются на фотографиях?
Есть несколько распространенных форм, которые можно найти на фотографиях, включая треугольники, круги, квадраты и прямоугольники. Эти формы могут добавить визуальный интерес и помочь создать ощущение баланса и гармонии в композиции.
Должна ли геометрия присутствовать на каждой фотографии?
Нет, геометрия не обязательно должна быть на каждой фотографии. Хотя включение геометрии в вашу фотографию может помочь создать визуальный интерес и ощущение баланса, это не является требованием для каждой фотографии, и его следует использовать вдумчиво и намеренно, чтобы улучшить композицию.
Геометрия в композиции
Первый урок, Правило третей, представил широко используемый принцип, который помогает решить *куда поместить предмет*. Вторая, «Простота», заключалась в том, чтобы убрать ненужное и сконцентрироваться на важном.
Предыдущие аспекты более или менее воспринимали предмет или основной интерес фотографии как данность. Этот другой: его цель — дать представление о том, «что фотографировать», не с точки зрения предметов, а с точки зрения того, что искать в предметах или композициях. Чтобы выйти за пределы трех «К» (что изображения с детьми, животными или красивыми женщинами обычно побеждают изображения без них; спросите Чака, что означает «К»), мы остаемся на несколько абстрактном уровне. Геометрия играет важную роль в фотографии, так как помогает создавать интересные композиции и придает изображениям ощущение баланса. Понимая, как использовать основные геометрические формы и линии, фотографы могут добавлять эффектные визуальные элементы к своим фотографиям.
Теперь мы рассмотрим геометрические элементы и то, как их использовать в композиции.
Для чего это нужно?
Геометрические элементы редко бывают очень хорошими предметами, начальными или второстепенными. Вместо этого они выполняют вспомогательную роль, помогая собрать картину воедино. У них есть по крайней мере три общих и очень важных применения:
Ведущая линияВедущая линия делает то, о чем говорит: она ведет взгляд от одной части изображения к другой: от переднего плана к заднему, второстепенному подчинены основному предмету (но очень редко наоборот). Ведущая линия добавляет движения статичному изображению и связывает вместе различные элементы. Диагонали и дуги или другие незамкнутые кривые являются хорошими направляющими линиями.
Пространственный разделитель Пространственный разделитель делит изображение на отдельные области, которые вместе образуют композицию. Не все изображения основаны на областях, но иногда области могут создавать сильную композицию даже при отсутствии четких точек интереса. Треугольники особенно полезны в качестве пространственных разделителей, но и другие элементы (диагонали, незамкнутые кривые) также могут выполнять эту роль.
Треугольники особенно полезны в качестве пространственных разделителей, но и другие элементы (диагонали, незамкнутые кривые) также могут выполнять эту роль.
Элемент обрамления служит для фокусировки внимания на главном объекте. Обычно он закрывает как минимум два края изображения и может сильно вторгаться в него, иногда занимая большую часть его пространства. Чтобы это работало, обрамляющий элемент должен иметь некоторые собственные интересные характеристики: цвет, текстуру или форму. Смелые геометрические формы могут очень хорошо работать в качестве элементов обрамления: особенно хорошо работают треугольники или дуги. Обычно элементы обрамления должны быть в более низком ключе и более приглушенными, чем основной объект: они предназначены не для отвлечения, а для фокусировки, даже если фактическая точка изображения является элементом обрамления, например, в некоторых примерах Фальшивого Субъекта. .
Что это значит?
Это не математика, поэтому мы упрощаем. Геометрические элементы — это простые узнаваемые формы, такие как квадраты, круги, треугольники, линии и кривые. Композиционно одни геометрические формы имеют больше возможностей, чем другие: квадраты и круги, например, более статичны и поэтому менее интересны, чем треугольники или незамкнутые кривые.
Геометрические элементы — это простые узнаваемые формы, такие как квадраты, круги, треугольники, линии и кривые. Композиционно одни геометрические формы имеют больше возможностей, чем другие: квадраты и круги, например, более статичны и поэтому менее интересны, чем треугольники или незамкнутые кривые.
Некоторые геометрические фигуры имеют особенно большой композиционный потенциал:
- Диагонали
- Треугольники
- Дуги
- S-кривые
Мы сосредоточимся на этих формах и их использовании.
Диагональ Изображение с диагональным элементом почти всегда динамичнее и сильнее, чем такое же изображение без него. В то время как вертикали и горизонтали обычно делят пространство на области, диагонали соединяют. Действительно, одним из наиболее распространенных и эффективных способов использования диагонали является «ведущая линия» — то, что соединяет главный объект с второстепенным, заставляя глаз двигаться внутри кадра. В этой роли диагонали могут быть сильными компонентами перспективы и глубины, придающими изображению трехмерность.
В этой роли диагонали могут быть сильными компонентами перспективы и глубины, придающими изображению трехмерность.
Вот картина, составленная из диагоналей, используемых в качестве направляющих линий и для создания трехмерности:
Линии чугунных перил, трамвайных путей и тросов ведут взгляд от статуи к приближающемуся трамваю. Ощущение глубины усиливается малой глубиной резкости.
Вот изображение, составленное вокруг диагонали, используемой в качестве направляющей линии и разделителя пространства, но не в первую очередь как показатель перспективы:
Простая диагональ — одна из самых универсальных геометрических фигур, используемых в композициях. Ищите их и делайте из них лучшее. Однако, поскольку диагональ представляет собой линию и часто одновременно входит и выходит из кадра, важно положить на нее что-нибудь, чтобы взгляд не убегал за пределы кадра. Использование его в качестве ведущей линии, например, от главного объекта к второстепенному или от переднего плана к заднему, — хороший способ организовать это.
Треугольник — это замкнутая кривая, имеющая хотя бы одну диагональ. Будучи закрытым, он не будет уводить взгляд за пределы кадра. Тем не менее, особенно равносторонний треугольник намного более статичен, чем диагональ. Сам по себе, и особенно в середине кадра, он может сделать композицию статичной и скучной. Иногда треугольные области могут создавать необычные изображения, как, например, это:
Однако настоящие треугольники встречаются довольно редко. Вместо того, чтобы искать их, треугольник можно использовать более абстрактно: для размещения ваших основных и второстепенных объектов в кадре или с помощью трех дополнительных точек интереса, чтобы сформировать «рамку» для вашего основного объекта.
ДугаДуга может быть прекрасным композиционным элементом. В незамкнутом виде может служить ведущей линией, притягивающей взгляд к главному объекту (фото Шоста Сулонена)…
…пространственным разделителем. ..
..
… или обрамляющим элементом, фокусирующим внимание на основной предмет:
Особенно если он асимметричный, он может создать динамичную и интересную композицию. Если вы видите дугу, внимательно изучите сцену и найдите элементы, которые сбалансируют (обычно) асимметричную композицию, созданную дугой, и попытайтесь найти способ наилучшим образом использовать дугу — не просто включайте ее, сконцентрируйтесь. на него и его назначение в композиции: ведущая линия, связующее звено, разделитель пространства или обрамляющий элемент?
S-образная криваяS-образная кривая представляет собой кривую в форме буквы S. Это композиционное золото. Если вы его видите, вы *знаете*, что это хорошая картина. S-образная кривая — едва ли не единственная геометрическая форма, которая может стоять отдельно в качестве основного объекта, но ее также можно использовать в качестве направляющей линии, элемента кадра или чего-либо еще.
Обе фотографии Мелани Кипп.


 Сборник готовых решений – прекрасный мотиватор, позволяющий сбалансировать интенсивную работу и необходимый полноценный отдых, получить высокую оценку и впоследствии стремиться удержать полученный результат.
Сборник готовых решений – прекрасный мотиватор, позволяющий сбалансировать интенсивную работу и необходимый полноценный отдых, получить высокую оценку и впоследствии стремиться удержать полученный результат. Двугранный угол. Перпендикулярность плоскостей
Двугранный угол. Перпендикулярность плоскостей
 04.2020
6410
0
04.2020
6410
0
 2. Линейные операции над векторами: сложение и вычитание векторов, умножение вектора на число. Свойства операций над векторами.
3. Компланарные векторы. Условия компланарности. Разложение вектора по трём некомпланарным векторам.
Критерии оценивания (процент правильных ответов):
— если Вы наборали 85-100%, то Вам выставляется оценка «отлично»;
— если Вы наборали 65-84%, то Вам выставляется оценка «хорошо»;
— если Вы наборали 40-64%, то Вам выставляется оценка «удовлетворительно»;
— если Вы наборали менее 40%, то Вам выставляется оценка «неудовлетворительно».
В случае, если Вы успешно прошли тест, набрав более 65% баллов, то Вы можете скачат сертификат о прохождении теста.
2. Линейные операции над векторами: сложение и вычитание векторов, умножение вектора на число. Свойства операций над векторами.
3. Компланарные векторы. Условия компланарности. Разложение вектора по трём некомпланарным векторам.
Критерии оценивания (процент правильных ответов):
— если Вы наборали 85-100%, то Вам выставляется оценка «отлично»;
— если Вы наборали 65-84%, то Вам выставляется оценка «хорошо»;
— если Вы наборали 40-64%, то Вам выставляется оценка «удовлетворительно»;
— если Вы наборали менее 40%, то Вам выставляется оценка «неудовлетворительно».
В случае, если Вы успешно прошли тест, набрав более 65% баллов, то Вы можете скачат сертификат о прохождении теста.

 Стереометрия в задачах ЕГЭ.
Стереометрия в задачах ЕГЭ.
 08.2020
1080
0
08.2020
1080
0
 10.2021
5284
0
10.2021
5284
0

 Аксиомы стереометрии. Некоторые следствия из аксиом. Тест 1
Аксиомы стереометрии. Некоторые следствия из аксиом. Тест 1
 05.2019
5004
0
05.2019
5004
0
 04.2020
787
0
04.2020
787
0

 Делимость чисел;
2.Многочлены. Алгебраические уравнения;
3.Степень с действительным показателем;
4.Степенная функция;
5.Показательная функция;
6.Логарифмическая функция
Делимость чисел;
2.Многочлены. Алгебраические уравнения;
3.Степень с действительным показателем;
4.Степенная функция;
5.Показательная функция;
6.Логарифмическая функция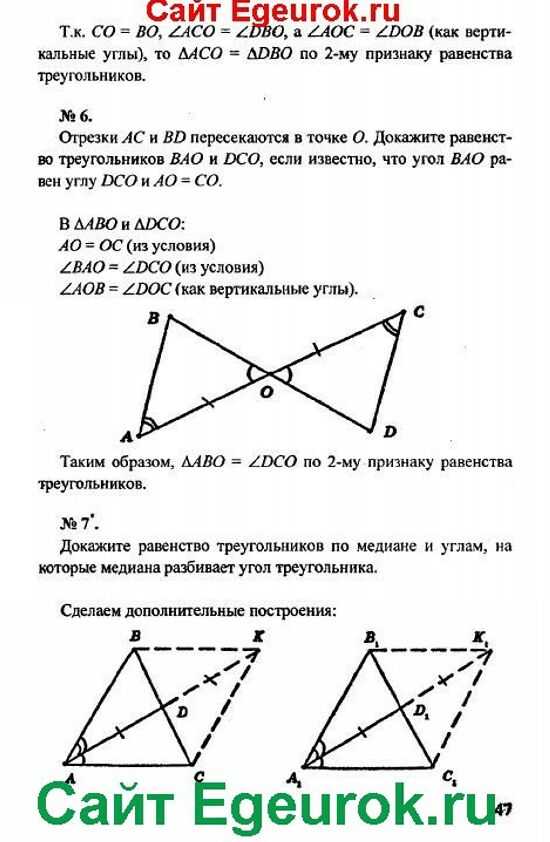 Основные понятия и утверждения геометрии. Позволяет оценить знания теории учащихся 9-10 кл.
Основные понятия и утверждения геометрии. Позволяет оценить знания теории учащихся 9-10 кл. Задачи.
Задачи.


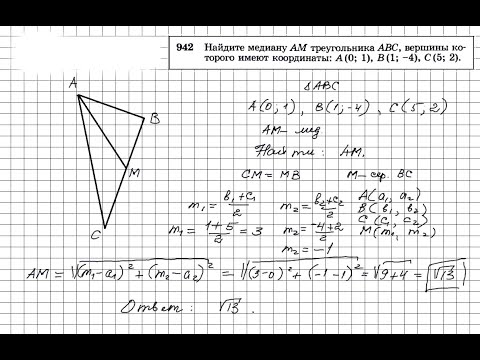

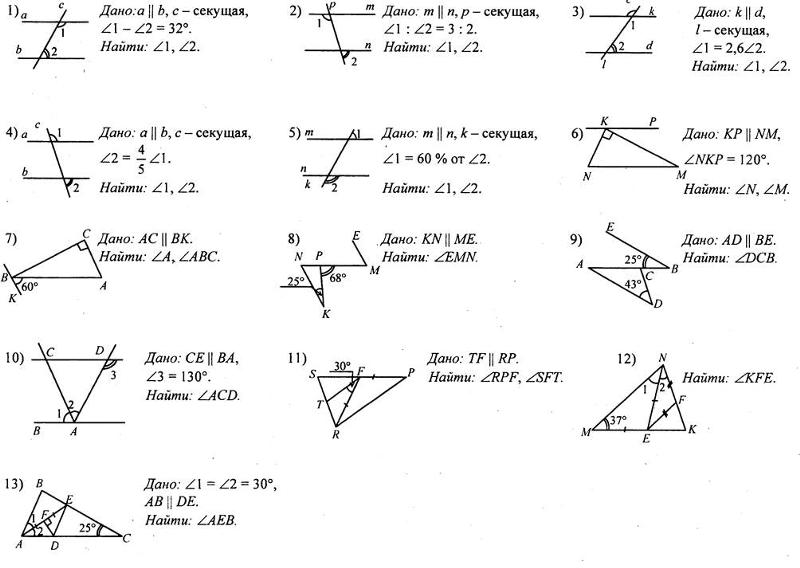


 В своей настольной игре Саша придумал задачку, которую с трудом смог решить мой муж, его дедушка, кандидат наук. Такой алгоритм и смекалка, что даже ученому пришлось постараться!
В своей настольной игре Саша придумал задачку, которую с трудом смог решить мой муж, его дедушка, кандидат наук. Такой алгоритм и смекалка, что даже ученому пришлось постараться!



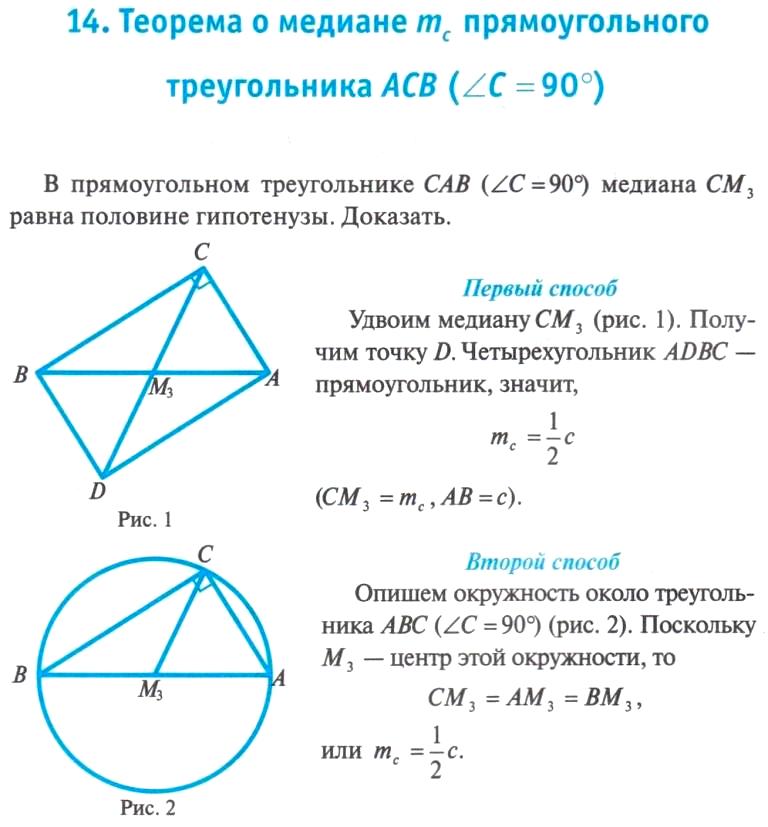



 Присоединяйтесь к Schoolhouse для бесплатного обучения геометрии с сообществом, которое поддержит вас!
Присоединяйтесь к Schoolhouse для бесплатного обучения геометрии с сообществом, которое поддержит вас! Сессии будут проходить в 18:00 по центральному поясному времени каждый понедельник-четверг, пока серия не закончится. Однако первая неделя занятий будет состоять только из занятий по средам и четвергам.
Сессии будут состоять из:
— Слайд-шоу, проходящее по содержанию
— Практика Проблемы
— Короткое домашнее задание
— Игры для практики Контент, изучаемый в конце каждых 2 модулей
Примечание. По мере продолжения серии будут добавляться дополнительные сеансы. Я ожидаю, что серия будет завершена к концу второй недели мая, как раз к финалу.
Сессии будут проходить в 18:00 по центральному поясному времени каждый понедельник-четверг, пока серия не закончится. Однако первая неделя занятий будет состоять только из занятий по средам и четвергам.
Сессии будут состоять из:
— Слайд-шоу, проходящее по содержанию
— Практика Проблемы
— Короткое домашнее задание
— Игры для практики Контент, изучаемый в конце каждых 2 модулей
Примечание. По мере продолжения серии будут добавляться дополнительные сеансы. Я ожидаю, что серия будет завершена к концу второй недели мая, как раз к финалу. Мы подробно рассмотрим все концепции в среднем темпе, чтобы у вас было полное понимание предмета.
Эта серия предназначена для того, чтобы предоставить вам широкие возможности для практики и улучшения ваших навыков с помощью разнообразных практических упражнений, которые бросят вам вызов и помогут укрепить вашу уверенность в геометрии.
Чтобы получить максимальную отдачу от этого курса, рекомендуется, чтобы учащиеся имели знания по предварительной алгебре.
К концу этой серии у вас будет прочная основа в геометрии, которая подготовит вас к вашим будущим курсам по этому предмету.
ПРИМЕЧАНИЕ. В будущем будет добавлено больше сеансов
Мы подробно рассмотрим все концепции в среднем темпе, чтобы у вас было полное понимание предмета.
Эта серия предназначена для того, чтобы предоставить вам широкие возможности для практики и улучшения ваших навыков с помощью разнообразных практических упражнений, которые бросят вам вызов и помогут укрепить вашу уверенность в геометрии.
Чтобы получить максимальную отдачу от этого курса, рекомендуется, чтобы учащиеся имели знания по предварительной алгебре.
К концу этой серии у вас будет прочная основа в геометрии, которая подготовит вас к вашим будущим курсам по этому предмету.
ПРИМЕЧАНИЕ. В будущем будет добавлено больше сеансов Мы предлагаем бесплатные онлайн-репетиторские занятия по математике, а также подготовку к SAT и AP. Если вы хотите присоединиться к сеансу, зарегистрируйте учетную запись, чтобы начать.
Мы предлагаем бесплатные онлайн-репетиторские занятия по математике, а также подготовку к SAT и AP. Если вы хотите присоединиться к сеансу, зарегистрируйте учетную запись, чтобы начать. Однако, если вам нужна помощь по геометрии, запишитесь на сеанс репетиторства Schoolhouse — это совершенно бесплатно!
Однако, если вам нужна помощь по геометрии, запишитесь на сеанс репетиторства Schoolhouse — это совершенно бесплатно!

 2
2
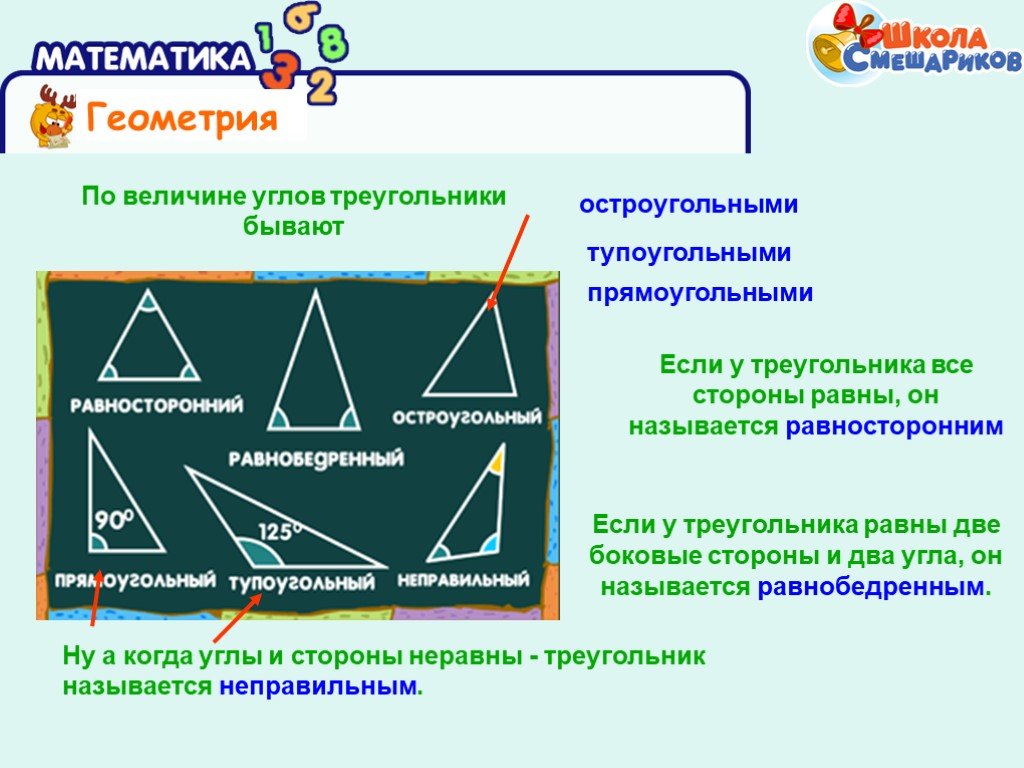
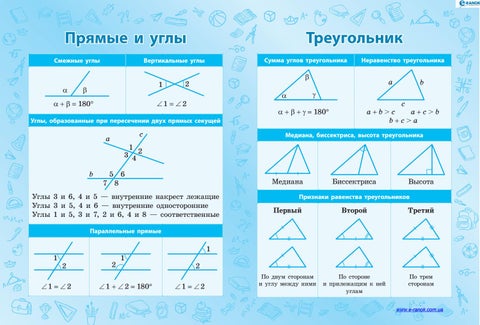
 Если хоть один из углов треугольника прямой или тупой, то фигуру уже нельзя считать произвольной.
Если хоть один из углов треугольника прямой или тупой, то фигуру уже нельзя считать произвольной.
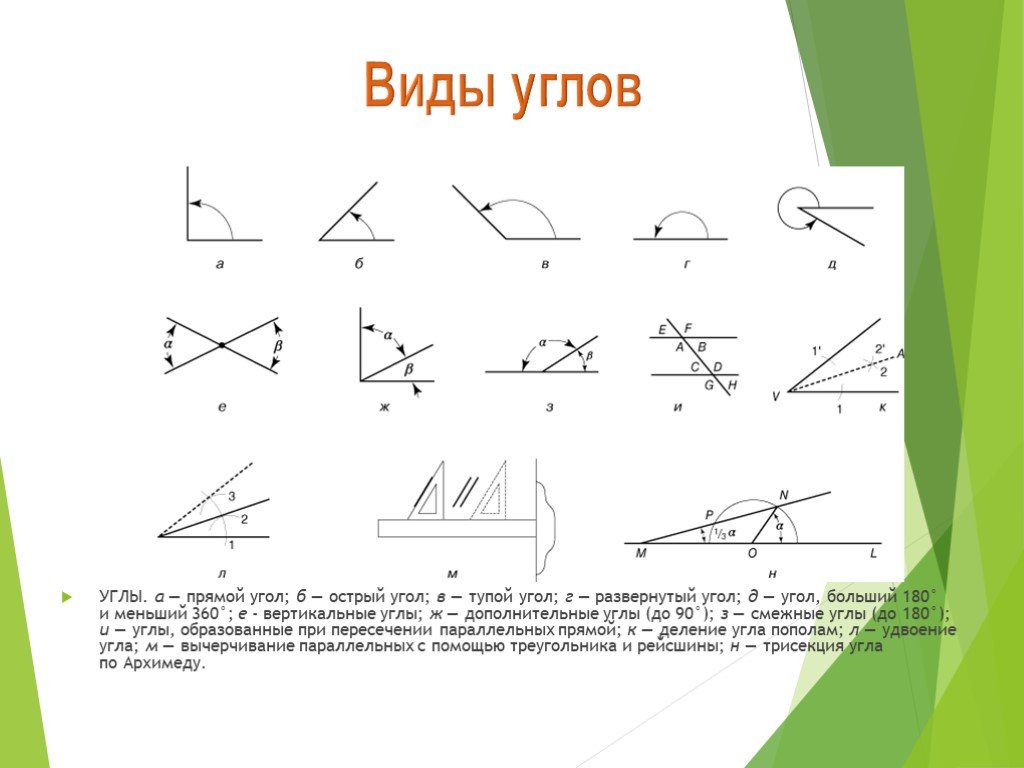
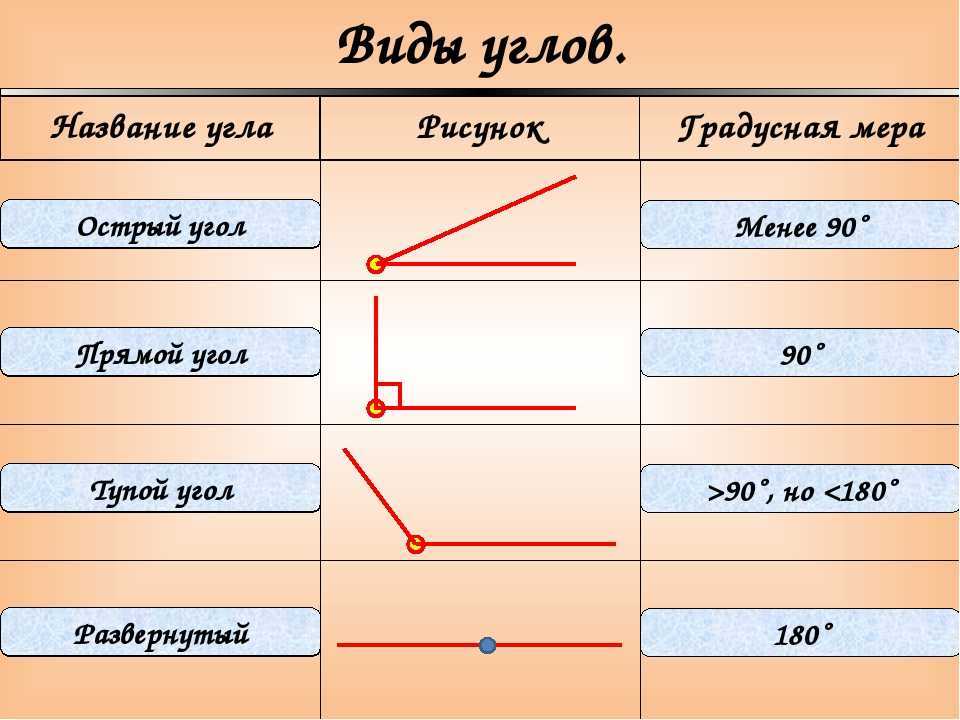
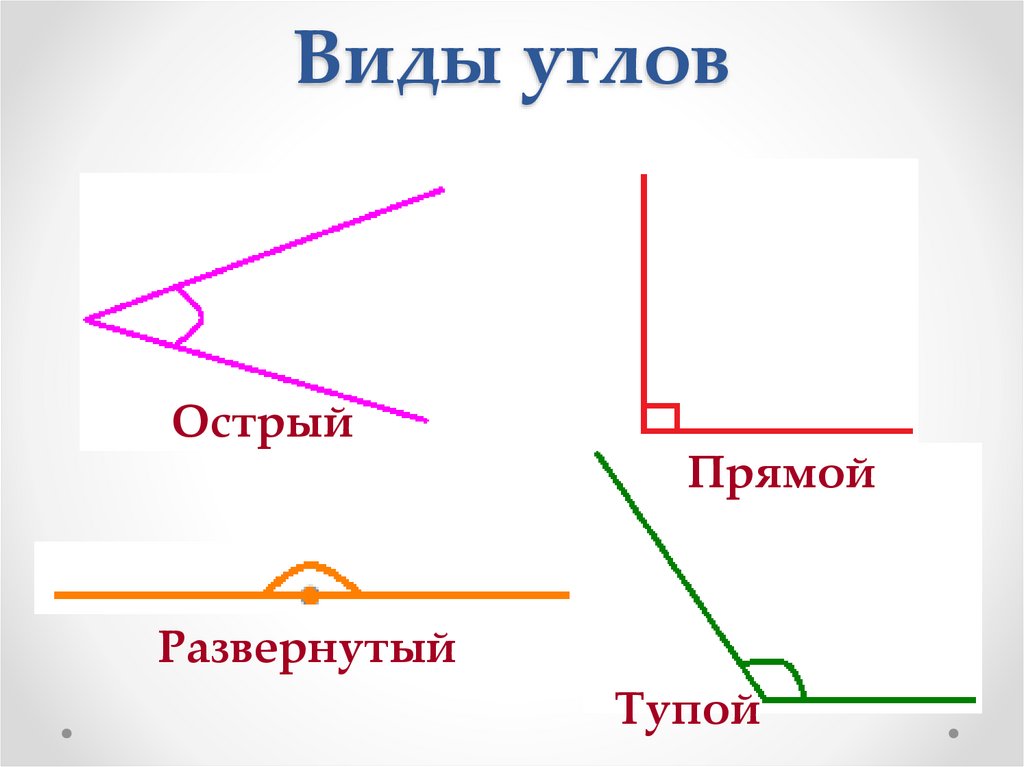 Существуют различные типы углов в геометрии, такие как острый угол, тупой угол, прямой угол, рефлекторный угол и прямой угол. Например, острый угол — это угол, который меньше 90°, а тупой угол — это угол, который больше 90°. Существуют также некоторые специальные типы пар углов. Давайте узнаем о различных типах углов в деталях.
Существуют различные типы углов в геометрии, такие как острый угол, тупой угол, прямой угол, рефлекторный угол и прямой угол. Например, острый угол — это угол, который меньше 90°, а тупой угол — это угол, который больше 90°. Существуют также некоторые специальные типы пар углов. Давайте узнаем о различных типах углов в деталях. В зависимости от размера углы классифицируют следующим образом. На следующем рисунке показаны различные виды углов, описанные ниже.
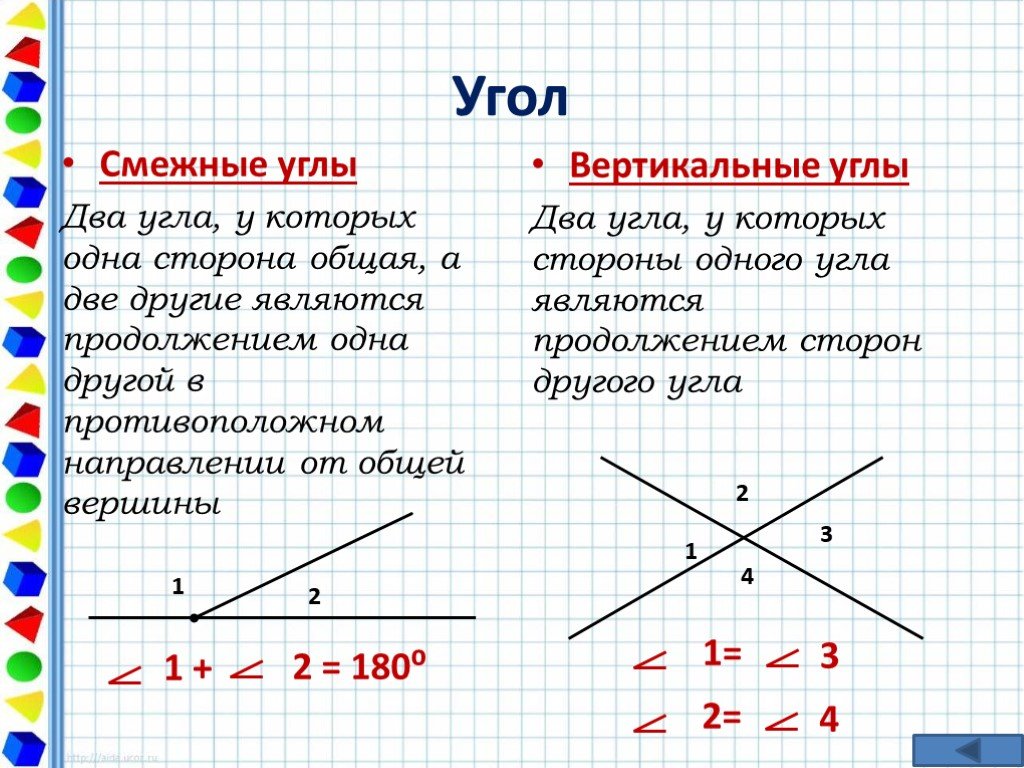
В зависимости от размера углы классифицируют следующим образом. На следующем рисунке показаны различные виды углов, описанные ниже.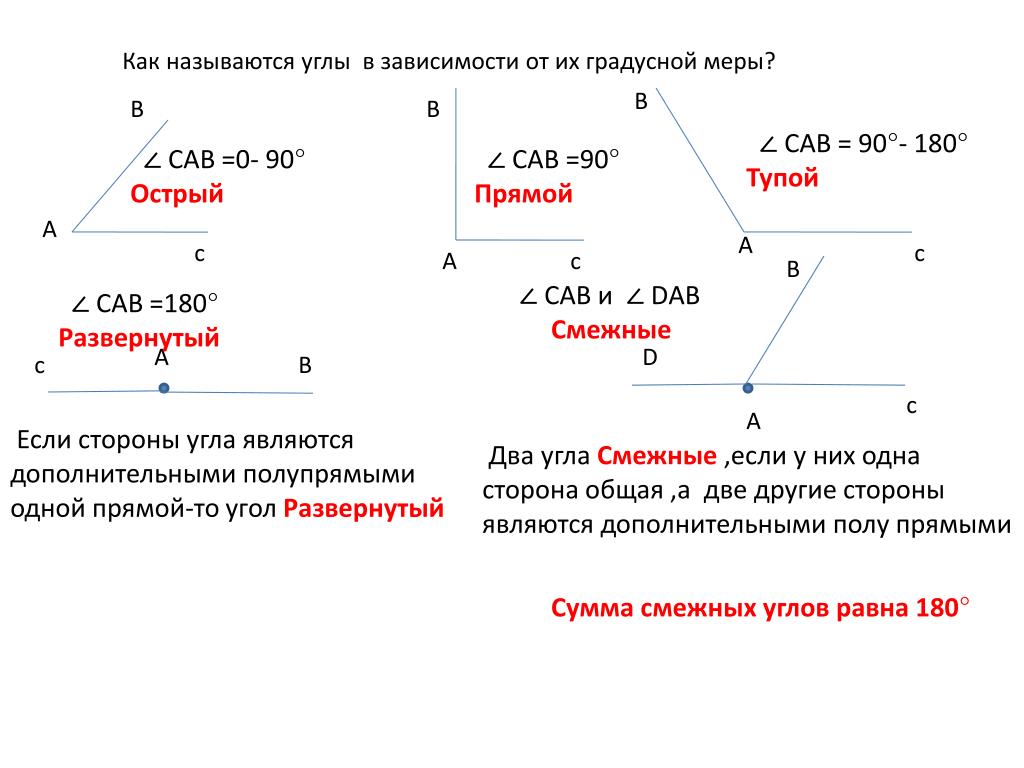 Под прямым углом два луча противоположны друг другу. Прямой угол может быть образован путем соединения двух смежных прямых углов или, другими словами, два прямых угла составляют прямой угол. На рисунке ∠SRT представляет собой угол 180° или прямой угол.
Под прямым углом два луча противоположны друг другу. Прямой угол может быть образован путем соединения двух смежных прямых углов или, другими словами, два прямых угла составляют прямой угол. На рисунке ∠SRT представляет собой угол 180° или прямой угол. На рисунке ниже при повороте стороны 1(AB) против часовой стрелки на угол θ образуется положительный угол.
На рисунке ниже при повороте стороны 1(AB) против часовой стрелки на угол θ образуется положительный угол.
 В зависимости от поворота углы делятся на положительные и отрицательные.
В зависимости от поворота углы делятся на положительные и отрицательные.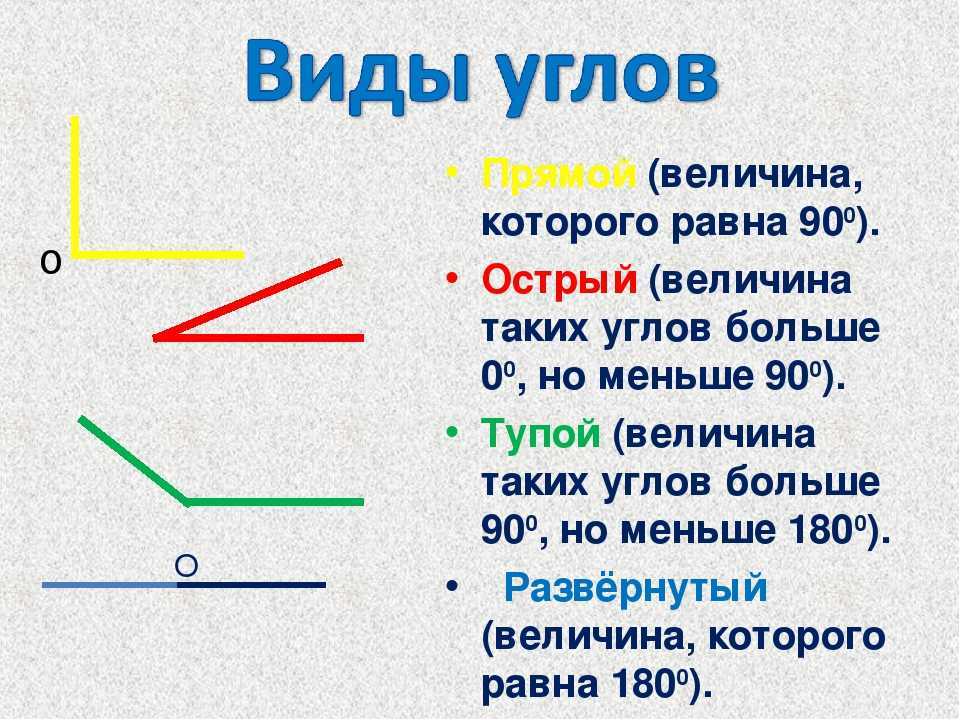

 Обратите внимание на рисунок, на котором вершина O отмечена как точка соединения двух плеч.
Обратите внимание на рисунок, на котором вершина O отмечена как точка соединения двух плеч.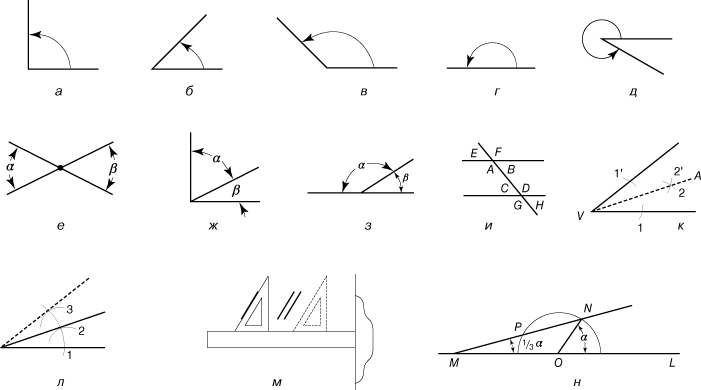 Прямой угол легко заметить, так как он образует форму буквы L.
Прямой угол легко заметить, так как он образует форму буквы L. Другими словами, положительные углы — это те углы, которые повернуты от основания в направлении против часовой стрелки.
Другими словами, положительные углы — это те углы, которые повернуты от основания в направлении против часовой стрелки.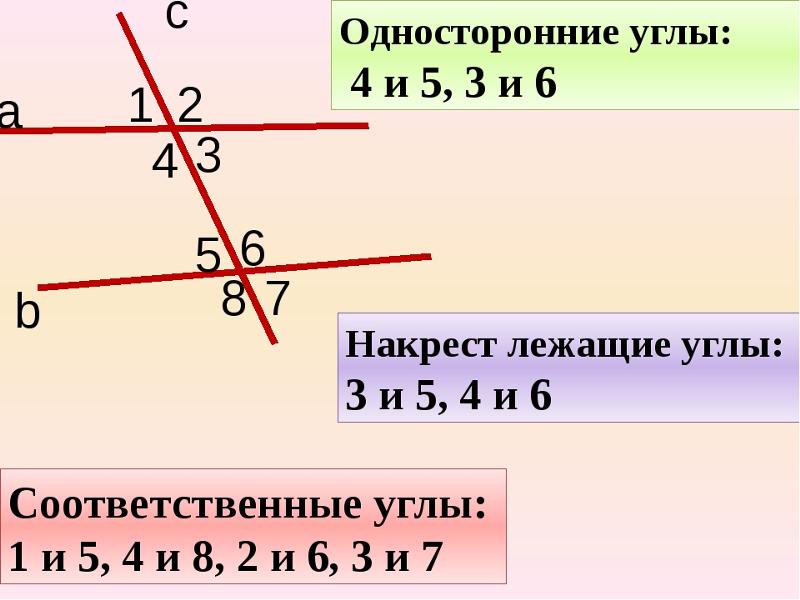
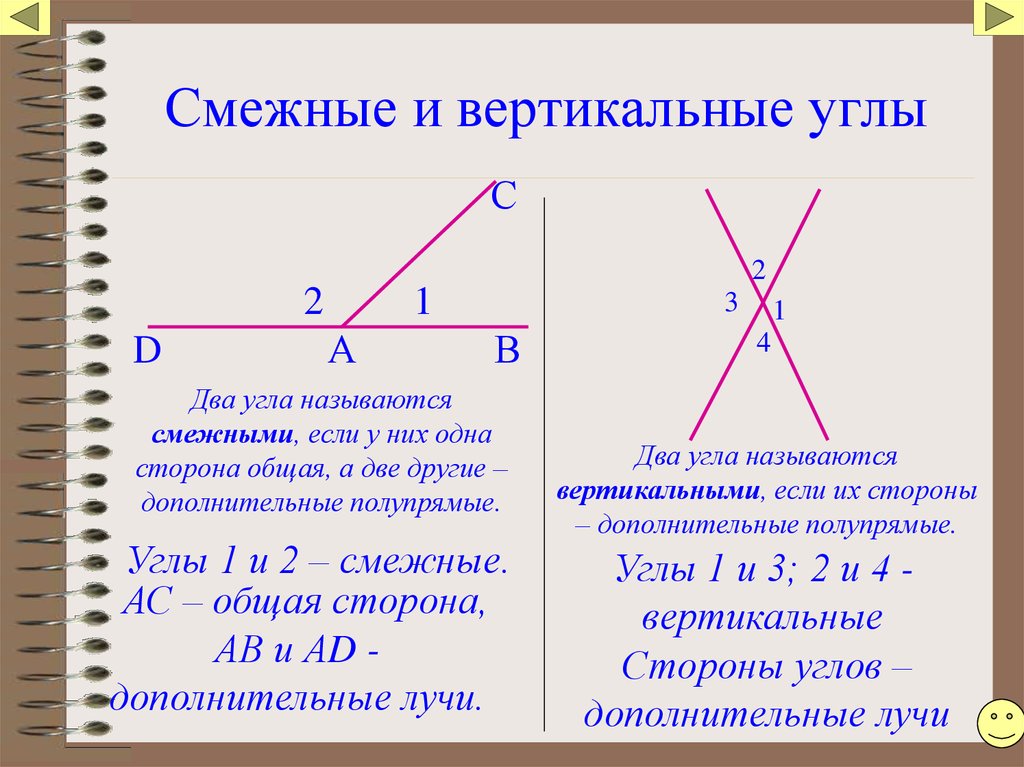


 «Отверстие» между этими двумя лучами называется «углом», который обозначается символом ∠. Углы обычно измеряются в градусах и выражаются как 60°, 90° и так далее.
«Отверстие» между этими двумя лучами называется «углом», который обозначается символом ∠. Углы обычно измеряются в градусах и выражаются как 60°, 90° и так далее.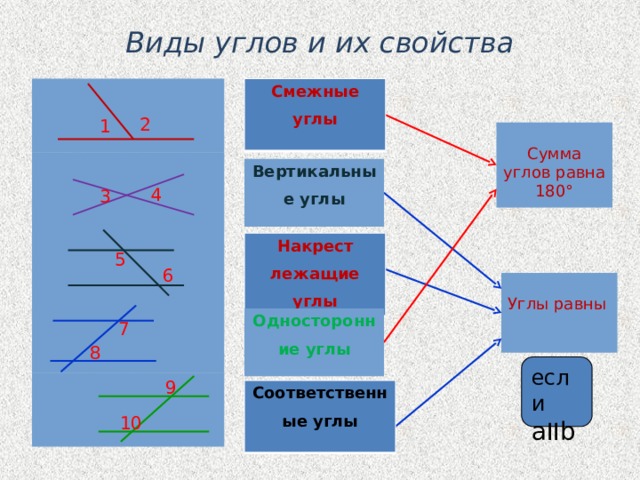
 Соотношение между этими величинами определяется формулой 1c = 15″.[3]
Соотношение между этими величинами определяется формулой 1c = 15″.[3]


 Инфо» : справочник. — 2003.
Инфо» : справочник. — 2003. справочный материал ниже).
справочный материал ниже). )
) 8481368 prad
8481368 prad сейчас ()
геометрия = Satellite.at(t)
подточка = геометрия.подточка()
печать (подпункт.широта)
печать('\п')
печать (подпункт.долгота)
время сна(1)
сейчас ()
геометрия = Satellite.at(t)
подточка = геометрия.подточка()
печать (подпункт.широта)
печать('\п')
печать (подпункт.долгота)
время сна(1)
 org/skyfield/api-units.html#skyfield.units.Angle
org/skyfield/api-units.html#skyfield.units.Angle широта)
lng = преобразовать (подточка.долгота)
печать (широта, долгота)
время сна(1)
широта)
lng = преобразовать (подточка.долгота)
печать (широта, долгота)
время сна(1)
 1: Измерение углов — Математика LibreTexts
1: Измерение углов — Математика LibreTexts Это позволяет использовать радианы в вычислениях в ситуациях, когда градусная мера неуместна. 9{7}\)
Это позволяет использовать радианы в вычислениях в ситуациях, когда градусная мера неуместна. 9{7}\) 

 Измеряется высота как и другая фигура, в километрах, сантиметрах, миллиметрах и пр.
Измеряется высота как и другая фигура, в километрах, сантиметрах, миллиметрах и пр.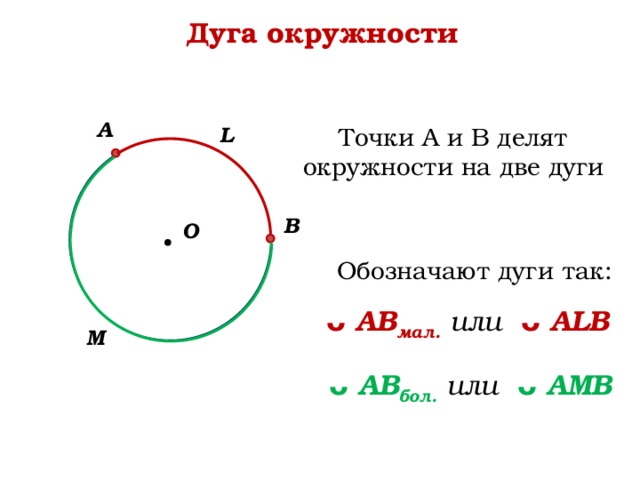 Определения, условные обозначения, хитрости.
Определения, условные обозначения, хитрости.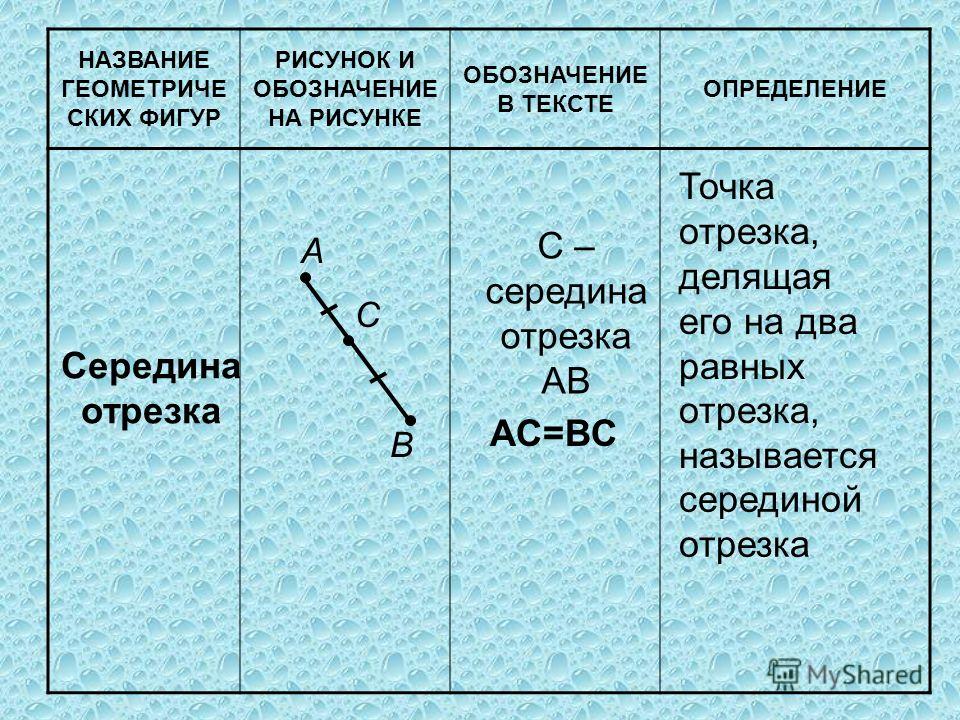

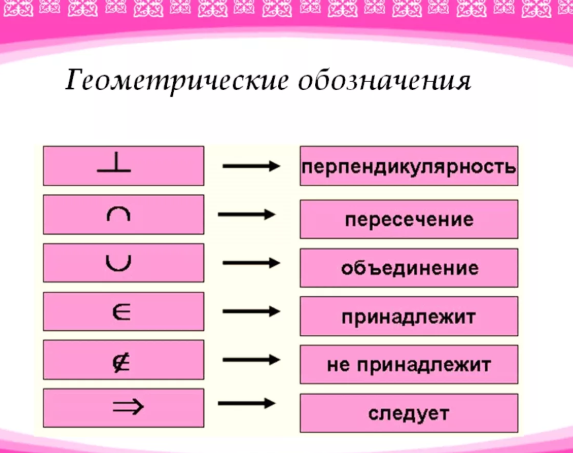 Как правило, она обозначается буквой В.
Как правило, она обозначается буквой В.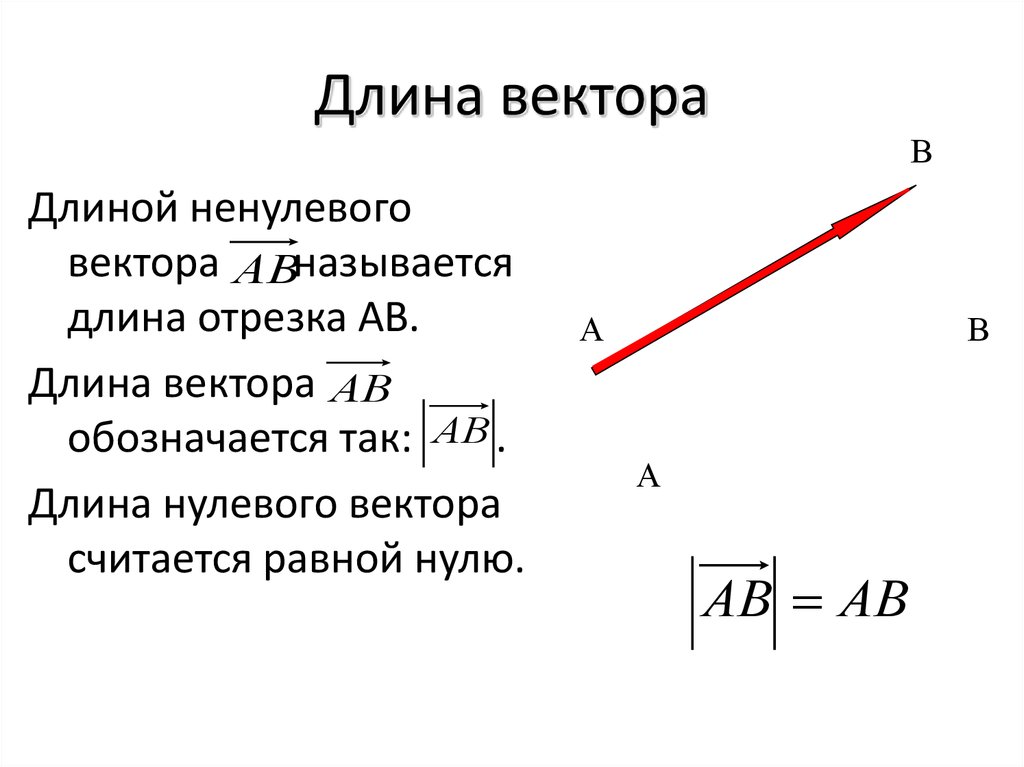 Вокруг прямоугольника всегда можно описать окружность. Эти свойства работают и в обратном направлении.
Вокруг прямоугольника всегда можно описать окружность. Эти свойства работают и в обратном направлении.
 Например, длина линейки, приведенная ниже, говорит нам о ее длине.
Например, длина линейки, приведенная ниже, говорит нам о ее длине. Измерения варьируются от человека к человеку и от объекта к объекту.
Измерения варьируются от человека к человеку и от объекта к объекту.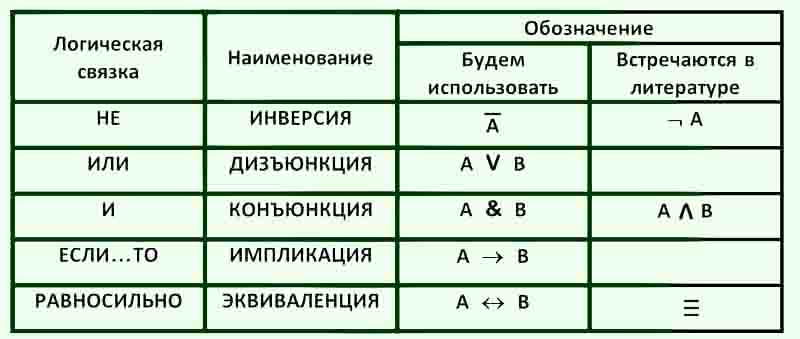 д.
д.  Единицей СИ для измерения длины является метр (м). Метр является базовой единицей длины.
Единицей СИ для измерения длины является метр (м). Метр является базовой единицей длины.
 Например, на рисунке ниже длина карандаша от 0 до 10 см.
Например, на рисунке ниже длина карандаша от 0 до 10 см.
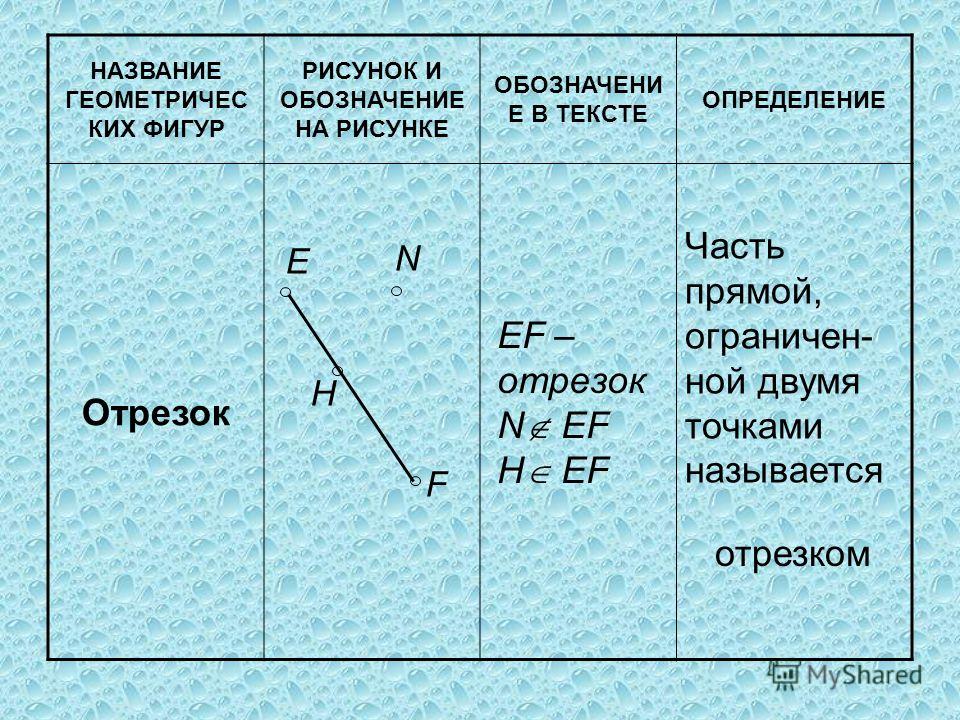 измерение длины линейкой?
измерение длины линейкой?  Пусть $A$ — точка
который движется по оси $x$ между точками $(0, 0)$ и $(4, 0)$. Пусть $B$ будет
точка, которая движется по прямой $y = 2$ между точками $(0, 2)$ и $(4, 2)$.
Рассмотрим все возможные пути, состоящие из отрезков $PA,AB$ и $BQ$.
Какова наименьшая возможная длина такого пути?
Пусть $A$ — точка
который движется по оси $x$ между точками $(0, 0)$ и $(4, 0)$. Пусть $B$ будет
точка, которая движется по прямой $y = 2$ между точками $(0, 2)$ и $(4, 2)$.
Рассмотрим все возможные пути, состоящие из отрезков $PA,AB$ и $BQ$.
Какова наименьшая возможная длина такого пути?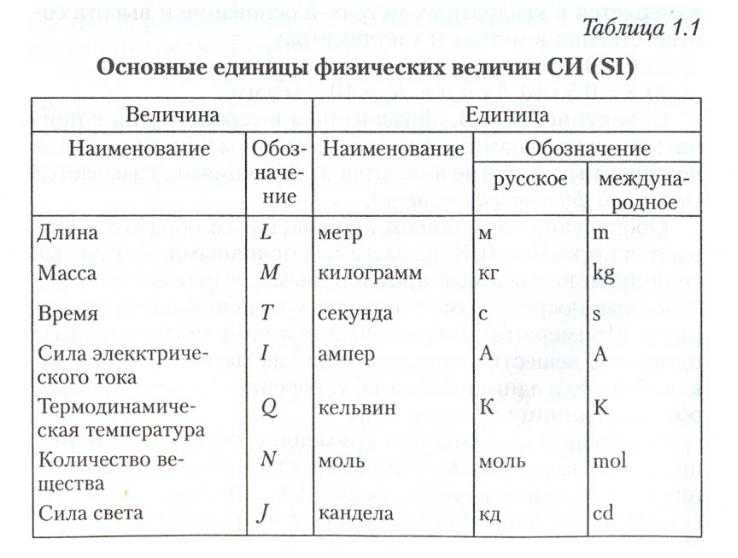
 рис. 8).
рис. 8).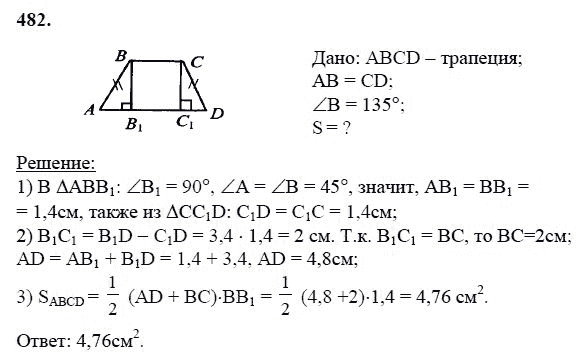 Мы знаем, как выразить через дуги вписанные углы, которые на них опираются. Поэтому попробуем выразить угол через вписанные углы. Для этого соединим точки и . Получим два вписанных угла и (см. рис. 10).
Мы знаем, как выразить через дуги вписанные углы, которые на них опираются. Поэтому попробуем выразить угол через вписанные углы. Для этого соединим точки и . Получим два вписанных угла и (см. рис. 10).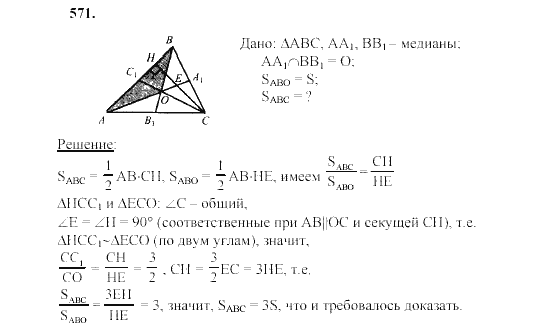 Это свойство лошадей или их необходимый признак. Но назвать признаком наличие головы нельзя: она есть у людей, у собак и т. д.
Это свойство лошадей или их необходимый признак. Но назвать признаком наличие головы нельзя: она есть у людей, у собак и т. д. рис. 11).
рис. 11). 12. Четырехугольник , где сумма углов и равна
12. Четырехугольник , где сумма углов и равна Там рассуждения совершенно аналогичны (изменится только знак неравенства).
Там рассуждения совершенно аналогичны (изменится только знак неравенства). Теоремы синусов и косинусов).
Теоремы синусов и косинусов). Как быть? Если бы у нас не было больше никакой информации об угле, то на этом нам бы пришлось остановиться. Действительно, при данном значении косинуса у синуса может быть два значения (вертикальная прямая пересекает окружность в двух точках с противоположными ординатами) (см. рис. 18).
Как быть? Если бы у нас не было больше никакой информации об угле, то на этом нам бы пришлось остановиться. Действительно, при данном значении косинуса у синуса может быть два значения (вертикальная прямая пересекает окружность в двух точках с противоположными ординатами) (см. рис. 18). Видим, что окружность пересекается горизонтальной прямой в двух точках (см. рис. 20).
Видим, что окружность пересекается горизонтальной прямой в двух точках (см. рис. 20).
 Или, зная три стороны, можно найти каждый угол, точнее – его косинус.
Или, зная три стороны, можно найти каждый угол, точнее – его косинус. Выполните их самостоятельно. У вас должно получиться, что во втором случае косинус наибольшего треугольника равен (треугольник прямоугольный), а в третьем – косинус угла отрицательный (треугольник тупоугольный).
Выполните их самостоятельно. У вас должно получиться, что во втором случае косинус наибольшего треугольника равен (треугольник прямоугольный), а в третьем – косинус угла отрицательный (треугольник тупоугольный). рис. 26).
рис. 26).

 Мы собрали онлайн-сервисы с занятиями для восьмиклассников по алгебре и геометрии. Актуальность учебных программ и их стоимость проверяются каждый день.
Мы собрали онлайн-сервисы с занятиями для восьмиклассников по алгебре и геометрии. Актуальность учебных программ и их стоимость проверяются каждый день. /курс
/курс
 /курс
/курс
 9 / 5
9 / 5
 8 / 5
8 / 5 8 / 5
8 / 5 9 / 5
9 / 5 8 / 5
8 / 5 Здесь можно подготовиться к ЕГЭ, ОГЭ и олимпиадам на курсах, улучшить оценки по школьным предметам, пройти подготовку к поступлению в ВУЗ, а также школа подойдет для тех, кто выбрал домашнее/семейное обучение (экстернат). Фоксфорд ведет свою деятельность на основании государственной лицензии, входит в состав онлайн-университета Нетология и является участником Сколково.
Здесь можно подготовиться к ЕГЭ, ОГЭ и олимпиадам на курсах, улучшить оценки по школьным предметам, пройти подготовку к поступлению в ВУЗ, а также школа подойдет для тех, кто выбрал домашнее/семейное обучение (экстернат). Фоксфорд ведет свою деятельность на основании государственной лицензии, входит в состав онлайн-университета Нетология и является участником Сколково. /курс
/курс /курс
/курс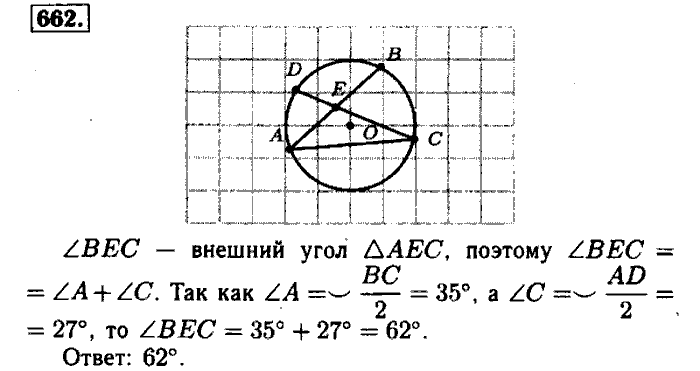 Домашние задания тоже сдаются онлайн.
Домашние задания тоже сдаются онлайн.
 Теперь, чтобы получить все преимущества, вы должны подписаться на один из онлайн-курсов по математике и согласовать график обучения и учебный план по математике с репетиторами.
Теперь, чтобы получить все преимущества, вы должны подписаться на один из онлайн-курсов по математике и согласовать график обучения и учебный план по математике с репетиторами. Но после наблюдения за тем, как мой сын быстро выучил математику благодаря этим методам обучения, я убежден, что Брайтерли точно знает, что делает.
Но после наблюдения за тем, как мой сын быстро выучил математику благодаря этим методам обучения, я убежден, что Брайтерли точно знает, что делает. Однако с тех пор, как мы подписались на Brighterly, я больше не думаю об этом, потому что Brighterly помогает с домашним заданием.
Однако с тех пор, как мы подписались на Brighterly, я больше не думаю об этом, потому что Brighterly помогает с домашним заданием. Вот причины, по которым это место особенное:
Вот причины, по которым это место особенное:
 Такой подход делает обучение более эффективным.
Такой подход делает обучение более эффективным. Дети развивают творческие способности, находя уникальные способы решения математических задач 8-го класса.
Дети развивают творческие способности, находя уникальные способы решения математических задач 8-го класса. Дети также могут избегать разговоров со своим учителем, потому что им стыдно, что они не понимают методов решения математических задач.
Дети также могут избегать разговоров со своим учителем, потому что им стыдно, что они не понимают методов решения математических задач.
 Если вам нужен эксперт, который поможет вашему ребенку в изучении математики, загляните в Brighterly. Их онлайн-курс по математике для 8-го класса может сделать обучение детей увлекательным и увлекательным.
Если вам нужен эксперт, который поможет вашему ребенку в изучении математики, загляните в Brighterly. Их онлайн-курс по математике для 8-го класса может сделать обучение детей увлекательным и увлекательным.
 openupresources.org › curricula › unit-5
openupresources.org › curricula › unit-5 ЛЕКЦИОН/ТАРЕЯ.
ЛЕКЦИОН/ТАРЕЯ.

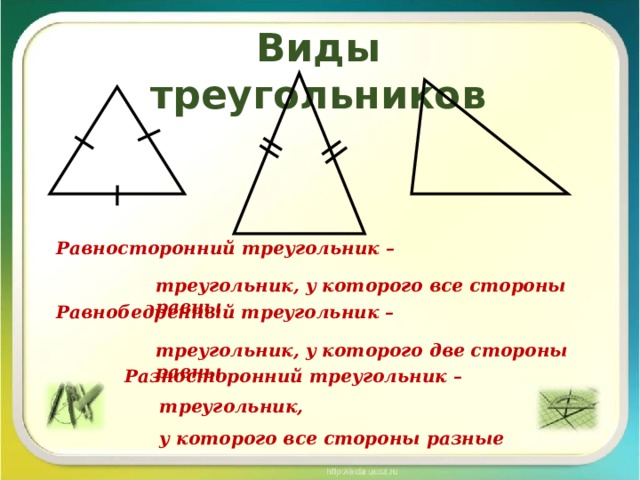

 Получаем, что можно изменять градусную меру углов четырехугольника, не меняя длины его сторон. Можно менять величины углов у пятиугольников, шестиугольников и многоугольников с большим количеством сторон.
Получаем, что можно изменять градусную меру углов четырехугольника, не меняя длины его сторон. Можно менять величины углов у пятиугольников, шестиугольников и многоугольников с большим количеством сторон. п.
п.

 «Жесткость».
«Жесткость».  А задумаешься…, нет, вовсе не простая, мы ещё многое о ней не знаем. Не умеем вычислять площади треугольников, не знаем о признаках равенства и подобии треугольников, о признаках равенства прямоугольных треугольников, не знаем и не умеем применять теоремы косинусов, синусов, и многое ещё осталось загадочным для вас.
А задумаешься…, нет, вовсе не простая, мы ещё многое о ней не знаем. Не умеем вычислять площади треугольников, не знаем о признаках равенства и подобии треугольников, о признаках равенства прямоугольных треугольников, не знаем и не умеем применять теоремы косинусов, синусов, и многое ещё осталось загадочным для вас.
 \\circ$. Второй — по величине в два раза больше первого. Чему равен третий угол?»}}}]}
\\circ$. Второй — по величине в два раза больше первого. Чему равен третий угол?»}}}]} \circ$.
\circ$.  \circ$.
\circ$.




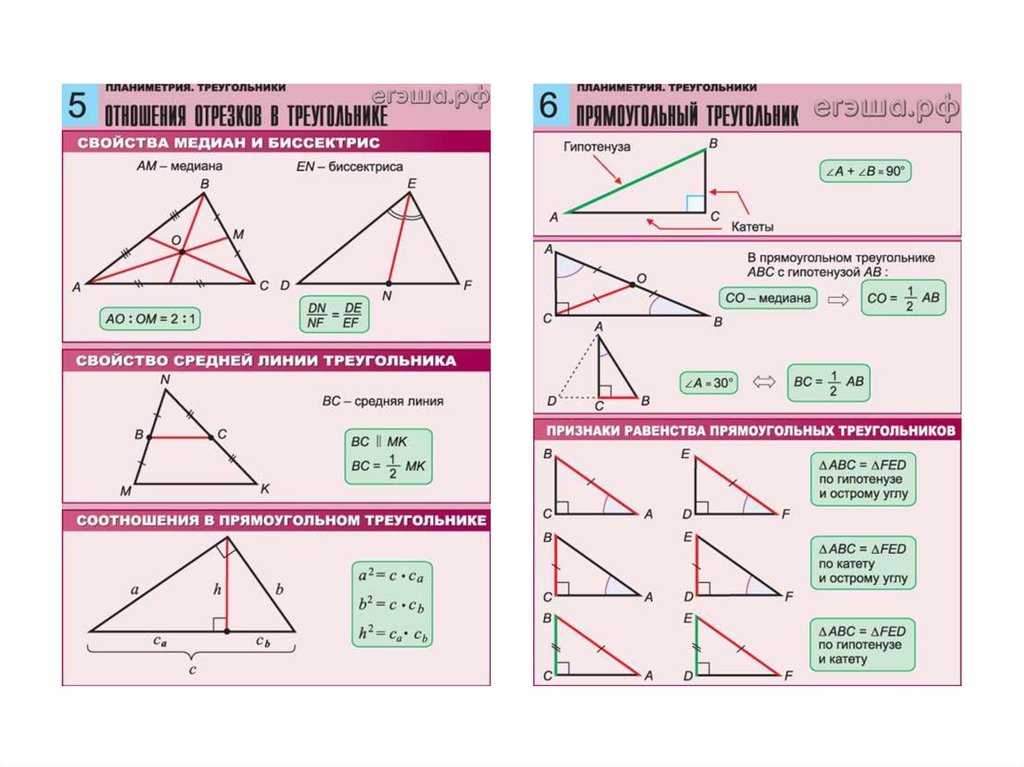




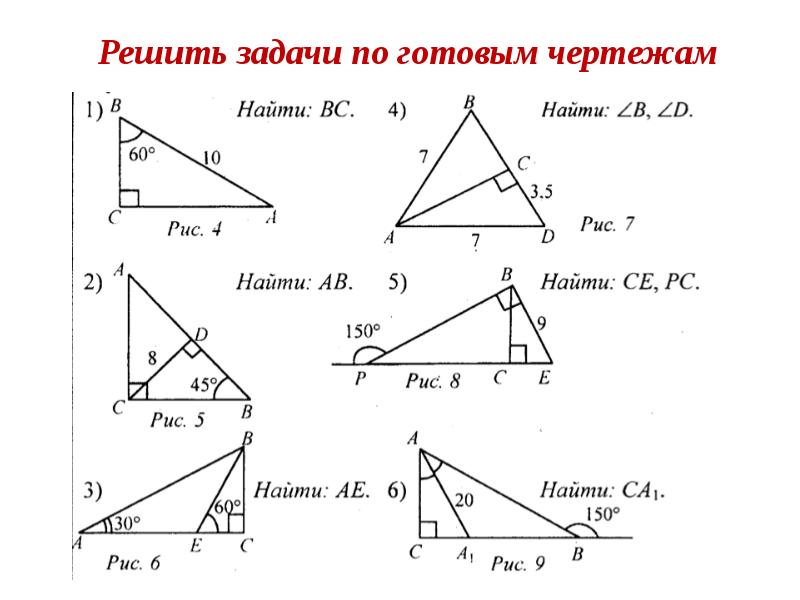 Ею пользуются многие учащиеся различных учебных заведений. Она полностью бесплатная, поэтому с её помощью можно решить многие уравнения и задания. Там можно вписывать какие-то значения, редактировать их, менять вводные, а также решать задания по фото.
Ею пользуются многие учащиеся различных учебных заведений. Она полностью бесплатная, поэтому с её помощью можно решить многие уравнения и задания. Там можно вписывать какие-то значения, редактировать их, менять вводные, а также решать задания по фото. Снизу есть красный круг, его нужно нажать, чтобы сделать снимок.
Снизу есть красный круг, его нужно нажать, чтобы сделать снимок.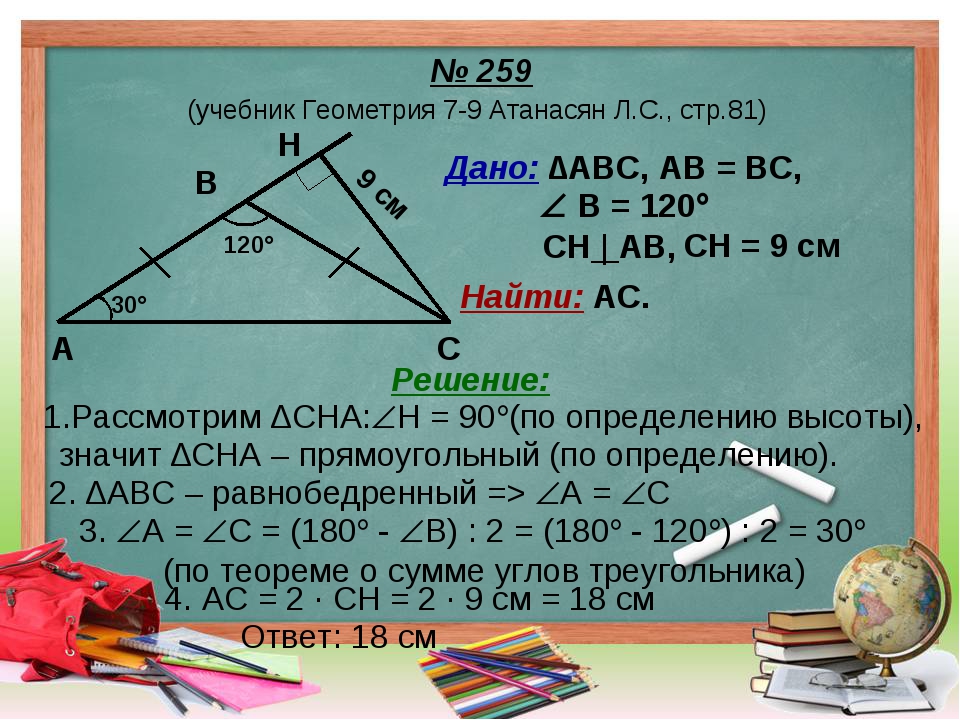 Решите объем, площадь поверхности и периметр. Пошаговые решения, предварительный просмотр в реальном времени, калькулятор веса и экспорт изображений!
Решите объем, площадь поверхности и периметр. Пошаговые решения, предварительный просмотр в реальном времени, калькулятор веса и экспорт изображений!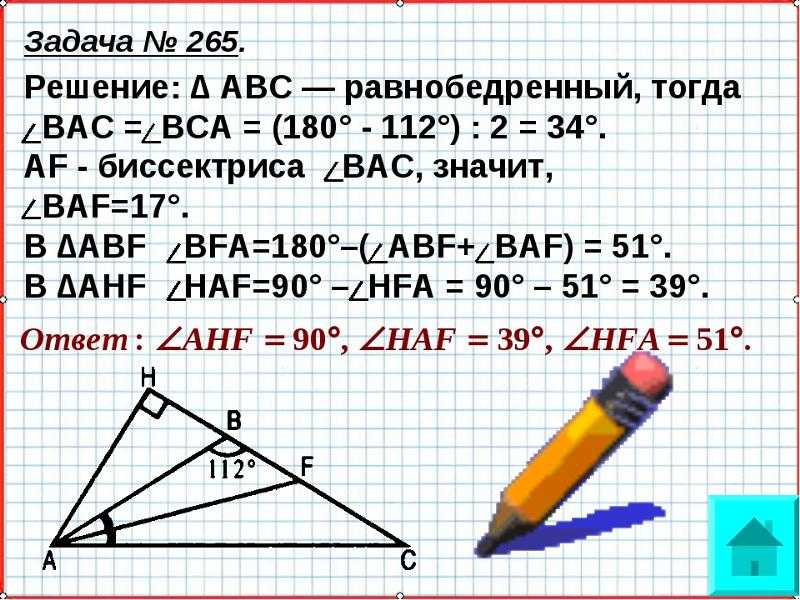 ..
.. Это очень легко понять и дает вам ответы. Но не хватает нескольких вещей. Он не просто дает объем трехмерных фигур и не содержит всей треугольной пирамиды (пирамиды с треугольным основанием). Кроме того, это удивительно и работает очень хорошо.
Это очень легко понять и дает вам ответы. Но не хватает нескольких вещей. Он не просто дает объем трехмерных фигур и не содержит всей треугольной пирамиды (пирамиды с треугольным основанием). Кроме того, это удивительно и работает очень хорошо. Я просмотрел кучу этих приложений, и большинство из них были либо плохо спроектированы, либо нефункциональны, либо стоили слишком дорого. И я устал от того, что сейчас все по подписке!
Я просмотрел кучу этих приложений, и большинство из них были либо плохо спроектированы, либо нефункциональны, либо стоили слишком дорого. И я устал от того, что сейчас все по подписке! 

 Эти новые идеи дают учащимся возможность постоянно применять накопленные знания и навыки по алгебре. Курс завершается изучением многочисленных свойств, связанных с окружностями, и введением в тригонометрию.
Эти новые идеи дают учащимся возможность постоянно применять накопленные знания и навыки по алгебре. Курс завершается изучением многочисленных свойств, связанных с окружностями, и введением в тригонометрию. …………………… 70%
…………………… 70% com ожидают решения.
com ожидают решения.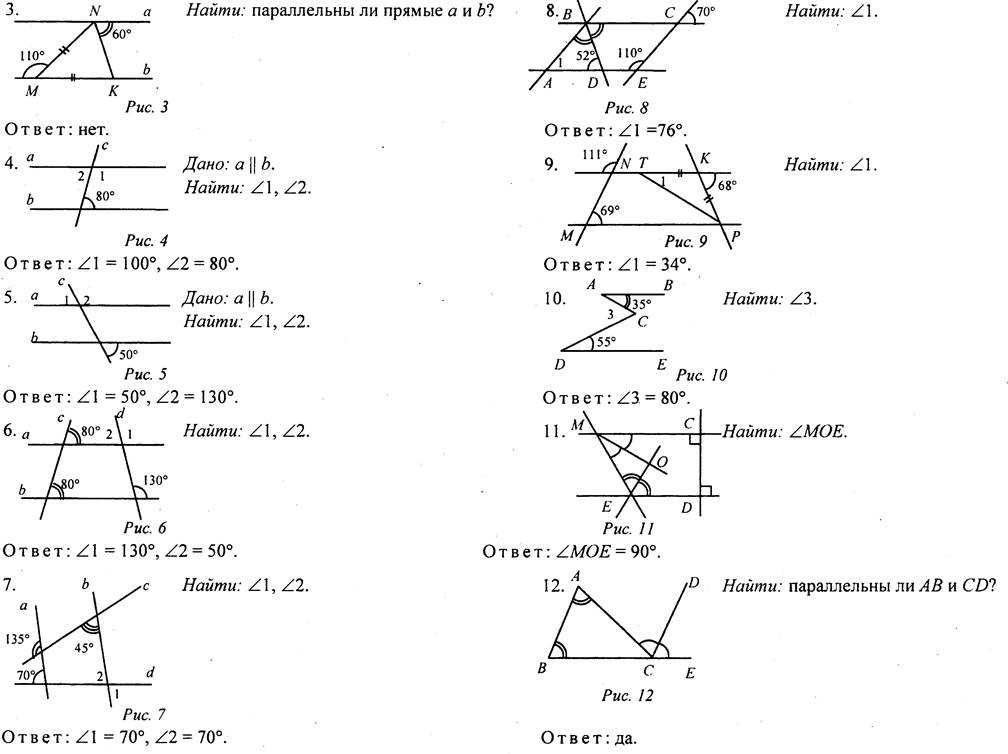

 Уровень сложности: средняя школа.
Уровень сложности: средняя школа.





 ГеоГебра,
iPad.
ГеоГебра,
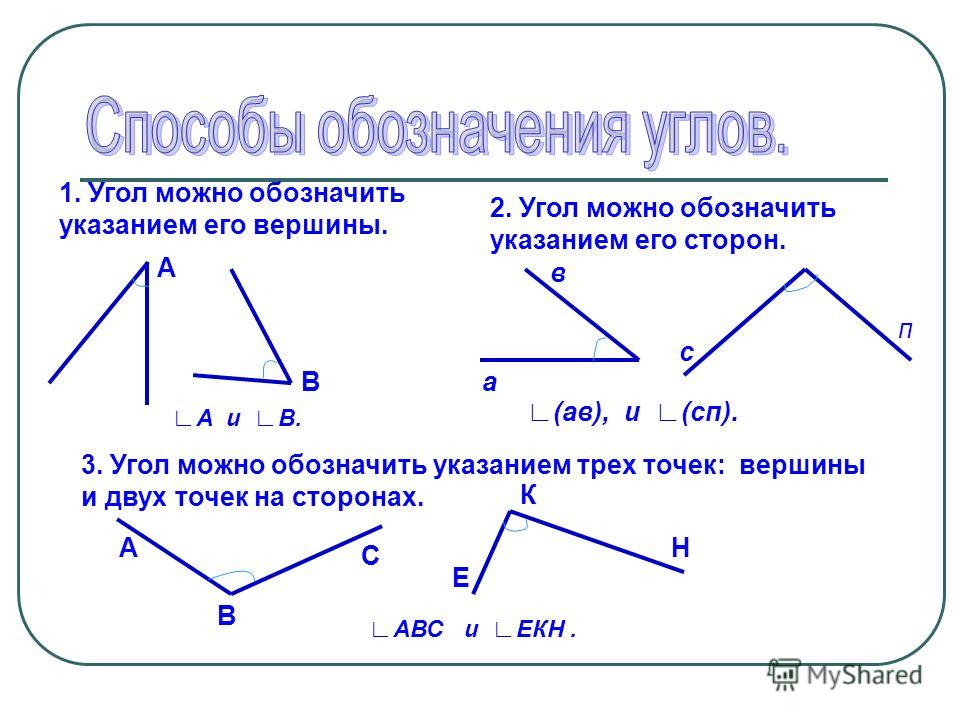
iPad. Вторая — это точка которая принадлежит лучу или другими словами — через которую луч проходит.
Вторая — это точка которая принадлежит лучу или другими словами — через которую луч проходит. В геометрии вместо слова угол часто пишут специальный значок.
В геометрии вместо слова угол часто пишут специальный значок.
 Великолепно, восторг! Преимущества мы оценили сразу. С
начала нового учебного года будем активно пользоваться. Поэтому никаких пожеланий у
нас пока нет, одни благодарности. Очень простая и понятная инструкция, что
немаловажно! Благодарю Вас и Ваших коллег за этот важный труд. Очень приятно, когда
коллеги понимают, как можно «упростить» работу учителя.
Великолепно, восторг! Преимущества мы оценили сразу. С
начала нового учебного года будем активно пользоваться. Поэтому никаких пожеланий у
нас пока нет, одни благодарности. Очень простая и понятная инструкция, что
немаловажно! Благодарю Вас и Ваших коллег за этот важный труд. Очень приятно, когда
коллеги понимают, как можно «упростить» работу учителя. 0
0