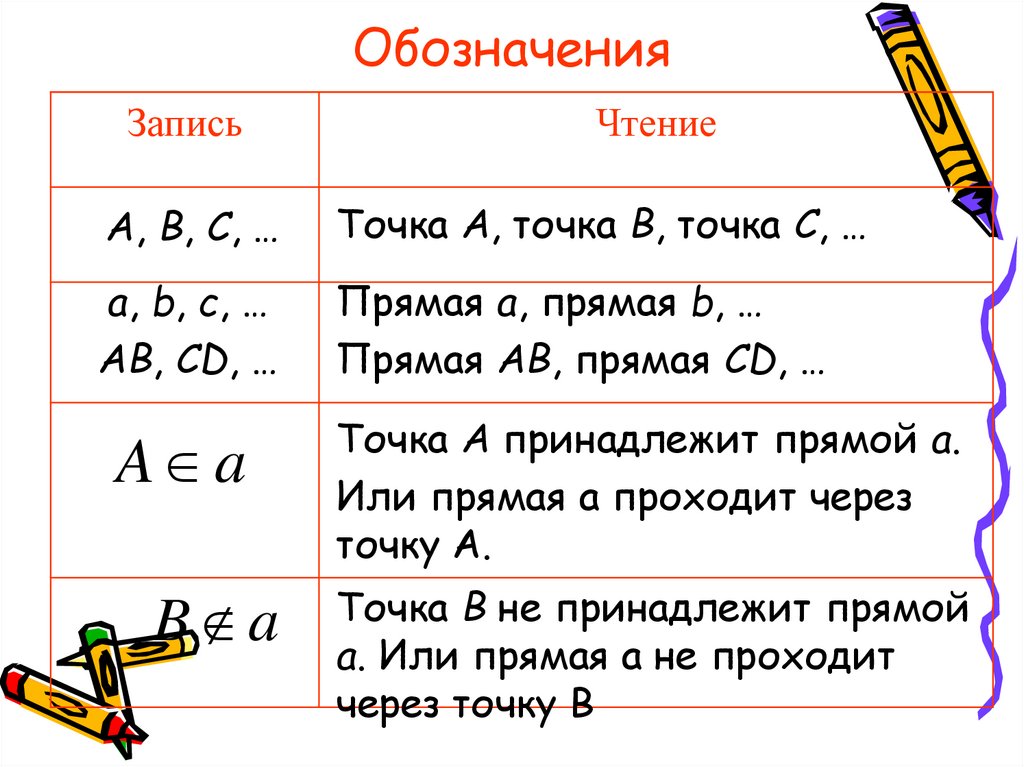
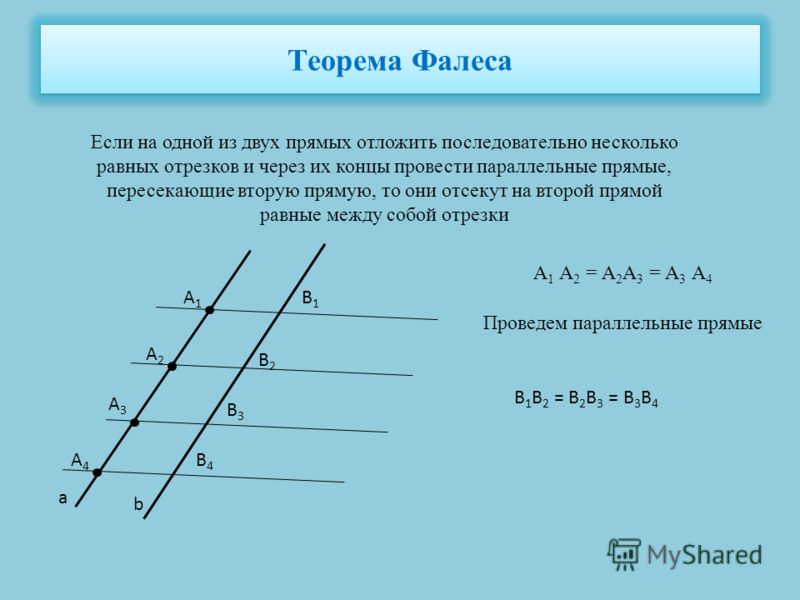
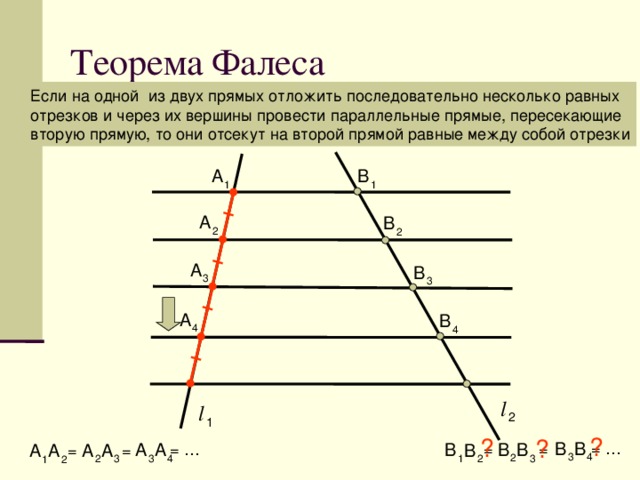
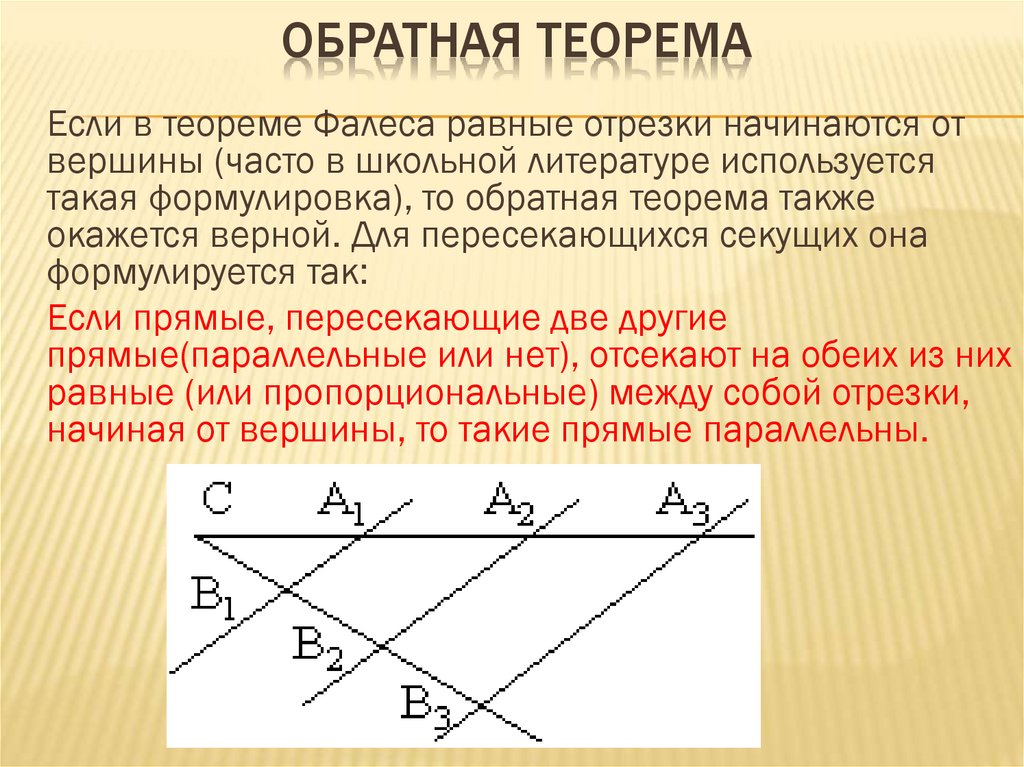
Точка, линия, прямая, луч, отрезок, ломанная
Точка — это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса. В рамках задачи важно только его местоположениеТочка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать
точка A, точка B, точка C
ABCточка 1, точка 2, точка 3
123Можно нарисовать на листке бумаги три точки "А" и предложить ребёнку провести линию через две точки "А". Но как понять через какие? AAAЛиния — это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет
Обозначается строчными (маленькими) латинскими буквами
линия a, линия b, линия c
abcЛиния может быть
- замкнутой, если её начало и конец находятся в одной точке,
- разомкнутой, если её начало и конец не соединены
замкнутые линии
разомкнутые линии
Ты вышел из квартиры, купил в магазине хлеб и вернулся обратно в квартиру.Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку. Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку. Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
- самопересекающейся
- без самопересечений
самопересекающиеся линии
линии без самопересечений
- прямой
- ломанной
- кривой
прямые линии
ломанные линии
кривые линии
Прямая линия — это линия которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороныДаже когда виден небольшой участок прямой, предполагается, что она бесконечно продолжается в обе стороны
Обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой
прямая линия a
aпрямая линия AB
BAПрямые могут быть
- пересекающимися, если имеют общую точку.
 Две прямые могут пересекаться только в одной точке.
Две прямые могут пересекаться только в одной точке.- перпендикулярными, если пересекаются под прямым углом (90°).
- параллельными, если не пересекаются, не имеют общей точки.
параллельные линии
пересекающиеся линии
перпендикулярные линии
Луч — это часть прямой, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторонуУ луча света на картинке начальной точкой является солнце
солнышко
Точка разделяет прямую на две части — два луча A A
Луч обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается луч, а вторая — точка, лежащая на луче
луч a
aлуч AB
BAЛучи совпадают, если
- расположены на одной и той же прямой,
- начинаются в одной точке,
- направлены в одну сторону
лучи AB и AC совпадают
лучи CB и CA совпадают
CBAОтрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину.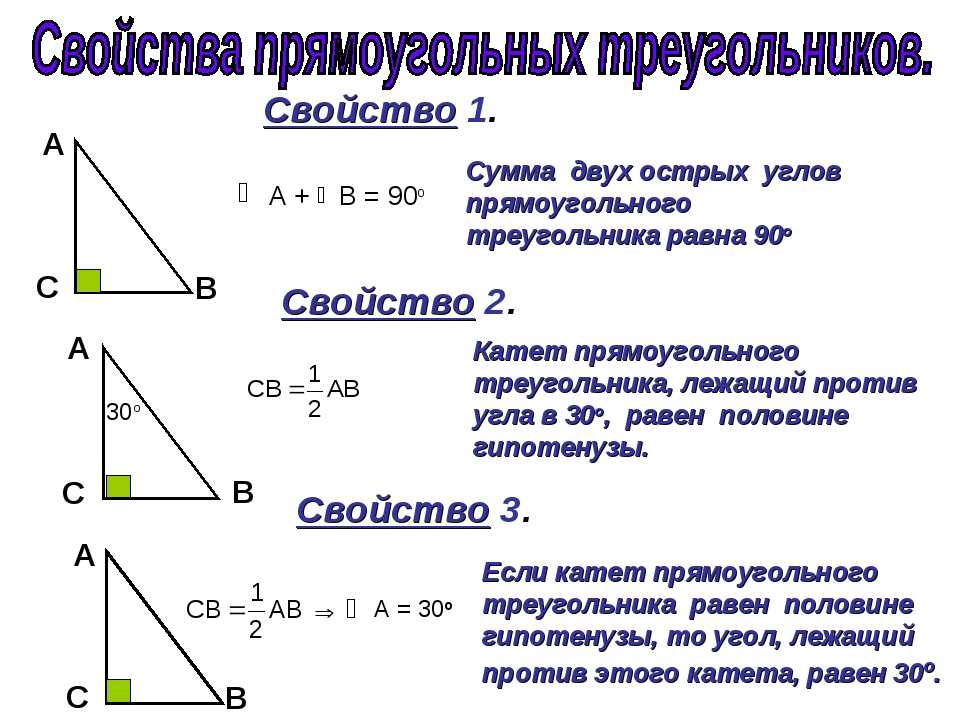 Длина отрезка — это расстояние между его начальной и конечной точками
Длина отрезка — это расстояние между его начальной и конечной точкамиЧерез одну точку можно провести любое число линий, в том числе прямых
Через две точки — неограниченное количество кривых, но только одну прямую
кривые линии, проходящие через две точки
BAпрямая линия AB
BAОт прямой «отрезали» кусочек и остался отрезок. Из примера выше видно, что его длина — наикратчайшее расстояние между двумя точками. ✂ BA✂
Отрезок обозначается двумя заглавными(большими) латинскими буквами, где первая — это точка, с которой начинается отрезок, а вторая — точка, которой заканчивается отрезок
отрезок AB
BAЗадача: где прямая, луч, отрезок, кривая?Ломанная линия — это линия, состоящая из последовательно соединённых отрезков не под углом 180°
Длинный отрезок «поломали» на несколько коротких
Звенья ломаной (похожи на звенья цепи) — это отрезки, из которых состоит ломанная. Смежные звенья — это звенья, у которых конец одного звена является началом другого. Смежные звенья не должны лежать на одной прямой.
Смежные звенья — это звенья, у которых конец одного звена является началом другого. Смежные звенья не должны лежать на одной прямой.
Вершины ломаной (похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная.
Обозначается ломанная перечислением всех её вершин.
ломанная линия ABCDE
вершина ломанной A, вершина ломанной B, вершина ломанной C, вершина ломанной D, вершина ломанной E
звено ломанной AB, звено ломанной BC, звено ломанной CD, звено ломанной DE
звено AB и звено BC являются смежными
звено BC и звено CD являются смежными
звено CD и звено DE являются смежными
ABCDE646212752Длина ломанной — это сумма длин её звеньев: ABCDE = AB + BC + CD + DE = 64 + 62 + 127 + 52 = 305
Задача: какая ломанная длиннее, а у какой больше вершин? У первой линии все звенья одинаковой длины, а именно по 13см.Многоугольник — это замкнутая ломанная линияУ второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.
Стороны многоугольника (помогут запомнить выражения: «пойти на все четыре стороны», «бежать в сторону дома», «с какой стороны стола сядешь?») — это звенья ломанной. Смежные стороны многоугольника — это смежные звенья ломанной.
Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.
Обозначается многоугольник перечислением всех его вершин.
замкнутая ломанная линия, не имеющая самопересечения, ABCDEF
многоугольник ABCDEF
вершина многоугольника A, вершина многоугольника B, вершина многоугольника C, вершина многоугольника D, вершина многоугольника E, вершина многоугольника F
вершина A и вершина B являются соседними
вершина B и вершина C являются соседними
вершина C и вершина D являются соседними
вершина D и вершина E являются соседними
вершина E и вершина F являются соседними
вершина F и вершина A являются соседними
сторона многоугольника AB, сторона многоугольника BC, сторона многоугольника CD, сторона многоугольника DE, сторона многоугольника EF
сторона AB и сторона BC являются смежными
сторона BC и сторона CD являются смежными
сторона CD и сторона DE являются смежными
сторона DE и сторона EF являются смежными
сторона EF и сторона FA являются смежными
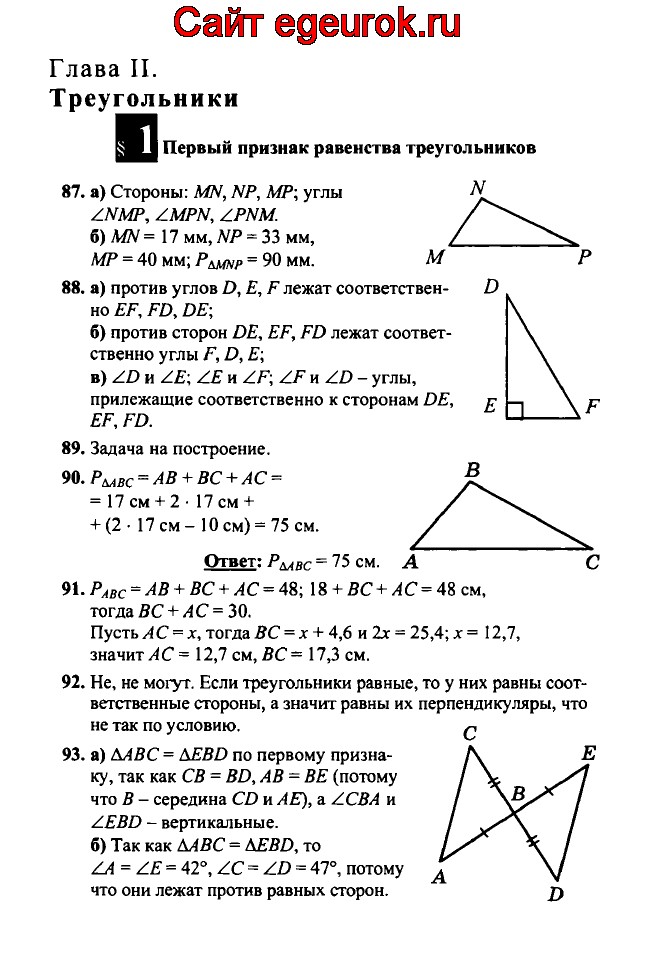
ABCDEF120605812298141Периметр многоугольника — это длина ломанной: P = AB + BC + CD + DE + EF + FA = 120 + 60 + 58 + 122 + 98 + 141 = 599
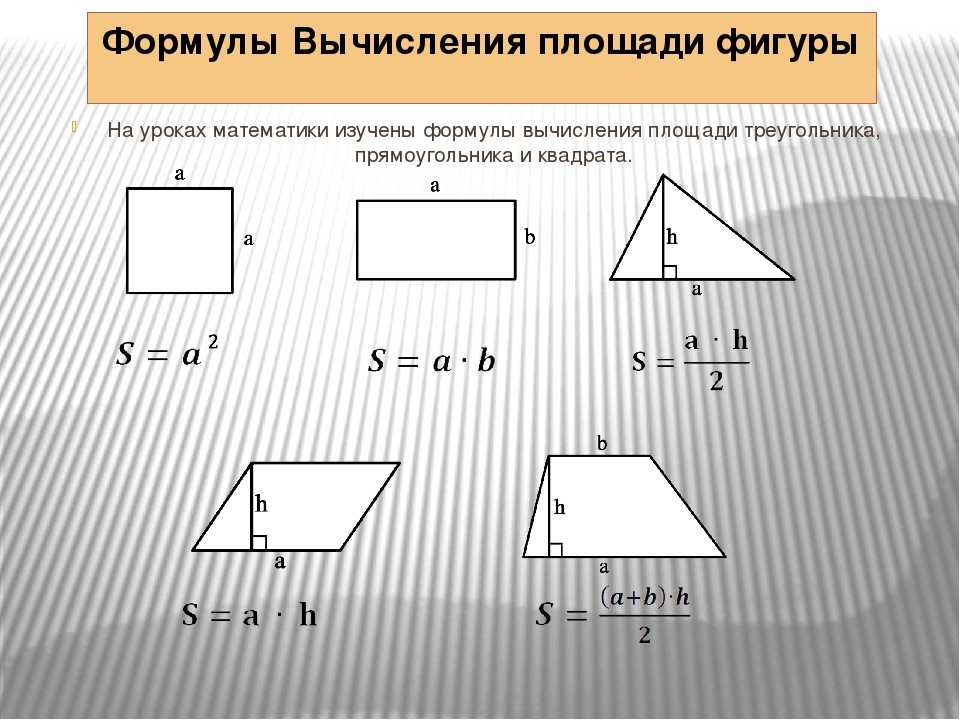
Многоугольник с тремя вершинами называется треугольником, с четырьмя — четырёхугольником, с пятью — пятиугольником и т. д.
д.
треугольники
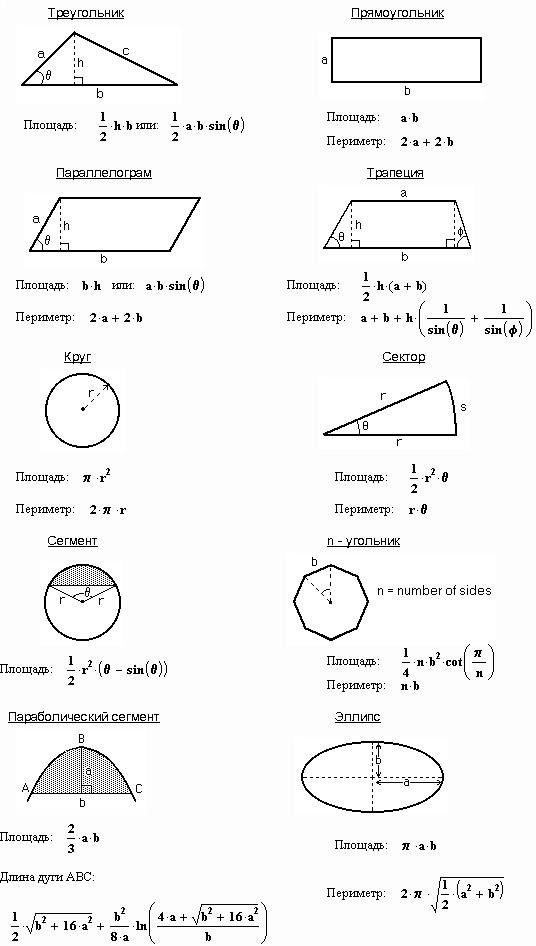
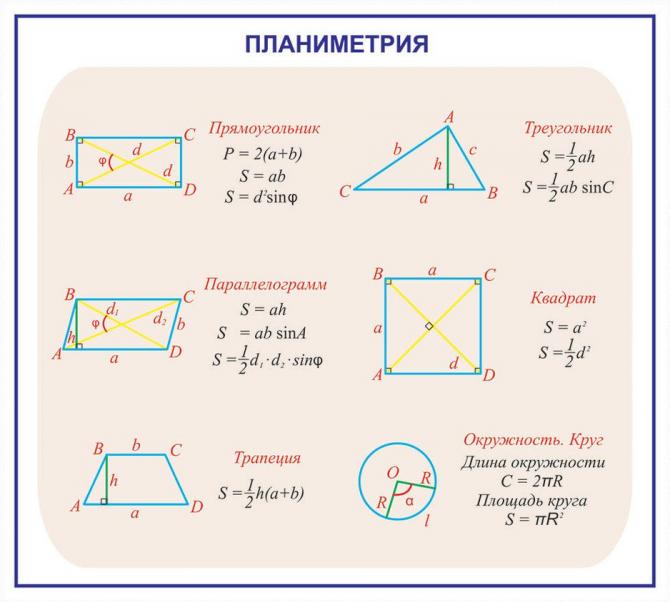
четырёхугольники: квадрат, прямоугольник, дельтоид, ромб, параллелограмм, трапеция
пятиугольники
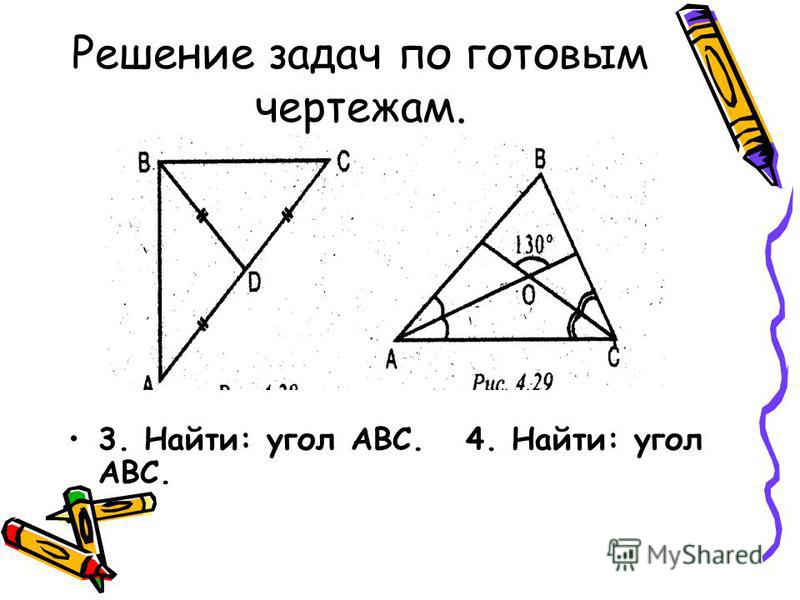
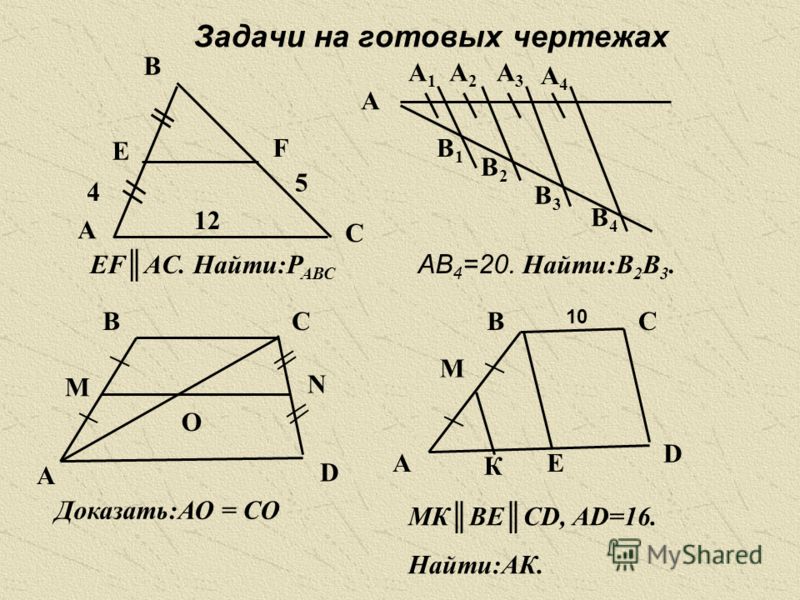
Отрезок
Отрезок. Длина отрезка. Треугольник.
1. В этом параграфе вы познакомитесь с некоторыми понятиями геометрии. Геометрия — наука об «измерении земли». Это слово происходит от латинских слов: geo – земля и metr — мера, мерить. В геометрии изучаются различные геометрические объекты, их свойства, их связи с окружающим миром. Простейшие геометрические объекты – это точка, линия, поверхность. Более сложные геометрические объекты, например, геометрические фигуры и тела, образованы из простейших.
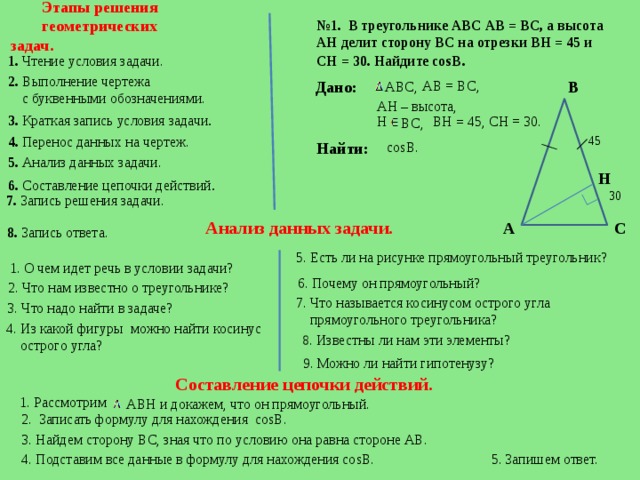
Если приложить к двум точкам А и В линейку и вдоль нее провести линию, соединяющую эти точки, то мы получим отрезок, который называют АВ или ВА (читаем: «а – бэ», «бэ– а»). Точки А и В называются концами отрезка (рисунок 1). Расстояние между концами отрезка, измеренное в единицах длины, называется длиной отрезка.
Единицы длины: м – метр, см — сантиметр, дм – дециметр, мм – миллиметр, км – километр и др. (1 км = 1000 м; 1м =10 дм; 1 дм = 10 см; 1 см = 10 мм). Для измерения длины отрезков используют линейку, рулетку. Измерить длину отрезка, значит, выяснить, сколько раз в нем укладывается та или иная мера длины.
Равными называются два отрезка, которые можно совместить, наложив один на другой (рисунок 2). Например, можно вырезать реально или мысленно один из отрезков и приложить к другому так, чтобы совпали их концы. Если отрезки АВ и СК равны, то пишут АВ = СК. Равные отрезки имеют равные длины. Верно обратное: два отрезка, имеющие равные длины, равны. Если два отрезка имеют различные длины, то они не равны. Из двух неравных отрезков меньше тот, который составляет часть другого отрезка. Сравнивать отрезки наложением можно, используя циркуль.
Если мысленно продлить отрезок АВ в обе стороны до бесконечности, то мы получим представление о прямой АВ (рисунок 3). Любая точка, лежащая на прямой, разбивает ее на два луча (рисунок 4). Точка С разбивает прямую АВ на два луча СА и СВ. Тоска С называется началом луча.
Любая точка, лежащая на прямой, разбивает ее на два луча (рисунок 4). Точка С разбивает прямую АВ на два луча СА и СВ. Тоска С называется началом луча.
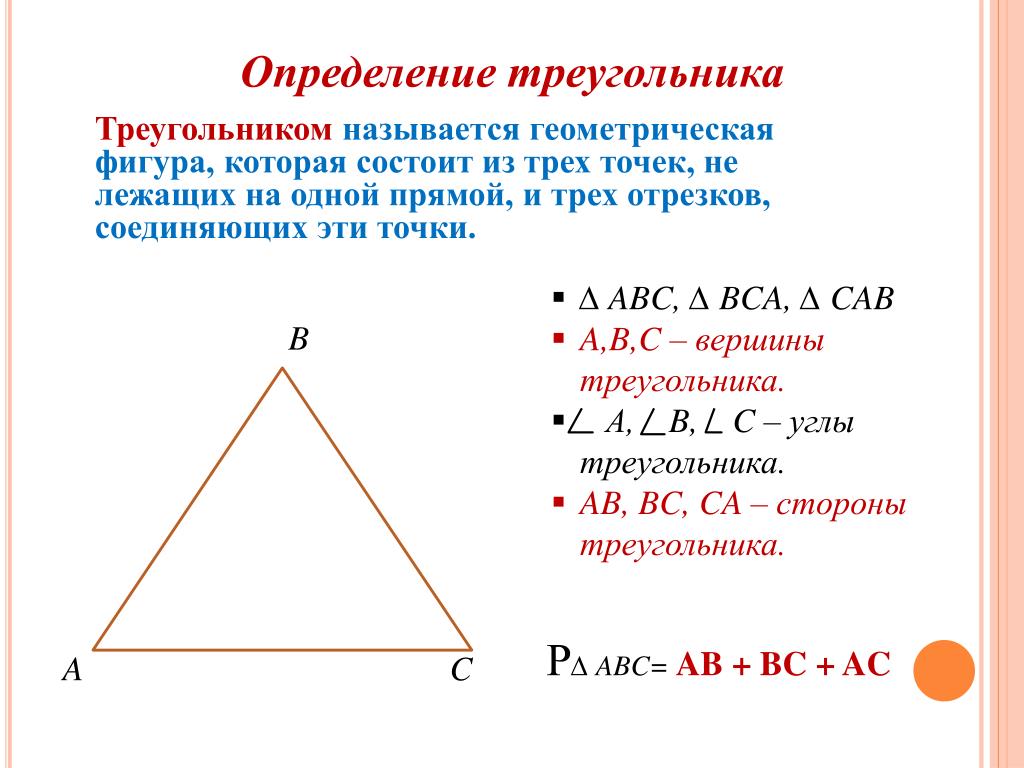
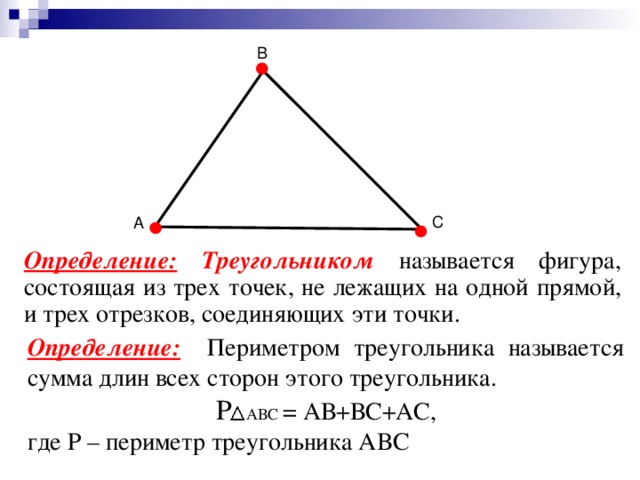
2. Если три точки, не лежащие на одной прямой, соединить отрезками, то получим фигуру, называемую треугольником. Данные точки называются вершинами треугольника, а отрезки, их соединяющие, сторонами треугольника (рисунок 5). FNM — треугольник, отрезки FN, NM, FM – стороны треугольника, точки F, N, M – вершины треугольника. Стороны всех треугольников обладают следующим свойством: длина любой из сторон треугольника всегда меньше суммы длин двух других его сторон.
Если мысленно продлить во все стороны, например, поверхность крышки стола, то получим представление о плоскости. Точки, отрезки, прямые, лучи располагаются на плоскости (рисунок 6).
Блок 1. Дополнительный
Мир, в котором мы живем, все, что нас окружает, древние называли природой или космосом.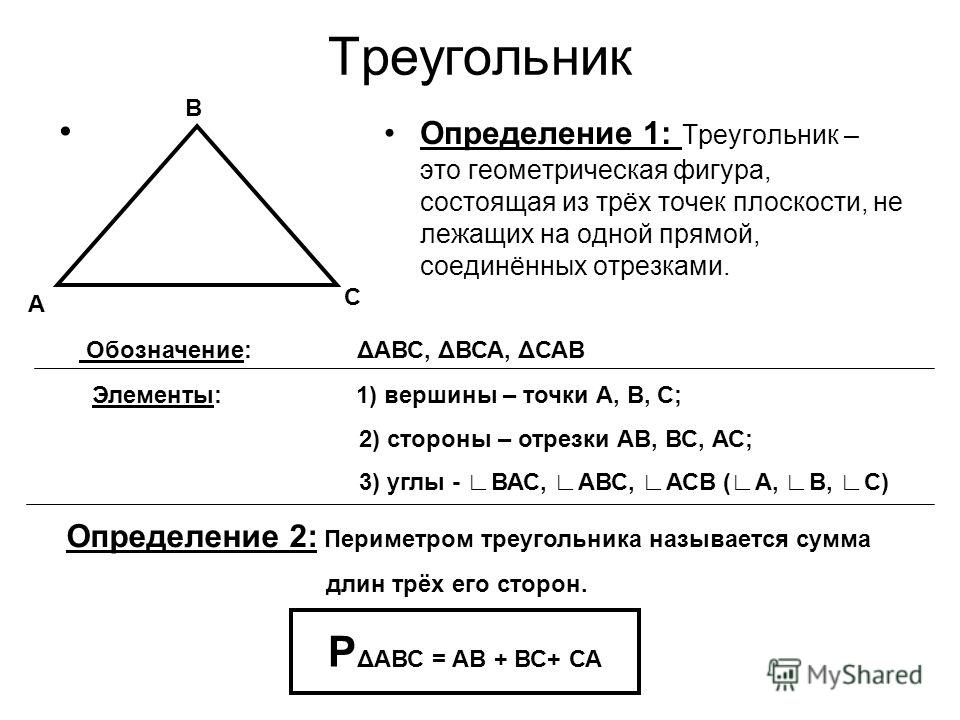 Пространство, в котором мы живем, считается трехмерным, т.е. имеет три измерения. Их часто называют: длина, ширина и высота (например, длина комнаты 4 м, ширина комнаты 2 м и высота 3 м).
Пространство, в котором мы живем, считается трехмерным, т.е. имеет три измерения. Их часто называют: длина, ширина и высота (например, длина комнаты 4 м, ширина комнаты 2 м и высота 3 м).
Представление о геометрической (математической) точке дает нам звезда на ночном небе, точка в конце этого предложения, след от иглы и т.д. Однако все перечисленные объекты имеют размеры, в отличие от них размеры геометрической точки считаются равными нулю (её измерения равны нулю). Поэтому реальную математическую точку можно лишь мысленно представить. Можно также сказать, в каком месте она находится. Поставив авторучкой в тетради точку, мы не изобразим геометрическую точку, но будем считать, что построенный объект есть геометрическая точка (рисунок 6). Точки обозначают заглавными буквами латинского алфавита: A, B, C, D, (читают «точка а, точка бэ, точка цэ, точка дэ») (рисунок 7).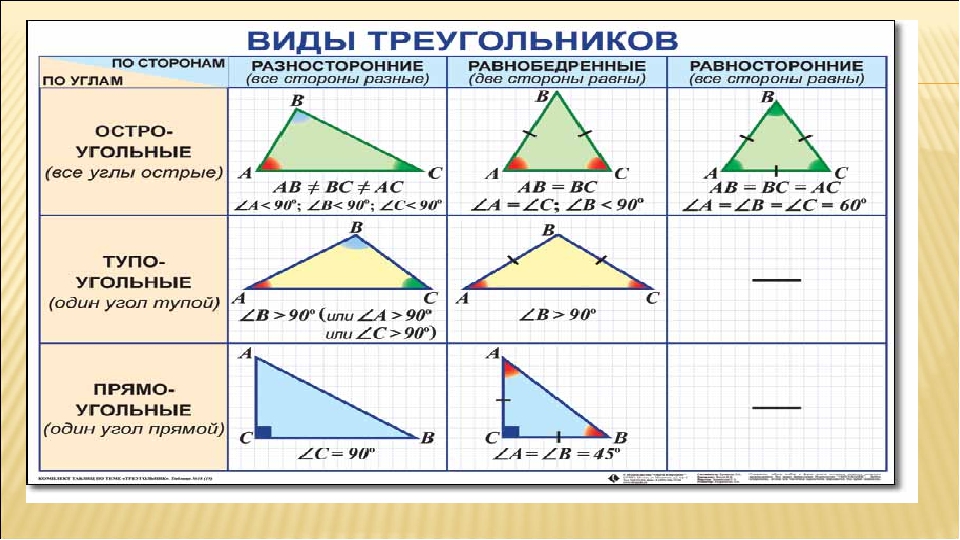
Провода, висящие на столбах, видимая линия горизонта (граница между небом и землей или водой), русло реки, изображенное на карте, гимнастический обруч, струя воды, бьющая из фонтана дают нам представление о линиях.
Различают замкнутые и незамкнутые линии, гладкие и негладкие линии, линии с самопересечением и без самопересечения (рисунки 8 и 9).
Лист бумаги, лазерный диск, оболочка футбольного мяча, картон упаковочной коробки, новогодняя пластиковая маска и т.д. дают нам представление о поверхностях (рисунок 10). Когда красят пол комнаты или автомобиль, то покрывают краской именно поверхность пола или автомобиля.
Тело человека, камень, кирпич, головка сыра, мяч, ледяная сосулька и т.д. дают нам представление о геометрических телах (рисунок 11).
Наиболее простая из всех линий – это прямая. Приложим к листу бумаги линейку и проведем карандашом вдоль неё прямую линию.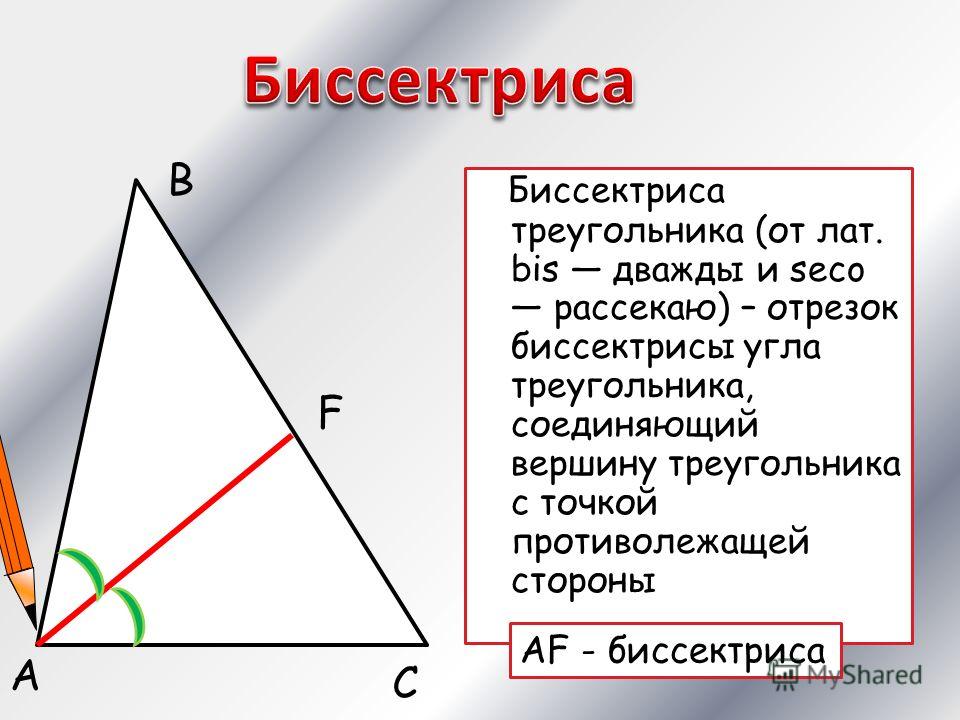 Мысленно продолжив эту линию до бесконечности в обе стороны, мы получим представление о прямой. Считают, что прямая имеет одно измерение – длину, а два других ее измерения равны нулю (рисунок 12).
Мысленно продолжив эту линию до бесконечности в обе стороны, мы получим представление о прямой. Считают, что прямая имеет одно измерение – длину, а два других ее измерения равны нулю (рисунок 12).
При решении задач прямую изображают в виде линии, которую проводят вдоль линейки карандашом или мелом. Прямые обозначаются строчными латинскими буквами: a, b, n, m (рисунок 13). Можно обозначать прямую также двумя буквами, соответствующими точкам, лежащим на ней. Например, прямую n на рисунке 13 можно обозначить: АВ или ВА, АD или DА, DВ или ВD.
Точки могут лежать на прямой (принадлежать прямой) и не лежать на прямой (не принадлежать прямой). На рисунке 13 изображены точки A, D, B, лежащие на прямой AB (принадлежащие прямой AB). При этом пишут . Читают: точка A принадлежит прямой AB, точка В принадлежит AB, точка D принадлежит АВ. Точка D принадлежит также и прямой m, ее называют общей точкой. В точке D прямые AB и m пересекаются. Точки P и R не принадлежат прямым AB и m:
В точке D прямые AB и m пересекаются. Точки P и R не принадлежат прямым AB и m:
Через любые две точки всегда можно провести прямую и причем только одну.
Из всех видов линий, соединяющих любые две точки, наименьшую длину имеет отрезок, концами которого служат данные точки (рисунок 14).
Фигура, которая состоит из точек и соединяющих их отрезков называется ломаной (рисунок 15). Отрезки, образующие ломаную, называются звеньями ломаной, а их концы — вершинами ломаной. Называют (обозначают) ломаную, перечисляя по порядку все ее вершины, например, ломаная ABCDEFG. Длиной ломаной называется сумма длин ее звеньев. Значит, длина ломаной ABCDEFG равна сумме: AB + BC + CD + DE + EF + FG.
Замкнутая ломаная называется многоугольником, ее вершины называются вершинами многоугольника, а ее звенья сторонами многоугольника (рисунок 16).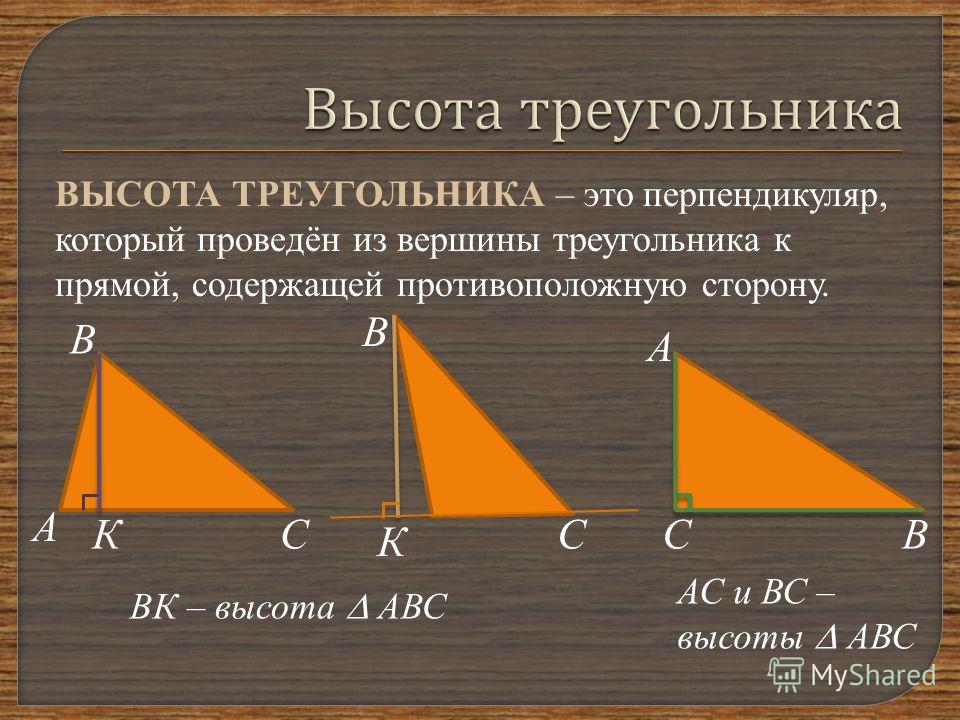 Называют (обозначают) многоугольник, перечисляя по порядку все его вершины, начиная с любой, например, многоугольник (семиугольник) ABCDEFG , многоугольник (пятиугольник) RTPKL:
Называют (обозначают) многоугольник, перечисляя по порядку все его вершины, начиная с любой, например, многоугольник (семиугольник) ABCDEFG , многоугольник (пятиугольник) RTPKL:
Сумма длин всех сторон многоугольника называется периметром многоугольника и обозначается латинской буквой p (читаем: пэ). Периметры многоугольников на рисунке 13:
PABCDEFG = AB + BC + CD + DE + EF + FG + GA.
PRTPKL = RT + TP + PK + KL + LR.
Мысленно продлив поверхность крышки стола или оконного стекла до бесконечности во все стороны, получим представление о поверхности, которая называется плоскостью (рисунок 17). Обозначают плоскости малыми буквами греческого алфавита: α, β, γ, δ,… (читаем: плоскость альфа, бетта, гамма, дельта, и т.д.).
Блок 2. Словарь.
Составьте словарь новых терминов и определений из §2. Для этого в пустые строки таблицы впишите слова из списка терминов, приведенного ниже. В таблице 2 укажите номера терминов в соответствии с номерами строк. Рекомендуется перед заполнением словаря еще раз внимательно просмотреть §2 и блок 2.1.
В таблице 2 укажите номера терминов в соответствии с номерами строк. Рекомендуется перед заполнением словаря еще раз внимательно просмотреть §2 и блок 2.1.
Блок 3. Установите соответствие (УС).
Геометрические фигуры.
Блок 4. Самопроверка.
Измерение отрезка с помощью линейки.
Напомним, что измерить отрезок АВ в сантиметрах, значит, сравнить его с отрезком длиной 1см и узнать, сколько таких отрезков по 1см помещается в отрезке АВ. Чтобы измерить отрезок в других единицах длины, поступают подобным же образом.
Для выполнения заданий работайте по плану, приведенному в левой колонке таблицы. При этом правую колонку рекомендуем закрыть листом бумаги. Затем вы сможете сопоставить свои выводы с решениями, приведенными в таблице справа.
Блок 5. Установление последовательности действий (УП).
Построение отрезка заданной длины.
Вариант 1. В таблице записан перепутанный алгоритм (перепутанный порядок действий) построения отрезка заданной длины (например, построим отрезок ВС = 7см). В левом столбце указание к действию в правом результат выполнения этого действия. Переставьте строки таблицы так, чтобы получился верный алгоритм построения отрезка заданной длины. Запишите верную последовательность действий.
Вариант 2. В следующей таблице приведен алгоритм построения отрезка КМ = n см, где вместо n можно подставить любое число. В этом варианте нет соответствия между действием и результатом. Поэтому необходимо установить последовательность действий, затем для каждого действия выбрать его результат. Ответ запишите в виде: 2а, 1в, 4б и т.д.
Вариант 3. Используя алгоритм варианта 2, постройте в тетради отрезки при n = 3 см, n = 10 см, n = 12 см.
Блок 6. Фасетный тест.
Отрезок, луч, прямая, плоскость.
В задачах фасетного теста используются рисунки и записи под номерами 1 – 12, приведённые в таблице 1. Из них формируются данные задач. Затем к ним добавляются требования задач, которые в тесте помещены после соединительного слова «ТО». Ответы к задачам помещены после слова «РАВНО». Набор задач приведён в таблице 2. Например, задача 6.15.19 составляется следующим образом: «ЕСЛИ в задаче используется рисунок 6, затем к нему добавляется условие под номером 15, требование задачи стоит под номером 19.»
Содержание теста.
13) построить четыре точки так, чтобы каждые три из них не лежали на одной прямой;
14) провести через каждые две точки прямую;
15) каждую из поверхностей коробки продлить мысленно во все стороны до бесконечности;
ТО:
16) количество различных отрезков на рисунке;
17) количество различных лучей на рисунке;
18) количество различных прямых на рисунке;
19) количество получившихся различных плоскостей;
20) длина отрезка АС в сантиметрах;
21) длина отрезка АВ в километрах;
22) длина отрезка DC в метрах;
23) периметр треугольника PRQ;
24) длина ломаной QPRMN;
25) частное периметров треугольников RMN и PRQ;
26) длина отрезка ED;
27) длина отрезка BE;
28) количество получившихся точек пересечения прямых;
29) количество получившихся треугольников;
30) количество частей, на которые оказалась разделена плоскость;
31) периметр многоугольника, выраженный в метрах;
32) периметр многоугольника, выраженный в дециметрах;
33) периметр многоугольника, выраженный в сантиметрах;
34) периметр многоугольника, выраженный в миллиметрах;
35) периметр многоугольника, выраженный в километрах;
РАВНО (равна, имеет вид):
а) 70; б) 4; в) 217; г) 8; д) 20; е) 10; ж) 8∙b; з) 800∙b; и) 8000∙b; к) 80∙b; л) 63000; м) 63; н) 63000000; о) 3; п) 6; р) 630000; с) 6300000; т) 7; у) 5; ф) 22; х) 28
Блок 7. Давай поиграем.
Давай поиграем.
7.1. Математический лабиринт.
Лабиринт состоит из десяти комнат с тремя дверьми каждая. В каждой из комнат находится по одному геометрическому объекту (он нарисован на стене комнаты). Сведения об этом объекте находятся в «путеводителе» по лабиринту. Читая его, надо переходить в ту комнату, о которой написано в путеводителе. Проходя по комнатам лабиринта, рисуйте свой маршрут. В двух последних комнатах имеются выходы.
Путеводитель по лабиринту
- Войти в лабиринт надо через комнату, где находится геометрический объект, у которого нет начала, но есть два конца.
- Геометрический объект этой комнаты не имеет размеров, он подобен далёкой звезде на ночном небе.
- Геометрический объект этой комнаты составлен из четырёх отрезков, имеющих три общие точки.
- Этот геометрический объект состоит из четырёх отрезков с четырьмя общими точками.
- В этой комнате находятся геометрические объекты, каждый из которых имеет начало, но не имеет конца.

- Здесь два геометрических объекта, не имеющих ни начала, ни конца, но с одной общей точкой.
- Представление об этом геометрическом объекте даёт полет артиллерийских снарядов
(траектория движения).
- В этой комнате находится геометрический объект с тремя вершинами, но это не горные
вершины.
- Об этом геометрическом объекте даёт представление полёт бумеранга (охотничье
оружие коренных жителей Австралии). В физике эту линию называют траекторией
движения тела.
- Представление об этом геометрическом объекте даёт поверхность озера в
безветренную погоду.
Теперь можете выходить из лабиринта.
В лабиринте находятся геометрические объекты: плоскость, незамкнутая линия, прямая, треугольник, точка, замкнутая линия, ломаная, отрезок, луч, четырёхугольник.
7.2. Периметр геометрических фигур.
В рисунках выделите геометрические фигуры: треугольники, четырёхугольники, пяти – и шестиугольники. С помощью линейки (в миллиметрах) определите периметры некоторых из них.
7.3. Эстафета геометрических объектов.
В заданиях эстафеты есть пустые рамки. В них запишите пропущенное слово. Затем перенесите это слово в другую рамку, куда показывает стрелка. При этом можно изменять падеж этого слова. Проходя по этапам эстафеты, выполняйте требуемые построения. Если эстафету пройдёте правильно, то в конце получите слово: периметр.
7.4. Крепость геометрических объектов.
Прочитайте § 2, выпишите из его текста названия геометрических объектов. Затем впишите эти слова в пустые клетки «крепости».
Что такое Сиде? Определение Факты и примеры
Сторона в математике
Представьте, если бы у нас не было линий, соединяющих точки. Не было бы форм! Линии и точки составляют все плоские формы, которые мы видим, такие как квадраты, прямоугольники и треугольники.
Когда мы говорим о стороне, мы используем ее для описания различных сторон объекта, например стороны монеты или стороны страницы.
Мы также используем слово «бок», чтобы описать, где что-то расположено по отношению к другому объекту.
Например, «магазин находится на левой стороне улицы». Однако сторона в математике имеет другое значение.
Сторона в математике означает линию, которая образует часть плоской фигуры. Давайте лучше поймем это с точки зрения геометрии.
Определение стороны в математике?
Сторона в математике — это аспект геометрической формы. Формы, которые мы видим, состоят из линий (отрезков) и точек (вершин). Эти отрезки соединяются друг с другом в вершинах, образуя фигуру. Эти отрезки называются сторонами.
Сторона в геометрии определяется как отрезок, соединяющий две вершины формы или двумерной фигуры.
Другими словами, сторона в математике — это линия, соединяющая две точки фигуры. Форма здесь означает двумерную (плоскую) форму, такую как прямоугольник, квадрат или треугольник.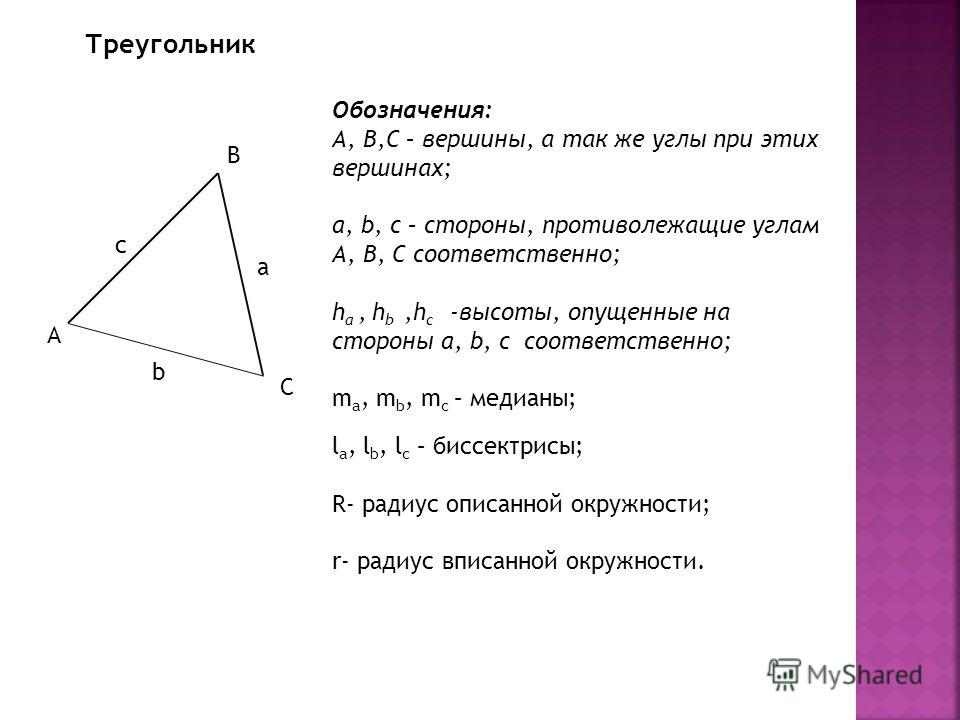
Вот, например, прямоугольник имеет четыре стороны.
Стороны в двумерных фигурах
Многоугольник — это замкнутая фигура, состоящая из трех или более отрезков. Эти фигуры обычно называют в зависимости от того, сколько у них сторон. Например, у треугольника 3 стороны, у четырехугольника 4 стороны, а у пятиугольника 5 сторон.
Если все стороны многоугольника равны, он называется правильным многоугольником.
Например, у равностороннего треугольника три равные стороны, у квадрата четыре равные стороны, а у правильного шестиугольника шесть равных сторон. Эти формы являются некоторыми примерами правильных многоугольников.
Давайте петь!
У всех двухмерных фигур есть сторона.
У кого-то три, у кого-то пять.
Вы можете назвать их всех по бокам!
Давай сделаем это!
Покажите ребенку изображения разных двухмерных фигур. Попросите их посчитать количество сторон, которые у них есть, и назовите их имена. Вы можете дополнительно объяснить, как эти фигуры были названы в зависимости от количества сторон, которые у них есть.
Вы можете дополнительно объяснить, как эти фигуры были названы в зависимости от количества сторон, которые у них есть.
Решенные примеры
Пример 1. Сколько сторон у треугольника?
Решение : Треугольник имеет три стороны.
Пример 2: Если многоугольник имеет 5 сторон, как он называется?
Решение . Многоугольник с 5 сторонами называется пятиугольником.
Пример 3. Является ли квадрат многоугольником?
Решение : Да, квадрат является многоугольником, потому что это замкнутая фигура с 4 сторонами. Многоугольник – это замкнутая фигура с тремя или более сторонами.
Пример 4. Является ли прямоугольник четырехугольником?
Решение : Да, прямоугольник является четырехугольником, потому что это замкнутая фигура с четырьмя сторонами. Замкнутая фигура с четырьмя сторонами — это многоугольник, известный как четырехугольник.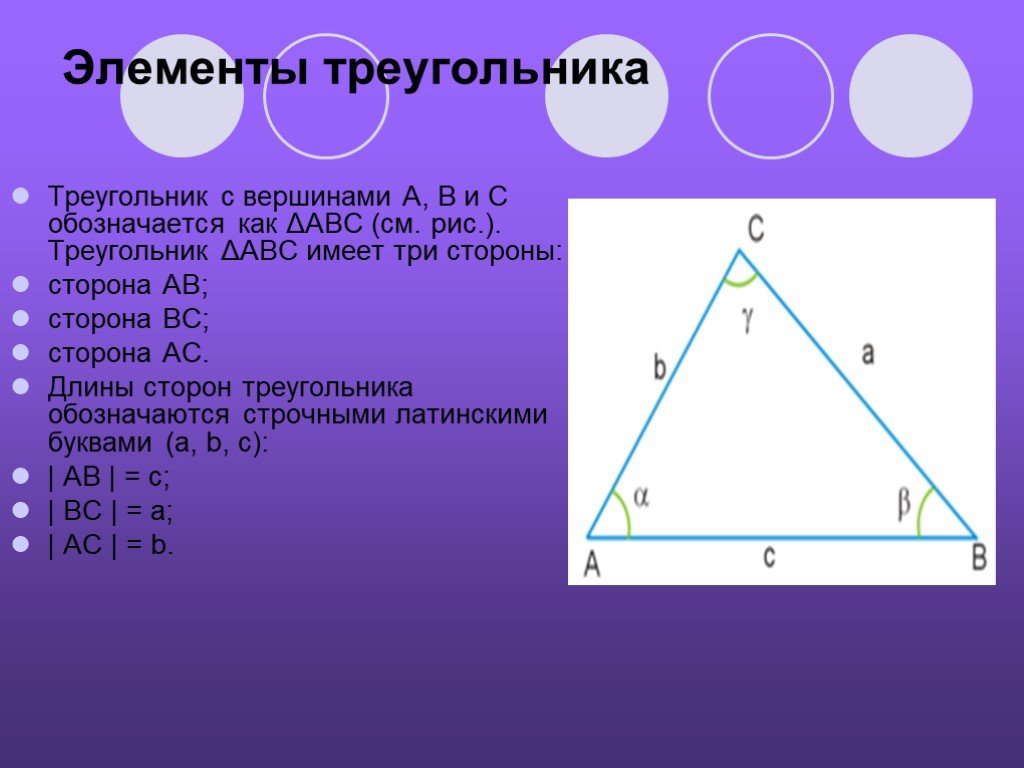
Практические задачи
1
Замкнутая фигура имеет 5 отрезков, соединенных в вершинах. Как это называется?
Квадрат
Прямоугольник
Пятиугольник
Четырехугольник
Правильный ответ: Пятиугольник
5 линий, соединенных в вершинах, означают, что фигура имеет 5 сторон. Замкнутая фигура с 5 сторонами называется пятиугольником.
2
Многоугольник имеет четыре стороны. Какая из следующих форм это?
Треугольник
Пятиугольник
Прямоугольник
Шестиугольник
Правильный ответ: Прямоугольник
Это прямоугольник, потому что прямоугольник является четырехугольником. Многоугольник с четырьмя сторонами называется четырехугольником, который может быть квадратом, прямоугольником или другой замкнутой фигурой с четырьмя сторонами.
3
Как называется замкнутая фигура с тремя или более сторонами?
Треугольник
Объемная фигура
Квадрат
Многоугольник
Правильный ответ: Многоугольник
Многоугольник – это замкнутая фигура, имеющая три или более сторон.
4
Двумерные фигуры состоят из отрезков, соединенных в точках. Как называются отрезки прямой?
Вершины
Ребра
Стороны
Многоугольники
Правильный ответ: Стороны
Стороны — это отрезки, которые соединяются в вершинах, образуя двумерные фигуры.
5
Многоугольник состоит из трех отрезков, которые соединяются друг с другом в трех точках. Как это называется?
Треугольник
Многоугольник
Пятиугольник
Четырехугольник
Правильный ответ: Треугольник
Треугольник – это многоугольник с тремя сторонами.
Часто задаваемые вопросы
Может ли открытая фигура иметь стороны?
Да, отрезки незамкнутой формы также называются сторонами. И открытые, и закрытые формы имеют стороны.
Как называются стороны трехмерной фигуры?
Стороны трехмерной фигуры в геометрии называются ребрами.

 Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
 Две прямые могут пересекаться только в одной точке.
Две прямые могут пересекаться только в одной точке. У второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.
У второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.
 a, b, с – стороны треугольника α – угол треугольника, противолежащий стороне a β – угол треугольника, противолежащий
a, b, с – стороны треугольника α – угол треугольника, противолежащий стороне a β – угол треугольника, противолежащий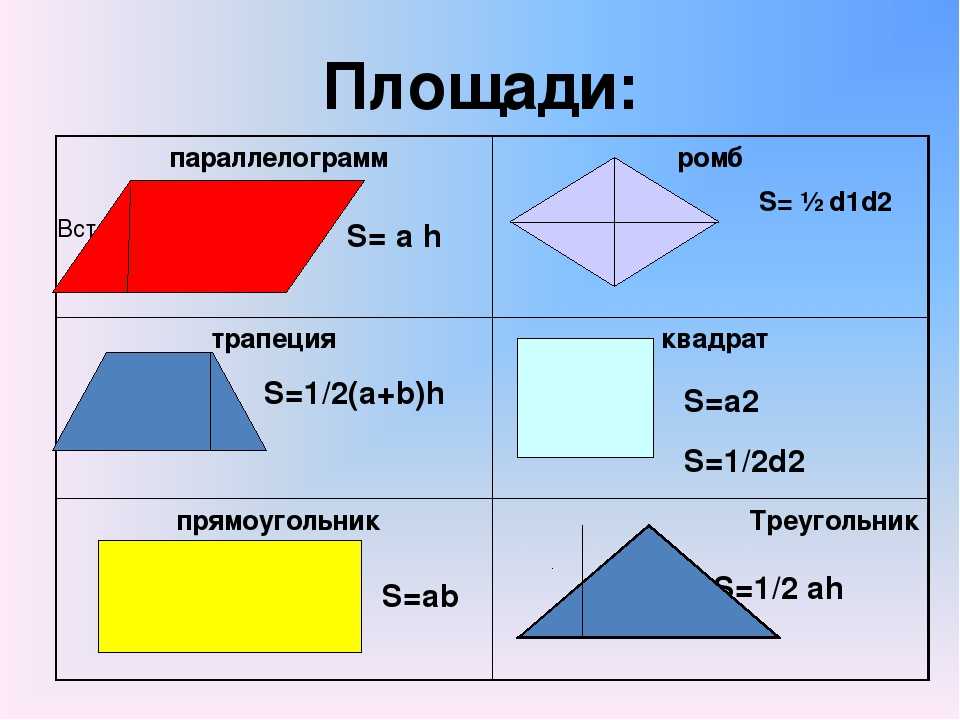
 Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.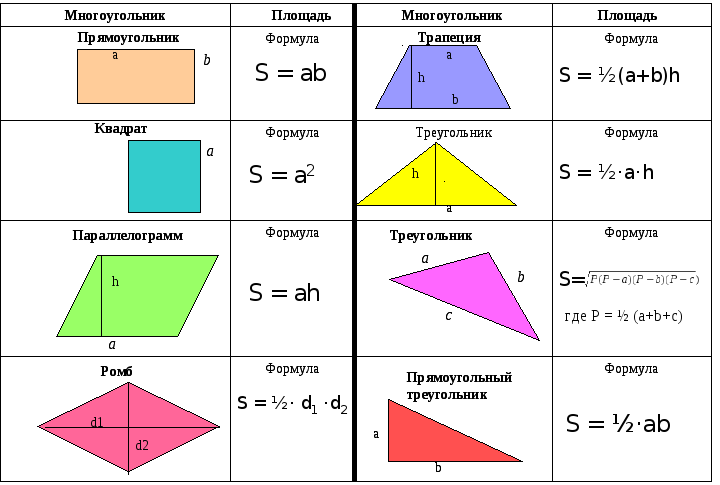
 Формула площади равнобедренной
трапеции через стороны и угол
Формула площади равнобедренной
трапеции через стороны и угол Формула площади равнобедренной
трапеции через среднюю линию, боковую
сторону и угол при основании
Формула площади равнобедренной
трапеции через среднюю линию, боковую
сторону и угол при основании


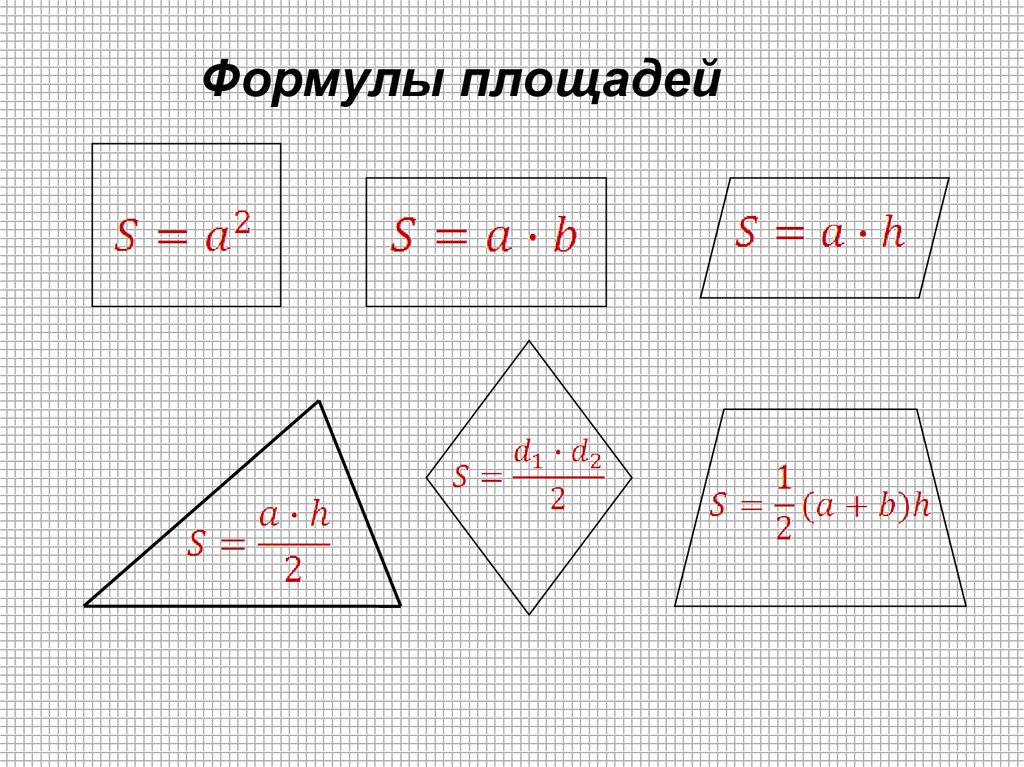
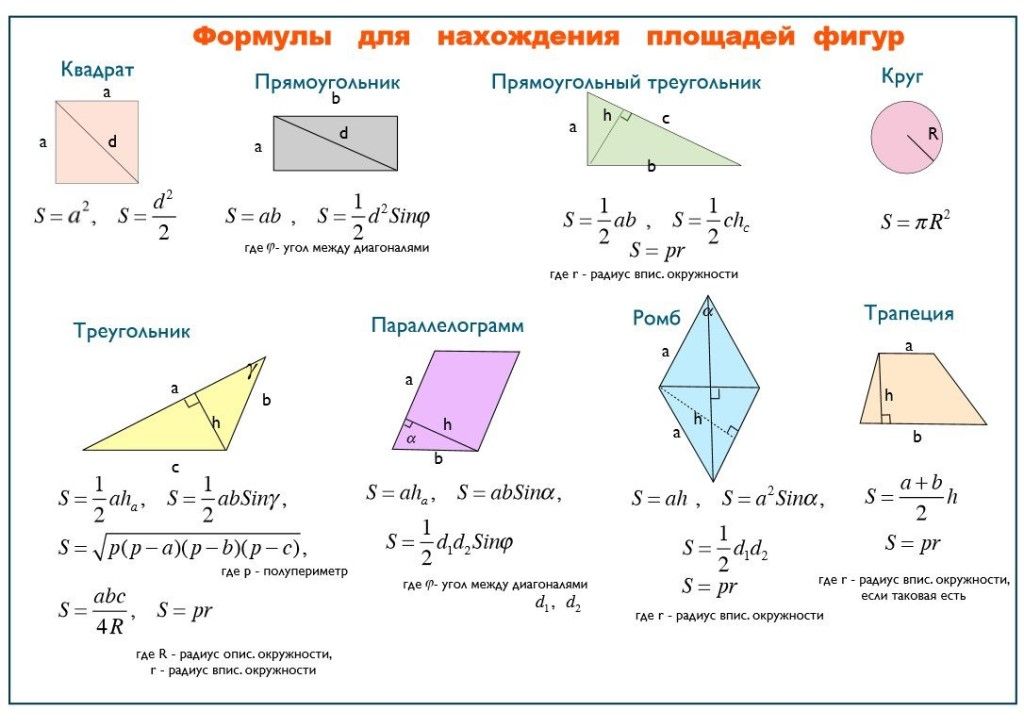
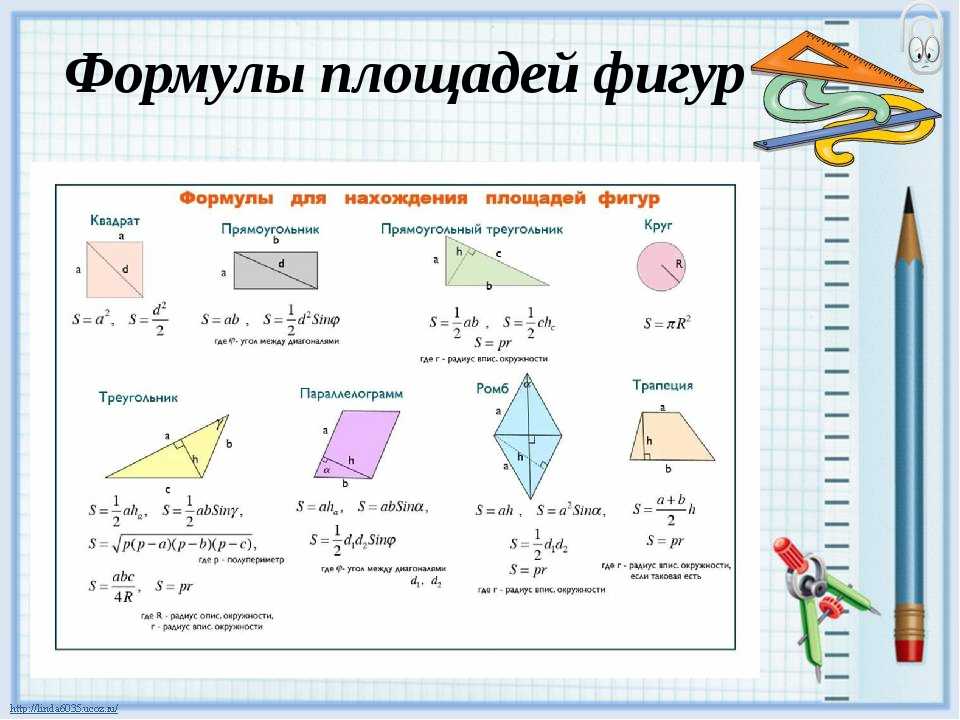
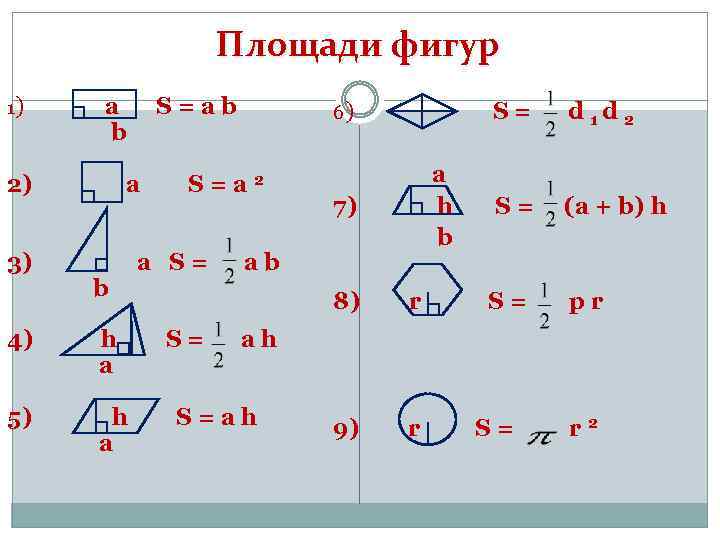
 В указанном ниже случае: Площадь = АВ × ВС.
В указанном ниже случае: Площадь = АВ × ВС.
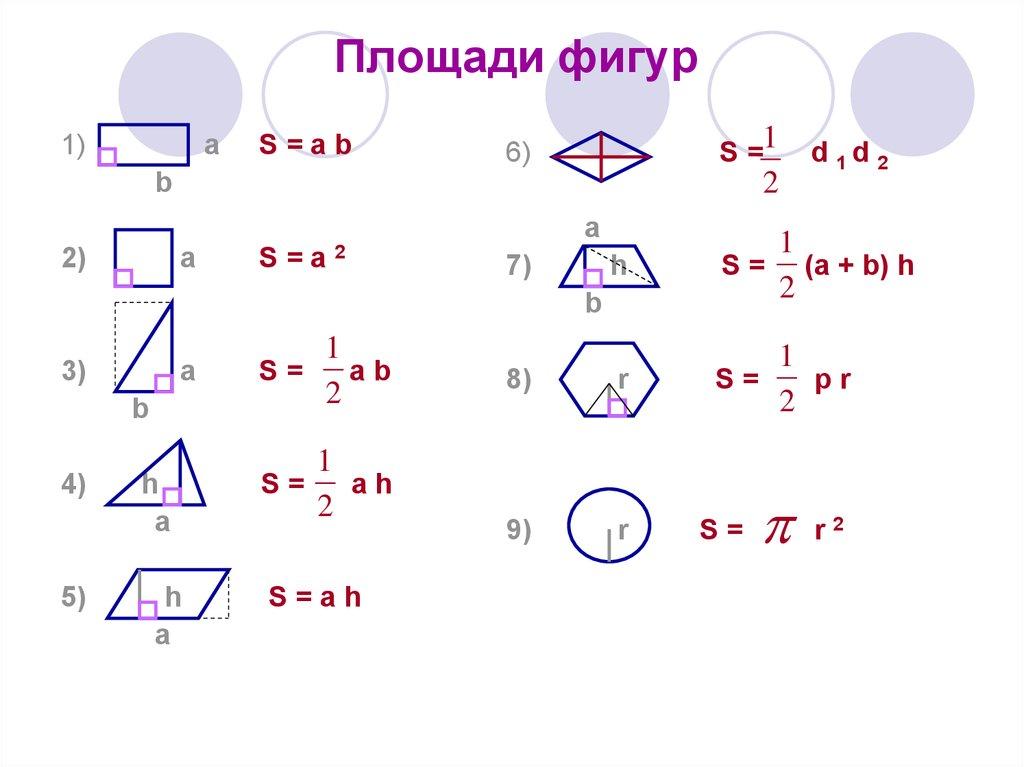
 см, потому что а=4 см, b=3 см, а S=4*3=12 кв. .м.
см, потому что а=4 см, b=3 см, а S=4*3=12 кв. .м.


 Следовательно, мы можем сделать следующее:
Следовательно, мы можем сделать следующее: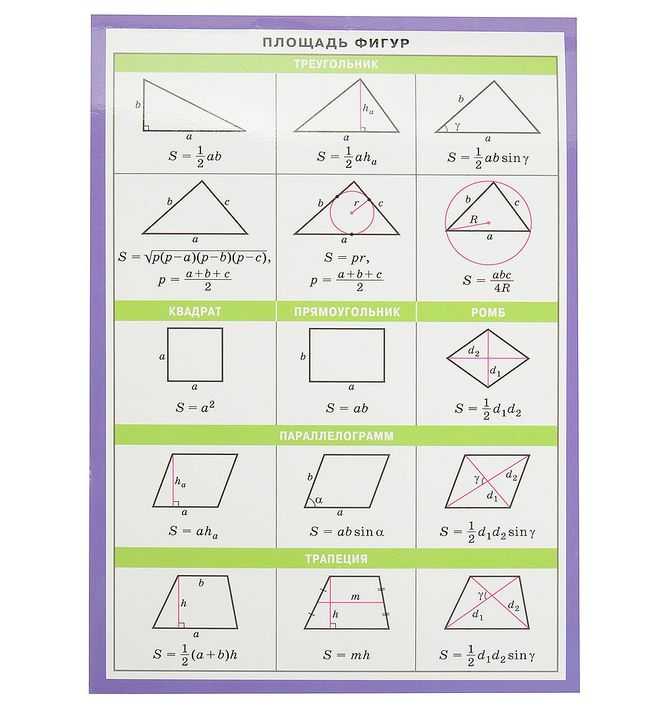
 М.И. Моро, М.А.Бантова и др. Математика: Учебник. 3 класс: В 2 ч., ч. 2. М., «Просвещение», 2012.
М.И. Моро, М.А.Бантова и др. Математика: Учебник. 3 класс: В 2 ч., ч. 2. М., «Просвещение», 2012. Величина площади выражается количеством квадратных единиц, входящих в нее.
Величина площади выражается количеством квадратных единиц, входящих в нее.
 Каждый урок создан учителями-практиками высокой квалификации, сопровождается текстом и чертежами, проверочными тестами, интерактивными тренажерами и контрольными вопросами по изученной теме.
Каждый урок создан учителями-практиками высокой квалификации, сопровождается текстом и чертежами, проверочными тестами, интерактивными тренажерами и контрольными вопросами по изученной теме.
 Ответы даются оперативно и по существу.
Ответы даются оперативно и по существу.







 Он остается пригодным для использования, но интервалы и размеры шрифта не позволяют использовать преимущества больших экранов. Это приложение, скорее всего, будет использоваться на телефонах учащихся, но школы, которые, как правило, больше полагаются на планшетные устройства, должны знать, что оно не точно воспроизводит работу с телефоном.
Он остается пригодным для использования, но интервалы и размеры шрифта не позволяют использовать преимущества больших экранов. Это приложение, скорее всего, будет использоваться на телефонах учащихся, но школы, которые, как правило, больше полагаются на планшетные устройства, должны знать, что оно не точно воспроизводит работу с телефоном.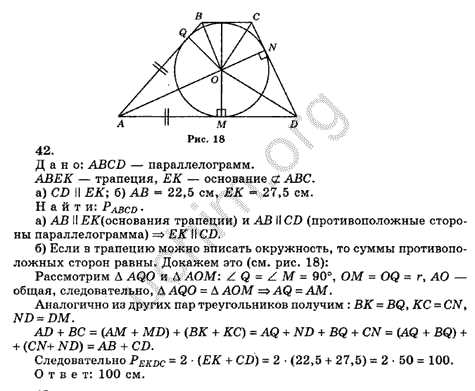

 Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма его противоположных углов равна 180 градусов.
Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма его противоположных углов равна 180 градусов.



 Эти правила получили название «правила естественного вывода» или «производные правила вывода».
Эти правила получили название «правила естественного вывода» или «производные правила вывода».

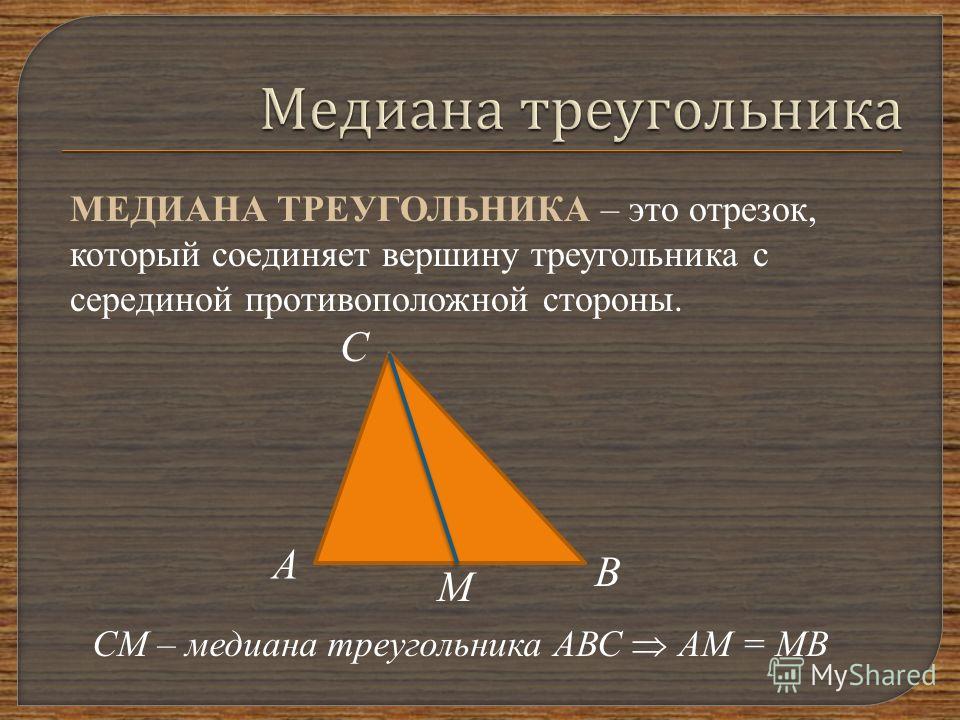
 1), где АА1, ВВ1, СС1 – медианы, а М0 – точка их пересечения.
1), где АА1, ВВ1, СС1 – медианы, а М0 – точка их пересечения.
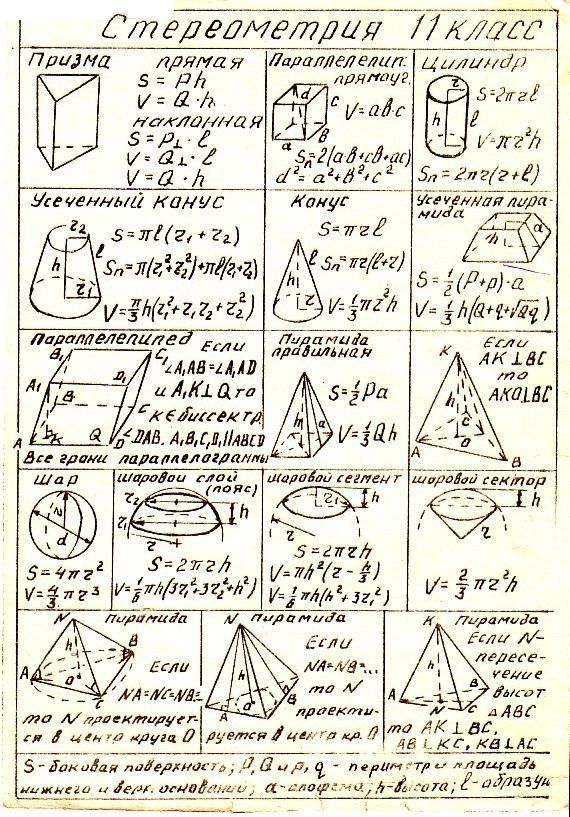
 14-недельный базовый курс геометрии от School Yourself можно пройти вместе с курсом старшей школы, и он может служить углубленным учебным пособием по геометрии для дополнительной практики и мастерства. Изучите все основы геометрии, в том числе, как вычислять площади сложных фигур, как измерять углы, как доказывать и применять теорему Пифагора, как применять свойства треугольников и четырехугольников и как применять геометрические формулы. Курс является самостоятельным, поэтому студенты могут переходить к любому разделу по мере необходимости.
14-недельный базовый курс геометрии от School Yourself можно пройти вместе с курсом старшей школы, и он может служить углубленным учебным пособием по геометрии для дополнительной практики и мастерства. Изучите все основы геометрии, в том числе, как вычислять площади сложных фигур, как измерять углы, как доказывать и применять теорему Пифагора, как применять свойства треугольников и четырехугольников и как применять геометрические формулы. Курс является самостоятельным, поэтому студенты могут переходить к любому разделу по мере необходимости. Вы можете быть удивлены количеством рабочих мест и профессий, которые требуют практических знаний геометрии для выполнения повседневных задач. Ниже приведены несколько примеров профессий, требующих понимания геометрии для выполнения повседневных задач.
Вы можете быть удивлены количеством рабочих мест и профессий, которые требуют практических знаний геометрии для выполнения повседневных задач. Ниже приведены несколько примеров профессий, требующих понимания геометрии для выполнения повседневных задач. Некоторые роботы созданы с диапазоном зрения для обнаружения объектов, поэтому измерение углов и восприятие являются повседневными задачами в этой профессии.
Некоторые роботы созданы с диапазоном зрения для обнаружения объектов, поэтому измерение углов и восприятие являются повседневными задачами в этой профессии.

 Ему же принадлежит теорема, что вписанный угол,
опирающийся на диаметр окружности- прямой.
Ему же принадлежит теорема, что вписанный угол,
опирающийся на диаметр окружности- прямой. В ее основу они
положили простейшие геометрические свойства,
подсказанные опытом. Остальные свойства
выводились из простейших с помощью рассуждений.
В ее основу они
положили простейшие геометрические свойства,
подсказанные опытом. Остальные свойства
выводились из простейших с помощью рассуждений.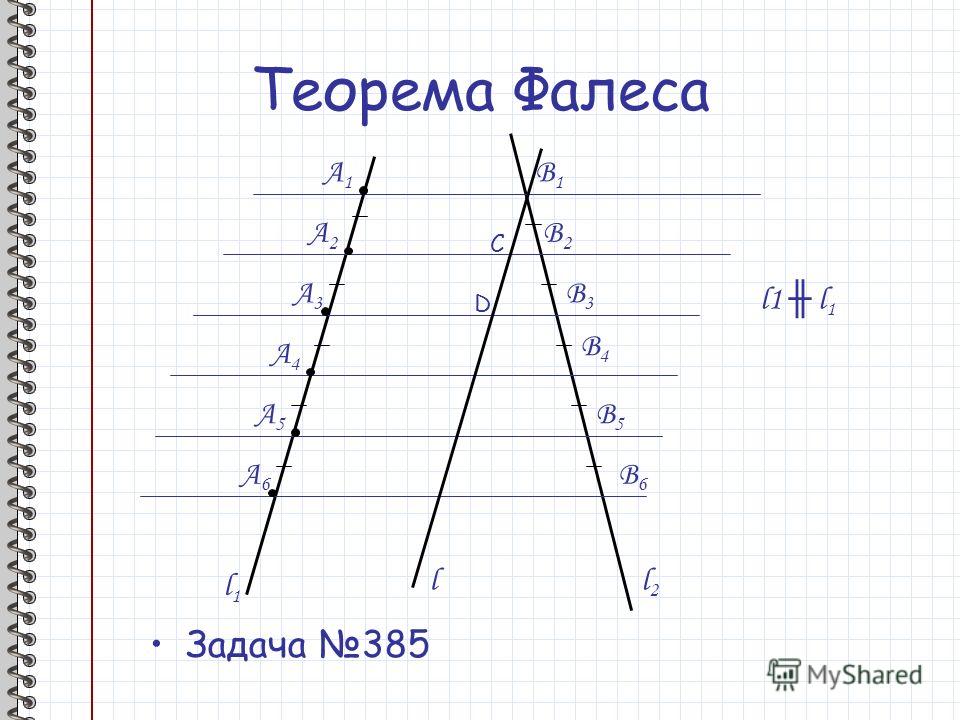 Построим данный
отрезок АВ.
Построим данный
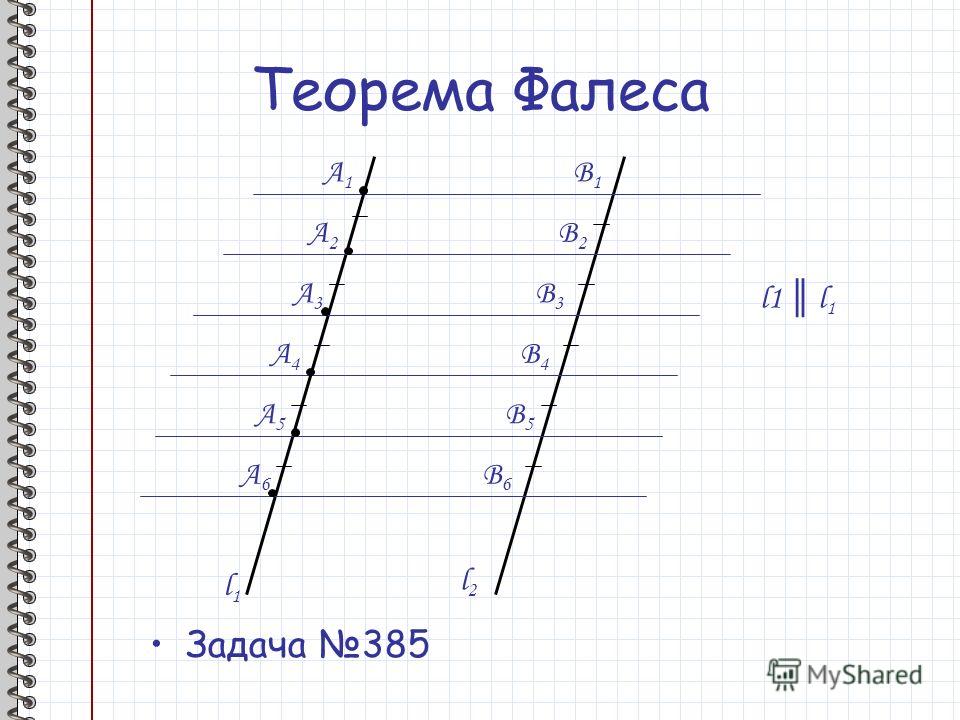
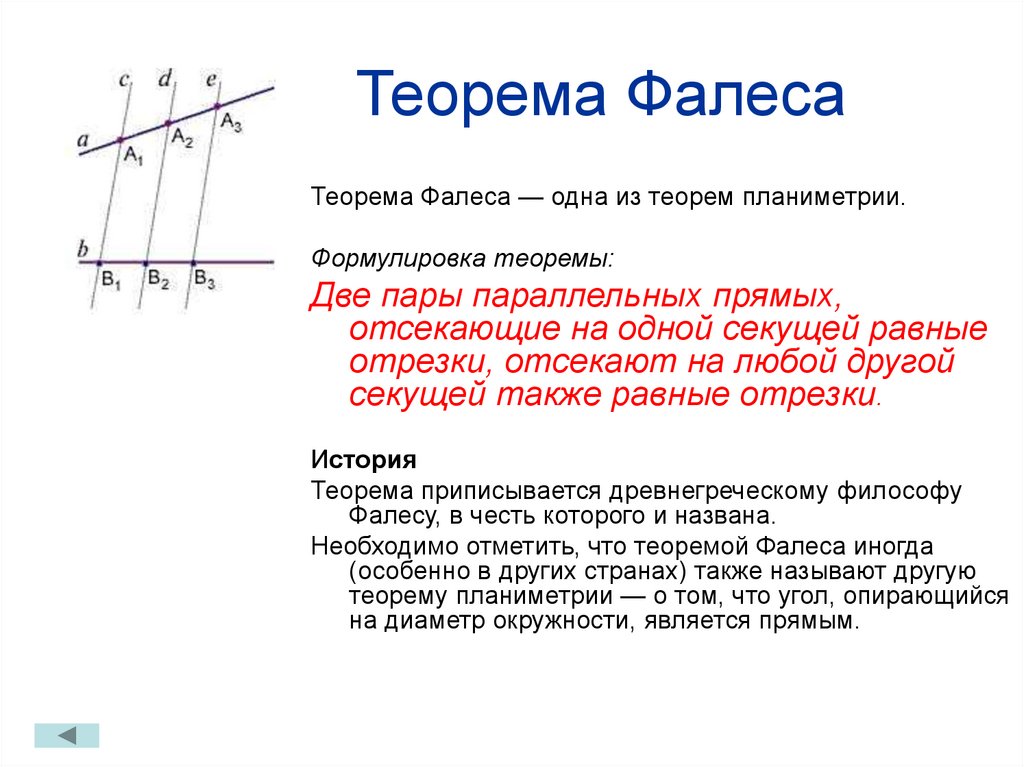
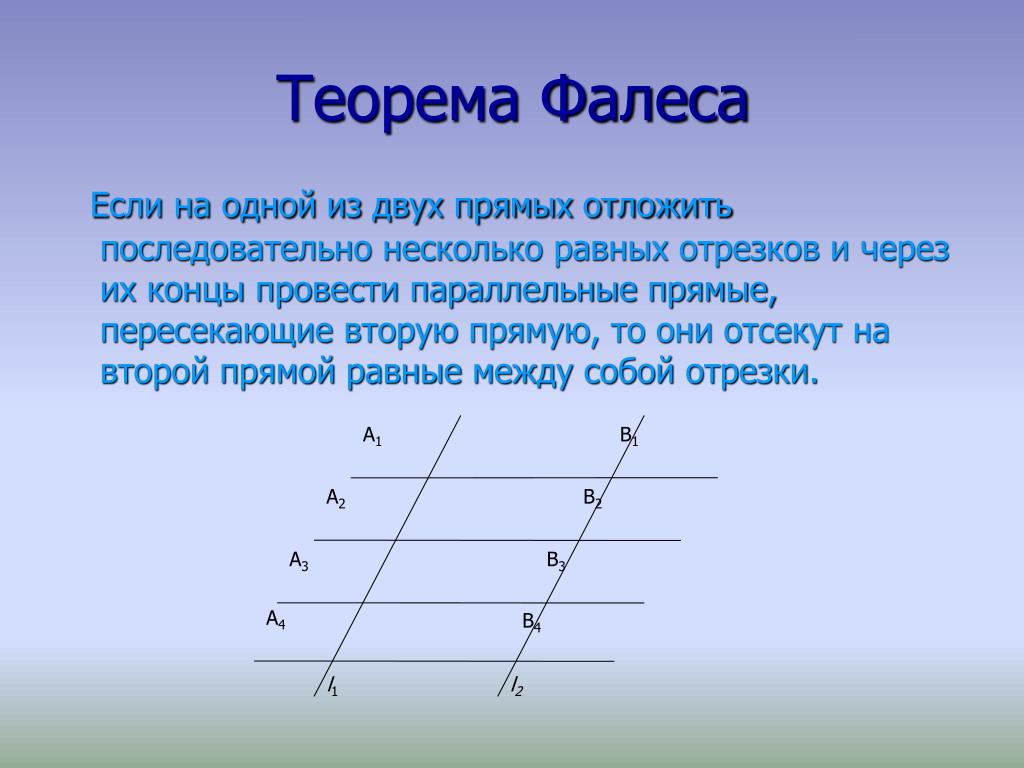
отрезок АВ. на 7 равных частей. Выучить теорему Фалеса.
на 7 равных частей. Выучить теорему Фалеса.

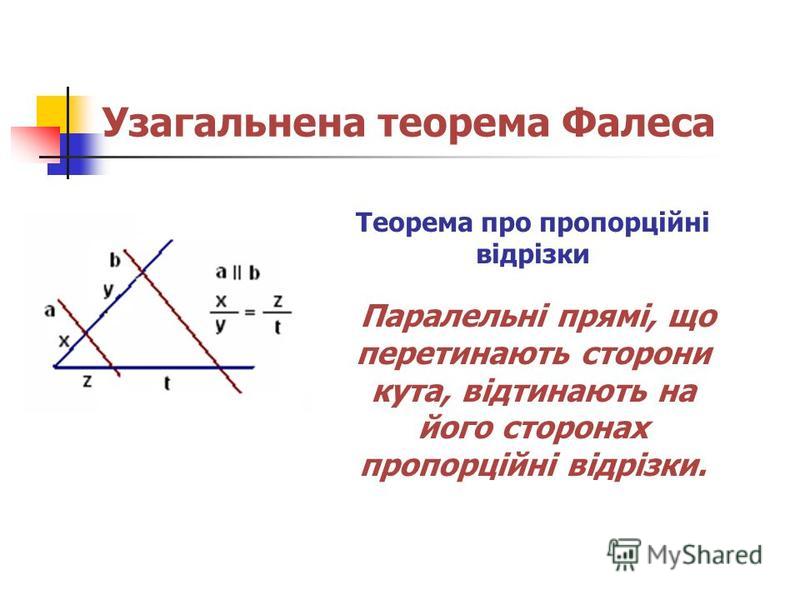
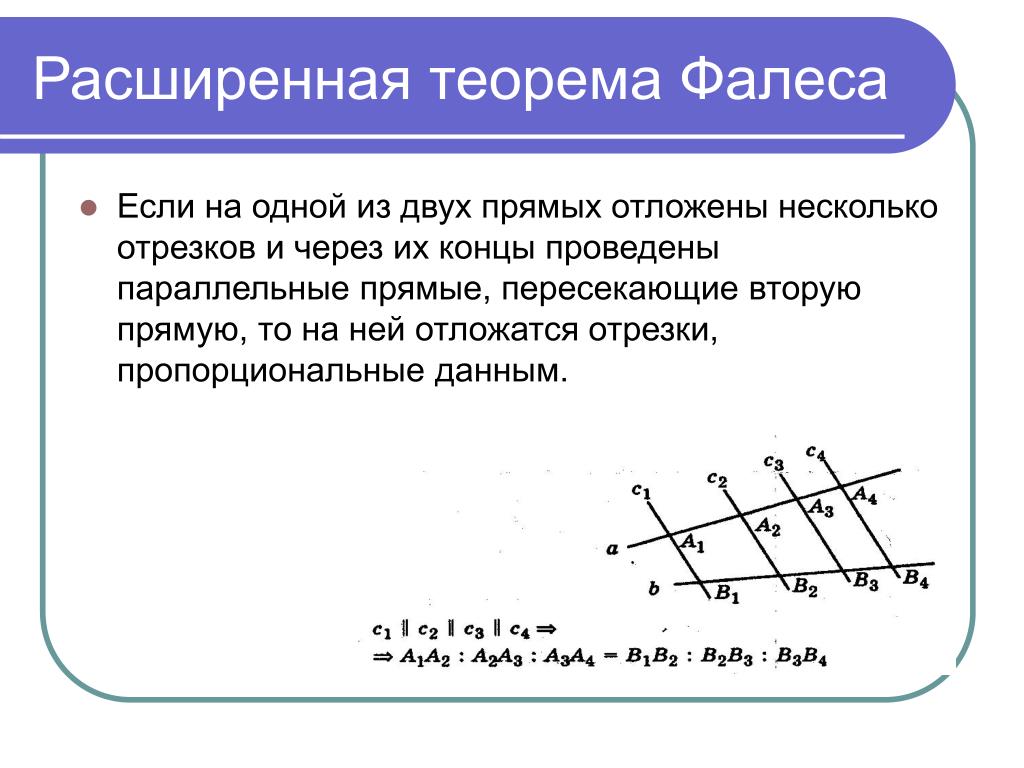
 Разобьем отрезок X1X3 на b одинаковых частей. (При этом точка X2 окажется одной из точек деления.) Проведем через каждую точку деления прямые, параллельные n1, n2 и n3. (Одна из этих прямых совпадет с прямой n2.)
Разобьем отрезок X1X3 на b одинаковых частей. (При этом точка X2 окажется одной из точек деления.) Проведем через каждую точку деления прямые, параллельные n1, n2 и n3. (Одна из этих прямых совпадет с прямой n2.) Из нашего построения следует также, что
Из нашего построения следует также, что

 Для первого равенства это ясно сразу, а для второго это становится очевидным после того, как мы через точку Y1 проведем прямую m, параллельную прямой x.
Для первого равенства это ясно сразу, а для второго это становится очевидным после того, как мы через точку Y1 проведем прямую m, параллельную прямой x.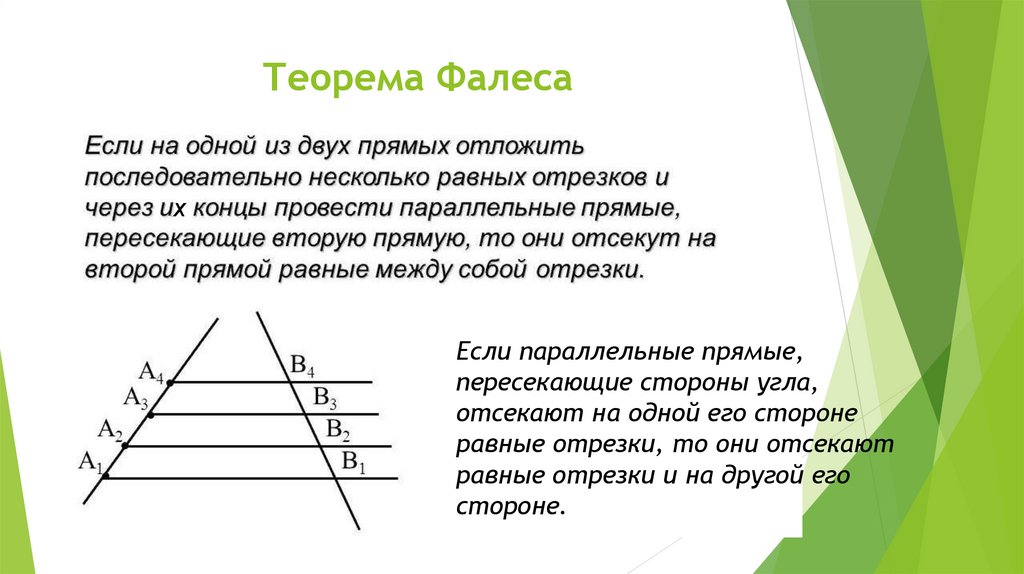 Следовательно, она совпадает с прямой n1. Таким образом, прямая n1 параллельна прямой n2.
Следовательно, она совпадает с прямой n1. Таким образом, прямая n1 параллельна прямой n2.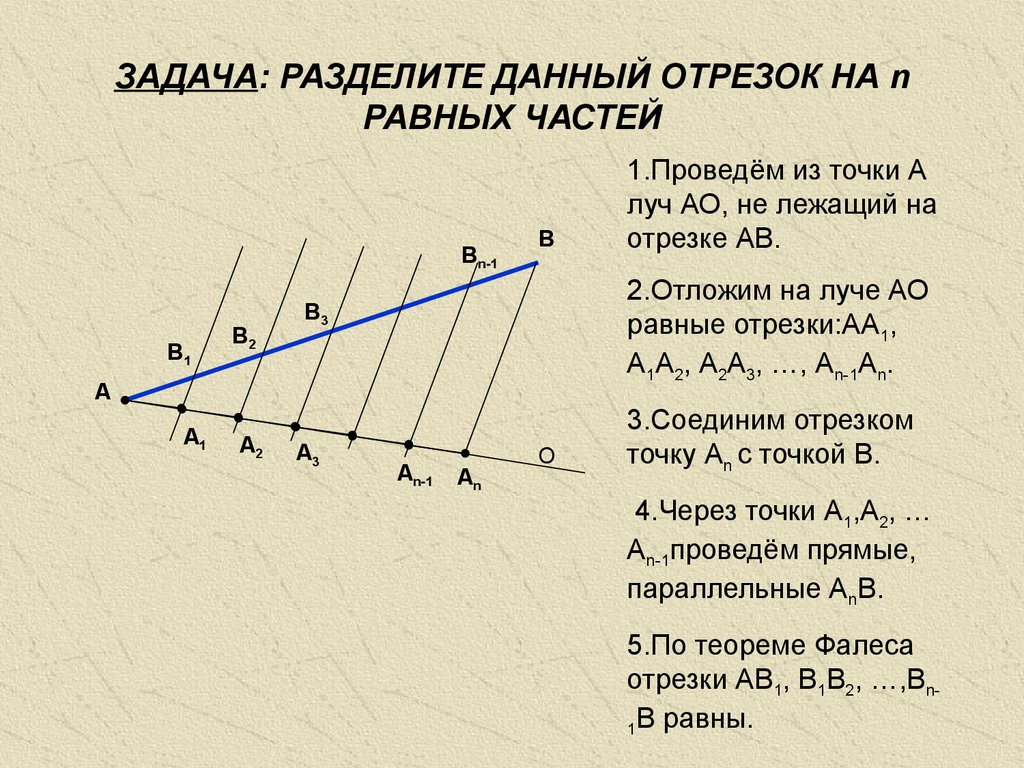 Умножим это расстояние на число k, равное 1/1000. Мысленно отложим от точки O отрезок длиной x2 = kx1 вдоль луча, направленного на данный объект. В том месте на бумаге, где находится второй конец отрезка, сделаем отметку карандашом. Проделаем такую процедуру со всеми примечательными точками на местности, используя всё время одно и то же значение параметра k. Если какие-либо из этих точек соединены между собой забором или стеной или же чем-то подобным, то между соответствующими метками на бумаге также проведем линии.
Умножим это расстояние на число k, равное 1/1000. Мысленно отложим от точки O отрезок длиной x2 = kx1 вдоль луча, направленного на данный объект. В том месте на бумаге, где находится второй конец отрезка, сделаем отметку карандашом. Проделаем такую процедуру со всеми примечательными точками на местности, используя всё время одно и то же значение параметра k. Если какие-либо из этих точек соединены между собой забором или стеной или же чем-то подобным, то между соответствующими метками на бумаге также проведем линии.
 Мы отметили, что такие прямые нигде не пересекаются. Докажем теперь, что если прямые лежат в одной плоскости и не параллельны (то есть угол между ними отличен от нуля), то тогда они обязательно где-нибудь пересекутся.
Мы отметили, что такие прямые нигде не пересекаются. Докажем теперь, что если прямые лежат в одной плоскости и не параллельны (то есть угол между ними отличен от нуля), то тогда они обязательно где-нибудь пересекутся.

 Он считал, что Земля представляет собой плоскую массу, плавающую в огромном море.
Он считал, что Земля представляет собой плоскую массу, плавающую в огромном море.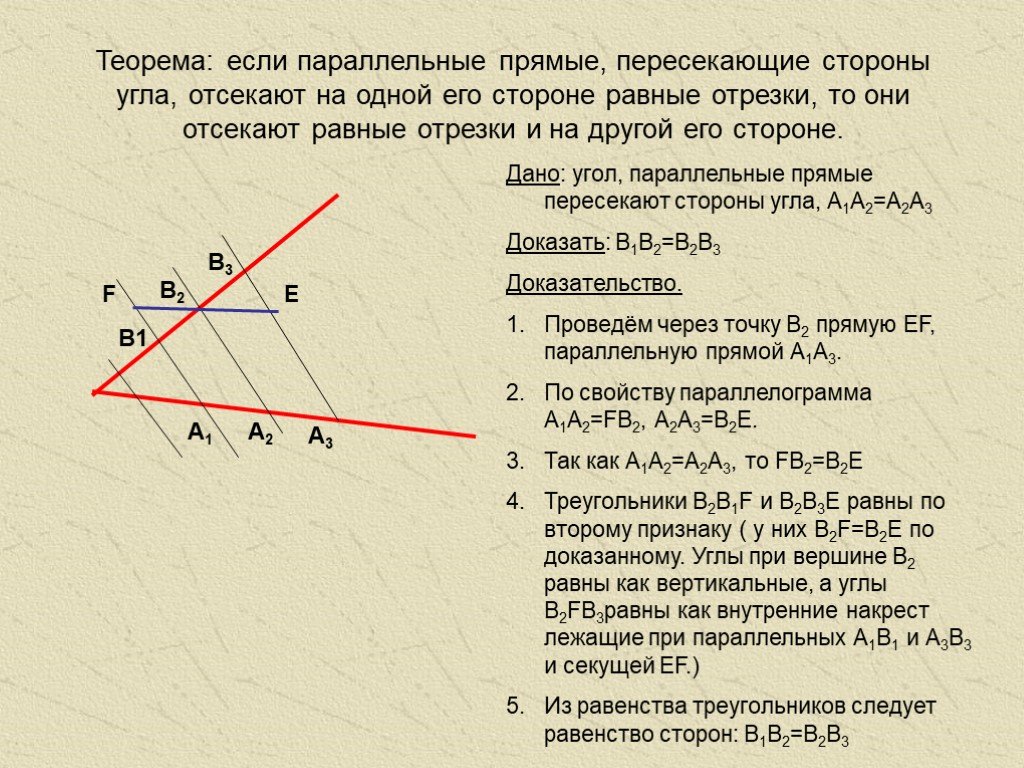 (современная Турция)
(современная Турция)
 Тем не менее, он начал мыслить научно и рационально еще в те времена, когда люди считали, что за все несут ответственность боги.
Тем не менее, он начал мыслить научно и рационально еще в те времена, когда люди считали, что за все несут ответственность боги.

 Философ ХХ века Бертран Рассел идет дальше и говорит, что западная философия начинается с Фалеса. Насколько нам известно, Фалес был первым математиком, увидевшим необходимость дедуктивных рассуждений. Другие жители древнего мира, например, вавилоняне и египтяне, определенно знали некоторые жемчужины геометрии и успешно использовали их в технике и промышленности. Однако именно Фалес хотел доказать эти факты с помощью дедуктивных рассуждений, начиная с набора аксиом и делая выводы посредством дедукции. Фалес тоже хотел понять мир не через мифологию, а через человеческий разум. Он часто ассоциируется с фразой «Все есть вода». Для современного уха это звучит нелепо и слишком упрощенно. Однако мы также можем рассматривать это выражение как означающее, что мир может быть понят людьми через несколько основных принципов. Это был огромный отход от мышления древнего мира. К сожалению, мы не можем прочитать ни одного из оригинальных сочинений Фалеса, так как они утеряны во времени. То, что мы знаем о нем и его работах, мы получили от других греческих философов.
Философ ХХ века Бертран Рассел идет дальше и говорит, что западная философия начинается с Фалеса. Насколько нам известно, Фалес был первым математиком, увидевшим необходимость дедуктивных рассуждений. Другие жители древнего мира, например, вавилоняне и египтяне, определенно знали некоторые жемчужины геометрии и успешно использовали их в технике и промышленности. Однако именно Фалес хотел доказать эти факты с помощью дедуктивных рассуждений, начиная с набора аксиом и делая выводы посредством дедукции. Фалес тоже хотел понять мир не через мифологию, а через человеческий разум. Он часто ассоциируется с фразой «Все есть вода». Для современного уха это звучит нелепо и слишком упрощенно. Однако мы также можем рассматривать это выражение как означающее, что мир может быть понят людьми через несколько основных принципов. Это был огромный отход от мышления древнего мира. К сожалению, мы не можем прочитать ни одного из оригинальных сочинений Фалеса, так как они утеряны во времени. То, что мы знаем о нем и его работах, мы получили от других греческих философов.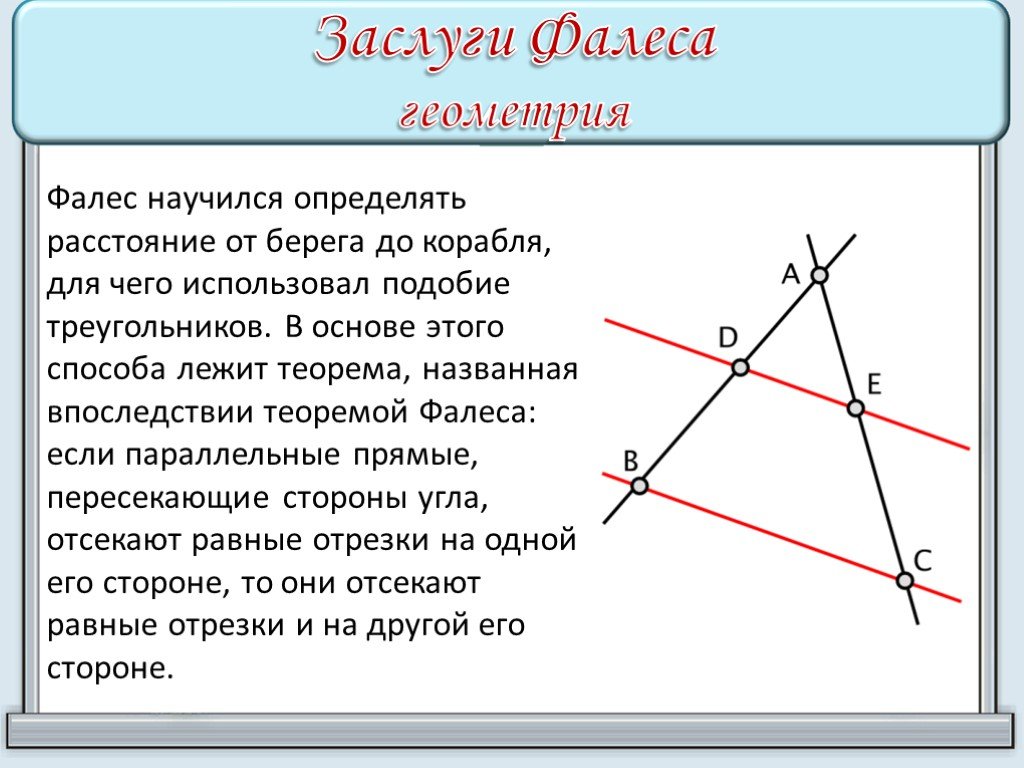 Узнайте больше о Фалесе.
Узнайте больше о Фалесе.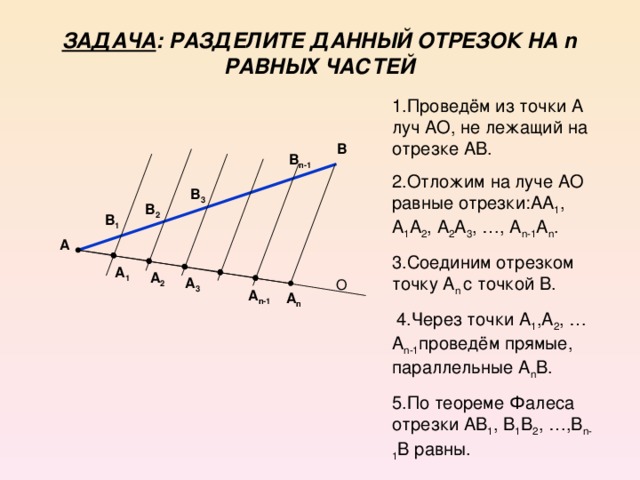

 Вот доказательство этого драгоценного камня: обозначьте углы вашего треугольника A, B, C и нарисуйте параллельные линии L и M на изображении ниже
Вот доказательство этого драгоценного камня: обозначьте углы вашего треугольника A, B, C и нарисуйте параллельные линии L и M на изображении ниже Мы поговорим об этом подробнее в разделе, посвященном делению угла пополам и трисечению угла позже или . Прямо сейчас просто вспомните, как разделить угол пополам с помощью линейки и циркуля. Возможно, вам придется просмотреть свои школьные заметки.
Мы поговорим об этом подробнее в разделе, посвященном делению угла пополам и трисечению угла позже или . Прямо сейчас просто вспомните, как разделить угол пополам с помощью линейки и циркуля. Возможно, вам придется просмотреть свои школьные заметки. Предположим, что мы находимся на суше в точке А, а корабль выходит в море в точке В.
Предположим, что мы находимся на суше в точке А, а корабль выходит в море в точке В.
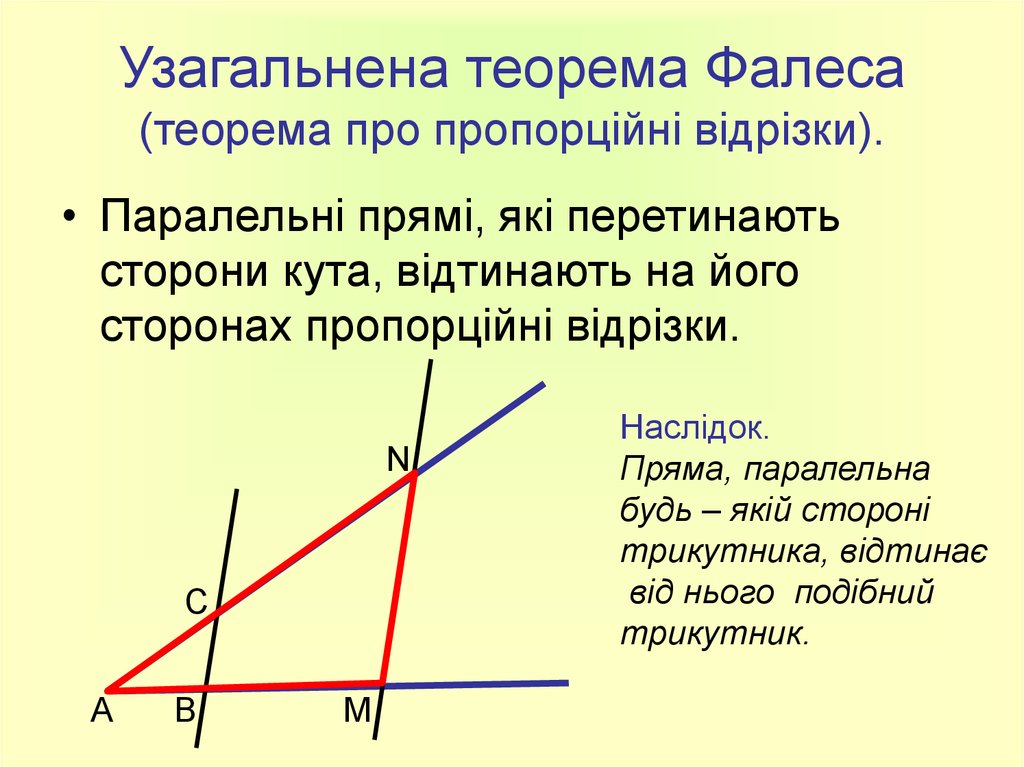
 Биссектриса делит противоположную сторону на части, пропорциональные прилежащим к ней сторонам.
Биссектриса делит противоположную сторону на части, пропорциональные прилежащим к ней сторонам.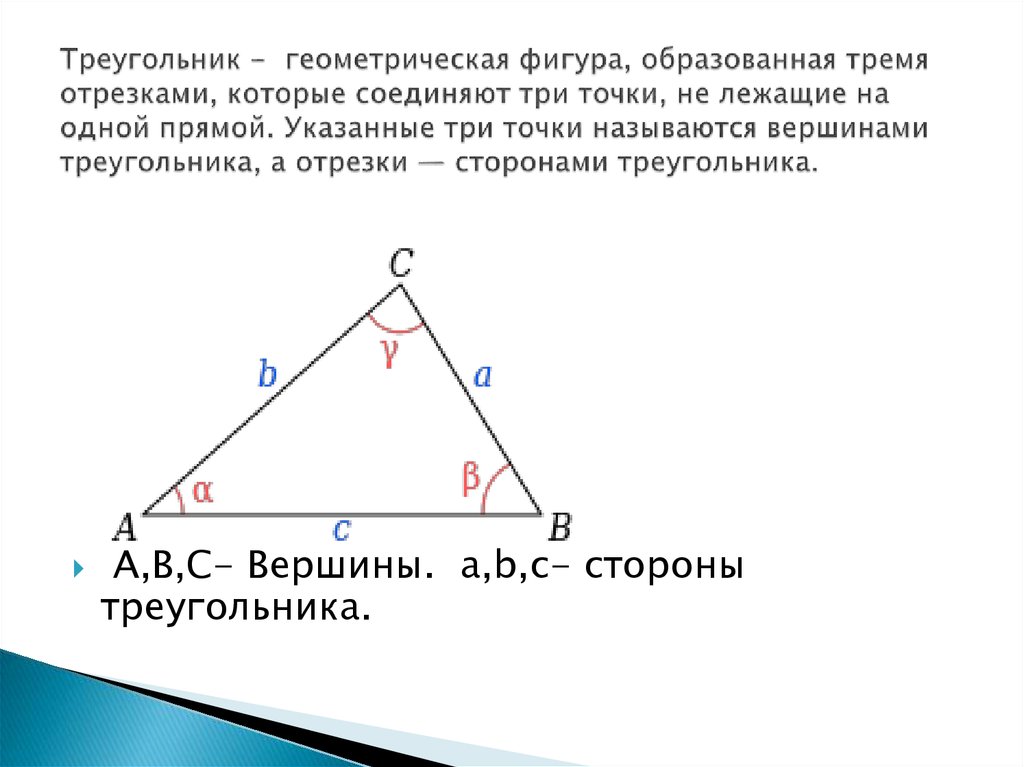

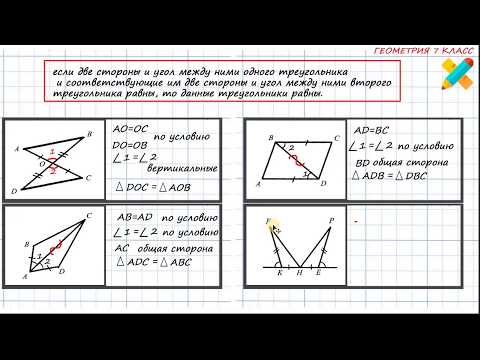
 Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.


 Основание — это нижний край треугольника, а высота — это вертикальная линия, идущая от основания к противоположному углу в 90 градусов.
Основание — это нижний край треугольника, а высота — это вертикальная линия, идущая от основания к противоположному углу в 90 градусов.
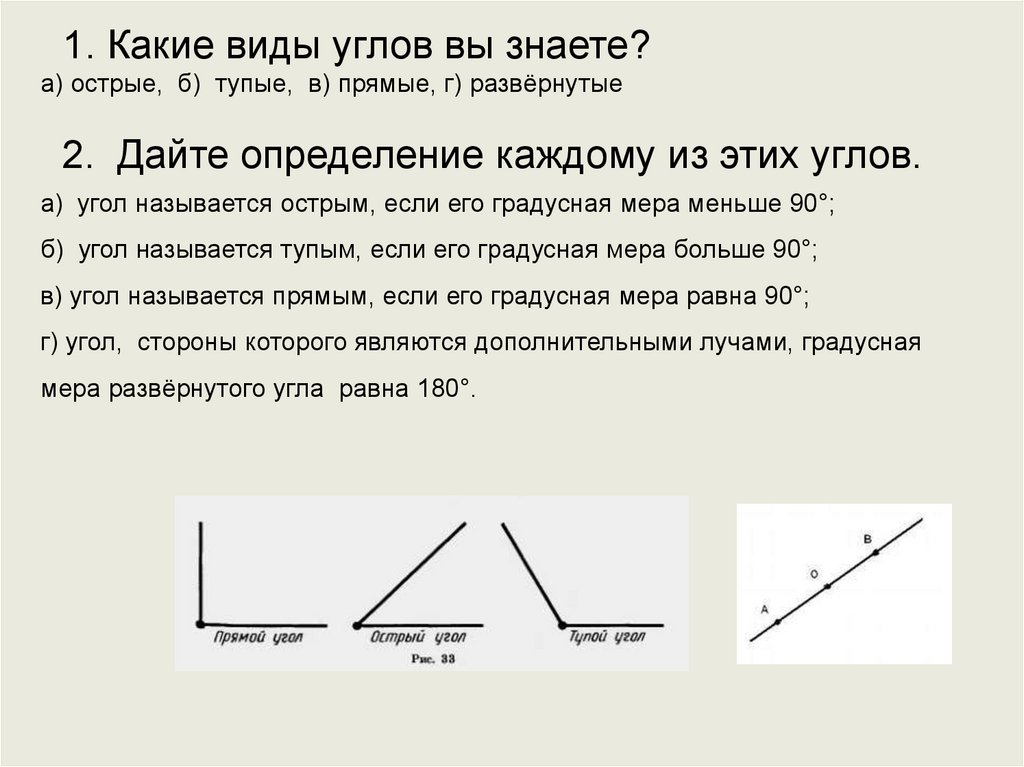

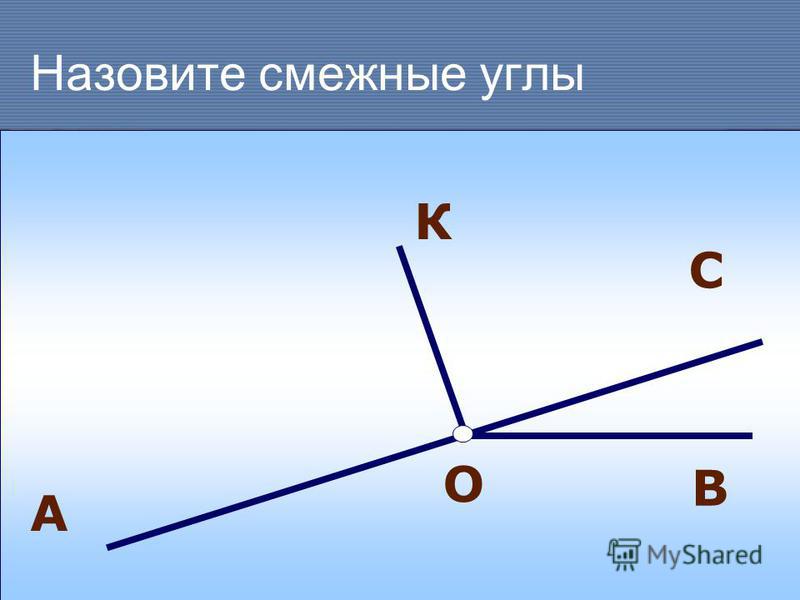
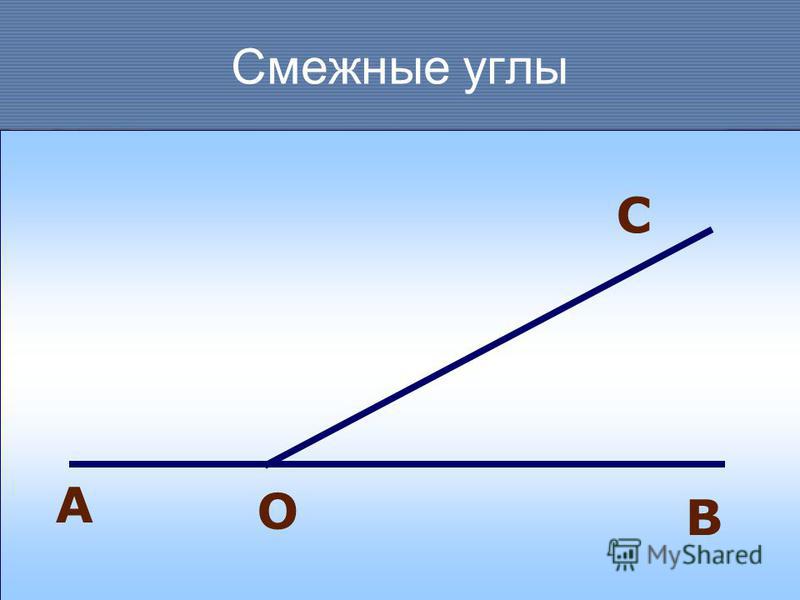 Каким свойством они обладают?
Каким свойством они обладают? Из
двух смежных углов один больше другого на . Найдите больший их этих углов.
Из
двух смежных углов один больше другого на . Найдите больший их этих углов.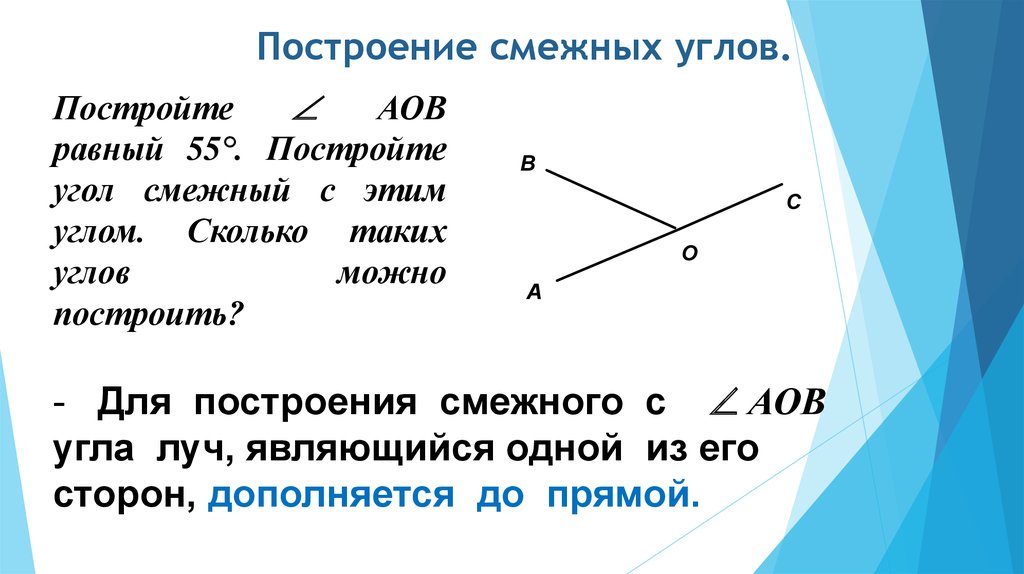
 Найдите их градусные меры. Чему равен
наименьший из них?
Найдите их градусные меры. Чему равен
наименьший из них? Соотношения величин трёх из шести
образовавшихся углов указаны на рисунке. Найдите их градусные меры. Чему равен
наибольший из них?
Соотношения величин трёх из шести
образовавшихся углов указаны на рисунке. Найдите их градусные меры. Чему равен
наибольший из них? Соотношения величин трёх из шести образовавшихся
углов указаны на рисунке. Найдите их градусные меры. Чему равен наибольший из
них?
Соотношения величин трёх из шести образовавшихся
углов указаны на рисунке. Найдите их градусные меры. Чему равен наибольший из
них?
 Найдите эти углы.
Найдите эти углы.
 Известны углы между некоторыми из них: . Найдите углы между
остальными парами прямых.
Известны углы между некоторыми из них: . Найдите углы между
остальными парами прямых. Найдите градусную меру
большего из смежных углов.
Найдите градусную меру
большего из смежных углов.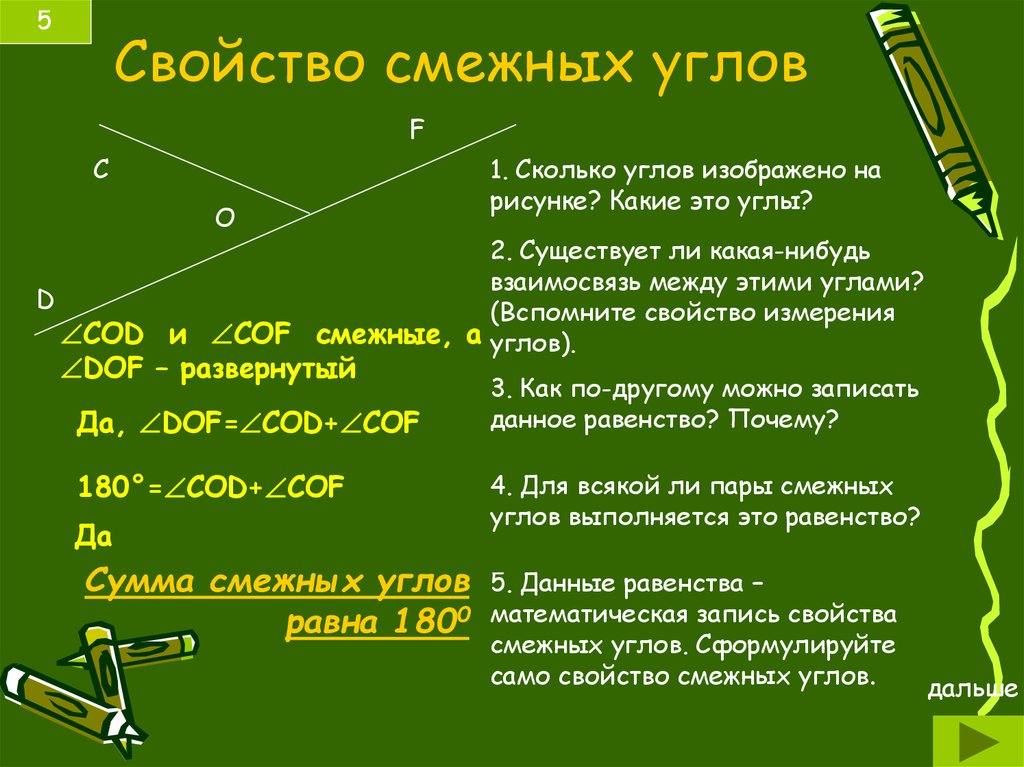 Найдите градусную меру
угла .
Найдите градусную меру
угла . Каждый из углов и является смежным с углом
. Найдите угол , если угол равен . Сделайте рисунок.
Каждый из углов и является смежным с углом
. Найдите угол , если угол равен . Сделайте рисунок. Углы и – вертикальные, луч – биссектриса угла . Найдите угол , если . Сделайте чертёж.
Углы и – вертикальные, луч – биссектриса угла . Найдите угол , если . Сделайте чертёж. \circ.\)
\circ.\)
 \circ.\)
\circ.\)
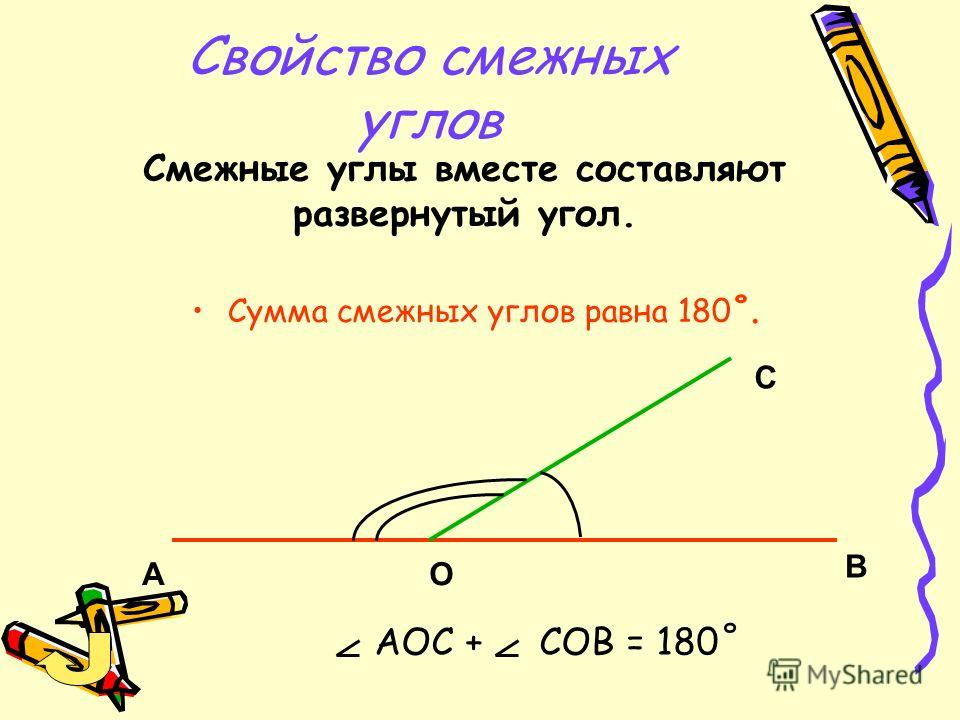

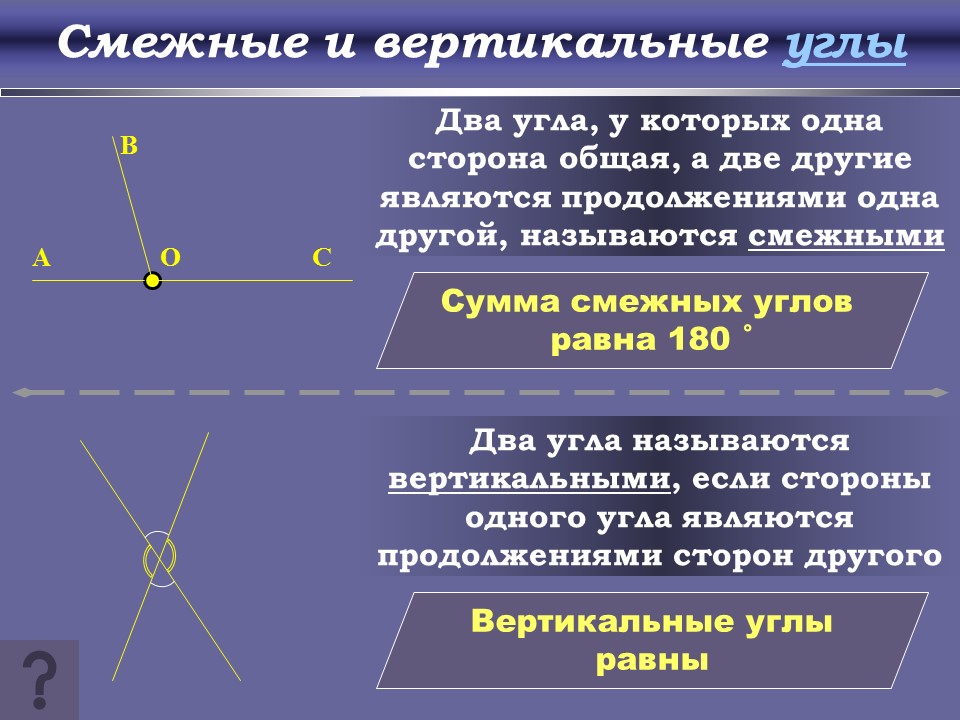
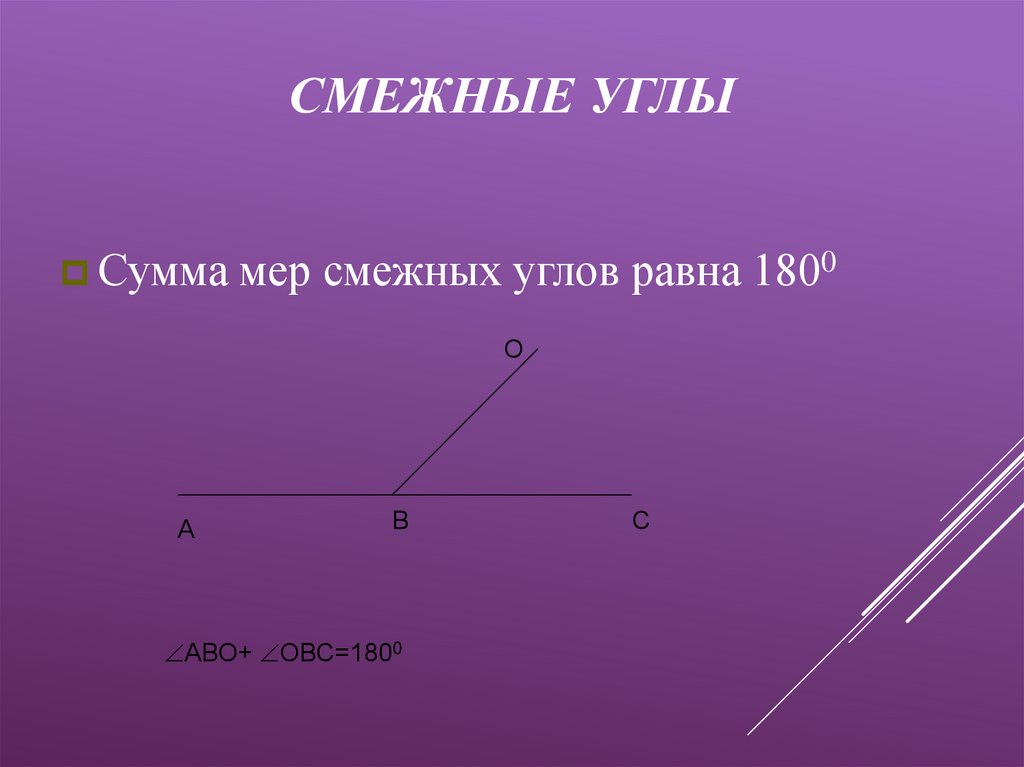
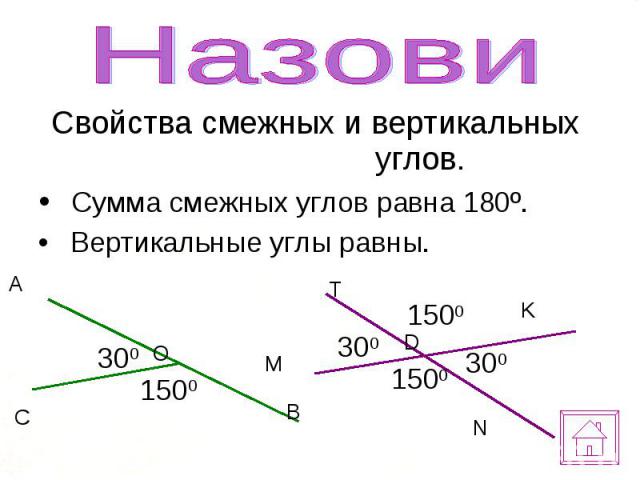
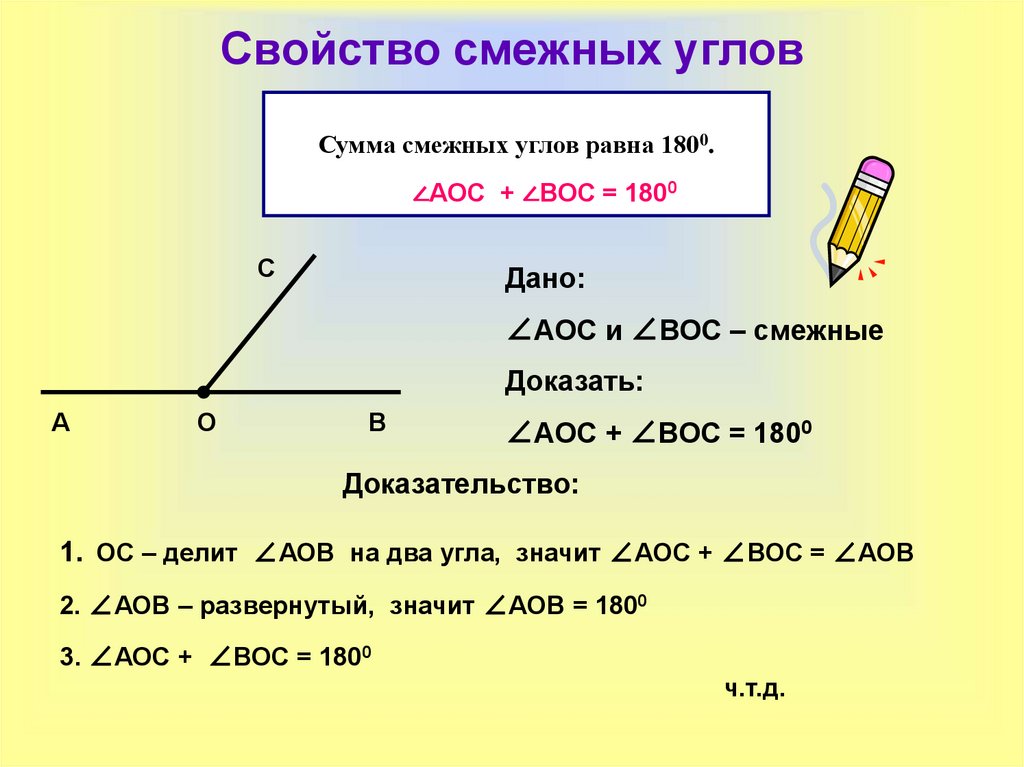
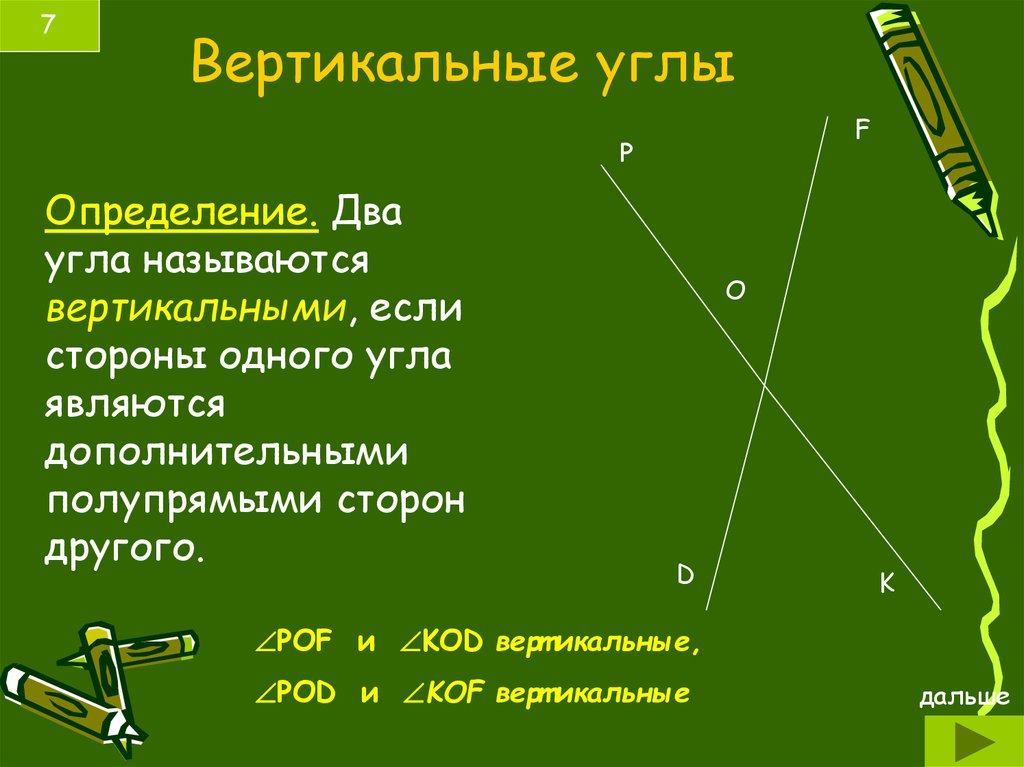 Все линейные пары углов являются дополнительными, поэтому сумма всегда дает 180 градусов . Если углы смежные и в сумме дают 180 градусов, можно с уверенностью утверждать, что они представляют собой линейную пару смежных углов.
Все линейные пары углов являются дополнительными, поэтому сумма всегда дает 180 градусов . Если углы смежные и в сумме дают 180 градусов, можно с уверенностью утверждать, что они представляют собой линейную пару смежных углов.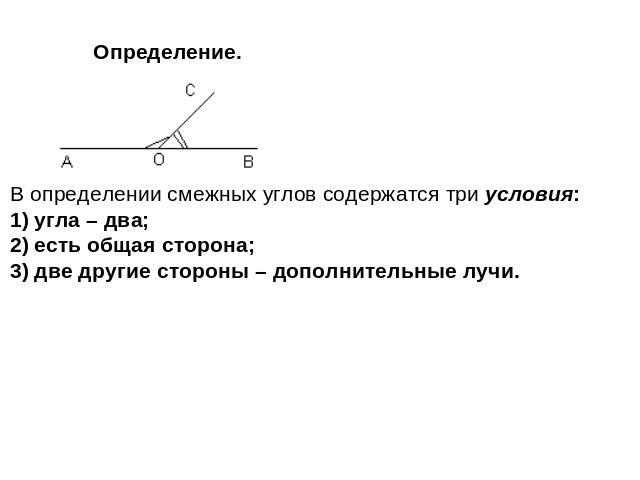 Что такое смежные углы?
Что такое смежные углы? Однако не все смежные углы являются линейными парами.
Однако не все смежные углы являются линейными парами.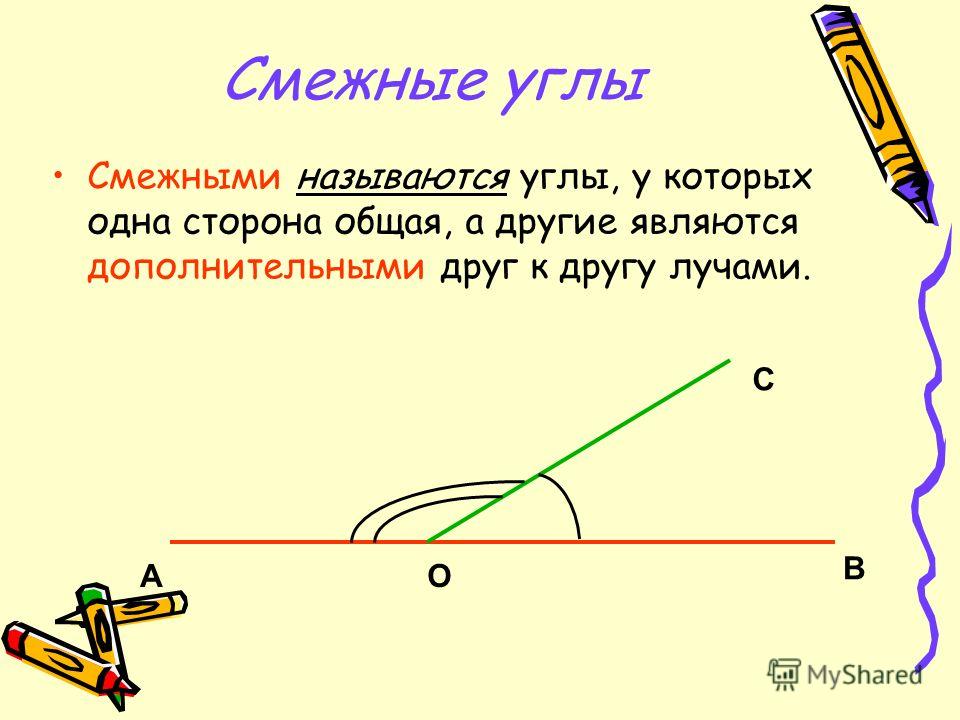 Также мы узнаем о наиболее важных свойствах смежных углов и рассмотрим несколько примеров.
Также мы узнаем о наиболее важных свойствах смежных углов и рассмотрим несколько примеров. Кроме того, углы также имеют общую сторону, сторону ОС.
Кроме того, углы также имеют общую сторону, сторону ОС.
 Площадь всего круга равна πR² = π, так
как R=1. Остается узнать, какая часть
круга изображена. Поскольку длина всей
окружности равна 2πR = 2π (так как R=1), а
длина дуги данного сектора равна 2,
следовательно, длина дуги в π раз меньше,
чем длина всей окружности. Угол, на
который опирается эта дуга, также в π
раз меньше, чем полный круг (то есть 360
градусов). Значит, и площадь сектора
будет в π раз меньше, чем площадь всего
круга.
Площадь всего круга равна πR² = π, так
как R=1. Остается узнать, какая часть
круга изображена. Поскольку длина всей
окружности равна 2πR = 2π (так как R=1), а
длина дуги данного сектора равна 2,
следовательно, длина дуги в π раз меньше,
чем длина всей окружности. Угол, на
который опирается эта дуга, также в π
раз меньше, чем полный круг (то есть 360
градусов). Значит, и площадь сектора
будет в π раз меньше, чем площадь всего
круга. Дело
в том, что когда-то экзамен по геометрии
в школе был обязательным, а сейчас —
нет. В результате у большинства
абитуриентов знания по геометрии
близки к нулю.
Дело
в том, что когда-то экзамен по геометрии
в школе был обязательным, а сейчас —
нет. В результате у большинства
абитуриентов знания по геометрии
близки к нулю. Вершины и стороны. Высоты, медианы,
биссектрисы (определения).
Вершины и стороны. Высоты, медианы,
биссектрисы (определения). б) три биссектрисы.
в) три медианы.
б) три биссектрисы.
в) три медианы. Окружность и круг. Длина окружности.
Площадь круга. Длина дуги и площадь
сектора.
Окружность и круг. Длина окружности.
Площадь круга. Длина дуги и площадь
сектора.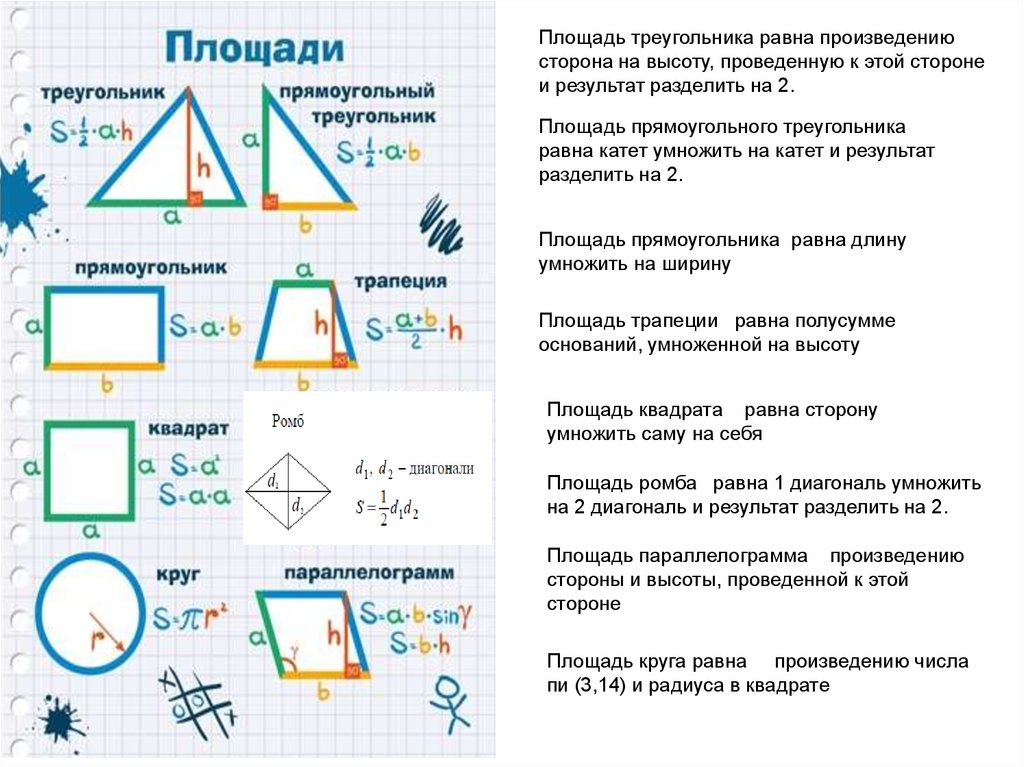
 Определим, что такое синус
и косинус, а также тангенс и котангенс
острого угла. Это основы тригонометрии.
Определим, что такое синус
и косинус, а также тангенс и котангенс
острого угла. Это основы тригонометрии.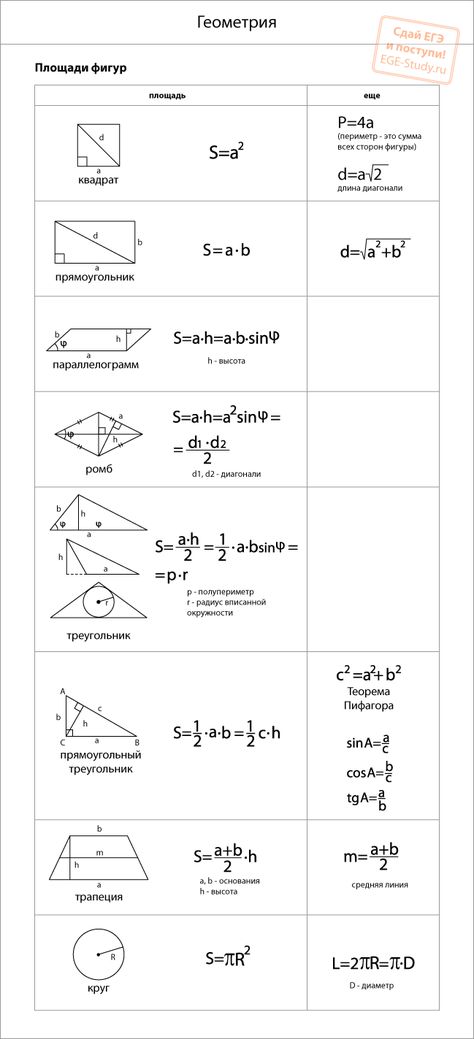
 Это теорема
Пифагора: a2 + b2 = с2.
Это теорема
Пифагора: a2 + b2 = с2. Клетки на бумаге позволяют выполнять разные чертежи с помощью линейки. Но нужно помнить свойства геометрических фигур, ведь именно они позволяют использовать клетки в полной мере.
Клетки на бумаге позволяют выполнять разные чертежи с помощью линейки. Но нужно помнить свойства геометрических фигур, ведь именно они позволяют использовать клетки в полной мере.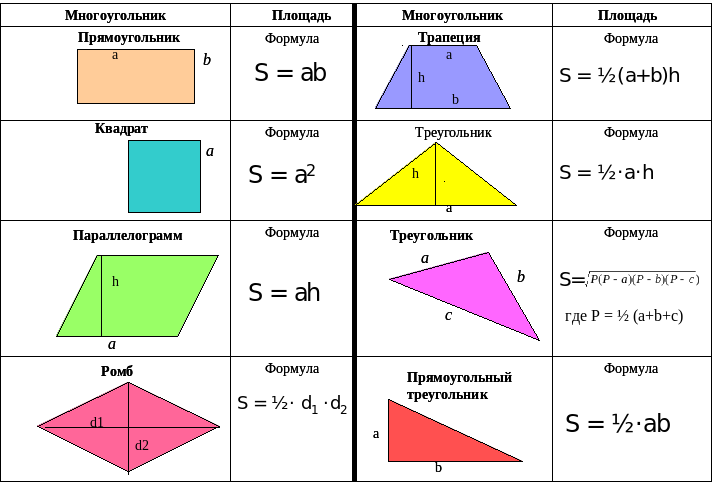

 Если радиус окружности равен 14 см. Найдите площадь данного круга.
Если радиус окружности равен 14 см. Найдите площадь данного круга.  Найти периметр квадрата, длина которого 5 см.
Найти периметр квадрата, длина которого 5 см. 
 После того, как вы вычислили периметр одного прямоугольного треугольника, вы должны вычислить второй, чтобы получить размеры исходного треугольника.
После того, как вы вычислили периметр одного прямоугольного треугольника, вы должны вычислить второй, чтобы получить размеры исходного треугольника.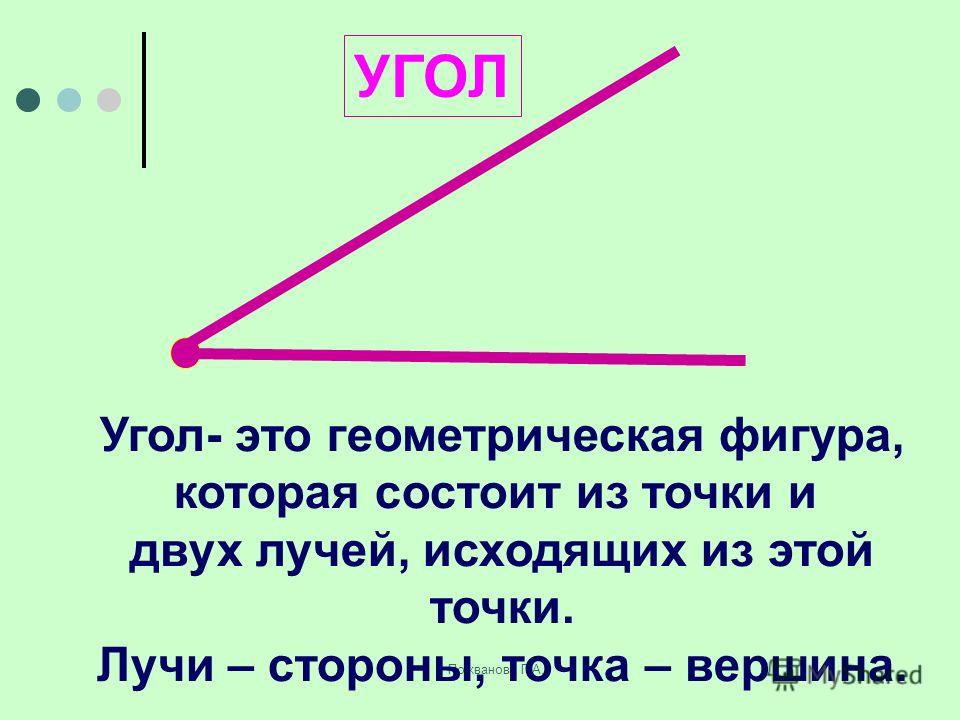
 Жрецы считали, что свой дневной путь Солнце совершает за 180 «шагов», и, значит, один «шаг» равен 1/180 развернутого угла.
Жрецы считали, что свой дневной путь Солнце совершает за 180 «шагов», и, значит, один «шаг» равен 1/180 развернутого угла.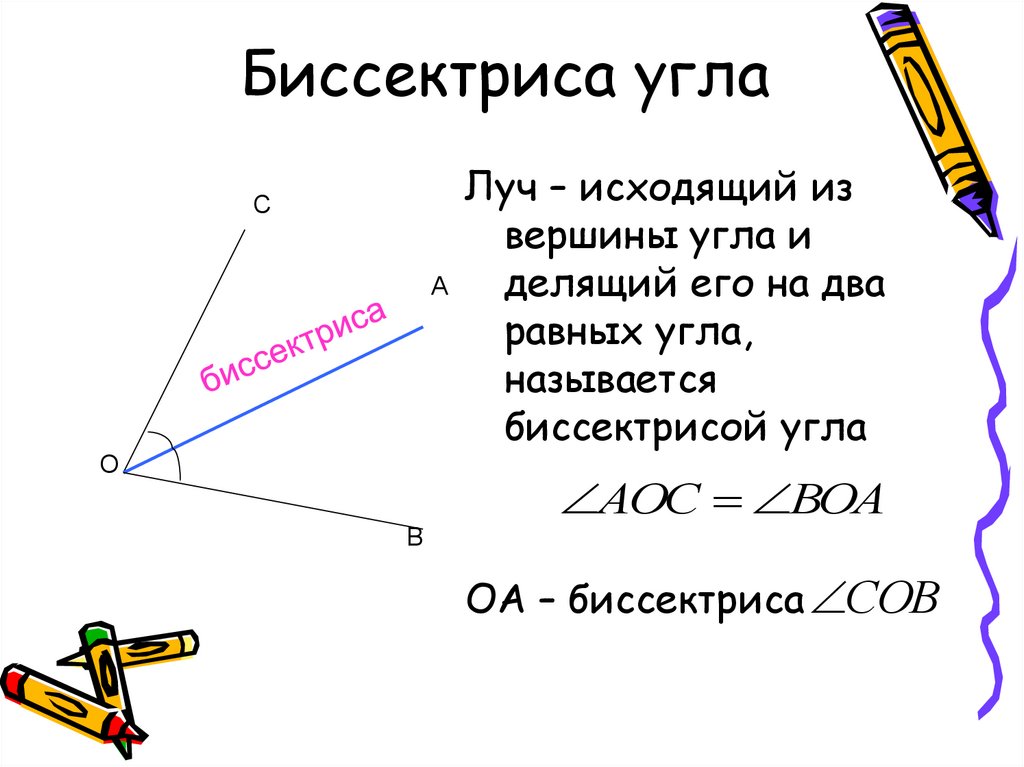
 Геометрически, угол — это часть плоскости, которая включена между двумя лучами, начинающимися из общей точки.
Геометрически, угол — это часть плоскости, которая включена между двумя лучами, начинающимися из общей точки. Когда угол прямой, говорят, что стороны, которые его формируют, перпендикулярны.
Когда угол прямой, говорят, что стороны, которые его формируют, перпендикулярны. .
. , Хайме П., Чавес М., Гальегос М. и Родригес С. (2006). Геометрия и тригонометрия. Порог издания.
, Хайме П., Чавес М., Гальегос М. и Родригес С. (2006). Геометрия и тригонометрия. Порог издания. Определение: Фигура, образованная двумя линиями или лучами, расходящимися из общей точки (вершины).
Определение: Фигура, образованная двумя линиями или лучами, расходящимися из общей точки (вершины).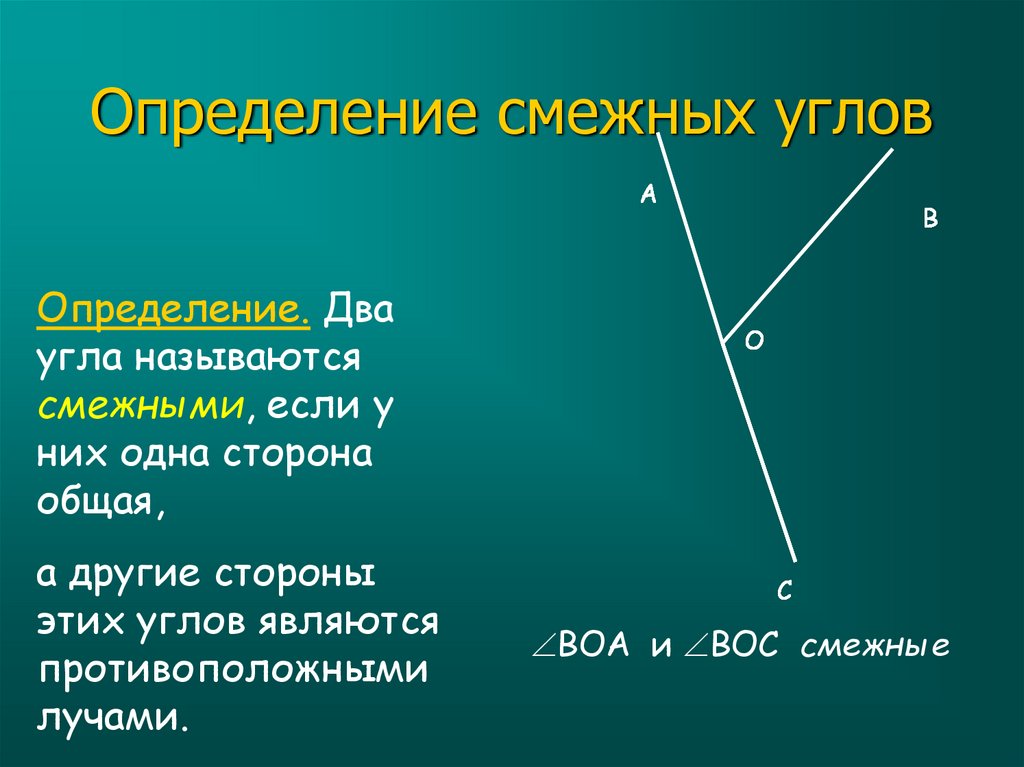 С другой стороны, вычисление sin() и т. д. становится очень простым.
С другой стороны, вычисление sin() и т. д. становится очень простым.