| Анилин | 0…20…40…60…80…100…140…180 | 1037…1023…1007…990…972…952…914…878 |
| Антифриз 65 (ГОСТ 159-52) | -60…-40…0…20…40…80…120 | 1143…1129…1102…1089…1076…1048…1011 |
| Ацетон C3H6O | 0…20 | 813…791 |
| Белок куриного яйца | 20 | 1042 |
| Бензин | 20 | 680-800 |
| Бензол C6H6 | 7…20…40…60 | 910…879…858…836 |
| Бром | 20 | 3120 |
| Вода | 0…4…20…60…100…150…200…250…370 | 999,9…1000…998,2…983,2…958,4…917…863…799…450,5 |
| Вода морская | 20 | 1010-1050 |
| Вода тяжелая | 10…20…50…100…150…200…250 | 1106…1105…1096…1063…1017…957…881 |
| Водка | 0…20…40…60…80 | 949…935…920…903…888 |
| Вино крепленое | 20 | 1025 |
| Вино сухое | 20 | 993 |
| Газойль | 20…60…100…160…200…260…300 | 848…826…801…761…733…688…656 |
| Глицерин C3H5(OH)3 | 20…60…100…160…200…240 | 1260…1239…1207…1143…1090…1025 |
| ГТФ (теплоноситель) | 27…127…227…327 | 980…880…800…750 |
| Даутерм | 20…50…100…150…200 | 1060…1036…995…953…912 |
| Желток яйца куры | 20 | 1029 |
| Карборан | 27 | 1000 |
| Керосин | 20 | 802-840 |
| Кислота азотная HNO3 (100%-ная) | -10…0…10…20…30…40…50 | 1567…1549…1531…1513…1495…1477…1459 |
| Кислота пальмитиновая C16H32O2 (конц.) | 62 | 853 |
| Кислота серная H2SO4 (конц.) | 20 | 1830 |
| Кислота соляная HCl (20%-ная) | 20 | 1100 |
| Кислота уксусная CH3COOH (конц.) | 20 | 1049 |
| Коньяк | 20 | 952 |
| Креозот | 15 | 1040-1100 |
| Кровь человека | 37 | 1050-1062 |
| Ксилол C8H10 | 20 | 880 |
| Купорос медный (10%) | 20 | 1107 |
| Купорос медный (20%) | 20 | 1230 |
| Ликер вишневый | 20 | 1105 |
| Мазут | 20 | 890-990 |
| Масло арахисовое | 15 | 911-926 |
| Масло машинное | 20 | 890-920 |
| Масло моторное Т | 20 | 917 |
| Масло оливковое | 15 | 914-919 |
| Масло подсолнечное (рафинир.) | -20…20…60…100…150 | 947…926…898…871…836 |
| Мед (обезвоженный) | 20 | 1621 |
| Метилацетат CH3COOCH3 | 25 | 927 |
| Молоко | 20 | 1030 |
| Молоко сгущенное с сахаром | 20 | 1290-1310 |
| Нафталин | 230…250…270…300…320 | 865…850…835…812…794 |
| Нефть | 20 | 730-940 |
| Олифа | 20 | 930-950 |
| Паста томатная | 20 | 1110 |
| Патока вареная | 20 | 1460 |
| Патока крахмальная | 20 | 1433 |
| ПАБ | 20…80…120…200…260…340…400 | 990…961…939…883…837…769…710 |
| Пиво | 20 | 1008-1030 |
| ПМС-100 | 20…60…80…100…120…160…180…200 | 967…934…917…901…884…850…834…817 |
| ПЭС-5 | 20…60…80…100…120…160…180…200 | 998…971…957…943…929…902…888…874 |
| Пюре яблочное | 0 | 1056 |
| Раствор поваренной соли в воде (10%-ный) | 20 | 1071 |
| Раствор поваренной соли в воде (20%-ный) | 20 | 1148 |
| Раствор сахара в воде (насыщенный) | 0…20…40…60…80…100 | 1314…1333…1353…1378…1405…1436 |
| Ртуть | 0…20…100…200…300…400 | 13596…13546…13350…13310…12880…12700 |
| Сероуглерод | 0 | 1293 |
| Силикон (диэтилполисилоксан) | 0…20…60…100…160…200…260…300 | 971…956…928…900…856…825…779…744 |
| Сироп яблочный | 20 | 1613 |
| Скипидар | 20 | 870 |
| Сливки молочные (жирность 30-83%) | 20 | 939-1000 |
| Смола | 80 | 1200 |
| Смола каменноугольная | 20 | 1050-1250 |
| Сок апельсиновый | 15 | 1043 |
| Сок виноградный | 20 | 1056-1361 |
| Сок грейпфрутовый | 15 | 1062 |
| Сок томатный | 20 | 1030-1141 |
| Сок яблочный | 20 | 1030-1312 |
| Спирт амиловый | 20 | 814 |
| Спирт бутиловый | 20 | 810 |
| Спирт изобутиловый | 20 | 801 |
| Спирт изопропиловый | 20 | 785 |
| Спирт метиловый | 20 | 793 |
| Спирт пропиловый | 20 | 804 |
| Спирт этиловый C2H5OH | 0…20…40…80…100…150…200 | 806…789…772…735…716…649…557 |
| Сплав натрий-калий (25%Na) | 20…100…200…300…500…700 | 872…852…828…803…753…704 |
| Сплав свинец-висмут (45%Pb) | 130…200…300…400…500..600…700 | 10570…10490…10360…10240…10120..10000…9880 |
| Стекло жидкое | 20 | 1350-1530 |
| Сыворотка молочная | 20 | 1027 |
| Тетракрезилоксисилан (CH3C6H4O)4Si | 10…20…60…100…160…200…260…300…350 | 1135…1128…1097…1064…1019…987…936…902…858 |
| Тетрахлордифенил C12H6Cl4 (арохлор) | 30…60…150…250…300 | 1440…1410…1320…1220…1170 |
| Толуол | 0…20…50…80…100…140 | 886…867…839…810…790…744 |
| Топливо дизельное | 20…40…60…80…100 | 879…865…852…838…825 |
| Топливо карбюраторное | 20 | 768 |
| Топливо моторное | 20 | 911 |
| Топливо РТ | -60…-40…0…20…40…60…100…140…160…200 | 836…821…792…778…764…749…720…692…677…648 |
| Топливо Т-1 | -60…-40…0…20…40…60…100…140…160…200 | 867…853…824…819…808…795…766…736…720…685 |
| Топливо Т-2 | -60…-40…0…20…40…60…100…140…160…200 | 824…810…781…766…752…745…709…680…665…637 |
| Топливо Т-6 | -60…-40…0…20…40…60…100…140…160…200 | 898…883…855…841…827…813…784…756…742…713 |
| Топливо Т-8 | -60…-40…0…20…40…60…100…140…160…200 | 847…833…804…789…775…761…732…703…689…660 |
| Топливо ТС-1 | -60…-40…0…20…40…60…100…140…160…200 | 837…823…794…780…765…751…722…693…879…650 |
| Углерод четыреххлористый (ЧХУ) | 20 | 1595 |
| Уроторопин C6H12N2 | 27 | 1330 |
| Фторбензол | 20 | 1024 |
| Хлорбензол | 20 | 1066 |
| Этилацетат | 20 | 901 |
| Этилбромид | 20 | 1430 |
| Этилиодид | 20 | 1933 |
| Этилхлорид | 0 | 921 |
| Эфир | 0…20 | 736…720 |
| Эфир Гарпиуса | 27 | 1100 |
thermalinfo.ru
Плотность жидкости
Любая жидкость обладает собственными неповторимыми свойствами и характеристиками. В физике принято рассматривать ряд явлений, которые связаны с этим специфическими характеристиками.

Рисунок 1. Плотность жидкостей. Автор24 — интернет-биржа студенческих работ
Жидкости обычно разделяют на две основные категории:
- капельные или малосжимаемые;
- газообразные или сжимаемые.

Рисунок 2. Вычисление плотности жидкости. Автор24 — интернет-биржа студенческих работ
Эти классы жидкостей имеют принципиальные различия между собой. Так капельные жидкости существенно отличаются от газообразных. Они обладают определенным объемом. Его величина не будет изменяться под действием каких-либо внешних сил. В газообразном состоянии жидкости могут занимать весь объем, который у них имеется. Также подобный класс жидкости может в значительной степени изменять свой собственный объем, если на него влияют определенные внешние силы.
У жидкостей любого типа есть три свойства, с которыми они не могут расстаться:
- плотность;
- вязкость;
- сила поверхностного натяжения.
Эти свойства способны влиять на многочисленные законы их движения, поэтому они имеют главное значение в процессе изучения и применения знаний на практике.
Понятие плотности жидкости
Масса, которая заключена в единицу объема, называется плотностью жидкости. Если поступательно повышать единицу давления, то объем воды будет стремиться к уменьшению от первоначальной его величины. Разница значений составляет примерно 1 к 20000. Такой же порядок чисел будет иметь коэффициент объемного сжатия для иных капельных жидкостей. Как правило, на практике установлено, что серьезных изменений давления не происходит, поэтому принято не использовать на практике сжимаемость воды при расчете удельного веса и плотности в зависимости от давления.
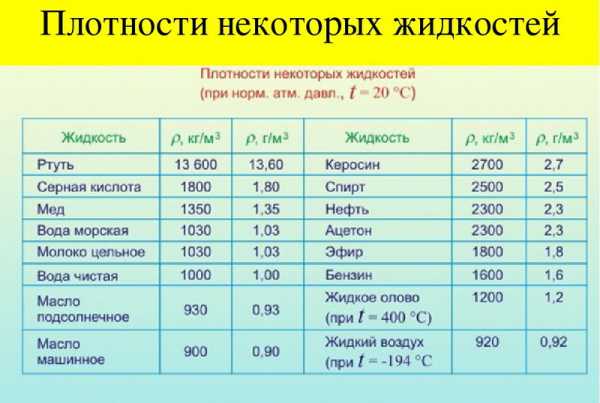
Рисунок 3. Плотности различных жидкостей. Автор24 — интернет-биржа студенческих работ
Для расчетов плотности жидкости вводится понятие температурного расширения для капельных жидкостей. Оно характеризуется коэффициентом температурного расширения, которое выражает увеличение объема жидкости при увеличении температурного режима на 10 градусов по шкале Цельсия.
Таким образом, формируется показатель плотности для определенной жидкости. Ее принято учитывать при различном атмосферном давлении, температурных показателях. Выше представлена таблица, которая показывает плотности основных видов жидкостей.
Плотность воды
Самой распространенной и привычной человеку жидкостью является вода. Рассмотрим основные характеристики по плотности и вязкости этого вещества. Плотность воды в естественных условиях будет равна 1000 кг/м3. Этот показатель применяется для дистиллированной воды. Для морской воды значение по плотности чуть выше — 1030 кг/м3. Подобная величина не является конечной и плотно связана с температурой. Идеальные показатели можно зафиксировать при температуре около 4 градусов Цельсия. Если производить вычисления над кипящей водой при температуре 100 градусов, то плотность довольно сильно сократится и составит примерно 958 кг/м3. Установлено, что обычно в процессе нагревания любых жидкостей их плотность уходит в сторону уменьшения.
Плотность воды также довольно близка к ряду распространенных продуктов питания. Ее можно сравнить с вином, раствором уксуса, обезжиренным молоком, сливками, сметаной. Некоторые виды продуктов имеют более высокие показатели по плотности. Однако немало среди продуктов питания и напитков таких, которые существенно могут уступить классической воде. Среди них обычно выделяют спирты, а также нефтепродукты, включая мазут, керосин и бензин.
Если необходимо рассчитать плотность некоторых газов, тогда используется уравнения состояния идеальных газов. Это необходимо в тех случаях, когда поведение реальных газов существенно отличается от поведения идеальных газов и процесса сжижения не происходит.
Объем газа обычно зависит значений давления и температуры. Разности давлений, которые вызывают существенные изменения плотности газов, возникают при движении на больших скоростях. Обычно несжимаемый газ проявляется на скоростях, которые превышаю сто метров в секунду. Рассчитывается соотношение скорости движения жидкости со скоростью звука. Это позволяет соотносить многие показатели при подтверждении плотности того или иного вещества.
Вязкость жидкостей
Еще одним свойством любой жидкости является вязкость. Это такое состояние жидкости, которое способно оказывать сопротивление сдвига или иной внешней силы. Известно, что реальные жидкости обладают подобными свойствами. Она определяется в виде внутреннего трения при относительном перемещении частиц жидкости, находящихся рядом.
Существуют не только легко подвижные жидкости, но и более вязкие вещества. К первой группе обычно относят воздух и воду. У тяжелых масел сопротивление происходит на ином уровне. Вязкость может охарактеризовать степенью текучести жидкости. Также такой процесс называют подвижностью ее частиц, и он зависит от плотности вещества. Вязкость жидкостей в лабораторных условиях определяют вискозиметрами. Если вязкость жидкости в большей степени зависит только от прилагаемой температуры, то принято различать несколько основных параметров веществ. При увеличении температуры вязкости капельной жидкости стремится к уменьшению. Вязкость газообразной жидкости при схожих условиях только возрастает.
Сила внутреннего трения в жидкостях возникает при пропорциональности скорости градиента к площади слоев, которые осуществляют трение. При этом трение в жидкостях принято различать от процесса трения в иных телах твердого типа. В твердых телах сила трения будет зависеть от нормального давления, а не от площади трущихся поверхностей.
Аномальные и идеальные жидкости
Различают два вида жидкостей, исходя из их внутренних характеристик:
- аномальные жидкости;
- идеальные жидкости.
Определение 1
Аномальными жидкостями называют такие жидкости, которые не подчиняются закону вязкости Ньютона. Подобные жидкости способны начинать движение после момента касательного напряжения при прохождении предельного порога по минимуму. Такой процесс также называют начальным напряжением сдвига. Эти жидкости не могут двигаться при небольших напряжениях и испытывают упругие деформации.
К идеальным жидкостям относят воображаемую жидкость, которая не подвержена любым сжатиям и деформациям, то есть она лишена свойства вязкости. Для ее расчета необходимо вводить определенные поправочные коэффициенты.
spravochnick.ru
Таблица плотности жидкостей — 2mb.ru
Таблица плотности жидкостей позволяет узнать, какую плотность имеют различные вещества при определенной температуре.
Эта таблица широко применяется в физике при решении задач различной сложности. Единицы измерения плотности (ρ) – (1 г/л = 103 кг/м3). Плотность – это отношение массы вещества к занимаемому им объему.
| Вещество | Температура, °С | ρ |
|---|---|---|
| Ацетон | 20 | 0,792 |
| Бензин | 20 | 0,68–0,72 |
| Бензол | 0 | 0,899 |
| Вода | 4 | 1 |
| Глицерин | 20 | 1,26 |
| Керосин | 20 | 0,82 |
| 2-Ксилол | 20 | 0,88 |
| Кислота | ||
| → азотная | 20 | 1,502 |
| → пальмитиновая | 62 | 0,853 |
| → уксусная | 20 | 1,049 |
| Масло | ||
| → вазелиновое | 20 | 0,8 |
| → креозот | 15 | 1,04–1,10 |
| → машинное | 20 | 0,90–0,92 |
| → парафиновое | 20 | 0,87–0,88 |
| → скипидарное | 20 | 0,87 |
| Метилацетат | 25 | 0,9274 |
| Молоко | 20 | 1,03 |
| Морская вода | 20 | 1,01–1,05 |
| Нефть | 20 | 0,81–0,85 |
| Пентан | 20 | 0,626 |
| Ртуть | 0 | 13,596 |
| Спирт амиловый | 20 | 0,814 |
| Спирт | ||
| → бутиловый | 20 | 0,80978 |
| → изобутиловый | 20 | 0,8011 |
| → изопропиловый | 20 | 0,7854 |
| → пропиловый | 20 | 0,8044 |
| → метиловый | 20 | 0,7928 |
| → этиловый | 20 | 0,7893 |
| Сероуглерод | 0 | 1,293 |
| Углерод четыре хлористый | 20 | 1,595 |
| Фторбензол | 20 | 1,024 |
| Хлорбензол | 20 | 1,066 |
| Хлороформ | 20 | 1,489 |
| Эфир | 0 | 0,736 |
| Этилацетат | 20 | 0,901 |
| Этилбромид | 20 | 1,43 |
| Этилиодид | 20 | 1,933 |
| Этилхлорид | 0 | 0,9214 |
2mb.ru
| °С | кг/м 3 | |
| Анилин | 0…20…40…60…80…100…140…180 | 1037…1023…1007…990…972…952…914…878 |
| Антифриз 65 (ГОСТ 159-52) | -60…-40…0…20…40…80…120 | 1143…1129…1102…1089…1076…1048…1011 |
| Ацетон C 3 H 6 O | 0…20 | 813…791 |
| Белок куриного яйца | 20 | 1042 |
| Бензин | 20 | 680-800 |
| Бензол C6H6 | 7…20…40…60 | 910…879…858…836 |
| Бром | 20 | 3120 |
| Вода | 0…4…20…60…100…150…200…250…370 | 999,9…1000…998,2…983,2…958,4…917…863…799…450,5 |
| Вода морская | 20 | 1010-1050 |
| Вода тяжелая | 10…20…50…100…150…200…250 | 1106…1105…1096…1063…1017…957…881 |
| Водка | 0…20…40…60…80 | 949…935…920…903…888 |
| Вино крепленое | 20 | 1025 |
| Вино сухое | 20 | 993 |
| Газойль | 20…60…100…160…200…260…300 | 848…826…801…761…733…688…656 |
| Глицерин C3H5(OH)3 | 20…60…100…160…200…240 | 1260…1239…1207…1143…1090…1025 |
| ГТФ (теплоноситель) | 27…127…227…327 | 980…880…800…750 |
| Даутерм | 20…50…100…150…200 | 1060…1036…995…953…912 |
| Желток яйца куры | 20 | 1029 |
| Карборан | 27 | 1000 |
| Керосин | 20 | 802-840 |
| Кислота азотная HNO 3 (100%-ная) | -10…0…10…20…30…40…50 | 1567…1549…1531…1513…1495…1477…1459 |
| Кислота пальмитиновая C 16 H 32 O 2 (конц.) | 62 | 853 |
| Кислота серная H 2 SO 4 (конц.) | 20 | 1830 |
| Кислота соляная HCl (20%-ная) | 20 | 1100 |
| Кислота уксусная CH 3 COOH (конц.) | 20 | 1049 |
| Коньяк | 20 | 952 |
| Креозот | 15 | 1040-1100 |
| Кровь человека | 37 | 1050-1062 |
| Ксилол C 8 H 10 | 20 | 880 |
| Купорос медный (10%) | 20 | 1107 |
| Купорос медный (20%) | 20 | 1230 |
| Ликер вишневый | 20 | 1105 |
| Мазут | 20 | 890-990 |
| Масло арахисовое | 15 | 911-926 |
| Масло машинное | 20 | 890-920 |
| Масло моторное Т | 20 | 917 |
| Масло оливковое | 15 | 914-919 |
| Масло подсолнечное (рафинир.) | -20…20…60…100…150 | 947…926…898…871…836 |
| Мед (обезвоженный) | 20 | 1621 |
| Метилацетат CH 3 COOCH 3 | 25 | 927 |
| Молоко | 20 | 1030 |
| Молоко сгущенное с сахаром | 20 | 1290-1310 |
| Нафталин | 230…250…270…300…320 | 865…850…835…812…794 |
| Нефть | 20 | 730-940 |
| Олифа | 20 | 930-950 |
| Паста томатная | 20 | 1110 |
| Патока вареная | 20 | 1460 |
| Патока крахмальная | 20 | 1433 |
| ПАБ | 20…80…120…200…260…340…400 | 990…961…939…883…837…769…710 |
| Пиво | 20 | 1008-1030 |
| ПМС-100 | 20…60…80…100…120…160…180…200 | 967…934…917…901…884…850…834…817 |
| ПЭС-5 | 20…60…80…100…120…160…180…200 | 998…971…957…943…929…902…888…874 |
| Пюре яблочное | 0 | 1056 |
| Раствор поваренной соли в воде (10%-ный) | 20 | 1071 |
| Раствор поваренной соли в воде (20%-ный) | 20 | 1148 |
| Раствор сахара в воде (насыщенный) | 0…20…40…60…80…100 | 1314…1333…1353…1378…1405…1436 |
| Ртуть | 0…20…100…200…300…400 | 13596…13546…13350…13310…12880…12700 |
| Сероуглерод | 0 | 1293 |
| Силикон (диэтилполисилоксан) | 0…20…60…100…160…200…260…300 | 971…956…928…900…856…825…779…744 |
| Сироп яблочный | 20 | 1613 |
| Скипидар | 20 | 870 |
| Сливки молочные (жирность 30-83%) | 20 | 939-1000 |
| Смола | 80 | 1200 |
| Смола каменноугольная | 20 | 1050-1250 |
| Сок апельсиновый | 15 | 1043 |
| Сок виноградный | 20 | 1056-1361 |
| Сок грейпфрутовый | 15 | 1062 |
| Сок томатный | 20 | 1030-1141 |
| Сок яблочный | 20 | 1030-1312 |
| Спирт амиловый | 20 | 814 |
| Спирт бутиловый | 20 | 810 |
| Спирт изобутиловый | 20 | 801 |
| Спирт изопропиловый | 20 | 785 |
| Спирт метиловый | 20 | 793 |
| Спирт пропиловый | 20 | 804 |
| Спирт этиловый C 2 H 5 OH | 0…20…40…80…100…150…200 | 806…789…772…735…716…649…557 |
| Сплав натрий-калий (25%Na) | 20…100…200…300…500…700 | 872…852…828…803…753…704 |
| Сплав свинец-висмут (45%Pb) | 130…200…300…400…500..600…700 | 10570…10490…10360…10240…10120..10000…9880 |
| Стекло жидкое | 20 | 1350-1530 |
| Сыворотка молочная | 20 | 1027 |
| Тетракрезилоксисилан (CH 3 C 6 H 4 O) 4 Si | 10…20…60…100…160…200…260…300…350 | 1135…1128…1097…1064…1019…987…936…902…858 |
| Тетрахлордифенил C 12 H 6 Cl 4 (арохлор) | 30…60…150…250…300 | 1440…1410…1320…1220…1170 |
| Толуол | 0…20…50…80…100…140 | 886…867…839…810…790…744 |
| Топливо дизельное | 20…40…60…80…100 | 879…865…852…838…825 |
| Топливо карбюраторное | 20 | 768 |
| Топливо моторное | 20 | 911 |
| Топливо РТ | -60…-40…0…20…40…60…100…140…160…200 | 836…821…792…778…764…749…720…692…677…648 |
| Топливо Т-1 | -60…-40…0…20…40…60…100…140…160…200 | 867…853…824…819…808…795…766…736…720…685 |
| Топливо Т-2 | -60…-40…0…20…40…60…100…140…160…200 | 824…810…781…766…752…745…709…680…665…637 |
| Топливо Т-6 | -60…-40…0…20…40…60…100…140…160…200 | 898…883…855…841…827…813…784…756…742…713 |
| Топливо Т-8 | -60…-40…0…20…40…60…100…140…160…200 | 847…833…804…789…775…761…732…703…689…660 |
| Топливо ТС-1 | -60…-40…0…20…40…60…100…140…160…200 | 837…823…794…780…765…751…722…693…879…650 |
| Углерод четыреххлористый (ЧХУ) | 20 | 1595 |
| Уроторопин C 6 H 12 N 2 | 27 | 1330 |
| Фторбензол | 20 | 1024 |
| Хлорбензол | 20 | 1066 |
| Этилацетат | 20 | 901 |
| Этилбромид | 20 | 1430 |
| Этилиодид | 20 | 1933 |
| Этилхлорид | 0 | 921 |
| Эфир | 0…20 | 736…720 |
| Эфир Гарпиуса | 27 | 1100 |
zygar.ru
| ЗАДАЧНИК ОНЛ@ЙН БИБЛИОТЕКА 1 БИБЛИОТЕКА 2 Плотность — есть скалярная физическая величина. Определяется, как отношение массы тела к его объёму. ϱ = m / V
Измерение плотностиДля измерения плотности используются:
… 2 >> следующая страница | Плотность газов и паров. Плотность сухого воздуха. Плотность жидкостей. Плотность металлов и сплавов.Плотность газов и паровпри температуре 0o C и нормальном атмосферном давлении
Как видим из таблицы наибольшую плотность пара у Хлороформа. Водород имеет наименьшую плотность из газов. Плоность сухого воздухапри различной температуре t и нормальном атмосферном давлениии
Плотность жидкостей
Примечание. Значения плотностей жидкостей даны при нормальном атмосферном давлении и температуре 20oC (если не указана иная температура). Плотность металлов и сплавовпри температуре 20oC
Плотность сжиженных газов и расплавленных металлов
* Жидкий водород — наименее плотная жидкость. Плотность твердых тел
Примечание. Значения плотностей даны при температуре 20о С (если не указана иная температура). Плотность некоторых сельскохозяйственных продуктов
Плотность некоторых пластмасс
Плотность различных пород дерева
Плоность (средняя насыпная) некоторых материалов и продуктов
|
www.kilomol.ru
Энциклопедия сантехника Физические свойства жидкостей
Жидкости. В природе различают четыре вида состояния вещества: твердое, жидкое, газообразное и плазменное. Основное отличие жидкостей от твердых тел заключается в их текучести, т.е. способности легко принимать форму сосуда, в который жидкость поместили, при этом объем жидкости не изменяется. Газ тоже обладает текучестью, но при этом занимает любой предоставленный ему объем. В сосудах жидкость образует свободную поверхность, а газ аналогичной поверхностью не обладает. Однако с точки зрения механики и жидкость, и газ подчиняются одним и тем же закономерностям в случае, если сжимаемостью газа можно пренебречь. Поэтому в гидравлике под термином «жидкость» понимаются и собственно жидкости (которые часто называют капельными жидкостями), и газы (газообразные жидкости).
Основные свойства жидкости (при рассмотрении задач механики жидкости) — это плотность, способность изменять свой объем при нагревании (охлаждении) и изменениях давления, вязкость жидкости. Рассмотрим каждое из свойств жидкости подробнее.
Плотность жидкости. Плотностью жидкости ρ называется ее масса, заключенная в единице объема:
где m — масса жидкости; W — объем жидкости.
Единица измерения плотности — кг/м3.
Так как вода является наиболее распространенной в природе жидкостью, в качестве примера количественного значения параметра, определяющего то или иное свойство жидкости, будем приводить значение рассматриваемого параметра для воды.
Плотность воды при 4 °С ρв = 1000 кг/м3. Плотность жидкости уменьшается при увеличении температуры. Однако для воды эта закономерность справедлива только с 4 °С, в чем проявляется одно из аномальных свойств воды.
Удельный вес. Удельный вес γ — это вес жидкости, приходящийся на единицу объема:
где G — вес жидкости в объеме W.
Единица измерения удельного веса — Н/м3.
Удельный вес воды при температуре 4 °С γв= 9810 Н/м3.
Плотность и удельный вес связаны между собой соотношением
где g — ускорение свободного падения (g=9,81 м/с2).
Вообще плотность и удельный вес отичаются лиш тем, что у плотности сила веса измеряется в килограммах, а у удельного веса в ньютонах. Килограммы легко переводятся в ньютоны и обратно. Вообще эти параметры нам помогут вычислять массу в любых объемах.
Температурное расширение. Это свойство жидкости характеризуется изменением объема при изменении температуры, которое определяется температурным коэффициентом объемного расширения жидкости βt:
где W — начальный объем жидкости; ΔW — Изменение объема после уменьшения или увеличения температуры; Δt — изменение температуры.
Знак Δ означает разницу между начальной величиной и конечной величиной. |
Единица измерения βt; — град-1,
для воды,при t=20 °С βt = 0,00015 [1/°С].
Это свойство нужно обязательно знать! В будущем нам придется вычислять количество жидкости которое будет увеличиваться в замкнутой системе отопления. И при этом мы сможем посчитать на сколько литров нам необходим раширительный бак для системы отопления.Получается, что этот параметр βt показывает изменение величины объема на единицу температуры. То есть, если температура изменилась на 10 градусов, то объем увеличится в 10раз от величины βt.
Сжимаемость. Это свойство жидкости менять свой объем при изменении давления, которое характеризуется коэффициентом объемного сжатия βp :
где W — начальный объем жидкости; ΔW — изменение объема после изменения давления; ΔP — изменение давления.
Единица измерения βp — Па-1 Коэффициент объемного сжатия капельных жидкостей мало меняется в зависимости от давления и температуры.
Для воды βp = 5×10-10 Па-1
Вы только не путайте давление с плотностью. Так как буквы похожи, я и сам сначало об этом подумал. О давлении будет рассказано в следующих статьях. Вообще я сейчас не рекомендую вникать в понятие сжимаемость, так как вы возможно незнакомы с понятием давления и поэтому возможно несможите понять связь.
Величина, обратная коэффициенту объемного сжатия, называется модулем упругости жидкости Е и определяется по формуле:
для воды E=2×109 Па.
Вязкость жидкости — свойство жидкостей оказывать сопротивление сдвигу. Это свойство проявляется только при движении жидкостей. Вязкость характеризует степень текучести жидкости. Наряду с легко подвижными жидкостями (вода, спирт, воздух и др.) существуют очень вязкие жидкости (глицерин, машинные масла и др.).
Я предлогаю понять вязкость следующем образом: Представте жидкое вещество ввиде находящихся в ней большого количество мелких шариков, атомов, малекул, кому как угодно. И представте, что их начинает ктото толкать. И во время толкания шарики начинают терется друг об друга сопротивляясь перемещению. Дык вот, а теперь представим ситуацию когда эти шарики стали липкими и тогда эти шарики будут еще сильнее сопротивлятся сдвигу. И вот чем сильнее они буду сопротивлятся сдвигу об друг друга, тем сильнее будет вязкость.
Вязкость жидкости характеризуется динамической вязкостью μ.
И. Ньютон выдвинул гипотезу о силе трения F, возникающей между двумя слоями жидкости на поверхности их раздела площадью ω, согласно которой сила внутреннего трения в жидкости не зависит от давления, прямо пропорциональна площади соприкосновения слоев ω и быстроте изменения скорости в направлении, перпендикулярном направлению движения слоев, и зависит от рода жидкости.
Пусть жидкость течет по плоскому дну параллельными ему слоями
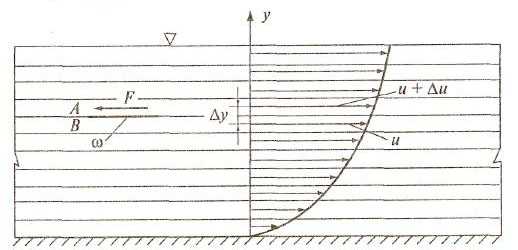
Вследствие тормозящего влияния дна слои жидкости будут двигаться с разными скоростями. Скорости слоев Показаны стрелками. Рассмотрим два слоя жидкости, середины которых расположены на расстоянии Δу друг от друга. Слой А движется со скоростью u, а слой В со скоростью u + Δu.
На площадке ω вследствие вязкости возникает сила сопротивления F. Согласно гипотезе Ньютона эта сила
коэффициент пропорциональности μ, в этой формуле и является динамической вязкостью, отношение Δu/Δy называется градиентом скорости.
Таким образом, динамическая вязкость является силой трения, приходящейся на единицу площади соприкосновения слоев жидкости при градиенте скорости, равном единице.
Размерность μ — Па • с.
Гипотеза И. Ньютона, представленная в формуле, экспериментально подтверждена и математически оформлена в дифференциальном виде
основоположником гидравлической теории смазки Н.П. Петровым и в настоящее время носит название закона внутреннего трения Ньютона.
В гидравлических расчетах часто удобнее пользоваться другой величиной, характеризующей вязкость жидкости, — ν:
Эта величина называется кинематической вязкостью. Размерность v — м2/с
Название «кинематическая вязкость» не несет особого физического смысла, так как название было предложено потому, что размерность v похожа на размерность скорости.
Вязкость жидкости зависит как от температуры, так и от давления. Кинематическая вязкость капельных жидкостей уменьшается с увеличением температуры, а вот вязкость газов, наоборот, возрастает с увеличением температуры. Кинематическая вязкость жидкостей при давлениях, встречающихся в большинстве случаев на практике, мало зависит от давления, а вязкость газов с возрастанием давления уменьшается.
Вязкость жидкости измеряют с помощью вискозиметров различных конструкций.
Жидкости, для которых справедлив закон внутреннего тяготения Ньютона, называют ньютоновскими. Существуют жидкости, которые не подчиняются закономерности формулам, к ним относятся растворы полимеров, гидросмеси из цемента, глины, мела и др. Такие жидкости относятся к неньютоновским.
Вообще для меня понятие вязкость , несколько смутное понятие, потому что нехвотает примеров как находится вязкость в реальных условиях, а не ввымышленных как описано выше. Меня берет сомнение площадь соприкосновения с жидкостью. Тут описана площадь просто как ввиде листа. А мне нужно было бы, площадь ввиде замкнутой трубы. В будущем я найду задачи по вязкости и объяснюдетали расчетов сопротивления в трубопроводе.
Я кстати уже нашел формулы которые нужны сантехникам и инженерам, опишу их в других статьях. Пишите коментарии, я обязательно отвечу на ваши вопросы и постараюсь подкорректировать статьи под вашы нужды.
Следующий раздел: Гидростатическое давление
| Если Вы желаете получать уведомления о новых полезных статьях из раздела: Сантехника, водоснабжение, отопление, то оставте Ваше Имя и Email. | ||
Все о дачном доме
Водоснабжение
Обучающий курс. Автоматическое водоснабжение своими руками. Для чайников.
Неисправности скважинной автоматической системы водоснабжения.
Водозаборные скважины
Ремонт скважины? Узнайте нужен ли он!
Где бурить скважину — снаружи или внутри?
В каких случаях очистка скважины не имеет смысла
Почему в скважинах застревают насосы и как это предотвратить
Прокладка трубопровода от скважины до дома
100% Защита насоса от сухого хода
Отопление
Обучающий курс. Водяной теплый пол своими руками. Для чайников.
Теплый водяной пол под ламинат
Обучающий Видеокурс: По ГИДРАВЛИЧЕСКИМ И ТЕПЛОВЫМ РАСЧЕТАМ
Водяное отопление
Виды отопления
Отопительные системы
Отопительное оборудование, отопительные батареи
Система теплых полов
Личная статья теплых полов
Принцип работы и схема работы теплого водяного пола
Проектирование и монтаж теплого пола
Водяной теплый пол своими руками
Основные материалы для теплого водяного пола
Технология монтажа водяного теплого пола
Система теплых полов
Шаг укладки и способы укладки теплого пола
Типы водных теплых полов
Все о теплоносителях
Антифриз или вода?
Виды теплоносителей (антифризов для отопления)
Антифриз для отопления
Как правильно разбавлять антифриз для системы отопления?
Обнаружение и последствия протечек теплоносителей
Как правильно выбрать отопительный котел
Тепловой насос
Особенности теплового насоса
Тепловой насос принцип работы
Про радиаторы отопления
Способы подключения радиаторов. Свойства и параметры.
Как рассчитать колличество секций радиатора?
Рассчет тепловой мощности и количество радиаторов
Виды радиаторов и их особенности
Автономное водоснабжение
Схема автономного водоснабжения
Устройство скважины Очистка скважины своими руками
Опыт сантехника
Подключение стиральной машины
Полезные материалы
Редуктор давления воды
Гидроаккумулятор. Принцип работы, назначение и настройка.
Автоматический клапан для выпуска воздуха
Балансировочный клапан
Перепускной клапан
Трехходовой клапан
Трехходовой клапан с сервоприводом ESBE
Терморегулятор на радиатор
Сервопривод коллекторный. Выбор и правила подключения.
Виды водяных фильтров. Как подобрать водяной фильтр для воды.
Обратный осмос
Фильтр грязевик
Обратный клапан
Предохранительный клапан
Смесительный узел. Принцип работы. Назначение и расчеты.
Расчет смесительного узла CombiMix
Гидрострелка. Принцип работы, назначение и расчеты.
Бойлер косвенного нагрева накопительный. Принцип работы.
Расчет пластинчатого теплообменника
Рекомендации по подбору ПТО при проектировании объектов теплоснабжения
О загрязнение теплообменников
Водонагреватель косвенного нагрева воды
Магнитный фильтр — защита от накипи
Инфракрасные обогреватели
Радиаторы. Свойства и виды отопительных приборов.
Виды труб и их свойства
Незаменимые инструменты сантехника
Интересные рассказы
Страшная сказка о черном монтажнике
Технологии очистки воды
Как выбрать фильтр для очистки воды
Поразмышляем о канализации
Очистные сооружения сельского дома
Советы сантехнику
Как оценить качество Вашей отопительной и водопроводной системы?
Профрекомендации
Как подобрать насос для скважины
Как правильно оборудовать скважину
Водопровод на огород
Как выбрать водонагреватель
Пример установки оборудования для скважины
Рекомендации по комплектации и монтажу погружных насосов
Какой тип гидроаккумулятора водоснабжения выбрать?
Круговорот воды в квартире
фановая труба
Удаление воздуха из системы отопления
Гидравлика и теплотехника
Введение
Что такое гидравлический расчет?
Физические свойства жидкостей
Гидростатическое давление
Поговорим о сопротивлениях прохождении жидкости в трубах
Режимы движения жидкости (ламинарный и турбулентный)
Гидравлический расчет на потерю напора или как рассчитать потери давления в трубе
Местные гидравлические сопротивления
Профессиональный расчет диаметра трубы по формулам для водоснабжения
Как подобрать насос по техническим параметрам
Профессиональный расчет систем водяного отопления. Расчет теплопотерь водяного контура.
Гидравлические потери в гофрированной трубе
Теплотехника. Речь автора. Вступление
Процессы теплообмена
Тплопроводность материалов и потеря тепла через стену
Как мы теряем тепло обычным воздухом?
Законы теплового излучения. Лучистое тепло.
Законы теплового излучения. Страница 2.
Потеря тепла через окно
Факторы теплопотерь дома
Начни свое дело в сфере систем водоснабжения и отопления
Вопрос по расчету гидравлики
Конструктор водяного отопления
Диаметр трубопроводов, скорость течения и расход теплоносителя.
Вычисляем диаметр трубы для отопления
Расчет потерь тепла через радиатор
Мощность радиатора отопления
Расчет мощности радиаторов. Стандарты EN 442 и DIN 4704
Расчет теплопотерь через ограждающие конструкции
Найти теплопотери через чердак и узнать температуру на чердаке
Подбираем циркуляционный насос для отопления
Перенос тепловой энергии по трубам
Расчет гидравлического сопротивления в системе отопления
Распределение расхода и тепла по трубам. Абсолютные схемы.
Расчет сложной попутной системы отопления
Расчет отопления. Популярный миф
Расчет отопления одной ветки по длине и КМС
Расчет отопления. Подбор насоса и диаметров
Расчет отопления. Двухтрубная тупиковая
Расчет отопления. Однотрубная последовательная
Расчет отопления. Двухтрубная попутная
Расчет естественной циркуляции. Гравитационный напор
Расчет гидравлического удара
Сколько выделяется тепла трубами?
Собираем котельную от А до Я…
Система отопления расчет
Онлайн калькулятор Программа расчет Теплопотерь помещения
Гидравлический расчет трубопроводов
История и возможности программы — введение
Как в программе сделать расчет одной ветки
Расчет угла КМС отвода
Расчет КМС систем отопления и водоснабжения
Разветвление трубопровода – расчет
Как в программе рассчитать однотрубную систему отопления
Как в программе рассчитать двухтрубную систему отопления
Как в программе рассчитать расход радиатора в системе отопления
Перерасчет мощности радиаторов
Как в программе рассчитать двухтрубную попутную систему отопления. Петля Тихельмана
Расчет гидравлического разделителя (гидрострелка) в программе
Расчет комбинированной цепи систем отопления и водоснабжения
Расчет теплопотерь через ограждающие конструкции
Гидравлические потери в гофрированной трубе
Гидравлический расчет в трехмерном пространстве
Интерфейс и управление в программе
Три закона/фактора по подбору диаметров и насосов
Расчет водоснабжения с самовсасывающим насосом
Расчет диаметров от центрального водоснабжения
Расчет водоснабжения частного дома
Расчет гидрострелки и коллектора
Расчет Гидрострелки со множеством соединений
Расчет двух котлов в системе отопления
Расчет однотрубной системы отопления
Расчет двухтрубной системы отопления
Расчет петли Тихельмана
Расчет двухтрубной лучевой разводки
Расчет двухтрубной вертикальной системы отопления
Расчет однотрубной вертикальной системы отопления
Расчет теплого водяного пола и смесительных узлов
Рециркуляция горячего водоснабжения
Балансировочная настройка радиаторов
Расчет отопления с естественной циркуляцией
Лучевая разводка системы отопления
Петля Тихельмана – двухтрубная попутная
Гидравлический расчет двух котлов с гидрострелкой
Система отопления (не Стандарт) — Другая схема обвязки
Гидравлический расчет многопатрубковых гидрострелок
Радиаторная смешенная система отопления — попутная с тупиков
Терморегуляция систем отопления
Разветвление трубопровода – расчет
Гидравлический расчет по разветвлению трубопровода
Расчет насоса для водоснабжения
Расчет контуров теплого водяного пола
Гидравлический расчет отопления. Однотрубная система
Гидравлический расчет отопления. Двухтрубная тупиковая
Бюджетный вариант однотрубной системы отопления частного дома
Расчет дроссельной шайбы
Что такое КМС?
Конструктор технических проблем
Температурное расширение и удлинение трубопровода из различных материалов
Требования СНиП ГОСТы
Требования к котельному помещению
Вопрос слесарю-сантехнику
Полезные ссылки сантехнику
—
Сантехник — ОТВЕЧАЕТ!!!
Жилищно коммунальные проблемы
Монтажные работы: Проекты, схемы, чертежи, фото, описание.
Если надоело читать, можно посмотреть полезный видео сборник по системам водоснабжения и отопления
infobos.ru
4. Основные свойства жидкости Плотность
Плотность жидкости  ,
так же как любых других тел, представляет
собой массу
единицы объёма, и для бесконечно малого
объёма жидкости dV массой dM может быть
определена по формуле:
,
так же как любых других тел, представляет
собой массу
единицы объёма, и для бесконечно малого
объёма жидкости dV массой dM может быть
определена по формуле:
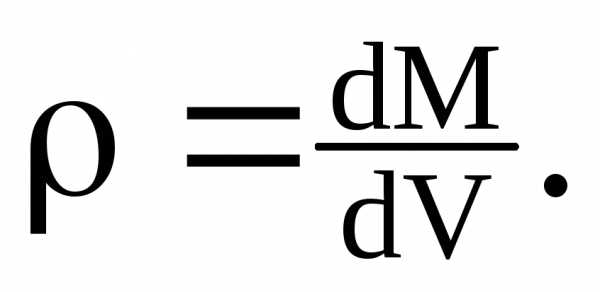
Для однородных жидкостей можно считать, что
где M – масса жидкости,
V – объём жидкости.
Единицы измерения:
[кг/м3], [кг/дм3], [кг/л], [г/см3].
П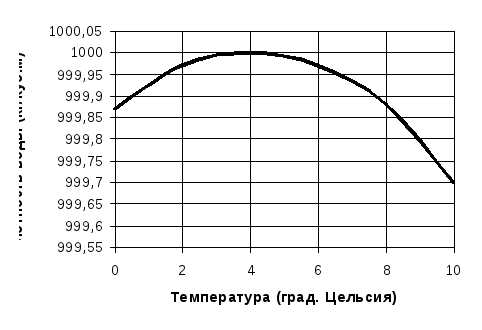 лотность
жидкости зависит от температуры и
давления. Все жидкости, кроме воды,
характеризуются уменьшением плотности
с ростом температуры. Плотность воды
имеет максимум приt
= 4 оC и уменьшается при любых других
температурах. В этом проявляется одно
из аномальных свойств воды. Температура,
при которой плотность воды максимальная,
с увеличением давления уменьшается.
Так, при давлении 14
МПа вода имеет максимальную плотность при 0,6 оC.
лотность
жидкости зависит от температуры и
давления. Все жидкости, кроме воды,
характеризуются уменьшением плотности
с ростом температуры. Плотность воды
имеет максимум приt
= 4 оC и уменьшается при любых других
температурах. В этом проявляется одно
из аномальных свойств воды. Температура,
при которой плотность воды максимальная,
с увеличением давления уменьшается.
Так, при давлении 14
МПа вода имеет максимальную плотность при 0,6 оC.
Плотность пресной воды равна 1000 кг/м3, солёной морской воды — 1020 ÷ 1030, нефти и нефтепродуктов – 650 ÷ 900 кг/м3, ртути – 13596 кг/м3.
При изменении давления плотность жидкостей изменяется незначительно. В большинстве случаев плотность жидкости в расчётах можно принимать постоянной. Однако встречаются случаи, когда изменением плотности пренебрегать нельзя, т.к. это может привести к значительным ошибкам.
Удельный вес
Удельным весом
жидкости  —
называется вес единицы её объёма. Эта
величина выражается формулой для
бесконечно малого объёма жидкости dV с весом dG:
—
называется вес единицы её объёма. Эта
величина выражается формулой для
бесконечно малого объёма жидкости dV с весом dG:
Для однородных жидкостей можно считать:
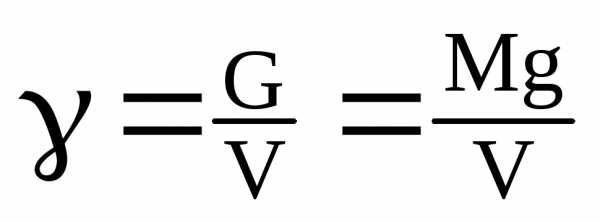 ,
,
где G – вес жидкости.
Удельный вес жидкости и плотность связаны соотношением:
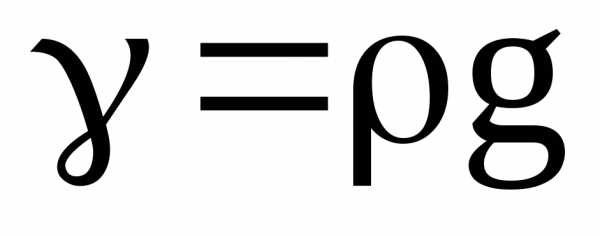 ,
,
где g – ускорение свободного падения.
Единицы измерения: [Н/м3], [Н/дм3], [Н/л], [Н/см3], 1Н=1кг•м/с2.
Значение ускорения свободного падения g на земле изменяется от 9,831 м/с2 на полюсах до 9,781 м/с2 на экваторе.
Относительный удельный вес
Иногда удобно использовать такую характеристику жидкости, которая называется «относительный удельный вес». Это отношение удельного веса жидкости к удельному весу пресной воды
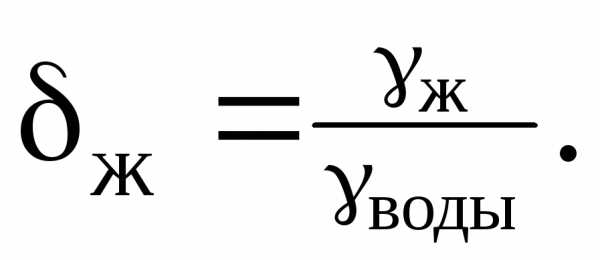
Единицы измерения: Относительный удельный вес — величина безразмерная.
Сжимаемость жидкости
Сжимаемость жидкости это свойство жидкостей изменять свой объём при изменении давления.
Сжимаемость характеризуетсякоэффициентом объёмного сжатия (сжимаемости) βP, представляющим собой относительное изменение объёма жидкости V при изменении давления P на единицу.
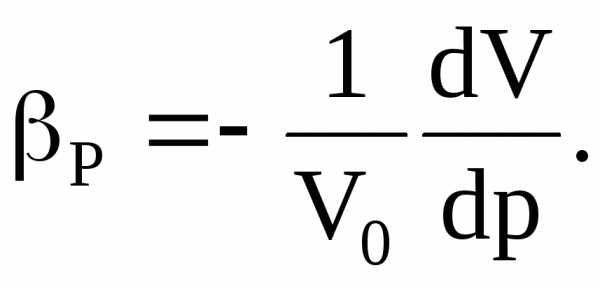
Знак минус в формуле указывает, что при увеличении давления объём жидкости уменьшается.
Единицы измерения: Па-1 (Паскаль. 1Па=1Н/м2).
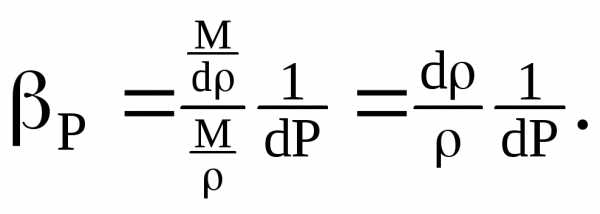
Отсутствие знака минус в этом выражении означает, что увеличение давления приводит к увеличению плотности.
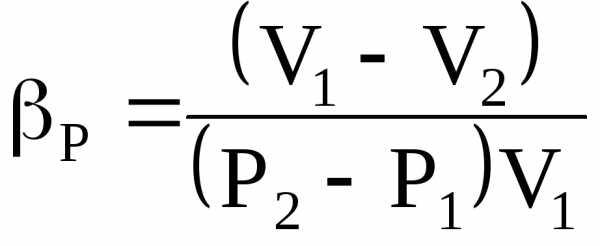
Величина, обратная
коэффициенту сжимаемости, или, по-другому,
коэффициенту объёмного сжатия 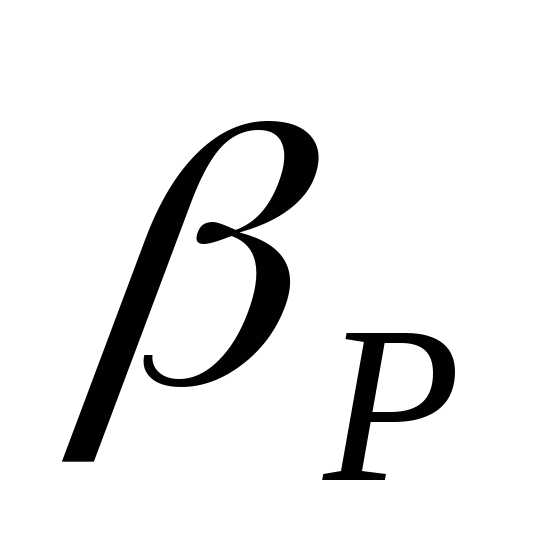 ,
обозначается
,
обозначается
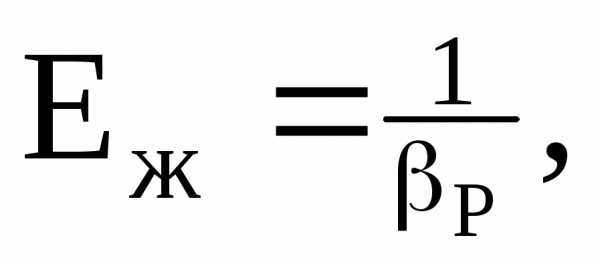
и называется объёмным модулем упругости жидкости.
Тогда предыдущая формула примет вид
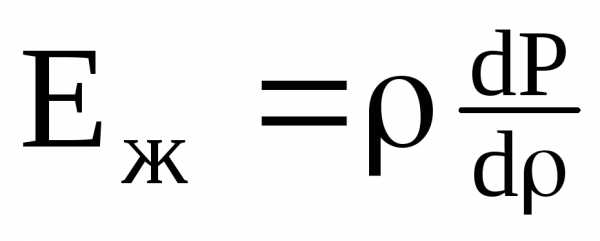 .
.
Это выражение называется законом Гука для жидкости.
Единицы измерения: [Па], [МПа], [кГс/ см2].
Модуль упругостиЕж зависит от температуры и давления. Поэтому различают два модуля упругости: адиабатический и изотермический. Первый имеет место при быстротекущих процессах без теплообмена. Процессы, происходящие в большинстве гидросистем, происходят с теплообменом, поэтому чаще используется изотермический модуль упругости. Примерная форма зависимостей Eж от P и t0 представлена на графиках. Всё это говорит о том, что жидкости не вполне точно следуют закону Гука.
Приведём несколько примеров значений модулей упругости.
Минеральные масла, используемые в технологических машинах с гидравлическим приводом, при t0 = 20 оC имеют объёмные модули упругости 1,35·103 ÷ 1,75·103 МПа (меньшее значение относится к более легкому маслу), бензин и керосин – приблизительно 1,3·103 МПа, глицерин — 4,4·103 МПа, ртуть – в среднем 3,2·103 МПа.
В практике эксплуатации гидравлических систем имеются случаи, когда вследствие действия того или иного возмущения в жидкости может значительно изменяться давление. В таких случаях пренебрежение сжимаемостью приводит к существенным погрешностям.
studfiles.net

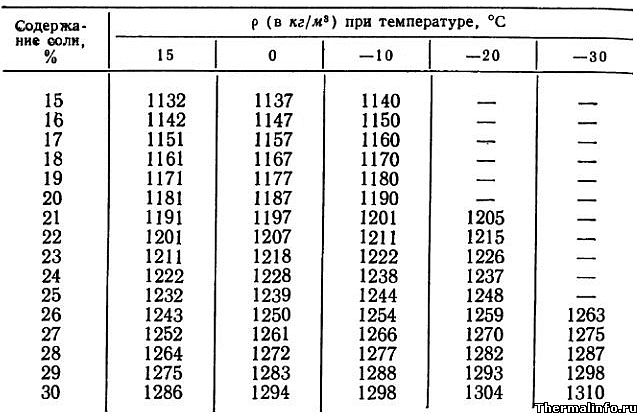


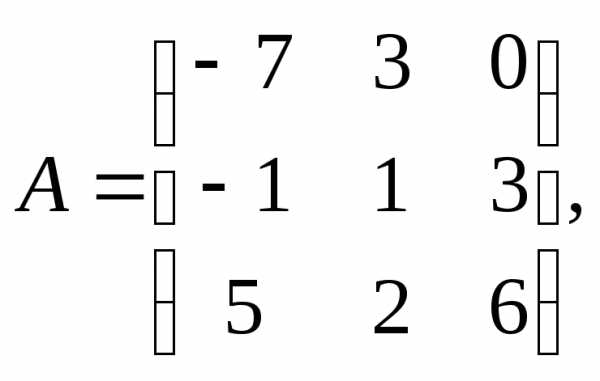
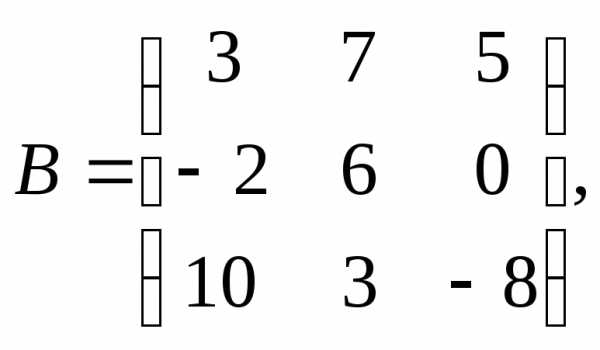 α = 6, β = 3.
α = 6, β = 3.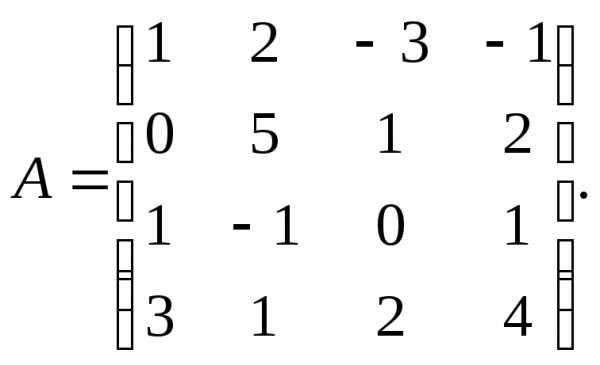 3.
3. 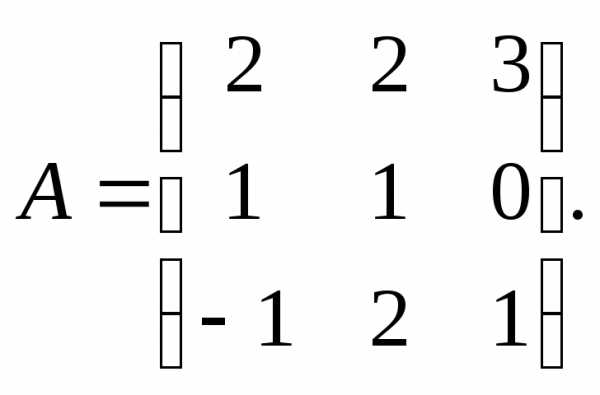
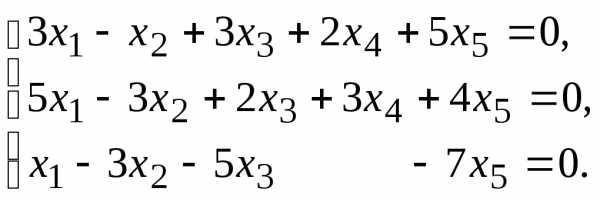


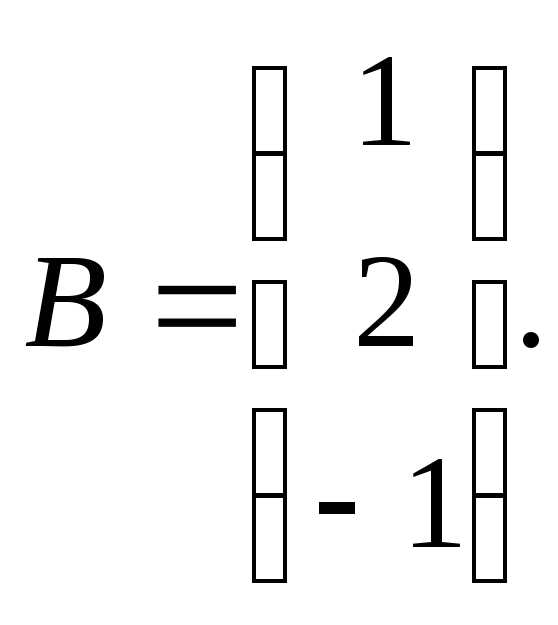 7.
7.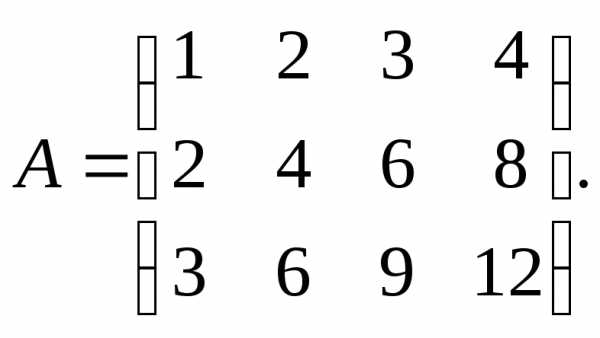 9.
9.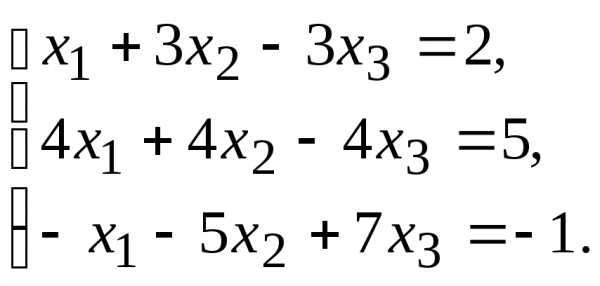
 11.
11. 13.
13. 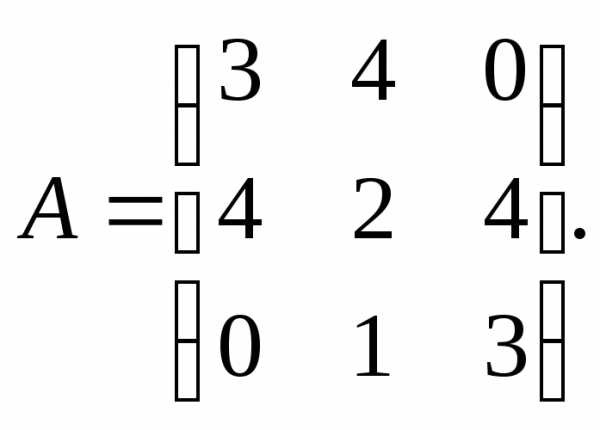
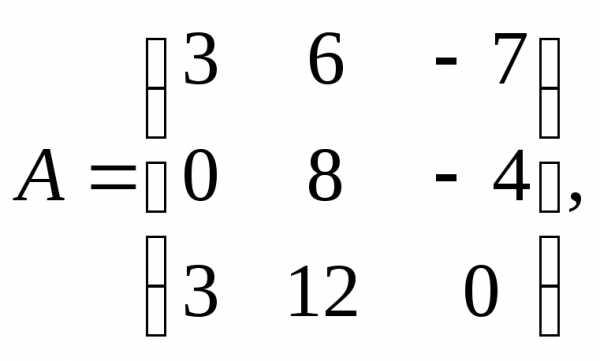
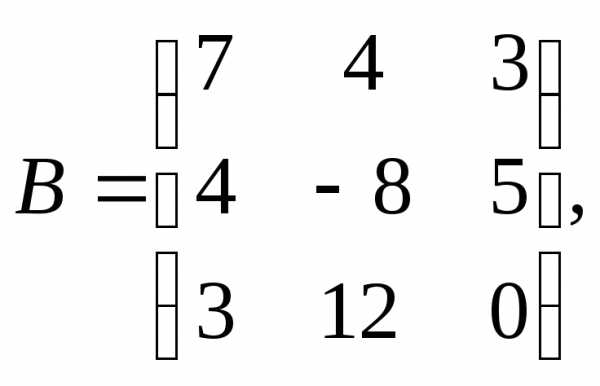 α = 2, β = 4.
α = 2, β = 4.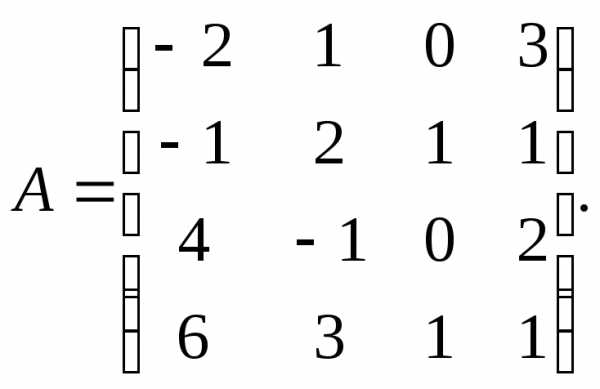 3.
3. 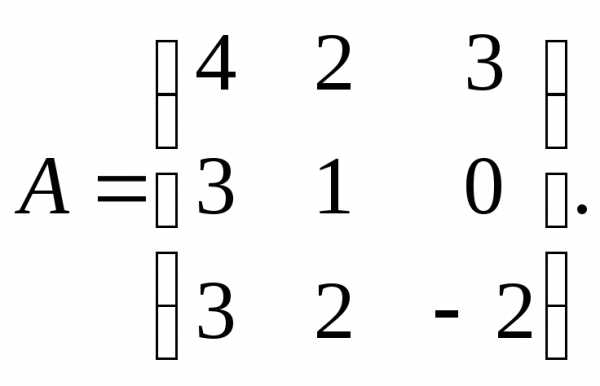
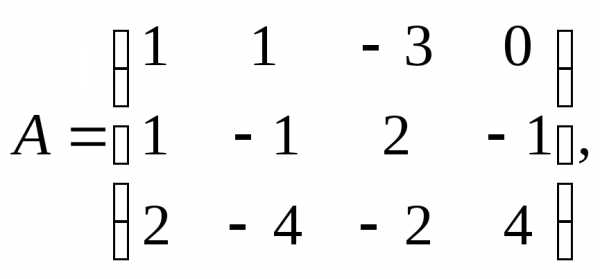
 7.
7.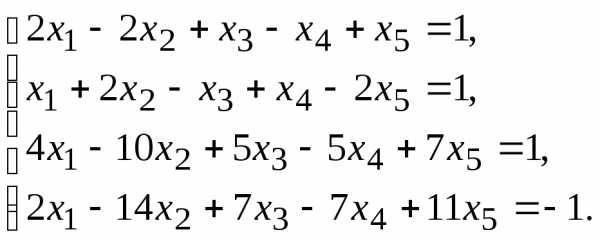
 9.
9.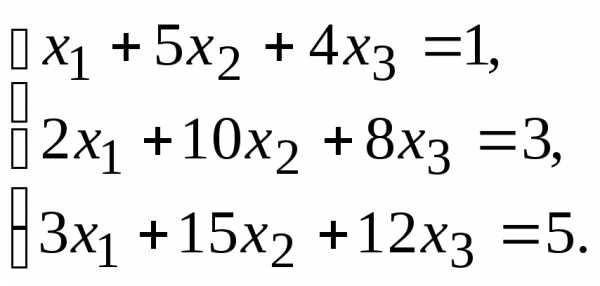
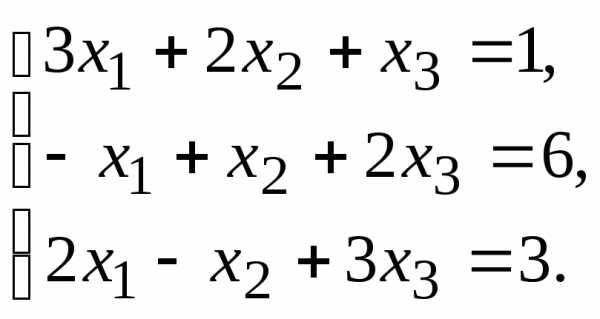 11.
11.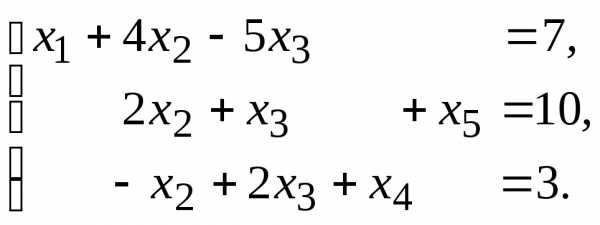 13.
13.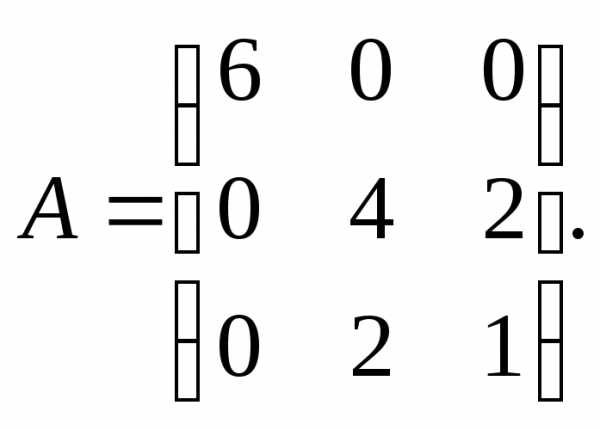
 α = – 2, β =
5.
α = – 2, β =
5.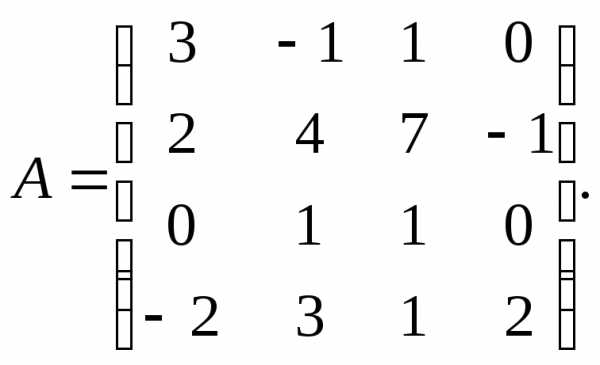 3.
3.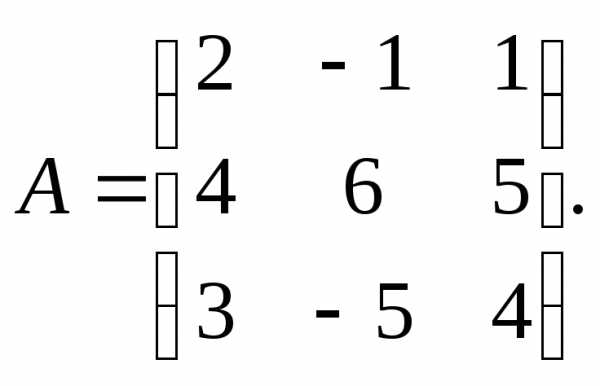

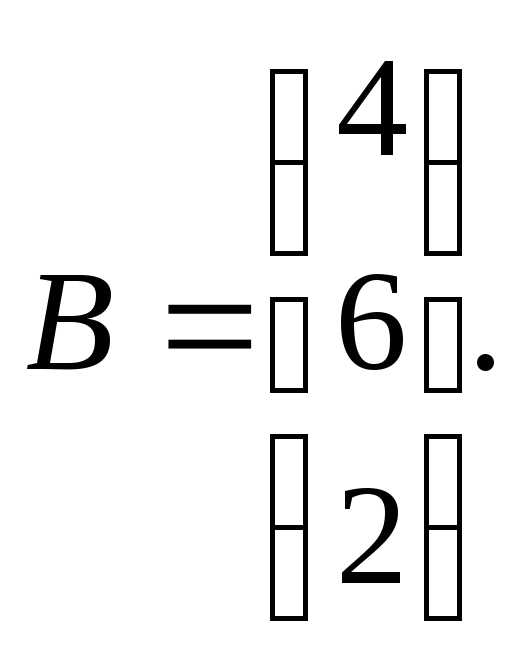 7.
7.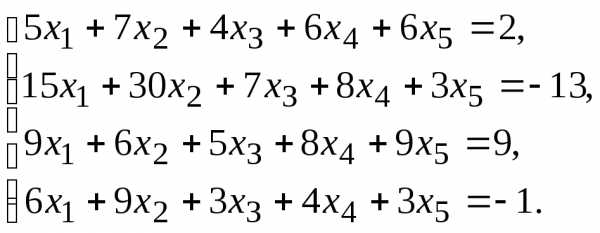
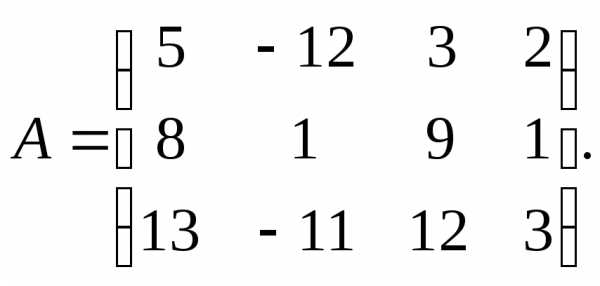 9.
9.
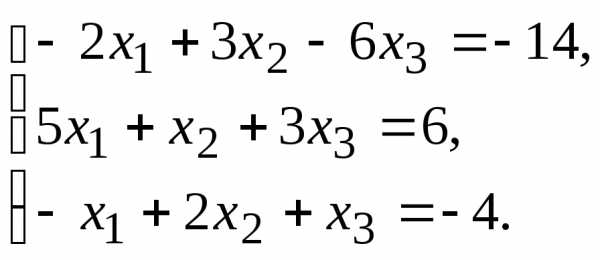 11.
11. 13.
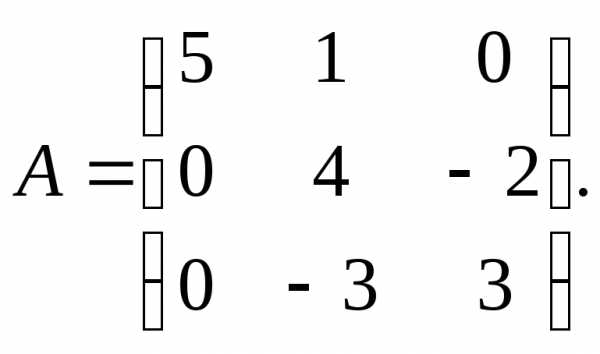
13. 
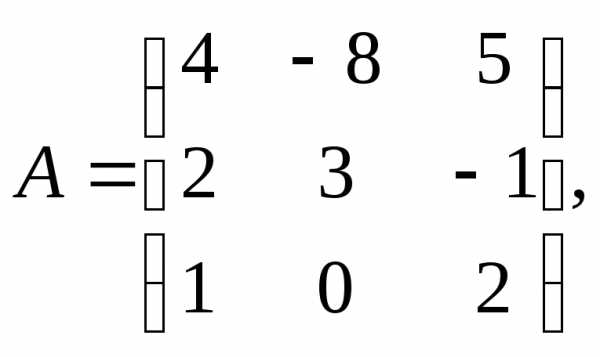
 α = 4, β =
α = 4, β = 
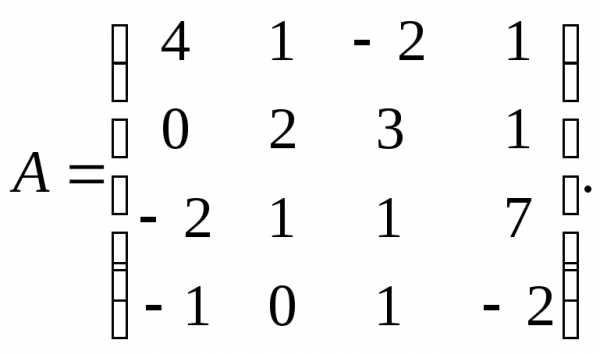 3.
3. 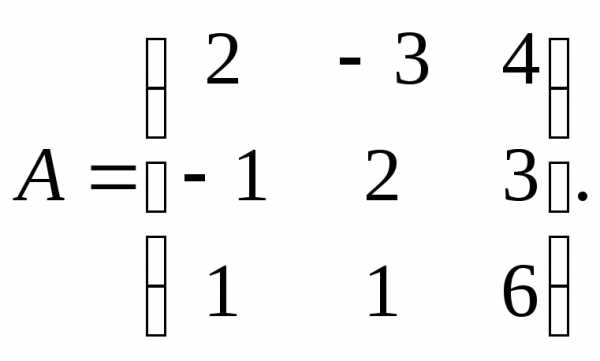
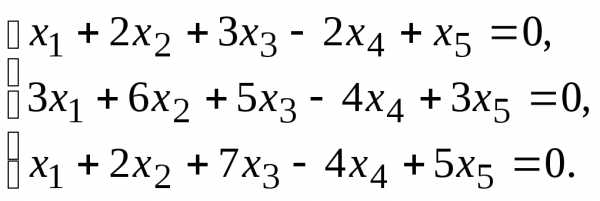

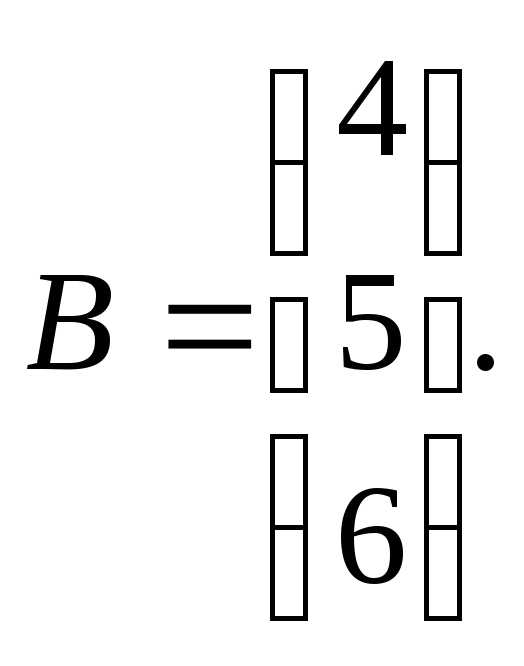 7.
7.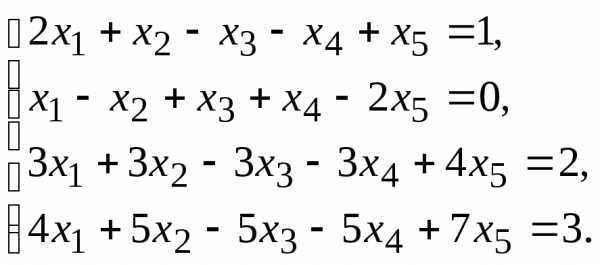
 9.
9.
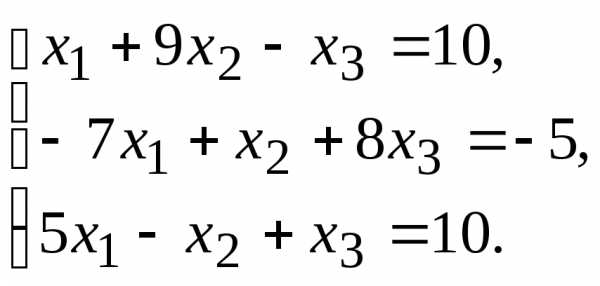 11.
11.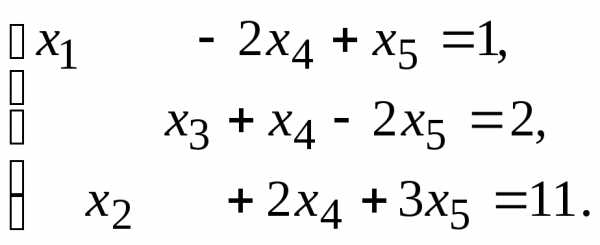 13.
13.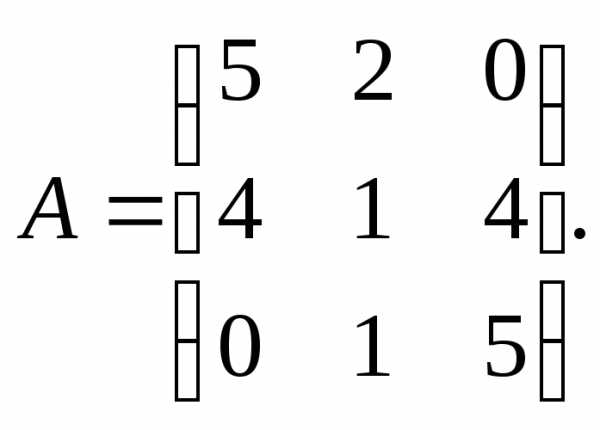
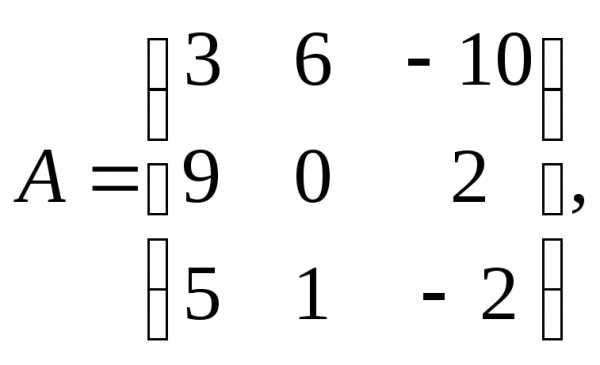
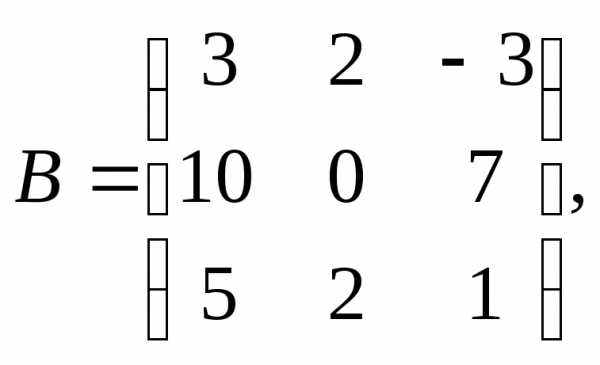 α = 3, β = 5.
α = 3, β = 5.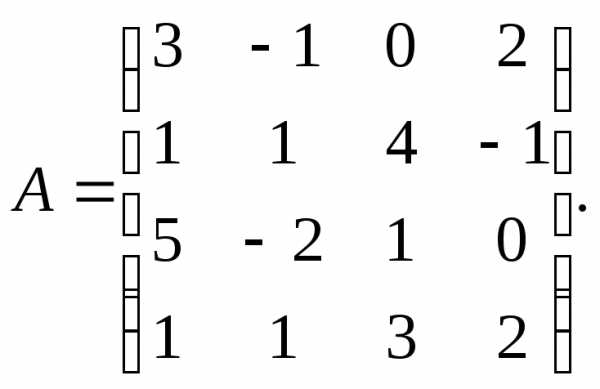 3.
3.
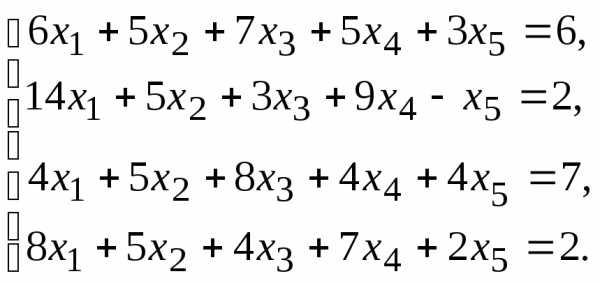
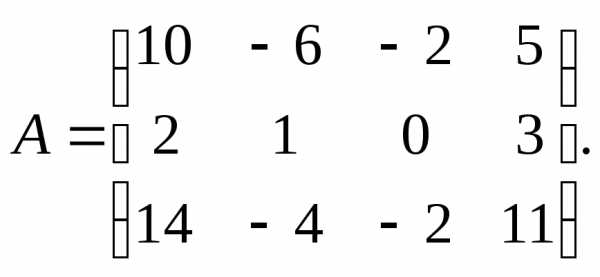 9.
9.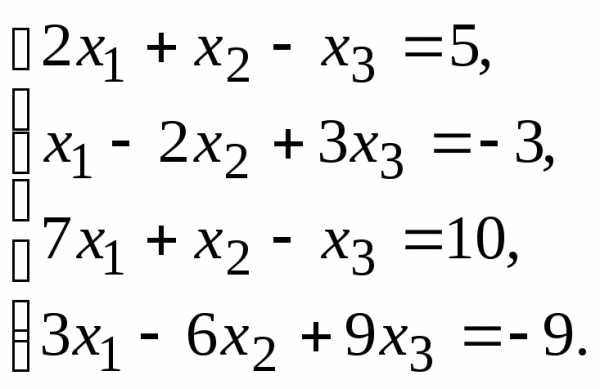
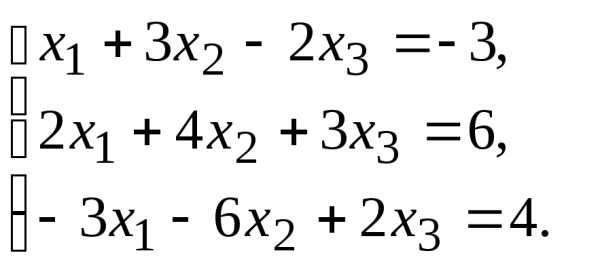 11.
11.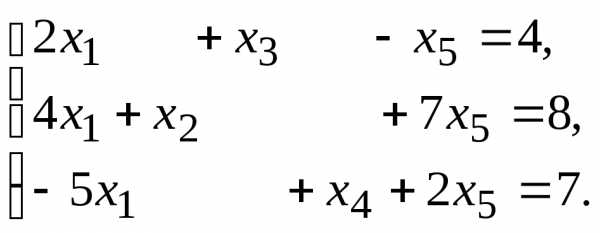 13.
13.
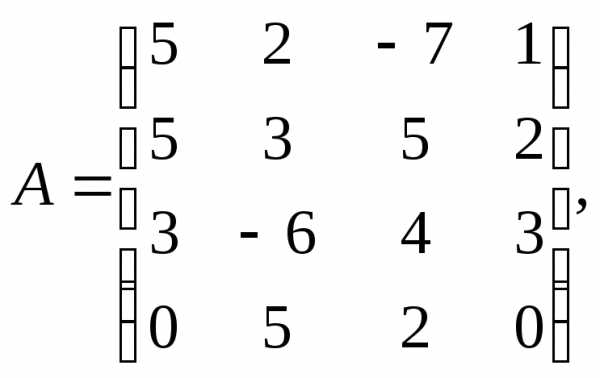
 α = – 2, β =
3.
α = – 2, β =
3.

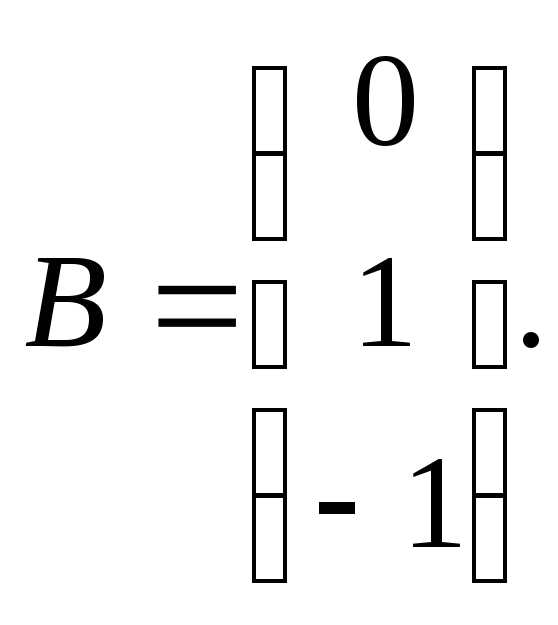 7.
7.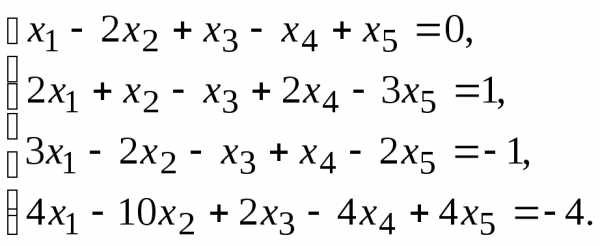
 9.
9.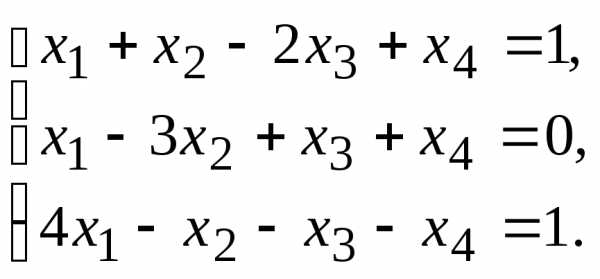
 11.
11. 13.
13.

 α= –
5,β = 3.
α= –
5,β = 3.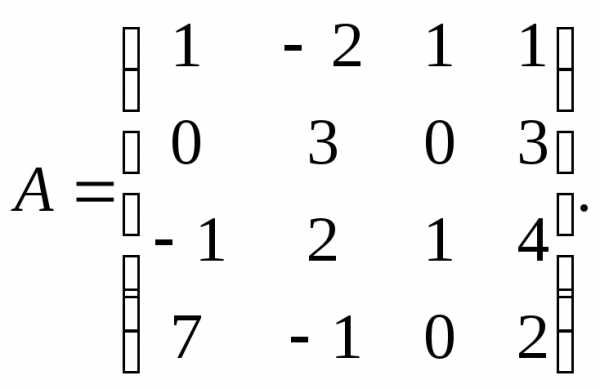 3.
3.

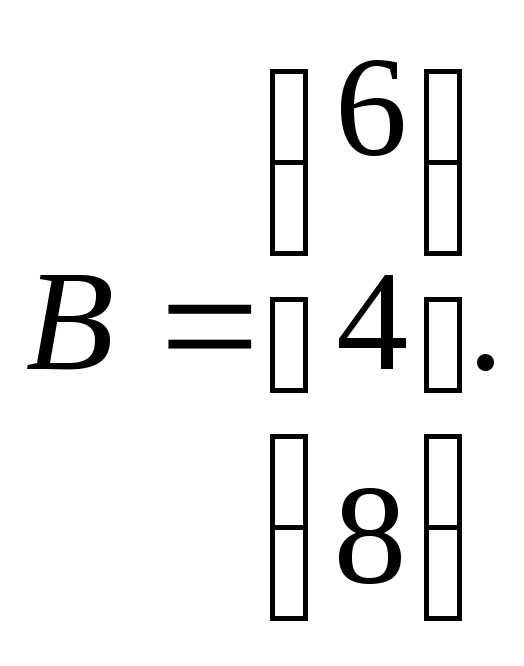 7.
7.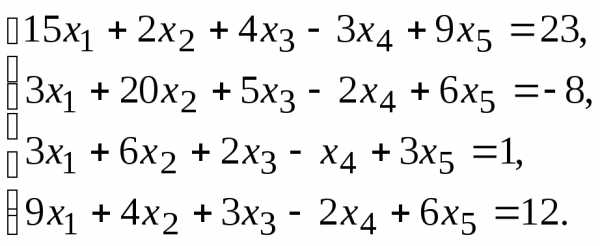
 9.
9.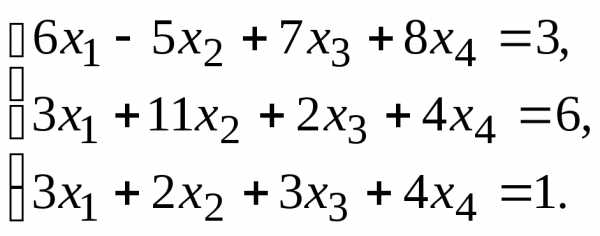
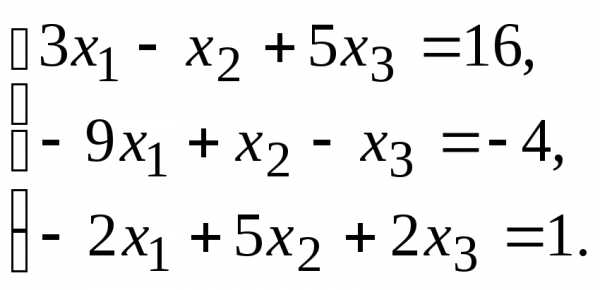 11.
11.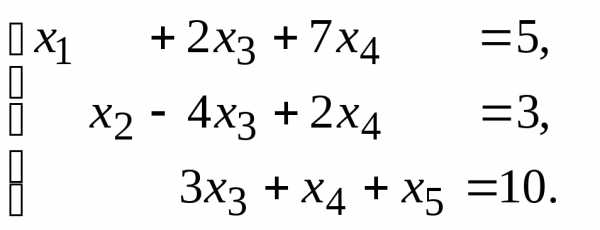 13.
13.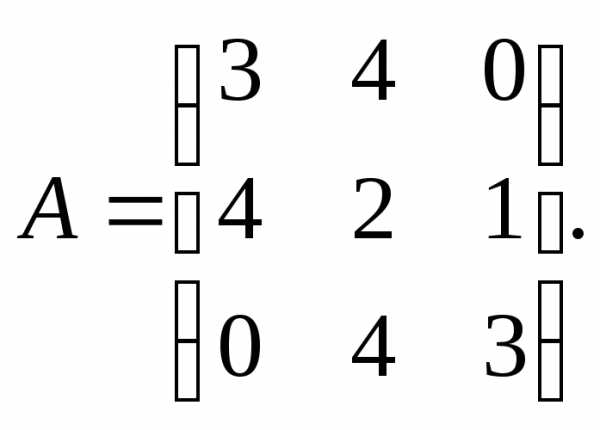
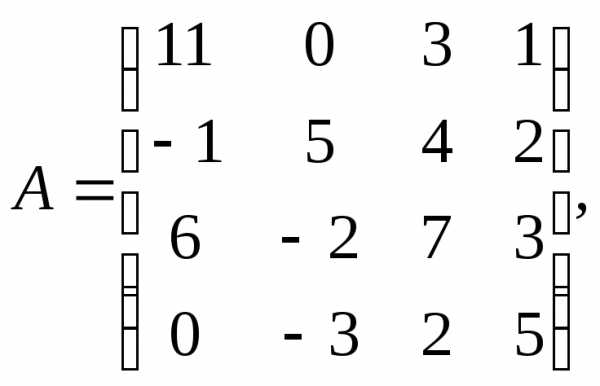
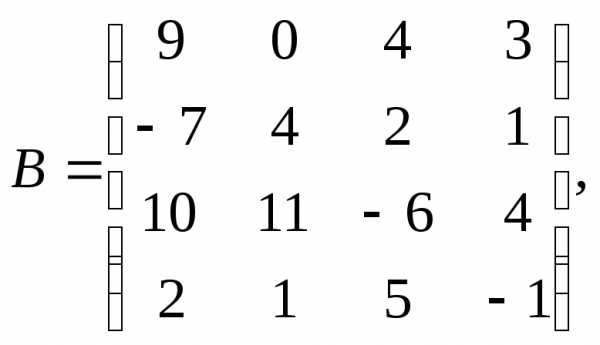 α= 10,β
= – 3.
α= 10,β
= – 3. 3.
3.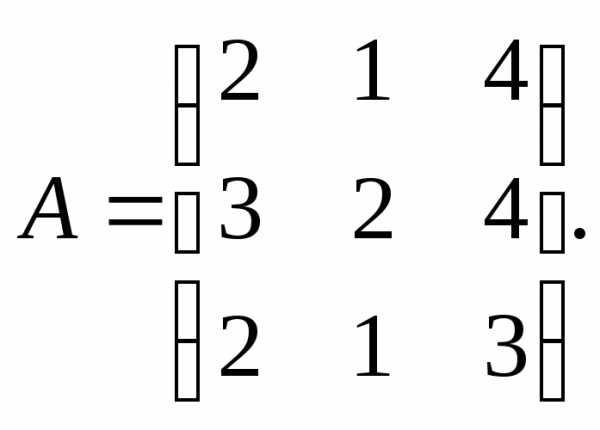

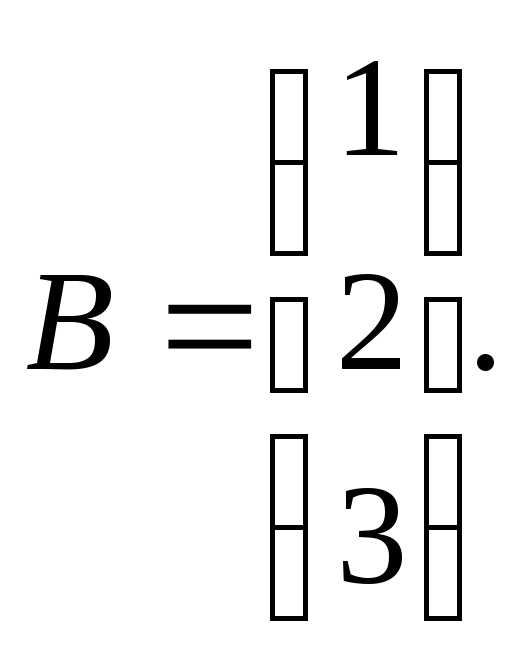 7.
7.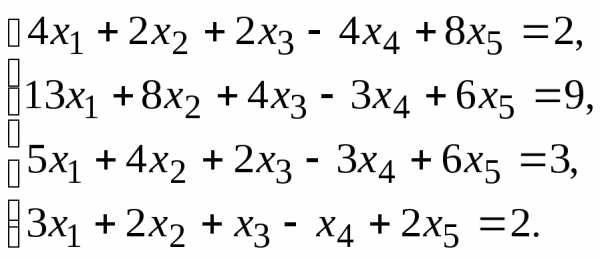
 9.
9.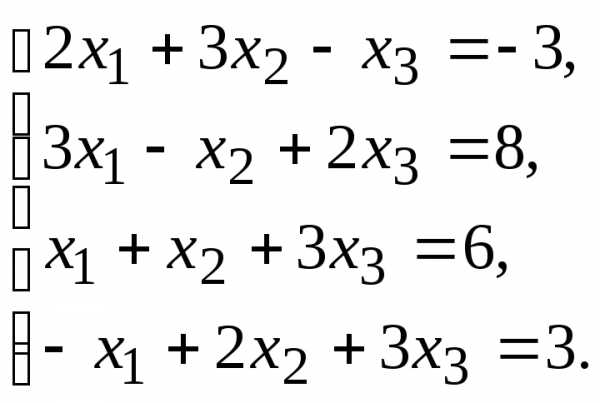
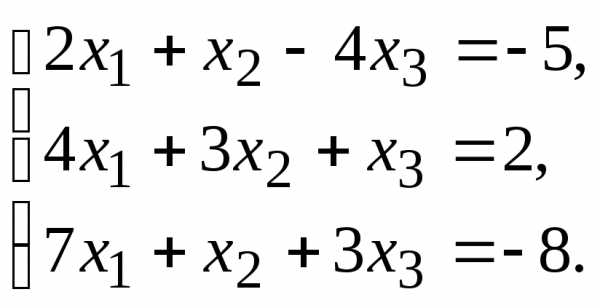 11.
11.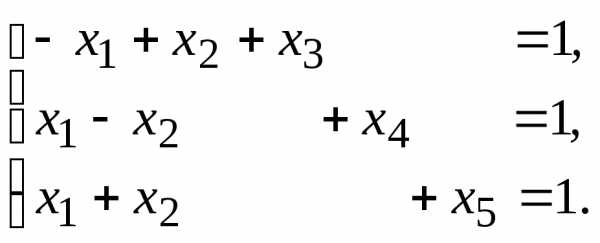 13.
13.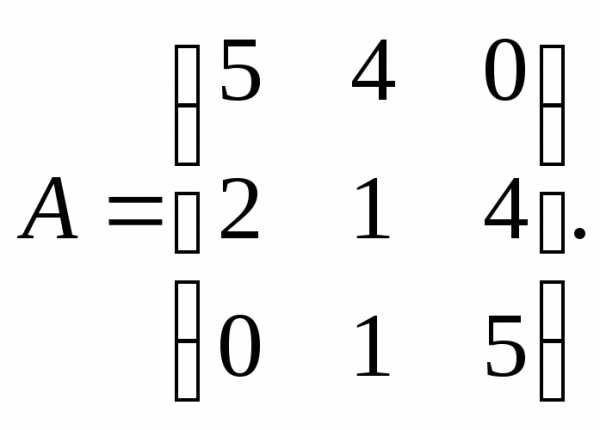
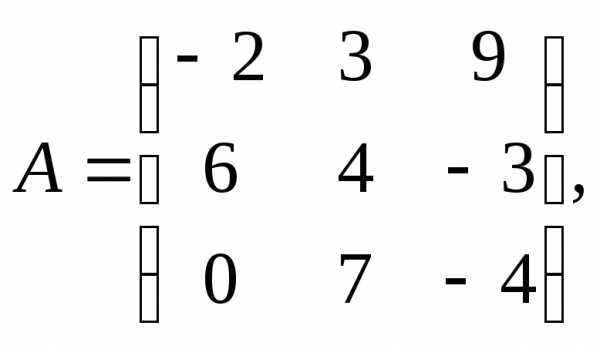
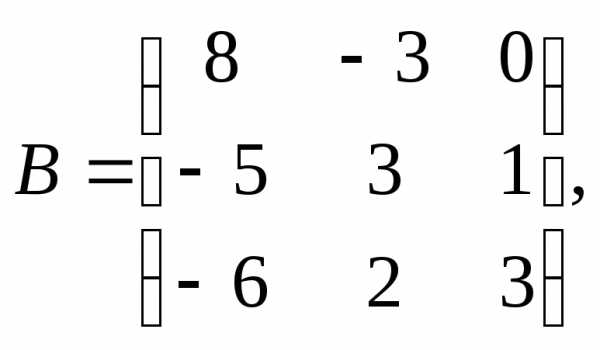 α= – 3,β = 10.
α= – 3,β = 10. 3.
3. 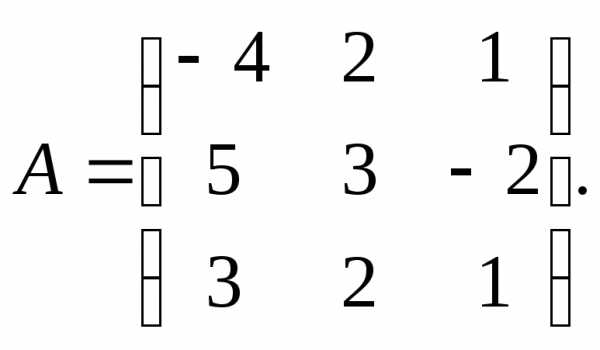

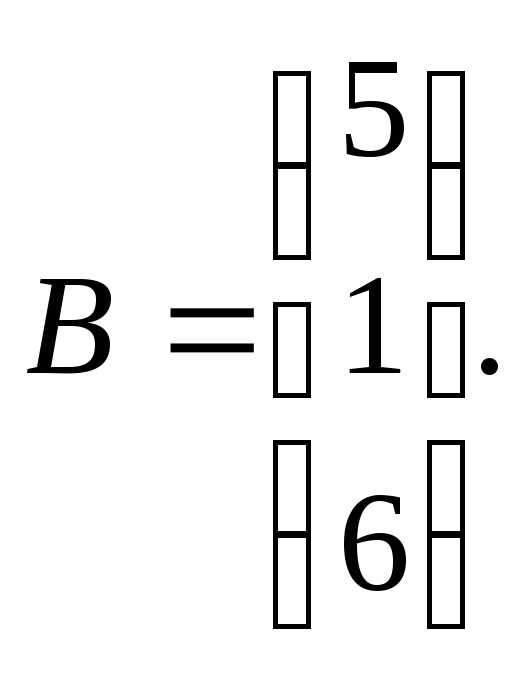 7.
7.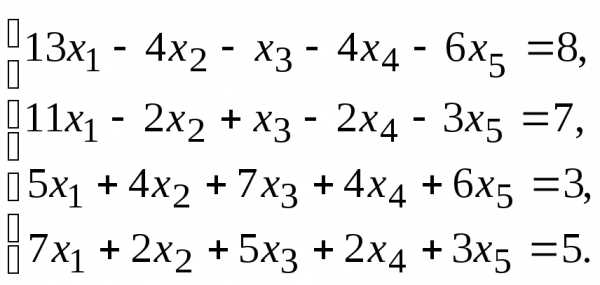
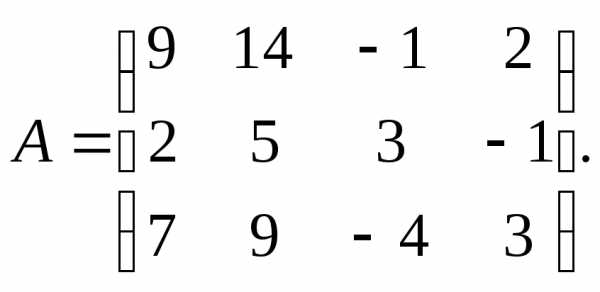 9.
9.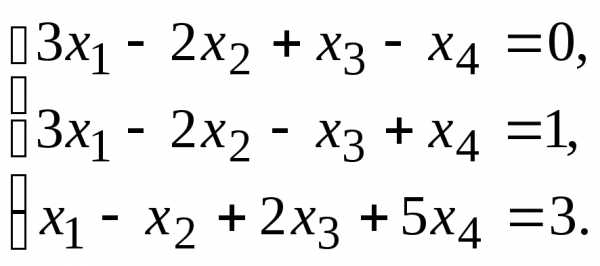
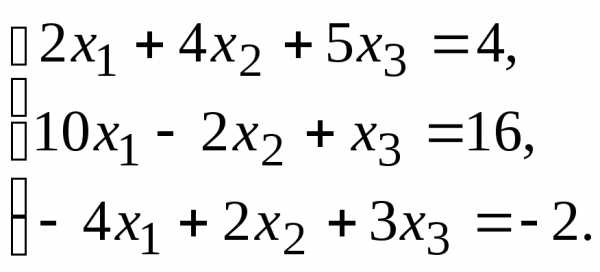 11.
11.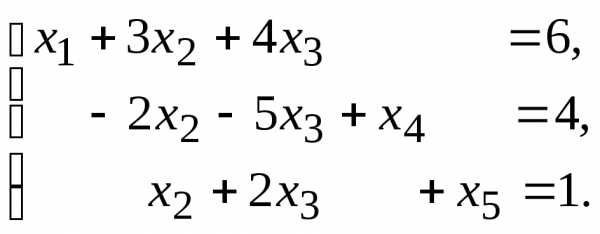 13.
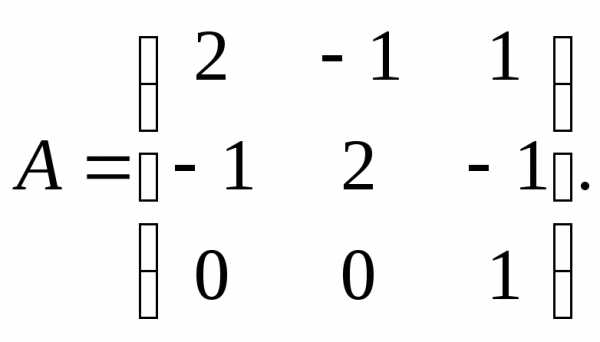
13.
 α= –
6,β = 4.
α= –
6,β = 4. 3.
3.

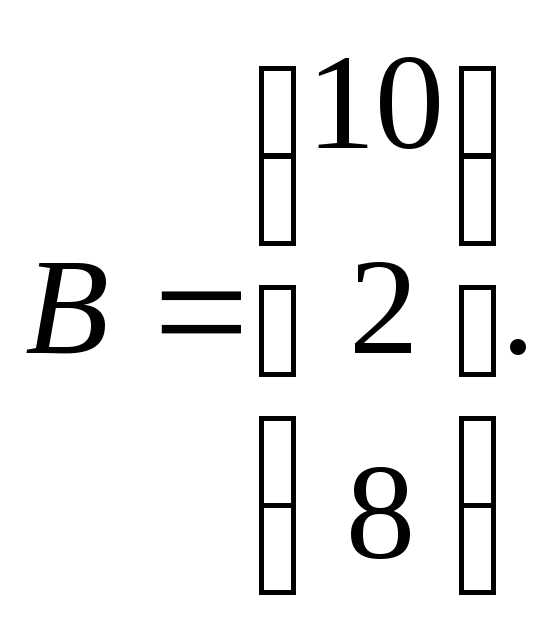 7.
7.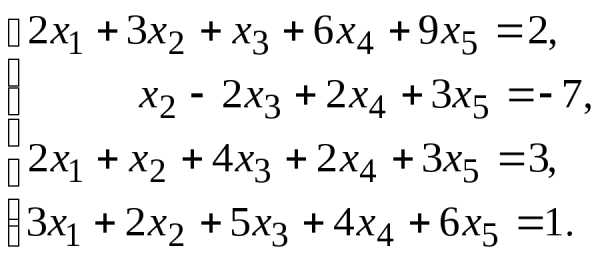
 9.
9.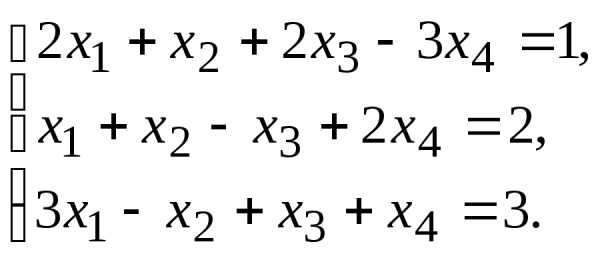
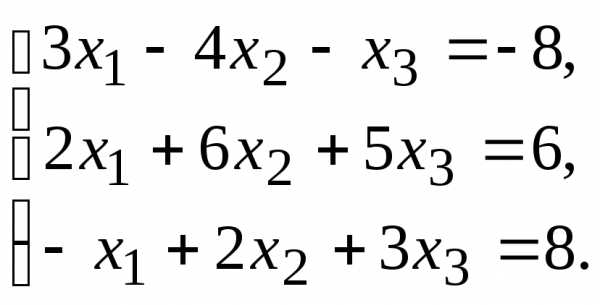 11.
11. 13.
13.
 α= –
2,β = 3.
α= –
2,β = 3.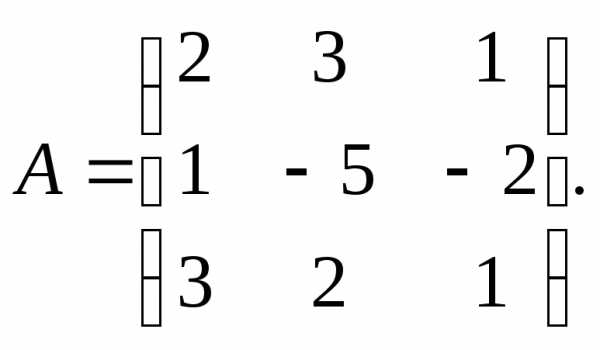
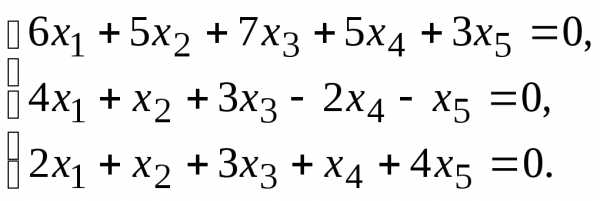
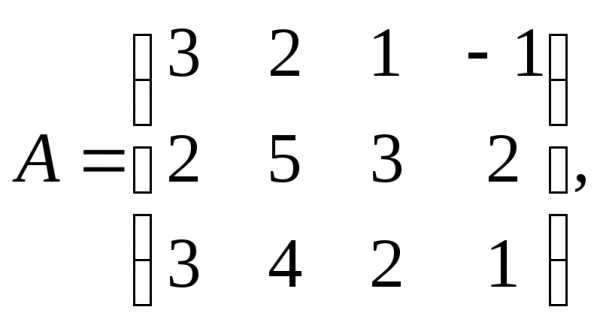
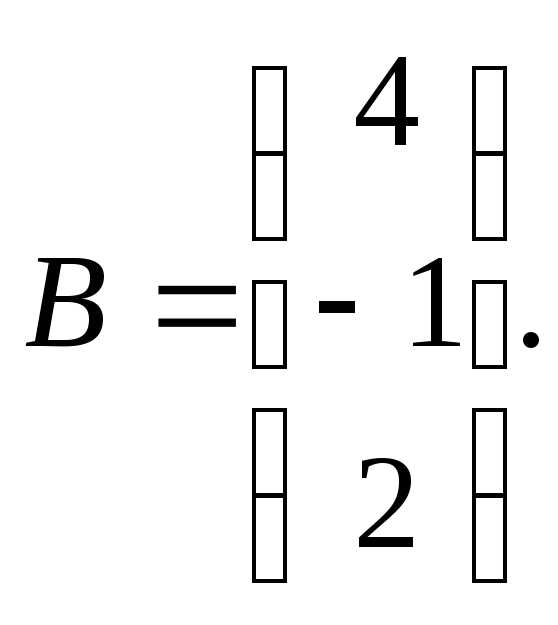 7.
7.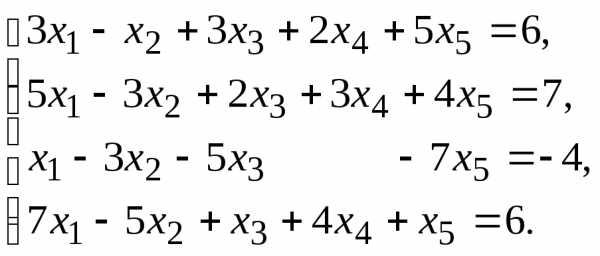
 9.
9.
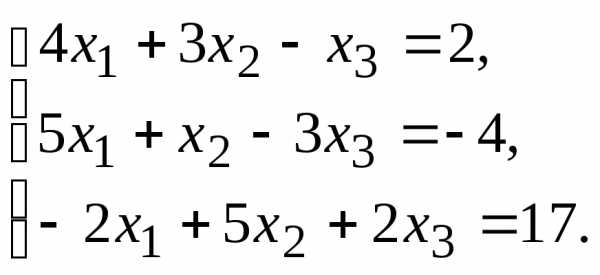 11.
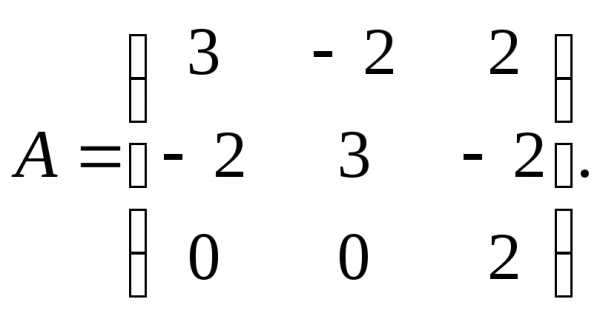
11. 13.
13.
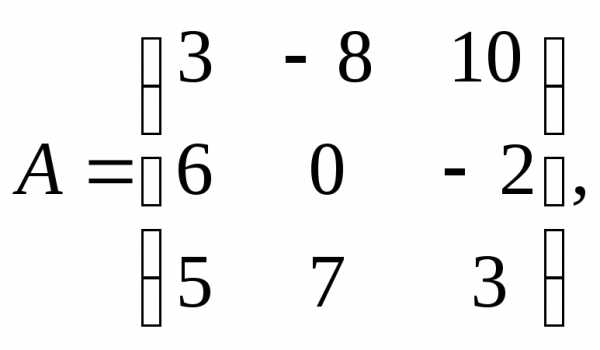
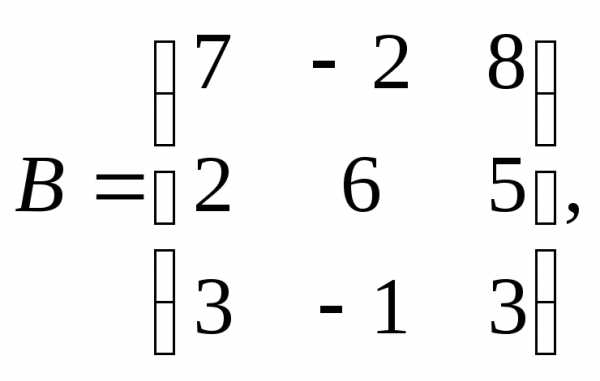 α= 9,β
= – 3.
α= 9,β
= – 3.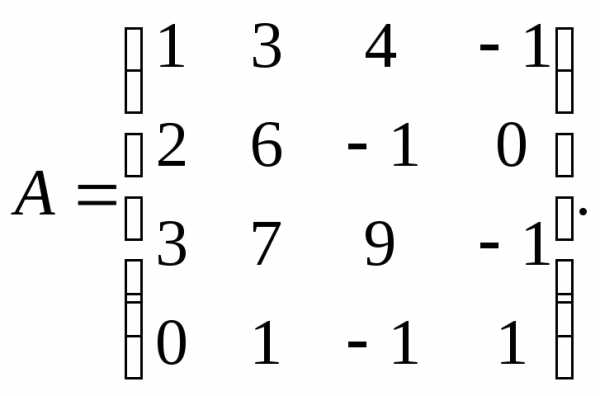 3.
3.
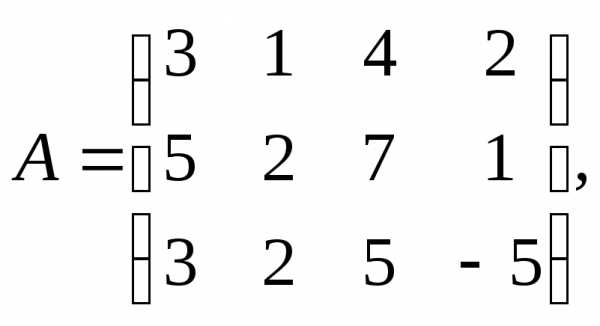
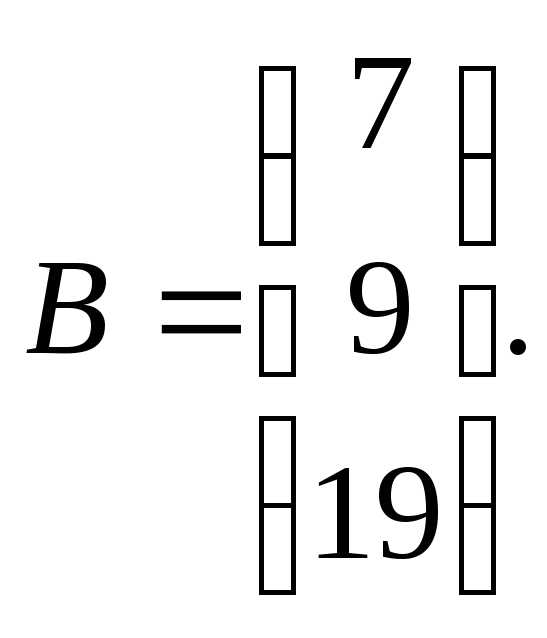 7.
7. 
 9.
9.
 11.
11.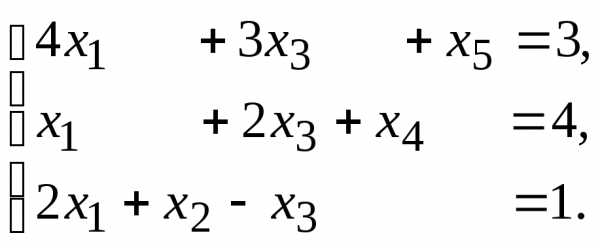 13.
13.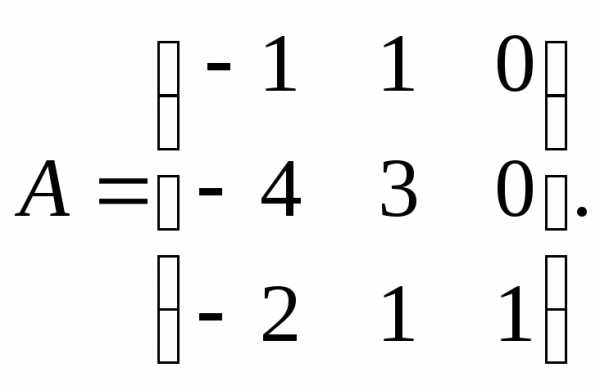
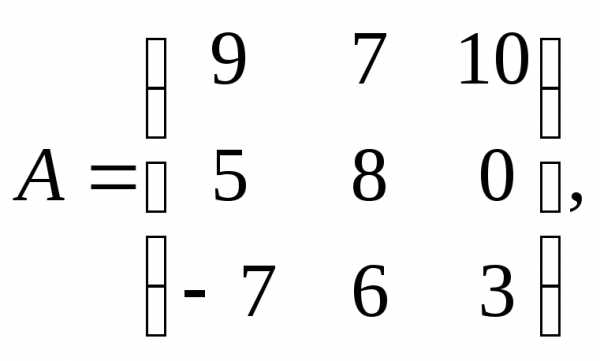
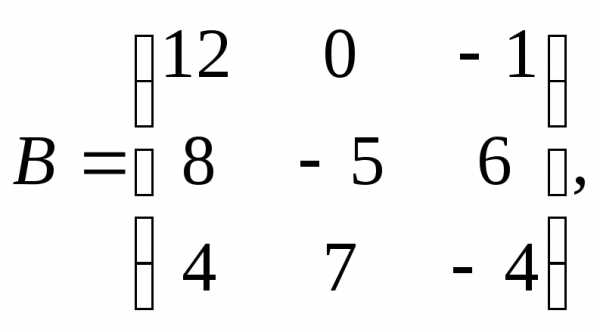 α = – 10, β = –
2.
α = – 10, β = –
2.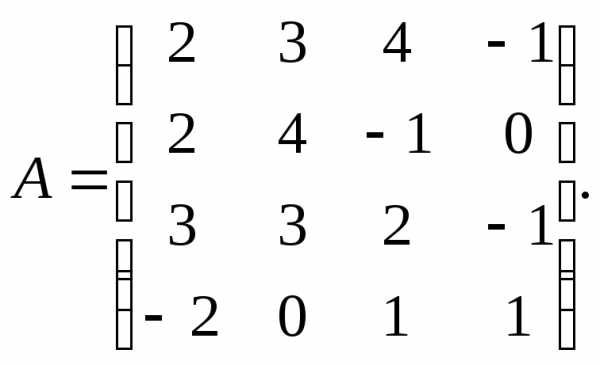 3.
3.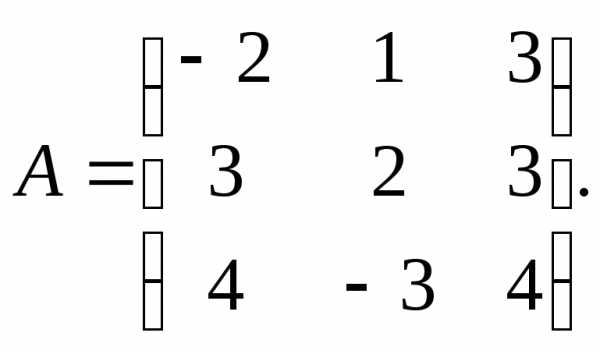
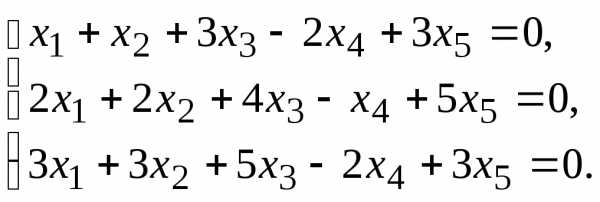

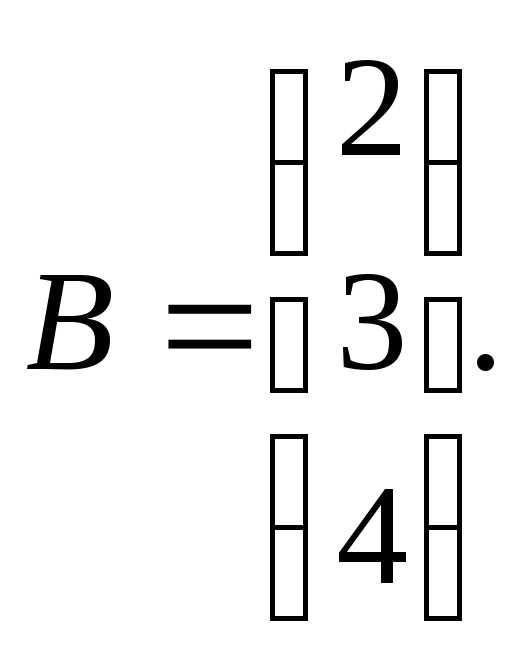 7.
7.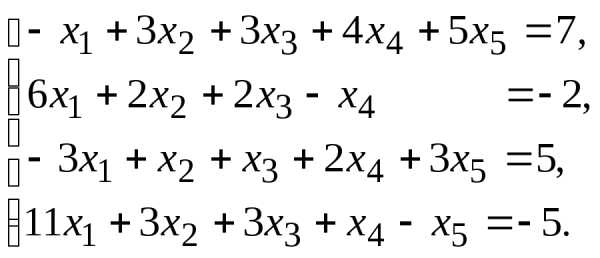
 9.
9.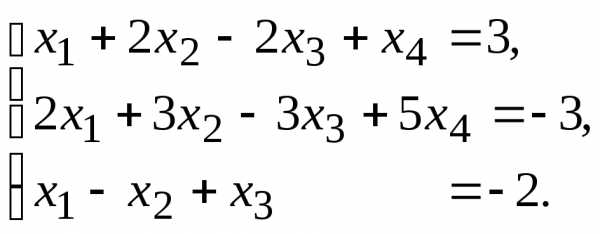
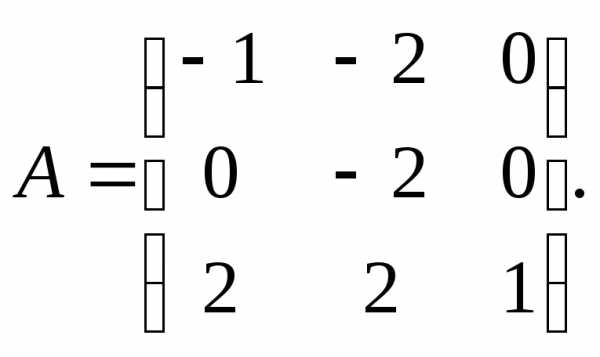
 11.
11. 13.
13.
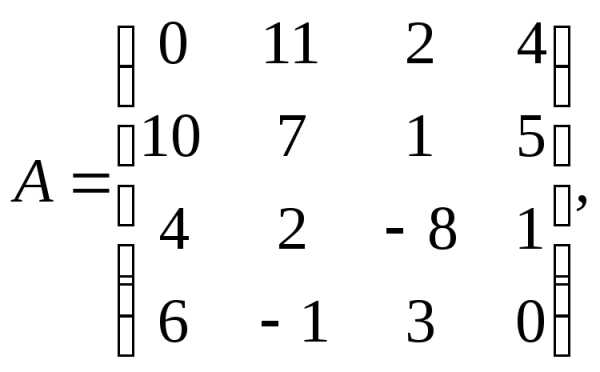
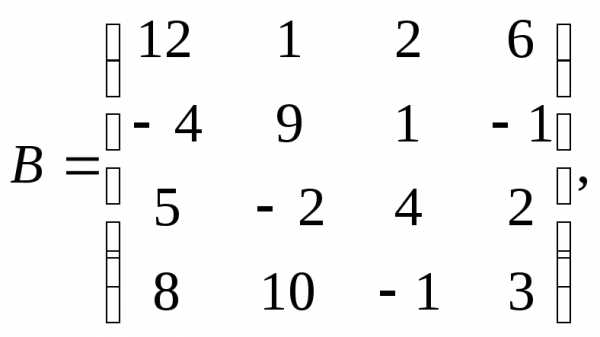 α = – 2, β =
4.
α = – 2, β =
4.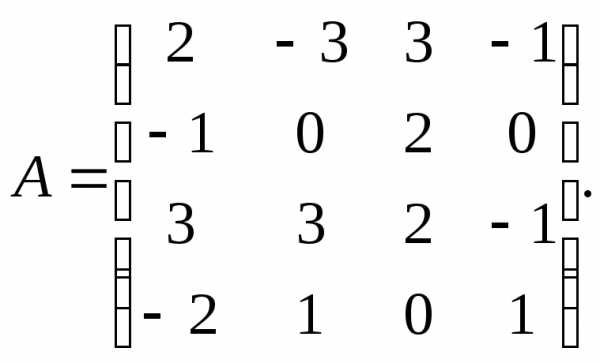 3.
3.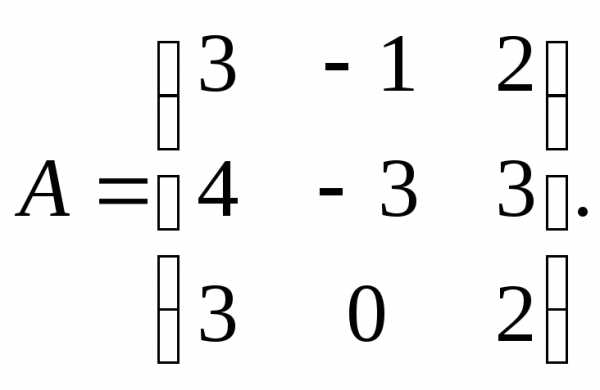
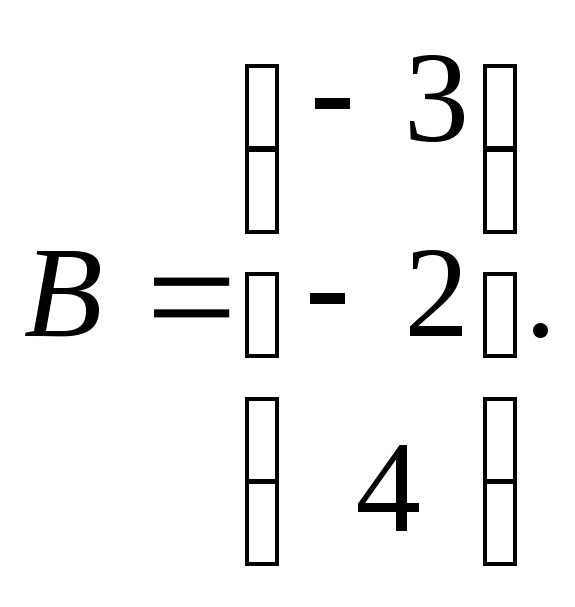 7.
7.
 9.
9.
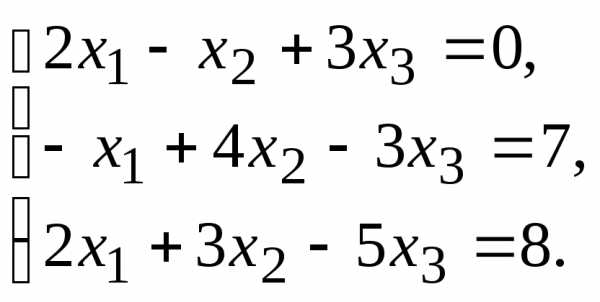 11.
11. 13.
13.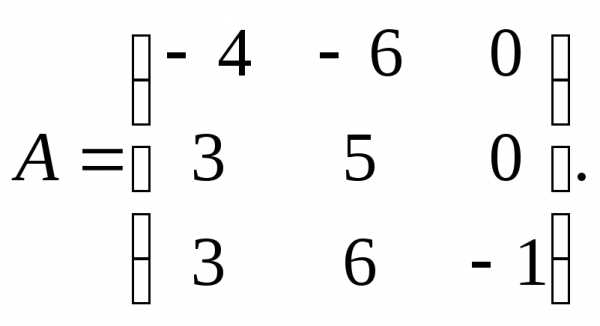
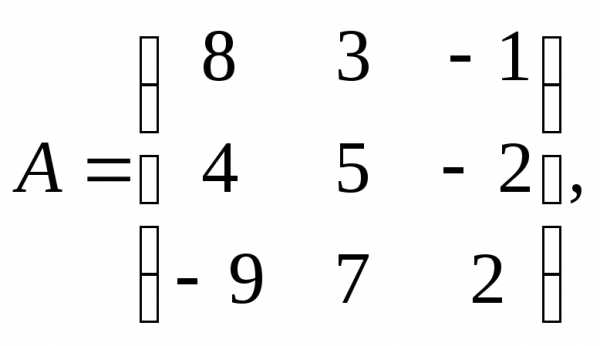
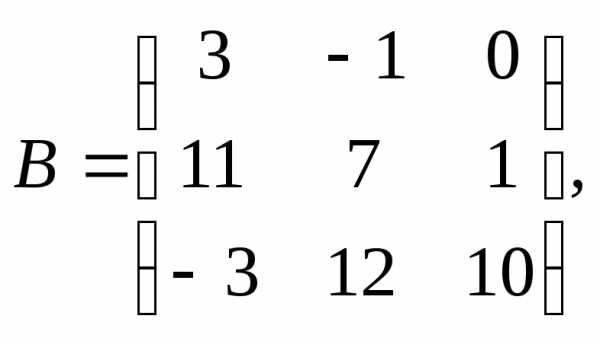 α = – 9, β =
5.
α = – 9, β =
5. 3.
3.

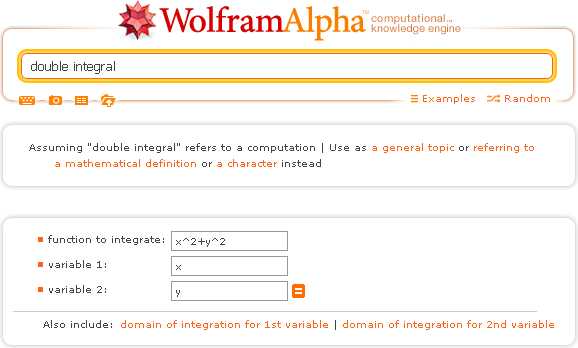
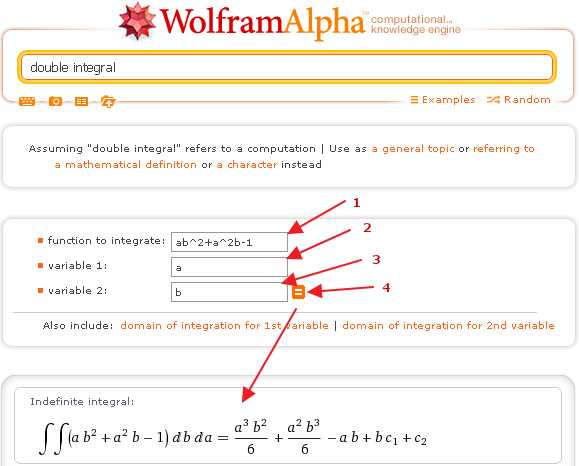


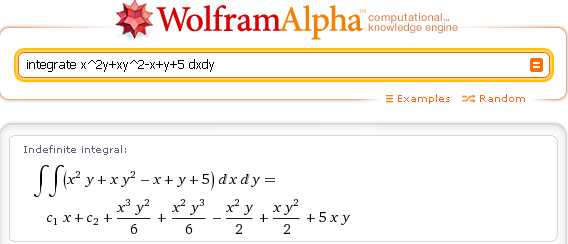




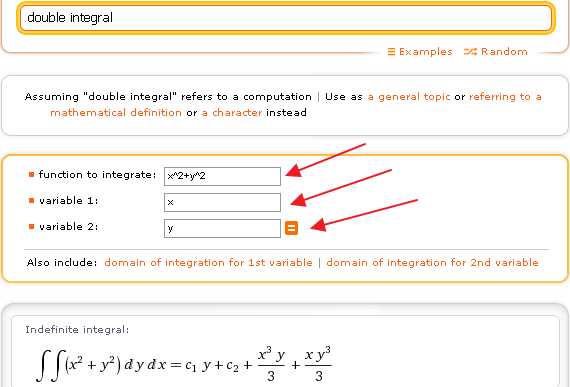



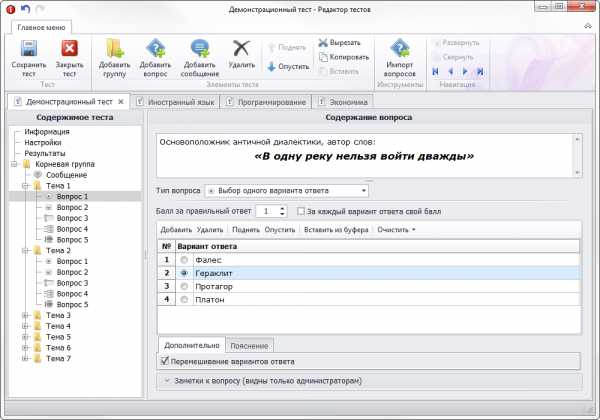
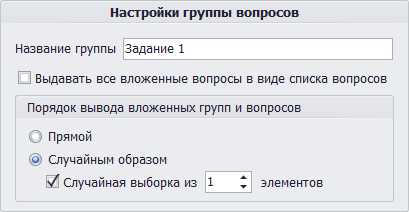
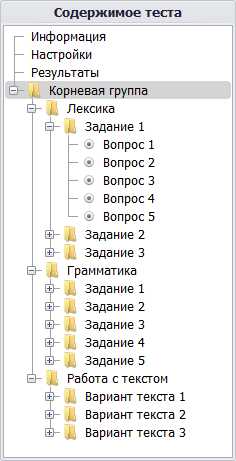
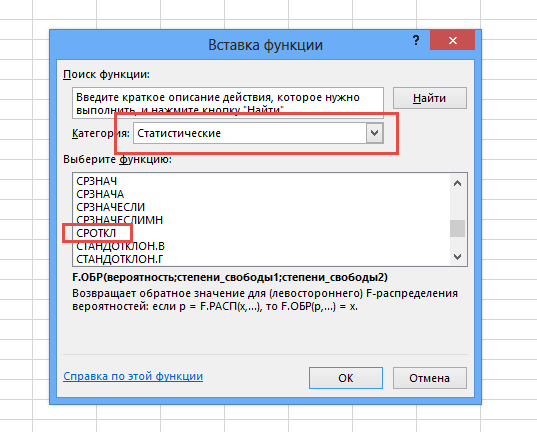
 Амплитуда и фаза факториала комплексного аргумента.
Амплитуда и фаза факториала комплексного аргумента. Пи-функция, определённая для всех вещественных чисел, кроме отрицательных целых, и совпадающая при натуральных значениях аргумента с факториалом.
Пи-функция, определённая для всех вещественных чисел, кроме отрицательных целых, и совпадающая при натуральных значениях аргумента с факториалом.









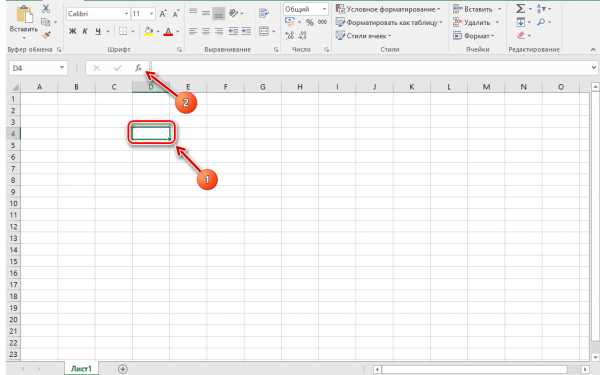

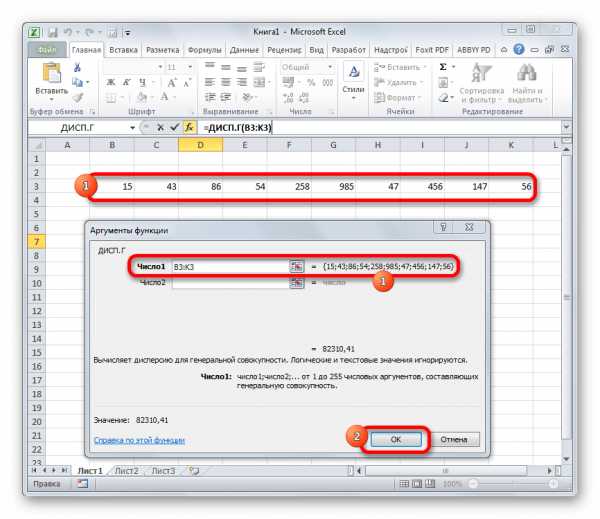

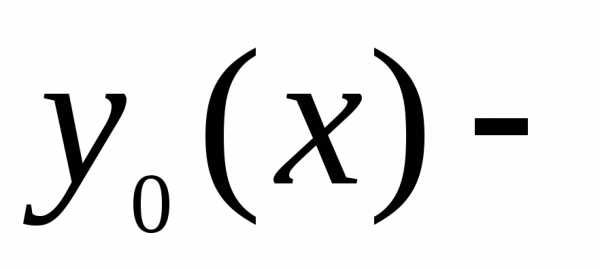 общее
решение уравнения (17), а
общее
решение уравнения (17), а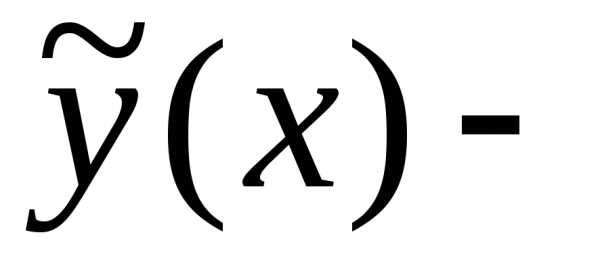 частное
решение уравнения (17). Иными словами,
общее решение линейного неоднородного
уравнения есть сумма общего решения
линейного однородного решения и одного
из частных решений линейного неоднородного
уравнения.
частное
решение уравнения (17). Иными словами,
общее решение линейного неоднородного
уравнения есть сумма общего решения
линейного однородного решения и одного
из частных решений линейного неоднородного
уравнения.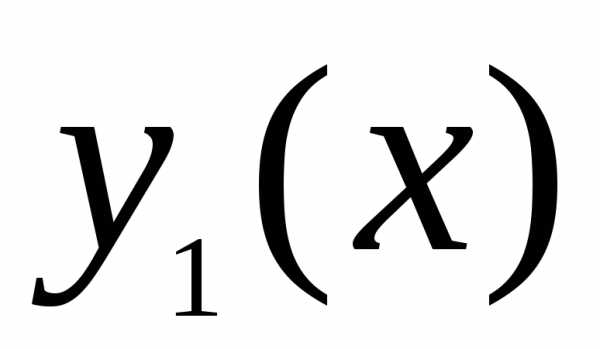 и
и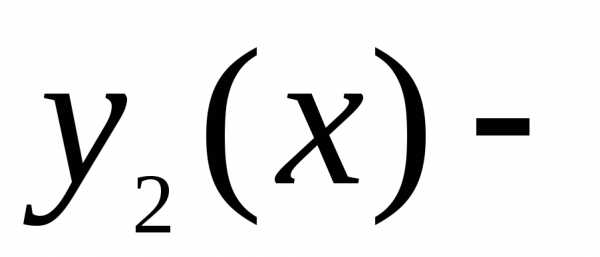 решения
дифференциальных уравнений:исоответственно. Это означает, что, разбив
правую часть линейного неоднородного
дифференциального уравнения на сумму
двух слагаемых, можно свести его решение
к решению двух более простых дифференциальных
уравнений.
решения
дифференциальных уравнений:исоответственно. Это означает, что, разбив
правую часть линейного неоднородного
дифференциального уравнения на сумму
двух слагаемых, можно свести его решение
к решению двух более простых дифференциальных
уравнений. ,
,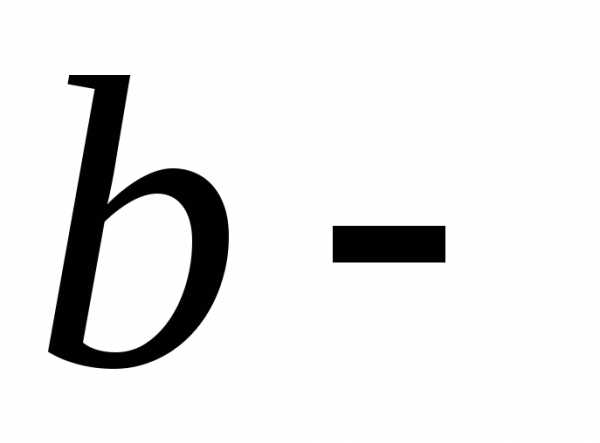 постоянные числа,
постоянные числа, 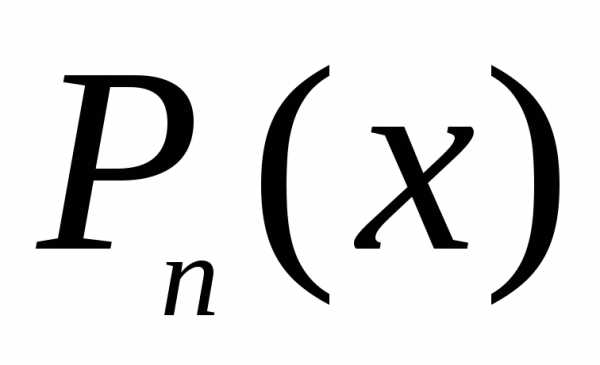 ,
,  многочлены порядка
многочлены порядка 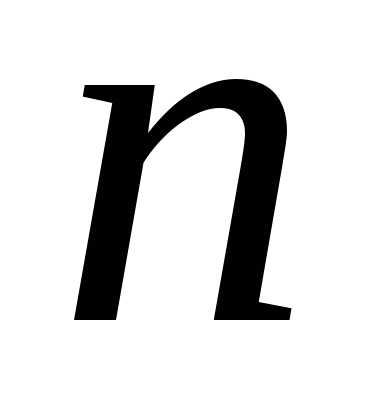 и
и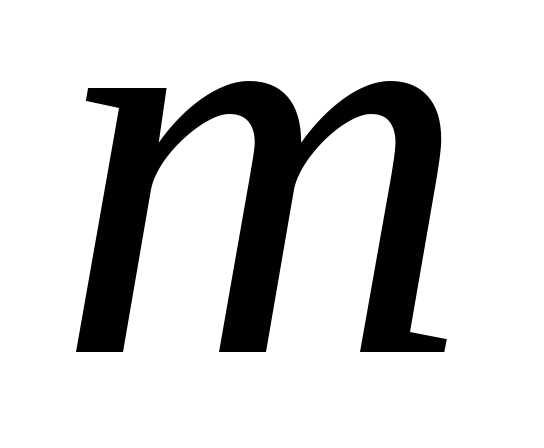 .
.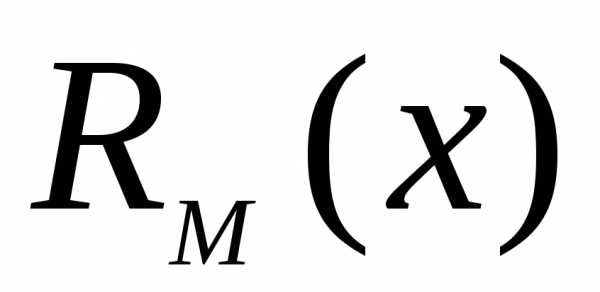 и
и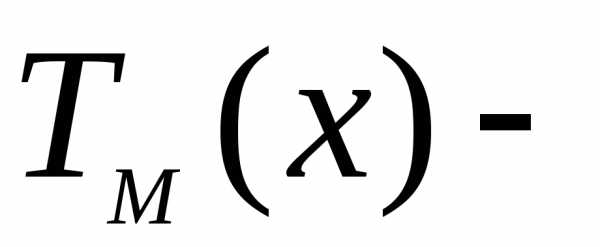 многочлены степени
многочлены степени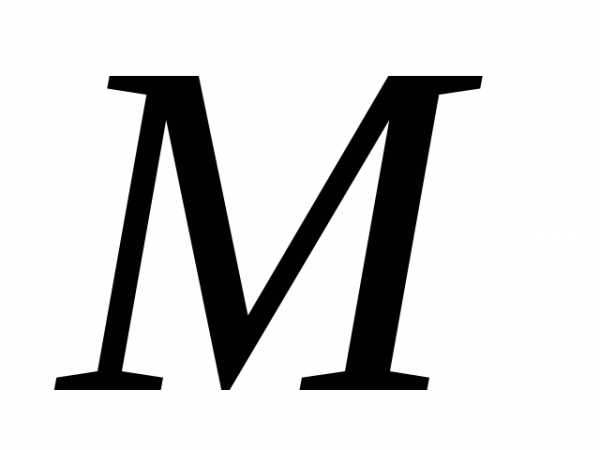 с неопределенными коэффициентами (их
число равно
с неопределенными коэффициентами (их
число равно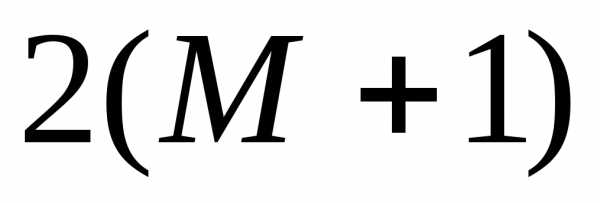 ).
Степень множителя
).
Степень множителя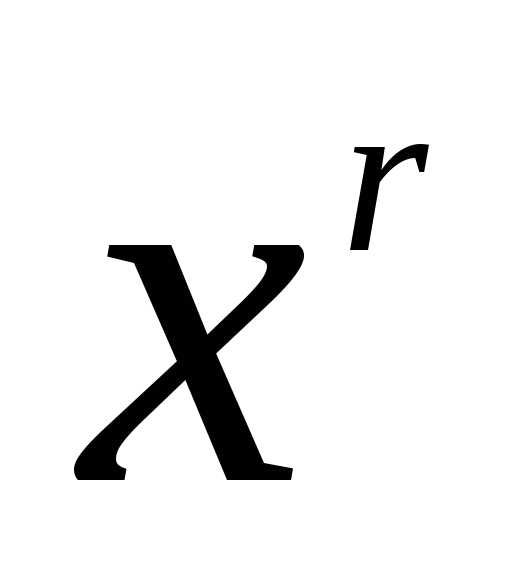 определяется
по следующему правилу.
определяется
по следующему правилу.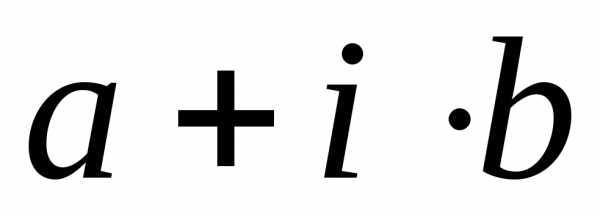 (комплексное при
(комплексное при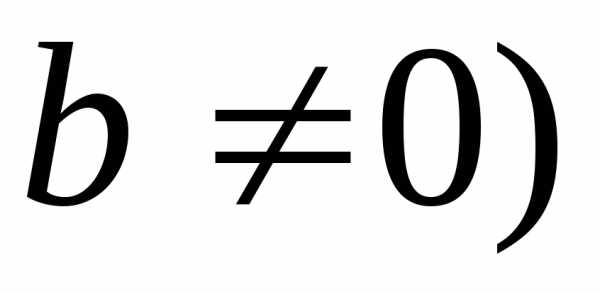 не совпадает ни с одним из корней
характеристического уравнения (18), то
не совпадает ни с одним из корней
характеристического уравнения (18), то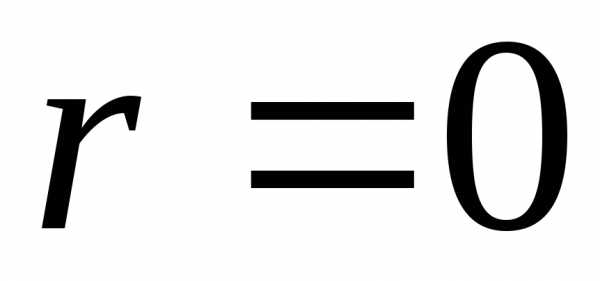 .
Если контрольное число совпадает с
одним из корней характеристического
уравнения, то
.
Если контрольное число совпадает с
одним из корней характеристического
уравнения, то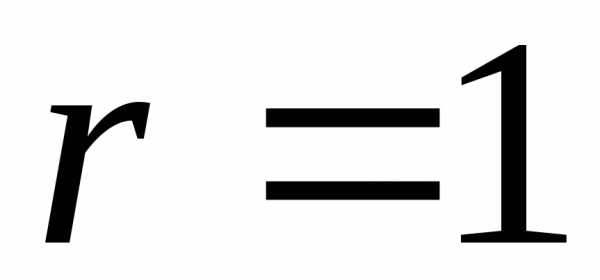 .
Наконец, если контрольное число совпадает
с корнем характеристического уравнения
и этот корень кратный, то
.
Наконец, если контрольное число совпадает
с корнем характеристического уравнения
и этот корень кратный, то .
Очевидно, что последний случай возможен
только при
.
Очевидно, что последний случай возможен
только при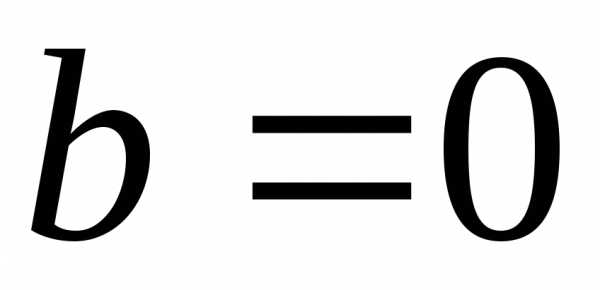 ,
так как кратный корень может быть только
вещественным.
,
так как кратный корень может быть только
вещественным.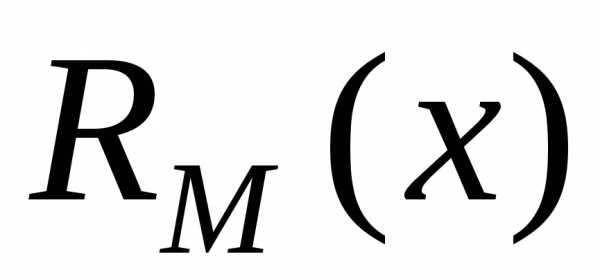 и
и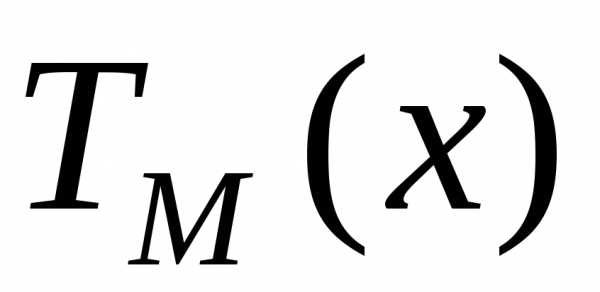 следует подставить выражение (20) в
уравнение (17), предварительно найдя его
производные
следует подставить выражение (20) в
уравнение (17), предварительно найдя его
производные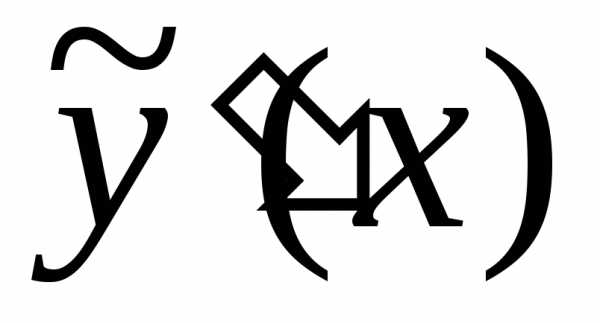 и
и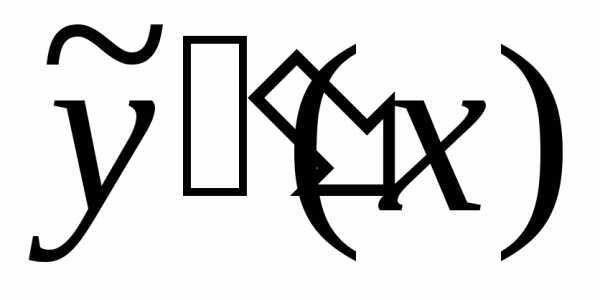 .
Неопределенные коэффициенты находятся
из системы линейных алгебраических
уравнений, к которым сведется уравнение
(17) после подстановки в него выражения
(20).
.
Неопределенные коэффициенты находятся
из системы линейных алгебраических
уравнений, к которым сведется уравнение
(17) после подстановки в него выражения
(20).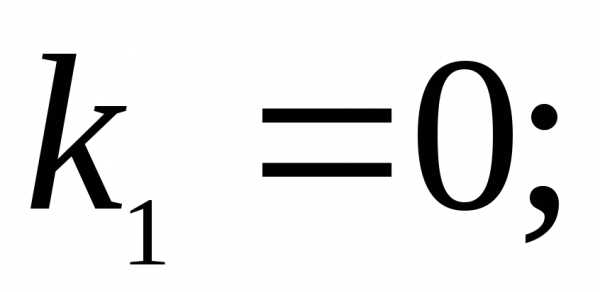
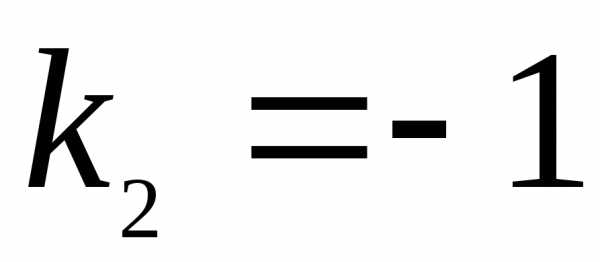 .
Общее решение однородного уравнения
записывается в форме:,
где
.
Общее решение однородного уравнения
записывается в форме:,
где и
и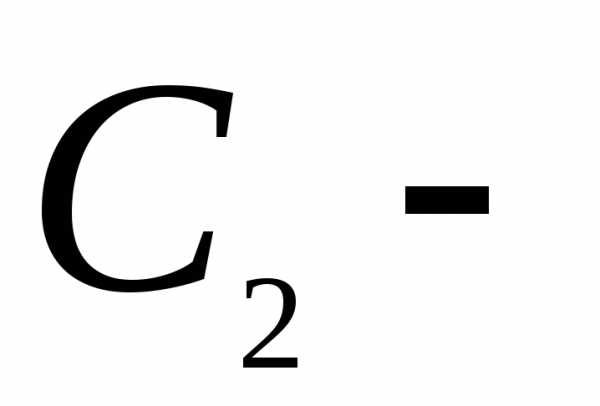 произвольные постоянные.
произвольные постоянные.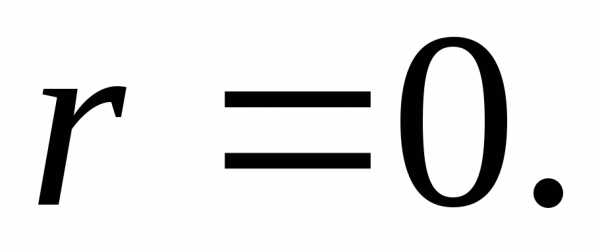 Таким образом, формула (20) дает:.
Найдем производные
Таким образом, формула (20) дает:.
Найдем производные .
.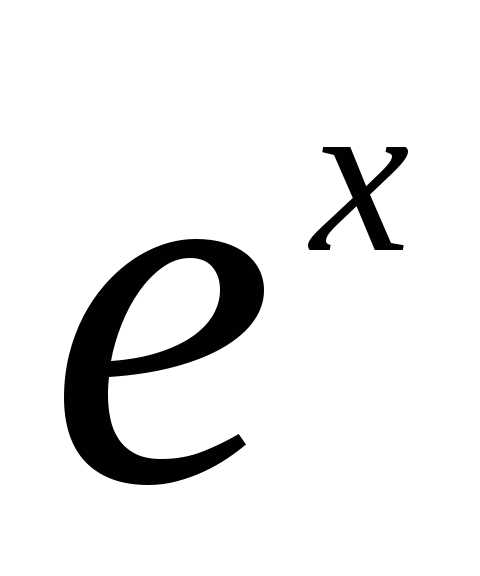 и приводя подобные, получаем:
и приводя подобные, получаем: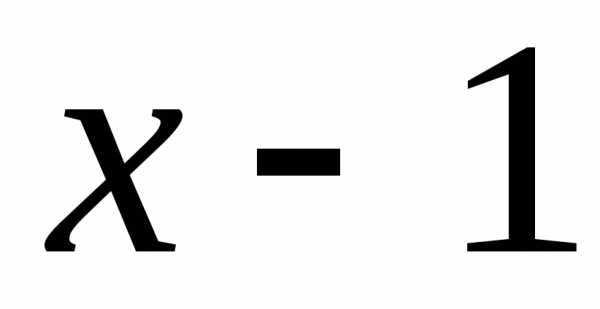 .
.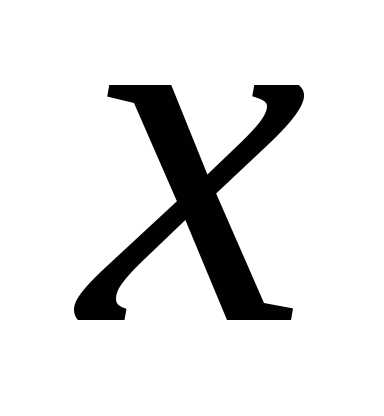 ,
что возможно лишь при выполнении
следующих условий:
,
что возможно лишь при выполнении
следующих условий: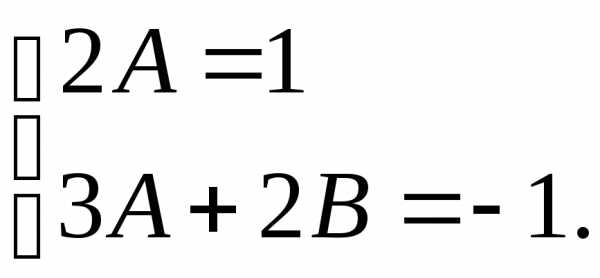

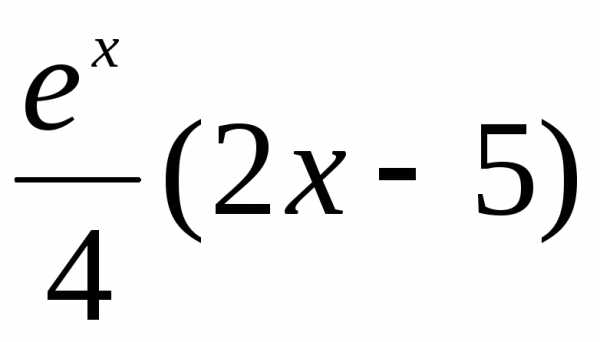 .
. и
и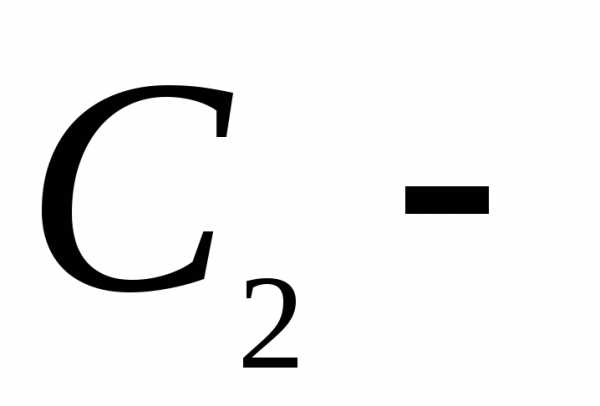 произвольные постоянные.
произвольные постоянные.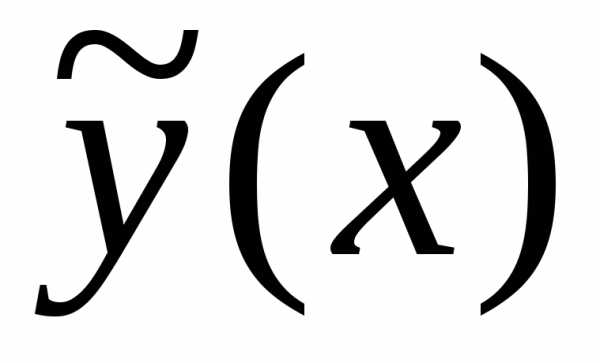 :
: возможно только в том случае, когда
коэффициенты при функцияхв левой и правой частях уравнения будут
одинаковы. Это условие приводит к системе
уравнений:
возможно только в том случае, когда
коэффициенты при функцияхв левой и правой частях уравнения будут
одинаковы. Это условие приводит к системе
уравнений: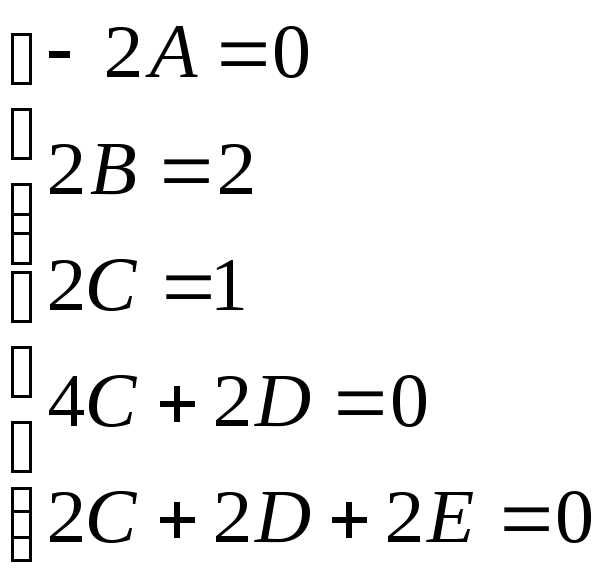
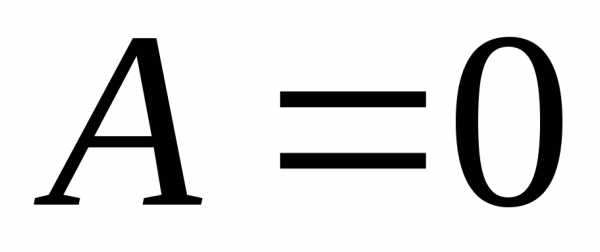 ;
;  ;
; 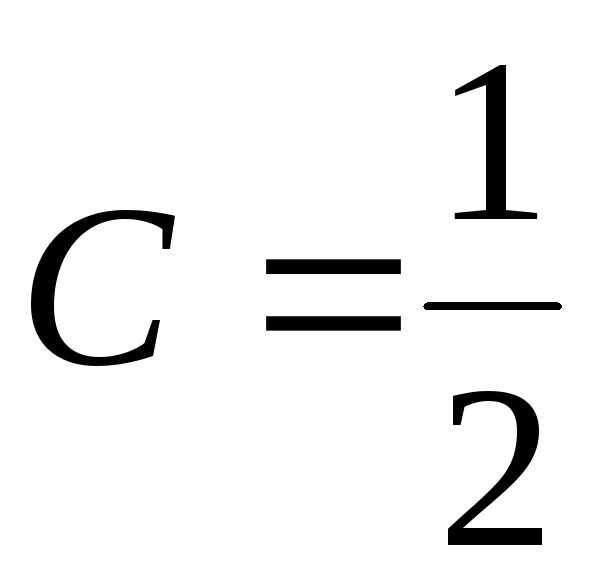 ;;
;;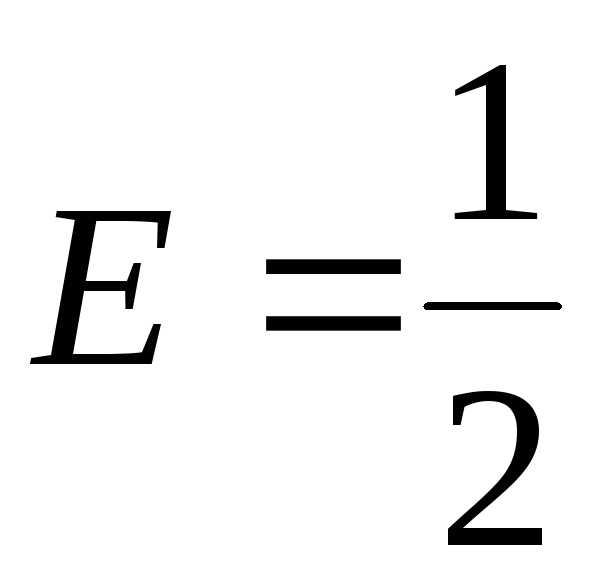 .
.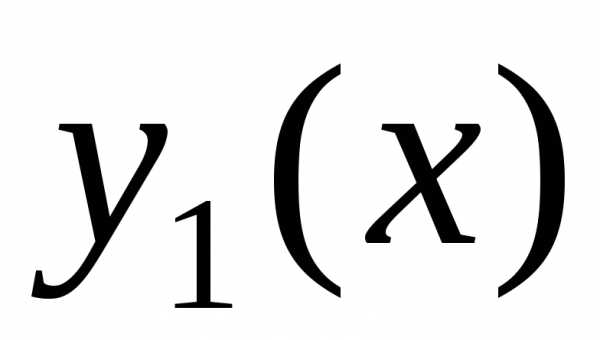 и
и однородного дифференциального уравнения.
Частное решение неоднородного
дифференциального уравнения ищется в
виде их линейной комбинации, в которой
произвольные постоянные
однородного дифференциального уравнения.
Частное решение неоднородного
дифференциального уравнения ищется в
виде их линейной комбинации, в которой
произвольные постоянные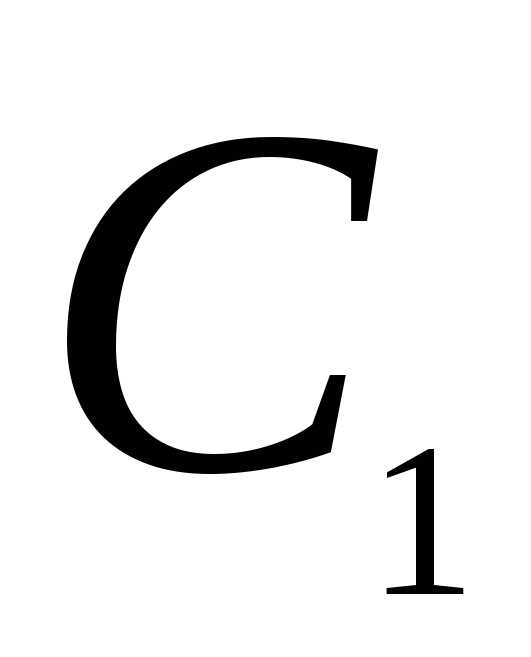 и
и заменяются на неизвестные функции
заменяются на неизвестные функции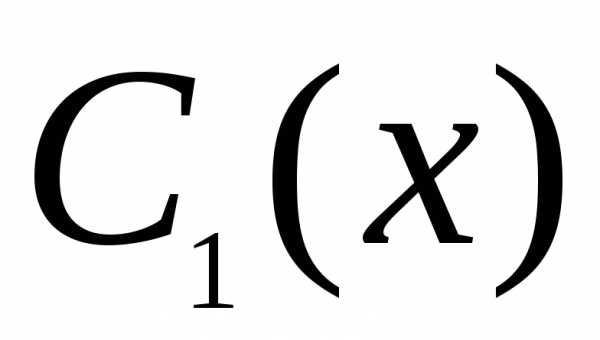 и
и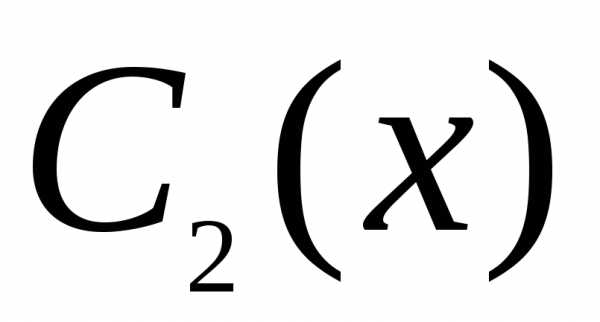 :
:
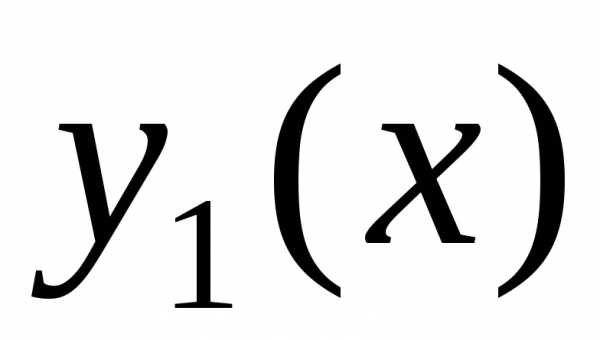 и
и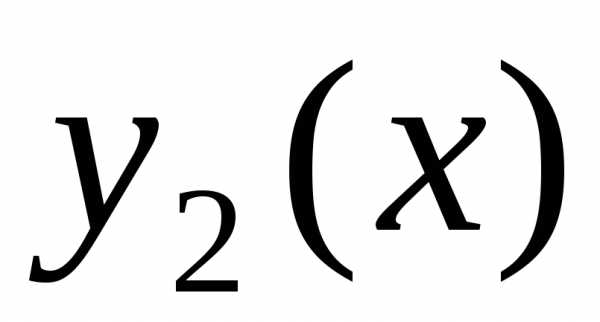 являются решениями однородного
дифференциального уравнения (12), выражения
в третьей и четвертой скобках в (23)
тождественно равны нулю. Наложим на
пока неопределенные функции
являются решениями однородного
дифференциального уравнения (12), выражения
в третьей и четвертой скобках в (23)
тождественно равны нулю. Наложим на
пока неопределенные функции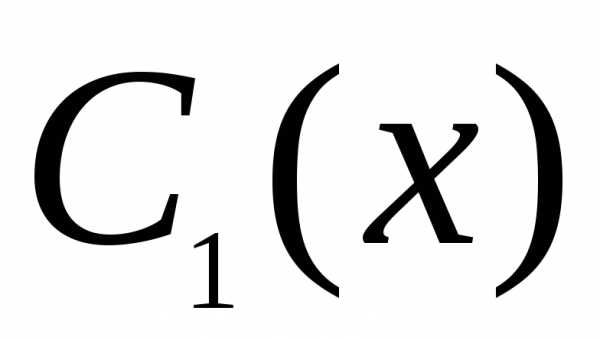 и
и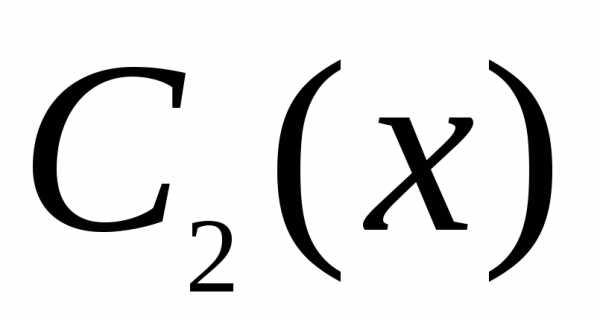 следующее условие:
следующее условие: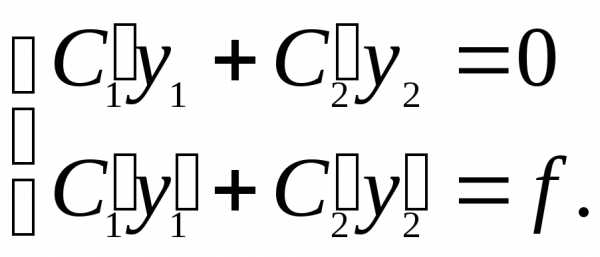 (25)
(25) и
и ,
и отличен от нуля, система всегда имеет
единственное решение.
,
и отличен от нуля, система всегда имеет
единственное решение.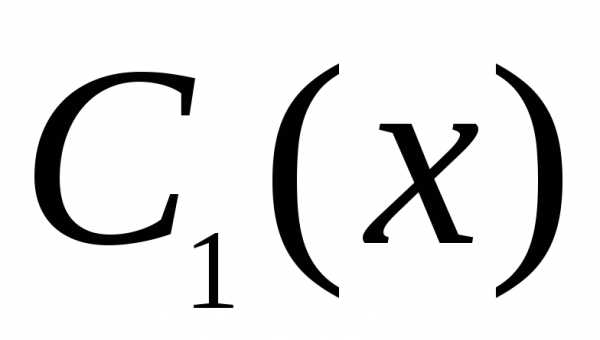 и
и ,
то есть проинтегрировать полученные
из (25) функции
,
то есть проинтегрировать полученные
из (25) функции и
и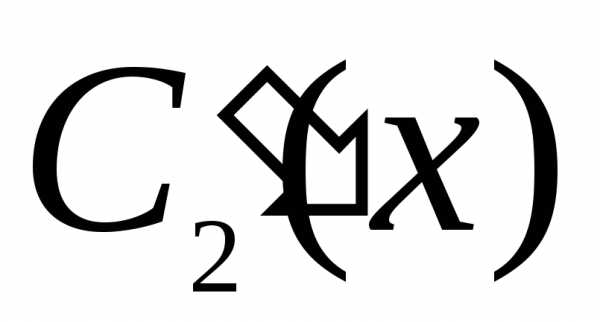 )
и, подставить их в выражение для
)
и, подставить их в выражение для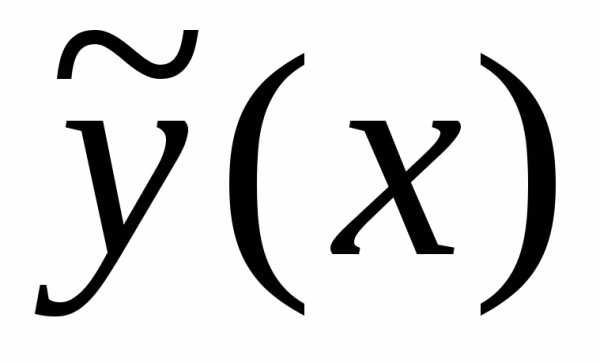 .
.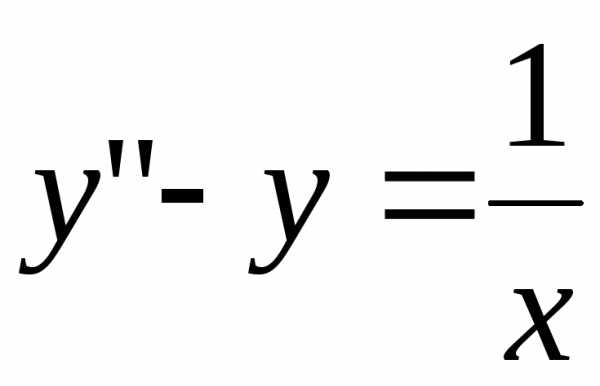 .
.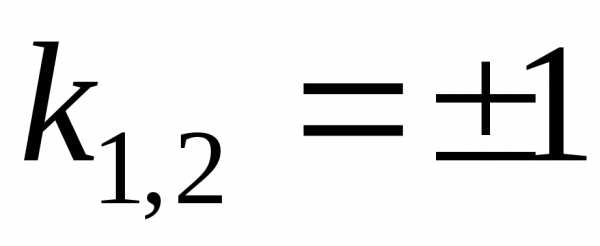 ,
и общее решение записывается в виде:
,
и общее решение записывается в виде: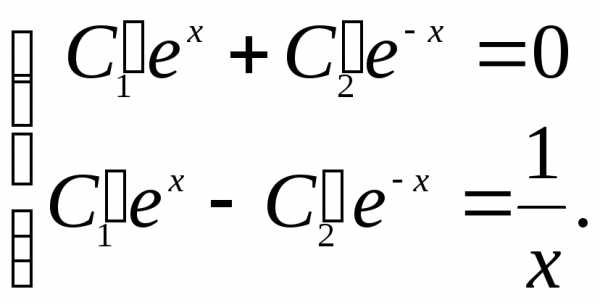
 и
и 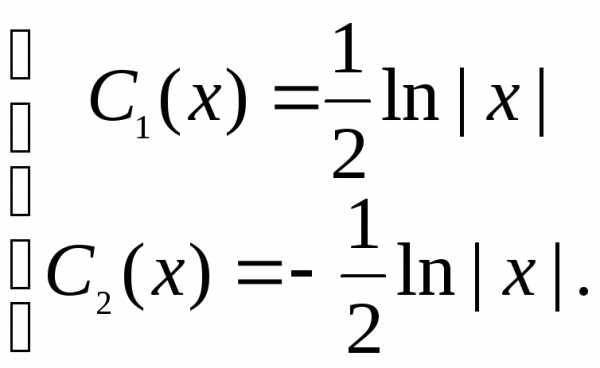
 ,
то общее решение однородного уравнения
имеет вид:
,
то общее решение однородного уравнения
имеет вид: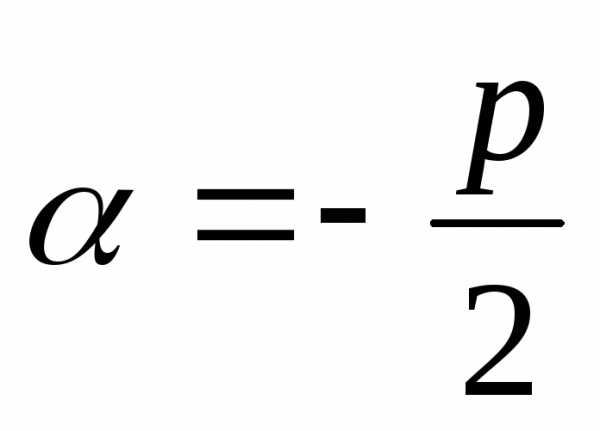 ,
,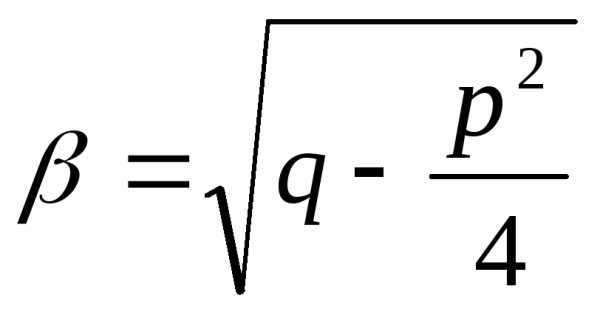 .
. .
.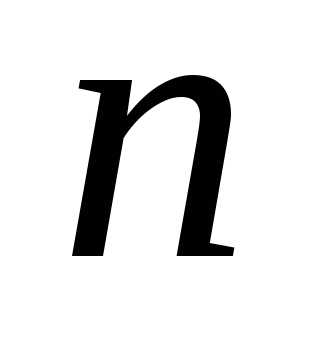 ,
то частное решение линейного неоднородного
уравнения имеет вид:
,
то частное решение линейного неоднородного
уравнения имеет вид: с неизвестными коэффициентами, которые
нужно найти,
с неизвестными коэффициентами, которые
нужно найти,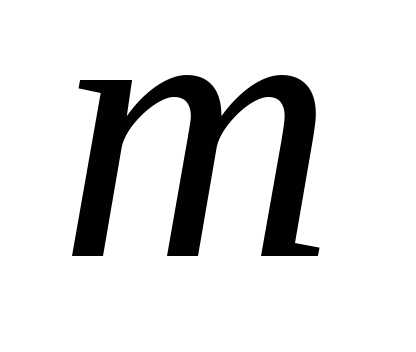 – число корней характеристического
уравнения, равных нулю.
– число корней характеристического
уравнения, равных нулю. – многочлен степени
– многочлен степени с неизвестными коэффициентами,
с неизвестными коэффициентами,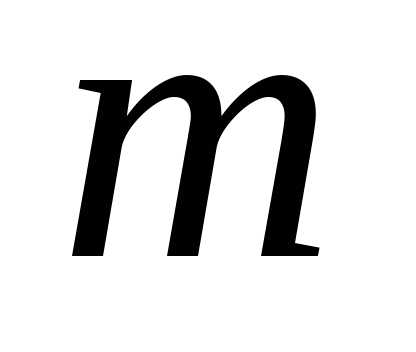 – кратность корня характеристического
уравнения
– кратность корня характеристического
уравнения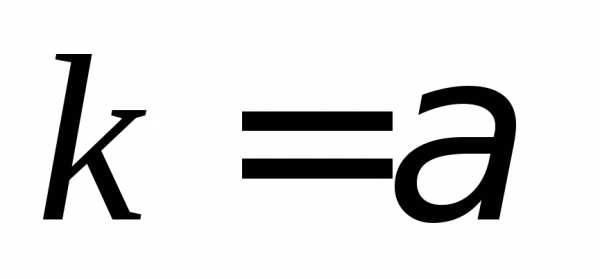 .
. ,
, и
и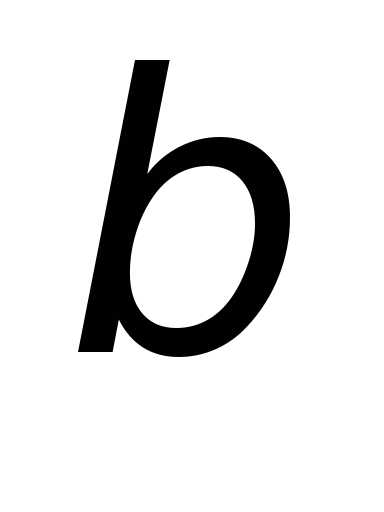 – известные числа, то частное решение
линейного неоднородного уравнения
имеет вид:
– известные числа, то частное решение
линейного неоднородного уравнения
имеет вид: ,
, – неизвестные коэффициенты,
– неизвестные коэффициенты,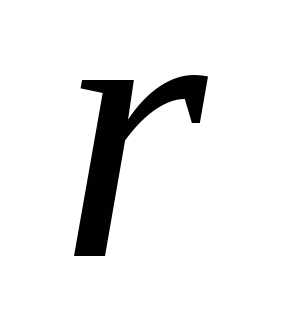 – число корней характеристического
уравнения, равных
– число корней характеристического
уравнения, равных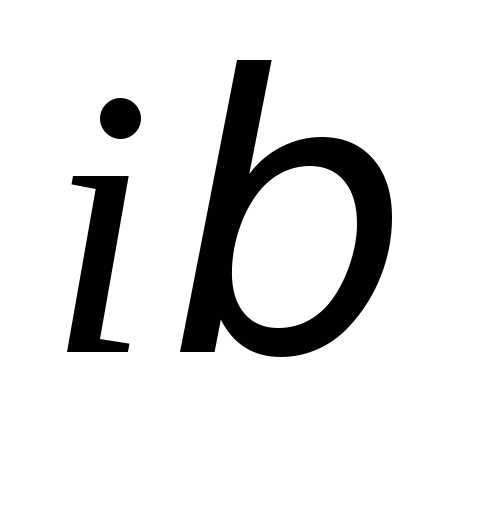 .
. и
и :,
:,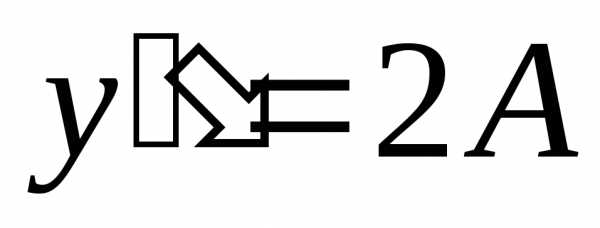 .
.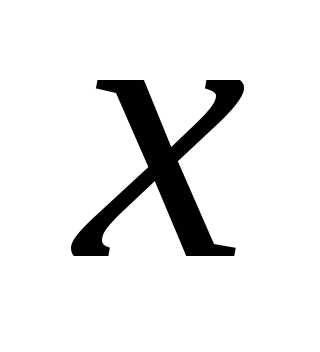 ,
получим систему алгебраических уравнений:
,
получим систему алгебраических уравнений:
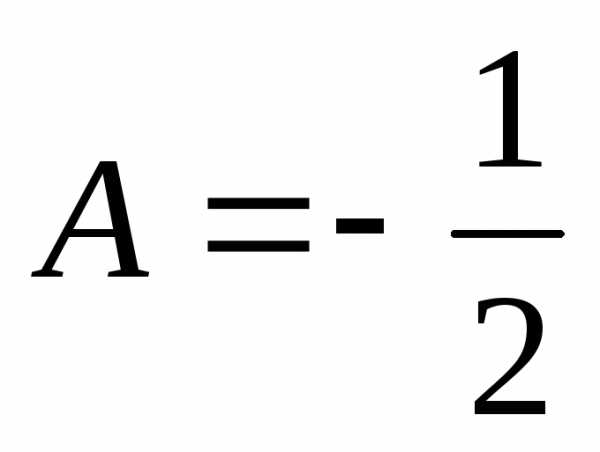 ,
,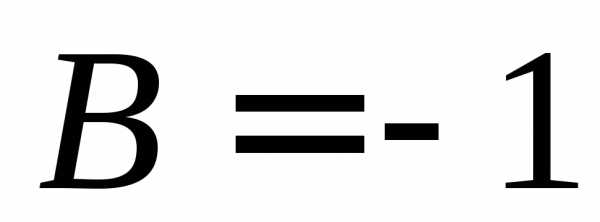 .
Итак,.
Тогда общее решение неоднородного
уравнения примет вид:
.
Итак,.
Тогда общее решение неоднородного
уравнения примет вид: = 1 не является корнем характеристического
уравнения, то частное решение неоднородного
уравнения необходимо искать в виде:.
Подставив
ив исходное уравнение, получим:
= 1 не является корнем характеристического
уравнения, то частное решение неоднородного
уравнения необходимо искать в виде:.
Подставив
ив исходное уравнение, получим: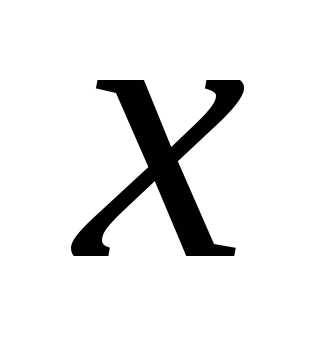 ,
получим систему уравнений:
,
получим систему уравнений:
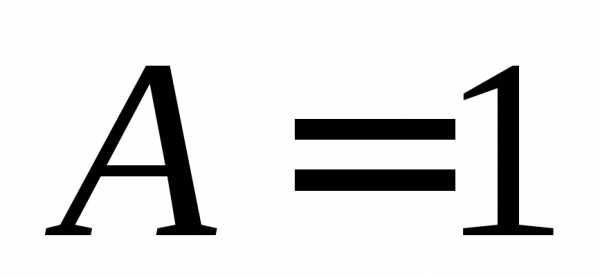 ,
,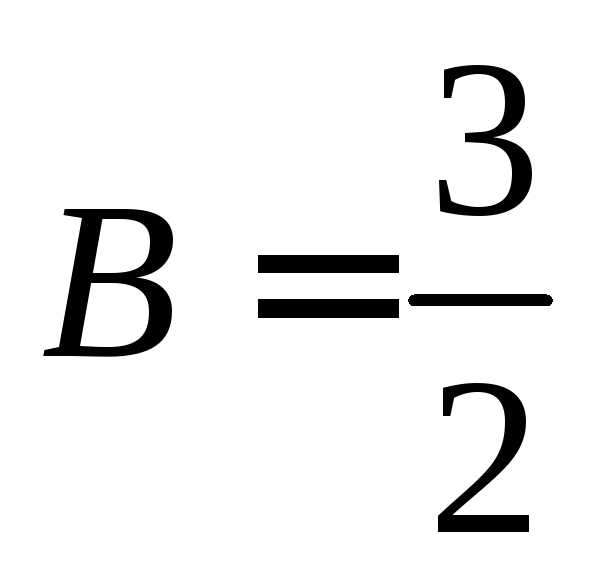 .
. ,
,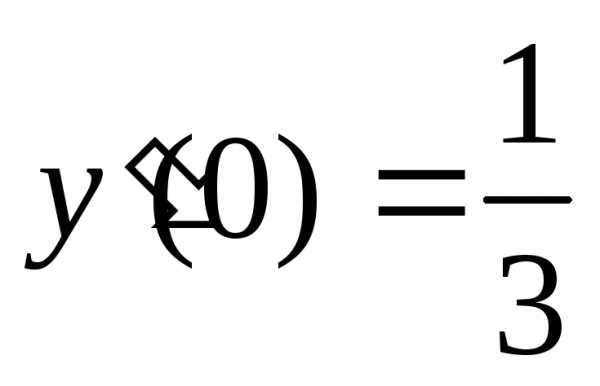 .
. и
и :
: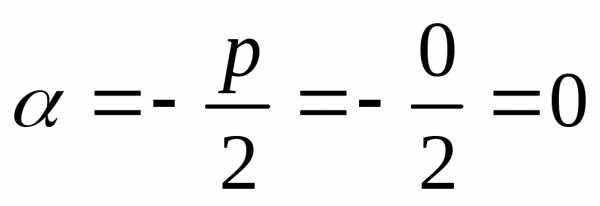 ,.
,. и
и в исходное уравнение, получим:
в исходное уравнение, получим: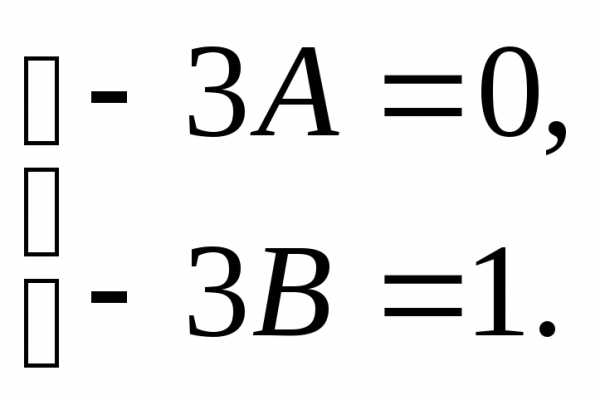
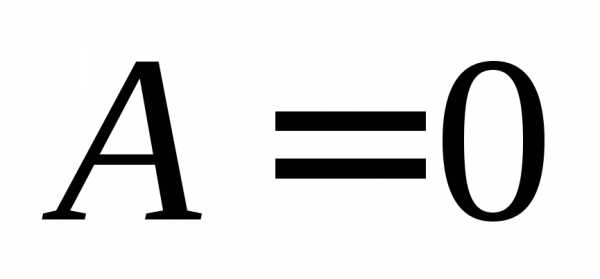 ,
,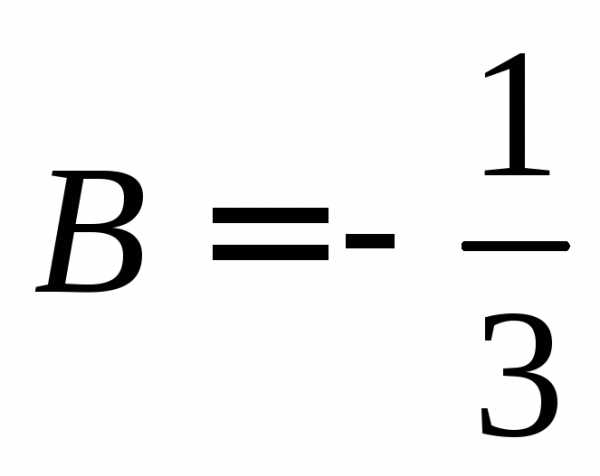 .
.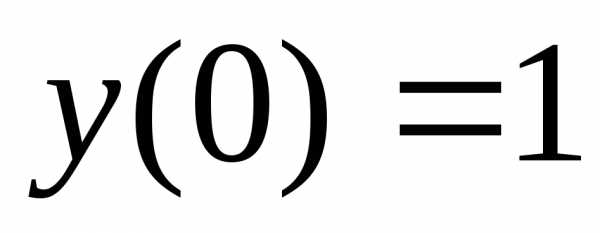 ,
,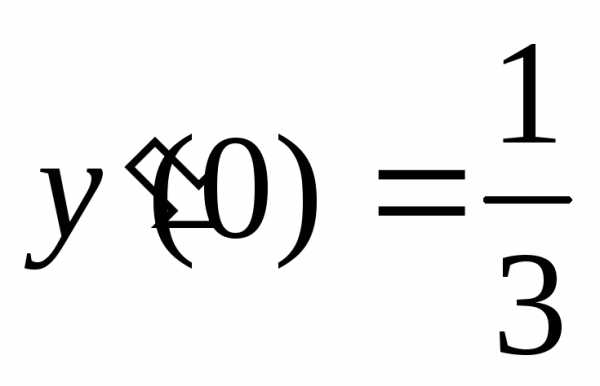 ,
имеет вид:
,
имеет вид: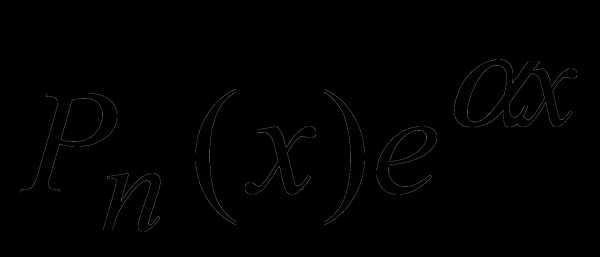 , где
, где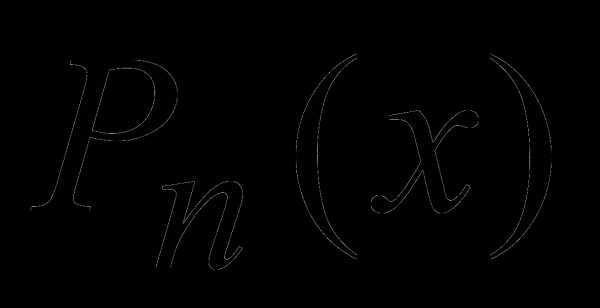 – многочлен n-ной степени:
– многочлен n-ной степени: , получим:
, получим: не является корнем характеристического уравнения, то и слева в уравнении (9) – полином n-ного порядка, приравнивая коэффициенты при равных степенях х слева и справа в (9), получим n+1 уравнение с n+1 неизвестной , найдем их и получим частное решение (8).
не является корнем характеристического уравнения, то и слева в уравнении (9) – полином n-ного порядка, приравнивая коэффициенты при равных степенях х слева и справа в (9), получим n+1 уравнение с n+1 неизвестной , найдем их и получим частное решение (8). есть однократный корень характеристического уравнения (7) (резонанс).
есть однократный корень характеристического уравнения (7) (резонанс). , и слева — полином (n+1)-й степени, а справа – n-й степени, и мы не сможем его найти.
, и слева — полином (n+1)-й степени, а справа – n-й степени, и мы не сможем его найти. есть двукратный корень характеристического уравнения,
есть двукратный корень характеристического уравнения, 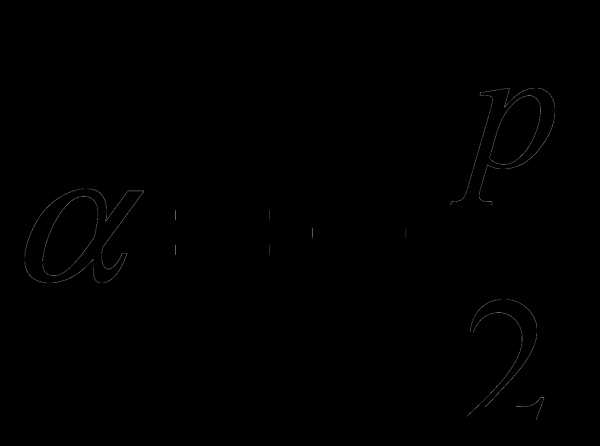 .
. ;
;  .
. подставим это решение и его производные ; в уравнение:
подставим это решение и его производные ; в уравнение: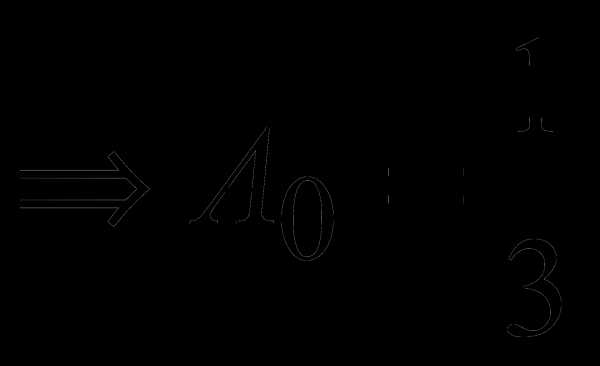 ;
; 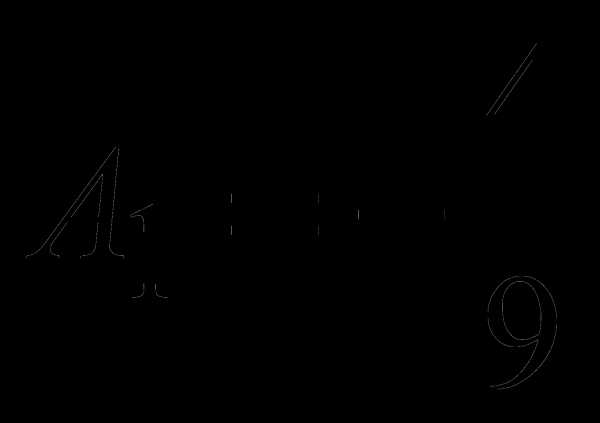 ;
;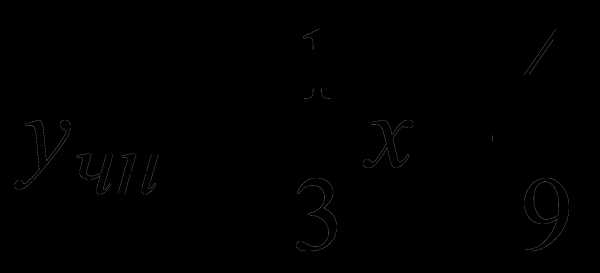 .
. ;
; ;
; 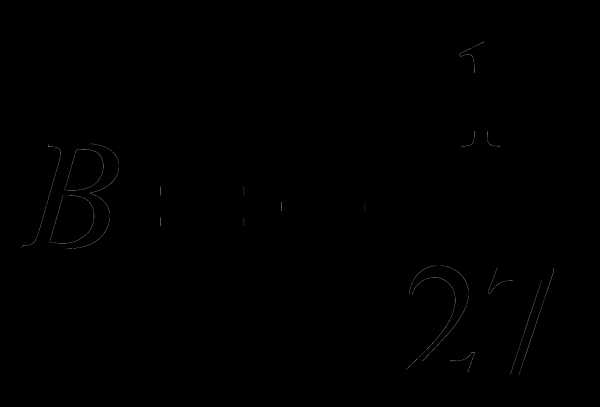 ;
;  .
. ;
; 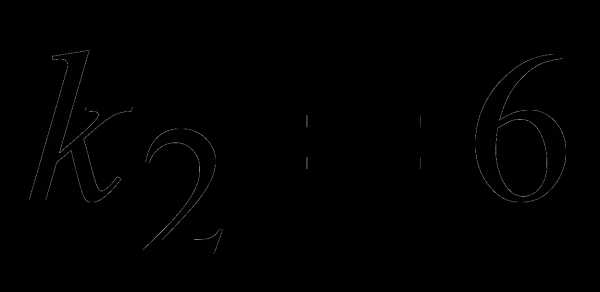 ;
; даёт резонанс
даёт резонанс ;
; 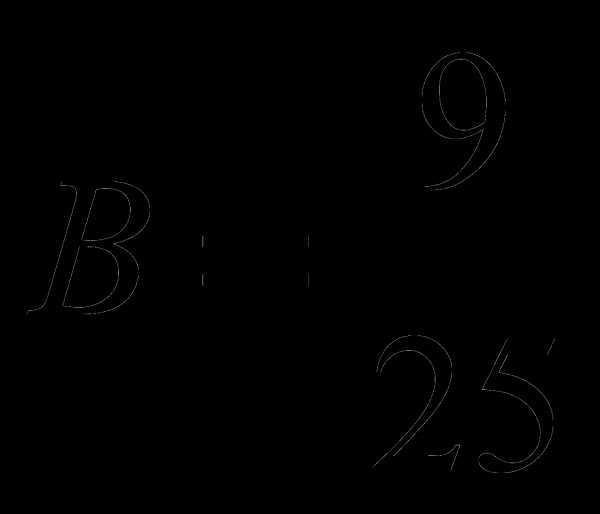 ;
;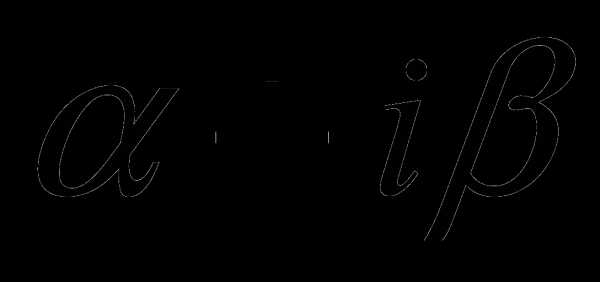 не является корнем характеристического уравнения, то частное решение уравнения (12) надо искать в виде
не является корнем характеристического уравнения, то частное решение уравнения (12) надо искать в виде и
и 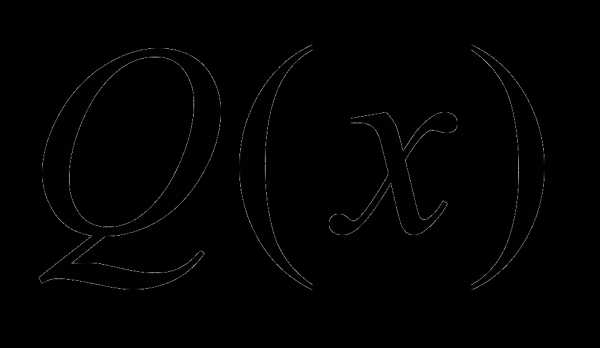 .
. есть корень характеристического уравнения, то частное решение ищем в виде
есть корень характеристического уравнения, то частное решение ищем в виде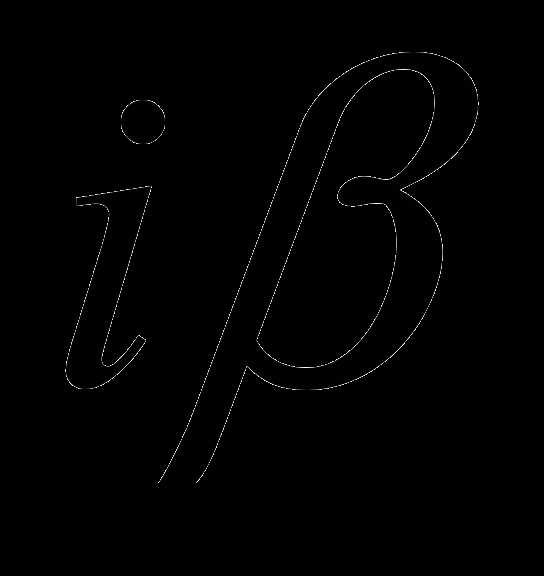 — не является корнем характеристического уравнения, то частное решение ищем в виде
— не является корнем характеристического уравнения, то частное решение ищем в виде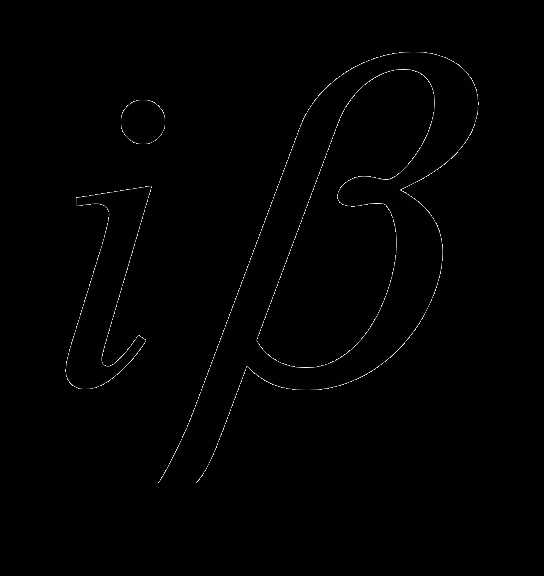 — корень характеристического уравнения, то частное решение уравнения (15) ищем в виде
— корень характеристического уравнения, то частное решение уравнения (15) ищем в виде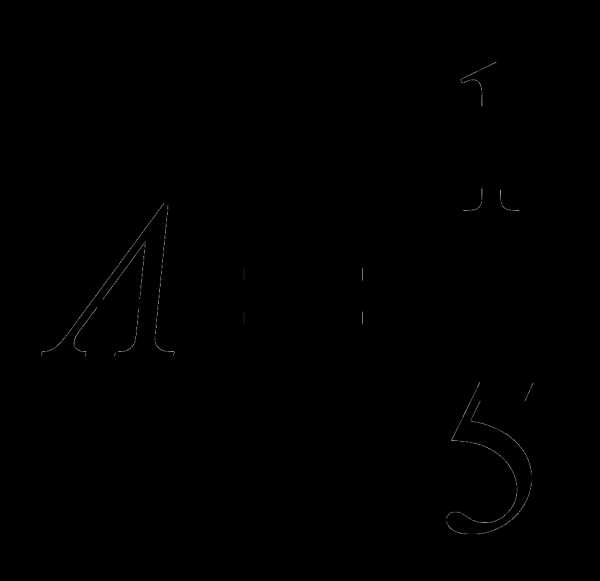 ;
;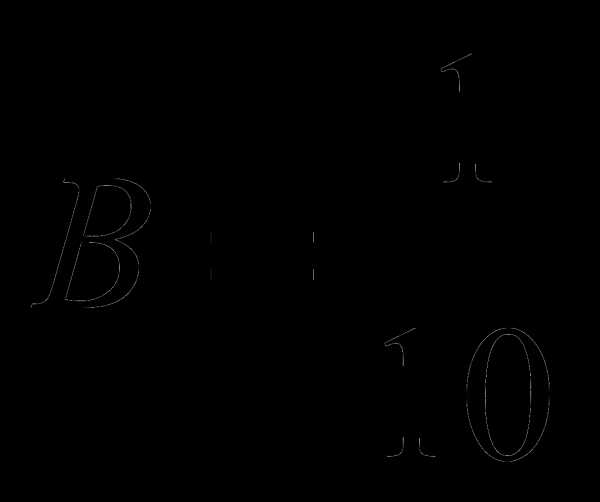 ;
; ; корень
; корень 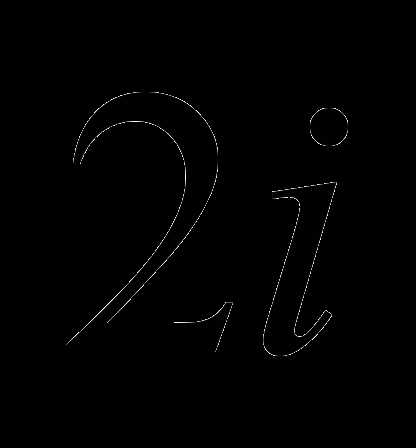 — даёт резонанс с правой частью, ; ;
— даёт резонанс с правой частью, ; ; 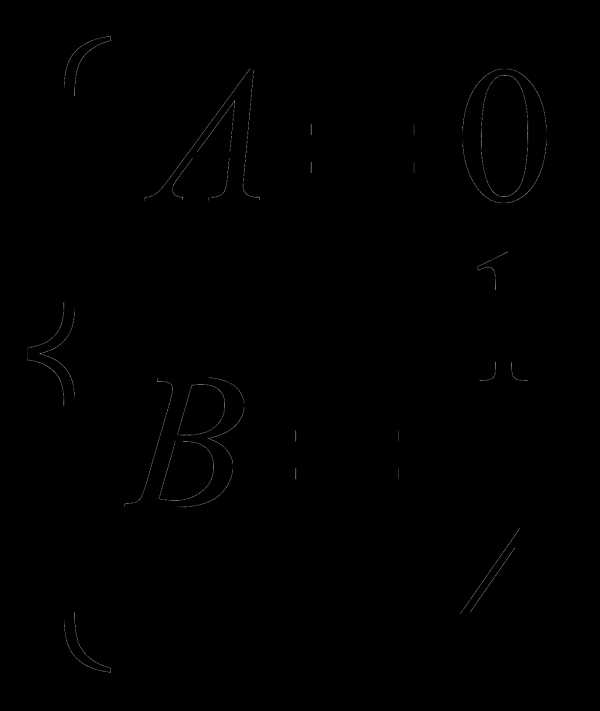
 ;
; 
 — но он не является корнем характеристического уравнения, резонанса нет:
— но он не является корнем характеристического уравнения, резонанса нет: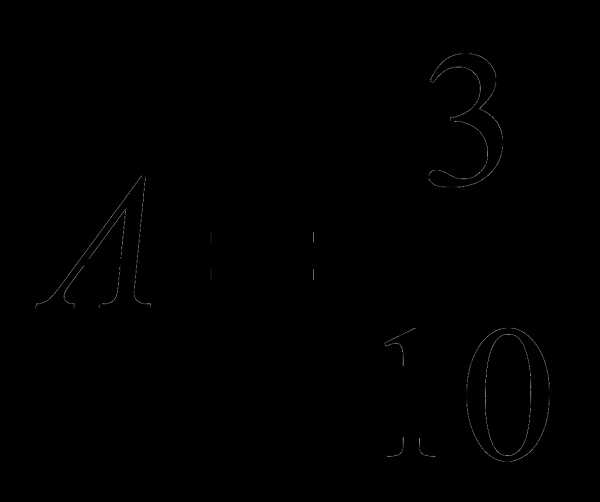 ;
;  ;
;