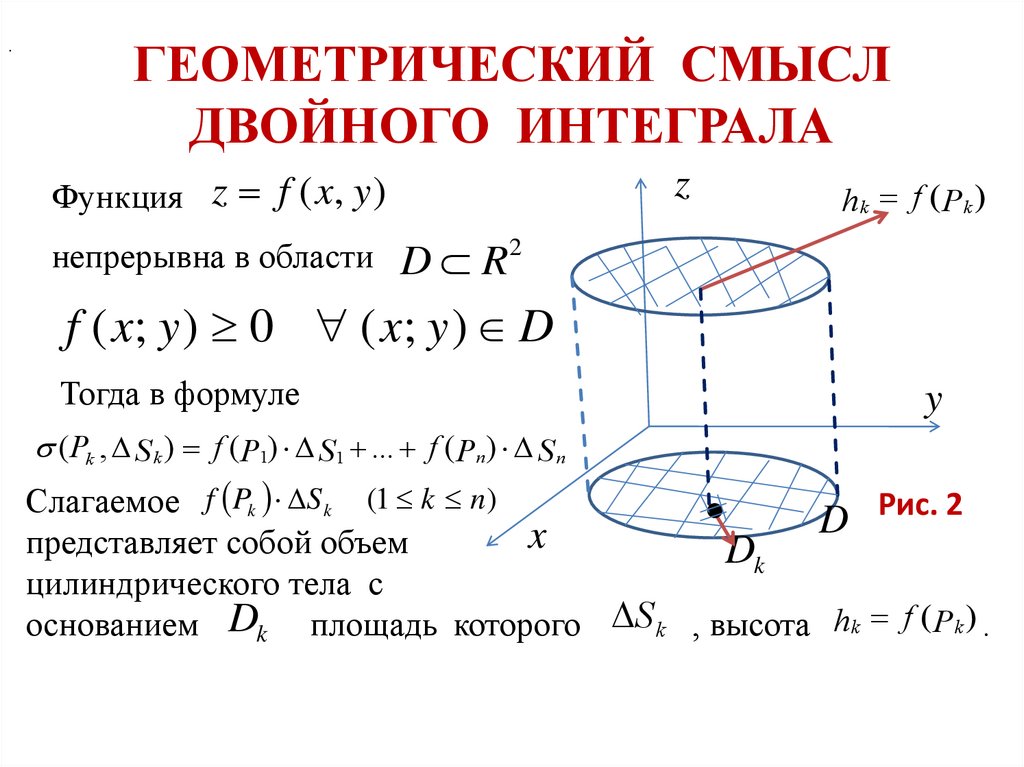
Геометрический и физический смысл определённого интеграла. — Мегаобучалка
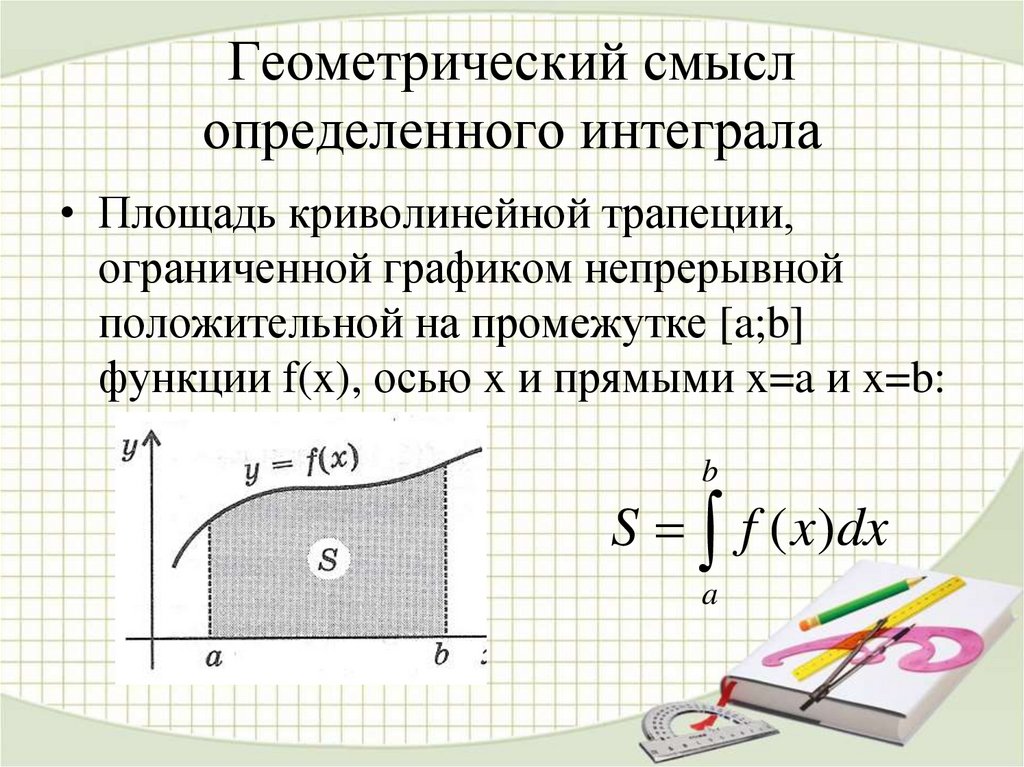
Геометрический смысл определенного интеграла. Если f ( x ) непрерывна и положительна на [ a , b ], то интеграл представляет собой площадь криволинейной трапеции, ограниченной линиями y = 0, x = a , x = b , y = f ( x ) (см. рис. 5.).
Физический смысл определенного интеграла: пусть материальная точка M движется вдоль числовой оси со скоростью V ( t ), V ( t )≥0 . Тогда путь, пройденный точкой за промежуток времени от t = a до t = b , равен определенному интегралу от скорости: S =
Замена переменной в определённом интеграле.
Пусть для вычисления интеграла от непрерывной функции сделана подстановка х = φ(t).
Теорема 1. Если: 1) функция х = φ(t) и ее производная х’ =φ’(t) непрерывны при t ϵ [α;β]; 2) множеством значений функции х = φ(t) при t ϵ [α,β] является отрезок [а; b ]; 3) φ(α) = а и φ(β) = b, то = * φ ’( t ) dt
Формула называется формулой замены переменной в определенном интеграле. Отметим, что:
Отметим, что:
1) при вычислении определенного интеграла методом подстановки возвращаться к старой переменной не требуется
2) часто вместо подстановки х = φ(t) применяют подстановку t = g(x)
3) не следует забывать менять пределы интегрирования при замене переменных!
Интегрирование по частям при вычислении определённого интеграла.
Пусть U(x) и V(x) — дифференцируемые функции. Тогда d ( U ( x ) V ( x )) = U ( x ) dV ( x ) + V ( x ) dU ( x ) . Поэтому U ( x ) dV ( x ) = d ( U ( x ) V ( x )) – V ( x ) dU ( x ) . Вычисляя интеграл от обеих частей последнего равенства, с учетом того, что ∫ d ( U ( x ) V ( x ))= U ( x ) V ( x )+ C , получаем соотношение
Называемое формулой интегрирования по частям. Понимают его в том смысле, что множество первообразных, стоящее в левой части, совпадает со множеством первообразных, получаемых по правой части.
Понимают его в том смысле, что множество первообразных, стоящее в левой части, совпадает со множеством первообразных, получаемых по правой части.
Вычисление площадей плоских фигур в прямоугольных и полярных координатах
Допустим, что фигура D предполагает наличие границы ծ D : y = f ( x ), x = a , x = b ( a < b ), f ( x )ϵ C [ a , b ]
D является криволинейной трапецией и , при условии, что f ( x )>0 на [ a , b ].
Если D находится ниже оси [ a , b ] (рис. 18.1), то
Под полярной системой координат понимается совокупность т. O (полюса) и исходящей из данной точки направленной полупрямой l (полярной оси). В качестве полярных координат т. M обозначают числа (полярный радиус) и (полярный угол) (рис. а).
Вычисление длины дуги плоской кривой.
Кривой линией l -наз. непрерывное отображение отрезка трехмерного пространства. Кривая наз. плоской если она целиком лежит в какой-то плоскости.
Кривая наз. плоской если она целиком лежит в какой-то плоскости.
Замечание: Кривую L можно задавать в виде( параметрическое задание кривой) :
На плоскости бывает задана в таком виде: или в явном виде y = f ( x ) a Предположим, что функция y = f ( x ) непрер. дифференц. Разобьем отрезок [ a , b ] на n частичных отрезков и рассм.точки на кривой с координатами. Рассмотрим ломаную соверш.в этих точках, тогда длина кривой L =
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации — обмен информацией между организацией и её внешней средой… Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении. Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного… Интересное: Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений… Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов… Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция | ⇐ ПредыдущаяСтр 2 из 2 1. 2. Если переменная сила F=f(x) действует в направлении оси Ox (f(x) – непрерывна на [a; b]), то работа этой силы на отрезке [a; b] оси Ох равна . 3. Если функция f(x) непрерывна и неотрицательна на отрезке [a; b], то геометрически представляет собой площадь криволинейной трапеции, ограниченной сверху графиком функции y=f(x), снизу – отрезком [a; b] оси Ох, с боков – отрезками прямых x=a, x=b. Пример 3.5.11.Найти площадь фигуры, ограниченной параболой и гиперболой . ○ Найдем точки пересечения параболы и гиперболы, для этого решим систему уравнений: ; ; ; , ; , . Таким образом, заданные кривые пересекаются в точках А(1; 0) и В(3; 4) (рис. 3.27). Следовательно, 4,58 (кв. ед.). ● Замена переменной в определенном интеграле Формула замены переменной в определенном интеграле: , где , α и β определяются из условий соответственно. Пример 3.5.12. Вычислить . ○ ● Теорема 3.5.6. (Теорема о среднем)Если функция f(x) непрерывна на отрезке [a; b], то в интервале (a; b) найдется такая точка с, что . Интегрирование по частям в определенном интеграле Пусть u=u(x), v=v(x) – непрерывно дифференцируемые на отрезке [a; b] функции. Тогда . Определенный интеграл с переменным верхним пределом Пусть функция f(x) непрерывна на отрезке [a; b]. , где х – любая точка из [a; b]. Если F(x) – первообразная функции f(x), т.е. F′(x)=f(x), то согласно формуле Ньютона-Лейбница имеем: . Отсюда . Таким образом, производная определенного интеграла с переменным верхним пределом по этому пределу равна значению подынтегральной функции от этого предела.
Несобственные интегралы Интегралы с одним или обоими бесконечными пределами получили название несобственных интегралов первого рода. Здесь также, как при вычислении определенных интегралов, можно на практике использовать формулу Ньютона-Лейбница, однако следует помнить, что символ ∞ – не число, а условное обозначение неограниченного возрастания (или убывания) аргумента в процессе его изменения. То есть, со строгих позиций, вычисление несобственного интеграла первого рода – это вычисление некоторого предела, с постоянным использованием теорем о бесконечно малых и бесконечно больших величинах. Таким образом: ; ; . То есть, символы бесконечности условно заменяются буквенными параметрами, применяется формула Ньютона-Лейбница, после чего обычным образом вычисляются указанные пределы. Если в результате такого расчета получится конечное число А (включая 0), то ответ следует записать в форме: интеграл сходится к значению А. Если же результатом будет +∞ (или –∞) или предел не существует, то ответ: интеграл расходится. В практических вычислениях, вполне допустимо не использовать в явной форме операторы lim, но не следует забывать о том, что на самом деле вычисляются пределы, а не конкретные числовые значения. Следующим видом несобственных интегралов являются интегралы от функций с разрывом на одном конце (или обоих концах) интервала интегрирования или с разрывом внутри интервала интегрирования. Например: , и т.п. Такие интегралы носят название несобственных интегралов второго рода. Эти интегралы очень опасны, т. Вычисление несобственных интегралов второго рода осуществляется приведением к интегралам первого рода (или сумме таких интегралов), то есть, ставится задача вычисления предела относительно точки, в которой подынтегральная функция разрывна.
Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой. |
Геометрическая интерпретация определенных интегралов
- Математические сомнения
- Определенные интегралы
Объяснение определенного интеграла математическим уравнением определенно сбивает с толку всех на начальном уровне, но геометрическая интерпретация ни для кого не создает проблем. Итак, всем всегда рекомендуется понимать концепцию определенного интегрирования по геометрической системе.
График функции необходим для объяснения понятия определенного интеграла в геометрической системе. Итак, давайте сначала нарисуем график для функции, а затем выполним еще несколько геометрических шагов для подготовки графика для поддержки геометрической интерпретации.
- Пусть $x$ — переменная, представляющая действительные числа по горизонтальной оси $x$.
- Давайте рассмотрим функцию, и это функция в терминах $x$. Итак, в математике это записывается как $f(x)$. Соответствующие значения функции для всех значений $x$ отложены по вертикальной оси $y$.
 Таким образом, математическая связь между значениями $x$ и соответствующими значениями функции $f(x)$ выражается кривой.
Таким образом, математическая связь между значениями $x$ и соответствующими значениями функции $f(x)$ выражается кривой. - Теперь возьмем точку $P$ на оси $x$ и проведем прямую, пересекающую кривую в точке $Q$. Аналогичным образом рассмотрим другую точку на оси $x$, обозначенную как $R$, а затем проведем прямую линию, пересекающую кривую в точке $S$. Помните, что две прямые линии должны быть перпендикулярны горизонтальной оси.
- Предположим, что $x$-координата точек $P$ и $R$ обозначена через $a$ и $b$ соответственно.
Интерпретация
Образуется замкнутая геометрическая фигура $PQSR$. Площадь замкнутой геометрической формы равна площади, ограниченной кривой функции $f(x)$, прямыми $x = a$ и $x = b$ и осью $x$.
Область $PQSR$ не является идеальным четырехугольником. Таким образом, найти площадь области по формулам площади невозможно, потому что она не является ни квадратом, ни прямоугольником, ни каким-либо другим четырехугольником. Однако разбиение области на несколько прямоугольников одинаковой длины помогает нам найти ее площадь. Итак, разделите область на несколько прямоугольников одинаковой длины, как показано на рисунке.
Итак, разделите область на несколько прямоугольников одинаковой длины, как показано на рисунке.
Теперь длина каждого прямоугольника одинакова, и его можно обозначить дифференциальным элементом $\Delta x$ согласно дифференциальному исчислению, но ширина каждого прямоугольника различна. Однако площадь любого прямоугольника можно вычислить по формуле его площади. Интегрирование площадей всех прямоугольников — это концепция нахождения всей площади области $PQSR$.
Площадь каждого прямоугольника может быть легко вычислена по формуле площади прямоугольника, но мы можем заметить, что мы игнорируем некоторые части области над прямоугольниками. По этой причине сумма площадей всех прямоугольников не равна в точности площади замкнутой геометрической фигуры $PQSR$.
Если мы уменьшим длину каждого прямоугольника наполовину, то игнорируемая часть области всех прямоугольников уменьшится по сравнению с предыдущим случаем. Теперь сумма площадей всех прямоугольников близка к площади области $PQSR$, но не совсем равна. Однако сумма площадей всех прямоугольников текущего случая больше площадей всех прямоугольников предыдущего случая.
Однако сумма площадей всех прямоугольников текущего случая больше площадей всех прямоугольников предыдущего случая.
Два случая показали, что уменьшение длины прямоугольника минимизирует неучтенную площадь над каждым прямоугольником. Следовательно, если длина каждого прямоугольника приблизительно равна нулю, то не учитываемая площадь над каждым прямоугольником также равна нулю. В этом случае сумма площадей всех прямоугольников в точности равна площади замкнутой геометрической фигуры $PQSR$.
Теперь разделите область области $PQSR$ на несколько прямоугольников одинаковой длины.
- Длина каждого прямоугольника очень мала, приблизительно равна нулю, а его длина математически обозначается дифференциалом $dx$. Из-за очень маленькой длины прямоугольник выглядит как прямая линия. Помните, что для удобства мы показываем на рисунке только два прямоугольника.
- Ширина каждого прямоугольника является переменной, и ее можно узнать, сравнив ширину двух прямоугольников.
 Однако ширину любого прямоугольника можно вычислить с помощью функции $f(x)$.
Однако ширину любого прямоугольника можно вычислить с помощью функции $f(x)$.
Следовательно, площадь одного прямоугольника равна произведению длины и ширины прямоугольника.
$A_R$ $\,=\,$ $dx \times f(x)$
$\имплицит$ $A_R$ $\,=\,$ $f(x) \times dx$
$\ ,\,\,\следовательно\,\,\,\,\,\,$ $A_R$ $\,=\,$ $f(x)dx$
Площадь каждого прямоугольника выражается приведенной выше формулой математически. Итак, складываем площади всех прямоугольников, и их сумма обозначается интегральным символом в исчислении.
$\implies$ $A$ $\,=\,$ $\displaystyle \int{f(x)}\,dx$
Функция $f(x)$ является непрерывной функцией. Таким образом, кривая продолжается бесконечно в обоих направлениях. Интеграл от произведения $f(x)$ и $dx$ вычисляет площадь под всей кривой.
В этом случае площадь под кривой должна быть рассчитана между пределами. Итак, границы должны быть определены, чтобы найти интеграл функции. По этой причине границы $a$ и $b$ отображаются ниже и выше символа интеграла соответственно. {\displaystyle b} {f(x)}\,dx$
{\displaystyle b} {f(x)}\,dx$
Интеграл функции $f(x)$ от $a$ до $b$ точно вычисляет площадь, ограниченную кривой $f(x)$, линиями $x = a$ и $x = b$, и горизонтальная ось $x$.
| Определенный интеграл Ваш браузер не поддерживает видео тег. Интегральное понятие связано с понятием площади. Хотя Кавальери не знал термина «функция», мы можем сказать, что одним из его вкладов было рассмотрение проблемы вычисления функции. площадь, ограниченная графиком положительной функции, осью x и двумя вертикальными линиями («криволинейная трапеция» или «площадь под кривой»): Мы хотим присвоить этой области число, которое представляет ее площадь, когда функция положительна. Мы будем называть это число определенным интегралом f между a и b. Этот интеграл не всегда представляет собой площадь «криволинейной трапеции». Это только случай
когда f неотрицательно.
Когда f отрицательно, интеграл будет минус площадь. В общем,
интеграл — это площадь криволинейной трапеции, лежащей над осью x, уменьшенная на площадь частей, которые
лежат ниже оси x. Если мы хотим интегрировать линейные функции, проблема проста. Проблема усложняется, когда график функции не является линией. «Мы будем следовать идее Архимеда. Она состоит в том, чтобы аппроксимировать функцию f горизонтальными (постоянными) функциями, а площадь под f — функцией сумма маленьких прямоугольников» (Ланг) В этих случаях мы хотим построить определенный интеграл (число) как результат некоторого предельного процесса. Мы можем начать делить [a,b] на подынтервалы и взять сумма площадей некоторых прямоугольников, аппроксимирующих функцию f в различных точках отрезка. Площадь этих прямоугольников аппроксимирует интеграл. Интеграция – это процесс суммирования. Это обозначение, которое мы используем: Символ S (удлиненная буква S для суммы) называется знаком интеграла и был введен Лейбницем в 1675 году. Процесс, в результате которого получается результат, называется
интеграция. Числа а и b, которые стоят перед знаком интеграла, называются нижним и верхним пределами интегрирования. Лейбниц использовал этот символ, потому что считал интеграл суммой бесконечного числа прямоугольников с высотой f (x) и «бесконечно малым». ширина. Его с готовностью приняли многие ранние математики, потому что им нравилось думать об интегрировании как о своего рода «процесс суммирования», который позволял им складывать вместе бесконечно много «бесконечно малых величин». Мы попытаемся показать некоторые идеи, лежащие в основе строгого определения интеграла, данного Бернхардом Риманом (1826-1866). P является разбиением [a,b]. Раздел определяет некоторые подынтервалы. Ширина этих подынтервалов может быть разной: Учитывая раздел [a,b], мы можем добавить больше чисел к разделу, и тогда мы получим новый раздел с небольшими интервалами. Если мы добавьте достаточное количество промежуточных чисел, тогда интервалы можно сделать сколь угодно малыми. Одним из ограничений является использование регулярных подразделений интервала. В этом случае основания прямоугольников равны: Для каждого i мы выбираем некоторую точку x i * в [x i , x i+1 ]. «Основная идея, которую мы собираемся осуществить, состоит в том, что по мере того, как мы будем делать интервалы нашего разбиения все меньше и меньше, сумма площадей прямоугольников приблизится к пределу, и этот предел можно использовать для определения площади под кривой» (Ланг). Мы можем выбрать, что x i * будет точкой в середине подынтервала (как в матлете и в предыдущих примерах). Одним из популярных вариантов является x i * , равный x i , левому концу подынтервала. Тогда высота прямоугольника будет f(x i ): Или мы можем выбрать x i * равным x i+1 , правому концу подынтервала. Тогда высота прямоугольника будет f(x я+1 ): Выбор этих x i * в [x i , x i+1 ] является произвольным. Любая из этих сумм называется суммой Римана функции f для P. Геометрическая интерпретация: «Это общая площадь n прямоугольников, которая лежит частично под графиком f и частично над ним. Из-за каким бы образом ни были выбраны высоты прямоугольников, мы не можем с уверенностью сказать, меньше ли та или иная сумма Римана или больше интеграла. Но кажется, что перекрытие не должно иметь большого значения; если основания всех прямоугольников узкие достаточно, то сумма Римана должна быть близка к интегралу». (Спивак) Если мы увеличим количество прямоугольников, мы (интуитивно) будем иногда ближе к значению, которое является определенным интегралом. Тогда можно сказать, что определенный интеграл является пределом сумм Римана при стремлении числа подразделений к бесконечности и ширины каждого подинтервала стремится к нулю. И неважно, какую точку x i * мы выберем в каждом подинтервале. «Мораль этой басни состоит в том, что все, что выглядит как хорошее приближение к интегралу, на самом деле им является, при условии, что все длины
интервалы в разбиении достаточно малы». В математике мы можем изменить функцию и количество прямоугольников. Хотя в каждом интервале высота прямоугольника может быть любым значением функции в точке подынтервала, здесь мы рассматриваем только одну простую возможность: x i * является средней точкой подынтервала. В этом случае суммы Римана называются средними суммами Римана. «Интегралы большинства функций невозможно точно определить (хотя их можно вычислить с любой желаемой степенью точности). путем вычисления нижней и верхней сумм). Тем не менее [как мы узнаем позже, например, при изучении основной теоремы исчисления] интеграл от многих функций может быть вычисляется очень легко» (Спивак). Аксиоматический подход к интегралу (вслед за Сержем Лангом) В своей книге «Первый курс исчисления», прежде чем объяснять суммы Римана, он подчеркивает важность двух свойств, которые будут определять интеграл. для f на [a,b]: Пусть a, b — два числа, причем a удовлетворяющие следующим свойствам: Свойство 1. Лучшие смартфоны на Android в 2022 году Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей. 1740 0 Документация
Схемотехника
CAD / CAM
Статьи MathCAD 12
MatLab
OrCAD
P CAD
AutoCAD
MathCAD 8 — 11 При умножении следует помнить, что матрицу размерности MxN допустимо умножать только на матрицу размерности
NxP (р может быть любым). В результате получается матрица размерности
MхP. Чтобы ввести символ умножения, нужно нажать клавишу со звездочкой <*> или воспользоваться панелью инструментов
Matrix (Матрица), нажав на ней кнопку Dot Product (Умножение). Умножение матриц обозначается по умолчанию точкой, как показано в листинге 7.5. Листинг 7.5. Перемножение матриц Обратите внимание (нижняя строка листинга 7.5), что попытка перемножить матрицы
А и В несоответствующего (одинакового 2х3) размера оказалась безрезультатной: после введенного знака равенства находится пустой местозаполнитель, а само выражение в редакторе Mathcad выделяется красным цветом. При установке курсора на это выражение появляется сообщение о несовпадении числа строк первой матрицы с числом столбцов второй матрицы. Еще один пример, относящийся к умножению вектора на матрицу-строку и, наоборот, строки на вектор, приведен в листинге 7.6. ВНИМАНИЕ! Тот же самый оператор умножения действует на два вектора по-другому (см. разд. 7.2.2). Листинг 7.6. Умножение вектора и строки Аналогично сложению матриц со скаляром определяется умножение и деление матрицы на скалярную величину (листинг 7.7). Символ умножения вводится так же, как и в случае умножения двух матриц. На скаляр можно умножать матрицу любой размерности. Листинг 7.7. Умножение матрицы на скалярную величину Нравится Твитнуть Теги MathCad
САПР Сюжеты MathCad Глава 1 Основы работы с системой Mathcad 11 10102 0 Глава 10 Работа с информационными ресурсами Mathcad 11 7088 0 Глава 2 Работа с файлами Mathcad 11 12833 0 Комментарии (0) Вы должны авторизоваться, чтобы оставлять комментарии. Вход О проекте
Использование материалов
Контакты Новости
Статьи
База знаний Радиомастер При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster.ru обязательна. 0.2357 s Последнее обновление: 17.01.2023 Рассмотрим расспространенную задачу — умножение матриц. Например, у нас есть следующие матрицы a11 a12 a13 a21 a22 a23 a31 a32 a33 b11 b12 b13 b21 b22 b23 b31 b32 b33 То результат перемножения матриц будет равен a11*b11 + a12*b21 + a13*b31 a11*b12 + a12*b22 + a13*b32 a11*b13 + a12*b23 + a13*b33 a21*b11 + a22*b21 + a23*b31 a21*b12 + a22*b22 + a23*b32 a21*b13 + a22*b23 + a23*b33 a31*b11 + a32*b21 + a33*b31 a31*b12 + a32*b22 + a33*b32 a31*b13 + a32*b23 + a33*b33 То есть для получения элемента результирующей матрицы, элементы строки первой матрицы последовательно перемножаются на элементы столбцов второй матрицы, и результаты умножений складываются. С точки зрения псевдокода это выглядело бы так: Напишем программу для перемножения двух матриц размером 3×3. Для упрощения вывода результатов на консоль воспользуемся функции printf языка С. Итак, определим файл main.s со следующим кодом: Вкратце рассмотрим данный код. Прежде всего в секции .data определены три матрицы. Матрицы A и B состоят из 9 элементов типа Для упрощения работы определяем две дополнительные константы: Вначале определяем значения для прохода по строкам: В W1 помещаем счетчик строк, то есть число 3 (надо пройти по трем строкам матрицы А). В регистр X4 загружается адрес матрицы A (адрес первого ее элемента) и в X19 помещается
адрес матрицы С, в которую будем сохранять результат. Дальше начинаем цикл для прохода по строкам и определяем значения для прохода по столбцам матрицы B: В регистр X5 помещается адрес матрицы В, а в W2 — счетчик столбцов (то есть надо пройтись по 3 столбцам матрицы В). Затем начинаем цикл по столбцам В регистр Х7 помещаем число 0 — этот регистр будет накапливать значения для одного элемента матрицы С. Кроме того, в W0 помещается счетчик цикла — надо перемножить 3 элемента из строки матрицы А и столбца марицы B.
Регистр Х12 будет указывать на адрес текущего элемента строки матрицы А, а Х6 — на адрес текущего элемента столбца матрицы В. Далее перемножаем все элементы текущей строки матрицы А и текущего столбца матрицы В: Для перемножения в W9 загружаем элемент по адресу X12, при этом увеличиваем данный адрес на #WDSIZE (4) байт, то есть адрес будет указываать на следующий элемент текущей строки
матрицы А. Аналогично в W10 загружаем элемент по адресу X6, при этом увеличиваем данный адрес на #(N*WDSIZE) (12) байт, то есть адрес будет указываать на следующий элемент текущего столба
матрицы В. Инструкция SMADDL перемножает значения W9 и W10 и прибавляет к содержимому в регистре X7. И пока не пройдем по всем 3 элементам текущих строки и столбца,
продолжаем данные действия. Таким образом, в цикле Далее для вычисления элемента матрицы C в следующем столбце переходим к следующему столбцу матрицы B: При этом полученный результат из X7 сохраняем в текущей элемент матрицы С, адрес которого хранится в Х19. При этом данный адрес увеличиваем на 4 байта, чтобы в следующий раз сохранить
значение для следующего элемента матрицы С. Также увеличиваем адрес в X5 на #WDSIZE байт, то есть переходим к новому столбцу матрицы В и уменьшаем счетчик столбцов в регистре W2. Если все столбцы матрицы В пройдены, то переходим к новой строке матрицы А: Для этого изменяем адрес в Х4 на #(N*WDSIZE) байт (по сути на 12 байт — размер строки), уменьшаем счетчик строк в W1 и переходим к следующей строке. Если все строки перебраны, то переходим к печати на консоль — проходим по трем строкам матрицы С и единосременно с помощью строки форматирования Поскольку в данном случае используется функция языка С, скомпилируем приложение с помощью следующей команды: После запуска программа отобразит нам результирующую матрицу: НазадСодержаниеВперед Бала Прия С
в Разработка
|
Последнее обновление:
1 июля 2022 г. Поделись на: Сканер безопасности веб-приложений Invicti — единственное решение, обеспечивающее автоматическую проверку уязвимостей с помощью Proof-Based Scanning™. В этом уроке вы узнаете, как умножить две матрицы на Питоне. Вы начнете с изучения условия правильного умножения матриц и напишете пользовательскую функцию Python для умножения матриц. Далее вы увидите, как можно добиться того же результата, используя вложенные генераторы списков. Наконец, вы приступите к использованию NumPy и его встроенных функций для более эффективного выполнения матричного умножения. Прежде чем писать код Python для умножения матриц, давайте вернемся к основам умножения матриц. Матрица Умножение двух матриц A и B допустимо, только если количество столбцов в матрице A равно , равному количеству строк в матрице B . Вероятно, вы уже сталкивались с этим условием умножения матриц раньше. Однако задумывались ли вы когда-нибудь, почему это так? Ну, это из-за того, как работает умножение матриц. Взгляните на изображение ниже. В нашем общем примере матрица A имеет м рядов и n столбцов. А матрица B имеет n строк и p столбцов. Элемент с индексом (i, j) результирующей матрицы C является скалярным произведением строки i матрицы A и столбца j матрицы B. Итак, чтобы получить элемент с определенным индексом в результирующей матрице C вам нужно будет вычислить скалярное произведение соответствующей строки и столбца в матрицах A и B соответственно. Повторяя вышеописанный процесс, вы получите матрицу произведения C формы m x p — с m строками и p столбцами, как показано ниже. А скалярное произведение или скалярное произведение между двумя векторами a и b задается следующим уравнением. Подведем итоги: Если присмотреться, то n — это количество столбцов в матрице A, а также количество строк в матрице B. И именно поэтому вам нужно количество столбцов в матрице A должно быть равным числу строк в матрице B . Надеюсь, вы понимаете условие выполнения матричного умножения и то, как получить каждый элемент в матрице произведения. Давайте продолжим писать код Python для умножения двух матриц. В качестве первого шага давайте напишем пользовательскую функцию для умножения матриц. Эта функция должна выполнять следующие действия: Шаг 1 : Создайте две матрицы целых чисел, используя функцию NumPy Шаг 2: Идем дальше и определяем функцию Перейдем к разбору определения функции. Объявить C как глобальную переменную : По умолчанию все переменные внутри функции Python имеют локальную область видимости. И вы не можете получить к ним доступ извне функции. Чтобы сделать матрицу продукта C доступной извне, нам придется объявить ее как глобальную переменную. Просто добавьте глобальный квалификатор Проверка правильности умножения матриц: Используйте атрибут формы Использовать вложенные циклы для вычисления значений: Чтобы вычислить элементы результирующей матрицы, мы должны перебрать строки матрицы A, и внешний цикл ▶️ Теперь, когда мы узнали, как работает функция Python для умножения матриц, давайте вызовем функцию с матрицами A и B, которые мы сгенерировали ранее. Поскольку умножение матриц между A и B допустимо, функция Вот понимание вложенного списка для умножения матриц. Сначала это может показаться сложным. Но мы будем шаг за шагом разбирать понимание вложенного списка. Давайте сосредоточимся на анализе одного списка и определим, что он делает. Мы будем использовать следующий общий шаблон для понимания списка: ▶️ Ознакомьтесь с нашим руководством «Понимание списков в Python — с примерами», чтобы получить более глубокое понимание. Прежде чем продолжить, обратите внимание, что мы хотели бы построить результирующую матрицу C по одной строке за раз. Шаг 1: Вычисление одного значения в матрице C Для заданной строки i матрицы A и столбца j матрицы B приведенное ниже выражение дает запись с индексом (i, j) в матрице C. Если Шаг 2: Построить одну строку в матрице C Наша следующая цель — построить всю строку. Для строки 1 в матрице A вам нужно перебрать все столбцы в матрице B, чтобы получить одну полную строку в матрице C. Вернуться к шаблону понимания списка. А вот и первое понимание списка. Шаг 3: Постройте все строки и получите матрицу C Далее вам нужно будет заполнить матрицу произведения C, вычислив остальные строки. А для этого нужно перебрать все строки в матрице A. Еще раз вернуться к пониманию списка и сделать следующее. И вот наше окончательное понимание вложенного списка.
for A_row in A] Пришло время проверить результат! ✔ Если вы присмотритесь, это эквивалентно вложенным циклам for, которые мы использовали ранее, только более лаконично. Вы также можете сделать это более эффективно, используя некоторые встроенные функции. Давайте узнаем о них в следующем разделе. Обратите внимание, насколько этот метод проще, чем два метода, которые мы изучали ранее. На самом деле вместо В Python Он работает с двумя матрицами и, как правило, с N-мерными массивами NumPy и возвращает матрицу произведения. Примечание: Для использования оператора Вот как вы можете его использовать. Обратите внимание, что матрица произведения C такая же, как та, которую мы получили ранее. Если вы когда-либо сталкивались с кодом, который использует Вы увидите, что Однако, согласно документам NumPy, вы должны использовать Напомним из предыдущего раздела, что элемент с индексом (i, j) матрицы произведения C является скалярным произведением строки i матрицы A и столбца j матрицы B. Поскольку NumPy неявно передает эту операцию скалярного произведения всем строкам и всем столбцам, вы получаете результирующую матрицу произведения. Но чтобы ваш код был читабельным и чтобы избежать двусмысленности, используйте вместо этого 🎯 В этом уроке вы узнали следующее. На этом мы завершаем обсуждение умножения матриц в Python. В качестве следующего шага узнайте, как проверить, является ли число простым в Python. Или решить интересные задачи на строки Python. Приятного обучения!🎉 Спасибо нашим спонсорам В этом уроке мы рассмотрим различные способы выполнения умножения матриц с использованием массивов NumPy. Также мы узнаем, как ускорить процесс умножения с помощью графического процессора и другие горячие темы, так что давайте начнем! Прежде чем мы двинемся дальше, лучше рассмотреть некоторые основные термины матричной алгебры. Вектор: Алгебраически вектор представляет собой набор координат точки в пространстве. Матрица: Матрица (множественное число матриц) представляет собой двумерное расположение чисел или набор векторов. Скалярное произведение: Скалярное произведение – это математическая операция между 2 векторами одинаковой длины . С четким пониманием этих терминов мы готовы к работе. Начнем с простой формы умножения матриц — между матрицей и вектором. Прежде чем мы продолжим, давайте сначала поймем, как создать матрицу с помощью NumPy. Метод array() NumPy используется для представления векторов, матриц и многомерных тензоров. Давайте определим 5-мерный вектор и матрицу 3 × 3, используя NumPy. Вывод: При умножении матрицы на вектор следует помнить о следующих моментах: Вывод: Теперь мы поняли умножение матрицы на вектор; было бы легко вычислить умножение двух матриц. Рассмотрим умножение m x n матрицы A на n x p матрицу B: Вывод: Вы можете установить любое другое целое число в качестве начального числа, но я предлагаю установить его на 42 для этого урока, чтобы ваши выходные данные соответствовали показанным на выходных снимках экрана. Теперь умножим две матрицы, используя Метод np.matmul() . Результирующая матрица должна иметь форму 3 x 4. Вывод: Умножение трех матриц будет состоять из двух операций умножения 2 матриц, и каждая из двух операций будут следовать тем же правилам, которые обсуждались в предыдущем разделе. Допустим, мы перемножаем три матрицы A, B и C, и произведение равно D = ABC. Полученная матрица будет иметь строк, равных количеству строк в A и столбцов равно количеству столбцов в C. Важным свойством операции умножения матриц является то, что является ассоциативным . Например, в нашем примере умножения трех матриц D = ABC не имеет значения, выполняем ли мы сначала AB или BC. Результат: Выполним умножение в обоих порядках и проверим свойство ассоциативности. Вывод: Трехмерная матрица — это не что иное, как набор (или стек) множества двумерных матриц, точно так же, как двумерная матрица представляет собой набор/стек множества одномерных векторов. Таким образом, матричное умножение трехмерных матриц включает в себя многократное умножение двумерных матриц, что в конечном итоге сводится к скалярному произведению между их векторами строк и столбцов. Рассмотрим пример матрицы A формы (3,3,2), умноженной на другую трехмерную матрицу B формы (3,2,4). Вывод: Умножение матриц между этими двумя включает три умножения между соответствующими двумерными матрицами A и B, имеющими формы (3,2) и (2,4) соответственно. В частности, первое умножение будет между A[0] и B[0], второе умножение будет между A[1] и B[1] и, наконец, третье умножение будет между A[2] и БИ 2]. Результат каждого отдельного умножения двумерных матриц будет иметь форму (3,4). Следовательно, конечным продуктом двух трехмерных матриц будет матрица формы (3,3,4). Давайте реализуем это с помощью кода. Вывод: Кроме ‘np.matmul ()’ существует два других способа выполнения матричного умножения — метод np.dot() и оператор ‘@’ , каждый из которых предлагает некоторые различия/гибкость в операциях матричного умножения. Вы можете использовать этот метод для нахождения скалярного произведения векторов, но если мы передадим две двумерные матрицы, то он будет вести себя аналогично методу ‘np. Давайте рассмотрим пример: Вывод: Разница между np.dot() и np.matmul() заключается в их работе с трехмерными матрицами. np.dot() для двух трехмерных матриц A и B возвращает произведение суммы по последней оси A и предпоследней оси B. Итак, если A имеет форму (a, b, c), а B имеет форму (d, c, e), то результат np.dot(A, B) будет иметь форму (a, d, b,e), отдельный элемент которого в позиции (i,j,k,m) определяется как: Проверим на примере: Вывод: Вывод: Оператор @, представленный в Python 3.5, выполняет ту же операцию, что и «np.matmul()». Давайте рассмотрим более ранний пример np.matmul() с использованием оператора @ и увидим тот же результат, что и ранее: Вывод: Раньше нам приходилось вызывать np.matmul() несколько раз и передавать их результаты в качестве параметра следующему вызову. Вывод: До сих пор мы выполняли умножение матрицы на вектор или другую матрицу. Но что происходит, когда мы выполняем умножение матриц на скалярное или одно числовое значение? Результат такой операции получается путем умножения каждого элемента матрицы на скалярное значение. Таким образом, выходная матрица имеет ту же размерность, что и входная матрица. Обратите внимание, что ‘np.matmul()’ не позволяет умножать матрицу на скаляр. Вы можете добиться этого, используя np.dot() или с помощью оператора ‘*’. Давайте посмотрим на это на примере кода. Вывод: Иногда нам нужно сделать умножение соответствующих элементов двух матриц, имеющих одинаковую форму. Этого можно добиться, вызвав функцию Multi() NumPy или используя оператор ‘*’ . Вывод: На самом деле умножение матриц на скаляр также включает передачу скалярного значения в матрицу формы, равной матричному операнду при умножении. Это означает, что когда мы умножаем матрицу формы (3,3) на скалярное значение 10, NumPy создаст другую матрицу формы (3,3) с постоянными значениями десять во всех позициях в матрице и выполнит поэлементно умножение двух матриц. Давайте разберемся с этим на примере: Вывод: Подобно тому, как мы можем возвести скалярное значение в степень, мы можем проделать ту же операцию с матрицами. Например, если мы возведем матрицу A в степень n, она будет равна матричному умножению n матриц, каждая из которых будет матрицей A. Эта операция обеспечивается в Python методом linalg.matrix_power() NumPy, который принимает базовую матрицу и целочисленную степень в качестве параметров. Давайте посмотрим на пример в Python: Вывод: Вывод: В связи с этой операцией возникает важный вопрос: Что происходит, когда мощность равна 0? Это матрица идентичности. Таким образом, возведение матрицы n x n в степень 0 приводит к единичной матрице I формы n x n. Давайте быстро проверим это на Python, используя нашу предыдущую матрицу A. Вывод: Точно так же, как мы могли бы выполнять поэлементное умножение матриц, мы также можем выполнять поэлементное возведение в степень, т. Этого можно добиться в Python с помощью стандартного оператора экспоненты ‘ ** ’ — пример оператора, перегружающего . Опять же, мы можем предоставить одну постоянную степень для всех элементов в матрице или матрицу степеней для каждого элемента в базовой матрице. Давайте посмотрим на примеры того и другого в Python: 9полномочия:\n{}, shape={}\n».format(C, C.shape)) Вывод: Предположим, у нас есть матрица 5 x 6 A и другую матрицу 3 x 3 B. Очевидно, мы не можем перемножить эти две вместе из-за несоответствия размеров Но что, если мы хотим умножить подматрицу 3×3 в матрице A на матрицу B, сохраняя при этом другие элементы в A неизменными? Давайте посмотрим это в действии. Вывод: Также нет необходимости перезаписывать исходную матрицу. Мы также можем записать результат в новую матрицу, сначала скопировав исходную матрицу в новую матрицу, а затем записав произведение в позиции подматрицы. Мы знаем, что NumPy ускоряет матричные операции, распараллелив множество вычислений и используя возможности параллельных вычислений нашего ЦП. Однако современным приложениям нужно нечто большее. ЦП предлагают ограниченные вычислительные возможности, и этого недостаточно для большого количества необходимых нам вычислений, как правило, в таких приложениях, как глубокое обучение. Именно здесь на сцену выходят графические процессоры. Они предлагают большие вычислительные возможности и превосходную инфраструктуру параллельных вычислений, которая помогает нам сэкономить значительное количество времени, выполняя сотни тысяч операций за доли секунды. В этом разделе мы рассмотрим, как можно выполнять умножение матриц на графическом процессоре вместо центрального процессора и сэкономить при этом много времени. NumPy не предлагает функции для умножения матриц на графическом процессоре. Поэтому мы должны установить некоторые дополнительные библиотеки, которые помогут нам достичь нашей цели. Сначала мы установим библиотеки « scikit-cuda » и « PyCUDA », используя установку pip. Если на вашем компьютере нет графического процессора, вы можете попробовать ноутбуки Google Colab и включить доступ к графическому процессору; это бесплатно для использования. Теперь мы напишем код для генерации двух матриц 1000×1000 и выполнения матричного умножения между ними двумя методами: Во втором методе мы будем генерировать матрицы на процессоре; затем мы будем хранить их на графическом процессоре (используя PyCUDA’s ‘ gpuarray.to_gpu() ‘метод) перед выполнением умножения между ними. Мы будем использовать модуль « time » для вычисления времени вычислений в обоих случаях. Вывод: На некоторых старых аппаратных системах вы можете получить ошибку памяти, но если вам повезет, это будет работать в течение длительного времени (зависит от вашей системы). Теперь давайте выполним то же самое умножение на графическом процессоре и посмотрим, как отличается время вычислений между ними. Вывод: В этом уроке мы рассмотрели, как происходит умножение двух матриц, управляющие им правила и как их реализовать в Python. Мы также рассмотрели поэлементные вычисления в матрицах, такие как поэлементное матричное умножение или поэлементное возведение в степень. Интегральные функции: В выражениях можно применять следующие операции: Другие функции: Постоянные: Пересечение уклона Деллисия С. решение для y-перехвата? Подписаться
І
3 Подробнее Отчет Автор:
Лучшие новыеСамые старые Грейди К.
ответил 18/12/12 Репетитор Новое в Византе Молодой, целеустремленный инженер со страстью к физике и математике. Смотрите таких репетиторов Смотрите таких репетиторов Чтобы найти точку пересечения уравнения по оси y, нам нужно установить значение x равным 0 и найти значение y. Результирующее значение y — это значение, при котором функция пересекает ось y. Это был твой вопрос? Голосовать за 0 голос против Подробнее Отчет Тамара Дж.
ответил 18/12/12 Репетитор 4.9
(51) Репетиторство по математике — алгебра и исчисление (все уровни) См. таких репетиторов Смотрите таких репетиторов Насколько я понимаю, у вас есть квадратичная функция — ƒ(x) = (1/2)x 2 или y = (1/2)x 2 — и вы ищете найдите точку пересечения этой функции с осью y, которая является точкой, в которой функция пересекает ось y (или, другими словами, это точка, в которой x=0). Чтобы найти точку пересечения y, мы просто подставляем 0 вместо x в уравнение функции и находим y. ƒ(x) = (1/2)x 2 , x = 0 = (1/2)(0) = 0 Таким образом, поскольку ƒ(0)=0, отрезок y находится в точке (0, 0). Голосовать за 0 голос против Подробнее Отчет Задайте вопрос бесплатно Получите бесплатный ответ на быстрый вопрос. Найдите онлайн-репетитора сейчас Выберите эксперта и встретьтесь онлайн. Приводится подробное решение 19 варианта, включающее решения задач по теории вероятности под номерами: 5-10, 12, 13, 15-17, 19, 20. Фотографии. МЭИ, 2 курс, Высшая математика. Сборник заданий по специальным курсам высшей математики. Чудесенко В. Ф. Решение задач из сборника Чудесенко по теории вероятностей, 14 вариант. Задания 1, 2, 3, 4, 5, 7, 8, 9, 12, 13, 15, 19, 20. Решение примеров из задачника Чудесенко номера заданий — 8,13 13,13 8,11 13,11 8,22 13,22 8,12 13,12 8,10 13,10 8,2 13,2 8,15 13,15 8,17 13,17 8,3 13,3 8,4 13,4 8,8 13,8 3,13 3,11 3,22 3,12 3,10 3,2 3,15 3,17 3,3 3,4 3,8 3,5 3,24 8,5 13,5 8,24 13,24 Все задачи Решенные варианты по задачнику Чудесенко. 3 вариант. 8 вариант. 9 вариант. 10 вариант. 12 вариант. 17 вариант. 18 вариант. 25 вариант. Решенные варианты по задачнику Чудесенко. 3 вариант. Решены номера 1-15. 8 вариант. Решены номера 7, 12, 19, 21-23, 25, 30-33. 9 вариант. Все номера решены. 10 вариант. Решены номера 1, 3, 12, 16, 21, 23, 34. 12 вариант. Решены номера 1-16. 17 вариант. Все номера решены. 18 вариант. Решены номера 1, 3, 4, 7-9, 12, 15, 17, 19-21, 27, 33, 34, 36. 25 вариант. Решены номера 1-37. Полностью решены задачи: 16, 18, 20, 21, 22, 25, 27, 28 Отсканированная тетрадь. Решены полностью правильно без сомнений! Самостоятельно. Задания 1-4, 8-9, 12-15, 17, 19 (двумя способами), 21, 22. Отсканированная тетрадь. Все очень ясно и понятно. На записи преподавателя можно не обращать внимания. Арзамасский политехнический институт, ст. Теория функций комплексного переменного и операционное исчисление Имя файла соответствует варианту ТР типового расчета Решено 30 вариантов не со всеми примерами. Решение задач для РГР по предмету Теория вероятностей и Матстатистика по задачнику Чудесенко В.Ф. 17 вариант. для студентов 3 курса. Признаки делимости Чтобы понять делится ли одно число на другое не обязательно проводить сложные вычисления или иметь при
себе калькулятор. Математики придумали специальные правила, который помогут вам узнать делятся ли числа нацело друг на друга.
Эти правила называются признаками делимости. Число делится на 2, если его последняя цифра делится на 2 или является нулём. Примеры: Число делится на 4, если две его последние цифры нули или образуют число,
делящееся на 4. Примеры: Число делится на 8, если три последние его цифры нули или образуют число,
делящееся на 8. Примеры: Признаки делимости Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте». Оставить комментарий: 31 мая 2018 в 11:03 math-prosto.ru/ru/pages/delimost/delimost/ Суммы там должны отличаться не ровно на 11, а число, кратное 11 (в том числе и ноль, кстати говоря :D). Проблема в том, что по Вашему признаку число 90904 не будет делиться на 11. Не верите? А Вы проверьте! 😉 31 мая 2018 в 14:13 Благодарим за ваше наблюдение. Вы правы, число будет делиться на 11, если разница между суммами цифр на нечетных местах кратно 11. Случай, когда разница между суммами равна нулю, в уроке описан: Изменения в урок будут внесены в ближайшее время. 8 сентября 2015 в 0:09 Спасибо! Приходится «обновлять» знания… Вроде знаю, а пояснить грамотно уже не получается… Спасибо, за «возрождение» моего математического языка. 2 сентября 2016 в 14:58 Оглавление Время чтения:
5 минут 252 Разберемся как определить, что число может делиться на 4, рассмотрим формулировку признака. Рассмотрим признак делимости на 4, правило и примеры использования признака при вычислении. Для начала, чтобы узнать делится ли однозначное натуральное число на 4 без остатка, можно разделить его прямым путем на 4. Среди этих чисел только 4 и 8. Так же можно поступить с двузначными числами, трехзначными и т.п. Но по мере увеличения разрядов в числе проводить деление для проверки делимости на 4 становится все сложнее. Тогда на помощь приходит Признак делимости на 4, с которым более подробно ознакомимся. Его суть заключается в проверке делимости на 4 одной или двух последних цифр многозначного натурального числа. Рассмотрим, что это значит более подробно. Некоторое значение a может быть поделено на 4 только если одна или две крайние правые цифры в записи числа a могут быть поделены на 4 без остатка. Если же в записи некоторого числа a 2 цифры с правого края не могут быть поделены на 4 без остатка, то и все число a невозможно поделить на 4. Примеры 1 — 2 Какие из натуральных чисел 484 788, 89 336, 53 869 делятся на 4? Решение:У числа 484 788 две крайние правые цифры 88 делятся на 4 без остатка, значит и 484 788 может быть поделено на 4 без остатка. 89 336 имеет 2 крайние правые цифры 36, а 36 делится на 4, значит и 89 336 можно поделить на 4. 53 869 имея две крайние цифры 69, не делится на 4, так как 69 не делимо без остатка на 4. Ответ: числа 484 788 и 89 336 делятся на 4. В случае если в исходном числе предпоследняя цифра ноль, то необходимо отбросить его из рассмотрения и ориентироваться на последнюю цифру в числе. Делится ли на 4 натуральные числа 888 709 и 79 508? Решение: У числа 888 709 две крайние правые цифры 09, поэтому ноль отбрасываем и ориентируемся на цифру 9, которая на 4 не делится. 79 508 имеет две крайние цифры 08, поэтому ноль отбрасываем, рассматриваем только цифру 8, которая на 4 делится без остатка. Ответ: 888 709 на 4 не делится, а 79 508 может быть поделено на 4. Если рассматривать числа, в конце записи которых находятся сразу два ноля, то они делятся на 4. Это доказывается тем, что 100 делится без остатка на 4, получается 25. Это утверждение можно доказать с помощью правила умножения числа на сто. Если а — это произвольное многозначное число, в записи которого справа находятся два ноля. То есть оно равно а1*100, где а1 — это сумма а, если отбросить два ноля, расположенные справа в записи. Например, 777 800= 7 778*100. Полученное произведение а1*100 имеет один из множителей цифру 100, она без остатка может быть поделена на 4, то есть 100:4=25. Правило Правило признака делимости на 4, можно сформулировать таким образом: Рассмотрим такой момент, придумаем любое натуральное число а и представим его в виде суммы а=а1*100+а0, где а1 — это сумма а, из записи которого откинуты две цифры с правой стороны, а0 — это 2 цифры с правого края из записи числа а. Если рассматривать одно или двузначные числа, то в данном случае а=а0. Вспомним и сформулируем свойства делимости: На основании данных свойств постараемся сформулировать теорему делимости на 4 и докажем ее правоту. Нет времени решать самому? Наши эксперты помогут! Контрольная | от 300 ₽ | Реферат | от 500 ₽ | Курсовая | от 1 000 ₽ | Доказательство Поясним доказательство признака делимости на 4 в виде достаточного и необходимого условия делимости на 4. Сформулируем теорему: Необходимым и достаточным условием для делимости целого натурального числа а на 4 является факт делимости 2 цифр числа а, расположенных в конце записи, на 4. Доказательство теоремы: Предположим, что а равно 0, тогда теорема не нуждается в доказательстве. Для всех остальных натуральных чисел а, будем применять модуль числа а, которое является положительным: Учитывая тот факт, что произведение a1*100 всегда делится на 4, при этом опираясь на свойства делимости можно сделать вывод о том, что если а делится на 4, то и модуль а можно поделить на 4. Из равенства \[|a|=a_{1} * 100+a_{0}\] следует, что а0 делится на 4. Этим мы доказали необходимость. Из равенства \[|a|=a_{1} * 100+a_{0}\] можно сделать вывод, что модуль числа а делится на 4, а это означает, что и само а можно поделить на 4. Этим мы докажем достаточность. Иногда возникает необходимость проверить делится ли число на 4, если оно представлено в виде некоторого выражения, значение которого сначала надо вычислить. В этом случае необходимо: Формула бинома Ньютона поможет в решении таких задач. Примеры 3 — 5 Необходимо вычислить делится ли на 4 выражение 9n−12n+7, если n – это некоторое натуральное число? Решение: Для начала необходимо представить 9 в виде суммы 8+1, далее мы сможем применить формулу бинома Ньютона: \[\begin{aligned} Произведение, которое получилось в результате преобразований, имеет один из множителей 4, а выражение в скобках — это натуральное число. Итак, мы сможем утверждать, что исходное выражение 9n+12n+7 можно поделить на 4, при условии, что n – это любое натуральное значение. Ответ: исходное выражение может быть поделено на 4 без остатка. К решению данного выражения можно применить метод математической индукции. Необходимо доказать, что выражение 9n+12n−7 можно без остатка поделить на 4, при соблюдении условия, что n – это любое натуральное. Решение: Предположим, что n=1, тогда мы сможем решить выражение таким образом 91+12∗1−7=4, а это означает, что 4 делится на 4 без остатка. Далее предположим, что n=k, и при этом значении выражение 9n+12n−7, будет делиться без остатка на 4. Получаем выражение 9k+12k−7 и оно без остатка делится на 4. Далее докажем, что выражение 9n+12n+7 можно поделить на 4, при условии, что n=k+1, но с учетом того, что выражение 9k+12k−7 делится на 4. 9k+1−12(k+1)+7=9∗9k−12k−5=9∗(9k−12k+7)+96k−68=9∗(9k−12k+7)+4∗(24k−17) В итоге преобразований получаем сумму, где первое слагаемое 9∗(9k−12k+7) может быть поделено на 4 без остатка, имея ввиду наше предположение о том, что 9k−12k+7 делится на 4, а второе слагаемое в выражении имеет вид 4∗(24k−17) и содержит множитель 4, исходя из этого можно сделать вывод, что оно тоже делимо на 4. Соответственно и вся исходная сумма может быть поделена на 4. Ответ: с помощью математической индукции мы доказали, что 9n−12n+7 можно поделить на 4, если n – это любое натуральное число. Мы можем использовать еще один вариант для того, чтобы доказать делимость без остатка некоторого выражения на 4. Этот подход предполагает следующее: Необходимо доказать, что значение выражения n*(n2+1)*(n+3)*(n2+4) при условии, что n это целое, делится на 4. Решение: Предположим, что n=4*m, тогда получаем выражение: 4m*((4m)2+1)*(4m+3)*((4m)2+4)=4m*(16m2+1)*(4m+3)*4*(4m2+1) Произведение, которое получилось в результате преобразований, содержит множитель 4, а все остальные множители – это целые числа, исходя из этого можно утверждать, что все выражение делится на 4. Предположим, что n=4*m+1, тогда получаем выражение: (4m+1)*((4m+1)2+1)*(4m+1+3)*((4m+1)2+4)=(4m*1)+((4m+1)2+1)*4(m+1)*((4m+1)2+4) В полученном произведении есть множитель 4, что свидетельствует о том, что исходное выражение делится на 4. Если же предположить, что n=4*m+2, то получаем: (4m+2)*((4m+2)2+1)+(4m+2+3)*((4m+2)2+4)=2*(2m+1)+(16m2+16m+5)*(4m+5)*8*(2m2+2m+1) В данном произведении получаем один из множителей 8, а 8 делится на 4, значит и все выражение делится на 4. Рассмотрим вариант, если что n=4*m+3, то получаем следующее выражение: (4m+3)*((4m+3)2+1)*(4m+3+3)*((4m+3)2+4)=(4m+3)*2*(8m2+12m+5)*2*(2m+3)*(16m2+24m+13)=4*(4m+3)*(8m2+12m+5)*(16m2+24m+13) Оценить статью (59 оценок): Поделиться спросил Изменено
2 года, 2 месяца назад Просмотрено
2к раз Я пытаюсь помочь своей дочери выучить математику. Она борется с множителями, которая заключается в том, чтобы выяснить, какие числа входят в большее число (деление). Я уже узнал, что при суммировании чисел, если они составляют 3, оно может делиться на 3. Я пытаюсь выяснить, есть ли правило для 4. Я думаю, что нет. https://www.quora.com/Why-does-the-divisibility-rule-for-the-number-4-work показывает следующее Правило делимости на 4 в любом большом числе, если разряды десятков и единиц делятся на, то все число делится на 4. Это не имеет смысла. 56 делится на 4. Однако 2 числа в сумме дают 11, поэтому их нельзя разделить на 4. На это вполне может быть получен ответ «нет», но есть ли какая-либо закономерность/метод, который я могу использовать для определения того, число делится на 4, если оно меньше 100 (и больше 4) Как понять это правило делимости на $4$:
это не говорит к добавить последние две цифры; это просто говорит посмотреть на последние две цифры. Например, если вы хотите узнать, делится ли $2389080349$ на $4$, вам просто нужно определить, делится ли $49$ на $4$. (Это не так.) Десятки четные и единицы $0$, $4$ или $8$ (т.е. делятся на $4$) или десятки нечетные и единицы $2$ или $6$ (четные, но не делятся на $4$). Признак делимости на $4$ задано любое целое число $n$, учитывая две последние цифры; если это двузначное число делится на $4$, то делится и $n$. Пример. Рассмотрим 96. Так как 96$ делится на 4$, то и 196$ делится на Причина: 196$ = 100 + 96$. Наконец, что касается вашего последнего вопроса, предположим, что у вас есть число 8. Описывая $8$ как $08$, тест применим и к однозначным числам. Суть в том, что 100 делится на 4. Итак, имеем: $12345678956 = (123456789)(100) + 56 = (123456789)(25)(4) + (14)(4) = ( (123456789)(25)+14)(4)$$ Следовательно, если первые две цифры делятся на четыре, то и все число делится на четыре. На самом деле остаток при делении на четыре равен остатку при делении только двух последних цифр, потому что 3 цифры и далее имеют нулевой остаток. Здесь есть правило делимости числа $4$. Вот оно: Чтобы выяснить, делится ли число на четыре, вам сначала нужно посмотреть на две последние цифры, и если они делятся на четыре вместе, вы можете предположить, что все число делится на $4$ . Почему это работает? Что ж, 100 долларов делятся на четыре, любое числовое значение разряда, превышающее разряд сотен, кратно 100 долларам. Например, в числе $2375$ 2$ в тысячном разряде означает $2000$, а 100\умножить на 20=2000$, поэтому $2000$ кратно $100$. Если мы затем добавим две цифры ниже разряда сотен, мы можем сказать, что если все цифры над разрядом единиц и разрядом десятков делятся на четыре, если две оставшиеся цифры также делятся на четыре, это не изменится. что-либо! Надеюсь, это помогло вам ответить на ваш вопрос. Эти правила делимости помогают определить, когда положительные целые числа делятся на определенные другие целые числа. Все эти правила применимы только для базы 10 — для других баз есть свои, разные версии этих правил. https://youtu.be/bIipw2XSMgU Число делится на тогда и только тогда, когда последние цифры числа делятся на . Так, в частности, число делится на 2 тогда и только тогда, когда его разряд единиц делится на 2, т. Доказательство Число делится на 3 или 9 тогда и только тогда, когда сумма его цифр делится на 3 или 9 соответственно. Обратите внимание, что это , а не работает для более высоких степеней 3. Например, сумма цифр 1899 делится на 27, но 1899 не делится на 27. Доказательство Число делится на тогда и только тогда, когда последние цифры делятся на эту степень числа 5. Доказательство Правило 1: Разбиение на 3-значные числа справа (). Переменная сумма () делится на 7 тогда и только тогда, когда она делится на 7. Доказательство Правило 2: Обрежьте последнюю цифру , удвойте эту цифру и вычтите ее из остального числа (или наоборот). делится на 7 тогда и только тогда, когда результат делится на 7. Доказательство Правило 3: «Хвостовая делимость». Если число представляет собой степень 10, определите его как степень 10. Показатель степени — это количество нулей, которое должно быть в конце числа, чтобы оно делилось на эта сила 10. Пример:
Число должно иметь 6 нулей в конце, чтобы оно делилось на 1 000 000, потому что . Число делится на 11 тогда и только тогда, когда сумма переменных цифр делится на 11. Доказательство Число делится на , где простая факторизация , если число делится на каждое из . Например, мы проверим, делится ли 55682168544 на 36. Первичная факторизация 36 должна быть . Таким образом, мы должны проверить делимость на 4 и 9, чтобы узнать, делится ли оно на 36. Таким образом, число делится и на 4, и на 9 и должно делиться на 36. Для каждого простого числа, отличного от 2 и 5, существует правило, аналогичное правилу 2 делимости на 7. Для общего простого числа существует такое число, что целое число делится на тогда и только тогда, когда усечение последней цифры, умножение ее на и вычитание из оставшегося числа дает нам результат, кратный . Правило 1: Обрежьте последнюю цифру, умножьте ее на 4 и прибавьте к остальной части числа. Результат делится на 13 тогда и только тогда, когда исходное число делилось на 13. Этот процесс можно повторить для больших чисел, как и со вторым правилом делимости для 7. Доказательство Правило 2: Разбиение на 3-значные числа справа (). Переменная сумма () делится на 13 тогда и только тогда, когда она делится на 13. Доказательство Усеките последнюю цифру, умножьте ее на 5 и вычтите из оставшегося старшего числа. Доказательство Усеките последнюю цифру, умножьте ее на 2 и прибавьте к оставшемуся старшему числу. Число делится тогда и только тогда, когда делится результат. Это можно повторить и для больших чисел. Доказательство Усеките последнюю цифру, умножьте ее на 3 и прибавьте к оставшемуся старшему числу. Число делится тогда и только тогда, когда делится результат. Это можно повторить и для больших чисел. Доказательство Почему 49? Для извлечения надоедливого из корня. Полезно до 2300. Округлите до ближайших 50, назовите это, и вычтите исходное число, назовите это. Если , то делится на 49. Примеры: 49. Округлить: . Разница: . ? Да! 1501. Округлить: . Разница: . ? Нет! 1470. Округлить: .
Посмотреть всех экспертов из раздела Учеба и наука > Математика 1. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Area
Площадь области, ограниченной графиком функции, осью x и двумя вертикальными границами, может быть определена непосредственно путем вычисления определенного интеграла. Если f(x ) ≥ 0 на [ a, b ], то площадь ( A ) области, лежащей ниже графика f(x ), выше оси x , и между строками x = a и x = b
Рисунок 1 Нахождение площади под неотрицательной функцией.
Если f(x ) ≤ 0 на [ a, b ], то площадь ( A ) области, лежащей над графиком f(x ), ниже оси x , а между строками x = a и x = b равно
Рисунок 2 Нахождение площади над отрицательной функцией.
Если f(x ) ≥ 0 на [ a, c ] и f(x ) ≤ 0 на [ c, b ], то площадь ( A ) области, ограниченной графом f(x ), ось x и линии x = a и x = b будут определяться следующими определенными интегралами:
Рисунок 3 Область, ограниченная функцией, знак которой меняется.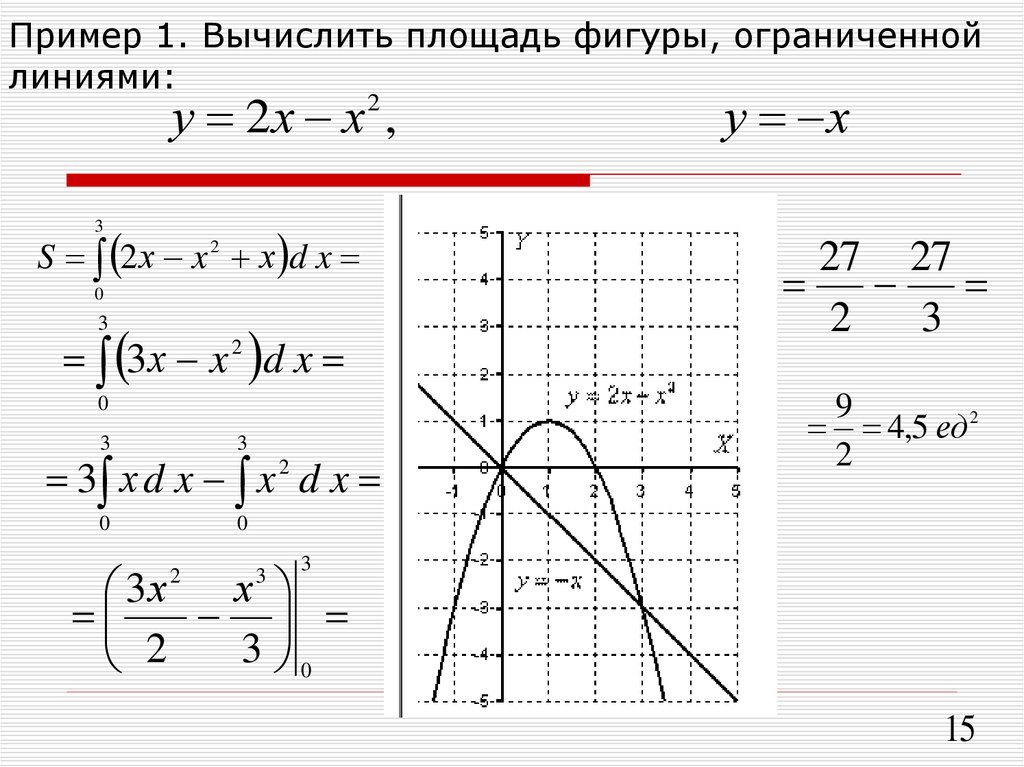
Обратите внимание, что в этой ситуации необходимо было бы определить все точки, в которых график f(x ) пересекает ось x и знак f(x ) на каждом соответствующем интервале.
Для некоторых задач, требующих площади областей, ограниченных графиками двух или более функций, необходимо определить положение каждого графика относительно графиков других функций области. Возможно, потребуется найти точки пересечения графиков, чтобы определить пределы интегрирования. Например, если f(x ) ≥ g ( x ) на [ a, b ], затем площадь ( A ) области между графиками f(x ) и g ( x ) и линии x = a и x = b равно
Рисунок 4 Область между двумя функциями.
Обратите внимание, что аналогичное обсуждение может быть проведено для площадей, определяемых графиками функций y , y — ось, а линии y = a и y = b .
Пример 1: Найдите площадь области, ограниченной y = x 2 , осью x , x = -2 и x = 3.
Поскольку f(x ) ≥ 0 на [–2,3], площадь ( A ) равна
Пример 2: Найдите площадь области, ограниченной y = x 3 + x 2 – 6 x и ось x .
Установив y = 0, чтобы определить, где график пересекает ось x , вы обнаружите, что
Поскольку f ( x ) ≥ 0 на [–3,0] и f ( x ) ≤ 0 на [0,2] (см. рис. 5), площадь ( A ) регион
Рисунок 5 Диаграмма для примера 2.
Пример 3: Найдите площадь, ограниченную y = x 2 и y = 8 – x 2 .
Поскольку y = x 2 и y = 8 – x 2 , вы находите, что
, следовательно, кривые пересекаются в точках (–2,4) и (2,4). ← Предыдущий вопрос
Следующий вопрос → Найти площадь плоской фигуры, ограниченной y = √x, x ∈ [0, 1], y = x 2 , x ∈ [1, 2] и y = –x 2 + 2x + 4, х ∈ [0, 2]. +1 голос ← Предыдущий вопрос
Следующий вопрос → Площадь, ограниченная кривыми y = √x, 2y + 3 = x и осью x в первом квадранте, равна (a) 9 (b) 27/4 (c) 36 (d) 18 спросил
14 декабря 2019 г.
в исчислении интегралов
к
Джей01
(39,7 тыс. баллов) Область, ограниченная кривой y = f(x) и линиями x = 0, y = 0 и x = t, лежит в интервале спросил
14 декабря 2019 г. спросил
14 декабря 2019 г.
в исчислении интегралов
к
Абхилаша01
(37,7 тыс. баллов) Площадь области, ограниченной кривой y = f(x), осью x и линиями x = a и x = b, где – < ∞ < a < b < –2, равна спросил
14 декабря 2019 г.
в исчислении интегралов
к
Абхилаша01
(37,7 тыс. баллов) Площадь области между кривыми y = √((1 + sin x)/cos x) и y = √((1 – sin x)/cos x), ограниченной линиями x = 0 и x = π /4 это спросил
14 декабря 2019 г.
в исчислении интегралов
к
Абхилаша01
(37,7 тыс. баллов) Потому что 8 – x 2 ≥ x 2 92 + 2x + 4, x ∈ [0, 2]. — Sarthaks eConnect
Потому что 8 – x 2 ≥ x 2 92 + 2x + 4, x ∈ [0, 2]. — Sarthaks eConnect 1 ответ
Похожие вопросы
 в исчислении интегралов
к
Абхилаша01
(37,7 тыс. баллов)
9х и х = 0 и х = е
в исчислении интегралов
к
Абхилаша01
(37,7 тыс. баллов)
9х и х = 0 и х = е Категории
 6к)
6к)

 ..
.. Путь S, пройденный точкой по прямой за время T – t0 со скоростью v=v(t) (v(t) непрерывна на [t0; T]), есть .
Путь S, пройденный точкой по прямой за время T – t0 со скоростью v=v(t) (v(t) непрерывна на [t0; T]), есть .
 Рассмотрим интеграл
Рассмотрим интеграл
 к. часто выглядят вполне безобидно (по невнимательности забываем особые точки подынтегральной функции), но применение формулы Ньютона-Лейбница приводит к неверным результатам.
к. часто выглядят вполне безобидно (по невнимательности забываем особые точки подынтегральной функции), но применение формулы Ньютона-Лейбница приводит к неверным результатам. ..
.. Таким образом, математическая связь между значениями $x$ и соответствующими значениями функции $f(x)$ выражается кривой.
Таким образом, математическая связь между значениями $x$ и соответствующими значениями функции $f(x)$ выражается кривой. Однако ширину любого прямоугольника можно вычислить с помощью функции $f(x)$.
Однако ширину любого прямоугольника можно вычислить с помощью функции $f(x)$. Когда плоская фигура ограничена прямыми линиями, легко вычислить ее площадь.
Однако области, ограниченные изогнутыми линиями, сложнее найти (и даже определить).
9n) от n=1 до n=9.
Общий результат для произвольного n был получен Ферма.
Когда плоская фигура ограничена прямыми линиями, легко вычислить ее площадь.
Однако области, ограниченные изогнутыми линиями, сложнее найти (и даже определить).
9n) от n=1 до n=9.
Общий результат для произвольного n был получен Ферма.

 Значение f(x i * )
можно рассматривать как высоту прямоугольника.
Значение f(x i * )
можно рассматривать как высоту прямоугольника.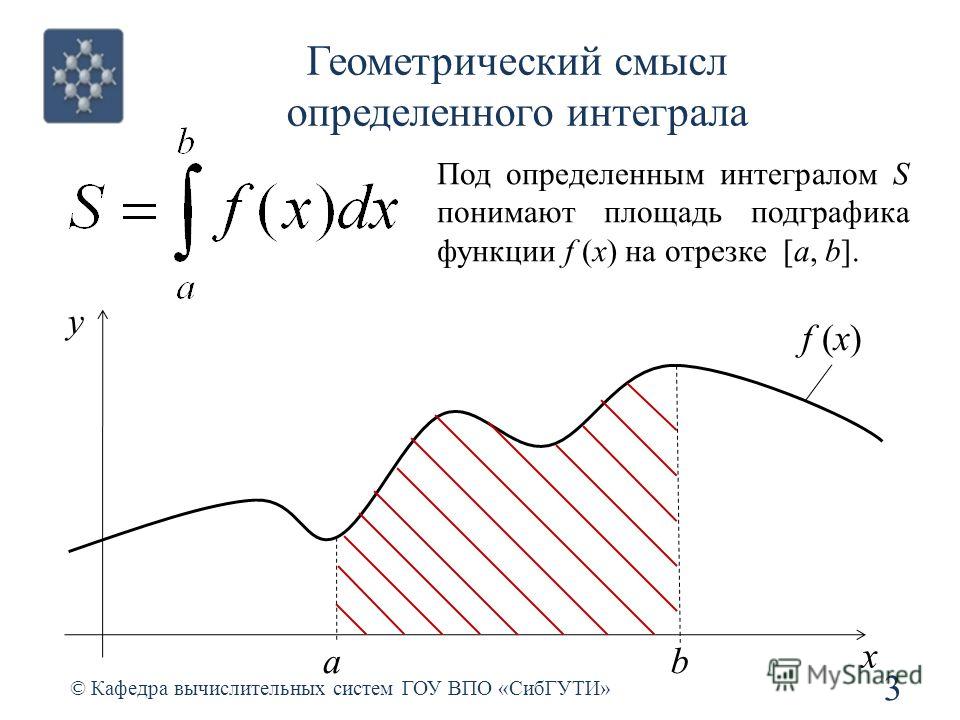 Затем Риман считал
Затем Риман считал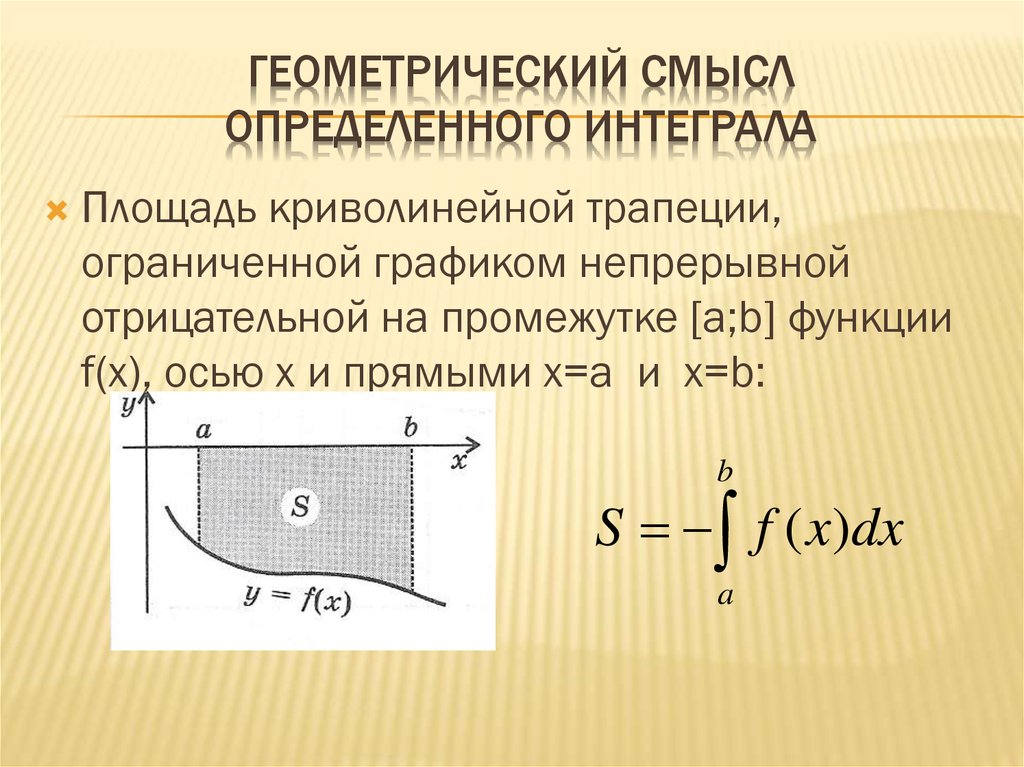 (Спивак)
(Спивак)
 4.3. Сортировка элементов матриц
4.3. Сортировка элементов матриц
 ru
ru
 equ N, 3 // Размер матрицы
.equ WDSIZE, 4 // размер элемента в байтах
main:
STR LR, [SP, #-16]! // сохраняем значение регистра LR
STP X19, X20, [SP, #-16]! // сохраняем значения регистров X19 и X20
MOV W1, #N // помещаем в W1 индекс строки
LDR X4, =A // В X4 адрес текущей строки матрицы А
LDR X19, =C // В X19 адрес материцы С
rowloop:
LDR X5, =B // первый столбец матрицы B
MOV W2, #N // индекс столбца (считаем в обратном порядке до 0)
colloop:
MOV X7, #0 // регистр для накопления результата - по умолчанию равен 0
MOV W0, #N // счетчик цикла
MOV X12, X4 // в X12 помещаем адрес строки для перемножения элементов
MOV X6, X5 // в X6 помещаем адрес столбца для перемножения элементов
dotloop: // Цикл для умножения элементов текущей строки матрицы A на элементы текущего столбца матрицы B
LDR W9, [X12], #WDSIZE // загружаем A[row, i] и увеличиваем адрес в X12 на #WDSIZE байт
LDR W10, [X6], #(N*WDSIZE) // загружаем в W10 данные из B[i, col]
SMADDL X7, W9, W10, X7 // умножаем и сохраняем результат в X7
SUBS W0, W0, #1 // уменьшаем счетчик на 1
B.
equ N, 3 // Размер матрицы
.equ WDSIZE, 4 // размер элемента в байтах
main:
STR LR, [SP, #-16]! // сохраняем значение регистра LR
STP X19, X20, [SP, #-16]! // сохраняем значения регистров X19 и X20
MOV W1, #N // помещаем в W1 индекс строки
LDR X4, =A // В X4 адрес текущей строки матрицы А
LDR X19, =C // В X19 адрес материцы С
rowloop:
LDR X5, =B // первый столбец матрицы B
MOV W2, #N // индекс столбца (считаем в обратном порядке до 0)
colloop:
MOV X7, #0 // регистр для накопления результата - по умолчанию равен 0
MOV W0, #N // счетчик цикла
MOV X12, X4 // в X12 помещаем адрес строки для перемножения элементов
MOV X6, X5 // в X6 помещаем адрес столбца для перемножения элементов
dotloop: // Цикл для умножения элементов текущей строки матрицы A на элементы текущего столбца матрицы B
LDR W9, [X12], #WDSIZE // загружаем A[row, i] и увеличиваем адрес в X12 на #WDSIZE байт
LDR W10, [X6], #(N*WDSIZE) // загружаем в W10 данные из B[i, col]
SMADDL X7, W9, W10, X7 // умножаем и сохраняем результат в X7
SUBS W0, W0, #1 // уменьшаем счетчик на 1
B. NE dotloop // если W0 не равно 0, то переходим к dotloop для перемножения новых элементов матриц
STR W7, [X19], #4 // сохраняем результат из W7 в X19 - C[row, col] = W7, увеличиваем адрес в X19 на 4 байта
ADD X5, X5, #WDSIZE // Переходим к следующему столбцу в матрице B - увеличиваем адрес в X5 на #WDSIZE байт
SUBS W2, W2, #1 // увеличиваем счетчик столбцов
B.NE colloop // если не все столбцы прошли, то переходим обратно к colloop
ADD X4, X4, #(N*WDSIZE) // к адресу в X4 прибавляем #(N*WDSIZE) байт для перехода к адресу новой строки
SUBS W1, W1, #1 // уменьшаем счетчик строк
B.NE rowloop // если еще есть строки, переходим обратно к rowloop
MOV W20, #3 // проходим по трем строкам
LDR X19, =C // адрес результирующей матрицы C
// выводим матрицу с помощью функции printf языка C
printloop:
LDR X0, =prtstr // загружаем строку форматирования для функции printf
LDR W1, [X19], #WDSIZE // первый элемент текущей строки матрицы
LDR W2, [X19], #WDSIZE // второй элемент текущей строки матрицы
LDR W3, [X19], #WDSIZE // третий элемент текущей строки матрицы
BL printf // Вызыв функции printf
SUBS W20, W20, #1 // уменьшаем счетчик строк
B.
NE dotloop // если W0 не равно 0, то переходим к dotloop для перемножения новых элементов матриц
STR W7, [X19], #4 // сохраняем результат из W7 в X19 - C[row, col] = W7, увеличиваем адрес в X19 на 4 байта
ADD X5, X5, #WDSIZE // Переходим к следующему столбцу в матрице B - увеличиваем адрес в X5 на #WDSIZE байт
SUBS W2, W2, #1 // увеличиваем счетчик столбцов
B.NE colloop // если не все столбцы прошли, то переходим обратно к colloop
ADD X4, X4, #(N*WDSIZE) // к адресу в X4 прибавляем #(N*WDSIZE) байт для перехода к адресу новой строки
SUBS W1, W1, #1 // уменьшаем счетчик строк
B.NE rowloop // если еще есть строки, переходим обратно к rowloop
MOV W20, #3 // проходим по трем строкам
LDR X19, =C // адрес результирующей матрицы C
// выводим матрицу с помощью функции printf языка C
printloop:
LDR X0, =prtstr // загружаем строку форматирования для функции printf
LDR W1, [X19], #WDSIZE // первый элемент текущей строки матрицы
LDR W2, [X19], #WDSIZE // второй элемент текущей строки матрицы
LDR W3, [X19], #WDSIZE // третий элемент текущей строки матрицы
BL printf // Вызыв функции printf
SUBS W20, W20, #1 // уменьшаем счетчик строк
B. NE printloop // если есть еще строки, переходим обратно к printloop
MOV X0, #0 // код возврата из функции
LDP X19, X20, [SP], #16 // восстанавливаем значение регистров
LDR LR, [SP], #16 // восстанавливаем регистр LR
RET // выход из функции
.data
// первая матрица
A: .word 1, 2, 3
.word 4, 5, 6
.word 7, 8, 9
// вторая матрица
B: .word 9, 8, 7
.word 6, 5, 4
.word 3, 2, 1
// результирующая матрица
C: .fill 9, 4, 0
prtstr: .asciz "%3d %3d %3d\n"
NE printloop // если есть еще строки, переходим обратно к printloop
MOV X0, #0 // код возврата из функции
LDP X19, X20, [SP], #16 // восстанавливаем значение регистров
LDR LR, [SP], #16 // восстанавливаем регистр LR
RET // выход из функции
.data
// первая матрица
A: .word 1, 2, 3
.word 4, 5, 6
.word 7, 8, 9
// вторая матрица
B: .word 9, 8, 7
.word 6, 5, 4
.word 3, 2, 1
// результирующая матрица
C: .fill 9, 4, 0
prtstr: .asciz "%3d %3d %3d\n"


 NE dotloop // если W0 не равно 0, то переходим к dotloop для перемножения новых элементов матриц
NE dotloop // если W0 не равно 0, то переходим к dotloop для перемножения новых элементов матриц
 NE colloop // если не все столбцы прошли, то переходим обратно к colloop
NE colloop // если не все столбцы прошли, то переходим обратно к colloop



 И каждый столбец в матрице B также имеет n элементов.
И каждый столбец в матрице B также имеет n элементов.
 "
"  В противном случае функция возвращает сообщение об ошибке.
В противном случае функция возвращает сообщение об ошибке.



 dot(A, B)
dot(A, B) 
 Мы научимся перемножать матрицы разных размеров вместе.
Мы научимся перемножать матрицы разных размеров вместе.


 random.seed()’, чтобы сделать генератор случайных чисел детерминированным.
random.seed()’, чтобы сделать генератор случайных чисел детерминированным. 
 format(B, B.shape))
print("Матрица C:\n{}, shape={}\n".format(C, C.shape))
format(B, B.shape))
print("Матрица C:\n{}, shape={}\n".format(C, C.shape)) 

 matmul()’ и будет возвращать результат матричного умножения две матрицы.
matmul()’ и будет возвращать результат матричного умножения две матрицы.
 matmul()’ и ‘np.dot()’ состоит в том, что ‘np.matmul()’ не допускает умножения на скаляр (мы обсудим это в следующий раздел), в то время как ‘np.dot()’ разрешает это.
matmul()’ и ‘np.dot()’ состоит в том, что ‘np.matmul()’ не допускает умножения на скаляр (мы обсудим это в следующий раздел), в то время как ‘np.dot()’ разрешает это.

 random.seed (42)
A = np.random.randint (0, 10, размер = (3,3))
B = np.random.randint (0, 10, размер = (3,3))
print("Матрица A:\n{}\n".format(A))
печать ("Матрица B:\n{}\n".format(B))
C = np.multiply(A,B) # или A * B
print("Поэлементное умножение A и B:\n{}".format(C))
random.seed (42)
A = np.random.randint (0, 10, размер = (3,3))
B = np.random.randint (0, 10, размер = (3,3))
print("Матрица A:\n{}\n".format(A))
печать ("Матрица B:\n{}\n".format(B))
C = np.multiply(A,B) # или A * B
print("Поэлементное умножение A и B:\n{}".format(C)) 

 format(B, B.shape))
format(B, B.shape))  е. возводить каждый отдельный элемент матрицы в некоторую степень.
е. возводить каждый отдельный элемент матрицы в некоторую степень.

 Эти библиотеки помогают нам выполнять вычисления на графических процессорах на базе CUDA. Чтобы установить эти библиотеки с вашего терминала, если на вашем компьютере установлен графический процессор.
Эти библиотеки помогают нам выполнять вычисления на графических процессорах на базе CUDA. Чтобы установить эти библиотеки с вашего терминала, если на вашем компьютере установлен графический процессор.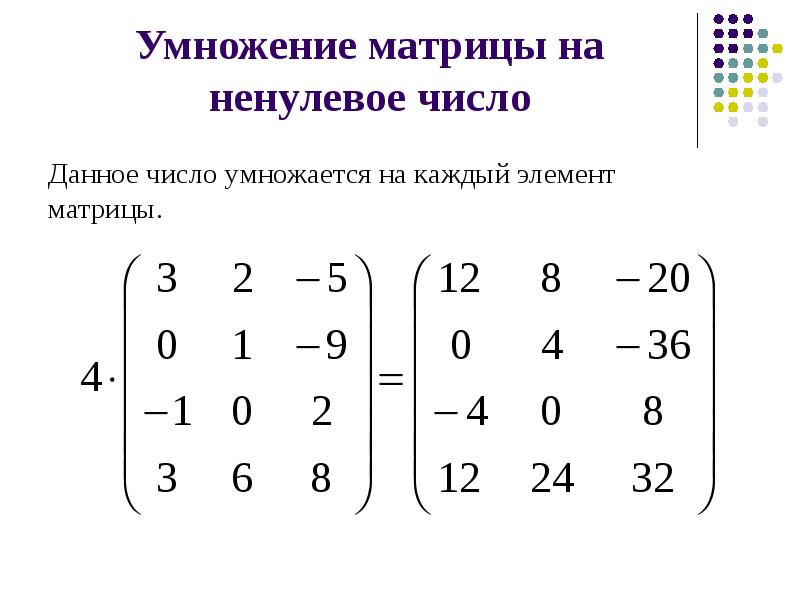
 to_gpu(x)
y_gpu = gpuarray.to_gpu(y)
тик = время.время()
#выполнение умножения
z_gpu = linalg.mdot(x_gpu, y_gpu)
ток = время.время()
time_taken = toc - тик #время в секундах
print("Время, затраченное на GPU (в мс) = {}".format(time_taken*1000))
to_gpu(x)
y_gpu = gpuarray.to_gpu(y)
тик = время.время()
#выполнение умножения
z_gpu = linalg.mdot(x_gpu, y_gpu)
ток = время.время()
time_taken = toc - тик #время в секундах
print("Время, затраченное на GPU (в мс) = {}".format(time_taken*1000)) 
 {2}+2 x-3}
{2}+2 x-3} 2 равен 0,9.0003
2 равен 0,9.0003 Это значение для y является точкой пересечения с осью y. то есть
Это значение для y является точкой пересечения с осью y. то есть
 81 МБ
81 МБ
 преподаватель Калиничев Р. А. Специальность 230401.5 «Прикладная математика», 5 семестр. Теория вероятностей. Вариант № 25. Страниц 39, решенные задания с 1 по 37 включительно.
преподаватель Калиничев Р. А. Специальность 230401.5 «Прикладная математика», 5 семестр. Теория вероятностей. Вариант № 25. Страниц 39, решенные задания с 1 по 37 включительно.




 Это значит, что все произведение а1*100 можно поделить на 4.
Это значит, что все произведение а1*100 можно поделить на 4.

 Поэтому можно сделать вывод о том, что это произведение без остатка можно поделить на 4.
Поэтому можно сделать вывод о том, что это произведение без остатка можно поделить на 4.


 Я также знаю правила для 2, 5, 6, 9 и 10.
Я также знаю правила для 2, 5, 6, 9 и 10. Поскольку $4$ делит $100$, число делится на $4$ тогда и только тогда, когда его последние две цифры (десятки и единицы) делятся на $4$. Ответ Роберта Исраэля дает метод определения того, делится ли двузначное число на 4 доллара, и правило гласит, что это практически все, что вам нужно.
Поскольку $4$ делит $100$, число делится на $4$ тогда и только тогда, когда его последние две цифры (десятки и единицы) делятся на $4$. Ответ Роберта Исраэля дает метод определения того, делится ли двузначное число на 4 доллара, и правило гласит, что это практически все, что вам нужно. Число слева (которое всегда будет иметь место, даже если оно равно $0$) делится на $4$; следовательно, достаточно рассмотреть только число, представленное двумя последними цифрами целого числа $n$.
Число слева (которое всегда будет иметь место, даже если оно равно $0$) делится на $4$; следовательно, достаточно рассмотреть только число, представленное двумя последними цифрами целого числа $n$.
 2 Правило делимости на 3 и 9
2 Правило делимости на 3 и 9 е. если число оканчивается на 0, 2, 4, 6 или 8.
е. если число оканчивается на 0, 2, 4, 6 или 8. Примечание. Это говорит вам только о том, делится ли оно, а НЕ остаток. Возьмите число, скажем, 12345. Посмотрите на последнюю цифру и добавьте или вычтите число, кратное 7, чтобы получить ноль. В этом случае мы получаем 12380 или 12310 (оба допустимы, я использую первое). Отрежьте конечные 0 и повторите. 1238 — 28 ==> 1210 ==> 121 — 21 ==> 100 ==> 1 НЕТ. Обычно работает с числами, относительно простыми по основанию (и ОТЛИЧНО работает с двоичными числами). Вот тот, который работает. 12348 — 28 ==> 12320 ==> 1232 +28 ==> 1260 ==> 126 + 14 ==> 14 УРА!
Примечание. Это говорит вам только о том, делится ли оно, а НЕ остаток. Возьмите число, скажем, 12345. Посмотрите на последнюю цифру и добавьте или вычтите число, кратное 7, чтобы получить ноль. В этом случае мы получаем 12380 или 12310 (оба допустимы, я использую первое). Отрежьте конечные 0 и повторите. 1238 — 28 ==> 1210 ==> 121 — 21 ==> 100 ==> 1 НЕТ. Обычно работает с числами, относительно простыми по основанию (и ОТЛИЧНО работает с двоичными числами). Вот тот, который работает. 12348 — 28 ==> 12320 ==> 1232 +28 ==> 1260 ==> 126 + 14 ==> 14 УРА!
 Правило делимости 2 для 7 говорит, что для , . Правило делимости для 11 эквивалентно выбору . Правило делимости на 3 эквивалентно выбору . Эти правила также можно найти при соответствующих условиях в системах счисления, отличных от 10. Также обратите внимание, что эти правила существуют в двух формах: если заменяется, то вычитание может быть заменено сложением. Мы видим один пример этого в правиле делимости для 13: мы могли бы умножить на 9и вычитать, а не умножать на 4 и добавлять.
Правило делимости 2 для 7 говорит, что для , . Правило делимости для 11 эквивалентно выбору . Правило делимости на 3 эквивалентно выбору . Эти правила также можно найти при соответствующих условиях в системах счисления, отличных от 10. Также обратите внимание, что эти правила существуют в двух формах: если заменяется, то вычитание может быть заменено сложением. Мы видим один пример этого в правиле делимости для 13: мы могли бы умножить на 9и вычитать, а не умножать на 4 и добавлять. Число делится тогда и только тогда, когда делится результат. Процесс можно повторить для любого числа.
Число делится тогда и только тогда, когда делится результат. Процесс можно повторить для любого числа.
 2
2 Используйте функцию СУММ, преобразуя все числа, которые необходимо вычесть, в их отрицательные значения. Например, функция СУММ(100,-32,15,-6) возвращает результат 77.
Используйте функцию СУММ, преобразуя все числа, которые необходимо вычесть, в их отрицательные значения. Например, функция СУММ(100,-32,15,-6) возвращает результат 77.
 Каждый аргумент может быть диапазон, ссылка на ячейку, массив, константа или формулалибо результатом выполнения другой функции. Например, СУММ(A1:A5) суммирует все числа в диапазоне ячеек A1–A5. Другим примером является сумм(A1, A3, A5), которая суммирует числа, содержащиеся в ячейках A1, A3 и A5 (аргументы — A1, A3 и A5).
Каждый аргумент может быть диапазон, ссылка на ячейку, массив, константа или формулалибо результатом выполнения другой функции. Например, СУММ(A1:A5) суммирует все числа в диапазоне ячеек A1–A5. Другим примером является сумм(A1, A3, A5), которая суммирует числа, содержащиеся в ячейках A1, A3 и A5 (аргументы — A1, A3 и A5). Для начала необходимо создать таблицу со значениями. Обратите внимание на то, что каждая ячейка таблицы имеет свой адрес, который определяется буквой и цифрой. Каждая буква соответствует столбцу, а каждая цифра — строке.
Для начала необходимо создать таблицу со значениями. Обратите внимание на то, что каждая ячейка таблицы имеет свой адрес, который определяется буквой и цифрой. Каждая буква соответствует столбцу, а каждая цифра — строке. Затем поставьте знак «=» и по очереди вводите адрес каждой ячейки, содержимое которой нужно просуммировать, не забывая ставить знак «+» между ними. К примеру, у вас должно получиться: «=A1+B7+C2+B3+E5». После того как будет введён адрес последней ячейки, нажмите на клавиатуре «Enter» и вы получите сумму всех отмеченных чисел. Необязательно вводить каждый адрес вручную. Достаточно кликнуть по определённой ячейке и в поле для формул сразу отобразится её адрес, ставьте после него «+» и переходите к следующей.
Затем поставьте знак «=» и по очереди вводите адрес каждой ячейки, содержимое которой нужно просуммировать, не забывая ставить знак «+» между ними. К примеру, у вас должно получиться: «=A1+B7+C2+B3+E5». После того как будет введён адрес последней ячейки, нажмите на клавиатуре «Enter» и вы получите сумму всех отмеченных чисел. Необязательно вводить каждый адрес вручную. Достаточно кликнуть по определённой ячейке и в поле для формул сразу отобразится её адрес, ставьте после него «+» и переходите к следующей. В открывшемся окне в разделе «Вставить» отметьте «Значения», а в разделе «Операция» выберите сложить. В результате все данные просуммируются.
В открывшемся окне в разделе «Вставить» отметьте «Значения», а в разделе «Операция» выберите сложить. В результате все данные просуммируются. Эксель позволяет решать сложные уравнения, выполнять инженерный и статистический анализ. Постепенно овладевая базовыми функциями и инструментами программы, вы научитесь выполнять всё больше операций в редакторе Excel. Пишите в комментариях помогла ли вам статья разобраться с возникшими вопросами и делитесь своим опытом с другими пользователями.
Эксель позволяет решать сложные уравнения, выполнять инженерный и статистический анализ. Постепенно овладевая базовыми функциями и инструментами программы, вы научитесь выполнять всё больше операций в редакторе Excel. Пишите в комментариях помогла ли вам статья разобраться с возникшими вопросами и делитесь своим опытом с другими пользователями.


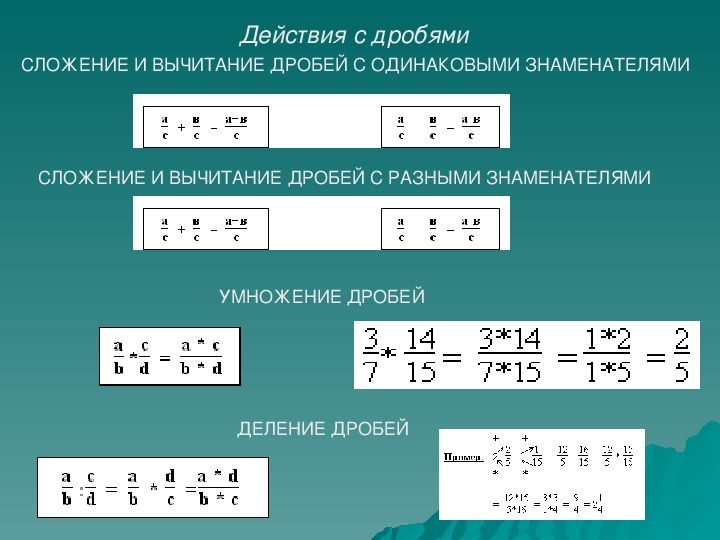



 9{2} =16\cdot 3+16=64\), поэтому \(A = 8\).
9{2} =16\cdot 3+16=64\), поэтому \(A = 8\). 9{-1} \left(\dfrac{3}{5} \right)\приблизительно 0,927\text{ или }C=2\pi -0,927=5,356\nonnumber\]
9{-1} \left(\dfrac{3}{5} \right)\приблизительно 0,927\text{ или }C=2\pi -0,927=5,356\nonnumber\]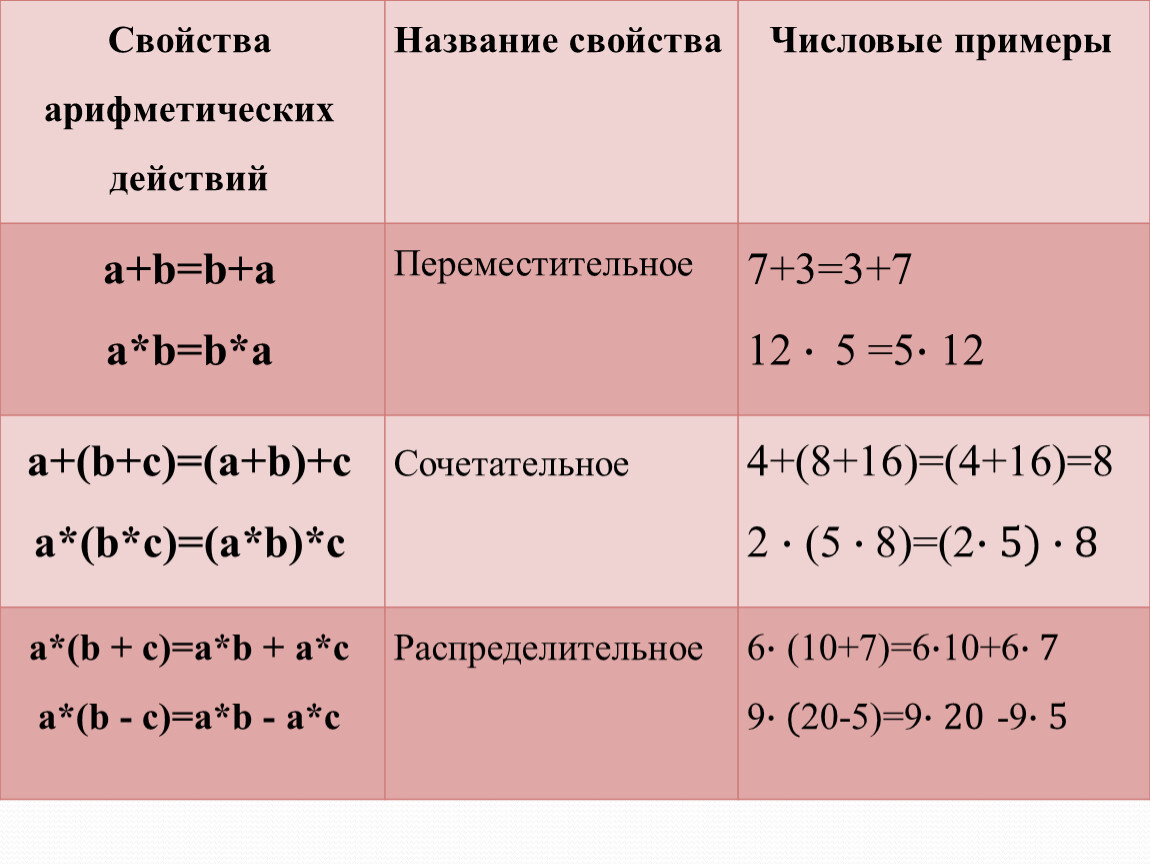


 Используйте это вместе с идентичностью суммы синусов, чтобы доказать идентичность суммы и произведения для \(\sin\left(u\right)-\sin\left(v\right)\).
Используйте это вместе с идентичностью суммы синусов, чтобы доказать идентичность суммы и произведения для \(\sin\left(u\right)-\sin\left(v\right)\).
 Первый фактор, \(\cos\left(\pi {\kern 1pt} t\right)\), имеет период \(P=\dfrac{2\pi}{\pi} =2\), поэтому решение интервал \(0\le t<2\) представляет собой один полный цикл этой функции.
Первый фактор, \(\cos\left(\pi {\kern 1pt} t\right)\), имеет период \(P=\dfrac{2\pi}{\pi} =2\), поэтому решение интервал \(0\le t<2\) представляет собой один полный цикл этой функции.
 opentextbookstore.com/details.php?id=30
opentextbookstore.com/details.php?id=30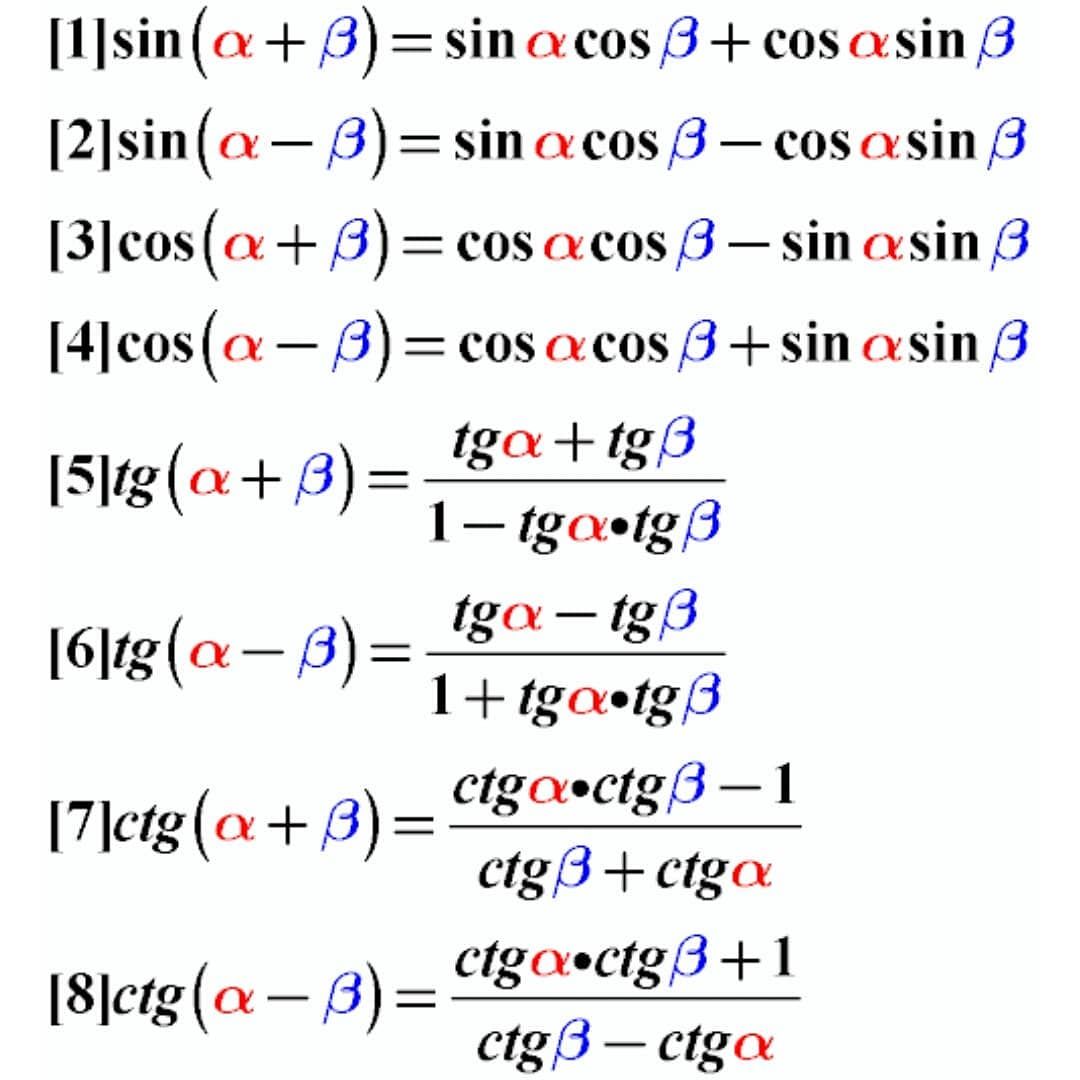 Такие вопросы не предназначены для проверки, а вместо этого используются для получения знаний, которые помогут в курсах математики более высокого уровня.
Такие вопросы не предназначены для проверки, а вместо этого используются для получения знаний, которые помогут в курсах математики более высокого уровня.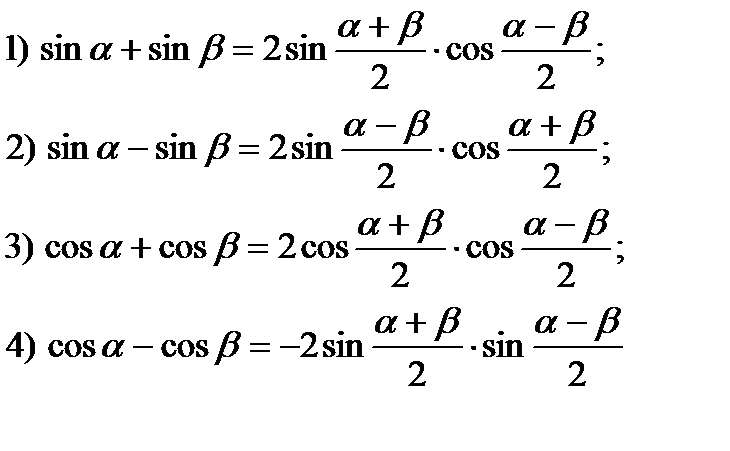


 MATH. СОДЕРЖАНИЕ.HSF.TF.C).
MATH. СОДЕРЖАНИЕ.HSF.TF.C).
 Такие вопросы не предназначены для проверки, а вместо этого используются для получения знаний, которые помогут в курсах математики более высокого уровня.
Такие вопросы не предназначены для проверки, а вместо этого используются для получения знаний, которые помогут в курсах математики более высокого уровня.

 HSF.TF.C).
HSF.TF.C).
 Нам нужен наименьший из этих четырех корней x. При этом другие три корня это 2k — x, 2k-1 + x и 2k — 2k-1 — x
Нам нужен наименьший из этих четырех корней x. При этом другие три корня это 2k — x, 2k-1 + x и 2k — 2k-1 — x
 Форма отчета
Форма отчета
 Используйте наш ‘Конвертер Джипег в ПДФ’, чтобы сохранить каждое Джипег изображение в виде ПДФ документа. Это самый быстрый способ конвертировать фотографии и сканы Джипег в ПДФ онлайн.
Используйте наш ‘Конвертер Джипег в ПДФ’, чтобы сохранить каждое Джипег изображение в виде ПДФ документа. Это самый быстрый способ конвертировать фотографии и сканы Джипег в ПДФ онлайн.
 Выберите файлы для конвертации.
Выберите файлы для конвертации. Ваши данные. Вы в контроле.
Ваши данные. Вы в контроле. Этот формат часто используется в цифровых картах памяти камер. Файл JPG – отличный формат, так как нередко удается сжимать файлы до 1/10 размера исходного файла, что особенно хорошо для экономии трафика.
Этот формат часто используется в цифровых картах памяти камер. Файл JPG – отличный формат, так как нередко удается сжимать файлы до 1/10 размера исходного файла, что особенно хорошо для экономии трафика. Пропорции сжатия 10:1 или 20:01 дают незначительное ухудшение качества изображения.
Пропорции сжатия 10:1 или 20:01 дают незначительное ухудшение качества изображения. pdf
pdf Он не кодирует информацию, относящуюся к программному обеспечению, аппаратному обеспечению или операционной системе, используемой для создания или просмотра документа.
Он не кодирует информацию, относящуюся к программному обеспечению, аппаратному обеспечению или операционной системе, используемой для создания или просмотра документа. com и aspose.cloud
com и aspose.cloud  Вы можете сделать это онлайн за считанные секунды бесплатно.
Вы можете сделать это онлайн за считанные секунды бесплатно.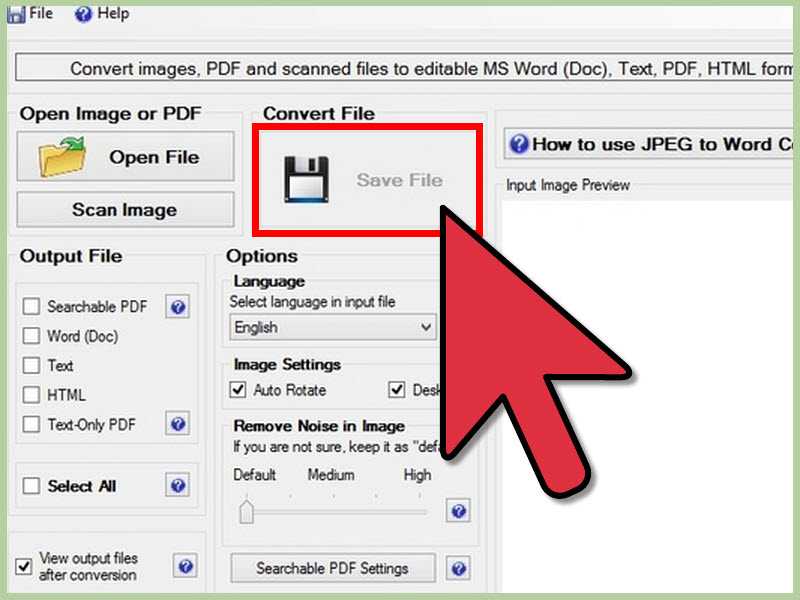
 Используйте наше бесплатное приложение, чтобы уменьшить нагрузку при работе как с документами, так и с файлами изображений.
Используйте наше бесплатное приложение, чтобы уменьшить нагрузку при работе как с документами, так и с файлами изображений.
 Вы можете получить результат в течение нескольких секунд.
Вы можете получить результат в течение нескольких секунд.
 03.2023, 14:23:23 • Подано по адресу:
Онлайн PDF-инструменты
• Проверенные решения
03.2023, 14:23:23 • Подано по адресу:
Онлайн PDF-инструменты
• Проверенные решения Бесплатно скачайте его, чтобы попробовать.
Бесплатно скачайте его, чтобы попробовать. С помощью этого бесплатного онлайн-конвертера JPEG в PDF вы можете легко конвертировать JPEG в PDF онлайн и сохранять результат на своем компьютере, чтобы использовать его в любое время. Нажмите кнопку «Изображение в PDF» и просто загрузите изображение в формате JPEG из любой области хранения, а затем преобразуйте его в PDF, и это так просто. Важно отметить, что качество PDF после преобразования является первоклассным и стандартным и может быть прочитано любой программой для чтения PDF. HiPDF — очень эффективный инструмент, доступный на всех платформах.
С помощью этого бесплатного онлайн-конвертера JPEG в PDF вы можете легко конвертировать JPEG в PDF онлайн и сохранять результат на своем компьютере, чтобы использовать его в любое время. Нажмите кнопку «Изображение в PDF» и просто загрузите изображение в формате JPEG из любой области хранения, а затем преобразуйте его в PDF, и это так просто. Важно отметить, что качество PDF после преобразования является первоклассным и стандартным и может быть прочитано любой программой для чтения PDF. HiPDF — очень эффективный инструмент, доступный на всех платформах. Основное преимущество заключается в том, что вам не нужно устанавливать какое-либо программное обеспечение на свой компьютер, чтобы он выполнял преобразование в высококачественный PDF.
Основное преимущество заключается в том, что вам не нужно устанавливать какое-либо программное обеспечение на свой компьютер, чтобы он выполнял преобразование в высококачественный PDF.

 Веб-страница преобразования JPG в PDF имеет простой в использовании интерфейс, который позволяет конвертировать JPG за считанные секунды.
Веб-страница преобразования JPG в PDF имеет простой в использовании интерфейс, который позволяет конвертировать JPG за считанные секунды. Если ваши файлы превышают это значение, они не будут преобразованы в PDF.
Если ваши файлы превышают это значение, они не будут преобразованы в PDF.
 Никто не имеет доступа к вашим файлам. Преобразование файлов (включая WORD в EXCEL) абсолютно безопасно.
Никто не имеет доступа к вашим файлам. Преобразование файлов (включая WORD в EXCEL) абсолютно безопасно. Вы получите ссылку для скачивания, как только файл будет конвертирован.
Вы получите ссылку для скачивания, как только файл будет конвертирован. com
а также
aspose.cloud
com
а также
aspose.cloud

 Наш конвертер DOCX в Эксель совершенно бесплатен.
Наш конвертер DOCX в Эксель совершенно бесплатен.
 Вы можете скачать результат сразу или отправить ссылку на скачивание Эксель на свой e-mail позже.
Вы можете скачать результат сразу или отправить ссылку на скачивание Эксель на свой e-mail позже. Форма отчета
Форма отчета

 Без регистрации и капчи. Здесь вы можете конвертировать документы онлайн и сохранять их в нужном вам формате на свой компьютер или любое другое устройство.
Без регистрации и капчи. Здесь вы можете конвертировать документы онлайн и сохранять их в нужном вам формате на свой компьютер или любое другое устройство. Мы поддерживаем множество популярных форматов для работы, все возможные форматы изображений, форматы мультимедийных файлов и т. д. Наш инструмент преобразования Word в Excel прост в использовании: выберите нужный тип файла, затем определите выходной формат вашего документа, загрузите файл и нажмите ‘Загрузить’.
Мы поддерживаем множество популярных форматов для работы, все возможные форматы изображений, форматы мультимедийных файлов и т. д. Наш инструмент преобразования Word в Excel прост в использовании: выберите нужный тип файла, затем определите выходной формат вашего документа, загрузите файл и нажмите ‘Загрузить’. Наш сервис работает на любой ОС, включая Windows, Mac и Linux.
Наш сервис работает на любой ОС, включая Windows, Mac и Linux.
 Вы можете получить результат в течение нескольких секунд.
Вы можете получить результат в течение нескольких секунд.