Скалярное произведение векторов: теория и решения задач
- Определения и смысл скалярного произведения векторов
- Нахождение скалярного произведения через координаты перемножаемых векторов
- Свойства скалярного произведения векторов
- Матричное представление скалярного произведения векторов и произведение n-мерных векторов
- Угол между двумя векторами
- Применения скалярного произведения векторов
- Скалярное произведение векторов Калькулятор онлайн
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Найти скалярное произведение векторов можно несколькими различными способами. Способ зависит от того, какие условия даны в задаче. Поэтому существуют несколько определений скалярного произведения.
В задаче могут в явном или неявном виде присутствовать длины перемножаемых векторов
и косинус угла между ними. В этом случае действует следующее определение.
Определение 1. Скалярным произведением векторов называется число (скаляр), равное произведению длин (модулей) этих векторов на косинус угла между ними. Формула скалярного произведения векторов согласно определению 1: (1)
Можно встретить и другое название этой операции: внутреннее произведение.
Скалярное произведение вектора на себя называется скалярным квадратом.
Справедливо и другое определение, полностью равносильное определению 1.
Определение 2. Скалярным произведением векторов называется число (скаляр), равное произведению длины одного их этих векторов на проекцию другого вектора на ось, определяемую первым из указанных векторов. Формула согласно определению 2:
(2)
или
(3)
Но в задаче могут в явном или неявном виде присутствовать координаты перемножаемых
векторов. Как на плоскости, так и в пространстве. Тогда справедливо следующее определение.
Как на плоскости, так и в пространстве. Тогда справедливо следующее определение.
Определение 3. Скалярное произведение векторов — это число, равное сумме попарных произведений их соответствующих координат.
Два перемножаемых вектора могут быть представлены также в виде матриц: первый вектор — в виде матрицы-строки, а второй — в виде матрицы-столбца:
.
В этом случае верно следующее определение.
Определение 4. Скалярное произведение векторов, представленных в виде матрицы-строки и матрицы-столбца представляет собой произведение этих матриц.
Почему скалярное произведение векторов называется именно скалярным и что представляет собой?
Чем оно отличается от результатов других операций над векторами? Что такое скаляр? Скаляр — это число.
И скалярное произведение векторов — это тоже число. Этим оно и отличается от уже рассмотренной суммы векторов, и от векторного произведения векторов, которое ещё предстоит рассмотреть. В отличие от
скалярного произведения, сумма векторов — это вектор, и векторное произведение — тоже вектор.
Этим оно и отличается от уже рассмотренной суммы векторов, и от векторного произведения векторов, которое ещё предстоит рассмотреть. В отличие от
скалярного произведения, сумма векторов — это вектор, и векторное произведение — тоже вектор.
На этом уроке будем решать распространённые задачи не только на непосредственное вычисление скалярного произведения, но и на выяснение ортогональности (перпендикулярности) векторов, вида угла (тупой, острый, прямой) между векторами, вычисление скалярного произведения векторов, которые даны в координатах, вычисление длин диагоналей параллелограма, построенного на вектора. Но все по порядку. Перед каждым видом задач будем обращать внимание на то, что на этот счёт гласит теория. По ходу урока вам пригодится онлайн-калькулятор для проверки решения задач на скалярное произведение векторов.
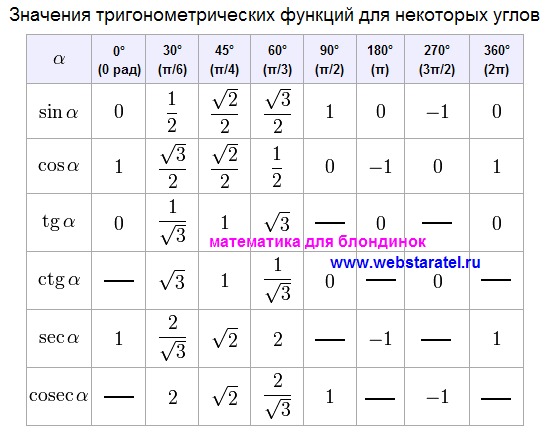
- Пригодится: тригонометрическая таблица (синусы, косинусы, тангенсы и котангенсы распространенных углов)
Если в задаче и длины векторов, и угол между ними преподнесены «на блюдечке с голубой каёмочкой», то условие задачи и её решение выглядят так:
Пример 1. Даны векторы .
Найти скалярное произведение векторов
, если их длины и угол между ними представлены
следующими значениями:
Даны векторы .
Найти скалярное произведение векторов
, если их длины и угол между ними представлены
следующими значениями:
Решение:
Задачу с применением этой формулы решим после следующего важного теоретического пункта.
То же самое число можно получить, если перемножаемые векторы заданы своими координатами. Повторим определение для этого случая.
Определение 3. Скалярное произведение векторов — это число, равное сумме попарных произведений их соответствующих координат.
На плоскости
Если два вектора и на плоскости определены своими двумя декартовыми прямоугольными координатами
и
,
то скалярное произведение этих векторов равно сумме попарных произведений их соответствующих координат:
.
Пример 2. Найти численную величину проекции вектора на ось, параллельную вектору .
Решение. Находим скалярное произведение векторов, складывая попарные произведения их координат:
.
Теперь нам требуется приравнять полученное скалярное произведение произведению длины вектора на проекцию вектора на ось, параллельную вектору (в соответствии с формулой ).
Находим длину вектора как квадратный корень из суммы квадратов его координат:
.
Составляем уравнение и решаем его:
Ответ. Искомая численная величина равна минус 8.
Для самопроверки можно использовать онлайн калькулятор Скалярное произведение векторов и косинус угла между ними.
В пространстве
Если два вектора и в пространстве определены своими тремя декартовыми прямоугольными координатами
и
,
то скалярное произведение этих векторов также равно сумме попарных произведений их соответствующих координат, только координат уже три:
.
Задача на нахождение скалярного произведения рассмотренным способом — после разбора свойств скалярного произведения. Потому что в задаче потребуется определить, какой угол образуют перемножаемые векторы.
Алгебраические свойства
1. (переместительное свойство: от перемены местами перемножаемых векторов величина их скалярного произведения не меняется).
2. (сочетательное относительно числового множителя свойство: скалярное произведение вектора, умноженного на некоторый множитель, и другого вектора, равно скалярному произведению этих векторов, умноженному на тот же множитель).
3. (распределительное относительно суммы векторов свойство: скалярное произведение суммы двух векторов на третий вектор равно сумме скалярных произведений первого вектора на третий вектор и второго вектора на третий вектор).
4. (скалярный квадрат вектора больше нуля),
если — ненулевой вектор, и ,
если — нулевой вектор.
Геометрические свойства
В определениях изучаемой операции мы уже касались понятия угла между двумя векторами. Пора уточнить это понятие.
На рисунке выше видны два вектора, которые приведены к общему началу. И первое, на что нужно обратить внимание: между этими векторами существуют два угла — φ1 и φ2. Какой из этих углов фигурирует в определениях и свойствах скалярного произведения векторов? Сумма рассмотренных углов равна 2π и поэтому косинусы этих углов равны. В определение скалярного произведения входит только косинус угла, а не значение его выражения. Но в свойствах рассматривается только один угол. И это тот из двух углов, который не превосходит π, то есть 180 градусов. На рисунке этот угол обозначен как φ1.
1. Два вектора называют ортогональными и угол между этими векторами — прямой (90 градусов или π/2), если скалярное произведение этих векторов равно нулю:
.
Ортогональностью в векторной алгебре называется перпендикулярность двух векторов.
2. Два ненулевых вектора составляют острый угол (от 0 до 90 градусов, или, что тоже самое — меньше π/2) тогда и только тогда, когда их скалярное произведение положительно.
3. Два ненулевых вектора составляют тупой угол (от 90 до 180 градусов, или, что то же самое — больше π/2) тогда и только тогда, когда их скалярное произведение отрицательно.
- Пригодится: тригонометрическая таблица (синусы, косинусы, тангенсы и котангенсы распространенных углов)
Пример 3. В координатах даны векторы:
.
Вычислить скалярные произведения всех пар данных векторов. Какой угол (острый, прямой, тупой) образуют эти пары векторов?
Решение. Вычислять будем путём сложения произведений соответствующих координат.
Вычислять будем путём сложения произведений соответствующих координат.
.
Получили отрицательное число, поэтому векторы образуют тупой угол.
.
Получили положительное число, поэтому векторы образуют острый угол.
.
Получили положительное число, поэтому векторы образуют острый угол.
.
Получили нуль, поэтому векторы образуют прямой угол.
.
Получили положительное число, поэтому векторы образуют острый угол.
.
Получили положительное число, поэтому векторы образуют острый угол.
Для самопроверки можно использовать онлайн калькулятор Скалярное произведение векторов и косинус угла между ними.
Пример 4. Даны длины двух векторов и угол между ними:
.
Определить, при каком значении числа векторы и ортогональны (перпендикулярны).
Решение. Перемножим векторы по правилу умножения многочленов:
.
Теперь вычислим каждое слагаемое:
.
Составим уравнение (равенство произведения нулю), приведём подобные члены и решим уравнение:
Ответ: мы получили значение λ = 1,8, при котором векторы ортогональны.
- Пригодится: тригонометрическая таблица (синусы, косинусы, тангенсы и котангенсы распространенных углов)
Пример 5. Доказать, что вектор ортогонален (перпендикулярен) вектору
Решение. Чтобы проверить ортогональность, перемножим векторы и как многочлены, подставляя вместо его выражение, данное в условии задачи:
.
Для этого нужно каждый член (слагаемое) первого многочлена умножить на каждый член второго и полученные произведения сложить:
.
В полученном результате дробь за счёт сокращается. Получается следующий результат:
.
Вывод: в результате умножения получили нуль, следовательно, ортогональность (перпендикулярность) векторов доказана.
Решить задачу самостоятельно, а затем посмотреть решение
Пример 6. Даны длины векторов и , a угол между этими векторами равен π/4. Определить, при каком значении μ векторы и взаимно перпендикулярны.
Посмотреть правильное решение и ответ.
Для самопроверки можно использовать онлайн калькулятор Скалярное произведение векторов и косинус угла между ними.
Иногда выигрышным для наглядности является представление двух перемножаемых векторов
в виде матриц. Тогда первый вектор представлен в виде матрицы-строки, а второй — в виде матрицы-столбца:
Тогда первый вектор представлен в виде матрицы-строки, а второй — в виде матрицы-столбца:
Тогда скалярное произведение векторов будет произведением этих матриц:
Результат тот же, что и полученный способом, который мы уже рассмотрели. Получили одно единственное число, и произведение матрицы-строки на матрицу-столбец также является одним единственным числом.
В матричной форме удобно представлять произведение абстрактных n-мерных векторов. Так, произведение двух четырёхмерных векторов будет произведением матрицы-строки с четырьмя элементами на матрицу-столбец также с четырьмя элементами, произведение двух пятимерных векторов — произведением матрицы-строки с пятью элементами на матрицу-столбец также с пятью элементами и так далее.
Пример 7. Найти скалярные произведения пар векторов
и
,
используя матричное представление.
Решение. Первая пара векторов. Представляем первый вектор в виде матрицы-строки, а второй — в виде матрицы-столбца. Находим скалярное произведение этих векторов как произведение матрицы-строки на матрицу-столбец:
Аналогично представляем вторую пару и находим:
Как видим, результаты получились те же, что и у тех же пар из примера 2.
Вывод формулы косинуса угла между двумя векторами очень красив и краток.
Чтобы выразить скалярное произведение векторов
(1)
в координатной форме, предварительно найдём скалярные произведение ортов. Скалярное произведение вектора на само себя по определению:
То, что записано в формуле выше, означает: скалярное произведение вектора на самого себя равно квадрату его длины. Косинус нуля равен единице, поэтому квадрат каждого орта будет равен единице:
Так как векторы
попарно перпендикулярны, то попарные произведения ортов будут равны нулю:
Теперь выполним умножение векторных многочленов:
Подставляем в правую часть равенства значения соответствующих скалярных произведений ортов:
Получаем формулу косинуса угла между двумя векторами:
- Пригодится: тригонометрическая таблица (синусы, косинусы, тангенсы и котангенсы распространенных углов)
Пример 8. Даны три точки A(1;1;1), B(2;2;1), C(2;1;2).
Даны три точки A(1;1;1), B(2;2;1), C(2;1;2).
Найти угол .
Решение. Находим координаты векторов:
,
.
По формуле косинуса угла получаем:
Следовательно, .
Для самопроверки можно использовать онлайн калькулятор Скалярное произведение векторов и косинус угла между ними.
Пример 9. Даны два вектора
и
Найти сумму, разность, длину, скалярное произведение и угол между ними.
Решение.
1.Сумма
2.Разность
3.Длина
4.Скалярное произведение
5.Угол между и :
Решить задачи самостоятельно, а затем посмотреть решения
Пример 10. Определить, какой угол (острый, тупой или прямой) образуют
и
.
Определить, какой угол (острый, тупой или прямой) образуют
и
.
Посмотреть правильное решение и ответ.
Для самопроверки можно использовать онлайн калькулятор Скалярное произведение векторов и косинус угла между ними.
Пример 11. Определить угол треугольника ABC при вершине A, если , , .
Посмотреть правильное решение и ответ.
Пример 12. На векторах и построен параллелограмм. Вычислить длины диагоналей параллелограмма, если , , угол .
Посмотреть правильное решение и ответ.
- Пригодится: тригонометрическая таблица (синусы, косинусы, тангенсы и котангенсы распространенных углов)
Пример 13. Среди векторов
Найти а) коллинеарные; б) ортогональные.
Решение.
а) проверим пропорциональность соответствующих координат векторов — условие коллинеарности (повторение материала предыдущей части темы «Векторы»).
Для векторов и :
Равенство не выполняется.
Для векторов и :
Равенство выполняется.
Для векторов и :
Равенство не выполняется.
Наше исследование показало, что коллинеарны векторы и .
б) найдём скалярные произведения векторов.
Наше исследование показало, что ортогональны векторы и и и .
Расчёт работы постоянной силы
Посмотрите ещё раз на рисунок в начале статьи. Пусть материальная
точка перемещается прямолинейно из начала координат в конец вектора B под
действием постоянной силы F = A, образующей угол
с перемещением S = A. Из физики известно, что работа силы F при перемещении S равна
.
Таким образом, работа постоянной силы при прямолинейном перемещении её точки
приложения равна скалярному произведению вектора силы F = B на
вектор перемещения S = A.
Из физики известно, что работа силы F при перемещении S равна
.
Таким образом, работа постоянной силы при прямолинейном перемещении её точки
приложения равна скалярному произведению вектора силы F = B на
вектор перемещения S = A.
Скалярное произведение векторов позволяет находить угол между двумя векторами. Поэтому оно часто встречается в последующих разделах математики, особенно, аналитической геометрии. Стоит ли говорить о том, что нахождение скалярного произведения векторов — фундаментальный навык для любого будущего инженера, проектирующего всё что угодно, от гладильных досок и лестниц-стремянок до зданий, или для программиста, собирающегося разрабатывать игры?
Экономический смысл скалярного произведения векторов
В экономических задачах можно рассматривать скалярное произведение вектора цен p
на вектор объёма проданных товаров x . Скалярное произведение px в этом случае даёт суммарную стоимость проданных товаров x при ценах p . Например, если объём всех товаров, проданных предприятием, выражается вектором x = (400; 750; 200; 300), элементы которого означают соответственно количество товаров различных групп, а цены в одних и тех же денежных единицах заданы в соответствующем порядке вектором p = (3; 2,1; 1,2; 0,5), то скалярное произведение
Например, если объём всех товаров, проданных предприятием, выражается вектором x = (400; 750; 200; 300), элементы которого означают соответственно количество товаров различных групп, а цены в одних и тех же денежных единицах заданы в соответствующем порядке вектором p = (3; 2,1; 1,2; 0,5), то скалярное произведение
выражает суммарную стоимость всех товаров x.
| Назад | Листать | Вперёд>>> |
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Векторы
Поделиться с друзьями
Начало темы «Векторы»
Векторы: определения и действия над векторами
Сложение векторов: длина суммы векторов и теорема косинусов
Продолжение темы «Векторы»
Линейная зависимость векторов
Базис системы векторов. Аффинные координаты
Векторное и смешанное произведение векторов
«Скалярное произведение векторов.
 Угол между векторами». 9-й класс
Угол между векторами». 9-й класс- Кононова Анастасия Владимировна, заместитель директора по УВР, учитель математики
Разделы: Математика
Класс: 9
Цели урока:сформировать понятия скалярного произведения векторов, угла между векторами.
Задачи:
- рассмотреть следствия из теоремы о скалярном произведении в координатах, свойства скалярного произведения векторов; показать применение скалярного произведения векторов при решении задач;
- формировать навыки нахождения скалярного произведения и угла между векторами;
- способствовать воспитанию ответственности,
организованности, самостоятельности.

Тип урока: урок совершенствования ЗУН
Вид урока: традиционный урок с применением компьютера
Оборудования: компьютер, демонстрационный материал
ХОД УРОКА
I. Организационный момент
Приветствие, психологический настрой на урок (Приложение 1. Слайд 1)
Добрый день! Добрый час!
Начинаем мы сейчас
Наш урок очередной.
И не легкий, и не сложный,
Очень нужный нам сейчас
В подготовке к ОГЭ!
II. Актуализация знаний учащихся
1) Устная работа №8 – Угол между векторами (Приложение 2, материал с сайта matvaz.ru), №9 – Скалярное произведение векторов (Приложение 3, материал с сайта matvaz.ru)
2) Проверка домашнего задания (Приложение 4)
П. 101-104, №1041, стр.269
101-104, №1041, стр.269
№1041
Дано:
– векторы
Найти:
Решение:
Ответ:
Инд тесты на сайте uztest.ru
3) Контроль усвоения материала (самостоятельная работа) (Приложение 5)
Вспомнить формулу нахождения координаты вектора через координаты его начала и конца: Каждая координата вектора равна разности соответствующих координат его конца и начала
Вариант 1
А1. Даны точки А(2; 4), В(5; 8), С(–7; –1), D(5; 8).
Найдите скалярное произведение векторов .
А2. Даны векторы .
Найдите скалярное произведение векторов.
А3. Вычислите скалярное произведение векторов,
если , а угол
между ними равен 60о.
Вариант 2
А1. Даны точки А(2; 4), В(–1; 6), С(–4; –2), D(3;
2). Найдите скалярное произведение
векторов и
.
А2. Даны векторы . Найдите скалярное произведение
векторов.
А3. Вычислите скалярное произведение векторов,
если , а угол
между ними равен 30о.
Ответы: (Слайд 2)
Вариант 1
А1. 72 А2. 37 А3.13,5
Вариант 2
А1. –13 А2.–13 А3.
III. Изучение нового материала.
Сообщение темы урока, сформулировать цели урока (Слайд 3)
(Слайд 4)
Ненулевые векторы и перпендикулярны тогда и только тогда,
когда
(Слайд 5)
Косинус угла ? между ненулевыми векторами и выражается формулой
(Слайд 6)
Для любых векторов и любого числа k справедливы соотношения:
IV. Применение знаний
Решить задачи №55, 57 из рабочей тетради (Приложение 6)
Коллективно решить №1047(а), 1044 (а,в), 1045, 1047(в) (Слайд
7)
V. Рефлексия
Подведение итогов урока. Оценить работы учащихся
V. Домашняя работа
Домашняя работа
(Слайд 8)
П.101-104, №1051 Стр.270.
(Слайд 9)
Индивидуальные задания: 1) выполнить тест №3 (задания №11 ОГЭ), выполнить тест №4 (задания №21 ОГЭ), составленные на сайте uztest.ru, задания на карточках: №54, 56 из рабочей тетради (Приложение 7)
Геометрия
. Что представляет собой скалярное произведение двух векторов?
Как указывалось в других ответах, точечный продукт $\vec{a} \cdot \vec{b}$ связан с углом $\theta$ между $\vec{a}$ и $\vec{b} $ through:
$$\vec a \cdot \vec b = \Vert\vec a\Vert_2 \, \Vert\vec b\Vert_2 \, \cos \theta$$
Предположим, что $a$ и $b $ указывают в аналогичных направлениях, т. е. $\theta \leq 90°$, мы можем визуализировать, что означает это отношение (с этого момента пропуская векторные стрелки и нижний индекс евклидовой нормы):
$p$ — вектор, полученный ортогональной проекцией $a$ на $b$. Поскольку $\cos$ — это отношение между соседним катетом ($p$) и гипотенузой ($a$) в прямоугольном треугольнике, т. е.
Поскольку $\cos$ — это отношение между соседним катетом ($p$) и гипотенузой ($a$) в прямоугольном треугольнике, т. е.
$$\cos \theta = \frac{\Vert p \Vert }{\Vert a \Vert},$$
получаем для скалярного произведения:
$$a \cdot b = \Vert a \Vert \, \Vert b \Vert \, \frac{\Vert p \ Vert}{\Vert a \Vert} = \Vert p \Vert \Vert b \Vert$$
Итак, скалярное произведение — это длина вектора $p$, проекция $a$ на $b$, умножается на длину $b$. Если $a$ и $b$ направлены в противоположные стороны, т. е. $90° < \theta \leq 180°$, скалярное произведение будет отрицательным: $a \cdot b = - \Vert p \Vert \Vert b \Vert$
угол $\theta$ сам по себе не задан. По определению:
$$a \cdot b = \sum_i a_i b_i$$
Итак, нам нужно найти связь между этим и косинусом. Из определения скалярного произведения видно, что оно масштабируется пропорционально входным векторам, поэтому для неединичных векторов $u$ и $v$ с соответствующими единичными векторами $\hat{u}$ и $\hat{ v}$:
$$u \cdot v = \Vert u \Vert \hat{u} \cdot \Vert v \Vert \hat{v} = \Vert u \Vert \Vert v \Vert \hat{u} \cdot \ hat{v}. $$
$$
Для простоты будем считать $a$ и $b$ единичными векторами. Таким образом, нам нужно только показать
$$a \cdot b = \cos \theta$$
или, по определению $\cos$, нам нужно показать:
$$a \cdot b = \ Vert p \Vert $$
Вычислим длину проекции $p$, используя $a$ и $b$. Мы можем начать с использования теоремы Пифагора: 92\\ &= 2 — (2 — 2 \sum_i b_i a_i) \\ &= 2 \sum_i b_i a_i \\ \Vert p \Vert &= \sum_i b_i a_i \end{выравнивание} $$
четв.е.д.
Скалярный продукт — исчисление 3
Все ресурсы исчисления 3
6 Диагностические тесты 373 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 5 6 7 8 9 … 17 18 Следующая →
Исчисление 3 Помощь » Векторы и векторные операции » Скалярный продукт
Оцените скалярное произведение между , и .
Возможные ответы:
Правильный ответ:
Объяснение:
Все, что нам нужно сделать, это умножить подобные компоненты.
Сообщить об ошибке
Оценить скалярное произведение , и .
Возможные ответы:
Правильный ответ:
Объяснение:
Все, что нам нужно сделать, это перемножить одинаковые компоненты и сложить их вместе.
Сообщить об ошибке
Найдите скалярное произведение следующих векторов: ответ:
Объяснение:
Чтобы найти скалярное произведение двух векторов
, мы вычисляем
, поэтому для
у нас есть
Сообщить об ошибке
Какова длина вектора
?
Возможные ответы:
Правильный ответ:
Объяснение:
Мы можем вычислить длину вектора, взяв квадратный корень из скалярного произведения и , поэтому длина равна:
Сообщить об ошибке
Найдите скалярное произведение следующих векторов:
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти скалярное произведение двух векторов
, мы вычисляем
, поэтому для
у нас есть
Сообщить об ошибке
Какова длина вектора
?
Возможные ответы:
Правильный ответ:
Объяснение:
Мы можем вычислить длину вектора, взяв квадратный корень из скалярного произведения и , поэтому длина равна:
Сообщить об ошибке определение скалярного произведения двух векторов с действительным знаком?
Возможные ответы:
Все они могут быть использованы
, где – угол между .
Правильный ответ:
Объяснение:
неверно. Это говорит о том, что нужно сложить вместе все компоненты двух векторов. Два других определения обычно используются при вычислении углов между векторами и другими объектами, а также могут быть получены друг из друга.
Сообщить об ошибке
Что из следующего верно относительно скалярного произведения двух векторов?
Возможные ответы:
Скалярное произведение двух векторов никогда не является скаляром.
Ни одно из других утверждений не верно.
тогда и только тогда, когда ортогональны.
Скалярное произведение двух векторов никогда не бывает отрицательным.
является корректным, если каждый вектор имеет одинаковую размерность
Правильный ответ:
тогда и только тогда, когда ортогональны.
Объяснение:
Это утверждение верно; его можно получить из определения, установив острый угол между векторами равным ; требование ортогональности. Кроме того, если любой из векторов имеет длину, векторы по-прежнему называются ортогональными.
Сообщить об ошибке
Что такое скалярное произведение векторов и ?
Возможные ответы:
Правильный ответ:
Объяснение:
Пусть вектор представлен как , а вектор представлен как .
Скалярное произведение векторов и равно .
В этой задаче
Сообщить об ошибке
Что такое скалярное произведение векторов и ?
Возможные ответы:
Не существует
Правильный ответ:
9000 3
Объяснение:
Пусть вектор представлен как , а вектор представлен как .


 То есть, для простоты понимания, мы говорим, что умножаем «накрест».
То есть, для простоты понимания, мы говорим, что умножаем «накрест». В простых множителях числа 12 осталось только число 3. Но оно присутствует в простых множителях числа 24. Вычеркиваем число 3 из обоих рядов, при этом для числа 16 никаких действий не предполагается.
В простых множителях числа 12 осталось только число 3. Но оно присутствует в простых множителях числа 24. Вычеркиваем число 3 из обоих рядов, при этом для числа 16 никаких действий не предполагается.




 работать по профессии.
работать по профессии. Вы также просматриваете другие совпадающие названия должностей.
Вы также просматриваете другие совпадающие названия должностей.


 …
… Действительные профили Express Entry, созданные в период с 18 мая 2022 г. по 18 мая 2023 г. с…
Действительные профили Express Entry, созданные в период с 18 мая 2022 г. по 18 мая 2023 г. с… {\circ}
\]
{\circ}
\] {\circ}.\]
{\circ}.\]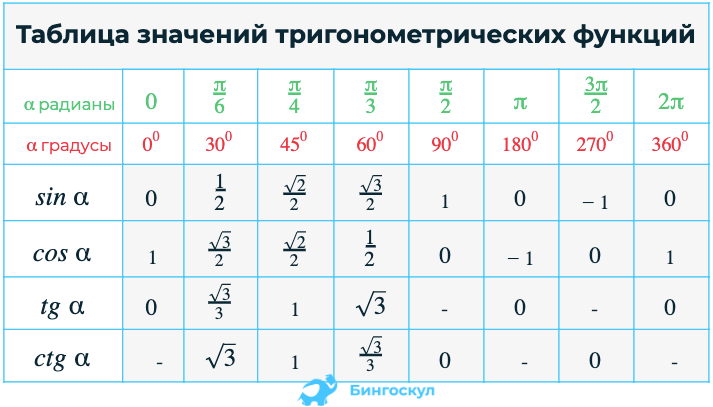
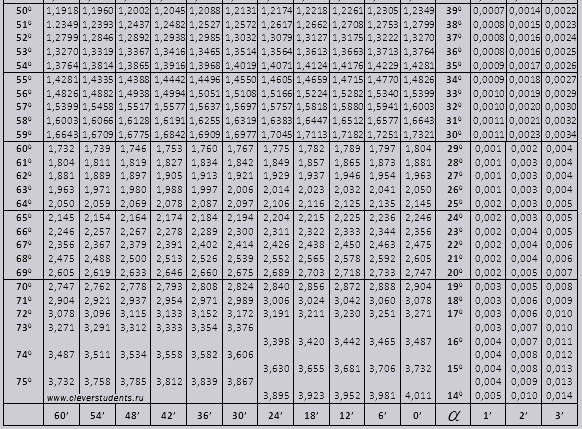
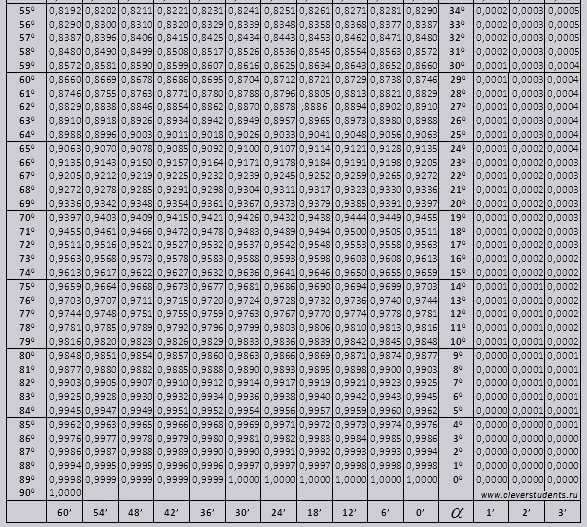
 Для того чтобы посчитать значение 16 ° 32 минуты. В таблице находим значение нужного угла, которое ближе всего по значению подходит к заданному. Это sin16 30 =0.2840. Так как 16 32=16 30+2, то в столбце, выбираем нужную поправку, которая находится на пересечении со строкой, со значением 16 градусов стоит 0,0006, то есть
Для того чтобы посчитать значение 16 ° 32 минуты. В таблице находим значение нужного угла, которое ближе всего по значению подходит к заданному. Это sin16 30 =0.2840. Так как 16 32=16 30+2, то в столбце, выбираем нужную поправку, которая находится на пересечении со строкой, со значением 16 градусов стоит 0,0006, то есть 6361 Так как 50 33=50 30+3, то в нужном столбце выбираем значение 3. Далее находим значение 0,0007, и записываем следующее уравнение:
6361 Так как 50 33=50 30+3, то в нужном столбце выбираем значение 3. Далее находим значение 0,0007, и записываем следующее уравнение: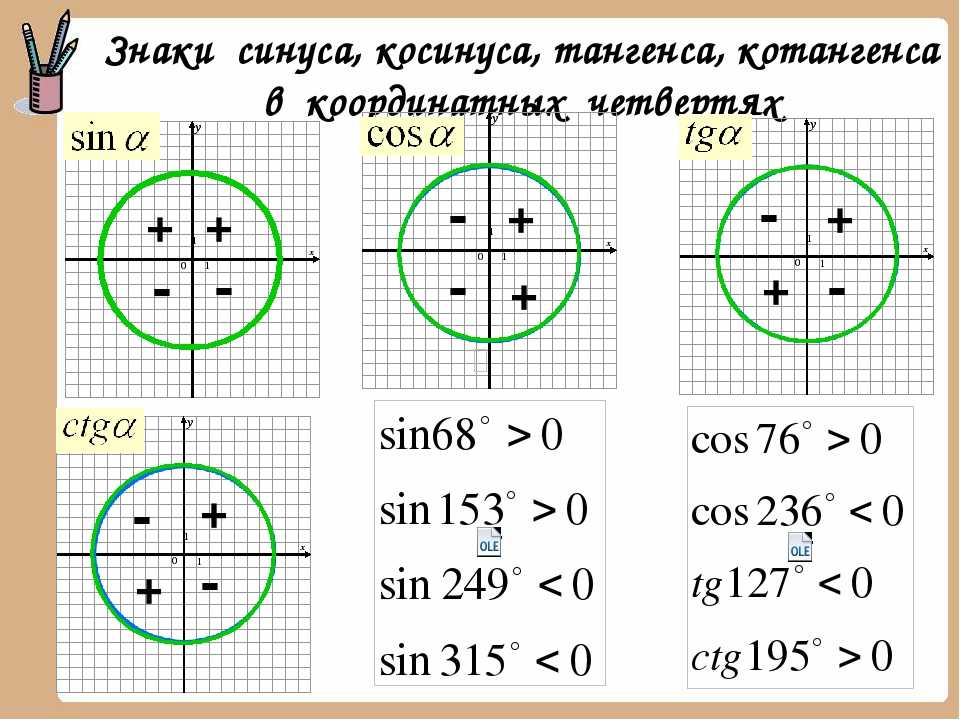 6361 +(- 0 . 0007) = 0,6454
6361 +(- 0 . 0007) = 0,6454 они записаны в первом столбике. Далее применяя \[\frac{\sqrt{x}}{2}\] можно вычислить данные для углов, которые нам необходимы. Вычисленные значения, записываются в таблицу.
они записаны в первом столбике. Далее применяя \[\frac{\sqrt{x}}{2}\] можно вычислить данные для углов, которые нам необходимы. Вычисленные значения, записываются в таблицу. {\circ}=\frac{1}{\frac{1}{2}}=2\]
{\circ}=\frac{1}{\frac{1}{2}}=2\]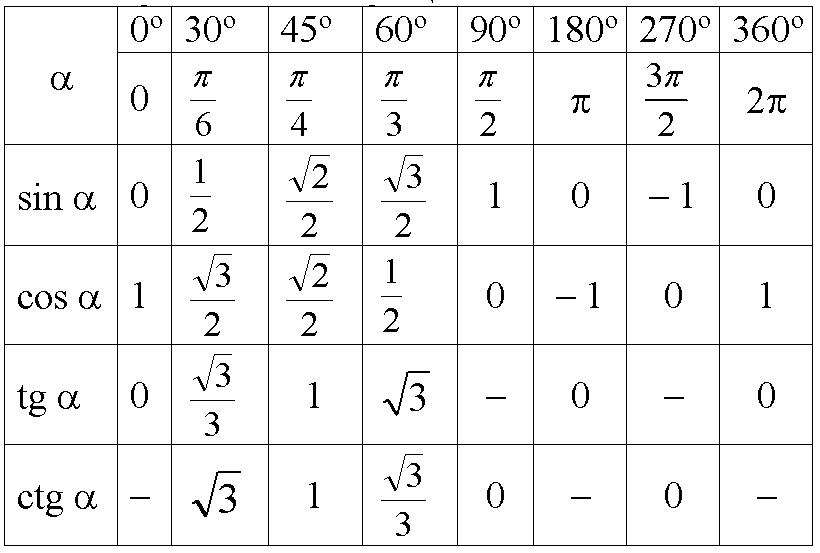 {\circ}=\frac{4}{6}=0,67\]
{\circ}=\frac{4}{6}=0,67\]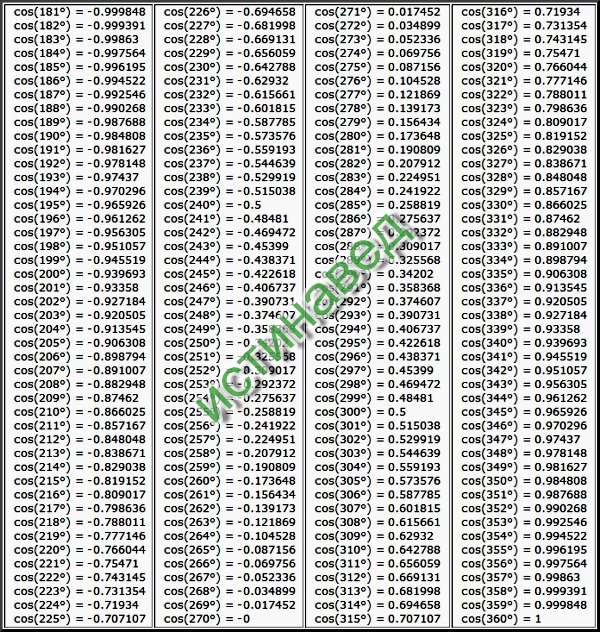 Применяя для решения огромные формулы и функции можно растеряться и не сразу сообразить, как производить их расчет. Однако досконально рассмотрев и изучив каждый раздел, становится понятно, что все достаточно просто и громоздкие таблицы освоить можно быстро и легко.
Применяя для решения огромные формулы и функции можно растеряться и не сразу сообразить, как производить их расчет. Однако досконально рассмотрев и изучив каждый раздел, становится понятно, что все достаточно просто и громоздкие таблицы освоить можно быстро и легко.
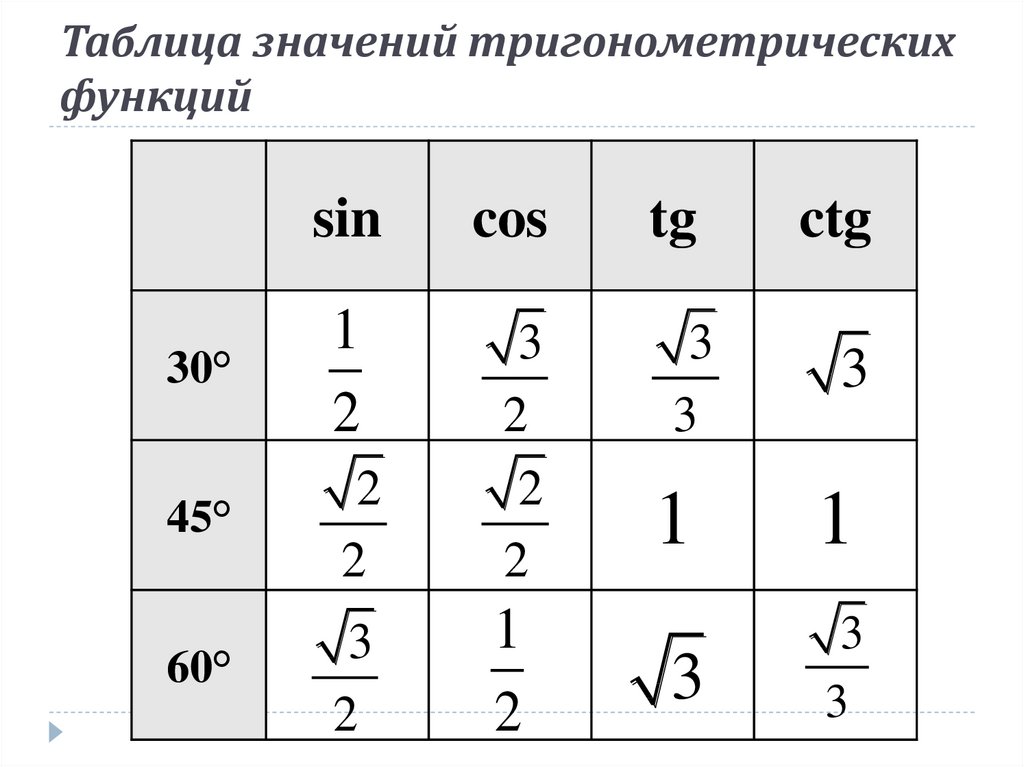
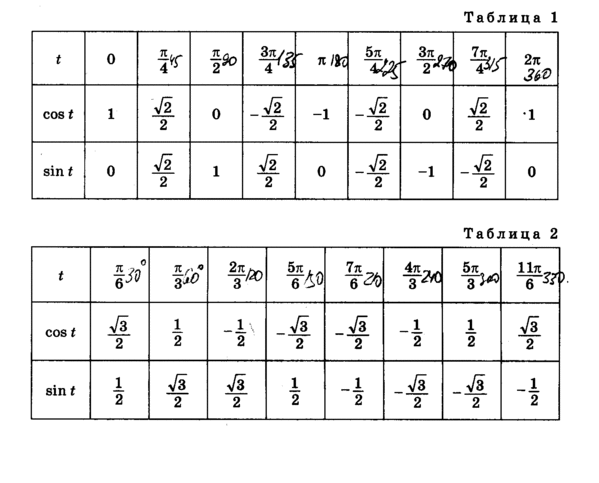
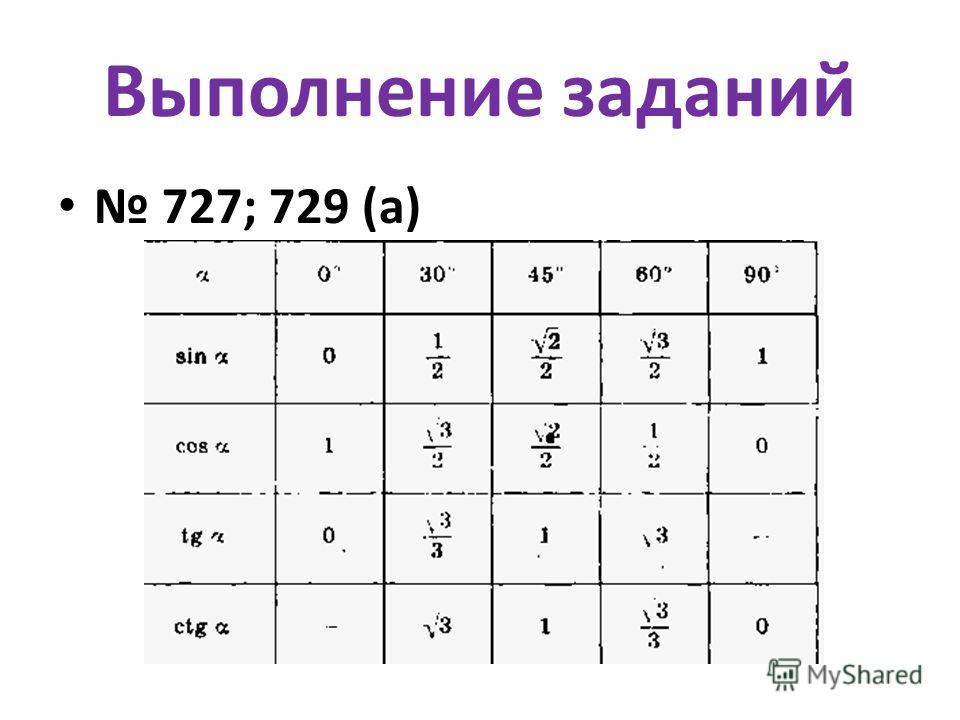
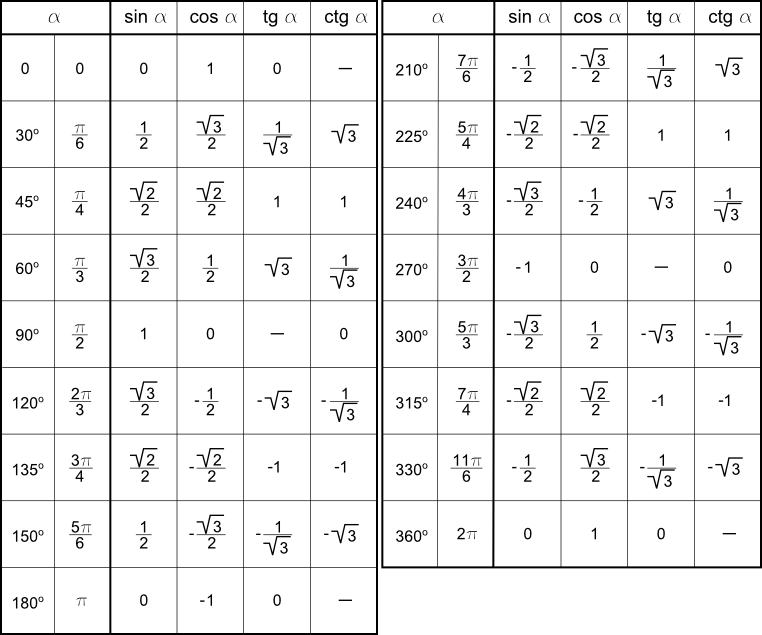
 Аналогично находим косинус 60 градусов, синус 60 градусов (еще раз, в пересечении колонки sin (синус) и строки 60 градусов находим значение sin 60 = √3/2) и т.д. Точно так же находятся значения синусов, косинусов и тангенсов других «популярных» углов.
Аналогично находим косинус 60 градусов, синус 60 градусов (еще раз, в пересечении колонки sin (синус) и строки 60 градусов находим значение sin 60 = √3/2) и т.д. Точно так же находятся значения синусов, косинусов и тангенсов других «популярных» углов.
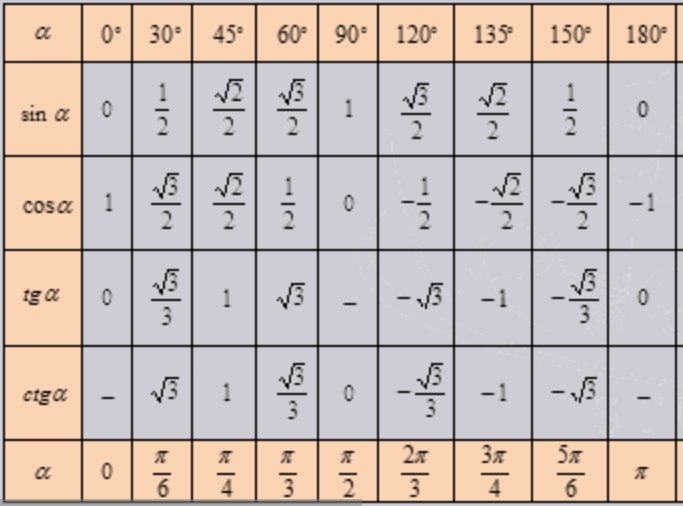 Если же прочерка нет — клетка пуста, значит мы еще не внесли нужное значение. Мы интересуемся, по каким запросам к нам приходят пользователи и дополняем таблицу новыми значениями, несмотря на то, что текущих данных о значениях косинусов, синусов и тангенсов самых часто встречающихся значений углов вполне достаточно для решения большинства задач.
Если же прочерка нет — клетка пуста, значит мы еще не внесли нужное значение. Мы интересуемся, по каким запросам к нам приходят пользователи и дополняем таблицу новыми значениями, несмотря на то, что текущих данных о значениях косинусов, синусов и тангенсов самых часто встречающихся значений углов вполне достаточно для решения большинства задач.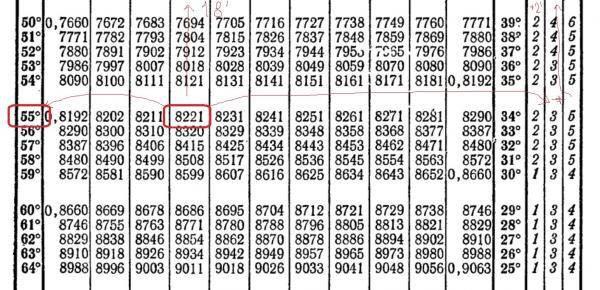
 Если снова смотреть по рисунку выше, то cos ∠ABC = AB / BC
Если снова смотреть по рисунку выше, то cos ∠ABC = AB / BC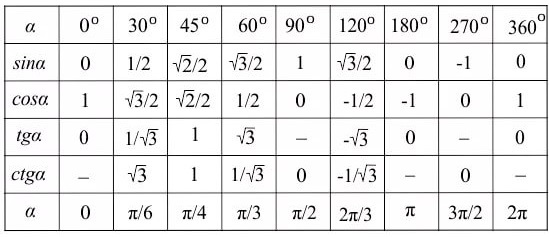
 Сложив два косинуса — «колобка», получаем пару косинусов- «колобков». А вычитая, колобков точно не получим. Получаем пару синусов. Еще и с минусом впереди.
Сложив два косинуса — «колобка», получаем пару косинусов- «колобков». А вычитая, колобков точно не получим. Получаем пару синусов. Еще и с минусом впереди.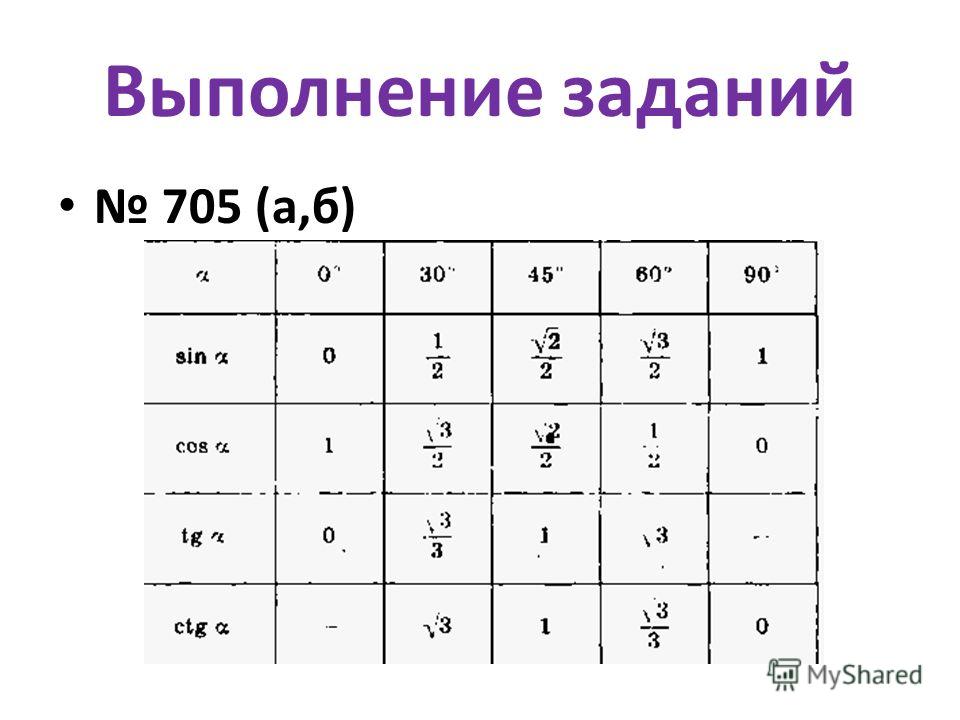

 (2)
(2) Решим уравнение
Решим уравнение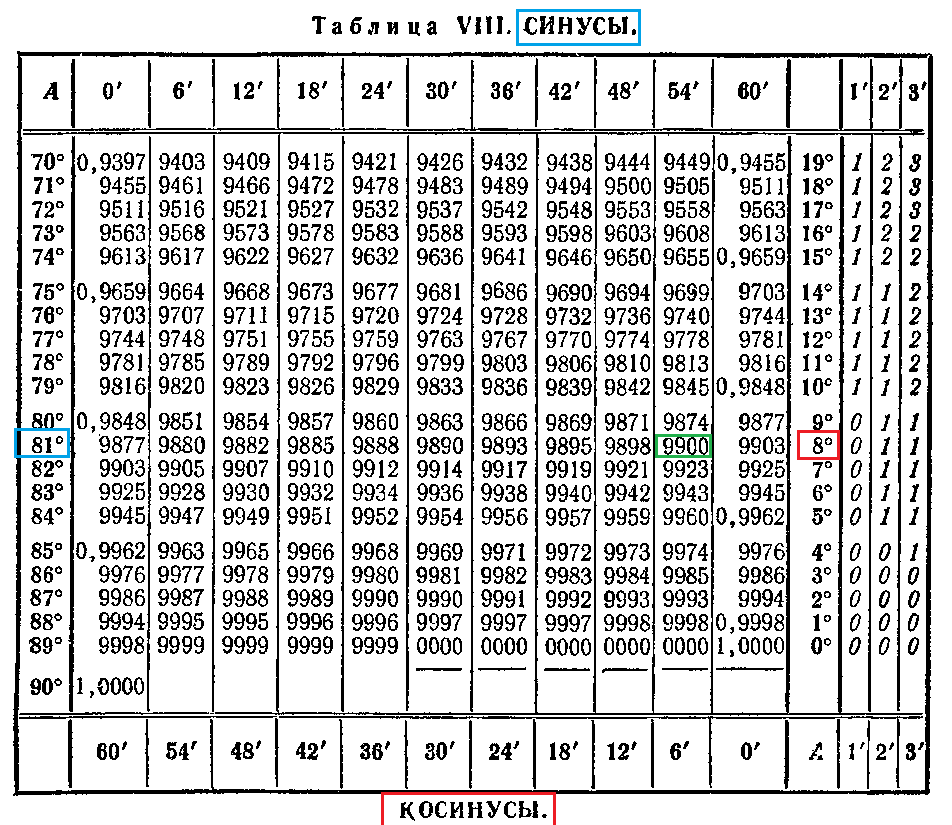
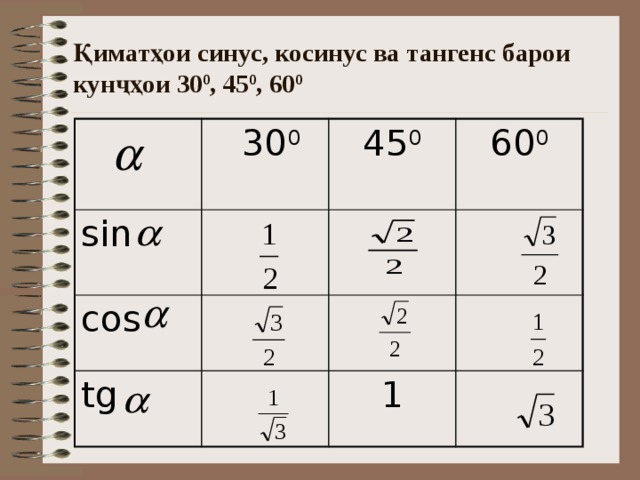
 Запишем их в таблицу, а ниже дадим вывод этих формул и приведем необходимые пояснения.
Запишем их в таблицу, а ниже дадим вывод этих формул и приведем необходимые пояснения. Оно позволяет сумму квадратов синуса и косинуса одного угла заменять единицей. Не менее часто основное тригонометрическое тождество используется и в обратном порядке: единица заменяется суммой квадратов синуса и косинуса какого-либо угла.
Оно позволяет сумму квадратов синуса и косинуса одного угла заменять единицей. Не менее часто основное тригонометрическое тождество используется и в обратном порядке: единица заменяется суммой квадратов синуса и косинуса какого-либо угла. Так формула справедлива для любых , отличных от (иначе в знаменателе будет нуль, а деление на нуль мы не определяли), а формула — для всех , отличных от , где z
— любое .
Так формула справедлива для любых , отличных от (иначе в знаменателе будет нуль, а деление на нуль мы не определяли), а формула — для всех , отличных от , где z
— любое . com
com Синус угла определяется в контексте прямоугольного треугольника: для указанного угла это отношение длины стороны, противоположной этому углу, к длине самой длинной стороны треугольника (деленное на нее). (так называемая гипотенуза).
Синус угла определяется в контексте прямоугольного треугольника: для указанного угла это отношение длины стороны, противоположной этому углу, к длине самой длинной стороны треугольника (деленное на нее). (так называемая гипотенуза). Это была таблица хорд (обсуждавшаяся ранее) для каждой дуги от 1/2° до 180° с интервалами в 1/2°. Также он объяснил, как интерполировать между заданными углами.
Это была таблица хорд (обсуждавшаяся ранее) для каждой дуги от 1/2° до 180° с интервалами в 1/2°. Также он объяснил, как интерполировать между заданными углами.
 С помощью этого шага мы можем построить таблицы триггеров для триггерных функций с шагом 1°.
С помощью этого шага мы можем построить таблицы триггеров для триггерных функций с шагом 1°.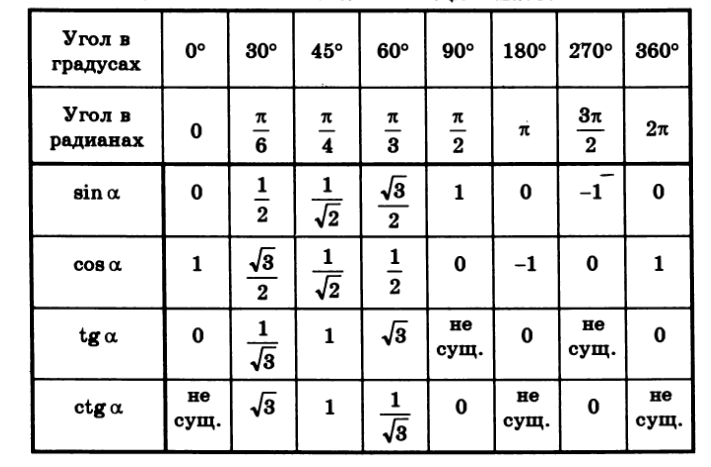
 Сначала преобразуйте 45° в радианы, чтобы получить π /4, что равно 0,78539816 в восьми разрядах. Затем вычислить значение
Сначала преобразуйте 45° в радианы, чтобы получить π /4, что равно 0,78539816 в восьми разрядах. Затем вычислить значение

 Также можете поделиться им с друзьями, разместив ссылку у себя на странице или отправив в мессенджеры.
Также можете поделиться им с друзьями, разместив ссылку у себя на странице или отправив в мессенджеры. Эта задача представляется нетривиальной. Если вы используете аналитические формулы для оценки объема жидкости в разных резервуарах и резервуарах или других физических телах, это может быть сложно и утомительно. Тем не менее, вычислить объем элементарных тел можно было бы проще. Например, всего несколько математических формул помогут вам рассчитать объем трубопровода. Стандартная единица измерения объема жидкости в трубах – м³. Но наше онлайн-приложение дает результаты в литрах, за исключением расчета площади трубы, которая дается в м². При расчете необходимо указать внутренний диаметр, наружный диаметр трубы и ее длину. 92*л.
Эта задача представляется нетривиальной. Если вы используете аналитические формулы для оценки объема жидкости в разных резервуарах и резервуарах или других физических телах, это может быть сложно и утомительно. Тем не менее, вычислить объем элементарных тел можно было бы проще. Например, всего несколько математических формул помогут вам рассчитать объем трубопровода. Стандартная единица измерения объема жидкости в трубах – м³. Но наше онлайн-приложение дает результаты в литрах, за исключением расчета площади трубы, которая дается в м². При расчете необходимо указать внутренний диаметр, наружный диаметр трубы и ее длину. 92*л. е. системы отопления, за определенный период времени. Если вы используете пластиковые трубы, пропускная способность трубы постоянна и не изменится со временем, потому что пластик устойчив к коррозии внутри. Обратная ситуация может возникнуть в случае использования металлических труб. Важно знать техническое задание на обслуживание собранных элементов, используемых при подключении сантехнического оборудования. Это обеспечит стабильную подачу воды, когда вы откроете кран в ванной. Это очень важный вопрос для трубопроводов системы отопления, так как используемая горячая вода даже ускоряет процесс возникновения коррозии. Следует принять к сведению, что длина трубопровода влияет на пропускную способность трубы.
е. системы отопления, за определенный период времени. Если вы используете пластиковые трубы, пропускная способность трубы постоянна и не изменится со временем, потому что пластик устойчив к коррозии внутри. Обратная ситуация может возникнуть в случае использования металлических труб. Важно знать техническое задание на обслуживание собранных элементов, используемых при подключении сантехнического оборудования. Это обеспечит стабильную подачу воды, когда вы откроете кран в ванной. Это очень важный вопрос для трубопроводов системы отопления, так как используемая горячая вода даже ускоряет процесс возникновения коррозии. Следует принять к сведению, что длина трубопровода влияет на пропускную способность трубы. 20×0,20
20×0,20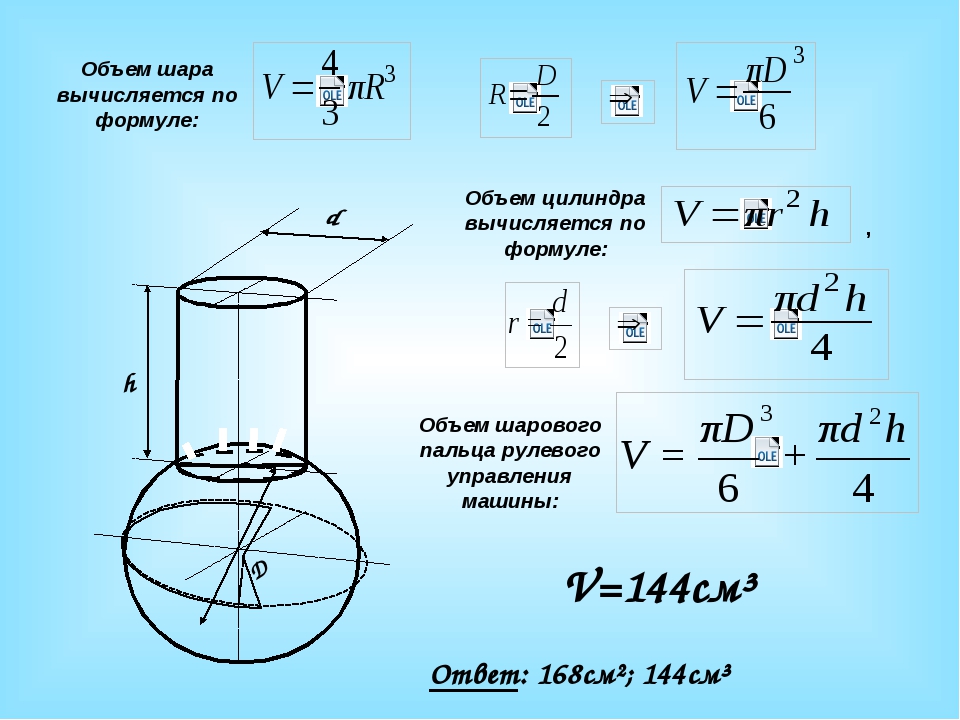


 2. Ускорение научно-технической
революции техники и технологии. Жизненный
цикл технического изделия сократился
настолько, что «опыт» не успевал
накапливаться и требовалось применение
более развитого математического
аппарата.
3. Развитие ЭВМ, размерность и сложность
реальных инженерных задач не позволяло
использовать аналитические методы.
Теория
принятия решений является определенной
ветвью других более общих наук: теория
систем, системный анализ, кибернетика,
а с другой, является синтезом определенных
фундаментальных более частных наук
исследование операций, оптимизация,
теория массового обслуживания, создав
при этом и собственную методологию.
Инженерное
дело теснейшим образом связано с
совокупностями объектов, которые принято
называть сложными системами, которые
характеризуются многочисленными и
разнообразными по типу связями между
отдельно существующими элементами
системы и наличием у системы функции
назначения, которой нет у составляющих
ее частей. На первый взгляд каждая
сложная система имеет уникальную
организацию.
2. Ускорение научно-технической
революции техники и технологии. Жизненный
цикл технического изделия сократился
настолько, что «опыт» не успевал
накапливаться и требовалось применение
более развитого математического
аппарата.
3. Развитие ЭВМ, размерность и сложность
реальных инженерных задач не позволяло
использовать аналитические методы.
Теория
принятия решений является определенной
ветвью других более общих наук: теория
систем, системный анализ, кибернетика,
а с другой, является синтезом определенных
фундаментальных более частных наук
исследование операций, оптимизация,
теория массового обслуживания, создав
при этом и собственную методологию.
Инженерное
дело теснейшим образом связано с
совокупностями объектов, которые принято
называть сложными системами, которые
характеризуются многочисленными и
разнообразными по типу связями между
отдельно существующими элементами
системы и наличием у системы функции
назначения, которой нет у составляющих
ее частей. На первый взгляд каждая
сложная система имеет уникальную
организацию. Однако более детальное
изучение способно выделить общее в
системе команд ЭВМ, в процессах
проектирования машины, самолета и
космического корабля.
Наиболее
общий термин «теория систем»
относится ко всевозможным аспектам
исследования систем. Ее основными
частями являются:
1. системный анализ, который понимается
как исследование проблемы принятия
решения в сложной системе,
2. кибернетика, которая рассматривается
как наука об управлении и преобразовании
информации.
Однако более детальное
изучение способно выделить общее в
системе команд ЭВМ, в процессах
проектирования машины, самолета и
космического корабля.
Наиболее
общий термин «теория систем»
относится ко всевозможным аспектам
исследования систем. Ее основными
частями являются:
1. системный анализ, который понимается
как исследование проблемы принятия
решения в сложной системе,
2. кибернетика, которая рассматривается
как наука об управлении и преобразовании
информации. Дадим
основные определения системного
анализа.
Элемент — некоторый объект
(материальный, энергетический,
информационный), который обладает рядом
важных для нас свойств, но внутреннее
строение (содержание) которого
безотносительно к цели рассмотрения.
Связь — важный для целей рассмотрения
обмен между элементами веществом,
энергией, информацией.
Система — совокупность элементов,
которая обладает следующими признаками:
·
связями, которые позволяют посредством
переходов по ним от элемента к элементу
соединить два любых элемента совокупности;
·
свойством, отличным от свойств отдельных
элементов совокупности.
Практически любой объект с определенной
точки зрения может быть рассмотрен как
система. Вопрос состоит в том, насколько
целесообразна такая точка зрения.
Большая система — система, которая
включает значительное число однотипных
элементов и однотипных связей.
Дадим
основные определения системного
анализа.
Элемент — некоторый объект
(материальный, энергетический,
информационный), который обладает рядом
важных для нас свойств, но внутреннее
строение (содержание) которого
безотносительно к цели рассмотрения.
Связь — важный для целей рассмотрения
обмен между элементами веществом,
энергией, информацией.
Система — совокупность элементов,
которая обладает следующими признаками:
·
связями, которые позволяют посредством
переходов по ним от элемента к элементу
соединить два любых элемента совокупности;
·
свойством, отличным от свойств отдельных
элементов совокупности.
Практически любой объект с определенной
точки зрения может быть рассмотрен как
система. Вопрос состоит в том, насколько
целесообразна такая точка зрения.
Большая система — система, которая
включает значительное число однотипных
элементов и однотипных связей. Для расчетов на прочность по методу
конечных элементов элементами системы
считаются небольшие участки трубы, а
связь имеет силовой (энергетический)
характер — каждый элемент действует на
соседние. Сложная система — система,
которая состоит из элементов разных
типов и обладает разнородными связями
между ними. В качестве примера можно
привести ЭВМ, лесной трактор или судно.
Для сложной системы автоматизированный
режим считается более предпочтительным,
чем автоматический. Например, посадка
самолета или захват дерева харвестерной
головкой выполняется при участии
человека, а автопилот или бортовой
компьютер используется лишь на
относительно простых операциях. Типична
также ситуация, когда решение, выработанное
техническими средствами, утверждается
к исполнению человеком.
Структура системы — расчленение
системы на группы элементов с указанием
связей между ними, неизменное на все
время рассмотрения и дающее представление
о системе в целом. Указанное расчленение
может иметь материальную, функциональную,
алгоритмическую или другую основу.
Для расчетов на прочность по методу
конечных элементов элементами системы
считаются небольшие участки трубы, а
связь имеет силовой (энергетический)
характер — каждый элемент действует на
соседние. Сложная система — система,
которая состоит из элементов разных
типов и обладает разнородными связями
между ними. В качестве примера можно
привести ЭВМ, лесной трактор или судно.
Для сложной системы автоматизированный
режим считается более предпочтительным,
чем автоматический. Например, посадка
самолета или захват дерева харвестерной
головкой выполняется при участии
человека, а автопилот или бортовой
компьютер используется лишь на
относительно простых операциях. Типична
также ситуация, когда решение, выработанное
техническими средствами, утверждается
к исполнению человеком.
Структура системы — расчленение
системы на группы элементов с указанием
связей между ними, неизменное на все
время рассмотрения и дающее представление
о системе в целом. Указанное расчленение
может иметь материальную, функциональную,
алгоритмическую или другую основу. Пример материальной структуры —
структурная схема сборного моста,
которая состоит из отдельных, собираемых
на месте секций и указывает только эти
секции и порядок их соединения. Пример
функциональной структуры — деление
двигателя внутреннего сгорания на
системы питания, смазки, охлаждения,
передачи крутящего момента. Пример
алгоритмической структуры — алгоритм
программного средства, указывающего
последовательность действий или
инструкция, которая определяет действия
при отыскании неисправности технического
устройства.
Пример материальной структуры —
структурная схема сборного моста,
которая состоит из отдельных, собираемых
на месте секций и указывает только эти
секции и порядок их соединения. Пример
функциональной структуры — деление
двигателя внутреннего сгорания на
системы питания, смазки, охлаждения,
передачи крутящего момента. Пример
алгоритмической структуры — алгоритм
программного средства, указывающего
последовательность действий или
инструкция, которая определяет действия
при отыскании неисправности технического
устройства.  е. неравноправных
связей между элементами, когда воздействие
в одном из направлений оказывают гораздо
большее влияние на элемент, чем в другом.
Виды иерархических структур разнообразны,
но важных для практики иерархических
структур всего две — древовидная и
ромбовидная.
е. неравноправных
связей между элементами, когда воздействие
в одном из направлений оказывают гораздо
большее влияние на элемент, чем в другом.
Виды иерархических структур разнообразны,
но важных для практики иерархических
структур всего две — древовидная и
ромбовидная.
 В отличие от большинства
научных дисциплин, стремящихся к
формализации, системный анализ допускает,
что в определенных ситуациях неформализуемые
решения, принимаемые человеком, являются
более предпочтительными. Следовательно,
системный анализ рассматривает в
совокупности формализуемые и
неформализуемые процедуры, и одной из
его задач является определение их
оптимального соотношения.
Формализуемые
стороны отдельных операций лежат в
области прикладной математики и
использования ЭВМ. В ряде случаев
математическими методами исследуется
связное множество процедур и производится
само моделирование принятие решения.
Все это позволяет говорить о математической
основе системного анализа. Такие области
прикладной математики, как исследование
операций и системное программирование,
наиболее близки к системной постановке
вопросов.
Практическое
приложение системного анализа чрезвычайно
обширно по содержанию. Важнейшими
разделами являются научно-технические
разработки и различные задачи экономики.
Ссылки на системность исследований,
анализа, подхода включает биологию,
экологию, военное дело, психологию,
социологию, медицину, управление
государством и регионом, лесное и
сельское хозяйство, обучение и многое
другое.
В отличие от большинства
научных дисциплин, стремящихся к
формализации, системный анализ допускает,
что в определенных ситуациях неформализуемые
решения, принимаемые человеком, являются
более предпочтительными. Следовательно,
системный анализ рассматривает в
совокупности формализуемые и
неформализуемые процедуры, и одной из
его задач является определение их
оптимального соотношения.
Формализуемые
стороны отдельных операций лежат в
области прикладной математики и
использования ЭВМ. В ряде случаев
математическими методами исследуется
связное множество процедур и производится
само моделирование принятие решения.
Все это позволяет говорить о математической
основе системного анализа. Такие области
прикладной математики, как исследование
операций и системное программирование,
наиболее близки к системной постановке
вопросов.
Практическое
приложение системного анализа чрезвычайно
обширно по содержанию. Важнейшими
разделами являются научно-технические
разработки и различные задачи экономики.
Ссылки на системность исследований,
анализа, подхода включает биологию,
экологию, военное дело, психологию,
социологию, медицину, управление
государством и регионом, лесное и
сельское хозяйство, обучение и многое
другое.
 14 МБ
14 МБ
 82 КБ
82 КБ Следует подчеркнуть, что окончательное решение принимает лицо ответственное за принятие решений, причём его выбор не всегда совпадает с рекомендуемым. Некоторые разделы ТиМПР: математическое программирование (линейное программирование, нелинейное…
Следует подчеркнуть, что окончательное решение принимает лицо ответственное за принятие решений, причём его выбор не всегда совпадает с рекомендуемым. Некоторые разделы ТиМПР: математическое программирование (линейное программирование, нелинейное…
 Основные классы однокритериальных задач принятия решений в условиях определенности. Моделирование задач принятия решений. Задача использования ресурсов. Задачи линейного программирования транспортного типа. Задачи упорядоче…
Основные классы однокритериальных задач принятия решений в условиях определенности. Моделирование задач принятия решений. Задача использования ресурсов. Задачи линейного программирования транспортного типа. Задачи упорядоче… 5 КБ
5 КБ При изучении сложных систем (социальных, биологических, экологических и др. ) указанный способ формализации их целей позволяет в не…
При изучении сложных систем (социальных, биологических, экологических и др. ) указанный способ формализации их целей позволяет в не… -Рос. гос. техн. ун-т. Новочеркасск, 2002, 276 с. Оглавление: Методологические основы процессов принятия решений. Применение метода ветвей и границ для решения детерминированных задач теории принятия решений. Методы и модели теории расписаний. Применение метода динамического программирования для решения детерминированных задач теории принятия решений. Вероятностные модели теории принятия решений. Принятие решений в условиях н…
-Рос. гос. техн. ун-т. Новочеркасск, 2002, 276 с. Оглавление: Методологические основы процессов принятия решений. Применение метода ветвей и границ для решения детерминированных задач теории принятия решений. Методы и модели теории расписаний. Применение метода динамического программирования для решения детерминированных задач теории принятия решений. Вероятностные модели теории принятия решений. Принятие решений в условиях н…



 Направление идей через эти шесть шагов поможет управлять и улучшать решения организации, создавая эффективный поток направления и непрерывности.
Направление идей через эти шесть шагов поможет управлять и улучшать решения организации, создавая эффективный поток направления и непрерывности.


 (если это что-то «предварительное»)
(если это что-то «предварительное»)



 Используйте его как ограниченный по времени период, чтобы честно проанализировать решения, принятые за день, и подумать, почему одни из них оказались лучше (или хуже), чем другие.
Используйте его как ограниченный по времени период, чтобы честно проанализировать решения, принятые за день, и подумать, почему одни из них оказались лучше (или хуже), чем другие. 

 Они чувствуют себя хорошо.
Они чувствуют себя хорошо.  Составьте план на год вперед и даже на пять лет вперед. Важно не зацикливаться только на немедленных результатах своих решений.
Составьте план на год вперед и даже на пять лет вперед. Важно не зацикливаться только на немедленных результатах своих решений.  Запишите свои цели
Запишите свои цели 


 Это может уменьшить ваши собственные предубеждения и раскрыть возможности, которые вы не рассматривали.
Это может уменьшить ваши собственные предубеждения и раскрыть возможности, которые вы не рассматривали. 

 Предел определяется как значение, которого достигает функция, когда входные данные приближаются к указанному числу. Пределы используются для анализа поведения данной функции.
Предел определяется как значение, которого достигает функция, когда входные данные приближаются к указанному числу. Пределы используются для анализа поведения данной функции. 
 Нам нужно подставить значение переменной в заданную функцию, чтобы получить ответ.
Нам нужно подставить значение переменной в заданную функцию, чтобы получить ответ.  Напомним, что определение
производная дается пределом 9n, n, inf)
Напомним, что определение
производная дается пределом 9n, n, inf)  В случае неопределенных пределов MATLAB ® возвращает
В случае неопределенных пределов MATLAB ® возвращает 
 2
2



 Урок 29,
Петерсон, Учебник, часть 2
Урок 29,
Петерсон, Учебник, часть 2

 2$.
2$.
 2$.
2$. — 2006. — Vol. 90, № 517. — P. 132—134.
— 2006. — Vol. 90, № 517. — P. 132—134.
 Важными аспектами этой формы являются радиус, диаметр, окружность и объем.
Важными аспектами этой формы являются радиус, диаметр, окружность и объем. Теперь высоту цилиндра также можно назвать диаметром сферы, потому что мы предполагаем, что эта сфера идеально помещается в цилиндре. Следовательно, можно сказать, что высота цилиндра = диаметру сферы = 2r. Итак, в формуле площадь поверхности Сферы = 2πrh; «h» можно заменить диаметром, то есть 2r. Следовательно, площадь поверхности сферы равна 2πrh = 2πr(2r) = 4πr 2
Теперь высоту цилиндра также можно назвать диаметром сферы, потому что мы предполагаем, что эта сфера идеально помещается в цилиндре. Следовательно, можно сказать, что высота цилиндра = диаметру сферы = 2r. Итак, в формуле площадь поверхности Сферы = 2πrh; «h» можно заменить диаметром, то есть 2r. Следовательно, площадь поверхности сферы равна 2πrh = 2πr(2r) = 4πr 2 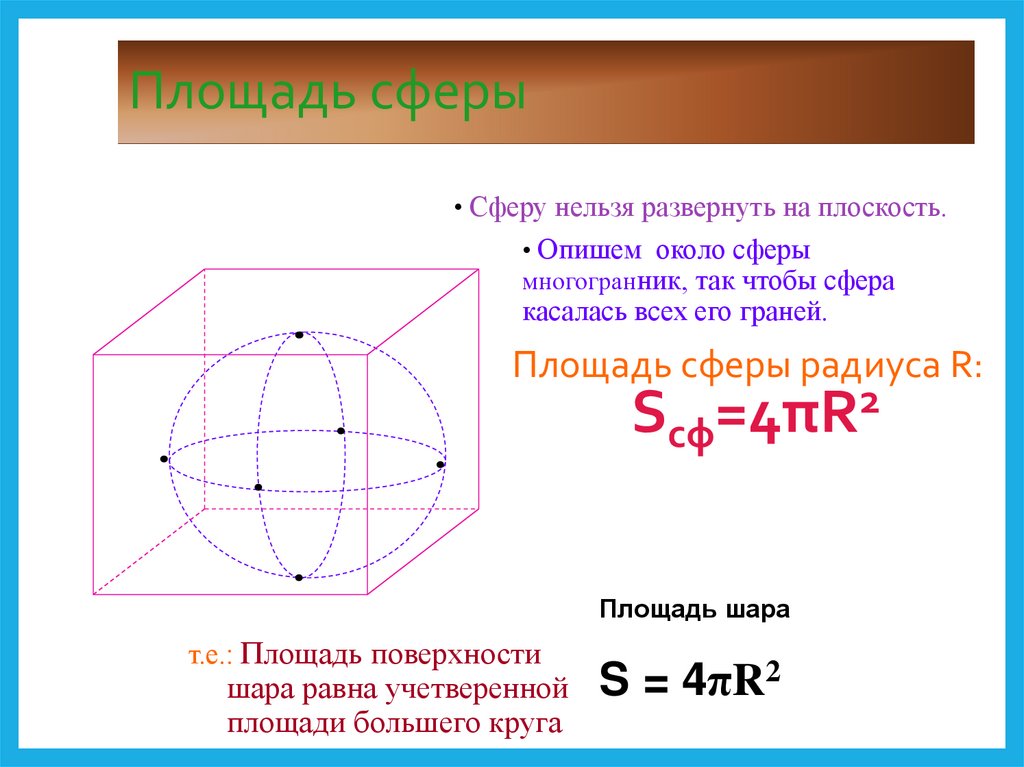 Шаги для расчета площади поверхности сферы приведены ниже.
Шаги для расчета площади поверхности сферы приведены ниже. Следовательно, формула площади криволинейной поверхности сферы выражается как Площадь криволинейной поверхности сферы = 4πr 2 ; где «r» — радиус сферы.
Следовательно, формула площади криволинейной поверхности сферы выражается как Площадь криволинейной поверхности сферы = 4πr 2 ; где «r» — радиус сферы.

 Когда мы пишем формулу площади поверхности сферы, мы пишем площадь поверхности сферы = 4πr 2 = 4(πr 2 ) = 4 × площадь круга.
Когда мы пишем формулу площади поверхности сферы, мы пишем площадь поверхности сферы = 4πr 2 = 4(πr 2 ) = 4 × площадь круга. Он дает отношение между площадью поверхности сферы и диаметром сферы.
Он дает отношение между площадью поверхности сферы и диаметром сферы.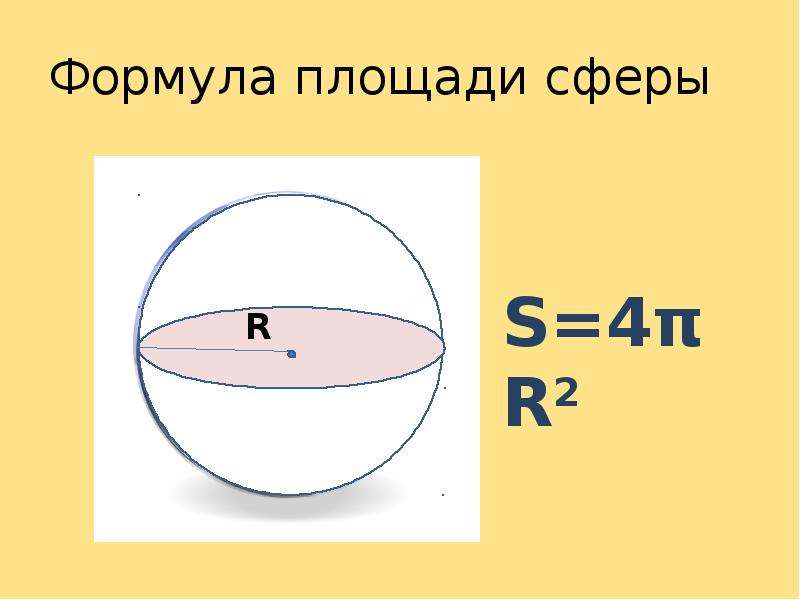 Попробуйте калькулятор площади поверхности сферы от Cuemath и получите ответы за несколько секунд.
Попробуйте калькулятор площади поверхности сферы от Cuemath и получите ответы за несколько секунд. \_\квадрат
\конец{выравнивание} \]
\_\квадрат
\конец{выравнивание} \]
 Неточно, в зависимости от уровня огранки
Неточно, в зависимости от уровня огранки
 В последующем, начиная с года, следующего за годом получения сертификата, не реже одного раза в два года, физическое лицо, имеющее сертификат профессионального бухгалтера банка, обязано подтверждать свою квалификацию. Подтверждение квалификации профессиональными бухгалтерами проводится в форме тестирования.
В последующем, начиная с года, следующего за годом получения сертификата, не реже одного раза в два года, физическое лицо, имеющее сертификат профессионального бухгалтера банка, обязано подтверждать свою квалификацию. Подтверждение квалификации профессиональными бухгалтерами проводится в форме тестирования.
 ..
.. RSYa’
if(!$(s).height()) saa()
}, 5000)
})
RSYa’
if(!$(s).height()) saa()
}, 5000)
})
 » онлайн (675 вопросов)
» онлайн (675 вопросов) » онлайн (90 вопросов)
» онлайн (90 вопросов) )» онлайн (307 вопросов)
)» онлайн (307 вопросов) » онлайн (303 вопроса)
» онлайн (303 вопроса) )» онлайн (322 вопроса)
)» онлайн (322 вопроса) » онлайн (233 вопроса)
» онлайн (233 вопроса) » онлайн (1765 вопросов)
» онлайн (1765 вопросов) » онлайн (173 вопроса)
» онлайн (173 вопроса) » онлайн (541 вопрос)
» онлайн (541 вопрос) pro 2013-2021
pro 2013-2021




 Сертификаты включают дебеты и кредиты, корректирующие записи, финансовые отчеты, балансовый отчет, отчет о прибылях и убытках, отчет о движении денежных средств, оборотный капитал и ликвидность, финансовые коэффициенты, банковскую выверку и расчет заработной платы. Нажмите здесь, чтобы узнать больше.
Сертификаты включают дебеты и кредиты, корректирующие записи, финансовые отчеты, балансовый отчет, отчет о прибылях и убытках, отчет о движении денежных средств, оборотный капитал и ликвидность, финансовые коэффициенты, банковскую выверку и расчет заработной платы. Нажмите здесь, чтобы узнать больше.  Собственник вкладывает в бизнес личные деньги.
Собственник вкладывает в бизнес личные деньги. (Если компания является корпорацией, то Обыкновенных акций счет(а) увеличится.)
(Если компания является корпорацией, то Обыкновенных акций счет(а) увеличится.)


 Таким образом, общая сумма активов не изменится.
Таким образом, общая сумма активов не изменится.


 Собственный капитал владельца (акционеров) будет уменьшен при использовании запасов.
Собственный капитал владельца (акционеров) будет уменьшен при использовании запасов.