Тесты Глава 25 Налог на прибыль с ответами и объяснением
Это демонстрационный вариант, полная версия доступна при условии подписки на закрытый контент и включает более 280 тестов и задач, сгруппированных по следующим разделам:
ОБЩАЯ ИНФОРМАЦИЯ
Какие хозяйствующие субъекты выступают в роли налогоплательщика и налогового агента, в чем состоят основные элементы налога, как организуется налоговый учет, что представляет собой налоговая учетная политика?
ДОХОДЫ И РАСХОДЫ
Налоговая база по налогу на прибыль исчисляется как разница между налогооблагаемыми доходами и расходами, принимаемыми при налогообложении прибыли. Какие статьи затрат полностью или частично исключаются при формировании налоговой базы? Зачем расходы делятся на прямые и косвенные? Какой метод следует применять для учета доходов и расходов – метод начисления или кассовый метод?
АМОРТИЗИРУЕМОЕ ИМУЩЕСТВО
Стоимость амортизируемого имущества списывается на расходы через амортизационные начисления.
Что относится к такому имуществу, с какой целью оно распределяется по амортизационным группам? Как ускорить списание стоимости основных средств на расходы, варьируя учетной методологией в дозволенных законом пределах?
НАЛОГОВЫЕ РЕЗЕРВЫ
Налоговое законодательство предоставляет налогоплательщику право на создание резервов. Как формируются, используются и восстанавливаются налоговые резервы?
РАСЧЕТ НАЛОГА
Как производится расчет налога на практике? По каким сделкам и операциям убытки признаются в особом порядке? Каким образом учитываются налоговые убытки прошлых лет? Что такое инвестиционный налоговый вычет и каковы условия его применения?
УПЛАТА НАЛОГА
По налогу на прибыль предусмотрена авансовая система оплаты. Как рассчитать авансы по налогу на прибыль? Можно ли выбрать способ уплаты авансовых платежей? Как распределить платежи между региональными бюджетами при наличии территориально обособленных подразделений?
ДЕКЛАРАЦИЯ ПО НАЛОГУ НА ПРИБЫЛЬ
Сведения о сформированной налоговой базе, исчисленном налоге и предстоящих налоговых платежах отражаются в налоговой декларации.
Как заполнить эту форму?
ИТОГОВОЕ ТЕСТИРОВАНИЕ
Какие операции производственной компании, помимо продажи готовой продукции, однозначно влекут за собой признание доходов от реализации для целей налогообложения прибыли?
| Продажа излишков материалов | |
| Компенсация виновным лицом суммы причиненного ущерба | |
| Сдача в аренду офисных помещений | |
| Уступка права требования дебиторской задолженности | |
| Обмен объекта основных средств на партию товаров | |
| Передача земельного участка в качестве вложения в уставный капитал другой организации |
Проверка
Развернуть ответ
В течение отчетного периода в производство переданы сырье и материалы стоимостью 14900ДЕ, начислена заработная плата производственным рабочим с отчислениями на социальные нужды в размере 7800ДЕ, учтена амортизация по производственному оборудованию на сумму 2300ДЕ. Согласно учетной политике компании все указанные затраты для целей налога на прибыль относятся к прямым расходам.
Согласно учетной политике компании все указанные затраты для целей налога на прибыль относятся к прямым расходам.
На начало и конец отчетного периода остатки незавершенного производства равны нулю. По состоянию на начало отчетного периода остатки готовой продукции отсутствуют. На дату завершения отчетного периода на складе осталось 30% готовой продукции, выпущенной из производства.
Рассчитайте сумму прямых расходов, списанных на уменьшение доходов от реализации в отчетном периоде.
Ваш ответ
Проверка
Развернуть ответ
Объект основных средств введен в эксплуатацию в апреле 2017 года и продан в январе 2023 года. Для начисления амортизации компания применяет линейный метод. Сколько месяцев амортизировалось имущество?
Ваш ответ
Проверка
Развернуть ответ
Первоначальная стоимость основного средства 209950ДЕ. Ввод в эксплуатацию – апрель 2021. Срок полезного использования 85 мес. В январе 2023 объект был реализован за 140000ДЕ.
В январе 2023 объект был реализован за 140000ДЕ.
Рассчитайте сумму убытка от реализации основного средства, которую можно признать в качестве расходов, уменьшающих налоговую базу за 1 квартал 2023 года.
Ваш ответ
Проверка
Развернуть ответ
Найдите ошибки в начислении и использовании резерва на ремонт основных средств.
| Компания, начисляя резерв на капитальный ремонт доменных печей, не начисляет резерв на ремонты по остальным основным средствам, так как они проводятся на основании графиков планово-предупредительных ремонтов, имеют невысокую стоимость и равномерно распределяются в течение года по отчетным периодам, т.е. не оказывают существенного влияния на себестоимость производимой продукции. | |
В конце года компания формирует за счет расходов налогового периода резерв на текущий ремонт, предстоящий в новом году. В течение следующего года все расходы на ремонт списываются за счет резерва. | |
| Компания, срок существования которой составляет 2 года, создает резерв на предстоящий дорогостоящий капитальный ремонт здания производственного цеха. | |
| В конце года остаток неиспользованного резерва на текущий ремонт компания относит на уменьшение прочих расходов периода. |
Проверка
Развернуть ответ
Имеется следующая информация о доходах и расходах компании, отраженных в ее отчете о прибылях и убытках за отчетный год:
Выручка от реализации 198000ДЕ
Себестоимость 135600ДЕ
Общехозяйственные расходы 20700ДЕ
Коммерческие расходы 2700ДЕ
Прочие доходы 4500ДЕ
Прочие расходы 7800ДЕ
Прочие доходы и расходы компании, признанные в бухгалтерском учете, не связаны с реализацией.
Дополнительно известно, что в составе себестоимости отражена амортизация производственного оборудования, принятого в эксплуатацию в мае со сроком полезного использования 7 лет, на сумму 1750ДЕ, а в общехозяйственных расходах учтены расходы на проведение корпоративных праздников на сумму 590ДЕ.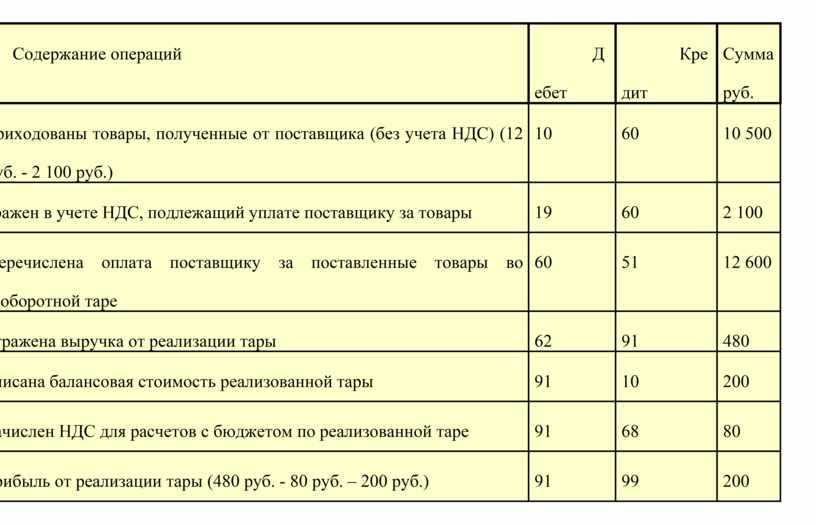 Кроме того, в отчетном году компания начала строительство производственного здания. Источником финансирования являются собственные средства и средства, заимствованные у банка. Сумма процентов по инвестиционному кредиту, начисленных в отчетном периоде, составила 400ДЕ. Указанная сумма была капитализирована в стоимости объекта незавершенного строительства.
Кроме того, в отчетном году компания начала строительство производственного здания. Источником финансирования являются собственные средства и средства, заимствованные у банка. Сумма процентов по инвестиционному кредиту, начисленных в отчетном периоде, составила 400ДЕ. Указанная сумма была капитализирована в стоимости объекта незавершенного строительства.
В налоговом учете по приобретенному в мае оборудованию была применена 30% амортизационная премия. В конце отчетного года была восстановлена неиспользованная сумма налогового резерва на ремонт основных средств, равная 340ДЕ.
На основе имеющейся информации определите сумму налога на прибыль к уплате за отчетный год.
Ваш ответ
Проверка
Развернуть ответ
1 квартал 2022
Налоговая база компании по итогам первого квартала 2022 года составила 5170ДЕ. Авансовые платежи за этот отчетный период равны 0ДЕ.
Заполните расчетную таблицу по начислению налоговых платежей в первом квартале 2022 года.
Расчет налоговых платежей
| Показатели | Значение |
|---|---|
| Налоговая база для исчисления налога | |
| Ставка налога — всего (%) | 20 |
| Сумма исчисленного налога — всего | |
| Сумма начисленных авансовых платежей за отчетный (налоговый) период — всего | |
| Сумма налога к доплате | |
| Сумма налога к уменьшению | |
| Сумма ежемесячных авансовых платежей, подлежащих уплате в квартале, следующем за текущим отчетным периодом |
Проверка
Развернуть ответ
Известна налоговая база за первый квартал 2018 года и сумма накопленного налогового убытка на начало 2018 года. Продолжите заполнение налоговой декларации за указанный отчетный период.
Лист 02
Расчет налога
| Показатели | Код строки | Сумма |
|---|---|---|
Налоговая база (стр. 060 — стр.070 — стр.080 — стр.400 Приложения №2 к Листу 02 + стр.100 Листов 05 + стр.530 Листа 06) 060 — стр.070 — стр.080 — стр.400 Приложения №2 к Листу 02 + стр.100 Листов 05 + стр.530 Листа 06) | 100 | 452000 |
| Сумма убытка или части убытка, уменьшающего налоговую базу за отчетный (налоговый) период (стр.150 Приложения №4 к Листу 02) | 110 | |
| Налоговая база для исчисления налога (стр.100 — стр.110) | 120 | |
в том числе в бюджет субъекта РФ (с учетом положений пункта 1 статьи 284 НК РФ) | 130 | Х |
| Ставка налога — всего, (%) | 140 | 20 |
в том числе: | 150 | 3 |
в бюджет субъекта РФ | 160 | 17 |
в бюджет субъекта РФ (с учетом положений пункта 1 статьи 284 НК РФ) | 170 | Х |
| Сумма исчисленного налога — всего | 180 | |
в том числе: | 190 | |
в бюджет субъекта РФ | 200 |
Приложение №4 к Листу 02
Расчет суммы убытка или части убытка, уменьшающего налоговую базу
| Показатели | Код строки | Сумма |
|---|---|---|
| Остаток неперенесенного убытка на начало налогового периода | 010 | 800210 |
в том числе | 040 | 152110 |
за 2016 год | 050 | 648100 |
Налоговая база за отчетный (налоговый) период (стр. 100 Листа 02 или стр.060 Листа 05) 100 Листа 02 или стр.060 Листа 05) | 140 | |
| Сумма убытка или части убытка, уменьшающего налоговую базу за отчетный (налоговый) период — всего | 150 | |
| Остаток неперенесенного убытка на конец налогового периода — всего | 160 |
Проверка
Развернуть ответ
Подписаться?
Налоги и налогообложение. Тема 6. Налог на прибыль организаций. Тест для самопроверки – пройти тест онлайн бесплатно
Авторам
8-800-333-85-44
Оформить заявку
Вход
- Справочник
- Онлайн-калькуляторы
- Тесты с ответами
Выполним любые типы работ
- Дипломные работы
- Курсовые работы
- Рефераты
- Контрольные работы
- Отчет по практике
- Эссе
Налогообложение
Налогообложение
Налогообложение
Налогообложение
Налогообложение
Налогообложение
Налогообложение
Налогообложение
Налогообложение
Контрольная работа
от 1 дня /
от 100 руб
Курсовая работа
от 5 дней /
от 1800 руб
Дипломная работа
от 7 дней /
от 7950 руб
Реферат
от 1 дня /
от 700 руб
Онлайн-помощь
от 1 дня /
от 300 руб
Оставляй заявку — и мы пройдем все тесты за тебя!
Викторина по подоходному налогу Вопросы и ответы для викторин и рабочих листов
Поиск среди миллионов викторин
ВИКТОРИНА
Прочее
54%
точность
234
играет
Джессика Де Ла Круз
7 лет
Джессика Де Ла Круз
234
играет
20 вопросов
Устройства учащихся не требуются. Узнать больше
Узнать больше
20 вопросы
Показать ответы
См. предварительный просмотр
1. Множественный выбор
30 секунд
1 балл удерживать деньги из зарплаты работника?
Федеральный подоходный налог
Налог на социальное обеспечение
Налог Medicare
Все вышеперечисленное
2. Множественный выбор
30 секунд 90 003
1 балл
Фред зарабатывает 10 долларов в час как библиотекарь помощник.
 Если бы мы работали 40 часов на прошлой неделе, его зарплата составила бы
Если бы мы работали 40 часов на прошлой неделе, его зарплата составила быРавно 400 долларов
Менее 400 долларов
Больше 400 долларов
Найдено в налоговой таблице
3. Множественный выбор
30 секунд
1 балл
Что из следующего не влияет на сумму вашего удержания федерального налога?
Сумма вашего заработка
Ваши пособия по медицинскому страхованию
Ваше семейное положение
Количество удерживаемых вами пособий
4. Множественный выбор
900 55 30 секунд
1 pt
Что из перечисленного ниже не является вознаграждением работникам?
Медицинское страхование
Оплачиваемый отпуск
Пенсионный план
Годовой оклад
5.
 Множественный выбор
Множественный выбор30 секунд 9 0003
1 pt
Форма W-4 используется для
Применить для минимальной заработной платы
Заявление об удержании пособий
Подача федерального подоходного налога
Расчет социального налога
6. Множественный выбор
30 секунд
1 pt
Поскольку федеральный подоходный налог является(n)_____ , Фил платил федеральный налог по более высокой ставке, когда его заработная плата повысился.
Регрессивный налог
Прогрессивный налог
Пропорциональный налог
Налог на прибыль
7. Множественный выбор
30 секунд
1 балл
Налоги на социальное обеспечение и Medicare являются частью ____?
FDIC
SIPC
IRS
FICA
8.
 Множественный выбор
Множественный выбор30 секунд 900 03
1 pt
Тайлер заметил, что из его зарплаты удержаны налоги и некоторые льготы. Эти удержания также называются ________?
Расходы
Удержания
Сбавки
Скидки
9. Множественный выбор
30 секунд
1 балл
Социальный налог является прогрессивным налогом?
Верно
Ложно
10. Множественный выбор
30 секунд
1 точка
Физические лица обязаны подавать отчет о своих доходах и налогах, которые причитаются федеральному правительству в (н)
Налоговая таблица
Форма W-2
Федеральная налоговая декларация
Форма W-4
11.
 Множественный выбор
Множественный выбор30 секунд 9 0003
1 балл
Что из следующего является примером федеральной налоговой декларации?
Форма 1040EZ
W-2
W-4
Форма 10-K
12. Множественный выбор
900 55 30 секунд
1 pt
Работодатель Линды прислал ей (n) _____, в котором указаны ее заработок и сумма, удержанная из ее зарплаты.
Форма W-4
Форма W-2
Форма I-9
1040 Форма
13. Множественный выбор
30 секунд
1 балл
Сумма заработанных и незаработанный доход в течение определенного периода времени, если ваш _____?
Чистая прибыль
Валовой доход
Доход от капитала
Доход от инвестиций
14.
 Множественный выбор
Множественный выбор30 секунд
1 pt
Что обычно называют самым важным налоговым днем в году?
15 августа
15 апреля
30 декабря
30 июня
15. Множественный выбор
3 0 секунд
1 pt
Что означает IRS?
Служба возврата инвестиций
Государственная процентная ставка
Стандарт доходов и арендной платы
Налоговая служба
16. Множественный выбор
30 секунд
1 балл
Налоги на заработную плату состоят из:
Федеральный подоходный налог и подоходный налог штата
Налог на социальное обеспечение и налог на медицинское обслуживание
Зарплата брутто и нетто
Пенсионные взносы и страховые выплаты
17.
 Множественный выбор
Множественный выбор30 секунд
1 pt
Конституция Соединенных Штатов всегда предоставляла право повышать подоходный налог .
Верно
Ложно
18. Множественный выбор
30 секунд
1 точка
Регрессивный налог изымает наибольший процент дохода из какой группы?
Среднедоходные
Малообеспеченные
Высокодоходные
Бездоходные
19. Множественный выбор
30 секунд
1 pt
Единый налог аналогичен a
Пропорциональный налог
Прогрессивный налог
Регрессивный налог
Ничего из вышеперечисленного
20.
 Множественный выбор
Множественный выбор30 секунд
1 балл
Прогрессивный налог взимает меньшую долю дохода с групп с низкими доходами, чем с групп с высокими доходами.
Верно
Ложно
Рассказать обо всех вопросах с бесплатной учетной записью
Уже есть учетная запись?
Ответы на 13 общих налоговых вопросов
Примечание редактора: Credit Karma получает компенсацию от сторонних рекламодателей, но это не влияет на мнение наших редакторов. Наши сторонние рекламодатели не просматривают, не одобряют и не одобряют наш редакционный контент. Это точно, насколько нам известно, когда публикуется.
Мы считаем важным, чтобы вы понимали, как мы зарабатываем деньги. Это довольно просто, на самом деле. Предложения финансовых продуктов, которые вы видите на нашей платформе, исходят от компаний, которые платят нам. Деньги, которые мы зарабатываем, помогают нам предоставлять вам доступ к бесплатным кредитным рейтингам и отчетам, а также помогают нам создавать другие наши замечательные инструменты и учебные материалы.
Деньги, которые мы зарабатываем, помогают нам предоставлять вам доступ к бесплатным кредитным рейтингам и отчетам, а также помогают нам создавать другие наши замечательные инструменты и учебные материалы.
Компенсация может зависеть от того, как и где продукты появляются на нашей платформе (и в каком порядке). Но поскольку мы обычно зарабатываем деньги, когда вы находите предложение, которое вам нравится, и получаете его, мы стараемся показать вам предложения, которые, по нашему мнению, вам подходят. Вот почему мы предоставляем такие функции, как ваши шансы на одобрение и оценки экономии.
Конечно, предложения на нашей платформе не представляют все доступные финансовые продукты, но наша цель — показать вам как можно больше отличных вариантов.
Эта статья была проверена нашими редакторами и Дженнифер Самуэль, старшим специалистом по продуктам Credit Karma. Он был обновлен на 2020 налоговый год.
Правила федерального подоходного налога в США очень сложны.

Это верно независимо от того, подаете ли вы налоговую декларацию впервые или являетесь практикующим налоговым юристом с многолетним опытом. Фактически, даже Служба защиты налогоплательщиков IRS признает, что самой серьезной проблемой, с которой сталкиваются налогоплательщики, является сложность налогового кодекса.
Чтобы помочь вам сориентироваться при подаче налоговой декларации, у нас есть ответы на некоторые из наиболее распространенных налоговых вопросов прямо здесь.
- Как узнать, должен ли я подавать налоговую декларацию?
- С какого дохода я должен платить налоги?
- Какой статус регистрации выбрать?
- Есть ли у меня иждивенцы?
- Как узнать свою налоговую категорию и налоговую ставку?
- Какую налоговую форму следует использовать?
- Должен ли я использовать стандартный вычет или детализировать?
- В чем разница между налоговым кредитом и налоговым вычетом?
- На какие вычеты и кредиты я могу претендовать?
- Когда должны быть уплачены налоги?
- Как подать налоговую декларацию?
- Когда я получу возмещение?
- Что делать, если я не могу заплатить причитающийся налог?
1.
 Как узнать, должен ли я подавать налоговую декларацию?
Как узнать, должен ли я подавать налоговую декларацию? Необходимость подачи налоговой декларации зависит от нескольких факторов, в том числе от вашего валового дохода, статуса подачи, возраста и от того, являетесь ли вы иждивенцем в чьей-либо федеральной налоговой декларации. И вам, возможно, придется подать заявление, даже если вы не должны платить какие-либо налоги.
Чтобы получить более конкретную информацию о том, кто должен подавать документы, ознакомьтесь с публикацией IRS 501. Для большинства людей валовой доход является основным фактором для подачи требований. Например, в 2020 году порог подачи заявок для одиноких людей моложе 65 лет составлял 12 400 долларов. Для супружеских пар, подавших совместную регистрацию, сумма составляла 24 800 долларов, если оба супруга были моложе 65 лет9.0003
Если вы были указаны как иждивенец на основании чьей-либо декларации и имели доход, вам, возможно, также придется подать заявление, даже если ваш доход был намного ниже общего порога. Публикация 501 содержит более подробную информацию о том, когда иждивенцы должны подавать документы.
Публикация 501 содержит более подробную информацию о том, когда иждивенцы должны подавать документы.
Вам также необходимо подать налоговую декларацию, если ваш доход от индивидуальной предпринимательской деятельности составляет не менее 400 долларов США или вы отвечаете другим особым требованиям, таким как получение не облагаемых налогом чаевых, получение денег от освобожденных от налогов церквей или задолженность по альтернативному минимальному налогу. Публикация IRS 501 подробно описывает эти и другие особые ситуации.
Узнайте, кто должен подавать федеральную налоговую декларацию
2. С какого дохода я должен платить налоги? Согласно IRS, доход включает деньги, имущество или услуги. Любой доход подлежит налогообложению, если только закон специально не освобождает его от уплаты налогов, и все налогооблагаемые доходы должны быть указаны в вашей налоговой декларации. Некоторый необлагаемый налогом доход также должен быть указан, даже если вы не будете платить налоги с него.
Публикация IRS 525 содержит подробную информацию о том, что считается налогооблагаемым доходом, а что нет, и это длинный список. Не все налогооблагаемые доходы рассматриваются одинаково. Заработанный доход, как и ваша заработная плата, облагается налогом по-разному, поскольку вы платите с него налог на социальное обеспечение, налог на Medicare, а также подоходный налог штата и федеральный налог.
Нетрудовой доход, такой как алименты или пособия по социальному обеспечению, не облагается налогом на заработную плату, но вы платите с него федеральный налог, а иногда и подоходный налог штата. А некоторые виды незаработанного дохода облагаются налогом по более низкой ставке прироста капитала, чем ваша обычная ставка налога.
С налоговыми декларантами обращаются по-разному в зависимости от статуса семьи. Чтобы сообщить IRS о том, какие правила применяются к вам, вам нужно будет выбрать статус подачи. Их пять: холостые, состоящие в браке, подающие совместную регистрацию, состоящие в браке, подающие по отдельности, глава семьи и квалифицированный вдовец (вдовец) с ребенком на иждивении.
Ваш статус подачи влияет на вашу налоговую ставку, стандартные вычеты и право на определенные вычеты и кредиты. IRS предоставляет интерактивный инструмент, помогающий налогоплательщикам выбрать статус подачи.
4. Есть ли у меня иждивенцы?Иждивенец — это лицо, за содержание которого вы несете ответственность. Если вы можете претендовать на иждивенца, вы можете получить право на определенные налоговые льготы, включая налоговый кредит на детей. Вы также можете претендовать на статус главы семьи.
У вас может быть иждивенец, если …
- У вас есть соответствующий требованиям ребенок младше 19 лет или младше 24 лет, если он посещает школу полный рабочий день. Ваш ребенок должен либо прожить с вами более полугода, либо подпадать под действие исключения, и не должен обеспечивать более половины своей поддержки. Ваш ребенок также не может подавать совместную налоговую декларацию, за исключением требования возмещения.
- У вас есть подходящий родственник.
 Ваш квалифицированный родственник либо должен состоять с вами в определенных семейных отношениях, либо должен проживать с вами в течение всего года. Вы должны обеспечить более половины их поддержки, они должны зарабатывать очень мало, и никто другой не может считать их иждивенцами.
Ваш квалифицированный родственник либо должен состоять с вами в определенных семейных отношениях, либо должен проживать с вами в течение всего года. Вы должны обеспечить более половины их поддержки, они должны зарабатывать очень мало, и никто другой не может считать их иждивенцами.
Налоговое управление США предоставляет Интерактивный помощник по налогам, который поможет вам определить, есть ли у вас иждивенец.
5. Как узнать свою налоговую категорию и налоговую ставку?В США действует прогрессивная налоговая система, поэтому не все ваши доходы обязательно облагаются налогом по одинаковой ставке. Налоговые категории относятся к диапазону доходов, облагаемых налогом по определенным ставкам, в то время как ваша предельная налоговая ставка является самой высокой налоговой группой, применимой к вашему доходу.
В соответствии с действующим налоговым законодательством существует семь налоговых категорий. Чтобы узнать, к какой из них вы относитесь, и какова ваша налоговая ставка, вам нужно знать свой доход. Затем вы можете использовать таблицы налоговых ставок IRS для налогового года, чтобы определить свою категорию, какова ваша предельная налоговая ставка и какую сумму налога вы можете заплатить.
Затем вы можете использовать таблицы налоговых ставок IRS для налогового года, чтобы определить свою категорию, какова ваша предельная налоговая ставка и какую сумму налога вы можете заплатить.
Каковы рамки федерального подоходного налога в 2020 году?
6. Какую налоговую форму мне следует использовать?Начиная с 2018 налогового года, единая форма 1040 заменила предыдущие три версии — формы 1040, 1040EZ и 1040A.
Упрощенная форма 1040, которую вы будете использовать для подачи индивидуального федерального подоходного налога за 2020 год, вдвое меньше последних форм и использует подход «стандартных блоков» для упрощения процесса подачи. Налогоплательщикам с более сложной налоговой ситуацией может потребоваться представить дополнительные формы (называемые «расписаниями»), но все 150 миллионов индивидуальных налогоплательщиков США начинают с одной и той же базовой формы.
7. Должен ли я использовать стандартный вычет или детализировать? Вычеты уменьшают налогооблагаемый доход. У вас есть выбор между стандартным вычетом или перечислением ваших вычетов. Когда вы детализируете, вы уменьшаете налогооблагаемый доход на сумму определенных расходов, подлежащих вычету в соответствии с налоговым законодательством США. Например, если вы платите проценты по ипотеке, вы можете вычесть уплаченные проценты, но только в том случае, если вы перечислите их по пунктам.
У вас есть выбор между стандартным вычетом или перечислением ваших вычетов. Когда вы детализируете, вы уменьшаете налогооблагаемый доход на сумму определенных расходов, подлежащих вычету в соответствии с налоговым законодательством США. Например, если вы платите проценты по ипотеке, вы можете вычесть уплаченные проценты, но только в том случае, если вы перечислите их по пунктам.
Чтобы решить, какие вычеты использовать, сравните значение стандартного вычета с общей стоимостью ваших постатейных вычетов. На 2020 год стандартные суммы вычетов составляют:
- 12 400 долларов США, если вы подаете заявление как холост или состоите в браке и подаете заявление отдельно
- 18 650 долларов США, если вы подаете заявление как глава семьи
- 24 800 долларов США, если вы подаете заявление как состоящее в браке, подающее заявление совместно
Поскольку налоговая реформа значительно увеличила стандартный вычет, детализированный отчисления не превышают стандартную сумму отчислений для вашего статуса подачи.
Как налоговые кредиты, так и налоговые вычеты могут уменьшить сумму налога, которую вы должны заплатить. Вычеты уменьшают сумму дохода, с которого вы платите налоги, что, в свою очередь, может уменьшить ваш налог. Кредиты — это доллар за долларом снижение суммы налога, который вы должны.
Если ваш доход составил 30 000 долларов США и вы получили вычет в размере 1000 долларов США, вам не нужно платить налог с этой 1000 долларов дохода. Вычет может сэкономить вам 200 долларов (при ставке налога 20% на эту 1000 долларов).
Напротив, кредит в размере 1000 долларов уменьшит фактическую сумму налога, которую вы должны уплатить, на эту 1000 долларов. Таким образом, если вы должны 3000 долларов налогов, теперь вы должны 2000 долларов и сэкономите 1000 долларов.
9. На какие вычеты и кредиты я могу претендовать? Вычеты и кредиты, на которые вы имеете право претендовать, зависят от вашей ситуации. Вот некоторые вычеты, на которые вы можете претендовать, даже если вы не перечисляете.
Вот некоторые вычеты, на которые вы можете претендовать, даже если вы не перечисляете.
- Взносы в индивидуальные пенсионные фонды, включая IRA, SEP-IRA, Simple IRA и соло 401(k)s (поэтапный отказ от них при более высоких доходах)
- 50% налогов на самозанятость
- Проценты по студенческой ссуде до $2,500
- Плата за обучение и высшее образование до 4000 долларов США, если ваш доход соответствует ограничениям
- Взносы на медицинские сберегательные счета, сделанные из личных средств
Вычеты, на которые вы можете претендовать, только если вы перечислите:
- Максимум 10 000 долларов США по совокупности уплаченных налогов штата и местных налогов (налоги ОСВ)
- Проценты на сумму до 1 миллиона долларов США по приемлемой ипотечной задолженности по кредитам, взятым до 15 декабря 2017 года, и до 750 000 долларов США по соответствующей ипотеке задолженность по кредитам, взятым после этого
- Вычет на медицинские расходы, но только если они составляют не менее 7,5% вашего дохода
- Вычет на благотворительные взносы, которые не превышают установленный процент от дохода
И, наконец, кредиты, на которые вы можете претендовать.
- Налоговый вычет за заработанный доход предоставляется американцам с низким доходом. Помощник IRS EITC может помочь вам определить, соответствуете ли вы требованиям.
- Налоговый вычет на детей предоставляет зачет в размере до 2000 долларов США на каждого ребенка в налоговых годах с 2018 по 2024 год. До 1400 долларов США из этой суммы подлежат возврату. Право на участие в программе постепенно прекращается при доходе в размере 200 000 долларов США для одиноких заявителей и 400 000 долларов США для супружеских пар, подающих совместную заявку.
- Налоговый кредит по уходу за детьми и иждивенцами оценивается в размере 20–35% от суммы разрешенных расходов на уход, до 3000 долларов США в виде расходов на уход за одним лицом, имеющим на это право. Налогоплательщик, ухаживающий за двумя или более иждивенцами, может претендовать на максимальный кредит в размере 6000 долларов.
- Американская налоговая льгота на альтернативные возможности обеспечивает максимальный кредит в размере 2500 долларов США на отвечающие требованиям расходы на образование, выплаченные правомочным учащимся.
 Кредит доступен только для оплаты обучения в течение первых четырех лет послесреднего образования, и существуют ограничения по доходу.
Кредит доступен только для оплаты обучения в течение первых четырех лет послесреднего образования, и существуют ограничения по доходу. - Кредит на обучение в течение всей жизни обеспечивает максимальный кредит в размере 2000 долларов США в год для покрытия расходов на послесреднее образование. Существуют также ограничения по доходам, и кредит составляет только 20% квалификационных расходов, но не более 10 000 долларов США.
В зависимости от вашей ситуации, возможно, вы можете потребовать другие вычеты и кредиты.
10. Когда уплачиваются налоги?Каждый год вы должны подавать налоговую декларацию по федеральному подоходному налогу за предыдущий календарный год до налогового дня. Обычно срок подачи документов истекает 15 апреля или около того, хотя, если 15 число выпадает на выходной или праздничный день, крайний срок может быть перенесен на следующий рабочий день.
БЫСТРЫЕ ФАКТЫ
Как получить расширение для регистрации?
Вы можете запросить продление срока подачи федеральной налоговой декларации на шесть месяцев. В большинстве случаев IRS может предоставить автоматическое продление подачи.
В большинстве случаев IRS может предоставить автоматическое продление подачи.
Обратите внимание, что продление срока подачи не дает вам больше времени для уплаты причитающихся налогов. Уплата налога должна быть произведена в налоговый день, и несвоевременная уплата может привести к тому, что вам грозят проценты и штрафы на невыплаченную сумму. Подробнее о заполнении расширений читайте здесь.
ПоказатьСкрыть
11. Как подать налоговую декларацию?У вас есть несколько вариантов подачи декларации.
- Почта: Адрес для отправки декларации зависит от штата, в котором вы живете (Налоговое управление США предлагает список адресов) составляет $72 000 или меньше
- Бесплатная подача налоговых деклараций через Интернет: С такой услугой, как Credit Karma
- Самостоятельно: С платным программным обеспечением для подготовки налоговых деклараций
- Специалист по налогообложению: Если у вас более сложная ситуация
Как бы вы ни выбрали подачу декларации, имейте в виду, что подача декларации в электронном виде имеет несколько преимуществ. Если вам причитается возмещение, вы можете получить его раньше через электронный файл, поскольку IRS обрабатывает электронные декларации быстрее, чем бумажные.
Если вам причитается возмещение, вы можете получить его раньше через электронный файл, поскольку IRS обрабатывает электронные декларации быстрее, чем бумажные.
По данным IRS, большинство возмещений выдается в течение 21 дня для налогоплательщиков, которые подали документы в электронной форме и которые получают возмещение напрямую. Возврат занимает до шести недель, если вы представили бумажные декларации. Требование определенных кредитов или вычетов может задержать ваш возврат. Вы можете проверить статус вашего возмещения на веб-сайте IRS «Где мой возврат».
13. Что делать, если я не могу заплатить причитающийся налог?Если вы не можете позволить себе платить налоги, обязательно подайте налоговую декларацию и примите меры для выплаты того, что вы должны. Несвоевременная подача и/или уплата налогов приведет к начислению процентов и штрафов.
Если вы не можете позволить себе выплатить всю причитающуюся сумму к установленному сроку, Налоговое управление США предлагает несколько вариантов оплаты, которые могут вам помочь, включая соглашения о рассрочке.

 Как заполнить эту форму?
Как заполнить эту форму? Если бы мы работали 40 часов на прошлой неделе, его зарплата составила бы
Если бы мы работали 40 часов на прошлой неделе, его зарплата составила бы Множественный выбор
Множественный выбор Множественный выбор
Множественный выбор Множественный выбор
Множественный выбор Множественный выбор
Множественный выбор Множественный выбор
Множественный выбор Множественный выбор
Множественный выбор Кредит доступен только для оплаты обучения в течение первых четырех лет послесреднего образования, и существуют ограничения по доходу.
Кредит доступен только для оплаты обучения в течение первых четырех лет послесреднего образования, и существуют ограничения по доходу. Форма отчета
Форма отчета
 Будьте уверены, что ваши файлы хранятся на надежных серверах и защищены от любого несанкционированного доступа.
Будьте уверены, что ваши файлы хранятся на надежных серверах и защищены от любого несанкционированного доступа. co
co DOCX (Office Open XML) является преемником устаревшего формата DOC.
DOCX (Office Open XML) является преемником устаревшего формата DOC.


 Но, вы можете скачать это средство по ссылке с моего сайта.
Но, вы можете скачать это средство по ссылке с моего сайта.


 Есть простое решение для изменения формата в операционной системе Windows: необходимо поменять расширение файла «.docx» на «doc».
Есть простое решение для изменения формата в операционной системе Windows: необходимо поменять расширение файла «.docx» на «doc». Сделать это можно разными способами с помощью программ на компьютере, на онлайн сервисах в интернете, используя средства Windows.
Сделать это можно разными способами с помощью программ на компьютере, на онлайн сервисах в интернете, используя средства Windows. Наша бесплатная служба преобразования проанализирует содержимое исходного файла DOCX до мельчайших деталей и воссоздаст содержимое в целевом формате DOC.
Наша бесплатная служба преобразования проанализирует содержимое исходного файла DOCX до мельчайших деталей и воссоздаст содержимое в целевом формате DOC.

 Сколько метров провода осталось в мотке?
Сколько метров провода осталось в мотке?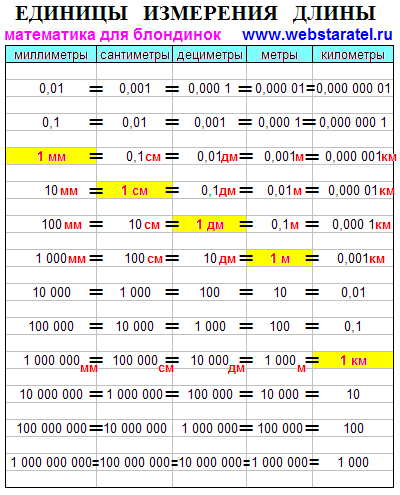

 Они связаны с:
Они связаны с:



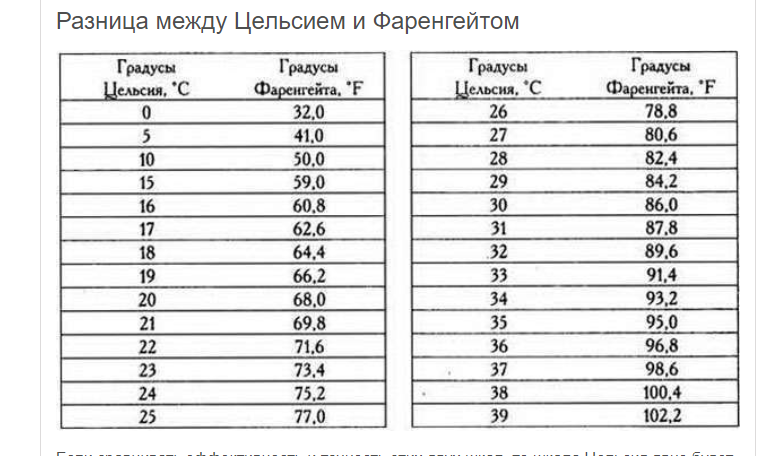
 Чтобы преобразовать 1 градус в миллиметры, используйте приведенную ниже формулу прямого преобразования.
Чтобы преобразовать 1 градус в миллиметры, используйте приведенную ниже формулу прямого преобразования.  S.) — Ссылка (Gunter’s; Геодезист) LNK (RE) — Link (Ramsden’s; Engineer’s) LS — Световой-секундный — Световой годM — Метр (базовая единица СИ)MIL — Мил (Швеция и Норвегия)MILE DATA — Мили (тактические или данные)MK — MickeyNAIL — Гвоздь (ткань)NL — Морская лигаNM — НанометрNMI — Морские милиNMI I — Морская миляP — PalmPC — ParsecPICA — PicaPM — Пикометр (бикрон, клеймо)POINT — точка (американский, английский)PT — PaceQUART — QuarterSHAKU — Shaku (Japan)SPT — SpatTH — Мил (тыс.) TWP — TwipUM — Микрометр (стар. микрон) XU — X единица измерения; siegbahnABA — Электромагнитная единица AbampereAMP — Ампер (базовая единица Si)ESU — Esu в секунду Статампер (CgsABC — Абкулон Электромагнитная единицаATU — Атомная единица зарядаCLM — КулонFRD — ФарадейMAH — Миллиампер-часSTT — Статкулон Франклин ЭлектростABV — Абвольт (единица Cgs)STV — Статвольт ( Cgs Unit)VLT — Вольт (Si Unit)ACF — Акр-футыACI — Акры-дюймыBIB — Баррели (нефтяные)BII — Баррели (британские)BIU — Баррели (Us Dry)BKT — Ведра (британские)BRO — Галлоны (пивные)BUD — Бушели (Us Dry Level)BUI — Бушели (Imperial)BUU — Бушели (Us Dry Heaped)CMB — CoombsCMI — Cubic MilesCP — CupsCRF — Cord-FootsCRW — Cords (Дрова)CUF — Cubic FathomsCUI — Cubic InchsCUT — Cubic FootsCUY — Cubic ЯрдыDSI — тире (имперские фунты)DSS — десертные ложки (имперские фунты)DSU — тире (США)FBM — борд-футыFFT — пятые FID — жидкие драхмы (имперские)FIS — жидкие скрукле (имперские)FLB — бочки (США, жидкие)FLU — жидкие драмы ( Us) Us FluidramFRK — FirkinsGAI — галлоны (имперские единицы)GAU — галлоны (Us Dry)GAW — галлоны (Us Fluid Wine)GLU — Teacups (gills)GTT — DropsHDI — Hogsheads (Imperial)HHU — Hogsheads (Us)JGR — Jiggers ( Bartending)KLD — KilderkinsLMD — LambdasLOD — LoadsLST — LastsM3 — Кубические метры (Si Unit)MII — Minims (Imperial)MIU — Minims (Us)OZF — Унции (Fluid Us Food NutritioPER — PerchsPKI — Pecks (Imperial)PKU — Pecks (Us) Сухой)PNI — пинчи (британские)PNU — пинчи (американские)PON — PonysPOT — Pottle QuartersPP — стыковые трубыPTI — пинты (британские)PUD — пинты (Us Dry)PUF — пинты (Us Fluid)QRF — Quart S (Us Fluid) QRT — Кварталы QTI — Кварты (британские)QTU — Кварты (Us Dry)RGS — Реестр TonsSCI — Мешки (британские) BagsSCU — Мешки(Us)SHT — Shots (Us)SM — SeamsSTK — Забастовки (Imperial)STU — Забастовки (Us) )TBC — столовые ложки (канадские)TBF — столовые ложки (обычные в США)TBM — столовые ложки (метрические)TBS — столовые ложки (в австралийских единицах измеренияTCA — чайные ложки (канадские) TFD — столовые ложки (Us Food NutritionTIM — чайные ложки (британские)TMF — Timber FootsTMT — чайные ложки ( Метрическая система)TND – тонны (водоизмещение)TNT – тонны (воды)TNW – тонны (фрахт)TSC – чайные ложки (стандарт США)TSF – чайные ложки (США Food Nutrition) WEY — Wey (Us)ACM — Атмосфера-кубический фут в минутуACS — Атмосфера-кубический фут в секунду SecoATC — Атмосфера-кубический сантиметр PeATH — Атмосфера-кубический фут в часBTJ — BTU (Международная таблица) В расчете на BTN — BTU (Международная таблица) В расчете на BTS — БТЕ (международная таблица) по CAS — Калория (международная таблица) ERS — Эрг в секундуFMF — Фут-фунт-сила в минутуFT — Фут-фунт-сила в часFTO — Фут-фунт-сила в секундуHPS — Лошадиная силаLAM — Литр-атмосфера в час MinuteLSC — LusecLTS — Литр атмосферы в секундуPNC — PonceletSQL — Прямой эквивалент квадратного фута TC — Тонна кондиционирования воздухаTMS — Атмосфера-кубический сантиметр PeTRM — Тонна охлаждения (ImperialTRR — Тонна охлаждения (It)AMU — Единица атомной массы UnifiedAT — Анализ тонны (Короткий)ATS — Ton Assay (Длинный)BAC — Bag (Coffee)BDM — Bag (Portland Cement)BRG — BargeCLV — CloveCRT — CrithCT — Carat (Metric)DA — DaltonDRT — Dram (Apothecary Troy)DWT — PennyweightGAM — GammaGR — GrainGV — GraveKIP — KipLB — Фунт (метрический)LBA — ФунтLBT — Фунт (тройской)LBV — Фунт (Avoirdupois)ME — Атомная единица массы Электрон RMRK — MarkMTE — MiteMTM — Клещ (метрический)OZ — Унция (Us Food Nutrition LabelOZT — Унция (аптечная тройка)OZZ — унция (Avoirdupois)PNN — PointQ — квинтал (метрическая система)QR — четверть (неформальная)QRI — четверть (имперская)QRL — четверть длинная (неформальная)SAP — Scruple (аптекарь)SH — тонна короткаяSLG — слаг Geepound HylSLH — SheetST — StoneSWT — Вес в сотни (центум) oTON — Тонна LongWY — WeyZTR — ZentnerARE — AresBD — BoardsBHE — Эквивалент мощности котла DBR — BarnsBRN — BaronysCDA — Cuerda Pr SurveysCRD — CordsCRI — Circular InchsCRM — Circular MilsDNM — DunamsGNT — GunthasHD — HidesRO — RoodsSCT — SectionsSHD — СараиSII — Square Link Gunters InternatiSLR — Square Link RamsdensSQC — Square Chains InternationalSQM — Square Mil Square ThousSQR — Square Rod/Pole/PerchsSRR — Square RoofingsSTR — StremmasTWN — TownshipsYLN — YardlandsARM — Arcminute MoaARS — ArcsecondCNS — Centesimal Second Of ArcCNT — Столетняя минута ArcDOA — Градус (дуги)GRA — Град Градиан GonOCT — OctantQRD — QuadrantSGN - SignSXT — Секстантµ — Угловой MilATA — Атмосфера (техническая)ATM — Атмосфера (стандартная)BAR — BarBRY — Бари (единица Cgs)CMH — Сантиметр Of MercuryCMW – сантиметр водяного столба (4 °C)FTH – фут ртутного столба (условный)FTW – фут водяного столба (392 °F)IMC — Дюйм ртутного столба (условный)INW — Дюйм водяного столба (392 °F)KM — Килограмм-сила на квадратный дюймKSI — Кип на квадратный дюймLTP — Длинная тонна на квадратный футMHG — Микрометр ртутного столбаMMH — Миллиметр ртутного столбаMMW — Миллиметр воды (398 °C)PA — Паскаль (единица Si)PD — фунт на квадратный футPSF — фунт на квадратный футPSI — фунт на квадратный дюймPZ — пьеза (единица Mts)STP — короткая тонна на квадратный футTOR — ТоррATN — атомная единица ForceDYN — Dyne (Cgs Unit)KFF — Килограмм-сила Kilopond Grave-KI — Kip Kip-ForceMGF — Milligrave-Force Gravet-ForceOZC — Унция-силаPDL — PoundalSN — Sthene (единица Mts)TNF — Long Ton-ForceTNL — Short Ton- ForceAUC — атомная единица времениCTN — CenturyCYC — каллипический циклDEC — DecadeFN — FortnightHEL — HelekHIP — гиппархический циклJFF — JiffyKEH — Ke (четверть часа) LSR — Luster LustrumMD — MillidayMLL — MillenniumMMN — MomentMOF — Month (Full)MOG — Month (Greg) Av)MOH — месяц (полый)MOS — месяц (синодический)MTN — метонический цикл EnneadecaeterisOC — OctaeterisPLN — планковское времяSGM — SigmaSHK — ShakeSTH — сотический циклSVD — SvedbergYR — год (общий)YRG — год (григорианский)YRJ — год (юлианский) YRL – год (високосный)YRM – год (среднетропический)B39- Британская термальная единица (39 °F)B59 — Британская термальная единица (59 °F)B60 — Британская термальная единица (60 °F)B63 — Британская термальная единица (63 °F)BOE — эквивалент барреля нефтиBRT — Британская термальная единица ( Iso)BTI — Британская термальная единица (InternatBTM — Британская термальная единица (средняя)BTT — Британская термальная единица (ThermochC15 — Калория (15 °C)C20 — Калория (20 °C)C98 — Калория (398 °C)CAM — Калория ( Среднее значение)CFT — Кубический фут атмосферы CHU — Тепловая единица ЦельсияCL — Калория (Us Fda)CLTH — Калория (термохимическая)CN — Кубический фут природного газаCTA — Кубический сантиметр атмосферыCYD — Кубический ярд атмосферы StandEH — Атомная единица энергии ХартриFTD — Foot-PoundalIMG — Галлон-атмосфераKCA — Большая килокалорияKWH — Киловатт-час Board Of Trade ULTM — Литр-атмосфераQD — QuadRDB — Therm (Ec)RY — RydbergTCE — Тонна угольного эквивалентаTHR — Therm (Us)THU — ThermieTN — Тонна TntTOE — Тонна нефтяного эквивалентаBAN — Ban HartleyBSH — Bit ShannonCD — Candela (Si Base Unit) CandleCPD — Candlepower (New)JK — Si UnitNAT — Nat Nip NepitNBL — NibbleBQ — Беккерель (Si Unit)CI — CurieRD — Rutherford (H)C — Скорость света в вакуумеFPF — фарлонг в две неделиFPH — фут в часIPH — дюйм в часIPM — дюйм в минутуIPS — дюйм в секундуMCH — число МахаMPM — миля в минутуMPS — миля в секундуMS — метр в секунду (единица Си)SPS — скорость звука в AirCDF — Кандела на квадратный футCDI — Кандела на квадратный дюймCDM — Кандела на квадратный метр (Si UFL — FootlambertLMB — LambertSB — Stilb (Cgs Unit)CEL — ЦельсийDDE — Градус DelisleDNE — Градус НьютонаFAN — ФаренгейтGMR — Регулятор газа MarkKEL — Kelvin’sRAN — RankineREA — ReaumurRME — Градус RømerCFM — Кубический фут в минутуFTS — Кубический фут в секундуGPD — Галлон (жидкость США) в суткиGPH — Галлон (жидкость США) в часGPM — Галлон (жидкость США) в минутуINM — Кубический дюйм в минутуINS — Кубический дюйм в секундуLPM — Литр в минутуMQS — кубический метр в секунду (Si UniCM — кулон-метрDB — DebyeEA0 — атомная единица электрического диполяFC — фут-канделя люмен на квадрат FoLMN — люмен на квадратный дюймLX — люкс (единица Si)PH — Phot (единица Cgs)FHP — фут в секунду Час в секундуFMS — фут в минуту в секундуFP — фут в секунду в квадратеG — стандартная гравитацияGAL — галлон GalileoIP — дюйм в минуту в секунду в секундуIP2 — дюйм в секунду в квадратеKNS — узел в секундуMM — миля в минуту в секундуMP — миля в час в секундуMP2 — миля в секунду Секунда в квадратеMSA — метр на секунду в квадрате (Si UFT2 — квадратный фут в секундуM2S — квадратный метр в секунду (Si UnSTX — Стокс (единица Cgs)FTP — фут-фунт)MKG — метр-килограмм-силаNEM — ньютон-метр (единица Si)GML — грамм на секунду MillilitreLAB — фунт (эквивалентный) на галлонLBF — фунт (эквивалентный) на кубический LBI — фунт (экспериментальный) на кубический LBL — фунт (экспериментальный) на галлонOFT — унция (экспериментальный) на кубический OG — унция (эвердупуа) на галлон ) Per GallonOIN — Унция (Avoirdupois) на кубический SFT — Slug на кубический футGSS — Gauss (Cgs Unit)TSL — Tesla (Si Unit)GY — Grey (Si Unit)RDD — RadLBH — Pound Per Foot HourLBS — Фунт на фут в секундуLFT — Фунт-сила-секунда на квадрат LIN — Фунт-сила-секунда на квадрат PAS — Паскаль-секунда (единица Si)PSU — Пуаз (единица Cgs)MX — Максвелл (единица Cgs)WB — Вебер (единица Si)REM — Рентген-эквивалент ManSV — Sievert (Единица Си)
S.) — Ссылка (Gunter’s; Геодезист) LNK (RE) — Link (Ramsden’s; Engineer’s) LS — Световой-секундный — Световой годM — Метр (базовая единица СИ)MIL — Мил (Швеция и Норвегия)MILE DATA — Мили (тактические или данные)MK — MickeyNAIL — Гвоздь (ткань)NL — Морская лигаNM — НанометрNMI — Морские милиNMI I — Морская миляP — PalmPC — ParsecPICA — PicaPM — Пикометр (бикрон, клеймо)POINT — точка (американский, английский)PT — PaceQUART — QuarterSHAKU — Shaku (Japan)SPT — SpatTH — Мил (тыс.) TWP — TwipUM — Микрометр (стар. микрон) XU — X единица измерения; siegbahnABA — Электромагнитная единица AbampereAMP — Ампер (базовая единица Si)ESU — Esu в секунду Статампер (CgsABC — Абкулон Электромагнитная единицаATU — Атомная единица зарядаCLM — КулонFRD — ФарадейMAH — Миллиампер-часSTT — Статкулон Франклин ЭлектростABV — Абвольт (единица Cgs)STV — Статвольт ( Cgs Unit)VLT — Вольт (Si Unit)ACF — Акр-футыACI — Акры-дюймыBIB — Баррели (нефтяные)BII — Баррели (британские)BIU — Баррели (Us Dry)BKT — Ведра (британские)BRO — Галлоны (пивные)BUD — Бушели (Us Dry Level)BUI — Бушели (Imperial)BUU — Бушели (Us Dry Heaped)CMB — CoombsCMI — Cubic MilesCP — CupsCRF — Cord-FootsCRW — Cords (Дрова)CUF — Cubic FathomsCUI — Cubic InchsCUT — Cubic FootsCUY — Cubic ЯрдыDSI — тире (имперские фунты)DSS — десертные ложки (имперские фунты)DSU — тире (США)FBM — борд-футыFFT — пятые FID — жидкие драхмы (имперские)FIS — жидкие скрукле (имперские)FLB — бочки (США, жидкие)FLU — жидкие драмы ( Us) Us FluidramFRK — FirkinsGAI — галлоны (имперские единицы)GAU — галлоны (Us Dry)GAW — галлоны (Us Fluid Wine)GLU — Teacups (gills)GTT — DropsHDI — Hogsheads (Imperial)HHU — Hogsheads (Us)JGR — Jiggers ( Bartending)KLD — KilderkinsLMD — LambdasLOD — LoadsLST — LastsM3 — Кубические метры (Si Unit)MII — Minims (Imperial)MIU — Minims (Us)OZF — Унции (Fluid Us Food NutritioPER — PerchsPKI — Pecks (Imperial)PKU — Pecks (Us) Сухой)PNI — пинчи (британские)PNU — пинчи (американские)PON — PonysPOT — Pottle QuartersPP — стыковые трубыPTI — пинты (британские)PUD — пинты (Us Dry)PUF — пинты (Us Fluid)QRF — Quart S (Us Fluid) QRT — Кварталы QTI — Кварты (британские)QTU — Кварты (Us Dry)RGS — Реестр TonsSCI — Мешки (британские) BagsSCU — Мешки(Us)SHT — Shots (Us)SM — SeamsSTK — Забастовки (Imperial)STU — Забастовки (Us) )TBC — столовые ложки (канадские)TBF — столовые ложки (обычные в США)TBM — столовые ложки (метрические)TBS — столовые ложки (в австралийских единицах измеренияTCA — чайные ложки (канадские) TFD — столовые ложки (Us Food NutritionTIM — чайные ложки (британские)TMF — Timber FootsTMT — чайные ложки ( Метрическая система)TND – тонны (водоизмещение)TNT – тонны (воды)TNW – тонны (фрахт)TSC – чайные ложки (стандарт США)TSF – чайные ложки (США Food Nutrition) WEY — Wey (Us)ACM — Атмосфера-кубический фут в минутуACS — Атмосфера-кубический фут в секунду SecoATC — Атмосфера-кубический сантиметр PeATH — Атмосфера-кубический фут в часBTJ — BTU (Международная таблица) В расчете на BTN — BTU (Международная таблица) В расчете на BTS — БТЕ (международная таблица) по CAS — Калория (международная таблица) ERS — Эрг в секундуFMF — Фут-фунт-сила в минутуFT — Фут-фунт-сила в часFTO — Фут-фунт-сила в секундуHPS — Лошадиная силаLAM — Литр-атмосфера в час MinuteLSC — LusecLTS — Литр атмосферы в секундуPNC — PonceletSQL — Прямой эквивалент квадратного фута TC — Тонна кондиционирования воздухаTMS — Атмосфера-кубический сантиметр PeTRM — Тонна охлаждения (ImperialTRR — Тонна охлаждения (It)AMU — Единица атомной массы UnifiedAT — Анализ тонны (Короткий)ATS — Ton Assay (Длинный)BAC — Bag (Coffee)BDM — Bag (Portland Cement)BRG — BargeCLV — CloveCRT — CrithCT — Carat (Metric)DA — DaltonDRT — Dram (Apothecary Troy)DWT — PennyweightGAM — GammaGR — GrainGV — GraveKIP — KipLB — Фунт (метрический)LBA — ФунтLBT — Фунт (тройской)LBV — Фунт (Avoirdupois)ME — Атомная единица массы Электрон RMRK — MarkMTE — MiteMTM — Клещ (метрический)OZ — Унция (Us Food Nutrition LabelOZT — Унция (аптечная тройка)OZZ — унция (Avoirdupois)PNN — PointQ — квинтал (метрическая система)QR — четверть (неформальная)QRI — четверть (имперская)QRL — четверть длинная (неформальная)SAP — Scruple (аптекарь)SH — тонна короткаяSLG — слаг Geepound HylSLH — SheetST — StoneSWT — Вес в сотни (центум) oTON — Тонна LongWY — WeyZTR — ZentnerARE — AresBD — BoardsBHE — Эквивалент мощности котла DBR — BarnsBRN — BaronysCDA — Cuerda Pr SurveysCRD — CordsCRI — Circular InchsCRM — Circular MilsDNM — DunamsGNT — GunthasHD — HidesRO — RoodsSCT — SectionsSHD — СараиSII — Square Link Gunters InternatiSLR — Square Link RamsdensSQC — Square Chains InternationalSQM — Square Mil Square ThousSQR — Square Rod/Pole/PerchsSRR — Square RoofingsSTR — StremmasTWN — TownshipsYLN — YardlandsARM — Arcminute MoaARS — ArcsecondCNS — Centesimal Second Of ArcCNT — Столетняя минута ArcDOA — Градус (дуги)GRA — Град Градиан GonOCT — OctantQRD — QuadrantSGN - SignSXT — Секстантµ — Угловой MilATA — Атмосфера (техническая)ATM — Атмосфера (стандартная)BAR — BarBRY — Бари (единица Cgs)CMH — Сантиметр Of MercuryCMW – сантиметр водяного столба (4 °C)FTH – фут ртутного столба (условный)FTW – фут водяного столба (392 °F)IMC — Дюйм ртутного столба (условный)INW — Дюйм водяного столба (392 °F)KM — Килограмм-сила на квадратный дюймKSI — Кип на квадратный дюймLTP — Длинная тонна на квадратный футMHG — Микрометр ртутного столбаMMH — Миллиметр ртутного столбаMMW — Миллиметр воды (398 °C)PA — Паскаль (единица Si)PD — фунт на квадратный футPSF — фунт на квадратный футPSI — фунт на квадратный дюймPZ — пьеза (единица Mts)STP — короткая тонна на квадратный футTOR — ТоррATN — атомная единица ForceDYN — Dyne (Cgs Unit)KFF — Килограмм-сила Kilopond Grave-KI — Kip Kip-ForceMGF — Milligrave-Force Gravet-ForceOZC — Унция-силаPDL — PoundalSN — Sthene (единица Mts)TNF — Long Ton-ForceTNL — Short Ton- ForceAUC — атомная единица времениCTN — CenturyCYC — каллипический циклDEC — DecadeFN — FortnightHEL — HelekHIP — гиппархический циклJFF — JiffyKEH — Ke (четверть часа) LSR — Luster LustrumMD — MillidayMLL — MillenniumMMN — MomentMOF — Month (Full)MOG — Month (Greg) Av)MOH — месяц (полый)MOS — месяц (синодический)MTN — метонический цикл EnneadecaeterisOC — OctaeterisPLN — планковское времяSGM — SigmaSHK — ShakeSTH — сотический циклSVD — SvedbergYR — год (общий)YRG — год (григорианский)YRJ — год (юлианский) YRL – год (високосный)YRM – год (среднетропический)B39- Британская термальная единица (39 °F)B59 — Британская термальная единица (59 °F)B60 — Британская термальная единица (60 °F)B63 — Британская термальная единица (63 °F)BOE — эквивалент барреля нефтиBRT — Британская термальная единица ( Iso)BTI — Британская термальная единица (InternatBTM — Британская термальная единица (средняя)BTT — Британская термальная единица (ThermochC15 — Калория (15 °C)C20 — Калория (20 °C)C98 — Калория (398 °C)CAM — Калория ( Среднее значение)CFT — Кубический фут атмосферы CHU — Тепловая единица ЦельсияCL — Калория (Us Fda)CLTH — Калория (термохимическая)CN — Кубический фут природного газаCTA — Кубический сантиметр атмосферыCYD — Кубический ярд атмосферы StandEH — Атомная единица энергии ХартриFTD — Foot-PoundalIMG — Галлон-атмосфераKCA — Большая килокалорияKWH — Киловатт-час Board Of Trade ULTM — Литр-атмосфераQD — QuadRDB — Therm (Ec)RY — RydbergTCE — Тонна угольного эквивалентаTHR — Therm (Us)THU — ThermieTN — Тонна TntTOE — Тонна нефтяного эквивалентаBAN — Ban HartleyBSH — Bit ShannonCD — Candela (Si Base Unit) CandleCPD — Candlepower (New)JK — Si UnitNAT — Nat Nip NepitNBL — NibbleBQ — Беккерель (Si Unit)CI — CurieRD — Rutherford (H)C — Скорость света в вакуумеFPF — фарлонг в две неделиFPH — фут в часIPH — дюйм в часIPM — дюйм в минутуIPS — дюйм в секундуMCH — число МахаMPM — миля в минутуMPS — миля в секундуMS — метр в секунду (единица Си)SPS — скорость звука в AirCDF — Кандела на квадратный футCDI — Кандела на квадратный дюймCDM — Кандела на квадратный метр (Si UFL — FootlambertLMB — LambertSB — Stilb (Cgs Unit)CEL — ЦельсийDDE — Градус DelisleDNE — Градус НьютонаFAN — ФаренгейтGMR — Регулятор газа MarkKEL — Kelvin’sRAN — RankineREA — ReaumurRME — Градус RømerCFM — Кубический фут в минутуFTS — Кубический фут в секундуGPD — Галлон (жидкость США) в суткиGPH — Галлон (жидкость США) в часGPM — Галлон (жидкость США) в минутуINM — Кубический дюйм в минутуINS — Кубический дюйм в секундуLPM — Литр в минутуMQS — кубический метр в секунду (Si UniCM — кулон-метрDB — DebyeEA0 — атомная единица электрического диполяFC — фут-канделя люмен на квадрат FoLMN — люмен на квадратный дюймLX — люкс (единица Si)PH — Phot (единица Cgs)FHP — фут в секунду Час в секундуFMS — фут в минуту в секундуFP — фут в секунду в квадратеG — стандартная гравитацияGAL — галлон GalileoIP — дюйм в минуту в секунду в секундуIP2 — дюйм в секунду в квадратеKNS — узел в секундуMM — миля в минуту в секундуMP — миля в час в секундуMP2 — миля в секунду Секунда в квадратеMSA — метр на секунду в квадрате (Si UFT2 — квадратный фут в секундуM2S — квадратный метр в секунду (Si UnSTX — Стокс (единица Cgs)FTP — фут-фунт)MKG — метр-килограмм-силаNEM — ньютон-метр (единица Si)GML — грамм на секунду MillilitreLAB — фунт (эквивалентный) на галлонLBF — фунт (эквивалентный) на кубический LBI — фунт (экспериментальный) на кубический LBL — фунт (экспериментальный) на галлонOFT — унция (экспериментальный) на кубический OG — унция (эвердупуа) на галлон ) Per GallonOIN — Унция (Avoirdupois) на кубический SFT — Slug на кубический футGSS — Gauss (Cgs Unit)TSL — Tesla (Si Unit)GY — Grey (Si Unit)RDD — RadLBH — Pound Per Foot HourLBS — Фунт на фут в секундуLFT — Фунт-сила-секунда на квадрат LIN — Фунт-сила-секунда на квадрат PAS — Паскаль-секунда (единица Si)PSU — Пуаз (единица Cgs)MX — Максвелл (единица Cgs)WB — Вебер (единица Si)REM — Рентген-эквивалент ManSV — Sievert (Единица Си)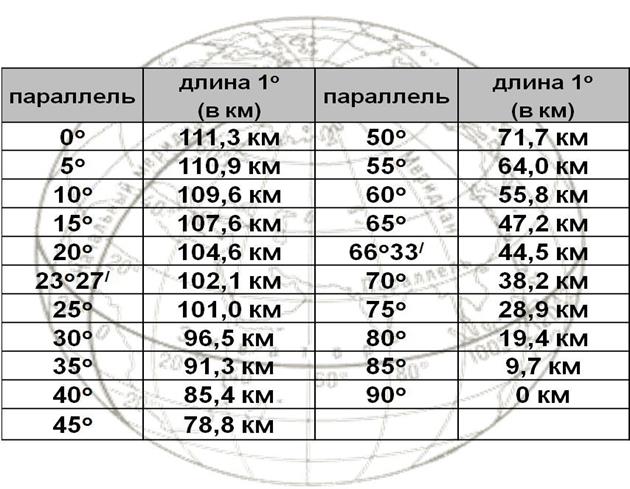 S.) — Ссылка (Гюнтера; Сюрвейерская)LNK (RE) — Ссылка (Рамсденская; Инженерная)LS — Световая секундаLY — Световая- yearM — метр (базовая единица СИ)MIL — мил (Швеция и Норвегия)MILE DATA — мили (тактические или данные)MK — MickeyNAIL — гвоздь (ткань)NL — морская лигаNM — нанометрNMI — морская миляNMI I — морская миляP — PalmPC — ParsecPICA — PicaPM — пикометр (бикрон, клеймо) POINT — точка (американский, английский) PT — PaceQUART — QuarterSHAKU — Shaku (японский) SPT — SpatTH — Mil (тыс.)TWP — TwipUM — микрометр (стар.: микрон)XU — единица X; siegbahnABA — Электромагнитная единица AbampereAMP — Ампер (базовая единица Si)ESU — Esu в секунду Статампер (CgsABC — Абкулон Электромагнитная единицаATU — Атомная единица зарядаCLM — КулонFRD — ФарадейMAH — Миллиампер-часSTT — Статкулон Франклин ЭлектростABV — Абвольт (единица Cgs)STV — Статвольт ( Cgs Unit)VLT — Вольт (Si Unit)ACF — Акр-футыACI — Акры-дюймыBIB — Баррели (нефтяные)BII — Баррели (британские)BIU — Баррели (Us Dry)BKT — Ведра (британские)BRO — Галлоны (пивные)BUD — Бушели (Us Dry Level)BUI — Бушели (Imperial)BUU — Бушели (Us Dry Heaped)CMB — CoombsCMI — Cubic MilesCP — CupsCRF — Cord-FootsCRW — Cords (Дрова)CUF — Cubic FathomsCUI — Cubic InchsCUT — Cubic FootsCUY — Cubic ЯрдыDSI — тире (имперские фунты)DSS — десертные ложки (имперские фунты)DSU — тире (США)FBM — борд-футыFFT — пятые FID — жидкие драхмы (имперские)FIS — жидкие скрукле (имперские)FLB — бочки (США, жидкие)FLU — жидкие драмы ( Us) Us FluidramFRK — FirkinsGAI — галлоны (имперские единицы)GAU — галлоны (Us Dry)GAW — галлоны (Us Fluid Wine)GLU — Teacups (gills)GTT — DropsHDI — Hogsheads (Imperial)HHU — Hogsheads (Us)JGR — Jiggers ( Bartending)KLD — KilderkinsLMD — LambdasLOD — LoadsLST — LastsM3 — Кубические метры (Si Unit)MII — Minims (Imperial)MIU — Minims (Us)OZF — Унции (Fluid Us Food NutritioPER — PerchsPKI — Pecks (Imperial)PKU — Pecks (Us) Сухой)PNI — пинчи (британские)PNU — пинчи (американские)PON — PonysPOT — Pottle QuartersPP — стыковые трубыPTI — пинты (британские)PUD — пинты (Us Dry)PUF — пинты (Us Fluid)QRF — Quart S (Us Fluid) QRT — Кварталы QTI — Кварты (британские)QTU — Кварты (Us Dry)RGS — Реестр TonsSCI — Мешки (британские) BagsSCU — Мешки(Us)SHT — Shots (Us)SM — SeamsSTK — Забастовки (Imperial)STU — Забастовки (Us) )TBC — столовые ложки (канадские)TBF — столовые ложки (обычные в США)TBM — столовые ложки (метрические)TBS — столовые ложки (в австралийских единицах измеренияTCA — чайные ложки (канадские) TFD — столовые ложки (Us Food NutritionTIM — чайные ложки (британские)TMF — Timber FootsTMT — чайные ложки ( Метрическая система)TND – тонны (водоизмещение)TNT – тонны (воды)TNW – тонны (фрахт)TSC – чайные ложки (стандарт США)TSF – чайные ложки (США Food Nutrition) WEY — Wey (Us)ACM — Атмосфера-кубический фут в минутуACS — Атмосфера-кубический фут в секунду SecoATC — Атмосфера-кубический сантиметр PeATH — Атмосфера-кубический фут в часBTJ — BTU (Международная таблица) В расчете на BTN — BTU (Международная таблица) В расчете на BTS — БТЕ (международная таблица) по CAS — Калория (международная таблица) ERS — Эрг в секундуFMF — Фут-фунт-сила в минутуFT — Фут-фунт-сила в часFTO — Фут-фунт-сила в секундуHPS — Лошадиная силаLAM — Литр-атмосфера в час MinuteLSC — LusecLTS — Литр атмосферы в секундуPNC — PonceletSQL — Прямой эквивалент квадратного фута TC — Тонна кондиционирования воздухаTMS — Атмосфера-кубический сантиметр PeTRM — Тонна охлаждения (ImperialTRR — Тонна охлаждения (It)ACR — AcresCMK — Квадратные сантиметрыFTK — Квадратные футыHAR — ГектарыINK — Квадратные дюймыKMK — Квадратные километрыMIK — Квадратные милиMTK — Квадратные метрыYDK — Квадратные ярдыAMU — Унифицированная атомная единица массыAT — Тонна анализа (краткая)ATS — Тонна анализа (длинная)BAC — Мешок (Кофе)BDM — Мешок (портландцемент)BRG — BargeCLV — CloveCRT — CrithCT — Carat (Metric)DA — DaltonDRT — Dram (Apothecary Troy)DWT — PennyweightGAM — GammaGR — GrainGV — GraveKIP — KipLB — Pound (Metric)LBA — PoundLBT — Pound (Troy)LBV — Pound (Avoirdupois)ME — Атомная единица массы Электрон RMRK — MarkMTE — MiteMTM — Клещ (метрический) OZ — Унция (этикетка питания США OZT — Унция (аптечная Троя) OZZ — Унция (Avoirdupois) PNN — PointQ — Квинтал (метрический) QR — Квартал (неофициальный) QRI — Quarter (Imperial)QRL — Quarter Long (Informal)SAP — Scruple (Apothecary)SH — Ton ShortSLG — Slug Geepound HylSLH — SheetST — StoneSWT — Hundredweight (центум веса oTON — Ton LongWY — WeyZTR — ZentnerANN — YearsDAY — DaysHUR — HoursMCS — MicrosecondsMIN — MinutesMLS — MillisecondsMON — MonthsSEC — SecondsWEE — WeeksARE — AresBD — BoardsBHE — эквивалент мощности котла DBR — BarnsBRN — BaronysCDA — Cuerda Pr SurveysCRD — CordsCRI — Circular InchsCRM — Circular MilsDNM — DunamsGNT — GunthasHD — HidesRO — RoodsSCT — SectionsSHD — ShedsSs — Square Link Gunters InternatiSLR — Square Link RamsdensSQC — Square Chains InternationalSQM — Square Mil Square ThousSQR — Square Rod/Pole/PerchsSRR — Square RoofingsSTR — StremmasTWN — TownshipsYLN — YardlandsARM — Arcminute MoaARS — ArcsecondCNS — Centesimal Second Of ArcCNT — Centesimal Minute Of ArcDOA — Degree (Дуги)GRA — Grad Gradian GonOCT — OctantQRD — QuadrantSGN - SignSXT — Sextantµ — Угловой MilATA — Атмосфера (Техническая)ATM — Атмосфера (Стандартная)BAR — BarBRY — Бари (единица Cgs)CMH — Сантиметр ртутного столбаCMW — Сантиметр водяного столба ( 4 °C)FTH — фут ртутного столба (условный)FTW — фут водяного столба (392 °F)IMC — Дюйм ртутного столба (условный)INW — Дюйм водяного столба (392 °F)KM — Килограмм-сила на квадратный дюймKSI — Кип на квадратный дюймLTP — Длинная тонна на квадратный футMHG — Микрометр ртутного столбаMMH — Миллиметр ртутного столбаMMW — Миллиметр воды (398 °C)PA — Паскаль (единица Si)PD — фунт на квадратный футPSF — фунт на квадратный футPSI — фунт на квадратный дюймPZ — пьеза (единица Mts)STP — короткая тонна на квадратный футTOR — ТоррATN — атомная единица ForceDYN — Dyne (Cgs Unit)KFF — Килограмм-сила Kilopond Grave-KI — Kip Kip-ForceMGF — Milligrave-Force Gravet-ForceOZC — Унция-силаPDL — PoundalSN — Sthene (единица Mts)TNF — Long Ton-ForceTNL — Short Ton- ForceAUC — атомная единица времениCTN — CenturyCYC — каллипический циклDEC — DecadeFN — FortnightHEL — HelekHIP — гиппархический циклJFF — JiffyKEH — Ke (четверть часа) LSR — Luster LustrumMD — MillidayMLL — MillenniumMMN — MomentMOF — Month (Full)MOG — Month (Greg) Av)MOH — месяц (полый)MOS — месяц (синодический)MTN — метонический цикл EnneadecaeterisOC — OctaeterisPLN — планковское времяSGM — SigmaSHK — ShakeSTH — сотический циклSVD — SvedbergYR — год (общий)YRG — год (григорианский)YRJ — год (юлианский) YRL – год (високосный)YRM – год (среднетропический)B39- Британская термальная единица (39 °F)B59 — Британская термальная единица (59 °F)B60 — Британская термальная единица (60 °F)B63 — Британская термальная единица (63 °F)BOE — эквивалент барреля нефтиBRT — Британская термальная единица ( Iso)BTI — Британская термальная единица (InternatBTM — Британская термальная единица (средняя)BTT — Британская термальная единица (ThermochC15 — Калория (15 °C)C20 — Калория (20 °C)C98 — Калория (398 °C)CAM — Калория ( Среднее значение)CFT — Кубический фут атмосферы CHU — Тепловая единица ЦельсияCL — Калория (Us Fda)CLTH — Калория (термохимическая)CN — Кубический фут природного газаCTA — Кубический сантиметр атмосферыCYD — Кубический ярд атмосферы StandEH — Атомная единица энергии ХартриFTD — Foot-PoundalIMG — Галлон-атмосфераKCA — Большая килокалорияKWH — Киловатт-час Board Of Trade ULTM — Литр-атмосфераQD — QuadRDB — Therm (Ec)RY — RydbergTCE — Тонна угольного эквивалентаTHR — Therm (Us)THU — ThermieTN — Тонна TntTOE — Tone Of Oil EquivalentBAN — Ban HartleyBSH — Bit ShannonCD — Candela (Si Base Unit) CandleCPD — Candlepower (New)JK — Si UnitNAT — Nat Nip NepitNBL — NibbleBIT — BitsBYT — BytesEBI — ExabitsEBY — ExabytesGBI — GigabitsGBY — GigabytesKBI — KilobitsKBY — KilobytesMBI — МегабитыMBY — МегабайтыPBI — ПетабитыPBY — ПетабайтыTBI — ТерабитыTBY — ТерабайтыBLL — Баррели (нефть)CMQ — Кубические сантиметрыFTQ — Кубические футыGLI — Галлоны (Великобритания)GLL — Галлоны (жидкости США)LTR — ЛитрыMLT — МиллилитрыMTQ — Кубические метрыOZI — Унции UKBQ — Беккерели ( Si Unit)CI — КюриRD — Резерфорд (H)BTU — BTUCAL — КалорииERG — ErgEVL — Электрон ВольтFPD — Фут-фунтHPH — Лошадиная сила-часIPD — Дюйм-фунтJOU — ДжоульC — Скорость света в вакуумеFPF — Фарлонг в две неделиFPH — Фут в часIPH — Inch Per HourIPM — Inch Per MinuteIPS — Inch Per SecondMCH — Mach NumberMPM — Mile Per MinuteMPS — Mile Per SecondMS — Метр в секунду (Si Unit)SPS — Скорость звука в AirCDF — Candela Per Square FootCDI — Candela Per Square InchCDM — Candela Per Квадратный метр (Si UFL — FootlambertLMB — LambertSB — Stilb (Cgs Unit)CEL — ЦельсийDDE — Градус DelisleDNE — Градус НьютонаFAN — ФаренгейтGMR — Регулирующий газ MarkKEL — Kelvin’sRAN — RankineREA — ReaumurRME — Градус RømerCFM — Кубический фут в минутуFTS — Кубический фут в минуту SecondGPD — галлон (жидкость США) в суткиGPH — галлон (жидкость США) в часGPM — галлон (жидкость США) в минутуINM — кубический дюйм в минутуINS — кубический дюйм в секундуLPM — литр в минутуMQS — кубический метр в секунду (Si UniCM — кулоновый метрDB — DebyeEA0 — атомная единица электрического диполя CMT — сантиметр DMT — дециметрыFOT — футыINH — дюймыKMT — километрыMMT — миллиметрыMTR — метрыSMI — милиYRD — ярдыCTM — каратыGRM — граммыKGM — килограммыLBR — фунтыMGM — миллиграммыONZ — унции TNE — тонны (метрические)DEG — градусыGRD — градыRAD - RadiansFC — Фут-канд Люмен на квадрат FoLMN — Люмен на квадратный дюймLX — Люкс (Единица Si)PH — Фот (Единица Cgs)FHP — Фут в час в секундуFMS — Фут в минуту в секундуFP — Фут в секунду в квадратеdG — Стандартная сила тяжестиGAL — Gal GalileoIP — Дюйм в минуту в секундуIP2 — дюйм в секунду в квадратеKNS — узел в секундуMM — миля в минуту в секундуMP — миля в час в секундуMP2 — миля в секунду в квадратеMSA — метр в секунду в квадрате (Si UFPM — футы/минутыFPS — футы/секундыKMH — километры/ ЧасKMS — Километры/секундыKNT — УзлыMPH — Мили/часMTS — Метры/секундыFT2 — Квадратный фут в секундуM2S — Квадратный метр в секунду (Si UnSTX — Стокс (единица Cgs)FTP — Foot-PoundalMKG — Метр Килограмм-силаNEM — Ньютон-метр (Единица Si )GCC — граммы/кубический сантиметрKCC — килограммы/кубический сантиметрKLI — килограммы/литрKMC — килограммы/кубический метрOCI — унции/кубический дюймOGL — унции/галлонPCF — фунты/кубический футPCI — фунты/кубический дюймPGL — фунты/галлонGML — грамм на миллилитрLAB — фунт (Avoirdupois) Per GallonLBF — фунт (Avoirdupois) на кубический LBI — фунт (Avoirdupois) на кубический LBL — фунт (Avoirdupois) на галлонOFT — унция (Avoirdupois) на кубический OG — унция (Avoirdupois) на галлонOGA — унция (Avoirdupois) на галлонOIN — Унция (Avoirdupois) на кубический SFT — Слаг на кубический футGSS — Гаусс (единица Cgs)TSL — Тесла (единица Si)GY — Грей (единица Si)RDD — RadJCM — Джоули/сантиметрKGF — Килограмм-силаNWN — НьютоныPFC — Фунт силыLBH — Фунт Per Foot HourLBS — Фунт на фут-секундуLFT — Фунт-сила-секунда на квадрат LIN — Фунт-сила-секунда на квадрат PAS — Паскаль-секунда (единица Si)PSU — Пуаз (единица Cgs)MX — Максвелл (единица Cgs)WB — Вебер (Si) Единица)REM — Рентген-эквивалент ManSV — Зиверт (Единица Si)
S.) — Ссылка (Гюнтера; Сюрвейерская)LNK (RE) — Ссылка (Рамсденская; Инженерная)LS — Световая секундаLY — Световая- yearM — метр (базовая единица СИ)MIL — мил (Швеция и Норвегия)MILE DATA — мили (тактические или данные)MK — MickeyNAIL — гвоздь (ткань)NL — морская лигаNM — нанометрNMI — морская миляNMI I — морская миляP — PalmPC — ParsecPICA — PicaPM — пикометр (бикрон, клеймо) POINT — точка (американский, английский) PT — PaceQUART — QuarterSHAKU — Shaku (японский) SPT — SpatTH — Mil (тыс.)TWP — TwipUM — микрометр (стар.: микрон)XU — единица X; siegbahnABA — Электромагнитная единица AbampereAMP — Ампер (базовая единица Si)ESU — Esu в секунду Статампер (CgsABC — Абкулон Электромагнитная единицаATU — Атомная единица зарядаCLM — КулонFRD — ФарадейMAH — Миллиампер-часSTT — Статкулон Франклин ЭлектростABV — Абвольт (единица Cgs)STV — Статвольт ( Cgs Unit)VLT — Вольт (Si Unit)ACF — Акр-футыACI — Акры-дюймыBIB — Баррели (нефтяные)BII — Баррели (британские)BIU — Баррели (Us Dry)BKT — Ведра (британские)BRO — Галлоны (пивные)BUD — Бушели (Us Dry Level)BUI — Бушели (Imperial)BUU — Бушели (Us Dry Heaped)CMB — CoombsCMI — Cubic MilesCP — CupsCRF — Cord-FootsCRW — Cords (Дрова)CUF — Cubic FathomsCUI — Cubic InchsCUT — Cubic FootsCUY — Cubic ЯрдыDSI — тире (имперские фунты)DSS — десертные ложки (имперские фунты)DSU — тире (США)FBM — борд-футыFFT — пятые FID — жидкие драхмы (имперские)FIS — жидкие скрукле (имперские)FLB — бочки (США, жидкие)FLU — жидкие драмы ( Us) Us FluidramFRK — FirkinsGAI — галлоны (имперские единицы)GAU — галлоны (Us Dry)GAW — галлоны (Us Fluid Wine)GLU — Teacups (gills)GTT — DropsHDI — Hogsheads (Imperial)HHU — Hogsheads (Us)JGR — Jiggers ( Bartending)KLD — KilderkinsLMD — LambdasLOD — LoadsLST — LastsM3 — Кубические метры (Si Unit)MII — Minims (Imperial)MIU — Minims (Us)OZF — Унции (Fluid Us Food NutritioPER — PerchsPKI — Pecks (Imperial)PKU — Pecks (Us) Сухой)PNI — пинчи (британские)PNU — пинчи (американские)PON — PonysPOT — Pottle QuartersPP — стыковые трубыPTI — пинты (британские)PUD — пинты (Us Dry)PUF — пинты (Us Fluid)QRF — Quart S (Us Fluid) QRT — Кварталы QTI — Кварты (британские)QTU — Кварты (Us Dry)RGS — Реестр TonsSCI — Мешки (британские) BagsSCU — Мешки(Us)SHT — Shots (Us)SM — SeamsSTK — Забастовки (Imperial)STU — Забастовки (Us) )TBC — столовые ложки (канадские)TBF — столовые ложки (обычные в США)TBM — столовые ложки (метрические)TBS — столовые ложки (в австралийских единицах измеренияTCA — чайные ложки (канадские) TFD — столовые ложки (Us Food NutritionTIM — чайные ложки (британские)TMF — Timber FootsTMT — чайные ложки ( Метрическая система)TND – тонны (водоизмещение)TNT – тонны (воды)TNW – тонны (фрахт)TSC – чайные ложки (стандарт США)TSF – чайные ложки (США Food Nutrition) WEY — Wey (Us)ACM — Атмосфера-кубический фут в минутуACS — Атмосфера-кубический фут в секунду SecoATC — Атмосфера-кубический сантиметр PeATH — Атмосфера-кубический фут в часBTJ — BTU (Международная таблица) В расчете на BTN — BTU (Международная таблица) В расчете на BTS — БТЕ (международная таблица) по CAS — Калория (международная таблица) ERS — Эрг в секундуFMF — Фут-фунт-сила в минутуFT — Фут-фунт-сила в часFTO — Фут-фунт-сила в секундуHPS — Лошадиная силаLAM — Литр-атмосфера в час MinuteLSC — LusecLTS — Литр атмосферы в секундуPNC — PonceletSQL — Прямой эквивалент квадратного фута TC — Тонна кондиционирования воздухаTMS — Атмосфера-кубический сантиметр PeTRM — Тонна охлаждения (ImperialTRR — Тонна охлаждения (It)ACR — AcresCMK — Квадратные сантиметрыFTK — Квадратные футыHAR — ГектарыINK — Квадратные дюймыKMK — Квадратные километрыMIK — Квадратные милиMTK — Квадратные метрыYDK — Квадратные ярдыAMU — Унифицированная атомная единица массыAT — Тонна анализа (краткая)ATS — Тонна анализа (длинная)BAC — Мешок (Кофе)BDM — Мешок (портландцемент)BRG — BargeCLV — CloveCRT — CrithCT — Carat (Metric)DA — DaltonDRT — Dram (Apothecary Troy)DWT — PennyweightGAM — GammaGR — GrainGV — GraveKIP — KipLB — Pound (Metric)LBA — PoundLBT — Pound (Troy)LBV — Pound (Avoirdupois)ME — Атомная единица массы Электрон RMRK — MarkMTE — MiteMTM — Клещ (метрический) OZ — Унция (этикетка питания США OZT — Унция (аптечная Троя) OZZ — Унция (Avoirdupois) PNN — PointQ — Квинтал (метрический) QR — Квартал (неофициальный) QRI — Quarter (Imperial)QRL — Quarter Long (Informal)SAP — Scruple (Apothecary)SH — Ton ShortSLG — Slug Geepound HylSLH — SheetST — StoneSWT — Hundredweight (центум веса oTON — Ton LongWY — WeyZTR — ZentnerANN — YearsDAY — DaysHUR — HoursMCS — MicrosecondsMIN — MinutesMLS — MillisecondsMON — MonthsSEC — SecondsWEE — WeeksARE — AresBD — BoardsBHE — эквивалент мощности котла DBR — BarnsBRN — BaronysCDA — Cuerda Pr SurveysCRD — CordsCRI — Circular InchsCRM — Circular MilsDNM — DunamsGNT — GunthasHD — HidesRO — RoodsSCT — SectionsSHD — ShedsSs — Square Link Gunters InternatiSLR — Square Link RamsdensSQC — Square Chains InternationalSQM — Square Mil Square ThousSQR — Square Rod/Pole/PerchsSRR — Square RoofingsSTR — StremmasTWN — TownshipsYLN — YardlandsARM — Arcminute MoaARS — ArcsecondCNS — Centesimal Second Of ArcCNT — Centesimal Minute Of ArcDOA — Degree (Дуги)GRA — Grad Gradian GonOCT — OctantQRD — QuadrantSGN - SignSXT — Sextantµ — Угловой MilATA — Атмосфера (Техническая)ATM — Атмосфера (Стандартная)BAR — BarBRY — Бари (единица Cgs)CMH — Сантиметр ртутного столбаCMW — Сантиметр водяного столба ( 4 °C)FTH — фут ртутного столба (условный)FTW — фут водяного столба (392 °F)IMC — Дюйм ртутного столба (условный)INW — Дюйм водяного столба (392 °F)KM — Килограмм-сила на квадратный дюймKSI — Кип на квадратный дюймLTP — Длинная тонна на квадратный футMHG — Микрометр ртутного столбаMMH — Миллиметр ртутного столбаMMW — Миллиметр воды (398 °C)PA — Паскаль (единица Si)PD — фунт на квадратный футPSF — фунт на квадратный футPSI — фунт на квадратный дюймPZ — пьеза (единица Mts)STP — короткая тонна на квадратный футTOR — ТоррATN — атомная единица ForceDYN — Dyne (Cgs Unit)KFF — Килограмм-сила Kilopond Grave-KI — Kip Kip-ForceMGF — Milligrave-Force Gravet-ForceOZC — Унция-силаPDL — PoundalSN — Sthene (единица Mts)TNF — Long Ton-ForceTNL — Short Ton- ForceAUC — атомная единица времениCTN — CenturyCYC — каллипический циклDEC — DecadeFN — FortnightHEL — HelekHIP — гиппархический циклJFF — JiffyKEH — Ke (четверть часа) LSR — Luster LustrumMD — MillidayMLL — MillenniumMMN — MomentMOF — Month (Full)MOG — Month (Greg) Av)MOH — месяц (полый)MOS — месяц (синодический)MTN — метонический цикл EnneadecaeterisOC — OctaeterisPLN — планковское времяSGM — SigmaSHK — ShakeSTH — сотический циклSVD — SvedbergYR — год (общий)YRG — год (григорианский)YRJ — год (юлианский) YRL – год (високосный)YRM – год (среднетропический)B39- Британская термальная единица (39 °F)B59 — Британская термальная единица (59 °F)B60 — Британская термальная единица (60 °F)B63 — Британская термальная единица (63 °F)BOE — эквивалент барреля нефтиBRT — Британская термальная единица ( Iso)BTI — Британская термальная единица (InternatBTM — Британская термальная единица (средняя)BTT — Британская термальная единица (ThermochC15 — Калория (15 °C)C20 — Калория (20 °C)C98 — Калория (398 °C)CAM — Калория ( Среднее значение)CFT — Кубический фут атмосферы CHU — Тепловая единица ЦельсияCL — Калория (Us Fda)CLTH — Калория (термохимическая)CN — Кубический фут природного газаCTA — Кубический сантиметр атмосферыCYD — Кубический ярд атмосферы StandEH — Атомная единица энергии ХартриFTD — Foot-PoundalIMG — Галлон-атмосфераKCA — Большая килокалорияKWH — Киловатт-час Board Of Trade ULTM — Литр-атмосфераQD — QuadRDB — Therm (Ec)RY — RydbergTCE — Тонна угольного эквивалентаTHR — Therm (Us)THU — ThermieTN — Тонна TntTOE — Tone Of Oil EquivalentBAN — Ban HartleyBSH — Bit ShannonCD — Candela (Si Base Unit) CandleCPD — Candlepower (New)JK — Si UnitNAT — Nat Nip NepitNBL — NibbleBIT — BitsBYT — BytesEBI — ExabitsEBY — ExabytesGBI — GigabitsGBY — GigabytesKBI — KilobitsKBY — KilobytesMBI — МегабитыMBY — МегабайтыPBI — ПетабитыPBY — ПетабайтыTBI — ТерабитыTBY — ТерабайтыBLL — Баррели (нефть)CMQ — Кубические сантиметрыFTQ — Кубические футыGLI — Галлоны (Великобритания)GLL — Галлоны (жидкости США)LTR — ЛитрыMLT — МиллилитрыMTQ — Кубические метрыOZI — Унции UKBQ — Беккерели ( Si Unit)CI — КюриRD — Резерфорд (H)BTU — BTUCAL — КалорииERG — ErgEVL — Электрон ВольтFPD — Фут-фунтHPH — Лошадиная сила-часIPD — Дюйм-фунтJOU — ДжоульC — Скорость света в вакуумеFPF — Фарлонг в две неделиFPH — Фут в часIPH — Inch Per HourIPM — Inch Per MinuteIPS — Inch Per SecondMCH — Mach NumberMPM — Mile Per MinuteMPS — Mile Per SecondMS — Метр в секунду (Si Unit)SPS — Скорость звука в AirCDF — Candela Per Square FootCDI — Candela Per Square InchCDM — Candela Per Квадратный метр (Si UFL — FootlambertLMB — LambertSB — Stilb (Cgs Unit)CEL — ЦельсийDDE — Градус DelisleDNE — Градус НьютонаFAN — ФаренгейтGMR — Регулирующий газ MarkKEL — Kelvin’sRAN — RankineREA — ReaumurRME — Градус RømerCFM — Кубический фут в минутуFTS — Кубический фут в минуту SecondGPD — галлон (жидкость США) в суткиGPH — галлон (жидкость США) в часGPM — галлон (жидкость США) в минутуINM — кубический дюйм в минутуINS — кубический дюйм в секундуLPM — литр в минутуMQS — кубический метр в секунду (Si UniCM — кулоновый метрDB — DebyeEA0 — атомная единица электрического диполя CMT — сантиметр DMT — дециметрыFOT — футыINH — дюймыKMT — километрыMMT — миллиметрыMTR — метрыSMI — милиYRD — ярдыCTM — каратыGRM — граммыKGM — килограммыLBR — фунтыMGM — миллиграммыONZ — унции TNE — тонны (метрические)DEG — градусыGRD — градыRAD - RadiansFC — Фут-канд Люмен на квадрат FoLMN — Люмен на квадратный дюймLX — Люкс (Единица Si)PH — Фот (Единица Cgs)FHP — Фут в час в секундуFMS — Фут в минуту в секундуFP — Фут в секунду в квадратеdG — Стандартная сила тяжестиGAL — Gal GalileoIP — Дюйм в минуту в секундуIP2 — дюйм в секунду в квадратеKNS — узел в секундуMM — миля в минуту в секундуMP — миля в час в секундуMP2 — миля в секунду в квадратеMSA — метр в секунду в квадрате (Si UFPM — футы/минутыFPS — футы/секундыKMH — километры/ ЧасKMS — Километры/секундыKNT — УзлыMPH — Мили/часMTS — Метры/секундыFT2 — Квадратный фут в секундуM2S — Квадратный метр в секунду (Si UnSTX — Стокс (единица Cgs)FTP — Foot-PoundalMKG — Метр Килограмм-силаNEM — Ньютон-метр (Единица Si )GCC — граммы/кубический сантиметрKCC — килограммы/кубический сантиметрKLI — килограммы/литрKMC — килограммы/кубический метрOCI — унции/кубический дюймOGL — унции/галлонPCF — фунты/кубический футPCI — фунты/кубический дюймPGL — фунты/галлонGML — грамм на миллилитрLAB — фунт (Avoirdupois) Per GallonLBF — фунт (Avoirdupois) на кубический LBI — фунт (Avoirdupois) на кубический LBL — фунт (Avoirdupois) на галлонOFT — унция (Avoirdupois) на кубический OG — унция (Avoirdupois) на галлонOGA — унция (Avoirdupois) на галлонOIN — Унция (Avoirdupois) на кубический SFT — Слаг на кубический футGSS — Гаусс (единица Cgs)TSL — Тесла (единица Si)GY — Грей (единица Si)RDD — RadJCM — Джоули/сантиметрKGF — Килограмм-силаNWN — НьютоныPFC — Фунт силыLBH — Фунт Per Foot HourLBS — Фунт на фут-секундуLFT — Фунт-сила-секунда на квадрат LIN — Фунт-сила-секунда на квадрат PAS — Паскаль-секунда (единица Si)PSU — Пуаз (единица Cgs)MX — Максвелл (единица Cgs)WB — Вебер (Si) Единица)REM — Рентген-эквивалент ManSV — Зиверт (Единица Si)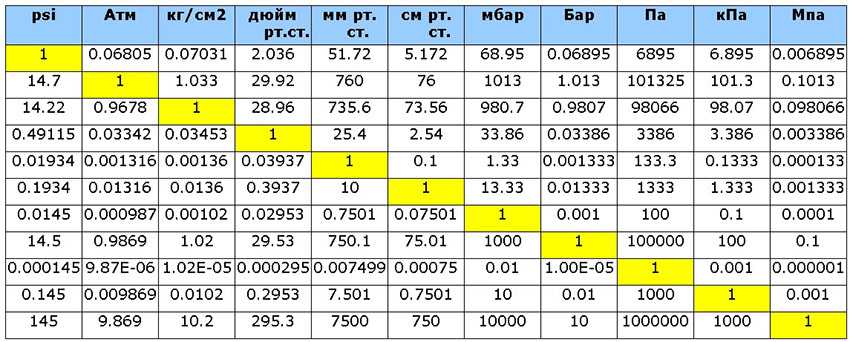 5 шт. 10 шт. 20 шт. 50 шт. 100 шт. 200 шт.
5 шт. 10 шт. 20 шт. 50 шт. 100 шт. 200 шт. Des Maquis du Grésivaudan, 38700, Ла-Тронш, Франция.
Des Maquis du Grésivaudan, 38700, Ла-Тронш, Франция. 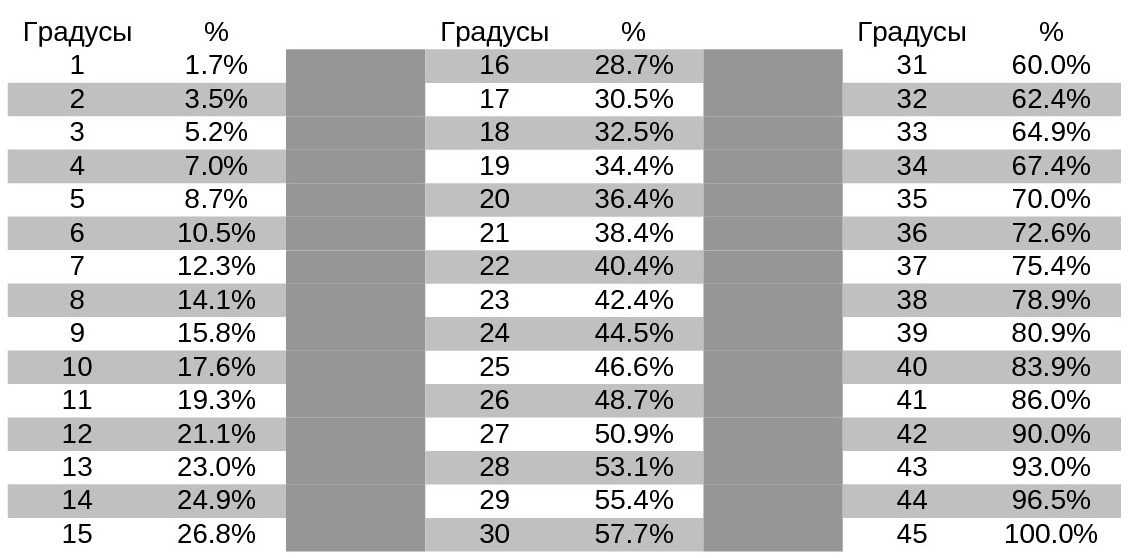 .
.
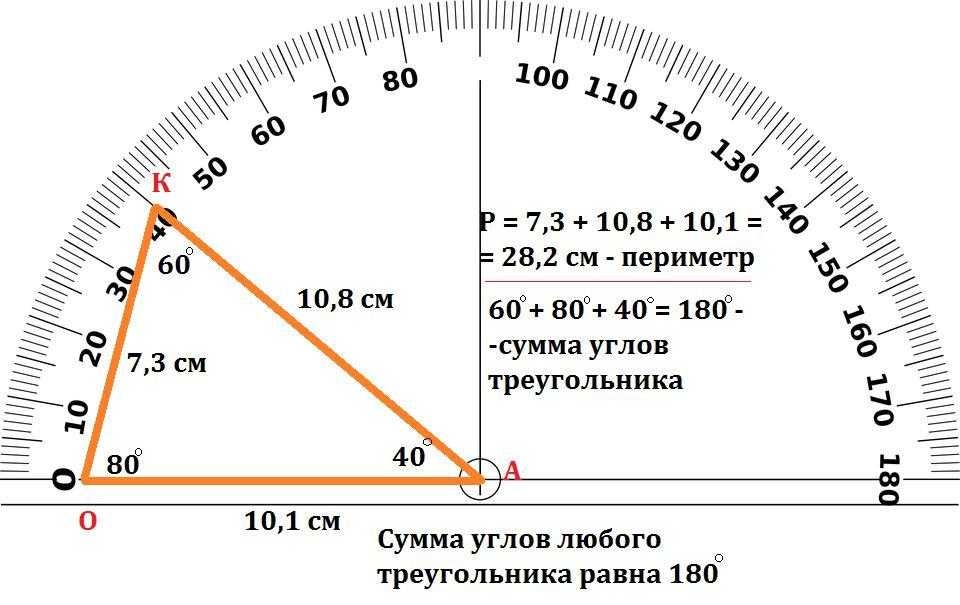
 Наша гипотеза заключалась в том, что одной степени коррекции соответствует одна степень раскрытия.
Наша гипотеза заключалась в том, что одной степени коррекции соответствует одна степень раскрытия.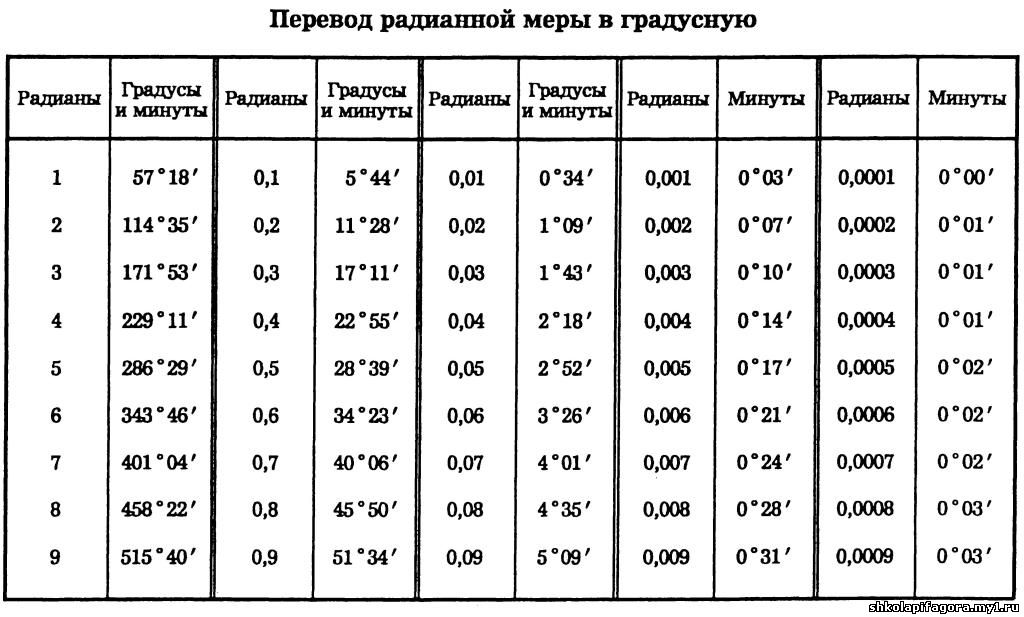 Таким образом, мы достигли желаемой гиперкоррекции 2°-6° в 92% случаев на основании наших послеоперационных рентгенограмм и в 100% случаев на основе интраоперационных измерений с компьютерной навигацией.
Таким образом, мы достигли желаемой гиперкоррекции 2°-6° в 92% случаев на основании наших послеоперационных рентгенограмм и в 100% случаев на основе интраоперационных измерений с компьютерной навигацией.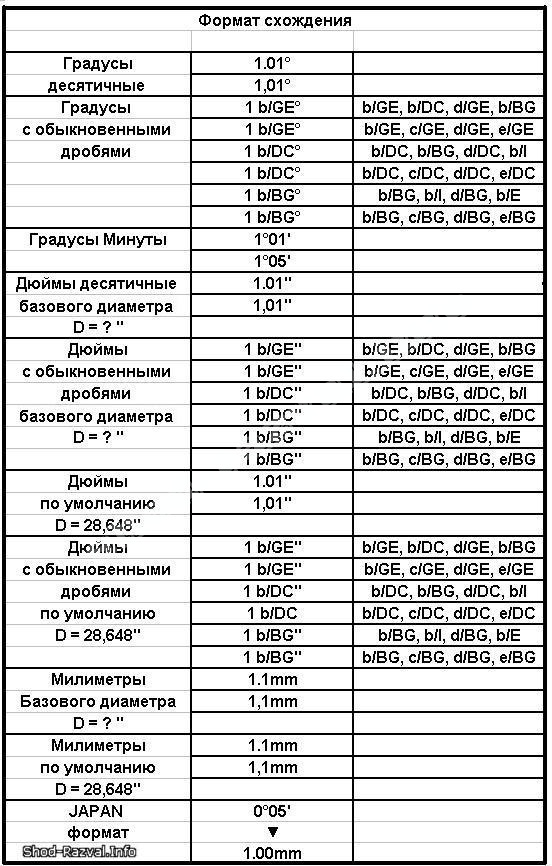
 Частота и факторы риска несращения в 41 случае.
Частота и факторы риска несращения в 41 случае.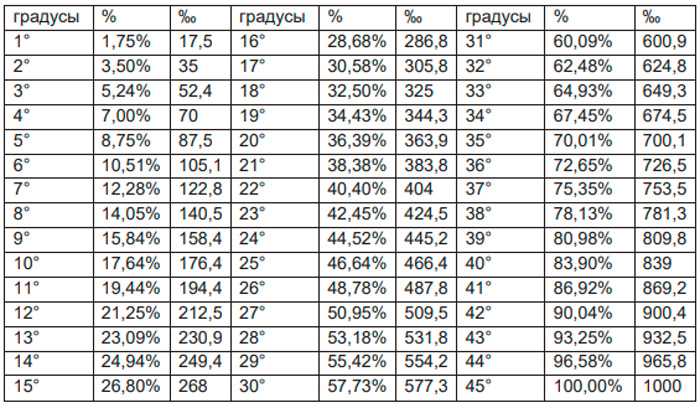
 Л., Джеймс С.Л., Ларсон Р.Л., Слокум Д.Б. (1988)Проксимальная остеотомия большеберцовой кости у пациентов в возрасте пятидесяти лет и младше. J Bone Joint Surg Am 70: 977–982
—
DOI
Л., Джеймс С.Л., Ларсон Р.Л., Слокум Д.Б. (1988)Проксимальная остеотомия большеберцовой кости у пациентов в возрасте пятидесяти лет и младше. J Bone Joint Surg Am 70: 977–982
—
DOI

 Следовательно, мы будем интегрировать по x.
Следовательно, мы будем интегрировать по x.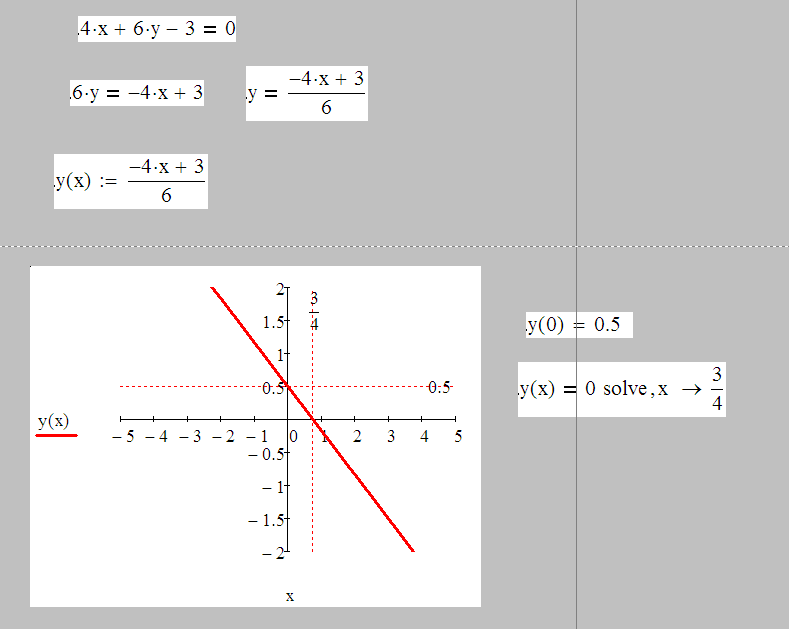 Объем представляет собой интеграл площади круга (πr 2 ), умноженный на его толщину (dx) от 0 до 2.
Объем представляет собой интеграл площади круга (πr 2 ), умноженный на его толщину (dx) от 0 до 2. ответил 30.05.20
ответил 30.05.20


 График функции
График функции
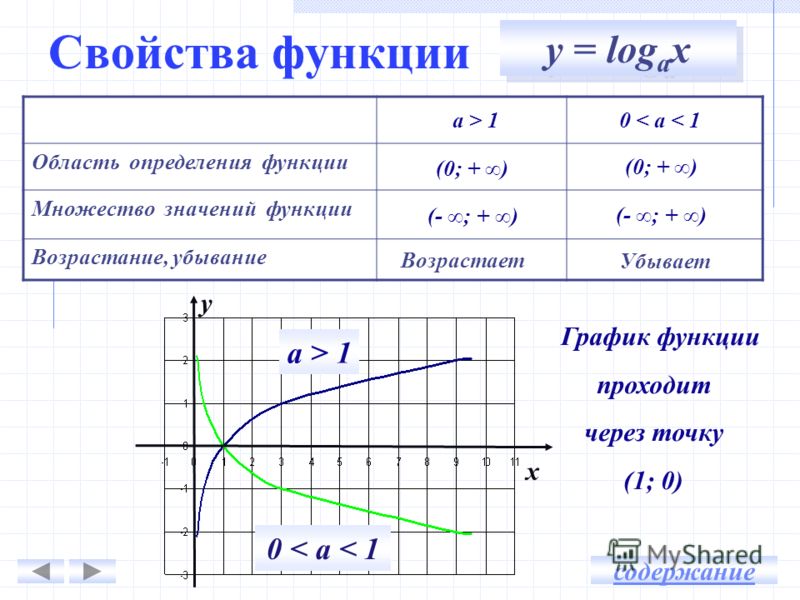 Такую запись можно читать как «\(y\ \)равен \(f\) от\(\ x\)».
Такую запись можно читать как «\(y\ \)равен \(f\) от\(\ x\)».


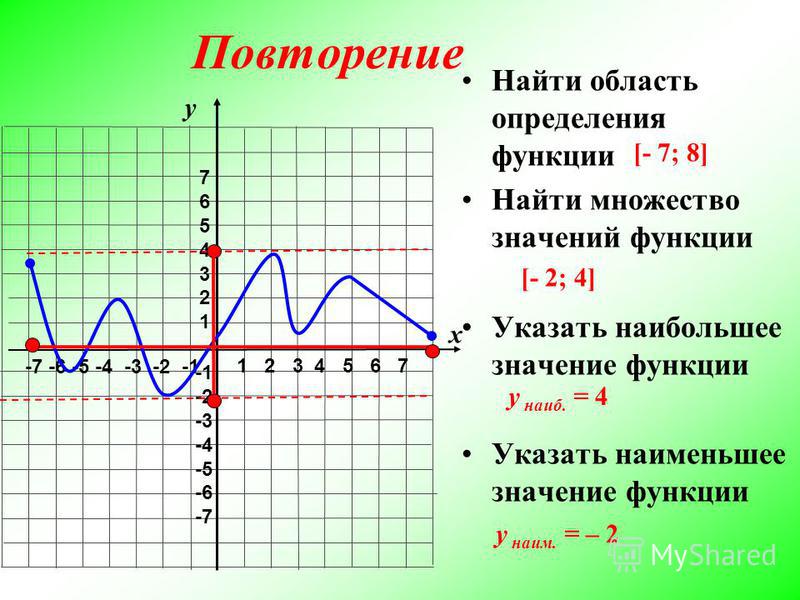 {2}–\ 4.\)
{2}–\ 4.\)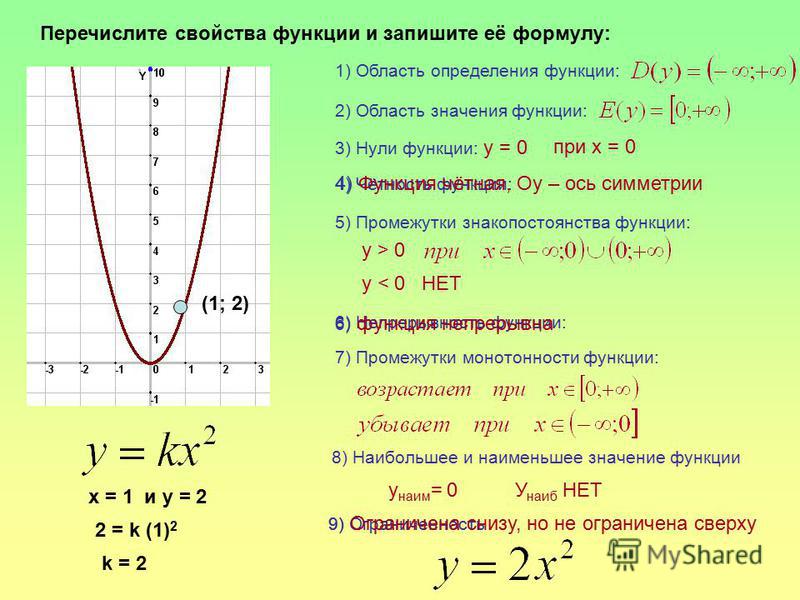 Точка принадлежит графику функций, если её координате x соответствует координата соответствует координата y именно как \(y\ = \ 8\ + \ x.\)
Точка принадлежит графику функций, если её координате x соответствует координата соответствует координата y именно как \(y\ = \ 8\ + \ x.\)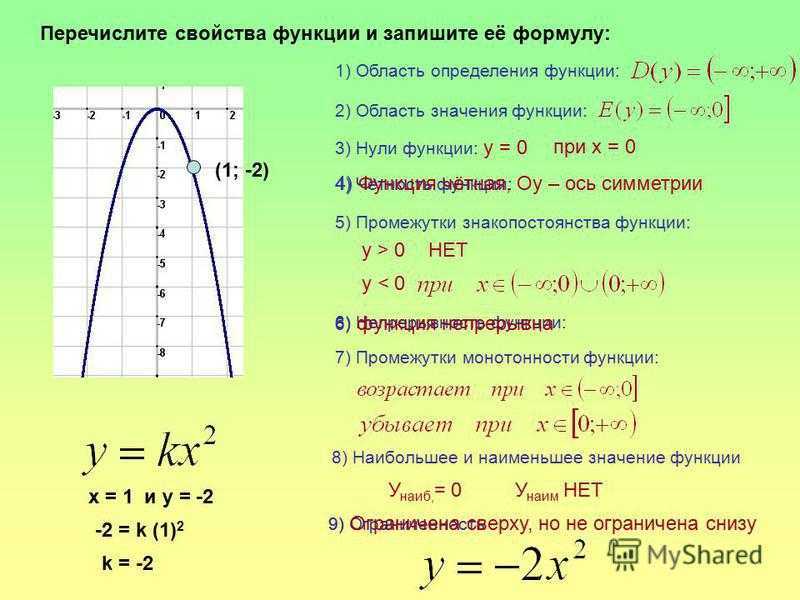 Функции повсеместно используются в математике и необходимы для формулирования физических отношений в естественных науках. Современное определение функции впервые дал в 1837 году немецкий математик Петер Дирихле:
Функции повсеместно используются в математике и необходимы для формулирования физических отношений в естественных науках. Современное определение функции впервые дал в 1837 году немецкий математик Петер Дирихле: Набор значений x называется доменом функции, а набор значений f ( x ), порожденных значениями в домене, называется диапазоном функции. В дополнение к f ( x ), другие сокращенные символы, такие как g ( x ) и P ( x ), часто используются для представления функций независимой переменной x , особенно когда характер функция неизвестна или не определена.
Набор значений x называется доменом функции, а набор значений f ( x ), порожденных значениями в домене, называется диапазоном функции. В дополнение к f ( x ), другие сокращенные символы, такие как g ( x ) и P ( x ), часто используются для представления функций независимой переменной x , особенно когда характер функция неизвестна или не определена.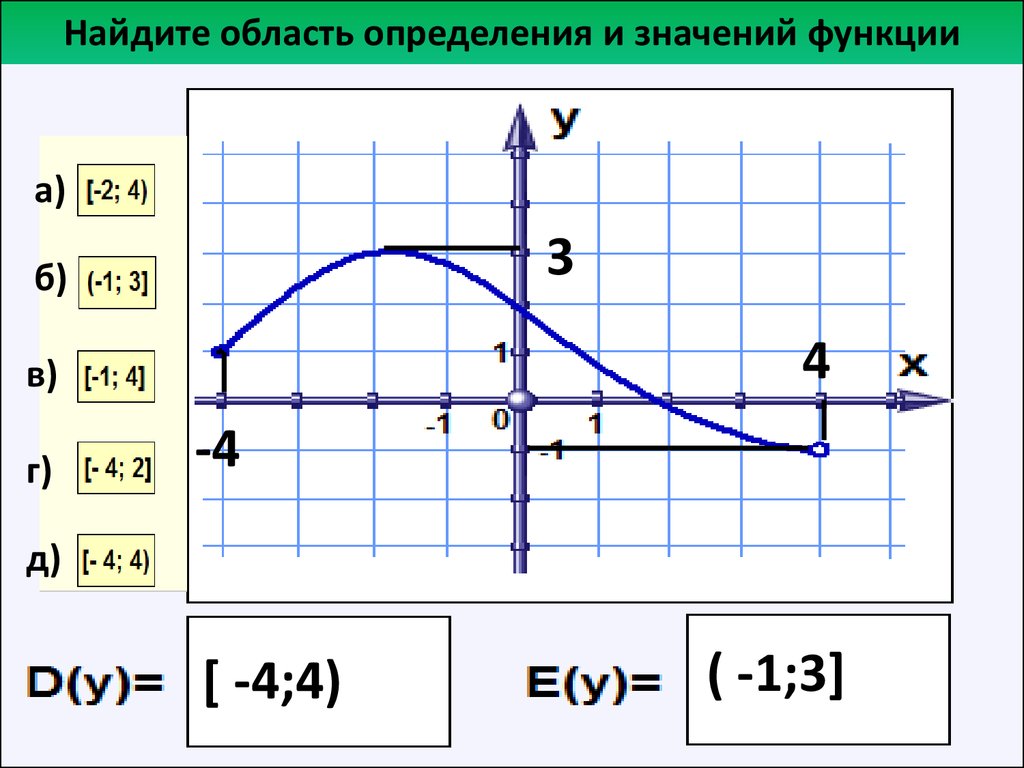 В этих примерах физические ограничения заставляют независимые переменные быть положительными числами. Когда независимым переменным также разрешено принимать отрицательные значения — таким образом, любое действительное число — функции известны как функции с действительными значениями.
В этих примерах физические ограничения заставляют независимые переменные быть положительными числами. Когда независимым переменным также разрешено принимать отрицательные значения — таким образом, любое действительное число — функции известны как функции с действительными значениями. ) Полиномиальные функции изучались с древнейших времен из-за их универсальности — практически любое отношение, включающее действительные числа, может быть точно аппроксимировано с помощью полиномиальная функция. Полиномиальные функции характеризуются наибольшей степенью независимой переменной. Для таких степеней от одного до пяти обычно используются специальные названия: линейная, квадратичная, кубическая, квартическая и квинтическая для высших степеней, равных 1, 2, 3, 4 и 5 соответственно.
) Полиномиальные функции изучались с древнейших времен из-за их универсальности — практически любое отношение, включающее действительные числа, может быть точно аппроксимировано с помощью полиномиальная функция. Полиномиальные функции характеризуются наибольшей степенью независимой переменной. Для таких степеней от одного до пяти обычно используются специальные названия: линейная, квадратичная, кубическая, квартическая и квинтическая для высших степеней, равных 1, 2, 3, 4 и 5 соответственно. Затем график функции состоит из точек с координатами ( x , y ), где y = f ( x ). Например, на рисунке показан график кубического уравнения f ( x ) = x 3 − 3 x + 2.
Затем график функции состоит из точек с координатами ( x , y ), где y = f ( x ). Например, на рисунке показан график кубического уравнения f ( x ) = x 3 − 3 x + 2. Вероятно, наиболее важной из экспоненциальных функций является y = e x , иногда пишут y = exp ( x ), в которой e (2,718 2818…) является основой природного система логарифмов (ln). По определению x — это логарифм, и, таким образом, существует логарифмическая функция, обратная экспоненциальной функции. В частности, если y = e x , тогда x = ln y . Неалгебраические функции, такие как экспоненциальные и тригонометрические функции, также известны как трансцендентные функции.
Вероятно, наиболее важной из экспоненциальных функций является y = e x , иногда пишут y = exp ( x ), в которой e (2,718 2818…) является основой природного система логарифмов (ln). По определению x — это логарифм, и, таким образом, существует логарифмическая функция, обратная экспоненциальной функции. В частности, если y = e x , тогда x = ln y . Неалгебраические функции, такие как экспоненциальные и тригонометрические функции, также известны как трансцендентные функции. 2$ в $\R$.
Возможно, вы сталкивались с функциями в более абстрактных условиях, таких как
хорошо; это наша цель. В нескольких последних разделах главы мы
использовать функции для изучения некоторых интересных тем теории множеств.
2$ в $\R$.
Возможно, вы сталкивались с функциями в более абстрактных условиях, таких как
хорошо; это наша цель. В нескольких последних разделах главы мы
использовать функции для изучения некоторых интересных тем теории множеств. На данный момент все
необходимо интуитивное понимание концепции и способа
показывает, что две функции равны.)
На данный момент все
необходимо интуитивное понимание концепции и способа
показывает, что две функции равны.) Если эта точка $(a,b)$, то
$f(a)=b$. $\квадрат$
Если эта точка $(a,b)$, то
$f(a)=b$. $\квадрат$ ) $\square$
) $\square$ Это называется композиция из
две функции. Заметьте, что $f$ — это первая функция, которая
применяется к элементу $a$, хотя он указан справа. Этот
нарушение обычного правила слева направо иногда вызывает
путаница. $\квадрат$
9+\cup\{0\}\to \R$ определяется выражением
$(g\circ f)(x)=\sin\sqrt x$. Обратите внимание, что $(f\circ g)(x)=\sqrt{\sin x}$
имеет смысл только для таких $x$, что $\sin x\ge 0$.
В общем, $f\circ g$ и $g\circ f$ не обязательно равны, и (поскольку
в этом случае) их не обязательно определять в одних и тех же точках.
$\квадрат$
Это называется композиция из
две функции. Заметьте, что $f$ — это первая функция, которая
применяется к элементу $a$, хотя он указан справа. Этот
нарушение обычного правила слева направо иногда вызывает
путаница. $\квадрат$
9+\cup\{0\}\to \R$ определяется выражением
$(g\circ f)(x)=\sin\sqrt x$. Обратите внимание, что $(f\circ g)(x)=\sqrt{\sin x}$
имеет смысл только для таких $x$, что $\sin x\ge 0$.
В общем, $f\circ g$ и $g\circ f$ не обязательно равны, и (поскольку
в этом случае) их не обязательно определять в одних и тех же точках.
$\квадрат$ 1.10. Если $A\subseteq B$, $f\colon A\to B$ является функцией включения
(пример 4.1.6) и $g\colon B\to C$ — функция, то
$g\circ f\colon A\to C$ называется ограничением от $g$ до $A$ и обычно записывается
$г\верт_А$. Для всех $a\in A$
$$ г\верт_А(а)=г(ф(а))=г(а),
$$
поэтому $g\vert_A$ — это та же самая функция, что и $g$, но с меньшим
домен.
$\квадрат$
1.10. Если $A\subseteq B$, $f\colon A\to B$ является функцией включения
(пример 4.1.6) и $g\colon B\to C$ — функция, то
$g\circ f\colon A\to C$ называется ограничением от $g$ до $A$ и обычно записывается
$г\верт_А$. Для всех $a\in A$
$$ г\верт_А(а)=г(ф(а))=г(а),
$$
поэтому $g\vert_A$ — это та же самая функция, что и $g$, но с меньшим
домен.
$\квадрат$
 Можно ли открыть такой замок?
Можно ли открыть такой замок? Докажите, что отношение отрезков ВМ и BN равно отношению радиусов окружностей.
Докажите, что отношение отрезков ВМ и BN равно отношению радиусов окружностей. Пусть — угол между лучом и положительной полуосью абсцисс (при совпадении данного луча с положительной полуосью абсцисс будем считать, что = 00):
Пусть — угол между лучом и положительной полуосью абсцисс (при совпадении данного луча с положительной полуосью абсцисс будем считать, что = 00):
 е.
е. Скалярное произведение векторов
Скалярное произведение векторов Тангенс определяется как отношение длины противоположной стороны или перпендикуляра прямого угла к углу и длине прилежащей стороны. Функция касательной в тригонометрии используется для вычисления наклона линии между началом координат и точкой, определяющей пересечение гипотенузы и высоты прямоугольного треугольника. В этой статье мы обсудим значения тангенса 0 и как получить значение тангенса 0 градусов.
Тангенс определяется как отношение длины противоположной стороны или перпендикуляра прямого угла к углу и длине прилежащей стороны. Функция касательной в тригонометрии используется для вычисления наклона линии между началом координат и точкой, определяющей пересечение гипотенузы и высоты прямоугольного треугольника. В этой статье мы обсудим значения тангенса 0 и как получить значение тангенса 0 градусов.
 Известно, что отношение синуса и косинуса одного и того же угла дает тангенс этого же угла. Итак, если у нас есть значение sin 0° градусов и cos 0° градусов, то значение tan 0° градусов можно вычислить очень легко.
Известно, что отношение синуса и косинуса одного и того же угла дает тангенс этого же угла. Итак, если у нас есть значение sin 0° градусов и cos 0° градусов, то значение tan 0° градусов можно вычислить очень легко.
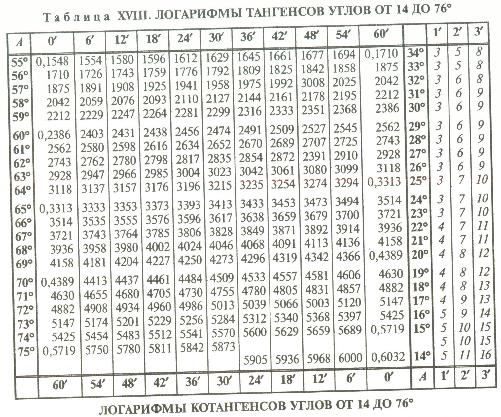

 1 Найдите вершину y = x 2 -2x+2
1 Найдите вершину y = x 2 -2x+2 В нашем случае координата x равна 1.0000
В нашем случае координата x равна 1.0000  Поскольку
Поскольку  3 Решение x 2 -2x+2 = 0 по квадратичной формуле .
3 Решение x 2 -2x+2 = 0 по квадратичной формуле .
 11 Найти радиус сходимости и область сходимости степенного ряда:
11 Найти радиус сходимости и область сходимости степенного ряда: Из приведенных примеров
Из приведенных примеров
 Из этого условия определяем
Из этого условия определяем Хотя едва ли возможно сделать y точно равным нулю, предельное значение y приближается к нулю, потому что мы можем сделать y настолько малым, насколько это возможно, выбрав большие значения x.
Хотя едва ли возможно сделать y точно равным нулю, предельное значение y приближается к нулю, потому что мы можем сделать y настолько малым, насколько это возможно, выбрав большие значения x. .
. 
 В противном случае при x-3 > 1 ряд расходится.
В противном случае при x-3 > 1 ряд расходится.

 Назовите групповой реагент и перечислите катионы, входящие в IV группу.
2. Укажите цвет гидроксидов катионов IV
Назовите групповой реагент и перечислите катионы, входящие в IV группу.
2. Укажите цвет гидроксидов катионов IV
 Следующие тождества с двумя переменными называются тождествами тригонометрического сложения .
Следующие тождества с двумя переменными называются тождествами тригонометрического сложения .
 Эти формулы приведения полезны при переписывании синусов углов, превышающих 90 °, как функций острых углов.
Эти формулы приведения полезны при переписывании синусов углов, превышающих 90 °, как функций острых углов. Задача 3
Задача 3 Таким образом, эта 1 над косинусом альфа и косинусом бета будет распределена по обоим этим терминам в числителе: синус альфа, косинус бета над косинусом альфа, косинус бета косинус бета отменит, и у меня будет синус альфа над косинусом альфа минус . Вот что происходит с первым сроком.
Таким образом, эта 1 над косинусом альфа и косинусом бета будет распределена по обоим этим терминам в числителе: синус альфа, косинус бета над косинусом альфа, косинус бета косинус бета отменит, и у меня будет синус альфа над косинусом альфа минус . Вот что происходит с первым сроком. Задача говорит найти тангенс 15 градусов? Итак, сначала вы хотите выразить 15 градусов как некоторую разницу, которая включает в себя хорошие углы, особые углы. Например, тангенс 45 минус 30. На самом деле позвольте мне пойти с 60 минус 45, позвольте мне сказать вам, почему. Если вы помните тангенс 30 градусов, это 1 над корнем 3, а тангенс 60 градусов это корень 3, я не хочу, чтобы в моих ответах была 1 над корнем 3, поэтому я собираюсь держаться подальше от этого, но даст мне немного более приятный ответ, так что это тангенс 60 градусов минус 45 градусов.
Задача говорит найти тангенс 15 градусов? Итак, сначала вы хотите выразить 15 градусов как некоторую разницу, которая включает в себя хорошие углы, особые углы. Например, тангенс 45 минус 30. На самом деле позвольте мне пойти с 60 минус 45, позвольте мне сказать вам, почему. Если вы помните тангенс 30 градусов, это 1 над корнем 3, а тангенс 60 градусов это корень 3, я не хочу, чтобы в моих ответах была 1 над корнем 3, поэтому я собираюсь держаться подальше от этого, но даст мне немного более приятный ответ, так что это тангенс 60 градусов минус 45 градусов.