Тест: Простые и сложные высказывания. Булевые функции
Тест: Простые и сложные высказывания. Булевые функции — Информатика 10 классАнглийский язык
Астрономия
Белорусский язык
Биология
География
ИЗО
Информатика
История
Итальянский язык
Краеведение
Литература
Математика
Музыка
Немецкий язык
ОБЖ
Обществознание
Окружающий мир
ОРКСЭ
Русский язык
Технология
Физика
Физкультура
Химия
Черчение
Для учителей
Дошкольникам
VIP — доступ
- Предметы »
- Информатика »
- 10 класс »
- Простые и сложные высказывания. Булевые функции
Простые и сложные высказывания. Булевые функции
Информатика 10 класс | Автор: | ID: 9198 | Дата: 28.2.2017
Помещать страницу в закладки могут только зарегистрированные пользователи
Зарегистрироваться
Вопрос №
1
СКН-форма не существует у формулы алгебры высказываний, если она …
тождественно истинная
тождественно ложная
выполнимая
опровержимая
Вопрос №
2
СДН-форма не существует у формулы алгебры высказываний, если она …
тождественно истинная
тождественно ложная
выполнимая
опровержимая
Вопрос №
3
Высказывание – это
Любое предложение
Утверждение, истинность или ложность которого нельзя установить в любой момент времени
Утверждение, истинность или ложность которого можно установить в любой момент времени
Вопрос №
4
Выбрать пример, не являющийся высказыванием:
«Откройте книгу»
«Волки и зайцы – дикие животные»
«Идёт урок информатики»
«некоторые лекарства опаснее самих болезней»
Вопрос №
5
Высказывание «Все растения съедобны»:
Простое и истинное
Сложное и истинное
Простое и ложное
Вопрос №
6
Знаком в логике обозначается следующая операция:
Инверсия
Дизъюнкция
Конъюнкция
Вопрос №
7
Знаком в логике обозначается следующая операция:
Инверсия
Импликация
Конъюнкция
Дизъюнкция
Вопрос №
8
Логическая операция с использованием ключевых слов «Если…то…», называется
Дизъюнкция
Импликация
Инверсия
Конъюнкция
Вопрос №
9
Выбрать пример, не являющийся высказыванием:
«Никакая причина не извиняет невежливость»
«Спортом заниматься полезно»
«Как твоя фамилия?»
«Все птицы зимой улетают на юг»
Вопрос №
10
Высказывание «Прозвенел звонок и закончился урок»:
Простое и истинное
Сложное и истинное
Простое и ложное
Сложное и ложное
Показать ответы
Получение сертификата
о прохождении теста
Доступно только зарегистрированным пользователям
© TestEdu. ru 2013-2022
ru 2013-2022
E-mail администратора: [email protected]
Основные понятия формальной логики — презентация онлайн
Похожие презентации:
Пиксельная картинка
Информационная безопасность. Методы защиты информации
Электронная цифровая подпись (ЭЦП)
Этапы доказательной медицины в работе с Pico. Первый этап
История развития компьютерной техники
От печатной книги до интернет-книги
Краткая инструкция по CIS – 10 шагов
Информационные технологии в медицине
Информационные войны
Моя будущая профессия. Программист
1. Основные понятия формальной логики
Формальная логика — наука о формах и законахмышления. Законы логики отражают в сознании
человека свойства, связи и отношения объектов
окружающего мира. Логика как наука позволяет
строить формальные модели окружающего мира,
отвлекаясь от содержательной стороны.
Высказывание — это любое предложение
какого-либо языка (утверждение),
содержание которого можно определить как
истинное или ложное.

Всякое высказывание или истинно, или
ложно; быть одновременно и тем и другим
оно не может.
Суждения — это форма мышления, в которой утверждается
или отрицается связь между предметом и его признаком,
отношения между предметами или факт существования
предмета и которая может быть либо истинной, либо ложной.
Языковой формой выражения суждения является
повествовательное предложение. Вопросительные и
побудительные предложения суждениями не являются.
Суждения рассматриваются не с точки зрения их смысла и
содержания, а только с точки зрения их истинности или
ложности. Истинным будет суждение, в котором связь понятий
правильно отражает свойства и отношения реальных объектов.
«Дважды два равно четырем» — истинное суждение, а вот
«Процессор предназначен для печати» — ложное. Суждения
могут быть простыми и сложными. «Весна наступила, и грачи
прилетели» — сложное суждение, состоящее из двух простых.
Простые суждения (высказывания) выражают связь двух
понятий.
 Сложные — состоят из нескольких простых суждений
Сложные — состоят из нескольких простых сужденийУмозаключение — прием мышления, позволяющий на
основе одного или нескольких суждений-посылок получить
новое
суждение
(знание
или
вывод).
Примерами умозаключений являются доказательства
теорем в геометрии. Посылками умозаключения по
правилам формальной логики могут быть только истинные
суждения. Тогда и умозаключение будет истинным. Иначе
можно прийти к ложному умозаключению.
Логические величины—понятия, выражаемые словами:
ИСТИНА, ЛОЖЬ (true, false).
Следовательно, истинность высказываний
выражается,через логические величины.
Логическое выражение — это символическая запись
высказывания, состоящая из логических величин
(констант или переменных), объединенных логическими
операциями (связками).
Связки «НЕ», «И», «ИЛИ» заменяются логическими
операциями инверсия, конъюнкция, дизъюнкция. Это
основные логические операции, при помощи которых
можно записать любое логическое выражение.

Конъюнкция — логическое умножение (от латинского conjunctio — союз, связь):
• в естественном языке соответствует союзу «И»
;
• в алгебре высказываний обозначение «&»
;
• в языках программирования обозначение «And».
Конъюнкция — это логическая операция, ставящая в соответствие каждым двум
простым (или исходным) высказываниям составное высказывание, являющееся
истинным тогда и только тогда, когда оба исходных высказывания истинны. Если
хотя бы одно из составляющих высказываний ложно, то и полученное из них с
помощью союза «И» сложное высказывание также считается ложным.
Дизъюнкция — логическое сложение (от латинского disjunctio — разобщение,
различие):
• в естественном языке соответствует союзу «ИЛИ»
;
• в алгебре высказываний обозначение «V» или «+»
;
• в языках программирования обозначение «Or».
Дизъюнкция — это логическая операция, которая каждым двум простым (или
исходным) высказываниям ставит в соответствие составное высказывание,
являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны
и истинным, когда хотя бы одно из двух образующих его высказываний истинно
Инверсия — отрицание (от латинского disjunctio — разобщение, различие):
• в естественном языке соответствует словам «неверно, что.
 ..» и частице
..» и частице«не»
;
• в алгебре высказываний обозначение «¬» или «-»
;
• в языках программирования обозначение «Not».
Отрицание — логическая операция, которая с помощью связки «не» каждому
исходному высказыванию ставит в соответствие составное высказывание,
заключающееся в том, что исходное высказывание отрицается.
Логическое следование (импликация):
Высказывание, составленное из двух
высказываний при помощи связки «если …, то
…», называется логическим следованием,
импликацией (импликация от латинского
implico — тесно связываю).
Эквивалентность (логическое тождество):
Высказывание, составленное из двух
высказываний при помощи связки «тогда и
только тогда, когда», называется
эквивалентностью (эквивалентность логическое тождество, равнозначность,
взаимная обусловленность. )
13. Примеры:
+ Пример 1. Определить участника преступления, исходя издвух посылок:
1) «Если Иванов не участвовал или Петров участвовал, то
Сидоров участвовал»;
2) «Если Иванов не участвовал, то Сидоров не участвовал».

Решение
Составим выражения:
I — «Иванов участвовал в преступлении»;
P — «Петров участвовал в преступлении»;
S — «Сидоров участвовал в преступлении».
Запишем посылки в виде формул:
Тогда
+ Проверим результат, используя таблицу истинности:
+
Ответ: Иванов участвовал в преступлении.
1.
Выберите пример, являющийся высказыванием:
a) «Не могли бы вы передать мне соль?»
b) «Н. В. Гоголь писал «Мертвые души» в Риме.»
c) «Солнце есть спутник Земли.»
d) «Некоторые лекарства опаснее самих болезней»
e) «Сегодня замечательная погода!»
2) Запишите высказывания в виде логических выражений
1.число 17 нечетное и двухзначное, и простое
2.Неверно, что корова – хищное животное
3.Если Маша – сестра Саши, то Саша – брат Маши
4.Если компьютер включен, то можно на нем работать
5.Водительские права можно получить права тогда и только
тогда, когда тебе исполнится 18 лет
English Русский Правила
Что такое заявления? Определение и примеры
Давайте рассмотрим несколько примеров утверждений и не-утверждений, чтобы определить, какие предложения образуют утверждения.
© Патрик Жирар, Университет Окленда
Говоря об утверждениях, мы начнем с нескольких примеров утверждений и не-утверждений.
| Выписки | Неутверждения |
|---|---|
| Поезда всегда опаздывают. | Добро пожаловать в Оклендский университет! |
| Прыжки в багажник — основная причина автомобильных аварий. | Как перестать прятаться? |
| Я люблю бананы, потому что в них нет костей. | Когда машина впереди достигает объекта, убедитесь, что вы можете сосчитать до четырех крокодилов , прежде чем вы достигнете того же объекта. |
Итак, что делает что-то заявлением?
- Определение : Утверждения — это предложения, которые либо истинны, либо ложны.
Таким образом, утверждение является утверждением о том, что нечто имеет место или не имеет место. Утверждение истинно, если то, что оно утверждает, имеет место, и ложно, если то, что оно утверждает, не имеет места.
Например, утверждение «Поезда всегда опаздывают» истинно только в том случае, если оно описывает случай, т. е. если на самом деле случай, что поезда всегда опаздывают. Это ложь в Окленде. Иногда поезда приходят вовремя, а иногда рано. Кто-то может нетерпеливо жаловаться, что поезда всегда опаздывают, чтобы выразить свое недовольство системой поездов, но, строго говоря, то, что они говорят, — ложь.
Это правда, что у бананов нет костей, и я люблю бананы, но я люблю бананы, потому что они вкусные и полезные, а не потому, что у них нет костей. Таким образом, я бы сказал что-то ложное, если бы сказал: «Мне нравятся бананы, потому что в них нет костей». Вот почему «мне нравятся бананы, потому что в них нет костей» — это утверждение. Это предложение, которое либо истинно, либо ложно, в данном случае ложно.
Однако говорить о том, что фраза «Добро пожаловать в Оклендский университет!» не имеет смысла! является либо истинным, либо ложным. Разве вы не были бы озадачены, если бы кто-то ответил «правда» в ответ на приветствие? Это не будет подходящим ответом. «Как мне перестать прятаться?» это вопрос; предложение не выражает ничего истинного или ложного.
«Как мне перестать прятаться?» это вопрос; предложение не выражает ничего истинного или ложного.
Наконец, «Когда машина впереди достигает объекта, убедитесь, что вы можете сосчитать до четырех крокодилов , прежде чем доберетесь до того же объекта». это совет. Он советует вам убедиться, что вы можете сосчитать до четырех крокодилов (один крокодил, два крокодила,…, четыре крокодила), прежде чем вы достигнете того же объекта, что и машина впереди вас. Попробуй это! Вы будете гораздо более безопасным водителем (это верное утверждение!).
Таким образом, предложения, которые могут быть истинными или ложными, являются высказываниями. Довольно просто. Но все может быть сложнее. Посмотрим, как.
Что-то может быть утверждением, даже если мы не знаем, истинно оно или ложно. Все, что имеет значение в утверждениях, это то, что они могут быть истинными или ложными, а не то, что мы знаем, истинны они или ложны. Например:
- Иван Слотвский, знаменитый ирландский строитель Мадрида, в этот самый момент ест бифштексы с ветчиной и чатни.

Правда или ложь? Я не знаю. Но это то, что может быть правдой или ложью.
Вот еще один:
- Когда-нибудь в следующие 39 лет у меня будет жуткая соседка.
Пока все хорошо. Мне повезло, и у меня не было жуткого соседа по соседству. Но это утверждение верно, если однажды в следующие 39 лет у меня появится жуткий сосед. В противном случае утверждение ложно. Но я не знаю, верно это утверждение или нет. Независимо от того, что имеет значение, так это то, что это предложение является истинным или ложным.
Другой пример:
- Vero входит в состав Promina
Я понятия не имею, что такое Веро или Промина. Но предложение выражает нечто, что либо истинно, либо ложно.
Одно и то же утверждение может быть истинным в одних случаях и ложным в других. То есть утверждения не всегда истинны или всегда ложны.
Вот пример:
- Я киви.
Это утверждение верно для Тима и неверно для Патрика. Или заявление
Или заявление
- Патрик счастлив в браке.
было ложным до того, как Патрик женился, оно верно сейчас (пока я это печатаю) и может стать ложным в будущем.
Одна из трудностей с утверждениями состоит в том, что иногда они могут выражать две разные вещи. Мы называем эти неоднозначных утверждения . Вот пример:
- Джон приветствовал всех с улыбкой.
Какие два состояния дел может описывать это утверждение? Попробуйте ответить на этот вопрос для себя, прежде чем продолжить.
Ответ:
- Джон улыбался, а затем поприветствовал всех. В данном случае это правда, что он всех встречал улыбкой – своей улыбкой.
- Может быть, были улыбающиеся и не улыбающиеся люди, а Джон приветствовал только тех, кто улыбался.
Таким образом, предложение «Джон приветствовал всех с улыбкой» можно использовать для описания двух разных вещей. Вот что делает его двусмысленным.
Будьте осторожны с этим. Если вы используете двусмысленные утверждения, вы рискуете, что другие неправильно поймут то, что вы говорите. В некоторых случаях то, что другие думают, что вы говорите, может сильно отличаться от того, что вы пытались выразить. Например, Тим — ранняя пташка. Каждое утро он встает рано и всегда раньше жены. Теперь предположим, что он попытался выразить это, сказав:
Если вы используете двусмысленные утверждения, вы рискуете, что другие неправильно поймут то, что вы говорите. В некоторых случаях то, что другие думают, что вы говорите, может сильно отличаться от того, что вы пытались выразить. Например, Тим — ранняя пташка. Каждое утро он встает рано и всегда раньше жены. Теперь предположим, что он попытался выразить это, сказав:
- Я избиваю свою жену каждый день.
Это наверняка будет воспринято неправильно. Старайтесь не использовать двусмысленные предложения!
Во втором списке не утверждений у нас были вопросы и команды, и обычно это не утверждения.
- Если люди произошли от обезьян, почему у нас до сих пор есть обезьяны?
Этот вопрос не выражает ничего, что может быть истинным или ложным. Нет смысла отвечать «правда» или «ложь», когда вы это слышите. Это не заявление. Обратите внимание, что часть предложения является утверждением, а именно «люди произошли от обезьян». Это ложное утверждение. Люди не эволюционировали от обезьян. Люди, обезьяны и человекообразные обезьяны в целом имеют общего предка, которого больше нет. Несмотря на то, что часть вопроса содержит ложное утверждение, это не делает сам вопрос чем-то истинным или ложным.
Люди не эволюционировали от обезьян. Люди, обезьяны и человекообразные обезьяны в целом имеют общего предка, которого больше нет. Несмотря на то, что часть вопроса содержит ложное утверждение, это не делает сам вопрос чем-то истинным или ложным.
Однако иногда, в особом контексте, один и тот же вопрос может использоваться для выражения утверждения. Можете ли вы представить себе контекст, в котором кто-то мог бы использовать этот вопрос, чтобы выразить что-то, что является правдой или ложью? Если это так, то, по-видимому, человек использовал бы вопрос, чтобы выразить, что утверждение о том, что люди произошли от обезьян, ложно, поскольку обезьяны все еще существуют. Мы называем вопросы, которые используются для выражения утверждений риторический вопрос . Когда вы видите риторический вопрос, вы всегда должны перефразировать его как утверждение. В нашем случае заявление будет примерно таким:
- Люди не произошли от обезьян, потому что у нас все еще есть обезьяны.

Таким образом, утверждения являются типами предложений, которые либо истинны, либо ложны. Предложения неоднозначны, если они могут использоваться для выражения нескольких утверждений. Когда у вас есть двусмысленное предложение, вам нужно решить, для выражения какого утверждения оно используется. Вопросы, команды и советы обычно не являются утверждениями, потому что они не выражают ничего истинного или ложного. Но иногда люди используют их риторически для выражения утверждений. Мы видели пример вопроса, который сам по себе не является утверждением, но может использоваться для выражения утверждения. Когда вы видите риторические вопросы, всегда перефразируйте их как утверждения.
© Патрик Жирар, Университет Окленда
Логические и математические операторы — рабочие примеры
Иногда в математике важно определить, что является противоположностью данному математическому утверждению. Это обычно называют «отрицанием» утверждения. Следует иметь в виду, что если утверждение истинно, то его отрицание ложно (а если утверждение ложно, то его отрицание истинно).
Следует иметь в виду, что если утверждение истинно, то его отрицание ложно (а если утверждение ложно, то его отрицание истинно).
Давайте рассмотрим некоторые из наиболее распространенных отрицаний.
Отрицание «A
или B».Прежде чем дать ответ, попробуем сделать это для примера.
Рассмотрим утверждение «Вы либо богаты, либо счастливы». Чтобы это утверждение было ложным, вы не можете быть богатым и вы не можете быть счастливым. Другими словами, наоборот, быть не богатым и не счастливым. Или, если мы перепишем его в терминах исходного утверждения, мы получим «Вы не богаты и не счастливы».
Если мы допустим, что А будет утверждением «Вы богаты», а В будет утверждением «Вы счастливы», то отрицание «А или В» станет «Не А и не В».
В общем случае мы имеем одно и то же утверждение: Отрицание «А или В» есть утверждение «Не А и Не В».
Отрицание «A
и B».
Опять же, давайте сначала проанализируем пример.
Рассмотрим утверждение «Я и богат, и счастлив». Чтобы это утверждение было ложным, я мог быть либо небогатым , либо несчастливым. Если мы допустим, что А будет утверждением «я богат», а В будет утверждением «я счастлив», то отрицание «А и В» станет «я не богат».0034 или Я недоволен» или «Не А и не Б».
Отрицание «
Если А, , то В».Чтобы опровергнуть утверждение вида «Если А, то В», мы должны заменить его утверждением « А и не В ». Сначала это может показаться запутанным, поэтому давайте рассмотрим простой пример, чтобы понять, почему это правильно.
Рассмотрим утверждение «Если я богат, то я счастлив». Для этого
Если бы утверждение было ложным, мне нужно было бы быть богатым и несчастливым. Если
— это утверждение «Я богат», а Б — это утверждение «Я счастлив»,
тогда отрицание «A $\Rightarrow$ B» есть «я богат» = A, и «я
я недоволен» = не Б.
Таким образом, отрицание «, если А, , затем В» становится «А , а не В».
Пример.
Теперь давайте рассмотрим утверждение, включающее некоторую математику. Возьмем утверждение «Если n четно, то $\frac{n}{2}$ — целое число». Чтобы это утверждение было ложным, нам нужно было бы найти четное целое число $n$, для которого $\frac{n}{2}$ не было целым числом. Таким образом, противоположным этому утверждению является утверждение, что «$n$ четно, а $\frac{n}{2}$ не является целым числом».
Отрицание «Для каждого…», «Для всех…», «Существует…»
Иногда встречаются такие фразы, как «для каждого», «для любого», «для любого». все» и «существует» в математических утверждениях.
Пример.
Рассмотрим утверждение «Для всех целых чисел $n$ либо $n$ четно, либо
$n$ нечетно».
Хотя формулировка немного отличается, это утверждение формы «Если А, то Б». Мы можем переформулировать это предложение следующим образом: «Если $n$ — любое целое число, то либо $n$ четно, либо $n$ нечетно».
Мы можем переформулировать это предложение следующим образом: «Если $n$ — любое целое число, то либо $n$ четно, либо $n$ нечетно».
Как бы мы опровергли это утверждение? Чтобы это утверждение было ложным, все, что нам нужно, это найти единственное целое число, которое не является четным и не нечетным. Другими словами, отрицание — это утверждение «Существует целое число $n$, такое что $n$ нечетно и $n$ нечетно».
В общем, при отрицании утверждения, включающего «для всех», «для каждого», фраза «для всех» заменяется на «существует». Точно так же при отрицании утверждения, включающего «существует», фраза «существует» заменяется на «для каждого» или «для всех».
Пример. Отрицайте утверждение «Если все богатые люди счастливы, то все бедные несчастны».
Во-первых, это высказывание имеет форму «Если А, то В», где А — высказывание «Все богатые люди счастливы», а В — высказывание «Все бедняки грустны». Таким образом, отрицание имеет форму «А, а не В».




 Если же в первом столбце нет ненулевых элементов, то определитель равен нулю.
Если же в первом столбце нет ненулевых элементов, то определитель равен нулю.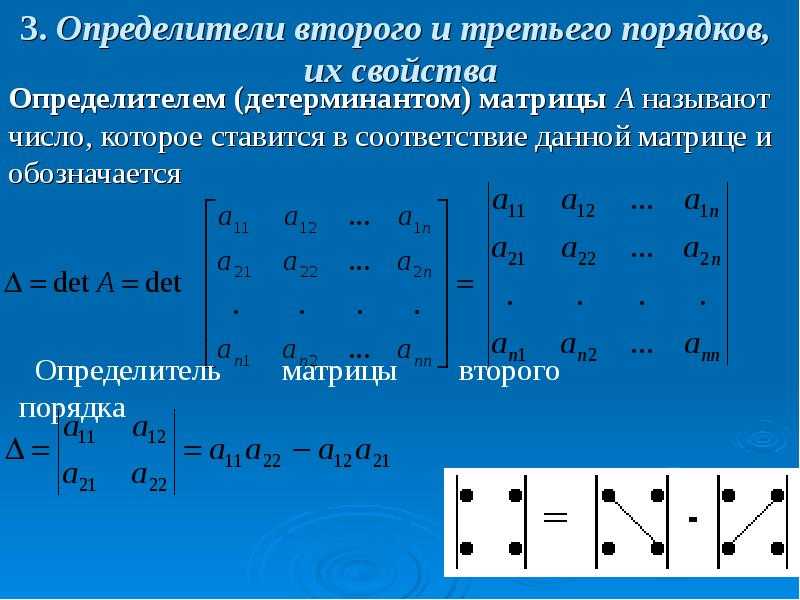 Нам понадобится программа построения минора, получающегося вычеркиванием первой строки и k-го столбца.
Нам понадобится программа построения минора, получающегося вычеркиванием первой строки и k-го столбца. .n]
where n = length matrix - 1
.n]
where n = length matrix - 1
 При этом, если встретилась строка с номером n1, принудительно подставляется строка n2 (и наоборот). Остальные строки остаются на месте.
При этом, если встретилась строка с номером n1, принудительно подставляется строка n2 (и наоборот). Остальные строки остаются на месте. Она нужна в случае, когда очередной диагональный элемент оказался равным нулю.
Она нужна в случае, когда очередной диагональный элемент оказался равным нулю. Функция mkzero формирует нули в очередном столбце матрицы:
Функция mkzero формирует нули в очередном столбце матрицы: Теперь можно составить парадную функцию приведения матрицы к верхней треугольной форме:
Теперь можно составить парадную функцию приведения матрицы к верхней треугольной форме: Определители квадратных матриц.
Определители квадратных матриц. Т.е. определитель матрицы — это число, характеризующее матрицу (параметр). Для каждой квадратной матрицы можно рассчитать число по ее элементам по определенной формуле, которое будет ее характеризовать.
Т.е. определитель матрицы — это число, характеризующее матрицу (параметр). Для каждой квадратной матрицы можно рассчитать число по ее элементам по определенной формуле, которое будет ее характеризовать. Для того, чтобы использовать такой способ, предварительно рассчитывают миноры и алгебраические дополнения. Минором Mij элемента аij называется определитель n-1 порядка, а алгебраическое дополнение это произведение Аij = (-1)i+j Mij
Для того, чтобы использовать такой способ, предварительно рассчитывают миноры и алгебраические дополнения. Минором Mij элемента аij называется определитель n-1 порядка, а алгебраическое дополнение это произведение Аij = (-1)i+j Mij
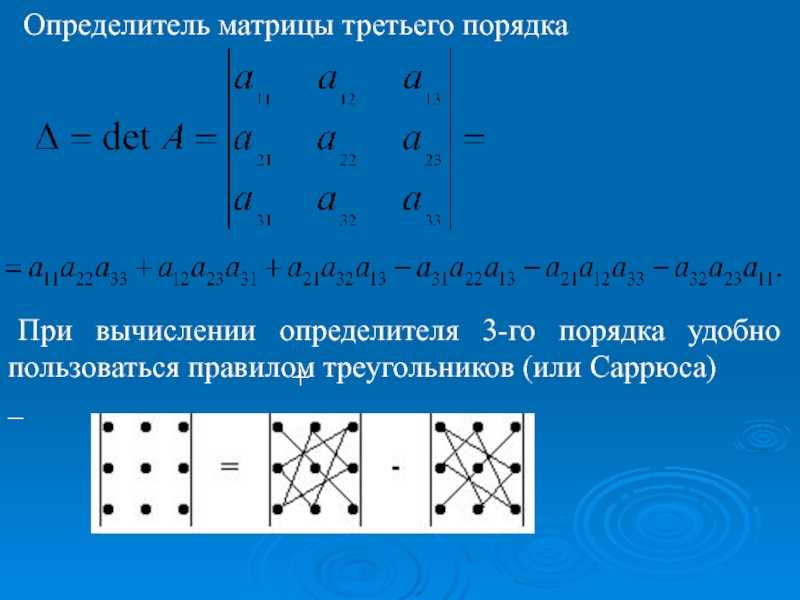
 mathtask.ru
mathtask.ru {1+3}$. 9{4} \times {\begin{vmatrix} e_{21} & e_{22} \\ e_{31} & e_{32} \\ \end{vmatrix}}$
{1+3}$. 9{4} \times {\begin{vmatrix} e_{21} & e_{22} \\ e_{31} & e_{32} \\ \end{vmatrix}}$



 Для количественного выражения этой зависимости введено понятие об ионной силе раствора I, которая численно равна полусумме произведений концентрации CM каждого иона на квадрат его заряда Z:
Для количественного выражения этой зависимости введено понятие об ионной силе раствора I, которая численно равна полусумме произведений концентрации CM каждого иона на квадрат его заряда Z: 10-3 моль/л; (Cl—) = 8,36 .10-3 моль/л.
10-3 моль/л; (Cl—) = 8,36 .10-3 моль/л. 12] = 0,155.
12] = 0,155. 
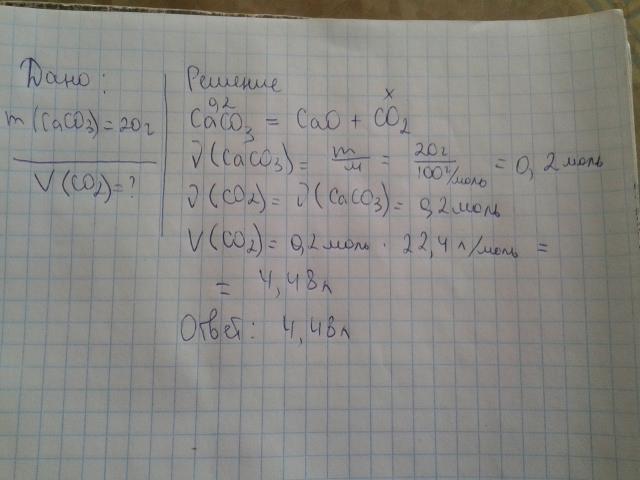 {23}\) репрезентативных частиц. Репрезентативной частицей \(\ce{CO_2}\) является молекула, а для \(\ce{Na_2S}\) это формульная единица.
{23}\) репрезентативных частиц. Репрезентативной частицей \(\ce{CO_2}\) является молекула, а для \(\ce{Na_2S}\) это формульная единица. Таким образом, \(1 \: \text{моль}\) нитрата кальция содержит \(1 \: \text{моль}\) из \(\се{Са}\) атомов, \(2 \: \text{ моль}\) из \(\ce{N}\) атомов и \(6 \: \text{mol}\) из \(\ce{O}\) атомов.
Таким образом, \(1 \: \text{моль}\) нитрата кальция содержит \(1 \: \text{моль}\) из \(\се{Са}\) атомов, \(2 \: \text{ моль}\) из \(\ce{N}\) атомов и \(6 \: \text{mol}\) из \(\ce{O}\) атомов.
 Массы атомов можно взять из периодической таблицы.
Массы атомов можно взять из периодической таблицы.


 008\, g\, H}{1 \,\отмена{моль\,Н}} \справа)\, = 3,024\,г\, Н\]
008\, g\, H}{1 \,\отмена{моль\,Н}} \справа)\, = 3,024\,г\, Н\] Напоминаем, что мы можем сделать свои собственные коэффициенты пересчета, пока верх и низ равны друг другу. Точно так же я могу дать вам четыре четверти или 1 доллар, если я дам вам моль \(\ce{H_{3}PO_{4}}) Я дал вам 3 моля H, 1 моль P и 4 моля O. Поскольку это правда, существует дополнительный набор коэффициентов преобразования, которые мы можем использовать:
Напоминаем, что мы можем сделать свои собственные коэффициенты пересчета, пока верх и низ равны друг другу. Точно так же я могу дать вам четыре четверти или 1 доллар, если я дам вам моль \(\ce{H_{3}PO_{4}}) Я дал вам 3 моля H, 1 моль P и 4 моля O. Поскольку это правда, существует дополнительный набор коэффициентов преобразования, которые мы можем использовать: е.м.) – это масса одной молекулы соединения
е.м.) – это масса одной молекулы соединения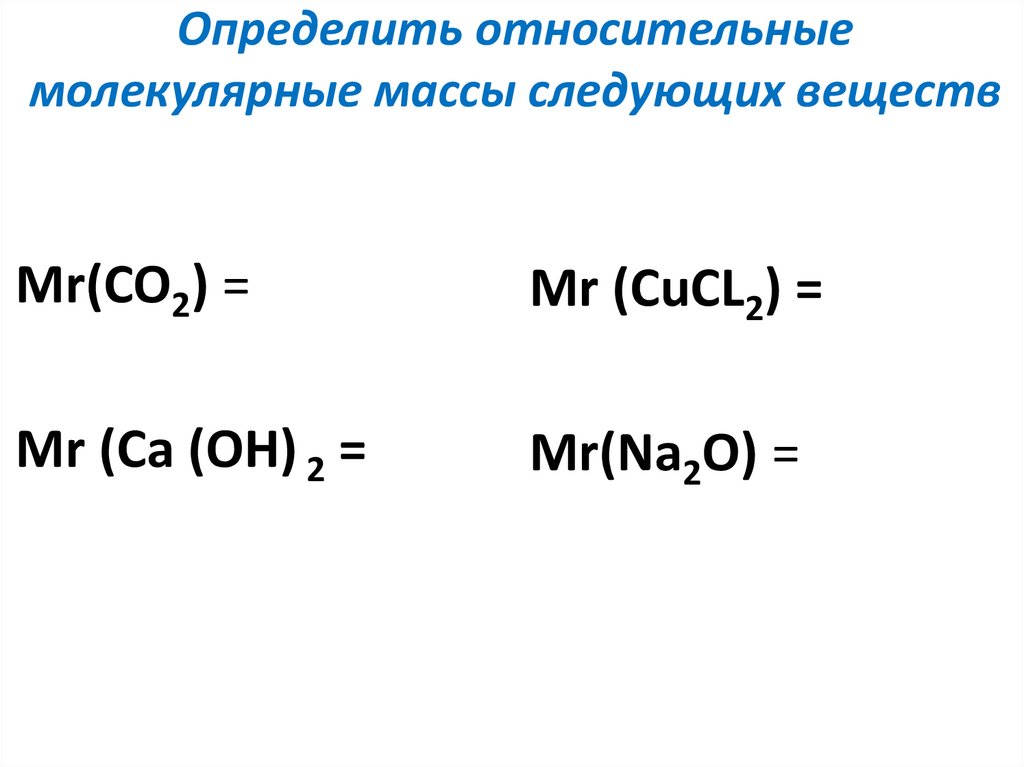


 Нитрат кальция также имеет нейтральный рН, что помогает поддерживать баланс рН почвы.
Нитрат кальция также имеет нейтральный рН, что помогает поддерживать баланс рН почвы.
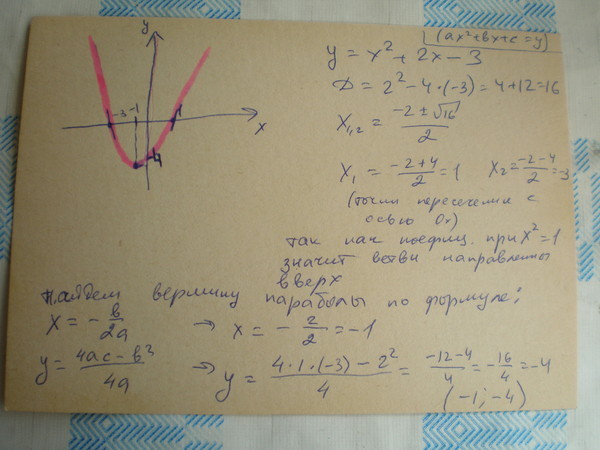

 Если присмотреться, то биноминальные коэффициенты — это ни что иное как числа из соответствующего ряда треугольника Паскаля.
Если присмотреться, то биноминальные коэффициенты — это ни что иное как числа из соответствующего ряда треугольника Паскаля. Такая ситуация возникает в случае, если преподаватели должны участвовать в разных конкурсах. При «ручном» решении нам пришлось бы использовать стандартные формулы для комбинаторики, однако проще воспользоваться свойствами треугольника Паскаля.
Такая ситуация возникает в случае, если преподаватели должны участвовать в разных конкурсах. При «ручном» решении нам пришлось бы использовать стандартные формулы для комбинаторики, однако проще воспользоваться свойствами треугольника Паскаля. Используйте наш калькулятор для построения сетки необходимой вам размерности для решения самых разных математических задач.
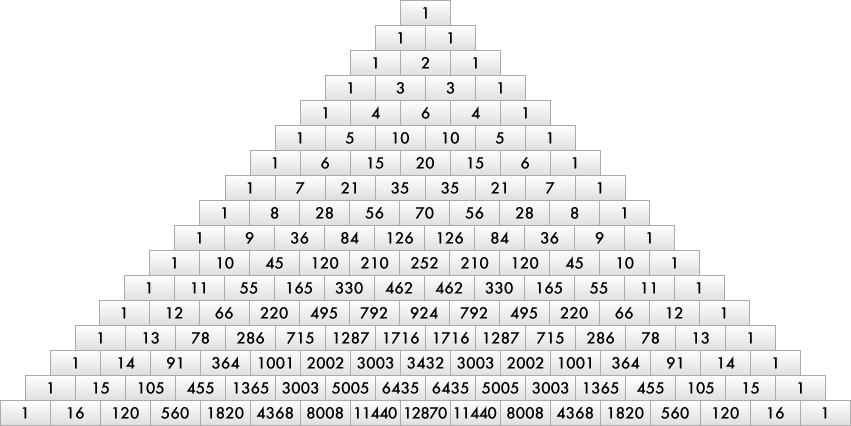
Используйте наш калькулятор для построения сетки необходимой вам размерности для решения самых разных математических задач. , составим следующую Таблицу — Треугольник Паскаля:
, составим следующую Таблицу — Треугольник Паскаля:


 Но прежде чем мы начнем описывать шаблоны треугольников Паскаля, давайте начнем с основ.
Но прежде чем мы начнем описывать шаблоны треугольников Паскаля, давайте начнем с основ.
 У вас есть список из двадцати ваших любимых фильмов, и ваш партнер сказал вам выбрать три, которые ему могут понравиться. Что ж, это лучшие фильмы из существующих , так что ясно, что они понравятся каждому из них, и не так уж важно, какие из них вы выберете. Кроме того, порядок, в котором вы их смотрите, также не имеет значения. Так сколько вариантов?
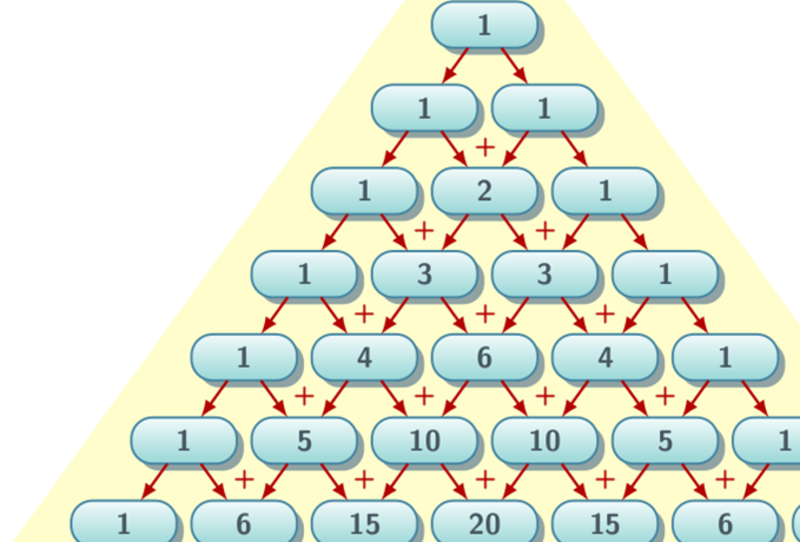
У вас есть список из двадцати ваших любимых фильмов, и ваш партнер сказал вам выбрать три, которые ему могут понравиться. Что ж, это лучшие фильмы из существующих , так что ясно, что они понравятся каждому из них, и не так уж важно, какие из них вы выберете. Кроме того, порядок, в котором вы их смотрите, также не имеет значения. Так сколько вариантов? Однако треугольник часто вводится с помощью гораздо более простого правила . Обратите внимание, что кроме единиц на дальних концах треугольника, каждое из остальных чисел является суммой двух, стоящих прямо над ним.
Однако треугольник часто вводится с помощью гораздо более простого правила . Обратите внимание, что кроме единиц на дальних концах треугольника, каждое из остальных чисел является суммой двух, стоящих прямо над ним.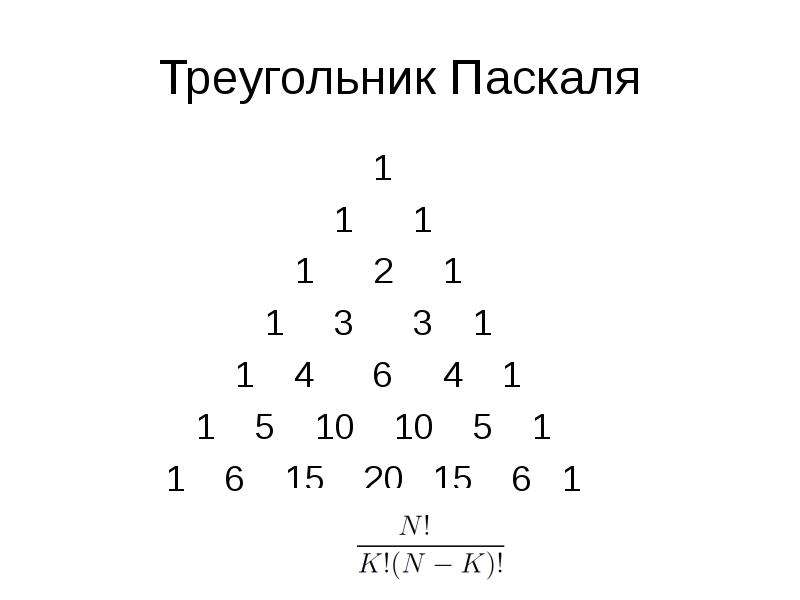 Это снова магия или математика? Что ж, давайте попробуем понять, что здесь происходит.
Это снова магия или математика? Что ж, давайте попробуем понять, что здесь происходит.
 д., и поэтому существует гораздо больше комбинаций, чтобы это произошло.
д., и поэтому существует гораздо больше комбинаций, чтобы это произошло.
















 $$
$$
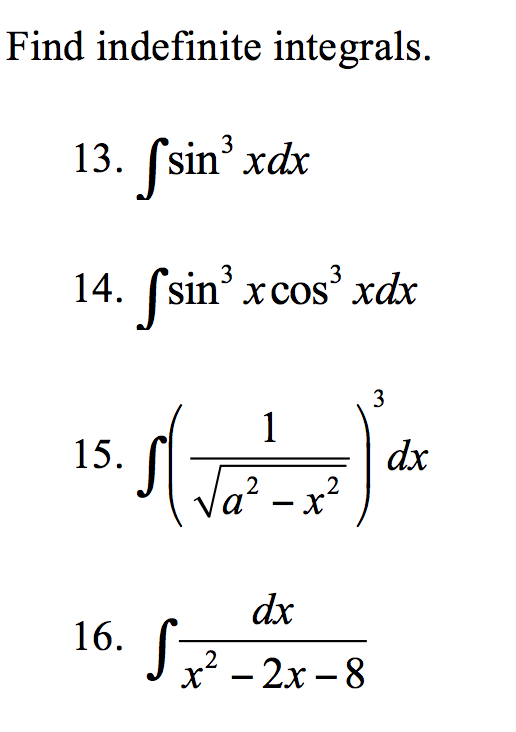 3{x}}+\frac{3\tg{x}}{8\cos{x}}+\frac{3}{8}\ln\left|\tg\left(\frac{\pi}{4}+\frac{x}{2}\right)\right|+C
$$
3{x}}+\frac{3\tg{x}}{8\cos{x}}+\frac{3}{8}\ln\left|\tg\left(\frac{\pi}{4}+\frac{x}{2}\right)\right|+C
$$
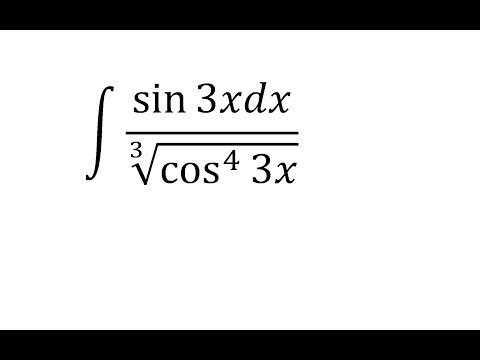 Далее мы докажем, что интегрирование sin 3x дается выражением (-1/3) cos 3x + C, используя формулу sin 3x. Прежде чем доказывать интеграл от sin 3x, выведем интеграл от куба sin x, то есть sin 3 x. Мы будем использовать следующие формулы для доказательства интеграла sin 3 x:
Далее мы докажем, что интегрирование sin 3x дается выражением (-1/3) cos 3x + C, используя формулу sin 3x. Прежде чем доказывать интеграл от sin 3x, выведем интеграл от куба sin x, то есть sin 3 x. Мы будем использовать следующие формулы для доказательства интеграла sin 3 x: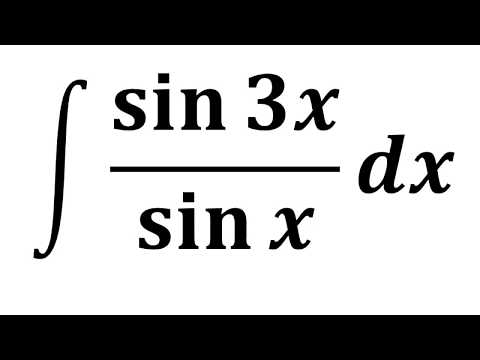 cos 2 x dx
cos 2 x dx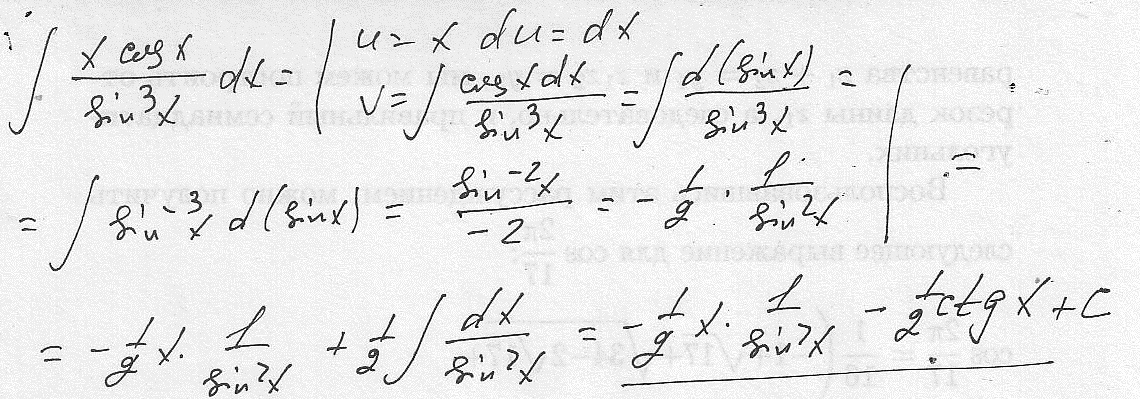 9\frac{\pi}{2}\\&=\left ( -\frac{1}{3}\cos 3\frac{\pi}{2}+C \right )-\left ( -\frac{ 1}{3}\cos 3(0)+C\right )\\&=-\frac{1}{3}\cos \frac{3\pi}{2}+C + \frac{1}{ 3}\cos 0-C\\&= -\frac{1}{3}(0)+\frac{1}{3}(1)\\&=\frac{1}{3}\end{ align}\)
9\frac{\pi}{2}\\&=\left ( -\frac{1}{3}\cos 3\frac{\pi}{2}+C \right )-\left ( -\frac{ 1}{3}\cos 3(0)+C\right )\\&=-\frac{1}{3}\cos \frac{3\pi}{2}+C + \frac{1}{ 3}\cos 0-C\\&= -\frac{1}{3}(0)+\frac{1}{3}(1)\\&=\frac{1}{3}\end{ align}\)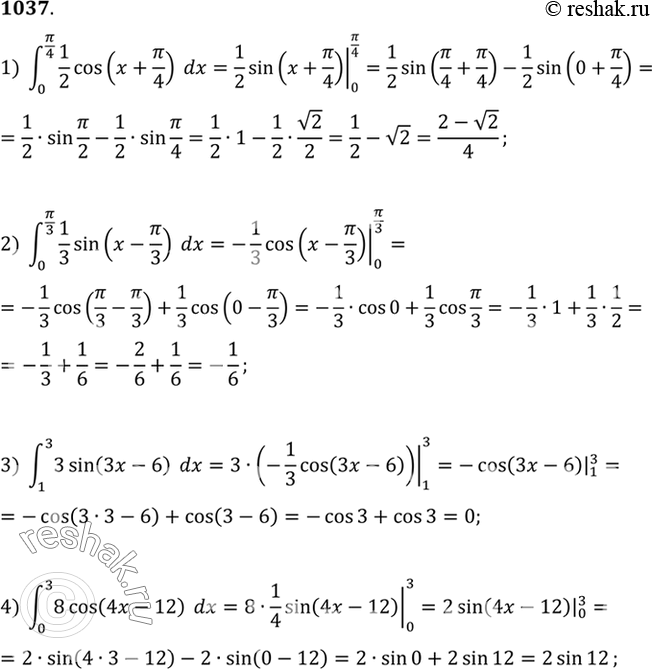

 Основные свойства определенного интеграла40 Определенный интеграл от
Основные свойства определенного интеграла40 Определенный интеграл от Теорема о среднем значении функции
Теорема о среднем значении функции
 5, не 7,5
5, не 7,5
 Поэтому он называется определенным интегралом.
Поэтому он называется определенным интегралом. 
 Чек следующие определенные интегралы:
Чек следующие определенные интегралы:
 symbolab.com › … › Integral Applications
symbolab.com › … › Integral Applications В основном площадь под …
В основном площадь под …
 Например:
Например: — М.: Айрис-пресс, 2008. — 176 с. — (Высшее образование)
— М.: Айрис-пресс, 2008. — 176 с. — (Высшее образование)
 Основными командами являются:
Основными командами являются: Если вам не нужна эта функция (например, вы привыкли устанавливать обновления вручную или используете сетевое соединение с ограничением по трафику), вы можете деактивировать ее следующим образом.
Если вам не нужна эта функция (например, вы привыкли устанавливать обновления вручную или используете сетевое соединение с ограничением по трафику), вы можете деактивировать ее следующим образом. Зависимости разрешены.
================================================================================
Пакет Архитектура Версия Репозиторий Размер
================================================================================
Установка:
midori x86_64 0.5.12-0.2.fc26 fedora 1.3 M
Результат транзакции
================================================================================
Установка 1 Пакет
Объем загрузки: 1.3 M
Объем изменений: 6.2 M
Продолжить? [д/Н]: y
Загрузка пакетов:
midori-0.5.12-0.2.fc26.x86_64.rpm 621 kB/s | 1.3 MB 00:02
--------------------------------------------------------------------------------
Общий размер 277 kB/s | 1.3 MB 00:04
Проверка транзакции
Проверка транзакции успешно завершена.
Идет проверка транзакции
Тест транзакции проведен успешно
Выполнение транзакции
Подготовка : 1/1
Установка : midori-0.
Зависимости разрешены.
================================================================================
Пакет Архитектура Версия Репозиторий Размер
================================================================================
Установка:
midori x86_64 0.5.12-0.2.fc26 fedora 1.3 M
Результат транзакции
================================================================================
Установка 1 Пакет
Объем загрузки: 1.3 M
Объем изменений: 6.2 M
Продолжить? [д/Н]: y
Загрузка пакетов:
midori-0.5.12-0.2.fc26.x86_64.rpm 621 kB/s | 1.3 MB 00:02
--------------------------------------------------------------------------------
Общий размер 277 kB/s | 1.3 MB 00:04
Проверка транзакции
Проверка транзакции успешно завершена.
Идет проверка транзакции
Тест транзакции проведен успешно
Выполнение транзакции
Подготовка : 1/1
Установка : midori-0. 5.12-0.2.fc26.x86_64 1/1
Запуск скриплета: midori-0.5.12-0.2.fc26.x86_64 1/1
Проверка : midori-0.5.12-0.2.fc26.x86_64 1/1
Установлено:
midori.x86_64 0.5.12-0.2.fc26
Выполнено!
5.12-0.2.fc26.x86_64 1/1
Запуск скриплета: midori-0.5.12-0.2.fc26.x86_64 1/1
Проверка : midori-0.5.12-0.2.fc26.x86_64 1/1
Установлено:
midori.x86_64 0.5.12-0.2.fc26
Выполнено! 2 M
Продолжить? [д/Н]: y
Проверка транзакции
Проверка транзакции успешно завершена.
Идет проверка транзакции
Тест транзакции проведен успешно
Выполнение транзакции
Подготовка : 1/1
Удаление : midori-0.5.12-0.2.fc26.x86_64 1/1
Запуск скриплета: midori-0.5.12-0.2.fc26.x86_64 1/1
Проверка : midori-0.5.12-0.2.fc26.x86_64 1/1
Удален:
midori.x86_64 0.5.12-0.2.fc26
Выполнено!
2 M
Продолжить? [д/Н]: y
Проверка транзакции
Проверка транзакции успешно завершена.
Идет проверка транзакции
Тест транзакции проведен успешно
Выполнение транзакции
Подготовка : 1/1
Удаление : midori-0.5.12-0.2.fc26.x86_64 1/1
Запуск скриплета: midori-0.5.12-0.2.fc26.x86_64 1/1
Проверка : midori-0.5.12-0.2.fc26.x86_64 1/1
Удален:
midori.x86_64 0.5.12-0.2.fc26
Выполнено! x86_64 : A lightweight GTK+ web browser
midori.i686 : A lightweight GTK+ web browser
x86_64 : A lightweight GTK+ web browser
midori.i686 : A lightweight GTK+ web browser copyright1}}
copyright1}} Некоторые функции, которые отличают DNF от yum:
Некоторые функции, которые отличают DNF от yum: Тем не менее, обновление dnf предпочтительнее, так как оно работает точно так же, как yum — обновление устаревает.
Тем не менее, обновление dnf предпочтительнее, так как оно работает точно так же, как yum — обновление устаревает.

 timer: Загружает пакеты, но не устанавливает их
timer: Загружает пакеты, но не устанавливает их

 Задание №16
Задание №16 Температура убывает с ростом высоты со средним вертикальным градиентом 0,65°/100 м
Температура убывает с ростом высоты со средним вертикальным градиентом 0,65°/100 м Температура с высотой понижается со средним вертикальным градиентом (0,25—0,3)°/100 м. Основным энергетическим процессом является лучистый теплообмен. Сложные фотохимические процессы с участием свободных радикалов, колебательно возбуждённых молекул и т. д. обусловливают свечение атмосферы.
Температура с высотой понижается со средним вертикальным градиентом (0,25—0,3)°/100 м. Основным энергетическим процессом является лучистый теплообмен. Сложные фотохимические процессы с участием свободных радикалов, колебательно возбуждённых молекул и т. д. обусловливают свечение атмосферы. Температура растёт до высот 200—300 км, где достигает значений порядка 1500 К, после чего остаётся почти постоянной до больших высот. Под действием ультрафиолетовой и рентгеновской солнечной радиации и космического излучения происходит ионизация воздуха («полярные сияния») — основные области ионосферы лежат внутри термосферы. На высотах свыше 300 км преобладает атомарный кислород. Верхний предел термосферы в значительной степени определяется текущей активностью Солнца. В периоды низкой активности происходит заметное уменьшение размеров этого слоя.
Температура растёт до высот 200—300 км, где достигает значений порядка 1500 К, после чего остаётся почти постоянной до больших высот. Под действием ультрафиолетовой и рентгеновской солнечной радиации и космического излучения происходит ионизация воздуха («полярные сияния») — основные области ионосферы лежат внутри термосферы. На высотах свыше 300 км преобладает атомарный кислород. Верхний предел термосферы в значительной степени определяется текущей активностью Солнца. В периоды низкой активности происходит заметное уменьшение размеров этого слоя.


 00
00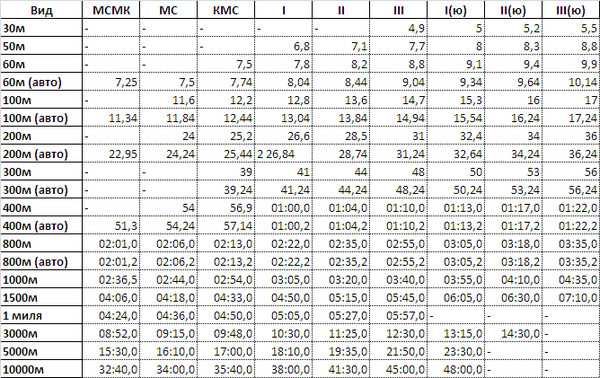 864
864 764
764 024
024 3 km
3 km 2 km
2 km Метр (м) — единица длины, используемая в метрической системе.
Километр (км) — единица длины, используемая в метрической системе.
Метр (м) — единица длины, используемая в метрической системе.
Километр (км) — единица длины, используемая в метрической системе. знаки для более коротких расстояний в Соединенном Королевстве и ноги широко используются в строительстве и недвижимости в Канаде).
знаки для более коротких расстояний в Соединенном Королевстве и ноги широко используются в строительстве и недвижимости в Канаде). В 1960 году метр был определен как 1 650 763,73 длины волны света от определенного перехода в криптоне-86.
В 1983 окончательное определение метра было принято как длина пути, пройденного светом в вакууме за 1/299 792 458 секунды.
В 1960 году метр был определен как 1 650 763,73 длины волны света от определенного перехода в криптоне-86.
В 1983 окончательное определение метра было принято как длина пути, пройденного светом в вакууме за 1/299 792 458 секунды.
 Основными исключениями являются Соединенное Королевство, Либерия, Мьянма и Соединенные Штаты Америки, где миля остается стандартной частью имперской системы.
Основными исключениями являются Соединенное Королевство, Либерия, Мьянма и Соединенные Штаты Америки, где миля остается стандартной частью имперской системы. 35, оставив километр в качестве признанной единицы длины вместо мириаметра.
35, оставив километр в качестве признанной единицы длины вместо мириаметра.