Решение задач и уравнений (продолжение) 10 класс онлайн-подготовка на Ростелеком Лицей
Тема: Преобразование тригонометрических выражений
Урок: Решение задач и уравнений (продолжение)
1. Введение. Определение и пример однородного тригонометрического уравнения второй степени
На уроке рассматривается методика решения однородных тригонометрических уравнений второй и первой степени, решаются задачи и уравнения с применением данной методики.
Определение: уравнение вида
называется однородным тригонометрическим уравнением второй степени относительно функций синус и косинус.
Пример: ,
2. Методика решения однородных тригонометрических уравнений второй степени
· Разделить обе части уравнения на старшую степень одной из функций, например, , рассмотрев оба случая, т. е. когда и когда
е. когда и когда
· Решить полученное квадратное уравнение относительно тригонометрической функции.
3. Решение однородного тригонометрического уравнения второй степени
Решить уравнение:
Решение:
1-й случай.
, т.к.
2-й случай.
Ответ:
4. Решение уравнения, приводимого к однородному тригонометрическому уравнению
Решить уравнение:
Решение: данное уравнение равносильно
Применяя методику решения для полученного однородного уравнения, имеем:
Первая система не имеет решений, вторая дает совокупность двух уравнений
Ответ:
5. Определение и пример однородного тригонометрического уравнения первой степени
Определение: уравнение вида
называется однородным тригонометрическим уравнением первой степени относительно функций синус и косинус.
Пример:
6. Решение примера
Решение примера однородного тригонометрического уравнения первой степени выполняется по аналогичной методике.
1)
Решение системы проиллюстрировано на рисунке 1.
Рис. 1.
2)
Ответ:
7. Однородное тригонометрическое уравнение второй степени в общем виде при a≠0
8. Решение частных случаев однородного тригонометрического уравнения второй степени
1) Решить уравнение:
Решение:
Ответ:
2) Решить уравнение:
Решение:
Ответ:
3) Решить уравнение:
Решение:
1-й способ.
Объединяя решения (см. рис. 2), получим:
Рис. 2.
2.
Ответ:
2-й способ.
Используя формулы понижения степени, получаем:
Ответ:
9. Итог урока
На уроке рассматривались решения однородных уравнений.
На следующем уроке продолжается решение задач и уравнений.
Список рекомендованной литературы
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М. Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.
7. Звавич Л.И., Шляпочник Л.Я., Чинкина Алгебра и начала анализа. 8-11 кл.: Пособие для школ и классов с углубленным изучением математики (дидактические материалы).-М.: Дрофа, 2002.
8. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
9. Карп А.П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
10. Глейзер Г.И. История математики в школе. 9-10 классы (пособие для учителей).-М.: Просвещение, 1983
Дополнительные веб-ресурсы
1. Интернет-портал Mathematics. ru (Источник).
ru (Источник).
2. Портал Естественных Наук (Источник).
3. Интернет-портал exponenta.ru (Источник).
Сделай дома
№№ 23.14(а, б), 23.15(a), 23.17(a) (Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.)
Элективный курс по математике «Практикум по решению задач» 10 класс
Муниципальное казенное общеобразовательное учреждение
Новохоперского муниципального района
Воронежской области
« Ярковская средняя общеобразовательная школа»
«Согласовано» Заместитель директора по УВР __________М.О. Перова «____»____________2019г.
| «Утверждаю» Директор_______________Н.Ю.Хромова Приказ №__от «____»_______2019г.
|
Обсуждена на заседании методического объединения Протокол № ___ от«____»________2019г.
|
|
РАБОЧАЯ ПРОГРАММА
элективного курса
«Практикум по решению задач»
10_ класс,
базовый уровень
Составитель:
учитель математики Токарева Н. В.
В.
с. Ярки
2019 год
1.Пояснительная записка
Рабочая программа элективного курса «Практикум по решению задач» для 10 класса составлена на основе:
1. Федерального компонента государственного стандарта общего образования (от 05.03.2004 года №1089).
2. Программы общеобразовательных учреждений. Алгебра и начала математического анализа, 10-11классы.-сост. Бурмистрова Т.А.- : Просвещение, 2008
3. Учебного плана МКОУ «Ярковская СОШ».
Общая характеристика элективного курса
Основная задача обучения математики в школе – обеспечить прочное и сознательное овладение учащимися системой математических знаний и умений, необходимых в повседневной жизни и трудовой деятельности каждого человека, достаточных для изучения смежных дисциплин и продолжения образования.
Содержание данной программы нацелено на
формирование практических навыков решения математических задач, на развитие у
учащихся алгоритмической культуры. Программа расширяет представления учащихся о
математике как универсальном языке науки, средстве моделирования явлений и
процессов, знакомит с универсальными методами решения алгебраических задач,
способствует развитию логического мышления и математической интуиции.
Программа расширяет представления учащихся о
математике как универсальном языке науки, средстве моделирования явлений и
процессов, знакомит с универсальными методами решения алгебраических задач,
способствует развитию логического мышления и математической интуиции.
В процессе изучения данного элективного курса старшеклассники познакомятся с различными приёмами построения графиков функций; приобретут навыки рационального поиска решения таких задач и выстраивания алгоритмов, а в дальнейшем смогут реализовать полученные знания и умения при подготовке к ЕГЭ, поступлению в вуз и продолжению образования.
Актуальность
данной программы обусловлена ее практической значимостью. Учащиеся могут
применить полученные знания и практический опыт при решении практических задач
из других естественнонаучных дисциплин. Целесообразность введения данного элективного
курса состоит и в том, что содержание курса, форма его организации помогут
школьнику через практические занятия оценить свой потенциал с точки зрения
образовательной перспективы и предоставят ему возможность работать на уровне
повышенных возможностей. Элективный курс «Практикум по решении задач»
позитивно влияет на мотивацию старшеклассника к учению, развивает его учебную
мотивацию по предметам естественно-математического цикла
Элективный курс «Практикум по решении задач»
позитивно влияет на мотивацию старшеклассника к учению, развивает его учебную
мотивацию по предметам естественно-математического цикла
Задания, предлагаемые программой данного элективного курса, носят исследовательский характер и способствуют развитию навыков рационального мышления, способности прогнозирования результатов деятельности.
Разделяется на два отдельных раздела «Алгебра» и «Геометрия». Основным направлением курса является подготовка обучающихся к успешной сдаче экзаменов в форме ЕГЭ.
Обучающиеся не всегда могут самостоятельно повторять и систематизировать весь материал, пройденный за предыдущие года обучения, поэтому испытывают трудности при решении задач. На занятиях этого предмета есть возможность устранить пробелы ученика по тем или иным темам. Учитель оказывает помощь при систематизации материала, готовит правильно оформлять то или иное задание.
Цели и задачи курса:
Основные цели курса:
· оказание индивидуальной, систематической помощи выпускнику при систематизации, обобщении теории курса алгебры, геометрию;
·
создание
условий для развития творческого потенциала при решении задач.
Основные задачи курса:
Обучающие:
· Сформировать умения решать задания повышенной сложности;
· Расширить сферу математических знаний учащихся;
Развивающие:
· развитие умения уметь самостоятельно работать с таблицами и справочной литературой;
· развитие умения составлять алгоритмы решения текстовых и геометрических задач;
· развитие умения решать тригонометрические, показательные и логарифмические уравнения и неравенства;
· развитие умения применять различные методы исследования элементарных функций и построения их графиков;
Воспитательные:
· рассмотреть практическую значимость использования математических знаний в повседневной жизни, а также как прикладного инструмента в будущей профессиональной деятельности;
· создать положительную мотивацию обучения;
·
воспитание
аккуратности, последовательности в действиях, умение чётко выражать свои мысли.
Методы, формы и средства обучения, применяемые педагогические технологии.
Основная форма организации образовательного процесса – классно-урочная
система, а также используются следующие формы работы:
· организация взаимной проверки заданий;
· взаимные задания групп;
Предусматривается применение следующих технологий обучения:
· элементы проблемного обучения
· технологии уровневой дифференциации
· здоровьесберегающие технологии
· ИКТ
Место предмета в учебном плане школы.
Элективный курс «Практикум по решению задач.» рассчитан на 17 часов (1 час в неделю в течение одного полугодия) для работы с учащимися 10 класса.
2. Содержание курса
Тема 1. Уравнения и неравенства
Способы решения различных уравнений
(линейных, квадратных и сводимых к ним, дробно-рациональных). Способы решения
различных неравенств (числовых, линейных, квадратных). Метод интервалов.
Область определения выражения.
Способы решения
различных неравенств (числовых, линейных, квадратных). Метод интервалов.
Область определения выражения.
Тема 2. Текстовые задачи
Задачи на проценты. Задачи на движение, на концентрацию, на смеси и сплавы, на работу, задачи про кредиты и вклады
Тема 3. Формулы тригонометрии
Формулы приведения, сложения, двойных углов и их применение. Применение основных тригонометрических формул к преобразованию выражений.
Тема 4. Степенная функция
Обобщить понятие степенной функцией с действительным показателем, ее свойства и умение строить ее график; знакомство с разными способами решения иррациональных уравнений; обобщение понятия степени числа и корня n-й степени.
Тема 5. Задачи с геометрическим содержанием
Действия с геометрическими фигурами,
координатами и векторами. Планиметрические задачи на нахождение геометрических
величин (длин, углов, площадей).
3. Учебно-тематический план
№ п/п | Название темы | Количество часов |
1 | Уравнения и неравенства | 3 |
2 | Текстовые задачи | 4 |
3 | Формулы тригонометрии | 3 |
4 | Степенная функция | 3 |
5 | Задачи с геометрическим содержанием | 3 |
6 | Итоговый контроль | 1 |
ВСЕГО: | 17 ч | |
4. Требования к уровню подготовки обучающихся
Требования к уровню подготовки обучающихся
В результате изучения элективного курса «Практикум по решению задач» обучающиеся должны:
ü уметь решать задания различной сложности;
ü уметь самостоятельно работать с таблицами и справочной литературой;
ü уметь составлять алгоритмы решения типичных задач;
ü уметь решать тригонометрические, показательные и логарифмические уравнения и неравенства;
ü знать методы исследования элементарных функций
ü знать, как используются математические формулы, примеры их применения для решения математических и практических задач;
ü знать, как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
ü уметь использовать математические знания в повседневной жизни, а также как прикладного инструмента в будущей профессиональной деятельности.
5. Учебно-методическое обеспечение:
- Учебно-наглядные пособия
- Компьютер
- Мультимедийный проектор
- Интерактивная доска
6. Список
литературы
Список
литературы
Учебно-методический комплект учителя:
1. В.В. Вавилов, И.И. Мельников, С.Н. Олехник, П.И. Пасиченко «Задачи по математике. Уравнения и неравенства». М., 1987.
2. М.Л. Галицкий, A.M. Гольдман, Л.И. Звавич «Сборник задач по алгебре». М, 1992.
3. Газета «Математика» (приложение к газете «Первое Сентября»). № 12, 1996, № 7, 1998, № 36, № 41, 2002.
4. И.Н. Гельфанд «Функции и графики (основные приёмы)». М., 1968.
5. С.И. Колесникова «Подготовка к ЕГЭ. Математика. Решение сложных задач ЕГЭ». М.,2005.
6. Под редакцией А.И. Прилепко «Сборник задач по математике для поступающих в вузы». М., 1989.
7. СВ. Дворянинов, С.А. Письменная «Функции, графики, задачи с параметром». Самара, 1998.
8. О.Ю. Черкасов, А.Г. Якушев «Математика: интенсивный курс подготовки к экзамену». М., 2006.
9.
М. И. Шабунин «Пособие по математике для
поступающих в вузы». М., 1999.
И. Шабунин «Пособие по математике для
поступающих в вузы». М., 1999.
Учебно-методический комплект ученика:
7. Под редакцией А.Г. Мордковича «Алгебра и начала анализа.». 10 -11 кл. в 1,2 ч. М., 2009.
8. Под редакцией Ф.Ф.Лысенко Математика ЕГЭ — 2010. “Учебно-тренировочные тесты”. Легион, Ростов –на-Дону, 2010.
9. С.В. Богатырёв, Ю.Н. Неценко, Т.П. Шаповалова Тренировочные материалы для подготовки к ЕГЭ по математике. Самара ГО СИПКРО, 2009.
10. Б.М. Ивлев, A.M. Абрамов, Ю.П. Дудницын, С.И. Шварцбурд «Задачи повышенной трудности по алгебре и началам анализа». М., 1990.
11. М.Л. Галицкий, A.M. Гольдман, Л.И. Звавич «Сборник задач по алгебре». М, 1992.
Приложение
Календарно-тематическое планирование элективного курса
«Практикум по решению задач» для 10 класса
№ п/п | Содержание учебного материала | Кол-во часов | Дата проведения | |
по плану | факт | |||
| Тема 1.
|
|
| |
1 | Способы решения линейных, квадратных и дробно-рациональных уравнений. | 1 | 06.09.19 |
|
2 | Способы решения линейных, квадратных неравенств. Метод интервалов. | 1 | 13.09.19 |
|
3 | Способы решения систем уравнений и неравенств. | 1 | 20. |
|
| Тема 2. Текстовые задачи (4 часа) |
|
| |
4 | Решение задач на «проценты», на «концентрацию», на «смеси и сплавы». | 1 | 27.09.19 |
|
5 | Задачи на «движение», на «работу». | 1 | 04.10.19 |
|
6 | Решение комбинаторных задач. | 1 | 11.10.19 |
|
7 | Решение экономических задач | 1 | 18.10.19 |
|
| Тема 3. Формулы тригонометрии (3 часа)
|
|
| |
8 | Основные тригонометрические формулы и их применение. | 1 | 25.10.19 |
|
9 | Преобразование
выражений с помощью формул тригонометрии. | 1 | 01.11.19 |
|
10 | Применение основных тригонометрических формул к преобразованию выражений. | 1 | 15.11.19 |
|
| Тема 4. Степенная функция (3 часа)
|
|
| |
11 | Степенная функция, ее свойства и график. | 1 | 22.11.19 |
|
12 | Преобразование
степенных и иррациональных выражений. | 1 | 29.11.19 |
|
13 | Решение иррациональных уравнений. | 1 | 06.12.19 |
|
| Тема 5. Задачи с геометрическим содержанием (3 часа)
|
|
| |
14 | Действия с геометрическими фигурами, координатами и векторами. | 1 | 13.12.19 |
|
15 | Планиметрические
задачи на нахождение геометрических величин (длин, углов, площадей). | 1 | 20.12.19 |
|
16 | Простейшие стереометрические задачи на нахождение площадей поверхностей многогранников. | 1 | 27.12.19 |
|
17 | Резерв | 1 |
|
|
ИТОГО: | 17 |
|
| |
Вопросы и решения по математике для 10 класса
The Smarter Balanced Assessment Consortium (SBAC) — это стандартизированный тест, который включает в себя ряд вопросов, улучшенных новыми технологиями.
Некоторые из них: Множественный выбор — один правильный ответ, Множественный выбор — несколько правильных ответов, Сопоставление таблиц, Перетаскивание, Горячий текст, Заполнение таблицы, Графики, Уравнения / числа, Расширенный построенный ответ, Короткий ответ и многое другое. .
Эта страница содержит несколько примеров вопросов, а также ссылки на практические тесты по математике для 10 класса, которые дают вам представление о вопросах, которые ваши учащиеся, скорее всего, увидят в тесте. После каждого примерного вопроса следует объяснение ответа. Объяснение включает в себя важные аспекты задачи, которые вам, возможно, потребуется рассмотреть для навыков, процессов и информации, которые должны знать ваши студенты.
Сфера: 10 класс >> Число и количество – Система реальных чисел
Пример вопроса: Оценка 9 150/300
- 18
- 9
- 3
- 81
Объяснение ответа: 9 150/300 = 9 1/2 = квадратный корень из 9 = 3. В задаче с рациональным показателем степени числитель указывает степень, а знаменатель — корень. Однако в этой задаче показатель степени можно уменьшить, поэтому сначала мы должны уменьшить его. Показатель степени 150/300 = 1/2. Итак, проблема становится 9в 1/2 степени. Знаменатель равен 2, поэтому мы извлекаем квадратный корень из 9, что равно 3. Числитель равен 1, поэтому мы возводим 3 в первую степень, и ответ равен 3.
В задаче с рациональным показателем степени числитель указывает степень, а знаменатель — корень. Однако в этой задаче показатель степени можно уменьшить, поэтому сначала мы должны уменьшить его. Показатель степени 150/300 = 1/2. Итак, проблема становится 9в 1/2 степени. Знаменатель равен 2, поэтому мы извлекаем квадратный корень из 9, что равно 3. Числитель равен 1, поэтому мы возводим 3 в первую степень, и ответ равен 3.
Стандарты: HSN.RN.A.1
Щелкните здесь, чтобы попрактиковаться: Число и количество – система действительных чисел Вопросы по математике 10 класса
Область: 10 класс >> Число и количество – количества
Пример вопроса: Перепишите x 1/2 в радикальной форме.
- √х
- √x 2
- 1/√x
- -√x
Объяснение ответа: В задаче с рациональным показателем степени числитель указывает степень, а знаменатель — корень. Поскольку проблема в том, x 1/2 , знаменатель равен 2, что означает, что мы должны извлечь квадратный корень, а числитель равен 1, поэтому мы должны возвести это в первую степень, иначе не будет показателя степени, поскольку показатель степени 1 редко встречается. использовал. Таким образом, ответ представляет собой квадратный корень из x, записанный как √x.
использовал. Таким образом, ответ представляет собой квадратный корень из x, записанный как √x.
. Стандарты: HSN.RN.A.1. Вопрос: Полностью упростить i(7−i)
- 7i−i 2
- 1+7i
- 6и
- −1+7i
Объяснение ответа: i(7−i)=i*7−i*i=7i−i 2 =7i−(−1)=7i+1=1+7i
Начните с использования метода распределения. Теперь упростим -i 2 =1 по определению. Теперь переставьте и поставьте действительную часть первой, а мнимую последней, чтобы она выглядела как a+bi.
Стандарты: HSN.CN.A.2
Нажмите здесь, чтобы попрактиковаться: 10 класс.
Пример вопроса: Вектор в стандартной форме имеет компоненты. Что такое начальная точка?
- (0, 0)
- (3, 10)
- (6, 20)
- Недостаточно информации
Ответ Объяснение: Поскольку вектор находится в стандартном положении, мы знаем, что начальная точка (0, 0) или начало координат.
Стандарты: HSN.VM.A.2
Нажмите здесь, чтобы потренироваться: Число и количество – векторные и матричные величины0012
Предмет: 10 класс >> Алгебра – Видение структуры в выражениях
Пример вопроса: Какое выражение эквивалентно 9x 2 – 16y 2 ?
- (3x – 4 года) (3x – 4 года)
- (3x + 4г) (3x + 4г)
- (3x + 4 года) (3x – 4 года)
- (3x – 4 года) 2
Объяснение ответа: Студент должен распознать выражение как разность двух полных квадратов
Стандарты: HSA.SSE.A.2
Нажмите здесь, чтобы попрактиковаться: Алгебра – Видение структуры в выражениях Вопросы по математике для 10 класса
Область: 10 класс >> Алгебра – арифметика с полиномами и рациональными выражениями
Пример вопроса: Вычислить f(x)=−a 3 +6a−7 при a = – 1 и указать остаток.
- -14
- -12
- 14
- 12
Объяснение ответа: студент должен подставить – 1 в функцию следующим образом −(−1) 3 +6(−1)−7=−12 и найти значение, чтобы получить остаток
Стандарты: HSA. APR.B. 2
APR.B. 2
Щелкните здесь для практики: Алгебра – арифметика с полиномами и рациональными выражениями Вопросы для 10 класса Математика
Предмет: 10 класс >> Алгебра – составление уравнений
Пример вопроса: Соотношение персонала и гостей в гала было 3 на 5. Всего в бальном зале было 576 человек. Сколько гостей было на гала?
- 276
- 300
- 360
- 216
Объяснение ответа: Установите пропорцию гостей к общему количеству людей, 8/5 = x/576. Решите перекрестным умножением. 8x = 2880. Разделите обе части на 8. Таким образом, x = 360.
. Стандарты: HSA.CED.A.3.0009
Пример вопроса: Решите квадратное уравнение x 2 +10x=−25.
- -10
- 10
- 5
- -5
Объяснение ответа: Эту задачу можно легко решить, перестроив уравнение так, чтобы оно решалось относительно нуля, а затем разложить на множители, как показано:
x 2 +10x=−25 25=0
(x+5)(x+5)=0
Поскольку оба коэффициента абсолютно одинаковы, у вас будет только одно решение этой проблемы.
x+5=0
x=−5
Стандарты: HSA.REI.B.4
Щелкните здесь, чтобы попрактиковаться: Алгебра – Рассуждения с помощью уравнений и неравенств. Вопросы для 10 класса по математике
83 Область знаний : 10 класс >> Функции – интерпретация функций
Пример вопроса: Какой график может представлять график функции f(x)=sin(x)?
Объяснение ответа: График функции sin всегда выглядит как волна. Функция sin может быть только D.
Стандарты: HSF.IF.C.7
Щелкните здесь, чтобы попрактиковаться: Функции – Интерпретация функций Вопросы для 10 класса по математике
Домен: 10 класс > > Функции – построение функций
Пример вопроса: Опишите, как график g(x)=x 3 – 5 может быть получен сдвигом f(x) = x 3 + 2.
- Сдвиг вправо 7 единиц
- Сдвиг влево 7 единиц
- Сдвиг вверх на 7 единиц
- Сдвиг вниз на 7 единиц
Объяснение ответа: Единственное, что изменилось в двух уравнениях, это точка пересечения с осью y, которая управляет сдвигом по вертикали (вверх или вниз). Чтобы получить график g(x), сдвинув график f(x), вы должны сдвинуть f(x) вниз на 7 единиц, чтобы измениться с +2 на -5.
Чтобы получить график g(x), сдвинув график f(x), вы должны сдвинуть f(x) вниз на 7 единиц, чтобы измениться с +2 на -5.
Стандарты: HSF.BF.B.3
Нажмите здесь, чтобы потренироваться: Функции – Построение функций Вопросы для 10 класса Математика
Домен: 10 класс >> Функции – интерпретация функций
Пример вопроса: Решите 3 x =12, используя логарифмическую форму.
- х = ln12/ln3
- х = пер(4)
- х = пер(9)
- Ни один из этих
Объяснение ответа:
Решите с использованием журналов следующим образом:
3 x =12
x=log(основание 3) 12
x=ln12/ln3
02 Щелкните здесь, чтобы попрактиковаться: Функции — интерпретация функций Вопросы для 10 класса по математике
Область: 10 класс >> Функции — тригонометрические функции
Пример вопроса: В единичном круге видно, что tan(5π/4) =1 . Каково значение cos(5π/4)?
Каково значение cos(5π/4)?
- −√2/2
- не определено
- √2/2
- -1
Объяснение ответа:
Тригонометрическое отношение косинуса равно отношению длины прилежащей стороны к длине гипотенузы. Длина смежной стороны — это значение x в точке на единичной окружности. Гипотенуза — это радиус единичной окружности, поэтому гипотенуза равна 1. Таким образом, значение отношения косинуса любого угла в единичной окружности — это значение x точки на единичной окружности, соответствующей этому углу. Тригонометрическое отношение тангенса равно длине противолежащей стороны, деленной на длину прилежащей стороны. Длина противоположной стороны — это значение y в точке единичной окружности, а длина соседней стороны — это значение x в точке единичной окружности. Гипотенуза — это радиус единичной окружности, поэтому гипотенуза равна 1. Таким образом, значение отношения тангенсов любого угла в единичной окружности — это отношение yx от точки на единичной окружности, соответствующей этому углу. В этом вопросе тангенс(5π/4)=1. Это отношение берется из точки (−2/√2, −2/√2), которая соответствует углу величиной 5π/4 радиана. Таким образом, используя приведенную выше информацию, значение cos(5π4) совпадает со значением x в точке (−2/√2, −2/√2). Следовательно, значение cos(5π/4) =-2/√2.
В этом вопросе тангенс(5π/4)=1. Это отношение берется из точки (−2/√2, −2/√2), которая соответствует углу величиной 5π/4 радиана. Таким образом, используя приведенную выше информацию, значение cos(5π4) совпадает со значением x в точке (−2/√2, −2/√2). Следовательно, значение cos(5π/4) =-2/√2.
. Стандарты: HSF.TF.A.2. будут координатами точки S после применения следующего правила: (x+3, y -2)?
- (1, -4)
- (-2, -2)
- (2, -2)
- (3, -2)
Объяснение ответа: Ответ: B
Объяснение: Данное правило преобразования заключается в перемещении точки на 3 единицы вправо и на 2 единицы вниз, как показано на следующей диаграмме:
Стандарты:
Нажмите здесь, чтобы попрактиковаться: Геометрия – Вопросы на соответствие для 10 класса Математика
Область: 10 класс >> Геометрия – подобие, прямоугольные треугольники и тригонометрия
Пример вопроса: По какому свойству углы BAX и TSX могут быть признаны равными?
- Соответствующие углы
- Вертикальные уголки
- Альтернативные внутренние углы
- Равные углы
Объяснение ответа: Ответ: A
Несмотря на то, что они равны, вопрос задает свойство. Поскольку они находятся в соответствующих местах с поперечной (AX), правильный ответ: A
Поскольку они находятся в соответствующих местах с поперечной (AX), правильный ответ: A
Стандарты: HSG.SRT.A.3
Нажмите здесь, чтобы попрактиковаться: Геометрия — подобие, прямоугольные треугольники и тригонометрия Вопросы для оценки 10 Математика
Домен: 10 класс >> Геометрия – Окружности
Пример вопроса: Каково правило перевода и масштабный коэффициент расширения, когда Окружность F→Окружность F′ ?
- (x,y)→1/4(x,y+10)
- (х, у)→4(х, у+10)
- (х, у)→1/4(х+10,у)
- (х, у) → 1/4 (х, у-10)
Ответ Объяснение: Исходный круг F имеет центр в точке (−5,−6) с радиусом 4 единицы. Перемещенный/расширенный круг F’ имеет центр в точке (−5,4) с радиусом 1 единица. Это означает, что центр был перемещен вверх на 10 единиц. В качестве преобразования этот перевод записывается как (x,y)→(x,y+10). Окружность F также расширилась в 1/4 раза, потому что радиус был уменьшен с 4 единиц до 1 единицы. В качестве преобразования это расширение записывается как (x, y) → 1/4 (x, y). Соединяя перевод и расширение вместе, правило (x, y) → 1/4 (x, y + 10).
В качестве преобразования это расширение записывается как (x, y) → 1/4 (x, y). Соединяя перевод и расширение вместе, правило (x, y) → 1/4 (x, y + 10).
Стандарты:
Щелкните здесь, чтобы попрактиковаться: Геометрия – круги Вопросы для 10 класса Математика
Область: 10 класс >> Геометрия – Выражение геометрических свойств с помощью уравнений
Пример1 Вопрос 2: 900 Число 1 линия на рисунке ниже делит отрезок EF на две части с отношением их длин 3:1?
- -5
- -3
- -2
- -1
Объяснение ответа: На числовой прямой на рисунке точка E находится в точке -7, а точка F в точке 1. Таким образом, длина отрезка EF равна 8. Разделить отрезок на две части с отношением их длин 3:1, измените соотношение на 3x:1x, чтобы разрешить изменение положения на числовой прямой. Затем установите сумму двух частей равной 8 и найдите x. 3x+1x=8;4x=8;x=2. Теперь, когда вы знаете, что x=2, найдите 3x, равное 6. Найдите значение на числовой прямой, прибавив 6 к позиции точки E. −7 +6=-1. Значение на числовой прямой, которая делит отрезок EF в отношении 3:1, равно -1.
Найдите значение на числовой прямой, прибавив 6 к позиции точки E. −7 +6=-1. Значение на числовой прямой, которая делит отрезок EF в отношении 3:1, равно -1.
Стандарты: HSG.GPE.B.6
Нажмите здесь, чтобы попрактиковаться: Геометрия – Выражение геометрических свойств с помощью уравнений Пример вопроса: Каков объем показанной ниже призмы?
- 1350 см 3
- 1350 см
- 675 см 3
- 675 см
Объяснение ответа: Используйте формулу объема пирамиды:
V=1/2.a.c.h
В этом случае длина 15см, длина основания 10см, высота 9см. Следовательно:
V=1/2.15.10.9=675 см 3
Стандарты: HSG.GMD.A.3
Нажмите здесь, чтобы попрактиковаться: Геометрия – геометрические измерения и размеры Вопросы для 901 класса
МатематикаДомен: 10 класс >> Геометрия – Моделирование с помощью геометрии
Пример вопроса: Компания отправляет сферические пресс-папье в кубических коробках. Окружность пресс-папье 9π см. Если коробка соответствует сфере точно так, что стороны сферы касаются коробки, каков объем наименьшей коробки, которую компания может использовать для доставки?
Окружность пресс-папье 9π см. Если коробка соответствует сфере точно так, что стороны сферы касаются коробки, каков объем наименьшей коробки, которую компания может использовать для доставки?
- 81 см 3
- 81 см 3
- 729 см 3
- 1009 π см 3
Объяснение ответа:
Обратите внимание, что диаметр сферы будет таким же, как сторона куба. Используя значение окружности, можно определить диаметр пресс-папье.
C = πd9π
см = πd9
см = d
Так как диаметр равен сторонам {\dots}
V=s 3
V=(9 см) 3
V=729 см 3
Стандарты: HSG.MG.A.3
Нажмите здесь для практики: Геометрия – Моделирование с помощью геометрии Вопросы для 10 класса Математика
Область: 10 класс >> Статистика и вероятность – интерпретация категориальных и количественных данных
Пример вопроса: Какой тип функции, представленной ниже, показывает корреляцию между двумя переменными?
- Линейный
- Экспоненциальный
- Квадратичный
- Полярный
Ответ Объяснение: Обратите внимание, что тренд графика (красный) между точками данных образует линию.
Стандарты: HSS.ID.A.4
Нажмите здесь, чтобы попрактиковаться: Статистика и вероятность – интерпретация категориальных и количественных данных. & Обоснование выводов
Пример вопроса: В исследовательском проекте о поведении домашних животных была выбрана случайная выборка из 400 кошек. Исследование показало, что 60% кошек предпочитают спать внутри дома. Курица была любимой едой для 35% этих кошек. Исследование также показало, что у 85% кошек, которые предпочитали спать вне дома, было другое любимое блюдо. Сколько кошек в выборке больше всего любили курицу и предпочитали спать внутри?
- 84
- 56
- 160
- 156
Объяснение ответа: Если в выборке 400 кошек и 60% кошек предпочитают спать внутри, то 400.0.60=240 кошек предпочитают спать внутри, а 160 кошек предпочитают спать снаружи. Далее, если любимым блюдом 35% тех кошек, которые предпочли спать внутри, была курица, то 240,0,35=84 кошки в выборке предпочли спать внутри и имели курицу в качестве своего любимого блюда.
Стандарты: HSS.IC.B.6
Нажмите здесь, чтобы попрактиковаться: Статистика и вероятность – выводы и обоснование выводов Правила вероятности
Пример вопроса: В студенческом совете есть одна предстоящая вакансия. Школа проводит выборы и имеет восемь равновероятных кандидатов. Класс статистики AP хочет смоделировать результаты выборов, поэтому учащиеся должны выбрать подходящий метод моделирования. Они намерены провести испытания с симуляцией. Какой из этих методов будет наиболее подходящим?
- Вращение колеса с восемью равными ячейками
- Подбросьте монету восемь раз за каждые выборы
- Бросить кости
- Бросьте четыре кубика
Объяснение ответа: В вопросе говорится, что существует восемь равновероятных кандидатов. Это означает, что каждый кандидат имеет одинаковые шансы на победу на выборах. Только вращающееся колесо с восемью равными ячейками может имитировать эту ситуацию, потому что у колеса есть равные шансы приземлиться на каждой ячейке.
Стандарты: HSS.IC.A.1
Нажмите здесь, чтобы попрактиковаться: Статистика и вероятность – Условная вероятность и правила вероятности Вопросы для 10 класса по математике Использование вероятности для принятия решений
Пример вопроса:
Используя приведенную выше диаграмму Венна, найдите P(C или E).
- 1/3
- 7/24
- 5/24
- Ни один из этих
Ответ Объяснение: Просто подсчитайте точки данных в кругах C и E. Их 8 из 24 общих точек данных, и, уменьшая, мы получаем 8/24=1/3.
Стандарты: HSS.CP.B.7
Нажмите здесь, чтобы попрактиковаться: Статистика и вероятность – Использование вероятности для принятия решений Вопросы для 10 класса по математике принимать решения
Пример вопроса: Статистик, работающий в Sweet Shop USA, получил задание выяснить, какова вероятность того, что аппарат для помадки выйдет из строя и в процессе работы будет испорчена целая партия помадки. Каждая неисправность машины обходится компании в 250 долларов. Статистики подсчитали, что вероятность того, что 1 из 20 партий помадки будет потеряна из-за неисправности машины, составляет 1. Какова ожидаемая величина этих убытков за один месяц, если компания производит 20 партий помадки каждый день?
Каждая неисправность машины обходится компании в 250 долларов. Статистики подсчитали, что вероятность того, что 1 из 20 партий помадки будет потеряна из-за неисправности машины, составляет 1. Какова ожидаемая величина этих убытков за один месяц, если компания производит 20 партий помадки каждый день?
- 3750 долларов
- 150 000 долларов США
- 7500 $
- $375
Объяснение ответа: Поскольку в большинстве месяцев 30 дней, будем считать, что в месяце 30 дней. Мы можем использовать E(x)=x1p1+x2p2+…+xipi или просто рассчитать следующим образом:
E(X)=0,05*250*30=$375
здесь, чтобы попрактиковаться: Статистика и вероятность – использование вероятности для принятия решений. Вопросы для 10 класса по математике
Десятый класс (10 класс) Стратегии решения проблем Вопросы для тестов и рабочих листов
Из них можно создавать печатные тесты и рабочие листы. Стратегии решения проблем для 10 класса вопроса!
Выберите один или несколько вопросов, установив флажки над каждым вопросом. Затем нажмите кнопку добавить выбранные вопросы в тест , прежде чем перейти на другую страницу.
Затем нажмите кнопку добавить выбранные вопросы в тест , прежде чем перейти на другую страницу.
Кейт купила в магазине манго. Она также купила некоторые другие продукты. Если ее общий счет составил 22 доллара, и она знает, что купила около 3 фунтов манго, что из следующего потребуется, чтобы узнать, сколько манго стоит фунт?
- Стоимость других ее продуктов.
- Количество манго, которое она купила.
- Вес каждого манго.
- Стоимость каждого манго.

[математика](3 «фунт»)/1 хх (16 «унций») / (1 «фунт») хх (28,3 «г»)/(1 «унция») = 1358,4 «г» «[/math]
Математически, почему 3 можно умножить на множители [математика] (16 \»oz») / (1 \»lb»)[/math] и [математика](28,3 \»g») /(1 \ «унция») ?[/math]
- Поскольку это размерный анализ, обычные правила математики не применяются.
- Поскольку необходимые единицы сокращаются, проблем нет.
- Потому что каждый из этих множителей равен единице (числитель и знаменатель равны, но в разных единицах).

- По мультипликативному свойству равенства.
: Используйте анализ размерностей, чтобы определить, сколько минут в году. При необходимости округлить до ближайшей минуты.
- 525 600 минут
- 21 900 минут
- 8760 минут
- 913 минут
Транспортная компания берет зарядку в размере 65 долларов в час плюс плата, которая зависит от расстояния между местами перемещения объектов (35 долларов за каждую милю). Какие переменные было бы полезно определить, если бы нужно было создать выражение, определяющее общую стоимость переезда?
Какие переменные было бы полезно определить, если бы нужно было создать выражение, определяющее общую стоимость переезда?
- Одна переменная: C, стоимость перемещения.
- Одна переменная: t для количества времени.
- Две переменные: C для общей стоимости и t для количества времени.
- Две переменные: t для количества времени и d для пройденного расстояния.
Потолок комнаты Кары протекает. Она ставит ведро под капельницу. Через час воды около полулитра. Она возвращается еще через 3 часа, и там около 2 литров воды. Если она хочет определить, сколько воды будет через 12 часов, какое количество или количества ей нужно будет определить?
Она ставит ведро под капельницу. Через час воды около полулитра. Она возвращается еще через 3 часа, и там около 2 литров воды. Если она хочет определить, сколько воды будет через 12 часов, какое количество или количества ей нужно будет определить?
- Скорость прилива воды, литров в час.
- Количество воды в ведре, литров.
- Количество воды в ведре в литрах и количество прошедшего времени в часах.
- Размер ведра в литрах и скорость капель в литрах в час.
Карл сажает огород, но ему нужно построить вокруг него забор, чтобы олени не могли съесть растения. У него есть 30-метровое ограждение, и он хочет оградить территорию площадью 50 квадратных метров, чтобы разместить там все растения, которые он хочет выращивать. Если бы Карлу нужно было создать математическую модель, чтобы помочь ему понять, как правильно построить ограждение, какие переменные было бы полезно создать?
У него есть 30-метровое ограждение, и он хочет оградить территорию площадью 50 квадратных метров, чтобы разместить там все растения, которые он хочет выращивать. Если бы Карлу нужно было создать математическую модель, чтобы помочь ему понять, как правильно построить ограждение, какие переменные было бы полезно создать?
- Одна переменная, длина стороны сада.
- Одна переменная, общий периметр сада.
- Две переменные, длина и ширина сада.
- Две переменные: количество забора, которое у него есть, и площадь сада.
Роб пишет контрольную по физике. Для одной из задач ему нужна формула гравитационной силы для силы притяжения между двумя объектами. Он не уверен, что правильно его помнит. Он считает, что это 93[/математика].
Для одной из задач ему нужна формула гравитационной силы для силы притяжения между двумя объектами. Он не уверен, что правильно его помнит. Он считает, что это 93[/математика].
Аарон — тренер по хоккею в старшей школе для мальчиков, и в этом году он проводит пробы для хоккейной команды. Он надеется разработать модель, которая поможет ему определить, какие игроки лучше всего подходят для команды. Какие из следующих переменных будут важны для этой модели? Выберите все подходящие.
- Хоккейное мастерство.
- Количество занятий, которые посещает студент.
- Какие фильмы он любит.

- Намерен ли студент поступать в университет после окончания средней школы.
Мишель — полицейский, пытающийся смоделировать схемы преступности в определенном районе. Она хочет знать, когда обычно совершаются преступления и какие виды преступной деятельности наиболее распространены. Она надеется использовать это, чтобы лучше предсказать, как охранять этот район. Какие из следующих величин было бы важно включить в эту модель? Выберите все подходящие.
- Количество сделанных звонков до 9-1-1 из этого района.
- При звонках в службу 9-1-1 из этого района.

- Имена людей, арестованных в этом районе.
- Криминальная история людей, арестованных в этом районе.
Колина попросили создать математическую модель популяции пингвинов на отдаленном острове. Он хочет иметь возможность предсказывать рост колонии пингвинов. Он решает, что важные переменные и величины, которые следует учитывать в модели, включают: доступность пищи, присутствие хищников, текущее количество пингвинов и исторические темпы роста популяции пингвинов. Верен ли список Колина? Почему или почему нет?
- Да, это правильная модель, и нет более важных факторов для рассмотрения.

- Нет, эта модель не учитывает многие важные переменные, такие как климат, водные течения, болезни и многие другие.
- Нет, важны только текущее количество пингвинов и исторические темпы роста популяции. Все остальные факторы просто усложняют проблему.
- Ни правильный, ни неправильный. Любая проблема реального мира может быть смоделирована несколькими способами и с разной степенью сложности.
Мика и двое его друзей отправляются в путешествие из Хьюстона, штат Техас, в Сент-Луис, штат Иллинойс, что составляет около 778 миль. Автомобиль, на котором они ездят, расходует около 26,4 миль на галлон, а стоимость бензина составляет около 2,50 долларов за галлон. Они будут делить расходы поровну, какова стоимость поездки на человека (при условии, что газ является единственной стоимостью). Используйте анализ размерностей, чтобы выбрать приведенное ниже выражение, которое правильно дает стоимость этой поездки на человека.
Автомобиль, на котором они ездят, расходует около 26,4 миль на галлон, а стоимость бензина составляет около 2,50 долларов за галлон. Они будут делить расходы поровну, какова стоимость поездки на человека (при условии, что газ является единственной стоимостью). Используйте анализ размерностей, чтобы выбрать приведенное ниже выражение, которое правильно дает стоимость этой поездки на человека.
- [математика]3 хх 778 хх 26,4 хх 2,5[/математика]
- [математика]1/3 хх 778 хх 26,4 хх 2,5[/математика]
- [математика]1/3 хх 778 хх 1/26,4 хх 2,5[/математика]
- [математика]1/3 хх 778 хх 1/26,4 хх 1/2,5[/математика]
Анжела каждый год продает выпечку на летнем рынке. Двумя основными хлебобулочными изделиями являются яблочные пироги и кексы с шоколадной карамелью. К сожалению, она не ведет очень точных записей и не может точно вспомнить, по какой цене продала каждую из них в прошлом году. Она помнит, что однажды продала 50 кексов и 30 оборотов и заработала около 135 долларов. В другой день она продала 40 кексов и 40 оборотов и заработала 140 долларов. Если бы ей нужно было создать модель для определения того, по какой цене она продала каждое выпечное изделие, какие переменные было бы целесообразно создать?
Двумя основными хлебобулочными изделиями являются яблочные пироги и кексы с шоколадной карамелью. К сожалению, она не ведет очень точных записей и не может точно вспомнить, по какой цене продала каждую из них в прошлом году. Она помнит, что однажды продала 50 кексов и 30 оборотов и заработала около 135 долларов. В другой день она продала 40 кексов и 40 оборотов и заработала 140 долларов. Если бы ей нужно было создать модель для определения того, по какой цене она продала каждое выпечное изделие, какие переменные было бы целесообразно создать?
- Только одна переменная, средняя стоимость хлебобулочных изделий.
- Две переменные, одна для затрат на производство выпечки, а другая для общего дохода от выпечки.
- Две переменные, одна для общего количества проданных оборотов, а другая для общего количества проданных кексов.

- Две переменные, одна для стоимости оборота, а другая для стоимости кекса.
где [math]d, d_0[/math] — расстояния, измеренные в метрах; [math]v_0[/math] — скорость, измеряемая в метрах в секунду; [math]t[/math] — время, измеряемое в секундах; а [math]a[/math] — ускорение, измеряемое в метрах в секунду в квадрате.
Она решает использовать размерный анализ, чтобы определить, правильно это или нет. Она считает, что каждый член должен иметь одни и те же единицы измерения, и, поскольку член в левой части уравнения и первый член в правой части уравнения выражены в метрах, два других члена также должны быть. Второй член в правой части уравнения равен 9.2/1 = «м»[/математика].
Второй член в правой части уравнения равен 9.2/1 = «м»[/математика].
Поскольку все члены выражены в метрах, она решает, что уравнение, которое она записала, верно. Права ли она, и если нет, то какую ошибку она сделала?
- Да, она правильная.
- Нет. Она предположила, что все термины должны иметь одни и те же единицы измерения, в то время как все термины должны быть без единиц измерения.
- Нет. Хотя переменная [math]t[/math] возведена в квадрат, единицы измерения — нет. Следовательно, единицами последнего члена являются м/с, которые отличаются от остальных членов.
- Нет.
 4[/математика].
4[/математика].
Ханна хочет купить комнатное растение для своей квартиры. Какие из следующих факторов важно исследовать, чтобы определить, какое растение целесообразно купить? Выберите все подходящие.
- Количество солнечного света, которое получит растение.
- Размер квартиры.
- Поставит ли она растение на пол или на стол.
- Средняя температура ее квартиры.
Кент хочет вырастить помидоры на заднем дворе, чтобы консервировать их на зиму. Он надеется получить около 9л консервированных помидоров. Он знает, что примерно каждые 3 фунта свежих помидоров дают одну кварту консервированных помидоров. Какие количества были бы полезны для определения количества томатов, которое нужно посадить Кенту?
Он надеется получить около 9л консервированных помидоров. Он знает, что примерно каждые 3 фунта свежих помидоров дают одну кварту консервированных помидоров. Какие количества были бы полезны для определения количества томатов, которое нужно посадить Кенту?
- Среднее количество томатов, которое производит томатное растение.
- Средний вес томатов, которые производит томатное растение.
- Сколько времени нужно, чтобы консервировать один фунт помидоров.
- Средний вес одной банки помидоров.



 Уравнения и неравенства (3 часа)
Уравнения и неравенства (3 часа) 09.19
09.19





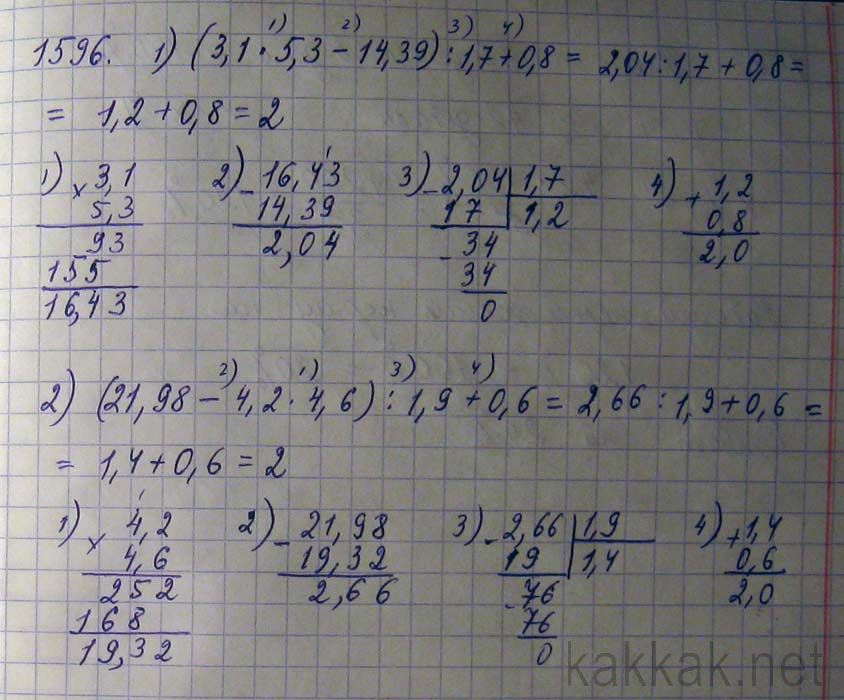

 4[/математика].
4[/математика]. 4. Плотность распределения
4. Плотность распределения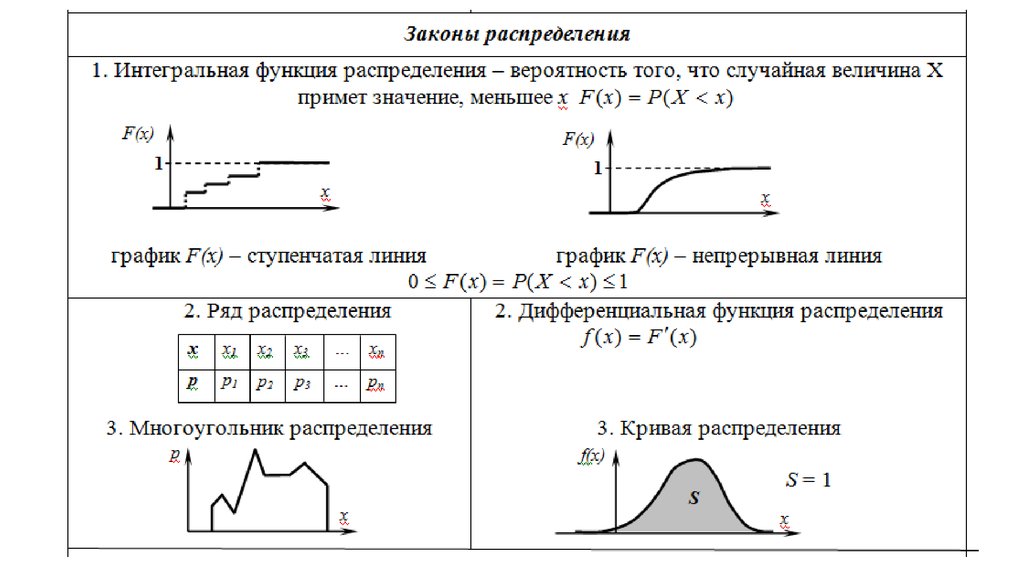 Системы случайных величин
Системы случайных величин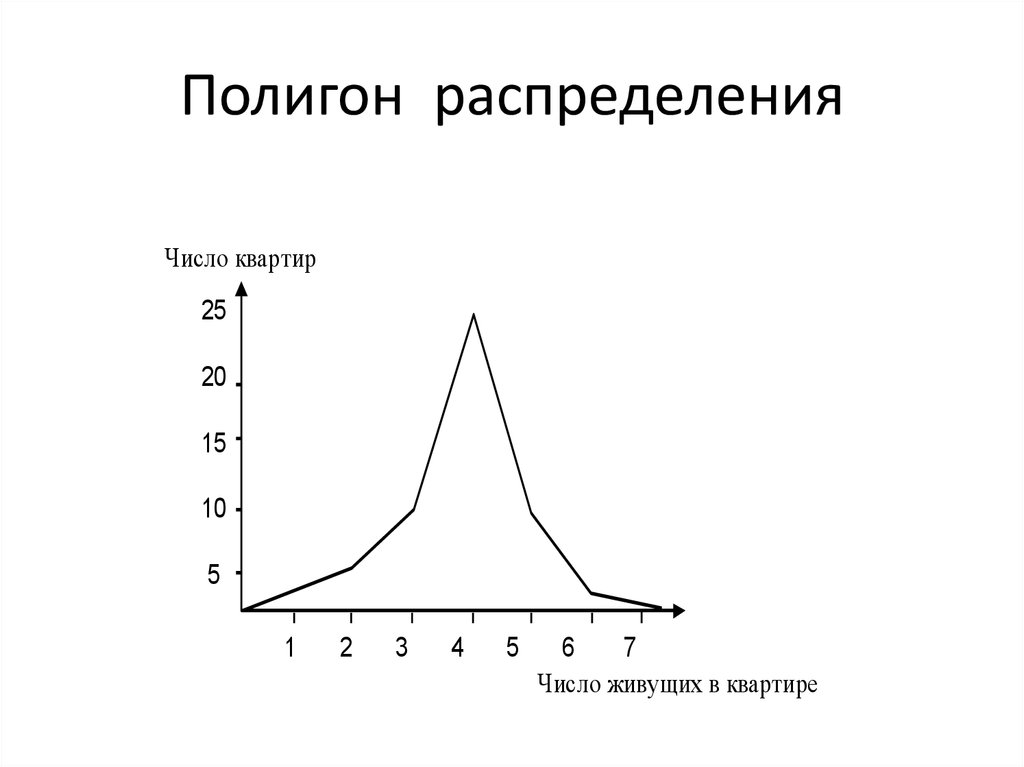 Общая запись нормального закона для системы произвольного числа случайных величин
Общая запись нормального закона для системы произвольного числа случайных величин Композиция законов распределения
Композиция законов распределения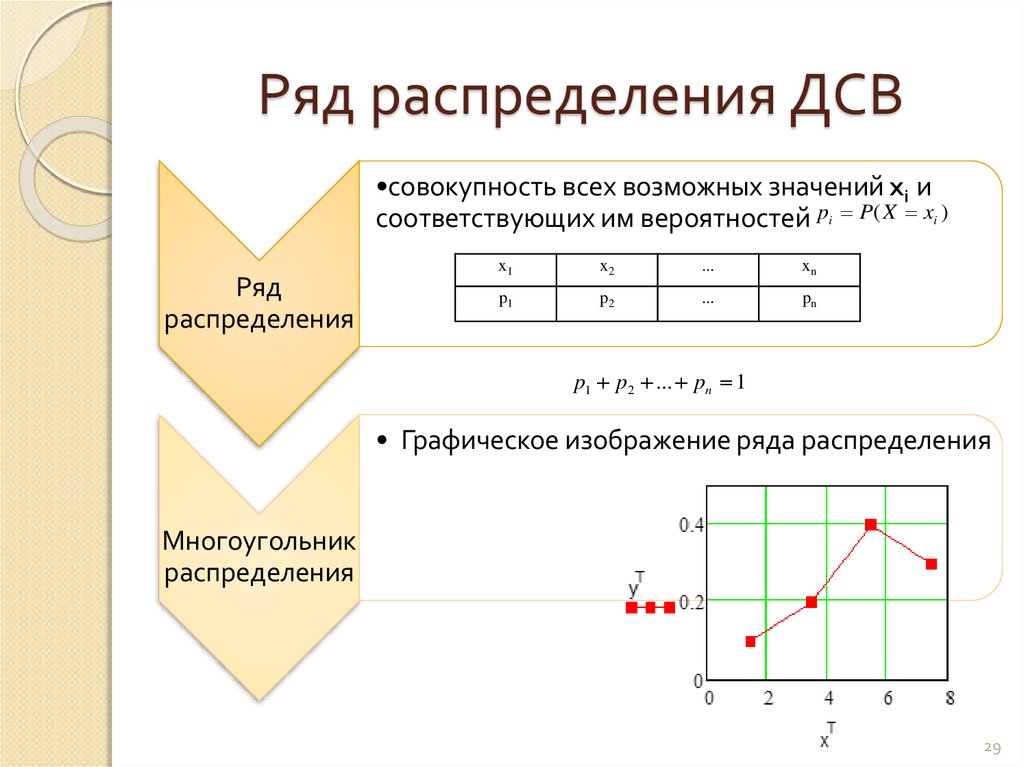 3. Доверительный интервал. Доверительная вероятность
3. Доверительный интервал. Доверительная вероятность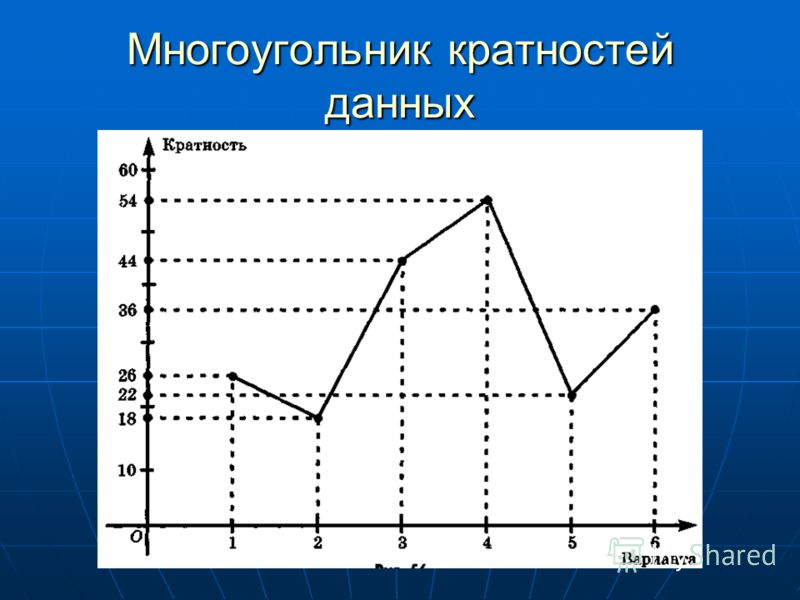 7.2. Производная от случайной функции
7.2. Производная от случайной функции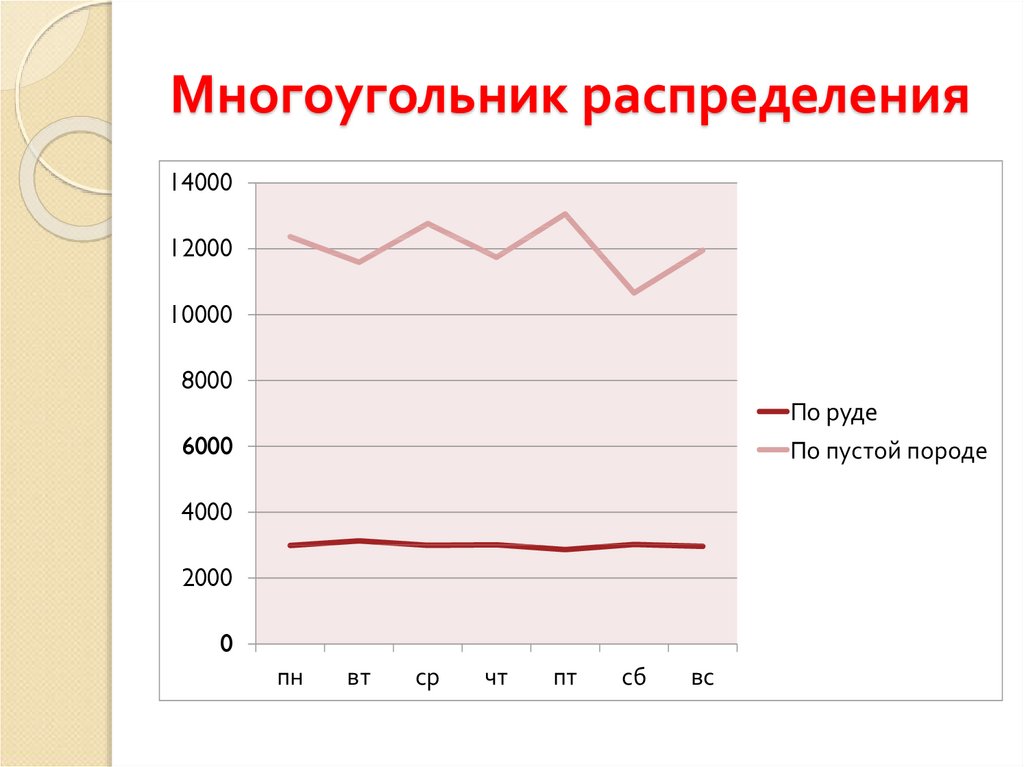 7. Эргодическое свойство стационарных случайных функций
7. Эргодическое свойство стационарных случайных функций 3. Поток событий. Простейший поток и его свойства
3. Поток событий. Простейший поток и его свойства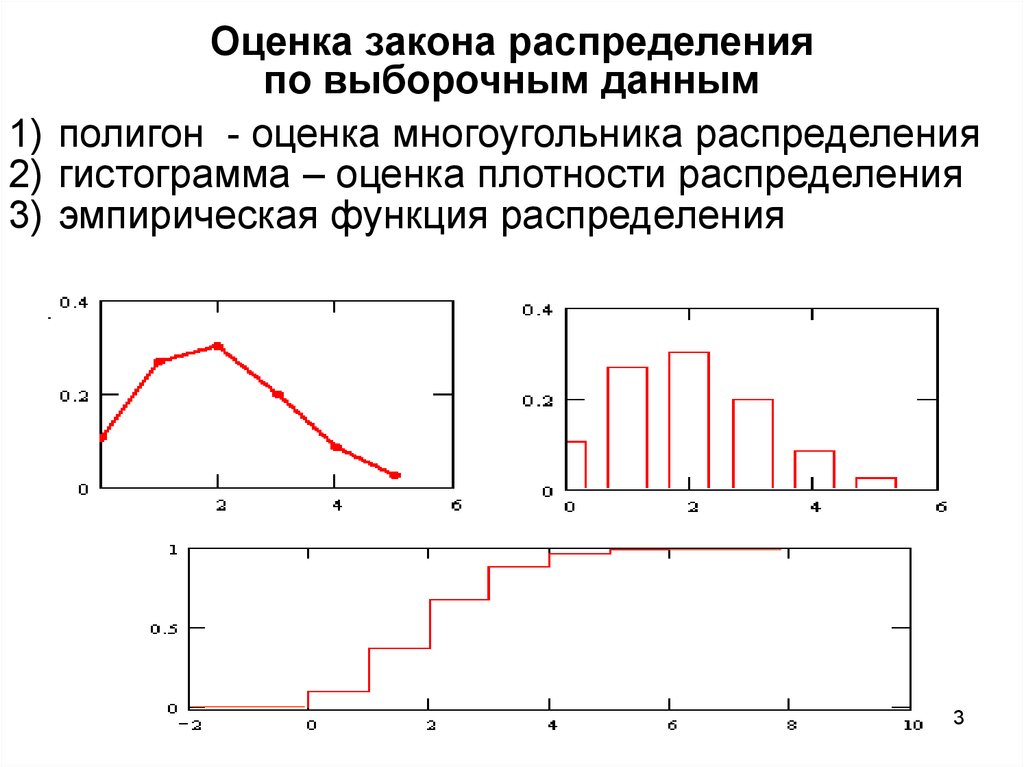 [16]
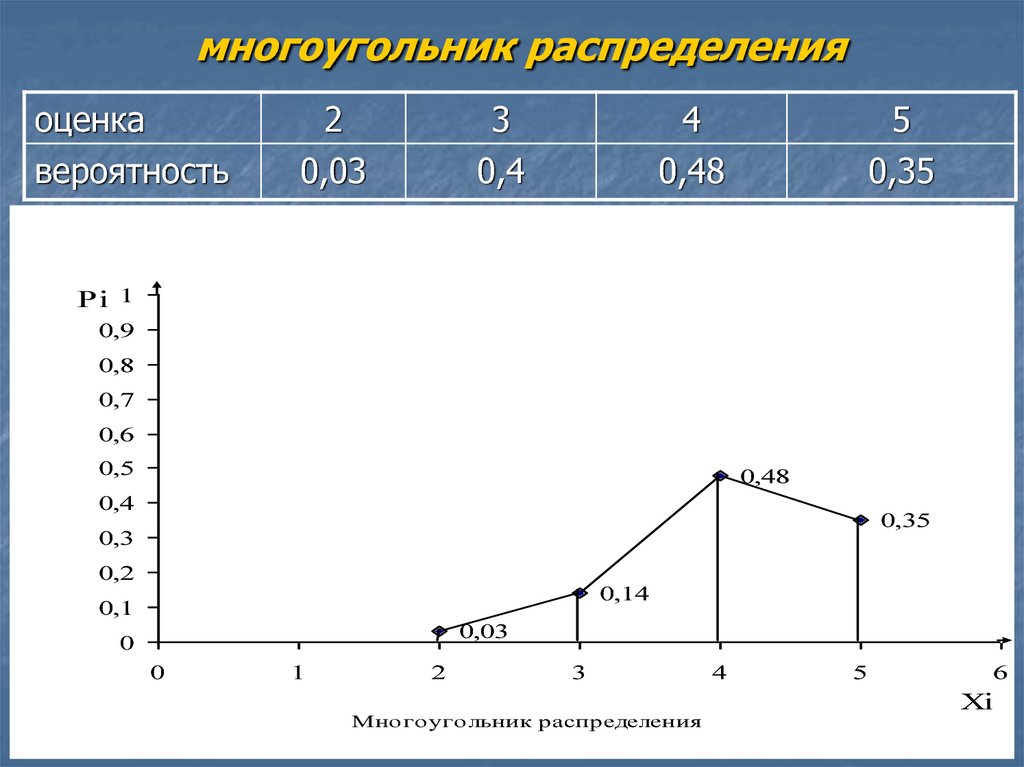
[16]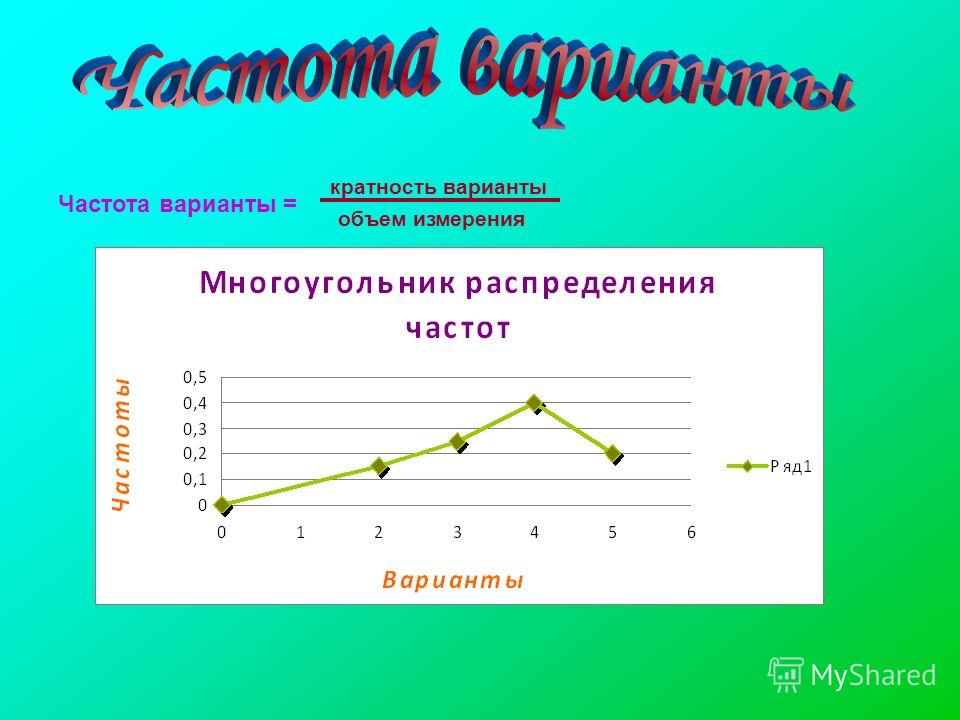 Полученную фигуру называют многоугольником распределения.
[21]
Полученную фигуру называют многоугольником распределения.
[21]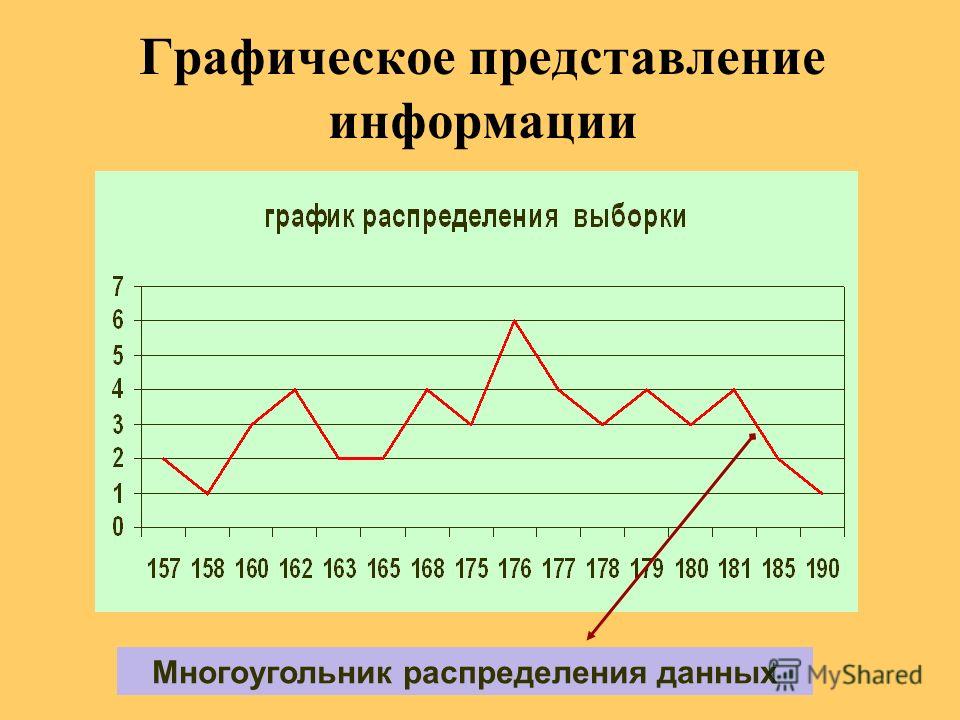 [24]
[24]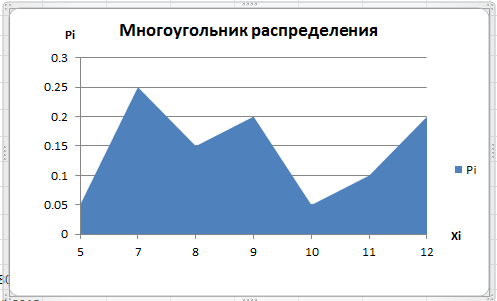 ) и аналитически.
[27]
) и аналитически.
[27]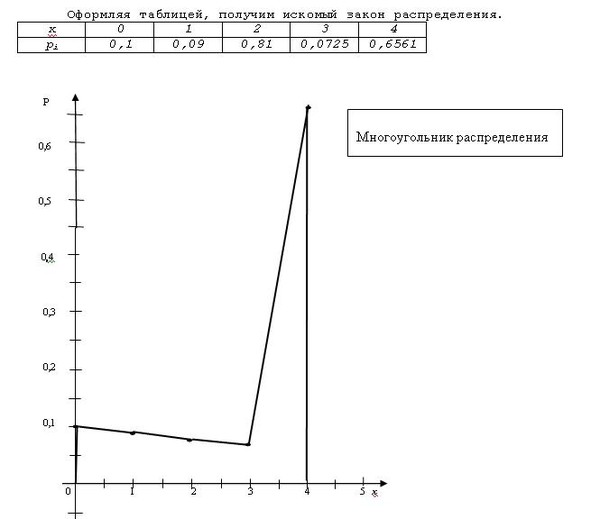 [29]
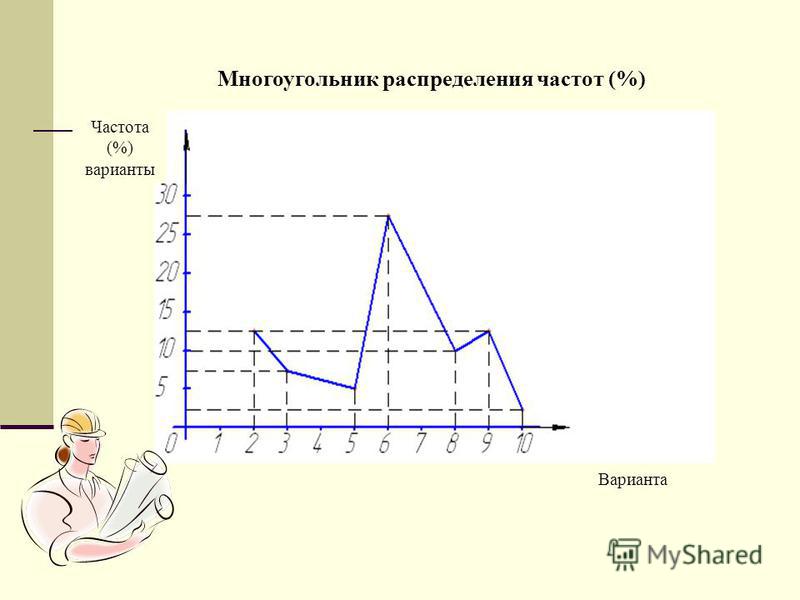
[29]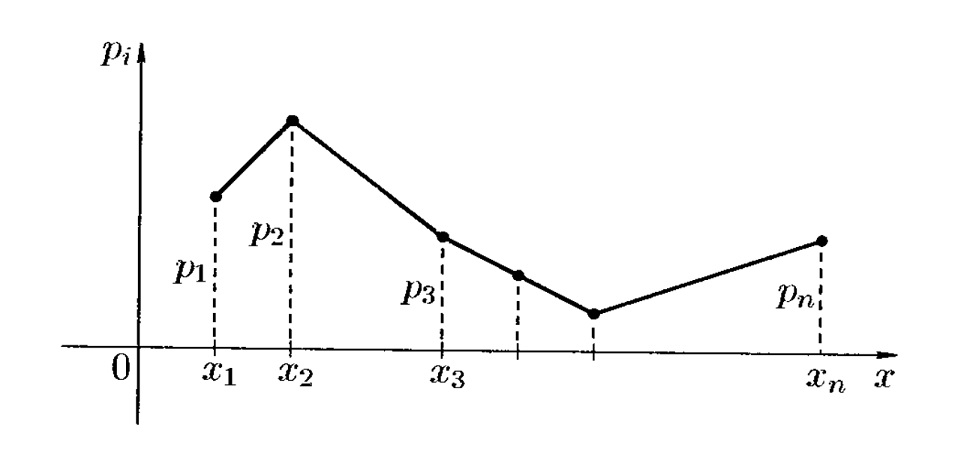 Они служат той же цели, что и гистограммы, но особенно полезны для сравнения наборов данных. Полигоны частот также хорошо подходят для отображения кумулятивных частотных распределений.
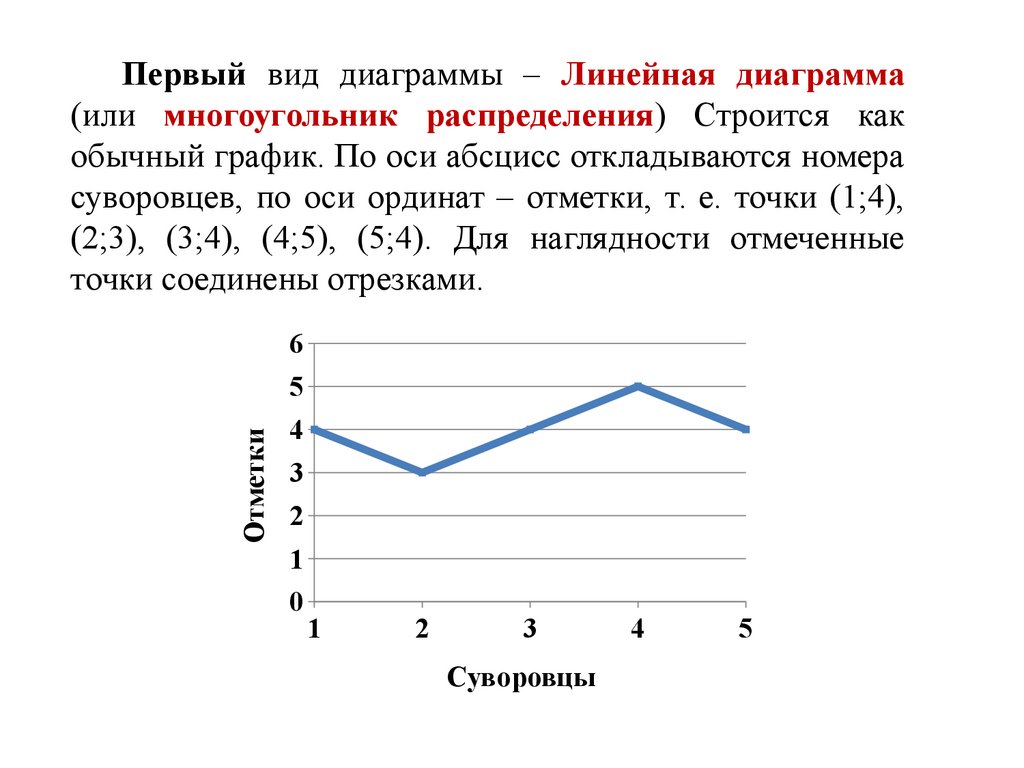
Они служат той же цели, что и гистограммы, но особенно полезны для сравнения наборов данных. Полигоны частот также хорошо подходят для отображения кумулятивных частотных распределений.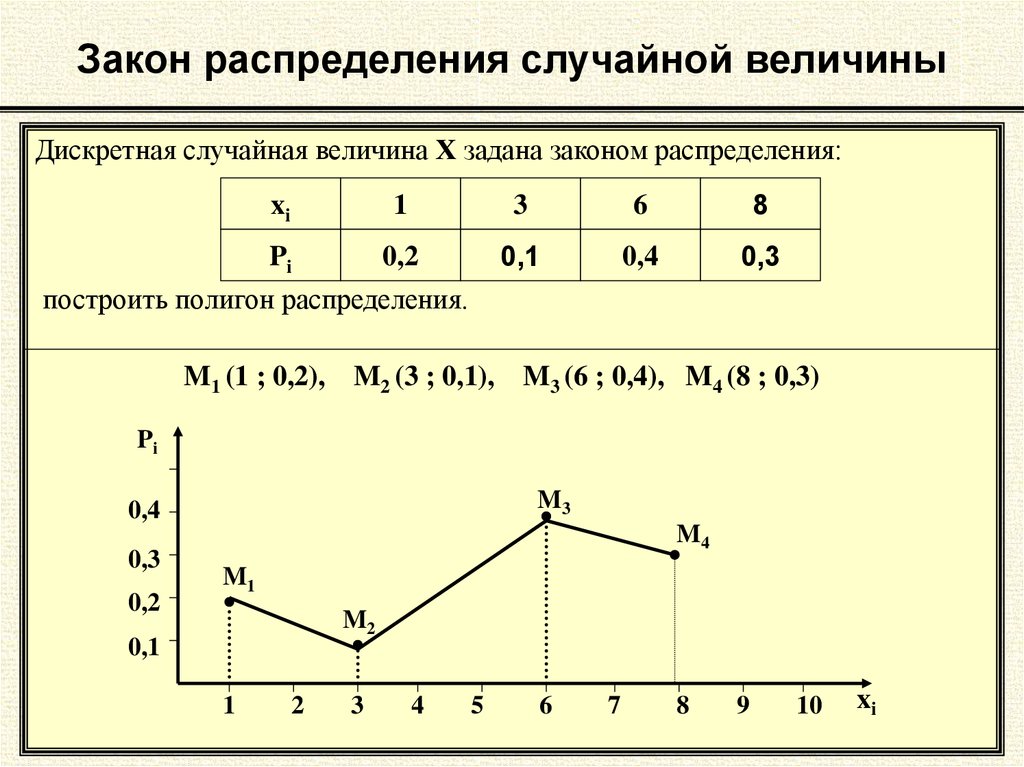
 5
5 В этом интервале три балла. В интервале, окружающем \(85\), есть \(147\) баллов.
В этом интервале три балла. В интервале, окружающем \(85\), есть \(147\) баллов.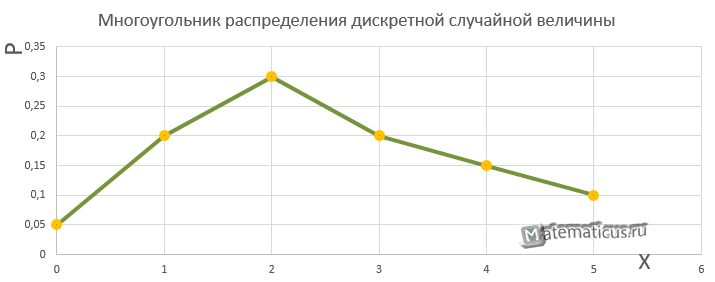 Поскольку тест прошли \(642\) студентов, суммарная частота за последний интервал равна \(642\).
Поскольку тест прошли \(642\) студентов, суммарная частота за последний интервал равна \(642\).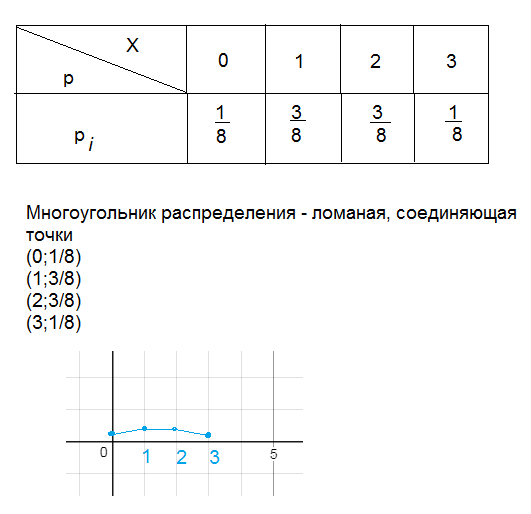 Это показано на рисунке \(\PageIndex{4}\) с использованием тех же данных из задачи курсора. Разница в распределениях для двух целей снова очевидна.
Это показано на рисунке \(\PageIndex{4}\) с использованием тех же данных из задачи курсора. Разница в распределениях для двух целей снова очевидна.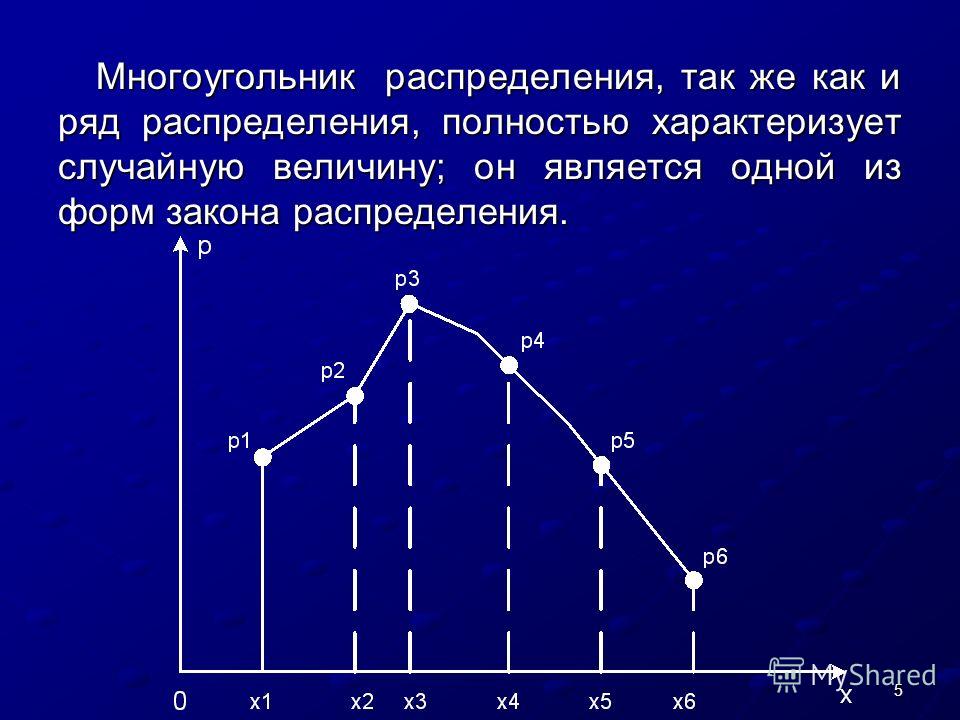 com
com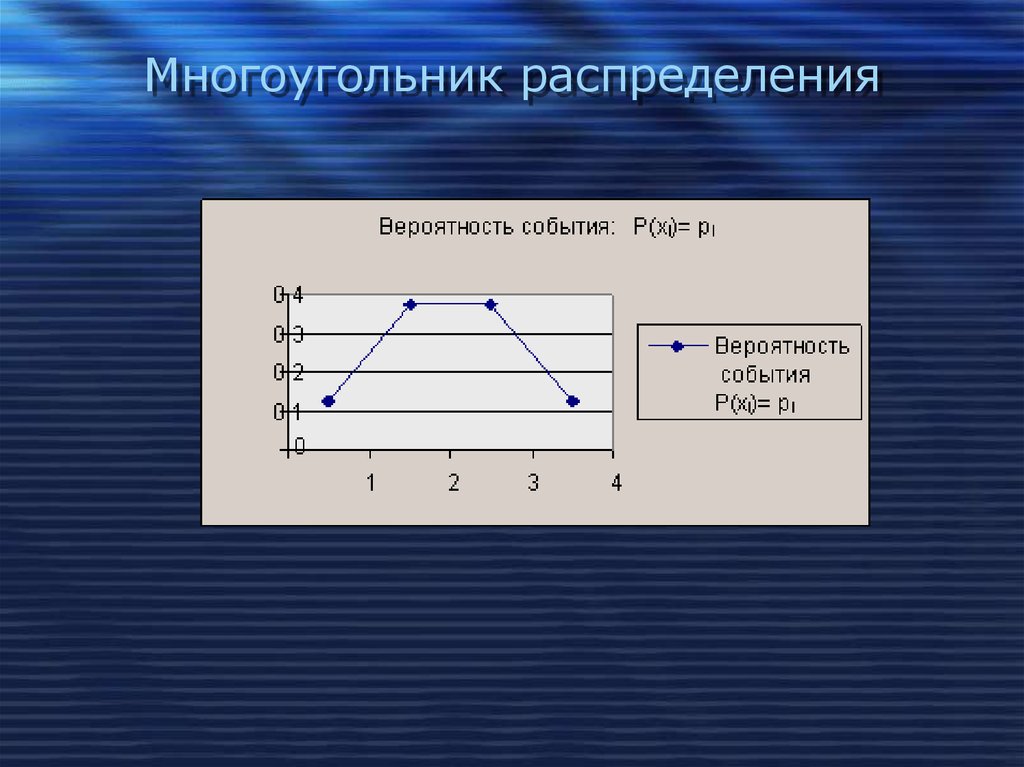
 На обычном графике ось X представляет значение в наборе данных, а ось Y показывает количество вхождений каждой категории. При построении графика многоугольника частот наиболее важным аспектом является средняя точка, которая называется интервалом класса или метками класса. Кривая частотного многоугольника может быть построена с гистограммой или без нее. Для рисования с помощью гистограммы мы сначала рисуем прямоугольные столбцы на интервалах классов и соединяем середины столбцов, чтобы получить многоугольники частот. Вот шаги для построения частотного многоугольника без гистограммы:
На обычном графике ось X представляет значение в наборе данных, а ось Y показывает количество вхождений каждой категории. При построении графика многоугольника частот наиболее важным аспектом является средняя точка, которая называется интервалом класса или метками класса. Кривая частотного многоугольника может быть построена с гистограммой или без нее. Для рисования с помощью гистограммы мы сначала рисуем прямоугольные столбцы на интервалах классов и соединяем середины столбцов, чтобы получить многоугольники частот. Вот шаги для построения частотного многоугольника без гистограммы: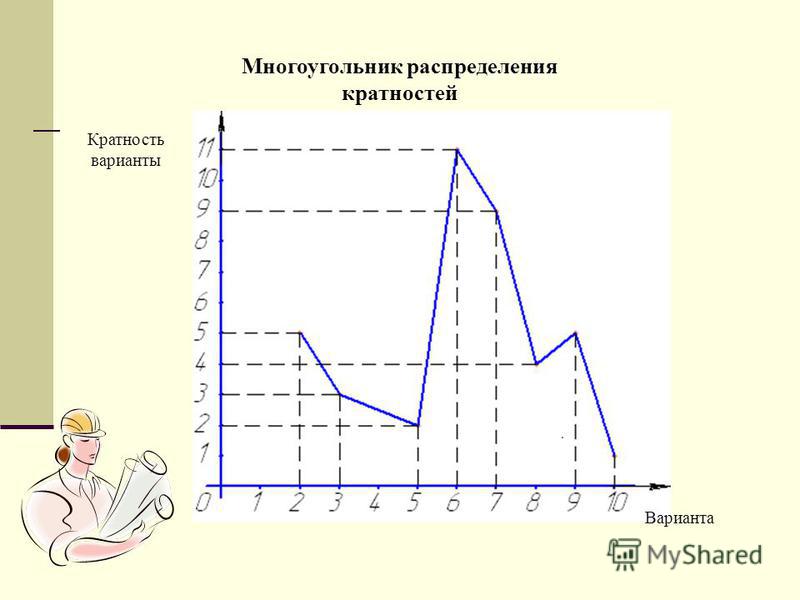 Он должен быть нанесен на сам классный знак, а не на верхний или нижний предел.
Он должен быть нанесен на сам классный знак, а не на верхний или нижний предел.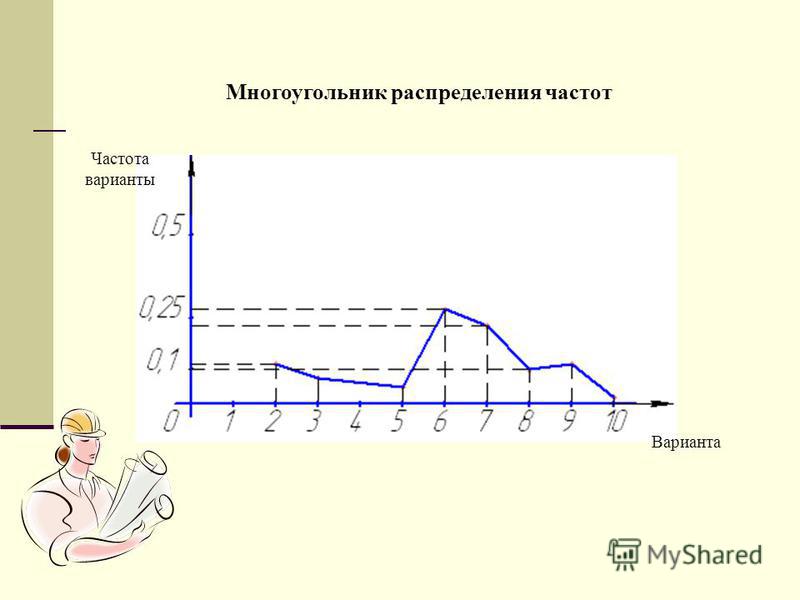
 В этом случае до 44,5 и после 104,5. По оси абсцисс отложены баллы, а по оси у — частота. Следовательно, график полигонов частот будет выглядеть так:
В этом случае до 44,5 и после 104,5. По оси абсцисс отложены баллы, а по оси у — частота. Следовательно, график полигонов частот будет выглядеть так:
 В этом случае до 135, а после 205. ABCDEFGH представляет данные графически в виде многоугольника частот, т.е. это средние точки. Следовательно, график полигонов частот будет выглядеть так:
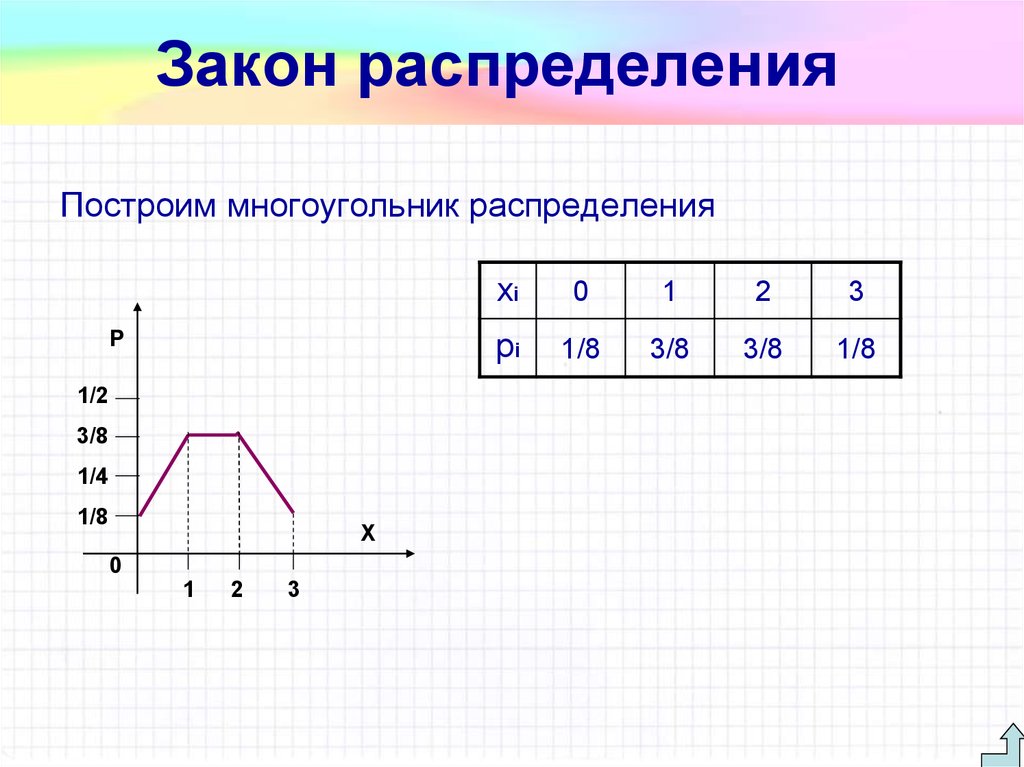
В этом случае до 135, а после 205. ABCDEFGH представляет данные графически в виде многоугольника частот, т.е. это средние точки. Следовательно, график полигонов частот будет выглядеть так: Кривая может быть построена с гистограммой и без нее. Полигональная диаграмма частот помогает отображать максимумы и минимумы данных частотного распределения. Чтобы получить кривую для многоугольника частот, нам нужно найти метку класса или среднюю точку из интервалов классов.
Кривая может быть построена с гистограммой и без нее. Полигональная диаграмма частот помогает отображать максимумы и минимумы данных частотного распределения. Чтобы получить кривую для многоугольника частот, нам нужно найти метку класса или среднюю точку из интервалов классов.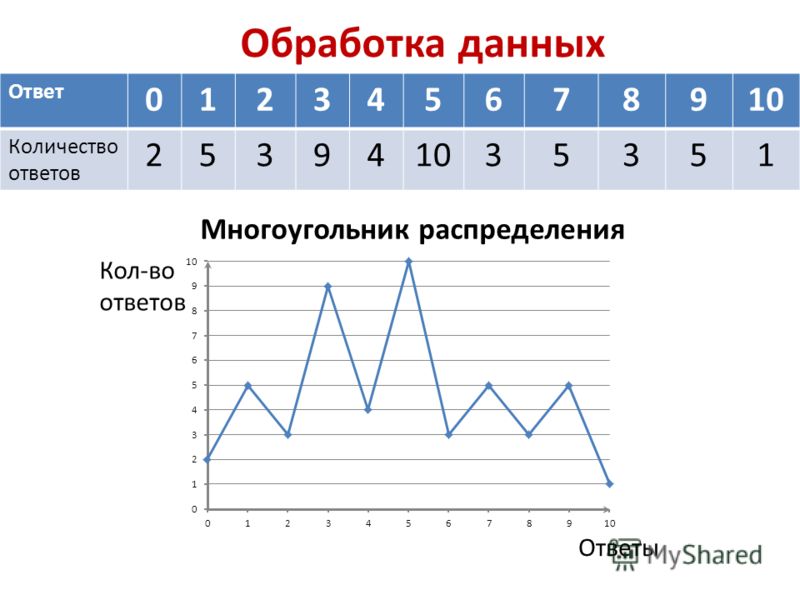





 Загрузите оригинальный файл из личного кабинета Wildberries в формате xlsx.
Загрузите оригинальный файл из личного кабинета Wildberries в формате xlsx.
 Нажмите кнопку «Приостановить».
Нажмите кнопку «Приостановить». Вкладка «Отчеты Wildberries» пропадет из раздела «Операции». Новые комиссии и возвраты от маркетплейса нужно будет учитывать вручную.
Вкладка «Отчеты Wildberries» пропадет из раздела «Операции». Новые комиссии и возвраты от маркетплейса нужно будет учитывать вручную.
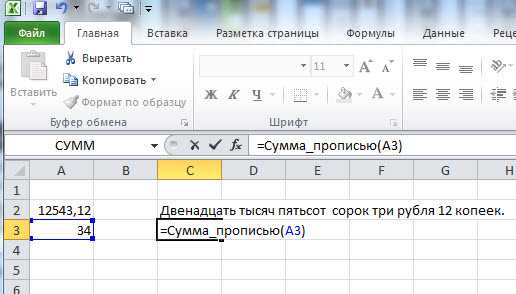
 Бесплатный онлайн калькулятор «Сумма прописью онлайн» мгновенно переведет сумму, записанную цифрами, в сумму прописью на различных языках мира. Также есть перевод даты в пропись и пропись дробных чисел. Наш калькулятор быстро и грамотно напишет за вас сумму прописью. Вам потребуется лишь ввести число/дату в специальное поле.
Бесплатный онлайн калькулятор «Сумма прописью онлайн» мгновенно переведет сумму, записанную цифрами, в сумму прописью на различных языках мира. Также есть перевод даты в пропись и пропись дробных чисел. Наш калькулятор быстро и грамотно напишет за вас сумму прописью. Вам потребуется лишь ввести число/дату в специальное поле. делай что дальше. делай что дальше.
делай что дальше. делай что дальше. решения по финансированию продаж. До прихода в Amount Адам был президентом и главным операционным директором в компании Avant, которую он помог превратить в ведущую в отрасли цифровую платформу потребительского кредитования. Ранее Адам был одним из первых сотрудников Enova International, где он сыграл решающую роль в построении и масштабировании международного бизнеса цифрового кредитования компании. Адам имеет степень бакалавра Северо-Западного университета.
решения по финансированию продаж. До прихода в Amount Адам был президентом и главным операционным директором в компании Avant, которую он помог превратить в ведущую в отрасли цифровую платформу потребительского кредитования. Ранее Адам был одним из первых сотрудников Enova International, где он сыграл решающую роль в построении и масштабировании международного бизнеса цифрового кредитования компании. Адам имеет степень бакалавра Северо-Западного университета. Его предыдущий опыт включает время в качестве директора в Centerview Partners и время в Keefe, Bruyette & Woods, крупнейшем в стране специализированном инвестиционном банке, специализирующемся на секторе финансовых услуг. Сэм с отличием окончил Бакнеллский университет со степенью в области компьютерных наук и инженерии.
Его предыдущий опыт включает время в качестве директора в Centerview Partners и время в Keefe, Bruyette & Woods, крупнейшем в стране специализированном инвестиционном банке, специализирующемся на секторе финансовых услуг. Сэм с отличием окончил Бакнеллский университет со степенью в области компьютерных наук и инженерии. Радж имеет степень магистра компьютерных наук Университета Джорджа Мейсона и степень магистра делового администрирования Мэрилендского университета в Колледж-Парке.
Радж имеет степень магистра компьютерных наук Университета Джорджа Мейсона и степень магистра делового администрирования Мэрилендского университета в Колледж-Парке.
 Меган 14 лет занимается цифровым кредитованием, в последнее время руководя маркетинговой стратегией и реализацией цифровой платформы потребительского кредитования Avant. До прихода в Avant Меган руководила маркетингом CashNetUSA, ведущего бренда Enova International в США.
Меган 14 лет занимается цифровым кредитованием, в последнее время руководя маркетинговой стратегией и реализацией цифровой платформы потребительского кредитования Avant. До прихода в Avant Меган руководила маркетингом CashNetUSA, ведущего бренда Enova International в США. До прихода в Amount Сандип был директором по кредитам и аналитике в Linear Financial Technologies/Fundation, признанном финтех-стартапе, предлагающем лучшие в своем классе кредитные решения для малого бизнеса. До Fundation Сандип занимал ключевые руководящие и управленческие должности в сфере управления кредитами и продуктами в Capital One и Citigroup. Он имеет степень бакалавра ИИТ Бомбея и аспирантуру по поведенческой экономике Университета Джорджа Мейсона. Sandip увлечен внедрением инновационных продуктов и кредитов в масштабе меняющейся экосистемы финансовых услуг.
До прихода в Amount Сандип был директором по кредитам и аналитике в Linear Financial Technologies/Fundation, признанном финтех-стартапе, предлагающем лучшие в своем классе кредитные решения для малого бизнеса. До Fundation Сандип занимал ключевые руководящие и управленческие должности в сфере управления кредитами и продуктами в Capital One и Citigroup. Он имеет степень бакалавра ИИТ Бомбея и аспирантуру по поведенческой экономике Университета Джорджа Мейсона. Sandip увлечен внедрением инновационных продуктов и кредитов в масштабе меняющейся экосистемы финансовых услуг.
 Система онлайн-платежей может быть использована для оплаты залогов любой суммы.
Система онлайн-платежей может быть использована для оплаты залогов любой суммы. 
 / дебетовой карты, которую вы хотите использовать. Вы можете использовать несколько кредитных/дебетовых карт для оплаты полной суммы залога. Несколько человек также могут внести части одной и той же суммы залога.
/ дебетовой карты, которую вы хотите использовать. Вы можете использовать несколько кредитных/дебетовых карт для оплаты полной суммы залога. Несколько человек также могут внести части одной и той же суммы залога. 
 m. and 1 a.m.
m. and 1 a.m. 
 Вы можете складывать отдельные значения, диапазоны ячеек, ссылки на ячейки или данные всех этих трех видов.
Вы можете складывать отдельные значения, диапазоны ячеек, ссылки на ячейки или данные всех этих трех видов. Можно указать до 255 чисел.
Можно указать до 255 чисел.

 Гораздо лучше использовать отдельные диапазоны, например:
Гораздо лучше использовать отдельные диапазоны, например: Выберите соответствующую ячейку или соответствующий диапазон и нажмите клавиши CTRL+1, чтобы открыть диалоговое окно Формат ячеек, затем щелкните вкладку Число и выберите нужный формат, указав при этом нужное количество десятичных знаков.
Выберите соответствующую ячейку или соответствующий диапазон и нажмите клавиши CTRL+1, чтобы открыть диалоговое окно Формат ячеек, затем щелкните вкладку Число и выберите нужный формат, указав при этом нужное количество десятичных знаков.



 Кроме того, функция игнорирует пустые ячейки и текстовые значения.
Кроме того, функция игнорирует пустые ячейки и текстовые значения. д.) необязательны.
д.) необязательны. Выберите ячейку A8.
Выберите ячейку A8.  Он возвращает 58,8 в ячейке C2.
Он возвращает 58,8 в ячейке C2.

 Функция СУММ используется, когда необходимо найти сумму указанных ячеек.
Функция СУММ используется, когда необходимо найти сумму указанных ячеек. Оно указывает функцию, которая будет использоваться для ПРОМЕЖУТОЧНОГО ИТОГА. арифметические операции, такие как среднее, произведение, сумма, стандартное отклонение, дисперсия и т. д., в определенном диапазоне. Подробнее. Используемые функции могут быть AVERAGE, MAX, MIN, COUNT, STDEV, SUM и так далее.
Оно указывает функцию, которая будет использоваться для ПРОМЕЖУТОЧНОГО ИТОГА. арифметические операции, такие как среднее, произведение, сумма, стандартное отклонение, дисперсия и т. д., в определенном диапазоне. Подробнее. Используемые функции могут быть AVERAGE, MAX, MIN, COUNT, STDEV, SUM и так далее.

 Для того чтобы это произошло, химические связи веществ разрываются, а составляющие их атомы отделяются и перестраиваются в новые вещества с новыми химическими связями. Когда этот процесс происходит, мы называем его химической реакцией. А химическая реакция — это процесс, в котором одно или несколько веществ превращаются в одно или несколько новых веществ.
Для того чтобы это произошло, химические связи веществ разрываются, а составляющие их атомы отделяются и перестраиваются в новые вещества с новыми химическими связями. Когда этот процесс происходит, мы называем его химической реакцией. А химическая реакция — это процесс, в котором одно или несколько веществ превращаются в одно или несколько новых веществ.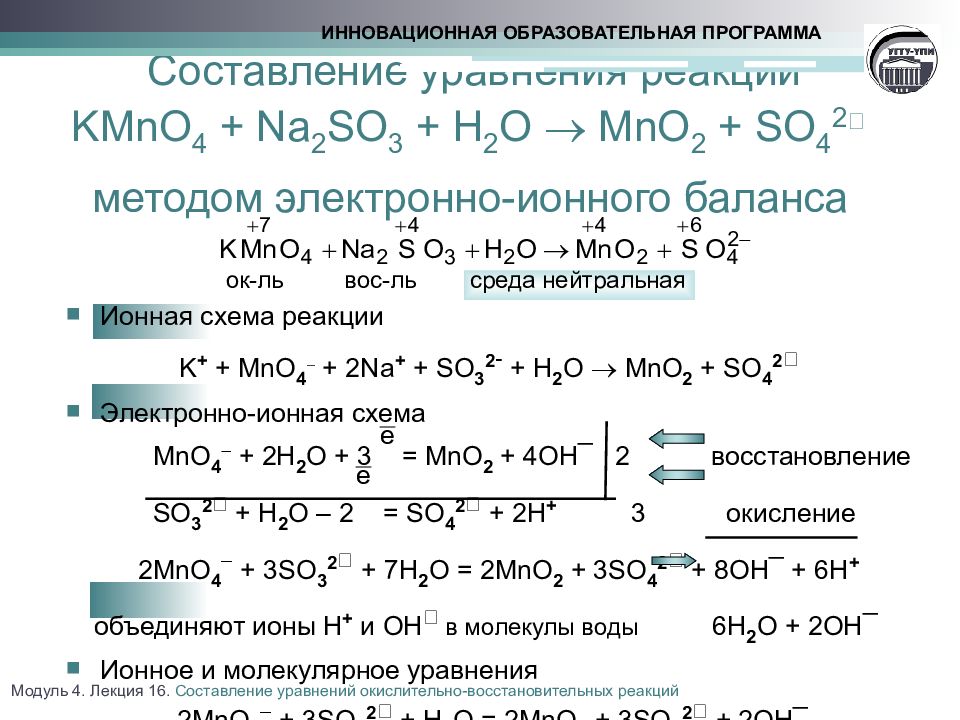 Общее уравнение реакции:
Общее уравнение реакции:
 Есть семь элементов, которые считаются двухатомными, а это означает, что они всегда встречаются в природе парами. Они включают в себя те элементы, которые перечислены в таблице.
Есть семь элементов, которые считаются двухатомными, а это означает, что они всегда встречаются в природе парами. Они включают в себя те элементы, которые перечислены в таблице.

 9: Chemical Equations распространяется по незадекларированной лицензии, автором, ремиксом и/или куратором является LibreTexts.
9: Chemical Equations распространяется по незадекларированной лицензии, автором, ремиксом и/или куратором является LibreTexts. SO2+h3S→h3O+S
SO2+h3S→h3O+S ..
..
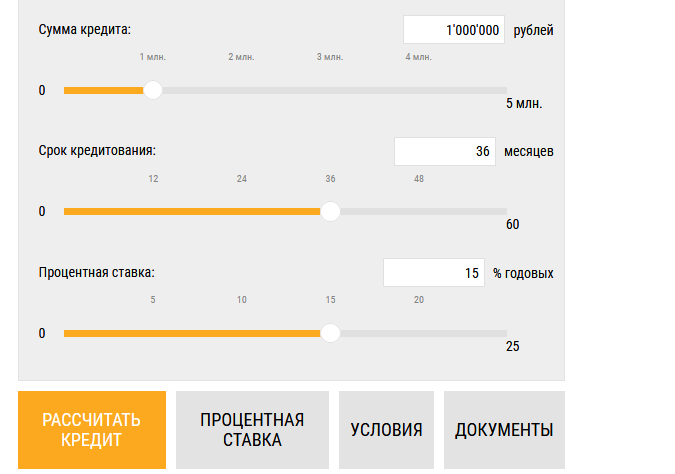
 Нажмите «Подать заявку», чтобы увидеть варианты, как можно получить скидку
Нажмите «Подать заявку», чтобы увидеть варианты, как можно получить скидку Также скидку дает комплексное страхование недвижимости, жизни и трудоспособности.
Также скидку дает комплексное страхование недвижимости, жизни и трудоспособности.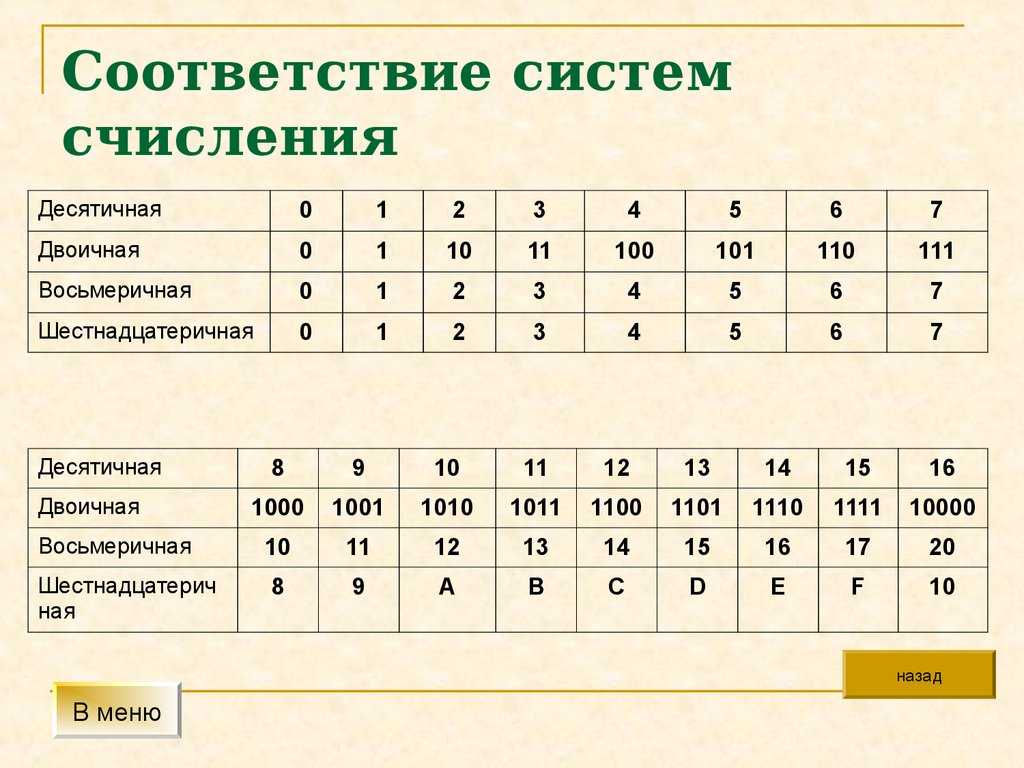
 Вы можете сделать это с клавиатуры, если кликните на цену
Вы можете сделать это с клавиатуры, если кликните на цену
 CITIZEN SR-135
CITIZEN SR-135 00
00 с контейнером Maped I-gloo 1 отв.
с контейнером Maped I-gloo 1 отв.
 Для пятидесятичного числа требуется пятнадцать символов, таких как: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E.
Для пятидесятичного числа требуется пятнадцать символов, таких как: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E. Используется двадцать один символ: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I, J и K.
Используется двадцать один символ: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I, J и K. В этой системе используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9., A, B, C, D, E, F, G, H, I, J, K, L, M, N, O и P.
В этой системе используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9., A, B, C, D, E, F, G, H, I, J, K, L, M, N, O и P. Цифры в этом основании могут быть представлены арабскими цифрами 0-9 и латинскими буквами A-T.
Цифры в этом основании могут быть представлены арабскими цифрами 0-9 и латинскими буквами A-T. Выбор 36 удобен тем, что цифры можно представить с помощью арабских цифр 0-9 и латинских букв A-Z.
Выбор 36 удобен тем, что цифры можно представить с помощью арабских цифр 0-9 и латинских букв A-Z.

 Потом снова проверить,
если то, что получилось, делится на 7, то и само число делится на 7.
Потом снова проверить,
если то, что получилось, делится на 7, то и само число делится на 7.
 Потом снова проверить,
если то, что получилось, делится на 11, то и само число делится на 11.
Потом снова проверить,
если то, что получилось, делится на 11, то и само число делится на 11.
 На 12 число делится, если оно одновременно делится на
3 и на 4. На 15 число делится, если оно одновременно делится на 3 и на 5. На
18 число делится, если оно одновременно делится на 2 и на 9.
На 12 число делится, если оно одновременно делится на
3 и на 4. На 15 число делится, если оно одновременно делится на 3 и на 5. На
18 число делится, если оно одновременно делится на 2 и на 9.
 Поэтому и цифры 0, 2, 4, 6, 8 называют чётными, а цифры 1, 3, 5, 7, 9 — нечётными. Все полные десятки делятся на 2 без остатка (т.е. они четны). Значит, любое натуральное число чётно лишь в том случае, когда в рязряде единиц стоит чётная цифра, и нечётно, когда в разряде единиц стоит нечётная цифра.
Поэтому и цифры 0, 2, 4, 6, 8 называют чётными, а цифры 1, 3, 5, 7, 9 — нечётными. Все полные десятки делятся на 2 без остатка (т.е. они четны). Значит, любое натуральное число чётно лишь в том случае, когда в рязряде единиц стоит чётная цифра, и нечётно, когда в разряде единиц стоит нечётная цифра. От четырёх десятков останется 4 яйца.
От четырёх десятков останется 4 яйца. Без фактического деления, как мы можем угадать числа, делящиеся на 4 или нет? В этой статье вы изучите делящиеся на 4 или правила делимости на 4. В этой статье будет рассмотрено правило делимости на 4 с примерами и то, как его можно использовать для проверки, делится ли число на 4.
Без фактического деления, как мы можем угадать числа, делящиеся на 4 или нет? В этой статье вы изучите делящиеся на 4 или правила делимости на 4. В этой статье будет рассмотрено правило делимости на 4 с примерами и то, как его можно использовать для проверки, делится ли число на 4.
 Если да, то данное число будет делиться на 4. Если нет, то проверьте второе условие, приведенное ниже. Нули должны стоять в разряде единиц и десятков.
Если да, то данное число будет делиться на 4. Если нет, то проверьте второе условие, приведенное ниже. Нули должны стоять в разряде единиц и десятков. 00
00 делится на заданное фиксированное число (делитель). Правило делимости 4 определяется как данное число делится на 4, если последние две цифры данного числа являются нулями или кратны 4.
делится на заданное фиксированное число (делитель). Правило делимости 4 определяется как данное число делится на 4, если последние две цифры данного числа являются нулями или кратны 4.



 Онлайн калькулятор расстояния между точками
Онлайн калькулятор расстояния между точками Найди правильный ответ.
Найди правильный ответ. Калькулятор вычисления силы, массы и ускорения.
Калькулятор вычисления силы, массы и ускорения. Для плоского, цилиндрического и сферического конденсаторов
Для плоского, цилиндрического и сферического конденсаторов На этом уроке мы рассмотрим скалярное произведение векторов и решим задачи на вычисление скалярного произведения.
На этом уроке мы рассмотрим скалярное произведение векторов и решим задачи на вычисление скалярного произведения.
 Рассмотрим следующую задачу.
Рассмотрим следующую задачу. К одной и той же точке приложены две силы и , действующие под углом друг к другу, причем . Найти величину равнодействующей силы .
К одной и той же точке приложены две силы и , действующие под углом друг к другу, причем . Найти величину равнодействующей силы . ru (Источник).
ru (Источник). 
 Мы можем выразить это с помощью уравнения:
Мы можем выразить это с помощью уравнения: Если, с другой стороны, вы хотите умножить векторы в 2D-пространстве, вы должны опустить третий член формулы.
Если, с другой стороны, вы хотите умножить векторы в 2D-пространстве, вы должны опустить третий член формулы. В данном случае он равен
В данном случае он равен 

 Поскольку они оба параллельны, результат является просто произведением их длин.
Поскольку они оба параллельны, результат является просто произведением их длин. Формула тройного произведения может быть выражена как:
Формула тройного произведения может быть выражена как: Как мы знаем из предыдущего раздела, это проекция
Как мы знаем из предыдущего раздела, это проекция  Если мы хотим найти
Если мы хотим найти 
 Значит, он равен нулю для двух взаимно перпендикулярных векторов. И это обозначается символом «.» между двумя векторами. Основное различие между точечным и перекрестным произведением заключается в том, что произведение точечной операции представляет собой одно число, а результатом перекрестной операции является вектор.
Значит, он равен нулю для двух взаимно перпендикулярных векторов. И это обозначается символом «.» между двумя векторами. Основное различие между точечным и перекрестным произведением заключается в том, что произведение точечной операции представляет собой одно число, а результатом перекрестной операции является вектор. Здесь у нас есть пример:
Здесь у нас есть пример:

 Например, к такому виду:
Например, к такому виду:
 Обычно это можно сделать несколькими способами. Поступим так:
Обычно это можно сделать несколькими способами. Поступим так: То есть, если бы у нас внизу получилось что-нибудь вроде (0 0 11 |23)
, и, соответственно, 11x 3 = 23, x 3 = 23/11, то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.
То есть, если бы у нас внизу получилось что-нибудь вроде (0 0 11 |23)
, и, соответственно, 11x 3 = 23, x 3 = 23/11, то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований. 4 –0.6 0.6
4 –0.6 0.6

 Если же при
Если же при

 Такой процесс преобразования уравнений системы для последовательного исключения неизвестных переменных называется прямым ходом метода Гаусса . После завершения прямого хода метода Гаусса из последнего уравнения находитсяx n , с помощью этого значения из предпоследнего уравнения вычисляется x n-1 , и так далее, из первого уравнения находится x 1 . Процесс вычисления неизвестных переменных при движении от последнего уравнения системы к первому называется обратным ходом метода Гаусса .
Такой процесс преобразования уравнений системы для последовательного исключения неизвестных переменных называется прямым ходом метода Гаусса . После завершения прямого хода метода Гаусса из последнего уравнения находитсяx n , с помощью этого значения из предпоследнего уравнения вычисляется x n-1 , и так далее, из первого уравнения находится x 1 . Процесс вычисления неизвестных переменных при движении от последнего уравнения системы к первому называется обратным ходом метода Гаусса .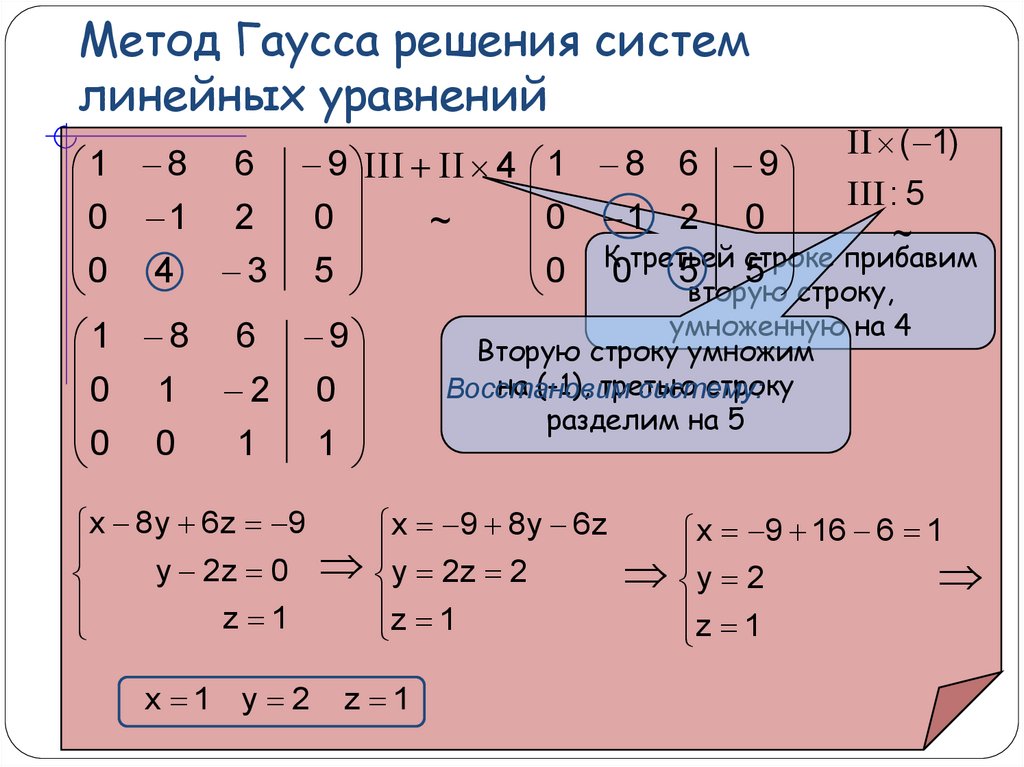


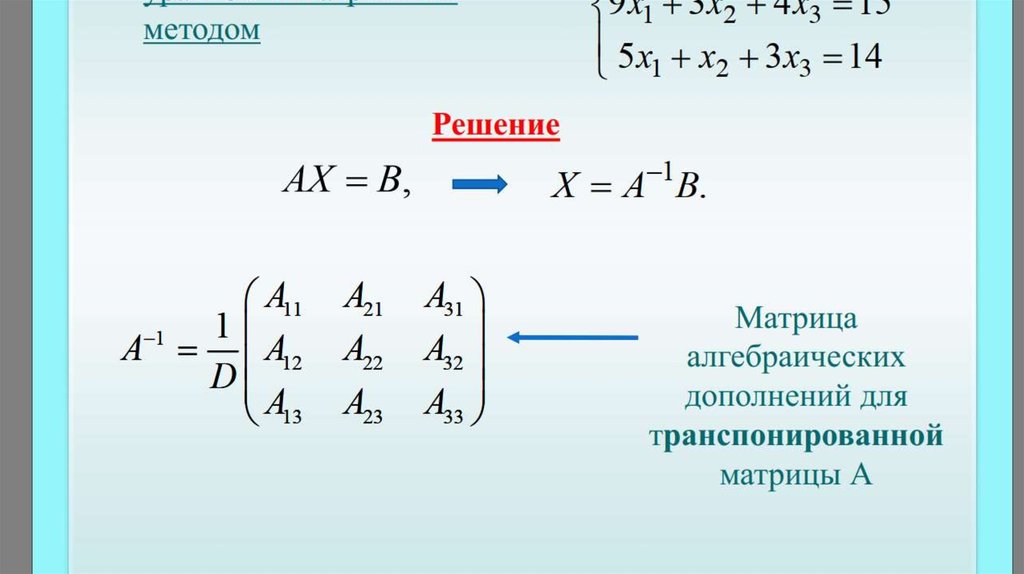 Наиболее часто программисты разрабатывают специальные программы-вычислители линейной алгебры, сюда входит и система линейных уравнений. Метод Гаусса позволяет высчитать все существующие решения. Также используются и другие упрощенные формулы и методики.
Наиболее часто программисты разрабатывают специальные программы-вычислители линейной алгебры, сюда входит и система линейных уравнений. Метод Гаусса позволяет высчитать все существующие решения. Также используются и другие упрощенные формулы и методики. В нашем случае ранг матрицы 2. Матрица А будет состоять из коэффициентов, находящихся возле неизвестных, а в расширенную матрицу вписываются и коэффициенты, находящиеся за знаком «=».
В нашем случае ранг матрицы 2. Матрица А будет состоять из коэффициентов, находящихся возле неизвестных, а в расширенную матрицу вписываются и коэффициенты, находящиеся за знаком «=». Канонический вид подразумевает, что все элементы матрицы, которые расположены по главной диагонали, становятся единицами, а оставшиеся — нулями.
Канонический вид подразумевает, что все элементы матрицы, которые расположены по главной диагонали, становятся единицами, а оставшиеся — нулями. Получается, что в каждом ряду необходимо оставить одну переменную со значением «1», остальные привести к нулевому виду. Для более точного понимания необходимо рассмотреть метод Гаусса на примерах.
Получается, что в каждом ряду необходимо оставить одну переменную со значением «1», остальные привести к нулевому виду. Для более точного понимания необходимо рассмотреть метод Гаусса на примерах. Для этого вторую строку отнимаем от первой и получаем необходимый ответ — решение СЛАУ. Или, как показано на рисунке, вторую строку умножаем на коэффициент -1 и прибавляем к первой строке элементы второго ряда. Это одно и то же.
Для этого вторую строку отнимаем от первой и получаем необходимый ответ — решение СЛАУ. Или, как показано на рисунке, вторую строку умножаем на коэффициент -1 и прибавляем к первой строке элементы второго ряда. Это одно и то же. Для этого умножаем первое уравнение на -1 и прибавляем к нему второе уравнение. Важно запомнить, что первую строку мы переписываем в изначальном виде, а вторую — уже в измененном.
Для этого умножаем первое уравнение на -1 и прибавляем к нему второе уравнение. Важно запомнить, что первую строку мы переписываем в изначальном виде, а вторую — уже в измененном. Из результата видно, что вторая строка тоже приведена к необходимой нам форме. Осталось проделать еще несколько операций и убрать коэффициенты неизвестных из первой строки.
Из результата видно, что вторая строка тоже приведена к необходимой нам форме. Осталось проделать еще несколько операций и убрать коэффициенты неизвестных из первой строки. Таким образом, получается такая же расширенная матрица, которую мы пишем вручную.
Таким образом, получается такая же расширенная матрица, которую мы пишем вручную.
 Наш калькулятор умеет решать онлайн как обычную определенную, так и неопределенную систему линейных уравнений методом Гаусса, которая имеет бесконечное множество решений. В этом случае в ответе вы получите зависимость одних переменных через другие, свободные. Также можно проверить систему уравнений на совместность онлайн, используя решение методом Гаусса.
Наш калькулятор умеет решать онлайн как обычную определенную, так и неопределенную систему линейных уравнений методом Гаусса, которая имеет бесконечное множество решений. В этом случае в ответе вы получите зависимость одних переменных через другие, свободные. Также можно проверить систему уравнений на совместность онлайн, используя решение методом Гаусса.
 Калькулятор работает при температуре воздуха от -50°F до 50°F.
Калькулятор работает при температуре воздуха от -50°F до 50°F. Результатом охлаждения ветром является увеличение скорости потери тепла. Физиологической реакцией организма на повышенную скорость теплоотдачи является выделение большего количества тепла для поддержания температуры поверхности, что приводит к восприятию более низких температур из-за большей теплоотдачи.
Результатом охлаждения ветром является увеличение скорости потери тепла. Физиологической реакцией организма на повышенную скорость теплоотдачи является выделение большего количества тепла для поддержания температуры поверхности, что приводит к восприятию более низких температур из-за большей теплоотдачи.
 К ним относятся:
К ним относятся:

 При необходимости можно добавить слои, например, синтетическую или пуховую куртку для дополнительной изоляции.
При необходимости можно добавить слои, например, синтетическую или пуховую куртку для дополнительной изоляции. Находящиеся под угрозой исчезновения южные косатки зависят от этого лосося в качестве добычи, что делает эту среду обитания важной и для китов. Прибрежная среда обитания также является краеугольным камнем региональной экономики, поддерживая рыболовство, разведение моллюсков, туризм и многое другое.
Находящиеся под угрозой исчезновения южные косатки зависят от этого лосося в качестве добычи, что делает эту среду обитания важной и для китов. Прибрежная среда обитания также является краеугольным камнем региональной экономики, поддерживая рыболовство, разведение моллюсков, туризм и многое другое. Продолжающаяся потеря прибрежной среды обитания, столь тесно связанная с выживанием лосося, остается самым большим риском для зарегистрированного в Пьюджет-Саунд чавычи.
Продолжающаяся потеря прибрежной среды обитания, столь тесно связанная с выживанием лосося, остается самым большим риском для зарегистрированного в Пьюджет-Саунд чавычи.
 использовать.
использовать. Мы также готовы проявлять гибкость в отношении того, как инициаторы проекта получают кредиты на среду обитания, чтобы компенсировать воздействия или дебеты, связанные с развитием. Мы понимаем, что это новый подход, при котором существует лишь несколько природоохранных банков. Мы работаем над тем, чтобы улучшить это. А пока мы можем помочь разными способами:
Мы также готовы проявлять гибкость в отношении того, как инициаторы проекта получают кредиты на среду обитания, чтобы компенсировать воздействия или дебеты, связанные с развитием. Мы понимаем, что это новый подход, при котором существует лишь несколько природоохранных банков. Мы работаем над тем, чтобы улучшить это. А пока мы можем помочь разными способами: )
)
 Представление калькулятора для каждого проекта настоятельно рекомендуется.
Представление калькулятора для каждого проекта настоятельно рекомендуется.

 Если после изучения
примеров решения задач
у Вас останутся вопросы, то Вы всегда можете задать их на
форуме, и не забывайте про наши
онлайн калькуляторы для
решения задач по геометрии и другим предметам!
Если после изучения
примеров решения задач
у Вас останутся вопросы, то Вы всегда можете задать их на
форуме, и не забывайте про наши
онлайн калькуляторы для
решения задач по геометрии и другим предметам!