что такое, чем отличаются друг от друга, как найти, примеры решения
Что такое делители и кратные числа
Определение 1Деление — математическое действие, которое определяет, сколько раз одно число содержится в другом. Обратной операцией является умножение.
Выделяют следующие компоненты деления:
- делимое;
- делитель;
- частное.
Делимое — число, которое делят на несколько частей.
Делитель — число, которое показывает, на сколько частей нужно разделить делимое.
Частное — число, которое является результатом деления.
a:b =c , где a — делимое, b — делитель, c — частное.
Умножение частного на делитель дает делимое.
Чтобы получить делитель, нужно делимое разделить на частное.
Делимое = частное * делитель
Дельтель = делимое / частное
Пример 1Например, нужно поровну разделить 16 мандаринов между двумя детьми. Для этого 16:2=8. Таким образом, каждый ребенок получит по 8 мандаринов.
Для этого 16:2=8. Таким образом, каждый ребенок получит по 8 мандаринов.
16 в этом примере является делимым, 2 — делителем, 8 — частным. Шестнадцать поделили на две части, по восемь в каждой. Или восемь содержится в 16 два раза. Или 2 содержится в 16 восемь раз. Деление прошло без остатка — нацело. Тогда число 2 является делителем числа 16.
Определение 3Делителем числа a называется такое число b, на которое a делится нацело.
Пример 2Например, 9:4=2 (остаток 5).
В примере 9 — делимое, 4 — делитель, 2 — неполное частное, 5 — остаток.
Остаток от деления — число, которое меньше делителя. Образуется при делении с остатком. Значит, в примере 9:4=2 (остаток 5) — число 4 не является делителем числа 9.
УпражнениеЗадание: найдите такую пару делителей числа 144, если один из делителей равен 2.
Объяснение:
Пусть неизвестный делитель равен x. Чтобы найти еще один делитель, если какой-то известен, нужно данное нам число разделить на известный делитель.
Чтобы найти еще один делитель, если какой-то известен, нужно данное нам число разделить на известный делитель.
Тогда представим решение данной задачи в виде уравнения:
144:x = 2;
x = 144:2;
x=72.
72 — целое число, без остатка.
Проверка:
Произведение делителей должно дать в результате 144:
72*2 = 144 — верно, значит, 72 — корень уравнения и делитель 144.
Ответ: числа 2 и 72 — делители 144.
Определение 4Число называют кратным, если оно делится на данное число нацело, без остатка.
Пример 3Например, 15:3 нацело.
15:3=5.
Тогда число 15 является кратным 3.
Пишут: 15 кратно 3.
Слово «кратно» синонимично слову «делится».
Фразу «15 кратно 3» можно в уме заменить на «15 делится на 3 нацело».
Примечание 1Основные понятия и определения
Определение 5Делитель — это число, на которое данное число делится нацело. Делитель всегда меньше или равен числу.
Делитель всегда меньше или равен числу.
Делится нацело = без остатка.
Наименьшим делителем любого числа является единица.
Наибольшим делителем числа является само число.
Делителем нуля будет любое число, но сам 0 делителем не будет.
При делении нуля на любое число получаем 0. А делить на ноль нельзя.
У единицы только один делитель — единица.
Другие числа, кроме 1, имеют не меньше двух делителей.
Определение 6Кратное — число, которое делится на данное число нацело. Всегда больше или равно числу.
Наименьшее кратное числа является равным самому числу.
Наибольшее кратное подобрать нельзя, потому что ряд натуральных чисел бесконечен. У любого натурального числа бесконечное множество кратных.
Ноль является кратным для любого числа. При умножении на ноль всегда получается ноль.
Когда одно число делится нацело на другое, то первое число — кратное второго, а второе — делитель первого.
Примечание 2a:b=c, где а — кратное b и c — делитель a
Чем отличаются друг от друга, как найти
Делитель отличается от кратного тем, что:
- делитель — это число, НА которое делится заданное число;
- кратное — это число, которое само ДЕЛИТСЯ НА заданное число.
Чтобы найти делители числа, нужно данное число разложить на множители.
Разложить на множители — представить число в виде произведения целых чисел.
Чтобы проверить, является ли одно число делителем другого, нужно разделить число на данное нам.
Для нахождения кратного числа заданному числу, нужно это число последовательно умножать на натуральные числа. Каждое полученное число будет кратно — будет делиться — заданному.
Делители и кратные связаны между собой. Например, делителем числа 15 является 3 и число, кратное 3, равно 15.
Примеры решения задач
Задача 1Необходимо найти делители числа 14.
Решить задание можно двумя способами.
Способ 1:
Последовательно делим 14 на натуральные числа от 1 до 14. Помним, что делитель всегда меньше или равен заданному числу.
Выбираем такие числа в качестве делителя, при делении на которые мы не получили остаток: 1, 2, 7, 14.
Ответ: делители числа 14: 1, 2, 7, 14.
Способ 2:
Представим 14 в виде произведения чисел:
14 = 14*1 = 2*7
Делителями будут множители, так как можем разделить 14 нацело на каждый из них.
Ответ: делители 14: 1, 2, 7, 14.
Задача 2Найдите три числа, кратных 7.
Решение:
Чтобы найти число, кратное данному, нужно это число умножить на любое натуральное число.
7*1 = 7 — семь кратно семи;
7*2=14— 14 кратно 7;
7*3=21— 21 кратно 7.
Ответ: числа, кратные 7: 7, 14, 21.
Задача 3Самостоятельно проверьте, 225 кратно 3 или нет.
Чтобы проверить, кратно ли одно число другому, нужно разделить числа друг на друга.
225:3=75.
75 — целое число, при делении нет остатка. Тогда 225 кратно 3.
Задача 4Найдите любое число, делителями которого являются числа 7 и 8.
Самый простой способ, если в задании не оговорены еще какие-либо условия, просто перемножить эти делители:
7*8=56
Ответ: 56.
ДЕЛЕНИЕ НА 8: НАЦЕЛО И С ОСТАТКОМ
Примеры.
Открыть в полном размере
‹
›
Благодарен вашему журналу за публикацию моего материала о признаке делимости целых чисел на 7 (см. «Наука и жизнь» № 10, 1997 г.). Рискну предложить еще один новый признак делимости, но уже на 8.
Я перелистал много книг по занимательной математике, но такого признака не нашел нигде.
Общепринятый
признак делимости на 8 выглядит так:
число делится на 8 в том и только в
том случае, если его последние три
цифры образуют число, делящееся на
8.
Этот способ деления основан на том, что все числа, кратные 1000, делятся на 8 без остатка.
Значит, определение признака делимости на 8 любых многозначных целых чисел сводится в итоге к определению признака делимости на 8 трехзначных чисел.
Трехзначные числа и будем рассматривать.
Б. А. Кордемский сводит делимость уже трехзначных чисел к делимости двузначных (образованных цифрами сотен и десятков): «На 8 делится всякое трехзначное число, у которого двузначное число, образованное цифрами сотен и десятков, сложенное с половиной числа единиц, делится на 4».
Он приводит пример с числом 592. Применяя к нему признак делимости, получаем:
59 + 1 = 60,
где 1 — это 2:2, половина числа единиц.
Число 60 делится на 4, значит, число 592 делится на 8 без остатка.
При данном методе
определения остатка от деления
надо учитывать, что трехзначные
числа, оканчивающиеся нечетной
цифрой (1, 3, 5, 7, 9), надо сначала
«округлить» в разряде единиц
до ближайшей большей или меньшей
четной цифры и в конечном
результате опять же учесть эту
единицу, то есть прибавить ее или
отнять.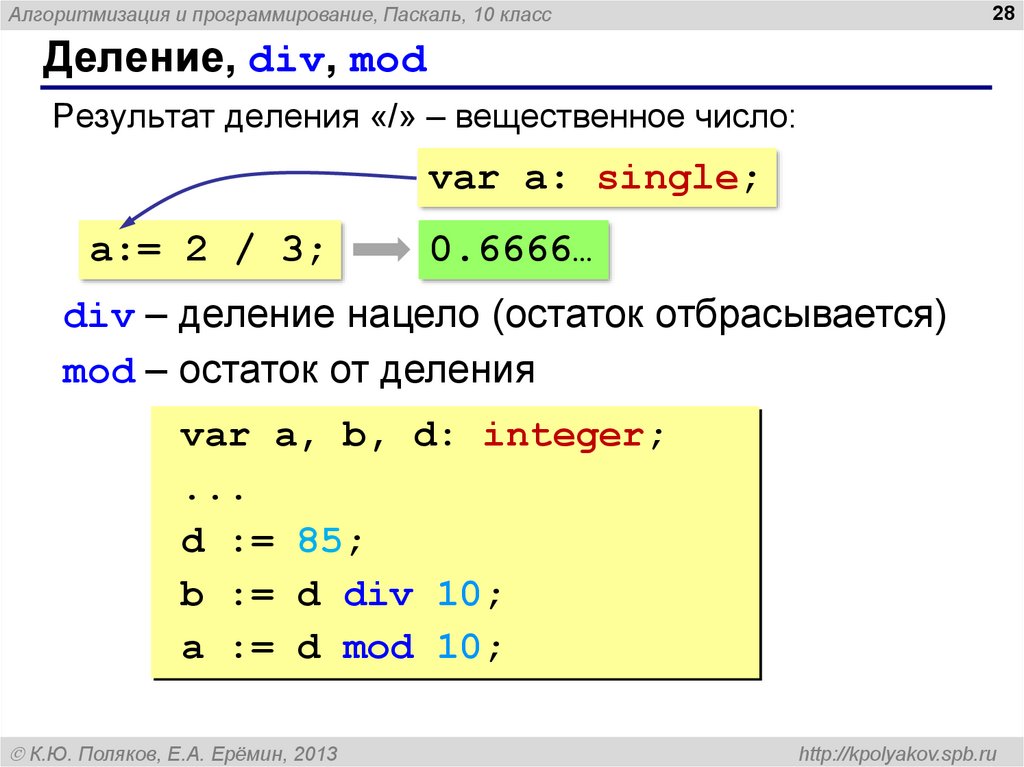 Это первое.
Это первое.
Второе: в некоторых случаях сумма двузначного числа, образованного цифрами сотен и десятков, и половины единиц будет также трехзначным числом, что опять же не совсем удобно. Это будет происходить с рядом чисел в промежутке от 968 до 999.
Однако всех этих неудобств — прибавления (вычитания) 1 и оперирования трехзначными числами — можно избежать.
Вспомним, что четное число сотен — 2, 4, 6, 8 (200, 400, 600, 800) делится на 8 без остатка. Следовательно, у таких, к примеру, чисел, как 059, 237, 461, 632, 844, определить остаток от деления на 8 можно сразу по двузначному числу, составленному из десятков и единиц, то есть по числам 59, 37, 61, 32, 44. Достаточно в уме разделить эти двузначные числа на 8.
Если цифры сотен в
трехзначных исходных числах
нечетны (1, 3, 5, 7, 9), то опять же делим
на 8 двузначные числа, образованные
десятками и единицами, но в этом
случае прибавляем (или отнимаем) к
двузначным числам цифру 4. Этот факт
следует из того, что все целые
нечетные сотни (100, 300, 500, 700, 900) при
делении на 8 дают один остаток — 4.
Этот факт
следует из того, что все целые
нечетные сотни (100, 300, 500, 700, 900) при
делении на 8 дают один остаток — 4.
Для примера возьмем числа 165, 371, 587, 716, 923. «Превратим» их в двузначные числа, прибавляя (можно отнимая) 4:
69, 75, 91, 20, 27.
Делить эти двузначные числа на 8 опять же просто. Остатки от делений и будут остатками от деления на 8 исходных трехзначных чисел.
А как поступить, если трехзначное число 997?
Выше говорилось, что цифру 4 можно не только прибавлять, но и отнимать от двузначного числа. Значит, делить на 8 будем уже число 93: 97- 4 = 93.
Так происходит «избавление» от трехзначных чисел.
Обобщая все
вышесказанное, алгоритм
упрощенного признака делимости на 8
целых чисел можно записать так:
отделяем, отсчитывая справа, три
цифры исходного числа; если третья
справа цифра четная (0, 2, 4, 6, 8), то
делим на 8 только число,
образованное двумя крайними
правыми цифрами; остаток от этого
деления и будет остатком от деления
на 8 всего исходного числа; если
третья справа цифра в исходном
числе нечетная (1, 3, 5, 7, 9), делим на 8 число,
образованное двумя крайними
правыми цифрами, плюс (минус) 4;
остаток от деления этой суммы и
даст остаток от деления на 8 всего
исходного целого числа.
Как видно, этот признак делимости совсем прост, и для его освоения понадобятся минимальные усилия и знание элементарной арифметики.
Литература
Кордемский Б. А. Математическая смекалка. М., 1991.
Воробьев Н. Н. Признаки делимости. М., 1980.
Гарднер М. Математические досуги. М., 1995.
Делимое
Когда делимое делится на делитель, а частное представляет собой целое число без остатка, говорят, что делимое делится на делитель.
На рисунке ниже показано, что 8 делится на 2, но не на 3. Слева мы видим, что 8 можно без остатка разделить на 4 группы по 2. С другой стороны, 8 нельзя разделить на 3 группы. Только 2 группы могут содержать 3 объекта, а третья группа может содержать только 2 объекта.
Примеры
Определите, являются ли следующие элементы делимыми.
1. 48 ÷ 8:
48 &дел. 8 = 6
48 делится на 8.
2. 32 ÷ 5:
32 &дел.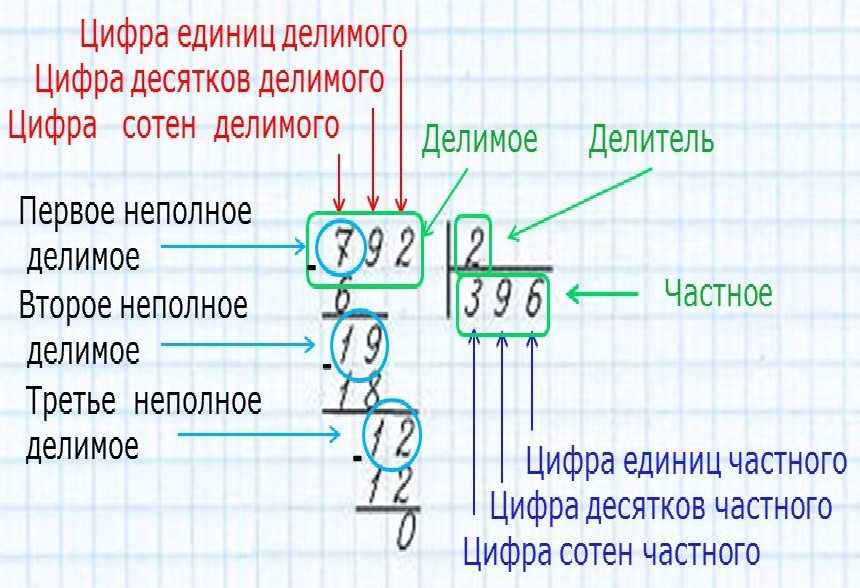 5 = 6 R2
5 = 6 R2
32 не делится на 5.
Определение того, делится ли число на определенное целое путем деления вручную и проверки остатка, может очень быстро стать утомительным, поскольку числа становятся больше. К счастью, есть несколько быстрых тестов, с помощью которых можно проверить, делится ли заданное число на определенные целые числа. В некоторых случаях выполнить деление может быть быстрее, но в других эти тесты могут сэкономить время. Ниже приведены тесты на делимость чисел от 1 до 10.
Признак делимости на 1
Все числа делятся на 1. Независимо от того, что это за число, при делении его на 1 получится одно и то же число.
Признак кратности 2
Если цифра в разряде единиц (последняя цифра) числа четная (0, 2, 4, 6, 8), то число делится на 2.
Пример
Проверить, следующие числа делятся на 2.
1. 5568:
8 делится на 2, поэтому 5568 делится на 2.
2. 527:
7 не делится на 2, поэтому 527 не делится на 2.
Делимость на 3
Найдите сумму всех цифр в числе. Если сумма цифр числа делится на 3, то это число делится на 3.
Пример
Проверить, делятся ли следующие числа на 3.
1. 273:
2 + 7 + 3 = 12
12 делится на 3, поэтому 273 делится на 3.
2. 323:
3 + 2 + 3 = 8
8 не делится на 3, поэтому 323 не делится на 3.
Делимость на 4
Если число, состоящее из двух последних цифр числа, делится на 4, то это число делится на 4.
Пример
Проверить, делятся ли следующие числа на 4.
1. 428:
28 ÷ 4 = 7
28 делится на 4, поэтому 428 делится на 4.
2. 1055:
55 ÷ 4 = 13 R3
55 не делится на 3, поэтому 1055 не делится на 3.
Признак кратности 5
Если последняя цифра в числе 5 или 0, то число делится на 5.
Пример
Проверить, делятся ли следующие числа на 5.
1. 3325:
Последняя цифра числа 3325 — 5, поэтому число 3325 делится на 5.
2. 325270:
Последняя цифра числа 325270 — 0, поэтому число 325270 делится на 5.
3. 4872: 900 03
Последняя цифра в 4872 не равно ни 0, ни 5, поэтому оно не делится на 5.
Признак кратности 6
Если число делится и на 2, и на 3, то оно делится и на 6.
Пример
Проверить, делятся ли следующие числа на 6.
1. 2358:
2358 &дел ; 2 = 1179
2358 &дел; 3 = 786
2358 делится и на 2, и на 3, поэтому оно делится на 6. Обратите внимание, что мы могли бы также использовать тесты на делимость для 2 и 3, а не решать задачу деления; вывод был бы таким же. 8 — четное число, поэтому 2358 делится на 2. 2 + 3 + 5 + 8 = 18, что делится на 3, поэтому 2358 делится на 3.
2. 4528:
4528 ÷ 2 = 2264
4528 &дел; 3 = 1509 R1
4528 делится на 2, но не на 3, поэтому 4528 не делится на 6.
3. 123:
123 ÷ 3 = 41
123 &дел; 2 = 61 R1
123 делится на 3, но не на 2, поэтому 123 не делится на 6. продукт от исходного номера. Если результат делится на 7, то исходное число делится на 7.
продукт от исходного номера. Если результат делится на 7, то исходное число делится на 7.
Пример
Проверить, делятся ли следующие числа на 7.
1. 567:
7 × 2 = 14
56 — 14 = 42
42 ÷ 7 = 6
42 делится на 7, значит, 567 делится на 7. &дел; 7 = 5 R3
38 не делится на 7, поэтому 548 не делится на 7.
Делимость на 8
Если последние 3 цифры в числе равны 0, число делится на 8. Если последние 3 цифры цифры не равны 0, но число, образованное последними 3 цифрами исходного числа, делится на 8, тогда исходное число делится на 8.
Пример
Проверить, делятся ли следующие числа на 8.
1. 231968:
968 ÷ 8 = 121
968 делится на 8, значит, 231968 делится на 8.
2. 347823000:
делится на 8.
Делимость на 9
Если сумма цифр числа делится на 9, тогда число делится на 9. И наоборот, число, которое дважды делится на 3, делится на 9.
Пример
Проверить, делятся ли следующие числа на 9.
1. 2349:
2 + 3 + 4 + 9 = 18
18 делится на 9, поэтому 2349 делится к 9.
2 405
405 &дел; 3 = 135
135 &дел; 3 = 45
405 делится на 3 дважды, поэтому 405 делится на 9.
Делимость на 10
Если последняя цифра в числе 0, то число делится на 10.
Пример
Проверить, делятся ли на 10 следующие числа. некоторые случаях проверка делимости может быть более утомительной, чем выполнение деления. Показаны только тесты на делимость от 1 до 10, поскольку они относительно просты.
Делитель — определение, формула, свойства, примеры
A делитель — это число, которое делится на другое число. Без делителя мы не можем делить числа. При делении используются четыре важных термина: делимое, делитель, частное и остаток. Деление — это метод равномерного распределения предметов по группам. Число, которое необходимо разделить, называется делимым, а общее количество равных групп, на которые оно должно быть разделено, называется делителем. Число, которое не учитывается без образования группы, называется «остатком».
Число, которое не учитывается без образования группы, называется «остатком».
| 1. | Что такое делитель? |
| 2. | Как найти делитель? |
| 3. | Формула делителя |
| 4. | Факты о делителях |
| 5. | Разница между делителем и множителями |
| 6. | Часто задаваемые вопросы о делителях |
Что такое делитель?
Делитель делит число на равные группы. Число, которое делится, называется делимым , а число, на которое оно делится, называется делителем .
Делитель Значение
Число, которое делится на другое число с остатком или без него, называется делителем.
Существуют разные способы записи задачи на деление. На следующем рисунке показаны различные способы выражения деления и показано, как идентифицировать делитель, делимое и частное.
Как найти делитель?
Без делителей деление невозможно. Это означает, что определить делитель довольно просто. Например, если нам нужно разделить число 35 на 5, его можно представить как 35 ÷ 5 = 7. Здесь число 35 — делимое, число 5 — делитель , а число 7 — частное .
Иногда мы знаем значение делимого и частного и нам нужно найти делитель. В этом случае мы используем формула делителя . Давайте узнаем о формуле делителя в следующем разделе.
Формула делителя
Формула делителя формируется для двух ситуаций — с остатком или без остатка:
- Если остаток равен 0, то Делитель = Дивиденд ÷ Частное.
- Если остаток не равен 0, то Делитель = (Дивиденд — Остаток) ÷ Частное
Пример 1: Найдите делитель, если делимое равно 48, а частное равно 4.
Решение: Мы знаем, что делимое = 48, частное = 4. Итак, применим формулу делителя Делитель = Делимое ÷ Частное. Подставляя известные значения в формулу, получаем Делитель = 48 ÷ 4 = 12. Следовательно, делитель = 12.
Подставляя известные значения в формулу, получаем Делитель = 48 ÷ 4 = 12. Следовательно, делитель = 12.
Пример 2: Найдите делитель, если делимое равно 59, частное 11, а остаток равен 4.
Решение: Мы знаем, что делимое = 59, частное = 11, остаток = 4. Итак, применим формулу делителя Делитель = (Дивиденд — Остаток) ÷ Частное. Подставив известные значения в формулу, получим, Делитель = (59- 4) ÷ 11 = 55 ÷ 11 = 5. Следовательно, делитель = 5.
Факты о делителях
Вот список некоторых фактов, связанных с делителем.
- Если частное равно делимому, то делитель равен 1. Например, 45 ÷ 1 = 45
- Когда делимое и делитель равны в задаче на деление, частное равно 1. Например, 45 ÷ 45 = 1
- Частным называется число, которое получается при делении делимого на делитель, а любое число, оставшееся после деления, называется остатком.
- Остаток всегда меньше делителя.
- Когда остаток равен нулю, это означает, что делитель полностью разделил делимое.

- Если делитель больше делимого, результирующее число будет десятичным числом. Например, 45 ÷ 100 = 0,45· .
Разница между множителем и делителем
Мы знаем, что делитель — это число, на которое делится делимое. Когда делитель полностью делит делимое и не оставляет остатка, этот делитель также называется множителем этого числа. Таким образом, все делители числа являются делителями, но не всегда все делители должны быть делителями числа.
Пример 1: Множители 8 = 1, 2, 4 и 8. Это означает, что 8 полностью делится на 1, 2, 4, 8. Следовательно, все эти множители в данном случае являются делителями.
Пример 2: Разделите 12 на 5. Если мы разделим 12 на 5, мы получим 2 в качестве частного, а остаток равен 2. Это означает, что 12 ÷ 5 = 2, остаток = 2. В этом случае делитель равен 5, но 12 не делится полностью на 5. Таким образом, 5 не является делителем 12, но является делителем 12, так как дает остаток 2.
Следовательно, все делители являются делителями, но не все делители являются факторами.
Важные советы по делителю
Ниже приведены некоторые важные советы, связанные с делителем, которые мы изучили в этой статье.
- Делитель не может быть равен нулю, потому что при делении числа на ноль результат не определен.
- Задача на деление остается верной, даже если поменять местами частное и делитель.
- Когда ноль делится на любой делитель, в частном всегда получается ноль.
☛Статьи по теме
- Дивизион Формула
- Формула остатка делителя дивиденда
- Деление десятичных дробей
Часто задаваемые вопросы о делителях
Что такое делитель в математике?
Число, на которое делится другое число, называется делителем . Например, когда мы делим 20 на 4, мы получаем 5. Когда мы записываем это как 20 ÷ 4 = 5, здесь 4 — это число, на которое делится число 20. Следовательно, 4 называется делителем.
Следовательно, 4 называется делителем.
Является ли число делителем самого себя?
Да, число является делителем самого себя, потому что число может полностью делиться само на себя. Это означает, что частное будет равно 1. Например, 23 ÷ 23 = 1
Что такое делитель в дроби?
Дробь представляется в виде p/q, (где q не равно 0). Здесь знаменатель q является делителем. Например, в дроби 6/2 знаменатель 2 является делителем.
Что такое формула делителя?
Мы используем формулу делителя, когда знаем значение делимого и частного. У нас есть два сценария, чтобы найти делитель.
- Если остаток равен 0, то Делитель = Делимое ÷ Частное.
- Если остаток не равен 0, то Делитель = (Дивиденд — Остаток) ÷ Частное
Чему равен делитель в факте деления 30 ÷ 15 = 2?
Делитель — это число, на которое делится другое число. Здесь 30 делится на 15. Следовательно, 15 — делитель.
В чем разница между делителем и дивидендом?
Делитель делит число на равные группы.


 Наш онлайн-инструмент позволяет быстро и легко конвертировать единицы времени без лишних усилий. Вы можете перевести часы в минуты, минуты в секунды, дни в часы и многое другое.
Наш онлайн-инструмент позволяет быстро и легко конвертировать единицы времени без лишних усилий. Вы можете перевести часы в минуты, минуты в секунды, дни в часы и многое другое. Например, можно узнать сколько секунд в 1 году или сколько минут в 1 дне.
Например, можно узнать сколько секунд в 1 году или сколько минут в 1 дне. Это может предотвратить или отсрочить многие проблемы со здоровьем, которые, кажется, приходят с возрастом. Это также помогает вашим мышцам стать сильнее, чтобы вы могли продолжать заниматься своими повседневными делами, не становясь зависимыми от других.
Это может предотвратить или отсрочить многие проблемы со здоровьем, которые, кажется, приходят с возрастом. Это также помогает вашим мышцам стать сильнее, чтобы вы могли продолжать заниматься своими повседневными делами, не становясь зависимыми от других.

 Это заставит вас дышать тяжелее, а сердце биться чаще. Вы также заметите, что сможете говорить, но не напевать слова любимой песни.
Это заставит вас дышать тяжелее, а сердце биться чаще. Вы также заметите, что сможете говорить, но не напевать слова любимой песни. Важно, чтобы вы занимались физическими упражнениями, которые подходят вам и вашим способностям.
Важно, чтобы вы занимались физическими упражнениями, которые подходят вам и вашим способностям. Вы можете:
Вы можете:
 Только примерно каждый пятый взрослый и подросток получает достаточно упражнений для поддержания хорошего здоровья. Повышение активности может помочь всем людям лучше думать, чувствовать и спать, а также легче выполнять повседневные задачи. И если вы ведете малоподвижный образ жизни, лучше всего начать с меньшего количества сидения.
Только примерно каждый пятый взрослый и подросток получает достаточно упражнений для поддержания хорошего здоровья. Повышение активности может помочь всем людям лучше думать, чувствовать и спать, а также легче выполнять повседневные задачи. И если вы ведете малоподвижный образ жизни, лучше всего начать с меньшего количества сидения.

 Они потребуют большего количества усилий. Вы, вероятно, согреетесь и начнете потеть. Вы не сможете много говорить, не запыхавшись.
Они потребуют большего количества усилий. Вы, вероятно, согреетесь и начнете потеть. Вы не сможете много говорить, не запыхавшись. Даже если вы в течение многих лет вели сидячий образ жизни, сегодня тот день, когда вы можете начать вносить здоровые изменения в свою жизнь. Поставьте достижимую цель на сегодня. Вы можете работать над рекомендуемой суммой, увеличивая время по мере того, как становитесь сильнее. Не позволяйте мышлению «все или ничего» удерживать вас от того, что вы можете делать каждый день.
Даже если вы в течение многих лет вели сидячий образ жизни, сегодня тот день, когда вы можете начать вносить здоровые изменения в свою жизнь. Поставьте достижимую цель на сегодня. Вы можете работать над рекомендуемой суммой, увеличивая время по мере того, как становитесь сильнее. Не позволяйте мышлению «все или ничего» удерживать вас от того, что вы можете делать каждый день.

 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
 Тестирование с мгновенной проверкой. Учимся — с интересом!)
Тестирование с мгновенной проверкой. Учимся — с интересом!) Достаточно известный факт, что график показательной функции у = а х непременно пересекается с прямой у = b и притом исключительно в одной точке. Абсцисса точки пересечения и будут корнем уравнения .
Достаточно известный факт, что график показательной функции у = а х непременно пересекается с прямой у = b и притом исключительно в одной точке. Абсцисса точки пересечения и будут корнем уравнения .
 Именно по этой причине и оговорено условие a > 0 .
Именно по этой причине и оговорено условие a > 0 . к. 2 3 = 8
к. 2 3 = 8 Теперь рассмотрев примеры решения логарифмов мы можем переходить к логарифмическим уравнениям. Примеры решения логарифмических уравнений мы более подробно рассмотрим в статье: » «. Не пропустите!
Теперь рассмотрев примеры решения логарифмов мы можем переходить к логарифмическим уравнениям. Примеры решения логарифмических уравнений мы более подробно рассмотрим в статье: » «. Не пропустите!

 Так мы приходим к равенству b p =a p·log a b
, из которого по определению логарифма заключаем, что log a b p =p·log a b
.
Так мы приходим к равенству b p =a p·log a b
, из которого по определению логарифма заключаем, что log a b p =p·log a b
.
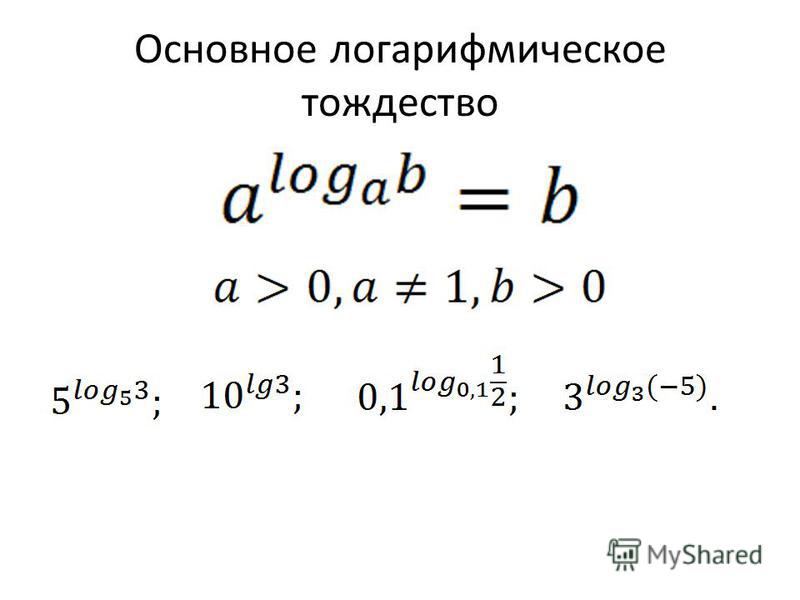
 Предположим, что при a 1 >1
, a 2 >1
и a 1 1
справедливо log a 1 b≤log a 2 b
. По свойствам логарифмов эти неравенства можно переписать как и соответственно, а из них следует, что log b a 1 ≤log b a 2
и log b a 1 ≥log b a 2
соответственно. Тогда по свойствам степеней с одинаковыми основаниями должны выполняться равенства b log b a 1 ≥b log b a 2
и b log b a 1 ≥b log b a 2
, то есть, a 1 ≥a 2
. Так мы пришли к противоречию условию a 1
Предположим, что при a 1 >1
, a 2 >1
и a 1 1
справедливо log a 1 b≤log a 2 b
. По свойствам логарифмов эти неравенства можно переписать как и соответственно, а из них следует, что log b a 1 ≤log b a 2
и log b a 1 ≥log b a 2
соответственно. Тогда по свойствам степеней с одинаковыми основаниями должны выполняться равенства b log b a 1 ≥b log b a 2
и b log b a 1 ≥b log b a 2
, то есть, a 1 ≥a 2
. Так мы пришли к противоречию условию a 1
 04.2013, 13:04
04.2013, 13:04  04.2013, 13:10
04.2013, 13:10 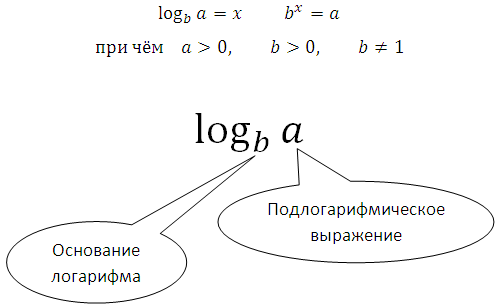 Частичными суммами и оценивайте.
Частичными суммами и оценивайте. Если нужно точнее, несколько членов сохраните без изменения, а в последующих дроби замените на первую из них (самую большую).
Если нужно точнее, несколько членов сохраните без изменения, а в последующих дроби замените на первую из них (самую большую). 04.2013, 13:31
04.2013, 13:31 
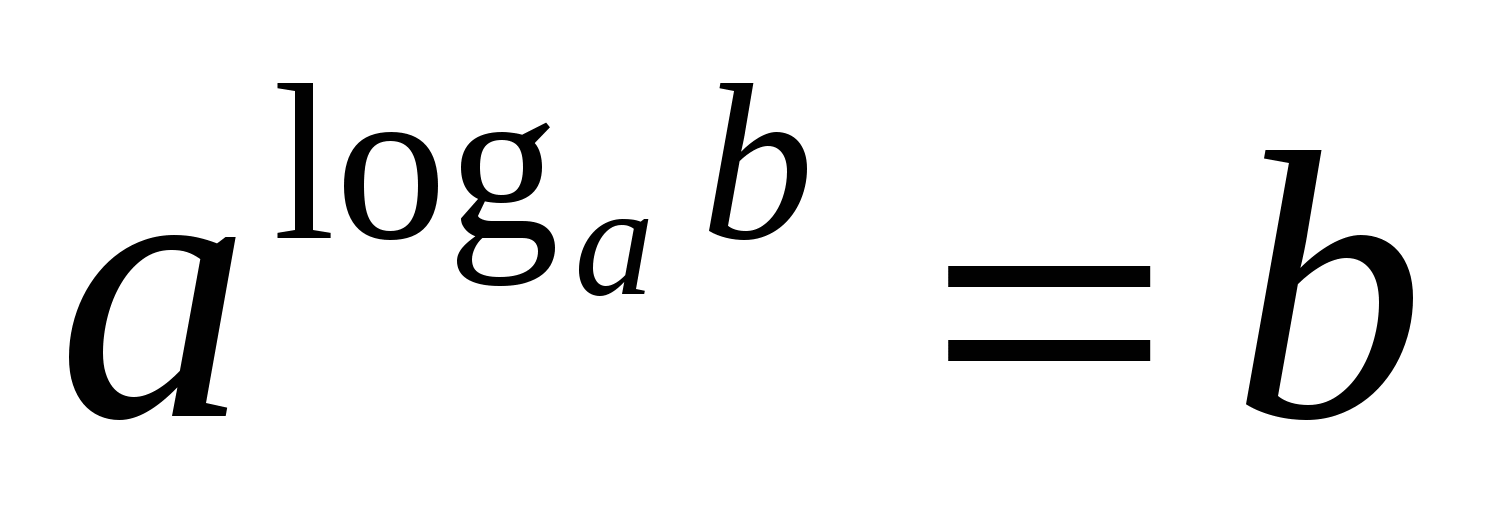 04.2013, 14:37
04.2013, 14:37  04.2013, 14:43
04.2013, 14:43  Логарифмическая функция определяется следующим образом:
Логарифмическая функция определяется следующим образом: Два свойства:
Два свойства:
 Мы обсудили два метода нахождения предела. Выбор метода решения проблемы зависит от сложности проблемы. Большинство проблем эффективно решаются с помощью правила Ло Хоспиталя. Но некоторые вопросы требуют базового метода для их решения. Мы также обсудили алгебру пределов. Понимание этой концепции является обязательным для всех, потому что она разбивает сложные проблемы на более простые.
Мы обсудили два метода нахождения предела. Выбор метода решения проблемы зависит от сложности проблемы. Большинство проблем эффективно решаются с помощью правила Ло Хоспиталя. Но некоторые вопросы требуют базового метода для их решения. Мы также обсудили алгебру пределов. Понимание этой концепции является обязательным для всех, потому что она разбивает сложные проблемы на более простые. Помните, чего не могут экспоненциальные функции: они не могут выводить отрицательное число вместо 9.0166 ф ( х ). Функция, на которую мы обратили внимание, когда думали об экспоненциальных функциях, была f ( x ) = 4 x .
Помните, чего не могут экспоненциальные функции: они не могут выводить отрицательное число вместо 9.0166 ф ( х ). Функция, на которую мы обратили внимание, когда думали об экспоненциальных функциях, была f ( x ) = 4 x .
 14159..
14159.. 5 класс.
5 класс. 10 — 11 класс.
10 — 11 класс.
 Она также пишет биографии для Story Terrace.
Она также пишет биографии для Story Terrace. В действительности 10-процентные инвестиции удвоятся за 7,3 года ((1,10 7,3 = 2).
В действительности 10-процентные инвестиции удвоятся за 7,3 года ((1,10 7,3 = 2). 11
11 Наиболее важное свойство числа e связано с наклоном экспоненциальной и логарифмической функций, и его первые несколько цифр равны 2,718281828. 9н
2 = (1 + г) п
Наиболее важное свойство числа e связано с наклоном экспоненциальной и логарифмической функций, и его первые несколько цифр равны 2,718281828. 9н
2 = (1 + г) п
 Формула:
Формула: io/ru/number/least-common-multiple-lcm-of/50—70
io/ru/number/least-common-multiple-lcm-of/50—70 2014 Апрель; 70 (4): 637-643.
2014 Апрель; 70 (4): 637-643. Льежуа 11 , Дэвид Берд 12 , Артур Собер 13 , Пол Нгхием 14
Льежуа 11 , Дэвид Берд 12 , Артур Собер 13 , Пол Нгхием 14 

 1016/j.jaad.2013.11.031
1016/j.jaad.2013.11.031 Бичакджян 5 , Натали Зейтуни 6 , Джеффри Э. Гершенвальд 7 , Вернон Сондак 8 , Кларк К. Отли 9 , Зигрид С. Ю. 10 , Тимоти М. Джонсон 5 , Нанетт Дж. Льежуа 11 , Дэвид Берд 12 , Артур Собер 13 , Пол Нгхием 14
Бичакджян 5 , Натали Зейтуни 6 , Джеффри Э. Гершенвальд 7 , Вернон Сондак 8 , Кларк К. Отли 9 , Зигрид С. Ю. 10 , Тимоти М. Джонсон 5 , Нанетт Дж. Льежуа 11 , Дэвид Берд 12 , Артур Собер 13 , Пол Нгхием 14 
 Ли Моффита и Университет Южной Флориды, Тампа, Флорида.
Ли Моффита и Университет Южной Флориды, Тампа, Флорида. Электронный адрес:
Электронный адрес: 


 Отношение размера первичной опухоли к поражению регионарных узлов.
Отношение размера первичной опухоли к поражению регионарных узлов. 
 Патологическая стадия узлов уменьшалась с возрастом у обоих полов. Столбики погрешностей представляют биномиальную стандартную ошибку. Данные от 4809показаны самцы и 3036 самок. Частота оценки патологических узлов значительно различалась в зависимости от возраста и пола (молодые и пожилые мужчины, p
Патологическая стадия узлов уменьшалась с возрастом у обоих полов. Столбики погрешностей представляют биномиальную стандартную ошибку. Данные от 4809показаны самцы и 3036 самок. Частота оценки патологических узлов значительно различалась в зависимости от возраста и пола (молодые и пожилые мужчины, p


 2002 декабрь; 979: 166-77; обсуждение 188-96.
2002 декабрь; 979: 166-77; обсуждение 188-96. 2002 декабрь; 979: 166-77; обсуждение 188-96.
2002 декабрь; 979: 166-77; обсуждение 188-96. Рекрутированные антигеном, находящимся в нелимфоидных тканях, инфильтрирующие лимфоциты часто организуются в виде фолликулоподобных структур, содержащих зародышевые центры, подобные таковым во вторичных лимфоидных фолликулах лимфатических узлов. Эти экстранодальные третичные лимфоидные фолликулы обнаруживаются при различных аутоиммунных заболеваниях. Обследованы 153 пациента с затяжным лимфостазом нижней конечности, обусловленным лимфатическим поражением, возникшим вследствие бактериального воспаления мягких тканей или механической травмы мягких тканей и костей. У 10% больных с поствоспалительным и у 25% с посттравматическим лимфостазом методом лимфосцинтиграфии выявляли «новообразованные» лимфатические узлы. Они располагались по ходу крупных икроножных и бедренных вен. Хотя в этих областях обычно выявляются рассеянные узлы, количество и общая масса визуализируемых узлов значительно превышали таковые у здоровых людей. Расчетная площадь поверхности «новообразованных» узлов достигала 50-70% от площади ипсилатеральных паховых узлов.
Рекрутированные антигеном, находящимся в нелимфоидных тканях, инфильтрирующие лимфоциты часто организуются в виде фолликулоподобных структур, содержащих зародышевые центры, подобные таковым во вторичных лимфоидных фолликулах лимфатических узлов. Эти экстранодальные третичные лимфоидные фолликулы обнаруживаются при различных аутоиммунных заболеваниях. Обследованы 153 пациента с затяжным лимфостазом нижней конечности, обусловленным лимфатическим поражением, возникшим вследствие бактериального воспаления мягких тканей или механической травмы мягких тканей и костей. У 10% больных с поствоспалительным и у 25% с посттравматическим лимфостазом методом лимфосцинтиграфии выявляли «новообразованные» лимфатические узлы. Они располагались по ходу крупных икроножных и бедренных вен. Хотя в этих областях обычно выявляются рассеянные узлы, количество и общая масса визуализируемых узлов значительно превышали таковые у здоровых людей. Расчетная площадь поверхности «новообразованных» узлов достигала 50-70% от площади ипсилатеральных паховых узлов. Гистологическая оценка узловых биоптатов у трех таких пациентов выявила, у одного, структуру лимфатического узла без дифференциации на корковую и медуллярную области, а у второго — фолликулоподобную структуру в расширенном лимфатическом сосуде. Сгусток лимфы, удаленный из другого расширенного сосуда, содержал агрегат лимфоцитов/дендритных клеток. «Вновь образованные» узлы, вероятно, происходят из первичных лимфоидных фолликулов и/или агрегатов лимфоидных клеток, формирующихся в ответ на хроническую стимуляцию микробными продуктами и аутоантигенами из поврежденных тканей. Обнаружение «новообразованных» лимфатических узлов на конечности свидетельствует о продолжающемся воспалительном процессе и требует соответствующей терапии.
Гистологическая оценка узловых биоптатов у трех таких пациентов выявила, у одного, структуру лимфатического узла без дифференциации на корковую и медуллярную области, а у второго — фолликулоподобную структуру в расширенном лимфатическом сосуде. Сгусток лимфы, удаленный из другого расширенного сосуда, содержал агрегат лимфоцитов/дендритных клеток. «Вновь образованные» узлы, вероятно, происходят из первичных лимфоидных фолликулов и/или агрегатов лимфоидных клеток, формирующихся в ответ на хроническую стимуляцию микробными продуктами и аутоантигенами из поврежденных тканей. Обнаружение «новообразованных» лимфатических узлов на конечности свидетельствует о продолжающемся воспалительном процессе и требует соответствующей терапии.
 Лимфология. 1983.
PMID: 6664116
Лимфология. 1983.
PMID: 6664116 , июнь; 43 (6): 811-27.
Дж Нукл Мед. 2002.
PMID: 12050328
Обзор.
, июнь; 43 (6): 811-27.
Дж Нукл Мед. 2002.
PMID: 12050328
Обзор.

 В этом случае для оклейки над окнами и дверями Вам потребуется дополнительный рулон.
В этом случае для оклейки над окнами и дверями Вам потребуется дополнительный рулон.
 В среднем, кубический метр почти всей древесины весит 700 кг.
В среднем, кубический метр почти всей древесины весит 700 кг. 
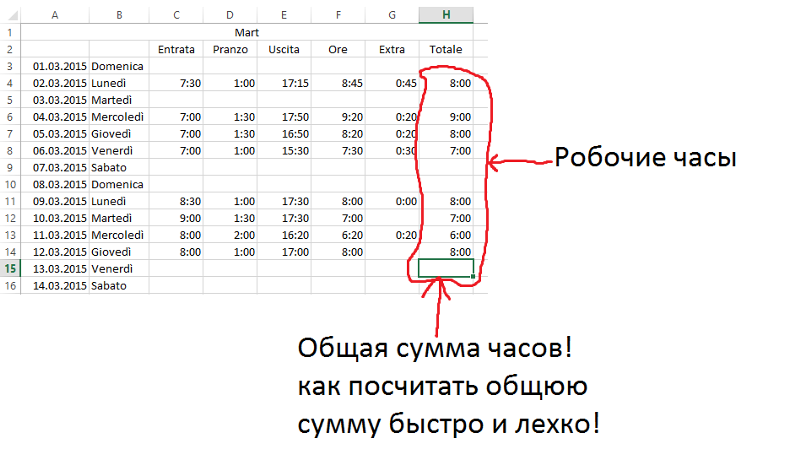
 время отключения. Затем просто разделите свой доход на общее количество часов, которые вы подсчитали. (Большинство людей, по его словам, тратят около 2500 часов в год на работу с полной занятостью.)
время отключения. Затем просто разделите свой доход на общее количество часов, которые вы подсчитали. (Большинство людей, по его словам, тратят около 2500 часов в год на работу с полной занятостью.)

 д.)
д.) Когда дело доходит до денег, вы потратите , это может означать, что вы с радостью заплатите дополнительные 200 долларов, чтобы вернуться домой из отпуска пораньше, чтобы успеть расслабиться.
Когда дело доходит до денег, вы потратите , это может означать, что вы с радостью заплатите дополнительные 200 долларов, чтобы вернуться домой из отпуска пораньше, чтобы успеть расслабиться.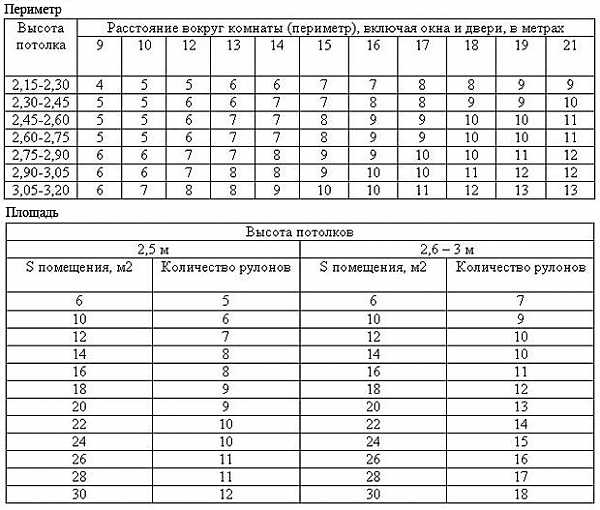 Включите все свои потоки доходов, от алиментов до прибыли от инвестиций и доходов от аренды.
Включите все свои потоки доходов, от алиментов до прибыли от инвестиций и доходов от аренды.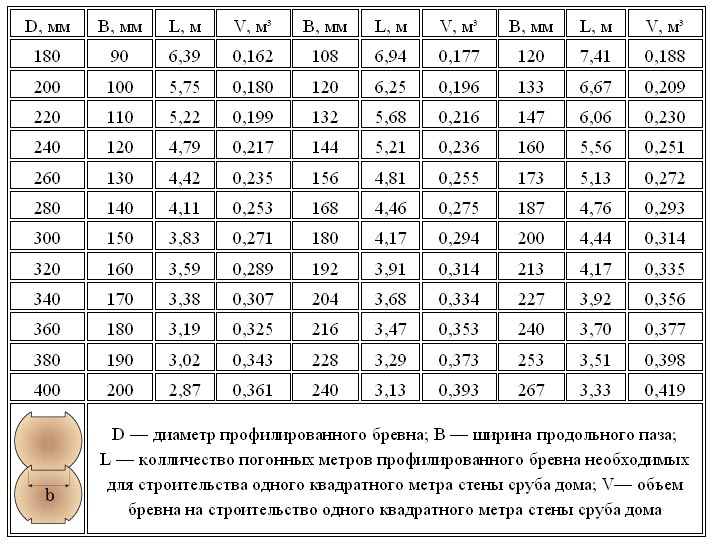 Правило 28/36 процентов — это проверенное практическое правило доступности жилья, которое устанавливает базовый уровень того, что вы можете позволить себе платить каждый месяц. Предположим, что вы зарабатываете 4000 долларов в месяц. Это означает, что ваш платеж по ипотеке должен составлять не более 1120 долларов (28 процентов от 4000 долларов), а сумма других ваших долгов не должна превышать 1440 долларов в месяц (36 процентов от 4000 долларов). Что вы делаете с тем, что осталось? Вам нужно будет определить бюджет, который позволяет вам платить за предметы первой необходимости, такие как еда и транспорт, желания, такие как развлечения и обеды вне дома, и цели сбережений, такие как выход на пенсию.
Правило 28/36 процентов — это проверенное практическое правило доступности жилья, которое устанавливает базовый уровень того, что вы можете позволить себе платить каждый месяц. Предположим, что вы зарабатываете 4000 долларов в месяц. Это означает, что ваш платеж по ипотеке должен составлять не более 1120 долларов (28 процентов от 4000 долларов), а сумма других ваших долгов не должна превышать 1440 долларов в месяц (36 процентов от 4000 долларов). Что вы делаете с тем, что осталось? Вам нужно будет определить бюджет, который позволяет вам платить за предметы первой необходимости, такие как еда и транспорт, желания, такие как развлечения и обеды вне дома, и цели сбережений, такие как выход на пенсию. Если у вас осталось только 500 долларов после покрытия других расходов, вы, вероятно, слишком сильно напрягаетесь. Помните, что есть и другие важные финансовые цели, и вы хотите жить по средствам. Тот факт, что кредитор предлагает вам предварительное одобрение на большую сумму денег, не означает, что вы должны тратить так много на свой дом.
Если у вас осталось только 500 долларов после покрытия других расходов, вы, вероятно, слишком сильно напрягаетесь. Помните, что есть и другие важные финансовые цели, и вы хотите жить по средствам. Тот факт, что кредитор предлагает вам предварительное одобрение на большую сумму денег, не означает, что вы должны тратить так много на свой дом. Это, в свою очередь, привело к росту ставок по ипотечным кредитам. Повышение ставок часто ослабляет энтузиазм покупателей жилья или даже полностью вытесняет их с рынка, что в конечном итоге снижает стоимость домов. Однако, если вы все еще хотите купить дом, более высокие процентные ставки означают, что ваши ежемесячные платежи по ипотеке будут выше. Например, при 3-процентной процентной ставке ипотека в размере 600 000 долларов будет стоить около 2,9 доллара.90 в месяц. При ставке 6 процентов тот же кредит будет стоить 4058 долларов. (После падения до 3,08 процента в конце 2020 года фиксированные ставки по 30-летней ипотеке в середине февраля 2023 года колебались на уровне около 6,5 процента.)
Это, в свою очередь, привело к росту ставок по ипотечным кредитам. Повышение ставок часто ослабляет энтузиазм покупателей жилья или даже полностью вытесняет их с рынка, что в конечном итоге снижает стоимость домов. Однако, если вы все еще хотите купить дом, более высокие процентные ставки означают, что ваши ежемесячные платежи по ипотеке будут выше. Например, при 3-процентной процентной ставке ипотека в размере 600 000 долларов будет стоить около 2,9 доллара.90 в месяц. При ставке 6 процентов тот же кредит будет стоить 4058 долларов. (После падения до 3,08 процента в конце 2020 года фиксированные ставки по 30-летней ипотеке в середине февраля 2023 года колебались на уровне около 6,5 процента.) Если ваш кредитный рейтинг ниже — например, 640 — ваша ставка может быть выше 6 процентов. В этом случае ежемесячный платеж для покрытия основного долга и процентов может быть на 300 долларов дешевле для более высокого кредитного рейтинга. Чтобы узнать свой кредитный рейтинг, проверьте свой кредитный отчет в одном из трех больших агентств: Equifax, Experian и TransUnion.
Если ваш кредитный рейтинг ниже — например, 640 — ваша ставка может быть выше 6 процентов. В этом случае ежемесячный платеж для покрытия основного долга и процентов может быть на 300 долларов дешевле для более высокого кредитного рейтинга. Чтобы узнать свой кредитный рейтинг, проверьте свой кредитный отчет в одном из трех больших агентств: Equifax, Experian и TransUnion. Если вы хотите уменьшить соотношение долга к доходу до подачи заявки на ипотеку — что, вероятно, является хорошей идеей — погасите свои кредитные карты и другие повторяющиеся долги, такие как студенческие ссуды и платежи за автомобиль.
Если вы хотите уменьшить соотношение долга к доходу до подачи заявки на ипотеку — что, вероятно, является хорошей идеей — погасите свои кредитные карты и другие повторяющиеся долги, такие как студенческие ссуды и платежи за автомобиль. Используя правило 28 процентов, ваши платежи по ипотеке должны составлять не более 19 600 долларов США в год, что соответствует ежемесячному платежу в размере 1 633 долларов США. Имея в виду это волшебное число, вы можете позволить себе дом за 305 000 долларов с процентной ставкой 5,35% в течение 30 лет. Но вам нужно будет внести первоначальный взнос в размере 20 процентов.
Используя правило 28 процентов, ваши платежи по ипотеке должны составлять не более 19 600 долларов США в год, что соответствует ежемесячному платежу в размере 1 633 долларов США. Имея в виду это волшебное число, вы можете позволить себе дом за 305 000 долларов с процентной ставкой 5,35% в течение 30 лет. Но вам нужно будет внести первоначальный взнос в размере 20 процентов. И не забудьте подумать о том, что взносы по ипотечному страхованию могут повлиять на ваш бюджет. Если вы делаете первоначальный взнос менее 20 процентов по обычному кредиту, вам нужно будет заплатить за частное ипотечное страхование или PMI.
И не забудьте подумать о том, что взносы по ипотечному страхованию могут повлиять на ваш бюджет. Если вы делаете первоначальный взнос менее 20 процентов по обычному кредиту, вам нужно будет заплатить за частное ипотечное страхование или PMI. Если ваша оценка 580 или выше, вы можете поставить всего 3,5 процента. Однако существуют ограничения на кредиты FHA. В большинстве районов в 2023 году ссуда FHA не может превышать 472 030 долларов США для дома на одну семью. В более дорогих районах эта цифра может достигать 1089 долларов.,300. Вам также необходимо учитывать, как взносы по ипотечному страхованию, обязательные для всех кредитов FHA, повлияют на ваши платежи.
Если ваша оценка 580 или выше, вы можете поставить всего 3,5 процента. Однако существуют ограничения на кредиты FHA. В большинстве районов в 2023 году ссуда FHA не может превышать 472 030 долларов США для дома на одну семью. В более дорогих районах эта цифра может достигать 1089 долларов.,300. Вам также необходимо учитывать, как взносы по ипотечному страхованию, обязательные для всех кредитов FHA, повлияют на ваши платежи.
 .К счастью, существуют программы, разработанные специально для тех, кто впервые покупает жилье. В зависимости от того, где вы живете и сколько вы зарабатываете, вы можете претендовать на помощь с вашим авансовым платежом и/или закрывающими расходами.
.К счастью, существуют программы, разработанные специально для тех, кто впервые покупает жилье. В зависимости от того, где вы живете и сколько вы зарабатываете, вы можете претендовать на помощь с вашим авансовым платежом и/или закрывающими расходами. Вы также можете сосредоточиться на увеличении своего дохода, договорившись о повышении заработной платы на вашей текущей работе или устроившись на вторую работу для дополнительного заработка. В любом случае вы продемонстрируете кредитору, что у вас больше денег, что снижает риск.
Вы также можете сосредоточиться на увеличении своего дохода, договорившись о повышении заработной платы на вашей текущей работе или устроившись на вторую работу для дополнительного заработка. В любом случае вы продемонстрируете кредитору, что у вас больше денег, что снижает риск.
 Этот счет сильно различается в зависимости от оценки вашей собственности и ее местонахождения. Например, средний счет налога на недвижимость для дома на одну семью в Нью-Джерси составлял 9 долларов.476 в 2021 году. По данным ATTOM, эта цифра почти в 10 раз превышает средний счет налога на недвижимость в размере 901 доллара для домовладельцев в Западной Вирджинии.
Этот счет сильно различается в зависимости от оценки вашей собственности и ее местонахождения. Например, средний счет налога на недвижимость для дома на одну семью в Нью-Джерси составлял 9 долларов.476 в 2021 году. По данным ATTOM, эта цифра почти в 10 раз превышает средний счет налога на недвижимость в размере 901 доллара для домовладельцев в Западной Вирджинии.

 Часть 2 . Содержит задачи по основам математического анализа, а также дифференциальному и . .
Часть 2 . Содержит задачи по основам математического анализа, а также дифференциальному и . .  Сборник задач по математике для ВТУЗов . Часть 4 . Теория вероятностей и математическая статистика .
Сборник задач по математике для ВТУЗов . Часть 4 . Теория вероятностей и математическая статистика . 
 .
. 
 ctgα = AC:BC.
ctgα = AC:BC.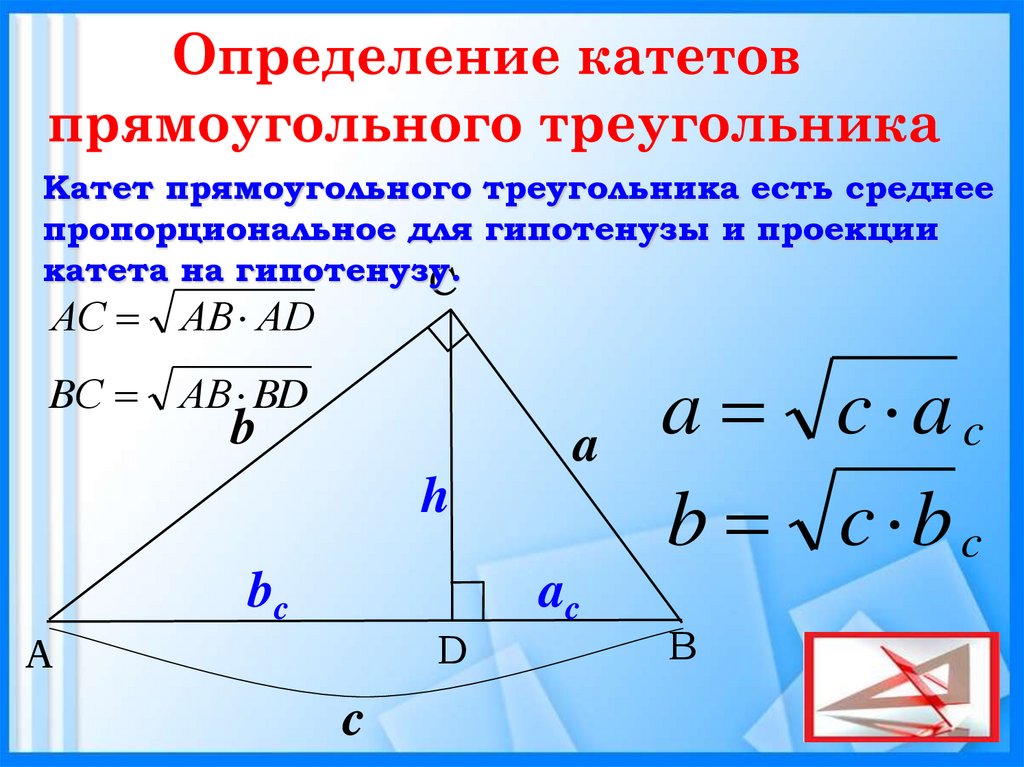
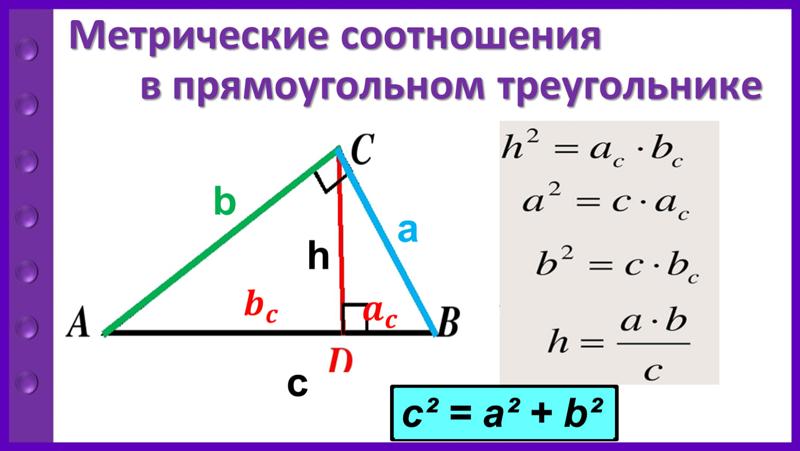
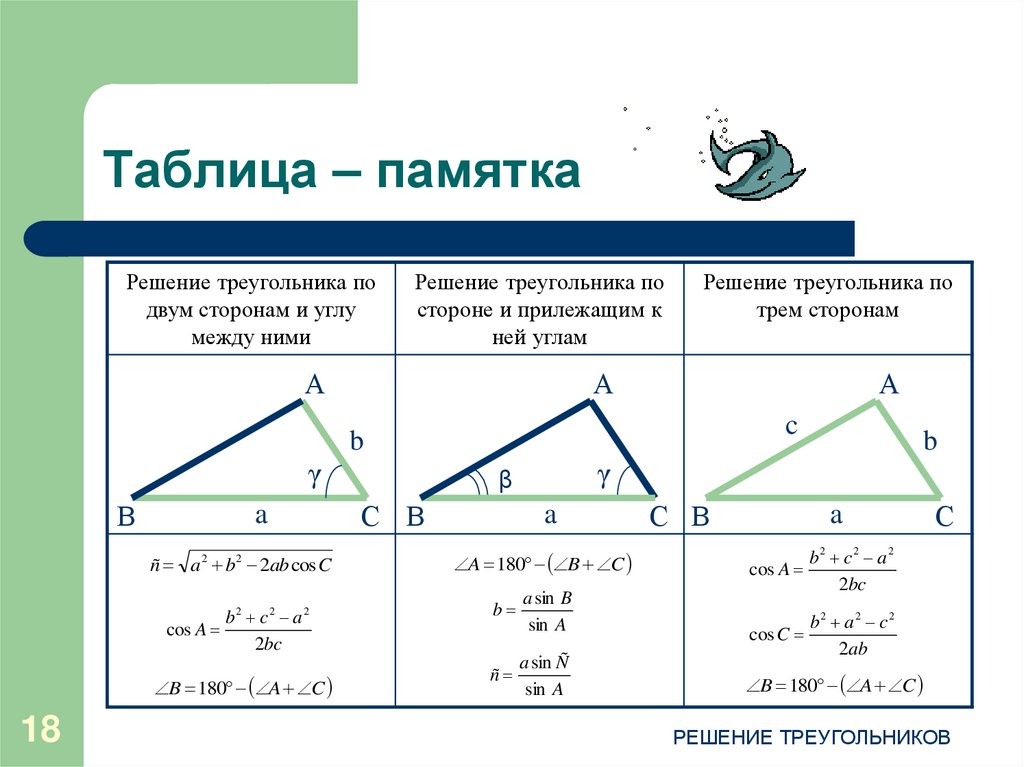 2=q*p\)
2=q*p\)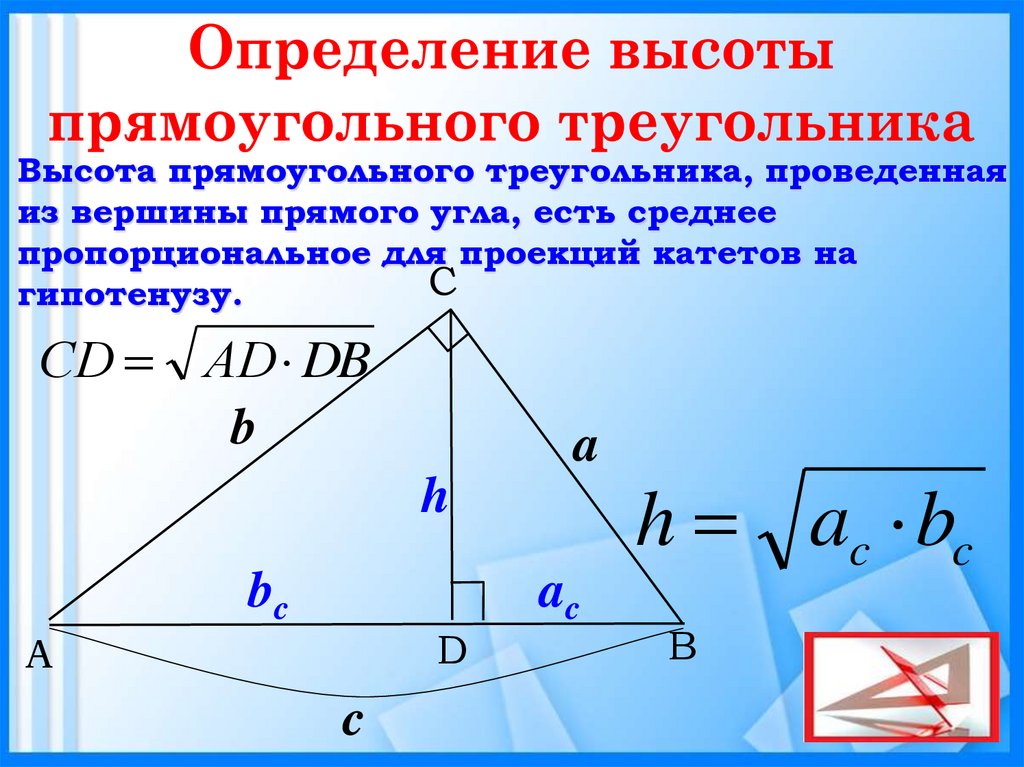 Тригонометрическое уравнение
Тригонометрическое уравнение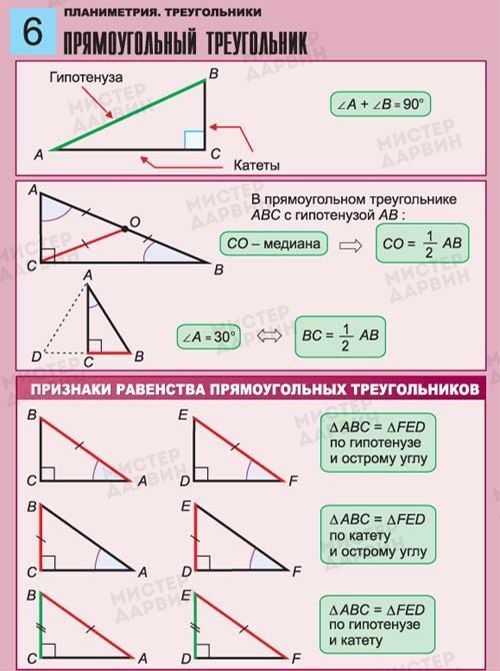 Пусть прямой угол обозначен C , а гипотенуза c. Пусть A и B обозначают два других угла, а a и b стороны, противоположные им соответственно.
Пусть прямой угол обозначен C , а гипотенуза c. Пусть A и B обозначают два других угла, а a и b стороны, противоположные им соответственно. Теорема Пифагора даст нам гипотенузу. Например, если A = 10 и B = 24, затем C 2 = A 2 + B 2 = 100024 2 +24 2 = 100+576 = 676. Квадратный корень из 676 равен 26, поэтому c = 26. (Приятно привести примеры, когда из квадратных корней получаются целые числа; в жизни это обычно не так.)
Теорема Пифагора даст нам гипотенузу. Например, если A = 10 и B = 24, затем C 2 = A 2 + B 2 = 100024 2 +24 2 = 100+576 = 676. Квадратный корень из 676 равен 26, поэтому c = 26. (Приятно привести примеры, когда из квадратных корней получаются целые числа; в жизни это обычно не так.) Поскольку грех A = a/c, мы знаем c = a /sin A = 15/sin 41. Используя калькулятор, это 15/0,6561 = 22,864. Кроме того, tan A = a/b, , поэтому b = a /tan A = 15/tan 41 = 15/0,8693 = 17,256. Используете ли вы синус, косинус или тангенс, зависит от того, какую сторону и угол вы знаете.
Поскольку грех A = a/c, мы знаем c = a /sin A = 15/sin 41. Используя калькулятор, это 15/0,6561 = 22,864. Кроме того, tan A = a/b, , поэтому b = a /tan A = 15/tan 41 = 15/0,8693 = 17,256. Используете ли вы синус, косинус или тангенс, зависит от того, какую сторону и угол вы знаете. Арктангенс 0,2455 равен 13,79., поэтому угол A равен 13,79°. (Если хотите, вы можете преобразовать 0,79 градуса в минуты и секунды.)
Арктангенс 0,2455 равен 13,79., поэтому угол A равен 13,79°. (Если хотите, вы можете преобразовать 0,79 градуса в минуты и секунды.) Они в значительной степени избыточны, но стоит знать, что они собой представляют на случай, если вы столкнетесь с ними. Обратите внимание, что котангенсы являются тангенсами дополнительных углов, а это означает, что cot A = tan B, и косекансы являются секущими дополнительных углов, а это означает, что csc A = sec B.
Они в значительной степени избыточны, но стоит знать, что они собой представляют на случай, если вы столкнетесь с ними. Обратите внимание, что котангенсы являются тангенсами дополнительных углов, а это означает, что cot A = tan B, и косекансы являются секущими дополнительных углов, а это означает, что csc A = sec B.  Итак, секанс — это линия, проведенная из центра круга к касательной AC. Причина, по которой его называют секущим, заключается в том, что он пересекает круг, а слово «секанс» происходит от латинского слова, означающего «разрезание».
Итак, секанс — это линия, проведенная из центра круга к касательной AC. Причина, по которой его называют секущим, заключается в том, что он пересекает круг, а слово «секанс» происходит от латинского слова, означающего «разрезание».
 Каковы высота и расстояние до второго здания.
Каковы высота и расстояние до второго здания.
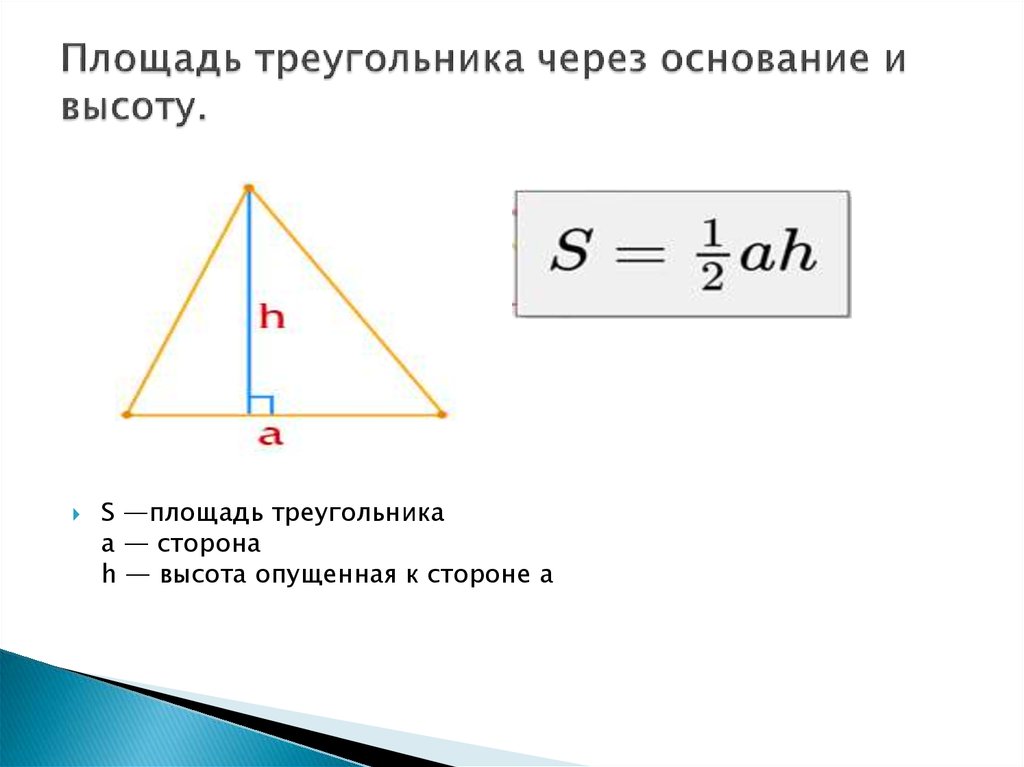 Вот два.
Вот два. Вы можете использовать касательные, чтобы найти две части стороны AB и сложить их вместе.
Вы можете использовать касательные, чтобы найти две части стороны AB и сложить их вместе.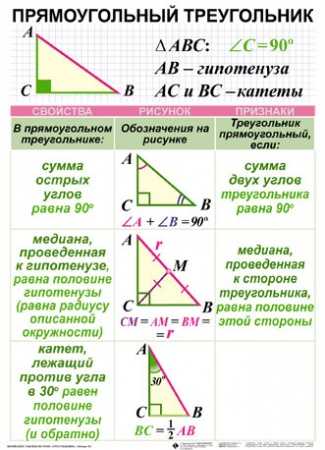
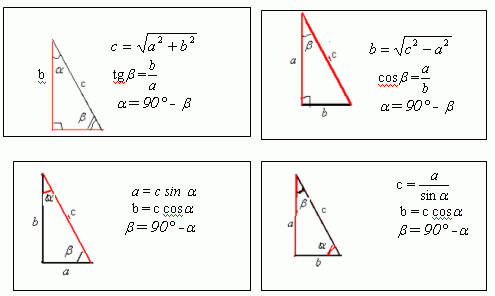 Теорема Пифагора третья сторона треугольника.
Теорема Пифагора третья сторона треугольника.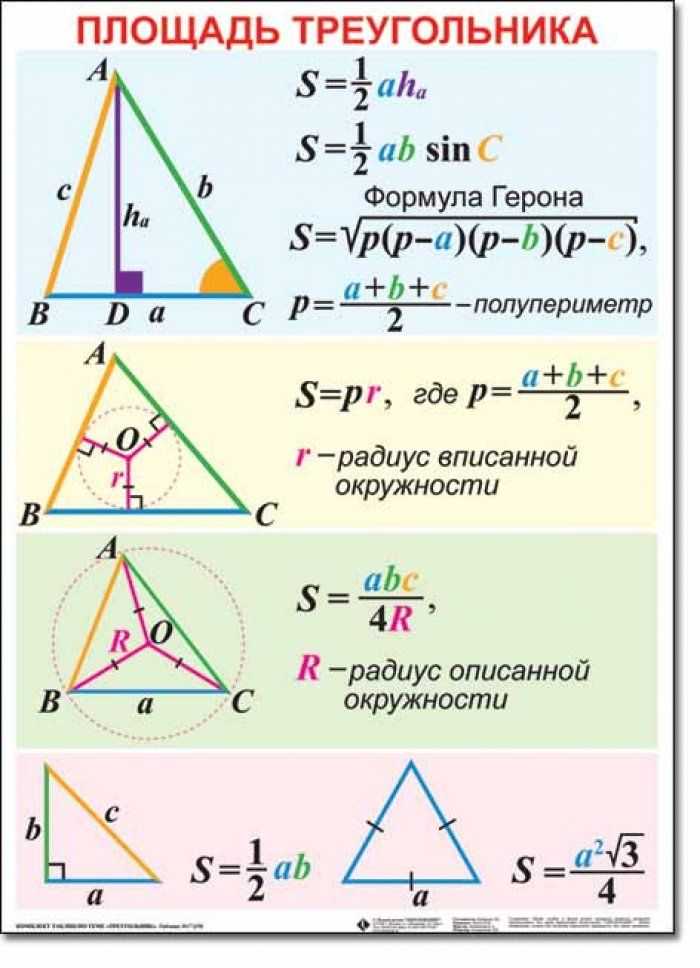

 Вы, наверное, заметили, как Кроули часто выбирал две стороны прямоугольного треугольника целыми числами, а третья тоже оказывалась целым числом. Как и в задаче 26, где все три прямоугольных треугольника имели целые числа в качестве сторон, а именно 9:40:41, 12:35:37 и 7:24:25. Кроме того, в начале этой страницы был треугольник 5:12:13 (на самом деле 10:24:26, но он похож на треугольник 5:12:13). И, без сомнения, вы уже знаете о прямоугольном треугольнике 3:4:5.
Вы, наверное, заметили, как Кроули часто выбирал две стороны прямоугольного треугольника целыми числами, а третья тоже оказывалась целым числом. Как и в задаче 26, где все три прямоугольных треугольника имели целые числа в качестве сторон, а именно 9:40:41, 12:35:37 и 7:24:25. Кроме того, в начале этой страницы был треугольник 5:12:13 (на самом деле 10:24:26, но он похож на треугольник 5:12:13). И, без сомнения, вы уже знаете о прямоугольном треугольнике 3:4:5.
 Для формул прямоугольного треугольника свойства должны быть более конкретными. Если какой-либо из углов треугольника является прямым углом (размером 90º), такой треугольник называется прямоугольным треугольником или просто прямоугольным треугольником. Формулы прямоугольного треугольника помогут вам выполнять различные вычисления, связанные с периметром, площадью и т. д. прямоугольного треугольника.
Для формул прямоугольного треугольника свойства должны быть более конкретными. Если какой-либо из углов треугольника является прямым углом (размером 90º), такой треугольник называется прямоугольным треугольником или просто прямоугольным треугольником. Формулы прямоугольного треугольника помогут вам выполнять различные вычисления, связанные с периметром, площадью и т. д. прямоугольного треугольника.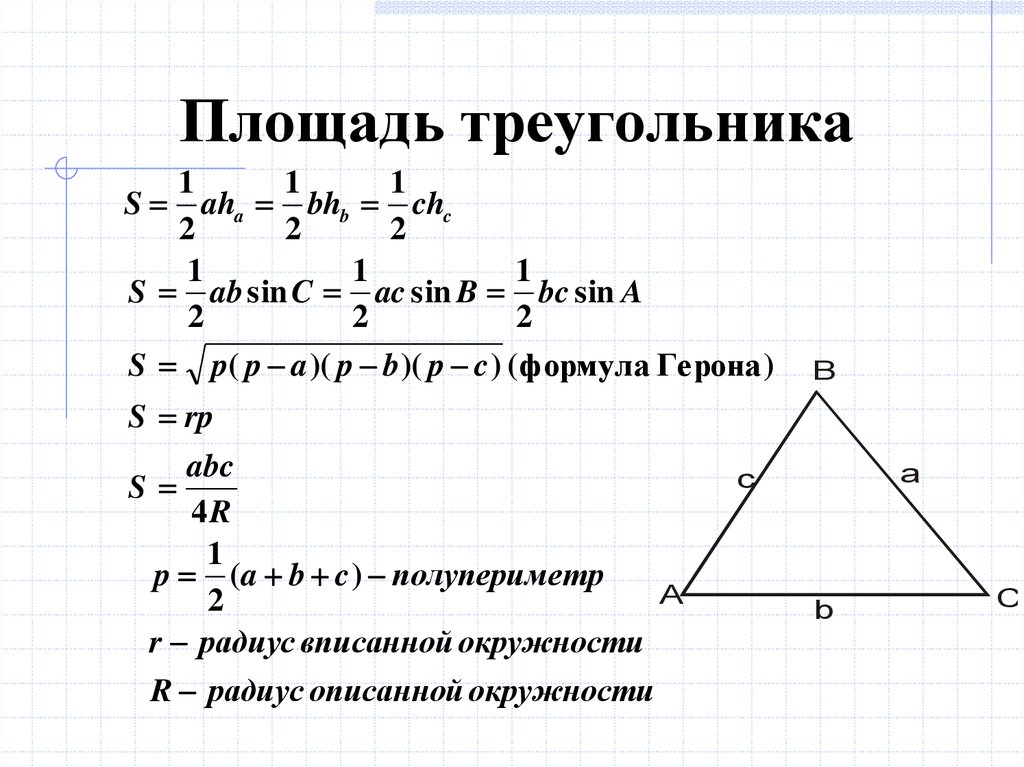 Квадрат гипотенузы равен сумме квадратов двух других катетов.
Квадрат гипотенузы равен сумме квадратов двух других катетов. Найти:
Найти: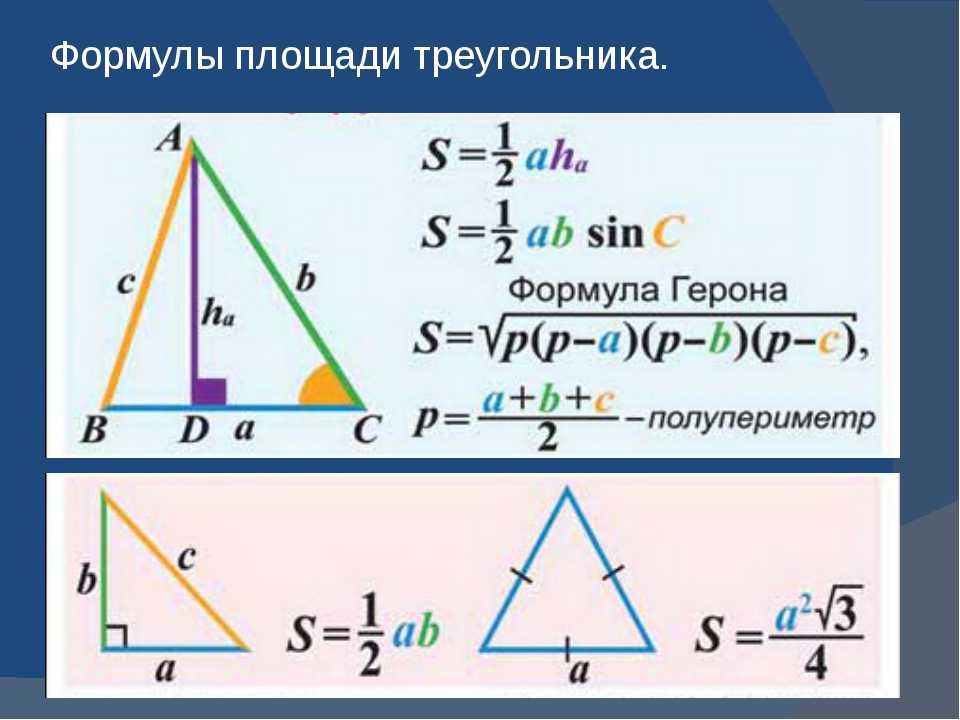 Найдите его площадь.
Найдите его площадь.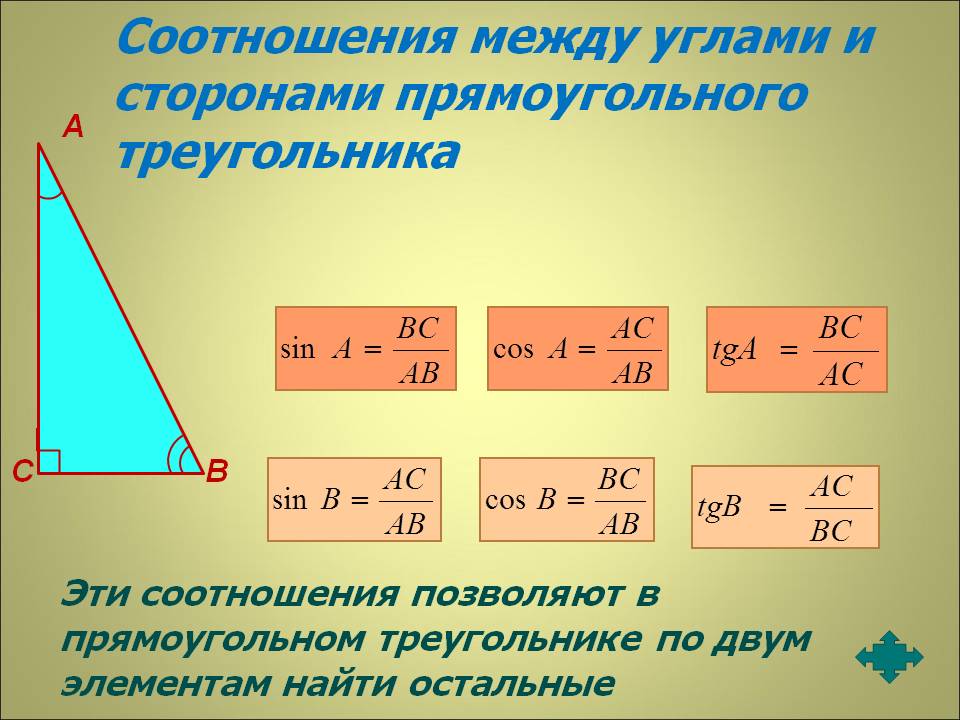 5 единиц
5 единиц
 Зная любую сторону и площадь:
Зная любую сторону и площадь: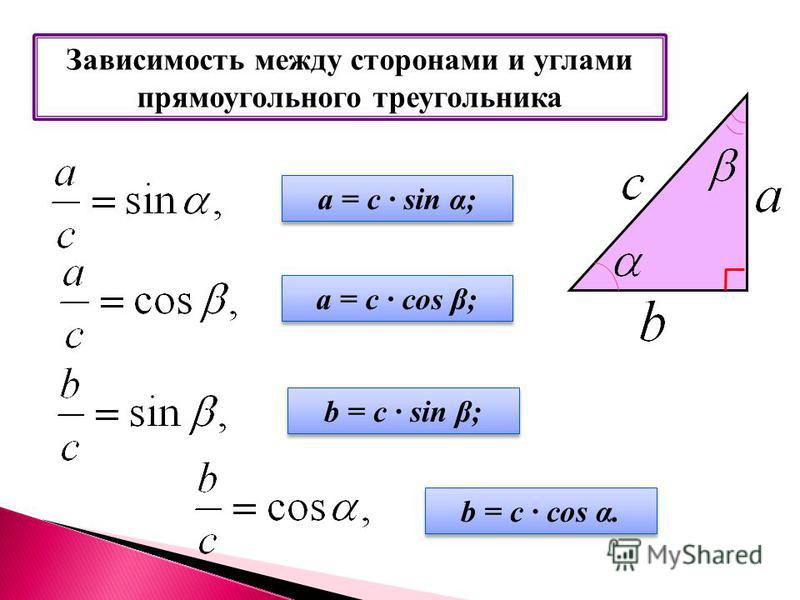
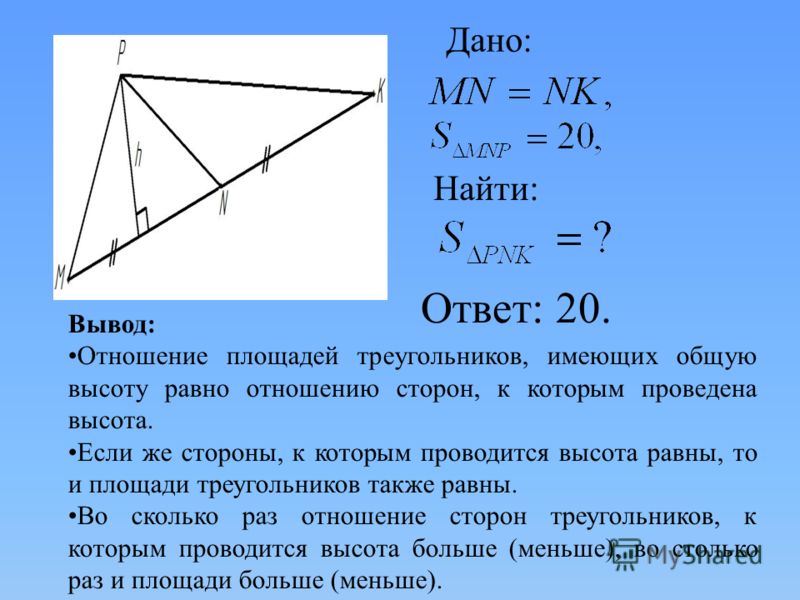
 Поэтому сверху и снизу вы будете наблюдать одинаковую картину на обоих соотношениях.
Поэтому сверху и снизу вы будете наблюдать одинаковую картину на обоих соотношениях.
 к. у них углы равны 30, 60 и 90°). Это видео, а именно знания
к. у них углы равны 30, 60 и 90°). Это видео, а именно знания

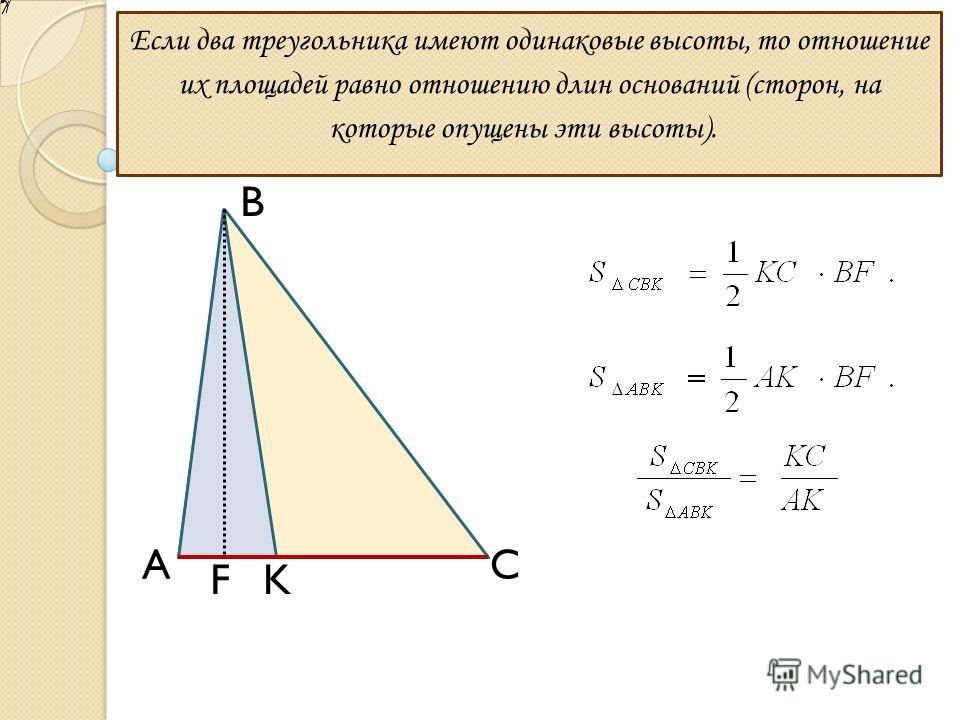
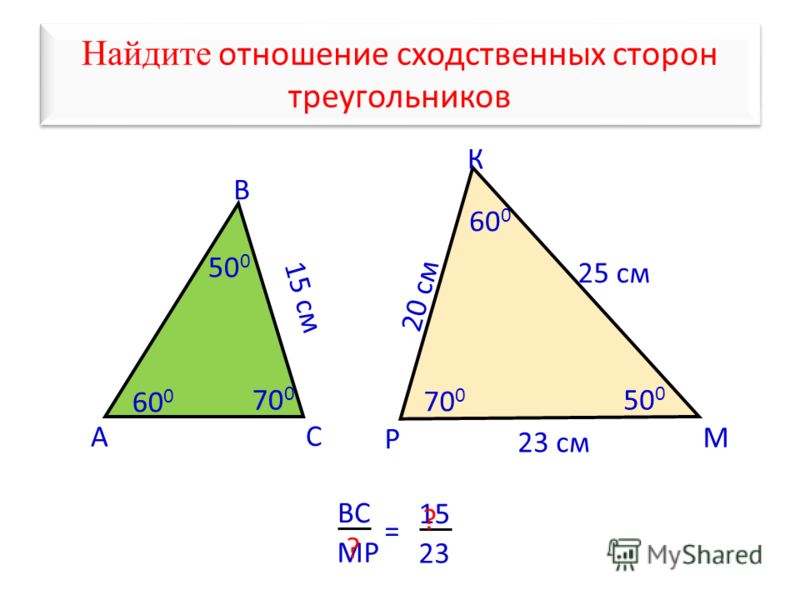 к. это то же самое, что и х². Теперь, если мы вычтем
к. это то же самое, что и х². Теперь, если мы вычтем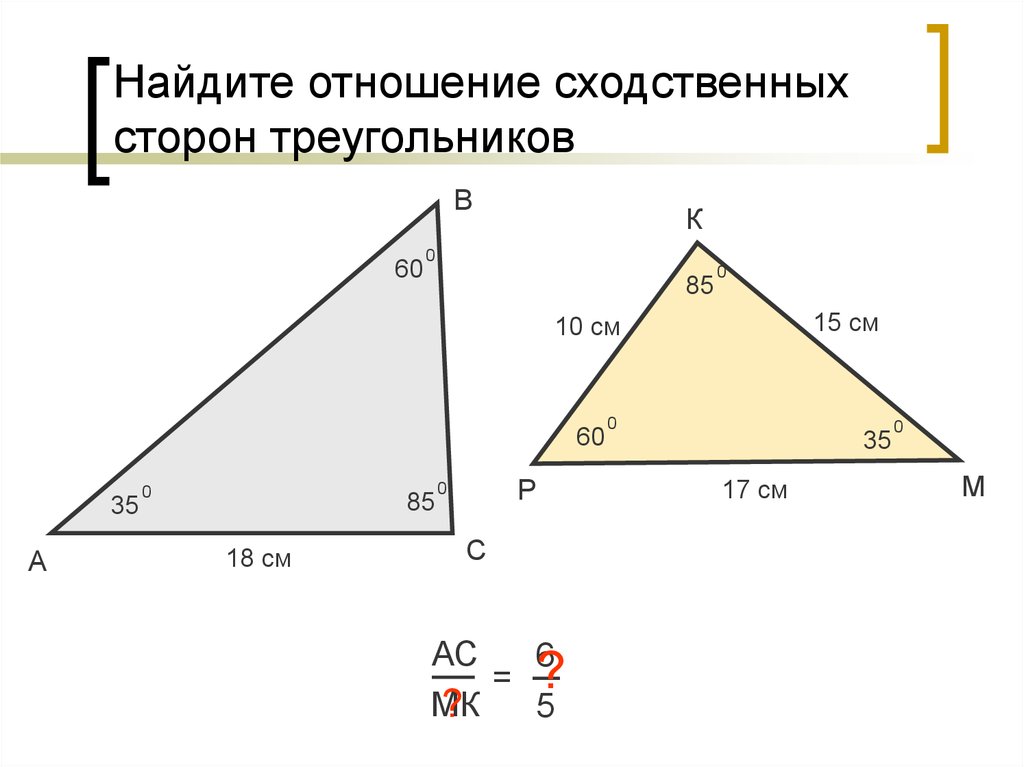
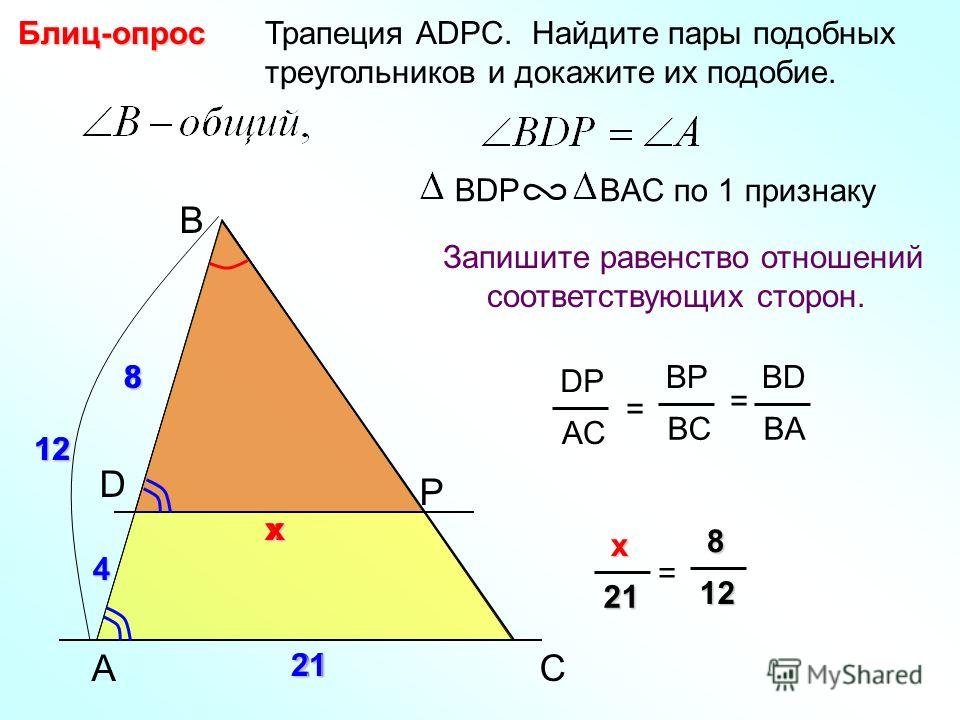 Какие углы
Какие углы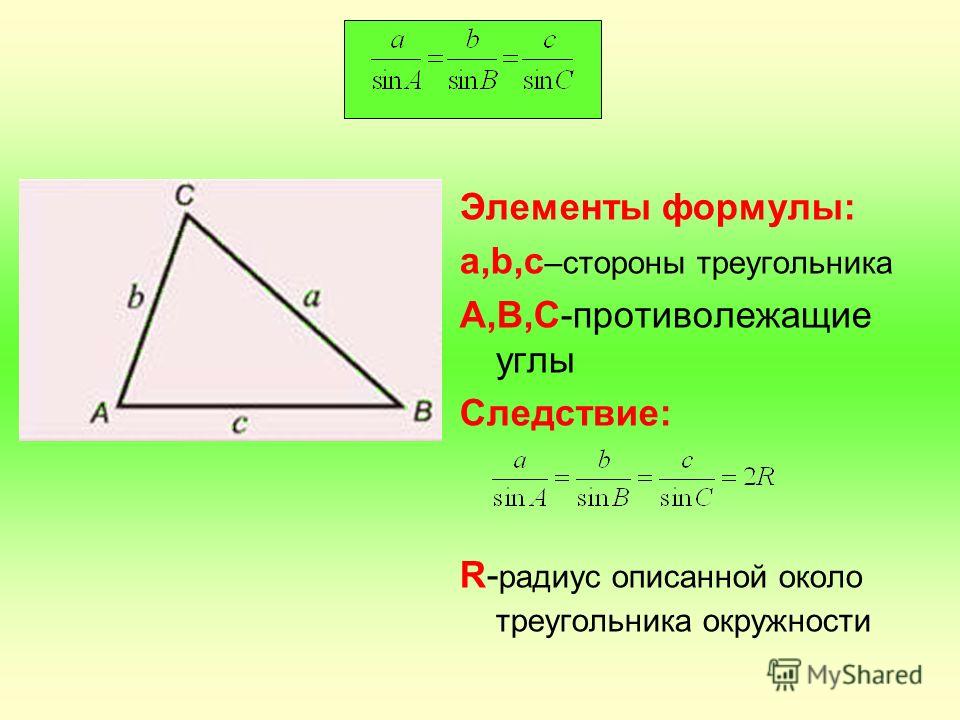 ..
..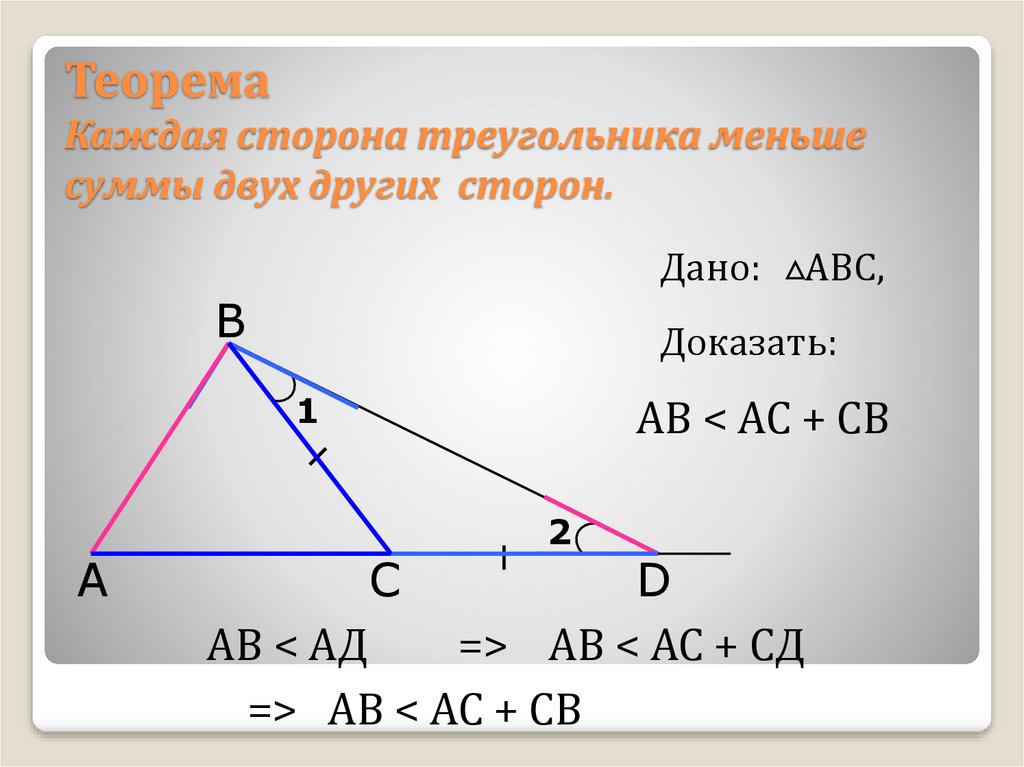 Если периметр треугольника равен 27 см, найдите длину каждой стороны.
Если периметр треугольника равен 27 см, найдите длину каждой стороны.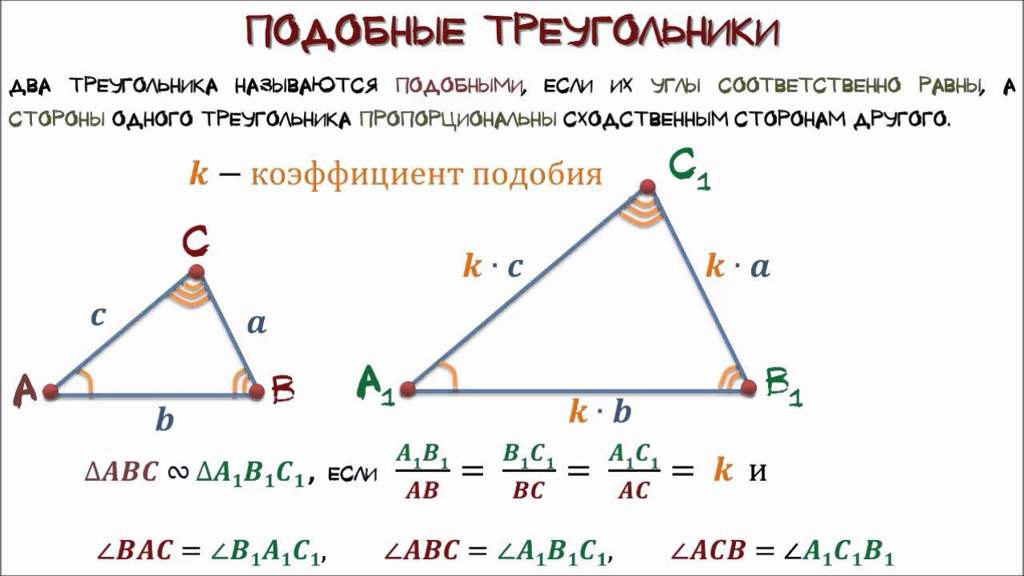 Итак, прежде всего, отложите наши проблемы на 5 плюс 4 равно 9фут 9 х равно 27 Следовательно. Ваш бывший будет 27 разделить на 9, если Алексис. Красиво и дают бой по бокам. Таким образом, мы должны умножить 3 на них. Итак, прежде всего три на три — это первый признак зрелости, время на сторону равно 9 и победа над Ирис, которая даст вам шесть сантиметров.
И последняя третья сторона — Коридор 3, который даст вам стороны танка. Спасибо вам, ребята. Понравилось видео и подписались на мой канал? Большое спасибо
Итак, прежде всего, отложите наши проблемы на 5 плюс 4 равно 9фут 9 х равно 27 Следовательно. Ваш бывший будет 27 разделить на 9, если Алексис. Красиво и дают бой по бокам. Таким образом, мы должны умножить 3 на них. Итак, прежде всего три на три — это первый признак зрелости, время на сторону равно 9 и победа над Ирис, которая даст вам шесть сантиметров.
И последняя третья сторона — Коридор 3, который даст вам стороны танка. Спасибо вам, ребята. Понравилось видео и подписались на мой канал? Большое спасибо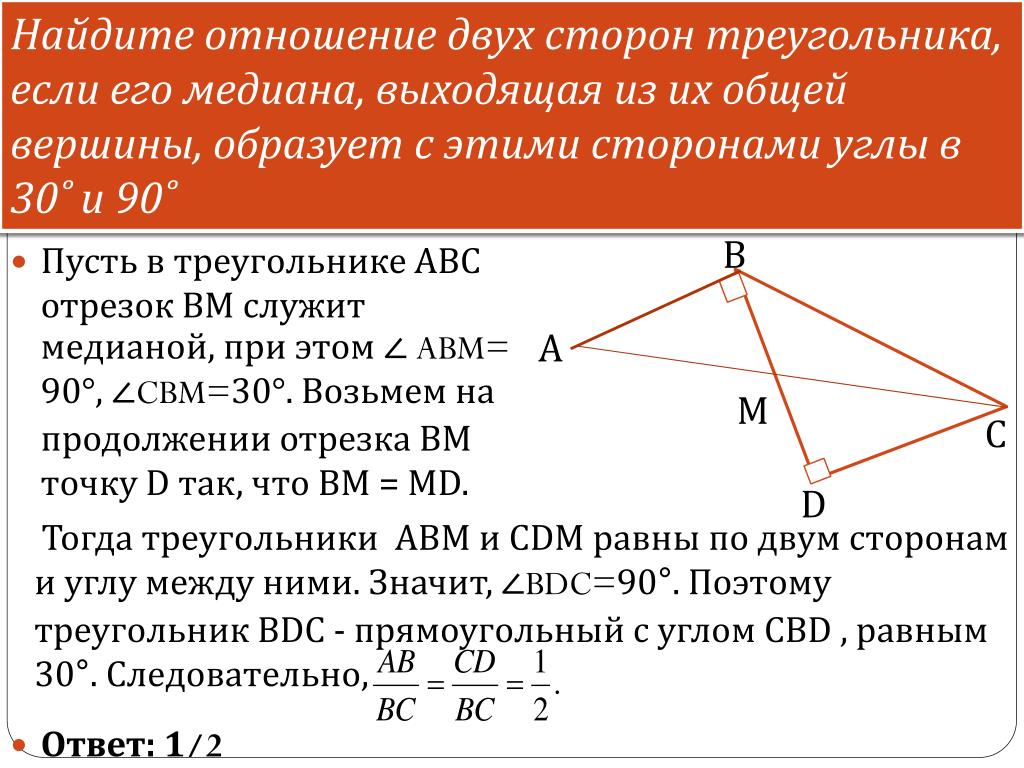 Сколько …
Сколько …