Таблица косинусов углов, вычислить косинус угла
Угол
Косинусом острого угла считается отношение величины прилежащего катета к величине гипотенузы. Прилежащим является катет, расположенный на одной из сторон угла.
cos (A) = в / с
где в — прилежащий катет;
с — гипотенуза.
Рассчитать косинус угла
cos (°) =
Таблица косинусов 1° — 180°
|
|
|
Таблица косинусов 180° — 360°
|
|
|
Синус 30 градусов, sin 30
Автор Admin На чтение 4 мин Просмотров 2.9к. Опубликовано
Синус 30 градусов равняется одной второй или ноль целых пять десятых.
sin 30° = 1/2 или sin 30° = 0,5
В радианной мере измерения углов синусу 30 градусов соответствует синус π/6:
sin 30° = sin π/6
Как это ни странно, но справедливо и обратное равенство, которое утверждает, что синус π/6 (синус пи на 6) равняется синусу 30 градусов:
sin π/6 . sin 30°
sin 30°
Равняется синус пи / 6 так же одной второй или ноль целых пять десятых.
sin π/6 = 1/2 или sin π/6 = 0,5
Это было для блондинок. Для брюнеток и лысых академиков математических наук можно записать всё это в общем виде, пусть распутывают:
sin 30° = sinπ/6 = 1/2 = 0,5
Для полного счастья здесь явно не хватает картинки синуса 30 градусов. А вот и она:
Надеюсь, первую часть задачи я решил и мне удалось объяснить блондинкам, чему равен синус тридцати градусов. Теперь нужно решить вторую половину задачи, с которой не в состоянии справиться даже вся академия математических наук, вместе взятая. Нужно в Интернете найти блондинок, которые ищут синус 30 градусов. Попробую вооружиться логикой блондинок и перечислю ниже поисковые запросы, которые блондинки могут вводить в поисковые системы при поиске ответа на вопрос: чему равен синус 30 градусов? И так, поисковые запросы, разбавленные моими комментариями, дабы поисковые системы не отлучили мое творение от блондинок.
Синус — это математики сверяют свои знания с Интернетом.
Синус, косинус — появилось начальство математиков, чтобы проверить, как математики сверили свои знания.
Синус угла — это очкастые ботаники, будущие Билы Гейтсы, чешут свои умные репы и пытаются вспомнить школьный курс математики.
Синус градусов — шустрые школьники мимоходом забрасывают свой вопрос, что бы побыстрее разделаться с этой бякой и продолжить игру.
Таблица синусов, тангенсов — добросовестные школьники и добропорядочные брюнетки соскребли все свои познания в тригонометрии и пытаются сверить их с Интернетом.
Значение синуса — математики, после долгих блужданий по сайтам с блондинками, наконец-то поняли, как лучше сформулировать поисковый запрос.
Значения косинусов и синусов — математики вдруг вспомнили, что не синусом единым живет тригонометрия.
Синус чему равен? — а вот и первые признаки присутствия блондинок в Интернете с их подкупающей непосредственностью общения, даже с компьютером.
Синусы и косинусы углов. Таблица значений синусов. Синус угла равен — это мамы пытаются проверить, как их чада сделали уроки.
Как найти синус? — это уже типичный вопрос растерянной блондинки.
Синус острого угла. Синус и косинус 30 — мамы с трудом, но уже начинают понимать, что требуется найти в задаче.
Синус числа — бедные мамы, они даже не подозревают, что углы можно измерять радианами.
Синус альфа — мамы вспомнили, какой буквой когда-то в школе они сами обозначали углы.
Калькулятор синусов — на помощь беспомощным мамам приходят умные папы.
Как найти синус угла? — умные папы нашли калькулятор синуса, теперь нужно узнать, как же этой штукой пользоваться.
Геометрия синус, косинус. Скачать таблицу синусов. Значения синусов углов — это чада оторвались от своих виртуальных игр и пытаются доказать умным папам, что папы не правильно нажимают на кнопочки калькулятора, потому что синус угла не может равняться трем банкам пива. Вычисления синуса — математики-теоретики пытаются слямзить результаты работы математиков-прикладников.
Вычисления синуса — математики-теоретики пытаются слямзить результаты работы математиков-прикладников.
Вычислить синус — это математики-прикладники тырят результаты работы своих коллег.
Синус бесконечности — это уже физики пытаются проверить расчеты математиков.
Нахождение синуса — блондинки пытаются узнать, где живут синусы.
Тригонометрический синус — все с удивлением обнаружили, что синусы бывают не только в математике.
Сколько синус 30 — ноль целых пять десятых.
Скольки равен sin 30 — стольки же, ноль пять.
Сколько будет синус 30? — вопрос, конечно, интересный…
ышт 30 — можно и так, только лучше переключаться на английский язык.
Таблица sin альфа 30градусов — здесь не совсем таблица, но и сину, с и 30 градусов точно есть.
Числа из которых синусы натуральные — математики, блондинка задала вопрос. Есть варианты ответов? Честь мундира поставлена на кон.
Кто может объяснить, почему синус 30 градусов равен 1/2? — ну, вундеркинды, блондинка задала вопрос. Кто осмелится ответить?
Кто осмелится ответить?
синус какого угла равен одной второй? — Синус тридцати градусов. Это если просто. Если по математической науке — тогда нужно добавлять периодичность этой тригонометрической функции.
Значение cos 30 — Расчет, тригонометрическая таблица и часто задаваемые вопросы
- Математика
- Значение cos 30
Какова важность и актуальность cos 30?
Что такое тригонометрические отношения?
Тригонометрические соотношения — это соотношения сторон треугольника, взятых одновременно по две. Эти соотношения дают отношение одной стороны треугольника к другой. Чтобы тригонометрические отношения были допустимы, один из углов треугольника должен быть прямым. Если мы предположим, что угол отсчета по горизонтали противоположен прямому углу, то горизонтальное сечение или ось x прямого угла называется основанием треугольника, а вертикальная сторона или ось y известна как соседняя сторона. Отрезок, соединяющий концы обеих стрелок, называется гипотенузой.
Отрезок, соединяющий концы обеих стрелок, называется гипотенузой.
Отношение прилежащей стороны к гипотенузе называется синусом (обычно -sin)
Отношение основания к гипотенузе называется косинусом (обычно -cos)
Отношение прилежащей стороны к основанию равно называется тангенсом (обычно тангенсом)
[Изображение будет загружено в ближайшее время]
Представление Cos 30°:
Когда берется отношение основания исходного угла к гипотенузе, это дает нам значение косинуса отношения под этим конкретным углом. Когда этот угол равен 30°, тогда значение называется cos 30. Значение cos 30 равно значению sin 60, поскольку они дополняют друг друга в треугольнике. Следовательно, значение sin 30 можно использовать и с cos 60, учитывая эту закономерность, мы можем заключить, что sin (90-х) = cos х; где x может быть любым углом.
Производная Cos 30°:
Чтобы получить значение cos 30°, давайте посмотрим на образовавшийся треугольник и проанализируем его.
Если рассматривать углы, то один из углов всегда равен 90°, а два других угла остаются дополняющими друг друга. Если мы должны взять значение cos 30°, это означает, что один из углов равен 30°, а значит, другой угол равен 180° — (90° + 30°), что равно 60°. Теперь, используя свойство прямоугольного треугольника с одним углом 30°, мы можем видеть, что длина гипотенузы в два раза больше, чем длина прилежащего катета, вдвое меньше длины гипотенузы.
Пусть гипотенуза равна x; тогда соседняя сторона имеет значение x/2.
Используя теорему Пифагора гипотенуза² = основание² + смежная² x² = adj²+(x/2)²
Что равно,
x² — (x/2)² =adj²
Упрощая, получаем,
( ¾ )x² =adj²
Отсюда значение adj²/x² = ¾ ;
Что дает нам adj/x = \[\sqrt{3}\]/2
И поскольку мы знаем, что отношение смежных с гипотенузой равно косинусу, следовательно, значение cos 30° равно \[\sqrt{3 }\]/2
Забавные факты:
Еще один способ запомнить значение cos 30° — запомнить его дробное значение π/6 , как оно обозначается в круговой системе или системе координат.
Примеры задач:
Решение. Мы знаем, что значение cos 30° равно \[\sqrt{3}\]/2; Следовательно, мы можем использовать это для вычисления смежной стороны треугольника, т.е. кврт{3}\]/2 = 6\[\кварт{3}\]
Следовательно, одна сторона равна 6\[\sqrt{3}\],
Теперь, по теореме Пифагора, гипотенуза = смежная²+основание²
12² = (6\[\sqrt{3}\])²+ основание² → 12²-(6\[\sqrt{3}\])² = основание²
база = \[\sqrt{144-108}\] = \[\sqrt{36}\] = 6 ;
Следовательно, две стороны равны 6 и 6 \[\sqrt{3}\].
Задача 2: Реактивный самолет во время испытаний летит со скоростью 1,5 Маха, как только взлетает. Между тем, он преодолевает расстояние в 2000 метров после того, как оказался рядом с вами. Теперь вам нужно посмотреть под углом 30°, чтобы увидеть самолет и вычислить высоту самолета.
Решение: Поскольку вы смотрите на него под углом 30°, это означает, что угол возвышения по отношению к земле составляет 30°. Поскольку высота выступает в качестве смежной стороны прямоугольного треугольника, мы можем вычислить высоту с помощью тригонометрии.
Поскольку высота выступает в качестве смежной стороны прямоугольного треугольника, мы можем вычислить высоту с помощью тригонометрии.
Cos Cos 30° = \[\frac{adjacent}{гипотенуза}\] = \[\frac{altitude}{2000}\]
\[\sqrt{3}\]/2 = \[\frac {altitude}{2000}\] ⇒altitude 1000\[\sqrt{3}\]
Отсюда видно, что самолет достиг высоты 1000\[\sqrt{3}\]м
Решение: Чтобы вычислить расстояние от лестницы до стены, нам нужно сначала найти прямоугольный треугольник, одна из сторон которого является путем пожарного. Путь образует примыкание к лестнице, тогда как сама лестница является гипотенузой, а стена вместе с ней выступает в качестве основания. Следовательно, теперь мы можем применить тригонометрию для вычисления смежных.
Используя cos 30° = \[\sqrt{3}\]/2
\[\sqrt{3}\]/2 = \[\frac{adjacent}{гипотенуза}\] = \[\frac{ соседний {20}\]сосед = 20\[\sqrt{3}\]/2 = 10\[\sqrt{3}\]
Следовательно, пожарный должен пройти расстояние 10\[\sqrt{3}\]м до добраться до ступеньки лестницы.
Дата последнего обновления: 29 мая 2023
•
Всего просмотров: 328.8k
•
Просмотров сегодня: 5.86k
Недавно обновленные страницы
90 094 LCM 3 и 4, и как найти наименьшее общее кратноеЧто такое простые проценты? — Пример, формула, решенные примеры и часто задаваемые вопросы
Линейные графики — определение, решенные примеры и практические задачи
Числа в словах
Дробь в процентах
Теорема Коши о среднем значении: введение, история и решенные примеры
НОК 3 и 4 и как найти наименьшее общее кратное
Что такое простые проценты? — Пример, формула, решенные примеры и часто задаваемые вопросы
Линейные графики — определение, решенные примеры и практические задачи
Числа в словах
Доля в процентах
Теорема Коши о среднем значении: введение, история и примеры решений
Актуальные темы
Таблица косинусов | Кубенс
Таблица косинусов значений косинусов углов, записанных в таблице от 0° до 360°.
С помощью таблицы косинусов можно произвести расчет, даже если под рукой не окажется научного калькулятора.
Чтобы найти косинус искомого угла, достаточно воспользоваться таблицей.
Таблица косинусов в радианах
| α | 0 | №6 | №4 | №3 | №2 | № | 3π2 | 2π |
| потому что α |
Таблица косинусов — Наровне таблица синусов изучается в начале тригонометрии. Без понимания таблицы косинусов будет очень сложно изучать тригонометрию и применять тригонометрические формулы.
Тригонометрические функции имеют большое практическое значение в геометрии. По сути это только показатели отношения различных сторон прямоугольного треугольника друг к другу, они могут помочь в решении большинства задач, результат которых сводится к решениям прямоугольных треугольников.
Одной из основных тригонометрических функций является косинус. Поэтому в этой таблице косинусов можно найти любое значение косинуса.
Таблица косинусов углов от 0° до 180°
| cos(0°) = 1 cos(1 градус) = 0,999848 cos(2°) = 0,999391 cos(3°) = 0,99863 cos(4°) = 0,997564 cos(5° ) = 0,996195 cos(6°) = 0,994522 cos(7°) = 0,992546 cos(8°) = 0,9 cos(9°) = 0,987688 cos(10°) = 0,98480 8 cos(11°) = 0,981627 cos(12°) = 0,978148 cos(13°) = 0,97437 cos(14°) = 0,970296 cos(15°) = 0,965926 cos(16°) = 0,9612 62 cos(17°) = 0,956305 cos(18°) = 0,951057 cos(19°) = 0,945519 cos(20°) = 0,939693 cos(21°) = 0,93358 cos(22°) = 0,927184 cos(23°) = 0,920505 9 0214 cos(24°) = 0,913545 cos(25°) = 0, 8 cos(26°) = 0,898794 cos(27°) = 0,891007 cos(28°) = 0,882948 cos(29°) = 0,87462 cos(30°) = 0,866025 соз( 31°) = 0,857167 cos(32°) = 0,848048 cos(33°) = 0,838671 cos(34°) = 0,829038 cos(35°) = 0,819152 cos(36°) = 0,809017 cos(37° ) = 0,798636 cos(38°) = 0,788011 cos(39°) = 0,777146 cos(40°) = 0,766044 cos(41°) = 0,75471 cos(42°) = 0,743145 cos(43°) = 0,731354 cos( 44°) = 0,71934 cos (45°) = 0,707107 | cos(46°) = 0,694658 cos(47°) = 0,681998 cos(48°) = 0,669131 cos(49°) = 0,656059 cos(50°) = 0,642788 co s(51°) = 0,62932 cos (52°) = 0,615661 cos(53°) = 0,601815 cos(54°) = 0,587785 cos(55°) = 0,573576 cos(56°) = 0,559193 cos(57°) = 0,544639 соз(58 °) = 0,529919 cos(59°) = 0,515038 cos(60°) = 0,5 cos(61°) = 0,48481 cos(62°) = 0,469472 cos(63°) = 0,453 99 cos(64°) = 0,438371 cos(65°) = 0,422618 cos(66°) = 0,406737 cos(67°) = 0,390731 cos(68°) = 0,374607 cos(69°) = 0,3583 68 cos(70°) = 0,34202 cos(71°) = 0,325568 cos(72°) = 0,309017 cos(73°) = 0,292372 cos(74°) = 0,275637 cos(75°) = 0,258819 cos(76°) = 0,241922 соз( 77°) = 0,224951 cos(78°) = 0,207912 cos(79°) = 0,190809 cos(80°) = 0,173648 cos(81°) = 0,156434 cos(82°) = 0,139173 902 14 cos(83°) = 0,121869 cos(84°) = 0,104528 cos(85°) = 0,087156 cos(86°) = 0,069756 cos(87°) = 0,052336 cos(88°) = 0,034899 cos(89°) = 0,017452 cos (90°) = 0 | cos(91°) = -0,017452 cos(92°) = -0,034899 cos(93°) = -0,052336 cos(94°) = -0,069756 cos(95°) = -0,087156 co с(96°) = -0,104528 cos(97°) = -0,121869 cos(98°) = -0,139173 cos(99°) = -0,156434 cos(100°) = -0,173648 cos(101°) = — 0,190809 cos(102°) = -0,207912 cos(103°) = -0,224951 cos(104°) = -0,241922 cos(105°) = -0,258819 cos(106°) = -0 .  275637 275637 cos(107 °) = -0,292372 cos(108°) = -0,309017 cos(109°) = -0,325568 cos(110°) = -0,34202 cos(111°) = -0,358368 cos(112°) = -0,374607 cos(113°) = -0,390731 cos(114°) = -0,406737 cos(115°) = -0,422618 cos(116°) = -0,438371 cos(117°) = -0,45399 cos(118°) = -0,469472 cos(119°) = -0,48481 9021 4 cos(120 °) = -0,5 cos(121°) = -0,515038 cos(122°) = -0,529919 cos(123°) = -0,544639 cos(124°) = -0,559193 cos(125°) ) = — 0,573576 cos(126°) = -0,587785 cos(127°) = -0,601815 cos(128°) = -0,615661 cos(129°) = -0,62932 cos(130°) = -0. 642788 потому(131 °) = -0,656059 cos(132°) = -0,669131 cos(133°) = -0,681998 cos(134°) = -0,694658 cos(135°) = -0,707107 | cos(136°) = -0,71934 cos(137°) = -0,731354 cos(138°) = -0,743145 cos(139°) = -0,75471 cos(140°) = -0,766044 902 14 cos(141° ) = -0,777146 cos(142°) = -0,788011 cos(143°) = -0,798636 cos(144°) = -0,809017 cos(145°) = -0,819152 cos(146°) = -0,829038 cos(147°) = -0,838671 cos(148°) = -0,848048 cos(149°) = -0,857167 cos(150°) = -0,866025 cos(151°) = -0,87462 cos(152°) = -0,882948 cos(153°) = -0,891007 cos(154°) = -0,898794 cos(155°) = -0, 8 902 14 cos(156° ) = -0,913545 cos(157°) = -0,920505 cos(158°) = -0,927184 cos(159°) = -0,93358 cos(160°) = -0,939693 cos(161°) = -0,945519 cos(162°) = -0,951057 cos(163°) = -0,956305 cos(164°) = -0,961262 cos(165°) = -0,965926 cos(166°) = -0,970296 cos (167°) = -0,97437 cos(168°) = -0,978148 cos(169°) = -0,981627 cos(170°) = -0,984808 cos(171°) = -0,987688 cos(172°) = -0,9 cos(173°) = -0,992546 90 214 cos(174° ) = -0,994522 cos(175°) = -0,996195 cos(176°) = -0,997564 cos(177°) = -0,99863 cos(178°) = -0,999391 cos(179°) = -0,999848 cos(180°) = -1 |
Cos 0 (косинус нуля)
равно (равно единице)
1 косинус (мера косинуса)
равно
3 косинус (косинус трех)
равно
косинус 90 (косинус 90 градусов)
= 0 (равно нулю)
косинус 30 (косинус 30 градусов)
равно
45 косинус (косинус 45 градусов)
равен
Косинус 60 (косинус 60 градусов)
равен
Таблица косинусов углов от 181° до 360°
902 08cos(182°) = -0,999391
cos(183°) = -0,99863
cos(184°) = -0,997564
cos(185°) = -0,996195
cos(186°) = -0,994522
cos(187°) = -0,992546
cos(188°) = -0,990 268
потому что(189 °) = -0,987688
cos(190°) = -0,984808
cos(191°) = -0,981627
cos(192°) = -0,978148
cos(193°) = -0,97437
cos(194°) = -0,970296
cos(195°) = -0,965926
cos(196°) = -0,961262
cos(197°) = -0,956305
cos(198°) = -0,951057
cos(199°) = -0,945519 9 0214 cos(200° ) = -0,939693
cos(201°) = -0,93358
cos(202°) = -0,927184
cos(203°) = -0,920505
cos(204°) = -0,913545
cos(205°) = -0,
8
cos(206°) = -0,898 794
потому(207 °) = -0,891007
cos(208°) = -0,882948
cos(209°) = -0,87462
cos(210°) = -0,866025
cos(211°) = -0,857167
cos(212°) = -0,848048
cos(213°) = -0,838671
cos(214°) = -0,829038
cos(215°) = -0,819152
cos(216°) = -0,809017
cos(217°) = -0,798636 9 0214 cos(218° ) = -0,788011
cos(219°) = -0,777146
cos(220°) = -0,766044
cos(221°) = -0,75471
cos(222°) = -0,743145
cos(223°) = -0,731354
cos(224°) = -0,71934 9021 4 cos(225° ) = -0,707107
cos(227°) = -0,681998
cos(228°) = -0,669131
cos(229°) = -0,656059
cos(230°) = -0,642788 9 0214 cos(231° ) = -0,62932
cos(232°) = -0,615661
cos(233°) = -0,601815
cos(234°) = -0,587785
cos(235°) = -0,573576
cos(236°) = -0,559193
cos(237°) = -0,544639
cos(238°) = -0,529919
cos(239°) = -0,515038
cos(240°) = -0,5
cos(241°) = -0,48481
cos(242°) = -0,46 9472
потому( 243°) = -0,45399
cos(244°) = -0,438371
cos(245°) = -0,422618
cos(246°) = -0,406737
cos(247°) = -0,390731
cos(24) 8°) = — 0,374607
cos(249°) = -0,358368
cos(250°) = -0,34202
cos(251°) = -0,325568
cos(252°) = -0,309017
cos(253°) = -0.

Онлайн конвертер pdf to jpg: Конвертировать PDF в JPG — быстрый, онлайн, бесплатный
Преобразование PDF в JPG в автономном режиме в простых шагах
Хотите конвертировать между форматами файлов, например, из PDF в JPG, о чем вы думаете? Большинство пользователей выйдут в интернет и сразу же будут искать онлайн-фильтр, конвертирующий PDF-файлы в JPG. Однако это может быть не самый надежный и безопасный способ для многих пользователей, у которых нет стабильного подключения к Интернету. В этой статье мы предоставим вам несколько эффективных и простых способов конвертировать файлы PDF в файлы JPG в автономном режиме.
В этой статье
Метод 1. Как конвертировать PDF в JPG в автономном режиме (самый простой способ)
Метод 2. Как конвертировать PDF в JPG в автономном режиме бесплатно (Windows)
Метод 3. Как конвертировать PDF в JPG Офлайн бесплатно (Mac)
Способ 4. Преобразование PDF в JPG Офлайн и онлайн
Способ 1. Как конвертировать PDF в JPG офлайн (самый простой способ)
Первый способ — самый простой и рекомендуемый, если вы ищете для надежного автономного конвертера PDF в JPG. Мы будем использовать сторонний инструмент, известный как Wondershare PDFelement — PDF Editor. Wondershare PDFelement — это армия из одного человека, так как это универсальный PDF-редактор, который позволяет легко управлять PDF-файлами на нескольких устройствах, будь то мобильные устройства, планшеты, веб-сайты или настольные компьютеры. Вот пошаговые подробные инструкции о том, как конвертировать PDF в JPG с помощью PDFelement.
Мы будем использовать сторонний инструмент, известный как Wondershare PDFelement — PDF Editor. Wondershare PDFelement — это армия из одного человека, так как это универсальный PDF-редактор, который позволяет легко управлять PDF-файлами на нескольких устройствах, будь то мобильные устройства, планшеты, веб-сайты или настольные компьютеры. Вот пошаговые подробные инструкции о том, как конвертировать PDF в JPG с помощью PDFelement.
Попробуйте бесплатно Попробуйте бесплатно КУПИТЬ СЕЙЧАС КУПИТЬ СЕЙЧАС
Шаг 1 Загрузите и установите PDF бесплатно PDF Converter
Самый первый шаг, с которого начинается процесс, — это загрузка и установка PDF Converter на свой компьютер. Вы можете скачать установочный файл с официального сайта и установить его в соответствии с инструкциями, приведенными в руководстве. После установки запустите его на своем компьютере.
Шаг 2. Добавление PDF-файлов в автономном режиме
Перейдите в главное меню и нажмите «Файл», а затем выберите «Открыть PDF». Откроется окно с просьбой выбрать файл PDF с вашего компьютера, который вы хотите преобразовать в JPG в автономном режиме. Выберите файл PDF и нажмите кнопку «Открыть», чтобы загрузить этот файл в автономный конвертер PDF.
Откроется окно с просьбой выбрать файл PDF с вашего компьютера, который вы хотите преобразовать в JPG в автономном режиме. Выберите файл PDF и нажмите кнопку «Открыть», чтобы загрузить этот файл в автономный конвертер PDF.
Шаг 3 Преобразование PDF в JPG в автономном режиме
Теперь вам нужно начать процесс преобразования, нажав кнопку «Преобразовать» в меню, которое появляется вверху. После нажатия этой кнопки вы увидите различные варианты, теперь найдите «В изображение» и нажмите на нее. Появится окно «Сохранить как», в котором вас попросят ввести имя файла и выбрать место для сохранения. Вы также можете изменить тип изображения на PNG, JPG, BMP, GIF, TIFF и JPEG. После предоставления всей этой информации нажмите кнопку «Сохранить», и ваш файл PDF будет преобразован в выбранный вами формат файла.
Шаг 4 Настройте качество изображения (необязательно)
Существует дополнительная функция, связанная с качеством изображения. Вы можете настроить качество изображения в соответствии с вашими требованиями, зайдя в настройки в PDFelement. Пользователь может добавить цвет границы, увеличить или уменьшить масштаб, а DPI можно настроить по мере необходимости. Выбранные страницы могут быть преобразованы. Пользователь может конвертировать нечетные или четные страницы или указанные страницы из файла PDF в JPG в автономном режиме. После настройки качества изображения нажмите кнопку «Применить».
Пользователь может добавить цвет границы, увеличить или уменьшить масштаб, а DPI можно настроить по мере необходимости. Выбранные страницы могут быть преобразованы. Пользователь может конвертировать нечетные или четные страницы или указанные страницы из файла PDF в JPG в автономном режиме. После настройки качества изображения нажмите кнопку «Применить».
Если вам интересно, предназначен ли Wondershare PDFelement — PDF Editor только для преобразования PDF? Нет, это не просто автономный конвертер PDF. Есть и много других особенностей.
Попробуйте бесплатно Попробуйте бесплатно КУПИТЬ СЕЙЧАС КУПИТЬ СЕЙЧАС
Ссылка ниже дает вам одну из лучших платформ для работы с PDF-файлами.
Пакетное преобразование
Пакетное преобразование — наиболее полезная функция PDFelement, которая позволяет пользователю одновременно конвертировать несколько файлов в файлы любого другого формата. Вы можете выбрать папку или группу PDF-файлов и сразу же начать их преобразование в JPG в автономном режиме одним щелчком мыши.
Вы можете выбрать папку или группу PDF-файлов и сразу же начать их преобразование в JPG в автономном режиме одним щелчком мыши.
Редактирование PDF-файлов
PDFelement имеет полнофункциональный редактор, который поможет вам редактировать любой PDF-файл. Пользователь может создавать PDF-формы и даже интерактивные PDF-формы. Эта функция позволяет сделать ваш PDF-файл более интерактивным.
Аннотировать PDF
PDFelement — один из самых удивительных и надежных инструментов аннотирования PDF, доступных в автономном режиме. Если мы сравним его цену в соответствии с его функциями, он будет стоить гораздо дешевле с той же функцией, которую Adobe Acrobat и Foxit предоставляют по более высоким ценам. Вы можете сделать свой PDF-файл более профессиональным, добавляя заметки, выделяя области или текст, зачеркивая, подчеркивая, добавляя ссылки и многое другое.
Заполнение форм
С помощью PDFelement можно легко создать заполняемую форму в формате PDF. Заполняемая форма содержит кнопки, флажки, кнопки, экспорт данных, импорт данных, поле со списком, переключатели, списки и многие другие функции, которые сделают заполняемую форму PDF более активной.
Заполняемая форма содержит кнопки, флажки, кнопки, экспорт данных, импорт данных, поле со списком, переключатели, списки и многие другие функции, которые сделают заполняемую форму PDF более активной.
Попробуйте бесплатно Попробуйте бесплатно КУПИТЬ СЕЙЧАС КУПИТЬ СЕЙЧАС
Способ 2. Как бесплатно конвертировать PDF в JPG в автономном режиме (Windows)
Не хотите использовать какой-либо автономный инструмент для конвертации PDF в JPG? Как я могу сделать автономное преобразование из PDF в JPG. Что ж, вы можете использовать простой ручной способ, и вам не потребуется никаких инструментов. Этот метод рекомендуется, если в вашем PDF-файле очень мало страниц, но если он содержит много страниц, вам следует использовать метод, описанный выше.
Шаг 1 Щелкните правой кнопкой мыши файл PDF в Windows
Шаг 1. Откройте проводник на своем компьютере и найдите файл PDF, который вы хотите преобразовать в JPG, щелкните файл правой кнопкой мыши и выберите веб-браузер для просмотра это. Все веб-браузеры имеют встроенную программу просмотра PDF.
Все веб-браузеры имеют встроенную программу просмотра PDF.
Шаг 2 Откройте PDF-файл в браузере
После открытия PDF-файла в веб-браузере нажмите кнопку «По размеру экрана» и откройте инструмент «Ножницы» в Windows.
Шаг 3 Преобразование PDF в JPG в автономном режиме бесплатно
Здесь вы можете легко сделать скриншоты всех страниц, которые вы хотите преобразовать в JPG, и сохранить их в упорядоченном виде, пронумеровав их соответствующим образом. Это самый простой способ конвертировать PDF в JPG без подключения к Интернету или инструментов.
Метод 3: как бесплатно конвертировать PDF в JPG в автономном режиме (Mac)
Preview — это средство просмотра изображений, а также средство просмотра PDF на Mac. Каким-то образом у него есть некоторые функции редактирования, которые могут помочь пользователю редактировать изображения или другие документы. Приложение предварительного просмотра можно найти в доке вашего Mac, и если это программа для просмотра PDF по умолчанию, вам просто нужно выполнить шаги, указанные ниже:
Шаг 1 Откройте PDF в автономном режиме на Mac
Шаг 1. Нажмите на любой файл PDF, который вы хотите открыть, выберите файл из появившегося окна и нажмите «Открыть». После того, как файл открыт в режиме предварительного просмотра, перейдите в главное меню и нажмите «Файл».
Нажмите на любой файл PDF, который вы хотите открыть, выберите файл из появившегося окна и нажмите «Открыть». После того, как файл открыт в режиме предварительного просмотра, перейдите в главное меню и нажмите «Файл».
Шаг 2 Преобразование PDF в JPG в автономном режиме на Mac
Появится список параметров, и здесь вам нужно будет выбрать параметр «Экспорт». Запишите имя, под которым вы хотите сохранить этот файл, и в раскрывающемся списке «Формат» выберите JPEG и нажмите кнопку «Сохранить». Вы также можете настроить качество изображения в появившихся настройках.
JPEG-файл этого PDF-файла будет сохранен в том же месте с добавленным вами именем. Теперь вы можете открыть и просмотреть преобразованный файл PDF в JPG и поделиться им с кем угодно.
Преобразование PDF в JPG Офлайн или онлайн, что лучше?
Зачем конвертировать PDF в JPG в автономном режиме? Должны ли вы использовать автономный конвертер PDF в JPG или онлайн-инструмент? В этой таблице перечислены преимущества преобразования PDF в JPG в автономном режиме и онлайн.
PDF в JPG Офлайн | PDF в JPG онлайн |
Преобразование PDF без подключения к Интернету Преобразование PDF в JPG без ограничения размера файла Преобразование PDF в JPG в высоком качестве Более безопасный. Нет необходимости входить в систему. Ваши файлы сохраняются локально на ваших устройствах. | Преобразование PDF без загрузки программы Бесплатное использование с ограничением размера |
Заключение
Преобразование PDF в JPG в автономном режиме становится необходимым, когда у вас возникают проблемы с Интернетом. В такой ситуации автономные конвертеры PDF в JPG являются наиболее надежным решением, которое можно использовать. Wondershare PDFelement — один из самых профессиональных и удивительных автономных инструментов для конвертации PDF, который вы можете использовать для таких целей.
Конвертер PDF в JPG [100% бесплатно PDF в JPG]
Бесплатно конвертируйте PDF-страницы в отдельные изображения с помощью нашего онлайн-конвертера PDF в JPG.
Что такое конвертер PDF в JPG?
PDF to JPG — самый мощный инструмент для обработки PDF, который позволяет извлекать содержимое файла PDF в формате JPG. Этот инструмент принимает PDF-файл и позволяет вынуть все его страницы в виде изображений.
Конвертер PDF в JPG предназначен для людей, которые хотят отправить одну или несколько страниц PDF кому-либо через Интернет. Сделать снимок экрана этих страниц можно, но это довольно трудоемко и требует от вас больших усилий.
С конвертером PDF в JPG вы можете легко конвертировать PDF в изображения. Вам просто нужно ввести файл PDF в инструмент, и он обрабатывает весь процесс преобразования изображений PDF в JPG за вас.
#1 Конвертер PDF в JPG онлайн
Конвертер PDF в JPG — это инструмент номер один, предлагающий невероятную производительность бесплатно. Этот инструмент не влияет на качество изображения, и вы можете загрузить весь PDF-файл в формате JPG.
Этот инструмент не влияет на качество изображения, и вы можете загрузить весь PDF-файл в формате JPG.
Если вы загружаете сразу несколько страниц, файлы предоставляются вам в виде файла .zip. Таким образом, вы можете быть уверены, что вся ваша информация останется в безопасности. Этот конвертер PDF в JPG является инструментом № 1, поскольку он прост в использовании и предлагает замечательную производительность. И если вы хотите сделать шаг вперед и преобразовать любой URL-адрес в PDF, вы можете проверить URL-адрес в PDF Converter онлайн для этого.
Зачем конвертировать PDF в JPG?
Есть много причин, по которым вы захотите конвертировать PDF в JPG с помощью нашего конвертера. Если вы хотите поделиться с кем-то определенной частью информации, вместо отправки всего PDF-файла вы можете взять необходимую информацию и отправить ее получателю.
Конвертер PDF в JPG поможет вам в этом. Этот инструмент преобразует PDF в изображения, и вы можете поделиться теми, которыми хотите поделиться с получателем. Кроме того, если вы хотите пойти в другом направлении и преобразовать изображения в документы PDF, вы можете использовать для этого PNG в PDF.
Кроме того, если вы хотите пойти в другом направлении и преобразовать изображения в документы PDF, вы можете использовать для этого PNG в PDF.
Как конвертировать PDF в JPG с помощью SEO Tools Center Конвертер PDF в JPG?
- Прежде всего, перейдите на домашнюю страницу и выберите инструмент для преобразования PDF в JPG по адресу: https://seotoolscentre.com/pdf-to-jpg-converter здесь.
- Загрузите PDF-документ из памяти ПК или телефона.
- Вы также можете перетащить файл PDF с диска Google или Dropbox и нажать Преобразовать сейчас .
- Нажмите кнопку «Преобразовать файл PDF», чтобы начать.
- Подождите несколько секунд, загрузите преобразованные файлы.
- Конвертер выдаст вам результат в виде изображений, которые вы можете скачать.
Особенности конвертера PDF в JPG от SEOToolsCentre
Простое преобразование PDF в JPG
Если вы хотите преобразовать PDF-файл в высококачественные изображения, онлайн-конвертер PDF в JPG может помочь вам в этом. Простой пользовательский интерфейс этого конвертера поможет сделать преобразование невероятно простым для вас. Это быстрый и мощный конвертер PDF в JPG, обеспечивающий превосходное качество изображения без ущерба для размера файла.
Простой пользовательский интерфейс этого конвертера поможет сделать преобразование невероятно простым для вас. Это быстрый и мощный конвертер PDF в JPG, обеспечивающий превосходное качество изображения без ущерба для размера файла.
Аналогичным образом, если вы хотите преобразовать документ PDF в съедобный текстовый документ вместо формата JPG, вы можете попробовать конвертер PDF в Word для выполнения преобразования.
Веб-приложение с быстрой обработкой
Онлайн-сервис конвертации PDF в JPG — это веб-приложение, которое вы можете использовать, не устанавливая ничего на свой ПК. Обработка для этого инструмента происходит в облаке, поэтому он использует очень мало ваших системных ресурсов. Высокая скорость обработки этого инструмента возможна из-за того, что он не зависит от собственных системных ресурсов.
Работает во всех операционных системах
Универсальные функции совместимости этого приложения являются основной причиной его успеха. Неважно, какая у вас операционная система и какой веб-браузер вы используете, конвертер PDF в JPG работает на всех новейших ПК и мобильных устройствах. Конвертер Word в PDF от SEO Tools Center также является веб-приложением, которое работает во всех основных операционных системах и веб-браузерах.
Конвертер Word в PDF от SEO Tools Center также является веб-приложением, которое работает во всех основных операционных системах и веб-браузерах.
Безопасная и надежная обработка
Конвертер PDF в JPG обеспечивает безопасную и надежную обработку. Мы не храним ваши PDF-файлы на наших серверах. Как только вы добавите PDF-файл и получите из него файлы JPG с помощью нашего инструмента, загруженные файлы и информация будут удалены из этого приложения. Конвертер TXT в PDF от SEO Tools Center работает точно так же. Мы верим в прозрачность, поэтому вам не придется беспокоиться о рисках безопасности с нашим конвертером PDF в JPG.
Часто задаваемые вопросы о конвертере PDF в JPG от SEOToolsCentre
Как преобразовать документ PDF в формат файла JPEG?
Вы можете использовать инструмент преобразования PDF в JPG от SEO Tools Center, чтобы преобразовать PDF-документы в JPEG. Этот инструмент позволяет конвертировать входной файл PDF и выводить все его страницы в виде изображений JPG высокого качества.
Как бесплатно сохранить PDF-документ в формате JPG?
Вы можете использовать бесплатный конвертер PDF в JPG от SEO Tools Center, чтобы бесплатно конвертировать PDF в JPG. Этот инструмент совершенно бесплатный, и вам не нужно тратить деньги на покупку подписки для использования этого приложения.
Как сохранить файл PDF в виде изображения JPG?
Если вы хотите сохранить PDF в виде изображения, мы предлагаем вам воспользоваться конвертером PDF в JPG от Центра инструментов SEO. Этот инструмент на 100% бесплатный и предлагает невероятно высокую скорость обработки. Поскольку это веб-приложение, вам не нужно загружать стороннее приложение на свой компьютер или телефон, чтобы использовать этот конвертер.
Как преобразовать PDF в JPG в 2021 году?
Конвертер PDF в JPG — ваш лучший выбор для преобразования PDF в JPG в 2021 году. Этот инструмент прост в использовании и имеет интерактивный пользовательский интерфейс, который делает преобразование PDF в JPG невероятно простым для пользователя.
Найдите вероятность того что случайно выбранное целое число из первого миллиона: Национальный исследовательский университет «Высшая школа экономики»
Вычисление вероятности — Умскул Учебник
На этой странице вы узнаете- Как кот может быть одновременно жив и мертв?
- Можно ли всегда выигрывать спор с монеткой?
- Если рандомно ответить на вопрос теста, какой шанс угадать ответ?
Какова вероятность выиграть в лотерею? Исследователи подсчитали: один на восемь миллионов. «Или выиграю, или проиграю», — решаю я, покупая лотерейный билет. Так понятие вероятности преследует нас в обычной жизни. И не только в лотерее. Давайте разберемся подробнее.
ВероятностьВыходя утром из дома, мы задумываемся: брать ли с собой зонт? Проверяем прогноз погоды — вероятность выпадения осадков 2%. Зонтик нам сегодня вряд ли понадобится. В пути нас настигает ливень…
Прогноз погоды — самый яркий пример вероятности. Он не всегда бывает точный, не всегда сбывается. Мы не можем с уверенностью сказать, что будет завтра. Зато можем по совокупности факторов определить, на какую погоду стоит ориентироваться.
Теория вероятности — один из разделов математики, в котором изучаются модели случайных экспериментов.
Случайными экспериментами называются такие, результаты которых неизвестны заранее. Подбрасывая монетку, мы не знаем, что выпадет — орел или решка. Только поймав монетку, мы узнаем результат.
| Как кот может быть одновременно жив и мертв? Ученый по имени Эрвин Шредингер провел мысленный эксперимент. Он поместил кота в закрытый ящик, в котором был расположен механизм, содержащий атомное ядро и ёмкость с ядовитым газом. По эксперименту с вероятностью 0,5 ядро распадется, емкость с газом откроется и кот умрет. Но при этом с вероятностью 0,5 ядро не распадается и кот останется жив. Пока ящик закрыт, мы не знаем результат эксперимента — такой эксперимент в математике можно назвать случайным. Тем временем кот находится одновременно в двух состояниях: он и жив, и мертв. |
Рассмотрим чуть подробнее пример с монеткой. Есть всего два варианта, какое событие может произойти:
Есть всего два варианта, какое событие может произойти:
- выпадет орел;
- выпадет решка.
Эти два события образуют множество элементарных событий.
Множество элементарных событий — множество всех возможных результатов случайного эксперимента.
В случае выше их всего два. А если мы будем подбрасывать игральную кость, то их будет уже 6. Множество элементарных событий будет менять в зависимости от ситуации.
Допустим, мы поспорили с друзьями, что выпадет орел. Для нас это событие будет благоприятным, поскольку мы выиграем спор. Второе событие будет неблагоприятным, потому что спор будет проигран.
Как найти вероятность, что мы выиграем спор? Нужно разделить число благоприятных событий на общее число событий. Таким образом, мы получили классическое определение вероятности.
Вероятность — отношение количества благоприятных событий к количеству всех возможных событий.
Пусть m — количество благоприятных исходов, а n — количество всех событий. Получаем следующую формулу.
Получаем следующую формулу.
\(P = \frac{m}{n}\)
Вероятность можно обозначить, как P(x), где х — некоторое событие.
Заметим, что количество благоприятных исходов должно быть либо меньше, либо равно количеству всех исходов. Если благоприятных событий больше, чем всех, значит, мы нашли не все множество элементарных событий.
Когда вероятность равна 1, то такое событие точно наступит. Иначе говоря, мы можем быть уверены на 100% — оно произойдет.
| Можно ли всегда выигрывать спор с монеткой? Можно, если хитро сформулировать условия. Например: «Орел — я выиграл, решка — ты проиграл». Вероятность выигрыша в этом случае будет равна \(P = \frac{2}{2} = 1\), то есть мы точно выиграем спор. Однако вероятность не так проста, и даже здесь подготовила ловушку. В редких случаях есть и третий вариант событий — монетка встанет на ребро. Вероятность такого события составляет \(\frac{1}{6000}\). |
Вероятность всегда будет меньше или равна 1. Но ее можно выразить и через проценты. Для этого достаточно умножить полученный результат на 100%.
Пример 1. На ресепшене одного из отелей стоит ваза с конфетами. В вазе 56 яблочных конфет, 49 апельсиновых и 35 малиновых. Гость отеля наугад тянет конфету. Какова вероятность, что ему попадется апельсиновая конфета?
Решение. Найдем, сколько всего конфет в вазе: 56 + 49 + 35 = 140. Вероятность вытащить апельсиновую конфету будет равна
\(\frac{49}{140} = 0,35\)
Выразим в процентах:
0,35 * 100% = 35%
Задача решена. Обычно в ответе пишут значение вероятности через дробное число, а не проценты. Поэтому получаем следующий ответ.
Ответ: 0,35
Чтобы выразить вероятность через проценты в одно действие, достаточно воспользоваться следующей формулой.
\(P = \frac{m}{n} * 100%\)
Но что, если нам нужно найти вероятность для более сложных экспериментов? Первым делом нужно определить, какие события перед нами.
Равновозможные и противоположные событияКогда мы бросаем игральную кость, вероятность выпадения любого из чисел равна 16. То есть вероятности выпадения чисел равны между собой. Такие события называются равновозможными.
Равновозможные события — такие события, что по условиям опыта ни одно из них не является более возможным, чем другие.
Вероятности появления событий равны.
Для игрального кубика существует всего шесть событий, которые могут произойти: выпадет число 1, 2, 3, 4, 5 или 6. Все эти события образуют полную группу событий.
Полная группа событий — такая группа событий, если в результате опыта обязательно появится хотя бы одно из них.
В результате подбрасывания монеты выпадет либо орел, либо решка. То есть полная группа событий состоит из двух событий.
Мы подбросили монету и выпал орел. Следовательно, не выпала решка.
А если не выпадет орел? Обязательно выпадет решка. Эти события будут называться противоположными.
Противоположные события — такие события, если при не наступлении одного обязательно наступает второе.
Обозначим событие “выпала решка” как A. Противоположное ему событие “выпал орел” обозначим как \(\overline{A}\).
Заметим, что вероятность события A равняется 12, как и вероятность события \(\overline{A}\). Чему равна их сумма?
\)\frac{1}{2} + \frac{1}{2} = 1\)
Так мы вывели связь между противоположными событиями. Поскольку они всегда образуют полную группу событий, то сумма их вероятностей будет равна 1.
\(P(A) + P(\overline{A}) = 1\)
Какие еще примеры противоположных событий можно назвать? Ясная и дождливая погода. Если наступает одно из этих событий, то второе уже не может наступить.
Если наступает одно из этих событий, то второе уже не может наступить.
Допустим, у нас есть два события: сегодня пойдет снег и сегодня пойдет дождь. Что будет, если мы их объединим?
Объединение событий — событие, состоящее из всех элементарных исходов, благоприятствующих хотя бы одному из событий.
В этом случае мы получим событие, которое будет выполняться при любом из исходов: и если пойдет снег, и если не пойдет снег.
Объединение событий обозначается знаком \(\cup\). Объединение событий А и В можно записать как \(A \cup B\).
Рассмотрим немного другой пример. В первое событие входит, что Илья получит пятерку по физике, а второе событие — Антон получит пятерку по физике. А как можно назвать событие, если оба мальчика получат пятерку по физике?
Пересечение событий — событие, состоящее из всех элементарных исходов, благоприятствующих обоим событиям.
Пересечение событий обозначается знаком \(\cap\). Пересечение событий А и В можно записать как \(A \cap B\).
Пересечение событий А и В можно записать как \(A \cap B\).
Рассмотрим два события: “чайник исправно работает” и “чайник сломался”. Могут ли эти события существовать одновременно? Нет, поскольку появление одного из них исключает появление другого.
Такие события называются несовместными. Название само говорит, что события не могут существовать одновременно.
Несовместные события — такие события, появление одного из которых исключает появление другого.
Решим небольшую задачу. На экзамене есть несколько билетов. С вероятностью 0,5 попадется билет по планиметрии. С вероятностью 0,3 попадется билет по экономике. При этом не существует билетов, которые включают обе эти темы. С какой вероятностью на контрольной попадется билет по одной из этих тем?
Представим билеты в виде схемы. Заметим, что нам нужно объединить два из трех кругов, то есть сложить их вероятности.
Следовательно, вероятность будет равна 0,5 + 0,3 = 0,8.
Сформулируем определение суммы вероятностей двух несовместных событий.
Если события А и В несовместны, то вероятность их объединения равна сумме их вероятностей:
\(P(A \cup B) = P(A) + P(B)\)
Если существуют несовместные события, то существуют и совместные.
Совместные события — события, наступление одного из которых не исключает наступления другого.
В магазине работают два консультанта. Один из них занят общением с клиентом. Означает ли это, что второй консультант тоже занят? Нет, поскольку они работают независимо друг от друга. Если занят первый консультант, второй может быть как занят, так и нет.
Подбросим игральный кубик и рассмотрим два вида событий. Пусть событие А — это “выпадет число 2”, событие В — “выпадет четное число”.
Найдем вероятность события А: \(\frac{1}{6}\).
Для события В всего три благоприятных исхода из шести: выпадет число 2, 4 или 6. Тогда вероятность наступления события В равна \(\frac{3}{6} = \frac{1}{2}\)
Тогда вероятность наступления события В равна \(\frac{3}{6} = \frac{1}{2}\)
Исключают ли события А и В друг друга? Нет, поскольку если произойдет событие А, произойдет и событие В. Когда произойдет событие В, есть вероятность, что произойдет и событие А.
Найдем объединение совместных событий на примере кругов. Если мы наложим их друг на друга, то в середине получится как бы два слоя. Проверить это можно, если наложить друг на друга два листа бумаги.
А нужно получить вот такую картину:
Поэтому для объединения двух кругов нам нужно будет исключить одну из серединок.
Если события А и В совместны, то вероятность их объединения равна сумме их вероятностей без вероятности их пересечения:
\(P(A \cup B) = P(A) + P(B) — P(A \cap B)\)
В каких случаях нужно пользоваться формулой со сложением? Достаточно, чтобы задачу можно было сформулировать с помощью “или”. Например, нужно, чтобы выпали темы по планиметрии или по экономике.
Прогуляемся в магазин за булочками. В упаковке две булочки, а сама упаковка непрозрачная, то есть увидеть булочки до вскрытия упаковки мы не можем.
Известно, что на заводе, где изготавливаются булочки, 5 из 100 булочек подгорают. Значит, 95 из 100 булочек не подгорают. По классическому определению вероятности находим, что вероятность каждой булочки не подгореть равна \(\frac{95}{100} = 0,95\).
Какова вероятность, что в упаковке попадутся только не подгорелые булочки? Как найти вероятность сразу для двух булочек?
Ответим на вопрос: зависят ли булочки друг от друга?
Если подгорит одна из булочек в упаковке, не обязательно подгорит другая. Следовательно, булочки не зависят друг от друга. Такие события называются независимыми.
Независимые события — такие события, появление одного из которых не зависит от появления другого события.
Определим вероятность независимых событий.
Пусть вероятность, что подгорела первая булочка, будет равна Р(А) = 0,95, а вероятность для второй булочки будет равна Р(В) = 0,95.
А чтобы найти вероятность независимых событий, нужно воспользоваться следующей формулой:
\(P(A \cap B) = P(A) * P(B)\)
Тогда вероятность, что булочки в одной упаковке не подгорят, равняется P = 0,95 * 0,95 = 0,9025.
В каком случае нужно пользоваться этой формулой? Нужно подставить союз “и”.
Мы хотим, чтобы в упаковке первая булочка была не подгорелой и вторая булочка была не подгорелой.
Приведем еще один пример. В здании два автомата с кофе на разных этажах. Даже если сломается один из них, работа второго не будет зависеть от первого.
Но если автоматы стоят рядом и включены в одну розетку, то при поломке одного из них есть вероятность выхода из строя розетки, а значит, и второй автомат тоже сломается. Такие события будут зависимыми: появление одного из них зависит от появления другого.
Предположим, что в мешке лежит семь кубиков: два из них оранжевые, а пять — фиолетовые. Из мешка дважды вытаскивают кубики. Какова вероятность, достать во второй раз именно фиолетовый кубик?
Нужная последовательность может быть в двух случаях:
- сначала вытащат фиолетовый кубик и потом снова фиолетовый;
- сначала вытащат оранжевый кубик, а потом фиолетовый.
Разберем первый случай. Вероятность в первый раз вытащить фиолетовый кубик равна \(\frac{5}{7}\). После этого в мешке останется шесть кубиков, четыре из которых будут фиолетовые.
Вероятность вытащить во второй раз фиолетовый кубик равна \(\frac{5}{7} * \frac{4}{6} = \frac{20}{42} = \frac{10}{21}\).
Теперь рассмотрим второй случай. Вероятность в первый раз достать оранжевый кубик равна \(\frac{2}{7}\). В мешке останется шесть кубиков, пять из которых будут фиолетовыми.
Вероятность вытащить во второй раз фиолетовый кубик будет уже равна \(\frac{2}{7} * \frac{5}{6} = \frac{10}{42} = \frac{5}{21}\).
В этом примере очень наглядно видно, что вероятность напрямую зависит от того, какой кубик попался первым. Следовательно, эти события зависимы.
Как отличить зависимые и независимые события? Если после наступления первого события меняется количество благоприятных и всех исходов, то такие события — зависимые. Если количество благоприятных и всех исходов не меняется, то события независимые.
Условная вероятность — вероятность некоторого события В при условии наступления некоторого события А.
Условная вероятность обозначается P(B|A). В нашем примере условной вероятностью будет вычисление, что во второй раз попадется именно фиолетовый кубик.
Найдем вероятность двух зависимых событий. Формула похожа на ту, что используется для независимых событий. Но в этот раз нам нужно применить условную вероятность.
Вероятность появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие уже наступило:
\(P(A \cap B) = P(A) * P(B | A)\)
Формула БернуллиРассмотрим случаи, когда испытание повторяется многократно. 8} \approx 0,1\)
8} \approx 0,1\)
- Вероятность — отношение количества благоприятных событий к количеству всех возможных событий.
- События могут быть противоположными. Противоположные события — такие события, если при не наступлении одного обязательно наступает второе.
- События можно разделить на совместные и несовместные. Несовместные события — такие события, появление одного из которых исключает появление другого. Если события А и В несовместны, то вероятность их объединения равна сумме их вероятностей: P(A \(\cup) B) = P(A) + P(B). Совместные события — события, наступление одного из которых не исключает наступления другого. Если события А и В совместны, то вероятность их объединения равна сумме их вероятностей без вероятности их пересечения: P(A \cup B) = P(A) + P(B) — P(A \cap B).
- События также можно разделить на независимые и зависимые. Независимые события — такие события, появление одного из которых не зависит от появления другого события.
 Вероятность независимых событий можно найти по формуле P(A \cap B) = P(A) * P(B). Зависимые события — это события, появление одного из которых зависит от появления другого. Вероятность появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие уже наступило. P(A \cap B) = P(A) * P(B | A).
Вероятность независимых событий можно найти по формуле P(A \cap B) = P(A) * P(B). Зависимые события — это события, появление одного из которых зависит от появления другого. Вероятность появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие уже наступило. P(A \cap B) = P(A) * P(B | A). - Условная вероятность — вероятность некоторого события В при условии наступления некоторого события А.
Задание 1.
Какие события являются несовместными?
- Подбрасывание монетки.
- Брак батареек в одной упаковке.
- “Миша идет” и “Миша стоит”.
- Случайное вытаскивание конфет из вазы.
Задание 2.
Алена делает ошибку при решении задач по математике с вероятностью 0,17. С какой вероятностью она не сделает ошибку при решении задачи?
- 0,17
- 1
- 0,83
- 1,17
Задание 3.
Артем решал задачи на вероятность. Ниже приведены его ответы. В какой из задач он точно совершил ошибку?
- 1
- 0,216
- 0,45
- 1,5
Задание 4.
В упаковке три шариковые ручки. С вероятностью 0,1 такая ручка не будет писать. Найдите вероятность, что все три ручки в упаковке пишут.
- 0,3
- 0,001
- 2,7
- 0,729
Задание 5.
Перед Дашей лежит несколько карточек. Она случайно переворачивает одну из них. С вероятностью 0,5 на карточке окажется рисунок природы. С вероятностью 0,27 на карточке окажется мотивационная цитата. Карточек и с рисунком, и с цитатой нет. Найдите вероятность, что Дана перевернет карточку или с рисунком, или с цитатой.
- 0,77
- 0,135
- 0,23
- -0,23
Ответы: 1. — 3 2. — 3 3. — 4 4. — 4 5. — 1
Вероятность с использованием перестановок и комбинаций
Результаты обучения
- Вычисление условной вероятности события
- Используйте теорему Байе для вычисления условной вероятности
- Рассчитать ожидаемое значение события
Мы можем использовать перестановки и комбинации, чтобы помочь нам ответить на более сложные вопросы вероятности.
примеры
Выбран 4-значный PIN-код. Какова вероятность того, что нет повторяющихся цифр?
Показать решение
Попробуйте
Пример
В лотерее одного штата 48 шаров с номерами от 1 до 48 помещаются в автомат, и шесть из них вытягиваются случайным образом. Если шесть выпавших номеров совпадают с номерами, выбранными игроком, игрок выигрывает 1 000 000 долларов. В этой лотерее порядок выпадения номеров не имеет значения. Вычислите вероятность того, что вы выиграете приз в миллион долларов, если купите один лотерейный билет.
Показать решение
Пример
В лотерее штата из предыдущего примера, если пять из шести выпавших номеров совпадают с номерами, выбранными игроком, игрок выигрывает второй приз в размере 1000 долларов. Вычислите вероятность того, что вы выиграете второй приз, если купите один лотерейный билет.
Показать решение
Предыдущие примеры показаны в следующем видео.
примера
Вычислите вероятность случайного извлечения пяти карт из колоды и получения ровно одного туза.
Показать решение
Пример
Вычислите вероятность случайного извлечения пяти карт из колоды и получения ровно двух тузов.
Показать решение
Просмотрите следующее для дальнейшей демонстрации этих примеров.
Попробуйте
Давайте сделаем паузу, чтобы рассмотреть известную задачу теории вероятностей:
Предположим, у вас есть комната, полная 30 человек. Какова вероятность того, что есть хотя бы один общий день рождения?
Какова вероятность того, что есть хотя бы один общий день рождения?
Угадайте ответ на приведенную выше задачу. Было ли ваше предположение довольно низким, около 10%? Это кажется интуитивным ответом (возможно, 30/365?). Давайте посмотрим, стоит ли нам прислушиваться к своей интуиции. Однако начнем с более простой задачи.
пример
Предположим, в комнате находятся три человека. Какова вероятность того, что у этих трех человек есть хотя бы один общий день рождения?
Показать решение
Предположим, в комнате находятся пять человек. Какова вероятность того, что среди этих пяти человек есть хотя бы один общий день рождения?
Показать решение
Предположим, в комнате 30 человек. Какова вероятность того, что среди этих 30 человек есть хотя бы один общий день рождения?
Показать решение
Ниже подробно рассматривается проблема дня рождения.
Если вам нравится делать ставки, и если вы можете убедить 30 человек раскрыть свои дни рождения, вы можете выиграть немного денег, поспорив с другом, что в комнате будет по крайней мере два человека с одинаковым днем рождения в любое время. вы находитесь в комнате на 30 и более человек. (Конечно, вам нужно убедиться, что ваш друг не изучал вероятность!) Вы не гарантированно выиграете, но вы должны выигрывать более чем в половине случаев.
Это один из многих противоречивых результатов теории вероятностей; то есть это идет вразрез с нашими внутренними инстинктами.
Попробуйте
Предположим, в комнате находятся 10 человек. Какова вероятность того, что среди этих 10 человек есть хотя бы один общий день рождения?
3.2.2 Вероятностная выборка
Содержание
Текст начинается
Тематическая навигация
- 3 Сбор и обработка данных
- 3.
 2 Отбор проб
2 Отбор проб- 3.2.1 Отбор проб
- 3.2.2 Вероятностная выборка
- 3.2.3 Невероятностная выборка
- 3.
Под вероятностной выборкой понимается отбор выборки из совокупности, когда этот отбор основан на принципе рандомизации, то есть случайного отбора или случайности. Вероятностная выборка более сложна, требует больше времени и обычно дороже, чем невероятностная выборка. Однако, поскольку единицы из совокупности выбираются случайным образом и можно рассчитать вероятность выбора каждой единицы, можно получить надежные оценки и сделать статистические выводы о совокупности.
Существует несколько различных способов выбора вероятностной выборки.
При выборе плана вероятностной выборки цель состоит в том, чтобы свести к минимуму ошибку выборки оценок наиболее важных переменных обследования, одновременно сводя к минимуму время и затраты на проведение обследования. Некоторые операционные ограничения также могут повлиять на этот выбор, например, характеристики инструментария обследования.
Некоторые операционные ограничения также могут повлиять на этот выбор, например, характеристики инструментария обследования.
В данном разделе каждый из этих методов будет кратко описан и проиллюстрирован примерами.
Простая случайная выборка
В простой случайной выборке (SRS) каждая единица выборки совокупности имеет равные шансы быть включенной в выборку. Следовательно, каждая возможная выборка также имеет равные шансы быть отобранной. Чтобы выбрать простую случайную выборку, вам необходимо перечислить все единицы в генеральной совокупности обследования.
Пример 1 Чтобы взять простую случайную выборку из телефонной книги, каждая запись должна быть последовательно пронумерована. Если бы в телефонной книге было 10 000 записей и размер выборки составлял 2 000, то компьютер должен был бы случайным образом сгенерировать 2 000 номеров от 1 до 10 000. Все числа будут иметь одинаковые шансы быть сгенерированными компьютером. 2000 телефонных записей, соответствующих 2000 сгенерированным компьютером случайным числам, составили бы выборку.
SRS можно сделать с заменой или без. SRS с заменой означает, что существует вероятность того, что выбранная телефонная запись может быть выбрана дважды или более. Обычно подход SRS проводится без замены, поскольку он более удобен и дает более точные результаты. В остальной части текста SRS будет использоваться для обозначения SRS без замены, если не указано иное.
СРС является наиболее часто используемым методом. Преимущество этого метода заключается в том, что он не требует никакой информации об инструментарии обследования, кроме полного списка единиц обследуемой совокупности вместе с контактной информацией. Кроме того, поскольку SRS является простым методом и его теория хорошо известна, существуют стандартные формулы для определения размера выборки, оценок и т. д., и эти формулы просты в использовании.
д., и эти формулы просты в использовании.
С другой стороны, этот метод требует списка всех единиц совокупности. Если такого списка еще не существует, а целевая аудитория велика, его создание может быть очень дорогим или нереалистичным. Если список уже существует и содержит вспомогательную информацию по объектам, то SRS не использует информацию, позволяющую повысить эффективность других методов (например, стратифицированной выборки). Если сбор должен производиться лично, SRS может предоставить выборку, которая слишком распределена по нескольким регионам, что может увеличить затраты и продолжительность обследования.
Пример 2 Представьте, что у вас есть кинотеатр, и вы предлагаете специальный фестиваль фильмов ужасов в следующем месяце. Чтобы решить, какие фильмы ужасов показать, вы опрашиваете кинозрителей, какие из перечисленных фильмов им нравятся больше всего. Чтобы составить список фильмов, необходимых для вашего опроса, вы решаете выбрать 10 из 100 лучших фильмов ужасов всех времен. Один из способов выбрать образец — написать все названия фильмов на листках бумаги и поместить их в пустую коробку. Затем нарисуйте 10 названий, и у вас будет образец. Используя этот подход, вы обеспечите равную вероятность выбора каждого фильма. Вы даже можете рассчитать эту вероятность выбора, разделив размер выборки (n=10) на размер совокупности 100 лучших фильмов ужасов всех времен (N=100). Эта вероятность будет равна 0,10 (10/100) или 1 из 10.
Один из способов выбрать образец — написать все названия фильмов на листках бумаги и поместить их в пустую коробку. Затем нарисуйте 10 названий, и у вас будет образец. Используя этот подход, вы обеспечите равную вероятность выбора каждого фильма. Вы даже можете рассчитать эту вероятность выбора, разделив размер выборки (n=10) на размер совокупности 100 лучших фильмов ужасов всех времен (N=100). Эта вероятность будет равна 0,10 (10/100) или 1 из 10.
Систематическая выборка
Систематическая выборка означает наличие пробела или интервала между каждой выбранной единицей в выборке. Например, вы можете выполнить следующие действия:
- Пронумеруйте единицы на вашем кадре от 1 до N (где N — это общая численность населения).
- Определите интервал выборки ( K ), разделив количество единиц в совокупности на желаемый размер выборки. Например, чтобы выбрать выборку в 100 человек из совокупности в 400 человек, вам потребуется интервал выборки 400/100 = 4.
 Следовательно, K = 4. Вам нужно будет выбрать одну единицу из каждых четырех единиц, чтобы получить в общей сложности 100 единиц в вашей выборке.
Следовательно, K = 4. Вам нужно будет выбрать одну единицу из каждых четырех единиц, чтобы получить в общей сложности 100 единиц в вашей выборке. - Случайным образом выберите число от 1 до K . Это число называется , случайное начало , и это будет первое число, включенное в вашу выборку. Если вы выберете 3, третья единица на вашем кадре будет первой единицей, включенной в вашу выборку; если вы выберете 2, ваша выборка начнется со второго устройства на вашей раме.
- Выберите каждые Kth (в данном случае, каждую четвертую) единицу после этого первого числа. Например, выборка может состоять из следующих единиц, чтобы составить выборку из 100: 3 (случайное начало), 7, 11, 15, 19 … 395, 399 (до N , что в данном случае равно 400). ).
В приведенном выше примере вы можете видеть, что можно выбрать только четыре возможных образца, соответствующих четырем возможным случайным стартам:
1, 5, 9, 13 … 393, 397
2, 6, 10, 14 … 394, 398
3, 7, 11, 15 … 395, 399
4, 8, 12, 16 … 396, 400
Каждый член населения принадлежит только к одному из четыре образца, и каждый образец имеет одинаковый шанс быть выбранным. Из этого мы видим, что каждая единица имеет один шанс из четырех быть выбранным в выборке. Это такая же вероятность, как если бы была выбрана простая случайная выборка из 100 единиц. Основное отличие состоит в том, что в случае SRS любая комбинация из 100 единиц может составить выборку, в то время как при систематической выборке имеется только четыре возможных выборки. Порядок единиц в кадре будет определять возможные выборки для систематической выборки. Если совокупность случайным образом распределена в основе, систематическая выборка должна давать результаты, аналогичные простой случайной выборке.
Из этого мы видим, что каждая единица имеет один шанс из четырех быть выбранным в выборке. Это такая же вероятность, как если бы была выбрана простая случайная выборка из 100 единиц. Основное отличие состоит в том, что в случае SRS любая комбинация из 100 единиц может составить выборку, в то время как при систематической выборке имеется только четыре возможных выборки. Порядок единиц в кадре будет определять возможные выборки для систематической выборки. Если совокупность случайным образом распределена в основе, систематическая выборка должна давать результаты, аналогичные простой случайной выборке.
Этот метод часто используется в промышленности, где изделие выбирается для испытаний с производственной линии, чтобы гарантировать, что машины и оборудование имеют стандартное качество. Например, тестер на заводе-изготовителе может выполнять проверку качества каждого 20-го продукта на сборочной линии. Тестер может выбрать случайное начало между числами 1 и 20. Это определит первый тестируемый продукт; после этого каждый 20-й продукт будет протестирован.
Это определит первый тестируемый продукт; после этого каждый 20-й продукт будет протестирован.
Интервьюеры могут использовать этот метод выборки при опросе людей для выборочного обследования. Исследователь рынка может выбрать, например, каждого 10-го человека, который входит в конкретный магазин, после случайного выбора первого человека. Инспектор может опросить жителей каждого пятого дома на улице после случайного выбора одного из первых пяти домов.
Преимущества систематической выборки заключаются в том, что отбор выборки не может быть проще: вы получаете только одно случайное число, случайное начало, а остальная часть выборки следует автоматически. Самым большим недостатком метода систематической выборки является то, что если в способе размещения совокупности в списке есть какой-либо периодический признак, и этот периодический признак каким-то образом совпадает с интервалом выборки, возможные выборки могут не быть репрезентативными для совокупности. Это можно увидеть на следующем примере:
Пример 3 Предположим, вы управляете большим продуктовым магазином и у вас есть список сотрудников в каждом отделе. Продуктовый магазин разделен на следующие 10 секций: гастроном, пекарня, кассы, склад, мясной прилавок, продукты, аптека, фотосалон, цветочный магазин и химчистка. В каждой секции работает 10 сотрудников, включая менеджера (всего 100 сотрудников). Ваш список упорядочен по разделам, где сначала указан менеджер, а затем остальные сотрудники в порядке убывания старшинства.
Продуктовый магазин разделен на следующие 10 секций: гастроном, пекарня, кассы, склад, мясной прилавок, продукты, аптека, фотосалон, цветочный магазин и химчистка. В каждой секции работает 10 сотрудников, включая менеджера (всего 100 сотрудников). Ваш список упорядочен по разделам, где сначала указан менеджер, а затем остальные сотрудники в порядке убывания старшинства.
Если вы хотите опросить своих сотрудников о том, что они думают об их рабочей среде, вы можете выбрать небольшую выборку, чтобы ответить на ваши вопросы. Если вы используете метод систематической выборки и ваш интервал выборки равен 10, вы можете выбрать только руководителей или только новых сотрудников в каждом разделе. Этот тип выборки не даст вам полной или адекватной картины мыслей ваших сотрудников.
Выборка с вероятностью, пропорциональной размеру
Вероятностная выборка требует, чтобы каждый член обследуемой совокупности имел известную вероятность включения в выборку, но не требует, чтобы эта вероятность была одинаковой для всех. Если в основе имеется информация о размере каждой единицы (например, количество работников для каждого предприятия) и если эти единицы различаются по размеру, эту информацию можно использовать при формировании выборки для повышения эффективности. Это известно как 9Выборка 0099 с вероятностью, пропорциональной размеру (PPS). При использовании этого метода чем больше размер единицы, тем выше вероятность ее включения в выборку. Для повышения эффективности этого метода необходимо, чтобы измерение размера было точным. Это более сложный метод выборки, который не будет подробно обсуждаться здесь.
Если в основе имеется информация о размере каждой единицы (например, количество работников для каждого предприятия) и если эти единицы различаются по размеру, эту информацию можно использовать при формировании выборки для повышения эффективности. Это известно как 9Выборка 0099 с вероятностью, пропорциональной размеру (PPS). При использовании этого метода чем больше размер единицы, тем выше вероятность ее включения в выборку. Для повышения эффективности этого метода необходимо, чтобы измерение размера было точным. Это более сложный метод выборки, который не будет подробно обсуждаться здесь.
Стратифицированная выборка
При использовании стратифицированной выборки совокупность делится на однородные взаимоисключающие группы, называемые стратами, а затем из каждой страты отбираются независимые выборки. Любой из методов выборки, упомянутых в этом разделе, может быть использован для выборки внутри каждой страты. Метод выборки может варьироваться от одной страты к другой. Совокупность может быть стратифицирована по любой переменной, значение которой доступно для всех единиц основы выборки до формирования выборки (например, возраст, пол, провинция проживания, доход).
Совокупность может быть стратифицирована по любой переменной, значение которой доступно для всех единиц основы выборки до формирования выборки (например, возраст, пол, провинция проживания, доход).
Зачем создавать слои? Есть много причин, главная из которых заключается в том, что это может сделать стратегию выборки более эффективной. В предыдущем разделе упоминалось, что для оценки определенной точности требуется больший размер выборки для характеристики, которая сильно варьируется от одной единицы к другой, чем для характеристики с меньшей изменчивостью. Например, если бы каждый человек в совокупности имел одинаковую заработную плату, то выборки одного человека было бы достаточно, чтобы получить точную оценку средней заработной платы.
В этом заключается идея повышения эффективности, полученного с помощью стратификации. Если вы создаете страты, в которых единицы имеют сходные характеристики и значительно отличаются от единиц в других стратах, вам потребуется только небольшая выборка из каждой страты, чтобы получить точную оценку общего дохода для этой страты. Затем вы можете объединить эти оценки, чтобы получить точную оценку общего дохода для всего населения. Если бы вы использовали SRS для всего населения без стратификации, выборка должна была бы быть больше, чем сумма всех размеров выборок страты, чтобы получить оценку общего дохода с тем же уровнем точности.
Затем вы можете объединить эти оценки, чтобы получить точную оценку общего дохода для всего населения. Если бы вы использовали SRS для всего населения без стратификации, выборка должна была бы быть больше, чем сумма всех размеров выборок страты, чтобы получить оценку общего дохода с тем же уровнем точности.
Еще одним преимуществом является то, что стратифицированная выборка обеспечивает достаточный размер выборки для представляющих интерес подгрупп населения. При стратификации совокупности каждая страта становится независимой совокупностью, и для каждой из них рассчитывается размер выборки.
Пример 4 Предположим, вы хотите оценить, сколько старшеклассников работают неполный рабочий день на национальном уровне и уровне провинции. Если бы вы выбрали простую случайную выборку из 25 000 человек из списка всех старшеклассников в Канаде (при условии, что такой список был доступен для выбора), вы бы получили немногим более 100 человек с Острова Принца Эдуарда, поскольку они составляют менее 0,5% населения Канады. Эта выборка, вероятно, не будет достаточно большой для подробного анализа, который вы планировали. Разделение вашего списка по провинциям, а затем определение размера выборки, необходимого для каждой провинции, позволит вам получить требуемый уровень точности для Острова Принца Эдуарда, а также для каждой из других провинций.
Эта выборка, вероятно, не будет достаточно большой для подробного анализа, который вы планировали. Разделение вашего списка по провинциям, а затем определение размера выборки, необходимого для каждой провинции, позволит вам получить требуемый уровень точности для Острова Принца Эдуарда, а также для каждой из других провинций.
Стратификация наиболее полезна, когда стратифицирующие переменные
- просты в работе,
- легко заметить,
- тесно связаны с темой опроса.
Кластерная выборка
Иногда слишком дорого иметь слишком разбросанную географическую выборку. Командировочные расходы могут стать дорогими, если интервьюерам приходится опрашивать людей из одного конца страны в другой. Чтобы сократить расходы, статистики могут выбрать 9Метод кластерной выборки 0099 .
Кластерная выборка делит совокупность на группы или кластеры. Несколько кластеров выбираются случайным образом для представления общей совокупности, а затем все единицы внутри выбранных кластеров включаются в выборку. В выборку не включены единицы из невыбранных кластеров. Они представлены представителями выбранных кластеров. Это отличается от стратифицированной выборки, когда некоторые единицы выбираются из каждой страты. Примерами кластеров являются фабрики, школы и географические районы, такие как избирательные округа.
В выборку не включены единицы из невыбранных кластеров. Они представлены представителями выбранных кластеров. Это отличается от стратифицированной выборки, когда некоторые единицы выбираются из каждой страты. Примерами кластеров являются фабрики, школы и географические районы, такие как избирательные округа.
Предположим, вы представитель спортивной организации и хотите узнать, в каких видах спорта участвуют учащиеся 11-х (или 4-х) классов по всей Канаде. Было бы слишком дорого и долго опрашивать каждого канадца в 11-м классе или даже пару учеников из каждого класса 11-го класса в Канаде. Вместо этого случайным образом выбираются 100 школ со всей Канады. Эти 100 школ являются отобранными кластерами. Затем опрашиваются все учащиеся 11-х классов во всех 100 кластерах.
Кластерная выборка создает «карманы» единиц выборки, а не распределяет выборку по всей территории, что позволяет снизить затраты на операции по сбору. Еще одна причина использования кластерной выборки заключается в том, что иногда список всех единиц генеральной совокупности недоступен, в то время как список всех кластеров либо доступен, либо его легко создать.
В большинстве случаев кластерная выборка менее эффективна, чем SRS . Это главный недостаток метода. По этой причине обычно лучше обследовать большое количество небольших скоплений, а не небольшое количество больших скоплений. Почему? Поскольку соседние единицы имеют тенденцию быть более похожими, в результате получается выборка, которая не отражает весь спектр мнений или ситуаций, присутствующих в генеральной совокупности. В примере 5 учащиеся одной и той же школы, как правило, занимаются одними и теми же видами спорта, то есть теми, для которых в их школе имеются возможности.
Еще один недостаток кластерной выборки заключается в том, что у вас нет полного контроля над окончательным размером выборки. Поскольку не во всех школах одинаковое количество учащихся 11-х классов, и вы должны опросить каждого учащегося в своей выборке, окончательный размер может быть больше или меньше, чем вы ожидали.
Многоэтапная выборка
Многоэтапная выборка аналогична кластерной выборке, за исключением того, что она включает выборку в каждом выбранном кластере, а не включает все единицы из выбранных кластеров. Этот тип выборки требует как минимум двух этапов. На первом этапе выявляются и отбираются большие кластеры. На втором этапе единицы выбираются из выбранных кластеров с использованием любого из методов вероятностной выборки. В этом контексте кластеры называются первичными единицами выборки (ПЕВ), а единицы внутри кластеров называются вторичными единицами выборки (ВЕВ). При наличии более двух этапов в рамках SSE выбираются третичные единицы выборки (TSU), и процесс продолжается до тех пор, пока не будет получена окончательная выборка.
Этот тип выборки требует как минимум двух этапов. На первом этапе выявляются и отбираются большие кластеры. На втором этапе единицы выбираются из выбранных кластеров с использованием любого из методов вероятностной выборки. В этом контексте кластеры называются первичными единицами выборки (ПЕВ), а единицы внутри кластеров называются вторичными единицами выборки (ВЕВ). При наличии более двух этапов в рамках SSE выбираются третичные единицы выборки (TSU), и процесс продолжается до тех пор, пока не будет получена окончательная выборка.
В примере 5 кластерная выборка будет выбирать 100 школ, а затем опрашивать каждого учащегося 11 класса из этих школ. Вместо этого вы можете выбрать больше школ, получить список всех учащихся 11-х классов из этих выбранных школ и выбрать случайную выборку учащихся 11-х классов из каждой школы. Это будет двухэтапный план выборки. Школы будут иметь PSU , а учащиеся — SSU .
Вы также можете получить список всех классов 11 класса в выбранных школах, выбрать случайную выборку классов из каждой из этих школ, получить список всех учащихся в выбранных классах и, наконец, выбрать случайную выборку учащихся из каждого выбранного класса. Это будет трехэтапный план выборки. Школы были бы PSU , классы будут иметь номер SSU , а студенты будут иметь номер TSU . Каждый раз, когда добавляется этап, процесс усложняется.
Теперь представьте, что в каждой школе учится в среднем 80 11-классников. Тогда кластерная выборка даст вашей организации выборку из примерно 8000 учащихся (100 школ x 80 учащихся). Если вам нужна большая выборка, вы можете выбрать школы с большим количеством учащихся. Для меньшей выборки вы можете выбрать школы с меньшим количеством учащихся. Одним из способов контроля размера выборки может быть разделение школ на большие, средние и малые размеры (с точки зрения количества учащихся 11-х классов) и выборка школ из каждой страты. это называется стратифицированная кластерная выборка .
это называется стратифицированная кластерная выборка .
В качестве альтернативы можно использовать трехэтапную схему. Вы должны выбрать выборку из 400 школ, затем выбрать два класса 11 класса в каждой школе и, наконец, выбрать 10 учащихся в классе. Таким образом, вы все равно получите выборку из примерно 8000 учащихся (400 школ x 2 класса x 10 учащихся), но выборка будет более разбросанной.
Из этого примера видно, что при многоступенчатой выборке у вас все еще есть преимущество более концентрированной выборки для снижения затрат. Однако выборка не такая концентрированная, как кластерная выборка, и размер выборки, необходимый для получения заданного уровня точности, все равно будет больше, чем для 9-кратной выборки.0135 SRS , так как этот метод менее эффективен. Тем не менее, многоэтапная выборка может сэкономить много времени и усилий по сравнению с SRS , поскольку вам не нужно иметь список всех учащихся 11-х классов. Все, что вам нужно, это список классов из 400 школ и список учеников из 800 классов.
Все, что вам нужно, это список классов из 400 школ и список учеников из 800 классов.
Многоэтапная выборка
Многоэтапная выборка собирает основную информацию из большой выборки единиц, а затем собирает более подробную информацию для подвыборки этих единиц. Наиболее распространенной формой многоэтапной выборки является двухэтапная выборка (или двойная выборка), но также возможны три или более этапов.
Многоэтапный отбор проб сильно отличается от многоступенчатого отбора проб, несмотря на схожесть их названий. Хотя многоэтапная выборка также включает в себя получение двух или более выборок, все выборки берутся из одного и того же кадра. Выбор подразделения на втором этапе обусловлен его выбором на первом этапе. Единица, не выбранная на первом этапе, не будет частью выборки на втором этапе. Как и в случае многоэтапной выборки, чем больше фаз используется, тем сложнее план выборки и ее оценка.
Многоэтапная выборка полезна, когда в основе выборки отсутствует вспомогательная информация, которую можно было бы использовать для стратификации совокупности или для исключения части совокупности.
Предположим, что организации требуется информация о животноводческих фермах в Альберте, но в инструментарии обследования перечислены все типы ферм — крупного рогатого скота, молочные, зерновые, свиноводческие, птицеводческие и сельскохозяйственные. Ситуация усложняется тем, что инструментарий обследования не предоставляет никакой вспомогательной информации по перечисленным там хозяйствам.
Простой опрос, единственным вопросом которого будет «Часть или вся ваша ферма посвящена животноводству?» можно было провести. При наличии только одного вопроса это обследование должно иметь низкую стоимость интервью (особенно если оно проводится по телефону) и, следовательно, организация должна быть в состоянии составить большую выборку. После того, как первая выборка составлена, можно взять вторую, меньшую выборку среди фермеров, занимающихся выращиванием крупного рогатого скота, и задать этим фермерам более подробные вопросы. Используя этот метод, организация избегает затрат на съемочные единицы, которые не входят в эту конкретную область (например, фермеры, не занимающиеся животноводством).
В примере 7 данные, собранные на первом этапе, использовались для исключения единиц, не входящих в целевую совокупность. В другом контексте эти данные можно было бы использовать для повышения эффективности второй фазы, например, путем создания пластов. Многоэтапная выборка также может использоваться для уменьшения нагрузки на респондентов или в случае очень разных затрат, связанных с разными вопросами опроса, как показано в следующем примере.
Пример 8В ходе обследования состояния здоровья участникам задают несколько основных вопросов об их питании, привычках курения, физических упражнениях и употреблении алкоголя. Кроме того, опрос требует, чтобы респонденты подвергали себя некоторым прямым физическим тестам, таким как бег на беговой дорожке или измерение артериального давления и уровня холестерина.
Заполнение анкет или опрос участников являются относительно недорогими процедурами, но медицинские тесты требуют наблюдения и помощи квалифицированного врача, а также использования оборудованной лаборатории, что может быть довольно дорогостоящим.
График функции y 2x в квадрате рисунок: как построить график функции y 2x в квадрате
Работа № 4. Вариант 2. № 4. ГДЗ Алгебра 9 класс Кузнецова. Помогите выяснить, проходит ли график через точку – Рамблер/класс
Работа № 4. Вариант 2. № 4. ГДЗ Алгебра 9 класс Кузнецова. Помогите выяснить, проходит ли график через точку – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
а) Постройте график функции у = 2х — 4.
б) Проходит ли график через точку В(-45; -86)?
ответы
a) y = 2x — 4.
График — прямая.
б) B (-45; -86).
y(-45) = 2 ∙ (-45) — 4 = -90 — 4 = -94; -94 ≠ -86.
Равенство неверно, т. о. точка В не принадлежит графику.
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
ЕГЭ
10 класс
11 класс
Химия
похожие вопросы 5
Напишите гдз по алгебре Мордкович 7 класс! Надо решить №32.20!
Решите уравнение:
●32.20. а) х2 — 3x + 2 = 0; в) х2 — 6x + 8 = 0;
б) x2 + 8х + 15 = 0; г) x2 (Подробнее…)
ГДЗАлгебраМордкович А.Г.7 класс
Будет ли введено устное собеседование по русскому языку на ГИА?
Подскажите, будет ли введено устное собеседование по русскому языку на ГИА? Как это будет проходить? (Подробнее. ..)
..)
НовостиГИАЭкзамены9 классРусский язык
3. Вычислите… 6 класс А.П. Ершова Математика. К 2. Вариант А 1
3.
Вычислите: (Подробнее…)
ГДЗМатематика6 классЕршова А.П.
Радиус основания цилиндра равен 2. В этот цилиндр наклонно к оси вписан квадрат со стороной 4 так, что все вершины его находятся на окружностях осн
Радиус основания цилиндра равен 2. В этот цилиндр наклонно к оси вписан квадрат со стороной 4 так, что все вершины его находятся на (Подробнее…)
ВыпускнойЕГЭГДЗ
Помогите упростить № 443 ГДЗ Математика 6 класс Никольский С.М.
Упростите запись по образцу (Подробнее…)
ГДЗМатематика6 классНикольский С.М.
Написать уравнение линейной функции по графику прямой | Колледж Алгебра |
Графики линейных функций
Напомним, что в разделе «Линейные функции» мы написали уравнение для линейной функции по графику. Теперь мы можем расширить наши знания о построении графиков линейных функций для более тщательного анализа графиков. Начните с рассмотрения рисунка 8. Мы сразу видим, что график пересекает ось y в точке (0, 4), так что это y -перехват.
Теперь мы можем расширить наши знания о построении графиков линейных функций для более тщательного анализа графиков. Начните с рассмотрения рисунка 8. Мы сразу видим, что график пересекает ось y в точке (0, 4), так что это y -перехват.
Рисунок 8
Затем мы можем рассчитать наклон, найдя подъем и уклон. Мы можем выбрать любые две точки, но давайте посмотрим на точку (-2, 0). Чтобы добраться от этой точки до перехвата y- , мы должны продвинуться на 4 единицы вверх (подъем) и вправо на 2 единицы (бег). Таким образом, наклон должен быть
м=подъем=42=2м=\frac{\text{подъем}}{\text{прогон}}=\frac{4}{2}=2\\m=подъем=24=2
Подстановка наклона и пересечения y- в форму пересечения наклона линии дает
у=2х+4у=2х+4\\у=2х+4
Как: Имея график линейной функции, найдите уравнение, описывающее эту функцию.

- Определите точку пересечения y- уравнения.
- Выберите две точки для определения уклона.
- Замените точку пересечения y- и наклон в форму линии с пересечением наклона.
Пример 4. Сопоставление линейных функций с их графиками
Сопоставьте каждое уравнение линейных функций с одной из линий на рисунке 9.
f(x)=2x+3f\влево(x\вправо)=2x+3\\f(x)=2x+3
g(x)=2x−3g\left(x\right)=2x — 3\\g(x)=2x−3
h(x)=−2x+3h\left(x\right)=-2x+3\\h(x)=−2x+3
j(x)=12x+3j\left(x\right)=\frac{1}{2}x+3\\j(x)=21x+3
Рисунок 9
Решение
Проанализируйте информацию для каждой функции.
- Эта функция имеет наклон 2 и y — точка пересечения 3.
 Она должна проходить через точку (0, 3) и наклоняться вверх слева направо. Мы можем использовать две точки, чтобы найти наклон, или мы можем сравнить его с другими перечисленными функциями. Функция g имеет тот же наклон, но другую точку пересечения y-. Линии I и III имеют одинаковый наклон, потому что они имеют одинаковый наклон. Строка III не проходит через (0, 3), поэтому f должна быть представлена линией I.
Она должна проходить через точку (0, 3) и наклоняться вверх слева направо. Мы можем использовать две точки, чтобы найти наклон, или мы можем сравнить его с другими перечисленными функциями. Функция g имеет тот же наклон, но другую точку пересечения y-. Линии I и III имеют одинаковый наклон, потому что они имеют одинаковый наклон. Строка III не проходит через (0, 3), поэтому f должна быть представлена линией I. - Эта функция также имеет наклон 2, но y — пересечение –3. Он должен проходить через точку (0, –3) и наклоняться вверх слева направо. Он должен быть представлен линией III.
- Эта функция имеет наклон –2 и точку пересечения y-, равную 3. Это единственная функция, указанная с отрицательным наклоном, поэтому она должна быть представлена линией IV, поскольку она наклонена вниз слева направо.
- Эта функция имеет наклон
12\frac{1}{2}\\21
и точку пересечения y- 3. Она должна проходить через точку (0, 3) и наклоняться вверх слева направо . Линии I и II проходят через (0, 3), но наклон j меньше наклона f , поэтому линия для j должна быть более плоской. Эта функция представлена линией II.
Она должна проходить через точку (0, 3) и наклоняться вверх слева направо . Линии I и II проходят через (0, 3), но наклон j меньше наклона f , поэтому линия для j должна быть более плоской. Эта функция представлена линией II.
Теперь мы можем перемаркировать линии, как показано на рисунке 10.
Рисунок 10
Нахождение пересечения линии размером x
До сих пор мы находили точки пересечения y- функции: точки, в которых график функции пересекает ось y . Функция также может иметь x — точка пересечения, — координата x точки пересечения графика функции с осью x . Другими словами, это входное значение, когда выходное значение равно нулю.
Чтобы найти точку пересечения x , установите функцию f ( x ) равной нулю и найдите значение x . Например, рассмотрим показанную функцию.
f(x)=3x−6f\влево(x\вправо)=3x — 6\\f(x)=3x−6
Установить функцию равной 0 и найти x .
{0=3x−66=3×2=xx=2\begin{cases}0=3x — 6\qquad \\ 6=3x\qquad \\ 2=x\qquad \\ x=2\qquad \end{cases }\\⎩
⎨
⎧0=3x−66=3×2=xx=2
График функции пересекает ось x в точке (2, 0).
Вопросы и ответы
Все ли линейные функции имеют x точек пересечения?
Нет. Однако линейные функции вида y = c , где c — ненулевое действительное число, являются единственными примерами линейных функций без пересечения x . Например, y = 5 — это горизонтальная линия, расположенная на 5 единиц выше оси x . Эта функция не имеет x -перехватов .
Например, y = 5 — это горизонтальная линия, расположенная на 5 единиц выше оси x . Эта функция не имеет x -перехватов .
Рисунок 11
A Общее примечание:
x — точка пересечения78 ф ( x ) = 0. Его можно решить с помощью уравнения 0 = m x + b .
Пример 5: Нахождение точки пересечения
xНахождение точки пересечения x
f(x)=12x−3f\left(x\right)=\frac{1}{2}x — 3 \\f(x)=21x−3
.
Решение
Установите функцию равной нулю для решения x .
{0=12x−33=12×6=xx=6\begin{case}0=\frac{1}{2}x — 3\\ 3=\frac{1}{2}x\\ 6=x \\ х=6\конец{случаи}\\⎩
⎨
⎧0=21x−33=21x6=xx=6
График пересекает ось x в точке (6, 0).
Рис. 12. График линейной функции
f(x)=12x−3f\left(x\right)=\frac{1}{2}x — 3\\f(x)=21 х-3
.
Попробуйте 4
Найдите точку пересечения x
f(x)=14x−4f\left(x\right)=\frac{1}{4}x — 4\\f(x) =41x−4
. Решение
Описание горизонтальных и вертикальных линий
Есть два особых случая линий на графике — горизонтальные и вертикальные линии. Горизонтальная линия указывает постоянный выход или y -значение. На рисунке 13 мы видим, что выход имеет значение 2 для каждого входного значения. Таким образом, изменение объема производства между любыми двумя точками равно 0. В формуле наклона числитель равен 0, поэтому наклон равен 0. Если мы используем m = 0 в уравненииf(x)=mx+bf \left(x\right)=mx+b\\f(x)=mx+b
, уравнение упрощается доf(x)=bf\left(x\right)=b\\f(x)=b
. Другими словами, значение функции является константой. Этот график представляет функцию
Другими словами, значение функции является константой. Этот график представляет функциюf(x)=2f\left(x\right)=2\\f(x)=2
.Рис. 13. Горизонтальная линия, представляющая функцию
f(x)=2f\left(x\right)=2\\f(x)=2
.
Рисунок 14
Вертикальная линия указывает на постоянное значение или значение x . Мы видим, что входное значение для каждой точки на линии равно 2, но выходное значение меняется. Поскольку это входное значение сопоставляется более чем с одним выходным значением, вертикальная линия не представляет функцию. Обратите внимание, что между любыми двумя точками изменение входных значений равно нулю. В формуле наклона знаменатель будет равен нулю, поэтому наклон вертикальной линии не определен.
Обратите внимание, что вертикальная линия, такая как на рис. 15 , , имеет точку пересечения x , но не имеет точки пересечения y-, если это не линия x = 0. Этот график представляет линию x = 2.
Этот график представляет линию x = 2.Рис. 15. Вертикальная линия x = 2, которая не представляет функцию.
A Общее примечание: горизонтальные и вертикальные линии
Линии могут быть горизонтальными или вертикальными.
A горизонтальная линия — это линия, заданная уравнением вида
f(x)=bf\left(x\right)=b\\f(x)=b
.
Вертикальная линия — это линия, заданная уравнением вида
x=ax=a\\x=a
.
Пример 6. Написание уравнения горизонтальной линии
Напишите уравнение линии, изображенной на рисунке 16. Рис. 160078 г = –4.
Пример 7. Написание уравнения вертикальной линии
Напишите уравнение линии, изображенной на рисунке 17.
Рисунок 17
Раствор
Константа x -значение равно 7, поэтому уравнение x = 7.
Лицензии и атрибуты
Контент по лицензии CC, совместно используемый ранее
- Precalculus. Автор : Джей Абрамсон и др. Предоставлено : ОпенСтакс. Расположен по адресу : https://openstax.org/books/precalculus/pages/1-introduction-to-functions. Лицензия : CC BY: Attribution . Условия лицензии.
Привет
Меня зовут Женева, и у меня возникли проблемы с графическим отображением уравнений типа y=2x+1, что является моей домашней работой. Я не знаю, как это сделать. Я учусь в 8 классе, изучаю курс алгебры 9 класса I.
СпасибоПривет Женева,
Иногда, особенно после небольшого опыта, вы можете сказать по «форме» уравнения, какова «форма» графика. Если вы можете определить форму, это упрощает построение графика, но сейчас давайте просто попробуем построить его, не зная формы заранее. Для этого я буду использовать таблицу значений. Я собираюсь выбрать некоторые значения для переменной x, вычислить соответствующее значение y и затем записать свои результаты в таблицу. Так, например, когда x = 1, то y = 2 1 + 1 = 3, а когда x = 2, то y = y = 2 2 + 1 = 5. Вот моя таблица, включающая эти два значения x и еще несколько.
х и 1 3 2 5 3 7 0 1 -1 -1 -2 -3 Теперь я нанес эти точки на свой график.

Конвертер жпг в ворд: Конвертировать JPG в DOC (WORD) онлайн — Convertio
JPG в Word — лучший онлайн-конвертер JPG в Word
Неограниченный
Этот конвертер JPG в Word является бесплатным и позволяет вам использовать его неограниченное количество раз и конвертировать JPG в Word.
Быстро
Его обработка преобразования является мощной. Таким образом, для преобразования всех выбранных JPG требуется меньше времени.
Охрана
Мы гарантируем, что ваши JPG очень безопасны. Почему, потому что мы нигде не загружаем JPG на Сервер.
Добавить несколько файлов
С помощью этого инструмента вы можете легко конвертировать несколько JPG одновременно. Вы можете конвертировать JPG в Word и сохранить его.
Удобный для пользователя
Этот инструмент предназначен для всех пользователей, дополнительные знания не требуются. Таким образом, конвертировать JPG в Word легко.
Мощный инструмент
Вы можете получить доступ к инструменту JPG to Word или использовать его онлайн в Интернете, используя любой браузер из любой операционной системы.

Как конвертировать JPG в Word онлайн?
- Выберите JPG, который вы хотите преобразовать в конвертере JPG в Word.
- Вы можете настроить качество JPG, настройки, связанные с предварительным просмотром страницы и т. Д.
- Вы можете легко вращать JPG с помощью ротатора соответственно.
- Кроме того, вы можете добавлять или удалять файлы JPG из списка.
- Наконец, загрузите преобразованное слово из конвертера JPG в Word.
Это простой способ конвертировать JPG в Word с помощью конвертера JPG в Word. Это простой способ конвертировать из JPG в текстовый файл с помощью этого инструмента JPG в текст. Итак, выберите изображение JPG, которое вы хотите преобразовать в слово, в этом инструменте JPG в слово.
Лучший и простой способ конвертировать JPG в файл Word онлайн с помощью инструмента JPG в Word. Это простой инструмент для преобразования JPG в слово с помощью этого инструмента для преобразования JPG в слово.
 Для преобразования JPG в текстовый файл вы должны выбрать изображение JPG, которое вы хотите преобразовать в слово в этом инструменте. После выбора JPG в этом инструменте вы увидите, что этот инструмент автоматически конвертирует все выбранные изображения JPG в файлы Word в инструменте. Вы также можете добавить больше изображений JPG, которые хотите преобразовать в файлы Word. Кроме того, вы можете удалить изображения JPG, которые не хотите преобразовывать в слово. С помощью этого инструмента вы можете одновременно конвертировать несколько изображений JPG в файлы Word. Теперь нажмите кнопку «преобразовать в слово», а затем легко загрузите все преобразованные в текстовые файлы на свое устройство. Наконец, используя этот инструмент JPG to word, вы можете просто конвертировать изображения JPG в файлы word онлайн.
Для преобразования JPG в текстовый файл вы должны выбрать изображение JPG, которое вы хотите преобразовать в слово в этом инструменте. После выбора JPG в этом инструменте вы увидите, что этот инструмент автоматически конвертирует все выбранные изображения JPG в файлы Word в инструменте. Вы также можете добавить больше изображений JPG, которые хотите преобразовать в файлы Word. Кроме того, вы можете удалить изображения JPG, которые не хотите преобразовывать в слово. С помощью этого инструмента вы можете одновременно конвертировать несколько изображений JPG в файлы Word. Теперь нажмите кнопку «преобразовать в слово», а затем легко загрузите все преобразованные в текстовые файлы на свое устройство. Наконец, используя этот инструмент JPG to word, вы можете просто конвертировать изображения JPG в файлы word онлайн.- Выберите JPG, который вы хотите преобразовать в слово, в инструменте JPG в слово.
- Теперь просмотрите выбранные изображения JPG в инструменте.
- Вы также можете добавлять / удалять файлы изображений JPG.

- Кроме того, вы также можете определить собственное имя файла.
- Наконец, загрузите файлы Word и конвертируйте их с помощью инструмента JPG в Word.
Конвертер изображений в Word (2023)
Конвертер изображений в Word (2023) — Онлайн и 100% бесплатноВыберите язык текста (Для достижения наилучших результатов)
Все загруженные файлы навсегда удаляются с сервера в течение часа.
Загружая документ, вы соглашаетесь с условиями использования нашего сервиса.
Оригинальные макет и формат будут сохранены как по волшебству!
Читаю текст.
 Это может занять некоторое время…
Это может занять некоторое время…Работает на основе технологии оптического распознавания символов (OCR).
report this adКак работает этот инструмент
Этот онлайн-инструмент преобразует отсканированные файлы или изображения текстовых документов в редактируемые документы Word с помощью технологии оптического распознавания символов (OCR). Все документы Word преобразуются с сохранением исходного макета документа и столбцов. Чем крупнее и четче отсканированный текст, тем лучше будут результаты. В большинстве случаев мы достигаем свыше 99% точности распознования текста в изображениях.
Его можно использовать бесплатно, регистрация не требуется.Применение
Этот инструмент идеально подходит для преобразования нередактируемых отсканированных документов (таких как отсканированные контракты, счета-фактуры, квитанции или текстовые архивы) в оцифрованный текст, который в дальнейшем можно редактировать, задавать в поиске и форматировать.

Поддерживаемые файлы
Просто перетащите любой файл PNG, JPG или многостраничный PDF-документ, содержащий изображения текста, в форму, и ваш файл будет мгновенно преобразован в документ Word, который вы можете редактировать.
Ограничения
Вы можете использовать этот инструмент без ограничений. Инструмент поддерживает файлы до 10 МБ и отсканированные PDF-документы до 30 страниц. Если вам нужно разделить PDF-файл на файлы меньшего размера, вы можете сделать это здесь. При этом нет никаких ограничений по количеству использования.
Конфиденциальность
Мы серьезно относимся к соблюдению конфиденциальности; ваши данные в безопасности. Все загруженные файлы навсегда удаляются с наших серверов в течение 1 часа. Если вы хотите получить дополнительные сведения, ознакомьтесь с нашей политикой конфиденциальности .

Конвертер JPG в Word — Преобразование Jpeg/изображения в Word
О конвертере JPG в Word
Конвертер JPG в Word выходит за рамки простого преобразования формата в редактируемый документ. Этот конвертер изображений в Word поддерживает несколько форматов, включая JPG, PNG, GIF, TIFF, BMP и TGA. С помощью этого средства вы можете преобразовать изображение размером до 5 МБ в Word.
Как конвертировать JPG в Word?
Следующие шаги позволят вам без проблем использовать этот конвертер JPG в Word.
- Загрузите изображения, нажав кнопку «Загрузить».
- Сейчас! Нажмите на кнопку «Преобразовать в Word».
- Бум! Вы получите желаемый результат в мгновение ока.
(Примечание: вы можете загрузить файл JPG с облачного хранилища, нажав кнопку «Из Google Диска и Dropbox».)
Конвертер JPG в Word — Почему?
Преобразование JPG в Word становится необходимым при извлечении текста из изображений.
 Использование конвертера JPEG в Word может устранить необходимость в том, чтобы специалисты по вводу данных выполняли эту работу за вас за считанные секунды.
Использование конвертера JPEG в Word может устранить необходимость в том, чтобы специалисты по вводу данных выполняли эту работу за вас за считанные секунды.Преобразование JPEG в Word онлайн без электронной почты
С помощью этого конвертера вы можете конвертировать JPEG в Doc онлайн. В отличие от других инструментов, доступных в Интернете, эта утилита не просит вас указать адрес электронной почты для получения результатов. После того, как эта утилита завершит процесс преобразования, необходимо нажать кнопку загрузки.
Преобразование нескольких файлов JPG одновременно
Конвертер JPG в Word позволяет пользователям упростить извлечение текста из изображений. Если вам нужно преобразовать несколько файлов JPG в Word, вам не следует полагаться на конвертер, который позволяет конвертировать только один файл за раз. Этот конвертер позволяет одновременно конвертировать несколько изображений в документы Word.
Преобразование изображений в редактируемые файлы Word
Когда дело доходит до редактирования печатных документов, это кажется геркулесовой задачей.
 Проблемы превышают еще больше, когда вы теряете цифровую версию печатных документов. Тем не менее, вам не нужно преодолевать такие большие проблемы, так как преобразование изображений в редактируемые файлы Word теперь возможно благодаря этому конвертеру JPG в редактируемый Word. Это средство поможет вам преобразовать отсканированные документы в редактируемые файлы Word, не требуя от вас затрат времени и усилий.
Проблемы превышают еще больше, когда вы теряете цифровую версию печатных документов. Тем не менее, вам не нужно преодолевать такие большие проблемы, так как преобразование изображений в редактируемые файлы Word теперь возможно благодаря этому конвертеру JPG в редактируемый Word. Это средство поможет вам преобразовать отсканированные документы в редактируемые файлы Word, не требуя от вас затрат времени и усилий.Лучшее для студентов и преподавателей
Бесплатный конвертер фотографий в Word может помочь людям, работающим в различных областях. Будучи студентом, у вас могут быть рукописные заметки, которые необходимо отправить учителям в цифровом формате. Вместо того, чтобы тратить время на создание документа с нуля, вы можете делать снимки рукописного текста и преобразовывать их в файлы Word с помощью этого инструмента. Кроме того, предприятия также могут использовать это бесплатное средство для преобразования своих отсканированных документов в редактируемый формат.
Конвертер JPG в Word — Особенности
Наш онлайн-конвертер JPG в Word позволяет без проблем преобразовывать изображения в высококачественные файлы Word.
 Другие важные функции нашего конвертера изображений в Word обсуждаются ниже.
Другие важные функции нашего конвертера изображений в Word обсуждаются ниже.- Неограниченное количество преобразований
Наш онлайн-конвертер изображений в Word позволяет преобразовать неограниченное количество файлов JPG в файлы Word. Использование этого бесплатного онлайн-конвертера JPG в Word не требует никаких затрат. Вы можете конвертировать столько изображений в Word, сколько пожелаете, без какой-либо оплаты.
- Без водяного знака
При использовании других онлайн-инструментов вы, возможно, заметили, что результирующий файл может содержать водяной знак или визуальный символ. Вам может быть сложно делиться файлами JPG с другими, так как это может выглядеть непрофессионально. Наш конвертер изображений в Word позволяет конвертировать изображения в Word без водяных знаков.
- Точное преобразование
Качество текста в изображении, которое вы хотите преобразовать в формат Doc, остается неизменным при использовании этого онлайн-конвертера JPEG в Word.
 Наш инструмент обеспечивает надежное и безошибочное преобразование редактируемых документов JPG в Word.
Наш инструмент обеспечивает надежное и безошибочное преобразование редактируемых документов JPG в Word.- Поддержка всех платформ
Конвертер JPEG в Word — это веб-утилита, для которой не требуется программное обеспечение или плагины. Это средство поддерживается всеми операционными системами, такими как iOS, Android, Mac, Windows и Linux. Вам не нужно специальное устройство для преобразования файлов с помощью этого инструмента. Вам необходимо стабильное подключение к Интернету, чтобы получить доступ и использовать этот конвертер JPG в Word.
- Облачная поддержка
Многие пользователи хранят свои данные в облачном хранилище вместо того, чтобы загружать свои устройства. Если изображение, которое вы хотите преобразовать в Word, хранится в вашей учетной записи облачного хранилища, нет необходимости загружать его на свое устройство. Конвертер JPG в Word поддерживает облачное преобразование; следовательно, вы можете легко загрузить файл прямо из своей учетной записи Dropbox или Google Drive с помощью этого инструмента.

- Регистрация не требуется
Преобразователь изображения в документ не требует регистрации для извлечения текста из изображения на этом веб-сайте. Удобный интерфейс этого инструмента устраняет все препятствия, помогая вам легко конвертировать JPG в Word. Однако, если у вас есть изображение и вы хотите преобразовать его в текстовую форму, вы можете использовать наш конвертер изображений в текст.
- Многоязычная поддержка
Этот конвертер изображений в Word доступен по всему миру. Следовательно, вы можете найти эту утилиту на том языке, который кажется вам подходящим. Кроме того, вы можете извлекать текст из изображений на нескольких языках. Помимо английского, онлайн-конвертер JPG в Word поддерживает многие другие языки, в том числе французский, китайский, испанский, португальский, голландский, итальянский, русский и японский.
- Извлечение на основе ИИ
Это утилита на основе ИИ, которая эффективно извлекает текст из изображения и представляет его в редактируемом документе.
 Этот инструмент не пропустит ни одно слово Word на вашем изображении и грамотно преобразует весь текст в файл Word.
Этот инструмент не пропустит ни одно слово Word на вашем изображении и грамотно преобразует весь текст в файл Word.Мы уважаем вашу конфиденциальность
Возможно, вы были свидетелями того, как люди обычно нервничают по поводу конфиденциальности своих конфиденциальных или личных изображений, загружая их в онлайн-инструмент. Но вам больше не нужно беспокоиться, так как наш онлайн-конвертер JPG в Word гарантирует вам секретность и конфиденциальность загруженного файла изображения. Все файлы, которые вы загрузите в наш инструмент для конвертации, будут удалены с серверов сразу после завершения обработки. Кроме того, никакая третья сторона не может получить доступ к вашим загруженным изображениям в любом случае. Таким образом, вы можете без колебаний использовать нашу программу для бесплатного конвертирования JPG в Word онлайн.
Часто задаваемые вопросы
- Как преобразовать JPEG в редактируемый документ Word?
Вам необходимо получить доступ к конвертеру этой фотографии в Word, загрузить файл JPEG, который вы хотите преобразовать, и нажать кнопку «Преобразовать в Word», чтобы получить редактируемый документ Word.

- Сколько времени занимает преобразование JPG в Word?
Преобразование JPG в Word с помощью этого онлайн конвертера JPG в редактируемый формат занимает пару секунд.
- Могу ли я преобразовать изображение в Word в Linux, Mac OS или Android?
Конвертер JPG в Word, предлагаемый на SmallSEOTools, совместим со всеми устройствами. Поскольку это веб-утилита, вы можете легко конвертировать JPEG в документ на устройствах Linux, Android, Mac, Windows или iOS, не сталкиваясь с какими-либо трудностями.
- Могу ли я преобразовать снимок экрана в файл Word онлайн?
Да! Этот бесплатный онлайн-конвертер JPG в doc позволяет конвертировать снимки экрана в файл Word. Все, что вам нужно сделать, это загрузить скриншот, который вы хотите преобразовать, и нажать данную кнопку, чтобы начать процесс.
- Какой браузер следует использовать для преобразования изображения в Word?
Нет ограничений на использование определенного браузера для преобразования JPG в Word с помощью этого онлайн-инструмента.
 Все веб-браузеры поддерживают этот инструмент; следовательно, независимо от того, используете ли вы Chrome, Explorer, Firefox, Opera или Safari, вы можете быстро и безопасно получить доступ к JPEG для документов и выполнить необходимые преобразования.
Все веб-браузеры поддерживают этот инструмент; следовательно, независимо от того, используете ли вы Chrome, Explorer, Firefox, Opera или Safari, вы можете быстро и безопасно получить доступ к JPEG для документов и выполнить необходимые преобразования.- Безопасно ли конвертировать JPG в Word с помощью бесплатного конвертера?
Да! Преобразование JPEG в Word безопасно с помощью бесплатного онлайн-инструмента, предлагаемого на SmallSEOTools. С помощью этого инструмента пользователям не нужно беспокоиться о сохранении своих изображений в базе данных. После преобразования файла пользователя в Word он автоматически удаляется с серверов и баз данных.
- Как преобразовать изображения рукописного текста в Word?
Вы можете конвертировать рукописные текстовые изображения в Word с помощью конвертера изображений в Word. В этом случае вы должны щелкнуть четкое изображение рукописного текста, который хотите преобразовать.
 Люди, использующие этот инструмент с мобильных устройств, могут напрямую захватывать изображение текста, который они хотят преобразовать.
Люди, использующие этот инструмент с мобильных устройств, могут напрямую захватывать изображение текста, который они хотят преобразовать.- Как преобразовать изображение в документ на мобильном телефоне?
Вам не нужно загружать программное обеспечение на свой мобильный телефон, чтобы преобразовать изображение в документ. Доступ к этому объекту можно легко получить через браузер по умолчанию на вашем мобильном телефоне. После доступа к конвертеру JPG в Word вы должны загрузить изображение, которое хотите преобразовать, и нажать кнопку «Преобразовать в Word», чтобы начать процесс. Результаты отобразятся на вашем экране в считанные секунды.
Конвертер JPG в WORD Бесплатно. JPG в слово онлайн.
Создание редактируемых документов Word из изображений JPG
Питаться от aspose.com и aspose.cloud
Выберите файлы JPG или перетащите файлы JPG
Google Диск Дропбокс
Использовать пароль
Этот пароль будет применяться ко всем документам
Использовать распознавание текста Использовать распознавание текста
АрабскийКитайский упрощенныйАнглийскийФранцузскийНемецкийИтальянскийПерсидскийПольскийПортугальскийРусскийИспанский For the OCR algorithm to work correctly, text and tables must not be rotated down or sideways.»/>
Если вам нужно конвертировать несколько JPG в один Word, используйте Merger
Загружая свои файлы или используя наш сервис, вы соглашаетесь с нашими Условиями обслуживания и Политикой конфиденциальности
Сохранить как
DOCXTXTDOCDOTDOCMDOTXDOTMRTFODTOTT
КОНВЕРТИРОВАТЬ
Ваши файлы были успешно преобразованы
СКАЧАТЬ
Загрузить в Google Загрузить в Dropbox
Преобразование других документов Отправить по электронной почте
Ответьте на наш опросВы хотите сообщить об этой ошибке на форум Aspose, чтобы мы могли изучить и решить проблему? Вы получите уведомление по электронной почте, когда ошибка будет исправлена.
 Форма отчета
Форма отчетаGoogle Таблицы
Слияние почты Облачный APIJPG в Word онлайн
Преобразование JPG в Word онлайн с помощью OCR (распознавание текста в картинке). Во время преобразования «JPG в Word» каждое изображение будет преобразовано в редактируемый документ Word. Эта услуга на 100% бесплатна.
Форматы документов JPG и Word являются одними из наиболее распространенных форматов файлов. JPG широко используется в веб-дизайне и фотографии, тогда как формат Word является стандартом де-факто в офисной работе. Из-за высокого спроса на оба формата нам часто нужно конвертировать JPG в Word и наоборот.
Конвертировать JPG в Word Online
В некотором смысле файлы JPG и Word совершенно разные. Изображение JPG представляет собой двоичный файл, а документ Word представляет собой текстовый (XML) файл. Офисные пакеты обычно не предоставляют простого способа конвертировать JPG в редактируемый Word, но у нас есть эффективное решение.
Конвертер JPG в Word онлайн
Наш сервис конвертирует JPG в Word с помощью OCR — распознавания текста в картинке.
 Используйте наш «Конвертер JPG в Word», чтобы сохранить каждое изображение JPG в виде редактируемого документа Word. Это самый быстрый способ конвертировать фотографии и сканы в формат Word онлайн.
Используйте наш «Конвертер JPG в Word», чтобы сохранить каждое изображение JPG в виде редактируемого документа Word. Это самый быстрый способ конвертировать фотографии и сканы в формат Word онлайн.FAQ
Как бесплатно конвертировать JPG в Word?
Просто воспользуйтесь нашим конвертером JPG в Word. Вы получите выходные файлы Word одним щелчком мыши.
Сколько файлов JPG можно преобразовать в формат Word за один раз?
Вы можете конвертировать до 10 файлов JPG одновременно.
Каков максимально допустимый размер файла JPG?
Размер каждого файла JPG не должен превышать 10 МБ.
Какими способами можно получить результат в формате Word?
После завершения преобразования JPG в Word вы получите ссылку для скачивания. Вы можете скачать результат сразу или отправить ссылку на скачивание ворда на почту позже.
Как долго мои файлы будут храниться на ваших серверах?
Все пользовательские файлы хранятся на серверах Aspose в течение 24 часов.

Как построить график функции онлайн с модулем: Построение графиков с модулем онлайн · Как пользоваться Контрольная Работа РУ
Построение графиков квадратичной функции, содержащей модуль
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Построение графиков квадратичной функции, содержащей модуль
2. Актуализация опорных знаний
1.
2.
3.
4.
5.
6.
7.
8.
Определение квадратичной функции
Алгоритм построения квадратичной функции
Как, зная график функции y=f(x) построить графики следующих
функций:
y=f(-x)
y=-f(x)
y=f(x+m)
y=f(x)+n
y=f(x+m)+n
y=kf(x)
y=|f(x)|
y=f(|x|)3.
 Устно Дан график функции y = x2 – 4x + 3. Составьте формулу функции, график которой:1) симметричен данному относительно оси:
Устно Дан график функции y = x2 – 4x + 3. Составьте формулу функции, график которой:1) симметричен данному относительно оси:
а) x;
б) y;
2) получается из данного параллельным переносом на
1а) y = –x2 + 4x – 3;
1б) y = x2 + 4x + 3
2
y = x2 – 6x + 6;
(1; 2)
3) получается из данного растяжением в 2 раза от оси
а) x;
б) y
4) получается из данного сжатием в 2 раза к оси
а) x;
б) y
3а) y = 0,25×2 – 2x + 3;
3б) y = 2×2 – 8x + 6;
4а) y = 4×2 – 8x + 3
4б) y = 0,5×2 – 2x + 1,5;
Найдите соответствия:
у х2 5
у 0,3х
2
у ( х 3)
2
у х 2 5
25. Построить график функции y=|-2×2 +8x -6|
1. Построим график функции y= -2×2 +8x -6
Ветви параболы направлены вниз
Вершина в точке:
b
8
2,
2a
4
y0 8 16 6 2
xo
Ось симметрии: х=2
Нули функции
Х1 =1, Х2 =3
х
0
1
2
3
4
у
-6
-0
2
0
-6
2. отразим части параболы,
расположенные в нижней части
полуплоскости, симметрично
относительно оси абсцисс.
Применение преобразований при построении графика функции
Y
2
Построим график функции y =| — 2 x +6 x -2 |
1.Сначала построим график функции
y = — 2 x 2+8 x -6
Преобразуем трехчлен:
2 x 8 x 6 2 x 4 x 3
2
2
2 x 2 2 x 2 4 4 3
2 x 2 1 2 x 2 2
2
2
6
2
1
0
-1
-2
y 2 x 2 2
2
-3
-4
-5
-6
2. отразим части параболы, расположенные в
нижней части полуплоскости, симметрично
относительно оси абсцисс.
1
x7. Аналитическое построение
Построить график функции y=|x|x
По определению модуля: y = x2 ,x>0
— x2 ,x<0
x>0
y
0
x<0
x8. Построим график функции y=|x2-5x|+x-3 с помощью узловых точек
x2-5x=0, x(x-5)=0, x=0 илиx=5
|
||
x=0или x=5 разбивают числовую
прямую на три промежутка
0
5
I. x=-1;
(-1)2 -5(-1)>0
y=x2-5x+x-3 =x2-4x-3
Строим параболу и выделяем ту часть,
которая находится на промежутке ;0
II. x=1;
x=1;
12 -5*1<0,
y=-x2+5x+x-3 =-x2 +6x-3
Строим параболу и выделяем ту часть,
которая находится на промежутке 0;5
III. x=6;
62 -5*6>0
y=x2-4x-3 Эту параболу уже строили, поэтому
выделим ту часть,
которая находится на промежутке 5;
Выделенные части являются графиком
функции
|||
x9. Постройте графики функций:
Вариант 1
а) y=|x2 -4|
б) y=|2x-x2 |
Вариант 2
а)y=|x2 -1|
б) y=|x2 +2x-1|
Вариант 3
Вариант 4
а) y=|(x-3)2 -1| б) а) y=|-(x+2)2 +3|
y=x2 -|x-1|
б) y=|2+4|x|-x2|10. Проверь себя !
Вариант 1
Вариант 2
а) y=|x2 -4|
а) y=|x2 -1|
б) y=|x2 +2x-1|
б) y=|2x-x2 |
Вариант3
Вариант 4
а) y=|(x-3)2 -1|
а) y=|-(x+2)2 +3|
б) y=x2 -|x-1|
б) y=|2+4|x|-x2|11. Основные преобразования графиков:
параллельные переносы;
симметрии относительно осей координат;
растяжения (сжатия) от (к) осей (осям) координат;
преобразования, связанные с модулями.
12. Алгоритм построения графика функции у = ах2 + bх +с.
1. Определить направление ветвей параболы.
2. Найти координаты вершины параболы
(т; п).
3. Провести ось симметрии.
4. Определить точки пересечения графика
функции с осью Ох, т.е. найти нули
функции.
5. Составить таблицу значений функции
с учетом оси симметрии параболы.13. Перенос вдоль оси ординат
График функции y= f (x) + b при b >0
можно получить параллельным переносом вдоль
оси ординат графика функции y= f (x) на b
единиц вверх.
y= x2 +2
Y
2
1
y=x2
0 1
График функции y=f(x)-b при b>0 можно
получить параллельным переносом вдоль оси
ординат графика функции y=f(x) на b единиц
вниз
x
Y
1
0 1
-2
y=x2
x
y= x2 -214. Перенос вдоль оси ординат
График функции y= f(x)+b при b >0
можно получить так :
1. построить график функции y= f (x)
2.перенести ось абсцисс на b единиц
вверх
Y
2
На b
вверх
0
0
1
x
1
x
Y
График функции y=f(x)-b при b>0
можно получить так:
1. построить график функции y=f(x)
построить график функции y=f(x)
2 перенести ось абсцисс на единиц вниз
1
Вниз
На b
0
-2
0
x
1
x15. Перенос вдоль оси абсцисс
График функции y= f (x + c) можно получить
параллельным переносом вдоль оси абсцисс графика
функции y= f (x) на |c| единиц влево при c >0 .
Y
y=x2
1
-2
0
1
x
y=(x+2)2
График функции y=f(x+c) можно получить
параллельным переносом вдоль оси абсцисс графика
функции y=f(x) на |c| единиц вправо при c<0
y=x2
Y
y=(x-2)2
1
0
1
2
x16. Перенос вдоль оси абсцисс
График функции y= f (x + c) при c >0
можно получить так :
1. построить график функции y= f (x)
2.перенести ось ординат на |b| единиц
вправо
y
1
0
График функции y=f(x+c) при c<0
можно получить так:
1. Построить график функции y=f(x)
2. Перенести ось ординат на |c| единиц
влево
y
y
1
1
y
1
1 0
x
0
0 1
x17.
 Сжатие ( растяжение ) графика вдоль оси ординатГрафик функции y= b f (x)
Сжатие ( растяжение ) графика вдоль оси ординатГрафик функции y= b f (x)
при b>1 можно получить
растяжением графика функции
y= f (x) вдоль оси ординат
y=2×2
Y
1
y=x2
0 1
График функции y=bf(x) при
0<b<1 можно получить сжатием
графика функции y=f(x) вдоль
оси ординат
x
y=0,5×2
Y
1
0 1
y=x2
x18. Симметрия относительно оси абсцисс
Чтобы построить график фунуции y= -f(x):
1. Строим график функции y=f(x)
2. Отражаем его симметрично относительно оси
абсцисс.
y=x2
0 1
x
y=-x219. график функции y = f(|x|), y = |f(x)|
график функции y = f(|x|) получается из графика функции y = f(x)
следующим преобразованием:
1)
точки графика, имеющие неотрицательные абсциссы – неподвижны;
2) точки графика, имеющие отрицательные абсциссы заменяются на
точки, полученные из неподвижных отражением относительно оси y.
график функции y = |f(x)| получается из графика функции y = f(x)
следующим преобразованием:
1)
точки графика, имеющие неотрицательные ординаты – неподвижны;
2) точки графика, имеющие отрицательные ординаты, отражаются
относительно оси x.
20. Функция, содержащая операцию « взятие модуля»
y
Чтобы построить график функции y= |f( x) |:
1. Строим график функции y= f(x),
2.Часть графика, расположенную в верхней
полуплоскости сохраняем.
3. Часть графика, расположенную в нижней
полуплоскости. отображаем симметрично
относительно оси абсцисс в верхнюю
полуплоскость.
0
xEnglish Русский Правила
Основные правила преобразования графиков функций 9 класс онлайн-подготовка на Ростелеком Лицей
Введение
Наверняка многие из вас могут быстро и правильно построить графики некоторых функций, не прибегая к вычислениям значений точек. Всем известно, что график функции – это прямая, а график функции – это парабола. Но как построить, например, график функции , не вычисляя значения точек? Для этого существуют правила преобразования графиков функций.
Преобразование симметрии относительно оси
OxПредположим, что у нас есть функция (график этой функции – это парабола) и необходимо построить график функции .
 Вычислим значения некоторых точек для графиков этих функций.
Вычислим значения некоторых точек для графиков этих функций.Из таблиц видно, что одним и тем же значениям аргумента соответствуют противоположные значения функций. Графически это означает, что графики расположены симметрично относительно оси абсцисс. То есть заданная парабола () зеркально отобразится относительно оси (см. Рис. 1).
Рис. 1. Графики функций и
Таким образом, если у нас есть произвольный график , то для построения графика необходимо график симметрично отразить относительно оси (см. Рис. 2). Такое преобразование называется преобразованием симметрии относительно оси .
Рис. 2. Преобразование симметрии относительно оси
Преобразование симметрии – зеркальное отражение относительно прямой.
 График получается из графика функции преобразованием симметрии относительно оси .
График получается из графика функции преобразованием симметрии относительно оси .На рисунке 3 показаны примеры симметрии относительно оси .
Рис. 3. Симметрия относительно оси Ox
Параллельный перенос вдоль оси OyПредположим, что у нас есть функция (график этой функции – это парабола) и необходимо построить график функции . Вычислим значения некоторых точек для графиков этих функций.
Из таблиц видно, что при одних и тех же значениях аргумента значения функции у графика больше на 3 единицы. Графически это означает, что график функции находится на 3 единицы выше, чем график функции (см. Рис. 4).
Рис.
 4. Графики функций и
4. Графики функций и График получается из графика функции параллельным переносом последнего вдоль оси ординат на единиц вверх, если , и на единиц вниз, если (см. Рис. 5, 6).
Рис. 5. Параллельный перенос вдоль оси (при )
Рис. 6. Параллельный перенос вдоль оси (при )
Растяжение от оси Ox и сжатие к оси OxПредположим, что у нас есть функция (график этой функции – это парабола) и необходимо построить график функции . Вычислим значения некоторых точек для графиков этих функций.
Из таблиц видно, что при одних и тех же значениях аргумента значения функции у графика больше в 2 раза.
 Графически это означает, что график функции сужается по сравнению с графиком функции (см. Рис. 7).
Графически это означает, что график функции сужается по сравнению с графиком функции (см. Рис. 7).Рис. 7. Графики функций и
Если необходимо построить график функций , то из таблиц видно, что при одних и тех же значениях аргумента значения функции у графика меньше в 2 раза, чем у . Графически это означает, что график функции расширяется по сравнению с графиком функции (см. Рис. 8).
Рис. 8. Графики функций и
Чтобы построить график функции , где и , нужно ординаты точек заданного графика умножить на . Такое преобразование называется растяжением от оси с коэффициентом , если , и сжатием к оси, если (см.
 Рис. 9, 10).
Рис. 9, 10).Рис. 9. Растяжение от оси
Рис. 10. Сжатие к оси
Параллельный перенос вдоль оси OxПредположим, что у нас есть функция , необходимо построить график функции . Вычислим значения некоторых точек для графиков этих функций.
Из таблиц видно, что одинаковым значениям функции соответствуют значения аргумента, отличающиеся на 2 единицы. Это означает, что график данной функции переместился на 2 единицы относительно оси ординат влево (см. Рис. 11), так как для получения одинаковых значений функций приходится брать значения аргумента на 2 меньше:
, при
при
Следовательно, если необходимо было построить график функции , то сдвиг на 3 единицы относительно оси ординат был бы вправо (по сравнению с графиком функции ) (см.
 Рис. 11).
Рис. 11).Рис. 11. Графики функций , и
График получается из графика функции параллельным переносом последнего на единиц влево, если , и на единиц вправо, если (см. Рис. 12, 13).
Рис. 12. Параллельный перенос влево при
Рис. 13. Параллельный перенос вправо при
Обратите внимание на то, что по этому принципу из графика не построить график , ведь мы добавили 1 не ко всем вхождениям в это выражение.
 А вот график построить можно, сдвинув исходный график на 1 влево (см. Рис. 14).
А вот график построить можно, сдвинув исходный график на 1 влево (см. Рис. 14).Рис. 14. Графики функции и
Растяжение от оси Oy и сжатие к оси OyГрафик функции , где и , получается из графика функции сжатием с коэффициентом к оси (если указанное «сжатие» фактически является растяжением с коэффициентом ) (см. Рис. 15, 16).
Рис. 15. Сжатие к оси
Рис.
 16. Растяжение от оси
16. Растяжение от оси Подобное преобразование мы уже рассматривали в случае построения графика функции .
Преобразование симметрии относительно оси OyРанее мы рассматривали преобразование симметрии относительно оси Ox, то есть функция умножалась на (-1). Рассмотрим случай, когда на (-1) умножается только аргумент.
В этом случае график симметрично отображается относительно оси ординат, так как значения функций будут одинаковы при противоположных значениях аргумента:
для функции :
при
при
для функции :
при
при
График получается из графика функции преобразованием симметрии относительно оси (см.
 Рис. 17).
Рис. 17).Рис. 17. Преобразование симметрии относительно оси Oy
Построение графиков и
Пусть дан график , построим график . Для начала раскроем модуль по определению:
Следовательно, те точки, в которых значения функции положительны или равны 0, остаются на месте, а все точки, в которых значения отрицательны, – отражаются относительно оси (см. Рис. 18).
Рис.
 18. Графики функций и (красным цветом выделена общая часть этих графиков)
18. Графики функций и (красным цветом выделена общая часть этих графиков)Для того чтобы построить график , нужно часть исходного графика, лежащую выше оси , оставить без изменения, а нижнюю отразить наверх относительно оси .
Пусть дан график , построим график . Для начала раскроем модуль по определению:
Следовательно, все точки с положительными или равными нулю абсциссами остаются без изменения, а все точки с отрицательными – заменяются точками с противоположными абсциссами (см. Рис. 19).
Рис.
 19. Графики функций и (красным цветом выделена общая часть этих графиков)
19. Графики функций и (красным цветом выделена общая часть этих графиков)Для того чтобы построить график , нужно часть исходного графика, соответствующую значениям , оставить без изменений и отразить ее относительно оси для значений .
Задача 1Построить график функции .
Решение
Построим график заданной функции последовательно (см. Рис. 20):
1. Строим график .
2.
 График получается из графика параллельным переносом последнего на 2 единицы вправо.
График получается из графика параллельным переносом последнего на 2 единицы вправо.3. График получается из графика функции параллельным переносом последнего вдоль оси ординат на 3 единицы вверх.
Рис. 20. Иллюстрация к задаче
Мы могли бы сделать операции в обратном порядке, то есть сначала поднять график на 3 единицы вверх, а потом получившийся график сдвинуть вправо на 2 единицы (см. Рис. 21).
Рис. 21. Иллюстрация к задаче
Обратите внимание, что не все графики функций можно строить в произвольном порядке.
 Например, для построения графика сначала нужно построить график , затем график (растяжение от оси ), а далее – график (параллельный перенос вдоль оси ординат) (см. Рис. 22). Если же сделать в другой последовательности, то есть построить , то далее на 2 придется умножить всё выражение.
Например, для построения графика сначала нужно построить график , затем график (растяжение от оси ), а далее – график (параллельный перенос вдоль оси ординат) (см. Рис. 22). Если же сделать в другой последовательности, то есть построить , то далее на 2 придется умножить всё выражение.– ПРАВИЛЬНО
– НЕПРАВИЛЬНО
Рис. 22. Иллюстрация к задаче
Пример
Построить график .
Решение
1.
 Строим график (гипербола) (см. Рис. 23).
Строим график (гипербола) (см. Рис. 23).2. Строим график (из аргумента вычитается 2, следовательно, сдвигаем график на 2 единицы вправо) (см. Рис. 23).
3. Строим график (домножение функции на (-1), следовательно, отражаем график относительно оси ) (см. Рис. 24).
4. Строим график (добавление 2 к функции, следовательно, сдвигаем график на 2 единицы вверх) (см. Рис. 24).
5. Строим график (модуль функции, следовательно, отражаем нижнюю часть графика относительно оси , а верхнюю оставляем без изменений) (см. Рис. 25).
Рис.
 23. Иллюстрация к задаче
23. Иллюстрация к задачеРис. 24. Иллюстрация к задаче
Рис. 25. Иллюстрация к задаче (искомый график)
Список литературы
1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений. – 4-е изд. – М.: Мнемозина, 2002. – 192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. – 4-е изд.
 – М.: Мнемозина, 2002. – 143 с.: ил.
– М.: Мнемозина, 2002. – 143 с.: ил.3. Макарычев Ю.Н. Алгебра. 9 класс : учеб.для учащихся общеобразоват. учреждений / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, И.Е. Феоктистов. – 7-е изд., испр. и доп. – М.: Мнемозина, 2008.
5. Виленкин Н.Я., Сурвилло Г.С. и др. Алгебра 9 кл. С углубленным изучением математики. – М.: Просвещение, 2006.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Интернет-сайт учебного центра «Резольвента» (Источник)
2. Интернет-сайт «Инфоурок» (Источник)
3.
 Интернет-сайт YouTube (Источник)
Интернет-сайт YouTube (Источник)Домашнее задание
1. Упражнения 64, 66, 68 (б, г), 69 (в, ж), 70 (и) (стр. 65-69) Виленкин Н.Я., Сурвилло Г.С. и др. Алгебра 9 кл. (Источник).
2. Даны графики функций: а) ; б) ; в)
Какое уравнение будет иметь функция, график которой образуется из данных графиков функций: 1. при параллельном переносе вверх на 3 единицы; 2. при растяжении в 3 раза; 3. при параллельном переносе вправо на 3 единицы?
3. Постройте график функции .
Как построить график экспоненциальной функции — Объяснение!
Пошаговые примерыБольше примеров
Purplemath
Построение графика экспоненциальной функции похоже на построение графика, который вы делали ранее.
 Однако по природе экспоненциальных функций их точки, как правило, либо очень близки к одному фиксированному значению, либо слишком велики, чтобы их можно было удобно изобразить на графике.
Однако по природе экспоненциальных функций их точки, как правило, либо очень близки к одному фиксированному значению, либо слишком велики, чтобы их можно было удобно изобразить на графике.На самом деле будет всего несколько точек, которые «разумно» использовать для рисования вашего изображения.
Содержание продолжается ниже
MathHelp.com
Чтобы выбрать разумные точки, вам потребуется хорошее понимание общего поведения экспоненты, чтобы вы могли заполнить пробелы.
Какое основное свойство экспонент?
Помните, что основное свойство экспонент состоит в том, что они изменяются в заданной пропорции в течение заданного интервала. Например, медицинский изотоп, который распадается наполовину по сравнению с предыдущим количеством каждые двадцать минут, и бактериальная культура, которая удваивается каждый день, демонстрируют экспоненциальное поведение, потому что за заданный промежуток времени (двадцать минут и один день соответственно) количество изменилась в постоянной пропорции (в полтора и два раза соответственно).

(Примечание: многие [«самые»?] экспоненты будут иметь беспорядочное время удвоения/уменьшения пополам, поэтому часто полезнее работать с точки зрения утроения, учетверения и т. д. времени, или данное упражнение может полностью игнорировать проблему , Если основание экспоненты не равно 2 [или ½], то не ожидайте, что время удвоения/уменьшения пополам будет подчеркнуто — или же не ожидайте, что время удвоения/уменьшения пополам будет хорошим аккуратным целым числом.)
Эта черта — наличие фиксированного времени деления пополам или удвоения — является основной для экспоненциальных функций. Но это может сделать график немного рискованным.
Такое поведение можно увидеть в любой базовой экспоненциальной функции, поэтому мы будем использовать y = 2 x как представление всего класса функций:
В левой части x -ось, график отображается на оси x . Но ось x представляет y = 0. Сможете ли вы когда-нибудь превратить 2 в 0, возведя его в степень? Конечно, нет.
 И положительная 2 не может превратиться в отрицательное число, если возвести его в степень.
И положительная 2 не может превратиться в отрицательное число, если возвести его в степень.Итак, линия, несмотря на свой внешний вид, никогда не опускается ниже оси x в отрицательные значения y ; график y = 2 x всегда фактически выше оси x , даже если только на исчезающе малую величину.
Так почему он выглядит так, как будто он прямо на оси? Помните, что делают отрицательные экспоненты: они говорят вам перевернуть основание на другую сторону дробной черты. Итак, если, скажем, x = -4, приведенная выше экспоненциальная функция даст нам 2 −4 , что равно 2 4 = 16, а затем перевернуто снизу, чтобы получить 1/16, что довольно мало.
По характеру экспонент каждый раз, когда мы возвращаемся назад (то есть всякий раз, когда мы двигаемся дальше влево) на 1 по оси x , линия только наполовину меньше высоты над осью x , чем она. было для предыдущего значения x .
 То есть, в то время как y = 1/16 для x = −4, линия будет только вдвое короче, при y = 1/32, для x = -5.
То есть, в то время как y = 1/16 для x = −4, линия будет только вдвое короче, при y = 1/32, для x = -5.Таким образом, хотя линия на самом деле никогда не касается и не пересекает ось x , она чертовски близка! Вот почему, говоря практически, левая часть основной экспоненты имеет тенденцию быть направленной вдоль оси. Если вы увеличите график достаточно близко, вы в конечном итоге сможете увидеть, что график действительно выше оси x , но достаточно близко, чтобы не иметь никакого значения, по крайней мере, в том, что касается графика.
Если вы используете ТАБЛИЦУ или другую подобную функцию своего графического калькулятора для поиска точек на графике, вы должны знать, что ваш калькулятор вернет y — значение 0 для сильно отрицательных значений x . Ваш калькулятор может содержать только определенное количество знаков после запятой, и в конце концов он просто сдается и говорит: «Эй, ноль уже достаточно близко»:
Но вы не должны забывать, что это всего лишь признак ограничений технологии.
 Как я часто говорю своим ученикам: «Ученик умный, калькулятор глупый». Вы должны помнить, что независимо от того, что говорит калькулятор, график все равно находится выше оси x ; значения и по-прежнему положительны, хотя и очень, очень, очень малы.
Как я часто говорю своим ученикам: «Ученик умный, калькулятор глупый». Вы должны помнить, что независимо от того, что говорит калькулятор, график все равно находится выше оси x ; значения и по-прежнему положительны, хотя и очень, очень, очень малы.Давайте снова посмотрим на график y = 2 x :
Вы можете видеть, что в правой части оси x график взлетает до небес. Это опять-таки из-за удвоения экспоненты. Как только функции начинают заметно расти, они продолжают удваиваться, поэтому очень быстро становятся очень большими.
Обычно вы не будете наносить много точек в левой части графика, потому что y -значения настолько близки к нулю, что точки графика становятся неотличимыми от оси x . Вы будете рисовать ту сторону графика, которая движется поверх оси.
И, как правило, вы не будете строить много точек в правой части графика, потому что значения и становятся слишком большими.
 Вот почему я подробно рассказал об общей форме и поведении экспоненты: вам понадобятся эти знания, чтобы помочь вам в построении графика, поэтому убедитесь, что вы достаточно хорошо его понимаете.
Вот почему я подробно рассказал об общей форме и поведении экспоненты: вам понадобятся эти знания, чтобы помочь вам в построении графика, поэтому убедитесь, что вы достаточно хорошо его понимаете.Что нужно знать при построении экспоненты:
- Переменная функции будет в степени.
- Число, на котором стоит сила, называется базовым.
- Экспоненциальные функции имеют время удвоения (или деления пополам).
- Графики обычно выглядят довольно горизонтально для одной половины.
- Для второй половины графики обычно растут безумно быстро.
- С недоверием относитесь к тому, что говорит вам ваш калькулятор.
- Рисуйте аккуратно и аккуратно.
URL: https://www.purplemath.com/modules/graphexp.htm
Page 2Page 3Page 4
Изучение функций и их графиков учащимися с помощью Desmos – Technology Tools for Higher Education, The Practical Handbook Series
Ана Дафф
Desmos Graphing Calculator — это открытый онлайн-инструмент с широкими числовыми и визуальными универсальными возможностями.
 Он позволяет пользователю отображать и маркировать точки на декартовой плоскости, демонстрировать решения уравнений и неравенств, графически отображать функции и создавать регрессионные модели из наборов данных, среди прочих возможностей. Он имеет мощный встроенный инструмент калькулятора и инструмент ползунка, который позволяет пользователю создавать динамические визуальные эффекты, иллюстрирующие изменения или привлекающие внимание к определенным компонентам.
Он позволяет пользователю отображать и маркировать точки на декартовой плоскости, демонстрировать решения уравнений и неравенств, графически отображать функции и создавать регрессионные модели из наборов данных, среди прочих возможностей. Он имеет мощный встроенный инструмент калькулятора и инструмент ползунка, который позволяет пользователю создавать динамические визуальные эффекты, иллюстрирующие изменения или привлекающие внимание к определенным компонентам.Преимущества обучения с помощью Desmos
- Открытый и бесплатный ресурс, не требующий регистрации или подписки
- Позволяет статическую и динамическую графическую демонстрацию и количественный анализ 2-мерных моделей
- Демонстрации и мероприятия могут быть предварительно созданы
- Требует от пользователей легко приобретаемых технологических навыков
- Позволяет легко обмениваться демонстрациями с другими пользователями
Ресурсы
- Ноутбук или мобильное устройство (Android или iOS)
- Интернет-браузер или приложение Desmos Graphing Calculator
Шаг 1. Создайте учетную запись на Desmos.com (необязательно)
Перейдите на сайт Desmos.com и перейдите по ссылке, чтобы начать построение графиков. У вас есть возможность создать учетную запись и войти в систему, что позволит вам сохранять, называть и искать свою работу. Последующие шаги реализации будут основываться на предположении, что вы вошли в свою учетную запись, чтобы воспользоваться этими функциями. Тем не менее, графическая функциональность Desmos не ограничивается владельцами учетных записей, и в этом случае можно сохранить доступ к своей работе, создав ссылку для общего доступа и сохранив ее на потом.
Шаг 2. Откройте графический калькулятор Desmos и создайте график
Нажмите «График без названия» и введите название графика (доступно только для зарегистрированных пользователей). Введите краткое описание действия: поместите курсор в строку 1, нажмите +
(Добавить элемент), затем примечание « » и добавьте описание в строку 1.
Шаг 3. Укажите функцию, компоненты функции или данные, которые должны быть смоделированы функцией
Desmos позволяет пользователю явно указывать функцию(и) и моделировать данные с помощью функции, используя регрессию. Если задание используется как часть оценивания, попросите учащихся импортировать случайно сгенерированные данные (например, из документа Excel), чтобы получить вариативность в результирующих функциях.
Шаг 4. Создайте набор инструкций
Пусть результаты обучения определяют ваш набор инструкций. Обратите внимание, что задачи могут включать статическое и динамическое исследование модели, включая визуализацию изменений с помощью ползунка. Для лучшего прогресса задания можно организовать по папкам и руководствоваться примечаниями инструктора, встроенными в график Desmos. Оба могут быть добавлены, нажав на
+ (Добавить элемент), затем папку или заметку.
Шаг 4.
 Предложите учащимся ознакомиться с учебными пособиями по графическим инструментам Desmos
Предложите учащимся ознакомиться с учебными пособиями по графическим инструментам DesmosВ разделе «Справка» представлен большой банк интерактивных обучающих ресурсов для новых и опытных пользователей Desmos. Учащиеся могут научиться создавать ползунки и таблицы, определять ограничения домена и диапазона и выполнять регрессию, следуя простым интерактивным турам, предоставляемым Desmos. Библиотека видеоуроков обширна и легкодоступна для поиска, а руководство пользователя Desmos содержит основное руководство по инструментам Desmos.
Шаг 5. Предоставьте учащимся график(ы)
Нажмите на инструмент «Поделиться своим графиком» в левом верхнем углу. Созданная ссылка направит учащихся к диаграмме и позволит каждому учащемуся просматривать и изменять ее отдельно от других пользователей и не затрагивать созданную вами диаграмму. Обратите внимание, что вы также можете использовать этот инструмент для сохранения изображения графика (за некоторыми исключениями) и встраивания его в другие платформы.

Шаг 6. Включите калькулятор Desmos Graph Calculator в оценки
Включайте результаты исследования и извлеченные уроки учащимися в оценки с помощью инструмента «Поделиться своим графиком», с помощью которого учащиеся делятся ссылками или изображениями своей работы непосредственно или как часть отдельного документа для отправки. Обратите внимание, что ссылка будет включать диаграмму в том виде, в каком она была на момент создания ссылки.
- Избегайте путаницы, сводя к минимуму двусмысленность. Разработайте инструкции, соответствующие результатам обучения. Разбейте активность на компоненты и организуйте их по папкам. Направляйте учащихся к конкретным ресурсам по мере необходимости, выполняя задания по темам, которые могут нуждаться в пояснении. Воспользуйтесь обширной библиотекой видеороликов с практическими рекомендациями от Desmos и ее пользователей (доступных через любую поисковую систему с «Desmos + тема по выбору») в качестве ресурса для учащихся по конкретным задачам.

- Помните о времени и требуемых навыках. Проверьте, сколько времени у вас уйдет на выполнение задания, а затем умножьте время на три. На протяжении всего теста размышляйте о своих знаниях учащихся, о диапазоне их навыков, связанных с технологиями и содержанием, и соответствующим образом корректируйте задание.
- Поощряйте решение проблем и устранение неполадок с помощью одноранговой поддержки — Покажите учащимся, как делиться работой с помощью инструмента «Поделитесь своим графиком», чтобы обращаться за помощью к другим во время занятия. Наблюдение за работой учащегося поможет определить, где учащийся допустил ошибку или наткнулся на камень преткновения.
Цифровые ресурсы
Руководство пользователя Desmos
Примеры изучения функций через Desmos в действии:
- Демонстрация односторонних пределов
- Пример метода Ньютона
- Демонстрация функций и производных
- Данные моделирования с использованием примера функций
Экичи, Селил, и Плайли, Крис.
 «Моделирование динамики населения на основе запросов с помощью логистических дифференциальных и разностных уравнений». ПРИМУС 29.6 (2019): 553–570. Веб.
«Моделирование динамики населения на основе запросов с помощью логистических дифференциальных и разностных уравнений». ПРИМУС 29.6 (2019): 553–570. Веб.Годин, Шон. «В чем проблема? Ищем лжецов». Бюллетень — Математическая ассоциация Онтарио 56.4 (2018): 11–13. Веб.
Хойлс, Селия. «Преобразование математических практик учащихся и учителей с помощью цифровых технологий». Исследования в области математического образования. 20.3 1–20. Веб.
Набб, Кейт, и Муравска, Жаклин. «Мотивация исчисления с помощью одного вопроса». ПРИМУС 29.10 (2019): 1140–1153. Веб.
Шахриари, Рази и др. «Влияние использования технологий на понимание студентами исчисления и алгебры в колледже». Издательство диссертаций ProQuest, 2019 г.. Веб.
Ана Дафф — научный сотрудник факультета бизнеса и информационных технологий Технического университета Онтарио, где она преподает математику на первом курсе. Ее исследовательский опыт связан с математикой, в которой она имеет докторскую степень.

Разложить на множители икс в квадрате минус икс минус один: 1. 2. 3. 4. 5. 6. Разложить на множители x^2-64 (х в квадрате минус 64)
Алгебра Разложение квадратного трёхчлена на множители
Материалы к уроку
Конспект урока
Пусть требуется разложить на множители квадратный трехчлен два икс квадрат минус десять икс плюс восемь.
Сначала вынесем за скобки старший коэффициент два. Для того чтобы разложить на множители квадратный трехчлен икс квадрат минус пять икс плюс четыре, представим минус пять икс в виде разности одночленов минус икс и минус четыре икс и применим способ группировки… Получим произведение двух множителей, первый из которых равен разности между икс и четыре, а второй разности между икс и один.
Значит, два икс квадрат минус десять икс плюс восемь равно удвоенному произведению полученных множителей. При икс равном четырем и икс равном одному произведение, а следовательно и трехчлен, обращаются в нуль. Значит, числа четыре и один являются его корнями.

Итак, мы представили квадратный трехчлен в виде произведения числа два, то есть старшего коэффициента, и двух линейных множителей. Первый из них представляет собой разность между переменной икс и первым корнем трехчлена, второй – разность между переменной икс и вторым корнем трехчлена.
Такое разложение можно получить для любого квадратного трехчлена, имеющего корни. При этом считают, что если дискриминант квадратного трехчлена равен нулю, то этот трехчлен имеет два равных корня.
Теорема. Если икс первое и икс второе – корни квадратного трехчлена а икс квадрат плюс бэ икс плюс цэ, то а икс квадрат плюс бэ икс плюс цэ равно произведению старшего коэффициента и двух линейных множителей, первый из которых равен разности между икс и первым корнем трехчлена, а второй разности между икс и вторым корнем трехчлена.
Вынесем за скобки в многочлене а икс квадрат плюс бэ икс плюс цэ множитель а. Так как корни квадратного трехчлена являются корнями соответствующего ему квадратного уравнения, то по теореме Виета сумма корней равна минус бэ деленному на а, произведение корней равно цэ деленному на а.
 Подставим эти значения в наше выражение… и получим произведение двух линейных множителей, первый из которых равен разности между икс и первым корнем, второй – разности между икс и вторым корнем.
Подставим эти значения в наше выражение… и получим произведение двух линейных множителей, первый из которых равен разности между икс и первым корнем, второй – разности между икс и вторым корнем.Итак, получили, что квадратный трехчлен а икс квадрат плюс бэ икс плюс цэ равен произведению старшего коэффициента и двух линейных множителей, первый из которых равен разности между икс и первым корнем, второй – разности между икс и вторым корнем…
Существует правило: если квадратный трехчлен не имеет корней, то его нельзя разложить на множители, являющиеся многочленами первой степени.2
Докажем это.
Пусть квадратный трехчлен а икс квадрат плюс бэ икс плюс цэ не имеет корней. Предположим, что его можно представить в виде произведения многочленов первой степени: ка икс плюс эм… и.. пэ икс плюс ку, где ка, эм, пэ и ку – некоторые числа, причем ка и пэ не равны нулю. Данное произведение обращается в нуль при икс равном минус эм, деленное на ка и икс равном минус ку деленное на пэ.
 При этих значениях.. икс обращается в нуль и трехчлен а икс квадрат плюс бэ икс плюс цэ, то есть числа минус эм деленное на ка и ку деленное на пэ, являются его корнями. Мы пришли к противоречию, так как по условию этот трехчлен корней не имеет.
При этих значениях.. икс обращается в нуль и трехчлен а икс квадрат плюс бэ икс плюс цэ, то есть числа минус эм деленное на ка и ку деленное на пэ, являются его корнями. Мы пришли к противоречию, так как по условию этот трехчлен корней не имеет.Пример первый. Разложить на множители квадратный трехчлен три икс квадрат плюс пять икс минус два.
Решив уравнение три икс квадрат плюс пять икс минус два равно нулю, найдем корни трехчлена. Первый корень будет равен одной третьей, второй корень равен минус двум.
По теореме о разложении квадратного трехчлена на множители получим утроенное произведение разности между икс и первым корнем.. и.. суммы икс и второго корня.
Полученный результат можно записать иначе, если умножить число три на двучлен икс минус одна третья.
Пример второй. Разложим на множители квадратный трехчлен минус пять икс квадрат плюс двадцать икс минус двадцать.
Приравняем данный трехчлен к нулю и решим полученное уравнение.
 Оба его корня равны двум. Значит, трехчлен можно представить в виде произведения числа минус пять и двух равных линейных множителей икс минус два. Это выражение мы можем записать как произведение числа минус пять и квадрата разности чисел икс и два.
Оба его корня равны двум. Значит, трехчлен можно представить в виде произведения числа минус пять и двух равных линейных множителей икс минус два. Это выражение мы можем записать как произведение числа минус пять и квадрата разности чисел икс и два.Пример третий. Сократим дробь, числитель которой равен сумме чисел два икс и один, а знаменатель равен квадратному трехчлену два икс квадрат минус семь икс минус четыре.
Разложим знаменатель на множители. Его корни равны минус одна вторая и четыре. Поэтому знаменатель можно представить в виде произведения линейных множителей, первый из которых равен два икс плюс один, второй – икс минус четыре.
Значит, если в дроби знаменатель записать в виде множителей и сократить эту дробь, то получится дробь, числитель которой равен одному, а знаменатель — разности чисел икс и четыре.
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитораОставить заявку на подбор
3-8Mathway | Популярные задачи
1 Множитель x^2-4 2 Множитель 4x^2+20x+16 3 График y=-x^2 4 Вычислить 2+2 5 Множитель x^2-25 6 Множитель x^2+5x+6 7 Множитель x^2-9 8 Множитель x^3-8 9 Вычислить квадратный корень из 12 10 Вычислить квадратный корень из 20 11 Вычислить квадратный корень из 50 12 Множитель x^2-16 13 Вычислить квадратный корень из 75 14 Множитель x^2-1 15 Множитель x^3+8 16 Вычислить -2^2 17 Вычислить квадратный корень из (-3)^4 18 Вычислить квадратный корень из 45 19 Вычислить квадратный корень из 32 20 Вычислить квадратный корень из 18 21 Множитель x^4-16 22 Вычислить квадратный корень из 48 23 Вычислить квадратный корень из 72 24 Вычислить квадратный корень из (-2)^4 25 Множитель x^3-27 26 Вычислить -3^2 27 Множитель x^4-1 28 Множитель x^2+x-6 29 Множитель x^3+27 30 Множитель x^2-5x+6 31 Вычислить квадратный корень из 24 32 Множитель x^2-36 33 Множитель x^2-4x+4 34 Вычислить -4^2 35 Множитель x^2-x-6 36 Множитель x^4-81 37 Множитель x^3-64 38 Вычислить 4^3 39 Множитель x^3-1 40 График y=x^2 41 Вычислить 2^3 42 Вычислить (-12+ квадратный корень из -18)/60 43 Множитель x^2-6x+9 44 Множитель x^2-64 45 График y=2x 46 Множитель x^3+64 47 Вычислить (-8+ квадратный корень из -12)/40 48 Множитель x^2-8x+16 49 Вычислить 3^4 50 Вычислить -5^2 51 Множитель x^2-49 52 Вычислить (-20+ квадратный корень из -75)/40 53 Множитель x^2+6x+9 54 Множитель 4x^2-25 55 Вычислить квадратный корень из 28 56 Множитель x^2-81 57 Вычислить 2^5 58 Вычислить -8^2 59 Вычислить 2^4 60 Множитель 4x^2-9 61 Вычислить (-20+ квадратный корень из -50)/60 62 Вычислить (-8+ квадратный корень из -20)/24 63 Множитель x^2+4x+4 64 Множитель x^2-10x+25 65 Вычислить квадратный корень из -16 66 Множитель x^2-2x+1 67 Вычислить -7^2 68 График f(x)=2^x 69 Вычислить 2^-2 70 Вычислить квадратный корень из 27 71 Вычислить квадратный корень из 80 72 Множитель x^3+125 73 Вычислить -9^2 74 Множитель 2x^2-5x-3 75 Вычислить квадратный корень из 40 76 Множитель x^2+2x+1 77 Множитель x^2+8x+16 78 График y=3x 79 Множитель x^2+10x+25 80 Вычислить 3^3 81 Вычислить 5^-2 82 График f(x)=x^2 83 Вычислить квадратный корень из 54 84 Вычислить (-12+ квадратный корень из -45)/24 85 Множитель x^2+x-2 86 Вычислить (-3)^3 87 Множитель x^2-12x+36 88 Множитель x^2+4 89 Вычислить квадратный корень из (-8)^2 90 Множитель x^2+7x+12 91 Вычислить квадратный корень из -25 92 Множитель x^2-x-20 93 Вычислить 5^3 94 Множитель x^2+8x+15 95 Множитель x^2+7x+10 96 Множитель 2x^2+5x-3 97 Вычислить квадратный корень квадратный корень из 116 98 Множитель x^2-x-12 99 Множитель x^2-x-2 100 Вычислить 2^2 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92-х-1$? Задавать вопрос
спросил
Изменено 7 лет, 4 месяца назад
Просмотрено 12 тысяч раз
$\begingroup$
Я знаю, что вы не можете иметь все целые числа, но как вы все равно это учитываете?
Wolfram|Alpha дает мне $-\frac{1}{4} (1+\sqrt{5}-2 x) (-1+\sqrt{5}+2 x)$.

Корень 4 степени из x 4 3x: Mathway | Популярные задачи
10 класс квадратные уравнения: «Решение уравнений» (10 класс, повторение)
Кейс «Квадратные уравнения с параметром» для учащихся 10 класса
Кейс «Квадратные уравнения в гостях у параметра»
учителя математики МАОУ «Гимназия №87»
Ленинского района города Саратова
Заико Ильи Валерьевича
с 4 февраля по 27 марта 2020 года
Кейс «Квадратные уравнения в гостях у параметра»
Уравнения для меня важнее потому, что
политика – для настоящего,
а уравнения – для вечности.

Альберт Эйнштейн
Что такое параметр?
В повседневной жизни мы очень часто сталкиваемся с понятием параметра: параметры загрузки Windows 10, параметры бытовых приборов, параметры автомобиля. Рассмотрение параметров — это всегда выбор. Покупая какую-то вещь, мы внимательно изучаем ее основные характеристики. Так, приобретая компьютер, мы обращаем внимание на следующие его параметры: производительность, габариты, состав комплектующих, цену и многое другое. Перед выбором мы стоим и в различных жизненных ситуациях. Вспомним сказку: В чистом поле стоит столб, а на столбу написаны слова: «Кто поедет от столба сего прямо, тот будет голоден и холоден; кто поедет в правую сторону, тот будет здрав и жив, а конь его будет мертв; а кто поедет в левую сторону, тот сам будет убит, а конь его жив и здрав останется!» Иван-царевич прочел эту надпись и поехал в правую сторону, держа на уме: хоть конь его и убит будет, зато сам жив останется и со временем сможет достать себе другого коня.
 (“Иван-царевич и серый волк” Русская народная сказка). Здесь от выбора зависит
жизнь Ивана-царевича.
(“Иван-царевич и серый волк” Русская народная сказка). Здесь от выбора зависит
жизнь Ивана-царевича.Но это в сказке, а что же собой представляет параметр в математике? Какую роль он играет при решении уравнений? Какими методами решаются уравнения с параметрами?
Что такое параметр в математике?
Параметр (от греческого – отмеривающий) в математике – величина, числовые значения которой позволяют выделить определённый элемент из множества элементов того же рода. (Большой энциклопедический словарь)
Так, например, в декартовых прямоугольных координатах уравнением определяется множество всех окружностей радиуса 1 на плоскости xOy; полагая, например, ,
выделяют из этого множества вполне определённую окружность единичного радиуса с центром в точке , — и, следовательно, являются параметрами окружности в рассматриваемом множестве элементов того же рода.
История возникновения уравнений с параметром
Задачи на уравнения с параметром встречались уже в астрономическом трактате «Ариабхаттиам», составленном в 499 г.
 индийским математиком и астрономом Ариабхаттой. Другим индийским ученым,
Брахмагупта в VII веке было изложено общее правило решения квадратных
уравнений, приведенных к единой канонической форме: .
В
уравнении коэффициенты, кроме параметра a, могут быть и отрицательными. В
теоретической части книги «Китаб аль-джебр ва-ль-мукабала» Аль-Хорезми дает
классификацию линейных и квадратных уравнений с параметрами. Автор выделяет 6
видов уравнений, выражая их следующим образом:
индийским математиком и астрономом Ариабхаттой. Другим индийским ученым,
Брахмагупта в VII веке было изложено общее правило решения квадратных
уравнений, приведенных к единой канонической форме: .
В
уравнении коэффициенты, кроме параметра a, могут быть и отрицательными. В
теоретической части книги «Китаб аль-джебр ва-ль-мукабала» Аль-Хорезми дает
классификацию линейных и квадратных уравнений с параметрами. Автор выделяет 6
видов уравнений, выражая их следующим образом:1) «Квадраты равны корням», т. е.
2) «Квадраты равны числу», т. е. .
3) «Корни равны числу», т. е. .
4) «Квадраты и числа равны корням», т. е. .
5) «Квадраты и корни равны числу», т. е. .
6) «Корни и числа равны квадратам», т. е. .
Формулы решения квадратных уравнений по Аль-Хорезми в Европе были впервые изложены в «Книге абака», написанной в 1202 г. итальянским математиком Леонардо Фибоначчи. Вывод формулы решения квадратного уравнения с параметром в общем виде имеется у Виета, однако он признавал только положительные корни.
 Итальянские математики Тарталья, Кардано,
Бомбелли среди первых в ХII в. учитывают, помимо положительных, и отрицательные
корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых
способ решения квадратных уравнений принял современный вид.
Итальянские математики Тарталья, Кардано,
Бомбелли среди первых в ХII в. учитывают, помимо положительных, и отрицательные
корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых
способ решения квадратных уравнений принял современный вид.1) Определение. Квадратным уравнением называется уравнение вида:
,
где коэффициенты a, b, c – любые действительные числа, причем .
2) Решение квадратного уравнения по формулам.
3) Теорема обратная теореме Виета. Если числа таковы, что их произведение равно , а сумма равна , то эти числа являются корнями квадратного уравнения .
4) Графиком квадратичной функции является парабола с вершиной в точке , ветви которой направлены вверх, если или вниз, если . Абсциссы, обозначим их , общих точек параболы и оси Ox являются нулями квадратичной функции.
5) Поскольку корнем квадратного уравнения можно считать значение переменной x, при котором соответствующий квадратный трёхчлен принимает значение равное нулю, то каждый корень такого уравнения является нулём квадратичной функции и наоборот.
 Поэтому, количество корней
квадратного уравнения равно количеству нулей соответствующей квадратичной
функции, а значит и количеству общих точек параболы и оси абсцисс.
Поэтому, количество корней
квадратного уравнения равно количеству нулей соответствующей квадратичной
функции, а значит и количеству общих точек параболы и оси абсцисс. Таблица количества общих точек параболы и оси абсцисс в зависимости от дискриминанта D соответствующего квадратного уравнения .
Таблица 1*.
* здесь — абсциссы общих точек параболы и оси Ox, — абсцисса вершины параболы.
6) Теорема 1 (о равносильной замене неравенства). Неравенство равносильно совокупности систем и
7) Теорема 2 (о равносильной замене неравенства). Неравенство равносильно совокупности систем и
Исследовать расположение корней квадратного уравнения относительно точки в зависимости от значений его параметров-коэффициентов, решая подходящие для этого задания.

Задание 1. Найдём все значения параметра a, при которых только один корень квадратного уравнения больше 2.
Решение. Перепишем уравнение следующим, привычным для нас, образом
.
Так как свободный член этого уравнения можно представить в виде произведения , то есть , а второй коэффициент, взятый с противоположным знаком, можно представить в виде суммы , то есть , то, по теореме обратной теореме Виета, числа 3 и являются корнями заданного уравнения. Поскольку, согласно условию задачи, только один корень должен быть больше 2, и таким корнем уже является число 3, то второй корень должен, либо совпадать с первым, то есть , либо не превосходить число 2, то есть , поэтому искомыми значениями параметра a являются решения совокупности
Решим эту совокупность, имеем
Таким образом, интересующие нас значения параметра a образуют множество .
Ответ. .
Задание 2 (для самостоятельного решения).
 Найдите все значения
параметра m, при которых один из корней уравнения находится между числами 0 и 2, а второй
– между числами 3 и 5.
Найдите все значения
параметра m, при которых один из корней уравнения находится между числами 0 и 2, а второй
– между числами 3 и 5.Решение.
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
________________________________________________________________________
Ответ.
 __________________________________________________________________
__________________________________________________________________Указание: если не удалось подобрать корни с опорой на теорему обратную теореме Виета, решите это уравнение по формулам, то есть найдите его дискриминант и корни.
Задание 3. При каких значениях параметра a число 2 находится между корнями квадратного уравнения ?
Решение. В двух предыдущих заданиях поиск корней квадратного уравнения был связан либо с привлечением теоремы обратной теореме Виета, либо с нахождением дискриминанта. Поэтому поступим аналогичным образом и в этом задании, то есть найдём действительные корни заданного уравнения, если они существуют, например, по формулам.
Имеем, .
И далее,
Так как условие: «число 2 находится между корнями квадратного уравнения» прямо указывает на существование двух различных корней, то дискриминант должен быть положительным. Кроме того, в силу очевидного соотношения , должны выполняться неравенства: .
 А стало быть, искомыми значениями
параметра a являются решения системы неравенств:
А стало быть, искомыми значениями
параметра a являются решения системы неравенств:Вы никогда не сумеете решить возникшую проблему, если сохраните то же мышление и тот же подход, который привёл вас к этой проблеме.
Альберт Эйнштейн
Совершенно очевидно, что решение этой системы связано с немалыми техническими трудностями. Поэтому для настоящей задачи выбранный приём не оправдан. Однако способом преодоления возникшей трудности может стать изменение подхода к толкованию условия нашей задачи.
И такой подход основан на простой геометрической интерпретации. Графиком левой части заданного уравнения, то есть графиком квадратного трёхчлена , является парабола, ветви которой направлены вверх.
 Поскольку, согласно условию задачи, число
2 находится между корнями заданного квадратного уравнения, то парабола должна пересекать ось абсцисс в точках,
расположенных по разные стороны от точки этой оси с координатой 2 (смотри
рисунок 1). А значит, рисунок 1 – перевод условия данной задачи на графический
язык.
Поскольку, согласно условию задачи, число
2 находится между корнями заданного квадратного уравнения, то парабола должна пересекать ось абсцисс в точках,
расположенных по разные стороны от точки этой оси с координатой 2 (смотри
рисунок 1). А значит, рисунок 1 – перевод условия данной задачи на графический
язык.Составим аналитическую запись приведённого рисунка, то есть найдём описывающие его соотношения (уравнения, неравенства). Для этого, рассматривая всевозможные параболы (с ветвями, направленными вверх), пересекающие ось абсцисс в точках, расположенных по разные стороны от точки 2 (постройте на рисунке 1 ещё такие параболы), будем сравнивать с нулём значение квадратичной функции при x=2. В результате мы заметим, что в каждом таком случае , поэтому требование будет как необходимым, так и достаточным для того, чтобы число 2 находилось между корнями заданного уравнения. А значит, искомыми значениями параметра a являются решения неравенства , то есть неравенства .
 Решите это неравенство самостоятельно
Решите это неравенство самостоятельно________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Итак, интересующие нас значения параметра a образуют множество .
Ответ. .
Задание 4 (для самостоятельного решения). При каких значениях параметра a корни уравнения расположены по разные стороны от числа (-1)?
Решение.

_______________________________
_______________________________
_________________________________
_________________________________
_________________________________
_________________________________
_________________________________
_________________________________
_________________________________
_________________________________
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
________________________________________________________________________________________________________________________________________________________________________________________________________________________Ответ.
 __________________________________________________________________
__________________________________________________________________С понятийной точки зрения будет чрезвычайно полезным обобщить рассмотренные выше задачи, то есть найти условия, при которых число p лежит между нулями квадратичной функции . И снова обратимся к геометрической трактовке. Поскольку из условия задания следует, что дискриминант D больше нуля, то в зависимости от знака старшего коэффициента достаточно рассмотреть два случая: a>0 и a<0 (смотри рисунок 2).
Каждый из этих случаев полностью описывается следующими условиями: для рисунка 2(а) имеем, а для рисунка 2(б) — Заметим, что здесь нет необходимости требовать ещё выполнение условия D>0, это условие является лишним (избыточным), потому как неравенства системы гарантируют существование двух различных нулей квадратичной функции .
Поскольку совокупность этих двух систем, согласно теореме 2, равносильна неравенству , то справедливо следующее утверждение.

Утверждение 1. Для того, чтобы число p находилось между нулями квадратичной функции (корнями квадратного уравнения ), необходимо и достаточно выполнения неравенства .
Далее, попытаемся построить критерий, обеспечивающий положение заданного числа p вне корневого промежутка.
Для начала, заполняя пропуски, найдём условия, при которых нули квадратичной функции будут меньше числа p. И для этого снова обратимся к геометрическому толкованию поставленной задачи.
Графиком квадратичной функции является _____________, ветви которой направлены вверх, если ________ или вниз, если _______. Парабола может имеет с осью Ox либо одну общую точку и в этом случае дискриминант D, соответствующего квадратного трёхчлена, равен ____________, либо две общие точки и тогда дискриминант D будет _________________. Для удобства абсциссы общих точек параболы и оси Ox обозначим через ().
Теперь в декартовой прямоугольной системе координат xOy построим две параболы с ветвями направленными вверх: первую — имеющую с осью абсцисс одну общую точку, вторую – две общие точки, расположенные левее уже отмеченной на оси Ox точки с координатой p.

Из рисунка 3 видно, что:
1) старший коэффициент a ________;
2) дискриминанта D ______________; 3) и кроме того, согласно рисунку, значение квадратичной функции в точке x=p, в сравнении с нулём, будет __________________________, то есть .
Подумайте, достаточно ли этих условий, чтобы общие точки параболы и оси Ox располагались левее точки с абсциссой p? Для этого попытайтесь построить параболу, имеющую с осью Ox общие точки расположенные, наоборот, правее точки с абсциссой p, для которой выполнялось бы каждое из трёх условий 1) – 3).
Очевидно, что примером такой параболы может стать парабола, проходящая через точки оси Ox с абсциссами 5 и 10, поскольку для неё выполняются все вышеперечисленные условия 1) — 3). Однако, в этом случае, нули квадратичной функции будут больше числа p. А значит, выполнимость всех условий 1) – 3) не гарантирует расположение нулей квадратичной функции слева от точки p.
Окончательно зафиксировать точку p в нужном положении позволяет неравенство , где , то есть x0 – абсцисса вершины параболы .
 А значит, следующая
система полностью описывает рисунок 3.
А значит, следующая
система полностью описывает рисунок 3.Задание 5 (для самостоятельного решения). Рассуждая аналогичным образом, найдите условия, при которых нули квадратичной функции с отрицательным старшим коэффициентом будут меньше числа p.
Решение.
_______________________________
_______________________________
_________________________________
_________________________________
_________________________________
_________________________________
_________________________________
_________________________________
_________________________________
_________________________________
_________________________________
_________________________________
_________________________________
_________________________________
_________________________________
_________________________________
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
________________________________________________________________________________________________________________________________________________
________________________________________________________________________________________________________________________________________________
________________________________________________________________________________________________________________________________________________________________________________________________________________________Ответ.
 Система гарантирует
расположение нулей
Система гарантирует
расположение нулейквадратичной функции с отрицательным старшим коэффициентом слева от точки p.
Как и ранее, согласно теореме 1 о равносильной замене неравенства, совокупность полученных систем и равносильна системе
Это и есть необходимое и достаточное условие того, что число p больше нулей квадратичной функций. Сформулируем его в таком виде.
Утверждение 2. Для того чтобы число p было больше нулей квадратичной функции (корней квадратного уравнения ), необходимо и достаточно выполнение следующей системы неравенств:
Задание 6 (для самостоятельного решения). Сформулируйте необходимое и достаточное условие того, что число p меньше нулей квадратичной функции .
Решение.
________________________________
________________________________
________________________________
________________________________
________________________________
________________________________
________________________________
________________________________
________________________________
________________________________
_________________________________
_________________________________
_________________________________
_________________________________
_________________________________
_________________________________
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
________________________________________________________________________ ________________________________________________________________________________________________________________________________________________
Итак, результатом решения задания 6 является построенное необходимое и достаточное условие того, что число p меньше нулей квадратичной функции, которое можно сформулировать следующим образом.

Утверждение 3. Для того чтобы число p было меньше нулей квадратичной функции (корней квадратного уравнения ), необходимо и достаточно выполнение следующей системы неравенств:
Задание 7 (для самостоятельного решения). Найдите все значения параметра a, при которых все корни уравнения больше .
Задание 8 (для самостоятельного решения). Найдите все значения параметра а, при каждом из которых: 1) только один корень уравнения удовлетворяет неравенству ; 2) все корни уравнения удовлетворяет неравенству .
Выберите одно из двух заданий и решите его.
________________________________
________________________________
________________________________
________________________________
________________________________
________________________________
________________________________
________________________________
________________________________
________________________________
_________________________________
_________________________________
_________________________________
_________________________________
_________________________________
_________________________________
________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
________________________________________________________________________ ________________________________________________________________________________________________________________________________________________
________________________________________________________________________
____________________________________________________________________________________________________________________________________________
_______________________________________________________________________
Ответ.
 Искомые значения
параметра a образуют множество__________________
Искомые значения
параметра a образуют множество__________________В двух трёх предложениях опишите, чем Вы занимались на занятии, что Вам запомнилось? Какие результаты были Вами получены? Какой из этих результатов был в большей степени получен Вами самостоятельно?
________________________________________________________________________
________________________________________________________________________ ________________________________________________________________________________________________________________________________________________
________________________________________________________________________________________________________________________________________________
________________________________________________________________________
Заполните таблицу вариантов расположения нулей квадратичной функции на числовой прямой и соответствующих им условий.

Таблица.
Расположение нулей квадратичной функции на числовой прямой
Необходимое и достаточное условие
В заключении, с целью систематизации приобретённых знаний, будет чрезвычайно полезным исправить ошибки в первой блок-схеме – осмыслить их – запомнить – оформить свою мысль – применить знания на практике, заполнив вторую блок-схему.

О квадратных уравнениях в правильном порядке / Хабр
Как вам преподавали квадратные уравнения в школе? Это был 7-8 класс, примерно. Вероятнее всего, вам рассказали что есть формулы корней через дискриминант, что направление ветвей зависит от старшего коэффициента. Через пару занятий дали теорему Виета. Счастливчикам еще рассказали про метод переброски. И на этом решили отпустить.
Вы довольны такой базой? Вам не рассказали ни геометрический смысл, ни как это получить.
Спустя некоторое время обдумывания сей несправедливости, я решил написать эту статью и тем самым закрыть гештальт о фрагментарности знаний.
Вы не найдете здесь ничего нового по факту, но, возможно, это даст посмотреть на такое простое понятие с другой стороны.
Начнем с конца
Когда я перечислял темы, касающиеся квадратных уравнений, я делал это примерно в том же порядке, в котором изучают их в школе. Но такой порядок не оправдан с точки зрения обучения, и вот почему:
Дискриминант дается просто как данность (за редким исключением, когда показывают вывод этих формул через приведение к полному квадрату)
Мощнейшая по своей сути теорема Виета дается в конце и только как эвристический способ решения
Гораздо проще начать с теоремы Виета.

Рассмотрим квадратный трехчлен
В силу основной теоремы алгебры (примем её как данность, так как её действительно тяжело доказать), мы знаем, что у этого уравнения должно быть два корня. Допустим, что это некоторые числа . Тогда можно переписать изначальное уравнение как выражение его корней:
Оба эти уравнения эквиваленты, так как они оба зануляются в (первое по определению , второе по построению).
Раскрывая скобки, мы получим следующее:
Откуда приравняв соответствующие коэффициенты с имеющимися, получим знаменитую систему:
Мы только что доказали теорему Виета на случай квадратного трехчлена. Это потрясающий результат: мы начинаем получать некоторую информацию о корнях, которые, как мы предположили, существуют. И этот результат мы будем использовать далее.
Геометрия параболы
Вершина
Здесь можно было бы рассказать весь первый курс алгебры университета: о фокусах, директрисах, о конических сечениях, первой и второй производной…
Но раз мы ограничились школьной программой (7-8 класс, если быть точным), то и рассуждения у нас будут простые.

Самая, на мой субъективный взгляд, интересная точка параболы – это её вершина. Она уникальным образом задает положение параболе и дает понимание о том, как устроены корни.
Но формулу для нее мы не знаем, до первых понятий о производной нам еще 3 года в среднем. Будем выкручиваться.
Парабола – симметричная фигура. До того момента, как мы сдвинули ее относительно оси , ось служит для нее осью симметрии. Когда же мы начинаем ее сдвигать, становится видно, что она продолжает быть симметричной, но уже относительно оси, проходящей через вершину.
Парабола, вершина и ось симметрииТогда от вершины в обе стороны до корней равные расстояния, а это значит, что вершина параболы лежит ровно между корнями. Тогда координата вершины это среднее между ее корнями
Пока что мы не знаем наши корни. Но благодаря теореме Виета мы знаем, чему равна сумма корней!
Потрясающий результат, который нам пригодится далее.
Ещё немного про корни
Мы знаем, что корни, графически, это те точки, в которых кривая пересекает ось .
 Очень полезное знание, учитывая, что смотря на параболу, исключительно визуально, мы понимаем что у нас может быть 3 случая:
Очень полезное знание, учитывая, что смотря на параболу, исключительно визуально, мы понимаем что у нас может быть 3 случая:Корней нет, при этом
Либо значение в вершине больше нуля и старший коэффициент больше нуля
Либо значение в вершине меньше нуля и старший коэффициент меньше нуля
Корень один, но кратности 2 (не забываем основную теорему алгебры), и значение в вершине равно нулю
Корня два
Второй случай тривиален, до третьего мы еще дойдем. Интересно математически взглянуть на первый. Найдем значение квадратного трехчлена в вершине:
И теперь все же рассмотрим первый случай: парабола висит над осью ветвями вверх.
Первый случайДомножим первое неравенство на . Учитывая, что , знак неравенства сменится на противоположный:
Это условие, при котором корней нет.
Рассмотрим вкратце противоположный случай: парабола висит под осью ветвями вниз.
Второй случайКакая-то магия.
 Получается, что это условие инвариантно относительно положения параболы. Но тем оно лучше.
Получается, что это условие инвариантно относительно положения параболы. Но тем оно лучше.На данном этапе прошу заметить, что это только условие отсутствия действительных корней. Да, это похоже на дискриминант, но давайте представим, что вы этого не знаете.
Понятие дискриминанта
Мы уже многое поняли о корнях: в какой они связи с коэффициентами, когда они не существуют, каким образом они лежат относительно вершины. Все это безумно полезно, но это все до сих пор не способ найти значения алгебраически.
Давайте будем отталкиваться от того, что мы уже знаем: от вершины. Если бы мы каким-то образом знали расстояние между корнями, то могли бы однозначно найти и сами корни.
Таки что мешает нам это сделать? Но как настоящие математики, давайте находить квадрат расстояния между корнями. Не теряя общности, будем считать, что – больший корень. Тогда
Пока что выглядит не очень, но на что-то это очень сильно похоже. Не видите? Давайте выделим полный квадрат, но по сумме, а не по разности: добавим , но чтобы все осталось в точности так же, это же и вычтем.

Все еще не видите? Воспользуемся снова теоремой Виета:
Мы получили квадрат расстояния между корнями с учетом растяжения коэффициентом .
Так мы теперь можем найти корни! Вершина параболы да половину расстояния между корнями в обе стороны:
Или, немного преобразовав
Квадрат расстояния между корнями квадратного трехчлена и есть дискриминант.
В общем случае, дискриминант — более сложное понятие, связанное с кратными корнями. Но для квадратного уравнения в 7 классе этого достаточно.
Теперь, если рассуждать о дискриминанте как о расстоянии, становится логично и понятно, почему если он равен нулю, то корень всего один; а если отрицательный, то действительных корней вообще нет.
Заключение
Заметьте, что единственное, что мы предположили, что корня два и они существуют. Единственное, что приняли на веру, это основную теорему алгебры. До всего остального мы дошли исключительно умозрительными заключениями и простейшей алгеброй.

Как по мне, это именно то, как должны преподавать эту тему в школе.
4.3 Решение квадратных уравнений | Уравнения и неравенства
Квадратное уравнение — это уравнение, в котором показатель степени переменной не превышает \(\text{2}\). Следующее примеры квадратных уравнений:
Квадратные уравнения отличаются от линейных уравнений тем, что линейное уравнение имеет только одно решение, а квадратное уравнение имеет не более двух решений. Однако существуют особые ситуации, когда квадратное уравнение имеет либо одно решение, либо не имеет решений. 9{2} + bx + c = 0\) иметь вид \(\left(rx + s\right)\left(ux + v\right) = 0\).
Два решения: \(\left(rx + s\right) = 0\) или \(\left(ux + v\right) = 0\), поэтому \(x= -\dfrac{s}{r}\) или \(x = -\dfrac{v}{u}\) соответственно.
Проверьте ответ, подставив его обратно в исходное уравнение.
 9{2} + Ьх + с = 0\)
9{2} + Ьх + с = 0\)Факторизовать
\[\влево(х + 1\вправо)\влево(3x — 1\вправо) = 0\]Решите для обоих факторов
У нас есть
\начать{выравнивать*} х + 1 & = 0 \\ \поэтому х & = -1 \конец{выравнивание*}
ИЛИ
\начать{выравнивать*} 3х — 1 & = 0 \ \следовательно, x & = \frac{1}{3} \конец{выравнивание*} 9{2} & = 0 \конец{выравнивание*}
Квадратное уравнение является полным квадратом
Это пример особой ситуации, когда существует только одно решение квадратного уравнения. уравнения, потому что оба фактора одинаковы.
\начать{выравнивать*} х — 1 & = 0 \\ \поэтому х & = 1 \конец{выравнивание*}
Проверьте ответ, подставив обратно в исходное уравнение 9{2} — 6x — 8 & = 0 \\ (3x + 2)(3x — 4) & = 0 \\ 3х+2&=0\ х & = -\фракция{2}{3} \\ \текст{или} & \\ 3х — 4 & = 0 \ х & = \ гидроразрыва {4} {3} \\ \поэтому x = -\frac{2}{3} & \text{ или } x = \frac{4}{3} \end{выравнивание*}
9{2} — 9 & = 0 \\ (2у — 3)(2у + 3) & = 0 \\ 2у — 3&=0\ у & = \ гидроразрыва {3} {2} \\ \текст{или} & \\ 2у+3&=0\ y & = -\frac{3}{2} \\ \поэтому y = \frac{3}{2} & \text{ или } y = -\frac{3}{2} \end{выравнивание*}\(4x^{2} + 16x — 9{2} + 16x — 9 & = 0 \\ (2х — 1)(2х + 9) & = 0 \\ 2х — 1 & = 0 \ х & = \ гидроразрыва {1} {2} \\ \текст{или} & \\ 2х+9&=0\ y & = -\frac{9}{2} \\ \следовательно, x = \frac{1}{2} & \text{ или } x = -\frac{9}{2} \end{выравнивание*}
9{2} + 58x — 48 & = 0 \\ (5х — 6)(3х — 8) & = 0 \\ 5х — 6 & = 0 \ х & = \ гидроразрыва {6} {5} \\ \текст{или} & \\ 3х — 8 & = 0 \ х & = \ гидроразрыва {8} {3} \\ \следовательно, x = \frac{6}{5} & \text{ или } x = \frac{8}{3} \end{выравнивание*} 9{2} + 5x — 6 & = 0 \\ (7x + 6)(2x — 1) & = 0 \\ 7х+6&=0\ х & = -\ гидроразрыва {6} {7} \\ \текст{или} & \\ 2х — 1 & = 0 \ х & = \ гидроразрыва {1} {2} \\ \поэтому x = -\frac{6}{7} & \text{ или } x = \frac{1}{2} \end{выравнивание*} 92 -17 лет + 4 &= 0\\ (4у-1)(у-4)&= 0\\ \поэтому y = \frac{1}{4} &\text{ или } y = 4 \конец{выравнивание*}\(\dfrac{1}{2}(b — 1) = \dfrac{1}{3}\left(\dfrac{2}{b} + 4\right)\)
Примечание \(b \neq 0\)
\начать{выравнивать*} \frac{1}{2}(b — 1) &= \frac{1}{3}\left(\frac{2}{b} + 4\right) \\ 3(b — 1) &= 2\влево(\frac{2}{b} + 4\вправо) \\ 3b — 3 &= \frac{4}{b} + 8 \\ 3b^2 — 3b &= 4 + 8b \\ 3b^2 — 11b — 4 &= 0 \\ (3b + 1)(b — 4) &= \\ \поэтому b = -\frac{1}{3}b &\text{ или } b = 4 \конец{выравнивание*} 92 — 9) &= 0 \\ (б-2)(б+2)(б-3)(б+3) &= 0 \\ \поэтому b = \pm 2 &\text{ или } b = \pm 3 \end{align*}
\(\dfrac{a + 1}{3a — 4} + \dfrac{9}{2a + 5} + \dfrac{2a + 3}{2a + 5} = 0\)
\begin{выравнивание*} \frac{a + 1}{3a — 4} + \frac{9}{2a + 5} + \frac{2a + 3}{2a + 5} & = 0 \\ \frac{(a + 1)(2a + 5) + 9(3a — 4) + (2a + 3)(3a — 4)}{(3a — 4)(2a + 5)} & = 0 \\ 2а^{2} + 7а + 5 + 27а — 36 + 6а^{2} + а — 12 & = 0 \\ 8а^{2} + 35а — 43 & = 0 \\ (8а + 43)(а — 1) & = 0 \\ 8а+43&=0\ а & = -\frac{43}{8} \\ \текст{или} & \\ а — 1 & = 0 \\ а & = 1 \\ \поэтому a = -\frac{43}{8} & \text{ или } a = 1 \end{выравнивание*} 92 — 2x — 3}{x+1} &= 0 \\ \frac{(x+1)(x-3)}{x+1} &= 0 \\ \поэтому х &= 3 \конец{выравнивание*}
\(x + 2 = \dfrac{6x -12}{x- 2}\)
Примечание \(x \neq 2\)
\начать{выравнивать*} х + 2 &= \frac{6x-12}{x- 2} \\ (х+2)(х-2) &= 6х — 12 \\ х^2 — 4 &= 6х — 12\\ х^2 — 6х + 8 & = 0 \\ (х — 2)(х — 4) & = 0 \\ \поэтому х &= 4 \конец{выравнивание*} 9{2} — 6а&=0\ 3а(3а — 2) & = 0 \\ 3а & = 0 \\ а & = 0 \\ \текст{или} & \\ 3а — 2&=0\ а & = \ гидроразрыва {2} {3} \\ \следовательно, a = 0 & \text{ или } a = \frac{2}{3} \конец{выравнивание*}
РешенияNCERT для математики класса 10 Глава 4 Квадратные уравнения Пример 4.
 1
1Решения NCERT Математика класса 10 Глава 4 Квадратные уравнения — Вот все решения NCERT по математике класса 10 Глава 4 Квадратные уравнения. Это решение содержит вопросы, ответы, изображения, пошаговое объяснение полной главы 4 под названием «Квадратные уравнения в классе 10». 4 Квадратные уравнения. После того, как вы изучили урок, вы должны искать ответы на его вопросы из учебника. Здесь вы можете получить полные решения NCERT для математики класса 10, глава 4, квадратные уравнения в одном месте.
- Класс 10 Квадратные уравнения по математике Пример 4.1
- प्रश्नावली 4.1 का हल हिंदी में
- Квадратные уравнения по математике, класс 10, пр. 4.2
- प्रश्नावली 4.2 का हल हिंदी में
- Квадратные уравнения по математике, класс 10, пр. 4.3
- प्रश्नावली 4.3 का हल हिंदी में
- Квадратные уравнения по математике, класс 10, пр. 4.4
- प्रश्नावली 4.4 का हल हिंदी में
- Дополнительные вопросы по квадратным уравнениям 10 класса
Решения NCERT для математики класса 10 Глава 4 Квадратные уравнения Ex 4.
 1 являются частью решений NCERT для математики класса 10. Здесь мы дали решения NCERT для математики класса 10, глава 4, квадратные уравнения, пример 4.1.
1 являются частью решений NCERT для математики класса 10. Здесь мы дали решения NCERT для математики класса 10, глава 4, квадратные уравнения, пример 4.1.Доска CBSE Учебник НЦЕРТ Класс Класс 10 Субъект Математика Глава Глава 4 Название раздела Квадратные уравнения Упражнение Пример 4.1 Количество решенных вопросов 2 Категория Решения NCERT Упр. 4.1 Класс 10 Математика Вопрос 1.
Проверьте, являются ли следующие уравнения квадратными: ) (3-x)
(iii) (x – 2) (x + 1) = (x – 1) (x + 3)
(iv) (x – 3) (2x + 1) = x (x + 5)
(в) (2х – 1) (х – 3) = (х + 5) (х – 1)
(vi) x 2 + 3x + 1 = (x – 2) 2
(vii) (x + 2) 3 = 2x(x 2 – 1)
(viii) x 3 -4x 2 -x + 1 = (x-2) 3
Решение:
Решения NCERT Класс 10 Математика Глава 4 Квадратные уравнения — Видео
Решения NCERT Класса 1 Математика глава 4 Квадратные уравнения здесь.

Упражнение 4.1 Класс 10 Математика Вопрос 2.
Представьте следующие ситуации в виде квадратных уравнений:
(i) Площадь прямоугольного участка составляет 528 м 2 . Длина участка (в метрах) более чем в два раза превышает его ширину. Нам нужно найти длину и ширину участка.
(ii) Произведение двух последовательных положительных целых чисел равно 306. Нам нужно найти целые числа.
(iii) Мать Рохана старше его на 26 лет. Произведение их возраста (в годах) через 3 года будет равно 360. Мы хотели бы найти нынешний возраст Рохана.
(iv) Поезд проехал расстояние 480 км с постоянной скоростью. Если бы скорость была на 8 км/ч меньше, то на преодоление того же расстояния ушло бы на 3 часа больше. Нам нужно найти скорость поезда.
Нам нужно найти скорость поезда.
Решение:
Неправильный результат NCVT 2019
Решения NCERT, класс 10, математика, глава 4, квадратные уравнения
, класс 10, математика, глава 4, решения квадратных уравнений приведены ниже в формате PDF. Вы можете просмотреть их в Интернете или загрузить PDF-файл для дальнейшего использования.
или сохраните изображения решений и распечатайте их, чтобы они всегда были под рукой при подготовке к экзамену. Нажмите здесь, чтобы загрузить решения NCERT для класса 10 по математике, глава 4, квадратные уравнения.
NCERT Solutions для класса 10 Математика Глава 4 Квадратичные уравнения (Hindi Medium) EX 4,1
Класс 10 Математические квадратичные уравнения. переменная x представляет собой уравнение вида ax2 + bx + c = 0, где a, b, c — действительные числа, а a ≠ 0.
Любое уравнение вида P(x) = 0, где P(x) — это многочлен степени 2, является квадратным уравнением.
Нуль(и)/корень(и) квадратного уравнения
Вещественное число α называется корнем квадратного уравнения ax 2 + bx + c = 0, a ≠ 0, если aα 2 + bα + c = 0,
Можно сказать, что x = α является решением квадратного уравнения или что α удовлетворяет квадратному уравнению.
Нули квадратного полинома ax 2 + bx + c = 0 и корни уравнения ax 2 + bx + c = 0 совпадают. Квадратное уравнение имеет не более двух корней/нулей.Связь между нулями и коэффициентом квадратного уравнения
Если α и β — нули квадратного уравнения ax 2 + bx + c = 0, где a, b, c — действительные числа и a ≠ 0, то
Методы решения квадратных уравнений
Ниже приведены методы, используемые для решения квадратных уравнений:
(i) Факторизация
(ii) Заполнение квадрата
(iii) Квадратная формулаМетоды факторизации
В этом62 методом находим корни квадратного уравнения (ax
2 + bx + c = 0) путем разложения LHS на два линейных множителя и приравнивания каждого множителя к нулю, например,
6x 2 – x – 2 = 0
⇒ 6x 2 + 3x – 4x – 2 = 0 …(i)
⇒ 3x (2x + 1) – 2(2x + 1) = 0
⇒ (3x – 2) (2x + 1) = 0
⇒ 3x – 2 = 0 или 2x + 1 = 0
Необходимое условие : Произведение 1-го и последнего членов уравнения. (i) должно быть равно произведению 2-го и 3-го членов того же уравнения.
(i) должно быть равно произведению 2-го и 3-го членов того же уравнения.Метод завершения квадрата
Это метод преобразования L.H.S. квадратного уравнения, не являющегося полным квадратом, в сумму или разность полного квадрата и константы путем сложения и вычитания подходящих постоянных членов. например,
(1) x 2 + 4x – 5 = 0
⇒ x 2 + 2(2)(x) -5 = 0
⇒ x 2 + 2(2)(x) + (2) 2 – (2) 2 – 5 = 0
⇒ (х + 2) 2 – 4 – 5 = 0
⇒ (х + 2) 2 – 9 = 0
⇒ х + 2 ± 3
⇒ x = -5, 1
(2) 3x 2 – 5x + 2 = 0Квадратная формула
Рассмотрим квадратное уравнение: ax 2 + bx + c = 0.
Если b 2 – 4ac ≥ 0, то корни приведенного выше уравнения имеют вид:Природа корней
Для квадратного уравнения ax 2 + bx + c = 0
(a ≠ 0), значение (b 2 – 4ac) называется дискриминантом уравнения и обозначается как D.
9 х в квадрате: решить уравнение: 9-x(в квадрате)<0 - Школьные Знания.com

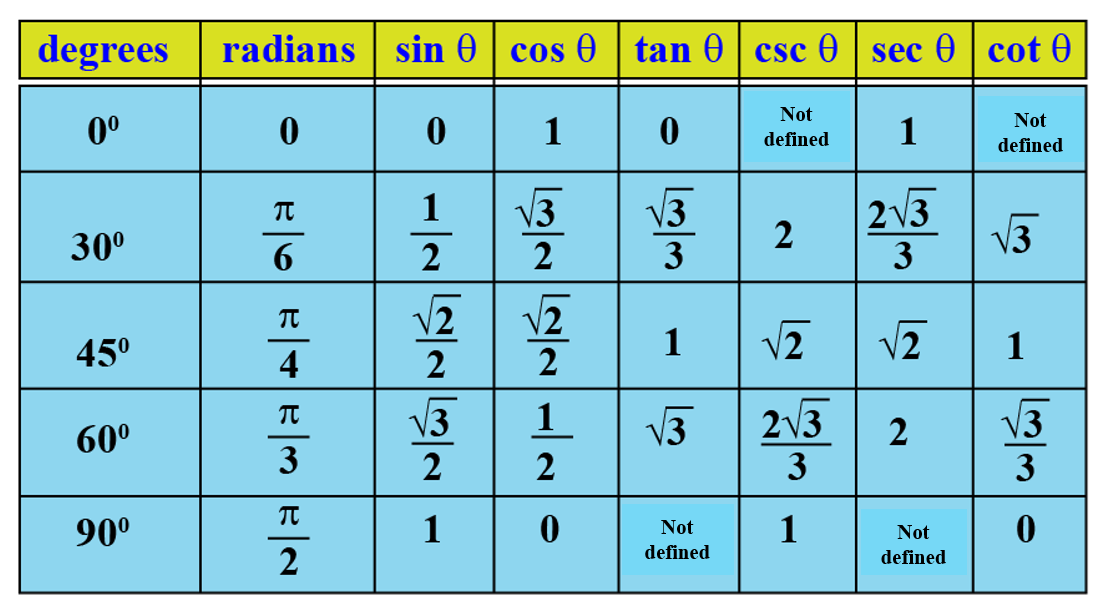 9063
9063 6691
6691 3584
3584 0349
0349 4067
4067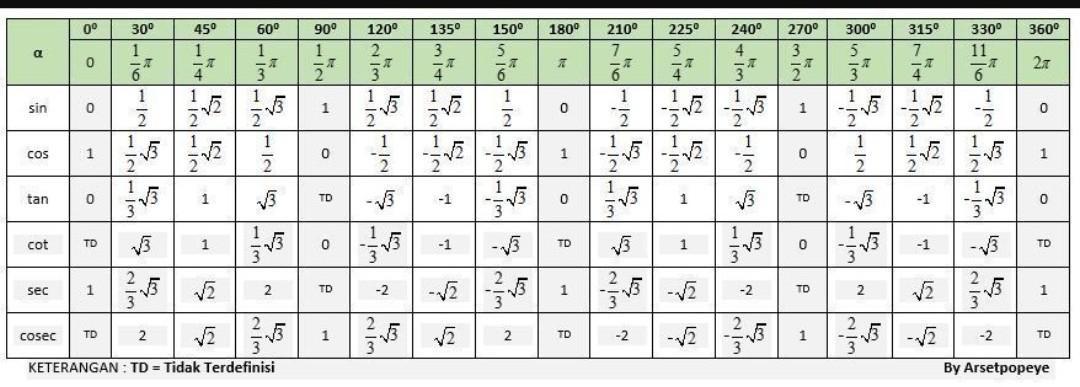 6947
6947 9135
9135 9994
9994 9613
9613 788
788 5
5 1736
1736 225
225 5592
5592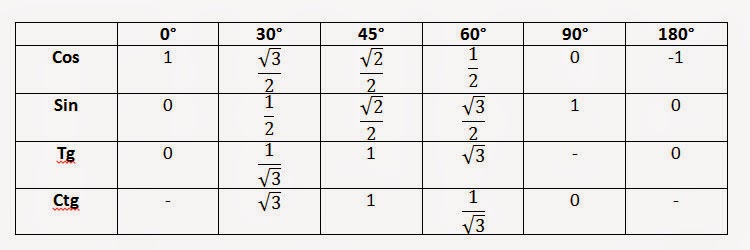 8387
8387 9848
9848 То есть за миллион бросков это может случиться 150 раз или 1 раз в 2 дня, если подкидывать монету каждый день по 8 часов в течение года. Чтобы монета встала на ребро два раза подряд, придется подбрасывать ее в том же темпе около 35 лет.
То есть за миллион бросков это может случиться 150 раз или 1 раз в 2 дня, если подкидывать монету каждый день по 8 часов в течение года. Чтобы монета встала на ребро два раза подряд, придется подбрасывать ее в том же темпе около 35 лет. Вероятность независимых событий можно найти по формуле P(A \cap B) = P(A) * P(B). Зависимые события — это события, появление одного из которых зависит от появления другого. Вероятность появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие уже наступило. P(A \cap B) = P(A) * P(B | A).
Вероятность независимых событий можно найти по формуле P(A \cap B) = P(A) * P(B). Зависимые события — это события, появление одного из которых зависит от появления другого. Вероятность появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие уже наступило. P(A \cap B) = P(A) * P(B | A).  2 Отбор проб
2 Отбор проб Следовательно, K = 4. Вам нужно будет выбрать одну единицу из каждых четырех единиц, чтобы получить в общей сложности 100 единиц в вашей выборке.
Следовательно, K = 4. Вам нужно будет выбрать одну единицу из каждых четырех единиц, чтобы получить в общей сложности 100 единиц в вашей выборке. Она должна проходить через точку (0, 3) и наклоняться вверх слева направо. Мы можем использовать две точки, чтобы найти наклон, или мы можем сравнить его с другими перечисленными функциями. Функция g имеет тот же наклон, но другую точку пересечения y-. Линии I и III имеют одинаковый наклон, потому что они имеют одинаковый наклон. Строка III не проходит через (0, 3), поэтому f должна быть представлена линией I.
Она должна проходить через точку (0, 3) и наклоняться вверх слева направо. Мы можем использовать две точки, чтобы найти наклон, или мы можем сравнить его с другими перечисленными функциями. Функция g имеет тот же наклон, но другую точку пересечения y-. Линии I и III имеют одинаковый наклон, потому что они имеют одинаковый наклон. Строка III не проходит через (0, 3), поэтому f должна быть представлена линией I. Она должна проходить через точку (0, 3) и наклоняться вверх слева направо . Линии I и II проходят через (0, 3), но наклон j меньше наклона f , поэтому линия для j должна быть более плоской. Эта функция представлена линией II.
Она должна проходить через точку (0, 3) и наклоняться вверх слева направо . Линии I и II проходят через (0, 3), но наклон j меньше наклона f , поэтому линия для j должна быть более плоской. Эта функция представлена линией II.

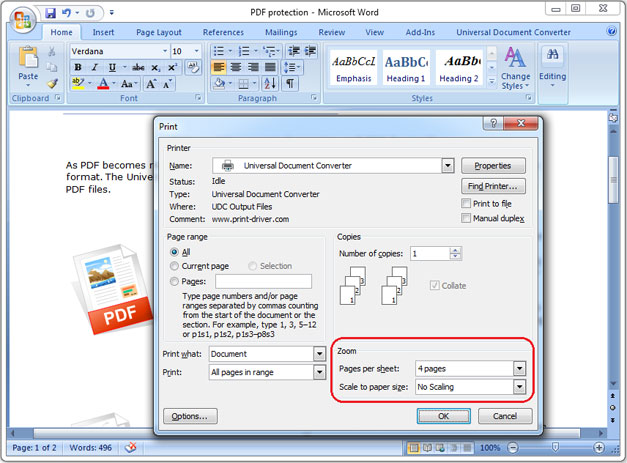 Для преобразования JPG в текстовый файл вы должны выбрать изображение JPG, которое вы хотите преобразовать в слово в этом инструменте. После выбора JPG в этом инструменте вы увидите, что этот инструмент автоматически конвертирует все выбранные изображения JPG в файлы Word в инструменте. Вы также можете добавить больше изображений JPG, которые хотите преобразовать в файлы Word. Кроме того, вы можете удалить изображения JPG, которые не хотите преобразовывать в слово. С помощью этого инструмента вы можете одновременно конвертировать несколько изображений JPG в файлы Word. Теперь нажмите кнопку «преобразовать в слово», а затем легко загрузите все преобразованные в текстовые файлы на свое устройство. Наконец, используя этот инструмент JPG to word, вы можете просто конвертировать изображения JPG в файлы word онлайн.
Для преобразования JPG в текстовый файл вы должны выбрать изображение JPG, которое вы хотите преобразовать в слово в этом инструменте. После выбора JPG в этом инструменте вы увидите, что этот инструмент автоматически конвертирует все выбранные изображения JPG в файлы Word в инструменте. Вы также можете добавить больше изображений JPG, которые хотите преобразовать в файлы Word. Кроме того, вы можете удалить изображения JPG, которые не хотите преобразовывать в слово. С помощью этого инструмента вы можете одновременно конвертировать несколько изображений JPG в файлы Word. Теперь нажмите кнопку «преобразовать в слово», а затем легко загрузите все преобразованные в текстовые файлы на свое устройство. Наконец, используя этот инструмент JPG to word, вы можете просто конвертировать изображения JPG в файлы word онлайн.
 Это может занять некоторое время…
Это может занять некоторое время…
 Использование конвертера JPEG в Word может устранить необходимость в том, чтобы специалисты по вводу данных выполняли эту работу за вас за считанные секунды.
Использование конвертера JPEG в Word может устранить необходимость в том, чтобы специалисты по вводу данных выполняли эту работу за вас за считанные секунды. Проблемы превышают еще больше, когда вы теряете цифровую версию печатных документов. Тем не менее, вам не нужно преодолевать такие большие проблемы, так как преобразование изображений в редактируемые файлы Word теперь возможно благодаря этому конвертеру JPG в редактируемый Word. Это средство поможет вам преобразовать отсканированные документы в редактируемые файлы Word, не требуя от вас затрат времени и усилий.
Проблемы превышают еще больше, когда вы теряете цифровую версию печатных документов. Тем не менее, вам не нужно преодолевать такие большие проблемы, так как преобразование изображений в редактируемые файлы Word теперь возможно благодаря этому конвертеру JPG в редактируемый Word. Это средство поможет вам преобразовать отсканированные документы в редактируемые файлы Word, не требуя от вас затрат времени и усилий. Другие важные функции нашего конвертера изображений в Word обсуждаются ниже.
Другие важные функции нашего конвертера изображений в Word обсуждаются ниже. Наш инструмент обеспечивает надежное и безошибочное преобразование редактируемых документов JPG в Word.
Наш инструмент обеспечивает надежное и безошибочное преобразование редактируемых документов JPG в Word.
 Этот инструмент не пропустит ни одно слово Word на вашем изображении и грамотно преобразует весь текст в файл Word.
Этот инструмент не пропустит ни одно слово Word на вашем изображении и грамотно преобразует весь текст в файл Word.
 Все веб-браузеры поддерживают этот инструмент; следовательно, независимо от того, используете ли вы Chrome, Explorer, Firefox, Opera или Safari, вы можете быстро и безопасно получить доступ к JPEG для документов и выполнить необходимые преобразования.
Все веб-браузеры поддерживают этот инструмент; следовательно, независимо от того, используете ли вы Chrome, Explorer, Firefox, Opera или Safari, вы можете быстро и безопасно получить доступ к JPEG для документов и выполнить необходимые преобразования. Люди, использующие этот инструмент с мобильных устройств, могут напрямую захватывать изображение текста, который они хотят преобразовать.
Люди, использующие этот инструмент с мобильных устройств, могут напрямую захватывать изображение текста, который они хотят преобразовать. Форма отчета
Форма отчета Используйте наш «Конвертер JPG в Word», чтобы сохранить каждое изображение JPG в виде редактируемого документа Word. Это самый быстрый способ конвертировать фотографии и сканы в формат Word онлайн.
Используйте наш «Конвертер JPG в Word», чтобы сохранить каждое изображение JPG в виде редактируемого документа Word. Это самый быстрый способ конвертировать фотографии и сканы в формат Word онлайн.
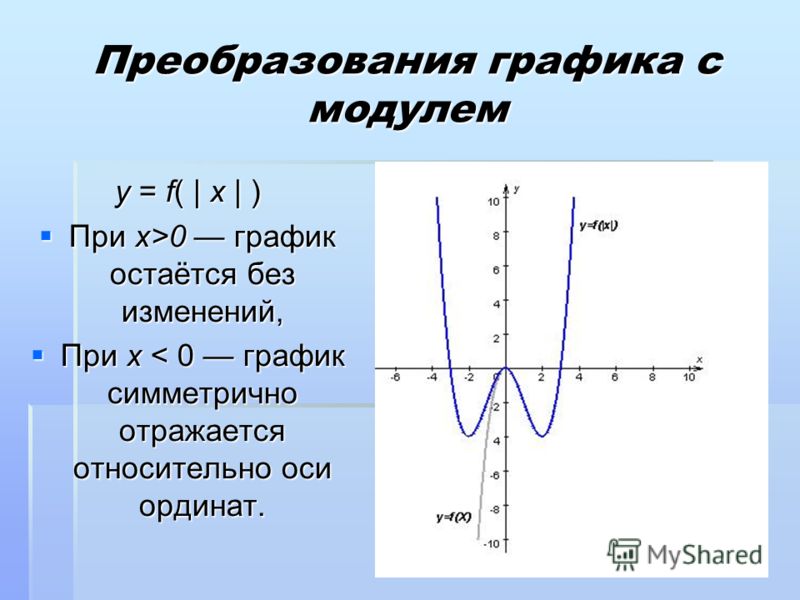
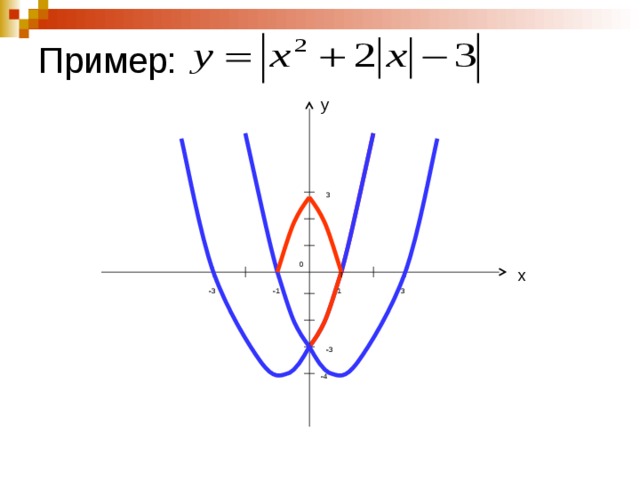 x=1;
x=1;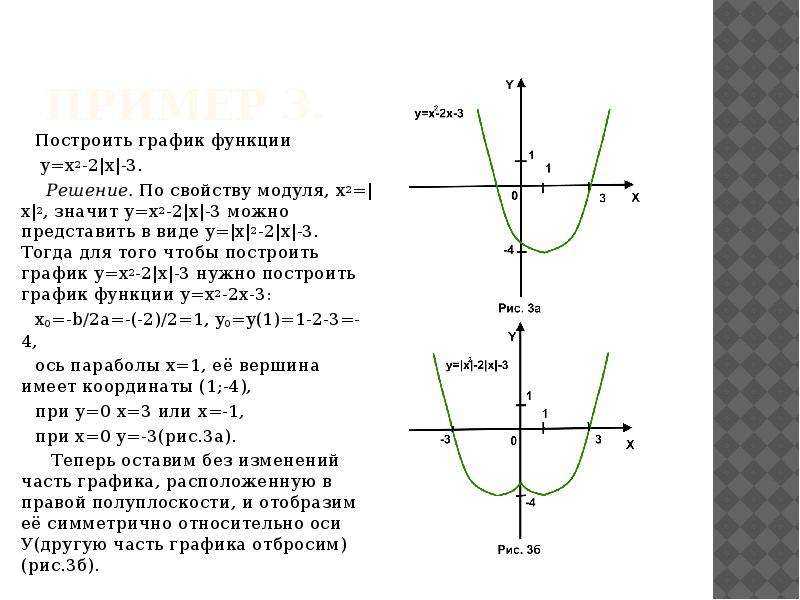
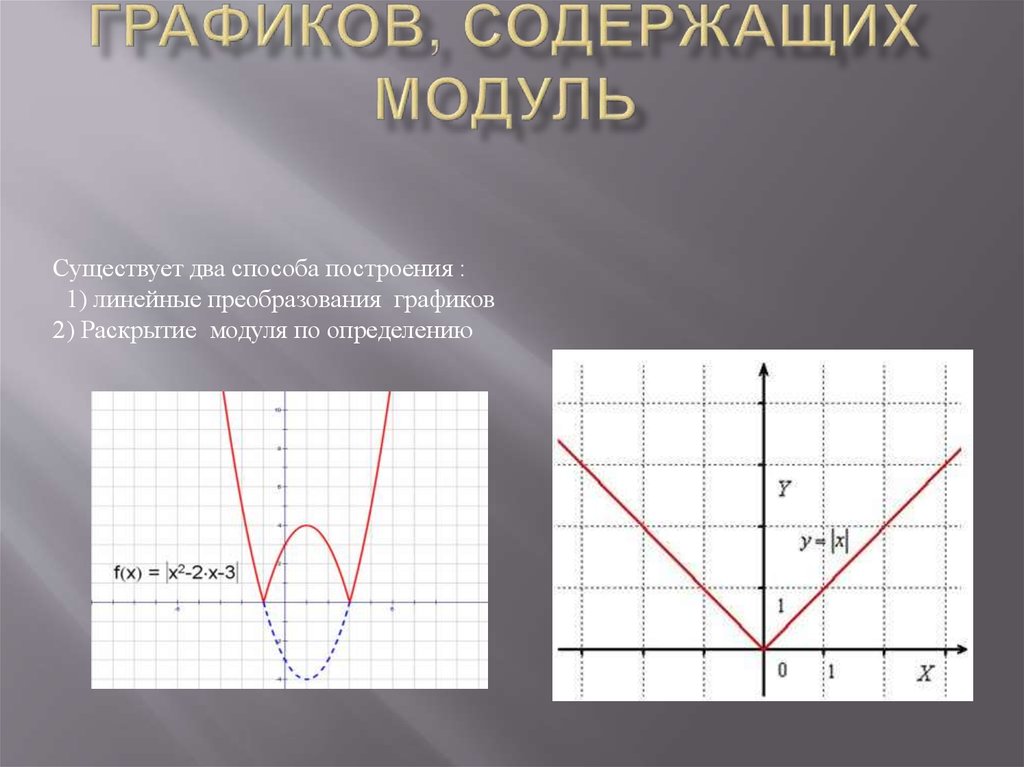 построить график функции y=f(x)
построить график функции y=f(x) Сжатие ( растяжение ) графика вдоль оси ординатГрафик функции y= b f (x)
Сжатие ( растяжение ) графика вдоль оси ординатГрафик функции y= b f (x)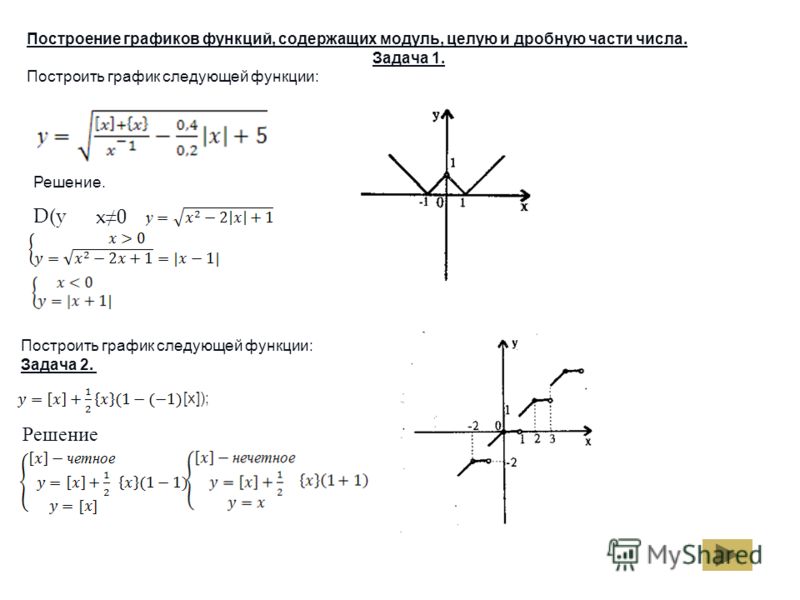
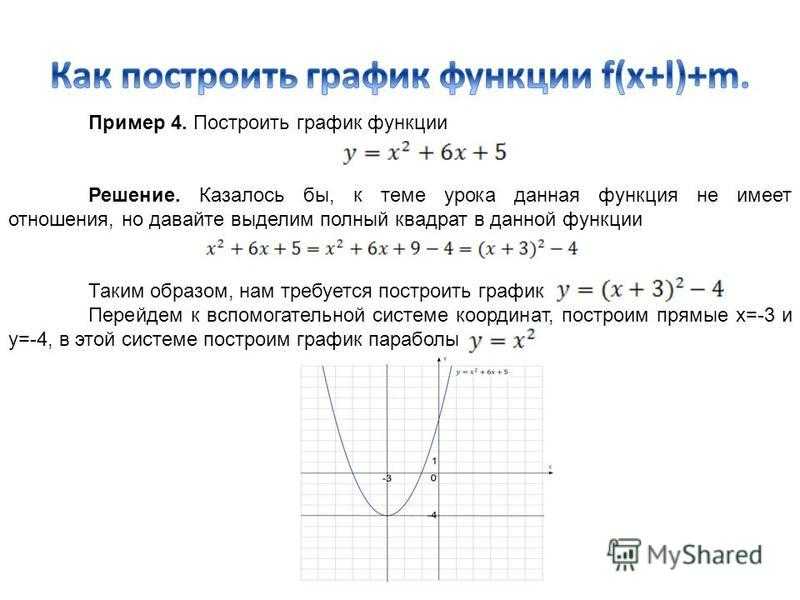 Вычислим значения некоторых точек для графиков этих функций.
Вычислим значения некоторых точек для графиков этих функций.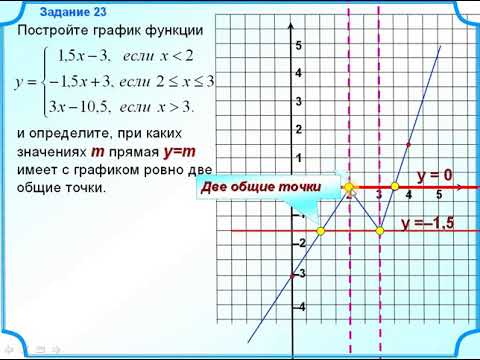 График получается из графика функции преобразованием симметрии относительно оси .
График получается из графика функции преобразованием симметрии относительно оси .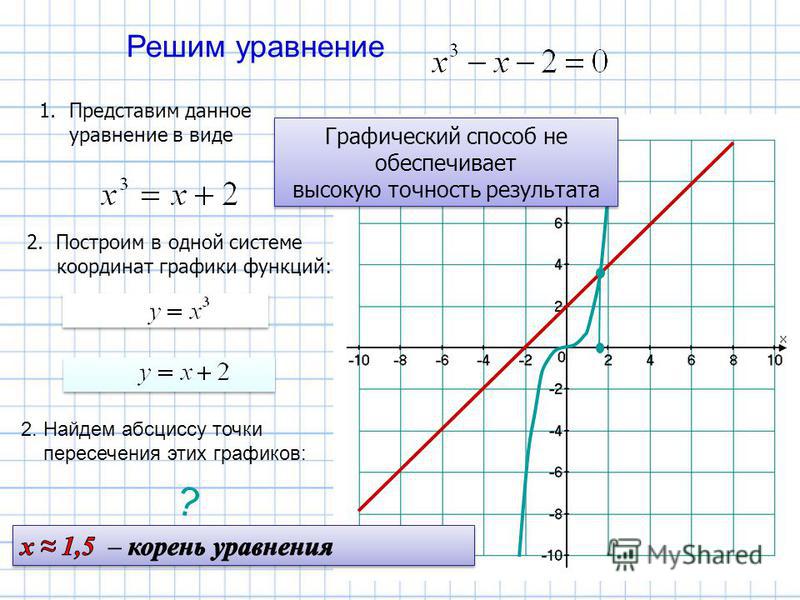 4. Графики функций и
4. Графики функций и  Графически это означает, что график функции сужается по сравнению с графиком функции (см. Рис. 7).
Графически это означает, что график функции сужается по сравнению с графиком функции (см. Рис. 7). Рис. 9, 10).
Рис. 9, 10). Рис. 11).
Рис. 11). А вот график построить можно, сдвинув исходный график на 1 влево (см. Рис. 14).
А вот график построить можно, сдвинув исходный график на 1 влево (см. Рис. 14).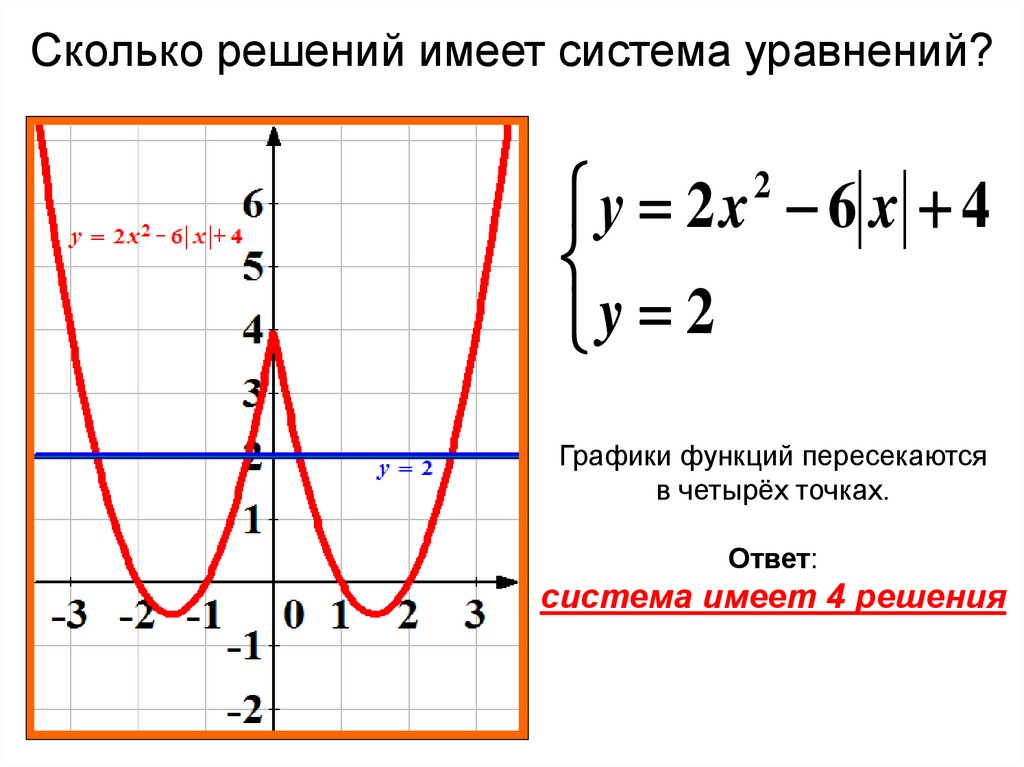 16. Растяжение от оси
16. Растяжение от оси  Рис. 17).
Рис. 17).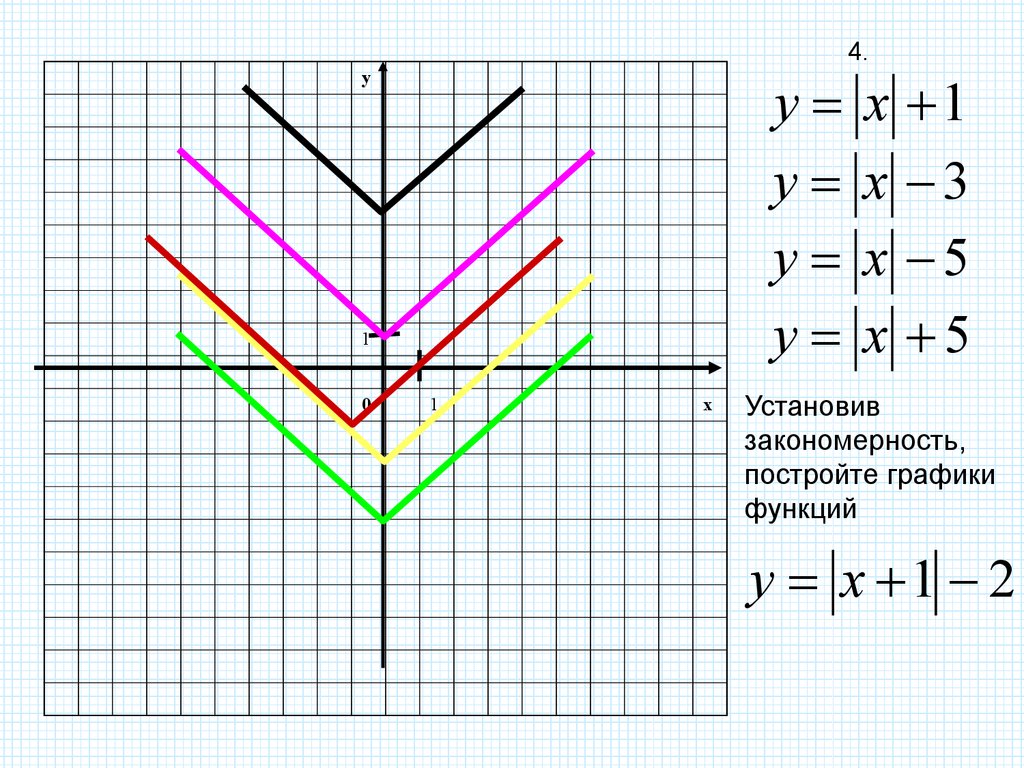 18. Графики функций и (красным цветом выделена общая часть этих графиков)
18. Графики функций и (красным цветом выделена общая часть этих графиков)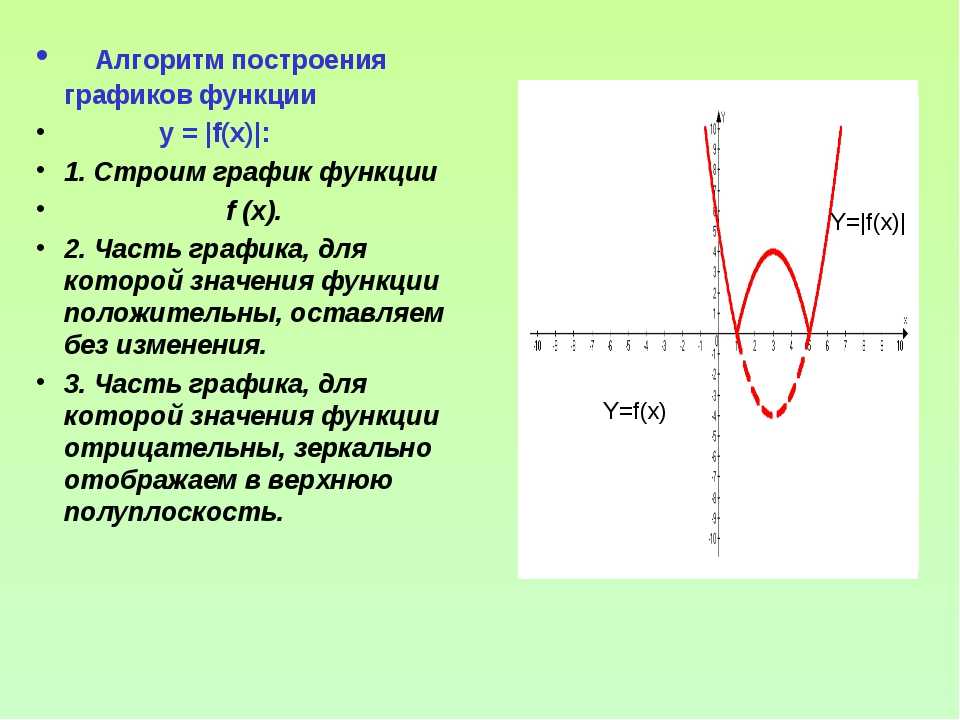 19. Графики функций и (красным цветом выделена общая часть этих графиков)
19. Графики функций и (красным цветом выделена общая часть этих графиков)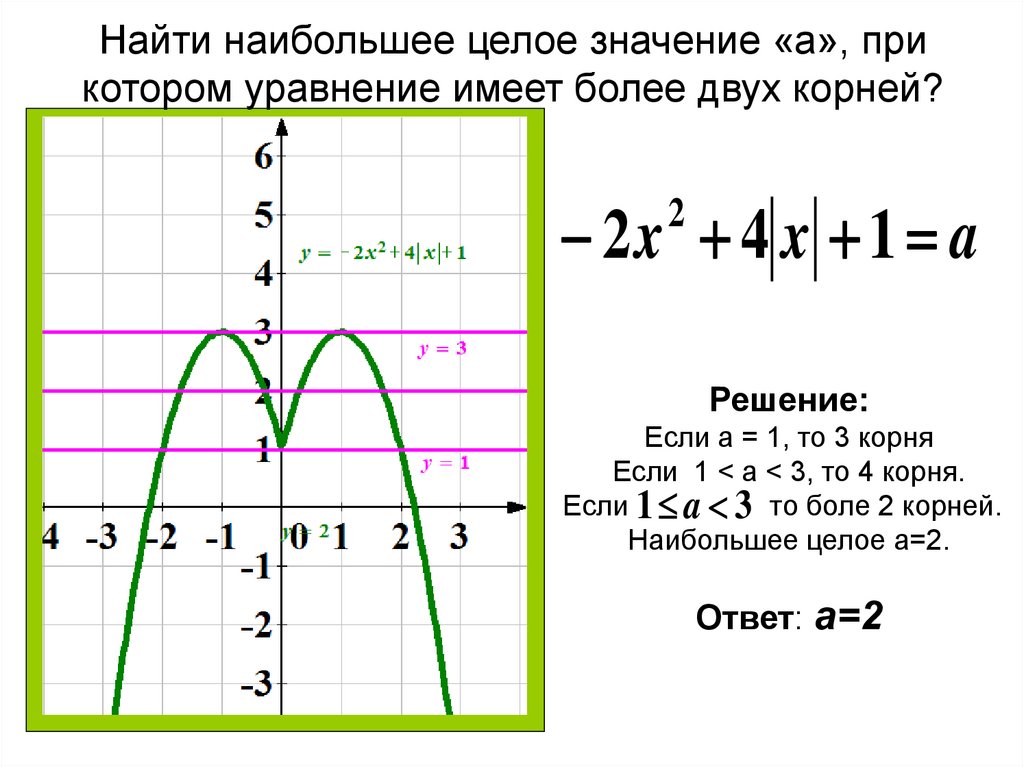 График получается из графика параллельным переносом последнего на 2 единицы вправо.
График получается из графика параллельным переносом последнего на 2 единицы вправо.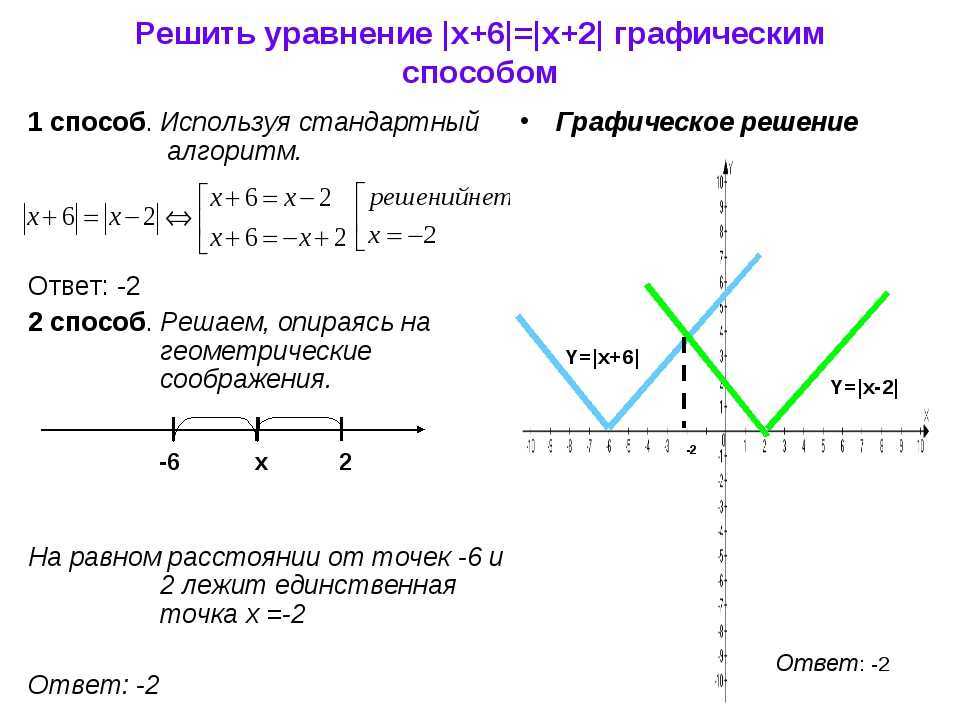 Например, для построения графика сначала нужно построить график , затем график (растяжение от оси ), а далее – график (параллельный перенос вдоль оси ординат) (см. Рис. 22). Если же сделать в другой последовательности, то есть построить , то далее на 2 придется умножить всё выражение.
Например, для построения графика сначала нужно построить график , затем график (растяжение от оси ), а далее – график (параллельный перенос вдоль оси ординат) (см. Рис. 22). Если же сделать в другой последовательности, то есть построить , то далее на 2 придется умножить всё выражение.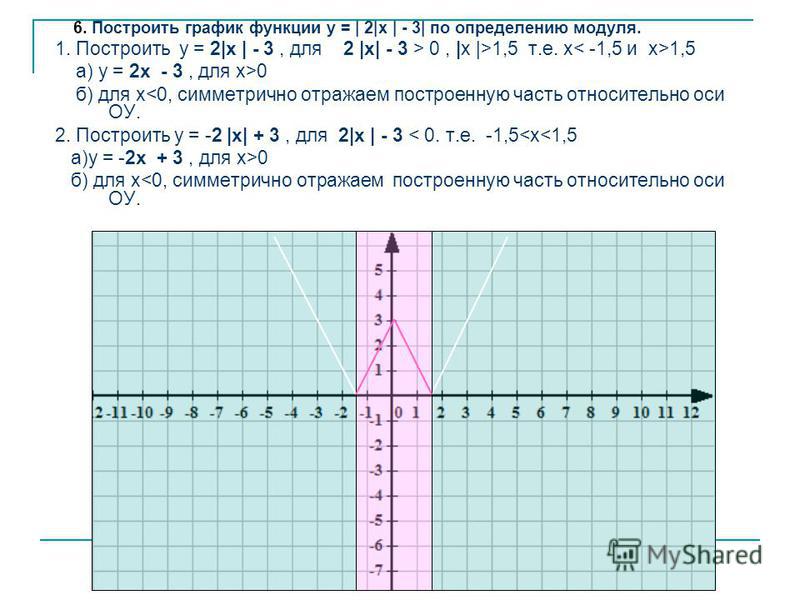 Строим график (гипербола) (см. Рис. 23).
Строим график (гипербола) (см. Рис. 23).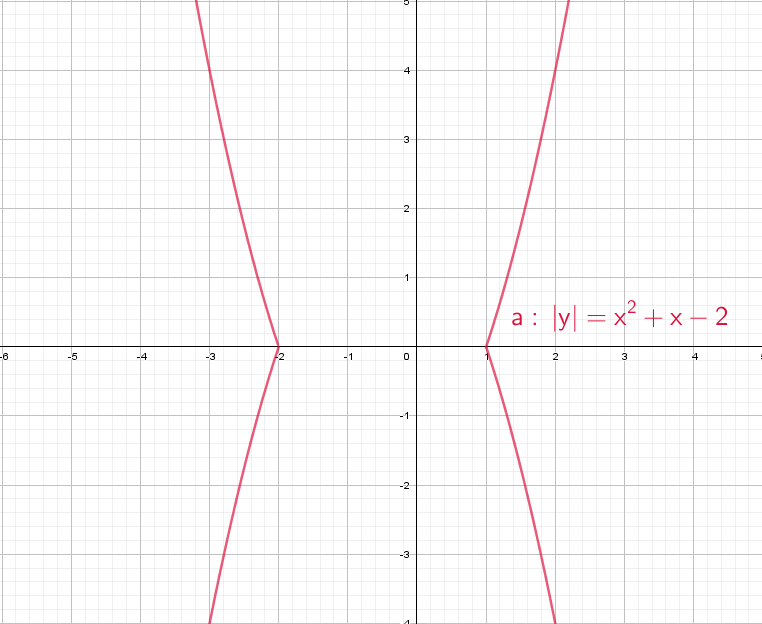 23. Иллюстрация к задаче
23. Иллюстрация к задаче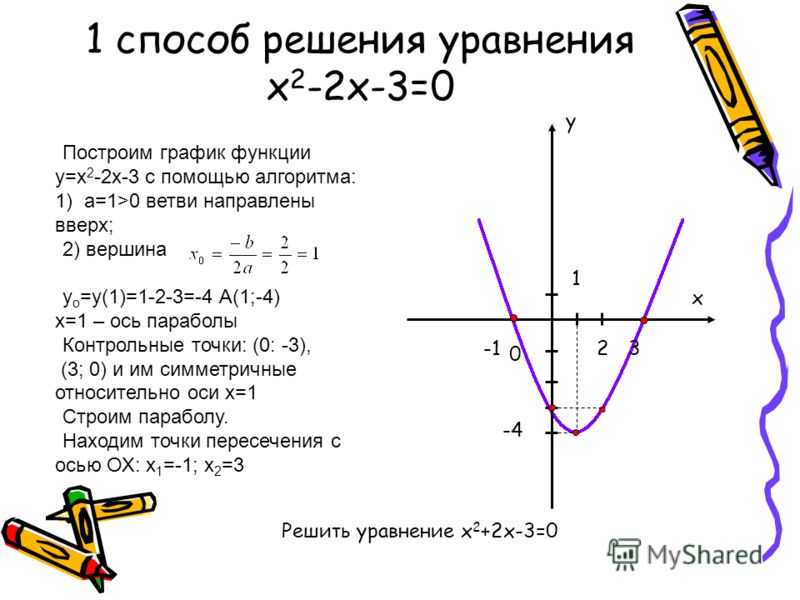 – М.: Мнемозина, 2002. – 143 с.: ил.
– М.: Мнемозина, 2002. – 143 с.: ил.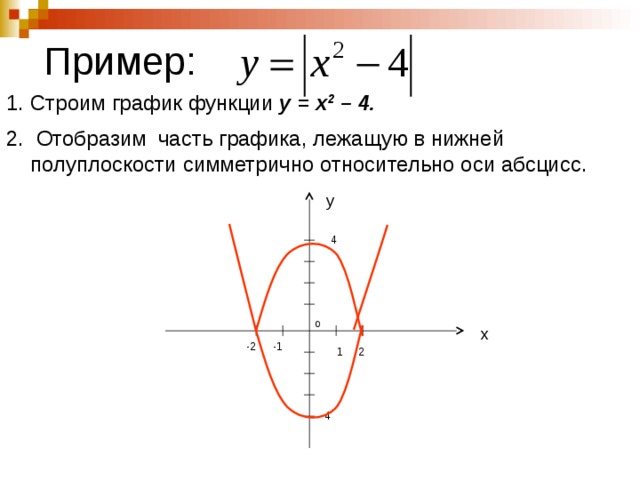 Интернет-сайт YouTube (Источник)
Интернет-сайт YouTube (Источник) Однако по природе экспоненциальных функций их точки, как правило, либо очень близки к одному фиксированному значению, либо слишком велики, чтобы их можно было удобно изобразить на графике.
Однако по природе экспоненциальных функций их точки, как правило, либо очень близки к одному фиксированному значению, либо слишком велики, чтобы их можно было удобно изобразить на графике.
 И положительная 2 не может превратиться в отрицательное число, если возвести его в степень.
И положительная 2 не может превратиться в отрицательное число, если возвести его в степень.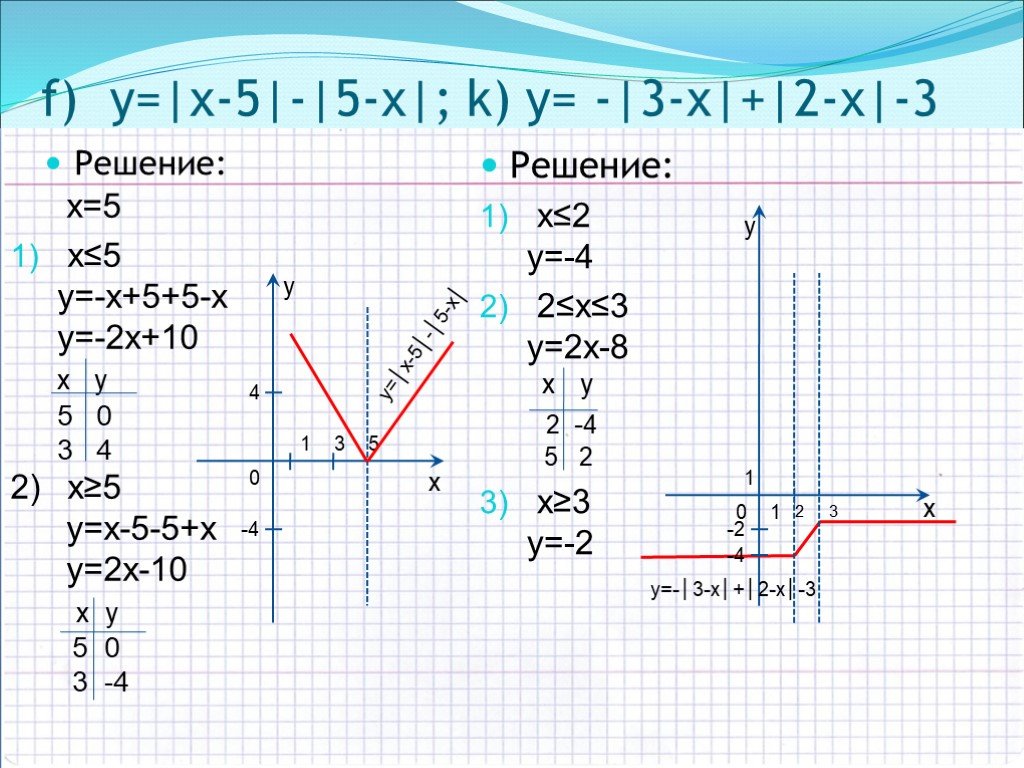 То есть, в то время как y = 1/16 для x = −4, линия будет только вдвое короче, при y = 1/32, для x = -5.
То есть, в то время как y = 1/16 для x = −4, линия будет только вдвое короче, при y = 1/32, для x = -5. Как я часто говорю своим ученикам: «Ученик умный, калькулятор глупый». Вы должны помнить, что независимо от того, что говорит калькулятор, график все равно находится выше оси x ; значения и по-прежнему положительны, хотя и очень, очень, очень малы.
Как я часто говорю своим ученикам: «Ученик умный, калькулятор глупый». Вы должны помнить, что независимо от того, что говорит калькулятор, график все равно находится выше оси x ; значения и по-прежнему положительны, хотя и очень, очень, очень малы.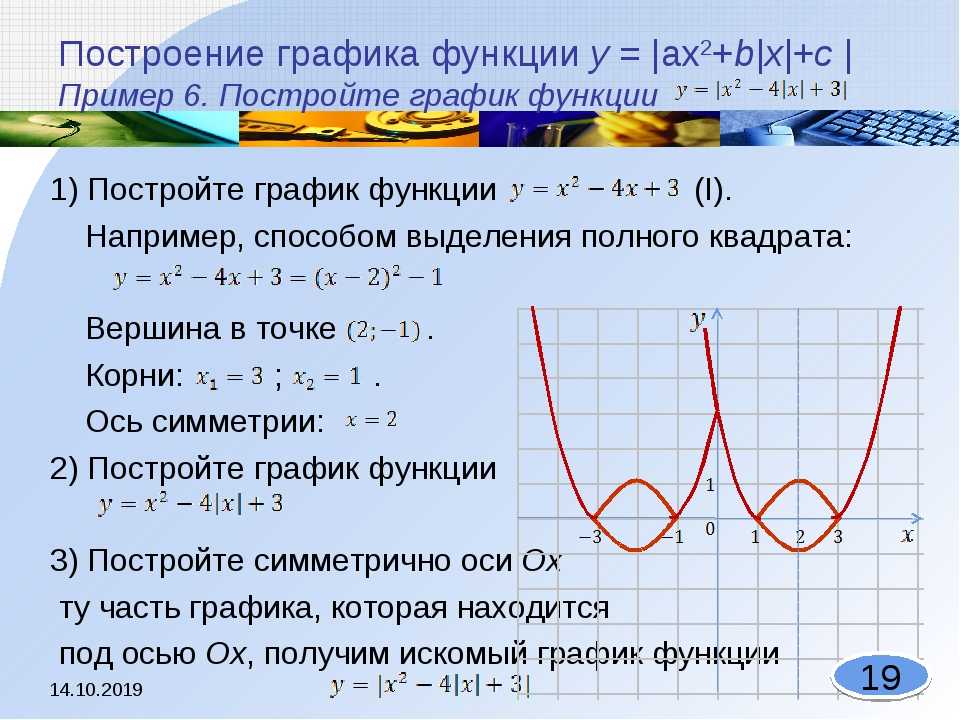 Вот почему я подробно рассказал об общей форме и поведении экспоненты: вам понадобятся эти знания, чтобы помочь вам в построении графика, поэтому убедитесь, что вы достаточно хорошо его понимаете.
Вот почему я подробно рассказал об общей форме и поведении экспоненты: вам понадобятся эти знания, чтобы помочь вам в построении графика, поэтому убедитесь, что вы достаточно хорошо его понимаете.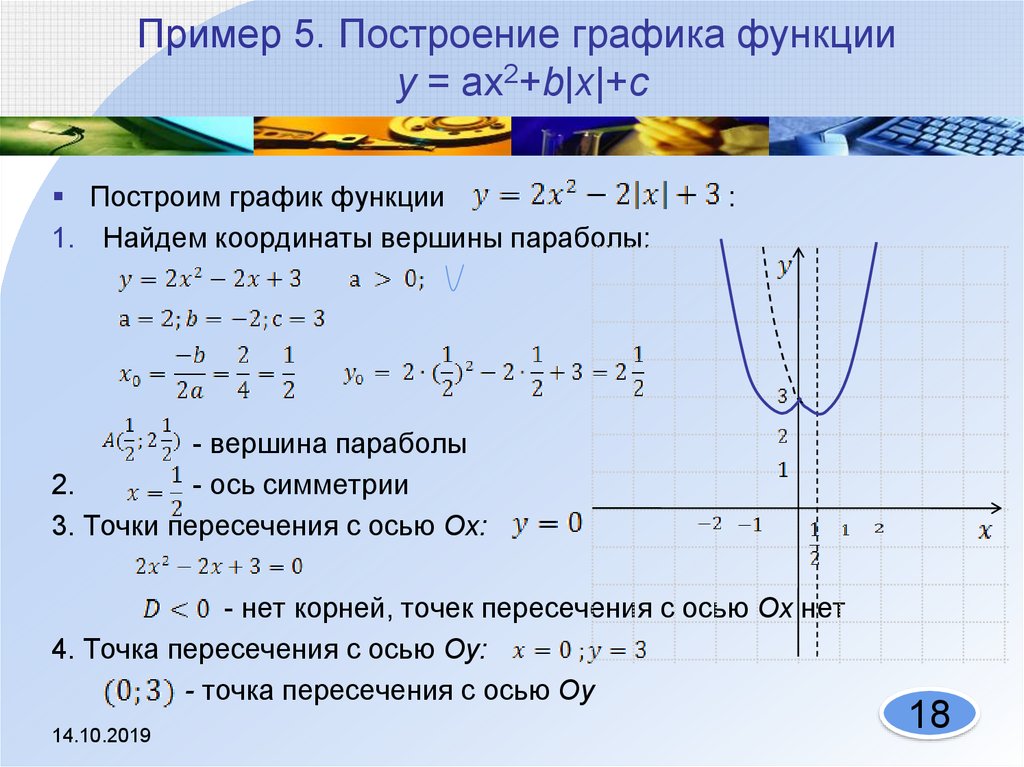 Он позволяет пользователю отображать и маркировать точки на декартовой плоскости, демонстрировать решения уравнений и неравенств, графически отображать функции и создавать регрессионные модели из наборов данных, среди прочих возможностей. Он имеет мощный встроенный инструмент калькулятора и инструмент ползунка, который позволяет пользователю создавать динамические визуальные эффекты, иллюстрирующие изменения или привлекающие внимание к определенным компонентам.
Он позволяет пользователю отображать и маркировать точки на декартовой плоскости, демонстрировать решения уравнений и неравенств, графически отображать функции и создавать регрессионные модели из наборов данных, среди прочих возможностей. Он имеет мощный встроенный инструмент калькулятора и инструмент ползунка, который позволяет пользователю создавать динамические визуальные эффекты, иллюстрирующие изменения или привлекающие внимание к определенным компонентам.
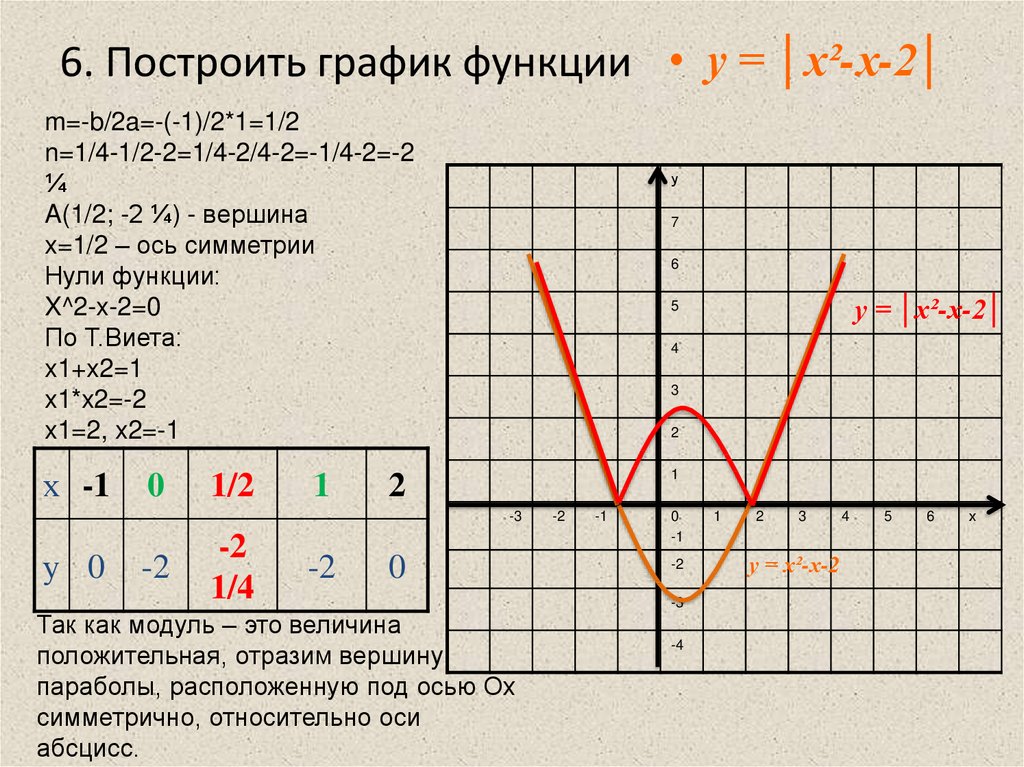 Предложите учащимся ознакомиться с учебными пособиями по графическим инструментам Desmos
Предложите учащимся ознакомиться с учебными пособиями по графическим инструментам Desmos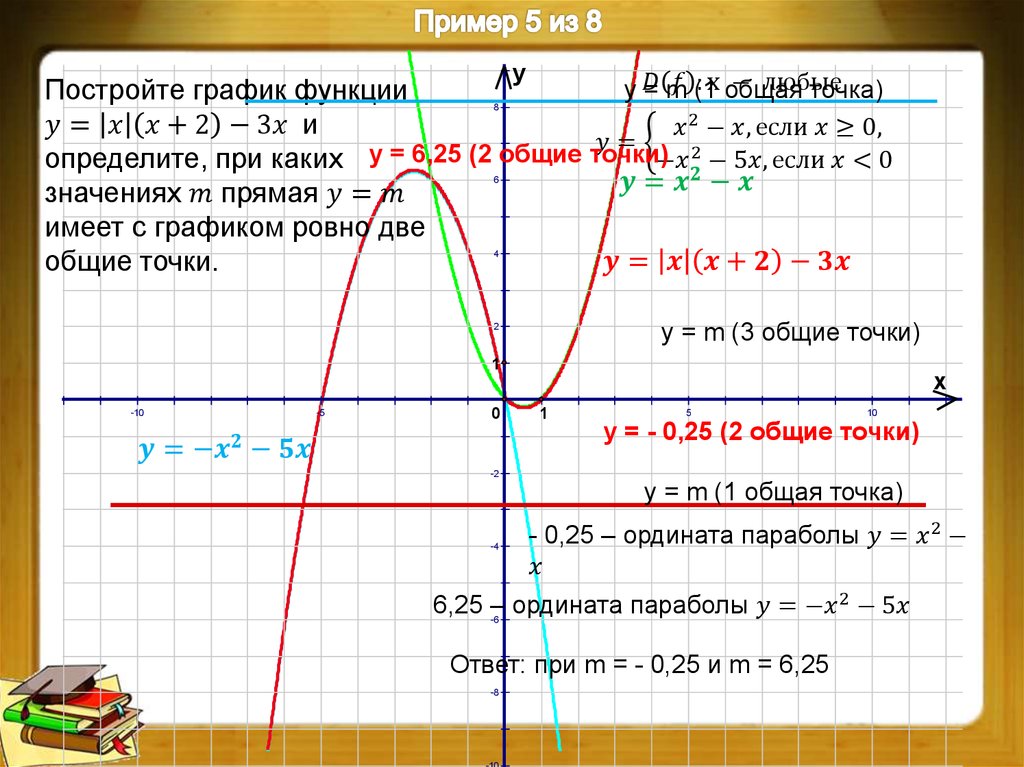
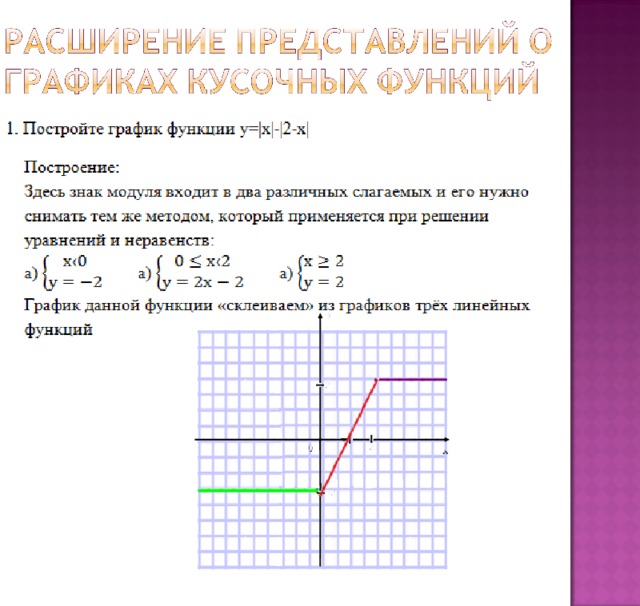
 «Моделирование динамики населения на основе запросов с помощью логистических дифференциальных и разностных уравнений». ПРИМУС 29.6 (2019): 553–570. Веб.
«Моделирование динамики населения на основе запросов с помощью логистических дифференциальных и разностных уравнений». ПРИМУС 29.6 (2019): 553–570. Веб.
 Подставим эти значения в наше выражение… и получим произведение двух линейных множителей, первый из которых равен разности между икс и первым корнем, второй – разности между икс и вторым корнем.
Подставим эти значения в наше выражение… и получим произведение двух линейных множителей, первый из которых равен разности между икс и первым корнем, второй – разности между икс и вторым корнем. При этих значениях.. икс обращается в нуль и трехчлен а икс квадрат плюс бэ икс плюс цэ, то есть числа минус эм деленное на ка и ку деленное на пэ, являются его корнями. Мы пришли к противоречию, так как по условию этот трехчлен корней не имеет.
При этих значениях.. икс обращается в нуль и трехчлен а икс квадрат плюс бэ икс плюс цэ, то есть числа минус эм деленное на ка и ку деленное на пэ, являются его корнями. Мы пришли к противоречию, так как по условию этот трехчлен корней не имеет. Оба его корня равны двум. Значит, трехчлен можно представить в виде произведения числа минус пять и двух равных линейных множителей икс минус два. Это выражение мы можем записать как произведение числа минус пять и квадрата разности чисел икс и два.
Оба его корня равны двум. Значит, трехчлен можно представить в виде произведения числа минус пять и двух равных линейных множителей икс минус два. Это выражение мы можем записать как произведение числа минус пять и квадрата разности чисел икс и два.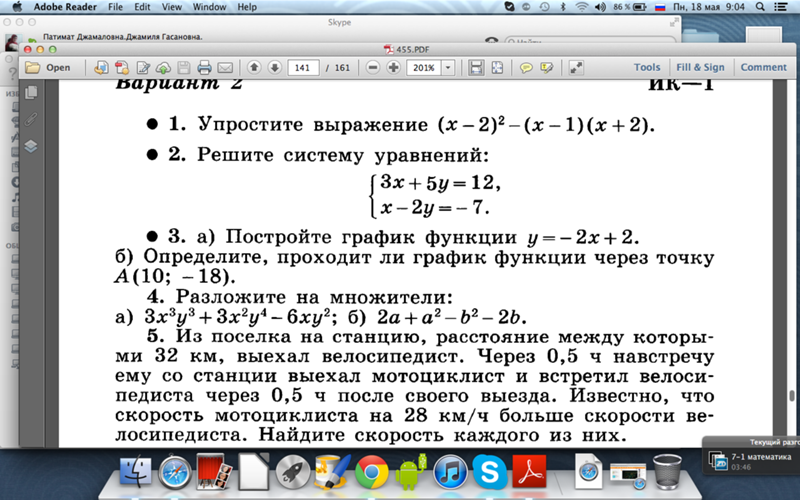
 (“Иван-царевич и серый волк” Русская народная сказка). Здесь от выбора зависит
жизнь Ивана-царевича.
(“Иван-царевич и серый волк” Русская народная сказка). Здесь от выбора зависит
жизнь Ивана-царевича. индийским математиком и астрономом Ариабхаттой. Другим индийским ученым,
Брахмагупта в VII веке было изложено общее правило решения квадратных
уравнений, приведенных к единой канонической форме: .
В
уравнении коэффициенты, кроме параметра a, могут быть и отрицательными. В
теоретической части книги «Китаб аль-джебр ва-ль-мукабала» Аль-Хорезми дает
классификацию линейных и квадратных уравнений с параметрами. Автор выделяет 6
видов уравнений, выражая их следующим образом:
индийским математиком и астрономом Ариабхаттой. Другим индийским ученым,
Брахмагупта в VII веке было изложено общее правило решения квадратных
уравнений, приведенных к единой канонической форме: .
В
уравнении коэффициенты, кроме параметра a, могут быть и отрицательными. В
теоретической части книги «Китаб аль-джебр ва-ль-мукабала» Аль-Хорезми дает
классификацию линейных и квадратных уравнений с параметрами. Автор выделяет 6
видов уравнений, выражая их следующим образом: Итальянские математики Тарталья, Кардано,
Бомбелли среди первых в ХII в. учитывают, помимо положительных, и отрицательные
корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых
способ решения квадратных уравнений принял современный вид.
Итальянские математики Тарталья, Кардано,
Бомбелли среди первых в ХII в. учитывают, помимо положительных, и отрицательные
корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых
способ решения квадратных уравнений принял современный вид. Поэтому, количество корней
квадратного уравнения равно количеству нулей соответствующей квадратичной
функции, а значит и количеству общих точек параболы и оси абсцисс.
Поэтому, количество корней
квадратного уравнения равно количеству нулей соответствующей квадратичной
функции, а значит и количеству общих точек параболы и оси абсцисс. 
 Найдите все значения
параметра m, при которых один из корней уравнения находится между числами 0 и 2, а второй
– между числами 3 и 5.
Найдите все значения
параметра m, при которых один из корней уравнения находится между числами 0 и 2, а второй
– между числами 3 и 5.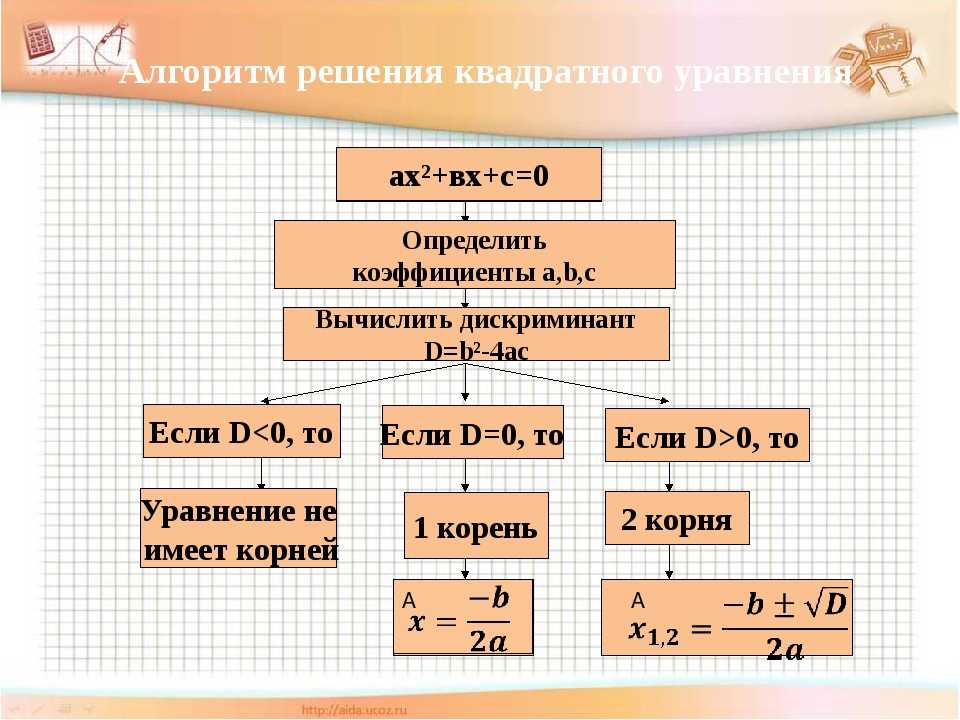 __________________________________________________________________
__________________________________________________________________ А стало быть, искомыми значениями
параметра a являются решения системы неравенств:
А стало быть, искомыми значениями
параметра a являются решения системы неравенств: Поскольку, согласно условию задачи, число
2 находится между корнями заданного квадратного уравнения, то парабола должна пересекать ось абсцисс в точках,
расположенных по разные стороны от точки этой оси с координатой 2 (смотри
рисунок 1). А значит, рисунок 1 – перевод условия данной задачи на графический
язык.
Поскольку, согласно условию задачи, число
2 находится между корнями заданного квадратного уравнения, то парабола должна пересекать ось абсцисс в точках,
расположенных по разные стороны от точки этой оси с координатой 2 (смотри
рисунок 1). А значит, рисунок 1 – перевод условия данной задачи на графический
язык. Решите это неравенство самостоятельно
Решите это неравенство самостоятельно
 __________________________________________________________________
__________________________________________________________________

 А значит, следующая
система полностью описывает рисунок 3.
А значит, следующая
система полностью описывает рисунок 3. Система гарантирует
расположение нулей
Система гарантирует
расположение нулей
 Искомые значения
параметра a образуют множество__________________
Искомые значения
параметра a образуют множество__________________



 Очень полезное знание, учитывая, что смотря на параболу, исключительно визуально, мы понимаем что у нас может быть 3 случая:
Очень полезное знание, учитывая, что смотря на параболу, исключительно визуально, мы понимаем что у нас может быть 3 случая: Получается, что это условие инвариантно относительно положения параболы. Но тем оно лучше.
Получается, что это условие инвариантно относительно положения параболы. Но тем оно лучше.

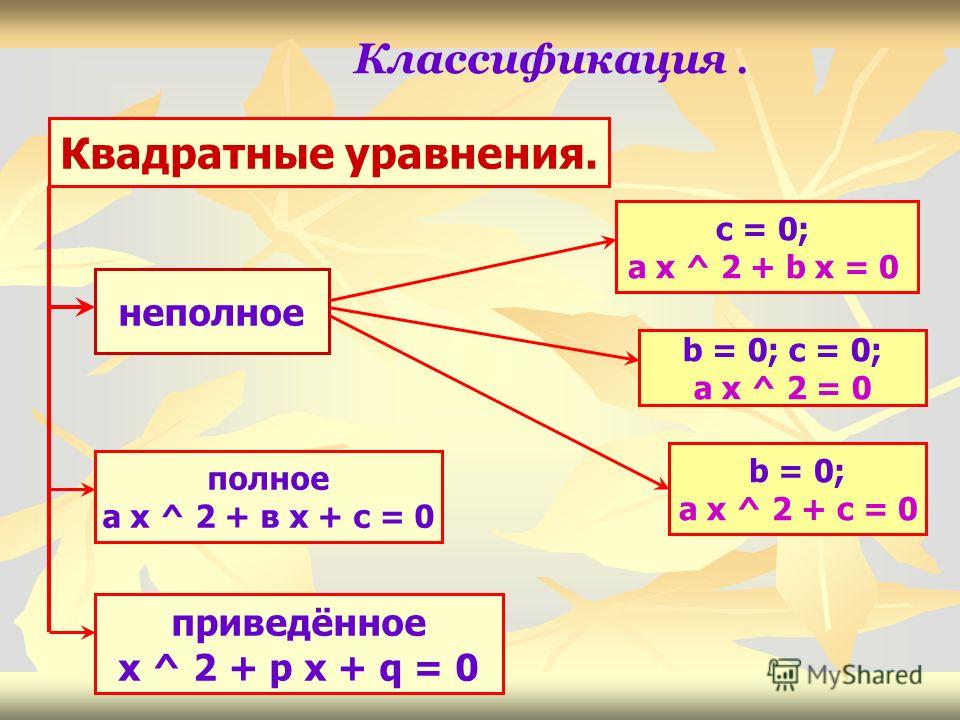 9{2} + Ьх + с = 0\)
9{2} + Ьх + с = 0\) 1
1 1 являются частью решений NCERT для математики класса 10. Здесь мы дали решения NCERT для математики класса 10, глава 4, квадратные уравнения, пример 4.1.
1 являются частью решений NCERT для математики класса 10. Здесь мы дали решения NCERT для математики класса 10, глава 4, квадратные уравнения, пример 4.1.
 Нам нужно найти скорость поезда.
Нам нужно найти скорость поезда. 
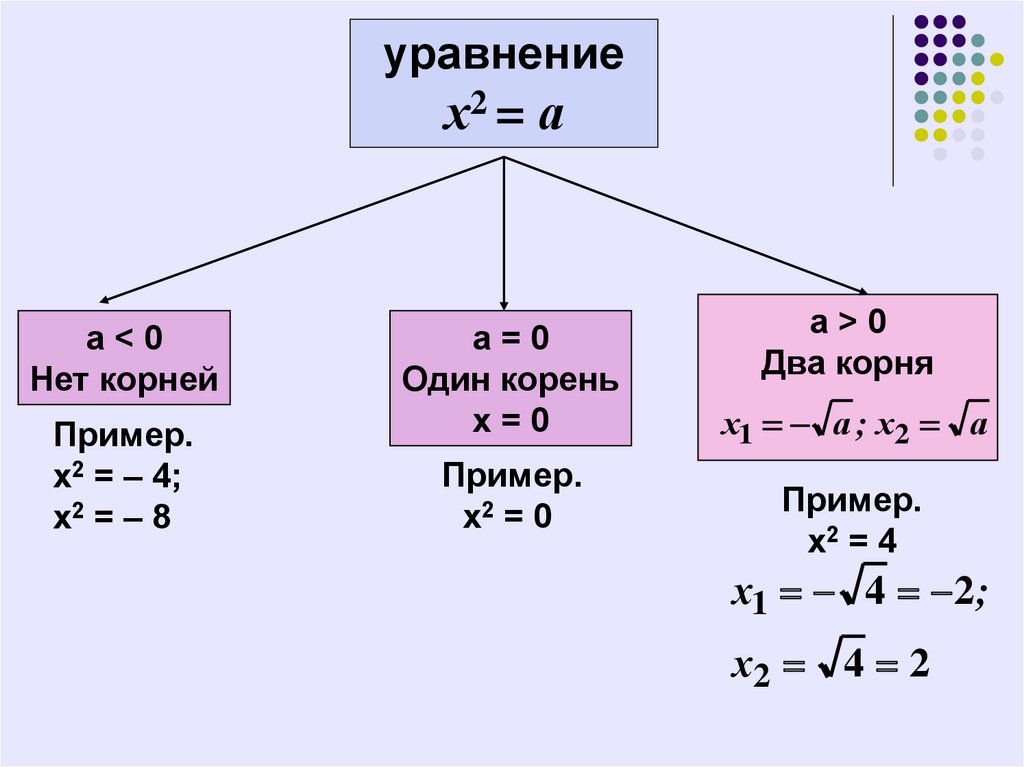 (i) должно быть равно произведению 2-го и 3-го членов того же уравнения.
(i) должно быть равно произведению 2-го и 3-го членов того же уравнения.