Таблица умножения на 3 — умножение числа 3 на 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Сколько будет трижды три? Девять. А откуда мы это знаем? Из таблицы умножения на 3. О ней и пойдет речь в этой статье.
Что такое таблица умножения на 3? Это список произведений двух множителей, один из которых постоянен и равен 3, а второй изменяется с 1 до 10. Результат такого произведения надо запомнить.
Содержание
Описание
Итак, перечислим все произведения и запишем их в виде списка:
3·1=3
3·2=6
3·3=9
3·4=12
3·5=15
3·6=18
3·7=21
3·8=24
3·9=27
3·10=30
Что означает эта таблица? Это повторяющееся сложение:
3·1=3
3·2=3+3=6
3·3=3+3+3=9
3·4=3+3+3+3=12
3·5=3+3+3+3+3=15
3·6=3+3+3+3+3+3=18
3·7=3+3+3+3+3+3+3=21
3·8=3+3+3+3+3+3+3+3=24
3·9=3+3+3+3+3+3+3+3+3=27
3·10=3+3+3+3+3+3+3+3+3+3=30
Когда вы будете учить таблицу умножения, то просто учите ее по частям — сначала три примера, потом повторите их так, что почувствуете что хорошо запомнили. Затем возьмите еще три примера, выучите только их, повторите. Теперь повторите уже шесть примеров. Затем добавьте оставшиеся четыре и повторите все шаги по запоминанию. Многократное повторение позволит вам легко и быстро все выучить. Для этого вы также можете использовать тренажеры.
Затем возьмите еще три примера, выучите только их, повторите. Теперь повторите уже шесть примеров. Затем добавьте оставшиеся четыре и повторите все шаги по запоминанию. Многократное повторение позволит вам легко и быстро все выучить. Для этого вы также можете использовать тренажеры.
Таблица Пифагора
Распространенный вид таблицы умножения — список. Но есть, действительно, таблица — со строками и столбцами. Она называется таблица Пифагора.
И выглядит так:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
Произведение находится на пересечении строки и столбца таблицы. В строке указывается первый множитель, в столбце — второй множитель.
В строке указывается первый множитель, в столбце — второй множитель.
Попробуйте сами заполнить строки и столбцы, на пересечении строки и столбцов должны стоять произведения чисел:
Попробуй свои знания таблицы умножения на 3 на нашем тренажере.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 3 |
Интересные факты
Интересные факты о таблице умножения на 3:
Сумма любых двух чисел из таблицы умножения на 3 всегда кратна 3. Действительно, сумма 3 и 6 равна 9, что кратно 3.
Можно использовать для решения задач с дробями. Например, чтобы найти 3/6, мы можем сократить числитель и знаменатель на 3 и получим ½=0,5. Следовательно, 3/6 = 0,5.
Если сложить цифры каждого из чисел в результате умножения, то получатся числа 3, 6, 9, 3, 6, 9,3, 6,9. Эта закономерность продолжается для всей таблицы умножения на 3:
3·1=3
3·2=6
3·3=9
3·4=12 (1+2=3)
3·5=15 (1+5=6)
3·6=18 (1+8=9)
3·7=21 (2+1=3)
3·8=24 (2+4=6)
3·9=27 (2+7=9)
3·10=30 (3+0=3)
Это свойство известно как «признак делимости» на 3.
Это может быть полезно для быстрого определения, является ли число кратным 3, без необходимости выполнять фактическое умножение.
Умножение на 3 можно применить к умножению на 6.
Действительно, умножим шесть на шесть.
Мы можем записать 6·4=3·2·4=3·8=24
То есть результат в умножении на 3 надо просто умножить на 2, чтобы получить результат умножения на 6
3·8=24
6·8=2·24=48
Деление
Так как деление — это обратная операция умножению, то 3 разделить на 3 будет 1. Составить таблицу деления на 3 :
3:3=1
6:3=2
9:3=3
12:3=4
15:3=5
18:3=6
21:3=7
24:3=8
27:3=9
30:3=10
Примеры применения
Решим несколько задач.
Задача 1. На первой грядке посадили 3 куста сирени, а на второй в пять раз больше, потому что она было подлиннее. Сколько кустов сирени посадили на второй грядке?
Решение:
Если в задаче стоит вопрос с предлогом «в», значит, речь идет об умножении или о делении.
«В …раз больше» — умножаем, «в … раз меньше» — делим.
У нас «в пять раз больше», значит, число кустов сирени на первой грядке умножаем на 5:
3·5=15
Ответ: 15
Задача 2. У Наташи было 15 бантиков, а у Маши в 3 раза меньше. Сколько бантиков было у Маши?
Решение: У Маши по условию задачи было «в 3 раза меньше, чем у Наташи». Значит, мы должны количество бантиков Наташи разделить на 3:
15:3=5 бантиков было у Маши.
Ответ: 5 бантиков .
Задача 3
Если у вас есть 3 яблока и вы хотите разделить их поровну на 3-х ваших друзей, сколько яблок получит каждый из друзей?
Решение:
Каждый из друзей получит 3:3= 1 яблоко.
Ответ: 1 яблоко.
Задача 4
Если у вас есть 6 уток и вы хотите разделить их на группы по 3 утки в каждой, сколько групп у вас будет?
Решение:
У вас будет 6:3=2 группы.
Ответ: 2 группы.
Задача 5
Если у вас есть 9 шариков и вы хотите разделить их поровну между 3 людьми, сколько шариков достанется каждому?
Решение:
Каждый человек получит 9 : 3 = 3 шарика.
Ответ: 3 шарика.
Задача 6
Ответьте на вопросы.
- 3 раза по 4 это какое число? Решение: 3 раза по 4 будет 12.
- 3 раза по 7 это какое число? Решение: 3 раза по 7 будет 21.
- 3 раза по 9 это какое число? Решение: 3 раза по 9 будет 27.
Задача 7
Рабочий в Индии зарабатывает по 3 рупии в час, сколько денег он заработает за 8 часов работы?
Решение: рабочий заработает 3 8=24 рупии.
Ответ: 24 рупии.
Задача 8
Найдите результат 12 умножить на 12 (для второклассников).
Решение: 12=3·4, а второй множитель представим в виде 12=10+2
Получается, 12·12= 3·4 (10+2)= 3·4·10+3·4·2=3·4·10+3·4·2=12·10+12·2=120+12+12=132+12=144.
Мы знаем, что чтобы умножить на 10 — это просто приписать ноль в конце числа.
Здесь мы использовали свойство: a·b=a (c+d), если b=c+d.
Ответ: 144.
Если вы поняли тему и готовы уже приступить к запоминанию, то используйте наши тренажеры. Начинать лучше с того тренажера, в котором второй множитель располагается по возрастанию.
Где применяется
Учить таблицу необходимо, она есть везде. Вот часть разделов математики, где ее знание просто необходимо:
- Арифметика
- Алгебра
- Геометрия
- Тригонометрия
- Статистика
- Вероятность
- Дискретная математика
- Комбинаторика
- Теория чисел
- Теория графов
- Теория игр
- Математическое моделирование
- Дифференциальные уравнения
- Линейная алгебра
- Функциональный анализ
- Векторное исчисление
- Комплексный анализ
- Тензорный анализ
- Математическая логика и теория множеств.

Арифметику, алгебру, геометрию, тригонометрию, комбинаторику, вероятность проходят в школе, а остальные разделы в ВУЗе. Таблица умножения — это фундаментальное знание в математике. На нем будет строиться ваша успеваемость в алгебре, геометрии, тригонометрии и других разделах математики.
Онлайн тренажеры таблицы умножения на 3
Онлайн тренажер по возрастанию
Онлайн тренажер по убыванию
Онлайн тренажер в разброс
Онлайн тренажер — вписать ответ в окошки.
Таблица умножения
Таблица умноженияВсё о таблице умножения и способах её запоминания.
Содержание
Этот сайт посвящён таблице умножения, способам её понять и выучить, мнемотехникам для запоминания и всему, что с ней связано:
- Тренажёры и приложения
- Как выучить
- Распечатать
- Игры и развлечения
- Множители
- Виды
- История и факты
- Фото
- Видео
- Стихи и песни
В этом разделе мы собрали тренажёры, проверочные тесты и задания, которые можно проходить онлайн, чтобы тренировать навыки умножения.
- Онлайн-тренажёр
- Кому подходят тренажеры?
- Как правильно повторять?
- Что еще важно знать?
- Как учить таблицу умножения?
- Техники и лайфхаки для запоминания и проверки таблицы умножения
- Проверка знания таблицы умножения
- Задания на таблицу умножения
- Приложения
- Интерактивная таблица умножения
- Проверочные тесты
Для быстрого и лёгкого запоминания таблицы Пифагора существуют способы, приёмы и мнемотехники, которые вы сможете найти в специальном разделе на сайте.
- Как выучить легко и быстро
- Законы умножения
- Свойства умножения
- Что такое умножение
- Презентация таблицы умножения
- Таблица умножения на пальцах
- Зачем учить таблицу умножения?
- Книга Узоровой О.В. «Таблица умножения за 3 дня»
- Таблица умножения в игровой форме
- Мнемотехники
- Способы выучить таблицу умножения
Часть родителей и педагогов предпочитают обучать детей таблице умножения с помощью печатных материалов: таблиц, карточек, мнемокарточек, самодельных игр. Это особенно актуально, если ребенок проводит слишком много времени в гаджетах.
Это особенно актуально, если ребенок проводит слишком много времени в гаджетах.
- Карточки по таблице умножения
- Таблица умножения
- Примеры из таблицы умножения без ответов
- Таблица умножения без ответов вразброс
- Таблица умножения А4
- Таблица умножения на 12
- Сделай таблицу умножения
- Игра на пальцы
Учить таблицу умножения можно и в игровой форме с помощью стихов, песен, раскрасок. Когда процесс обучения идёт играючи, удовольствие получает и ребёнок, и родитель или педагог.
- Настольные игры
- Приложения для Android и iOS
- Компьютерные игры
- Дополнительные инструменты
- Игра «Monkey Multiplier»
- Игры для запоминания таблицы умножения
- Раскраска таблицы умножения
Чтобы запомнить таблицу Пифагора, удобно делить задачу на части, другими словами, учить умножения на конкретные множители по отдельности. Мы собрали материалы и тренажёры для каждого множителя на отдельной странице.
Мы собрали материалы и тренажёры для каждого множителя на отдельной странице.
- Умножение на 0
- Умножение на 1
- Умножение на 2
- Умножение на 3
- Умножение на 4
- Умножение на 5
- Умножение на 6
- Умножение на 7
- Умножение на 8
- Умножение на 9
- Умножение на 10
- Умножение на 11
- Умножение на 12
- Умножение до 20, 30 и 100
Существует множество видов таблиц умножения. Мы подробно разбираем каждый по отдельности в данном разделе.
- Китайская таблица умножения
- Таблица умножения и деления
- Древняя таблица умножения на фрагментах бамбуковых полосок
- Таблица на костях Напьера
- Таблица Пифагора
- Древнерусское умножение
- Таблица сокращенного умножения
- Умножение на пальцах
- Пирамида умножения
- Арийское умножение
- Ведический квадрат
- Китайское умножение с линиями
- Японское умножение с кругами
- Умножение степеней
- Умножение дробей
- Сокращённое умножение
- Умножение в столбик
Самые старые из известных таблиц умножения использовались вавилонянами около 4000 лет назад. С тех пор таблицы умножения менялись, совершенствовались, переосмысливались. В этом разделе вы найдете много интересных фактов из истории таблиц умножения.
С тех пор таблицы умножения менялись, совершенствовались, переосмысливались. В этом разделе вы найдете много интересных фактов из истории таблиц умножения.
- История таблицы умножения
- Кто придумал таблицу умножения
- Интересные факты
- День таблицы умножения — 2 октября
- Таблица Пифагора и таблица умножения
- В каком классе учат таблицу умножения?
Мы предлагаем вам небольшую подборку стихов о таблице умножения от разных авторов, а также полезные советы в использовании этого метода для родителей и педагогов:
- Стихи и песни о таблице умножения
- Таблица умножения в стихах — Андрей Усачев
- Таблица умножения — Марина Казарина
- Таблица умножения — Тим Собакин
- Двойка за урок – беда — Владимир Трофимов
- Умножения таблицу — Юлия Прокопьева
- Музыкальные таблицы умножения
В этом разделе мы собираем различные фотографии таблиц умножения, мемы, гифки, ведь это тоже часть современной культуры изучения пифагоровой таблицы.
- Древние версии таблицы умножения на камнях
- Таблица умножения на папирусе в Древнем Китае
- Таблица на костях Непера
- Таблица Пифагора
- Древнерусская таблица умножения
- Машина Паскаля
- Арифмометры, помогающие умножать
- Таблица умножения на задней стороне тетради
- Как выглядела таблица умножения в СССР
- Как умножают в Китае
- Футболки с таблицей умножения
- Настольные игры для запоминания таблицы умножения
- Компьютерные игры
- Игры и приложения для смартфонов
- Кубики с таблицей умножения
- Распечатки для изучения таблиц умножения
- «Лягушка» игра на пальцы
- Круги для умножения
- Шпаргалки с таблицей умножения
- Мемы с таблицей умножения
Изучать таблицу умножения, а также узнавать педагогические методики, помогающие с ней работать, можно и видеоформате. Для этого на сайте есть подборки видео роликов, посвященных данной теме.
Для этого на сайте есть подборки видео роликов, посвященных данной теме.
- Таблица умножения. Круто!
- Устный счет. Как легко и быстро умножать в уме числа до 100 и до 1000
- 10 глупых вопросов математику
- Можно ли доверять математике?
- Лайфхак как быстро выучить таблицу умножения
- Самые важные идеи математики
- Как объяснить деление в столбик? Деление чисел уголком
- Как стать лучше в математике
- Как выучить таблицу умножения за 3 дня
- Зачем нужна математика?
- Музыкальные таблицы умножения
Что такое таблицы умножения? Определение, таблицы умножения, пример
Введение
Таблица умножения — это список кратных числу. Можно получить таблицу умножения любого числа, добавляя одно и то же число на каждом следующем шаге. Например, если мы хотим разработать таблицу времени для 2, мы начинаем с 2, а затем прибавляем 2 на каждом шаге. Ответ, полученный на каждом шаге, кратен 2 и известен как факт умножения.
Ответ, полученный на каждом шаге, кратен 2 и известен как факт умножения.
Вот как будет выглядеть таблица умножения на 2.
Таблица умножения 2:
Другой способ получить таблицу умножения любого числа — просто умножить это число. Например, 2 х 1 = 2, 2 х 2 = 4, 2 х 3 = 6 и так далее.
Родственные игры
Примеры таблиц умножения
Помимо 2, таблицы умножения на 5 и 10 полезны для детей. Эти числа могут помочь детям запомнить и другие таблицы умножения.
Таблица умножения на 50005
2 партии по 5 = 5 + 5 = 10
3 партии по 5 = 5 + 5 + 5 = 15
4 партии по 5 = 5 + 5 + 5 + 5 = 20 и так далее…
Раз Таблица 10
Таким же образом таблица умножения 10 требует прибавления 10 к каждому лоту.
1 партия по 10 = 10
2 партии по 10 = 10 + 10 = 20
3 партии по 10 = 20 + 10 = 30
4 партии по 10 = 30 + 10 = 40 и так далее 9005…
Взгляните на схему.
Связанные рабочие листы
Чем полезны таблицы умножения?
Запоминание таблицы умножения имеет множество преимуществ. Некоторые из них обсуждаются ниже:
Некоторые из них обсуждаются ниже:
- Учащийся, хорошо разбирающийся в таблицах умножения, может решать математические задачи на умножение быстрее, чем те, кто их не знает.
- Понимание математических понятий становится более простым для учащихся, когда они хорошо разбираются в таблицах умножения.
- Таблица умножения помогает учащимся не только умножать, но и складывать.
- Кроме того, это повышает уверенность студентов.
- Запоминание таблицы умножения также улучшает память детей.
- Таблицы умножения также необходимы для выполнения быстрых повседневных вычислений в математических задачах в классе.
Интересные факты
- Первые таблицы умножения были использованы 4000 лет назад вавилонянами.
- Раньше они использовали глиняные таблички для решения своих математических задач.
- С развитием цивилизации им понадобился более простой и легкий способ решения повседневных математических задач, таких как таблицы умножения.

Советы, как легко выучить таблицы умножения
Дети часто считают, что заучивание таблиц им не легко. Тем не менее, изучение таблицы умножения может быть простым и увлекательным с использованием соответствующих методов. Вот как:
- Сначала начните изучать простую таблицу умножения, а более сложные оставьте на потом. Например, некоторые простые таблицы умножения — это 2, 5, 9 и 10. Как только они освоят эту технику, они смогут перейти к сложным таблицам, таким как 3, 4, 7 и 8.
- Запоминание упрощается с картинками. Таблица умножения может помочь детям учиться лучше и быстрее.
- Быстрая проверка таблицы каждый день также может помочь запомнить их.
- Есть несколько приемов, которым стоит научиться за несколькими столами. Использование таких уловок может облегчить процесс.
Например:
Таблица умножения на 1:
Принятие того, кто вы есть, — это как раз то, о чем эта таблица умножения. Какое бы число вы ни умножали на 1, результатом будет само число.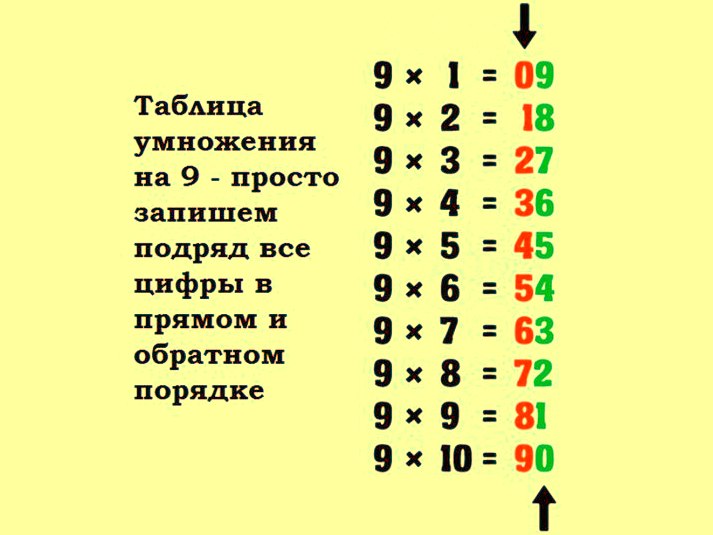
Таблица умножения 2
Число 2 — это то, что мы называем «Двойное или ничего». Любое число, которое вы умножаете на 2, удваивается или просто добавляется само к себе.
Таблица умножения на 3
Вот самый простой способ попрактиковаться в таблице умножения на 3. Если вы хотите умножить число на 3, сначала умножьте его на 2, а затем прибавьте к нему такое же число.
Таблица умножения 4
Время для удвоения удвоения. Из этого нет простого выхода. Если вы хотите умножить число на 4, удвойте его один раз, а затем удвойте то, что получится!
Таблица умножения на 5
Любое число, на которое вы хотите умножить 5, прикрепите к его концу 0, а затем половину его.
Таблица умножения на 6
Эта таблица работает как просто таблица 3. Если вы хотите найти произведение числа на 6, вернитесь к своим 5, умножьте это число на 5, а затем добавьте то же число.
Таблица умножения на 7
Самый простой трюк — не забывать добавлять группу из 7 столько раз, сколько раз мы умножаем число 7.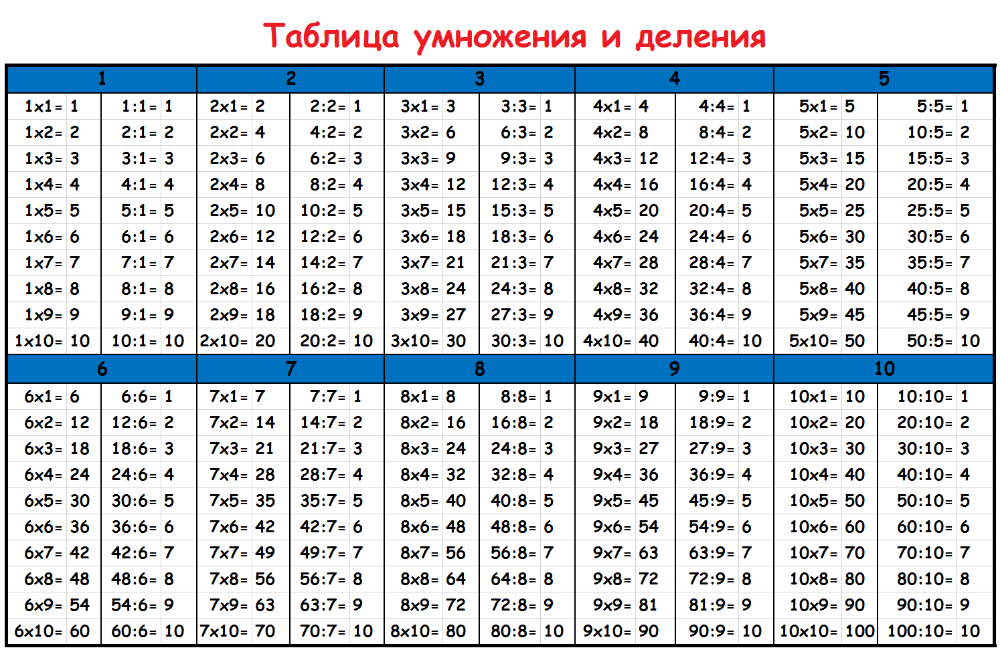
Таблица умножения на 8
Самый простой способ выучить таблицу умножения на 8 — добавить группы «8» для всех кратных, как в вашей таблице умножения на 7.
Таблица умножения на 9
Простой способ чтобы запомнить эту таблицу умножения, нужно использовать факты 10.
Чтобы умножить число на 9, добавьте ноль в конце числа, а затем вычтите то же число.
Еще одна хитрость заключается в том, что все продукты можно считать состоящими из двух столбцов. Первый столбец имеет числа от 0 до 9в порядке возрастания, а второй столбец имеет числа от 9 до 0 в порядке убывания.
Таблица умножения на 10
Это самый простой вариант. Просто добавьте ноль в конце любого числа, которое вы умножаете на 10, и вы получите ответ.
Решенные примеры
Сознательно или бессознательно таблицы умножения имеют множество повседневных применений. Рассмотрим примеры, приведенные ниже:
Пример 1:
Узнайте, что мы можем написать вместо вопросительного знака?
7×3=?
7 умножить на 3 означает 3 лота по 7 или 7 лотов по 3.
Или мы можем посчитать иначе,
день. Сколько литров молока он купил за 5 дней?
В нашей повседневной жизни мы сталкиваемся с вопросами, упомянутыми выше. Чтобы ответить на них в один миг, важно знать концепцию таблицы умножения.
Следовательно, если Сэм покупает 2 литра молока за один день, его дневное потребление составляет 2 x 1 = 2 литра.
Расчет его потребления за 5 дней составит 2 x 5 = 10 литров.
Следовательно, ответ 10 литров.
Пример 03:
Парул учится по 4 часа в день. Сколько часов она учится в неделю?
Есть 7 дней в неделю. Итак, нужно найти часы занятий Парула за 7 дней.
Обычные часы Парул, посвященные учебе, составляют 4 x 1 = 4 часа.
Количество часов, которые Парул посвящает учебе в неделю, составляет 4 х 7 = 28 часов.
Поэтому Парул учится 28 часов в неделю.
Практические задачи
1
8 раз 7 = _____ ?
56
65
45
Ничего из вышеперечисленного
Правильный ответ: 56
8 x 7 = 56
2
часовСюзан работает каждый день 5.
 Сколько часов она работает за 3 дня?
Сколько часов она работает за 3 дня?12 часов
15 часов
14 часов
10 часов
Правильный ответ: 15 часов
Количество рабочих часов Сюзан в один день = 5 x 1 = 5 часов
Количество рабочих часов Сюзан за 3 дня = 5 х 3 = 15 часов
3
Сколько будет 4 умножить на 6?
34
24
18
14
Правильный ответ: 24
4 x 6 = 24.
4
Сэм съедает 3 шоколадки за час. Сколько шоколадок он съел за 7 часов?
22
21
45
Ничего из вышеперечисленного
Правильный ответ: 21
3 x 7 = 21 шоколадка лучший контент для классов К-8. Начните учиться прямо сейчас!
Часто задаваемые вопросы
Таблица умножения и таблица умножения одинаковы?
Да, таблицы умножения также известны как таблицы умножения.
Как лучше всего выучить таблицу умножения на 9?
Растопырить перед собой все 10 пальцев. Опустите левый мизинец вниз. Теперь у вас 9 пальцев, что означает 9 х 1 = 09. Теперь, чтобы найти 9 х 2, опустите левый безымянный палец. У вас остался 1 палец, пробел и 8 пальцев, то есть 1 и 8. Это 9.x 2 = 18. Этот трюк работает для всей таблицы.
Опустите левый мизинец вниз. Теперь у вас 9 пальцев, что означает 9 х 1 = 09. Теперь, чтобы найти 9 х 2, опустите левый безымянный палец. У вас остался 1 палец, пробел и 8 пальцев, то есть 1 и 8. Это 9.x 2 = 18. Этот трюк работает для всей таблицы.
Какие таблицы умножения необходимо знать детям?
Дети до 5-го класса должны знать таблицу умножения до 12. Таблицы умножения на 2, 5 и 10 являются основными таблицами умножения, которые просты и необходимы для запоминания других таблиц умножения.
Какая самая сложная таблица умножения?
Из таблицы умножения от 1 до 10 Расписание 7 обычно считается самым трудным для изучения детьми.
Математическая таблица из 4-х — Выучить таблицу умножения для детей
- Почему вашему ребенку нужно выучить эту таблицу
- Что такое таблица умножения на 4 в математике?
- Таблица умножения на 4 для детей
- Таблица 4 умножения для детей
- Советы по изучению и запоминанию таблицы умножения 4 для детей
- Простые вопросы для детей: пересмотрите таблицу из 4
- Словесные задачи по таблице умножения на 4 для детей
- Часто задаваемые вопросы
Если учащиеся помнят свои таблицы умножения, они могут легко решать математические задачи, выполняя домашнюю работу или готовясь к тестам. В результате после изучения 2 и 3 таблиц становится важным знание таблицы умножения на 4. Эта статья содержит 4 таблицы умножения на английском языке от 1 до 20 (4 умножения на 20), которые учащиеся могут выучить и использовать для решения задач во время практики. Студенты поймут таблицу умножения 4 с последовательной практикой. Кроме того, заучивание таблиц наизусть позволяет вашему ребенку быстро выполнять умножение, что имеет решающее значение для дальнейших сложных расчетов по математике.
В результате после изучения 2 и 3 таблиц становится важным знание таблицы умножения на 4. Эта статья содержит 4 таблицы умножения на английском языке от 1 до 20 (4 умножения на 20), которые учащиеся могут выучить и использовать для решения задач во время практики. Студенты поймут таблицу умножения 4 с последовательной практикой. Кроме того, заучивание таблиц наизусть позволяет вашему ребенку быстро выполнять умножение, что имеет решающее значение для дальнейших сложных расчетов по математике.
Почему вашему ребенку необходимо выучить эту таблицу
- Когда учащийся запоминает таблицу умножения, ему легче решать математические задачи.
- Понимание таблицы четырех поможет вашему ребенку легче отслеживать четные числа.
- В реальной жизни таблица умножения на 4 часто используется во многих повседневных действиях и вычислениях.
Что такое таблица умножения на 4 в математике?
В математике таблица умножения на четыре — это таблица умножения на 4, которую можно выразить с помощью различных математических операций, включая сложение и умножение. Взгляните на четыре таблицы ниже, чтобы лучше понять, как это может быть выражено в различных операциях.
Взгляните на четыре таблицы ниже, чтобы лучше понять, как это может быть выражено в различных операциях.
| 4 х 1 = 4 | 4 |
| 4 х 2 = 8 | 4+4=8 |
| 4 х 3 = 12 | 4+4+4=12 |
| 4 х 4 = 16 | 4+4+4+4=16 |
| 4 х 5 = 20 | 4+4+4+4+4=20 |
| 4 х 6 = 24 | 4+4+4+4+4+4=24 |
| 4 х 7 = 28 | 4+4+4+4+4+4+4=28 |
| 4 х 8 = 32 | 4+4+4+4+4+4+4+4=32 |
| 4 х 9 = 36 | 4+4+4+4+4+4+4+4+4=36 |
| 4 х 10 = 40 | 4+4+4+4+4+4+4+4+4+4=40 |
| 4 х 11 = 44 | 4+4+4+4+4+4+4+4+4+4+4=44 |
| 4 х 12 = 48 | 4+4+4+4+4+4+4+4+4+4+4+4=48 |
Таблица умножения 4 для детей
По мере развития ребенка ему необходимо выучить таблицу от 4 до 20. Вот таблица от 4 до 20, чтобы помочь вашему ребенку выучить ее с легкостью.
| 4 х 1 = 4 | 4 х 11 = 44 |
| 4 х 2 = 8 | 4 х 12 = 48 |
| 4 х 3 = 12 | 4 х 13 = 52 |
| 4 х 4 = 16 | 4 х 14 = 56 |
| 4 х 5 = 20 | 4 х 15 = 60 |
| 4 х 6 = 24 | 4 х 16 = 64 |
| 4 х 7 = 28 | 4 х 17 = 68 |
| 4 х 8 = 32 | 4 х 18 = 72 |
| 4 х 9 = 36 | 4 х 19 = 76 |
| 4 х 10 = 40 | 4 х 20 = 80 |
Таблица умножения на 4 для детей
Таблицу умножения на четыре легко выучить, а самый быстрый способ выучить таблицу умножения на четыре — запомнить ее. Чтобы помочь вашему ребенку запомнить четыре таблицы умножения, используйте приведенные ниже схемы таблицы умножения на 4. Вы можете сделать его наглядным, разместив в таком месте, где ребенок может легко его увидеть, помогая ему пересматривать таблицу.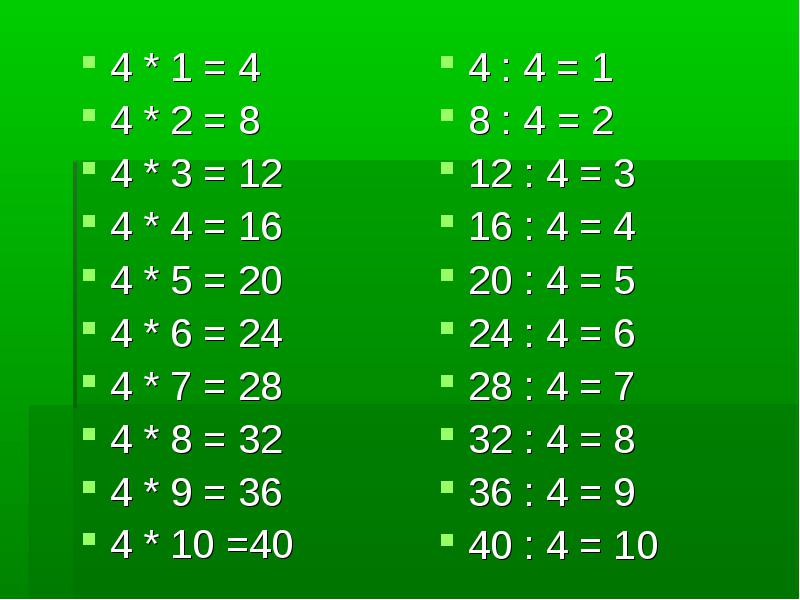
Таблица умножения на 4 До 10
Визуальное представление любого понятия является хорошим способом обучения. Упомянутая выше таблица четырех умножений до 10.
Таблица умножения на 4 до 20
Поскольку вашему ребенку удобно пользоваться таблицей умножения на 4 до 10, вы можете познакомить его с таблицей умножения на 4 до 20. Найдите график для этого выше.
Советы по изучению и запоминанию таблицы умножения на 4 для детей
Некоторым детям может быть сложно запомнить таблицу умножения на четыре, и им может потребоваться помощь в ее изучении. Вот несколько трюков с таблицей умножения на 4, стратегии, методы и математические игры для обучения, которые предоставят вашим детям простой способ выучить таблицу умножения на 4. Это поможет родителям в обучении таблицы умножения на 4 своих детей в веселый способ.
- Использование реальных предметов для обучения: После изучения таблиц умножения на 2 и 3 дети понимают основные понятия умножения к тому времени, когда они изучают таблицу умножения на 4.
 Они понимают, что при умножении одного числа на другое результат умножается на множитель. Это упрощает запоминание таблицы четырех. Если у вашего ребенка все еще есть проблемы, продемонстрируйте ему, как умножать на четыре с реальными предметами. Например, соберите и положите перед ребенком три маленькие кучки шариков, по 4 шарика в каждой. Теперь попросите ребенка сосчитать количество шариков в каждой кучке. Теперь объясните им, что у них три раза по 4 шарика. Это означает, что у них есть 4 + 4 + 4 шарика, что равно 12 шарикам.
Они понимают, что при умножении одного числа на другое результат умножается на множитель. Это упрощает запоминание таблицы четырех. Если у вашего ребенка все еще есть проблемы, продемонстрируйте ему, как умножать на четыре с реальными предметами. Например, соберите и положите перед ребенком три маленькие кучки шариков, по 4 шарика в каждой. Теперь попросите ребенка сосчитать количество шариков в каждой кучке. Теперь объясните им, что у них три раза по 4 шарика. Это означает, что у них есть 4 + 4 + 4 шарика, что равно 12 шарикам. - Показать связь между таблицами 2 и 4: Изучать таблицу умножения на 2 проще для детей. Вы можете показать связь между таблицами 2 и 4, выполнив простое упражнение. Во-первых, попросите ребенка сделать три столбца на бумаге и назвать их столбцами 1, 2 и 3. На втором этапе попросите их написать 2 раза таблицу в столбце 1. На третьем этапе попросите их еще больше умножить полученное произведение на 2. Каким бы ни был ответ, обратите внимание, что в столбце 3.
 У вас будет таблица умножения на 4. Ниже приведен пример того же самого.
У вас будет таблица умножения на 4. Ниже приведен пример того же самого.
| Столбец 1 | Столбец 2 | Столбец 3 |
| 2 х 1= 2 | 2 х 2= 4 | 4 х 1= 4 |
| 2 х 2= 4 | 4 х 2= 8 | 4 х 2= 8 |
| 2 х 3= 6 | 6 х 2= 12 | 4 х 3= 12 |
| 2 х 4= 8 | 8 х 2= 16 | 4 х 4 = 16 |
| 2 х 5= 10 | 10 х 2=20 | 4 х 5= 20 |
| 2 х 6= 12 | 12 х 2= 24 | 4 х 6 = 24 и т. |
- Для совершенствования таблицы четырех требуется практика: Единственный способ для вашего ребенка выучить таблицу умножения четырех — это практика. Напишите на бумаге таблицу четырехкратного умножения и попросите ребенка прочитать ее вслух. Поощряйте ребенка регулярно заполнять рабочие листы, чтобы помочь им вспомнить, что они узнали. Вознаграждайте их за заполнение тренировочного листа и правильный ответ на вопрос. Проверьте их математические способности, проверяя их время от времени.
Простые вопросы для детей: повторение таблицы из 4-х
Повторение очень важно для детей, чтобы запомнить то, что они изучают. Вот несколько простых вопросов, которые вы можете задать своим детям, чтобы повторить таблицу 4.
- Что такое 4 x 4?
Ответ: 16
- Перечислите все двузначные числа, кратные 4, под номером 25
Ответ: 12, 16, 20, 24
- Заполните пропуски
a) _ x 4 = 32,
Ответ: равно 8
b) 4 x _ = 56
Ответ: равно 14
- Сколько будет 8 раз?
- 90 90 90 90
18, 2, 13, 24, 56, 27, 20, 37, 32, 48
Ответ: равно 24, 56, 20, 32 и 48
Ответ: 32
Словесные задачи по таблице умножения на 4 для детей
В предыдущем разделе мы видели несколько простых вопросов на повторение. Теперь давайте рассмотрим некоторые сложные словесные задачи, которые помогут вашим детям углубить понимание таблицы четырех.
Теперь давайте рассмотрим некоторые сложные словесные задачи, которые помогут вашим детям углубить понимание таблицы четырех.
1. Сколько всего печенья, если есть 10 упаковок печенья, по 4 печенья в каждой?
Решение: Используя многократное сложение, мы получаем 4+4+4+4+4+4+4+4+4+4=40.
Тогда 10 умножить на 4, т. е. 10 × 4 = 40.
Следовательно, имеется 40 бисквитов.
2. В коробке четыре груши. Сколько груш будет в 5 ящиках?
Решение: Используя многократное сложение, мы получим 4+4+4+4+4 = 20
Тогда 5 умножить на 4, т. е. 4 × 5 = 20
Следовательно, груш 20.
3. Найдите значение ‘x’ с помощью таблицы умножения на 4, если x умножить на 4 = 36. значение x равно 9.
Часто задаваемые вопросы
Вот некоторые часто задаваемые вопросы о таблице 4s.
1. Как получить таблицу 4?
Как объяснялось выше, таблица 4 получается путем многократного добавления числа 4 к предыдущему ответу, например:
4 x 1 = 4
4 x 2 = прибавление 2 два раза = (4+4)= 8
4 x 3 = прибавление 2 три раза = (4+4+4) = 12
4 x 4 = прибавление 2 четыре раза = (4+4+4+4) = 16
4 x 5 = прибавление 2 пять раз = (4+4+4+4+4) = 20 и так далее.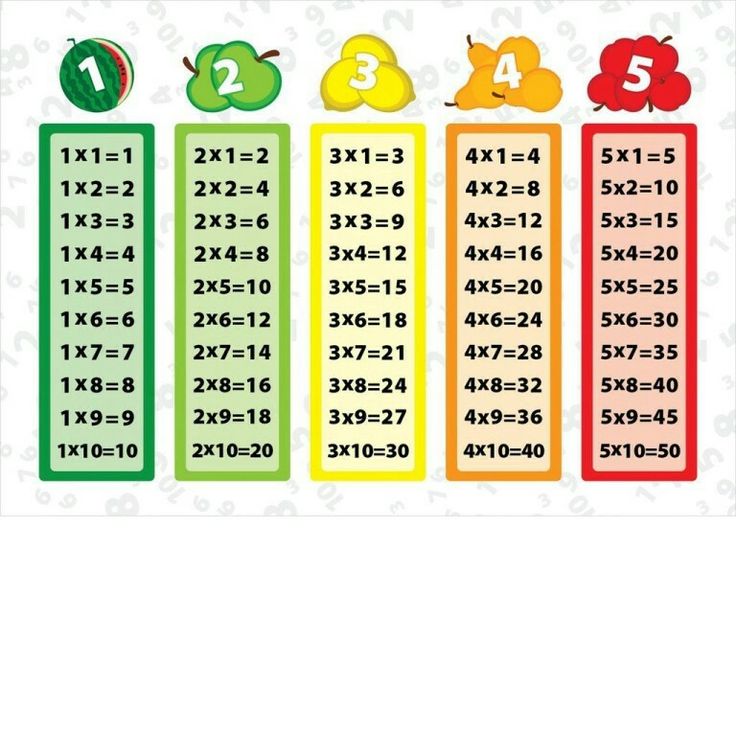

 Это может быть полезно для быстрого определения, является ли число кратным 3, без необходимости выполнять фактическое умножение.
Это может быть полезно для быстрого определения, является ли число кратным 3, без необходимости выполнять фактическое умножение.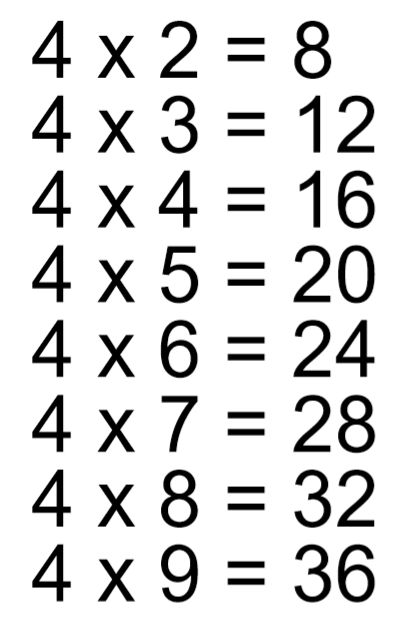 «В …раз больше» — умножаем, «в … раз меньше» — делим.
«В …раз больше» — умножаем, «в … раз меньше» — делим.

 Они понимают, что при умножении одного числа на другое результат умножается на множитель. Это упрощает запоминание таблицы четырех. Если у вашего ребенка все еще есть проблемы, продемонстрируйте ему, как умножать на четыре с реальными предметами. Например, соберите и положите перед ребенком три маленькие кучки шариков, по 4 шарика в каждой. Теперь попросите ребенка сосчитать количество шариков в каждой кучке. Теперь объясните им, что у них три раза по 4 шарика. Это означает, что у них есть 4 + 4 + 4 шарика, что равно 12 шарикам.
Они понимают, что при умножении одного числа на другое результат умножается на множитель. Это упрощает запоминание таблицы четырех. Если у вашего ребенка все еще есть проблемы, продемонстрируйте ему, как умножать на четыре с реальными предметами. Например, соберите и положите перед ребенком три маленькие кучки шариков, по 4 шарика в каждой. Теперь попросите ребенка сосчитать количество шариков в каждой кучке. Теперь объясните им, что у них три раза по 4 шарика. Это означает, что у них есть 4 + 4 + 4 шарика, что равно 12 шарикам. У вас будет таблица умножения на 4. Ниже приведен пример того же самого.
У вас будет таблица умножения на 4. Ниже приведен пример того же самого. д.
д.
 Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.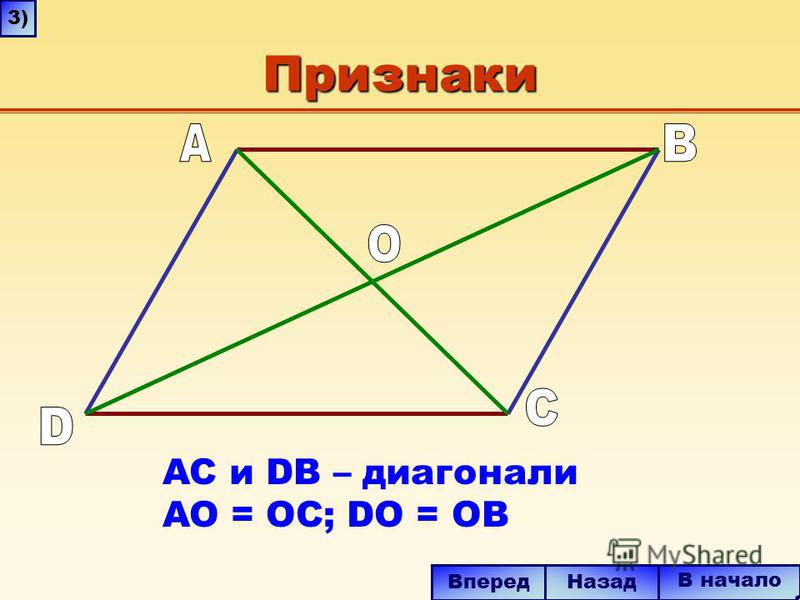 А.
А. 
 к. АК – биссектриса,
к. АК – биссектриса, 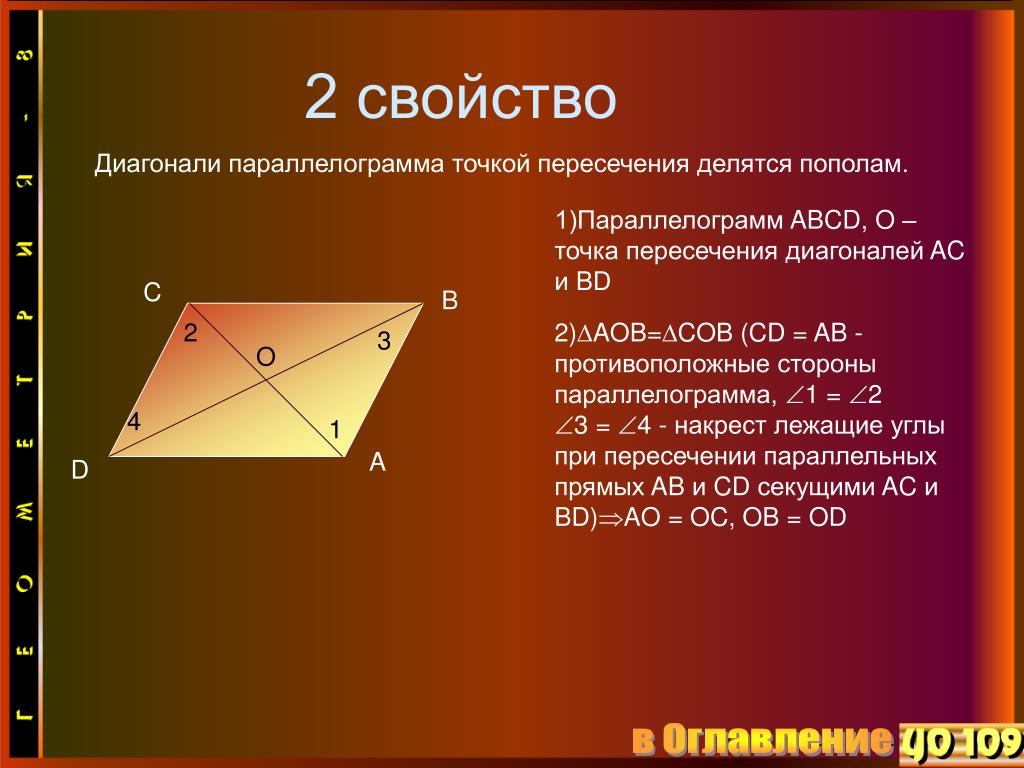
 к. АК – биссектриса
к. АК – биссектриса 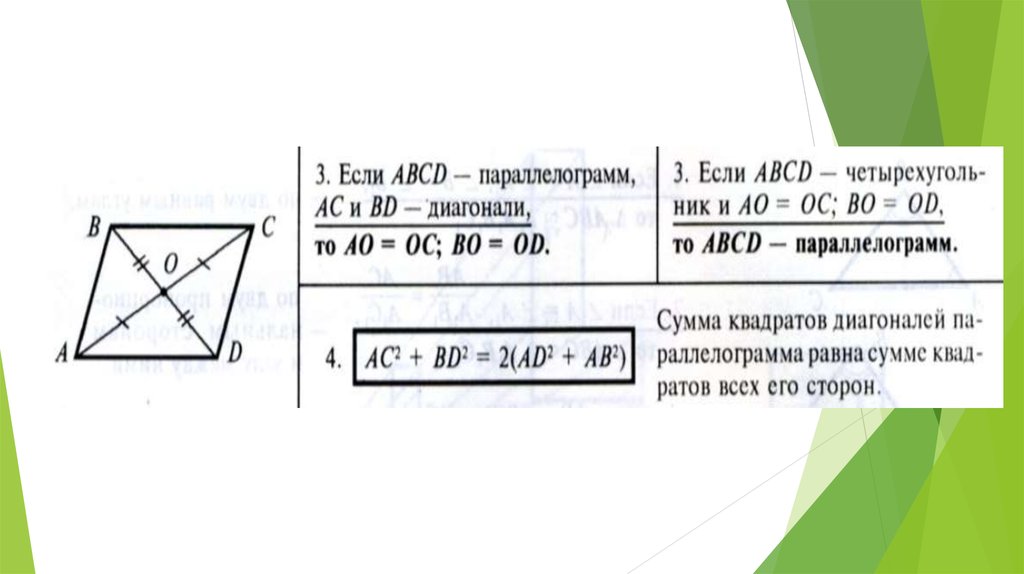 к. АN
— биссектриса
к. АN
— биссектриса 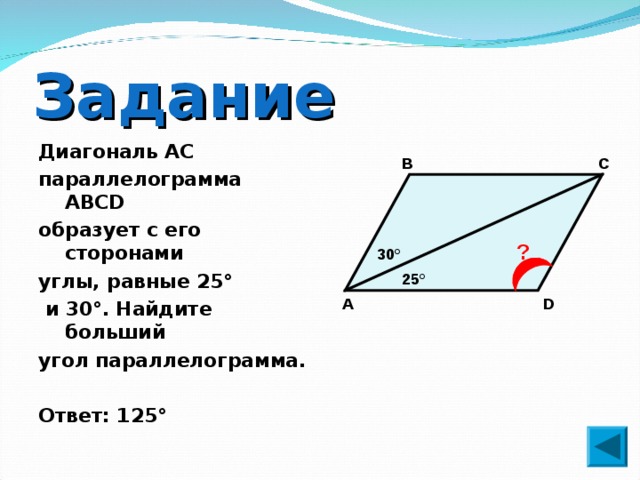 Все звенья работают на сжатие.
Все звенья работают на сжатие.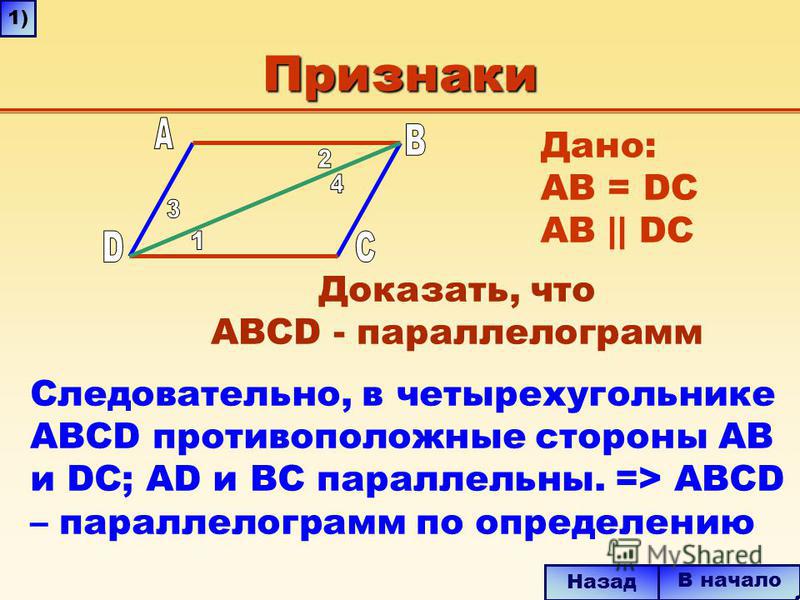
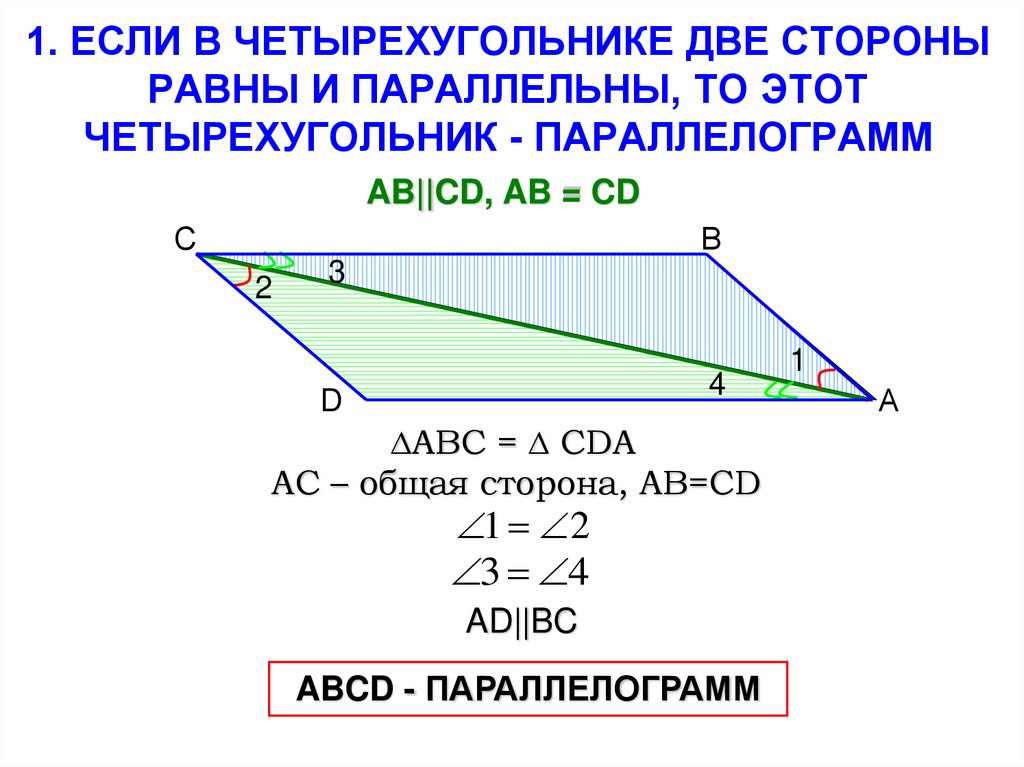
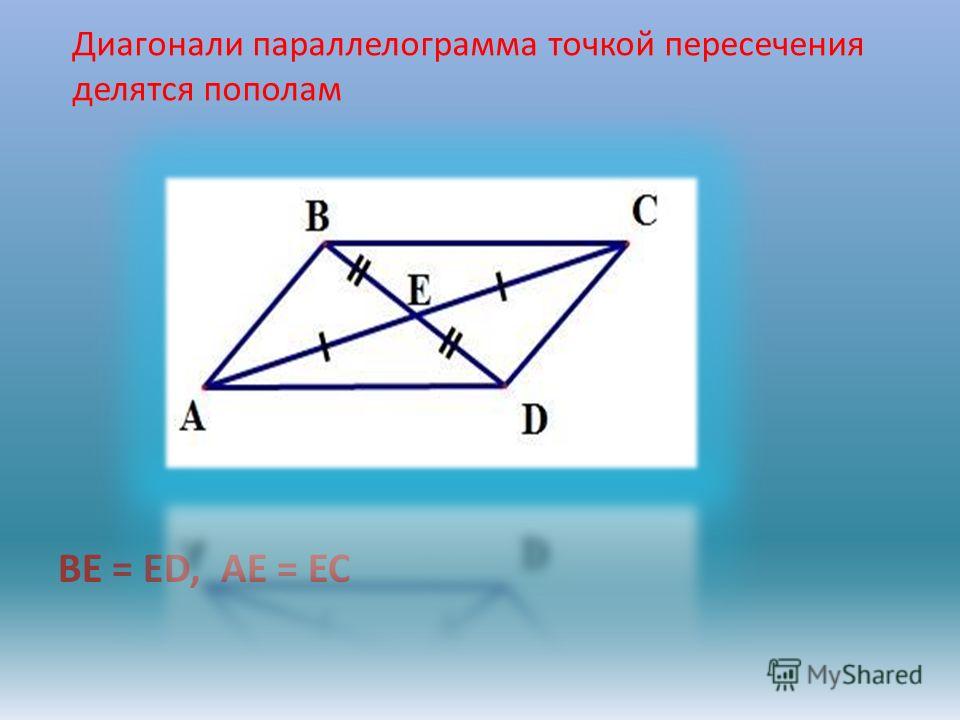 То есть, BO = OD
(напротив углов \angle 2
и \angle 1
) и AO = OC
(напротив углов \angle 3
и \angle 4
соответственно).
То есть, BO = OD
(напротив углов \angle 2
и \angle 1
) и AO = OC
(напротив углов \angle 3
и \angle 4
соответственно). {\circ}
говорит и о том, что AD || BC
.
{\circ}
говорит и о том, что AD || BC
.


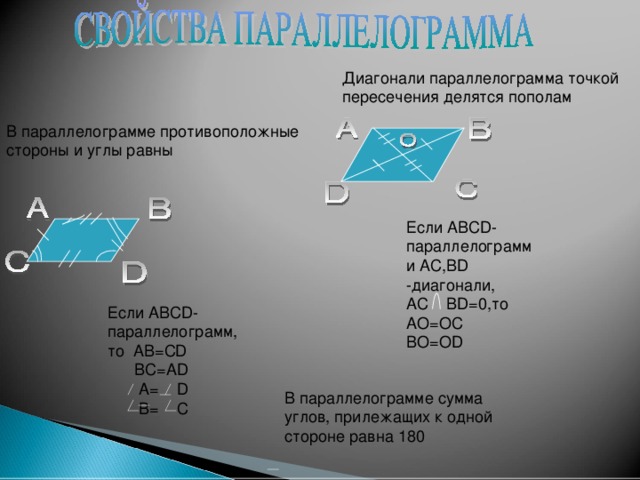
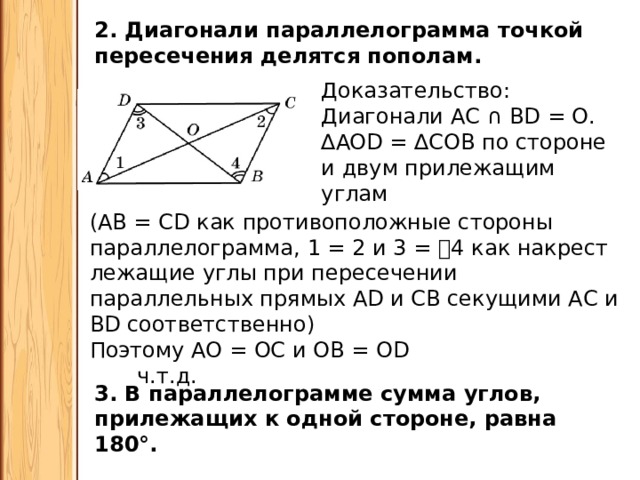
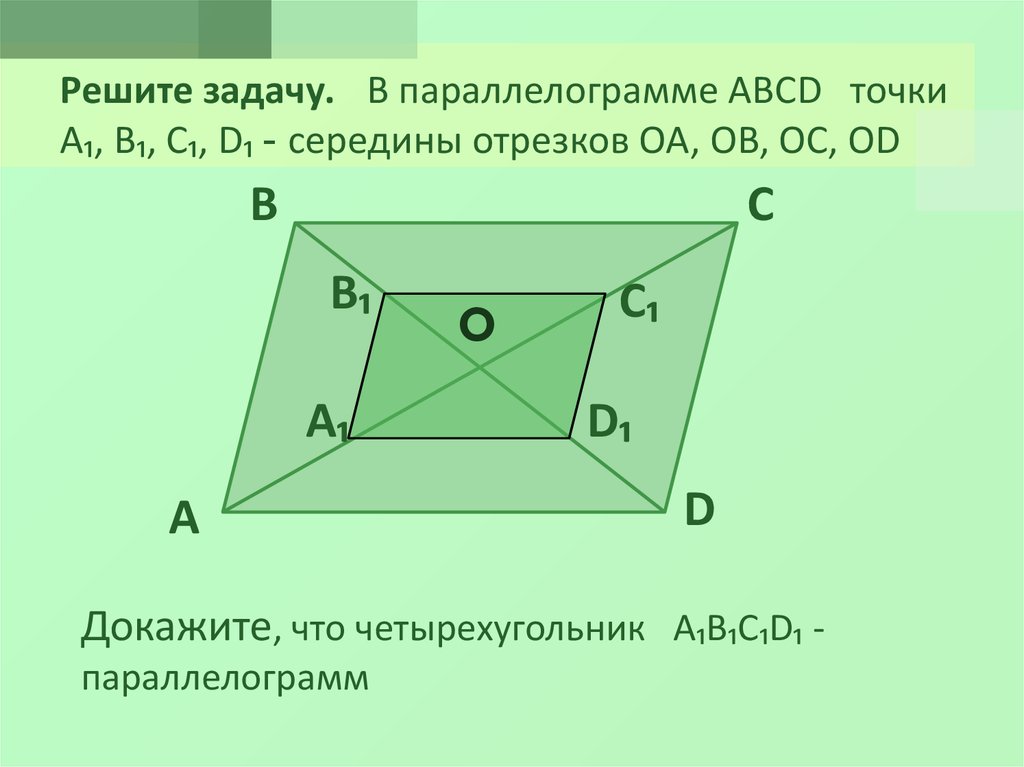
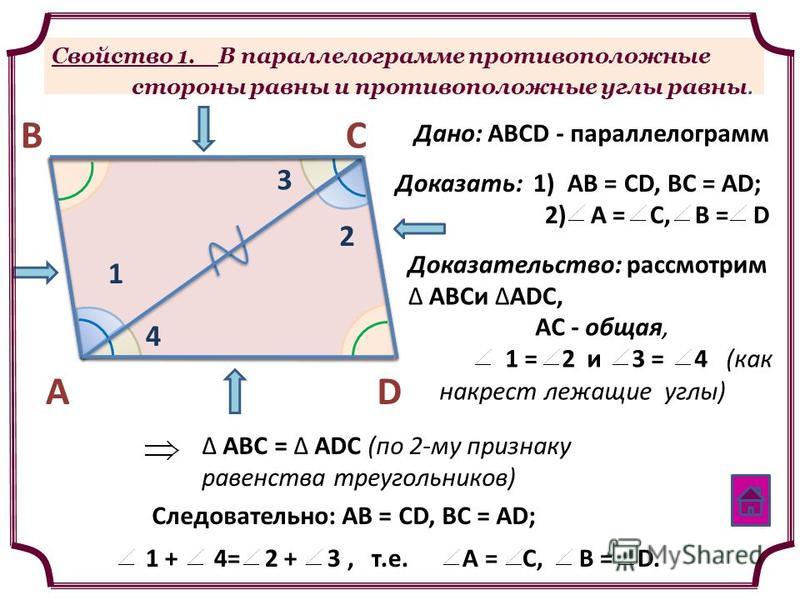
 Рассмотрим в параллелограмме ABCD треугольники ABC и ADC, полученные в результате проведения диагонали AC.
Рассмотрим в параллелограмме ABCD треугольники ABC и ADC, полученные в результате проведения диагонали AC. Рассмотрим образованные ими треугольники ABE и CDE.
Рассмотрим образованные ими треугольники ABE и CDE.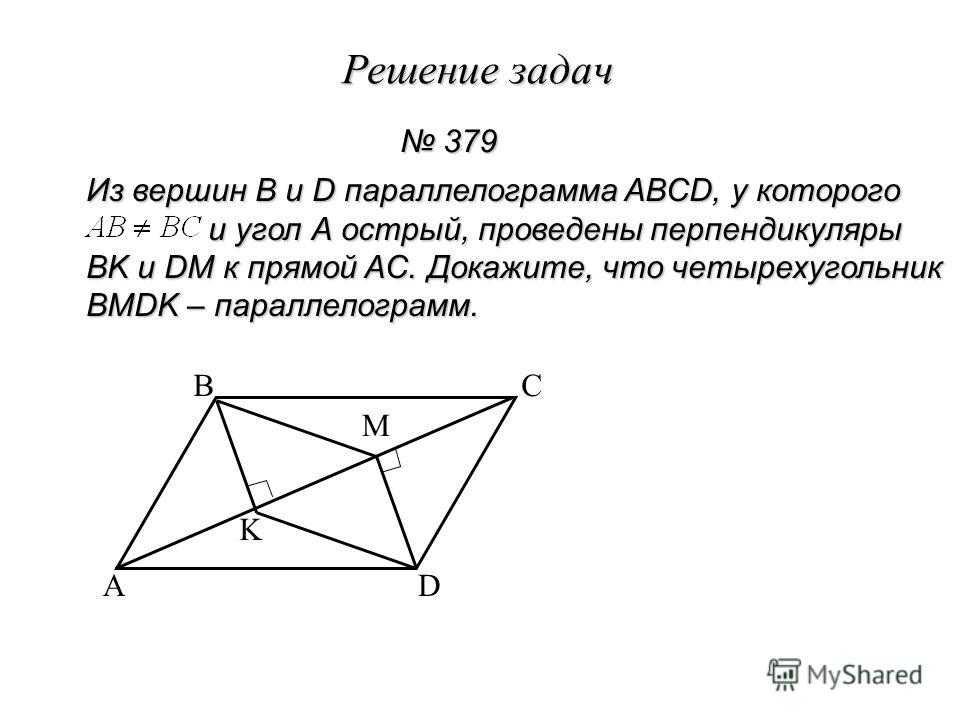
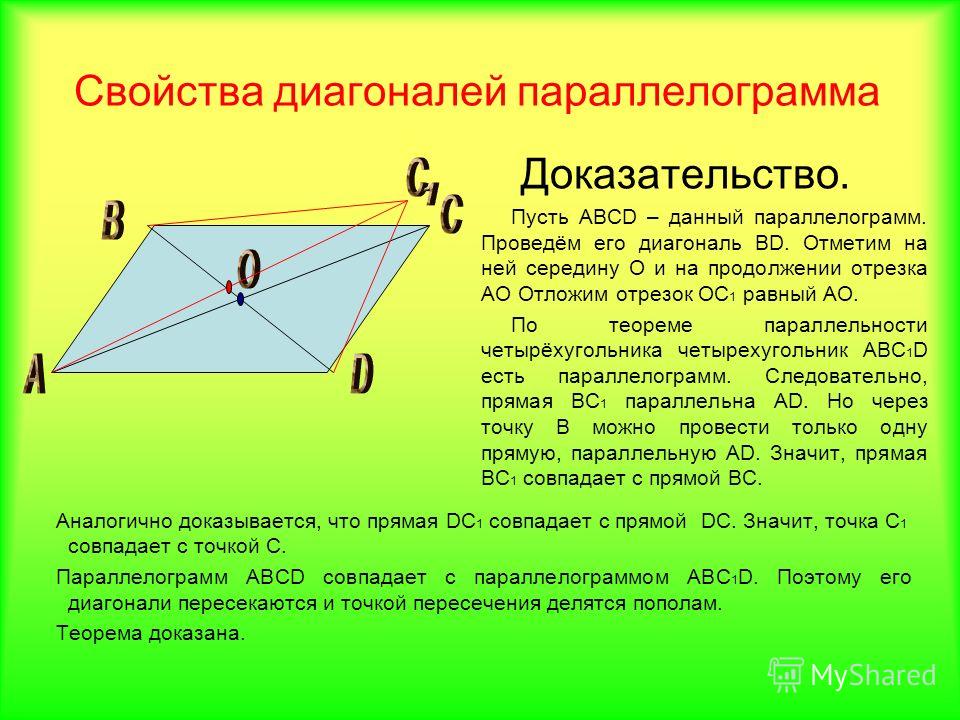 ВЕ = СF. Следовательно, прямая ВС || AD. (*)
ВЕ = СF. Следовательно, прямая ВС || AD. (*)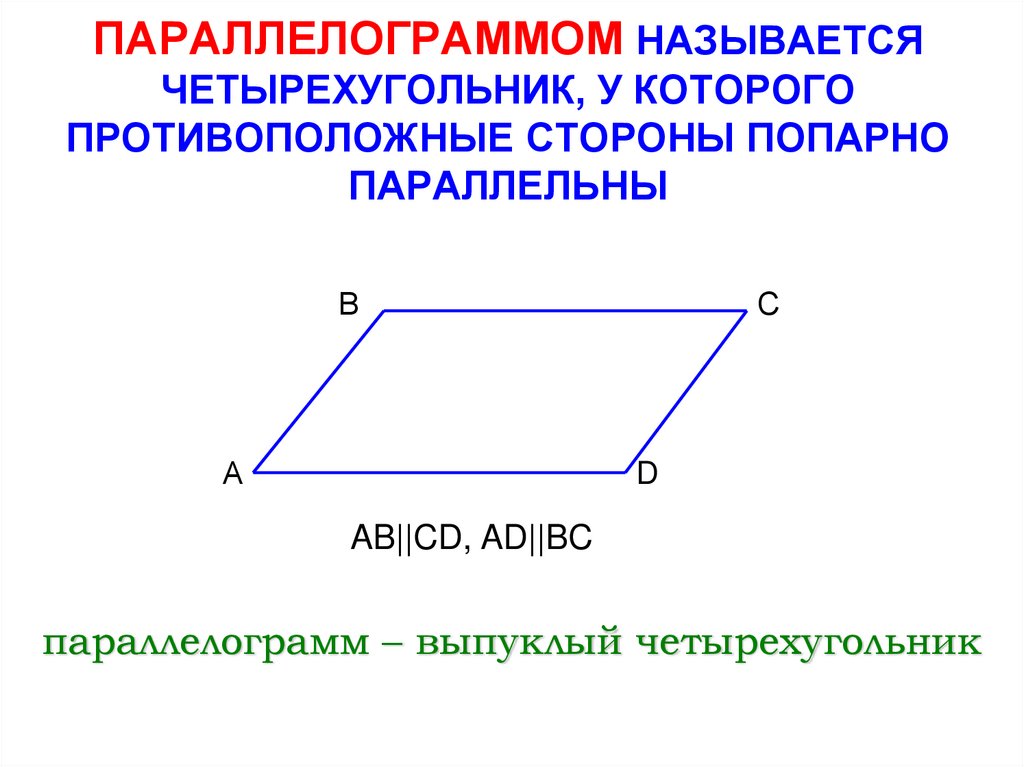
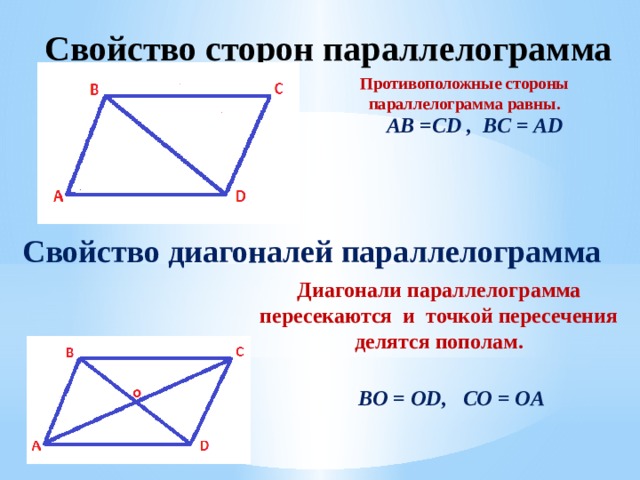
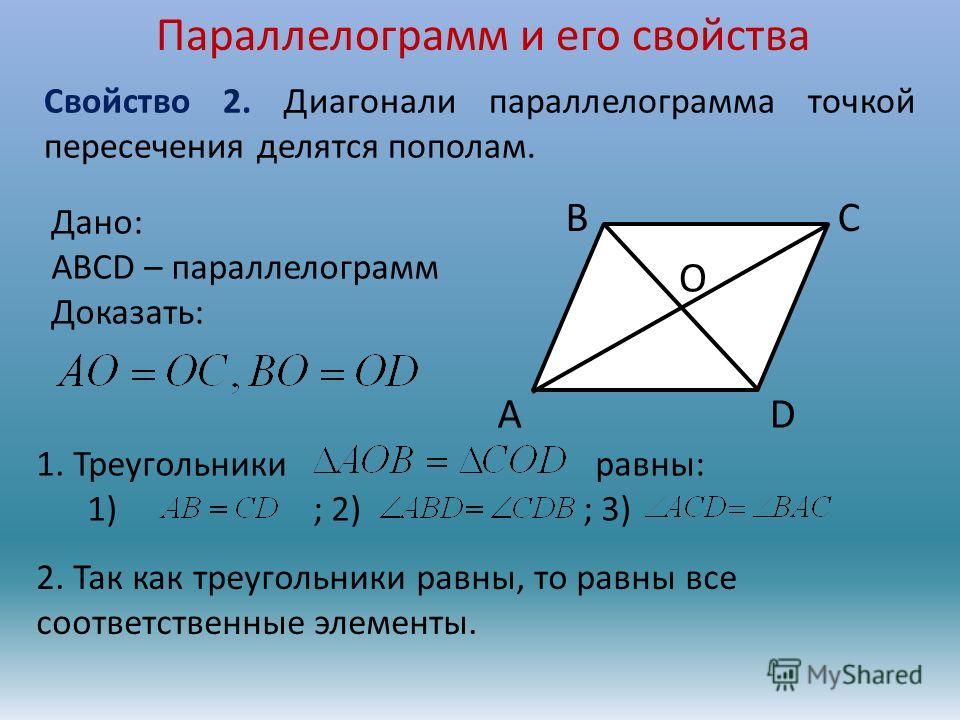 Используя соотношение между сторонами и диагоналями параллелограмма запишем равенство
Используя соотношение между сторонами и диагоналями параллелограмма запишем равенство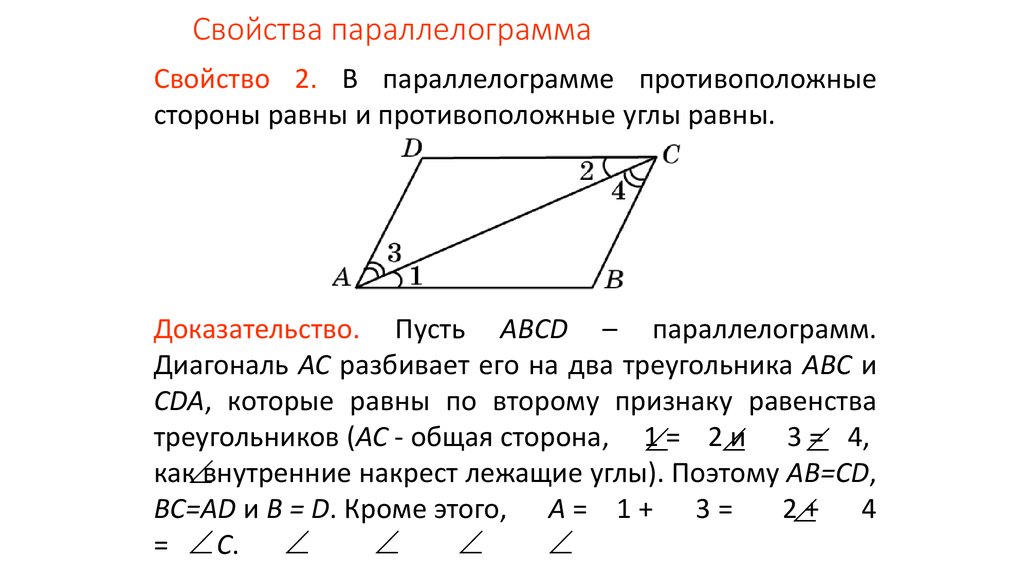

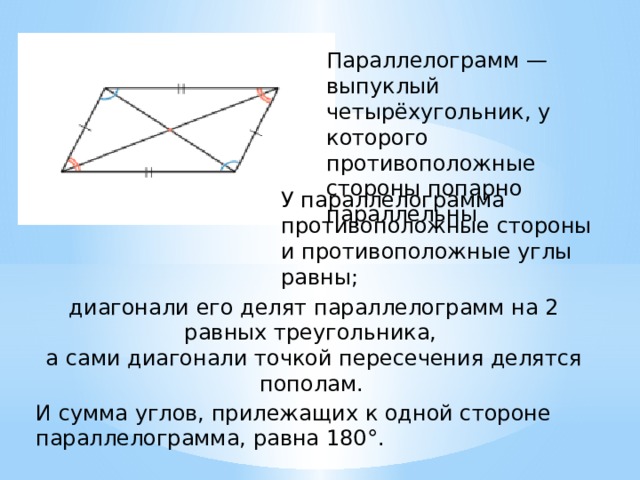
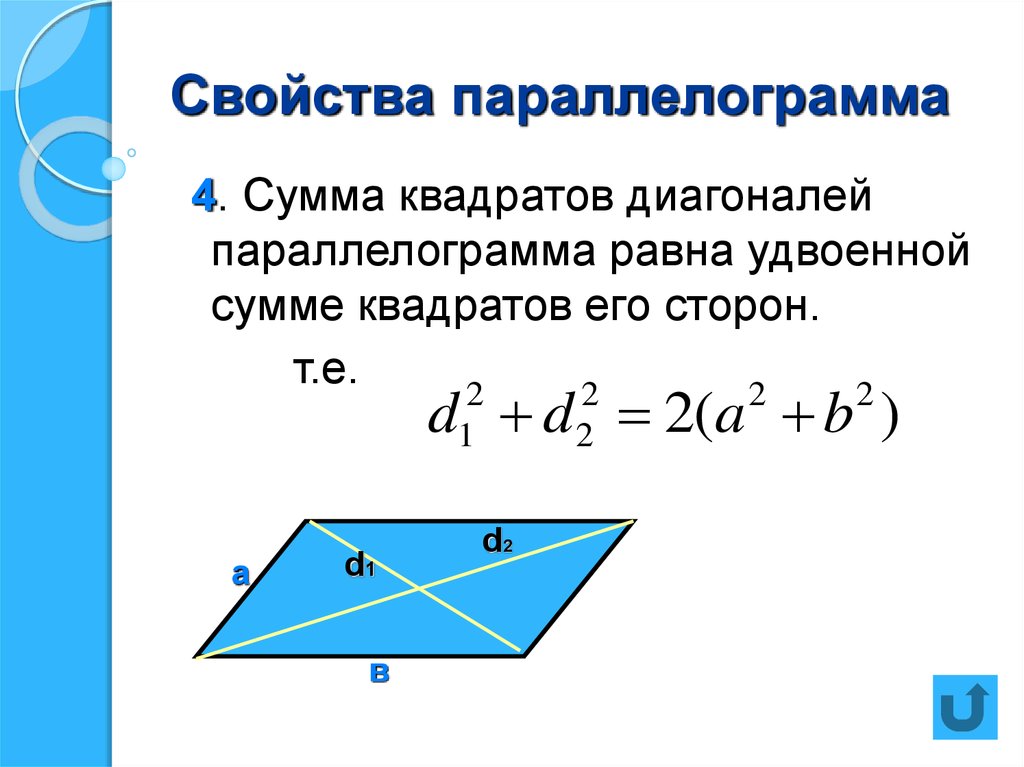 }Следовательно, по определению $1$, данный четырехугольник является параллелограммом.
}Следовательно, по определению $1$, данный четырехугольник является параллелограммом.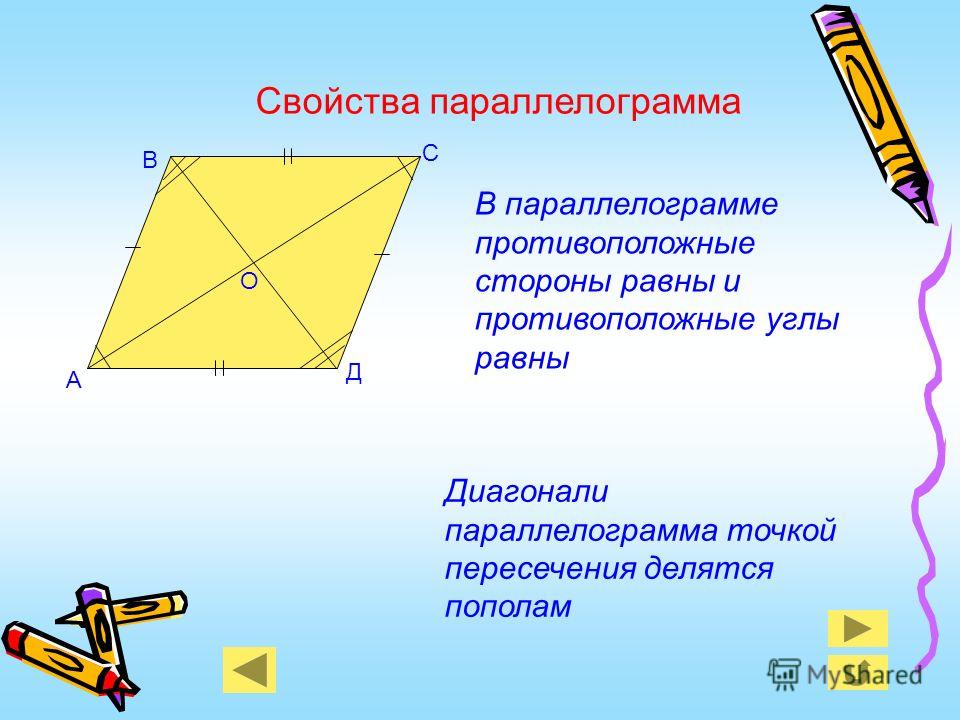

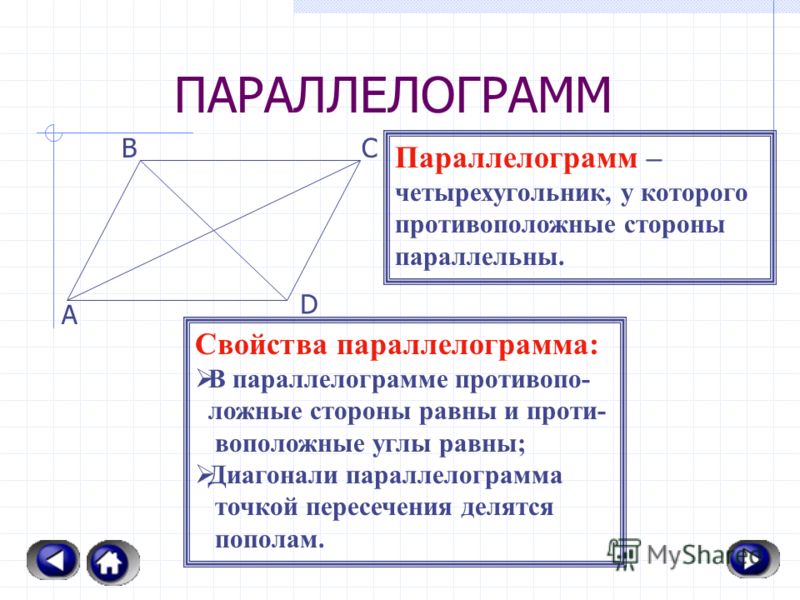 То есть, BO = OD
(напротив углов \angle 2
и \angle 1
) и AO = OC
(напротив углов \angle 3
и \angle 4
соответственно).
То есть, BO = OD
(напротив углов \angle 2
и \angle 1
) и AO = OC
(напротив углов \angle 3
и \angle 4
соответственно).


 Отсюда происходит интуитивное представление о желании последовательности или функции чего-либо; в рамках математического анализа это понятие желания находит свое формализацию в математических определениях предела функции и предела последовательности.
Отсюда происходит интуитивное представление о желании последовательности или функции чего-либо; в рамках математического анализа это понятие желания находит свое формализацию в математических определениях предела функции и предела последовательности.
 Общая формула этого правила приведена ниже.
Общая формула этого правила приведена ниже. (н.д.). Что такое правило Лопиталя? . Академия Хана.
(н.д.). Что такое правило Лопиталя? . Академия Хана. также: Область определения функции — Асимптота функции — Экстремум функции
также: Область определения функции — Асимптота функции — Экстремум функции


 )
) )
) )
) )
) )
) )
) )
) )
) )
) )
) )
) )
) )
) )
) )
) )
) )
) ответил 08.06.19
ответил 08.06.19 Это оставляет нам:
Это оставляет нам: 9
(705)
9
(705) Никаких пакетов или подписок, платите только за то время, которое вам нужно.
Никаких пакетов или подписок, платите только за то время, которое вам нужно.


 03.2020 домашнее задание):
03.2020 домашнее задание):

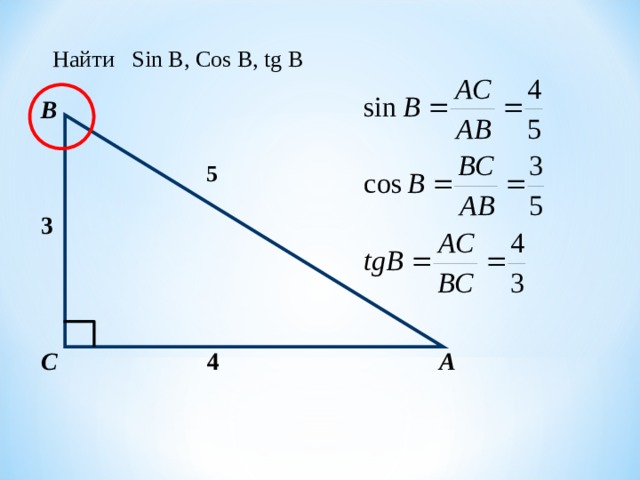
 Найдите значение выражения
Найдите значение выражения

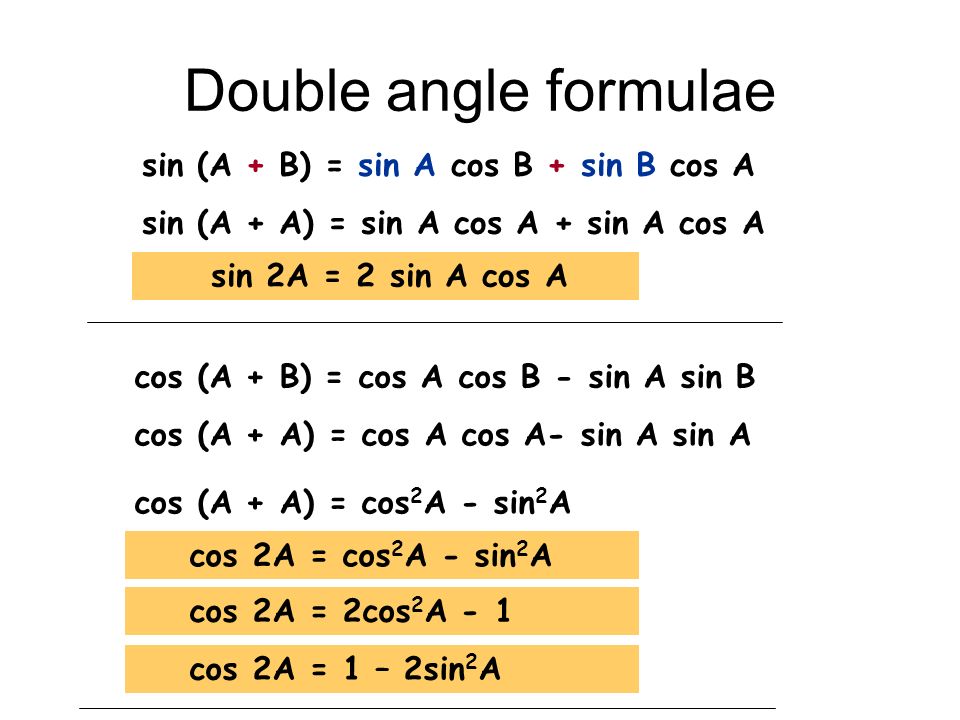
 Найдите tg2 t, если 5sin2 t + 12cos2 t = 6.
Найдите tg2 t, если 5sin2 t + 12cos2 t = 6.
 Найдите значение выражения
Найдите значение выражения

 Счет в пределах 10
Счет в пределах 10






 Причем для целой части мы будем последовательно делить на 2, а для дробной умножать на 2.
Причем для целой части мы будем последовательно делить на 2, а для дробной умножать на 2. Если в результате умножения целая часть не равна нулю, тогда необходимо заменить значение целой части на ноль. В результате будет получено число из целых частей произведений, записанное слева направо.
Если в результате умножения целая часть не равна нулю, тогда необходимо заменить значение целой части на ноль. В результате будет получено число из целых частей произведений, записанное слева направо. 8
8 8
8 1012 из двоичной системы в десятичную систему счисления
1012 из двоичной системы в десятичную систему счисления 62510
62510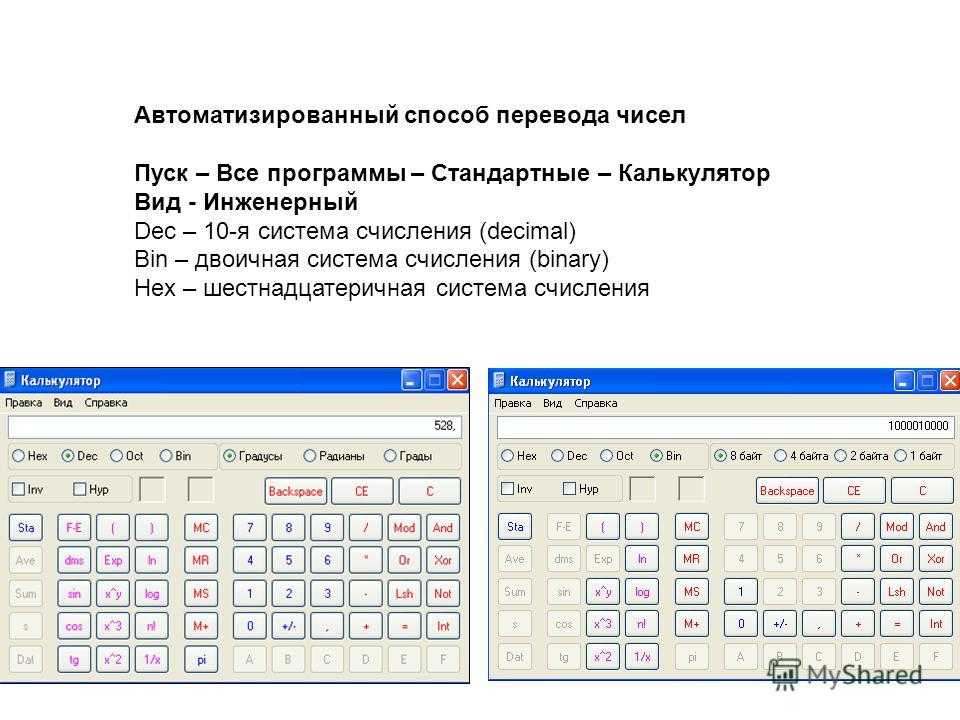 Графит
Графит 0 Калькулятор
0 Калькулятор 0118, Положения об иммиграции и защите беженцев и Инструкции министра, изданные в соответствии с IRPA s.10.3. Этот инструмент будет время от времени обновляться в соответствии с изменениями в Министерских инструкциях, регулирующих экспресс-въезд.
0118, Положения об иммиграции и защите беженцев и Инструкции министра, изданные в соответствии с IRPA s.10.3. Этот инструмент будет время от времени обновляться в соответствии с изменениями в Министерских инструкциях, регулирующих экспресс-въезд.
 ..
.. ..НетДа
..НетДа ..Аудирование:Выбрать…Чтение:Выбрать…Письмо:Выбрать…
..Аудирование:Выбрать…Чтение:Выбрать…Письмо:Выбрать…
 Чтобы получить его, человек должен оценить свою подготовку, обменяться опытом и навыками, а затем сдать сертификационный экзамен.
Чтобы получить его, человек должен оценить свою подготовку, обменяться опытом и навыками, а затем сдать сертификационный экзамен.
 .. НетДа
.. НетДа Степень бакалавра (трехгодичная программа в университете, колледже, торговом или техникуме или другом институте). Два или более сертификата, диплома или степени. Один должен быть для программы продолжительностью три или более лет. Степень магистра или профессиональная степень, необходимая для практики по лицензированной профессии. Университетская степень доктора наук (PhD)
Степень бакалавра (трехгодичная программа в университете, колледже, торговом или техникуме или другом институте). Два или более сертификата, диплома или степени. Один должен быть для программы продолжительностью три или более лет. Степень магистра или профессиональная степень, необходимая для практики по лицензированной профессии. Университетская степень доктора наук (PhD)

 Точка Р лежит внутри угла D, и РК = РМ. Докажите, что луч DР – биссектриса угла МDК.
Точка Р лежит внутри угла D, и РК = РМ. Докажите, что луч DР – биссектриса угла МDК.

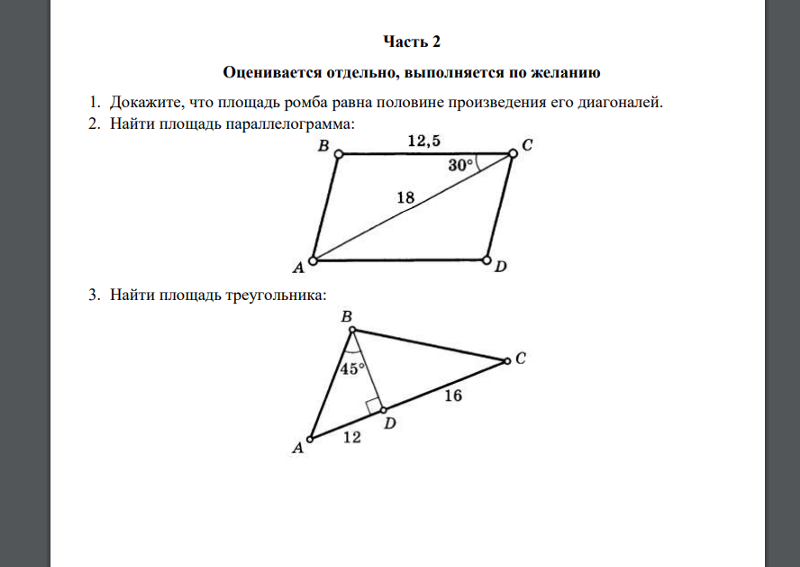
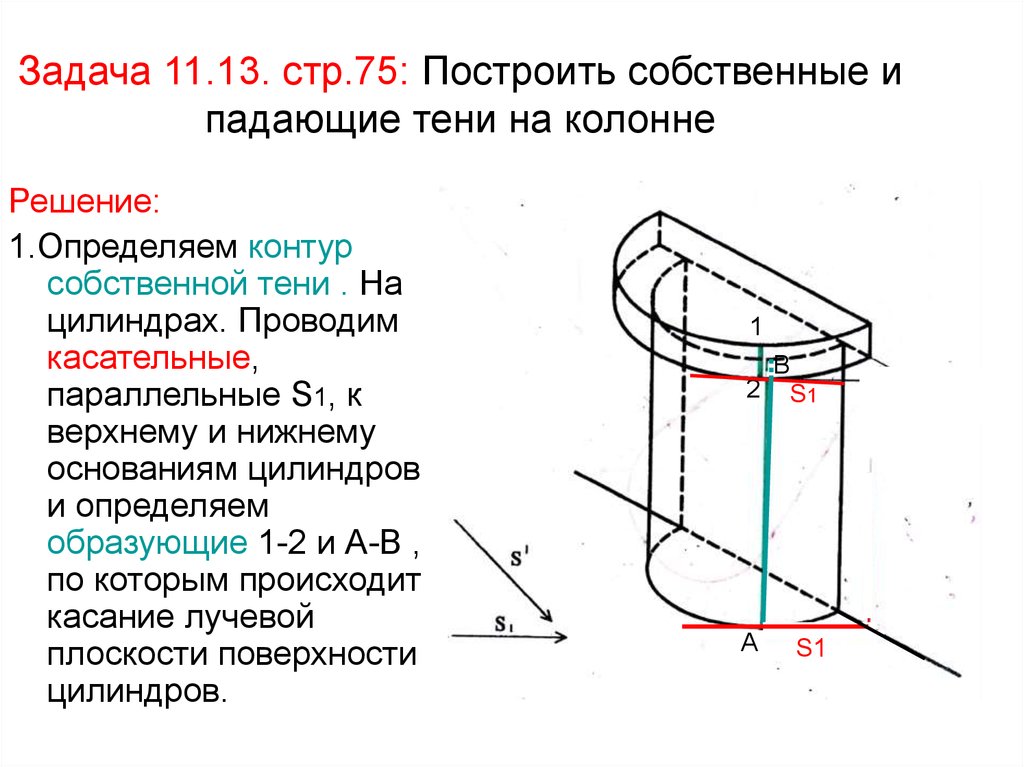 2. Найдите площадь полной поверхности цилиндра.
2. Найдите площадь полной поверхности цилиндра.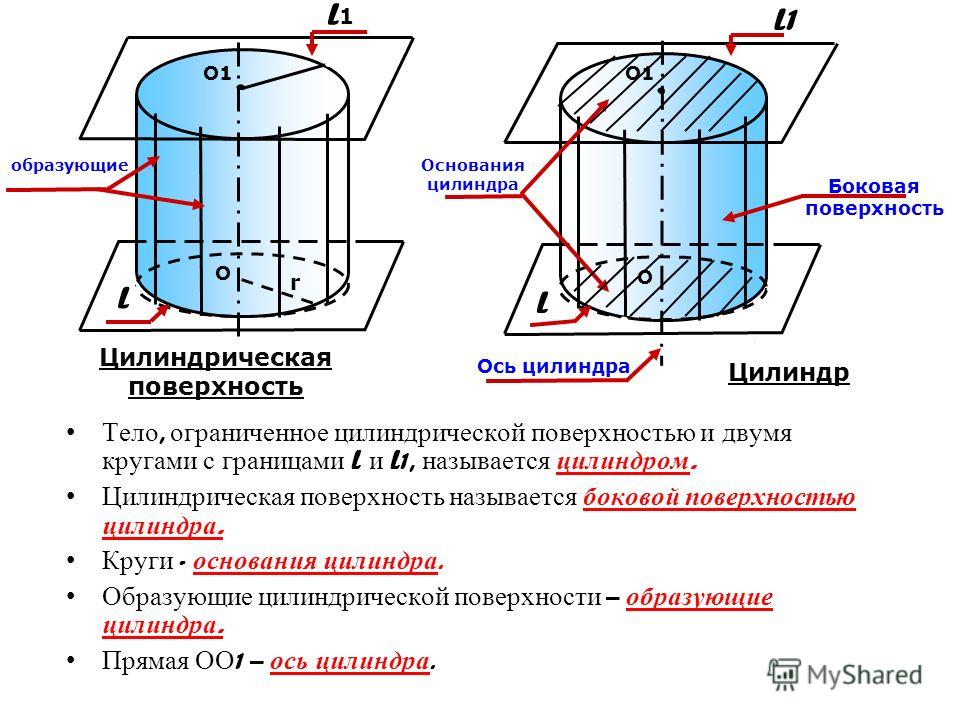

 4 :: Tl.Rulate.ru
4 :: Tl.Rulate.ru Пускай сейчас большая часть штатов и разрознена, но старые праздники до сих пор стоят на особом счету у кочевых народов Америки.
Пускай сейчас большая часть штатов и разрознена, но старые праздники до сих пор стоят на особом счету у кочевых народов Америки. К счастью, наши запасы были ещё полны, поэтому я с чистой душей сделал себя оладьи.
К счастью, наши запасы были ещё полны, поэтому я с чистой душей сделал себя оладьи. — Заявила девушка, своим тоном показывая, что возражения не принимаются.
— Заявила девушка, своим тоном показывая, что возражения не принимаются. — Пришли со мной поболтать или к малышкам?
— Пришли со мной поболтать или к малышкам?



 {-1}$.
Инверсия $B$:
9{-1}_{i, j}=A_{i, j}$, если $B_{ij} \neq 0$.
{-1}$.
Инверсия $B$:
9{-1}_{i, j}=A_{i, j}$, если $B_{ij} \neq 0$. (См. документы для
(См. документы для 


