Множества. Решение задач с помощью кругов Эйлера. 5, 6, 7 класс
Братунова Вера Дмитриевкна, преподаватель математики и информатики, Гимназия-детсад им. С. Демиреля, мун. Комрат, АТО Гагауз Ери, Республика Молдова
Множества. Решение задач с помощью кругов Эйлера
Классы: 5, 6, 7
Ключевые слова: круги Эйлера
Пояснительная записка
Очень часто решение задачи помогает найти рисунок. Использование рисунка делает решение простым и наглядным.
В данной разработке приведены примеры решения задач с помощью кругов Эйлера. Это не просто занимательная и интересная штука, но и весьма полезный метод решения задач. Они помогают быстро и просто решить даже достаточно сложные или просто запутанные на первый взгляд задачи.
С данным способом решения задач учащихся можно познакомить как на уроках, так и на кружковых занятиях.
Главной
целью этой работы является помощь учителям математики для подготовки учащихся к
олимпиадам, а также к экзаменам.
Основные понятия
Понятие множества − одно из первичных в математике. Поэтому очень трудно дать ему какое-либо определение, которое бы не заменяло слово «множество» каким-нибудь равнозначным выражением, например, совокупность, собрание элементов и т.д. Элементы множества − это то, из чего это множество состоит, например, каждый ученик вашего класса есть элемент множества школьников.
Пересечение множеств в теории множеств — это множество, которому принадлежат те и только те элементы, которые одновременно принадлежат всем данным множествам.
Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Леонардом Эйлером. Используется в математике, логике, менеджменте и других прикладных направлениях.
2. Решение задач с помощью кругов Эйлера
2.1. «Обитаемый остров» и «Стиляги»
Некоторые ребята из нашего класса
любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров»,
11 человек — фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и
«Стиляги». Сколько человек смотрели только фильм «Стиляги»?
Известно, что 15 ребят смотрели фильм «Обитаемый остров»,
11 человек — фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и
«Стиляги». Сколько человек смотрели только фильм «Стиляги»?
Решение:
Чертим два множества таким образом:
6 человек, которые смотрели фильмы «Обитаемый остров» и «Стиляги», помещаем в пересечение множеств.
1. 15 — 6 = 9 — человек, которые смотрели только «Обитаемый остров»,
2. 11- 6 = 5 — человек, которые смотрели только «Стиляги».
Получаем:
Ответ: 5 человек.
2.2. Задача про библиотеки
Каждый из 35 шестиклассников является читателем, по крайней мере, одной из двух библиотек: школьной и районной. Из них 25 человек берут книги в школьной библиотеке, 20 — в районной.
Сколько шестиклассников:
1. Являются читателями обеих библиотек;
2. Не являются читателями районной библиотеки;
3. Не являются читателями школьной библиотеки;
4. Являются
читателями только районной библиотеки;
Являются
читателями только районной библиотеки;
5. Являются читателями только школьной библиотеки?
Решение:
Чертим два множества таким образом:
1) 20+ 25 — 35 = 10 (человек) — являются читателями обеих библиотек. На схеме это общая часть кругов. Мы определили единственную неизвестную нам величину. Теперь, глядя на схему, легко даем ответы на поставленные вопросы.
2) 35 — 20 = 15 (человек) — не являются читателями районной библиотеки,
3) 35 — 25 = 10 (человек) — не являются читателями школьной библиотеки,
4) 35- 20 = 10 (человек) — являются читателями только районной библиотеки,
5) 35- 20 = 15 (человек) — являются читателями только школьной библиотеки.
Очевидно, что вопросы 2 и 5, а также 3 и 4 — равнозначны и ответы на них совпадают.
Ответ: 10 человек; 15 человек; 10 человек; 10
человек; 15 человек.
2.3. Гарри Поттер, Рон и Гермиона
На полке стояло 26 волшебных книг по заклинаниям, все они были прочитаны. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал только Рон?
Решение:
Учитывая условия задачи, сделаем чертеж:
Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги — Гермиона, то 11 — 4 — 2 = 5 — книг прочитал только Гарри.
Следовательно, 26 — 7 — 2 — 5 — 4 = 8 — книг прочитал только Рон.
Ответ: 8 книг.
2.4. Задача про любимые мультфильмы
Шестиклассники
заполняли анкету с вопросами об их любимых мультфильмах. Оказалось, что
большинству из них нравятся «Белоснежка и семь гномов», «Губка Боб Квадратные
Штаны» и «Волк и теленок».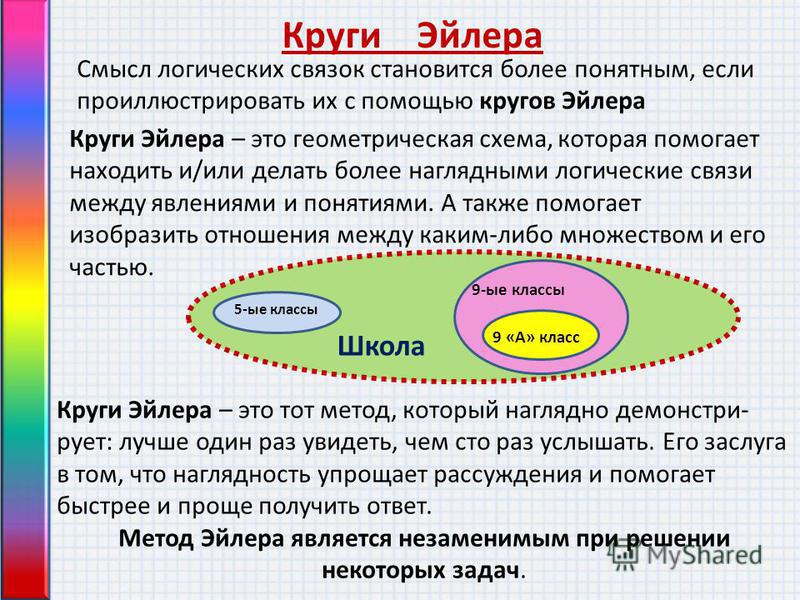 В классе 38 учеников. «Белоснежка и семь гномов»
нравится 21 ученику. Причем трем среди них нравятся еще и «Волк и теленок»,
шестерым — «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три
мультфильма. У «Волка и теленка» 13 фанатов, пятеро из которых назвали в анкете
два мультфильма. Надо определить, скольким же шестиклассникам нравится «Губка
Боб Квадратные Штаны».
В классе 38 учеников. «Белоснежка и семь гномов»
нравится 21 ученику. Причем трем среди них нравятся еще и «Волк и теленок»,
шестерым — «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три
мультфильма. У «Волка и теленка» 13 фанатов, пятеро из которых назвали в анкете
два мультфильма. Надо определить, скольким же шестиклассникам нравится «Губка
Боб Квадратные Штаны».
Решение:
Чертим три круга, таким образом:
Из условия знаем, что трем ученикам нравиться и «Белоснежка и семь гномов», и «Волк и теленок», шестерым — «Белоснежка и семь гномов» и «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма.
Мы помним, что по условиям задачи среди фанатов мультфильма «Волк и теленок» пятеро ребят выбрали два мультфильма сразу, т.е. 5 — 3 = 2 — ученика выбрали «Волк и теленок» и «Губка Боб Квадратные Штаны».
1) 21 — 3 — 1 — 6 = 11 — учеников выбрали только «Белоснежка и семь гномов»,
2) 13 — 3 — 1 — 2 = 7 — учеников выбрали — «Волк и теленок»,
3) 38 — (11 + 3 + 1 + 2 + 6 + 7) =
8 — ребят выбрали «Губка Боб Квадратные Штаны».
4) 8 + 2 + 1 + 6 = 17 — человек выбрали мультик «Губка Боб Квадратные Штаны».
Ответ: 17 учеников.
2.5. Задача про Крейсер и Линкор
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети интернет.
Запрос | Найдено страниц, тыс. |
Крейсер и Линкор | 7000 |
Крейсер | 4800 |
Линкор | 4500 |
Какое
количество страниц (в тысячах) будет найдено по запросу Крейсер и Линкор?
(Считается, что все вопросы выполняются практически одновременно, так что набор
страниц, содержащих все искомые слова, не изменялся за время выполнения
запросов. )
)
Решение:
При помощи кругов Эйлера изобразим условия задачи.
1) 4800 + 4500 — 7000 = 2300 (тыс. страниц) — найдено по запросу Крейсер и Линкор,
2) 4800 — 2300 = 2500 (тыс. страниц) — найдено по запросу Крейсер,
3) 4500 — 2300 = 2200 (тыс. страниц) — найдено по запросу Линкор.
Ответ: 2300 тыс. страниц.
2.6. Задача про блондинок
Каждый ученик класса — либо девочка, либо блондин, либо любит математику. В классе 20 девочек, из них 12 блондинок, но одна блондинка любит математику. Всего в классе 24 ученика — блондина, математику из них любят 12, а всего учеников (мальчиков и девочек), которые любят математику, 17, из них 6 девочек. Сколько учеников в данном классе?
Решение:
Изобразим с помощью кругов Эйлера данные из задачи:
1) 12 — 1 = 11 (учеников) — девочек блондинок,
2) 12 — 1 = 11 (учеников) — блондины и любят математику,
3) 6 — 1 = 5 (учеников) — девочек, которые любят математику,
4) 20 — 11 — 1 — 5 = 3 (ученика) — девочки,
5) 24 — 11 — 1 — 11 = 1 (ученик) — блондин,
6) 17- 5 — 1 — 11 = 0 (учеников) — любят математику,
7) 3 + 1 + 0 + 5 + 11 + 11 + 1 =
32 (ученика) — всего в классе.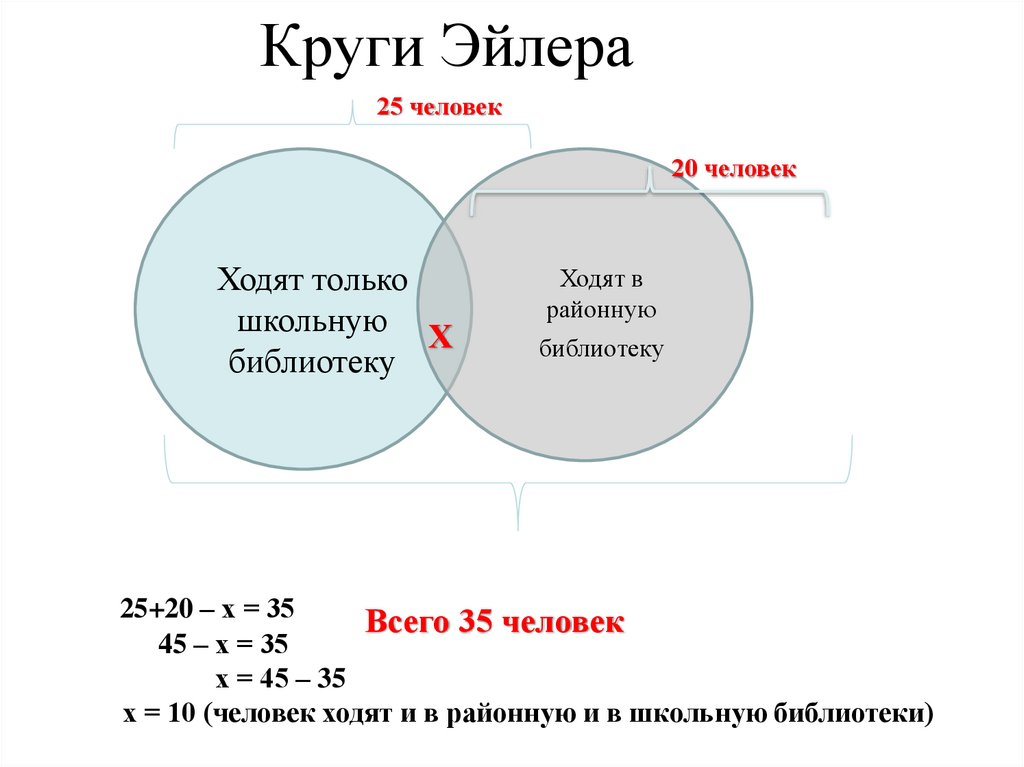
Ответ: 32 ученика.
2.7. Задача про кружки
В трёх седьмых классах 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?
Решение:
Учитывая условия задачи, сделаем чертеж:
1) 10 — 3 = 7 (ребят) — посещают драмкружок и хор,
2) 6 — 3 = 3 (ребят) — поют в хоре и занимаются спортом,
3) 8 — 3 = 5 (ребят) — занимаются спортом и посещают драмкружок,
4) 27 — 7 — 3 — 5 = 12 (ребят) — посещают драмкружок,
5) 32 — 7 3 — 3 = 19 (ребят) — поют в хоре,
6) 22 — 5 — 3 — 3 = 11 (ребят) — увлекаются спортом,
7) 70 — (12 + 19 + 11 + 5+ 7 + 3 +
3) = 10 (ребят) — не поют в хоре, не увлекаются спортом и не занимаются в
драмкружке.
Ответ: 10 человек и 11 человек.
Задачи для самостоятельного решения
1. На фирме работают 67 человек. Из них 47 знают английский язык, 35 — немецкий язык, а 23 — оба языка. Сколько человек фирмы не знают ни английского, ни немецкого языков?
2. Из 40 учащихся нашего класса 32 любят молоко, 21 — лимонад, а 15 — и молоко, и лимонад. Сколько ребят в нашем классе не любят ни молоко, ни лимонад?
3. 12 моих одноклассников любят читать детективы, 18 — фантастику, трое с удовольствием читают и то, и другое, а один вообще ничего не читает. Сколько учеников в нашем классе?
4. Из тех 18 моих одноклассников, которые любят смотреть триллеры, только 12 не прочь посмотреть и мультфильмы. Сколько моих одноклассников смотрят одни «мультики», если всего в нашем классе 25 учеников, каждый из которых любит смотреть или триллеры, или мультфильмы, или и то и другое?
5. Из 29 мальчишек нашего двора
только двое не занимаются спортом, а остальные посещают футбольную или
теннисную секции, а то и обе. Футболом занимается 17 мальчишек, а теннисом —
19. Сколько футболистов играет в теннис? Сколько теннисистов играет в футбол?
Из 29 мальчишек нашего двора
только двое не занимаются спортом, а остальные посещают футбольную или
теннисную секции, а то и обе. Футболом занимается 17 мальчишек, а теннисом —
19. Сколько футболистов играет в теннис? Сколько теннисистов играет в футбол?
6. В одном классе 25 учеников. Из них 7 любят груши, 11 — черешню. Двое любят груши и черешню; 6 — груши и яблоки; 5 — яблоки и черешню. Но есть в классе два ученика, которые любят все и четверо таких, что не любят фруктов вообще. Сколько учеников этого класса любят яблоки?
7. В конкурсе красоты участвовали 22 девушки. Из них 10 было красивых, 12 — умных и 9 — добрых. Только 2 девушки были и красивыми, и умными; 6 девушек были умными и одновременно добрыми. Определите, сколько было красивых и в то же время добрых девушек, если я скажу вам, что среди участниц не оказалось ни одной умной, доброй и вместе с тем красивой девушки?
8. В нашем классе 35 учеников. За
первую четверть пятерки по русскому языку имели 14 учеников; по математике —
12; по истории — 23. По русскому и математике — 4; по математике и истории — 9;
по русскому языку и истории — 5. Сколько учеников имеют пятерки по всем трем
предметам, если в классе нет ни одного ученика, не имеющего пятерки хотя бы по
одному из этих предметов?
По русскому и математике — 4; по математике и истории — 9;
по русскому языку и истории — 5. Сколько учеников имеют пятерки по всем трем
предметам, если в классе нет ни одного ученика, не имеющего пятерки хотя бы по
одному из этих предметов?
9. Из 100 человек 85 знают английский язык, 80 — испанский, 75 — немецкий. Все владеют, по крайней мере, одним иностранным языком. Среди них нет таких, которые знают два иностранных языка, но есть владеющие тремя языками. Сколько человек из этих 100 знают три языка?
10. Из сотрудников фирмы 16 побывали во Франции, 10 — в Италии, 6 — в Англии; в Англии и Италии — 5; в Англии и Франции — 6; во всех трех странах — 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работают 19 человек, и каждый из них побывал хотя бы в одной из названных стран?
Список использованных источников
1. Баженов И.И, Порошкин А.Г.,
Тимофеев А.Ю., Яковлев В.Д. Задачи для школьных математических кружков: учеб.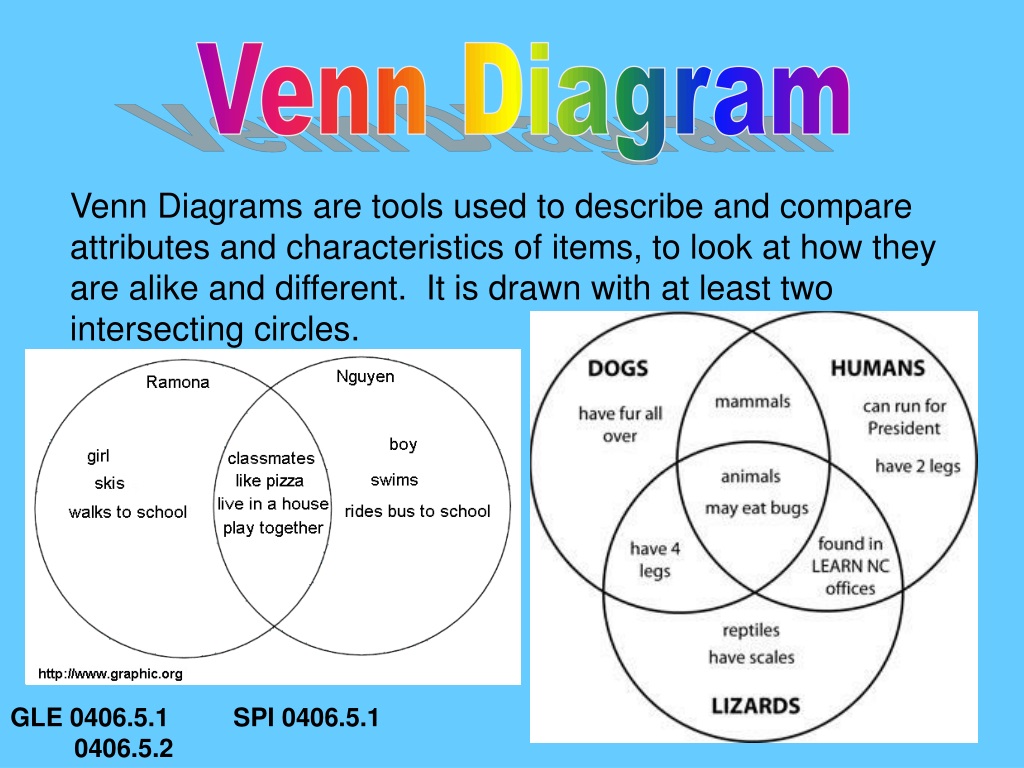 пособие / Сыктывкар: Сыктывкарский университет, 2006.
пособие / Сыктывкар: Сыктывкарский университет, 2006.
2. Марков И.С. Новые олимпиады по математике — Ростов н/Д: Феникс, 2005.
3. https://ru.wikipedia.org/wiki/
4. http://logika.vobrazovanie.ru
5. http://www.otvet-prost.ru/load/diskretnaja_matematika/na_krugi_ehjlera/zadacha_na_krugi_ehjlera/18-1-0-22
6. http://urok.1sept.ru/articles/550092/
7. http://www.tutoronline.ru/blog/reshit-zadachu-pomogut-krugi-jejlera
Презентация по теме «Круги Эйлера»
Соотношения между множествами принято
иллюстрировать с помощью кругов.
Эти круги называют кругами Эйлера
по имени ученого, который придумал
метод решения задач с их помощью.
Леонардо Эйлер (1707 – 1783)
Знаменитый математик, механик, физик и астроном, Л.Эйлер родился в 1707 году, он вырос в Швейцарии, а работал в основном в России и Германии. За свою жизнь Л.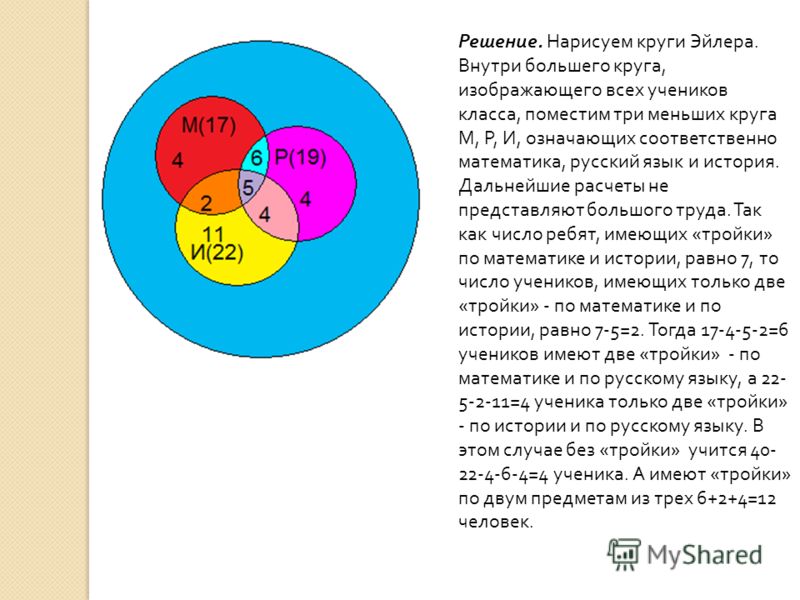 Эйлер написал более 850 научных работ. В одной из них и появились круги, которые, по его словам, «очень подходят для того, чтобы облегчить наши размышления».
Эйлер написал более 850 научных работ. В одной из них и появились круги, которые, по его словам, «очень подходят для того, чтобы облегчить наши размышления».
Рассмотрим, действительно ли это так ?
Запишем на символическом языке соотношения между множествами.
А и В
А и С
С и В
А, В и С
А B
С
A C
А
B C
В
A B C
A является подмножеством множества В, а В является подмножеством множества С
Пересечение множеств.
Пересечение множеств А и В — это множество, состоящее из элементов, входящих одновременно в А и В.
Пересечение А и В –
записывают с помощью символа
А В
В
А
А В
Пересечение множеств.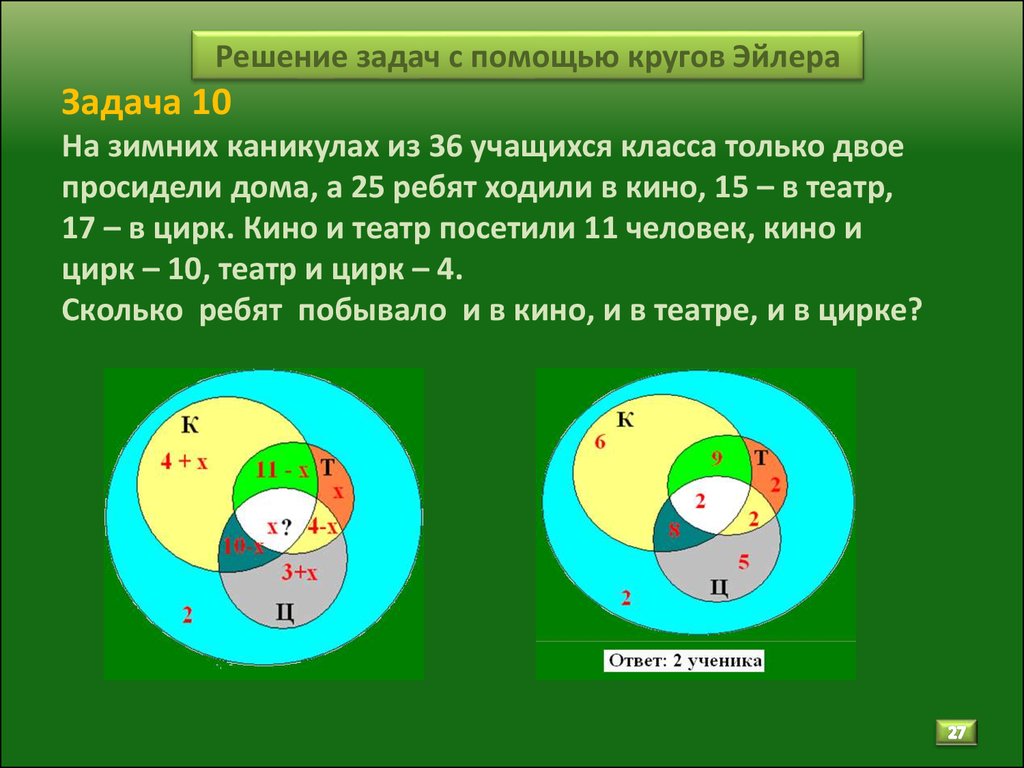
Пусть А = { 2, 4, 6} , a B = { 2, 4, 6, 8, 10}
Пересечение множеств А и В
А В = А
В
А
Объединение множеств.
Объединением множеств А и B называют множество, состоящее из элементов, входящих хотя бы в одно из множеств А или В.
Объединение множеств А и В обозначают символом
В
А
Объединение множеств.
Пусть А = { 2, 4, 6} , a B = { 2, 4, 6, 8, 10}
Объединение множеств А и В
А В = В
В
А
Рассмотрим, как можно решить задачу с помощью кругов Эйлера
Задача: По результатам опроса 52 шестиклассников было установлено, что 23 из них собирают значки, 35 собирают марки, а 16 – и значки, и марки. Остальные не увлекаются коллекционированием. Сколько человек не увлекаются коллекционированием?
Решение:
З
?
Собирают значки
М
Собирают марки
Собирают и значки и марки
Не увлекаются
коллекционированием
Решение задачи ( продолжение)
1) Значки и марки собирают 16 человек. Впишем число 16 в пересечение кругов З и М.
Впишем число 16 в пересечение кругов З и М.
2) Значки собирают 23 человека. Тогда только значки собирают: 23-16 = 7 человек. Впишем число 7 в свободную часть круга З
3) Только марки собирают: 35-16 = 19 человек. Занесем число 19 в схему.
4) Теперь мы можем узнать, сколько человек занимаются коллекционированием: 16+7+19 = _______ человека
5) Не занимаются коллекционированием:
52 — __ = __________ человек.
Ответ: _____ человек.
З
7
М
16
19
№ 227,стр.87 ПРТ
Результаты опроса жильцов дома о том, смотрели ли они в новогоднюю ночь основные телеканалы — Первый канал и Россию — 1.
Используя данные на схеме, ответьте на вопросы:
25
Р-1
П
46
43
31
№ 227,стр.87 ПРТ
1.Сколько человек не смотрело ни тот, ни другой канал?
2. Сколько человек включало то один, то другой канал?
Сколько человек включало то один, то другой канал?
3. Сколько человек смотрело только Первый канал?
4. Сколько человек смотрело канал Россия-1?
5. Сколько человек смотрело хотя бы один из этих каналов?
25
(25)
Р-1
П
(46)
46
(43)
43
31
(31+46)
(120)
Задание . На полке стояло 25 волшебных книг по заклинаниям, все они были прочитаны Гермионой, Гарри Поттером или Роном.
При этом не было не одной книги, которую бы прочитали все.
4 книги прочитали и Гарри Поттер, и Рон.
Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер.
Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитали только Гарри Поттер и только Рон?
1. Обозначим: P- множество книг, прочитанных Гарри Поттером;
R-множество книг, прочитанных Роном;
G- множество книг, прочитанных Гермионой
2. Расставим известные данные в круги Эйлера.
Расставим известные данные в круги Эйлера.
3. Найдем количество книг, которые прочитал только Гарри Поттер: 11 — 4 — 2 = 5 книг. 6. А теперь, чтобы узнать количество прочитанных книг только Роном, нужно из всего количества книг вычесть известное количество прочитанных книг: 25 ― (11+7)= 7 книг прочел только Рон.
R
P
G
4
7
2
7
5
Мы работаем отлично, Отдохнуть не прочь сейчас. И зарядка к нам привычно На урок приходит в класс. Выше руки, выше пятки Улыбнитесь веселей! Мы попрыгаем как зайки Сразу станем всех бодрей! Потянулись и вздохнули. Отдохнули? Отдохнули!
Встали и потянулись
Стряхнули руки
Подняли руки вверх
Работа по карточкам
Вариант 1
Из 40 учащихся шестых классов 32 любят молоко, 21 — лимонад, а 15 и молоко и лимонад.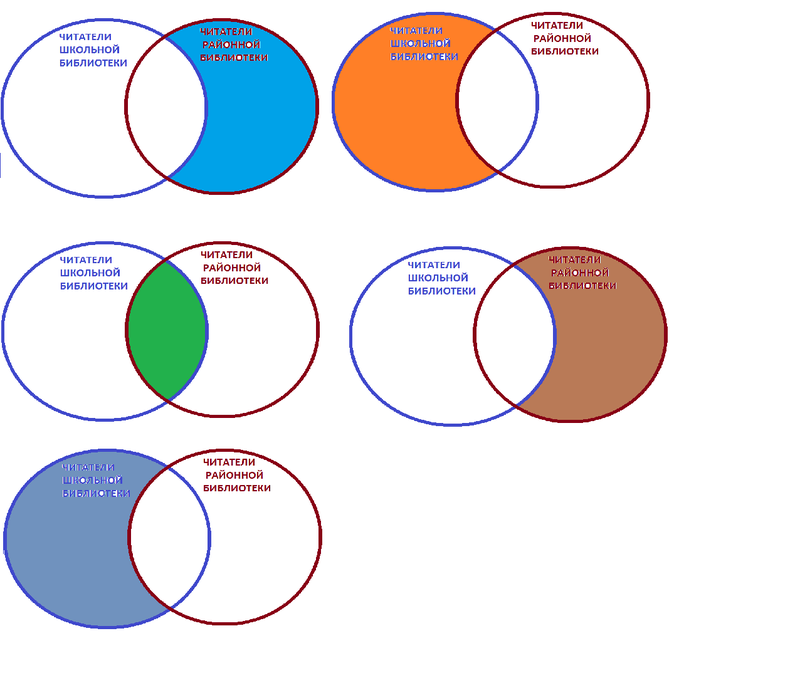 Сколько ребят не любят ни лимонад, ни молоко?
Сколько ребят не любят ни лимонад, ни молоко?
Вариант 2
12 шестиклассников любят читать детективы, 18-фантастику, трое с удовольствием читают и то и другое, а один вообще ничего не читает. Сколько учеников в шестом классе?
Ответ: 2 ученика
Ответ: 28 учеников.
№ 231,стр.90 ПРТ
В математической олимпиаде для 6-кл. участвовали 50 человек. Из них арифметическую задачу решили 40 человек, а геометрическую — 20.
Покажите на схеме решение задачи.
Г
А
10
30
10
Давайте обсудим
- Что называют объединением множеств?
Приведите пример.
2. Что называют пересечением множеств?
Приведите пример.
3. Пусть С-множество чисел, кратных 9, и D-множество чисел, кратных 3. Какое соотношение связывает эти множества?
4. Понравилось вам использовать метод кругов Эйлера для решения задач?
Понравилось вам использовать метод кругов Эйлера для решения задач?
Как анализировать аргументы с помощью диаграмм Эйлера
На экзамене по конечной математике вас могут попросить проанализировать аргумент с помощью визуального подхода с использованием диаграммы Эйлера. Эта изобразительная техника используется для проверки правильности аргумента.Аргумент может быть классифицирован как допустимый или недопустимый. Действительный аргумент возникает в ситуациях, когда, если посылки верны, то и заключение должно быть верным. И аргумент может быть верным, даже если вывод ложный.
Следующий аргумент имеет две предпосылки: (1) «У всех собак есть блохи». (2) «Хэнк — собака». Вывод таков, что, следовательно, у Хэнка блохи.Эти аргументы обычно имеют следующий формат с предпосылками, перечисленными первыми, и выводом, подчеркнутым горизонтальной линией:
Используя диаграмму Эйлера для анализа этого аргумента, нарисуйте круг, содержащий все объекты, на которых есть блохи. Внутри круга поместите еще один круг, чтобы содержать всех собак. А внутри круга собак посади Хэнка. Рисунок иллюстрирует этот подход.
Внутри круга поместите еще один круг, чтобы содержать всех собак. А внутри круга собак посади Хэнка. Рисунок иллюстрирует этот подход.
У бедного Хэнка блохи.
Этот аргумент не обязательно верен, потому что вы знаете, что не у всех собак есть блохи. Все это показывает, что аргумент равен действительный . Если обе посылки верны, то и заключение должно быть верным.
Теперь рассмотрим аргумент, включающий прямоугольники и треугольники. Многоугольник — это фигура, состоящая из отрезков, соединенных концами.
При анализе правильности этого аргумента диаграмма Эйлера начинается с круга, содержащего все многоугольники, как показано здесь.
Два типа полигонов.
Два круга нарисованы внутри большего круга — один содержит прямоугольники, а другой — треугольники. Два круга не пересекаются, потому что у прямоугольников четыре стороны, а у треугольников три стороны.
Аргумент недействителен . Прямоугольники — это не треугольники, даже иногда.
Прямоугольники — это не треугольники, даже иногда.
Аргументы могут иметь более двух посылок. Например:
Одна диаграмма Эйлера, которая может представить эту ситуацию, имеет три пересекающихся круга, как показано здесь.
Президент Авраам Линкольн и другие юристы штата Иллинойс.
Как видно из диаграммы, могут быть президенты, родившиеся в Кентукки, которые не были юристами в Иллинойсе, и могут быть президенты, которые были юристами в Иллинойсе, но не родились в Кентукки. Аргумент равен неверный . Чтобы быть действительным, оно всегда должно быть истинным.
Эта статья из книги:
- Конечная математика для чайников,
Об авторе книги:
Мэри Джейн Стерлинг является автором Алгебра I для чайников, учебник по алгебре для чайников, и многие другие Для чайников книг. Она преподавала в Университете Брэдли в Пеории, штат Иллинойс, более 30 лет, преподавая алгебру, бизнес-расчеты, геометрию и конечную математику.
Она преподавала в Университете Брэдли в Пеории, штат Иллинойс, более 30 лет, преподавая алгебру, бизнес-расчеты, геометрию и конечную математику.
Эту статью можно найти в категории:
- Расчет и анализ,
17.9: Оценка дедуктивных аргументов с помощью диаграмм Эйлера
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 41408
- Дэвид Липпман
- Колледж Пирса через OpenTextBookStore
Мы можем визуально интерпретировать дедуктивный аргумент с помощью диаграммы Эйлера, которая по сути является тем же самым, что и диаграмма Венна. Это может облегчить определение того, является ли аргумент действительным или недействительным.
Это может облегчить определение того, является ли аргумент действительным или недействительным.
Пример 31
Рассмотрим дедуктивный аргумент «Все кошки — млекопитающие, а тигр — кошка, поэтому тигр — млекопитающее». Является ли этот аргумент действительным?
Решение
Помещения:
Все кошки млекопитающие.
Тигр — это кошка.
Вывод:
Тигр — млекопитающее.
Обе посылки верны. Чтобы увидеть, что посылки должны логически вести к заключению, мы можем использовать диаграмму Венна. Исходя из первой посылки, мы рисуем множество кошек как подмножество множества млекопитающих. Из второй посылки нам говорят, что тигр содержится в множестве кошек. Из этого мы видим на диаграмме Венна, что тигр также должен быть внутри множества млекопитающих, так что вывод верен.
Анализ аргументов с помощью диаграмм Эйлера
Чтобы проанализировать аргумент с помощью диаграммы Эйлера:
1) Нарисуйте диаграмму Эйлера на основе предпосылок аргумента
2) Аргумент недействителен, если есть способ нарисовать диаграмму что делает вывод ложным
3) Аргумент действителен, если нельзя построить диаграмму, чтобы сделать вывод ложным
4) Если посылок недостаточно для определения местоположения элемента или множества, упомянутых в заключении, то аргумент неверный.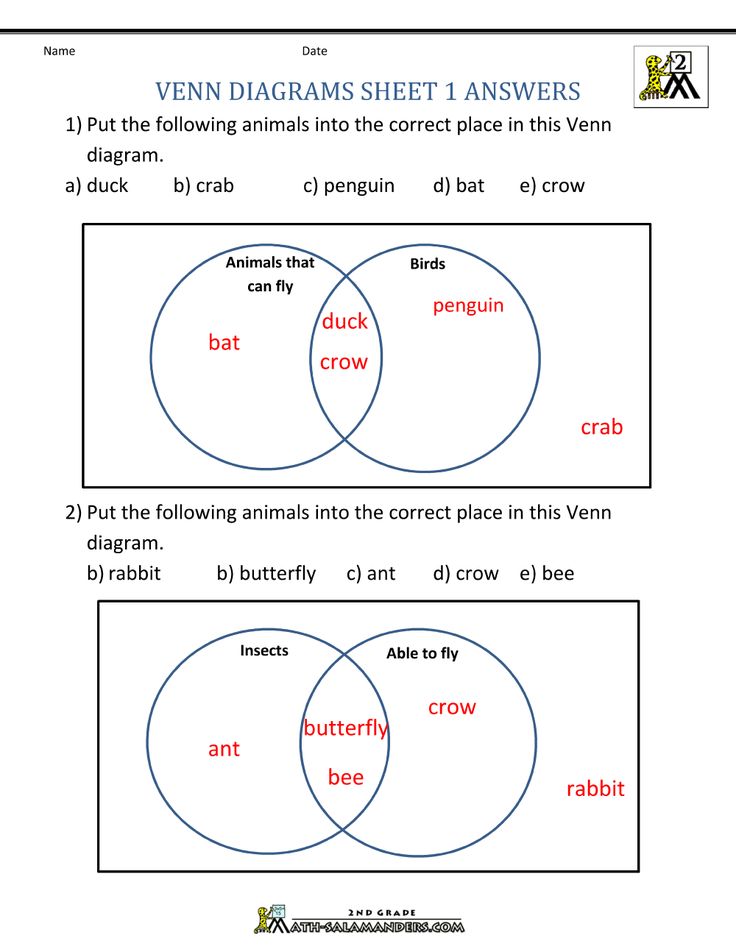
Попробуйте сейчас 9
Определите правильность этого аргумента:
\(\begin{array} {ll} \text{Предпосылка:} & \text{Все кошки боятся пылесосов.} \\ \text {Предпосылка:} & \text{Макс — кошка.} \\ \text{Вывод:} & \text{Макс боится пылесосов.} \end{array}\)
- Ответ
Действителен. Кошки — это подмножество существ, которых пугают пылесосы. Макс входит в набор котов, значит, он тоже должен быть в наборе существ, которых пугают пылесосы.
Пример 32
\(\begin{array} {ll} \text{Предпосылка:} & \text{Все пожарные знают СЛР.} \\ \text{Посылка:} & \text{Джилл знает СЛР.} \ \ \text{Вывод:} & \text{Джилл — пожарный.} \end{array}\)
Решение
Из первой посылки мы знаем, что все пожарные находятся внутри набора тех, кто знает СЛР. (Пожарные — это подмножество людей, знающих СЛР.) Из второй посылки мы знаем, что Джилл является членом этой большей группы, но у нас недостаточно информации, чтобы узнать, является ли она также членом меньшей подгруппы, т. е. пожарные.
е. пожарные.
Поскольку вывод не обязательно следует из посылок, это неверный аргумент. Возможно, что Джилл — пожарный, но структура аргумента не позволяет сделать вывод, что это определенно так.
Важно отметить, что действительно ли Джилл пожарный или нет, не имеет значения для оценки обоснованности аргумента; нас интересует, достаточно ли посылок для доказательства вывода.
Попробуйте сейчас 10
Определите правильность этого аргумента:
\(\begin{array} {ll} \text{Посылка:} & \text{Все велосипеды имеют два колеса.} \\ \text{Посылка:} & \text{Это У Harley-Davidson два колеса.} \\ \text{Вывод:} & \text{Этот Harley-Davidson — велосипед.} \end{array}\)
- Ответ
Недействительно. Множество велосипедов является подмножеством множества транспортных средств с двумя колесами; Harley-Davidson входит в число двухколесных транспортных средств, но не обязательно в меньший круг.
Попробуйте сейчас 11
Определите правильность этого аргумента:
\(\begin{array} {ll} \text{Предпосылка:} & \text{Нет фиолетовых коров. } \\ \text{Предпосылка: } & \text{Фидо не корова.} \\ \text{Вывод:} & \text{Фидо фиолетовый.} \end{массив}\)
} \\ \text{Предпосылка: } & \text{Фидо не корова.} \\ \text{Вывод:} & \text{Фидо фиолетовый.} \end{массив}\)
- Ответ
Недействительно. Поскольку фиолетовых коров нет, мы знаем, что набор коров и набор фиолетовых вещей не пересекаются. Мы знаем, что Фидо не находится в наборе коров, но этого недостаточно, чтобы сделать вывод, что Фидо находится в наборе фиолетовых вещей.
Помимо этих категориальных стилевых посылок вида «все ___», «некоторые ____» и «нет ____», также часто встречаются условные посылки.
Пример 33
\(\begin{array} {ll} \text{Предпосылка:} & \text{Если вы живете в Сиэтле, вы живете в Вашингтоне.} \\ \text{Предпосылка:} & \text{Маркус не живет в Сиэтле.} \\ \text{Вывод:} & \text{Маркус не живет в Вашингтоне.} \end{array}\)
Решение
Из первой посылки мы знаем, что множество людей, живущих в Сиэтле, находится внутри множества тех, кто живет в Вашингтоне. Из второй посылки мы знаем, что Маркус не входит в набор Сиэтла, но у нас недостаточно информации, чтобы узнать, живет ли Маркус в Вашингтоне или нет.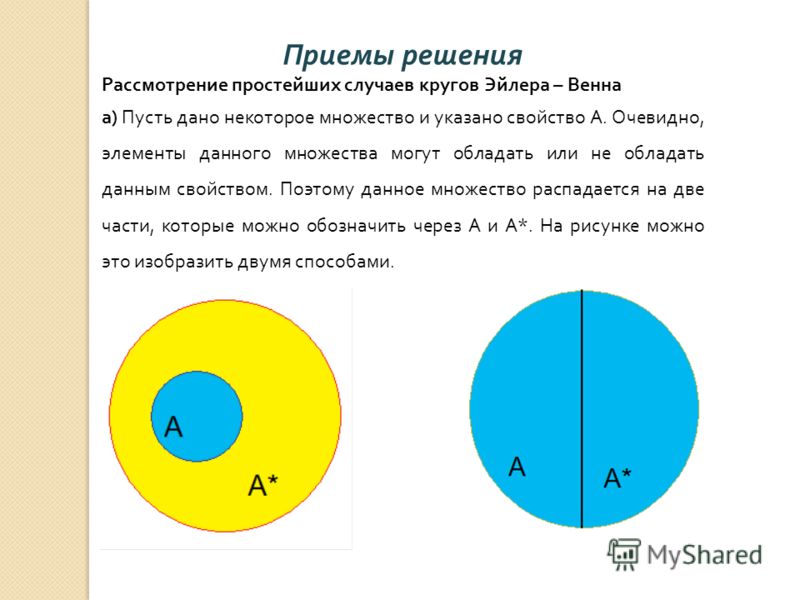 Это неверный аргумент.
Это неверный аргумент.
Попробуй сейчас 12
Определите правильность этого аргумента:
\(\begin{array} {ll} \text{Предпосылка:} & \text{Если у вас есть помада на воротнике, то вы изменяешь мне.} \\ \text{Предпосылка:} & \text{Если ты мне изменяешь, я разведусь с тобой.} \\ \text{Предпосылка:} & \text{ У тебя нет помады на губах воротник.} \\ \text{Вывод:} & \text{Я с вами не разведусь.} \end{array}\)
- Ответить
Недействительно. Помада на твоем воротнике — это подмножество сценариев, в которых ты изменяешь, а обман — это подмножество сценариев, в которых я разведусь с тобой. Хотя прекрасно, что у тебя на воротнике нет помады, ты все равно можешь мне изменять, и я разведусь с тобой. На самом деле, даже если ты мне не изменяешь, я могу развестись с тобой по другой причине. Тебе лучше привести себя в форму.
Эта страница называется 17.9: Оценка дедуктивных аргументов с помощью диаграмм Эйлера распространяется под лицензией CC BY-SA 3.

 rope)родрод (США, геодезический)перчполь (англ. pole)морская сажень, фатомсажень (США, геодезическая)локотьярдфутфут (США, геодезический)линклинк (США, геодезический)локоть (брит.)хендпядьфингернейльдюймдюйм (США, геодезический)ячменное зерно (англ. barleycorn)тысячнаямикродюймангстрематомная единица длиныикс-единицафермиарпанпайкатипографский пункттвиплокоть (шведский)морская сажень (шведская)калибрсантидюймкенаршинactus (Др. Рим.)vara de tareavara conuqueravara castellanaлокоть (греческий)long reedreedдлинный локотьладонь«палец»планковская длинаклассический радиус электронаборовский радиусэкваториальный радиус Землиполярный радиус Землирасстояние от Земли до Солнцарадиус Солнцасветовая наносекундасветовая микросекундасветовая миллисекундасветовая секундасветовой чассветовые суткисветовая неделяМиллиард световых летРасстояние от Земли до Луныкабельтов (международный)кабельтов (британский)кабельтов (США)морская миля (США)световая минутастоечный юнитгоризонтальный шагцицеропиксельлиниядюйм (русский)вершокпядьфутсаженькосая саженьверстамежевая верста
rope)родрод (США, геодезический)перчполь (англ. pole)морская сажень, фатомсажень (США, геодезическая)локотьярдфутфут (США, геодезический)линклинк (США, геодезический)локоть (брит.)хендпядьфингернейльдюймдюйм (США, геодезический)ячменное зерно (англ. barleycorn)тысячнаямикродюймангстрематомная единица длиныикс-единицафермиарпанпайкатипографский пункттвиплокоть (шведский)морская сажень (шведская)калибрсантидюймкенаршинactus (Др. Рим.)vara de tareavara conuqueravara castellanaлокоть (греческий)long reedreedдлинный локотьладонь«палец»планковская длинаклассический радиус электронаборовский радиусэкваториальный радиус Землиполярный радиус Землирасстояние от Земли до Солнцарадиус Солнцасветовая наносекундасветовая микросекундасветовая миллисекундасветовая секундасветовой чассветовые суткисветовая неделяМиллиард световых летРасстояние от Земли до Луныкабельтов (международный)кабельтов (британский)кабельтов (США)морская миля (США)световая минутастоечный юнитгоризонтальный шагцицеропиксельлиниядюйм (русский)вершокпядьфутсаженькосая саженьверстамежевая верста )морская лига (международная)лига (статутная)миляморская миля (брит.)морская миля (международная)миля (статутная)миля (США, геодезическая)миля (римская)1000 ярдовфарлонгфарлонг (США, геодезический)чейнчейн (США, геодезический)rope (англ. rope)родрод (США, геодезический)перчполь (англ. pole)морская сажень, фатомсажень (США, геодезическая)локотьярдфутфут (США, геодезический)линклинк (США, геодезический)локоть (брит.)хендпядьфингернейльдюймдюйм (США, геодезический)ячменное зерно (англ. barleycorn)тысячнаямикродюймангстрематомная единица длиныикс-единицафермиарпанпайкатипографский пункттвиплокоть (шведский)морская сажень (шведская)калибрсантидюймкенаршинactus (Др. Рим.)vara de tareavara conuqueravara castellanaлокоть (греческий)long reedreedдлинный локотьладонь«палец»планковская длинаклассический радиус электронаборовский радиусэкваториальный радиус Землиполярный радиус Землирасстояние от Земли до Солнцарадиус Солнцасветовая наносекундасветовая микросекундасветовая миллисекундасветовая секундасветовой чассветовые суткисветовая неделяМиллиард световых летРасстояние от Земли до Луныкабельтов (международный)кабельтов (британский)кабельтов (США)морская миля (США)световая минутастоечный юнитгоризонтальный шагцицеропиксельлиниядюйм (русский)вершокпядьфутсаженькосая саженьверстамежевая верста
)морская лига (международная)лига (статутная)миляморская миля (брит.)морская миля (международная)миля (статутная)миля (США, геодезическая)миля (римская)1000 ярдовфарлонгфарлонг (США, геодезический)чейнчейн (США, геодезический)rope (англ. rope)родрод (США, геодезический)перчполь (англ. pole)морская сажень, фатомсажень (США, геодезическая)локотьярдфутфут (США, геодезический)линклинк (США, геодезический)локоть (брит.)хендпядьфингернейльдюймдюйм (США, геодезический)ячменное зерно (англ. barleycorn)тысячнаямикродюймангстрематомная единица длиныикс-единицафермиарпанпайкатипографский пункттвиплокоть (шведский)морская сажень (шведская)калибрсантидюймкенаршинactus (Др. Рим.)vara de tareavara conuqueravara castellanaлокоть (греческий)long reedreedдлинный локотьладонь«палец»планковская длинаклассический радиус электронаборовский радиусэкваториальный радиус Землиполярный радиус Землирасстояние от Земли до Солнцарадиус Солнцасветовая наносекундасветовая микросекундасветовая миллисекундасветовая секундасветовой чассветовые суткисветовая неделяМиллиард световых летРасстояние от Земли до Луныкабельтов (международный)кабельтов (британский)кабельтов (США)морская миля (США)световая минутастоечный юнитгоризонтальный шагцицеропиксельлиниядюйм (русский)вершокпядьфутсаженькосая саженьверстамежевая верста
 В странах, где не пользуются метрической системой, например в США и Великобритании, используют такие единицы как дюймы, футы и мили.
В странах, где не пользуются метрической системой, например в США и Великобритании, используют такие единицы как дюймы, футы и мили. Первоначально она измерялась как дуга в одну минуту по меридиану, то есть 1/(60×180) меридиана. Это облегчало вычисления широты, так как 60 морских миль равнялись одному градусу широты. Когда расстояние измеряется в морских милях, скорость часто измеряют в морских узлах. Один морской узел равен скорости движения в одну морскую милю в час.
Первоначально она измерялась как дуга в одну минуту по меридиану, то есть 1/(60×180) меридиана. Это облегчало вычисления широты, так как 60 морских миль равнялись одному градусу широты. Когда расстояние измеряется в морских милях, скорость часто измеряют в морских узлах. Один морской узел равен скорости движения в одну морскую милю в час. Один парсек — это расстояние от Солнца до другого астрономического объекта, например планеты, звезды, луны, или астероида, с углом в одну угловую секунду. Одна угловая секунда — 1/3600 градуса, или примерно 4,8481368 мкрад в радианах. Парсек можно вычислить используя параллакс — эффект видимого изменения положения тела, в зависимости от точки наблюдения. При измерениях прокладывают отрезок E1A2 (на иллюстрации) от Земли (точка E1) до звезды или другого астрономического объекта (точка A2). Шесть месяцев спустя, когда Солнце находится на другой стороне Земли, прокладывают новый отрезок E2A1 от нового положения Земли (точка E2) до нового положения в пространстве того же самого астрономического объекта (точка A1). При этом Солнце будет находиться на пересечении этих двух отрезков, в точке S. Длина каждого из отрезков E1S и E2S равна одной астрономической единице. Если отложить отрезок через точку S, перпендикулярный E1E2, он пройдет через точку пересечения отрезков E1A2 и E2A1, I. Расстояние от Солнца до точки I — отрезок SI, он равен одному парсеку, когда угол между отрезками A1I и A2I — две угловые секунды.
Один парсек — это расстояние от Солнца до другого астрономического объекта, например планеты, звезды, луны, или астероида, с углом в одну угловую секунду. Одна угловая секунда — 1/3600 градуса, или примерно 4,8481368 мкрад в радианах. Парсек можно вычислить используя параллакс — эффект видимого изменения положения тела, в зависимости от точки наблюдения. При измерениях прокладывают отрезок E1A2 (на иллюстрации) от Земли (точка E1) до звезды или другого астрономического объекта (точка A2). Шесть месяцев спустя, когда Солнце находится на другой стороне Земли, прокладывают новый отрезок E2A1 от нового положения Земли (точка E2) до нового положения в пространстве того же самого астрономического объекта (точка A1). При этом Солнце будет находиться на пересечении этих двух отрезков, в точке S. Длина каждого из отрезков E1S и E2S равна одной астрономической единице. Если отложить отрезок через точку S, перпендикулярный E1E2, он пройдет через точку пересечения отрезков E1A2 и E2A1, I. Расстояние от Солнца до точки I — отрезок SI, он равен одному парсеку, когда угол между отрезками A1I и A2I — две угловые секунды.
 В некоторых странах, например в Канаде, где принята метрическая система, ярды используют для измерения ткани и длины бассейнов и спортивных полей и площадок, например, полей для гольфа и футбола.
В некоторых странах, например в Канаде, где принята метрическая система, ярды используют для измерения ткани и длины бассейнов и спортивных полей и площадок, например, полей для гольфа и футбола. Перемещение и длина одинаковы по величине только если тело двигалось по прямой.
Перемещение и длина одинаковы по величине только если тело двигалось по прямой.
 Иногда термин «длина» относится только к определенному размеру объекта. Например, можно отрезать кусок каната, длина которого будет меньше его толщины. В физике термин «длина» обычно используется как синоним «расстояния».
Иногда термин «длина» относится только к определенному размеру объекта. Например, можно отрезать кусок каната, длина которого будет меньше его толщины. В физике термин «длина» обычно используется как синоним «расстояния». », то есть «…умножить на десять в степени…». Компьютерная экспоненциальная запись широко используется в научных, математических и инженерных расчетах.
», то есть «…умножить на десять в степени…». Компьютерная экспоненциальная запись широко используется в научных, математических и инженерных расчетах. com на YouTube
com на YouTube единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева
единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева rope)родрод (США, геодезический)перчполь (англ. pole)морская сажень, фатомсажень (США, геодезическая)локотьярдфутфут (США, геодезический)линклинк (США, геодезический)локоть (брит.)хендпядьфингернейльдюймдюйм (США, геодезический)ячменное зерно (англ. barleycorn)тысячнаямикродюймангстрематомная единица длиныикс-единицафермиарпанпайкатипографский пункттвиплокоть (шведский)морская сажень (шведская)калибрсантидюймкенаршинactus (Др. Рим.)vara de tareavara conuqueravara castellanaлокоть (греческий)long reedreedдлинный локотьладонь«палец»планковская длинаклассический радиус электронаборовский радиусэкваториальный радиус Землиполярный радиус Землирасстояние от Земли до Солнцарадиус Солнцасветовая наносекундасветовая микросекундасветовая миллисекундасветовая секундасветовой чассветовые суткисветовая неделяМиллиард световых летРасстояние от Земли до Луныкабельтов (международный)кабельтов (британский)кабельтов (США)морская миля (США)световая минутастоечный юнитгоризонтальный шагцицеропиксельлиниядюйм (русский)вершокпядьфутсаженькосая саженьверстамежевая верста
rope)родрод (США, геодезический)перчполь (англ. pole)морская сажень, фатомсажень (США, геодезическая)локотьярдфутфут (США, геодезический)линклинк (США, геодезический)локоть (брит.)хендпядьфингернейльдюймдюйм (США, геодезический)ячменное зерно (англ. barleycorn)тысячнаямикродюймангстрематомная единица длиныикс-единицафермиарпанпайкатипографский пункттвиплокоть (шведский)морская сажень (шведская)калибрсантидюймкенаршинactus (Др. Рим.)vara de tareavara conuqueravara castellanaлокоть (греческий)long reedreedдлинный локотьладонь«палец»планковская длинаклассический радиус электронаборовский радиусэкваториальный радиус Землиполярный радиус Землирасстояние от Земли до Солнцарадиус Солнцасветовая наносекундасветовая микросекундасветовая миллисекундасветовая секундасветовой чассветовые суткисветовая неделяМиллиард световых летРасстояние от Земли до Луныкабельтов (международный)кабельтов (британский)кабельтов (США)морская миля (США)световая минутастоечный юнитгоризонтальный шагцицеропиксельлиниядюйм (русский)вершокпядьфутсаженькосая саженьверстамежевая верста )морская лига (международная)лига (статутная)миляморская миля (брит.)морская миля (международная)миля (статутная)миля (США, геодезическая)миля (римская)1000 ярдовфарлонгфарлонг (США, геодезический)чейнчейн (США, геодезический)rope (англ. rope)родрод (США, геодезический)перчполь (англ. pole)морская сажень, фатомсажень (США, геодезическая)локотьярдфутфут (США, геодезический)линклинк (США, геодезический)локоть (брит.)хендпядьфингернейльдюймдюйм (США, геодезический)ячменное зерно (англ. barleycorn)тысячнаямикродюймангстрематомная единица длиныикс-единицафермиарпанпайкатипографский пункттвиплокоть (шведский)морская сажень (шведская)калибрсантидюймкенаршинactus (Др. Рим.)vara de tareavara conuqueravara castellanaлокоть (греческий)long reedreedдлинный локотьладонь«палец»планковская длинаклассический радиус электронаборовский радиусэкваториальный радиус Землиполярный радиус Землирасстояние от Земли до Солнцарадиус Солнцасветовая наносекундасветовая микросекундасветовая миллисекундасветовая секундасветовой чассветовые суткисветовая неделяМиллиард световых летРасстояние от Земли до Луныкабельтов (международный)кабельтов (британский)кабельтов (США)морская миля (США)световая минутастоечный юнитгоризонтальный шагцицеропиксельлиниядюйм (русский)вершокпядьфутсаженькосая саженьверстамежевая верста
)морская лига (международная)лига (статутная)миляморская миля (брит.)морская миля (международная)миля (статутная)миля (США, геодезическая)миля (римская)1000 ярдовфарлонгфарлонг (США, геодезический)чейнчейн (США, геодезический)rope (англ. rope)родрод (США, геодезический)перчполь (англ. pole)морская сажень, фатомсажень (США, геодезическая)локотьярдфутфут (США, геодезический)линклинк (США, геодезический)локоть (брит.)хендпядьфингернейльдюймдюйм (США, геодезический)ячменное зерно (англ. barleycorn)тысячнаямикродюймангстрематомная единица длиныикс-единицафермиарпанпайкатипографский пункттвиплокоть (шведский)морская сажень (шведская)калибрсантидюймкенаршинactus (Др. Рим.)vara de tareavara conuqueravara castellanaлокоть (греческий)long reedreedдлинный локотьладонь«палец»планковская длинаклассический радиус электронаборовский радиусэкваториальный радиус Землиполярный радиус Землирасстояние от Земли до Солнцарадиус Солнцасветовая наносекундасветовая микросекундасветовая миллисекундасветовая секундасветовой чассветовые суткисветовая неделяМиллиард световых летРасстояние от Земли до Луныкабельтов (международный)кабельтов (британский)кабельтов (США)морская миля (США)световая минутастоечный юнитгоризонтальный шагцицеропиксельлиниядюйм (русский)вершокпядьфутсаженькосая саженьверстамежевая верста Его длина составляет 319 метров или 1047 футов.
Его длина составляет 319 метров или 1047 футов. В странах, где не пользуются метрической системой, например в США и Великобритании, используют такие единицы как дюймы, футы и мили.
В странах, где не пользуются метрической системой, например в США и Великобритании, используют такие единицы как дюймы, футы и мили. Первоначально она измерялась как дуга в одну минуту по меридиану, то есть 1/(60×180) меридиана. Это облегчало вычисления широты, так как 60 морских миль равнялись одному градусу широты. Когда расстояние измеряется в морских милях, скорость часто измеряют в морских узлах. Один морской узел равен скорости движения в одну морскую милю в час.
Первоначально она измерялась как дуга в одну минуту по меридиану, то есть 1/(60×180) меридиана. Это облегчало вычисления широты, так как 60 морских миль равнялись одному градусу широты. Когда расстояние измеряется в морских милях, скорость часто измеряют в морских узлах. Один морской узел равен скорости движения в одну морскую милю в час. Один парсек — это расстояние от Солнца до другого астрономического объекта, например планеты, звезды, луны, или астероида, с углом в одну угловую секунду. Одна угловая секунда — 1/3600 градуса, или примерно 4,8481368 мкрад в радианах. Парсек можно вычислить используя параллакс — эффект видимого изменения положения тела, в зависимости от точки наблюдения. При измерениях прокладывают отрезок E1A2 (на иллюстрации) от Земли (точка E1) до звезды или другого астрономического объекта (точка A2). Шесть месяцев спустя, когда Солнце находится на другой стороне Земли, прокладывают новый отрезок E2A1 от нового положения Земли (точка E2) до нового положения в пространстве того же самого астрономического объекта (точка A1). При этом Солнце будет находиться на пересечении этих двух отрезков, в точке S. Длина каждого из отрезков E1S и E2S равна одной астрономической единице. Если отложить отрезок через точку S, перпендикулярный E1E2, он пройдет через точку пересечения отрезков E1A2 и E2A1, I. Расстояние от Солнца до точки I — отрезок SI, он равен одному парсеку, когда угол между отрезками A1I и A2I — две угловые секунды.
Один парсек — это расстояние от Солнца до другого астрономического объекта, например планеты, звезды, луны, или астероида, с углом в одну угловую секунду. Одна угловая секунда — 1/3600 градуса, или примерно 4,8481368 мкрад в радианах. Парсек можно вычислить используя параллакс — эффект видимого изменения положения тела, в зависимости от точки наблюдения. При измерениях прокладывают отрезок E1A2 (на иллюстрации) от Земли (точка E1) до звезды или другого астрономического объекта (точка A2). Шесть месяцев спустя, когда Солнце находится на другой стороне Земли, прокладывают новый отрезок E2A1 от нового положения Земли (точка E2) до нового положения в пространстве того же самого астрономического объекта (точка A1). При этом Солнце будет находиться на пересечении этих двух отрезков, в точке S. Длина каждого из отрезков E1S и E2S равна одной астрономической единице. Если отложить отрезок через точку S, перпендикулярный E1E2, он пройдет через точку пересечения отрезков E1A2 и E2A1, I. Расстояние от Солнца до точки I — отрезок SI, он равен одному парсеку, когда угол между отрезками A1I и A2I — две угловые секунды.
 В некоторых странах, например в Канаде, где принята метрическая система, ярды используют для измерения ткани и длины бассейнов и спортивных полей и площадок, например, полей для гольфа и футбола.
В некоторых странах, например в Канаде, где принята метрическая система, ярды используют для измерения ткани и длины бассейнов и спортивных полей и площадок, например, полей для гольфа и футбола. Перемещение и длина одинаковы по величине только если тело двигалось по прямой.
Перемещение и длина одинаковы по величине только если тело двигалось по прямой.
 Иногда термин «длина» относится только к определенному размеру объекта. Например, можно отрезать кусок каната, длина которого будет меньше его толщины. В физике термин «длина» обычно используется как синоним «расстояния».
Иногда термин «длина» относится только к определенному размеру объекта. Например, можно отрезать кусок каната, длина которого будет меньше его толщины. В физике термин «длина» обычно используется как синоним «расстояния». », то есть «…умножить на десять в степени…». Компьютерная экспоненциальная запись широко используется в научных, математических и инженерных расчетах.
», то есть «…умножить на десять в степени…». Компьютерная экспоненциальная запись широко используется в научных, математических и инженерных расчетах. com на YouTube
com на YouTube Аббревиатура: mm
Аббревиатура: mm
 0E-7 километр
0E-7 километр Дроби округляются до ближайшей восьмой дроби.
Дроби округляются до ближайшей восьмой дроби. Это РАВНОЕ значение длины, равное 1 миллиметру, но в альтернативной единице длины в километрах.
Это РАВНОЕ значение длины, равное 1 миллиметру, но в альтернативной единице длины в километрах.  000014 km
000014 km

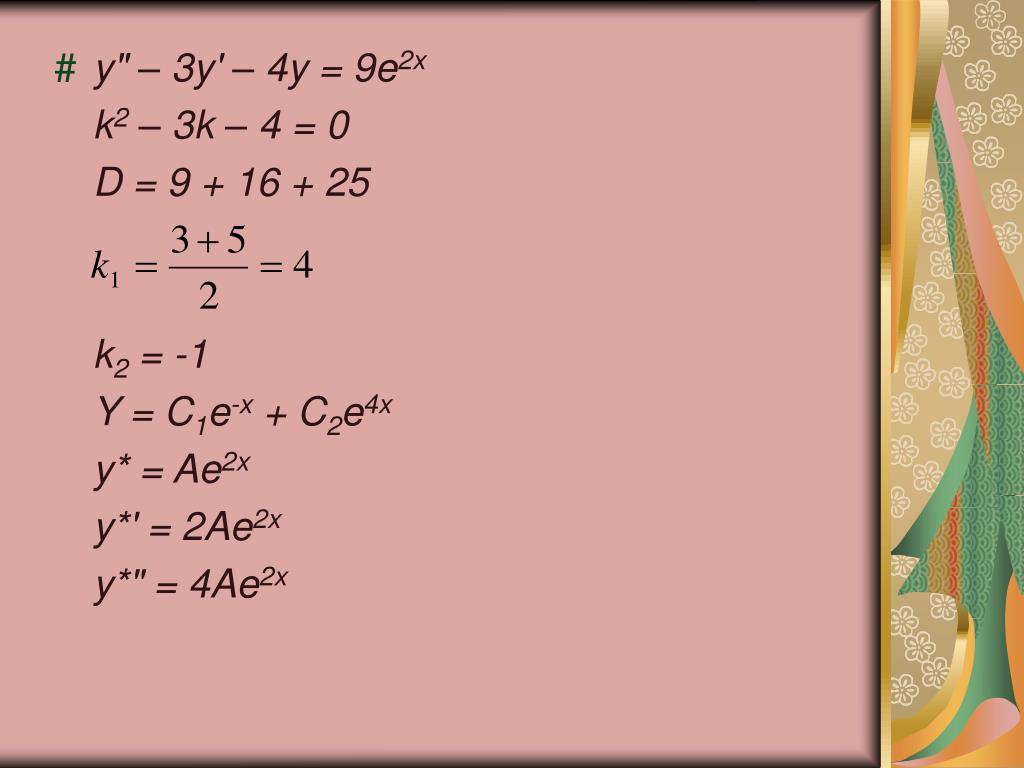

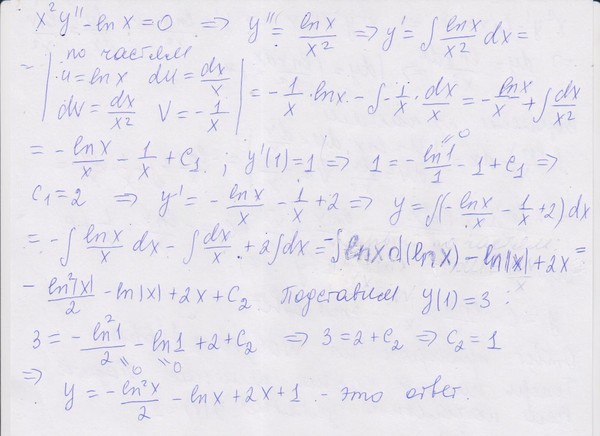



 Применяя различные методы, решить уравнения 601–611: x2y» — xy’ + y = ln x/x + x/ln x.
Применяя различные методы, решить уравнения 601–611: x2y» — xy’ + y = ln x/x + x/ln x. ..
.. ..
..
 Так, например, если вы нашли $2$ в качестве нуля полинома, то вы должны использовать $(r-2)$, чтобы попытаться уменьшить полином до квадратного, если это возможно, или до чего-то, что можно разложить на множители. 9{nd}$ Порядок линейных уравнений с постоянными коэффициентами однородных обыкновенных дифференциальных уравнений, и то же самое относится к более высокому порядку.
Так, например, если вы нашли $2$ в качестве нуля полинома, то вы должны использовать $(r-2)$, чтобы попытаться уменьшить полином до квадратного, если это возможно, или до чего-то, что можно разложить на множители. 9{nd}$ Порядок линейных уравнений с постоянными коэффициентами однородных обыкновенных дифференциальных уравнений, и то же самое относится к более высокому порядку.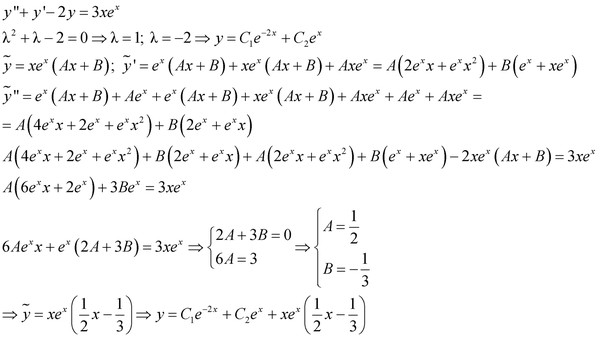 Наши корни будут $r=-3$ (с кратностью 2), потому что один и тот же корень встречается дважды, это означает необходимость умножения линейной комбинации решения на соответствующее количество степеней $’x’$ или $’t ‘$ в зависимости от вашей независимой переменной в ODE. Давайте рассмотрим еще несколько примеров.
Наши корни будут $r=-3$ (с кратностью 2), потому что один и тот же корень встречается дважды, это означает необходимость умножения линейной комбинации решения на соответствующее количество степеней $’x’$ или $’t ‘$ в зависимости от вашей независимой переменной в ODE. Давайте рассмотрим еще несколько примеров.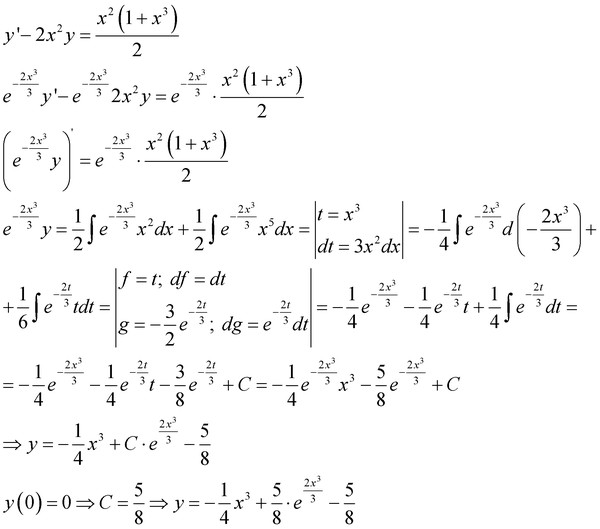
 Сколько всего книг было в магазине?
Сколько всего книг было в магазине?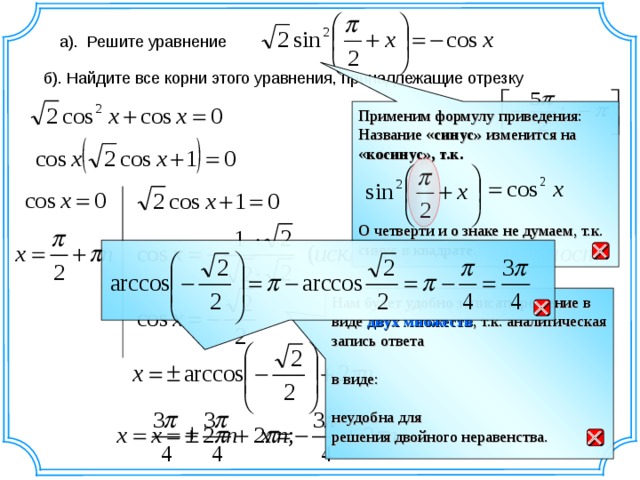
 В статье представлена информация о функции, включая ее домен, диапазон и ключевые данные, относящиеся к построению графиков, дифференцированию и интегрированию.
В статье представлена информация о функции, включая ее домен, диапазон и ключевые данные, относящиеся к построению графиков, дифференцированию и интегрированию. 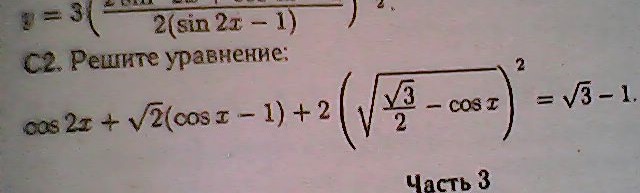 2 График функции с первообразной
2 График функции с первообразной
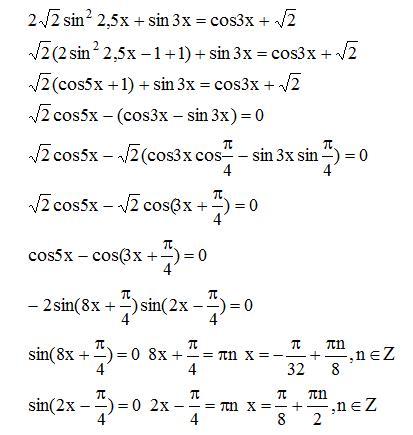

 Как было подсчитано ранее, имеем:
Как было подсчитано ранее, имеем: Значение функции во всех этих точках равно .
Значение функции во всех этих точках равно .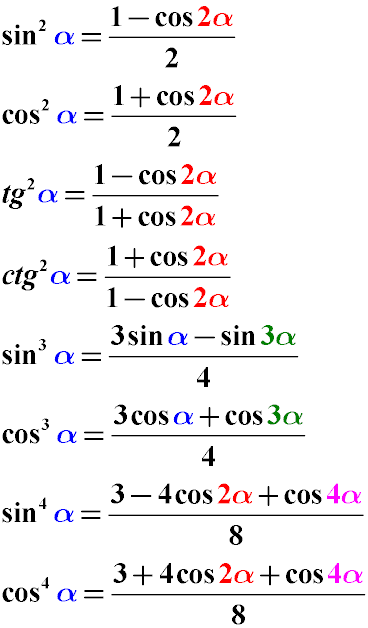

 Также на достаточно большом интервале среднее значение близко к 1/2:
Также на достаточно большом интервале среднее значение близко к 1/2:

 1 Критические точки
1 Критические точки


 Как было подсчитано ранее, имеем:
Как было подсчитано ранее, имеем: Значение функции во всех этих точках равно .
Значение функции во всех этих точках равно .

 Также на достаточно большом интервале среднее значение близко к 1/2:
Также на достаточно большом интервале среднее значение близко к 1/2:
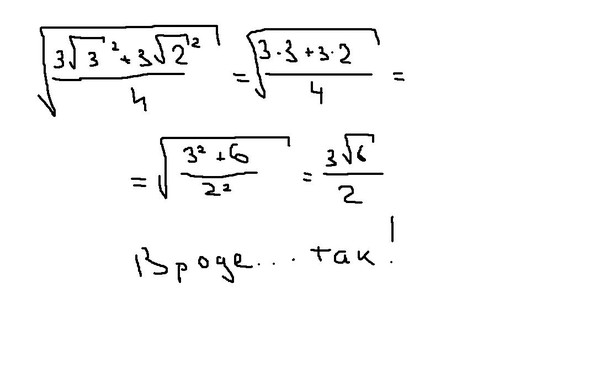
 6 GHz с 16 ГБ ОЗУ. Среди математических констант только было вычислено более точно.
6 GHz с 16 ГБ ОЗУ. Среди математических констант только было вычислено более точно. Множество чисел вида , где — рациональные числа, образует алгебраическое поле. Оно обозначается и является подполем поля вещественных чисел.
Множество чисел вида , где — рациональные числа, образует алгебраическое поле. Оно обозначается и является подполем поля вещественных чисел. Скорость сходимости здесь меньше, чем у метода Ньютона, но вычисления гораздо проще. Выпишем несколько первых приближений:
Скорость сходимости здесь меньше, чем у метода Ньютона, но вычисления гораздо проще. Выпишем несколько первых приближений:



 п.
п.
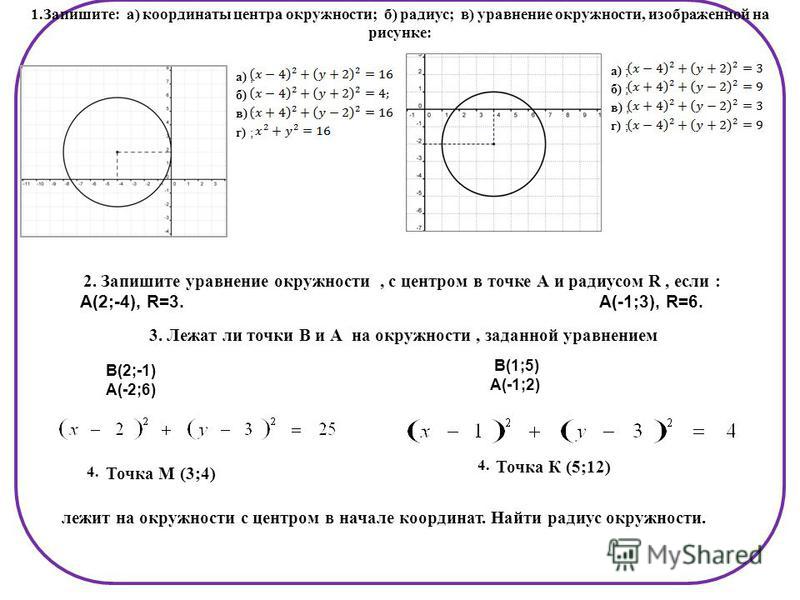 Составить уравнение окружности, если ее центр находится в точке С(5;4) и окружность отсекает от прямой х+2у-3=0 хорду, длина которой равна 8.
Составить уравнение окружности, если ее центр находится в точке С(5;4) и окружность отсекает от прямой х+2у-3=0 хорду, длина которой равна 8.
 Это уравнение используется во многих задачах окружностей в координатной геометрии.
Это уравнение используется во многих задачах окружностей в координатной геометрии.
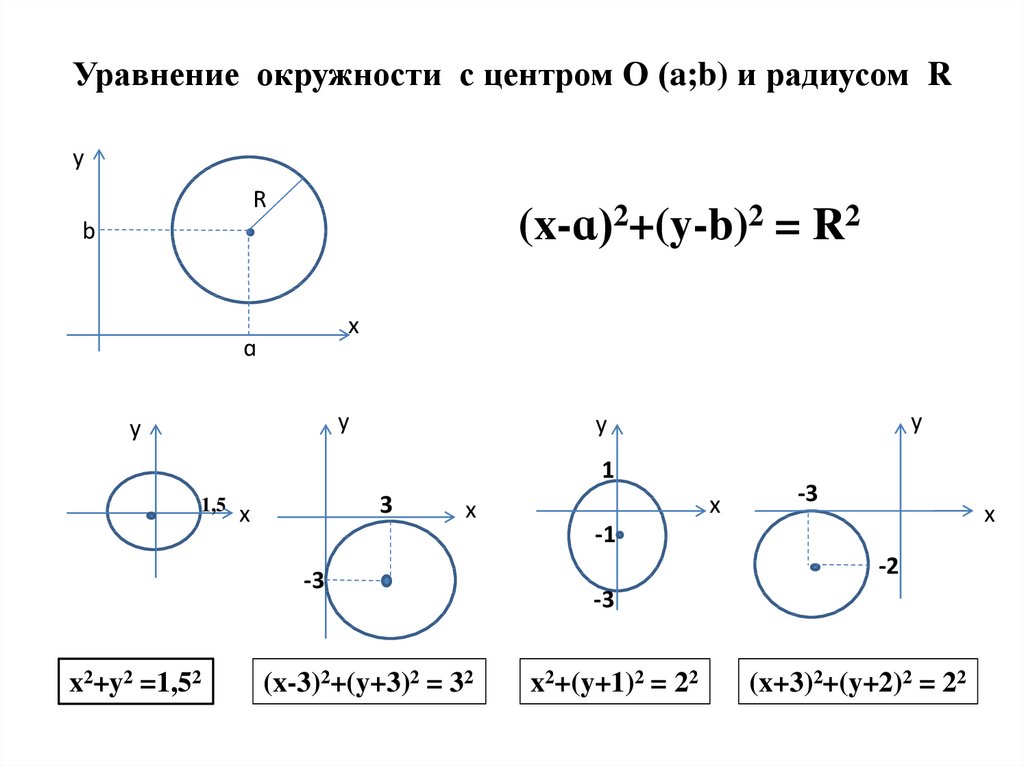
 Существуют различные формы представления уравнения окружности,
Существуют различные формы представления уравнения окружности,
 2\).
2\). Мы изучили формы представления уравнения окружности при заданных координатах центра окружности. Существуют определенные особые случаи, основанные на положении окружности в координатной плоскости. Давайте узнаем о методе нахождения уравнения окружности для общего и этих частных случаев. 92} = г\).
Мы изучили формы представления уравнения окружности при заданных координатах центра окружности. Существуют определенные особые случаи, основанные на положении окружности в координатной плоскости. Давайте узнаем о методе нахождения уравнения окружности для общего и этих частных случаев. 92} = г\). (x, y) — произвольная точка на окружности.
(x, y) — произвольная точка на окружности. Применим формулу расстояния между этими точками. 92\)
Применим формулу расстояния между этими точками. 92\) Итак, радиус r = 4,
Итак, радиус r = 4, В уравнении окружности нет члена \(xy\).
В уравнении окружности нет члена \(xy\).
 С Cuemath вы будете учиться визуально и будете удивлены результатами.
С Cuemath вы будете учиться визуально и будете удивлены результатами.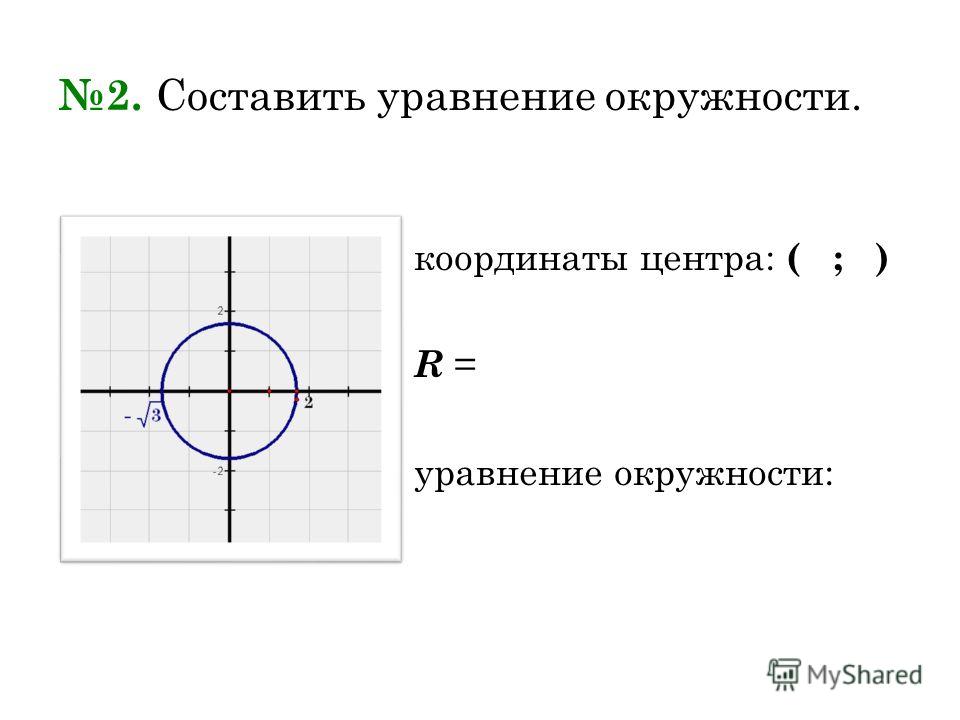 2 = 2\).
2 = 2\). Существуют разные формы уравнения окружности:
Существуют разные формы уравнения окружности: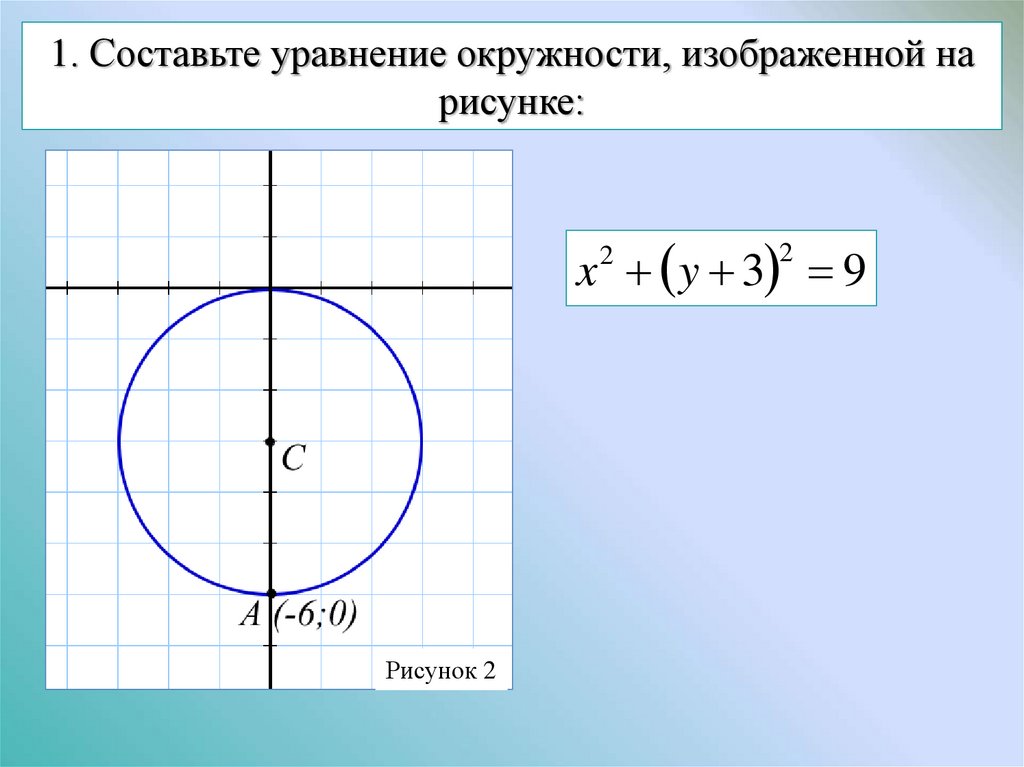
 ХХ ст.? Як вони вирішувалися?»
ХХ ст.? Як вони вирішувалися?» Г. характеризуються пропорційно розвиненими частинами тіла, міцним здоров’ям, високою продуктивністю і відтворювальною здатністю.
Б. характеризуються тонкою шкірою, яка вкрита коротким ніжним волоссям, слаборозвиненою тонковолокнистою мускулатурою, слабким розвитком підшкірної жирової тканини, мають тонкий, але міцний скелет.
Г. характеризуються пропорційно розвиненими частинами тіла, міцним здоров’ям, високою продуктивністю і відтворювальною здатністю.
Б. характеризуються тонкою шкірою, яка вкрита коротким ніжним волоссям, слаборозвиненою тонковолокнистою мускулатурою, слабким розвитком підшкірної жирової тканини, мають тонкий, але міцний скелет. через все аресты, сделанные вчера.
через все аресты, сделанные вчера. Система VINE также позволяет гражданину зарегистрироваться для получения уведомления об освобождении заключенного. Для получения дополнительной информации о системе VINE посетите страницу справки
Система VINE также позволяет гражданину зарегистрироваться для получения уведомления об освобождении заключенного. Для получения дополнительной информации о системе VINE посетите страницу справки 03.23 в 11:15
03.23 в 11:15  5(2)(C) UNLAW POSS SCH III, IV, V, ЗА ИСКЛЮЧЕНИЕМ КЕТАМИНА ИЛИ ФЛУНИТРАЗЕПАМА
5(2)(C) UNLAW POSS SCH III, IV, V, ЗА ИСКЛЮЧЕНИЕМ КЕТАМИНА ИЛИ ФЛУНИТРАЗЕПАМА  Номер бронирования: IN202302549
Номер бронирования: IN202302549  07.72
07.72  03.23 в 16:00
03.23 в 16:00  00
00 03.23 в 09:00
03.23 в 09:00  Номер бронирования: IN202300240
Номер бронирования: IN202300240  03.23 в 22:02
03.23 в 22:02  Номер бронирования: IN202302537
Номер бронирования: IN202302537  08.83
08.83  00
00 Номер бронирования: IN202302546
Номер бронирования: IN202302546  09.88
09.88 
 у.)
углекислого газа в раствор, содержа
у.)
углекислого газа в раствор, содержа (По произведениям Дж. Роулинг.)
(По произведениям Дж. Роулинг.)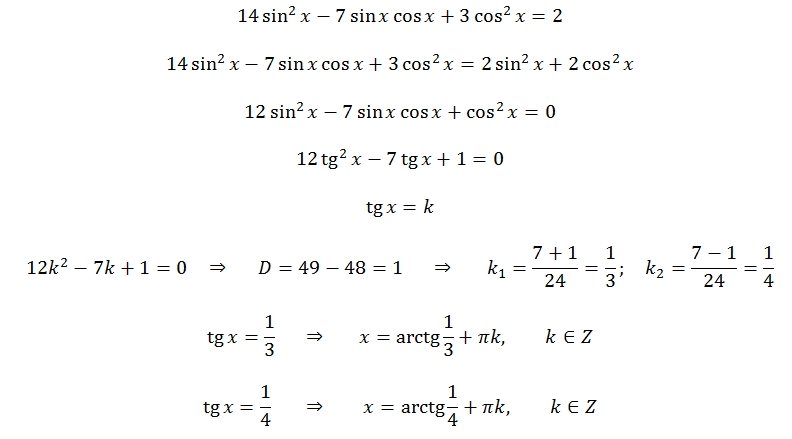 )/3
)/3
 ответил 22.07.22
92 +2y + 1 = 0
ответил 22.07.22
92 +2y + 1 = 0

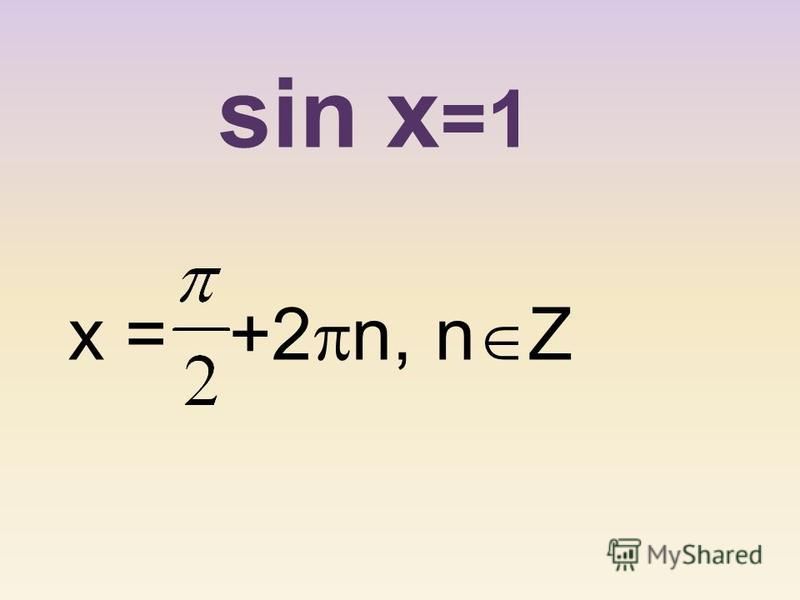 )
) )
)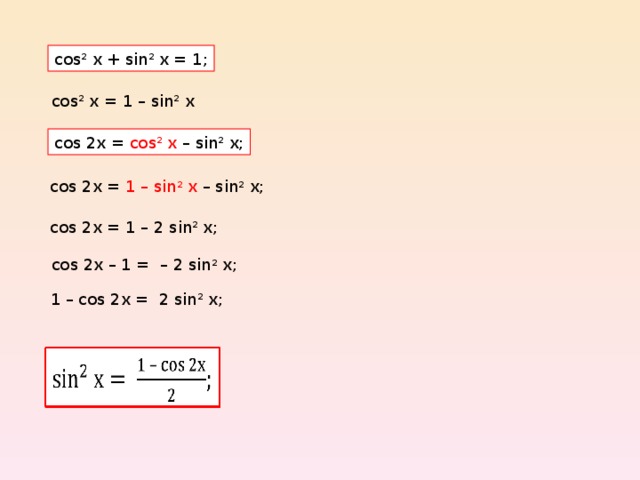 )
) )
) )
)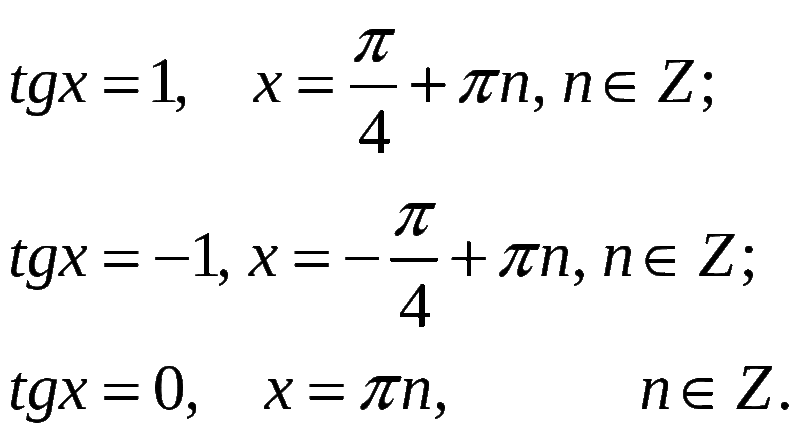 )
) )
) 2
2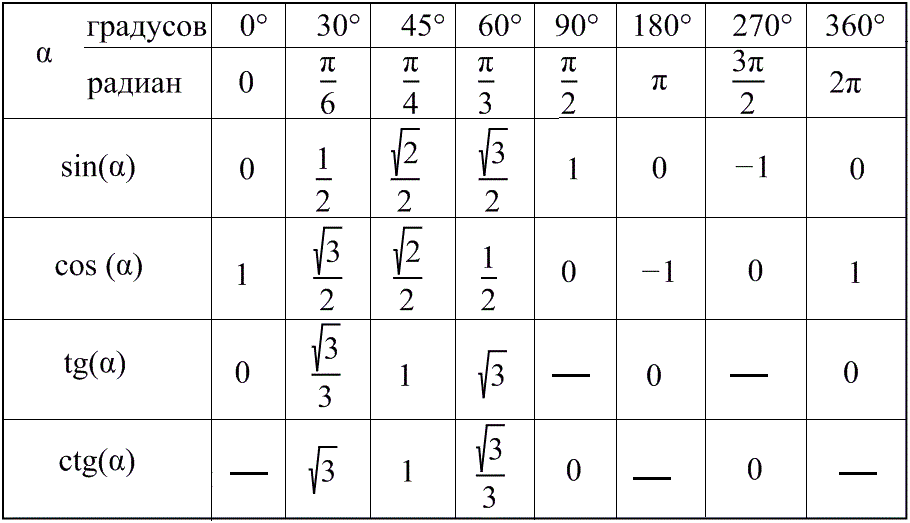 3
3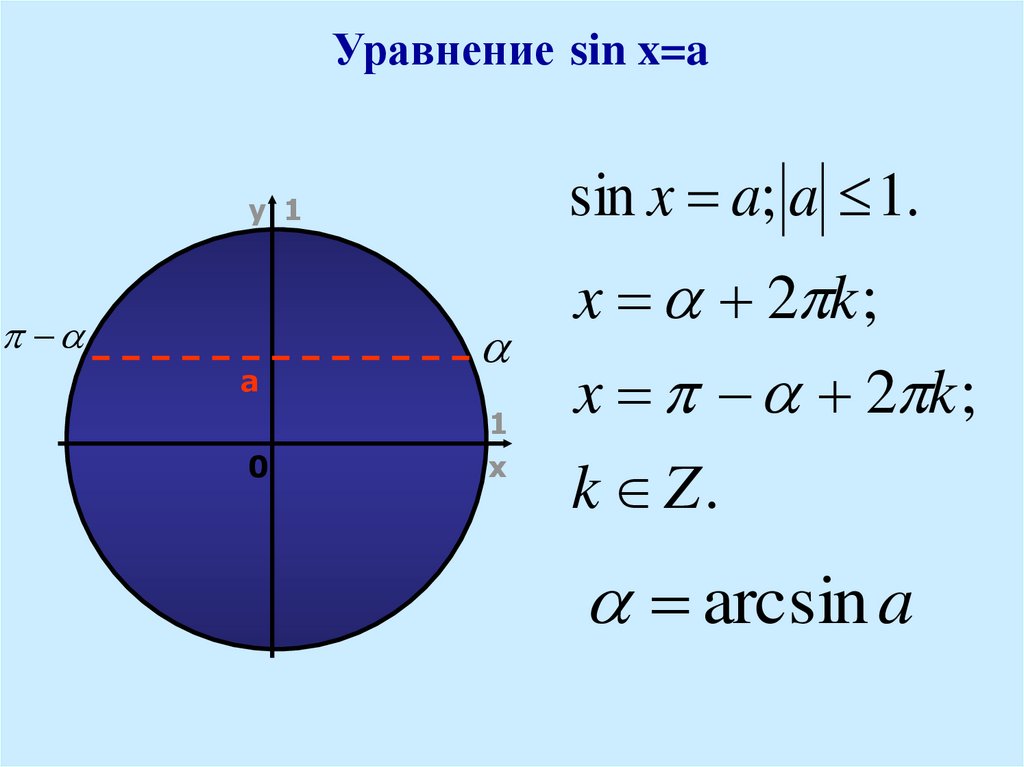 14159..
14159..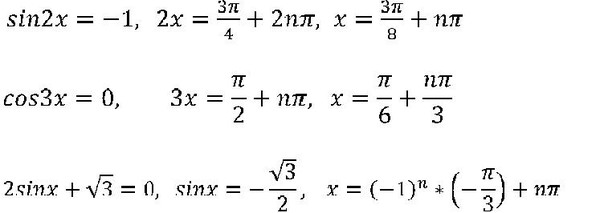

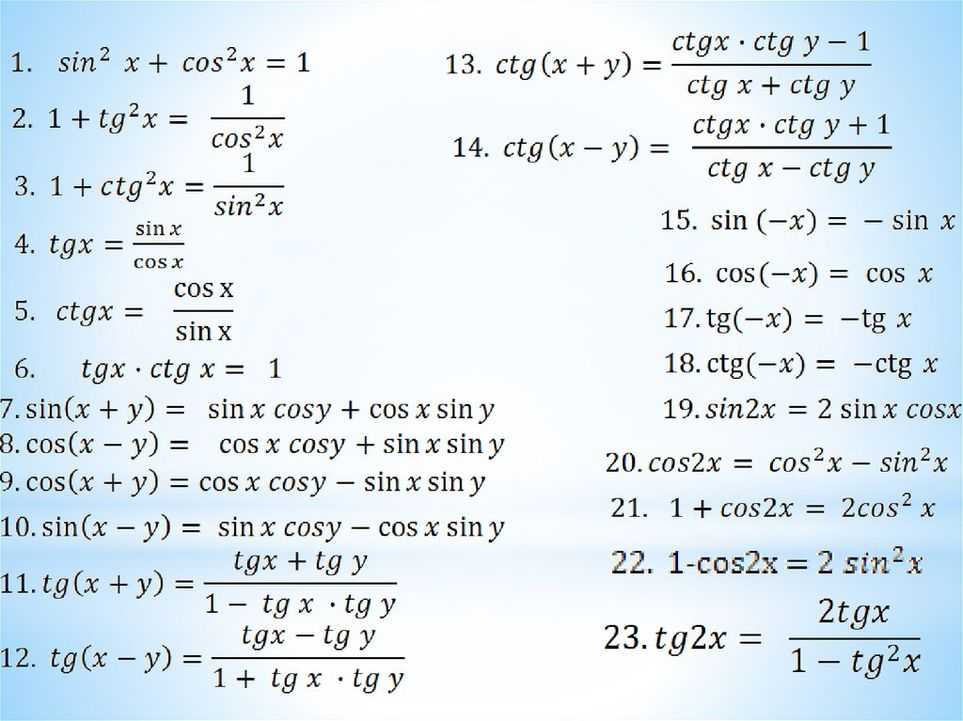 Поэтому мы можем найти sin x, используя квадратичную формулу. а = 1, б = -5 или с = 4,
Поэтому мы можем найти sin x, используя квадратичную формулу. а = 1, б = -5 или с = 4,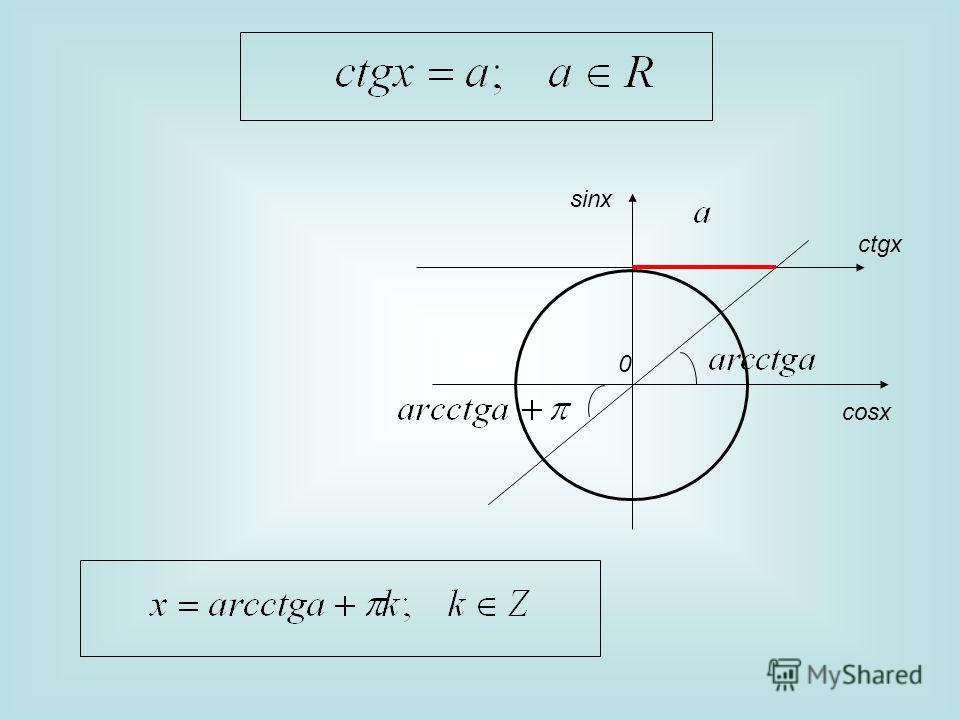
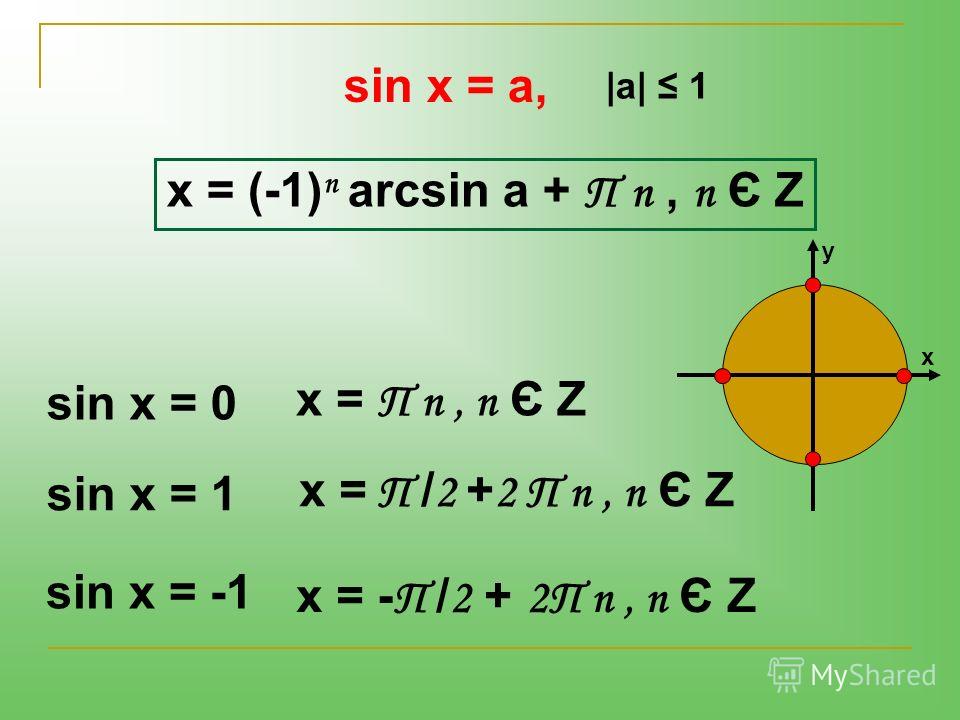
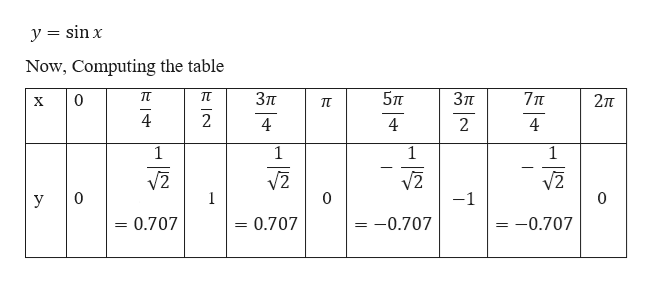 поэтому полное решение:
поэтому полное решение:  Изначально вопрос должен был решаться алгебраически, но я решил изменить его на аналитический из-за комментариев и ответов.
Изначально вопрос должен был решаться алгебраически, но я решил изменить его на аналитический из-за комментариев и ответов. 7}{7!} + \cdots $$ 94}{7!} + \cdots) = 0 $$
7}{7!} + \cdots $$ 94}{7!} + \cdots) = 0 $$
 Симметричные кривые называются ветвями параболы.
Симметричные кривые называются ветвями параболы. Что касается построения графика, старший коэффициент « a » указывает, насколько «толстой» или насколько «худой» будет парабола.
Что касается построения графика, старший коэффициент « a » указывает, насколько «толстой» или насколько «худой» будет парабола.

 )
)
 Но для графических целей десятичная аппроксимация «(−0,2, −2,1)» может быть более полезной, поскольку ее легче найти на осях.
Но для графических целей десятичная аппроксимация «(−0,2, −2,1)» может быть более полезной, поскольку ее легче найти на осях.