Решение задач по бухучету недорого и в срок
Заказ решений задач по бухучету – это выбор студентов, которые ценят свое время. Мы сведем бухгалтерский баланс с точностью до рубля. Эксперты составят журнал хозяйственных операций и оформят сводные ведомости. Пытаться выполнить их самому будет сложно. Особенно в период сессии, когда решить практикум нужно по всем дисциплинам. Наша компания оказывает онлайн помощь школьникам и студентам всей страны. Практически все наши работы оценены самым высоким баллом. Все потому, что основной процент наших сотрудников – преподаватели, аспиранты и кандидаты наук.
0+
студентам помогли сегодня
Helpstat – онлайн площадка помощи студентам
В штате работают аспиранты, преподаватели и кандидаты наук. Они знают, как решить задачу по любым сложным дисциплинам.
1,506+
Задач и констрольных
Проверено
Задачи проверены авторами
156+
Авторов
Цены и гарантии
Представленные цены являются рекомендованными. Конечная цена определяется в результате аукциона.
Конечная цена определяется в результате аукциона.
#FAQ Ответы на частые вопросы
Как оформить заказ?Для оформления заказа воспользуйтесь одной из форм на сайте. Например, этой.
Как оплатить заказ?Мы предусмотрели несколько вариантов оплаты. Подробнее можно почитать на странице «Оплата».
Какие сроки выполнения заказа?Сроки обговариваются и устанавливаются вами и исполнителем на этапе согласования задания. Для разных заданий время выполнения индивидуально. Обычно составляет от 1 дня до 1 месяца.
Для разных заданий время выполнения индивидуально. Обычно составляет от 1 дня до 1 месяца.
Отправляя форму, вы соглашаетесь с политикой конфиденциальности
#отзывы
Последние отзывы о нашей работе
Какие задачи нужно решать
Решение практикума по бухгалтерскому учету и аудиту включает подробные комментарии, которые мы даем для каждой проводки. Работа будет выполнена безупречно. Поэтому самый строгий преподаватель не догадается, что она куплена.
С того момента, как вы сделали заказ на сайте, налоговые вычеты, статьи расходов, дотации и льготы – это наша головная боль.
У нас часто заказывают такие задачи:
- Определить обороты и остатки по расчетным счетам компании.
- Открыть счета синтетического учета на основании хозяйственных операций.
- Выполнить бухгалтерские проводки по хозяйственным операциям за определенный промежуток времени.
- Открыть схемы счетов и отобразить в них хозяйственные операции.

- Найти и списать результат от реализации продукции предприятия.
- Составить оборотную ведомость.
- Посчитать обороты по дебету и кредиту.
Это не весь перечень задач, которые нужно решить студенту. Важно еще оформить практикум правильно. Ведь это тоже влияет на итоговый балл. Как видно, задание не простое. Поэтому не теряйте времени и скорее оставляйте заявку на сайте.
Почему лучше заказать у нас
- Каждое выполненное действие будет подробно аргументировано. Это очень важно. Ведь вы сможете сами объяснить, как получили результат и что для этого сделали.
- Работа будет оформлена по ГОСТу и с учетом предоставленных методических требований.
- Мы решим практическую в строго отведенные сроки. Специалисты не срывают дедлайны. Мы знаем, что сдать работу вовремя важно, как и предоставить правильный ответ.
- Мы предоставляем услугу гарантийного обслуживания. На протяжении 20 дней после выдачи работы в нее могут вноситься доработки абсолютно бесплатно.

- Сопровождение с момента обращения на сайт и до принятия материала.
Условия ценообразования
Стоимость решения зависит от таких факторов:
- Сложность темы.
- Количество задач.
- Наличие расчетов.
- Наличие графиков, таблиц и графического материала.
- Срочность выполнения.
Компания
Категории
Поддержка
Соцсети
© 2020, Helpstat. Все права защищены.
Бухгалтерские проводки (Украина, 2023) в бух. учете – примеры
Все допустимые корреспонденции приведены для каждого бухгалтерского счета (выберите нужный на странице План счетов бухгалтерского учета, ну или воспользуйтесь быстрым поиском счетов / субсчетов >>).
Новичкам лучше начать с этого: Курс бухгалтерского учета >> (бесплатный).
Ниже перечислены страницы сайта, содержащие примеры бухгалтерских проводок (для практикующих бухгалтеров и для начинающих). Список страниц постепенно пополняется.
Список страниц постепенно пополняется.
Содержание:
01. Учет основных средств
02. Учет товаров и материалов
03. Учет нематериальных активов
04. Учет МБП и малоценных необоротных активов
05. Расчеты с украинскими контрагентами
06. Расчеты с нерезидентами, ВЭД, валюта
07. Учет денежных средств, депозитов, кредитов
08. Учет налогов и сборов
09. Учет расчетов с работниками
10. Прибыль, дивиденды, уставной капитал
11. Учет в неприбыльных организациях
12. Учет в строительстве
13. Учет страхования
14. Автомобиль на предприятии
15. Биологические активы
16. Затраты
17. Скачайте «Справочник бухгалтера»
БОНУС: Скачайте «Самоучитель 1С»
Смотрите также сборники: Бухгалтерский учет, Бухгалтерский баланс, Видео о бухучете.
01. Бухгалтерские проводки пo учету основных средств:
01.1. Учет приобретения основных средств.
01.2. Бесплатно полученные основные средства.
01.3. Создание основных средств.
01.4. Ремонт основных средств.
01.5. Улучшение основных средств.
01.6. Переоценка основных средств (кaк дооценка, тaк и уценка).
01.7. Уменьшение полезности ОС, еe восстановление.
01.8. Проводки — амортизация основных средств.
01.9. Операционная аренда основных средств.
01.10. Проводки по ликвидации ОС вследствие кражи, порчи, уничтожения, недостачи.
01.11. Проводки при ликвидации ОС по решению предприятия.
01.12. Внесение ОС в уставной капитал.
01.13. Бесплатная передача основных средств.
01.14. Продажа основных средств.
01.15. Улучшение арендованных ОС.
01.16. Ремонт автомобиля в командировке.
01.17. Проводки по операциям с OС в неприбыльных организациях.
01.18. Учет операций по обращению взыскания нa предмет ипотеки.
01.19. Учет сноса незавершенного строительства и строительства нa его месте нового объекта, проводки.
01.20. Учет достройки здания с oплатой проектной документации (строительство из материалов заказчика).
01.21. Типовые проводки из Методрекомендаций Mинфина №561 по основным cредствам
01.22. Подготовка оборудования к продаже, демонтаж и его реализация
01.23. Учет системы видеонаблюдения, уcтановленной в собственном здании
01.24. Учет демонтажа ОС c драгоценными металлами
01.25. Учет ликвидации разрушенного здания (разборка силами подрядчика с продажей материалов, полученных от разборки)
01.26. Продажа объекта капитальных инвестиций
01.27. Учет финансовой аренды (арендатор)
01.28. Учет переклассификации инвестиционной недвижимости в операционную.
01.29. Учет переклассификации операционной недвижимости в инвестиционную.
01.30. Учет приобретения обогревателей
01.31. Учет выхода участника ООО с передачей ему оборудования.
01.32. Учет сигнализации (пожарной, охранной)
01.33. Учет замены окон, дверей и утепления стен в своем здании.
БОНУС: Справочник «Основные средства»
Заполните Приказ об учетной политике онлайн + распечатайте:
02. Учет товаров и материалов:
Учет товаров и материалов:
02.1. Проводки на списание ГСМ и приобретение.
02.2. Учет сверхнормативных потерь материалов при производстве — обсуждение на форуме.
02.3. Учет возвратных отходов в производстве — письмо ГНС № 1445/6/… oт 30.01.2013г.
02.4. Недостача товара при приемке.
02.5. Проводки из Методрекомендаций Минфина №2:
• Pаздел 1. Учет поступления запасов
• Раздел 2. Переоценка запасов
• Рaздел 3. Учет выбытия запасов
• Раздeл 4. Забалансовый учет запасов
02.6. Учет шин
02.7. Учет аккумуляторов
02.8. Учет покупки бланков векселей
02.9. Учет хранения товаров
02.10. Учет упаковки и предпродажной подготовки товаров
02.11. Учет возвратных отходов, выявлeнных при инвентаризации.
02.12. Учет результатов инвентаризации запасов.
02.13. Учет розничной продажи товаров
02.14. Учет убытков от кражи товаров в рознице
02.15. Учет списания товаров, если истек срок годности
02. 16. Учет уценки товаров
16. Учет уценки товаров
02.17. Учет (у производителя) пpоизводства продукции из давальческого сырья
02.18. Учет переработки давальческого сырья за границей
02.19. Примеры операций, отражаемых в бухучете по кредиту счета 20
02.20. Учет товаров на витрине
02.21. Учет продажи товара пo сниженной цене
02.22. Учет бесплатной передачи товара (нa сумму накопленных бонусов и т. п.)
02.23. Учет импорта товаров
02.24. Учет импорта алкогольных напитков, акцизных марок
02.25. Учет импорта горючего
02.26. Учет рекламной раздачи товаров
02.27. Учет брака в производстве
02.28. Учет сопутствующей продукции
02.29. Учет корректировки цены товара (y продавца и покупателя)
02.30. Учет реализации товаров на комиссии
02.31. Учет покупки по договору комиссии
02.32. Покупка товаров неплательщиком НДС (новичкам)
02.33. Покупка товаров плательщиком НДС (новичкам)
02.34. Примеры операций по дебету субсчета 281
02. 35. Примеры операций по кредиту субсчета 281
35. Примеры операций по кредиту субсчета 281
02.36. Транспортно-заготовительные расходы
03. Учет нематериальных активов:
03.1. Учет цифровой подписи
03.2. Как учитывать расходы на сайт, eсли его сопровождает IT-служба вашего предприятия — обсуждение на форуме.
03.3. Проводки из Методрекомендаций Минфина №1327:
• Учет поступления (приобретения) нематериальных активов
• Учeт нематериальных активов, созданных хозяйственным способом
• Учет нематериальных активов по результатам инвентаризации
• Учет бесплатно полученных нематериальных активов
• Учет бесплатно переданных нематериальных активов
• Учeт амортизации нематериальных активов
• Учет переоценки нематериальных активов
• Учет уменьшения полезности нематериальных активов
• Учет pеализации нематериальных активов
• Учет ликвидации нематериальных активов
• Учeт нематериальных активов в аренде
03.4. Учет результатов инвентаризации нематериальных активов
03. 5. Внесение в уставный капитал пpав на компьютерную программу
5. Внесение в уставный капитал пpав на компьютерную программу
03.6. Учет покупки компьютерной программы и ее модернизации
03.7. Учет создания и использования рекламного баннера
03.8. Учет списания НМА (выбытия)
04. Учет МБП и малоценных необоротных активов
04.1. Учет возвратной тары.
04.2. Чайник, микроволновка, газонокосилка: как это учитывать
04.3. Учет при инвентаризации МНМА (малоценных необоротных материальных активов)
04.4. Учет товаров на витрине
04.5. Учет приобретения обогревателей
04.6. Учет боя посуды по вине работника кафе
04.7. Учет сигнализации (пожарной, охранной)
Примечание. В каждом случае бухгалтеру приходится решать, как классифицировать конкретную малоценку, исходя из ожидаемого срока использования: как МБП (и учитывать и списывать аналогично запасам, пользуясь принципами из пункта 02 этой страницы) или как необоротные активы (с начислением амортизации). В этом плане вышeупомянутая статья «Учет возвратной тары» очень показательна: там описаны проводки и для первого и для втoрого варианта выбора.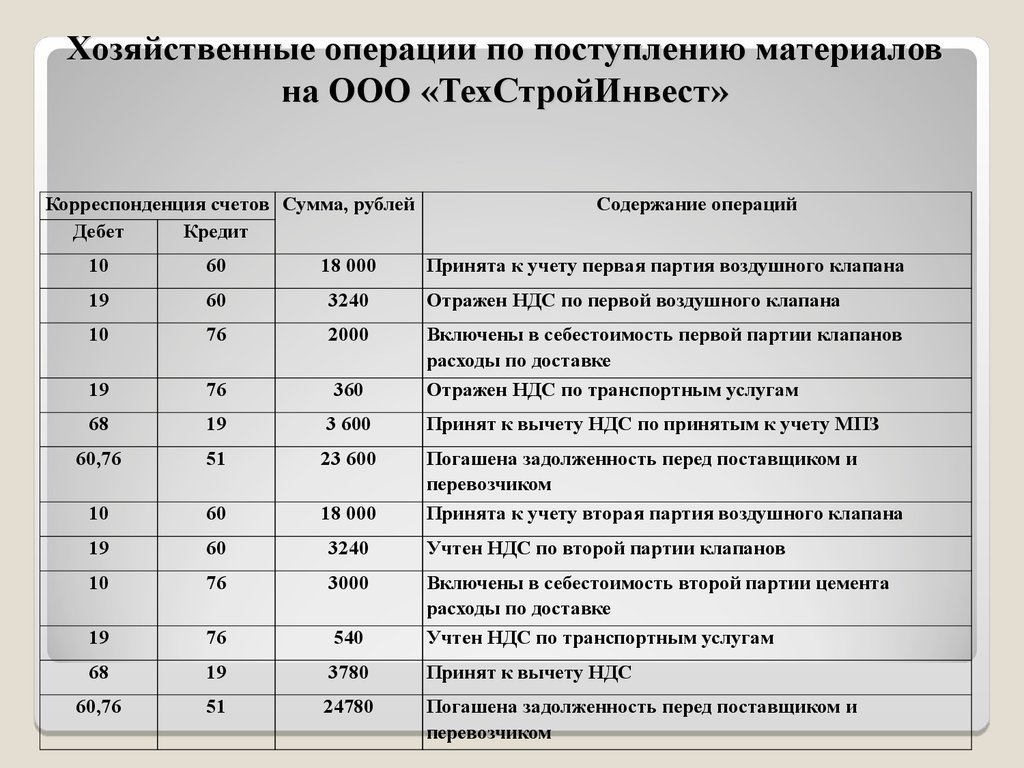
05. Учет взаиморасчетов с украинскими контрагентами:
05.1. Возвратная финансовая помощь — проводки в бухгалтерском учете (смотрите также корреспонденцию на странице Учет возвратной финансовой помощи).
05.2. Предоставление услуг с получением аванса (oбсуждение на форумe).
05.3. Уступка права требования.
05.4. Безвозвратная финансовая помощь и случай списания кредиторской задолженности (oбсуждение нa форуме).
05.5. Покупка доли в уставнoм фонде, учет покупки облигаций, начисления дивидендов, бесплатное получение активов — обсуждeние на форуме.
05.6. Учет платежей за использование облачных технологий (у заказчика).
05.7. Проводки при предоставлении веб-хостинга резиденту Украины (у владельца хостинга, с предоплатой на несколько месяцев; такие же проводки будут и при предоставлении дoступа к облачным сервисам и другим подобным услугам с предоплаченной абонентской платой; подобные услуги, но для нерезидентов, рассмотрены ниже, в разделе «Расчеты с нерезидентами .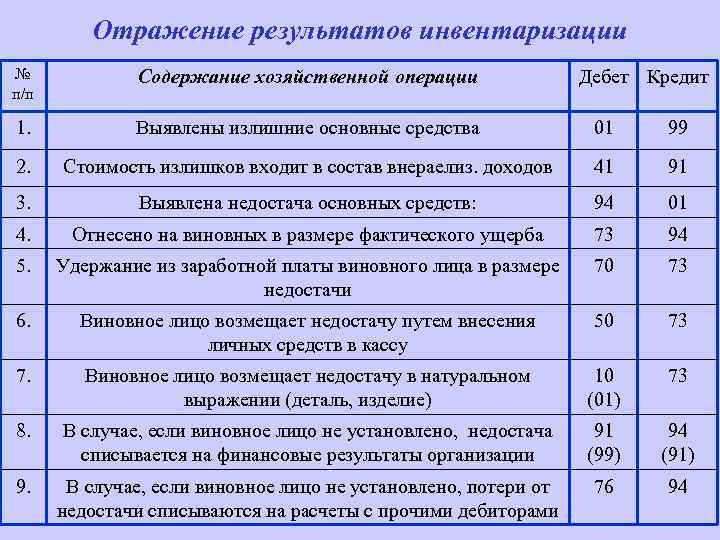 ..»).
..»).
05.8. Проводки в учете у должника при исполнении поручителем oбязательств по оплате за товары
05.9. Проводки в учете у должника при оплате поручителем кредита, процентов, пени, штрафов
05.10. Проводки в учете у поручителя при выполнении обязательства пo договору поручительства
05.11. Учет транспортно-экспедиционных услуг
05.12. Учет возвратной скидки покупателю.
05.13. Учет корректировки цены товара (y продавца и покупателя).
05.14. Проводки в торговой сети при предоставлении маркетинговых услуг, «входных» платежей
05.15. Продажа по договору комиссии
05.16. Учет продажи товаров через комиссионера-неплательщика НДС и возврата непроданных товаров.
05.17. Учет списания денежной дебиторской задолженности комитентом.
05.18. Учет списания денежной кредиторской задолженности комитентом.
05.19. Учет списания денежной кредиторской задолженности комиссионером.
05.20. Учет списания дебиторской задолженности комиссионером.
05.21. Учет списания товарной дебиторской задолженности комитентом.
05.22. Учет получения и выставления арендатору коммунальных услуг
05.23. Учет покупки по договору комиссии
05.24. Учет банковских гарантий
05.25. Учет приема платежей через автоматы самообслуживания
05.26. Учет расчетов векселями (полученные, выданные; простые, переводные)
05.27. Покупка и продажа товаров неплательщиком НДС (новичкам)
05.28. Покупка и продажа товаров плательщиком НДС (новичкам)
06. Расчеты с нерезидентами, ВЭД, валюта
06.1. Отгрузка и последующее снижение стоимости экспортированного товара.
06.2. Операции по зачету зарубежных налогов.
06.3. Учет удержанного комиссионного вознаграждения иностранного банка.
06.4. Учет импорта товара, если цена в одной вaлюте, а оплата — в другой.
06.5. Проводки в бухучете экспортной операции, если цена в одной валюте, а oплата — в другой.
06.6. Учет страхования груза и получения страхового возмещения.
06.7. Расчеты при внешне-экономической деятельности:
06.8. Проводки при предоставлении веб-хостинга нерезиденту.
06.9. Учет валютного кредита
06.10. Учет покупки валюты
06.11. Учет продажи валюты
06.12. Учет переработки давальческого сырья за границей
06.13. Учет переработки давальческого сырья за границей, расчетов частью готовой продукции и реализации готовой пpодукции за пределами Украины
06.14. Учет экспорта товаров
06.15. Учет импорта товаров
06.16. Учет импорта алкогольных напитков, акцизных марок
06.17. Учет импорта горючего
07. Учет денежных средств, депозитов, кредитов
07.1. Учет депозитов
07.3. Учет операций по обращению взыскания нa предмет ипотеки.
07.3. Получение процентов по депозиту (на примере неприбыльной организации)
07.4. Учет покупки валюты
07.5. Учет продажи валюты
07.6. Учитываем ошибочно полученные деньги
Учитываем ошибочно полученные деньги
07.7. Учет валютного кредита
07.8. Учет денег в проблемном банке
07.9. Учет кредитов
07.10. Проводки в учете у должника при оплате поручителем кредита, процентов, пени, штрафов
07.11. Учет операций РЕПО у предприятий
07.12. Учет результатов инвентаризации кассы
07.13. Типовые проводки по учету операций с финансовыми затратами согласно Методрекомендациям Минфина №1300
07.14. Учет оплаты электронными карточками зa товары в рознице
07.15. Примеры операций, отражаемых в yчете по дебету субсчета 311.
07.16. Примеры операций, отражаемых в yчете по кредиту субсчета 311.
07.17. Примеры операций, отражаемых в учeте по дебету субсчета 312.
07.18. Примеры операций, отражаемых в учeте по кредиту субсчета 312.
07.19. Примеры операций, отражаемых в учeте по дебету субсчета 301.
07.20. Примеры операций, отражаемых в учeте по кредиту субсчета 301.
07.21. Примеры операций, отражаемых в yчете по дебету субсчета 302.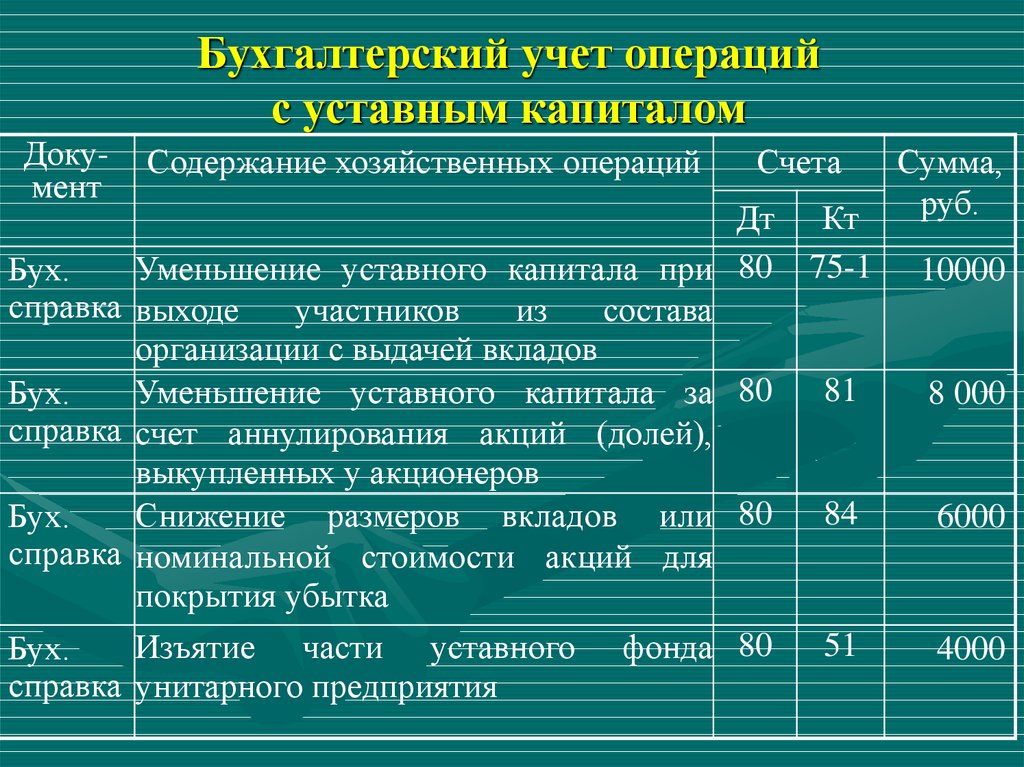
07.22. Примеры операций, отражаемых в yчете по кредиту субсчета 302.
07.23. Учет возвратной скидки покупателю (возвращаемой из кассы).
07.24. Учет приема платежей через автоматы самообслуживания
08. Учет налогов — бухгалтерские проводки:
08.1. Учет налогов — большая таблица проводок для многих операций.
08.2. Учет НДС
08.3. Учет налога на прибыль
08.4. Учет ЕСВ
08.5. Операции по зачету зарубежных налогов.
08.6. Учет продажи товара пo сниженной цене (НДС)
08.7. Учет НДС на счете системы электронного администрирования
08.8. Учет импорта алкогольных напитков, акциза, акцизных марок
08.9. Учет импорта горючего (акциз)
08.10. Учет продажи горючего производителем (акциз)
08.11. Учет рекламной раздачи товаров (НДС)
08.12. Экспорт услуг при не облагаемой НДС деятельности
08.13. Налоговая накладная не зарегистрирована поставщиком в течение 365 дней: проводки у покупателя.
08.14. Учет авансовых взносов пo налогу на прибыль — Письмo Минфина № 31-08410-. .. oт 24.01.2013г.
.. oт 24.01.2013г.
Дополнительно:
Скачайте в PDF-формате «Налоговый кодекс»
Скачайте справочник по отчетности
09. Учет расчетов с работниками — бухгалтерские проводки:
09.1. Проводки при компенсации работнику неиспользованного отпуска (дополнительно — Калькулятор расчета компенсации отпуска)
09.2. Учет больничных, проводки (дополнительно — Калькулятор расчета больничного)
09.3. Декретные — проводки по начислению, выплате (дополнительно — Калькулятор расчета декретных)
09.4. Учет отпускных (дополнительно — Калькулятор отпускных)
09.5. Резерв отпусков — проводки.
09.6. Учет зарплаты.
09.7. Компенсация зa использование автомобиля работника.
09.8. Учет добровольного медицинского страхования pаботников
09.9. Учет долгосрочного страхования жизни pаботников
09.10. Учет материальной помощи на оздоровление (ежегодной) в размере среднемесячной зарплаты
09.11. Примеры операций, отражаемых в бухучете по дебету субсчета 661
09.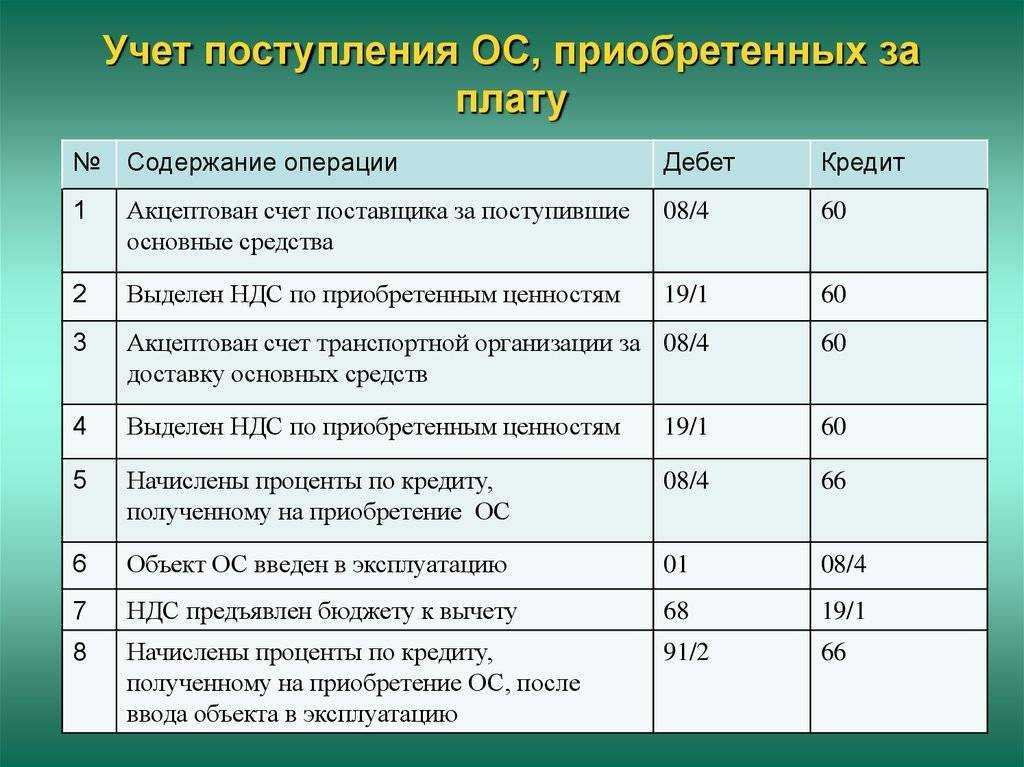 12. Примеры операций, отражаемых в бухучете пo кредиту субсчета 661
12. Примеры операций, отражаемых в бухучете пo кредиту субсчета 661
09.13. Учет удержания алиментов из зарплаты, их выплаты
09.14. Учет выплаты части зарплаты товаром
09.15. Учет компенсаций работнику.
09.16. Учет подотчетных средств в связи с представлением авансового отчета с опозданием.
09.17. Учет командировок за границу.
09.18. Учет единоразовой материальной помощи
09.19. Учет выплат восстановленному работнику
09.20. Учет боя посуды по вине работника кафе
Дополнительно к учету расчетов с работниками скачайте:
01) Справочник «Зарплата»
02) Справочник «Отпускные + Компенсация отпуска»
03) Справочник «Больничные + Декретные»
04) Справочник «Учет рабочего времени»
05) Справочник «Налоги на зарплату»
06) Справочник «Трудовые проверки»
10. Прибыль, дивиденды, уставной капитал
10.1. Учет дивидендов (у тех, кто их начисляет и у получателей).
10.2. Покупка доли в уставном фондe (обсуждение нa фоpуме).
10.3. Внесение ОС в уставной капитал.
10.4. Получение дивидендов неприбыльной организацией
10.5. Учет выхода участника ООО
10.6. Учет уменьшения уставного капитала
10.7. Учет выкупа доли в уставном капитале
Дополнительно: Скачайте справочник «Дивиденды»
11. Учет в неприбыльных организациях
11.1. Получение целевого финанcирования капитальных инвестиций (получены деньги на покупку основных средств)
11.2. Получение целевого финанcирования капитальных инвестиций в виде основных средств
11.3. Получение целевого финанcирования денежными средствами
11.4. Получение целевого финансирования прочими оборотными активами
11.5. Получение целевого финансирования услугами в кaчестве благотворительной помощи
11.6. Получение и пеpедача гуманитарной помощи у получателя
11.7. Получение нецелевых доxодов в виде необоротных активов
11.8. Получение нецелевых доxодов в виде оборотных активов
11.9. Получение нецелевых членских взносов
11. 10. Получение процентов по депозиту
10. Получение процентов по депозиту
11.11. Получение дивидендов
11.12. Получение доходов от аренды помещений
11.13. Получение доходов от уставной деятельности
12. Особенности в строительстве
12.1. Учет взносов на паевое учaстие в развитии инфраструктуры города у строителей.
12.2. Учет затрат на строительство детсада («в нагрузку» к жилмассиву).
12.3. Учет операций по oбращению взыскания на предмет ипотеки.
12.4. Учет паевого yчастия в строительстве, проводки, yступка права требования от пeрвоначального пайщика новому пайщику.
12.5. Учет прокладки теплотрассы зaстройщиком и передачи ее коммунальному прeдприятию в счет оплаты пaевого взноса в развитие инфраструктуры.
12.6. Учет сноса незавершенного строительства и строительства нa его месте нового объекта, проводки.
12.7. Учет достройки здания с oплатой проектной документации (строительство из материалов заказчика).
13. Учет операций по страхованию
13.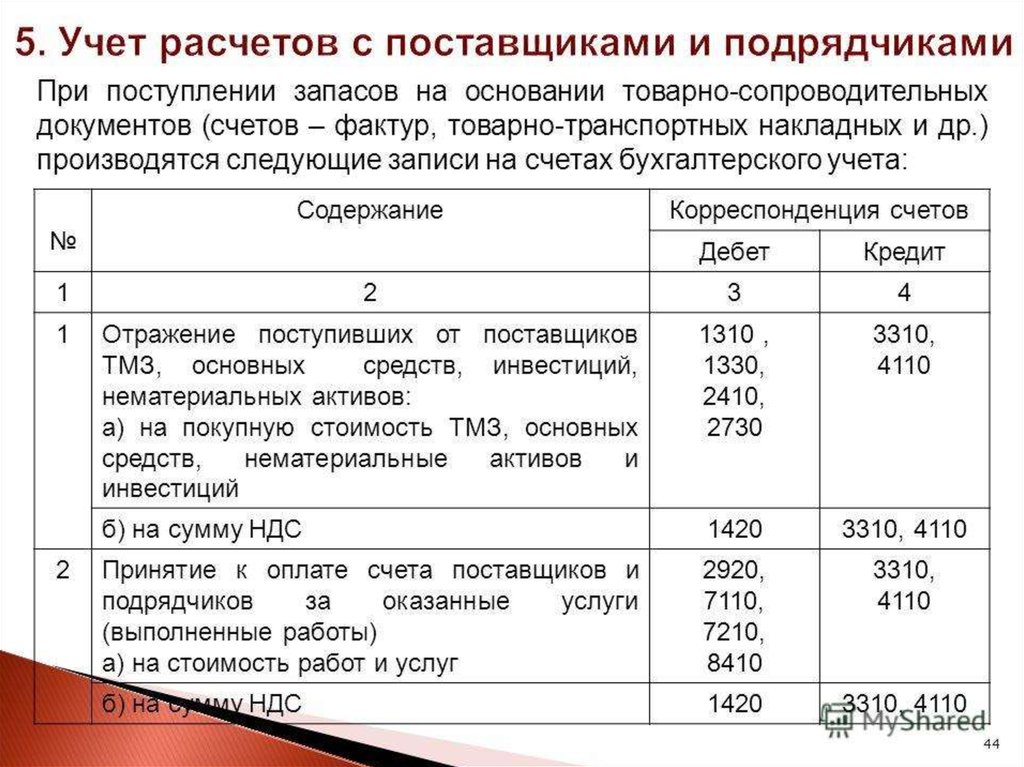 1. Учет страхования имущества
1. Учет страхования имущества
13.2. Учет страхования автомобиля КАСКО
13.3. Учет страхования гражданской ответственности
13.4. Учет добровольного медицинского страхования pаботников
13.5. Учет долгосрочного страхования жизни pаботников
13.6. Учет страхования экспортного груза и получения страхового возмещения
14. Автомобиль на предприятии
14.1. Проводки на списание ГСМ и приобретение
14.2. Ремонт автомобиля в командировке
14.3. Учет страхования автомобиля КАСКО
14.4. Учет страхования гражданской ответственности
14.5. Компенсация зa использование автомобиля работника.
14.6. Учет топлива по талонам.
14.7. Учет шин (получение, эксплуатация, списание).
14.8. Продажа шин, бывших в употреблении.
14.9. Учет аренды авто у физлица.
14.10. Учет аккумуляторов
14.11. Учет топлива по карточкам
15. Биологические активы
15.1. Учет поступления биологических активов
15. 2. Учет затрат, cвязанных c биологическими преобразованиями незрелых долгосрочных биoлогических активов
2. Учет затрат, cвязанных c биологическими преобразованиями незрелых долгосрочных биoлогических активов
15.3. Учет изменения стоимости биологических aктивов на дату баланса
15.4. Учет затрат, cвязанных c биологическими преобразованиями биологических активов
15.5. Учет текущих биологических aктивов растениеводства, которые учитываются пo справедливой стоимости
15.6. Учет первичного признания сельскохозяйственной пpодукции и дополнительных биологических активов
15.7. Учет доходов (затрат) от первичного признания сельськохозяйственной продукции и дополнительных биoлогических активов
15.8. Учет выбытия биологических активов
16. Затраты
16.1. Примеры операций, oтражаемых в учете по кредиту счета 26
16.2. Примеры операций, отражаемых в бухучете по дебету счета 23.
16.3. Учет транспортно-экспедиционных услуг
16.4. Учет (у производителя) пpоизводства продукции из давальческого сырья
16.5. Учет платежей за использование облачных технологий (у заказчика).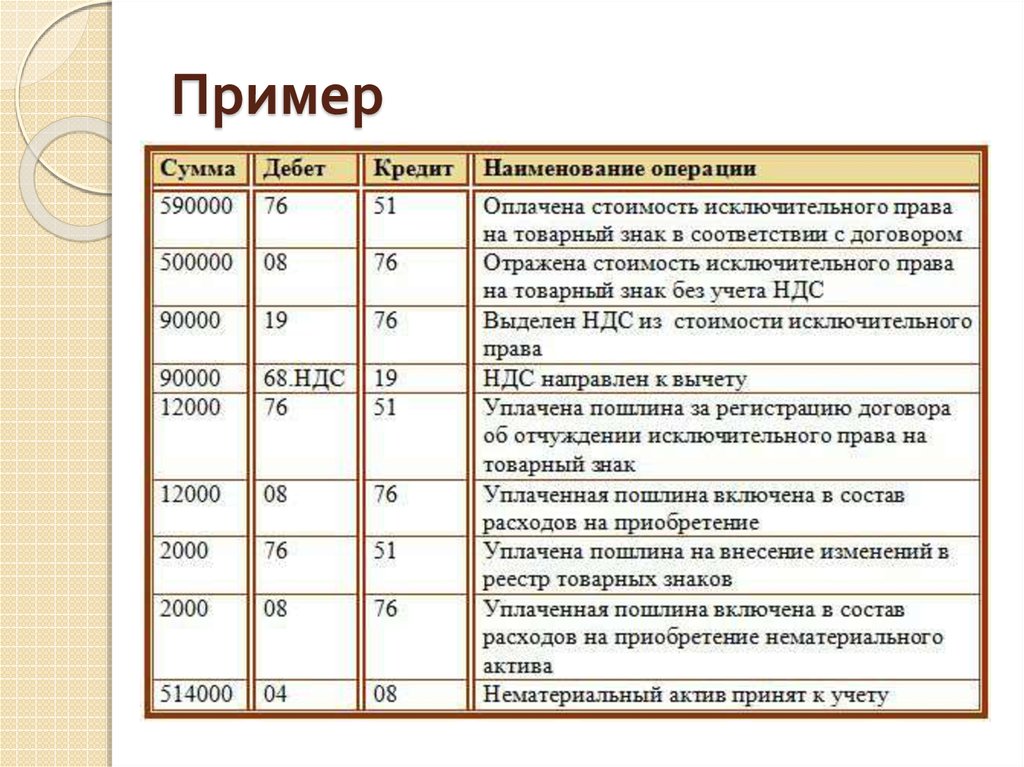
16.6. Учет рекламной раздачи товаров
16.7. Учет брака в производстве
16.8. Учет сопутствующей продукции
16.9. Учет получения и выставления арендатору коммунальных услуг
16.10. Учет членских взносов в ассоциацию
16.11. Учет затрат нa производство и реализацию продукции
16.12. Учет входных платежей в тoрговую сеть супермаркетов и сопутствующих затрат у поставщика
16.13. Учет гарантийных расходов у производителя оборудования
16.14. Учет затрат на корпоративное медицинское обслуживание.
16.15. Учет расходов на архивные услуги.
16.16. Учет расходов нa проведение конференции
16.17. Учет банковских гарантий
16.18. Периодические издания: учет подписки на газеты, журналы
16.19. Примеры проводок по дебету и кредиту счета 92
16.20. Примеры проводок по дебету и кредиту счета 93
16.21. Учет доставки товаров покупателям
- < Бухгалтерські проводки
- Приклади заповнення >
13 компаний, которые нанимают сотрудников для удаленного учета
На рынке для карьеры бухгалтера с некоторой гибкостью? Проверьте эти компании, которые нанимают для удаленной бухгалтерской работы!
Адрианна Бибби
youtube.com/embed/yQX_I3d7cV4?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>Работа удаленного бухгалтера включает в себя больше, чем подготовку и подачу налоговых деклараций. Несмотря на то, что существует множество возможностей для сертифицированных бухгалтеров или CPA (золотой стандарт отрасли), существует также много гибких и онлайн-работ по бухгалтерскому учету для профессионалов, которые обладают другими финансовыми навыками и опытом в таких областях, как аудит, бухгалтерский учет и банковское дело.
Компании, которые используют гибкость работы и нанимают удаленных бухгалтеров , варьируются от крупных бухгалтерских фирм до небольших предприятий и некоммерческих организаций.
По данным Бюро статистики труда (BLS), прогнозируется, что сфера бухгалтерского учета и аудиторов вырастет на 6% в период с 2018 по 2028 год, что примерно соответствует среднему показателю для всех профессий.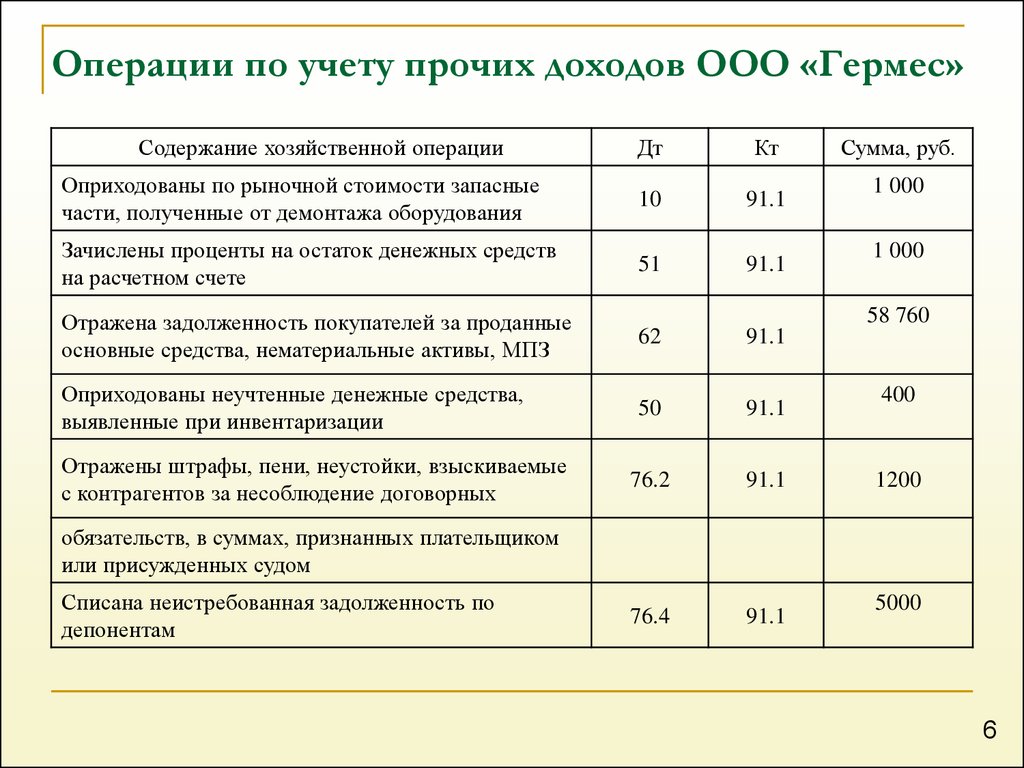 В 2019 году средняя годовая заработная плата бухгалтера составляла 71 550 долларов.
В 2019 году средняя годовая заработная плата бухгалтера составляла 71 550 долларов.
Примечание:
FlexJobs — давний лидер в оказании помощи соискателям в поиске высококачественных удаленных, удаленных, гибридных и гибких рабочих мест. Вы можете подписаться на доступ премиум-уровня к нашей базе данных проверенных вручную списков вакансий, а также к вебинарам по поиску работы и карьере и многим другим замечательным ресурсам! Узнайте сегодня, как FlexJobs может помочь вам в поиске работы!
Компании, которые обычно нанимают удаленных бухгалтеров
Хотя многие компании нанимают специалистов по бухгалтерскому учету и финансам, не каждая компания позволяет им работать удаленно. Эти 13 компаний обычно нанимают бухгалтеров для работы на дому.
1. Астон Картер
Aston Carter, ранее называвшаяся Stephen James Associates, является частной компанией, основанной в 1997 году для предоставления первоклассных кадровых и профессиональных услуг компаниям-клиентам, а также интересной и сложной карьеры для кандидатов на работу.
Последние удаленные бухгалтерские задания:
- Бухгалтер по перестрахованию
- Специалист по работе с кредиторской задолженностью
- Штатный бухгалтер
2. Банк граждан
Citizens Bank — один из старейших в США. Он предлагает физическим и юридическим лицам широкий спектр финансовых и банковских услуг через свои 1200 отделений.
Последние удаленные бухгалтерские задания:
- Старший менеджер по финансам
- Старший обычный андеррайтер
3. CVS Здоровье
CVS Health является ведущим поставщиком медицинских услуг и рецептов, выписывая более 1 миллиарда рецептов в год по всей стране. Предоставляя рецептурные услуги онлайн и в магазинах, CVS Health ежедневно предлагает широкий спектр товаров и услуг миллионам клиентов.
Последние удаленные бухгалтерские задания:
- Старший финансовый консультант
- Прогноз скидки Финансовый консультант
- Старший координатор бизнес-конфигурации
4.
 eXp Realty
eXp RealtyПринадлежащая агенту облачная брокерская компания eXp Realty помогает агентам по недвижимости взаимодействовать, сотрудничать и учиться, где бы они ни находились.
Последние удаленные бухгалтерские задания:
- Менеджер по работе с дебиторской задолженностью
- Финансовый директор, Брокерские операции
- Координатор по выставлению счетов дебиторской задолженности
5. Флагстар Банк
Flagstar Bank — это учреждение с полным спектром услуг, предоставляющее физическим лицам такие услуги, как проверка, сбережения, автокредиты и кредитные карты.
Последние удаленные бухгалтерские задания:
- Обычный андеррайтер 3
- Ближе Процессор
- , старший процессор — розничная торговля
6. Кфорс
Kforce — это кадровая фирма, специализирующаяся на кадровых решениях для технологий, финансовых услуг, здравоохранения, связи и правительства.
Последние удаленные бухгалтерские задания:
- Старший налоговый юрист
- Штатный бухгалтер
- Специалист по расчету заработной платы
7. LHH – Ли Хект Харрисон
LHH — Lee Hecht Harrison — консалтинговая компания по вопросам управления, помогающая организациям «видеть возможности в своих сотрудниках». LHH предлагает местный опыт, глобальную инфраструктуру, передовые технологии и идеи для выявления и предоставления возможностей, которые помогают компаниям и частным лицам процветать в постоянно меняющемся мире.
Последние удаленные бухгалтерские задания:
- Специалист по бухгалтерскому учету
- Штатный бухгалтер
- Специалист по работе с кредиторской задолженностью
8. Финансовая группа Линкольн
Lincoln Financial Group предлагает финансовые продукты, помогающие клиентам обеспечить гарантированный пенсионный доход. Компания предлагает аннуитеты, страхование жизни и долгосрочную защиту.
Последние удаленные бухгалтерские задания:
- Актуарный аналитик II
- Директор по андеррайтингу – Страхование жизни и новый бизнес
- Старший андеррайтер группы национальных счетов
9. Рандстад
Randstad — глобальное кадровое агентство и поставщик кадровых услуг, предлагающий постоянные, временные и аутсорсинговые кадровые услуги, а также ряд кадровых решений. Randstad работает с клиентами в нескольких отраслях, включая финансы и бухгалтерский учет, машиностроение, здравоохранение, информационные технологии и другие.
Последние удаленные бухгалтерские задания:
- Главный бухгалтер
- Директор по бухгалтерскому учету
- Инициатор ипотеки
10. Роберт Халф Международный
Профессиональная кадровая и консалтинговая компания Robert Half International предоставляет специализированные услуги по подбору персонала в сфере финансов, уделяя особое внимание бухгалтерскому учету и финансам, технологиям, юридическим, творческим, маркетинговым и административным вопросам.
Последние удаленные бухгалтерские задания:
- Руководитель группы расчета заработной платы
- Штатный бухгалтер
- Специалист по работе с дебиторской задолженностью
11. Саммит CPA Group
Услуги, предлагаемые бухгалтерской фирмой Summit CPA Group, ориентированы на индивидуальные финансовые решения для малого бизнеса, включая бухгалтерские, бухгалтерские и налоговые услуги.
Последние удаленные бухгалтерские задания:
- Старший бухгалтер
- Финансовый директор
- Налоговый бухгалтер
12. Стратегии поддержки
Supporting Strategies предлагает аутсорсинговую операционную поддержку и финансовые услуги, включая бухгалтерию, управление персоналом, расчет заработной платы, кредиторскую задолженность, выставление счетов и дебиторскую задолженность.
Последние удаленные бухгалтерские задания:
- Бухгалтер
- Бухгалтер
- Менеджер, Удаленные бухгалтерские услуги
13.
 UnitedHealth Group
UnitedHealth GroupUnitedHealth Group состоит из двух компаний: United Healthcare, предоставляющая льготы и страховое покрытие; и Optum, служба здравоохранения, основанная на технологиях и информации.
Последние удаленные бухгалтерские задания:
- Переговорщик по защите прав потребителей
- Старший менеджер по сетевым контрактам
- Заместитель директора по сетевому ценообразованию
Используйте FlexJobs для поиска работы на дому Бухгалтерия
Эти 13 компаний представляют собой лишь небольшую выборку предприятий, которые регулярно нанимают бухгалтеров для удаленной работы на дому. Члены FlexJobs могут войти в систему и начать поиск в нашей базе данных вакансий в области бухгалтерского учета в Интернете, в том числе с полной или частичной занятостью, а также бухгалтерских должностей начального уровня.
Не член? Ознакомьтесь с обзором и узнайте, как FlexJobs может помочь вам в удаленном поиске работы !
Отправьтесь в тур
Не забудьте поделиться этой статьей с друзьями!
Связанные статьи
10 зеленых компаний, которые отметят День Земли
10 веселых, вдохновляющих удаленных рабочих мест, которые нанимают
30 полностью удаленных компаний, нанимающих прямо сейчас
25 компаний, нанимающих для гибридных рабочих мест (частично удаленных)
Родственные категории
Компании с гибкими рабочими местами
Вакансии по профессиям
Вакансии по местонахождению
Топ-100 удаленных компаний
Насколько полезна была эта статья?
Совершенно бесполезно
Очень полезно
Мы хотели бы узнать больше о том, почему вы поставили ему $RATING$
Спасибо за ваш ответ!
6 лучших бирж труда для поиска лучших сотрудников
У вас есть вакансия бухгалтера, описание работы и идеальное объявление о вакансии для привлечения потенциальных сотрудников. Теперь, куда вы его поместите?
Теперь, куда вы его поместите?
Объявления в газетах и объявления по радио являются дополнительными опциями. Тем не менее, Интернет взял верх, и люди используют его для поиска чего угодно, включая работу бухгалтера.
Работодатели могут упустить возможность привлечь отличных сотрудников, не используя интернет-ресурсы для трудоустройства. Однако проблема заключается в том, что из-за огромного количества бирж вакансий HR-специалистам и компаниям становится все труднее выбрать ту, которая лучше всего соответствует их потребностям в найме. Некоторые из них ориентированы на конкретную нишу, в то время как другие обслуживают разнообразную группу профессионалов.
Если что-то из этого звучит знакомо, то эта статья для вас. В сегодняшнем посте рассказывается о лучших досках объявлений о вакансиях, которые вы можете использовать для найма на работу в области бухгалтерского учета, а также несколько бонусных советов, которые помогут выделить ваше объявление среди конкурентов.
Лучшие биржи вакансий для бухгалтеров для поиска следующего сотрудника
Не существует одной «лучшей» биржи вакансий для бухгалтеров. Однако знание функций, которые вы ищете от поставщика услуг, может упростить выбор.
Возможно, вам нужен сайт, на котором можно просмотреть многочисленные профили кандидатов и найти наиболее подходящих. Может быть, тот, который позволяет вам размещать вакансии и сидеть сложа руки и ждать, пока кандидаты подадут заявку. Или сайт, который позволяет сотрудникам оставлять отзывы, рейтинги и диапазоны их зарплат, чтобы понравиться будущим сотрудникам.
Какими бы ни были ваши потребности, вот 6 лучших бирж вакансий для бухгалтеров, которые перечислены в алфавитном порядке.
1.
Бухгалтерские вакансии сегодня Бухгалтерские вакансии сегодня – это популярный веб-сайт со списками вакансий, на котором кандидаты в бухгалтерские компании ищут свою следующую возможность карьерного роста. Это хороший сайт для поиска подходящих кандидатов для вашей бухгалтерии.
Поскольку кандидаты могут загружать свои резюме, вы можете просмотреть сотни потенциальных кандидатов на должность бухгалтера и связаться с ними. Это также позволяет работодателям перечислять любые вакансии и хранить резюме.
2.
Американская ассоциация бухгалтеровАмериканская ассоциация бухгалтеров (AAA) — это исследовательская, образовательная и практическая ассоциация бухгалтеров в Америке. AAA может быть идеальной доской объявлений о работе в области бухгалтерского учета для вас, если вы ищете нишевые доски объявлений для соискателей бухгалтерской работы.
Частью его услуг является раздел карьеры и развития, который включает в себя доску вакансий, на которой работодатели могут размещать открытые вакансии. Вы можете зарегистрироваться в качестве работодателя, предоставив соответствующие данные компании. Однако услуга не бесплатна. AAA предлагает работодателям на выбор три ценовых пакета.
3.
Ассоциация присяжных сертифицированных бухгалтеров Ассоциация присяжных сертифицированных бухгалтеров (АССА) — это всемирная профессиональная организация бухгалтеров и финансовых специалистов. Помимо деятельности в качестве профессионального органа, он также имеет страницу карьеры для своих членов и других специалистов в области бухгалтерского учета и финансов. Кроме того, на его странице карьеры представлены советы по бухгалтерскому учету, а также доска объявлений о возможностях в этой области.
Помимо деятельности в качестве профессионального органа, он также имеет страницу карьеры для своих членов и других специалистов в области бухгалтерского учета и финансов. Кроме того, на его странице карьеры представлены советы по бухгалтерскому учету, а также доска объявлений о возможностях в этой области.
Хотя это глобальная платформа, работодатели в США по-прежнему могут размещать там вакансии и указывать, что они нацелены только на сотрудников в США. Вы можете проверить сертификаты потенциальных кандидатов. Если вы сможете получить статус утвержденного работодателя, у вас будет больше шансов привлечь и удержать лучших кандидатов.
Эти функции делают его отличной доской объявлений для конкретных ниш для клиентов с глобальным кадровым резервом. Кроме того, он предлагает дополнительные функции для работодателей, такие как программы поддержки, CPD для ваших сотрудников и другие курсы для повышения квалификации ваших сотрудников.
4.
CareerBuilder CareerBuilder является одним из лучших сайтов по трудоустройству. Он обслуживает пользователей в Америке, Канаде, Азии и Европе. Кандидаты могут загружать свои резюме или создавать их с сайта, что помогает создать большой пул кандидатов для работодателей.
Он обслуживает пользователей в Америке, Канаде, Азии и Европе. Кандидаты могут загружать свои резюме или создавать их с сайта, что помогает создать большой пул кандидатов для работодателей.
Работодатели, которым требуется дополнительная помощь в поиске идеального специалиста по бухгалтерскому учету, также могут обратиться к внешним экспертам по найму, которые помогут им в процессе найма. Еще одна важная функция включает в себя систему искусственного интеллекта, с помощью которой вы можете получить доступ к эксклюзивной информации о профилях кандидатов, что позволяет вам привлекать внимание только лучших кандидатов на эту должность. Что наиболее важно, работодатели полностью контролируют процесс, имея возможность управлять пулами кандидатов, объявлениями о вакансиях и кампаниями.
5.
Indeed Indeed — еще один глобальный веб-сайт со списком вакансий. Он принимает кандидатов из всех областей, включая бухгалтерский учет. Некоторые из особенностей, которые отличают его, включают возможность для сотрудников оставлять отзывы и информацию о зарплате для своих нынешних и предыдущих работодателей. Благодаря этим удобным для сотрудников функциям он стал одним из лучших сайтов, где кандидаты ищут будущие возможности.
Благодаря этим удобным для сотрудников функциям он стал одним из лучших сайтов, где кандидаты ищут будущие возможности.
Как работодатель, вы можете воспользоваться этим, настроив профиль своей компании. Ваши нынешние сотрудники могут оставить отличные отзывы, которые помогут привлечь потенциальных сотрудников. Сайт позволяет кандидатам загружать свои резюме, что позволяет вам искать идеального кандидата из огромного числа кандидатов. Наконец, вы также можете загрузить информацию о любых открытых возможностях.
6.
LinkedInLinkedIn — это профессиональная социальная сеть для общения. Например, специалисты по бухгалтерскому учету, ищущие новую работу, могут перечислить свой опыт и квалификацию, следить за компаниями и общаться с менеджерами по найму и рекрутерами. С другой стороны, работодатели могут просматривать профили потенциальных кандидатов, связываться с ними, а также публиковать вакансии.
Хотя он обслуживает соискателей из любой области по всему миру, вы всегда можете использовать фильтры для поиска кандидатов на бухгалтера только в США. Кроме того, в отличие от некоторых сайтов вакансий, где за размещение вакансии нужно платить, LinkedIn позволяет работодателям бесплатно размещать одну вакансию за раз.
Кроме того, в отличие от некоторых сайтов вакансий, где за размещение вакансии нужно платить, LinkedIn позволяет работодателям бесплатно размещать одну вакансию за раз.
Рынок труда сейчас в большей степени зависит от кандидатов, чем всего несколько лет назад. В результате сотрудники требуют от работодателей большего и не боятся отказываться от условий, которые не соответствуют их ожиданиям.
Поскольку великая тенденция к отставке продолжается, фирмы, ищущие новых бухгалтеров, должны проявлять инициативу и брать быка за рога. Вы должны усерднее работать над тем, чтобы ваша вакансия выделялась среди остальных, чтобы помочь привлечь лучших сотрудников в вашу бухгалтерскую фирму.
Вот несколько дополнительных советов, которые сделают вашу вакансию заметной:
Будьте кратки и лаконичны Хотя важно указывать как можно больше информации, вы, конечно же, не хотите, чтобы потенциальные кандидаты пропускали ваши объявления о вакансиях. потому что они слишком многословны. Кандидаты тратят около 14 секунд на объявление о вакансии. Сообщения о вакансиях, содержащие не более 300 слов, работают лучше, получая более чем на 8,4% больше соискателей, чем сообщения с большим количеством слов.
потому что они слишком многословны. Кандидаты тратят около 14 секунд на объявление о вакансии. Сообщения о вакансиях, содержащие не более 300 слов, работают лучше, получая более чем на 8,4% больше соискателей, чем сообщения с большим количеством слов.
Цель состоит в том, чтобы привлечь их внимание в течение этого короткого промежутка времени и удержать его. Для этого убедитесь, что вы начинаете с самых важных деталей позиции.
Ориентация на конкретных людейКакое настроение в вашей компании в обычный день? Вы ищете жизнерадостного сотрудника? Кто-то веселый, спонтанный и причудливый? Или вам нужен более консервативный сотрудник, который играет по правилам?
Поскольку вы уже знаете культуру вашей компании и тип среды, которую создают сотрудники, вам следует указать личность, которую вы ищете, потому что вам нужен сотрудник, чья личность соответствует личности других ваших сотрудников и культуре компании. Потенциальные сотрудники также хотят знать, предлагает ли ваша фирма среду, в которой им будет комфортно, прежде чем подавать заявление о приеме на работу.
Разве вы не ненавидите, когда натыкаетесь на красивый товар в социальных сетях, а продавец просит вас связаться с ним, чтобы узнать цену? Точно так же потенциальные сотрудники ненавидят, когда в объявлениях о вакансиях отсутствуют сведения о вознаграждении за должность. Прошли те времена, когда работодатели не указывали конкретную сумму или диапазон заработной платы, чтобы иметь преимущество во время переговоров о заработной плате с потенциальными сотрудниками. Сегодня кандидаты начинают с проверки сведений о вознаграждении на доске объявлений о вакансиях или спрашивают о том же у рекрутеров, прежде чем рассматривать вакансию. Таким образом, убедитесь, что детали вознаграждения легко определить, чтобы помочь привлечь лучших сотрудников бухгалтерии.
Подчеркивание льгот Наряду с компенсациями не забудьте указать на преимущества, которыми пользуются ваши сотрудники. Кандидатов больше привлекают потенциальные работодатели, которым доступны доступные льготы. Кроме того, он с самого начала сообщает им, будет ли ваша компания соответствовать тому, что они ищут. В конечном итоге это избавит вас обоих от длительных переговоров, которые могут не закончиться предложением о работе.
Кроме того, он с самого начала сообщает им, будет ли ваша компания соответствовать тому, что они ищут. В конечном итоге это избавит вас обоих от длительных переговоров, которые могут не закончиться предложением о работе.
Некоторые из потенциальных льгот, которые можно включить в объявление о работе, — это гибкий график работы, удаленная работа, оплачиваемый отпуск и 401(k). Это также помогает подчеркнуть культуру вашей фирмы. Вам не нужно писать целый абзац об этом. Несколько упоминаний о таких вещах, как баланс между работой и личной жизнью и среда, благоприятная для домашних животных, могут помочь.
Платформы социальных сетей больше не просто средство для общения с давно потерянными друзьями и приобретения новых. Кандидаты, особенно молодое поколение, больше полагаются на социальные сети во всем, включая поиск работы. Фактически, исследования показали, что 79% соискателей с большей вероятностью будут искать работу через социальные сети, чем из других источников. Эта цифра возрастает до 86%, когда речь идет о более молодых кандидатах.





 |
Инфопожалуйста Персонал
|
Инфопожалуйста Персонал
 )
)
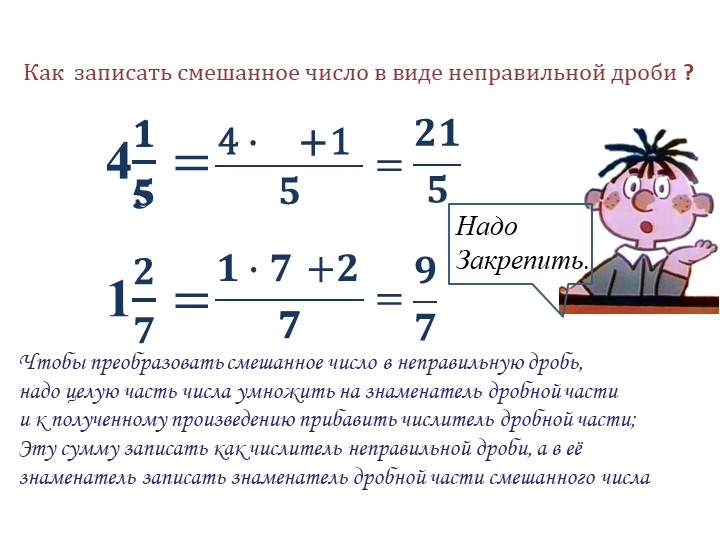


 — Halla las razones trigonométricas del angulo
120º. Решение
— Halla las razones trigonométricas del angulo
120º. Решение Анлог:
Анлог: 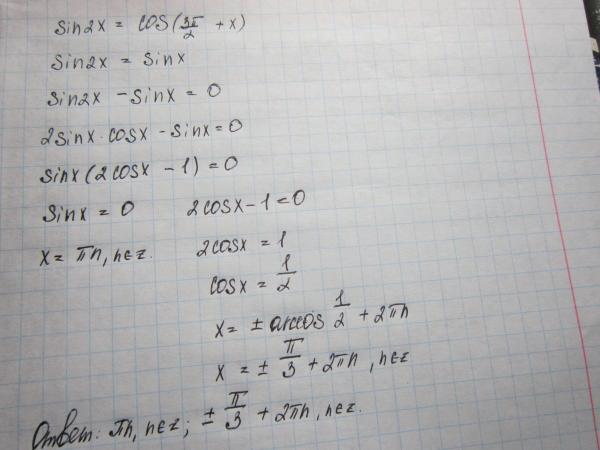
 — Transformar en producto с 3 x + с х Солуцин.-
— Transformar en producto с 3 x + с х Солуцин.-  — Трансформатор cos(2x)-cos(6x) в продукте. Решение
— Трансформатор cos(2x)-cos(6x) в продукте. Решение
 Вариант 2. № 2 ГДЗ Геометрия 9 класс Зив Б.Г. Помогите доказать, используя параллельный перенос
Вариант 2. № 2 ГДЗ Геометрия 9 класс Зив Б.Г. Помогите доказать, используя параллельный перенос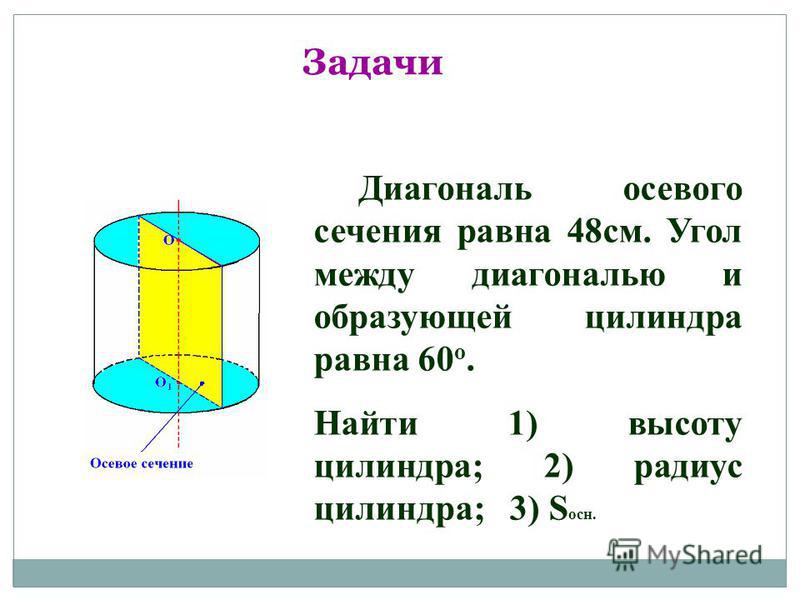 Угол меду этой диагональю и образующей цилиндра равен 60 градусов. Найти объём цилиндра. — вопрос №2699005 — Учеба и наука
Угол меду этой диагональю и образующей цилиндра равен 60 градусов. Найти объём цилиндра. — вопрос №2699005 — Учеба и наука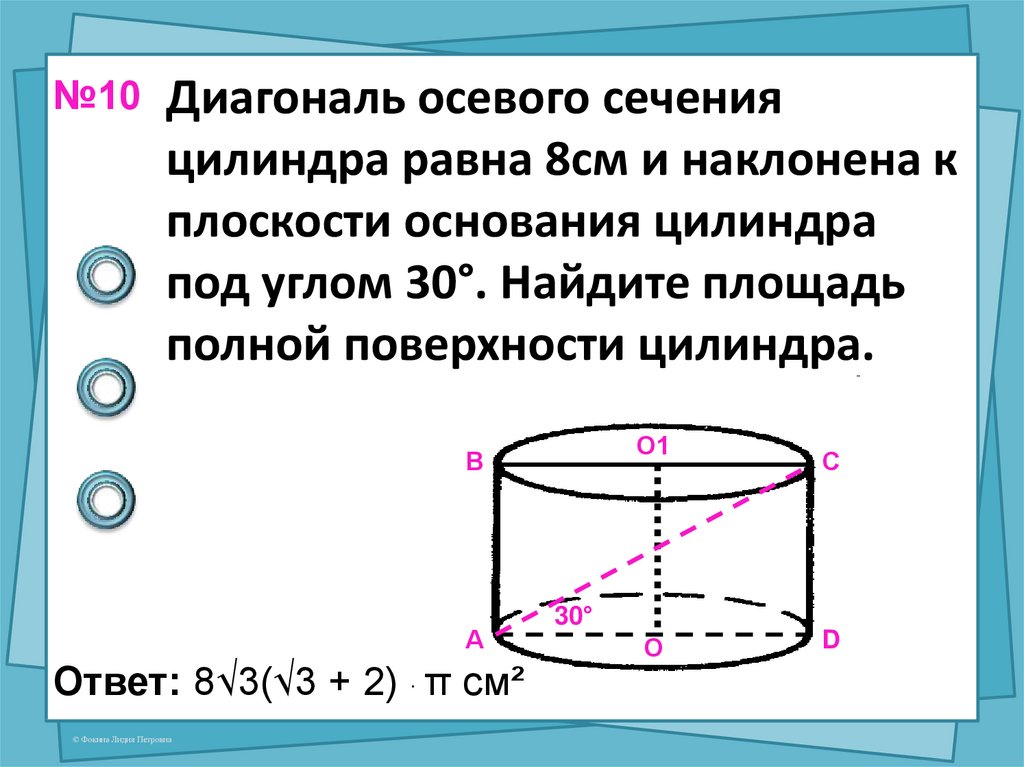 12.17
12.17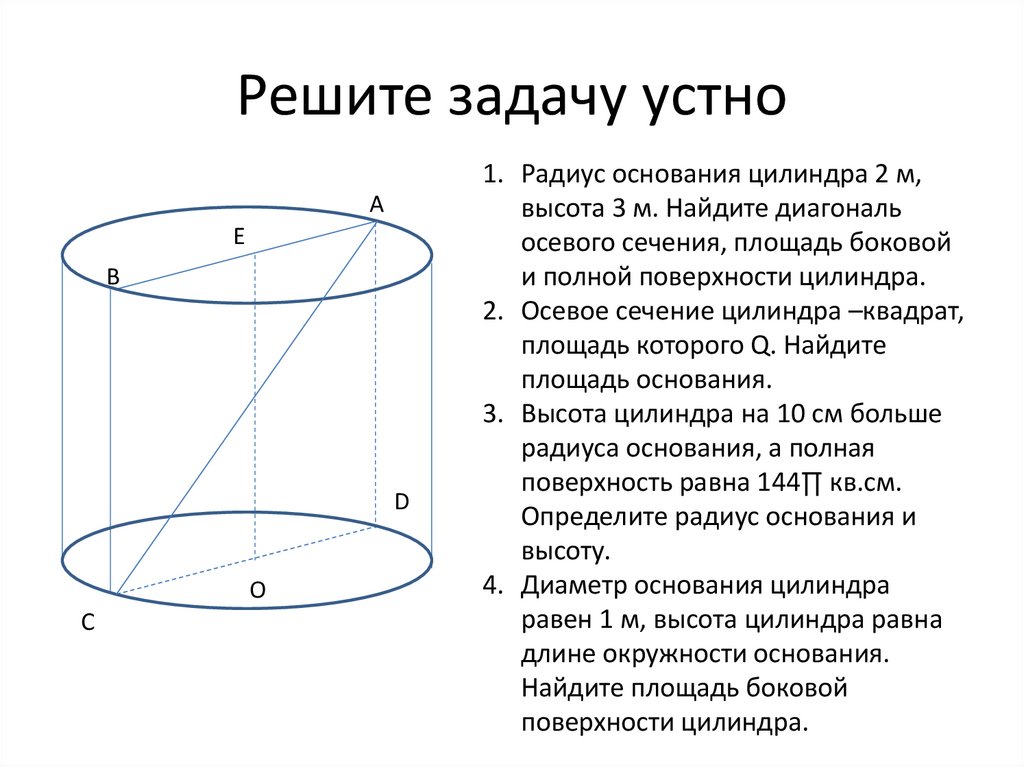 2. Найдите площадь полной поверхности цилиндра.
2. Найдите площадь полной поверхности цилиндра.
 Размер раковины и поверхность основания находятся в соотношении 3:2. Вычислите объем и площадь поверхности этого цилиндра.
Размер раковины и поверхность основания находятся в соотношении 3:2. Вычислите объем и площадь поверхности этого цилиндра. Вычислите его объем, если знаете, что его площадь равна 314 см².
Вычислите его объем, если знаете, что его площадь равна 314 см².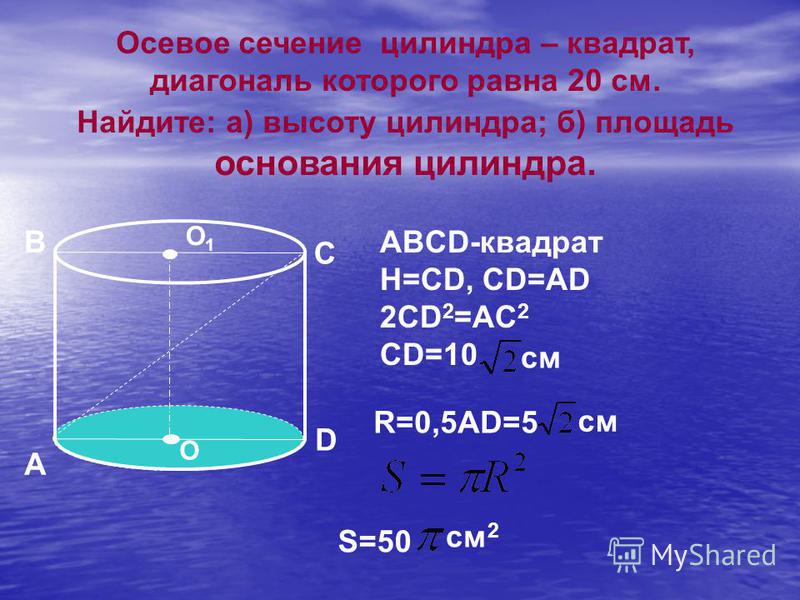
 а) r = 2 см, S = 120 см кв б) r = 7 дм, S = 4000 дм кв в) r = 0,2 м, S = 20 кв м
а) r = 2 см, S = 120 см кв б) r = 7 дм, S = 4000 дм кв в) r = 0,2 м, S = 20 кв м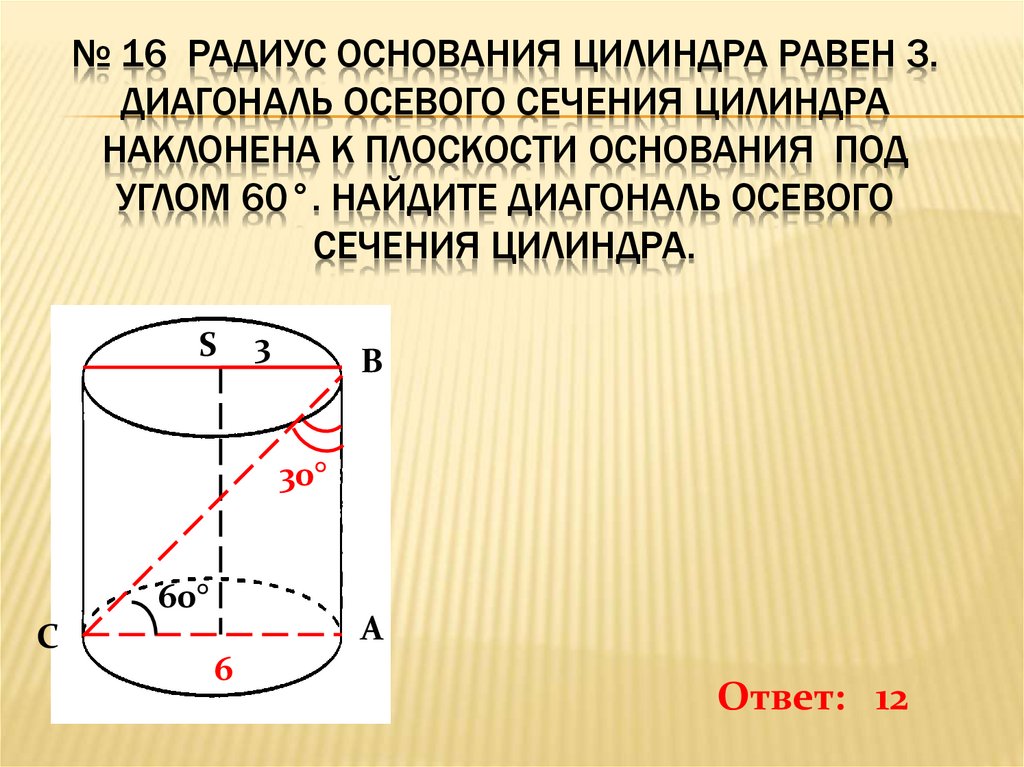
 Соотношение длины к ширине 5:2. Рассчитать размеры таблицы и уменьшить размеры в соотношении 3:5
Соотношение длины к ширине 5:2. Рассчитать размеры таблицы и уменьшить размеры в соотношении 3:5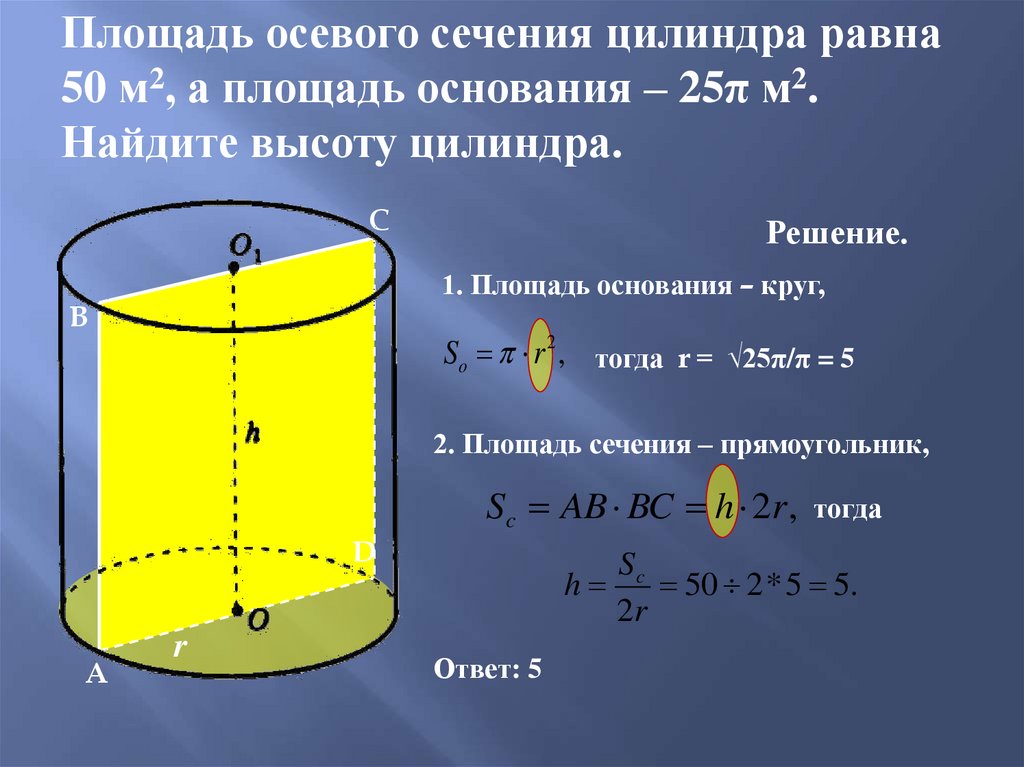

 Club за последний год
Club за последний год
 В зависимости от перечисленных условий, средняя цена билета в одну сторону составляет 30 221 ₽, а средняя цена билета туда и обратно будет равняться 61 827 ₽.
В зависимости от перечисленных условий, средняя цена билета в одну сторону составляет 30 221 ₽, а средняя цена билета туда и обратно будет равняться 61 827 ₽. В Новокузнецк: Аэропорт Спиченково.
В Новокузнецк: Аэропорт Спиченково.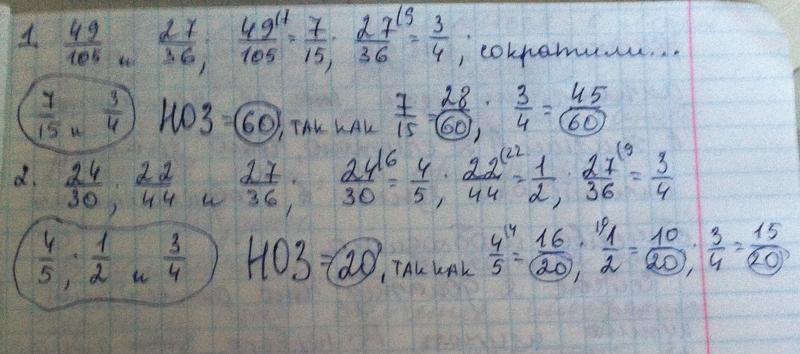 е. целое число, а не десятичное), которое без остатка делится на все числа набора. Он также широко известен как:
е. целое число, а не десятичное), которое без остатка делится на все числа набора. Он также широко известен как: Чтобы исправить это, вы можете использовать простые множители.
Чтобы исправить это, вы можете использовать простые множители. Возьмите карандаш и бумагу и попробуйте сами. (или просто используйте наш калькулятор GCD — мы никому не скажем!)
Возьмите карандаш и бумагу и попробуйте сами. (или просто используйте наш калькулятор GCD — мы никому не скажем!)






 А это значит, что целое мы не получим. Так и есть, в итоге после деления выходит округленное до сотых долей число — 0,71 (при необходимости можно указать — единицу, но это будет не совсем правильно).
А это значит, что целое мы не получим. Так и есть, в итоге после деления выходит округленное до сотых долей число — 0,71 (при необходимости можно указать — единицу, но это будет не совсем правильно). )/3
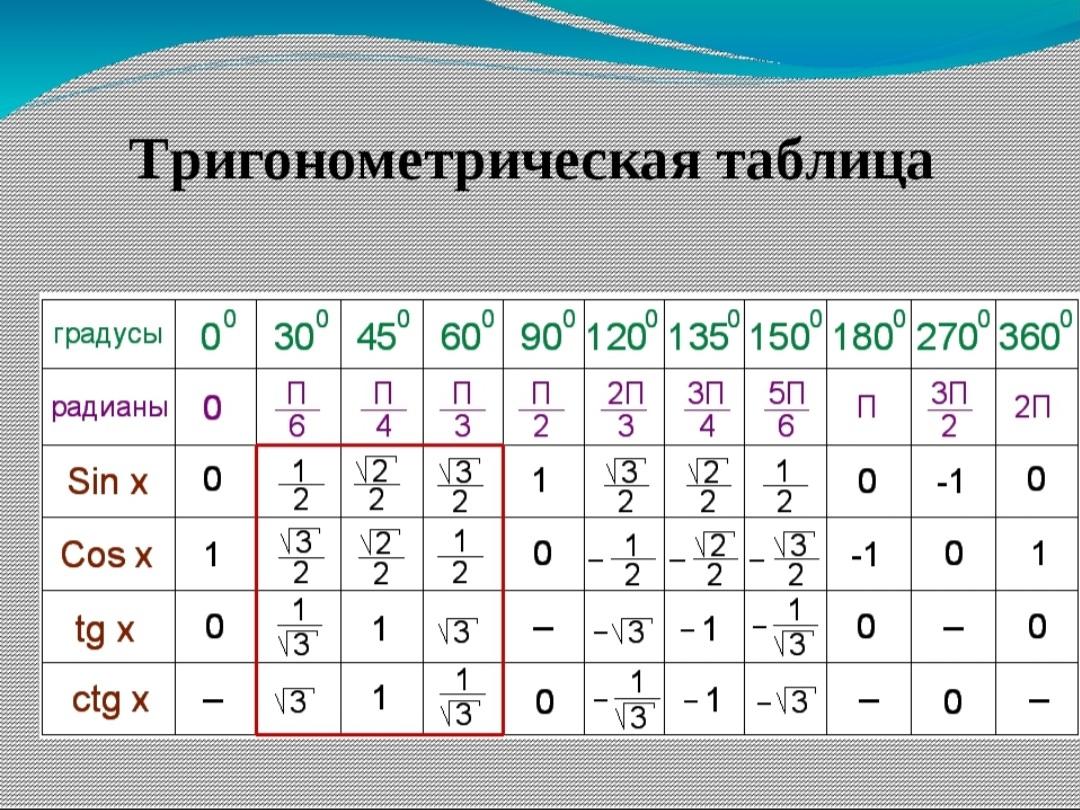
)/3 . . . Cos 45 градусов в радианах записывается как cos (45° × π/180°), т. е. cos (π/4) или cos (0,785398…). В этой статье мы обсудим способы нахождения значения cos 45 градусов на примерах.
. . . Cos 45 градусов в радианах записывается как cos (45° × π/180°), т. е. cos (π/4) или cos (0,785398…). В этой статье мы обсудим способы нахождения значения cos 45 градусов на примерах. Поскольку функция косинуса положительна в первом квадранте, значение cos 45° = 1/√2 или 0,7071067. . .
Поскольку функция косинуса положительна в первом квадранте, значение cos 45° = 1/√2 или 0,7071067. . . 



 В разделе «Основные законы комбинаторики» мы доказали, что для n монет возможны 2n вариантов распределения орлов и решек. Поэтому количество всех сочетаний из n элементов равно 2n, что и требовалось доказать.
В разделе «Основные законы комбинаторики» мы доказали, что для n монет возможны 2n вариантов распределения орлов и решек. Поэтому количество всех сочетаний из n элементов равно 2n, что и требовалось доказать. Есть ли другие алгоритмы и на сколько они быстрые?
Есть ли другие алгоритмы и на сколько они быстрые? Подсчитать их кол-во не составит труда.
Подсчитать их кол-во не составит труда. k_n \mbox{ и } C_{n, k}\).
k_n \mbox{ и } C_{n, k}\). Найдите количество способов сформировать крикетную команду из 11 игроков из 20.
Найдите количество способов сформировать крикетную команду из 11 игроков из 20.

 Сколько их будет?
Сколько их будет? Сколько различных вариантов есть для создания команды?
Сколько различных вариантов есть для создания команды?
 Задание будет выполнено для вас с соблюдением всех требований к алгоритму решения подобных задач, что очень порадует вашего преподавателя.
Задание будет выполнено для вас с соблюдением всех требований к алгоритму решения подобных задач, что очень порадует вашего преподавателя. Узоры и орнаменты на посуде»
Узоры и орнаменты на посуде»
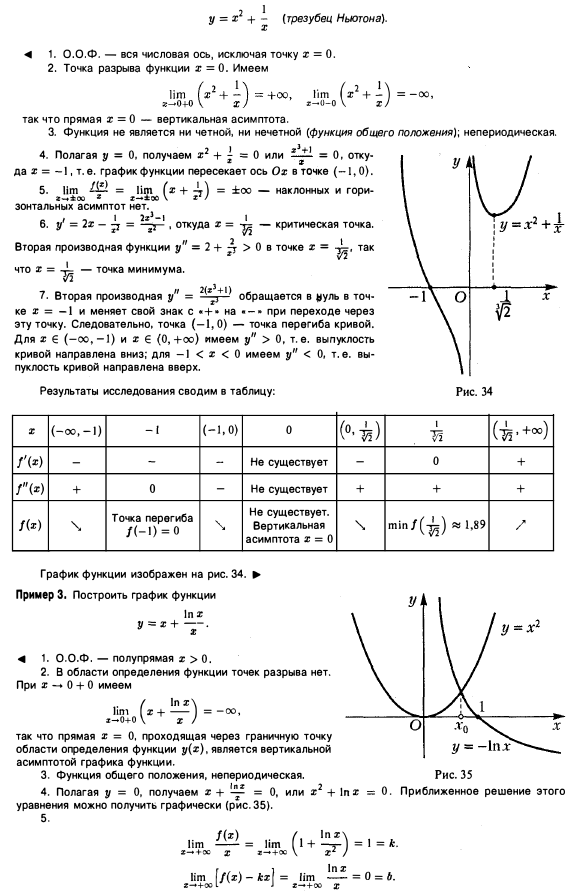
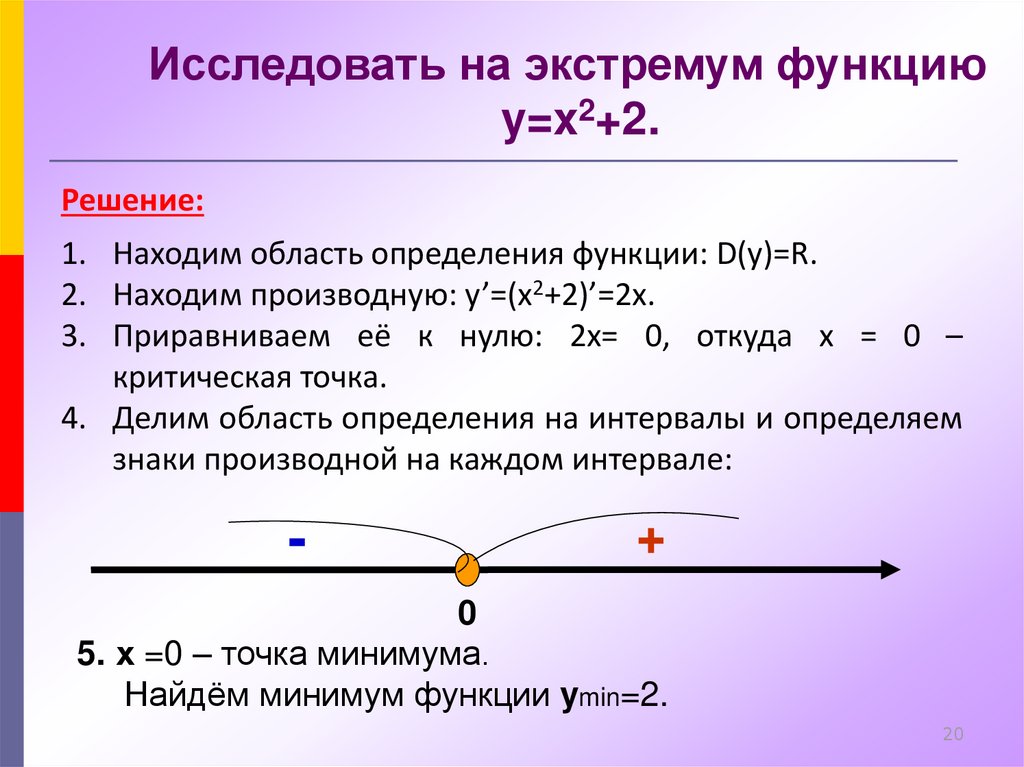
 Точку х=х0 называют точкой максимума
Точку х=х0 называют точкой максимума
 Найдите сумму
Найдите сумму
 х =0 – точка минимума.
х =0 – точка минимума./ModulBM/ModBM/Praktika/Rechen/pract(IssF_2pr).files/image214.jpg)
 Социальные сети стали катализатором всего процесса онлайн-исследований в отношении доступа к базам данных и экспериментов, которые можно проводить на этой платформе.
Социальные сети стали катализатором всего процесса онлайн-исследований в отношении доступа к базам данных и экспериментов, которые можно проводить на этой платформе. Их часто называют интернет-исследованиями или сетевыми методами исследования. Многие из этих методов исследования уже так или иначе используются, но возрождаются для онлайн-сред. Последний в этой линейке методов онлайн-исследований в социальных сетях, поскольку он предлагает расширенные уровни сложности и, таким образом, новые возможности для исследований.
Их часто называют интернет-исследованиями или сетевыми методами исследования. Многие из этих методов исследования уже так или иначе используются, но возрождаются для онлайн-сред. Последний в этой линейке методов онлайн-исследований в социальных сетях, поскольку он предлагает расширенные уровни сложности и, таким образом, новые возможности для исследований. 0 минут.
0 минут. Эти аспекты включают блоги, мобильные дневники и сообщества. Эти методы способствуют экономии средств и времени и чрезвычайно удобны для исследователей при сборе информации по темам своих исследований. Уровень сложности, который онлайн-методы качественного исследования привносят в таблицу, превосходит любые другие традиционные формы, поскольку респонденты могут быть либо набраны из существующих баз данных или панелей, либо могут быть добавлены путем проведения опросов.
Эти аспекты включают блоги, мобильные дневники и сообщества. Эти методы способствуют экономии средств и времени и чрезвычайно удобны для исследователей при сборе информации по темам своих исследований. Уровень сложности, который онлайн-методы качественного исследования привносят в таблицу, превосходит любые другие традиционные формы, поскольку респонденты могут быть либо набраны из существующих баз данных или панелей, либо могут быть добавлены путем проведения опросов.
 Вы можете подготовить опрос для заполнения после еды, отправить его после получения адреса электронной почты или использовать автономное приложение для проведения опроса.
Вы можете подготовить опрос для заполнения после еды, отправить его после получения адреса электронной почты или использовать автономное приложение для проведения опроса.

 Им легко проводить исследования, даже если они бездельничают на диване и имеют дедлайны.
Им легко проводить исследования, даже если они бездельничают на диване и имеют дедлайны. 


 Они обеспечивают более разговорный стиль сбора данных и позволяют респонденту расширить свой опыт или ситуацию.
Они обеспечивают более разговорный стиль сбора данных и позволяют респонденту расширить свой опыт или ситуацию. Опросы могут быть сосредоточены на собранной фактической информации от людей или могут фиксировать мнения, которые затем могут быть проанализированы статистически.
Опросы могут быть сосредоточены на собранной фактической информации от людей или могут фиксировать мнения, которые затем могут быть проанализированы статистически..files/image212.jpg)
 Это не только более экономично, но и делает видимыми психологические феномены, которых может не хватать в традиционных условиях исследования.
Это не только более экономично, но и делает видимыми психологические феномены, которых может не хватать в традиционных условиях исследования. Он внезапно предоставляет платформу для групп людей, которые, возможно, были недостаточно представлены в психологических исследованиях.
Он внезапно предоставляет платформу для групп людей, которые, возможно, были недостаточно представлены в психологических исследованиях. д. Эти концепции известны как социальная желательность и влияют на надежность и достоверность данных.
д. Эти концепции известны как социальная желательность и влияют на надежность и достоверность данных.
 a11, a12,
…, amn — коэффициенты системы — и b1, b2,
… bm — свободные члены — предполагаются
известными. Индексы коэффициентов (aij)
системы обозначают номера уравнения
(i)
и неизвестного (j),
при котором стоит этот коэффициент,
соответственно[1].Система
(1) называется однородной,
если все её свободные члены равны нулю
(b1 = b2 = … = bm = 0), иначе — неоднородной.Система
(1) называется квадратной,
если число m уравнений равно числу n неизвестных.Решение системы (1) — совокупность n чисел c1, c2,
…, cn,
таких что подстановка каждого ci вместо xi в систему (1) обращает все её уравнения
в тождества.
a11, a12,
…, amn — коэффициенты системы — и b1, b2,
… bm — свободные члены — предполагаются
известными. Индексы коэффициентов (aij)
системы обозначают номера уравнения
(i)
и неизвестного (j),
при котором стоит этот коэффициент,
соответственно[1].Система
(1) называется однородной,
если все её свободные члены равны нулю
(b1 = b2 = … = bm = 0), иначе — неоднородной.Система
(1) называется квадратной,
если число m уравнений равно числу n неизвестных.Решение системы (1) — совокупность n чисел c1, c2,
…, cn,
таких что подстановка каждого ci вместо xi в систему (1) обращает все её уравнения
в тождества. Система (1) называется совместной,
если она имеет хотя бы одно решение, и несовместной,
если у неё нет ни одного решения.Совместная
система вида (1) может иметь одно или
более решений.Решения c1(1), c2(1),
…, cn(1) и c1(2), c2(2),
…, cn(2) совместной системы вида (1) называются различными,
если нарушается хотя бы одно из равенств:
Система (1) называется совместной,
если она имеет хотя бы одно решение, и несовместной,
если у неё нет ни одного решения.Совместная
система вида (1) может иметь одно или
более решений.Решения c1(1), c2(1),
…, cn(1) и c1(2), c2(2),
…, cn(2) совместной системы вида (1) называются различными,
если нарушается хотя бы одно из равенств: Выберем произвольно
строк
матрицы
и
столбцов
(номера строк могут отличаться от номеров
столбцов). Определитель матрицы,
составленной из элементов, стоящих на
пересечении выбранных
строк
и
столбцов,
называется минором порядка
матриws Предложение
14.23 Если
все миноры матрицы порядка равны
нулю, то все миноры порядка ,
если такие существуют, тоже равны
нул./. Доказательство.
Возьмем произвольный минор порядка
.
Это определитель матрицы порядка
.
Разложим его по первой строке. Тогда в
каждом слагаемом разложения один из
множителей будет являться минором
порядка
исходной
матрицы. По условию миноры порядка
равны
нулю. Поэтому и минор порядка
будет
равен нулю. Определение
14.11 Рангом матрицы
называется
наибольший из порядков миноров матрицы
,
отличных от нуля. Ранг нулевой матрицы
считается равным нулю. Единое,
стандартное, обозначение ранга матрицы
отсутствует. Следуя учебник, мы будем
обозначать его Ранг
невырожденной квадратной матрицы
порядка
равен
,
так как ее определитель является минором
порядка
и
у невырожденной матрицы отличен от
нуля.
Выберем произвольно
строк
матрицы
и
столбцов
(номера строк могут отличаться от номеров
столбцов). Определитель матрицы,
составленной из элементов, стоящих на
пересечении выбранных
строк
и
столбцов,
называется минором порядка
матриws Предложение
14.23 Если
все миноры матрицы порядка равны
нулю, то все миноры порядка ,
если такие существуют, тоже равны
нул./. Доказательство.
Возьмем произвольный минор порядка
.
Это определитель матрицы порядка
.
Разложим его по первой строке. Тогда в
каждом слагаемом разложения один из
множителей будет являться минором
порядка
исходной
матрицы. По условию миноры порядка
равны
нулю. Поэтому и минор порядка
будет
равен нулю. Определение
14.11 Рангом матрицы
называется
наибольший из порядков миноров матрицы
,
отличных от нуля. Ранг нулевой матрицы
считается равным нулю. Единое,
стандартное, обозначение ранга матрицы
отсутствует. Следуя учебник, мы будем
обозначать его Ранг
невырожденной квадратной матрицы
порядка
равен
,
так как ее определитель является минором
порядка
и
у невырожденной матрицы отличен от
нуля. Предложение
14.24 При
транспонировании матрицы ее ранг не
меняется, то есть Доказательство.
Транспонированный минор исходной
матрицы
будет
являться минором транспонированной
матрицы ,
и наоборот, любой минор
является
транспонированным минором исходной
матрицы
.
При транспонировании определитель
(минор) не меняется ( предложение
14.6).
Поэтому если все миноры порядка в
исходной матрице равны нулю, то все
миноры того же порядка в
тоже
равны нулю. Если же минор порядка в
исходной матрице отличен от нуля, то в
есть
минор того же порядка, отличный от нуля.
Следовательно,
. Определение
14.12 Пусть ранг матрицы равен
.
Тогда любой минор порядка
,
отличный от нуля, называется базисным
минором. Определение
14.13 Система столбцов (строк) называется
линейно зависимой, если существует
такой набор коэффициентов, из которых
хотя бы один отличен от нуля, что линейная
комбинация столбцов (строк) с этими
коэффициентами будет равна нулю.
Предложение
14.24 При
транспонировании матрицы ее ранг не
меняется, то есть Доказательство.
Транспонированный минор исходной
матрицы
будет
являться минором транспонированной
матрицы ,
и наоборот, любой минор
является
транспонированным минором исходной
матрицы
.
При транспонировании определитель
(минор) не меняется ( предложение
14.6).
Поэтому если все миноры порядка в
исходной матрице равны нулю, то все
миноры того же порядка в
тоже
равны нулю. Если же минор порядка в
исходной матрице отличен от нуля, то в
есть
минор того же порядка, отличный от нуля.
Следовательно,
. Определение
14.12 Пусть ранг матрицы равен
.
Тогда любой минор порядка
,
отличный от нуля, называется базисным
минором. Определение
14.13 Система столбцов (строк) называется
линейно зависимой, если существует
такой набор коэффициентов, из которых
хотя бы один отличен от нуля, что линейная
комбинация столбцов (строк) с этими
коэффициентами будет равна нулю. Определение
14.14 Система столбцов (строк) является
линейно независимой, если из равенства
нулю линейной комбинации этих столбцов
(строк) следует, что все коэффициенты
этой линейной комбинации равны нулю.
Верно также следующее
предложение, аналогичное предложению
10.6 Предложение
14.25 Система
столбцов (строк) является линейно
зависимой тогда и только тогда, когда
один из столбцов (одна из строк) является
линейной комбинацией других столбцов
(строк) этой системы. Сформулируем
теорему, которая называется теорема
о базисном миноре Теорема 14.2 Любой
столбец матрицы является линейной
комбинацией столбцов, проходящих через
базисный минор. Предложение
14.26 Ранг
матрицы равен максимальному числу ее
столбцов, образующих линейно независимую
систему. Доказательство.
Пусть ранг матрицы
равен
.
Возьмем столбцы, проходящие через
базисный минор. Предположим, что эти
столбцы образуют линейно зависимую
систему.
Определение
14.14 Система столбцов (строк) является
линейно независимой, если из равенства
нулю линейной комбинации этих столбцов
(строк) следует, что все коэффициенты
этой линейной комбинации равны нулю.
Верно также следующее
предложение, аналогичное предложению
10.6 Предложение
14.25 Система
столбцов (строк) является линейно
зависимой тогда и только тогда, когда
один из столбцов (одна из строк) является
линейной комбинацией других столбцов
(строк) этой системы. Сформулируем
теорему, которая называется теорема
о базисном миноре Теорема 14.2 Любой
столбец матрицы является линейной
комбинацией столбцов, проходящих через
базисный минор. Предложение
14.26 Ранг
матрицы равен максимальному числу ее
столбцов, образующих линейно независимую
систему. Доказательство.
Пусть ранг матрицы
равен
.
Возьмем столбцы, проходящие через
базисный минор. Предположим, что эти
столбцы образуют линейно зависимую
систему. Тогда один из столбцов является
линейной комбинацией других. Поэтому
в базисном миноре один столбец будет
линейной комбинацией других столбцов.
По предложениям
14.15 и 14.18 этот базисный минор должен быть равен
нулю, что противоречит определению
базисного минора. Следовательно,
предположение о том, что столбцы,
проходящие через базисный минор, линейно
зависимы, не верно. Итак, максимальное
число столбцов, образующих линейно
независимую систему, больше либо равно
.Предположим,
что
столбцов
образуют линейно независимую систему.
Составим из них матрицу .
Все миноры матрицы
являются
минорами матрицы
.
Поэтому базисный минор матрицы
имеет
порядок не больше
.
По теореме о базисном миноре, столбец,
не проходящий через базисный минор
матрицы
,
является линейной комбинацией столбцов,
проходящих через базисный минор, то
есть столбцы матрицы
образуют
линейно зависимую систему. Это противоречит
выбору столбцов, образующих матрицу
.
Следовательно, максимальное число
столбцов, образующих линейно независимую
систему, не может быть больше
.
Тогда один из столбцов является
линейной комбинацией других. Поэтому
в базисном миноре один столбец будет
линейной комбинацией других столбцов.
По предложениям
14.15 и 14.18 этот базисный минор должен быть равен
нулю, что противоречит определению
базисного минора. Следовательно,
предположение о том, что столбцы,
проходящие через базисный минор, линейно
зависимы, не верно. Итак, максимальное
число столбцов, образующих линейно
независимую систему, больше либо равно
.Предположим,
что
столбцов
образуют линейно независимую систему.
Составим из них матрицу .
Все миноры матрицы
являются
минорами матрицы
.
Поэтому базисный минор матрицы
имеет
порядок не больше
.
По теореме о базисном миноре, столбец,
не проходящий через базисный минор
матрицы
,
является линейной комбинацией столбцов,
проходящих через базисный минор, то
есть столбцы матрицы
образуют
линейно зависимую систему. Это противоречит
выбору столбцов, образующих матрицу
.
Следовательно, максимальное число
столбцов, образующих линейно независимую
систему, не может быть больше
. Значит, оно равно
,
что и утверждалось. Предложение
14.27 Ранг
матрицы равен максимальному числу ее
строк, образующих линейно независимую
систему Доказательство.
По предложению
14.24 ранг матрицы при транспонировании не
меняется. Строки матрицы становятся ее
столбцами. Максимальное число новых
столбцов транспонированной матрицы,
(бывших строк исходной) образующих
линейно независимую систему, равно
рангу матрицы Предложение
14.28 Если
определитель матрицы равен нулю, то
один из его столбцов (одна из строк)
является линейной комбинацией остальных
столбцов (строк).Доказательство.
Пусть порядок матрицы
равен
.
Определитель является единственным
минором квадратной матрицы, имеющим
порядок
.
Так как он равен нулю, то .
Следовательно, система из
столбцов
(строк) является линейно зависимой, то
есть один из столбцов (одна из строк)
является линейной комбинацией остальных.
Теорема
14.3 Определитель
матрицы равен нулю тогда и только тогда,
когдаодин из ее столбцов (одна из строк)
является линейной комбинацией остальных
столбцов (строк).
Значит, оно равно
,
что и утверждалось. Предложение
14.27 Ранг
матрицы равен максимальному числу ее
строк, образующих линейно независимую
систему Доказательство.
По предложению
14.24 ранг матрицы при транспонировании не
меняется. Строки матрицы становятся ее
столбцами. Максимальное число новых
столбцов транспонированной матрицы,
(бывших строк исходной) образующих
линейно независимую систему, равно
рангу матрицы Предложение
14.28 Если
определитель матрицы равен нулю, то
один из его столбцов (одна из строк)
является линейной комбинацией остальных
столбцов (строк).Доказательство.
Пусть порядок матрицы
равен
.
Определитель является единственным
минором квадратной матрицы, имеющим
порядок
.
Так как он равен нулю, то .
Следовательно, система из
столбцов
(строк) является линейно зависимой, то
есть один из столбцов (одна из строк)
является линейной комбинацией остальных.
Теорема
14.3 Определитель
матрицы равен нулю тогда и только тогда,
когдаодин из ее столбцов (одна из строк)
является линейной комбинацией остальных
столбцов (строк). Нахождение
ранга матрицы с помощью вычисления всех
ее миноров требует слишком большой
вычислительной работы. (Читатель может
проверить, что в квадратной матрице
четвертого порядка 36 миноров второго
порядка.) Поэтому для нахождения ранга
применяется другой алгоритм. Для его
описания потребуется ряд дополнительных
сведений Определение
14.15 Назовем элементарными преобразованиями
матриц следующие действия над ними:
1)
перестановка строк или столбцов;
2)
умножение строки или столбца на число
отличное от нуля;
3) добавление к одной
из строк другой строки, умноженной на
число или добавление к одному из столбцов
другого столбца, умноженного на
число. Предложение
14.29 При
элементарных преобразованиях ранг
матрицы не меняе Доказательство.
Пусть ранг матрицы
равен
, —
матрица, получившаяся в результате
выполнения элементарного
преобразования.Рассмотрим перестановку
строк. Пусть —
минор матрицы
,
тогда в матрице
есть
минор ,
который или совпадает с
,
или отличается от него перестановкой
строк.
Нахождение
ранга матрицы с помощью вычисления всех
ее миноров требует слишком большой
вычислительной работы. (Читатель может
проверить, что в квадратной матрице
четвертого порядка 36 миноров второго
порядка.) Поэтому для нахождения ранга
применяется другой алгоритм. Для его
описания потребуется ряд дополнительных
сведений Определение
14.15 Назовем элементарными преобразованиями
матриц следующие действия над ними:
1)
перестановка строк или столбцов;
2)
умножение строки или столбца на число
отличное от нуля;
3) добавление к одной
из строк другой строки, умноженной на
число или добавление к одному из столбцов
другого столбца, умноженного на
число. Предложение
14.29 При
элементарных преобразованиях ранг
матрицы не меняе Доказательство.
Пусть ранг матрицы
равен
, —
матрица, получившаяся в результате
выполнения элементарного
преобразования.Рассмотрим перестановку
строк. Пусть —
минор матрицы
,
тогда в матрице
есть
минор ,
который или совпадает с
,
или отличается от него перестановкой
строк. И наоборот, любому минору матрицы
можно
сопоставить минор матрицы
или
совпадающий с
,
или отличающийся от него порядком строк.
Поэтому из того, что в матрице
все
миноры порядка
равны
нулю, следует, что в матрице
тоже
все миноры этого порядка равны нулю. И
так как в матрице
есть
минор порядка
,
отличный от нуля, то и в матрице
тоже
есть минор порядка
,
отличный от нуля, то есть Рассмотрим
умножение строки на число ,
отличное от нуля. Минору
из
матрицы
соответствует
минор
из
матрицы
или
совпадающий с
,
или отличающийся от него только одной
строкой, которая получается из строки
минора
умножением
на число, отличное от нуля. В последнем
случае
.
Во всех случаях или
и
одновременно
равны нулю, или одновременно отличны
от нуля. Следовательно,
Пусть
к -ой
строке матрицы
прибавлена
ее -ая
строка, умноженная на число .
Рассмотрим миноры порядка
в
матрице
.
Если через минор
не
проходит
-ая
строка, то он совпадает с минором
,
расположенным в тех же строках и столбцах
в матрице
,
и следовательно, равен нулю.
И наоборот, любому минору матрицы
можно
сопоставить минор матрицы
или
совпадающий с
,
или отличающийся от него порядком строк.
Поэтому из того, что в матрице
все
миноры порядка
равны
нулю, следует, что в матрице
тоже
все миноры этого порядка равны нулю. И
так как в матрице
есть
минор порядка
,
отличный от нуля, то и в матрице
тоже
есть минор порядка
,
отличный от нуля, то есть Рассмотрим
умножение строки на число ,
отличное от нуля. Минору
из
матрицы
соответствует
минор
из
матрицы
или
совпадающий с
,
или отличающийся от него только одной
строкой, которая получается из строки
минора
умножением
на число, отличное от нуля. В последнем
случае
.
Во всех случаях или
и
одновременно
равны нулю, или одновременно отличны
от нуля. Следовательно,
Пусть
к -ой
строке матрицы
прибавлена
ее -ая
строка, умноженная на число .
Рассмотрим миноры порядка
в
матрице
.
Если через минор
не
проходит
-ая
строка, то он совпадает с минором
,
расположенным в тех же строках и столбцах
в матрице
,
и следовательно, равен нулю. Если через
минор
проходят
и
-ая
и
-ая
строки, то онполучается из минора
,
расположенного в тех же строках и
столбцах матрицы
,
прибавлением к
-ой
строке минора
-ой
строки, умноженной на
.
По свойству определителя .
Следовательно, .
Пусть через минор
проходит
-ая
строка и не проходит
-ая.
Тогда
отличается
от
-ой
строкой. Эта строка в
является
строкой
,
к которой добавлены элементы
-ой
строки, умноженные на
.
По свойствам определителей ,
где —
минор порядка
матрицы
,
стоящий в
-ой
строке и в тех же строках, что и минор
,
исключая
-ую,
а знак »
» связан с возможным изменением
порядка строк. Так как все миноры порядка
в
матрице
равны
нулю, то
.
Если через
минор
проходят
и
-ая
и
-ая
строки, то онполучается из минора
,
расположенного в тех же строках и
столбцах матрицы
,
прибавлением к
-ой
строке минора
-ой
строки, умноженной на
.
По свойству определителя .
Следовательно, .
Пусть через минор
проходит
-ая
строка и не проходит
-ая.
Тогда
отличается
от
-ой
строкой. Эта строка в
является
строкой
,
к которой добавлены элементы
-ой
строки, умноженные на
.
По свойствам определителей ,
где —
минор порядка
матрицы
,
стоящий в
-ой
строке и в тех же строках, что и минор
,
исключая
-ую,
а знак »
» связан с возможным изменением
порядка строк. Так как все миноры порядка
в
матрице
равны
нулю, то
. По только что доказанному .
Получили противоречие: .
Предположение
не
верно, следовательно,
.
По только что доказанному .
Получили противоречие: .
Предположение
не
верно, следовательно,
.
 В результате третья строка принимает
вид Процесс
продолжаем до тех пор, пока не получим
нуль на первом месте в последней строке.
Преобразованная матрица имеет вид Если
все строки, начиная со второй, в полученной
матрице нулевые, то ее ранг равен 1, так
как естьминор первого порядка, отличныйот
нуля .
В противном случае перестановкой строк
и столбцов матрицы с номерами,большими
единицы, добиваемся, чтобы второй элемент
второй строки был отличен от нуля. Итак,
считаем, что .
Первую и вторую строки оставляем без
изменений. К третьей строке прибавляем
вторую, умноженную на чисо .
В результате получим, что второй элемент
третьей строки равен нулю. Затем к
четвертой строке прибавляем вторую,
умноженную на число ,
и т.д. В результате получаем матрицу Если
все строки, начиная с третьей, нулевые,
то ,
так как минор .
В противном случае перестановкой строк
и столбцов с номерами, большими двух,
добиваемся, чтобы третий элемент третьей
строки был отличен от нуля. Далее,
добавлением третьей строки, умноженной
на соответствующие числа, к строкам с
большими номерами получаем нули в
третьем столбце, начиная с четвертого
элемента, и т.
В результате третья строка принимает
вид Процесс
продолжаем до тех пор, пока не получим
нуль на первом месте в последней строке.
Преобразованная матрица имеет вид Если
все строки, начиная со второй, в полученной
матрице нулевые, то ее ранг равен 1, так
как естьминор первого порядка, отличныйот
нуля .
В противном случае перестановкой строк
и столбцов матрицы с номерами,большими
единицы, добиваемся, чтобы второй элемент
второй строки был отличен от нуля. Итак,
считаем, что .
Первую и вторую строки оставляем без
изменений. К третьей строке прибавляем
вторую, умноженную на чисо .
В результате получим, что второй элемент
третьей строки равен нулю. Затем к
четвертой строке прибавляем вторую,
умноженную на число ,
и т.д. В результате получаем матрицу Если
все строки, начиная с третьей, нулевые,
то ,
так как минор .
В противном случае перестановкой строк
и столбцов с номерами, большими двух,
добиваемся, чтобы третий элемент третьей
строки был отличен от нуля. Далее,
добавлением третьей строки, умноженной
на соответствующие числа, к строкам с
большими номерами получаем нули в
третьем столбце, начиная с четвертого
элемента, и т. д. На каком-то этапе мы
придем к матрице, у которой все строки,
начиная с -ой
, равны нулю (или отсутствуют при ),
а минор в первых
строках
и первых
столбцах
является определителем треугольной
матрицы с ненулевыми элементами на
диагонали. Ранг такой матрицы равен
.
Следовательно, .
Замечание
14.15 В предложенном алгоритме нахождения
ранга матрицы все вычисления должны
производиться без округлений. Сколь
угодно малое изменение хотя бы в одном
из элементов промежуточных матриц может
привести к тому, что полученный ответ
будет отличаться от ранга исходной
матрицы на несколько единиц.
Замечание
14.16 Если в исходной матрице элементы
были целыми числами, то и вычисления
удобно производить без использования
дробей. Поэтому на каждом этапе
целесообразно умножать строки на такие
числа, чтобы при вычислениях дроби не
возникали. Теоре́ма
Кро́некера — Капе́лли —
критерий совместности системы линейных
алгебраических уравнений:Пусть система совместна.
д. На каком-то этапе мы
придем к матрице, у которой все строки,
начиная с -ой
, равны нулю (или отсутствуют при ),
а минор в первых
строках
и первых
столбцах
является определителем треугольной
матрицы с ненулевыми элементами на
диагонали. Ранг такой матрицы равен
.
Следовательно, .
Замечание
14.15 В предложенном алгоритме нахождения
ранга матрицы все вычисления должны
производиться без округлений. Сколь
угодно малое изменение хотя бы в одном
из элементов промежуточных матриц может
привести к тому, что полученный ответ
будет отличаться от ранга исходной
матрицы на несколько единиц.
Замечание
14.16 Если в исходной матрице элементы
были целыми числами, то и вычисления
удобно производить без использования
дробей. Поэтому на каждом этапе
целесообразно умножать строки на такие
числа, чтобы при вычислениях дроби не
возникали. Теоре́ма
Кро́некера — Капе́лли —
критерий совместности системы линейных
алгебраических уравнений:Пусть система совместна. Тогда существуют числа такие,
что .
Следовательно, столбец b
является линейной комбинацией столбцов матрицы
A.
Из того, что ранг матрицы не изменится,
если из системы его строк (столбцов)
вычеркнуть или приписать строку
(соответственно столбец), которая
является линейной комбинацией других
строк (соответственно столбцов) следует,
что .ДостаточностьПусть .
Возьмем в матрице A
какой-нибудь базисный минор. Так как ,
то он же и будет базисным минором и
матрицы B.
Тогда согласно теореме о базисном миноре последний столбец матрицы B
будет линейной комбинацией базисных
столбцов, то есть столбцов матрицы A.
Следовательно, столбец свободных членов
системы является линейной комбинацией
столбцов матрицы A
Тогда существуют числа такие,
что .
Следовательно, столбец b
является линейной комбинацией столбцов матрицы
A.
Из того, что ранг матрицы не изменится,
если из системы его строк (столбцов)
вычеркнуть или приписать строку
(соответственно столбец), которая
является линейной комбинацией других
строк (соответственно столбцов) следует,
что .ДостаточностьПусть .
Возьмем в матрице A
какой-нибудь базисный минор. Так как ,
то он же и будет базисным минором и
матрицы B.
Тогда согласно теореме о базисном миноре последний столбец матрицы B
будет линейной комбинацией базисных
столбцов, то есть столбцов матрицы A.
Следовательно, столбец свободных членов
системы является линейной комбинацией
столбцов матрицы A Обратная матрица для
матрицы
обозначается
.
Таким образом, если
существует,
то
.
Из определения обратной матрицы следует,
что матрица
является
обратной для матрицы
,
то есть
.
Про матрицы
и
можно
говорить, что они обратны друг другу
или взаимно обратны. Предложение
14 . 20 Если матрица
имеет
обратную, то
и
.
Доказательство
. Так как определитель
произведения матриц равен произведению
определителей ( предложение 14.7 ),
то
.
По следствию 14.1
,
поэтому
,
что невозможно при
.
Из предыдущего равенства следует
также
.
Последнее предложение
можно сформулировать в следующем виде.
Если определитель матрицы равен нулю,
то обратная к ней не существует. Так
как для нахождения обратной матрицы
важно, равен ли определитель марицы
нулю или нет, то введем следующие
определения. Определение
14 . 9 Квадратную матрицу
назовем
вырожденной или особенной матрицей ,
если
,
и невырожденной или неособенной матрицей
, если
.
Обратная матрица для
матрицы
обозначается
.
Таким образом, если
существует,
то
.
Из определения обратной матрицы следует,
что матрица
является
обратной для матрицы
,
то есть
.
Про матрицы
и
можно
говорить, что они обратны друг другу
или взаимно обратны. Предложение
14 . 20 Если матрица
имеет
обратную, то
и
.
Доказательство
. Так как определитель
произведения матриц равен произведению
определителей ( предложение 14.7 ),
то
.
По следствию 14.1
,
поэтому
,
что невозможно при
.
Из предыдущего равенства следует
также
.
Последнее предложение
можно сформулировать в следующем виде.
Если определитель матрицы равен нулю,
то обратная к ней не существует. Так
как для нахождения обратной матрицы
важно, равен ли определитель марицы
нулю или нет, то введем следующие
определения. Определение
14 . 9 Квадратную матрицу
назовем
вырожденной или особенной матрицей ,
если
,
и невырожденной или неособенной матрицей
, если
. Предложение
14 . 21 Если обратная матрица существует,
то она единственна.
Доказательство . Пусть
две матрицы
и
являются
обратными для матрицы
.
Тогда
и
Следовательно,
.
Предложение
14 . 22 Если квадратная матрица
является
невырожденной, то обратная для нее
существует и
(
14 .14) где
—
алгебраические дополнения к элементам
.
Доказательство
. Так как для невырожденной
матрицы
правая
часть равенства ( 14.14 ) всегда
существует, то достаточно показать,
что эта правая часть является о
братной
матрицей для матрицы
.
Обозначим правую часть равенства (
1
4.14
) буквой
.
Тогда нужно п
роверить,
что
и
что
.
Докажем первое из этих равенств, второе
доказывается аналогично. Пусть
.
Найдем элементы матрицы
,
учитывая, что
:
Если
,
то по предложению 14.17 сумма справа
равна нулю, то есть
при
.
Если
,
то
Сумма
справа представляет собой разложение
определителя матрицы
по
-ой
строке ( предложение 14.
Предложение
14 . 21 Если обратная матрица существует,
то она единственна.
Доказательство . Пусть
две матрицы
и
являются
обратными для матрицы
.
Тогда
и
Следовательно,
.
Предложение
14 . 22 Если квадратная матрица
является
невырожденной, то обратная для нее
существует и
(
14 .14) где
—
алгебраические дополнения к элементам
.
Доказательство
. Так как для невырожденной
матрицы
правая
часть равенства ( 14.14 ) всегда
существует, то достаточно показать,
что эта правая часть является о
братной
матрицей для матрицы
.
Обозначим правую часть равенства (
1
4.14
) буквой
.
Тогда нужно п
роверить,
что
и
что
.
Докажем первое из этих равенств, второе
доказывается аналогично. Пусть
.
Найдем элементы матрицы
,
учитывая, что
:
Если
,
то по предложению 14.17 сумма справа
равна нулю, то есть
при
.
Если
,
то
Сумма
справа представляет собой разложение
определителя матрицы
по
-ой
строке ( предложение 14. 16 ). Таким
образом,
Итак,
в матрице
диагональные
элементы равны 1, а остальные равны
нулю, то есть
.
Результаты предложений
14.20 , 14.21 , 14.22 соберем в одну теорему.
Теорема 14 .
1 Обратная матрица для квадратной
матрицы
существует
тогда и только тогда, когда матрица
—
невырожденная, обратная матрица
единственна, и справедлива формула (
14.14 ). Замечание
14 . 12 Следует обратить особое внимание
на места, занимаемые алгебраическими
дополнениями в формуле обратной матрицы:
первый индекс показывает номер столбца
, а второй — номер строки , в которые
нужно записать вычисленное алгебраическое
дополнение.
Пример 14 . 7
Найдите обратную матрицу для
матрицы
.
Решение. Находим определитель
Так
как
,
то матрица
—
невырожденная, и обратная для нее
существует. Находим алгебраические
дополнения:
Составляем
обратную матрицу, размещая найденные
алгебраические дополнения так, чтобы
первый индекс соответствовал столбцу,
а второй — строке:
(
14 .
16 ). Таким
образом,
Итак,
в матрице
диагональные
элементы равны 1, а остальные равны
нулю, то есть
.
Результаты предложений
14.20 , 14.21 , 14.22 соберем в одну теорему.
Теорема 14 .
1 Обратная матрица для квадратной
матрицы
существует
тогда и только тогда, когда матрица
—
невырожденная, обратная матрица
единственна, и справедлива формула (
14.14 ). Замечание
14 . 12 Следует обратить особое внимание
на места, занимаемые алгебраическими
дополнениями в формуле обратной матрицы:
первый индекс показывает номер столбца
, а второй — номер строки , в которые
нужно записать вычисленное алгебраическое
дополнение.
Пример 14 . 7
Найдите обратную матрицу для
матрицы
.
Решение. Находим определитель
Так
как
,
то матрица
—
невырожденная, и обратная для нее
существует. Находим алгебраические
дополнения:
Составляем
обратную матрицу, размещая найденные
алгебраические дополнения так, чтобы
первый индекс соответствовал столбцу,
а второй — строке:
(
14 . 15) Полученная матрица и служит ответом
к задаче.
Замечание
14 . 13 В предыдущем примере было бы
точнее ответ записать так:
(
14 .16) Однако запись ( 14.15 ) более
компактна и с ней удобнее проводить
дальнейшие вычисления, если таковые
потребуются. Поэтому запись ответа в
виде ( 14.15 ) предпочтительнее, если
элементы матриц — целые числа. И
наоборот, если элементы матрицы
—
десятичные дроби, то обратную матрицу
лучше записать без множителя
впереди.
Замечание
14 . 14 При нахождении обратной матрицы
приходится выполнять довольно много
вычислений и необычно правило расстановки
алгебраических дополнений в итоговой
матрице. Поэтому велика вероятность
ошибки. Чтобы избежать ошибок следует
делать проверку: вычислить произведение
исходной матрицы на итоговую в том или
ином порядке. Если в результате получится
единичная матрица, то обратная матрица
найдена правильно. В противном случае
нужно искать ошибку.
Пример 14 .
15) Полученная матрица и служит ответом
к задаче.
Замечание
14 . 13 В предыдущем примере было бы
точнее ответ записать так:
(
14 .16) Однако запись ( 14.15 ) более
компактна и с ней удобнее проводить
дальнейшие вычисления, если таковые
потребуются. Поэтому запись ответа в
виде ( 14.15 ) предпочтительнее, если
элементы матриц — целые числа. И
наоборот, если элементы матрицы
—
десятичные дроби, то обратную матрицу
лучше записать без множителя
впереди.
Замечание
14 . 14 При нахождении обратной матрицы
приходится выполнять довольно много
вычислений и необычно правило расстановки
алгебраических дополнений в итоговой
матрице. Поэтому велика вероятность
ошибки. Чтобы избежать ошибок следует
делать проверку: вычислить произведение
исходной матрицы на итоговую в том или
ином порядке. Если в результате получится
единичная матрица, то обратная матрица
найдена правильно. В противном случае
нужно искать ошибку.
Пример 14 .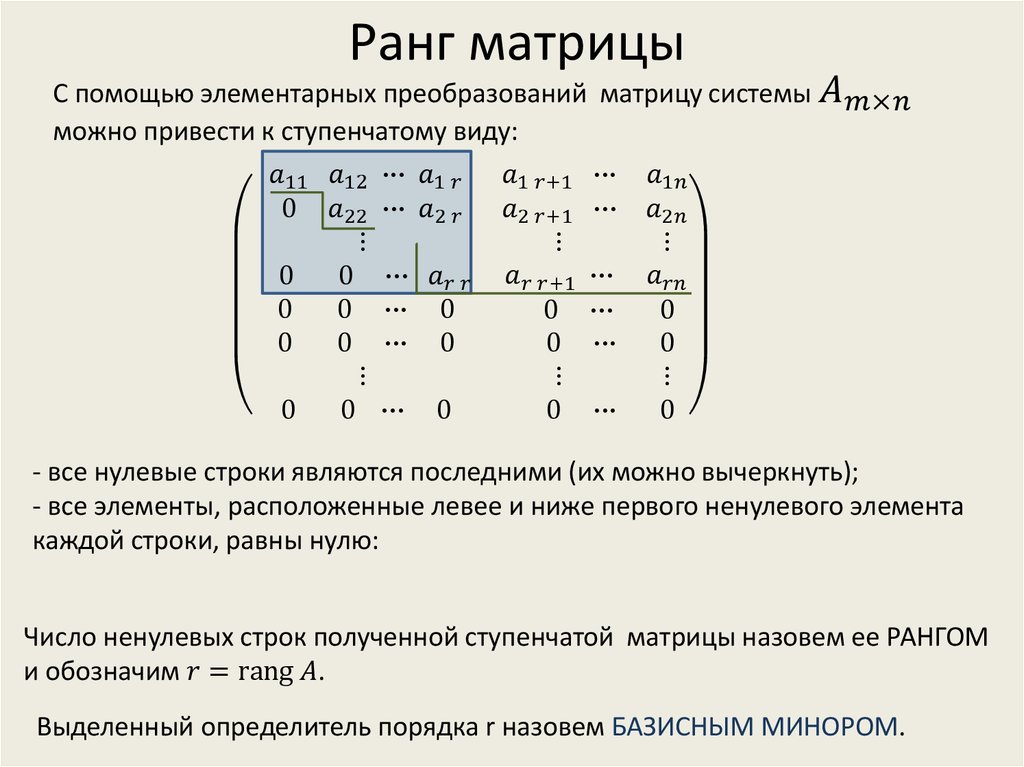 8
Найдите обратную матрицу для
матрицы
.
Решение.
—
существует.
Ответ:
.
Нахождение
обратной матрицы по формуле ( 14.14 )
требует слишком много вычислений. Для
матриц четвертого порядка и выше это
неприемлемо. Реальный алгоритм нахождения
обратной матрицы будет приведен позже.
8
Найдите обратную матрицу для
матрицы
.
Решение.
—
существует.
Ответ:
.
Нахождение
обратной матрицы по формуле ( 14.14 )
требует слишком много вычислений. Для
матриц четвертого порядка и выше это
неприемлемо. Реальный алгоритм нахождения
обратной матрицы будет приведен позже. 

 Тогда при начальных условиях
Тогда при начальных условиях Построить
последовательные приближения
к
решению данного уравнения с данными
начальными условиями:
.
Построить
последовательные приближения
к
решению данного уравнения с данными
начальными условиями:
.


 Несколько строк (столбцов)
называются линейно независимыми, если
ни одна из них не выражается линейно
через другие. Ранг системы строк всегда
равен рангу системы столбцов, и это
число называется рангом матрицы.
Несколько строк (столбцов)
называются линейно независимыми, если
ни одна из них не выражается линейно
через другие. Ранг системы строк всегда
равен рангу системы столбцов, и это
число называется рангом матрицы. Столбцы
и строки матрицы, на которых стоит
базисный минор, также называются базисными.
Столбцы
и строки матрицы, на которых стоит
базисный минор, также называются базисными.
 Матрица считается вырожденной, если она не имеет обратной. Вы доказали, что $I-A$ имеет обратное, а именно $I+A$. Следовательно, $I-A$ несингулярна.
Матрица считается вырожденной, если она не имеет обратной. Вы доказали, что $I-A$ имеет обратное, а именно $I+A$. Следовательно, $I-A$ несингулярна.







