Налоги и налогообложение в Казахстане Тест с ответами
1. Налог, установленный в 15 веке в Казахском ханстве в виде натуральной повинности, заключавшаяся в поставке мяса ханской семье в зимнее время
• согым
2. К универсальному налогу относится:
• НДС
3. Налоговый патент считается не действительным
• на всей территории районов, городов РК и за пределами РК
4. Способность лица исполнять обязанности и осуществлять права налогоплательщика
• налоговая дееспособность
5. Метод оценки ТМЗ по ценам последних покупок
• метод ЛИФО
6. Налог на транспортные средства на автобусы исчисляется в зависимости
• от количества посадочных мест и месячного расчетного показателя на момент платежа
7. Общая теория налогов, характеризующая налоги в роли главного рычага регулирования экономики:
• кейнсианская теория
8. Какой из данных процессов не характерен для налогообложения
Какой из данных процессов не характерен для налогообложения
• возвратность
9. Налоговое обязательство состоит из следующих этапов
• возникновение, исполнение, прекращение
10. Объектом обложения налогом на добычу полезных ископаемых является:
• физический объем добытых недропользователем за налоговый период сырой нефти, газового конденсата и природного газа
11. Плательщики единого земельного налога уплачивают социальный налог за каждого работника по ставке
• 20% от МРП
12. Способ уплаты корпоративного подоходного налога в Республике Казахстан
• уплата налога по декларации
13. Легальные пути уменьшения налогового бремени
• переложение налога
14. Освобождение налогоплательщика, от налогового бремени, или уменьшение его тяжести, по сравнению с обычным режимом
• льгота
15. Пени за несвоевременную уплату налогов начисляются в размере
Пени за несвоевременную уплату налогов начисляются в размере
• 2,5-кратной официальной ставки рефинансирования
16. Неправомерная форма уклонения от уплаты налога
• сокрытие объектов налогообложения
17. Автобусы свыше 25 посадочных мест облагаются по ставке
• 20 МРП
18. Система целенаправленных действий и определенных экономических, правовых и организационно-контрольных мероприятий государства в области налогов и налогообложения
• налоговая политика
19. Регулирующая функция подразделяется на:
• стимулирующую, дестимулирующую и воспроизводственную
20. Сколько периодов выделяют в системе налогообложения
• 3
21. Налог взимаемый с продаж и включаемый в цену товара
• НДС
22. Условная точка в налогообложении, в которой достигается оптимальная для плательщиков и государственной казны доля валового национального продукта, перераспределяемого через бюджетную систему
• налоговый предел
23. К элементам налогового механизма не относится:
К элементам налогового механизма не относится:
• налоговая политика
24. Комплексные проверки проводятся:
• не чаще одного раза в год
25. Налоговая политика, проводимая с расчетом на перспективу
• налоговая стратегия
26. При переводе в течении налогооблагаемого периода населенного пункта из одной категории в другую в текущем году, земельный налог взимается:
• по ранее установленным ставкам до момента перевода, дальше до конца года по ставкам установленным для новой категории населения
27. Предельная норма амортизации для зданий, сооружении (за исключением нефтяных, газовых скважин и передаточных устройств):
• 10
28. Базовые налоговые ставки на земли населенных пунктов устанавливаются:
• в расчете на 1 кв. метр площади
29. Метод расчета при котором НДС исчисляется в виде доли от предварительно рассчитанной величины добавленной стоимости:
• прямой
30. Ответственности за нарушение налогового законодательства
Ответственности за нарушение налогового законодательства
• уголовная, финансовая, административная
31. Функция налога, которая направлена через установление налогового бремени, препятствий, для развития экономических процессов
• дестимулирующая
32. Налоговая система, при которой доходы юридических и физических лиц облагаются одинаково
• глобальная
33. Платеж, устанавливаемый в рамках налогооблагаемого законодательства органами местного самоуправления и зачисляемый в местный бюджет
• сбор
34. Стадии налогового производства
• исчисление и уплата налога
35. Декларация по налогу на транспортные средства представляется:
• 31 марта, года следующего за отчетным периодом
36. К общим теориям налогообложения не относится:
• теория единого налога
37. Официальное заявление налогоплательщика о наличии объекта налогоплательщика, величине налоговой базы и размера налогового платежа за соответствующий налоговый период
Официальное заявление налогоплательщика о наличии объекта налогоплательщика, величине налоговой базы и размера налогового платежа за соответствующий налоговый период
• налоговая декларация
38. К подакцизным товарам относятся:
• табачные изделия
39. Метод, при котором сумма НДС, относимая в зачет, определяется исходя из удельного веса облагаемого оборота в общей сумме оборота
• пропорциональный метод
40. По импортируемым товарам установленные ставки акцизов применяются:
• к таможенной стоимости или физическому объему в натуральном выражении ввозимых подакцизных товаров
41. К стадиям процесса исчисления налога не относится:
• определение субъекта налога
42. По признаку использования налоги подразделяются на:
• общие и специальные
43. Декларация по социальному налогу представляется:
• ежеквартально не позднее 15 числа второго месяца, следующего за отчетным кварталом
44. По товарам, необлагаемым таможенной пошлиной, акцизом и другими сборами, но подлежащим обложению таможенным сбором НДС определяется по формуле:
По товарам, необлагаемым таможенной пошлиной, акцизом и другими сборами, но подлежащим обложению таможенным сбором НДС определяется по формуле:
• НДС = ((ТСТ + ТС) * 15%) / 100%
45. Если среднемесячные платежи за квартал по роялти составляют более 1000 МРП, то отчетным периодом является:
• календарный месяц
46. Объектами налогообложения фиксированным налогом являются:
• игровой автомат без выигрыша, предназначенный для проведения игры с одним игроком; игровой автомат без выигрыша, предназначенный для проведения игры с участием более одного игрока
• персональный компьютер, используемый для проведения игры; игровая дорожка; карт; бильярдный стол
47. При невозможности определить бал бонитета земельных участков, размер налога определяется:
• исходя из балл бонитета смежно-расположенных земель
48. Часть дохода или стоимости, выраженная в облагаемых единицах, к которой применяется ставка налога
• налогооблагаемая база
49. При отсутствии какого элемента налога, налог считается установленным
При отсутствии какого элемента налога, налог считается установленным
• льготы
50. Принцип налогообложения, при котором в кассу государства должна поступать сумма, соразмерная той, которая убывает из кармана налогоплательщика
• равномерность
51. Налогоплательщик имеет право
• обжаловать решения налоговых органов в определенном порядке
52. По результатам налоговой проверки при отсутствии нарушений составляется:
• справка
53. Доходы адвокатов и частных нотариусов облагаются индивидуальным подоходным налогом по ставке
• 10%
54. В зависимости от источников налоговый контроль подразделяется на виды:
• документальный, визуальный
55. Налоговые органы обязаны учитывать выдаваемые патенты
• в специальных журналах
56. Налог на транспортные средства на летательные аппараты исчисляется:
• в процентах от минимального расчетного показателя на момент платежа, с каждого киловатта мощности
57. Налоговой теорией и практикой выделены 4 вида причин уклонения от налогов, кроме
Налоговой теорией и практикой выделены 4 вида причин уклонения от налогов, кроме
• политических
58. Принцип налогообложения, согласно которому каждый должен участвовать в поддержке государства соразмерно своему доходу, которым он пользуется под охраной государства
• равномерность
59. Ставка налога на транспортные средства на легковые автомобили с объемом двигателя свыше 2500 см3 по 3000 м3
• 8 МРП
60. Плательщиками налога на транспортные средства являются:
• физические лица, имеющие транспортные средства на праве хозяйственного ведения
• юридические лица, имеющие транспортные средства на праве собственности, хозяйственного ведения
61. Ставка сбора с аукционных продаж
• 3%
62. Совокупный годовой доход налогоплательщика — нерезидента состоит из:
• доходов, полученных из казахстанских источников
63. Деяние заключенное в сознательном нежелании уплаты, установленных законодательных сборов, налогов и других платежей
Деяние заключенное в сознательном нежелании уплаты, установленных законодательных сборов, налогов и других платежей
• налоговые правонарушения
64. Минимальный расчетный показатель на 2009 г.
• 1273 тенге
65. Ставка налога на транспортные средства на мотор-вагонный подвижной состав, используемый для организации перевозок пассажиров по магистральным и станционным путям узкой и широкой колеи
• 1% от МРП с каждого киловатта общей мощности транспортного средства
66. Убытки от предпринимательской деятельности переносятся на срок до …
• 3 лет
67. Ставка налога на транспортные средства на легковые автомобили с объемом двигателя свыше 1500 см3 по 2000 м3
• 3 МРП
68. К плательщикам налога на имущество относятся плательщики:
• индивидуальные предприниматели, имеющие объект налогообложения на праве собственности
• физические лица, имеющие объект налогообложения на праве собственности
• юридические лица, имеющие объект налогообложения на праве собственности, хозяйственного ведения
69. Ставка налога на транспортные средства на мотоциклы, мотороллеры, мощность двигателя которых не более 55 кВт
Ставка налога на транспортные средства на мотоциклы, мотороллеры, мощность двигателя которых не более 55 кВт
• 1 МРП
70. Расчетная сумма по индивидуальному подоходному налогу определяется как:
• доходы, полученные в виде оплаты труда, умноженные на ставку индивидуального подоходного налога
71. Мировоззренческое учение о восприятии налога как осознанной общественной необходимости
• философия налога
72. При определенных условиях, налогоплательщик — индивидуальный предприниматель уменьшает сумму налога, подлежащую уплате по упрощенной декларации, на сумму за каждого работника в размере
• 1,5% от суммы налога
73. Совокупность налогов, пошлин и сборов, взимаемых на территории государства в соответствии с Налоговым кодексом
• налоговая система
74. Ставка налога увеличивается с ростом налогооблагаемой базы при:
• прогрессивном обложении
75. Предельная норма амортизации компьютеров и оборудования для обработки информации
Предельная норма амортизации компьютеров и оборудования для обработки информации
• 40
76. Ставки налога на добычу полезных ископаемых на сырую нефть, включая газовый конденсат, до 250 000 тонн включительно: Ставки налога на добычу полезных ископаемых на сырую нефть, включая газовый конденсат, до 500 000 тонн включительно:
• 9%
77. По вновь отведенным земельным участкам налог исчисляется:
• начиная с месяца, следующего за отчетным
78. Право государства устанавливать любые налоги в любом размере на любые объекты и проводить любую налоговую политику в пределах своей территории
• налоговый суверенитет
79. Под государственной пошлиной понимается:
• обязательный платеж
80. Ставки налога на добычу полезных ископаемых на сырую нефть, включая газовый конденсат, до 1000 000 тонн включительно:
• 10%
81. Что является отчетным периодом по НДС, если среднемесячные платежи по НДС более 1000 МРП
Что является отчетным периодом по НДС, если среднемесячные платежи по НДС более 1000 МРП
• календарный месяц
82. В зависимости от времени своего осуществления налоговый контроль подразделяется на виды:
• предварительный, текущий, последующий
83. Косвенные налоги подразделяются на налоги
• индивидуальные и универсальные
84. Размеры минимальных и максимальных базовых ставок фиксированного налога на персональный компьютер, используемый для проведения игры:
• 1 и 4 МРП
85. К косвенным налогам относится:
• акцизы
86. Элемент налогового механизма
• налоговый контроль
87. В совокупный годовой доход юридического лица включаются:
• доходы от уступки требования долга
• доходы по сомнительным обязательствам
88. Базовые ставки на земли населенных пунктов для городов областного значения
• 85% от ставки, уставленной для областного центра
89. Количество плат, взимаемых в Республике Казахстан с 01.01.2010 года
Количество плат, взимаемых в Республике Казахстан с 01.01.2010 года
• 9
90. Земли населенных пунктов, отведенные под территории рынков, подлежат налогообложению по базовым ставкам на земли населенных пунктов, увеличенным
• в 10 раз
91. Способ уплаты налогов, при котором взимание осуществляется на основе описи или реестра, содержащего перечень типичных сведений об оценке и средней доходности объекта обложения
• кадастровый
92. Физические лица уплачивают земельный налог не позднее
• 1 октября текущего года
93. Вид косвенного налога, устанавливаемого или на часть определенных товаров (услуг), или в расчете на единицу товарной массы
• акцизы
94. Ставка налога уменьшается с ростом налогооблагаемой базы при:
• регрессивном обложении
95. Ставка налога на транспортные средства на легковые автомобили с объемом двигателя свыше 2000 см3 по 2500 см3
• 5 МРП
96. Налогообложение недропользователей, исходя из основных видов контрактов, разделяется на:
Налогообложение недропользователей, исходя из основных видов контрактов, разделяется на:
• 2 модели
97. В случае наличия налогоплательщика по НДС с облагаемых и необлагаемых оборотов в зачет принимается сумма НДС определяемая:
• раздельным и пропорциональным методами
98. Налоги, поступающие в строго определенный бюджет
• закрепленные
99. Ставка налога на транспортные средства по летательным аппаратам:
• 4% от МРП с каждого киловатта мощности
100. Предприятие берет оборудование в лизинг. Кто в данном случае платит налог на имущество?
• арендатор
Готовый тест по дисциплине «Налоговое право» для АНО ПО ОСЭК (sdo.i-spo.ru).
или напишите нам прямо сейчас
Написать в WhatsApp
Вопрос 1
К косвенным налогам относятся:
Выберите один ответ:
a. НДС, подоходный налог, налог на рекламу
НДС, подоходный налог, налог на рекламу
b. акцизы, таможенные пошлины, налог с оборота
c. подоходный налог, НДС, земельный налог
Выберите один ответ:
a. юридические факты, которые обуславливают обязанность субъекта заплатить налог
b. количественное выражение объекта налогообложения
c. имущество (земля, автомобили, другое имущество) и нематериальные блага (государственная символика), с наличием которых закон связывает возникновение налоговых обязательств
Вопрос 3
Равный метод налогообложения означает, что:
Выберите один ответ:
a. с ростом налоговой базы средняя налоговая ставка снижается.
b. для каждого налогоплательщика установлена равная сумма налога;
c. с ростом налоговой базы средняя налоговая ставка возрастает;
d. для каждого налогоплательщика установлена равная ставка налога;
Вопрос 4
По налоговому законодательству РФ юридические лица считаются резидентами, если они:
Выберите один ответ:
a. имеют имущество на территории РФ
имеют имущество на территории РФ
b. находятся на территории РФ
c. созданы на территории России по российскому законодательству
Вопрос 5
Укажите верные утверждения в отношении региональных налогов (допускаются несколько ответов):
Выберите один или несколько ответов:
a. поступают исключительно в региональный бюджет;
b. устанавливаются законами субъекта РФ;
c. устанавливаются Налоговым кодексом РФ и законами субъектов РФ;
d. при их установлении органами субъектов РФ определяются налоговые льготы, налоговые ставки в переделах, установленных Налоговым кодексом РФ, порядок и сроки уплаты налога.
Вопрос 6
По налоговому законодательству РФ физические лица считаются резидентами, если они находятся на территории РФ более:
Выберите один ответ:
a. 58 суток в календарном году
b. 93 суток в календарном году
c. 183 суток в календарном году
183 суток в календарном году
Вопрос 7
При установлении законодательными (представительны¬ми) органами субъектов РФ регионального налога налоговые льготы могут быть предусмотрены:
Выберите один ответ:
a. да, только для определенных категорий налогоплательщиков.
b. да;
c. нет;
Вопрос 8
В Российской Федерации устанавливаются следующие виды налогов и сборов:
Выберите один ответ:
a. федеральные налоги и сборы, налоги и сборы субъектов Российской Федерации и местные налоги и сборы
b. федеральные налоги и сборы, налоги и сборы субъектов Российской Федерации
c. федеральные налоги и сборы, налоги и сборы субъектов Российской Федерации, налоги и сборы свободных экономических зон РФ
Вопрос 9
Налог на рекламу в РФ относится к налогам и сборам:
Выберите один ответ:
a. федеральным
федеральным
b. региональным
c. местным
Вопрос 10
Налог на имущество организаций в РФ относится к налогам и сборам:
Выберите один ответ:
a. смешанным
b. региональным
c. местным
Вопрос 11
Какой из российских налогов, введенный Петром I, действует в модифицированной форме в настоящее время?
Выберите один ответ:
a. с капитала
b. подушный
c. с церковных верований
Вопрос 12
Ставка налога – это:
Выберите один ответ:
a. размер налога, приходящийся на единицу налогообложения
b. сумма денег, которую платит налогоплательщик, за вычетом налоговых льгот
c. установленный государством размер налога за вычетом налоговых льгот
Вопрос 13
К региональным налогам и сборам относится налог (до¬пускаются несколько ответов):
Выберите один или несколько ответов:
a. на имущество организаций;
на имущество организаций;
b. транспортный.
c. на имущество физических лиц;
d. на игорный бизнес;
Вопрос 14
Местные налоги и сборы обязательны к уплате:
Выберите один ответ:
a. если они установлены Налоговым кодексом РФ и соответствующими законами на территории соответствующего муниципального образования;
b. если они установлены соответствующими законами на территории субъекта РФ и муниципального образования;
c. во всех муниципальных образованиях РФ, если они установлены главой Налогового кодекса РФ;
d. если они установлены соответствующими законами на территории субъекта РФ.
Вопрос 15
При установлении налогов должны быть определены
Выберите один ответ:
a. все элементы налогообложения
b. ставка налогообложения
ставка налогообложения
c. субъекты налогообложения
Вопрос 16
Законодательство по налогам и сборам РФ включает в себя:
Выберите один ответ:
a. Налоговый кодекс РФ и федеральные законы;
b. Налоговый кодекс РФ, федеральные законы, законы субъектов РФ, нормативно-правовые акты представительных органов местного самоуправления о налогах и сборах, принятых в соответствии с Налоговым кодексом РФ;
c. только Налоговый кодекс РФ;
d. Налоговый кодекс РФ, федеральные законы, законы субъектов РФ, нормативно-правовые акты представительных органов местного самоуправления о налогах и сборах, постановления Правительства РФ и письма министерств и ведомств, в том числе органа, уполномоченного осуществлять функции по контролю и надзору в области налогов и сборов.
Вопрос 17
Резким отличием российской налоговой системы от зарубежных налоговых систем является/являются
Выберите один ответ:
a. низкая доля подоходного налога с физических лиц и высокая доля налога на прибыль предприятий
низкая доля подоходного налога с физических лиц и высокая доля налога на прибыль предприятий
b. высокие доли налога с оборота и налога с продаж и низкая доля подоходного налога с физических лиц
c. высокая доля подоходного налога с физических лиц и низкая доля налога на прибыль предприятий
d. примерно равные доли подоходного налога с физических лиц и налога на прибыль предприятий
Вопрос 18
Количество уровней в налоговой системе государства зависит от:
Выберите один ответ:
a. государственного устройства
b. уровня экономического развития
c. географического положения
Вопрос 19
Из перечисленных ниже налогов укажите прямые личные налоги:
Выберите один или несколько ответов:
a. акциз.
b. земельный;
c. на имущество физических лиц;
d. на доходы физических лиц;
Вопрос 20
Налог на игорный бизнес в РФ относится к налогам и сборам:
Выберите один ответ:
a. федеральным
федеральным
b. региональным
c. местным
или напишите нам прямо сейчас
Написать в WhatsApp
77% американцев не прошли этот тест из 4 вопросов по налогам
Снова пришло время налогов, и многие американцы не понимают, как налоговая реформа может повлиять на них.
Закон о сокращении налогов и создании рабочих мест, принятый в декабре 2017 года, внес радикальные изменения, и многие налогоплательщики могли ознакомиться с деталями. Одно исследование показало, что 28 процентов точно не понимают, что именно изменил закон, а 48 процентов говорят, что они даже не знают, в какой налоговой категории они сейчас находятся. закона, чтобы выяснить, что именно сбивает с толку американцев, и 77 процентов из 501 респондента не смогли. «Проходной балл означает, что вы ответили правильно более чем на половину вопросов», — отмечается на сайте.
«Большинство американцев нуждаются в переподготовке перед подачей налоговой декларации», — заключает GOBankingRates.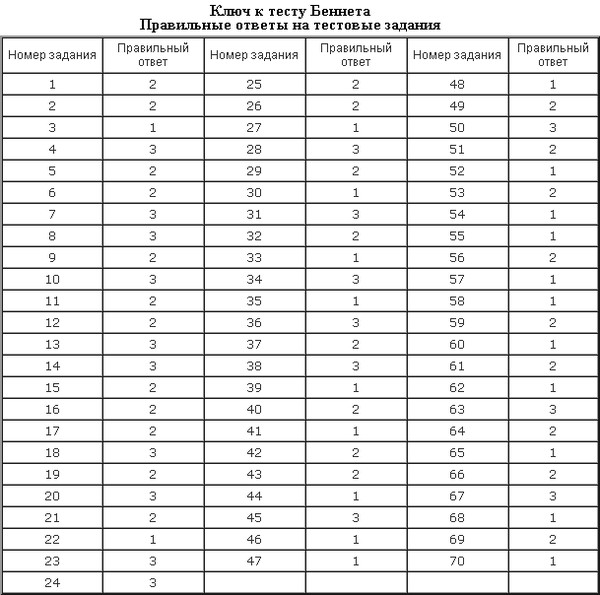 «Эти результаты, по-видимому, указывают на то, что многие налогоплательщики плохо информированы».
«Эти результаты, по-видимому, указывают на то, что многие налогоплательщики плохо информированы».
Ниже приведены вопросы, а также правильные ответы и доля респондентов, ответивших на каждый из них правильно:
1. Сколько составляет стандартный вычет за одного заявителя в 2019 году?
Ответ : 12 000 долларов
Процент респондентов, ответивших правильно : 17,8
Налоговый вычет — это определенная сумма денег, которую налоговая служба позволяет вам вычесть из общего дохода до расчета налогов.
Вы можете выбрать стандартный вычет, фиксированную сумму, устанавливаемую IRS каждый год, которая «с поправкой на инфляцию и варьируется в зависимости от вашего статуса подачи», отмечает агентство. Вы также можете детализировать или индивидуализировать свои вычеты, что может уменьшить ваш налогооблагаемый доход на основе определенных допустимых расходов или убытков от стихийных бедствий, которые вы могли понести в течение года.
Стандартный вычет теперь составляет 12 000 долларов для одиночных регистраторов. В прошлом году это было 6350 долларов.
В отчете IRS за 2018 год отмечается, что «большинство налогоплательщиков требуют стандартного вычета», но у каждого варианта есть свои плюсы и минусы, в зависимости от вашей ситуации. Вот как выбрать, что лучше для вас.
2. Каков размер штрафа за отсутствие медицинской страховки в 2019 году?
Ответ : $0
Процент респондентов, ответивших правильно : 51,7
Это был единственный вопрос, на который большинство респондентов ответили правильно, причем более половины «правильно отметили, что отмена «индивидуального мандата» — налогового штрафа за отсутствие медицинской страховки — является одним из новых изменений в налоговом законодательстве» говорит GOBankingRates.
В предыдущие годы вы могли платить взнос, если вы, ваш супруг или ваши иждивенцы должны были платить, но не имели соответствующей медицинской страховки.
Имейте в виду, что, несмотря на то, что новый закон устраняет эти виды штрафов в будущем, когда вы подаете заявку в этом году, вы все равно можете быть на крючке из-за любой оставшейся суммы 2017 и корректировки на инфляцию, которые будут определены.
3. Сколько различных налоговых категорий предусмотрено для налогоплательщиков в 2019 году?
Ответ : 7
Процент респондентов, ответивших правильно : 10
Налоговая реформа внесла изменения в семь налоговых категорий, которые определяют ставку, которую вы платите за часть вашего дохода. Конгресс скорректировал ставки и уровни доходов, соответствующие каждому из них.
NerdWallet: Налоговые категории и ставки для одиночных регистраторов — нажмите, чтобы увеличить
Когда налогоплательщики подавали декларации в 2018 году, диапазоны составляли 10 процентов, 15 процентов, 25 процентов, 28 процентов, 33 процента, 35 процентов и 39,6 процента. Скобки, которые применяются в этом году, составляют 10 процентов, 12 процентов, 22 процента, 24 процента, 32 процента, 35 процентов и 37 процентов.
Скобки, которые применяются в этом году, составляют 10 процентов, 12 процентов, 22 процента, 24 процента, 32 процента, 35 процентов и 37 процентов.
Эти правила применяются только к федеральным подоходным налогам, отмечает NerdWallet в своем налоговом исследовании 2018 года: «В вашем штате могут быть другие скобки, фиксированный подоходный налог или вообще отсутствие подоходного налога».
4. Какова ставка налога для самой высокой налоговой категории в 2019 г.?
Ответ : 37 процентов
Процент респондентов, ответивших правильно : 12,8
Ставка для самой высокой налоговой категории снизилась с 39,6 процента до 37 процентов.
В то время как в целом американцы получили низкие баллы в викторине, миллениалы старшего возраста, похоже, «более согласны с изменениями, включенными в новый законопроект», — говорит GOBankingRates. Респонденты в возрасте от 25 до 34 лет имели самый высокий проходной балл — 27 процентов. У лиц в возрасте от 55 до 64 лет был самый низкий процент сдачи: 16 процентов.
У лиц в возрасте от 55 до 64 лет был самый низкий процент сдачи: 16 процентов.
«Это может быть просто признаком времени», что американцы мало знают о своих налогах, говорит GOBankingRates.
Тем не менее, полезно и важно быть в курсе: некоторые заявители могут столкнуться с более низким возмещением из-за изменений в налоговом законодательстве. И около 30 миллионов могут фактически быть должны деньги IRS.
«Оставаясь в неведении относительно основ налогового законодательства, вы можете получить потенциально неприятный сюрприз при подаче заявления», — пишет GOBankingRates, или это может заставить вас «планировать возмещение, которое не материализуется».
Понравилась эта история? Подпишитесь на CNBC Make It на YouTube!
Не пропустите: 30 миллионов человек могут получить налоговый счет, а не возмещение, в этом году — вот 3 шага, которые нужно предпринять, если вы один из них
Вопросы и Ответы об оценке недвижимости
Уважаемый покупатель,
Оценка имущества и налогообложение исторически вызывали затруднения у владельцев собственности. Эта информация предназначена как простой в использовании источник информации о том, как оценивается ваша собственность, что делать, если вы считаете, что стоимость вашей собственности ошибочна, и какие специальные программы налоговых льгот доступны. Включены ответы на наиболее часто задаваемые вопросы об оценке недвижимости.
Эта информация предназначена как простой в использовании источник информации о том, как оценивается ваша собственность, что делать, если вы считаете, что стоимость вашей собственности ошибочна, и какие специальные программы налоговых льгот доступны. Включены ответы на наиболее часто задаваемые вопросы об оценке недвижимости.
Сотрудники SDAT всегда готовы ответить на ваши вопросы. Пожалуйста, свяжитесь с вашим местным офисом оценки для получения более подробной информации.
Что такое оценка?
Оценка — это оценка текущей рыночной стоимости вашей собственности, определенная Департаментом оценки и налогообложения. Местные органы власти будут применять свои налоговые ставки к оценке при определении вашего годового счета по налогу на имущество.
Как вы определяете стоимость моей собственности, отраженную в уведомлении?
Новая рыночная стоимость, о которой вас уведомляют, представляет собой оценку рыночной стоимости, основанную на сравнительном анализе затрат и продаж. Проще говоря, стоимостной подход представляет собой оценочную стоимость земли плюс оценку стоимости восстановления сооружений (за вычетом амортизации). Подход, основанный на продажах, основан на оценке стоимости, основанной на недавних продажах сопоставимой недвижимости.
Проще говоря, стоимостной подход представляет собой оценочную стоимость земли плюс оценку стоимости восстановления сооружений (за вычетом амортизации). Подход, основанный на продажах, основан на оценке стоимости, основанной на недавних продажах сопоставимой недвижимости.
Как я могу прочитать уведомление об оценке?
Цифры в уведомлении об оценке предназначены для информирования владельцев собственности об их старой и новой рыночной стоимости и возможных кредитах. Чтение описания уведомления может помочь вам лучше понять процесс оценивания. Более подробное объяснение можно получить, связавшись с местным отделом оценки и получив полезные брошюры, опубликованные Департаментом, или зайдя на наш веб-сайт по адресу www.dat.state.md.us в разделе «Недвижимость».
Что такое список продаж?
Список продаж — это список всех продаж, используемый для оценки отдельных свойств. Информация в списке продаж идентифицирует и описывает недвижимость для продажи.
Что такое сопоставимая недвижимость?
Сопоставимая недвижимость – это недавно проданная недвижимость, аналогичная оцениваемой недвижимости. Чем больше они напоминают собственность, тем больше цена продажи представляет стоимость непроданной собственности.
Как вы получаете введенные значения, указанные в уведомлении?
Увеличение вашей оценки от старой рыночной стоимости до новой рыночной стоимости делится поровну в течение трех лет. Поэтапный ввод предназначен для распределения увеличения стоимости вашей собственности в течение следующих трех лет, чтобы полное увеличение не облагалось налогами в течение одного года. Это не прогноз рыночной стоимости имущества на будущую дату.
Почему необходимо проводить переоценку имущества?
Каждые 3 года недвижимость переоценивается, поэтому каждый владелец недвижимости платит соответствующую долю местных налогов. Стоимость недвижимости растет и падает с течением времени. Переоценка необходима, чтобы отразить текущую рыночную стоимость имущества.
Стоимость недвижимости растет и падает с течением времени. Переоценка необходима, чтобы отразить текущую рыночную стоимость имущества.
Программа налоговых льгот для домовладельцев — это программа по освобождению от налога на имущество штата, которая позволяет предоставлять налоговые льготы на имущество домохозяйствам, общий валовой доход которых ниже стандарта, установленного законом. Эта программа предоставляет налоговые льготы на недвижимость для домовладельцев всех возрастов в зависимости от их доходов. В дополнение к государственной программе местные органы власти теперь могут дополнять сумму, субсидируемую государством.
Как на меня повлияют местные предельные оценки?
Каждый округ и муниципалитет должен ограничить увеличение налогооблагаемой базы до 10 % или меньше по сравнению с налогооблагаемой базой за предыдущий год. Чем ниже процент, установленный местным самоуправлением, тем большую экономию получает владелец недвижимости. Если, например, округ устанавливает верхний предел налогообложения в размере 4%, местный налог увеличится не более чем на 4% по сравнению с налоговым счетом за предыдущий год, если округ использует ту же налоговую ставку. Если округ использует постоянную ставку налога на прибыль, ваш налоговый счет будет еще меньше.
Если, например, округ устанавливает верхний предел налогообложения в размере 4%, местный налог увеличится не более чем на 4% по сравнению с налоговым счетом за предыдущий год, если округ использует ту же налоговую ставку. Если округ использует постоянную ставку налога на прибыль, ваш налоговый счет будет еще меньше.
Что такое налоговый кредит на недвижимость в приусадебном доме?
Налоговая льгота на имущество приусадебного участка, обычно называемая Предел оценки, представляет собой программу для домовладельцев, соответствующих требованиям, которая ограничивает налогообложение значительного ежегодного повышения оценки основного места жительства владельца собственности. Для целей налогообложения штата любое ежегодное повышение оценки дома или приусадебного участка, превышающее 10%, не облагается налогом. Округа и муниципалитеты могут ограничивать увеличение налогов для целей местного налогообложения до уровня менее 10% в год.
Что такое постоянная ставка налога на прибыль?
Государственный департамент оценки и налогообложения (SDAT) по закону обязан установить постоянную ставку налога на прибыль для каждого округа и местной юрисдикции. Это важный инструмент защиты прав потребителей для уведомления домовладельцев, когда юрисдикция решает увеличить доход.
По мере роста стоимости недвижимости общие налоговые поступления увеличиваются, если округа решат не применять постоянную ставку налога на прибыль. Если юрисдикция решает не применять постоянную ставку налога на доход, она должна объявить о своем намерении сделать это и провести публичные слушания для обсуждения увеличения налоговых поступлений.
Любое увеличение дохода, полученное в результате принятия ставки налога на недвижимость, превышающей постоянную ставку налога на прибыль, является увеличением налога, даже если принятая ставка налога такая же, как ставка налога в предыдущем году.
В то время как SDAT оценивает стоимость вашей собственности, юрисдикция определяет размер налога, который вы будете платить.
*Примечание:* Муниципалитеты освобождаются от требований в отношении рекламы и публичных слушаний, если сохранение налоговой ставки предыдущего года принесет менее 25 000 долларов дополнительного дохода сверх суммы дохода, которая будет получена за счет применения постоянной ставки налога на прибыль .
*Пример: * Общая сумма налогооблагаемого дохода для *города Балтимора *на 01.07.2020 составила 41 027 419 000 долларов США. Ставка налога составляла 2 * 0,2480 * на 100 долларов оценочной стоимости, в результате чего доход от налога на недвижимость для * города Балтимор * составил 922 296 379 долларов.
Город Балтимор решил сохранить текущую налоговую ставку и не применять постоянную доходность. Общая налогооблагаемая база *города Балтимора* на 01.07.2021 составила 41 587 521 000 долларов США. Сохранение текущей налоговой ставки привело к увеличению налога на * 12,59 долларов США.1,0093* новых налоговых поступлений.
Сохранение текущей налоговой ставки привело к увеличению налога на * 12,59 долларов США.1,0093* новых налоговых поступлений.
Если бы город Балтимор решил принять постоянную ставку налога на прибыль, это привело бы к сохранению текущих налоговых поступлений.
Как повышение оценки повлияет на мои налоги?
Ваш налоговый счет основан на расходных потребностях вашего местного округа или муниципалитета. Увеличение оценки не обязательно влечет за собой увеличение налогов. Ваш налоговый счет является прямым результатом бюджетных потребностей вашего местного подразделения.
Что мне делать, если у меня есть вопрос о моих налогах?
Департамент оценки и налогообложения оценивает имущество в качестве услуги местным органам власти. Департамент не занимается установлением ставок местных налогов, на основе которых рассчитывается налоговый счет. Поэтому ваши вопросы относительно налогов должны быть адресованы вашим местным чиновникам.
Что мне делать, если я не согласен с моей оценкой?
Владельцы могут обжаловать общую новую рыночную стоимость в течение 45 дней с даты уведомления. Решение об апелляции должно основываться на том, отражает ли Общая рыночная стоимость (стоимость земли и здания вместе) рыночную стоимость имущества. Для вашего удобства ваша апелляция может быть подана в письменном виде, обсуждена на слушании по телефону или на личном слушании с оценщиком.
Как подать апелляцию?
К уведомлению об оценке прилагается форма апелляции, в которой объясняется процесс апелляции. Инструкции прилагаются, чтобы помочь вам заполнить форму.
Как проводятся слушания?
Слушания на первом уровне (уровень супервайзера) носят неформальный характер. Оценщик проверит данные об имуществе и объяснит основу оценки. Это возможность для собственника выявить ошибки в оценке или предоставить дополнительную информацию об имуществе.
Почему стоимость моего дома выросла, если я ничего с ним не сделал?
Стоимость вашего дома может увеличиться из-за инфляции и других нормальных факторов, влияющих на рынок недвижимости. Ваша недвижимость оценивается каждые три года. Новая рыночная стоимость отражает изменения на рынке недвижимости с момента последней оценки.
Существуют ли другие уровни апелляции?
Да, если вы не удовлетворены решением, принятым в результате слушания Надзорным органом, вы можете подать апелляцию в Апелляционный совет по оценке налога на имущество, а затем в Налоговый суд Мэриленда. Оба являются отдельными и независимыми агентствами от Департамента оценки и налогообложения.
Как вы можете говорить, что моя собственность стоит 175 000 долларов, если три года назад я заплатил за нее всего 150 000 долларов?
Текущая оценка отражает изменения на рынке недвижимости с момента ее приобретения. Продажи, имевшие место за последние три года, указывают на то, что рыночная стоимость вашей собственности увеличилась.
Продажи, имевшие место за последние три года, указывают на то, что рыночная стоимость вашей собственности увеличилась.
Что произойдет, если рынок недвижимости пойдет вниз?
Департамент постоянно следит за рынком по всему штату. Все сделки купли-продажи обрабатываются через местные офисы оценки по мере регистрации сделок. Цена продажи каждой собственности сравнивается с ее оценкой. Департамент уменьшает взносы, если наблюдается тенденция к снижению.
Моя страховая компания только что оценила мой дом. Почему она намного ниже моей общей рыночной стоимости?
Оценка для целей страхования от пожара не включает землю.
Как оценивается земля?
Земля оценивается на основе рыночного подхода или метода сравнительных продаж, а также метода распределения. Свойства продажи анализируются и сравниваются. Единицы сравнения, такие как квадратные футы, площадь в акрах и передний фут, используются для определения стоимости земли на основе продажи недвижимости. Эта стоимость земли затем применяется к объектам недвижимости, не подлежащим продаже, на основе их сопоставимости.
Эта стоимость земли затем применяется к объектам недвижимости, не подлежащим продаже, на основе их сопоставимости.
Почему у моего соседа с гораздо большим участком стоимость земли лишь немного выше?
Рыночные условия отражаются в стоимости земли. При оценке участков под застройку небольшой размер участка под застройку обычно не указывает на значительную разницу в стоимости участка. На стоимость земли могут влиять такие факторы, как местоположение и топография.
При оценке имущества анализируются все экономические и физические факторы, влияющие на стоимость. Ставки на землю и стоимость улучшений отражают различные индивидуальные различия в свойствах. Ставки на землю у воды обычно различаются в зависимости от многих факторов, таких как глубина воды и местоположение.
Как вы оцениваете землю для кондоминиума?
Стоимость земли, относящаяся к отдельному кондоминиуму, основана на принципе распределения. За землю закреплен процент от общей стоимости.
За землю закреплен процент от общей стоимости.
Карта налога на недвижимость неправильно отражает мой земельный участок.
Отдел недвижимости SDAT проводит оценку имущества; предоставляет информацию об оценке; и ведет наши записи на основе официальных записей, зарегистрированных в Land Records.
Департамент планирования штата Мэриленд (MDP), отдел планирования данных и исследований, отвечает за ведение налоговых карт для 23 округов штата Мэриленд. Налоговые карты предназначены для предоставления графического представления недвижимого имущества путем отражения границ отдельных участков по отношению к прилегающему недвижимому имуществу.
Карты, предоставленные MDP, НЕ должны толковаться или использоваться как «юридическое описание». Это не продукт исследования, и его нельзя использовать для проектирования, модификации или строительства улучшений недвижимого имущества или для определения поймы. MDP не гарантирует точность или полноту картографической информации.

 (Архивное фото)
(Архивное фото)
 comFeminaETimesGraziaZoomTravel DestinationsBombay TimesCricbuzz.comFilmfareOnline SongsTVLifestyleLongwalks AppNewspaper SubscriptionFood NewsTimes PrimeWhats Hot
comFeminaETimesGraziaZoomTravel DestinationsBombay TimesCricbuzz.comFilmfareOnline SongsTVLifestyleLongwalks AppNewspaper SubscriptionFood NewsTimes PrimeWhats Hot Проверьте наш календарь, чтобы узнать о местах проведения встреч и подробностях.
Проверьте наш календарь, чтобы узнать о местах проведения встреч и подробностях.

 55 МБ
55 МБ Ж. Н. Горбатович, А. С. Семенкова, Е. А. Шинкевич — Мн.: БГТУ, 2006. — 78 с. Приведены основные теоретические сведения, примеры решения задач, задачи для самостоятельного решения. Учебно-методическое пособие предназначено для оказания помощи студентам заочной формы обучения при самостоятельном изучении следующих тем курса «Неопределенный интеграл», «Определенный интеграл», «Не…
Ж. Н. Горбатович, А. С. Семенкова, Е. А. Шинкевич — Мн.: БГТУ, 2006. — 78 с. Приведены основные теоретические сведения, примеры решения задач, задачи для самостоятельного решения. Учебно-методическое пособие предназначено для оказания помощи студентам заочной формы обучения при самостоятельном изучении следующих тем курса «Неопределенный интеграл», «Определенный интеграл», «Не… ..
.. Часть 2 содержит контрольные задания (5-8 контрольные работы и образцы их решения) для студентов-заочников инженерных и инженерно-экономических специальностей приборостроительного факультета.rn
Часть 2 содержит контрольные задания (5-8 контрольные работы и образцы их решения) для студентов-заочников инженерных и инженерно-экономических специальностей приборостроительного факультета.rn
 Включает программу 1 семестра, соответствующую ГОС.
Включает программу 1 семестра, соответствующую ГОС.
 Начала математического анализа: предел числовой последовательности, предел и непрерывность функции
Начала математического анализа: предел числовой последовательности, предел и непрерывность функции 00.00 Технологии материалов
00.00 Технологии материалов 
 Рекомендуем заменить его на один из предложенных.
Рекомендуем заменить его на один из предложенных. Процесс подачи заявки очень прост, и онлайн-курсы можно пройти индивидуально для продолжения образования или для онлайн-магистерской программы. Ниже вы найдете описания наших онлайн-курсов по математике для выпускников.
Процесс подачи заявки очень прост, и онлайн-курсы можно пройти индивидуально для продолжения образования или для онлайн-магистерской программы. Ниже вы найдете описания наших онлайн-курсов по математике для выпускников.
 Приложения к технике и науке. Не может быть принято за диплом магистра или доктора философии. студенты, изучающие математику или прикладную математику. Кредит для этого курса и MA 401 не допускается.
Приложения к технике и науке. Не может быть принято за диплом магистра или доктора философии. студенты, изучающие математику или прикладную математику. Кредит для этого курса и MA 401 не допускается. Различные подходы к изучению геометрии, включая векторную геометрию, трансформационную геометрию и аксиоматику. Не может быть принято за диплом магистра или доктора философии. студенты, изучающие математику или прикладную математику.
Различные подходы к изучению геометрии, включая векторную геометрию, трансформационную геометрию и аксиоматику. Не может быть принято за диплом магистра или доктора философии. студенты, изучающие математику или прикладную математику. Курс может быть пройден для получения кредита выпускника для продления сертификата учителями средней школы. Кредит на получение степени магистра может быть разрешен только для студентов, обучающихся математике.
Курс может быть пройден для получения кредита выпускника для продления сертификата учителями средней школы. Кредит на получение степени магистра может быть разрешен только для студентов, обучающихся математике. Билинейные формы.
Билинейные формы.
 Семинары дают вам возможность подробно изучить конкретный аспект вашего предмета, а также обсудить и обменяться идеями с однокурсниками.
Как правило, они требуют предварительного изучения.
Семинары дают вам возможность подробно изучить конкретный аспект вашего предмета, а также обсудить и обменяться идеями с однокурсниками.
Как правило, они требуют предварительного изучения.


 Число прибежавших раньше Миши в три раза больше тех, кто прибежал после него. А
Число прибежавших раньше Миши в три раза больше тех, кто прибежал после него. А

 к. можно учитывать и другие факторы – см. выше).
к. можно учитывать и другие факторы – см. выше).
 И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.
И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.

 Разрешите получать регулярные обновления!
Разрешите получать регулярные обновления!
 Она должна проходить через точку (0, 3) и наклоняться вверх слева направо. Мы можем использовать две точки, чтобы найти наклон, или мы можем сравнить его с другими перечисленными функциями. Функция g имеет тот же наклон, но другую точку пересечения y-. Линии I и III имеют одинаковый наклон, потому что они имеют одинаковый наклон. Линия III не проходит через (0, 3), поэтому f должно быть представлено линией I.
Она должна проходить через точку (0, 3) и наклоняться вверх слева направо. Мы можем использовать две точки, чтобы найти наклон, или мы можем сравнить его с другими перечисленными функциями. Функция g имеет тот же наклон, но другую точку пересечения y-. Линии I и III имеют одинаковый наклон, потому что они имеют одинаковый наклон. Линия III не проходит через (0, 3), поэтому f должно быть представлено линией I. Она должна проходить через точку (0, 3) и наклоняться вверх слева направо. Линии I и II проходят через (0, 3), но наклон j меньше, чем наклон f , поэтому линия для j должна быть более плоской. Эта функция представлена линией II.
Она должна проходить через точку (0, 3) и наклоняться вверх слева направо. Линии I и II проходят через (0, 3), но наклон j меньше, чем наклон f , поэтому линия для j должна быть более плоской. Эта функция представлена линией II.
 Например, y = 5 — это горизонтальная линия, расположенная на 5 единиц выше оси x . Эта функция не имеет x -перехватов .
Например, y = 5 — это горизонтальная линия, расположенная на 5 единиц выше оси x . Эта функция не имеет x -перехватов .
 Этот график представляет функцию
Этот график представляет функцию
 Часть вторая
Часть вторая Частное решение.
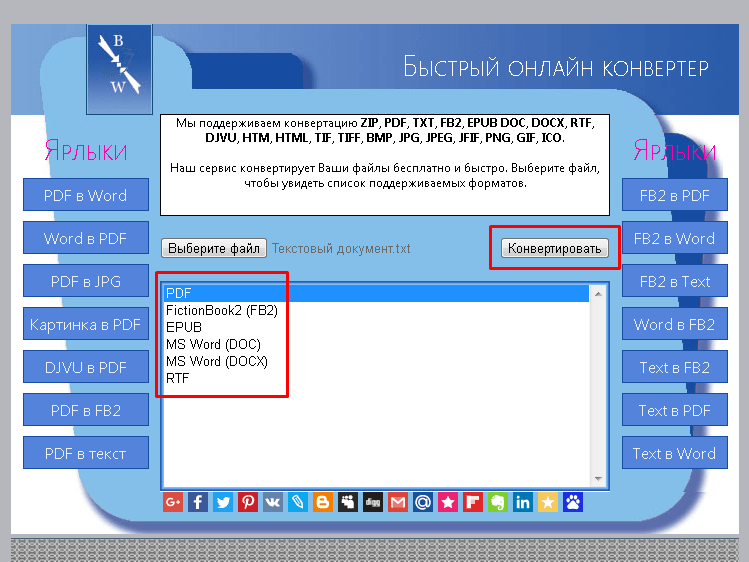
Частное решение. Но чаще всего пользователям нужна лишь конвертация, которую мы и предоставляем на отдельной странице.
Но чаще всего пользователям нужна лишь конвертация, которую мы и предоставляем на отдельной странице. Угол между ними.
Угол между ними.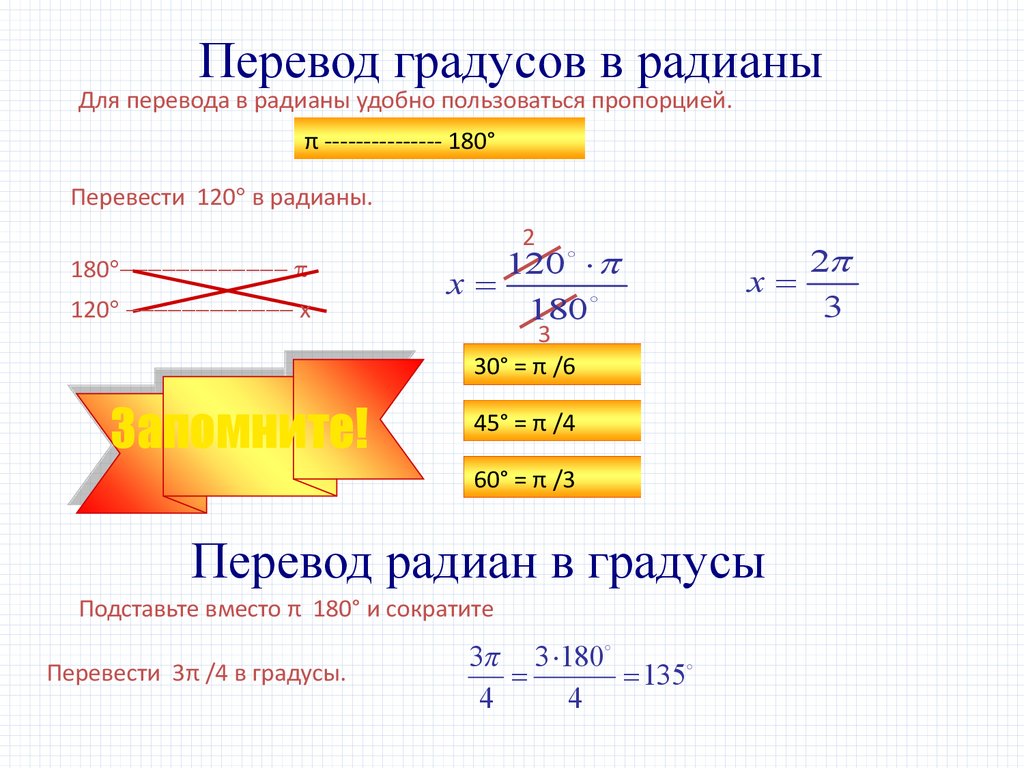 Матрица смежности онлайн
Матрица смежности онлайн
 д.
Эти ресурсы основаны на стандартах IEEE и 3GPP. Он также имеет академический раздел, который охватывает колледжи и университеты по инженерным дисциплинам и дисциплинам MBA.
д.
Эти ресурсы основаны на стандартах IEEE и 3GPP. Он также имеет академический раздел, который охватывает колледжи и университеты по инженерным дисциплинам и дисциплинам MBA.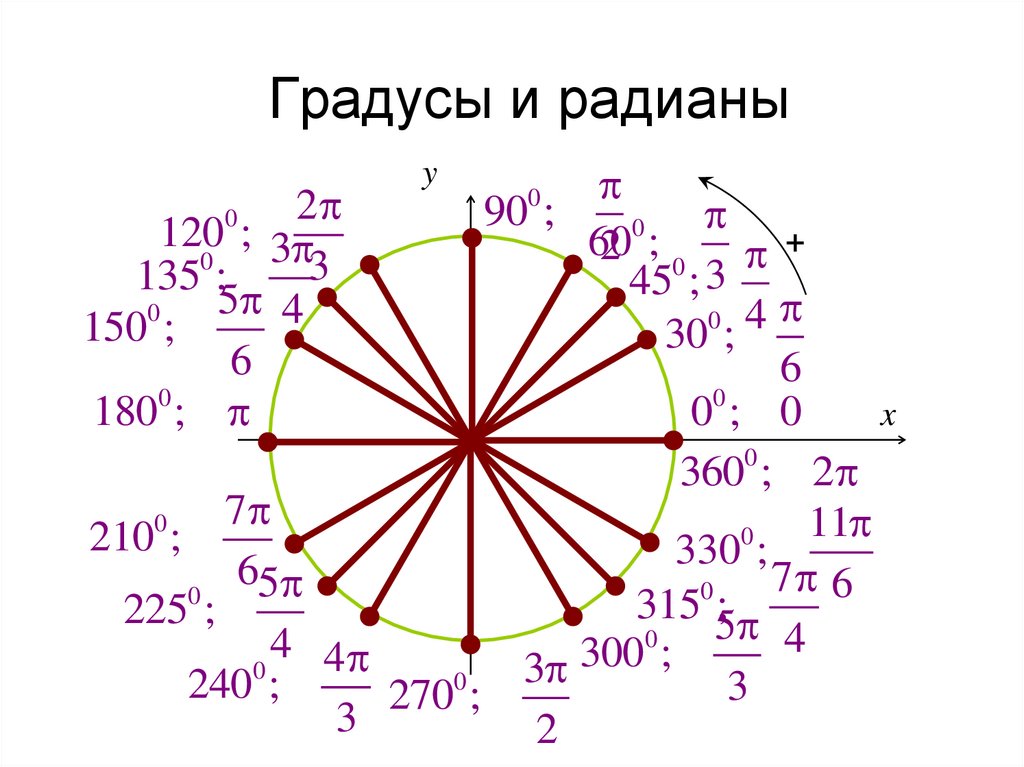 д. , стандарты.
Он также охватывает статьи, связанные с испытаниями и измерениями, посвященные испытаниям на соответствие, используемым для испытаний устройств на соответствие RF/PHY. СМ. УКАЗАТЕЛЬ СТАТЕЙ >>.
д. , стандарты.
Он также охватывает статьи, связанные с испытаниями и измерениями, посвященные испытаниям на соответствие, используемым для испытаний устройств на соответствие RF/PHY. СМ. УКАЗАТЕЛЬ СТАТЕЙ >>. Архитектура сотового телефона.
Подробнее➤
Архитектура сотового телефона.
Подробнее➤ Он охватывает учебные пособия по таким темам, как
сотовая связь, WLAN (11ac, 11ad), wimax, bluetooth, zigbee, zwave, LTE, DSP, GSM, GPRS,
GPS, UMTS, CDMA, UWB, RFID, радар, VSAT, спутник, беспроводная сеть, волновод, антенна, фемтосота, тестирование и измерения, IoT и т. д.
См. ИНДЕКС УЧЕБНЫХ ПОСОБИЙ >>
Он охватывает учебные пособия по таким темам, как
сотовая связь, WLAN (11ac, 11ad), wimax, bluetooth, zigbee, zwave, LTE, DSP, GSM, GPRS,
GPS, UMTS, CDMA, UWB, RFID, радар, VSAT, спутник, беспроводная сеть, волновод, антенна, фемтосота, тестирование и измерения, IoT и т. д.
См. ИНДЕКС УЧЕБНЫХ ПОСОБИЙ >>
 ИНДЕКС испытаний и измерений >>
ИНДЕКС испытаний и измерений >> 


 866
866 750
750 750
750 5
5 Кроме того, в формулах можно использовать и более сложные математические функции – например, тригонометрические функции для вычисления площадей и объёмов, или логические функции, позволяющие получить нужное значение в зависимости от выполнения того или иного условия.
Кроме того, в формулах можно использовать и более сложные математические функции – например, тригонометрические функции для вычисления площадей и объёмов, или логические функции, позволяющие получить нужное значение в зависимости от выполнения того или иного условия.
 число2 – возвращает результат возведения числа1 в степень число2.
число2 – возвращает результат возведения числа1 в степень число2. Номер – это порядковый номер выбираемого значения, он должен быть целым числом. Количество аргументов – не более 29. Например, результатом функции ВЫБОР(А;5;6;7) будет число 5, если переменная А равна 1; число 6, если переменная А равна 2; число 7, если переменная А равна 3. Аналогично для функции CHOOSE.
Номер – это порядковый номер выбираемого значения, он должен быть целым числом. Количество аргументов – не более 29. Например, результатом функции ВЫБОР(А;5;6;7) будет число 5, если переменная А равна 1; число 6, если переменная А равна 2; число 7, если переменная А равна 3. Аналогично для функции CHOOSE.


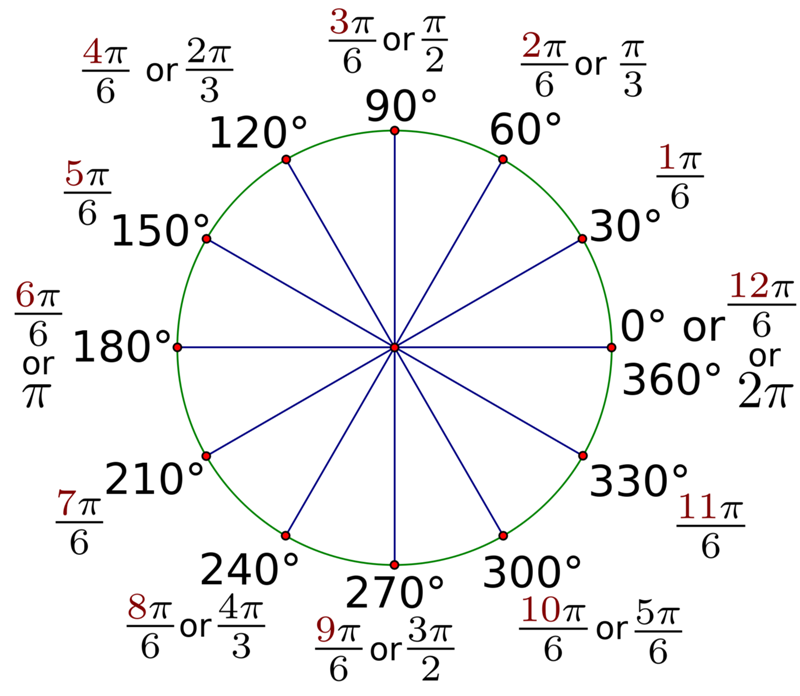
 К концу этой статьи вы будете иметь глубокое представление о функции RADIANS, ее синтаксисе, примерах, советах и рекомендациях, распространенных ошибках и связанных формулах.
К концу этой статьи вы будете иметь глубокое представление о функции RADIANS, ее синтаксисе, примерах, советах и рекомендациях, распространенных ошибках и связанных формулах.
 Поэтому перед использованием этих тригонометрических функций необходимо использовать функцию РАДИАНЫ для преобразования градусов в радианы.
Поэтому перед использованием этих тригонометрических функций необходимо использовать функцию РАДИАНЫ для преобразования градусов в радианы. Если оно выражено в других единицах, сначала преобразуйте его в градусы.
Если оно выражено в других единицах, сначала преобразуйте его в градусы. Синтаксис функции TAN: =TAN(угол), где угол указывается в радианах.
Синтаксис функции TAN: =TAN(угол), где угол указывается в радианах.
 (2x-5)-9)
(2x-5)-9)
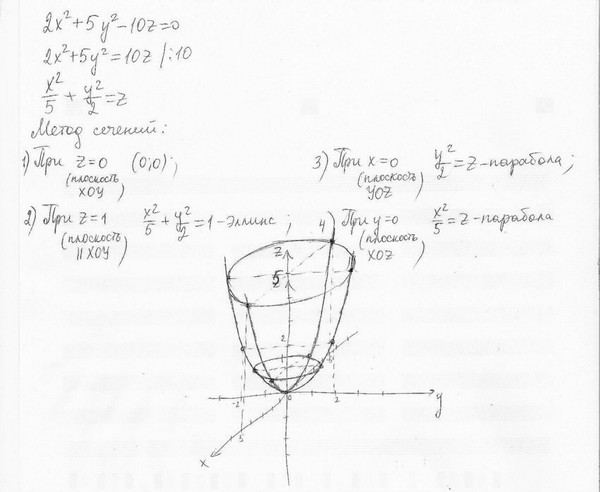 Этому уравнению удовлетворяет только одна точка О(0,0).
Этому уравнению удовлетворяет только одна точка О(0,0).
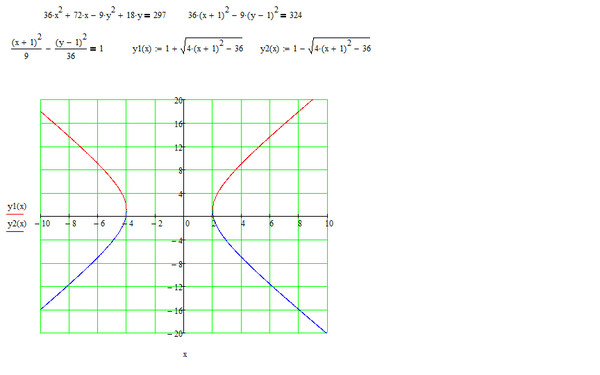


 Решением является такие значения х, при котором данное уравнение становится тождеством. В… … Экономический словарь
Решением является такие значения х, при котором данное уравнение становится тождеством. В… … Экономический словарь 2–16. Определить выражение этой функции в новой системе координат, если координатные оси повернуты на угол –45 градусов.
2–16. Определить выражение этой функции в новой системе координат, если координатные оси повернуты на угол –45 градусов.

 )
) Определить длины отрезков, на которые рассе-кает спираль Архимеда р = 3Θ луч, выходящий из полюса и наклоненный к полярной оси под углом Θ = π/6.
Сделать чертеж.
Определить длины отрезков, на которые рассе-кает спираль Архимеда р = 3Θ луч, выходящий из полюса и наклоненный к полярной оси под углом Θ = π/6.
Сделать чертеж. Из треугольника BMN: k – угловой коэффициент прямой. k x by NB MN tg bkxy
Из треугольника BMN: k – угловой коэффициент прямой. k x by NB MN tg bkxy M)(11 xxkyy
M)(11 xxkyy 1 yx
1 yx

 Как только мы узнаем какую-либо форму уравнения прямой, легко переформулировать уравнение в других формах, если это необходимо.
Как только мы узнаем какую-либо форму уравнения прямой, легко переформулировать уравнение в других формах, если это необходимо.
 (Найдите уравнение прямой, проходящей через точку (\(2, 7\)) и имеющей наклон \(3\).) Покажите, что две формы уравнений эквивалентны.
(Найдите уравнение прямой, проходящей через точку (\(2, 7\)) и имеющей наклон \(3\).) Покажите, что две формы уравнений эквивалентны.

 Но сначала мы должны научиться находить наклон линии в стандартной форме путем проверки.
Но сначала мы должны научиться находить наклон линии в стандартной форме путем проверки.

 deanza.edu/faculty/bloomroberta/math21/afm3files.html.html
deanza.edu/faculty/bloomroberta/math21/afm3files.html.html
 Далее, это уравнение может быть решено и упрощено до стандартной формы/формы пересечения наклона/формы пересечения уравнения прямой.
Далее, это уравнение может быть решено и упрощено до стандартной формы/формы пересечения наклона/формы пересечения уравнения прямой. Все это можно преобразовать и представить в стандартной форме.
Все это можно преобразовать и представить в стандартной форме.
 Кроме того, чтобы использовать это уравнение линейного калькулятора, нам нужно указать значения наклона m и точки пересечения с осью c, чтобы получить ответ уравнения линии в форме наклона и точки пересечения и в стандартной форме.
Кроме того, чтобы использовать это уравнение линейного калькулятора, нам нужно указать значения наклона m и точки пересечения с осью c, чтобы получить ответ уравнения линии в форме наклона и точки пересечения и в стандартной форме.



 В большинстве случаев уравнение линии с наклоном m и точкой (x 1 , у 1 ) на нем находится по формуле y — y 1 = m × (x — x 1 ).
В большинстве случаев уравнение линии с наклоном m и точкой (x 1 , у 1 ) на нем находится по формуле y — y 1 = m × (x — x 1 ).
 Любая упорядоченная пара (x, y), лежащая на прямой, удовлетворяет этому уравнению.
Любая упорядоченная пара (x, y), лежащая на прямой, удовлетворяет этому уравнению. Здесь m — наклон линии. Далее это уравнение можно окончательно решить и представить в стандартной форме в виде ax + by + c = 0. Найдем уравнение прямой, проходящей через точку (2, 1) и имеющей наклон 3. Искомое уравнение линии с использованием этой одноточечной формы (y — 1) = 3 (x — 2), что при упрощении дает окончательное уравнение в стандартной форме как 3x — y — 5 = 0
Здесь m — наклон линии. Далее это уравнение можно окончательно решить и представить в стандартной форме в виде ax + by + c = 0. Найдем уравнение прямой, проходящей через точку (2, 1) и имеющей наклон 3. Искомое уравнение линии с использованием этой одноточечной формы (y — 1) = 3 (x — 2), что при упрощении дает окончательное уравнение в стандартной форме как 3x — y — 5 = 0
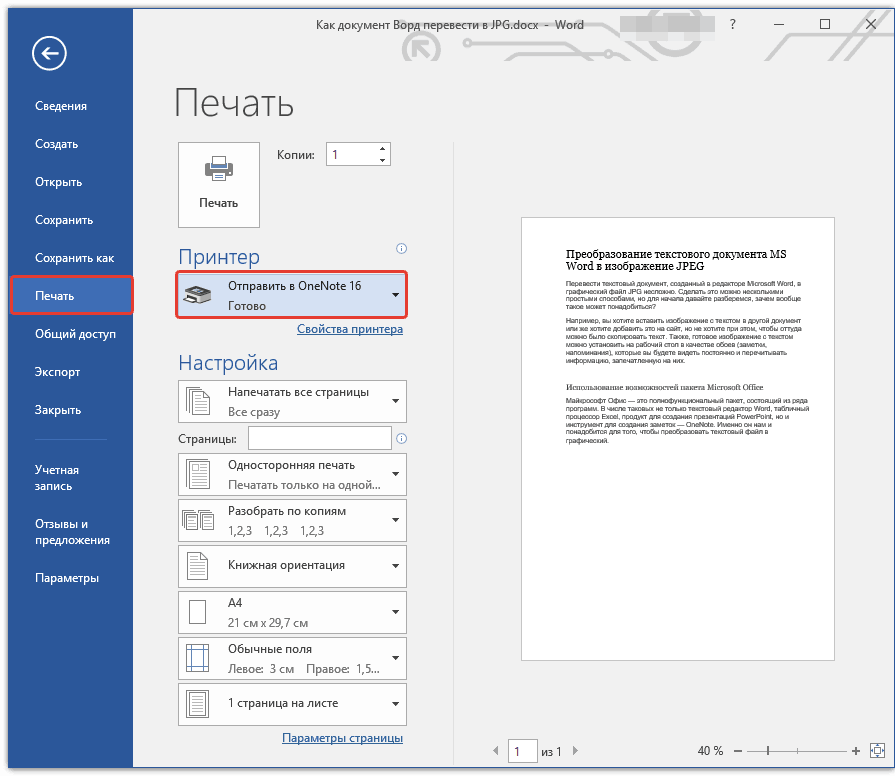
 Документы Word (в форматах doc и docx) требуют наличие на компьютере программы Microsoft Word или приложения, поддерживающее открытие файлов в данных форматах.
Документы Word (в форматах doc и docx) требуют наличие на компьютере программы Microsoft Word или приложения, поддерживающее открытие файлов в данных форматах.
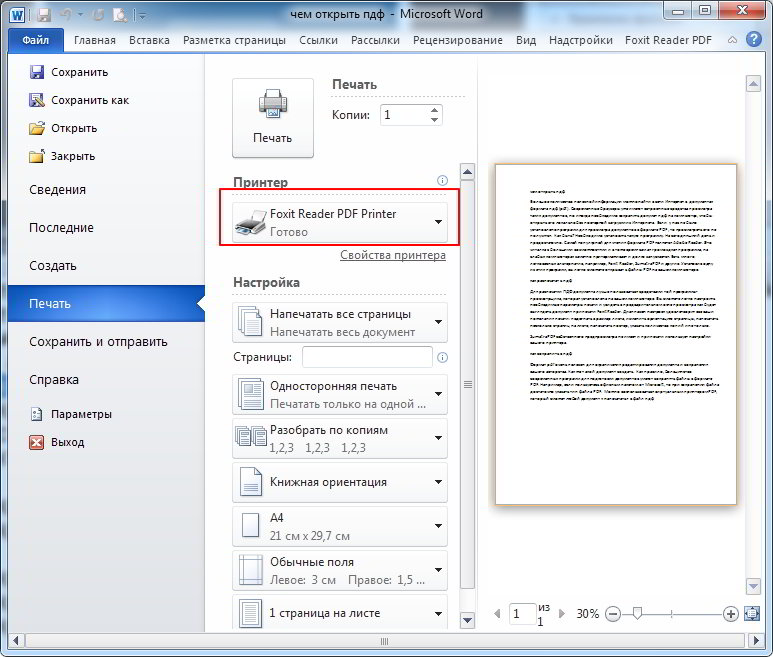 Нажмите на кнопку «Параметры…» для выбора других настроек.
Нажмите на кнопку «Параметры…» для выбора других настроек.
 Укажите имя для файла, выберите место сохранения, настройки оптимизации, при необходимости, измените другие параметры.
Укажите имя для файла, выберите место сохранения, настройки оптимизации, при необходимости, измените другие параметры. Данные программы поддерживают открытие файлов MS Word. В данных программах имеется функциональная возможность для сохранения документа в формате PDF.
Данные программы поддерживают открытие файлов MS Word. В данных программах имеется функциональная возможность для сохранения документа в формате PDF.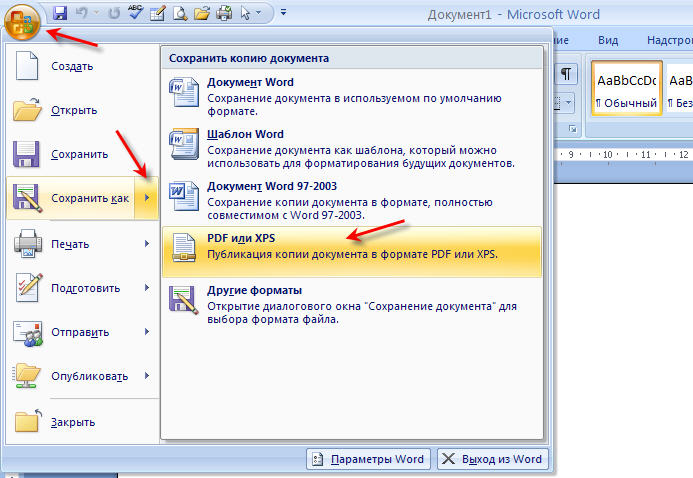 Об этом способе я уже подробно писал в этой статье.
Об этом способе я уже подробно писал в этой статье.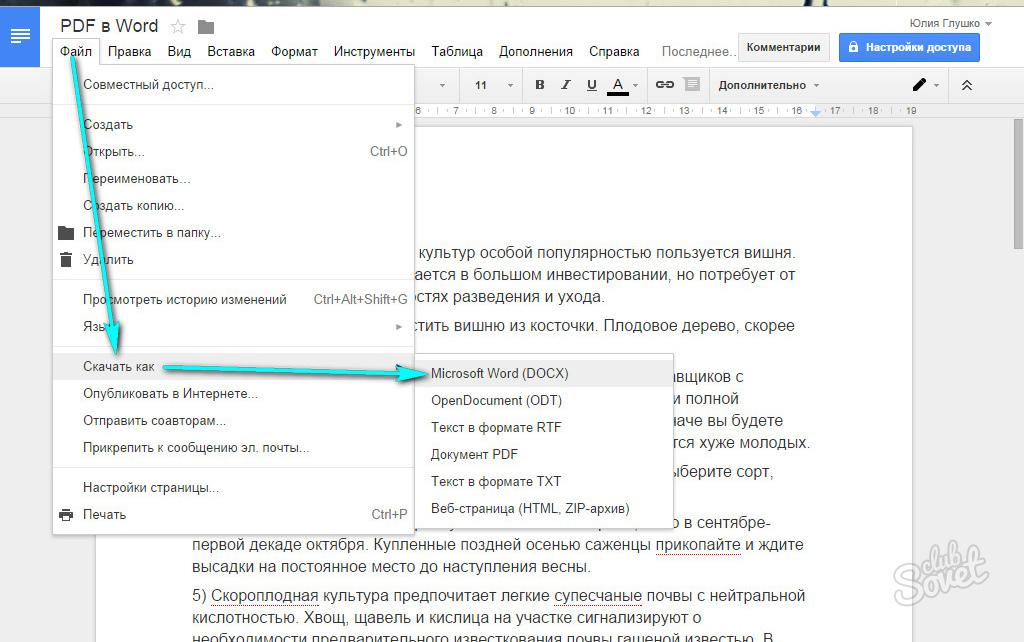
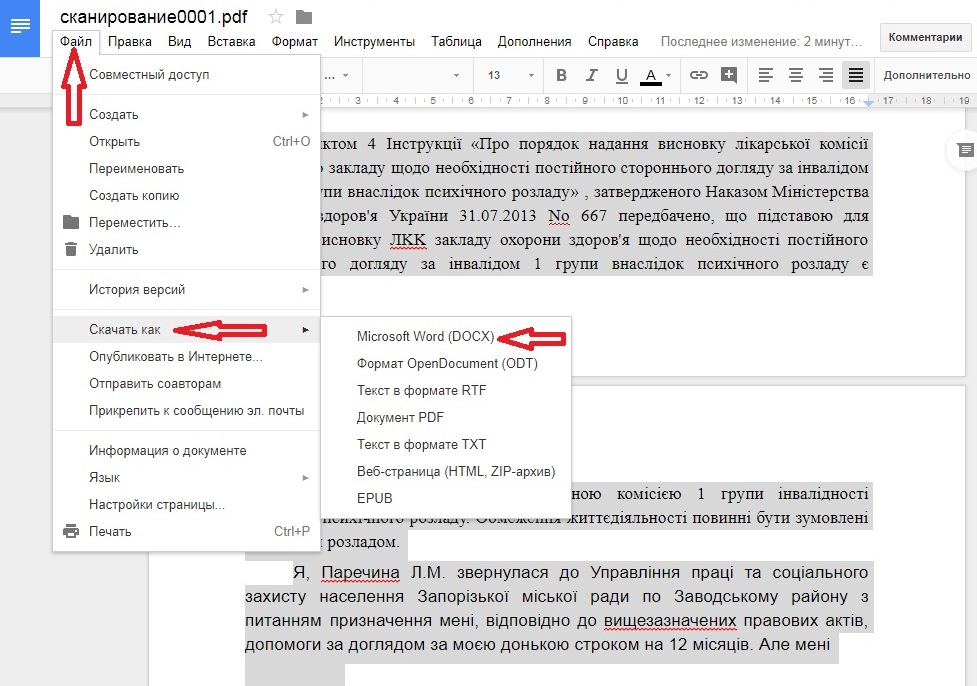
 docx и .doc сейчас довольно широко распространены. Он стал своего рода стандартом для передачи текстов (или текстов с картинками, картинками, таблицами) между разными пользователями, между разными компьютерами. Поэтому может потребоваться создать файлы Word, чтобы их можно было отправить кому-нибудь. Microsoft Word — самый популярный текстовый редактор, и почти каждый пользователь, если не работал в нем, наверняка слышал об этой программе.
docx и .doc сейчас довольно широко распространены. Он стал своего рода стандартом для передачи текстов (или текстов с картинками, картинками, таблицами) между разными пользователями, между разными компьютерами. Поэтому может потребоваться создать файлы Word, чтобы их можно было отправить кому-нибудь. Microsoft Word — самый популярный текстовый редактор, и почти каждый пользователь, если не работал в нем, наверняка слышал об этой программе. Размер двух одинаковых PDF-документов на экране может отличаться.
Размер двух одинаковых PDF-документов на экране может отличаться.
 04.2023, 17:06:35 • Подано по адресу:
Как сделать Windows
• Проверенные решения
04.2023, 17:06:35 • Подано по адресу:
Как сделать Windows
• Проверенные решения
 Точно так же пользователи могут удалить текст из файла PDF или заменить его новым текстом, сохранив при этом то же форматирование. PDFelement также можно использовать для преобразования PDF-файлов во множество других форматов, создания новых заполняемых форм, заполнения существующих форм и их цифровой подписи с использованием защищенных серверов PDFelement.
Точно так же пользователи могут удалить текст из файла PDF или заменить его новым текстом, сохранив при этом то же форматирование. PDFelement также можно использовать для преобразования PDF-файлов во множество других форматов, создания новых заполняемых форм, заполнения существующих форм и их цифровой подписи с использованием защищенных серверов PDFelement. Вы также можете выбрать папку и назвать файл по своему усмотрению.
Вы также можете выбрать папку и назвать файл по своему усмотрению.
 Кроме того, это позволит вам подписать ваш PDF-файл и защитить его паролем.
Кроме того, это позволит вам подписать ваш PDF-файл и защитить его паролем.
 Это самый простой способ преобразовать Word в PDF.
Это самый простой способ преобразовать Word в PDF.
 (Подробнее…)
(Подробнее…)
 Тогда верно неравенство .
Тогда верно неравенство .
 » подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела. Математические выражения решают сложные задачи, находя их значение.
Математические выражения решают сложные задачи, находя их значение. 9{2}-30\вправо)+50\).
9{2}-30\вправо)+50\). Есть четыре вида скобок.
Есть четыре вида скобок.

 Используйте обычный порядок операций с абсолютными значениями, примените абсолютное значение и рассмотрите внешние члены. 9{2}+2(1)(2)\)
Используйте обычный порядок операций с абсолютными значениями, примените абсолютное значение и рассмотрите внешние члены. 9{2}+2(1)(2)\)  Два типа выражений — это арифметические выражения и алгебраические выражения. Арифметическое/числовое выражение представляет собой математическое выражение, состоящее из чисел и одного или нескольких символов операций.
Два типа выражений — это арифметические выражения и алгебраические выражения. Арифметическое/числовое выражение представляет собой математическое выражение, состоящее из чисел и одного или нескольких символов операций.
 Числовое выражение — это математическое выражение, состоящее из чисел и одного или нескольких символов операций. Сложение, вычитание, умножение и деление являются примерами символов операций.
Числовое выражение — это математическое выражение, состоящее из чисел и одного или нескольких символов операций. Сложение, вычитание, умножение и деление являются примерами символов операций.



 Алгебраическое выражение
5
(
Икс
+
9
)
является нет эквивалентно алгебраическому выражению,
5
Икс
+
9.
Алгебраическое выражение
5
(
Икс
+
9
)
является нет эквивалентно алгебраическому выражению,
5
Икс
+
9.
 Комбинированный способ.1) 64а-а3= а(64-а2)= а(8-а)(8+а)
Комбинированный способ.1) 64а-а3= а(64-а2)= а(8-а)(8+а)

 92 + х — 6), теперь найдем неполную дробь
разложение следующим образом.
92 + х — 6), теперь найдем неполную дробь
разложение следующим образом.